Charged colloids at low ionic strength macro- or microphase separation
胶体电位5分钟入门

Electrokinetics and Colloid BehaviorZeta potential can help you understand and control colloidal suspensions. Examples include complex biological systems such as blood and functional ones like paint.Colloidal suspensions can be as thick as paste (like cement) or as dilute as the turbidity particles in a lake. Water, milk, wine, clay,dyes, inks, paper and pharmaceu-ticals are good examples of useful colloidal systems. Water is a com-mon suspending liquid, although non-aqueous liquids are used as well. In many cases, the perform-ance of a suspension can be im-proved by understanding the effect of colloidal behavior on such prop-erties as viscosity, settling and effective particle size.We can often tailor the charac-teristics of a suspension by under-standing how individual colloids interact with one another. At times we may want to maximize thebehavior of concentrated suspen-sions. On standing, a weak matrix of flocculant particles is formed.This prevents the closely packed sediment that would form and cause “caking” problems if the par-ticles were highly stabilized and remained completely discrete.Surface forces at the interface of the particle and the liquid are very important because of the micro-scopic size of the colloids. One of the major surface effects is elec-trokinetic. Each colloid carries a “like” electrical charge which pro-duces a force of mutual electro-static repulsion between adjacent particles. If the charge is high enough, the colloids will remain discrete, disperse and in suspen-sion. Reducing or eliminating the charge has the opposite effect —the colloids will steadily agglomer-ate and settle out of suspension or form an interconnected matrix.This agglomeration causes the characteristics of the suspension to change.Particle charge can be controlled by modifying the suspending liq-uid. Modifications include chang-ing the liquid’s pH or changing the ionic species in solution. Another,more direct technique is to use sur-face active agents which directly adsorb to the surface of the colloid and change its characteristics.Uncharged Particles are free to collide and aggregate.repulsive forces between them in order to keep each particle discrete and prevent them from gathering into larger, faster settling agglom-erates. Examples include pharma-ceuticals and pastes. Sometimes we have the opposite goal and want to separate the colloid from the liquid. Removing the repulsive forces allows them to form large flocs that settle fast and filter eas-ily. Viscosity is another property that can be modified by varying the balance between repulsion and at-traction.In some cases, an in-between state of weak aggregation can be the best solution. Paints are a good example. Here, the weak aggrega-tion causes viscosity to be a func-tion of shear rate. Stirring will produce enough shear to reduce the viscosity and promote blend-ing.Reversible aggregation is also useful in controlling the settlingThe Interaction of ColloidsZeta Potential:A Complete Course in 5 MinutesCharged Particlesrepel each other.The diffuse layer can be visualized as a charged atmosphere surrounding the colloid.The Double LayerThe double layer model is used to visualize the ionic environment in the vicinity of a charged colloid and explains how electrical repul-sive forces occur. It is easier to understand this model as a se-quence of steps that would take place around a single negative col-loid if its neutralizing ions were suddenly stripped away.We first look at the effect of the colloid on the positive ions (often called counter-ions) in solution. Initially, attraction from the nega-tive colloid causes some of the posi-tive ions to form a firmly attached layer around the surface of the colloid; this layer of counter-ions isknown as the Stern layer.Additional positive ions are stillattracted by the negative colloid,but now they are repelled by theStern layer as well as by otherpositive ions that are also trying toapproach the colloid. This dynamicequilibrium results in the forma-tion of a diffuse layer of counter-ions. They have a high concentra-tion near the surface which gradu-ally decreases with distance, untilit reaches equilibrium with thecounter-ion concentration in thesolution.In a similar, but opposite, fash-ion there is a lack of negative ionsin the neighborhood of the surface,because they are repelled by thenegative colloid. Negative ions arecalled co-ions because they havethe same charge as the colloid.Their concentration will graduallyincrease with distance, as the re-pulsive forces of the colloid arescreened out by the positive ions,until equilibrium is again reached.The diffuse layer can be visual-ized as a charged atmosphere sur-rounding the colloid. The chargedensity at any distance from thesurface is equal to the difference inconcentration of positive and nega-tive ions at that point. Chargedensity is greatest near the colloidand gradually diminishes towardzero as the concentration of posi-tive and negative ions merge to-gether.The attached counter-ions in theStern layer and the charged at-mosphere in the diffuse layer arewhat we refer to as the doublelayer. The thickness of this layerdepends upon the type and concen-tration of ions in solution.Two Ways to Visualize the Double LayerThe left view shows the change in charge density around the colloid. The right shows the distribution of positive and negative ions around the charged colloid.Zeta PotentialThe double layer is formed in order to neutralize the charged col-loid and, in turn, causes an elec-trokinetic potential between the surface of the colloid and any point in the mass of the suspending liq-uid. This voltage difference is on the order of millivolts and is re-ferred to as the surface potential.The magnitude of the surface potential is related to the surface charge and the thickness of the double layer. As we leave the sur-face, the potential drops off roughly linearly in the Stern layer and then exponentially through the diffuse layer, approaching zero at the imaginary boundary of the double layer. The potential curve is useful because it indicates the strength of the electrical force between par-ticles and the distance at which this force comes into play.A charged particle will move with a fixed velocity in a voltage field.This phenomenon is called electro-phoresis. The particle’s mobility is related to the dielectric constant and viscosity of the suspending liq-uid and to the electrical potential at the boundary between the mov-ing particle and the liquid. This boundary is called the slip plane and is usually defined as the point where the Stern layer and the dif-fuse layer meet. The Stern layer isThe electrokinetic potential between the surface of the colloid and any point in the mass of the suspending liquid is referred to as the surface potential.Zeta Potential vs. Surface Potential The relationship between zeta potential and surface potential depends on the level of ions in the solution.Variation of Ion Density in the Diffuse LayerThe figures above are two representa-tions of the change in charge density through the diffuse layer. One shows the variation in positive and negative ion concentration with distance from a negative colloid. The second shows the net effect — the difference in positive and negative charge density.considered to be rigidly attached to the colloid, while the diffuse layer is not. As a result, the electrical potential at this junction is related to the mobility of the particle and is called the zeta potential .Although zeta potential is an intermediate value, it is sometimes considered to be more significant than surface potential as far as electrostatic repusion is concerned.Zeta potential can be quantified by tracking the colloidal particles through a microscope as they mi-grate in a voltage field.The Balance ofRepulsion & AttractionThe DLVO Theory (named after Derjaguin, Landau, Verwey and Overbeek) is the classical explana-tion of the stability of colloids in suspension. It looks at the balance between two opposing forces — elec-trostatic repulsion and van der Waals attraction — to explain why some colloidal systems agglomer-ate while others do not.Electrostatic repulsion becomes significant when two colloids ap-proach each other and their double layers begin to interfere. Energy is required to overcome this repul-sion. An electrostatic repulsion curve is used to indicate the energy that must be overcome if the par-ticles are to be forced together. It has a maximum value when they are almost touching and decreases to zero outside the double layer.The maximum energy is related to the surface potential and the zeta potential.The DLVO theory explains the tendency of colloids to agglomerate or remain discrete.The height of the barrier indicates how stable the system is. In order to agglomerate, two particles on a collision course must have suffi-cient kinetic energy due to their velocity and mass, to “jump over”this barrier. If the barrier is cleared, then the net interaction is all attractive, and as a result the particles agglomerate. This inner region is after referred to as an energy trap since the colloids can be considered to be trapped together by van der Waals forces.In many cases we can alter the environment to either increase or decrease the energy barrier, de-pending upon our goals. Various methods can be used to achieveElecrostatic Repulsion is always shown as a positive curve.Van der Waals attraction is ac-tually the result of forces between individual molecules in each col-loid. The effect is additive; that is,one molecule of the first colloid has a van der Waals attraction to each molecule in the second colloid. This is repeated for each molecule in the first colloid, and the total force is the sum of all of these. An attrac-tive energy curve is used to indi-cate the variation in van der Waals force with distance between the particles.The DLVO theory explains the tendency of colloids to agglomerate or remain discrete by combining the van der Waals attraction curve with the electrostatic repulsion curve to form the net interaction energy curve. At each distance,the smaller value is subtracted from the larger to get the net energy.The net value is then plotted —above if repulsive and below if at-tractive — and a curve is formed. If there is a repulsive section, then the point of maximum repulsive energy is called the energy barrier.Van der Waals Attraction is shown asa negative curve.subtracting the attraction curve from the repulsion curve.In many cases we can alter the environment to either increase or decrease the energy barrier, depending upon our goals.Effect of Type and Concentration ofElectrolytesSimple inorganic electrolytes can havea significant impact on zeta potential.The effect depends on the relativevalence of the ions and on theirconcentration. Relative valence canalso be thought of as the type ofelectrolyte, with type being the ratiobetween the valences of the cationand the anion.In this example, the zeta potential of adilute suspension of colloidal silica wasmodified by adding different electro-lytes. Aluminum chloride is a 3:1electrolyte and its trivalent cationseasily push the zeta potential towardzero. Contrast this with the effect ofpotassium sulfate, a 1:2 electrolyte.First the zeta potential becomesincreasingly negative until a plateau isreached at about 50 mg/L. At about500 mg/L, the zeta potential begins todecrease because the ions arecompressing the double layer. environment, or pH, or addingsurface active materials to directlyaffect the charge of the colloid. Ineach case, zeta potential measure-ments can indicate the impact ofthe alteration on overall stability.Nothing is ever as simple as itfirst seems. There are other effectsthat must be considered wheneveryou work with particle stability.Steric stabilization is the most sig-nificant one. Usually this involvesthe adsorption of polymers on par-ticle surfaces. You can visualizethe adsorbed layer as a barrieraround each particle, preventingthem from coming close enough forvan der Waals attraction to causeflocculation. Unlike electrostaticstabilization, there are no longrange repulsive forces and the par-ticles are subject to attractive forcesuntil the outer portions of the stericmolecules contact each other.Mechanical bridging by poly-mers can be an effective floccu-lating technique. Some long chainpolymers are large enough to ad-sorb to the surface of several par-ticles at the same time, bindingthem together in spite of the elec-trostatic forces that would normallymake them repel each other.In practice, a combination of ef-fects can be used to create stablesystems or to flocculate them. Forinstance, stable dispersions can becreated by a combination of electro-static repulsion and steric hin-drance. Electronegative disper-sions can be flocculated using longchain cationic polymers which si-multaneously neutralize chargeand bridge between adjacent par-ticles.CeramicsSlip casting is used in volume production of ceramic ware. A sus-pension of clay is prepared and poured into porous molds, which draw off the water from the clay particles by capillary action. A fil-ter cake of clay forms as the water is drawn off. The structure of theControl of Slip CastingClay suspensions for slip casting must have their viscosity minimized so that they pour readily and release trapped air bubbles easily. The above figure shows the effect of pH on the apparent viscosity and zeta potential of thoria (ThO 3). Note that a maximum zeta potential corresponds to a low appar-ent viscosity.Clays & Drilling FluidsClays are an essential part of paper, adhesives, ointments, rub-ber and synthetic plastics. In each of these systems, we have to deal with dispersions of clay in water or other fluids. Clay colloid chemis-try helps us to tailor their charac-teristics to fit the task.Clays are also used as drilling fluids in water well and petroleum well production. They are called drilling muds and are chemically conditioned to vary their proper-ties during drilling. A highly charged suspension is desirable for the initial drilling operation. This keeps the clay colloids discrete, al-lowing them to penetrate into the porous wall of the drilled hole and clog the soil pores, forming a thin,impermeable cake which prevents the loss of drilling fluid. Later, the clay charge may be reduced to form a flocculated suspension in order to keep it from clogging the lower,pumping zone of the well.Minerals & OresMany raw mineral ores such as those for copper, lead, zinc and tungsten are separated by first grinding the ore, mixing it with a collector and suspending it in wa-ter. The next step is flotation. Air is bubbled through the mixture and the collector causes the mineral particles to adhere to the bubbles so that they can be recovered at the surface. The efficiency of this proc-ess depends upon the degree of adsorption between the collector and the mineral and can be con-trolled by the zeta potential of the particles. In another interesting application, zeta potential studies have been used to minimize the viscosity of coal slurries.Determining Point of Zero Charge These experiments with alpha-alumina show good correlation between the point of zero charge as determined by zeta potential and the point of maxi-mum subsidence rate. Subsidence rate is a measure of the degree of coagulation.Zeta Potential ApplicationsAdhesivesAgricultural Chemicals AsbestosAtomic EnergyBeverages Biochemistry BiomedicinePharmaceuticalsThe physical properties of a pharmaceutical suspension affect the user’s response to the product.A successful suspension will not cake and will, therefore enjoy a long shelf life. With fine colloids this can be achieved by adding a suspending agent to increase the zeta potential, and produce maxi-mum repulsion between adjacent particles. This highly dispersed system will settle very slowly, but any that do settle will pack tightly and aggravate caking.Another, and sometimes more effective, approach is to formulate a weakly flocculated suspension. The suspended particles form light, fluffy agglomerates held together by van der Waals forces. The floc-culated particles settle rapidly forming a loosely adhering mass with a large sediment height in-stead of a cake. Gentle agitation will easily resuspend the particles. Weak flocculation requires a zeta potential of almost zero.Fluidization of an AntacidSuspensionFluidization is an alternative toflocculation. A negatively chargedcolloidal polyelectrolyte is used as a“fluidizing” agent. The polyelectrolyteadsorbs onto the surfaces of insolubleparticles and deflocculates them oncethe zeta potential exceeds the criticalvalue.This graph illustrates the fluidization ofan aluminum hydroxide suspensionusing carrageenan sodium as the“fluidizing” agent. The drops in zetapotential and viscosity of the suspen-sion correlate quite well with eachother and are produced by an increasein the concentration of carrageenan.PaintsThe pigments in paint must bewell dispersed in order for the paintto perform successfully. If the pig-ment agglomerates, then the paintwill seem to have larger pigmentparticles and may fail color qual-ity. Gloss and texture are also af-fected by the degree of dispersionbetween the particles in the paint.Zeta potential measurements canbe used in this application to con-trol the composition of the paintand the dosage of additive requiredfor an optimum dispersion.CoalDairy Products DetergentsDry Powder Technology Dyestuffs Emulsions FibersFoodsLatex Production Petrochemicals Petroleum Photographic Emulsions PigmentsWater and Wastewater CoagulationZeta potential is a convenient way to optimize coagulant dosage in water and wastewater treat-ment. The most difficult suspended solids to remove are the colloids. Due to their small size, they easily escape both sedimentation and fil-tration. The key to effective colloid removal is reduction of their zeta potential with coagulants, such as alum, ferric chloride and/or cati-onic polymers. Once the charge is reduced or eliminated, then no re-pulsive forces exist and gentle agi-tation in a flocculation basin causes numerous successful colloid colli-sions. Microflocs form and grow into visible floc particles that settle rapidly and filter easily.PapermakingRetention of fines and fibers canbe increased through zeta poten-tial control. This reduces theamount of sludge produced by thewastewater treatment facility aswell as the load on white waterrecycle systems. Zeta potentialmeasurements also assist the pa-permaker in understanding theeffect of various paper ingredientsas well as the physical characteris-tics of the paper particles them-selves.Zeta Potential Control of Alum DoseThere is no single zeta potential thatwill guarantee good coagulation forevery treatment plant. It will usually bebetween 0 and -10 mV but the targetvalue is best set by test, using pilotplant or actual operating experience.Once the target ZP is established, thenthese correlations are no longernecessary, except for infrequentchecks. Just take a sample from therapid mix basin and measure the zetapotential. If the measured value ismore negative than the target ZP, thenincrease the coagulant dose (and vice-versa).In this example a zeta potential of -3mV corresponds to the lowest filteredwater turbidity and would be used asthe target ZP.Synthetic Size Retention in Paper-makingThe point of maximum size retentioncorresponds to a zeta potential of +4,which can be considered the optimumZP. More positive or more negativevalues of the zeta potential cause adrop in the percent of size retained.Operating at the optimum value resultsin titanium oxide savings, improvedsheet formation, increased wire life,improved sizing, pitch control, andbiocide reduction.Order a CatalogOur catalog describes our instru-ments and accessories in depth, and will help you select the appropriate configuration.Zeta-Meter, Inc.765 Middlebrook AvenuePO Box 3008Staunton, VA 24402, USA Telephone...............540-886-3503 Toll-Free (USA).......800-333-0229 Fax..........................540-886-3728。
Pennsylvania, USA. Part 2 Geochemical controls on constituent concentrations

Dissolved metals and associated constituents in abandonedcoal-mine discharges,Pennsylvania,USA.Part 2:Geochemical controls on constituent concentrationsCharles A.Cravotta IIIU.S.Geological Survey,215Limekiln Road,New Cumberland,PA 17070,United StatesAvailable online 7October 2007AbstractWater-quality data for discharges from 140abandoned mines in the Anthracite and Bituminous Coalfields of Pennsyl-vania reveal complex relations among the pH and dissolved solute concentrations that can be explained with geochemical equilibrium models.Observed values of pH ranged from 2.7to 7.3in the coal-mine discharges (CMD).Generally,flow rates were smaller and solute concentrations were greater for low-pH CMD samples;pH typically increased with flow rate.Although the frequency distribution of pH was similar for the anthracite and bituminous discharges,the bituminous dis-charges had smaller median flow rates;greater concentrations of SO 4,Fe,Al,As,Cd,Cu,Ni and Sr;comparable concen-trations of Mn,Cd,Zn and Se;and smaller concentrations of Ba and Pb than anthracite discharges with the same pH values.The observed relations between the pH and constituent concentrations can be attributed to (1)dilution of acidic water by near-neutral or alkaline ground water;(2)solubility control of Al,Fe,Mn,Ba and Sr by hydroxide,sulfate,and/or carbonate minerals;and (3)aqueous SO 4-complexation and surface-complexation (adsorption)reactions.The forma-tion of AlSO þ4and AlHSO 2þ4complexes adds to the total dissolved Al concentration at equilibrium with Al(OH)3and/or Al hydroxysulfate phases and can account for 10–20times greater concentrations of dissolved Al in SO 4-laden bitumi-nous discharges compared to anthracite discharges at pH of 5.Sulfate complexation can also account for 10–30times greater concentrations of dissolved Fe III concentrations at equilibrium with Fe(OH)3and/or schwertmannite (Fe 8O 8(OH)4.5(SO 4)1.75)at pH of 3–5.In contrast,lower Ba concentrations in bituminous discharges indicate that elevated SO 4concentrations in these CMD sources could limit Ba concentrations by the precipitation of barite (BaSO 4).Coprecip-itation of Sr with barite could limit concentrations of this element.However,concentrations of dissolved Pb,Cu,Cd,Zn,and most other trace cations in CMD samples were orders of magnitude less than equilibrium with sulfate,carbonate,and/or hydroxide minerals.Surface complexation (adsorption)by hydrous ferric oxides (HFO)could account for the decreased concentrations of these divalent cations with increased pH.In contrast,increased concentrations of As and,to a lesser extent,Se with increased pH could result from the adsorption of these oxyanions by HFO at low pH and desorption at near-neutral pH.Hence,the solute concentrations in CMD and the purity of associated ‘‘ochres ”formed in CMD settings are expected to vary with pH and aqueous SO 4concentration,with potential for elevated SO 4,As and Se in ochres formed at low pH and elevated Cu,Cd,Pb and Zn in ochres formed at near-neutral pH.Elevated SO 4content of ochres could enhance the adsorption of cations at low pH,but decrease the adsorption of anions such as As.Such information on envi-ronmental processes that control element concentrations in aqueous samples and associated precipitates could be useful in0883-2927/$-see front matter Published by Elsevier Ltd.doi:10.1016/j.apgeochem.2007.10.003E-mail address:cravotta@Available online at Applied Geochemistry 23(2008)203–226Applied Geochemistrythe design of systems to reduce dissolved contaminant concentrations and/or to recover potentially valuable constituents in mine effluents.Published by Elsevier Ltd.1.IntroductionAbandoned coal-mine discharges(CMD)can becorrosive or encrusting and can impair aquatic hab-itat,water-delivery systems,bridges,and associatedinfrastructure(Barnes and Clarke,1969;Winlandet al.,1991;Earle and Callaghan,1998;Bighamand Nordstrom,2000;Houben,2003).Although dis-solved SO4,Fe,Al,and Mn are widely recognized asmineral constituents of concern,numerous tracemetals have also been documented in CMD,partic-ularly in strongly acidic,low-pH solutions(Hymanand Watzlaf,1997;Rose and Cravotta,1998;Nord-strom and Alpers,1999;Nordstrom,2000;Nord-strom et al.,2000;Cravotta,2008).The dissolvedmetals and associated constituents in CMD can betoxic to aquatic and terrestrial organisms.Generally,the toxicity of a dissolved element increases with itsconcentration after nutritional requirements,ifany,are met(Smith and Huyck,1999).The pH of a solution is an important measure forevaluating aquatic toxicity and corrosiveness.Theseverity of toxicity or corrosion tends to be greaterunder low-pH or high-pH conditions than at near-neutral pH,because the solubility of many metalscan be described as amphoteric,with a greater ten-dency to dissolve as cations at low pH or anionicspecies at high pH(Langmuir,1997).For example,Al hydroxide and aluminosilicate minerals havetheir minimum solubility at pH6–7(Nordstromand Ball,1986;Bigham and Nordstrom,2000),and brief exposure to relatively low concentrationsof dissolved Al can be toxic tofish and other aquaticorganisms(Baker and Schofield,1982;Elder,1988).Accordingly,the U.S.Environmental ProtectionAgency(2000,2002a,b)recommends pH 6.5–9.0for protection of freshwater aquatic life and pH6.5–8.5for public drinking supplies.Nevertheless,pH is not the sole determinant of metals solubility.Anions including SO2À4;HCOÀ3and,less com-monly,ClÀcan be elevated above background con-centrations in CMD(Cravotta,2008),and polyvalent cations such as Al3+and Fe3+tend to associate with such ions of opposite charge(Ball and Nordstrom,1991;Nordstrom,2004).Ion-pair formation,or aqueous-complexation reactions,between dissolved cations and anions can increase the total concentration of metals in a solution at equi-librium with a mineral and can affect the bioavailabil-ity and toxicity of metal ions in aquatic ecosystems (e.g.Rose et al.,1979;Langmuir,1997;Sparks, 2005).Eventually,the solutions can become satu-rated,or reach equilibrium,with respect to various sulfate,carbonate,or hydroxide minerals that estab-lish limits for the dissolved metal concentrations.Dissolved trace elements,such as Pb and Cu,in natural waters can be limited to concentrations lower than expected on the basis of trace-mineral solubility because of surface complexation,or adsorption,of the elements onto solid surfaces (Rose et al.,1979).Hydrous Fe III,Al,and Mn III–IV oxides that precipitate in oxidizing CMD environ-ments are important sorbents because of their large surface areas,tendencies to form colloids and to coat other geological materials,and potential for the oxide surfaces to have variable electrostatic charges(Hem,1977,1978,1985;Loganathan and Burau,1973;McKenzie,1980;Davis and Kent, 1990;Kooner,1993;Coston et al.,1995;Langmuir, 1997;Webster et al.,1998;Kairies et al.,2005; Sparks,2005).Surface hydroxyl groups at the solu-tion interface tend to dissociate at high pH or to protonate at low pH,giving rise to a negative or positive surface charge,respectively.Cations,such as Cd,Cu,Pb,Ni and Zn,tend to be adsorbed by the negatively charged oxide surfaces at near-neu-tral pH,whereas oxyanions,such as sulfate,arse-nate,arsenite,selenate,selenite and borate,tend to be adsorbed by the positively charged surfaces at lower pH(Dzombak and Morel,1990;Davis and Kent,1990;Stumm and Morgan,1996;Drever, 1997;Langmuir,1997).These conditions for adsorption are consistent with reported enrichment of CMD ochres and streambed coatings with Cd, Cu,Pb,Ni and Zn at near-neutral pH and with S and As at low pH(Winland et al.,1991;Hedin et al.,1994;Rose and Ghazi,1997;Cravotta and Trahan,1999;Cravotta and Bilger,2001;Cravotta et al.,2001;Hedin,2003;Kairies et al.,2005;Crav-otta,2005,2008).This report examines relationships between pH, SO4,and metal concentrations in CMD samples204 C.A.Cravotta III/Applied Geochemistry23(2008)203–226from abandoned coal mines in the Bituminous and Anthracite Coalfields of Pennsylvania.Similarities and differences in theflow rate and chemistry between the anthracite and bituminous CMD sam-ples are examined.The potential formation of aque-ous complexes,surface complexes,and stability of possible solid phases in contact with aqueous solu-tions are evaluated with respect to thermodynamic equilibrium at near-surface temperature and pres-sure conditions.Additionally,ratios of Br/Cl are used to evaluate potential for mixing of fresh ground water with road salts or deep brine.A companion report by Cravotta(2008)describes the chemical and hydrological data in more detail and examines the correlations betweenflow rate,pH,constituent concentrations,and constituent loadings.2.Methods of sampling and analysisThe study area description,a map showing the sampling locations,and details on the site character-istics and methods of data collection and chemical analysis are given in the companion report by Crav-otta(2008).Essential information on sampling and analytical methods is summarized below.2.1.Water-quality sampling and analysisIn summer and fall1999,water-quality samples from140abandoned,discharging coal mines in the Anthracite and Bituminous Coalfields of Penn-sylvania were collected by the U.S.Geological Sur-vey(USGS)for analysis of chemical concentrations and loading.The140discharges,including99from bituminous mines and41from anthracite mines, were selected among thousands of CMD sources statewide based on their geographic distribution, accessibility,and potential for substantial loadings of dissolved metals.Most of the sampled discharges were from underground mines.All the CMD sources were discharging by gravity when sampled. Flow was measured at each site by use of a current meter or bucket and stopwatch.To minimize effects from aeration,electrodes were immersed and samples were collected as close as possible to the point of discharge.Field data forflow rate,temperature,specific conductance (SC),dissolved O2(DO),pH and redox potential (Eh)were measured at each site when samples were collected in accordance with standard methods (Rantz et al.,1982a,b;Wood,1976;U.S.Geological Survey,variously dated;Ficklin and Mosier,1999).All meters were calibrated in thefield using elec-trodes and standards that had been thermally equil-ibrated to sample temperatures.Field pH and Eh were determined using a combination Pt and Ag/ AgCl electrode with a pH sensor.The electrode was calibrated in pH2.0,4.0and7.0buffer solu-tions and in ZoBell’s solution(Wood,1976;U.S. Geological Survey,variously dated).Values for Eh were corrected to25°C relative to the standard hydrogen electrode in accordance with methods of Wood(1976)and Nordstrom(1977).An unfiltered subsample for analysis of alkalinity was capped leaving no head space and stored on ice.Alkalinity was analyzed in the laboratory within 48h of sampling by titration with H2SO4to the end-point pH of4.5(American Public Health Associa-tion,1998;Kirby and Cravotta,2005a,b).The pH before and during alkalinity titrations was measured using a liquid-filled combination Ag/AgCl pH elec-trode calibrated in pH4.0,7.0,and10.0buffer solu-tions.The net acidity of the CMD samples was computed fromfield pH,alkalinity and dissolved Fe,Mn,and Al concentrations(Kirby and Cravotta, 2005b;Cravotta,2008).Subsamples for analysis of‘‘dissolved”constitu-ents werefiltered through a0.45-l m pore-size nitro-cellulose capsulefilter using the clean-sampling methods of Horowitz et al.(1994).Although colloi-dal particles could pass through0.45-l m pore-sizefil-ters,constituent concentrations in thefiltered samples are interpreted hereinafter as dissolved sol-utes.The subsample for cation analyses was pre-served with trace-element grade HNO3to pH<2. Anions(SO4,Cl,F,NO3,NO2and PO4)infiltered, refrigerated samples were analyzed by ion chroma-tography(IC)(Fishman and Friedman,1989;Crock et al.,1999).Concentrations of major cations and trace metals in thefiltered,acidified samples were determined using inductively coupled plasma optical emission spectroscopy(ICP-OES)and inductively coupled plasma mass spectrometry(ICP-MS)(Fish-man and Friedman,1989;Crock et al.,1999).Results for replicate analyses were averaged before evalua-tion.When values for one or more replicates were reported as not detected,the lowest reported value or the lowest non-detect value was used as the result.putation of aqueous complexation and mineral saturationActivities of aqueous species,partial pressure of CO2(P CO2),and mineral-saturation index(SI)C.A.Cravotta III/Applied Geochemistry23(2008)203–226205values were calculated using the WATEQ4F version 2.63computer program(Ball and Nordstrom, 1991).The activities of Fe II and Fe III species were computed on the basis of the measured Eh,Fe con-centration,and temperature of the samples.Nord-strom(1977)and Nordstrom et al.(1979)have shown there is good agreement between the mea-sured Eh and that predicted by the Fe II/Fe III couple in acidic mine waters.For the90samples that hadalkalinity>0,the P CO2was computed on the basisof measured pH,alkalinity,and -puted SI values for silicate,oxide,carbonate and sulfate minerals that could be present in coal depos-its or associated wall rocks or that may form as solutions oxidized or evaporated at the land surface were summarized as a function of pH.Stability diagrams were developed to evaluate the potential for equilibrium of specific elements(Ca, Mg,Al,Fe,Mn,Ba,Cd,Cu,Pb,Sr,Zn)with respect to hydroxide,sulfate and carbonate minerals(solubility)for specified ranges of pH,Eh,P CO2,SO4and Cl.The theoretical stability boundaries for min-erals and aqueous species computed with spread-sheet models were plotted as reference lines or curves on‘‘pC–pH”and‘‘Eh–pH”diagrams(e.g. Snoeyink and Jenkins,1981;Drever,1997;Lang-muir,1997).Then,data on sample pH,Eh,or activ-ities of uncomplexed cations(Al3+,Fe3+,Fe2+)and major aqueous complexes computed with WATEQ4F were plotted as points on the stability diagrams.Reactions and associated equilibrium constants for relevant species and solids in the spreadsheet models were obtained mostly from the WATEQ4F thermodynamic database(Nordstrom et al.,1990;Ball and Nordstrom,1991;Drever, 1997)and supplemented with other data for Fe III minerals(Bigham et al.,1996;Yu et al.,1999).Ther-modynamic data that were used are summarized in the Appendix(Tables A1–A3).Equilibrium reac-tions and associated thermodynamic data for hydroxide,sulfate,and carbonate minerals and aqueous species involving SO4,CO3,Fe III and Al are given in Table A1.Speciation and solubility data for Al,Ba,Ca,Cd,Co,Cu,Fe II,Fe III,Mg,Mn II, Ni,Pb II,Sr and Zn are summarized in Table A2; detailed reactions for Pb II with data from Table A2are provided as an example in Table A3.putation of surface complexationAdsorption and desorption,or surface complexa-tion,of cations and anions on hydrous ferric hydroxide(HFO)particles were evaluated using adiffuse double-layer modeling approach with PHREEQC(Parkhurst and Appelo,1999),sur-face-complexation data from Dzombak and Morel (1990),and aqueous speciation data from Ball and Nordstrom(1991).Although the concentrations of dissolved solutes in the models could be specified based on the known ranges for the CMD samples, knowledge of the amounts and properties of the sor-bent HFO was lacking.Models were developed for different cations and anions byfirst modifying an example for Zn adsorption on HFO(‘‘example8”of Parkhurst and Appelo,1999)that implicitly spec-ified the HFO surface assemblage in equilibrium with a solution offixed composition.The HFO solid was specified as0.09g kgÀ1solution,with a specific surface area of600m2gÀ1consisting of5Â10À6 moles of strong binding sites and2Â10À4moles of weak binding sites.With data from Dzombak and Morel(1990),additional sorbate elements were considered(cations:Ba,Ca,Cd,Co,Cu,Mn II,Ni, Pb II,Sr;anions:As,B,Cr,Se,S,V).Aqueous spe-ciation and adsorption distribution were computed for a constant concentration of the sorbate element and a range of pH values.Plots were created to summarize the percentage of the sorbate element distributed between the solution and sorbent as a function of pH.The models developed for anion adsorption simulated a NaCl background matrix, whereas those for cation adsorption also specified initial concentrations of SO2À4and HCOÀ3to iden-tify effects of metal complexes with OHÀ,ClÀ,SO2À4and CO2À3species.3.Results–characteristics of anthracite and bituminous CMD samplesData on theflow rates,pH,acidity,alkalinity and selected solute concentrations for the140 CMD samples collected in1999from abandoned coal mines in the Anthracite and Bituminous Coal-fields of Pennsylvania are summarized in Table1 and Figs.1and2.Sampledflow rates at the140 CMD sites ranged from0.028to2.210L sÀ1.The anthracite discharges had greater medianflow rates than the bituminous discharges(Table1).Further-more,median and maximumflow rates for the anthracite mine discharges generally exceeded those for the bituminous mines for the same pH class interval(Fig.1).Generally,flow rate and alkalinity increased with pH,whereas acidity,SO4and metal concentrations206 C.A.Cravotta III/Applied Geochemistry23(2008)203–226decreased(Fig.1).These trends imply(1)neutral-ization of CMD did not result solely by mineral dis-solution but also involved dilution of initially acidic water by alkaline ground water or surface water or (2)decreased pyrite oxidation because of decreased contact time with increasedflows.Regardless of the cause,mines with largeflows tended to be less acidic and have greater pH than those with smallflows. Largerflow rates for anthracite discharges than bituminous discharges reflect differences in the phys-iographic and geologic settings between the two coalfields(Berg et al.,1989;Edmunds,1999;Eggle-ston et al.,1999)and indicate that,on average,the anthracite mines have larger recharge areas and more extensiveflooded volumes compared to the bituminous mines.Because anthracite mine com-plexes historically connected multiple coalbeds and extended beneath valleys to hundreds of meters below the regional water table,their mined areas and associated discharge volumes tend to be sub-stantially greater than those from contemporaneous surface mines or bituminous mines that access one or two coalbeds within isolated hilltops.Thefield pH of the140CMD samples ranged from 2.7to7.3,with the majority either acidic (pH 2.5–4)or near neutral(pH6–7)(Table1, Fig.1).This bimodal frequency distribution of pH for the CMD samples was discussed in detail by Cravotta et al.(1999)and Kirby and Cravotta (2005a,b).Although the minimum and maximum pH values were associated with bituminous mine discharges,the median pH values of5.1and5.2 were similar for the41anthracite and99bituminous discharges,respectively(Table1).Table1Summary of hydrochemical characteristics of discharges from140abandoned coal mines in Pennsylvania,1999aCoalfield and number of samples Flowrate(L sÀ1)Temperature(°C)Specific(l S cmÀ1)Redoxpotential,Eh(mV)pH,field Alkalinity(mg LÀ1asCaCO3)Net acidity b(mg LÀ1asCaCO3)Hardness c(mg LÀ1asCaCO3)Sulfate,SO4(mg LÀ1)Anthracite N=4164.011.4692390 5.1343244260 (0.028;2.21)(8.8;26.6)(131;2050)(170;770)(3.0;6.3)(0;120)(À79;588)(23;770)(34;1300)Bituminous N=9912.512.01480390 5.21476433580(0.227;278)(9.0;16.5)(495;3980)(140;800)(2.7;7.3)(0;510)(À326;1587)(117;1811)(120;2000)Calcium,Ca(mg LÀ1)Magnesium,Mg(mg LÀ1)Sodium,Na(mg LÀ1)Potassium,K(mg LÀ1)Chloride,Cl(mg LÀ1)Silica,SiO2(mg LÀ1)Aluminum,Al(mg LÀ1)Iron,Fe(mg LÀ1)Manganese,Mn(mg LÀ1)Anthracite N=413735 6.1 1.8 6.3130.2815 2.9(3.3;180)(3.6;87)(0.69;67)(0.7;3.9)(0.1;110)(5.8;51)(0.007;26)(0.046;312)(0.019;19)Bituminous N=991103823 3.37.719 1.543 2.3 (19;410)(8.5;210)(1.0;500)(0.5;12)(0.4;460)(8.2;67)(0.008;108)(0.16;512)(0.12;74) Arsenic,As(l g LÀ1)Barium,Ba(l g LÀ1)Cadmium,Cd(l g LÀ1)Copper,Cu(l g LÀ1)Lead,Pb(l g LÀ1)Nickel,Ni(l g LÀ1)Selenium,Se(l g LÀ1)Strontium,Sr(l g LÀ1)Zinc,Zn(l g LÀ1)Anthracite N=410.62180.120.850.68830.4190130(<0.03;15)(13;31)(<0.01;2.1)(0.4;91)(<0.05;11)(19;620)(<0.2;3.9)(27;2700)(3.0;1000)Bituminous N=992.0130.12 2.20.10900.61000140 (0.1;64)(2.0;39)(<0.01;16)(0.4;190)(<0.05;4.6)(2.6;3200)(<0.2;7.6)(47;3600)(0.6;10,000)a Median(minimum;maximum);L sÀ1,liters per second;°C,degrees Celsius;l S cmÀ1,microsiemens per centimeter;mV,millivolts; mg LÀ1,milligrams per liter;l g LÀ1,micrograms per liter.Sample site locations shown in Fig.1of Cravotta(2008).Detailed data available from Cravotta(2008).b Net acidity=(acidity,computedÀAlkalinity,measured)per Kirby and Cravotta(2005b).Acidity,computed(mg LÀ1 CaCO3)=50Á(10(3ÀpH)+3ÁC Al/26.98+2ÁC Fe/55.85+2ÁC Mn/54.94),where C Al,C Fe,and C Mn are dissolved aluminum,iron,and manganese concentration,respectively,in milligrams per liter.c Hardness(mg LÀ1CaCO3)=2.5ÁC Ca+4.1ÁC Mg,where C Ca and C Mg are dissolved calcium and magnesium concentration, respectively,in milligrams per liter.C.A.Cravotta III/Applied Geochemistry23(2008)203–226207Alkalinity concentrations ranged from0 (pH64.4;50samples)to510mg LÀ1as CaCO3 (Table1).Computed net acidity concentrations, which exclude contributions from dissolved CO2, ranged fromÀ326to1587mg LÀ1as CaCO3(Table 1).Concentrations of dissolved SO4(34–2000 mg LÀ1),Fe(0.046–512mg LÀ1),Al(0.007–108 mg LÀ1)and Mn(0.019–74mg LÀ1)varied signifi-cantly(Table1).Generally,the highest concentra-tions of acidity,SO4,Fe,Al,Mn and most other metals were associated with low-pH samples. Although a few samples were saturated with DO (10–12mg LÀ1),median concentrations of DO gener-ally were low(<2mg LÀ1)throughout the range of pH(Fig.1),consistent with the predominance of dis-solved Fe II and Mn II species in most CMD samples.The bituminous discharges generally contained greater concentrations of total dissolved solids than the anthracite discharges as a whole(Table1)or with the same pH values(Figs.1and2)as indicated by greater median and maximum values for specific conductance and concentrations of alkalinity,acid-ity,hardness,SO4,Fe,Al,Mn,and other solutes, including Cd,Cu,Ni,Sr and Zn.In contrast,the median concentrations of dissolved Ba and Pb in bituminous discharges were less than those for the anthracite discharges(Table1,Fig.2).As noted above,relatively low concentrations of dissolved mineral constituents in the anthracite discharges could result from dilution of initially acidic CMD with a freshwater source containing limited dis-solved solids.Such dilution could affect aqueous speciation and mineral solubilities.4.Discussion–geochemical controls on constituent concentrationsThe widespread occurrence of SO4,Fe,Mn,Al, As,Ba,Cd,Cu,Pb,Ni,Se,Sr and Zn in CMD sam-ples(Figs.1and2)results from the mobilization of these constituents by the weathering of pyrite and associated minerals in coal and surrounding sedimen-tary wall rocks.Under oxidizing conditions,pyrite oxidation produces H2SO4that reacts with carbon-208 C.A.Cravotta III/Applied Geochemistry23(2008)203–226ate,silicate and oxide minerals along pathways downflow from the pyrite (e.g.Cravotta,1994;Blowes and Ptacek,1994).Generally,the pH,alka-linity,and concentrations of alkali and alkaline earth cations increase because of the wall rock reactions,whereas SO 4concentrations remain constant.On the other hand,reducing conditions also can lead to increased pH but with corresponding decreases in the concentrations of SO 4and certain metals (Stumm and Morgan,1996;Drever,1997;Langmuir,1997).Hence,concentrations of dissolved metals and other trace constituents can increase or decrease as the CMD approaches neutrality.Such variations in sol-ute concentrations can be explained by geochemical processes including oxidation and reduction,mineral dissolution and precipitation,aqueous-complexa-tion,and surface-complexation (adsorption and desorption)reactions.4.1.Aqueous complexation and mineral solubility controls of constituents in CMD samplesAlthough Fe III and Al hydroxide minerals are insoluble at near-neutral pH,most divalent cations,including Fe II ,Mn,Cu,Cd,Pb and Zn,form rela-tively soluble hydroxides (Fig.3).Precipitation of Cu II ,Fe II ,and other divalent metal hydroxides gen-erally will not limit the dissolved metal concentra-tions until solutions become highly alkaline (pH >9).Furthermore,as demonstrated later,aqueouscomplexation with SO 2À4;CO 2À3;HCO À3;Cl À,and/or other anions can increase the dissolved metal concentration at equilibrium with its hydroxide.Nevertheless,observed concentrations of dissolved Fe II ,Cu,Cd,Pb,Zn,and other trace metals tend to be substantially lower than these solubility limits.Within the pH range of CMD,many trace metals can be adsorbed by hydrous Fe III ,Al and Mn IV oxi-des (e.g.Dzombak and Morel,1990;Davis and Kent,1990;Kooner,1993;Coston et al.,1995;Web-ster et al.,1998)and/or precipitate as sulfate or car-bonate minerals.Although most trace metals are capable of forming pure sulfate or carbonate phases,Cd,Cu,Pb,Zn,Ba and Sr commonly sub-stitute for Ca,Mg and Fe in calcite (CaCO 3),arago-nite (CaCO 3),dolomite (CaMg(CO 3)2),ankerite (Ca(Fe,Mg)(CO 3)2)and siderite (FeCO 3)(Hanshaw and Back,1979;Veizer,1983;Mozley,1989).2 945 23 15 1313114 713 91818217.52.53.0 3.54.0 4.55.0 5.56.0 6.57.025034568101520253040B A R I U M ,μg .L -1294523 15 1 3 1311471391818 2 1200.050.070.10.20.30.50.712357107.52.53.0 3.54.0 4.55.0 5.56.0 6.57.0L E A D ,μg .L -12 9 4 5 2 315 1 313 11 4 713 91818 210.220,0000.51251020501002005001,0002,0005,00010,000Z I N C ,μg .L -17.52.53.0 3.54.0 4.55.0 5.56.0 6.57.029452315131311471391818217.52.53.0 3.54.0 4.55.0 5.56.0 6.57.00.012000.020.050.10.20.5125102050100A R S E N I C ,μg .L -1pH CLASS INTERVAL MIDPOINT pH CLASS INTERVAL MIDPOINT pH CLASS INTERVAL MIDPOINT29452315131311471391818210.3300.0.50.7123571020305070100200C O P P E R , μg .L -17.52.53.0 3.54.0 4.55.0 5.56.0 6.57.0294523151313114713918182155,000710203050701002003005007001,0002,0003,000N I C K E L ,μg .L -17.52.53.0 3.54.0 4.55.0 5.56.0 6.57.029452315131311471391818210.003300.0050.010.020.030.050.10.20.30.512351020C A D M I U M , μg .L -17.52.53.0 3.54.0 4.55.0 5.56.0 6.57.0S E L E N I U M ,μg .L -17.52.5 3.0 3.5 4.0 4.5 5.0 5.5 6.0 6.57.029452315131311471391818210.07100.10.20.30.40.50.71234572945231513131147139181821205,0003050701002003005007001,0002,0003,000S T R O N T I U M ,μg .L -17.52.53.0 3.54.0 4.55.0 5.56.0 6.57.0Fig. 2.Boxplots showing concentrations of selected trace elements as a function of pH for 140abandoned mine discharges in Pennsylvania,1999:(A)As;(B)Ba;(C)Cd;(D)Cu;(E)Pb;(F)Ni;(G)Se;(H)Sr;(I)Zn.Shaded box,bituminous;open box,anthracite.C.A.Cravotta III /Applied Geochemistry 23(2008)203–226209。
藤壶附着对低合金高强度钢牺牲阳极保护效果的影响

表面技术第52卷第8期腐蚀与防护藤壶附着对低合金高强度钢牺牲阳极保护效果的影响蔡凡帆1,2,3,4,黄彦良1,2,4,邢少华5,许勇1,2,3,4,王秀通1,2,4(1.中国科学院海洋研究所 海洋环境腐蚀与生物污损重点实验室,山东 青岛 266071;2.青岛海洋科学与技术国家实验室海洋腐蚀与防护开放工作室,山东 青岛 266237;3.中国科学院大学,北京 100049;4.中国科学院海洋大科学研究中心,山东 青岛 266071;5.中国船舶重工集团公司第七二五研究所,山东 青岛 266237)摘要:目的探索藤壶附着对低合金高强度钢阴极保护效果的影响,研究海洋中大型污损生物附着下金属材料的腐蚀规律。
方法在青岛胶州湾进行腐蚀挂板实海暴露实验,运用纱网箱隔离藤壶幼虫作为对照组。
在暴露6个月和12个月后回收腐蚀挂板,研究藤壶附着后挂板腐蚀形貌、腐蚀产物和阴极保护效率的变化。
在室内进行模拟实验,研究牺牲阳极对存在藤壶附着的钢的保护效果。
结果在施加牺牲阳极保护后,藤壶附着下的钢表面具有更明显的局部腐蚀坑,且多位于藤壶附着的边缘位置。
藤壶附着对牺牲阳极保护效率的影响有限,藤壶附着钢的极化电位相较于无藤壶附着钢的极化电位更负,保护电流密度更小。
藤壶附着钢的未附着区域的保护电流密度(63.9 μA/cm2)比无藤壶附着钢(46.3 μA/cm2)的保护电流密度高。
XRD 谱、拉曼光谱和SEM图表明,藤壶附着不影响腐蚀产物或沉积物的组成。
结论在牺牲阳极保护下,处于藤壶附着边缘和中心位置的钢,可作为氧浓差电池的阳极,在自催化的协同作用下,腐蚀过程加速,形成了严重的局部腐蚀。
同时,藤壶附着可使钢的有效工作面积下降,导致藤壶附着下钢试样的无藤壶附着区域与不存在藤壶附着的钢试样相比,具有更高的保护电流密度和更负的极化电位。
关键词:藤壶;低合金高强度钢;牺牲阳极;局部腐蚀;保护效率;遮蔽作用中图分类号:TG174.41 文献标识码:A 文章编号:1001-3660(2023)08-0226-11DOI:10.16490/ki.issn.1001-3660.2023.08.017Effect of Barnacle Adhesion on Cathodic Protection of Low AlloyHigh Strength Steel by Sacrificial AnodeCAI Fan-fan1,2,3,4, HUANG Yan-liang1,2,4, XING Shao-hua5,XU Yong1,2,3,4, WANG Xiu-tong1,2,4(1. Key Laboratory of Marine Environmental Corrosion and Bio-fouling, Institute of Oceanology, Chinese Academy of Science,Shandong Qingdao 266071, China; 2. Open Studio for Marine Corrosion and Protection, Qingdao National Laboratory for收稿日期:2022-07-29;修订日期:2022-09-19Received:2022-07-29;Revised:2022-09-19基金项目:国家自然科学基金(41976033)Fund:National Natural Science Foundation of China (41976033)作者简介:蔡凡帆(1998—),男,硕士,主要研究方向为生物污损。
the hydrogen bond in the solid state
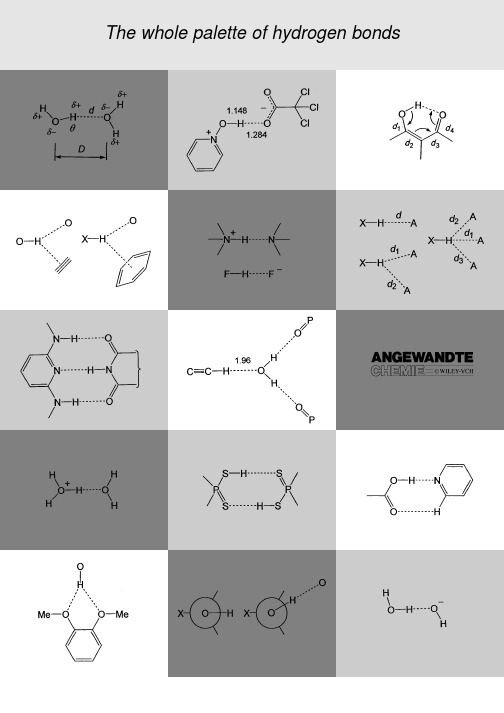
1.IntroductionThe hydrogen bond was discovered almost 100years ago,[1]but still is a topic of vital scientific research.The reason forthis long-lasting interest lies in the eminent importance ofhydrogen bonds for the structure,function,and dynamics of avast number of chemical systems,which range from inorganicto biological chemistry.The scientific branches involved arevery diverse,and one may include mineralogy,materialscience,general inorganic and organic chemistry,supramo-lecular chemistry,biochemistry,molecular medicine,andpharmacy.The ongoing developments in all these fields keepresearch into hydrogen bonds developing in parallel.In recentyears in particular,hydrogen-bond research has stronglyexpanded in depth as well as in breadth,new concepts havebeen established,and the complexity of the phenomenaconsidered has increased dramatically.This review is intendedto give a coherent survey of the state of the art,with a focus onthe structure in the solid state,and with weight put mainly on the fundamental aspects.Numerous books [2±9]and reviews on the subject have appeared earlier,so a historical outline is not necessary.Much of the published numerical material is somewhat outdated and,therefore,this review contains some numerical data that have been newly retrieved from the most relevant structural database,the Cambridge Structural Data-base (CSD).[10]It is pertinent to recall here the earlier ™classical∫view on hydrogen bonding.One may consider the directional inter-action between water molecules as the prototype of all hydrogen bonds (Scheme 1,definitions of geometric parameters are also in-cluded).The large difference in electro-negativity between the H and O atoms makes the O ÀH bonds of a water molecule inherently polar,with partial atomic charges of around 0.4on each H atom and À0.8on the O atom.Neighboring water molecules orient in such a way that local dipoles O d ÀÀH d point at negative partial charges O d À,that is,at the electron lone pairs of the filled p orbitals.In the resulting The Hydrogen Bond in the Solid StateThomas Steiner*In memory of JanKroon[*]Dr.T.SteinerInstitut f¸r Chemie–KristallographieFreie Universit‰t BerlinTakustrasse 6,14195Berlin (Germany)Fax:( 49)30-838-56702E-mail:steiner@chemie.fu-berlin.deREVIEWSREVIEWS T.SteinerOÀH¥¥¥j O interaction,the intermolecular distance is short-ened by around1äcompared to the sum of the van der Waals radii for the H and O atoms[11](1ä 100pm),which indicates there is substantial overlap of electron orbitals to form a three-center four-electron bond.Despite significant charge transfer in the hydrogen bond,the total interaction is dominantly electrostatic,which leads to pronounced flexibil-ity in the bond length and angle.The dissociation energy is around3±5kcal molÀ1.This brief outline of the hydrogen bond between water molecules can be extended,with only minor modifications,to analogous interactions XÀH¥¥¥A formed by strongly polar groups X dÀÀH d on one side,and atoms A dÀon the other (X O,N,halogen;A O,N,S,halide,etc.).Many aspects of hydrogen bonds in structural chemistry and structural biology can be readily explained at this level,and it is certainly the relative success of these views that made them dominate the perception of the hydrogen bond for decades.This dominance has been so strong in some periods that research on hydrogen bonds differing too much from the one between water molecules was effectively impeded.[8]Today,it is known that the hydrogen bond is a much broader phenomenon than sketched above.What can be called the™classical hydrogen bond∫is just one among many–a very abundant and important one,though.We know of hydrogen bonds that are so strong that they resemble covalent bonds in most of their properties,and we know of others that are so weak that they can hardly be distinguished from van der Waals interactions.In fact,the phenomenon has continuous transition regions to such different effects as the covalent bond,the purely ionic,the cation±p,and the van der Waals interaction.The electrostatic dominance of the hydrogen bond is true only for some of the occurring configurations,whereas for others it is not.The H¥¥¥A distance is not in all hydrogen bonds shorter than the sum of the van der Waals radii.For an XÀH group to be able to form hydrogen bonds,X does not need to be™very electroneg-ative∫,it is only necessary that XÀH is at least slightly polar. This requirement includes groups such as CÀH,PÀH,and some metal hydrides.XÀH groups of reverse polarity, X d ÀH dÀ,can form directional interactions that parallel hydrogen bonds(but one can argue that they should not be called so).Also,the counterpart A does not need to be a particularly electronegative atom or an anion,but only has to supply a sterically accessible concentration of negative charge. The energy range for dissociation of hydrogen bonds covers more than two factors of ten,about0.2to40kcal molÀ1,and the possible functions of a particular type of hydrogen bond depend on its location on this scale.These issues shall all be discussed in the following sections.For space reasons,it will not be possible to cover all aspects of hydrogen bonding equally well.Therefore,some important fields,for which recent guiding reviews are available,will not be discussed in great length.One example is the role of hydrogen bonds in molecular recognition patters(™supra-molecular synthons∫),[12]and the use of suitably robust motifs for the construction of crystalline archtitectures with desired properties(™crystal engineering∫).[13,14]This area includes the interplay of hydrogen bonds with other intermolecular forces, with whole arrays of such forces,and hierarchies within such an interplay.The reader interested in this complexfield is referred to the articles of Desiraju,[12,13]Leiserowitz et al.,[15] and others.[16]A further topic which could not be covered here is the symbolic description of hydrogen bond networks using tools of graph theory,[17]in particular the™graph set analy-sis∫.[18]An excellent guiding review is also available in this case.[19]For hydrogen bonding in biological structures,the interested reader is referred to the book of Jeffrey and Saenger,[5]and for theoretical aspects to the book of Scheiner[7]as well as other recent reviews.[20]Results obtained with experimental methods other than diffraction will be touched upon only briefly,and will possibly leave some readers dissatisfied.The role of hydrogen bonding in special systems will not be discussed at all,simply because there are too many of them.2.Fundamentals2.1.Definition of the Hydrogen BondBefore discussing the hydrogen bond itself,the matter of hydrogen bond definitions must be addressed.This is an important point,because definitions of terms often limit entire fields.It is,also,a problematic point because very different hydrogen bond definitions have been made,and partREVIEWS Solid-State Hydrogen Bondsof the literature relies quite uncritically on the validity(or thevalue)of the particular definition that is adhered to.Time has shown that only very general and flexibledefinitions of the term™hydrogen bond∫can do justice tothe complexity and chemical variability of the observedphenomena,and include the strongest as well as the weakestspecies of the family,and inter-as well as intramolecularinteractions.A far-sighted early definition is that of Pimenteland McClellan,who essentially wrote that™...a hydrogenbond exists if1)there is evidence of a bond,and2)there isevidence that this bond sterically involves a hydrogen atomalready bonded to another atom∫.[2]This definition leaves thechemical nature of the participants,including their polaritiesand net charges,unspecified.No restriction is made on theinteraction geometry except that the hydrogen atom must besomehow™involved∫.The crucial requirement is the existenceof a™bond∫,which is itself not easy to define.The methods totest experimentally if requirements1and2are fulfilled arelimited.For crystalline compounds,it is easy to see withdiffraction experiments whether an H atom is involved,but itis difficult to guarantee that a given contact is actually™bonding∫.A drawback of the Pimentel and McClellan definition isthat in the strict sense it includes pure van der Waals contacts(which can be clearly™bonding∫,with energies of severaltenths of a kcal molÀ1),and it also includes three-center two-electron interactions where electrons of an XÀH bond are donated sideways to an electron-deficient center(™agosticinteraction∫).From a modern viewpoint,it seems advisable tomodify point2,such as by requiring that XÀH acts as a proton (not electron)donor.Therefore,the following definition is proposed:An XÀH¥¥¥A interaction is called a™hydrogen bond∫,if 1.it constitutes a local bond,and2.XÀH acts as proton donor to A.The second requirement is related to the acid/base proper-ties of XÀH and A,and has the chemical implication that a hydrogen bond can at least in principle be understood as an incipient proton-transfer reaction from XÀH to A.It excludes, for example,pure van der Waals contacts,agostic interactions, so-called™inverse hydrogen bonds∫(see Section8),and B-H-B bridges.As a matter of fact,point2should be interpreted liberally enough to include symmetric hydrogen bonds XÀHÀX,where donor and acceptor cannot be distin-guished.The direction of formal or real electron transfer in a hydrogen bond is reverse to the direction of proton donation.Apart from general chemical definitions,there are manyspecialized definitions of hydrogen bonds that are based oncertain sets of properties that can be studied with a particulartechnique.For example,hydrogen bonds have been definedon the basis of interaction geometries in crystal structures(short distances,fairly™linear angles∫q),certain effects in IRabsorption spectra(red-shift and intensification of n XH,etc.),or certain properties of experimental electron density distri-butions(existence of a™bond critical point∫between H andA,with numerical parameters within certain ranges).All suchdefinitions are closely tied to a specific technique,and may be quite useful in the regime accessible to it.Nevertheless,theyare more or less useless outside that regime,and many amisunderstanding in the hydrogen bond literature has beencaused by applying such definitions outside their region ofapplicability.The practical scientist often requires a technical definition,and automated data treatment procedures for identifyinghydrogen bonds cannot be done without.It is not within thescope of this article to discuss any set of threshold values thata™hydrogen bond∫must pass in any particular type oftechnical definition.It is only mentioned that the™van derWaals cutoff∫definition[21]for identifying hydrogen bonds ona structural basis(requiring that the H¥¥¥A distance issubstantially shorter than the sum of the van der Waals radiiof H and A)is far too restrictive and should no longer beapplied.[5,6,8]If distance cutoff limits must be used,XÀH¥¥¥A interactions with H¥¥¥A distances up to3.0or even3.2äshould be considered as potentially hydrogen bonding.[6]Anangular cutoff can be set at>908or,somewhat moreconservatively,at>1108.A necessary geometric criterionfor hydrogen bonding is a positive directionality preference,that is,linear XÀH¥¥¥A angles must be statistically favored over bent ones(this is a consequence of point2of the above definition).[22]2.2.Further TerminologyA large part of the terminology concerning hydrogen bonds is not uniformly used in the literature,and still today, terminological discrepancies lead to misunderstanding be-tween different authors.Therefore,some of the technical terms used in this review need to be explicitly defined.In a hydrogen bond XÀH¥¥¥A,the group XÀH is called the donor and A is called the acceptor(short for™proton donor∫and™proton acceptor∫,respectively).Some authors prefer the reverse nomenclature(XÀH electron acceptor,Y electron donor),which is equally justified.In a simple hydrogen bond,thedonor interacts with one acceptor(Scheme2a).Since the hydro-gen bond has a long range,adonor can interact with two andthree acceptors simultaneously(Scheme2b,c).Hydrogen bondswith more than three acceptorsare possible in principle,but areonly rarely found in practice be-cause they require very highspatial densities of acceptors.The terms™bifurcated∫and™tri-furcated∫are commonly used todescribe the arrangements inScheme2b and c,respectively.The term™two-centered∫hydro-gen bond is an alternative descrip-tor for XÀH¥¥¥A(Scheme2a)where the H-atom is bonded totwo other atoms,and is itself notX H AX HAX H AAAAb)c)a)dd1d2d1d2d3Scheme2.Different typesof hydrogen bridges.a)Nor-mal hydrogen bond with oneacceptor.b)Bifurcated hy-drogen bond;if the twoH¥¥¥A separations are dis-tinctly different,the shorterinteraction is called majorcomponent,and the longerone the minor component ofthe bifurcated bond.c)Tri-furcated hydrogen bond.REVIEWST.Steiner counted as a center.Consequently,the arrangements in Scheme 2b and 2c may be called ™three-∫and ™four-centered∫hydrogen bonds,respectively.[5,6]This terminology is logical,but leads to confusion from the point of view of regarding hydrogen bonds O ÀH ¥¥¥O as ™three-center four-electron∫interactions,where the H-atom is counted as a center.A bifurcated hydrogen bond (Scheme 2b)is then termed ™three-centered∫,but also represents a ™four-center six-electron∫interaction.To avoid such ambiguities,the older term ™bifurcated∫is used here.There is particular confusion concerning the terms attrac-tive and repulsive .Some authors use these terms to character-ize forces,and others to characterize energies.In the latter case,an ™attractive interaction∫is taken as a synonym for ™bonding interaction∫,that is,one that requires the input of energy to be broken.Following well-founded recommenda-tions,[23]the terms ™attractive∫and ™repulsive∫are used here exclusively to describe forces.Negative and positive bond energies are indicated by the terms ™stabilizing∫(or ™bond-ing∫)and ™destabilizing∫,respectively.The schematic hydro-gen bond potential in Figure 1shows that a stabilizing interaction (that is,with E <0)is associated with a repulsive force if it is shorter than the equilibrium distance (see figure legend for further details).[8]Figure 1.Schematic representation of a typical hydrogen bond potential.[8]A hydrogen bond length differing from d 0implies a force towards a geometry of lower energy,that is,by attraction if d >d 0and repulsion if d <d 0.Note that the interaction can at the same time be ™stabilizing∫(or ™bonding∫)and ™repulsive∫!The distortions from d 0occurring in practice are limited by the energy penalties that have to be paid,and in crystals,only a few hydrogen bonds have energies differing by more than 1kcal mol À1from optimum.Hydrogen bonds are sometimes called ™nonbonded inter-actions∫.At least to this author,this appears a contradiction in terms which should be avoided.2.3.Constituent InteractionsThe hydrogen bond is a complexinteraction composed of several constituents that are different in their natures.[6,7]Most popular are partitioning modes that essentially follow those used by Morokuma.[24]The total energy of a hydrogen bond (E tot )is split into contributions from electrostatics (E el ),polarization (E pol ),charge transfer (E ct ),dispersion (E disp ),and exchange repulsion (E er ),somewhat different,but still related,partitioning schemes are also in use.The distance and angular characteristics of these constituents are very different.The electrostatic term is directional and of long range (diminishing only slowly as Àr À3for dipole ±dipole and as Àr À2for dipole ±monopole interactions).Polarization de-creases faster (Àr À4)and the charge-transfer term decreases even faster,approximately following e Àr .According to natural bond orbital analysis,[25]charge transfer occurs from an electron lone pair of A to an antibonding orbital of X ÀH,that is n A 3s *XH .The dispersion term is isotropic with a distance dependence of Àr À6.The exchange repulsion term increases sharply with reducing distance (as r À12).The dispersion and exchange repulsion terms are often combined into an isotropic ™van der Waals∫contribution that is approx-imately described by the well-known Lennard ±Jones poten-tial (E vdW $A r À12ÀB r À6).Depending on the particular chem-ical donor ±acceptor combination,and the details of the contact geometry,all these terms contribute with different weights.It cannot be globally stated that the hydrogen bond as such is dominated by this or that term in any case.Some general conclusions can be drawn from the overall distance characteristics.In particular,it is important that of all the constituents,the electrostatic contribution reduces slowest with increasing distance.The hydrogen bond potential for any particular donor ±acceptor combination (Figure 1)is,there-fore,dominated by electrostatics at long distances,even if charge transfer plays an important role at optimal geometry.Elongation of a hydrogen bond from optimal geometry always makes it more electrostatic in nature.In ™normal∫hydrogen bonds E el is the largest term,but a certain charge-transfer contribution is also present.The van der Waals terms too are always present,and for the weakest kinds of hydrogen bonds dispersion may contribute as much as electrostatics to the total bond energy.Purely ™electrostatic plus van der Waals∫models can be quite successful despite their simplicity for hydrogen bonds of weak to intermediate strengths.[26]Such simple models fail for the strongest types of hydrogen bonds,for which their quasi-covalent nature has to be fully considered (see Section 7).2.4.Energies The energy of hydrogen bonds in the solid state cannot be directly measured,and this circumstance leaves open ques-tions in many structural putational chemistry,on the other hand,produces results on hydrogen bond energies at an inflationary rate,[7,20]many obtained at high levels of theory and even more in rather routine calculations using black-box methods.Theoretical studies are not the topic of the present review,but an idea of typical results can be gained from the collection of calculated values listed in Table 1.[27]It appears that hydrogen bond energies cover more than two orders of magnitude,about À0.2to À40kcal mol À1.On a logarithmic scale,the bond energy of the water dimer is roughly in the middle.REVIEWS Solid-State Hydrogen BondsThe values in Table1are computed for dimers in optimal geometry undisturbed by their surroundings.In the solid state, hydrogen bonds are practically never in optimal geometry, and are always influenced by their environment.There are numerous effects from the close and also from the remote surrounding that may considerably increase or lower hydro-gen bond energies(™crystal-field effects∫).Hydrogen bonds do not normally occur as isolated entities but form networks. Within these networks,hydrogen bond energies are not additive(see Section4).In such cases,it is not reasonable to split up the network into individual hydrogen bonds and to calculate energies for each one.In this sense,calculated hydrogen bond energies should always be taken with caution.2.5.Transition to Other Interaction TypesAs outlined previously,the hydrogen bond is composed of several constituent interactions which are variant in their contributing weights.Chemical variation of donor and/or acceptor,and possibly also of the environment,can gradually change a hydrogen bond to another interaction type.This shall be detailed here for the most important cases.The transition to pure van der Waals interaction is very common.The polarity of XÀH or A(or both)in the array X dÀÀH d ¥¥¥A dÀcan be reduced by suitable variation of X or A.This reduces the electrostatic part of the interaction, whereas the van der Waals component is much less affected. In consequence,the van der Waals component gains relative weight,and the angular characteristics gradually change from directional to isotropic.Since the polarities of X dÀÀH d or A dÀcan be reduced to zero continuously,the resulting transition of the interaction from hydrogen bond to van der Waals type is continuous too.Such a behavior was actually demonstrated for the directionality of CÀH¥¥¥O C interactions,which gradually disappears when the donor is varied from C CÀH to C CH2to CÀCH3(see Figure8,Section3.2).[22]At the acceptor side of a hydrogen bond,sulfur is typical of an atom that allows continuous variation of the partial charge from S dÀto S d .Therefore,one can create a continuum of chemical situations between the S atom acting as a fairly strong hydrogen bond acceptor,and being inert to hydrogen bonding (the extreme cases are ionic species such as XÀSÀand X S ÀY).At the other end of the energy scale,there is a continuous transition to covalent bonding.[28]In the so-called symmetric hydrogen bonds XÀHÀX,where an H atom is equally shared between two chemically identical atoms X,no distinction can be made between a donor and an acceptor,or a™covalent∫XÀH and™noncovalent∫H¥¥¥X bond(found experimentally for X F,O,and possibly N).In fact,this situation can be conveniently described as a hydrogen atom forming two covalent bonds with bond orders s 1³2.In crystals(and also in solution),all intermediate cases exist between the extremes XÀH¥¥¥¥¥¥IX and XÀHÀX.Strongly covalent hydrogen bonds will be discussed in greater detail in Section7,and the bond orders(™valences∫)of H¥¥¥O over the whole distance range will be given in Section9(Table7).There is also a gradual transition from hydrogen bonding to purely ionic interactions.If in an interaction X dÀÀH d ¥¥¥Y dÀÀH d the net charges on XÀH and YÀH are zero,the electrostatics are of the dipole±dipole type.In general, however,the net charges are not zero.Alcoholic OÀH groups have a partial negative charge in addition to their dipole moment,ammonium groups have a positive net charge,and so on.This situation leads to ionic interactions between the charge centers with the energy having a rÀ1distance depend-ence.If the charges are large,the ionic behavior may become dominant.For fully charged hydrogen bond partners,ener-getics are typically dominated by the Coulombic interaction between the charge centers,but the total interaction still remains directional,with XÀH not oriented at random but pointing at A.An important example are the so-called salt-bridges between primary ammonium and carboxylate groups in biological structures,[5]N ÀH¥¥¥OÀ.If weakly polar XÀH groups are attached to a charged atom,such as the methyl groups in the N Me4ion,they are often involved in short contacts to an approaching counterion,N ÀXÀH¥¥¥AÀ.[8] Although these interactions are directional and may still be classified as a kind of hydrogen bond,their dominant part is certainly the ionic bond N ¥¥¥AÀ.Finally,there is a transition region between the hydrogen bond and the cation±p interaction.In the pure cation±p interaction a spherical cation such as K contacts the negative charge concentration of a p-bonded moiety such as a phenyl ring.This can be considered an electrostatic monopole±quadrupole interaction.The bond energy isÀ19.2kcal molÀ1 for the example of K ¥¥¥benzene.[29]A pure p-type hydrogen bond X dÀÀH d ¥¥¥Ph is formally a dipole±quadrupole inter-action with much lower energies of only a few kcal molÀ1 (Table1).If charged hydrogen bond donors such as NH4 interact with p-electron clouds,local dipoles are oriented atTable1.Calculated hydrogen bond energies(kcal molÀ1)in some gas-phase dimers.[a]Dimer Energy Ref.[FÀHÀF]À39[27a] [H2OÀHÀOH2] 33[27b] [H3NÀHÀNH3] 24[27b] [HOÀHÀOH]À23[27a]NH4 ¥¥¥OH219[27c]NH4 ¥¥¥Bz17[27d] HOH¥¥¥ClÀ13.5[27c]O CÀOH¥¥¥O CÀOH7.4[27e] HOH¥¥¥OH2 4.7;5.0[27f,g]N CÀH¥¥¥OH2 3.8[27h] HOH¥¥¥Bz 3.2[27i]F3CÀH¥¥¥OH2 3.1[27j]MeÀOH¥¥¥Bz 2.8[27k]F2HCÀH¥¥¥OH2 2.1;2.5[27f,j] NH3¥¥¥Bz 2.2[27i]HC CH¥¥¥OH2 2.2[27h]CH4¥¥¥Bz 1.4[27i]FH2CÀH¥¥¥OH2 1.3[27f,j] HC CH¥¥¥C CHÀ 1.2[27l] HSH¥¥¥SH2 1.1[27m]H2C CH2¥¥¥OH2 1.0[27l]CH4¥¥¥OH20.3;0.5;0.6;0.8[27f,n±p] C CH2¥¥¥C C0.5[27l]CH4¥¥¥FÀCH30.2[27q] [a]For computational details,see the original literature.Bz benzyl.REVIEWS T.Steinerthe p face,[30]but the energetics are dominated by the charge±quadrupole interaction[27d](NH4 ¥¥¥Bz experimentally:À19.3kcal molÀ1).[29]If the XÀH groups of the cation are only weakly polar,they may also orient at the p face and cause some modulation of the dominant cation±p interaction,but this modulation fades to zero with decreasing XÀH polarity.2.6.Incipient Proton Transfer ReactionA very important way of looking at hydrogen bonds is to regard them as incipient proton-transfer reactions. From this viewpoint,a stable hydrogen bond XÀH¥¥¥Y is a ™frozen∫stage of the reaction XÀH¥¥¥Y>XÀ¥¥¥HÀÀ Y(orX ÀH¥¥¥Y>X¥¥¥HÀÀ Y,etc.).This means that a partial bond H¥¥¥Y is already established and the XÀH bond is concomitantly weakened.[31]In the case of strong hydrogen bonds,the stage of proton transfer can be quite advanced.In some hydrogen bonds the proton position is not stable at X or Y,but proton transfer actually takes place with high rates.In other cases these rates are small or negligible.The interpretation of hydrogen bonds as an incipient chemical reaction is complementary to electrostatic views on hydrogen bonding.It brings into play acid±base consid-erations,proton affinities,the partially covalent nature of the H¥¥¥Y bond,and turns out to be a very powerful concept for understanding the stronger types of hydrogen bonds in particular.For example,the partial H¥¥¥Y bond can only become strong if its orientation roughly coincides with the orientation of the full HÀY bond that would be formed upon proton transfer.Approach in different orientations may still be favorable in electrostatic terms,but results only in moderately strong hydrogen bonds.This view also helps in deciding whether a particular type of XÀH¥¥¥A interaction may be classified as a hydrogen bond or not(compare the definition in Section2.1).Only if it may be thought of as a frozen proton-transfer reaction,may it be called a hydrogen bond.2.7.Location of the H AtomAn atom is constituted of a nucleus and its electron shell. Normally,the centers of gravity of the nucleus and electron shell coincide well,and this common center is called the ™location∫of the atom.For H atoms,however,this is generally not the case.In a covalent bond with a more electronegative atom,the average position of the single electron of the H atom is displaced towards that other atom. The centers of gravity of the nucleus and electron no longer coincide,and this leads to a conceptual problem:what should be taken as the™location∫of the atom?It is not chemically reasonable to consider one of the two centers of gravity as the ™right∫location of the atom,and the other as™wrong∫,but one must accept that a point-atom model is simplistic in this situation.[32,33]In practice,this leads to unpleasant complica-tions.X-ray diffraction experiments determine electron-density distributions and locate the electron-density maxima of the atoms.Neutron diffraction,on the other hand,locates the nuclei.The results of the two techniques for H atoms often differ by more than0.1ä.[34]Neither of the two results is more true than the other,but they are complementary and both represent useful pieces of information.Nevertheless,neutron diffraction results are much more precise and reliable,and allow the proton positions to be located as accurately as other nuclei.It has become a practice in the analysis of X-ray diffraction results to™normalize∫the XÀH bonds by shifting the position found for the H atom(that is,the position of the electron center of gravity)along the XÀH vector to the average neutron-determined internuclear distance,namely,to the approximate position of the proton.[35]This theoretical position is then used for the calculation of hydrogen bond parameters.The currently used standard bond lengths are: OÀH 0.983,NÀH 1.009,CÀH 1.083,BÀH 1.19,and SÀH 1.34ä;a more complete list can be found in ref.[8]. The normalization procedure is generally reasonable,well suited to smooth out the large experimental uncertainty of X-ray diffraction data,and is particularly useful in statistical database analysis.Nevertheless,one must be aware that it is not a correction in the strict sense,instead it replaces a certain structural feature(the location of the electron center of gravity)by a chemically different one(the proton position). Furthermore,the internuclear XÀH bond length is fairly constant only in weak and moderate hydrogen bonds,whereas it is significantly elongated in strong ones.In the latter situation,the elongation should at least in principle be taken into account in the normalization.This requires,however, knowledge of the relationship between the relevant XÀH and H¥¥¥A distances(see Section3.6).[36]2.8.Charge Density PropertiesThe precise mapping of the distribution of charge density in hydrogen-bonded systems is a classical topic in structural chemistry,[37]with a large number of individual studies reported.[38]Currently,Baders quantum theory of atoms in molecules(AIM)is the most frequently used formalism in theoretical analyses of charge density.[39]Each point in space is characterized by a charge density1(r),and further quantities such as the gradient of1(r),the Laplacian function of1(r), and the matrixof the second derivatives of1(r)(Hessian matrix).The relevant definitions and the topology of1(r)in a molecule or molecular complexcan be best understood with the help of an illustration(Figure2;see figure legend for details).[40]The thin lines represent lines of steepest ascent through1(r)(trajectories).If there is a chemical bond between two atoms(such as a hydrogen bond),they are directly connected by a trajectory called the™bond path∫.The point with the minimal1value along the bond path is called the™bond critical point∫(BCP).It represents a saddle point of 1(r)(strictly speaking,trajectories terminate at the BCP,so that the bond path represents a pair of trajectories each of which connects a nucleus with the BCP).Different kinds of chemical bonds have different numerical properties at the BCP,such as different electron density1BCP and different。
Studies on metal ions-DNA interactions- Specific behaviour of reiterative DNA sequences

I. INTRODUCTION Metal ions are present in practically all biological materials: they are known to bind tightly to membranes (Warren et al., 1965) and they participate to the stabilization of numerous biological structures. Various protein-metal ions complexes have been described (Frieden, 1968) and several enzymatic reactions depend on metal ions presence (Eichhorn et al., 1969). The association of divalent metal ions with ribosomes is a well established fact. Many metal ions are found in intimate association with nucleic acids in their natural environment and these ions may stabilize the structure of nucleic acids. They are required for virtually all biological processes in which nucleic acid are engaged. But in this last case, it is often difficult to know if metal ions are localized on proteins, on nucleic acids, between the two or really inside the double helical DNA. In some investigations the results of metal determinations in carefully isolated DNA preparations indicate that some metal ions are originally bound to the nucleic acid part of the chromatin areas. Studies of the interactions of metal ions-DNA have been made at two levels: addition of metal ions to natural DNA preparations and studies of the metal-DNA complexes obtained, and search for metal ions already present in DNA molecules extracted from various biological materials. It early became apparent in these investigations that metal ions are involved in the stabilization of the Watson-Crick double helix (Wacker and Vallee, 1959). In fact metal ions, under a variety of conditions, may produce quite different effects upon the structure of DNA, as shown, for instance, for the opposite influence on DNA melting temperature according to the studied metal ion. In this work, all the known aspects of the interaction metal ion-DNA sequences are described. Among these aspects, two open new areas of biological research: (1) A specificity exists in the metal-DNA complexes, depending on the nature of the metal, the nature of the DNA sequence and on various environmental conditions. This specificity is more strict than a recognition of one metal by one base. (2) Analysis of metal ions repartition on DNA molecules extracted from various biological materials show that metal ions are not bound at random on DNA; they are concentrated on some reiterative DNA sequences. Although many efforts have been spent on the study of reiterative components of eukaryotic DNAs, very little can be said with certainty about their function in the genome. At present, it appears most likely that the function of these reiterative components is mainly in chromosome folding or in influencing their mutual affinity (Walker, 1973). Some years ago, we proposed a model of quantitative control of genetic information where reiterative DNA sequences would be active regulation areas when scattered in the genome and potentially active ones when clustered in constitutive heterochromatin areas (Guill6 and Qu~tier, 1973). In the present work, numerous experimental facts are described which enable us to conceive a functional model, where the metal ion-reiterative DNA sequence complexes play a major role in regulation processes. The application of this functional model may allow us to imagine plausible and experimentally testable solutions to numerous problems including differentiation determinism, wound healing mechanisms and tumour disease establishment. Although little is known about the biochemical aspects of the toxicity of heavy metal ions and about the mechanism of their uptake into the cell, the existence and the properties of specific metal ion-reiterative DNA complexes may be partly responsible for the toxic effects of these metal ions.
化合物的logp-pka的测量和使用指导

Introduction / pH / Activity / pH measurement / pKa / LogP / Partition Solvents / Use of LogP / Methods / RefsA guide to Log P and pKa measurements andtheir useBy Mark Earll BSc(Hons) CChem MRSC (C) Copyright 1999-2006, All rights reserved.Return to Mark's Analytical Chemistry Index PageWinner of ACD Labs "Star Pick" AwardNB: You should have MDL's Chime installed to see these pages at their best!Disclaimer: This article is for guidance and educational purposes only. The author can accept no responsibility for loss or damage however caused. The author recommends that manufacturers advice be consulted exclusively when using any laboratory products.PREFACE TO 2006 REVISION: This page was written in 1999 and can be seen as summarising my practical knowledge of the field at that time. Things have moved onparticularly in the area of high throughput measurements. For the latest in high throughput pKa and LogP measurements I suggest you contact Sirius Analytical Instruments and for high throughput permeability contact Pion Inc . I will continue to add things to this site on the use of physical chemistry measurements in QSAR modelling. Please see section 1.7. to 1.9.Table of Contents:Introduction / pH / Activity / pH measurement / pKa / LogP / Partition Solvents / Use of LogP / Methods / Refs / TopIntroductionz Introduction z ContentszUnderstanding pKa and Log P measurements.{The pH scale {Activity {Practical pH measurement {pKa or Dissociation Constant {Log P and Partition Coefficients {Choice of partition solvent{How are LogP results related to activity? {How are LogP results related to solubility? {What do LogP values mean in practice?zMeasurement strategyzLogP/pKa measurement techniques{Aqueous Titration using Sirius instruments {Yesuda-Shedlovsky experiment {Ion Pair Log P's {pKa by Manual Titration {pKa by U.V. Spectroscopy {pKa by Solubility Method {Filter Probe Measurements {Log D and Log P by Filter Probe Method {Log P by Shake Flask {Log P by HPLCz ReferenceszAppendix 1 - Calculating Log D and % ionisedzAppendix 2 - Worked example calculationsThe followingJavascript calculators will help you calculate % ionised and Log D from pKa and Log P values:Percent Ionised Log DTable of pKa values: (Coming soon)The pKa or 'Dissociation Constant' is a measure of the strength of an acid or a base. The pKa allows you to determine the charge on a molecule at any given pH.The Partition Coefficient is a measure of how well a substance partitions between a lipid (oil) and water. pKa and Log P measurements are useful parameters for use in understanding the behaviour of drug molecules. Different ionic species of a molecule differ in physical chemical and biological properties and so it is important to be able to predict which ionic form of the molecule is present at the site of action. The Partition Coefficient is also a very useful parameter which may be used in combination with the pKa to predict the distribution of a drug compound in a biological system. Factors such as absorption, excretion and penetration of the CNS may be related to the Log P value of a drug and in certain cases predictions made.The measurement of pKa and Log P values are not straightforward. Experiments must be very carefully performed under standard conditions to ensure the results are valid and require interpretation of data which takes time and experience. In addition no one method is available for all compounds due to problems of insolubility, lack of removable protons and extreme values.This guide gives the theoretical basis of the pKa and LogP parameters as well as describing the techniques that can be used to measure them indicating which methods are appropriate for problem samples. I have also briefly indicated the use of these measurements in rational drug design.For more information please see the References section.Introduction / pH / Activity / pH measurement / pKa / LogP / Partition Solvents / Use of LogP / Methods / Refs / Top 1.0 Understanding pKa and Log P measurements.1.1 The pH scaleArrhenius 1887 was the first person to give a definition of an acid and a base, namely that an Acid gives rise to excess of H+ in aq solution whereas a Base gives rise to excess of OH- in solution. This was refined by Bronsted-Lowry in 1923 such that a proton donor was defined as an acid and a proton acceptor as a base They also introduced the familiar concept of the conjugate Acid - Base pair. The final refinement to Acid Base theory was completed by Lewis in 1923 who extended the concept to an Acids being an e -pair acceptor and a base a e -pair donor.The pH concept was introduced in 1909 by the Danish chemist S.P.L.SorensonpH is defined by the negative logarithm of the hydrogen ion activity:where aH = activity of the hydrogen ionThe pH scale derives from the characteristics of the auto-dissociation of Water. Pure water has a low conductivity and is only slightly ionised however does Water dissociate slightly into Hydronium ions and hydroxide ions:orThe concentration of H+ and OH- ions, which are equal, are 1x 10-7 ions per litre The equilibrium constant (or ion product ) for the dissociation of water, Kw, isby taking logs of both side we get:Using the standard abbreviation p for {-log10} we get:This equation sets the pH scale to 0-14, which gives a convenient way to express 14 orders of magnitude of [H+]. Any solution with pH>7 contains excess hydroxyl ions and is alkaline; those with pH<7 are acidic, containing excess hydrogen ionspH scaleIntroduction / pH / Activity / pH measurement / pKa / LogP / Partition Solvents / Use of LogP / Methods / Refs / Top1.2 ActivityA complication arises in electrochemistry due to the non-ideal nature of ions in solution. The activity of an ion at infinite dilution is equal to its concentration but as the concentration increases ionic attraction and incomplete hydration results in a drop in effective concentration. This means the law of Mass Action is only valid when activities are used in place of concentrationsActivity is defined as the "apparent concentration" of an ionic species, due to the attraction which ions can exert on one another and the incomplete hydration of ions in solutions that are too concentrated. The lower the concentration the less the interaction becomes. At infinite dilution activity coefficients approach unityThe activity of a species X is equal to the product of its concentration and its activity coefficient,The pH from an electrode relates to {H+} not [H+] though below Ionic strength of 0.01 these terms are very close between pH 2 and pH 10Introduction / pH / Activity / pH measurement / pKa / LogP / Partition Solvents / Use of LogP / Methods / Refs / Top1.3 Practical pH measurementA pH electrode consists of a pH sensor which varies in proportion to the {H+} of the solution and a reference electrode which provides a stable constant voltage. The output is in mV which needs to be converted to pH units.Where Ec = reference potentialNf = Nernstian slope factor = Nf=2.3RT/nF = 59.1 at 25 CWhere R=Gas constantT=abs Temp in KelvinF=faraday constantn=Valance factorAs can be seen from the equation the slope factor is temperature dependentthe pH is derived from:At pH 7 where {H+}={OH-} the voltage from the electrode is zero, this is called the Isopotential Point. In theory this point is temperature independent. IUPAC-NBS operational pH scale is defined as the pH relative to a standard buffer measured using hydrogen electrode. In practice a pH electrode is calibrated with a standard pH 7.00 buffer to determine the isoelectric point and a standard buffer at either pH 4 or 9 to determine the slope. Conventional pH meters will read accurately over a range 2.5 - 11. Beyond this their accuracy is dubious.In recent years Sirius Analytical Instruments have produced a series of dedicated pKa/LogP instruments. In the PCA 101 pKa instrument the calibration is carried out in a more sophisticated way adding empirical correction factors at the extreme ends of the pH spectrum where the electrode behaviour is non-ideal. In this way measurements at pH 1 or 13 are possible. This is based on the work of Alex Avdeef (1)Introduction / pH / Activity / pH measurement / pKa / LogP / Partition Solvents / Use of LogP / Methods / Refs / Top 1.4 pKa or dissociation constantBronsted was the first to show the advantage of expressing the ionisation of both acids and bases the same scale. He made an important distinction between Strong and weak bases:Strong acids and bases - defined as completely ionised in pH range 0-14Weak acids and bases - defined as incompletely ionised in pH range 0-14The pKa or ionisation constant is defined as the negative logarithm of the equilibrium coefficient of the neutral and charged forms of a compound. This allows the proportion of neutral and charged species at any pH to be calculated, as well as the basic or acidic properties of the compound to be defined."Thermodynamic Ionisation Constants" require the use of activities, being an "Infinite Dilution" definition. The measurement of activities is highly impractical, so in practice a high ionic strength swamping background electrolyte is used to give a "Constant Ionic Medium" pH definition. This is closely related to the thermodynamic definition. Such pKa values are independent of concentration and are of the type usually quoted in the literature.Thermodynamic Ionisation constantsfor acids:where{ } = activity in Mole litre-1pKa = -log10(Ka)for basespKa = -log10(Ka)At a given temp these are Thermodynamic Ionisation constants, which are independent of concentration. KTa. Since log 1 = 0 the pKa corresponds to the pH at which the concentration of ionised and neutral forms are equal.Ionisation constants that measured by Spectroscopy are "Concentration Ionisation Constants" These constants are measured ignoring activity effects and are dependent on concentration. It is therefore important that the concentration of the compound measured is quoted. Comparison of different compounds is only valid if their concentrations are identical.Concentration Ionisation constantswhere [] = concThese result from spectroscopic measurements where concentrations are used due to the beer lambert law.The "Thermodynamic" Ionisation Coefficient is related to the "Concentration" Ionisation Coefficient by:where f=activity coefficientpKa values are temperature dependent in a non-linear and unpredictable way. Samples measured by potentiometry are held at a constant temperature using a water jacket and thermostated water bath. Spectroscopic values are measured at ambient temperature. No pKa value should ever be quoted without the temperature. There is the additional question of whether pKa values should be measured at biological temperature as well as the standard 25 degrees. The former would have more meaning to biologists and the latter to chemists. Standard practice is to measure pKa’s at 25’CA useful formula for calculating the % ionisation of a compound at a particular pH from its pKa is(Where charge = 1 for bases and -1 for acids)% ionised plots of an Acid and a Base with a pKa of 8.0:Introduction / pH / Activity / pH measurement / pKa / LogP / Partition Solvents / Use of LogP / Methods / Refs / Top1.5 Log P and Partition CoefficientsThe Partition Coefficient itself is a constant. It is defined as the ratio of concentration of compound in aqueous phase to the concentration in an immiscible solvent, as the neutral molecule . In practical terms the neutral molecule exists for bases > 2 pKa units above the pKa and for acids > 2 pKa units below. In practice the Log P will vary according to the conditions under which it is measured and the choice of partitioning solvent.Partition CoefficientPartition Coefficient, P = [Organic] / [Aqueous] Where [] = concentration Log P= log 10 (Partition Coefficient)NOTE:Log P = 1 means 10:1 Organic:Aqueous Log P = 0 means 1:1 Organic:Aqueous Log P = -1 means 1:10 Organic:AqueousLog D is the log distribution coefficient at a particular pH. This is not constant and will vary according to the protogenic nature of the molecule. Log D at pH 7.4 is often quoted to give an indication of the lipophilicity of a drug at the pH of blood plasma.Distribution CoefficientDistribution Coefficient, D = [Unionised] (o) / [Unionised] (aq) + [Ionised] (aq) Log D = log 10 (Distribution Coefficient )LogD is related to LogP and the pKa by the following equations:for acids for basesAcid withpKa = 8.0Base with pKa = 8.0The graphs below show the distribution plots of an acid a base and a zwitterionIon Pair PartitioningIn practice not only neutral molecules but also ion pairs may partition. The charged species may pair with a reagent ion or even, in certain cases, itself. This leads to great complication of the experimental determination. Both the Log P and the LogD values may be affected if one or more of the charged species partitions. Ion pairing effects may be fully determined with the Sirius PCA101 or GL-pKa instrument, but at least two to three titrations need to be carried out. Ion pairing effects will cause errors in any spectroscopic measurements.Both the ionic strength and the type of counter ion used in solution have a pronounced effect on the ion pairing phenomenon. The high ionic strength used in the potentiometric determinations in the Sirius PCA101 instrument tends to encourage ion pairing effects. The spectroscopic measurements of Log P are measured at a much lower ionic strength, hence comparisons will be invalid.The question arises how valid is the use of a background electrolyte? Typically 0.1M of a background electrolyte is used. This is very close to the biological level of 0.16M. The type of electrolyte is also called into question. 0.15 M KCl is generally used due to its similarity with NaCl. NaCl cannot be used because of the "sodium effect" on the electrode at high pH. Measurements in KCl have been found to match those in NaCl almost exactly. Initially the Sirius Instruments used KNO 3, as used in thedevelopment of Metal Ligand binding titrations, from which the titrimetric method was developed. KNO 3 is obviously alien to most biological systems.Introduction / pH / Activity / pH measurement / pKa / LogP / Partition Solvents / Use of LogP / Methods / Refs / Top1.6 Choice of Partition solventThe choice of partition solvent has been subject to debate in recent years. The most commonly used solvent has been octan-1-ol after the work of Leo and Hansch at Pomona college California. Octanol was chosen as a simple model of a phospholipid membrane; however it has shown serious shortcomings in predicting Blood-brain barrier or skin penetration. More recently a group at ICI in 1989, (Leahy, Taylor and Wait) have proposed the use of four critical solvents for modelling biological membranes. These are octanol, chloroform, cyclohexane and propylene glycol dipelargonate (PGDP). Log P values measured in these different solvents show differences principally due to hydrogen bonding effects. Octanol candonate and accept hydrogen bonds whereas cyclohexane is inert. Chloroform can donate hydrogen bonds whereas PGDP can only accept them.Acid pKa = 8Base pKa =8Zwitterion pKa (base) = 5.6 & (acid) = 7.0Octanolamphiprotic (H-bonding)Which solvent to use is debatable; however delta log P values have been found to be useful in several QSAR studies.Liposomes.Recently partitioning experiments have been carried out with Liposomes. Liposomes are self assemblingmodel membranes composed of phopholipid groups such as phosphatadylcholine. The lipid molecule isChloroformproton donor (H-bonding)PGDPproton acceptor (H-bonding)AlkaneinertPhospholipidPhospholipid Model: (ref 8)log P (octanol-water) - logP (PGDP-water) predicts cardioselectivity in oxypropanolamines (ref 5)log P (octanol-water) - logP (alkane-water)has been suggested reflects hydrogen bonding capacity, which has implications for skin penetration. Compounds with high log P values and low H bonding capacity can readily get past ester/phosphate groups in skin membranes. (ref 6)log P (octanol-water) -logP (cyclohexane-water)correlates inversely with Log(Cbrain/Cblood) for a series of H2-receptor histamine antagonists (ref 7)dissolved in chloroform and deposited by evaporation onto a large surface such as a large round bottomed flask. The liposome is then hydrated by adding water and agitated. The lipids then self assemble to form lipid bilayers which form spheres, often concentric (multilammellar). For partitioning experiments it has been found that Unilamellar (single layer) liposomes are required. These can be formed by a a combination of freeze-thawing and extrusion through a fine filter or french press under pressure.Neutral LogP values from liposomes tend to be very similar to those measured in octanol but the ion-pair LogP values differ. The "Surface Ion Pair" log P is found to be much higher in bases, zwitterions and amphophiles. The values for acids tend to be similar to the octanol values. This reflects the increased potential for partitioning of molecules with basic groups into membranes.QSAR studies have found improved correlations with liposome derived "Surface Ion Pair" LogP values. It should be realised that for some compounds it is not possible to make measurements due to insolubility, impurity or instability reasons. It is practically impossible to make measurements on highly insoluble compounds, although pKa values may sometimes be measurable by aqueous-methanol titrations. In practical terms results become meaningless for compounds with extreme insolubility.Introduction / pH / Activity / pH measurement / pKa / LogP / Partition Solvents / Use of LogP / Methods / Refs / Top 1.7 How are Log P results related to biological activity?Relationships between Log P and activity are often found in series where structural modifications have not significantly affected the pKa values. Hansch in 1964 showed that these relationships were often parabolic hence the relationship often leads to an optimum value for the log P for a desired activity or selective distribution. Relationships of the type:Activity= m log P + k’ (linear)Activity= m log P - c(log P)2 - k(parabolic)Activity= m log P - c(blog P +1) - k (rectilinear) (where m, k and c are constants)are generated using regression analysis to correlate observed biological data with measured partition coefficients.The best way of relating LogP, pKa and other physico-chemical data to biological activity is using Multivariate techniques such as Principal Components Analysis and Partial Least Squares Regression. To understand these techniques and for software to do this please visit Umetrics at It must be remembered that measured log P values only correlate with activity in certain instances. The use of organic solvents to model complex biolipids is very simplistic and cannot explain phenomena such as the large difference in activity between molecules of wildly different structures or between enantiomers. In these cases it is very useful to combine physical measurements with molecular modelling, molecular property and spectroscopic data and use multivariate analysis.For both CNS penetration and gastric absorption many studies show a parabolic relationship with an optimum Log P value of around 2 ± 1. Evidence for this comes from a wide variety of experiments in the literature from brain concentration of radiolabelled compounds to CNS behavioural studies. Recently more sophisticated analysis of molecular properties such as "Partial Charged Surface Area" (PSA) and the hydrogen bonding properties of molecules have lead to better predictions of oral absorption.Although lipophilicity is just one of many factors involved in biological activity it is often one of the most influential. In PLS regression of molecular properties vs biological activity measurements of LogP almost always features in the more important coefficients. It is also a good idea to add a LogP squared to any regression analysis to take account of the non linearity mentioned above.1.8 How are Log P results related to solubility?Log P’s of neutral immiscible liquids run parallel with their solubilities in water; however for solids solubility also depends on the energy required to break the crystal lattice. Bannerjee, Yalkowsky and Valvoni (1980) Envir.Sci.Tech ,14,1227 have suggested the following empirical equation to relate solubility, melting point and Log P:where S is the solubility in water in micromoles per litre.It is therefore possible to have compounds with high Log P values which are still soluble on account oftheir low melting point. Similarly it is possible to have a low Log P compound with a high melting point, which is very insoluble.In cases of precipitation when titrating a basic compound, the solubility of the free base may be calculated using the equation:1.9 What do Log P values mean in practice?From a survey of the literature, it is possible to obtain some general guidelines about the optimum Log P values for certain classes of drugs. When designing drug molecules some thought should be given to the following:Studies have found: (bear in mind these may not apply to your class of chemicals)z OptimumCNS penetration around Log P = 2 +/- 0.7 (Hansch) z Optimum Oral absorption around Log P = 1.8 z Optimum Intestinal absorption Log P =1.35 z Optimum Colonic absorption LogP = 1.32 z Optimum Sub lingual absorption Log P = 5.5 zOptimum Percutaneous Log P = 2.6 (& low mw)Formulation and dosing forms:z Low Log P (below 0) Injectable z Medium (0-3) Oralz High (3-4) TransdermalzVery High (4-7) Toxic build up in fatty tissuesDrug Clearance and Toxicityz Increasing LogD 7.4 above 0 will decrease renal clearance and increase metabolic clearance. z High Log D7.4 compounds will tend to be metabolised by P450 enzymes in the liver. z A high degree of ionisation keeps drugs out of cells and decreases systemic toxicity. z pKa in range 6 to 8 is advantageous for membrane penetration.zDrugs should be designed with the lowest possible Log P , to reduce toxicity, non-specific binding, increase ease of formulation and bioavailability. Drugs should also be as low mw as possible to lower the risk of allergic reactions. (See principle of minimum hydrophobicity )Physiological pH values:zStomach 2Where: = solubility at= solubility of free basez Kidneys 4.2 (variable)z Small Intestine Fed 5.0 Fasted 6.8z Duodenal Mucus 5.5z Plasma 7.4Principle of minimum hydrophobicityTaken from the introductory chapter in "Lipophilicity in Drug Action and Toxicology" VCH 1995 Vol 4p22-24 Bernard Testa, Vladimir Pliska and Han van de Waterbeemd."Both parabolic and bilinear relationships allow one to derive the optimum value of log P for transport to a givenlocation, within the time of a biological assay. Evidence for an optimum lipophilicity for CNS depressants wasfound by 1968. Hancsh was then able to assert that in order for drugs to gain rapid access to the CNS, theyshould preferably have a logP value near 2.0. Subsequently, studies on anesthetics, hypnotics and other CNSagents have lead to the "Principle of Minimum Hydrophobicity in Drug Design" The thrust of this is to keepdrugs out of the CNS, and thereby avoid CNS related side effects such as depression, weird dreams andsedation, one should design drugs so that logP is considerably lower than 2.0. This ploy has been successful inthe new generation of non-sedative antihistamines.That we require drugs to have lower rather than higher lipophilicity depends also on other observations madeover the past 30 years. Many studies on plants animals, fish various organelles such as liver microsomes, andenzymes have shown a linear increase in toxicity or inhibitory action in a series of compounds as LogP or piincreases.A very high lipophilicity should also be avoided because of adverse effects on protein binding and on drugabsorption, including solubility.Linear and sometimes parabolic relationships have been found between lipophilicity and drug metabolism, eitherin whole animals, in liver microsomes, or by specific enzymes such as cytochrome P450. Metabolism can beundesirable for two reasons; it may limit drug bioavailability, or it may produce toxic metabolites.The ideal drug candidate, going into human studies, should have already been designed with the idea of keepinglipophilicity as low as possible, provided this can be done without loss of affinity to the target receptor." Lipinski's "Rule of 5" for DrugsChris Lipinski of Pfizer derived an easy to use 'rule of thumb' for drug likeness in molecules after surveying the worlds marketed drugs.The rule states that for reasonable absorptionz Keep H-Bond donors below 5 (sum of OH and NHs)z Keep mW below 500z Log P should be below 5z No more than 10 H bond acceptors (sum of Ns and Os)Like all rules they are there to be broken and a number of exceptions exist. I have personally worked on a couple of well-absorbed drugs which broke this rule but as a general guide it works well. Remember that you may have charge in your molecule so that LogD(7.4) or LogD(5.5) is really the important parameter rather than Log P. Keeping LogD(7.4) around 2 seem generally good advice. Manipulating the pKa can be a way of improving a molecule.Clarke-Delaney "Guide of 2" for AgrochemicalsErik Clarke and John Delaney of Syngenta have derived a set of guidelines for agrochemicalsz Mw 200-400z Mpt <200z LogPoct <2z pKa (base) 7+/- 2z Log Sw 2+/-1z Stability alerts <2For other attempts at rules for agrochemicals see references 19 and 20 RefsIntroduction / pH / Activity / pH measurement / pKa / LogP / Partition Solvents / Use of LogP / Methods / Refs / Top 2.0 Measurement StrategyThe strategy for measuring pKa and Log P is determined by the solubility of a compound. The compound must be soluble (and stable) during any procedure to ensure equilibrium is maintained.Typically in titration methods the compound is titrated towards the direction of its neutral form, resulting in a dramatic drop in solubility. Often several experiments are required to determine the concentration required for the compound to stay in solution. Data collected while precipitation is occurring produces incorrect results. Sometimes if sufficient data is collected while the compound is in solution the pKa may still be calculated.The pKa's of poorly soluble compounds must be measured in aqueous-methanol solution. If several titrations are carried out with different ratios of Methanol:Water the Yesuda-Shedlovsky equation can reveal the theoretical pKa in purely aqueous solution.Log P determination of poorly soluble compounds is a problem. Provided the Log P is high enough the compound may be determined by titration, adding the sample to the octanol first. The compound will then back partition into the aqueous layer. If this fails then spectroscopic methods have to be employed since more dilute solutions may be used.Substances submitted for pKa and LogP need to be pure, of accurately known composition and be submitted as free bases or inorganic acid salts. In general no reliable measurements can be made on organic acid salts.A good strategy is to submit compounds in a series. The reasons for this are:z to compare and contrast the properties of a closely related series, using directly comparabletechniques.z to find a common measurement strategy for all the compounds in a seriesz to identify experimental problems common to the seriesz to prevent unnecessary measurements, only key members of the series should be chosenz to ensure reagents with short shelf lives, and apparatus can be preparedIntroduction / pH / Activity / pH measurement / pKa / LogP / Partition Solvents / Use of LogP / Methods / Refs / Top 3.0 Log P/pKa measurement techniques:Method Measures Advantage Disadvantage Concrequired Sample sizeSirius Potentiometric pKa/Log P pKa, Log P,Log PappRapid, Convenient Insoluble or neutralsamples cannot bemeasured0.0001M(0.1mM)1-5 mgSirius Yesuda-Shedlovsky pKa pKa for insoluble samples Takes three or moretitrations0.0005M(0.5mM)5mgSirius Ion Pair Log P LogP, Log P(ip)Predict Log D moreaccurately Takes three or moretitrations0.0001M(0.1mM)3-15 mgManual potentiometric pKa pKa Simple, rapid Not for low oroverlapping pKa's>0.0025M(2.5mM)50 mgpKa by UV pKa pKa for poorly soluble orscarce compounds Slow0.000025M(25uM)6 mgpKa by Solubility pKa pKa for very insolublecompounds Slow, Low accuracy Below0.0005M(0.5mM)10 mgLogP by Filter Probe Log P Log P for poorly solublecompounds, Reliable > Log P of0.2.Messy, Slow to setup, requires care.Inaccurate below LogP of 0.20.000025M(25uM)6 mg。
高分子物理名词解释

高分子物理名词解释Θ溶剂(Θ solvent):链段-溶剂相互吸引刚好抵消链段间空间排斥的溶剂,形成高分子溶液时观察不到远程作用,该溶剂中的高分子链的行为同无扰链2.7Θ温度(Θ temperature):溶剂表现出Θ溶剂性质的温度2.7Argon理论(Argon theory):一种银纹扩展过程的模型,描述了分子链被伸展将聚合物材料空化的过程5.3Avrami方程(Avrami equation):描述物质结晶转化率与时间关系的方程:--α,α为转化率,K与n称Avrami常数(Avrami constants) 4.8 =Kt1n)ex p(Bingham流体(Bingham liquid):此类流体具有一个屈服应力σy,应力低于σy时不产生形变,当应力大于σy时才发生流动,应力高于σy的部分与应变速率呈线性关系3.13 Boltzmann叠加原理(Blotzmann superposition principle):Boltzmann提出的粘弹性原理:认为样品在不同时刻对应力或应变的响应各自独立并可线性叠加 3.8Bravais晶格(Bravais lattice):结构单元在空间的排列方式4.1Burger's模型(Burger's model):由一个Maxwell模型和一个Kelvin模型串联构成的粘弹性模型3.7Cauchy应变(Cauchy strain):拉伸引起的相对于样品初始长度的形变分数,又称工程应变3.16Charpy冲击测试(Charpy impact test):样品以简支梁形式放置的冲击强度测试,测量样品单位截面积的冲击能5.4Considère构图(Considère construction):以真应力对工程应作图以判定细颈稳定性的方法5.2Eyring模型(Eyring model):一种描述材料形变过程的分子模型,认为形变是结构单元越过能垒的跳跃式运动5.2Flory-Huggins参数(Flory-Huggins interaction parameter):描述聚合物链段与溶剂分子间相互作用的参数,常用χ表示,物理意义为一个溶质分子被放入溶剂中作用能变化与动能之比2.11.2Flory构图(Flory construction):保持固定拉伸比所需的力f对实验温度作图得到,由截距确定内能对拉伸力的贡献,由斜率确定熵对拉伸力的贡献2.16.2Flory特征比(characteristic ratio):无扰链均方末端距与自由连接链均方末端距的比值2.4 Griffith理论(Griffith theory):一种描述材料断裂机理的理论,认为断裂是吸收外界能量产生新表面的过程5.4Hencky应变(Hencky strain):拉伸引起的相对于样品形变分数积分,又称真应变3.16 Hermans取向因子(Hermans orientation factor):描述结构单元取向程度的参数,是结构单元与参考方向夹角余弦均方值的函数4.8, 4.10Hoffman-Weeks作图法(Hoffman-Weeks plot):一种确定平衡熔点的方法。
胶体悬液中白云母与铁铝氧化物表面双电层的相互作用

胶体悬液中白云母与铁铝氧化物表面双电层的相互作用王艳平;徐仁扣;李九玉【摘要】@@ 白云母是一种原生矿物,也是土壤中常见的层状硅酸盐矿物,其负电荷主要由四面体结构中的Al置换Si而来[1].在通常的pH条件下,白云母带负电荷,可变电荷土壤中的铁、铝氧化物带正电荷.当白云母与铁、铝氧化物存在于同一悬液体系中时,带相反电荷的胶体颗粒之间可以发生相互作用.Qafoku和Sumner[2]提出可变电荷土壤中带相反电荷的胶体颗粒表面双电层重叠的假说.【期刊名称】《土壤学报》【年(卷),期】2011(048)003【总页数】4页(P650-653)【关键词】扩散双电层;zeta电位;白云母;铁铝氧化物;胶体颗粒相互作用【作者】王艳平;徐仁扣;李九玉【作者单位】土壤与农业可持续发展国家重点实验室(中国科学院南京土壤研究所),南京,210008;中国科学院研究生院,北京,100049;土壤与农业可持续发展国家重点实验室(中国科学院南京土壤研究所),南京,210008;中国科学院研究生院,北京,100049;土壤与农业可持续发展国家重点实验室(中国科学院南京土壤研究所),南京,210008;中国科学院研究生院,北京,100049【正文语种】中文【中图分类】S153白云母是一种原生矿物,也是土壤中常见的层状硅酸盐矿物,其负电荷主要由四面体结构中的Al置换Si而来[1]。
在通常的 pH条件下,白云母带负电荷,可变电荷土壤中的铁、铝氧化物带正电荷。
当白云母与铁、铝氧化物存在于同一悬液体系中时,带相反电荷的胶体颗粒之间可以发生相互作用。
Qafoku和Sumner[2]提出可变电荷土壤中带相反电荷的胶体颗粒表面双电层重叠的假说。
Hou等[3]在高岭石与铁铝氧化物混合胶体悬液体系中的研究结果表明,带相反电荷胶体颗粒的扩散层的重叠降低了高岭石表面的有效负电荷密度,使得混合体系的zeta电位向正值方向位移。
Tombácz[4]在蒙脱石与氧化铁的混合体系中也观察到类似的现象。
Photonic Crystal Carbohydrate Sensors Low Ionic Strength Sugar Sensing

Photonic Crystal Carbohydrate Sensors:Low Ionic StrengthSugar SensingSanford A.Asher,*,†Vladimir L.Alexeev,†Alexander V.Goponenko,†Anjal C.Sharma,†Igor K.Lednev,†Craig S.Wilcox,†and David N.Finegold ‡Contribution from the Department of Chemistry,Che V ron Science Center,Uni V ersity of Pittsburgh,Pittsburgh,Pennsyl V ania 15260,and Department of Pediatrics,Uni V ersity of Pittsburgh Medical School,Uni V ersity of Pittsburgh,Pittsburgh,Pennsyl V ania 15260Received July 30,2002;E-mail:asher@Abstract:We developed a carbohydrate sensing material,which consists of a crystalline colloidal array (CCA)incorporated into a polyacrylamide hydrogel (PCCA)with pendent boronic acid groups.The embedded CCA diffracts visible light,and the PCCA diffraction wavelength reports on the hydrogel volume.This boronic acid PCCA responds to species containing vicinal cis diols such as carbohydrates.This PCCA photonic crystal sensing material responds to glucose in low ionic strength aqueous solutions by swelling and red shifting its diffraction as the glucose concentration increases.The hydrogel swelling results from a Donnan potential due to formation of boronate anion;the boronic acid p K a decreases upon glucose binding.This sensing material responds to glucose and other sugars at <50µM concentrations in low ionic strength solutions.IntroductionThere is an ever-increasing demand for continuous,nonin-vasive glucose monitoring due to the increasing number of people diagnosed with diabetes mellitus 1(type 1,insulin-dependent diabetes).The need for minimally invasive glucose sensing has also increased due to the recognition that the long-term health of diabetes mellitus patients is dramatically improved by careful glucose monitoring and control.2The development of accurate,reliable,continuous,and noninvasive glucose sensors would significantly improve the lives of diabetic patients and decrease their risk of hypoglycemia.These sensors would have to operate reliably at the physiological pH values and ionic strengths of bodily fluids and would have to be immune from interference by other species present.This need for glucose sensors has motivated the investigation of numerous approaches,which were recently reviewed.2In the work here we describe a new photonic crystal carbohydrate sensing hydrogel material (PCCA,Figure 1)which can be used to detect sugars in low ionic strength solutions.This material consists of a polyacrylamide hydrogel with an embedded crystalline colloidal array (CCA).We previously demonstrated the use of this photonic crystal sensor motif to sense metal cations,pH,ionic strength,and glucose.3-5Our previously demonstrated glucose sensor utilized glucose oxidase (GOD)as the molecular recognition element.The GOD conversion of glucose to gluconic acid reduced the GOD FAD prosthetic group,which became negatively charged.The forma-tion of these covalently bound hydrogel anions resulted in a Donnan potential that resulted in an osmotic pressure that caused the hydrogel to swell,which red shifted the Bragg diffraction.3,5Unfortunately,the utility of this motif for measuring glucose was limited because it did not function at high ionic strength,its response depended upon the oxygen concentration (which reoxidized the FAD),and the accompanying production of hydrogen peroxide could be problematic for many applications.We developed a new class of glucose sensing materials by attaching phenylboronic acid to our PCCA photonic crystal hydrogels.The use of boronic acid derivatives to sense,target,and separate diol-containing substances has been exploited for a long time (for recent reviews see refs 6and 7).Polymers con-taining boronic acid groups are widely used for affinity puri-fication.8-10Hydrogels with attached boronic acid moieties 11-15†Department of Chemistry.‡Department of Pediatrics.(1)(a)Clark,C.M.,Jr.Diabetes Care 1998,21(Suppl.3),C1-C2.(b)Davidson,M.B.Diabetes Care 1998,21,2152-2160.(2)Pickup,J.;McCartney,L.;Rolinski,O.;Birch,D.Br.Med.J.1999,319,1289-1293.(3)Holtz,J.H.;Asher,S.A.Nature.1997,389,829-832.(6)James,T.D.;Shinkai,S.Top.Curr.Chem.2002,218,159-200.(7)James,T.D.;Sandanayake,K.R.A.S.;Shinkai,S.Supramol.Chem.1995,6,141-157.(8)Hageman,J.H.;Kuehn,G.D.Boronic Acid Matrices for the AffinityPurification of Glycoproteins and Enzymes.In Methods in Molecular Biology:Practical Protein Chromatography ;Kenney,A.,Fowell,S.,Eds.;The Human Press Inc.:Totowa,NJ,1992;Vol.11,Chapter 4,pp 45-71.(9)Hageman,J.H.;Kuehn,G.D .Anal.Biochem .1977,80,547-554.(10)Maestas,R.R.;Prieto,J.R.;Kuehn,G.D.;Hageman,J.H.J.Chromatogr.1980,189,225-231.(11)Miyazaki,H.;Kikuchi,A.;Koyama,Y.;Okano,T.;Sakurai,Y.;Kataoka,mun.1993,195,829-836.(12)Kikuchi,A.;Suzuki,K.;Okabayashi,O.;Hoshino,H.;Kataoka,K.;Sakurai,Published on Web 02/22/2003have been used to bind cis diol-containing substances and lymphocytes.In addition,boronic acid derivatives have been polymerized in the presence of sugars to create imprinted sugar binding sites.16-18Kikuchi et al.12previously demonstrated that polymer hy-drogel volume changes could be actuated by boronic acid -sugar complexation.These hydrogel volume changes were utilized in a boronic acid -polymer membrane electrochemical detection scheme,where the hydrogel volume changes controlled ion diffusion to the electrode.12More recently,Arnold et al.19demonstrated an electrochemical conductometric glucose sensor that monitored the glucose concentration in whole blood and plasma.The detection scheme utilized the fact that glucose complexation to boronic acid releases protons and increases the local ionic strength.Sugar-induced boronic acid hydrogel swelling was used in a quartz crystal microbalance sugar sensing study by the Shinkai group.13,14In fact,the Sakurai group 20,21proposed that this glucose-induced boronic acid hydrogel swelling could be used for insulin delivery purposes.Boronic acid derivatives have been synthesized that change their absorbance upon binding of cis diols.22-25For instance,Lavigne et al.25demonstrated a boronic acid-based colorimetric chemosensing ensemble to sense tartrate and malate.These deri-vatives can be utilized for colorimetric sugar sensing.In fact,boronic acid -sugar complexes can be used to control the pitch and resulting diffraction of a cholesteric liquid crystal.26It may be possible to design a detection scheme utilizing this approach.Our PCCA photonic crystal glucose sensing hydrogel also utilizes color changes to report on sugar binding.These color changes result from shifts in the wavelength of Bragg diffracted light from the CCA incorporated into a hydrogel matrix.The PCCA volume depends on the concentration of bound sugars.These PCCA volume changes alter the CCA spacing,which alters the Bragg diffraction condition.3-5This report is the first in a series of papers devoted to the use of boronic acids as molecular recognition elements in PCCA.Our objective is to utilize these photonic crystal glucose sensing materials for in vivo glucose sensors in the form of contact lenses to sense glucose concentration in a tear fluid or in the form of subcutaneous inserts to report glucose concentration in an interstitial fluid.In this publication we describe our first glucose sensing motif,which utilizes 3-aminophenylboronic acid as the molecular recognition agent.This carbohydrate sensor responds only in low ionic strength solutions.In subsequent papers we will describe a more sophisticated boronic acid complexation motif,which shows selecti V ity for glucose and is responsive at physiological pH values and ionic strengths.(14)Kanekiyo,Y.;Sano,M.;Iguchi,R.;Shinkai,S.J.Polym.Sci.,Part A:Polym.Chem.2000,38,1302-1310.(15)Gabai,R.;Sallacan,N.;Chegel,V.;Bourenko,T.;Katz,E.;Willner,I.J.Phys.Chem.B 2001,105,8196-8202.(16)Wulff,G.Pure Appl.Chem.1982,54,2093-2102.(17)Glad,M.;Norrlo ¨w,O.;Sellergren,B.;Siegbahn,N.;Mosbach,K.J.Chromatogr.1985,347,11-23.(18)Wulff,G.Angew.Chem.,Int.Ed.Engl.1995,34,1812-1832.(19)Arnold,F.H.;Zheng,W.;Michaels,A.S.J.Membr.Sci.2000,167,227-239.(20)Kitano,S.;Koyama,Y.;Kataoka,K.;Okano,T.;Sakurai,Y.J.Controlled(22)Davis,C.J.;Lewis,P.T.;McCarroll,M.E.;Read,M.W.;Cueto,R.;Strongin,.Lett.1999,1,331-334.(23)Koumoto,K.;Shinkai,S.Chem.Lett.2000,856-857.(24)Ward,C.J.;Patel,P.;Ashton,P.R.;James,mun.2000,229-230.Figure 1.Polymerized crystalline colloidal array photonic crystal sensing materials consist of an embedded crystalline colloidal array (CCA)surrounded by a polymer hydrogel network which contains a molecular recognition element.The embedded CCA of polystyrene colloidal particles efficiently diffracts light of a wavelength determined by the array lattice constant.As shown by spectra on the right,diffracted wavelength red shifts result from hydrogel volume increases induced by the interaction of the analyte with the molecular recognition element.Photonic Crystal Carbohydrate Sensors A R T I C L E SExperimental Section-D -(+)-Glucose,methyl-R -D -glucopyranoside,D -(+)-mannose,D -(-)-fructose,and D -(+)-galactose were purchased from Sigma and were used as received.Tris-HCl (enzyme grade,supplied from USB,USA),NaCl (J.T.Baker),2,2-diethoxyacetophenone (DEAP,Acros Organics),acrylamide (AA,Fluka),N ,N ′-methylenebisacrylamide (bisAA,Fluka),3-aminophenylboronic acid hemisulfate (BA,Acros Organics),3-acetamidophenylboronic acid (Combi-Blocks Inc.,USA),hydrazine (Aldrich),NaNO 2(Fluka),HCl (J.T.Baker),NaOH (J.T.Baker),N ,N ,N ′,N ′-tetramethylethylenediamine (TEMED,Aldrich),and 1-[3-(dimethylamino)propyl]-3-ethylcarbodiimide hydrochloride (EDC,Aldrich)were used as received.Diffraction from the sensing materials was measured by using a SI 400(model 430/440)diode array spectrometer (Spectral Instruments,USA).UV spectra were measured by using a Perkin-Elmer Lambda 9UV/vis/NIR spectrometer.Preparation of CCAs.Highly charged monodisperse polystyrene colloids were prepared by emulsion polymerization as described elsewhere.27We used 5-10wt %suspensions of ∼140nm polystyrene colloidal particles.The suspensions were cleaned by dialysis against deionized water (17.5M Ω‚cm -1,Barnstead Nanopure Water Purifica-tion System)and by shaking with ion-exchange resin.The suspension became iridescent due to Bragg diffraction from the CCA upon shaking with ion-exchange resin.Each particle possesses ∼40000strong ionizable acid groups.Preparation of AA-PCCA.The PCCAs were synthesized by a free radical solution polymerization which utilized DEAP as a photoinitiator.A typical recipe utilized 100mg (1.4mmol)of AA,5mg (33.7µmol)of bisAA,2g of the CCA suspension (8-10wt %)in deionized water,and ∼50mg of ion-exchange resin.This polymerization mixture was shaken for 10-15min and deoxygenated by nitrogen bubbling.A 7.7µL sample of a 10%solution of DEAP in DMSO (3.84µmol of DEAP)was added to the AA -bisAA -CCA suspension,and the solution was shaken for an additional 10min and then centrifuged for 30s to precipitate the resin particles.This dispersion was injected into a cell consisting of two clean quartz disks separated by either a 125µm Parafilm film or by two 40µm Duraseal spacers.Photopolymerization was performed using UV mercury lamps [Black Ray (365nm)]for 40-60min.The cells were opened and the PCCAs were washed overnight in copious amounts of distilled water.If all of the bisacrylamide formed effecti V e 28hydrogel cross-links,the stoichi-ometry would yield a ∼0.03M cross-link density.In contrast,the elastic measurements of Lee and Asher 4indicate a much smaller effecti V e cross-link density of ∼1.5mM.Chemical Modification of Hydrogel Backbone.The synthetic procedures are shown in Scheme 1.1.Azide Route .The PCCA hydrogel backbone was functionalized with acyl azide groups to facilitate the attachment of 3-aminophenyl-boronic acid.The hydrazine treatment was performed as previously described.29-31The PCCA was immersed in 25mL of a 6M aqueous hydrazine solution at 47°C for 1h to generate PCCA-containing acyl hydrazine side chains.After repeated washing with 0.1M aqueous NaCl and with cold water,the gel was immersed for 20min in a cold aqueous nitrous acid solution formed by mixing 32mL of 0.25M HCl with 10mL of 1M NaNO2.This hydrazine treatment should also convert some (<2%)of the amides to carboxyl groups.29,31The resulting acyl azide gel was then repeatedly washed with 0.1M NaCl and cold water.We attached BA by immersing the acyl azide-functionalized PCCA in a 0.2M 3-aminophenylboronic acid solution (pH 8.5)in an ice bath for 1-2days.The remaining azide groups were removed by treating the IPCCA with 0.1M NH 4OH for 20min.302.Hydrolysis Route .Another route to the AA -BA PCCA involves hydrolysis of the PCCA amide groups.The PCCAs were placed in a 0.1N NaOH solution containing 10%v/v TEMED for 1.5-2h.The hydrolyzed PCCAs were then extensively washed with water and immersed in a solution containing 25mM EDC and 25mM 3-ami-nophenylboronic acid for 2-4h,to obtain the AA -BA PCCA.These PCCAs were repeatedly washed with distilled water.Because of carboxyl ionization,the washed hydrolyzed gels exten-sively swell in water and diffract in the IR region.The gel diffraction after BA attachment returned almost to that of the original nonhydro-lyzed PCCA,indicating that most of the carboxyl groups formed amide bonds with BA.Atomic emission determination of the boron content (Desert Analytics Co.)indicates that our procedure incorporates 0.27mmol of BA per g of dry PCCA.ResultsFigure 2shows the glucose concentration dependence of diffraction of the phenylboronic acid PCCA sensor in 2mM Tris buffer at pH 8.5.The spectral peaks derive from diffraction of normally incident light by the fcc 111planes of the embedded CCA.3-5In the absence of glucose the sensor shows a symmetric diffraction peak at 496nm,indicating that it diffracts blue-green light.This diffraction peak red shifts as the glucose concentration increases;the sensor diffracts green light at 506nm for 1mM glucose,orange light at 576nm for 20mM glucose,and red light at 624nm for 100mM glucose,for example.Thus,this sensor responds to glucose by changing its diffraction wave-length;the color changes are visually evident and can be used to visually estimate the glucose concentration.(27)Reese,C.E.;Guerrero,C.D.;Weissman,J.M.;Lee,K.;Asher,S.A.J.(29)Inman,J.R.;Dintzis,H.M.Biochemistry 1969,8,4074-4082.(30)Weith,H.L.;Wiebers,J.L.;Gilham,P.T.Biochemistry 1970,9,4396-4401.Scheme 1.Two Routes to Chemically Modify the PCCA Hydrogel BackboneA R T I C L E SAsher et al.The response of the sensor to glucose decreases upon addition of NaCl and ceases for NaCl concentrations greater than 10mM.In addition,the sensor response decreases for pH values below pH )8.5;the sensor becomes unresponsive to glucose at pH <7.The sensor swells as the pH increases to pH 9.5because all of the boronic acids titrate to boronates.Thus,the sensor becomes unresponsive to glucose at pH >9.5.We examined the dependence of the diffraction wavelength on glucose concentration in distilled water and found a detection limit of approximately 50µM for the sensors described herein.We can readily decrease the detection limit by decreasing the hydrogel cross-linking or increasing the concentration of boronic acid groups.3-5The glucose-induced diffraction red shifts originate from hydrogel swelling due to the formation of anionic boronate groups upon glucose binding (Scheme 2);the p K a of phenyl-boronic acid derivatives drops upon diol binding 6,7,19,32-39(also see Appendix).The diffracted wavelength changes linearly with changes in the embedded fcc 111plane CCA lattice constant,which varies as the 1/3power of the hydrogel volume.Figure 3shows the concentration dependence of the linear deformation factor,R )λ/λo )(V /V °)1/3,for this PCCA forglucose,fructose,mannose,galactose,and methyl-R -D -glucopy-ranoside,where V is the equilibrium volume of the PCCA at the defined sugar concentration and V °is the volume in the absence of the sugar.All of the sugars increase the PCCA linear deformation factor as their concentrations increase.The re-sponses of these sensors are fully reversible;decreases in the sugar concentration blue shift the diffraction.The maximum red shift occurs for fructose,which has the largest K 4association constant.The other sugars have significantly lower boronate K 4association constants and different K 3boronic acid associa-tion constants 32(Table 1).DiscussionThe glucose-induced PCCA diffraction shift results from formation of anionic boronate -glucose complexes,which are covalently linked to the PCCA hydrogel.At low ionic strengths significant differences can occur between the concentrations of ions in the PCCA and in the surrounding sample solution.This difference results in a Donnan potential that forces the gel to swell and the diffraction to red shift.3-5As shown by the solid lines in Figure 3,we successfully modeled the PCCA response (32)Lorand,J.P.;Edwards,J.O..Chem.1959,24,769-774.(33)Sienkiewicz,P.A.;Roberts,D.C.J.Inorg.Nucl.Chem.1980,42,1559-1575.(34)Singhal,R.P.;DeSilva,S.S.M.Ad V .Chromatogr.1992,31,293-335.(35)Singhal,R.P.;Ramamurthy,B.;Govindraj,N.;Sarwar,Y.J.Chromatogr.1991,543,17-38.(36)Soundararajan,S.;Badawi,M.;Kohlrust,C.M.;Hageman,J.H.Anal.Biochem.1989,178,125-134.(37)James,T.D.;Linnane,P.;Shinkai,mun.1996,281-288.Scheme 2.Equilibria Associated with 3-Acetamidophenylboronic Acid Glucose BindingFigure 2.Glucose concentration dependence of diffraction of the boronic acid PCCA sensor in 2mM Tris-HCl buffer at pH 8.5.The diffraction peaks are labeled with their glucose concentrations (mM).Figure 3.D -Glucose,D -fructose,D -mannose,D -galactose,and methyl-R -D -glucopyranoside concentration dependence of the linear deformation factor,R )λ/λo )(V /V °)1/3,for this PCCA.The solid lines are fits to the theoretical model as discussed in the text.We were unable to find a published value for the association constant of methyl-R -D -glucopyranoside to phenylboronic acid derivative.Photonic Crystal Carbohydrate SensorsA R T I C L E SThe equilibrium volume of our PCCA is determined by the condition that the total hydrogel osmotic pressure ΠT )0.The total osmotic pressure is the sum of the osmotic pressures due to the free energy of mixing,ΠM ,the hydrogel network elastic restoring force,ΠE ,and the osmotic pressure associated with the mobile ion concentration inside and outside the gel,Πion (Donnan potential):ΠT )ΠM +ΠE +ΠIon ,wherewhere R is universal gas constant,T is the temperature, is theFlory -Huggins interaction parameter for the polymer network and the solution,V s is the molar volume of the solvent,n cr is the effective number of cross-linked chains in the network,V is the existing volume of the gel,V m is the volume of the relaxed network,V 0is the volume of the dry polymer network,c +and c -are the concentrations of mobile cations and anions insidethe gel,and c +/and c -/are the concentrations outside the gel.In the case here we use the simplifying conditions that all ionic species are singly charged and the anion/cation stoichiometry is unity.We utilize the crucial assumptions 4that the hydrogel polym-erization occurred under conditions where the cross-linked chain length distribution is in its statistically most probable configura-tion(s)such that the volume of the prepared gel (before washing)is equal to V m .We utilize the hydrogel cross-link density obtained previously (n cr /V m )1.46×10-3M)and the Flory -Huggins interaction parameter )0.49for polyacrylamide.40As elaborated by Flory,28the concentration of ions inside the gel can be calculated by utilizing the requirement of electro-neutrality in the gel and by equating the product of the activities of the ions inside and outside the gel.Thus,if the system contains only monovalent ions,the difference between concen-trations of mobile anions and cations in the gel will be equal to the charge covalently attached to the polymer network.We expect that the only ionic species bound to the gel are the phenylboronates:c +)c B +c BG +c s and c -)c s ,where c B and c BG are the concentrations of the phenylboronate anion and of the phenylboronate -glucose anion complex attached to the gel.c s is the electrolyte concentration in the gel.Theconcentrations of boronate species were calculated from the reactions of Scheme 2(see details in the Appendix)taking into account the pH within the gel (which due to the Donnan potential differs from the pH of the external solution).We also include the boronic acid concentration changes due to hydrogel volume changes.The pH inside the gel was calculated by recognizing that identical water activities in the gel and in the reservoir require that [H +][OH -])[H +]*[OH -]*and that the other electrolyte activities (electrolyte CA )C ++A -)must be identical inside and outside the gel.Assuming that ion activities are equal to concentrations,the equality of the chemical potential of the electrolytes requires that the products of concentration of cations and anions inside and outside the gel be equal:Since the diffraction wavelength λD is directly proportional to V 1/3,solving the set of eqs 1,2,and 4for the value of V for which ΠT )0determines the dependence of the diffracted wavelength on the glucose concentration,provided that we know the solution electrolyte concentration and the ionization equi-libria of the boronic acid species.The electrolyte concentrations are determined by the 2mM Tris buffer equilibrium at the pH )8.5conditions used and the extent of boronic acid ionization.The charge covalently bound to the gel is determined by the glucose-dependent boronic acid -boronate ionization equilbria.An extensive body of literature exists on the mechanism of carbohydrate -phenylboronic acid complexation.6,7,19,41-47The equilibria are extraordinarily complex due to the multiple sugar conformations in solution and due to the fact that binding can be bis-bidentate for sugars with multiple cis diols.Even in the simplest case four different species may occur in the glucose binding equilibrium (Scheme 2).We are able to successfully model the dependence of the diffraction wavelength on the sugar concentration (Figure 3)by utilizing eqs 1,2,and 4,by assuming the simple sugar binding equilibria of Scheme 2and by fitting for the sugar binding equilibrium constants (Table 1).The values calculated from fitting differ somewhat from those measured for phenylboronic acid derivatives in solution.To compare the values for glucose,we (re)measured the equilibrium glucose binding constants and p K a values for 3-acetamidophe-nylboronic acid and 3-aminophenylboronic acid (Appendix).We find that the K 4equilibrium binding value found for PCCA boronate glucose binding is 4-fold smaller than to 3-acetamidophenylboronic acid in solution as well as bound to(41)James,T.D.;Sandanayake,K.R.A.S.;Shinkai,S.Angew.Chem.,Int.Ed.Engl.1996,35,1911-1922.(42)Norrild,J.C.;Eggert,H.J.Am.Chem.Soc.1995,117,1479-1484.(43)Norrild,J.C.;Eggert,H.J.Chem.Soc.,Perkin Trans.21996,2583-2588.(44)Bielecki,M.;Eggert,H.;Norrild,J.C.J.Chem.Soc.,Perkin Trans.21999,449-455.(45)Eggert,H.;Frederiksen,J.;Morin,C.;Norrild,.Chem.1999,64,3486-3846.Table 1.Sugar Binding Equilibrium Constants to Boronic Acid Derivatives and to the Boronic Acid Derivative Bound to the PCCAsugarPCCA K 3/M -1K 3/M -1PCCA K 4/M -1K 4/M -1fructose <1020004370a mannose 1290172a glucose 28<1b150600b50-160a 630c galactose<1100276aaFor 3-aminophenylboronic acid in solution by Lorand et al.32b For 3-acetamidophenylboronic acid in solution as measured here.c Phenylbo-ronic acid attached by an amide linkage at the 3-position to an acrylamide hydrogel.21Since c +/)c -/we will define c +/)c -/)c s /and c +‚c -)c +/‚c -/Further,[H +]/[H +]*)c s //c s and ΠIon )RT (c B +c BG -2(c s /-c s ))(4)ΠM )-∂∆G M ∂V )-RTV s [ln (1-V 0V )+V 0V + (V 0V)2](1)ΠE )-∂∆G E ∂V )-RT ‚n cr V m [(V mV)1/3-12V m V](2)ΠIon )RT (c ++c --c +/-c -/)(3)A R T I C L E SAsher et al.the acrylamide hydrogel of Shiino et al.21In contrast,the K3 value for boronic acid glucose binding is much larger than for 3-acetamidophenylboronic acid in solution.These differences may result from the different environment of the phenylboronic acid moieties in the PCCA and because some of the boronate binding sites may not be accessible to glucose in the PCCA.In addition,the effective boronic acid p K a may be higher in our PCCA.ConclusionsWe developed a photonic crystal hydrogel carbohydrate sensing material,which consists of a polyacrylamide hydrogel PCCA with pendent boronic acid groups.This material responds to sugars in low ionic strength aqueous solutions by red shifting its diffraction as the sugar concentration increases.This swelling of the hydrogel network results from an osmotic pressure generated by boronic acid ionization due to the boronic acid p K a decrease caused by glucose binding.We quantitatively modeled the response of our carbohydrate sensor to various sugars by extending hydrogel volume phase transition theory. The color of these sensors can be visually evaluated to determine sugar concentration.This sensing motif does not operate in high ionic strength solution since the Donnan potential becomes swamped at high ion concentrations.In a subsequent publication we will describe another boronic acid PCCA sensor that is selective for glucose and operates at high ionic strength that may prove useful for development of noninvasive or minimally invasive in vivo glucose sensors for patients with diabetes mellitus. AppendixWe determined the equilibrium constants shown in Scheme 2for phenylboronic acid,3-acetamidophenylboronic acid,and 3-aminophenylboronic acid in aqueous solution by examining the pH dependence of their absorption spectra(Figure4).All derivatives show absorption bands between190and325nm which derive from the perturbed transitions of the benzene aromatic rings.The high pH257nm phenylboronate band(Figure4),which has the low molar absorptivity of max≈200 M-1cm-1,characteristic of the forbidden substituted benzene L b transition,shows the characteristic vibronic progression of the benzenoid symmetric ring breathing vibration at∼900cm-1 in the excited state.48Formation of the phenylboronic acid at lower pH doubles the oscillator strength and red shifts this band by∼9nm(Figure4A).A much larger change occurs for the phenylboronate L a band,which appears as a shoulder at207 nm and red shifts to217nm in the phenylboronic acid form. Obviously the boronate and boronic acid aromatic ring substit-uents only weakly perturb the aromatic ring excited state structure and boronic acid is more perturbing than boronate. Dramatic absorption spectral changes occur upon amide or amine substitution in3-acetamidophenylboronic acid(Figure 4B)and3-aminophenylboronic acid(Figure4C and D),which indicates significantly stronger benzene ring electronic transition perturbations.The spectra resemble those substituted derivatives such as cresolate,for example.48The weak L b bands red shift out to260-300nm,while the stronger L a bands shift to∼240 nm.The fully allowed benzenoid B a,b bands shift down to just above200nm.The low pH3-acetamidophenylboronic acid weak L b bandat∼285nm appears to blue shift into a shoulder of the highpH9.9acetamidophenylboronate derivative(Figure4B).Littlechange occurs in the strong240nm L a band,while the higherenergy207nm B a,b band of3-acetamidophenylboronate redshifts∼5nm in the boronic acid derivative.3-Aminophenylboronic acid(Figure4C and D)shows a muchricher pH spectral dependence since both the boronic acid andthe amine substituents ionize(Scheme3).The lowest pH absorp-tion spectrum of3-aminophenylboronic acid shows a very weakL b-like absorption at∼265nm with max<300M-1cm-1withvibronic fine structure.This indicates little perturbation of theelectronic structure of the aromatic ring by the protonated amineand boronic acid substituents.In contrast,as the pH increases,the amine deprotonates and a much stronger294nm absorptionL b band appears( max≈1700M-1cm-1)with an L a band at ∼240nm and the B a,b band at∼205nm.Thus,the amine sub-stituent significantly perturbs the electronic structure.Formationof the boronate at higher pH significantly blue shifts each band.The pH absorption titrations show clear isosbestic pointsindicating simple titration behaviors except at the highest pHFigure4.pH dependence of absorption spectra of phenylboronic acid derivatives(1cm path length).(A)0.05mM phenylboronic acid aqueous solution at pH 4.5, 5.7,7.8,8.3,9.7,10.3,and11.1Inset:1mM phenylboronic acid aqueous solutions at pH4.5,5.5,6.9,7.7,8.6,10.3, and11.3.(B)0.05mM3-acetamidophenyl boronic aqueous solutions at pH4.0,5.5,7.5,8.4,9.0,and9.9.(C)1µM3-aminophenyl boronic acid aqueous solutions at pH3.6,4.1,and4.5.Inset:1mM at pH3.5,4.5,5.1, and5.75.(D)1µM3-aminophenyl boronic acid aqueous solutions at pH 5.3,6.0,6.9,7.8,9.0,and10.0.Inset:1mM3-aminophenyl boronic acid aqueous solutions at pH6.1,7.6,7.9,8.5,8.7,9.0,9.6,and10.6. Scheme3.Equilibria between Neutral and Charged3-Aminophenylboronic AcidPhotonic Crystal Carbohydrate Sensors A R T I C L E S。
Charge heterogeneity profiling of monoclonal antibodies using low ionic strength IEC

Journal of Chromatography A,1317 (2013) 148–154Contents lists available at ScienceDirectJournal of ChromatographyAj o u r n a l h o m e p a g e :w w w.e l s e v i e r.c o m /l o c a t e /c h r o maCharge heterogeneity profiling of monoclonal antibodies using low ionic strength ion-exchange chromatography and well-controlled pH gradients on monolithic columnsMohammad Talebi a ,Anna Nordborg a ,Andras Gaspar a ,Nathan cher b ,Qian Wang b ,Xiaoping Z.He b ,Paul R.Haddad a ,Emily F.Hilder a ,∗aPfizer Analytical Research Centre (PARC)and Australian Centre for Research on Separation Science (ACROSS),School of Chemistry,University of Tasmania,Hobart,Tasmania,Australia bAnalytical R&D,Pfizer BioTherapeutics Pharmaceutical Sciences,Chesterfield,MO,USAa r t i c l ei n f oArticle history:Received 13May 2013Received in revised form 13August 2013Accepted 16August 2013Available online 21 August 2013Keywords:pH gradient Ion exchangeMonoclonal antibodies Polymer monolithImaged capillary isoelectric focussingLiquid chromatography–mass spectrometrya b s t r a c tIn this work,the suitability of employing shallow pH gradients generated using single component buffer systems as eluents through cation-exchange (CEX)monolithic columns is demonstrated for the high-resolution separation of monoclonal antibody (mAb)charge variants in three different biopharma-ceuticals.A useful selection of small molecule buffer species is described that can be used within very narrow pH ranges (typically 1pH unit)defined by their buffer capacity for producing controlled and smooth pH profiles when used together with porous polymer ing very low ionic strength eluents also enabled direct coupling with electrospray ionisation mass spectrometry.The results obtained by the developed pH gradient approach for the separation of closely related antibody species appear to be consistent with those obtained by imaged capillary isoelectric focusing (iCE)in terms of both resolu-tion and separation profile.Both determinants of resolution,i.e.,peak compression and peak separation contribute to the gains in resolution,evidently through the Donnan potential effect,which is increased by decreasing the eluent concentration,and also through the way electrostatic charges are distributed on the protein surface.Retention mechanisms based on the trends observed in retention of proteins at pH values higher than the electrophoretic p I are also discussed using applicable theories.Employing monolithic ion-exchangers is shown to enable fast method development,short analysis time,and high sample throughput owing to the accelerated mass transport of the monolithic media.The possibility of short analysis time,typically less than 15min,and high sample throughput is extremely useful in the assessment of charge-based changes to the mAb products,such as during manufacturing or storage.© 2013 Elsevier B.V. All rights reserved.1.IntroductionThe advances in biotechnology in the last quarter of the 20th century have led to the development of new technologies for the production of complex biomolecules which could potentially be used in human health care in the areas of diagnostics,prevention and treatment of diseases.Qualities,such as high (target)selec-tivity,the ability to initiate immune recognition of the target,and long circulation half lives,have made the development of human-ised mAbs the fastest growing segment of therapeutic drugs [1,2].In the production of mAbs the final product often exhibits a number of variations from the expected or desired structure.These alterations may result from either known or novel types of posttranslational∗Corresponding author.Tel.:+61362267670.E-mail address:emily.hilder@.au (E.F.Hilder).modifications or from spontaneous,non-enzymatic protein degra-dation which bring about charge and size mon modifications of the primary sequence include N-glycosylation,methionine oxidation,proteolytic fragmentation,and deamidation [3].It has been shown that charge variants of therapeutic proteins can have significantly different bioactivity.For example,Harris et al.[4]showed that deamidated variants of recombinant human mAbs had reduced potency in a bioactivity assay.As protein charge het-erogeneity is an important factor in quality assessment of protein therapeutics,regulatory authorities such as the International Con-ference on Harmonisation (ICH)have set criteria for monitoring and characterising the degree and profile of variations to ensure lot-to-lot consistency and product stability [5].Considering the large size of antibodies and the minor struc-tural diversity between the variants,the existence of these variants imposes a great challenge for their separation.Ion-exchange (IEX)chromatography is a non-denaturing technique used widely to0021-9673/$–see front matter © 2013 Elsevier B.V. All rights reserved./10.1016/j.chroma.2013.08.061M.Talebi et al./J.Chromatogr.A1317 (2013) 148–154149separate and isolate protein charge variants for subsequent charac-terisation.However,when operating under a salt gradient approach (classical mode),IEX chromatography has been shown to exhibit limited selectivity when complex proteins with the same number of effective charges are to be separated[6]and lack of robustness when carboxypeptidase B(CPB)-treated mAbs are to be analysed [7].Capillary isoelectric focusing(CIEF)is another separation tech-nique used frequently to assess charge heterogeneity of proteins in which a complex mixture of ampholytes(polyionic organic elec-trolytes)is used to establish a pH gradient into a capillary with the aid of an electricfield.The electricfield causes protein isoforms to focus along the capillary according to their isoelectric point where they have zero net charge and then mobilise towards an on-column detector located at one end of the capillary.Due to the distortion of the pH gradient,which affects reproducibility in migration time and peak area,the mobilisation step often requires optimisation[8]. The introduction of imaged capillary electrophoresis(iCE),where imaging is performed of an entire capillary,has overcome this issue by eliminating the need for the mobilisation step through single point detection.While CIEF is perhaps the most powerful of the known separation technologies for charge variants,the difficulty of collecting fractions when compared to IEX chromatography has confined the method to be suitable for monitoring of variants but not for their preparative separation or isolation(peak identifica-tion)[2,6].Also,some authors believe that while the separations are consistent between the two methods,CIEF is not as precise as IEX chromatography and therefore cannot be considered as a suitable replacement[9].To the contrary,however,some have con-cluded that CE techniques could be superior to IEX chromatography in terms of both separation speed and obtainable high resolution and therefore could constitute a routine tool for assessing charge heterogeneity of proteins[8,10].Developed by Sluyterman et al.[11–15]in the late1970s, chromatofocusing(internal pH gradient)is recognised as the chromatographic analogy to IEF[9],mitigating many of the short-comings of classical IEX chromatography and combining some unique features of both methods.Chromatofocusing has been demonstrated to be useful for separating protein isoforms due to its high resolving power and ability to retain the protein native state[7,16].There are however some limitations to this technique such as the cost of polyampholyte buffers employed,the necessity of column regeneration after each separation,and the inflexibility in controlling pH gradient slope[7,17,18].Alternatively,pH gra-dient can be conducted externally by pre-column mixing of two eluting buffers at different pH values consisting of common buffer species.As the slope and profile of the pH gradient can be easily controlled by changing the elution program with less dependence on the buffer composition and column chemistry,this manner of introducing pH gradients should allow for more convenient method development and optimisation[17,18].The externally induced pH gradient has been applied for separation of deamidated variants of a mAb[3],resolving C-terminal lysine isoforms of a mAb after treat-ing with carboxypeptidase B[7]and also for the analysis of charge variants of full-length mAbs[9].Currently,particle-packed columns represent the most common stationary phases for high performance liquid chromatography. Despite immense popularity,their application for rapid and effi-cient separation of macromolecules is not as convenient as for small molecules.This is mostly because of slow diffusional mass transfer of large solutes and also the large void volume existing between the packed particles[19].Additionally,biocompatibility of stationary phases has become a new challenge when analysing biomolecules(including peptide and proteins).As defined by Li et al.[20],a biocompatible stationary phase material should be able to resist non-specific adsorption of biomolecules and preserve the bioactivity of the target biomolecules.These challenges are well met by employing monolithic media.Mass transfer in monolithic sorbents is mostly dominated by convection,rather than diffusion, and is therefore fast,even for large biomolecules.On the other hand,the expected biocompatibility of the most frequently used polymers in making porous monoliths,i.e.,poly(meth)acrylate and polyacrylamide,make these stationary phases highly suited for use in protein separation applications.We recently reviewed advances in polymer monoliths for IEX chromatography of biomolecules and addressed the importance of reducing non-specific interactions between analyte and stationary phase[21].While IEX chromatog-raphy of proteins using monolithic columns is frequently seen in the literature[22–24],very little effort has been directed towards employing this technique for separation of large proteins,such as mAbs.In continuing our recent efforts to resolve charge variants of mAbs with the aid of IEX monolithic columns[25];the maximum achievable resolution for mAb isoforms was pursued in this work using CEX columns in combination with simple,yet efficient,buffer systems.Unlike previous reports[6,9,18,26],we operated IEX chro-matography employing shallow pH profiles over a limited pH range (typically1pH unit)generated by single component buffer sys-tems at very low ionic strength.The suitability of the proposed buffer system in direct coupling of IEX chromatography to MS was also demonstrated.Due to their size and complexity,mAbs are typically characterised by two or more orthogonal separation methods[9].Therefore,the performance of the developed method was also assessed by comparing the results with those obtained by iCE.It was hoped that similar charge heterogeneity profiles could be achieved for mAbs analysed under two different separation mechanisms.2.Experimental2.1.Reagents and chemicalsThe buffering species used in this work,including imidazole,piperazine dihydrochloride hydrate(PDH),and tris(hydroxymethyl)aminomethane(Tris),diethanolamine(DEA) and ammonium hydroxide(AMH),28%(v/v)were all obtained from Sigma–Aldrich(Sydney,Australia)and triethanolamine(TEA) was from BDH(Poole,England).Sodium chloride,hydrochloric acid and sodium hydroxide(98.8%),methanol(LC–MS grade)were also from Sigma.All chemicals were of analytical grade unless specified otherwise.For iCE experiments,pharmalyte pH3–10,sucrose and urea were obtained from Sigma–Aldrich,while methyl cellulose (1%)and the Chemical Test Kit were from ProteinSimple(formerly Convergent Bioscience,Toronto,ON,Canada).The p I markers including p I s 5.13, 6.14,7.2and9.5were also obtained from ProteinSimple.Samples of three different IgG2mAb formulations, which are referred to as mAb1,mAb2and mAb3,were prepared by recombinant DNA technology at Pfizer Inc.2.2.ChromatographyThe IEX chromatography was performed on a Dionex DX-500liquid chromatograph(Thermo Fisher Scientific,Lane Cove, Australia)consisting of a GP50Gradient Pump,AD25UV/Vis Absorbance Detector,AS50Thermal Compartment and AS50 Autosampler.Detection was performed at280nm.Flow-rate was 1mL/min,the injection volume was10L and the column com-partment temperature was set at30◦C.Instrument control and data acquisition were performed using Dionex Chromeleon soft-ware,version6.80SR5.Chromatograms were transferred to ASCII files and redrawn using Origin8.1(Northampton,MA).150M.Talebi et al./J.Chromatogr.A1317 (2013) 148–154 The monolithic IEX columns used were ProSwift TM SCX-1S andProSwift TM WCX-1S(4.6mm×50mm)and the packed column wasProPac WCX-10,4mm×250mm,all from Dionex.The monolithiccolumns are methacrylates-based with sulfonic acid and carboxylicacid functionality for SCX and WCX,respectively.The ProPac WCXis a tentacle type ion-exchanger bearing carboxylate groups.Unless otherwise stated,mobile phases were generally preparedby dissolving appropriate amounts of the buffer components inwater prior to splitting into two aliquots denoted as eluent A andB.The pH of each portion was then adjusted with concentratedsodium hydroxide or hydrochloric acid.The elution was performedby a linearly ascending pH gradient from0%to100%eluent B fol-lowed by isocratic elution for3min before returning the eluentcomposition to the starting condition(100%eluent A).The gradi-ent volumes were10and30mL for monolithic and packed columns,corresponding to about14and10column volumes,respectively.For each elution,the column was pre-equilibrated with at leastthree column volumes of eluent A prior to sample introduction.Before measurement of peak areas,each sample chromatogram was subtracted from the relevant blank injection prepared from eluent A.Fractions of the column eluent were collected every1min and the offline pH measurement was carried out using a pH metre model labCHEM-CP from TPS(Springwood,QLD,Australia).All eluents were prepared using water purified via a Milli-Q water purification system(Millipore,Bedford,MA)andfiltered through a0.2m nylonfilter prior to use.mAb samples were ana-lysed as received without buffer exchange or any other sample pretreatment process.After dilution in eluent A to a concentra-tion of approximately0.3mg/mL,samples were stored at5◦C until analysed.2.3.Liquid chromatography–mass spectrometry(LC–MS)CEX chromatography was carried out using a ProSwift TM WCX-1S(4.6mm×50mm)column under pH gradient mode.5mM AMH buffer containing20%(v/v)methanol at pH9.5was used as eluent A and at pH10.5as eluent B.pH of eluents was adjusted before mixing with methanol.Elution was performed by running a linear gradient of eluent A to eluent B in20min at aflow-rate of0.4mL/min,which was split(1:100)before introducing into MS.Hyphenated with the CEX chromatography,electrospray ioni-sation time offlight(ESI-TOF)mass spectrometry was performed on a micrOTOF-Q mass spectrometer(Bruker Daltonics,Melbourne, Australia)equipped with an Agilent G1385A microflow nebuliser (Agilent technologies,Melbourne,Australia).The instrument was run in a positive ion mode with m/z range of500–10,000and a capillary voltage of4500V(−500V end plate offset).Drying gas flow of5L/min at300◦C was used with a20.3psi nebuliser gas pressure.The instrument was tuned and calibrated using an Agi-lent ES Tuning Mix(catalogue no.G2431A)in enhanced quadratic mode.The deconvolution of ESI mass spectra was performed usinga maximum entropy algorithm(Bruker Daltonics).2.4.Imaged capillary electrophoresis(iCE)iCE profiles of mAbs were obtained using an iCE280analyser with operational software from Convergent Bioscience,equipped with an Alcott719AL autosampler.A transparent capillary column (50mm,100m i.d.)was used with its inner surface coated with fluorocarbon to minimise electroosmoticflow.The test solutions were prepared using various amounts of p I markers,pharmalyte, 1%methyl cellulose,5M urea,20%sucrose,and mAb samples. Throughout the analysis,the capillary was kept at ambient tem-perature while the autosampler was set at8or15◦C,depending on the mAb sample analysed.The injection volume was35L and the Fig.1.pH gradient profiles obtained for mAb1and mAb2.The mobile phase com-position was12.5mM DEA and12.5mM TEA to either pH7.75(eluent A)or pH 10(eluent B).Gradient:0–100%B in10min,100%B for3min.Column:ProSwift SCX-1S(4.6mm×50mm);Detection:UV at280nm;Flow-rate:1mL/min;Column compartment temperature:30◦C.analysis was performed by applying a sample transfer time of100s, pre-focusing at1500V for duration of1min followed by focus-ing for5min at3kV.Detection was performed at280nm.Further details of the iCE conditions used are provided in the Supporting Information.3.Results and discussionWith the aim of improving the resolution,a series of new buffer systems based on both organic and inorganic buffer species were designed and applied using monolithic columns.To obtain suffi-cient binding of the proteins to the cation-exchanger,the lower pH of the gradient was chosen to be at least1pH unit below the elec-trophoretic p I values of mAbs,that is8.8for mAb1,8.5for mAb2 and8.4for mAb3.3.1.TEA-DEA buffer systemThefirst successful buffer system in eluting two of the mAbs of interest was prepared by mixing equimolar amounts of TEA (p K a7.76)and DEA(p K a8.88)resulting in a system buffering the pH range of approximately7.5–10.Fig.1shows the separation achieved for mAb1and mAb2on a ProSwift SCX-1S column using this buffer system in the pH range of7.75–10with each buffer com-ponent at a concentration of12.5mM.A somewhat linear pH profile for this system over the studied pH range was achieved(Fig.1).No elution was observed for mAb3.Acidic isoforms(p I lower than the main component)are observed for mAb1,while basic isoforms are more pronounced for mAb2.Indications of additional isoforms are also present,but as barely discernible shoulders of the main peaks.The effect offlattening the pH gradient profile on chromato-graphic resolution was of special interest in this study.As the pH gradient slope is reduced there is more time for differential move-ment of the isoforms through the column,which could lead to better resolution[6].In chromatofocusing,it is possible to generate shallow gradient slopes by limiting the pH range of the gradient or reducing the concentration of the mobile phase buffer components [12,15,27].Data presented later in this study show that these two strategies in obtaining higher resolution are also applicable to the external pH gradient approach.M.Talebi et al./J.Chromatogr.A 1317 (2013) 148–154151Fig.2.The effect of eluent concentration (DEA)on the elution profile of mAb2.(A)20mM,pH 9–10;(B)10mM,pH 9–10;(C)5mM,pH 9.2–10.2.For elution to occur at 5mM concentration,more basic pH range is required.Other conditions as in Fig.1.3.2.DEA buffer systemAs seen in Fig.1,elution of mAbs in the TEA-DEA buffer system occurred around the end of the pH range applied.The pH of eluent A was therefore increased from 7.5to 9.A simultaneous reduc-tion in gradient slope was achieved as the gradient time remained unchanged at 10min.In addition,because of its negligible buffer capacity in the new pH range,TEA was removed from the buffer system.The influence of buffer concentration within the range 20–5mM on separation efficiency of mAb2isoforms is shown in Fig.2.A decrease in buffer concentration at the same gradient slope results in an increase in the resolution of the charge variants from the main peak.For elution at 5mM,a further increase in working pH range from 9–10to 9.2–10.2is required.These findings are in agreement with Farnan and Moreno [9],who achieved improved separation efficiency and higher resolution for mAb isoforms by a 4-fold decrease in the concentration of buffer composition.The impact of column chemistry on separation efficiency was also evaluated for mAb1(Fig.3)and mAb2(Fig.S1in the Supporting Information).As can be seen,a trivial impact of column chemistry on the selectivity is recognisable.However,there are more promi-nent fluctuations in the pH profile and a longer titration time for the weak cation exchanger (see pH profiles).As the workingpHparison of separation of variants for mAb1on ProSwift WCX-1S and ProSwift SCX-1S columns.Eluent:5mM DEA,pH9.2–10.2.Fig.4.Interrelationship between eluent concentration and pH range on separation efficiency of mAb1.The gradient slope was 0.1pH units/min.Eluent:5mM AMH,pH 9.2–10.2(A);2.5mM AMH,pH 9.5–10.5(B).range is high enough to ensure full ionisation of the carboxylic group of the weak cation exchanger (p K a ∼5),the reason for dif-ferences in the pH profile might be due to the different chemistries of the stationary phases [25].3.3.AMH buffer systemAlthough suitable for resolving the isoforms of given mAbs,the low volatility of DEA might limit its application for mass spectro-metric detection.In order to address this issue,we explored the use of AMH which is a volatile buffer species with p K a 9.25.For this buffer,acceptable chromatographic resolution of protein isoforms was obtained for even lower concentrations than 5mM (Fig.4).This indicates that the focusing effect of the buffer system increases by decreasing the concentration.Based on earlier results,the optimum pH range had to be adjusted when decreasing the eluent concen-tration to allow maximum separation efficiency.Fig.5displays the effect of eluent pH range and gradient slope on resolving mAb1isoforms.By maintaining the gradient slope at 0.1pH units/min,it was found that although the fine structure of the acidicregionFig.5.Influence of operational pH range and gradient slope on resolution of mAb1variants.Eluent:2.5mM AMH.pH range and gradient slope:9.3–10.3and 0.1(A);9.5–10.5and 0.1(B);9.7–10.5and 0.08pH units/min (C).152M.Talebi et al./J.Chromatogr.A1317 (2013) 148–154 remains unaltered(Fig.5,traces A and B),basic variants previouslyhidden within the threshold of the major peak were clearly resolvedwhen the pH range was raised0.2pH units further from9.3–10.3to9.5–10.5.This step-wise optimisation protocol illustrates the pos-sibilities offered when using a pH gradient over a narrow pH range,in that it enables not only formation of controlled pH profile,butalso permits thefine tuning of pH within the range defined by theapplied buffer system to obtain the desired separation efficiency.Interestingly,it was found that low ionic strength eluents gen-erated a significant back-pressure with the ProPac WCX-10column(pressure upper limit=120bar).Once eluted with5mM AMH pH9.5at0.5mL/min,the initial back-pressure of94bar was monitoredand found to increase gradually.This behaviour is most likely dueto the osmotic pressure generated from the difference between thewater content of the very dilute eluent and the IEX sorbent.Unlikethe packed column,the higher permeability and rigid structure ofmonolithic ion-exchangers resulting from their porous propertiespermits fast generation of pH gradients at moderate and stableback-pressure(<70bar)even at very low buffer concentrations,as well as minimising column titration times(typically less than5min).These merits offer a rapid analysis time that is applicablefor high-throughput process development.While quite successful in resolving charge heterogeneity ofmAb1and mAb2,the simplified buffer systems failed to elute mAb3unless the eluent ionic strength was increased through addition ofa salt.Rozhkova[7]has previously reported the suitability of con-ducting pH gradient separation of mAb variants by adding NaClinto eluents.Accordingly,2.5mM AMH eluents,pH9–10contain-ing different concentrations of NaCl ranging from20to40mMwere used for eluting mAb3.Results indicate partial resolving ofthe main component from part of the acidic species(Fig.S2inthe SI).Basic variants,however,remained entirely hidden underthe wide shoulder of the major peak.One possible explanation forthis strong retention might be the differences in modification site,type of modification,and/or degree of modification occurring inthe protein[2],all of which influence the strength of interactionsbetween the protein molecule and the ion-exchanger.These modi-fications vary from those that change the number of charge residueson the surface of the protein to those being less connected to thecharge but can change antibody conformation.Deamidation,forexample,is one possible modification which is likely to have aneffect on retention of a protein by affecting the number of posi-tively charge groups over the surface of a protein and hence itsbinding to a cation-exchanger[3].Further investigation is requiredto confidently determine the characteristics of the mAb variants.3.4.Effects of eluent concentration and pH on resolutionThe overriding consideration in this work was towards maxi-mum achievable resolution for mAb isoforms.pH and ionic strengthare two major characteristics of the eluent governing the elutionand separation of proteins in pH gradient IEX chromatography.Here,we take advantage of the general expressions proposed bySluyterman and Elgersma[14]for the pH gradient approach toexplain the interplay between these two parameters and theireffects on separation efficiency.Peak width and peak separation are the two determinants ofresolution.The width of a protein band in terms of pH units can bewritten as:( pH)2≈D(d pH/dV)ϕ(dZ/d pH)(1)where D denotes the diffusion coefficient of a protein,d pH/dV the pH gradient slope andϕis equivalent to the dimensionless Donnan potential[14].This equation implies that an increase in peak focusing is consistent with the lower ionic strength(buffer concentration)used,which increases the absolute value ofϕ.Evi-dence of this inference can be seen in Fig.2,in which the resolution gain for the mAb2main isoform can be related to the focusing effect obtained by decreasing the ionic strength.In fact,the capability of focusing eluent bands is known as one inherent advantage of pH gradient IEX chromatography over conventional salt gradient at afixed pH[18],in which the absence of a focusing effect can be partly related to the lack of the Donnan potential,as a result of the high salt concentration involved.Trace C in Fig.2indicates that while employing the same pH range is likely to maintain the dZ/d pH unchanged,the positive effect of this kinetic factor on peak width can be highlighted by shifting up the pH range further,which along with more decrease in ionic strength leads to an even greater increase in resolution.The dominating effect of dZ/d pH on peak focusing can also be seen by comparing traces A and B in Fig.5 where there is likely no significant difference between the Don-nan potentials due to the constant eluent concentration(2.5mM). As should be expected,the peaks became broader when the pH gradient slope(d pH/dV),as another determinant of peak width in Eq.(1),decreased further from0.1(trace B)to0.08pH unit mL−1 (trace C)by keeping the other conditions unchanged,probably due to the domination of another kinetic determinant,i.e.,diffusion coefficient of protein(D).This therefore suggests that the rate of titrating the ion-exchanger with pH has become lower than the equilibrium state of protein molecules,which could compromise the peak focusing gains from shallower gradients.The contribution of the other factor governing resolution,i.e., peak separation,appears to be the main influence on resolution gains for isoforms in Fig.4,where the peak focussing for main iso-forms seems to be compromised,despite the expected focussing effects as the eluent concentration decreases and the pH range shifts up further.In fact,almost all of the posttranslational mod-ifications and degradations can change surface charge properties of an antibody,either directly by changing the number of charged groups or indirectly by introducing conformational alterations[2]. According to the electrostatic model developed by Tsonev and Hirsh [6]there is a relationship between the magnitude of a shift in electrophoretic p I and the relative charge distribution in a given protein.This,in turn,implies that isoforms can be resolved based on their apparent isoelectric point(p I app,being the pH at which the protein is eluted from the column)[12]when titrating by a gra-dient of pH,relating the resolution achieved in Fig.4to a greater separation of the peaks(for more discussion on p I app and retention mechanism see SI).Similar arguments based on the distribution of charges on the surface of a protein have also been used by other workers to explain the trends observed in resolution for chromato-focusing of-lactoglobulin A and B[12],and haemoglobin variants [12,28].3.5.Loading capacityThe loading capacity of the proposed approach for the separa-tion of mAb charge variants was also assessed.While some minor loss of resolution occurred when a sample load of about118g mAb1was injected onto the column,the overall separation pat-tern and thefine structure of the acidic region remained unaltered (Fig.S3in the SI).By considering the low ionic strength of the buffer system employed,a significant potential of this approach for scale up can be seen,enabling it to be used along with classical IEX chromatography for preparative purposes.3.6.Profiling charge heterogeneity of mAbs by iCETo assess the resolving power offered by the developed proce-dure,analysis of mAbs by iCE was also included in the study.The difference in separation mechanism of each technique can offer。
SAT考试 数学物理化学生物专业必备词汇

remainder余数
factorial阶乘
power乘方
radical sign, root sign根号
round to四舍五入
to the nearest四舍五入
2.有关集合
union并集
proper subset真子集 solution set解集
even integer, even number偶数
integer, whole number整数
positive whole number正整数
negative whole number负整数
consecutive number连续整数
real number, rational number实数,有理数
boundary 界限
cathode rays 阴极射线
cathode-ray oscilloscope (C.R.O) 阴极电子示波器
ceramic 陶器制品
charge-clouds 电子云
charge-to-mass ratio(e/m) 质荷比(质谱分析时样品质量的测量以质量与其离子电荷之比表示)
unit单位,位
几何部分
1.所有的角
alternate angle内错角 vulgar fraction,common fraction普通分数
simple fraction简分数
complex fraction繁分数
numerator分子 denominator分母
(least)common denominator(最小)公分母
exponent指数,幂
base乘幂的底数,底边
Colloid Chemistry and Surface Chemistry(胶体化学和表面化学)专业英语.

colloids include the metal sols. Lyophilic colloids generally have some chemical similarity to the solvent, such as –OH groups able to form hydrogen bonds.
▪ Surface active agent, surfactant (表面活性剂)
▪ Anionic surfactant
▪ Cationic surfactant ▪ Micelle (胶束) ▪ Surface film ▪ Monomolecular film
▪ Detergent (洗涤剂) ▪ Electrophoresis (电泳) ▪ Electroosmosis (电渗) ▪ Isoelectric point (等电点) ▪ Sol (溶胶) ▪ Aerosol (气溶胶) ▪ Gel (凝胶) ▪ Agar gel (琼脂糖凝胶)
Surfactant molecules or ions can cluster together as micelles, which are colloid-sized clusters of molecules, for their hydrophobic tails tend to congregate, and their hydrophilic heads provide protection. Micelles form only above the critical micelle concentration (CMC) and above the Krafft temperature.
离子强度 英文

离子强度英文Ionic strength is a crucial parameter in various scientific fields, including chemistry, biochemistry, and environmental science. It refers to the concentration of ions in a solution, which can significantly impact the behavior of substances dissolved in that solution. The ionic strength of a solution is determined by the types and concentrations of ions present, as well as their respective charges.离子强度是化学、生物化学和环境科学等各种科学领域中的一个关键参数。
它指的是溶液中离子的浓度,这可以显著影响溶解在该溶液中的物质的行为。
溶液的离子强度由存在的离子的类型、浓度以及它们的电荷共同决定。
In chemistry, ionic strength plays a vital role in determining the stability of chemical reactions and the solubility of compounds. Higher ionic strength can promote the dissociation of ionic compounds into their constituent ions, while lower ionic strength may lead to precipitation or the formation of complexes. Understanding the ionic strength of a solution is essential fordesigning effective chemical processes and controlling reaction outcomes.在化学中,离子强度在决定化学反应的稳定性和化合物的溶解度方面起着至关重要的作用。
Microchip电子产品说明书

TREE 3: POWER MANAGEMENT 2Supervisors & Voltage Detectors Unique Strengths (So What)Broad Portfolio(It's likely we have your part)Small Packages: SOT-23 and SC-70 (Saves space)Industrial Standard Crosses (Replace high priced and poor delivery suppliers)Battery Management Unique Strengths (So What)Wide variety of charging solutions for Li-Ion batteries(We have the solution for you)Small SOT-23, MSOP, DFN and QFN packages (Saves space)DC-DC Converter (So What)Low-voltage operation (Saves Power)PFM/PWM Auto switch mode (PFM at low loads reduces current, saves power)Small SOT-23 packaging (Saves space)Step-down, Step-up (Efficiently increase or decrease voltage) Charge Pumps (So What)Low-voltage operation (Battery operation)Small SOT-23 packaging (Saves space)Step-down, Step-up (Efficiently increase or decrease voltage)Doubling & Inverting (Meets V OUT needs) Low-Frequency capable (Reduces EMI)Low-Current Operation (Saves power)LDO Unique Strengths (So What)Hundreds of voltages, currents, packages (We have a match for the need)0.5% V OUT accuracy (Fills precision need)Up to 1.5A output current(Able to power high load applications)Op Amp Unique Strengths (So What)Low current versus GBWP (Saves power)TC and MCP6XXX devices RR-I/O (Expands usable voltage range)MCP604X 1.4V operation(Two alkaline cells 90% used =1.8V)MCP644X, 450 nA operation (Use the batteries even longer)Comparators Unique Strengths (So What)Low current versus propagation delay (Saves power)Integrated Features (Saves space)1.8V and 1.4V operation (That stuff about the batteries)Programmable Gain Amplifier Unique Strengths (So What)MUX inputWide bandwidth (2 to 12 MHz) (Reduces demand on MCU I/O)System control of gain(Changes easier through software configurable hardware)TREE 5: LINEARTemperature Sensor Unique Strengths (So What)Wide variety of solutions: logic, voltage and digital output products(Multiple sensor needs met)Small packages (Saves space)Low operating current(Saves power, smaller supply)Field or factory programmable (Low cost vs. flexibility)Programmable hysteresis (Stop system cycling)Multi-drop capability (Great for large systems)Beta compensation (Compatible with processor substrate diodes)Resistance error correction (Compensates for measurement error from long PCB traces)Fan Controllers Unique Strengths (So What)Closed loop fan control (Adjust to meet target speed even on aging fans)Integrated temperature sensing (Consolidate thermal management)Multiple temperature measurements drive one fan (Consolidate thermal management)Built-in ramp rate control and spin up alogorithm (Quick time to market, lower acoustic noise)Ability to detect/predict failure of less expensive 2-wire fans (Saves system cost)Unique solutions for extending fan life and reducing acoustic noise(Less power, nuisance and long fan life)TREE 6: MIXED-SIGNALADC Unique Strengths (So What)Low current at max sampling rate (Saves power, system cost)Small SOT-23 and MSOP packages (Saves space)Up to 24-bit resolution(Ideal for precision sensitive designs)Differential & single ended inputs (Able to cover various design needs)Up to 6 ADC per device(Save board space, system cost)DAC Unique Strengths (So What)Low Supply Current (Saves power)Low DNL & INL (Better accuracy)Extended Temperature Range(Suitable for wide temperature applications)Digital Potentiometers Unique Strengths (So What)64/256 tap (6-bit to 8-bit resolution)(Sufficient resolution for most applications)Non-volatile Memory(Remembers last wiper setting on power up)WiperLock™ Technology(Locks NV memory setting-better than OTP)Small SOT-23 and 2 × 3 DFN packages (Saves space)Low CostMOSFET Drivers (So What)4.5V up to 30V Supply voltages (Fills many application needs)Up to 12A Peak output current(Able to meet demanding design needs)Outstanding robustness and latch-upi mmunity (Ours work when the others burn up)Low-FOM MOSFETs(Support high-efficency applications)TREE 4: POWER MANAGEMENT 3LIN Unique Strengths(So What)Compliant with LIN Bus Specs 1.3, 2.0, 2.1 andSAE J2602 (Allows for reliable interoperability)High EMI Low EME (Meets OEM requirements)On-board V REG available(Saves space, allows for MCU V CC flexibility)CAN Unique Strengths(So What)Simple SPI CAN controller is an easy way toadd CAN Ports (Short design cycles)High speed transceiver meets ISO-11898 (Drop inreplacement for industry standard transceivers)Low-cost, easy-to-use development tools(Tools easy to buy/use, quick design)I/O Expanders Unique Strengths(So What)Configurable inputs (interrupt configuration flexibility)Interrupt on pin change, or change fromregister default (interrupt source flexibility)Can disable automatic address incrementingwhen accessing the device(allows continual access to the port)The 16-bit devices can operate in 8-bit or 16-bitmode (easy to interface to 8-bit or 16-bit MCUs)IrDA Unique Strengths (So What)IrDA protocol handler embedded on chip(Complex design issue solved)Low cost developer's kit available to assistInfrared design-in (Quick design cycle)Small, cost-effective way of replacing serial links(No more wires)Enables system to wirelessly communicatewith PDA (Wireless connectivity solution) TREE 8: INTERFACEAnalog & InterfaceQuestion TreesAnalog & Interface Development ToolsDemonstration Boards, Evaluation Kits and AccessoriesAnalog & Interface LiteratureADM00313EV: MCP73830L 2 × 2 TDFN Evaluation BoardADM00352: MCP16301 High Voltage Buck Converter 600 mA Demonstration BoardADM00360: MCP16301 High Voltage Buck Coverter 300 mA D2PAK Demonstration BoardADM00427: MCP16323 Evaluation Board (Supports MCP16321 and MCP16322)ARD00386: MCP1640 12V/50 mA Two Cells Input Boost Converter Reference DesignMCP1252DM-BKLT: MCP1252 Charge Pump Backlight Demonstration BoardMCP1256/7/8/9EV: MCP1256/7/8/9 Charge Pump Evaluation BoardMCP1630RD-LIC1: MCP1630 Li-Ion Multi-Bay Battery Charger Reference DesignMCP1630DM-NMC1: MCP1630 NiMH Battery Charger Demonstration BoardMCP1640EV-SBC: MCP1640 Sync Boost Converter Evaluation BoardMCP1640RD-4ABC: MCP1640 Single Quad-A Battery Boost Converter Reference DesignMCP1650DM-LED1: MCP165X 3W White LED Demonstration BoardMCP1726EV: MCP1726 LDO Evaluation BoardMCP73831EV: MCP73831 Evaluation KitMCP7383XEV: MCP73837/8 AC/USB Dual Input Battery Charger Evaluation BoardMCP7383XRD-PPM: MCP7383X Li-Ion System Power Path Management Reference DesignMCP7384XEV: MCP7384X Li-Ion Battery Chager Evaluation BoardMCP73871EV: MCP73871 Load Sharing Li-Ion Battery Charger Evaluation BoardTC1016/17EV: TC1016/17 LDO Evaluation BoardVSUPEV: SOT-23-3 Voltage Supervisor Evaluation BoardPowerManagementThermalManagementMCP9700DM-PCTL: MCP9700 Thermal Sensor PICtail Demonstration BoardMCP9800DM-PCTL: MCP9800 Thermal Sensor PICtail Demonstration BoardTC72DM-PICTL: TC72 Digital Temperature Sensor PICtail Demonstration BoardTC74DEMO: TC74 Serial Daughter Thermal Sensor Demonstration BoardTC1047ADM-PCTL: TC1047A Temperature-to-Voltage Converter PICtail™ Demonstration BoardSerial GPIODM-KPLCD: GPIO Expander Keypad and LCD Demonstration BoardMCP23X17: MCP23X17 16-bit GPIO Expander Evaluation BoardInterface MCP2515DM-BM: MCP2515 CAN Bus Monitor Demonstration BoardMCP2515DM-PTPLS: MCP2515 PICtail™ Plus Daughter BoardMCP2515DM-PCTL: MCP2515 CAN Controller PICtail Demonstration BoardMCP215XDM: MCP215X/40 Data Logger Demonstration BoardMCP2140DM-TMPSNS: MCP2140 IrDA® Wireless Temp Demonstration BoardLinear ADM00375: MCP6H04 Evaluation BoardARD00354: MCP6N11 Wheatstone Bridge Reference DesignMCP651EV-VOS: MCP651 Input Offset Evaluation BoardMCP661DM-LD: MCP661 Line Driver Demo BoardMCP6S22DM-PCTL: MCP6S22 PGA PICtail Demonstration BoardMCP6S2XEV: MCP6S2X PGA Evaluation BoardMCP6SX2DM-PCTLPD: MCP6SX2 PGA Photodiode PICtail Demonstration BoardMCP6SX2DM-PCTLTH: MCP6SX2-PGA Thermistor PICtail Demonstration BoardMCP6V01RD-TCPL: MCP6V01 Thermocouple Auto-Zero Ref DesignMCP6XXXDM-FLTR: Active Filter Demo BoardPIC16F690DM-PCTLHS: Humidity Sensor PICtail Demonstration BoardMixed-Signal MCP3221 DM-PCTL: MCP3221 12-bit A/D PICtail Demonstration BoardMCP3421DM-BFG: MCP3421 Battery Fuel Gauge Demonstration BoardMCP3551DM-PCTL: MCP3551 PICtail Demonstration BoardMCP355XDM-TAS: MCP355X Tiny Application Sensor Demonstration BoardMCP355XDV-MS1: MCP3551 Sensor Demonstration BoardMCP402XEV: MCP402X Digital Potentiometer Evaluation BoardMCP4725EV: MCP4725, 12-bit Non-Volatile DAC Evaluation Board (Preferred One)MCP4725DM-PTPLS: MCP4725, 12-bit Non-Volatile DAC PICtail Demonstration BoardADM00398: MCP3911 ADC Evaluation Board for 16-bit MicrocontrollersCorporate Microchip Product Line Card - DS00890Brochures Analog and Interface Product Selector Guide - DS21060Low Cost Development Tools Solutions Guide - DS51560Analog and Interface Guide (Volume 1) - DS00924Analog and Interface Guide (Volume 2) - DS21975Cards Analog Highlights Card - DS21972Microchip Op Amp Discovery Card - DS21947Analog & Interface Question Trees - DS21728Mirochip SAR and Delta-Sigma ACD Discovery Card - DS22101Software Tools MAPS - Microchip Advanced Product SelectorAnalog & Interface Treelink Products PresentationDesign Guides Analog-to-Digital Converter Design Guide - DS21841Digital Potentiometers Design Guide - DS22017Programmable Gain Amplifiers (PGAs), Operational Amplifiersand Comparators Design Guide - DS21861Interface Products Design Guide - DS21883Signal Chain Design Guide - DS21825Power Solutions Design Guide - DS21913Temperature Sensor Design Guide - DS21895Voltage Supervisors Design Guide - DS51548DS21728JPowerManagementLDO & SwitchingRegulatorsCharge PumpDC/DC ConvertersPower MOSFETDriversPWM ControllersSystem SupervisorsVoltage DetectorsVoltage ReferencesLi-Ion/Li-PolymerBattery ChargersUSB Port PowerControllersMixed-SignalA/D ConverterFamiliesDigitalPotentiometersD/A ConvertersV/F and F/VConvertersEnergyMeasurement ICsCurrent/DC PowerMeasurement ICsInterfaceCAN PeripheralsInfraredPeripheralsLIN TransceiversSerial PeripheralsEthernet ControllersUSB PeripheralLinearOp AmpsInstrumentationAmpsProgrammableGain AmplifiersComparatorsSafety & SecurityPhotoelectricSmoke DetectorsIonization SmokeDetectorsIonization SmokeDetector Front EndsPiezoelectricHorn DriversThermalManagementTemperatureSensorsFan Control& HarwareManagementMotor DriveStepper and DC3Ф BrushlessDC Motor DriverTREE 7: MOTOR DRIVE Stepper Unique Strenghts(So What)Industrial standard footprint(Footprint compatible to industrial leaders)Perfect PIC® MCU companion chip(Solid field support)Micro-stepping ready(Enhanced performance)Integration protections(Simplify software development)3-Phase BLDC Unique Strengths(So What)Full-wave sinusoidal(Quiet operation, low mechanical vibration)Sensorless operation (Minimum externalcomponents, no software required)Thin form factor(Fits space concerned applications)Information subject to change. The Microchip name and logo, the Microchip logo, dsPIC, PIC are registered trademarks and MiWi, PICtail and ZENA are trademarks ofMicrochip Technology Incorporated in the U.S.A. and other countries. All other trademarks mentioned herein are property of their respective companies.© 2012, Microchip Technology Incorporated. All Rights Reserved.。
电位滴定法测定胶原的表观解离平衡常数

文章编号:1004-1656(2016)08-1141-04电位滴定法测定胶原的表观解离平衡常数王㊀力1,2,周继博2,张文华2*(1.四川大学皮革化学与工程教育部重点实验室,四川㊀成都㊀610065;2.四川大学制革清洁技术国家工程实验室,四川㊀成都㊀610065)摘要:论文采用电位滴定法测定不同离子强度下胶原蛋白的表观解离平衡常数,根据Katchalsk-Spitnik方程作图和计算㊂结果表明:随着离子强度的增大,胶原的表观解离常数随之减小,其值分别为:7.94(0mol㊃L-1NaCl)㊁7.90(0.1mol㊃L-1NaCl)㊁7.90(0.2mol㊃L-1NaCl)和7.88(0.4mol㊃L-1NaCl),离子强度对胶原的表观解离常数影响较小㊂关键词:胶原;电位滴定;解离常数;离子强度中图分类号:O657.1㊀㊀文献标志码:ADetermination of apparent dissociation constantof collagen by potentiometric methodWANG Li1,2,ZHOU Ji-bo1,ZHANG Wen-hua1*(1.The Key Laboratory of Leather Chemistry and Engineering of Ministry of Education,Sichuan University,Chengdu610065,China;2.National Engineering Laboratory for Clean Technology of Leather Manufacture,Sichuan University,Chengdu610065,China)Abstract:The apparent dissociation constants of collagen under different ionic strength were determined by potentiometric titration, and the data were analyzed based on Katchalsk-Spitnik equation.The results indicate that collagen s apparent dissociation constant decreases slightly with the increase of ionic strength,and the value is7.94(0mol㊃L-1NaCl),7.90(0.1mol㊃L-1NaCl),and7.90 (0.2mol㊃L-1NaCl),7.88(0.4mol㊃L-1NaCl)respectively.The ionic strength has a weak influence on apparent dissociation con-stants of collagen.Key words:collagen;potentiometric titration;dissociation constant;ionic strength㊀㊀胶原蛋白是一类具有三股螺旋结构的可再生天然高分子,其结构可调㊁生物相容性好,广泛应用于制革㊁医药和组织工程等领域[1-4]㊂有关胶原蛋白的研究报道很多,大多集中在交联改性的方式与应用性能的研究[5-6]㊂事实上,胶原是一种典型的两性高分子,以分布最广的I型胶原为例,胶原肽链中碱性氨基酸和酸性氨基酸分别占氨基酸总数的21.2%和9.4%[7],这些侧链官能团的存在形态在胶原交联改性中起着关键作用㊂例如金属离子与胶原之间的交联需要酸性官能团一定程度的解离,而碱性基团去质子化才能使醛与胶原发生有效交联[8]㊂由于胶原蛋白固有的两性,在水溶液中官能团的解离不仅与该基团的酸(碱)性强弱有关,而且受其他碱(酸)性官能团的影响,而收稿日期:2015-10-28;修回日期:2016-02-27基金项目:国家高技术研究发展计划项目(2013AA06A306)资助联系人简介:张文华(1970-),女,教授,主要从事制革化学及皮化材料分子设计研究㊂E-mail:zhangwh@化学研究与应用第28卷外部条件如温度㊁pH㊁离子强度也会影响其解离㊂由于胶原在水溶液中的解离过程及平衡十分复杂,因此对其溶液中解离常数的测定及其相关溶液配位化学作用的研究较为困难㊂本文利用聚合酸解离模型[9-10],采用电位滴定法测定了胶原蛋白的表观解离平衡常数,为进一步深入开展胶原交联作用机理研究提供了理论基础㊂1㊀实验部分1.1㊀试剂与仪器邻苯二甲酸氢钾㊁氢氧化钠㊁氯化钠等均为分析纯,成都市科龙化工试剂厂;胶原蛋白I型,分子量为30ˑ104,成都贝斯特试剂有限公司;ZDJ-5自动电位滴定仪,上海仪电科学仪器股份有限公司㊂1.1㊀实验方法1.2.1㊀氢氧化钠溶液的配制与标定㊀0.1mol㊃L-1氢氧化钠储备液配置:称取110g氢氧化钠,溶于100mL去离子水(煮沸除二氧化碳)中,摇匀,注入聚乙烯容器中,密闭放置至溶液清亮㊂用塑料管量取上层清液5.4mL,稀释至1000mL,按照GB/T601-2002用邻苯二甲酸氢钾溶液标定[11]㊂配置好的氢氧化钠溶液使用前用去离子水准确稀释10倍后使用㊂1.2.2㊀胶原溶液的滴定㊀准确称取胶原蛋白I型1.0g,溶于一定量的脱二氧化碳的去离子水中,胶原完全溶解后,分别加入0mL㊁10mL㊁20mL㊁40 mL的离子强度调节剂(1mol㊃L-1NaCl溶液),稀释至100mL,恒温(25.0ʃ0.5)ħ㊂此时溶液的离子强度I分别为0mol㊃L-1㊁0.1mol㊃L-1㊁0.2mol㊃L-1㊁0.4mol㊃L-1㊂分别移取20mL溶液于50mL 烧杯,用0.01mol㊃L-1的氢氧化钠标准溶液滴定,绘制pH-V曲线并根据经验方程作图和计算胶原的表观解离常数㊂2㊀结果与讨论2.1㊀胶原的解离平衡机理胶原侧链含有较多羧基和氨基,羧基在水溶液中易发生解离释放出质子H+变成-COO-,而氨基在水溶液中易接收H+形成-NH3+,因此胶原是一种两性电解质㊂在水溶液中,胶原的解离包括侧链羧基和质子化氨基的解离,两者互相影响㊂但在宏观上,胶原的解离可看作一级解离,其解离平衡式为:Col+H2췍췍=O Col-+H3O+(1)其表观解离平衡常数的定义为:K a=[Col-][H+][Col](2)式中,[Col-]㊁[H+]㊁[Col]分别表示平衡时解离胶原㊁氢离子和胶原的浓度㊂2.2㊀胶原的滴定曲线pH-V胶原溶液的浓度均为10g㊃L-1,不同离子强度介质溶液中胶原滴定结果见图1㊂胶原是一种两性聚合物,有一定的缓冲作用,滴定曲线的pH突变性减缓㊂随着离子强度增加,滴定曲线的pH变化趋缓,终点pH略有降低㊂这可能是强电解质NaCl加入胶原溶液后产生了盐效应,使胶原电离的侧链-COO-与H+结合形成胶原分子的机会减小,从而使胶原分子的浓度减小,胶原解离度增大[13]㊂事实上,制革过程发现金属离子如铬(III),在一定浓度的NaCl存在下能与皮胶原产生更强的交联[14]㊂图1㊀不同离子强度溶液中胶原的滴定曲线Fig.1㊀Titration curve of collagen in differentionic strengthen in the solution 2.3㊀胶原的电位滴定模型Katchalsk和Spitnik报道聚合酸的滴定曲线可以用一个经验等式[10]来描述:pH=p K a-n lg1-αα(3)式中:α为聚合酸的解离度,p K a和n为常数㊂由方程(3)计算实验数据结果见图2和表1㊂2411第8期王㊀力,等:电位滴定法测定胶原的表观解离平衡常数表1㊀胶原表观解离平衡常数计算结果(25ħ)Table1㊀Calculated results of dissociationconstants of collagen at25ħC(NaCl)/(mol㊃L-1)表观p K a n R2p K0 0.007.941.11180.99957.84 0.107.901.12810.99917.83 0.207.901.09830.99907.81 0.407.881.08290.99907.81㊀㊀随着离子强度增大,胶原的表观解离常数随之减小,胶原的表观解离常数分别为:7.94(0mol㊃L-1NaCl)㊁7.90(0.1mol㊃L-1NaCl)㊁7.90(0.2mol ㊃L-1NaCl)和7.88(0.4mol㊃L-1NaCl),盐浓度从0到0.1mol㊃L-1,胶原表观p K a差值为0.04,而盐浓度从0.1mol㊃L-1到0.4mol㊃L-1增大4倍,胶原表观p K a减少0.02,表明胶原作为较弱的两性电解质,其表观解离常数受溶液中盐浓度的影响较小㊂胶原是由三条各含1000多个氨基酸的α肽链相互缠绕形成的棒状分子,以I型胶原的氨基酸序列为例(如图3所示),胶原肽链中的酸性氨基酸和碱性氨基酸大都对应地集中出现在一定的区段而不是均匀分布于整个肽链[12]㊂图2㊀不同盐浓度下胶原的Katchalsky-Spitnik方程Fig.2㊀The Katchalsky-Spitnik equationfor collagen under different ionstrength图3㊀I型胶原α链中的酸性㊁碱性氨基酸及Gly-Pro-Hyp-序列的分布矩形黑色框表示连续的Gly-Pro-Hyp序列,螺旋链上端的垂线表示酸性氨基酸,下部的黑点表示碱性氨基酸残基[12]Fig.3㊀The distribution of acidic amino acid,basic amino acid and the sequence ofGly-Pro-Hyp-inα-chain of type I collagenThe black rectangle means successiveGly-Pro-Hyp-,the vertical line means acidic amino acid and black spot means basic amino acid[12]㊀㊀对于这类结构较为伸展有一定刚性的聚合物分子,Katchalsky认为其p K和n分别由两部分构成[10]:3411化学研究与应用第28卷p K =p K 0+e 2DjbkTlg 1+6κsb (4)n =1+2.3e22DjbkT lg1+6κsb(5)式中,p K o 为固有解离常数;e 为电子电荷;D为介质的介电常数;j 为带可解离基团的单体数;κ为德拜半径的倒数;s 为每个统计元内单体的数量;b 为单体的流线形长度㊂据此,可以计算胶原蛋白的固有解离常数p K 0,见表1㊂显然与球状柔性高分子不同,胶原肽链上大多数带电荷的解离基团距离较远,因此盐溶液构成的静电场对胶原表观解离常数影响较小,同时胶原蛋白的固有解离常数趋近于表观解离常数㊂3㊀结论本文用电位滴定法测定了胶原的表观解离常数,研究了离子强度对胶原表观解离常数的影响㊂结果表明:胶原的表观解离常数随着溶液中离子强度的增加略有减小,胶原的表观解离常数值为7.94ʃ0.06㊂参考文献:[1]Song E,Kim S Y,Chun T,et al.Collagen scaffolds derivedfrom a marine source and their biocompatibility[J].Bio-materials ,2006,27(15):2951-2961.[2]王晓敏,李旭东,张志斌.胶原-羟基磷灰石复合骨组织引导再生膜的制备及性能研究[J].化学研究与应用,2010,22(10):1301-1304.[3]Tsai S W,Chen C C,Liou H M,et al.Preparation andcharacterization of microspheres comprised of collagen,chondroitin sulfate,and apatite as carriers for the osteo-blast-like cell MG63[J].J Biomed Mater Res ,2010,93(1):115-122.[4]Dorotka R,Windberger U,Macfelda K,et al.Repair of ar-ticular cartilage defects treated by microfracture and athree-dimensional collagen matrix[J].Biomaterials ,2005,26(17):3617-3629.[5]Hafezi F,Mrochen M,Iseli H P,et al.Collagen crosslink-ing with ultraviolet-A and hypoosmolar riboflavin solutionin thin corneas[J].J Cataract Refr Surg ,2009,35(4):621-624.[6]Duan X,Sheardown H.Dendrimer crosslinked collagen asa corneal tissue engineering scaffold:mechanical propertiesand corneal epithelial cell interactions[J].Biomaterials ,2006,27(26):4608-4617.[7]Bowes J H,Kenten R H.The amino-acid composition and titration curve of collagen[J].Biochem J ,1948,43(3):358.[8]王伟,马建中,杨宗邃,等.皮革鞣剂及鞣制机理综述[J].中国皮革,1997,26(8):27-32.[9]Katchalsky A,Spitnik P.Potentiometric titrations of poly-methacrylic acid[J].J Polym Sci ,1947,2:432-446.[10]Katchalsky A,Shavit N,Eisenberg H.Dissociation ofweak polymeric acids and bases[J].J Polym Sci ,1954,13:69-84.[11]中华人民共和国国家质量监督检验检疫局.GB /T601-2002氢氧化钠标准滴定溶液[S].北京:中国标准出版社,2002.[12]詹怀宇,李志强,蔡再生.纤维化学与物理[M].北京:科学出版社,2005:375-377.[13]何玉萼,袁永明,童冬梅,等.物理化学(下册)[M].北京:化学工业出版社,2006:124-133.[14]Xiangyi W,Zhang W,Bi S.Effect of neutral salt on pick-ling and tanning-a study based on assembly behaviour of collagen[J].J Soc Leather Tech Chem (JSLTC ),2014,98(1):30-34.(责任编辑㊀李㊀方)4411。
化学专业术语英语对照

化学专业术语英语对照来源:发布时间:2011年4月7日爆炸界限explosionlimits霍根-华森图Hougen-WatsonChart德拜和法尔肯哈根效应DebyeandFalkenhageneffect德拜-休克尔极限公式Debye-Huckel’slimitingequation 德拜立方公式Debyecubicformula聚沉值coagulationvalue聚沉coagulation聚(合)电解质polyelectrolyte精馏rectify键焓bondenthalpy触变thixotropy解离化学吸附dissociationchemicaladsorption简并度degeneracy感胶离子序lyotropicseries催化剂catalyst隔离法theisolationmethod隔离系统isolatedsystem道尔顿定律Daltonlaw道尔顿分压定律Daltonpartialpressurelaw超电势overpotential缔合化学吸附associationchemicaladsorption 等温等容位Helmholtzfreeenergy等温等压位Gibbsfreeenergy等温方程equationatconstanttemperature等焓线isenthalpicline等焓过程isenthalpicprocess等几率定理theoremofequalprobability焦耳定律Joule';slaw焦耳-汤姆生效应Joule-Thomsoneffect焦耳-汤姆生实验Joule-Thomsonexperiment焦耳-汤姆生系数Joule-Thomsoncoefficient焦耳Joule敞开系统opensystem菲克扩散第一定律Fick’sfirstlawofdiffusion 粗分散系统thickdispersesystem第三定律熵third-lawentropy第二类永动机perpetualmachineofthesecondkind 第一类永动机perpetualmachineofthefirstkind 盖斯定律Hesslaw盖·吕萨克定律Gay-Lussaclaw焓enthalpy混合熵entropyofmixing混合物mixture接触角contactangle接触电势contactpotential弹式量热计bombcalorimeter常见术语基态能级energylevelatgroundstate基希霍夫公式Kirchhoffformula基元反应elementaryreactions高会溶点upperconsolutepoint高分子溶液macromolecularsolution胶凝作用demulsification胶核colloidalnucleus胶束micelle胶冻brothjelly胶体粒子colloidalparticles胶体化学collochemistry胶体分散系统dispersionsystemofcolloid胶体colloid胶团micelle积分溶解热integrationheatofdissolution盎萨格电导理论Onsager’s theoryofconductance爱因斯坦-斯托克斯方程Einstein-Stokesequation爱因斯坦光化当量定律Einstein’slawofphotochemicalequivalence浸湿功immersionwettingwork浸湿immersionwetting格罗塞斯-德雷珀定律Grotthus-Draoer’slaw根均方速率root-mean-squarespeed费米-狄拉克统计Fermi-Diracstatistics绝热量热计adiabaticcalorimeter绝热指数adiabaticindex绝热过程adiabaticprocess绝对熵absoluteentropy绝对温标absolutetemperaturescale绝对反应速率理论absolutereactionratetheory结晶热heatofcrystallization结线tieline科尔劳施离子独立运动定律Kohlrausch’sLawofIndependentMigrationofIons 界面张力surfacetension界面interfaces玻色-爱因斯坦统计Bose-Einsteinstatistics玻尔兹曼熵定理Boltzmannentropytheorem玻尔兹曼常数Boltzmannconstant玻尔兹曼分布Boltzmanndistribution玻尔兹曼公式Boltzmannformula独立子系统independentparticlesystem活度activity活化控制activationcontrol活化能activationenergy活化络合物理论activatedcomplextheory标准熵standardentropy标准摩尔燃烧焓standardmolarcombustionenthalpy标准摩尔熵standardmolarentropy标准摩尔焓函数standardmolarenthalpyfunction标准摩尔吉布斯自由能函数standardmolarGibbsfreeenergyfunction 标准摩尔生成焓standardmolarformationenthalpy标准摩尔生成吉布斯函数standardmolarformationGibbsfunction标准摩尔反应熵standardmolarreactionentropy标准摩尔反应焓standardmolarreactionenthalpy标准摩尔反应吉布斯函数standardGibbsfunctionofmolarreaction 标准氢电极standardhydrogenelectrode标准态standardstate标准状况standardcondition标准压力standardpressure标准电极电势standardelectrodepotential标准电动势standardelectromotiveforce标准平衡常数standardequilibriumconstant柯诺瓦洛夫-吉布斯定律Konovalov-Gibbslaw查理定律Charle’slaw挥发度volatility恒容摩尔热容molarheatcapacityatconstantvolume恒容热heatatconstantvolume恒沸混合物constantboilingmixture恒压摩尔热容molarheatcapacityatconstantpressure恒压热heatatconstantpressure恒外压constantexternalpressure封闭系统closedsystem复合反应compositereaction饱和蒸气压saturatedvaporpressure饱和蒸气saturatedvapor饱和液体saturatedliquids饱和吸附量saturatedextentofadsorption非基元反应non-elementaryreactions非依时计量学反应timeindependentstoichiometricreactions 非体积功non-volumework规定熵stipulatedentropy表面活性剂surfactants表面质量作用定律surfacemassactionlaw表面张力surfacetension表面吸附量surfaceexcess表面过程控制surfaceprocesscontrol表面surfaces表观摩尔质量apparentmolecularweight表观活化能apparentactivationenergy表观迁移数apparenttransferencenumber范德华常数vanderWaalsconstant范德华气体vanderWaalsgases范德华方程vanderWaalsequation范德华力vanderWaalsforce范特霍夫渗透压公式van’tH offequationofosmoticpressure 范特霍夫规则van’tHoffrule范特霍夫方程van’tHoffequation环境熵变entropychangeinenvironment环境environment波义尔温度Boyletemperature波义尔点Boylepoint波义尔定律Boylelaw法拉第常数faradayconstant法拉第定律Faraday’slaw泊Poise沸点升高elevationofboilingpoint沸点boilingpoint构型熵configurationalentropy定域子系统localizedparticlesystem定容摩尔热容molarheatcapacityunderconstantvolume 定容温度计ConstantvoIumethermometer定压摩尔热容molarheatcapacityunderconstantpressure 定压温度计constantpressurethermometer孤立系统isolatedsystem固溶胶solidsol固相线solidphaseline固态混合物solidsolution单链反应straightchainreactions单分子层吸附理论monomoleculelayeradsorption单分子反应unimolecularreaction附加压力excesspressure阿累尼乌斯活化能Arrheniusactivationenergy阿累尼乌斯电离理论Arrheniusionizationtheory阿累尼乌斯方程Arrheniusequation阿伏加德罗常数Avogadro’number阿伏加德罗定律Avogadrolaw阿马格定律Amagatlaw沉降电势sedimentationpotential沉降平衡sedimentationequilibrium沉降sedimentation极限摩尔电导率limitingmolarconductivity极化作用polarization极化曲线polarizationcurves极化电极电势polarizationpotentialofelectrode杠杆规则leverrule低熔冰盐合晶cryohydric低共熔混合物eutecticmixture低共熔点eutecticpoint低会溶点lowerconsolutepoint亨利常数Henryconstant亨利定律Henrylaw过程process过渡状态理论transitionstatetheory过热液体overheatedliquid过饱和蒸气oversaturatedvapor过饱和溶液oversaturatedsolution过冷液体overcooledliquid过冷水super-cooledwater负极negativepole负吸附negativeadsorption安托万常数Antoineconstant安托万方程Antoineequation多方过程polytropicprocess多分子层吸附理论adsorptiontheoryofmulti-molecularlayers吉布斯函数判据Gibbsfunctioncriterion吉布斯函数Gibbsfunction吉布斯-杜亥姆方程Gibbs-Duhemequation吉布斯吸附公式Gibbsadsorptionformula吉布斯自由能Gibbsfreeenergy吉布斯-亥姆霍兹方程Gibbs-Helmhotzequation 吉氏函数Gibbsfunction动力学控制kineticscontrol动力学方程kineticequations共轭溶液conjugatesolution共沸温度azeotropictemperature光谱熵spectrum entropy光敏反应photosensitizedreactions光反应photoreaction光化学第二定律thesecondlawofactinochemistry 光化学第一定律thefirstlawofactinochemistry 价数规则ruleofvalence产率yield亥姆霍兹函数判据Helmholtzfunctioncriterion 亥姆霍兹函数Helmholtzfunction亥姆霍兹自由能Helmholtzfreeenergy亥氏函数Helmholtzfunction节流膨胀系数coefficientofthrottlingexpansion节流膨胀throttlingexpansion节流过程throttlingprocess艾林方程Eryingequation电解池electrolyticcell电量计coulometer电渗析electrodialysis电渗electroosmosis电流效率currentefficiency电泳electrophoresis电极种类typeofelectrodes电极电势electrodepotential电极反应reactionsontheelectrode电迁移率electromobility电迁移electromigration电池常数cellconstant电池电动势electromotiveforceofcells电池反应cellreaction电导率conductivity电导conductance电动势的温度系数temperaturecoefficientofelectromotiveforce 电动电势zetapotential电功electricwork电化学极化electrochemicalpolarization电化学electrochemistry甘汞电极calomelelectrode弗罗因德利希吸附经验式Freundlichempiricalformulaofadsorption 布朗运动brownianmovement对称数symmetrynumber对应状态原理principleofcorrespondingstate对行反应reversiblereactions对比摩尔体积reducedmolevolume对比温度reducedtemperature对比体积reducedvolume对比压力reducedpressure卡诺循环Carnotcycle卡诺定理Carnottheorem半衰期halftimeperiod半电池halfcell功函workcontent功work计量系数stoichiometriccoefficient计量式stoichiometricequation比浓粘度reducedviscosity比表面吉布斯函数specificsurfaceGibbsfunction比表面功specificsurfacework开尔文公式Kelvinformula反渗透reverseosmosis反应速率常数constantofreactionrate反应速率rateofreaction反应热heatofreaction反应进度extentofreaction反应级数reactionorders反应分子数molecularity反电动势back化学热力学chemicalthermodynamics化学亲合势chemicalaffinity化学势判据chemicalpotentialcriterion化学势chemicalpotential化学吸附chemisorptions化学动力学chemicalkinetics化学反应进度extentofchemicalreaction化学反应计量系数stoichiometriccoefficientofchemicalreaction 化学反应计量式stoichiometricequationofchemicalreaction分解电压decompositionvoltage分散相dispersionphase分散系统dispersesystem分配定律distributionlaw分体积定律partialvolumelaw分体积partialvolume分压定律partialpressurelaw分压partialpressure分布数distributionnumbers分布distribution分子蒸馏moleculardistillation分子间力intermolecularforce分子反应力学mechanicsofmolecularreactions不可逆相变化irreversiblephasechange不可逆过程热力学thermodynamicsofirreversibleprocesses 不可逆过程irreversibleprocess广度性质extensiveproperty广延量extensivequantity广延性质extensiveproperty几率因子stericfactor二级相变secondorderphasechange二级反应secondorderreaction丁达尔效应Dyndalleffectζ电势zetapotentialpVT性质pVTpropertyHLB法hydrophile-lipophilebalancemethodDLVO理论DLVOtheoryBET公式BETformula可能的电解质potentialelectrolyte可逆电池reversiblecell可逆过程reversibleprocess可逆过程方程reversibleprocessequation可逆体积功reversiblevolumework可逆相变reversiblephasechange克拉佩龙方程Clapeyronequation克劳修斯不等式Clausiusinequality克劳修斯-克拉佩龙方程Clausius-Clapeyronequation控制步骤controlstep库仑计coulometer扩散控制diffusioncontrolled拉普拉斯方程Laplace’sequation拉乌尔定律Raoultlaw兰格缪尔-欣谢尔伍德机理Langmuir-Hinshelwoodmechanism 兰格缪尔吸附等温式Langmuiradsorptionisothermformula 雷利公式Rayleighequation冷冻系数coefficientofrefrigeration冷却曲线coolingcurve离解热heatofdissociation离解压力dissociationpressure离域子系统non-localizedparticlesystems离子的标准摩尔生成焓standardmolarformationofion离子的电迁移率mobilityofions离子的迁移数transportnumberofions离子独立运动定律lawoftheindependentmigrationofions离子氛ionicatmosphere离子强度ionicstrength理想混合物perfectmixture理想气体idealgas理想气体的绝热指数adiabaticindexofidealgases理想气体的微观模型micro-modelofidealgas理想气体反应的等温方程isothermalequationofidealgaseousreactions理想气体绝热可逆过程方程adiabaticreversibleprocessequationofidealgase 理想气体状态方程stateequationofidealgas理想稀溶液idealdilutesolution理想液态混合物perfectliquidmixture粒子particles粒子的配分函数partitionfunctionofparticles连串反应consecutivereactions链的传递物chaincarrier链反应chainreactions量热熵calorimetricentropy量子统计quantumstatistics量子效率quantumyield临界参数criticalparameter临界常数criticalconstant临界点criticalpoint临界胶束浓度criticalmicelleconcentration临界摩尔体积criticalmolarvolume临界温度criticaltemperature临界压力criticalpressure临界状态criticalstate零级反应zeroorderreaction流动电势streamingpotential流动功flowwork笼罩效应cageeffect路易斯-兰德尔逸度规则Lewis-Randallruleoffugacity 露点dewpoint露点线dewpointline麦克斯韦关系式Maxwellrelations麦克斯韦速率分布Maxwelldistributionofspeeds麦克斯韦能量分布MaxwelIdistributionofenergy毛细管凝结condensationincapillary毛细现象capillary phenomena米凯利斯常数Michaelisconstant摩尔电导率molarconductivity摩尔反应焓molarreactionenthalpy摩尔混合熵moleentropyofmixing摩尔气体常数molargasconstant摩尔热容molarheatcapacity摩尔溶解焓moledissolutionenthalpy摩尔稀释焓moledilutionenthalpy内扩散控制internaldiffusionscontrol内能internalenergy内压力internalpressure能级energylevels能级分布energyleveldistribution能量均分原理principleoftheequipartitionofenergy 能斯特方程Nernstequation能斯特热定理Nernstheattheorem凝固点freezingpoint凝固点降低loweringoffreezingpoint凝固点曲线freezingpointcurve凝胶gelatin凝聚态condensedstate凝聚相condensedphase浓差超电势concentrationover-potential浓差极化concentrationpolarization浓差电池concentrationcells帕斯卡pascal泡点bubblepoint泡点线bubblepointline配分函数partitionfunction配分函数的析因子性质propertythatpartitionfunctiontobeexpressedasap roductoftheseparatepartitionfunctionsforeachkindofstate碰撞截面collisioncrosssection碰撞数thenumberofcollisions偏摩尔量partialmolequantities平衡常数(理想气体反应)equilibriumconstantsforreactionsofidealgases 平动配分函数partitionfunctionoftranslation平衡分布equilibriumdistribution平衡态equilibriumstate平衡态近似法equilibriumstateapproximation平衡状态图equilibriumstatediagram平均活度meanactivity平均活度系统meanactivitycoefficient平均摩尔热容meanmolarheatcapacity平均质量摩尔浓度meanmassmolarity平均自由程meanfreepath平行反应parallelreactions破乳demulsification铺展spreading普遍化范德华方程universalvanderWaalsequation其它功theotherwork气化热heatofvaporization气溶胶aerosol气体常数gasconstant气体分子运动论kinetictheoryofgases气体分子运动论的基本方程foundamentalequationofkinetictheoryofgases 气溶胶aerosol气相线vaporline迁移数transportnumber潜热latentheat强度量intensivequantity强度性质intensiveproperty亲液溶胶hydrophilicsol氢电极hydrogenelectrodes区域熔化zonemelting热heat热爆炸heatexplosion热泵heatpump热功当量mechanicalequivalentofheat热函heatcontent热化学thermochemistry热化学方程thermochemicalequation热机heatengine热机效率efficiencyofheatengine热力学thermodynamics热力学第二定律thesecondlawofthermodynamics热力学第三定律thethirdlawofthermodynamics热力学第一定律thefirstlawofthermodynamics热力学基本方程fundamentalequationofthermodynamics 热力学几率thermodynamicprobability热力学能thermodynamicenergy热力学特性函数characteristicthermodynamicfunction 热力学温标thermodynamicscaleoftemperature热力学温度thermodynamictemperature热熵thermalentropy热效应heateffect熔点曲线meltingpointcurve熔化热heatoffusion溶胶colloidalsol溶解焓dissolutionenthalpy溶液solution溶胀swelling乳化剂emulsifier乳状液emulsion润湿wetting润湿角wettingangle萨克尔-泰特洛德方程Sackur-Tetrodeequation 三相点triplepoint三相平衡线triple-phaseline熵entropy熵判据entropycriterion熵增原理principleofentropyincrease渗透压osmoticpressure渗析法dialyticprocess生成反应formationreaction升华热heatofsublimation实际气体realgas舒尔采-哈迪规则Schulze-Hardyrule松驰力relaxationforce松驰时间timeofrelaxation速度常数reactionrateconstant速率方程rateequations速率控制步骤ratedeterminingstep塔费尔公式Tafelequation态-态反应state-statereactions唐南平衡Donnanequilibrium淌度mobility特鲁顿规则Troutonrule特性粘度intrinsicviscosity体积功volumework统计权重statisticalweight统计热力学statisticthermodynamics统计熵statisticentropy途径path途径函数pathfunction外扩散控制externaldiffusioncontrol完美晶体perfectcrystalline完全气体perfectgas微观状态microstate微态microstate韦斯顿标准电池Westonstandardbattery维恩效应Wieneffect维里方程virialequation维里系数virialcoefficient稳流过程steadyflowprocess稳态近似法stationarystateapproximation 无热溶液athermalsolution无限稀溶液solutionsinthelimitofextremedilution物理化学PhysicalChemistry物理吸附physisorptions吸附adsorption吸附等量线adsorptionisostere吸附等温线adsorptionisotherm吸附等压线adsorptionisobar吸附剂adsorbent吸附量extentofadsorption吸附热heatofadsorption吸附质adsorbate析出电势evolutionordepositionpotential析因子性质propertythatpartitionfunctiontobeexpressedasaproductof 稀溶液的依数性colligativepropertiesofdilutesolutions稀释焓dilutionenthalpy系统system系统点systempoint系统的环境environmentofsystem相phase相变phasechange相变焓enthalpyofphasechange相变化phasechange相变热heatofphasechange相点phasepoint相对挥发度relativevolatility相对粘度relativeviscosity相律phaserule相平衡热容heatcapacityinphaseequilibrium相图phasediagram相倚子系统systemofdependentparticles悬浮液suspension循环过程cyclicprocess压力商pressurequotient压缩因子compressibilityfactor压缩因子图diagramofcompressibilityfactor亚稳状态metastablestate盐桥saltbridge盐析saltingout阳极anode杨氏方程Young’sequation液体接界电势liquidjunctionpotential液相线liquidphaselines一级反应firstorderreaction一级相变firstorderphasechange依时计量学反应timedependentstoichiometricreactions逸度fugacity逸度系数coefficientoffugacity阴极cathode荧光fluorescence永动机perpetualmotionmachine永久气体Permanentgas有效能availableenergy原电池primarycell原盐效应salteffect增比粘度specificviscosity憎液溶胶lyophobicsol沾湿adhesionalwetting沾湿功theworkofadhesionalwetting真溶液truesolution真实电解质realelectrolyte真实气体realgas真实迁移数truetransferencenumber振动配分函数partitionfunctionofvibration振动特征温度characteristictemperatureofvibration 蒸气压下降depressionofvaporpressure正常沸点normalpoint正吸附positiveadsorption支链反应branchedchainreactions直链反应straightchainreactions指前因子pre-exponentialfactor质量作用定律massactionlaw制冷系数coefficientofrefrigeration中和热heatofneutralization轴功shaftwork转动配分函数partitionfunctionofrotation转动特征温度characteristictemperatureofvibration 转化率convertratio转化温度conversiontemperature状态state状态方程stateequation状态分布statedistribution状态函数statefunction准静态过程quasi-staticprocess准一级反应pseudofirstorderreaction自动催化作用auto-catalysis自由度degreeoffreedom自由度数numberofdegreeoffreedom自由焓freeenthalpy自由能freeenergy自由膨胀freeexpansion组分数componentnumber最低恒沸点lowerazeotropicpoint最高恒沸点upperazeotropicpoint最佳反应温度optimalreactiontemperature 最可几分布mostprobabledistribution最可几速率mostpropablespeed化学专业术语英语对照来源:发布时间:2011年4月7日爆炸界限explosionlimits霍根-华森图Hougen-WatsonChart德拜和法尔肯哈根效应DebyeandFalkenhageneffect德拜-休克尔极限公式Debye-Huckel’slimitingequation 德拜立方公式Debyecubicformula聚沉值coagulationvalue聚沉coagulation聚(合)电解质polyelectrolyte精馏rectify键焓bondenthalpy触变thixotropy解离化学吸附dissociationchemicaladsorption简并度degeneracy感胶离子序lyotropicseries催化剂catalyst隔离法theisolationmethod隔离系统isolatedsystem道尔顿定律Daltonlaw道尔顿分压定律Daltonpartialpressurelaw超电势overpotential缔合化学吸附associationchemicaladsorption等温等容位Helmholtzfreeenergy等温等压位Gibbsfreeenergy等温方程equationatconstanttemperature等焓线isenthalpicline等焓过程isenthalpicprocess等几率定理theoremofequalprobability焦耳定律Joule';slaw焦耳-汤姆生效应Joule-Thomsoneffect焦耳-汤姆生实验Joule-Thomsonexperiment焦耳-汤姆生系数Joule-Thomsoncoefficient焦耳Joule敞开系统opensystem菲克扩散第一定律Fick’sfirstlawofdiff usion 粗分散系统thickdispersesystem第三定律熵third-lawentropy第二类永动机perpetualmachineofthesecondkind 第一类永动机perpetualmachineofthefirstkind 盖斯定律Hesslaw盖·吕萨克定律Gay-Lussaclaw焓enthalpy混合熵entropyofmixing混合物mixture接触角contactangle接触电势contactpotential弹式量热计bombcalorimeter常见术语基态能级energylevelatgroundstate基希霍夫公式Kirchhoffformula基元反应elementaryreactions高会溶点upperconsolutepoint高分子溶液macromolecularsolution胶凝作用demulsification胶核colloidalnucleus胶束micelle胶冻brothjelly胶体粒子colloidalparticles胶体化学collochemistry胶体分散系统dispersionsystemofcolloid胶体colloid胶团micelle积分溶解热integrationheatofdissolution盎萨格电导理论Onsager’stheoryofconductance爱因斯坦-斯托克斯方程Einstein-Stokesequation爱因斯坦光化当量定律Einstein’slawofphotochemicalequivalence 浸湿功immersionwettingwork浸湿immersionwetting格罗塞斯-德雷珀定律Grotthus-Draoer’slaw根均方速率root-mean-squarespeed费米-狄拉克统计Fermi-Diracstatistics绝热量热计adiabaticcalorimeter绝热指数adiabaticindex绝热过程adiabaticprocess绝对熵absoluteentropy绝对温标absolutetemperaturescale绝对反应速率理论absolutereactionratetheory结晶热heatofcrystallization结线tieline科尔劳施离子独立运动定律Kohlrausch’sLawofIndependentMigrationofIons 界面张力surfacetension界面interfaces玻色-爱因斯坦统计Bose-Einsteinstatistics玻尔兹曼熵定理Boltzmannentropytheorem玻尔兹曼常数Boltzmannconstant玻尔兹曼分布Boltzmanndistribution玻尔兹曼公式Boltzmannformula独立子系统independentparticlesystem活度activity活化控制activationcontrol活化能activationenergy活化络合物理论activatedcomplextheory标准熵standardentropy标准摩尔燃烧焓standardmolarcombustionenthalpy标准摩尔熵standardmolarentropy标准摩尔焓函数standardmolarenthalpyfunction标准摩尔吉布斯自由能函数standardmolarGibbsfreeenergyfunction 标准摩尔生成焓standardmolarformationenthalpy标准摩尔生成吉布斯函数standardmolarformationGibbsfunction标准摩尔反应熵standardmolarreactionentropy标准摩尔反应焓standardmolarreactionenthalpy标准摩尔反应吉布斯函数standardGibbsfunctionofmolarreaction 标准氢电极standardhydrogenelectrode标准态standardstate标准状况standardcondition标准压力standardpressure标准电极电势standardelectrodepotential标准电动势standardelectromotiveforce标准平衡常数standardequilibriumconstant柯诺瓦洛夫-吉布斯定律Konovalov-Gibbslaw查理定律Charle’slaw挥发度volatility恒容摩尔热容molarheatcapacityatconstantvolume恒容热heatatconstantvolume恒沸混合物constantboilingmixture恒压摩尔热容molarheatcapacityatconstantpressure恒压热heatatconstantpressure恒外压constantexternalpressure封闭系统closedsystem复合反应compositereaction饱和蒸气压saturatedvaporpressure饱和蒸气saturatedvapor饱和液体saturatedliquids饱和吸附量saturatedextentofadsorption非基元反应non-elementaryreactions非依时计量学反应timeindependentstoichiometricreactions 非体积功non-volumework规定熵stipulatedentropy表面活性剂surfactants表面质量作用定律surfacemassactionlaw表面张力surfacetension表面吸附量surfaceexcess表面过程控制surfaceprocesscontrol表面surfaces表观摩尔质量apparentmolecularweight表观活化能apparentactivationenergy表观迁移数apparenttransferencenumber范德华常数vanderWaalsconstant范德华气体vanderWaalsgases范德华方程vanderWaalsequation范德华力vanderWaalsforce范特霍夫渗透压公式van’tHoffequationofosmoticpressure 范特霍夫规则van’tHoffrule范特霍夫方程van’tHoffequation环境熵变entropychangeinenvironment环境environment波义尔温度Boyletemperature波义尔点Boylepoint波义尔定律Boylelaw法拉第常数faradayconstant法拉第定律Faraday’slaw泊Poise沸点升高elevationofboilingpoint沸点boilingpoint构型熵configurationalentropy定域子系统localizedparticlesystem定容摩尔热容molarheatcapacityunderconstantvolume定容温度计ConstantvoIumethermometer定压摩尔热容molarheatcapacityunderconstantpressure定压温度计constantpressurethermometer孤立系统isolatedsystem固溶胶solidsol固相线solidphaseline固态混合物solidsolution单链反应straightchainreactions单分子层吸附理论monomoleculelayeradsorption 单分子反应unimolecularreaction附加压力excesspressure阿累尼乌斯活化能Arrheniusactivationenergy阿累尼乌斯电离理论Arrheniusionizationtheory 阿累尼乌斯方程Arrheniusequation阿伏加德罗常数Avogadro’number阿伏加德罗定律Avogadrolaw阿马格定律Amagatlaw沉降电势sedimentationpotential沉降平衡sedimentationequilibrium沉降sedimentation极限摩尔电导率limitingmolarconductivity极化作用polarization极化曲线polarizationcurves极化电极电势polarizationpotentialofelectrode杠杆规则leverrule低熔冰盐合晶cryohydric低共熔混合物eutecticmixture低共熔点eutecticpoint低会溶点lowerconsolutepoint亨利常数Henryconstant亨利定律Henrylaw过程process过渡状态理论transitionstatetheory过热液体overheatedliquid过饱和蒸气oversaturatedvapor过饱和溶液oversaturatedsolution过冷液体overcooledliquid过冷水super-cooledwater负极negativepole负吸附negativeadsorption安托万常数Antoineconstant安托万方程Antoineequation多方过程polytropicprocess多分子层吸附理论adsorptiontheoryofmulti-molecularlayers 吉布斯函数判据Gibbsfunctioncriterion吉布斯函数Gibbsfunction吉布斯-杜亥姆方程Gibbs-Duhemequation吉布斯吸附公式Gibbsadsorptionformula吉布斯自由能Gibbsfreeenergy吉布斯-亥姆霍兹方程Gibbs-Helmhotzequation 吉氏函数Gibbsfunction动力学控制kineticscontrol动力学方程kineticequations共轭溶液conjugatesolution共沸温度azeotropictemperature光谱熵spectrum entropy光敏反应photosensitizedreactions光反应photoreaction光化学第二定律thesecondlawofactinochemistry 光化学第一定律thefirstlawofactinochemistry 价数规则ruleofvalence产率yield亥姆霍兹函数判据Helmholtzfunctioncriterion 亥姆霍兹函数Helmholtzfunction亥姆霍兹自由能Helmholtzfreeenergy亥氏函数Helmholtzfunction节流膨胀系数coefficientofthrottlingexpansion 节流膨胀throttlingexpansion节流过程throttlingprocess艾林方程Eryingequation电解池electrolyticcell电量计coulometer电渗析electrodialysis电渗electroosmosis电流效率currentefficiency电泳electrophoresis电极种类typeofelectrodes电极电势electrodepotential电极反应reactionsontheelectrode电迁移率electromobility电迁移electromigration电池常数cellconstant电池电动势electromotiveforceofcells电池反应cellreaction电导率conductivity电导conductance电动势的温度系数temperaturecoefficientofelectromotiveforce 电动电势zetapotential电功electricwork电化学极化electrochemicalpolarization电化学electrochemistry甘汞电极calomelelectrode弗罗因德利希吸附经验式Freundlichempiricalformulaofadsorption 布朗运动brownianmovement对称数symmetrynumber对应状态原理principleofcorrespondingstate对行反应reversiblereactions对比摩尔体积reducedmolevolume对比温度reducedtemperature对比体积reducedvolume对比压力reducedpressure卡诺循环Carnotcycle卡诺定理Carnottheorem半衰期halftimeperiod半电池halfcell功函workcontent功work计量系数stoichiometriccoefficient计量式stoichiometricequation比浓粘度reducedviscosity比表面吉布斯函数specificsurfaceGibbsfunction比表面功specificsurfacework开尔文公式Kelvinformula反渗透reverseosmosis反应速率常数constantofreactionrate反应速率rateofreaction反应热heatofreaction反应进度extentofreaction反应级数reactionorders反应分子数molecularity反电动势back化学热力学chemicalthermodynamics化学亲合势chemicalaffinity化学势判据chemicalpotentialcriterion化学势chemicalpotential化学吸附chemisorptions化学动力学chemicalkinetics化学反应进度extentofchemicalreaction化学反应计量系数stoichiometriccoefficientofchemicalreaction 化学反应计量式stoichiometricequationofchemicalreaction分解电压decompositionvoltage分散相dispersionphase分散系统dispersesystem分配定律distributionlaw分体积定律partialvolumelaw分体积partialvolume分压定律partialpressurelaw分压partialpressure分布数distributionnumbers分布distribution分子蒸馏moleculardistillation分子间力intermolecularforce分子反应力学mechanicsofmolecularreactions不可逆相变化irreversiblephasechange不可逆过程热力学thermodynamicsofirreversibleprocesses 不可逆过程irreversibleprocess广度性质extensiveproperty广延量extensivequantity广延性质extensiveproperty几率因子stericfactor二级相变secondorderphasechange二级反应secondorderreaction丁达尔效应Dyndalleffectζ电势zetapotentialpVT性质pVTpropertyHLB法hydrophile-lipophilebalancemethodDLVO理论DLVOtheoryBET公式BETformula可能的电解质potentialelectrolyte可逆电池reversiblecell可逆过程reversibleprocess可逆过程方程reversibleprocessequation可逆体积功reversiblevolumework可逆相变reversiblephasechange克拉佩龙方程Clapeyronequation克劳修斯不等式Clausiusinequality克劳修斯-克拉佩龙方程Clausius-Clapeyronequation控制步骤controlstep库仑计coulometer扩散控制diffusioncontrolled拉普拉斯方程Laplace’sequation拉乌尔定律Raoultlaw兰格缪尔-欣谢尔伍德机理Langmuir-Hinshelwoodmechanism 兰格缪尔吸附等温式Langmuiradsorptionisothermformula 雷利公式Rayleighequation冷冻系数coefficientofrefrigeration冷却曲线coolingcurve离解热heatofdissociation离解压力dissociationpressure离域子系统non-localizedparticlesystems离子的标准摩尔生成焓standardmolarformationofion离子的电迁移率mobilityofions离子的迁移数transportnumberofions离子独立运动定律lawoftheindependentmigrationofions离子氛ionicatmosphere离子强度ionicstrength理想混合物perfectmixture理想气体idealgas理想气体的绝热指数adiabaticindexofidealgases理想气体的微观模型micro-modelofidealgas理想气体反应的等温方程isothermalequationofidealgaseousreactions理想气体绝热可逆过程方程adiabaticreversibleprocessequationofidealgase 理想气体状态方程stateequationofidealgas理想稀溶液idealdilutesolution理想液态混合物perfectliquidmixture粒子particles粒子的配分函数partitionfunctionofparticles连串反应consecutivereactions链的传递物chaincarrier链反应chainreactions量热熵calorimetricentropy量子统计quantumstatistics量子效率quantumyield临界参数criticalparameter临界常数criticalconstant临界点criticalpoint临界胶束浓度criticalmicelleconcentration临界摩尔体积criticalmolarvolume临界温度criticaltemperature临界压力criticalpressure临界状态criticalstate零级反应zeroorderreaction流动电势streamingpotential流动功flowwork笼罩效应cageeffect路易斯-兰德尔逸度规则Lewis-Randallruleoffugacity 露点dewpoint露点线dewpointline麦克斯韦关系式Maxwellrelations麦克斯韦速率分布Maxwelldistributionofspeeds麦克斯韦能量分布MaxwelIdistributionofenergy毛细管凝结condensationincapillary毛细现象capillary phenomena米凯利斯常数Michaelisconstant摩尔电导率molarconductivity摩尔反应焓molarreactionenthalpy摩尔混合熵moleentropyofmixing摩尔气体常数molargasconstant摩尔热容molarheatcapacity摩尔溶解焓moledissolutionenthalpy摩尔稀释焓moledilutionenthalpy内扩散控制internaldiffusionscontrol内能internalenergy内压力internalpressure能级energylevels能级分布energyleveldistribution能量均分原理principleoftheequipartitionofenergy 能斯特方程Nernstequation能斯特热定理Nernstheattheorem凝固点freezingpoint凝固点降低loweringoffreezingpoint凝固点曲线freezingpointcurve凝胶gelatin凝聚态condensedstate凝聚相condensedphase浓差超电势concentrationover-potential浓差极化concentrationpolarization浓差电池concentrationcells帕斯卡pascal泡点bubblepoint泡点线bubblepointline配分函数partitionfunction配分函数的析因子性质propertythatpartitionfunctiontobeexpressedasap roductoftheseparatepartitionfunctionsforeachkindofstate碰撞截面collisioncrosssection碰撞数thenumberofcollisions偏摩尔量partialmolequantities平衡常数(理想气体反应)equilibriumconstantsforreactionsofidealgases 平动配分函数partitionfunctionoftranslation平衡分布equilibriumdistribution平衡态equilibriumstate平衡态近似法equilibriumstateapproximation平衡状态图equilibriumstatediagram平均活度meanactivity平均活度系统meanactivitycoefficient平均摩尔热容meanmolarheatcapacity平均质量摩尔浓度meanmassmolarity平均自由程meanfreepath平行反应parallelreactions破乳demulsification铺展spreading普遍化范德华方程universalvanderWaalsequation。
定量分析10电解质对化学平衡的影响EFFECT OF ELECTROLYTES ON CHEMICAL EQUILIBRIA

aX =x[X] where, aX is the activity nd x is a dimensionless quantity called the activity coefficient.
…continued…
sulfate, or sodium perchlorate, is added to this solution,
the color of the triiodide ion becomes less intense. This
decrease in color intensity indicates that the concentration of I3- has decreased and that the equilibrium has been shifted to the left by the added
4. At any given ionic strength, the activity coefficients of ions of the same charge are approximately equal. The small variations that do exist can be correlated with the effective diameter of the hydrated ions.
Hydrophobic derivatives of chitosan

ELSEVIER
International Journal oules 19 (1996) 21-28
Biological Macromolecules
S ' I 1 U C l l I I ~ FUNCIION A / ~ ~
Keywords: Chitosan derivative; Hydrophobic; Characterization; Rheological behaviour
1. Introduction Hydrophobic associating water soluble polymers represent a new class of industrially important macromolecules. They possess unusual rheological characteristics which are thought to arise from the intermolecular association of neighbouring hydrophobic substituants [1] which are incorporated into the polymer molecule through chemical grafting [2,3] or suitable copolymerisation procedures [4]. The hydrophobic associations give rise to a three-dimensional polymer network. Self assembly or aggregation of amphiphilic polymers is of growing interest with respect to biological importance and pharmaceutical or biotechnological applications [5]. Recently, solution properties of block copolymer micelles [6] or self-aggregates or hydrophobized water soluble polymers [7] have been extensively studied. Biopolymers and various synthetic charged or non-ionic polymers have been used as hydrophilic backbone to prepare amphiphilic polymers by hydrophobic substitution. Among these water soluble polymers, naturally occurring polysaccharides which are
原子电离残存窗口

National Laboratory of Science and Technology on Computational Physics, Institute of Applied Physics and Computational Mathematics, Beijing 100088, China 2 HEDPS, Center for Applied Physics and Technology, Peking University, Beijing 100084, China 3 Graduate School, China Academy of Engineering Physics, Beijing 100088, China (Received 21 December 2012; published 20 March 2013) We find a fraction of atoms remain unionized after the laser pulse when the tunneled electrons are released in a certain window of initial field phase and transverse velocity. The survival window shifts with laser polarization ellipticity and its width varies with respect to laser intensity and atomic ionization potential. Neutral atom yield can be calculated by summing up tunneling probabilities in the window. Our theory can quantitatively reproduce the distribution of the survival yields vs laser ellipticity observed for helium in experiment. For other atom species with smaller ionization potential such as magnesium, our theory predicts a wider distribution than the strong-field approximation model while closer to the three-dimensional semiclassical electron ensemble simulations, indicating the important role of the Coulomb effects. DOI: 10.1103/PhysRevA.87.033415 I. INTRODUCTION PACS number(s): 32.80.Rm, 42.50.Hz, 33.80.Rv
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
a r X i v :c o n d -m a t /0006289v 1 [c o n d -m a t .s o f t ] 19 J u n 2000Charged colloids at low ionic strength:macro-or microphase separation?Patrick B.WarrenUnilever Research Port Sunlight,Bebington,Wirral,CH633JW,UK.Phase separation in charged systems may involve the replacement of critical points by microphase separated states,or charge-density-wave states.A density functional theory for highly charged colloids at low ionic strength is developed to examine this possibility.It is found that the lower critical solution point is most susceptible to microphase separation.Moreover the tendency can be quantified,and related to the importance of small ion entropy in suppressing phase separation at low added salt.The theory also gives insights into the colloid structure factor in these systems.PACS:05.20.-y,64.75.+g,82.70.DdThere has been much interest recently in statistical physics in charged soft matter systems.Whilst much of this is biologically inspired (eg DNA condensation [1]),there has also been a long standing controversy in the colloid science community over the anomalous behaviour of charge stabilised colloidal suspensions at low ionic strengths [2].Recently [3,4],it has been suggested that the anomalies in these systems may be understood in terms of a miscibility gap which is the analogue of the vapour-liquid coexistence in the restricted primitive model (RPM)of 1:1electrolytes [5].Arguably a theo-retical consensus is emerging,although there remain a number of competing theories [6].In all these examples,the crucial role of the counterions should not be underestimated.For the case of charged colloidal suspensions,for example,the theories show that the overall phase stability is almost entirely due to the entropy of the counterions [3,4].The same effect can be said to underpin the solubility of many water-soluble polymers [7].The basic point is that bulk phase separa-tion in a charged system must be into electrically neutral phases.If this involves significant fractionation of coun-terions,an entropic penalty will be incurred which tends to suppress phase separation.Clearly though,if bulk phase separation is suppressed,a possibility still exists to undergo microphase separa-tion ,where electroneutrality can be broken locally.Crit-ical points are particularly susceptible to this,as first shown by Nabutovskii,Nemov and Peisakhovich (NNP)using a Landau-Ginzburg theory [8].Consider density fluctuations at wavevector q .At q →0,fluctuations are restricted to elecrically neutral combinations,but for q >0fluctuations can violate electroneutrality increas-ingly easily.Thus one might expect some softening of the modes.Indeed,if the only terms to O (q 2)come from the long range Coulomb law,the analysis below implies that all partial structure factors have a minimum at q =0.Since the q =0partial structure factors diverge as one approaches a critical point,this suggests there must ex-ist regions around critical points where a divergence at q >0occurs first,indicative that the critical behaviour is preempted by microphase separation.However,thereare often other terms arising at O (q 2)from elsewhere which destroy the phenomenon.A closely analogous mi-crophase separation for polyelectrolytes in poor solvents has also been examined [9],but in the present study mi-crophase separation is driven purely by electrostatic ef-fects.Let us start by constructing a simplified but physically motivated model for the anomalous behaviour in charged colloidal suspensions.Consider the macroions as spheres of charge Z ,diameter 2a ,and number density ρM (vol-ume fraction φ=4πa 3ρM /3).There are small counte-rions and coions at number densities ρ−and ρ+respec-tively.The solvent is a dielectric continuum.Without loss of generality,I suppose the small ions are univalent,and there is only one species of counterion [10].Since the coions come from added salt,it will be convenient to write ρ+=ρS .Overall,the system is electrically neu-tral and ρ−=ρS +ZρM ,but δρ±will be retained for fluctuations.Each macroion polarises the surrounding electrolyte solution,and becomes surrounded by a ‘double layer’.It has been shown by many workers [3,11,12]that the self energy of the macroion with its double layer,in Debye-H¨u ckel theory,is (Z 2l B kT/2a )×h (κa ).In this l B =e 2/ǫkT is the Bjerrum length,the function h (x )=1/(1+x )[13],and the Debye screening length,κ−1,is given by κ2=8πl B ρI where 2ρI =ρ−+ρ+=ZρM +2ρS is (twice)the ionic strength.This energy has a well known interpretation:it corresponds exactly to a spherical ca-pacitor ,charged ±Ze ,with one plate at the macroion surface and the second a distance κ−1away [14].The simplest model free energy based on this is F/V kT =ρS log ρS +(ρS +ZρM )log(ρS +ZρM )+ρM log ρM +ρM (Z 2l B /2a )h (κa ).(1)The first three terms are the ideal terms,and the last is the self energy of macroions at number density ρM .The most important omission from this is the contribution from the macroion-macroion interactions.Whilst this plays a significant role in structuring the macroions,it has been demonstrated elsewhere [4]that it is less signif-icant than the self energy,as regards the appearance ofa miscibility gap.Moreover,by leaving this contribution out of the theory,we will see quite clearly how structure can develop in the system in the absence of pair interac-tions.A typical phase diagramcorresponding totheabove free energy is shown in Fig.1,for Z =103and 2a =100nm.It comprises a simple miscibility gap,limited above and below by critical solution points as the salt concentration is varied.The gap occurs at very low ionic strengths,and only appears if the charge on the macroions is sufficiently high (Zl B /a >∼13.4for 2a in the range 10–1000nm).Now,the NNP scenario could occur at either crit-ical point.To examine this therefore,I construct a density functional theory to correspond to the free energy introduced above.The ideal terms become kT d 3r ρi (r )log ρi (r )(i =+,−,M),and I intro-duce the ansatz that the self energy generalises in the obvious way to d 3r ρM (r )f self N (r )where f selfN =(Z 2l B kT/2a )h (κa )is the self energy per particle evalu-ated using the local ionic strength at the particle centre,κ2=8πl B ρI (r ).Finally,an electrostatic contrbution has to be added:l B kT d 3r d 3r ′ρZ (r )ρZ (r ′)/|r −r ′|,where ρZ (r )=ZρM (r )+ρ+(r )−ρ−(r )is the local charge den-sity.To examine the stability of the system against mi-crophase separation,expand the above density functional about the homogeneous state to quadratic order.For fluctuations at a wavevector q this results inδF2ρS +|δρ−|22ρM+2πl B2a8π2l 2B a 4ρM h 1(κa )|δρI |2(2)−2πl B a 2h 2(κa )(δρM δρ∗I +δρ∗M δρI )The functions are h 1(x )=(1+3x )/(x 3(1+x )3)and h 2(x )=1/(x (1+x )2).From this the macroion structure factor S (q )= |δρM (q )|2 is extracted in the standard way [15].The behaviour of S (q )is examined as a func-tion of φand ρS ,looking for the unstable regions in the (φ,ρS )-plane where 1/S (q )<0.At q =0the spinodal instability region corresponding to the free energy in Eq.(1)is recovered.For q >0the region of instability always expands .This is because the q -dependence arises solely from the long range elec-trostatic term,thus,as alluded to above,S (q )always has a minimum at q =0.But a clear difficulty emerges when the behaviour for large q is examined,since the instability region expands to fill the entire plane;there is no effective penalty against microphase separation at vanishingly small wavelengths.00.020.042040ρI (r )=d 3r ′w (|r −r ′|)ρI (r ′)where w (r )is a smoothing kernel of range a [17],but equally onemight smooth κor f selfN .All forms result in the appear-ance of extra multiplicative factors,w 1(qa )and w 2(qa ),in the last two terms of Eq.(2).The w i (qa )are related to the Fourier transform of w (r ),and satisfy w i →1at q →0,w i →0at q →∞.(More generally I ex-pect h i (κa,qa )such that h i →0for qa →∞.)With this ansatz ,progress can be made without developing a detailed theory by investigating various possibilities for w i .The results reported below have been carried out assuming w 1=w 2=exp(−αq 2a 2)with αa numerical prefactor of order unity.Very similar results are obtained for w i =1/(1+αq 2a 2).Typical results from this modified theory are shown in Figs.2and 3,for α=1.In Fig.2,the spinodal insta-bility at q =0is recovered as before.For q >0,the instability region is again expanded in the vicinity of the lower critical point,but is now reduced in the vicinity of the upper critical point.For qa ≫1the instability dis-appears completely,since the self energy which drives the instability is now insensitive to short wavelength fluctu-ations.Below the lower critical point,therefore,there is a region (delimited by the heavy dashed line in Fig.2)where S (q )diverges at some q ∗>0,corresponding to the appearance of microphases.10101010−610−510−4α.All the results discussedabove were at α=1.If α<∼0.338,microphases ap-pear at the upper critical point too.On the other hand,if α>∼1.961microphase separation at the lower critical point disappears.One would expect increasing αto sup-press microphase separation,since greater smoothing is bound to reduce q ∗,but the difference between the two critical points is suggestive.These critical values of αare more general than the assumed form of w i (q ),since they only depend on the q 2coefficient in the expansion w i (q )=1−αq 2a 2+O (q 4)[20].They are a measure of the susceptibility of the critical point to replacement by microphases (if αcould be treated as a control variable,the critical values would correspond to Lifshitz points in the phase diagram).00.20.40.60.810.000.050.100.150.01.50.00.51.0ψvanishes as one ap-proaches the critical point.Recall that ∆cause the interface can acquire a dipole moment den-sity(per unit area).In the present system,a dipole moment density appears to arise because the jump in small ion densities is spread out more broadly than the jump in macroion densities(although this remains to be confirmed with a detailed calculation[21]).Remarkably, one can calculate∆ψvanishes as∆φ/φcrit as the critical points are approached,with a constant of proportionality≈8.00for the upper critical solution point,and≈16.9for the lower one.This again indicates the growing importance of small ion entropy (broadening the jump in small ion densities)as the lower critical point is approached.Note that∆ψ.I thank C.Holmes and M.E.Cates for useful discus-sions,and P.Schurtenberger for sending data prior to publication.。
