Lepton-Number Violating Heavy Meson Decays轻子数违反重介子衰变
python的海豹运算符

python的海豹运算符
海豹运算符(walrus operator)是Python 3.8版本引入的一种新的运算符,用来在表达式中同时执行赋值操作。
它的符号是“:=”,它的主要作用是将表达式的结果赋值给变量,并且在同一时间使用这个结果。
这个特性主要用于简化代码和提高可读性。
举个例子,假设我们想要计算一个列表的长度,并且希望在之后使用这个长度值,我们可以这样写:
python.
if (n := len(a)) > 10:
print(f"List is too long ({n} elements, expected <= 10)")。
在这个例子中,海豹运算符“:=”将len(a)的结果赋值给变量n,然后这个n的值可以在后续的代码中直接使用,避免了重复计算len(a)的操作。
海豹运算符在循环中也非常有用,比如在迭代过程中同时赋值和使用元素的情况下。
例如:
python.
while (command := input("> ")) != "quit":
print(f'You entered: {command}')。
这样可以在循环中同时获取用户输入并且检查输入是否为"quit",从而避免了重复调用input函数。
总的来说,海豹运算符的引入使得Python的代码更加简洁和易读,但是在使用时也要注意不要滥用,以免降低代码的可读性。
希望这个回答能够全面解答你关于海豹运算符的问题。
第三届蓝桥杯省赛古堡算式

第三届蓝桥杯省赛古堡算式题⽬描述:福尔摩斯到某古堡探险,看到门上写着⼀个奇怪的算式:ABCDE * ? = EDCBA他对华⽣说:“ABCDE应该代表不同的数字,问号也代表某个数字!”华⽣:“我猜也是!”于是,两⼈沉默了好久,还是没有算出合适的结果来。
请你利⽤计算机的优势,找到破解的答案。
把 ABCDE 所代表的数字写出来。
答案写在“解答.txt”中,不要写在这⾥!思路:最开始就是想直接爆⼒求解好了,结果发现判断不同太⿇烦,然后采⽤了全排列#include<stdio.h>int d[10] = { 0,1,2,3,4,5,6,7,8,9 };void swap(int *a, int *b) {int temp;temp = *a;*a = *b;*b = temp;}void perm(int i) {if (i==9) {int k;if ((d[0] * 10000 + d[1] * 1000 + d[2] * 100 + d[3] * 10 + d[4])*d[5] == (d[4] * 10000 + d[3] * 1000 + d[2] * 100 + d[1] * 10 + d[0])) { for (k = 0; k < 10; k++) {printf("%d ", d[k]);}printf("\n");}}else {int j;for (j = i; j <= 9; j++) {swap(&d[i], &d[j]);perm(i + 1);swap(&d[i], &d[j]);}}}int main() {perm(0);return0;}答案:21978。
nucleon number英文定义

nucleon number英文定义1. IntroductionThe concept of nucleon number is essential in the field of nuclear physics, as it helps to describe the structure and characteristics of atomic nuclei. In this article, we will explore the English definition of nucleon number, its significance, and its relevance in the study of nuclear processes and reactions.2. DefinitionThe nucleon number, also known as the mass number, is the total number of protons and neutrons present in the nucleus of an atom. It is denoted by the symbol "A" and is used to distinguish between different isotopes of a particular element. The nucleon number is a whole number and is always greater than or equal to the number of protons in the nucleus.3. SignificanceThe nucleon number plays a crucial role in determining the stability and properties of an atomic nucleus. Nuclei with the same number of protons but different nucleon numbers are known as isotopes. Isotopes of an element may have different nuclear properties and stability due to variations in theirnucleon numbers. For example, isotopes with a higher nucleon number may be more unstable and prone to radioactive decay.4. Relevance in nuclear reactionsIn nuclear reactions, the nucleon number is conserved. This means that the total nucleon number before and after a nuclear reaction rem本人ns the same. For example, in a nuclear fusion reaction, two lighter nucleibine to form a heavier nucleus, and the nucleon number is conserved in the process. Similarly, in nuclear fission, a heavy nucleus splits into two or more lighter nuclei, and the nucleon number is also conserved.5. CalculationThe nucleon number can be calculated by adding the number of protons and neutrons in the nucleus of an atom. Since the number of protons is the same as the atomic number (Z), the nucleon number (A) can be calculated using the formula:A = Z + NWhere A is the nucleon number, Z is the atomic number (number of protons), and N is the number of neutrons.6. ConclusionIn conclusion, the nucleon number is a fundamental concept in nuclear physics, which provides valuable information about the structure and stability of atomic nuclei. Its significance in distinguishing between isotopes and its conservation in nuclear reactions highlights its importance in the study of nuclear processes and reactions. Understanding the nucleon number is crucial for the advancement of nuclear science and technology.。
阿姆斯特朗数 检测代码

阿姆斯特朗数检测代码【原创版】目录1.阿姆斯特朗数的概念与背景2.阿姆斯特朗数的特性3.阿姆斯特朗数的应用领域4.检测阿姆斯特朗数的代码示例正文1.阿姆斯特朗数的概念与背景阿姆斯特朗数,又称自幂数、阿姆斯特朗自幂数或水仙花数,是指一个 n 位数,它的每个位上的数字的 n 次幂之和等于它本身。
阿姆斯特朗数是由美国数学家爱德华·卡西尼·阿姆斯特朗于 1937 年首次提出的。
阿姆斯特朗数的命名来源于水仙花,因为该数的形状类似于水仙花的花瓣。
2.阿姆斯特朗数的特性阿姆斯特朗数具有以下特性:(1)阿姆斯特朗数是一个 n 位数,每一位上的数字都不相同。
(2)阿姆斯特朗数的每一位上的数字的 n 次幂之和等于它本身。
(3)阿姆斯特朗数是唯一的,即对于每个 n,只有一个阿姆斯特朗数。
3.阿姆斯特朗数的应用领域阿姆斯特朗数在数学领域具有较高的理论价值,它可以用于研究数位数的规律、数的表示、数的性质等问题。
此外,阿姆斯特朗数在计算机科学领域也有一定的应用,如在编程设计中可以用来设计算法、测试程序等。
4.检测阿姆斯特朗数的代码示例下面是一个用 Python 编写的检测阿姆斯特朗数的代码示例:```pythondef is_armstrong_number(num):num_str = str(num)num_len = len(num_str)return num == sum(int(i) ** num_len for i in num_str) um = 153if is_armstrong_number(num):print(f"{num} 是阿姆斯特朗数")else:print(f"{num} 不是阿姆斯特朗数")```在这个示例中,我们定义了一个名为`is_armstrong_number`的函数,该函数接受一个整数参数`num`。
首先将`num`转换为字符串,然后获取字符串的长度`num_len`。
物理专业英语词汇
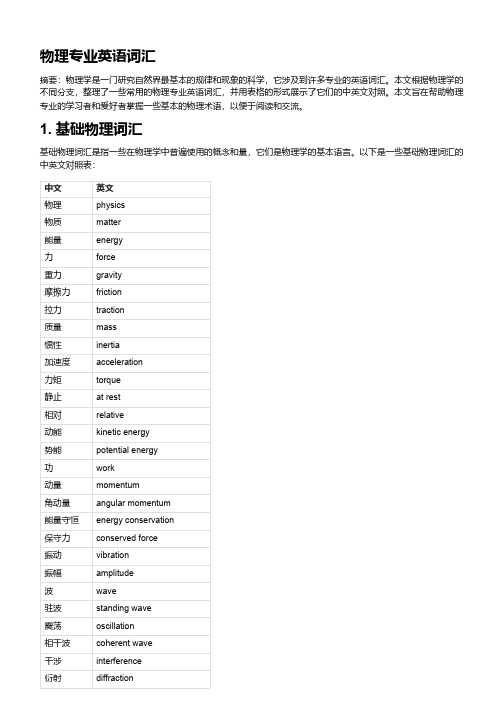
物理专业英语词汇摘要:物理学是一门研究自然界最基本的规律和现象的科学,它涉及到许多专业的英语词汇。
本文根据物理学的不同分支,整理了一些常用的物理专业英语词汇,并用表格的形式展示了它们的中英文对照。
本文旨在帮助物理专业的学习者和爱好者掌握一些基本的物理术语,以便于阅读和交流。
1. 基础物理词汇基础物理词汇是指一些在物理学中普遍使用的概念和量,它们是物理学的基本语言。
以下是一些基础物理词汇的中英文对照表:中文英文物理physics物质matter能量energy力force重力gravity摩擦力friction拉力traction质量mass惯性inertia加速度acceleration力矩torque静止at rest相对relative动能kinetic energy势能potential energy功work动量momentum角动量angular momentum能量守恒energy conservation保守力conserved force振动vibration振幅amplitude波wave驻波standing wave震荡oscillation相干波coherent wave干涉interference衍射diffraction轨道orbit速度velocity速率speed大小magnitude方向direction水平horizontal竖直vertical相互垂直perpendicular坐标coordinate直角坐标系Cartesian coordinate system极坐标系polar coordinate system2. 电学和磁学词汇电学和磁学是研究电荷、电流、电场、磁场等现象和规律的物理学分支,它们与光学、热学、原子物理等有着密切的联系。
以下是一些电学和磁学词汇的中英文对照表:中文英文电子electron电荷charge电流current电场electric field电通量electric flux电势electric potential导体conductor电介质dielectric绝缘体insulator电阻resistor电阻率resistivity电容capacitor3. 物理专业英语词汇物理专业英语词汇是指在物理学的学习和研究中经常使用的一些专业术语,它们涵盖了物理学的各个分支和领域,如力学、电磁学、光学、热学、量子力学等。
阿姆斯特朗数 检测代码

阿姆斯特朗数检测代码一、简介阿姆斯特朗数是一个在数学和计算机科学中常见的概念,它是指一个数字如果它是其因子和的结果也是数字自身,则称之为阿姆斯特朗数。
这种数在实际应用中有很多有趣的性质,例如它可以用于密码学和数学问题求解等。
二、代码实现以下是一个简单的Python代码实现,用于检测一个数字是否为阿姆斯特朗数:```pythondefis_armstrong(n):"""检测一个数字是否为阿姆斯特朗数"""ifn<1orn>2*10**9:#排除非整数和小于1的数returnFalsesum=0foriinrange(1,int(n**0.5)+1):#只考虑大于等于1的因子ifn%i==0:sum+=i*(n//i)**i#计算因子和returnsum==n```这段代码首先定义了一个名为`is_armstrong`的函数,它接受一个整数参数`n`,并返回一个布尔值,表示该数字是否为阿姆斯特朗数。
在函数内部,首先对输入数字进行了一些基本的检查,确保它是一个大于等于1的整数。
然后,使用一个循环遍历所有大于等于1的因子,并计算它们的和。
最后,比较因子和是否等于输入数字本身,如果相等则返回True,否则返回False。
三、测试为了验证代码的正确性,我们可以编写一些测试用例。
以下是一些示例测试用例:```pythonassertis_armstrong(23)#True,因为23是3的因子的因数和是7=23。
assertnotis_armstrong(2)#False,因为任何数的因子和都大于这个数本身。
assertnotis_armstrong(4)#False,因为4不是阿姆斯特朗数。
assertis_armstrong(37)#True,因为37是所有因子的因数和。
```四、总结通过以上代码实现和测试,我们可以检测一个数字是否为阿姆斯特朗数。
Nuclear physics aspects of double beta decay

Petr Vogel
Kellogg Radiation Laboratory 106-38 California Institute of Technology Pasadena, CA 91125, USA Lecture notes for course CLXX “MEASUREMENTS OF NEUTRINO MASS” Int. School of Physics “Enrico Fermi”, Varenna, June 2008
arXiv:0807.2457v1 [hep-ph] 15 Jul 2008
Summary. — Comprehensive description of the phenomenology of the ββ decay is given, with emphasis on the nuclear physics aspects. After a brief review of the neutrino oscillation results and of motivation to test the lepton number conservation, the mechanism of the 0νββ is discussed. Its relation to the lepton flavor violation involving charged leptons and its use as a diagnostic tool of the 0νββ mechanism is described. Next the basic nuclear physics of both ββ -decay modes is presented, and the decay rate formulae derived. The nuclear physics methods used, the nuclear shell model and the quasiparticle random phase approximation, are described next, and the choice of input parameters is discussed in the following section. Finally, the numerical values of the nuclear matrix elements, and their uncertainty, are presented. In the appendix the relation of the search for the neutrino magnetic moment to the Dirac versus Majorana nature of neutrinos is described. PACS 21.60.-n – . PACS 23.40.Bw – . PACS 23.40.Hc – .
Parton-Shower Simulations of R-parity Violating Supersymmetric Models

a r X i v :h e p -p h /9912407v 3 3 F eb 2000OUTP-99-26PRAL-TR-1999-080hep-ph/9912407Parton-Shower Simulations of R-parity Violating Supersymmetric Models H.Dreiner ∗1,P.Richardson †2,and M.H.Seymour ∗3∗Rutherford Appleton Laboratory,Chilton,Didcot OX110QX,U.K.†Department of Physics,Theoretical Physics,University of Oxford 1Keble Road,Oxford OX13NP,United Kingdom Abstract We study the colour connection structure of R-parity violating decays and pro-duction cross sections,and construct a Monte Carlo simulation of these processes including colour coherence effects.We then present some results from the imple-mentation of these processes in the HERWIG Monte Carlo event generator.We include the matrix elements for the two-body sfermion and three-body gaugino and gluino decays as well as the two-to-two resonant hard production processes in hadron-hadron collisions.1IntroductionIn the past few years there has been a large amount of interest in R-parity violating(R p) supersymmetric(SUSY)models,motivated by the possible explanations of various exper-imental discrepancies,e.g.[1–9].It has become clear that if we are to explore all possible channels for the discovery of supersymmetry then R p models must be investigated.For a recent review on R-parity violation see[10].In the Minimal Supersymmetric Standard Model(MSSM)a discrete multiplicative symmetry,R-parity(R p)is imposed,R p=(−1)3B+L+2S,(1) where B is the baryon number,L the lepton number and S the spin of the particle.All the Standard Model particles have R p=+1and their super-partners have R p=−1.The conservation of R-parity forbids the terms in the superpotential which violate baryon or lepton number1W R p=1E k+λ′ijkεab L i a Q j b2λ′′ijkεc1c2c3D j c2E i(U i)are the electron(down and up quark)SU(2)singlet superfields, and H n,n=1,2,are the Higgs superfields.We shall neglect the last term in Eqn.2 which mixes the lepton and Higgs SU(2)doublet superfields.For a recent summary of the bounds on the couplings in Eqn.2see[11].This superpotential gives interactions which violate either lepton or baryon number. For example thefirst term will give interactions of a slepton and two leptons which violates lepton number.The third term gives an interaction of two quarks and squark, which violates baryon number.When combined with the MSSM superpotential there are also terms involving the interactions of three sleptons/squarks and a Higgs which violate either lepton or baryon number.R p is imposed in the MSSM to avoid the simultaneous presence of the second two terms in Eqn.2.These lead to fast proton decay,in disagreement with the experimental lower bounds on the proton lifetime.However in order to guarantee proton stability it is sufficient to forbid only one set of these terms.This is achieved for example by lepton parity(L i,¯E i)→−(L i,¯E i),(3) (Q i,¯U i,¯D i,H1,H2)→(Q i,¯U i,¯D i,H1,H2),(4)which allows the third term in Eqn.2but forbids the remaining terms.Thus baryon number is violated(B)but lepton number is conserved and the proton is stable.Similarly there are symmetries such that lepton number is violated and baryon number is conserved.This also prevents proton decay.Both cases lead to very different phenomenology from the MSSM.In the MSSM the conservation of R p implies that1.Sparticles are produced in pairs.2.The lightest supersymmetric particle(LSP)is stable.3.Cosmological bounds on electric-or colour-charged stable relics imply that a stableLSP must be a neutral colour singlet[12].However,in the case of R p models we can have1.Single sparticle production.2.The LSP can decay.As the LSP is unstable it does not have to be a neutral coloursinglet.It can be any supersymmetric particle.3.Lepton or baryon number is violated.In the MSSM,as the LSP is stable,the experimental signatures of SUSY processes typically involve missing transverse energy in collider experiments.However,if R-parity is violated,and the LSP decays in the detector,the missing energy signatures of the MSSM no longer apply or are severely diluted.It therefore requires a different experimental search strategy.In particular,in the B case,where thefinal state is predominantly hadronic,it may be hard to extract a signal over the QCD background in hadron colliders.Despite the interest in R p and the potential experimental problems,there have been few experimental studies at hadron colliders.Thefirst systematic study of R p signatures at hadron colliders was presented in[13].More recent overviews of the search potential at the LHC and Run II of the Tevatron have been presented in[14,15].These studies have been limited by the fact that few simulations have been available.In hadron-hadron collisions the only available Monte Carlo event generator is ISAJET[16]where the R p decays can be implemented using the FORCE command,i.e.the decay mode of a given particle,e.g.the LSP,can be specified by hand.However there has been no simulation which includes all the decay modes and the single sparticle production processes.Here we present the calculations required to produce a Monte Carlo event generator for the two-body sfermion and three-body gaugino and gluino R p decay modes as well as all two-to-two R p resonant production processes in hadron-hadron collisions.We have only included those production processes where a resonance is possible,so for example processes which can only occur via a t-channel diagram are not included.However where a process can occur via a resonance all the diagrams including non-resonant s-channel and t-channel diagrams have been included.We also discuss colour coherence effects via the angular ordering procedure(which we describe in detail below),and some preliminary results from the implementation of these processes in the HERWIG Monte Carlo event generator[17]. Details of the implementation of supersymmetric processes with and without R p can be found in[18].After a general discussion of the angular ordering procedure in the Standard Model in Section2we discuss the extension to the R p decays and hard production processes inSection3.In Section4we describe the hadronization procedure which we adopt for the R p processes.We then present some preliminary results of the Monte Carlo simulation in Section5.We have made new calculations of all the necessary matrix elements,and include them as an appendix.2Monte Carlo SimulationsIn general a Monte Carlo event generator,for a process involving at least one hadron, consists of three parts.1.A hard scattering process,either of the incoming fundamental particles in leptoncollisions or of a parton extracted from a hadron in hadron initiated processes.2.A parton-shower phase where the partons coming into or leaving the hard processare evolved according to perturbative QCD.3.A hadronization model in which the partons left at the end of the parton-showerphase are formed into the hadrons which are observed.For processes with hadrons in the initial state after the removal of the partons in the hard process we are left witha hadron remnant.This remnant is also formed into hadrons by the hadronizationmodel.We now discuss these three stages in turn.2.1Hard ScatteringThe hard scattering process is described by a matrix element calculated to afixed order in perturbation theory,usually only leading order.The momenta of the particles involved in the collision can then be generated according to the matrix element.The Monte Carlo event generator then needs to take the results of this perturbative calculation,at a high scale,and generate the hadrons which are observed.2.2Parton ShowerIn a scattering process the incoming or outgoing partons can emit QCD radiation,e.g. q→gq and g→gg,or split into quark-antiquark pairs,g→q¯q.A full perturbative treatment of this part of an event is not possible.(If it were possible it would be included in the hard scattering matrix element.)We must therefore make an approximation and focus on the dominant contributions in the showering process.The emission of QCD radiation is enhanced for(a)Collinear Emission and for(b)Soft Emission.We discuss these two below in more detail.Our approximation will consist in focusing on these enhanced regions of radiation.We then discuss this in an explicit example.(a)Collinear EmissionIf we consider the emission of QCD radiation in the collinear limit then,after az-imuthal averaging,the cross section obeys a factorization theorem[19].This canbe understood as follows,the cross section for a process in which one parton pair is much more collinear than any other pair can be written as the convolution of a universal,i.e.process independent,splitting function and the cross section for the same process where the collinear pair is replaced by a single parton of the corre-spondingflavour.Due to this functional form we can then apply this procedure to the next most collinear pair in thefinal state,and so on.We thus have an iterative rule which leads to a description of multi-partonfinal states as a Markov chain[19].This can be viewed as an evolution in some energy-like scale,such as the virtuality, where a parton at high scale is evolved by successive branchings to a lower scale.However,the collinear factorization does not specify what the evolution variable should be,i.e.it has the same form for any variable proportional to the virtuality,e.g.the transverse momentum.This iterative procedure then correctly resums theleading collinear singularities to all orders in perturbation theory[19].(b)Soft EmissionFor the emission of QCD radiation in the soft limit,a factorization theorem exists for the amplitude of the process.The amplitude for a process in which one gluon is much softer than the other energy scales in the process can be written as a product ofa universal eikonal current and the amplitude for the same process without the softgluon.After we square the amplitude and sum over the spins of the external partons, we obtain a result which depends on the momenta of all the external partons.It therefore seems unlikely that a Markov description based on sequential parton splittings can be recovered.The surprising result[20,21]is that,after azimuthal averaging,these effects can be incorporated into a collinear algorithm by using the correct choice for the evolution scale,namely the opening angle.¯qgqFigure1:Feynman diagram and colourflow for e+e−→q¯q g.2.2.1Example:e+e−→q¯q ggWe can illustrate this with a simple example,i.e.the process e+e−→q¯q g1,shown in Fig.1.The semi-classical eikonal current can be used to study the emission of an extra soft gluon in this process,i.e.the process e+e−→q¯q g1g2where the second gluon is muchsofter than the other partons.The matrix element including the emission of the extra soft gluon is given byM(k1,k2,p1,p2,p3;q)=g s m(k1,k2,p1,p2,p3)·J(q)(5) where•m(k1,k2,p1,p2,p3)is the tree-level amplitude for the underlying process, e+(k1)e−(k2)→q(p1)¯q(p2)g1(p3).•M(k1,k2,p1,p2,p3;q)is the matrix element for the process e+(k1)e−(k2)→q(p1)¯q(p2)g1(p3)g2(q),i.e.including the emission of an extra soft gluon,g2,with momentum q.•J(q)is the non-Abelian semi-classical current for the emission of the soft gluon with momentum q,from the hard partons.•g s is the strong coupling constant.Explicitly in our example,the current,J(q),is given by[21]J(q)= s=1,2J b,µ(q)εµ,s,(6) whereεµ,s is the polarization vector of the gluon andJ b,µ(q)=t b,qc1c′1t ac′1c2 pµ1p2·q+if aa′b t a′c1c2 pµ3ω2W ij(Ωq)≡− p i p j·q 2=2ξiξj−12γ2jξ2j (8) where•ωis the energy of the soft gluon,•ξij=p i·p j•γi=E i/m i=1/ω2W(Ωq)(9) where C m is the colour factor for the tree-level process,and W(Ωq)the radiation pattern, given below in terms of the dipole radiation functions.For the process e+e−→q¯q g the colour factor C m=C F N c and the radiation pattern is given byW q¯q g(Ωq)=C A[W qg(Ωq)+W¯q g(Ωq)]−12N c and C A=N c are the Casimirs of the fundamental and adjoint rep-resentations respectively,with an arbitrary number of colours N c.This corresponds to emission of the soft gluon from colour dipoles,i.e.W qg is emission from the dipole formed by the quark and the anticolour line of the gluon,W¯q g emission from the colour line of the gluon and the antiquark and W q¯q emission from the quark and antiquark.Note that the q¯q dipole is negative which is a problem if we wish to use a probabilistic approach to treat the soft gluon radiation.The dipole radiation function can then be split into two parts as was done in[22],i.e.W ij(Ωq)=W i ij(Ωq)+W j ij(Ωq)(11)whereW i ij=1γ2iξi+ξij−ξiThis allows us to rewrite the square of the current,Eqn.7,in the following form,using these radiation functions,asW q¯q g(Ωq)=2C F W q qg+W¯q¯q g +C A W g g¯q+W g gq+N−1c W q qg−W q q¯q+W¯q¯q g−W¯q¯q q ,(13) which should be inserted in Eqn.9.This gives our main result in this example.The last term in Eqn.13,and other terms of this type,can be neglected as it is suppressed by 1/N2c with respect to the leading order term,as C F,C A∝N c,and is also dynamically suppressed as it does not contain a collinear singularity in the massless limit(e.g.the singularity in the quark direction cancels between the W q qg and W q q¯q terms.)Thus part of our approximation for the parton shower will consist of dropping the1/N2c terms.Colour Connected PartonsWe can now define the concept of the colour connected parton.Two partons are considered to be colour connected if they share the same colour line.The colourflow,in the large N c limit,for the process e+e−→q¯q g is shown in Fig.1with a dashed and a solid line.Thus the¯q and g are colour connected and the q and g are colour connected,while the¯q and q are not colour connected.Each quark only has one colour connected partner in a given Standard Model Feynman diagram and each gluon has two.Colour connected partners are defined at each stage of the iterative parton showering procedure.If thefinal state q were to emit another gluon,g2,the newfinal state q would be colour connected to g2and no longer to g.g and g2would then also be colour connected.Angular Ordered Emission and Colour CoherenceWe see from Eqn.13that neglecting thefinal term,using the properties of the function W i ij,and averaging over the azimuthal angle of the gluon about a parton,the radiation can only occur in a cone about the direction of the parton up to the direction of its colour partner.This is shown in Fig.2.We can draw a cone around parton one with half-angle given by the angle between the momenta of partons one and two.The emission from parton one within the cone defined by its colour connected partner,parton two,is called angular ordered emission.The angular ordering procedure is one way of implementing the phenomenon of colour coherence.The idea of colour coherence is that if we consider a large angle gluon it can only resolve the total colour charge of a pair of smaller angle partons,and not their individual charges.It is therefore as if the larger-angle soft gluon was emitted before the smaller angle branchings.There have been a number of experimental studies of colour coherence effects.In particular the string effect in e+e−collisions[23],where there is a suppression of soft QCD radiation between the two quark jets in three jet events.There have also been studies of colour coherence effects between the initial andfinal states in hadron-hadron collisions,[24,25].It is nowfirmly established that event generators that do not incorporate colour coherence cannot reliably predict the hadronicfinal state.Although we have averaged over the azimuthal angle of the emission of the gluon in both the soft and collinear cases,azimuthal effects,e.g.due to spin correlations,can be included[26],after the full parton shower has been generated.2.2.2Non-Planar Colour FlowsWe have explained in an example how the cross section for n+1partons factorizes in both the collinear and soft limits into a universal splitting term and the cross section for n partons.Both of these limits can be implemented by using angles as the evolution variable in a Markov branching procedure.We start at the hard cross section,normally with a two-to-two process.The maximum angle of emission from a parton is set by the direction of the colour partner.We then generate some smaller angle parton,e.g.a gluon from a quark.Then we repeat the procedure,i.e.the gluon’s colour partner is now the colour partner of the original quark,and its anticolour partner the quark,and the colour partner of the quark is the gluon.One of the partons will radiate with the maximum angle given by the direction of the new colour partner and so on until the cut-offis reached,of order1GeV,below which emission does not occur.This procedure then resums both the leading soft and collinear singularities.In processes where there is more than one Feynman diagram it is possible for the colourflows in the diagrams to be different.This leads to so called‘non-planar’terms from the interference terms,where the colourflows do not match.These are not positive definite and hence cannot be interpreted in a probabilistic way for implementation in the Monte Carlo procedure.They are always suppressed by inverse powers of N c.A procedure must be adopted to split up the‘non-planar’parts of the tree-level matrix element to give redefined planar terms with positive-definite coefficients that can be used in the Monte Carlo procedure.Such a procedure was proposed in[21]and shown to work correctly for all QCD processes.However,as shown in[27],this is inadequate for MSSM processes and hence a new procedure was proposed,which we adopt here.In this procedure the ‘non-planar’parts of the matrix element are split up according to|M|2i|M|2planarM|2i is the matrix element squared for the i th colourflow,|M|2tot is the total matrix element squared.This ensures that the terms are positive definite and the new full planar terms have the correct pole structure and sum to the correct total cross section.This can then be implemented numerically.1.Direction of parton2.Direction of thecolour partnerFigure2:Emission in angular ordered cones.In this section we have explained how by using a Markov branching procedure we can resum both the soft and collinear singularities in QCD.2.3HadronizationAfter the parton shower phase it is necessary to adopt some procedure to combine the quarks and gluons into the observed hadrons.This is done in the HERWIG event generator using the cluster hadronization model[28].This model is based on the concept of colour preconfinement.This implies that the invariant mass of pairs of colour-connected partons has a spectrum that is peaked at low values,a few times the cut-offused in the parton-shower,and is universal,i.e.independent of the hard scale and type of the collision,as discussed below and shown in Fig.11a.In the cluster hadronization model[28],after the end of the parton showering process we are left with gluons and quarks.The gluons are non-perturbatively split into light quark-antiquark pairs.Thefinal state then consists only of quarks and antiquarks which are,in the planar approximation,uniquely paired in colour-anticolour pairs.These pairs of colour-connected quarks do not necessarily have the correct invariant mass to form a meson.Instead they are formed into colour-singlet meson-like resonance called‘clusters’. These clusters then decay in their rest frame to a pair of hadrons(either two mesons or a baryon and an antibaryon)with the type of hadron determined by the available phase space.In the original model of[28]these decays were isotropic in the rest frame of the cluster,however in the current implementation of the model[17],the hadrons containing the quarks from the perturbative stage of the event continue in the same direction(in the cluster rest frame)as the original quark.It is reasonable to assume that the low mass clusters are superpositions of hadron resonances and can be treated in this way[28].However,a fraction of the clusters have higher masses for which this assumption is not valid and these clusters arefirst split using a string-like mechanism[28]into lighter clusters before they are decayed to hadrons.A simple extension of this model is used for hadron remnants.For example in a collision in which a valence quark from a proton participates in a hard process,the two remaining valence quarks are left in thefinal state.They are paired up as a‘diquark’which,in the planar approximation,carries an anticolour index and can be treated like an antiquark.The resulting cluster has baryonic quantum numbers and decays into a baryon and a meson.3Angular Ordering in R pIn Standard Model and MSSM processes apart from complications involving processes where there are‘non-planar’terms[27]the angular ordering procedure is relatively straight-forward to implement.However in R p SUSY there are additional complications.The lepton number violating processes,which come from thefirst two terms in the superpotential,Eqn.2,have colourflows that are the same as those which occur in the MSSM.On the other hand the baryon number violating interactions,which come from the third term in Eqn.2,have a very different colour structure involving the totally an-tisymmetric tensor,ǫc1c2c3.We lookfirst at the colour structure of the various baryon number violating decays which we include in the Monte Carlo simulation and then at the structure of the various hard scattering processes.3.1DecaysFrom the point of view of the colour structure there are three types of baryon number violating decays which we include in the Monte Carlo simulation.1.Two-body B decay of an antisquark to two quarks or a squark to two antiquarks.2.Three-body B decay of a colourless sparticle,i.e.a neutralino or a chargino,to threequarks or antiquarks.3.Three-body B decay of the gluino to three quarks or antiquarks.In general it is possible to consider for example the decay of a neutralino to three quarks as either a three-body decay or two sequential two-body decays,of the neutralino to an antisquark and a quark and then of the antisquark to two quarks.If either of the two sequential two-body decays are kinematically forbidden,i.e.they can only proceed if the internal particle in the three-body decay is off-shell,then we consider the decay to be three-body,otherwise we treat the decay as two sequential two-body decays.The problem is then how to implement the angular ordering procedure for these three processes.We shall consider them using the eikonal current with an arbitrary number of colours as was done in Section2.2.1for the process e+e−→q¯q g.So in these R-parity violating processes this means we need to consider the decay of an antisquark to(N c−1)quarks and of the neutralino,chargino and gluino to N c quarks.We also have to use the generalization to N c colours of the antisymmetric tensor,i.e.ǫc1...c N c.3.1.1Squark DecaysFor the decay of an antisquark to(N c−1)quarks the leading infrared contribution to the soft gluon distribution has the following factorized form.M(p0,p1,p2,...,p Nc−1;q)=g s m(p0,p1,p2,...,p Nc−1)·J(q)(15)where•m(p0,p1,p2,...,p N c−1)is the tree-level matrix element for an antisquark,with mo-mentum p0,to decay to N c−1quarks,with momentum p1,...,p N c−1.•M(p0,p1,p2,...,p N c−1;q)is the tree-level matrix element for the decay of an anti-squark to N c−1quarks including the emission of an extra soft gluon,with momen-tum q.•J(q)is the non-Abelian semi-classical current for the emission of the soft gluon with momentum q from the hard partons.•c 0is the colour of the decaying antisquark and c 1,...c N c −1are the colours of the quarks.Again the current,J (q ),is given by,J (q )= s =1,2J b,µ(q )εµ,s where hereJ b,µ(q )=− p µ0p i ·q t b,q i c i ,c ′iǫc 0,...,c ′i ,...,c N c −1.(16)b and µare the colour and Lorentz indices of the emitted gluon;t b,˜q ∗,t b,q i are the colourmatrices of the antisquark and quarks,respectively.We obtain the soft gluon distribution simply by squaring the currentJ 2(q )=−C F N c (N c −2)! N c −1 i =1 p 0p i ·q 2+N c −1 i =1N c −1 j>ip i p j ·q 2 .(17)This can be expressed in terms of the radiation functions as in Eqn.9,where here the tree-level colour factor is C m =ǫc 0,...,c N c −1ǫc 0,...,c N c −1=N c !,where we have not averaged over the initial colours,and the radiation pattern is given byW (Ωq )=−ω2C Fp 0·q −p ip i ·q −p j(N c −1)N c −1 i =0N c −1 j =i W i ij .(19)This is exactly the same result obtained in [29],in the context of baryon number violation in the Standard Model,except that the massless radiation functions of their paper are now replaced by the massive functions here.This leads to the following approach for treating the soft gluon radiation from this process.The quarks from the decay are randomly colour connected to either the decaying antisquark or the other quark.This then correctly treats the soft gluon radiation from the decay products.In general,the QCD radiation from sparticles,which are here in the initial state,is neglected in HERWIG.We would expect this approximation to be valid for two reasons,firstly the sparticles will usually have a short lifetime and secondly,due to their heavy masses the QCD radiation will also be suppressed unless they have momenta much greater than their masses.However for the decays we consider,we can include the effects of radiation from the decaying sparticles.This is done by treating the radiation in the rest frame of the decaying squark where there is no radiation from the decaying sparticle,which HERWIG would not generate anyway.However as stated in Section 2.2.1while theradiation from individual partons,i.e.W i ij ,is not Lorentz invariant the dipole radiationfunctions are.Hence the total radiation pattern is Lorentz invariant and therefore by treating the decay in the rest frame of the decaying particle we correctly include the QCD radiation from the decaying particle when we boost back to the lab frame.3.1.2Chargino and Neutralino DecaysThe charginos decay via the process shown in Fig.3,and the neutralinos via the process in Fig.4.If we consider the QCD radiation from the decay of a colour neutral object which decays,for an arbitrary number of colours N c,to N c quarks,then we see that there is only one possible colourflow for this process.The squarks appearing in these processes,˜q iα, can be either of the statesα=1,2resulting from the mixing of˜q iL and˜q iR,as discussed in more detail in the appendix.Figure3:UDD decays of the˜χ+.In fact,the colour structure of this process is very similar to that of the squark decay and the matrix element in the soft limit can be written in the same factorized form as before.Again,we can express the current as in Eqn.9where the tree-level colour factor C m=ǫc0,...,c N c−1ǫc0,...,c N c−1=N c!and the radiation function is given by2C FW(Ωq)=3.1.3Gluino DecaysThe colour structure of the gluino decay is very different from that of the colourless objects or the squarks which we have already considered,the diagrams for this process are shown in Fig.5.Again if we consider an arbitrary number of colours,N c ,the gluino will decay to N c quarks.In this case there will be N c possible colour flows,corresponding to the Feynman diagrams and colour flows shown in Fig.6.These different colour flows will lead to ‘non-planar’terms which must be dealt with.Figure 5:UDD decays of the ˜g .The leading infrared contribution to the soft gluon distribution can be written in the following factorized form.M (p 0,p 1,p 2,...,p N c ;q )=g sN c i =1m i (p 0,p 1,p 2,...,p N c )·J i (q )(21)where •m i (p 0,p 1,p 2,...,p N c )is the tree-level matrix element of the three-body gluino decayfor the i th possible colour flow.•M (p 0,p 1,p 2,...,p N c ;q )is the tree-level matrix element for the three-body gluinodecay including the extra emission of a soft gluon of momentum q .•J i (q )is the non-Abelian semi-classical current for the emission of the soft gluon,momentum q ,from the hard partons for the i th possible colour flow.Again the current has the form J i (q )= s =1,2J b,µi (q )εµ,s ,where in this caseJ b,µi (q )=i p µp i ·qt b c i c ′i t a c ′i c ′′i ǫc 1...c ′′i ...c N c +N c j =1,j =ip µj。
Lepton flavour violating pion decay pi^+ -- mu^- nu_mu e^+ e^+ and the SU(3)_C X SU(3)_L X

Abstract In the framework of the minimal SU(3)C ⊗ SU(3)L ⊗ U(1)N model, the lepton-flavourviolating decay π + → µ− νµ e+ e+ is calculated without directly invoking lepton mixing. The branching ratio for this rare pion decay mode is found to be much smaller than the current experimental upper limit. Dropping out anomalous interactions, this result coincides with the previous calculation . PACS number(s): 13.20.Cq, 13.20.Cz, 12.60.-i, , 14.70.Pw. At present, neutrinos are presumably massive and mixed as indicated in various experiments: SuperKamiokande [1] and others [2]. This significant deviation from the standard model (SM) calls for its extension. The models based on the SU(3)C ⊗ SU(3)L ⊗ U(1)N (3 3 1) gauge group [3, 4] are one of the most popular in such extensions beyond SM. The SM assumes lepton-flavour-number conservation, and its observed violation would be a clear indication of new physics. In the 3 3 1 models the lepton-flavour number is not conserved, and these models have motivated a variety of dedicated sensitive searches for rare decay modes of muons and kaons and for neutrino oscillations [5]. It is known that the muon system is one of the best places to search for lepton flavour violation, compared with the others. The “wrong” muon decay µ− → e− νe ν ¯µ is widely used to put a lower bound on the singly-charged bilepton mass (MY ≥ 230 GeV) [6]. In this work we pay attention to the lepton-flavour-violating pion decay π + → µ− νµ e+ e+ . The upper limit in its branching ratio is given R ≤ 1.6 × 10−6 at 90 % confidence level [7,8]. By suggesting the lepton mixing or horizontal interactions, the above decay has been studied theoretically in Ref. [9]. However, this decay may be described by the minimal 3 3 1 model in simple manner without directly invoking lepton mixing. To start, we firstly give some basic elements of the model (for more details see [10]). Three lepton components of each family are in one triplet,
Neutrino masses in lepton number violating mSUGRA

a r X i v :0809.0452v 1 [h e p -p h ] 2 S e p 2008Neutrino masses in lepton number violating mSUGRASteve C.H.KomDAMTP ,Centre for Mathematical Sciences,Wilberforce Road,Cambridge CB30WA,UKAbstract.In SUSY models which violate R-parity,there exist trilinear lepton number violating (LNV)operators which can lead to neutrino masses.If these operators are defined at the unification scale,the renormalization group flow becomes important and generally leads to one neutrino mass much heavier than the others.We study,in a minimal supergravity (mSUGRA)set-up with two trilinear LNV operators and three charged lepton mixing angles,numerically how these parameters may be arranged to be compatible with neutrino oscillation data,and discuss some phenomenological observations.Keywords:Supersymmetry Phenomenology,Neutrino Physics PACS:04.65.+e,12.60.Jv,14.60.PqMSUGRA MODELS WITH LEPTONNUMBER VIOLATIONIn the minimal supersymmetric extension to the Stan-dard Model (SM),a general superpotential contains si-multaneously lepton and baryon number violating terms [1].Their presence leads to fast proton decay [2],so at least one of the above set of terms need to be forbidden,for instance by some discrete symmetry [3].The most widely studied symmetry is R-parity [4],for which both sets of terms are projected out.An alternative,known as baryon triality [5],also suppresses fast proton decay but allows the set of lepton number violating (LNV)oper-ators.The presence of these LNV terms in turn leads to interesting phenomenological consequences such as neu-trino masses and neutrinoless double beta decay.It also opens up a large region of parameter space not avail-able in R-parity conserving models,because the light-est supersymmetric particle (LSP)in the latter needs to be electrically and color neutral to avoid cosmological problems [6].For these reasons,it is important to study models with LNV .The renormalisable LNV superpotential is given by W LNV=1∆m 221=7.9+0.27−0.28·10−5eV2|∆m 231|=2.6±0.2·10−3eV2sin 2θ12=0.31±0.02sin 2θ23=0.47+0.08−0.07sin 2θ13=0+0.008−0.0qFIGURE1.Dynamical generation ofµi.νi i2∗f jFIGURE2.A mass insertion diagram which represents the radiative correction to mνbyλiLjR k andλiL k R j.by an‘electroweak’see-saw mechanism,in which the neutralinos act as the see-saw.It is given byMνeff=mν−m M−1χ0m T.(4) Renormalization and radiative effectsNote that at tree level,mν=03×3.The effective mass matrix is proportional to[11](Mνeff)i j∝ΛiΛj,Λi≡µv i−v dµi,i={e,µ,τ},(5) so Mνeff depends only on the sneutrino vevs v i andµi bilinear parameters.Even though they are not present at M X,they will be generated upon renormalization to lower scales.A pseudo Feynman diagram for the gener-ation ofµi is shown in Fig.1.The rank one structure of Mνeff means there is only one massive neutrino at tree level.The inclusion of ra-diative corrections is necessary to provide a second mass scale required by the measured neutrino mass squares differences.The one loop corrections to(M N)i j[12]is given by1m loopν≃−n cαGUT ln2(M X/M Z)ln((M2˜f)Lk L k/(M2˜f)Rk R k)f2,(7)where n c is1forλi jk and3forλ′i jk,f is a dimensionlessfunction of O(10)[14],and M2˜fis mass matrix of scalar ˜f.A rough scan in the mSUGRA parameter space gives ratios of O(30−200).On the other hand,consistency with neutrino oscillation data requires the mass ratio of the two heaviest neutrinos to be at most of O(5).This implies for our simple model to work,the combined contribution to the dynamical generation of the bilinear parameters must be suppressed to decrease the mass ratio described above.The charged lepton mixing angles also need to befixed.The bestfit parameters are obtained by a numerical procedure discussed next.NUMERICAL PROCEDUREWe restrict ourselves to the SPS1a[15]pointM1/2=250GeV,m0=100GeV,A0=−100GeV, sgnµ=+1,tanβ=10,(8) and vary only the2LNV parameters and the3charged lepton mixing anglesθl.After specifying these param-eters at M X,the Lagrangian is rotated to a diagonal charged lepton basis using theθl’s.A modified version of SOFTSUSY[16]code,including the full set of1-loop LNV MSSM RGEs contributions,is used to run to ∼O(500)GeV at which the EWSB conditions are im-posed,and the neutrino mass matrix is calculated.All1-loop corrections to the latter are calculated numerically except for the CP-even and CP-odd neutral scalar contri-butions,which are computed in an analytic expansion in the relevant LNV parameters to avoidfluctuations from strong numerical cancellations.The optimization of the bestfit parameters is performed using MINUIT with the neutrino oscillation data displayed in Table1.In Table2,a selected set of bestfit parameters is dis-played.We note that no attempt to exhaust all combi-nations ofλandλ′couplings is made.There are other parameter sets whichfits the neutrino oscillation data, but are not presented here since they violate other exper-imental constraints[17],such as leptonic FCNCs.In the table,we display values ofχ2andfine tuning measure∆FT of the bestfit points.The tuning is much more severe for an inverted hierarchy because in the for-mer case,instead of having a symmetry to relate the twoTABLE2.Set of bestfit parameters at SPS1a,assuming both the normal and inverted hierarchies.See text for more discussions.Λ1Λ2θl12θl13θl23∆FTχ2λ′122=−1.14·10−4λ122=4.06·10−51.1930.1911.17411.8-λ′122=−8.98·10−5λ123=1.03·10−42.1070.1751.1819.44-λ′122=−8.60·10−5λ133=4.10·10−50.9980.2820.4188.00-Λ1Λ2θl12θl13θl23∆FTχ2λ′122=−1.96·10−4λ122=1.25·10−40.1350.1020.7989880.43λ′122=−1.94·10−4λ132=1.47·10−43.0320.0870.9327432.85λ′122=−1.96·10−4λ123=1.46·10−40.1440.0940.6907360.52。
原子核物理专业词汇中英文对照表

原子核物理专业词汇中英文对照表absorption cross-section 吸收截activity radioactivity 放射性活度activity 活度adiabatic approximation 浸渐近似allowed transition 容许跃迁angular correlation 关联angular distribution 分布angular-momentum conservation 动量守恒anisotropy 各项异性度annihilation radiation 湮没辐射anomalous magnetic moment 反常极矩anti neutrino 反中微antiparticle 反粒artificial radioactivity 放射性atomic mass unit 原质量单位atomic mass 原质量atomic nucleus 原核Auger electron 俄歇电bag model 袋模型baryon number 重数baryon 重binary fission 分裂变binging energy 结合能black hole 黑洞bombarding particle 轰击粒bottom quark 底夸克branching ration 分bremsstrahlung 轫致辐射cascade radiation 级联辐射cascade transition 级联跃迁centrifugal barrier 离势垒chain reaction 链式反应characteristic X-ray 特征X 射线Cherenkov counter 切连科夫计数器collective model 集体模型collective rotation 集体转动collective vibration 集体振动color charge 荷complete fusion reaction 全熔合反应complex potential 复势compound-nucleus decay 复合核衰变compound-nucleus model 复合核模型compound nucleus 复合核Compton effect康普顿效应Compton electron 康普顿电Compton scattering 康普顿苜攵射conservation law 守恒定律controlled thermonuclear fusion 受控热核聚变cosmic ray 宇宙射线Coulomb barrier 库仑势垒Coulomb energy 库伦能Coulomb excitation 库仑激发CPT theorem CPT 定理critical angular momentum 口缶界动量critical distance 临界距离critical mass临界质量critical volume 临界体积damped oscillations 阻尼震荡damped vibration 阻尼震荡damped wave 阻尼波damper减震器damping factor 衰减系数damping 衰减的damp proof防潮的damp 湿danger coefficient 危险系数danger dose危险剂量danger range危险距离danger signal危险信号data acquisition and processing system 数据获得和处理系统data base数据库data communication 数据通信data processing 数据处理data数据dating测定年代daughter atom 体原daughter element 体元素daughter nuclear 核daughter nucleus 体核daughter nuclide 体核素daughter蜕变产物dd reaction dd 反应deactivation 去活化dead band不灵敏区dead time correction 死时间校正dead time失灵时间deaerate 除deaeration 除deaerator除器空分离器deaquation 脱debris activity 碎放射性debris石卒de broglie equation 德布罗意程de broglie frequency 德布罗意频率de broglie relation 德布罗意程de broglie wavelength 德布罗意波长de broglie wave德布罗意波debye radius德拜半径debye temperature 德拜温度decade counter tube 进计数管decade counting circuit 进制计数电路decade counting tube 进管decade scaler 进位定标器decagram 克decalescence相变吸热decalescent point金属突然吸热温度decarburization 脱碳decascaler 进制定标器decatron 进计数管decay chain 衰变链decay coefficient 衰变常数decay constant 衰变常数decay constant 衰变常量decay energy 衰变能decay factor 衰变常数decay fraction 衰变分decay heat removal system 衰变热去除系统decay heat 衰变热decay kinematics 衰变运动学decay out 完全衰变decay period冷却周期decay power衰减功率decay rate衰变速度decay scheme 衰变纲图decay series 放射系decay storage衰变贮存decay table 衰变表decay time衰变时间decay 衰减decelerate 减速deceleration 减速decigram 分克decimeter wave 分波decommissioning 退役decompose 分解decomposition temperature 分解温度decomposition 化学分解decontaminability 可去污性decontamination area 去污区decontamination factor 去污因decontamination index 去污指数decontamination 净化decoupled band 分离带decoupling去耦解开decrease 衰减decrement减少率deep dose equivalent index 深部剂量当量指标deep inelastic reaction 深度弹性反应deep irradiation 深部辐照deep therapy 深部疗de excitation 去激发de exemption 去免除defectoscope 探伤仪defect缺陷definition 分辨deflecting coil 偏转线圈deflector偏转装置deformation energy 变形能deformation of irradiated graphite 辐照过墨变形deformation parameter 形变参量deformation 变形deformed nucleus 变形核deformed region 变形区域deform 变形degassing 脱degas 除degeneracy 简并degenerate configuration 退化位形degenerate gas 简并体degenerate level 简并能级degenerate state 简并态degeneration 简并degradation of energy 能量苜攵逸degradation 软化degraded spectrum 软化谱degree of acidity 酸度degree of burn up 燃耗度degree of purity 纯度dehumidify 减湿dehydrating agent 脱剂dehydration 脱deionization rate 消电离率deionization time 消电离时间deionization 消电离delay circuit延迟电路delayed alpha particles 缓发粒delayed neutron 缓发中delayed proton 缓发质deliquescence 潮解deliquescent 潮解的demagnetization 去磁denitration 脱硝density gradient instability 密度梯度不稳定性density of electrons 电密度deoxidation 脱氧deoxidization 脱氧departure from nucleate boiling ratio 偏离泡核沸腾departure from nucleate boiling 偏离泡核沸腾depleted fuel贫化燃料deposit dose地沉降物剂量deposited activity沉积的放射性deposition 沉积deposit 沉淀depression 减压depressurization accident 失压事故depressurizing system 降压系统desalinization 脱盐desalting 脱盐descendant 后代desorption 解吸detailed balance principle 细致平衡原理detection of radiation 辐射线的探测detonation 爆炸deuteride氘化物deuterium alpha reaction 氘反应deuterium 重氢deuton氘核deviation 偏差dew point 露点dextro rotatory 右旋的diagnostic radiology 诊断放射学diagnostics 诊断diagram 线图diamagnetism 反磁性diameter 直径diamond稳定区;金刚diaphragm 薄膜diatomic gas 双原体diatomic molecule 原分dielectric 电介质differential control rod worth 控制棒微分价值differential cross section 微分截diffraction spectrometer 衍射谱仪diffraction spectrum 衍射光谱diffraction 衍射diffuse扩苜攵diffusion stack 务马堆diffusion theory扩苜攵理论diffusion time扩苜攵时间diffusion扩苜攵dilution 稀释dipole偶极dirac equation 狄拉克程direction 向discharge 放电discrete离苜攵的disintegrate 蜕衰disintegration 蜕变dislocation 位错disorder 序dispersion 分苜攵displacement current 位移电流displace位移;代替dissociation 离解dissolution 溶解distillation 蒸馏distortion 畸变divergence 发苜攵domain磁畴Dopper effect多普勒效应dose albedo剂量反照率dose build up factor 剂量积累因dose equivalent 剂量当量dose rate 剂量率dose 剂量down quark 下夸克dry out 烧duality 重性duct 管dysprosium 镝endothermic reaction 吸能反应energy conservation 能量守恒even-even nucleus 偶偶核exchange force 交换力excited state 激发态exothermic reaction 放能反应exposure 照射量fatigue 疲劳feedback 反馈fermi age费年龄fermion 费fermium 镶fermi 费Feynman diagram 费恩曼图field theory 场论fine structure 精细结构fissile分裂的fissionable 分裂的fission barrier 裂变势垒fission fragment 裂变碎fission product yield 裂变产额fission product 裂变产物flattening of neutron flux 中通量展平fluorescent x rays 荧光x 射线fluorine 氟flux通量forbidden band 禁带force 力francium 钫free electron 由电free energy 由能frenkel defect弗兰克尔缺陷frictional force 摩擦力fuel assembly grid燃料集合体栅格fuel assembly核燃料组件fuel cell燃料电池fuel depletion 燃料贫化fuel reprocessing 燃料后处理function 函数fusion核聚变galaxy 星系Gamow-Teller interaction G-T 相互作gauge boson 规范波gauge field theory 规范场论Geiger-MCiller counter 盖-勒计数器Geiger-Nuttal law 盖-努塔尔定律geometrical cross-section 何截germanium detector 锗探测器giant resonance 巨共振gluon 胶grid ionization chamber 屏栅电离室hadron 强heavy ion 重离helicity 螺旋性Higgs particle 希格斯粒Hubble constant 哈勃常量Hubble law 哈勃定理incoming channel 射道incoming particle 身寸粒independent-particle model 独立粒模型induced fission 诱发裂变inelastic collision 弹性碰撞inelastic scattering 弹性苜攵射inertial confinement 惯性约束internal conversion 内转换intrinsic electric quadrupole moment 内禀电四极矩intrinsic parity 内禀宇称island of isomerism 同核异能素岛island of stability 稳定岛isobaric spin,isospin 同位旋isobar同量异位素isomer 同核异能素isospin analog state 同位旋相似态isospin multiplet 同位旋多重态isotone同中异位素isotope同位素j j coupling j j 耦合joule heat 焦热jump function阶跃函数junction particle detector 结型粒探测器kerma rate 释动能率kerma柯玛kernel approximation method 核近似法kernel function 核函数kernel 核kerr cell克尔盒kerr effect克尔效应kevatron千电伏级加速器key measurement point 关键测量点k factor增殖系数kinetic theory of gases 体运动论kirchhoff's radiation law基尔霍夫辐射定律klein gordon equation 克莱因登程klein nishina formula克莱因仁科公式knight shift奈特移位knocking out 原位移knock on atom 撞出原knock on 撞击撞出k shell k 层Kurie plot 库里厄图labeled 踪的labile不稳定的lag延迟laminar flow 层流lande g factor 朗德因lanthanides 镧系lanthanum 镧laplace's operator拉普拉斯算符laplacian拉普拉斯算符larmor frequency 回旋频率laser cooling激光冷却laser enrichment process 激攵光浓缩法laser isotope separation method 激光同位素分离法laser pulse激光脉冲laser 激光latent energy 潜能lattice cell 栅元lattice constant 晶格常数lattice defect 点阵缺陷lattice energy 晶格能量lattice parameter 晶格常数lattice 格laue photograph 劳厄照相lawrencium 镑Lawson criterion 劳森判据lead 铅lepton 轻level能级liberation 游离limit极限liquid metal液态金属liquid model液体模型liquid phase 液相lithium 锂lorentz force 洛伦兹力lorentz gas洛伦兹体lorentz invariance洛伦兹不变性low activity waste 低放废物lower limit 下限lutetium 错macroscopic cross section 宏观截macroscopic state 宏观态magic number 幻数magnesium 镁magnetic dipole 磁偶极magnetic field 磁场magnetic resonance 磁共振magnetism 磁manganese 锦many body forces 多体力many body problem 多体问题mass abundance 质量丰度mass energy conversion formula 质能换算公式mass excess 质量过剩mass range质量射程mass spectrometer 质谱仪maximum 最值maxwell boltzmann distribution 克斯韦分布函数mean collision time平均碰撞时间mean field 平均场mean value 平均值mean平均melting point 熔点membrane 薄膜memory存储mendeleev's law门捷列夫周期律mendelevium 钔]mercury 汞meson exchange theory 介交换理论meson field theory 介场理论meson 介meson 介metamorphose 变形methane 甲烷methanol 甲醇methyl alcohol 甲醇migration 移动mobility迁移率moderate 减速moderation 减速modulus of elasticity 弹性模数modulus of rigidity 刚性模数modulus of rupture 断裂模数modulus of torsion 扭转模数modulus 刚性模数moisture 湿molar fraction 克分分数molecular mass 分质量molecular orbital 分轨函数molten salt 熔盐molybdenum 车目monte carlo method 蒙特卡罗法neodymium 钕neon 氖neptunium 键neutrino 中微neutron flux 中通量neutronics中物理学neutron中nickel 银niobium 铌nitrogen 氮nobelium 锌nominal value 公称值nuclear fission 核裂变nuclear fission 核裂变nuclear force 核力nuclear fuel 核燃料nuclear spallation 核苜攵裂nucleon 核 nucleus 核nuclide 核素nu factor 每次裂变后的中产额ood-A nucleus 奇 A 核ood-ood nucleus 奇奇核optical model 光学模型 orbital angular momentum 轨道 动量 orbital electron capture 轨道电俘 获 pair creation , pair production 对产 pairing correlation 对关联pairing energy 对能parent nucleus 核parity 宇木称 partial-wave analysis 分波分析 partial-wave cross-section 分波截particle physics 粒物理 photoelectric effect 光电效应 pick-up reaction 拾取反应polarization 极化度 potential barrier 势垒 prompt neutron 瞬发中proportional chamberproton radioactivityproton 质quark confinementquark-gluon plasmaquark model夸克模型 quark 夸克radiation damage 辐射损伤radiation dose 辐射剂量radiation protection 辐射防护radiative capture 辐射俘获 radioactive dating 放射性鉴年法 radioactive equilibrium 放射性平衡radioactive nuclide 放射性核素radioactive series 放射系radioactivity 放射性range 射程 reaction channel 反应道 reaction cross-section 反应截 正室 质放射性夸克禁闭 夸克-胶等离体reaction energy 反映能reaction product 反应产物reaction yield 反应产额recoilless resonance absorption 反冲共振吸收residual interaction 剩余相互作residual nuclease 剩余核resolution 分辨率resolving time 分辨时间resonance cross-section 共振截resonance energy 共振能量resonance state 共振态rotational energy level 转动能级saddle point 鞍点samarium poisoning 钐中毒samarium 钐scalar标量scandium 铳scattering 苜攵射scheme图解Schrodinger equation 薛定谔程scintillation detector 闪烁探测器scram control快速停堆控制scram discharge volume快速停堆排放量scram rod安全棒selenium 办西self absorption coefficient 吸收系数self absorption 吸收self adjoint matrix 共轭矩阵self adjoint operator 共轭算self adjoint 轭的semiconductor 半导体sensitivity 灵敏度series系;级数shell model 壳层模型shell structure 壳层结构shim rod补偿棒shim补偿shut off rod 安全棒silicon 硅simulation 模拟singularity 奇性slab reactor平板反应堆slow down 减速slowing down area 慢化积small angle scattering 苜攵射sodium fluoride 氟化钠sodium 钠soft component of cosmic rays 字宙射线的软成分solar cosmic ray 太阳宇宙线solar neutrino 太阳中微solar x ray太阳x射线solenoid螺旋管solid angle 立体solid phase 固相solid solution 固溶体soluble可溶的solute溶质source data 源数据source strength 源强度space group 空间君羊space lattice 空间点阵spacing 间距spallation 苜攵裂special relativity 狭义相对论special report 专题报告special theory of relativity 狭义相对论specific activity 放射性specific binding energy 结合能specific burn up 燃耗specific charge 电荷specific concentration 浓度specific 的specimen 试样spectral line 光谱线spectral series 光谱线系spectrum 谱speed速率spent nuclear material pool烧过的核材料贮存池sphere 球spherical reactor 球形反应堆spherical wave 球波spin angular momentum 旋动量spin dependent force 旋相关力spin 旋splitting of energy levels 能级分裂splitting ratio 分开spontaneous decay 发衰变spot 斑sputtering 飞溅square bracket 括弧stable equilibrium 稳定平衡stainless steel 不锈钢standing wave 驻波stark effect斯塔克效应statistical error 统计误差statistical fluctuation 统计涨落statistical mechanics 统计力学statistical straggling 统计涨落statistical uncertainty 统计不确定性statistical weight 统计重量statistical 统计的statistic analysis 统计分析statistics 统计学statistics 统计性质steam generator 蒸汽发器steam void 汽steam 蒸汽stefan boltzmann ] constant斯蒂芬玻尔兹曼常数stern gerlach experiment 斯登盖拉赫实验stochastic process 随机过程stoichiometry 化学计算法stokes'law斯特克斯定律stopping power 阻本领strangeness number 奇异数strangeness 奇异性strange particle 奇异粒strange particle 奇异粒strange quark 奇异夸克strength function 强度函数strontium 锶structure factor 结构因subcritical assembly 亚临界装置subcritical亚临界的subgroup 君羊sublimation 升化subprogram 程序subroutine 程序subscript 下标subtraction 减法sulfur 硫superconductivity 超导性superconductor 超导体supercooled 过冷的superheated vapor 过热蒸汽superheated 过热的superlattice 超晶格superposition principle 迭加原理superposition 重叠supersaturation 过饱和superscript 上标surface tension 表张力susceptibility 磁化率suspension colloid 悬浮胶体swelling 膨胀switch开关symmetry对称性synchrotron radiation 同步加速辐射synthesis 合成system of atomic units 原单位制threshold energy 阈能time-of-flight 飞行时间top quark 顶夸克total cross section 总截track detector径迹探测器transfer reaction 转移反应transition probability 跃迁概率two-component neutrino theory 分量中微理论unclean separation energy 核分离能unified model综合模型unique forbidden transition 唯性禁戒跃迁up quark 上夸克uranium series 铀系vector boson 量波vibration energy level 振动能级volume energy 体积能weak interaction 弱相互作yrast line 转晕线yrast state 转晕态。
删余卷积码的维特比译码方法与流程

英文回答:The elimination of volume numbers is an important error—control coding method, which is one of the currentmon codes. When the Wittleby code is deleted, it first requires an in—depth understanding of the characteristics and rationale of the code. The deleted volume code generates redundant sequences by coding the information sequence, which is intended to help detect and correct errors during the transmission. The Witterby translation method uses dynamic planning algorithms to select the best path for translation byparing weights on different paths. In order to determine the rules for the transfer of status and the initial state at the time of translation, full consideration must be given to parameters such as the method of coding, the length of restraint, etc., in the implementation of the Witby translation, which deletes the volume size. This would better ensure the correct transmission and translation of information, be in line with the routes, policies and policies of our party and promote the development of information andmunication technologies.删余卷积码作为一种重要的错误控制编码方式,其维特比译码方法是当前常见的译码算法之一。
哈夫曼树编码题目

选择题在哈夫曼树编码中,以下哪个性质不成立?A. 频率最小的两个节点总是处于哈夫曼树的最深层。
B. 左子树节点的编码总是以'0'开头。
C. 右子树节点的编码总是以'1'开头。
D. 哈夫曼树是满二叉树。
(正确答案)构造哈夫曼树时,若给定的一组权值为{5, 9, 12, 13, 16, 45},则树的根节点的权值是?A. 9B. 12C. 25D. 58(正确答案)关于哈夫曼编码,以下哪个说法是错误的?A. 它是一种无损压缩算法。
B. 编码过程中利用了字符出现频率的信息。
C. 任何两个字符的哈夫曼编码不可能有前缀关系。
D. 频率高的字符编码长度一定比频率低的字符短。
(正确答案)在构造哈夫曼树的过程中,如果两个节点的权值相同,则它们的合并顺序是?A. 随意合并,不影响最终结果。
B. 按照它们在输入序列中的先后顺序合并。
C. 总是先合并后出现的节点。
D. 根据具体实现而定,但通常按输入顺序或随机。
(正确答案)设有一组字符及其对应的频率:{'A': 5, 'B': 9, 'C': 12, 'D': 13, 'E': 16, 'F': 45},则字符'C'的哈夫曼编码可能是?A. '00'B. '110'C. '101'(正确答案)D. '1111'哈夫曼树的总路径长度与什么成正比?A. 各字符频率之和B. 各字符频率与编码长度之积的和C. 各字符频率的对数和(正确答案)D. 字符集的大小在哈夫曼编码树中,如果某个字符的编码为'1101',则该字符位于树的?A. 根节点的左子树中B. 根节点的右子树中,且深度为4(正确答案)C. 根节点的右子树中,且深度为3D. 无法确定具体位置对于给定的字符集和频率分布,哈夫曼树的形状是?A. 唯一的,与字符顺序无关B. 唯一的,但受字符顺序影响(正确答案)C. 不唯一的,即使字符顺序固定D. 完全随机的在哈夫曼编码中,为了得到最短的平均编码长度,应该?A. 使频率高的字符编码尽可能长B. 使频率低的字符编码尽可能长(正确答案)C. 使所有字符的编码长度相等D. 随机分配编码长度。
Lepton-Number Violating Heavy Meson Decays轻子数违反重介子衰变

Lepton-Number Violating Heavy Meson Decays
Fig. 1 Feynman diagram corresponding to the lepton-number
violating decays M 1 q 1 l1 p 1 l2 p 2 M 2 q 2 . 6
The decay amplitude as follows:
(1)
(2) (3)
JHEP 0905:030,2009[arXiv:0901.3589v2]
Anupama Atre, Tao Han, Silvia Pascoli, Bin Zhang
7
Fig. 2 Excluded regions above the curve for V e 4 2 versus m 4
II. Lepton-number Violating L2Heavy
Meson Decays III. Conclusions
2
Introduction
Are neutrinos massless or massive? Are neutrinos Dirac or Majorana particles ?
Lepton-Number Violating Heavy Meson Decays
Jinmei Zhang Harbin Institute of Technology
Aug 26, 2009
The 4-th Conference of TeV Physics
Outline
I. Introduction
But they provide no information on the absolute neutrino mass scale.
Lepton-Number Violating Heavy Meson Decays轻子数违反重介子衰变

A detection in one of the heavy meson decay modes studied in our analysis would imply the existence of a Majorana neutrino.
branching fraction of
M11
M
22
.
14
Conclusions
We have calculated the decay widths and branching ratios of the leptonic-number violating heavy meson decays.
12
Fig. 6 Theoretically excluded regions inside the curve for the
branching
fraction
of
. M1e1
M
22
13
Fig. 7 Theoretically excluded regions inside the curve for the
term violates it by two units L2.
Thus, the experimental observation of lepton-number violating processes can be used the only signature for the Majoranar nature of neutrinos.
Reproduction numbers and sub-threshold endemic equilibria for compartmental models of disease trans

Reproduction numbers and sub-threshold endemicequilibria for compartmental models of disease transmissionP.van den Driesschea,1,James Watmough b,*,2aDepartment of Mathematics and Statistics,University of Victoria,Victoria,BC,Canada V8W 3P4b Department of Mathematics and Statistics,University of New Brunswick,Fredericton,NB,Canada E3B 5A3Received 26April 2001;received in revised form 27June 2001;accepted 27June 2001Dedicated to the memory of John JacquezAbstractA precise definition of the basic reproduction number,R 0,is presented for a general compartmental disease transmission model based on a system of ordinary differential equations.It is shown that,if R 0<1,then the disease free equilibrium is locally asymptotically stable;whereas if R 0>1,then it is unstable.Thus,R 0is a threshold parameter for the model.An analysis of the local centre manifold yields a simple criterion for the existence and stability of super-and sub-threshold endemic equilibria for R 0near one.This criterion,together with the definition of R 0,is illustrated by treatment,multigroup,staged progression,multistrain and vector–host models and can be applied to more complex models.The results are significant for disease control.Ó2002Elsevier Science Inc.All rights reserved.Keywords:Basic reproduction number;Sub-threshold equilibrium;Disease transmission model;Disease control1.IntroductionOne of the most important concerns about any infectious disease is its ability to invade a population.Many epidemiological models have a disease free equilibrium (DFE)at whichtheMathematical Biosciences 180(2002)29–48/locate/mbs*Corresponding author.Tel.:+1-5064587323;fax:+1-5064534705.E-mail addresses:pvdd@math.uvic.ca (P.van den Driessche),watmough@unb.ca (J.Watmough).URL:http://www.math.unb.ca/$watmough.1Research supported in part by an NSERC Research Grant,the University of Victoria Committee on faculty research and travel and MITACS.2Research supported by an NSERC Postdoctoral Fellowship tenured at the University of Victoria.0025-5564/02/$-see front matter Ó2002Elsevier Science Inc.All rights reserved.PII:S0025-5564(02)00108-630P.van den Driessche,J.Watmough/Mathematical Biosciences180(2002)29–48population remains in the absence of disease.These models usually have a threshold parameter, known as the basic reproduction number,R0,such that if R0<1,then the DFE is locally as-ymptotically stable,and the disease cannot invade the population,but if R0>1,then the DFE is unstable and invasion is always possible(see the survey paper by Hethcote[1]).Diekmann et al.[2]define R0as the spectral radius of the next generation matrix.We write down in detail a general compartmental disease transmission model suited to heterogeneous populations that can be modelled by a system of ordinary differential equations.We derive an expression for the next generation matrix for this model and examine the threshold R0¼1in detail.The model is suited to a heterogeneous population in which the vital and epidemiological parameters for an individual may depend on such factors as the stage of the disease,spatial position,age or behaviour.However,we assume that the population can be broken into homo-geneous subpopulations,or compartments,such that individuals in a given compartment are indistinguishable from one another.That is,the parameters may vary from compartment to compartment,but are identical for all individuals within a given compartment.We also assume that the parameters do not depend on the length of time an individual has spent in a compart-ment.The model is based on a system of ordinary equations describing the evolution of the number of individuals in each compartment.In addition to showing that R0is a threshold parameter for the local stability of the DFE, we apply centre manifold theory to determine the existence and stability of endemic equilib-ria near the threshold.We show that some models may have unstable endemic equilibria near the DFE for R0<1.This suggests that even though the DFE is locally stable,the disease may persist.The model is developed in Section2.The basic reproduction number is defined and shown to bea threshold parameter in Section3,and the definition is illustrated by several examples in Section4.The analysis of the centre manifold is presented in Section5.The epidemiological ramifications of the results are presented in Section6.2.A general compartmental epidemic model for a heterogeneous populationConsider a heterogeneous population whose individuals are distinguishable by age,behaviour, spatial position and/or stage of disease,but can be grouped into n homogeneous compartments.A general epidemic model for such a population is developed in this section.Let x¼ðx1;...;x nÞt, with each x i P0,be the number of individuals in each compartment.For clarity we sort the compartments so that thefirst m compartments correspond to infected individuals.The distinc-tion between infected and uninfected compartments must be determined from the epidemiological interpretation of the model and cannot be deduced from the structure of the equations alone,as we shall discuss below.It is plausible that more than one interpretation is possible for some models.A simple epidemic model illustrating this is given in Section4.1.The basic reproduction number can not be determined from the structure of the mathematical model alone,but depends on the definition of infected and uninfected compartments.We define X s to be the set of all disease free states.That isX s¼f x P0j x i¼0;i¼1;...;m g:In order to compute R0,it is important to distinguish new infections from all other changes inpopulation.Let F iðxÞbe the rate of appearance of new infections in compartment i,Vþi ðxÞbe therate of transfer of individuals into compartment i by all other means,and VÀi ðxÞbe the rate oftransfer of individuals out of compartment i.It is assumed that each function is continuously differentiable at least twice in each variable.The disease transmission model consists of non-negative initial conditions together with the following system of equations:_x i¼f iðxÞ¼F iðxÞÀV iðxÞ;i¼1;...;n;ð1Þwhere V i¼VÀi ÀVþiand the functions satisfy assumptions(A1)–(A5)described below.Sinceeach function represents a directed transfer of individuals,they are all non-negative.Thus,(A1)if x P0,then F i;Vþi ;VÀiP0for i¼1;...;n.If a compartment is empty,then there can be no transfer of individuals out of the compartment by death,infection,nor any other means.Thus,(A2)if x i¼0then VÀi ¼0.In particular,if x2X s then VÀi¼0for i¼1;...;m.Consider the disease transmission model given by(1)with f iðxÞ,i¼1;...;n,satisfying con-ditions(A1)and(A2).If x i¼0,then f iðxÞP0and hence,the non-negative cone(x i P0, i¼1;...;n)is forward invariant.By Theorems1.1.8and1.1.9of Wiggins[3,p.37]for each non-negative initial condition there is a unique,non-negative solution.The next condition arises from the simple fact that the incidence of infection for uninfected compartments is zero.(A3)F i¼0if i>m.To ensure that the disease free subspace is invariant,we assume that if the population is free of disease then the population will remain free of disease.That is,there is no(density independent) immigration of infectives.This condition is stated as follows:(A4)if x2X s then F iðxÞ¼0and VþiðxÞ¼0for i¼1;...;m.The remaining condition is based on the derivatives of f near a DFE.For our purposes,we define a DFE of(1)to be a(locally asymptotically)stable equilibrium solution of the disease free model,i.e.,(1)restricted to X s.Note that we need not assume that the model has a unique DFE. Consider a population near the DFE x0.If the population remains near the DFE(i.e.,if the introduction of a few infective individuals does not result in an epidemic)then the population will return to the DFE according to the linearized system_x¼Dfðx0ÞðxÀx0Þ;ð2Þwhere Dfðx0Þis the derivative½o f i=o x j evaluated at the DFE,x0(i.e.,the Jacobian matrix).Here, and in what follows,some derivatives are one sided,since x0is on the domain boundary.We restrict our attention to systems in which the DFE is stable in the absence of new infection.That is, (A5)If FðxÞis set to zero,then all eigenvalues of Dfðx0Þhave negative real parts.P.van den Driessche,J.Watmough/Mathematical Biosciences180(2002)29–4831The conditions listed above allow us to partition the matrix Df ðx 0Þas shown by the following lemma.Lemma 1.If x 0is a DFE of (1)and f i ðx Þsatisfies (A1)–(A5),then the derivatives D F ðx 0Þand D V ðx 0Þare partitioned asD F ðx 0Þ¼F 000 ;D V ðx 0Þ¼V 0J 3J 4;where F and V are the m Âm matrices defined byF ¼o F i o x j ðx 0Þ !and V ¼o V i o x jðx 0Þ !with 16i ;j 6m :Further ,F is non-negative ,V is a non-singular M-matrix and all eigenvalues of J 4have positive real part .Proof.Let x 02X s be a DFE.By (A3)and (A4),ðo F i =o x j Þðx 0Þ¼0if either i >m or j >m .Similarly,by (A2)and (A4),if x 2X s then V i ðx Þ¼0for i 6m .Hence,ðo V i =o x j Þðx 0Þ¼0for i 6m and j >m .This shows the stated partition and zero blocks.The non-negativity of F follows from (A1)and (A4).Let f e j g be the Euclidean basis vectors.That is,e j is the j th column of the n Ân identity matrix.Then,for j ¼1;...;m ,o V i o x jðx 0Þ¼lim h !0þV i ðx 0þhe j ÞÀV i ðx 0Þh :To show that V is a non-singular M-matrix,note that if x 0is a DFE,then by (A2)and (A4),V i ðx 0Þ¼0for i ¼1;...;m ,and if i ¼j ,then the i th component of x 0þhe j ¼0and V i ðx 0þhe j Þ60,by (A1)and (A2).Hence,o V i =o x j 0for i m and j ¼i and V has the Z sign pattern (see Appendix A).Additionally,by (A5),all eigenvalues of V have positive real parts.These two conditions imply that V is a non-singular M-matrix [4,p.135(G 20)].Condition (A5)also implies that the eigenvalues of J 4have positive real part.Ã3.The basic reproduction numberThe basic reproduction number,denoted R 0,is ‘the expected number of secondary cases produced,in a completely susceptible population,by a typical infective individual’[2];see also [5,p.17].If R 0<1,then on average an infected individual produces less than one new infected individual over the course of its infectious period,and the infection cannot grow.Conversely,if R 0>1,then each infected individual produces,on average,more than one new infection,and the disease can invade the population.For the case of a single infected compartment,R 0is simply the product of the infection rate and the mean duration of the infection.However,for more complicated models with several infected compartments this simple heuristic definition of R 0is32P.van den Driessche,J.Watmough /Mathematical Biosciences 180(2002)29–48insufficient.A more general basic reproduction number can be defined as the number of new infections produced by a typical infective individual in a population at a DFE.To determine the fate of a‘typical’infective individual introduced into the population,we consider the dynamics of the linearized system(2)with reinfection turned off.That is,the system _x¼ÀD Vðx0ÞðxÀx0Þ:ð3ÞBy(A5),the DFE is locally asymptotically stable in this system.Thus,(3)can be used to de-termine the fate of a small number of infected individuals introduced to a disease free population.Let wi ð0Þbe the number of infected individuals initially in compartment i and letwðtÞ¼w1ðtÞ;...;w mðtÞðÞt be the number of these initially infected individuals remaining in the infected compartments after t time units.That is the vector w is thefirst m components of x.The partitioning of D Vðx0Þimplies that wðtÞsatisfies w0ðtÞ¼ÀV wðtÞ,which has the unique solution wðtÞ¼eÀVt wð0Þ.By Lemma1,V is a non-singular M-matrix and is,therefore,invertible and all of its eigenvalues have positive real parts.Thus,integrating F wðtÞfrom zero to infinity gives the expected number of new infections produced by the initially infected individuals as the vector FVÀ1wð0Þ.Since F is non-negative and V is a non-singular M-matrix,VÀ1is non-negative[4,p.137 (N38)],as is FVÀ1.To interpret the entries of FVÀ1and develop a meaningful definition of R0,consider the fate of an infected individual introduced into compartment k of a disease free population.The(j;k)entry of VÀ1is the average length of time this individual spends in compartment j during its lifetime, assuming that the population remains near the DFE and barring reinfection.The(i;j)entry of F is the rate at which infected individuals in compartment j produce new infections in compartment i. Hence,the(i;k)entry of the product FVÀ1is the expected number of new infections in com-partment i produced by the infected individual originally introduced into compartment k.Fol-lowing Diekmann et al.[2],we call FVÀ1the next generation matrix for the model and set R0¼qðFVÀ1Þ;ð4Þwhere qðAÞdenotes the spectral radius of a matrix A.The DFE,x0,is locally asymptotically stable if all the eigenvalues of the matrix Dfðx0Þhave negative real parts and unstable if any eigenvalue of Dfðx0Þhas a positive real part.By Lemma1, the eigenvalues of Dfðx0Þcan be partitioned into two sets corresponding to the infected and uninfected compartments.These two sets are the eigenvalues of FÀV and those ofÀJ4.Again by Lemma1,the eigenvalues ofÀJ4all have negative real part,thus the stability of the DFE is determined by the eigenvalues of FÀV.The following theorem states that R0is a threshold parameter for the stability of the DFE.Theorem2.Consider the disease transmission model given by(1)with fðxÞsatisfying conditions (A1)–(A5).If x0is a DFE of the model,then x0is locally asymptotically stable if R0<1,but un-stable if R0>1,where R0is defined by(4).Proof.Let J1¼FÀV.Since V is a non-singular M-matrix and F is non-negative,ÀJ1¼VÀF has the Z sign pattern(see Appendix A).Thus,sðJ1Þ<0()ÀJ1is a non-singular M-matrix;P.van den Driessche,J.Watmough/Mathematical Biosciences180(2002)29–483334P.van den Driessche,J.Watmough/Mathematical Biosciences180(2002)29–48where sðJ1Þdenotes the maximum real part of all the eigenvalues of the matrix J1(the spectral abscissa of J1).Since FVÀ1is non-negative,ÀJ1VÀ1¼IÀFVÀ1also has the Z sign pattern.Ap-plying Lemma5of Appendix A,with H¼V and B¼ÀJ1¼VÀF,we have ÀJ1is a non-singular M-matrix()IÀFVÀ1is a non-singular M-matrix:Finally,since FVÀ1is non-negative,all eigenvalues of FVÀ1have magnitude less than or equal to qðFVÀ1Þ.Thus,IÀFVÀ1is a non-singular M-matrix;()qðFVÀ1Þ<1:Hence,sðJ1Þ<0if and only if R0<1.Similarly,it follows thatsðJ1Þ¼0()ÀJ1is a singular M-matrix;()IÀFVÀ1is a singular M-matrix;()qðFVÀ1Þ¼1:The second equivalence follows from Lemma6of Appendix A,with H¼V and K¼F.The remainder of the equivalences follow as with the non-singular case.Hence,sðJ1Þ¼0if and only if R0¼1.It follows that sðJ1Þ>0if and only if R0>1.ÃA similar result can be found in the recent book by Diekmann and Heesterbeek[6,Theorem6.13].This result is known for the special case in which J1is irreducible and V is a positive di-agonal matrix[7–10].The special case in which V has positive diagonal and negative subdiagonal elements is proven in Hyman et al.[11,Appendix B];however,our approach is much simpler(see Section4.3).4.Examples4.1.Treatment modelThe decomposition of fðxÞinto the components F and V is illustrated using a simple treat-ment model.The model is based on the tuberculosis model of Castillo-Chavez and Feng[12,Eq.(1.1)],but also includes treatment failure used in their more elaborate two-strain model[12,Eq.(2.1)].A similar tuberculosis model with two treated compartments is proposed by Blower et al.[13].The population is divided into four compartments,namely,individuals susceptible to tu-berculosis(S),exposed individuals(E),infectious individuals(I)and treated individuals(T).The dynamics are illustrated in Fig.1.Susceptible and treated individuals enter the exposed com-partment at rates b1I=N and b2I=N,respectively,where N¼EþIþSþT.Exposed individuals progress to the infectious compartment at the rate m.All newborns are susceptible,and all indi-viduals die at the rate d>0.Thus,the core of the model is an SEI model using standard inci-dence.The treatment rates are r1for exposed individuals and r2for infectious individuals. However,only a fraction q of the treatments of infectious individuals are successful.Unsuc-cessfully treated infectious individuals re-enter the exposed compartment(p¼1Àq).The diseasetransmission model consists of the following differential equations together with non-negative initial conditions:_E¼b1SI=Nþb2TI=NÀðdþmþr1ÞEþpr2I;ð5aÞ_I¼m EÀðdþr2ÞI;ð5bÞ_S¼bðNÞÀdSÀb1SI=N;ð5cÞ_T¼ÀdTþr1Eþqr2IÀb2TI=N:ð5dÞProgression from E to I and failure of treatment are not considered to be new infections,but rather the progression of an infected individual through the various compartments.Hence,F¼b1SI=Nþb2TI=NB B@1C CA and V¼ðdþmþr1ÞEÀpr2IÀm Eþðdþr2ÞIÀbðNÞþdSþb1SI=NdTÀr1EÀqr2Iþb2TI=NB B@1C CA:ð6ÞThe infected compartments are E and I,giving m¼2.An equilibrium solution with E¼I¼0has the form x0¼ð0;0;S0;0Þt,where S0is any positive solution of bðS0Þ¼dS0.This will be a DFE if and only if b0ðS0Þ<d.Without loss of generality,assume S0¼1is a DFE.Then,F¼0b100;V¼dþmþr1Àpr2Àm dþr2;givingVÀ1¼1ðdþmþr1Þðdþr2ÞÀm pr2dþr2pr2m dþmþr1and R0¼b1m=ððdþmþr1Þðdþr2ÞÀm pr2Þ.A heuristic derivation of the(2;1)entry of VÀ1and R0are as follows:a fraction h1¼m=ðdþmþr1Þof exposed individuals progress to compartment I,a fraction h2¼pr2=ðdþr2Þof infectious individuals re-enter compartment E.Hence,a fractionh1of exposed individuals pass through compartment I at least once,a fraction h21h2passthroughat least twice,and a fraction h k 1h k À12pass through at least k times,spending an average of s ¼1=ðd þr 2Þtime units in compartment I on each pass.Thus,an individual introduced into com-partment E spends,on average,s ðh 1þh 21h 2þÁÁÁÞ¼s h 1=ð1Àh 1h 2Þ¼m =ððd þm þr 1Þðd þr 2ÞÀm pr 2Þtime units in compartment I over its expected lifetime.Multiplying this by b 1gives R 0.The model without treatment (r 1¼r 2¼0)is an SEI model with R 0¼b 1m =ðd ðd þm ÞÞ.The interpretation of R 0for this case is simpler.Only a fraction m =ðd þm Þof exposed individuals progress from compartment E to compartment I ,and individuals entering compartment I spend,on average,1=d time units there.Although conditions (A1)–(A5)do not restrict the decomposition of f i ðx Þto a single choice for F i ,only one such choice is epidemiologically correct.Different choices for the function F lead to different values for the spectral radius of FV À1,as shown in Table 1.In column (a),treatment failure is considered to be a new infection and in column (b),both treatment failure and pro-gression to infectiousness are considered new infections.In each case the condition q ðFV À1Þ<1yields the same portion of parameter space.Thus,q ðFV À1Þis a threshold parameter in both cases.The difference between the numbers lies in the epidemiological interpretation rather than the mathematical analysis.For example,in column (a),the infection rate is b 1þpr 2and an exposed individual is expected to spend m =ððd þm þr 1Þðd þr 2ÞÞtime units in compartment I .However,this reasoning is biologically flawed since treatment failure does not give rise to a newly infected individual.Table 1Decomposition of f leading to alternative thresholds(a)(b)Fb 1SI =N þb 2TI =N þpr 2I 0000B B @1C C A b 1SI =N þb 2TI =N þpr 2I m E 000B B @1C C A Vðd þm þr 1ÞE Àm E þðd þr 2ÞI Àb ðN ÞþdS þb 1SI =N dT Àr 1E Àqr 2I þb 2TI =N 0B B @1C C A ðd þm þr 1ÞE ðd þr 2ÞI Àb ðN ÞþdS þb 1SI =N dT Àr 1E Àqr 2I þb 2TI =N 0B B @1C C A F0b 1þpr 200 0b 1þpr 2m 0 V d þm þr 10Àm d þr 2d þm þr 100d þr 2 q (FV À1)b 1m þpr 2mðd þm þr 1Þðd þr 2Þffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffib 1m þpr 2mðd þm þr 1Þðd þr 2Þs 36P.van den Driessche,J.Watmough /Mathematical Biosciences 180(2002)29–484.2.Multigroup modelIn the epidemiological literature,the term‘multigroup’usually refers to the division of a het-erogeneous population into several homogeneous groups based on individual behaviour(e.g., [14]).Each group is then subdivided into epidemiological compartments.The majority of mul-tigroup models in the literature are used for sexually transmitted diseases,such as HIV/AIDS or gonorrhea,where behaviour is an important factor in the probability of contracting the disease [7,8,14,15].As an example,we use an m-group SIRS-vaccination model of Hethcote[7,14]with a generalized incidence term.The sample model includes several SI multigroup models of HIV/ AIDS as special cases[8,15].The model equations are as follows:_I i ¼X mj¼1b ijðxÞS i I jÀðd iþc iþ iÞI i;ð7aÞ_S i ¼ð1Àp iÞb iÀðd iþh iÞS iþr i R iÀX mj¼1b ijðxÞS i I j;ð7bÞ_Ri¼p i b iþc i I iþh i S iÀðd iþr iÞR i;ð7cÞfor i¼1;...;m,where x¼ðI1;...;I m;S1;...;S m;R1;...;R mÞt.Susceptible and removed individu-als die at the rate d i>0,whereas infected individuals die at the faster rate d iþ i.Infected in-dividuals recover with temporary immunity from re-infection at the rate c i,and immunity lasts an expected1=r i time units.All newborns are susceptible,and a constant fraction b i are born into each group.A fraction p i of newborns are vaccinated at birth.Thereafter,susceptible individuals are vaccinated at the rate h i.The incidence,b ijðxÞdepends on individual behaviour,which determines the amount of mixing between the different groups(see,e.g.,Jacquez et al.[16]). The DFE for this model isx0¼ð0;...;0;S01;...;S0m;R01;...;R0mÞt;whereS0 i ¼b i d ið1Àp iÞþr iðÞd iðd iþh iþr iÞ;R0 i ¼b iðh iþd i p iÞd iðd iþh iþr iÞ:Linearizing(7a)about x¼x0givesF¼S0i b ijðx0ÞÂÃandV¼½ðd iþc iþ iÞd ij ;where d ij is one if i¼j,but zero otherwise.Thus,FVÀ1¼S0i b ijðx0Þ=ðd iÂþc iþ iÞÃ:P.van den Driessche,J.Watmough/Mathematical Biosciences180(2002)29–4837For the special case with b ij separable,that is,b ijðxÞ¼a iðxÞk jðxÞ,F has rank one,and the basic reproduction number isR0¼X mi¼1S0ia iðx0Þk iðx0Þd iþc iþ i:ð8ÞThat is,the basic reproduction number of the disease is the sum of the‘reproduction numbers’for each group.4.3.Staged progression modelThe staged progression model[11,Section3and Appendix B]has a single uninfected com-partment,and infected individuals progress through several stages of the disease with changing infectivity.The model is applicable to many diseases,particularly HIV/AIDS,where transmission probabilities vary as the viral load in an infected individual changes.The model equations are as follows(see Fig.2):_I 1¼X mÀ1k¼1b k SI k=NÀðm1þd1ÞI1;ð9aÞ_Ii¼m iÀ1I iÀ1Àðm iþd iÞI i;i¼2;...;mÀ1;ð9bÞ_Im¼m mÀ1I mÀ1Àd m I m;ð9cÞ_S¼bÀbSÀX mÀ1k¼1b k SI k=N:ð9dÞThe model assumes standard incidence,death rates d i>0in each infectious stage,and thefinal stage has a zero infectivity due to morbidity.Infected individuals spend,on average,1=m i time units in stage i.The unique DFE has I i¼0,i¼1;...;m and S¼1.For simplicity,define m m¼0. Then F¼½F ij and V¼½V ij ,whereF ij¼b j i¼1;j6mÀ1;0otherwise;&ð10ÞV ij¼m iþd i j¼i;Àm j i¼1þj;0otherwise:8<:ð11ÞLet a ij be the(i;j)entry of VÀ1.Thena ij¼0i<j;1=ðm iþd iÞi¼j;Q iÀ1k¼jm kQ ik¼jðm kþd kÞj<i:8>>><>>>:ð12ÞThus,R0¼b1m1þd1þb2m1ðm1þd1Þðm2þd2Þþb3m1m2ðm1þd1Þðm2þd2Þðm3þd3ÞþÁÁÁþb mÀ1m1...m mÀ2ðm1þd1Þ...ðm mÀ1þd mÀ1Þ:ð13ÞThe i th term in R0represents the number of new infections produced by a typical individual during the time it spends in the i th infectious stage.More specifically,m iÀ1=ðm iÀ1þd iÀ1Þis the fraction of individuals reaching stage iÀ1that progress to stage i,and1=ðm iþd iÞis the average time an individual entering stage i spends in stage i.Hence,the i th term in R0is the product of the infectivity of individuals in stage i,the fraction of initially infected individuals surviving at least to stage i,and the average infectious period of an individual in stage i.4.4.Multistrain modelThe recent emergence of resistant viral and bacterial strains,and the effect of treatment on their proliferation is becoming increasingly important[12,13].One framework for studying such sys-tems is the multistrain model shown in Fig.3,which is a caricature of the more detailed treatment model of Castillo-Chavez and Feng[12,Section2]for tuberculosis and the coupled two-strain vector–host model of Feng and Velasco-Hern a ndez[17]for Dengue fever.The model has only a single susceptible compartment,but has two infectious compartments corresponding to the two infectious agents.Each strain is modelled as a simple SIS system.However,strain one may ‘super-infect’an individual infected with strain two,giving rise to a new infection incompartment。
超级记忆编码完整版

A alien 外星人,aluminium 铝,aircraft 飞行器,angle 三角,ash 灰,arrow 矢,alarm 闹钟,angel安琪儿,apple 苹果,alcohol 酒精B bean豆子,bee 蜜蜂,birdcage 鸟笼,balsam 香油brush 刷,book 书,ballon 气球,bat 蝙蝠,bamboo 竹子,bag 包C chain 链条, clips 夹子,crab 螃蟹 cactus 仙人掌,cheese 奶酪,cow 母牛,camel骆驼,couch 沙发,cap 帽子,cigar 雪茄D dinosaur 恐龙,deer 鹿,Durian 榴莲, duck 鸭子,disk 圆盘,dove 鸽子,drum 鼓,detergent 洗衣粉,dolphin 海豚,dog 狗E elephant 大象,eel 鳝鱼,eraser 橡皮擦,earthenware陶器,essay 文章,explosive 炸药,elk 麋,engine 引擎,emperor 皇帝,eagle 鹰F flask 瓶,fly 苍蝇,faeces 粪,feather 羽毛,faucet 水龙头,fuel 燃料,foam 泡沫,fork 叉子,fibre 纤维,frog 蛙G grain 谷物,gyve 手铐,garlic 大蒜,goose 鹅,ghost 鬼魂,gourds 葫芦,glove 手套,ganja大麻,grape 葡萄, ginger 生姜H honey 蜂蜜,hail 冰雹,horn 号角,hanger 衣架,heroin 海洛因,Haw 山楂,hammer 锤,hat 帽子,herb 草,hag 女巫I idiot 傻瓜,indicator 指示器,iron 铁,ice 冰,insect 虫,ivy 常春藤,ivory 象牙,ink 墨水,imposture 骗子,ingot 铸块J javelin 标枪,jeans 牛仔裤,jar 罐子,jesus 耶稣,jasmine 茉莉,jewel 宝石,jam 果酱,jade 玉,jeep吉普车,jug大壶K kali 甘蓝,killer 杀手,kernel果仁,knapsack 背包,keys钥匙,knife小刀, koala树袋熊,Kite 风筝,kohlrabi大头菜,kangaroo袋鼠L lion狮子,lighter打火机,lizard 蜥蜴,lantern 提灯, lice 虱子,leaf 叶子,lemon柠檬,lock 锁,lamb羊羔,Longan 龙眼M melon 甜瓜,mantis 螳螂,magnet 磁铁,mice,老鼠,mask 面具,macaw 金刚鹦鹉,mummy 木乃伊,match 火柴,mobile 风铃,mango 芒果N neon 霓虹灯,neep萝卜,narcissus 水仙,nymph 蛹,necklace 项链,navvy 挖土机,nylon 尼龙,net 网,nipper 手铐,naggy小马O onion 洋葱,olive橄榄,orange 橘子,oven烤箱,ostrich 鸵鸟,owl 枭,猫头鹰,omelette 煎蛋,otter 水獭,opal 猫眼石,oscillation 摆钟P peony 牡丹,pear 梨子,parrot 鹦鹉,pecan 山核桃,pistol 手枪,prawn 虾,Plum 梅子,Peach 桃子,pulp果肉酱,pig 猪Q quoit 金属环,quilt 被子,quartz 石英,queen 女王 ,quicksilver 水银,quince 温柏树,quail 鹌鹑,quet 海鸥,quip 名言,quadrangle 四边形R rhinestone 水晶石,roe 鱼卵,rye 黑麦,rosin 松香,rose 玫瑰花,raven 大乌鸦,ram 雄绵羊,roach 蟑螂,robot 机器人,,rouge口红,S snake 蛇,seal 海豹,Sorosis 桑果,scissor剪刀,shoes 鞋,swallow 燕子,snail 蜗牛,suitcase箱子,spider 蜘蛛,Sugarcane 甘蔗T tin 罐头,tea茶,tower 塔,tank 坦克,trousers 裤子,towel 纸巾,番茄,turkey 火鸡,tobacco 烟草,tiger 虎U unique独特的,ungainly笨拙的,unregenerate不知悔改的,ulcer 道德败坏,unspotted清白的,unwield笨重的,unkempt不整洁的,untoward 不幸的,upright正直的,ugly 难看的V violinist 小提琴家,villager 村民,virago 悍妇,versifier 诗人,viewer 观众,venus 美人,valian坏蛋,veteran老兵,vampire 吸血鬼,vegetarian 素食者W wallet 钱包,wire电线,wreath 花圈,walrus 海象,whistle 口哨,whale 鲸,,Walnut 核桃,watch 手表,wolf 狼,wing翅膀曾郑左卓翟詹甄张赵周邹钟朱祝杨严俞袁余尹虞易叶雍阎岳姚郁习项萧肖谢辛邢萧胥徐薛许项邢。
菲利普斯密码提示码l-10

菲利普斯密码提示码l-10
菲利普斯密码提示码L-10是一种复杂的密码系统,用于保护和加密生物学实验数据。
它是由Thomas Philips博士提出的,包括以下几个主要组件:DNA和RNA序列:分子生物学实验的关键步骤是在DNA中提取特定的序列,作为一种可以用来产生理想的RNA序列的模板。
称为“菲利普斯序列提供者(FSP)”的机器人将被招募,以确保DNA序列的精确性,这样就可以使用DNA来指导RNA的合成。
借助菲利普斯代码,微生物可以被安全地加以保护,避免不可预知的外部因素因素的影响。
计算机技术也会被用来帮助菲利普斯密码提示码L-10。
为了使机器人能够正确识别DNA序列,通常会使用经过培训的人工智能算法来分析输入信息以及特定基因的相似性。
这样,任何破坏DNA序列的错误就会被发现和消除。
联合使用人工智能算法和机器人可以帮助生物学实验数据更加可靠可信。
当然,菲利普斯密码提示码L-10还有另一个重要组成部分,即密码生成器。
该密码生成器可以使用对特定基因的研究结果来生成独特的密码,以帮助保护和加密实验数据。
如果再次破解密码,实验数据就会无法识别。
菲利普斯密码提示码L-10的应用越来越广泛,从全球研究组织到大型医药公司,都开始采用这一技术,以提高实验过程的安全性和准确性。
未来,随着人工智能技术的进一步深入研究,菲利普斯密码提示码L-10可能会得到更多的应用,以确保生物学实验数据的安全和准确。
Geant4基础知识

Geant4基础知识Geant4基础知识G4模拟粒⼦过程:建⽴⼀次模拟,在 G4 中称为⼀次Run;Run 建⽴后,需要对⼏何结构、物理过程进⾏初始化;初始化完成后就开始模拟过程了,⾸先发射⼀个粒⼦。
在G4 中,发射⼀个(或⼀系列)粒⼦到所有次级粒⼦死亡的过程成为⼀次 Event。
⽽每次发射的初始粒⼦则有粒⼦发射器进⾏控制。
⽽在每⼀个event过程中,粒⼦与材料反应后会可能⽣成多个次级粒⼦,每个粒⼦都会有⼀条径迹,称之为 track;⽽每⼀个粒⼦(初始的或次级的)的径迹⼜是由很多步组成的,称之为step。
G4模拟的基本算法:A Run Start -> 初始化物理模型/⼏何模型-> An Event Start -> 调⽤粒⼦发射器发射粒⼦-> A Track Start-> A Step Start-> A Step End-> Next Step Start-> ……-> All Step End-> A Track End-> Next Track Start-> ……-> All Track End-> An Event End -> Next Event Start-> ……-> All Event End(All Primaries Shot) -> A Run End -> Next Run Start-> ……1) main()中应该包括的内容Geant4是⼀个探测器模拟⼯具, 但它对于某个特定的模拟程序没有固定的main()函数, ⽤户在建⽴模拟程序的过程中需要提供⾃⼰的main()函数. ⼀个最基本的main()函数需要包括以下⼏个⽅⾯:G4RunManager(模拟整个过程)G4VUserDetectorConstruction(定义探测器材料, ⼏何形状, 灵敏区和读出⽅案)G4VUserPhysicsList(定义粒⼦种类和物理过程, 还有截断参数)G4VUserPrimaryGeneratorAction(定义了源粒⼦的种类, 能量, 出射⽅向等)⼀个最简单的main()函数如下:#include ""#include ""#include ""#include ""#include ""int main(){Geant4的类结构Geant4程序代码是根据这个类结构建⽴起来的, 类结构如下图所⽰. 下⾯就是Geant4中每个类的简单说明.1) Run 和 Event这些类与模拟事件相关, 产⽣次级粒⼦, 为粒⼦径迹模拟器提供粒⼦.2) Tracking 和 Track根据粒⼦在探测器材料中的物理过程模拟粒⼦运⾏的轨迹, 给出粒⼦特定时间段在空间的位置, 或者粒⼦空间时间的分布.3) Geometry, Magnetic Field 和 CAD-Interface这三个类就是⽤来描述探测器⼏何结构和探测器中电磁场的分布. 为了使探测器⼏何结构可以在CAD系统中进⾏修改, Geant4的⼏何体模型完全与ISOSTEP标准⼀致. 将来Geant4中⼏何结构的设计将从程序设计中独⽴出来. ⾯向对象设计的⽅法可以让⽤户在不影响程序其他部分的同时改变⼏何参数和场.4) Particle Definition 和 Matter这两个类⽤于定义粒⼦和探测器材料.5) Physics它提供了粒⼦与探测器材料相互作⽤时所发⽣物理过程的模型, 允许⽤户为每次反应或每个反应道添加物理模型. ⽤户根据粒⼦的种类, 探测器材料和能量范围选择不同的物理模型. Geant4有电磁物理过程和强⼦物理过程模型, 同时也提供了散射截⾯数据库.6) Hits 和 Digitization这个两个类⽤于对⽤户定义的灵敏区内的响应进⾏采样和分析.7) Visualization它显⽰了探测器⼏何形状, 粒⼦轨迹和碰撞过程. 由于采⽤了⾯向对象设计技术来设计可视化部分, 这允许⽤户独⽴开发可视化⼯具, 如: OpenGL 和OpenInventor(为X11和Windows设计), DAWN, Postscript(via DAWN)和VRML.8) Interfaces⽀持可视化⽤户界⾯以及和外加程序的交流(OODBMS, reconstruction等).①User Verbose output class,定义了⼀个verbosity 变量;②Run manager,定义了⼀个运⾏管理器runManager;③User Initialization class es (mandatory),设置两个强制类ExN02DetectorConstruction 和ExN02PhysicsList;④User Action classes,设置⽤户⼲涉类 ExN02PrimaryGeneratorAction、ExN02RunAction、 ExN02EventAction和ExN02SteppingAction;⑤Initialize G4 kernel,“runManager->Initialize()”,初始化GEANT4 内核。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
4
The answer to the second question:
The Dirac mass term preserves the lepton number, and the Majorana mass
Lepton-Number Violating Heavy Meson Decays
Jinmei Zhang Harbin Institute of Technology
Aug 26, 2009
The 4-th Conference of TeV Physics
Outline
I. Introduction
term violates it by two units L2.
Thus, the experimental observation of lepton-number violating processes can be used the only signature for the Majoranar nature of neutrinos.
We have sampled the constrain on branching ratios as a function of the Majorana neutrino mass.
A detection in one of the heavy meson decay modes studied in our analysis would imply the existence of a Majorana neutrino.
The experiments at the current LHC may have the opportunity to discover it.
15
Thank You!
16
12
Fig. 6 Theoretically excluded regions inside the curve for the
branching
fraction
of
. M1e1
M
22
13
Fig. 7 Theoretically excluded regions inside the curve for the
II. Lepton-number Violating L2Heavy
Meson Decays III. Conclusions
2
Introduction
Are neutrinos massless or massive? Are neutrinos Dirac or Majorana particles ?
from
M1e1
M
22
searches.
10
Table 1 The decay modes of the leptonic-number violatong.
11
Fig. 5 Theoretically excluded regions tion of . M1e1e2M2
5
Lepton-Number Violating Heavy Meson Decays
Fig. 1 Feynman diagram corresponding to the lepton-number
violating decays M 1 q 1 l1 p 1 l2 p 2 M 2 q 2 . 6
3
The answer to the first question:
During the past few years, neutrino oscillation experiments have provided us with very convincing evidence that neutrinos are not strictly massless as predicted in the SM, but are massive.
branching fraction of
M11
M
22
.
14
Conclusions
We have calculated the decay widths and branching ratios of the leptonic-number violating heavy meson decays.
The decay amplitude as follows:
(1)
(2) (3)
JHEP 0905:030,2009[arXiv:0901.3589v2]
Anupama Atre, Tao Han, Silvia Pascoli, Bin Zhang
7
Fig. 2 Excluded regions above the curve for V e 4 2 versus m 4
from M1e1e2 M2searches.
8
Fig. 3 Excluded regions above the curve for Ve4V 4 versus m 4 from M1e12M2searches.
9
Fig. 4 Excluded regions above the curve for V 4 2 versus m 4
