青岛二中2016年自主招生考试

合集下载

笔试面试合格按比例顺序择优认定一本线上

辽宁省 557
数字媒体技术
山东省 557
翻译(英语)
毕业中学
测试内容
北京市日坛中学
笔试+面试
北京大学附属中学
笔试+面试
北京汇文中学
笔试+面试
邯郸市第一中学
笔试+面试
山东省青岛第十九中学笔试+面试
临沂第一中学（校本部）笔试+面试
绵阳中学实验学校
笔试+面试
浙江师范大学附属中学笔试+面试
郑州外国语新枫杨学校笔试+面试
谢奕帆四川省 596
陈蕴
浙江省 606
钱乐琦浙江省 622
张皓琳河南省 610
王紫菡河南省 530
付苏汉清湖南省 591
张诗琪辽宁省 618
马婧骁山东省 584
姜雨萌山东省 586
欧小亮贵州省 577
唐富强河北省 522
王梓阳河南省 492
宋大巍河南省 543
翻译(汉英法)
青岛开发区第一中学笔试+面试合格
合格按比例顺序择优认定一本线上自主招生
合格按比例顺序择优认定一本线上自主招生
合格按比例顺序择优认定一本线上自主招生
合格按比例顺序择优认定一本线上自主招生
合格按比例顺序择优认定一本线上自主招生
合格按比例顺序择优认定一本线上自主招生
王茜
山东省 609
朱文昕山东省 558
姓名罗天佐陈重之张天佐王学禹宋宇飞郁沛哲罗嘉琪胡泽嵚宋泽源王琛闫敬萱张惠文雷羽添陈莺歌宋悠扬郝子玥刘维维田青晗张小爽李宇轩曾依雪肖薇袁琳朱惟祎王婉宁王映茹马榕刘雅萱房晓婧

2016年青岛市中考自主招生青岛二中录取各学校学生名额

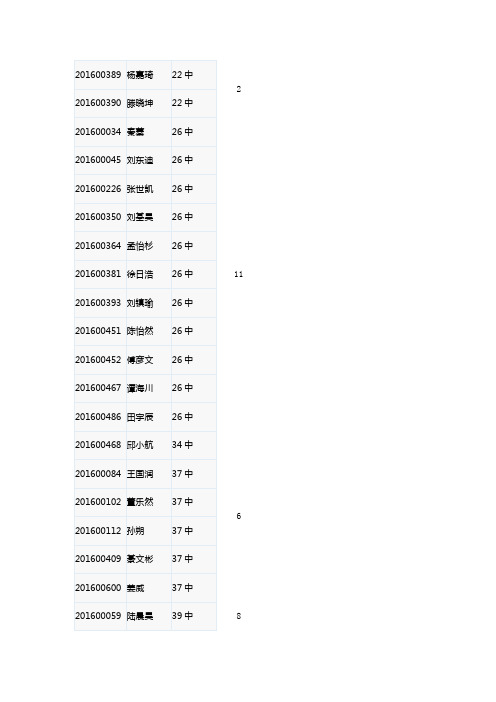
2 201600390 滕晓坤 22中 201600034 秦蓁 26中 11201600045 刘东迪 26中 201600226 张世凯 26中 201600350 刘基昊 26中 201600364 孟怡杉 26中 201600381 徐日浩 26中 201600393 刘镇瑜 26中 201600451 陈怡然 26中 201600452 傅彦文 26中 201600467 谭海川 26中 201600486 田宇辰 26中 201600468 邱小航 34中 6 201600084 王国润 37中 201600102 董乐然 37中 201600112 孙朔 37中 201600409 綦文彬 37中 201600600 姜威 37中 201600059 陆晨昊 39中 8201600133 戚恒源39中201600177 王嵩尧39中201600213 雷铠璐39中201600214 黄俊恺39中201600399 刘懿涟39中201600487 李依洵39中201600453 宗逸静43中 1201600107 谢秉圻44中2 201600445 屈凡博44中201600131 邹雪辰47中 1 201600138 宣民祺51中3 201600492 李炳萱51中201600612 张還51中201600094 刘新一53中 1 201600236 荣天毅57中 1 201600219 孙源59中2 201600567 费嘉琪59中201600032 韩方循5中2 201600387 李昀衡5中201600086 金建良 63中 2 201600470 杨笑源 63中 201600461 孙睿谦 65中 2 201600511 程舒扬 65中 201600023 周玄 7中 5 201600353 殷子豪 7中 201600398 马业伟 7中 201600412 郭笑言 7中 201600441 徐楷湲 7中201600292 赵许帆长泰学校1 201600394 肖航超银中学市北7201600630 董傲超银中学市北201600106 刘予欣超银中学四方201600318 盛浩超银中学四方201600373 曹源超银中学四方201600418 刘一唯超银中学四方201600433 肖乐兮超银中学四方201600118 李玉玺二实验 5 201600168 郝良瑀二实验 201600316 姜雨宏二实验 201600457 胡天同二实验 201600472 何凯琦二实验 201600010 邓天然青大附中 21201600031 崔扬青大附中 201600036 刘昱辰青大附中 201600110 盛婧妍青大附中 201600115 王雪莹青大附中 201600123 庞宇轩青大附中 201600135 赵景煜青大附中 201600152 孙松雨青大附中 201600165 张靖唯青大附中 201600180 康哲雨青大附中 201600183 肖瑶青大附中201600202 于卓浩青大附中201600203 兰浩中青大附中201600245 李子潇青大附中201600268 戴天元青大附中201600382 李名昊青大附中201600403 李泽超青大附中201600423 李晟昊青大附中201600448 张功昊青大附中201600485 孟雨泽青大附中201600626 孙铭浚青大附中201600026 周江南实验初中201600100 麻晨翔实验初中201600134 王子鸣实验初中201600142 裴雨欣实验初中201600148 颜鸿宇实验初中15 201600150 董小鹏实验初中201600227 于搏涛实验初中201600338 胡凯宇实验初中201600385 周子于实验初中201600442 李嘉麟实验初中201600454 王子成实验初中201600508 黄家铭实验初中201600534 赵晋科实验初中201600548 崔渐超实验初中201600621 于笑涵实验初中201600037 郭正智荣李沧2 201600466 蔡德沛智荣李沧。

2016青岛二中自招数学试题(含详细答案)

即
三、渐入佳境
（阅读预备知识，完成相应题目）
第8题预备知识：二次函数的图象与轴交点的横坐标分别为 .
时，则 ;
时，则
8．求使得为正整数的所有实数的值.
第9题预备知识：圆的切线与过切点的弦所形成的角（弦切角），
等于其所夹弧对的圆周角（如图）.
9．在中，为斜边，其内切圆分别与边，，切于，，，线段是的高.
11．中，的对边分别为，函数的最小值为，且是关于的方程的两根.
（1）求证：是直角三角形；（2）求实数的值；
（3）若此三角形外接圆面积为，求内接正方形的边长.
12．已知点，，
（1）求经过、、三点的抛物线顶点和抛物线与轴另一交点的坐标；
（2）若在线段上有一动点（不在端点），分别以点、为圆心，、为半径作圆，在⊙ 与⊙ 上各有一动点、，求的范围；
,则 ,
当时,解得 .综上得 .
9.解：(1)设，，在中，因为，
所以，又，所以
(2)由预备知识可知，因为，且
所以，即
（3）由（2）知，且所以为等腰直角三角形，所以
又，，所以 ≌ 所以，所以点在的平分线上.
10.解：（1）由题意，得
当时， .
（2）由题意，得点所在的反比例函数表达式为，图象在第一、三象限，且关于原点对称，函数图象过原点，也关于原点对称，若函数图象有交点，则，不妨设在第一象限的交点为，则第三象限交点为，，所以，，，又因为点在图象上，所以，即，所以的面积为定值 .
二、拾阶而上
5．解方程 .
6．自行车选手甲、乙、丙三人同时从点出发沿着，，三条直线段行进，选手甲在这三条直线上行进的速度分别为，， ( )，选手乙在这三条直线上行进的速度分别为，， ( )，选手丙在这三条直线上行进的速度分别为，， ( ).若三名选手同时到达终点，求的大小.

2023-2024学年山东省青岛市青岛第二中学高一上学期10月月考数学试题+答案解析(附后)

2023-2024学年山东省青岛市青岛第二中学高一上学期10月月考数学试题✽一、单选题：本题共8小题，每小题5分，共40分。

在每小题给出的选项中，只有一项是符合题目要求的。

1.已知集合，则下列结论错误的是( )A. B. C. D.2.已知集合，且A中至少有一个奇数，则这样的集合A的个数为( )A. 11B. 12C. 13D. 143.设集合，其中N为自然数集，，，则下列结论正确的是( )A. B.C. D.4.设，则“”是“”的( )A. 充分不必要条件B. 必要不充分条件C. 充要条件D. 既不充分也不必要条件5.若“”是假命题，则a的取值范围为( )A. B. C. D.6.近来牛肉价格起伏较大，假设第一周、第二周的牛肉价格分别为a元/斤、b元/斤，学校甲食堂和乙食堂购买牛肉的方式不同，甲食堂每周购买6000元钱的牛肉，乙食堂每周购买80斤牛肉，甲食堂、乙食堂两次平均单价为分别记为，，则下列结论正确的是( )A. B.C. D. ，的大小无法确定7.已知，，，则的最小值为( )A. B. C. D.8.对于集合A，B，我们把集合叫做集合A与B的差集，记作若集合，集合，且，则实数a的取值范围是( )A. B. C. D.二、多选题：本题共4小题，共20分。

在每小题给出的选项中，有多项符合题目要求。

全部选对的得5分，部分选对的得2分，有选错的得0分。

9.已知全集，，，，，，则下列选项正确的为( )A. B. A的不同子集的个数为8C. D.10.下列说法中，错误的是( )A. 若，，则B. 若，，则C. “对，恒成立”是“”的必要不充分条件D. 设，则的最小值为211.若关于x的不等式的解集为，则的值可以是( )A. B. C. D. 112.已知正实数a，b满足，则下列选项正确的是( )A. 的最大值为2B. 的最小值为C. 的最大值为3D. 的最小值为2三、填空题：本题共4小题，每小题5分，共20分。

2022年山东省青岛二中自主招生物理试题

2022年山东省青岛二中自主招生物理试题学校:___________姓名：___________班级：___________考号：___________一、单选题1．物理中这样定义“位移”，物体由初始位置A到终止位置B间的线段长度即位移的大小，由A指向B即位移的方向，速度定义为“物体通过的位移与发生这段位移所用时间的比值”，其方向与位移方向相同。

他采访了运输器材的卡车司机，得到了如下数据：汽车由器材站到达直线距离120km外的公园用了5h，卸货后原路返回，往返共用了12h，汽车上的导航记录本次运动总共走过的路程是480km。

据此以下分析正确的是（）A．汽车在本次运动的全过程中速度大小为20km/hB．汽车在去公园的过程中速度大小为48km/hC．汽车在由公园返回的过程中速度大小为24km/hD．汽车在本次运动的全过程中速度大小为0km/h二、多选题2．他找到一根匀质的、租细均匀的长木杆，在杆中间安装了水平转轴（忽略阻力），做成一个等臂的杠杆。

他又找了两个相同的厚壁气球及不计质量的细线，将充入空气后的气球分别挂在杠杆两端离转轴等距的地方，杠杆保持水平平衡。

一段时间后左侧气球因缓慢漏气瘪了，如图所示。

以下分析正确的是（）A．杠杆仍将保持水平平衡B．右侧气球受到空气的浮力较大，所以杠杆会向左倾斜C．若想让杠杆再次水平平衡，可将右侧气球的悬点向左移动D．若仅降低右侧气球内气体的温度，可能让杠杆再次水平平衡三、单选题3．他用冰制成一个焦距为f的凸透镜，将点亮的火炬模型、凸透镜、光屏等依图示次序放在光具座上组装成研究透镜成像规律的装置，以下判断正确的是（）A．移动火炬时，火炬移动的速度大于像移动的速度B．光屏上可以得到与火炬等大、正立的实像C．成清晰实像的时候，光屏与火炬之间的距离一定大于4fD．若固定火炬和光屏，仅移动它们之间的透镜，可能无法成清晰的实像4．闭合电路中的部分导体做切割磁感线运动时会严生感应电流。

2016年全国自主招生500强中学排行榜

2016年全国自主招生500强中学排行榜》名单排名省市学校名称1山东山东省泰安第一中学2山东山东省莱芜市第一中学3山东山东省实验中学4湖南湖南师大附中5河北石家庄市第二中学6湖南长沙市雅礼中学7河北保定市第一中学8山东临沂第一中学9山东山东省日照第一中学10湖南湖南省长沙市第一中学11湖南长郡中学12山东山东省青岛第五十八中学13重庆西南大学附属中学校14江苏南京师范大学附属中学15山东济宁市第一中学16山东山东省青岛第二中学17河北邯郸市第一中学18吉林东北师范大学附属中学19山东山东省聊城第一中学20河北衡水第一中学21辽宁大连市育明高级中学22河南郑州外国语学校23北京中国人民大学附属中学24四川四川省成都市树德中学25四川成都市第七中学26辽宁鞍山市第一中学27山东东平高级中学28河北临城县临城中学29湖南株洲市第二中学30山东巨野县第一中学31湖南宁乡县第一高级中学32河北张家口市第一中学33江苏南京市金陵中学34山东肥城市第一高级中学35湖南长沙市南雅中学36四川成都市第七中学高新校区37北京北京市顺义牛栏山第一中学38辽宁本溪市高级中学39四川四川省成都市石室中学40湖南益阳市第一中学41湖北华中师范大学第一附属中学42安徽蚌埠第二中学43山东山东省北镇中学44河北邢台市第一中学45安徽安徽省淮北市第一中学46湖南长沙市明德中学47山西山西省实验中学48黑龙江大庆第一中学49山东山东省泰安第二中学50四川四川省绵阳中学51河南郑州市第一中学52河北保定市第三中学53江苏江苏省扬州中学54山西太原市第五中学校55山东山东省宁阳第一中学56山东山东省青岛第九中学57辽宁本溪市第一中学58辽宁大连市第二十四中学59辽宁盘锦市高级中学60山东山东省聊城第三中学61湖南长沙麓山国际实验学校62山东东营市胜利第一中学63湖北武汉市第二中学64北京北京师范大学附属实验中学65山东山东省章丘市第四中学66山东临清市第一中学67河北河北衡水中学68山东济宁市兖州区第一中学69山西山西大学附属中学校70江苏江苏省如皋中学71河北石家庄市第一中学72安徽铜陵市第一中学73北京北京市十一学校74安徽合肥市第八中学75辽宁沈阳市第二中学76吉林吉林市第一中学校77河北唐山市第一中学78北京北京市第一O一中学79辽宁辽宁省实验中学80江苏江苏省泰兴中学81江苏无锡市第一中学82山东东营市第一中学83四川成都市实验外国语学校84山东山东师范大学附属中学85辽宁大连市第八中学86江苏江苏省盐城中学87河南洛阳市第一高级中学88山东山东省新泰市第一中学89吉林长春吉大附中实验学校90北京北京市第四中学91山东山东省泰安英雄山中学92四川四川省成都市第十二中学93四川四川省成都市石室中学北湖校区94四川四川省宜宾市第三中学校95四川成都外国语学校96重庆重庆市巴蜀中学校97安徽合肥市第一中学98安徽马鞍山市第二中学99湖南湘潭县第一中学100江苏江苏省镇江第一中学101山东莱芜市莱城区凤城高级中学102四川绵阳中学实验学校103湖北武汉市第六中学104江苏江苏省海门中学105陕西陕西省西安中学106四川成都树德中学（光华校区）107湖北湖北省宜昌市夷陵中学108山东济南市历城第二中学109江苏江苏省南通中学110四川遂宁市安居育才中学校111安徽安庆市第一中学112四川成都七中万达学校113四川四川省绵阳南山中学114山东肥城市泰西中学115安徽安徽省宿州市第二中学116北京北方交通大学附属中学117江苏常州市第一中学118河南河南省实验中学119北京清华大学附属中学120湖南长沙市周南中学121黑龙江哈尔滨师范大学附属中学122山东济宁市育才中学123辽宁辽宁师范大学附属中学124山东山东省潍坊第一中学125山东沂水县第一中学126北京北京大学附属中学127安徽安徽省滁州中学128安徽合肥市第六中学129湖北湖北省黄石市第二中学130江苏江苏省宜兴中学131山东莘县第一中学132四川成都市实验外国语学校（西区）133山东德州市第一中学134江苏南京师范大学附属中学江宁分校135江苏江苏省南菁高级中学136陕西西北工业大学附属中学137广东华南师范大学附属中学138江苏江苏省靖江高级中学139湖南浏阳市第一中学140河南郑州外国语新枫杨学校141北京北京理工大学附属中学142山西朔州市朔城区第一中学143安徽芜湖市第一中学144河南安阳市第一中学145辽宁东北育才学校高中部146山东肥城市第六高级中学147辽宁阜新市实验中学148山东武城县第二中学149湖北襄阳市第五中学150重庆重庆市第一中学校151山东邹平县第一中学152山东临沭第一中学153四川绵阳南山中学实验学校154贵州盘县第二中学155江苏扬州大学附属中学156山东淄博实验中学157江苏江苏省射阳中学158四川绵阳东辰国际学校159江苏江苏省常州高级中学160江苏江苏省启东中学161山东山东省济钢高级中学162北京首都师范大学附属中学163四川四川省宜宾市第一中学校164北京北京市第五中学165黑龙江大庆外国语学校166内蒙古自治区呼和浩特市第二中学167江苏南京市第一中学(高中）168山东山东省菏泽第一中学169山东泗水县第一中学170山东威海市第一中学171江苏徐州市第一中学172北京北京市第八中学173四川成都七中嘉祥外国语学校174江苏江苏省新海高级中学175江苏江苏省兴化中学176四川四川师范大学附属中学177山西忻州市第一中学校178重庆重庆南开中学179湖南鼎城区第一中学180湖南娄底市第三中学181山东寿光市第一中学182湖南株洲市南方中学183湖北武汉市武钢三中184湖北湖北省武昌实验中学185湖北黄冈中学186江苏江苏省常熟中学187辽宁辽河油田第一高级中学188山东山东省泰安第一中学（虎山路校区）189山东山东省郓城第一中学190浙江浙江省湖州中学191安徽安徽省宿城第一中学192辽宁阜新市高级中学193江苏江苏省苏州中学校194江苏江苏省宿迁中学195江苏江苏省镇江中学196山东山东省莒南第一中学197浙江台州市第一中学198湖北武汉市第十一中学199山东阳谷县第一中学200北京北京师范大学第二附属中学201北京北京市八一中学202北京北京市第二中学203河南南阳市第一中学校204黑龙江齐齐哈尔市实验中学205山东山东省青岛第一中学206山东莘县实验高级中学207新疆维吾尔自治区乌鲁木齐市第一中学208浙江浙江省瑞安中学209重庆重庆市第八中学校210辽宁东北育才双语学校211广东广东实验中学212湖南湖南师范大学附属中学213江苏江苏省天一中学214湖南冷水江市第一中学215黑龙江哈尔滨市第三中学校216江苏江苏省丹阳高级中学217浙江宁波市效实中学218广东深圳中学219安徽安徽省宣城中学220安徽安徽师范大学附属中学221北京北京汇文中学222山东东营市胜利第二中学223河北邯郸市第四中学224江苏江苏省阜宁中学225江苏江苏省淮阴中学226江苏江苏省梁丰高级中学227河南新乡市第一中学228安徽安徽省淮南第二中学229黑龙江大庆市实验中学230湖南衡阳市第八中学231江苏江苏省通州高级中学232山东山东省淄博第四中学233陕西陕西师范大学附属中学234四川四川省南充高级中学235陕西西安高新第一中学236北京北京师范大学附属中学237四川成都市铁路中学校238山东东营市河口区第一中学239湖南湖南广益实验中学240江苏南京市第十三中学241山东寿光现代中学242陕西西安市铁一中学243甘肃西北师范大学附属中学244山东章丘市第五中学245山东邹城市第一中学246辽宁大连理工大学附属高级中学247广西壮族自治区贵港市高级中学248辽宁锦州市锦州中学249山东莒县第一中学250山东利津县第一中学251山东青岛第三十九中学252天津天津市实验中学253湖南郴州市第一中学254江苏江苏省滨海中学255江苏江苏省江都中学256山东鄄城县第一中学257辽宁辽阳石油化纤公司高级中学258山东临沂第四中学259江苏南京市中华中学（高中）260四川郫县第一中犀浦校区261四川成都市第二十中学校262黑龙江哈尔滨市第九中学校263湖北湖北省沙市中学264江苏江苏省东台中学265江苏江苏省华罗庚中学266江苏江苏省泗洪中学267江西江西省景德镇一中268山东山东省日照实验高级中学269安徽萧县实验高级中学270浙江浙江省温州中学271安徽安徽省濉溪中学272河北黄骅市中学273江苏江苏省如东高级中学274辽宁辽宁省实验中学营口分校275山东临沭县实验中学276江苏南京市第二十九中学(高中部)277河南南阳市第五中学校278四川四川省成都市新都一中279山西太原市第十二中学校280天津天津市第一中学281江苏无锡市大桥实验学校282湖北襄阳市第四中学283北京北京市第三十五中学284江西赣州中学285江苏江苏省运河中学286河南焦作市第一中学287湖南娄底市第一中学288河南汝阳县第一高级中学289天津天津市南开中学290湖北武汉市第三中学291浙江浙江省桐乡市高级中学292湖南湖南省长沙县实验中学293江苏江苏省邗江中学294山东新泰中学295江苏新沂市第一中学296湖南长沙市实验中学297河南安阳正一中学298黑龙江大庆铁人中学299湖南湖南省湘潭市第一中学300四川四川省广元中学301山西太原成成中学校302河北威县第一中学303山西盐湖区运城中学校304山东济南市长清第一中学305江苏江苏省太仓高级中学306福建厦门大学附属实验中学307山西山西省运城市康杰中学308浙江浙江省杭州高级中学309广东中山纪念中学310安徽安徽省阜阳第一中学311安徽当涂县第一中学312安徽固镇县第一中学313辽宁葫芦岛市第一高级中学314上海华东师范大学第二附属中学315江苏江苏省丰县中学316江苏江苏省高淳高级中学317江苏江苏省泰州中学318山东莒县第二中学319山东聊城市水城中学320山东青岛经济技术开发区第一中学321四川四川省南充高级中学嘉陵校区322四川四川省郫县第一中学323湖北武汉中学324北京北京市第一七一中学325湖南湖南省隆回第一中学326安徽蒙城县第一中学327陕西西安交通大学附属中学328河南许昌高级中学329山东曹县第一中学330辽宁东北育才学校331内蒙古自治区鄂尔多斯市第一中学332福建福建省福州第三中学333河北河北乐亭第一中学334湖南湖南省长沙县第一中学335湖北江汉油田广华中学336湖南浏阳市田家炳实验中学337山东青岛市胶州市第一中学338四川四川省成都市龙泉驿区第一中学校339四川成都树德中学（外国语校区）340河北河北定州中学341湖南衡山县岳云中学342江苏江苏省沛县中学343河北曲周第一中学344山东山东省蒙阴第一中学345湖南邵东县第一中学346天津天津市新华中学347安徽安徽省六安第一中学348内蒙古自治区包钢第一中学349内蒙古自治区包头市第九中学350四川成都市华阳中学351辽宁大连市第二十三中学352辽宁丹东市第二中学353福建福建省漳州第一中学354广西壮族自治区广西师范大学附属外国语学校355黑龙江哈尔滨市第三中学校群力校区356安徽合肥一六八中学357湖北湖北省天门中学358安徽黄山市屯溪第一中学359浙江宁波中学360河南商丘市第一高级中学361四川四川省双流县中学362河北唐山市第二中学363天津天津市武清区杨村第一中学364陕西西安市曲江第一中学365山东阳信县第二高级中学366河南郑州市第七中学367河南郑州市第十一中学368贵州遵义市第四中学369江苏江苏省句容高级中学370江苏江苏省震泽中学371江苏金陵中学河西分校372河南洛阳理工学院附属中学373河南平顶山市第一中学374山东山东省垦利第一中学375山东山东省烟台第四中学376湖北武汉外国语学校377浙江浙江省杭州第二中学378安徽安徽省界首市第一中学379山东费县第二中学380河北河北易县中学381河南河南师范大学附属中学382山东莱阳市第一中学383江西萍乡中学384河北秦皇岛市第一中学385山东青岛市胶州市实验中学386湖北十堰市第一中学387吉林四平市第一高级中学388湖南桃江县第一中学389河南项城市第一高级中学390安徽安徽省亳州市第一中学391安徽安徽省宁国中学392湖南北京师范大学株洲附属学校393辽宁大连市第十二中学394福建福建省福州第一中学395湖北湖北省水果湖高级中学396湖南湖南省娄底市第五中学397湖南湖南省永州市第一中学398山东济南市历城第一中学399江苏江苏省昆山中学400江苏江苏省锡山高级中学401山西晋城市第一中学校402广西壮族自治区柳州高级中学403江西南昌市第二中学404山东山东省潍坊第四中学405四川四川省成都市盐道街中学406河北张家口市宣化第一中学407河北张家口市正博高级中学408山西大同市第一中学校409湖北恩施市第一中学410安徽肥东县第一中学411山东费县实验中学412湖南湖南省地质中学413湖南湖南省永州市第四中学414安徽淮北市实验高级中学415江苏江苏省姜堰中学416江苏江苏省沭阳高级中学417江西江西省九江第一中学418黑龙江齐齐哈尔市齐齐哈尔中学419山东山东省广饶县第一中学420山东山东省莱芜市第四中学421山东山东省沂南第二中学422浙江绍兴市第一中学423安徽寿县第一中学424四川四川省成都市玉林中学425江苏泰兴市第一高级中学426河南卫辉市第一中学427湖北武汉钢铁公司第三子弟中学428江苏盐城市第一中学429安徽安徽省舒城中学430安徽安庆市第二中学431辽宁鞍山市第八中学432北京北京市第八十中学433北京北京市第一六一中学434湖南常德芷兰实验学校435河北邯郸市致远中学436河南河南省南阳市油田第一中学437江苏江苏省灌南高级中学438江苏江苏省仪征中学439吉林辽源市第五中学校440广西壮族自治区南宁市第三中学441天津天津市宝坻区第一中学442陕西咸阳彩虹学校443安徽安徽省淮南第一中学444北京北京市中关村中学445山东冠县第一中学446河北邯郸市第三中学（河北邯郸外国语学校）447河南河南省驻马店高级中学448湖南衡阳市第一中学449湖北湖北省仙桃中学450江苏江苏省前黄高级中学451江苏江苏省苏州实验中学452江西江西省会昌中学453江苏南京师范大学附属扬子中学454山东青岛市崂山区第一中学455山东山东省冠县武训高级中学456山东山东省沂南第一中学457湖北武汉市洪山高级中学458湖北宜昌市第一中学459河北张家口市第四中学460新疆维吾尔自治区兵团二中461河北磁县第一中学462山东东明县第一中学463福建福建省厦门第一中学464河南河南省开封高级中学465湖北湖北省荆州中学466山东济宁市兖州区实验高级中学467江苏江苏省赣榆高级中学468江苏江苏省溧水高级中学469江苏江苏省睢宁高级中学470湖南涟源市第一中学471山东山东省泰山中学472山东山东省诸城第一中学473四川四川省彭州中学474四川西南交通大学附属中学475湖北咸丰县第一中学476湖北宜昌市葛洲坝中学477山东枣庄市第一中学478吉林长春市十一高中479浙江浙江省杭州学军中学480北京中央民族大学附属中学481山东淄博市临淄中学482陕西宝鸡中学483内蒙古自治区北京师范大学乌兰察布集宁附属中学484辽宁大连市第一中学485河北高碑店市第一中学486河北河北正中实验中学487江苏江苏省清江中学488江苏江苏省泗阳中学489江西江西省吉安市第一中学490湖北荆门市龙泉中学491辽宁辽阳市第一高级中学492贵州盘县第一中学493山东山东省枣庄市第八中学494浙江绍兴市柯桥区柯桥中学495四川四川省成都列五中学496四川四川省成都市石室天府中学497江苏苏州工业园区星海实验中学498山西太原市外国语学校499天津天津市耀华中学500湖北武汉市新洲区第一中学500四川西昌市第一中学500湖南新化县第一中学500辽宁义县高级中学500云南玉溪第一中学500湖南长沙市望城区第一中学。

2016年自主招生备考讲座

2021/3/5
山东省平度第一中学物理组
4
2021/3/5
山东省平度第一中学物理组
5
一中2014年自招情况
1 2 3 4 5 6 7
许展玮通过清华自招耿佳雨通过北大自招李子龙通过北大自招林贞贞通过复旦自招刘蒙露通过山大自招万大千通过山大自招焦思涵通过山大自招
2021/3/5
山东省平度第一中学物理组
38
2021/3/5
山东省平度第一中学物理组
39
什么样的学生适合报考自主招生 40
• 自主招生考
•
与
•
高考矛盾吗？
2021/3/5
山东省平度第一中学物理组
41
备战自主招生考与高考矛盾吗？
• 1.自主招生考的难度、深度、广度都超过6月高考； • 2.自主招生考的加深、拓展都是在高考的基础上延展开来的； • 3.参加自主招生考“站得高，看得远”，有利于高考； • 4.自主招生考与高考完全可以做到“两不误，双保险”！
84
其长安大学
27
他
陕西师范大学
4
西北农林科技大学
59
2021/3/5
76
华东师范大学
3
19
上海外国语大学
2
6
上海财经大学
1
145
苏州大学
24
20
南京航空航天大学 36
14
南京理工大学
12
8
中国矿业大学
129
23
河海大学
28
24
江南大学
52
30
南京农业大学
35
32
中国药科大学
32
其他
59

【考试必备】2018-2019年最新青岛二中初升高自主招生考试数学模拟精品试卷【含解析】【5套试卷】

2018-2019年最新青岛二中自主招生考试数学模拟精品试卷（第一套）考试时间：90分钟总分：150分一、选择题（本题有12小题，每小题3分，共36分）下面每小题给出的四个选项中，只有一个是正确的，请你把正确选项前的字母填涂在答题卷中相应的格子内．注意可以用多种不同的方法来选取正确答案．1．下列事件中，必然事件是( )A．掷一枚硬币，正面朝上B．a是实数，|a|≥0C．某运动员跳高的最好成绩是20.1米D．从车间刚生产的产品中任意抽取一个，是次品2、如图是奥迪汽车的标志，则标志图中所包含的图形变换没有的是（）A．平移变换 B．轴对称变换 C．旋转变换 D．相似变换3．如果□３3ab＝3a2b，则□内应填的代数式()A．ab B．3ab C．a D．3a4．一元二次方程x(x－2)＝0根的情况是( )A．有两个不相等的实数根B．有两个相等的实数根C．只有一个实数根D．没有实数根5、割圆术是我国古代数学家刘徽创造的一种求周长和面积的方法：随着圆内接正多边形边数的增加，它的周O长和面积越来越接近圆周长和圆面积，“割之弥细，所失弥少，割之又割，以至于不可割，则与圆周合体而无所失矣”。

试用这个方法解决问题：如图，⊙的内接多边形周长为 3 ，⊙O的外切多边形周长为3.4，则下列各数中与此圆的周长最接近的是（）A．6 B．8 C．10 D．176、今年5月，我校举行“庆五四”歌咏比赛，有17位同学参加选拔赛，所得分数互不相同，按成绩取前8名进入决赛，若知道某同学分数，要判断他能否进入决赛，只需知道17位同学分数的（）A.中位数B.众数C.平均数D.方差7．如图，数轴上表示的是某不等式组的解集，则这个不等式组可能是( )A.x＋1>0，x－3>0B.x＋1>0，3－x>0C.x＋1<0，x－3>0D.x＋1<0，3－x>08．已知二次函数的图象(0≤x≤3)如图所示，关于该函数在所给自变量取值范围内，下列说法正确的是( )A．有最小值0，有最大值 3B．有最小值－1，有最大值0C．有最小值－1，有最大值 3D．有最小值－1，无最大值9．如图，矩形OABC的边OA长为2 ，边AB长为1，OA在数轴上，以原点O为圆心，对角线OB的长为半径画弧，交正半轴于一点，则这个点表示的实数是( )水平面主视方向A ．2.5B ．2 2C. 3 D. 510．青岛二中广场有一喷水池，水从地面喷出，如图，以水平地面为x 轴，出水点为原点，建立平面直角坐标系，水在空中划出的曲线是抛物线y ＝－x 2＋4x (单位：米)的一部分，则水喷出的最大高度是( )A ．4米B ．3米C ．2米D ．1米11、两个大小不同的球在水平面上靠在一起，组成如图所示的几何体，则该几何体的左视图是（）（A ）两个外离的圆（B ）两个外切的圆（C ）两个相交的圆（D ）两个内切的圆12．已知二次函数y ＝ax 2＋bx ＋c (a ≠0)的图象如图所示，有下列结论：①b 2－4ac >0；②abc >0；③8a ＋c >0；④9a ＋3b ＋c <0.其中，正确结论的个数是( )A ．1B ．2C ．3D ．4 二、填空题（本小题有6小题，每小题4分，共24分）要注意认真看清题目的条件和要填写的内容，尽量完整地填写答案13．当x ______时，分式13－x有意义．14．在实数范围内分解因式：2a 3－16a ＝________.15．在日本核电站事故期间，我国某监测点监测到极微量的人工放射性核素碘－131，其浓度为0.0000963贝克/立方米．数据“0.0000963”用科学记数法可表示为________．16．如图，C岛在A岛的北偏东60°方向，在B岛的北偏西45°方向，则从C岛看A、B两岛的视角∠ACB＝________.17．若一次函数y＝(2m－1)x＋3－2m的图象经过一、二、四象限，则m的取值范围是________．18．将一些半径相同的小圆按如图所示的规律摆放，请仔细观察，第n个图形有________个小圆. (用含n的代数式表示)三、解答题（本大题7个小题，共90分）19．（本题共2个小题，每题8分，共16分）（1）.计算：(2011－1)0＋18sin45°－2－1（2）．先化简，再计算：x2－1 x2＋x÷x－2x－1x，其中x是一元二次方程x2－2x－2＝0的正数根．20．（本题共2个小题，每题6分，共12分）（1）.如图，用两段等长的铁丝恰好可以分别围成一个正五边形和一个正六边形，其中正五边形的边长为(x2＋17) cm，正六边形的边长为(x2＋2x) cm(其中x>0)．求这两段铁丝的总长．（2）．描述证明海宝在研究数学问题时发现了一个有趣的现象：将上图横线处补充完整，并加以证明．21．（本题12分）某初中学校欲向高一级学校推荐一名学生，根据规定的推荐程序：首先由本年级200名学生民主投票，每人只能推荐一人(不设弃权票)，选出了票数最多的甲、乙、丙三人．票数结果统计如图一：其次，对三名候选人进行了笔试和面试两项测试．各项成绩如下表所示：测试项目测试成绩/分测试成绩/分测试成绩/分甲乙丙笔试929095面试859580图二是某同学根据上表绘制的一个不完全的条形图．请你根据以上信息解答下列问题：(1)补全图一和图二；(2)请计算每名候选人的得票数；(3)若每名候选人得一票记1分，投票、笔试、面试三项得分按照2∶5∶3的比确定，计算三名候选人的平均成绩，成绩高的将被录取，应该录取谁？22．（本题12分）如图，已知直线AB与x轴交于点C，与双曲线y＝kx交于A(3，203)、B(－5，a)两点．AD⊥x轴于点D，BE∥x轴且与y轴交于点E.(1)求点B的坐标及直线AB的解析式；(2)判断四边形CBED的形状，并说明理由．23、（本题12分）如图，△ABC内接于⊙O，且AB=AC，点D在⊙O上，AD⊥AB于点A， AD与BC交于点E，F在DA的延长线上，且AF=AE．（1）试判断BF与⊙O的位置关系，并说明理由；(2）若⊙O的半径为2．∠F=60，求弓形AB的面积24．（本题12分）已知双曲线y ＝k x与抛物线y ＝ax 2＋bx ＋c 交于A (2,3)、B (m,2)、c (－3，n )三点．(1)求双曲线与抛物线的解析式；(2)在平面直角坐标系中描出点A 、点B 、点C ，并求出△ABC 的面积．O FEABDC25．（本题共2个小题，每题7分，共14分）（1）观察下列算式：① 1 3 3－22＝3－4＝－1② 2 3 4－32＝8－9＝－1③ 3 3 5－42＝15－16＝－1④ __________________________……(1)请你按以上规律写出第4个算式；(2)把这个规律用含字母的式子表示出来；(3)你认为(2)中所写出的式子一定成立吗？并说明理由．（2）如图，在直角坐标系中，O为坐标原点. 已知反比例函数y＝kx(k>0)的图象经过点A(2，m)，过点A作AB⊥x轴于点B，且△AOB的面积为1 2 .(1)求k和m的值；(2)点C(x，y)在反比例函数y＝kx的图象上，求当1≤x≤3时函数值y的取值范围；(3)过原点O的直线l与反比例函数y＝kx的图象交于P、Q两点，试根据图象直接写出线段PQ长度的最小值.2018-2019年最新青岛二中自主招生考试数学模拟精品试卷答案（第一套）1.答案 B解析据绝对值的意义，一个数的绝对值是一个非负数，|a|≥0.2.C3.答案 C解析□＝3a2b÷3ab＝a.4.答案 A解析x(x－2)＝0，x＝0或x－2＝0，x1＝0，x2＝2，方程有两个不相等的实数根．5.C6.A7.答案 B解析观察数轴，可知－1<x<3，只有x＋1>0，3－x>0的解集为－1<x<3.8.答案 C解析当0≤x≤3时，观察图象，可得图象上最低点(1，－1)，最高点(3,3)，函数有最小值－1，最大值3.9.答案 D解析在Rt△OAB中，∠OAB＝90°，所以OB＝12＋22＝ 510.答案 A解析y＝－x2＋4x＝－(x－2)2＋4，抛物线开口向下，函数有最大值4.11.D12.答案 D解析由图知：抛物线与x 轴有两个不同的交点，则△＝b 2－4ac >0，故①正确．抛物线开口向上，得a >0；又对称轴为直线x ＝－b2a＝1，b ＝－2a <0.抛物线交y 轴于负半轴，得c <0，所以abc >0，②正确．根据图象，可知当x ＝－2时，y >0，即4a －2b ＋c >0，把b ＝－2a 代入，得4a －2(－2a )＋c ＝8a ＋c >0，故③正确．当x ＝－1时，y <0，所以x ＝3时，也有y <0，即9a ＋3b ＋c <0，故④正确．二．填空题13.答案≠3解析因为分式有意义，所以3－x ≠0，即x ≠3. 14.答案2a (a ＋2 2)(a －22)15.答案9.63310－5解析0.0000963＝9.63310－5.16.答案105°解析如图，∵(60°＋∠CAB )＋(45°＋∠ABC )＝180°，∴∠CAB ＋∠ABC ＝75°，在△ABC 中，得∠C ＝105°.17.答案m <12解析因为直线经过第一、二、四象限，所以2m －1<0，3－2m >0，解之，得m <12.18.答案n (n ＋1)＋4或n 2＋n ＋4解析第1个图形有2＋4＝(132＋4)个小圆，第2个图形6＋4＝(233＋4)个小圆，第3个图形有12＋4＝(334＋4)个小圆，……第n 个图形有[n (n ＋1)＋4]个小圆．三、解答题（本大题7个小题，共90分）19．（本题共2个小题，每题8分，共16分）（1）.解：原式＝1＋32322－12＝312.（2）解：原式＝x＋1x－1x x＋1÷x2－2x＋1x＝x－1x2xx－12＝1x－1.解方程得x2－2x－2＝0得，x1＝1＋3>0，x2＝1－3<0.当x＝1＋3时，原式＝11＋3－1＝13＝33.20.（1）.解：由已知得，正五边形周长为5(x2＋17) cm，正六边形周长为6(x2＋2x) cm.因为正五边形和正六边形的周长相等，所以5(x2＋17)＝6(x2＋2x)．整理得x2＋12x－85＝0，配方得(x＋6)2＝121，解得x1＝5，x2＝－17(舍去)．故正五边形的周长为53(52＋17)＝210(cm)．又因为两段铁丝等长，所以这两段铁丝的总长为420 cm.答：这两段铁丝的总长为420 cm.（2）解：如果ab＋ba＋2＝ab，那么a＋b＝ab.证明：∵ab＋ba＋2＝ab，∴a2＋b2＋2abab＝ab，∴a2＋b2＋2ab＝(ab)2，∴(a＋b)2＝(ab)2，∵a>0，b>0，a＋b>0，ab>0，∴a＋b＝ab.21.解：(1)乙30%；图二略．(2)甲的票数是：200334%＝68(票)，乙的票数是：200330%＝60(票)，丙的票数是：200328%＝56(票)，(3)甲的平均成绩：x 1＝6832＋9235＋85332＋5＋3＝85.1，乙的平均成绩：x 2＝6032＋9035＋95332＋5＋3＝85.5，丙的平均成绩：x 3＝5632＋9535＋80332＋5＋3＝82.7，∵乙的平均成绩最高，∴应该录取乙．22.解：(1)∵双曲线y ＝k x 过A (3，203)，∴k ＝20.把B (－5，a )代入y ＝20x，得a ＝－4.∴点B 的坐标是(－5，－4). 设直线AB 的解析式为y ＝mx ＋n ，将A (3，203)、B (－5，－4)代入得，203＝3m ＋n ，－4＝－5m ＋n ，解得：m ＝43，n ＝83.∴直线AB 的解析式为：y ＝43x ＋83.(2)四边形CBED 是菱形．理由如下：易求得点D 的坐标是(3,0)，点C 的坐标是(－2,0)．∵BE //x 轴，∴点E 的坐标是(0，－4)．而CD ＝5, BE ＝5, 且BE //CD . ∴四边形CBED 是平行四边形. 在Rt △OED 中，ED 2＝OE 2＋OD2,∴ED ＝32＋42＝5，∴ED ＝CD . ∴四边形CBED 是菱形.23.解：证明：（1）BF 与⊙O 相切，连接OB 、OA ，连接BD ，∵AD ⊥AB ，∴∠BAD=90°，∴BD 是直径，∴BD 过圆心. ∵AB=AC ，∴∠ABC=∠C ，∵∠C=∠D ，∴∠ABC=∠D ，∵AD ⊥AB ，∴∠ABD+∠D=90°，∵AF=AE ，∴∠EBA=∠FBA ，∴∠ABD+∠FBA=90°，∴OB ⊥BF ，∴BF 是⊙O 切线.(2)∵∠F=600，∴∠D=900-∠F=300,∴∠AOB=600,∴△AOB 为等边三角形..S 弓形AB=33224336026022.24.解：(1)把点A (2,3)代入y ＝kx得：k ＝6.∴反比例函数的解析式为：y ＝6x.把点B (m,2)、C (－3，n )分别代入y ＝6x得：m ＝3，n ＝－2.把A (2,3)、B (3,2)、C (－3，－2)分别代入y ＝ax 2＋bx ＋c 得：4a ＋2b ＋c ＝3，9a ＋3b ＋c ＝2，9a －3b ＋c ＝－2，解之得a ＝－13，b ＝23，c ＝3.∴抛物线的解析式为：y ＝－13x 2＋23x ＋3.(2)描点画图(如图)：S △ABC ＝12(1＋6)35－123131－123634＝352－12－12＝5.25.（1）.解：(1)436－52＝24－25＝－1.(2)答案不唯一．如n ()n ＋2－()n ＋12＝－1.(3)n ()n ＋2－()n ＋12＝n 2＋2n －()n 2＋2n ＋1＝n 2＋2n －n 2－2n －1 ＝－1. 所以一定成立．（2）解：(1)∵A (2，m )，∴OB ＝2，AB ＝m ，∴S △A OB ＝12OB 2AB ＝12323m ＝12，∴m ＝12.∴点A 的坐标为(2，12)．把A (2，12)代入y ＝k x ，得12＝k2，∴k ＝1.(2)∵当x ＝1时，y ＝1；当x ＝3时，y ＝13，又∵反比例函数y ＝1x在x >0时，y 随x 的增大而减小，∴当1≤x ≤3时，y 的取值范围为13≤y ≤1.(3) 由图象可得，线段PQ 长度的最小值为 22.。

青岛二中自主招生物理试题及答案

青岛⼆中⾃主招⽣物理试题及答案青岛⼆中2016年⾃主招⽣考试物理试题欢迎同学们参加青岛⼆中的⾃主招⽣考试，请认真阅读下列说明：1、请将答案书写在答题卡上指定区域，在本试卷上答题⽆效；2、请按每⼩题的要求做答，作图题请⽤铅笔或中性笔画图；简答题要⾔简意赅；计算题解答时请写出必要的⽅程式和重要的演算步骤。

有数值计算的题，答案中必须明确写出数值和单位。

第⼀部分：物理与校园（本部分含9⼩题，共48分，请按各⼩题要求作答）1．（4分）图1为青岛⼆中校园内照⽚（1）图中有禁鸣标志，禁鸣是在哪个环节控制噪声？（2）图中有限速标志，按此规定，汽车在学校沿环路⾏驶1km⾄少需要多少秒？图12．（4分）学校元旦晚会前，⼩明同学不⼩⼼松开了⼀只充满⽓但未扎⼝的⽓球，⽓球飞出去了。

⼩明认为这个过程中⽓球除受重⼒外，不再受到其它物体的作⽤。

⼩明想的是否正确？如不正确，⽓球的施⼒物体是什么？3．（4分）我校每年都要举⾏⾜球⽐赛，⼀次⽐赛中⼩明同学踢出的任意球绕过⼈墙，进⼊球门，这类球俗称⾹蕉球。

假设⾜球的轨迹如图2所⽰。

你认为⾜球飞⾏过程中左侧还是右侧相对空⽓的速度⼤？4．（4分）为保证学⽣的安全，校内安装的摄像头（如图3）内部光学元件的作⽤相当于凸透镜。

如果在⼀块玻璃中有⼀形状如凸透镜的空⽓泡，如图4所⽰，完成它的光路图。

图2 图3 图4 5．（4分）⽆之海及钟楼是学校⼭海⽂化的表征，湖中倒映钟楼，恰似⼀个平⾯镜的影像（如图5）。

上述情形可简化为下⾯模型，如图6中P为⼀不透光的箱⼦，点光源在S处，试⽤作图法画出点光源在箱⼦右侧所照亮地⾯的光路图，并在地⾯上⽤阴影线段标出范围。

图5 图6 图76．（6分）教学楼前的达礼路是⼀段粗糙斜⾯，如图7所⽰。

假设斜⾯长为L，与⽔平⾯的夹⾓θ=30o，将重100N的物体沿斜⾯匀速推上，若斜⾯的机械效率为η=80%，物体所受斜⾯的摩擦⼒多⼤？7．（6分）教学楼每层设有电热⽔器（如图8），若该电热⽔器的铭牌如图9所⽰，请计算把20o C的⼀箱⽔烧开需要多长时间?（⽔的⽐热容c =4.2×103J/kg·o C,⽔的密度ρ=1.0×103kg/m3）图8 图98．（8分）礼堂顶灯设计美轮美奂（如图10），如果某部分彩灯电路如图11所⽰，电源电压为3.0V，L1、L2、L3为三个相同规格的⼩灯泡，⼩灯泡的伏安特性曲线如图12所⽰．当开关闭合后，求：（2）L1消耗的功率多⼤？9．（8分）⽆之海是⼀个⽔⽣动植物的乐园，每年都会在湖内放养鱼苗。

2021年山东省青岛市第二中学自主招生物理试题(含答案)

2021年山东省青岛二中自主招生物理试题一、填空题（共7小题，每小题3分，满分21分）1．（3分）历史攻关十余载，一朝升空即告成。

“天问一号”带着民族的寄托与希望，踏上了我国探索火星的征程。

“天问一号”飞船由“长征五号”运载火箭发射升空，在飞行过程中，请回答以下问题：（1）火箭刚刚发射处于加速上升阶段时，其动能增大、重力势能、机械能。

（2）火箭在大气中加速到较高速度后，整流罩会剧烈发热。

造成发热的主要原因是。

（3）火箭脱离大气后，与飞船分离，之后进入地火转移轨道。

在转移过程中，发动机即使关闭，飞船也会向火星飞去，原因是。

2．（3分）火星车在火星表面行进时遇一障碍物，通过车顶部的射灯，投下障碍物的影子，原理如图。

灯距火星表面的高度AB为H，通过传感器测得AD的长度为l，影子DE的长为x，则障碍物的高度h为多少？3．（3分）重力常数是影响行星环境的关键参数之一。

在测定行星重力常数时，经常用到单摆（将小球用长度远大于小球直径的轻细线悬挂在一个固定位置的装置）。

下列数据是研究单摆的周期T与摆长L（从悬点到小球中心的距离）的关系时测得的。

（1）请根据这些数据分析T与L成正比还是与成正比？T（s） 1.31 1.42 1.52 1.56 1.73 1.84 1.92L（m）0.420.500.570.600.720.840.92（）0.650.710.7550.770.850.920.96（2）如图，长为l的细绳下方悬挂一个小球a，绳的另一端固定在天花板上O点处，在O点正下方的O′处有一细铁钉。

将小球向右拉开，使细绳与竖直方向成一小角度后由静止释放并开始计时。

当小球a摆至最低位置时，细绳会受到铁钉的阻挡，在此瞬间小球速度大小不变（不计空气阻力）。

①对比在O′处无细铁钉与O′处有细铁钉小球的运动情况，小球两次达到的最大高度是否相同？请说明原因。

②设O′处无细铁钉，小球从图示位置开始释放到第一次回到初位置的时间为T1；O′处有细铁钉时，小球从图示位置开始释放到第一次回到初位置的时间为T2，则T1：T2＝。

山东省青岛第二中学2024-2025学年高二上学期第一次月考数学试题

山东省青岛第二中学2024-2025学年高二上学期第一次月考数学试题一、单选题1．已知空间向量()1,3,5a =-r ，()2,,b x y =r ，且//a b r r ，则x y -=（）A ．16-B ．16C ．4D ．4-2．已知点()2,3A -，()3,2B --，若过点()1,1P -的直线与线段AB 相交，则该直线斜率的取值范围是（）A ．32,,43⎛⎤⎡⎫-∞-+∞ ⎪⎥⎢⎝⎦⎣⎭U B ．][43,,32⎛⎫-∞-⋃+∞ ⎪⎝⎭ C ．34,23⎡⎤-⎢⎥⎣⎦D ．43,32⎡⎤-⎢⎥⎣⎦ 3．已知空间向量()1,,2a n =r ，()2,1,2b =-r ，若3a b -r r 与b r 垂直，则a r 等于（）A B C D ．24．设A ，B 为两个随机事件，以下命题正确的为（）A ．若A ，B 是对立事件，则()1P AB =B ．若A ，B 是互斥事件，11(),()32P A P B ==，则1()6P A B += C ．若11(),()32P A P B ==，且1()3P AB =，则A ，B 是独立事件 D ．若A ，B 是独立事件，12(),()33P A P B ==，则1()9P AB = 5．已知点()0,1P -关于直线10x y -+=对称的点Q 在圆22:50C x y mx +++=上，则m =（） A ．4 B ．5 C ．-4 D ．-56．连掷两次骰子得到的点数分别为m 和n ，记向量(),a m n =v 与向量()1,1b =-v 的夹角为θ，则0,2πθ⎛⎤∈ ⎥⎝⎦的概率是（） A ．512 B ．12 C ．712D ．56 7．边长为1的正方形ABCD 沿对角线AC 折叠，使14AD BC ⋅=u u u r u u u r ，则三棱锥D ABC -的体积为（）A B C D 8．已知空间向量a r ，b r ，c r 两两的夹角均为60o ，且2a b ==r r ，4c =r .若向量x r ，y r 满足()x x a x b ⋅+=⋅r r r r r ，()y y a y c ⋅+=⋅r r r r r ，则x y -r r 的最大值是（）A ．1+B ．1C ．D ．2二、多选题9．下列说法正确的是（）A ．8个数据的平均数为5，另3个数据的平均数为7，则这11个数据的平均数是6111B ．若样本数据1x ，2x ，L ，10x 的平均数为2，则数据121x -，221x -，L ，1021x -的平均数为3C ．一组数据4，3，2，6，5，8的60%分位数为6D ．某班男生30人、女生20人，按照分层抽样的方法从该班共抽取10人答题.若男生答对题目的平均数为10，方差为1；女生答对题目的平均数为15，方差为0.5，则这10人答对题目的方差为6.810．已知m ∈R ，若过定点A 的动直线1:20l x my m -+-=和过定点B 的动直线2:420l mx y m +-+=交于点P （P 与A ，B 不重合），则以下说法正确的是（）A ．B 点的坐标为()2,4-B ．22PA PB +为定值C ．PAB S V 最大值为252D ．2PA PB +的最大值为11．在棱长为1的正方体1111ABCD A B C D -中，1BP xBB yBC =+u u u r u u u r u u u r ，x ，()0,1y ∈，11AQ z AC =u u u r u u u r ，[]0,1z ∈，若直线1A P 与11A B 的夹角为45o ，则下列说法正确的是（）A ．线段1A PB 1AQ PQ +的最小值为1C ．对任意点P ，总存在点Q ，使得1⊥D Q CPD ．存在点P ，使得直线1A P 与平面11ADD A 所成的角为60o三、填空题12．已知()11,0,1n =-u r ，()2,3,2n m =-u u r ，()30,1,1n =-u u r ，若{}123,,n n n u r u u r u u r 不能构成空间的一个基底，则m =.13．已知半径为1的圆经过点()3,4，则其圆心到直线3430x y --=距离的最大值为. 14．在长方体1111ABCD A B C D -中，已知异面直线1AC 与11B C ，1AC 与11C D 所成角的大小分别为60o 和45o ，E 为1CC 中点，则点E 到平面1A BC 的距离为.15．平面直角坐标系中，矩形的四个顶点为，O 0,0 ，()8,0A ，()8,6B ，C 0,6 ，光线从OA 边上一点()04,0P 沿与x 轴正方向成θ角的方向发射到AB 边上的1P 点，被AB 反射到BC 上的2P 点，再被BC 反射到OC 上的3P 点，最后被OC 反射到x 轴上的()4,0P t 点，若()4,6t ∈，则tan θ的取值范围是.四、解答题16．已知直线()1:220l x m y +-=，2:220l mx y +-=，且满足12l l ⊥，垂足为C .(1)求m 的值及点C 的坐标.(2)设直线1l 与x 轴交于点A ，直线2l 与x 轴交于点B ，求ABC V 的外接圆方程. 17．在信道内传输0，1信号，信号的传输相互独立.发送0时，收到1的概率为()1101p p <<，收到0的概率为11p -；发送1时，收到0的概率为()2201p p <<，收到1的概率为21p -.现有两种传输方案：单次传输和三次传输.单次传输是指每个信号只发送1次，三次传输是指每个信号重复发送3次.收到的信号需要译码，译码规则如下：单次传输时，收到的信号即为译码（例如，若收到1，则译码为1，若收到0，则译码为0）；三次传输时，收到的信号中出现次数多的即为译码（例如，若依次收到1，0，1，则译码为1，若依次收到1，1，1，则译码为1）.(1)已知13p 4=，223p =，（i ）若采用单次传输方案，重复发送信号0两次，求至少收到一次0的概率；（ii ）若采用单次传输方案，依次发送0，0，1，判断事件“第三次收到的信号为1”与事件“三次收到的数字之和为2”是否相互独立，并说明理由；(2)若发送1，采用三次传输方案时译码为0的概率不大于采用单次传输方案时译码为0的概率，求2p 的取值范围.18．如图，四面体ABCD 中，ABC V 为等边三角形，且2AB =，ADC △为等腰直角三角形，且90ADC ∠=o .(1)当BD（i ）求二面角D AC B --的正弦值；（ii ）当P 为线段BD 中点时，求直线AD 与平面APC 所成角正弦值；(2)当2BD =时，若()01DP DB λλ=<<u u u r u u u r ，且PH ⊥平面ABC ，H 为垂足，CD 中点为M ，AB中点为N ；直线MN 与平面APC 的交点为G ，当三棱锥P ACH -体积最大时，求MG GN的值.。

2016年招生计划和安排

附件12016年初中学业水平考试安排附件22016年市内三区普通高中报名要求一、网上志愿填报（一）报名时间。

5月19日（星期四）8:00-5月21日（星期六）20:00（二）网上志愿填报网址。

青岛市初中学业水平考试（高中阶段学校招生）管理平台（/）（三）有关要求。

1.考生须在规定的时间内登陆报名网址进行报名。

2.考生网上报名需选择自己的报考志愿（含是否服从分配）、填写监护人的有关信息和考生的其他信息。

其中考生第一志愿、监护人有关信息、联系电话、家庭住址、邮政编码等信息为必填内容。

3.考生报名信息填报完成并确认提交后，应同时打印《青岛市初中学业水平考试（高中阶段学校招生）网上报名信息表》。

普通高中志愿填报后不能再修改。

4.网上报名结束后，考生须在规定时间内，持相关材料到第一志愿普通高中学校现场确认报名。

届时，学生加分优待项目信息由第一志愿学校录入。

5.考生如对网上报名系统信息有异议（不含普通高中志愿信息），可在现场确认时提出，由第一志愿学校受理。

二、现场确认（一）普通高中现场确认报名地点及时间。

1.地点：第一志愿普通高中学校。

2.时间：5月22日（星期日）上午8:00至下午6:00。

5月23日（星期一）补充现场确认（二）现场确认报名需携带的证件和材料。

1.《青岛市初中学业水平考试（高中阶段学校招生）网上报名信息表》一份（通过网上报名系统打印）；2.综合素质发展评价档案（含《综合素质发展评价表》、《中学生综合素质发展评价手册》、学生成长的标志性成果、至少一份研究性学习报告等）。

其中，标志性成果包括市级及以上教育部门组织或参与组织的各类比赛、评优获奖证书原件及复印件、能够反映个人成长的其他成果资料等；3.享受加分优待政策有关证件原件及复印件。

以上各种证件的原件，由第一志愿学校查验后返还考生，证件复印件及其他报名材料由报名学校保存在考生的报名档案袋中。

（三）普通高中学校通过“青岛市初中学业水平考试（高中阶段学校招生）管理平台”组织现场确认，考生报名信息填报完毕后，打印两份报名信息表，一份经学生或家长签字确认后粘贴到普通高中招生报名档案袋上，一份交由学生或家长留存。

山东省青岛第二中学2020年自主招生考试笔试试题

青岛二中2020年自主招生考试（笔试）亲爱的同学，欢迎选择青岛二中。

港口是一个地区通往世界各地的桥梁，它推动了城市经济的发展和繁荣。

为了更深入地了解港口，青岛二中“求是”社团组织学生到某港口进行项目式学习。

同学们分为四个小组，从物理和化学两个学科角度，对恒温仓储、装卸效率、运输安全、环境保护及消毒等方面展开探究。

通过考察，同学们收获颇丰，但也有一些困惑。

回校以后他们根据搜集的资料，设计实验，尝试解决这些问题。

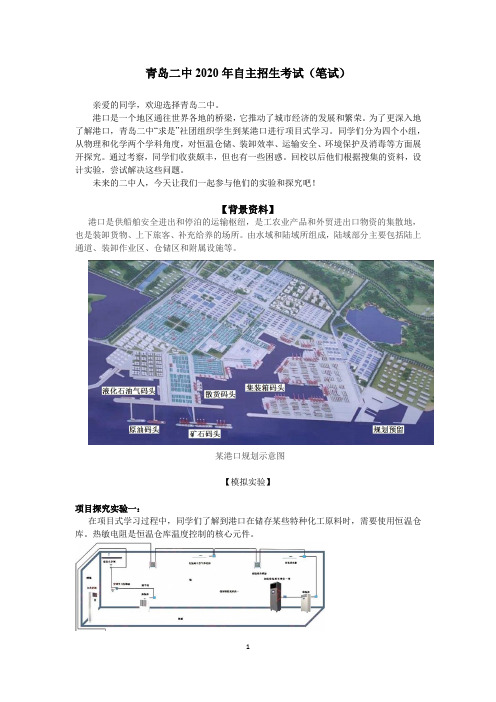
未来的二中人，今天让我们一起参与他们的实验和探究吧！【背景资料】港口是供船舶安全进出和停泊的运输枢纽，是工农业产品和外贸进出口物资的集散地，也是装卸货物、上下旅客、补充给养的场所。

由水域和陆域所组成，陆域部分主要包括陆上通道、装卸作业区、仓储区和附属设施等。

某港口规划示意图【模拟实验】项目探究实验一：在项目式学习过程中，同学们了解到港口在储存某些特种化工原料时，需要使用恒温仓库。

热敏电阻是恒温仓库温度控制的核心元件。

恒温仓库示意图如何更加全面地了解热敏电阻的特性，更有效地利用热敏电阻保持港口仓库恒温，同学们设计了以下实验：实验1.同学从网络上查询到电子体温计和空调温控装置都用到了热敏电阻，并查阅到一些数据。

如图为某热敏电阻阻值随温度变化的图像，若将此热敏电阻制成的电子体温计用绝缘膜包好置于正常人腋窝中央测量体温，请计算此时热敏电阻的阻值。

实验2.若将实验1中的热敏电阻与电压为6V的电源、阻值为650Ω的定值电阻、开关、电流表串联构成一个闭合回路，欲使通过电流表的最小电流为5mA，则对热敏电阻的温度有什么要求，请写出具体的求解过程实验3.若用图示电路测量某一特定温度下热敏电阻的阻值，请完成以下任务：（1）开关接1，调节电阻箱和滑动变阻器滑片P到适当位置，记下；（2）开关接2，调整，保持不变，记下（3）则R T可表示为实验4. 为了更好地了解热敏电阻，同学们找来了空调温控装置。

下图为模拟空调温控装置原理的简单电路，控制电路的电源电压为4V，L为阻值不计的线圈，R T为热敏电阻，其电流随电压变化的图像如图x所示，当控制电路中的电流大于等于某一值时，会接通受控电路使空调工作。

青岛二中2017年自主招生考试

青岛二中2017年自主招生考试物理试题1.（8分）“辽宁号”航空母舰，简称“辽宁舰”，是中国人民解放军海军第一艘可以搭载固定翼飞机的航空母舰。

辽宁舰满载排水量为67000吨，全长304.5米，宽37米（飞行甲板最大宽是70米）。

求：（1）辽宁舰满载时所受的浮力是多少牛顿？（2）航母在航行中需要不断补给物资，这个艰巨的任务是由中国先进的补给舰“高邮湖”舰来完成。

如图所示，在航行补给时“辽宁号”与“高邮湖”舰不能靠的太近，否则外部的水会把两舰挤在一起，请大家分析其原因。

2. （14分）青岛二中教学楼东大厅有一个长为L=m的平面镜竖直挂在墙上，=m，一同学站立于镜前，其眼睛离地高度h=m、离墙水镜子上边缘离地高度h2平距离a=1m，求该同学在镜面内能看到的地面上x坐标轴上的范围？3.青岛二中学生团队活动丰富多彩、小组成员积极探索。

某次自然MT（Magnet Team简称MT）团队进行合金实验，他们取相等质量、密度分别是ρ1和ρ2的金属甲与金属乙制成合金，请计算他们制造的这种合金的密度是多大？（设合金体积等于合成前金属甲和金属乙的总体积）4.青岛二中是全国绿色先进学校和国际生态学校。

在节能和环保方面，学校采取了一系列的方法。

例如在一些公共场所使用的光控开关控制照明系统（如右图所示）。

光控开头可采用光敏电阻来控制，光敏电阻是随着光的照度而发生变化的元件（照度可以反映光的强弱，光越强照度越大，照度单位为1x）。

某光①明阻值随照度变化的特点。

②如图所示，当A、B两端所加电压上升至2V时，控制开关自动启动照明系统，请利用下列器材设计一个简单电路，给A、B两端提供电压，要求当天色渐暗照度降低至1.0（1x）时启动照明系统，在虚线框内完成电路原理图。

（不考虑控制开关对所设计电路的影响，光敏电阻用表示）提供的器材如下：电源电压3V；定值电阻：R1=10kΩ，R2=20kΩ，R3=40kΩ（限选其中之一并在图中标出）开关S及导线若干。

解读青岛中考改革三大变化

解读青岛中考改革三大变化解读青岛中考改革三大变化青岛中考等级制“大事记”2013年，市教育局正式印发《青岛市初中学生学业考试与普通高中招生改革方案》的通知，首次表明从2015年中考开始实行学业成绩等级评价制度。

2014年6月24日，市教育局召开新闻通气会，公布等级制实施的主要思路和基本原则。

2014年7月9日，市教育局发布公告，暂缓实行等级制。

2014年8月3日，市教育局发布公告，拟对青岛中考改革召开听证会。

2014年8月18日，市教育局发布“市内三区初中学生学业考试与普通高中招生改革有关事项的说明(征求意见稿)”。

解读一：分数制、等级制如何并行?2013年，青岛市教育局印发《青岛市初中学生学业考试与普通高中招生改革方案》的通知，首次表明从2015年中考开始实行学业成绩等级评价制度。

一石激起千层浪，该方案公示后，很多家长担心出现“一刀切”、“不公正”等现象，并在网络上热烈讨论。

对此，青岛市教育局在广泛征求意见、充分调研论证的基础上，决定对市内三区初中学生学业考试与普通高中招生改革方案进行了调整和完善，实行分数制与等级制并行，条件成熟后再实行完全等级制评价与录取。

那么，分数制和等级制如何并行?根据市教育局公布的征求意见稿，调整后的方案将改变“单一模式”，单纯的“以考分论成败”或者“按照等级排序”的方式将不会出现。

学生考试成绩，将以分数和等级同步体现，分数相同的前提下，则按照等级高低进行排序，择优录取。

在具体操作中，青岛将调整考试科目成绩呈现方式和普通高中录取方式。

、数学、英语、物理、化学、历史、地理、生物8个科目考试成绩以分数和等级(分ABCDE五个等级,各等级所占比例分别为10%、20%、30%、35%、5%)两种形式呈现，思想品德、体育与健康、信息技术3个科目以等级(分及格、不及格两个等级)形式呈现。

普通高中录取总分780分。

其中，120分、数学120分、英语120分、物理100分、化学80分、历史80分、地理80分、生物80分。

2024年山东省青岛市普通高中自主招生物理试卷(含答案)

2024年山东省青岛市普通高中自主招生物理试卷一、单选题：本大题共14小题，共28分。

1.唐代诗人李白在《早发白帝城》中写到“两岸猿声啼不住，轻舟已过万重山”，其中描写轻舟的运动情况所选择的参照物是( )A. 舟B. 万重山C. 舟上的李白D. 水流2.下列关于声现象的说法正确的是( )A. 响度与声源振动的频率有关B. “未见其人，先闻其声”，是因为声速比光速大C. 摩托车上安装消声器是为了在传播过程中减弱噪声D. 超声波能粉碎人体内的“结石”，是因为声波能够传递能量3.把干净的玻璃板吊在弹簧测力计的下面，读出测力计的示数。

使玻璃板水平接触水面，然后稍稍用力向上拉玻璃板，如图所示，则弹簧测力计的示数将( )A. 不变B. 变大C. 变小D. 无法确定4.如图所示，小明在实验课上自制气压计，取一个瓶子，装入适量带色的水，再取一根两端开口的透明玻璃管，在管壁上刻度，穿过橡胶塞插入水中，从管口向瓶内吹入少量的气体，水沿玻璃管上升到瓶口以上。

关于自制气压计，下列说法正确的是( )A. 大气压在数值上等于玻璃管内水柱产生的压强B. 小明提着瓶子从一楼到楼顶，玻璃管内水柱高度逐渐升高C. 小明提着瓶子从一楼到楼顶，瓶内气体压强始终小于外界大气压D. 若瓶外是标准大气压，则瓶子内外的气压差为105Pa5.如图所示，在“探究平面镜成像的特点”实验中，下列说法正确的是( )A. 用玻璃板代替平面镜，能使蜡烛成像更清晰B. 把光屏放在恰当的位置可以承接到蜡烛的像C. 只将玻璃板沿其所在的平面向左移动2cm，像的位置保持不变D. 只将玻璃板向蜡烛方向倾斜，使玻璃板与竖直方向夹角为30°，则像和蜡烛的连线与玻璃板夹角为60°6.如图所示，体育课上，小明在老师的指导下进行爬杆训练。

他以0.2m/s的速度匀速爬上3m高的竖直杆，又以0.5m/s的速度匀速下杆。

已知小明的质量为60kg，在本次爬杆训练过程中，下列说法正确的是( )A. 上杆过程中小明的机械能不变B. 上杆过程中小明受到的摩擦力方向竖直向下C. 下杆过程中小明受到的摩擦力和上杆过程中的摩擦力相等D. 下杆过程中小明所受重力做功的功率为30W7.2024年4月25日20时58分，“神舟十八号”载人飞船搭载“长征二号F遥十八”运载火箭在酒泉卫星发射中心升空，由叶光富、李聪、李广苏三名航天员组成全新飞行乘组，与“神舟十七号”乘组在空间站胜利会师。

【精选试卷】青岛第二中学中考数学解答题专项练习经典习题(含答案解析)

一、解答题1．已知点A在x轴负半轴上，点B在y轴正半轴上，线段OB的长是方程x2﹣2x﹣8=0的解，tan∠BAO=12．（1）求点A的坐标；（2）点E在y轴负半轴上，直线EC⊥AB，交线段AB于点C，交x轴于点D，S△DOE=16．若反比例函数y=kx的图象经过点C，求k的值；（3）在（2）条件下，点M是DO中点，点N，P，Q在直线BD或y轴上，是否存在点P，使四边形MNPQ是矩形？若存在，请直接写出点P的坐标；若不存在，请说明理由．2．已知：如图，△ABC为等腰直角三角形∠ACB＝90°，过点C作直线CM，D为直线CM上一点，如果CE＝CD且EC⊥CD．（1）求证：△ADC≌△BEC；（2）如果EC⊥BE，证明：AD∥EC．3．距离中考体育考试时间越来越近，某校想了解初三年级1500名学生跳绳情况，从中随机抽查了20名男生和20名女生的跳绳成绩，收集到了以下数据：男生：192、166，189，186，184，182，178，177，174，170，188，168，205，165，158，150，188，172，180，188女生：186，198，162，192，188，186，185，184，180，180，186，193，178，175，172，166，155，183，187，184．根据统计数据制作了如下统计表：个数x150≤x＜170170≤x＜185185≤x＜190x≥190男生5852女生38a3两组数据的极差、平均数、中位数、众数如表所示：极差平均数中位数众数男生55178b c女生43181184186（1）请将上面两个表格补充完整：a＝____，b＝_____，c＝_____；（2）请根据抽样调查的数据估计该校初三年级学生中考跳绳成绩能得满分（185个及以上）的同学大约能有多少人？（3）体育组的江老师看了表格数据后认为初三年级的女生跳绳成绩比男生好，请你结合统计数据，写出支持江老师观点的理由．4．问题：探究函数y＝x+2x的图象和性质．小华根据学习函数的方法和经验，进行了如下探究，下面是小华的探究过程，请补充完整：（1）函数的自变量x的取值范围是：____；（2）如表是y与x的几组对应值，请将表格补充完整：x…﹣3﹣2﹣32﹣1−121213223…y…﹣323﹣3−256﹣3﹣412412256323…（3）如图，在平面直角坐标系中描点并画出此函数的图象；（4）进一步探究：结合函数的图象，写出此函数的性质（一条即可）．5．如图1，在直角坐标系中，一次函数的图象l1与y轴交于点A（0 , 2），与一次函数y＝x﹣3的图象l2交于点E（m ,﹣5）．（1）m=__________；（2）直线l1与x轴交于点B，直线l2与y轴交于点C，求四边形OBEC的面积；（3）如图2，已知矩形MNPQ，PQ＝2，NP＝1，M（a，1），矩形MNPQ的边PQ在x 轴上平移，若矩形MNPQ与直线l1或l2有交点，直接写出a的取值范围_____________________________6．某烘焙店生产的蛋糕礼盒分为六个档次，第一档次(即最低档次)的产品每天生产76件，每件利润10元，调查表明：生产提高一个档次的蛋糕产品，该产品每件利润增加2元(1)若生产第五档次的蛋糕，该档次蛋糕每件利润为多少元？(2)由于生产工序不同，蛋糕产品每提高一个档次，一天产量会减少4件．若生产的某档次产品一天的总利润为1024元，该烘焙店生产的是第几档次的产品？7．如图，在平面直角坐标系中，小正方形格子的边长为1，Rt△ABC三个顶点都在格点上，请解答下列问题：(1)写出A，C两点的坐标；(2)画出△ABC关于原点O的中心对称图形△A1B1C1；(3)画出△ABC绕原点O顺时针旋转90°后得到的△A2B2C2，并直接写出点C旋转至C2经过的路径长．8．已知：如图，点E，A，C在同一条直线上，AB∥CD，AB=CE，AC=CD．求证：BC=ED．9．今年5月份，我市某中学开展争做“五好小公民”征文比赛活动，赛后随机抽取了部分参赛学生的成绩，按得分划分为A，B，C，D四个等级，并绘制了如下不完整的频数分布表和扇形统计图：等级成绩（s）频数（人数）A90＜s≤1004B80＜s≤90xC70＜s≤8016D s≤706根据以上信息，解答以下问题：（1）表中的x= ；（2）扇形统计图中m= ，n=，C等级对应的扇形的圆心角为度；（3）该校准备从上述获得A等级的四名学生中选取两人做为学校“五好小公民”志愿者，已知这四人中有两名男生（用a1，a2表示）和两名女生（用b1，b2表示），请用列表或画树状图的方法求恰好选取的是a1和b1的概率．10．如图，AB为⊙O的直径，C为⊙O上一点，∠ABC的平分线交⊙O于点D，DE⊥BC 于点E．（1）试判断DE与⊙O的位置关系，并说明理由；（2）过点D作DF⊥AB于点F，若BE=33，DF=3，求图中阴影部分的面积．，，，四人随机分成甲、乙两组参加羽毛球比赛，每组两人．11．将A B C D（1）A在甲组的概率是多少？，都在甲组的概率是多少？（2）A B12．为培养学生良好学习习惯，某学校计划举行一次“整理错题集”的展示活动，对该校部分学生“整理错题集”的情况进行了一次抽样调查，根据收集的数据绘制了下面不完整的统计图表．整理情况频数频率非常好0.21较好700.35一般m不好36请根据图表中提供的信息，解答下列问题：（1）本次抽样共调查了名学生；（2）m=；（3）该校有1500名学生，估计该校学生整理错题集情况“非常好”和“较好”的学生一共约多少名？（4）某学习小组4名学生的错题集中，有2本“非常好”（记为A1、A2），1本“较好”（记为B），1本“一般”（记为C），这些错题集封面无姓名，而且形状、大小、颜色等外表特征完全相同，从中抽取一本，不放回，从余下的3本错题集中再抽取一本，请用“列表法”或“画树形图”的方法求出两次抽到的错题集都是“非常好”的概率．13．如图，BD是△ABC的角平分线，过点D作DE∥BC交AB于点E，DF∥AB交BC于点F．（1）求证：四边形BEDF为菱形；（2）如果∠A=90°，∠C=30°，BD=12，求菱形BEDF的面积．14．小慧和小聪沿图①中的景区公路游览．小慧乘坐车速为30 km/h的电动汽车，早上7：00从宾馆出发，游玩后中午12：00回到宾馆．小聪骑车从飞瀑出发前往宾馆，速度为20 km/h，途中遇见小慧时，小慧恰好游完一景点后乘车前往下一景点．上午10：00小聪到达宾馆．图②中的图象分别表示两人离宾馆的路程s(km)与时间t(h)的函数关系．试结合图中信息回答：(1)小聪上午几点钟从飞瀑出发？(2)试求线段AB，GH的交点B的坐标，并说明它的实际意义；(3)如果小聪到达宾馆后，立即以30 km/h的速度按原路返回，那么返回途中他几点钟遇见小慧？15．先化简，再求值：(2)(2)(4)a a a a +-+-，其中14a =． 16．矩形ABCD 的对角线相交于点O ．DE ∥AC ，CE ∥BD ． (1)求证：四边形OCED 是菱形；(2)若∠ACB ＝30°，菱形OCED 的而积为83，求AC 的长．17．如图，AD 是ABC ∆的中线，AE BC ∥，BE 交AD 于点F ，F 是AD 的中点，连接EC .（1）求证：四边形ADCE 是平行四边形；（2）若四边形ABCE 的面积为S ，请直接写出图中所有面积是13S 的三角形.18．如图，点B 、C 、D 都在⊙O 上，过点C 作AC ∥BD 交OB 延长线于点A ，连接CD ，且∠CDB=∠OBD=30°，DB=63cm ．（1）求证：AC 是⊙O 的切线；（2）求由弦CD 、BD 与弧BC 所围成的阴影部分的面积．（结果保留π）19．4月18日，一年一度的“风筝节”活动在市政广场举行，如图，广场上有一风筝A ，小江抓着风筝线的一端站在D 处，他从牵引端E 测得风筝A 的仰角为67°，同一时刻小芸在附近一座距地面30米高(BC ＝30米)的居民楼顶B 处测得风筝A 的仰角是45°，已知小江与居民楼的距离CD ＝40米，牵引端距地面高度DE ＝1.5米，根据以上条件计算风筝距地面的高度(结果精确到0.1米，参考数据：sin67°≈1213，cos67°≈513，tan67°≈125，2≈1.414)．20．甲乙两人做某种机械零件，已知甲每小时比乙多做4个，甲做120个所用的时间与乙做100个所用的时间相等，求甲乙两人每小时各做几个零件？21．甲、乙两公司为“见义勇为基金会”各捐款60000元．已知甲公司的人数比乙公司的人数多20℅，乙公司比甲公司人均多捐20元．甲、乙两公司各有多少人？22．“安全教育平台”是中国教育学会为方便学长和学生参与安全知识活动、接受安全提醒的一种应用软件.某校为了了解家长和学生参与“防溺水教育”的情况，在本校学生中随机抽取部分学生作调查，把收集的数据分为以下4类情形：A ．仅学生自己参与；B ．家长和学生一起参与；C ．仅家长自己参与；D ．家长和学生都未参与.请根据图中提供的信息，解答下列问题：（1）在这次抽样调查中，共调查了________名学生；（2）补全条形统计图，并在扇形统计图中计算C 类所对应扇形的圆心角的度数；（3）根据抽样调查结果，估计该校2000名学生中“家长和学生都未参与”的人数. 23．如图，点D 在以AB 为直径的⊙O 上，AD 平分BAC ∠，DC AC ⊥，过点B 作⊙O 的切线交AD 的延长线于点E ． (1)求证：直线CD 是⊙O 的切线． (2)求证：CD BE AD DE ⋅=⋅．24．荆门市是著名的“鱼米之乡”．某水产经销商在荆门市长湖养殖场批发购进草鱼和乌鱼（俗称黑鱼）共75千克，且乌鱼的进货量大于40千克．已知草鱼的批发单价为8元/千克，乌鱼的批发单价与进货量的函数关系如图所示．（1）请直接写出批发购进乌鱼所需总金额y （元）与进货量x （千克）之间的函数关系式；（2）若经销商将购进的这批鱼当日零售，草鱼和乌鱼分别可卖出89%、95%，要使总零售量不低于进货量的93%，问该经销商应怎样安排进货，才能使进货费用最低？最低费用是多少？25．阅读材料：小明在学习二次根式后，发现一些含根号的式子可以写成另一个式子的平方，如：232212+=（），善于思考的小明进行了以下探索：设(2a b 2m 2+=+（其中a b m n 、、、均为整数），则有22a b 2m 2n 2+=++∴22a m 2n b 2mn =+=，．这样小明就找到了一种把部分a b 2+法．请你仿照小明的方法探索并解决下列问题：当a b m n 、、、均为正整数时，若(2a b 3m 3+=+，用含m 、n 的式子分别表示a b 、，得a ＝，b ＝；（2）利用所探索的结论，找一组正整数a b m n 、、、，填空：＋＝( ＋3)2；（3）若(233a m +=＋，且ab m n 、、、均为正整数，求a 的值．26．“端午节”是我国的传统佳节，民间历来有吃“粽子”的习俗．我市某食品厂为了解市民对去年销量较好的肉馅粽、豆沙馅粽、红枣馅粽、蛋黄馅粽（以下分别用A 、B 、C 、D 表示）这四种不同口味粽子的喜爱情况，在节前对某居民区市民进行了抽样调查，并将调查情况绘制成如下两幅统计图（尚不完整）．请根据以上信息回答：（1）本次参加抽样调查的居民有多少人？（2）将两幅不完整的图补充完整；（3）若居民区有8000人，请估计爱吃D 粽的人数；（4）若有外型完全相同的A 、B 、C 、D 粽各一个，煮熟后，小王吃了两个．用列表或画树状图的方法，求他第二个吃到的恰好是C 粽的概率．27．在一次中学生田径运动会上，根据参加男子跳高初赛的运动员的成绩（单位：m ），绘制出如下的统计图①和图②，请根据相关信息，解答下列问题：（Ⅰ）图1中a 的值为；（Ⅱ）求统计的这组初赛成绩数据的平均数、众数和中位数；（Ⅲ）根据这组初赛成绩，由高到低确定9人进入复赛，请直接写出初赛成绩为1.65m 的运动员能否进入复赛． 28．解方程：x 21x 1x-=-. 29．已知222111x x xA x x ++=---. （1）化简A ；（2）当x 满足不等式组1030x x -≥⎧⎨-<⎩，且x 为整数时，求A 的值.30．计算：（1）2（m ﹣1）2﹣（2m+1）（m ﹣1）（2）（1﹣1x+2）÷x 2−1x+2【参考答案】2016-2017年度第*次考试试卷参考答案**科目模拟测试一、解答题1．2．3．4．5．6．7．8．9．10．11．12．13．14．15．16．17．18．19．20．21．22．23．24．25．26．27．28．29．30．2016-2017年度第*次考试试卷参考解析【参考解析】**科目模拟测试一、解答题1．（1）（-8，0）（2）k=-19225（3）（﹣1，3）或（0，2）或（0，6）或（2，6）【解析】【分析】（1）解方程求出OB的长，解直角三角形求出OA即可解决问题；（2）求出直线DE、AB的解析式，构建方程组求出点C坐标即可；（3）分四种情形分别求解即可解决问题；【详解】解：（1）∵线段OB的长是方程x2﹣2x﹣8=0的解，∴OB=4，在Rt△AOB中，tan∠BAO=12 OBOA=，∴OA=8，∴A（﹣8，0）．（2）∵EC⊥AB，∴∠ACD=∠AOB=∠DOE=90°，∴∠OAB+∠ADC=90°，∠DEO+∠ODE=90°，∵∠ADC=∠ODE，∴∠OAB=∠DEO，∴△AOB∽△EOD，∴OA OB OE OD=，∴OE：OD=OA：OB=2，设OD=m，则OE=2m，∵12•m•2m=16，∴m=4或﹣4（舍弃），∴D（﹣4，0），E（0，﹣8），∴直线DE的解析式为y=﹣2x﹣8，∵A（﹣8，0），B（0，4），∴直线AB的解析式为y=12x+4，由28142y xy x--⎧⎪⎨+⎪⎩＝＝，解得24585xy⎧-⎪⎪⎨⎪⎪⎩＝＝，∴C（245-，85），∵若反比例函数y=kx的图象经过点C，∴k=﹣192 25．（3）如图1中，当四边形MNPQ是矩形时，∵OD=OB=4，∴∠OBD=∠ODB=45°，∴∠PNB=∠ONM=45°，∴OM=DM=ON=2，∴BN=2，2，∴P（﹣1，3）．如图2中，当四边形MNPQ是矩形时（点N与原点重合），易证△DMQ是等腰直角三角形，OP=MQ=DM=2，P（0，2）；如图3中，当四边形MNPQ是矩形时，设PM交BD于R，易知R（﹣1，3），可得P （0，6）如图4中，当四边形MNPQ是矩形时，设PM交y轴于R，易知PR=MR，可得P（2，6）．综上所述，满足条件的点P坐标为（﹣1，3）或（0，2）或（0，6）或（2，6）；【点睛】考查反比例函数综合题、一次函数的应用、矩形的判定和性质、相似三角形的判定和性质等知识，解题的关键是灵活运用所学知识解决问题.2．（1）详见解析；（2）详见解析．【解析】【分析】（1）根据两锐角互余的关系可得∠ACD＝∠BCE，利用SAS即可证明△ADC≌△BEC；（2）由△ADC≌△BEC可得∠ADC＝∠E＝90°，根据平行线判定定理即可证明AD//EC.【详解】（1）∵EC⊥DM，∴∠ECD＝90°，∴∠ACB＝∠DCE=90°，∴∠ACD+∠ACE=90°，∠BCE+∠ACE=90°，∴∠ACD＝∠BCE，∵CD＝CE，CA＝CB，∴△ADC≌△BEC（SAS）．（2）由（1）得△ADC≌△BEC，∵EC⊥BE，∴∠ADC＝∠E＝90°，∴AD⊥DM，∵EC⊥DM，∴AD∥EC．【点睛】本题考查全等三角形的判定和性质，等腰直角三角形的性质等知识，解题的关键是正确寻找全等三角形全等的条件，属于中考常考题型．3．（1）a＝6，b＝179，c＝188；(2)600；（3）详见解析.【解析】【分析】（1）依据中位数以及众数的定义即可将上面两个表格补充完整；（2）依据样本中能得满分（185个及以上）的同学所占的比例，即可估计该校初三年级学生中考跳绳成绩能得满分的人数；（3）依据两组数据的极差和平均数的大小，即可得到结论．【详解】（1）满足185≤x＜190的数据有：186，188，186，185，186，187．∴a＝6，20名男生的跳绳成绩排序后最中间的两个数据为178和180，（178+180）＝179，∴b＝1220名男生的跳绳成绩中出现次数最多的数据为188，∴c＝188，故答案为：6；179；188；（2）∵20名男生和20名女生的跳绳成绩中，185个及以上的有16个，＝∴该校初三年级学生中考跳绳成绩能得满分（185个及以上）的同学大约能有1500×1640 600（人）；（3）理由：初三年级的女生跳绳成绩的极差较小，而平均数较大．【点睛】本题考查了用样本估计总体，中位数，众数，正确的理解题意是解题的关键．一般来说，用样本去估计总体时，样本越具有代表性、容量越大，这时对总体的估计也就越精确．4．（1）x≠0；（2）3，3；（3）详见解析；（4）此函数有最小值和最大值．【解析】【分析】（1）由分母不为零，确定x的取值范围即可；（2）将x＝1，x＝2代入解析式即可得答案；（3）描点画图即可；（4）观察函数图象有最低点和最高点，得到一个性质；【详解】（1）因为分母不为零，∴x≠0；故答案为a≠0．（2）x＝1时，y＝3；x＝2时，y＝3；故答案为3，3．（3）如图：（4）此函数有最小值和最大值；【点睛】本题考查了函数自变量的取值范围：自变量的取值范围必须使含有自变量的表达式都有意义．5．（1）-2；（2）317；（3）−47≤a≤127或3≤a≤6. 【解析】【分析】（1）根据点E 在一次函数图象上，可求出m 的值；（2）利用待定系数法即可求出直线l 1的函数解析式，得出点B 、C 的坐标，利用S 四边形OBEC ＝S △OBE ＋S △OCE 即可得解；（3）分别求出矩形MNPQ 在平移过程中，当点Q 在l 1上、点N 在l 1上、点Q 在l 2上、点N 在l 2上时a 的值，即可得解．【详解】解：（1）∵点E （m ，−5）在一次函数y ＝x−3图象上，∴m−3＝−5，∴m ＝−2；（2）设直线l 1的表达式为y ＝kx ＋b （k≠0），∵直线l 1过点A （0，2）和E （−2，−5），∴{b =2−2k +b =−5 ，解得{b =2k =72， ∴直线l 1的表达式为y ＝72x ＋2，当y ＝72x ＋2=0时，x=−47 ∴B 点坐标为(−47，0)，C 点坐标为（0，−3），∴S 四边形OBEC ＝S △OBE ＋S △OCE ＝12×47×5＋12×2×3＝317；（3）当矩形MNPQ 的顶点Q 在l 1上时，a 的值为−47；矩形MNPQ 向右平移，当点N 在l 1上时，72x ＋2＝1，解得x ＝−27，即点N （−27，1）， ∴a 的值为−27＋2＝127；矩形MNPQ 继续向右平移，当点Q 在l 2上时，a 的值为3，矩形MNPQ 继续向右平移，当点N 在l 2上时，x−3＝1，解得x ＝4，即点N （4，1）， ∴a 的值为4＋2＝6，综上所述，当−47≤a≤127或3≤a≤6时，矩形MNPQ 与直线l 1或l 2有交点．【点睛】本题主要考查求一次函数解析式，两条直线相交、图形的平移等知识的综合应用，在解决第（3）小题时，只要求出各临界点时a 的值，就可以得到a 的取值范围．6．（1该档次蛋糕每件利润为18元;（2）该烘焙店生产的是四档次的产品．【解析】【分析】（1）依题意可求出产品质量在第五档次的每件的利润．（2）设烘焙店生产的是第x 档次的产品，根据单件利润×销售数量=总利润，即可得出关于x 的一元二次方程，解之即可得出结论．【详解】（1）10＋2×（5－1）＝18（元）．答：该档次蛋糕每件利润为18元．（2）设烘焙店生产的是第x 档次的产品，根据题意得：[10＋2（x －1）]×[76－4(x －1）]＝1024，整理得：x 2﹣16x ＋48＝0，解得：x 1＝4，x 2＝12（不合题意，舍去）．答：该烘焙店生产的是四档次的产品．【点睛】本题考查了一元二次方程的应用，解题的关键是：（1）根据数量关系，列式计算；（2）根据单件利润×销售数量=总利润，列出关于x 的一元二次方程．7．(1)A 点坐标为(﹣4，1)，C 点坐标为(﹣1，1)；(2)见解析；．【解析】【分析】(1)利用第二象限点的坐标特征写出A ，C 两点的坐标；(2)利用关于原点对称的点的坐标特征写出A 1、B 1、C 1的坐标，然后描点即可；(3)利用网格特点和旋转的性质画出点A 、B 、C 的对应点A 2、B 2、C 2，然后描点得到△A 2B 2C 2，再利用弧长公式计算点C 旋转至C 2经过的路径长．【详解】解：(1)A 点坐标为(﹣4，1)，C 点坐标为(﹣1，1)；(2)如图，△A1B1C1为所作；(3)如图，△A2B2C2为所作，OC2213+10，点C旋转至C29010π⋅⋅10π．【点睛】本题考查了作图﹣旋转变换：根据旋转的性质可知，对应角都相等都等于旋转角，对应线段也相等，由此可以通过作相等的角，在角的边上截取相等的线段的方法，找到对应点，顺次连接得出旋转后的图形．也考查了弧长公式．8．见解析【解析】【分析】首先由AB∥CD，根据平行线的性质可得∠BAC=∠ECD，再由条件AB=CE，AC=CD可证出△BAC和△ECD全等，再根据全等三角形对应边相等证出CB=ED.【详解】证明：∵AB∥CD，∴∠BAC=∠ECD，∵在△BAC和△ECD中，AB=EC，∠BAC=∠ECD ，AC=CD，∴△BAC≌△ECD（SAS）.∴CB=ED.【点睛】本题考查了平行线的性质，全等三角形的判定和性质.9．（1）14；（2）10、40、144；（3）恰好选取的是a1和b1的概率为16．【解析】【分析】（1）根据D组人数及其所占百分比可得总人数，用总人数减去其他三组人数即可得出x的值；（2）用A、C人数分别除以总人数求得A、C的百分比即可得m、n的值，再用360°乘以C等级百分比可得其度数；（3）首先根据题意列出表格，然后由表格求得所有等可能的结果与恰好选取的是a1和b1的情况，再利用概率公式即可求得答案．【详解】（1）∵被调查的学生总人数为6÷15%=40人，∴x=40﹣（4+16+6）=14，故答案为14；（2）∵m%=440×100%=10%，n%=1640×10%=40%，∴m=10、n=40，C等级对应的扇形的圆心角为360°×40%=144°，故答案为10、40、144；（3）列表如下：a1和b1的有2种结果，∴恰好选取的是a1和b1的概率为21 126．【点睛】本题考查的是条形统计图和扇形统计图的综合运用，列表法或树状图法求概率，读懂统计图，从不同的统计图中得到必要的信息是解决问题的关键．条形统计图能清楚地表示出每个项目的数据；扇形统计图直接反映部分占总体的百分比大小；概率=所求情况数与总情况数之比．10．（1）DE与⊙O相切，理由见解析；（2）阴影部分的面积为2π．【解析】【分析】（1）直接利用角平分线的定义结合平行线的判定与性质得出∠DEB=∠EDO=90°，进而得出答案；（2）利用勾股定理结合扇形面积求法分别分析得出答案．【详解】（1）DE与⊙O相切，理由：连接DO，∵DO=BO，∴∠ODB=∠OBD，∵∠ABC 的平分线交⊙O 于点D ，∴∠EBD=∠DBO，∴∠EBD=∠BDO，∴DO∥BE，∵DE⊥BC，∴∠DEB=∠EDO=90°，∴DE 与⊙O 相切；（2）∵∠ABC 的平分线交⊙O 于点D ，DE⊥BE，DF⊥AB，∴DE=DF=3， 3 223+33（）=6， ∵sin∠DBF=31=62， ∴∠DBA=30°，∴∠DOF=60°， ∴sin60°=33DF DO DO == 3则3 260(23)1333322ππ⨯-= 【点睛】此题主要考查了切线的判定方法以及扇形面积求法等知识，正确得出DO 的长是解题关键． 11．（1）12（2）16【解析】解：所有可能出现的结果如下：甲组乙组结果（1）所有的结果中，满足A 在甲组的结果有3种，所以A 在甲组的概率是12，··· 2分（2）所有的结果中，满足A B ，都在甲组的结果有1种，所以A B ，都在甲组的概率是16．利用表格表示出所有可能的结果，根据A 在甲组的概率=3162， A B ，都在甲组的概率=1612．（1）200；（2）52；（3）840人；（4）16【解析】分析：（1）用较好的频数除以较好的频率．即可求出本次抽样调查的总人数；（2）用总人数乘以非常好的频率，求出非常好的频数，再用总人数减去其它频数即可求出m 的值；（3）利用总人数乘以对应的频率即可；（4）利用树状图方法，利用概率公式即可求解．详解：（1）本次抽样共调查的人数是：70÷0.35=200（人）；（2）非常好的频数是：200×0.21=42（人），一般的频数是：m=200﹣42﹣70﹣36=52（人），（3）该校学生整理错题集情况“非常好”和“较好”的学生一共约有：1500×（0.21+0.35）=840（人）；（4）根据题意画图如下：∵所有可能出现的结果共12种情况，并且每种情况出现的可能性相等，其中两次抽到的错题集都是“非常好”的情况有2种，∴两次抽到的错题集都是“非常好”的概率是21= 126．点睛：此题考查的是用列表法或树状图法求概率．列表法可以不重复不遗漏的列出所有可能的结果，适合于两步完成的事件；树状图法适合两步或两步以上完成的事件；解题时要注意此题是放回实验还是不放回实验．用到的知识点为：概率=所求情况数与总情况数之比．13．(1)见解析;(2)243.【解析】【分析】（1）根据平行四边形的和菱形的判定证明即可；（2）根据含30°的直角三角形的性质和勾股定理以及菱形的面积解答即可．【详解】证明：（1）∵DE∥BC，DF∥AB，∴四边形BFDE是平行四边形，∵BD是△ABC的角平分线，∴∠EBD=∠DBF，∵DE∥BC，∴∠EDB=∠DBF，∴∠EBD=∠EDB，∴BE=ED，∴平行四边形BFDE是菱形；（2）连接EF，交BD于O，∵∠BAC=90°，∠C=30°，∴∠ABC=60°，∵BD平分∠ABC，∴∠DBC=30°，∴BD=DC=12，∵DF ∥AB ，∴∠FDC=∠A=90°，∴DF=124333DC ==，在Rt △DOF 中，OF=()222243623DF OD -=-=， ∴菱形BFDE 的面积=12×EF •BD ＝12×12×43=243．【点评】此题考查了菱形的判定和性质，熟练掌握菱形的判定和性质是解题的关键．14．（1）小聪上午7：30从飞瀑出发；（2）点B 的实际意义是当小慧出发1.5 h 时，小慧与小聪相遇，且离宾馆的路程为30 km.；（3）小聪到达宾馆后，立即以30 km/h 的速度按原路返回，那么返回途中他11：00遇见小慧．【解析】【分析】（1）由时间=路程÷速度，可得小聪骑车从飞瀑出发到宾馆所用时间为：50÷20=2.5（小时），从10点往前推2.5小时，即可解答；（2）先求GH 的解析式，当s=30时，求出t 的值，即可确定点B 的坐标；（3）根据50÷30=53（小时）=1小时40分钟，确定当小慧在D 点时，对应的时间点是10：20，而小聪到达宾馆返回的时间是10：00，设小聪返回x 小时后两人相遇，根据题意得：30x+30（x ﹣）=50，解得：x=1，10+1=11点，即可解答．【详解】（1）小聪骑车从飞瀑出发到宾馆所用时间为：50÷20=2.5（小时）， ∵上午10：00小聪到达宾馆，∴小聪上午7点30分从飞瀑出发．（2）3﹣2.5=0.5，∴点G 的坐标为（0.5，50），设GH 的解析式为s kt b =+，把G （0.5，50），H （3，0）代入得；150{230k b k b +=+=，解得：20{60k b =-=， ∴s=﹣20t+60，当s=30时，t=1.5，∴B 点的坐标为（1.5，30），点B 的实际意义是当小慧出发1.5小时时，小慧与小聪相遇，且离宾馆的路程为30km ；（3）50÷30=53（小时）=1小时40分钟，12﹣53=1103， ∴当小慧在D 点时，对应的时间点是10：20，而小聪到达宾馆返回的时间是10：00，设小聪返回x 小时后两人相遇，根据题意得：30x+30（x ﹣13）=50，解得：x=1， 10+1=11=11点，∴小聪到达宾馆后，立即以30km/h 的速度按原路返回，那么返回途中他11点遇见小慧． 15．44a -，3-．【解析】试题分析：根据平方差公式和单项式乘以多项式可以对原式化简，然后将a=14代入化简后的式子，即可解答本题．试题解析：原式=2244a a a -+-=44a -；当a=14时，原式=1444⨯-=14-=3-．考点：整式的混合运算—化简求值． 16．（1）证明见解析；（2）8．【解析】【分析】（1）熟记菱形的判定定理，本题可用一组邻边相等的平行四边形是菱形．（2）因为∠ACB=30°可证明菱形的一条对角线和边长相等，可证明和对角线构成等边三角形，然后作辅助线，根据菱形的面积已知可求解．【详解】解：（1）∵DE ∥AC ，CE ∥BD∴四边形OCED 是平行四边形∵四边形ABCD 是矩形∴AO ＝OC ＝BO ＝OD∴四边形OCED 是菱形（2）∵∠ACB ＝30°，∴∠DCO ＝90°－30°＝60°又∵OD ＝OC∴△OCD 是等边三角形过D 作DF ⊥OC 于F ，则CF=12OC ，设CF=x ，则OC=2x ，AC=4x ．在Rt △DFC 中，tan60°=DF FC，∴．∴OC•DF=83．∴x=2．∴AC=4×2=8．【点睛】本题考查了矩形的性质，对角线相等且互相平分，菱形的判定和性质，以及解直角三角形等知识点．17．（1）见解析；（2）ABD ∆，ACD ∆，ACE ∆，ABE ∆【解析】【分析】（1）首先证明△AFE ≌△DFB 可得AE=BD ，进而可证明AE=CD ，再由AE ∥BC 可利用一组对边平行且相等的四边形是平行四边形可得四边形ADCE 是平行四边形；（2）根据面积公式解答即可．【详解】证明：∵AD 是△ABC 的中线，∴BD=CD ，∵AE ∥BC ，∴∠AEF=∠DBF ，在△AFE 和△DFB 中，AEF DBF AFE BFD AF DF ＝＝＝∠∠⎧⎪∠∠⎨⎪⎩，∴△AFE ≌△DFB （AAS ），∴AE=BD ，∴AE=CD ，∵AE ∥BC ，∴四边形ADCE 是平行四边形；（2）∵四边形ABCE 的面积为S ，∵BD=DC ，∴四边形ABCE 的面积可以分成三部分，即△ABD 的面积+△ADC 的面积+△AEC 的面积=S ，∴面积是12S 的三角形有△ABD ，△ACD ，△ACE ，△ABE ．【点睛】此题主要考查了平行四边形的判定，全等三角形的判定和性质．等腰三角形的判定和性质等知识，解题的关键是正确寻找全等三角形解决问题.18．（1）证明见解析；（2）6πcm 2．【解析】【分析】连接BC ，OD ，OC ，设OC 与BD 交于点M ．（1）求出∠COB 的度数，求出∠A 的度数，根据三角形的内角和定理求出∠OCA 的度数，根据切线的判定推出即可；（2）证明△CDM ≌△OBM ，从而得到S 阴影=S 扇形BOC ．【详解】如图，连接BC ，OD ，OC ，设OC 与BD 交于点M ．（1）根据圆周角定理得：∠COB=2∠CDB=2×30°=60°，∵AC ∥BD ，∴∠A=∠OBD=30°，∴∠OCA=180°﹣30°﹣60°=90°，即OC ⊥AC ，∵OC 为半径，∴AC 是⊙O 的切线；（2）由（1）知，AC 为⊙O 的切线，∴OC ⊥AC ．∵AC ∥BD ，∴OC ⊥BD ．由垂径定理可知，MD=MB=12．在Rt △OBM 中， ∠COB=60°，OB=cos30MB ︒==6．在△CDM 与△OBM 中3090CDM OBM MD MBCMD OMB ︒︒⎧∠=∠=⎪=⎨⎪∠=∠=⎩， ∴△CDM ≌△OBM （ASA ），∴S △CDM =S △OBM∴阴影部分的面积S 阴影=S 扇形BOC =2606360π⋅=6π（cm 2）．考点：1．切线的判定；2.扇形面积的计算．19．风筝距地面的高度49.9m．【解析】【分析】作AM⊥CD于M，作BF⊥AM于F，EH⊥AM于H．设AF=BF=x，则CM=BF=x，DM=HE=40-x，AH=x+30-1.5=x+28.5，在Rt△AHE中，利用∠AEH的正切列方程求解即可.【详解】如图，作AM⊥CD于M，作BF⊥AM于F，EH⊥AM于H．∵∠ABF=45°，∠AFB=90°，∴AF=BF，设AF=BF=x，则CM=BF=x，DM=HE=40-x，AH=x+30-1.5=x+28.5，在Rt△AHE中，tan67°=AH HE，∴1228.5 540xx+=-，解得x≈19.9 m．∴AM=19.9+30=49.9 m．∴风筝距地面的高度49.9 m．【点睛】本题考查了解直角三角形的应用，解决此问题的关键在于正确理解题意得基础上建立数学模型，把实际问题转化为数学问题.20．甲每小时做24个零件，乙每小时做20个零件．【解析】【分析】设甲每小时做x个零件，则乙每小时做（x-4）个零件，根据工作时间=工作总量÷工作效率结合甲做120个所用的时间与乙做100个所用的时间相等，即可得出关于x的分式方程，解之经检验后即可得出结论．【详解】解：设甲每小时做x个零件，则乙每小时做（x﹣4）个零件，根据题意得：1201004x x=-，解得：x=24，经检验，x=24是分式方程的解，∴x﹣4=20．答：甲每小时做24个零件，乙每小时做20个零件．【点睛】本题考查了分式方程的应用，找准等量关系，正确列出分式方程是解题的关键．21．甲公司有600人，乙公司有500人.【解析】分析：根据题意，可以设乙公司人数有x人，则甲公司有(1+20%)x人；由乙公司比甲公司人均多捐20元列分式方程，解之即可得出答案.详解：设乙公司有x人，则甲公司就有（1+20％）x人，即1.2x人，根据题意，可列方程：60000x600001.2x-=20解之得：x=500经检验：x=500是该方程的实数根.22．（1）400；（2）补全条形图见解析；C类所对应扇形的圆心角的度数为54°；（3）该校2000名学生中“家长和学生都未参与”有100人.【解析】分析：（1）根据A类别人数及其所占百分比可得总人数；（2）总人数减去A、C、D三个类别人数求得B的人数即可补全条形图，再用360°乘以C 类别人数占被调查人数的比例可得；（3）用总人数乘以样本中D类别人数所占比例可得．详解：（1）本次调查的总人数为80÷20%=400人；（2）B类别人数为400-（80+60+20）=240，补全条形图如下：。

青岛二中高中自主招生试题附答案

高中自主招生试题数学一．选择题（共12小题）1．已知抛物线y=﹣x2﹣2x+3与x轴交于A、B两点，将这条抛物线的顶点记为C，连接AC、BC，则tan∠CAB的值为（）A．B．C． D．22．如图，把八个等圆按相邻两两外切摆放，其圆心连线构成一个正八边形，设正八边形内侧八个扇形（无阴影部分）面积之和为S1，正八边形外侧八个扇形（阴影部分）面积之和为S2，则=（）A．B．C．D．13．已知直线y=﹣x+3与坐标轴分别交于点A，B，点P在抛物线y=﹣（x﹣）2+4上，能使△ABP为等腰三角形的点P的个数有（）A．3个B．4个C．5个D．6个4．如图，在Rt△AOB中，∠AOB=90°，OA=3，OB=2，将Rt△AOB绕点O顺时针旋转90°后得Rt△FOE，将线段EF绕点E逆时针旋转90°后得线段ED，分别以O，E为圆心，OA、ED长为半径画弧AF和弧DF，连接AD，则图中阴影部分面积是（）A．πB．C．3+πD．8﹣π5．若关于x的一元二次方程（k﹣1）x2+4x+1=0有两个不相等的实数根，则k的取值范围是（）A．k＜5 B．k＜5，且k≠1 C．k≤5，且k≠1 D．k＞56．如图，在Rt△ABC中，∠C=90°，AC=4，BC=7，点D在边BC上，CD=3，⊙A的半径长为3，⊙D与⊙A相交，且点B在⊙D外，那么⊙D的半径长r的取值范围是（）A．1＜r＜4 B．2＜r＜4 C．1＜r＜8 D．2＜r＜87．若关于x的方程+=3的解为正数，则m的取值范围是（）A．m＜B．m＜且m≠C．m＞﹣D．m＞﹣且m≠﹣8．实数a，b在数轴上对应点的位置如图所示，化简|a|+的结果是（）A．﹣2a+b B．2a﹣b C．﹣b D．b9．如图，已知A，B是反比例函数y=（k＞0，x＞0）图象上的两点，BC∥x轴，交y轴于点C，动点P从坐标原点O出发，沿O→A→B→C（图中“→”所示路线）匀速运动，终点为C，过P作PM⊥x轴，垂足为M．设三角形OMP的面积为S，P点运动时间为t，则S关于t的函数图象大致为（）A．B．C．D．10．如图，⊙O的半径为1，AD，BC是⊙O的两条互相垂直的直径，点P从点O出发（P点与O点不重合），沿O→C→D 的路线运动，设AP=x，sin∠APB=y，那么y与x之间的关系图象大致是（）A．B．C．D．11．一个整数的所有正约数之和可以按如下方法求得，如：6=2×3，则6的所有正约数之和（1+3）+（2+6）=（1+2）×（1+3）=12；12=22×3，则12的所有正约数之和（1+3）+（2+6）+（4+12）=（1+2+22）×（1+3）=28；36=22×32，则36的所有正约数之和（1+3+9）+（2+6+18）+（4+12+36）=（1+2+22）×（1+3+32）=91．参照上述方法，那么200的所有正约数之和为（）A．420 B．434 C．450 D．46512．如图，在Rt△ABC中，∠C=90°，以顶点A为圆心，适当长为半径画弧，分别交AC，AB于点M，N，再分别以点M，N为圆心，大于MN的长为半径画弧，两弧交于点P，作射线AP交边BC于点D，若CD=4，AB=15，则△ABD 的面积是（）A．15 B．30 C．45 D．60题号 1 2 3 4 5 6 7 8 9 10 11 12 答案二．选择题（共6小题）第13题第14题第15题第17题13．如图，三个正方形的边长分别为2，6，8；则图中阴影部分的面积为．14．如图，已知正方形ABCD边长为1，∠EAF=45°，AE=AF，则有下列结论：①∠1=∠2=22.5°；②点C到EF的距离是；③△ECF的周长为2；④BE+DF＞EF．其中正确的结论是．（写出所有正确结论的序号）15．如图，分别以边长等于1的正方形的四边为直径作半圆，则图中阴影部分的面积为．16．已知∠AOB=60°，点P是∠AOB的平分线OC上的动点，点M在边OA上，且OM=4，则点P到点M与到边OA 的距离之和的最小值是．17．如图，C为半圆内一点，O为圆心，直径AB长为2cm，∠BOC=60°，∠BCO=90°，将△BOC绕圆心O逆时针旋转至△B′OC′，点C′在OA上，则边BC扫过区域（图中阴影部分）的面积为cm2．18．如图，一次函数y=﹣x+b与反比例函数y=（x＞0）的图象交于A，B两点，与x轴、y轴分别交于C，D两点，连结OA，OB，过A作AE⊥x轴于点E，交OB于点F，设点A的横坐标为m．（1）b=（用含m的代数式表示）；（2）若S△OAF+S四边形EFBC=4，则m的值是．三．解答题（共7小题）19．先化简，再求值：÷•，其中a=2016．20．为了提高学生书写汉字的能力，增强保护汉字的意识，某校举办了首届“汉字听写大赛”，学生经选拔后进入决赛，测试同时听写100个汉字，每正确听写出一个汉字得1分，本次决赛，学生成绩为x（分），且50≤x＜100，将其按分数段分为五组，绘制出以下不完整表格：组别成绩x（分）频数（人数）频率一50≤x＜60 2 0.04二60≤x＜70 10 0.2三70≤x＜80 14 b四80≤x＜90 a 0.32五90≤x＜100 8 0.16请根据表格提供的信息，解答以下问题：（1）本次决赛共有名学生参加；（2）直接写出表中a=，b=；（3）请补全下面相应的频数分布直方图；（4）若决赛成绩不低于80分为优秀，则本次大赛的优秀率为．21．某网店销售某款童装，每件售价60元，每星期可卖300件，为了促销，该网店决定降价销售．市场调查反映：每降价1元，每星期可多卖30件．已知该款童装每件成本价40元，设该款童装每件售价x元，每星期的销售量为y 件．（1）求y与x之间的函数关系式；（2）当每件售价定为多少元时，每星期的销售利润最大，最大利润多少元？（3）若该网店每星期想要获得不低于6480元的利润，每星期至少要销售该款童装多少件？22．某公司今年如果用原线下销售方式销售一产品，每月的销售额可达100万元．由于该产品供不应求，公司计划于3月份开始全部改为线上销售，这样，预计今年每月的销售额y（万元）与月份x（月）之间的函数关系的图象如图1中的点状图所示（5月及以后每月的销售额都相同），而经销成本p（万元）与销售额y（万元）之间函数关系的图象图2中线段AB所示．（1）求经销成本p（万元）与销售额y（万元）之间的函数关系式；（2）分别求该公司3月，4月的利润；（3）问：把3月作为第一个月开始往后算，最早到第几个月止，该公司改用线上销售后所获得利润总额比同期用线下方式销售所能获得的利润总额至少多出200万元？（利润=销售额﹣经销成本）23．如图，在Rt△ABC中，∠BAC=90°，O是AB边上的一点，以OA为半径的⊙O与边BC相切于点E．（1）若AC=5，BC=13，求⊙O的半径；（2）过点E作弦EF⊥AB于M，连接AF，若∠F=2∠B，求证：四边形ACEF是菱形．24．如图，抛物线y=ax2+bx+c经过△ABC的三个顶点，与y轴相交于（0，），点A坐标为（﹣1，2），点B是点A关于y轴的对称点，点C在x轴的正半轴上．（1）求该抛物线的函数关系表达式．（2）点F为线段AC上一动点，过F作FE⊥x轴，FG⊥y轴，垂足分别为E、G，当四边形OEFG为正方形时，求出F 点的坐标．（3）将（2）中的正方形OEFG沿OC向右平移，记平移中的正方形OEFG为正方形DEFG，当点E和点C重合时停止运动，设平移的距离为t，正方形的边EF与AC交于点M，DG所在的直线与AC交于点N，连接DM，是否存在这样的t，使△DMN是等腰三角形？若存在，求t的值；若不存在请说明理由．25．如图1，已知一次函数y=x+3的图象与x轴、y轴分别交于A、B两点，抛物线y=﹣x2+bx+c过A、B两点，且与x 轴交于另一点C．（1）求b、c的值；（2）如图1，点D为AC的中点，点E在线段BD上，且BE=2ED，连接CE并延长交抛物线于点M，求点M的坐标；（3）将直线AB绕点A按逆时针方向旋转15°后交y轴于点G，连接CG，如图2，P为△ACG内一点，连接PA、PC、PG，分别以AP、AG为边，在他们的左侧作等边△APR，等边△AGQ，连接QR①求证：PG=RQ；②求PA+PC+PG的最小值，并求出当PA+PC+PG取得最小值时点P的坐标．参考答案与试题解析一．选择题（共12小题）1．（2016•陕西）已知抛物线y=﹣x2﹣2x+3与x轴交于A、B两点，将这条抛物线的顶点记为C，连接AC、BC，则tan∠CAB的值为（）A ．B ．C ．D．2【考点】抛物线与x轴的交点；锐角三角函数的定义．【分析】先求出A、B、C坐标，作CD⊥AB于D，根据tan∠ACD=即可计算．【解答】解：令y=0，则﹣x2﹣2x+3=0，解得x=﹣3或1，不妨设A（﹣3，0），B（1，0），∵y=﹣x2﹣2x+3=﹣（x+1）2+4，∴顶点C（﹣1，4），如图所示，作CD⊥AB于D．在RT△ACD中，tan∠CAD===2，故答案为D．【点评】本题考查二次函数与x轴交点坐标，锐角三角函数的定义，解题的关键是熟练掌握求抛物线与x轴交点坐标的方法，记住锐角三角函数的定义，属于中考常考题型．2．（2016•玉林）如图，把八个等圆按相邻两两外切摆放，其圆心连线构成一个正八边形，设正八边形内侧八个扇形（无阴影部分）面积之和为S1，正八边形外侧八个扇形（阴影部分）面积之和为S2，则=（）A ．B ．C ．D．1【考点】扇形面积的计算；正多边形和圆．【分析】先根据正多边形的内角和公式可求正八边形的内角和，根据周角的定义可求正八边形外侧八个扇形（阴影部分）的内角和，再根据半径相等的扇形面积与圆周角成正比即可求解．【解答】解：∵正八边形的内角和为（8﹣2）×180°=6×180°=1080°，正八边形外侧八个扇形（阴影部分）的内角和为360°×8﹣1080°=2880°﹣1080°=1800°，∴==．故选：B．【点评】考查了扇形面积的计算，求不规则的图形的面积，可以转化为几个规则图形的面积的和或差来求．3．（2016•桂林）已知直线y=﹣x+3与坐标轴分别交于点A，B，点P在抛物线y=﹣（x ﹣）2+4上，能使△ABP为等腰三角形的点P的个数有（）A．3个 B．4个 C．5个 D．6个【考点】二次函数图象上点的坐标特征；一次函数图象上点的坐标特征；等腰三角形的判定．【分析】以点B为圆心线段AB长为半径做圆，交抛物线于点C、M、N点，连接AC、BC，由直线y=﹣x+3可求出点A、B的坐标，结合抛物线的解析式可得出△ABC等边三角形，再令抛物线解析式中y=0求出抛物线与x轴的两交点的坐标，发现该两点与M、N重合，结合图形分三种情况研究△ABP为等腰三角形，由此即可得出结论．【解答】解：以点B为圆心线段AB长为半径做圆，交抛物线于点C、M、N点，连接AC、BC，如图所示．令一次函数y=﹣x+3中x=0，则y=3，∴点A的坐标为（0，3）；令一次函数y=﹣x+3中y=0，则﹣x+3=0，解得：x=，∴点B 的坐标为（，0）．∴AB=2．∵抛物线的对称轴为x=，∴点C的坐标为（2，3），∴AC=2=AB=BC，∴△ABC为等边三角形．令y=﹣（x ﹣）2+4中y=0，则﹣（x ﹣）2+4=0，解得：x=﹣，或x=3．∴点E 的坐标为（﹣，0），点F的坐标为（3，0）．△ABP为等腰三角形分三种情况：①当AB=BP时，以B点为圆心，AB长度为半径做圆，与抛物线交于C、M、N三点；②当AB=AP时，以A点为圆心，AB长度为半径做圆，与抛物线交于C、M两点，；③当AP=BP时，作线段AB的垂直平分线，交抛物线交于C、M两点；∴能使△ABP为等腰三角形的点P的个数有3个．故选A．【点评】本题考查了二次函数与坐标轴的交点坐标、等腰三角形的判定、一次函数与坐标轴的交点坐标以及等边三角形的判定定理，解题的关键是依照题意画出图形，利用数形结合来解决问题．本题属于中档题，难度不小，本题不需要求出P点坐标，但在寻找点P的过程中会出现多次点的重合问题，由此给解题带来了难度．4．（2016•桂林）如图，在Rt△AOB中，∠AOB=90°，OA=3，OB=2，将Rt△AOB绕点O顺时针旋转90°后得Rt△FOE，将线段EF绕点E逆时针旋转90°后得线段ED，分别以O，E为圆心，OA、ED长为半径画弧AF和弧DF，连接AD，则图中阴影部分面积是（）A．πB ． C．3+πD．8﹣π【考点】扇形面积的计算；旋转的性质．【分析】作DH⊥AE于H，根据勾股定理求出AB，根据阴影部分面积=△ADE的面积+△EOF的面积+扇形AOF的面积﹣扇形DEF的面积、利用扇形面积公式计算即可．【解答】解：作DH⊥AE于H，∵∠AOB=90°，OA=3，OB=2，∴AB==，由旋转的性质可知，OE=OB=2，DE=EF=AB=，△DHE≌△BOA，∴DH=OB=2，阴影部分面积=△ADE的面积+△EOF的面积+扇形AOF的面积﹣扇形DEF的面积=×5×2+×2×3+﹣=8﹣π，故选：D．【点评】本题考查的是扇形面积的计算、旋转的性质、全等三角形的性质，掌握扇形的面积公式S=和旋转的性质是解题的关键．5．（2016•桂林）若关于x的一元二次方程（k﹣1）x2+4x+1=0有两个不相等的实数根，则k的取值范围是（）A．k＜5 B．k＜5，且k≠1 C．k≤5，且k≠1 D．k＞5【考点】根的判别式；一元二次方程的定义．【分析】根据方程为一元二次方程且有两个不相等的实数根，结合一元二次方程的定义以及根的判别式即可得出关于k的一元一次不等式组，解不等式组即可得出结论．【解答】解：∵关于x的一元二次方程（k﹣1）x2+4x+1=0有两个不相等的实数根，∴，即，解得：k＜5且k≠1．故选B．【点评】本题考查了根的判别式以及一元二次方程的定义，解题的关键是得出关于k的一元一次不等式组．本题属于基础题，难度不大，解决该题型题目时，根据方程根的个数结合一元二次方程的定义以及根的判别式得出不等式组是关键．6．（2016•上海）如图，在Rt△ABC中，∠C=90°，AC=4，BC=7，点D在边BC上，CD=3，⊙A的半径长为3，⊙D与⊙A相交，且点B在⊙D外，那么⊙D的半径长r的取值范围是（）A．1＜r＜4 B．2＜r＜4 C．1＜r＜8 D．2＜r＜8【考点】圆与圆的位置关系；点与圆的位置关系．【分析】连接AD，根据勾股定理得到AD=5，根据圆与圆的位置关系得到r＞5﹣3=2，由点B在⊙D外，于是得到r＜4，即可得到结论．【解答】解：连接AD，∵AC=4，CD=3，∠C=90°，∴AD=5，∵⊙A的半径长为3，⊙D与⊙A相交，∴r＞5﹣3=2，∵BC=7，∴BD=4，∵点B在⊙D外，∴r＜4，∴⊙D的半径长r的取值范围是2＜r＜4，故选B．【点评】本题考查了圆与圆的位置关系，点与圆的位置关系，设点到圆心的距离为d，则当d=r时，点在圆上；当d＞r时，点在圆外；当d＜r时，点在圆内．7．（2016•潍坊）若关于x 的方程+=3的解为正数，则m的取值范围是（）A．m ＜B．m ＜且m ≠C．m ＞﹣ D．m ＞﹣且m ≠﹣【考点】分式方程的解．【分析】直接解分式方程，再利用解为正数列不等式，解不等式得出x的取值范围，进而得出答案．【解答】解：去分母得：x+m﹣3m=3x﹣9，整理得：2x=﹣2m+9，解得：x=，∵关于x 的方程+=3的解为正数，∴﹣2m+9＞0，解得：m ＜，当x=3时，x==3，解得：m=，故m的取值范围是：m ＜且m ≠．故选：B．【点评】此题主要考查了分式方程的解以及不等式的解法，正确解分式方程是解题关键．8．（2016•潍坊）实数a，b在数轴上对应点的位置如图所示，化简|a |+的结果是（）A．﹣2a+b B．2a﹣b C．﹣b D．b【考点】二次根式的性质与化简；实数与数轴．【分析】直接利用数轴上a，b的位置，进而得出a＜0，a﹣b＜0，再利用绝对值以及二次根式的性质化简得出答案．【解答】解：如图所示：a＜0，a﹣b＜0，则|a |+=﹣a﹣（a﹣b）=﹣2a+b．故选：A．【点评】此题主要考查了二次根式的性质以及实数与数轴，正确得出各项符号是解题关键．9．（2016•衡阳）如图，已知A，B是反比例函数y=（k＞0，x＞0）图象上的两点，BC∥x轴，交y 轴于点C，动点P从坐标原点O出发，沿O→A→B→C（图中“→”所示路线）匀速运动，终点为C，过P 作PM⊥x轴，垂足为M．设三角形OMP的面积为S，P点运动时间为t，则S关于t的函数图象大致为（）A ．B ．C ．D ．【考点】动点问题的函数图象．【专题】反比例函数及其应用．【分析】结合点P的运动，将点P的运动路线分成O→A、A→B、B→C三段位置来进行分析三角形OMP 面积的计算方式，通过图形的特点分析出面积变化的趋势，从而得到答案．【解答】解：设∠AOM=α，点P运动的速度为a，当点P从点O运动到点A的过程中，S==a2•cosα•sinα•t2，由于α及a均为常量，从而可知图象本段应为抛物线，且S随着t的增大而增大；当点P从A运动到B时，由反比例函数性质可知△OPM 的面积为k，保持不变，故本段图象应为与横轴平行的线段；当点P从B运动到C过程中，OM的长在减少，△OPM的高与在B点时相同，故本段图象应该为一段下降的线段；故选：A．【点评】本题考查了反比例函数图象性质、锐角三角函数性质，解题的关键是明确点P在O→A、A→B、B→C三段位置时三角形OMP的面积计算方式．10．（2016•烟台）如图，⊙O的半径为1，AD，BC是⊙O的两条互相垂直的直径，点P从点O出发（P 点与O点不重合），沿O→C→D的路线运动，设AP=x，sin∠APB=y，那么y与x之间的关系图象大致是（）A ．B ．C ．D ．【考点】动点问题的函数图象．【专题】动点型；函数思想．【分析】根据题意分1＜x ≤与＜x≤2两种情况，确定出y与x的关系式，即可确定出图象．【解答】解：当P在OC上运动时，根据题意得：sin∠APB=，∵OA=1，AP=x，sin∠APB=y，∴xy=1，即y=（1＜x ≤），当P 在上运动时，∠APB=∠AOB=45°，此时y=（＜x≤2），图象为：故选C．【点评】此题考查了动点问题的函数图象，列出y与x的函数关系式是解本题的关键．11．（2016•日照）一个整数的所有正约数之和可以按如下方法求得，如：6=2×3，则6的所有正约数之和（1+3）+（2+6）=（1+2）×（1+3）=12；12=22×3，则12的所有正约数之和（1+3）+（2+6）+（4+12）=（1+2+22）×（1+3）=28；36=22×32，则36的所有正约数之和（1+3+9）+（2+6+18）+（4+12+36）=（1+2+22）×（1+3+32）=91．参照上述方法，那么200的所有正约数之和为（）A．420 B．434 C．450 D．465【考点】规律型：数字的变化类．【分析】在类比推理中，200的所有正约数之和可按如下方法得到：根据200=23×52，可得200的所有正约数之和为（1+2+22+23）（1+5+52），即可得出答案．【解答】解：200的所有正约数之和可按如下方法得到：因为200=23×52，所以200的所有正约数之和为（1+2+22+23）×（1+5+52）=465．故选（D）．【点评】本题属于类比推理的问题，类比推理的一般方法是：找出两类事物之间的相似性或一致性；用一类事物的性质去推测另一类事物的性质，得出一个明确的猜想．解决问题的关键是认真观察、仔细思考、善用联想，探寻变化规律．12．（2016•淮安）如图，在Rt△ABC中，∠C=90°，以顶点A为圆心，适当长为半径画弧，分别交AC，AB于点M，N，再分别以点M，N 为圆心，大于MN的长为半径画弧，两弧交于点P，作射线AP交边BC于点D，若CD=4，AB=15，则△ABD的面积是（）A．15 B．30 C．45 D．60【考点】角平分线的性质．【分析】判断出AP是∠BAC的平分线，过点D作DE⊥AB于E，根据角平分线上的点到角的两边距离相等可得DE=CD，然后根据三角形的面积公式列式计算即可得解．【解答】解：由题意得AP是∠BAC的平分线，过点D作DE⊥AB于E，又∵∠C=90°，∴DE=CD，∴△ABD的面积=AB•DE=×15×4=30．故选B．【点评】本题考查了角平分线上的点到角的两边距离相等的性质以及角平分线的画法，熟记性质是解题的关键．二．选择题（共6小题）13．（2016•广安）如图，三个正方形的边长分别为2，6，8；则图中阴影部分的面积为21．【考点】三角形的面积．【分析】根据正方形的性质来判定△ABE∽△ADG，再根据相似三角形的对应线段成比例求得BE的值；同理，求得△ACF∽△ADG，AC：AD=CF：DG，即CF=5；然后再来求梯形的面积即可．【解答】解：如图，根据题意，知△ABE∽△ADG，∴AB：AD=BE：DG，又∵AB=2，AD=2+6+8=16，GD=8，∴BE=1，∴HE=6﹣1=5；同理得，△ACF∽△ADG，∴AC：AD=CF：DG，∵AC=2+6=8，AD=16，DG=8，∴CF=4，∴IF=6﹣4=2；∴S梯形IHEF=（IF+HE）•HI=×（2+5）×6=21；所以，则图中阴影部分的面积为21．【点评】本题主要考查的是相似三角形的判定及性质、以及梯形面积的计算，解决本题的关键是利用三角形的性质定理与判定定理．14．（2016•玉林）如图，已知正方形ABCD边长为1，∠EAF=45°，AE=AF，则有下列结论：①∠1=∠2=22.5°；②点C到EF 的距离是；③△ECF的周长为2；④BE+DF＞EF．其中正确的结论是①②③．（写出所有正确结论的序号）【考点】四边形综合题．【专题】综合题．【分析】先证明Rt△ABE≌Rt△ADF得到∠1=∠2，易得∠1=∠2=∠22.5°，于是可对①进行判断；连结EF、AC，它们相交于点H ，如图，利用Rt△ABE≌Rt△ADF得到BE=DF ，则CE=CF，接着判断AC 垂直平分EF，AH平分∠EAF，于是利用角平分线的性质定理得到EB=EH，FD=FH，则可对③④进行判断；设BE=x，则EF=2x，CE=1﹣x，利用等腰直角三角形的性质得到2x=（1﹣x），解得x=﹣1，则可对④进行判断．【解答】解：∵四边形ABCD为正方形，∴AB=AD，∠BAD=∠B=∠D=90°，在Rt△ABE和Rt△ADF中，∴Rt△ABE≌Rt△ADF，∴∠1=∠2，∵∠EAF=45°，∴∠1=∠2=∠22.5°，所以①正确；连结EF、AC，它们相交于点H，如图，∵Rt△ABE≌Rt△ADF，∴BE=DF，而BC=DC，∴CE=CF，而AE=AF，∴AC垂直平分EF，AH平分∠EAF，∴EB=EH，FD=FH，∴BE+DF=EH+HF=EF，所以④错误；∴△ECF的周长=CE+CF+EF=CE+BE+CF+DF=CB+CD=1+1=2，所以③正确；设BE=x，则EF=2x，CE=1﹣x，∵△CEF为等腰直角三角形，∴EF=CE，即2x=（1﹣x），解得x=﹣1，∴EF=2（﹣1），∴CH=EF=﹣1，所以②正确．故答案为①②③．【点评】本题考查了四边形的综合题：熟练掌握正方形的性质和角平分线的性质定理．解决本题的关键是证明AC垂直平分EF．15．（2016•毕节市）如图，分别以边长等于1的正方形的四边为直径作半圆，则图中阴影部分的面积为π﹣1．【考点】扇形面积的计算．【分析】如图，作辅助线；首先求出半圆O的面积，其次求出△ABP的面积；观察图形可以发现：阴影部分的面积=4（S半圆O﹣S△ABP），求出值，即可解决问题．【解答】解：如图，连接PA、PB、OP；则S半圆O==，S△ABP=AB•OP=×1×=，由题意得：图中阴影部分的面积=4（S 半圆O ﹣S △ABP ） =4（﹣）=π﹣1，故答案为：π﹣1．【点评】该题主要考查了正方形的性质、圆的面积公式、三角形的面积公式等知识点及其应用问题；解题的关键是作辅助线，将阴影部分的面积转化为规则图形的面积和或差．16．（2016•潍坊）已知∠AOB=60°，点P 是∠AOB 的平分线OC 上的动点，点M 在边OA 上，且OM=4，则点P 到点M 与到边OA 的距离之和的最小值是 2 ．【考点】轴对称﹣最短路线问题．【分析】过M 作MN′⊥OB 于N′，交OC 于P ，即MN′的长度等于点P 到点M 与到边OA 的距离之和的最小值，解直角三角形即可得到结论．【解答】解：过M 作MN′⊥OB 于N′，交OC 于P ，则MN′的长度等于PM +PN 的最小值，即MN′的长度等于点P 到点M 与到边OA 的距离之和的最小值， ∵∠ON′M=90°，OM=4， ∴MN′=OM•sin60°=2，∴点P 到点M 与到边OA 的距离之和的最小值为2．【点评】本题考查了轴对称﹣最短路线问题，解直角三角形，正确的作出图形是解题的关键． 17．（2016•烟台）如图，C 为半圆内一点，O 为圆心，直径AB 长为2cm ，∠BOC=60°，∠BCO=90°，将△BOC 绕圆心O 逆时针旋转至△B′OC′，点C′在OA 上，则边BC 扫过区域（图中阴影部分）的面积为π cm 2．【考点】扇形面积的计算；旋转的性质．【分析】根据已知条件和旋转的性质得出两个扇形的圆心角的度数，再根据扇形的面积公式进行计算即可得出答案．【解答】解：∵∠BOC=60°，△B′OC′是△BOC 绕圆心O 逆时针旋转得到的， ∴∠B′OC′=60°，△BCO=△B′C′O ， ∴∠B′OC=60°，∠C′B′O=30°， ∴∠B′OB=120°， ∵AB=2cm ，∴OB=1cm ，OC′=， ∴B′C′=，∴S 扇形B′OB ==π，S 扇形C′OC ==，∵∴阴影部分面积=S 扇形B′OB +S △B′C′O ﹣S △BCO ﹣S 扇形C′OC =S 扇形B′OB ﹣S 扇形C′OC =π﹣=π；故答案为：π．【点评】此题考查了旋转的性质和扇形的面积公式，掌握直角三角形的性质和扇形的面积公式是本题的关键．18．（2016•丽水）如图，一次函数y=﹣x +b 与反比例函数y=（x ＞0）的图象交于A ，B 两点，与x 轴、y 轴分别交于C ，D 两点，连结OA ，OB ，过A 作AE ⊥x 轴于点E ，交OB 于点F ，设点A 的横坐标为m ．（1）b= m + （用含m 的代数式表示）；（2）若S △OAF +S 四边形EFBC =4，则m 的值是．【考点】反比例函数与一次函数的交点问题．【分析】（1）根据待定系数法点A 的纵坐标相等列出等式即可解决问题．（2）作AM ⊥OD 于M ，BN ⊥OC 于N ．记△AOF 面积为S ，则△OEF 面积为2﹣S ，四边形EFBC 面积为4﹣S ，△OBC 和△OAD 面积都是6﹣2S ，△ADM 面积为4﹣2S=2（2﹣s ），所以S △ADM =2S △OEF ，推出EF=AM=NB ，得B （2m ，）代入直线解析式即可解决问题．【解答】解：（1）∵点A 在反比例函数y=（x ＞0）的图象上，且点A 的横坐标为m ， ∴点A 的纵坐标为，即点A 的坐标为（m ，）．令一次函数y=﹣x +b 中x=m ，则y=﹣m +b ， ∴﹣m +b= 即b=m +．故答案为：m +．（2）作AM ⊥OD 于M ，BN ⊥OC 于N ．∵反比例函数y=，一次函数y=﹣x +b 都是关于直线y=x 对称， ∴AD=BC ，OD=OC ，DM=AM=BN=CN ，记△AOF 面积为S ，则△OEF 面积为2﹣S ，四边形EFBC 面积为4﹣S ，△OBC 和△OAD 面积都是6﹣2S ，△ADM 面积为4﹣2S=2（2﹣s ）， ∴S △ADM =2S △OEF ，由对称性可知AD=BC ，OD=OC ，∠ODC=∠OCD=45°，△AOM ≌△BON ，AM=NB=DM=NC ， ∴EF=AM=NB ， ∴EF 是△OBN 的中位线， ∴N （2m ，0），∴点B 坐标（2m ，）代入直线y=﹣x +m +， ∴=﹣2m +m +，整理得到m 2=2， ∵m ＞0， ∴m=．故答案为．【点评】本题考查反比例函数与一次函数图象的交点、对称等知识，解题的关键是利用对称性得到很多相等的线段，学会设参数解决问题，属于中考填空题中的压轴题．三．选择题（共7小题）19．（2016•黄石）先化简，再求值：÷•，其中a=2016．【考点】分式的化简求值．【分析】先算除法，再算乘法，把分式化为最简形式，最后把a=2016代入进行计算即可．【解答】解：原式=••=（a ﹣1）•=a +1，当a=2016时，原式=2017．【点评】本题考查的是分式的化简求值，在解答此类问题时要注意把分式化为最简形式，再代入求值． 20．（2016•毕节市）为了提高学生书写汉字的能力，增强保护汉字的意识，某校举办了首届“汉字听写大赛”，学生经选拔后进入决赛，测试同时听写100个汉字，每正确听写出一个汉字得1分，本次决赛，学生成绩为x （分），且50≤x ＜100，将其按分数段分为五组，绘制出以下不完整表格：组别成绩x （分）频数（人数）频率一 50≤x ＜60 2 0.04 二60≤x ＜70100.2三70≤x＜8014b四80≤x＜90a0.32五90≤x＜10080.16请根据表格提供的信息，解答以下问题：（1）本次决赛共有50名学生参加；（2）直接写出表中a=16，b=0.28；（3）请补全下面相应的频数分布直方图；（4）若决赛成绩不低于80分为优秀，则本次大赛的优秀率为48%．【考点】频数（率）分布直方图；频数（率）分布表．【专题】探究型；统计与概率．【分析】（1）根据表格中的数据可以求得本次决赛的学生数；（2）根据（1）中决赛学生数，可以求得a、b的值；（3）根据（2）中a的值，可以将频数分布直方图补充完整；（4）根据表格中的数据可以求得本次大赛的优秀率．【解答】解：（1）由表格可得，本次决赛的学生数为：10÷0.2=50，故答案为：50；（2）a=50×0.32=16，b=14÷50=0.28，故答案为：16，0.28；（3）补全的频数分布直方图如右图所示，（4）由表格可得，决赛成绩不低于80分为优秀率为：（0.32+0.16）×100%=48%，故答案为：48%．【点评】本题考查频数分布直方图、频数分布表，解题的关键是明确题意，找出所求问题需要的条件．21．（2016•咸宁）某网店销售某款童装，每件售价60元，每星期可卖300件，为了促销，该网店决定降价销售．市场调查反映：每降价1元，每星期可多卖30件．已知该款童装每件成本价40元，设该款童装每件售价x元，每星期的销售量为y件．（1）求y与x之间的函数关系式；（2）当每件售价定为多少元时，每星期的销售利润最大，最大利润多少元？（3）若该网店每星期想要获得不低于6480元的利润，每星期至少要销售该款童装多少件？【考点】二次函数的应用；一元二次不等式．【分析】（1）根据售量y（件）与售价x（元/件）之间的函数关系即可得到结论．（2））设每星期利润为W元，构建二次函数利用二次函数性质解决问题．（3）列出不等式先求出售价的范围，再确定销售数量即可解决问题．【解答】解：（1）y=300+30（60﹣x）=﹣30x+2100．（2）设每星期利润为W元，W=（x﹣40）（﹣30x+2100）=﹣30（x﹣55）2+6750．∴x=55时，W最大值=6750．∴每件售价定为55元时，每星期的销售利润最大，最大利润6750元．（3）由题意（x﹣40）（﹣30x+2100）≥6480，解得52≤x≤58，当x=52时，销售300+30×8=540，当x=58时，销售300+30×2=360，∴该网店每星期想要获得不低于6480元的利润，每星期至少要销售该款童装360件．【点评】本题考查二次函数的应用，一元二次不等式，解题的关键是构建二次函数解决最值问题，学会利用图象法解一元二次不等式，属于中考常考题型．22．（2016•无锡）某公司今年如果用原线下销售方式销售一产品，每月的销售额可达100万元．由于该产品供不应求，公司计划于3月份开始全部改为线上销售，这样，预计今年每月的销售额y（万元）。