2第二章-土体应力计算
土力学

(3)地基土可视为半无限体。地基土在水平和深度方向上相 对于建筑物基础的尺寸而言,可视为是无限延伸的,因此,地 基土符合半无限体的假设。
pmax
2P 3Kb
3(L
2P 2 e)b
e>b/6: 出现拉应力区
3.2.4 基底附加压力
p0 p ch p 0h
例题:某矩形基础底面尺寸l=2.4m, b=1.6m,埋深2.0m,所受荷载设计值 m=100kN·m,F=450kN,其他条件见图。 试求基底压力和基底附加压力。
z
3P
2
z3 R5
z
3P
2
(r 2
z3 z2 )5/2
3
2
1 [(r / z)2 1]5/ 2
P z2
z
P z2
查表3.1
3.3.2 竖向分布荷载地基附加应力
若在半无限体表面作用一分布荷载p(x,y),如图所示。计 算土中某点M(x,y,z)的竖向应力σz。
在基底取微元面积dF=dξdη,则作 用在dF上的集中力:
a 点:z = 0 m,σcz=γz=0; b 点:z = 2 m,σcz=γz=19 ×2=38 kPa c 点:z = 5 m , σcz =∑γihi=19 ×2+10 ×3=68 kPa, d 点:z = 9 m,σcz =∑γihi=19 ×2+10 ×3+7.1 ×4=96.4 kPa
土体应力计算知识点总结

土体应力计算知识点总结土体应力计算是岩土工程中的重要内容,它对于工程设计、施工和监测都起着至关重要的作用。
通过对土体内部的应力状态进行分析和计算,可以为工程的安全性和稳定性提供重要参考,并指导工程的设计和施工过程。
本文将对土体应力计算的相关知识点进行总结和分析,希望可以对读者有所帮助。
1. 土体的内部应力状态土体内部的应力状态包括有效应力和孔隙水压力,有效应力是由于土体的自重和外部载荷引起的土体颗粒间的相互作用产生的应力,而孔隙水压力则是由土体中的水分引起的压力。
有效应力和孔隙水压力的分布对土体的力学性质和变形特性有着重要影响,因此对其进行合理的计算和分析是土体力学研究的重要内容。
2. 应力计算的相关理论在进行土体内部应力计算时,需要涉及到一些基本的理论知识,如莫尔-库伦准则、孔隙水压力的计算方法、应力传递的原理等。
莫尔-库伦准则是描述土体内部剪切应力和正应力之间关系的重要理论,它对于土体内部应力的分析和计算有着重要的指导作用。
而孔隙水压力的计算方法涉及到水文和渗流的知识,需要结合土壤的渗透特性和水文条件进行综合考虑。
应力传递的原理则是描述土体内部应力传递过程的基本规律,对于分析土体内部应力状态有着重要的指导意义。
3. 应力计算的相关方法在进行土体内部应力计算时,可以采用不同的方法,如弹性理论方法、极限平衡方法、有限元方法等。
弹性理论方法是描述土体内部应力分布的基本方法,它基于弹性力学理论,以均匀弹性和线弹性为假设,通过解析方法来进行应力计算。
极限平衡方法则是一种应用力学平衡原理来计算土体内部应力状态的方法,它可以考虑土体内部的非弹性变形和塑性变形,适用于分析较复杂的土体结构。
有限元方法是一种数值方法,通过离散化土体结构,构建有限元模型,利用计算机进行数值计算,可以对土体内部应力状态进行较为精确的分析和计算。
4. 土体内部应力计算的应用土体内部应力计算在工程实践中有着广泛的应用,如用于岩土工程的设计、地下工程的施工和监测等。
岩土力学中应力计算

的原因 附加应力 土 中
由于外荷(静的或动的) 在土体内部引起的应力, 记为σZ。
应 力
有效应力
土粒所传递的粒间应力, 记为σ′。
按其传
递方式
孔隙水压力
土中水传递的 孔隙应力, 记
孔隙应力 孔隙气压力
为u。
土中气传递的 孔隙应力。
土中应力计算的基本假定
假定地基土是均匀、连续、各向同性的半无限弹性体。
【解】
本例题天然地面下第一层粉质黏土厚6m,其中地下水位以 上和以下的厚度分别为3.6m和2.4m;第二层为黏土层。依 次 计算2.5m、3.6m、5m、6m、9m各深度处的土中竖向自重 应 力,计算过程及自重应力分布图一并列于下图中。
粉 质 黏 土
黏 土
习题2-1图
三、土中附加应力计算
上部 结构
应力矩阵
ij yxx
xy y
xz yz
zx zy z
三维应力状态(轴对称应力状态)
应力条件
x y c
xy yz zx 0
水压 力c
应
c 0 0
力 矩
ij
0
c
0
阵
0 0 z
轴向力F
z
试 样
y
x
x y c
2、二维应力状态(平面应变状态)
o
y
z
x
1、当位于地下水位以下的土为砂土时,土中水为自由 水,计算时用土的浮重度。
2、当位于地下水位以下的土为坚硬黏土时(IL ≤ 0) , 在饱和坚硬黏土中只含有结合水,对土体没有浮力 的作用,计算自重应力时应采用饱和重度。
3、地下水位以下黏土,当 IL > 1时,土处于流动状态, 土粒间存在大量的自由水,用土的浮重度。
土体中的应力计算

x 0xy 0 xz x 0yx y 0 yz y ij = 0zy z 0zx
理论研究和工程实践中广泛应用
三、土的应力-应变关系的假定
1、室内测定方法及一般规律
轴对称问题 常规三轴试验 侧限压缩试验
特殊应力状态
一维问题
2、应力计算时的基本假定 1)连续性假定 2)均质、各向同性假定 3)线性变形体假定 4)半无限体假定
x y ; z xy , yz , zx 0
x y ; z xy , yz , zx 0
x y , z ; x y , z
二、地基中常见的应力状态----三维问题图解
z
zx
xy
x
o x z
y yz
y
x xy xz ij = yx y yz zx zy z
本章重点
1、应力状态及应力应变关系
地基中的应力状态 土力学中应力符号的规定 应力应变关系 强度问题 变形问题
2、自重应力
建筑物修建以前,地基中由土体 本身的有效重量所产生的应力。 建筑物修建以后,建筑物重 量等外荷载在地基中引起的 应力,所谓的“附加”是指 在原来自重应力基础上增加 的压力。
3、附加应力
碎散体 非线性 弹塑性 成层土 各向异性
① 连续介质(宏观平均) ② 线弹性体(应力较小时)
线弹性体
③ 均匀一致各向同性体 (土层性质变化不大时)
Δσ
加 载
卸 载
E、
与(x, y, z)无关 与方向无关
εp
εe
ε
§3.2 土体自重应力的计算
一、水平地基中的自重应力
定义:在修建建筑物以前,地基中由土体本身的有效重量而 产生的应力。
土体中的应力计算

土体中的应力计算在土体中,应力是指单位面积上的力的作用,可以分为垂直应力和水平应力。
垂直应力是指垂直于土体中其中一点的力的作用,通常用σ表示,单位为N/m²或Pa;水平应力是指与土体中其中一点切向的力的作用,通常用τ表示,单位为N/m²或Pa。
在计算土体中的应力时,需要先确定作用力的大小和方向。
作用力可以分为自重应力、表面荷载和边界条件所引起的应力。
自重应力是由土体自身的重力引起的应力,可以通过土体的密度和重力加速度来计算;表面荷载是由于外界施加在土体上的荷载,可以通过荷载的大小和分布情况来计算;边界条件所引起的应力是由于土体边界的约束而产生的应力,可以根据边界条件的空间限制来计算。
计算垂直应力时,需要将作用力作用在单位面积上,即垂直应力等于作用力的大小除以土体的面积。
例如,对于自重应力来说,垂直应力可以通过土体的密度乘以重力加速度来计算。
而对于表面荷载来说,垂直应力可以通过荷载的大小和分布情况来计算。
计算水平应力时,需要考虑土体的弹性特性。
根据弹性理论,水平应力的大小与垂直应力的大小和土体的弹性模量有关。
弹性模量是反映土体抵抗应力的能力的指标,可以通过试验或经验公式估算得到。
一般来说,弹性模量越大,土体的抵抗应力能力越强,水平应力的大小也越大。
在应力计算时,还需要考虑土体的变形特性。
土体的变形可以分为弹性变形和塑性变形两种。
弹性变形是指在荷载作用后,土体恢复到无荷载状态时的变形,是可逆的,可以通过应力和应变之间的线性关系进行计算。
而塑性变形是指在荷载作用后,土体不完全恢复到无荷载状态时的变形,是不可逆的,需要通过试验或经验公式来确定。
总之,土体中的应力计算是根据应力平衡原理和弹性力学原理进行的,需要考虑土体的类型、作用力的大小和方向以及土体的弹性和变形特性。
通过合理的应力计算,可以为土壤工程和土木工程的设计和施工提供基础数据。
土体应力计算

第2章 土体应力计算2.1 自重应力 2.1.1 地基中的自重应力自重应力是由于地基土体本身的有效重量而产生的。
研究地基的自重应力是为了确定地基土体的应力状态。
计算地基中的自重应力时,一般将地基作为半无限弹性体来考虑,地基中的自重应力状态属于侧限应力状态,其内部任一水平面和垂直面上,均只有正应力而无剪应力。
1)垂直向自重应力.......设地基中某单元距地面的距离为Z ,如图2-1所示,土的容重为 γ,则该单元上的垂向自重应力等于其单位面积上土柱的有效 重量,即:(2-1)单位以kPa 计。
从式(5-1)很容易得出,垂向自重应力随深度的增加而加大。
在均质地基中,垂直自重应力沿某一铅垂线上的分布是一条向下倾斜的直线,如图2-2所示。
若计算点在地下水位以下,由于水对土体有浮力作用,水下部分土柱的有效重量应采用土的浮容重γˊ计算。
如图2-2(a )中位于地下水位以下的某点,在水位以下深度为 ,其竖向自重应力为:(2-2)式中,浮容重为 (2-3 )分析式(2-2)可知,自重应力的分布仍为直线,在地下水位处 发生转折,分布图见2-2(b )若地基是由几种不同容重的土层组成时,如图2-2(b ),则任意深度Z 处的自重应力为:∑==++=ni ii sz h h h 12211γγγσ szσz sz γσ=i h 2'1h h s z γγσ+=ωγγγ-=sat '(2-4)式中,n 为地基中土的层数;为第i 层土的容重,单位:kN ∕ ; 为第i 层土的厚度,单位:m.。
成层土地基自重应力沿铅直线的分布图见图2-2(b),它是一条折线, 其转折点位于各不同容重土层的分界面上。
2)水平向自重应力 、在地面以下深度Z 处,由土的自重而产生的水平向应力,大小等于该点土的自重应力与土的侧压力系数 之乘积,即(2-5)土的静止侧压力系数 是指土体在无侧向变形条件下,水平向有效应力与垂直向有效应力之比值。
第二章 土体中的应力

其中 cosβ=z/R1,同样可求得 x
2 p
R1
cos
sin 2
五、条形荷载作用 1.均布条形荷载作用
xz
zx
2 p R1
cos2
s in
z
p
[sin
1
cos1
sin
2
cos2
(1
2 )]
同理得: x
p
[ sin(1
2 ) cos(1
2 ) (1
2 )]
xz
p
说明;经常用到的是竖向自重应力,为简单起见,一律简写成 c ,即 c z 。
2.成层土条件下自重应力
设各层土的土层厚度分别为 h1、h2、h3,容重分别为 1、 2、 3,如图。分层
不影响对称性,仍用前述的方法截取土柱体,分段求合力,得 P=P1+P2+P3
即:P F 1 h1 F 2 h2 F 3 h3 由此得: c 1 h1 2 h2 3 h3
三、圆形面积上的荷载
1.均布荷载圆心点下
z
A
3 pZ3 2 R5
dF
o
p
ro
o
0
2 0
3 Z3
z
2 R5
dF
f( ) ro
0 —均布圆形荷载作用时中心点下的竖向附加应力系数其中的 ro 为荷载作用面半径,z 计算点至荷载作用面的距离。
2. 均布荷载任意点下
z p
其中
f(r , z) ro ro
=
M/N,则
pm ax
m in
N Lb
(1
6e L
)
(e
L) 6
此时,基底反力呈梯形或三角形分布,如图,当 e>L/6 时,按上式计算基底出现拉力,而基底只能承压不能受拉,
《土力学》课程导学

《土力学》课程导学1.《土力学》课程特点和学习方法《土力学》形成一门完整的学科才80余年的历史。
土是一种多孔松散介质,是由固态、液态、气态物质组成的三相体系。
土不同于其他各种连续体材料,天然土体物理力学性质十分复杂,受土的成因、物质成分、环境变动等因素影响很大。
因此研究《土力学》课题时不能完全沿用其它力学课程的研究方法。
为了实用的目的,本科阶段学习的《土力学》教材中常常采用一些简单的、理想化的假定来描述土的性质,如计算土中应力时,常假定地基土是各向同性的、均匀的弹性体;当研究土的渗透性和变形时,假设土是连续的多孔介质;研究土的强度时,又假定土体为理想的刚塑性体。
学习中希望能够体会针对不同理论或方法的简化假定条件,要注意灵活应用不可生搬硬套,依据基本理论解决工程问题时也常常要做出某些比较符合实际的简化假定,但不要背离该理论原先的假定前提。
《土力学》已形成一定的理论体系,尽管现代《土力学》理论发展迅速,由“初等”向“高等”发展,但到目前为止,土的许多性质还未被很好的认识,还难以全面客观模拟和概括天然土体的各种力学行为的全貌。
《土力学》初学者往往有新名词多、头绪多,有分块“割裂”连贯性差的感觉。
其实不然,课程各章有相对独立性,但全课程内容的关联性和综合性很强,有其完整体系。
学习中要突出重点,兼顾全面。
要做到融会贯通,学会由此及彼由表及里,建议采取概念—理论—方法—应用—拓展的学习路径。
结合理论学习要进行各种物理力学试验,通过试验培养技能并深化理论学习,掌握计算参数的确定方法与原理,着重基本概念的理解和各知识点的贯通。
另外,通过一定量的例题和练习,了解相关的工程地质知识、建筑结构和施工知识及与其后续课程的关系。
学习和运用《土力学》基本理论和基本原理时,必须有“体系观”而且还应有“动态观”。
所谓“体系观”就是不只是能够看见树木,更要看到森林,应该既能够从“微观”试样单元入手讨论土体的变形、强度和渗透性,又能够揉合知识从“宏观”入手解决工程系统中的《土力学》问题。
土力学完整课件土中应力计算

积分,得
z t p
Y
t f (m l / b, n z / b)
三角分布矩形荷载角点下的竖向附加应 力系数.可查表. 注意l—荷载不变化边 的长度; b—荷载变化边的长度.
水平均布荷载
q
z
x z
2
2 pz 3
2
2
(二)条形荷载下的附加应力计算 1.均布条形荷载下的附加应力 p O x b/2 b/2 z x M z 2. 三角形荷载的附加应力 pt O x b z x M z
z u p
z x u f u m , n b b
l
pmax pmin
基础底面的抵 抗矩;矩形截 面W=(bl2)/6
讨论:
N 6e pmax 1 bl l min
当e<l/6时,pmax,pmin>0,基底压力呈梯形分布 当e=l/6时,pmax>0,pmin=0,基底压力呈三角形分布 当e>l/6时,pmax>0,pmin<0,基底出现拉应力,基底压力重分布
F=400kN/m 0.1m M=20kN •m/m
3.基底中点下附加压 力计算
1.5m 2m 112.6kPa
0 =18.5kN/m3
292.0kPa
179.4kPa
112.6kPa
分析步骤Ⅳ:
F=400kN/m 0.1m M=20kN •m/m
1.5m
1m 1m 2m 2m 2m
0 =18.5kN/m3
3. r 0 ,随 z 从 0 开始增大, z 先随之增大,后随之减小;
地基中的应力计算

地基中的应力计算地基是地下工程中最基本的构造部分,承受着上部结构的重量和荷载,承担着巨大的压力作用。
在地基设计中,应力计算是非常重要的一部分,它能够提供地基承载力和安全性的评估。
本文将介绍地基中应力计算的方法和计算公式。
首先,需要了解地基中的应力是如何形成的。
地基承受的主要应力有自重应力、活载荷载应力和附加应力。
自重应力是由于地基材料本身的重量所引起的应力,可以通过材料的密度和重力加速度计算得到。
活载荷载应力是由上部结构的荷载所引起的应力,可以根据上部结构的设计荷载计算得到。
附加应力是由于地基中存在的其他因素所引起的应力,比如建筑物的自身形变引起的应力。
接下来,我们介绍如何计算地基中的应力。
地基中的应力计算可以根据不同的地基类型和荷载情况采用不同的方法。
下面以均质土壤的地基为例,介绍几种常用的应力计算方法。
1.利用铁索计算应力:铁索是一种常用的应力计算工具,可以通过测量铁索的伸长量来计算地基中的应力。
首先,在地基中铺设一根长度合适的铁索,然后测量并记录铁索的伸长量。
根据该伸长量和铁索的初始长度,可以通过应力-应变关系计算得到地基中的应力。
2.利用试孔计算应力:试孔是另一种用于计算地基中应力的方法。
首先,在地基中进行试孔,并记录试孔的深度和直径。
然后,根据试孔的直径和土壤的剪切强度,可以计算得到地基中的应力分布情况。
3.利用数值模拟计算应力:数值模拟是一种常用的计算地基应力的方法,它可以通过建立地基的有限元模型来模拟地基的应力分布情况。
首先,需要根据地基的实际情况建立有限元模型,然后通过数值计算方法求解得到地基中的应力。
综上所述,地基中的应力计算是地基设计的重要环节,可以通过铁索、试孔和数值模拟等多种方法进行计算。
在进行应力计算时,需要考虑地基的类型、荷载情况和材料特性等因素,确保计算结果的准确性和可靠性。
地基中的应力计算对于确保地基的稳定性和安全性具有重要意义,是地基设计中不可或缺的一环。
应力计算

§4.3 地基中附加应力的计算 一. 竖直集中力作用下的附加应力计算-布辛内斯克课题
z
3P 2
z3 R5
zy
3P 2
yz 2 R5
zx
Ph
分解为竖直向和水平向荷 载,水平荷载引起的基底 水平应力视为均匀分布。
根据上述概念,基底平均附加压力p0 可按下式计算
p0 p cd p md (1-19)
式中 p—基底平均压力,kPa;
cd—基底处土中自重应力,kPa; m—基底标高以上天然土层的加权平均重
度,kN/m3; d—从天然地面算起的基础埋深,m。
P A
1
6e B
pmin
P 1 A
6e B
pmax
min
P A
1
6e B
P
矩形面积单向偏心荷载
P
P
土不能承 受拉应力
B
B
e
e
x
Lx
L
y
y
pmax
pmin 0 pmax
pmin 0
e<B/6: 梯形
e=B/6: 三角形
B
压力调整
Ke
基底
x
L
压力
K=B/2-e
合力
与总
3K y pmin 0
荷载 相等
pmax
2P
2P
pmax 3KL 3(B 2 e)L
e>B/6: 出现拉应力区
条形基础竖直偏心荷载
e P
B
p(x) P Mx BI
pmax
min
P 1 B
第二章 土体中的应力计算

• [思考题答案] 按给出的资料,计算并绘制地 基中的自重应力 沿深度的分布曲线。 (假定,地下水位位于标高为141.0处。)
2.2
基底压力
• 基底压力:上部结构荷载和基础自重通过 基础传递,在基础底面处施加于地基上的 单位面积压力。 • 基底反力:反向施加于基础底面上的压力
基底压力、反力
• 基底压力 建筑物上部结构荷载和基础自重通过基础传 基底压力:
讨论: 讨论:
p max p min = F + G 6e 1± bl l
当e<l/6时,pmax,pmin>0,基底压力呈梯形分布 时 , 当e=l/6时,pmax>0,pmin=0,基底压力呈三角形分布 时 , , 当e>l/6时,pmax>0,pmin<0,基底出现拉应力,基底压力重分布 时 , ,基底出现拉应力, pmax e<l/6 pmin pmax e=l/6 pmax pmin<0 基底压力重分布 pmax e>l/6 pmin=0
2.2.1 基底压力的分布规律
(1)情况1 情况1
EI=0
(a) 理想柔性基础
(b) 堤坝下基底压力
图2-1 柔性基础 基础抗弯刚度EI=0,相当于绝对柔性基础 基底压力分布与作用荷载分布相同。 基底压力分布与作用荷载分布相同。
(2)情况2 EI=∞ 情况2 刚度很大(即EI=∞),可视为刚性基础(大块混凝土实体结构) 。 荷载小,呈中央小而边缘大的情形。 荷载小,呈中央小而边缘大的情形。 随作用荷载增大,呈抛物线分布。 随作用荷载增大,呈抛物线分布。 作用荷载继续增大,发展为钟形分布。 作用荷载继续增大,发展为钟形分布。
例题见教材P29 例题见教材P29 [例2-2]解题思路: 2]解题思路: 解题思路 1)求基础自重 G=γGAd 2)求外荷F=P+Q 3)求基础的合力距M:M=M/+Q∙e0 4)求合力距的偏心距e :M=(F+G)∙e p F + G 6e 5)求基底压力 = 1 ±
土力学清华版第2章 土体中的应力计算
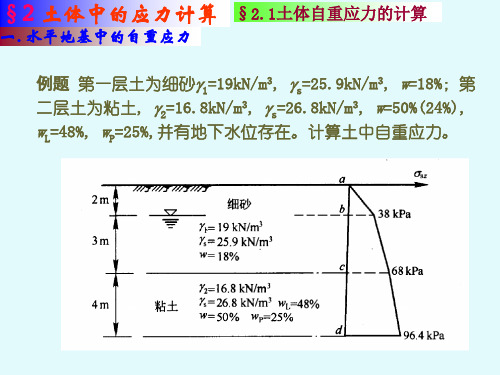
94.0 83.8 57.0 31.6 18.9 12.3
1200 1200 1600 1600 1600
25.6 44.8 60.2 71.7 83.2
88.9 70.4 44.3 25.3 15.6
114.5 115.2 104.5 97.0 98.8
0.970 0.960 0.954 0.948 0.944
a点:z=0,sz= z=0; b点:z=2m,sz=192=38kPa; c点:z=5m,sz=192+103=68kPa; d点:z=9m,sz=192+103+7.14=96.4kPa 分布如图:
§2 土体中的应力计算
§2.3地基中附加应力的计算
例题 土体表面作用一集中力F=200kN,计算地面深度 z=3m处水平面上的竖向法向应力z分布,以及距F作用点 r=1m处竖直面上的竖向法向应力z分布。
§3.3 地基的最终沉降量计算 四、例题分析 5.计算基础中点下地基中附加应力
7.2
6.确定沉降计算深度zn 根据σz = 0.2σc的确定原则,由计算结果,取zn=7.2m 7.最终沉降计算 根据e-σ曲线,计算各层的沉降量
§3土的压缩性与地基沉降计算
z( m ) 0 1.2 2.4 4.0 5.6 7.2 h σc σz σz+ σc e1 ( kPa ) ( mm ) (kPa) (kPa) (kPa) (kPa)
§2.3地基中附加应力的计算
四. 矩形面积三角形分布荷载作用下的附加应力计算
三角形分布荷载AFD作用在aeOh和ebfO上: z2=z2(aeOh)+
z2(ebfO)=p1(t1+t2)
z2=33.3(0.021+0.045)=2.2kPa
土力学与地基基础——第二章

pi 1 z Ki 2 2 z z i 1
n
K P
i 1 i i
n
2.3 地基中的附加应力
讨论:集中力荷载产生的竖向附加应力在地基
2.3 地基中的附加应力
(d)o点在荷载面角点外侧 把荷载面看成由I(ohce)、Ⅳ(ogaf)两个面积中扣除 Ⅱ(ohbf)和Ⅲ(ogde)而成的,所以
z ( Kc1 Kc 2 Kc3 Kc 4 ) p0
2.3 地基中的附加应力
例题 以角点法计算矩形基础甲的基底中心点
垂线下不同深度处的地基附加应力的分布,基 础埋深1.5m,集中力为1940KN,并考虑两相邻 基础乙的影响(两相邻柱距为6m,荷载同基础 甲)。
(b)o点在荷载面内
z ( Kc1 Kc 2 Kc 3 Kc 4 ) p0
(c)o点在荷载面边缘外侧 此时荷载面abcd可看成是由I(ofbg)与Ⅱ(ofah)之差和 Ⅲ(oecg)与Ⅳ(oedh)之差合成的,所以
z ( Kc1 Kc 2 Kc 3 Kc 4 ) p0
如果基础砌置在天然地面上,那末全部基底压 力就是新增加于地基表面的基底附加压力。一 般天然土层在自重作用下的变形早巳结束,因 此只有基底附加压力才能引起地基的附加应力 和变形。
2.2 基底压力
基底压力为均匀分布时:
p0 p 0 p 0 d
基底压力为梯形分布时:
p0 max p0 min
2.1 地基中的自重应力
什么时候考虑土体在自重下的自重应力? 土层一般形成至今有很长的时间,自重应力下
土体中的应力计算共45页文档

L
y
矩形面积偏心荷载
P b
ey
x
ex
p(x,y)PMxyMyx A Ix Iy
Mx P ey; My P ex
L
y
pP A
pmax
P16e A b
当ey 0, ex e
pmax
m in
P A
1
6e b
pmin
P16e A b
11
pmax
min
P16e A b
P
矩形面积单向偏心荷载
竖直中心
荷载条件 竖直偏心
倾斜偏心
P
矩 形
基 础 形 状条
形
L b
pP A
P—集中力
P’ b
pP b
P’—单位长 度上的荷载
P
x y
o
L
b
p(x,y)PMxyMyx
A Ix
Iy
P’
b
p(x)P Mx bI
P L
b
PPvPh
P’ b
PPvPh
13
§4.4竖直集中力作用下的附加应力计算
土力学中应力符号的规定
P
P
土不能承 受拉应力
b
b
e
e
x
Lx
L
y
y
p max
pmin0 p max
pmin0
e<b/6: 梯形
e=b/6: 三角形
b
压力调整
Ke
x
L
K=b/2-e
3K y pmin0
基底 压力 合力 与总 荷载 相等
p max
pmax32KPL3(b22P e)L
e>b/6: 出现拉应力区
第2章土体应力计算

查表2-2
角点法计算地基附加应力
计算点在基底内 p
III IV
II o
I
III o II
IV
I
z
M
z K cⅠKcⅡ KcⅢ K cⅣ p
矩形面积基底受三角形分布荷载时角点下的附加应力
bl
z 0 0 d z z ( pt , m, n)
z Kt1 pt
z Kt 2 pt
x
K
x s
pn
Ksx ,Ktz为条形基底竖向附 加应力系数, 均为m ,n的 函数,其中m=x/b, n=z/b,可查表2-6、27得到
x
K
z t
pt
注意原点位置
见例题2-3
第5节 土坝(堤)自重应力和坝基附加应力
➢ 自重应力:
坝身任意点自重应力均等于单位面积上该计算点以上土柱 的有效重度与土柱高度的乘积。
n
cz 1h1 2h2 nhn ihi i 1
194.1kPa
第三节 基底压力与基底附加应力
1.柔性基础的底面压力分布与作用的荷载分布形状相同;刚性基础的底面 压力分布形状同荷载大小有关,还与基础埋深及土的性质有关。
2.基底压力的简化计算法
1)中心荷载时:
P
N
F
2)偏心荷载时:
力沿深度呈折线分布
h3 3
1 h1 + 2h2 + 3h3
三、水平向自重应力
天然地面
z
cy
cz cx
cz z
cx cy K0 cz
静止侧压 力系数
四、例题分析
【例】一地基由多层土组成,地质剖面如下图所示,试计算
并绘制自重应力σcz沿深度的分布图
土体中的应力计算—附加应力的计算(土力学课件)

z 2 p
x
p x
z z
x z
二、条形面积受均布荷载土中附加应力
2.条形面积受三角形荷载作用下的附加应力
土中任意点所受的附加应力
z 3 p
-x 0
z x
p x
z
注意坐标系的建立,以荷载0为坐标原点,向荷 载增大的方向为正方向。
二、条形面积受均布荷载土中附加应力
3.圆形面积均布荷载作用下的竖向附加应力
(1)距离地面越深, 附加应力的分布范围 越广,r/z=2.5范围内。
(2)在距地面为z的平 面上,集中力作用线 下的附加应力最大, 向两侧逐渐减小。
集中力作用下附加应力分布图
一、竖直集中荷载作用下的地基附加应力计算
1、附加应力分布规律
(3)距P作用线为r竖直 线上的附加应力随深 度先增加再减小。
171
332 kPa
134
条形荷载作用下土中附加应力
(1)p1=134kPa
+x
+x
+(x 2)p2=198kPa
-x
z x1 x/b z/b
x2 x/b z/b
00 0 0 1
134 1 0.5 0 0.500 99 233
1 0 0 0.5 0.820 110 1 0.5 0.5 0.410 81 191
条形荷载作用下 土中附加应力
条形荷载作用下土中附加应力
条形荷载作用下土中附加应力
1.条形面积受均布荷载作用下的土中竖向附加应力
土中任意点所受的附加应力 x
z 2 p
2 ——条形均布荷载作用
下的竖向附加应力系数
2 (x / b, z / b)
第二章土体应力计算
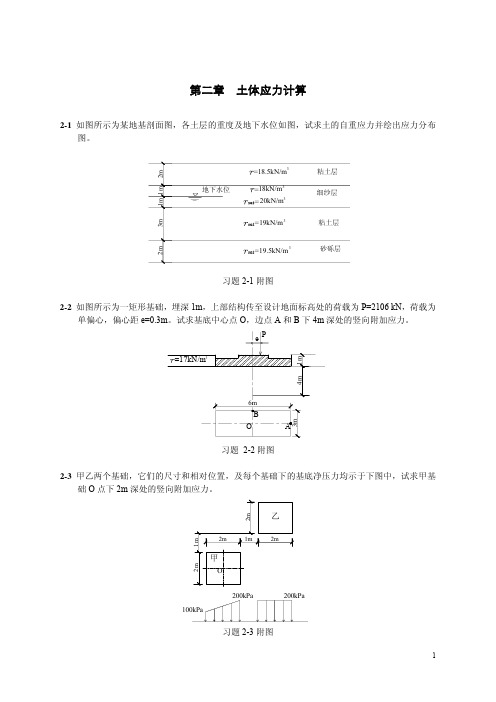
第二章 土体应力计算2-1如图所示为某地基剖面图,各土层的重度及地下水位如图,试求土的自重应力并绘出应力分布图。
习题2-1附图2-2如图所示为一矩形基础,埋深1m,上部结构传至设计地面标高处的荷载为P=2106 kN,荷载为单偏心,偏心距e=0.3m。
试求基底中心点O,边点A和B下4m深处的竖向附加应力。
习题 2-2附图2-3甲乙两个基础,它们的尺寸和相对位置,及每个基础下的基底净压力均示于下图中,试求甲基础O点下2m深处的竖向附加应力。
200kPa200kPa100kPa习题2-3附图2-4 某挡土墙建于图示地基上,埋深2m ,尺寸如图所示。
墙受上部竖向荷载和墙身自重为F v =1000kN/m ,其作用位置距墙前趾A 点为3.83m ;墙背受有总水平推力F h =350 kN/m ,其作用点距墙底为3.5m 。
(不计墙后填土影响)试求: (1)M ,N 点的竖向自重应力; (2)M ,N 点处的竖向附加应力。
习题 2-4附图2-5 某矩形基础长度分别3m 和2m ,基础剖面和地基条件如图所示。
试求基础中点O 及其以下点M和N 的自重应力、竖向附加应力以及静孔隙水应力。
习题 2-5附图2-6 粉质粘土层下部有承压水,测压管水位高出地下水位1.5m ,形成向上的稳定渗流,现在地表突然加无限均布荷载p=40kPa ,试按图所示数据计算施加p 后瞬间(t=0),A 点的垂直有效应力'z σ。
习题 2-6附图2-7 试绘出下图所示两种情况下土中总应力、有效应力及孔隙水压力分布图。
习题 2-7附图2-8 绘出下图所示自重应力分布图及作用在基岩层面处的水土总压力。
3习题 2-8附图2-9 从钻孔中获得下列资料:0~-3m ,细砂,饱和密度ρsat =1.92 t/m 3;-3~-7m ,粘土,饱和密度ρsat =2t/m 3,7.0m 以下为中砂。
试计算和绘制自重应力随深度的变化图。
(地下水位在地面±0.00处)2-10 已知某均布受荷面积如图所示,求深度10m 处A 点与O 点的竖向附加应力比值。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
P σz = K 2 z
称为竖向集中力作用竖向附 加应力系数。
一、附加应力基本解答
注意:上述公式在集中力作用点处是不适用的, 因为当R=0时,应力及位移均趋于无穷大,此 刻土已发生塑性变形,按弹性理论解已不适用 了。 事实上集中力是不存在的,因为基础总有 一定的面积,上面的荷载总是面积荷载。求解 时利用集中力的解答在作用面积上分块叠加或 积分。
三、倾斜偏心荷载作用下的基底压力
三、倾斜偏心荷载作用下的基底压力
当基础底面受到倾斜的偏心荷载作用时,先将倾斜偏心的 合力R分解为竖向分量Fv 和水平分量Fh ,其中Fv=Rcosβ, Fh =Rsinβ, β为倾斜荷载与竖向线之间的倾角。 对于竖向分量作用下的基底反力计算,同前文 对于水平分量Fh引起的基底反力可按下式计算 矩形基底 ph= Fh/lb 条形基底 ph= Fh/b
二、刚性基础下基底压力分布
e<L/6时,基 底压力成梯形 分布; e=L/6时,基 底压力为三角 形分布;
二、刚性基础下基底压力分布
e>L/6时,基底压力pmin<0,由于地基与基础之间不能承 受拉力,此时基底与地基局部脱离而使基底压力重新分布。 根据基底压力与偏心荷载相平衡的条件,三角形反力分布 如图(e)中的实线所示,形心应在P+G的合力Fv作用线上, 由此可计算基础边缘的最大压力pmax为 pmax=2Fv/3kb 式中:k——单向偏心荷载作用点至具有最大压力的基底边 缘的距离,k=(L/2-e)。
第1节 概述 节
按土体中土骨架和土中孔隙(水、气)的应力承担作用原理 或应力传递方式可分为有效应力和孔隙应(压)力 有效应力和孔隙应( 有效应力和孔隙应 有效应力——由土骨架传递(或承担)的应力。 孔隙应力——由土中孔隙流体水和气体传递(或承担) 的应力。 对于饱和土体,由于孔隙应力是通过土中孔隙水来传递 的,它不会使土体产生变形,土体的强度也不会改变。 孔隙应力分为:静孔隙应力和超静孔隙应力。
第二章 土体应力计算
概 述 地基中的自重应力 基底压力与基底附加应力 地基中的附加应力计算 土坝(堤)自重应力荷坝基附加应力
第1节 概述 节
支撑建筑物荷载的土层称为地基 地基。 地基 与建筑物基础底面直接接触的土层称为持力层 持力层。 持力层 将持力层下面的土层称为下卧层 下卧层。 下卧层 自重应力和附加应力; 土体的应力按引起的原因分为自重应力和附加应力 自重应力和附加应力 自重应力——由土体自身重量所产生的应力。 附加应力——由外荷(静的或动的)引起的土中应力。
四、基底附加应力——基底净压力
实际工程中,基础总是埋置在天然地面以下一定 的深度,势必要进行基坑开挖,这样一来就意味 着加了一个负荷载。因此,应在基底压力中扣除 基底标高处原有土的自重应力,才是基础底面下 真正施加于地基的压力,称为基底附加应力或基 基底附加应力或基 底净压力。 底净压力
四、基底附加应力——基底净压力
式中,各层土容重地下水位以上取天然容重;地下水位以 下砂土、粉土、粘性土液性指数大于1时取浮容重;粘性 土液性指数小于等于0时取天然容重,在0~1之间时依最 不利原则取天然或浮容重。 自重应力分布图为分段线性,可有突变否?
第3节 基底压力与基底附加应力 节
基底压力:指上部结构荷载和基础自重通过基础传递, 基底压力 在基础底面处施加于地基上的单位面积压力。 基底反力:地基反向施加于基础底面上的压力。 基底反力 基底附加应力:是指基底压力扣除因基础埋深所开挖的 基底附加应力 自重应力之后在基底处施加于地基上的单位面积压力。 一、柔性基础与刚性基础基底压力分布特征 基底压力的分布和大小与荷载的性质(中心或偏心、倾斜 等)及大小等有关,也与基础的刚度有关。
第2节 地基中的自重应力 节
第2节 地基中的自重应力 节
若地基是由多层土所组成,设 各层的厚度为hi ,则地基中第n 层底面处的竖向土自重应力
地面 h1
σ c = γ 1h1 + γ 2 h2 + ...... + γ n hn
= ∑γ h i i i =1
n
hi hn
σcz σcy σcx
第2节 地基中的自重应力 节
四、基底附加应力——基底净压力
对于基底压力p为均布情况
p
d
rd
对于基底压力为梯形分布情况
第4节 地基中的附加应力计算 节
附加应力:由于外荷载 附加应力 作用,在地基中产生的 应力增量。 计算方法:假定地基土 计算方法 是均质的、各向同性的、 半无限的弹性体(即在 深度和水平方向上都是 无限的)。 应力计算可分为空间问 题和平面问题。
(一)中心荷载下的基底压力 中心荷载作用下的基础,上部结构荷载P与基础自重G的 合力Fv通过基底形心,基底压力为均匀分布。平均基底压 力为
二、刚性基础下基底压力分布
(二)偏心荷载下的基底压力 对于单向偏心荷载作用下的矩 形面积基底的刚性基础,如图 (a),(b)所示。两端边缘最大压力 pmax与最小压力pmin可按下式计 算:
一、柔性基础与刚性基础基底压力分布特 征
柔性基础:刚度较小,基底压力与其上的荷载大小及分布相 同;
一、柔性基础与刚性基础基底压力分布特 征
刚性基础:刚度较大,基底压力分布随上部荷载的大小 、基础的埋深及土的性质而异。
当基础尺寸不太大,荷载也较小时,可假定基底压力为直线分布
二、刚性基础下基底压力分布
第2节 地基中的自重应力 节
假设土体为均匀连续介质,并为 地面 半无限空间体,在距地表深度z处, 土体的自重应力为: σcz = γz z σcx = σcy = K0σcz σcz K0——静止侧压力系数,它是土 体在无侧向变形条件下有效小主 σcx σcy 应力σ’3与有效大主应力σ’1之比 与土层的应力历史及土的类型有关; 正常固结粘土:K0 =1-sinφ’ 对一般地基K0 =0.5左右
一、附加应力基本解答
(一)竖向集中力作 用下地基附加应力: : 半无限空间体弹性力 学基本解 由布辛内斯克解答得 σz的表达式
3F z 3 ⋅ 5 由图中的几何关系,得
R = r2 + z2
3P z 3 σz = ⋅ 5 2π R
式中
3P z3 3 1 P σz = = 2 2 5/ 2 2π (r + z ) 2π [(r / z)2 +1]5/ 2 z 2
