中考专题复习之四边形-完美版2

合集下载

专题43四边形(2) 中考数学真题分项汇编系列2(学生版)

专题43四边形（2）（全国一年）学校:___________姓名：___________班级：___________考号：___________一、单选题1．（2020·贵州遵义中考真题）如图，在菱形ABCD中，AB＝5，AC＝6，过点D作DE⊥BA，交BA的延长线于点E，则线段DE的长为（）A．125B．185C．4 D．2452．（2020·北京中考真题）正五边形的外角和为（）A．180°B．360°C．540°D．720°3．（2020·贵州黔东南中考真题）如图，将矩形ABCD沿AC折叠，使点B落在点B′处，B′C交AD于点E，若∠1＝25°，则∠2等于（）A．25°B．30°C．50°D．60°4．（2020·浙江温州中考真题）如图，在△ABC中，∠A＝40°，AB＝AC，点D在AC边上，以CB，CD为边作□BCDE，则∠E的度数为（）A．40°B．50°C．60°D．70°5．（2020·山东德州中考真题）如图，小明从A点出发，沿直线前进8米后向左转45°，再沿直线前进8米，又向左转45°……照这样走下去，他第一次回到出发点A时，共走路程为（）A ．80米B ．96米C ．64米D ．48米6．（2020·江苏无锡中考真题）正十边形的每一个外角的度数为（）A ．36︒B ．30C ．144︒D ．150︒7．（2020·江苏连云港中考真题）如图，将矩形纸片ABCD 沿BE 折叠，使点A 落在对角线BD 上的A '处．若24DBC ︒∠=，则'∠A EB 等于（）．A ．66︒B ．60︒C ．57︒D ．48︒8．（2020·山东泰安中考真题）将含30°角的一个直角三角板和一把直尺如图放置，若150∠=︒，则2∠等于（）A ．80°B ．100°C ．110°D ．120°9．（2020·四川南充中考真题）如图，面积为S 的菱形ABCD 中，点O 为对角线的交点，点E 是线段BC 单位中点，过点E 作EF ⊥BD 于F ，EG ⊥AC 与G ，则四边形EFOG 的面积为（）A ．14SB ．18SC ．112SD ．116S 10．（2020·四川泸州中考真题）下列命题是假命题的是（）A ．平行四边形的对角线互相平分B ．矩形的对角线互相垂直C ．菱形的对角线互相垂直平分D ．正方形的对角线互相垂直平分且相等11．（2020·山东临沂中考真题）如图，P 是面积为S 的ABCD 内任意一点，PAD △的面积为1S ，PBC 的面积为2S ，则（）A ．122S S S +> B ．122S S S +< C ．122S S S += D ．12S S +的大小与P 点位置有关12．（2020·山东菏泽中考真题）如果顺次连接四边形的各边中点得到的四边形是矩形，那么原来四边形的对角线一定满足的条件是（）A ．互相平分B ．相等C ．互相垂直D ．互相垂直平分13．（2020·湖南衡阳中考真题）如图,在四边形ABCD 中,AC 与BD 相交于点O ,下列条件不能判定四边形ABCD 为平行四边形的是（）A ．AB ∥DC ,AB =DC B ．AB =DC ,AD =BCC ．AB ∥DC ,AD =BC D ．OA=OC ,OB =OD14．（2020·河南中考真题）如图，在ABC ∆中，90ACB ∠=︒．边BC 在x 轴上，顶点,A B 的坐标分别为()2,6-和()7,0．将正方形OCDE 沿x 轴向右平移当点E 落在AB 边上时，点D 的坐标为（）A ．3,22⎛⎫ ⎪⎝⎭B ．()2,2C ．11,24⎛⎫ ⎪⎝⎭D ．()4,215．（2020·贵州贵阳中考真题）菱形的两条对角线长分别是6和8，则此菱形的周长是（）A ．5B ．20C ．24D ．3216．（2020·天津中考真题）如图，四边形OBCD 是正方形，O ，D 两点的坐标分别是()0,0，()0,6，点C 在第一象限，则点C 的坐标是（）A ．()6,3B ．()3,6C ．()0,6D ．()6,617．（2020·山东青岛中考真题）如图，将矩形ABCD 折叠，使点C 和点A 重合，折痕为EF ，EF 与AC 交于点.O 若5AE =，3BF =，则AO 的长为（）A 5B 352C ．25D ．4518．（2020·贵州黔东南中考真题）如图，正方形ABCD的边长为2，O为对角线的交点，点E、F分别为BC、AD的中点．以C为圆心，2为半径作圆弧BD，再分别以E、F为圆心，1为半径作圆弧BO、OD，则图中阴影部分的面积为（）A．π﹣1 B．π﹣2 C．π﹣3 D．4﹣π19．（2020·贵州黔东南中考真题）若菱形ABCD的一条对角线长为8，边CD的长是方程x2﹣10x+24＝0的一个根，则该菱形ABCD的周长为（）A．16 B．24 C．16或24 D．4820．（2020·新疆中考真题）如图，在△ABC中，∠A=90°，D是AB的中点，过点D作BC的平行线，交AC 于点E，作BC的垂线交BC于点F，若AB=CE，且△DFE的面积为1，则BC的长为（）A．5B．5 C．45D．1021．（2020·贵州铜仁中考真题）如图，正方形ABCD的边长为4，点E在边AB上，BE＝1，∠DAM＝45°，点F在射线AM上，且AF2，过点F作AD的平行线交BA的延长线于点H，CF与AD相交于点G，连接EC、EG、EF．下列结论：①△ECF的面积为172；②△AEG的周长为8；③EG2＝DG2+BE2；其中正确的是（）A．①②③B．①③C．①②D．②③22．（2020·贵州铜仁中考真题）如图，在矩形ABCD中，AB＝3，BC＝4，动点P沿折线BCD从点B开始运动到点D，设点P运动的路程为x，△ADP的面积为y，那么y与x之间的函数关系的图象大致是（）A．B．C．D．23．（2020·浙江宁波中考真题）如图，在Rt△ABC中，∠ACB＝90°，CD为中线，延长CB至点E，使BE＝BC，连结DE，F为DE中点，连结BF．若AC＝8，BC＝6，则BF的长为（）A．2 B．2.5 C．3 D．424．（2020·浙江台州中考真题）如图，已知线段AB ，分别以A ，B 为圆心，大于12AB 同样长为半径画弧，两弧交于点C ，D ，连接AC ，AD ，BC ，BD ，CD ，则下列说法错误的是（）A ．AB 平分∠CAD B ．CD 平分∠ACBC ．AB ⊥CD D ．AB=CD25．（2020·浙江台州中考真题）下是关于某个四边形的三个结论：①它的对角线相等；②它是一个正方形；③它是一个矩形．下列推理过程正确的是（）A ．由②推出③，由③推出①B ．由①推出②，由②推出③C ．由③推出①，由①推出②D ．由①推出③，由③推出②26．（2020·浙江衢州中考真题）如图，把一张矩形纸片ABCD 按所示方法进行两次折叠，得到等腰直角三角形BEF ，若BC =1，则AB 的长度为（）A ．2B ．212+C ．512+D ．4327．（2020·浙江金华中考真题）如图，四个全等的直角三角形拼成“赵爽弦图”，得到正方形ABCD 与正方形EFGH .连结EG ，BD 相交于点O ，BD 与HC 相交于点P .若GO=GP ，则ABCDEFGH S S 正方形正方形的值是（）A ．12B ．22+C ．52D ．15428．（2020·四川乐山中考真题）如图，在菱形ABCD 中，4AB =，120BAD ∠=︒，O 是对角线BD 的中点，过点O 作OE CD ⊥ 于点E ，连结OA ．则四边形AOED 的周长为（）A ．923+B ．93+C ．723+D ．829．（2020·四川乐山中考真题）如图，在平面直角坐标系中，直线y x =-与双曲线k y x=交于A 、B 两点，P 是以点(2,2)C 为圆心，半径长1的圆上一动点，连结AP ，Q 为AP 的中点．若线段OQ 长度的最大值为2，则k 的值为（）A ．12-B ．32-C ．2-D ．14- 30．（2020·四川遂宁中考真题）如图，在平行四边形ABCD 中，∠ABC 的平分线交AC 于点E ，交AD 于点F ，交CD 的延长线于点G ，若AF ＝2FD ，则BE EG的值为（）A ．12B ．13C ．23D ．3431．（2020·四川遂宁中考真题）如图，在Rt △ABC 中，∠C ＝90°，AC ＝BC ，点O 在AB 上，经过点A 的⊙O 与BC 相切于点D ，交AB 于点E ，若CD ＝2，则图中阴影部分面积为（）A ．4﹣2πB ．2﹣2πC ．2﹣πD ．1﹣4π 32．（2020·山东德州中考真题）下列命题：①一组对边平行，另一组对边相等的四边形是平行四边形； ②对角线互相垂直且平分的四边形是菱形；③一个角为90°且一组邻边相等的四边形是正方形；④对角线相等的平行四边形是矩形．其中真命题的个数是（）A ．1B ．2C ．3D ．4 33．（2020·江苏无锡中考真题）如图，在四边形ABCD 中()AB CD >，90ABC BCD ∠=∠=︒，3AB =，3BC =，把Rt ABC ∆沿着AC 翻折得到Rt AEC ∆，若3tan 2AED ∠=，则线段DE 的长度为（）A 6B 7C 3D 27 34．（2020·四川自贡中考真题）如图，在平行四边形ABCD 中，==AD 2,AB 6B 是锐角，AE BC ⊥于点E ，F 是AB 的中点，连接DF EF 、；若90EFD ∠=，则AE 的长为（）A ．2B ．5C ．322D ．33235．（2020·重庆中考真题）如图，在平面直角坐标系中，矩形ABCD 的对角线AC 的中点与坐标原点重合，点E 是x 轴上一点，连接AE ．若AD 平分OAE ∠，反比例函数(0,0)k y k x x=>>的图象经过AE 上的两点A ，F ，且AF EF =，ABE △的面积为18，则k 的值为（）A ．6B ．12C ．18D ．2436．（2020·江苏苏州中考真题）如图，在扇形OAB 中，已知90AOB ∠=︒，2OA =，过AB 的中点C 作CD OA ⊥，CE OB ⊥，垂足分别为D 、E ，则图中阴影部分的面积为（）A ．1π-B ．12π-C ．12π-D ．122π- 37．（2020·黑龙江绥化中考真题）如图，四边形ABCD 是菱形，E 、F 分别是BC 、CD 两边上的点，不能．．保证．．ABE △和ADF 一定全等的条件是（）A ．BAF DAE ∠=∠B ．EC FC = C ．AE AF =D ．BE DF =38．（2020·黑龙江绥化中考真题）如图，在Rt ABC 中，CD 为斜边AB 的中线，过点D 作DE AC ⊥于点E ，延长DE 至点F ，使EF DE =，连接,AF CF ，点G 在线段CF 上，连接EG ，且180,2,3CDE EGC FG GC ∠+∠=︒==．下列结论：①12DE BC =；②四边形DBCF 是平行四边形；③EF EG =；④25BC =．其中正确结论的个数是（）A ．1个B ．2个C ．3个D ．4个39．（2020·四川甘孜中考真题）如图，菱形ABCD 中，对角线AC ，BD 相交于点O ，E 为AB 的中点．若菱形ABCD 的周长为32，则OE 的长为（）A ．3B ．4C ．5D ．640．（2020·安徽中考真题）已知点,,A B C 在O 上．则下列命题为真命题的是（）A ．若半径OB 平分弦AC ．则四边形OABC 是平行四边形B ．若四边形OABC 是平行四边形．则120ABC ∠=︒C ．若120ABC ∠=︒．则弦AC 平分半径OBD ．若弦AC 平分半径OB ．则半径OB 平分弦AC41．（2020·山东聊城中考真题）如图，在Rt ABC △中，2AB =，30C ∠=︒，将Rt ABC △绕点A 旋转得到Rt A B C '''∆，使点B 的对应点B '落在AC 上，在B C ''上取点D ，使2B D '=，那么点D 到BC 的距离等于（）．A ．3213⎛⎫+ ⎪ ⎪⎝⎭B ．313+C ．31-D ．31+42．（2020·山东菏泽中考真题）如图，将ABC 绕点A 顺时针旋转角α，得到ADE ，若点E 恰好在CB 的延长线上，则BED ∠等于（）A ．2αB ．23αC ．αD ．180α︒-43．（2020·湖南怀化中考真题）在矩形ABCD 中，AC 、BD 相交于点O ，若AOB 的面积为2，则矩形ABCD 的面积为（）A ．4B ．6C ．8D ．1044．（2020·黑龙江中考真题）如图，菱形ABCD 的两个顶点A ，C 在反比例函数k y x=的图象上，对角线AC ，BD 的交点恰好是坐标原点O ，已知()1,1B -，120ABC ∠=︒，则k 的值是（）A ．5B ．4C ．3D ．245．（2020·黑龙江中考真题）如图，菱形ABCD 的对角线AC 、BD 相交于点O ，过点D 作DH AB ⊥于点H ，连接OH ，若6OA =，48ABCD S =菱形，则OH 的长为（）A ．4B ．8C ．13D ．646．（2020·湖北襄阳中考真题）已知四边形ABCD 是平行四边形，AC ，BD 相交于点O ，下列结论错误的是（）A ．OA OC =，OB OD =B ．当AB CD =时，四边形ABCD 是菱形C ．当90ABC ∠=︒时，四边形ABCD 是矩形D ．当AC BD =且AC BD ⊥时，四边形ABCD 是正方形47．（2020·黑龙江牡丹江中考真题）如图，在平面直角坐标系中，O 是菱形ABCD 对角线BD 的中点，//AD x 轴且4=AD ，60A ∠=︒，将菱形ABCD 绕点O 旋转，使点D 落在x 轴上，则旋转后点C 的对应点的坐标是（）A ．(0,23)B ．(2,4)-C ．(23,0)D ．(0,23)或(0,23)-48．（2020·黑龙江牡丹江中考真题）如图，在矩形ABCD 中，3AB =，10BC =，点E 在BC 边上，DF AE ⊥，垂足为F ．若6DF =，则线段EF 的长为（）A ．2B ．3C ．4D ．549．（2020·江苏南京中考真题）如图，在平面直角坐标系中，点P 在第一象限，⊙P 与x 轴、y 轴都相切，且经过矩形AOBC 的顶点C ，与BC 相交于点D ，若⊙P 的半径为5，点A 的坐标是(0,8)，则点D 的坐标是（）A ．(9,2)B ．(9,3)C ．(10,2)D ．(10,3)50．（2020·湖南湘西中考真题）如图，在平面直角坐标系xOy 中，矩形ABCD 的顶点A 在x 轴的正半轴上，矩形的另一个顶点D 在y 轴的正半轴上，矩形的边,,AB a BC b DAO x ==∠=．则点C 到x 轴的距离等于（）A ．cos sin a x b xB ．cos cos a x b xC ．sin cos a x b xD ．sin sin a x b x51．（2020·山东潍坊中考真题）如图，点E 是ABCD 的边AD 上的一点，且12DE AE =，连接BE 并延长交CD 的延长线于点F ，若3,4DE DF ==，则ABCD 的周长为（）A ．21B ．28C ．34D ．4252．（2020·浙江温州中考真题）如图，在Rt △ABC 中，∠ACB ＝90°，以其三边为边向外作正方形，过点C 作CR ⊥FG 于点R ，再过点C 作PQ ⊥CR 分别交边DE ，BH 于点P ，Q ．若QH ＝2PE ，PQ ＝15，则CR 的长为（）A ．14B ．15C ．83D ．6553．（2020·浙江台州中考真题）把一张宽为1cm 的长方形纸片ABCD 折叠成如图所示的阴影图案，顶点A ，D 互相重合，中间空白部分是以E 为直角顶点，腰长为2cm 的等腰直角三角形，则纸片的长AD （单位：cm ）为（）A ．732+B ．742+C ．832+D ．82+54．（2020·浙江中考真题）四边形具有不稳定性，对于四条边长确定的四边形．当内角度数发生变化时，其形状也会随之改变．如图，改变正方形ABCD 的内角，正方形ABCD 变为菱形ABC ′D ′．若∠D ′AB ＝30°，则菱形ABC ′D ′的面积与正方形ABCD 的面积之比是（）A ．1B ．12C ．22D ．32 55．（2020·浙江嘉兴中考真题）已知二次函数y ＝x 2，当a ≤x ≤b 时m ≤y ≤n ，则下列说法正确的是（） A ．当n ﹣m ＝1时，b ﹣a 有最小值B ．当n ﹣m ＝1时，b ﹣a 有最大值C ．当b ﹣a ＝1时，n ﹣m 无最小值D ．当b ﹣a ＝1时，n ﹣m 有最大值56．（2020·山东泰安中考真题）如图，点A ，B 的坐标分别为(2,0),(0,2)A B ，点C 为坐标平面内一点，1BC =，点M 为线段AC 的中点，连接OM ，则OM 的最大值为（）A 21B 122C ．221D ．122257．（2020·山东泰安中考真题）如图，矩形ABCD 中，,AC BD 相交于点O ，过点B 作BF AC ⊥交CD 于点F ，交AC 于点M ，过点D 作//DE BF 交AB 于点E ，交AC 于点N ，连接,FN EM ．则下列结论： ①DN BM =；②//EM FN ；③AE FC =；④当AO AD =时，四边形DEBF 是菱形．其中，正确结论的个数是（）A ．1个B ．2个C ．3个D ．4个58．（2020·江苏无锡中考真题）如图，等边ABC ∆的边长为3，点D 在边AC 上，12AD =，线段PQ 在边BA 上运动，12PQ =，有下列结论：①CP 与QD 可能相等；②ΔAQD 与BCP ∆可能相似；③四边形PCDQ 面积的最大值为31316；④四边形PCDQ 周长的最小值为3732+．其中，正确结论的序号为（） A ．①④ B ．②④ C ．①③ D ．②③59．（2020·四川达州中考真题）如图，45BOD ∠=︒，BO DO =，点A 在OB 上，四边形ABCD 是矩形，连接AC 、BD 交于点E ，连接OE 交AD 于点F ．下列4个判断：①OE 平分BOD ∠；②OF BD =；③2DF AF =；④若点G 是线段OF 的中点，则AEG △为等腰直角三角形．正确判断的个数是（）A ．4B ．3C ．2D ．1二、填空题60．（2020·甘肃兰州中考真题）如图，M 、N 是正方形ABCD 的边CD 上的两个动点，满足AM BN =，连接AC 交BN 于点E ，连接DE 交AM 于点F ，连接CF ，若正方形的边长为6，则线段CF 的最小值是______．61．（2020·西藏中考真题）如图，已知平行四边形ABCD ，以点A 为圆心，适当长为半径画弧分别交AB ，AD 于点E ，F ，再分别以点E ，F 为圆心，大于12EF 的长为半径画弧，两弧在∠DAB 的内部相交于点G ，画射线AG 交DC 于H ．若∠B ＝140°，则∠DHA ＝_____．62．（2020·西藏中考真题）如图，在矩形ABCD 中，E 为AB 的中点，P 为BC 边上的任意一点，把PBE △沿PE 折叠，得到PBE △，连接CF ．若AB ＝10，BC ＝12，则CF 的最小值为_____．63．（2020·广西河池中考真题）如图，菱形ABCD 的周长为16，AC ，BD 交于点O ，点E 在BC 上，OE ∥AB ，则OE 的长是_____．64．（2020·辽宁大连中考真题）如图，在平面直角坐标系中，正方形ABCD 的顶点A 与D 在函数(0)k y x x=>的图象上，AC x ⊥轴，垂足为C ，点B 的坐标为(0,2)，则k 的值为______．65．（2020·辽宁大连中考真题）如图，矩形ABCD 中，6,8AB AD ==，点E 在边AD 上，CE 与BD 相交于点F ．设DE x =，BF y =，当08x 时，y 关于x 的函数解析式为_____．66．（2020·辽宁鞍山中考真题）如图，在菱形ABCD 中，60ADC ∠=︒，点E ，F 分别在AD ，CD 上，且AE DF =，AF 与CE 相交于点G ，BG 与AC 相交于点H ．下列结论：①ACF CDE △≌△；②2CG GH BG =⋅；③若DF 2CF =，则7CE GF =；④234ABCG S BG =四边形．其中正确的结论有_______．（只填序号即可）67．（2020·辽宁鞍山中考真题）如图，在ABCD 中，点E 是CD 的中点，AE ，BC 的延长线交于点F ．若ECF △的面积为1，则四边形ABCE 的面积为________．68．（2020·辽宁铁岭中考真题）如图，以AB 为边，在AB 的同侧分别作正五边形ABCDE 和等边ABF ，连接,FE FC ，则EFA 的度数是____________．69．（2020·辽宁铁岭中考真题）如图，45MON ︒∠=，正方形1ABB C ，正方形1121A B B C ，正方形2232A B B C ，正方形3343A B B C ，…，的顶点123,,,,⋯A A A A ，在射线OM 上，顶点1234,,,,,⋯B B B B B ，在射线ON 上，连接2AB 交11A B 于点D ，连接13A B 交22A B 于点1D ，连接24A B 交33A B 于点2D ，…，连接11B D 交2AB 于点E ，连接22B D 交13A B 于点1E ，…，按照这个规律进行下去，设ACD △与1B DE 的面积之和为1111,S AC D 与211B D E 的面积之和为2222,S A C D 与322B D E 的面积之和为3S ，…，若2AB =，则n S 等于__________．（用含有正整数n 的式子表示）70．（2020·辽宁铁岭中考真题）一张菱形纸片ABCD 的边长为6cm ，高AE 等于边长的一半，将菱形纸片沿直线MN 折叠，使点A 与点B 重合，直线MN 交直线CD 于点F ，则DF 的长为____________cm ． 71．（2020·江苏泰州中考真题）如图所示的网格由边长为1个单位长度的小正方形组成，点A 、B 、C 、在直角坐标系中的坐标分别为()3,6，()3,3-，()7,2-，则ABC 内心的坐标为______．72．（2020·辽宁丹东中考真题）如图，在四边形ABCD 中，AB BC ⊥，AD AC ⊥，AD AC =，105BAD ∠=︒，点E 和点F 分别是AC 和CD 的中点，连接BE ，EF ，BF ，若8CD =，则BEF ∆的面积是_________．73．（2020·辽宁丹东中考真题）如图，在矩形1OAA B 中，3OA =，12AA =，连接1OA ，以1OA 为边，作矩形121OA A B 使12123A A OA =，连接2OA 交1A B 于点C ；以2OA 为边，作矩形232OA A B ，使23223A A OA =，连接3OA 交21AB 于点1C ；以3OA 为边，作矩形343OA A B ，使34323A A OA =，连接4OA 交32AB 于点2C ；…按照这个规律进行下去，则201920202022C C A ∆的面积为_________．74．（2020·黑龙江鹤岗中考真题）在矩形ABCD 中，1AB =，BC a =，点E 在边BC 上，且35BE a =，连接AE ，将ABE ∆沿AE 折叠．若点B 的对应点B '落在矩形ABCD 的边上，则折痕的长为______． 75．（2020·黑龙江鹤岗中考真题）如图，在边长为4的正方形ABCD 中将ABD ∆沿射线BD 平移，得到EGF ∆，连接EC 、GC ．求EC GC +的最小值为______．76．（2020·内蒙古呼伦贝尔中考真题）如图，在平面直角坐标系中，正方形OABC 的顶点O 与坐标原点重合，点C 的坐标为（0,3），点A 在x 轴的正半轴上．直线1y x =-分别与边,AB OA 相交于,D M 两点，反比例函数(0)ky x x=>的图象经过点D 并与边BC 相交于点N ，连接MM ．点P 是直线DM 上的动点，当时，点P的坐标是________________．CP MN77．（2020·山东滨州中考真题）如图，点P是正方形ABCD内一点，且点P到点A、B、C的距离分别为23,2,4则正方形ABCD的面积为________78．（2020·内蒙古鄂尔多斯中考真题）如图，已知正方形ABCD，点M是边BA延长线上的动点（不与点△平移得到，若过点E作EH⊥AC，H为垂足，则有以下结论：A重合），且AM＜AB，△CBE由DAM①点M位置变化，使得∠DHC＝60°时，2BE＝DM；②无论点M运动到何处，都有DM＝2HM；③在点M的运动过程中，四边形CEMD可能成为菱形；④无论点M运动到何处，∠CHM一定大于135°．以上结论正确的有_____（把所有正确结论的序号都填上）．79．（2020·内蒙古鄂尔多斯中考真题）如图，AB是⊙O的直径，弦CD⊥AB，垂足为E，∠BCD＝30°，CD＝3S阴影＝_____．80．（2020·内蒙古鄂尔多斯中考真题）如图，平面直角坐标系中，菱形ABCD 在第一象限内，边BC 与x 轴平行，A ，B 两点的纵坐标分别为6，4，反比例函数y ＝kx（x ＞0）的图象经过A ，B 两点，若菱形ABCD 的面积为25，则k 的值为_____．81．（2020·云南中考真题）已知四边形ABCD 是矩形，点E 是矩形ABCD 的边上的点，且EA EC =．若6AB =，210AC =，则DE 的长是___．82．（2020·辽宁营口中考真题）如图，在菱形ABCD 中，对角线AC ，BD 交于点O ，其中OA ＝1，OB ＝2，则菱形ABCD 的面积为_____．83．（2020·湖南益阳中考真题）若一个多边形的内角和是540°，则该多边形的边数是_____． 84．（2020·内蒙古赤峰中考真题）一个n 边形的内角和是它外角和的4倍，则n =______． 85．（2020·湖南湘西中考真题）若多边形的内角和是外角和的2倍，则该多边形是_____边形. 86．（2020·江苏淮安中考真题）已知直角三角形斜边长为16，则这个直角三角形斜边上的中线长为__________．87．（2020·四川凉山中考真题）如图，ABCD ◊的对角线AC 、BD 相交于点O ，//OE AB 交AD 于点E ，若OA=1，AOE ∆的周长等于5，则ABCD ◊的周长等于__________．88．（2020·浙江舟山中考真题）如图所示，平行四边形ABCD的对角线AC、BD相交于点O，试添加一个条件：，使得平行四边形ABCD为菱形．89．（2020·江苏镇江中考真题）如图，点P是正方形ABCD内位于对角线AC下方的一点，∠1＝∠2，则∠BPC 的度数为_____°．∠=_____°．90．（2020·辽宁大连中考真题）如图，菱形ABCD中，40ACD︒∠=，则ABC91．（2020·四川凉山中考真题）如图，矩形ABCD中，AD=12，AB=8，E是AB上一点，且EB=3，F是∆沿EF对折后，点B落在点P处，则点P到点D的最短距为．BC上一动点，若将EBF92．（2020·四川绵阳中考真题）如图，在平面直角坐标系xOy中，一次函数的图象与反比例函数y＝kx（k＜0）的图象在第二象限交于A（﹣3，m），B（n，2）两点．（1）当m＝1时，求一次函数的解析式；（2）若点E在x轴上，满足∠AEB＝90°，且AE＝2﹣m，求反比例函数的解析式．93．（2020·四川绵阳中考真题）如图，四边形ABCD中，AB∥CD，∠ABC＝60°，AD＝BC＝CD＝4，点M是四边形ABCD内的一个动点，满足∠AMD＝90°，则点M到直线BC的距离的最小值为_____．94．（2020·江苏宿迁中考真题）如图，在△ABC中，AB=AC，∠BAC的平分线AD交BC于点D，E为AB 的中点，若BC=12，AD=8，则DE的长为_____．95．（2020·江苏宿迁中考真题）如图，在矩形ABCD中，AB=1，AD3P为AD上一个动点，连接BP，线段BA与线段BQ关于BP所在的直线对称，连接PQ，当点P从点A运动到点D时，线段PQ在平面内扫过的面积为_____．96．（2020·辽宁沈阳中考真题）如图，在矩形ABCD 中，6AB =，BC B =，对角线,AC BD 相交于点O ，点P 为边AD 上一动点，连接OP ，以OP 为折痕，将AOP 折叠，点A 的对应点为点E ，线段PE 与OD 相交于点F ．若PDF 为直角三角形，则DP 的长__________．97．（2020·辽宁沈阳中考真题）如图，在平行四边形ABCD 中，点M 为边AD 上一点，2AM MD =，点E ，点F 分别是,BM CM 中点，若6EF =，则AM 的长为__________．。

2022年中考数学专题复习：四边形

板块八【四边形中考】2022年长沙中考板块精炼【高频考点】1.多边形的内角和与外角和的关系与计算；2.特殊四边形：平行四边形、矩形、菱形、正方形的性质与判定，以及综合应用；【真题训练】一、选择题1.（2021常德）一个多边形的内角和为1800°，则这个多边形的边数为（）A．9B．10C．11D．122.（2021株洲）如图所示，四边形ABCD是平行四边形，点E在线段BC的延长线上，若∠DCE＝132°，则∠A＝（）A．38°B．48°C．58°D．66°3. （2021北京）下列多边形中，内角和最大的是（）A．B．C．D．4.（2021株洲）如图所示，在正六边形ABCDEF内，以AB为边作正五边形ABGHI，则∠F AI＝（）A．10°B．12°C．14°D．15°5.（2021娄底）如图，点E、F在矩形ABCD的对角线BD所在的直线上，BE＝DF，则四边形AECF是（）A．平行四边形B．矩形C．菱形D．正方形6. （2021福建）如图，点F在正五边形ABCDE的内部，△ABF为等边三角形，则∠AFC等于（）A．108°B．120°C．126°D．132°7.（2021湘西）如图，在菱形ABCD中，E是AC的中点，EF∥CD，交AD于点F，如果EF＝5.5，那么菱形ABCD的周长是（）A．11B．22C．33D．448. （2021安徽）如图，在菱形ABCD中，AB＝2，∠A＝120°，过菱形ABCD的对称中心O分别作边AB，BC的垂线，交各边于点E，F，G，H，则四边形EFGH的周长为（）A．3B．2+23C．3D．1+239.（2021常德）如图，已知F、E分别是正方形ABCD的边AB与BC的中点，AE与DF交于P．则下列结论成立的是（）A．BE＝12AE B．PC＝PD C．∠EAF+∠AFD＝90°D．PE＝EC10.（2021怀化）如图，菱形ABCD的四个顶点均在坐标轴上，对角线AC、BD交于原点O，AE⊥BC于E点，交BD于M点，反比例函数33yx（x＞0）的图象经过线段DC的中点N，若BD＝4，则ME的长为（）A．ME＝53B．ME＝43C．ME＝1D．ME＝2311.（2021郴州）如图，在边长为4的菱形ABCD中，∠A＝60°，点P从点A出发，沿路线A→B→C→D运动．设P点经过的路程为x，以点A，D，P为顶点的三角形的面积为y，则下列图象能反映y与x的函数关系的是（）A．B．C．D．12.（2021衡阳）如图，矩形纸片ABCD，AB＝4，BC＝8，点M、N分别在矩形的边AD、BC上，将矩形纸片沿直线MN折叠，使点C落在矩形的边AD上，记为点P，点D落在G处，连接PC，交MN于点Q，连接CM．下列结论：①四边形CMPN是菱形；②点P与点A重合时，MN＝5；③△PQM的面积S的取值范围是4≤S≤5．其中所有正确结论的序号是（）A．①②③B．①②C．①③D．②③二、填空题13.（2021益阳）如图，已知四边形ABCD是平行四边形，从①AB＝AD，②AC＝BD，③∠ABC＝∠ADC中选择一个作为条件，补充后使四边形ABCD成为菱形，则其选择是（限填序号）．14.（2021长沙）如图，菱形ABCD的对角线AC，BD相交于点O，点E是边AB的中点，若OE＝6，则BC的长为.15. （2021邵阳）如图，在矩形ABCD中，DE⊥AC，垂足为点E．若sin∠ADE＝45，AD＝4，则AB的长为．16.（2021衡阳）如图1，菱形ABCD的对角线AC与BD相交于点O，P、Q两点同时从O点出发，以1厘米/秒的速度在菱形的对角线及边上运动．点P的运动路线为O—A—D —O，点Q的运动路线为O—C—B—O．设运动的时间为x秒，P、Q间的距离为y厘米，y与x的函数关系的图象大致如图2所示，当点P在A—D段上运动且P、Q两点间的距离最短时，P、Q两点的运动路程之和为厘米．17.（2021张家界）如图，在正方形ABCD外取一点E，连接DE，AE，CE，过点D作DE的垂线交AE于点P，若DE＝DP＝1，PC＝6．下列结论：①△APD≌△CED；②AE⊥CE；③点C到直线DE的距离为6；④S正方形ABCD＝5+22，其中正确结论的序号为．18.（2021北京）如图，在矩形ABCD中，点E，F分别在BC，AD上，AF＝EC．只需添加一个条件即可证明四边形AECF是菱形，这个条件可以是（写出一个即可）．19.（2021湘潭）如图，在▱ABCD 中，对角线AC ，BD 相交于点O ，点E 是边AB 的中点．已知BC ＝10，则OE ＝．20.（2021兰州）如图，在矩形ABCD 中，AB ＝1，AD ＝3．①以点A 为圆心，以不大于AB 长为半径作弧，分别交边AD ，AB 于点E ，F ，再分别以点E ，F 为圆心，以大于12EF 长为半径作弧，两弧交于点P ，作射线AP 分别交BD ，BC 于点O ，Q ；②分别以点C ，Q 为圆心，以大于12CQ 长为半径作弧，两弧交于点M ，N ，作直线MN 交AP 于点G ，则OG 长为．三、解答题21.（2021长沙）如图，□ABCD 的对角线AC ，BD 相交于点O ，△OAB 是等边三角形，AB ＝4.(1)求证：□ABCD 是矩形； (2)求AD 的长.O QP E D22.（2021怀化）已知：如图，四边形ABCD为平行四边形，点E、A、C、F在同一直线上，AE＝CF．求证：（1）△ADE≌△CBF；（2）ED∥BF．23. （2021湘潭）如图，矩形ABCD中，E为边BC上一点，将△ABE沿AE翻折后，点B 恰好落在对角线AC的中点F上．（1）证明：△AEF≌△CEF；（2）若AB＝3，求折痕AE的长度．23.（2021株洲）如图所示，在矩形ABCD中，点E在线段CD上，点F在线段AB的延长线上，连接EF交线段BC于点G，连接BD，若DE＝BF＝2．（1）求证：四边形BFED是平行四边形；（2）若tan∠ABD＝23，求线段BG的长度．24.（2021郴州）如图，四边形ABCD中，AB＝DC，将对角线AC向两端分别延长至点E，F，使AE＝CF．连接BE，DF，若BE＝DF．证明：四边形ABCD是平行四边形．25. （2021衡阳）如图，点E为正方形ABCD外一点，∠AEB＝90°，将Rt△ABE绕A点逆时针方向旋转90°得到△ADF，DF的延长线交BE于H点．（1）试判定四边形AFHE的形状，并说明理由；（2）已知BH＝7，BC＝13，求DH的长．26.（2021邵阳）如图，在正方形ABCD中，对角线AC，BD相交于点O，点E，F是对角线AC上的两点，且AE＝CF．连接DE，DF，BE，BF．（1）证明：△ADE≌△CBF．（2）若AB＝4，AE＝2，求四边形BEDF的周长．27.（2021岳阳）如图，在四边形ABCD中，AE⊥BD，CF⊥BD，垂足分别为点E，F．（1）请你只添加一个条件（不另加辅助线），使得四边形AECF为平行四边形，你添加的条件是；（2）添加了条件后，证明四边形AECF为平行四边形．28.（2021张家界）如图，在矩形ABCD中，对角线AC与BD相交于点O，∠AOB＝60°，对角线AC所在的直线绕点O顺时针旋转角α（0°＜α ＜120°），所得的直线l分别交AD，BC于点E，F．（1）求证：△AOE≌△COF；（2）当旋转角α为多少度时，四边形AFCE为菱形？试说明理由．29.（2020长沙）在矩形ABCD中，E为DC边上一点，把△ADE沿AE翻折，使点D恰好落在BC边上的点F.(1)求证：△ABF∽△FCE；(2)若AB＝23，AD＝4，求EC的长；(3)若AE－DE＝2EC，记∠BAF＝α，∠F AE＝β.求tanα＋tanβ的值．板块八【四边形中考】2022年长沙中考板块精炼【答案或简析】【高频考点】1.多边形的内角和与外角和的关系与计算；2.特殊四边形：平行四边形、矩形、菱形、正方形的性质与判定，以及综合应用；【真题训练】一、选择题1.（2021常德）一个多边形的内角和为1800°，则这个多边形的边数为（）A．9B．10C．11D．12【答案或简析】D.2.（2021株洲）如图所示，四边形ABCD是平行四边形，点E在线段BC的延长线上，若∠DCE＝132°，则∠A＝（）A．38°B．48°C．58°D．66°【答案或简析】B.3. （2021北京）下列多边形中，内角和最大的是（）A．B．C．D．【答案或简析】D.4.（2021株洲）如图所示，在正六边形ABCDEF内，以AB为边作正五边形ABGHI，则∠F AI＝（）A．10°B．12°C．14°D．15°【答案或简析】B.5.（2021娄底）如图，点E、F在矩形ABCD的对角线BD所在的直线上，BE＝DF，则四边形AECF是（）A．平行四边形B．矩形C．菱形D．正方形【答案或简析】A.6. （2021福建）如图，点F在正五边形ABCDE的内部，△ABF为等边三角形，则∠AFC等于（）A．108°B．120°C．126°D．132°【答案或简析】C.7.（2021湘西）如图，在菱形ABCD中，E是AC的中点，EF∥CD，交AD于点F，如果EF＝5.5，那么菱形ABCD的周长是（）A．11B．22C．33D．44【答案或简析】D.8. （2021安徽）如图，在菱形ABCD中，AB＝2，∠A＝120°，过菱形ABCD的对称中心O分别作边AB，BC的垂线，交各边于点E，F，G，H，则四边形EFGH的周长为（）A．3+3B．2+23C．2+3D．1+23【答案或简析】B.9.（2021常德）如图，已知F、E分别是正方形ABCD的边AB与BC的中点，AE与DF交于P．则下列结论成立的是（）A．BE＝12AE B．PC＝PD C．∠EAF+∠AFD＝90°D．PE＝EC【答案或简析】C.10.（2021怀化）如图，菱形ABCD的四个顶点均在坐标轴上，对角线AC、BD交于原点O，AE⊥BC于E点，交BD于M点，反比例函数33yx（x＞0）的图象经过线段DC的中点N，若BD＝4，则ME的长为（）A．ME＝53B．ME＝43C．ME＝1D．ME＝23【答案或简析】D.解：过N作y轴和x轴的垂线NG，NH，设N（b，a），∵反比例函数y＝33x（x＞0）的图象经过点N，∴ab 3，∵四边形ABCD是菱形，∴BD⊥AC，DO＝12BD＝2，∵NH⊥x轴，NG⊥y轴，∴四边形NGOH是矩形，∴NG∥x轴，NH∥y轴，∵N为CD的中点，∴DO•CO＝2a•2b＝4ab43∴CO23∴tan∠CDO＝33 OCDO．∴∠CDO＝30°，∴∠DCO＝60°，∵四边形ABCD是菱形，∴∠ADC＝∠ABC＝2∠CDO＝60°，∠ACB＝∠DCO＝60°，∴△ABC是等边三角形，∵AE⊥BC，BO⊥AC，∴AE＝BO＝2，∠BAE＝30°＝∠ABO，∴AM＝BM，∴OM＝EM，∵∠MBE＝30°，∴BM＝2EM＝2OM，∴3EM＝OB＝2，∴ME＝23，故选：D．11.（2021郴州）如图，在边长为4的菱形ABCD中，∠A＝60°，点P从点A出发，沿路线A→B→C→D运动．设P点经过的路程为x，以点A，D，P为顶点的三角形的面积为y，则下列图象能反映y与x的函数关系的是（）A．B．C．D．【答案或简析】A.12.（2021衡阳）如图，矩形纸片ABCD，AB＝4，BC＝8，点M、N分别在矩形的边AD、BC上，将矩形纸片沿直线MN折叠，使点C落在矩形的边AD上，记为点P，点D落在G处，连接PC，交MN于点Q，连接CM．下列结论：①四边形CMPN是菱形；②点P与点A重合时，MN＝5；③△PQM的面积S的取值范围是4≤S≤5．其中所有正确结论的序号是（）A．①②③B．①②C．①③D．②③【答案或简析】C.二、填空题13.（2021益阳）如图，已知四边形ABCD是平行四边形，从①AB＝AD，②AC＝BD，③∠ABC＝∠ADC中选择一个作为条件，补充后使四边形ABCD成为菱形，则其选择是（限填序号）．【答案或简析】①.14.（2021长沙）如图，菱形ABCD的对角线AC，BD相交于点O，点E是边AB的中点，若OE＝6，则BC的长为.【答案或简析】12.15. （2021邵阳）如图，在矩形ABCD中，DE⊥AC，垂足为点E．若sin∠ADE＝45，AD＝4，则AB的长为．【答案或简析】3.16.（2021衡阳）如图1，菱形ABCD的对角线AC与BD相交于点O，P、Q两点同时从O点出发，以1厘米/秒的速度在菱形的对角线及边上运动．点P的运动路线为O—A—D —O，点Q的运动路线为O—C—B—O．设运动的时间为x秒，P、Q间的距离为y厘米，y与x的函数关系的图象大致如图2所示，当点P在A—D段上运动且P、Q两点间的距离最短时，P、Q两点的运动路程之和为厘米．【答案或简析】23317.（2021张家界）如图，在正方形ABCD外取一点E，连接DE，AE，CE，过点D作DE的垂线交AE于点P，若DE＝DP＝1，PC＝6．下列结论：①△APD≌△CED；②AE⊥CE；③点C到直线DE的距离为6；④S正方形ABCD＝5+22，其中正确结论的序号为．【答案或简析】B.18.（2021北京）如图，在矩形ABCD中，点E，F分别在BC，AD上，AF＝EC．只需添加一个条件即可证明四边形AECF是菱形，这个条件可以是（写出一个即可）．【答案或简析】例如AE=EC.19.（2021湘潭）如图，在▱ABCD中，对角线AC，BD相交于点O，点E是边AB的中点．已知BC＝10，则OE＝．【答案或简析】5.20.（2021兰州）如图，在矩形ABCD中，AB＝1，AD＝3．①以点A为圆心，以不大于AB长为半径作弧，分别交边AD，AB于点E，F，再分别以点E，F为圆心，以大于12EF 长为半径作弧，两弧交于点P，作射线AP分别交BD，BC于点O，Q；②分别以点C，Q为圆心，以大于12CQ长为半径作弧，两弧交于点M，N，作直线MN交AP于点G，则OG长为．【答案或简析】524三、解答题21.（2021长沙）如图，□ABCD的对角线AC，BD相交于点O，△OAB是等边三角形，AB＝4.(1)求证：□ABCD是矩形；(2)求AD的长.【答案或简析】（1）证明：∵△AOB为等边三角形，OQPE D∴∠BAO ＝∠AOB ＝60°，OA ＝OB ， ∵四边形ABCD 是平行四边形 ∴OB ＝OD ＝12BD ，OA ＝OC ＝12AC ， ∴BD ＝AC ，∴▱ABCD 是矩形；（2）解：∵▱ABCD 是矩形， ∴∠BAD ＝90°， ∵∠ABO ＝60°，∴∠ADB ＝90°﹣60°＝30°， ∴AD ＝3AB ＝43．22. （2021怀化）已知：如图，四边形ABCD 为平行四边形，点E 、A 、C 、F 在同一直线上，AE ＝CF ．求证：（1）△ADE ≌△CBF ；（2）ED ∥BF ．【答案或简析】证明：（1）∵四边形ABCD 为平行四边形， ∴DA ＝BC ，DA ∥BC ， ∴∠DAC ＝∠BCA ，∵∠DAC +∠EAD ＝180°，∠BCA +∠FCB ＝180°， ∴∠EAD ＝∠FCB ，在△ADE 和△CBF 中，,,,AE CF EAD FCB AD CB ， ∴△ADE ≌△CBF （SAS ）；（2）由（1）知，△ADE ≌△CBF ， ∴∠E ＝∠F ， ∴ED ∥BF ．23. （2021湘潭）如图，矩形ABCD 中，E 为边BC 上一点，将△ABE 沿AE 翻折后，点B恰好落在对角线AC 的中点F 上．（1）证明：△AEF ≌△CEF ；（2）若AB ＝3，求折痕AE 的长度．【答案或简析】（1）证明：∵四边形ABCD 是矩形，∴∠B ＝90°，∵将△ABE 沿AE 翻折后，点B 恰好落在对角线AC 的中点F 上，∴∠AFE ＝∠B ＝90°，AF ＝CF ， ∵∠AFE +∠CFE ＝180°，∴∠CFE ＝180°﹣∠AFE ＝90°，在△AEF 和△CEF 中，,,,AF CF AFE CFE EF EF ∠∠， ∴△AEF ≌△CEF （SAS ）．（2）解：由（1）知，△AEF ≌△CEF ， ∴∠EAF ＝∠ECF ，由折叠性质得，∠BAE ＝∠EAF ， ∴∠BAE ＝∠EAF ＝∠ECF ， ∵∠B ＝90°，∴∠BAC +∠BCA ＝90°， ∴3∠BAE ＝90°， ∴∠BAE ＝30°，在Rt △ABE 中，AB ＝3，∠B ＝90°，∴AE ＝32cos3032AB ．23.（2021株洲）如图所示，在矩形ABCD 中，点E 在线段CD 上，点F 在线段AB 的延长线上，连接EF 交线段BC 于点G ，连接BD ，若DE ＝BF ＝2．（1）求证：四边形BFED 是平行四边形；（2）若tan ∠ABD ＝23，求线段BG 的长度．【答案或简析】证明：（1）∵四边形ABCD 是矩形， ∴DC ∥AB ，又∵DE ＝BF ，∴四边形DEFB 是平行四边形；（2）∵四边形DEFB 是平行四边形， ∴DB ∥EF ， ∴∠ABD ＝∠F ，∴tan ∠ABD ＝tan F ＝23， ∴23BG BF ，又∵BF ＝2， ∴BG ＝43．24.（2021郴州）如图，四边形ABCD 中，AB ＝DC ，将对角线AC 向两端分别延长至点E ，F ，使AE ＝CF ．连接BE ，DF ，若BE ＝DF ．证明：四边形ABCD 是平行四边形．【答案或简析】证明：在△BEA 和△DFC 中，,,,AB DC AE CF BE DF ∴△BEA ≌△DFC （SSS ）， ∴∠EAB ＝∠FCD ， ∴∠BAC ＝∠DCA ， ∴AB ∥DC ， ∵AB ＝DC ，∴四边形ABCD 是平行四边形．25. （2021衡阳）如图，点E 为正方形ABCD 外一点，∠AEB ＝90°，将Rt △ABE 绕A 点逆时针方向旋转90°得到△ADF ，DF 的延长线交BE 于H 点．（1）试判定四边形AFHE 的形状，并说明理由；（2）已知BH ＝7，BC ＝13，求DH 的长．【答案或简析】（1）四边形AFHE 是正方形，理由如下：由旋转得∠AEB =∠AED =90°，AE =AF ,∠DAF =∠EAB. ∴∠AFH =90°.∵四边形ABCD 是正方形， ∴∠DAB =90°，∴∠F AE =∠F AB +∠BAE =∠F AB +∠DAF =∠DAB =90°， ∴∠AEB =∠AFB =∠F AE =90°，∴四边形AFHE 是矩形. 又∵AE =AF ，∴四边形AFHE 是正方形. （2）连接BD ，由题意得，BC =CD =13, ∴在Rt △BCD 中，BD =22132CD CB .∵四边形AFHE 是正方形， ∴∠EHD =90°，∴∠DHB =90°，在Rt △DHB 中，DH =22,BD BH又∵BH =7,∴DH =17.26.（2021邵阳）如图，在正方形ABCD 中，对角线AC ，BD 相交于点O ，点E ，F 是对角线AC 上的两点，且AE ＝CF ．连接DE ，DF ，BE ，BF ．（1）证明：△ADE ≌△CBF ．（2）若AB ＝4，AE ＝2，求四边形BEDF 的周长．【答案或简析】（1）证明：由正方形对角线平分每一组对角可知：∠DAE ＝∠BCF ＝45°，在△ADE 和△CBF 中，,,,AD BC DAE BCF AE CF ∠∠ ∴△ADE ≌△CBF （SAS ）．（2）解：∵AB ＝AD ＝42， ∴BD ＝228AB AD ，由正方形对角线相等且互相垂直平分可得：AC ＝BD ＝8，DO ＝BO ＝4，OA ＝OC ＝4，又AE ＝CF ＝2，∴OA ﹣AE ＝OC ﹣CF ，即OE ＝OF ＝4﹣2＝2，故四边形BEDF 为菱形． ∵∠DOE ＝90°， ∴DE ＝22224225DO EO ．∴4DE ＝85，故四边形BEDF 的周长为85．27.（2021岳阳）如图，在四边形ABCD 中，AE ⊥BD ，CF ⊥BD ，垂足分别为点E ，F ．（1）请你只添加一个条件（不另加辅助线），使得四边形AECF 为平行四边形，你添加的条件是；（2）添加了条件后，证明四边形AECF 为平行四边形．【答案或简析】解：（1）添加条件为：AE ＝CF ，故答案为：AE ＝CF ；（2）证明：∵AE ⊥BD ，CF ⊥BD ， ∴AE ∥CF ， ∵AE ＝CF ，∴四边形AECF 为平行四边形．28.（2021张家界）如图，在矩形ABCD 中，对角线AC 与BD 相交于点O ，∠AOB ＝60°，对角线AC 所在的直线绕点O 顺时针旋转角α（0°＜ α ＜120°），所得的直线l 分别交AD ，BC 于点E ，F ．（1）求证：△AOE ≌△COF ；（2）当旋转角α为多少度时，四边形AFCE 为菱形？试说明理由．【答案或简析】证明：（1）∵四边形ABCD 是矩形， ∴AD ∥BC ，AO ＝CO ， ∴∠AEO ＝∠CFO ，在△AOE 和△COF 中，,,,AEO CFO AOE COF AO CO ∠∠∠∠， ∴△AOE ≌△COF （AAS ）；（2）当α＝90°时，四边形AFCE 为菱形，理由：∵△AOE ≌△COF ， ∴OE ＝OF ，又∵AO ＝CO ，∴四边形AFCE 为平行四边形，又∵∠AOE ＝90°，∴四边形AFCE 为菱形．29.（2020长沙）在矩形ABCD 中，E 为DC 边上一点，把△ADE 沿AE 翻折，使点D 恰好落在BC 边上的点F . (1)求证：△ABF ∽△FCE ；(2)若AB ＝23，AD ＝4，求EC 的长；(3)若AE －DE ＝2EC ，记∠BAF ＝α，∠F AE ＝β.求tan α＋tan β的值．【答案或简析】(1)证明：∵四边形ABCD 是矩形， ∴∠B ＝∠C ＝∠D ＝90°， ∴∠CEF ＋∠EFC ＝90°， ∵△AEF 由△AED 翻折得到， ∴∠AFE ＝∠D ＝90°， ∴∠AFB ＋∠EFC ＝90°， ∴∠CEF ＝∠AFB ， ∴△ABF ∽△FCE ； (2)∵四边形ABCD 是矩形， ∴AB ＝CD ＝23，AD ＝BC ＝4，设CE ＝x ，则DE ＝23－x ， ∵△AEF 由△AED 翻折得到， ∴AD ＝AF ＝4，DE ＝EF ＝23－x ，在Rt △ABF 中，BF ＝AF 2－AB 2＝42－（23）2＝2， ∴CF ＝BC －BF ＝4－2＝2，在Rt △CEF 中，EF 2＝CE 2＋CF 2，即(23－x )2＝x 2＋22，解得x ＝233，即EC ＝233；(3)如解图，设EC ＝x ，DE ＝a ，则易得EF ＝a ，AB ＝a ＋x ， ∵AE －DE ＝2EC ，∴AE －a ＝2x ，即AE ＝2x ＋a ，由勾股定理得：AF ＝AE 2－EF 2＝（2x ＋a ）2－a 2＝4ax ＋4x 2， CF ＝EF 2－CE 2＝a 2－x 2，由(1)知∠CEF ＝∠AFB ，∴∠BAF ＝∠CFE ＝α，∴cos ∠BAF ＝AB AF ＝a ＋x 4ax ＋4x 2，cos ∠CFE ＝CFEF ＝a 2－x 2a ，∴a ＋x 4ax ＋4x2＝a 2－x 2a ， a ＋x4x （a ＋x ）＝（a ＋x ）（a －x ）a，a (a ＋x )＝(a ＋x )4x （a －x ）， a ＝4ax －4x 2，整理得(a －2x )2＝0， ∴a ＝2x ，∴sin ∠CFE ＝CE EF ＝x a ＝x 2x ＝12，即∠CFE ＝∠BAF ＝α＝30°，∴∠DAF ＝60°， ∴∠EAF ＝β＝30°.∴tan α＋tan β＝tan 30°＋tan 30°＝233.。

中考四边形综合知识点总结

中考四边形综合知识点总结一、四边形的性质1. 任意四边形的内角和为360度2. 对角线互相垂直的四边形是矩形3. 对边平行且相等的四边形是平行四边形4. 有一对对边平行的四边形是梯形5. 有一对对边相等的四边形是菱形6. 对角线相等的四边形是菱形7. 有一对对边互相垂直且相等的四边形是正方形8. 矩形和菱形都是平行四边形二、矩形1. 定义：有四个顶点和四条边的四边形2. 性质：内角和为360度，对角线长度相等，对角线互相垂直，相邻边互相垂直且相等3. 公式：周长=2*(长+宽)，面积=长*宽三、平行四边形1. 定义：有四个顶点和四条边的四边形，对边平行且相等2. 性质：内角和为360度，对角线互相平分，对边互相相等3. 公式：周长=2*(a+b)，面积=底*高四、梯形1. 定义：有四个顶点和四条边的四边形，有一对对边平行2. 性质：内角和为360度，底边平行，上底和下底长度相等，两个底边平行线段的中线互相平行3. 公式：周长=上底+下底+两腰，面积=(上底+下底)*高/2五、菱形1. 定义：有四个顶点和四条边的四边形，对边互相平行且相等2. 性质：内角和为360度，对角线相等，对角线互相平分，对角线互相垂直3. 公式：周长=4*边长，面积=对角线1*对角线2/2六、正方形1. 定义：有四个顶点和四条边的四边形，对角线相等，对边互相平行且相等2. 性质：内角和为360度，对角线相等，对角线互相垂直，边互相平行且相等3. 公式：周长=4*边长，面积=边长^2七、计算题1. 计算四边形的周长和面积2. 计算梯形的高3. 根据题目条件运用四边形的性质进行计算4. 判断四边形的类型和性质八、应用题1. 根据实际场景运用四边形的性质进行解决问题2. 通过综合应用四边形的知识解决问题3. 运用数学推理和逻辑思维解答四边形的实际问题以上就是中考四边形综合知识点总结，希望对大家有所帮助。

《四边形中考复习》课件

《四边形中考复习》PPT课件
四边形中考复习PPT课件导言
• 介绍课程目的和安排 • 简要介绍四边形的概念
矩形
定义与性质
介绍矩形的定义和基本性质
周长和面积公式
探讨矩形的周长和面积计算方法
角度和对角线
讲解矩形的角度和对角线的特点 Nhomakorabea平行四边形
1
定义与性质
介绍平行四边形的定义和基本性质
周长和面积公式
2
探讨平行四边形的周长和面积计算方法
3
高度和对角线
讲解平行四边形的高度和对角线的特点
菱形
定义与性质
介绍菱形的定义和基本性质
周长和面积公式
探讨菱形的周长和面积计算方法
对角线和角度
讲解菱形的对角线和角度的特点
梯形
1 定义与性质
介绍梯形的定义和基本性质
2 周长和面积公式
探讨梯形的周长和面积计算方法
3 高度和中线
讲解梯形的高度和中线的特点
总结
1
复习四种四边形的定义、性质和
公式
常见四边形的应用实例
2
加深对四边形知识的理解和掌握
展示四边形在实际问题中的应用
3
准备好中考
提醒学生及时复习巩固知识，为中考做好准备

2020初中数学中考专题复习——四边形中的线段最值问题专项训练2(附答案详解)

【详解】
解：∵在△ABC中，AB=6，AC=8，BC=10，
∴AB2+AC2=BC2，
即∠BAC=90°．
又PE⊥AB于E，PF⊥AC于F，
∴四边形AEPF是矩形，
∴EF=AP．
∵M是EF的中点，
∴AM= EF= AP,
因为AP的最小值即为直角三角形ABC斜边上的高
AP= ,
∴AM的最小值是．
故选C．
②根据对称性：连接ED交BC于点P，此时AP+EP＝AD，最小，再过点D作DF垂直AC的延长线于点F，根据勾股定理即可求解．
【详解】
如图所示：
（1）∵BD∥CE，CD∥BE，
∴四边形BDCE是平行四边形，
∵CE⊥AB，
∴∠BEC＝90°，
∴四边形BECD是矩形；
（2）①当BE的长为时，四边形BECD是菱形．理由如下：
6．C
【解析】
【分析】
根据勾股定理的逆定理可以证明∠BAC=90°，根据直角三角形斜边上的中线等于斜边的一半，则AM= EF，要求AM的最小值，即求EF的最小值；根据三个角都是直角的四边形是矩形得四边形AEPF是矩形，根据矩形的对角线相等，得EF=AP，则EF的最小值即为AP的最小值，根据垂线段最短知：AP的最小值即等于直角三角形ABC斜边上的高．
【详解】
设与AC交于点O，作 ⊥ 于，如图所示：
在Rt△ABC中，∠BAC=90 ，∠ACB=45 ，
∴ ，
∵四边形PAQC是平行四边形，
∴ ，
∵ ⊥ ，∠ACB=45 ，
∴ ，
当与重合时，OP的值最小，则PQ的值最小，
∴PQ的最小值
故选：A．
【点睛】
本题考查了勾股定理的运用、平行四边形的性质以及垂线段最短的性质，利用垂线段最短求线段的最小值是解题的关键．

中考专题复习四边形综合专题

谢湘君中考专题复习·四边形综合专题1、如图，在菱形ABCD中， AB=2，∠ ABC=60°，对角线AC、BD相交于点O，将对角线旋转角α（0°＜α＜90°）后得直线l ，直线 l 与 AD、 BC两边分别相交于点 E 和点（1）求证：△ AOE≌△ COF；（2）当α =30°时，求线段EF的长度．AC所在的直线绕点F．O顺时针解：（ 1）∵四边形ABCD是菱形，∴AD∥ BC，AO=OC，∴AECF＝ OEOF＝ AOOC＝ 1，∴ AE=CF， OE=OF，在△ BCD是菱形，∠ ABC=60°，∴∠ OAD=60°，∴∠ AEO=90°，在 Rt △ AOB中，sin ∠ ABO=AOAB=A△AOE和△ COF中，AO＝ COOE＝OFAE＝ CF ∴△ AOE≌△ COF．（2）当α =30°时，即∠ AOE=30°，∵四边形A12，∴ AO=1，在 Rt △ AEO中，cos∠ AOE=cos30° =OEAO=32，∴OE=32，∴EF=2OE=3．2、如图，在Rt△ ABC中，∠ C＝ 90o， BD是Rt△ ABC的一条角一平分线，点O、E、F 分别在 BD、BC、AC上，且四边形 OECF是正方形，（1）求证：点 O在∠ BAC的平分线上；（2）若 AC＝ 5， BC＝12，求 OE的长AMDO FBC第22题图E【试题分析】（1）考察角平分线定理的性质，及直角三角形全等的判断方法，“HL”（2）利用全等得到线段AM＝BE， AM＝AF，利用正方形OECF，得到四边都相等，从而利用OE与 BE、AF 及 AB的关系求出 OE的长解：（ 1）过点 O作 ON⊥ AB于点 M∵正方形OECF∴OE＝ EC＝CF＝ OF，OE⊥ BC于 E， OF⊥AC于 F∵BD平分∠ ABC， OM⊥ AB于 M，OE⊥ BC于 E∴OM ＝ OE ＝OF∵OM ⊥ AB 于 M ， OE ⊥BC 于 E ∴∠ AMO ＝ 90°，∠ AFO ＝ 90°OMOF∴点 O 在∠ BAC 的平分线上∵∴ Rt △ AMO ≌ Rt △ AFO ∴∠ MA0＝∠ FAO AOAO（2）方法一：∵ R t △ ABC 中，∠ C ＝90°， AC ＝ 5， BC ＝12∴ AB ＝ 13 易证： BE ＝BM ， AM ＝AF又 BE ＝ BC －CE ， AF ＝： AC － CF ，而 CE ＝CF ＝ OE 故： BE ＝ 12－ OE ， AF ＝ 5－ OE 显然： BM ＋AM ＝ AB即： BE ＋AF ＝ 1312－ OE ＋ 5－OE ＝ 13 解得 OE ＝ 2 方法二利用面积法： S △ ABC ＝ 1 ACBC2S △ ABC ＝ 1BCOE1AC OE1BA OE222从而解得。

中考总复习《四边形》共28页文档

▪
27、只有把抱怨环境的心情，化为上进的力量，才是成功的保证。——罗曼·罗兰
▪
28、知之者不如好之者，好之者不如乐之者。——孔子
▪பைடு நூலகம்
29、勇猛、大胆和坚定的决心能够抵得上武器的精良。——达·芬奇
▪
30、意志是一个强壮的盲人，倚靠在明眼的跛子肩上。——叔本华
谢谢！
28
中考总复习《四边形》
51、山气日夕佳，飞鸟相与还。 52、木欣欣以向荣，泉涓涓而始流。
53、富贵非吾愿，帝乡不可期。 54、雄发指危冠，猛气冲长缨。 55、土地平旷，屋舍俨然，有良田美池桑竹之属，阡陌交通，鸡犬相闻。
▪
26、要使整个人生都过得舒适、愉快，这是不可能的，因为人类必须具备一种能应付逆境的态度。——卢梭

2023中考数学专题复习——第七章四边形

2023中考专题复习——第七章四边形时间：45分钟满分：80分一、选择题(每题4分，共32分)1．下列各组条件中，不能判断一个四边形是平行四边形的是() A．两组对边分别平行的四边形B．两组对角分别相等的四边形C．两条对角线互相平分的四边形D．一组对边平行另一组对边相等的四边形2．如图，在△ABC中，∠A＝90°，点M，N分别为边AB和AC的中点，若AB ＝2，AC＝4，则MN的长度为()A．2 3 B. 3 C．2 5 D. 5(第2题)(第3题)3．如图，在▱ABCD中，连接AC，已知∠BAC＝40°，∠ACB＝80°，则∠BCD＝()A．80°B．100°C．120°D．140°4．如图，四边形ABCD是菱形，其中A，B两点的坐标分别为A(0，3)，B(4，0)，则点D的坐标为()A．(0，1) B．(0，－1)C．(0，2) D．(0，－2)(第4题)(第5题)5．如图，在正方形ABCD的外侧作等边三角形CDE，连接AE，则∠DAE的度数是()A．15°B．20°C．12.5°D．10°6．如图，在矩形ABCD中，AB＝4，BC＝8，对角线AC，BD相交于点O，过点O作OE⊥AC交AD于点E，则DE的长是()A．3 B．5 C．2.4 D．2.5(第6题)(第7题)7．如图，在▱ABCD中，AB＝BC＝5，对角线BD＝8，则▱ABCD的面积为() A．20 B．24 C．40 D．488．将两张全等的矩形纸片和另两张全等的正方形纸片按如图方式不重叠地放置在矩形ABCD内，其中矩形纸片和正方形纸片的周长相等．若知道图中阴影部分的面积，则一定能求出()A．正方形纸片的面积B．四边形EFGH的面积C. △BEF的面积D. △AEH的面积(第8题)(第9题)二、填空题(每题4分，共16分)9．如图是以正方形的边长为直径，在正方形内画半圆得到的图形，则此图形的对称轴有________条．10．在平面直角坐标系xOy中，已知点A(2，0)，B(5，4)，若四边形OABC是平行四边形，则▱OABC的周长等于________．11．如图，在Rt△ABC中，AC＝3，BC＝4，点D为斜边AB上一动点，DE⊥BC，DF⊥AC，垂足分别为E，F，则线段EF的最小值为________．(第11题)(第12题)12．如图，四边形ABCD是菱形，点E，F分别在边AB，AD上，且AE＝DF，连接BF与DE相交于点G，已知AF＝2DF，若FG ＝3，则GB＝________．三、解答题(共32分)13．(8分)如图，在四边形ABCD中，BE⊥AC，DF⊥AC，垂足分别为E，F，且BE＝DF，AF＝CE.求证：四边形ABCD为平行四边形．(第13题)14．(24分)如图，已知在矩形ABCD中，点M，N分别是边AD，BC的中点，点P，Q分别是边BM，DN的中点．(1)求证：BM∥DN；(2)求证：四边形MPNQ是菱形；(3)当矩形ABCD的边AB与AD满足什么数量关系时，四边形MPNQ为正方形？请说明理由．3(第14题)答案一、1.D 2.D 3.C 4.D 5.A 6.A7.B8.C二、9.410.1411.12 512. 63点拨：如图，过点F作FP∥AB，交DE于点P，则△DFP∽△DAE.∵AF＝2DF，∴FPAE＝DFDA＝13.∵四边形ABCD是菱形，∴AB＝AD.∵AE＝DF，∴BE＝AF，∴BE＝2AE，∴FPBE＝FP2AE＝16.∵FP∥AB，∴△FPG∽△BEG，∴GFGB＝FPBE＝16，∴GB＝6GF＝6 3.(第12题)三、13.证明：∵AF＝CE，∴AF－EF＝CE－EF，即AE＝CF.∵BE⊥AC，DF⊥AC，∴∠AEB＝∠CFD＝90°.∵BE＝DF，∴△ABE≌△CDF.∴AB＝CD，∠BAE＝∠DCF.∴AB∥CD.∴四边形ABCD为平行四边形．14．(1)证明：∵四边形ABCD是矩形，∴AD∥BC，AD＝BC.∵点M，N分别为边AD，BC的中点，∴DM＝BN，∴四边形DMBN是平行四边形．∴BM∥DN.(2)证明：由(1)可知四边形DMBN是平行四边形，∴BM＝DN，BM∥DN.5∵点P，Q分别为边BM，DN的中点，∴MP＝NQ.∴四边形MPNQ是平行四边形．如图，连接MN.(第14题)由(1)可知AD∥BC，AD＝BC.∵点M，N分别为边AD，BC的中点，∴DM＝CN，∴四边形DMNC是平行四边形．由题可知∠C＝90°，∴四边形DMNC是矩形，∴∠DMN＝∠C＝90°.∵点Q是边DN的中点，∴MQ＝NQ，∴四边形MPNQ是菱形．(3)解：当矩形ABCD的边AB与AD满足AB＝12AD时，四边形MPNQ为正方形．理由：∵AB＝12AD，点M是边AD的中点，∴AB＝AM.易得矩形ABNM是正方形．∵P为正方形ABNM对角线BM的中点，∴∠NPM＝90°.由(2)知四边形MPNQ是菱形，∴四边形MPNQ是正方形．。

中考四边形综合复习

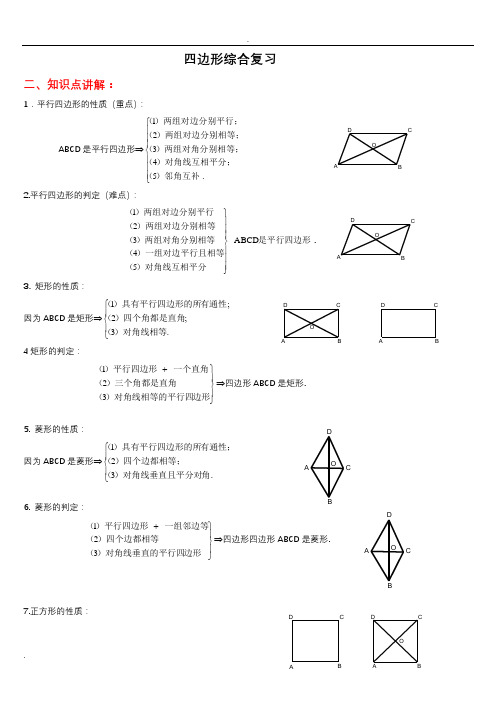
C D CD O四边形综合复习二、知识点讲解：1．平行四边形的性质（重点）：ABCD 是平行四边形⇒⎪⎪⎪⎩⎪⎪⎪⎨⎧.54321）邻角互补（）对角线互相平分；（）两组对角分别相等；（）两组对边分别相等；（）两组对边分别平行；（ 2.平行四边形的判定（难点）：是平行四边形）对角线互相平分（）一组对边平行且相等（）两组对角分别相等（）两组对边分别相等（）两组对边分别平行（ABCD 54321⎪⎪⎪⎭⎪⎪⎪⎬⎫. 3. 矩形的性质：因为ABCD 是矩形⇒⎪⎩⎪⎨⎧.3;2;1）对角线相等（）四个角都是直角（有通性）具有平行四边形的所（ 4矩形的判定：⎪⎭⎪⎬⎫+边形）对角线相等的平行四（）三个角都是直角（一个直角）平行四边形（321⇒四边形ABCD 是矩形.5. 菱形的性质：因为ABCD 是菱形⇒⎪⎩⎪⎨⎧.321角）对角线垂直且平分对（）四个边都相等；（有通性；）具有平行四边形的所（6. 菱形的判定：⎪⎭⎪⎬⎫+边形）对角线垂直的平行四（）四个边都相等（一组邻边等）平行四边形（321⇒四边形四边形ABCD 是菱形.7.正方形的性质：ABDOCABDOCAD BCAD BC OCDBAOCDBAOABCD 是正方形⇒⎪⎩⎪⎨⎧.321分对角）对角线相等垂直且平（角都是直角；）四个边都相等，四个（有通性；）具有平行四边形的所（8. 正方形的判定：⎪⎭⎪⎬⎫++++一组邻边等矩形）（一个直角）菱形（一个直角一组邻边等）平行四边形（321⇒四边形ABCD 是正方形.三、典型例题：1.下列四边形中，两条对角线一定不相等的是（）A ．正方形B ．矩形C ．等腰梯形D ．直角梯形 2．下列四个命题中，假命题是（）A ．两条对角线互相平分且相等的四边形是正方形B ．菱形的一条对角线平分一组对角C ．顺次连结四边形各边中点所得的四边形是平行四边形D ．等腰梯形的两条对角线相等3.在下列命题中，正确的是（）A ．一组对边平行的四边形是平行四边形B ．有一个角是直角的四边形是矩形C ．有一组邻边相等的平行四边形是菱形D ．对角线互相垂直平分的四边形是正方形 4.顺次连结任意四边形各边中点所得四边形一定是 ( )A ．平行四边形B ．菱形C ．矩形D ．正方形 5.下列命题中，真命题是（）Ａ．两条对角线相等的四边形是矩形Ｂ．两条对角线互相垂直的四边形是菱形Ｃ．两条对角线互相垂直且相等的四边形是正方形Ｄ．两条对角线互相平分的四边形是平行四边形6.7. 8. 9.10.例1.ABCD 中，已知对角线AC 和BD 相交于点O ， △AOB•的周长为15，AB=6，那么对角线AC+BD=_______．例2中， E、F•是对角线AC 上的两点，请你再添加一个条件，使四边形DEBF 是平行四边形，你添加的条件是 ,说明你的理由。

中考数学专题训练第12讲四边形2(解析版)

四边形题型一平行四边形的判定与性质1．（2021·四川·达州中学九年级期中）关于平行四边形ABCD 的叙述.正确的是（） A ．若AB BC ⊥.则平行四边形ABCD 是菱形 B ．若AC BD ⊥.则平行四边形ABCD 是正方形 C ．若AC BD =.则平行四边形ABCD 是矩形 D ．若AB AD =.则平行四边形ABCD 是正方形【答案】C【解析】解：解：A 、错误．若AB ⊥BC .则平行四边形ABCD 是矩形.B 、错误．若AC ⊥BD .则平行四边形ABCD 是菱形.C 、正确．D 、错误．若AB ＝AD .则平行四边形ABCD 是菱形.故选：C ．2．如图.四边形ABCD 和四边形DBCE 都是平行四边形.点R 在CE 上.且CR ＝14CE .则△APD .△DPQ .△QRC 的面积比为（）A ．15：9：4B ．25：9：4C ．16：9：4D ．5：3：2【答案】A【解析】∵四边形ABCD 及四边形DBCE 都是平行四边形 ∴AD =BC =DE .BD ∥CE∴D 点是AE 的中点.AP ：PR =AD ：DE ∴P 点是AR 的中点 ∴DP 是△ARE 的中位线 ∴DP RE =12∵CR CE =14∴CR RE =13∴CR DP =23∵BD ∥CE ∴△CRQ ∽△DPQ ∴CRQ DPQS CR SDP ⎛⎫== ⎪⎝⎭249.RQ PQ =23 即DPQCRQ SS =94.PQ PR AP ==3355∵△ADP 与△DPQ 等高 ∴DPQ ADPS PQ SAP ==35即ADPDPQCRQSS S ==51534ADPDPQCRQSS S=::15:9:4故选：A ．3．（2021·江苏·无锡市天一实验学校九年级期中）如图.点O 为正方形ABCD 对角线BD 的中点.BE 平分∠DBC 交DC 于点E .延长BC 到点F .使FC EC =.连接DF 交BE 的延长线于点H .连接OH 交DC 于点G .连接H C ．则以下五个结论中①12OH BF =.②60CHF ∠=︒.③()22BC GH =+.④2HF HE HB =⋅.正确结论有（）A ．1B ．2C ．3D ．4【答案】B【解析】∵四边形ABCD 是正方形.,90,45,2BC CD BCD DBC BD BC ∴=∠=︒∠=︒=．∵BE 平分∠DBC .14522.52DBH HBF ∴∠=∠=⨯︒=︒.67.5BEC ∴∠=︒．在和中.BC CD BCE DCF CE CF =⎧⎪∠=∠⎨⎪=⎩BCE DCF ∴≌△△.,67.5EBC CDF BEC CFD ∴∠=∠∠=∠=︒．BEC DEH ∠=∠.BEC EBC DEH FDC ∴∠+∠=∠+∠.90DHB ∴∠=︒．在DBH △和中.DBH HBFBH BHBHD BHF ∠=∠⎧⎪=⎨⎪∠=∠⎩DBH HBF ∴△≌△.,2DH HF BD BF BC ∴===.∴点H 是DF 的中点.∴1,2OH BF CH FH ==.故①正确.67.5HCF CFD ∴∠=∠=︒.180267.545CHF ∴∠=︒-⨯︒=︒.故②错误.2BC CF BC +=. )21BC CF ∴=．2CF GH =.(222BC GH ∴=+.故③错误.,90CE CF ECF =∠=︒.45EFC ∴∠=︒.67.54522.5EFH ∴∠=︒-︒=︒.FBE EFH ∴∠=∠． 90BHF FHE ∠=∠=︒.BHF ∴△△∽FFHE ∴△△. HB HFHF HE∴=. 2HF HE HB ∴=⋅.故④正确.综上所述.正确的有①.④. 故选：B ．4．（2021·吉林朝阳·九年级期中）如图.平行四边形ABCD 的对角线AC 、BD 相交于点O .//OE AB 交AD 于点E ．若2OA =.AOE △的周长为10.则平行四边形ABCD 的周长为（）A ．16B ．32C ．36D ．40【答案】B【解析】解：∵ AOE △的周长是10.且2OA =. ∴+=1028OE AE -=.又∵对角线AC 、BD 相交于点O . ∴O 是BD 的中点. ∵//OE AB . ∴12OE AB =.点E 为AD 的中点. ∴AB =2OE .AD =2AE .∵四边形ABCD 是平行四边形. ∴,AB DC AD BC ==.∴24,24AD BC AD AE AB DC AB OE +==+== .∴+444()4832AD BC AB DC AE OE AE OE ++=+=+=⨯=．故选：B ．5．如图.△ABC 的中线BD 、CE 交于点O .连接OA .点G 、F 分别为OC 、OB 的中点.BC =8.AO =6.则四边形DEFG 的周长为（）A ．12B ．14C ．16D ．18【答案】B【解析】BD ∴.CE 是的中线.D ∴是AC 中点.E 是AB 中点.//ED BC ∴且12ED BC =. F 是BO 的中点.G 是CO 的中点.//FG BC ∴且12FG BC =,142ED FG BC ∴===. 同理132GD EF AO ===. ∴四边形DEGF 的周长为343414+++=．故选B ．6．如图.将▱DEBF 的对角线EF 向两端延长.分别至点A 和点C .且使AE ＝CF .连接AB .BC .AD .CD ．求证：四边形ABCD 为平行四边形．以下是证明过程.其顺序已被打乱. ①∴四边形ABCD 为平行四边形.②∵四边形DEBF 为平行四边形.∴OD =OB .OE =OF . ③连接BD .交AC 于点O .④又∵AE =CF .∴AE +OE =CF +OF .即OA =OC 正确的证明步骤是（）A ．①②③④B ．③④②①C ．③②④①D ．④③②①【答案】C【解析】连接BD .交AC 于点O .如图∵四边形DEBF 为平行四边形∴OD =OB .OE =OF ∵AE =CF ∴AE +OE =CF +OF 即OA =OC∴四边形ABCD 为平行四边形故正确的证明步骤是：③②④① 故选：C ．7．如图.点E 、F 、G 、H 分别是四边形ABCD 边AB 、BC 、CD 、DA 的中点.则下列说法： ①若AC ＝BD .则四边形EFGH 为矩形. ②若AC ⊥BD .则四边形EFGH 为菱形.③若四边形EFGH 是平行四边形.则AC 与BD 互相平分. 其中正确的个数是（）A ．0B ．1C ．2D ．3【答案】A【解析】解：∵点E 、F 、G 、H 分别是四边形ABCD 边AB 、BC 、CD 、DA 的中点.∴12EH BD =.//EH BD .12FG BD =.//FG BD .12EF AC =.//EF AC .12HG AC =.//HG AC .∴EH FG =.//EH FG .∴四边形EFGH 是平行四边形. ①当AC BD =时.EF EH =. ∴四边形EFGH 是菱形. ②当AC BD ⊥时.90HEF ∠=︒. ∴四边形EFGH 是矩形.③当四边形EFGH 是平行四边形.则AC 与BD 不一定互相平分. 正确的个数为0个. 故选A ．8．如图.在平行四边形ABCD 中.60B ∠=︒.4AB =.6AD =.E 是AB 边的中点.F 是线段BC上的动点.将EBF△沿EF所在直线折叠得到EB F'△.连接B D'.则B D'的最小值是（）A．2102-B．6 C．4 D．2132-【答案】D【解析】解：如图.B’的运动轨迹是以E为圆心.以BE的长为半径的圆．所以.当B’点落在DE上时.B’D取得最小值．过点D作DG⊥BA交BA延长线于G.∴∠DGA=90°.∵四边形ABCD是平行四边形.∠B=60°.∴AD∥BC.∴∠GAD=60°.∴∠ADG=30°.∴132AG AD==∴2233DG AD AG=-=.∵E是AB的中点.AB=4.∴AE=BE=2.∴GE=AE+AG=5∴22213DE DG EG=+=由折叠的性质可知2B E BE'==∴DB’＝2132-．故选D．9．（2021·浙江·温州市第十二中学九年级期中）如图. 中.,6,AB AC BC AD BC==⊥于点,4,D AD P=是半径为2的⊙A上一动点. 连结PC.若E 是PC 的中点. 连结DE . 则DE 长的最大值为（）A ．3B ．3.5C ．4D ．4.5【答案】B【解析】解：如图.可知P 在BA 延长线与⊙A 的交点时此时DE 长的最大.证明如下：连接BP ,∵,6,AB AC BC AD BC ==⊥, ∴BD =DC , ∵E 是PC 的中点.∴DE //BP , 12DE BP =,所以当BP 的长最大时.DE 长的最大.由题意可知P 在BA 延长线与⊙A 的交点时BP 的长最大此时DE 长的最大. ∵BC =6,AD =4, ∴BD =DC =3,BA =5, ∵⊙A 的半径为2.即AP =2, ∴BP =5+2=7,∴13.52DE BP ==.故选：B.10．如图.折叠ABCD.折痕经过点B.交AD边于点P.点C落在BA的延长线上的点F处.点D落在点E处.得到四边形APEF.若ABCD的面积为8.有以下结论：①AB AP=.②若AP PD=.则四边形APEF是菱形.③设四边形APEF的面积为y.四边形BCDP的面积为x.则y与x的函数关系式为()=-<<.y x x2848④若4BC=.则点P到AB的距离为1．其中正确的个数为（）A．4 B．3 C．2 D．1【答案】A【解析】解：由折叠知：∠C＝∠F.∠ABP＝∠CBP.∵平行四边形ABCD.∴∠C＝∠BAD.CD＝AB.∴∠F＝∠BAD.∴EF∥AP.∵AD∥BC.∴∠APB＝∠PBC.∴∠ABP＝∠APB.∴AB＝AP.故①正确.由折叠可知.CD＝EF.PD＝EP.∴AP＝EF.∴四边形APEF是平行四边形.∵AP PD=.∴AP＝EP.∴平行四边形APEF是菱形.故②正确.∵四边形BCDP的面积为x.∴S APEF+S ABCD＝2x.∴y ＝2x ﹣8（4＜x ＜8）.故③正确. 设点P 到AB 的距离为h . ∴S ABCD ＝S 四边形BPEF +S △ABP . ∴8＝11()22h BF PE h AB ⨯⨯++⨯⨯.∴8＝()118+8,22h h PE AB h ⨯⨯⨯+=.∴h ＝1.故④正确.故选：A11．（2021·陕西碑林·九年级期中）在平行四边形ABCD 中.点E .F .G 分别是AD .BC .CD 的中点.BE ⊥EG .AD ＝25.AB ＝3.则AF 的长为______．【答案】4【解析】解：连接AC 、EC .如图所示： ∵四边形ABCD 是平行四边形. ∴AD ＝BC .AD ∥BC .即AE ∥CF ∵点E .F 分别是AD .BC 的中点.∴AE =12AD .12CF BC =∴AE ＝CF .AE ∥CF .∴四边形AFCE 是平行四边形. ∴AF ＝CE . ∵AD ∥BC .∴∠EAQ =∠BCQ .∠AEQ =∠CBQ . ∴△AEQ ∽△CBQ .∴1122ADAQ EQ AE CQ BQ CB BC ====.设AQ ＝a .EQ ＝b .则CQ ＝2a .BQ ＝2b . ∵点E .G 分别是AD .CD 的中点. ∴EG 是△ACD 的中位线. ∴EG ∥AC .∵BE ⊥EG . ∴BE ⊥AC .由勾股定理得：BQ 2=AB 2﹣AQ 2＝BC 2﹣CQ 2. 即9﹣a 2＝()225﹣4a 2. ∴3a 2＝11. ∴a 2＝113. ∴BQ 2＝4b 2＝（25）2﹣4×113＝163. ∴b 2＝1614343⨯=. 在Rt △EQC 中.CE 2＝EQ 2+CQ 2＝b 2+4a 2＝16. ∴CE ＝4. ∴AF ＝4．故答案为：4．12．（2021·湖北云梦·九年级期中）如图.AB 、AC 、BC 都是⊙O 的弦.OM ⊥AB .ON ⊥AC .垂足分别为M 、N .若MN ＝1.则BC 的长为 ___．【答案】2【解析】解：∵OM ⊥AB .ON ⊥AC .垂足分别为M 、N .OM 过圆心O .ON 过圆心O . ∴AN ＝CN .AM ＝BM . ∴MN ＝12BC . ∵MN ＝1. ∴BC ＝2. 故答案为：2．13．（2021·上海杨浦·九年级期中）如图.已知AD 是△ABC 的中线.G 是△ABC 的重心.联结BG 并延长交边AC 于点E .联结DE .那么S △ABC ：S △GED 的值为____．【答案】12【解析】解：∵G 是△ABC 的重心 ∴点D 为BC 的中点.点E 是AC 的中点 ∴BE 、AD 为的中线.DE 为中位线∴DE AD ∥.12DE AD = ∴GDE GAB △∽△ ∴12GE DE GB AB == ∴2=BG GE .即3BE GE =由三角形面积公式得到3BDE GDE S S =△△ ∵点D 为BC 的中点 ∴26BCE BDE GDE S S S ==△△△ ∵点E 是AC 的中点 ∴212BC A C DE B E G S S S ==△△△ ∴:12ABC GED S S =△△ 故答案为1214．（2021·上海市文来中学九年级期中）如图.三边的中点分别为D .E .F ．联结CD交AE 于点G .交EF 于点H .则::DG GH CH =______．【答案】2：1：3【解析】解：∵E.F分别为CB、CA的中点. ∴EF是△ABC的中位线.∴1//,2EF AB EF AB=.∴△CHE∽△CDB.∴12 CH CE EHCD CB BD===.∴CH=DH. ∵AD=DB.∴12 HEAD=.∵//EF AB.∴△EGH∽△AGD.∴12 HG EHDG AD==.∴DG：GH：CH=2：1：3. 故答案为：2：1：3．15．（2021·福建·龙岩初级中学九年级期中）已知：A (-3.0).B (0.3).C是平面内任意一点.AC=1. D是BC的中点.则DO的取值范围是_____________．【答案】321321 22OD【解析】解：如图.由AC=1.A (-3.0). C∴在以A为圆心.1为半径的A上.作B 关于原点O 的对称点1,B 则10,3,B 连接1B A 并延长与圆交于1,,C C 则此时1B C 最长.当C 与1C 重合.1B C 最短.13,0,0,3,0,3,A B B 1AOB 为等腰直角三角形.1145,OAB OB A2213332,AB111321,321,BC BC ∴=-=+ D 为BC 的中点.1,OB OBDO ∴为1BCB △的中位线.11,2DO B C ∴=OD ∴最大时为32+1,2最小时为321,2 OD ∴的范围为：321321.22OD 故答案为：321321.22OD 16．（2021·江苏江阴·九年级期中）如图.矩形ABCD 中.AB ＝3.AD ＝4.点E 从点B 出发.以1单位每秒的速度向点C 运动.DF ＝53.G .H 分别是AE .EF 的中点.在点E 的整个运动过程中.当AE ⊥EF 时.点E 的运动时间为____秒.线段GH 扫过的图形面积为____．【答案】256【解析】解：设当AE ⊥EF 时.点E 的运动时间为t 秒.则BE t = . ∵矩形ABCD 中.AB =3.AD =4.∴3490CD AB BC AD B C ====∠=∠=︒，， . ∴490CE BC BE t BAE BEA =-=-∠+∠=︒， . ∵DF ＝53. ∴43CF CD DF =-= . ∵AE ⊥EF .∴90AEF ∠=︒ . ∴90BEA CEF ∠+∠=︒ . ∴BAE CEF ∠=∠ . ∴ .∴BE ABCF CE= . ∴BE CE AB CF = .∴()4433t t -=⨯ .整理得：2440t t -+= .解得：122t t == , 即当AE ⊥EF 时.点E 的运动时间为2秒.此时.线段GH 扫过的图形为图中阴影部分.点M 、N 分别为点G 、H 的初始位置.如图：则点M 、点G 、点N 、点H 分别为AB 、AE 、BF 、EF 的中点. ∴MG 、NH 分别是△ABE 、△FBE 的中位线. ∴111//1//22MG BE MG BE NH BE NH BE ====，，， . ∴1,//MG NH MG NH MG AB ==⊥， . ∴四边形MNHG 是平行四边形. 延长HN 交AB 于点P .如图. 则PN ⊥AB .且1322PM BM PB AB PB PB =-=-=- . ∵点H 是EF 中点.//PH BC .∴()11152322233PB FC DC DF ⎛⎫==⨯-=⨯-= ⎪⎝⎭.∴325236PM =-= .∴55==1=66S MG PM ⨯阴影部分 .即线段GH 扫过的图形面积为56,故答案为:2.56．17．（2021·浙江·杭州市杭州中学九年级期中）如图.在平行四边形ABCD 中.DE 交BC 于F.交AB的延长线于E.且∠EDB＝∠C．（1）求证：△ADE∽△DBE.（2）若DE＝210cm.AE＝8cm.求DC的长．【答案】（1）见解析.（2）3cm【解析】（1）证明：平行四边形ABCD中.∠A＝∠C. ∵∠EDB＝∠C.∴∠A＝∠EDB.又∠E＝∠E.∴△ADE∽△DBE.（2）解：平行四边形ABCD中.DC＝AB.由（1）得△ADE∽△DBE.∴DE BEAE DE=.22(210)58DEBEAE===（cm）.AB＝AE﹣BE＝8﹣5＝3（cm）.∴DC＝AB＝3（cm）．18．（2021·江苏滨湖·九年级期中）如图.在平行四边形ABCD中.点E在BC上.∠C＝∠DEA．（1）求证：△ADE∽△DEC.（2）若CE＝2.DE＝4.求EB的长．【答案】（1）见解析（2）6．【解析】（1）证明：∵四边形ABCD是平行四边形.AD//BC.∴∠ADE＝∠DEC.又∵∠DEA＝∠C.∴△ADE∽△DEC.（2）解：∵△ADE∽△DEC.∴DE AD EC DE=.∵CE＝2.DE＝4.∴424AD =.∴AD＝8=BC．∴EB=BC-CE=8-2=6．19．如图.已知菱形ABCD的对角线相交于点O.延长AB至点E.使BE=AB.连结CE．(1)求证：BD=EC．(2)当∠DAB=60°时.四边形BECD为菱形吗?请说明理由．【答案】（1）见解析.（2）四边形BECD是菱形．理由见解析【解析】（1）证明：四边形ABCD是菱形.∴AB=CD.AB∥CD.又∵BE=AB.∴BE=CD.BE∥CD.∴四边形BECD是平行四边形.∴BD=EC.（2）解：结论：四边形BECD是菱形．理由：∵四边形ABCD是菱形.∴AD=AB.∵∠DAB=60°.∴△ADB.△DCB都是等边三角形.∴DC=DB.∵四边形BECD是平行四边形.∴四边形BECD是菱形．20．在△ABC中.AB＝AC.点D在BC边上.O是AC边的中点.CE//AD.交DO的延长线于点E.连接AE．（1）如图1.求证：四边形ADCE 是平行四边形.（2）如图2.若点D 是BC 边的中点.在不添加任何辅助线的情况下.请直接写出图中所有的直角三角形．【答案】（1）见解析.（2）,,,,ABD ACD ADE ACE CDE △△△△△ 【解析】解：（1）∵CE //AD . ∴∠CED =∠ADE . ∵O 是AC 边的中点. ∴OA =OC .∴在△COE 和△AOD 中.CEO ADE COE AOD OC OA ∠=∠⎧⎪∠=∠⎨⎪=⎩. ∴△COE ≌△AOD (AAS ). ∴CE =AD . 又∵CE //AD .∴四边形ADCE 是平行四边形. （2）∵点D 是BC 边的中点. ∴DC =DB .又由（1）可知四边形ADCE 是平行四边形. ∴DC =AE .DC //AE . ∴DB =AE . 又∵DB //AE .∴四边形DBAE 是平行四边形. ∴AB =DE . 又∵AB =AC . ∴DE =AC .∵四边形ADCE 是平行四边形. ∴平行四边形ADCE 是矩形.∴∠DCE =∠CEA =∠EAD =∠ADC =90°. ∴∠BDA =90°.∴直接三角形有：,,,,ABD ACD ADE ACE CDE △△△△△．21．（2021·河南·郑州市第二初级中学九年级期中）如图.在▱ABCD 中.点E 、F 分别在边AD 、BC 上.且∠ABE ＝∠CDF ．（1）探究四边形BEDF 的形状.并说明理由.（2）连接AC .分别交BE 、DF 于点G 、H .连接BD 交AC 于点O ．若23AG OG =.AE ＝4.求BC 的长．【答案】（1）四边形ABCD 是平行四边形.理由见解析.（2）16 【解析】解：（1）四边形BEDF 是平行四边形.理由如下： ∵四边形ABCD 是平行四边形. ∴∠ABC =∠ADC .AD ∥BC . 又∵∠ABE =∠CDF . ∴∠EBF =∠EDF . ∴∠DFC =∠EDF =∠EBF . ∴BE ∥DF .∴四边形BEDF 是平行四边形. （2）设2AG a =. ∵23AG OG =. ∴3OG a =.∴5AO AG OG a =+=. ∵四边形ABCD 是平行四边形. ∴AO =OC .AD ∥BC . ∴210AC AO a ==. ∴8CG AC AG a =-=. ∵AD ∥BC . ∴△AGE ∽△CGB . ∴4BC CGAE AG==.∴416BC AE==．22．如图.在Rt△ABC中.∠C＝90°.AC＝8.BC＝6.动点P从点A出发.沿AB以每秒5个单位长度的速度向终点B运动．当点P不与点A重合时.过点P作PD⊥AC于点D.以AP.AD为边作▱APED．设点P的运动时间为t秒．（1）线段AD的长为（用含t的代数式表示）．（2）当点E落在BC边上时.求t的值．（3）连结BE.当tan∠CBE＝13时.求t的值．（4）若线段PE的中点为Q.当点Q落在△ABC一边垂直平分线上时.直接写出t的值．【答案】（1）4t.（2）当点E落在BC边上时.t的值为1.（3）67t=或109t=.（4）满足条件的t的值为23或2533或1．【解析】解：（1）如图1中.在Rt △ABC 中.∵∠C ＝90°.AC ＝8.BC ＝6. ∴2210AB AC BC =+=.∵PD ⊥AC .∴cos AD AC A AP AB ==. ∴8510AD t =., ∴4AD t =.3DP t =.故答案为：4t .（2）如图2中.当点E 落在BC 上时.∵四边形APED 是平行四边形.∴5DE AP t ==.∴DE AB ∥.∴A CDE ∠=∠.∵C C ∠=∠.∴.由（1）可得：4AD PE t ==.∴DE CD AB AC =. ∴584108t t -=. 解得：1t ＝. ∴当点E 落在BC 边上时.t 的值为1.（3）①如图中.当01t <<时.延长PE 交BC 于点F .∵90C CDP DPE ∠=∠=∠=︒.∴四边形CDPF 为矩形.∴84PF CD t ==-.3CF DP t ==.∴84488EF PF PE PF AD t t t =-=-=--=-.63BF BC CF t =-=-.在Rt △BEF 中.881tan 633EF t CBE BF t -∠===-. 解得：67t =.②如图中.当12t <≤时.PE 交BC 于点F .连接BE .∵四边形APED 是平行四边形.四边形CDPF 为矩形.∴84PF CD t ==-.4PE AD t ==.3CF DP t ==.∴()48488EF PE PF t t t =-=--=-.63BF BC CF t =-=-.在Rt △BEF 中. 881tan 633EF t CBE BF t -∠===-. 解得：109t =. 综上可得：67t =或109t =. （4）①如图中.当点Q 落在线段AC 的垂直平分线MN 上时.由题意：4cos cos 5PQ QPN A PN ∠=∠==. 可得24555t t =-. 解得t ＝23.②如图中.当点Q 落在线段AB 的垂直平分线MN 上时.由题意：4 cos cos5PNQPN APQ∠=∠==.可得554 25tt-=.解得t＝25 33.③如图中.当点Q落在线段BC的垂直平分线上时.AP＝PB.此时t＝1.综上所述.满足条件的t的值为23或2533或1．题型二矩形的判定与性质1．（2021·山东陵城·九年级期中）如图.AB是⊙O的直径.弦MN∥AB.分别过M.N作AB 的垂线.垂足为C.D．以下结论：①AC＝BD.②AM BN=.③若四边形MCDN是正方形.则MN＝12AB.④若M为的中点.则D为OB中点.所有正确结论的序号是（）A．①②③B．①②④C．①②D．①②③④【答案】B【解析】解：如图所示.连接OM.ON.BN.∵MC⊥AB.ND⊥AB.∴∠OCM=∠ODN=90°.∵MN∥AB.∴∠CMN+∠MCD=180°.∴∠CMN=90°.∴四边形CMND 是矩形.∴CM =DN .又∵OM =ON .∴Rt △OCM ≌Rt △ODN （HL ）.∴OC =OD .∠COM =∠DON .∴OA -OC =OB -OD 即AC =BD .AM BN = .故①②正确.当四边形MCDN 是正方形时.MC =CD .∵OC =OD .∴CM =2OC . ∴225OM OC CM OC =+=.∴2255AB OM OC MN ===.故③错误.若M 是的中点.∴∠AOM =∠MON =∠BON =60°.∵ON =OB .∴△ONB 是等边三角形.∵ND ⊥OB .∴OD =BD .故④正确.故选B ．2．如图.在ABC ∆中.90B ∠=︒.12AB =.5BC =.D 为边AC 上一动点.DE AB ⊥于点E .DF BC ⊥于点F .则EF 的最小值为（）A ．4.8B ．6013C ．3013D ．13【答案】B 【解析】解：如图.连接BD ．∵在△ABC 中.AB ＝12.BC ＝5.90B ∠=︒.∴AB 2+BC 2＝AC 2.即AC =22125=13+．又∵DE ⊥AB 于点E .DF ⊥BC 于点F .∴四边形EDFB 是矩形.∴EF ＝BD ．∵BD 的最小值即为Rt △ABC 斜边上的高.∴1122AB BC AC BD ⋅=⋅.即125601313AB BC BD AC ⋅⨯===. ∴EF 的最小值为6013. 故选B ．3．（2021·浙江·瑞安市安阳实验中学九年级开学考试）如图.四边形ABCD 和AEFG 均为正方形.点G 在对角线BD 上.点F 在边BC 上.连结BE .记AEB △和的面积分别为1S 和2S ．若9AD =.1223S S =.则BE 的长为（）A ．3B 924C ．4D ．32【答案】D 【解析】解：如图.过点G 作MN ⊥BC .垂足为点N .交AD 于点M .∵四边形ABCD 为正方形.∴AD ＝AB ＝9.∠BAD ＝90°.//AD BC .∴∠ADB ＝∠ABD ＝45°.∵MN ⊥BC .//AD BC .∴∠GMD ＝∠GMA ＝∠GNB ＝90°.又∵∠BAD ＝90°.∴四边形ABNM 为矩形.∴BN ＝AM .MN ＝AB ＝9.∵∠GMD ＝90°.∠ADB ＝45°.∴∠MGD ＝∠MDG ＝45°.∴设MG ＝MD ＝x .则BN ＝AM ＝AD －MD ＝9－x .GN ＝MN －MG ＝9－x .∴AM ＝GN .∵四边形AEFG 为正方形.∴AE ＝AG .∠EAG ＝∠AGF ＝90°.∴∠EAG ＝∠DAB .∴∠EAB ＋∠BAG ＝∠DAG ＋∠BAG .∴∠EAB ＝∠DAG .在△ABE 和△ADG 中.AB AD BAE DAG AE AG =⎧⎪∠=∠⎨⎪=⎩. ∴BAE ≌DAG （SAS ）.∴1ABE ADG S S S ==△△.BE ＝DG .∵∠AGF ＝∠GMA ＝90°.∴∠AGM ＋∠FGN ＝∠AGM ＋∠GAM ＝90°.∴∠FGN ＝∠GAM .在△FGN 和△GAM 中.FGN GAM GN AMGNF AMG ∠=∠⎧⎪=⎨⎪∠=∠⎩. ∴△FGN ≌△GAM （ASA ）.∴FN ＝GM ＝x .∴BF ＝BN －FN ＝9－x －x ＝9－2x .∵1223S S =. ∴112322AD MG BF GN ⨯⋅=⨯⋅.∴11293(92)(9)22x x x ⨯⨯=⨯--.解得：13x =.213.5x =（不符合题意.舍去）.∴MG ＝MD ＝3.∴DG ＝2232MG MD +=.∴BE ＝DG ＝32.故选：D ．4．（2021·陕西·西安市汇文中学九年级开学考试）如图.在中.90BAC ∠=︒.6AB =.8AC =.P 为边BC 上一动点.PE AB ⊥于E .PF AC ⊥于F .M 为EF 的中点.则PM 的最小值为（）A ．2.4B ．2.5C ．4.8D ．5【答案】A 【解析】解：连结AP .如图所示：∵∠BAC =90°.AB =6.AC =8.∴BC 226810+==5.∵PE ⊥AB .PF ⊥AC .90BAC ∠=︒∴四边形AFPE 是矩形.∴EF =AP ．∵M 是EF 的中点.∴PM =12AP .根据直线外一点到直线上任一点的距离.垂线段最短.即AP ⊥BC 时.AP 最短.同样PM 也最短. ∴当AP ⊥BC 时.AP =6810⨯=4.8. ∴AP 最短时.AP =4.8.∴当PM 最短时.PM =12AP =2.4．故选A ．5．如图所示.在Rt ABC 中.90ABC ∠=︒.3,4AB BC ==.在Rt ABC 中.90MPN ∠=︒.点P 在AC 上.PM 交AB 于点E .PN 交BC 于点F ．当2PE PF =时.AP 的值为（）．A ．1B ．2C ．3D ．4【答案】C 【解析】解：∵在Rt ABC 中.90ABC ∠=︒.3,4AB BC ==.∴AC 2222345AB BC ++=.过P 作PH ⊥BC 于H .PQ ⊥AB 于Q .则∠PQB =∠PHB =∠B =90°.∴四边形PQBH 是矩形.∴PH=BQ .∠QPH =90°=∠MPN .PQ ∥BC .∴∠EPH +∠QPE =∠EPH +∠HPF =90°.∴∠QPE =∠HPF .∴△PQE ∽△PHF .∴PQ PE PH PF =.又PE =2PF . ∴PQ =2PH =2BQ .∵PQ ∥BC .∴△AQP ∽△ABC .∴AQ PQ AP AB BC AC==. 设BQ =x .则AQ =3﹣x .PQ =2x .∴32345x x AP -==. 解得：65x =.AP =3. 故选：C ．6．（2021·黑龙江牡丹江·模拟预测）如图.矩形ABCD 的边CD 上有一点E .∠DAE ＝22.5°.EF ⊥AB .垂足为F .将△AEF 绕着点F 顺时针旋转.使得点A 的对应点M 落在EF 上.点E 恰好落在点B 处.连接BE ．下列结论：①BM ⊥AE .②四边形EFBC 是正方形.③∠EBM ＝30°.④():221:1BFM BCEM S S =+四边形．其中结论正确的序号是（）A ．①②B ．①②③C ．①②④D ．③④【答案】C 【解析】解：如图.延长BM 交AE 于N .连接AM .∵EF ⊥AB .∴∠AFE ＝∠EFB ＝90°.∵∠DAE ＝22.5°.∴∠EAF ＝90°－∠DAE ＝67.5°.∵将△AEF 绕着点F 顺时针旋转得△MFB .∴MF ＝AF .FB ＝FE .∠FBM ＝∠AEF ＝∠DAE ＝22.5°.∴∠EAF ＋∠FBM ＝90°.∴∠ANB ＝90°.∴BM ⊥AE .故①正确.∵四边形ABCD 是矩形.∴∠ABC ＝∠C ＝90°.∵∠EFB ＝90°.∴四边形EFBC 是矩形.又∵EF ＝BF .∴矩形EFBC 是正方形.故②正确.∴∠EBF ＝45°.∴4522.522.5EBM EBF FBM ∠=∠-∠=︒-︒=︒.故③错误.∵∠AFM ＝90°.AF ＝FM .∴∠MAF ＝45°.2AM FM .∴67.54522.5EAM ∠=︒-︒=︒.∴AEM MAE ∠=∠. ∴2EM AM FM ==. ∴)21EF EM FM FM =+=. ∴()21EFB BFM S S =：:1. 又∵四边形BCEF 是正方形.∴S 四边形BCEF ＝2S △EFB .∴():21:1BFM BCEM S S =+△四边形故④正确. ∴正确的是：①②④.故选：C ．7．已知点A 是抛物线y ＝ax －4ax ＋4a ＋3（a ＞0）的图象上的一点（1）当a ＝2时.该抛物线的顶点坐标为___________.（2）过点A 作AC ⊥x 轴于点C .以AC 为斜边作Rt △ABC 和Rt △DAC .使得BC ∥AD .则BD 的最小值为___________【答案】（2.3） 3【解析】解：（1）当2a =时.22811y x x =-+=22(2)3x -+.∴抛物线的顶点坐标为：（2.3）.（2）∵ABC 和DAC △都为直角三角形.∵BC AD ∥.∴四边形ABCD 为矩形.∴对角线BD AC =.即AC 最短时.BD 最短.∵0a >.224164(43)120b ac a a a a ∆=-=-+=-<.∴抛物线开口向上.抛物线与x 轴没有交点.最低点为顶点.当0y =时.24430ax ax a -++=.即2(2)4430a a a a --++=得2(2)30a x -+=.∴无论a 为任何数.顶点坐标都为（2.3）.∴当AC 最短时.即为顶点到x 轴得距离.即为3.∴BD 最小值为3．8．（2021·山西太原·九年级期中）如图.在平行四边形ABCD 中.对角线AC 与BD 相交于点O .△ABO 是等边三角形.BC ＝8．AE 平分∠BAD 交BC 于点E .连接OE ．请从A .B 两题中任选一题作答（1）线段AE 的长等于_______．（2）线段OE 的长等于________．【答案】863 46423-## 【解析】解：∵四边形ABCD 是平行四边形.∴OA =OC .OB =OD .∵△ABO 是等边三角形.∴OA =OB .∠ABO =∠BAO =60°.∴OA =OC =OB =OD .即AC =BD .∴平行四边形ABCD 是矩形.在Rt △ACB 中.∠ACB =30°.BC =8．∴AC =2AB .222AB BC AC +=,∴()22282AB AB +=,∴AB =833. （1）∵AE 平分∠BAD 交BC 于点E .∴∠BAE =45°.∴△ABE 是等腰直角三角形.∴AE =22863AB BE +=. 故答案为：863. （2）过点E 作FF ⊥OC 于点F .∵△ABO 是等边三角形.∴AB =OB 83.∠ABO =∠BAO =60°.∠OBC =∠OCB =30°. ∴∠BOE =280013︒-︒=75°. ∴∠EOF =180°-60°-75°=45°.∴△OEF 是等腰直角三角形.∴OF =EF .∵△ABE 是等腰直角三角形.∴AB=BE=833.∴EC=BC-BE=8383 -.在Rt△CEF中.∠ECF=30°.∴EF=12EC=4343．∴OE=2EF=46423-．故答案为：46 423-．9．（2021·辽宁·沈阳市实验学校九年级期中）如图.矩形ABCD中.对角线AC、BD相交于点O.过点O作OE⊥BD交AD于点E．已知AB＝2.△DOE的面积为54.则AE的长为 ___．【答案】1.5【解析】解：如图所示.由题可得.OE为对角线BD的垂直平分线.∴BE DE=.54BOE DOES S==.∴522 BDE BOES S==.∴15 22 DE AB=.又∵2AB=.∴52 DE=.∴52BE =. 在Rt ABE △中.22 1.5AE BE AB =-=.故答案是：1.5．10．如图.正方形ABCD 中.点E 是对角线BD 上一点.且BE ＝2DE .连接AE 并延长交CD 于G .点F 是BC 边上一点.且CF ＝2BF .连接AF 、EF 、FG ．下列四个结论：①DG ＝CG .②AF ＝AG .③S △ABF ＝S △FCG .④AE ＝EF ．其中正确的结论是 ___．（写出所有正确结论的序号）【答案】①③④【解析】解：正方形,ABCD//,,AB CD AB CD ∴=而2,BE DE =1,2DG DE EG AB BE AE∴=== 11,22DG AB CD ∴== ,DG CG ∴= 故①正确.如图.设BF =m .而CF ＝2BF .则CF =2m .AB =AD =3m .DG =CG =32m .在Rt △ABF 中. 2210,AF AB BF m =+=而2235,2AG AD DG m =+= ,AF AG ∴≠ 故②错误.过点E 作AB 的平行线.交AD 于M .交BC 于N . 可得四边形MNCD 是矩形.△AME ∽△ADG . 2,3AM AE AD AG ∴== ∵AD =3m . ∴AM =2m .DM =m .NC =m . 则BN =BC -NC =2m .FN =BN -BF =m .∵MD ∥BN .∴△MDE ∽NBE . 且相似比12.∴ME =m .EN =2m .在Rt △EFN 中. EF = 225,EN FN m +=在Rt △AME 中. 225,AE AM AE m =+=,AE EF ∴= 故④正确. 2211311333,2,2222222ABF FCG SAB BF m m m S FC CG m m m ==⨯⨯===⨯= ,ABF FCG S S ∴= 故③正确.综上：正确的有：①③④故答案为：①③④11．（2021·四川内江·中考真题）如图.矩形ABCD 中.6AB =.8BC =.对角线BD 的垂直平分线EF 交AD 于点E 、交BC 于点F .则线段EF 的长为 __．【答案】152【解析】解：如图：四边形ABCD 是矩形.90A ∴∠=︒.又6AB =.8AD BC ==.2210BD AB AD ∴=+=.EF 是BD 的垂直平分线.5OB OD ∴==.90BOF ∠=︒.又90C ∠=︒.BOF BCD ∴∆∆∽.∴OF BO CD BC =. ∴568=OF . 解得.154OF =. 四边形ABCD 是矩形.//AD BC ∴.90A ∠=︒.EDO FBO ∴∠=∠.EF 是BD 的垂直平分线.BO DO ∴=.EF BD ⊥.在DEO ∆和BFO ∆中.EDO FBO BO DOEOD FOB ∠=∠⎧⎪=⎨⎪∠=∠⎩. ()DEO BFO ASA ∴∆≅∆.OE OF ∴=.1522EF OF ∴==．故答案为：152． 12．（2021·辽宁于洪·九年级期中）如图.在矩形ABCD 中.E 为C 边上一点.把△ADE 沿AE 翻折.使点D 恰好落在BC 边上的点F 处．若AB ＝8.BC ＝10.则EC ＝___.P .Q 分别是AE .AD 上的动点.PD ＋PQ 的最小值＝___．【答案】3 8【解析】解：∵四边形ABCD 是矩形.∴AB=CD=8.AD=BC=10.∠C=∠B=90°.设EC=x.则EF=ED=8-x.∵由翻折可知AF=AD=10.∴2222BF AF AB=-=-=.1086,∴CF=BC-BF=10-6=4.∵在Rt△EFC中.EF2=EC2+CF2.∴（8-x）2=x2+42.解得.x=3.∴EC的长为3.如图.作FQ′⊥AD于点Q′.交AE于点P′.连结DP′.连结QF.交AE于点P.连结DF、DP.由翻折得.AE垂直平分DF.∴PD=PF.P′D=P′F.∴PD+PQ=PF+PQ=QF.P′D+P′Q′=P′F+P′Q′=Q′F.由“两点之间.线段最短”可知.线段QF的长即表示PD+PQ的最小值.由“垂线段最短”可知.当点Q与点Q′重合时.QF=Q′F.此时QF的值最小.PD+PQ的最小值.∵∠FQ′A=∠Q′AB=∠B=90°.∴四边形ABFQ′是矩形.∴Q′F=AB=8.∴PD+PQ的最小值是8．故答案为：3.8．13．如图.平行四边形ABCD的对角线AC、BD交于点O.分别过点C、D作CF∥BD.DF∥AC.连接BF交AC于点E．（1）求证：△FCE≌△BOE.（2）当△ADC 满足什么条件时.四边形OCFD 为菱形？请说明理由．【答案】（1）见解析.（2）当△ADC 满足∠ADC =90°时.四边形OCFD 为菱形．【解析】（1）证明：∵CF ∥BD .DF ∥AC .∴四边形OCFD 是平行四边形.∠OBE =∠CFE .∴OD =CF .∵四边形ABCD 是平行四边形.∴OB =OD .∴OB =CF .在△FCE 和△BOE 中.OBE CFE BEO FEC OB CF ∠=∠⎧⎪∠=∠⎨⎪=⎩. ∴△FCE ≌△BOE （AAS ）.（2）解：当△ADC 满足∠ADC =90°时.四边形OCFD 为菱形.理由如下：∵∠ADC =90°.四边形ABCD 是平行四边形.∴四边形ABCD 是矩形.∴OA =OC .OB =OD .AC =BD .∴OC =OD .∴四边形OCFD 为菱形．14．如图.在矩形ABCD 中.点O 为对角线AC 的中点.过点O 作EF AC ⊥ 交BC 于点E .交AD 于点F .连接AE .CF ．（1）求证：四边形AECF是菱形.（2）连接OB.若4AB=.5AF=.求OB的长．【答案】（1）见解析.（2）25【解析】证明：（1）∵O是AC的中点.且EF⊥AC. ∴AF=CF.AE=CE.OA=OC.∵四边形ABCD是矩形.∴AD∥BC.∴∠AFO=∠CEO.在△AOF和△COE中.AFO CEOAOF COEOA OC∠=∠⎧⎪∠=∠⎨⎪=⎩.∴△AOF≌△COE（AAS）.∴AF＝CE.∴AF＝CF＝CE＝AE.∴四边形AECF是菱形.（2）如图.连接BO.∵AB＝4.AF＝AE＝EC＝5.∴BE2225163AE AB--.∴BC＝8.∴AC22166445AB BC++=∵AO＝CO.∠ABC＝90°.∴BO＝12AC＝515．（2021·辽宁凌海·九年级期中）如图.在平行四边形ABCD中.对角线AC、BD相交于点O.以AC为斜边的等腰直角三角形AEC的边CE与AD交于点F.连接OE.使得OE OD．在AD上截取AH CD=.连接EH、ED．（1）判断四边形ABCD的形状.并说明理由. （2）若2AB=.6BC=.求EH的长．【答案】（1）矩形.理由见解析.（2）22【解析】解：（1）四边形ABCD是矩形.理由如下：∵四边形ABCD是平行四边形.∴OA=OC=12AC.OB=OD=12BD.∵△AEC是等腰直角三角形.∴OE⊥AC.OE=12AC=OA.∵OE=OD.∴OA=OD.∴AC=BD.∴平行四边形ABCD是矩形.（2）∵平行四边形ABCD是矩形. ∴AD=BC=6.∠ADC=90°.CD=AB=2. ∵AH=CD.∴AH=2.∴DH=AD－AH=4.∵∠AEC=∠ADC=90°.∴∠DCF＋∠DFC=∠EAF＋∠AFE=90°∵∠AFE=∠DFC.∴∠DCF=∠EAF.∴△AEH≌△CED（SAS）.∴EH=ED.∠AEH=∠DEC.∵∠AEH＋∠HEC=∠AEC=90°. ∴∠CED＋∠HEC=∠HED=90°. ∴EH2＋ED2=DH2.∴2EH2=DH2.∴EH=22DH=22×4=22．16．（2021·福建永安·九年级期中）如图.平行四边形ABCD的对角线AC、BD相交于点O.过点A作AF⊥CD.垂足为F.延长DC到点E.使CE＝DF.连接BE．（1）求证：四边形ABEF是矩形.（2）若AB＝5.CF＝2.AC⊥BD.连接OE.求OE的长．【答案】（1）证明见详解.（2）25【解析】（1）证明：∵在平行四边形ABCD中.∴AB∥CD且AB=CD,∵CD=DF+FC,EF=CE+FC.又∵CE=DF.∴CD=EF=AB,∴AB∥EF,AB=EF,∴四边形AFEB是平行四边形.又∵AF⊥CD.∴AFEB平行四边形是矩形.（2）解：在ABCD平行四边形中.∵AC⊥BD.∴ABCD平行四边形是菱形.∴AD=AB.BO=DO.∵AB=5.CF=2,AB=CD,∴DF=5-2=3=CE,∴DE=DC+CE=5+3=8.在Rt ADF中由勾股定理可得：2222534 AF AD DF=-=-=. ∴BE=AF=4.∴BD=224845=+.∴1252OE BD．17．（2021·福建永安·九年级期中）如图.点F在四边形ABCD的边AB上.（1）如图①.当四边形ABCD是正方形时.过点B作BE⊥CF.垂足为O.交AD于点E．求证：BE＝CF.（2）当四边形ABCD是矩形.AD＝6.AB＝8时.①如图②.点P是BC上的一点.过点P作PE⊥CF.垂足为O.点O恰好落在对角线BD上.求OCOE的值.②如图③.点P是BC上的一点.过点P作PE⊥CF.垂足为O.点O恰好落在对角线BD上.延长EP、AB交于点G.当BG＝2时.DE＝．【答案】（1）见解析.（2）①34.②83【解析】证明：（1）在正方形ABCD中. ∠A=∠ABC=90°.AB=CB.∴∠FBO+∠OBC=90°.∵BE⊥CF.∴∠BOC=90°.∴∠BCO+∠OBC=90°.∴∠FBO=∠BCO.∴△ABE≌△BCF（ASA）.∴BE=CF.（2）①如图.过点O作MN∥AB交AD、BC于点M、N.在矩形ABCD中.AB∥CD.AD∥BC.∠ABC=90°.∴MN∥CD.∴四边形ABNM和DMNC为矩形.∴MN=AB=8.设ON=a.BN=b.则OM=8-a.DM=CN=6-b.∵△DOM∽△BON.∴DM OMBN ON= .即68b ab a--= .解得：34ba.∴6384b ba a-==-.∵PE⊥CF.∴∠EOM+∠CON=90°. ∵∠OCN+∠CON=90°. ∴∠OCN=∠EOM.∴△EOM∽△OCN.∴OC CNOE OM= .∴即6384 OC bOE a-==-.②在矩形ABCD中.AB∥CD .AD∥BC.∠ABC=90°∴COD FOB.DOE BOP.∴OD CD OB BF =.OD DE OB BP =. ∴CD DE BF BP =. ∴DE BP CD BF=. ∵∠ABC =90°.∴∠BFC +∠BCF =90°∵CF PE ⊥ .∴∠FOG =90°.∴∠G +∠BFC =90°.∴∠G =∠BCF .∵∠PBG =∠CBF =90°.∴△PBG ∽△FBC .∴2163BP BG BF BC ===. ∴13DE CD =. ∴1833DE CD ==． 18．（2021·上海市徐汇中学九年级期中）如图.矩形ABCD 中.AB =4.点E 是边AD 的中点.点F 是对角线BD 上一动点.∠ADB =30°.连结EF .作点D 关于直线．．EF 的对称点P .（1）若EF ⊥BD .求DF 的长;（2）若PE ⊥BD .求DF 的长;（3）直线PE 交BD 于点Q .若△DEQ 是锐角三角形.请直接写出DF 长的取值范围.【答案】（1）3.（2）2或6.（3）263DF <<-或68DF <．【解析】解：（1）如图1.矩形ABCD 中.90BAD ∴∠=︒.30ADB ∠=︒.4AB =. 43AD ∴=.点E 是AD 中点.∴23DE =.EF BD ⊥.∴△EFD 为直角三角形. ∵23DE =.30ADB ∠=︒ ∴3cos 2DF ADB DE ∠== 3DF ∴=．（2）第一种情况.如图2.则60PED ∠=︒.由对称性可得.EF 平分PED ∠.30DEF ∴∠=︒.30DEF EDF ∴∠=∠=︒∴是等腰三角形.过点F 作FM ⊥EDDM =EM =132DE ∵在Rt △DMF 中.3DM =30ADB ∠=︒∴2DF =第二种情况.如图3.延长PE 交BD 于M∵PE BD ⊥∴∠EMD =90°∵30ADB ∠=︒∴60DEM ∠=︒∴120PED ∠=︒.∵点D 关于直线EF 的对称点P∴FE 垂直平分PD 交PD 于H∴∠HED =60°.∠HDE =30°∴∠HDF =60°∴∠EFD =30° ∴是等腰三角形.∴FE 垂直平分DF∵在Rt △DME 中.23DE =.30ADB ∠=︒∴3DM =∵26DF DM ==．∴6DF =．综上：DF 的长为2或6（3）∵是锐角三角形∴当PE ⊥BD 时DF 最小.当PE ⊥AD 时.DF 最大由（2）可得当90DQE ∠=︒时.2DF =（如图2）或6（如图3）．当90DEQ ∠=°时.第①种情况.如图4.EF 平分PED ∠.45DEF ∠=︒.过点F 作FM AD ⊥于点M .设EM a =.则FM a =.3DM a =.323a a ∴+=.33a ∴=-.623DF =-.2623DF ∴<<-．第②种情况.如图5.EF 平分AEQ ∠.45MEF ∠=︒.过点F 作FM AD ⊥于点M .设EM a =.则FM a =.3DM a =.33a a -=33a ∴=623DF =+6238+>.DF 最大值为8.68DF ∴<．综上：2623DF <<-68DF <．题型三菱形的判定与性质1．如图.菱形ABCD 的边长是5.两对角线交于点O .且AO 、BO 的长分别是关于x 的方程x 2+（2m +1）x +m 2﹣4＝0的两根.则m 为（）A ．﹣4B ．2C ．2或﹣4D ．﹣2或4【答案】A 【解析】解：设OA ＝α.OB ＝β.则α+β＝﹣（2m +1）＞0.即12m <-,αβ＝m 2﹣4. Δ＝（2m +1）2﹣4（m 2﹣4）≥0.解得m ≥﹣174. ∴m 的范围为m ≥﹣174. ∵四边形ABCD 是菱形.∴AC ⊥BD .在Rt △AOB 中：OA 2+OB 2＝AB 2.即α2+β2＝52.∴（α+β）2﹣2αβ＝25.∴[﹣（2m +1）]2﹣2（m 2﹣4）＝2m 2+4m ﹣16＝0.（m +4）（m ﹣2）＝0.解得m 1＝﹣4.m 2＝2(舍去).∴m 的值为﹣4.故选：A ．2．如图.在▱ABCD 中.AB ＝BC ＝5．对角线BD ＝8.则▱ABCD 的面积为（）A ．20B ．24C ．40D ．48【答案】B 【解析】解：如图所示.连接AC 交BD 于O .在ABCD 中.5AB BC ==.∴四边形ABCD 是菱形.AC BD ∴⊥. 又对角线8BD =.4BO ∴=.在Rt △AOB 中.2222543AO AB BO =-=-=.26AC AO .∴菱形ABCD 的面积为11862422BD AC ⨯=⨯⨯=．故选：B ．3．（2021·四川雅安·九年级期末）如图.在平行四边形ABCD 中.对角线AC 的垂直平分线分别与AD .AC .BC 相交于点E .O .F ．下列结论正确的个数有（）①四边形AFCE 为菱形.②△ABF ≌△CDE .③当F 为BC 中点时.∠ACD ＝90°．A ．0个B ．1个C ．2个D ．3个【答案】D 【解析】解：∵四边形ABCD 为平行四边形.∴AD //BC .AD ＝BC .AB ＝CD .∠B ＝∠D .AB //CD .∴∠EAC ＝∠FCA .∵EF 垂直平分AC .∴OA ＝OC .EA ＝EC .∴∠EAC ＝∠ECA .∴∠FCA ＝∠ECA .在△AOE 和△COF 中.EAO FCO OA OCAOE COF ∠=∠⎧⎪=⎨⎪∠=∠⎩.。

九年级数学中考专题(空间与图形)-第十讲《四边形(二)》课件(北师大版)

B
E
参考答案
一、填空题： 1、180；2、20cm；3、3；4、；5、200 提示：4题过点P作矩形任一边的垂线，利用勾股定理求解； 5题连结AC，证△ABE≌△ACF得AE＝AF，从而△AEF 是等边三角形. 6、 2 1 ；7、2 1 ；8、②
参考答案
二、DDBBA 三、解答题： 14、可证△DEA≌△ABF 15、略证：AE平分∠BAC，且EG⊥AB， EC⊥AC，故EG＝EC，易得∠AEC＝∠CEF， ∵CF＝EC，EG＝CF，又因EG⊥AB，CD⊥AB，故EG∥CF.四边形GECF是平行四边形，又因EG ＝FG，故GECF是菱形.
A
D G B E F C
能力训练
16、如图，以△ABC的三边为边在BC的同一侧分别作三个等边三角形，即△ABD、△BCE、△ACF.请回答下列问题（不要求证明）：（1）四边形ADEF是什么四边形？（2）当△ABC满足什么条件时，四边形ADEF是矩形？（3）当△ABC满足什么条件时，以A、D、E、F为顶点的四边形不存在？ E F D
第十讲四边形（二）
复习目标
1．复习矩形、菱形、正方形的判定与性质. 2．复习运用矩形、菱形、正方形的判定和性质解决相关的证明和计算问题.
知识要点
1．矩形的四个角都是直角，对角线相等；菱形的四条边相等，对角线互相垂直平分. 2. 三个角是直角的四边形，或对角线相等的平行四边形是矩形;四边相等的四边形，或对角线互相垂直的平行四边形是菱形. 3. 是矩形又是菱形的四边形是正方形.正方形既具有矩形的性质又具有菱形的性质.
典型例题
例1 如图，已知矩形ABCD中，对角线AC、BD 相交于点O，AE⊥BD，垂足为E， ∠DAE∶∠BAE＝3∶1，求∠EAC的度数. 分析：本题充分利用矩形对角线把矩形分成四个等腰三角形的基本图形进行求解. 答案：45° A D

新版初三总复习四边形专题复习-新版.pdf

中考四边形专题【知识要点】一一般四边形1．四边形的内角和与外角和定理：（1）四边形的内角和等于360°；（2）四边形的外角和等于360°.2．多边形的内角和与外角和定理：（1）n 边形的内角和等于(n -2)180°；（2）任意多边形的外角和等于360°.3．若n 是多边形的边数，则对角线条数公式是：2)3n(n .二平行四边形的判定与性质1. 平行四边形定义：两组对边分别平行的四边形叫做平行四边形。

2. 平行四边形是中心对称图形，对称中心是两条对角线的交点。

3．平行四边形的性质：因为ABCD 是平行四边形.54321）邻角互补（）对角线互相平分；（）两组对角分别相等；（）两组对边分别相等；（）两组对边分别平行；（4.平行四边形的判定：是平行四边形）对角线互相平分（）一组对边平行且相等（）两组对角分别相等（）两组对边分别相等（）两组对边分别平行（ABCD 54321.三矩形的判定与性质1. 矩形定义1：有一个角是直角的平行四边形叫做矩形2. 矩形定义2：有三个角是直角的四边形叫做矩形3. 矩形既是中心对称图形又是轴对称图形，对称中心是两条对角线的交点，对称轴是各边的垂直平分线。

4.矩形的性质：因为ABCD 是矩形.3;2;1）对角线相等（）四个角都是直角（有通性）具有平行四边形的所（5. 矩形的判定：边形）对角线相等的平行四（）三个角都是直角（一个直角）平行四边形（321四边形ABCD 是矩形.四菱形的判定与性质1. 菱形定义1：有一组邻边相等的平行四边形叫做菱形.2. 菱形定义2：四条边都相等的四边形叫做菱形。

3. 菱形既是中心对称图形又是轴对称图形，对称中心是两条对角线的交点，对称轴是对角线所在的直线。

4．菱形的性质：因为ABCD 是菱形A BCD 1234AB CDABDOCABD OCADBCADBCOCDBAO.321角）对角线垂直且平分对（）四个边都相等；（有通性；）具有平行四边形的所（5．菱形的判定：边形）对角线垂直的平行四（）四个边都相等（一组邻边等）平行四边形（321四边形四边形ABCD 是菱形.五正方形的判定与性质1. 正方形定义1：有一组邻边相等的矩形叫做正方形。

2020年九年级数学中考复习：四边形专题复习教案

2020年九年级数学中考复习：四边形专题复习教案一、教学目标通过本教案的学习，学生将能够：1.了解四边形的定义和性质；2.掌握四边形的分类和特征；3.理解四边形的面积和周长的计算方法；4.能够解决与四边形相关的问题。

二、知识概述四边形是指由四条线段组成的封闭图形。

常见的四边形包括矩形、正方形、平行四边形和菱形等。

在九年级数学中，掌握四边形的定义、分类和性质是非常重要的，同时还需要熟练掌握四边形的面积和周长的计算方法。

2.1 四边形的定义和性质四边形是由四条线段构成的封闭图形，它有以下性质：•四边形的内角和等于360°；•对角线互相垂直的四边形是矩形；•有一对对边相等且互相平行的四边形是平行四边形；•有4个边长相等的四边形是正方形；•有一对对边相等且对角线互相垂直的四边形是菱形。

2.2 四边形的分类和特征根据边长和角度的特征，四边形可以分为以下几类：•矩形：具有四个内角都是直角的四边形；•正方形：具有四个边长相等且四个内角都是直角的四边形；•平行四边形：具有相对的两边平行的四边形；•菱形：具有四个边长相等且对角线互相垂直的四边形。

2.3 四边形的面积和周长的计算方法•矩形的面积等于长乘以宽；•正方形的面积等于边长的平方；•平行四边形的面积等于底边乘以高；•菱形的面积等于对角线的乘积的一半。

四边形的周长等于各边长的和。

三、教学重点与难点3.1 教学重点•四边形的定义和性质；•四边形的分类和特征；•四边形的面积和周长的计算方法。

3.2 教学难点•理解和应用四边形的性质；•熟练计算不同类型四边形的面积和周长。

4.1 导入与导入教师通过原生实例或者图片，引入四边形的概念，让学生了解四边形的定义。

4.2 教学内容4.2.1 四边形的定义和性质1.讲解四边形的定义和性质，介绍四边形的内角和等于360°的性质；2.分类介绍矩形、正方形、平行四边形和菱形的特征和性质。

4.2.2 四边形的面积和周长的计算方法1.讲解不同类型四边形的面积计算方法：矩形、正方形、平行四边形和菱形；2.讲解四边形的周长计算方法。

2024年中考第一轮复习特殊平行四边形2

在 Rt△ AFE 中,EF= 2 + 2 =2 15.
3.[2019·上海]如图25-7,在正方形ABCD中,E是边AD的中点.将△ABE沿直线BE
翻折,点A落在点F处,连结DF,那么∠EDF的正切值是
图25-7
.
[答案]2
1
[解析] 如图所示,由折叠可得 AE=FE,∠AEB=∠FEB= ∠AEF,
■ 知识梳理
1.定义:顺次连结四边形各边中点所得的四边形称为中点四边形.
2.任意四边形的中点四边形是① 平行四边形 .
对角线相等的四边形的中点四边形是② 菱形
.
对角线垂直的四边形的中点四边形是③ 矩形
.
对角线互相垂直且相等的四边形的中点四边形是④ 正方形 .
考向一
中点四边形
例1 如图25-4,D,E分别是不等边三角形ABC(即AB≠BC≠AC)的边AB,AC的中点
1
2
∵AC=BD=8,AE=CF=2,∴OD=4,OE=OF= (8-2-2)=2.
由勾股定理,得 DE= 2 + 2 = 42 + 22 =2 5,
∴四边形 BEDF 的周长=4DE=4×2 5=8 5.
■ 知识梳理
图25-2
考点二
中点四边形
4.顺次连结任意四边形各边的中点,所得的四边形一定是
,O是△ABC所在平面上的动点,连结OA,OB,OC,点G,F分别是OB,OC的中点,顺
次连结点D,G,F,E.
(1)当点O在△ABC的内部时,求证:四边形DGFE是平行四边形;
解:(1)证明:∵D,E 分别是 AB,AC 的中点,
1
∴DE∥BC,且 DE=2BC.
1
同理,GF∥BC,且 GF=2BC,

中考数学考点系统复习第五章四边形第二节矩形、菱形、正方形

∵OB＝OD，EF∥AD，∴AE＝BE＝4， ∵FG⊥BE，∴EG＝BG＝2，
在 Rt△BGF 中，BF＝4，BG＝2，根据勾股定理得，FG＝ 42－22＝2 3，
在 Rt△AGF 中，AG＝6， AF＝ AG2＋FG2＝ 62＋（2 3）2＝4 3. ∴AF 的长为 4 3.
15．(2020·德州)如图，在▱ABCD 中，对角线 BD⊥AD，AB＝10，AD＝6，
的面积是 1，则 AB 的长为
( C)
A．1
B. 2
C．2
D．2 2
18．(2021·阜新)如图，折叠矩形纸片 ABCD，使点 B 的对应点 E 落在 CD
边上，GH 为折痕，已知 AB＝6，BC＝10.当折痕 GH 最长时，线段 BH 的长
为 6. ． 8
19．(2021·呼和浩特)如图，四边形 ABCD 是平行四边形，BE∥DF，且分别交对角线 AC 于点 E，F. (1)求证： △ABE≌△CDF； (2)当四边形 ABCD 分别是矩形和菱形时，请分别说出四边形 BEDF 的形状．(无需说明理由)
坐标是 O(0，0)，点 B 的坐标是(0，1)，且 BC＝ 5，则点 A 的坐标是 ((22，，0)． 0)
11.(2021·中山区模拟)如图，正方形 ABCD 的边长为 4，点 E 在对角线 BD 上，且 DE＝DA，EF⊥AB，垂足为 F，则 EF 的长为 44－－22 2 .
12.(2020·遂宁)如图，在△ABC 中，AB＝AC，点 D，E 分别是线段 BC， AD 的中点，过点 A 作 BC 的平行线交 BE 的延长线于点 F，连接 CF. (1)求证：△BDE≌△FAE； (2)求证：四边形 ADCF 为矩形．
∵AB＝AC，∴AD⊥BC， ∴∠ADC＝90°，∴四边形 ADCF 为矩形．