第三章一元一次方程知识点梳理及典型例题牛园园
人教版七年级数学上册—第3章一元一次方程单元总结

第三章 一元一次方程知识点一 :一元一次方程的概念1.方程的定义:含有未知数的等式.①未知数;②等式. 2.一元一次方程的定义:只.含有一个..未知数(元),未知数的最高次数是.....1.,等号两边都是整式的方程叫一元一次方程. 一元一次方程的一般形式....:ax+b=0(a 、b 为常数,且a≠0,即末知数的系数一定不能为0). 3.方程的解:使方程等号左、右两边相等的未知数的值. 4.解方程:求方程的解的过程. 例题:1. (1)下列方程中是一元一次方程的是( )A .23x y =B .()7561x x +=-C .()21112x x +-= D .12x x-= (2)下列各式中,是一元一次方程的是( )A. 6x y -=B. 1223x x --= C. 34x - D. 21x x += 2.(1)已知2x1-m +4=0是一元一次方程,则m= ________.(2)已知方程04)2(1||=+--a xa 是一元一次方程,则=a __________(3)若2(21)30a x bx c +--=是关于x 的一元一次方程,则一定有( )A. 12a =-,0b ≠,c 为任意数 B. 12a =-,b 、c 为任意数 C. 12a =-,0,0b c ≠= D. 12a =,0,0bc =≠(4)若2(1)(1)30k x k x -+++=是关于x 的一元一次方程,求k 的值3.下列说法:①等式是方程; ②x=4是方程5x+20=0的解; ③x=-4和x=6都是方程│x-1│=5的解.其中说法 正确的是___ _.(填序号)4.(1)下列方程中,解为4的方程是( )A. 104x x =-B. 5(2)2(27)x x +=+C.62355y y -=+ D. 50.594x x =+ (2)已知4x =-是方程231x a x +=-的解,则a 的值是 5.根据条件列出方程(1)某数的2倍,再减去1等于5 (2)某数的3倍与它的12的和等于106.(1)买4本练习本和5支铅笔一共用了4.9元,已知铅笔每支0.5元,练习本每本多少元?若设练习本每本x 元,则可列方程为(2)一辆汽车从A 地到B 地后,用去了邮箱里的汽油的25%,还剩40升,邮箱里原有汽油多少升?若设邮箱里原有汽油x 升,可列方程为知识点二:等式的基本性质等式的性质1:等式两边都加(或减)同一个数(或式子),结果仍相等.即:如果a =b ,那么a ±c =b ±c等式的性质2:等式两边都乘同一个数,或除以同一个不为0的数,结果仍相等.即:如果a =b ,那么ac =bc ;如果a =b (c ≠0),那么c a =cb 例题:1.(1)若a b =,则下列式子正确的有( )①22a b -=- ②1132a b =③3344a b -=- ④5151a b -=-. A.1个 B.2个 C.3个 D.4个(2)如果ma mb =,那么在下列变形中,不一定成立的是( )A. 11ma mb +=+B. 33ma mb -=-C. 1122ma mb -=- D. a b = (3)下列变形中,正确的是()A.若ac=bc ,那么a=bB.若cbc a =,那么a=b C.a =b ,那么a=b D.若a 2=b 2那么a=b (4)运用等式的性质进行变形,正确的是( )A.如果a b =,那么a c b c +=-;B.如果a bc c=,那么a b = C.如果a b =,那么a bc c= D.如果23a a =,那么3a = 2.(1)给出下面四个方程及其变形:①48020x x +=+=变形为;②x x x +=-=-75342变形为;③253215x x ==变形为;④422x x =-=-变形为;其中变形正确的是( ) A .①③④ B .①②④C .②③④D .①②③(2)下列各式的变形中,错误的是 ( )A. 260x +=变形为26x =-B.312x x +=-变形为322x x +=- C. 2(4)2x --=-变形为41x -= D. 1122x +-=变形为11x -+=3.用适当的数或式子填空,使所得结果仍是等式,并说明是根据等式的哪一条性质以及怎样变形的; (1)如果810x +=,那么10x =- (2)如果437x x =+,那么4x - =7 (3)如果38x -=,那么x = (3)如果123x =-,那么 =-6 4.完成下列解方程: (1)1343x -= 解:两边 ,根据 得13343x --= 于是13x -=两边 ,根据 得x =(2)5234x x -=+解:两边 ,根据 ,得 =3x+6 两边 ,根据 ,得2x=两边 ,根据 ,得x= 5.根据下列变形,填写过程及理由21100.10.2x -= 解:20101012x -=( ) 20510x -= ( )2015x = ( )34x = ( )6.利用等式的性质解下列方程并检验 (1)1262x += (2)1543x --= (3)328x -=-7.当x 为何值时,式子453x -与31x +的和等于9?8.列方程并求解:一个两位数,个位上的数字比十位上的数字大2,个位与十位上的数字之和是10,求这个两位数(提示,设个位上的数字为x )9.如果方程21x a x +=-的解是x=-4,求32a -的值10.等式2(2)10a x ax -++=是关于x 的一元一次方程,求这个方程的解知识点三:一元一次方程的解法(一般步骤、注意事项) 1.解方程的一般步骤:把含未知数的项归在方程的一边,把常数项归到方程的另一边,将方程化为最简的形式ax b =(0)a ≠,然后根据方程两边都除以a ,化为bx a=的形式。
新人教版七年级数学上册第三章《一元一次方程》知识点和题型总结

新人教版七年级数学上册第三章《一元一次方程》应知应会知识点和题型总结一、方程定义【一元一次方程的认识】1.下列各式:①3x+2y=1②m-3=6③x/2+2/3=0.5④x 2+1=2⑤z/3-6=5z ⑥(3x-3)/3=4⑦5/x+2=1⑧x+5中,一元一次方程的个数是( )A.1 B.2 C.3 D.42.下列各式中是一元一次方程的是( )。
A.1232x y -=-B.2341x x x -=-C.1123y y -=+D.1226x x -=+ 3.下列方程①313262-=+x x ②4532x x =+③2(x+1)+3=x1 ④3(2x+5)-2(x-1)=4x+6.一元一次方程共有( )个. A.1 B.2 C.3 D.4【利用定义求参数】4.如果(m-1)x |m| +5=0是一元一次方程,那么m = .【列方程】5.根据“x 的3倍与5的和比x 的13多2”可列方程( )。
A 、3525x x +=- B 、3523x x +=+ C 、3(523x x +=-) D 、3(523x x +=+) 二、方程的解【方程解的应用】1.若x=1是方程k (x-2)=2的解,则k= .2.已知3是关于x 的方程mx+1=0的根,那么m=3.一个一元一次方程的解为2,请写出这个一元一次方程 .4.若关于x 的一元一次方程23132x k x k ---=的解是1x =-,则k 的值是()A .27B .1C .1311- D .0 5.已知方程3x 2x -9x+m=0的一个根是1,则m 的值是 。
6.方程2152x kx x -+=-的解为-1时,k 的值为( )。
A.10 B.-4 C.-6 D.-87.y=1是方程12()23m y y --=的解,求关于x 的方程(4)2(3)m x mx +=+的解。
8.已知x=-1是关于x 的方程328490x x kx -++=的一个解,求23159k k --5的值。
人教版七年级数学上册—第3章一元一次方程单元总结

第三章 一元一次方程知识点一 :一元一次方程的概念1.方程的定义:含有未知数的等式.①未知数;②等式. 2.一元一次方程的定义:只.含有一个..未知数(元),未知数的最高次数是.....1.,等号两边都是整式的方程叫一元一次方程. 一元一次方程的一般形式....:ax+b=0(a 、b 为常数,且a≠0,即末知数的系数一定不能为0). 3.方程的解:使方程等号左、右两边相等的未知数的值. 4.解方程:求方程的解的过程. 例题:1. (1)下列方程中是一元一次方程的是( )A .23x y =B .()7561x x +=-C .()21112x x +-= D .12x x-= (2)下列各式中,是一元一次方程的是( )A. 6x y -=B. 1223x x --= C. 34x - D. 21x x += 2.(1)已知2x1-m +4=0是一元一次方程,则m= ________.(2)已知方程04)2(1||=+--a xa 是一元一次方程,则=a __________(3)若2(21)30a x bx c +--=是关于x 的一元一次方程,则一定有( )A. 12a =-,0b ≠,c 为任意数 B. 12a =-,b 、c 为任意数 C. 12a =-,0,0b c ≠= D. 12a =,0,0bc =≠(4)若2(1)(1)30k x k x -+++=是关于x 的一元一次方程,求k 的值3.下列说法:①等式是方程; ②x=4是方程5x+20=0的解; ③x=-4和x=6都是方程│x-1│=5的解.其中说法 正确的是___ _.(填序号)4.(1)下列方程中,解为4的方程是( )A. 104x x =-B. 5(2)2(27)x x +=+C.62355y y -=+ D. 50.594x x =+ (2)已知4x =-是方程231x a x +=-的解,则a 的值是 5.根据条件列出方程(1)某数的2倍,再减去1等于5 (2)某数的3倍与它的12的和等于106.(1)买4本练习本和5支铅笔一共用了4.9元,已知铅笔每支0.5元,练习本每本多少元?若设练习本每本x 元,则可列方程为(2)一辆汽车从A 地到B 地后,用去了邮箱里的汽油的25%,还剩40升,邮箱里原有汽油多少升?若设邮箱里原有汽油x 升,可列方程为知识点二:等式的基本性质等式的性质1:等式两边都加(或减)同一个数(或式子),结果仍相等.即:如果a =b ,那么a ±c =b ±c等式的性质2:等式两边都乘同一个数,或除以同一个不为0的数,结果仍相等.即:如果a =b ,那么ac =bc ;如果a =b (c ≠0),那么c a =cb 例题:1.(1)若a b =,则下列式子正确的有( )①22a b -=- ②1132a b =③3344a b -=- ④5151a b -=-. A.1个 B.2个 C.3个 D.4个(2)如果ma mb =,那么在下列变形中,不一定成立的是( )A. 11ma mb +=+B. 33ma mb -=-C. 1122ma mb -=- D. a b = (3)下列变形中,正确的是()A.若ac=bc ,那么a=bB.若cbc a =,那么a=b C.a =b ,那么a=b D.若a 2=b 2那么a=b (4)运用等式的性质进行变形,正确的是( )A.如果a b =,那么a c b c +=-;B.如果a bc c=,那么a b = C.如果a b =,那么a bc c= D.如果23a a =,那么3a = 2.(1)给出下面四个方程及其变形:①48020x x +=+=变形为;②x x x +=-=-75342变形为;③253215x x ==变形为;④422x x =-=-变形为;其中变形正确的是( ) A .①③④ B .①②④C .②③④D .①②③(2)下列各式的变形中,错误的是 ( )A. 260x +=变形为26x =-B.312x x +=-变形为322x x +=- C. 2(4)2x --=-变形为41x -= D. 1122x +-=变形为11x -+=3.用适当的数或式子填空,使所得结果仍是等式,并说明是根据等式的哪一条性质以及怎样变形的; (1)如果810x +=,那么10x =- (2)如果437x x =+,那么4x - =7 (3)如果38x -=,那么x = (3)如果123x =-,那么 =-6 4.完成下列解方程: (1)1343x -= 解:两边 ,根据 得13343x --= 于是13x -=两边 ,根据 得x =(2)5234x x -=+解:两边 ,根据 ,得 =3x+6 两边 ,根据 ,得2x=两边 ,根据 ,得x= 5.根据下列变形,填写过程及理由21100.10.2x -= 解:20101012x -=( ) 20510x -= ( )2015x = ( )34x = ( )6.利用等式的性质解下列方程并检验 (1)1262x += (2)1543x --= (3)328x -=-7.当x 为何值时,式子453x -与31x +的和等于9?8.列方程并求解:一个两位数,个位上的数字比十位上的数字大2,个位与十位上的数字之和是10,求这个两位数(提示,设个位上的数字为x )9.如果方程21x a x +=-的解是x=-4,求32a -的值10.等式2(2)10a x ax -++=是关于x 的一元一次方程,求这个方程的解知识点三:一元一次方程的解法(一般步骤、注意事项) 1.解方程的一般步骤:把含未知数的项归在方程的一边,把常数项归到方程的另一边,将方程化为最简的形式ax b =(0)a ≠,然后根据方程两边都除以a ,化为bx a=的形式。
七年级数学上册第三章一元一次方程知识点总结归纳完整版

(名师选题)七年级数学上册第三章一元一次方程知识点总结归纳完整版单选题1、下列图中所示的球、圆柱、正方体的重量分别都相等,三个天平分别都保持平衡,那么第三个天平中,右侧秤盘上所放正方体的个数应为( )A .5B .4C .3D .2答案:A分析:设一个球的质量为a ,一个圆柱体的质量为b ,一个正方体的质量为c ,根据天平平衡的条件可得2a =5b ,2c =3b ,再根据等式的性质得到3a =5c 即可.解:设一个球的质量为a ,一个圆柱体的质量为b ,一个正方体的质量为c ,由题意得,2a =5b ,2c =3b ,即a =52b ,c =32b ,∴3a =152b ,5c =152b , 即3a =5c ,∴右侧秤盘上所放正方体的个数应为5,故选:A .小提示:本题考查认识立体图形、等式的性质,掌握等式的性质是解决问题的前提.2、将连续奇数1,3,5,7,9,…排成如图所示的数表,若将十字形框上下左右移动,可框出另外五个数,则框出的五个数之和可以是( )A.2020B.2022C.2023D.2025答案:D分析:先设中间的数为2x+1(x为整数),进而得到该数上方、下方、左边、右边的数分别为(2x+1)-10、(2x+1)+10、(2x+1)-2、(2x+1)+2,然后求得框出的五个数之和,即可得到答案.解:设中间的数为2x+1(x为整数),则该数上方、下方、左边、右边的数分别为(2x+1)-10、(2x+1)+10、(2x+1)-2、(2x+1)+2,∴框出的五个数之和为(2x+1)+(2x+1)-10+(2x+1)+10+(2x+1)-2+(2x+1)+2=10x+5,∵x为整数,∴10x+5是5的倍数,且个位数字为5,故选:D.小提示:本题考查了代数式的表示,属于数字的变化规律类题型,解题的关键是会用含有未知数的式子表示框出的5个数.3、小明解方程x+12−1=x−23的步骤如下:解:方程两边同乘6,得3(x+1)−1=2(x−2)①去括号,得3x+3−1=2x−2②移项,得3x−2x=−2−3+1③合并同类项,得x=−4④以上解题步骤中,开始出错的一步是()A.①B.②C.③D.④答案:A分析:按照解一元一次方程的一般步骤进行检查,即可得出答案.解:方程两边同乘6,得3(x+1)−6=2(x−2)①∴开始出错的一步是①,故选:A.小提示:本题考查了解一元一次方程,熟练掌握解一元一次方程的一般步骤以及注意事项是解决问题的关键.4、“曹冲称象”是流传很广的故事,如图.按照他的方法:先将象牵到大船上,并在船侧面标记水位,再将象牵出.然后往船上抬入20块等重的条形石,并在船上留3个搬运工,这时水位恰好到达标记位置.如果再抬入1块同样的条形石,船上只留1个搬运工,水位也恰好到达标记位置.已知搬运工体重均为120斤,设每块条形石的重量是x斤,则正确的是()A.依题意3×120=x−120B.依题意20x+3×120=(20+1)x+120C.该象的重量是5040斤D.每块条形石的重量是260斤答案:B分析:利用题意找出等量关系,将等量关系中的量用已知数和未知数的代数式替换即可得出结论.解:根据题意可得方程;20x+3×120=(20+1)x+120则A错误,B正确;解上面的方程得:x=240,故D错误;∴大象的重量是20×240+3×120=5160(斤)故C错误,故选:B.小提示:本题主要考查一元一次方程的应用,根据题意真确列出方程是解题的关键.5、若x=2是关于x的一元一次方程ax−b=3的解,则4a−2b+1的值是()A.7B.8C.−7D.−8答案:A分析:将x=2代入ax-b=3中,得2a-b=3,整体代入代数式即可得到答案.解:将x=2代入ax-b=3中,得2a-b=3,∴4a−2b+1=2(2a-b)+1=2×3+1=7,故选A.小提示:此题考查了方程的解,已知式子的值求代数式的值,正确理解方程的解是解题的关键.6、解一元一次方程的过程就是通过变形,把一元一次方程转化为x=a的形式,下面是解方程2x−0.30.5−x+0.40.3=1的主要过程,方程变形对应的依据错误的是()解:原方程可化为20x−35−10x+43=1(①)去分母,得3(20x−3)−5(10x+4)=15(②)去括号,得60x−9−50x−20=15(③)移项,得60x−50x=15+9+20(④)合并同类项,得10x=44(合并同类项法则)系数化为1,得x=4.4(等式的基本性质2)A.①分数的基本性质B.②等式的基本性质2C.③乘法对加法的分配律D.④加法交换律答案:D分析:方程利用分数的基本性质化简,再利用等式的基本性质2两边乘以15去分母,去括号后利用等式的基本性质1移项,合并后将x系数化为1,即可求出解.解:原方程可化为20x−35−10x+43=1(①)去分母,得3(20x −3)−5(10x +4)=15( ② )去括号,得60x −9−50x −20=15( ③ )移项,得60x −50x =15+9+20(等式的基本性质1 )合并同类项,得10x =44(合并同类项法则)系数化为1,得x =4.4(等式的基本性质2).故选:D .小提示:本题考查了解一元一次方程,熟练掌握运算法则是解本题的关键.7、小明早上8点从家骑车去图书馆,计划在上午11点30分到达图书馆.出发半小时后,小明发现若原速骑行,将迟到10分钟,于是他加速继续骑行,平均每小时多骑行1千米,恰好准时到达,则小明原来的速度是( )A .12千米/小时B .17千米/小时C .18千米/小时D .20千米/小时答案:C分析:设原来的速度是x 千米/小时,则提高速度后为x +1千米/小时,根据出发半小时后,发现按原速行驶要迟到10分钟,将速度每小时增加1千米,恰好准时到达,分别表示路程建立方程求解即可.解:设小明原来的速度是x 千米/小时,则提高速度后为x +1千米/小时,由题意得(3.5+16)x =12x +(x +1)×(3.5−0.5),解得:x =18.答:小明原来的速度是18千米/小时.故选:C小提示:此题考查一元一次方程的实际运用,利用行程问题中的速度、时间、路程之间的等量关系是解决问题的关键.8、有一所寄宿制学校,开学安排宿舍时,如果每间宿舍安排住4人,就会空出5间宿舍;如果每间宿舍安排住3人,就有100人没床位,那么在学校住宿的学生有多少人?设在学校住宿的学生有x 人,根据题意可列方程为( )A .x 4+5=x−1003B .x 4+5=x 3−100C .x+54=x−1003D .x 4−5=x−1003答案:A分析:根据宿舍间数一定即可列出方程.解:根据题意得:x4+5=x−1003故选:A.小提示:本题考查了一元一次方程的实际应用,理解题意,找准等量关系,列出方程是解决本题的关键.9、轮船在河流中来往航行于A、B两码头之间,顺流航行全程需7小时,逆流航行全程需9小时,已知水流速度为每小时3km,求A、B两码头间的距离.若设A、B两码头间距离为x,则所列方程为()A.x7+3=x9−3B.x7−3=x9+3C.x7+3=x9D.x7−3=x9答案:B分析:根据顺流速度减去水流速度等于逆流速度加上水流速度列出方程即可.解:设A、B两码头间距离为x,由题意得:x7−3=x9+3,故选:B.小提示:此题考查一元一次方程的应用,列方程解应用题的关键是找出题目中的相等关系.10、已知一项工程,甲单独完成需要5天,乙单独完成需要10天,现先由甲单独做2天,然后再安排乙与甲合作完成剩下的部分,则完成这项工程共耗时( )A.1天B.2天C.3天D.4天答案:D分析:设完成这项工程共耗时x天,则甲工作了x天,乙工作了(x﹣2)天,根据总工作量=甲完成的工作量+乙完成的工作量,即可得出关于x的一元一次方程,解之即可得出结论.解:设完成这项工程共耗时x天,则甲工作了x天,乙工作了(x﹣2)天,根据题意得:x5+x−210=1,解得:x=4.即完成这项工程共耗时4天.故选:D小提示:本题考查了一元一次方程的应用,找准等量关系,正确列出一元一次方程是解题的关键.填空题11、已知A=2x−5,B=3x+3,若A比B大7,则x的值为________.答案:-15分析:根据“A比B大7”列出方程,进而求解即可.解:根据题意可得:A=B+7,由此可得出关于x的方程2x−5=3x+3+7,移项,得:2x−3x=3+7+5,合并同类项,得:−x=15,系数化为1,得:x=−15,所以答案是:-15.小提示:此题考查了一元一次方程的简单应用,熟练掌握解一元一次方程的步骤是解本题的关键.12、当x=________时,整式3x−1与2x+1互为相反数;答案:0分析:利用互为相反数两数之和为0列出方程,求出方程的解即可得到x的值.解:∵代数式3x−1与2x +1互为相反数,∴3x−1+2x +1=0,解得x=0.所以答案是:0.小提示:此题考查了解一元一次方程,以及相反数,熟练掌握解一元一次方程的解法是解题的关键.13、在0,1,2,3中,_______是方程2x–1=–5x+6的解.答案:1分析:根据解一元一次方程的方法移项合并,把x系数化为1,即可求出解.解:2x–1=–5x+6移项,得2x+5x=1+6,合并同类项,得7x=7,系数化为1,得x=1,所以答案是:1.小提示:本题主要考查解一元一次方程,解题的关键是掌握解一元一次方程的基本步骤:去分母、去括号、移项、合并同类项、系数化为1.14、若x|m|﹣10=2是关于x的一元一次方程,则m的值是 _____.答案:±1分析:只含有一个未知数(元),并且未知数的指数是1(次)的方程叫做一元一次方程.它的一般形式是ax+b=0(a,b是常数且a≠0).解:根据题意,有|m|=1,∴m=±1,所以答案是:±1.小提示:本题主要考查了一元一次方程的一般形式,只含有一个未知数,且未知数的指数是1,一次项系数不是0,这是这类题目考查的重点.15、已知5x2−5x−3=7,利用等式的基本性质,x2−x的值为___________.答案:2分析:首先根据等式的性质1,两边同时+3得5x2−5x=10,再根据等式的性质2,两边同时除以5即可得到答案.解:5x2−5x−3=7,根据等式的性质1,两边同时+3得:5x2−5x−3+3=7+3,即:5x2−5x=10,根据等式的性质2,两边同时除以5得:5x2−5x5=105,∴x2−x=2,故填:2.小提示:此题主要考查了等式的性质,关键是掌握等式的性质:性质1、等式两边加同一个数(或式子)结果仍得等式;性质2、等式两边乘同一个数或除以一个不为零的数,结果仍得等式.解答题16、粤港澳大湾区自动驾驶产业联盟积极推进自动驾驶出租车应用落地工作,无人化是自动驾驶的终极目标.某公交集团拟在今明两年共投资9000万元改装260辆无人驾驶出租车投放市场.今年每辆无人驾驶出租车的改装费用是50万元,预计明年每辆无人驾驶出租车的改装费用可下降50%.(1)求明年每辆无人驾驶出租车的预计改装费用是多少万元;(2)求明年改装的无人驾驶出租车是多少辆.答案:(1)明年每辆无人驾驶出租车的预计改装费用是25万元;(2)明年改装的无人驾驶出租车是160辆.分析:(1)根据今年每辆无人驾驶出租车的改装费用是50万元,预计明年每辆无人驾驶出租车的改装费用可下降50%,列出式子即可求出答案;(2)根据“某公交集团拟在今明两年共投资9000万元改装260辆无人驾驶出租车投放市场”列出方程,求解即可.解:(1)依题意得:50×(1-50%)=25(万元)(2)设明年改装的无人驾驶出租车是x辆,则今年改装的无人驾驶出租车是(260-x)辆,依题意得:50×(260−x)+25x=9000解得:x=160答:(1)明年每辆无人驾驶出租车的预计改装费用是25万元;(2)明年改装的无人驾驶出租车是160辆.小提示:本题考查了一元一次方程的实际应用问题,解题的关键是找到数量关系,列出方程.17、解下列方程:(1)x−1=1−x;(2)2x+13+1=x+32.答案:(1)x=1;(2)x=1分析:(1)按照移项、合并同类项、系数化为1的步骤解方程即可得;(2)按照去分母、去括号、移项、合并同类项的步骤解方程即可得.解:(1)x−1=1−x,移项,得x+x=1+1,合并同类项,得2x=2,系数化为1,得x=1;(2)2x+13+1=x+32,方程两边同乘以6去分母,得2(2x+1)+6=3(x+3),去括号,得4x+2+6=3x+9,移项,得4x−3x=9−2−6,合并同类项,得x=1.小提示:本题考查了解一元一次方程,熟练掌握解方程的步骤是解题关键.18、阅读材料:我们把绝对值符号内含有未知数的方程叫做“含有绝对值的方程”.如:|x|=2,|2x﹣1|=3,…都是含有绝对值的方程.怎样求含有绝对值的方程的解呢?基本思路是:含有绝对值的方程→不含有绝对值的方程.我们知道,由|x|=2,可得x=2或x=﹣2.【例】解方程:|2x﹣1|=3.我们只要把2x﹣1看成一个整体就可以根据绝对值的意义进一步解决问题.解:根据绝对值的意义,得2x﹣1=3或2x﹣1=﹣3.解这两个一元一次方程,得x=2或x=﹣1.根据以上材料解决下列问题:(1)解方程:|3x﹣2|=4;(2)拓展延伸:解方程|x﹣2|=|3x+2|.答案:(1)x=2或x=−23(2)x=-2或x=0分析:先去绝对值转化成一元一次方程求解.(1)解:根据绝对值的意义得:3x-2=4或3x-2=-4.解得:x=2或x=−23;(2)由绝对值的意义得:x-2=3x+2或x-2+3x+2=0.解得:x=-2或x=0.小提示:本题考查含绝对值的一元一次方程的解法,理解绝对值的意义是求解本题的关键.。
第三章一元一次方程知识点梳理及典型例题牛园园

第三章 一元一次方程知识要点梳理及典型例题一.元一次方程及解的概念 1、一元一次方程的概念只含有一个未知数,并且未知数的次数都是1的方程叫做一元一次方程。
一元一次方程的标准形式是:ax+b=0(其中x 是未知数,a,b 是已知数,且a ≠0)。
典型例题:下列方程是一元一次方程的是( )A.x+y=1B.250x x += C.3x+7=16 D.1532x-= 做题要点:判断一元一次方程必须满足的3个条件: 只含有一个未知数; 未知数的次数是1次; 整式方程。
2、方程的解使方程左右两边的值相等的未知数的值叫做方程的解。
典型例题:以x 为未知数的方程)2(21x a ax -=-的解是x=3,求a 的值。
做题要点:将方程的解代入方程,得到一个以a 为未知数的新方程,解得a 的值。
二.方程变形——解方程的重要依据 1、等式的基本性质等式的性质1:等式两边加(或减)同一个数(或式子),结果仍相等。
即:如果,那么;(c 为一个数或一个式子)。
等式的性质2:等式两边乘同一个数,或除以同一个不为0的数,结果仍相等。
即:如果,那么;如果,那么典型例题:1)、下列等式变形中不正确的是( ) A 、若x=y,则x+5=y+5 B.若x ya a= ,则x=y C.若-3x=-3y ,则x=y D.mx=my,x=y2)、若2x+1=8,那么4x+2= 。
2、分数的基本的性质分数的分子、分母同时乘以或除以同一个不为0的数,分数的值不变。
即://a am a mb bm b m==(其中m ≠0) 注:分数的基本的性质主要是用于将方程中的小数系数(特别是分母中的小数)化为整数, 如方程:30.5x - -40.2x + =1.6,将其化为的形式: 10(3)10(4)1.652x x -+-=。
方程的右边没有变化,这要与“去分母”区别开。
典型例题三.解一元一次方程的一般步骤 1、解一元一次方程的基本思路通过对方程变形,把含有未知数的项归到方程的一边,把常数项归到方程的另一边,最终把方程“转化”成x =a 的形式。
新人教版七年级上期末复习《第三章一元一次方程》知识点+易错题(含答案)

2019年七年级数学上册期末复习一元一次方程知识点+易错题一元一次方程知识点总结一、等式与方程1.等式:(1)定义:含有等号的式子叫做等式.(2)性质:①等式两边同时加上(或减去)同一个整式,等式的值不变.若a b=那么a c b c+=+②等式两边同时乘以一个数或除以同一个不为0的整式,等式的值不变.若a b=那么有ac bc=或a c b c÷=÷(0c≠)③对称性:若a b=,则b a=.④传递性:若a b=,b c=则a c=.(3)拓展:①等式两边取相反数,结果仍相等.如果a b=,那么a b-=-②等式两边不等于0时,两边取倒数,结果仍相等.如果0a b=≠,那么11 a b =③等式的性质是解方程的基础,很多解方程的方法都要运用到等式的性质.如移项,运用了等式的性质①;去分母,运用了等式的性质②.④运用等式的性质,涉及除法运算时,要注意转换后除数不能为0,否则无意义.2.方程:(1)定义:含有未知数的等式叫做方程.(2)说明:①方程中一定有含一个或一个以上未知数,且方程是等式,两者缺一不可.②未知数:通常设x、y、z为未知数,也可以设别的字母,全部小写字母都可以.未知数称为元,有几个未知数就叫几元方程.一道题中设两个方程时,它们的未知数不能一样!③“次”:方程中次的概念和整式的“次”的概念相似.指的是含有未知数的项中,未知数次数最高的项对应的次数,也就是方程的次数.未知数次数最高是几就叫几次方程.④方程有整式方程和分式方程.整式方程:方程的两边都是关于未知数的整式的方程叫做整式方程.分式方程:分母中含有未知数的方程叫做分式方程.二、一元一次方程1.一元一次方程的概念:(1)定义:只含有一个未知数(元)且未知数的指数是1(次)的整式方程叫做一元一次方程.(2)一般形式:0ax b+=(a,b为常数,x为未知数,且0a≠).(3)注意:①该方程为整式方程.②该方程有且只含有一个未知数.③该方程中未知数的最高次数是1.④化简后未知数的系数不为0.如:212x x-=,它不是一元一次方程.⑤未知数在分母中时,它的次数不能看成是1次.如13xx+=,它不是一元一次方程.2.一元一次方程的解法:(1)方程的解:能使方程左右两边相等的未知数的值叫做方程的解,一般写作:“?x=”的形式.(2)解方程:求出方程的解的过程,也可以说是求方程中未知数的值的过程,叫解方程.(3)移项:①定义:从方程等号的一边移到等号另一边,这样的变形叫做移项.②说明:Ⅰ移项的标准:看是否跨过等号,跨过“=”号才称为移项;移项一定改变符号,不移项的不变.Ⅱ移项的依据:移项实际上就是对方程两边进行同时加减,根据是等式的性质①.Ⅲ移项的原则:移项时一般把含未知数的项向左移,常数项往右移,使左边对含未知数的项合并,右边对常数项合并,方便求解.(4)解一元一次方程的一般步骤及根据:①去分母——等式的性质②②去括号——分配律③移项——等式的性质①④合并——合并同类项法则⑤系数化为1——等式的性质②⑥检验——把方程的解分别代入方程的左右边看求得的值是否相等(在草纸上)(5)一般方法:①去分母,程两边同时乘各分母的最小公倍数.②去括号,一般先去小括号,再去中括号,最后去大括号.但顺序有时可依据情况而定使计算简便,本质就是根据乘法分配律.③移项,方程中含有未知数的项移到方程的另一边,其余各项移到方程的另一边移项时别忘记了要变号.(一般都是把未知数移到一起)④合并同类项,合并的是系数,将原方程化为ax b=(0a≠)的形式.⑤系数化1,两边都乘以未知数的系数的倒数.⑥检验,用代入法,在草稿纸上算.(6)注意:(对于一元一次方程的一般步骤要熟练掌握,更要观察所求方程的形式、特点,灵活变化解题步骤)①分母是小数时,根据分数的基本性质,把分母转化为整数,局部变形;②去分母时,方程两边各项都乘各分母的最小公倍数,Ⅰ此时不含分母的项切勿漏乘,即每一项都要乘Ⅱ分数线相当于括号,去分母后分子各项应加括号(整体思想);③去括号时,不要漏乘括号内的项,不要弄错符号;④移项时,切记要变号,不要丢项,有时先合并再移项,以免丢项;⑤系数化为1时,方程两边同乘以系数的倒数或同除以系数,不要弄错符号(打草稿认真计算);⑥不要生搬硬套解方程的步骤,具体问题具体分析,找到最佳解法;⑦分数、小数运算时不能嫌麻烦,不要跳步,一步步仔细算.(7)补充:分数的基本性质:与等式基本性质②不同.分数的分子分母两个整体同时乘以同一个不为0的数或除以同一个不为0的数,分数的值不变.3.一元一次方程的应用:(1)解决实际应用题的策略:①审题:就是多读题,读懂题,读的时候一定沉下心去,不能慌不要急躁,要细,一个字一个字的精读,要慢,边读边思考.找到已知条件,未知条件,找到数量关系和等量关系,可以用笔在题目中标注下来重要信息和数量关系,审题往往伴随下个步骤.②设出适当未知数,往往问什么设什么,有时也间接设未知数,然后用未知数通过关系表示出其他相关的量.③找出等量关系,用符号语言表示就是列出方程.(2)分析问题方法:①文字关系分析法,找关键字词句分析实际问题中的数量关系②表格分析法,借助表格分析分析实际问题中的数量关系③示意图分析法,通过画图帮助分析实际问题中的数量关系(3)设未知量方法:一个应用题,往往涉及到几个未知量,为了利用一元一次方程来解应用题,我们总是设其中一个未知量为x,并用这个未知数的代数式去表示其他的未知量,然后列出方程.①设未知量的原则就是设出的量要便于分析问题,与其它量关系多,好表示其它量,好表示等量关系;②有直接设未知量和间接设未知量,还有不常见的辅助设未知量.(4)找等量关系的方法:“等量关系”特指数量间的相等关系,是数量关系中的一种.数学题目中常含有多种等量关系,如果要求用方程解答时,就需找出题中的等量关系.①标关键词语,抓住关键句子确定等量关系.(比如多,少,倍,分,共)解题时只要找出这种关键语句,正确理解关键语句的含义,就能确定等量关系.②紧扣基本公式,利用基本关系确定等量关系就是根据常见的数量关系确定等量关系.(比如体积公式,单价×数量=总价,单产量×数量=总产量,速度×时间=路程,工效×时间=工作总量等.这些常见的基本数量关系,就是等量关系)③通过问题中不变的量,相等的量确定等量关系.就是用不同的方法表示同一个量,从而建立等量关系.④借助线段图确定等量关系。
第三章 一元一次方程单元总结(人教版)(解析表)

第三章一元一次方程单元总结【思维导图】【知识要点】知识点一一元一次方程的基础等式的概念:用等号表示相等关系的式子。
方程的概念:含有未知数的等式叫做方程。
特征:它含有未知数,同时又是—个等式。
一元一次方程的概念:只含有一个未知数(元),未知数的次数都是1的方程叫做一元一次方程。
【特征】1. 只含有一个未知数x2. 未知数x的次数都是13. 等式两边都是整式。
方程的解的概念:能使方程中等号左右两边相等的未知数的值叫方程的解。
一元方程的解又叫根。
【典型例题】1.(2018·湖南省地质中学初一期中)下列方程中,是一元一次方程的是( )A. B. C. D.【答案】A【详解】A. ,是一元一次方程;B. ,分母有未知数,不是一元一次方程;C. ,两个未知数,不是一元一次方程;D. 未知数的指数是2,不是一元一次方程;故选A.【名师点睛】本题考查一元一次方程的识别,熟练掌握一元一次方程的定义是解题关键. 2.(2018·福建省福州第十九中学初一期中)解是x=的方程是()A.2﹣4x=1B.3x+2=5C.x=2D.4x﹣2=6x﹣3 【答案】D【详解】A.解方程2﹣4x=1得:x=,即A项错误,B.解方程3x+2=5得:x=1,即B项错误,C.解方程x=2得:x=4,即C项错误,D.解方程4x﹣2=6x﹣3得:x=,即D项正确,故选:D.【名师点睛】本题考查了一元一次方程的解,正确掌握解一元一次方程的方法是解题的关键.3.(2018·太原市期末)已知x=2是2x+a=5的解,则a的值为()A.1B.C.﹣1D.【答案】A【详解】解:将x=2代入方程得:4+a=5,解得:a=1,故选:A.【名师点睛】本题考查了一元一次方程的解,方程的解即为能使方程左右两边相等的未知数的值.知识点二等式的性质(解一元一次方程的基础)等式的性质1:等式两边(或减)同一个数(或式子),结果仍相等。
表示为:如果a=b,则a±c=b±c等式的性质2:等式两边乘同一个数,或除以同一个不为零的数,结果仍相等。
七年级数学上册第三章一元一次方程3.1.1一元一次方程(图文详解)

人教版七年级数学上册第三章一元一次方程
请你判断下列给定的t的值中,哪个是方程2t+1=7-t 的解?
(1)t=-2 (2)t=2 (3)t=1 根据方程的解的定义,我们得到t=2是方程2t+1=7-t 的解.
人教版七年级数学上册第三章一元一次方程
1.方程x=3是下列哪个方程的解?( C )
(A)3x+9=0
人教版七年级数学上册第三章一元一次方程
你知道什么 叫方程吗?
含有未知数的等式—方程
你能举出一些 方程的例子?
练习:
判断下列式子是不是方程,正确的打“√”,错误的打”×”:
(1) 1+2=3 (2) 1+2x=4 (3) x+1-3
(×) (4) x 2 1 (×)
(√) (5) x+y=2
4.已知数x-5与2x-4的值互为相反数,列出关于x的方程. 解:由题意得:(x-5)+(2x-4)=0.
人教版七年级数学上册第三章一元一次方程
1.方程、方程的解、一元一次方程的概念. 2.根据实际问题中的等量关系,用一元一次方程表示问 题中的数量关系. 注:分析实际问题中的数量关系,利用其中的相等关系 列出方程,是用数学解决实际问题的一种方法.
秀水两地之间,距青山50千米,距秀水70千米,
王家庄到翠湖的路程有多远?
回顾:路程=速度×时间 速度=路程÷时间
时间=路程÷速度
人教版七年级数学上册第三章一元一次方程
分析:若知道王家庄到翠湖的路程(比如x千米), 用含x的式子表示关于路程的数量: 那么王家庄距青山_(__x_-_5_0_)_千米,王家庄距秀水(_x_+_7_0_)_千米. 有关时间的数量: 从王家庄到青山行车___3__小时,王家庄 到秀水行车__5__小时.
七年级数学上册第三章一元一次方程知识点总结归纳

七年级数学上册第三章一元一次方程知识点总结归纳单选题1、已知x=y,字母m为任意有理数,下列等式不一定成立的是()A.x+m=y+m B.x−m=y−m C.mx=my D.x1+m =y1+m答案:D解析:根据等式的基本性质对各选项分析判断后利用排除法求解.解:A、等式两边同时加上m,依据等式的基本性质1,∴所得等式成立;B、等式两边同时加上﹣m,依据等式的基本性质1,∴所得等式成立;C、等式两边同时乘以m,依据等式的基本性质2,∴所得等式成立;D、等式两边同时除以1+m,而1+m有可能为0,则所得等式无意义,∴此等式不一定成立.故选:D.小提示:本题主要考查了等式的基本性质,等式性质:1、等式的两边同时加上或减去同一个数或字母,等式仍成立;2、等式的两边同时乘以或除以同一个不为0数或字母,等式仍成立.2、若x=1是方程3−m+x=6x的解,则关于y的方程m(y−3)−2=m(2y−5)的解是()A.y=−10B.y=3C.y=43D.y=4答案:B解析:根据x=1为已知方程的解,将x=1代入方程求出m的值,代入所求方程即可求出y的值.将x=1代入已知方程得:3﹣m+1=6,解得:m=-2.所求方程化为-2(y﹣3)﹣2=-2(2y﹣5),解得:y=3.故选B.小提示:本题考查了解一元一次方程,其步骤为:去分母,去括号,移项合并,将未知数系数化为1,求出解.3、若x=1是方程3−m+x=6x的解,则关于y的方程m(y−3)−2=m(2y−5)的解是()A.y=−10B.y=3C.y=4D.y=43答案:B解析:根据x=1为已知方程的解,将x=1代入方程求出m的值,代入所求方程即可求出y的值.将x=1代入已知方程得:3﹣m+1=6,解得:m=-2.所求方程化为-2(y﹣3)﹣2=-2(2y﹣5),解得:y=3.故选B.小提示:本题考查了解一元一次方程,其步骤为:去分母,去括号,移项合并,将未知数系数化为1,求出解.4、某件商品先按成本价加价50%后标价,再以九折出售,售价为135元,若设这件商品的成本价是x元,根据题意,可得到的方程是()A.(1+50%)x×90%=135B.(1+50%)x×90%=135−xC.(1+50%x)×90%=135D.(1+50%x)×90%=135−x答案:A解析:设这件商品的成本价为x元,售价=标价×90%,据此列方程.解:标价为x(1+50%),九折出售的价格为(1+50%)x×90%,可列方程为(1+50%)x×90%=135.故选:A.小提示:本题考查了由实际问题抽象出一元一次方程,解答本题的关键是读懂题意,设出未知数,找出合适的等量关系,列方程.5、一货轮往返于上、下游两个码头,逆流而上38个小时,顺流而下需用32个小时,若水流速度为8千米/时,则下列求两码头距离x的方程正确的是()A.x−832=x+838B.x32−8=x38+8C.x32−x38=82D.2x32+38=12(x32+x38)答案:B解析:根据题意分别表示出顺流和逆流时船的速度,然后列方程即可.解:∵逆流而上38个小时,∴逆流时船本身的速度可以表示为x38千米/时,∵顺流而下需用32个小时,∴顺流时船本身的速度可以表示为x32千米/时,∵静水的速度是不变的,∴可列方程为x32−8=x38+8.故选:B.小提示:此题考查了一元一次方程中的航行问题,解题的关键是根据题意分析出顺流和逆流时船的速度.6、下列式子中,是方程的是()A.x−1≠0B.3x−2C.2+3=5D.3x=6答案:D解析:根据方程的定义,对选项逐个判断即可.解:A.不是等式,故不是方程,选项不符合题意;B.是多项式,不是等式,故不是方程,选项不符合题意;C.不含未知数,故不是方程,选项不符合题意;D.是含有未知数的等式,故是方程,选项符合题意;故选D.小提示:此题考查了方程的定义,含有未知数的等式叫做方程,掌握方程的定义是解题的关键.7、《增删算法统宗》记载:“有个学生资性好,一部孟子三日了,每日增添一倍多,问若每日读多少?”其大意是:有个学生天资聪慧,三天读完一部《孟子》,每天阅读的字数是前一天的两倍,问他每天各读多少个字?已知《孟子》一书共有34 685个字,设他第一天读x个字,则下面所列方程正确的是( ).A.x+2x+4x=34 685B.x+2x+3x=34 685C .x +2x +2x =34 685D .x +12x +14x =34 685答案:A解析:设他第一天读x 个字,根据题意列出方程解答即可.解:设他第一天读x 个字,根据题意可得:x +2x +4x =34685,故选A .小提示:此题考查由实际问题抽象出一元一次方程,解答本题的关键是读懂题意,设出未知数,找出合适的等量关系,列方程.8、下列方程中,解是x =2的方程是( )A .3x=x+3B .-x+3=0C .5x-2=8D .2x=6答案:C解析:根据一元一次方程的解的概念解答即可.A 、由原方程,得2x=3,即x=1.5;故本选项错误;B 、由原方程移项,得x=3;故本选项错误;C 、由原方程移项、合并同类项,5x=10,解得x=2;故本选项正确;D 、两边同时除以2,得x=3;故本选项正确.故选C .小提示:本题考查了一元一次方程的解的定义,方程的解就是能使方程的左右两边相等的未知数的值.填空题9、若a,b为常数,无论k为何值时,关于x的一元一次方程(b+1)x=12−4ka,它的解总是1,则a,b的值分别是_______.答案:a=0,b=11解析:将方程的解代入原方程,并化简.因为无论k为何值,它的解总是1,即可列出{4a=011−b=0,解出a和b即可.把x=1代入方程得b+1=12−4ka,化简得4ka=11−b,∵k的值为全体实数,∴4a=0,且11−b=0,∴a=0,b=11.小提示:本题考查一元一次方程的解.理解方程的解的定义“能够使方程左右两边相等的未知数的值”是解答本题的关键.10、当a=__________时,方程ax−13+x+a2=1解是x=1?答案:1解析:将x=1代入方程,再解一元一次方程即可.由题意,将x=1代入得:a−13+1+a2=1两边同乘以6得2(a−1)+3(1+a)=6去括号得2a−2+3+3a=6移项、合并同类项得5a=5系数化为1得a=1所以答案是:1.小提示:本题考查了方程的解、解一元一次方程,掌握方程的解法是解题关键.11、关于x的方程mx2m﹣1+(m﹣1)x-2=0如果是一元一次方程,则其解为_____.答案:x=2或x=−2或x=-3.解析:利用一元一次方程的定义判断即可.解:∵关于x的方程mx2m﹣1+(m﹣1)x﹣2=0如果是一元一次方程,(1)当2m﹣1=1,即m=1,即x﹣2=0解得:x=2,(2)当m=0时,−x−2=0,解得:x=−2(3)当2m-1=0,即m=12时,方程为12−12x−2=0解得:x=-3,故答案为x=2或x=-2或x=-3.小提示:此题考查了一元一次方程的定义,熟练掌握一元一次方程的定义是解本题的关键.12、明代数学家程大位的《算法统宗》中有这样一个问题(如图),其大意:有一群人分银子,如果每人分七两银子,那么剩余四两;如果每人分九两银子,那么还差八两.请问所分的银子共有________两.(注:明代时1斤=16两,故有“半斤八两”这个成语)答案:46解析:可设有x人,根据有一群人分银子,如果每人分七两,则剩余四两;如果每人分九两,则还差八两,根据所分的银子的总两数相等可列出方程,求解即可.解:设有x人,依题意有7x+4=9x−8,解得x=6,故7x+4=42+4=46,即所分的银子共有46两,所以答案是:46.小提示:本题考查了一元一次方程的应用,解题关键是要读懂题目的意思,根据题目中所分的银子的总两数相等的等量关系列出方程,再求解.13、如果5x n−2=3是一元一次方程,那么n=________.答案:3解析:若一个整式方程经过化简变形后,只含有一个未知数,并且未知数的次数都是1,系数不为0,则这个方程是一元一次方程.据此可得出关于n的方程,继而可求出n的值.解:根据题意,得n-2=1,解得n=3.所以答案是:3.小提示:本题考查了一元一次方程的概念和解法.一元一次方程的未知数的指数为1.解答题14、某校开展校园艺术节系列活动,派小明到文体超市购买若干个文具袋作为奖品.这种文具袋标价每个10元,请认真阅读结账时老板与小明的对话图片,解决下面两个问题:(1)求小明原计划购买文具袋多少个?(2)学校决定,再次购买钢笔和签字笔共50支作为补充奖品,其中钢笔标价每支8元,签字笔标价每支6元.经过沟通,这次老板给予8折优惠,合计272元.问小明购买了钢笔和签字笔各多少支?答案:(1)小明原计划购买文具袋17个;(2)小明购买了钢笔20支,签字笔30支.解析:(1)设未知数后可以根据等量关系“实际购买文具袋(比原计划多1个)的花费×0.85=原计划购买文具袋的花费-17”列方程求解;(2)设未知数后可以根据等量关系“钢笔和签字笔的总价×0.8(或80%)=272”列方程求解.解:(1)设小明原计划购买文具袋x个,则实际购买了(x+1)个,由题意得:10(x+1)×0.85=10x−17.解得:x=17;答:小明原计划购买文具袋17个;(2)设小明购买了钢笔y支,则购买签字笔(50−y)支,由题意得:[8y+6(50−y)]×80%=272,解得:y=20,则:50−y=30.答:小明购买了钢笔20支,签字笔30支.小提示:本题考查一元一次方程的应用,根据题目中的等量关系设未知数列方程求解是解题关键.15、如图,一块长5厘米、宽2厘米的长方形纸板,一块长4厘米、宽1厘米的长方形纸板,一块小正方形以及另两块长方形的纸板,恰好拼成一个大正方形,求大正方形的面积.答案:大正方形的面积是36cm2解析:设小正方形的边长为x,然后表示出大正方形的边长,利用正方形的面积相等列出方程求得小正方形的边长,然后求得大正方形的边长即可求得面积.设小正方形的边长为x,则大正方形的边长为4+(5−x)cm或(x+1+2)cm,根据题意得:4+(5−x)=(x+1+2),解得:x=3,∴4+(5−x)=6,∴大正方形的面积为36cm2.答:大正方形的面积为36cm2.小提示:本题考查了一元一次方程的应用,解题的关键是设出小正方形的边长并表示出大正方形的边长.11。
七年级《第三章 一元一次方程》知识点总结

第三章一元一次方程3.1 从算式到方程3.1.1 一元一次方程含有未知数的等式叫做方程.方程都只含有一个未知数(元)x,未知数x的指数都是1(次),这样的方程叫做一元一次方程.方程的解:使方程左右两边相等的未知数的值,叫做方程的解.解方程是求出使方程中等号左右两边相等的未知数的值的过程.3.1.2 等式的性质等式的性质1:等式两边加(或减)同一个数(或式子),结果仍相等.等式的性质2.等式两边乘同一个数,或除以同一个不为0的数,结果仍相等.3.2 解一元一次方程(一)——合并同类项与移项把等式一边的某项变号后移到另一边,叫做移项.【说明】1.一般情况,将含有未知数的项移到等号的左边,常数项移到等号的右边.2.从左边移到右边,或从右边移到左边,移动的那一项的符号要改变.3.合并同类项同整式合并同类项一样,将未知数x的系数相加,作为合并后的项的系数,x照写不变.常数项的合并,按照有理数的基本运算进行合并.3.3 解一元一次方程(二)——去括号与去分母去括号:(同整式中的去括号)去分母:分子分母同时乘以分母的最小公倍数,通过约分,将含有分母的方程转化成为不含分母的方程.【说明】1.所选的乘数是所有的分母的最小公倍数.(用短除法找最小公分母)2.用最小公倍数去乘方程两边时,不要漏掉等号两边不含字母的“项”.3.去掉分母时,分数线也同时去掉,分子上的多项式要用括号括起来.4.解方程的类型:①简易方程;②有括号的方程;③有分母的括号;④含参方程;⑤含绝对值的方程;⑥比例式方程.3.4 实际问题与一元一次方程分析实际问题中的数量关系,利用其中的相等关系列出方程,是用数学解决实际问题的一种方法.列方程解应用题的一般步骤:①认真审题,弄清题意(注意单位是否统一).②根据问题设出未知数.(一般是问什么,设什么,也可以间接设未知数)③找出题中的等量关系,列方程.④解方程.⑤检验:一是检验是否是方程的解;二是检验是否符合实际问题.⑥写答语.常见问题的等量关系:行程问题: 距离=速度·时间 时间距离速度= 速度距离时间=; 工程问题: 工作量=工作效率·工作时间 工时工作量工效= 工效工作量工时=;顺水逆水问题: 顺流速度=静水速度+水流速度,逆流速度=静水速度-水流速度;水流速度=(顺水速度-逆水速度)÷2商品利润问题:售价=定价×10几折, %100⨯-=成本成本售价利润率;利润问题常用等量关系: 售价-进价=利润配套问题:两个量之间满足某种倍数关系分配问题:分配总量保持不变。
七年级数学上册第三章一元一次方程知识点梳理

(名师选题)七年级数学上册第三章一元一次方程知识点梳理单选题1、下列等式变形错误..的是()A.若a=b,则a1+x2=b1+x2B.若a=b,则3a=3bC.若a2=b2,则a=b D.若a=b,则am =bm(m<0)答案:C分析:利用等式的性质对每个式子进行变形即可解答.解:A. 若a=b,∵1+x2≠0,∴a1+x2=b1+x2正确,该选项不符合题意;B. 若a=b,则3a=3b正确,该选项不符合题意;C. 若a2=b2,则|a|=|b|,则C选错误,该选项符合题意;D. 若a=b,a=b,则am =bm(m<0)正确,该选不项符合题意.故选:C小提示:本题主要考查了等式的性质.等式的两边都加上或者减去同一个数或同一个整式,所得结果仍是等式;等式的两边都乘以或者除以同一个数(除数不为零),所得结果仍是等式.2、解方程3x−12=1−x+33时,去分母结果正确的是()A.3(3x−1)=1−2(x+3)B.3(3x−1)=1−(x+3) C.2(3x−1)=6−3(x+3)D.3(3x−1)=6−2(x+3)答案:D分析:根据等式的性质,把方程3x−12=1−x+33的等号的左右两边分别乘6,判断出去分母结果正确的是哪个即可.解:解方程3x−12=1−x+33时,去分母结果正确的是:3(3x-1)=6-2(x+3).故选:D.小提示:此题主要考查了解一元一次方程的方法,注意等式的性质的应用.3、我们把|a b c d |称为二阶行列式,且|a b c d |=ad −bc ,如|123−4|=1×(−4)-2×3=-10.若|−472m|=6,则m 的值为( )A .8B .-2C .2D .-5答案:D分析:根据二阶行列式的定义列式得一个关于m 的一元一次方程,求出m 的值即可.根据题意得|−472m|=-4m -2×7, ∵|−472m|=6, ∴-4m -2×7=6,解得m =-5.故选:D小提示:本题主要考查了利用定义新运算解一元一次方程,解题的关键是读懂题意,正确的列方程.4、已知下列方程:①x −2=2x ;②0.3x =1;③x 2=5x +1;④x 2−4x =3;⑤x =6;⑥x +2y =0.其中一元一次方程的个数是( )A .2B .3C .4D .5答案:B分析:根据一元一次方程的定义进行判断即可.解:①x −2=2x 是分式方程,故①不符合题意;②0.3x =1,即0.3x −1=0,符合一元一次方程的定义.故②符合题意;③x 2=5x +1,即9x +2=0,符合一元一次方程的定义.故③符合题意; ④x 2−4x =3的未知数的最高次数是2,它属于一元二次方程.故④不符合题意;⑤x =6,即x −6=0,符合一元一次方程的定义.故⑤符合题意;⑥x +2y =0中含有2个未知数,属于二元一次方程.故⑥不符合题意.综上所述,一元一次方程的个数是3个.故选:B .小提示:本题主要考查了一元一次方程的一般形式,只含有一个未知数,且未知数的指数是1,一次项系数不是0.5、下列方程变形中,正确的是()A.x−2−4x−33=1,去分母,得3(x−2)−(4x−3)=1B.1+x=4,移项,得x=4−1C.2x−(1−3x)=5,去括号,得2x−1−3x=5D.2x=−3,两边都除以2,得x=−23答案:B分析:根据去分母、去括号、移项、系数化1等基本步骤逐项判断即可.解:A,x−2−4x−33=1,去分母,得3(x−2)−(4x−3)=3,故本选项错误,不合题意;B,1+x=4,移项,得x=4−1,故本选项正确,符合题意;C,2x−(1−3x)=5,去括号,得2x−1+3x=5,故本选项错误,不合题意;D,2x=−3,两边都除以2,得x=−32,故本选项错误,不合题意;故选B.小提示:本题考查解一元一次方程,解题的关键是掌握去分母、去括号、移项、系数化1等基本步骤.6、方程3x=a的解是()A.方程有唯一解x=3a B.方程有唯一解x=a3C.当a≠0方程有唯一解x=a3D.当a=0时方程有无数多个解答案:B分析:根据解一元一次方程的步骤,把未知数的系数化为1,即可得出答案解:∵3x=a∴方程有唯一解x=a3;故选:B小提示:本题考查了解一元一次方程,熟练掌握解方程的步骤是解题的关键7、将连续的奇数1、3、5、7、9、11等,按一定规律排成如图:图中的T字框框住了四个数字,若将T字框上下左右移动,按同样的方式可框住另外的四个数.若将T字框上下左右移动,则框住的四个数的和不可能得到的数是()A.34B.62C.118D.158答案:A分析:由题意,设T字框内处于中间且靠上方的数为2n﹣1,则框内该数左边的数为2n﹣3,右边的为2n+1,下面的数为2n﹣1+10,故T字框内四个数的和为:8n+6.由题意,设T字框内处于中间且靠上方的数为2n﹣1,则框内该数左边的数为2n﹣3,右边的为2n+1,下面的数为2n﹣1+10,∴T字框内四个数的和为:2n﹣3+2n﹣1+2n+1+2n﹣1+10=8n+6.故T字框内四个数的和为:8n+6.A、由题意,令框住的四个数的和为34,则有:8n+6=34,解得n=3.5.不满足整数的条件.故框住的四个数的和不能等于34,故本选项符合题意;B、由题意,令框住的四个数的和为62,则有:8n+6=62,解得n=7.满足整数的条件.故本选项不符合题意;C、由题意,令框住的四个数的和为118,则有:8n+6=118,解得n=14.满足整数的条件.故本选项不符合题意;D、由题意,令框住的四个数的和为158,则有:8n+6=158,解得n=19.满足整数的条件.故本选项不符合题意;故选:A.小提示:此题主要考查了一元一次方程的应用,关键是正确理解题意,找出题目中的等量关系,设出未知数,列出方程.8、解方程x2−x−26=1−x−13,下列去分母变形正确的是()A.3x−x+2=6−2(x−1)B.3x−x−2=6−2(x−1) C.3x−(x+2)=1−2(x−1)D.3x−x+2=3−2(x−1)答案:A分析:把方程两边同时乘以6去分母即可.解:x2−x−26=1−x−13把方程两边同时乘以6得:3x−(x−2)=6−2(x−1)即3x−x+2=6−2(x−1),故选A.小提示:本题主要考查了解一元一次方程,解题的关键在于能够熟练掌握去分母的方法.9、已知(m−2)x|m|−1=5是关于x的一元一次方程,则m的值为( )A.-2B.±2C.2D.0答案:A分析:根据一元一次方程的定义即可求出答案.只含有一个未知数(元),且未知数的次数是1,这样的整式方程叫一元一次方程.解:∵(m−2)x|m|−1=5是关于x的一元一次方程,∴{m−2≠0|m|−1=1,解得m=−2.故选:A.小提示:本题考查一元一次方程,解题的关键是正确运用一元一次方程的定义.10、某种商品因换季准备打折出售,若按定价的七五折出售将赔25元,若按定价的九折出售将赚20元,则这种商品的定价为()A.280元B.300元C.320元D.200元答案:B分析:设这种商品的定价为x元,根据题意可直接列方程求解.设这种商品的定价为x元,由题意,得0.75x+25=0.9x﹣20,解得:x=300.故选:B.小提示:本题主要考查一元一次方程的实际应用,熟练掌握一元一次方程的应用是解题的关键.填空题11、已知x+2y−3=0,用含x的代数式表示y:__________,用含y的代数式表示x:_________.答案:y=3−xx=3−2y2分析:先把x当常数,求解函数值y,再把y当常数,求解自变量x,从而可得答案.解:∵x+2y−3=0,∴2y=−x+3,,∴y=3−x2∵x+2y−3=0,∴x=3−2y,,x=3−2y所以答案是:y=3−x2小提示:本题考查的是函数自变量与因变量之间的关系,掌握用含有一个变量的代数式表示另外一个变量是解题的关键.12、如图,在数轴上有A、B两个动点,O为坐标原点.点A、B从图中所示位置同时向数轴的负方向运动,A 点运动速度为每秒2个单位长度,B点运动速度为每秒3个单位长度,当运动___________秒时,点O恰好为线段AB中点.##0.8答案:45分析:设经过t秒,点O恰好是线段AB的中点,因为点B不能超过点O,所以0<t<2,经过t秒点A,B表示的数为,-2-2t,6-3t,根据题意可知-2-2t<0,6-3t>0,化简|-2-2t|=|6-3t|,即可得出答案.解:设经过t秒,点O恰好为线段AB中点,根据题意可得,经过t秒,点A表示的数为-2-2t,AO的长度为|-2-2t|,点B表示的数为6-3t,BO的长度为|6-3t|,因为点B不能超过点O,所以0<t<2,则|-2-2t|=|6-3t|,因为-2-2t<0,6-3t>0,所以,-(-2-2t)=6-3t,解得t=45.所以答案是:45.小提示:本题主要考查了数轴和绝对值的意义,解一元一次方程,根据题意列出等式应用绝对值的意义化简是解决本题的关键.13、若a,b为常数,无论k为何值时,关于x的一元一次方程(b+1)x=12−4ka,它的解总是1,则a,b 的值分别是_______.答案:a=0,b=11分析:将方程的解代入原方程,并化简.因为无论k为何值,它的解总是1,即可列出{4a=011−b=0,解出a 和b即可.把x=1代入方程得b+1=12−4ka,化简得4ka=11−b,∵k的值为全体实数,∴4a=0,且11−b=0,∴a=0,b=11.小提示:本题考查一元一次方程的解.理解方程的解的定义“能够使方程左右两边相等的未知数的值”是解答本题的关键.14、已知代数式5a+1与3(a−5)的值相等,那么a=______.答案:-8分析:根据题意列方程,然后进行解答即可得出a的值.解:根据题意得:5a+1=3(a-5),去括号得:5a+1=3a-15,移项合并同类项得:2a=-16,解得:a=-8.所以答案是:-8小提示:本题主要考查解一元一次方程,关键在于根据题意列出方程.15、如果△+△=★,〇=□+□,△=〇+〇+〇+〇,那么★÷□的值为_____.答案:16分析:根据题意可知★=2个△=8个〇=16个□,再代入★÷□即可计算求解.解:∵△+△=★,∴★=2个△,∵△=〇+〇+〇+〇,∴★=8个〇,∵〇=□+□,∴★=16个□,∴★÷□=16.所以答案是:16.小提示:本题考查了等式的性质与有理数的混合运算,由题得出★=16个□是解题关键.解答题16、若关于x的一元一次方程:kx-13-a=x-26-32的解是x=m,其中a,m,k为常数.(1)当a=m=2时,则k=______;(2)当a=2时,且m是整数,求正整数k的值;(3)是否存在m的值会使关于y的方程m(k-3)y=2+(3a-m)y无解,若存在请求m的值,若不存在请说明理由.答案:(1)54(2)k=1或2(3)m=-3分析:(1)将a=m=2代入一元一次方程:kx-13-a=x-26-32得出关于k的方程,解方程即可;(2)把a=2代入kx-13-2=x-26-32得:(2k-1)x=3,把x=m代入(2k-1)x=3得(2k-1)m=3,整理得出m=32k-1,根据m是整数,k为正整数,求出k=1或2 即可;(3)整理方程得:(mk-2m-3a)y=2,根据方程无解,得出mk-2m-3a=0,把x=m代入kx-13-a=x-26-32得km-1 3-a=m-26-32,整理方程得出2km=m+6a-9,把mk=2m+3a整体代入得2(2m+3a)=m+6a-9,解关于m的方程即可.(1)解:∵关于x的一元一次方程:kx-13-a=x-26-32的解是x=m,∴将a=m=2代入一元一次方程:kx-13-a=x-26-32得:2k-1 3-2=2-26-32,解得:k=54.所以答案是:54.(2)解:当a=2时,代入方程得kx-13-2=x-26-32,整理得:(2k-1)x=3,把x=m代入(2k-1)x=3得(2k-1)m=3,m=32k-1,∵m是整数,k为正整数,∴2k-1=1、3,∴k=1或2 .(3)解:整理方程得:(mk-2m-3a)y=2,∵无解,∴mk-2m-3a=0,即mk=2m+3a,把x=m代入kx-13-a=x-26-32得km-13-a=m-26-32,整理方程得2km=m+6a-9,把mk=2m+3a代入得2(2m+3a)=m+6a-9,解得m=-3.小提示:本题主要考查了解一元一次方程,熟练掌握解一元一次方程的一般步骤,是解题的关键.17、一艘轮船从甲码头到乙码头顺流而行,用了3h,从乙码头返回甲码头逆流而行,用了4h.已知水流的速度是3km/h,求船在静水中的平均速度.答案:船在静水中的平均速度为21km/h分析:设船在静水中的平均速度为x km/h,则顺流速度为(x+3)km/h,逆流速度为(x−3)km/h,根据题意,列出方程,即可求解.解:设船在静水中的平均速度为x km/h,则顺流速度为(x+3)km/h,逆流速度为(x−3)km/h,依题意,得3(x+3)=4(x−3),解得x=21.答:船在静水中的平均速度为21km/h.小提示:本题主要考查了一元一次方程的应用,明确题意,准确得到等量关系是解题的关键.18、定义:对于一个有理数x,我们把[x]称作x的对称数:若x≥0,则[x]=x−2,若x<0,则[x]=x+2:例:[1]=1−2=−1 , [−2]=−2+2=0.(1)求[2]+[−1]的值;(2)若x<−1时,解方程:[2x]+[x+1]=1答案:(1)1;.(2)x=-43分析:(1)根据对称数的定义求得即可;(2)根据对称数的定义化简方程,然后解方程即可.(1)解:[2]=2-2=0,[-1]=-1+2=1;∴[2]+ [-1]=0+1=1;(2)解:当x<-1时,方程为:2x+2+x+1+2=1,;解得:x=-43故方程的解为:x=-4.3小提示:本题考查了对称数的定义,代数式求值以及解一元一次方程,能够根据对称数的概念化简是解题的关键.。
【精选】人教版七年级上册数学第三章《一元一次方程》知识点+典型例题

【精选】人教版七年级上册数学第三章《一元一次方程》知识点+典型例题知识点、概念总结1.一元一次方程:只含有一个未知数,并且未知数的次数是1,并且含未知数项的系数不是零的整式方程是一元一次方程。
2.一元一次方程的标准形式:ax+b=0(x是未知数,a、b是已知数,且a≠0)。
3.条件:一元一次方程必须同时满足4个条件:(1)它是等式;(2)分母中不含有未知数;(3)未知数最高次项为1;(4)含未知数的项的系数不为0.4.等式的性质:等式的性质一:等式两边同时加一个数或减去同一个数或同一个整式,等式仍然成立。
等式的性质二:等式两边同时扩大或缩小相同的倍数(0除外),等式仍然成立。
等式的性质三:等式两边同时乘方(或开方),等式仍然成立。
解方程都是依据等式的这三个性质等式的性质一:等式两边同时加一个数或减同一个数,等式仍然成立。
5.合并同类项(1)依据:乘法分配律(2)把未知数相同且其次数也相同的相合并成一项;常数计算后合并成一项(3)合并时次数不变,只是系数相加减。
6.移项(1)含有未知数的项变号后都移到方程左边,把不含未知数的项移到右边。
(2)依据:等式的性质(3)把方程一边某项移到另一边时,一定要变号。
7.一元一次方程解法的一般步骤:使方程左右两边相等的未知数的值叫做方程的解。
一般解法:(1)去分母:在方程两边都乘以各分母的最小公倍数;(2)去括号:先去小括号,再去中括号,最后去大括号;(记住如括号外有减号的话一定要变号)(3)移项:把含有未知数的项都移到方程的一边,其他项都移到方程的另一边;移项要变号(4)合并同类项:把方程化成ax=b(a≠0)的形式;(5)系数化成1:在方程两边都除以未知数的系数a,得到方程的解x=b/a.8.同解方程如果两个方程的解相同,那么这两个方程叫做同解方程。
9.方程的同解原理:(1)方程的两边都加或减同一个数或同一个等式所得的方程与原方程是同解方程。
(2)方程的两边同乘或同除同一个不为0的数所得的方程与原方程是同解方程。
七年级数学上册第三章一元一次方程知识点总结(超全)

(名师选题)七年级数学上册第三章一元一次方程知识点总结(超全)单选题1、如果关于x的方程(m−2)x=8无解,那么m的取值范围()A.任意实数B.m>2C.m≠2D.m=2答案:D分析:根据ax=b中当a=0,b≠0方程无解可知当m-2=0时关于x的方程(m−2)x=8无解.解:由题意得:当m-2=0时关于x的方程(m−2)x=8无解,解得m=2,故选D.小提示:本题考查了解一元一次方程无解的情况,根据题意得出关于m-2=0是解题关键.2、一支球队参加比赛,开局9场保持不败,共积21分,比赛规定胜一场得3分,平一场得1分,则该队共胜的场数为()A.6场B.7场C.8场D.9场答案:A分析:设该队前9场比赛共平了x场,则胜了(9-x)场.根据共得21分列方程求解.解:设该队前9场比赛共平了x场,则胜了(9-x)场.根据题意得:3(9-x)+x=21,解得:x=3.9-x=6.答:该队前9场比赛共胜了6场.故选:A.小提示:本题考查了一元一次方程的应用,解题的关键是根据题意找到等量关系并正确的列出方程.3、若关于x的方程5x−m=2(x−2)+1的解是x=−2,则m的值为()A.-3B.-5C.-13D.5答案:A分析:把x=−2代入方程即可得到一个关于m的方程,解方程即可求解.解∶把x=−2代入方程5x−m=2(x−2)+1得∶5×(−2)−m=2×(−2−2)+1,解得m=-3.故选∶ A.小提示:本题考查了方程的解的定义,方程的解就是能使方程左右两边相等的未知数的值,理解定义是解题的关键.4、某校手工社团30名学生制作纸飞机模型,每人每小时可做20个机身或60个机翼,一个飞机模型要一个机身配两个机翼,为了使每小时制作的成品刚好配套,应该分配多少名学生做机身,多少名学生做机翼?设分配x名学生做机身,则可列方程为()A.20x=60(30−x)B.20x=2×60(30−x)C.2×20x=60(30−x)D.60x=20(30−x)答案:C分析:设分配x名学生做机身,根据一个飞机模型要一个机身配两个机翼,则飞机模型的个数乘以2等于机翼的个数,据此列出一元一次方程即可求解.设分配x名学生做机身,则可列方程为, 2×20x=60(30−x)故选C.小提示:本题考查了一元一次方程的应用,找到等量关系是解题的关键.5、疫情无情人有情,爱心捐款传真情.某校三个年级为疫情重灾区捐款,经统计,七年级捐款数占全校三个年级捐款总数的25,八年级捐款数是全校三个年级捐款数的平均数,已知九年级捐款1916元,求其他两个年级的捐款数若设七年级捐款数为x元,则可列方程为()A.x+65x+1916=52x B.25x+13x+1916=xC.x+25x+1916=3x D.x+25x+1916=52x答案:A分析:根据七年级的捐款为x元,可以求得三个年级的总的捐款数,然后即可得到八年级的捐款数,从而可以列出相应的方程,本题得以解决.解:由题意可得,七年级捐款数为x 元,则三个年级的总的捐款数为:x ÷25=52x ,故八年级的捐款为:52x 3=56x , 则x +56x +1916=52x ,故选:A .小提示:本题考查由实际问题抽象出一元一次方程,解答本题的关键是明确题意,列出相应的方程.6、新型冠状肺炎疫情正在全球蔓延肆虐,口罩成了人们生活中必不可少的物品.某口罩厂有26名工人,每人每天可以生产400个口罩面或500个口罩耳绳,一个口罩面需要配两个耳绳,为使每天生产的口罩刚好配套,设安排x 名工人生产口罩面,则下列所列方程正确的是( )A .2×500(26−x )=400xB .500(26−x )=400xC .500(26−x )=2×400xD .500(26−x )=400x答案:C分析:安排x 名工人生产口罩面,则(26−x )人生产耳绳,由一个口罩面需要配两个耳绳可知耳绳的个数是口罩面个数的2倍从而得出等量关系,就可以列出方程.解:设安排x 名工人生产口罩面,则(26−x )人生产耳绳,由题意得500(26−x )=2×400x .故选:C .小提示:本题考查了由实际问题抽象出一元一次方程,解答本题的关键是读懂题意,设出未知数,找出合适的等量关系,列方程.7、解一元一次方程12(x +1)=1−13x 时,去分母正确的是( )A .3(x +1)=1−2xB .2(x +1)=1−3xC .2(x +1)=6−3xD .3(x +1)=6−2x答案:D分析:根据等式的基本性质将方程两边都乘以6可得答案.解:方程两边都乘以6,得:3(x+1)=6﹣2x,故选:D.小提示:本题主要考查解一元一次方程,解题的关键是掌握解一元一次方程的步骤和等式的基本性质.8、已知一项工程,甲单独完成需要5天,乙单独完成需要10天,现先由甲单独做2天,然后再安排乙与甲合作完成剩下的部分,则完成这项工程共耗时( )A.1天B.2天C.3天D.4天答案:D分析:设完成这项工程共耗时x天,则甲工作了x天,乙工作了(x﹣2)天,根据总工作量=甲完成的工作量+乙完成的工作量,即可得出关于x的一元一次方程,解之即可得出结论.解:设完成这项工程共耗时x天,则甲工作了x天,乙工作了(x﹣2)天,根据题意得:x5+x−210=1,解得:x=4.即完成这项工程共耗时4天.故选:D小提示:本题考查了一元一次方程的应用,找准等量关系,正确列出一元一次方程是解题的关键.9、对于两个不相等的有理数a,b,我们规定符号min{a,b}表示a、b两数中较小的数,例如min{2,-4}=-4,则方程min{x,-x}=3x+4的解为()A.x=-1B.x=-2C.x=-1或x=-2D.x=1或x=2答案:B分析:根据题意可得:min{x,-x}=x或−x,所以x=3x+4或−x=3x+4,据此求出x的值即可.∵规定符号min{a,b}表示a、b两数中较小的数,∴当min{x,-x}表示为x时,则x=3x+4,解得x=−2,当min{x,-x}表示为−x时,则−x=3x+4,解得x=−1,∵x=−1时,最小值应为x,与min{x,-x}=−x相矛盾,故舍去,∴方程min{x,-x}=3x+4的解为x=−2,故选:B.小提示:本题主要考查一元一次方程的解法,能根据题意正确列出一元一次方程是解题的关键.−3=0;④x−y=6中,为一元一次方程的有()10、在方程①x+1=0;②1−x2=0;③1xA.4个B.3个C.2个D.1个答案:D分析:只含有一个未知数(元)并且未知数的指数是1 (次)的方程叫做一元一次方程,它的一般形式是ax+b=0 (a,b是常数且a≠0),根据此定义判断即可.①x+1=0;是一元一次方程,故①正确;②1−x2=0;不是一元一次方程,故②错误;−3=0;不是一元一次方程,故③错误;③1x④x−y=6不是一元一次方程,故④错误;为一元一次方程的有1个;故选:D.小提示:本题主要考查了一元一次方程的识别,注意三个要点:只含有一个未知数,且未知数的指数是1,一次项系数不是0,这是这类题目考查的重点.填空题11、某品牌旗舰店平日将某商品按进价提高40%后标价,在某次电商购物节中,为促销该商品,按标价8折销售,售价为2240元,则这种商品的进价是______元.答案:2000分析:设这种商品的进价是x元,根据提价之后打八折,售价为2240元,列方程解答即可.设这种商品的进价是x元,由题意得,(1+40%)x×0.8=2240,解得:x=2000,故答案为2000.小提示:本题考查了一元一次方程的应用——销售问题,弄清题意,熟练掌握标价、折扣、实际售价间的关系是解题的关键.12、若x|m|﹣10=2是关于x的一元一次方程,则m的值是 _____.答案:±1分析:只含有一个未知数(元),并且未知数的指数是1(次)的方程叫做一元一次方程.它的一般形式是ax+b=0(a,b是常数且a≠0).解:根据题意,有|m|=1,∴m=±1,所以答案是:±1.小提示:本题主要考查了一元一次方程的一般形式,只含有一个未知数,且未知数的指数是1,一次项系数不是0,这是这类题目考查的重点.13、已知5x2−5x−3=7,利用等式的基本性质,x2−x的值为___________.答案:2分析:首先根据等式的性质1,两边同时+3得5x2−5x=10,再根据等式的性质2,两边同时除以5即可得到答案.解:5x2−5x−3=7,根据等式的性质1,两边同时+3得:5x2−5x−3+3=7+3,即:5x2−5x=10,根据等式的性质2,两边同时除以5得:5x2−5x5=105,∴x2−x=2,故填:2.小提示:此题主要考查了等式的性质,关键是掌握等式的性质:性质1、等式两边加同一个数(或式子)结果仍得等式;性质2、等式两边乘同一个数或除以一个不为零的数,结果仍得等式.14、已知数轴上的点A,B表示的数分别为−2,4,P为数轴上任意一点,表示的数为x,若点P到点A,B的距离之和为7,则x的值为 _____.答案:−2.5或4.5分析:根据数轴上两点间的距离公式列出方程,求出方程的解即可得到x的值.解:根据题意得:|x+2|+|x-4|=7,当x<-2时,化简得:-x-2-x+4=7,解得:x=-2.5;当-2≤x<4时,化简得:x+2-x+4=7,无解;当x≥4时,化简得:x+2+x-4=7,解得:x=4.5,综上,x的值为-2.5或4.5.所以答案是:-2.5或4.5.小提示:此题考查了数轴,弄清数轴上两点间的距离公式是解本题的关键.15、若关于x的方程2kx+m3=x−nk6+2,无论k为任何数时,它的解总是x=1,那么m+n=_______.答案:52分析:先将x=1代入原方程得,根据无论k为任何数时(4+n)k=13−2m恒成立,可得k的系数为0,由此即可求出答案.解:将x=1代入2kx+m3=x−nk6+2,∴2k+m3=1−nk6+2,∴(4+n)k=13−2m,由题意可知:无论k为任何数时(4+n)k=13−2m恒成立,∴n+4=0,∴n=−4,m=132,∴m+n=52,所以答案是:52小提示:本题主要考查了一元一次方程,解题的关键是正确理解一元一次方程的解.解答题16、解方程:(1)3x−2(2x−1)=7(2)2x+13−5x−16=1答案:(1)x=−5(2)x=−3分析:(1)方程去括号,移项,合并,把x系数化为1,即可求出解;(2)方程去分母,去括号,移项,合并,把x系数化为1,即可求出解.(1)解:去括号得:3x−4x+2=7移项得:3x−4x=7−2合并同类项得:−x=5系数化为1得:x=−5(2):去分母得:2(2x+1)−(5x−1)=6去括号得:4x+2−5x+1=6移项合并同类项得:−x=3系数化为1得:x=−3小提示:此题考查了解一元一次方程,熟练掌握解方程的步骤是解本题的关键.17、解方程:(1)4−x3=x−35−1(2)5(x−3)−2(x−3)=0答案:(1)x=112(2)x=3分析:(1)根据解一元一次方程的步骤“去分母,去括号,移项、合并同类项,系数化为1”解答即可;(2)根据解一元一次方程的步骤“去括号,移项、合并同类项,系数化为1”解答即可.(1)4−x3=x−35−1解:去分母,得:5(4−x)=3(x−3)−15去括号,得:20−5x=3x−9−15移项、合并同类项,得:−8x=−44系数化为1,得:x=112(2)5(x−3)−2(x−3)=0解:去括号,得5x−15−2x+6=0移项、合并同类项得:3x=9系数化为1,得:x=3小提示:本题考查解一元一次方程.熟练掌握解一元一次方程的步骤是解题关键.18、解方程:(1)3x−1=8;(2)x+12−1=x−23.答案:(1)x=3(2)x=-1分析:(1)按解一元一次方程的一般步骤求解即可;(2)按解一元一次方程的一般步骤求解即可.(1)解:由原方程移项、合并同类项,得3x=9,解得x=3,所以,原方程的解为x=3;(2)解:去分母,得3(x+1)-6=2(x-2),去括号,得3x+3-6=2x-4,移项、合并同类项,得x=-1,所以,原方程的解为x=-1.小提示:本题考查了一元一次方程解法.解一元一次方程的一般步骤是:去分母,去括号,移项,合并同类项,系数化为1.。
人教新课标第三章一元一次方程知识点总结

1 1 的 两 边 同 ________________________ , 得 到 等 式 x , 这 是 依 据 8 2
______________________________________. 11、根据等式的性质解下列方程 (1) 2x 7 3 (2) 6 x 6 8 (3)
2
3
3.2—3.3 解一元一次方程 知识点归纳
一、方程中的合并同类项 解方程时,将含有未知数的几个项合成一项叫合并同类项,它的依据是乘法 的分配律,是分配律的逆用。 ※※★【注意】 (1)合并同类项的实质是系数的合并,字母及指数都不变 (2)在等号两边的同类项不能合并 (3)注意系数是负数的项的合并 (4)把常数项相加 二、系数化为 1 系数化为 1 的目的,是将形如 ax b(a 0) 化成 x 的形式,也就是求出方程 的解 x 。系数化为 1 的依据是等式性质 2,方程两边同时乘以系数 a(a 0) 的倒 数 ,或者同除以系数 a 本身。
D. x Байду номын сангаас 9
2
3、若关于 x 的方程 3x a x 1 的解是 x 2 ,则 a 的值为________. 4、如果关于 x 的方程 3x
5 2 k
6 0 是一元一次方程,则 k __________.
5、已知 x 1 是方程 mx 6 2 的解,则 m _________. 6、 x 的 8 倍加上 4 与 x 的 5 倍相等,列方程为_______________________. 7、已知方程 (a 4) x
※※※★★【注意】在解一元一次方程时,把系数化为
b a
b a
1 a
1 要注意一下几点:
新人教版七年级数学上册第三章一元一次方程知识与题型总结

每个学生都可以用的“超级数学学习笔记”一元一次方程知识框架与典型例题一、知识点知识点一:1、含有______________的等式是方程,使方程的等式两边的相等的值教方程的解,方程中含有____个未知数,未知数的_________________的方程称为一元一次方程(注意:方程一定是等式,等式不一定是方程)知识点二:等式的性质1 等式两边都______(或者减去)_________(或同一个式子)所得结果仍是____.等式的性质2 等式两边都______(或者除以)_________(或同一个式子)(除数或者除式不能为0),所得结果仍是____.知识点三:解方程的步骤:1、 如果有分母,先去____, (注意去分母时等式两边每一项都乘以最小公倍数)2、 后去_____,(去括号时,注意括号前面的符合)3、 再_____、(移项要变号)4、 ______得到标准形式ax=b(a ≠0),最后两边同除以______的系数。
(合并同类型)5、 易错知识辨析:(1)判断一个方程是不是一元一次方程,首先在整式方程前提下,化简后满足只含有一个未知数,并且未知数的次数是1,系数不等于0的方程,像21=x,()1222+=+x x 等不是一元一次方程. (2)解方程的基本思想就是应用等式的基本性质进行转化,要注意:①方程两边不能乘以(或除以)含有未知数的整式,否则所得方程与原方程不同解;②去分母时,不要漏乘没有分母的项;③解方程时一定要注意“移项”要变号.二、常考题型题型总结题型一:判定是不是方程1下列各式中:① 3+3=6 ② 123>+x ③ 39-x =7 ④ 122=-z z⑤ 0=m (6) 239=-π(7)236=-πx有______条是方程,其中__________(填写编号)是一元一次方程。
每个学生都可以用的“超级数学学习笔记”2、下列式子谁有资格进入住方程乐园?2973=+x ,62-=x x ,y x 21-,071<-x ,422=-y x ,224-=+- 3、判断是不是一元一次方程?2(x +100)=600 , (x +200)+ x +(x -448)=300644x +(x +4)=8, x +5=8 , x -2y =6 , 32x -2y =120题型二:判定是不是一元一次方程1、如果单项式121-2n a b +与213n m a b -是同类项,则n=___,m=____ 2 如果代数式3x-5与1-2x 的值互为相反数,那么x=____ 3 若方程3x-5=4x+1与3m-5=4(m+x)-2m 的解相同,求()200820m +的值4.关于x 的方程230m mx m ++-=是一个一元一次方程,则m =_______.5.关于x 的方程()112436x x m +=-+的解是116-,则()20021m -=_______. 6.关于x 的方程39x =与4x k +=解相同,则代数式212kk-的值为_______. 7.若关于x 的方程()23202k x kx -+-=k 是一元一次方程,则k =_______,方程的解为_______. 8.当x =_______时,代数式12x -与113x +-的值相等.9 若关于x 的一元一次方程231,32x k x k---=的解是x= -1,则k 的值是( )A 27B 1C 1311- D 011.已知方程112332x x x ---=+-与方程2224334kx xk +--=-的解相同,则k 的值为( ) A.0B.2C.1D.1-11.已知方程233mx x -=+的解满足10x -=,则m 的值是( ) A.6-B.12-C.6-或12-D.任何数12.已知当1a =,2b =-时,代数式10ab bc ca ++=,则c 的值为( ) A.12B.6C.6-D.12-13.(8分)解关于x 的方程()0b x x aa b a b+-=≠≠. 14.(10分)已知2ym my m +=-.每个学生都可以用的“超级数学学习笔记”(1)当4m =时,求y 的值;(2)当4y =时,求m 的值.15 已知x=- 2是方程22328x mx m -+=的解,求m 的值。
人教版七年级上册数学:第三章《一元一次方程》全章复习与巩固(提高)知识讲解(含答案)
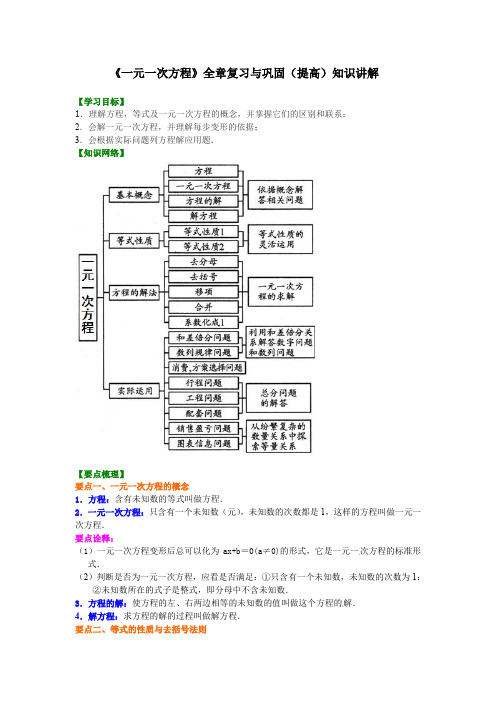
《一元一次方程》全章复习与巩固(提高)知识讲解【学习目标】1.理解方程,等式及一元一次方程的概念,并掌握它们的区别和联系;2.会解一元一次方程,并理解每步变形的依据;3.会根据实际问题列方程解应用题.【知识网络】【要点梳理】要点一、一元一次方程的概念1.方程:含有未知数的等式叫做方程.2.一元一次方程:只含有一个未知数(元),未知数的次数都是1,这样的方程叫做一元一次方程.要点诠释:(1)一元一次方程变形后总可以化为ax+b=0(a≠0)的形式,它是一元一次方程的标准形式.(2)判断是否为一元一次方程,应看是否满足:①只含有一个未知数,未知数的次数为1;②未知数所在的式子是整式,即分母中不含未知数.3.方程的解:使方程的左、右两边相等的未知数的值叫做这个方程的解.4.解方程:求方程的解的过程叫做解方程.要点二、等式的性质与去括号法则1.等式的性质:等式的性质1:等式两边加(或减)同一个数(或式子),结果仍相等.等式的性质2:等式两边乘同一个数,或除以同一个不为0的数,结果仍相等.2.合并法则:合并时,把系数相加(减)作为结果的系数,字母的指数不变.3.去括号法则:(1)括号外的因数是正数,去括号后各项的符号与原括号内相应各项的符号相同.(2)括号外的因数是负数,去括号后各项的符号与原括号内相应各项的符号相反. 要点三、一元一次方程的解法解一元一次方程的一般步骤:(1)去分母:在方程两边同乘以各分母的最小公倍数.(2)去括号:依据乘法分配律和去括号法则,先去小括号,再去中括号,最后去大括号.(3)移项:把含有未知数的项移到方程一边,常数项移到方程另一边.(4)合并:逆用乘法分配律,分别合并含有未知数的项及常数项,把方程化为ax =b (a ≠0)的形式.(5)系数化为1:方程两边同除以未知数的系数得到方程的解b x a=(a ≠0). (6)检验:把方程的解代入原方程,若方程左右两边的值相等,则是方程的解;若方程左右两边的值不相等,则不是方程的解.要点四、用一元一次方程解决实际问题的常见类型1.行程问题:路程=速度×时间2.和差倍分问题:增长量=原有量×增长率3.利润问题:商品利润=商品售价-商品进价4.工程问题:工作量=工作效率×工作时间,各部分劳动量之和=总量5.银行存贷款问题:本息和=本金+利息,利息=本金×利率×期数6.数字问题:多位数的表示方法:例如:32101010abcd a b c d =⨯+⨯+⨯+.【典型例题】类型一、一元一次方程的相关概念1.已知方程(3m -4)x 2-(5-3m )x -4m =-2m 是关于x 的一元一次方程,求m 和x 的值.【思路点拨】若一个整式方程经过化简变形后,只含有一个未知数,并且未知数的次数都是1,系数不为0,则这个方程是一元一次方程.【答案与解析】解:因为方程(3m -4)x 2-(5-3m )x -4m =-2m 是关于x 的一元一次方程,所以3m -4=0且5-3m ≠0.由3m -4=0解得43m =,又43m =能使5-3m ≠0,所以m 的值是43. 将43m =代入原方程,则原方程变为485333x ⎛⎫--⨯= ⎪⎝⎭,解得83x =-. 所以43m =,83x =-. 【总结升华】解答这类问题,一定要严格按照一元一次方程的定义.方程(3m -4)x 2-(5-3m )x -4m =-2m 2是关于x 的一元一次方程,就是说x 的二次项系数3m -4=0,而x的一次项系数5-3m≠0,m的值必须同时符合这两个条件.举一反三:【高清课堂:一元一次方程复习393349 等式和方程例3】【变式】下面方程变形中,错在哪里:(1)方程2x=2y两边都减去x+y,得2x-(x+y)=2y-(x+y), 即x-y=-(x-y).方程 x-y=-(x-y)两边都除以x-y, 得1=-1.(2)3721223x xx-+=+,去分母,得3(3-7x)=2(2x+1)+2x,去括号得:9-21x=4x+2+2x.【答案】(1)答:错在第二步,方程两边都除以x-y.(2)答:错在第一步,去分母时2x项没乘以公分母6.2.如果5(x+2)=2a+3与(31)(53)35a x a x+-=的解相同,那么a的值是________.【答案】7 11【解析】由5(x+2)=2a+3,解得275ax-=.由(31)(53)35a x a x+-=,解得95x a=-.所以27955aa-=-,解得711a=.【总结升华】因为两方程的解相同,可把a看做已知数,分别求出它们的解,令其相等,转化为求关于a的一元一次方程.举一反三:【变式】已知|x+1|+(y+2x)2=0,则y x=________.【答案】1类型二、一元一次方程的解法3.解方程:4621132x x-+-=.【答案与解析】解:去分母,得:2(4-6x)-6=3(2x+1).去括号,得:8-12x-6=6x+3.移项,合并同类项,得:-18x=1.系数化为1,得:118x=-.【总结升华】转化思想是初中数学中一种常见的思想方法,它能将复杂的问题转化为简单的问题,将生疏的问题转化为熟悉的问题,将未知转化为已知.事实上解一元一次方程就是利用方程的同解原理,将复杂的方程转化为简单的方程直至求出它的解.举一反三:【变式1】解方程26752254436z z z zz+---++=-【答案】解:把方程两边含有分母的项化整为零,得267522544443366z z z z z +++-=--+. 移项,合并同类项得:1122z =,系数化为1得:z =1. 【高清课堂:一元一次方程复习 393349 解方程例1(2)】 【变式2】解方程: 0.10.050.20.05500.20.54x x +--+=. 【答案】 解:把方程可化为:0.520.550254x x +--+=, 再去分母得:232x =-解得:16x =-4.解方程3{2x -1-[3(2x -1)+3]}=5.【答案与解析】解:把2x -1看做一个整体.去括号,得:3(2x -1)-9(2x -1)-9=5.合并同类项,得-6(2x -1)=14. 系数化为1得:7213x -=-,解得23x =-. 【总结升华】把题目中的2x -1看作一个整体,从而简化了计算过程.本题也可以考虑换元法:设2x -1=a ,则原方程化为3[a -(3a+3)]=5.类型三、特殊的一元一次方程的解法1.解含字母系数的方程5.解关于x 的方程:11()(2)34m x n x m -=+ 【思路点拨】这个方程化为标准形式后,未知数x 的系数和常数都是以字母形式出现的,所以方程的解的情况与x 的系数和常数的取值都有关系.【答案与解析】解:原方程可化为:(43)462(23)m x mn m m n -=+=+ 当34m ≠时,原方程有唯一解:4643mn m x m +=-; 当33,42m n ==-时,原方程无数个解; 当33,42m n =≠-时,原方程无解; 【总结升华】解含字母系数的方程时,一般化为最简形式ax b =,再分类讨论进行求解,注意最后的解不能合并,只能分情况说明.2.解含绝对值的方程6. 解方程|x -2|=3.【答案与解析】解:当x -2≥0时,原方程可化为x -2=3,得x =5.当x -2<0时,原方程可化为-(x -2)=3,得 x =-1.所以x =5和x =-1都是方程|x -2|=3的解.【总结升华】如图所示,可以看出点-1与5到点2的距离均为3,所以|x -2|=3的意义为在数轴上到点2的距离等于3的点对应的数,即方程|x -2|=3的解为x =-1和x =5.举一反三:【变式1】若关于x 的方程230x m -+=无解,340x n -+=只有一个解,450x k -+=有两个解,则,,m n k 的大小关系为: ( )A . m n k >> B.n k m >> C.k m n >> D.m k n >>【答案】A【变式2】若9x =是方程123x m -=的解,则__m =;又若当1n =时,则方程123x n -=的解是 .【答案】1; 9或3. 类型四、一元一次方程的应用7.李伟从家里骑摩托车到火车站,如果每小时行30千米,那么比火车开车时间早到15分钟;若每小时行18千米,则比火车开车时间迟到15分钟,现在李伟打算在火车开车前10分钟到达火车站,求李伟此时骑摩托车的速度应是多少?【思路点拨】本题中的两个不变量为:火车开出的时间和李伟从家到火车站的路程不变.【答案与解析】 解:设李伟从家到火车站的路程为y 千米,则有:151530601860y y +=-,解得:452y = 由此得到李伟从家出发到火车站正点开车的时间为4515213060+=(小时). 李伟打算在火车开车前10分钟到达火车站时,设李伟骑摩托车的速度为x 千米/时, 则有:452271010116060y x ===--(千米/时) 答:李伟此时骑摩托车的速度应是27千米/时.【总结升华】在解决问题时,当发现某种方法不能解决问题时,应该及时变换思维角度,如本题直接设未知数较难时,应迅速变换思维的角度,合理地设置间接未知数以寻求新的解决问题的途径和方法.8. 黄冈某地“杜鹃节”期间,某公司70名职工组团前往参观欣赏,旅游景点规定:①门票每人60元,无优惠;②上山游玩可坐景点观光车,观光车有四座和十一座车,四座车每辆60元,十一座车每人10元.公司职工正好坐满每辆车且总费用刚好为4920元时,问公司租用的四座车和十一座车各多少辆?【答案与解析】解:设四座车租x 辆,十一座车租70411x -辆,依题意得: 7047060601110492011x x -⨯++⨯⨯= 解得:x =1,704611x -= 答:公司租用的四座车和十一座车分别是1辆和6辆。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第三章一元一次方程知识要点梳理及典型例题一.元一次方程及解的概念1、一元一次方程的概念只含有一个未知数,并且未知数的次数都是1的方程叫做一元一次方程。
一元一次方程的标准形式是:ax+b=0(其中x是未知数,a,b是已知数,且a≠0)。
典型例题:下列方程是一元一次方程的是()A.x+y=1B.250x x+= C.3x+7=16 D.153 2x-=做题要点:判断一元一次方程必须满足的3个条件:只含有一个未知数;未知数的次数是1次;整式方程。
2、方程的解使方程左右两边的值相等的未知数的值叫做方程的解。
典型例题:以x为未知数的方程)2(21xaax-=-的解是x=3,求a的值。
做题要点:将方程的解代入方程,得到一个以a为未知数的新方程,解得a的值。
二.方程变形——解方程的重要依据1、等式的基本性质等式的性质1:等式两边加(或减)同一个数(或式子),结果仍相等。
即:如果,那么;(c为一个数或一个式子)。
等式的性质2:等式两边乘同一个数,或除以同一个不为0的数,结果仍相等。
即:如果,那么;如果,那么典型例题:1)、下列等式变形中不正确的是()A、若x=y,则x+5=y+5 B.若x ya a=,则x=yC.若-3x=-3y,则x=yD.mx=my,x=y2)、若2x+1=8,那么4x+2= 。
2、分数的基本的性质分数的分子、分母同时乘以或除以同一个不为0的数,分数的值不变。
即://a am a m b bmb m== (其中m ≠0)注:分数的基本的性质主要是用于将方程中的小数系数(特别是分母中的小数)化为整数, 如方程:30.5x - -40.2x + =1.6,将其化为的形式:10(3)10(4)1.652x x -+-=。
方程的右边没有变化,这要与“去分母”区别开。
典型例题三.解一元一次方程的一般步骤 1、解一元一次方程的基本思路通过对方程变形,把含有未知数的项归到方程的一边,把常数项归到方程的另一边,最终把方程“转化”成x =a 的形式。
2、解一元一次方程的一般步骤是注意:① 解方程时,表中有些变形步骤可能用不到,并且也不一定按照自上而下的顺序,要根据方程形式灵活安排求解步骤。
② 去分母时,不要漏乘没有分母的项。
6.003.02.05.05.01.24.0+-=+x x③ 去括号时,不要漏乘括号内的项,若括号前为“-”号,括号内各项要改变符号。
典型例题: 1、 x x x 2532421-+=- 2、 2(2x+1)=3(x-2)-(x-6)3、 67313x x +=+ 4、31632141+++=--x x x5、)33102(21)]31(311[2xx x x --=+--一元一次方程应用题专题总结一、列一元一次方程解应用题的一般步骤(1)审题,分析题中已知什么,未知什么,明确各量之间的关系,寻找等量关系. (2)设未知数,一般求什么就设什么为x ,但有时也可以间接设未知数.(3)列方程,把相等关系左右两边的量用含有未知数的代数式表示出来,列出方程. (4)解方程.(5)检验,看方程的解是否符合题意. (6)写出答案.二、解应用题的书写格式:设→根据题意→解这个方程→答。
(1)在一道应用题中,往往含有几个未知数量,应恰当地选择其中的一个,用字母x 表示出来,即所设的未知数,然后根据数量之间的关系,将其它几个未知数量用含x 的代数式表示。
(2)解应用题时,不能漏掉“答”,“设”和“答”中都必须写清单位名称。
(3)列方程时,要注意方程两边是同一个量,并且单位要统一。
(4)一般情况下,题目中所给的条件在列方程时不能重复使用,也不能漏掉不用。
三、典型例题:1. 和、差、倍、分问题:(1)倍数关系:通过关键词语“是几倍,增加几倍,增加到几倍,增加百分之几,增长率……”来体现。
(2)多少关系:通过关键词语“多、少、和、差、不足、剩余……”来体现。
例.某校共有学生1050人,女生占男生的一半,求男生的人数。
分析:等量关系为:男生人数+女生人数=学生总人数解:设男生人数为xx+0.5x=10501.两个村共有834人,甲村的人数比乙村的人数的一半还少111人,两村各有多少人?2.两组工人,按计划本月应共生产680个零件,实际第一组超额20%、第二组超额15%完成了本月任务,因此比原计划多生产118个零件。
问本月原计划每组各生产多少个零件?2. 劳力调配问题:这类问题要搞清人数的变化,常见题型有:(1)既有调入又有调出;(2)只有调入没有调出,调入部分变化,其余不变;(3)只有调出没有调入,调出部分变化,其余不变。
例. 甲、乙两车间各有工人若干,如果从乙车间调100人到甲车间,那么甲车间的人数是乙车间剩余人数的6倍;如果从甲车间调100人到乙车间,这时两车间的人数相等,求原来甲乙车间的人数。
分析:等量关系(1)原来甲车间的人数+100=(原来乙车间的人数-100)× 6(2)原来甲车间的人数-100=原来乙车间的人数+100解:设求原来乙车间的x人,由等量关系(2)得原来甲车间的人数=x+200,代入(1)中得方程x+200+100=(x-100)× 61.某厂一车间有64人,二车间有56人。
现因工作需要,要求第一车间人数是第二车间人数的一半。
问需从第一车间调多少人到第二车间?2.甲队人数是乙队人数的2倍,从甲队调12人到乙队后,甲队剩下来的人数是原乙队人数的一半还多15人。
求甲、乙两队原有人数各多少人?3. 比例分配问题:这类问题的一般思路为:设其中一份为x,利用已知的比,写出相应的代数式。
常用等量关系:总量=各部分之和, 比值相等。
例. 三个正整数的比为1:2:4,它们的和是84,那么这三个数中最大的数是几?解:设最小的数为x,则中间数为2x,最大数字为4xx+2x+4x=841.图纸上某零件的长度为32cm,它的实际长度是4cm,那么量得该图纸上另一个零件长度为12cm,求这个零件的实际长度。
2.一时期,日元与人民币的比价为25.2:1,那么日元50万,可以兑换人民币多少元?4. 数字问题(1)要搞清楚数的表示方法:一个二位数的十位数字为a,个位数字是b(其中a、b均为整数,且1≤a≤9, 0≤b≤9)则这个三位数表示为:10a+b。
(2)数字问题中一些表示:两个连续整数之间的关系,较大的比较小的大1;偶数用2n表示,连续的偶数用2n+2或2n—2表示;奇数用2n+1或2n—1表示。
例. 一个两位数,个位上的数是十位上的数的2倍,如果把十位与个位上的数对调,那么所得的两位数比原两位数大36,求原来的两位数分析:等量关系:(1)现在的两位数-原来的两位数=36(2)原来的两位数个位上的数=十位上的数×2解:原来的两位数十位上的数为x,则由(2)得原来的两位数个位上的数为2x现在的两位数=2x ×10+x,所以由(1)得方程(2x ×10+x ) - (x ×10+2x )=36现在的两位数 原来的两位数1.将连续的奇数1,3,5,7,9…,排成如下的数表:(1)十字框中的五个数的平均数与15有什么关系?(2)若将十字框上下左右平移,可框住另外的五个数,这五个数的和能等于315吗?若能,请求出这五个数;若不能,请说明理由.5. 工程问题:工程问题中的三个量及其关系为:工作总量=工作效率×工作时间经常在题目中未给出工作总量时,设工作总量为单位1,则 工作效率 =1工作时间例. 一件工程,甲独做需15天完成,乙独做需12天完成,现先由甲、乙合作3天后,甲有其他任务,剩下工程由乙单独完成,问乙还要几天才能完成全部工程?分析:设工程总量为单位1,等量关系为:甲、乙合作3天后+乙单独完成剩下工程=1解:设乙还要x 天才能完成全部工程111+3+x 1151212⨯⨯=()1.某工程由甲、乙两队完成,甲队单独完成需16天,乙队单独完成需12天。
如先由甲队做4天,然后两队合做,问再做几天后可完成工程的六分之五?2.有一个水池,用两个水管注水。
如果单开甲管,2小时30分注满水池,如果单开 乙管,5小时注满水池。
① 如果甲、乙两管先同时注水20分钟,然后由乙单独注水。
问还需要多少时间才能把 水池注满?② 假设在水池下面安装了排水管丙管,单开丙管3小时可以把一满池水放完。
如果三 管同时开放,多少小时才能把一空池注满水?3531211116. 行程问题:(1)行程问题中的三个基本量及其关系:路程=速度×时间。
(2)基本类型有①相遇问题;②追及问题;常见的还有:相背而行;行船问题;环形跑道问题。
(3)解此类题的关键是抓住甲、乙两物体的时间关系或所走的路程关系,一般情况下问题就能迎刃而解。
并且还常常借助画草图来分析,理解行程问题。
例. 甲、乙两站相距480公里,一列慢车从甲站开出,每小时行90公里,一列快车从乙站开出,每小时行140公里。
(1)慢车先开出1小时,快车再开。
两车相向而行。
问快车开出多少小时后两车相遇?(2)两车同时开出,相背而行多少小时后两车相距600公里?(3)两车同时开出,慢车在快车后面同向而行,多少小时后快车与慢车相距600公里?(4)两车同时开出同向而行,快车在慢车的后面,多少小时后快车追上慢车?(5)慢车开出1小时后两车同向而行,快车在慢车后面,快车开出后多少小时追上慢车?此题关键是要理解清楚相向、相背、同向等的含义,弄清行驶过程。
故可结合图形分析。
(1)分析:相遇问题,画图表示为:等量关系是:慢车路程+快车路程=480,慢车时间=快车时间+1小时解:设快车开出t小时后两车相遇140t+90(t+1)=480(2)分析:相背而行,画图表示为:等量关系是:慢车路程+快车路程+480=600,慢车时间=快车时间解:相背而行t小时后两车相距600公里140t+90t+480=600(3)分析:追及问题,画图表示为等量关系为:快车路程+480公里-慢车路程=600公里, 慢车时间=快车时间解:设x小时后两车相距600公里,140t+480-90t=600(4)分析:追及问题,画图表示为:等量关系为:慢车路程+480公里=快车路程, 慢车时间=快车时间解:设t小时后快车追上慢车90t+480=140t(5)分析:追及问题画图表示为:等量关系为:快车的路程=慢车走的路程+480公里,慢车时间=快车时间+1解:快车开出后t小时追上慢车140t=90(t+1)+4801. 某人从家里骑自行车到学校。
若每小时行15千米,可比预定的时间早到15分钟;若每小时行9千米,可比预定的时间晚到15分钟;求从家里到学校的路程有多少千米?2.与铁路平行的一条公路上有一行人与骑自行车的人同时向南行进。
