十字程序1

合集下载

设备日常保养,一级保养,二级保养,三级保养和十字作业内容

设备日常保养,一级保养,二级保养,三级保养和十字作业内容一、设备日常保养：1、清洁设备表面，保持设备干净整洁。

2、检查设备各部件是否松动或异常。

3、检查设备电源、电线是否完好无损。

4、检查设备油、水、气等管道是否畅通。

5、按照厂家要求添加或更换润滑油、冷却水等。

6、做好日常保养记录。

二、一级保养：1、清洁设备内部和外部，清除积尘和杂物。

2、检查设备各部件是否有磨损或异常。

3、检查设备液压、气压和润滑系统是否正常。

4、检查设备传动装置是否有松动或异常。

5、更换已磨损或损坏的部件，补充润滑油等。

6、做好一级保养记录。

三、二级保养：1、清洁设备内部和外部，清除积尘和杂物。

2、检查设备各部件是否有磨损或异常。

3、检查设备液压、气压和润滑系统是否正常。

4、检查设备传动装置是否有松动或异常。

5、更换已磨损或损坏的部件，补充润滑油等。

6、对设备进行调试和校准，确保设备精度和性能。

7、做好二级保养记录。

四、三级保养：1、对设备进行全面检查，发现并解决潜在问题。

2、对设备进行拆卸、清洗、检查和维修。

3、检查设备的电气、液压、气压系统是否正常。

4、更换已磨损或损坏的部件，补充润滑油等。

5、对设备进行调试和校准，确保设备精度和性能。

6、做好三级保养记录。

五、十字作业内容：1、清洁：保持设备表面和内部的清洁，清理积尘和杂物。

2、检查：检查设备的各部件是否松动或异常，发现并解决问题。

3、润滑：定期对设备进行润滑，保证设备的正常运行。

4、调整：对设备的各项参数进行定期检查和调整，确保设备的精度和性能。

5、安全：确保设备的安全防护装置完好无损，遵守安全操作规程。

六、设备一级保养主要内容：1、清洁保养：定期清洁设备的内部和外部，包括机身、控制面板、传感器等部分，以去除灰尘、污垢等杂质，避免对设备造成损害。

2、润滑维护：对设备的润滑部件进行定期检查和维护，确保润滑油的正常使用和更换，以减少设备的磨损和摩擦。

3、零部件检查：检查设备的关键零部件，如传动系统、电气元件等，确保其正常工作和运行。

因式分解十字相乘法1

因式分解十字相乘法一．选择题（共20小题）1．若关于x的二次三项式x2﹣kx﹣b因式分解为（x﹣1）（x﹣3），则k+b的值为（）A．﹣1B．1C．﹣7D．72．因式分解x2+mx+n时，甲看错了m的值，分解的结果是（x﹣6）（x+2），乙看错了n的值，分解的结果为（x+8）（x﹣4），那么x2+mx+n分解因式正确的结果为（）A．（x+3）（x﹣4）B．（x+4）（x﹣3）C．（x+6）（x﹣2）D．（x+2）（x﹣6）3．下列算式计算结果为x2﹣4x﹣12的是（）A．（x﹣3）（x+4）B．（x+6）（x﹣2）C．（x+3）（x﹣4）D．（x﹣6）（x+2）4．若x2+mx+n分解因式的结果是（x﹣2）（x+1），则m+n的值为（）A．3B．﹣3C．1D．﹣15．如果二次三项式x2﹣ax﹣9（a为整数）在整数范围内可以分解因式，那么a可取值的个数是（）A．2个B．3个C．4个D．无数个6．多项式x2﹣8x+m＝（x﹣9）（x﹣n），则m，n的值为（）A．m＝9，n＝1B．m＝9，n＝﹣1C．m＝﹣9，n＝﹣1D．m＝﹣9，n＝1 7．如果把二次三项式x2+2x+c分解因式得x2+2x+c＝（x﹣1）（x+3），那么常数c的值是（）A．3B．﹣3C．2D．﹣28．已知关于x的二次三项式2x2+bx+a分解因式的结果是（x+1）（2x﹣3），则代数式a b的值为（）A．﹣3B．﹣1C．﹣D．9．二次三项式x2﹣mx﹣12（m是整数），在整数范围内可分为两个一次因式的积，则m的所有可能值有（）个．A．4B．5C．6D．810．下列因式分解正确的是（）A．6a3﹣4a2+2a＝2a（3a2﹣2a）B．x2+x﹣12＝（x﹣4）（x+3）C．2（a﹣b）2﹣a+b＝（a﹣b）（2a﹣2b﹣1）D．（x﹣1）2﹣4＝（x+3）（x﹣5）11．下列因式分解错误的是（）A．3x﹣3y＝3（x﹣y）B．x2﹣4＝（x+2）（x﹣2）C．x2+6x﹣9＝（x+9）2D．﹣x2﹣x+2＝﹣（x﹣1）（x+2）12．把多项式x2+5x+m因式分解得（x+n）（x﹣2），则常数m，n的值分别为（）A．m＝﹣14，n＝7B．m＝14，n＝﹣7C．m＝14，n＝7D．m＝﹣14，n＝﹣7 13．下列因式分解正确的是（）A．x2﹣3x﹣2＝（x﹣1）（x﹣2）B．3x2﹣27＝3（x+3）（x﹣3）C．x3﹣x2﹣x＝x（x+1）（x﹣1）D．（x+2）（x﹣2）＝x2﹣414．若x2+mx﹣10＝（x﹣5）（x+n），则n m的值为（）A．﹣6B．8C．﹣D．15．若x2+mx﹣12＝（x+4）（x﹣n），则m的值是（）A．3B．﹣3C．1D．﹣116．下列各式因式分解正确的是（）A．x2+1＝（x+1）2B．x3﹣x＝x（x+1）（x﹣1）C．（x+1）（x+3）＝x2+4x+3D．x2+2x+1＝x（x+2）+117．若多项式x2﹣ax﹣1可分解为（x﹣2）（x﹣b），则a+b的值为（）A．2B．1C．﹣2D．﹣118．下列因式分解中，错误的是（）A．2x2﹣x＝x（2x﹣1）B．y2﹣x2＝（x+y）（y﹣x）C．x2﹣2x+4＝（x﹣2）2D．x2+x+＝（x+）219．下列因式分解正确的是（）A．a2+b2＝（a+b）2B．a2﹣2a+1＝a（a﹣2）+1C．a2﹣a﹣2＝（a+1）（a﹣2）D．（a﹣3）2＝a2﹣6a+920．如果x2+kx﹣2＝（x﹣1）（x+2），那么k应为（）A．3B．﹣3C．1D．﹣1二．填空题（共40小题）21．如果二次三项式x2+ax﹣6可以分解为（x﹣b）（x﹣2），则（a+b）2＝．22．在对某二次三项式进行因式分解时，甲同学因为看错了一次项系数而将其分解为2（x ﹣1）（x﹣9），乙同学因为看错了常数项而将其分解为2（x﹣2）（x﹣4），请写出正确的因式分解的结果．23．甲乙两人完成因式分解x2+ax+b时，甲看错了a的值，分解的结果是（x+6）（x﹣2），乙看错了b的值，分解的结果为（x﹣8）（x+4），那么x2+ax+b分解因式正确的结果为．24．若3x2﹣mx+n进行因式分解的结果为（3x+2）（x﹣1），则mn＝．25．把关于x的多项式x2+ax+b分解因式，得（x+1）（x﹣3），则ab＝．26．若x2﹣nx﹣6＝（x﹣2）（x+3），则常数n的值是．27．已知多项式x2+mx﹣6分解因式后为（x﹣6）（x+1），则m的值为．28．分解因式：（1）ax+ay＝；（2）＝；（3）＝．29．把多项式x2﹣6x+m分解因式得（x+3）（x﹣n），则m+n的值是．30．已知关于x的多项式x2+kx﹣3能分解成两个一次多项式的积，那么整数k的值为．31．关于x的二次三项式x2+mx+6因式分解的结果是（x+3）（x+2），则m＝．32．分解因式：（x2+x+1）（x2+x+2）﹣12＝．33．若关于x的二次三项式x2+ax﹣6可分解为（x+3）（x+b）．则a+b＝．34．如果二次三项式x2+px﹣6可以分解为（x+q）（x﹣2），那么p的值为，q的值为．35．若x2+2x﹣3＝（x﹣a）（x﹣b），则ab＝．36．在将x2+mx+n因式分解时，小刚看错了m的值，分解得（x﹣1）（x+6）；小芳看错了n 的值，分解得（x﹣2）（x+1），那么原式x2+mx+n正确分解为．37．把多项式x2+ax+b分解因式得（x+1）（x﹣3），则a＝，b＝．38．把多项式x2+ax+b因式分解得（x﹣1）（x+2），则a+b的值是．39．把多项式x3+2x2﹣3x因式分解，结果为．40．因式分解：b﹣2ab+2b＝．41．分解因式：＝．42．若x2+mx+n＝（x﹣2）（x﹣1），则m n＝．43．分解因式：x2﹣x﹣12＝．44．分解因式x2+ax+b，甲看错了a的值，分解的结果是（x+6）•（x﹣1），乙看错了b的值，分解的结果是（x﹣2）•（x+1），那么a+b的值是．45．把多项式x2+ax+b分解因式，得（x+1）（x﹣3），则a，b的值分别是．46．若x2+ax﹣2＝（x﹣1）（x+2），则a＝．47．把多项式18x2﹣12x+2分解因式的结果是．48．如果多项式x2+mx+n能因式分解为（x﹣2）（x+5），则m+n的值是．49．若：x2+mx﹣10＝（x+2）（x﹣5），则m＝．50．因式分解：（1）﹣x2+y2＝；（2）x2﹣2xy+y2＝；（3）a2﹣4a＝；（4）m2﹣6m+5＝．51．若多项式x2+mx﹣21可以分解为（x+3）（x﹣7），则m＝．52．关于x的二次三项式2x2+bx+c分解因式后为2（x﹣3）•（x+1），则b＝，c＝．53．如果多项式x2+mx+4可以分解成两个一次因式的积，那么整数m的值可取个．54．一个二次三项式分解因式后，其中一个因式为x+1，请写出一个满足条件的二次三项式：．55．因式分解：﹣2x2y+8xy﹣6y＝．56．请你写出一个既能提取公因式，同时又能用十字相乘法分解因式的多项式：．因式分解十字相乘法参考答案与试题解析一．选择题（共20小题）1．若关于x的二次三项式x2﹣kx﹣b因式分解为（x﹣1）（x﹣3），则k+b的值为（）A．﹣1B．1C．﹣7D．7【解答】解：根据题意得：x2﹣kx﹣b＝（x﹣1）（x﹣3）＝x2﹣4x+3，∴k＝4，b＝﹣3，则k+b＝1，故选：B．2．因式分解x2+mx+n时，甲看错了m的值，分解的结果是（x﹣6）（x+2），乙看错了n的值，分解的结果为（x+8）（x﹣4），那么x2+mx+n分解因式正确的结果为（）A．（x+3）（x﹣4）B．（x+4）（x﹣3）C．（x+6）（x﹣2）D．（x+2）（x﹣6）【解答】解：（x﹣6）（x+2）＝x2﹣6x+2x﹣12＝x2﹣4x﹣12，（x+8）（x﹣4）＝x2﹣4x+8x﹣32＝x2+4x﹣32，∵因式分解x2+mx+n时，甲看错了m的值，分解的结果是（x﹣6）（x+2），乙看错了n 的值，分解的结果为（x+8）（x﹣4），∴n＝﹣12，m＝4，∴x2+mx+n＝x2+4x﹣12＝（x+6）（x﹣2），故选：C．3．下列算式计算结果为x2﹣4x﹣12的是（）A．（x﹣3）（x+4）B．（x+6）（x﹣2）C．（x+3）（x﹣4）D．（x﹣6）（x+2）【解答】解：x2﹣4x﹣12＝（x+2）（x﹣6），4．若x2+mx+n分解因式的结果是（x﹣2）（x+1），则m+n的值为（）A．3B．﹣3C．1D．﹣1【解答】解：（x﹣2）（x+1）＝x2+x﹣2x﹣2＝x2﹣x﹣2，∵二次三项式x2+mx+n可分解为（x﹣2）（x+1），∴m＝﹣1，n＝﹣2，∴m+n＝﹣1+（﹣2）＝﹣3，故选：B．5．如果二次三项式x2﹣ax﹣9（a为整数）在整数范围内可以分解因式，那么a可取值的个数是（）A．2个B．3个C．4个D．无数个【解答】解：当﹣9＝﹣9×1时，﹣a＝﹣9+1，∴a＝8，当﹣9＝﹣1×9时，﹣a＝﹣1+9，∴a＝﹣8，∴如果二次三项式x2﹣ax﹣9（a为整数）在整数范围内可以分解因式，那么a可取值：±8，故选：A．6．多项式x2﹣8x+m＝（x﹣9）（x﹣n），则m，n的值为（）A．m＝9，n＝1B．m＝9，n＝﹣1C．m＝﹣9，n＝﹣1D．m＝﹣9，n＝1【解答】解：∵多项式x2﹣8x+m分解因式得（x﹣9）（x﹣n），∴﹣9﹣n＝﹣8，﹣9×（﹣n）＝m，解得：m＝﹣9，n＝﹣1，故选：C．7．如果把二次三项式x2+2x+c分解因式得x2+2x+c＝（x﹣1）（x+3），那么常数c的值是（）A．3B．﹣3C．2D．﹣2【解答】解：∵x2+2x+c＝（x﹣1）（x+3），（x﹣1）（x+3）＝x2+2x﹣3，∴c＝﹣3．8．已知关于x的二次三项式2x2+bx+a分解因式的结果是（x+1）（2x﹣3），则代数式a b的值为（）A．﹣3B．﹣1C．﹣D．【解答】解：由题意得：2x2+bx+a＝（x+1）（2x﹣3），2x2+bx+a＝2x2﹣3x+2x﹣3，2x2+bx+a＝2x2﹣x﹣3，∴b＝﹣1，a＝﹣3，∴a b＝（﹣3）﹣1＝﹣，故选：C．9．二次三项式x2﹣mx﹣12（m是整数），在整数范围内可分为两个一次因式的积，则m的所有可能值有（）个．A．4B．5C．6D．8【解答】解：若x2﹣mx﹣12（m为常数）可分解为两个一次因式的积，m的值可能是﹣1，1，﹣4，4，11，﹣11．共有6个．故选：C．10．下列因式分解正确的是（）A．6a3﹣4a2+2a＝2a（3a2﹣2a）B．x2+x﹣12＝（x﹣4）（x+3）C．2（a﹣b）2﹣a+b＝（a﹣b）（2a﹣2b﹣1）D．（x﹣1）2﹣4＝（x+3）（x﹣5）【解答】解：选项A，左边是三项，右边乘开是两项，故A不对；选项B，右边乘开结果为：x2﹣x﹣12，不等于左边，故B不对；选项C，2（a﹣b）2﹣（a﹣b）＝（a﹣b）（2a﹣2b﹣1），故C正确．选项D，观察发现，等式左边的常数项合并之后为﹣3，而右边的常数项为﹣15，两者不等，故D不对．故选：C．11．下列因式分解错误的是（）A．3x﹣3y＝3（x﹣y）B．x2﹣4＝（x+2）（x﹣2）C．x2+6x﹣9＝（x+9）2D．﹣x2﹣x+2＝﹣（x﹣1）（x+2）【解答】解：A．3x﹣3y＝3（x﹣y），故A不符合题意；B．x2﹣4＝（x+2）（x﹣2），故B不符合题意；C．x2+6x﹣9≠（x+9）2，故C符合题意；D．﹣x2﹣x+2＝﹣（x﹣1）（x+2），故D不符合题意；故选：C．12．把多项式x2+5x+m因式分解得（x+n）（x﹣2），则常数m，n的值分别为（）A．m＝﹣14，n＝7B．m＝14，n＝﹣7C．m＝14，n＝7D．m＝﹣14，n＝﹣7【解答】解：由题意得：x2+5x+m＝（x+n）（x﹣2），∴x2+5x+m＝x2+nx﹣2x﹣2n，∴x2+5x+m＝x2+（n﹣2）x﹣2n，∴n﹣2＝5，m＝﹣2n，∴n＝7，m＝﹣14，故选：A．13．下列因式分解正确的是（）A．x2﹣3x﹣2＝（x﹣1）（x﹣2）B．3x2﹣27＝3（x+3）（x﹣3）C．x3﹣x2﹣x＝x（x+1）（x﹣1）D．（x+2）（x﹣2）＝x2﹣4【解答】解：∵（x﹣1）（x﹣2）＝x2﹣3x+2≠x2﹣3x﹣2，故选项A分解错误；3x2﹣27＝3（x2﹣9）＝3（x+3）（x﹣3），故选项B分解正确；x（x+1）（x﹣1）＝x3﹣x≠x3﹣x2﹣x，故选项C分解错误；（x+2）（x﹣2）＝x2﹣4，该变形是整式乘法不是因式分解，故选项D错误．故选：B．14．若x2+mx﹣10＝（x﹣5）（x+n），则n m的值为（）A．﹣6B．8C．﹣D．【解答】解：（x﹣5）（x+n）＝x2+nx﹣5x﹣5n，∵x2+mx﹣10＝（x﹣5）（x+n），∴nx﹣5x＝mx，﹣5n＝﹣10，∴n﹣5＝m，n＝2，解得：m＝﹣3，n＝2，∴n m＝．故选：D．15．若x2+mx﹣12＝（x+4）（x﹣n），则m的值是（）A．3B．﹣3C．1D．﹣1【解答】解：x2+mx﹣12＝（x+4）（x﹣n），x2+mx﹣12＝x2+4x﹣nx﹣4n，x2+mx﹣12＝x2+（4﹣n）x﹣4n，∴m＝4﹣n，﹣4n＝﹣12，∴n＝3，m＝1，故选：C．16．下列各式因式分解正确的是（）A．x2+1＝（x+1）2B．x3﹣x＝x（x+1）（x﹣1）C．（x+1）（x+3）＝x2+4x+3D．x2+2x+1＝x（x+2）+1【解答】解：A．x2+1，不能分解，故A不符合题意；B．x3﹣x＝x（x+1）（x﹣1），故B符合题意；C．（x+1）（x+3）＝x2+4x+3，不是因式分解，故C不符合题意；D．x2+2x+1＝（x+1）2，故D不符合题意；故选：B．17．若多项式x2﹣ax﹣1可分解为（x﹣2）（x﹣b），则a+b的值为（）A．2B．1C．﹣2D．﹣1【解答】解：∵（x﹣2）（x﹣b）＝x2﹣bx﹣2x+2b＝x2﹣（b+2）x+2b＝x2﹣ax﹣1，∴b+2＝a，2b＝﹣1，∴b＝﹣0.5，a＝1.5，∴a+b＝1．故选：B．18．下列因式分解中，错误的是（）A．2x2﹣x＝x（2x﹣1）B．y2﹣x2＝（x+y）（y﹣x）C．x2﹣2x+4＝（x﹣2）2D．x2+x+＝（x+）2【解答】解：∵2x2﹣x＝x（2x﹣1），故A选项不符合题意；∵y2﹣x2＝（y+x）（y﹣x），故B选项不符合题意；∵x2﹣2x+4不能因式分解，故C选项符合题意；∵x2+x+＝（x+）2，故D选项不符合题意，故选：C．19．下列因式分解正确的是（）A．a2+b2＝（a+b）2B．a2﹣2a+1＝a（a﹣2）+1C．a2﹣a﹣2＝（a+1）（a﹣2）D．（a﹣3）2＝a2﹣6a+9【解答】解：A：（a+b）2＝a2+2ab+b2，等式不成立，故A错误；B：a2﹣2a+1＝（a﹣1）2，不符合因式分解的结果形式，故B错误；D：该选项是整式的乘法，不是因式分解，故D错误．故选：C．20．如果x2+kx﹣2＝（x﹣1）（x+2），那么k应为（）A．3B．﹣3C．1D．﹣1【解答】解：由题意得，x2+kx﹣2＝（x﹣1）（x+2）＝x2+x﹣2，则k＝1．故选：C．二．填空题（共40小题）21．如果二次三项式x2+ax﹣6可以分解为（x﹣b）（x﹣2），则（a+b）2＝4．【解答】解：根据题意得：x2+ax﹣6＝（x﹣b）（x﹣2）＝x2﹣（b+2）x+2b，∴a＝﹣（b+2），﹣6＝2b，解得：a＝1，b＝﹣3，则原式＝（1﹣3）2＝（﹣2）2＝4．故答案为：4．22．在对某二次三项式进行因式分解时，甲同学因为看错了一次项系数而将其分解为2（x ﹣1）（x﹣9），乙同学因为看错了常数项而将其分解为2（x﹣2）（x﹣4），请写出正确的因式分解的结果2（x﹣3）2．【解答】解：∵2（x﹣1）（x﹣9）＝2x2﹣20x+18，2（x﹣2）（x﹣4）＝2x2﹣12x+16，∵甲同学因为看错了一次项系数，∴多项式的二次项和常数项分别是2x2、18，∵乙同学因为看错了常数项，∴多项式的二次项和一次项分别是2x2、﹣12x，所以该二次三项式为：2x2﹣12x+18．2x2﹣12x+18＝2（x2﹣6x+9）＝2（x﹣3）2故答案为：2（x﹣3）223．甲乙两人完成因式分解x2+ax+b时，甲看错了a的值，分解的结果是（x+6）（x﹣2），乙看错了b的值，分解的结果为（x﹣8）（x+4），那么x2+ax+b分解因式正确的结果为（x ﹣6）（x+2）．【解答】解：因式分解x2+ax+b时，∵甲看错了a的值，分解的结果是（x+6）（x﹣2），∴b＝6×（﹣2）＝﹣12，又∵乙看错了b的值，分解的结果为（x﹣8）（x+4），∴a＝﹣8+4＝﹣4，∴原二次三项式为x2﹣4x﹣12，因此，x2﹣4x﹣12＝（x﹣6）（x+2），故答案为：（x﹣6）（x+2）．24．若3x2﹣mx+n进行因式分解的结果为（3x+2）（x﹣1），则mn＝﹣2．【解答】解：∵（3x+2）（x﹣1）＝3x2﹣x﹣2，∴3x2﹣mx+n＝3x2﹣x﹣2，∴m＝1，n＝﹣2，∴mn＝﹣2，故答案为：﹣2．25．把关于x的多项式x2+ax+b分解因式，得（x+1）（x﹣3），则ab＝6．【解答】解：由题意得：x2+ax+b＝（x+1）（x﹣3），∴x2+ax+b＝x2﹣2x﹣3，∴a＝﹣2，b＝﹣3，∴ab＝﹣2×（﹣3）＝6，故答案为：6．26．若x2﹣nx﹣6＝（x﹣2）（x+3），则常数n的值是﹣1．【解答】解：（x﹣2）（x+3）＝x2+3x﹣2x﹣6＝x2+x﹣6，∵x2﹣nx﹣6＝（x﹣2）（x+3），∴n＝﹣1，故答案为：﹣1．27．已知多项式x2+mx﹣6分解因式后为（x﹣6）（x+1），则m的值为﹣5．【解答】解：（x﹣6）（x+1）＝x2﹣5x﹣6，根据题意可得，x2+mx﹣6＝x2﹣5x﹣6，即m＝﹣5．故答案为：﹣5/28．分解因式：（1）ax+ay＝a（x+y）；（2）＝（a+）（a﹣）；（3）＝．【解答】解：（1）ax+ay＝a（x+y）；（2）＝（a+）（a﹣）；（3）＝．故答案为：（1）a（x+y）；（2）（a+）（a﹣）；（3）．29．把多项式x2﹣6x+m分解因式得（x+3）（x﹣n），则m+n的值是﹣18．【解答】解：由题意得：x2﹣6x+m＝（x+3）（x﹣n），x2﹣6x+m＝x2+3x﹣nx﹣3n，x2﹣6x+m＝x2+（3﹣n）x﹣3n，∴3﹣n＝﹣6，m＝﹣3n，∴n＝9，m＝﹣27，∴m+n＝﹣18，故答案为：﹣18．30．已知关于x的多项式x2+kx﹣3能分解成两个一次多项式的积，那么整数k的值为±2．【解答】解：∵﹣3＝﹣3×1或﹣3＝﹣1×3，∴k＝﹣3+1＝﹣2或k＝﹣1+3＝2，∴整数k的值为：±2，故答案为：±2．31．关于x的二次三项式x2+mx+6因式分解的结果是（x+3）（x+2），则m＝5．【解答】解：关于x的二次三项式x2+mx+6因式分解的结果是（x+3）（x+2），则（x+3）（x+2）＝x2+5x+6，故m＝5．故答案为：5．32．分解因式：（x2+x+1）（x2+x+2）﹣12＝（x2+x+5）（x+2）（x﹣1）．【解答】解：原式＝（x2+x）2+3（x2+x）﹣10＝（x2+x+5）（x2+x﹣2）＝（x2+x+5）（x+2）（x﹣1）．故答案为：（x2+x+5）（x+2）（x﹣1）．33．若关于x的二次三项式x2+ax﹣6可分解为（x+3）（x+b）．则a+b＝﹣1．【解答】解：（x+3）（x+b）＝x2+bx+3x+3b＝x2+（b+3）x+3b，∵x2+ax﹣6＝（x+3）（x+b），∴b+3＝a，3b＝﹣6，解得：a＝1，b＝﹣2，则a+b＝1﹣2＝﹣1，故答案为：﹣1．34．如果二次三项式x2+px﹣6可以分解为（x+q）（x﹣2），那么p的值为1，q的值为3．【解答】解：根据题意得：x2+px﹣6＝（x+q）（x﹣2）＝x2+（q﹣2）x﹣2q，∴p＝q﹣2，﹣2q＝﹣6，解得：p＝1，q＝3．故答案为：1，3．35．若x2+2x﹣3＝（x﹣a）（x﹣b），则ab＝﹣3．【解答】解：因为（x﹣a）（x﹣b）＝x2﹣（a+b）x+ab＝x2+2x﹣3，所以ab＝﹣3，故答案为：﹣3．36．在将x2+mx+n因式分解时，小刚看错了m的值，分解得（x﹣1）（x+6）；小芳看错了n 的值，分解得（x﹣2）（x+1），那么原式x2+mx+n正确分解为（x﹣3）（x+2）．【解答】解：（x﹣1）（x+6）＝x2+5x﹣6，∵小刚看错了m的值，∴n＝﹣6；（x﹣2）（x+1）＝x2﹣x﹣2，∵小芳看错了n的值，∴m＝﹣1．∴x2+mx+n＝x2﹣x﹣6＝（x﹣3）（x+2）．故答案为：（x﹣3）（x+2）．37．把多项式x2+ax+b分解因式得（x+1）（x﹣3），则a＝﹣2，b＝﹣3．【解答】解：（x+1）（x﹣3）＝x2﹣2x﹣3＝x2+ax+b，利用对应系数法，知道a＝﹣2，b＝﹣3故答案是：﹣2；﹣3．38．把多项式x2+ax+b因式分解得（x﹣1）（x+2），则a+b的值是﹣1．【解答】解：根据题意得：x2+ax+b＝（x﹣1）（x+2），则a＝2﹣1＝1，b＝﹣1×2＝﹣2，所以a+b＝1﹣2＝﹣1．故答案为：﹣1．39．把多项式x3+2x2﹣3x因式分解，结果为x（x+3）（x﹣1）．【解答】解：原式＝x（x2+2x﹣3）＝x（x+3）（x﹣1），故答案为：x（x+3）（x﹣1）．40．因式分解：b﹣2ab+2b＝b（a﹣2）2．【解答】解：原式＝b（a2﹣4a+4）＝b（a﹣2）2．故答案为：b（a﹣2）2．41．分解因式：＝b（a﹣3）2．【解答】解：a2b﹣2ab+3b＝b（a2﹣6a+9）＝b（a﹣3）2．故答案为：b（a﹣3）2．42．若x2+mx+n＝（x﹣2）（x﹣1），则m n＝9．【解答】解：∵（x﹣2）（x﹣1）＝x2﹣3x+2，∴x2+mx+n＝x2﹣3x+2，∴m＝﹣3，n＝2，∴m n＝（﹣3）2＝9，故答案为：9．43．分解因式：x2﹣x﹣12＝（x﹣4）（x+3）．【解答】解：原式＝（x﹣4）（x+3），故答案为：（x﹣4）（x+3）44．分解因式x2+ax+b，甲看错了a的值，分解的结果是（x+6）•（x﹣1），乙看错了b的值，分解的结果是（x﹣2）•（x+1），那么a+b的值是﹣7．【解答】解：根据题意得：a＝﹣1，b＝﹣6，则a+b＝﹣1﹣6＝﹣7，故答案为：﹣745．把多项式x2+ax+b分解因式，得（x+1）（x﹣3），则a，b的值分别是﹣2，﹣3．【解答】解：∵x2+ax+b＝（x+1）（x﹣3），∴x2+ax+b＝x2﹣2x﹣3．∴a＝﹣2，b＝﹣3．故答案为：﹣2，﹣3．46．若x2+ax﹣2＝（x﹣1）（x+2），则a＝1．【解答】解：由题意知，a＝﹣1+2＝1．故答案是：1．47．把多项式18x2﹣12x+2分解因式的结果是2（3x﹣1）2．【解答】解：18x2﹣12x+2＝2（9x2﹣6x+1）＝2（3x﹣1）2．故答案为：2（3x﹣1）2．48．如果多项式x2+mx+n能因式分解为（x﹣2）（x+5），则m+n的值是﹣7．【解答】解：（x﹣2）（x+5）＝x2+3x﹣10，所以m＝3，n＝﹣10，所以m+n＝3﹣10＝﹣7．故答案为：﹣7．49．若：x2+mx﹣10＝（x+2）（x﹣5），则m＝﹣3．【解答】解：∵（x+2）（x﹣5）＝x2﹣3x﹣10＝x2+mx﹣10，∴m＝﹣3，故答案为：﹣3．50．因式分解：（1）﹣x2+y2＝（y﹣x）（y+x）；（2）x2﹣2xy+y2＝（x﹣y）2；（3）a2﹣4a＝a（a﹣4）；（4）m2﹣6m+5＝（m﹣1）（m﹣5）．【解答】解：（1）﹣x2+y2＝y2﹣x2＝（y﹣x）（y+x）；故答案为：（y﹣x）（y+x）；（2）x2﹣2xy+y2＝（x﹣y）2；故答案为：（x﹣y）2；（3）a2﹣4a＝a（a﹣4）；故答案为：a（a﹣4）；（4）m2﹣6m+5＝（m﹣1）（m﹣5）；故答案为：（m﹣1）（m﹣5）．51．若多项式x2+mx﹣21可以分解为（x+3）（x﹣7），则m＝﹣4．【解答】解：∵（x+3）（x﹣7）＝x2﹣4x﹣21，又∵x2+mx﹣21＝（x+3）（x﹣7），∴x2﹣4x﹣21＝x2+mx﹣21．∴m＝﹣4．故答案为：﹣4．52．关于x的二次三项式2x2+bx+c分解因式后为2（x﹣3）•（x+1），则b＝﹣4，c＝﹣6．【解答】解：由题意得：2x2+bx+c＝2（x﹣3）（x+1），2x2+bx+c＝2（x2+x﹣3x﹣3），2x2+bx+c＝2x2﹣4x﹣6，∴b＝﹣4，c＝﹣6，故答案为：﹣4，﹣6．53．如果多项式x2+mx+4可以分解成两个一次因式的积，那么整数m的值可取4个．【解答】解：∵多项式x2+mx+4可以分解成两个一次因式的积，∴当m＝±4，±5时，符合题意，故整数m的值可取4个．故答案为：4．54．一个二次三项式分解因式后，其中一个因式为x+1，请写出一个满足条件的二次三项式：x2+4x+3（答案不唯一，满足题意即可）．【解答】解：∵（x+1）（x+3）＝x2+4x+3，∴一个二次三项式分解因式后，其中一个因式为x+1，写出一个满足条件的二次三项式为x2+4x+3（答案不唯一，满足题意即可）．故答案为：x2+4x+3（答案不唯一，满足题意即可）．55．因式分解：﹣2x2y+8xy﹣6y＝﹣2y（x﹣1）（x﹣3）．【解答】解：原式＝﹣2y（x2﹣4x+3）＝﹣2y（x﹣1）（x﹣3），故答案为：﹣2y（x﹣1）（x﹣3）56．请你写出一个既能提取公因式，同时又能用十字相乘法分解因式的多项式：x3+3x2﹣4x．【解答】解：∵x3+3x2﹣4x＝x（x2+3x﹣4）＝x（x+4）（x﹣1）故答案为：x3+3x2﹣4x（不唯一）。

文明礼仪十字用语

文明礼貌十字用语请、你好、谢谢、对不起、再见与他人交谈，重在交流信息，相互取长补短，同时也应注意尊重交谈对象。

在交谈中，态度要谦恭，语言要文明，另外还要注意避免出现10种情况：一是“闭嘴”，即一言不发，使交谈冷场；二是“插嘴”，即在他人说话的途中，突然插上一嘴，打断对方；三是“杂嘴”，即乱用语言、俚语、外语、术语、语言不标准，不规范; 四是“脏嘴”，即用语不文明，满口脏话；五是“荤嘴”，即出口带色，时刻将性事、艳事、绯闻、下流话挂在嘴上；六是“油嘴”，即交谈时油腔滑调，乱说幽默，取笑他人；七是“贫嘴”，即爱讲废话，爱饶舌，好起腻；八是“强嘴”，即爱与人争辩，好强词夺理，自以为一贯正确；九是“刀子嘴”，即讲话尖酸刻薄，肆无忌惮，恶语伤人；十是“长舌妇”，即爱传闲话，爱搬弄是非，爱打听小道消息；端庄坐姿*入座时应以轻盈和缓的步履，从容自如地走到座位前，然后轻而稳地从左侧入座，并将右脚与左脚自然摆放。

女士入座时，若着裙装，应将裙子稍微拢一下；*落座后，立腰、挺胸，上体自然挺直，上身微向前倾，重心垂直向下。

面带微笑，双目平视，嘴唇微闭，下颌微收。

双膝应并拢或微微分开，并视情况向一侧倾斜，手自然放在双膝上或椅子扶手上。

*起身时，右脚向后收半步，而后站起，轻稳离座；正确的站姿*平肩，直颈，下颌微向后收；两眼平视，精神饱满，面带微笑。

*直立，挺胸，收腹，略微收肩。

*两肩自然下垂，手指自然弯曲；两手亦可在前体交叉，一般是右手放在左手上，肘部应略向外张。

身体重心落于前脚掌。

*双脚分开，与肩同宽；或者脚可向后撤半步，但上体仍须保持正直；良好的走资*上体垂直，抬头，下巴与地面平行，两眼平视前方，精神饱满，面带微笑。

*双肩平稳，双肩前后自然协调摆动，手臂与身体的夹角一般在10度至15度 *跨步均匀，两脚两脚之间约一只脚到一只半脚，跨出的步子应是全脚掌着地，膝和脚腕不可过于僵直。

脚尖可微微分开，但脚尖、脚跟应与前进方向近乎一条直线，避免“外八字”或“内八字”迈步。

十字交叉法1ppt课件

1
则二种硫酸溶液所取体积比为1:1。
五、用两种物质中同一元素的质量分数求两物质的质量比
例6：FeO 中和FeBr2 的混合物中Fe 的质量百分率为50%，求两物质的质量比（13∶15）
解: ω(FeO)=56/72=7/9
ω(FeBr2)=56/216=7/27
FeO
7/9
13/54
13
1/2
FeBr2
0 0 . .2 6 1 3 ，此比为 C O 2 在二个反应中所耗的物质的量之比，根据二反应中系数关系得出 N a H C O 3 与 N a 2 C O 3 的物质的量之比为 3 ： 1 。
系数处理问题在求分量时，根据题给条件在原物质分子量前会产生系
7/27
5/18
15
所以: M(FeO):m(FeBr2)=13:15
练习:
1、实验室用密度为1.84 g·cm-3 98%的浓硫
酸与密度为1.1 g·cm-3 15%的稀硫酸混和配
制密度为1.4 g·cm-3 59%的硫酸溶液, 取浓、
稀硫酸的体积比最接近的值是( )
A、1:2
B、2:1
C、3:2
例4：标况下，氮气的密度为1.25 g·L-1，C2H6的密度为1.34 g·L-1，两种气体混合后，其密度为 1.30 g·L-1，求混合气中氮气和乙烷的体积比
解:
N2 1.25g/L
0.04
4
1.30g/l
C2H6 1.34g/l
0.05
5
故: V(N2):V(C2H6)=4:5
CH4与C3H8的混合气体密度与同温同压下C2H6的密度相等，混合气体中CH4与C3H8的体积比是（） A. 2:1 B. 3:1 C. 1:3 D. 1:1

实验1-十字路口交通信号灯的PLC控制

实验1 十字路口交通信号灯的PLC控制
1.交通灯设置
在十字路口的东、西、南、北装设红、绿、黄灯。

红、绿、黄灯按照一定时序轮流发光。

2.控制要求
信号灯受开关控制。

当单击启动按钮时，信号灯系统开始工作。

（1）南北向红灯、东西向绿灯同时亮
南北向红灯亮并维持30s；东西向绿灯亮并维持25s。

到25s时，东西向绿灯闪烁3s，闪烁周期为1s（亮0.5s，熄0.5s）。

绿灯闪烁3s后熄灭，东西向黄灯亮，并维持2s。

到2s时，东西向黄灯熄灭，东西向红灯亮；同时南北向红灯熄灭，南北向绿灯亮。

（2）东西向红灯、南北向绿灯同时亮
东西向红灯亮并维持30s；南北向绿灯亮并维持25s。

到25s时，南北向绿灯闪烁3s，闪烁周期1s（亮0.5s，熄0.5s）。

绿灯闪烁3s后熄灭，南北向黄灯亮，并维持2s。

到2s时，南北向黄灯熄，南北向红灯亮；同时东西向红灯熄灭，东西向绿灯亮。

如此周而复始循环，当单击停止按钮时，所有信号灯熄灭。

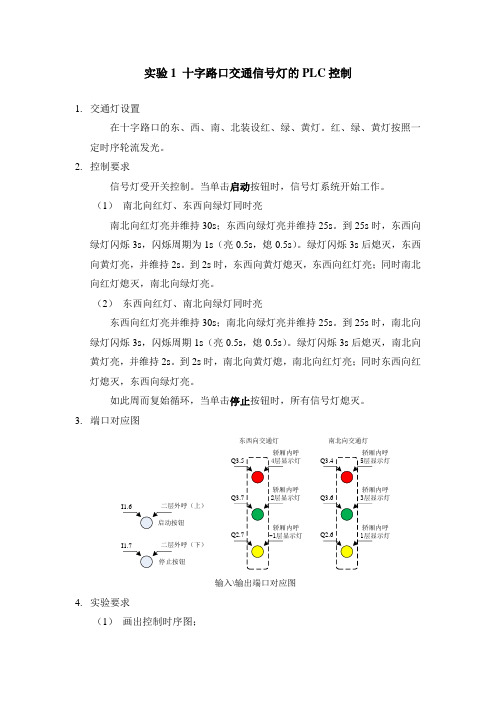
3.端口对应图
东西向交通灯
南北向交通灯
输入\输出端口对应图
4.实验要求
（1）画出控制时序图；
（2）编写PLC程序；。

公开课--十字相乘法(1)

--中英文学校数学科教学案课题：十字相乘法（1）课型：新授主备人：审核：使用时间： 2012 年 ____ 月日第周学习目标：会用十字相乘法进行二次项系数是“1”的二次三项式的因式分解；学习重点：能熟练应用十字相乘法进行二次项系数是“1”的二次三项的分解。

学习难点：在对二次项系数是“1”二次三项式分解因式时，合理分解常数项凑出一次项系数，并能正确区分它们的符号关系。

学习过程：一、前置学习：1、分解因式: 3222y xy y x +-2、用我们以前学过的方法你能分解多项式1072++x x 吗?3、计算下列各题：（1）)5)(2(++x x ＝（2）)3)(2(--x x ＝（3）)6)(4(+-x x ＝（4）)7)(5(-+x x ＝二、合作学习：1、多项式c bx ax ++2称为关于字母____的二次三项式，其中____称为二次项，____称为一次项，____称为常数项。

例如：322--x x 和652++x x 都是关于x 的二次三项式。

2、在多项式2286y xy x +-中，如果把____看作常数，就是关于____的二次三项式，如果把____看作常数，就是关于____的二次三项式。

3、在多项式3622+-ab b a 中，如果把_____看作一个整体，即______________,就是关于_____的二次三项式；同样，多项式12)(7)(2++++y x y x 中，把_____看作一个整体，就是关于_____的二次三项式。

1、将“前置学习第3题”等号左右两边调换位置后的等式写在右边空白处。

2、小组讨论：具有什么特点的二次三项式可以分解因式？（提示：观察展开前两因式中的常数与展开后的多项式中的常数有何关系？与展开后的多项式中的一次项系数又有什么关系？）3、对于二次项系数为“1”的二次三项式，你能用下面的数学表达式表示吗？请填空： __)__)(((___)(______)2++=++x x x x例1 分解因式（同学们自学第（1）题，尝试做第（2）题，并尝试小结归纳）（1） 232++x x （2） 672+-x x分析： x 1+ 分析: x ___x 2+ x ___x x x 3)1()2(+=+++ x 7________-=+)2)(1(++=x x 解：原式 ____)____)((x x =解：原式小结：当常数项为____数时,把它分解成两个____号因数的积，因式的符号与___________的符号相同。

6个简单实用的PLC程序实例分析

段时间内，咖啡指示灯闪动。 5.若投入硬币总值超过按钮所需的钱数(汽水 12 元，咖啡 15 元)时,
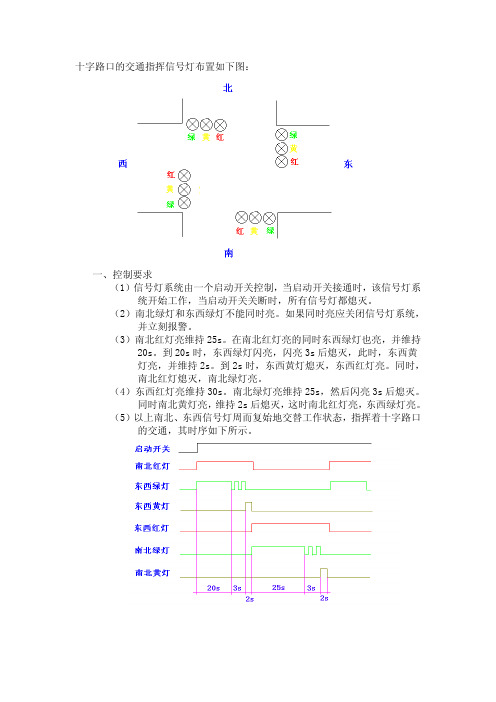
找钱指示灯亮,表示找钱动作,并退出多余的钱。参考答案:
１
２
３
４
５
设计程序,使两个气缸顺序动作,其顺序为:A1B1B0A0。（一）气控回路
(二)位移-步骤图 1 2 3 4 5=1
1 A 0 1 B 0 （三）I 型障碍信号分析
（四）PLC 接线
（五）定义符号地址（六）梯形图程序
自动售货机的 PLC 控制如下图所示的自动售货机示意图，其工作要求如下：
12
2
3、1
升上升到 3 层停
13
3
2、1
降
先降到 2 层暂停 2S 后，再降到 1 层停
14
任意任意
任意
楼层间运行时间必须小于 10S，否则停
多种液体自动混合装置的 PLC 控制如图所示为三种液体混合装置，SQ1、SQ2、SQ3 和 SQ4 为液面传感器，液面淹没时接通，液体 A、B、C 与混合液阀由电磁阀 YV1、YV2、YV3、 YV4 控制，M 为搅匀电动机，其控制要求如下：
3.停止操作按下停止按钮 SB2 后，要将当前的混合操作处理完毕后，才停止操作（停在初始状态）
参考程序：
霓虹灯广告屏控制器的设计用 PLC 对霓虹灯广告屏实现控制，其具体要求如下：
该广告屏中间 8 个灯管亮灭的时序为第 1 根亮→第 2 根亮→第 3 根亮→…→第 8 根亮，时间间隔为 1s，全亮后，显示 10s，再反过来从 8→7→…→1 顺序熄灭。全灭后，停亮 2s，再从第 8 根灯管开始亮起，顺序点亮 7→6→…→1，时间间隔为 1s，显示 20s，再从→2→…→8 顺序熄灭。全熄灭后，停亮 2s，再从头开始运行，周而复始。参巧梯形图程序：

沪科版数学七年级下册《十字相乘法》教学设计1

沪科版数学七年级下册《十字相乘法》教学设计1一. 教材分析《十字相乘法》是沪科版数学七年级下册中的一章节，主要介绍了十字相乘法的原理和应用。

本章节通过讲解十字相乘法，使学生能够掌握分解因式的方法，进一步提高他们的数学思维能力和解决问题的能力。

二. 学情分析学生在学习本章节之前，已经掌握了整式的乘法、因式分解等基础知识。

但学生在应用十字相乘法时，容易出错，对一些特殊情况进行处理不够灵活。

因此，在教学过程中，需要注重引导学生理解十字相乘法的原理，并通过大量练习让学生熟悉并掌握十字相乘法的应用。

三. 教学目标1.让学生理解十字相乘法的原理，掌握十字相乘法分解因式的步骤。

2.培养学生运用十字相乘法解决实际问题的能力。

3.提高学生的数学思维能力和解决问题的能力。

四. 教学重难点1.重点：十字相乘法的原理和应用。

2.难点：如何引导学生灵活运用十字相乘法解决实际问题。

五. 教学方法1.讲授法：讲解十字相乘法的原理和步骤。

2.案例分析法：分析具体例子，引导学生运用十字相乘法解决问题。

3.练习法：布置适量练习题，让学生巩固所学知识。

4.小组讨论法：分组讨论，培养学生的合作能力和交流能力。

六. 教学准备1.准备相关的教学PPT，展示十字相乘法的原理和应用。

2.准备一些具体的例子，用于讲解和练习。

3.准备一份详细的十字相乘法步骤指南，方便学生查阅。

七. 教学过程1.导入（5分钟）通过一个具体的问题引入十字相乘法，激发学生的兴趣。

2.呈现（10分钟）讲解十字相乘法的原理和步骤，让学生初步了解并掌握十字相乘法。

3.操练（15分钟）给学生发放练习题，让学生独立完成，巩固所学知识。

4.巩固（10分钟）讲解练习题的答案，分析学生容易出现的问题，并进行针对性讲解。

5.拓展（10分钟）给学生发放一些具有挑战性的题目，让学生小组讨论，共同解决问题。

6.小结（5分钟）对本节课的主要内容进行总结，强调十字相乘法的重点和难点。

7.家庭作业（5分钟）布置适量的家庭作业，让学生进一步巩固所学知识。

化学十字交叉法的原理及应用[1]

化学总结一、基本概念和基本理论（一）物质的变化和性质1.物质的变化：物理变化：没有生成其他物质的变化。

化学变化：生成了其他物质的变化。

两种变化常常同时发生。

物质发生化学变化时一定伴随物理变化；而发生物理变化不一定同时发生化学变化。

物质的三态变化（固、液、气）是物理变化。

物质发生物理变化时只是分子间的间隔发生变化，而分子本身没有发生变化；发生化学变化时，分子被破坏，分子本身发生变化。

化学变化的特征：生成了其他物质的变化。

2．物质的性质 (描述性质的语句中常有“能……”“可以……”等字)物理性质:颜色、状态、气味、熔点、沸点、硬度、密度、溶解性。

化学性质:通过化学变化表现出的性质。

如还原性、氧化性、酸性、碱性、可燃性、热稳定性。

元素的化学性质跟原子的最外层电子数关系最密切。

原子的最外层电子数决定元素的化学性质。

（二）物质的分类金属单质物混合物单质非金属单质酸性氧化物物质种类稀有气体氧化物碱性氧化物质纯净物元素种类无机物酸其他氧化物化合物碱有机物盐3.混合物：是由两种或两种以上的物质混合而成(或由不同种物质组成）例如，空气，溶液（盐酸、澄清的石灰水、碘酒、矿泉水），矿物（煤、石油、天然气、铁矿石、石灰石），合金（生铁、钢）注意：氧气和臭氧混合而成的物质是混合物，红磷和白磷混合也是混合物。

纯净物、混合物与组成元素的种类无关。

即一种元素组成的物质可能是纯净物也可能是混合物，多种元素组成的物质可能是纯净或混合物。

4.纯净物：由一种物质组成的。

例如：水、水银、蓝矾(CuSO4 ·5H2 O)都是纯净物冰与水混合是纯净物。

名称中有“某化某”“某酸某”的都是纯净物，是化合物。

5.单质：由同种（或一种）元素组成的纯净物。

例如:铁氧气（液氧）、氢气、水银。

6.化合物：由不同种（两种或两种以上）元素组成的纯净物。

名称中有“某化某”“某酸某”的是化合物。

7．有机物（有机化合物）：含碳元素外的化合物（除CO、CO2 和含碳酸根化合物外）无机物：不含碳元素的化合物以及CO、CO2 和含碳酸根的化合物8. 氧化物：由两种元素组成，其中一种是氧元素的化合物。

数控机床安装与调试3.2.1 机械十字滑台装调与检测

机械十字滑台的装调与检测根据提供的电机、联轴器、电机支座、轴承支座、直线导轨、滑块、等高块、滚珠丝杠、螺母、螺母支座、轴承、运动平台等，其中滚珠丝杠、轴承已装成组件，要求根据安装装配工艺要求和提供的零部件进一步自行完成十字滑台的装配，十字滑台机械安装几何精度检测单如下。

底座已经安放型材桌面上，图示为装配完成后的效果图，十字滑台安装流程。

（见下页）注：装配要求①导轨、滚珠丝杠平行度误差0.02mm；②Z轴运动相对于X轴运动的垂直度0.02mm；③工作台面的安装水平误差小于1格。

十字滑台装配完成后的效果图十字滑台安装流程一、安装底座平板1、在安装可调底脚以前，将4只可调底脚的内六角M8×25的螺栓拧至37mm 左右的高度（螺杆顶端到尼龙底座底部的距离），螺栓中间的螺母与尼龙底座间隙约为1mm，并将扁平螺母放到工作台的固定槽中；2、将底座平板4放在工作台上，将可调底脚安装到底座平板底部，对准扁平螺母与底座平板的固定孔，将M6×60的内六角螺栓拧进扁平螺母，留1mm的间隙，然后将水平仪放在底座平板上，调节可调底脚，达到水平要求后，将可调底脚上的螺母与尼龙底座固定紧，用M6×60的内六角螺栓将底座平板安装在铝质型材平台上。

二、安装Z轴部件（一）安装导轨1．将导轨5（650mm）中的一根安放到底座平板上，用两颗M4×20的内六角螺栓预紧该导轨的两端；2．以底座平板的侧面为粗基准，根据导轨安装孔中心到侧面的距离，调整导轨与底座侧面基本平行，将剩余的螺栓装上并将该导轨5固定到底座平板4上，后续的安装工作均以该直线导轨为安装基准(以下称该导轨为基准导轨)；3．将另一根导轨5（650mm）安放到底座上，用两颗M4×20的内六角螺栓预紧此导轨的两端，用游标卡尺初测导轨之间的平行度并进行粗调；4．将杠杆式百分表吸在导轨的滑块上，百分表的表头接触基准导轨的侧面，沿导轨移动滑块，通过橡胶榔头调整导轨，使得两导轨平行，将导轨固定在底座平板上。

汇报课(双脚跳跃--“十字跳”)教学设计1

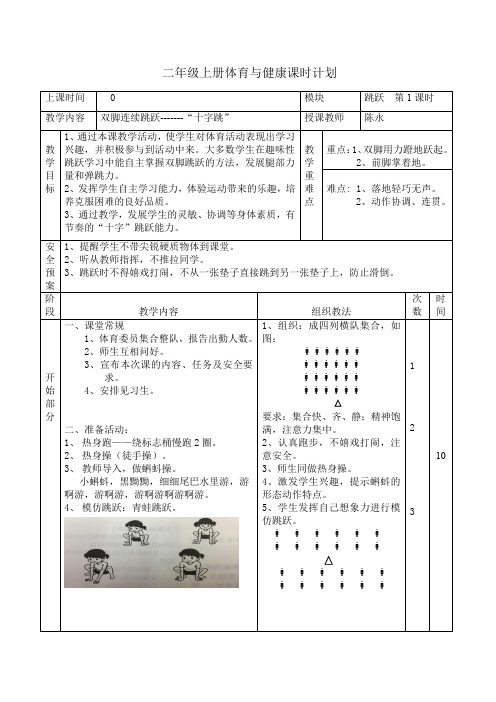
二年级上册体育与健康课时计划
教学内容
一、课堂常规
1、体育委员集合整队，报告出勤人数。

2、师生互相问好。

3、宣布本次课的内容、任务及安全要
求。

4、安排见习生。

二、准备活动：
1、热身跑——绕标志桶慢跑2圈。

2、热身操（徒手操）。

3、教师导入，做蝌蚪操。

小蝌蚪，黑黝黝，细细尾巴水里游，游
啊游，游啊游，游啊游啊游啊游。

4、模仿跳跃：青蛙跳跃。

一、学习双脚跳跃
动作方法：双脚自然姿势站立准备,跳跃时前脚掌着地发力向上跳起，落地时前脚掌着地；整个跳跃过程双臂屈肘画圈摆动，带动身体有节奏的跳跃。

1、教师选一名学生示范原地青蛙跳跃。

2、教师示范原地青蛙跳跃。

3、教师提问：老师和学生模仿的青蛙跳跃有什么不同？（落地是否发出声音）
4、怎样才能做到落地轻巧不发出声音？（前脚掌着地）
“十字跳”如下图：
二、手脚并用----爬行
动作方法：手脚协调并用向前爬行通过一定距离，爬行过程中手脚都在标志垫上，不触碰地面。

1、放松练习（拉伸）。

魔方复原方法架十字技巧三色定律 (1)

如何快速高效地转出“十”字（Cross ）快速高效地转出“十”字的确是一种艺术，而且只能通过练习和实践来学会它。

作为一个初学者，不能一拿起魔方就想着一下子找到转出“十”字的捷径（许多高手也有曾为此困惑过）更别提以最优的方法来解决它。

我希望通过这篇文章展示一些你在观察、摆弄魔方时寻找的东西，和学会它的技巧。

我也会给出各种情况下的一些例子。

但是，不要期盼一天之内就能掌握它！）以下分析显示了从各种可能初始状态下所需的步数概率，你可以指望最多在8 步以内转出“十”字。

另外要强调的是，几乎所有（99.95%）的情况能够在最多7 步以内搞定，平均你只需5 ～ 6 步转出“十”字。

所以如果你每次都能找到最少或接近最少步数并快速转动的话，在1.5 ～ 2 秒内转出一个“十”字是完全有可能的。

你应该知道的基本知识我的第一个也是最重要的建议是：总是在底层来转“十”字。

如果你现在的方法是在顶层来转“十”字，然后在在后面一些步骤中要上、下翻转魔方来完成最后一层的话，我建议你马上放弃这个习惯。

有些玩家更喜欢在左侧来拧“十”字，它和在底层转“十”字一样方便，但为了这篇文章的目的，我还将主要介绍在底层转“十”字，因为这是我最喜欢也是发现的最适用的方法。

在底层转“十”字是一个不错的主意，它让你对上层有很好的观察视角，这意味着在你转“十”字时能很容易地预测并找到F2L 用到的块。

这也意味着你不必在转的过程上、下翻转魔方，从而节约出宝贵的几秒种。

第二，彻底地搞清楚你的魔方上的颜色方案。

确定底层“十”字上每个棱块的颜色，你要知道各个棱块各自对面（正确位置相对面）的颜色（看正面和对面中心块），并且你要知道魔方四周各个方向上的颜色排列。

在我的魔方上，是红－橙，蓝－绿，如果我将红的对着我的话，那绿色就在右边，蓝色在左边，而橙色在后边。

这个知识会让你将精力集中在转魔方的其它方面。

学习你的魔方上的颜色方案并练习，直到习惯成自然。

相对位置和棱“翻转”的概念在你想看到给出的某一种状态就能在最短的时间里转出“十”字之前，相对位置的概念必须非常牢固的掌握在你脑海中。

一年级体育课教案十字接力-2024鲜版

一年级体育课教案十字接力•课程介绍与目标•热身活动与运动技能•团队协作与沟通目录•竞技比赛与策略部署•安全防护与急救措施•总结回顾与展望未来01课程介绍与目标十字接力是一种团队竞技项目，每队四人分别站在四个角上，通过接力棒传递完成比赛。

规则包括起跑、传棒、接棒等环节，要求运动员快速准确地完成动作。

比赛中，队员之间需要密切配合，发挥团队精神，争取最佳成绩。

十字接力定义及规则教学目标与意义教学目标教学意义课程安排与时间课程安排时间分配02热身活动与运动技能热身运动慢跑关节活动组织学生围绕操场进行慢跑，提升身体温度，为接下来的活动做好准备。

拉伸运动双手传球单手接球传球与接球的配合030201传球和接球技巧跑步姿势和呼吸调整正确的跑步姿势呼吸调整跑步练习03团队协作与沟通分组策略及角色分配团队协作意识培养强调团队目标的重要性，鼓励学生为团队胜利而努力。

通过共同完成任务，培养学生间的信任感和默契度。

及时肯定和鼓励团队中的协作行为，树立榜样。

提醒学生在接力过程中保持冷静，用简洁明了的语言传递信息。

鼓励学生之间互相交流，分享经验和技巧，提高团队整体实力。

教授学生正确的传接棒技术，强调语言沟通的重要性。

有效沟通技巧04竞技比赛与策略部署接力棒传递每位队员手持接力棒，跑到赛道中央后将接力棒传递给下一位队员，传递过程必须准确迅速。

赛道与队伍在操场上划定十字形赛道，每队四人分别站在四个角上，听到哨声后开始跑动。

比赛胜负以最先完成接力棒传递并返回起点的队伍为胜。

比赛规则解读策略制定及实施起跑策略01接力棒传递技巧02团队协作03竞技精神培养竞争意识通过比赛培养学生的竞争意识，让他们学会在竞争中发挥自己的潜力。

团队精神强调团队合作的重要性，让学生明白只有团结一致才能取得胜利。

尊重对手教育学生尊重对手，遵守比赛规则，培养良好的体育道德风尚。

05安全防护与急救措施安全防护装备使用穿着合适的运动鞋穿着适当的运动服装使用防护装备常见运动损伤处理擦伤和刮伤扭伤和拉伤鼻出血急救知识普及心肺复苏术（CPR）止血方法休克处理拨打急救电话06总结回顾与展望未来1 2 3接力跑的基本技术和规则团队协作和竞争意识运动技能和体能提升关键知识点总结学生自我评价报告大多数学生能够认识到自己在接力跑中的表现，并对接力棒传递和团队协作有更深的理解。

十字交叉法1

十字交叉法解题十字交叉法是进行二组分混和物平均量与组分量计算的一种简便方法。

凡可组成二元一次方程组（x+y=1;ax+by=c)的平均值问题都可用十字交叉法解决，所得的十字交叉法的比值就是方程组解得的x和y的比。

比值的单位取决于x和y的单位；通常中学常用的十字交叉法有溶液的百分比浓度十字交叉，结果得质量比；混合气体的平均分子量十字交叉，结果得物质的量比或体积比；同位素的平均相对原子质量十字交叉，结果得原子个数比；有机组成十字交叉，结果得物质的量比；使用过程中要灵活应用能解决更多的问题。

能用十字交叉法解答的常见题型一、用组分的式量与混合气的平均式量做十字交叉，求组分体积比或含量。

例1：已知H2和CO 的混合气，其平均式量是20，求混合气中H2和CO 的体积比。

（4∶9）解：H2 2 28－20 4╲╱—— 20 ——╱╲CO 28 20－2 9例2：已知CO、CO2混合气的平均式量是32，耱混合气中CO 的体积百分数。

（75%）解：CO 28 12 3╲╱—— 32 ——╱╲CO2 28 4 1例3. 体积为1L的干燥烧瓶中用排气法收集HCl后，测得瓶中的气体对氧气的相对密度为1.082，以此气体做喷泉实验，结束后进入烧瓶的液体体积是（）A. 1LB. 3/4LC. 1/2LD. 1/4L解析：两组分气体混合，体积分数不变，总体积等于组分体积之和，可用十字交叉法解题。

相对平均式量为：1.082×32=34.624，介于29和36.5之间，故烧瓶中是HCl、空气的混合气体。

有十字交叉关系：HCl气体与空气体积比为5.624：1.876＝3：1，答案是B。

例题14（MCE 1997—26）一定量的乙醇在氧气不足的情况下燃烧，得到CO、CO2和水的总质量为27.6g，若其中水的质量为10.8g，则CO的质量是[ ]A．1.4g B．2.2gC．4.4g D．在2.1g和4.4g之间【讲解并板书】此题考查有机物的不完全燃烧，解析过程中可运用十字交叉法：（方法一）CO与CO2总质量：27.6g-10.8g=16.8g生成CO、CO2共0.2 mol×2=0.4 molm（CO）=28 g/mol×0.05 mol=1.4 g答案：A例题15 （MCE 1999—21）右图中横坐标表示完全燃烧时耗用可燃气体X（X=A、B、C）的物质的量n（X），纵坐标表示消耗O2的物质的量n（O2），A、B是两种可燃性气体，C是A 和B图6-1的混合气体，则C中n（A）∶n（B）为[ ]A．2∶1 B．1∶2C．1∶1 D．任意比仔细地观察图示，认真地分析数据，热烈地进行讨论。

一元二次方程十字相乘法例题过程

一、引言一元二次方程是数学中常见的类型之一，解一元二次方程的方法有很多种，其中十字相乘法是一种常用的解题方法。

这种方法简单直观，适合初学者掌握。

下面我们将通过一些例题来演示一元二次方程十字相乘法的解题过程。

二、十字相乘法概述十字相乘法是解一元二次方程的一种常用方法，它的基本思想是将一元二次方程化简为两个一次方程的乘积，然后通过求解这两个一次方程来得到一元二次方程的解。

使用十字相乘法的关键是要找到适当的两个一次方程使其乘积等于一元二次方程。

下面我们将通过例题来详细演示十字相乘法的具体操作过程。

三、例题一题目：解一元二次方程x^2 + 5x + 6 = 0解答：1. 首先写出一元二次方程的标准形式：x^2 + 5x + 6 = 02. 找到适当的两个一次方程使其乘积等于一元二次方程：x^2 + 3x + 2x + 6 = 03. 将一元二次方程的中间项拆分为两个一次方程的和：x(x + 3) +2(x + 3) = 04. 将上式进行分组：(x + 3)(x + 2) = 05. 通过分解得到的两个一次方程求解得到：x + 3 = 0 或 x + 2 = 06. 得到方程的解：x = -3 或 x = -2四、例题二题目：解一元二次方程x^2 - 9x + 20 = 0解答：1. 首先写出一元二次方程的标准形式：x^2 - 9x + 20 = 02. 找到适当的两个一次方程使其乘积等于一元二次方程：x^2 - 4x - 5x + 20 = 03. 将一元二次方程的中间项拆分为两个一次方程的和：x(x - 4) - 5(x - 4) = 04. 将上式进行分组：(x - 4)(x - 5) = 05. 通过分解得到的两个一次方程求解得到：x - 4 = 0 或 x - 5 = 06. 得到方程的解：x = 4 或 x = 5五、例题三题目：解一元二次方程2x^2 + 7x - 15 = 0解答：1. 首先写出一元二次方程的标准形式：2x^2 + 7x - 15 = 02. 找到适当的两个一次方程使其乘积等于一元二次方程：2x^2 + 10x - 3x - 15 = 03. 将一元二次方程的中间项拆分为两个一次方程的和：2x(x + 5) - 3(x + 5) = 04. 将上式进行分组：(2x - 3)(x + 5) = 05. 通过分解得到的两个一次方程求解得到：2x - 3 = 0 或 x + 5 = 06. 得到方程的解：x = 3/2 或 x = -5六、总结通过以上例题的演示，我们可以清晰地了解到一元二次方程十字相乘法的解题过程。

十字法解一元二次方程

十字法解一元二次方程
十字法是一种求解一元二次方程的方法，通过将方程中的一些常数项按照一定的方式排列，然后进行计算，最终求解出方程的根。

具体步骤如下：
1. 将一元二次方程写成标准形式，即ax^2 + bx + c = 0，其中a、
b、c为已知常数。

2. 计算常数项c的因数，即找出两个数p和q，满足p*q=c。

3. 将系数b的值分解成两个数，满足p+q=b。

4. 写出方程的因式分解形式，即(x+p)(x+q)=0。

5. 根据因式分解形式，得到方程的两个解x=-p和x=-q。

这样就可以得到方程的两个解。

需要注意的是，如果方程不能被因式分解，那么十字法就无法使用，需要使用其他方法来求解方程的根。