2013数学建模优秀作品
2013高教社杯全国大学生数学建模竞赛获奖名单(本科组)

浙江
浙江大学
余昉恒
梁梓鹏
张宇轩
数模组
108
浙江
浙江大学
方子君
郭俊宏
任青
数模组
109
浙江
浙江大学
沈剑飞
张仑
李拜
数模组
110
浙江
温州大学
翁雯雯
赵环
赵妙妙
数模组
111
浙江
温州大学
徐晶
石珍妮
陈斯定
连新泽
112
浙江
温州大学瓯江学院
曹晖晖
姜冬丽
孔晓栋
徐徐
113
安徽
安庆师范学院
张启军
万杨
汪严随
郝庆一
114
安徽
湖北
三峡大学
韩雪晨
李欢欢
刘军
指导教师组
163
湖北
三峡大学
李金武
杨志巧
马舒
指导教师组
164
湖北
中南民族大学
刘琴
亓晓同
黄强
教练组
165
湖北
华中农业大学
汪伟平
白婷
刘凌览
牛晓辉
166
湖北
华中农业大学
胡曹园
李扶摇
刘志祥
李治
167
湖北
华中农业大学
鲍晨
郑田蔚宝
韩以超
谭劲英
168
湖北
华中农业大学
王泷
陈攀
唐功宇
李治
169
徐志丹
刘晓峰
35
山西
太原理工大学
钟维坚
冯艳
万建
贺衎
36
山西
中北大学
2013高教社杯全国大学生数学建模竞赛一等奖论文

承诺书我们仔细阅读了《全国大学生数学建模竞赛章程》和《全国大学生数学建模竞赛参赛规则》(以下简称为“竞赛章程和参赛规则”,可从全国大学生数学建模竞赛网站下载)。
我们完全明白,在竞赛开始后参赛队员不能以任何方式(包括电话、电子邮件、网上咨询等)与队外的任何人(包括指导教师)研究、讨论与赛题有关的问题。
我们知道,抄袭别人的成果是违反竞赛章程和参赛规则的,如果引用别人的成果或其他公开的资料(包括网上查到的资料),必须按照规定的参考文献的表述方式在正文引用处和参考文献中明确列出。
我们郑重承诺,严格遵守竞赛章程和参赛规则,以保证竞赛的公正、公平性。
如有违反竞赛章程和参赛规则的行为,我们将受到严肃处理。
我们授权全国大学生数学建模竞赛组委会,可将我们的论文以任何形式进行公开展示(包括进行网上公示,在书籍、期刊和其他媒体进行正式或非正式发表等)。
我们参赛选择的题号是(从A/B/C/D中选择一项填写): D我们的参赛报名号为(即为你队的电子文件名):所属学校(请填写完整的全名):参赛队员(打印并签名) :1.2.3.指导教师或指导教师组负责人(打印并签名):(论文纸质版与电子版中的以上信息必须一致,只是电子版中无需签名。
以上内容请仔细核对,提交后将不再允许做任何修改。
如填写错误,论文可能被取消评奖资格。
)日期: 2013 年 9 月 16 日赛区评阅编号(由赛区组委会评阅前进行编号):编号专用页赛区评阅编号(由赛区组委会评阅前进行编号):全国统一编号(由赛区组委会送交全国前编号):全国评阅编号(由全国组委会评阅前进行编号):公共自行车服务系统优化模型摘要本模型的解决是为了提高公共自行车的使用率。
问题一,根据附件1中的公共自行车数据可统计出各站点20天中每天及累计的借车频次和还车频次(见于附件1),并得出各个站点累计的借车频次和还车频次进行从小到大的排序(见于附件2)。
根据附件1,可以得知每次用车的时长的统计,并根据此统计数据使用EXCEL软件描绘每次用车时长的分布图,通过此图,可以得知:用车时间在0—60分钟的次数较多,在20分钟附近较为突出,超过60分钟的次数较少。
2013年全国大学生数学建模竞赛B题全国一等奖论文.

碎纸片的拼接复原【摘要】破碎文件的拼接在司法物证复原、历史文献修复以及军事情报获取等领域都有着重要的应用。
本文主要解决碎纸机切割后的碎纸片拼接复原问题。
针对第一问,附件1、2分别为沿纵向切割后的19张中英文碎纸片,本文在考虑破碎纸片携带信息量较大的基础上,利用MATLAB对附件1、2的碎纸片图像分别读入,以数字矩阵的方式进行存储。
利用数字矩阵中包含图像边缘灰度这一特征,本文采用贪心算法的思想,在首先确定原文件左右边界的基础上,以Manhattan距离来度量两两碎纸片边界差异度,利用计算机搜索依次从左往右搜寻最匹配的碎纸片进行横向配对并达成排序目的。
最终,本文在没有进行人工干预,成功地将附件1、2碎纸片分别拼接复原,得到复原图片见附录2.1、2.2,纵切中文及英文结果表分别如下:思想仍为贪心算法,整体思路为先对209张碎纸片进行聚类还原成11行,再对分好的每行进行横向排序,最后对排序好的各行进行纵向排序。
本文在充分考虑汉字与拉丁字母结构特征差异以及每块碎纸片携带信息减少的基础上,创新地提出一种特征线模型来分别描述汉字及拉丁文字母的特征用于行聚类。
对于行聚类后碎片的横向排序,本文综合了广义Jaccard系数、一阶差分法、二阶差分法、Spearman系数等来构建扩展的边界差异度模型,刻画碎片间的差异度。
对于计算机横向排序存在些许错误的情况,本文给出了人工干预的位置节点和方式。
对于横向排序后的各行,由于在一页纸上,文字的各行是均匀分布的,本文基于各行文字的特征线,在确定首行的位置后,估计出其他行的基准线位置,得到一页的基准线网格,并通过各行基准线在基准线网格上的适配实现纵向的排序。
最终,本文成功的将附件3、4碎纸片分别拼接复原得到复原图片及结果表见附录1.3、1.4、2.3、2.4,同时本文给出了横向排序中人工干预的位置节点和方式。
针对第三问,附件5为双面文件既横切又纵切后的209张碎片(包含正反面),即包含418张图像。
2013年全国大学生数学建模云南赛区获奖名单
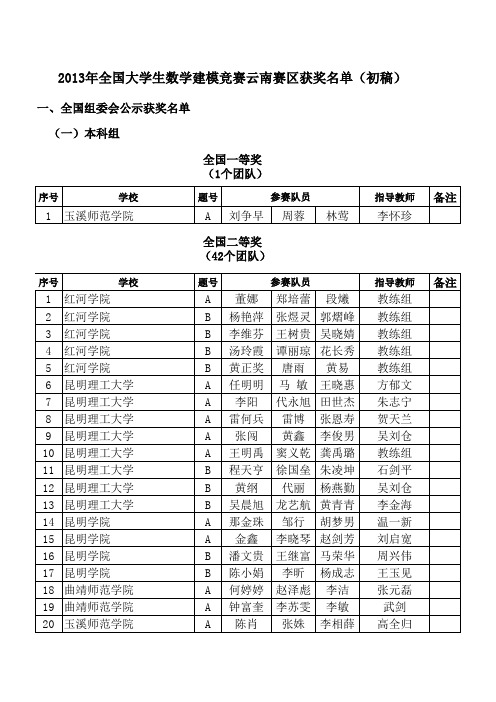
丁瑞敏 教练组 张李男 统计教练组 鲁瑶 尉洪 金姝含 数学教练组 凌硕豪 周维 刘强 李海燕 吴香兰 李海燕 和春元 李海燕 李超 教练组 赵刚 杨金华 王骏杰 杨金华 王淑文 吴萍萍 郑珊 付胜楠 王英杰 靳巧花 李建莹 段国定 杨明秋 王新 包玉仙 赵波 文正琴 施杰 方春渤 郑大川 吕姣兰 刘海鸿 顾文艳 胥成林 张营 教练组
董娜 杨艳萍 李维芬 汤玲霞 黄正奖 任明明 李阳 雷何兵 张闯 王明禹 程天亨 黄纲 吴晨旭 那金珠 金鑫 潘文贵 陈小娟 何婷婷 钟富奎 陈肖
郑培蕾 张煜灵 王树贵 谭丽琼 唐雨 马 敏 代永旭 雷博 黄鑫 窦义乾 徐国垒 代丽 龙艺航 邹行 李晓琴 王继富 李昕 赵泽彪 李苏雯 张姝
段爔 郭熠峰 吴晓婧 花长秀 黄易 王晓惠 田世杰 张恩寿 李俊男 龚禹璐 朱凌坤 杨燕勤 黄青青 胡梦男 赵剑芳 马荣华 杨成志 李洁 李敏 李相薛
A A A A A A A A A A A A A A A A A A A A A A A A A A A A A A A A A
董玲 赵玲玲 江俊杰 教练组 邓兰梅 王璐 班朝飞 王军 崇瑞 王齐 邵妍 资环教练组 史静怡 张星灿 李青 教练组 刘龙海 陆旭 邹骥 教练组 姚天昌 孙长义 徐大伟 吴晟 李欣美 高丽 辛彦蓉 罗建军 鲁佼佼 濮聪英 陈忍 李春娥 刘炜 黄源霖 刘丛高 郁湧 涂润润 胡菡 王里瑶 教练组 向艳梅 杨丽萍 段 敏 何俊 夏萧 母江艳 代云蔚 刘海鸿 施华英 杨美娟 徐刘全 邹欢 和建梅 姚依君 杨会云 卢方武 何志芳 倪飞 白杨林 晏林 杨启明 陶仿 潘佳斌 晏林 陈冠宇 李文涛 赵丽 贾丽丽 张明成 袁密 代超星 陈兴炼 解波 李继彪 夏恩鹏 教练组 段现涛 史红瑞 金 霞 冯云再 陈丽 陈兴翠 但磊 教练组 杨洪富 刘艳 苏智婷 刘海鸿 刘友义 李宗泽 吴桂鸿 吴晟 栾李媛 张益华 和春元 曾赤洁 卢绍国 谷峰雷 吴猛 柳士峰 严江 付靖玲 刘顺友 张洪波 李彬 陈晓琳 伍梦熊 蔡建春 卢珊 刘瑞 杜磊 王世普 刘翠 郑雪娇 牛佩飞 邵晶晶 杜红 普志红 龚方盛 高鑫 李雨青 黄茹芊 高佳羽 教练组 陈念念 张立娟 兰贵虹 教练组 刘旭 李世鹏 陈俊年 教练组
2013年高教社杯全国大学生数学建模竞赛辽宁赛区获奖名单
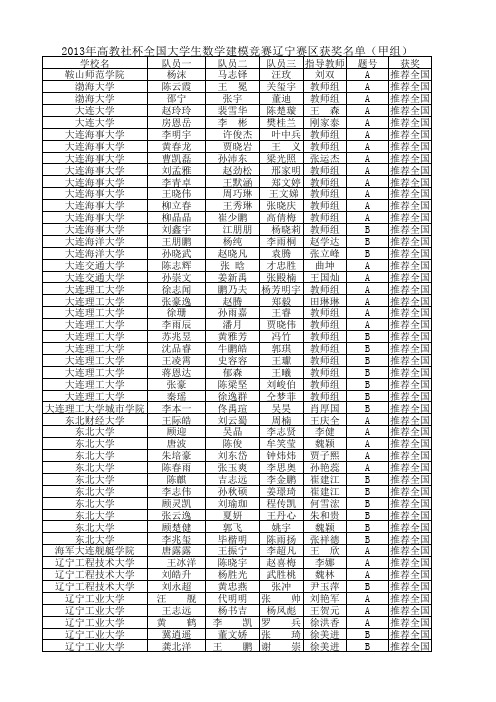
邱添 教师组
B
阚丹会 悦秋燕 孙晓坤
A
邵鹏
孟妮 高旭彬
B
吴旭
赵志强 教师组
B
曹子迁 俞珍珍 教师组
B
汤天耀 王德鹍 冯 杰
A
王博实 唐艺璇 王铁
B
张敬思 蒋浩邦 尹玉萍
A
何欣键 贾子钰 王磊
A
刘凯强 高梦云 尹玉萍
B
夏 冬 吴 迟 张晓薇
B
闫 硕 孙 俏 李莉莉
A
郑继敏 段恒昌 石鸿雁
A
宋永跃 宋方涛 王毅兵
大连大学
张晶
杨 晓 孟宪航 刚家泰
A
二等奖
大连大学
陈皓
梁 倩 房本旭 谭欣欣
B
二等奖
大连东软信息学院
郝婧
张子腾 李一鸣 梁艺多
B
二等奖
大连工业大学
马毅煌
何志童 曹金 黄徳智
A
二等奖
大连工业大学
王传宇
张营
王芯雨 张玉杰
A
二等奖
大连工业大学
王佳锴
梁嘉祯 杨挺 刘燕
A 二等奖
大连工业大学
王健丰
林敏慧 刘叶 于加武
2013年高教社杯全国大学生数学建模竞赛辽宁赛区获奖名单(甲组)
学校名
队员一
队员二 队员三 指导教师 题号 获奖
鞍山师范学院
杨沫
马志铎 汪玫 刘双
A 推荐全国
渤海大学
陈云霞
王 冕 关玺宇 教师组
A 推荐全国
渤海大学
邵宁
张宇
董迪 教师组
A 推荐全国
大连大学
赵玲玲
裴雪华 陈楚璇 王 森
A 推荐全国
2013年美国大学生数学建模大赛A题 一等奖

最终的布朗尼蛋糕盘Team #23686 February 5, 2013摘要Summary/Abstract为了解决布朗尼蛋糕最佳烤盘形状的选择问题,本文首先建立了烤盘热量分布模型,解决了烤盘形态转变过程中所有烤盘形状热量分布的问题。
又建立了数量最优模型,解决了烤箱所能容纳最大烤盘数的问题。
然后建立了热量分布最优模型,解决了烤盘平均热量分布最大问题。
最后,我们建立了数量与热量最优模型,解决了选择最佳烤盘形状的问题。
模型一:为了解决烤盘形态转变过程中所有烤盘形状热量分布的问题,我们假设烤盘的任意一条边为半无限大平板,结合第三边界条件下非稳态导热公式,建立了不同形状烤盘的热量分布模型,模拟出不同形状烤盘热量分布图。
最后得到结论:在烤盘由多边形趋于圆的过程中,烤焦的程度会越来越小。
模型二:为了解决烤箱所能容纳最大烤盘数的问题,本文建立了随烤箱长宽比变化下的数量最优模型。
求解得到烤盘数目N 随着烤箱长宽比和烤盘边数n 变化的函数如下:AL W L W cont cont cont N 4n2nsin 1222⎪⎭⎫ ⎝⎛⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎪⎪⎭⎫ ⎝⎛+⋅--=π模型三:本文定义平均热量分布H 为未超过某一温度时的非烤焦区域占烤盘边缘总区域的百分比。
为了解决烤盘平均热量分布最大问题,本文建立了热量分布最优模型,求解得到平均热量分布随着烤箱长宽比和形状变化的函数如下:n sin n cos -n 2nsin 22ntan1H ππδπδπ⎪⎪⎪⎪⎪⎭⎫⎝⎛⎪⎭⎫ ⎝⎛⋅-=A结论是:当烤箱长宽比为定值时,正方形烤盘在烤箱中被容纳的最多,圆形烤盘的平均热量分布最大。
当烤盘边数为定值时,在长宽比为1:1的烤箱中被容纳的烤盘数量最多,平均热量分布H 最大。
模型四:通过对函数⎪⎭⎫ ⎝⎛n ,L W N 和函数⎪⎭⎫⎝⎛n ,L W H 作无量纲化处理,结合各自的权重p 和()p -1,本文建立了数量和热量混合最优模型,得到烤盘边数n 随p值和LW的函数。
2013年全国研究生数学建模竞赛获奖名单

获华为特别奖的是10013009
90006007 90045019
10699002 90005008 10013009 10293014 90006018 10286030 90059005 10701007 10054019
D题
许放 肖帅芳 陶铭亮 阮智昊 宋歌 荆舒晟 林洪涛 陈智斌 唐艳梅 吴昊 尹辉 刘璧婷 何国玺 吴名强 袁光辉 蒋雪峰 郭慧敏 李海燕 刘天 何迎东 周诗雨 冉芸 董俊 李思佳 李子龙 罗永东 吴波亮 郑江 马烁 周少龙 肖玲 蔡淑娟
任丽 贵州大学 何伟 西北工业大学 谭索怡 国防科学技术大学 孙晓芹 山东财经大学 张艳欣 中国航天科工集团第二研究院 颜文超 上海交通大学 肖锦绣 西南交通大学 李鹏 中国石油大学(北京) 徐思军 宁波大学 程瑾 西南石油大学 罗晨 湖北工业大学 李秋影 吉林大学 魏杰 南京大学 余强 孙恒宇 叶尚斌 解放军电子工程学院 浙江工商大学 同济大学
获华为特别奖的是10248005
10248005 10247134 90005013 90005023 10287030 10286090 10256023 10319003 10595005 10079012 10287025 83221014 10613020 10252115 10558008 10418003 10699004 10533057 10422055 10269005 10335002 10561004 80132001 10358010 10004008
王丹华 王维 邵卿 谢婷 马文聪 张晓勇 陈余康
南京财经大学 江苏大学 上海大学 东华大学 天津大学 西南财经大学 复旦大学
姓名 李骥 余竹玛 田欣 卢梦凯 张成 刘友琼 陈其盛 林宝照 陈洪骏 胡在凰 时浩 李剑峰 严杰 曹海龙 黄国翔 时岩 罗杰华 张勇 孟飞
2013全国数学建模A题优秀作品

第六届“认证杯”数学中国数学建模网络挑战赛承诺书我们仔细阅读了第六届“认证杯”数学中国数学建模网络挑战赛的竞赛规则。
我们完全明白,在竞赛开始后参赛队员不能以任何方式(包括电话、电子邮件、网上咨询等)与队外的任何人(包括指导教师)研究、讨论与赛题有关的问题。
我们知道,抄袭别人的成果是违反竞赛规则的, 如果引用别人的成果或其他公开的资料(包括网上查到的资料),必须按照规定的参考文献的表述方式在正文引用处和参考文献中明确列出。
我们郑重承诺,严格遵守竞赛规则,以保证竞赛的公正、公平性。
如有违反竞赛规则的行为,我们将受到严肃处理。
我们允许数学中国网站()公布论文,以供网友之间学习交流,数学中国网站以非商业目的的论文交流不需要提前取得我们的同意。
我们的参赛队号为:2261参赛队员(签名) :队员1:张述平队员2:魏方征队员3:乔赛参赛队教练员(签名):参赛队伍组别:2261第六届“认证杯”数学中国数学建模网络挑战赛编号专用页参赛队伍的参赛队号:2261竞赛统一编号(由竞赛组委会送至评委团前编号):竞赛评阅编号(由竞赛评委团评阅前进行编号):2013年第六届“认证杯”数学中国数学建模网络挑战赛题目护岸框架减速效果的优化方案关键词护岸框架减速效果单因素方差分析最小二乘拟合回归分析摘要:四面六边透水框架是一种新型江河护岸工程技术,对于降低岸边流速、稳定河道、保护堤岸有显著的作用。
本文针对所引用参考文献中的图像、数据,从四面六边透水框架群框架尺寸、架空率和长度三方面出发,对框架群的水力特性及其影响因素进行分析,探讨三要素对减速效果的影响,建立三个模型,为这种“亲水”式生态防护技术在工程中推广运用提供参考依据。
模型一:架空率对减速效果影响的分析。
首先,利用单因素方差分析,推断出架空率对减速效果的影响较显著;其次,采取最小二乘法拟合曲线具体演示二者的发展趋势,并得到关系模型,依照此模型得出架空率对减速效果影响显著。
得出框架率ε=4.2~4.8 之间时,框架群的减速率比较高,能够使得框架群的阻水消能作用和“亲水”功能较好的结合起来。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
承诺书我们仔细阅读了《全国大学生数学建模竞赛章程》和《全国大学生数学建模竞赛参赛规则》(以下简称为“竞赛章程和参赛规则”,可从全国大学生数学建模竞赛网站下载)。
我们完全明白,在竞赛开始后参赛队员不能以任何方式(包括电话、电子邮件、网上咨询等)与队外的任何人(包括指导教师)研究、讨论与赛题有关的问题。
我们知道,抄袭别人的成果是违反竞赛章程和参赛规则的,如果引用别人的成果或其他公开的资料(包括网上查到的资料),必须按照规定的参考文献的表述方式在正文引用处和参考文献中明确列出。
我们郑重承诺,严格遵守竞赛章程和参赛规则,以保证竞赛的公正、公平性。
如有违反竞赛章程和参赛规则的行为,我们将受到严肃处理。
我们授权全国大学生数学建模竞赛组委会,可将我们的论文以任何形式进行公开展示(包括进行网上公示,在书籍、期刊和其他媒体进行正式或非正式发表等)。
我们参赛选择的题号是(从A/B/C/D中选择一项填写): A我们的参赛报名号为(如果赛区设置报名号的话):01034所属学校(请填写完整的全名):参赛队员(打印并签名) :1.2.3.指导教师或指导教师组负责人(打印并签名):(论文纸质版与电子版中的以上信息必须一致,只是电子版中无需签名。
以上内容请仔细核对,提交后将不再允许做任何修改。
如填写错误,论文可能被取消评奖资格。
)日期:2013 年 9 月16 日赛区评阅编号(由赛区组委会评阅前进行编号):编号专用页赛区评阅编号(由赛区组委会评阅前进行编号):赛区评阅记录(可供赛区评阅时使用):评阅人评分备注全国统一编号(由赛区组委会送交全国前编号):全国评阅编号(由全国组委会评阅前进行编号):车道被占用对城市道路通行能力的影响摘要车道被占用是研究城市交通的一个重要领域。
本题要求建立合理数学模型,成功解决某个道路被堵后交通情况变化的整个过程,为相关部门解决实际问题提供理论依据。
针对问题一,描述事故发生过程中实际交通能力的变化过程。
我们根据视频的分析得出此段路为二级公路。
按照二级路段的通行能力计算公式,在视频1中采集所需的数据,通过Excel 计算并绘制出图5-2。
实际通行能力呈周期性变化,且随着阻塞车辆的增加而降低,但达到一定程度后递减效果不再明显。
针对问题二,分析所占不同道对该横断面交通能力影响差异。
通过对附件3的分析,首先我们考虑的是不同道承担交通任务不同,进而导致需要换道的车辆数不同,换道会降低通行能力。
通过流体力学理论验证了我们的设想。
因此我们采用拟合的方式确定换道次数与实际交通能力的关系,利用Matlab 拟合结果为:23031025.776.66-+⋅⨯-=x N 仅一道和仅三道换道次数比为1.33,所以仅三道比通行比仅一道通行实际交通能力强,由图5-6也可验证此结论。
针对问题三,确定排队长度与横断面实际交通能力、事故持续时间、路段上游车流量的关系。
我们考虑到车流属于交通波,则有T y ω=,综合路口和交通带来的车流以60s 为一周期规律性变化,由此我们建立的交通波模型为:()()()()()()[]()()11211111t t k h t t t t k h k h t y B s ----+-=其中),()(N q f k h =,用0/=dt dy 便可求出极值点,得到了()()[]()()()1112114/k h t t k h k h y B s s -+-=,即车辆排队距离的表达式。
并利用视频1中的数据进行检验,检验结果相对误差为4.5%,在误差允许范围内,基本符合实际情况,可以推广使用。
针对问题四,事故发生在距离上游路口140m 处,上游车流量为1500h pcu / 来确定经过多久车辆长度达到140m 。
我们利用问题三的结论,把堵车距离作为已知量,堵车达到140m 的时间作为未知量。
综合路口状况和交通灯。
我们建立的模型为()()[]()()[]12112114/t k h t t k h k h t B s s +-+-=。
通过分析视频1,求出所需数据,得出车辆排队距离为140m 的时间为5分51秒。
本题综合了车辆变道的影响、路口状况的影响、交通灯变化规律的影响以及本段路的实况信息,建立了数学模型。
考虑较为全面,可以给交通管理部门正确引导车辆行驶、审批占道施工、设计道路渠化方案、设置路边停车位和设置非港湾式公交车站等提供理论依据。
关键词:换道行为;流体力学;Matlab 拟合;交通波一问题重述车道被占用是指因交通事故、路边停车、占道施工等因素,导致车道或道路横断面通行能力在单位时间内降低的现象。
由于城市道路具有交通流密度大、连续性强等特点,一条车道被占用,也可能降低路段所有车道的通行能力,即使时间短,也可能引起车辆排队,出现交通阻塞。
如处理不当,甚至出现区域性拥堵。
车道被占用的情况种类繁多、复杂,正确估算车道被占用对城市道路通行能力的影响程度,将为交通管理部门正确引导车辆行驶、审批占道施工、设计道路渠化方案、设置路边停车位和设置非港湾式公交车站等提供理论依据。
视频1(附件1)和视频2(附件2)中的两个交通事故处于同一路段的同一横断面,且完全占用两条车道。
请研究以下问题:(1)根据视频1(附件1),描述视频中交通事故发生至撤离期间,事故所处横断面实际通行能力的变化过程。
(2)根据问题1所得结论,结合视频2(附件2),分析说明同一横断面交通事故所占车道不同对该横断面实际通行能力影响的差异。
(3)构建数学模型,分析视频1(附件1)中交通事故所影响的路段车辆排队长度与事故横断面实际通行能力、事故持续时间、路段上游车流量间的关系。
(4)假如视频1(附件1)中的交通事故所处横断面距离上游路口变为140米,路段下游方向需求不变,路段上游车流量为1500pcu/h,事故发生时车辆初始排队长度为零,且事故持续不撤离。
请估算,从事故发生开始,经过多长时间,车辆排队长度将到达上游路口。
二基本假设模型假设(1)附件1、附近2中视频所取时间具有代表性,能反映客观事实;(2)事故发生具有偶然性,车流阻塞过程不存在人为干预;(3)只考虑四轮及以上的机动车、电瓶车的交通流量;(4)事故发生只会占用两个相邻车道;三符号说明N断面实际通行能力f各项修正系数if车道宽度修正系数wf车道硬路肩宽度修正系数hvf方向分布修正系数df路测干扰修正系数fμ临界车速mμ自由流车速jk发生事故前车流密度1k平静点车流密度1sk阻塞密度jk临界密度mt事故持续时间1t最大排对长度时间sy最大排队距离sq上游车流量l行驶车辆最小安全间距N基本通行能力最大四问题的分析本题从道路发生交通事故占用车道入手,要求建立模型解决占用后对通行能力的影响,占用不同车道对通行能力的影响,以及估算事故发生后车辆排队长度与相关参数的关系,并能准确计算车辆排队长度达到最大的时间针对问题一,描述事故发生过程中,实际交通能力的变化过程。
我们根据视频里的路面状况,首先确定公路的级别,进而确定所用的求解实际交通能力公式。
求出任意时间段的交通能力,再建立实际交通能力与时间的关系,得到实际交通能力变化过程。
针对问题二,分析所占不同道对该横断面交通能力影响差异。
通过对附件3的分析,首先我们考虑的是不同道承担交通任务不同,进而导致同一横断面不同车道发生事故对该横断面实际通行能力存在差异,因为需要换道的车辆数不同,换道会降低交通能力。
通过对实际交通能力对换道次数作图,得到仅一道和仅三道通行的差异。
针对问题三,确定排队长度与横断面实际交通能力、事故持续时间、路段上油车流量的关系。
我们考虑到车流属于交通波,应符合交通波模型,再综合路口和交通灯带来的车流规律性变化,求出了堵车距离的表达式。
针对问题四,事故发生在距离上游路口140m处,上游车流量为1500pcu/h 来确定经过多久车辆长度达到140m。
我们利用问题三的结论,把堵车距离作为已知量,堵车达到140m的时间作为未知量。
综合路口状况和交通灯,我们建立的模型为交通波模型。
通过分析附件一的视频,求出所需数据,从而得出结果。
五 模型的建立与求解5.1 问题一本题要求通过对附件一的认真观察及分析事故所处横断面实际通行能力的变化。
分析其作用是为了确定新建道路的等级,性质,主要技术指标和线形几何要求,确定现有道路系统或某一路段所存在的问题,针对问题提出改进方案和措施,为道路的改建和改善提供依据,作为交通枢纽的规划,设计及交通设施配置的依据,为制定交通组织,交通疏导,交通引导,交通量均衡,交通数量控制盒综合治理等交通系统管理方案提供依据,为制定交通管理,交通控制方案以及交通渠化,信号配时优化方案设计及选择等提供依据。
5.1.1 通行能力的计算首先,我们要知道什么是道路的实际通行能力,道路的通行能力是指在一定的时间段内和在通常的道路,交通,管制条件下,能合理的期望人和车辆通过道路某一断面或地点的最大交通数量。
通行能力一共分为三类,基本通行能力,实际通行能力和设计通行能力。
1.基本通行能力是指道路与交通处于理想情况下,每一条车道(或每一条道路) 在单位时间内能够通过的最大交通量。
作为理想的道路条件,主要是车道宽度应不小于3.65 m , 路旁的侧向余宽不小于1.75 m , 纵坡平缓并有开阔的视野、良好的平面线形和路面状况。
作为交通的理想条件, 主要是车辆组成单一的标准车型汽车, 在一条车道上以相同的速度,连续不断的行驶,各车辆之间保持与车速相适应的最小车头间隔, 且无任何方向的干扰。
在这样的情况下建立的车流计算模式所得出的最大交通量,即基本通行能力。
基本通行能力与行驶车辆之间的最小安全间距公式如下:)/(10006.3/36003600N 00h l VV l h t 辆最大===)(辆车安车安制反h l l V t V l l l l l /2546.320++Φ+=+++=安l 一般取用2m ,t 可取1s ,附着系数Φ与轮胎花纹,路面粗糙度,平整度,表面适度,行车速度等因素有关,如表5-1所示:表5-1 纵向附着系数与车速的关系表)/(h km V120 100 80 60 50 30 20 40 值Φ0.290.300.310.330.350.440.440.38对应表中的数据,对小车的安全长度进行计算,小汽车车辆长度一般采用6m 。
本题就把0l 取6m 。
2.计算可能通行能力N 是以基本通行能力为基础考虑到实际的道路和交通状况,确定其修正系数,再以此修正系数乘以前述的基本通行能力,即得实际道路、交通与一定环境条件下的可能通行能力[1]。
影响通行能力不同因素的修正系数为:1)道路条件影响通行能力的因素很多, 一般考虑影响大的因素, 其修正系数有: ①车道宽度修正系数1f ;②侧向净空的修正系数2f ;③纵坡度修正系数3f ;④视距不足修正系数5f ;⑤沿途条件修正系数6f 。
