Kernel methods and the exponential family
QuantStudio 6 qPCR仪器 (Applied Biosystems)快速入门指南说明书

protocol v1.09 QuantStudio 6 qPCR instrument (Applied Biosystems) quick start guideImportant notes-This document is only a quick start guide, please refer to the official instrument user manual for in depth instructions. Contact us if you have questions or need help with troubleshooting.-Check the compatibility of your mastermix with this instrument. In particular, the passive reference concentration is important. Mastermixes containing « high rox » concentrations should not be used with the QS6, rather choose the “low rox” version.Note:Many mastermixes contain a passive reference (most often ROX), which is a dye not involved in the qPCR reaction itself but used to normalize for putative volume differences between wells. If you don’t know if your mastermix includes ROX or its concentration, please check your mastermix user guide, or open a previous run, check the “Multicomponent plot” under “analysis” tab: A high ROX signal will typically appears around 1mio fluorescence units, while a “low rox” signal will show up around 100’000 units. If your mastermix does not contain rox at all, the signal will be flat at 0 unit. If the concentration of rox in your mastermix is too high, you can still save the analysis by unchecking the “rox passive dye” option during data analysis (see later).- Booking is done through the BBS GECF portal. Pricing is available on GECF web site.Starting the run-Wake-up the instrument from the touch screen (or switch on if needed). If the instrument was already on, make sure no run is still ongoing.-Open the “QuantStudio 6 and 7 Flex Real-Time PCR System software”.-“New Experiment” button “From template”.-Then, either use the relevant GECF template amongst the ones called “DontForgetToLoadPlate_QS6_384w...edt”. The templates are well suited for plates assembled with our Hamilton robot:[2]… Or open the “QS6 Flex” folder and choose the relevant generic template for your experimental design. In these templates, the volume in the well is 20 ul by default, therefore you’ll have to change it to 10 ul later on. - Click on “import” (at the top), select the txt file created by the Hamilton robot, click on “start import" and answer “yes”:Avoid non-standard characters in samples and detectors names.- If needed, in the “setup” tab on the left, “experiment properties” sub-tab:∙ choose the relevant dye chemistry (TaqMan or SYBR).∙ choose “Standard” or “Fast” settings (avoid “Fast” unless you have an assay and mastermix carefullyoptimized for “Fast” settings).∙ We recommend keeping the default “standard curve” setting for “experiment type” (this can bechanged after the run if needed, more in the analysis section of this guide):[3]-In the “setup” tab, “define” sub-tab, adjust the passive reference on the bottom (by default ROX is selected). - Press on the “Run method” button on the left of the screen. If needed, indicate “10 ul” as “Reaction Volume per Well”. Choose the cycling parameters (refer to your mastermix user guide). The melting curve (=dissociation curve) was added automatically from the template (only relevant for SYBR green).- Open the tray and insert your plate into the instrument. If the tray comes out empty, make sure a plate is not stuck inside.-Click on the “run” button on the left of the screen:[4]- Click on “start run”, selecting the instrument number that appears. Save your file in your own folder, and click again on the “start run” button if the run hasn’t started yet (the button becomes red when the run has begun):After the runAnalyzing the run- Make sure you don’t perform the analysis while another run is ongoing (for instance the run of the next user). If needed, we can provide you with the installation file for the QuantStudio software (PC only).- In the toolbar, choose “analysis” -> “analyze” to automatically set the threshold and background and calculate the Ct’s of your samples.-Inspect the amplification plot for putative issues, by selecting the samples in the table, and the detector/assay/gene/target in the drop-down list below the amplification plot:- You should check for each gene that the threshold and baseline were correctly assessed: 1) Check that the automatic threshold is in the exponential part of the amplification curve (appearing linear due to log scale);2) Check that the baseline is correctly set by checking for absence of aberrant behavior of the beginning ofthe curves, such as the ones depicted below:[5]- In case the automatically-set threshold and baseline need to be manually adjusted, press on the “analysis settings” button to adjust parameters manually.Melting curve analysisIf you used SYBR green, review the melting curves (“melt curve plot”) for absence of multiple peaks. Typical peaks will appear between approximately 77° and 88°. Secondary peaks lower than that may represent primer dimers, and higher may represent genomic DNA contamination (amplicon containing an intron).Detecting issues- The software automatically detects issues with the amplification and label the affected samples with a yellow triangle in the table. In addition a summary of all the detected issues is found in the “QC summary” tab. -For troubleshooting purpose, the “multicomponent plot” view can be useful since it shows raw signal for all[6]relevant channels (FAM/SYBR…, rox). You can select it here:Exporting dataData can be exported in excel format with the QS6 formatting, or with the formatting of other older instruments (options on top of the export window).Data analysisAbsolute quantification analysisIf your experiment includes a standard curve for absolute quantification of samples, it will be automatically calculated by the software and will appear in the Standard curve tab. Make sure your samples are within the range of the standard curve, and that the curve linear regression fits well enough the standard curve points.Relative quantification analysis (delta delta Ct)- The QS6 software can automatically calculate the delta delta Ct for relative quantification of gene expression. Most people use dedicated macros and software, but if you want to perform this analysis in the QS6 software, first convert the file into a relative quantification file in the setup tab (choose comparative Ct). After conversion, the exported txt file is much less broadly recognized by third party macros and software, therefore we recommend exporting a standard version of the Cts data before the conversion (see the “exporting data” section below).- Accurately using the delta delta Ct method requires that all your primer couples have a similar efficiency. A serial dilution of a sample or plasmid should be performed to calculate these efficiencies.-Contact us in case you need some help for the delta delta Ct analysis. We for instance provide access to the commercial Genex software, which allows selecting several housekeeping genes for normalization.Versions log-v1.04: initial release.-v1.05: many small changes as compared to initial draft, including analyses guidelines, and high/low rox recommendations.-v1.06: many minor changes. Addition of brief descriptions of melt curve analysis, and absolute/relative quantification analyses.-v1.07: Indicated not to perform an analysis while a run is ongoing.-v1.08: indicated to check no plate is stuck in the instrument when the plate holder goes out empty. Clarified how to tweak analysis settings for baseline issues.-v1.09: Clarified to avoid non-standard characters in samples/detectors names. Clarified how to book and where to find prices.[7]。
核酸适配体识别-荧光法检测赭曲霉素A

核酸适配体识别-荧光法检测赭曲霉素A段诺;吴世嘉;王周平【摘要】建立了核酸适配体识别-荧光探针技术检测赭曲霉素A(OTA)的新方法.基于微孔板上固定的核酸适配子与目标物质OTA结合时构象发生变化,导致预先与其互补杂交的FAM标记短链DNA解离,引起荧光信号发生变化,据此可实现对OTA 的定量检测.当微孔板包被亲和素浓度为25 mg/L、适配子浓度为50nmol/L,FAM标记互补短链DNA用量为150 nmol/L,OTA结合缓冲液为10 mmol/L HEPES(含120 mmol/L NaCl、5 mmol/L KCl、20 mmol/L MgCl2、20 mmol/L CaCl2,pH 7.0),45 ℃反应40 min时,可获得方法的最佳分析结果.在最佳实验条件下,对OTA的检测线性范围为2.0 ×10-8~1.0 ×10-5 g/L;检出限为1×10-8 g/L;相对标准偏差为2.6%(1×10-6 g/L,n=11).本方法选择性良好,操作简单,已成功应用于实际样品中OTA的检测.%A novel analytical method for the detection of Ochratoxin A(OTA) was established based on the aptamer recognition and fluorescent probe technology. The method was developed according to the fact that when the immobilized aptamer bond to the target OTA, it can induce the conformation change of aptamer and result in the dissociation of the carboxy-fluorescein(FAM)-tagged complementary DNA chain from aptamer, and finally lead to the fluorescent signals change. Based on it, OTA can be quantified. All the condition factors affecting the performance of the present method were investigated. The results show if the avidin concentration coated on the microplate is 25 mmg/L, the aptamer concentration is 50 nmol/L, the concentration of FAM-tagged complementary DNA chain is 150 nmol/L, 10mmol/L n-2-hydroxyethyl-piperazine-n-ethane sulfonic acid(HEPES) pH 7.0(contain 120 mmol/L NaCl, 5 mmol/L KCl, 20 mmol/L MgC12, 20 mmol/L CaCl2) was chosen as the binding buffer solution and the binding reaction was conducted at 45 ℃ for 40 min, the optimal analytical performance can be achieved. Under the optimal conditions, the linear range for the OTA concentration detection is 2.0 × 10- 11-1.0 × 10-8 g/mL with a detection limit of 1 × 10-11 g/mL. The RSD is 2.6% for 11 parallel measurements of 1 × 10-9 g/mL OTA. Meanwhile, the present method is highly selective for OTA and easy to be operated. It has been successfully applied to measure OTA content in real samples.【期刊名称】《分析化学》【年(卷),期】2011(039)003【总页数】5页(P300-304)【关键词】核酸适配体;荧光;分子识别;赭曲霉素A【作者】段诺;吴世嘉;王周平【作者单位】江南大学食品学院,食品科学与技术国家重点实验室,无锡,214122;江南大学食品学院,食品科学与技术国家重点实验室,无锡,214122;江南大学食品学院,食品科学与技术国家重点实验室,无锡,214122【正文语种】中文赭曲霉素(Ochratoxin,OT)是曲霉菌属和青霉菌属的某些菌种产生的空间代谢产物,基本结构为苯甲酸异香豆素,包含7种结构类似物。
一些常见的统计术语翻译

一些常见的统计术语翻译Absolute deviation, 绝对离差Absolute number , 绝对数Absolute r esiduals, 绝对残差Acceler ation arr ay, 加速度立体阵Acceler ation in an arbitr ary dir ection, 任意方向上的加速度Acceler ation nor mal, 法向加速度Acceler ation spac e dimension, 加速度空间的维数Acceler ation tangential, 切向加速度Acceler ation vector , 加速度向量Acceptable hypothesis, 可接受假设Accum ulation, 累积Accuracy, 准确度Actual fr equency, 实际频数Adaptive estimator , 自适应估计量Addition, 相加Addition theor em , 加法定理Additivity, 可加性Adjusted r ate, 调整率Adjusted value, 校正值Adm issible error , 容许误差Aggregation, 聚集性Alternative hypothesis, 备择假设Among gr oups, 组间Amounts, 总量Analysis of c orr elation, 相关分析Analysis of c ovarianc e, 协方差分析Analysis of r egr ession, 回归分析Analysis of time series, 时间序列分析Analysis of varianc e, 方差分析Angular tr ansfor mation, 角转换ANOVA (analysis of variance ), 方差分析ANOVA Models, 方差分析模型Arcing, 弧/ 弧旋Arcsine tr ansfor mation, 反正弦变换Area under the curve, 曲线面积AREG , 评估从一个时间点到下一个时间点回归相关时的误差ARIMA, 季节和非季节性单变量模型的极大似然估计Arithmetic grid paper , 算术格纸Arithmetic mean, 算术平均数Arrhenius r elation, 艾恩尼斯关系Assessing fit, 拟合的评估Associative laws, 结合律Asymmetric distribution, 非对称分布Asymptotic bias, 渐近偏倚Asymptotic efficiency, 渐近效率Asymptotic variance, 渐近方差Attributable risk, 归因危险度Attribute data, 属性资料Attribution, 属性Autoc orrelation, 自相关Autoc orrelation of residuals, 残差的自相关Aver age, 平均数Aver age c onfidenc e interval length, 平均置信区间长度Aver age growth r ate, 平均增长率Bar c hart, 条形图Bar gr aph, 条形图Base period, 基期Bayes' theorem , Bayes 定理Bell-shaped curve, 钟形曲线伯努力分布Ber noulli distribution,Best-trim estimator , 最好切尾估计量Bias, 偏性Binary logistic r egr ession, 二元逻辑斯蒂回归Binomial distribution, 二项分布Bisquare, 双平方Bivariate Corr elate, 二变量相关Bivariate nor mal distribution, 双变量正态分布Bivariate nor mal population, 双变量正态总体Biweight inter val, 双权区间Biweight M-estimator, 双权M 估计量Bloc k, 区组/ 配伍组BMDP(Biomedic al computer pr ograms), BMDP 统计软件包Boxplots, 箱线图/ 箱尾图Breakdown bound, 崩溃界/ 崩溃点Canonical c orrelation, 典型相关Caption, 纵标目Case-c ontrol study , 病例对照研究Categoric al variable, 分类变量Catenary, 悬链线Cauchy distribution, 柯西分布Cause-and-effect r elationship, 因果关系Cell, 单元Censoring, 终检Center of symmetry , 对称中心Centering and sc aling, 中心化和定标Centr al tendency, 集中趋势Centr al value, 中心值CHAID - x 2 Automatic Inter action Detector ,卡方自动交互检测Chanc e, 机遇Chanc e error , 随机误差Chanc e variable, 随机变量Char acteristic equation, 特征方程Char acteristic root, 特征根Char acteristic vector , 特征向量Chebshev criterion of fit, 拟合的切比雪夫准则Chernoff fac es, 切尔诺夫脸谱图Chi-square test, 卡方检验/咒2检验Choleskey dec omposition, 乔洛斯基分解Circle chart, 圆图Class interval, 组距Class mid-value, 组中值Class upper limit, 组上限Classified variable, 分类变量Cluster analysis, 聚类分析Cluster sampling, 整群抽样Code, 代码Coded data, 编码数据Coding, 编码Coefficient of c ontingency, 列联系数Coefficient of deter mination, 决定系数Coefficient of multiple c orr elation, 多重相关系数Coefficient of partial c orrelation, 偏相关系数Coefficient of pr oduction-moment c orrelation, 积差相关系数Coefficient of r ank corr elation, 等级相关系数Coefficient of r egr ession, 回归系数Coefficient of skewness, 偏度系数Coefficient of variation, 变异系数Cohort study, 队列研究Column, 列Column effect, 列效应Column factor , 列因素Combination pool, 合并Combinative table, 组合表Common factor , 共性因子Common regr ession coefficient, 公共回归系数Common value, 共同值Common varianc e, 公共方差Common variation, 公共变异Communality varianc e, 共性方差Compar ability, 可比性Comparison of bathes, 批比较Comparison value, 比较值Compartment model, 分部模型Compassion, 伸缩Complement of an event, 补事件Complete association, 完全正相关Complete dissociation, 完全不相关Complete statistic s, 完备统计量Completely r andomized design, 完全随机化设计Composite event, 联合事件Composite events, 复合事件Concavity, 凹性Conditional expectation, 条件期望Conditional likelihood, 条件似然Conditional pr obability, 条件概率Conditionally linear , 依条件线性Confidenc e interval, 置信区间Confidenc e lim it, 置信限Confidenc e lower lim it, 置信下限Confidenc e upper limit, 置信上限Confir matory Factor Analysis , 验证性因子分析Confir matory research, 证实性实验研究Confounding factor , 混杂因素Conjoint, 联合分析Consistency, 相合性Consistency chec k, 一致性检验Consistent asymptotic ally nor mal estimate, 相合渐近正态估计Consistent estimate, 相合估计Constr ained nonlinear r egr ession, 受约束非线性回归Constr aint, 约束Contam inated distribution, 污染分布Contam inated Gausssian, 污染高斯分布Contam inated nor mal distribution, 污染正态分布Contam ination, 污染Contam ination model, 污染模型Contingency table, 列联表Contour , 边界线Contribution r ate, 贡献率Control, 对照Controlled experiments, 对照实验Conventional depth, 常规深度Convolution, 卷积Corrected factor , 校正因子Corrected mean, 校正均值Correction coefficient, 校正系数Correctness, 正确性Correlation c oefficient, 相关系数Correlation index, 相关指数Correspondenc e, 对应Counting, 计数Counts, 计数/ 频数Covarianc e, 协方差Covariant, 共变Cox Regression, Cox 回归Criteria for fitting, 拟合准则Criteria of least squar es, 最小二乘准则Critic al r atio, 临界比Critic al r egion, 拒绝域Critic al value, 临界值Cr oss-over design, 交叉设计Cr oss-section analysis, 横断面分析Cr oss-section survey, 横断面调查Cr osstabs , 交叉表Cr oss-tabulation table, 复合表Cube r oot, 立方根Cumulative distribution function, 分布函数Cumulative probability, 累计概率Curvatur e, 曲率/ 弯曲Curvatur e, 曲率Curve fit , 曲线拟和Curve fitting, 曲线拟合Curvilinear r egression, 曲线回归Curvilinear r elation, 曲线关系Cut-and-try method, 尝试法Cycle, 周期Cyclist, 周期性D test, D 检验Data acquisition, 资料收集Data bank, 数据库Data c apacity, 数据容量Data deficiencies, 数据缺乏Data handling, 数据处理Data manipulation, 数据处理Data proc essing, 数据处理Data r eduction, 数据缩减Data set, 数据集Data sourc es, 数据来源Data tr ansfor mation, 数据变换Data validity, 数据有效性Data-in, 数据输入Data-out, 数据输出Dead time, 停滞期Degr ee of fr eedom, 自由度Degr ee of pr ecision, 精密度Degr ee of r eliability , 可靠性程度Degr ession, 递减Density function, 密度函数Density of data points,数据点的密度Dependent variable,应变量/ 依变量/ 因变量Dependent variable,因变量Depth, 深度Derivative matrix, 导数矩阵Derivative-fr ee methods, 无导数方法Design, 设计Deter minacy, 确定性Deter minant, 行列式Deter minant, 决定因素Deviation, 离差Deviation from aver age, 离均差Diagnostic plot, 诊断图Dichotomous variable, 二分变量Differential equation,微分方程Direct standardization, 直接标准化法Discr ete variable, 离散型变量DISCRIMINAN T, 判断Discriminant analysis, 判别分析Discriminant c oeffic ient, 判别系数Discriminant function, 判别值Disper sion, 散布/ 分散度Dispr oportional, 不成比例的Dispr oportionate sub-class numbers, 不成比例次级组含量Distribution free, 分布无关性/ 免分布Distribution shape, 分布形状Distribution-free method, 任意分布法Distributive laws, 分配律Distur banc e, 随机扰动项Dose response curve, 剂量反应曲线Double blind method, 双盲法Double blind trial, 双盲试验Double exponential distribution, 双指数分布Double logarithmic, 双对数Downward r ank, 降秩Dual-spac e plot, 对偶空间图DUD, 无导数方法新法Duncan's new multiple r ange method, 新复极差法/DuncanE-LEffect, 实验效应Eigenvalue, 特征值Eigenvector , 特征向量Ellipse, 椭圆Empiric al distribution, 经验分布Empiric al pr obability , 经验概率单位Enumer ation data, 计数资料Equal sun-class number , 相等次级组含量Equally likely , 等可能Equivarianc e, 同变性Error , 误差/ 错误Errorof estimate, 估计误差Error type I, 第一类错误Error type II, 第二类错误Estimand, 被估量Estimated err or mean squares, 估计误差均方Estimated err or sum of squar es, 估计误差平方和Euclidean distanc e,欧式距离Event, 事件Event, 事件Exc eptional data point, 异常数据点Expectation plane, 期望平面Expectation surfac e, 期望曲面Expected values, 期望值Experiment, 实验Experimental sampling, 试验抽样Experimental unit, 试验单位Explanatory variable, 说明变量Explor atory data analysis, 探索性数据分析Explore Summarize, 探索- 摘要Exponential curve, 指数曲线Exponential growth, 指数式增长EXSMOOTH, 指数平滑方法Extended fit, 扩充拟合Extr a par ameter ,附加参数Extr apolation, 外推法Extr eme observation, 末端观测值Extr emes, 极端值/ 极值F distribution, F分布 F test, F 检验Factor , 因素 / 因子Factor analysis, 因子分析Factor Analysis, 因子分析Factor scor e, 因子得分Factorial, 阶乘Factorial design, 析因试验设计False negative, 假阴性False negative error , 假阴性错误 Fam ily of distributions, 分布族 Fam ily of estimator s, 估计量族 Fanning, 扇面Fatality r ate, 病死率Field investigation, 现场调查Field survey , 现场调查Finite population, 有限总体 Finite-sample, 有限样本First derivative, 一阶导数First principal component,First quartile, 第一四分位数Fisher infor mation, 费雪信息量Fitted value, 拟合值Fourth, 四分点Frequency, 频率Frontier point, 界限点Function r elationship, 泛函关系Gaussian distribution, 高斯分布 / 正态分布Gini's mean difference,基尼均差 GLM (Gener al liner models), 通用线性模型Fitting a c urve, 曲线拟合 Fixed base,定基 Fluctuation, 随机起伏 For ec ast, 预测 Four fold table,四格表Fraction blow, 左侧比率Fractional error, 相对误差 Frequency polygon,频数多边图 Gamma distribution, 伽玛分布Gauss increment, 高斯增量Gauss-Newton incr ement, 高斯- 牛顿增量 Gener al census, 全面普查GENLOG (Gener alized liner models), 广义线性模型 Geometric mean,几何平均数 第一主成分Goodness of fit, 拟和优度/ 配合度Gradient of deter m inant, 行列式的梯度Graec o-Latin squar e, 希腊拉丁方Grand mean, 总均值Gross error s, 重大错误Gross-error sensitivity, 大错敏感度Group aver ages, 分组平均Grouped data, 分组资料Guessed mean, 假定平均数Half-life, 半衰期Hampel M-estimators, 汉佩尔M 估计量Happenstanc e, 偶然事件Har monic mean, 调和均数Hazar d function, 风险均数Hazar d r ate, 风险率Heading, 标目Heavy-tailed distribution, 重尾分布Hessian arr ay, 海森立体阵Heterogeneity , 不同质Heterogeneity of variance, 方差不齐Hier archic al classific ation, 组内分组Hier archic al clustering method, 系统聚类法High-lever age point, 高杠杆率点HILOGLINEAR, 多维列联表的层次对数线性模型Hinge, 折叶点Histogr am, 直方图Historical c ohort study, 历史性队列研究Holes, 空洞HOMALS, 多重响应分析Homogeneity of varianc e, 方差齐性Homogeneity test, 齐性检验Huber M-estimators, 休伯M 估计量Hyper bola, 双曲线Hypothesis testing, 假设检验Hypothetic al universe, 假设总体Impossible event, 不可能事件Independenc e, 独立性Independent variable, 自变量Index, 指标/ 指数Indir ect standardization, 间接标准化法Individual, 个体Infer enc e band, 推断带Infinite population, 无限总体Infinitely gr eat, 无穷大Infinitely small, 无穷小Influence curve, 影响曲线Intercept, 截距Interpolation, 内插法Invarianc e, 不变性Inverse matrix, 逆矩阵Inverse sine tr ansfor mation, 反正弦变换Iter ation, 迭代Jac obian deter m inant, 雅可比行列式Joint distribution function,分布函数 Joint probability, 联合概率Joint probability distribution,联合概率分布 K means method, 逐步聚类法Kaplan-Meier , 评估事件的时间长度Kaplan-Merier c hart, Kaplan-Merier图 Kendall's r ank c orrelation, Kendall等级相关 Kinetic, 动力学Kolmogor ov-Smirnove test, 柯尔莫哥洛夫 - 斯米尔诺夫检验Kruskal and Wallis test, Kr uskal 及 Wallis 检验 / 多样本的秩和检验 /H 检验 Kurtosis, 峰度Lac k of fit, 失拟Ladder of powers, 幂阶梯Lag, 滞后Lar ge sample, 大样本Lar ge sample test, 大样本检验Latin squar e, 拉丁方Latin squar e design, 拉丁方设计Leakage, 泄漏Least favor able c onfigur ation, 最不利构形Least favor able distribution, 最不利分布Least signific ant differ enc e, 最小显著差法Least squar e method, 最小二乘法Least-absolute-r esiduals estimates, Least-absolute-r esiduals fit, 最小绝对残差拟合 Least-absolute-r esiduals line, 最小绝对残差线 Legend, 图例L-estimator , L 估计量Infor mation capacity, 信息容量 Initial condition,初始条件 Initial estimate,初始估计值 Initial level,最初水平 Interaction,交互作用 Interaction terms, 交互作用项Interquartile range,四分位距 Interval estimation,区间估计 Intervals of equal probability, 等概率区间 Intrinsic c urvature,固有曲率Inverse probability,逆概率最小绝对残差估计L-estimator of loc ation, 位置L 估计量L-estimator of sc ale, 尺度L 估计量Level, 水平Life expectanc e, 预期期望寿命Life table, 寿命表Life table method, 生命表法Light-tailed distribution, 轻尾分布似然函数Likelihood function,似然比Likelihood r atio,line gr aph, 线图直线相关Linear corr elation,线性方程Linear equation,Linear pr ogr amm ing, 线性规划直线回归Linear regr ession,线性回归Linear Regression,Linear trend, 线性趋势Loading, 载荷Loc ation and sc ale equivarianc e, 位置尺度同变性Loc ation equivarianc e, 位置同变性Loc ation invarianc e, 位置不变性Loc ation sc ale family, 位置尺度族Log r ank test, 时序检验Logarithm ic curve, 对数曲线Logarithm ic nor mal distribution, 对数正态分布Logarithm ic sc ale, 对数尺度Logarithm ic tr ansfor mation, 对数变换Logic chec k, 逻辑检查Logistic distribution, 逻辑斯特分布Logit tr ansfor mation, Logit 转换LOGLINEAR, 多维列联表通用模型Lognor mal distribution, 对数正态分布Lost function, 损失函数Low corr elation, 低度相关Lower lim it, 下限Lowest-attained varianc e, 最小可达方差LSD, 最小显著差法的简称Lur king variable, 潜在变量M-RMain effect, 主效应Major heading, 主辞标目Marginal density function, 边缘密度函数Marginal pr obability, 边缘概率Marginal pr obability distribution, 边缘概率分布Matched data, 配对资料Matched distribution, 匹配过分布Matching of distribution, 分布的匹配Matching of tr ansfor mation, 变换的匹配Mathematic al expectation, 数学期望Mathematic al model, 数学模型Maximum L-estimator , 极大极小L 估计量Maximum likelihood method, 最大似然法Mean, 均数Mean squar es between groups, 组间均方Mean squar es within gr oup, 组内均方Means (Compar e means), 均值- 均值比较Median, 中位数Median effective dose, 半数效量Median lethal dose, 半数致死量Median polish, 中位数平滑Median test, 中位数检验Minimal sufficient statistic, 最小充分统计量Minimum distanc e estimation, 最小距离估计Minimum effective dose, 最小有效量Minimum lethal dose, 最小致死量Minimum varianc e estimator , 最小方差估计量MIN ITAB, 统计软件包Minor heading, 宾词标目Missing data, 缺失值Model specific ation, 模型的确定Modeling Statistic s , 模型统计Models for outliers, 离群值模型Modifying the model, 模型的修正Modulus of c ontinuity , 连续性模Mor bidity , 发病率Most favor able c onfigur ation, 最有利构形Multidimensional Sc aling (ASCAL), 多维尺度/ 多维标度Multinomial Logistic Regression , 多项逻辑斯蒂回归Multiple c omparison, 多重比较Multiple c orr elation , 复相关Multiple c ovarianc e, 多元协方差Multiple linear r egr ession, 多元线性回归Multiple r esponse , 多重选项Multiple solutions, 多解Multiplic ation theor em , 乘法定理Multir esponse, 多元响应Multi-stage sampling, 多阶段抽样Multivariate T distribution, 多元T 分布Mutual exclusive, 互不相容Mutual independenc e, 互相独立Natur al boundary, 自然边界Natur al dead, 自然死亡Natur al zer o, 自然零Negative c orr elation, 负相关Negative linear corr elation, 负线性相关Negatively skew ed, 负偏Newman-Keuls method, q 检验NK method, q 检验No statistic al signific ance, 无统计意义Nom inal variable, 名义变量Nonc onstancy of variability, 变异的非定常性Nonlinear regr ession, 非线性相关Nonpar ametric statistics, 非参数统计Nonpar ametric test, 非参数检验Nonpar ametric tests, 非参数检验Normal deviate, 正态离差Normal distribution, 正态分布Normal equation, 正规方程组Normal r anges, 正常范围Normal value, 正常值Nuisanc e par ameter , 多余参数/ 讨厌参数Null hypothesis, 无效假设Numeric al variable, 数值变量Objective function, 目标函数观察单位Observation unit,观察值Observed value,One sided test, 单侧检验One-way analysis of varianc e, 单因素方差分析Oneway ANOVA , 单因素方差分析Open sequential trial, 开放型序贯设计Optrim, 优切尾Optrim efficiency, 优切尾效率Order statistic s, 顺序统计量Or dered categories, 有序分类Or dinal logistic r egr ession , 序数逻辑斯蒂回归有序变量Or dinal variable,正交基Orthogonal basis,Orthogonal design, 正交试验设计Orthogonality c onditions, 正交条件ORTHOPLAN, 正交设计Outlier cutoffs, 离群值截断点Outlier s, 极端值OVE RALS , 多组变量的非线性正规相关Over shoot, 迭代过度Pair ed design, 配对设计Pair ed sample, 配对样本Pairwise slopes, 成对斜率Par abola, 抛物线Par allel tests, 平行试验Par ameter , 参数Par ametric statistic s, 参数统计Par ametric test, 参数检验Partial c orrelation, 偏相关Partial r egression, 偏回归Partial sorting, 偏排序Partials r esiduals, 偏残差Patter n, 模式Pear son curves, 皮尔逊曲线Peeling, 退层Perc ent bar gr aph, 百分条形图Perc entage, 百分比Perc entile, 百分位数Perc entile curves, 百分位曲线Periodicity , 周期性Per mutation, 排列P-estimator , P 估计量Pie graph, 饼图Pitman estimator , 皮特曼估计量Pivot, 枢轴量Planar , 平坦Planar assumption, 平面的假设PLANCARDS, 生成试验的计划卡Point estimation, 点估计Poisson distribution, 泊松分布Polishing, 平滑Polled standar d deviation, 合并标准差Polled varianc e, 合并方差Polygon, 多边图Polynomial, 多项式Polynomial c urve, 多项式曲线Population, 总体Population attributable risk,人群归因危险度Qualitative classific ation, 属性分类Qualitative method, 定性方法Quantile-quantile plot, Quantitative analysis, Quartile, 四分位数Quic k Cluster , 快速聚类Radix sort, 基数排序Random alloc ation, 随机化分组Random bloc ks design, 随机区组设计Random event, 随机事件Random ization, 随机化Range, 极差/ 全距Rank c orr elation, 等级相关Rank sum test, 秩和检验Rank test, 秩检验 Ranked data, 等级资料Rate, 比率Ratio, 比例 Positive c orrelation, 正相关Positively skewed, 正偏Posterior distribution, 后验分布Power of a test, 检验效能 Precision,精密度Predicted value, 预测值Preliminary analysis, 预备性分析Principal c omponent analysis, 主成分分析Prior distribution, 先验分布 Prior pr obability, Probabilistic model, probability, 概率Probability density Product moment, 先验概率概率模型, 概率密度 乘积矩 / 协方差Profile tr ace, 截面迹图Proportion, 比/ 构成比Proportion alloc ation in str atified random sampling, Proportionate, 成比例Proportionate sub-class numbers, 成比例次级组含量Prospective study , 前瞻性调查Proximities, 亲近性Pseudo F test, 近似 F 检验Pseudo model, 近似模型Pseudosigma, 伪标准差Purposive sampling, 有目的抽样QR dec omposition, QR 分解Quadratic approximation, 二次近似 按比例分层随机抽样分位数-分位数图 /Q-Q 图 定量分析Raw data, 原始资料Raw residual, 原始残差Rayleigh's test, 雷氏检验Rayleigh's Z, 雷氏Z 值Recipr ocal, 倒数Recipr ocal tr ansfor mation, 倒数变换Rec or ding, 记录Redesc ending estimators, 回降估计量Reducing dimensions, 降维Re-expression, 重新表达Refer enc e set, 标准组Region of acc eptanc e, 接受域Regr ession coefficient, 回归系数Regr ession sum of squar e, 回归平方和Rej ection point, 拒绝点Relative disper sion, 相对离散度Relative number , 相对数Reliability , 可靠性Repar ametrization, 重新设置参数Replication, 重复Report Summar ies, 报告摘要Residual sum of squar e, 剩余平方和Resistanc e, 耐抗性Resistant line, 耐抗线Resistant technique, 耐抗技术R-estimator of location, 位置R 估计量R-estimator of sc ale, 尺度R 估计量Retr ospective study, 回顾性调查Ridge tr ace, 岭迹Ridit analysis, Ridit 分析Rotation, 旋转Rounding, 舍入Row, 行Row effects, 行效应Row factor , 行因素RXC table, RXC 表S-ZSample, 样本Sample r egression c oefficient, 样本回归系数Sample size, 样本量Sample standar d deviation, 样本标准差Sampling error , 抽样误差SAS(Statistical analysis system ), SAS Scale, 尺度/ 量表Scatter diagr am, 散点图统计软件包Schematic plot, 示意图/ 简图Scor e test, 计分检验Screening, 筛检SEASON, 季节分析Sec ond derivative, 二阶导数Sec ond principal c omponent, 第二主成分SEM (Structur al equation modeling), 结构化方程模型Semi-logarithm ic gr aph, 半对数图Semi-logarithm ic paper , 半对数格纸Sensitivity c urve, 敏感度曲线Sequential analysis,贯序分析Sequential data set, 顺序数据集Sequential design, 贯序设计Sequential method, 贯序法Sequential test, 贯序检验法Serial tests, 系列试验Short-c ut method, 简捷法Sigmoid curve, S形曲线Sign function, 正负号函数Sign test, 符号检验Signed r ank, 符号秩Signific anc e test, 显著性检验Signific ant figur e, 有效数字Sim ple cluster sampling, 简单整群抽样Sim ple c orrelation, 简单相关Sim ple r andom sampling, 简单随机抽样Sim ple r egr ession, 简单回归simple table, 简单表Sine estimator , 正弦估计量Single-valued estimate, 单值估计Singular matrix, 奇异矩阵Skewed distribution, 偏斜分布Skewness, 偏度Slash distribution, 斜线分布Slope, 斜率Smirnov test, 斯米尔诺夫检验Source of variation, 变异来源Spear man r ank c orrelation, 斯皮尔曼等级相关Specific factor , 特殊因子Specific factor varianc e, 特殊因子方差Spectr a , 频谱Spherical distribution, 球型正态分布Spr ead, 展布SPSS(Statistical pac kage for the social scienc e), SPSS Spurious c orr elation, 假性相关Square root tr ansfor mation, 平方根变换Stabilizing variance, 稳定方差Standard deviation, 标准差Standard error , 标准误Standard error of differ ence, 差别的标准误Standard error of estimate, 标准估计误差Standard error of r ate, 率的标准误Standard nor mal distribution, 标准正态分布Standardization, 标准化Starting value, 起始值Statistic, 统计量Statistical c ontrol, 统计控制Statistical gr aph, 统计图Statistical inferenc e, 统计推断Statistical table, 统计表Steepest desc ent, 最速下降法Stem and leaf display, 茎叶图Step factor , 步长因子Stepwise r egr ession, 逐步回归Stor age, 存Strata, 层(复数)Stratified sampling, 分层抽样Stratified sampling, 分层抽样Strength, 强度Stringency , 严密性Structur al r elationship, 结构关系Studentized r esidual, 学生化残差/t 化残差Sub-class number s, 次级组含量Subdividing, 分割Sufficient statistic, 充分统计量Sum of pr oducts, 积和Sum of squares, 离差平方和Sur e event, 必然事件Survey, 调查Survival, 生存分析统计软件包Sum of squares about regr Sum of squares between gr Sum of squares of partial r ession, 回归平方和oups, 组间平方和egression, 偏回归平方和Survival r ate, 生存率Suspended r oot gr am, 悬吊根图Symmetry, 对称Systematic err or, 系统误差Systematic sampling, 系统抽样Tags, 标签Tail ar ea, 尾部面积Tail length, 尾长Tail weight, 尾重Tangent line, 切线Target distribution, 目标分布Taylor series, 泰勒级数Tendency of dispersion, 离散趋势Testing of hypotheses, 假设检验Theor etical frequency , 理论频数Time series, 时间序列Toler anc e interval, 容忍区间Toler anc e lower lim it, 容忍下限Toler anc e upper lim it, 容忍上限Torsion, 扰率Total sum of squar e, 总平方和Total variation, 总变异Transfor mation, 转换Treatment, 处理Trend, 趋势Trend of perc entage, 百分比趋势Trial, 试验Trial and err or method, 试错法Tuning c onstant, 细调常数Two sided test, 双向检验Two-stage least squar es, 二阶最小平方Two-stage sampling, 二阶段抽样Two-tailed test, 双侧检验Two-way analysis of varianc e, 双因素方差分析Two-way table, 双向表Type I err or, 一类错误/ a错误Type II err or,二类错误/ B错误UMVU, 方差一致最小无偏估计简称Unbiased estimate, 无偏估计Unc onstrained nonlinear r egr ession , 无约束非线性回归Unequal subclass number , 不等次级组含量Ungr ouped data, 不分组资料Unifor m coor dinate, 均匀坐标Unifor m distribution, 均匀分布Unifor m ly m inimum varianc e unbiased estimate, 方差一致最小无偏估计Unit, 单元Unor der ed categories, 无序分类Upper lim it, 上限Upwar d r ank, 升秩Vague conc ept, 模糊概念Validity , 有效性W test, W 检验W-estimation, W 估计量W-estimation of location,位置 W 估计量Width, 宽度 Wilcoxon paired test, 威斯康星配对法 / 配对符号秩和检验 Wild point, 野点 / 狂点Wild value, 野值 / 狂值Winsorized mean, 缩尾均值Withdr aw, 失访Youden's index, 尤登指数Z test, Z 检验Zer o corr elation, 零相关Z-tr ansfor mation, Z 变换 VARCOMP (Varianc e c omponent estimation), 方差元素估计 Variability , 变异性 Variable,变量 Varianc e,方差 Variation, 变异Varimax orthogonal rotation, 方差最大正交旋转 Volume of distribution,容积Weibull distribution, 威布尔分布 Weight, 权数Weighted Chi-squar e test, 加权卡方检验 /Coc hr an 检验 Weighted linear regression method, 加权直线回归 Weighted mean, 加权平均数Weighted mean squar Weighted sum of squarWeighting coefficient,Weighting method,e, 加权平均方差e, 加权平方和 权重系数 加权法。
应用地球化学元素丰度数据手册-原版

应用地球化学元素丰度数据手册迟清华鄢明才编著地质出版社·北京·1内容提要本书汇编了国内外不同研究者提出的火成岩、沉积岩、变质岩、土壤、水系沉积物、泛滥平原沉积物、浅海沉积物和大陆地壳的化学组成与元素丰度,同时列出了勘查地球化学和环境地球化学研究中常用的中国主要地球化学标准物质的标准值,所提供内容均为地球化学工作者所必须了解的各种重要地质介质的地球化学基础数据。
本书供从事地球化学、岩石学、勘查地球化学、生态环境与农业地球化学、地质样品分析测试、矿产勘查、基础地质等领域的研究者阅读,也可供地球科学其它领域的研究者使用。
图书在版编目(CIP)数据应用地球化学元素丰度数据手册/迟清华,鄢明才编著. -北京:地质出版社,2007.12ISBN 978-7-116-05536-0Ⅰ. 应… Ⅱ. ①迟…②鄢…Ⅲ. 地球化学丰度-化学元素-数据-手册Ⅳ. P595-62中国版本图书馆CIP数据核字(2007)第185917号责任编辑:王永奉陈军中责任校对:李玫出版发行:地质出版社社址邮编:北京市海淀区学院路31号,100083电话:(010)82324508(邮购部)网址:电子邮箱:zbs@传真:(010)82310759印刷:北京地大彩印厂开本:889mm×1194mm 1/16印张:10.25字数:260千字印数:1-3000册版次:2007年12月北京第1版•第1次印刷定价:28.00元书号:ISBN 978-7-116-05536-0(如对本书有建议或意见,敬请致电本社;如本社有印装问题,本社负责调换)2关于应用地球化学元素丰度数据手册(代序)地球化学元素丰度数据,即地壳五个圈内多种元素在各种介质、各种尺度内含量的统计数据。
它是应用地球化学研究解决资源与环境问题上重要的资料。
将这些数据资料汇编在一起将使研究人员节省不少查找文献的劳动与时间。
这本小册子就是按照这样的想法编汇的。
Kernels and regularization on graphs

Kernels and Regularization on GraphsAlexander J.Smola1and Risi Kondor21Machine Learning Group,RSISEAustralian National UniversityCanberra,ACT0200,AustraliaAlex.Smola@.au2Department of Computer ScienceColumbia University1214Amsterdam Avenue,M.C.0401New York,NY10027,USArisi@Abstract.We introduce a family of kernels on graphs based on thenotion of regularization operators.This generalizes in a natural way thenotion of regularization and Greens functions,as commonly used forreal valued functions,to graphs.It turns out that diffusion kernels canbe found as a special case of our reasoning.We show that the class ofpositive,monotonically decreasing functions on the unit interval leads tokernels and corresponding regularization operators.1IntroductionThere has recently been a surge of interest in learning algorithms that operate on input spaces X other than R n,specifically,discrete input spaces,such as strings, graphs,trees,automata etc..Since kernel-based algorithms,such as Support Vector Machines,Gaussian Processes,Kernel PCA,etc.capture the structure of X via the kernel K:X×X→R,as long as we can define an appropriate kernel on our discrete input space,these algorithms can be imported wholesale, together with their error analysis,theoretical guarantees and empirical success.One of the most general representations of discrete metric spaces are graphs. Even if all we know about our input space are local pairwise similarities between points x i,x j∈X,distances(e.g shortest path length)on the graph induced by these similarities can give a useful,more global,sense of similarity between objects.In their work on Diffusion Kernels,Kondor and Lafferty[2002]gave a specific construction for a kernel capturing this structure.Belkin and Niyogi [2002]proposed an essentially equivalent construction in the context of approx-imating data lying on surfaces in a high dimensional embedding space,and in the context of leveraging information from unlabeled data.In this paper we put these earlier results into the more principled framework of Regularization Theory.We propose a family of regularization operators(equiv-alently,kernels)on graphs that include Diffusion Kernels as a special case,and show that this family encompasses all possible regularization operators invariant under permutations of the vertices in a particular sense.2Alexander Smola and Risi KondorOutline of the Paper:Section2introduces the concept of the graph Laplacian and relates it to the Laplace operator on real valued functions.Next we define an extended class of regularization operators and show why they have to be es-sentially a function of the Laplacian.An analogy to real valued Greens functions is established in Section3.3,and efficient methods for computing such functions are presented in Section4.We conclude with a discussion.2Laplace OperatorsAn undirected unweighted graph G consists of a set of vertices V numbered1to n,and a set of edges E(i.e.,pairs(i,j)where i,j∈V and(i,j)∈E⇔(j,i)∈E). We will sometimes write i∼j to denote that i and j are neighbors,i.e.(i,j)∈E. The adjacency matrix of G is an n×n real matrix W,with W ij=1if i∼j,and 0otherwise(by construction,W is symmetric and its diagonal entries are zero). These definitions and most of the following theory can trivially be extended toweighted graphs by allowing W ij∈[0,∞).Let D be an n×n diagonal matrix with D ii=jW ij.The Laplacian of Gis defined as L:=D−W and the Normalized Laplacian is˜L:=D−12LD−12= I−D−12W D−12.The following two theorems are well known results from spectral graph theory[Chung-Graham,1997]:Theorem1(Spectrum of˜L).˜L is a symmetric,positive semidefinite matrix, and its eigenvaluesλ1,λ2,...,λn satisfy0≤λi≤2.Furthermore,the number of eigenvalues equal to zero equals to the number of disjoint components in G.The bound on the spectrum follows directly from Gerschgorin’s Theorem.Theorem2(L and˜L for Regular Graphs).Now let G be a regular graph of degree d,that is,a graph in which every vertex has exactly d neighbors.ThenL=d I−W and˜L=I−1d W=1dL.Finally,W,L,˜L share the same eigenvectors{v i},where v i=λ−1iW v i=(d−λi)−1L v i=(1−d−1λi)−1˜L v i for all i.L and˜L can be regarded as linear operators on functions f:V→R,or,equiv-alently,on vectors f=(f1,f2,...,f n) .We could equally well have defined Lbyf,L f =f L f=−12i∼j(f i−f j)2for all f∈R n,(1)which readily generalizes to graphs with a countably infinite number of vertices.The Laplacian derives its name from its analogy with the familiar Laplacianoperator∆=∂2∂x21+∂2∂x22+...+∂2∂x2mon continuous spaces.Regarding(1)asinducing a semi-norm f L= f,L f on R n,the analogous expression for∆defined on a compact spaceΩisf ∆= f,∆f =Ωf(∆f)dω=Ω(∇f)·(∇f)dω.(2)Both(1)and(2)quantify how much f and f vary locally,or how“smooth”they are over their respective domains.Kernels and Regularization on Graphs3 More explicitly,whenΩ=R m,up to a constant,−L is exactly thefinite difference discretization of∆on a regular lattice:∆f(x)=mi=1∂2∂x2if≈mi=1∂∂x if(x+12e i)−∂∂x if(x−12e i)δ≈mi=1f(x+e i)+f(x−e i)−2f(x)δ2=1δ2mi=1(f x1,...,x i+1,...,x m+f x1,...,x i−1,...,x m−2f x1,...,x m)=−1δ2[L f]x1,...,x m,where e1,e2,...,e m is an orthogonal basis for R m normalized to e i =δ, the vertices of the lattice are at x=x1e1+...+x m e m with integer valuedcoordinates x i∈N,and f x1,x2,...,x m=f(x).Moreover,both the continuous and the dis-crete Laplacians are canonical operators on their respective domains,in the sense that they are invariant under certain natural transformations of the underlying space,and in this they are essentially unique.Regular grid in two dimensionsThe Laplace operator∆is the unique self-adjoint linear second order differ-ential operator invariant under transformations of the coordinate system under the action of the special orthogonal group SO m,i.e.invariant under rotations. This well known result can be seen by using Schur’s lemma and the fact that SO m is irreducible on R m.We now show a similar result for L.Here the permutation group plays a similar role to SO m.We need some additional definitions:denote by S n the group of permutations on{1,2,...,n}withπ∈S n being a specific permutation taking i∈{1,2,...n}toπ(i).The so-called defining representation of S n consists of n×n matricesΠπ,such that[Ππ]i,π(i)=1and all other entries ofΠπare zero. Theorem3(Permutation Invariant Linear Functions on Graphs).Let L be an n×n symmetric real matrix,linearly related to the n×n adjacency matrix W,i.e.L=T[W]for some linear operator L in a way invariant to permutations of vertices in the sense thatΠ πT[W]Ππ=TΠ πWΠπ(3)for anyπ∈S n.Then L is related to W by a linear combination of the follow-ing three operations:identity;row/column sums;overall sum;row/column sum restricted to the diagonal of L;overall sum restricted to the diagonal of W. Proof LetL i1i2=T[W]i1i2:=ni3=1ni4=1T i1i2i3i4W i3i4(4)with T∈R n4.Eq.(3)then implies Tπ(i1)π(i2)π(i3)π(i4)=T i1i2i3i4for anyπ∈S n.4Alexander Smola and Risi KondorThe indices of T can be partitioned by the equality relation on their values,e.g.(2,5,2,7)is of the partition type [13|2|4],since i 1=i 3,but i 2=i 1,i 4=i 1and i 2=i 4.The key observation is that under the action of the permutation group,elements of T with a given index partition structure are taken to elements with the same index partition structure,e.g.if i 1=i 3then π(i 1)=π(i 3)and if i 1=i 3,then π(i 1)=π(i 3).Furthermore,an element with a given index index partition structure can be mapped to any other element of T with the same index partition structure by a suitable choice of π.Hence,a necessary and sufficient condition for (4)is that all elements of T of a given index partition structure be equal.Therefore,T must be a linear combination of the following tensors (i.e.multilinear forms):A i 1i 2i 3i 4=1B [1,2]i 1i 2i 3i 4=δi 1i 2B [1,3]i 1i 2i 3i 4=δi 1i 3B [1,4]i 1i 2i 3i 4=δi 1i 4B [2,3]i 1i 2i 3i 4=δi 2i 3B [2,4]i 1i 2i 3i 4=δi 2i 4B [3,4]i 1i 2i 3i 4=δi 3i 4C [1,2,3]i 1i 2i 3i 4=δi 1i 2δi 2i 3C [2,3,4]i 1i 2i 3i 4=δi 2i 3δi 3i 4C [3,4,1]i 1i 2i 3i 4=δi 3i 4δi 4i 1C [4,1,2]i 1i 2i 3i 4=δi 4i 1δi 1i 2D [1,2][3,4]i 1i 2i 3i 4=δi 1i 2δi 3i 4D [1,3][2,4]i 1i 2i 3i 4=δi 1i 3δi 2i 4D [1,4][2,3]i 1i 2i 3i 4=δi 1i 4δi 2i 3E [1,2,3,4]i 1i 2i 3i 4=δi 1i 2δi 1i 3δi 1i 4.The tensor A puts the overall sum in each element of L ,while B [1,2]returns the the same restricted to the diagonal of L .Since W has vanishing diagonal,B [3,4],C [2,3,4],C [3,4,1],D [1,2][3,4]and E [1,2,3,4]produce zero.Without loss of generality we can therefore ignore them.By symmetry of W ,the pairs (B [1,3],B [1,4]),(B [2,3],B [2,4]),(C [1,2,3],C [4,1,2])have the same effect on W ,hence we can set the coefficient of the second member of each to zero.Furthermore,to enforce symmetry on L ,the coefficient of B [1,3]and B [2,3]must be the same (without loss of generality 1)and this will give the row/column sum matrix ( k W ik )+( k W kl ).Similarly,C [1,2,3]and C [4,1,2]must have the same coefficient and this will give the row/column sum restricted to the diagonal:δij [( k W ik )+( k W kl )].Finally,by symmetry of W ,D [1,3][2,4]and D [1,4][2,3]are both equivalent to the identity map.The various row/column sum and overall sum operations are uninteresting from a graph theory point of view,since they do not heed to the topology of the graph.Imposing the conditions that each row and column in L must sum to zero,we recover the graph Laplacian.Hence,up to a constant factor and trivial additive components,the graph Laplacian (or the normalized graph Laplacian if we wish to rescale by the number of edges per vertex)is the only “invariant”differential operator for given W (or its normalized counterpart ˜W ).Unless stated otherwise,all results below hold for both L and ˜L (albeit with a different spectrum)and we will,in the following,focus on ˜Ldue to the fact that its spectrum is contained in [0,2].Kernels and Regularization on Graphs5 3RegularizationThe fact that L induces a semi-norm on f which penalizes the changes between adjacent vertices,as described in(1),indicates that it may serve as a tool to design regularization operators.3.1Regularization via the Laplace OperatorWe begin with a brief overview of translation invariant regularization operators on continuous spaces and show how they can be interpreted as powers of∆.This will allow us to repeat the development almost verbatim with˜L(or L)instead.Some of the most successful regularization functionals on R n,leading to kernels such as the Gaussian RBF,can be written as[Smola et al.,1998]f,P f :=|˜f(ω)|2r( ω 2)dω= f,r(∆)f .(5)Here f∈L2(R n),˜f(ω)denotes the Fourier transform of f,r( ω 2)is a function penalizing frequency components|˜f(ω)|of f,typically increasing in ω 2,and finally,r(∆)is the extension of r to operators simply by applying r to the spectrum of∆[Dunford and Schwartz,1958]f,r(∆)f =if,ψi r(λi) ψi,fwhere{(ψi,λi)}is the eigensystem of∆.The last equality in(5)holds because applications of∆become multiplications by ω 2in Fourier space.Kernels are obtained by solving the self-consistency condition[Smola et al.,1998]k(x,·),P k(x ,·) =k(x,x ).(6) One can show that k(x,x )=κ(x−x ),whereκis equal to the inverse Fourier transform of r−1( ω 2).Several r functions have been known to yield good results.The two most popular are given below:r( ω 2)k(x,x )r(∆)Gaussian RBF expσ22ω 2exp−12σ2x−x 2∞i=0σ2ii!∆iLaplacian RBF1+σ2 ω 2exp−1σx−x1+σ2∆In summary,regularization according to(5)is carried out by penalizing˜f(ω) by a function of the Laplace operator.For many results in regularization theory one requires r( ω 2)→∞for ω 2→∞.3.2Regularization via the Graph LaplacianIn complete analogy to(5),we define a class of regularization functionals on graphs asf,P f := f,r(˜L)f .(7)6Alexander Smola and Risi KondorFig.1.Regularization function r (λ).From left to right:regularized Laplacian (σ2=1),diffusion process (σ2=1),one-step random walk (a =2),4-step random walk (a =2),inverse cosine.Here r (˜L )is understood as applying the scalar valued function r (λ)to the eigen-values of ˜L ,that is,r (˜L ):=m i =1r (λi )v i v i ,(8)where {(λi ,v i )}constitute the eigensystem of ˜L .The normalized graph Lapla-cian ˜Lis preferable to L ,since ˜L ’s spectrum is contained in [0,2].The obvious goal is to gain insight into what functions are appropriate choices for r .–From (1)we infer that v i with large λi correspond to rather uneven functions on the graph G .Consequently,they should be penalized more strongly than v i with small λi .Hence r (λ)should be monotonically increasing in λ.–Requiring that r (˜L) 0imposes the constraint r (λ)≥0for all λ∈[0,2].–Finally,we can limit ourselves to r (λ)expressible as power series,since the latter are dense in the space of C 0functions on bounded domains.In Section 3.5we will present additional motivation for the choice of r (λ)in the context of spectral graph theory and segmentation.As we shall see,the following functions are of particular interest:r (λ)=1+σ2λ(Regularized Laplacian)(9)r (λ)=exp σ2/2λ(Diffusion Process)(10)r (λ)=(aI −λ)−1with a ≥2(One-Step Random Walk)(11)r (λ)=(aI −λ)−p with a ≥2(p -Step Random Walk)(12)r (λ)=(cos λπ/4)−1(Inverse Cosine)(13)Figure 1shows the regularization behavior for the functions (9)-(13).3.3KernelsThe introduction of a regularization matrix P =r (˜L)allows us to define a Hilbert space H on R m via f,f H := f ,P f .We now show that H is a reproducing kernel Hilbert space.Kernels and Regularization on Graphs 7Theorem 4.Denote by P ∈R m ×m a (positive semidefinite)regularization ma-trix and denote by H the image of R m under P .Then H with dot product f,f H := f ,P f is a Reproducing Kernel Hilbert Space and its kernel is k (i,j )= P −1ij ,where P −1denotes the pseudo-inverse if P is not invertible.Proof Since P is a positive semidefinite matrix,we clearly have a Hilbert space on P R m .To show the reproducing property we need to prove thatf (i )= f,k (i,·) H .(14)Note that k (i,j )can take on at most m 2different values (since i,j ∈[1:m ]).In matrix notation (14)means that for all f ∈Hf (i )=f P K i,:for all i ⇐⇒f =f P K.(15)The latter holds if K =P −1and f ∈P R m ,which proves the claim.In other words,K is the Greens function of P ,just as in the continuous case.The notion of Greens functions on graphs was only recently introduced by Chung-Graham and Yau [2000]for L .The above theorem extended this idea to arbitrary regularization operators ˆr (˜L).Corollary 1.Denote by P =r (˜L )a regularization matrix,then the correspond-ing kernel is given by K =r −1(˜L ),where we take the pseudo-inverse wherever necessary.More specifically,if {(v i ,λi )}constitute the eigensystem of ˜L,we have K =mi =1r −1(λi )v i v i where we define 0−1≡0.(16)3.4Examples of KernelsBy virtue of Corollary 1we only need to take (9)-(13)and plug the definition of r (λ)into (16)to obtain formulae for computing K .This yields the following kernel matrices:K =(I +σ2˜L)−1(Regularized Laplacian)(17)K =exp(−σ2/2˜L)(Diffusion Process)(18)K =(aI −˜L)p with a ≥2(p -Step Random Walk)(19)K =cos ˜Lπ/4(Inverse Cosine)(20)Equation (18)corresponds to the diffusion kernel proposed by Kondor and Laf-ferty [2002],for which K (x,x )can be visualized as the quantity of some sub-stance that would accumulate at vertex x after a given amount of time if we injected the substance at vertex x and let it diffuse through the graph along the edges.Note that this involves matrix exponentiation defined via the limit K =exp(B )=lim n →∞(I +B/n )n as opposed to component-wise exponentiation K i,j =exp(B i,j ).8Alexander Smola and Risi KondorFig.2.Thefirst8eigenvectors of the normalized graph Laplacian corresponding to the graph drawn above.Each line attached to a vertex is proportional to the value of the corresponding eigenvector at the vertex.Positive values(red)point up and negative values(blue)point down.Note that the assignment of values becomes less and less uniform with increasing eigenvalue(i.e.from left to right).For(17)it is typically more efficient to deal with the inverse of K,as it avoids the costly inversion of the sparse matrix˜L.Such situations arise,e.g.,in Gaussian Process estimation,where K is the covariance matrix of a stochastic process[Williams,1999].Regarding(19),recall that(aI−˜L)p=((a−1)I+˜W)p is up to scaling terms equiv-alent to a p-step random walk on the graphwith random restarts(see Section A for de-tails).In this sense it is similar to the dif-fusion kernel.However,the fact that K in-volves only afinite number of products ofmatrices makes it much more attractive forpractical purposes.In particular,entries inK ij can be computed cheaply using the factthat˜L is a sparse matrix.A nearest neighbor graph.Finally,the inverse cosine kernel treats lower complexity functions almost equally,with a significant reduction in the upper end of the spectrum.Figure2 shows the leading eigenvectors of the graph drawn above and Figure3provide examples of some of the kernels discussed above.3.5Clustering and Spectral Graph TheoryWe could also have derived r(˜L)directly from spectral graph theory:the eigen-vectors of the graph Laplacian correspond to functions partitioning the graph into clusters,see e.g.,[Chung-Graham,1997,Shi and Malik,1997]and the ref-erences therein.In general,small eigenvalues have associated eigenvectors which vary little between adjacent vertices.Finding the smallest eigenvectors of˜L can be seen as a real-valued relaxation of the min-cut problem.3For instance,the smallest eigenvalue of˜L is0,its corresponding eigenvector is D121n with1n:=(1,...,1)∈R n.The second smallest eigenvalue/eigenvector pair,also often referred to as the Fiedler-vector,can be used to split the graph 3Only recently,algorithms based on the celebrated semidefinite relaxation of the min-cut problem by Goemans and Williamson[1995]have seen wider use[Torr,2003]in segmentation and clustering by use of spectral bundle methods.Kernels and Regularization on Graphs9Fig.3.Top:regularized graph Laplacian;Middle:diffusion kernel with σ=5,Bottom:4-step random walk kernel.Each figure displays K ij for fixed i .The value K ij at vertex i is denoted by a bold line.Note that only adjacent vertices to i bear significant value.into two distinct parts [Weiss,1999,Shi and Malik,1997],and further eigenvec-tors with larger eigenvalues have been used for more finely-grained partitions of the graph.See Figure 2for an example.Such a decomposition into functions of increasing complexity has very de-sirable properties:if we want to perform estimation on the graph,we will wish to bias the estimate towards functions which vary little over large homogeneous portions 4.Consequently,we have the following interpretation of f,f H .As-sume that f = i βi v i ,where {(v i ,λi )}is the eigensystem of ˜L.Then we can rewrite f,f H to yield f ,r (˜L )f = i βi v i , j r (λj )v j v j l βl v l = iβ2i r (λi ).(21)This means that the components of f which vary a lot over coherent clusters in the graph are penalized more strongly,whereas the portions of f ,which are essentially constant over clusters,are preferred.This is exactly what we want.3.6Approximate ComputationOften it is not necessary to know all values of the kernel (e.g.,if we only observe instances from a subset of all positions on the graph).There it would be wasteful to compute the full matrix r (L )−1explicitly,since such operations typically scale with O (n 3).Furthermore,for large n it is not desirable to compute K via (16),that is,by computing the eigensystem of ˜Land assembling K directly.4If we cannot assume a connection between the structure of the graph and the values of the function to be estimated on it,the entire concept of designing kernels on graphs obviously becomes meaningless.10Alexander Smola and Risi KondorInstead,we would like to take advantage of the fact that ˜L is sparse,and con-sequently any operation ˜Lαhas cost at most linear in the number of nonzero ele-ments of ˜L ,hence the cost is bounded by O (|E |+n ).Moreover,if d is the largest degree of the graph,then computing L p e i costs at most |E | p −1i =1(min(d +1,n ))ioperations:at each step the number of non-zeros in the rhs decreases by at most a factor of d +1.This means that as long as we can approximate K =r −1(˜L )by a low order polynomial,say ρ(˜L ):= N i =0βi ˜L i ,significant savings are possible.Note that we need not necessarily require a uniformly good approximation and put the main emphasis on the approximation for small λ.However,we need to ensure that ρ(˜L)is positive semidefinite.Diffusion Kernel:The fact that the series r −1(x )=exp(−βx )= ∞m =0(−β)m x m m !has alternating signs shows that the approximation error at r −1(x )is boundedby (2β)N +1(N +1)!,if we use N terms in the expansion (from Theorem 1we know that ˜L≤2).For instance,for β=1,10terms are sufficient to obtain an error of the order of 10−4.Variational Approximation:In general,if we want to approximate r −1(λ)on[0,2],we need to solve the L ∞([0,2])approximation problemminimize β, subject to N i =0βi λi −r −1(λ) ≤ ∀λ∈[0,2](22)Clearly,(22)is equivalent to minimizing sup ˜L ρ(˜L )−r−1(˜L ) ,since the matrix norm is determined by the largest eigenvalues,and we can find ˜Lsuch that the discrepancy between ρ(λ)and r −1(λ)is attained.Variational problems of this form have been studied in the literature,and their solution may provide much better approximations to r −1(λ)than a truncated power series expansion.4Products of GraphsAs we have already pointed out,it is very expensive to compute K for arbitrary ˆr and ˜L.For special types of graphs and regularization,however,significant computational savings can be made.4.1Factor GraphsThe work of this section is a direct extension of results by Ellis [2002]and Chung-Graham and Yau [2000],who study factor graphs to compute inverses of the graph Laplacian.Definition 1(Factor Graphs).Denote by (V,E )and (V ,E )the vertices V and edges E of two graphs,then the factor graph (V f ,E f ):=(V,E )⊗(V ,E )is defined as the graph where (i,i )∈V f if i ∈V and i ∈V ;and ((i,i ),(j,j ))∈E f if and only if either (i,j )∈E and i =j or (i ,j )∈E and i =j .Kernels and Regularization on Graphs 11For instance,the factor graph of two rings is a torus.The nice property of factor graphs is that we can compute the eigenvalues of the Laplacian on products very easily (see e.g.,Chung-Graham and Yau [2000]):Theorem 5(Eigenvalues of Factor Graphs).The eigenvalues and eigen-vectors of the normalized Laplacian for the factor graph between a regular graph of degree d with eigenvalues {λj }and a regular graph of degree d with eigenvalues {λ l }are of the form:λfact j,l =d d +d λj +d d +d λ l(23)and the eigenvectors satisfy e j,l(i,i )=e j i e l i ,where e j is an eigenvector of ˜L and e l is an eigenvector of ˜L.This allows us to apply Corollary 1to obtain an expansion of K asK =(r (L ))−1=j,l r −1(λjl )e j,l e j,l .(24)While providing an explicit recipe for the computation of K ij without the need to compute the full matrix K ,this still requires O (n 2)operations per entry,which may be more costly than what we want (here n is the number of vertices of the factor graph).Two methods for computing (24)become evident at this point:if r has a special structure,we may exploit this to decompose K into the products and sums of terms depending on one of the two graphs alone and pre-compute these expressions beforehand.Secondly,if one of the two terms in the expansion can be computed for a rather general class of values of r (x ),we can pre-compute this expansion and only carry out the remainder corresponding to (24)explicitly.4.2Product Decomposition of r (x )Central to our reasoning is the observation that for certain r (x ),the term 1r (a +b )can be expressed in terms of a product and sum of terms depending on a and b only.We assume that 1r (a +b )=M m =1ρn (a )˜ρn (b ).(25)In the following we will show that in such situations the kernels on factor graphs can be computed as an analogous combination of products and sums of kernel functions on the terms constituting the ingredients of the factor graph.Before we do so,we briefly check that many r (x )indeed satisfy this property.exp(−β(a +b ))=exp(−βa )exp(−βb )(26)(A −(a +b ))= A 2−a + A 2−b (27)(A −(a +b ))p =p n =0p n A 2−a n A 2−b p −n (28)cos (a +b )π4=cos aπ4cos bπ4−sin aπ4sin bπ4(29)12Alexander Smola and Risi KondorIn a nutshell,we will exploit the fact that for products of graphs the eigenvalues of the joint graph Laplacian can be written as the sum of the eigenvalues of the Laplacians of the constituent graphs.This way we can perform computations on ρn and˜ρn separately without the need to take the other part of the the product of graphs into account.Definek m(i,j):=l ρldλld+de l i e l j and˜k m(i ,j ):=l˜ρldλld+d˜e l i ˜e l j .(30)Then we have the following composition theorem:Theorem6.Denote by(V,E)and(V ,E )connected regular graphs of degrees d with m vertices(and d ,m respectively)and normalized graph Laplacians ˜L,˜L .Furthermore denote by r(x)a rational function with matrix-valued exten-sionˆr(X).In this case the kernel K corresponding to the regularization operator ˆr(L)on the product graph of(V,E)and(V ,E )is given byk((i,i ),(j,j ))=Mm=1k m(i,j)˜k m(i ,j )(31)Proof Plug the expansion of1r(a+b)as given by(25)into(24)and collect terms.From(26)we immediately obtain the corollary(see Kondor and Lafferty[2002]) that for diffusion processes on factor graphs the kernel on the factor graph is given by the product of kernels on the constituents,that is k((i,i ),(j,j ))= k(i,j)k (i ,j ).The kernels k m and˜k m can be computed either by using an analytic solution of the underlying factors of the graph or alternatively they can be computed numerically.If the total number of kernels k n is small in comparison to the number of possible coordinates this is still computationally beneficial.4.3Composition TheoremsIf no expansion as in(31)can be found,we may still be able to compute ker-nels by extending a reasoning from[Ellis,2002].More specifically,the following composition theorem allows us to accelerate the computation in many cases, whenever we can parameterize(ˆr(L+αI))−1in an efficient way.For this pur-pose we introduce two auxiliary functionsKα(i,j):=ˆrdd+dL+αdd+dI−1=lrdλl+αdd+d−1e l(i)e l(j)G α(i,j):=(L +αI)−1=l1λl+αe l(i)e l(j).(32)In some cases Kα(i,j)may be computed in closed form,thus obviating the need to perform expensive matrix inversion,e.g.,in the case where the underlying graph is a chain[Ellis,2002]and Kα=Gα.Kernels and Regularization on Graphs 13Theorem 7.Under the assumptions of Theorem 6we haveK ((j,j ),(l,l ))=12πi C K α(j,l )G −α(j ,l )dα= v K λv (j,l )e v j e v l (33)where C ⊂C is a contour of the C containing the poles of (V ,E )including 0.For practical purposes,the third term of (33)is more amenable to computation.Proof From (24)we haveK ((j,j ),(l,l ))= u,v r dλu +d λv d +d −1e u j e u l e v j e v l (34)=12πi C u r dλu +d αd +d −1e u j e u l v 1λv −αe v j e v l dαHere the second equalityfollows from the fact that the contour integral over a pole p yields C f (α)p −αdα=2πif (p ),and the claim is verified by checking thedefinitions of K αand G α.The last equality can be seen from (34)by splitting up the summation over u and v .5ConclusionsWe have shown that the canonical family of kernels on graphs are of the form of power series in the graph Laplacian.Equivalently,such kernels can be char-acterized by a real valued function of the eigenvalues of the Laplacian.Special cases include diffusion kernels,the regularized Laplacian kernel and p -step ran-dom walk kernels.We have developed the regularization theory of learning on graphs using such kernels and explored methods for efficiently computing and approximating the kernel matrix.Acknowledgments This work was supported by a grant of the ARC.The authors thank Eleazar Eskin,Patrick Haffner,Andrew Ng,Bob Williamson and S.V.N.Vishwanathan for helpful comments and suggestions.A Link AnalysisRather surprisingly,our approach to regularizing functions on graphs bears re-semblance to algorithms for scoring web pages such as PageRank [Page et al.,1998],HITS [Kleinberg,1999],and randomized HITS [Zheng et al.,2001].More specifically,the random walks on graphs used in all three algorithms and the stationary distributions arising from them are closely connected with the eigen-system of L and ˜Lrespectively.We begin with an analysis of PageRank.Given a set of web pages and links between them we construct a directed graph in such a way that pages correspond。
A Tutorial on Spectral Clustering

Ulrike von Luxburg Max Planck Institute for Biological Cybernetics Spemannstr. 38, 72076 T¨ ubingen, Germany ulrike.luxburg@tuebingen.mpg.de
2
Similarity graphs
Given a set of data points x1 , . . . xn and some notion of similarity sij ≥ 0 between all pairs of data points xi and xj , the intuitive goal of clustering is to divide the data points into several groups such that points in the same group are similar and points in different groups are dissimilar to each other. If we do not have more information than similarities between data points, a nice way of representing the data is in form of the similarity graph G = (V, E ). Each vertex vi in this graph represents a data point xi . Two vertices are connected if the similarity sij between the corresponding data points xi and xj is positive or larger than a certain threshold, and the edge is weighted by sij . The problem of clustering can now be reformulated using the similarity graph: we want to find a partition of the graph such that the edges between different groups have very low weights (which means that points in different clusters are dissimilar from each other) and the edges within a group have high weights (which means that points within the same cluster are similar to each other). To be able to formalize this intuition we first want to introduce some basic graph notation and briefly discuss the kind of graphs we are going to study.
本书介绍了核方法Kernel记得上高等数理统计
本书第六章介绍了核方法(Kernel)。
记得上高等数理统计的时候,老师布置过关于核方法的一片小论文作业,只不过当时并没有重视,作业也是应付了事。
这两天读了这一章,觉得核方法是一种非常重要的工具。
当然,这一章中也有众多地方读不懂,慢慢继续读吧。
下面写点读书笔记和心得。
6.1节,先从最基本的一维核平滑说起。
所谓的平滑,我觉得可以这样理解。
对于一维变量及其相应,可以在二维空间中画一个散点图。
如果利用插值,将点连接起来,那么连线可能是曲折不平的。
所谓的平滑,就是用某种手段使得连线变得平滑光滑一点。
那么手段可以有多种,比如第五章介绍的样条平滑,是利用了正则化的方法,使得连线达到高阶可微,从而看起来比较光滑。
而本章要介绍的核方法,则是利用核,给近邻中的不同点,按照其离目标点的距离远近赋以不同的权重,从而达到平滑的效果。
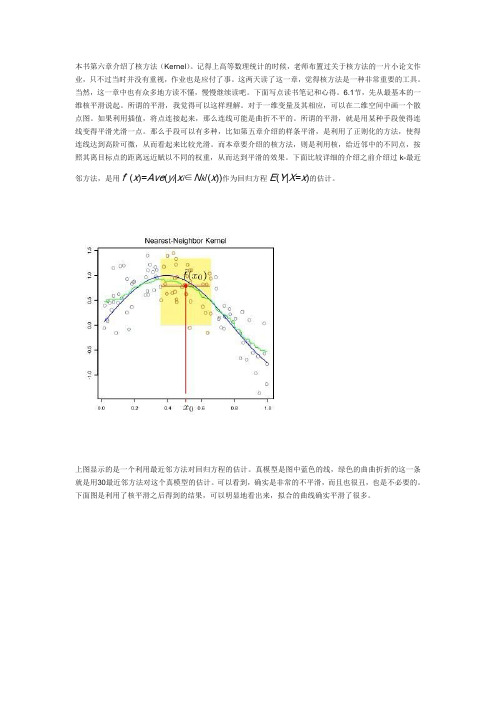
下面比较详细的介绍之前介绍过k-最近邻方法,是用fˆ(x)=Ave(y i|x i∈N k/(x))作为回归方程E(Y|X=x)的估计。
上图显示的是一个利用最近邻方法对回归方程的估计。
真模型是图中蓝色的线,绿色的曲曲折折的这一条就是用30最近邻方法对这个真模型的估计。
可以看到,确实是非常的不平滑,而且也很丑,也是不必要的。
下面图是利用了核平滑之后得到的结果,可以明显地看出来,拟合的曲线确实平滑了很多。
上面仅仅是一个核平滑的例子。
下面给出一维核平滑的一些具体的公式fˆ(x0)=∑Ni=1Kλ(x0,xi)yi∑Ni=1Kλ(x0,xi)这个就是利用核平滑对x0点的真实值的估计,可以看出,这其实是一个加权平均,相比起最近邻方法,这里的特殊的地方就是权重Kλ(x0,x)。
这个权重就称为核。
核函数有很多种,常用的包括Epanechnikov quadratic 核:Kλ(x0,x)=D(x−x0λ) with D(t)=34(1−t2),|t|<1这个图就是D(t)的图像,可以看出,随着离目标点的距离越来越远,所附加的权重也是平滑的越来越小。
From Data Mining to Knowledge Discovery in Databases

s Data mining and knowledge discovery in databases have been attracting a significant amount of research, industry, and media atten-tion of late. What is all the excitement about?This article provides an overview of this emerging field, clarifying how data mining and knowledge discovery in databases are related both to each other and to related fields, such as machine learning, statistics, and databases. The article mentions particular real-world applications, specific data-mining techniques, challenges in-volved in real-world applications of knowledge discovery, and current and future research direc-tions in the field.A cross a wide variety of fields, data arebeing collected and accumulated at adramatic pace. There is an urgent need for a new generation of computational theo-ries and tools to assist humans in extracting useful information (knowledge) from the rapidly growing volumes of digital data. These theories and tools are the subject of the emerging field of knowledge discovery in databases (KDD).At an abstract level, the KDD field is con-cerned with the development of methods and techniques for making sense of data. The basic problem addressed by the KDD process is one of mapping low-level data (which are typically too voluminous to understand and digest easi-ly) into other forms that might be more com-pact (for example, a short report), more ab-stract (for example, a descriptive approximation or model of the process that generated the data), or more useful (for exam-ple, a predictive model for estimating the val-ue of future cases). At the core of the process is the application of specific data-mining meth-ods for pattern discovery and extraction.1This article begins by discussing the histori-cal context of KDD and data mining and theirintersection with other related fields. A briefsummary of recent KDD real-world applica-tions is provided. Definitions of KDD and da-ta mining are provided, and the general mul-tistep KDD process is outlined. This multistepprocess has the application of data-mining al-gorithms as one particular step in the process.The data-mining step is discussed in more de-tail in the context of specific data-mining al-gorithms and their application. Real-worldpractical application issues are also outlined.Finally, the article enumerates challenges forfuture research and development and in par-ticular discusses potential opportunities for AItechnology in KDD systems.Why Do We Need KDD?The traditional method of turning data intoknowledge relies on manual analysis and in-terpretation. For example, in the health-careindustry, it is common for specialists to peri-odically analyze current trends and changesin health-care data, say, on a quarterly basis.The specialists then provide a report detailingthe analysis to the sponsoring health-care or-ganization; this report becomes the basis forfuture decision making and planning forhealth-care management. In a totally differ-ent type of application, planetary geologistssift through remotely sensed images of plan-ets and asteroids, carefully locating and cata-loging such geologic objects of interest as im-pact craters. Be it science, marketing, finance,health care, retail, or any other field, the clas-sical approach to data analysis relies funda-mentally on one or more analysts becomingArticlesFALL 1996 37From Data Mining to Knowledge Discovery inDatabasesUsama Fayyad, Gregory Piatetsky-Shapiro, and Padhraic Smyth Copyright © 1996, American Association for Artificial Intelligence. All rights reserved. 0738-4602-1996 / $2.00areas is astronomy. Here, a notable success was achieved by SKICAT ,a system used by as-tronomers to perform image analysis,classification, and cataloging of sky objects from sky-survey images (Fayyad, Djorgovski,and Weir 1996). In its first application, the system was used to process the 3 terabytes (1012bytes) of image data resulting from the Second Palomar Observatory Sky Survey,where it is estimated that on the order of 109sky objects are detectable. SKICAT can outper-form humans and traditional computational techniques in classifying faint sky objects. See Fayyad, Haussler, and Stolorz (1996) for a sur-vey of scientific applications.In business, main KDD application areas includes marketing, finance (especially in-vestment), fraud detection, manufacturing,telecommunications, and Internet agents.Marketing:In marketing, the primary ap-plication is database marketing systems,which analyze customer databases to identify different customer groups and forecast their behavior. Business Week (Berry 1994) estimat-ed that over half of all retailers are using or planning to use database marketing, and those who do use it have good results; for ex-ample, American Express reports a 10- to 15-percent increase in credit-card use. Another notable marketing application is market-bas-ket analysis (Agrawal et al. 1996) systems,which find patterns such as, “If customer bought X, he/she is also likely to buy Y and Z.” Such patterns are valuable to retailers.Investment: Numerous companies use da-ta mining for investment, but most do not describe their systems. One exception is LBS Capital Management. Its system uses expert systems, neural nets, and genetic algorithms to manage portfolios totaling $600 million;since its start in 1993, the system has outper-formed the broad stock market (Hall, Mani,and Barr 1996).Fraud detection: HNC Falcon and Nestor PRISM systems are used for monitoring credit-card fraud, watching over millions of ac-counts. The FAIS system (Senator et al. 1995),from the U.S. Treasury Financial Crimes En-forcement Network, is used to identify finan-cial transactions that might indicate money-laundering activity.Manufacturing: The CASSIOPEE trou-bleshooting system, developed as part of a joint venture between General Electric and SNECMA, was applied by three major Euro-pean airlines to diagnose and predict prob-lems for the Boeing 737. To derive families of faults, clustering methods are used. CASSIOPEE received the European first prize for innova-intimately familiar with the data and serving as an interface between the data and the users and products.For these (and many other) applications,this form of manual probing of a data set is slow, expensive, and highly subjective. In fact, as data volumes grow dramatically, this type of manual data analysis is becoming completely impractical in many domains.Databases are increasing in size in two ways:(1) the number N of records or objects in the database and (2) the number d of fields or at-tributes to an object. Databases containing on the order of N = 109objects are becoming in-creasingly common, for example, in the as-tronomical sciences. Similarly, the number of fields d can easily be on the order of 102or even 103, for example, in medical diagnostic applications. Who could be expected to di-gest millions of records, each having tens or hundreds of fields? We believe that this job is certainly not one for humans; hence, analysis work needs to be automated, at least partially.The need to scale up human analysis capa-bilities to handling the large number of bytes that we can collect is both economic and sci-entific. Businesses use data to gain competi-tive advantage, increase efficiency, and pro-vide more valuable services to customers.Data we capture about our environment are the basic evidence we use to build theories and models of the universe we live in. Be-cause computers have enabled humans to gather more data than we can digest, it is on-ly natural to turn to computational tech-niques to help us unearth meaningful pat-terns and structures from the massive volumes of data. Hence, KDD is an attempt to address a problem that the digital informa-tion era made a fact of life for all of us: data overload.Data Mining and Knowledge Discovery in the Real WorldA large degree of the current interest in KDD is the result of the media interest surrounding successful KDD applications, for example, the focus articles within the last two years in Business Week , Newsweek , Byte , PC Week , and other large-circulation periodicals. Unfortu-nately, it is not always easy to separate fact from media hype. Nonetheless, several well-documented examples of successful systems can rightly be referred to as KDD applications and have been deployed in operational use on large-scale real-world problems in science and in business.In science, one of the primary applicationThere is an urgent need for a new generation of computation-al theories and tools toassist humans in extractinguseful information (knowledge)from the rapidly growing volumes ofdigital data.Articles38AI MAGAZINEtive applications (Manago and Auriol 1996).Telecommunications: The telecommuni-cations alarm-sequence analyzer (TASA) wasbuilt in cooperation with a manufacturer oftelecommunications equipment and threetelephone networks (Mannila, Toivonen, andVerkamo 1995). The system uses a novelframework for locating frequently occurringalarm episodes from the alarm stream andpresenting them as rules. Large sets of discov-ered rules can be explored with flexible infor-mation-retrieval tools supporting interactivityand iteration. In this way, TASA offers pruning,grouping, and ordering tools to refine the re-sults of a basic brute-force search for rules.Data cleaning: The MERGE-PURGE systemwas applied to the identification of duplicatewelfare claims (Hernandez and Stolfo 1995).It was used successfully on data from the Wel-fare Department of the State of Washington.In other areas, a well-publicized system isIBM’s ADVANCED SCOUT,a specialized data-min-ing system that helps National Basketball As-sociation (NBA) coaches organize and inter-pret data from NBA games (U.S. News 1995). ADVANCED SCOUT was used by several of the NBA teams in 1996, including the Seattle Su-personics, which reached the NBA finals.Finally, a novel and increasingly importanttype of discovery is one based on the use of in-telligent agents to navigate through an infor-mation-rich environment. Although the ideaof active triggers has long been analyzed in thedatabase field, really successful applications ofthis idea appeared only with the advent of theInternet. These systems ask the user to specifya profile of interest and search for related in-formation among a wide variety of public-do-main and proprietary sources. For example, FIREFLY is a personal music-recommendation agent: It asks a user his/her opinion of several music pieces and then suggests other music that the user might like (<http:// www.ffl/>). CRAYON(/>) allows users to create their own free newspaper (supported by ads); NEWSHOUND(<http://www. /hound/>) from the San Jose Mercury News and FARCAST(</> automatically search information from a wide variety of sources, including newspapers and wire services, and e-mail rele-vant documents directly to the user.These are just a few of the numerous suchsystems that use KDD techniques to automat-ically produce useful information from largemasses of raw data. See Piatetsky-Shapiro etal. (1996) for an overview of issues in devel-oping industrial KDD applications.Data Mining and KDDHistorically, the notion of finding useful pat-terns in data has been given a variety ofnames, including data mining, knowledge ex-traction, information discovery, informationharvesting, data archaeology, and data patternprocessing. The term data mining has mostlybeen used by statisticians, data analysts, andthe management information systems (MIS)communities. It has also gained popularity inthe database field. The phrase knowledge dis-covery in databases was coined at the first KDDworkshop in 1989 (Piatetsky-Shapiro 1991) toemphasize that knowledge is the end productof a data-driven discovery. It has been popular-ized in the AI and machine-learning fields.In our view, KDD refers to the overall pro-cess of discovering useful knowledge from da-ta, and data mining refers to a particular stepin this process. Data mining is the applicationof specific algorithms for extracting patternsfrom data. The distinction between the KDDprocess and the data-mining step (within theprocess) is a central point of this article. Theadditional steps in the KDD process, such asdata preparation, data selection, data cleaning,incorporation of appropriate prior knowledge,and proper interpretation of the results ofmining, are essential to ensure that usefulknowledge is derived from the data. Blind ap-plication of data-mining methods (rightly crit-icized as data dredging in the statistical litera-ture) can be a dangerous activity, easilyleading to the discovery of meaningless andinvalid patterns.The Interdisciplinary Nature of KDDKDD has evolved, and continues to evolve,from the intersection of research fields such asmachine learning, pattern recognition,databases, statistics, AI, knowledge acquisitionfor expert systems, data visualization, andhigh-performance computing. The unifyinggoal is extracting high-level knowledge fromlow-level data in the context of large data sets.The data-mining component of KDD cur-rently relies heavily on known techniquesfrom machine learning, pattern recognition,and statistics to find patterns from data in thedata-mining step of the KDD process. A natu-ral question is, How is KDD different from pat-tern recognition or machine learning (and re-lated fields)? The answer is that these fieldsprovide some of the data-mining methodsthat are used in the data-mining step of theKDD process. KDD focuses on the overall pro-cess of knowledge discovery from data, includ-ing how the data are stored and accessed, howalgorithms can be scaled to massive data setsThe basicproblemaddressed bythe KDDprocess isone ofmappinglow-leveldata intoother formsthat might bemorecompact,moreabstract,or moreuseful.ArticlesFALL 1996 39A driving force behind KDD is the database field (the second D in KDD). Indeed, the problem of effective data manipulation when data cannot fit in the main memory is of fun-damental importance to KDD. Database tech-niques for gaining efficient data access,grouping and ordering operations when ac-cessing data, and optimizing queries consti-tute the basics for scaling algorithms to larger data sets. Most data-mining algorithms from statistics, pattern recognition, and machine learning assume data are in the main memo-ry and pay no attention to how the algorithm breaks down if only limited views of the data are possible.A related field evolving from databases is data warehousing,which refers to the popular business trend of collecting and cleaning transactional data to make them available for online analysis and decision support. Data warehousing helps set the stage for KDD in two important ways: (1) data cleaning and (2)data access.Data cleaning: As organizations are forced to think about a unified logical view of the wide variety of data and databases they pos-sess, they have to address the issues of map-ping data to a single naming convention,uniformly representing and handling missing data, and handling noise and errors when possible.Data access: Uniform and well-defined methods must be created for accessing the da-ta and providing access paths to data that were historically difficult to get to (for exam-ple, stored offline).Once organizations and individuals have solved the problem of how to store and ac-cess their data, the natural next step is the question, What else do we do with all the da-ta? This is where opportunities for KDD natu-rally arise.A popular approach for analysis of data warehouses is called online analytical processing (OLAP), named for a set of principles pro-posed by Codd (1993). OLAP tools focus on providing multidimensional data analysis,which is superior to SQL in computing sum-maries and breakdowns along many dimen-sions. OLAP tools are targeted toward simpli-fying and supporting interactive data analysis,but the goal of KDD tools is to automate as much of the process as possible. Thus, KDD is a step beyond what is currently supported by most standard database systems.Basic DefinitionsKDD is the nontrivial process of identifying valid, novel, potentially useful, and ultimate-and still run efficiently, how results can be in-terpreted and visualized, and how the overall man-machine interaction can usefully be modeled and supported. The KDD process can be viewed as a multidisciplinary activity that encompasses techniques beyond the scope of any one particular discipline such as machine learning. In this context, there are clear opportunities for other fields of AI (be-sides machine learning) to contribute to KDD. KDD places a special emphasis on find-ing understandable patterns that can be inter-preted as useful or interesting knowledge.Thus, for example, neural networks, although a powerful modeling tool, are relatively difficult to understand compared to decision trees. KDD also emphasizes scaling and ro-bustness properties of modeling algorithms for large noisy data sets.Related AI research fields include machine discovery, which targets the discovery of em-pirical laws from observation and experimen-tation (Shrager and Langley 1990) (see Kloes-gen and Zytkow [1996] for a glossary of terms common to KDD and machine discovery),and causal modeling for the inference of causal models from data (Spirtes, Glymour,and Scheines 1993). Statistics in particular has much in common with KDD (see Elder and Pregibon [1996] and Glymour et al.[1996] for a more detailed discussion of this synergy). Knowledge discovery from data is fundamentally a statistical endeavor. Statistics provides a language and framework for quan-tifying the uncertainty that results when one tries to infer general patterns from a particu-lar sample of an overall population. As men-tioned earlier, the term data mining has had negative connotations in statistics since the 1960s when computer-based data analysis techniques were first introduced. The concern arose because if one searches long enough in any data set (even randomly generated data),one can find patterns that appear to be statis-tically significant but, in fact, are not. Clearly,this issue is of fundamental importance to KDD. Substantial progress has been made in recent years in understanding such issues in statistics. Much of this work is of direct rele-vance to KDD. Thus, data mining is a legiti-mate activity as long as one understands how to do it correctly; data mining carried out poorly (without regard to the statistical as-pects of the problem) is to be avoided. KDD can also be viewed as encompassing a broader view of modeling than statistics. KDD aims to provide tools to automate (to the degree pos-sible) the entire process of data analysis and the statistician’s “art” of hypothesis selection.Data mining is a step in the KDD process that consists of ap-plying data analysis and discovery al-gorithms that produce a par-ticular enu-meration ofpatterns (or models)over the data.Articles40AI MAGAZINEly understandable patterns in data (Fayyad, Piatetsky-Shapiro, and Smyth 1996).Here, data are a set of facts (for example, cases in a database), and pattern is an expres-sion in some language describing a subset of the data or a model applicable to the subset. Hence, in our usage here, extracting a pattern also designates fitting a model to data; find-ing structure from data; or, in general, mak-ing any high-level description of a set of data. The term process implies that KDD comprises many steps, which involve data preparation, search for patterns, knowledge evaluation, and refinement, all repeated in multiple itera-tions. By nontrivial, we mean that some search or inference is involved; that is, it is not a straightforward computation of predefined quantities like computing the av-erage value of a set of numbers.The discovered patterns should be valid on new data with some degree of certainty. We also want patterns to be novel (at least to the system and preferably to the user) and poten-tially useful, that is, lead to some benefit to the user or task. Finally, the patterns should be understandable, if not immediately then after some postprocessing.The previous discussion implies that we can define quantitative measures for evaluating extracted patterns. In many cases, it is possi-ble to define measures of certainty (for exam-ple, estimated prediction accuracy on new data) or utility (for example, gain, perhaps indollars saved because of better predictions orspeedup in response time of a system). No-tions such as novelty and understandabilityare much more subjective. In certain contexts,understandability can be estimated by sim-plicity (for example, the number of bits to de-scribe a pattern). An important notion, calledinterestingness(for example, see Silberschatzand Tuzhilin [1995] and Piatetsky-Shapiro andMatheus [1994]), is usually taken as an overallmeasure of pattern value, combining validity,novelty, usefulness, and simplicity. Interest-ingness functions can be defined explicitly orcan be manifested implicitly through an or-dering placed by the KDD system on the dis-covered patterns or models.Given these notions, we can consider apattern to be knowledge if it exceeds some in-terestingness threshold, which is by nomeans an attempt to define knowledge in thephilosophical or even the popular view. As amatter of fact, knowledge in this definition ispurely user oriented and domain specific andis determined by whatever functions andthresholds the user chooses.Data mining is a step in the KDD processthat consists of applying data analysis anddiscovery algorithms that, under acceptablecomputational efficiency limitations, pro-duce a particular enumeration of patterns (ormodels) over the data. Note that the space ofArticlesFALL 1996 41Figure 1. An Overview of the Steps That Compose the KDD Process.methods, the effective number of variables under consideration can be reduced, or in-variant representations for the data can be found.Fifth is matching the goals of the KDD pro-cess (step 1) to a particular data-mining method. For example, summarization, clas-sification, regression, clustering, and so on,are described later as well as in Fayyad, Piatet-sky-Shapiro, and Smyth (1996).Sixth is exploratory analysis and model and hypothesis selection: choosing the data-mining algorithm(s) and selecting method(s)to be used for searching for data patterns.This process includes deciding which models and parameters might be appropriate (for ex-ample, models of categorical data are differ-ent than models of vectors over the reals) and matching a particular data-mining method with the overall criteria of the KDD process (for example, the end user might be more in-terested in understanding the model than its predictive capabilities).Seventh is data mining: searching for pat-terns of interest in a particular representa-tional form or a set of such representations,including classification rules or trees, regres-sion, and clustering. The user can significant-ly aid the data-mining method by correctly performing the preceding steps.Eighth is interpreting mined patterns, pos-sibly returning to any of steps 1 through 7 for further iteration. This step can also involve visualization of the extracted patterns and models or visualization of the data given the extracted models.Ninth is acting on the discovered knowl-edge: using the knowledge directly, incorpo-rating the knowledge into another system for further action, or simply documenting it and reporting it to interested parties. This process also includes checking for and resolving po-tential conflicts with previously believed (or extracted) knowledge.The KDD process can involve significant iteration and can contain loops between any two steps. The basic flow of steps (al-though not the potential multitude of itera-tions and loops) is illustrated in figure 1.Most previous work on KDD has focused on step 7, the data mining. However, the other steps are as important (and probably more so) for the successful application of KDD in practice. Having defined the basic notions and introduced the KDD process, we now focus on the data-mining component,which has, by far, received the most atten-tion in the literature.patterns is often infinite, and the enumera-tion of patterns involves some form of search in this space. Practical computational constraints place severe limits on the sub-space that can be explored by a data-mining algorithm.The KDD process involves using the database along with any required selection,preprocessing, subsampling, and transforma-tions of it; applying data-mining methods (algorithms) to enumerate patterns from it;and evaluating the products of data mining to identify the subset of the enumerated pat-terns deemed knowledge. The data-mining component of the KDD process is concerned with the algorithmic means by which pat-terns are extracted and enumerated from da-ta. The overall KDD process (figure 1) in-cludes the evaluation and possible interpretation of the mined patterns to de-termine which patterns can be considered new knowledge. The KDD process also in-cludes all the additional steps described in the next section.The notion of an overall user-driven pro-cess is not unique to KDD: analogous propos-als have been put forward both in statistics (Hand 1994) and in machine learning (Brod-ley and Smyth 1996).The KDD ProcessThe KDD process is interactive and iterative,involving numerous steps with many deci-sions made by the user. Brachman and Anand (1996) give a practical view of the KDD pro-cess, emphasizing the interactive nature of the process. Here, we broadly outline some of its basic steps:First is developing an understanding of the application domain and the relevant prior knowledge and identifying the goal of the KDD process from the customer’s viewpoint.Second is creating a target data set: select-ing a data set, or focusing on a subset of vari-ables or data samples, on which discovery is to be performed.Third is data cleaning and preprocessing.Basic operations include removing noise if appropriate, collecting the necessary informa-tion to model or account for noise, deciding on strategies for handling missing data fields,and accounting for time-sequence informa-tion and known changes.Fourth is data reduction and projection:finding useful features to represent the data depending on the goal of the task. With di-mensionality reduction or transformationArticles42AI MAGAZINEThe Data-Mining Stepof the KDD ProcessThe data-mining component of the KDD pro-cess often involves repeated iterative applica-tion of particular data-mining methods. This section presents an overview of the primary goals of data mining, a description of the methods used to address these goals, and a brief description of the data-mining algo-rithms that incorporate these methods.The knowledge discovery goals are defined by the intended use of the system. We can distinguish two types of goals: (1) verification and (2) discovery. With verification,the sys-tem is limited to verifying the user’s hypothe-sis. With discovery,the system autonomously finds new patterns. We further subdivide the discovery goal into prediction,where the sys-tem finds patterns for predicting the future behavior of some entities, and description, where the system finds patterns for presenta-tion to a user in a human-understandableform. In this article, we are primarily con-cerned with discovery-oriented data mining.Data mining involves fitting models to, or determining patterns from, observed data. The fitted models play the role of inferred knowledge: Whether the models reflect useful or interesting knowledge is part of the over-all, interactive KDD process where subjective human judgment is typically required. Two primary mathematical formalisms are used in model fitting: (1) statistical and (2) logical. The statistical approach allows for nondeter-ministic effects in the model, whereas a logi-cal model is purely deterministic. We focus primarily on the statistical approach to data mining, which tends to be the most widely used basis for practical data-mining applica-tions given the typical presence of uncertain-ty in real-world data-generating processes.Most data-mining methods are based on tried and tested techniques from machine learning, pattern recognition, and statistics: classification, clustering, regression, and so on. The array of different algorithms under each of these headings can often be bewilder-ing to both the novice and the experienced data analyst. It should be emphasized that of the many data-mining methods advertised in the literature, there are really only a few fun-damental techniques. The actual underlying model representation being used by a particu-lar method typically comes from a composi-tion of a small number of well-known op-tions: polynomials, splines, kernel and basis functions, threshold-Boolean functions, and so on. Thus, algorithms tend to differ primar-ily in the goodness-of-fit criterion used toevaluate model fit or in the search methodused to find a good fit.In our brief overview of data-mining meth-ods, we try in particular to convey the notionthat most (if not all) methods can be viewedas extensions or hybrids of a few basic tech-niques and principles. We first discuss the pri-mary methods of data mining and then showthat the data- mining methods can be viewedas consisting of three primary algorithmiccomponents: (1) model representation, (2)model evaluation, and (3) search. In the dis-cussion of KDD and data-mining methods,we use a simple example to make some of thenotions more concrete. Figure 2 shows a sim-ple two-dimensional artificial data set consist-ing of 23 cases. Each point on the graph rep-resents a person who has been given a loanby a particular bank at some time in the past.The horizontal axis represents the income ofthe person; the vertical axis represents the to-tal personal debt of the person (mortgage, carpayments, and so on). The data have beenclassified into two classes: (1) the x’s repre-sent persons who have defaulted on theirloans and (2) the o’s represent persons whoseloans are in good status with the bank. Thus,this simple artificial data set could represent ahistorical data set that can contain usefulknowledge from the point of view of thebank making the loans. Note that in actualKDD applications, there are typically manymore dimensions (as many as several hun-dreds) and many more data points (manythousands or even millions).ArticlesFALL 1996 43Figure 2. A Simple Data Set with Two Classes Used for Illustrative Purposes.。
(2008)Dimensionality reduction: A comparative review

L.J.P. van der Maaten ∗ , E.O. Postma, H.J. van den Herik
MICC, Maastricht University, P.O. Box 616, 6200 MD Maastricht, The Netherlands.
22 February 2008
the number of techniques and tasks that are addressed). Motivated by the lack of a systematic comparison of dimensionality reduction techniques, this paper presents a comparative study of the most important linear dimensionality reduction technique (PCA), and twelve frontranked nonlinear dimensionality reduction techniques. The aims of the paper are (1) to investigate to what extent novel nonlinear dimensionality reduction techniques outperform the traditional PCA on real-world datasets and (2) to identify the inherent weaknesses of the twelve nonlinear dimenisonality reduction techniques. The investigation is performed by both a theoretical and an empirical evaluation of the dimensionality reduction techniques. The identification is performed by a careful analysis of the empirical results on specifically designed artificial datasets and on the real-world datasets. Next to PCA, the paper investigates the following twelve nonlinear techniques: (1) multidimensional scaling, (2) Isomap, (3) Maximum Variance Unfolding, (4) Kernel PCA, (5) diffusion maps, (6) multilayer autoencoders, (7) Locally Linear Embedding, (8) Laplacian Eigenmaps, (9) Hessian LLE, (10) Local Tangent Space Analysis, (11) Locally Linear Coordination, and (12) manifold charting. Although our comparative review includes the most important nonlinear techniques for dimensionality reduction, it is not exhaustive. In the appendix, we list other important (nonlinear) dimensionality reduction techniques that are not included in our comparative review. There, we briefly explain why these techniques are not included. The outline of the remainder of this paper is as follows. In Section 2, we give a formal definition of dimensionality reduction. Section 3 briefly discusses the most important linear technique for dimensionality reduction (PCA). Subsequently, Section 4 describes and discusses the selected twelve nonlinear techniques for dimensionality reduction. Section 5 lists all techniques by theoretical characteristics. Then, in Section 6, we present an empirical comparison of twelve techniques for dimensionality reduction on five artificial datasets and five natural datasets. Section 7 discusses the results of the experiments; moreover, it identifies weaknesses and points of improvement of the selected nonlinear techniques. Section 8 provides our conclusions. Our main conclusion is that the focus of the research community should shift towards nonlocal techniques for dimensionality reduction with objective functions that can be optimized well in practice (such as PCA, Kernel PCA, and autoencoders).
美国应用生物系统公司实时荧光定量PCR技术

Calibrator Sample(基准样品)
目标基因 比如 内对照基因
IL-2 18S
得出相对于某一个样品的基因表达量, 1X sample. Treated vs. Untreated, 0 hr vs. 6 hr, Normal vs. Diseased…. Sample Calibrator 比如 处理后 处理前
荧光定量PCR原理
•TaqMan 探针法 •SYBR Green I 染料法
TaqMan 探针法
Polymerization
TaqMan® R Probe Q
5’ 3’ 5’
5’ 3’ 5’
Forward Primer
Reverse Primer
TaqMan 探针法
Displacement
R
5’ 3’ 5’
New Power SYBR Green PCR Master Mix and RT-PCR Reagents 高灵敏度SYBR Green PCR 混合试剂和逆转录PCR试剂
除模板和引物外, 该产品 已包含所有PCR反应所 需的全部试剂. 高灵敏度 , 高保真, 低背景. 可进行 实时PCR而不须用荧光 标记核苷酸探针.
ABI公司基因研究新技术报告会
9:00-9:50 9:50-10:40 11:00-12:00 实时荧光定量PCR技术的原理及应用进展 ABI公司分子生物学产品市场部经理 刘雪燕 基因突变和SNP分型技术进展 ABI公司分子生物学产品业务发展部部经理 杨林森 基因分析仪的应用 ABI公司分子生物学产品专家 陈云地 工作午餐 AB公司高内涵基因组分析试剂及其在肿瘤研究中的应用 ABI公司分子生物学产品业务发展部部经理 杨林森 基因和miRNA表达分析及其在干细胞研究中的应用 ABI公司分子生物学产品市场部经理 刘雪燕 定量PCR技术的应用 ABI公司分子生物学产品专家 陈云地 抽奖活动
基于网络分析和随机森林方法的肝细胞癌分期研究

Keywords
Hepatocellular Carcinoma, WGCNA, PPI Nபைடு நூலகம்twork, Random Forest
文章引用: 李鑫. 基于网络分析和随机森林方法的肝细胞癌分期研究[J]. 统计学与应用, 2019, 8(1): 95-107. DOI: 10.12677/sa.2019.81011
th th st
Abstract
Hepatocellular carcinoma (HCC) is an invasive malignant tumor. Although the diagnostic techniques and treatment levels of hepatocellular carcinoma have made great progress, the early diagnosis of HCC is still a huge challenge. In this paper, we attempt to analyze core genes associated with clinical staging by gene network for information on the discovery of early HCC patients and improving the diagnostic techniques and treatment levels of HCC. First, we selected the gene expression data of 219 patients with early postoperative HCC in the GEO database, performed differential expression analysis, and randomly divided the data into training set and test set. We use the genes of training set to clustering out five modules by weighted gene co-expression network (WGCNA), and performed functional enrichment and pathway enrichment analysis for each gene module. We found that the blue module is related to some biological processes such as cell proliferation, division, cycle and DNA replication initiation, replication, repair, and this module is also related to some pathways such as cell cycle, P53 signaling pathway, HTLV-I infection, hepatitis B. These processes and pathways are closely related to the occurrence and development of HCC. Therefore, we use the enriched genes of the module for PPI network analysis, and 10 core genes that we selected with high connectivity is BUB1B, CCNA2, CCNB1, CCNB2, CDC20, MAD2L1, MCM4, PCNA, RFC4, and TOP2A. Then through the supervised learning of core genes in random forests, a classification model of BCLC staging was established and then applied to the test set. The study found that the method has a great help for the classification of early patients, and the correct rate reached 95.52%, but for the patients in the middle and late stages. The classification effect is not very good. This study raises awareness of the pathogenesis and staging of HCC. And it provides a new direction for HCC targeted therapy.
论文的参考文献标准模版

参考文献标准模版一、参考文献书写格式1)期刊[序号] 主要作者. 文献题名[J]. 刊名,出版年份,卷号(期号):起止页码.例如:[1] 袁庆龙,候文义. Ni-P合金镀层组织形貌及显微硬度研究[J]. 太原理工大学学报,2001,32(1):51-53.2)专著[序号] 主要作者. 专著名[M].出版地:出版者,出版年份,起止页码.[4] 王芸生. 六十年来中国与日本[M]. 北京:三联书店,1980,161-172.3)专利文献[序号] 专利所有者. 专利题名[P]. 专利国别:专利号,发布日期.[7] 姜锡洲. 一种温热外敷药制备方案[P]. 中国专利:881056078,1983-08-12.4)报纸文章[序号] 主要作者. 文献题名[N]. 报纸名,出版日期(版次).[11] 谢希德. 创造学习的思路[N]. 人民日报,1998-12-25(10).二、文献名称标识期刊文章[J]、专著[M]、论文集[C]、学位论文[D]、专利[P]、标准[S]、报纸文章[N]、报告[R]、资料汇编[G]、其他文献[Z][1] 纪钢. 一种对周期性信号采样的新方法[J]. 仪表技术,1998,(4):31-34.[2] 李晓陆. 带通采样定理在降低功耗问题中的实际应用[J]. 桂林电子工业学院学报,2004,24(5):36-38.[3] 李思坤,苏显渝,陈文静. 一种新的小波变换空间载频条纹相位重建方法[J]. 中国激光,2010,37(12):3060-6065.[4] Wang Chuandan,Zhang Zhongpei,Li Shaoqian. INTERFERENCE MITIGATINGBASED ON FRACTIONAL FOURIER TRANSFORM IN TRANSFORM DOMAIN COMMUNICATION SYSTEM [J]. Journal of Electronics(China),电子科学学刊(英文版),2007(2):1327-1350.[5] S.C.Chan,T.S.Ng. TRANSFORM DOMAIN CONJUGATE GRADIENTALGORITHM FOR ADAPTIVE FILTERING [J]. Journal of Electronics(China),电子科学学刊(英文版),2000,17(1):69-76.[6] Li Ke,Shi Xinhua,Zhang Eryang. TRANSFORM DOMAIN SMART ANTENNASALGORITHM FOR MAI SUPPRESSION [J]. Journal of Electronics(China),电子科学学刊(英文版),2004,21(4):289-295.[7] 谢艾纾,徐成,赵利平,邓绍伟,赵嫦花. 变换域维纳滤波及其改进[J]. 计算机工程与应用,2011,11(24):1-8.[8] 焦李成,孙强. 多尺度变换域图像的感知与识别:进展和展望[J]. 计算机学报,2006,29(2):177-193.[9] 李栋. 模拟信号的数字化[J]. 中国新闻科技,1999(8):4-9.[10] 周超. 多带模拟信号的采样与重构[J]. 传感器与微系统,2011,30(5):83-85.[11] 山磊. 模拟信号的数字传输[J]. 南宁职业技术学院学报,2005,10(1):92-95.[12] 徐洪浩. 带限信号谱估计的一个新算法[J]. 哈尔滨船舶工程学院学报,1985(3):36-42.[13] 沈彩耀,李红波,张颋,曾繁景. 带限信号时延估计快速算法研究[J]. 信息工程大学学报,2007,8(1):77-80.[14] 王飞雪,郭桂蓉. 多通带带限信号的采样定理[C]. 第九届全国信号处理学术年会(CCSP-99),1999(10)-1.[15] 邓林旺,曹建航,何睿,倪琰. 一种模拟信号采样装置[P]. 比亚迪股份有限公司,2001(3)-2.[16] 木青. 高速A/D转换器的基本原理与结构比较[J]. 微电子学,1987,17(5):8-11.[17] 崔庆林,蒋和全. 高速A/D转换器动态参数的计算机辅助测试[J]. 微电子学,2004,34(5):505-509.[18] 王萍,石寅. 一种用于高速A/D转换器的高精度参考电压电阻网络[J]. 电子学报,2000,28(12):48-51.[19] 崔庆林,蒋和全. 高速A/D转换器测试采样技术研究[J]. 微电子学,2006,36(1):52-55.[20] David L. Donoho. Compressed sensing[J]. IEEE Transactions on InformationTheory,2006,52(4): 1289-1306[21] E.J. Candes and J Romberg. Quantitative robust uncertaninty principles and optimallysparse decompositions[J]. Foundations of Comput Math,2006,6(2) :227-254 [22] D. L. Donoho,Y Tsaig. Extensions of compressed sensing[J]. Signal Processing.2006,86(3) :533-548.[23] E.J. Candes. Monoscale ridgelets for the rep resentation of images with edges.Stanford:Stanford University,1999.[24] E.J. Candes and J Romberg. Practical signal recovery from random projections InProc.SPIE Computational Imaging,2005,5674:76-86[25] E.J.Candes. Compressive sampling.Int. Congress of Mathematics,2006,3:1433-1452[26] R. Baraniuk. Compressive sensing. IEEE Signal Processing Magazine,2007,24(4):448-121.[27] 石光明,刘丹化,高大化,刘哲,林杰,王良君.压缩感知理论及其研究进展[J].电子学报,2009,37(5):1070-1081.[28] Olshausen B A, Field D J. Emergency of simple-cell receptive field properties bylearning a sparse coding for natural images. Nature,1996,381(6583): 607-609. [29] Olshausen B A, Field D J. Sparse coding with an overcomplete basis set: a strategyemployed by V1? Visual Research,1997,37(33): 3311-3325.[30] 程文波,王华军. 信号稀疏表示的研究及应用[J].西南石油大学学报(自然科学版),2008,30(5):148-151.[31] 何昭水,谢胜利. 信号的稀疏性分析[J]. 自然科学进展,2006,16(9):1167-1173.[32] 李映,张艳宁,许星. 基于信号稀疏表示的形态成分分析:进展和展望[J]. 电子学报,2009,37(1):146-152.[33] 傅予力,谢胜利,何昭水. 稀疏信号的参数分析[J]. 武汉大学学报(工学版),2006,36(9):101-121.[34] 王世一编著. 《数字信号处理》(修订版). 北京理工大学出版社,1997.[35] Xiaoyan Xing,Lisheng Xu,Jilie Ding,Xiaobo Deng and Hailei Liu. The Preliminaryanalysis of Guizhou short-term climate change characteristics using the information theory[C]. 2010 International Conference on Remote Sensing (ICRS 2010),2010(10).[36] 廖斌,许刚,王裕国. 二维匹配跟踪自适应图像编码[J]. 计算机辅助设计与图形学学报,2003,15(9):1084-1090.[37] 尹忠科,王建英,Pierre Vandergheynst. 在低维空间实现的基于MP的图像稀疏分解. 电讯技术,2004,44(3):12-15.[38] M.Lustig,D.L.Donoho,J.M.Pauly. Sparse MRI:The application of compressedsensing for rapid MR imaging. Magnetic Resonance in Medicine. 2007,58(6):1182-1195.[39] Chen,S.A.Billings,and W. Luo. Orthogonal least squares and their application tonon-linear system identification. International Journal of Control,1989,50(5):1873-1896.[40] R. Baraniuk,P. Steeghs,Compressive radar imaging. IEEE Radar Conference,Waltham,Massachusetts,April 2007.[41] W. Bajwa,J. Haupt,A. Sayeed,etc. Compressive wireless sensing. Int. Conf. onInformation Processing in Sensor Networks(IPSN),Nashville,Tennessee,2006:134-142.[42] W. Bajwa,J. Haupt,A. Sayeed,etc. Compressive wireless sensing. Proceedings of thefifth International Conference on Information Processing in Sensor Networks,IPSN’06. New York: Association for Computing Machinery. 2006:134-142.[43] G.Quer,R.Masiero,D.Munaretto,etc. On the Interplay Between Routing and SignalRepresentation for Compressive Sensing in Wireless Sensor Networks. Information Throry and Applications Workshop(ITA 2009),San Diego,CA.[44] 黄萍莉,岳军. 图像传感器CCD技术[J]. 信息记录材料,2005,6(1):50-55.[45] 赵瑾娜. 攻擂方:CMOS技术前景无限[N]. 中国计算机报,2001-05-28(D03).[46] 青山. CMOS技术:还有很长的路要走[N]. 中国电子报,2001-03-16(006).[47] 俊平. CMOS技术有望再领风骚15年[N]. 电子资讯时报,2002-12-05(B04).[48] 陈辰. 基于CCD和CMOS技术的混合数字图像传感器技术兼有低成本和高性能两大优点[J]. 电子产品世界,1998,Z1:143.[49] 王东. 基于数码相机的CCD与CMOS技术[J]. 今日印刷,2002,8(12):56-59.[50] 康为民,李延彬,高伟志. 数字微镜阵列红外动态景象模拟器的研制[J]. 红外与激光工程,2008,37(5):753-756.[51] D. Takhar,V. Bansal,M. Wakin,etc. A compressed sensing camera: New theory andan implementation using digital micromirrors[C]. SPIE Electronic Imaging: Computational Imaging. San Jose. 2006[52] M. Duarte,M. Davenport,D. Takhar,etc. Single-pixel imaging via compressivesampling[C]. IEEE Signal Processing Magazine,2008,25(2):82-91.[53] CAO Wenhua,LIU Songhao,Wuyi University. Optical pulse compression using anonlinear optical loop mirror constructed from dispersion decreasing fiber[J]. Science in China(Series E: Technological Sciences),中国科学(E辑:技术科学)(英文版),2004,47(1):33-50.[54] 孟藏珍,袁俊泉,徐向东. 海杂波背景下自适应脉冲压缩的性能与分析[J]. 雷达科学与技术,2006,4(5):305-308.[55] 商枝江. 基于压缩感知的稀疏多径信道估计算法研究[D]. 电子科技大学,2011.[56] Emmanuel Candes,Justin Romberg,T. Tao,Robust uncertainty principles: exactsignal reconstruction from highly incomplete frequency information, IEEE Transactions on Information Theory,2006,52(2):489-509.[57] E. Candes,J. Romberg,T. Tao. Stable signal recovery from incomplete andinaccurate measurements. Communications on Pure and Applied Mathematics,2006,59(8):1207-1223.[58] Hong Fang,Quanbing Zhang,Sui Wei. A Method of image Reconstruction Based onSub-Gaussian Random Projection[J]. Journal of Computer Research and Development,2008,45(8):1402-1407.[59] Hong Fang,Quanbing Zhang,Sui Wei. Method of image reconstruction based on verysparse random projection[J]. Computer Engineering and Applications,2007,43(22):25-27.[60] E.Candes,T.Tao.Near optimal signal recovery from random projections: Universalencoding strategies?[J]. IEEE Transactions on Information Theory,2006,52(12): 5406-5425.[61] W.Yin,S.P.Morgan,J.Yang,Y.Zhang,Practical compressive sensing with Toeplitzand circulant matrices[C]. Rice University CAAM Technical Report TR10-01,Submitted to VCIP 2010.[62] W.Bajwa,J.Haupt,G.Raz,S.J.Wright,R.D.Nowak. Toeplitz-structured compressedsensing matrices[C]. Proceedings of the IEEE Workshop on Statistical Signal Processing,Washington D.C.,USA:IEEE,2007,294-298.[63] F.Sebert,Y.M.Zou,L.Ying. Toeplitz block matrices in compressed sensing and theirapplications in imaging. [C]. Proceedings of International Conference on Technology and Applications in Biomedicine,Washington D.C.,USA:IEEE,2008,47-50. [64] Holger Rauhut. Circulant and Toeplitz matrices in compressed sensing[C]. InProcessing SPARS’09,Saint Malo,2009.[65] Radu Berinde,Pintr Indyk,Sparse recovery using sparse random matrices,2008,preprint.[online],Available:/cs.[66] T.T.Do,T.D.Trany,L.Gan,Fast compressive with structurally random matrices,Proceedings of the IEEE International Conference on Acoustics[C]. Speech and signal Processing,Washington D.C.,USA:IEEE,2008,3369-3372.[67] Lorne Applebaum,Stephen Howard,Stephen Searle,Robert Calderbank,Chirpsensing codes: Deterministic compressed sensing measurements for fast recovery.2008,preprint.[online],Available:/cs.[68] Justin Romberg,compressive sensing by random convolution[J]. SIAM Jouranl onImagining Sciences,Nov.2009,2(4):1098-1128.[69] Richard Baraniuk,Mark Davenport,Ronald Dcvore,Michael Wakin. A simple proofof the restricted Isometry property for random matrices[J]. Comstructive Approximation, Dec.2008,28(3):253-263.[70] Richard Baraniuk. Compressive sensing. IEEE Signal Processing Magazine[J]. July2007,24(4):118-121.[71] E.Candes,T.Tao. Decoding by linear Programming[J]. IEEE Transactions onInformation Theory,2005,51(12):4203-4215.[72] Ronald,A. DeVore. Deterministic constructions of compressed sensing matrices[J].Journal of Complexity,2007,23(4-6):918-925.[73] P.Wojtaszczyk. Stability and instance optimality for Gaussian measurement incompressed sensing,Feb,2008.[74] 常彦勋. 有限域的本原元性质[J]. 数学杂志,1993,13(1):59-63.[75] 李海合,王三福. 有限域上的同余方程组[J]. 渭南师范学院学报,2009,24(5):9-10.[76] 白志东. 大维随机矩阵理论及其应用[R]. 东北师范大学,2009.[77] 李云龙. 一类凸规划最优解的形式表达式[J]. 哈尔滨科学技术大学学报,1993,17(1):78-83.[78] 陈景达,陈向晖. 特殊矩阵[M]. 北京:清华大学出版社,2001.[79] 张贤达. 矩阵分析与应用[M]. 北京:清华大学出版社,2004.[80] 胡星星. 线性规划的组合方向算法[D]. 杭州电子科技大学,2011.[81] S.B.Chen,D.L.Donoho,M.A.Saunders. Atomic decomposition by basis pursuit[J].SIAM Journal on Scientific Computing,1998,20(1):33-61.[82] Kim S,Koh K,Lustig M,Boyd S,Gorinevsky D. An interior-point method forlarge-scale l1 regularized least squares[C]. IEEE Journal of Selected Topics in Signal Processing,2007,1(4):606-617.[83] Fiqueiredo MAT,Nowak R D,Wright S J. Gradient projection for sparsereconstruction:Application to compressed sensing and other inverse problems[C].IEEE Journal of Selected Topics in Signal Processing,2007,1(4):586-598.[84] 伍杰. 求解对称非线性方程组的共轭梯度法[D]. 湖南大学,2010.[85] D. L. Donoho,Y Tsaig. Fast solution of l1-norm minimization problems when thesolution may be sparse[J]. Technical Report,Department of Statistics,Stanford University,USA,2008.[86] Tropp J,Gilbert A. Signal recovery from random measurements via orthogonalmatching pursuit[J]. Transactions on Information Theory,2007,53(12):4655-4666.[87] Needell D,Vershynin R. Uniform uncertainty principle and signal rccovery viaregularized orthogonal matching pursuit[J]. Found Comput Math,2008,in press. [88] Needell D,Tropp J A. CoSaMP:Iterative signal recovery from incomplete andinaccurate samples[J]. ACM Technical Report 2008-01,California Institute of Technology,Pasadena,2008.7.[89] Thong T Do,Lu Gan,Nam Nguyen and Trac D Tran. Sparsely adaptive matchingpursuit algorithm for practical compressed sensing[J]. Asilomar Conference on Signals Systems,and Computers,Pacific Grove,California,2008.10.[90] Dai W,Milenkovic O. Subspace pursuit for compressive sensing signalreconstruction[J]. 2008 5th International Symposium on Turbo Codes and Related Topics,TURBOCODING,2008:402-407.[91] 刘亚新,赵瑞珍,胡绍海,姜春晖. 用于压缩感知信号重建的正则化自适应匹配追踪算法[J]. 电子与信息学报,2010,32(11):2713-2717.[92] Kingsbury N G. Complex wavelets for shift invariant analysis and filtering of comlexwavelets for shift invariant analysis and filtering of signals[J]. Journal of Applied and Computational Harmonic Analysis,2001,10(3):234-253.[93] Herrity K.K,Gilbert A C,Tropp J A. Sparse approximation via iterative shareholding.In: Proceedings of the IEEE International Conference on Acoustics[C]. Speech and signal Processing,Washington D.C.,USA:IEEE,2006,624-627.[94] E.Candes,D.L.Donoho. New Tight Frames of Curvelets and Optimal Representationsof Objects with Piecewise C2 Singularities Communications on Pure and Applied Mathematics[C],2003,57(2):219-266.[95] Vinje W E,Gallant J L. Sparse coding and décor-relation in primary visual cortexduring natural vision[J]. Science,2000,287(5456): 1273-1276.[96] Olshausen B A,Field D J. Emergency of simple-cell receptive field properties bylearning a sparse coding for natural images[J]. Nature,1996,381(6583): 607-609.[97] Olshausen B A,Field D J. Sparse coding with an overcomplete basisset:a strategyemployed by V1? [J]. Visual Research,1997,37(33): 3311-3325.[98] V. K. Goyal,K. Alyson,et al. Compressive sampling and lossy compression[C].IEEE SIGNAL PROCESSING MAGAZINE,2008,25(2):48-56.[99] E. J. Candes,M. B. Wakin. An introduction to compressive sampling:Asending/sampling parading that goes against the common knowledge in data acquisition[C]. IEEE Signal Processing Magazine,2008,25(5):21-30.[100] 郭天圣. 基于小波变换的图像去噪研究[D]. 兰州理工大学,2010.[101] L.M.Bregman. The method of successive projection for finding a common point of convex sets[J]. Doklady Mathematics,1965,(6):688-692.[102] David L,Donoho,Yaakov Tsaig,Iddo Drori ,Jean-Luc Starck. Sparse Solution of Underdetermined Linear Equations by Stagewise Orthogonal Matching Pursuit[J],2006.[103] 王潇,尹忠科,王建英,杨郑. 应用基追踪的信号分离的算法[C]. 2008年中国西部青年通信学术会议论文集,2008(12):446-449.l-regularized [104] S.J.Kim,K.Koh,M.Lusting,et al. A method for large-scale1 least-squares[C]. IEEE Journal on Selected Topics in Signal Processing,2007,4(1):606-617.[105] I.Daubechies,M.Defrise,C.D.Mol. An iterative thresholding algorithm for linear inverse problems with a sparsely constraint[P]. Comm.Pure.,2004,57(11):1413-1457. [106] A.C.Gilbert,S.Guha,P.Indyk,et al. Near-optimal sparse Fourier representations via sampling[P]. Proceedings of the Annual ACM Symposium on Theory of Computing.Montreal,Que.,Canada: Association for Computing Machinery,2002:152-161.[107] A.C.Gilbert,S.Muthukrishnan,M.J.Strauss. Improved time bounds for neat-optimal sparse Fourier representation[P]. Proceedings of SPIE,Waveles XI,Belingham WA: International Society for Optical Engineering,2005,5914:1-15.[108] A.C.Gilbert,M.J.Strauss,J.Tropp. Algorithmic linear dimension reduction in thel1 norm for sparse vectors[N]. /files/cs/allerton2006GSTV.pdf. [109] A.C.Gilbert,M.J.Strauss,J.Tropp.One sketch for all:Fast algorithms for compressed sensing. Proceedings of the 39th Annual ACM Symposium on Theory of Computing,New York:Association for Computing Machiner,2007:237-246.[110] Takigawa I,Kudo M,Toyama J. Performance analysis of minimuml-norm1 solutions for underdetermined source separation[J]. IEEE Transactions on Signal Processing,2004,52(3): 582-591.。
高阶HBAM方法一般模型还可以

Bayesian Kernel Machine Regression工具包用户指南说明书

Package‘bkmrhat’October12,2022Title Parallel Chain Tools for Bayesian Kernel Machine RegressionVersion1.1.3Date2022-03-29Author Alexander Keil[aut,cre]Maintainer Alexander Keil<*************>Description Bayesian kernel machine regression(from the'bkmr'package)is a Bayesian semi-parametric generalized linear model approach underidentity and probit links.There are a number of functions in thispackage that extend Bayesian kernel machine regressionfits to allowmultiple-chain inference and diagnostics,which leverage functionsfrom the'future','rstan',and'coda'packages.Reference:Bobb,J.F.,Henn,B.C.,Valeri,L.,&Coull,B.A.(2018).Statisticalsoftware for analyzing the health effects of multiple concurrentexposures via Bayesian kernel machine regression.;<doi:10.1186/s12940-018-0413-y>.License GPL(>=3)Depends coda,R(>=3.5.0)Imports bkmr,data.table,future,rstanSuggests knitr,markdownVignetteBuilder knitrEncoding UTF-8Language en-USRoxygenNote7.1.2NeedsCompilation noRepository CRANDate/Publication2022-03-2908:50:05UTCR topics documented:as.mcmc.bkmrfit (2)12as.mcmc.bkmrfit as.mcmc.list.bkmrfit.list (3)ExtractPIPs_parallel (4)kmbayes_combine (5)kmbayes_combine_lowmem (6)kmbayes_continue (8)kmbayes_diagnose (9)kmbayes_parallel (10)kmbayes_parallel_continue (11)OverallRiskSummaries_parallel (12)predict.bkmrfit (12)PredictorResponseBivar_parallel (13)PredictorResponseUnivar_parallel (14)SamplePred_parallel (14)SingVarRiskSummaries_parallel (15)Index16 as.mcmc.bkmrfit Convert bkmrfit to mcmc object for coda MCMC diagnosticsDescriptionConverts a kmrfit(from the bkmr package)into an mcmc object from the coda package.The coda package enables many different types of single chain MCMC diagnostics,including geweke.diag, traceplot and effectiveSize.Posterior summarization is also available,such as HPDinterval and summary.mcmc.Usage##S3method for class bkmrfitas.mcmc(x,iterstart=1,thin=1,...)Argumentsx object of type kmrfit(from bkmr package)iterstartfirst iteration to use(e.g.for implementing burnin)thin keep1/thin%of the total iterations(at regular intervals)...unusedValueAn mcmc objectas.mcmc.list.bkmrfit.list3 Examples#following example from https://jenfb.github.io/bkmr/overview.htmlset.seed(111)library(coda)library(bkmr)dat<-bkmr::SimData(n=50,M=4)y<-dat$yZ<-dat$ZX<-dat$Xset.seed(111)fitkm<-kmbayes(y=y,Z=Z,X=X,iter=500,verbose=FALSE,varsel=FALSE)mcmcobj<-as.mcmc(fitkm,iterstart=251)summary(mcmcobj)#posterior summaries of model parameters#compare with default from bkmr package,which omits first1/2of chainsummary(fitkm)#note this only works on multiple chains(see kmbayes_parallel)#gelman.diag(mcmcobj)#lots of functions in the coda package to usetraceplot(mcmcobj)#will also fail with delta functions(when using variable selection)try(geweke.plot(mcmcobj))as.mcmc.list.bkmrfit.listConvert multi-chain bkmrfit to mcmc.list for coda MCMC diagnosticsDescriptionConverts a kmrfit.list(from the bkmrhat package)into an mcmc.list object from the coda pack-age.The coda package enables many different types of MCMC diagnostics,including geweke.diag, traceplot and effectiveSize.Posterior summarization is also available,such as HPDinterval and ing multiple chains is necessary for certain MCMC diagnostics,such as gelman.diag,and gelman.plot.Usage##S3method for class list.bkmrfit.listas.mcmc(x,...)Argumentsx object of type kmrfit.list(from bkmrhat package)...arguments to as.mcmc.bkmrfit4ExtractPIPs_parallelValueAn mcmc.list objectExamples#following example from https://jenfb.github.io/bkmr/overview.htmlset.seed(111)library(coda)dat<-bkmr::SimData(n=50,M=4)y<-dat$yZ<-dat$ZX<-dat$Xset.seed(111)future::plan(strategy=future::multisession,workers=2)#run2parallel Markov chains(more usually better)fitkm.list<-kmbayes_parallel(nchains=2,y=y,Z=Z,X=X,iter=1000,verbose=FALSE,varsel=FALSE)mcmcobj=as.mcmc.list(fitkm.list)summary(mcmcobj)#Gelman/Rubin diagnostics won t work on certain objects,#like delta parameters(when using variable selection),#so the rstan version of this will work better(does not give errors)try(gelman.diag(mcmcobj))#lots of functions in the coda package to useplot(mcmcobj)#both of these will also fail with delta functions(when using variable selection) try(gelman.plot(mcmcobj))try(geweke.plot(mcmcobj))closeAllConnections()ExtractPIPs_parallel Posterior inclusion probabilities by chainDescriptionPosterior inclusion probabilities by chainUsageExtractPIPs_parallel(x,...)Argumentsx bkmrfit.list object from kmbayes_parallel...arguments to ExtractPIPskmbayes_combine5Valuedata.frame with all chains togetherkmbayes_combine Combine multiple BKMR chainsDescriptionCombine multiple chains comprising BKMRfits at different starting values.Usagekmbayes_combine(fitkm.list,burnin=NULL,excludeburnin=FALSE,reorder=TRUE)comb_bkmrfits(fitkm.list,burnin=NULL,excludeburnin=FALSE,reorder=TRUE) Argumentsfitkm.list output from kmbayes_parallelburnin(numeric,or default=NULL)add in custom burnin(number of burnin iterations per chain).If NULL,then default to half of the chainexcludeburnin(logical,default=FALSE)should burnin iterations be excluded from thefinal chains?Note that all bkmr package functions automatically exclude burnin fromcalculations.reorder(logical,default=TRUE)ensures that thefirst half of the combined chain con-tains only thefirst half of each individual chain-this allows unaltered use ofstandard functions from bkmr package,which automatically trims thefirst halfof the iterations.This can be used for posterior summaries,but certain diag-nostics may not work well(autocorrelation,effective sample size)so the diag-nostics should be done on the individual chains#’@param...arguments toas.mcmc.bkmrfitDetailsChains are not combined fully sequentiallyValuea bkmrplusfit object,which inherits from bkmrfit(from the kmbayes function)with multiplechains combined into a single object and additional parameters given by chain and iters,which index the specific chains and iterations for each posterior sample in the bkmrplusfit objectExamples#following example from https://jenfb.github.io/bkmr/overview.htmlset.seed(111)library(bkmr)dat<-bkmr::SimData(n=50,M=4)y<-dat$yZ<-dat$ZX<-dat$Xset.seed(111)future::plan(strategy=future::multisession,workers=2)#run4parallel Markov chains(low iterations used for illustration)fitkm.list<-kmbayes_parallel(nchains=2,y=y,Z=Z,X=X,iter=500,verbose=FALSE,varsel=TRUE)#use bkmr defaults for burnin,but keep thembigkm=kmbayes_combine(fitkm.list,excludeburnin=FALSE)ests=ExtractEsts(bigkm)#defaults to keeping second half of samplesExtractPIPs(bigkm)pred.resp.univar<-PredictorResponseUnivar(fit=bigkm)risks.overall<-OverallRiskSummaries(fit=bigkm,y=y,Z=Z,X=X,qs=seq(0.25,0.75,by=0.05),q.fixed=0.5,method="exact")#additional objects that are not in a standard bkmrfit object:summary(bigkm$iters)#note that this reflects how fits are re-ordered to reflect burnin table(bigkm$chain)closeAllConnections()kmbayes_combine_lowmemCombine multiple BKMR chains in lower memory settingsDescriptionCombine multiple chains comprising BKMRfits at different starting values.This function writes some results to disk,rather than trying to process fully within memory which,in some cases,will result in avoiding"out of memory"errors that can happen with kmbayes_combine.Usagekmbayes_combine_lowmem(fitkm.list,burnin=NULL,excludeburnin=FALSE,reorder=TRUE)comb_bkmrfits_lowmem(fitkm.list,burnin=NULL,excludeburnin=FALSE,reorder=TRUE)Argumentsfitkm.list output from kmbayes_parallelburnin(numeric,or default=NULL)add in custom burnin(number of burnin iterations per chain).If NULL,then default to half of the chainexcludeburnin(logical,default=FALSE)should burnin iterations be excluded from thefinal chains?Note that all bkmr package functions automatically exclude burnin fromcalculations.reorder(logical,default=TRUE)ensures that thefirst half of the combined chain con-tains only thefirst half of each individual chain-this allows unaltered use ofstandard functions from bkmr package,which automatically trims thefirst halfof the iterations.This can be used for posterior summaries,but certain diag-nostics may not work well(autocorrelation,effective sample size)so the diag-nostics should be done on the individual chains#’@param...arguments toas.mcmc.bkmrfitDetailsChains are not combined fully sequentially(see"reorder")Valuea bkmrplusfit object,which inherits from bkmrfit(from the kmbayes function)with multiplechains combined into a single object and additional parameters given by chain and iters,which index the specific chains and iterations for each posterior sample in the bkmrplusfit objectExamples#following example from https://jenfb.github.io/bkmr/overview.htmlset.seed(111)library(bkmr)dat<-bkmr::SimData(n=50,M=4)y<-dat$yZ<-dat$ZX<-dat$Xset.seed(111)future::plan(strategy=future::multisession,workers=2)#run4parallel Markov chains(low iterations used for illustration)fitkm.list<-kmbayes_parallel(nchains=2,y=y,Z=Z,X=X,iter=500,verbose=FALSE,varsel=TRUE)8kmbayes_continue #use bkmr defaults for burnin,but keep thembigkm=kmbayes_combine_lowmem(fitkm.list,excludeburnin=FALSE)ests=ExtractEsts(bigkm)#defaults to keeping second half of samplesExtractPIPs(bigkm)pred.resp.univar<-PredictorResponseUnivar(fit=bigkm)risks.overall<-OverallRiskSummaries(fit=bigkm,y=y,Z=Z,X=X,qs=seq(0.25,0.75,by=0.05),q.fixed=0.5,method="exact")#additional objects that are not in a standard bkmrfit object:summary(bigkm$iters)#note that this reflects how fits are re-ordered to reflect burnin table(bigkm$chain)closeAllConnections()kmbayes_continue Continue sampling from existing bkmrfitDescriptionUse this when you’ve used MCMC sampling with the kmbayes function,but you did not take enough samples and do not want to start over.Usagekmbayes_continue(fit,...)Argumentsfit output from kmbayes...arguments to kmbayes_continueDetailsNote this does not fully start from the prior values of the MCMC chains.The kmbayes function does not allow full specification of the kernel function parameters,so this will restart the chain at the last values of allfixed effect parameters,and start the kernel r parmeters at the arithmetic mean of all r parameters from the last step in the previous chain.Valuea bkmrfit.continued object,which inherits from bkmrfit objects similar to kmbayes output,andwhich can be used to make inference using functions from the bkmr package.See Alsokmbayes_parallelkmbayes_diagnose9Examplesset.seed(111)dat<-bkmr::SimData(n=50,M=4)y<-dat$yZ<-dat$ZX<-dat$X##Not run:fitty1=bkmr::kmbayes(y=y,Z=Z,X=X,est.h=TRUE,iter=100)#do some diagnostics here to see if100iterations(default)is enough#add100additional iterations(for illustration-still will not be enough)fitty2=kmbayes_continue(fitty1,iter=100)cobj=as.mcmc(fitty2)varnames(cobj)##End(Not run)kmbayes_diagnose MCMC diagnostics using rstanDescriptionGive MCMC diagnostistics from the rstan package using the Rhat,ess_bulk,and ess_tail functions.Note that r-hat is only reported for bkmrfit.list objects from kmbayes_parallelUsagekmbayes_diagnose(kmobj,...)kmbayes_diag(kmobj,...)Argumentskmobj Either an object from kmbayes or from kmbayes_parallel...arguments to monitorExamplesset.seed(111)dat<-bkmr::SimData(n=50,M=4)y<-dat$yZ<-dat$ZX<-dat$Xset.seed(111)future::plan(strategy=future::multisession)fitkm.list<-kmbayes_parallel(nchains=2,y=y,Z=Z,X=X,iter=1000,10kmbayes_parallelverbose=FALSE,varsel=TRUE)kmbayes_diag(fitkm.list)kmbayes_diag(fitkm.list[[1]])#just the first chaincloseAllConnections()kmbayes_parallel Run multiple BKMR chains in parallelDescriptionFit parallel chains from the kmbayes function.These chains leverage parallel processing from the future package,which can speedfitting and enable diagnostics that rely on multiple Markov chains from dispersed initial values.Usagekmbayes_parallel(nchains=4,...)Argumentsnchains number of parallel chains...arguments to kmbayesValuea"bkmrfit.list"object,which is just an R list object in which each entry is a"bkmrfit"object kmbayesExamplesset.seed(111)dat<-bkmr::SimData(n=50,M=4)y<-dat$yZ<-dat$ZX<-dat$Xset.seed(111)future::plan(strategy=future::multisession,workers=2)#only50iterations fit to save installation timefitkm.list<-kmbayes_parallel(nchains=2,y=y,Z=Z,X=X,iter=50,verbose=FALSE,varsel=TRUE)closeAllConnections()kmbayes_parallel_continue11 kmbayes_parallel_continueContinue sampling from existing bkmr_parallelfitDescriptionUse this when you’ve used MCMC sampling with the kmbayes_parallel function,but you did not take enough samples and do not want to start over.Usagekmbayes_parallel_continue(fitkm.list,...)Argumentsfitkm.list output from kmbayes_parallel...arguments to kmbayes_continueValuea bkmrfit.list object,which is just a list of bkmrfit objects similar to kmbayes_parallelSee Alsokmbayes_parallelExamplesset.seed(111)dat<-bkmr::SimData(n=50,M=4)y<-dat$yZ<-dat$ZX<-dat$X##Not run:future::plan(strategy=future::multisession,workers=2)fitty1p=kmbayes_parallel(nchains=2,y=y,Z=Z,X=X)fitty2p=kmbayes_parallel_continue(fitty1p,iter=3000)cobj=as.mcmc.list(fitty2p)plot(cobj)##End(Not run)12predict.bkmrfit OverallRiskSummaries_parallelOverall summary by chainDescriptionOverall summary by chainUsageOverallRiskSummaries_parallel(x,...)Argumentsx bkmrfit.list object from kmbayes_parallel...arguments to OverallRiskSummariesValuedata.frame with all chains togetherpredict.bkmrfit Posterior mean/sd predictionsDescriptionProvides observation level predictions based on the posterior mean,or,alternatively,yields the pos-terior standard deviations of predictions for an observation.This function is useful for interfacing with ensemble machine learning packages such as SuperLearner,which utilize only point esti-mates.Usage##S3method for class bkmrfitpredict(object,ptype=c("mean","sd.fit"),...)Argumentsobjectfitted object of class inheriting from"bkmrfit".ptype"mean"or"sd.fit",where"mean"yields posterior mean prediction for every observation in the data,and"sd.fit"yields the posterior standard deviation forevery observation in the data....arguments to SamplePredPredictorResponseBivar_parallel13 Valuevector of predictions the same length as the outcome in the bkmrfit objectExamples#following example from https://jenfb.github.io/bkmr/overview.htmllibrary(bkmr)set.seed(111)dat<-bkmr::SimData(n=50,M=4)y<-dat$yZ<-dat$ZX<-dat$Xset.seed(111)fitkm<-kmbayes(y=y,Z=Z,X=X,iter=200,verbose=FALSE,varsel=TRUE)postmean=predict(fitkm)postmean2=predict(fitkm,Znew=Z/2)#mean difference in posterior meansmean(postmean-postmean2)PredictorResponseBivar_parallelBivariate predictor response by chainDescriptionBivariate predictor response by chainUsagePredictorResponseBivar_parallel(x,...)Argumentsx bkmrfit.list object from kmbayes_parallel...arguments to PredictorResponseBivarValuedata.frame with all chains together14SamplePred_parallel PredictorResponseUnivar_parallelUnivariate predictor response summary by chainDescriptionUnivariate predictor response summary by chainUsagePredictorResponseUnivar_parallel(x,...)Argumentsx bkmrfit.list object from kmbayes_parallel...arguments to PredictorResponseUnivarValuedata.frame with all chains togetherSamplePred_parallel Posterior samples of E(Y|h(Z),X,beta)by chainDescriptionPosterior samples of E(Y|h(Z),X,beta)by chainUsageSamplePred_parallel(x,...)Argumentsx bkmrfit.list object from kmbayes_parallel...arguments to SamplePredValuedata.frame with all chains togetherSingVarRiskSummaries_parallel15 SingVarRiskSummaries_parallelSingle variable summary by chainDescriptionSingle variable summary by chainUsageSingVarRiskSummaries_parallel(x,...)Argumentsx bkmrfit.list object from kmbayes_parallel...arguments to SingVarRiskSummariesValuedata.frame with all chains togetherIndexas.mcmc.bkmrfit,2,3,5,7as.mcmc.list.bkmrfit.list,3comb_bkmrfits(kmbayes_combine),5 comb_bkmrfits_lowmem(kmbayes_combine_lowmem),6 effectiveSize,2,3ess_bulk,9ess_tail,9ExtractPIPs,4ExtractPIPs_parallel,4gelman.diag,3gelman.plot,3geweke.diag,2,3HPDinterval,2,3kmbayes,5,7–10kmbayes_combine,5kmbayes_combine_lowmem,6 kmbayes_continue,8,8,11kmbayes_diag(kmbayes_diagnose),9 kmbayes_diagnose,9kmbayes_parallel,4,5,7–9,10,11–15 kmbayes_parallel_continue,11 mcmc,2mcmc.list,3,4monitor,9 OverallRiskSummaries,12 OverallRiskSummaries_parallel,12 predict.bkmrfit,12 PredictorResponseBivar,13 PredictorResponseBivar_parallel,13 PredictorResponseUnivar,14 PredictorResponseUnivar_parallel,14 Rhat,9SamplePred,12,14SamplePred_parallel,14SingVarRiskSummaries,15SingVarRiskSummaries_parallel,15summary.mcmc,2,3traceplot,2,316。
基于改进卷积神经网络的苹果叶部病害识别

2021年1月第45卷第1期安徽大学学报(自然科学版)Journal of Anhui University(Natural Science Edition)January2021Vol.45No.1doi:10.3969/j.issn.1000-2162.2021.01.008基于改进卷积神经网络的苹果叶部病害识别鲍文霞,吴刚,胡根生,张东彦,黄林生(安徽大学农业生态大数据分析与应用技术国家地方联合工程研究中心,安徽合肥230601.)摘要:针对苹果病害叶片图像病斑区域较小导致的传统卷积神经网络不能准确快速识别的问题,提出基于改进卷积神经网络的苹果叶部病害识别的网络模型•首先,将VGG16网络模型从ImagcNct数据集上学习到的先验知识迁移到苹果病害叶片数据集上;然后,在瓶颈层后采用选择性核(selective kernel,简称SK)卷积模块;最后,使用全局平均池化代替全连接层.实验结果表明:与其他传统网络模型相比,该模型能更准确快速捕获苹果病害叶片上微小的病斑•关键词:苹果叶部病害;图像识别;VGG16;SK卷积;迁移学习;全局平均池化中图分类号:TP391.41文献标志码:A 文章编号:10002162(2021)0-005307Apple leaf disease recognition based on improved convolutional neural networkBAO Wenxia,WU Gang,HU Gensheng,ZHANG Dongyan,HUANG Tlnsheng(National Engineering Research Center for Agro-Ecological Big Data Analysis&Application,Anhui University,Hefti230601,China.)Abstract:Aiming at the problem of small disease spots in apple leaf images,which couldn?t be accurately and quickly identified by using traditional convolutional neural networks,a network model based on improved convolutional neural network for apple leaf disease identification was proposed.First.,the prior knowledge learned from the VGG16network model was transferred from the ImageNet.dataset,to the apple disease leaf dataset.Then, after the bottleneck layer the selective kernel(SK)convolution module was adopted.Finally,the fully connected layer was replaced by Global average pooling.The experimental result,showed that,compared with other traditional network models,this model could capture the tiny spots on the diseased leaves of apples more accurately and quickly.Keywords:apple leaf disease;image recognition;VGG16;SK convolution;transfer learning;global average pooling快速、准确识别农作物病害对提高农作物的产量及质量具有重大意义.为了高效控制苹果病害,提高苹果的产量及质量,研究人员采用传统的机器学习方法识别各种类型的苹果叶片病害[12].传统方法需要大量的图像预处理及分割,工作量大且缺乏灵活性.由于病害区域的颜色、形状、纹理等信息复杂,收稿日期:20200522基金项目:国家自然科学基金资助项目(11771463);安徽省科技重大专项(6030701091);农业生态大数据分析与应用技术国家地方联合工程研究中心开放课题(A E2018009)作者简介:鲍文霞(980—),女,安徽铜陵人,安徽大学副教授,硕士生导师,博士,E-mail:bwxia@.54安徽大学学报(自然科学版)第45卷因此很难保证分割的区域为目标特征区域,这会导致特征提取的效率及识别的准确率降低•近年来,卷积神经网络(convolutional neural network,简称CNN)在模式识别领域取得了一定的成绩[-5]•与传统方法不同,CNN可自动从原始病害叶片图像数据中提取病斑特征,然后对提取的特征自动进行分类识别•Mohanty等[]在开源数据集PlantVillage[7]的基础上,使用GoogleNet[]和AlexNet[]识别14种农作物的26种病害,结果表明参数微调后的GoogleNet预训练模型的病虫害识别精度最高.孙俊等[0]以PlantVillage数据集及病害叶片图像为研究对象,通过对AlexNet网络进行改进,得到了较高的识别率.Baranwal等[1]通过具有2层卷积及2全连接层的网络,能识别苹果的3种病(黑星病、灰斑病及雪松锈病)害叶片.Geetharamani等[2]定义了1个卷积核大小为3X3的3层卷积,在每层卷积后接一个最大池化层,经3层卷积3层最大池化后,再通过2个全连接层进行特征融合,最后送入Softmax进行分类,分类精度高达96.46%.Ferentinos等[3]以复杂背景和简单背景下的病害叶片图像为研究对象,使用VGG16[4],GoogLeNet,AlexNet等网络模型进行训练,结果表明VGG16的效果最好.Guan等[5]先按病害严重程度对苹果灰斑病害叶片进行分级,后通过VGG16,VGG19, ResNet50[6],InceptionV3[7]的预训练模型进行迁移学习,结果表明迁移学习后的VGG16识别效果最好.研究表明,深度CNN网络模型在农作物病害叶片识别领域取得了较好的效果.但是•上述网络模型存在以下问题:①AlexNet,VGG16等网络模型通过全连接层进行特征融合、参数优化,延长了模型的收敛时间,当训练样本数不足时易导致模型过拟合•②寻找一个合适的网络层数需反复实验、比较,缺乏灵活性,选取的层数过浅易致欠拟合、过深易致过度拟合.③每层限定了卷积核的大小,不能针对植物病害叶片上病斑的不同尺度自适应调节卷积核的大小,降低了特征提取的效率•针对上述问题,该文利用在ImageNet数据集[8]上的预训练模型初始化瓶颈层的参数;在VGG16网络模型的基础上,去掉全连接层,在瓶颈层后采用选择性核(selective kernel,简称SK)卷积模块及全局平均池化,以减少模型的训练时间、提高识别的准确率•1数据集1.1数据集获取选取苹果的健康叶片图像及苹果叶片上发病概率较高的5种病(黑星病、灰斑病、雪松锈病、斑点落叶病和花叶病)害叶片图像为研究对象•其中健康、黑星病、灰斑病和雪松锈病叶片图像来自PlantVillage数据集,斑点落叶病和花叶病叶片图像来自Google网站.实验中所有图像的像素均为224X224,各类叶片图像如图1所示.(a)为健康叶片;(b)为病害程度一般的黑星病叶片,有少许黑色斑点;(c)为病害程度严重的黑星病叶片,有大量黑色斑点;(d)为灰斑病叶片;(e)为病害程度一般的雪松锈病叶片,有少量橘红色斑点;(f)为病害程度严重的雪松锈病叶片,表面接近枯萎,有大量病斑;(g)为斑点落叶病叶片,有褐色小圆点;(h)为花叶病叶片,病斑呈鲜黄色.图1各类叶片图像1.2数据增广通过数据增广,可增加噪声数据,提升模型的泛化能力,提高模型的鲁棒性•该文首先按4:1将原始数据集划分为训练集及测试集,对训练集中数据量小的病害类别进行数据增广,其具体操作有:图像随机旋转、裁剪、缩放,图像镜像操作、平移变换,图像亮度、对比度增强等[9].表1给出了不同类型的训第1期鲍文霞,等:基于改进卷积神经网络的苹果叶部病害识别55练集、增广后的训练集及测试集图像数•表1不同类型的训练集、增广后的训练集及测试集图像数类别图像数训练集增广后的训练集测试集健康1 3161 316329一般的黑星病29659274严重的黑星病20862452灰斑病497497124一般的雪松锈病17251643严重的雪松锈病4848012斑点落叶病4848012花叶病6036015总计2 6454 8656612改进的VGG16网络模型2.1网络模型结构在植物叶部病害识别领域,VGG16网络模型通过预训练模型得到了较好的识别结果[315].但是, VGG16网络模型中,一方面,卷积核大小均为3X3,不能自适应调整其感受野的大小;另一方面,其全 连接层复杂的参数优化操作会导致模型过拟合,且增加模型的训练时间•因此,该文在VGG16网络模 型的基础上,使用迁移学习的策略,利用预训练模型初始化瓶颈层参数,且在瓶颈层后接一个SK 卷积 模块,重新训练网络参数,使网络能根据输入特征图自适应选择卷积核,提高多尺度特征提取的水平,提 升对叶片微小病斑识别的能力.将全局平均池化代替全连接层,能加快网络模型的收敛、减少模型参数, 解决全连接层因大量参数优化而带来的过拟合问题•改进后的网络模型结构如图2所示,其中蓝色矩形 框表示卷积和激活操作,黄色矩形框表示池化操作,蓝色矩形框及黄色矩形框共同构成网络的瓶颈层,最右边长方形的长度表示该类病害出现概率的大小.改进后的网络模型结构■健康叶片I 雪松锈病一般雪松锈病严重灰斑病■黑星病一般黑星病严重斑点落叶病花叶病图22.2全局平均池化图3为全连接及全局平均池化示意图.特征提取后,全连接层产生了大量的参数,这些参数的优化 会加大模型的复杂度、延长模型的收敛时间、导致过拟合.通过采用全局平均池化,不仅可以解决全连接 层中过多参数优化导致的模型收敛速度较慢的问题,而且可以增强网络的抗过拟合能力[0]•通过特征 图像素的平均值得到1维特征向量,此过程没有涉及参数的优化,因此防止了过拟合•56安徽大学学报(自然科学版)第45卷平化4 局池 全均o o b o图 征 特s 特征图图3全连接(左)及全局平均池化(右)示意图2.3 卷积核的自适应选择传统CNN 大多在每一特征层上设置相同大小的卷积核[,4].尽管GoogleNet 在同一层采用多个卷 积核,但并不能根据输入特征图的大小自适应调整卷积核,影响了特征提取的效率.采用SKNt 21]中的 SK 卷积,能让网络根据输入特征图自适应选择大小适当的卷积核,从而提高特征提取的效率.SK 卷积 由分离、融合、选择3部分构成.(1)分离•分离操作中,利用多个卷积核对输入特征向量X 进行卷积,形成多个分支•对X 分别进 行大小为3X3和5X5的卷积操作,得到U € R H X W X C 和U 〃 € R H X W X C 两个特征向量.图4为SKNet 中 的SK 卷积示意图.刁 厂~㊉表示元素相加;表示元素相乘.图4 SKNet 中的SK 卷积示意图(2) 融合.设计门控机制,以分配流入下一个卷积层的信息流.在融合过程中,将前面卷积得到的' 和U 〃做如下式所示的像素融合u =U +u 〃. (1)对融合后的U ,通过全局平均池化压缩全局信息.图4中S 的第C 维度特征S c ,可由U 的第C 维度 特征经U c 全局平均池化后得到,如下式所示HWS c = /gp U c ) = ££u c a j ). ⑵全局平均池化后,将得到的特征送入全连接层处理,进一步压缩特征,以降低特征维度及提高特征 的提取效率•压缩后的特征为n =&(B(3s )), (3)其中:为函数ReLU ;B 表示批量归一化[1];n € R d x1,w s € R d ><C ,通过设置衰减比厂确定参数d 的 大小,其表达式为d = max(C/r L ) , (4)其中:L 的大小一般取32.(3) 选择.在Softmax 操作后,通过注意力机制[2],得到a ,软注意力向量为e " b e B z /匚、a =e A z +e B c z ,c — e A z + e B z , ⑸第1期鲍文霞,等:基于改进卷积神经网络的苹果叶部病害识别57其中:A,B e R CXd,A c表示A的第c行a为a的第c个元素;B c及b c同理•通过对应的权重矩阵及卷积核加权求和,得到输出特征为V1,V2,・・・V c],(6)其中:V c e R H X W V c=a U+b U,c+b c=1.3实验及其结果分析实验采用TensorFlow深度学习框架,其硬件及软件配置如表2所示.表2硬件及软件配置类别配置CPU Intel E5—2650V3GPU英伟达GTX1080Ti11GB内存128GB硬盘2TB操作系统Ubuntu16.04.02LTS(64位)3.1实验参数设置在训练过程中,使用随机梯度下降(stochastic gradient descent,简称SGD)的优化模型,使损失函数最小化.由于学习率过大导致模型学习不稳定、过小导致训练时间较长,因此将输入神经网络的训练图片的bach size设为32.虽然模型在开始时收敛速率较快,但随着训练的进行其收敛速率会逐步降低,因此,将初始学习率设为0.001;整个网络训练的epoch设为40;学习率下降间隔数设为8个epoch,其调整倍数为0.1.初始学习率可设置大一点,然后逐渐减少学习率,这样能避免因学习率过大而导致模型无法收敛.在SK卷积中,将路径数量n设为3,基数L设为32.3.2特征图可视化从特征图中,可更直观看到每层的特征•图5给出了苹果灰斑病图像及其特征图,为方便可视化,只列出25个通道特征图•(b)■S9BH HIIII ■■■■H■■■■B KHHai■■■■■IB■目■■■■■■3 3IBIH liaiB(d)(e)(a)为原图;(b),(c),(d),(e)分别为原图经图2中Conv1_1,Conv3_1,Conv5_1,Pool5操作后得到的特征图.图5苹果灰斑病图像及其特征图3.3不同网络模型性能对比为了验证笔者所提网络模型对苹果叶部病害识别的性能,需要比较同一条件下不同网络模型的识别准确率、训练时间•识别准确率的表达式为N-1工TP,P=-------------------------X100%,(7)工(TP,+FPQi=0其中:TP,表示第z种病害(包括健康叶片)分类正确数,FP,表示第z种病害(包括健康叶片)分类错误数N为病害总数•表3展示了增广后的训练集图像经不同网络模型训练后的识别准确率、生成的模型大小及训练时间.58安徽大学学报(自然科学版)第45卷表3不同网络模型性能对比网络模型识别准确率/%训练时间/s模型大小/MBAlexNet91.532768.16217.0GoogleNet93.042062.7347.1VGG1693.804561.24537.2VGG1993.504921.42558.4ResNet-5093.654859.2494.3SKNet-5093.955440.37186.0该文模型94.702138.5670.2由表3可知,不同CNN模型的识别准确率、训练时间以及模型大小存在较大差异•浅层模型AlexNet准确率只有91.53%,深层模型VGG16,VGG19,ResNet50的准确率分别达到了93.80%, 93.50%,93.65%,这得益于迁移学习的运用.通过加载预训练模型参数,充分学习到了苹果叶部病斑的特征,解决了由于训练样本不足而带来的过拟合问题•该文模型的准确率达到了94.70%,这是因为在VGG16模型的特征输出层采用了SK卷积模块,提升了模型的多尺度特征提取能力.AlexNet, VGG16,VGG19生成的模型较大,而该文模型生成的模型大小只有70.2MB,节省了计算成本.图6展示了不同网络模型经过不同训练轮数后的识别准确率.从图6中可以看出,与其他模型相比,该文模型收敛最快.这是因为全连接层的大量参数优化耗时较长,而全局平均池化无繁杂的参数优化操作,加快了模型的收敛速度.4结束语苹果病害初期叶片病斑相对较小,使用传统CNN不易准确识别.笔者在传统VGG16网络模型的基础上,提出了一个改进的网络模型,使用预训练模型初始化瓶颈层参数,采用SK卷积块及全局平均池化.该模型提高了识别微小病斑的能力,提升了叶部病害识别的准确率,加快了网络模型的收敛速度,降低了时间开销•参考文献:[1]ZHANG C L,ZHANG S W,YANG J C,et al Apple leaf disease identification using genetic algorithm andcorrelation based feature selection method[J].Int J Agric&Biol Eng,2017,10(2):74-83.[2]张云龙,袁浩,张晴晴,等•基于颜色特征和差直方图的苹果叶部病害识别方法[].江苏农业科学,2017,第1期鲍文霞,等:基于改进卷积神经网络的苹果叶部病害识别5945(14):17-174.[3]DYNMANN M,KARSTOFT H,MIDTIBY H S.Plant species classification using deep convolutional neuralnctwork[].Biosystems Engineering,2016,151:72-80.[4]AL.-SAFFAR A M,TAO H,TALB M A.Review of deep convolution neural network in image classification[C]//2017International Conference on Radar,Antenna,Microwave,Electronics,and Telecommunications,2018:26-31.[5]SLADOJEVIC S,ARSENOVIC M,ANDE2RLA A,ct al.Deep neural networks based recognition of plantdiseases by leaf image classificationJJ].Computational Intelligence and Neuroscience,2016(6):-11.[6]MOHANTY S P,HUGHES D P,SALATHE ing deep learning for image-based plant diseasedctcction[].Frontiers in Plant Science,2016,7:1419-143乙[7]LIU B,ZHANG Y,HE D J,ct al.Identification of apple leaf diseases based on deep convolutional neuralnetworks]」].Symmetry,2017,10(1):553-564.[8]SZEGEDY C,IIU W,JIA Y,ct al.Going deeper with con\91utions[C]//IEEE Conference on ComputerVision and Pattern Recognition,2014:-9.[9]KR1ZHEVSKY A,SUTSK EVER I,H INTON G E.ImagcNct classification with deep convolutional neuralnctworksEC]//Advances in Neural Information Processing Systems,202:1097-1105.[10]孙俊,谭文军,毛罕平,等.基于改进卷积神经网络的多种植物叶片病害识别[]•农业工程学报,2017,33(19):209-215.[11]BARANWAL S,KHANDE2LWAL S,ARORA A.Deep learning convolutional neural network for appleleaves disease detection[C]//International Conference on Sustainable Computing in Science,Technology&Management,2019:1-8.[12]GEET HARA MANI G,PANDIAN J A.Identification of plant leaf diseases using a nine-layer deepconvolutional neural nctwork[].Computers&Electrical Engineering,2019,76:323-338.[13]FERENTINOS K P.Deep learning models for plant disease detection and diagnosis[J].Computers andElectronics in Agriculture,2018,145:311-318.[14]SIMONYAN K,Z1SSERMAN A.Very deep convolutional networks for large-scale image recognition[EB/OL].[2020-05-03].https:///abs/1409.1556.[15]GUAN W,YU S,J1ANX1N W.Automatic image-based plant disease severity estimation using deep learning[EB/OL].[2020-05-06].https://dot org/10.1155/2017/2917536.[16]H EK,ZHANG X,RENS,ct al.Deep residual learning for image rccognition[C]//Procccdings of the IEEEConference on Computer Vision and Pattern Recognition,2016:770-778.[17]SZEGEDY C,VANHOUCKE V,IOFFE S,ct al.Rethinking the inception architecture for computer vision[C]//Proceedings of the2016IEEE Conference on Computer Vision and Pattern Recognition,2016:2818-2826.[18]MEHDIPOUR G M,YAN1KOGLU B,APTOULA E.Plant identification using deep neural networks viaoptimizatonoftransferlearningparameters[J].Neurocomputing,2017,235:228-235.[19]ZHANG D,CHEN P,ZHANG J,ct al.Classification of plant leaf diseases based on improved convolutionalneuralnetwork[J].Sensors,2019,19(19):4161-4180.[0]II X,WANG W,HU X,ct al.Selective kernel nctworks[C]//Proceedings of the2019IEEE Conference onComputer Vision and Pattern Recognition,2019:246-258.[21]NEWELL A,YANG K,DENG J.Stacked hourglass networks for human pose estimation[C]//EuropcanConference on Computer Vision,2016:483-499.[2]LIN M,CHEN Q,YAN work in nctwork[EB/OL].[2020-05-07].https:///abs/132.4400.(责任编辑郑小虎)。
IEEE参考文献格式

•Creating a reference list or bibliographyA numbered list of references must be provided at the end of thepaper. The list should be arranged in the order of citation in the text of the assignment or essay, not in alphabetical order. List only one reference per reference number. Footnotes or otherinformation that are not part of the referencing format should not be included in the reference list.The following examples demonstrate the format for a variety of types of references. Included are some examples of citing electronic documents. Such items come in many forms, so only some examples have been listed here.Print DocumentsBooksNote: Every (important) word in the title of a book or conference must be capitalised. Only the first word of a subtitle should be capitalised. Capitalise the "v" in Volume for a book title.Punctuation goes inside the quotation marks.Standard formatSingle author[1] W.-K. Chen, Linear Networks and Systems. Belmont, CA: Wadsworth,1993, pp. 123-135.[2] S. M. Hemmington, Soft Science. Saskatoon: University ofSaskatchewan Press, 1997.Edited work[3] D. Sarunyagate, Ed., Lasers. New York: McGraw-Hill, 1996.Later edition[4] K. Schwalbe, Information Technology Project Management, 3rd ed.Boston: Course Technology, 2004.[5] M. N. DeMers, Fundamentals of Geographic Information Systems,3rd ed. New York : John Wiley, 2005.More than one author[6] T. Jordan and P. A. Taylor, Hacktivism and Cyberwars: Rebelswith a cause? London: Routledge, 2004.[7] U. J. Gelinas, Jr., S. G. Sutton, and J. Fedorowicz, Businessprocesses and information technology. Cincinnati:South-Western/Thomson Learning, 2004.Three or more authorsNote: The names of all authors should be given in the references unless the number of authors is greater than six. If there are more than six authors, you may use et al. after the name of the first author.[8] R. Hayes, G. Pisano, D. Upton, and S. Wheelwright, Operations,Strategy, and Technology: Pursuing the competitive edge.Hoboken, NJ : Wiley, 2005.Series[9] M. Bell, et al., Universities Online: A survey of onlineeducation and services in Australia, Occasional Paper Series 02-A. Canberra: Department of Education, Science andTraining, 2002.Corporate author (ie: a company or organisation)[10] World Bank, Information and Communication Technologies: AWorld Bank group strategy. Washington, DC : World Bank, 2002.Conference (complete conference proceedings)[11] T. J. van Weert and R. K. Munro, Eds., Informatics and theDigital Society: Social, ethical and cognitive issues: IFIP TC3/WG3.1&3.2 Open Conference on Social, Ethical andCognitive Issues of Informatics and ICT, July 22-26, 2002, Dortmund, Germany. Boston: Kluwer Academic, 2003.Government publication[12] Australia. Attorney-Generals Department. Digital AgendaReview, 4 Vols. Canberra: Attorney- General's Department,2003.Manual[13] Bell Telephone Laboratories Technical Staff, TransmissionSystem for Communications, Bell Telephone Laboratories,1995.Catalogue[14] Catalog No. MWM-1, Microwave Components, M. W. Microwave Corp.,Brooklyn, NY.Application notes[15] Hewlett-Packard, Appl. Note 935, pp. 25-29.Note:Titles of unpublished works are not italicised or capitalised. Capitalise only the first word of a paper or thesis.Technical report[16] K. E. Elliott and C.M. Greene, "A local adaptive protocol,"Argonne National Laboratory, Argonne, France, Tech. Rep.916-1010-BB, 1997.Patent / Standard[17] K. Kimura and A. Lipeles, "Fuzzy controller component, " U.S. Patent 14,860,040, December 14, 1996.Papers presented at conferences (unpublished)[18] H. A. Nimr, "Defuzzification of the outputs of fuzzycontrollers," presented at 5th International Conference onFuzzy Systems, Cairo, Egypt, 1996.Thesis or dissertation[19] H. Zhang, "Delay-insensitive networks," M.S. thesis,University of Waterloo, Waterloo, ON, Canada, 1997.[20] M. W. Dixon, "Application of neural networks to solve therouting problem in communication networks," Ph.D.dissertation, Murdoch University, Murdoch, WA, Australia, 1999.Parts of a BookNote: These examples are for chapters or parts of edited works in which the chapters or parts have individual title and author/s, but are included in collections or textbooks edited by others. If the editors of a work are also the authors of all of the included chapters then it should be cited as a whole book using the examples given above (Books).Capitalise only the first word of a paper or book chapter.Single chapter from an edited work[1] A. Rezi and M. Allam, "Techniques in array processing by meansof transformations, " in Control and Dynamic Systems, Vol.69, Multidemsional Systems, C. T. Leondes, Ed. San Diego: Academic Press, 1995, pp. 133-180.[2] G. O. Young, "Synthetic structure of industrial plastics," inPlastics, 2nd ed., vol. 3, J. Peters, Ed. New York:McGraw-Hill, 1964, pp. 15-64.Conference or seminar paper (one paper from a published conference proceedings)[3] N. Osifchin and G. Vau, "Power considerations for themodernization of telecommunications in Central and Eastern European and former Soviet Union (CEE/FSU) countries," in Second International Telecommunications Energy SpecialConference, 1997, pp. 9-16.[4] S. Al Kuran, "The prospects for GaAs MESFET technology in dc-acvoltage conversion," in Proceedings of the Fourth AnnualPortable Design Conference, 1997, pp. 137-142.Article in an encyclopaedia, signed[5] O. B. R. Strimpel, "Computer graphics," in McGraw-HillEncyclopedia of Science and Technology, 8th ed., Vol. 4. New York: McGraw-Hill, 1997, pp. 279-283.Study Guides and Unit ReadersNote: You should not cite from Unit Readers, Study Guides, or lecture notes, but where possible you should go to the original source of the information. If you do need to cite articles from the Unit Reader, treat the Reader articles as if they were book or journal articles. In the reference list or bibliography use the bibliographical details as quoted in the Reader and refer to the page numbers from the Reader, not the original page numbers (unless you have independently consulted the original).[6] L. Vertelney, M. Arent, and H. Lieberman, "Two disciplines insearch of an interface: Reflections on a design problem," in The Art of Human-Computer Interface Design, B. Laurel, Ed.Reading, MA: Addison-Wesley, 1990. Reprinted inHuman-Computer Interaction (ICT 235) Readings and Lecture Notes, Vol. 1. Murdoch: Murdoch University, 2005, pp. 32-37. Journal ArticlesNote: Capitalise only the first word of an article title, except for proper nouns or acronyms. Every (important) word in the title of a journal must be capitalised. Do not capitalise the "v" in volume for a journal article.You must either spell out the entire name of each journal that you reference or use accepted abbreviations. You must consistently do one or the other. Staff at the Reference Desk can suggest sources of accepted journal abbreviations.You may spell out words such as volume or December, but you must either spell out all such occurrences or abbreviate all. You do not need to abbreviate March, April, May, June or July.To indicate a page range use pp. 111-222. If you refer to only one page, use only p. 111.Standard formatJournal articles[1] E. P. Wigner, "Theory of traveling wave optical laser," Phys.Rev., vol. 134, pp. A635-A646, Dec. 1965.[2] J. U. Duncombe, "Infrared navigation - Part I: An assessmentof feasability," IEEE Trans. Electron. Devices, vol. ED-11, pp. 34-39, Jan. 1959.[3] G. Liu, K. Y. Lee, and H. F. Jordan, "TDM and TWDM de Bruijnnetworks and shufflenets for optical communications," IEEE Trans. Comp., vol. 46, pp. 695-701, June 1997.OR[4] J. R. Beveridge and E. M. Riseman, "How easy is matching 2D linemodels using local search?" IEEE Transactions on PatternAnalysis and Machine Intelligence, vol. 19, pp. 564-579, June 1997.[5] I. S. Qamber, "Flow graph development method," MicroelectronicsReliability, vol. 33, no. 9, pp. 1387-1395, Dec. 1993.[6] E. H. Miller, "A note on reflector arrays," IEEE Transactionson Antennas and Propagation, to be published.Electronic documentsNote:When you cite an electronic source try to describe it in the same way you would describe a similar printed publication. If possible, give sufficient information for your readers to retrieve the source themselves.If only the first page number is given, a plus sign indicates following pages, eg. 26+. If page numbers are not given, use paragraph or other section numbers if you need to be specific. An electronic source may not always contain clear author or publisher details.The access information will usually be just the URL of the source. As well as a publication/revision date (if there is one), the date of access is included since an electronic source may change between the time you cite it and the time it is accessed by a reader.E-BooksStandard format[1] L. Bass, P. Clements, and R. Kazman. Software Architecture inPractice, 2nd ed. Reading, MA: Addison Wesley, 2003. [E-book] Available: Safari e-book.[2] T. Eckes, The Developmental Social Psychology of Gender. MahwahNJ: Lawrence Erlbaum, 2000. [E-book] Available: netLibrary e-book.Article in online encyclopaedia[3] D. Ince, "Acoustic coupler," in A Dictionary of the Internet.Oxford: Oxford University Press, 2001. [Online]. Available: Oxford Reference Online, .[Accessed: May 24, 2005].[4] W. D. Nance, "Management information system," in The BlackwellEncyclopedic Dictionary of Management Information Systems,G.B. Davis, Ed. Malden MA: Blackwell, 1999, pp. 138-144.[E-book]. Available: NetLibrary e-book.E-JournalsStandard formatJournal article abstract accessed from online database[1] M. T. Kimour and D. Meslati, "Deriving objects from use casesin real-time embedded systems," Information and SoftwareTechnology, vol. 47, no. 8, p. 533, June 2005. [Abstract].Available: ProQuest, /proquest/.[Accessed May 12, 2005].Note: Abstract citations are only included in a reference list if the abstract is substantial or if the full-text of the article could not be accessed.Journal article from online full-text databaseNote: When including the internet address of articles retrieved from searches in full-text databases, please use the Recommended URLs for Full-text Databases, which are the URLs for the main entrance to the service and are easier to reproduce.[2] H. K. Edwards and V. Sridhar, "Analysis of software requirementsengineering exercises in a global virtual team setup,"Journal of Global Information Management, vol. 13, no. 2, p.21+, April-June 2005. [Online]. Available: Academic OneFile, . [Accessed May 31, 2005].[3] A. Holub, "Is software engineering an oxymoron?" SoftwareDevelopment Times, p. 28+, March 2005. [Online]. Available: ProQuest, . [Accessed May 23, 2005].Journal article in a scholarly journal (published free of charge on the internet)[4] A. Altun, "Understanding hypertext in the context of readingon the web: Language learners' experience," Current Issues in Education, vol. 6, no. 12, July 2003. [Online]. Available: /volume6/number12/. [Accessed Dec. 2, 2004].Journal article in electronic journal subscription[5] P. H. C. Eilers and J. J. Goeman, "Enhancing scatterplots withsmoothed densities," Bioinformatics, vol. 20, no. 5, pp.623-628, March 2004. [Online]. Available:. [Accessed Sept. 18, 2004].Newspaper article from online database[6] J. Riley, "Call for new look at skilled migrants," TheAustralian, p. 35, May 31, 2005. Available: Factiva,. [Accessed May 31, 2005].Newspaper article from the Internet[7] C. Wilson-Clark, "Computers ranked as key literacy," The WestAustralian, para. 3, March 29, 2004. [Online]. Available:.au. [Accessed Sept. 18, 2004].Internet DocumentsStandard formatProfessional Internet site[1] European Telecommunications Standards Institute, 揇igitalVideo Broadcasting (DVB): Implementation guidelines for DVBterrestrial services; transmission aspects,?EuropeanTelecommunications Standards Institute, ETSI TR-101-190,1997. [Online]. Available: . [Accessed:Aug. 17, 1998].Personal Internet site[2] G. Sussman, "Home page - Dr. Gerald Sussman," July 2002.[Online]. Available:/faculty/Sussman/sussmanpage.htm[Accessed: Sept. 12, 2004].General Internet site[3] J. Geralds, "Sega Ends Production of Dreamcast," ,para. 2, Jan. 31, 2001. [Online]. Available:/news/1116995. [Accessed: Sept. 12,2004].Internet document, no author given[4] 揂憀ayman抯?explanation of Ultra Narrow Band technology,?Oct.3, 2003. [Online]. Available:/Layman.pdf. [Accessed: Dec. 3, 2003].Non-Book FormatsPodcasts[1] W. Brown and K. Brodie, Presenters, and P. George, Producer, 揊rom Lake Baikal to the Halfway Mark, Yekaterinburg? Peking to Paris: Episode 3, Jun. 4, 2007. [Podcast television programme]. Sydney: ABC Television. Available:.au/tv/pekingtoparis/podcast/pekingtoparis.xm l. [Accessed Feb. 4, 2008].[2] S. Gary, Presenter, 揃lack Hole Death Ray? StarStuff, Dec. 23, 2007. [Podcast radio programme]. Sydney: ABC News Radio. Available: .au/newsradio/podcast/STARSTUFF.xml. [Accessed Feb. 4, 2008].Other FormatsMicroform[3] W. D. Scott & Co, Information Technology in Australia:Capacities and opportunities: A report to the Department ofScience and Technology. [Microform]. W. D. Scott & CompanyPty. Ltd. in association with Arthur D. Little Inc. Canberra:Department of Science and Technology, 1984.Computer game[4] The Hobbit: The prelude to the Lord of the Rings. [CD-ROM].United Kingdom: Vivendi Universal Games, 2003.Software[5] Thomson ISI, EndNote 7. [CD-ROM]. Berkeley, Ca.: ISIResearchSoft, 2003.Video recording[6] C. Rogers, Writer and Director, Grrls in IT. [Videorecording].Bendigo, Vic. : Video Education Australasia, 1999.A reference list: what should it look like?The reference list should appear at the end of your paper. Begin the list on a new page. The title References should be either left justified or centered on the page. The entries should appear as one numerical sequence in the order that the material is cited in the text of your assignment.Note: The hanging indent for each reference makes the numerical sequence more obvious.[1] A. Rezi and M. Allam, "Techniques in array processing by meansof transformations, " in Control and Dynamic Systems, Vol.69, Multidemsional Systems, C. T. Leondes, Ed. San Diego: Academic Press, 1995, pp. 133-180.[2] G. O. Young, "Synthetic structure of industrial plastics," inPlastics, 2nd ed., vol. 3, J. Peters, Ed. New York:McGraw-Hill, 1964, pp. 15-64.[3] S. M. Hemmington, Soft Science. Saskatoon: University ofSaskatchewan Press, 1997.[4] N. Osifchin and G. Vau, "Power considerations for themodernization of telecommunications in Central and Eastern European and former Soviet Union (CEE/FSU) countries," in Second International Telecommunications Energy SpecialConference, 1997, pp. 9-16.[5] D. Sarunyagate, Ed., Lasers. New York: McGraw-Hill, 1996.[8] O. B. R. Strimpel, "Computer graphics," in McGraw-HillEncyclopedia of Science and Technology, 8th ed., Vol. 4. New York: McGraw-Hill, 1997, pp. 279-283.[9] K. Schwalbe, Information Technology Project Management, 3rd ed.Boston: Course Technology, 2004.[10] M. N. DeMers, Fundamentals of Geographic Information Systems,3rd ed. New York: John Wiley, 2005.[11] L. Vertelney, M. Arent, and H. Lieberman, "Two disciplines insearch of an interface: Reflections on a design problem," in The Art of Human-Computer Interface Design, B. Laurel, Ed.Reading, MA: Addison-Wesley, 1990. Reprinted inHuman-Computer Interaction (ICT 235) Readings and Lecture Notes, Vol. 1. Murdoch: Murdoch University, 2005, pp. 32-37.[12] E. P. Wigner, "Theory of traveling wave optical laser,"Physical Review, vol.134, pp. A635-A646, Dec. 1965.[13] J. U. Duncombe, "Infrared navigation - Part I: An assessmentof feasibility," IEEE Transactions on Electron Devices, vol.ED-11, pp. 34-39, Jan. 1959.[14] M. Bell, et al., Universities Online: A survey of onlineeducation and services in Australia, Occasional Paper Series 02-A. Canberra: Department of Education, Science andTraining, 2002.[15] T. J. van Weert and R. K. Munro, Eds., Informatics and theDigital Society: Social, ethical and cognitive issues: IFIP TC3/WG3.1&3.2 Open Conference on Social, Ethical andCognitive Issues of Informatics and ICT, July 22-26, 2002, Dortmund, Germany. Boston: Kluwer Academic, 2003.[16] I. S. Qamber, "Flow graph development method,"Microelectronics Reliability, vol. 33, no. 9, pp. 1387-1395, Dec. 1993.[17] Australia. Attorney-Generals Department. Digital AgendaReview, 4 Vols. Canberra: Attorney- General's Department, 2003.[18] C. Rogers, Writer and Director, Grrls in IT. [Videorecording].Bendigo, Vic.: Video Education Australasia, 1999.[19] L. Bass, P. Clements, and R. Kazman. Software Architecture inPractice, 2nd ed. Reading, MA: Addison Wesley, 2003. [E-book] Available: Safari e-book.[20] D. Ince, "Acoustic coupler," in A Dictionary of the Internet.Oxford: Oxford University Press, 2001. [Online]. Available: Oxford Reference Online, .[Accessed: May 24, 2005].[21] H. K. Edwards and V. Sridhar, "Analysis of softwarerequirements engineering exercises in a global virtual team setup," Journal of Global Information Management, vol. 13, no. 2, p. 21+, April-June 2005. [Online]. Available: AcademicOneFile, . [Accessed May 31,2005].[22] A. Holub, "Is software engineering an oxymoron?" SoftwareDevelopment Times, p. 28+, March 2005. [Online]. Available: ProQuest, . [Accessed May 23, 2005].[23] H. Zhang, "Delay-insensitive networks," M.S. thesis,University of Waterloo, Waterloo, ON, Canada, 1997.[24] P. H. C. Eilers and J. J. Goeman, "Enhancing scatterplots withsmoothed densities," Bioinformatics, vol. 20, no. 5, pp.623-628, March 2004. [Online]. Available:. [Accessed Sept. 18, 2004].[25] J. Riley, "Call for new look at skilled migrants," TheAustralian, p. 35, May 31, 2005. Available: Factiva,. [Accessed May 31, 2005].[26] European Telecommunications Standards Institute, 揇igitalVideo Broadcasting (DVB): Implementation guidelines for DVB terrestrial services; transmission aspects,?EuropeanTelecommunications Standards Institute, ETSI TR-101-190,1997. [Online]. Available: . [Accessed: Aug. 17, 1998].[27] J. Geralds, "Sega Ends Production of Dreamcast," ,para. 2, Jan. 31, 2001. [Online]. Available:/news/1116995. [Accessed Sept. 12,2004].[28] W. D. Scott & Co, Information Technology in Australia:Capacities and opportunities: A report to the Department of Science and Technology. [Microform]. W. D. Scott & Company Pty. Ltd. in association with Arthur D. Little Inc. Canberra: Department of Science and Technology, 1984.AbbreviationsStandard abbreviations may be used in your citations. A list of appropriate abbreviations can be found below:。
增强Kernel学习优化最大边缘投影的人脸识别

增强Kernel学习优化最大边缘投影的人脸识别郑翔;鲜敏;马勇【期刊名称】《计算机应用与软件》【年(卷),期】2015(000)009【摘要】针对传统的流形学习算法通常只考虑样本类内几何结构而忽略类间判别信息的问题,提出一种基于增强核学习的最大边缘投影(MMP)算法。
首先使用基于增强核学习非线性扩展的MMP采集人脸图像的非线性结构;然后利用核变换技术加强原始输入核函数的判别能力,并且借助于特征向量选择算法改善算法的计算效率;最后,利用基于乘性规则训练的支持向量机完成人脸的识别。
在Yale、ORL、PIE三大通用人脸数据库的组合数据集及AR上的实验验证了该算法的有效性。
实验结果表明,相比其他几种核学习算法,该算法取得了更好的识别效果。
%For the problem that traditional manifold learning methods usually consider intra-class geometry structure only but ignore the discriminative information of inter-classes,we propose an enhanced kernel learning-based maximum margin projection (MMP)algorithm. Firstly,we use MMP nonlinearly extended by enhanced kernel learning to collect the nonlinear structure of face image.Then,we use kernel transformation technology to enhance the discriminant ability of original inputted kernel function,and improve the computation efficiency of the proposed algorithm by feature vector selection algorithm.Finally,we use support vector machine trainedby multiplicative rules to finish the face recognition.The effectiveness ofthe proposed algorithm is verified by the experiments on AR and thecombination datasets of three com-mon face databases Yale,ORL and PIE.Experimental results show that the proposed algorithm has better recognition efficiency comparing with several other advanced approaches based on kernel learning.【总页数】5页(P314-318)【作者】郑翔;鲜敏;马勇【作者单位】四川工程职业技术学院计算机科学技术系四川德阳618000;四川工程职业技术学院计算机科学技术系四川德阳618000;四川工程职业技术学院计算机科学技术系四川德阳618000【正文语种】中文【中图分类】TP391【相关文献】1.基于优化投影矩阵的人脸识别技术研究 [J], 于爱华;白煌;孙斌斌;侯北平2.最大边缘准则图形嵌入在人脸识别中的应用 [J], 宋宇翔;胡伟3.基于加权最大类间边缘准则的人脸识别 [J], 秦春霞;任文杰;贺长伟;王欣4.最小化总投影误差优化一元回归分类的人脸识别 [J], 潘锋5.用于人脸识别的半监督优化局部保持投影 [J], 杨晓梅因版权原因,仅展示原文概要,查看原文内容请购买。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(1)
In the remaining of the paper the reproducing kernel Hilbert space, its dot product and its kernel k will be assumed to be given. In this case the so called feature space is given by the kernel and the dot product considered is the one of the r.k.h.s..
St´ ephane Canu1 and Alex J. Smola2 1- PSI - FRE CNRS 2645 INSA de Rouen, France St Etienne du Rouvray, France Stephane.Canu@insa-rouen.fr 2- Statistical Machine Learning Program National ICT Australia and ANU Alex.Smola@.au Abstract. The success of Support Vector Machine (SVM) gave rise to the development of a new class of theoretically elegant learning machines which use a central concept of kernels and the associated reproducing kernel Hilbert space (r.k.h.s.). Exponential families, a standard tool in statistics, can be used to unify many existing machine learning algorithms based on kernels (such as SVM) and to invent novel ones quite effortlessly. In this paper we will discuss how exponential families, a standard tool in statistics, can be used with great success in machine learning to unify many existing algorithms and to invent novel ones quite effortlessly. A new derivation of the novelty detection algorithm based on the one class SVM is proposed to illustrates the power of the exponential family model in a r.k.h.s.
∗ National ICT Australia is funded through the Australian Government’s Backing Australia’s Ability initiative, in part through the Australian Research Council. This work was supported by grants of the ARC and by the IST Programme of the European Community, under the Pascal Network of Excellence, IST-2002-506778.
n n
α i α j K (x i , y j ) ≥ 0
i=1 j =1
This definition is equivalent to Aronszajn definition of positive kernel. Proposition 1 (bijection between r.k.h.s. and Kernel) Corollary of proposition 23 in [3] and theorem 1.1.1 in [4]. There is a bijection between the set of all possible r.k.h.s. and the set of all positive kernels. Thus Mercer kernels are a particular case of a more general situation since every Mercer kernel is positive in the Aronszajn sense (definition 2) while the converse is false. One a the key property to be used here after is the reproducing ability in the r.k.h.s.. It is closely related with the fact than in r.k.h.s. functions are pointwise defined and the evaluation functional is continuous. Thus, because of this continuity Riesz theorem can be stated as follows ∀f ∈ H∀, x ∈ X, f (x) = f (.), k (x, .)
447
ESANN'2005 proceedings - European Symposium on Artificial Neural Networks Bruges (Belgium), 27-29 April 2005, d-side publi., ISBN 2-930307-05-6.
estimation and regression kernels based algorithms such as SVM are derived. In a final section new material is presented establishing the link between the kernel based one class SVM novelty detection algorithm and classical test theory. It is shown how this novelty detection can be seen a an approximation of a generalized likelihood ratio thus optimal test.
∗
1
Introduction
Machine learning is proving increasingly important tools in many fields such as text processing, machine vision, speech to name just a few. Among these new tools, kernel based algorithms have demonstrated their efficiency on many practical problems. These algorithms performed function estimation, and the functional framework behind these algorithm is now well known [1]. But still too little is known about the relation between these learning algorithms and more classical statistical tools such as likelihood, likelihood ratio, estimation and test theory. A key model to understand this relation is the generalized or non parametric exponential family. This exponential family is a generic way to represent any probability distribution since any distribution can be well approximated by an exponential distribution. The idea here is to retrieve learning algorithm by using the exponential family model with classical statistical principle such as the maximum penalized likelihood estimator or the generalized likelihood ratio test. To do so the paper (following [2]) is organized as follows. First section presents the functional frameworks and reproducing kernel Hilbert space. Then the exponential family on a r.k.h.s. is introduced and classification as well as deframework
Definition 1 (reproducing kernel Hilbert space (r.k.h.s.)) A Hilbert space (H, ., . H ) is a r.k.h.s. if it is defined on I RX (pointwise defined functions) and if the evaluation functional is continuous on H. For instance I Rn , the set Pk of polynomials of order k , as any finite dimensional set of genuine functions are r.k.h.s.. The set of sequences 2 is also a r.k.h.s.. Usual L2 (with Lebesgue measure) is not because it is not a set of pointwise functions. Definition 2 (positive kernel) A function from X × X to I R is a positive kernel if it is symmetric and if for any finite subset {xi }, i = 1, n of X and any sequence of scalar {αi }, i = 1, n
