河南省鹤壁市数学高三上学期理数一模试卷

合集下载

2020-2021学年河南省高三第一次模拟考试数学(理)试题及答案解析

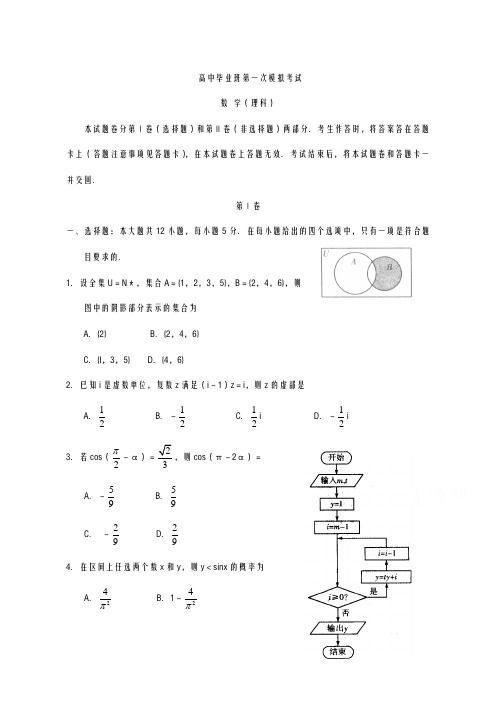
高中毕业班第一次模拟考试数学（理科）本试题卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分．考生作答时，将答案答在答题卡上（答题注意事项见答题卡），在本试题卷上答题无效．考试结束后，将本试题卷和答题卡一并交回．第Ⅰ卷一、选择题：本大题共12小题，每小题5分．在每小题给出的四个选项中，只有一项是符合题目要求的．1．设全集U ＝N ﹡，集合A ＝{1，2，3，5}，B ＝{2，4，6}，则图中的阴影部分表示的集合为A ．{2}B ．{2，4，6}C ．{l ，3，5}D ．{4，6}2．已知i 是虚数单位，复数z 满足（i －1）z ＝i ，则z 的虚部是A ．12B ．－12C ．12iD ．－12i 3．若cos （2π2，则cos （π－2α）＝ A ．－59 B ．59C ．－29 D ．29 4．在区间上任选两个数x 和y ，则y ＜sinx 的概率为A ．24π B ．1－24πC ．22πD ．1－22π5．将函数y ＝cos （2x ＋6π）图象上的点P （4π，t ）向右平移m （m ＞0）个单位长度得到点P '，若P '位于函数y ＝cos2x 的图象上，则A ．t ＝－12，m 的最小值为12πB ．t ＝32－，m 的最小值为12π C ．t ＝－12，m 的最小值为6π D ．t ＝32－，m 的最小值为6π 6．执行如图所示的程序框图，若输入m ＝4，t ＝3，则输出y ＝A ．61B ．62C ．183D ．1847．在31()n x x －的展开式中，所有项的二项式系数之和为4096，则其常数项为A ．－1 10B ．110C ．220D ．－2208．已知M 是抛物线C ：2y ＝2px （p ＞0）上一点，F 是抛物线C 的焦点．若｜MF ｜＝p ，K 是抛物线C 的准线与x 轴的交点，则∠MKF ＝A ．15°B ．30°C ．45°D ．60°9．函数f （x ）＝｜x ｜＋2a x （其中a ∈R ）的图象不可能是10．已知P 为矩形ABCD 所在平面内一点，AB ＝4，AD ＝3，PA 5PC ＝5PB uu r ·PD uu u r ＝A．－5 B．－5或0 C．5 D．0 11．某几何体的三视图如图所示，则该几何体的体积为A．16B．13C．1 D．212．已知函数f（x）＝（22x－x－1）x e，则方程e2＋tf（x）－9e＝0（t∈R）的根的个数为A．2 B．3C．4 D．5第Ⅱ卷本卷包括必考题和选考题两部分．第13～21题为必考题．每个试题考生都必须作答．第22～23题为选考题，考生根据要求作答．二、填空题：本大题共4小题，每小题5分．13．双曲线22221x ya b－＝（a＞0，b＞0）的一条渐近线与直线x－y＋3＝0平行，则此双曲线的离心率为______________．14．若实数x，y满足100,2,x yxy⎧⎪⎨⎪⎩－＋≤＞≤则221yx＋的取值范围是_______________15．《孙子算经》是我国古代内容极其丰富的数学名著，书中有如下问题：“今有圆窖，周五丈四尺，深一丈八尺．问受粟几何?”其意思为：“有圆柱形容器，底面圆周长五丈四尺，高一丈八尺，求此容器能装多少斛米．”则该圆柱形容器能装米_________斛．（古制1丈＝10尺，1斛＝1．62立方尺，圆周率π≈3）16．在△ABC 中，内角A ，B ，C 的对边分别为a ，b ，c ，且a ＞b ，a ＞c ．△ABC 的外接圆半径为1，a ＝3．若边BC 上一点D 满足BD ＝2DC ，且∠BAD ＝90°，则△ABC 的面积为______________.三、解答题：解答应写出文字说明，证明过程或演算步骤．17．（本小题满分12分）已知数列{n a }的前n 项和为n S ，且满足n a ＝2n S ＋1（n ∈N ﹡）．（Ⅰ）求数列{n a }的通项公式；（Ⅱ）若n b ＝（2n －1）·n a ，求数列{n b }的前n 项和n T ．18．（本小题满分12分）某市为了制定合理的节电方案，供电局对居民用电情况进行了调查，通过抽样，获得了某年200户居民每户的月均用电量（单位：度），将数据按照分成9组，制成了如图所示的频率分布直方图．（Ⅰ）求直方图中m 的值并估计居民月均用电量的中位数；（Ⅱ）从样本里月均用电量不低于700度的用户中随机抽取4户，用X 表示月均用电量不低于800度的用户数，求随机变量X 的分布列及数学期望．19．（本小题满分12分）如图，在三棱柱ABC －A 1B 1C 1中，CA ＝CB ，侧面ABB 1A 1是边长为2的正方形，点E ，F 分别在线段AA 1，A 1B 1上，且AE ＝12， A 1F ＝34，CE ⊥EF （Ⅰ）证明：平面ABB 1A 1⊥平面ABC ；（Ⅱ）若CA ⊥CB ，求直线AC 1与平面CEF 所成角的正弦值．20．（本小题满分12分）已知圆O ： 221x y ＋＝过椭圆C ：22221y x a b ＋＝(a ＞b ＞0)的短轴端点，P ，Q 分别是圆O 与椭圆C 上任意两点，且线段PQ 长度的最大值为3．（Ⅰ）求椭圆C 的方程；（Ⅱ）过点(0，t)作圆O 的一条切线交椭圆C 于M ，N 两点，求△OMN 的面积的最大值．21．（本小题满分12分）已知函数f （x ）＝2x ＋2ax ＋bcosx 在点（2π、f （2π））处的切线方程为y ＝34π．（Ⅰ）求a ，b 的值，并讨论f （x ）在上的增减性；（Ⅱ）若f （x 1）＝f （x 2），且0＜x 1＜x 2＜π，求证：12()2x x f '＋＜0．（参考公式cos θ－cos ϕ＝－2sin 2θϕ＋sin 2θϕ－）请考生在第22，23题中任选一题作答，如果多做，则按所做的第一题计分．作答时请写清题号．22．（本小题满分10分）选修4—4：坐标系与参数方程在平面直角坐标系xOy 中，直线l 的参数方程为12x t y ⎧⎪⎪⎨⎪⎪⎩＝＝1（t 为参数）．以坐标原点为极点，x 轴正半轴为极轴建立极坐标系，圆C 的极坐标方程为ρ＝2sin θ．（Ⅰ）判断直线l 与圆C 的交点个数；（Ⅱ）若圆C 与直线l 交于A ，B 两点，求线段AB 的长度．23．（本小题满分10分）选修4—5：不等式选讲已知函数f （x ）＝｜x ＋2｜－｜x －2｜＋m （m ∈R ）．（Ⅰ）若m ＝1，求不等式f （x ）≥0的解集；（Ⅱ）若方程f （x ）＝x 有三个实根，求实数m 的取值范围．。

2020-2021鹤壁市高中高三数学上期末第一次模拟试题(附答案)

2020-2021鹤壁市高中高三数学上期末第一次模拟试题(附答案)一、选择题1．已知数列{}n a 的前n 项和2n S n =，()1nn n b a =-则数列{}n b 的前n 项和n T 满足（） A ．()1nn T n =-⨯ B ．n T n = C ．n T n =-D ．,2,.n n n T n n ⎧=⎨-⎩为偶数，为奇数2．在ABC ∆中,,,a b c 分别为角,,A B C 所对的边,若 2?a bcos C =,则此三角形一定是( ) A ．等腰直角三角形 B ．直角三角形C ．等腰三角形D ．等腰三角形或直角三角形3．“干支纪年法”是中国历法上自古以来就一直使用的纪年方法，干支是天干和地支的总称，把干支顺序相配正好六十为一周，周而复始，循环记录，这就是俗称的“干支表”甲、乙、丙、丁、戊、己、庚、辛、癸等十个符号叫天干，子、丑、寅、卯、辰、巳、午、未、申、酉、戌、亥等十二个符号叫地支，如公元1984年农历为甲子年，公元1985年农历为乙丑年，公元1986年农历为丙寅年，则公元2047年农历为 A ．乙丑年B ．丙寅年C ．丁卯年D ．戊辰年4．已知实数x 、y 满足约束条件00134x y x ya a⎧⎪≥⎪≥⎨⎪⎪+≤⎩，若目标函数231x y z x ++=+的最小值为32，则正实数a 的值为（） A ．4B ．3C ．2D ．15．若ABC ∆的三个内角满足sin :sin :sin 5:11:13A B C =，则ABC ∆（）A ．一定是锐角三角形B ．一定是直角三角形C ．一定是钝角三角形D ．可能是锐角三角形，也可能是钝角三角形6．已知数列{}n a的首项110,1n n a a a +==+，则20a =（） A ．99B ．101C ．399D ．4017．在ABC ∆中，,,a b c 是角,,A B C 的对边，2a b =，3cos 5A =，则sinB =（） A ．25B ．35C ．45 D ．858．设x y ，满足约束条件70310,350x y x y x y +-⎧⎪-+⎨⎪--⎩，，………则2z x y =-的最大值为（）.A ．10B ．8C ．3D ．29．在△ABC 中，若1tan 15013A C BC ︒===，，，则△ABC 的面积S 是( ) A ．33- B ．33- C ．338+ D ．33+ 10．已知ABC ∆的三个内角、、A B C 所对的边为a b c 、、，面积为S ，且223tan 2S B =+，则A 等于（）A ．6π B ．4π C ．3π D ．2π 11．已知x 、y 满足约束条件50{03x y x y x -+≥+≥≤，则24z x y =+的最小值是（）A ．6-B ．5C ．10D ．10-12．在中，，，，则A ．B ．C ．D ．二、填空题13．已知实数，且，则的最小值为____14．数列{}n a 满足：1a a =（a R ∈且为常数），()()()*13343n n n n n a a a n N a a +⎧->⎪=∈⎨-≤⎪⎩，当100a =时，则数列{}n a 的前100项的和100S 为________.15．计算：23lim 123n n nn→+∞-=++++L ________16．在ABC ∆中，内角A ，B ，C 所对应的边长分别为a ，b ，c ，且2cos 3C =，cos cos 2b A a B +=，则ABC ∆的外接圆面积为__________．17．若正数,a b 满足3ab a b =++，则+a b 的取值范围_______________。

河南省鹤壁市高级中学高三数学上学期第一次段考试题理

鹤壁高中高三年级第一次段考理数试卷一、选择题（每题5分，共60分） 1．已知21)4tan(=-πα，则ααααcos sin cos sin -+的值为（） A ．21B ．2C ．22D ．-2 2．某几何体的三视图如图所示，图中的四边形都是边长为2的正方形，两条虚线互相垂直，则该几何体的体积是（）A ．163B ．203C ．86π-D ．83π-3．已知54sin ,135)cos(,02,20=-=-<<-<<αβαβππα,则=βsin （）.A ．725B ．725-C ．5665D ．5665-4．已知函数()sin 2f x x =向左平移6π个单位后，得到函数()y g x =，下列关于()y g x =的说法正确的是（）A ．图象关于点⎪⎭⎫⎝⎛0,3-π中心对称 B ．图象关于6π-=x 轴对称C ．在区间⎥⎦⎤⎢⎣⎡--6,125ππ单调递增 D ．在⎥⎦⎤⎢⎣⎡-3,6ππ单调递减 5．已知等差数列{}n a 的前n 项和为n S ，若42013OB a OA a OC =+u u u v u u u v u u u v，且,,A B C 三点共线（O 为该直线外一点），2016S 等于（）A ．2016B ．1008C ．20162D ．100826．设1k >,在约束条件1y xy kx x y ≥⎧⎪≤⎨⎪+≤⎩下，目标函数z x ky =+的最大值小于2,则k 的取值范围为（）A ．()1,12+ B ．()12,++∞ C ．()1,3 D ．()3,+∞ 7．等比数列{}n a 中，182,4a a ==，函数128()()()()f x x x a x a x a =---L ，则'(0)f =（）A ．62B ．92C ．122D ．1528．设等比数列{}n a ，n S 是数列{}n a 的前n 项和，143=S ，且81+a ，23a ，63+a 依次成等差数列，则31a a •等于（）A.4B.9C.16D.259．如图所示，正弦曲线x y sin =，余弦曲线x y cos =与两直线0=x ，π=x 所围成的阴影部分的面积为（）A ．1B ．2C ．2D ．2210．已知数列{}n a 是等差数列，oa 225tan 1=，1513a a =，设n S 为数列{(1)}n n a -的前n 项和，则2015S =（）A ．2015B ．2015-C ．3024D ．3022- 11．在ABC ∆中，已知BC A tan 2tan 1tan 1=+，则B cos 的最小值为（） A ．32 B ．42C ．31D ．2112．若关于x 的不等式()()211xa ax ex a ->->-有且仅有两个整数解，则实数a 的取值范围为A ．235,43e ⎛⎤-⎥⎝⎦ B ．31,2e ⎛⎤-- ⎥⎝⎦ C ．235,23e e ⎛⎤-- ⎥⎝⎦ D ．235,43e ⎛⎤-- ⎥⎝⎦二、填空题（每题5分，共20分）13.不等式2313x x a a +--≤-对任意实数x 恒成立，则实数a 的取值范围是 .14.已知数列{}n a 的前n 项和为n S ，若=24n n S a -，n N *∈，则n a =.15.若函数123)(23++-=x x a x x f 在区间)3,21(上有极值点，则实数a 的取值范围为 .16．设[)π2,0,,∈∈c R b a ，若对任意实数x 都有()c bx a x +=⎪⎭⎫⎝⎛-sin 33sin 2π，定义在区间 []0,3π上的函数sin 2y x =的图象与cos y x =的图象的交点横坐标为d ,则满足条件的有序实数组(),,,a b c d 的组数为 .三、解答题（17题10分，其余每题12分，共70分）17．（10分）已知→a 、→b 、→c 是同一平面内的三个向量，其中a r=（1，－2）.（1）若|c r |25=，且//c a r r ，求c r的坐标；（2）若|→b |=1，且→a +→b 与→a -2→b 垂直，求a r 与b r的夹角θ的余弦值.18.（12分）已知△ABC 的内角A ，B ，C 的对边分别为c b a ,,，且有S c b a 4222=-+,S 表示 ΔABC 的面积，（1）求角C 的大小；（2）若2c =，求22a b -的取值范围．19.（12分）已知函数()()()sin 0,0,0,f x A x b A b ωϕωϕπ=++>><<为常数的一段图象如图所示．（1）求函数()f x 的解析式；（2）若函数()f x 在y 轴右侧的极小值点的横坐标组成数列{}n a ，设右侧的第一个极小值点的横坐标为首项1a ，试求数列11n n a a +⎧⎫⎨⎬⎩⎭的前n 项和n S ．20．（12分）设函数)(3)(2R a e axx x f x∈+=．（1）若()x f 在0=x 处取得极值，确定a 的值，并求出此时曲线()x f y =在点))1(,1(f 处的切线方程；（2）若()x f 在),3[+∞上为减函数，求a 的取值范围．21．（12分）已知数列{}n a 的首项14a =，前n 项和为n S ，且13240n n S S n +---=（*n N ∈）.（1）求数列{}n a 的通项公式；（2）设函数23121()nn n n f x a x a x a x a x --=++++L ，)('x f 是函数()f x 的导函数，令'(1)n b f =，求数列{}n b 的通项公式.22．（12分）已知函数2()2ln f x x x ax =--，21()ln 3,g x a x x ax a R x=-+++∈．（1）当0a =时，求()f x 的极值；（2）令()()()h x f x g x =+，求函数()h x 的单调减区间；（3）如果12,x x 是函数()f x 的两个零点，且1214x x x <<，()f x '是()f x 的导函数，证明：122()03x x f +'>．鹤壁高中高三年级第一次段考理数答案一、选择题（每题5分，共60分） 1--5 BBDCB 6--10 ACCDD 11--12 DC 二、填空题（每题5分，共20分）),4[]1,.(13+∞⋃--∞ 14.12n + 15.)310,2( 16.28 三、解答题（17题10分，其余每题12分，共70分）17、解（1）设(),c x y =r ，则由→→a c //和52=→c 可得2212020y x x y ⋅+⋅=⎧⎨+=⎩，解得{24-==x y 或者{24=-=x y)4,2(-=∴→c 或)4,2(-=→c --------------------------------（5分）（2）Θ→a +→b 与→a -2→b 垂直，∴()(2)0a b a b +⋅-=r r r r 即2220,a a b b -⋅-=r r r r ∴ 3a b ⋅=r r，∴35cos ||||a b a b θ⋅==⋅r r r r -------------------------------（10分）18、解（1）由S c b a 4222=-+得：22214sin 2sin 2a b c ab C ab C +-=⨯= 即222sin 2a b c C ab+-=,从而有：tanC 1=,又因为角C 为△ABC 的内角，所以∠C＝45°.---------------------------------（4分）（2）由正弦定理得：sin a A ＝sin b B ＝sin C c222＝2，--------（6分） )10()4sin(2cos sin )43sin(2sin 2sin 2sin 222分-----------------------=-=--=-=-∴ππA A A A A B A b a又因为304A π<<，所以244πππ<-<-A ,所以－1<2sin 4π⎛⎫A -⎪⎝⎭<2，故a －22b的取值范围是()1,2---------（12分） 19、解：（1）由图可知，()51523,22A b +-=-===，因为54126T πππ⎛⎫=-⨯=⎪⎝⎭，所以2ω=，由“五点法”作图，262ππϕ⨯+=，解得6πϕ=，所以函数()f x 的解析式为()3sin 226f x x π⎛⎫=++ ⎪⎝⎭．．．．．．．．．．．．．．．．．．．．．．6分（2）易知{}n a 为等差数列，设其公差为d ，则d T π==，又函数()f x 在y 轴的右侧的第一个极值点横坐标为1a ，则有13262a ππ+=，得123a π=，所以()21133n a n n πππ⎛⎫=+-=- ⎪⎝⎭，-------（8分） 221111111111113333n n a a n n n n ππ+⎛⎫⎪==-⎪⎛⎫⎛⎫ ⎪-+--+- ⎪⎪⎝⎭⎝⎭⎝⎭，-------（10分） )12()46(9)31113113131312131213111(122分-----+=-+--++---+---=n n n n S n ππΛ20、解: （1） xx x x eax a x e e ax x e a x x f +-+-=+-+=')6(3)()3()6()(222 ∵)(x f 在0=x 处取得极值∴0)0(='f ，即0=a .当0=a 时xx e x x e x x x f )2(363)(2'--=+-=，)(x f ∴在)0,(-∞单调递减，在（0，2）单调递增，在),2(+∞单调递减故)(x f 在0=x 处取得极小值 ……………（4分）又e f 3)1('=，ef 3)1(=，则)(x f y =在1=x 处的切线方程为03=-ey x .--------------(6分) （2）由（1）知xe ax a x x f +-+-=')6(3)(2，因为)(x f 在),3[+∞上为减函数，0)('≤x f 在),3[+∞恒成立，即0)6(32≥---a x a x 在),3[+∞恒成立，即063)1(2≥-+-x x x a 在),3[+∞恒成立.---------------------------------------------------（8分）1632-+-≥∴x x x a 在),3[+∞恒成立.令[),2,1+∞∈-=t x t ，则)1(3332tt t t a --=+-≥令)1(3)(t t t g --=，则)(t g 在),2[+∞单调递减，29)2()(max -==g t g ----------------（10分） 29-≥∴a ------------------------（12分）21.（1）由13240n n S S n +---=，*()n N ∈，得132240n n S S n ---+-=(2)n ≥ 两式相减得1320n n a a +--=，可得113(1)(2)n n a a n ++=+≥又由已知214a =，∴2113(1)a a +=+，即{1}n a +是一个首项为5，公比3q =的等比数列，∴1*531()n n a n N -=⨯-∈.-----------------------（5分）（2）∵'111()2n n n f x a a x na x --=+++L ， ∴'11(1)2n n f a a na -=+++L120(531)2(531)(531)n n n --=⨯-+⨯-++⨯-L1230(1)5[323333]2n n n n n n ---+=+⨯+⨯++⨯-L -----------------（7分）令1230323333n n n S n ---=+⨯+⨯++⨯L ，则1213323333n n n S n --=+⨯+⨯++⨯L∴作差得：13324n n S +-=--，------------（9分）∴1'5315(6)(1)42n n n f +⨯-+=-即15315(6)42n n n n b +⨯-+=-----------------（12分）22.（1）当0a =时，2()2ln f x x x =-，故(1)(1)()2(0)x x f x x x+-'=>当01x <<时，()0f x '>，()f x 单调递增；当1x >时，()0f x '<，()f x 单调递减；故当1x =时，()f x 取极大值(1)1f =-，-----------（3分）（2）2222(2)1(21)(1)()ax a x x ax h x x x +---+'==，若0=a ，2'12)(xx x h -=，210,0)('<<<x x h 则. 若0≠a ，令()0h x '=得1211,2x x a =-=，若0>a ，由()0h x '<得102x <<，∴()h x 的单调减区间为1(0,)2；若0a <，①当2a <-时，112a -<，由()0h x '<得10x a <<-，或12x >，所以()h x 的单调减区间为11(0,),(,)2a -+∞；②当2a =-时，总有22(21)()0x h x x -'=-≤，故()h x 的单调减区间为(0,)+∞； ③当20a -<<时，112a ->，由()0h x '<得102x <<，或1x a>-，所以()h x 的单调减区间为11(0,),(,)2a-+∞；综上所述，当2a <-，()h x 的单调减区间为11(0,),(,)2a -+∞；当2a =-时，()h x 的单调减区间为(0,)+∞；当20a -<<时，()h x 的单调减区间为11(0,),(,)2a-+∞；当0a ≥时，()h x 的单调减区间为1(0,)2---------------（7分）（3）由题意知，2211112222()2ln 0,()2ln 0f x x x ax f x x x ax =--==--=两式相减，整理得所以2121212ln()x x a x x x x =-+-又因为a x xx f --=22)('， ),(31233ln 2)2(3226)32(2112121212212121'x x x x x x x x x x a x x x x x x f --⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡+----=-+-+=+∴ 令2133(1,4),()ln ,2x t t t t x t ϕ-=∈=-+则2(1)(4)()0(2)t t t t t ϕ--'=<+，所以()t ϕ在(1,4)上单调递减，故()(1)0t ϕϕ<=，又1221210,()03x x x x -<-->-，所以122()03x xf +'>．-------------（12分）。

河南省鹤壁市数学高三理数第一次模拟考试试卷

河南省鹤壁市数学高三理数第一次模拟考试试卷姓名:________班级:________成绩:________一、单选题 (共 12 题；共 24 分)1. （2 分） (2015 高二上·广州期末) 已知集合 A={y|y=2x}，B={y|y= A . {y|y≥0} B . {y|y＞0} C . {y|y≥1} D . {y|y＞1}}，则 A∩B 等于（）2. （2 分） (2019 高三上·东莞期末) 已知复数满足 A.2（为虚数单位），则（）B. C.D.3. （2 分）已知等差数列为（）满足：A.，且，，成等比数列，则数列的前项和B.C. 或D. 或 4. （2 分）曲线在 P 点处的切线平行于直线第 1 页共 15 页，则此切线方程是（）A.B.C.D.或5. （2 分）设直线值为（）A.1与函数B.的图像分别交于点，则当达到最小时的C.D. 6. （2 分） (2016 高二上·遵义期中) 动点 P 到点 M（1，0）与点 N（3，0）的距离之差为 2，则点 P 的轨迹是（） A . 双曲线 B . 双曲线的一支 C . 两条射线 D . 一条射线7. （2 分）在区间内，任取个数，则满足的概率为（）A.B.C.第 2 页共 15 页D.8. （2 分） (2016 高一下·南安期中) 如图，在四边形 ABCD 中，=0，=4，则（ +）•的值为（）=4， • = •A.2 B. C.4 D. 9. （2 分） (2017·南海模拟) 执行如图所示的程序框图中运算，输出的是（）第 3 页共 15 页A.0 B. C.D.10. （2 分） (2017 高三上·红桥期末) 已知双曲线 ﹣ =1（a＞0，b＞0）的两条渐近线与抛物线 y2=2px （p＞0）的准线分别交于 O、A、B 三点，O 为坐标原点．若双曲线的离心率为 2，△AOB 的面积为，则 p=（）A.1B. C.2 D.311. （2 分） (2018·孝义模拟) 在四面体中，为的重心，且直线与平面所成的角是上，则球的表面积是（），，若该四面体，底面，的顶点均在球的表面A.B.C.D.12. （2 分）下列函数中，既是偶函数又在单调递增的函数是（）A. B. C.第 4 页共 15 页D.二、填空题 (共 3 题；共 3 分)13. （1 分） (2019 高三上·广东期末) 二项式展开式中的常数项为________。

河南省鹤壁市高考数学一模试卷

河南省鹤壁市高考数学一模试卷姓名:________ 班级:________ 成绩:________一、填空题 (共12题；共12分)1. （1分） (2020高一上·南昌月考) 已知集合，，则________．2. （1分）(2017·大新模拟) 若复数z满足3+zi=z﹣3i（i为虚数单位），则复数z的模|z|=________．3. （1分） (2017高一下·蠡县期末) 已知数列满足，则 ________．4. （1分）(2014·重庆理) 函数f（x）=log2 • （2x）的最小值为________．5. （1分） (2016高三上·绍兴期末) 已知函数y=|x2﹣1|的图象与函数y=kx2﹣（k+2）x+2的图象恰有2个不同的公共点，则实数k的取值范围为________．6. （1分）已知直线x﹣2y+2=0经过椭圆的一个顶点和一个焦点，那么这个椭圆的方程为________，离心率为________。

7. （1分）(2018·宣城模拟) 已知各项都不相等的等差数列，满足，且，则数列项中的最大值为________．8. （1分） (2016高二上·诸暨期中) 已知棱长为1，各面均为等边三角形的四面体S﹣ABC，则它的表面积S=________，体积V=________．9. （1分） (2017高二下·汉中期中) i是虚数单位，若，则乘积ab的值是________．10. （1分） (2019高二上·沈阳月考) 如图，在杨辉三角形中，斜线1的上方，从1开始箭头所示的数组成一个锯齿形数列：1，3，3，4，6，5，10，…，记其前项和为，则 ________．11. （1分）(2016·上海文) 设a＞0,b＞0．若关于x,y的方程组无解，则的取值范围是________．12. （1分）已知函数f（x）=sin2x+2cos2x﹣1，将函数y=f（x）的图象上各点的横坐标伸长到原来的2倍，纵坐标不变，得到函数y=g（x）的图象，则g（x）的解析式为________．二、选择题 (共4题；共8分)13. （2分）将离心率为的双曲线的实半轴长和虚半轴长同时增加个单位长度，得到离心率为的双曲线，则（）A . 对任意的，B . 当时，；当时，C . 对任意的，D . 当时，；当时，14. （2分） (2019高一上·都匀期中) 函数的图象向左平移个单位，所得图象与的图象关于轴对称，则（）A .B .C .D .15. （2分） (2019高二下·吉林期末) 已知为定义在上的奇函数，当时，，则的值域为（）A .B .C .D .16. （2分）(2018·宁县模拟) 对于集合A，B，“ ”不成立的含义是A . B是A的子集B . A中的元素都不是B的元素C . A中至少有一个元素不属于BD . B中至少有一个元素不属于A三、解答题 (共5题；共55分)17. （10分） (2019高三上·岳阳月考) 如图所示多面体中，AD⊥平面PDC，ABCD为平行四边形，E，F分别为AD，BP的中点，AD= ，AP= ，PC= .（Ⅰ）求证：EF∥平面PDC；（Ⅱ）若∠CDP＝90°，求证BE⊥DP;（Ⅲ）若∠CDP＝120°，求该多面体的体积.18. （10分）我们给出如下定义：对函数y=f（x），x∈D，若存在常数C（C∈R），对任意的x1∈D，存在唯一的x2∈D，使得，则称函数f（x）为“和谐函数”，称常数C为函数f（x）的“和谐数”．（1）判断函数f（x）=x+1，x∈[﹣1，3]是否为“和谐函数”？答：________．（填“是”或“否”）如果是，写出它的一个“和谐数”：________．（2）证明：函数g（x）=lgx，x∈[10，100]为“和谐函数”，是其“和谐数”；（3）判断函数u（x）=x2 ，x∈R是否为和谐函数，并作出证明．19. （5分）(2017·上海模拟) 如图，O为总信号源点，A，B，C是三个居民区，已知A，B都在O的正东方向上，OA=10km，OB=20km，C在O的北偏西45°方向上，CO=5 km．（1）求居民区A与C的距离；（2）现要经过点O铺设一条总光缆直线EF（E在直线OA的上方），并从A，B，C分别铺设三条最短分光缆连接到总光缆EF．假设铺设每条分光缆的费用与其长度的平方成正比，比例系数为m（m为常数）．设∠AOE=θ（0≤θ＜π），铺设三条分光缆的总费用为w（元）．①求w关于θ的函数表达式；②求w的最小值及此时tanθ的值．20. （15分） (2016高二上·沙坪坝期中) 已知双曲线 =1（a＞0，b＞0）的右焦点为F（c，0）．（1）若双曲线的一条渐近线方程为y=x且c=2，求双曲线的方程；（2）以原点O为圆心，c为半径作圆，该圆与双曲线在第一象限的交点为A，过A作圆的切线，斜率为﹣，求双曲线的离心率．21. （15分）(2017·丰台模拟) 对于∀n∈N* ，若数列{xn}满足xn+1﹣xn＞1，则称这个数列为“K数列”．（Ⅰ）已知数列：1，m+1，m2是“K数列”，求实数m的取值范围；（Ⅱ）是否存在首项为﹣1的等差数列{an}为“K数列”，且其前n项和Sn满足？若存在，求出{an}的通项公式；若不存在，请说明理由；（Ⅲ）已知各项均为正整数的等比数列{an}是“K数列”，数列不是“K数列”，若，试判断数列{bn}是否为“K数列”，并说明理由．参考答案一、填空题 (共12题；共12分)答案：1-1、考点：解析：答案：2-1、考点：解析：答案：3-1、考点：解析：答案：4-1、考点：解析：答案：5-1、考点：解析：答案：6-1、考点：解析：答案：7-1、考点：解析：答案：8-1、考点：解析：答案：9-1、考点：解析：答案：10-1、考点：解析：答案：11-1、考点：解析：答案：12-1、考点：解析：二、选择题 (共4题；共8分)答案：13-1、考点：解析：答案：14-1、考点：解析：答案：15-1、考点：解析：答案：16-1、考点：解析：三、解答题 (共5题；共55分)答案：17-1、考点：解析：答案：18-1、答案：18-2、答案：18-3、考点：解析：答案：19-1、答案：19-2、考点：解析：答案：20-1、答案：20-2、考点：解析：考点：解析：。

河南省鹤壁市数学高三上学期理数教学质量监测试卷

河南省鹤壁市数学高三上学期理数教学质量监测试卷姓名:________ 班级:________ 成绩:________一、单选题 (共12题；共24分)1. （2分）已知集合，则为（）A . （1，2）B .C .D .2. （2分）如图所示，矩形长为6，宽为4，在矩形内随机地撒300颗黄豆，数得落在椭圆外的黄豆数为96颗，以此实验数据为依据可以估计出椭圆的面积约为（）A . 8.68B . 16.32C . 17.32D . 7.683. （2分）有下列关于三角函数的命题P1：∀x∈R，x≠kπ+（k∈Z），若tanx＞0，则sin2x＞0；P2：函数y=sin（x﹣）与函数y=cosx的图象相同；P3：∃x0∈R，2cosx0=3；P4：函数y=|cosx|（x∈R）的最小正周期为2π，其中真命题是（）A . P1 ， P4B . P2 ， P4C . P2 ， P3D . P1 ， P24. （2分） (2018高三上·大连期末) 《九章算术》之后，人们学会了用等差数列的知识来解决问题，《张丘建算经》卷上第题为：“今有女善织，日益攻疾（注：从第天开始，每天比前一天多织相同量的布），第一天织尺布，现一月（按天计）共织尺布”，则从第天起每天比前一天多织（）尺布A .B .C .D .5. （2分） (2016高一上·长春期中) 已知偶函数f（x）在[﹣1，0]上为单调增函数，则（）A . f（sin ）＜f（cos ）B . f（sin1）＞f（cos1）C . f（sin ）＜f（sin ）D . f（sin ）＞f（tan ）6. （2分） (1+2x) 6的展开式中，x的系数等于w，则函数的最小正周期是（）A .B .C .D .7. （2分）已知α是第四象限角tanα=﹣，则cosα=（）A .B . -C .D . -8. （2分）(2018·银川模拟) 如图程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”．执行该程序框图,若输入的a、b分别为14、18,则输出的a为（）A . 0B . 2C . 4D . 149. （2分）如图网格纸上小正方形的边长为l，粗实线画山的是某几何体的三视图，则这个几何体的体积为（）A . 2B . 3C . 4D . 510. （2分）已知f（x）=，则f（）的值是（）A . 0B . 1C .D . -11. （2分） (2017高二上·莆田月考) 已知点为椭圆上任意一点，则到直线的距离的最小值为（）A .B .C .D .12. （2分） (2016高一下·宿州期中) 设{an}是由正数组成的等比数列，公比q=2，且a1•a2•a3•…•a30=230 ，那么a3•a6•a9•…•a30等于（）A . 210B . 220C . 216D . 215二、填空题 (共4题；共4分)13. （1分）设，为单位向量．且、的夹角为，若=+3，=2，则向量在方向上的射影为________14. （1分） (2018高二上·莆田月考) 若x，y满足约束条件则z=x−2y的最小值为________.15. （1分）与双曲线共焦点，且过点的双曲线方程为________．16. （1分）设f（x）、g（x）是R上的可导函数，f′（x），g′（x）分别为f（x）、g（x）的导函数，且满足f′（x）g（x）+f（x）g′（x）＜0，则当a＜x＜b时，f（x）g（x）与f（b）g（b）的大小关系为________．三、解答题 (共7题；共70分)17. （5分） (2020高二上·青铜峡期末) 在中，内角所对的边分别为，已知．（Ⅰ）求角C的大小（Ⅱ）若，的面积为，求的周长．18. （10分）(2018·河北模拟) 已知在直角梯形中，，，将沿折起至，使二面角为直角.（1）求证：平面平面；（2）若点满足 , ，当二面角为45°时，求的值.19. （10分）(2017·鄂尔多斯模拟) 某联欢晚会举行抽奖活动，举办方设置了甲、乙两种抽奖方案，方案甲的中奖率为，中奖可以获得2分；方案乙的中奖率为，中奖可以获得3分；未中奖则不得分．每人有且只有一次抽奖机会，每次抽奖中奖与否互不影响，晚会结束后凭分数兑换奖品．（1）若小明选择方案甲抽奖，小红选择方案乙抽奖，记他们的累计得分为x，求x≤3的概率；（2）若小明、小红两人都选择方案甲或都选择方案乙进行抽奖，问：他们选择何种方案抽奖，累计得分的数学期望较大？20. （5分） (2016高三上·成都期中) 如图，设椭圆C：（a＞b＞0），动直线l与椭圆C只有一个公共点P，且点P在第一象限．（Ⅰ）已知直线l的斜率为k，用a，b，k表示点P的坐标；（Ⅱ）若过原点O的直线l1与l垂直，证明：点P到直线l1的距离的最大值为a﹣b．21. （10分） (2016高二下·潍坊期末) 已知函数f（x）=ax﹣lnx﹣1，若曲线y=f（x）在点（2，f（2））处的切线与直线2x+y﹣1=0垂直．（1）求a的值；（2）函数g（x）=f（x）﹣m（x﹣1）（m∈R）恰有两个零点x1，x2（x1＜x2），求函数g（x）的单调区间及实数m的取值范围．22. （20分）(2016·江苏) 【选做题】本题包括A、B、C、D四小题，请选定其中两小题，并在相应的答题区域内作答．若多做，则按作答的前两小题评分．解答时应写出文字说明、证明过程或演算步骤．（1）A．【选修4—1几何证明选讲】如图，在△ABC中，∠ABC=90°，BD⊥AC，D为垂足，E是BC的中点，求证：∠EDC=∠ABD.（2）B.【选修4—2：矩阵与变换】已知矩阵A= 矩阵B的逆矩阵B﹣1= ，求矩阵AB.（3）【选修4—4：坐标系与参数方程】在平面直角坐标系xOy中，已知直线l的参数方程为（t为参数），椭圆C的参数方程为（为参数）.设直线l与椭圆C相交于A，B两点，求线段AB的长.（4）D. 设a＞0，|x﹣1|＜，|y﹣2|＜，求证：|2x+y﹣4|＜a．23. （10分）(2016·柳州模拟) 已知函数f（x）=|x﹣a|+m|x+a|．（1）当m=a=﹣1时，求不等式f（x）≥x的解集；（2）不等式f（x）≥2（0＜m＜1）恒成立时，实数a的取值范围是{a|a≤﹣3或a≥3}，求实数m的集合．参考答案一、单选题 (共12题；共24分)1-1、2-1、3-1、4-1、5-1、6-1、7-1、8-1、9-1、10-1、11-1、12-1、二、填空题 (共4题；共4分)13-1、14-1、15-1、16-1、三、解答题 (共7题；共70分)17-1、18-1、18-2、19-1、19-2、20-1、21-1、21-2、22-1、22-2、22-3、22-4、23-1、23-2、。

河南省鹤壁市高中2022-2023学年高三上学期第三次模拟考试数学理科试题 (2)

一、单选题二、多选题1. 已知，，，则，，的大小关系为（）A．B．C．D．2. 欧拉公式（为虚数单位）是由瑞士著名数学家欧拉发现的，它将指数函数的定义域扩大到复数集，建立了三角函数和指数函数的关系，特别是当时，被认为是数学上最优美的公式.根据欧拉公式可知，表示的复数在复平面中位于（）A ．第一象限B ．第二象限C ．第三象限D ．第四象限3. 已知，，则（）A．B．C．D．4. 已知集合，，则（）A．B．C．D．5.若（，为虚数单位），则（）A．B．C．D．6.要测定古物的年代，可以用放射性碳法：在动植物的体内都含有微量的放射性．动植物死亡后，停止了新陈代谢，不再产生，且原来的会自动衰变．经过5730年，它的残余量只有原始量的一半．现用放射性碳法测得某古物中含量占原来的，推算该古物约是年前的遗物（参考数据：），则实数的值为（）A ．12302B ．13304C ．23004D ．240347. 等边的边长为，、是边的两个三等分点，则等于（）A．B．C．D．8.设为坐标原点，直线过定点，与抛物线交于两点，若，则抛物线的准线方程为（）A．B．C．D．9. 在棱长为1的正方体中，点E 为线段上一动点（不包含端点），则下列说法正确的有（）A ．平面B ．的最小值为C ．存在点E使得D ．点D到平面的距离为10. 已知平面向量，，则下列说法正确的是（）河南省鹤壁市高中2022-2023学年高三上学期第三次模拟考试数学理科试题 (2)河南省鹤壁市高中2022-2023学年高三上学期第三次模拟考试数学理科试题 (2)三、填空题四、解答题A．B．在方向上的投影向量为C ．与垂直的单位向量的坐标为D ．若向量与向量共线，则11. 已知函数，则（）A．的最小值为B．的图象关于点对称C ．直线是图象的一条对称轴D ．在区间上单调递减12. 已知双曲线：的左右焦点为，，左右顶点为，，过的直线交双曲线C 的右支于P ，Q 两点，设，，当直线绕着转动时，下列量保持不变的是（）A ．的周长B ．的周长与之差C．D．13. 圆的圆心到直线的距离为___________.14. 已知二项式的展开式中，只有第四项的二项式系数最大，则展开式中常数项为________．（用数字作答）15.若分式不论x取何值总有意义，则点关于x 轴的对称点在第______象限．16.已知函数（e 为自然对数的底数），其中．(1)试讨论函数的单调性；(2)若有两个极值点和，记过点，的直线的斜率为k ，同：是否存在a ，使得？若存在，求出a 的值，若不存在，请说明理由17.已知点，，动点满足直线与的斜率之积为，记动点的轨迹为曲线．（1）求的方程，并说明是什么曲线．（2）曲线与轴正半轴的交点为点，点是曲线上的一点（点不在坐标轴上），若直线与直线交于点，直线与直线交于点，求证：为等腰三角形．18. 已知椭圆的右焦点，且满足．(1)求椭圆E 的标准方程；(2)若E 上存在M ，N 两点关于直线对称，且满足（O 为坐标原点），求l 的方程．19. 如图是飞行棋部分棋盘图示，飞机的初始位置为0号格，抛掷一个质地均匀的骰子，若拋出的点数为1，2，飞机在原地不动；若抛出的点数为3，4，飞机向前移一格；若抛出的点数为5，6，飞机向前移两格.记抛掷骰子一次后，飞机到达1号格为事件.记抛两次骰子后，飞机到达2号格为事件.(1)求；(2)求.20. 已知离心率为的椭圆焦点在轴上，且椭圆个顶点构成的四边形面积为，过点的直线与椭圆相交于不同的两点、.（1）求椭圆的方程；（2）设为椭圆上一点，且（为坐标原点）.求当时，实数的取值范围.21. 已知函数的一段图象如图所示．（1）求函数的解析式；（2）函数在轴右侧的极小值点的横坐标组成数列，设右侧的第一个极小值点的横坐标为首项，试求数列的前项和．。

2024-2025学年河南省鹤壁市高中高三上学期第一次检测数学试题及答案

2025学年鹤壁市高中高三（上）第一次综合检测数学试题注意事项：1.答题前，考生务必用黑色碳素笔将自己的姓名、准考证号、考场号、座位号在答题卡上填写清楚。

2.每道选择题选出答案后，用2B 铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其他答案标号。

在试题卷上作答无效。

3.非选择题必须用黑色字迹钢笔或签字笔作答，答案必须写在答题卡各题目指定区域内相应位置上；如需改动，先划掉原来的答案，然后再写上新的答案；不准使用铅笔和涂改液。

不按以上要求作答的答案无效。

4.考试结束后，请将本试卷和答题卡一并交回。

一、单项选择题：本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.1.已知a ，b ∈R ，若m ，且不等式20x ax b −+<的解集为()1,2m ，则a b +=（）A.3B.43C.7D.112.设0.40.40.4log 0.5,0.3,0.5ab c −−==，则,,a b c 的大小关系是（）A.b c a >>B.c b a >>C.b a c >>D.c a b >>3.已知A B C D ，，，四点均在半径为R （R 为常数）的球O 的球面上运动，且,,AB AC AB AC AD BC =⊥⊥，若四面体 ABCD 的体积的最大值为43，则球 O 的表面积为（） A.2πB.3πC.9π4D.9π4.当π0,2x∈ 时，sin2a x ≥a 的取值范围为（）A.(]0,1B.1C.)1,+∞D.1,2+∞5.设1z ，2z 是复数，则下列命题中是假命题的是（）A.若12zz z =⋅，则12||||||z z z =⋅ B.若12zz z =⋅，则12z z z =⋅ C.若12||||z z =，则2212z z =D.若12||||z z =，则1122z z z z ⋅=⋅6.重庆八中味园食堂午餐情况监测数据表明，小唐同学周一去味园的概率为 35，周二去味园的概率为310，且小唐周一不去味园的条件下周二去味园的概率是周一去味园的条件下周二去味园的概率的2倍，则小唐同学周一、周二都去味园的概率为（） A.970B.950C.340D.3147.在长方体1111ABCD A B C D −中，122AB AD AA ==，点M 是线段11C D 上靠近1D 的四等分点，点N 是线段1CC 的中点，则平面AMN 截该长方体所得的截面图形为（） A.三角形B.四边形C.五边形D.六边形8.已知函数()f x 的导函数为()′f x ，记()1()f x f x ′=，()21(),f x f x ′=()1()n n f x f x +′=()n N ∗∈.若()sin f x x x =，则()()20192021f x f x +=（）A.2cos x −B.2sin x −C.2cos xD.2sin x二、多项选择题：本题共３小题，每小题６分，共18分.在每小题给出的选项中，有多项符合题目要求.全部选对的得6分，有选错的得0分，若只有2个正确选项，每选对1个得3分；若只有3个正确选项，每选对1个得2分.9.已知函数()sin221cos2x xf x x=−+，则（） A.函数()f x 一个周期是πB.函数()f x 递减区间为()πππ,π22k k k Z−+∈C.函数()f x 有无数多个对称中心D.过点()2,0作曲线()y f x =的切线有且只有一条10.已知函数()f x 的图象是由函数2sin cos y x x =的图象向右平移π6个单位得到，则（） A.()f x 的最小正周期为πB.()f x 在区间ππ,63−上单调递增C.()f x 的图象关于直线π3x =对称 D.()f x 的图象关于点π,06对称11.在三棱锥−P ABC 中，PA ⊥平面,,2,ABC AB BC AB BC PA ⊥==，点D 是三角形PAB 内的动点（含边界），AD CD ⊥，则下列结论正确的是（） A.PB 与平面ABC 所成角的大小为π3B.三棱锥C ABD −的体积最大值是2C.D 点的轨迹长度是2π3D.异面直线CD 与AB 所成角的余弦值范围是三、填空题：本大题共3个小题，每小题5分，共15分.12.对于函数()()cos 0f x x kx x =−≥，当该函数恰有两个零点时，设两个零点中最大值为α，当该函数恰有四个零点时，设这四个零点中最大值为β，求()()2221sin21cos21ααββαβ+++=− .13.已知P 是ABC 内一点，45,30ABP PBC PCB ACP °°∠=∠=∠=∠=，则tan BAP ∠= . 14.下图数阵的每一行最右边数据从上到下形成以1为首项，以2为公比的等比数列，每行的第n 个数从上到下形成以12n −为首项，以3为公比的等比数列，则该数阵第n 行()*n ∈N 所有数据的和n S = .四、解答题：本大题共5小题，共77分.解答应写出文字说明、证明过程或演算步骤.15.（13分）在某项比赛中，7位专业评委和7位观众评委分别给选手打分.针对某位选手，下面是两组评委的打分：A 组 42 45 48 53 52 47 49B 组48527066774951(1)选择一个可以度量每一组评分相似性的量，据此判断哪一组分数更可能是专业评委打的分数；(2)现从A 组评委所打分数中随机抽取2个分数，记为a ，b ，从B 组评委所打分数中随机抽取2个分数，记为c ，d .记事件:M a ，b 中有一个数据为48，事件:100N a b +=或100c d +=，判断事件M 与事件N 是否相互独立.16.（15分）如图，四边形ABCD内接于圆O，圆O的半径2R=，π2DAB ABC∠+∠=，2CD=.(1)求DBC∠的大小以及线段AB的长；(2)求四边形ABCD面积的取值范围.17.（15分）如图，在四棱锥PP−AAAAAAAA中，△PPAAAA为正三角形，底面AAAAAAAA为正方形，平面PPAAAA⊥平面AAAAAAAA，点MM是棱PPAA的中点，平面AAAAMM与棱PPAA交于点NN.（1）求证：MMNN//平面AAAAAAAA；（2）QQ为平面AAAANNMM内一动点，EE为线段AAAA上一点；①求证：NNQQ⊥AAPP；②当AAQQ+QQEE最小时，求MMMM MMQQ的值.18.（17分）已知抛物线2:=E y x ，过点()1,2T 的直线与抛物线E 交于,A B 两点，设抛物线E 在点,A B 处的切线分别为1l 和2l ，已知1l 与x 轴交于点2,M l 与x 轴交于点N ，设1l 与2l 的交点为P .(1)证明：点P 在定直线上；(2)若PMN 面积为P 的坐标； (3)若,,,P M N T 四点共圆，求点P 的坐标.19.（17分）设函数()f x 的导函数为()(),f x f x ′′的导函数为()(),f x f x ′′′′的导函数为()f x ′′′.若()00f x ′′=，且()00f x ′′′≠，则()()00,x f x 为曲线()y f x =的拐点.(1)判断曲线6y x =是否有拐点，并说明理由；(2)已知函数()535f x ax x =−，若f 为曲线()y f x =的一个拐点，求()f x 的单调区间与极值.数学参考答案一、单项选择题：本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.1.【答案】D【解析】根据不等式222x y xy +≤可得()22222244522a b a b a b ++≤=++，当且仅当222244a b a b ++=，即22a b =时等号成立，所以，52≤，所以52m =. 所以，不等式20x ax b −+<的解集为()1,5.根据一元二次不等式的解集与一元二次方程解的关系可知，1和5是方程20x ax b −+=的两个解，所以有1515a b +=×= ，所以65a b = = ，11a b +=. 故选：D. 2.【答案】A【解析】因为0.4log y x =在()0,+∞上单调递减，所以0.40.40.4log 1log 0.5log 0.4<<，即01a <<，因为0.4y x =在()0,+∞上单调递增，又11100.3,0.523−−==，即110.30.51−−>>，所以()()0.40.4110.40.0.513−−>>，即0.40.410.30.5−−>>，故1b c >>，所以b c a >>. 故选：A. 3.【答案】D【解析】因,,AB AC AB AC =⊥取BC 中点为N ，则AN BC ⊥，又AD BC ⊥，,AN AD ⊂平面AND ，AN AD A = ，则BC ⊥平面AND ，BC ⊂面ABC ，则平面ABC ⊥平面AND ，要使四面体ABCD 的体积最大，则有DN ⊥平面ABC ，且球心O 在DN 上.设球体半径为R ，则OAOD R ==，则()111332D ABC ABC V S DNBC AN R ON −=⋅=⋅⋅+，又注意到2BC AN =，22222AN OA ON R ON =−=−，则()()()22111333D ABC ABC V S DN AN R ON R ON R ON −=⋅=⋅+=+−. 注意到()()()()()33211122221422366363R ON R ON R R ON R ON R ON R ON R ON ++− +−=++−≤⋅=⋅.当且仅当22R ON R ON −=+，即3R ON =时取等号.又四面体 ABCD 的体积的最大值为43，则314436332R R ⋅=⇒= . 则球的表面积为24π9πR =. 故选：D4.【答案】D【解析】由sin2a x ≥2sin cos a x x ≥ 因为π0,2x∈ ，可得π0,24x ∈ ，所以sin cos 22x x <，可得2sin cos 2sin (cos sin )222x x xa x x ≥−，又因为22sin sin cos ,cos cos sin (cos sin )(cos sin )22222222x x x xx x x x x x ==−=+−，所以4sin cos (cos sin )2sin (cos sin (cos sin )22)2222222x x x x x x x xa x ≥−+−即2cos (c 1os sin )222x x xa +≥，因为2π2cos (cos sin )2sin cos sin cos 1)1222222s 42co x x x x x x x x x ++=+++==+，因为π0,2x ∈ ，可得ππ3π,444x +∈，所以πsin()4x +∈，则π)11]4x ++∈，则1]2，要使得不等式sin2a x ≥a ≥所以12a ≥，即实数a 的取值范围为1,2 +∞. 故选：D.5.【答案】C【解析】设1i z a b =+，2i z c d =+，其中,,,a b c d ∈R . 对于A ，12(i)(i)z z z a b c d ==++==12z z ⋅=，所以12z z z =⋅，故A 正确；对于B ，(i)(i)()()i z a b c d ac bd bc ad =++=−++，()()i z ac bd bc ad =−−+，()()()()12i i i z z a b c d ac bd bc ad ⋅=−−=−−+，所以12z z z =⋅，故B 正确；对于C ，1i z a b =+=，2i z c d =+= 由12||||z z =，得2222+=+a b c d .因为22212i z a b ab =−+，22222i z c d cd =−+，所以2212z z =不一定成立，如11z =，2i z =，此时12||||z z =，而211z =，221z =−，即2212z z ≠，故C 错误；对于D ，由12||||z z =，得2222+=+a b c d ，2211(i)(i)z z a b a b a b ⋅=+−=+，2222(i)(i)z z c d c d c d ⋅=+−=+，所以1122z z z z ⋅=⋅，故D 正确﹒故选C. 6.【答案】A【解析】设“小唐同学周一去味园”为事件A ，设“小唐周二去味园”为事件B ，则“小唐同学周一、周二都去味园”为事件AB ，由题意可知：33(),()510==P A P B ，且(|)2(|)=P B A P B A ，由全概率公式可知：()()()(|)(|)=+P B P B A P A P B A P A ，即343(|)(|)1055=+P B A P B A ，解得3(|)14=P B A ，所以()()339()|14570==×=P AB P B A P A . 故选：A 7.【答案】C【解析】延长MN 交DC 的延长线于点F ，连接AF 交BC 于点H ，连接NH ，延长NM 交1DD 的延长线于点E ，连接AE 交11A D 于点G ，连接GM ，则五边形AHNMG 为平面AMN 截该长方体所得的截面图形，不妨设1224AB AD AA ===，又点M 是线段11C D 上靠近1D 的四等分点，点N 是线段1CC 的中点，所以13C M =，11D M =，11C NNC ==，所以3CF =，又//CF AB ，所以43AB BH CF CH ==，又2BH CH +=，所以67CH =，又11D M ED DF ED =，即11172ED ED =+，解得113ED =，又11GD ED AD ED =，即1131223GD =+，解得127GD =，符合题意，即五边形AHNMG 为平面AMN 截该长方体所得的截面图形. 故选C.8.【答案】D 【解析】解：()sin f x x x =，则()1()sin cos f x f x x x x ′==+， ()21()cos cos sin 2cos sin f x f x x x x x x x x ′==+−=−， ()32()2sin sin cos 3sin cos f x f x x x x x x x x ′==−−−=−−， ()43()3cos cos sin 4cos sin f x f x x x x x x x x ′==−−+=−+， ()54()4sin sin cos 5sin cos f x f x x x x x x x x ′==++=+，所以猜想：()43()43sin cos k f x k x x x −=−+， ()42()42cos sin k f x k x x x −=−−，()41()41sin cos k f x k x x x −=−−−， 4()4cos sin k f x k x x x =−+，由201945051=×−，202145063=×−，所以()20192019sin cos f x x x x =−−， ()20212021sin cos f x x x x =+， ()()201920212sin f x f x x +=，故选：D .二、多项选择题：本题共３小题，每小题６分，共18分.在每小题给出的选项中，有多项符合题目要求.全部选对的得6分，有选错的得0分，若只有2个正确选项，每选对1个得3分；若只有3个正确选项，每选对1个得2分.9.【答案】BCD【解析】函数sin2()21cos2xx f x x=−+中，cos 21x ≠−，即2π2π,Z x k k ≠−+∈，解得ππ,Z 2x k k ≠−+∈，22sin cos ()tan 22cos 2x x x xf x x x =−=−，对于A ，显然(0)0f =，π(π)2f =，即(π)(0)f f ≠，A 错误；对于B ，由()tan 2xf x x =−，求导得211()02cos f x x ′=−<，因此函数()f x 递减区间为ππ(π,π)(Z)22k k k −+∈，B 正确；对于C ，由ππ(π)()tan(Z π)tan ,222k x x k f k x f k x x k x −−+=−−−=∈+，得函数()f x 图象关于点ππ(,)(Z)24k k k ∈成中心对称，有无数多个对称中心，C 正确；对于D ，设过点(2,0)的直线与曲线()y f x =相切于点000(,tan 2)x P x x −，则切线方程为0002011(tan )()(22)cos x y x x x x −−=−−，则()000200sin 1122cos 2cos x x x x x −+=−−，整理得000sin 2cos 223x x x −=−00π)234x x −=−，令函数π())234g x x x =−−+，当π4x ≤时，π3232x −≥−>π24x≤−，则()0g x >，即函数()g x 在π(,]4−∞上无零点，当πx ≥时，3232π3x −≤−<−，则()0g x <，即函数()g x 在[π,)+∞上无零点，当ππ4x <<时，π())24g x x ′=−−，又ππ7π2444x <−<，则πcos(2)41x −<−≤所以π)24x −<−，()0g x ′<，函数()g x 在π(,π)4上单调递减，显然π()0,(π)04g g ><，因此函数()g x 在π(,π)4上有唯一零点，从而方程00π)234x x −=−有唯一实根，过点()2,0作曲线()y f x =的切线有且只有一条，D 正确. 故选：BCD 10.【答案】AD 【解析】因为2sin cos sin 2yx x x =，向右平移π6个单位得()ππsin 2sin 263f x x x=−=−，则最小正周期为2ππ2T ==，故A 选项正确；令πππ2π22π232k x k −+≤−≤+，解得π5πππ1212k x k −+≤≤+，所以单调递增区间为π5ππ,π,Z 1212k k k−++∈，故B 选项错误；令ππ2π,32x k −=+解得5ππ,Z 122k x k =+∈，故C 选项错误；令π2π,3x k −=解得ππ,Z 6x k k =+∈所以函数()f x 的对称中心为ππ,0,Z 6k k +∈，故D 选项正确.故选：AD 11.【答案】ACD【解析】如图，把三棱锥−P ABC 补形成正四棱柱并建立空间直角坐标系A xyz −，对于A ，由PA ⊥平面ABC ，得PBA ∠是PB 与平面ABC所成的角，tan PAPBA AB∠= 因此π3PBA ∠=，A 正确；对于C ，由AD CD ⊥，得D 点的轨迹是以线段AC 为直径的球面与PAB 相交的一段圆弧及点B ，令,AC AB 的中点分别为,O E ，则OE ⊥平面PAB，1OE OD ==,1DE =，显然D 点所在圆弧所对圆心角大小为2π3，长度是2π3，C 正确；对于B ，由选项C 知，当DE AB ⊥时，D 点到平面ABC 距离最大，最大距离为1，因此三棱锥C ABD −的体积112212323C ABD D ABCV V −−=≤××××=，B 错误；对于D ，设2π(0)3AED θθ∠=<≤，则点(1cos ,0,sin )D θθ−，而(2,2,0)C ，于是(1cos ,2,sin )CD θθ=−−− ，又(2,0,0)AB =，令异面直线CD 与AB 所成的角大小为ϕ，则||cos |cos ,|||||CD AB CD AB CD AB ϕ⋅=〈〉==，令11cos [,2)2t θ=+∈，cos ϕ=1[,2)2t ∈上单调递增，因此t ≤D 正确. 故选：ACD三、填空题：本大题共3个小题，每小题5分，共15分.12.【答案】3−【解析】函数()()cos 0f x x kx x =−≥恰有两个零点等价于cos y x =与直线y kx =(0)x ≥有且只有两个交点，函数()()cos 0f x x kx x =−≥恰有四个个零点等价于cos y x =与直线y kx =(0)x ≥有且只有四个交点，cos y x =与直线y kx =(0)x ≥的图象如下：根据图象可知， cos y x =与直线y kx =(0)x ≥有且只有两个交点时，则cos y x =与y kx =在点A 处相切，且切点的横坐标为α，此时对应的函数解析式为cos y x =−，所以sin y x ′=，则sin k α=，又cos k αα−=，所以cos sin ααα−=，则()222cos 21sin cos 1sin2sin 2cos sin ααααααααα+ + ==−−同理，cos y x =与直线y kx =(0)x ≥有且只有四个交点时，则cos y x =与y kx =在点B 处相切，且切点的横坐标为β，此时对应的函数解析式为cos y x =，所以sin y x ′=−，则sin k β=−，又cos k ββ=，所以cos sin βββ=−，则()()22222222cos 1cos sin 1cos2sin 1cos 11sin βββββββββ+− +==−−−所以()()2221sin21cos231ααββαβ+++=−−故答案为：3−. 13.【答案】12/0.5 【解析】在PBC 中，30PBC PCB °∠=∠=，设1PB PC ==，由余弦定理可得2222cos1201113BC PB PC PB PC °=+−⋅=++=，可得BC = 在ABC 中，75ABC ABP PBC °∠=∠+∠=，所以18045BAC ABC ACB °∠=−∠−∠= ，由正弦定理得sin sin BC ABBAC ACB =∠∠，即sin 60AB =，可得AB = 在ABP 中，由余弦定理得222952cos 451322AP AB PB AB PB °=+−⋅=+−=，可得AP =222cos 2AP AB PB BAP AB AP +−∠==⋅可得sin BAP∠，因此sin1tancos2BAPBAPBAP∠∠==∠.故答案为：1214.【答案】32n n−【解析】因为每行的第n个数从上到下形成以12n−为首项，以3为公比的等比数列，所以0112231032323232n n n nnS−−−−=×+×+×++×,所以12301222233333n n nnnS−−−−×++++12123331322313nnn n n nnS−−=×=×−=−−.故答案为：32n n−.四、解答题：本大题共5小题，共77分.解答应写出文字说明、证明过程或演算步骤.15.（13分）【答案】(1)更可能是专业评委打的分数(2)事件M与事件N不独立.【解析】（1）可以用方差来度量每一组评委打分的相似性，方差越小，相似程度越高.42454853524749487Ax++++++=，48527066774951597Bx++++++=，所以A组数据的方差是22222222 1(4248)(4548)(4848)(5348)(5248)(4748)(4948) 7As=−+−+−+−+−+−+−887=，B组数据的方差是22222222 1(4859)(5259)(7059)(6659)(7759)(4959)(5159) 7Bs=−+−+−+−+−+−+−8287=，因为专业评委给分更符合专业规则，所以相似程度更高，因此组分数更可能是专业评委打的分数.（2）1627C2()C7P M==，:100:4852100,4753100N a b+=+=+=，100:4852100,4951100c d+=+=+=，各有两种，所以()21111722222222227777774C C C C C 2280C C C ?C C C 441P N ×−=+−==，事件MN ：当4852100a b +=+=时， ,c d 可以任意，有27C 种，当a ，b 中有一个数据为48，另一个不是52时，则100c d +=，有1152C C 种，所以21175222227777C C C 31()C C C C 441P MN =+=， ∴()()()P M P N P MN ≠，则事件M 与事件N 不独立.16.（15分）【答案】(1)π6DBC ∠=，AB =；(2) 【解析】（1）由题易知π2ABC ∠<,由正弦定理得21sin 242DC DBC R ∠===，π6DBC ∴∠=，πππ263DAB DBA DAB ABC DBC ∴∠+∠=∠+∠−∠=−=， 2ππ()3ADB DAB DBA ∴∠=−∠+∠=，2sin 4AB R ADB ∴=×∠=（2）方法一：延长AD ，BC ，交于点E .π2DAB ABC ∠+∠= ，π2AEB ∴∠=.设DAB α∠=，则11cos sin 6sin cos 3sin 222ABE S AE BE AB AB ααααα=×=××==△. 四边形ABCD 内接于圆O ，ECD DAB α∴∠=∠=，11sin cos 2sin cos sin 222CDE S DE CE CD CD ααααα∴=×=×==△， 2sin 2ABE CDE ABCD S S S α∴=−=四边形△△，ππ(,)63α∈ ，π2π2(,)33α∴∈，2]ABCD S ∴∈四边形，即四边形ABCD面积的取值范围是.方法二：连接OA ，OB ，OC ，OD ，由已知可得2π3AOB ∠=，OCD 是等边三角形.设AOD θ∠=，则π3BOC θ∠=−，OAD OBC OCD AOBCD S S S S ∴=++五边形△△△22211πsin sin()223R R Rθθ+−π[2sin sin()]3θθ=+−又212πsin 23AOBS R ==△AOB ABCD AOBCD S S S ∴−四边形五边形△ππ2[sin sin()]2sin()33θθθ=+−=+，π(0,)3θ∈ ，ππ2π(,)333θ∴+∈，2]ABCD S ∴∈四边形，即四边形ABCD 面积的取值范围是.17.（15分）【答案】（1）证明见解析；（2）①证明见解析；②12 .【解析】（1）证明：因为AAAA // AAAA ,AAAA ⊂ 平面AAAAPP ,AAAA ⊄ 平面AAAAPP , 所以AAAA // 平面AAAAPP ，又AAAA ⊂ 平面AAAANNMM ，平面AAAANNMM ∩ 平面AAAAPP =MMNN , 所以AAAA // MMNN .又AAAA ⊂平面AAAAAAAA ,MMNN ⊄ 平面AAAAAAAA ，所以MMNN // 平面AAAAAAAA .(2)解：①由平面PPAAAA ⊥ 平面AAAAAAAA ,AAAA ⊥AAAA , 又平面AAAAAAAA ∩ 平面PPAAAA =AAAA ，所以AAAA ⊥ 平面PPAAAA ，所以AAAA ⊥AAPP ，由（1），AAAA // MMNN ，故AAPP ⊥MMNN ，又MM 是棱PPAA 的中点，则NN 为棱PPAA 中点，△PPAAAA 为正三角形，所以AAPP ⊥NNAA ,MMNN ∩NNAA =NN ,MMNN ,NNAA ⊂ 平面AAAANNMM ，所以AAPP ⊥ 平面AAAANNMM ，且NNQQ ⊂ 平面AAAANNMM ，所以AAPP ⊥NNQQ .②因为AAPP ⊥NNQQ .且NN 为棱PPAA 中点，所以AAQQ =PPQQ ，所以AAQQ +QQEE =PPQQ +QQEE当QQ 为PPEE 与平面AAAANNMM 的交点时，(PPQQ +QQEE )mmmm mm =PPEE ，故当AAQQ +QQEE 最小时，PPEE 取得最小值，此时PPEE ⊥AAAA ，因为AAAA ⊥AAPP ，所以PPAA 2=PPAA 2+AAAA 2，同理PPAA 2=PPAA 2+AAAA 2=PPAA 2+AAAA 2=PPAA 2，当PPEE ⊥AAAA 时，可得EE 为AAAA 中点，取PPEE 中点TT ，连接MMTT ，如图：则有MMTT // AAEE 且MMTT =12AAEE =12EEAA ，有△MMTTQQ ∼△AAEEQQ ，所以MMMMMMQQ =MMMM EEQQ=12.18.（17分）【答案】(1)证明见解析； (2)()0,2−或()2,2； (3)1614,99【解析】（1）由2y x ，得2y x ′=，设()()()221122,,,,,P P A x x B x x P x y .所以1l 方程为：()21112yx x x x =−+，整理得：2112y x x x =−. 同理可得，2l 方程为：2222y x x x =−. 联立方程21122222y x x x y x x x =− =− ，解得12122P P x x x y x x +== . 因为点()1,2T 在抛物线内部，可知直线AB 的斜率存在，且与抛物线必相交，设直线AB 的方程为()12y k x =−+，与抛物线方程联立得：220x kx k −+−=，故1212,2x x k x x k +==−，所以,22P P kx y k ==−，可知22P P y x =−. 所以点P 在定直线22y x =−上. .（2）在12,l l 的方程中，令0y =，得12,0,,022x x M N，所以PMN面积()12121124P S MN y x x x x =⋅=−=故()()()()22221212121212432x x x x x x x x x x −=+−=，代入1212,2x x k x x k +==−可得：()()22484432k k k k −+−+=.整理得22(2)8(2)40k k −+−−=，解得：0k =或4k =. 所以点P 的坐标为()0,2−或()2,2.（3）抛物线焦点10,4F ，由1,02x M 得直线MF 斜率1112MF MP k x k =−=−，可知MF MP ⊥，同理NF NP ⊥，所以PF 是PMN 外接圆的直径. 若点T 也在该圆上，则TF TP ⊥. 由74TF k =，得直线TP 的方程为：()4127y x =−−+. 又点P 在定直线22y x =−上，联立两直线方程()412722y x y x =−−+ =− ，解得169149x y= = ，所以点P 的坐标为1614,99.19.（17分）【答案】(1)没有拐点，理由见解析.(2)单调递增区间为()(),1,1,−∞−+∞；单调递减区间为[]1,1−，极大值为2，极小值为2−.【解析】（1）解：由函数6y x =，可得5436,30,120y x y x y x ===′′′′′′，由4300x =，得0x =，又由31200x =，得0x =，所以曲线6y x =没有拐点. （2）解：由函数()535f x ax x =−，可得()()()4232515,20301023f x ax x f x ax x x ax =−=−=′′−′，因为f 为曲线()y f x =的一个拐点，所以0f =′′，所以12302a ×−=，解得3a =，经检验，当3a =时，0f ≠′′′，所以()()42221515151f x x x x x =′=−−. 当1x <−或1x >时，()0f x '>，则()f x 的单调递增区间为()(),1,1,−∞−+∞；当11x −≤≤时，()0f x ′≤，且()0f x ′=不恒成立，则()f x 的单调递减区间为[]1,1−，故当1x =−时，()f x 取得极大值，且极大值为2；当1x =时，()f x 取得极小值，且极小值为2−.。

河南省鹤壁市高级中学2022届高三数学上学期第一次模拟测试(8月段考)试题文

①B=∅，△=[2（a+1）]2﹣4（a2﹣1）=8a+8＜0，即a＜﹣1时，方程无解，满足题意；
②B={0}，即x2+2（a+1）x+a2﹣1=0有两个相等的实根0，
则有a+1=0且a2﹣1=0，解可得a=﹣1，
③B={﹣4}，即x2+2（a+1）x+a2﹣1=0有两个相等的实根﹣4，
则有a+1=4且a2﹣1=16，此时无解，
（1）若在上只有一个零点，求的取值范围；
（2）设为的极小值点，证明：
2022届高三年级数学（文）第一次模拟测试（答案）
一、选择题（每题5分）
1-5AAACC 6-10DABDC 11.C 12．C
12.解：在上是减函数，
时，，，时，，时，，
可知在递减，递增，又函数是连续的．
A．1.24 B．1.25 C．1.26 D．1.27
11．设函数的图像与的图像关于直线对称，且，则 ()
A． B． C． D．
12．已知函数，若函数与相同的值域，则实数的取值范围是（）
A． B． C． D．
二、填空题（每题5分）
13．命题“∀x＞0，x2+x＞1”的否定是_____．
20．已知 .
（1）求函数的单调递增区间；
（2）设的内角满足，若，求边上的高长的最大值.
21．已知点，过点作抛物线的两切线，切点为 .
（1）求两切点所在的直线方程；
（2）椭圆，离心率为，（1）中直线AB与椭圆交于点P，Q，直线的斜率分别为，，，若，求椭圆的方程.
22．已知函数．
17．设集合，若A∩B=B，求的取值范围．

河南省鹤壁市数学高三上学期理数第一次调查研究考试试卷

河南省鹤壁市数学高三上学期理数第一次调查研究考试试卷姓名:________ 班级:________ 成绩:________一、单选题 (共12题；共25分)1. （2分）已知集合，，则（）A .B .C .D .2. （2分）在复平面上，复数对应的点的坐标为（）A . (1,3)B . (3,1)C . (-1,3)D . (3,-1)3. （2分） (2016高一下·南安期中) 若多项式x2+x10=a0+a1(x+1)+...+a9(x+1)9+a10(x+1)10 ，则a9=（）A . 9B . 10C . -9D . -104. （2分）下列叙述中正确的是（）A . 从频率分布表可以看出样本数据对于平均数的波动大小B . 频数是指落在各个小组内的数据C . 每小组的频数与样本容量之比是这个小组的频率D . 组数是样本平均数除以组距5. （2分） (2018高一上·华安期末) 函数的零点一定位于区间（）A .B .C .D .6. （3分）已知x，y满足时，z=x﹣y的最大值为（）A . 4B . -4C . 0D . 27. （2分） (2018高一上·和平期中) 已知a=log20.3，b=20.3 ， c=0.32 ，则a，b，c三者的大小关系是（）A . b c aB . b a cC . a b cD . c b a8. （2分）(2019·西宁模拟) 若某程序框图如图所示，则该程序运行后输出的值是（）A . 5B . 4C . 3D . 29. （2分）已知外接圆的半径为1，圆心为O．若，且，则等于（）A .B .C .D . 310. （2分） (2015高二下·和平期中) 设函数y=f（x）在定义域内可导，其图象如图所示，则导函数y=f′（x）的图象只可能是下列情形中的（）A .B .C .D .11. （2分）(2017·新课标Ⅲ卷文) 已知函数f（x）=x2﹣2x+a（ex﹣1+e﹣x+1）有唯一零点，则a=（）A . ﹣B .C .D . 112. （2分） (2018高三上·湖南月考) 在△ABC中，∠ABC＝120°，AB＝3，BC＝1，D是边AC上的一点，则的取值范围是（）A .B .C .D .二、填空题 (共4题；共4分)13. （1分） (2019高二上·江都月考) 命题“ ”的否定是________.14. （1分） (2019高一下·上海月考) 己知，则________.15. （1分） (2019高一下·上海期中) 已知，， ________16. （1分） (2016高三上·辽宁期中) 已知△ABC的周长为，面积为，且，则角C的值为________．三、解答题 (共7题；共70分)17. （10分） (2019高一下·梅县期末) 单调递增的等差数列满足，且成等比数列.（1）求数列的通项公式；（2）设，求数列的前项和 .18. （10分）已知α是△ABC的一个内角，且，（Ⅰ）判断△ABC的形状；（Ⅱ）求sinα﹣cosα的值．19. （10分）(2020·济宁模拟) 如图1，四边形ABCD为矩形，BC=2AB，E为AD的中点，将 ABE、 DCE 分别沿BE、CE折起得图2，使得平面平面BCE，平面平面BCE.（1）求证：平面平面DCE；（2）若F为线段BC的中点，求直线FA与平面ADE所成角的正弦值.20. （10分） (2018高三上·扬州期中) 假定某人在规定区域投篮命中的概率为，现他在某个投篮游戏中，共投篮3次.（1）求连续命中2次的概率；（2）设命中的次数为X，求X的分布列和数学期望 .21. （10分）(2018·肇庆模拟) 已知函数，， .（Ⅰ）讨论的单调区间；（Ⅱ）若,且恒成立. 求的最大值.22. （10分） (2015高三上·天水期末) 在平面直角坐标系中，以原点为极点，x轴为极轴建立极坐标系，曲线C1的方程为（θ为参数），曲线C2的极坐标方程为C2：ρcosθ+ρsinθ=1，若曲线C1与C2相交于A、B两点．（1）求|AB|的值；（2）求点M（﹣1，2）到A、B两点的距离之积．23. （10分） (2019高二下·上饶期中) 已知为椭圆的左右焦点，点为其上一点，且有 .（1）求椭圆的标准方程；（2）过的直线与椭圆交于两点，求的面积的最大值.参考答案一、单选题 (共12题；共25分)答案：1-1、考点：解析：答案：2-1、考点：解析：答案：3-1、考点：解析：答案：4-1、考点：解析：答案：5-1、考点：解析：答案：6-1、考点：解析：答案：7-1、考点：解析：答案：8-1、考点：解析：答案：9-1、考点：解析：答案：10-1、考点：解析：答案：11-1、考点：解析：答案：12-1、考点：解析：二、填空题 (共4题；共4分)答案：13-1、考点：解析：答案：14-1、考点：解析：答案：15-1、考点：解析：答案：16-1、考点：解析：三、解答题 (共7题；共70分)答案：17-1、答案：17-2、考点：解析：答案：18-1、考点：解析：答案：19-1、答案：19-2、考点：解析：答案：20-1、答案：20-2、考点：解析：答案：21-1、考点：解析：答案：22-1、答案：22-2、考点：解析：答案：23-1、答案：23-2、考点：解析：。