五年级奥数题及答案：自然数(高等难度)

小学五年级奥数题100道及答案(完整版)

小学五年级奥数题100道及答案(完整版)1. 一个数除以5 余3，除以6 余4，除以7 余5，这个数最小是（）A. 208B. 203C. 200D. 198答案：A解析：这个数加上 2 就能被5、6、7 整除，5、6、7 的最小公倍数是210，所以这个数是210 - 2 = 208。

2. 有一个自然数，被10 除余7，被7 除余4，被4 除余1。

这个自然数最小是（）A. 137B. 107C. 131D. 101答案：C解析：这个数加上 3 就能被10、7、4 整除，10、7、4 的最小公倍数是140，所以这个数是140 - 3 = 137。

3. 一筐苹果，2 个一拿，3 个一拿，4 个一拿，5 个一拿都正好拿完而没有余数，这筐苹果最少应有（）A. 120 个B. 90 个C. 60 个D. 30 个答案：C解析：苹果数量是2、3、4、5 的公倍数，最小公倍数是60。

4. 把66 分解质因数是（）A. 66 = 1×2×3×11B. 66 = 6×11C. 66 = 2×3×11D. 2×3×11 = 66答案：C解析：分解质因数是把一个合数写成几个质数相乘的形式。

5. 两个质数的积一定是（）A. 质数B. 奇数C. 偶数D. 合数答案：D解析：两个质数相乘的积，除了1 和它本身以外还有这两个质数作为因数，所以是合数。

6. 一个合数至少有（）个因数。

A. 1B. 2C. 3D. 4答案：C解析：合数是指除了能被1 和本身整除外，还能被其他数（0 除外）整除的自然数。

所以一个合数至少有3 个因数。

7. 10 以内既是奇数又是合数的数是（）A. 7B. 8C. 9D. 5答案：C解析：9 不能被2 整除是奇数，同时除了1 和9 本身还有3 这个因数，所以是合数。

8. 下面算式中，结果最大的是（）A. 300÷8÷6×5B. 300÷(8÷6)×5C. 300÷(8÷6×5)D. 300÷8÷(6×5)答案：C解析：分别计算出每个选项的结果进行比较。

小学五年级数学奥数题100道及答案(完整版)

小学五年级数学奥数题100道及答案(完整版)题目1：计算：1 + 2 + 3 + 4 + 5 + …+ 99 + 100答案：5050解析：这是一个等差数列求和，公式为（首项+ 末项）×项数÷ 2 ，即（1 + 100）×100 ÷2 = 5050题目2：有三个连续自然数，它们的乘积是60，求这三个数。

答案：3、4、5解析：将60 分解质因数60 = 2×2×3×5 = 3×4×5题目3：一个数除以5 余3，除以6 余4，除以7 余5，这个数最小是多少？答案：208解析：这个数加上 2 就能被5、6、7 整除，5、6、7 的最小公倍数是210，所以这个数是210 - 2 = 208题目4：甲、乙两车同时从A、B 两地相向而行，在距A 地60 千米处第一次相遇。

各自到达对方出发地后立即返回，途中又在距A 地40 千米处相遇。

A、B 两地相距多少千米？答案：110 千米解析：第一次相遇时，两车共行了一个全程，甲行了60 千米。

第二次相遇时，两车共行了三个全程，甲行了60×3 = 180 千米。

此时甲距离 A 地40 千米，所以两个全程是180 + 40 = 220 千米，全程为110 千米。

题目5：鸡兔同笼，共有头48 个，脚132 只，鸡和兔各有多少只？答案：鸡30 只，兔18 只解析：假设全是鸡，有脚48×2 = 96 只，少了132 - 96 = 36 只脚。

每把一只鸡换成一只兔，脚多4 - 2 = 2 只，所以兔有36÷2 = 18 只，鸡有48 - 18 = 30 只。

题目6：小明从一楼到三楼用了18 秒，照这样计算，他从一楼到六楼需要多少秒？答案：45 秒解析：一楼到三楼走了 2 层楼梯，每层用时18÷2 = 9 秒。

一楼到六楼走5 层楼梯，用时5×9 = 45 秒。

（完整版）五年级奥数题100题（附答案）

（完整版）五年级奥数题100题（附答案）五年级奥数题100题（附答案）1. 765×213÷27＋765×327÷27解：原式=765÷27×(213+327)= 765÷27×540=765×20=153002. (9999＋9997＋...＋9001)-(1＋3＋ (999)解：原式=（9999-999）+（9997-997）+（9995-995）+……+(9001-1) =9000+9000+…….+9000 (500个9000) =45000003．19981999×19991998-19981998×19991999解：（19981998+1）×19991998-19981998×19991999=19981998×19991998-19981998×19991999+19991998=19991998-19981998=100004．(873×477-198)÷(476×874＋199)解：873×477-198=476×874＋199因此原式=15．2000×1999-1999×1998＋1998×1997-1997×1996＋…＋2×1解：原式＝1999×（2000－1998）＋1997×（1998－1996）＋…＋3×（4－2）＋2×1＝（1999＋1997＋…＋3＋1）×2＝2000000。

6．297＋293＋289＋…＋209解：（209+297）*23/2=58197．计算：解：原式=（3/2）*（4/3）*（5/4）*…*(100/99)*(1/2)*(2/3)*(3/4)*…*(98/99)=50*(1/99)=50/998.解：原式=（1*2*3）/(2*3*4)=1/49.有7个数，它们的平均数是18。

2019小学奥数试题含答案高难度五年级

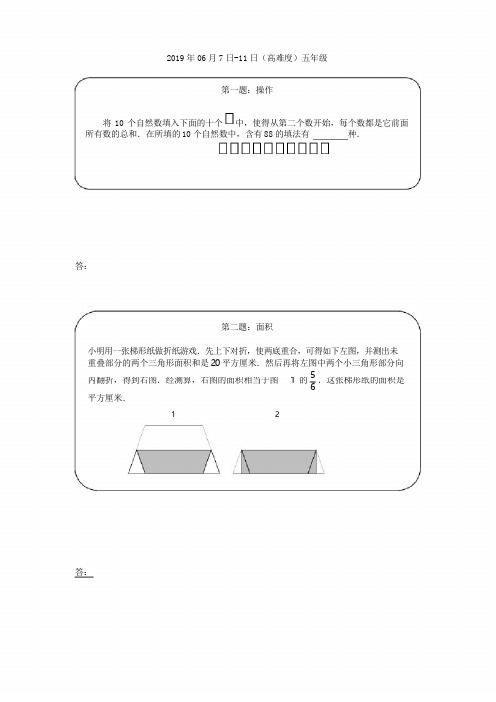
内翻折，得到右图．经测算，右图的面积相当于图 1 的．这张梯形纸的面积是2019 年 06 月 7 日-11 日（高难度）五年级第一题：操作将 10 个自然数填入下面的十个中，使得从第二个数开始，每个数都是它前面所有数的总和．在所填的 10 个自然数中，含有 88 的填法有种．答：第二题：面积小明用一张梯形纸做折纸游戏．先上下对折，使两底重合，可得如下左图，并测出未重叠部分的两个三角形面积和是 20 平方厘米．然后再将左图中两个小三角形部分向56平方厘米．12答：2第三题：假设法小明、小红、小华 3 名同学参加数学竞赛，共10 道题，答对一道题得10 分，答错一道题扣 3 分，如果这 3 名同学都回答了所有的题，小明得了87 分，小红得了 74 分，小华得了 9 分，那么他们三人一共答对了道题．答：计算：第四题：计算(22 + 42 + 62 + ⋅⋅⋅ + 1002 ) - (1 + 32 + 52 + ⋅⋅⋅ + 992 )1 +2 +3 + ⋅⋅⋅ + 9 + 10 + 9 + 8 + ⋅⋅⋅ + 3 + 2 + 1答：第五题：行程狼和狗是死对头，见面就要相互撕咬．一天，它们同时发现了对方，它们之间的距离狼要跑 568 步．如果狼跑 9 步的时间狗跑 7 步，狼跑 5 步的距离等于狗跑 4 步的距离，那么从它们同时奔向对方到相遇，狗跑了多少步？狼跑了多少步？答：将未重叠部分的两个三角形面积折半所减=1021=100积为20÷2=10平方厘米，所以左图的面积===501为10÷=60平方厘米，右图的面积为50600 013，．第一题答案：2019年06月7日-11日（高难度）五年级了3道题；他们三人一共答对了9+8+3=20道题．如果第一个数填的是，那么这十个数依次为：，，，，，，，，，．因为，所以88可能为，，，，即当，22，44，88时，出现88，所以有4种填法．第二题答案：第四题答案：原式(22-12)+(42-32)+(62-52)+⋅⋅⋅+(1002-992)少的面积即是右图的面积和左图的面积之(2+1)⨯(2-1)+(4+3)⨯(4-3)+(6+5)⨯(6-5)+⋅⋅⋅+(100+99)差，即左图的面积的，而折半所减少的面61+2+3+4+⋅⋅⋅+99+100505011001002第五题答案：平方厘米，而整张纸片的面积为右图的面积的2倍，所以这张梯形纸的面积是50⨯2=1平方厘米．第三题答案：如果某个同学10道题都答对了，那么他共得100分．由于答对一道题得10分，答错一道题扣3分，所以，一道答对的题如果变成答错，那么得分相应地减少10+3=13分．由于小明得了87分，比100分少10-8=7分，所以小明答错了13÷13=1道题，答对了9道题；小红得了74分，比100分少100-74=26分，所以小红答错了26÷13=2道题，答对了8道题；小华得了9分，比100分少100-9=91分，所以小华答错了91÷13=7道题，答对可以认为这里的路程单位有狼步，和狗步，为了便于计算我们需要统一成一种单位，由于它们间的路程是“狼步”所以把“狗步”转化为“狼步”为佳，由题目条件知，狼跑36步的时间狗跑28步，狼跑35步的距离等于狗跑28步的距离，也就是说，在相同的时间里，狼跑36“狼步”，狗跑35“狼步”．所以，相遇时，狼跑了：568÷(36+35)⨯36=288（步），狗跑了：288÷9⨯7=224（步）。

(完整word版)奥数题(高难度)

1.图形：（高等难度）如图，长方形ABCD中，E为的AD中点，AF与BE、BD分别交于G、H，OE垂直AD于E，交AF于O，已知AH=5cm，HF=3cm，求AG．图形答案：2.图形面积：（高等难度）直角三角形ABC的两直角边AC=8cm，BC=6cm，以AC、BC为边向形外分别作正方形ACD E与BCFG，再以AB为边向上作正方形ABMN，其中N点落在DE上，BM交CF于点T．问：图中阴影部分(与梯形BTFG)的总面积等于多少？应用题：（高等难度）3.我国某城市煤气收费规定：每月用量在8立方米或8立方米以下都一律收6.9元，用量超过8立方米的除交6.9元外，超过部分每立方米按一定费用交费，某饭店1月份煤气费是82.26元，8月份煤气费是40.02元，又知道8月份煤气用量相当于1月份的，那么超过8立方米后，每立方米煤气应收多少元应用题答案：4.乒乓球训练（逻辑）：（高等难度）甲、乙、丙三人用擂台赛形式进行乒乓球训练，每局2人进行比赛，另1人当裁判．每一局的输方去当下一局的裁判，而由原来的裁判向胜者挑战．半天训练结束时，发现甲共打了15局，乙共打了21局，而丙共当裁判5局．那么整个训练中的第3局当裁判的是_____ __．乒乓球训练（逻辑）答案：本题是一道逻辑推理要求较高的试题．首先应该确定比赛是在甲乙、乙丙、甲丙之间进行的．那么可以根据题目中三人打的总局数求出甲乙、乙丙、甲丙之间的比赛进行的局数．⑴丙当了5局裁判，则甲乙进行了5局；⑵甲一共打了15局，则甲丙之间进行了15-5=10局；⑶乙一共打了21局，则乙丙之间进行了21-5=16局；所以一共打的比赛是5+10+6=31局．此时根据已知条件无法求得第三局的裁判．但是，由于每局都有胜负，所以任意连续两局之间不可能是同样的对手搭配，就是说不可能出现上一局是甲乙，接下来的一局还是甲乙的情况，必然被别的对阵隔开．而总共31局比赛中，乙丙就进行了16局，剩下的甲乙、甲丙共进行了15局，所以类似于植树问题，一定是开始和结尾的两局都是乙丙，中间被甲乙、甲丙隔开．所以可以知道第奇数局(第1、3、5、……局)的比赛是在乙丙之间进行的．那么，第三局的裁判应该是甲．5.奇偶性应用：（高等难度）在圆周上有1987个珠子，给每一珠子染两次颜色，或两次全红，或两次全蓝，或一次红、一次蓝.最后统计有1987次染红，1987次染蓝.求证至少有一珠子被染上过红、蓝两种颜色奇偶性应用答案：假设没有一个珠子被染上过红、蓝两种颜色，即所有珠子都是两次染同色.设第一次染m个珠子为红色，第二次必然还仅染这m个珠子为红色.则染红色次数为2m次。

（完整版）小学五年级奥数题及答案（附精讲）

（完整版）⼩学五年级奥数题及答案（附精讲）⼩学五年级奥训练题及答案（精讲）⼀、⼯程问题1．⼀件⼯作，甲、⼄合做需4⼩时完成，⼄、丙合做需5⼩时完成。

现在先请甲、丙合做2⼩时后，余下的⼄还需做6⼩时完成。

⼄单独做完这件⼯作要多少⼩时？2．修⼀条⽔渠，单独修，甲队需要20天完成，⼄队需要30天完成。

如果两队合作，由于彼此施⼯有影响，他们的⼯作效率就要降低，甲队的⼯作效率是原来的五分之四，⼄队⼯作效率只有原来的⼗分之九。

现在计划16天修完这条⽔渠，且要求两队合作的天数尽可能少，那么两队要合作⼏天？3．甲⼄两个⽔管单独开，注满⼀池⽔，分别需要20⼩时，16⼩时.丙⽔管单独开，排⼀池⽔要10⼩时，若⽔池没⽔，同时打开甲⼄两⽔管，5⼩时后，再打开排⽔管丙，问⽔池注满还是要多少⼩时？4．⼀项⼯程，第⼀天甲做，第⼆天⼄做，第三天甲做，第四天⼄做，这样交替轮流做，那么恰好⽤整数天完⼯；如果第⼀天⼄做，第⼆天甲做，第三天⼄做，第四天甲做，这样交替轮流做，那么完⼯时间要⽐前⼀种多半天。

已知⼄单独做这项⼯程需17天完成，甲单独做这项⼯程要多少天完成？5．师徒俩⼈加⼯同样多的零件。

当师傅完成了1/2时，徒弟完成了120个。

当师傅完成了任务时，徒弟完成了4/5这批零件共有多少个？6．⼀批树苗，如果分给男⼥⽣栽，平均每⼈栽6棵；如果单份给⼥⽣栽，平均每⼈栽10棵。

单份给男⽣栽，平均每⼈栽⼏棵？7．⼀个池上装有3根⽔管。

甲管为进⽔管，⼄管为出⽔管，20分钟可将满池⽔放完，丙管也是出⽔管，30分钟可将满池⽔放完。

现在先打开甲管，当⽔池⽔刚溢出时，打开⼄,丙两管⽤了18分钟放完，当打开甲管注满⽔是，再打开⼄管，⽽不开丙管，多少分钟将⽔放完？8．某⼯程队需要在规定⽇期内完成，若由甲队去做，恰好如期完成，若⼄队去做，要超过规定⽇期三天完成，若先由甲⼄合作⼆天，再由⼄队单独做，恰好如期完成，问规定⽇期为⼏天？9．两根同样长的蜡烛，点完⼀根粗蜡烛要2⼩时，⽽点完⼀根细蜡烛要1⼩时，⼀天晚上停电，⼩芳同时点燃了这两根蜡烛看书，若⼲分钟后来点了，⼩芳将两⽀蜡烛同时熄灭，发现粗蜡烛的长是细蜡烛的2倍，问：停电多少分钟？⼆．鸡兔同笼问题1．鸡与兔共100只，鸡的腿数⽐兔的腿数少28条，,问鸡与兔各有⼏只？三．数字数位问题1．把1⾄2005这2005个⾃然数依次写下来得到⼀个多位数123456789.....2005,这个多位数除以9余数是多少?2．A和B是⼩于100的两个⾮零的不同⾃然数。

奥数题

1.种树挂牌：（高等难度）在10米长的一段马路的一侧种树，每隔1米种一棵，两头都种，共种11棵，如果把三块“爱护树木”的小牌任意挂在三棵树上，然后再把每两棵挂牌的树之间的距离是多少米算出来，看一看这三个距离（即多少米），至少有一个数是偶数，对吗？然后把三块小牌再挂在不同的三棵树上，再算算看。

种树挂牌答案：这三个距离数（即多少米）中，至少有一个数是偶数这话是对的，解答：这三个距离数（即多少米）中，至少有一个数是偶数这话是对的，A树和B树之间的距离AB=3（米）（奇数）B树和C树之间的距离BC=5（米）（奇数）A树和C 树之间的距离AC=3＋5=8（米）（偶数）这是为什么呢？可以这样想：假如距离AB和距离BC之中有一个为偶数，则自不待言，若AB和BC这两个距离都是奇数，则AB和BC之和必是偶数，因为两个奇数之和是偶数，所以说这三个距离中至少有一个是偶数。

2.小华买了一支铅笔，2块橡皮，2个笔记本，付了一元钱，售货员找个他五分钱，小华看了看一支铅笔的价格是8分，就说，叔叔，您把帐算错啦，想一想，小华为什么这么快就知道帐错了？找零问题答案：利用数的奇偶性判断，不用计算就可知道算错了，因为一支铅笔八分钱，是个偶数，另外，不论橡皮和练习本价钱是多少，两块橡皮两个本也肯定是偶数，所以小华应付的总钱数应当是个偶数，他付了1元就是100分，找回的钱是5分是个奇数，所以不需计算就知道算错了。

3.橡皮问题题目：（高等难度）小兰和小绿都有10块橡皮，小兰给小绿2块后，现在小绿比小兰多几块橡皮？橡皮问题题目答案：2×2=4(块)答：现在小绿比小兰多4块橡皮。

4.松树题目：（高等难度）明家门前有一排小树苗，柳树左边有6棵杨树，它的右边有10棵松树，这排小树苗一共有多少棵？松树题目答案：一共有17棵小树苗.5约数：（高等难度）100以内约数个数最多的自然数有五个，它们分别是几？约数答案：如果恰有一个质因数，那么约数最多的是=64，有7个约数；如果恰有两个不同质因数，那么约数最多的是×＝72和×3＝96，各有12个约数；如果恰有三个不同质因数，那么约数最多的是×3×5＝60，×3×7＝84和2××5=90，各有12个约数。

(完整)小学五年级奥数题100道带答案有解题过程

（完整）小学五年级奥数题100道带答案有解题过程姓名：__________班级：__________学号：__________1．一个数的3倍加上6，再减去9，结果是12，求这个数。

解：先从结果逆推，12加上9得到21，再减去6得15，最后除以3得到这个数是5。

思路：按照运算的逆顺序逐步还原。

2．有五个连续自然数的和是100，这五个连续自然数分别是多少？解：设中间的数为x，则这五个数依次是x-2，x-1，x，x+1，x+2，它们的和为5x=100，解得x=20，所以这五个连续自然数是18，19，20，21，22。

思路：利用连续自然数的特点设中间数简化计算。

3．一个长方形的周长是30厘米，长是宽的2倍，求这个长方形的面积。

解：设宽为x厘米，则长为2x厘米，根据周长公式可得（x+2x）×2=30，解得x=5，长为10厘米，面积为5×10=50平方厘米。

思路：根据周长公式列方程求解长和宽，再计算面积。

4．甲乙两数的和是25，甲数比乙数的2倍大1，求甲乙两数分别是多少？解：设乙数为x，则甲数为2x+1，根据和是25可列方程x+2x+1=25，解得x=8，甲数为17。

思路：通过设未知数表示甲乙两数，依据和的关系列方程。

5．一个三角形的面积是36平方厘米，底是9厘米，求高是多少厘米？解：根据三角形面积公式，面积×2÷底=高，即36×2÷9=8厘米。

思路：运用三角形面积公式的变形来求解高。

6．有一堆苹果，平均分给8个人，每人分5个后还剩下3个，这堆苹果一共有多少个？解：8×5+3=43个。

思路：先算出分出去的苹果数再加上剩余的。

7．小明和小红同时从相距500米的两地相向而行，小明每分钟走60米，小红每分钟走40米，几分钟后两人相遇？解：根据相遇时间=路程÷速度和，500÷（60+40）=5分钟。

思路：运用相遇问题的公式求解。

(word完整版)五年级奥数题100题(附答案)

五年级奥数题100题（附答案）1. 765×213÷27＋765×327÷27解：原式=765÷27×(213+327)= 765÷27×540=765×20=153002. (9999＋9997＋...＋9001)-(1＋3＋ (999)解：原式=（9999-999）+（9997-997）+（9995-995）+……+(9001-1) =9000+9000+…….+9000 (500个9000)=45000003．19981999×19991998-19981998×19991999解：（19981998+1）×19991998-19981998×19991999=19981998×19991998-19981998×19991999+19991998=19991998-19981998=100004．(873×477-198)÷(476×874＋199)解：873×477-198=476×874＋199因此原式=15．2000×1999-1999×1998＋1998×1997-1997×1996＋…＋2×1解：原式＝1999×（2000－1998）＋1997×（1998－1996）＋…＋3×（4－2）＋2×1＝（1999＋1997＋…＋3＋1）×2＝2000000。

6．297＋293＋289＋…＋209解：（209+297）*23/2=58197．计算：解：原式=（3/2）*（4/3）*（5/4）*…*(100/99)*(1/2)*(2/3)*(3/4)*…*(98/99)=50*(1/99)=50/998.解：原式=（1*2*3）/(2*3*4)=1/49.有7个数，它们的平均数是18。

五年级奥数题及答案

五年级奥数题及答案1.小学五年级奥数题及答案1、一件工作甲做6时、乙做12时可完成，甲做8时、乙做6时也可以完成。

如果甲做3时后由乙接着做，那么还需多少时间才能完成？解：甲做2小时的等于乙做6小时的，所以乙单独做需要6*3+12=30（小时）甲单独做需要10小时因此乙还需要（1-3/10）/（1/30）=21天才可以完成。

2、有一批待加工的零件，甲单独做需4天，乙单独做需5天，如果两人合作，那么完成任务时甲比乙多做了20个零件。

这批零件共有多少个？解：甲和乙的工作时间比为4：5，所以工作效率比是5：4工作量的比也5：4，把甲做的看作5份，乙做的看作4份那么甲比乙多1份，就是20个。

因此9份就是180个所以这批零件共180个3、挖一条水渠，甲、乙两队合挖要6天完成。

甲队先挖3天，乙队接着解：根据条件，甲挖6天乙挖2天可挖这条水渠的3/5所以乙挖4天能挖2/5因此乙1天能挖1/10，即乙单独挖需要10天。

甲单独挖需要1/（1/6-1/10）=15天。

2.小学五年级奥数题及答案1、一只野兔逃出80步后猎狗才追它，野兔跑8步的路程猎狗只需跑3步，猎狗跑4步的时间兔子能跑9步。

猎狗至少要跑多少步才能追上野兔？解：狗跑12步的路程等于兔跑32步的路程，狗跑12步的时间等于兔跑27步的时间。

所以兔每跑27步，狗追上5步（兔步），狗要追上80步（兔步）需跑［27×（80÷5）＋80］÷8×3＝192（步）。

2、甲、乙两人在铁路旁边以同样的速度沿铁路方向相向而行，恰好有一列火车开来，整个火车经过甲身边用了18秒，2分后又用15秒从乙身边开过。

问：（1）火车速度是甲的速度的几倍？（2）火车经过乙身边后，甲、乙二人还需要多少时间才能相遇？解：（1）设火车速度为a米／秒，行人速度为b米／秒，则由火车的是行人速度的11倍；（2）从车尾经过甲到车尾经过乙，火车走了135秒，此段路程一人走需1350×11=1485（秒），因为甲已经走了135秒，所以剩下的路程两人走还需（1485－135）÷2＝675（秒）。

最难小学奥数题100道及答案(完整版)

最难小学奥数题100道及答案(完整版)题目1：有三个连续的自然数，它们的乘积是60。

这三个数分别是多少？解题方法：将60 分解质因数，60 = 2×2×3×5 = 3×4×5答案：3、4、5题目2：在一个减法算式里，被减数、减数与差的和是180，减数比差大10。

差是多少？解题方法：因为被减数= 减数+ 差，所以被减数+ 减数+ 差= 2×被减数= 180，被减数= 90。

又因为减数-差= 10，减数+ 差= 90，所以差= （90 - 10）÷2 = 40答案：40题目3：甲乙两人同时从A、B 两地相向而行，第一次在离A 地75 千米处相遇，相遇后继续前进，到达目的地后又立即返回，第二次相遇在离 B 地55 千米处。

A、B 两地相距多少千米？解题方法：第一次相遇时，甲走了75 千米，两人共走了一个全程。

从开始到第二次相遇，两人共走了三个全程，所以甲走了75×3 = 225 千米。

此时甲走了一个全程多55 千米，所以全程为225 - 55 = 170 千米答案：170 千米题目4：一个数除以5 余3，除以6 余4，除以7 余5。

这个数最小是多少？解题方法：这个数加上 2 就能被5、6、7 整除，5、6、7 的最小公倍数是210，所以这个数是210 - 2 = 208答案：208题目5：有一堆苹果，平均分给5 个人多4 个，平均分给6 个人多5 个，平均分给7 个人多6 个。

这堆苹果最少有多少个？解题方法：如果这堆苹果再多1 个，就能正好平均分给5 个人、6 个人、7 个人。

5、6、7 的最小公倍数是210，所以这堆苹果最少有210 - 1 = 209 个答案：209 个题目6：一个长方体，如果高增加2 厘米，就变成一个正方体。

这时表面积比原来增加56 平方厘米。

原来长方体的体积是多少立方厘米？解题方法：增加的表面积是 4 个相同的长方形的面积，长方形的宽是2 厘米，长就是正方体的棱长，正方体棱长= 56÷4÷2 = 7 厘米，原长方体高= 7 - 2 = 5 厘米，体积= 7×7×5 = 245 立方厘米答案：245 立方厘米题目7：甲、乙、丙、丁四人拿出同样多的钱，合伙订购同样规格的若干件货物。

人教版2020年五年级奥数试题及答案

人教版2020年五年级奥数试题及答案试题一：数的规律问题：请找出符合下列规律的下一个数字：2, 6, 12, 20, __?答案：该数列的规律是每个数字等于前一个数字加上一个递增的偶数。

具体来说，2+4=6, 6+6=12, 12+8=20。

因此，下一个数字是20+10=30。

试题二：几何问题问题：一个长方形的长是15cm，宽是8cm，请问它的面积是多少？答案：长方形的面积计算公式是面积 = 长 ×宽。

所以，这个长方形的面积是 15cm × 8cm = 120cm²。

试题三：逻辑推理问题：有四个人A、B、C、D。

其中一人说的是真话，其他三人说的是假话。

A说：“B是说真话的。

”B说：“我是说真话的。

”C说：“我没说真话。

”D说：“C是说真话的。

”请问，哪个是说真话的人？答案：如果A说真话，那么B也应该说真话，这与题目条件冲突。

如果B说真话，那么A也应该说真话，这同样冲突。

如果C说真话，那么C自己说假话，这也不符合逻辑。

所以，D说真话，因为如果D说假话，那么C说真话，这与题目条件冲突。

试题四：算式填空问题：在数字1到9中，填入下面的等式，使等式成立：__ + __ + __ = __ + __。

答案：一个可能的答案是：1 + 2 + 3 = 4 + 2。

试题五：组合问题问题：有红、蓝、绿三色的珠子，每种颜色有一个。

如果要从中选出2个珠子，有多少种不同的组合方式？答案：这个问题可以用组合数学中的组合公式来解决。

组合公式是C(n, k) = n! / [k!(n-k)!]，其中n是总数，k是选出的数量，"!"表示阶乘。

所以，C(3, 2) = 3! / [2!(3-2)!] = (3×2×1) / (2×1×1) = 3。

因此，一共有3种不同的组合方式：红蓝、红绿、蓝绿。

---以上就是人教版2020年五年级奥数试题及答案的所有内容，希望对您有所帮助。

五年级奥数高等难度练习题二

1五年级奥数高等难度练习题二数字问题：（高等难度）（高等难度）任意写一个由数字1、2、3组成的三十位数，从这个三十位数中任意截取相邻三位，从这个三十位数中任意截取相邻三位，可得一个三位数。

可得一个三位数。

请证明，在从各个不同位置上截取的所有三位数中，一定有两个相等。

数字答案：由1,2,3组成一个3位数，共有位数，共有个不同三位数。

从一个30位数中截取3位数，共有位数，共有种不同截取方法。

那么，从不同位置截取的28个三位数中，必有其中2个是相同的三位数。

个是相同的三位数。

分苹果问题：（高等难度）（高等难度）把20个苹果分给3个小朋友，每人最少分3个，可以有多少种不同的分法？个，可以有多少种不同的分法？分苹果答案：先给每人2个，还有14个苹果，每人至少分一个，个苹果，每人至少分一个，1313个空插2个板，有个板，有种分法．种分法．数字推理问题：（高等难度）（高等难度）用1、2、3、4、6、7、8、9这8个数组成的2个四位数，使这两个数的差最小（大减小），这个差最小是多少？最小是多少？数字推理答案：若要让差最小，那么，让两数的千位只差1.1.；大数除去千位后的三位数要尽量小，小数除去千位后的；大数除去千位后的三位数要尽量小，小数除去千位后的三位数要尽量大。

三位数要尽量大。

1、2、3、4、6、7、8、9这8个数，能组成的最大三位数为987987，最小三位数为，最小三位数为123123。

但这样的话，剩下。

但这样的话，剩下的4、6差为2，显然不能得到最小差。

那么令千位为3、4，这样，剩余的数字组成的最大数为987987，最小，最小数为126126。

最小差为：。

最小差为： 4126-3987=139 4126-3987=139。

牛吃草问题：（高等难度）（高等难度）一片均匀生长的草地，可以供18头牛吃40天，或者供12头牛与36只羊吃25天，如果1头牛每天的吃草量相当于3只羊每天的吃草量。

五年级奥数大全附答案一

五年级奥数大全附答案一一、拓展提优试题1．（15分）一个自然数恰有9个互不相同的约数，其中3个约数A，B，C满足：①A+B+C＝79②A×A＝B×C那么，这个自然数是．2．（7分）爱尔兰作家刘易斯曾写过一篇反讽寓言，文中描述了一个名为尼亚特泊的野蛮国家．在这个国家里使用西巴巴数字．西巴巴数字的形状与通用的阿拉伯数字相同，但含义相反．如“0”表示“9”，“1”表示“8”，以次类推．他们写数字是从左到右，使用的运算符号也与我们使用的一样．例如，他们用62代表我们所写的37．按照尼亚特泊人的习惯，应怎样写837+742的和是419．【分析】“0”表示“9”，0+9＝9，“1”表示“8”，1+8＝9，由此可知西巴巴数字，表示的数字与正常数字的和都是9；由此找出837、742表示的数字，然后相加即可．3．将等边三角形纸片按图1所示步骤折叠3次（图1中的虚线是三边的中点的连线），然后沿两边的重点的边减去一角（如图2）．将剩下的纸片展开、平铺，得到的图形是A4．如图，甲、乙两人按箭头方向从A点同时出发，沿正方形ABCD的边行走，正方形ABCD的边长是100米，甲的速度是乙的速度的1.5倍，两人在E 点第一次相遇，则三角形ADE的面积比三角形BCE的面积大1000平方米．5．请从1、2、3、…、9、10中选出若干个数，使得1、2、3、…、19、20这20个数中的每个数都等于某个选出的数或某两个选出的数（可以相等）的和．那么，至少需要选出个数．6．甲、乙两人进行射击比赛，约定每中一发得20分，脱靶一发扣12分，两人各打10分，共得208分，最后甲比乙多得64分，乙打中发．7．定义新运算：a&b＝（a+1）÷b，求：2&（3&4）的值为．8．（8分）有四个人甲、乙、丙、丁，乙欠甲1元，丙欠乙2元，丁欠丙3元，甲欠丁4元．要想把他们之间的欠款结清，只因要甲拿出元．9．如图，若每个小正方形的边长是2，则图中阴影部分的面积是．10．（8分）如果两个质数的差恰好是2，称这两个质数为一对孪生质数．例如3和5是一对孪生质数，29和31也是一对孪生质数．在数论研究中，孪生质数是最热门的研究课题之一．华裔数学家张益唐在该课题的研究中取得了令人瞩目的成就，他的事迹激励着更多的青年学子投身数学研究．在不超过100的整数中，一共可以找到对孪生质数．11．用1、2、3、5、6、7、8、9这8个数字最多可以组成个质数（每个数字只能使用一次，且必须使用）．12．小明准备和面包饺子，他在1.5千克面粉中加入了5千克的水，发现面和得太稀了，奶奶告诉他，包饺子的面需要按照3份面，2份水和面，于是小明分三次加入相同分量的面粉，终于将面按按要求和好了，那么他每次加入了千克面粉．13．如图是一个由26个相同的小正方体堆成的几何体，它的底层由5×4个小正方体构成，如果把它的外表面（包括底面）全部涂成红色，那么当这个几何体被拆开后，有3个面是红色的小正方体有块．14．如图，在△ABC中，D、E分别是AB、AC的中点，且图中两个阴影部分（甲和乙）的面积差是5.04，则S＝．△ABC15．（7分）如图，按此规律，图4中的小方块应为个．【参考答案】一、拓展提优试题1．解：一个自然数N恰有9个互不相同的约数，则可得N＝x2y2，或者N＝x8，（1）当N＝x8，则九个约数分别是：1，x，x2，x3，x4，x5，x6，x7，x8，其中有3个约数A、B、C且满足A×A＝B×C，不可能．（2）当N＝x2y2，则九个约数分别是：1，x，y，x2，xy，y2，x2y，xy2，x2y2，其中有3个约数A、B、C且满足A×A＝B×C，①A＝x，B＝1，C＝x2，则x+1+x2＝79，无解．②A＝xy，B＝1，C＝x2y2，则xy+1+x2y2＝79，无解．③A＝xy，B＝x，C＝xy2，则xy+x+xy2＝79，无解．④A＝xy，B＝x2，C＝y2，则xy+x2+y2＝79，解得：，则N＝32×72＝441．⑤A＝x2y，B＝x2y2，C＝x2，则x2y+x2y2+x2＝79，无解．故答案为441．2．解：西巴巴数字8表示阿拉伯数字9﹣8＝1，西巴巴数字3表示阿拉伯数字9﹣3＝6，西巴巴数字7表示阿拉伯数字9﹣7＝2，西巴巴数字4表示阿拉伯数字9﹣4＝5，西巴巴数字2表示阿拉伯数字9﹣2＝7，所以837+742表示的正常算式为：162+257＝419．故答案为：419．3．解：找一剪刀与一等边三角形纸片，按题中所示步骤进行操作，最后得到的图形是A，故答案为：A．4．解：由于甲的速度是乙的速度的1.5倍所以两人速度比为：1.5：1＝3：2，所以两人在E点相遇时，甲行了：（100×4）×＝240（米）；乙行了：400﹣240＝160（米）；则EC＝240﹣100×2＝40（米），DE＝160﹣100＝60（米）；三角形ADE的面积比三角形BCE的面积大：60×100÷2﹣40×100÷2＝3000﹣2000，＝1000（平方米）．故答案为：1000．5．解：列举如下：1＝1；2＝2；3＝1+2；4＝2+2；5＝5；6＝1+5；7＝2+5；8＝8；9＝9；10＝10；11＝1+10；12＝2+10；13＝5+8；14＝7+7；15＝5+10；16＝8+8；17＝8+9；18＝8+10；19＝9+10；通过观察，可看出从1、2、3、…、9、10中选出若干个数分别为{1，2，5，8，9，10}；就能使得1、2、3、…、19、20这20个数中的每个数都等于某个选出的数或某两个选出的数（可以相等）的和．故至少需要选出6个数．故答案为6．6．解：假设全打中，乙得了：（208﹣64）÷2＝72（分），乙脱靶：（20×10﹣72）÷（20+12），＝128÷32，＝4（发）；打中：10﹣4＝6（发）；答：乙打中6发．故答案为：6．7．解：2&（3&4），＝（2+1）÷[（3+1）÷4]，＝3÷1，＝3；故答案为：3．8．解：根据分析，从甲开始，乙欠甲1元，故甲应得1元，甲欠丁4元，故甲应还4元；清算时，甲还应拿出4﹣1＝3元，此时甲的账就结清了；再看看丁的账，丁得到甲的4元后，还给丙3元，即可结清；再看看丙的账，丙得到丁的3元后，还给乙2元，丙的账也清了；再看看乙的账，乙得到丙的2元后，还给甲1元，乙的账也结清；综上，甲只须先拿出4元还给丁，后得到乙的1元，故而甲总共只须拿出3元．故答案是：3．9．解：根据分析，如图，将阴影部分进行剪切和拼接后得：此时，图中阴影部分的小正方形个数为：18个，每个小正方形的面积为：2×2＝4，故阴影部分的面积＝18×4＝72．故答案是：72．10．解：在不超过100的整数中，以下8组：3，5；5，7；11，13；17，19；29，31；41，43；59，61；71，73是孪生质数．故答案为8．11．解：可以组成下列质数：2、3、5、7、61、89，一共有6个．答：用1、2、3、5、6、7、8、9这8个数字最多可以组成 6个质数．故答案为：6．12．解：根据分析，因面和水的比为3：2，即每一份水需要：3÷2＝1.5份面粉，现在有5千克水，则需要面粉：5×1.5＝7.5千克，而现有面粉量为：1.5千克，故还须加：7.5﹣1.5＝6千克，分三次加入，则每次须加入：6÷3＝2千克．故答案是：2．13．解：依题意可知：第一层的共有4个角满足条件．第二层的4个角是4面红色，去掉所有的角块其余的符合条件．分别是3+2+3+2＝10（个）；共10+4＝14（个）；故答案为：1414．解：根据分析，S△BDC＝S△EBC⇒S△DOB＝S△EOC，∴S甲﹣S乙＝（S甲+S△DOB）﹣（S乙+S△EOC）＝5.04，又∵S△BDC ：S△DEC＝BC：DE＝2：1即：S△BDC＝2S△DEC∴S四边形DECB ＝3S△DEC；S△ADE＝S△DEC∴S△ABC ＝S四边形DECB+S△ADE＝4S△DEC，设S△DEC ＝X，则S△BDC＝2X，故有2X﹣X＝5.04，∴X＝5.04，S△ABC ＝4S△DEC＝4X＝4×5.04＝20.16故答案是：20.1615．解：因为图1中小方块的个数为1+2×3＝7个，图2中小方块的个数为1+（1+2）+3×4＝16个，图3中小方块的个数为1+（1+2）+（1+2+3）+4×5＝30个，所以图4中小方块的个数为1+（1+2）+（1+2+3）+（1+2+3+4）+5×6＝50个，故答案为：50．。

小学五年级奥数题及答案自然数

分析：先大概估计一下，30×30×30=27000，远小于42560.40×40×40=64000，远大于42560.因此，要求的三个自然数在30～40之间。
解：42560=26×5×7×19
=25×(5×7)×(19×2)
=32×35×38(合题意)
要求的三个自然数分别是32、35和38。
多做奥数题有助于我们数学思维的提升今天小编为同学们带来的小学五年级奥数题及答案希望同学们能认真去做
小学五年级奥数题及答案自然数
关于小学五年级奥题及答案自然数
多做奥数题有助于我们数学思维的提升，今天店铺为同学们带来的小学五年级奥数题及答案希望同学们能认真去做。
小学五年级奥数题及答案:自然数
三个自然数，最大的比最小的大6，另一个是它们的平均数，且三数的'乘积是42560.求这三个自然数。

小学五年级各类题型奥数题及答案

小学五年级各类题型奥数及答案面积计算(五年级奥数题)1、（05年三帆中学考题）右图中AB=3厘米，CD=12厘米，ED=8厘米，AF=7厘米.四边形ABDE的面积是( )平方厘米．2、如图，已知每个小正方形格的面积是1平方厘米，则不规则图形的面积是______．面积计算(答案)1、（05年三帆中学考题）右图中AB=3厘米，CD=12厘米，ED=8厘米，AF=7厘米.四边形ABDE的面积是( )平方厘米．解：阴影面积=1/2×ED×AF+1/2×AB×CD=1/2×8×7+1/2×3×12=28+18=46。

2、如图，已知每个小正方形格的面积是1平方厘米，则不规则图形的面积是______．解答：基本的格点面积的求解，可以用解答种这样的方法求解，当然也可以用格点面积公式来做，内部点有16个，周边点有8个，所以面积为16+8÷2-1=19图形面积(一)(五年级奥数题)1、（06年清华附中考题）如图，在三角形ABC中，D为BC的中点，E为AB上的一点，且BE=1 /3AB,已知四边形EDCA的面积是35，求三角形ABC的面积.2、正方形ABFD的面积为100平方厘米，直角三角形ABC的面积，比直角三角形（CDE的面积大30平方厘米，求DE的长是多少？ 04.jpg图形面积(一)(答案)1、（06年清华附中考题）如图，在三角形ABC中，D为BC的中点，E为AB上的一点，且BE=1 /3AB,已知四边形EDCA的面积是35，求三角形ABC的面积.解答：根据定理：所以四边形ACDE的面积就是6-1=5份，这样三角形35÷5×6=42。

2、正方形ABFD的面积为100平方厘米，直角三角形ABC的面积，比直角三角形（CDE的面积大30平方厘米，求DE的长是多少？解：公共部分的运用，三角形ABC面积-三角形CDE的面积=30，两部分都加上公共部分（四边形BCDF），正方形ABFD-三角形BFE=30，所以三角形BFE的面积为70，所以FE的长为70×2÷10=14，所以DE=4。