线性代数A卷
线性代数试题A及答案
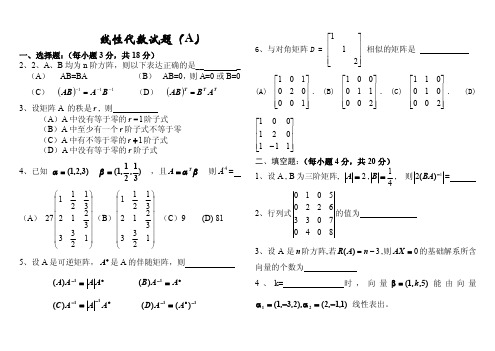
线性代数试题(A )一、选择题:(每小题3分,共18分)2、2、A 、B 均为n 阶方阵,则以下表达正确的是__ _ (A ) AB=BA (B ) AB=0,则A=0或B=0 (C ) ()111---=B A AB (D ) ()T T TA B AB =3、设矩阵A 的秩是r , 则(A )A 中没有等于零的1-r 阶子式 (B )A 中至少有一个r 阶子式不等于零 (C )A 中有不等于零的1+r 阶子式 (D )A 中没有等于零的r 阶子式4、已知 )3,2,1(=a )31,21,1(=b ,且b a T A = 则4A =(A ) 27÷÷÷÷÷÷øöççççççèæ1233321231211(B )÷÷÷÷÷÷øöççççççèæ1233321231211 (C )9 (D) 81 5、设A 是可逆矩阵,*A 是A 的伴随矩阵,则*-=A A A A 1)( *-=A A B 1)( *--=A AA C 11)( 11)()(-*-=A A D6、与对角矩阵D = úúúûùêêêëé211 相似的矩阵是 (A) úúúûùêêêëé100020101. (B) úúúûùêêêëé200110001. (C) úúúûùêêêëé200010011. (D) úúúûùêêêëé-111021001 二、填空题:(每小题4分,共20分)1、设A , B 为三阶矩阵, 2=A ,41=B , 则12-)(BA = 2、行列式8040703362205010的值为 3、设A 是n 阶方阵,若3-=n A R )(,则0=AX 的基础解系所含向量的个数为4、k= 时,向量)5,,1(k =b 能由向量)1,1,2(),2,3,1(21-=a -=a 线性表出。
12-13-1《线性代数试卷A》第一学期期末考试试卷

河南理工大学 2012-2013 学年第 1 学期《线性代数》试卷(A 卷)1.设()()(),,,,,,,,t 3,1321111321===βββ若321βββ,,线性相关,则t =.2.矩阵()nn ija ⨯=A 的全体特征值的和等于 , 全体特征值的积等于.3.设A 为4阶方阵,2-=A ,则A 3-= .4.()234321,,B ,A =⎪⎪⎪⎭⎫ ⎝⎛=,则=AB.5.设三阶方阵⎪⎪⎪⎭⎫ ⎝⎛--=120350002A ,则A 的逆矩阵1-A =.6.设3阶方阵A 按列分块为()321ααα,,A =,且Ad e t =5,又设()231215432ααααα,,B ++=,则B =.7.设⎪⎪⎪⎭⎫ ⎝⎛--=11334221xA ,x 为某常数,B 为3阶非零矩阵,且0AB =,则x = . 8.设三元非齐次线性方程组的系数矩阵的秩为2,已知21ηη,是它的两个解向量.且⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎭⎫ ⎝⎛=42232121ηη,该方程组的通解为.1.设A 与B 均为n 阶方阵,则下列结论中成立的为().(A) det(AB ) = 0,则0A =或0B =; (B) det(AB ) = 0,则det A = 0或det B = 0; (C) AB = 0,则0A =或0B =; (D) AB ≠ 0,则det A ≠ 0或det B ≠ 0.2. 设n 阶矩阵A 的行列式0≠A ,*A 是A 的伴随矩阵,则( ).(A) 2-=n *A A ; (B) 1+=n *A A ; (C) 1-=n *AA ;(D) 2+=n *AA .3. 已知A 、B 均为3阶方阵,且A 与B 相似,若A 的特征值为1,2,3,则()12-B 的特征值为( )(A) 2312,,; (B) 614121,,; (C) 321,,;(D) 3212,,.4. 向量组321,,βββ线性无关,324,,βββ线性相关,则有 .(A)1β可由324,,βββ线性表示; (B)3β可由42ββ,线性表示 ;(C)2β可由43ββ,线性表示;(D)4β可由32ββ,线性表示 .三、计算题1.(7分)计算行列式211112111121=n D .一、填空题,每小题4分二、选择题,每小题5分2.(7分)设⎪⎪⎪⎭⎫⎝⎛---=121011332A ,求1-A .3.(7分)求矩阵⎪⎪⎪⎪⎪⎭⎫⎝⎛---=1401131********12211A 的列向量组的一个最大线性无关组.4.(12分)λ取何值时,非齐次线性方程组⎪⎩⎪⎨⎧=++=++=++23213213211λλλλλx x x x x x x x x ,,(1)有唯一解;(2)无解;(3)有无穷多个解?5.(15分)已知二次型()322221321434x x x x x ,x ,x f ++=,求一个正交变换Py x =,把二次型()321x ,x ,x f 化为标准型.。
《线性代数》-期终A卷

杭州电子科技大学继续教育学院学生考试卷( A )卷A 表示方阵A 的行列式,r (A )表示矩阵A 的秩。
一、单项选择题(本大题共10小题,每小题2分,共20分)在每小题列出的四个备选项中只有一个是符合题目要求的,请将其代码填写在题后的括号内。
错选、多选或未选均无分。
1.3阶行列式011101110---=ij a 中元素a 21的代数余子式A 21=( ) A .-2 B .-1 C .-1D .22.若120231101λλ=0,则12λλ、必须满足( )A .1220λλ==,B 122λλ==C 122λλ=,可为任意数D 12λλ、均可为任意数 3.有矩阵3223,33,A B C ⨯⨯⨯,下列矩阵运算可行的是( ) A AC B ABC C BAC D AB BC -4.如果线性方程组12323331223(1)(3)(1)x x x x x x x λλλλλλ++=-⎧⎪-=-⎪⎨=-⎪⎪-=---⎩有唯一解,则λ=( )A 1或2B —1或3C 1或3D 1-或3- 5.设向量组α1, α2, α3, α4线性相关,则向量组中( ) A .必有一个向量可以表为其余向量的线性组合 B .必有两个向量可以表为其余向量的线性组合 C .必有三个向量可以表为其余向量的线性组合 D .每一个向量都可以表为其余向量的线性组合6.设A=1243⎛⎫⎪⎝⎭, B=12x y ⎛⎫ ⎪⎝⎭,则A 与B 可交换的充分必要条件是( ) A 1x y -= B 1x y -=- C x y = D 2x y = 7.下列矩阵不是初等矩阵的是( )A 100001010⎛⎫⎪⎪ ⎪⎝⎭ B001010100⎛⎫⎪- ⎪ ⎪⎝⎭ C 1001002001⎛⎫⎪⎪- ⎪ ⎪⎝⎭D100014001⎛⎫ ⎪- ⎪ ⎪⎝⎭8.已知向量组 123(1,2,1,1),(2,0,,0),(0,4,5,2)t ααα=-==--,的秩为2,则t =( ) A 3 B 3- C 2 D 2-9.四元线性方程组 1421400x x x x x ⎧+=⎪=⎨⎪-=⎩的基础解系是( )A (0,0,0,0)TB (0,0,2,0)TC (1,0,1)T- D (0,0,2,0)T和 (0,0,0,1)T10.三阶矩阵A 的特征值为 2,1,3.-则下列矩阵中非奇异矩阵是( ) A 2I -A B 2I+A C I -A D A -3I 二、填空题(本大题共10小题,每小题2分,共20分)请在每小题的空格中填上正确答案。
(完整版)线性代数测试试卷及答案

线性代数(A 卷)一﹑选择题(每小题3分,共15分)1。
设A ﹑B 是任意n 阶方阵,那么下列等式必成立的是( ) (A )AB BA = (B)222()AB A B = (C)222()2A B A AB B +=++ (D )A B B A +=+2。
如果n 元齐次线性方程组0AX =有基础解系并且基础解系含有()s s n <个解向量,那么矩阵A 的秩为( )(A) n (B) s (C ) n s - (D) 以上答案都不正确 3。
如果三阶方阵33()ij A a ⨯=的特征值为1,2,5,那么112233a a a ++及A 分别等于( ) (A) 10, 8 (B) 8, 10 (C) 10, 8-- (D) 10, 8--4。
设实二次型11212222(,)(,)41x f x x x x x ⎛⎫⎛⎫= ⎪ ⎪-⎝⎭⎝⎭的矩阵为A ,那么( )(A) 2331A ⎛⎫=⎪-⎝⎭ (B) 2241A ⎛⎫= ⎪-⎝⎭ (C) 2121A ⎛⎫= ⎪-⎝⎭(D) 1001A ⎛⎫= ⎪⎝⎭ 5. 若方阵A 的行列式0A =,则( ) (A ) A 的行向量组和列向量组均线性相关 (B )A 的行向量组线性相关,列向量组线性无关 (C ) A 的行向量组和列向量组均线性无关 (D )A 的列向量组线性相关,行向量组线性无关 二﹑填空题(每小题3分,共30分)1 如果行列式D 有两列的元对应成比例,那么该行列式等于 ;2。
设100210341A -⎛⎫⎪=- ⎪⎪-⎝⎭,*A 是A 的伴随矩阵,则*1()A -= ; 3. 设α,β是非齐次线性方程组AX b =的解,若λαμβ+也是它的解, 那么λμ+= ; 4. 设向量(1,1,1)T α=-与向量(2,5,)T t β=正交,则t = ; 5。
设A 为正交矩阵,则A = ;6。
设,,a b c 是互不相同的三个数,则行列式222111ab c a b c = ; 7。
中国海洋大学《线性代数》2016-2017学年第二学期期末试卷A卷

一、填空题(共 18分)1.设 A 是3阶方阵,|A|=3,A∗为 A 的伴随矩阵,则|3A−1|=( ),|A∗|=( ),|3A∗−7A−1|=( ).2.设α=(1,−2,3)T,β=(−1, 12,0),A=αβ,则|A100|=( ).3.设向量α=(1k 1)是矩阵A=(211121112) 的一个特征向量,则k=().4.A为3阶实对称矩阵,向量 ξ1=(1,2,5)T,ξ1=(k,2k,3)T是分别对应于特征值2和3的特征向量, 则 k=().5.设 η1,η2,η3为4元非齐次线性方程组 Ax=b 的三个解,r(A)=3,已知η1+η2=(3,4,5,6)T,η3=(1,2,3,4)T,则 Ax=b 的一般解为( ).二、选择题(共 6 题,每题 3分,共 18 分)1.设 M、P 为 n 阶矩阵,且 P 可逆,则下列运算不正确的是( ).A. |M|=|P−1MP|;B. |2E−M|=|2E−P−1MP|;C. |2E−M|=|2E−(P−1MP)T|;D. P−1MP=M.2.设 M、N、P 为同阶矩阵,下列结论成立的有( ).A. MN=NM;B. (M+N)−1=M−1+N−1;C. 若 MP=NP,则M=N;D. (M+N)T=M T+N T.3.设 A 为 m×n 矩阵,线性方程组 Ax=b 有解的充分条件为( ).A. 矩阵A 行满秩;B. 矩阵A 列满秩;C. 矩阵A 的秩小于其行数;D. 矩阵A 的秩小于其列数.4.设 A 是 n 阶实对称矩阵,P 是 n 阶可逆矩阵;若 n 维列向量 α 是 A 的属于特征值 λ 的特征向量,则矩阵 (P−1AP)T的属于特征值 λ 的特征向量是( ).A. P−1α;B. P Tα;C. Pα;D. (P−1)Tα.5.设向量 α,β,γ 线性无关,α,β,δ 线性相关,下列哪个成立().中国海洋大学《线性代数》2016-2017学年第二学期期末试卷A卷A. α 必可由 β,γ,δ 线性表示;B. β 必不可由 α,γ,δ 线性表示;C. δ 必可由 α,β,γ 线性表示;D. δ 必不可由 α,β,γ 线性表示.6.设 A 是 n (n ≥2)阶可逆矩阵,交换 A 的第1行与第2行得矩阵 B ;A ∗、B ∗分别为 A 、B 的伴随矩阵,则( ).A. 交换 A ∗的第一列与第二列得 B ∗;B. 交换 A ∗的第一行与第二行得 B ∗;C. 交换 A ∗的第一列与第二列得 −B ∗;D. 交换 A ∗的第一行与第二行得 −B ∗.三、计算题(共 4题,共 28 分)1.计算行列式的值:|−a 1a 10⋯000−a 2a 2⋯00⋮⋮⋮⋮⋮000⋯−a n a n 111⋯11|. 2.矩阵 A =(11−1−1111−11),矩阵 X 满足 A ∗X =A −1+2X ,其中 A ∗是 A 的伴随矩阵,求矩阵 X .3.已知 R 3的两组基 B 1={α1,α2,α3}和 B 2={β1,β2,β3},其中α1=(1,1,1)T ,α2=(0,1,1)T , α3=(0,0,1)T ;β1=(1,0,1)T ,β2=(0,1,−1)T ,β3=(1,2,0)T .(1)求基 B 1到基 B 2的过渡矩阵 A ;(2)已知 α 在基 B 1下的坐标向量为 (1,−2,−1)T ,求 α 在基 B 2下的坐标向量.4.求向量组 α1=(1,0,1,0), α2=(2,1,−3,7), α3=(4,1,−1,7), α4=(3,1,0,3), α5=(4,1,3,−1) 的秩,及其一个极大线性无关组,并将其余向量用极大线性无关组线性表示.四、证明题(共 1题,共 8 分)设 A 为 n 阶方阵,且 4A 2−I =O ,证明:(1) A 的特征值只能为− 1 2或 1 2;(2) r (2A +I )+r (2A −I )=n.五、解方程组(共1题,13分)当 λ 取何值时,线性方程组 {(1+λ)x 1+x 2+x 3=0x 1+(1+λ)x 2+x 3=3x 1+x 2+(1+λ)x 3=λ无解、有唯一解、有无穷多解?并在有无穷多解时求其通解.六、二次型(共1题,12分)二次型 f (x 1,x 2,x 3)=5x 12+5x 22+cx 32+2x 1x 2+4x 1x 3−4x 2x 3 的秩为2,(1)求 c ;(2)用正交变换法将二次型化为标准形,并写出对应的正交矩阵.一、填空题(共 18分)1.设 A 是3阶方阵,|A |=3,A ∗为 A 的伴随矩阵,则 |3A −1|=( ), |A ∗|=( ),|3A ∗−7A −1|=( ).解:|3A −1|=33|A−1|=331|A |=9;|A ∗|=|A |3−1=9; |3A ∗−7A −1|=|3|A |A −1−7A−1|=|2A −1|=23|A −1|= 8 3. 2.设 α=(1,−2,3)T ,β=(−1, 1 2,0),A =αβ,则 |A 100|=( ).解:A =αβ=(1−23)(−1, 1 2,0)= 1 2(−2104−20−630)⟹|A |=0 |A 100|=|A|100=0.3.设向量 α=(1k 1) 是矩阵 A =(211121112) 的一个特征向量,则 k =( ).解:设向量 α 是 A 的特征值 λ 对应的特征向量,则 Aα=λα,即 (211121112)(1k 1)=λ(1k 1)⟹{2+k +1=λ1+2k +1=λk ⟹(k −1)=λ(k −1)⟹{k −1=0⟹k =1,λ=4;k −1≠0⟹λ=1,k =−2. 4.A 为3阶实对称矩阵,向量 ξ1=(1,2,5)T ,ξ1=(k,2k,3)T 是分别对应于特征值2和3的特征向量, 则 k =( ).解:由题意知:ξ1,ξ2 正交,即 (ξ1,ξ2)=0⟹1∙k +2∙2k +5∙3=0从而 k =−3.5.设 η1,η2,η3 为4元非齐次线性方程组 Ax =b 的三个解,r (A )=3,已知 η1+η2=(3,4,5,6)T ,η3=(1,2,3,4)T ,则 Ax =b 的一般解为( ). 解:r (A )=3⟹Ax =0 的基础解系含有 4−r (A )=1 个向量.Ax =b 的一般解为 x =x 0+kξ;答案(1) x0可取 η3;(2)取 ξ=(η1−η3)+(η2−η3)=η1+η2−2η3=(1,0,−1,−2)T;于是,Ax=b 的一般解x=(1,2,3,4)T+k(1,0,−1,−2)T,k 任意.二、选择题(共 6 题,每题 3分,共 18 分)1.设 M、P 为 n 阶矩阵,且 P 可逆,则下列运算不正确的是( D ).A. |M|=|P−1MP|;B. |2E−M|=|2E−P−1MP|;C. |2E−M|=|2E−(P−1MP)T|;D. P−1MP=M.解:A. |M|=|P−1MP|=|P−1|∙|M|∙|P|=|M|;B. |2E−M|=|P−1|∙|2E−M|∙|P|=|P−1(2E−M)P|=|2E−P−1MP|;C. |2E−(P−1MP)T|=|(2E−P−1MP)T|=|2E−P−1MP|=|2E−M|;D. P−1MP=M结论不一定成立;MP不一定等于PM.2.设 M、N、P 为同阶矩阵,下列结论成立的有( D ).A. MN=NM;B. (M+N)−1=M−1+N−1;C. 若 MP=NP,则M=N;D. (M+N)T=M T+N T.3.设 A 为 m×n 矩阵,线性方程组 Ax=b 有解的充分条件为( A ).A. 矩阵A 行满秩;B. 矩阵A 列满秩;C. 矩阵A 的秩小于其行数;D. 矩阵A 的秩小于其列数.解:A 行满秩⟹r(A,b)=r(A)⟺Ax=b 有解.4.设 A 是 n 阶实对称矩阵,P 是 n 阶可逆矩阵;若 n 维列向量 α 是 A 的属于特征值 λ 的特征向量,则矩阵 (P−1AP)T的属于特征值 λ 的特征向量是( B ).A. P−1α;B. P Tα;C. Pα;D. (P−1)Tα.解:已知 Aα=λα,且 A T=A;记 P−1AP=Q,则 (P−1AP)T=Q T;则PQ=AP⟹Q T P T=P T A T,A 对称⟹Q T P T=P T A⟹Q T P Tα=P T Aα=λP Tα.5.设向量 α,β,γ 线性无关,α,β,δ 线性相关,下列哪个成立( C ).A. α 必可由 β,γ,δ 线性表示;B. β 必不可由 α,γ,δ 线性表示;C. δ 必可由 α,β,γ 线性表示;D. δ 必不可由 α,β,γ 线性表示.解:α,β,γ 线性无关,则 α,β 线性无关;又 α,β,δ 线性相关,则 δ 可由 α,β 线性表示,即 δ=k 1α+k 2β=k 1α+k 2β+0γ.6.设 A 是 n (n ≥2)阶可逆矩阵,交换 A 的第1行与第2行得矩阵 B ;A ∗、B ∗分别为 A 、B 的伴随矩阵,则( C ).A. 交换 A ∗的第一列与第二列得 B ∗;B. 交换 A ∗的第一行与第二行得 B ∗;C. 交换 A ∗的第一列与第二列得 −B ∗;D. 交换 A ∗的第一行与第二行得 −B ∗.解:A r 1↔r 2 ⇒ B ,则 B =E 12A ⟹{|B |=|E 12A|=−|A | B −1=(E 12A)−1=A −1E 12−1=A −1E 12于是 B ∗=|B |B −1=−|A |A −1E 12=−A ∗E 12;得 −B ∗=A ∗E 12⟺ 交换 A ∗的第1列和第2列得到 −B ∗.三、计算题(共 4题,共 28 分)1.计算行列式的值:|−a 1a 10⋯000−a 2a 2⋯00⋮⋮⋮⋮⋮000⋯−a n a n 111⋯11|. 解:行列式c 1+c 2+⋯+c n+10a 10⋯000−a 2a 2⋯00⋮⋮⋮ ⋮⋮000⋯−a n a n n +111⋯11|=(n +1)∙(−1)n+1+1|a 10⋯00−a 2a 2⋯00⋮⋮ ⋮⋮00⋯−a n a n| =(−1)n (n +1)a 1a 2⋯a n .2.矩阵 A =(11−1−1111−11),矩阵 X 满足 A ∗X =A −1+2X ,其中 A ∗是 A 的伴随 矩阵,求矩阵 X .解:A ∗X =A −1+2X ⟹(A ∗−2I )X =A −1⟹A (A ∗−2I )X =AA −1=I ⟹(|A |I −2A )X =I⟹X =(|A |I −2A)−1;又 |A |=4,则 |A |I −2A =(2−2222−2−222)=2(1−1111−1−111)=2B ,这里 B =(1−1111−1−111);从而 X =(2B)−1= 1 2B −1 由 (B,I )=(1−1111−1−111 1000 1 0001)初等行变换⇒ (1000 10001 1/21/2001/21/21/201/2)=(I,B −1), 得 B −1= 1 2(1100 11101),于是 X = 1 4(1100 11101). 3.已知 R 3的两组基 B 1={α1,α2,α3}和 B 2={β1,β2,β3},其中 α1=(1,1,1)T ,α2=(0,1,1)T , α3=(0,0,1)T ; β1=(1,0,1)T ,β2=(0,1,−1)T ,β3=(1,2,0)T .(1)求基 B 1到基 B 2的过渡矩阵 A ;(2)已知 α 在基 B 1下的坐标向量为 (1,−2,−1)T ,求 α 在基 B 2下的坐标向量. 解:仍记 B 1=(α1,α2,α3),B 2=(β1,β2,β3).(1)由 (β1,β2,β3)=(α1,α2,α3)A ,即得 B 2=B 1A ,于是,(B 1,B 2)=(1001011100121111−10)初等行变换⇒ (100101010−1110011−2−2)=(I,A )则基 B 1到基 B 2的过渡矩阵 A =(101−1111−2−2).(2)两种方法:已知 αB 1=(1,−2,−1)T方法1:α=B 1αB 1=(1,−1,−2)T ,又有 α=B 2αB 2,则求解该方程组(B 2,α)=(1010121−10|1−1−2)初等行变换⇒ (100010001|57−4),则 α 在基 B 2下的坐标向量 αB 2=(5,7,−4)T .方法2:因为 A αB 2=αB 1,求解该方程组(A ,αB 1)=(101−1111−2−2|1−2−1)初等行变换⇒ (100010001|57−4),则 α 在基 B 2下的坐标向量 αB 2=(5,7,−4)T .4.求向量组 α1=(1,0,1,0), α2=(2,1,−3,7), α3=(4,1,−1,7), α4=(3,1,0,3), α5=(4,1,3,−1) 的秩,及其一个极大线性无关组,并将其余向量用极大线性无关组线性表示.解:记矩阵A =(α1T ,α2T ,α3T ,α4T ,α5T )=(12434011111−3−1030773−1) 初等行变换 ⇒ (102000110−10001200000),则 (1)秩{α1,α2,α3,α4,α5}=3;(2)α1,α2,α4 是向量组 α1,α2,α3,α4,α5 的一个极大线性无关组;(3)α3=2α1+α2,α5=−α2+2α4.四、证明题(共 1题,共 8 分)设 A 为 n 阶方阵,且 4A 2−I =O ,证明:(1) A 的特征值只能为− 1 2或 1 2;(2) r (2A +I )+r (2A −I )=n. 证:(1)设 A 的特征值为 λ,则 4A 2−I 的特征值为 4λ2−1,因为 4A 2−I =O ,而零矩阵 O 的特征值均为0,于是有 4λ2−1=0⟹λ=− 1 2或 1 2; (2)4A 2−I =O ⟹(2A +I)(2A −I )=O ,则① r (2A +I )+r (2A −I )≤n ;② r (2A +I )+r (2A −I )=r (2A +I )+r (I −2A )≥r(2A +I +(I −2A ))=r (2I )=n ;于是,r (2A +I )+r (2A −I )=n .五、解方程组(共1题,13分)当 λ 取何值时,线性方程组{(1+λ)x 1+x 2+x 3=0x 1+(1+λ)x 2+x 3=3x 1+x 2+(1+λ)x 3=λ无解、有唯一解、有无穷多解?并在有无穷多解时求其通解.解:系数矩阵 A =(1+λ1111+λ1111+λ),b =(03λ).又 |A |=|1+λ1111+λ1111+λ|=λ2(λ+3)①当 |A |≠0,即当 λ≠0 且 λ≠−3 时,方程组有唯一解; ②当 λ=0 时,增广矩阵(A,b )=(111111111| 030)初等行变换⇒ (111000000| 030) 方程组出现矛盾方程,则原方程组无解;③当 λ=−3 时,增广矩阵(A,b )=(−2111−2111−2|03−3)初等行变换⇒ (10−101−1000| −1−20)=(U,d)取 x 3 为自由未知量,1)令 x 3=0,代入 Ux =d ,得原方程组的一个特解 x 0=(−1,−2,0)T ;2)令 x 3=1,代入 Ux =0,得 Ax =0 的一个基础解系 ξ=(1,1,1)T ;则原方程组的通解为 x =x 0+kξ=(−1−20)+k (111),k 任意;综上,{当 λ≠0 且 λ≠−3时,方程组有唯一解;当 λ=0 时,方程组无解;当 λ=−3时,方程组有无穷多解.六、二次型(共1题,12分)二次型 f (x 1,x 2,x 3)=5x 12+5x 22+cx 32+2x 1x 2+4x 1x 3−4x 2x 3 的秩为2, (1)求 c ;(2)用正交变换法将二次型化为标准形,并写出对应的正交矩阵.解:二次型对应的矩阵为 A =(51215−22−2c), (1)已知 r (A )=2⟹|A |=0,得 c =2;(2)A 的特征多项式 |λI −A |=|λ−5−1−2−1λ−52−22λ−2|=λ(λ−6)2,A 的特征值为 λ1=λ2=6,λ3=0;①对于 λ1=λ2=6,由(λ1I −A)x =0,即 (1−1−2−112−224)(x 1x 2x 3)=0,得基础解系 {ξ1=(1,1,0)T ξ2=(2,0,1)T , 1)正交化:取 β1=ξ1=(1,1,0)T ,令 β2=ξ2−(ξ2,β1)(β1,β1)β1=(1,−1,1)T , 2)单位化:令 η1=1‖β1‖β1=(1√2,1√2,0)T ; η2=1‖β2‖β2=(1√3,−1√31√3)T; ②对于特征值 λ3=0,由(λ3I −A)x =0⟺Ax =0,即 (51215−22−22)(x 1x 2x 3)=0,得基础解系为 ξ3=(−1,1,2)T ,单位化得:η3=1‖ξ3‖ξ3=(−1√6,1√6,2√6)T; ③记矩阵 Q =(η1,η2,η3)=( √2√3√6√2√3√60√3√6) ,则 Q 为正交阵, 且使得 Q T AQ =Q −1AQ =Λ=(660)④令 x =(x 1,x 2,x 3)T ,y =(y 1,y 2,y 3)T ,做正交变换 x =Qy ,原二次型就化成标准形 x T Ax =y T (Q T AQ )y =6y 12+6y 22.。
(完整版)线性代数试卷及答案详解

《线性代数A 》试题(A 卷)试卷类别:闭卷考试时间:120分钟考试科目:线性代数考试时间:学号:姓名:3的一组标准正交基,=___________《线性代数A》参考答案(A卷)一、单项选择题(每小题3分,共30分)二、填空题(每小题3分,共18分)1、 256;2、 132465798⎛⎫ ⎪--- ⎪ ⎪⎝⎭; 3、112211221122000⎛⎫⎪- ⎪ ⎪-⎝⎭; 4、; 5、 4; 6、 2 。
三. 解:因为矩阵A 的行列式不为零,则A 可逆,因此1X A B -=.为了求1A B -,可利用下列初等行变换的方法:231211201012010*******121011411033110331023211027210027810027801141010144010144001103001103001103---⎛⎫⎛⎫⎛⎫⎪⎪⎪-−−→-−−→-- ⎪ ⎪ ⎪ ⎪ ⎪ ⎪--⎝⎭⎝⎭⎝⎭-⎛⎫⎛⎫⎛⎫⎪⎪⎪−−→--−−→-−−→-- ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭―――――(6分)所以1278144103X A B -⎛⎫ ⎪==-- ⎪ ⎪⎝⎭.―――――(8分)四.解:对向量组12345,,,,ααααα作如下的初等行变换可得:1234511143111431132102262(,,,,)21355011313156702262ααααα--⎛⎫⎛⎫⎪ ⎪----- ⎪ ⎪=→ ⎪ ⎪--- ⎪ ⎪ ⎪ ⎪---⎝⎭⎝⎭111431212011310113100000000000000000000--⎛⎫⎛⎫⎪⎪---- ⎪ ⎪→→⎪ ⎪⎪ ⎪⎪ ⎪⎝⎭⎝⎭――――(5分)从而12345,,,,ααααα的一个极大线性无关组为12,αα,故秩12345{,,,,}ααααα=2(8分)且3122ααα=-,4123ααα=+,5122ααα=--――――(10分) 五.解:对方程组的增广矩阵进行如下初等行变换:221121121121110113011311101112002421120113400(2)(1)42p p p p p p p p p p p p p p p p p p p p p ---⎛⎫⎛⎫⎛⎫⎪ ⎪ ⎪−−→--−−→-- ⎪ ⎪ ⎪ ⎪ ⎪ ⎪--+--+⎝⎭⎝⎭⎝⎭-⎛⎫ ⎪−−→------- ⎪ ⎪-+-+⎝⎭(分)(1) 当10,(2)(1)0,p p p -≠-+-≠且时即1,2,p p ≠≠-且时系数矩阵与增广矩阵的秩均为3,此时方程组有唯一解.――――(5分) (2) 当1,p =时系数矩阵的秩为1,增广矩阵的秩为2,此时方程组无解.――――(6分)(3) 当2,p =-时此时方程组有无穷多组解. 方程组的增广矩阵进行初等行变换可化为1122112211221211033301112111033300001011011180000------⎛⎫⎛⎫⎛⎫⎪ ⎪ ⎪-−−→-−−→-- ⎪ ⎪ ⎪⎪ ⎪ ⎪---⎝⎭⎝⎭⎝⎭--⎛⎫⎪−−→------ ⎪ ⎪⎝⎭(分)故原方程组与下列方程组同解:132311x x x x -=-⎧⎨-=-⎩ 令30,x =可得上述非齐次线性方程组的一个特解0(1,1,0)Tξ=--;它对应的齐次线性方程组13230x x x x -=⎧⎨-=⎩的基础解系含有一个元素,令31,x =可得1(1,1,1)T ξ=为该齐次线性方程组的一个解,它构成该齐次线性方程组的基础解系.此时原方程组的通解为001101,,.k k k k ξξ+这里为任意常数――――(12分)六.解:(1)由于A的特征多项式2124||222(3)(6)421I A λλλλλλ----=-+-=+----故A 的特征值为13λ=-(二重特征值),36λ=。
全校各专业《线性代数》课程试卷及答案A卷

全校各专业《线性代数》课程试卷及答案A 卷试卷 A 考试方式 闭卷 考试时间(120分钟)一、选择题(本题共4小题,每小题4分,满分16分。
每小题给出的四个选项中,只有一项符合题目要求) 1、设A ,B 为n 阶方阵,满足等式0=AB,则必有( ) (A)0=A 或0=B ; (B)0=+B A ; (C )0=A 或0=B ; (D)0=+B A 。
2、A 和B 均为n 阶矩阵,且222()2A B A AB B +=++,则必有( ) (A) A E =; (B)B E =; (C ) A B =. (D) AB BA =。
3、设A 为n m ⨯矩阵,齐次方程组0=Ax 仅有零解的充要条件是( )(A) A 的列向量线性无关; (B) A 的列向量线性相关; (C ) A 的行向量线性无关; (D) A 的行向量线性相关. 4、 n 阶矩阵A 为奇异矩阵的充要条件是( ) (A) A 的秩小于n ; (B) 0A ≠;(C) A 的特征值都等于零; (D) A 的特征值都不等于零; 二、填空题(本题共4小题,每题4分,满分16分)5、若4阶矩阵A 的行列式5A =-,A *是A 的伴随矩阵,则*A = 。
6、A 为n n ⨯阶矩阵,且220A A E --=,则1(2)A E -+= 。
7、已知方程组⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎭⎫ ⎝⎛-+43121232121321x x x a a 无解,则a = 。
8、二次型2221231231213(,,)2322f x x x x x tx x x x x =++++是正定的,则t 的取值范围是 。
三、计算题(本题共2小题,每题8分,满分16分)9、计算行列式1111111111111111x x D y y+-=+-10、计算n 阶行列式121212333n n n n x x x x x x D x x x ++=+四、证明题(本题共2小题,每小题8分,满分16分。
完整版)线性代数试卷及答案

完整版)线性代数试卷及答案线性代数A试题(A卷)试卷类别:闭卷考试时间:120分钟考试科目:线性代数学号:______ 姓名:______题号得分阅卷人一.单项选择题(每小题3分,共30分)1.设A经过初等行变换变为B,则(B)。
(下面的r(A),r(B)分别表示矩阵A,B的秩)。
A) r(A)。
r(B);(D)2.设A为n(n≥2)阶方阵且|A|=,则(C)。
A) A中有一行元素全为零;(B) A中必有一行为其余行的线性组合;(C) A有两行(列)元素对应成比例;(D) A的任一行为其余行的线性组合。
3.设A,B是n阶矩阵(n≥2),AB=O,则下列结论一定正确的是: (D)A) A=O或B=O。
(B) B的每个行向量都是齐次线性方程组AX=O的解。
(C) BA=O。
(D) R(A)+R(B)≤n.4.下列不是n维向量组α1,α2.αs线性无关的充分必要条件是(A)A) 存在一组不全为零的数k1,k2.ks使得k1α1+k2α2+。
+ksαs≠O;(B) 不存在一组不全为零的数k1,k2.ks使得k1α1+k2α2+。
+ksαs=O(C) α1,α2.αs的秩等于s;(D) α1,α2.αs 中任意一个向量都不能用其余向量线性表示。
5.设n阶矩阵(n≥3)A=,若矩阵A的秩为n-1,则a必为()。
11;(C) -1;(D)。
(A) 1;(B)6.四阶行列式a1a2a3a4b1b2b3b4的值等于()。
A) a1a2a3a4+b1b2b3b4;(B) (a1a2-b1b2)(a3a4-b3b4);(C)a1a2a3a4-b1b2b3b4;(D) (a2a3-b2b3)(a1a4-b1b4)。
1.设A为四阶矩阵且A=b,则A的伴随矩阵A的行列式为b^3.(C)2.设A为n阶矩阵满足A+3A+In=O,In为n阶单位矩阵,则A=−A−3In。
(C)9.设A,B是两个相似的矩阵,则下列结论不正确的是A与B的行列式相同。
2020-2021(1)《线性代数A》A卷参考答案
3 ,1)T . 2
(3) 当 k 1时 R( A) 1; 当 k 2 时 R( A) 2; 当 k 1且 k 2 时 R( A) 3.
(12 分) (15 分)
P5
x1 3x2 2x3 x4 3
得 分
六、(12
分)求非齐次线性方程组
x1 x1
x2 x2
x4 x3
1 2
五
六
七
八
得分
阅卷人
得
一、 填空题(共 24 分,每小题 3 分)
分
1. n 阶行列式
1
2
n ( n 1)
(1) 2 1n .
n
3 5 2 1
2. 已 知 4 阶 行 列 式 D 1 1 1 3
0 5 1 3 ,D 的 (i, j) 元 的 代 数 余 子 式 记 作 Aij , 则
2 4 1 3
学院
考 专业 装
生
信
息 姓名
班级
栏 学号 线
订
集 美 大 学 试 卷 纸参考答案与评分标准
2020 — 2021 学年 第 一 学期
课程名称
适用 学院、专业、
年级
线性代数 A
试卷 卷别
考试 方式
A
闭卷 □√ 开卷 □
备注
1.本试卷共 8 页,答题前请检查;2.考试时间 120 分钟。
总分
题号
一
二
三
四
生
信
息 姓名
班级
栏 学号 线
订
1 2 3k
得
五、(15
分)设矩阵
A
1 k
2k 2
3 3
,
分
(1)求行列式 A ;
海南大学2012-2013《线性代数》 试题(A卷)

海南大学2012-2013学年度第二学期试卷科目:(工科类)《线性代数》试题(A 卷)姓名: 学 号: 学院: 专业班级:时限: 120 分钟 考试形式:闭卷笔试所有试卷均配有答题纸,考生应将答案写在答题纸上,写在试卷上一律无效大题号 一 二 三 四 五 六 七 八 总分 得分一、选择题:(每题3分,共15分)1.行列式0100002000034000=_____-24_____2. 设4阶方阵A 的秩为2,则其伴随矩阵A *的行列式为0___3. 设A 为m n ⨯矩阵,B 为n m ⨯矩阵,若m n >,则AB =____0___4.若n 元齐次线性方程组AX O =有n 个线性无关的解向量,则A =O5. 设三阶方阵A 有三个特征值1232,3,λλλ==,若 A =24,则3λ=4二、填空题(每题3分,共15分)1. 设A 为n 阶方阵,且AX O =有非零解,则矩阵A 必有一个特征值为( C )(A) 1 (B) -1 (C) 0 (D) 无法确定得分 阅卷教师得分 阅卷教师2. 设矩阵A 、B 都为n 阶方阵A =2,B =-3,则13A B *-=( D )(A) 6 (B) 6n (C) -6 (D) 16n --3.若可逆方阵A 满足2A A = ,则 A =( A )(A)1 (B) 0 (C) -1 (D)无法确定4. 设三阶行列式D 的第三行元素依次是1、-1、1,它们的代数余子式依次是2、8、-5,则D =( B ) (A ) 11 (B) -11 (C) 5 (D)-55. n 元非齐次线性方程组AX β=有解,其中A 为(1)n n +⨯的矩阵,则A β=( A )(A) 0 (B) 1 (C) -1 (D) 无法确定三 、计算题(14分)求非齐次线性方程组1234123412343133445980x x x x x x x x x x x x +--=⎧⎪--+=⎨⎪+--=⎩的通解。
线性代数试题(A 卷)

线性代数试题(A 卷)一、单项选择题1.如果将n 阶行列式中所有元素都变号,该行列式的值的变化情况为( ) (A) 不变; (B)变号;(C)若n 为奇数,行列式变号;若n 为偶数,行列式不变; (D)若n 为奇数,行列式不变;若n 为偶数,行列式变号. 2.设0λ是可逆矩阵A 的一个特征值,则( ) (A)0λ可以是任意一个数; (B)00>λ; (C)00≠λ; (D) 00<λ.3.设Ax=b 是一非齐次线性方程组,1η和2η是其任意2个解,则下列结论错误的是( )(A) 12ηη+是Ax=0的一个解; (B) 121122ηη+是Ax=b 的一个解;(C) 12ηη-是Ax=0的一个解;(D) 122ηη-是Ax=b 的一个解.4. 若1112α=-(,,),2764α=(,,),3000α=(,,),则向量组123,,ααα是( )(A) 线性相关; (B) 线性无关;(C) 可能线性相关,可能线性无关; (D) 秩123(,,)3ααα=.5.设100020004A ⎛⎫ ⎪= ⎪ ⎪⎝⎭,则A 的特征值为 ( )(A) 1,1,2 ; (B) 1,2,2 ; (C) 1,2,4 ; (D) 2,4,4.二、填空题(每小题4分,本大题共20分) 1. 排列32514的逆序数为 .2. 已知矩阵⎪⎪⎭⎫ ⎝⎛=1111A ,则矩阵=3A . 3. 设3阶方阵A 的元素全为1,则秩(A )为 .4.二次型12(,)f x x =22112264x x x x ++的矩阵是 .5.实对称矩阵A 为正定矩阵的充分必要条件是A 的所有特征值全是 .三、(本题10分)计算行列式ef cf bf de cd bd aeac ab ---.四、(本题10分)求方阵⎪⎪⎪⎪⎪⎭⎫ ⎝⎛2500380000120025 的逆矩阵.五、(本题12分) 求线性方程组 ⎪⎩⎪⎨⎧=++-=++-=++-211117847246373542432143214321x x x x x x x x x x x x 的通解.六、(本题12分)求三阶方阵⎪⎪⎪⎭⎫⎝⎛--=201034011A 的特征值及特征向量,并判断A 是否与对角形矩阵相似?七、(本题8分)设321,,ααα线性无关,证明3213221,,ααααααα++++也线性无关. 八、(本题8分)证明:若A 为n n ⨯阶非零矩阵,则秩(A )=1的充分必要条件是A 可写为一列向量与一行向量的积.参考答案和评分标准一、单项选择题(每小题4分,本大题共20分) 1.C ; 2.C ; 3. A ; 4. A ; 5. C 二、填空题(每小题4分,本大题共20分)1. 5 ;2、4444⎛⎫⎪⎝⎭;3. 1 ;4.⎥⎦⎤⎢⎣⎡4331 ;5.正数. 三、(本题10分)计算行列式efcf bf de cdbd aeacab ---.解:ef cfbf de cdbd aeac ab ---=ec b e c bec b adf ---……….…….…..…………(3分) =111111111---adfbce ……………………………………………………………………………….(6分) =abcdef 4……….………………………………………………………....……(10分)四、(本题10分)求方阵⎪⎪⎪⎪⎪⎭⎫⎝⎛2500380000120025的逆矩阵. 解:,21⎪⎪⎭⎫ ⎝⎛=A O O A A ,112251==A ,125382==A .……….……..……..(3分) ,5221111⎪⎪⎭⎫⎝⎛--==*-A A .……….……………………………………………(5分),8532212⎪⎪⎭⎫ ⎝⎛--==*-A A .…………………………………………..……..…(7分)⎪⎪⎪⎪⎪⎭⎫⎝⎛-=- 8 5-003-2000000 2- 1 521A .……….…………………………………….…(10分) 五、(本题12分) 求线性方程组 ⎪⎩⎪⎨⎧=++-=++-=++-211117847246373542432143214321x x x x x x x x x x x x 通解.解.对方程组的增广矩阵作初等行变换⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛--→⎪⎪⎪⎭⎫ ⎝⎛---=0000175100172021211117847246373542A ………………………..(4分) 于是方程组的同解方程组为⎪⎪⎩⎪⎪⎨⎧-=++=434217517221x x x x x ,42,x x 为自由未知量……………………..………..(8分) 所以方程组的通解为:21432117507200120101k k x x x x ⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛-+⎪⎪⎪⎪⎪⎭⎫ ⎝⎛+⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛ . …………….…..….(12分) 六、(本题12分)解:A 的特征方程为2134011||----+=-λλλλA E =0)1)(2(2=--λλ,……………..………....(2分)故A 的特征值为21=λ,132==λλ. ……………..………………….……..(5分)(1) 对于特征值21=λ,得到齐次线性方程组 ⎪⎩⎪⎨⎧=-=-=-0040312121x x x x x ,它的基础解系是⎪⎪⎪⎭⎫ ⎝⎛100, 所以属于特征值2的全部特征向量为,100⎪⎪⎪⎭⎫⎝⎛k (0≠k ).………..…….(7分)(2) 对于特征值132==λλ,得到齐次线性方程组 ⎪⎩⎪⎨⎧=--=-=-002402312121x x x x x x ,它的基础解系是⎪⎪⎪⎭⎫ ⎝⎛-121,所以属于特征值1的全部特征向量为,121⎪⎪⎪⎭⎫⎝⎛-k (0≠k ).………...(9分)因此A 不与对角形矩阵相似. .…………….…………………………….(12分) 七、(本题8分)设321,,ααα线性无关,证明3213221,,ααααααα++++也线性无关.证明:设0)()()(3213322211=++++++αααααααk k k ,………..…….(2分) 则有0)()()(3322321131=++++++αααk k k k k k k , ……………….(4分)321,,ααα 线性无关,⎪⎩⎪⎨⎧=+=++=+∴0003232131k k k k k k k ,0321===∴k k k ……….….(6分)所以3213221,,ααααααα++++线性无关. …………………………..….(8分) 八、(本题8分) 证明:若A 为n n ⨯阶非零矩阵,则秩(A )=1的充分必要条件是A 可写为一列向量与一行向量的积.证明:必要性:因为秩(A )=1,所以存在可逆矩阵P 和Q ,使得10010000(100)0000PAQ ⎛⎫⎛⎫⎪ ⎪⎪ ⎪== ⎪ ⎪⎪ ⎪⎝⎭⎝⎭,.……………………..….(2分)得到11)001(001--⎪⎪⎪⎪⎪⎭⎫⎝⎛=Q P A=)(2121n n b b b a a a ⎪⎪⎪⎪⎪⎭⎫ ⎝⎛,这里⎪⎪⎪⎪⎪⎭⎫ ⎝⎛n a a a 21=⎪⎪⎪⎪⎪⎭⎫⎝⎛-0011 P ,)(21n b b b =1)001(-Q 。
复旦大学《线性代数》2018-2019学年第二学期期末试卷A卷

复旦大学考试试卷2018——2019学年第二学期时间:100分钟《线性代数》课程32学时2学分考试形式:闭卷总分:100分一、填空题(每小题3分,共15分)1、设2()3f x x =-,矩阵⎪⎪⎭⎫⎝⎛-=3 4 0 1A ,则)(A f =.2、设B A ,为n 阶矩阵,如果有n 阶可逆矩阵P ,使成立,则称A 与B 相似.3、n 元非齐次线性方程组m n A x b ⨯=有唯一解的充分必要条件是.4、已知二次型()323121232221321662355,,x x x x x x x x x x x x f -+-++=,则二次型f 对应的矩阵A =.5、设4阶方阵A 满足:0,30,2T A E A AA E <+==(其中E 是单位矩阵),则A 的伴随矩阵*A 必有一个特征值为.二、选择题(每小题3分,共15分)1、已知4阶方阵A 的伴随矩阵为*A ,且A 的行列式A =3,则*A =().(A )81.(B )27.(C )12.(D )9.2、设A 、B 都是n 阶方阵,且A 与B 有相同的特征值,并且A 、B 都有n 个线性无关的特征向量,则()。
(A )A 与B 相似.(B )A =B .(C )B A ≠,但0||=-B A .(D )A 与B 不一定相似,但||||B A =.3、设n 阶方阵A 为正定矩阵,下面结论不正确的是().(A )A 可逆.(B )1-A 也是正定矩阵.(C )0||>A .(D )A 的所有元素全为正.4、若n 阶实方阵2A A =,E 为n 阶单位阵,则().(A )()()R A R A E n +->.(B )()()R A R A E n +-<.(C )()()R A R A E n +-=.(D )无法比较()()R A R A E n +-与的大小.5、设1234123400110111c c c c αααα-⎛⎫⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪ ⎪===-= ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭,,,,其中1234,,,c c c c 为任意常数,则下列向量组线性相关的为().(A )123ααα,,.(B )124ααα,,.(C )134ααα,,.(D )234ααα,,.三(本题满分10分)计算n (2n ≥)阶行列式n xa a a x a D aax=,n D 的主对角线上的元素都为x ,其余位置元素都为a ,且x a ≠.四(本题满分10分)设3阶矩阵,A B 满足关系:1100216,041007A BA A BA A -⎛⎫ ⎪ ⎪⎪=+= ⎪ ⎪ ⎪ ⎪⎝⎭且,求矩阵B .五(本题满分10分)设方阵A 满足220A A E --=(其中E 是单位矩阵),求11,(2)A A E --+.六(本题满分12分)已知向量组A :11412α⎛⎫ ⎪ ⎪= ⎪ ⎪⎝⎭,22131α⎛⎫ ⎪- ⎪= ⎪- ⎪⎝⎭,31541α⎛⎫ ⎪- ⎪= ⎪- ⎪-⎝⎭,43670α⎛⎫ ⎪- ⎪= ⎪- ⎪⎝⎭,(1)求向量组A 的秩;(2)求向量组A 的一个最大线性无关组,并把不属于该最大无关组的其它向量用该最大无关组线性表示.七(本题满分14分)设矩阵11111A ααββ⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦与矩阵000010002B ⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦相似,(1)求,αβ;(2)求正交矩阵P ,使1P AP B -=.八(本题满分14分)设有线性方程组为23112131231222322313233323142434x a x a x a x a x a x a x a x a x a x a x a x a ⎧++=⎪++=⎪⎨++=⎪⎪++=⎩(1)证明:若1a ,2a ,3a ,4a 两两不等,则此方程组无解.(2)设13a a k ==,24a a k ==-(0k ≠),且已知1β,2β是该方程组的两个解,其中1(1, 1, 1)T β=-,2(1, 1, 1)T β=-,写出此方程组的通解.参考答案一、填空题(每小题3分,共15分)1、-2 08 6⎛⎫ ⎪⎝⎭;2、1P AP B -=;3、()(,)R A R A b n ==;4、513153333-⎛⎫⎪-- ⎪ ⎪-⎝⎭;5、43二、选择题(每小题3分,共15分)BADCC三(本题满分10分,见教材P44习题第5题)解:后面1n -列都加到第1列,得(1)(1)(1)n x n a a a x n ax aD x n a a x+-+-=+-xaa x a a a n x a n x c111])1([])1([1-+===-+÷])1([)(0101001])1([1)()()(1223a n x a x ax ax a n x n c a c c a c c a c nn -+-=---+====--+-+-+.四、(本题满分10分,与典型题解P172例6类似)解:111121166()6416327161B A E ----⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫⎢⎥⎪ ⎪ ⎪ ⎪=-=-==⎢⎥ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦.五、(本题满分10分,见练习册P118第五大题第1小题和典型题解P173例7)解:212022A E A EA A E A E A -----=⇒=⇒=.22212112()202(2)()(4A E A A E A E A A E A A ------=⇒+=⇒+===)或34E A-六、(本题满分12分,见教材P89习题3第2题,或典型题解P178例6)解:1213101141560112134700002110000--⎛⎫⎛⎫⎪ ⎪---⎪ ⎪→→ ⎪ ⎪--- ⎪ ⎪-⎝⎭⎝⎭,12()2,,R A αα=为所求的一个最大线性无关组,且312412,2αααααα=-+=-+.七、(本题满分14分,见典型题解P190例14)解:(1)由,A B 相似知,,A B 有相同的特征值,而B 的特征值为0,1,2,故得A 的特征值为1230,1,2λλλ===,从而有0010E A E A ⎧⋅-=⎪⎨⋅-=⎪⎩,由此解得0α=,β=0.(2)对于10λ=,解()00E A X ⋅-=,得特征向量101-⎛⎫⎪⎪ ⎪⎝⎭,单位化得:⎪⎪⎪⎪⎪⎭⎫⎝⎛-=210211p ;对于21λ=,解()0E A X -=,得特征向量为⎪⎪⎪⎭⎫⎝⎛=0101p ;对于32λ=,解()20E A X -=,得特征向量为101⎛⎫⎪⎪ ⎪⎝⎭,单位化得:⎪⎪⎪⎪⎪⎭⎫⎝⎛=210211p 令()⎪⎪⎪⎪⎪⎭⎫⎝⎛-==2102101021021,,321p p p P ,则P 为正交阵,且使1P AP B -=.八、(本题满分14分,见教材P87例3.13)解:(1)增广矩阵B 的行列式是4阶范德蒙行列式:231112322223143332344411||()11ji i j a a a a a a B aa a a a a aa≤<≤==-∏由于1a ,2a ,3a ,4a 两两不等,知||0B ≠,从而()4R B =,但系数矩阵A 的秩()3R A ≤,故()()R A R B ≠,因此方程组无解.(2)13a a k ==,24a a k ==-(0k ≠)时,方程组变为23123231232312323123x kx k x k x kx k x k x kx k x k x kx k x k⎧++=⎪-+=-⎪⎨++=⎪⎪-+=-⎩即2312323123x kx k x k x kx k x k⎧++=⎨-+=-⎩因为1201kk k=-≠-,故()()2R A R B ==,所以方程组有解,且对应的齐次方程组的基础解系含3-2=1个解向量,又1β,2β是原非齐次方程组的两个解,故21(2, 0, 2)T ξββ=-=-是对应齐次方程组的解;由于0ξ≠,故ξ是它的基础解系。
线性代数试卷及答案 卷A

河南工业大学成教学院课程 线性代数 试卷专业班级: 卷A姓 名: 学 号:注:(1)不得在密封线以下书写班级、姓名。
(2)必须在密封线以下答题,不得另外加纸。
………………………………………密 封 线 ………………………………………………………一 .单项选择题(每题3分)1.若 111221226a a a a =,则 121122212020021a a a a -- 的值为( A )(A )12 (B) –12 (C) 18 (D) 02.设A 、B 都是n 阶矩阵,且AB=0,则下列一定成立的是( C )(A )A=0或B=0 (B) A 、B 都不可逆(C )A 、B 中至少有一个不可逆 (D )A+B=03. 若齐次线性方程组1231231230020kx x x x kx x x x x ++=⎧⎪+-=⎨⎪-+=⎩仅有零解,则( B )(A) 4k =或1K =- (B) K= 4-或K=1(C) 4K ≠且1K ≠- (D) 4K ≠-且1k ≠4. A 、B 均为n 阶可逆矩阵,则AB 的伴随矩阵()*AB =( D )(A) A B ** (B) 11||AB A B -- (C) 11B A -- (D) B A **5.设n 元齐次线性方程组0AX =的系数矩阵的秩为r ,则0AX =有非零解的充分必要条件是(D )(A )r n = (B ) r n ≥ (C ) r n > (D )r n <二 .填空题(每题3分)1.行列式 12342345_______32005000= 1602.若n n ⨯阶矩阵A 的行列式|A|=3,A *是A 的伴随矩阵,则A *__3^n-1____3. A 为n n ⨯阶矩阵,且2320A A E -+=,则1A -=______4. n1100⎡⎤=⎢⎥⎣⎦___1__(n 为正整数)5. 设1101A -⎡⎤=⎢⎥⎣⎦, 则1(2A)________=-三.计算题(共63分)1. 计算行列式12n12n 12nb a a a a b a a a a b a +++(12分)解:r2-r1、r3=r1、...ri-r1、...rn-r1D=|b+a1 a2 a3 ....................... an|-b b 0 0-b 0 b 0.............................-b 0 0 .......................... bc1+c2+c3+...+cj+...+cn=|b+a1+a2+...+an a2 ............... an|0 b ................. 0 ......................................0 0 .................... b=(b+Σai)*[b^(n-1)]=b^n+[b^(n-1)]*(a1+a2+...+an)2.3411231100250013A⎡⎤⎢⎥-⎢⎥=⎢⎥⎢⎥⎣⎦, 求1A-(12分)3 41 12 5解:令B= ,C= ,D= ,则原矩阵可以写为分块2 3 -1 1 1 3B C B ^-1 -B ^-1CD^-1 矩阵的形式A= ,它的逆矩阵易得为A^-1=0 D 0 D ^-1而利用伴随矩阵与逆矩阵的关系可以直接得到3 -4 3 -4B^-1=1/ B B *=1×=-2 3 -2 32 -53 -5D^-1=1/ D D *=1×=-1 3 -1 2-15 38计算可得-B^-1CD^-1=11 -283 -4 -22 37-2 3 16 -27所以A^-1= 0 0 3 -50 0 -1 23.求解齐次线性方程组1234123412342202220430x x x xx x x xx x x x+++=⎧⎪+--=⎨⎪---=⎩.(15分)解:基础解系为:1 2 2 1 2 2 1 0 -2 -5/32 1 -2 -2 -3 -6 -4 1 2 4/3 1 -1 -4 -3 0 0 0 0 0 0通解为:X12k1+5/3k2 2 5/3X=k1ξ1+ k2ξ2= X2 = -2k1-4/3k2 =k1 -2 +k2 -4/3X3 k1 1 0X4 k2 0 14.设211210111A-⎡⎤⎢⎥=⎢⎥⎢⎥-⎣⎦,311342B⎡⎤-=⎢⎥⎣⎦求解矩阵方程XA B=(12分)解:5. 计算矩阵3112322140511135524aA⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦的秩为3,求a (12分)解:r4-r2,r1-r3,r2-2r30 1 1 a-1 -20 2 1 -1 -61 0 1 1 50 1 2 4 0r1-r4,r2-2r40 0 -1 a-5 -20 0 -3 -9 -61 0 1 1 50 1 2 4 0r3*(-1/3), r1+r20 0 0 a-2 00 0 1 3 21 0 1 1 50 1 2 4 0交换行1 0 1 1 50 1 2 4 00 0 1 3 20 0 0 a-2 0因为 r(A)=3, 所以 a = 2.四.证明题(7分)设32=,证明5A E+可逆,并求1A E+(7分)A E-(5)解:(A+5E)【1/127(A^2-5A+25E)】=1/127(A+5E)(A^2-5A+25E)=1/127(A^3+5A^2-5A^2-25A+25A+125E)=1/127(A^3+125E)由于A^3=2E,所以1/127(A^3+125E)=1/127(127E)=E,所以(A+5E)可逆,且(A+5E)^-1=1/127(A^2-5A+25E)。
(完整版)线性代数试题套卷及答案

(线性代数) ( A 卷)专业年级: 学号: 姓名:一、单项选择题(本大题共5小题,每小题5分,共25分)在每小题列出的四个备选项中只有一个是符合题目要求的,请将其代码填写在题后的括号内。
错选、多选或未选均无分。
1.设为实矩阵,则线性方程组只有零解是矩阵为正定矩阵的n m A ⨯0=Ax )(A A T(A) 充分条件; (B) 必要条件; (C) 充要条件;(D) 无关条件。
2.已知为四维列向量组,且行列式 ,32121,,,,αααββ4,,,1321-==βαααA ,则行列式1,,,2321-==βαααB =+B A (A) ;(B) ;(C) ;(D) 。
4016-3-40-3.设向量组线性无关,且可由向量组线s ααα,,, 21)2(≥s s βββ,,, 21性表示,则以下结论中不能成立的是(A) 向量组线性无关;s βββ,,, 21(B) 对任一个,向量组线性相关;j αs j ββα,,, 2(C) 存在一个,向量组线性无关;j αs j ββα,,, 2(D) 向量组与向量组等价。
s ααα,,, 21s βββ,,, 214.对于元齐次线性方程组,以下命题中,正确的是n 0=Ax (A) 若的列向量组线性无关,则有非零解;A 0=Ax (B) 若的行向量组线性无关,则有非零解;A 0=Ax (C) 若的列向量组线性相关,则有非零解;A 0=Ax (D) 若的行向量组线性相关,则有非零解。
A 0=Ax 5.设为阶非奇异矩阵,为的伴随矩阵,则A n )2(>n *A A 题 号一二三总 分总分人复分人得 分得分评卷人√√(A) ;(B) ;A A A 11||)(-*-=A A A ||)(1=*-(C) ;(D) 。
111||)(--*-=A A A 11||)(-*-=A A A 二、填空题(本大题共5小题,每小题5分,共25分)请在每小题的空格中填上正确答案。
(完整版)线性代数试题套卷及答案

(线性代数) ( A 卷)专业年级: 学号: 姓名:一、单项选择题(本大题共5小题,每小题5分,共25分)在每小题列出的四个备选项中只有一个是符合题目要求的,请将其代码填写在题后的括号内。
错选、多选或未选均无分。
1.设n m A ⨯为实矩阵,则线性方程组0=Ax 只有零解是矩阵)(A A T为正定矩阵的(A) 充分条件; (B) 必要条件; (C) 充要条件; (D) 无关条件。
2.已知32121,,,,αααββ为四维列向量组,且行列式 4,,,1321-==βαααA ,1,,,2321-==βαααB ,则行列式 =+B A(A) 40; (B) 16-; (C) 3-; (D) 40-。
3.设向量组s ααα,,,21)2(≥s 线性无关,且可由向量组s βββ,,, 21线 性表示,则以下结论中不能成立的是(A) 向量组s βββ,,,21线性无关; (B) 对任一个j α,向量组s j ββα,,,2线性相关; (C) 存在一个j α,向量组s j ββα,,,2线性无关; (D) 向量组s ααα,,,21与向量组s βββ,,, 21等价。
4.对于n 元齐次线性方程组0=Ax ,以下命题中,正确的是(A) 若A 的列向量组线性无关,则0=Ax 有非零解; (B) 若A 的行向量组线性无关,则0=Ax 有非零解; (C) 若A 的列向量组线性相关,则0=Ax 有非零解; (D) 若A 的行向量组线性相关,则0=Ax 有非零解。
5.设A 为n 阶非奇异矩阵)2(>n ,*A 为A 的伴随矩阵,则√√(A) A A A 11||)(-*-=; (B) A A A ||)(1=*-;(C) 111||)(--*-=A A A ; (D) 11||)(-*-=A A A 。
二、填空题(本大题共5小题,每小题5分,共25分)请在每小题的空格中填上正确答案。
错填、不填均无分。
6. 列向量⎪⎪⎪⎭⎫ ⎝⎛-=111α 是矩阵⎪⎪⎪⎭⎫ ⎝⎛---=2135212b a A 的对应特征值λ的一个特征向量. 则λ= ,a = ,b = 。
线性代数A模拟卷

.
1
1
,
1
1 1 0
x1 2x2 1x3 1 3. 设ξ 1=(2,0,-1)T, ξ 2=(1,0,0)T为线性方程组 2x1 x2 2x3 2
ax1 bx2 cx3 5
的两个解向量,则方程的通解为
.
4. 向量组α 1=(1,2,-3)T, α 2=(-2,1, 0)T, α 3=(0,5,-6)T,线性
(2 )x1 2x2 2x3 1 2x1 (5 )x2 4x3 2
2x1 4x2 (5 )x3 1
六、(18分)设二次型f=2x12+3x22+3x32+4x2x3. 1.写出f的矩阵; 2.求A的特征值与特征向量; 3.用正交变换X=QY将f化为标准形,并写出正交矩阵Q.
(B) α 1一定不可由α 2,α 3,…,α s线性表示;
(C) 其中至少有一个向量可由其余s-1个向量线性表示.
5.n阶方阵A与对角阵相似,则(
).
(A)A有n个不同的特征值;(B) A有n个相同的特征值;(C) A有n
个线性无关的特征向量.
三、(14分)设n维向+2ααT,其中E 为n阶单位矩阵,求AB,A-1,B-1,并写出A-1与B-1的具体形式.
5.设α 1=(1,-2,5)T, α 2=(-2,4,-10)T,则(
).
(A)(α 1,α 2)=-60;(B) α 1 与α 2正交;(C) α 1,α 2线性相关.
三、(10分)求非齐次线性方程组
4
2x1 x1
2
x2 x2
x3 x4 2x3 x
1 4 2
线性代数A及答案

2005学年第2学期线性代数期末考试试卷( A 卷 )一. 填空题 (本题共有10个小题, 每小题3分)1. 设305021311121A ⎡⎤⎢⎥=-⎢⎥⎢⎥-⎣⎦,则矩阵A 的秩()r A =__________. 2. 设A 为3阶方阵,行列式2A =,则3A =________.3. 设矩阵20003101A x ⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦与400020002B ⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦相似,则x =_________. 4. 设A 是n 阶方阵且240A A E +-=, 则()1A E --=_________.5.()222,,2332f x y z x y z ayz =+++是正定二次型,则a 的取值范围是______.6. 若向量()1,2,0与(),,0x y 线性无关,则x 与y 的关系应为__________.7. 向量[]1,4,0,2T∂=与[]2,2,1,3Tβ=-的距离和内积分别为_________和___________.8. 设10246311A a -⎡⎤⎢⎥=⎢⎥⎢⎥-⎣⎦,B 为3阶非零矩阵,且0AB =,则a =___________.9. 设0是矩阵10102010A a ⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦的特征值,则a =___________. 10. 在MA TLAB 软件中,det(A ) 表示求__________.二. 选择题(本题共有5个小题, 每个小题都给出代号 (A), (B), (C), (D) 的四个结论, 其中只有一个结论是正确的。
每小题3分。
)1. 设A 是n 阶方阵,则下列4个式子中表明A 是正交矩阵的式子为( )(A) 1AA E -=(B) AA E = (C) 1TA A -=(D) 1A =±2. 已知,A B ,C 为n 阶方阵,则下列性质不正确的是( )(A) AB BA = (B) ()()AB C A BC =(C)()A B C AC BC +=+(D) ()C A B CA CB +=+3. 已知方程组Ax b =对应的齐次方程组为0Ax =,则下列命题正确的是( )(A) 若0Ax =只有零解,则Ax b =一定有唯一解。
《线性代数》2018-2019学年第一学期期末考试A卷

河海大学2018-2019学年第一学期期末考试《线性代数》试题(A)卷姓名:_______班级:_______学号:_______成绩:_______一、填空题(每空4分,共20分)1、已知A 为3阶方阵,且2A =-,则2A -=。
2、方阵A 的特征值为λ,方阵E A A B 322-+=,则B 的特征值为。
3、设A 为n 阶方阵,满足2A A E -=,则1A -=。
4、设12,ξξ是n 元非齐次线性方程组Ax b =的两个解,且A 的秩()R A 1=-n ,则Ax b =的通解x =。
5、二次型xz z y xy x f 44642222+--+-=的秩为,正定性为。
二、判断题(每小题2分,共10分)1、B A ,为n 阶方阵则BA AB =()2、设A 为)n m (n m <⨯矩阵,则b Ax =有无穷多解。
()3、向量组1A 是向量组A 的一部分,向量组1A 线性无关,则向量组A 一定线性相关;()4、设21,λλ是方阵A 的特征值,则21λλ+也是方阵A 的特征值。
()5、4个3维向量一定线性相关。
()三、计算:(每小题8分,共16分)1、已知4阶行列式1111201212112101---=D ,求4131211122A A A A +++.2、已知111121113A ⎛⎫ ⎪= ⎪ ⎪⎝⎭,试判断A 是否可逆。
若可逆,求1-A ,若不可逆,求A 的伴随矩阵A *四、计算:(每小题10分,共20分)1、求齐次线性方程组⎪⎪⎩⎪⎪⎨⎧=++-=++-=--+-=++-034220222402024321432143214321x x x x x x x x x x x x x x x x 的基础解系和它的通解。
2、已知线性方程组⎪⎩⎪⎨⎧=++=---=++a z y x z y x z y x 223320有解,求a ,并求全部解。
五、(10分)判断向量组⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛--=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-=1210,1012,0212,11014321αααα的线性相关性,并求它的一个最大无关组,并用最大无关组表示该组中其它向量。
线性代数试题A

线性代数试题一、单项选择题1. n 阶方阵A 与对角阵相似的充要条件是 ( ).(A) A 是实对称阵; (B) A 有n 个互异特征值; (C) A 有n 个线性无关的特征向量; (D) A 的特征向量两两正交. 2.二次型2221231213231002f x x x x x x x x x =+++-+是 ( ). (A) 正定的; (B) 负定的; (C) 半正定的; (D) 不定的. 3.n 阶方阵A 满足20A =,E 是n 阶单位阵,则 ( ).(A) 0E A -≠,但0E A +=; (B) 0E A -=,但0E A +≠; (C) 0E A -=,且0E A +=; (D) 0E A -≠,且0E A +≠.4.设矩阵⎪⎪⎪⎪⎪⎭⎫⎝⎛=0000100001000010A , 则3A 的秩为( ). A .2;B .3;C .1;D . 4.5.设向量组321,,ααα线性无关,则下列向量组线性相关的是( ) A. 133221αααααα---,,. B. 133221αααααα+++,,. C. 133221222αααααα---,,. D. 133221222αααααα+++,,.6.设矩阵⎪⎪⎪⎭⎫ ⎝⎛------=211121112A , ⎪⎪⎪⎭⎫ ⎝⎛=000010001B , 则A 与B ( )A. 合同且相似;B. 合同但不相似;C. 不合同但相似;D. 既不合同又不相似. 7.设A 是3阶方阵,将A 的第1列与第2列交换得B,再把B 的第2列加到第3列得C, 则满足AQ=C 的可逆矩阵Q 为( )A. ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡101001010;B. ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡100101010;C. ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡110001010;D. ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡100001110. 8.设321,,ααα均为3维列向量,记矩阵),,(321ααα=A ,)93,42,(321321321ααααααααα++++++=B ,若1=A ,则B =( ).A .0;B .1;C .2;D .3.9.n 阶矩阵M 的秩r n =的充分必要条件是M 中( ).A. 有一个r 阶子式不等于零;B.所有的r 阶子式都不等于零;C. 所有的1r +阶子式都不等于零;D. 有一个r 阶子式不等于零, 且所有1r +阶子式都等于零. 10. 如果0λ是n 阶矩阵A 的特征值, 那么必有( ).A. 00A E λ-=;B. 00A E λ-≠;C. 00A E λ-=;D. 00A E λ-≠.得分 评卷人二、填空题(本大题共10小题,每小题3分,共30分)请在每小题的空格中填上正确答案。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
线性代数试卷
一、选择题(4分 分)
1.设 、 均为n 阶方阵,则下列结论正确的是( ) (A) 且 (B) (C) 或 (D)
2.设非齐次线性方程组 有无穷多解,则 ( ).
(A )必有唯一解 (B)必定无解 (C )必有无穷多解 (D )A 、B 、C 都不正确 3.对n 阶方阵A 与B ,存在n 阶可逆阵P ,使得 ,则( ) (A ) 与 同时可逆或同时不可逆 (B ) (C )A 与B 有相同的特征向量 (D ) 4. 二次型 正定的一个充要条件是( )
(A) 可逆 (B)存在可逆矩阵 ,使得 (C)存在可逆矩阵 ,使 为对角阵 (D) 二、填空题(4分 分) 1.
2.
3.设 ,
,则
4.设 为三阶矩阵,且A =2,则
5.三阶矩阵 有特征值2、3、4,则
6.若
为正定阵,则k 的取值范围是 三、(14分)设n 阶矩阵 和 满足条件 (1)证明 为可逆矩阵.
(2)已知B=⎪⎪⎪
⎭
⎫
⎝⎛-200012031,求矩阵A.
四、(12分)设向量组α 1 = ,α 2 = ,α3= ,α 4 =
,
,判断向量组α1α2α3α4 的线性相关性;并求其秩和一个极大无关组.
五、(14分)求非齐次线性方程组
的通解.
六、(15分)用正交变换化二次型2
33231212
132134843),,(x x x x x x x x x x x f ++++=为标准型,并求正交变换矩阵.
七、(5分)设 为n 阶可逆的实反对称方阵,证明: 正定. 提示: 是反对称方阵
一选择(4分*4) 1 C 2 C 3 A 4 B
一填空(4分*6)
1、⎪⎪⎪⎪⎪
⎪⎭
⎫
⎝⎛--2100
021
23012 2、0 3、 ⎪⎪⎭
⎫ ⎝⎛-6402 4、 16 5、192 6、2>k 三、 (14分)解:(1)A B AB =-,A B I A =-)(两边同减I ,
I I B I A =--))((所以A-I 可逆 (2)由(1)知1)(--=-I B I A ,所以
⎪⎪⎪⎪⎪⎪⎭
⎫ ⎝
⎛
-=⎪⎪⎪⎭⎫ ⎝⎛⎪⎪⎭
⎫ ⎝⎛-+⎪⎪⎪⎭⎫ ⎝
⎛=-+=---20
0131021110230111)(111
I B I A 四、(12分)解:
()⎪⎪⎪
⎪⎪⎪
⎭⎫
⎝⎛-------→⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛--------=000000000011100011102101131102221210222012111
21011,,,,54321ααααα
53}
,
,,,{5
4321<=αααααr ,所以线性相关。
321,,ααα为一组极大无关组
五、(14分)解:()⎪⎪
⎪⎪
⎪
⎭⎫
⎝⎛---→⎪⎪⎪⎪⎪⎭⎫
⎝
⎛----=00000
10100050210
20
3
1
4122211233381301
71
1
11
B A 同解方程组⎪⎩⎪
⎨⎧-=+=--=1025324
3231x x x x x 3x 是自由未知量
取03=x ,得特解⎪⎪⎪⎪
⎪⎭
⎫ ⎝⎛--=*10052η
对应导出组解⎪⎩⎪
⎨⎧==-=0234
323
1x x x x x 3x 是自由未知量
令13=x ,得⎪⎪⎪⎪⎪⎭
⎫ ⎝⎛-=0123ξ 通解*
+=ηξk X ,k 为任意常数
六、(15分)解:⎪⎪⎪
⎭
⎫ ⎝⎛=324202423A
)8()1(3
24
224
2
32-+=--------=-λλλλ
λλA I ,令0=-A I λ,
得特征值8),(121=-=λλ二重
对11-=λ ()⎪⎪⎪
⎭
⎫ ⎝⎛→⎪⎪⎪⎭⎫ ⎝⎛---------=-0000002124242124241A I λ
解得31222x x x --= 31,x x 是自由未知量
令0,131==x x ,得⎪⎪⎪⎭⎫ ⎝⎛-=0211ξ;令1,031==x x ,得⎪⎪⎪
⎭⎫ ⎝⎛-=1202ξ
正交化 ⎪
⎪⎪⎭⎫ ⎝⎛-==02111ξβ ⎪⎪⎪
⎭
⎫ ⎝⎛--=-
=52451),(),(1111222ββββξξβ 对82=λ ⎪⎪⎪⎪
⎭
⎫ ⎝⎛
--→⎪⎪⎪⎭⎫ ⎝⎛------=-0002110101524282425)(2A I λ
解得⎪⎩⎪
⎨⎧==323
121x x x x 3x 是自由未知量 令13=x ,得基础解系⎪⎪⎪⎭⎫ ⎝⎛=212213ξ
标准化 ⎪
⎪⎪⎭
⎫
⎝⎛-==02151111ββγ ⎪⎪⎪⎭⎫ ⎝⎛-==
5245312
22ββγ ⎪⎪⎪⎭
⎫ ⎝⎛==
212313
33ξξγ
令⎪⎪⎪⎪⎪
⎪⎪⎭
⎫
⎝
⎛--==325
3503153252
3253451),,(321γγγT 作正交变换TY X = 得标准形2
322213218),,(y y y y y y f +--=
七、(5分)解:(1) 因为2
222)()()(A I A I I I A A T
T
-=--=-=-
所以2A I -是实对称矩阵
0≠∀X ,0≠AX ,则0>X X T ,0)()(>AX AX T
0)()()()(22>+=+=-=-AX AX X X X A A X X X X A X X X X A I X T T T T T T T T
则2A I -正定。
