武汉中考24题
2023年历年武汉市中考英语试题真题参考答案

武汉市新课程初中毕业生学业考试英语试题参照答案一、选择填空。
1-A 2-B 3-A 4-D 5-C 6-D 7-C 8-C 9-B 10-D11-A 12-C 13-B 14-C 15-A 16-C 17-D 18-C 19-C 20-B二、完形填空。
A1-A 2-D 3-C 4-D 5-AB 1-C 2-B 3-A 4-C 5-D 6-D 7-C 8-D 9-D 10-C 11-A 12-B 13-C 14-D 15-B三、阅读理解. A1-C 2-B 3-D 4-B 5-A B 1-A 2-C 3-C 4-A 5-CC 1-A 2-D 3-B 4-B 5-B四、阅读理解填词。
1 villages 2 together 3 enjoyed 4 heart 5 question 6 correctly 7 mean 8 already9 accepted 10 moved五、书面体现。
(范文)Mr. Smith is our English teacher. He is very kind to us and teaches very well. He fell ill last week and now he is in bed in hospital. Tomorrow is Saturday. We are going to see him together. We will meet at the school gate at 9:00 tomorrow morning. Then we’ll go to the hospital by bus. I think we should get him some flowers, because fresh and beautiful flowers will make him feel good and happy.武汉市新课程初中毕业生学业考试英语试题参照答案一、听力测试题(1-25小题)1. C2.B3.A4.C5.B6.A7.C8.C9.A 10.B 11.A 12.B 13.A 14.C15.B 16.B 17.A 18.C 19.A 20.B 21.A 22.B 23.C 24.B 25.C笔试部分二、选择填空(26-45小题)26.B 27.A 28.D 29.C 30.B 31.C 32.A 33.A 34.D 35.A 36.C 37.B 38.D39.B 40.A 41.D 42.A 43.C 44.B 45.C三、完形填空(46-65小题)46.D 47.A 48.C 49.B 50.D 51.B 52.D 53.B 54. B 55.C 56.D 57.C 58.A59.B 60.A 61.B 62.C 63.D 64. A 65.C四、阅读理解(66-80小题)66.B 67.A 68.D 69.B 70.C 71.A 72.C 73.D 74.A 75.B 76.C 77.A 78.D79.D 80. B五、阅读理解填词(81-90小题)81.kids 82.imagine 83.terrible 84.unusual 85.fit86.less 87. comfortable 88. movie 89.agreed 90.suggest六.书面体现One possible version:Wang Hong is a friendly girl and has a lot of hobbies. She often helps her parents with the housework. It’s her birthday this Saturday. Many classmates will go to her home for her birthday party. Some of them will ask their parents for some money to buy her gifts. But I don’t think it’s a good idea, becau se that’ll cost our parents’ money. I’m going to make a birthday card for her by myself. I’m sure she’ll like it.武汉市初中毕业生学业考试英语试卷参照答案一、听力测试题(1-25小题,每题1分,共25分)1.B2.B3.A4.C5.A6.B7.B8.A9.C 10.B 11.A 12.A 13.B 14.A 15.A16.B 17.C 18.A 19.C 20.C 21.C 22.A 23.C 24.B 25.A笔试部分二、选择填空(26-40小题,每题1分,共15分)26.D 27.C 28.C 29.A 30.B 31.A 32.A 33.D 34.D 35.B 36.D 37.A 38.B 39.C40.C三、完形填空(41-65小题,每题1分,共25分)41.A 42.D 43.A 44.C 45.B 46.D 47.B 48.C 49.C 50.B 51.B 52.A 53.C 54.D55.A 56.B 57.A 58.C 59.D 60.B 61.C 62.A 63.D 64.A 65.D四、阅读理解(66-80小题,每题2分,共30分)66.D 67.A. 68.C 69.B 70.A 71.A 72.D 73.D 74.C 75.B 76.B 77.B 78.A 79.A 80.C五、阅读理解填词(81-90小题,每题1分,共10分)81.lost 82.good 83.need 84.difficult 85.idea 86.knocked 87.heard 88.held 89.arms 90.help六、书面体现One possible version:Summer vacation is coming. We have different plans for it. Some of my classmates are going to visit some places of interest. Some are not going out, instead, they are going to do more reading and prepare for the future studies. Some want to do more sports to keep fit. I plan to go to Beijing to see the Olympic Games. Because it’s a good chance to make more friends and know more about the Olympic Games.+武汉市初中毕业生学业考试英语试卷参照答案:武汉市初中学业考试英语试题参照答案一、听力测试(1—25题,每题1分,共25分)1.A2.C3.B4.B5.C6.B7.C8.A9. A 10.C 11.C 12.B 13.B14.A 15.C 16.B 17.C 18.C 19.A 20.B 21.C 22.A 23.B 24.A 25.A二、选择填空(26—40小题,每题1分,共15分)26.C 27.D 28.A 29.D 30.B 31.B 32.C 33.D 34.A 35.C 36.B 37.A 38.C 39.D 40.B三、完形填空(41—55小题,每题1分,共15分)41.A 42.D 43.B 44.C 45.B 46.D 47.A 48.A 49.D 50.C 51.B 52.A 53.B 54.D 55.C四、阅读理解(56—70小题,每题2分,共30分)56.C 57.A 58.B 59.C 60.D 61.A 62.C 63.D 64.D 65.B 66.C 67.B 68.A69.D 70.B五、词与短语填空(71—75小题,每题2分,共10分)71. talk to 72. habit 73. Mad 74. get over 75. Sorry六、阅读理解填词(76—85小题,每题1分,共10分)76. broken 77. throw 78. left 79. ready 80. usually81. seats 82. belongs 83. mistake 84. voice 85. Successful七、书面体现(One possible version.)(共15分)Dear Tom,How are you recently? Now I’ll tell you something about my English teacher Mr. Lee.Mr. Lee is forty years old. He has a happy family. He’s outgoing and gets along well with us students. His classes are very interesting. After class, he often helps us with our English. He never smokes. He likes sports. He is especially good at playing chess.Most of my classmates like him and think that he’s n ot only a good teacher but also a good friend. I’m lokking forward to your reply.Yours,Li Ming武汉市初中毕业生学业考试英语试卷二、选择填空26-30 DBBAD 31-35 CCBBD 36-40 ACADA三、完形填空41-45 BCABD 46-50 CBADC 51-55 DACBD四、阅读理解56-60 CBAAD 61-65 ACCDB 66-70 CDBAC五、词与短语填空71.mind 72.need 73.mad 74.go back 75.polite六、阅读理解填词76.flew 77.Certainly 78.traffic 79.modern 80.written 81.little nguage83.another 84.believe 85.sent七、书面体现(One possible version)My hostess is Mrs.William.She is a middle-aged housewife whit blonde hair.I really like this outgoing woman.We get along well with each other.She always takes care of my daily life.She cooks and washes clothes for me.That makes me feel like at home.What’s more,she is very interested in Chinese history and culture.So she often reads books about China.She hopes to visit China one day.武汉市初中毕业生学业考试英语试卷参照答案16~20 CACBC21~25 BACCB二、选择填空(共15小题,每题1分,满分15分)26~30 CBAAC 31~35 DCCAC 36~40 DBABD三、完形填空(共15小题,每题1分,满分15分)41~45 BACAD 46~50 BCABD 51~55 ADBCA四、阅读理解(共15小题,每题2分,满分30分)56~60 BCACD 61~65 BBCAD 66~70 BDACC五、词与短语选择填空(本题共10分,每题2分)71.expensive 72.keep out 73.lead pare 75.cheap六、阅读理解填词(共10小题,每题1分,满分10分)76.drawing77.studied 78.calling 79.donated 80.writes 81.hear 82.books 83.reached84.flag 85.like七、书面体现(满分15分)It was fine last Sunday. I went to the Yard Sale in Changjiang Community. More than 200 people took tark in the activity .Some people sold used things such as bikes, toys, and clothes. Others sold cakes, cards and bookmarks made by themselves. Used books could be exchanged in the yard, too.I enjoyed myself there. In my opinion, it was a very good activity. We can not only make full use of used things, but also protect our environment in this way.参照答案听力(略)26-30DBDCB 31-35BADBC 36-40AACAD 41-45DCBDA 46-50CACBB 51-55DABCC 56-60DBCDA 61-65BBCDC 66-70BBCBC71-7576-85武汉中考英语答案:单项选择:26-30BBDCB 31-35DBCAC 36-40CBACD完形:DCBAC DBDAD CBDCA阅读:CBAAC BCBDA CBDCD nervous, compare, spend , grew up, worried, 填词:always, returning, honest, brushes,corner, nice, polite, collected, dear, manage。
2024年湖北武汉中考数学试卷试题解读及答案解析

2024年中考数学真题完全解读(武汉卷)审视2024年武汉市中考数学试卷,我们可以明显感受到与去年相比,题型与知识点的考查方式保持了一贯的稳定,整体难度适宜,而且考察手法愈发巧妙多变,要求学生对知识点有深入的理解和灵活的运用。
在历经三次模拟考试的磨砺后,24年的中考数学试卷不仅维持了知识点的连贯性,还在持续的创新与变化中,丰富了知识点的维度和命题的广度。
试卷的四大模块一一数与式、函数、几何图形、统计概率,分别占据了20分、34分、52分和14分的分值。
与23年相比,数与式部分稍有减少,具体体现在无理数的举例开放题上少了3分,而几何部分则增加了3分,主要涉及平行线和角的计算。
试卷的基础题、中档题和压轴题的分布与往年保持一致,基础题占据了约81分,即67.5%的比例,中档题和压轴题则分别占据了27分和12分,占比分别为22.5%和10%o然而,任何一份试卷都会给不同水平的学生带来不同程度的挑战。
例如,选择题第10题就需要学生巧妙运用函数对称性和数形结合的方法进行解答,而其他9题则较为常规。
填空第15题的几何小综合,无疑是今年考试的一个难点,涉及到面积的转化和相似的构造,这对于许多学生来说都是一大考验。
在解答题中,17〜22题延续了以往的考查方式,但21题对格点作图提出了更高的要求,需要学生对常规方法有更深入的理解和掌握;23题的几何大综合虽然整体考查方式未变,但第二问和第三问需要学生综合运用八九年级的几何知识点,进行巧妙的构造和推理;24题的二次函数大综合虽然思路清晰,但由于计算量巨大,对学生的计算能力提出了极大的挑战。
因此,学生在后期的备考中,需要巩固基础知识,立足课本,提高解题的熟练度和计算能力,这样才能在中考中应对自如,冲刺高分!姓题型新变化选择题、填空题、解答题的题量与分值相较于往年没有发生变化;罗列部分试题新思路第6题的一次函数应用题转变为了实际问题的函数图象;第10题是新载体,需考生结合函数对称性和数形结合的方法解题;第13题的分式计算演变成了分式方程;第15题是几何计算题,原为第16题的位置,被普遍认为是今年中考难度最高的一道题。
2021年中考物理专题24 杠杆问题必须练(原卷版)

专题24 杠杆问题必须练(共23道题)一、选择题1.(2020甘肃金昌)如图所示的生活用具中,使用时属于费力杠杆的是()A. 羊角锤B.筷子C. 起瓶器D.钢丝钳2. (2020广西河池)如图所示,轻质木杆AC可以绕O点转动,AB:OB=4:1,A端挂着重为300N的物体G,为了使木杆保持水平位置平衡,且物体G对水平地面的压力为100N,需要在B点施加竖直向下的力的大小为()A. 400NB. 600NC. 800ND. 1200N3.(2020黑龙江龙东农垦森工)如图是杠杆原理在生活中的应用,能省距离的是()A.用羊角锤起钉子B.用撬棒撬石头C.用启子起瓶盖D.用钓鱼竿钓鱼4. (2020黑龙江绥化)小明用独轮车搬运砖头,车箱和砖头的总质量是120kg,独轮车的有关尺寸如图所示。
推车时,下列说法正确的是()A. 独轮车是省力杠杆B. 动力臂是0.7mC. 阻力臂是0.3mD. 人手竖直向上的力F的大小是1500N 5.(2021重庆模拟)材料相同的甲、乙两个物体分别挂在杠杆A、B两端,O为支点(OA<OB),如图所示,杠杆处于平衡状态。
如果将甲、乙物体(不溶于水)浸没于水中,杠杆将会()A.A 端下沉B.B 端下沉C.仍保持平衡D.无法确定6.(2020河南)在如图所示的工具中,使用时属于费力杠杆的是()A. 瓶盖起子B. 食品夹C. 起钉锤D. 核桃夹7.(2020苏州)如图所示的工具中,在使用时属于省力杠杆的是()A .镊子B .开瓶器C .船桨D .钓鱼竿8.(2020湖北咸宁)下列的工具中,在使用时可以省距离的是( )A. 食品夹B. 裁纸刀C. 钢丝钳D. 核桃夹9. (2020四川达州)一轻质不等臂杠杆AOB 的左右两端分别吊着一实心铝块和铜块,此时杠杆在水平位置平衡。
现将铝块、铜块同时浸没在水中,如图所示。
已知:331.010kg/m ρ=⨯水,332.71k 0g/m ρ=⨯铝,338.910kg/m ρ=⨯铜,则下列判断正确的是( )A. A 端下降B. B 端下降C. 仍然平衡D. 无法判断10.小华发现一只虫子在长50cm 、质量10g 的刻度尺上向右爬行,她将刻度尺右端伸出水平课桌边缘23cm ,如图所示,当虫子爬行到距刻度尺右端3cm 处时,刻度尺刚好翻转,由此计算出虫子的质量约为( )(g =10N/kg 。
武汉中考24题参考答案与试题解析

武汉中考24题参考答案与试题解析1.(2013•武汉)已知四边形ABCD中,E,F分别是AB,AD边上的点,DE与CF交于点G.(1)如图①,若四边形ABCD是矩形,且DE⊥CF.求证:;(2)如图②,若四边形ABCD是平行四边形.试探究:当∠B与∠EGC满足什么关系时,使得成立?并证明你的结论;(3)如图③,若BA=BC=6,DA=DC=8,∠BAD=90°,DE⊥CF.请直接写出的值.压轴题.(1)根据矩形性质得出∠A=∠FDC=90°,求出∠CFD=∠AED,证出△AED∽△DFC即可;(2)当∠B+∠EGC=180°时,=成立,证△DFG∽△DEA,得出=,证△CGD∽△CDF,得出=即可得出答案;(3)过C作CN⊥AD于N,CM⊥AB交AB延长线于M,连接BD,设CN=x,△BAD≌△BCD,推出∠BCD=∠A=9证△BCM∽△DCN,求出CM=x,在Rt△CMB中,由勾股定理得出BM2+CM2=BC2,代入得出方程(x﹣2+(x)2=62,求出CN=,证出△AED∽△NFC,即可得出答案.(1)证明:∵四边形ABCD是矩形,∴∠A=∠FDC=90°,∵CF⊥DE,∴∠DGF=90°,∴∠ADE+∠CFD=90°,∠ADE+∠AED=90°,∴∠CFD=∠AED,∵∠A=∠CDF,∴△AED∽△DFC,∴=;(2)当∠B+∠EGC=180°时,=成立.证明:∵四边形ABCD是平行四边形,∴∠B=∠ADC,AD∥BC,∴∠B+∠A=180°,∵∠B+∠EGC=180°,∴∠A=∠EGC=∠FGD,∵∠FDG=∠EDA,∴△DFG∽△DEA,∴=,∵∠B=∠ADC,∠B+∠EGC=180°,∠EGC+∠DGC=180°,∴∠CGD=∠CDF,∵∠GCD=∠DCF,∴△CGD∽△CDF,∴=,∴=,∴=,即当∠B+∠EGC=180°时,=成立.(3)解:=.理由是:过C作CN⊥AD于N,CM⊥AB交AB延长线于M,连接BD,设CN=x,∵∠BAD=90°,即AB⊥AD,∴∠A=∠M=∠CNA=90°,∴四边形AMCN是矩形,∴AM=CN,AN=CM,∵在△BAD和△BCD中∴△BAD≌△BCD(SSS),∴∠BCD=∠A=90°,∴∠ABC+∠ADC=180°,∵∠ABC+∠CBM=180°,∴∠MBC=∠ADC,∵∠CND=∠M=90°,∴△BCM∽△DCN,∴=,∴=,∴CM=x,在Rt△CMB中,CM=x,BM=AM﹣AB=x﹣6,由勾股定理得:BM2+CM2=BC2,∴(x﹣6)2+(x)2=62,x=0(舍去),x=,CN=,∵∠A=∠FGD=90°,∴∠AED+∠AFG=180°,∵∠AFG+∠NFC=180°,∴∠AED=∠CFN,∵∠A=∠CNF=90°,∴△AED∽△NFC,∴===.2.(2012•武汉)已知△ABC中,AB=,AC=,BC=6(1)如图1,点M为AB的中点,在线段AC上取点N,使△AMN与△ABC相似,求线段MN的长;(2)如图2,是由100个边长为1的小正方形组成的10×10的正方形网格,设顶点在这些小正方形顶点的三角形为格点三角形.①请你在所给的网格中画出格点△A1B1C1与△ABC全等(画出一个即可,不需证明)②试直接写出所给的网格中与△ABC相似且面积最大的格点三角形的个数,并画出其中一个(不需证明).作图题;压轴题.(1)作MN∥BC交AC于点N,利用三角形的中位线定理可得MN的长;作∠ANM=∠B,利用相似可得的长;(2)①AC为两直角边长为4,8的直角三角形的斜边,2为两直角边长为2,4的两直角三角形的斜②以所给网格的对角线作为原三角形中最长的边,可得每条对角线处可作4个三角形与原三角形相似,那共有8个.解:(1)①∵△AMN∽△ABC,∴=∵M为AB中点,AB=2,∴AM=,∵BC=6,∴MN=3;②∵△AMN∽△ACB,∴=,∵BC=6,AC=4,AM=,∴MN=1.5;(2)①如图所示:②每条对角线处可作4个三角形与原三角形相似,那么共有8个.3.(2011•武汉)(1)如图1,在△ABC中,点D、E、Q分别在AB、AC、BC上,且DE∥BC,AQ交DE于点P,求证:=;(2)如图,△ABC中,∠BAC=90°,正方形DEFG的四个顶点在△ABC的边上,连接AG,AF分别交DE于M,N两点.①如图2,若AB=AC=1,直接写出MN的长;②如图3,求证:MN2=DM•EN.压轴题.(1)可证明△ADP∽△ABQ,△ACQ∽△ADP,从而得出=;(2)①根据三角形的面积公式求出BC边上的高,根据△ADE∽△ABC,求出正方形DEFG的边长,据等于高之比即可求出MN;②可得出△BGD∽△EFC,则DG•EF=CF•BG;又由DG=GF=EF,得GF2=CF•BG,再根据(1)==从而得出答案.(1)证明:在△ABQ和△ADP中,∵DP∥BQ,∴△ADP∽△ABQ,∴=,同理在△ACQ和△APE中,=,∴=.(2)①作AQ⊥BC于点Q.∵BC边上的高AQ=,∵DE=DG=GF=EF=BG=CF∴DE:BC=1:3又∵DE∥BC,∴AD:AB=1:3,∴AD=,DE=,∵DE边上的高为,MN:GF=:,∴MN:=:,∴MN=.故答案为:.②证明:∵∠B+∠C=90°∠CEF+∠C=90°,∴∠B=∠CEF,又∵∠BGD=∠EFC,∴△BGD∽△EFC,∴=,∴DG•EF=CF•BG,又∵DG=GF=EF,∴GF2=CF•BG,由(1)得==,∴×=•,∴()2=•,∵GF2=CF•BG,∴MN2=DM•EN.4.(2010•武汉)已知:线段OA⊥OB,点C为OB中点,D为线段OA上一点.连接AC,BD交于点P.(1)如图1,当OA=OB,且D为OA中点时,求的值;(2)如图2,当OA=OB,且时,求tan∠BPC的值.(3)如图3,当AD:AO:OB=1:n:时,直接写出tan∠BPC的值.压轴题.(1)过D作BO的平行线,根据平行线分线段成比例定理,在△ACO中ED:CO=AD:AO,在△PDE和△P 中,ED:BC=PE:PC,再根据C是BO的中点,可以求出PE:PC=1:2,再根据三角形中位线定理,点是AC的中点,利用比例变形即可求出AP与PC的比值等于2;(2)同(1)的方法,先求出PC=AC,再过D作DF⊥AC于F,设AD为a,利用勾股定理求出AC等2a,再利用相似三角形对应边成比例求出DF、AF的值,而PF=AC﹣AF﹣PC,也可求出,又∠BPC与∠F 是对顶角,所以其正切值便可求出.(3)根据(2)的方法,把相应数据进行代换即可求出.解:(1)过D作DE∥CO交AC于E,∵D为OA中点,∴AE=CE=,,∵点C为OB中点,∴BC=CO,,∴,∴PC==,∴=2;(2)过点D作DE∥BO交AC于E,∵,∴==,∵点C为OB中点,∴,∴,∴PC==,过D作DF⊥AC,垂足为F,设AD=a,则AO=4a,∵OA=OB,点C为OB中点,∴CO=2a,在Rt△ACO中,AC===2a,又∵Rt△ADF∽Rt△ACO,∴,∴AF=,DF=,PF=AC﹣AF﹣PC=2a﹣﹣=,tan∠BPC=tan∠FPD==.(3)与(2)的方法相同,设AD=a,求出DF=a,PF=a,所以tan∠BPC=.5.(2009•武汉)如图1,在Rt△ABC中,∠BAC=90°,AD⊥BC于点D,点O是AC边上一点,连接BO交AD于F,OE⊥OB交BC边于点E.(1)求证:△ABF∽△COE;(2)当O为AC的中点,时,如图2,求的值;(3)当O为AC边中点,时,请直接写出的值.几何综合题;压轴题.(1)要求证:△ABF∽△COE,只要证明∠BAF=∠C,∠ABF=∠COE即可.(2)作OH⊥AC,交BC于H,易证△ABF≌△COE,进而证明△ABF∽△HOF,根据相似三角形的对应边的比等,即可得出所求的值.同理可得(3)=n.(1)证明:∵AD⊥BC,∴∠DAC+∠C=90°.∵∠BAC=90°,∴∠BAF=∠C.∵OE⊥OB,∴∠BOA+∠COE=90°,∵∠BOA+∠ABF=90°,∴∠ABF=∠COE.∴△ABF∽△COE.(2)解:过O作AC垂线交BC于H,则OH∥AB,由(1)得∠ABF=∠COE,∠BAF=∠C.∴∠AFB=∠OEC,∴∠AFO=∠HEO,而∠BAF=∠C,∴∠FAO=∠EHO,∴△OEH∽△OFA,∴OF:OE=OA:OH又∵O为AC的中点,OH∥AB.∴OH为△ABC的中位线,∴OH=AB,OA=OC=AC,而,∴OA:OH=2:1,∴OF:OE=2:1,即=2;(3)解:=n.6.(2010•大田县)正方形ABCD中,点O是对角线AC的中点,P是对角线AC上一动点,过点P作PF⊥CD于点F.如图1,当点P与点O重合时,显然有DF=CF.(1)如图2,若点P在线段AO上(不与点A、O重合),PE⊥PB且PE交CD于点E.①求证:DF=EF;②写出线段PC、PA、CE之间的一个等量关系,并证明你的结论;(2)若点P在线段OC上(不与点O、C重合),PE⊥PB且PE交直线CD于点E.请完成图3并判断(1)中的结论①、②是否分别成立?若不成立,写出相应的结论.(所写结论均不必证明)压轴题;动点型.(1)由正方形的性质证得△BQP≌△PFE,从而得到DF=EF,由于△PCF和△PAG均为等腰直角三角形,故PA=PG,PC=CF,易得PA=EF,进而得到PC、PA、CE满足关系为:PC=CE+PA;(2)同(1)证得DF=EF,三条线段的数量关系是PA﹣PC=CE.解:(1)如图2,延长FP交AB于点Q,∵∠BQP=∠PFE=90°,∴△BQP≌△PFE,∴QP=EF,∵AQ=DF,∴DF=EF;②如图2,过点P作PG⊥AD.∵PF⊥CD,∠PCF=∠PAG=45°,∴△PCF和△PAG均为等腰直角三角形,∵四边形DFPG为矩形,∴PA=PG,PC=CF,∵PG=DF,DF=EF,∴PA=EF,∴PC=CF=(CE+EF)=CE+EF=CE+PA,即PC、PA、CE满足关系为:PC=CE+PA;(2)结论①仍成立;结论②不成立,此时②中三条线段的数量关系是PA﹣PC=CE.如图3:①∵PB⊥PE,BC⊥CE,∴B、P、C、E四点共圆,∴∠PEC=∠PBC,在△PBC和△PDC中有:BC=DC(已知),∠PCB=∠PCD=45°(已证),PC边公共边,∴△PBC≌△PDC(SAS),∴∠PBC=∠PDC,∴∠PEC=∠PDC,∵PF⊥DE,∴DF=EF;②同理:PA=PG=DF=EF,PC=CF,∴PA=EF=(CE+CF)=CE+CF=CE+PC即PC、PA、CE满足关系为:PA﹣PC=CE.7.(2007•武汉)填空或解答:点B、C、E在同一直线上,点A、D在直线CE的同侧,AB=AC,EC=ED,∠BAC=∠CED,直线AE、BD交于点F.(1)如图①,若∠BAC=60°,则∠AFB=60°;如图②,若∠BAC=90°,则∠AFB=45°;(2)如图③,若∠BAC=α,则∠AFB=90°(用含α的式子表示);(3)将图③中的△ABC绕点C旋转(点F不与点A、B重合),得图④或图⑤.在图④中,∠AFB与∠α的数量关系是∠AFB=90°;在图⑤中,∠AFB与∠α的数量关系是∠AFB=90°+.请你任选其中一个结论证明.压轴题;探究型.(1)由题意易得△ABC∽△EDC,进一步证得△BCD∽△ACE,进而可得∠AFB=∠CBD+∠AEC=∠CAE+∠AEC=∠ACB=60°,同理可得,∠AFB的大小;(2)同(1)的证明可得;(3)图四,由前面步骤可得∠AFB=180°﹣∠CAE﹣∠BAC﹣∠ABD=180°﹣∠BAC﹣∠ABC=∠ACB=90°图5,与前面步骤相同,可求得∠AFB=∠BDC+∠CDE+∠DEF=∠CDE+∠CED,代入数据求大小.解:(1)∵AB=AC,EC=ED,∠BAC=∠CED=60°,∴∠ACB=∠ECD,,∴∠BCD=∠ACE,∴△BCD∽△ACE,∴∠CBD=∠CAE,∴∠AFB=180°﹣∠CAE﹣∠BAC﹣∠ABD,=180°﹣∠BAC﹣∠ABC=∠ACB,∵AB=AC,∠BAC=α,∴∠ACB=90°﹣,∴∠AFB=90°﹣.故答案为:∠AFB=90°.(3)图4中:∠AFB=90°;图5中:∠AFB=90°+.∠AFB=90°的证明如下:∵AB=AC,EC=ED,∠BAC=∠CED,∴△ABC∽△EDC,∴∠ACB=∠ECD,,∴∠BCD=∠ACE,∴△BCD∽△ACE,∴∠CBD=∠CAE,∴∠AFB=180°﹣∠CAE﹣∠BAC﹣∠ABD,=180°﹣∠BAC﹣∠ABC=∠ACB,∵AB=AC,∠BAC=α,∴∠ACB=90°﹣,∴∠AFB=90°﹣.∠AFB=90°+的证明如下:∵AB=AC,EC=ED,∠BAC=∠CED,∴△ABC∽△EDC,∴∠ACB=∠ECD,,∴∠BCD=∠ACE,∴△BCD∽△ACE,∴∠BDC=∠AEC,∴∠AFB=∠BDC+∠CDE+∠DEF,=∠CDE+∠CED=180°﹣∠DCE,∵AB=AC,EC=ED,∠BAC=∠DEC=α,∴∠DCE=90°﹣,∴∠AFB=180°﹣(90°﹣)=90°+.。
近两年中考数学24、25题

近两年中考后两题评析一、考点分析:中考中第24、25题是综合性比较强的大题,往往也是学生最容易失分的题。
了解这类题的各种类型,掌握第三问得解题方法,各个击破。
二、教学目标:1. 通过与学生的交流,了解学生的做24、25题时的做题习惯、对考点相关知识点的掌握情况以 及薄弱的地 方,以便更好的查漏补缺。
2. 了解中考中较难的第24、25题的各种题型。
3. 掌握正确的解题方法三、教学内容 (一)第24题由最近几年武汉市的中考试题分析第24题的最常见题型一般是纯几何题,次类型的题主要是集锐角三角形,直角三角形,四边形,三角函数,全等,相似等知识的综合运用。
一般第一问比较简单,第二问第三问比较难,如何把握好这三问之间的关系是解的关键。
例题1 已知:线段OA ⊥OB ,点C 为OB 中点,D 为线段OA 上一点。
连结AC ,BD 交于点P .(1) 如图1,当OA=OB ,且D 为OA 中点时,求A P P C的值;(2) 如图2,当OA=OB ,且A D 1A O4=时,求tan ∠BPC 的值.(3) 如图3,当AD ∶AO ∶OB=1∶n ∶2n 时,直接写出tan ∠BPC的值.(图1) (图2) (图3) 解:(1) 延长AC 至点E ,使CE =CA ,连接BE ,∵C 为OB 中点, ∴△BCE ≅△OCA ,∴BE =OA ,∠E =∠OAC ,∴BE //OA , ∴△APD ~△EPB ,∴EP AP =EBAD 。
又∵D 为OA 中点,OA =OB ,∴EPAP =AOAD =21。
∴EPAP =APPC AP +2=21,∴PCAP =2。
(2) 延长AC 至点H ,使CH =CA ,连结BH ,∵C 为OB 中点, ∴△BCH ≅△OCA ,∴∠CBH =∠O =90︒,BH =OA 。
由AOAD =41,DCOPHA BABCD POE设AD =t ,OD =3t ,则BH =OA =OB =4t 。
2023湖北武汉中考英语试卷及答案

2023湖北武汉中考英语试卷及答案一、听力测试(共30分)第一部分听对话,回答问题听下面5段对话,每段对话后有一个小题,从题中所给的A、B、C三个选项中选出最佳选项。
1. What does the woman want to do tomorrow?A. Go shopping.B. Visit her friend.C. Stay at home.2. What is the relationship between the speakers?A. Doctor and patient.B. Teacher and student.C. Customer and shop assistant.3. What does the man want to do?A. Get a drink.B. Take a shower.C. Have a rest.4. Why is the woman going to London?A. For business.B. For vacation.C. For study.5. What is the man worried about?A. His test results.B. His health.C. His friend’s health.第二部分听对话和短文,回答问题听第6段材料,回答第6至7题。
6. Where are the speakers?A. In a hotel.B. On a train.C. In a museum.7. What does the man suggest they do?A. Visit the museum tomorrow.B. Have a picnic in the park.C. Go shopping in the city.听第7段材料,回答第8至10题。
8. What does the woman want to buy?A. A pair of shoes.B. A T-shirt.C. A skirt.9. What size does the woman wear in skirts?A. 8.B. 10.C. 12.10. What does the man suggest the woman do?A. Buy a different size.B. Look for other shops.C. Wait for a discount.听第8段材料,回答第11至13题。
武汉中考复习专题:沸腾实验

沸腾实验武汉原题:(2014武汉24题)(4分)在探究水沸腾时温度变化特点的实验中,用酒精灯给烧杯中的水加热,当水温接近90℃时,每隔1min记录一次温度,绘制了如图所示的水温与时间关系的图像。
(1)水沸腾时看到大量的“白气”不断地从烧杯上冒出,这些“白气”是由于水蒸气而形成的。
(2)由图象可知:水沸腾时温度变化的特点是方的气压(填“大于”、“等于”或“小于”)1标准大气压。
(2015武汉24题)(4分)小明和小华分别利用图甲所示的相同装置探究水沸腾时温度变化的特点,当水温接近90℃时,每隔0.5分钟记录一次温度,并绘制出了如图乙所示的水温与时间关系的图像。
(1)实验时,当看到水中有大量气泡不断上升、变大,到水面破裂开来,里面的散发到空气中,就表明水沸腾了。
(2)分析图乙可知,小华将水加热至沸腾的时间明显较长,最有可能的原因是(3)小明在第9分钟撤掉酒精灯后,发现有一段时间水温依然保持不变。
如图乙所示,这段时间内烧杯底部的温度(填“高于”“等于”或“低于”)杯内水的温度,原因是。
(2016武汉23题)(3分)某同学用如图甲所示的实验装置,比较不同物质的比热容和探究水沸腾时温度变化的特点。
将分别盛有相同质量的水和食用油的两个试管固定在铁架台上,温度传感器的探头与水和食用油良好接触,将温度传感器与计算机相连,计算机上显示的实验图线如图乙所示。
由图乙可知:水沸腾时吸热,温度(选填“升高”、“不变”或“降低”);加热2min 水吸收的热量(选填“大于”、“等于”或“小于”)食用油吸收的热量;食用油的比热容为J/(kg.℃)。
(2016武汉四调24题)(4 分)某同学用图甲所示的实验装置探究水沸腾时温度变化的特点。
(1)实验中观察到如图乙中a、b所示的两种情景,其中水沸腾时的情景为_________ (选填“a”或“b”)。
(2) 水沸腾时温度计示数如图丙所示,表明此时水的沸点为________℃,说明此时气压_________ (选填“大于”“等于”或“小于”)1 个标准大气压。
武汉中考题及答案

武汉九年级调研测试1.小明运用所学物理知识对生活中的一些物理量进行估测,以下估测中不符合实际的是()A.家用白炽灯灯丝电阻大约是20ΩB.成年人步行速度约1.0m/sC.中学生的体重约500ND.运动员举重时功率可达1kW2.小明对厨房中看到的一些现象进行了解释,其中不正确的是()A.用高压锅煮牛肉容易煮烂,是因为液体的沸点随气压增大而降低B.电饭煲使用三线插头,是为了让用电器的金属外壳和大地相连C.用煤气炉炒菜,是利用内能来加热物体D.能闻到饭菜的香味,这是分子无规则运动的结果3.下列措施中可在传播过程中控制噪声的是()4.下图是探究平面镜成像特点的实验装置,a为玻璃板,b为点燃的蜡烛,c是和b完全相同但未点燃的蜡烛。
则下列说法错误的是()A.沿水平桌面移动蜡烛c不能使c志b的像完全重合是因为玻璃板没有与桌面垂直放置B.眼睛透过玻璃板看见的“蜡烛c”实际上是光的折射所形成的虚像C.某同学发现镜中出现了b两个不重合的像是由于光在两个反射面上两次反射成像造成的D.为了保证实验效果应选择较厚的平板玻璃做实验5.下列关于运动和静止的说法正确的是()A.“嫦娥一号”从地球奔向月球,以地面为参照物,“嫦娥一号”是静止的B.飞机在空中加油,以受油机为参照物,加油机是静止的C.汽车在马路上行驶,以路灯为参照物,汽车是静止的D.小船顺流而下,以河岸为参照物,小船是静止的6.武汉市着手建立“绿色交通”体系,将建112条彩色自行车道,推行“低碳生活”。
到时候自行车会成为人们的重要交通工具,下列有关自行车的结构及使用的说法中正确的是()A.自行车的座垫做得较宽大是为了减小对臀部的压力B.自行车的龙头实际上是一个省力杠杆C.骑自行车上坡前用力蹬车是为了增大惯性D.骑自行车匀速下坡时动能和机械能均不变7.某家庭有父母与子女共四人,他们想采用投票表决的方式决定周末是否要外出旅游。
如果两个孩子都要去,而父母中只有一位要去,另一位愿留守在家中,那么他们就去旅游。
2023武汉中考数学24题

中考数学试题一、选择题1.如图,以A、B、C为顶点的三角形与以D、E、F为顶点的三角形相似,则这两个三角形的相似比为()A.2:1B.3:1C.4:3D.3:22.如图图形中是中心对称图形的为()A.B. C.D.3.对于反比例函数y=kx(k≠0),下列所给的四个结论中,正确的是()A.过图象上任一点P作x轴、y轴的垂线,垂足分别A,B,则矩形O APB的面积为k B.若点(2,4)在其图象上,则(−2,4)也在其图象上C.反比例函数的图象关于直线y=x和y=−x成轴对称D.当k>0时,y随x的增大而减小4.一元二次方程x2﹣3x=0的根是()A.x=3 B.x1=0,x2=﹣3C.x1=0,x2=√3 D.x1=0,x2=35.已知反比例函数y=kx(k≠0),当x<0时,y随x的增大而增大,那么一次函数y= kx−k的图象经过()。
A.第一,二,三象限B.第一,二,四象限C.第一,三,四象限D.第二,三,四象限6.在同一平面直角坐标系中,函数y=x﹣1与函数y=1的图象可能是()xA.B. C.D.7.如图,四边形ABCD是矩形,E是边BC延长线上的一点,AE与CD相交于点F,则图中的相似三角形共有()A.4对 B.3对C.2对D.1对8.一个由相同正方体堆积而成的几何体如图所示,从正面看,这个几何体的形状是()。
A.B.C.D.二、填空题(共24分)9.已知△ABC,若有|sinA−1|与(tanB−√3)2互为相反数,则∠C的度数2是。
(x<0)图象上的点,过点A作y轴10.如图,在平面直角坐标系中,点A是函数y=kx的垂线交y轴于点B,点C在x轴上,若△ABC的面积为1,则k的值为()。
11.把一张半径为2cm,圆心角为120°的扇形纸片卷成一个圆锥的侧面,那么这个圆锥的底面积是。
12.把一张半径为2cm,圆心角为120°的扇形纸片卷成一个圆锥的侧面,那么这个圆锥的底面积是。
2022年湖北武汉中考数学试卷

2022年湖北武汉中考数学试卷1.(2022·真题)实数2022的相反数是( )A.2022B.−2022C.12022D.−120222.(2022·真题)式子√x−1在实数范围内有意义,则x的取值范围是( )A.x≥0B.x≥−1C.x≥1D.x≤13.(2022·真题)不透明的袋子中只有4个黑球和2个白球,这些球除颜色外无其他差别,随机从袋子中一次摸出3个球,下列事件是不可能事件的是()A.3个球都是黑球B.3个球都是白球C.3个球中有黑球D.3个球中有白球4.(2022·真题)现实世界中,对称现象无处不在,中国的方块字中有些也具有对称性.下列美术字是轴对称图形的是( )A.B.C.D.5.(2022·真题)如图是由5个相同的小正方体组成的几何体,该几何体的左视图是( )A.B.C.D.6.(2022·真题)“漏壶”是一种中国古代计时器,在它内部盛一定量的水,不考虑水量变化对压力的影响,水从壶底小孔均匀漏出,壶内璧有刻度,人们根据壶中水面的位置计算时间,用x表示漏水时间,y 表示壶底到水面的高度,下列图象适合表示 y 与 x 的对应关系的是 ( )A .B .C .D .7. (2022·真题)从 1,2,3,4 四个数中随机选取两个不同的数,分别记为 a ,c ,则关于 x 的一元二次方程 ax 2+4x +c =0 有实数解的概率是 ( )A . 14B . 13C . 12D . 238. (2022·真题)已知反比例函数 y =k x 的图象分别位于第二、第四象限,A (x 1,y 1),B (x 2,y 2) 两点在该图象上.下列命题:①过点 A 作 AC ⊥x 轴,C 为垂足,连接 OA .若 △ACO 的面积是 3,则 k =−6;②若 x 1<0<x 2,则 y 1>y 2;③若 x 1+x 2=0,则 y 1+y 2=0.其中真命题个数是 ( )A . 0B . 1C . 2D . 39. (2022·真题)如图,AB 是 ⊙O 的直径,M ,N 是 AB⏜(异于 A ,B )上两点,C 是 MN ⏜ 上一动点,∠ACB 的平分线交 ⊙O 于点 D ,∠BAC 的平分线交 CD 于点 E .当点 C 从点 M 运动到点 N 时,则 C ,E 两点的运动路径长的比是 ( )A . √2B . π2C . 32D . √5210. (2022·真题)观察等式:2+22=23−2;2+22+23=24−2;2+22+23+24=25−2;⋯.已知按一定规律排列的一组数:250,251,252,⋯,299,2100.若 250=a ,用含 a 的式子表示这组数的和是 ( )A . 2a 2−2aB . 2a 2−2a −2C . 2a 2−aD . 2a 2+a11.(2022·真题)计算√16的结果是.12.(2022·真题)武汉市某气象观测点记录了5天的平均气温(单位:∘C),分别是25,20,18,23,27,这组数据的中位数是.13.(2022·真题)计算2aa2−16−1a−4的结果是.14.(2022·真题)如图,在平行四边形ABCD中,E,F是对角线AC上两点,AE=EF=CD,∠ADF=90∘,∠BCD=63∘,则∠ADE的大小是.15.(2022·真题)抛物线y=ax2+bx+c经过A(−3,0),B(4,0)两点,则关于x的一元二次方程a(x−1)2+c=b−bx的解是.16.(2022·真题)请回答下列各题:(1)问题背景:如图1,将△ABC绕点A逆时针旋转60∘得到△ADE,DE与BC交于点P可推出结论:PA+PC=PE.(2)问题解决:如图2,在△MNG中,MN=6,∠M=75∘,MG=4√2.点O是△MNG内一点,则点O到△MNG三个顶点的距离和的最小值是.17.(2022·真题)计算:(2x2)3−x2⋅x4.18.(2022·真题)如图,点A,B,C,D在一条直线上,CE与BF交于点G,∠A=∠1,CE∥DF.求证:∠E=∠F.19.(2022·真题)为弘扬中华传统文化,某校开展“汉剧进课堂”的活动.该校随机抽取部分学生,按四个类别:A表示“很喜欢”,B表示“喜欢”,C表示“一般”,D表示“不喜欢”,调查他们对汉剧的喜爱情况,将结果绘制成如下两幅不完整的统计图,根据图中提供的信息,解决下列问题.(1) 这次共抽取名学生进行调查统计,扇形统计图中,D类所对应的扇形圆心角的大小是.(2) 将条形统计图补充完整.(3) 该校共有1500名学生,估计该校表示“喜欢”的B类的学生大约有多少人?20.(2022·真题)如图是由边长为1的小正方形构成的网格,每个小正方形的顶点叫做格点.四边形ABCD的顶点在格点上,点E是边DC与网格线的交点.请选择适当的格点,用无刻度的直尺在网格中完成下列画图,保留连线的痕迹,不要求说明理由.(1) 如图1,过点A画线段AF,使AF∥DC,且AF=DC.(2) 如图1,在边AB上画一点G,使∠AGD=∠BGC.(3) 如图2,过点E画线段EM,使EM∥AB,且EM=AB.21.(2022·真题)已知AB是⊙O的直径,AM和BN是⊙O的两条切线,DC与⊙O相切于点E,分别交AM,BN于D,C两点.(1) 如图1,求证:AB2=4AD⋅BC.(2) 如图2,连接OE并延长交AM于点F,连接CF.若∠ADE=2∠OFC,AD=1,求图中阴影部分的面积.22.(2022·真题)某商店销售一种商品,经市场调查发现,该商品的周销售量y(件)是售价x(元/件)的一次函数,其售价,周销售量,周销售利润w(元)的三组对应值如下表:售价x(元/件)506080注:周销售利润=周销售量×(售价−进价)周销售量y(件)1008040周销售利润w(元)100016001600(1) ① 求y关于x的函数解析式(不要求写出自变量的取值范围);②该商品进价是元/件;当售价是元/件时,周销售利润最大,最大利润是元.(2) 由于某种原因,该商品进价提高了m元/件(m>0),物价部门规定该商品售价不得超过65元/件,该商店在今后的销售中,周销售量与售价仍然满足(1)中的函数关系.若周销售最大利润是1400元,求m的值.=n,M是BC边上一点,连接23.(2022·湖北武汉市·真题)在Rt△ABC中,∠ABC=90∘,ABBCAM.(1) 如图1,若n=1,N是AB延长线上一点,CN与AM垂直.求证:BM=BN.(2) 过点B作BP⊥AM,P为垂足,连接CP并延长交AB于点Q.①如图2,若n=1,求证:CPPQ =BMBQ.②如图3,若M是BC的中点,直接写出tan∠BPQ的值(用含n的式子表示).24.(2022·真题)已知抛物线C1:y=(x−1)2−4和C2:y=x2.(1) 如何将抛物线C1平移得到抛物线C2(2) 如图1,抛物线C1与x轴正半轴交于点A,直线y=−43x+b过点A,交抛物线C1于另一点B.请你在线段AB上取点P,过点P作直线PQ∥y轴交抛物线C1于点Q,连接AQ.①若AP=AQ,求点P的横坐标.②若PA=PQ,直接写出点P的横坐标.(3) 如图2,△MNE的顶点M,N在抛物线C2上,点M在点N右边,两条直线ME,NE与抛物线C2均有唯一公共点,ME,NE均与y轴不平行.若△MNE的面积为2,设M,N两点的横坐标分别为m,n,求m与n的数量关系.答案1. 【答案】B【解析】B选项符合相反数的定义.【知识点】相反数的定义2. 【答案】C【解析】要使√x−1有意义,∴x−1≥0,x≥1.【知识点】二次根式有意义的条件3. 【答案】B【解析】【分析】根据事件发生的可能性大小判断相应事件的类型.【解析】解:A、3个球都是黑球是随机事件;B、3个球都是白球是不可能事件;C、3个球中有黑球是必然事件;D、3个球中有白球是随机事件;故选:B.【点评】本题考查的是必然事件、不可能事件、随机事件的概念.必然事件指在一定条件下,一定发生的事件.不可能事件是指在一定条件下,一定不发生的事件,不确定事件即随机事件是指在一定条件下,可能发生也可能不发生的事件.【知识点】事件的分类4. 【答案】D【解析】根据轴对称图形的概念,能找到一条直线,沿这条直线折叠,直线两旁的部分能够完全重合的图形是轴对称图形,如图所示.【知识点】轴对称图形5. 【答案】A【解析】从左面看易得下面一层有2个正方形,上面一层左边有1个正方形,如图所示:故选A.【知识点】由立体图形到视图6. 【答案】A【解析】∵不考虑水量变化对压力的影响,水从壶底小孔均匀漏出,t表示漏水时间,y表示壶底到水面的高度,∴随t的增大而减小,符合一次函数图象【知识点】其他实际问题7. 【答案】C【解析】画树状图得:由树形图可知:一共有12种等可能的结果,其中使ac≤4的有6种结果,.故选C∴关于x的一元二次方程ax2+4x+c=0有实数解的概率为12【知识点】树状图法求概率8. 【答案】D【解析】①过点A作AC⊥x轴,C为垂足,连接OA.∵△ACO的面积为3,∴∣k∣=6,的图象分别位于第二、第四象限,∵反比例函数y=kx∴k<0,∴k=−6,正确,是真命题;② ∵反比例函数y=k的图象分别位于第二、第四象限,x∴在所在的毎一个象限y随着x的增大而增大,若x1<0<x2,则y1>0>y2,正确,是真命题;③当A,B两点关于原点对称时,x1+x2=0,则y1+y2=0,正确,是真命题,真命题有3个.【知识点】k对反比例函数的图象及性质的影响、命题的真假9. 【答案】A【解析】方法一:如图,连接EB.设OA=r.∵AB 是直径,∴∠ACB =90∘,∵E 是 △ACB 的内心,∴∠AEB =135∘,∵∠ACD =∠BCD ,∴AD =DB ,∴AD⏜=DB ⏜, ∴∠ADB =90∘,易知点 E 在以 D 为圆心 DA 为半径的圆上,运动轨迹是 GF⏜,点 C 的运动轨迹是 MN ⏜, ∵∠MON =2∠GDF ,设 ∠GDF =α,则 ∠MON =2α,∴MN⏜GF ⏜=2α⋅π⋅r 180α⋅π⋅√2r180=√2.方法二:如图所示,连接 AD ,BD ,∵ 点 E 是 ∠ACB 的平分线与 ∠BAC 的平分线的交点,∴∠ACD =∠BCD ,∠CAE =∠BAE .∵∠BAD =∠BCD ,∴∠BAD +∠BAE =∠ACD +∠CAE ,即 ∠DAE =∠AED ,∴AD =ED ,∴ 点 E 在以 D 为圆心,以 AD 为半径的圆上.又 ∵AB 是 ⊙O 的直径,CD 是 ∠ACB 的平分线,∴AD =BD ,∴AD =BD .设 ⊙ 的半径为 r ,∴AD =√2r ,∴ 点 E 的运动路径长是 90π⋅√2r 180=√22πr . ∵ 点 C 是 MN 上一动点,∴ 点 C 的运动路径长是 πr ,∴C ,E 两点的运动路径长的比是 πr:√22πr =√2:1.【知识点】弧长的计算10. 【答案】C【解析】∵2+22=23−2;2+22+23=24−2;2+22+23+24=25−2;⋯∴2+22+23+⋯+2n=2n+1−2,∴250+251+252+⋯+299+2100=(2+22+23+⋯+2100)−(2+22+23+⋯+249)=(2101−2)−(250−2),∵250=a,∴2101=(250)2⋅2=2a2,∴原式=2a2−a.【知识点】用代数式表示规律11. 【答案】4【解析】√16=4.【知识点】算术平方根的运算12. 【答案】23℃【解析】将数据重新排列为18,20,23,25,27,所以这组数据的中位数为23∘C.【知识点】中位数13. 【答案】1a+4【解析】原式=2a(a+4)(a−4)−a+4(a+4)(a−4) =2a−a+4(a+4)(a−4)=a−4(a+4)(a−4)=1a+4.【知识点】分式的加减14. 【答案】21°【解析】设∠ADE=x,∵AE=EF,∠ADF=90∘,∴∠DAE=∠ADE=x,DE=12AF=AE=EF,∵AE=EF=CD,∴DE=CD,∴∠DCE=∠DEC=2x,∵四边形ABCD是平行四边形,∴AD∥BC,∴∠DAE=∠BCA=x,∴∠DCE=∠BCD−∠BCA=63∘−x,∴2x=63∘−x,解得:x=21∘,即∠ADE=21∘.故答案为:21∘.【知识点】平行四边形及其性质15. 【答案】x1=−2,x2=5【解析】方法一:关于x的一元二次方程a(x−1)2+c=b−bx变形为a(x−1)2+b(x−1)+c=0,把抛物线y=ax2+bx+c沿x轴向右平移1个单位得到y=a(x−1)2+b(x−1)+c,∵抛物线y=ax2+bx+c经过点A(−3,0),B(4,0),∴抛物线y=a(x−1)2+b(x−1)+c与x轴的两交点坐标为(−2,0),(5,0),∴一元二方程a(x−1)2+b(x−1)+c=0的解为x1=−2,x2=5.方法二:∵抛物线y=ax2+bx+c经过A(−3,0),B(4,0)两点,∴方程ax2+bx+c=0的两个解分别是x1=−3,x2=4,∴关于x的一元二次方程a(x−1)2+c=b−bx,即a(x−1)2+b(x−1)+c=0中,x−1=−3或x−1=4,∴x1=−2,x2=5.【知识点】二次函数与方程16. 【答案】2√29【解析】(1)如图1,在BC上截取BG=PD,在△ABG和△ADP中,{AB=AD,∠B=∠D, BG=PD,∴△ABG≌△ADP(SAS),∴AG=AP,BG=DP,∴GC=PE.∵∠GAP=∠BAD=60∘,∴△AGP是等边三角形,∴AP=GP,∴PA+PC=GP+PC=GC=PE,∴PA+PC=PE.(2)如图2:以MG为边作等边三角形△MGD,以OM为边作等边△OME,连接ND,作DF⊥NM,交NM的延长线于F.∵△MGD和△OME是等边三角形,∴OE=OM=ME,∠DMG=∠OME=60∘,MG=MD,∴∠GMO=∠DME,在△GMO和△DME中,{OM=ME,∠GMO=∠DME, MG=MD,∴△GMO≌△DME(SAS),∴OG=DE,∴NO+GO+MO=DE+OE+NO,∴当D,E,O,M四点共线时,NO+GO+MO值最小,∵∠NMG=75∘,∠GMD=60∘,∴∠NMD=135∘,∴∠DMF=45∘,∵MG=4√2,∴MF=DF=4,∴NF=MN+MF=6+4=10,∴ND=√NF2+DF2=√102+42=2√29,∴MO+NO+GO最小值为2√29.【知识点】有一个角是60°的等腰三角形是等边三角形17. 【答案】(2x2)3−x2⋅x4 =8x6−x6=7x6.【知识点】积的乘方18. 【答案】∵CE∥DF,∴∠ACE=∠D,∵∠A=∠1,∴180∘−∠ACE−∠A=180∘−∠D=∠1,又∵∠E=180∘−∠ACE−∠A,∠F=180∘−∠D−∠1,∴∠E=∠F.【知识点】同位角相等19. 【答案】(1) 50;72∘(2) A类学生:50−23−12−10=5(人),条形统计图补充如下:(3) 该校表示“喜欢”的B类的学生大约有1500×2350=690(人),答:该校表示“喜欢”的B类的学生大约有690人.【解析】(1) 这次共抽取:12÷24%=50(人),D类所对应的扇形圆心角的大小360∘×1050=72∘.【知识点】扇形统计图、用样本估算总体、条形统计图20. 【答案】(1) 如图所示,线段AF即为所求.(2) 如图所示,点G即为所求.(3) 画图如图(2)所示.【知识点】勾股定理、垂直于同一直线的两直线平行、平行线的定义、等腰三角形“三线合一”21. 【答案】(1) 连接OC,OD,如图3所示,∵AM和BN是它的两条切线,∴AM⊥AB,BN⊥AB,∵AM∥BN,∴∠ADE+∠BCE=180∘,∵DC切⊙O于E,∴∠ODE=12∠ADE,∠OCE=12∠BCE,∴∠ODE+∠OCE=90∘,∴∠DOC=90∘,∴∠AOD+∠COB=90∘,∵∠AOD+∠ADO=90∘,∴∠AOD=∠OCB,∵∠OAD=∠OBC=90∘,∴△AOD∽△BCO,∴ADBO =OABC,∴OA2=AD⋅BC,∴(12AB)2=AD⋅BC,∴AB2=4AD⋅BC.(2) 连接OD,OC,如图4所示,∵∠ADE =2∠OFC ,∴∠ADO =∠OFC ,∵∠ADO =∠BOC ,∠BOC =∠FOC ,∴∠OFC =∠FOC ,∴CF =OC ,∴CD 垂直平分 OF ,∴OD =DF ,在 △COD 和 △CFD 中,{OC =CF,OD =DF,CD =CD,∴△COD ≌△CFD (SSS ),∴∠CDO =∠CDF ,∵∠ODA +∠CDO +∠CDF =180∘,∴∠ODA =60∘=∠BOC ,∴∠BOE =120∘,在 Rt △DAO ,AD =√33OA , Rt △BOC 中,BC =√3OB ,∴AD:BC =1:3,∵AD =1,∴BC =3,OB =√3,∴ 图中阴影部分的面积 =2S △OBC −S △OBE =2×12×√3×3−120π×(√3)2360=3√3−π.【知识点】切线的性质、两角分别相等、扇形面积的计算22. 【答案】(1) ① 设 y 与 x 的函数关系式为 y =kx +b (k ≠0),依题意有 {50k +b =100,60k +b =80,解得 {k =−2,b =200,所以 y 与 x 的函数关系式是 y =−2x +200.② 40;70;1800.(2) 依题意有w =(−2x +200)(x −40−m )=−2x 2+(2m +280)x −8000−200m =−2(x −m+1402)2+12m 2−60m +1800, 因为 m >0,所以对称轴 x =m+1402>70,因为−2<0,所以抛物线开口向下,因为x≤65,所以w随x的增大而增大,所以当x=65时,w有最大值(−2×65+200)(65−40−m),所以(−2×65+200)(65−40−m)=1400,所以m=5.【解析】(1) ②设该商品进价为a元,则根据表格可列(50−a)×100=1000元,解得a=40,因为w=(x−40)(−2x+200)=−2(x−70)2+1800,故当售价为70元/件时,最大利润为1800元.【知识点】利润问题23. 【答案】(1) 如图1中,延长AM交CN于点H.∵AM⊥CN,∴∠AHC=90∘,∵∠ABC=90∘,∴∠BAM+∠AMB=90∘,∠BCN+∠CMH=90∘,∵∠AMB=∠CMH,∴∠BAM=∠BCN,∵BA=BC,∠ABM=∠CBN=90∘,∴△ABM≌△CBN(ASA),∴BM=BN.(2) ①如图2中,作CH∥AB交BP的延长线于H.∵BP⊥AM,∴∠BPM=∠ABM=90∘,∵∠BAM+∠AMB=90∘,∠CBH+∠BMP=90∘,∴∠BAM=∠CBH,∵CH∥AB,∴∠HCB+∠ABC=90∘,∵∠ABC=90∘,∴∠ABM=∠BCH=90∘,∵AB=BC,∴△ABM≌△BCH(ASA),∴BM=CH,∵CH∥BQ,∴PCPQ =CHBQ=BMBQ.② 1n.【解析】(2) ②如图3中,作CH∥AB交BP的延长线于H,作CN⊥BH于N.不妨设BC=2m,则AB=2mn.则BM=CM=m,CH=mn ,BH=mn√1+4n2,AM=m√1+4n2,∵12⋅AM⋅BP=12⋅AB⋅BM,∴PB=√1+4n2,∵12⋅BH⋅CN=12⋅CH⋅BC,∴CN=√1+4n2,∵CN⊥BH,PM⊥BH,∴MP∥CN,∵CM=BM,∴PN=BP=√1+4n2,∵∠BPQ=∠CPN,∴tan∠BPQ=tan∠CPN=NCPN =√1+4n22mn√1+4n2=1n.【知识点】平行线分线段成比例定理、正切、角边角24. 【答案】(1) y=(x−1)2−4向左平移1个单位长度,再向上平移4个单位长度即可得到y=x2.(2) ① y=(x−1)2−4与x轴正半轴的交点A(3,0),∵直线y=−43x+b经过点A,∴b=4,∴y=−43x+4,y =−43x +4 与 y =(x −1)2−4 的交点为 −43x +4=(x −1)2−4 的解,∴x =3 或 x =−73,∴B (−73,649),设 P (t,−43t +4),且 −73<t <3,∵PQ ∥y 轴,∴Q (t,t 2−2t −3),当 AP =AQ 时,∣∣4−43t ∣∣=∣t 2−2t −3∣, 则有 −4+43t =t 2−2t −3,∴t =13,∴P 点横坐标为 13. ② −23.(3) 设经过 M 与 N 的直线解析式为 y =k (x −m )+m 2,∴{y =x 2,y =k (x −m )+m 2,则有 x 2−kx +km −m 2=0,Δ=k 2−4km +4m 2=(k −2m )2=0,∴k =2m ,直线 ME 的解析式为 y =2mx −m 2,直线 NE 的解析式为 y =2nx −n 2,∴E (m+n 2,mn),∴12[(n 2−mn )+(m 2−mn )]×(m −n )−12(n 2−mn )×(m+n 2−n)−12(m 2−mn )×(m −m+n 2)=2,∴(m −n )2−(m−n )22=4,∴(m −n )3=8,∴m −n =2.【解析】(2) ②当 AP =PQ 时,PQ =t 2+23t +7,PA =53(3−t ),∴t2+23t+7=53(3−t),∴t=−23,∴P点横坐标为−23.【知识点】二次函数与方程、二次函数的图象变换。
2024年武汉市中考数学试卷及答案
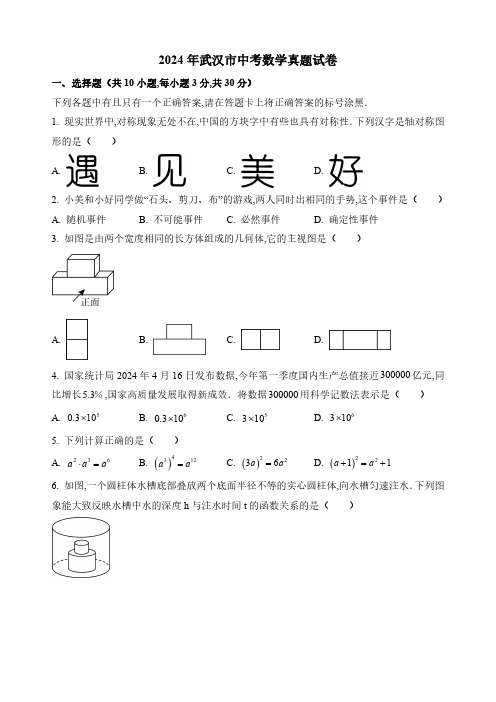
2024年武汉市中考数学真题试卷一、选择题(共10小题,每小题3分,共30分)下列各题中有且只有一个正确答案,请在答题卡上将正确答案的标号涂黑.1.现实世界中,对称现象无处不在,中国的方块字中有些也具有对称性.下列汉字是轴对称图形的是()A.B.C.D.2.小美和小好同学做“石头、剪刀、布”的游戏,两人同时出相同的手势,这个事件是()A.随机事件B.不可能事件C.必然事件D.确定性事件3.如图是由两个宽度相同的长方体组成的几何体,它的主视图是()A. B. C. D.4.国家统计局2024年4月16日发布数据,今年第一季度国内生产总值接近300000亿元,同比增长5.3%,国家高质量发展取得新成效.将数据300000用科学记数法表示是()A.50.310⨯ B.60.310⨯ C.5310⨯ D.6310⨯5.下列计算正确的是()A.236a a a⋅= B.()1432a a = C.()2236a a = D.()2211a a +=+6.如图,一个圆柱体水槽底部叠放两个底面半径不等的实心圆柱体,向水槽匀速注水.下列图象能大致反映水槽中水的深度h 与注水时间t 的函数关系的是()A. B. C. D.7.小美同学按如下步骤作四边形ABCD :①画MAN ∠;②以点A 为圆心,1个单位长为半径画弧,分别交AM ,AN 于点B ,D ;③分别以点B ,D 为圆心,1个单位长为半径画弧,两弧交于点C ;④连接BC ,CD ,BD .若44A ∠=︒,则CBD ∠的大小是()A.64︒B.66︒C.68︒D.70︒8.经过某十字路口的汽车,可能直行,也可能向左转或向右转,这三种可能性大小相同.若两辆汽车经过这个十字路口,则至少一辆车向右转的概率是()A.19B.13C.49D.599.如图,四边形ABCD 内接于O ,60ABC ∠=︒,45BAC CAD ∠=∠=︒,2AB AD +=,则O 的半径是()A.63B.223C.32D.2210.如图,小好同学用计算机软件绘制函数32331y x x x =-+-的图象,发现它关于点()1,0中心对称.若点()110.1,A y ,()220.2,A y ,()330.3,A y ,……,()19191.9,A y ,()20202,A y 都在函数图象上,这20个点的横坐标从0.1开始依次增加0.1,则1231920y y y y y +++++ 的值是()A.1-B.0.729- C.0 D.1二、填空题(共6小题,每小题3分,共18分)下列各题不需要写出解答过程,请将结果直接填写在答题卡指定的位置.11.中国是世界上最早使用负数的国家.负数广泛应用到生产和生活中,例如,若零上3℃记作3+℃,则零下2℃记作_________℃.12.某反比例函数kyx=具有下列性质:当0x>时,y随x的增大而减小,写出一个满足条件的k的值是__________.13.分式方程131x xx x+=--的解是______.14.黄鹤楼是武汉市著名的旅游景点,享有“天下江山第一楼”的美誉.在一次综合实践活动中,某数学小组用无人机测量黄鹤楼AB的高度,具体过程如下:如图,将无人机垂直上升至距水平地面102m的C处,测得黄鹤楼顶端A的俯角为45︒,底端B的俯角为63︒,则测得黄鹤楼的高度是__________m.(参考数据:tan632︒≈)15.如图是我国汉代数学家赵爽在注解《周髀算经》时给出的“赵爽弦图”,它是由四个全等的直角三角形和中间的小正方形MNPQ拼成的一个大正方形ABCD.直线MP交正方形ABCD的两边于点E,F,记正方形ABCD的面积为1S,正方形MNPQ的面积为2S.若(1)BE kAE k=>,则用含k的式子表示12SS的值是___________.16.抛物线2y ax bx c =++(a,b,c 是常数,0a <)经过()1,1-,(),1m 两点,且01m <<.下列四个结论:①0b >②若01x <<,则()()2111a xb xc -+-+>③若1a =-,则关于x 的一元二次方程22ax bx c ++=无实数解④点()11,A x y ,()22,B x y 在抛物线上,若1212x x +>-,12x x >,总有12y y <,则102m <≤.其中正确的是__________(填写序号).三、解答题(共8小题,共72分)下列各题需要在答题卡指定的位置写出文字说明、证明过程、演算步骤或画出图形.17.求不等式组3121x x x +>⎧⎨-≤⎩①②的整数解.18.如图,在ABCD Y 中,点E ,F 分别在边BC ,AD 上,AF CE =.(1)求证:C ABE DF≌△△(2)连接EF .请添加一个与线段相关的条件,使四边形ABEF 是平行四边形.(不需要说明理由)19.为加强体育锻炼,增强学生体质,某校在“阳光体育一小时”活动中组织九年级学生定点投篮技能测试,每人投篮4次,投中一次计1分.随机抽取m 名学生的成绩作为样本,将收集的数据整理并绘制成如下的统计图表.测试成绩扇形统计图测试成绩频数分布表成绩/分频数4123a2151b6根据以上信息,解答下列问题:(1)直接写出m ,n 的值和样本的众数(2)若该校九年级有900名学生参加测试,估计得分超过2分的学生人数.20.如图,ABC ∆为等腰三角形,O 是底边BC 的中点,腰AC 与半圆O 相切于点D ,底边BC 与半圆O 交于E ,F 两点.(1)求证:AB 与半圆O 相切(2)连接OA .若4CD =,2CF =,求sin OAC ∠的值.三个顶点都21.如图是由小正方形组成的34⨯网格,每个小正方形的顶点叫做格点.ABC是格点.仅用无刻度的直尺在给定网格中完成四个画图任务,每个任务的画线不得超过三条.的面积(1)在图(1)中,画射线AD交BC于点D,使AD平分ABC∠=∠(2)在(1)的基础上,在射线AD上画点E,使ECB ACB(3)在图(2)中,先画点F,使点A绕点F顺时针旋转90︒到点C,再画射线AF交BC于点G (4)在(3)的基础上,将线段AB绕点G旋转180︒,画对应线段MN(点A与点M对应,点B与点N对应).22.16世纪中叶,我国发明了一种新式火箭“火龙出水”,它是二级火箭的始祖.火箭第一级运行路径形如抛物线,当火箭运行一定水平距离时,自动引发火箭第二级,火箭第二级沿直线运行.某科技小组运用信息技术模拟火箭运行过程.如图,以发射点为原点,地平线为x 轴,垂直于地面的直线为y 轴,建立平面直角坐标系,分别得到抛物线2y ax x =+和直线12y x b =-+.其中,当火箭运行的水平距离为9km 时,自动引发火箭的第二级.(1)若火箭第二级的引发点的高度为3.6km .①直接写出a,b 的值②火箭在运行过程中,有两个位置的高度比火箭运行的最高点低1.35km ,求这两个位置之间的距离.(2)直接写出a 满足什么条件时,火箭落地点与发射点的水平距离超过15km .23.问题背景:如图(1),在矩形ABCD 中,点E ,F 分别是AB ,BC 的中点,连接BD ,EF ,求证:BCD FBE ∽△△.问题探究:如图(2),在四边形ABCD 中,AD BC ∥,90BCD ∠=︒,点E 是AB 的中点,点F 在边BC 上,2AD CF =,EF 与BD 交于点G ,求证:BG FG =.问题拓展:如图(3),在“问题探究”的条件下,连接AG ,AD CD =,AG FG =,直接写出EGGF的值.24.抛物线215222y x x =+-交x 轴于A ,B 两点(A 在B 的右边),交y 轴于点C .(1)直接写出点A ,B ,C 的坐标(2)如图(1),连接AC ,BC ,过第三象限的抛物线上的点P 作直线PQ AC ∥,交y 轴于点Q .若BC 平分线段PQ ,求点P 的坐标(3)如图(2),点D 与原点O 关于点C 对称,过原点的直线EF 交抛物线于E ,F 两点(点E 在x 轴下方),线段DE 交抛物线于另一点G ,连接FG .若90EGF ∠=︒,求直线DE 的解析式.2024年武汉市中考数学真题试卷解析一、选择题.题号12345678910答案CABCBDCDAD10.【解析】解:∵这20个点的横坐标从0.1开始依次增加0.1∴0.1 1.90.2 1.80.9 1.11222+++==⋅⋅⋅=∴123911190y y y y y y +++++= ∴12319201020y y y y y y y +++++=+ ,而()101,0A 即100y =∵32331y x x x =-+-当0x =时,1y =-,即()0,1-∵()0,1-关于点()1,0中心对称的点为()2,1即当2x =时,201y =∴12319201020011y y y y y y y +++++=+=+= 故选:D .二、填空题.11.【答案】2-12.【答案】1(答案不唯一)13.【答案】3x =-14.【答案】5115.【答案】221(1)k k +-【解析】解:作EG AN ⊥交AN 于点G ,不妨设MN a =,设1EG =四边形MNPQ 是正方形45PMN ∴∠=︒45EMG PMN ∴∠=∠=︒1EG MG ∴==在AEG △和ABN 中,EAG BAN ∠=∠,90AGE ANB ∠=∠=︒AEG ABN∴ ∽AE EG AG AB BN AN∴==(1)BE kAE k => (1)AB AE BE AE k ∴=+=+111AE AG AB BN AN k ∴===+1BN k∴=+由题意可知,ABN DAM△≌△1BN AM k∴==+11AG AM GM k k∴=-=+-=111AG AG k AN AM MN k a k ∴===++++21a k ∴=-2211AN AG GM MN k k k k∴=++=++-=+∴正方形ABCD 的面积222221222(1)()(1)(1)S AB BN AN k k k k k ==+=+++=++正方形MNPQ 的面积2222222(1)(1)(1)S MN a k k k ===-=+-222221(1)(1)(1)(1)k k k k S S +++-∴=1k >2(1)0k ∴+≠22121(1)k S S k +-∴=16.【答案】②③④【解析】解:∵2y ax bx c =++(a,b,c 是常数,0a <)经过()1,1-,(),1m 两点,且01m <<.∴对称轴为直线122b m x a -+=-=,11022m -+-<<∵02b x a =-<,a<0∴0b <,故①错误∵01m <<∴()11m -->,即()1,1-,(),1m 两点之间的距离大于1又∵a<0∴1x m =-时,1y >∴若01x <<,则()()2111a x b x c -+-+>,故②正确③由①可得11022m -+-<<,∴1022b -<<,即10b -<<当1a =-时,抛物线解析式为2y x bx c=-++设顶点纵坐标为224444ac b c b t a ---==-∵抛物线2y x bx c =-++(a,b,c 是常数,0a <)经过()1,1-∴11b c --+=∴2c b =+∴()222224411122144444c b b c t b c b b b --+===+=++=++-∵10b -<<,104->,对称轴为直线2b =-∴当0b =时,t 取得最大值为2,而0b <∴关于x 的一元二次方程22ax bxc ++=无解,故③正确④∵a<0,抛物线开口向下,点()11,A x y ,()22,B x y 在抛物线上,1212x x +>-,12x x >,总有12y y <又12124x x x +=>-∴点()11,A x y 离14x =-较远∴对称轴111224m -+-<≤-解得:102m <≤,故④正确.故答案为:②③④.三、解答题.17.【答案】整数解为:1,0,1-18.【答案】(1)见解析(2)添加AF BE =(答案不唯一)【小问1详解】证明:∵四边形ABCD 是平行四边形∴AB CD =,AD BC =,B D∠=∠∵AF CE=∴AD AF BC CE -=-即DF BE=在ABE 与CDF 中AB CD B D BE DF =⎧⎪∠=∠⎨⎪=⎩∴()SAS ABE CDF ≌【小问2详解】添加AF BE =(答案不唯一)如图所示,连接EF .∵四边形ABCD 是平行四边形∴AD BC ∥,即AF BE∥当AF BE =时,四边形ABEF 是平行四边形.19.【答案】(1)60m =,15n =,众数为3分(2)该校九年级有900名学生参加测试,估计得分超过2分的学生人数为450人【小问1详解】解:依题意,156025%m ==(人),6030%18a =⨯=(人),6012181569b =----=(人)∴9%100%15%60n =⨯=∴15n =∵3分的人数为18个,出现次数最多∴众数为3分【小问2详解】解:181290045060+⨯=(人)答:该校九年级有900名学生参加测试,估计得分超过2分的学生人数为450人.20.【答案】(1)见解析(2)45【小问1详解】证明:连接OA ,OD ,作ON AB ⊥交AB 于N ,如图ABC 为等腰三角形,O 是底边BC 的中点AO BC ∴⊥,AO 平分BAC∠AC 与半圆O 相切于点DOD AC∴⊥由ON AB⊥ ON OD∴=AC ∴是半圆O 的切线【小问2详解】解:由(1)可知AO BC ⊥,OD AC⊥90AOC ∴∠=︒,90ODC ∠=︒18090OAC OCA AOC ∴∠+∠=︒-∠=︒,18090COD OCA ODC ∠+∠=︒-∠=︒OAC COD∴∠=∠sin sin CDOAC COD OC∴∠=∠=又 OF OD =,2CF =∴在Rt ODC △中,4CD =,2OC OF FC OD =+=+ 222OC CD OD =+∴222(2)4OD OD +=+解得:3OD =442325CD CD sin OAC sin COD OC OD ∴∠=∠====++21.【答案】(1)作图见解析(2)作图见解析(3)作图见解析(4)作图见解析【小问1详解】解:如图所示,点D 即为所求.【小问2详解】解:如图所示,点E 即为所求.【小问3详解】解:如图所示.【小问4详解】解:如图所示.22.【答案】(1)①115a =-,8.1b =;②8.4km (2)2027a -<<【小问1详解】解:①∵火箭第二级的引发点的高度为3.6km∴抛物线2y ax x =+和直线12y x b =-+均经过点()9,3.6∴3.6819a =+,13.692b =-⨯+解得115a =-,8.1b =.②由①知,18.12y x =-+,2115y x x =-+∴22111515151524y x x x ⎛⎫=-+=--+ ⎪⎝⎭∴最大值15km 4y =当15 1.35 2.4km 4y =-=时则21 2.415x x -+=解得112x =,23x =又∵9x =时, 3.6 2.4y =>∴当 2.4km y =时则418. 2.12x +=-解得11.4x =()11.438.4km -=∴这两个位置之间的距离8.4km .【小问2详解】解:当水平距离超过15km 时火箭第二级的引发点为()9,819a +将()9,819a +,()15,0代入12y x b =-+,得181992a b +=-⨯+,10152b =-⨯+解得7.5b =,227a =-∴2027a -<<.23.【答案】问题背景:见解析;问题探究:见解析;问题拓展:5【详解】问题背景:∵四边形ABCD 是矩形∴90AB CD EBF C =∠=∠=︒,∵E ,F 分别是AB ,BC 的中点∴12BE BF AB BC ==即12BE BF CD BC ==∴BCD FBE∽△△问题探究:如图所示,取BD 的中点H ,连接,EH HC ∵E 是AB 的中点,H 是BD 的中点∴12EH AD =,EH AD ∥又∵2AD CF=∴EH CF=∵AD BC∥∴EH FC∥∴四边形EHCF 是平行四边形∴EF CH∥∴GFB HCB∠=∠又∵90BCD ∠=︒,H 是BD 的中点∴12HC BD BH ==∴HBC HCB∠=∠∴GBF GFB∠=∠∴GB GF=问题拓展:如图所示,过点F 作FM AD ⊥,则四边形MFCD 是矩形,连接AF∵2AD CF CD ==,∴12AM MD FC AD ===设2AD a =,则2MF CD a ==,AM a =在Rt AMF 中,()2225AF a a a =+=∵AG FG =,由(2)BG FG =∴AG BG=又∵E 是AB 的中点∴EF 垂直平分AB∴AF BF =,90BEG ∠=︒在,AFG BFG 中AG BG GF GF FA FB =⎧⎪=⎨⎪=⎩∴()SSS AFG BFG ≌设GBF GFB α∠=∠=,则GAF GFA α∠=∠=∴2BGE GBF GFB α∠=∠+∠=又∵AD BC∥∴2MAF AFB GFA GFB α∠=∠=∠+∠=∴MAF EGB∠=∠又∵90BEG AFM ∠=∠=︒∴BEG FMA ∽∴555EG EG AM GF BG AF a====.24.【答案】(1)()1,0A ,()5,0B -,50,2C ⎛⎫- ⎪⎝⎭(2)92,2P ⎛⎫-- ⎪⎝⎭(3)152y x =--【小问1详解】解:由215222y x x =+-当0x =时,52y =-,则50,2C ⎛⎫- ⎪⎝⎭当0y =,2152022x x +-=解得:125,1x x =-=∵A 在B 的右边∴()1,0A ,()5,0B -【小问2详解】解:设直线AC 的解析式为()0y kx b k =+≠将()1,0A ,50,2C ⎛⎫- ⎪⎝⎭代入得052k b b +=⎧⎪⎨=-⎪⎩解得:5252k b ⎧=⎪⎪⎨⎪=-⎪⎩∴直线AC 的解析式为5522y x =+∵PQ AC∥设直线PQ 的解析式为152y x b =+∵P 在第三象限的抛物线上设215,222P t t t ⎛⎫+- ⎪⎝⎭,()50t -<<∴215152222t b t t +=+-∴2115222t b t =--∴2150,222t Q t ⎛⎫-- ⎪⎝⎭设PQ 的中点为M ,则22352,22t t t M ⎛⎫+- ⎪ ⎪ ⎪⎝⎭由()5,0B -,50,2C ⎛⎫- ⎪⎝⎭,设直线BC 的解析式为152y k x =-将()5,0B -代入得15052k =--解得:112k =-∴直线BC 的解析式为1522y x =--∵BC 平分线段PQ∴M 在直线BC 上∴22351522222t t t +--⨯-=解得:122,0t t =-=(舍去)当2t =-时,21592222t t +-=-∴92,2P ⎛⎫-- ⎪⎝⎭【小问3详解】解:如图所示,过点G 作TS x ∥轴,过点,E F 分别作TS 的垂线,垂足分别为,T S∴90T S EGF ∠=∠=∠=︒∴90EGT FGS GFS ∠=︒-∠=∠∴ETG GSF∽∴ET TG GS FS=即ET FS GS TG⋅=⋅∵点D 与原点O 关于点50,2C ⎛⎫- ⎪⎝⎭对称∴()0,5D -设直线EF 的解析式为11y k x =,直线ED 的解析式为225y k x =-联立直线EF 与抛物线解析式11215222y k x y x x =⎧⎪⎨=+-⎪⎩可得,2112222k x x x =+-即()21152022x k x +--=联立直线ED 与抛物线解析式222515222y k x y x x =-⎧⎪⎨=+-⎪⎩可得,22125222k x x x -=+-即()22152022x k x +-+=设,E F x e x f ==,G x g =,∴5ef =-,5eg =,224e g k +=-∴f g=-()()221515122422222ET e e g g e g e g ⎛⎫=+--+-=++- ⎪⎝⎭()()221515122422222FS f f g g f g f g ⎛⎫=+--+-=++- ⎪⎝⎭∵ET FS GS TG ⋅=⋅∴()()()()()()114422g e f g e g e g f g f g --=++-⨯++-将f g =-代入得:5e g +=-∴2245k -=-∴212k =-∴直线DE 解析式为152y x =--.。
武汉中考数学第24题专题练习

F EA PBCD 图2武汉中考第24题一、内容分析:培养数学逻辑推理能力是新课标的要求,第24题便是近年来考查这种能力的一种新题型,它不仅开阔同学们的视野,而且发展了同学们发散思维,创新探索和逻辑推理能力和动手能力,这种题型考查学生逻辑推理的方式主要注意如下几方面:① 图形由特殊到一般;② 图形的位置由特殊到一般;③ 结论由特殊到一般.解决方法主要由“特殊到一般”的思路,结合旋转,全等或相似的相关性质,以及实践操作,观察猜想加以解决. 二、主要知识考点:1、图形旋转的性质;2、三角形全等或相似;3、实践作图; 三、结论类型: 1、 角度大小关系; 2、 线段大小和位置关系;3、 其它;四、题型变化引例:(08届4月调考题)如图所示,ABCD 为正方形。
(1)如图1,点P 为△ABC 的内心,问:DP 与DA 有何数量关系?证明你的结论; (2)如图2,若点E 在CB 边上(不与点C 、B 重合),点F 在BA 的延长线上,AF=CE ,点P 为△FBE 的内心,则DP 与DF 有何数量关系?证明你的结论; (3)如图3,若点E 在CB 的延长线上(不与点B 重合),点F 在BA 的延长线上,AF=CE ,点P 是△FEB 中与∠FEB 、∠FBE 相邻的两个外角平分线的交点。
完成图3,判断DP 与DF 之间的数量关系(直接写出结论,不证明)。
对照练习:1、如图1,正方形ABCD 中,∠FOE=90°顶点O 于D 点重合,交BC 边于E ,交BA 的延长线于F.(1)求证:OF=OE; (2)若O 点在直线BD 上运动,其它条件不变,上述结论是否仍然成立?试画图直接写出结论。
( (3)如图4,O 为正方形ABCD 对角线的中点,∠FOE=90°交BC 、CD 边于F 、E 点。
求证OE=OF 。
( (4)如图5、6,O 点在直线BD 上运动,OD :OB=1:n ,其它条件不变,(3)中结论是否还成立?若不成立,请直接写出OE :OF= 。
湖北省武汉市2024年中考物理试题(试题word答案扫描)

隐私★2024年6月21日2024年武汉市初中毕业生学业考试物理试卷武汉市教化科学探讨院命制2024.6.21第Ⅰ卷(选择题,共36分)一、选择题(本12包括小量,每小题只有1个正确选项。
每小题3分,共36分)9.学生们正在教室内上课,为了减小校内外汽车的噪声干扰,下列措施可行的是A.在校内四周植树B.将教室的窗户打开C.在教室内安装噪声监测装置D.每个学生都带一个防噪声耳罩10.关于运动和静止,下列说法正确的是A.,加油机在空中给受油机加油时,它们是相对运动的B.卡车和联合收割机收割庄稼时,它们是相对运动的C.两辆赛车在赛道上行驶时,它们是相对静止的D.“天宫一号”与“神舟八号”对接胜利时,它们是相对静止的11.如图所示,将凸透镜看作是眼睛的晶状体,光屏看作是眼睛的视网膜,烛焰看作是被眼睛视察的物体。
拿一个近视眼镜给“眼睛”戴上,光屏上出现烛焰清楚的像,而拿走近视眼镜则烛焰的像变得模糊。
在拿走近视眼镜后,为了能在光屏上重新得到清楚的像,下列操作可行的是A.将蜡烛远离凸透镜B.将光屏远离凸透镜C.将光屏靠近凸透镜D.将光屏和蜡烛同时远离凸透镜12.下列说法错误的是13、下列四幅图中,利用相关部件减小压强的是14、下图是探究阻力对物体运动的影响的试验装置,下列说法错误的A、每次试验时,应使小车滑到水平面时的初速度相等B、由于惯性,小车到达水平面后接着向前运动C、水平表面越粗糙,小车的速度减小得越快D、试验表明,力是维持物体运动的缘由15、如图所示,一辆在水平路面上匀速行驶的洒水车正在洒水作业,关于该洒水车,下列说法正确的是A、机械能不变,重力势能不变B、机械能变小,重力势能动能变小C、机械能不变,动能变小D、机械能变小,动能不变16、核电站利用核能发电,它的核心设备是核反应堆。
下列说法错误的是A、目前核电站都是通过聚变反应来利用核能B.核反应堆中发生的链式反应是可以限制的C、原子核分裂或聚合时释放出核能D、核能是一种不行再生的能源17、下列四幅图中,通电螺线管的极性标注正确的是18.下列装置中是利用电磁感应原理工作的是:19、下图是甲、乙两个电阻的电流I与电压U的关系图像,将它们并联接入电路,下列说法正确的是A、通过甲的电流大于通过乙的电流B、通过甲的电流小于通过乙的电流C、甲、乙并联的总电阻随它们两端电压的上升而减小D、甲、乙并联的总电阻随它们两端电压的上升而增大20、航模小组的某位同学在操场上利用如图所示的电动遥控飞机进行训练,他操作遥控器,使重为3N的飞机从水平地面由静止起先竖直上升,飞机先后经验加速、匀速、减速三个阶段,然后悬停在距离地面10m的高度处。
2020年湖北省武汉市中考化学试卷和答案解析

2020年湖北省武汉市中考化学试卷答案解析一、选择题(本题包括8小题,每小题只有一个选项符合题意。
每小题3分,共24分)1.(3分)下列物质中属于单质的是()A.五氧化二磷B.铜C.稀盐酸D.高锰酸钾解析:物质分为混合物和纯净物,混合物是由两种或两种以上的物质组成;纯净物是由一种物质组成。
纯净物又分为单质和化合物。
由同种元素组成的纯净物叫单质,铜属于单质;由两种或两种以上的元素组成的纯净物叫化合物。
氧化物是指由两种元素组成的化合物中,其中一种元素是氧元素。
参考答案:解:A、氧化物是指由两种元素组成的化合物中,其中一种元素是氧元素;五氧化二磷属于氧化物;故选项错误;B、由同种元素组成的纯净物叫单质,铜属于单质;故选项正确;C、稀盐酸属于化合物,故选项错误;D、高锰酸钾属于化合物,故选项错误;故选:B。
点拨:本考点考查了物质的分类,要加强记忆混合物、纯净物、单质、化合物、氧化物等基本概念,并能够区分应用。
本考点的基础性比较强,主要出现在选择题和填空题中。
2.(3分)下列实验操作正确的是()A.加热液体B.俯视读数C.倾倒液体D.检查气密性解析:A、根据给试管中的液体加热的方法进行分析判断。
B、根据量筒读数时视线要与凹液面的最低处保持水平进行分析判断。
C、根据向试管中倾倒液体药品的方法进行分析判断。
D、根据检查装置气密性的方法进行分析判断。
参考答案:解:A、给试管中的液体加热时,用酒精灯的外焰加热试管里的液体,且液体体积不能超过试管容积的,试管夹应夹在离试管口三分之一处,图中液体超过试管容积的,没有用酒精灯的外焰加热,手拿在试管夹的短柄上,图中所示操作错误。
B、量取液体时,视线与液体的凹液面最低处保持水平,图中视线没有与液体的凹液面最低处保持水平,操作错误。
C、向试管中倾倒液体药品时,瓶塞要倒放,标签要对准手心,瓶口紧挨;图中瓶塞没有倒放,标签没有对准手心,瓶口没有紧挨试管口,所示操作错误。
D、检查装置气密性的方法:把导管的一端浸没在水里,双手紧贴容器外壁,若导管口有气泡冒出,装置不漏气;图中所示操作正确。
2024年湖北省武汉市部分学校中考模拟数学试题4

2024年湖北省武汉市部分学校中考模拟数学试题4一、单选题1.2024-的相反数是( )A .2024B .2024-C .12024D .12024- 2.我国古代的二十四节气图标诸多呈现对称之美,下列图标是轴对称图形的是( ) A . B . C . D . 3.下列事件中是必然事件的是( )A .在十字交叉路口,遇到红灯亮起.B .射击运动员在进行一次射击时,能够精准地将子弹命中靶心.C .在平面内任意绘制一个三角形,其结构表现出稳定性.D .掷一枚硬币,国徽面朝上.4.计算()323a 的结果是( ) A .59a B .69a C .527a D .627a5.如图,一个几何体是由6个相同的小正方体组成的,它的主视图是( )A .B .C .D .6.如图,一条公路两次转弯后,和原来的方向相同.如果第一次的拐角A ∠是135︒,第二次的拐角B ∠的度数是( )A .45︒B .90°C .120︒D .135︒7.抛一枚质地均匀的正方体骰子,下列事件中发生的概率最大的是( )A .朝上的数字为奇数B .朝上的数字是3的倍数C .朝上的数字大于2D .朝上的数字是58.甲和乙两辆车从A 地同时出发,沿相同的路线匀速驶向B 地.在甲车行驶了2小时后,因发生故障停车进行维修.维修结束后,甲车继续以匀速驶向B 地,结果比乙车晚到了30分钟.甲、乙两车行驶的路程与离开A 地的时间的函数图象如图所示,当两车相距60km 时,乙车所行驶的时间是( )A .2hB .2h 或4hC .4h 或7hD .4h 或7h 或2h9.如图,进行下列尺规作图:①O e 六等分,依次得到,,,,,A B C D E F 六个分点;②分别以点,A D 为圆心,AC 长为半径画弧,G 是两弧的一个交点;③从点G 引出O e 的切线与AD 所在的直线围成三角形.此三角形的面积是( )A .4B .3C .6D .1210.已知()()1122,,,A x y B x y 是抛物线231y ax x =-+上的两点,其对称轴是直线0x x =,若1020x x x x ->-时,总有12y y >,同一坐标系中有()()2,3,4,3M N --,且抛物线与线段MN 有两个不相同的交点,则a 的取值范围是( )A .52a ≤-B .522a -<<C .728a ≤<D .728a ≤≤二、填空题11.微米和米都是长度的单位,其中1微米等于0.000001米.在日常生活中,我们经常需要将单位微米转换为米,以便于更好地理解和使用.30微米=米(用科学记数法表示). 12.已知在反比例函数k y x =的图象的每一支上,y 随x 的增大而增大,写出一个符合条件的k 的值是.13.计算2222111x x x x x -⎛⎫÷- ⎪+--⎝⎭的结果是. 14.如图,在龟山附近的小山AB 的顶部有一座通讯塔BC ,点,,A B C 位于同一直线上.在地面P 处,测得塔顶C 的仰角为42︒,塔底B 的仰角为35︒.已知通讯塔BC 的高度为29米,则小山AB 的高度为米.(结果取整数,参考数据:tan350.70,tan420.90︒≈︒≈.)15.如图,在ABC V 中,120A ∠=︒,点D 在AB 边上,15B ACD ∠=∠=︒.则ADC BDCS S V V 的值是.16.已知抛物线2y ax bx c =++(a ,b ,c 是常数,0a ≠)经过点()1,1--,()01,,当2x =-时,与其对应的函数值1y >,有下列结论:①0abc >;②242b ac a -<;③关于x 的方程230ax bx c ++-=有两个不等的实数根;④7a b c ++>.其中正确的是(填写序号).三、解答题17.求满足不等式组849322x x x x +>+⎧⎨≥-⎩①②的整数解. 18.如图,BE 是ABC V 的角平分线,点D 在AB 上,且DE BC ∥.(1)求证:DB DE=;(2)在BC上取一点F,连接EF,添加一个条件,使四边形BDEF为菱形,直接写出这个条件.19.每年的6月6日是我国的全国“爱眼日”,旨在倡导科学防控近视,关注青少年眼健康.在某校的“爱眼日”活动中,校方随机抽取了部分学生进行视力检测,以右眼视力值作为分组依据,将学生分为五组,并进行了数据收集和整理.以下是得到的尚不完整的统计图表:视力频数分布表请根据图表信息,解答下列问题:(1)本次调查活动共抽取了______人;表中a=______,b=______;(2)若该校共有学生2400人,且视力值为4.8及以上的为视力良好,请估计该校视力良好的有多少人?20.如图所示,BC为Oe的弦,点A位于优弧»BC上,连接AO并延长与BC交于点D,与Oe交于点F,连接AC,过点D作AC的垂线与AC相交于点E,然后连接,AB BF.(1)求证:DAB CDE∠=∠;(2)若5,3,2AC AD CD BD===,求Oe的半径.四、单选题21.如图,在每个小正方形的边长为1的网格中,ABCV的顶点,A C均落在格点上,点B在网格线上,以BC为直径的半圆与边AC相交于点D,仅用无刻度的直尺在给定网格中完成画图,画图过程用虚线表示.(1)在图1中,若2AB=,先画ABCV边AC上的高,再画点B关于AC的对称点B';(2)在图2中,若点B在离最近格点三分之一处,设P和Q分别为边AC与BC上的动点,当BP与PQ之和达到最小值时,画出点P和Q.五、解答题22.某商场经营某种商品,该商品的进价为30元/件,根据市场调查发现,该商品每周的销售量y(单位:件)与售价x(单位:元/件)(x为正整数)之间满足一次函数的关系,下表记录的是某三周的有关数据.(1)求y 关于x 的函数关系式(不求自变量的取值范围);(2)若某周该商品的销售量不少于700件,求这周该商场销售这种商品获得的最大利润;(3)规定这种商品的售价不超过进价的2倍,若商品的进价每件提高m 元(0m >)时,该商场每周销售这种商品的利润仍随售价的增大而增大,请直接写出m 的取值范围. 23.问题情境:在数学实践课程中,教师引导同学们围绕“菱形纸片的折叠”主题进行探索.已知菱形ABCD ,120BAD ∠=︒,点,E F 分别是,AB BC 边上的点,将菱形ABCD 沿EF 折叠.猜想证明:(1)如图1,设对角线AC 与BD 相交于点O ,若点B 的对应点与点O 重合,折痕EF 交BD 于点G .试直接写出四边形EBFO 的形状;问题解决:(2)如图2,若点B 的对应点恰好落在对角线AC 上的点M 处,若2,4CM AM ==,求线段FC 的长;(3)如图3,若点B 的对应点恰好落在CD 边上的点N 处,若点N 为CD 的一个三等分点()CN DN >,设DN a =,求FCN △的面积(用含a 的式子表示).24.如图,在平面直角坐标系中,已知抛物线2y ax bx c =++与x 轴交于点,A B ,与y 轴交于点C ,其对称轴为1x =-,点A 的坐标为 2,0 ,点53,2D ⎛⎫- ⎪⎝⎭在抛物线上.(1)求该抛物线的解析式;(2)如图1,点P 在y 轴上,且点P 在C 的下方,若45PDC ∠=︒,求点P 的坐标;(3)如图2,E 为线段CD 上的动点,射线OE 与线段AD 交于点M ,与抛物线交于点N ,求当MN OM取最大值时,点A D N ,,围成的三角形的面积.。
2020年湖北省武汉中考数学试卷(附答案与解析)

绝密★启用前2020年湖北省武汉市初中毕业生学业考试数 学亲爱的同学:在你答题前,请认真阅读下面的注意事项.1.本试卷由第I 卷(选择题)和第II 卷(非选择题)两部分组成.全卷共8页,三大题,满分120分.考试用时120分钟.2.答题前,请将你的姓名、准考证号填写在“答题卡”相应位置,并在“答题卡”背面左上角填写姓名和座位号.3.答第I 卷(选择题)时,选出每小题答案后,用2B 铅笔把“答题卡”上相应题目的答案标号涂黑.如需改动,用橡皮擦干净后,再选涂其他答案,答在“试卷”......上无效.... 4.答第II 卷(非选择题)时,答案用0.5毫米黑色笔迹签字笔书写在“答题卡”上,答在“试卷”上无效.......... 5.认真阅读答题卡上的注意事项. 预祝你取得优异成绩!第Ⅰ卷(选择题 共30分)一、选择题(共10小题,每小题3分,共30分)下列各题中有且只有一个正确答案,请在答题卡上将正确答案的标号涂黑. 1.2-的相反数是( )A .2-B .2C .12D .12-2.x 的取值范围是( )A .0x ≥B .2x -≥C .2x ≤D .2x ≥3.两个不透明的口袋中各有三个相同的小球,将每个口袋中的小球分别标号为1,2,3.从这两个口袋中分别摸出一个小球,则下列事件为随机事件的是( )A .两个小球的标号之和等于1B .两个小球的标号之和等于6C .两个小球的标号之和大于1D .两个小球的标号之和大于64.现实世界中,对称现象无处不在,中国的方块字中有些也只有对称性,下列汉字是轴对称图形的是( )ABCD5.下图是由4个相同的正方体组成的立体图形,它的左视图是( )ABCD6.某班从甲、乙、丙、丁四位选中随机选取两人参加校乒乓球比赛,恰好选中甲、乙两位选手的概率是( )A .13B .14C .16 D .18 7.若点()11,A a y -,()21,B a y +在反比例函数()0ky k x=<的图象上,且12y y >,则a 的取值范围是( )A .1a -<B .11a -<<C .1a >D .1a -<或1a >8.一个容器有进水管和出水管,每分钟的进水和出水是两个常数.从某时刻开始4 min 内只进水不出水,从第4 min 到第24 m in 内既进水又出水,从第24 m in 开始只出水不进水,容器内水量y (单位:L )与时间x (单位:min )之间的关系如图所示,则图中a 的值是 ( )(第8题)A .32B .34C .36D .38毕业学校_____________ 姓名________________ 考生号________________________________ _____________-------------在------------------此------------------卷------------------上-------------------答-------------------题-------------------无-------------------效----------------9.如图,在半径为3的O 中,AB 是直径,AC 是弦,D 是AC 的中点,AC 与BD 交于点E .若E 是BD 的中点,则AC 的长是( )(第9题)AB. C. D.10.下列图中所有小正方形都是全等的.图(1)是一张由4个小正方形组成的“L ”形纸片,图(2)是一张由6个小正方形组成的32⨯方格纸片.把“L ”形纸片放置在图(2)中,使它恰好盖住其中的4个小正方形,共有如图(3)中的4种不同放置方法,图(4)是一张由36个小正方形组成的66⨯方格纸片,将“L ”形纸片放置在图(4)中,使它恰好盖住其中的4个小正方形,共有n 种不同放置方法,则n 的值是( )A .160B .128C .80D .48第Ⅱ卷(非选择题 共90分)二、填空题(共6小题,每小题3分,共18分)下面各题不需要写出解答过程,请将结果直接填写在答题卡指定的位置. 11.________.12.热爱劳动,劳动最美!某合作学习小组6名同学一周居家劳动的时间(单位:h ),分别为:4,3,3,5,5,6.这组数据的中位数是________. 13.计算2223m nm n m n--+-的结果是________. 14.在探索数学名题“尺规三等分角”的过程中,有下面的问题:如图,AC 是平行四边形ABCD 的对角线,点E 在AC 上,AD AE BE ==,102D ∠=︒,则BAC ∠的大小是________.(第14题)15.抛物线2y ax bx c =++(a ,b ,c 为常数,0a <)经过()2,0A ,()4,0B -两点,下列四个结论:①一元二次方程20ax bx c ++=的根为12x =,24x =-; ②若点()15,C y -,()2,D y π在该抛物线上,则12y y <; ③对于任意实数t ,总有2at bt a b +-≤;④对于a 的每一个确定值,若一元二次方程2ax bx c p ++=(p 为常数,0p >)的根为整数,则p 的值只有两个.其中正确的结论是________(填写序号).16.如图,折叠矩形纸片ABCD ,使点D 落在AB 边的点M 处,EF 为折痕,1AB =,2AD =.设AM 的长为t ,用含有t 的式子表示四边形CDEF 的面积是________.(第16题)三、解答题(共8小题,共72分)下列各题需要在答题卡指定的位置写出文字说明、证明过程、演算步骤或画出图形. 17.(本小题满分8分)计算:()235423a a a a ⎡⎤⋅+÷⎢⎥⎣⎦. 18.(本小题满分8分)如图,直线EF 分别与直线AB ,CD 交于点E ,F .EM 平分BEF ∠,FN 平分CFE ∠,且EM FN ∥.求证:AB CD ∥.(第18题)19.(本小题满分8分)为改善民生;提高城市活力,某市有序推行“地摊经济”政策.某社区志愿者随机抽取该社区部分居民,按四个类别:A 表示“非常支持”,B 表示“支持”,C 表示“不关心”,D 表示“不支持”,调查他们对该政策态度的情况,将结果绘制成如下两幅不完整的统计图.根据图中提供的信息,解决下列问题:(1)这次共抽取了________名居民进行调查统计,扇形统计图中,D 类所对应的扇形圆心角的大小是________; (2)将条形统计图补充完整;(3)该社区共有2 000名居民,估计该社区表示“支持”的B 类居民大约有多少人?20.(本小题满分8分)在85⨯的网格中建立如图的平面直角坐标系,四边形OABC 的顶点坐标分别为()0,0O ,()3,4A ,()8,4B ,()5,0C .仅用无刻度的直尺在给定网格中按下列步骤完成画图,并回答问题:(1)将线段CB 绕点C 逆时针旋转90︒,画出对应线段CD ; (2)在线段AB 上画点E ,使45BCE ∠=︒(保留画图过程的痕迹); (3)连接AC ,画点E 关于直线AC 的对称点F ,并简要说明画法.(第20题)21.(本小题满分8分)如图,在Rt ABC △中,90ABC ∠=︒,以AB 为直径的O 交AC 于点D ,AE 与过点D 的切线互相垂直,垂足为E . (1)求证:AD 平分BAE ∠; (2)若CD DE =,求sin BAC ∠的值.(第21题)-------------在------------------此------------------卷------------------上-------------------答-------------------题-------------------无-------------------效----------------毕业学校_____________ 姓名________________ 考生号________________________________ _____________22.(本小题满分10分)某公司分别在A ,B 两城生产同种产品,共100件.A 城生产品的总成本y (万元)与产品数量x (件)之间具有函数关系2y ax bx c =++,当10x =时,400y =;当20x 时,1000y =.B 城生产产品的每件成本为70万元.(1)求a ,b 的值;(2)当A ,B 两城生产这批产品的总成本的和最少时,求A ,B 两城各生产多少件? (3)从A 城把该产品运往C ,D 两地的费用分别为m 万元/件和3万元/件;从B 城把该产品运往C ,D 两地的费用分别为1万元/件和2万元/件,C 地需要90件,D 地需要10件,在(2)的条件下,直接写出A ,B 两城总运费的和的最小值(用含有m 的式子表示).23.(本小题满分10分)问题背景 如图(1),已知A ABC DE ∽△△,求证:ABD ACE △∽△; 尝试应用 如图(2),在ABC △和ADE △中,90BAC DAE ∠=∠=︒,30ABC ADE ∠=∠=︒,AC 与DE 相交于点F .点D 在BC边上,ADBDDFCF的值; 拓展创新 如图(3),D 是ABC △内一点,30BAD CBD ∠=∠=︒,90BDC ∠=︒,4AB =,AC =AD 的长.(第23题)24.(本小题满分12分)将抛物线()2:2C y x =-向下平移6个单位长度得到抛物线1C ,再将抛物线1C 向左平移2个单位长度得到抛物线2C . (1)直接写出抛物线1C ,2C 的解析式;(2)如图(1),点A 在抛物线1C 对称轴l 右侧上,点B 在对称轴l 上,OAB △是以OB 为斜边的等腰直角三角形,求点A 的坐标;(3)如图(2),直线y kx =(0k ≠,k 为常数)与抛物线2C 交于E ,F 两点,M为线段EF 的中点;直线4y x k=-与抛物线2C 交于G ,H 两点,N 为线段GH 的中点.求证:直线MN 经过一个定点.(第24题)2020年湖北省武汉市初中毕业生学业考试数学答案解析一、 1.【答案】B【解析】因为220-+=,所以2-的相反数是2,故选B . 【考点】相反数 2.【答案】D20x ∴-≥, 2x ∴≥.故选D .【考点】二次根式有意义的条件 3.【答案】B【解析】解:从两个口袋中各摸一个球,其标号之和最大为6,最小为2, 选项A :“两个小球的标号之和等于1”为不可能事件,故选项A 错误; 选项B :“两个小球的标号之和等于6”为随机事件,故选项B 正确; 选项C :“两个小球的标号之和大于1”为必然事件,故选项C 错误; 选项D :“两个小球的标号之和大于6”为不可能事件,故选项D 错误. 故选:B .【考点】随机事件的概念,不可能事件的概念,必然事件的概念 4.【答案】C【解析】A 、不是轴对称图形,此项不符题意; B 、不是轴对称图形,此项不符题意; C 、是轴对称图形,此项符合题意; D 、不是轴对称图形,此项不符题意. 故选:C .【考点】轴对称图形的定义5.【答案】A【解析】根据图形可知左视图为.故选A . 【考点】三视图 6.【答案】C【解析】画树状图为:∴P (选中甲、乙两位)21126== 故选C .【考点】列表法或树状图法 7.【答案】B【解析】解:∵反比例函数()0ky k x=<, ∴图象经过第二、四象限,在每个象限内,y 随x 的增大而增大,①若点A 、点B 同在第二或第四象限, ∵12y y >,∴11a a -+>,此不等式无解; ②若点A 在第二象限且点B 在第四象限, ∵12y y >,∴1010a a -⎧⎨+⎩<>,解得:11a -<<;③由12y y >,可知点A 在第四象限且点B 在第二象限这种情况不可能. 综上,a 的取值范围是11a -<<. 故选:B .【考点】反比例函数的图象和性质 8.【答案】C【解析】设每分钟的进水量为 L b ,出水量为 L c 由第一段函数图象可知,2054b ==(L ) 由第二段函数图象可知,()()2016416435b c +---= 即201251235c +⨯-= 解得154c =(L ) 则当24x =时,()()15202445244454y =+-⨯--⨯=因此,45452412154a c -===解得()36min a = 故选:C .【考点】函数图象的应用 9.【答案】D【解析】解:连接DO 、DA 、DC 、OC ,设DO 与AC 交于点H ,如下图所示,∵D 是AC 的中点,∴DA DC =,∴D 在线段AC 的垂直平分线上, ∵OC OA =,∴O 在线段AC 的垂直平分线上, ∴DO AC ⊥,90DHC ∠=︒, ∵AB 是圆的直径,∴90BCA ∠=︒,∵E 是BD 的中点,∴DE BE =,且DEH BEC ∠=∠, ∴()AAS DHE BCE △≌△, ∴DH BC =,又O 是AB 中点,H 是AC 中点, ∴HO 是ABC △的中位线, 设OH x =,则2BC DH x ==, ∴33OD x ==,∴1x =, 即22BC x ==, 在Rt ABC △中,AC ==故选:D .【考点】圆周角定理,三角形全等,勾股定理 10.【答案】A【解析】由图可知,在66⨯方格纸片中,32⨯方格纸片的个数为54240⨯⨯=(个) 则404160n =⨯=, 故选:A .【考点】图形类规律探索 二、 11.【答案】333=-=,故答案为3.【考点】二次根式的性质 12.【答案】4.5【解析】将这组数据按从小到大进行排序为3,3,4,5,5,6,则这组数据的中位数是454.52+=,故答案为:4.5. 【考点】中位数 13.【答案】1m n- 【解析】原式()()()()()23m n m n m n m n m n m n ---+=+--()()223m n m n m n m n --++-=()()m nmn m n ++-=1m n=-. 故答案为:1m n-.【考点】分式的减法运算 14.【答案】26°【解析】解:设BAC x ∠= ∵平行四边形ABCD 的对角线 ∴DC AB ∥,AD BC =,AD BC ∥ ∴DCA BAC x ∠=∠= ∵AE BE =∴ EBA BAC x ∠=∠= ∴2BEC x ∠= ∵AD AE BE == ∴BE BC =∴ 2BCE BEC x ∠=∠= ∴3DCB BCE DCA x ∠=∠+∠= ∵AD BC ∥,102D ︒∠=∴180D DCB ∠+∠=︒,即1023180x ︒+=︒,解得26x =︒. 故答案为26°.【考点】平行四边形的性质,等腰三角形的判定和性质 15.【答案】①③【解析】抛物线2y ax bx c =++经过()2,0A ,()4,0B -两点∴一元二次方程20ax bx c ++=的根为12x =,24x =-,则结论①正确抛物线的对称轴为4212x -+==-∴3x =时的函数值与5x =-时的函数值相等,即为1y0a <∴当1x -≥时,y 随x 的增大而减小又13π-<<12y y ∴>,则结论②错误当1x =-时,y a b c =-+则抛物线的顶点的纵坐标为a b c -+,且0a b c -+>将抛物线2y ax bx c =++向下平移a b c -+个单位长度得到的二次函数解析式为()22y ax bx c a b c ax bx a b =++--+=+-+由二次函数图象特征可知,2y ax bx a b =+-+的图象位于x 轴的下方,顶点恰好在x 轴上 即0y ≤恒成立则对于任意实数t ,总有20at bt a b +-+≤,即2at bt a b +-≤,结论③正确将抛物线2y ax bx c =++向下平移p 个单位长度得到的二次函数解析式为2y ax bx c p =++-函数2y ax bx c p =++-对应的一元二次方程为20ax bx c p ++-=,即2ax bx c p ++= 因此,若一元二次方程2ax bx c p ++=的根为整数,则其根只能是11x =,23x =-或10x =,22x =-或121x x ==-对应的p 的值只有三个,则结论④错误 综上,结论正确的是①③ 故答案为:①③.【考点】二次函数的图象与性质(对称性、增减性),二次函数图象的平移问题,二次函数与一元二次方程的联系 16.【答案】211144t t -+ 【解析】设DE EM x ==, ∴()2222x x t =-+,∴244x t =+,设CF y =,连接FM ,∴2BF y =-,又∵FN y =,1NM =, ∴()()2222121y y t +=-+-,∴2244t y t =-+,∴四边形CDEF 的面积为:()221142412244t t t x y CD ⎛⎫+-++ ⎝=+⋅⎪⎭,故答案为:211144t t -+. 【考点】勾股定理的综合运用 三、17.【答案】解:原式()35829+=a a a +÷()8289=a a a +÷ 8210a a =÷ 610a =.【解析】根据同底数幂相乘、乘积的幂、幂的乘方、同底数幂相除运算法则逐步求解即可.【考点】整式的乘除中幂的运算法则 18.【答案】EM 平分BEF ∠,FN 平分CFE ∠12MEF BEF ∴∠=∠,12N E CF F E ∠=∠EM //FNMEF NFE ∠=∠∴1122BEF CFE ∴∠=∠,即BEF CFE ∠=∠ //AB CD ∴.【解析】先根据角平分线的定义可得11,22MEF BEF N CF FE E ∠=∠∠∠=,再根据平行线的性质可得MEF NFE ∠=∠,从而可得BEF CFE ∠=∠,然后根据平行线的判定即可得证.【考点】平行线的判定与性质,角平分线的定义 19.【答案】(1)6018︒(2)A 类居民的人数为60369312---=(名) 补全条形统计图如下所示:(3)表示“支持”的B 类居民的占比为36100%60%60⨯= 则200060%1200⨯=(名)答:该社区表示“支持”的B 类居民大约有1200人.【解析】(1)根据C 类的条形统计图和扇形统计图的信息可得出总共抽取的人数,再求出D 类居民人数的占比,然后乘以360︒即可得;(2)根据(1)的结论,先求出A 类居民的人数,再补全条形统计图即可; (3)先求出表示“支持”的B 类居民的占比,再乘以2000即可得. 【考点】条形统计图和扇形统计图的信息关联,画条形统计图20.【答案】解:(1)如图示,线段CD 是将线段CB 绕点C 逆时针旋转90︒得到的;(2)BCE ∠为所求的角,点E 为所求的点.(3)连接()5,0和()0,5点,与AC 的交点为F ,且F 为所求.【解析】(1)根据题意,将线段CD 是将线段CB 绕点C 逆时针旋转90︒即可; (2)连接BD ,并连接()4,2,()5,5点,两线段的交点即为所求的点E . (3)连接()5,0和()0,5点,与AC 的交点为F ,且F 为所求.【考点】作图旋转变换,正方形的性质,全等三角形的性质和轴对称的性质 21.【答案】(1)如图,连接OD 由圆的切线的性质得:OD DE ⊥AE DE ⊥//OD AE ∴ DAE ADO ∴∠=∠又OA OD =DAO ADO ∴∠=∠ DAE DAO ∴∠=∠则AD 平分BAE ∠; (2)如图,连接BD由圆周角定理得:90ADB ∠=︒90BDC ∴∠=︒ 90ABC ∠=︒ 90DAO C ∴∠+∠=︒ 90DAE ADE ∠+∠=︒ ADE C ∴∠=∠在ADE △和BCD △中,90E BDC DE CD ADE C ∠=∠=︒⎧⎪=⎨⎪∠=∠⎩()ADE BCD ASA ∴△≌△AD BC ∴=设AD BC a ==,CD x =,则AC AD CD a x =+=+,且0a >,0x >在ACB △和BCD △中,90C CABC BDC ∠=∠⎧⎨∠=∠=︒⎩ACB BCD ∴△∽△AC BC BC CD ∴=,即a x aa x+=解得2a x -=或02a x -=<(不符题意,舍去)经检验,x是所列分式方程的解AC a ∴=+=则在Rt ABC△中,sin BC BAC AC ∠===故sin BAC∠.【解析】(1)如图(见解析),先根据圆的切线的性质可得OD DE ⊥,再根据平行线的判定与性质可得DAE ADO ∠=∠,然后根据等腰三角形的性质可得DAO ADO ∠=∠,最后根据角平分线的定义即可得证;(2)如图(见解析),先根据角的和差、等量代换可得ADE C ∠=∠,再根据三角形全等的判定定理与性质可得AD BC =,设AD BC a ==,CD x =,然后根据相似三角形的判定与性质可得AC BCBC CD=,从而可求出x 的值,最后根据正弦三角函数的定义即可得.【考点】圆周角定理,圆的切线的性质,正弦三角函数,相似三角形的判定与性质 22.【答案】(1)由题意得:当产品数量为0时,总成本也为0,即0x =时,0y =则010010400400201000c a b c a b c =⎧⎪++=⎨⎪++=⎩,解得1300a b c =⎧⎪=⎨⎪=⎩故1a =,30b =;(2)由(1)得:230y x x =+设A ,B 两城生产这批产品的总成本的和为W 则()223070100700040x x x x W x ++-+==- 整理得:()2206600W x +=- 由二次函数的性质可知,当20x 时,W 取得最小值,最小值为6600万元此时1001002080x -=-=答:A 城生产20件,B 城生产80件;(3)设从A 城运往C 地的产品数量为n 件,A ,B 两城总运费的和为P ,则从A 城运往D 地的产品数量为()20n -件,从B 城运往C 地的产品数量为()90n -件,从B 城运往D 地的产品数量为()1020n -+件由题意得:20010200n n -⎧⎨-+⎩≥≥,解得1020n ≤≤()()()3209021020P mn n n n =+-+-+-+整理得:()2130P m n =-+根据一次函数的性质分以下两种情况:①当02m <≤时,在1020n ≤≤内,P 随n 的增大而减小则20n =时,P 取得最小值,最小值为()2021302090m m -+=+ ②当2m >时,在1020n ≤≤内,P 随n 的增大而增大则10n =时,P 取得最小值,最小值为()10213010110m m -+=+答:当02m <≤时,A ,B 两城总运费的和的最小值为()2090m +万元;当2m >时,A ,B 两城总运费的和的最小值为()10110m +万元.【解析】(1)先根据题意得出产品数量为0时,总成本y 也为0,再利用待定系数法即可求出a 、b 的值;(2)先根据(1)的结论得出y 与x 的函数关系式,从而可得出A ,B 两城生产这批产品的总成本的和,再根据二次函数的性质即可得;(3)设从A 城运往C 地的产品数量为n 件,A ,B 两城总运费的和为P ,先列出从A 城运往D 地的产品数量、从B 城运往C 地的产品数量、从B 城运往D 地的产品数量,再求出n 的取值范围,然后根据题干运费信息列出P 与n 的函数关系式,最后根据一次函数的性质求解即可得.【考点】利用待定系数法求二次函数的解析式,二次函数与一次函数的实际应用 23.【答案】问题背景:∵A ABC DE ∽△△, ∴BAC DAE ∠=∠,AB ACAD AE=, ∴BAD DAC CAE DAC ∠+∠=+∠, ∴BAD CAE ∠=∠, ∴ABD ACE △∽△; 尝试应用:连接CE ,数学试卷 第21页(共26页) 数学试卷 第22页(共26页)∵90BAC DAE ︒∠=∠=,30ABC ADE ︒∠=∠=, ∴BAC DAE △∽△,∴AB AD AC AE=, ∵BAD DAC CAE DAC ∠+∠=+∠, ∴BAD CAE ∠=∠, ∴ABD ACE △∽△,∴BD AD CE AE=, 由于30ADE ∠=︒,90DAE ∠=︒,∴tan30AE AD ︒==,即BD AD CE AE =,∵AD BD = ∴3AD CE=, ∵90BAC DAE ∠=∠=︒,30ABC ADE ∠=∠=︒, ∴60C E ∠=∠=︒, 又∵AFE DFC ∠=∠, ∴AFE DFC ∽△△, ∴AF EF DF CF =,即AF DFEF CF=, 又∵AFD EFC ∠=∠ ∴ADF ECF ∽△△, ∴3DF ADCF CE ==;拓展创新:AD =如图,在AD 的右侧作DAE BAC ∠=∠,AE 交BD 延长线于E ,连接CE ,∵ADE BAD ABD ∠=∠+∠,ABC ABD CBD ∠=∠+∠,30BAD CBD ∠=∠=︒, ∴ADE ABC ∠=∠, 又∵DAE BAC ∠=∠, ∴BAC DAE △∽△, ∴AB AC BCAD AE DE==, 又∵DAE BAC ∠=∠, ∴BAD CAE ∠=∠, ∴BAD CAE △∽△,∴=BD AB AD CE AC AE === 设CD x =,在直角三角形BCD 中,由于30CBD ∠=︒,∴BD =,2BC x =, ∴3CE x =,∴DE x ,∵AB BCAD DE =, ∴4AD =, ∴AD =【解析】问题背景:通过A ABC DE ∽△△得到AB ACAD AE =,AB ACAD AE=,再找到相等的数学试卷 第23页(共26页) 数学试卷 第24页(共26页)角,从而可证ABD ACE △∽△;尝试应用:连接CE ,通过BAC DAE △∽△可以证得ABD ACE △∽△,得到BD ADCE AE=,然后去证AFE DFC ∽△△,ADF ECF ∽△△,通过对应边成比例即可得到答案; 拓展创新:在AD 的右侧作DAE BAC ∠=∠,AE 交BD 延长线于E ,连接CE ,通过BAC DAE △∽△,BAD CAE △∽△,然后利用对应边成比例即可得到答案.【考点】相似三角形24.【答案】解:(1)∵抛物线()2:2C y x =-向下平移6个单位长度得到抛物线1C ,再将抛物线1C 向左平移2个单位长度得到抛物线2C , ∴抛物线1C 的解析式为:()226y x =--,即242y x x =--, 抛物线2C 的解析式为:()2226y x =-+-,即26y x =-.(2)如下图,过点A 作AC x ⊥轴于点C ,连接AD ,∵OAB △是等腰直角三角形, ∴ 45BOA ∠=︒,又∵90BDO BAO ∠=∠=︒, ∴点A 、B 、O 、D 四点共圆, ∴45BDA BOA ∠=∠=︒, ∴9045ADC BDA ∠=︒-∠=︒, ∴DAC △是等腰直角三角形,∴DC AC =.∵点A 在抛物线1C 对称轴l 右侧上,点B 在对称轴l 上, ∴抛物线1C 的对称轴为2x =, 设点A 的坐标为()2,42x x x --, ∴2DC x =-,2 42AC x x =--, ∴22 42x x x -=--,解得:5x =或0x =(舍去), ∴点A 的坐标为()5,3;同理,当点B 、点A 在x 轴的下方时,()2242x x x -=---,4x =或1x =-(舍去), ∴点A 的坐标为()4,2-,综上,点A 的坐标为()5,3或()4,2-.(3)∵直线y kx =(0k ≠,k 为常数)与抛物线2C 交于E ,F 两点, ∴26y kx y x =⎧⎨=-⎩,∴260x kx --=,设点E 的横坐标为E x ,点F 的横坐标为F x , ∴E F x x k +=,∴中点M 的横坐标22F M E x x x k+==, 中点M 的纵坐标22M y kx k==,∴点M 的坐标为2,22k k ⎛⎫⎪⎝⎭;同理可得:点N 的坐标为228,k k ⎛⎫- ⎪⎝⎭, 设直线MN 的解析式为y ax b =+(0a ≠),将2,22k k M ⎛⎫ ⎪⎝⎭、228,N k k ⎛⎫- ⎪⎝⎭代入得:数学试卷 第25页(共26页) 数学试卷 第26页(共26页)222282k ka b a b k k ⎧=+⎪⎪⎨⎪=-+⎪⎩, 解得:242k a k b ⎧-=⎪⎨⎪=⎩,∴直线MN 的解析式为24·2k ky x -=+(0k ≠), 不论k 取何值时(0k ≠),当0x =时,2y =, ∴直线MN 经过定点()0,2.【解析】(1)根据函数图象上下平移:函数值上加下减;左右平移:自变量左加右减写出函数解析式并化简即可;(2)先判断出点A 、B 、O 、D 四点共圆,再根据同弧所对的圆周角相等得到45BDA BOA ∠=∠=︒,从而证出DAC △是等腰直角三角形.设点A 的坐标为()2,42x xx --,把DC 和AC 用含x 的代数式表示出来,利用DC AC =列方程求解即可,注意有两种情况;(3)根据直线y kx =(0k ≠,k 为常数)与抛物线2C 交于E ,F 两点,联立两个解析式,得到关于x 的一元二次方程,根据根与系数的关系求出点M 的横坐标,进而求出纵坐标,同理求出点N 的坐标,再用待定系数法求出直线MN 的解析式,从而判断直线MN 经过的定点即可. 【考点】二次函数综合应用。
2022年湖北省武汉市中考数学真题(含解析)

z2022年湖北省武汉市中考数学试卷一、选择题1. 2022的相反数是( ) A.B. C. −2022 D. 20222. 彩民李大叔购买1张彩票,中奖.这个事件( ) A. 必然事件B. 确定性事件C. 不可能事件D. 随机事件3. 现实世界中,对称现象无处不在,中国的方块字中有些也具有对称性.下列汉字是轴对称图形的是( )A. B. C. D.4. 计算的结果是( )A.B.C.D.5. 如图是由4个相同的小正方体组成的几何体,它的主视图是( )A.B.C.D.6. 已知点,在反比例函数的图象上,且,则下列结论一定正确的是( ) A.B.C.D.7. 匀速地向一个容器内注水,最后把容器注满.在注水过程中,水面高度随时间的变化规律如图所示(图中为一折线).这个容器的形状可能是( )1202212022-是()342a 122a 128a 76a 78a ()11,A x y ()22,B x y 6y x=120x x <<120y y +<120y y +>12y y <12y y >h t OABCzA. B. C. D.8. 班长邀请,,,四位同学参加圆桌会议.如图,班长坐在⑤号座位,四位同学随机坐在①②③④四个座位,则,两位同学座位相邻的概率是( )A.B.C.D.9. 如图,在四边形材料中,,,,,.现用此材料截出一个面积最大的圆形模板,则此圆的半径是( )A.B.C.D.10. 幻方是古老数学问题,我国古代的《洛书》中记载了最早的幻方——九宫格.将9个数填入幻方的空格中,要求每一横行、每一竖列以及两条对角线上的3个数之和相等,例如图(1)就是一个幻方.图(2)是一个未完成的幻方,则与的和是( )A B C D A B 14131223ABCD AD BC !90A Ð=°9cm AD =20cm AB =24cm BC =110cm 138cm 10cm 的x yzA. 9B. 10C. 11D. 12二、填空题11._________.12. 某体育用品专卖店在一段时间内销售了20双学生运动鞋,各种尺码运动鞋销售量如下表.则这20双运动鞋的尺码组成的一组数据的众数是_________.尺码/销售量/双13104213. 计算:的结果是__. 14. 如图,沿方向架桥修路,为加快施工进度,在直线上湖的另一边的处同时施工.取,,,则,两点的距离是_________.15. 已知抛物线(,,是常数)开口向下,过,两点,且.下列四个结论:①; ②若,则; ③若点,在抛物线上,,且,则; ④当时,关于的一元二次方程必有两个不相等的实数根.其中正确的是_________(填写序号).的cm 2424.52525.52622193x x x ---AB AB D 150ABC Ð=°1600m BC =105BCD Ð=°C D m 2y ax bx c =++a b c ()1,0A -(),0B m 12m <<0b >32m =320a c +<()11,M x y ()22,N x y 12x x <121x x +>12y y >1a £-x 21ax bx c ++=z16. 如图,在中,,,分别以的三边为边向外作三个正方形,,,连接.过点作的垂线,垂足为,分别交,于点,.若,,则四边形的面积是_________.三、解答题17. 解不等式组请按下列步骤完成解答.(1)解不等式①,得_________; (2)解不等式②,得_________;(3)把不等式①和②的解集在数轴上表示出来:(4)原不等式组的解集是_________.18. 如图,在四边形中,,.(1)求的度数;(2)平分交于点,.求证:.19. 为庆祝中国共青团成立100周年,某校开展四项活动:项参观学习,项团史宣讲,项经典诵读,项文学创作,要求每名学生在规定时间内必须且只能参加其中一项活动.该校从全体学生中随机抽取部分学生,调查他们参加活动的意向,将收集的数据整理后,绘制成如下两幅不完整的统计图.Rt ABC !90ACB Ð=°AC BC >ABC !ABHL ACDE BCFG DF C AB CJ J DF LH I K 5CI =4CJ =AJKL 2532x x x -³-ìí<+î①②ABCD AD BC !80B Ð=°BAD ÐAE BAD ÐBC E 50BCD Ð=°AE DC !A B C Dz(1)本次调查的样本容量是__________,项活动所在扇形的圆心角的大小是_________,条形统计图中项活动的人数是_________;(2)若该校约有2000名学生,请估计其中意向参加“参观学习”活动的人数.20. 如图,以为直径的经过的顶点,,分别平分和,的延长线交于点,连接.(1)判断的形状,并证明你的结论;(2)若,的长.21. 如图是由小正方形组成的网格,每个小正方形的顶点叫做格点.的三个顶点都是格点.仅用无刻度的直尺在给定网格中完成画图,画图过程用虚线表示.B C AB O !ABC !C AE BE BAC ÐABC ÐAE O !D BD BDE !10AB =BE =BC 96´ABC !z(1)在图(1)中,,分别是边,与网格线的交点.先将点绕点旋转得到点,画出点,再在上画点,使;(2)在图(2)中,是边上一点,.先将绕点逆时针旋转,得到线段,画出线段,再画点,使,两点关于直线对称.22. 在一条笔直的滑道上有黑、白两个小球同向运动,黑球在处开始减速,此时白球在黑球前面处.小聪测量黑球减速后运动速度(单位:)、运动距离(单位:)随运动时间(单位:)变化的数据,整理得下表.运动时间 0 1 2 3 4 运动速度 10 9.5 9 8.5 8 运动距离9.751927.7536小聪探究发现,黑球的运动速度与运动时间之间成一次函数关系,运动距离与运动时间之间成二次函数关系.(1)直接写出关于函数解析式和关于的函数解析式(不要求写出自变量的取值范围)(2)当黑球减速后运动距离为时,求它此时的运动速度;(3)若白球一直..以的速度匀速运动,问黑球在运动过程中会不会碰到白球?请说明理由. 23. 问题提出:如图(1),中,,是的中点,延长至点,使,延长交于点,探究的值.D E AB AC B E 180°F F AC G DG BC !P AB BAC a Ð=AB A 2a AH AH Q P Q AC A 70cm 的v cm/s y cm t s /s t /cm/s v /cm y v t y t v t的y t 64cm 2cm/s ABC !AB AC =D AC BC E DE DB =ED AB F AFABz(1)先将问题特殊化.如图(2),当时,直接写出的值; (2)再探究一般情形.如图(1),证明(1)中的结论仍然成立.问题拓展:如图(3),在中,,是的中点,是边上一点,,延长至点,使,延长交于点.直接写出的值(用含的式子表示).24. 抛物线交轴于A ,两点(A 在的左边),是第一象限抛物线上一点,直线交轴于点.(1)直接写出A ,两点的坐标;(2)如图(1),当时,在抛物线上存在点(异于点),使,两点到的距离相等,求出所有满足条件的点的横坐标;(3)如图(2),直线交抛物线于另一点,连接交轴于点,点的横坐标为.求的值(用含的式子表示).60BAC Ð=°AFABABC !AB AC =D AC G BC ()12CG n BC n =<BC E DE DG =ED AB F AF ABn 223y x x =--x B B C AC y P B OP OA =D B B D AC D BP E CE y F C m FP OPm2022年湖北省武汉市中考数学试卷一、选择题1. 2022的相反数是( ) A.B.C. −2022D. 2022【答案】C 【解析】【分析】根据相反数的定义求解即可,只有符号不同的两个数互为相反数. 【详解】解:2022的相反数是−2022. 故选:C .【点睛】本题考查了相反数的定义,掌握相反数的定义是解题的关键. 2. 彩民李大叔购买1张彩票,中奖.这个事件是( ) A. 必然事件 B. 确定性事件 C. 不可能事件 D. 随机事件 【答案】D 【解析】【分析】直接根据随机事件的概念即可得出结论.【详解】购买一张彩票,结果可能为中奖,也可能为不中奖,中奖与否是随机的,即这个事件为随机事件. 故选:D .【点睛】本题考查了随机事件的概念,解题的关键是熟练掌握随机事件发生的条件,能够灵活作出判断.3. 现实世界中,对称现象无处不在,中国的方块字中有些也具有对称性.下列汉字是轴对称图形的是( )A. B.C. D.【答案】D 【解析】【分析】利用轴对称图形的概念可得答案.1202212022-z【详解】解:A .不是轴对称图形,故此选项不合题意; B .不是轴对称图形,故此选项不合题意; C .不是轴对称图形,故此选项不合题意; D .是轴对称图形,故此选项符合题意; 故选:D .【点睛】本题主要考查了轴对称图形,关键是掌握如果一个图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形叫做轴对称图形. 4. 计算的结果是( )A. B.C.D.【答案】B 【解析】【分析】直接运用幂的乘方、积的乘方计算即可. 【详解】解:.故答案为B .【点睛】本题主要考查了幂的乘方、积的乘方的运算,灵活运用相关运算法则成为解答本题的关键.5. 如图是由4个相同的小正方体组成的几何体,它的主视图是( )A.B.C. D.【答案】A 【解析】【分析】根据从正面所看得到的图形为主视图,据此解答即可.【详解】解:从正面可发现有两层,底层三个正方形,上层的左边是一个正方形. 故选:A .【点睛】本题主要考查了三视图的知识,掌握主视图是从物体的正面看得到的视图成为解()342a 122a 128a 76a 78a ()()()4134233228a a a ==z答本题的关键.6. 已知点,在反比例函数的图象上,且,则下列结论一定正确的是( ) A.B.C.D.【答案】C 【解析】【分析】把点A 和点B 的坐标代入解析式,根据条件可判断出、的大小关系. 【详解】解:∵点,)是反比例函数的图象时的两点, ∴. ∵, ∴. 故选:C .【点睛】本题主要考查反比例函数图象上点的坐标特征,掌握图象上点的坐标满足函数解析式是解题的关键.7. 匀速地向一个容器内注水,最后把容器注满.在注水过程中,水面高度随时间的变化规律如图所示(图中为一折线).这个容器的形状可能是( )A. B.C. D.【答案】A 【解析】【分析】根据函数图象的走势:较缓,较陡,陡,注水速度是一定的,上升的快慢跟容器()11,A x y ()22,B x y 6y x=120x x <<120y y +<120y y +>12y y <12y y >1y 2y ()11,A x y ()22,B x y 6y x=11226x y x y ==120x x <<120y y <<h tOABCz的粗细有关,越粗的容器上升高度越慢,从而得到答案.【详解】解:从函数图象可以看出:OA 段上升最慢,AB 段上升较快,BC 段上升最快,上升的快慢跟容器的粗细有关,越粗的容器上升高度越慢, ∴题中图象所表示的容器应是下面最粗,中间其次,上面最细; 故选:A .【点睛】本题考查了函数图象的性质在实际问题中的应用,判断出每段函数图象变化不同的原因是解题的关键.8. 班长邀请,,,四位同学参加圆桌会议.如图,班长坐在⑤号座位,四位同学随机坐在①②③④四个座位,则,两位同学座位相邻的概率是( )A.B.C.D.【答案】C 【解析】【分析】采用树状图发,确定所有可能情况数和满足题意的情况数,最后运用概率公式解答即可.【详解】解:根据题意列树状图如下:由上表可知共有12中可能,满足题意的情况数为6种 则,两位同学座位相邻的概率是 . 故选C.【点睛】本题主要考查了画树状图求概率,正确画出树状图成为解答本题关键. 9. 如图,在四边形材料中,,,,,.现用此材料截出一个面积最大的圆形模板,则此圆的半径是A B C D A B 14131223A B 61122=的ABCD AD BC !90A Ð=°9cm AD =20cm AB =24cm BC =z( )A.B.C.D.【答案】B 【解析】【分析】如图所示,延长BA 交CD 延长线于E ,当这个圆为△BCE 的内切圆时,此圆的面积最大,据此求解即可.【详解】解:如图所示,延长BA 交CD 延长线于E ,当这个圆为△BCE 的内切圆时,此圆的面积最大,∵,∠BAD =90°, ∴△EAD ∽△EBC ,∠B =90°, ∴,即, ∴, ∴EB =32cm , ∴,设这个圆的圆心为O ,与EB ,BC ,EC 分别相切于F ,G ,H ,∴OF =OG =OH ,∵, ∴, ∴, ∴, ∴此圆的半径为8cm , 故选B.110cm 138cm 10cm AD BC !EA AD EB BC=92024EA EA =+12cm EA=40cm EC ===EBC EOB COB EOC S S S S ++△△△△11112222EB BC EB OF BC OG EC OH ×=×+×+×()2432=243240OF ´++×8cm OF =z【点睛】本题主要考查了三角形内切圆半径与三角形三边的关系,勾股定理,正确作出辅助线是解题的关键.10. 幻方是古老的数学问题,我国古代的《洛书》中记载了最早的幻方——九宫格.将9个数填入幻方的空格中,要求每一横行、每一竖列以及两条对角线上的3个数之和相等,例如图(1)就是一个幻方.图(2)是一个未完成的幻方,则与的和是( )A. 9B. 10C. 11D. 12【答案】D 【解析】【分析】根据题意设出相应未知数,然后列出等式化简求值即可. 【详解】解:设如图表所示: x 6 20 22 z y nm根据题意可得:x +6+20=22+z +y ,整理得:x-y =-4+z ,x +22+n =20+z +n ,20+y +m =x +z +m , 整理得:x =-2+z ,y =2z -22, ∴x -y =-2+z -(2z -22)=-4+z , 解得:z =12,x y∴x +y =3z -24 =12 故选:D .【点睛】题目主要考查方程的应用及有理数加法的应用,理解题意,列出相应方程等式然后化简求值是解题关键.二、填空题11. 【答案】2【解析】【分析】根据二次根式的性质进行化简即可.【详解】解. 故答案为:2.【点睛】此题主要考查了二次根式的化简,注意.12. 某体育用品专卖店在一段时间内销售了20双学生运动鞋,各种尺码运动鞋的销售量如下表.则这20双运动鞋的尺码组成的一组数据的众数是_________.【答案】 【解析】【分析】直接根据众数的定义:一组数据中出现次数最多的数即为众数即可得出结论. 【详解】由表格可知:尺码的运动鞋销售量最多为双,即众数为. 故答案为:25.【点睛】本题考查了众数,解题的关键是熟练掌握众数的定义. 13. 计算:的结果是__. 【答案】. 【解析】 【分析】2=()()(0000a a a a a a ìï===íï-î>)<2525102522193x x x ---13x +z【详解】原式. 故答案为:. 14. 如图,沿方向架桥修路,为加快施工进度,在直线上湖的另一边的处同时施工.取,,,则,两点的距离是_________.【答案】【解析】【分析】如图所示:过点作于点,先求出,再根据勾股定理即可求出的长.【详解】如图所示:过点作于点,则∠BEC =∠DEC =90°, ,,∴∠BCE =90°-30°=60°, 又,,∴∠ECD =45°=∠D , ∴,,, ,即.23(3)(3)(3)(3)x x x x x x +=-+-+-23(3)(3)x x x x --=+-3(3)(3)x x x -=+-13x =+13x +AB AB D 150ABC Ð=°1600m BC =105BCD Ð=°C D m C CE BD ^E 800m CE =CD C CE BD ^E 150ABC Ð=°!30CBD \Ð=°105BCD Ð=°!45CDB \Ð=°CE DE =1600m BC =!111600800m 22CE BC \==´=22222CD CE DE CE \=+=CD ==z故答案为:【点睛】本题考查三角形内角和定理、等腰三角形的判定与性质、直角三角形的性质及勾股定理,解题的关键是熟练掌握相关内容并能灵活运用.15. 已知抛物线(,,是常数)开口向下,过,两点,且.下列四个结论: ①; ②若,则; ③若点,在抛物线上,,且,则; ④当时,关于的一元二次方程必有两个不相等的实数根. 其中正确的是_________(填写序号). 【答案】①③④ 【解析】【分析】首先判断对称轴,再由抛物线的开口方向判断①;由抛物线经过A (-1,0),,当时,,求出,再代入判断②,抛物线,由点,在抛物线上,得,,把两个等式相减,整理得,通过判断,的符号判断③;将方程写成a (x -m )(x +1)-1=0,整理,得,再利用判别式即可判断④.详解】解:抛物线过,两点,且,, ,2y ax bx c =++a b c ()1,0A -(),0B m 12m <<0b >32m =320a c +<()11,M x y ()22,N x y 12x x <121x x +>12y y >1a £-x 21ax bx c ++=02bx a=->(),0B m 32m =()312y a x x æö=+-ç÷èø32c a =-32a c+()()()2211y ax bx c a x x m ax a m x am =++=+-=+--()11,M x y ()22,N x y ()21111y ax a m x am =+--()22221y ax a m x am =+--()()1212121y y a x x x x m -=-++-12x x -121x x m ++-21ax bx c ++=()2110x m x m a+---=【!()1,0A -(),0B m 12m <<122b mx a -+\=-=!12m <<,即, 抛物线开口向下,,,故①正确;若,则,,,故②不正确;抛物线,点,在抛物线上,∴,,把两个等式相减,整理得, ,,, ,, ,故③正确;依题意,将方程写成a (x -m )(x +1)-1=0,整理,得, ,,,,, , 故④正确.综上所述,①③④正确. 故答案为;①③④.【点睛】本题考查二次函数图象与系数的关系,解题关键是掌握二次函数的性质,掌握二次函数与方程及不等式的关系.11022m -+\<<02ba->!0a <0b \>32m =()23131222y a x x ax ax a æö=+-=--ç÷èø32c a \=-3323202a c a a æö\+=+´-=ç÷èø!()()()2211y ax bx c a x x m ax a m x am =++=+-=+--()11,M x y ()22,N x y ()21111y ax a m x am =+--()22221y ax a m x am =+--()()1212121y y a x x x x m -=-++-120,a x x <<!121x x +>12m <<12120,10x x x x m \-<++->()()12121210y y a x x x x m \-=-++->12y y \>21ax bx c ++=()2110x m x m a+---=()()2214141m m m a a æö\D =----=++ç÷èø12m <<!1a £-()2419m \<+<44a³-()2410m a\++>z16. 如图,在中,,,分别以的三边为边向外作三个正方形,,,连接.过点作的垂线,垂足为,分别交,于点,.若,,则四边形的面积是_________.【答案】80 【解析】【分析】连接LC 、EC 、EB ,LJ ,由平行线间同底的面积相等可以推导出:,由,可得,故,证得四边形是矩形,可得,在正方形中可得:,故得出:.由,可得,即可求出,可得出【详解】连接LC 、EC 、EB ,LJ ,在正方形,,中Rt ABC !90ACB Ð=°AC BC >ABC !ABHL ACDE BCFG DF C AB CJ J DF LH I K 5CI =4CJ =AJKL JAL CAL BAE EAC S S S S ==!!!!,CAL EAB @!!CAL EAB S S =!!JAL CAL BAE EAC S S S S ===!!!!ALKJ 2ALJ ALKJ S S =!矩形ACDE 2EAC ACDE S S =!正方形2ALKJ S AC =矩形ACJ CBJ !"!CJ AJBJ CJ=8AJ=ABHL ACDE BCFG 90,ALK LAB EAC ACD BCF Ð=Ð=Ð=Ð=Ð=°. ∵,∴,∴, ∴, ∴.∵, ∴四边形矩形,∴. ∵,∴, ∴, ∵ ∴, ∴. ∵, ∴.∴∴.∵. ∴, ∵ ∴,∴, ∵,∴, ∴, ∵, ∴, ∴,∵,,,,,AL AB EA AC BC CF AC CD AE CD ====!,AB LH !,2EAC ACDE S S =!正方形CK LH ^90CKL Ð=°CK AB ^180CKL ALK Ð+Ð=°90CJA CJB Ð=Ð=°CK AL !CAL JAL S S =!!90JKL ALK JAL Ð=Ð=Ð=°ALKJ是2ALJ ALKJ S S =!矩形LAB EAC Ð=ÐLAB BAC EAC BAC Ð+Ð=Ð+ÐEAB CAL Ð=Ð,,AL AB EA AC ==CAL EAB @!!CAL EAB S S =!!AE CD !EAB EAC S S =!!JAL CAL BAE EAC S S S S ===!!!!22EAC ALKJ ACDE S S S AC ===!矩形正方形90,DCA BCF DCF BCD Ð=Ð=°Ð=Ð90DCF BCD Ð=Ð=°,,BC CF AC CD ==ABC DCF @!!,CAB CDF AB DF Ð=Ð=90,90ACB CJB Ð=°Ð=°90,90CAB ABC JCB CBJ Ð+Ð=°Ð+Ð=°CAB JCB Ð=ÐDCI JCB Ð=ÐDCI IDC Ð=Ð5ID CI ==90,90IDC DFC DIC ICF Ð+Ð=°Ð+Ð=°∴, ∴, ∴, ∴.设,∵ ∴, ∴, ∴,∴ ∵,∴, ∴, ∴, ∴.∴, ∴. 故答案为:80.【点睛】此题考查正方形的性质、矩形的性质与判定、相似三角形的判定与性质、勾股定理,平行线间同底的两个三角形,面积相等;难度系数较大,作出正确的辅助线并灵活运用相关图形的性质与判定是解决本题的关键.三、解答题17. 解不等式组请按下列步骤完成解答.(1)解不等式①,得_________; (2)解不等式②,得_________;(3)把不等式①和②的解集在数轴上表示出来:(4)原不等式组的解集是_________. 【答案】(1)ICF IFC Ð=Ð5IF CI ==10DF =10AB =,10AJ x BJ x ==-,,CAJ BCJ CJA CJB Ð=ÐÐ=ÐACJ CBJ !"!CJ AJBJ CJ=4104xx =-1228x x ==,,ACBC >AJ BJ >10x x >-5x >8x =222224880AC CJ AJ =+=+=280ALKJ S AC ==矩形2532x x x -³-ìí<+î①②3x ³-z(2)(3)详见解析 (4) 【解析】【分析】分别求出每一个不等式的解集,根据口诀“同大取大、同小取小、大小小大中间找、大大小小找不到”原则取所含不等式解集的公共部分,即确定为不等式组的解集. 【小问1详解】 解:解不等式①,得【小问2详解】 解:解不等式②,得【小问3详解】解:把不等式①和②的解集在数轴上表示出来:小问4详解】解:由图可得,原不等式组的解集是:【点睛】本题考查解一元一次不等式组,正确求出每一个不等式解集是基础,熟知“同大取大;同小取小;大小小大中间找;大大小小找不到”的原则是解答此题的关键. 18. 如图,在四边形中,,.(1)求的度数;(2)平分交于点,.求证:. 【答案】(1) (2)详见解析 【解析】【分析】(1)根据两直线平行,同旁内角互补,即可求解;(2)根据平分,可得.再由,可得1x <31x -£<3x ³-1x <【31x -£<ABCD AD BC !80B Ð=°BAD ÐAE BAD ÐBC E 50BCD Ð=°AE DC !100BAD Ð=°AE BAD Ð50DAE Ð=°AD BC !.即可求证.【小问1详解】 解:∵, ∴, ∵, ∴. 【小问2详解】证明:∵平分, ∴. ∵,∴. ∵, ∴. ∴.【点睛】本题主要考查了平行线的判定和性质,熟练掌握平行线的判定和性质定理是解题的关键19. 为庆祝中国共青团成立100周年,某校开展四项活动:项参观学习,项团史宣讲,项经典诵读,项文学创作,要求每名学生在规定时间内必须且只能参加其中一项活动.该校从全体学生中随机抽取部分学生,调查他们参加活动的意向,将收集的数据整理后,绘制成如下两幅不完整的统计图.(1)本次调查的样本容量是__________,项活动所在扇形的圆心角的大小是_________,条形统计图中项活动的人数是_________;(2)若该校约有2000名学生,请估计其中意向参加“参观学习”活动人数. 【答案】(1)80,,20 (2)大约有800人 【解析】【分析】(1)根据“总体=部分÷对应百分比”与“圆心角度数=360°×对应百分比”可求得样本50AEB DAE Ð=Ð=°AD BC !180B BAD Ð+Ð=°80B Ð=°100BAD Ð=°AE BAD Ð50DAE Ð=°AD BC !50AEB DAE Ð=Ð=°50BCD Ð=°BCD AEB Ð=ÐAE DC !A B CD B C 的54°z容量及B 项活动所在扇形的圆心角度数,从而求得C 项活动的人数;(2)根据“部分=总体×对应百分比”,用总人数乘以样本中“参观学习”的人数所占比例可得答案. 【小问1详解】解:样本容量:16÷20%=80(人), B 项活动所在扇形的圆心角:, C 项活动的人数:80-32-12-16=20(人); 故答案为:80,54°,20; 【小问2详解】 解:(人), 答:该校意向参加“参观学习”活动的学生大约有800人.【点睛】本题主要考查了条形统计图,扇形统计图,用样本估计总体,读懂图,找出对应数据,熟练掌握总体、部分与百分比之间的关系是解题的关键.20. 如图,以为直径的经过的顶点,,分别平分和,的延长线交于点,连接.(1)判断的形状,并证明你的结论; (2)若,的长. 【答案】(1)为等腰直角三角形,详见解析 (2) 【解析】【分析】(1)由角平分线的定义、结合等量代换可得,即;然后再根据直径所对的圆周角为90°即可解答;(2)如图:连接,,,交于点.先说明垂直平分.进123605480°´=°32200080080´=AB O !ABC !C AE BE BAC ÐABC ÐAE O !D BD BDE !10AB =BE =BC BDE !8BC =BED DBE Ð=ÐBD ED =OC CD OD OD BC F OD BCz而求得BD 、OD 、OB 的长,设,则.然后根据勾股定理列出关于t 的方程求解即可. 【小问1详解】解:为等腰直角三角形,证明如下: 证明:∵平分,平分, ∴,. ∵,, ∴. ∴. ∵为直径, ∴.∴是等腰直角三角形. 【小问2详解】解:如图:连接,,,交于点. ∵, ∴. ∵, ∴垂直平分.∵是等腰直角三角形,∴∵, ∴.设,则.在和中,.解得,. ∴. ∴.OF t =5DF t =-BDE !AEBAC ÐBE ABC ÐBAE CAD CBD Ð=Ð=ÐABE EBC Ð=ÐBED BAE ABE Ð=Ð+ÐDBE DBC CBE Ð=Ð+ÐBED DBE Ð=ÐBD ED =AB 90ADB Ð=°BDE !OC CD OD OD BC F DBC CAD BAD BCD Ð=Ð=Ð=ÐBD DC =OB OC =OD BC BDE !BE =BD =10AB =5OB OD ==OF t =5DF t =-Rt BOF !Rt BDF V 22225(5)t t -=--3t =4BF =8BC =z【点睛】本题主要考查了角平分线的定义、等腰三角形的判定与性质、勾股定理的应用、垂直平分线的判定与性质、圆的性质等知识点,灵活运用相关知识成为解答本题的关键. 21. 如图是由小正方形组成的网格,每个小正方形的顶点叫做格点.的三个顶点都是格点.仅用无刻度的直尺在给定网格中完成画图,画图过程用虚线表示.(1)在图(1)中,,分别是边,与网格线的交点.先将点绕点旋转得到点,画出点,再在上画点,使;(2)在图(2)中,是边上一点,.先将绕点逆时针旋转,得到线段,画出线段,再画点,使,两点关于直线对称. 【答案】(1)作图见解析 (2)作图见解析 【解析】【分析】(1)取格点,作平行四边形,利用平行四边形对角顶点关于对角线交点对称即可求点F ;平行四边形对边在网格中与格线的交点等高,连接等高点即可作出; (2)取格点,作垂直平分线即可作出线段AH ;利用垂直平分线的性质,证明三角形全等,作出,两点关于直线对称 【小问1详解】 解:作图如下:96´ABC!D E AB AC B E 180°F F AC G DG BC !P AB BAC a Ð=AB A 2a AH AH Q P Q AC DG BC !P Q ACz取格点,连接,且,所以四边形是平行四边形,连接,与AC 的交点就是点E ,所以BE =EF ,所以点F 即为所求的点;连接CF ,交格线于点M ,因为四边形ABCF 是平行四边形,连接DM 交AC 于一点,该点就是所求的G 点; 【小问2详解】 解:作图如下:取格点D 、E ,连接DE ,AC 平行于DE ,取格点R ,连接BR 并延长BR 交DE 于一点H ,连接AH ,此线段即为所求作线段;理由如下:取格点W 连接AW 、CW ,连接CR ,∴, ∴, ∵, ∴, ∴, ∴, ∵, ∴, ∵点是的中点, ∴点是的中点,F AF AF BC !AF BC =ABCFBF AWC RCB @!!WAC CRB Ð=Ð90WAC ACW Ð+Ð=°90CRB ACW Ð+Ð=°90RKC Ð=°AC BH ^DH CK !BK BCBH BD=C BD K BHz.com即, ∴垂直平分, ∴.连接,交AC 于点,连接交于点,则该点就是点关于直线的对称点.理由如下:∵垂直平分,∴是等腰三角形,, ∴ , ∴, ∴,∴,两点关于直线对称.【点睛】本题考查了用无刻度直尺在网格中作图的知识,找准格点作出平行四边形和垂直平分线是解决本题的关键.22. 在一条笔直的滑道上有黑、白两个小球同向运动,黑球在处开始减速,此时白球在黑球前面处.小聪测量黑球减速后的运动速度(单位:)、运动距离(单位:)随运动时间(单位:)变化的数据,整理得下表.运动时间1 2 3 4 运动速度 10 9.5 9 8.5 8 运动距离9.751927.7536小聪探究发现,黑球的运动速度与运动时间之间成一次函数关系,运动距离与运动时间之间成二次函数关系.(1)直接写出关于的函数解析式和关于的函数解析式(不要求写出自变量的取值范围)(2)当黑球减速后运动距离为时,求它此时的运动速度;(3)若白球一直..以的速度匀速运动,问黑球在运动过程中会不会碰到白球?请说明理由.BK KH =AC BH AB AH =PH M BM AH Q P AC AC BH BMH !PAM QAM Ð=ÐBMK AMQ HMK AMP Ð=Ð=Ð=ÐAMP AMQ @!!AP AQ =P Q AC A 70cm v cm/s y cm t s /s t /cm/s v /cm y v t y t v t y t 64cm 2cm/s【答案】(1), (2)(3)黑、白两球的最小距离为,大于0,黑球不会碰到白球 【解析】【分析】(1)根据黑球的运动速度与运动时间之间成一次函数关系,设表达式为v =kt +b ,代入两组数值求解即可;根据运动距离与运动时间之间成二次函数关系,设表达式为,代入三组数值求解即可;(2)当黑球减速后运动距离为时,代入(1)式中关于的函数解析式求出时间t ,再将t 代入关于的函数解析式,求得速度v 即可;(3)设黑白两球的距离为,得到,化简即可求出最小值,于是得到结论.【小问1详解】根据黑球的运动速度与运动时间之间成一次函数关系,设表达式为v =kt +b ,代入(0,10),(1,9.5)得,,解得, ∴, 根据运动距离与运动时间之间成二次函数关系,设表达式为,代入(0,0),(1,9.75),(2,19)得,解得,∴; 【小问2详解】 依题意,得, ∴, 解得,,;1102v t =-+21104y t t =-+6cm/s 6cm v t y t 2y at bt c =++64cm y t v t cm w 217028704w t y t t =+-=-+v t 109.5b k b =ìí=+î1210k b ì=-ïíï=î1102v t =-+y t 2y at bt c =++09.751942c a b a b=ìï=+íï=+î14100a b c ì=-ïï=íï=ïî21104y t t =-+2110644t t -+=2402560t t -+=18t =232t =z当时,;当时,(舍); 答:黑球减速后运动时的速度为. 【小问3详解】设黑白两球的距离为,, ∵,∴当时,的值最小为6, ∴黑、白两球的最小距离为,大于0,黑球不会碰到白球.【点睛】本题考查一次函数和二次函数的实际应用,待定系数法求解析式,解决本题的关键是明确题意求出函数表达式.23. 问题提出:如图(1),中,,是的中点,延长至点,使,延长交于点,探究的值.(1)先将问题特殊化.如图(2),当时,直接写出的值; (2)再探究一般情形.如图(1),证明(1)中的结论仍然成立.问题拓展:如图(3),在中,,是的中点,是边上一点,,延长至点,使,延长交于点.直接写出的值(用含的式子表示). 【答案】(1)[问题提出](1);(2)见解析 (2)[问题拓展]18t =6v =232t =6v =-64cm 6cm/s cm w 217028704w t y t t =+-=-+21(16)64t =-+104>16t =w 6cm ABC !AB AC =D AC BC E DE DB =ED AB F AFAB60BAC Ð=°AFABABC !AB AC =D AC G BC ()12CG n BC n=<BC E DE DG =ED AB F AFABn 1424n-z【解析】【分析】[问题探究](1)根据等边三角形的性质结合已知条件,求得,,根据含30度角的直角三角形的性质,可得,即可求解; (2)取的中点,连接.证明,可得,根据,证明,根据相似三角形的性质可得,进而可得; [问题拓展]方法同(2)证明,得出,,证明,得到,进而可得. 【小问1详解】[问题探究]:(1)如图,中,,是的中点,,是等边三角形, ,,,,,,,,, 30ADF ADB Ð=Ð=°90AFD Ð=°111,222AF AD AD AC AB ===BC H DH DBH DEC △≌△BH EC =DH AB !EDH EFB △∽△32FB EB DH EH ==14AF AB =DBH DEC △≌△GH EC =EDH EFB △∽△2+2FB EB nDH EH ==AF AB=24n-!ABC !AB AC =D AC 60BAC Ð=°ABC \!12AD AB =30ABD DBE \Ð=Ð=°60A Ð=°DB DE \=30E DBE \Ð=Ð=°180120DCE ACB Ð=°-Ð=°!18030ADF CDE E DCE \Ð=Ð=°-Ð-Ð=°60A Ð=°!90AFD \Ð=°12AF AD \=z . (2)证明:取的中点,连接.∵是的中点,∴,. ∵,∴,∴.∵,∴.∴.∴.∴.∴. ∵,∴.∴. ∴. ∴. 【小问2详解】[问题拓展]如图,取的中点,连接. 1124AD AF AB AB \==BC HDH D AC DH AB !12DH AB =AB AC =DH DC =DHC DCH Ð=ÐBD DE =DBH DEC Ð=ÐBDH EDC Ð=ÐDBH DEC △≌△BH EC =32EB EH =DH AB !EDH EFB △∽△32FB EB DH EH ==34FB AB =14AF AB =BC H DHz∵是的中点,∴,. ∵,∴,∴.∵,∴.∴.∴.∴.,∴. ∵,∴.∴. ∴. D AC DH AB !12DH AB =AB AC =DH DC =DHC DCH Ð=ÐDE DG =DGH DEC Ð=ÐGDH EDC Ð=ÐDGH DEC !!≌GH EC =HE CG \=!()12CG n BC n=<BC nCG \=()1BG n CG \=-()1111222n CE GH BC BG nCG n CG CG æö==-=--=-ç÷èø1221+22nCG EB BC CE n n EH EH n C CG G æö-+++====ç÷èøDH AB !EDH EFB △∽△2+2FB EB n DH EH ==24FB n AB +=z ∴. . 【点睛】本题考查了等边三角形的性质,全等三角形的性质与判定,相似三角形的性质与判定,等边对等角,掌握相似三角形的性质与判定是解题的关键.24. 抛物线交轴于A ,两点(A 在的左边),是第一象限抛物线上一点,直线交轴于点.(1)直接写出A ,两点的坐标;(2)如图(1),当时,在抛物线上存在点(异于点),使,两点到的距离相等,求出所有满足条件的点的横坐标; (3)如图(2),直线交抛物线于另一点,连接交轴于点,点的横坐标为.求的值(用含的式子表示). 【答案】(1),;(2)0,; (3). 【解析】【分析】(1)令求出x 的值即可知道A ,两点的坐标;(2)求出直线的解析式为,分情况讨论:①若点在下方时,②若点42244AF n n AB ---==\AF AB=24n -223y x x =--x B B C AC y P B OP OA =D B B D AC D BP E CE y F C m FP OPm ()1,0A -()3,0B 32-32+13m 223=0x x --B AC 1y x =+D AC。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
武汉中考调考24题
【中考题】
1.(2013•武汉)已知四边形ABCD中,E,F分别是AB,AD边上的点,DE与CF交于点G.
(1)如图①,若四边形ABCD是矩形,且DE⊥CF.求证:;
(2)如图②,若四边形ABCD是平行四边形.试探究:当∠B与∠EGC满足什么关系时,使
得成立?并证明你的结论;
(3)如图③,若BA=BC=6,DA=DC=8,∠BAD=90°,DE⊥CF.请直接写出的值.
2.(2012•武汉)已知△ABC中,AB=,AC=,BC=6
(1)如图1,点M为AB的中点,在线段AC上取点N,使△AMN与△ABC相似,求线段MN的长;
(2)如图2,是由100个边长为1的小正方形组成的10×10的正方形网格,设顶点在这些小正方形顶点的三角形为格点三角形.
①请你在所给的网格中画出格点△A1B1C1与△ABC全等(画出一个即可,不需证明)
②试直接写出所给的网格中与△ABC相似且面积最大的格点三角形的个数,并画出其中一个(不需证明).
3.(2011•武汉)(1)如图1,在△ABC中,点D、E、Q分别在AB、AC、BC上,且DE∥BC,
AQ交DE于点P,求证:=;
(2)如图,△ABC中,∠BAC=90°,正方形DEFG的四个顶点在△ABC的边上,连接AG,AF分别交DE于M,N两点.
①如图2,若AB=AC=1,直接写出MN的长;
②如图3,求证:MN2=DM•EN.
4.(2010•武汉)已知:线段OA⊥OB,点C为OB中点,D为线段OA上一点.连接AC,BD交于点P.
(1)如图1,当OA=OB,且D为OA中点时,求的值;
(2)如图2,当OA=OB,且时,求tan∠BPC的值.
(3)如图3,当AD:AO:OB=1:n:时,直接写出tan∠BPC的值.
5.(2009•武汉)如图1,在Rt△ABC中,∠BAC=90°,AD⊥BC于点D,点O是AC边上一点,连接BO交AD于F,OE⊥OB交BC边于点E.
(1)求证:△ABF∽△COE;
(2)当O为AC的中点,时,如图2,求的值;
(3)当O为AC边中点,时,请直接写出的值.
6.(2008•武汉)正方形ABCD中,点O是对角线AC的中点,P是对角线AC上一动点,过点P作PF⊥CD于点F.如图1,当点P与点O重合时,显然有DF=CF.
(1)如图2,若点P在线段AO上(不与点A、O重合),PE⊥PB且PE交CD于点E.
①求证:DF=EF;
②写出线段PC、PA、CE之间的一个等量关系,并证明你的结论;
(2)若点P在线段OC上(不与点O、C重合),PE⊥PB且PE交直线CD于点E.请完成图3并判断(1)中的结论①、②是否分别成立?若不成立,写出相应的结论.(所写结论均不
必证明)
7.(2007•武汉)填空或解答:点B、C、E在同一直线上,点A、D在直线CE的同侧,AB=AC,EC=ED,∠BAC=∠CED,直线AE、BD交于点F.
(1)如图①,若∠BAC=60°,则∠AFB=_________;如图②,若∠BAC=90°,则∠AFB=
_________;
(2)如图③,若∠BAC=α,则∠AFB=_________(用含α的式子表示);
(3)将图③中的△ABC绕点C旋转(点F不与点A、B重合),得图④或图⑤.在图④中,∠AFB 与∠α的数量关系是∠AFB=90°;在图⑤中,∠AFB与∠α的数量关系是_________.请你任选其中一个结论证明.。
