新版分数除法讲义+练习【精选】
新版分数除法易错题练习【精选】

分数除法易错题讲义一、选择题1.25米比30米少()A.B.C.2.把5米长的绳子平均分成8份,每份的长是()A.B.米C.米D.3.把10克盐放入100克水中,盐是盐水的()A.B.C.4.真分数除以真分数,商()A.>1 B.<1 C.不能确定5.一本书已看了全书的,则已看的页数比未看的页数少()A.B.C.D.6.千克的芝麻可榨千克油,每千克芝麻可榨油多少千克?正确列式是()A.÷B.÷C.×7.一个数的一半是,这个数是()A.B.C.8.一个数的是,求这个数,应列式为()A.×B.÷C.+D.﹣二.填空与判断9.(2014•临川区模拟)里有_________个,0.8里有_________个0.01.10.(2014•长沙模拟)甲数比乙数多,乙数比甲数少_________.11.(2013•毕节地区模拟)把2米长的铁丝平均截成5段,每段长米._________.(判断对错)12.将一根长5m的绳子平均分成6段,每段是这根绳子的_________,每段长_________米.13.甲数比乙数多,那乙数比甲数少._________.(判断对错)14.把7千克糖平均分装在9个袋子里,每袋是这些糖的_________,每袋重_________千克.15.(2012•翠屏区模拟)一个不为0的数除以一个分数,得到的商一定比这个数大._________.16.(2010•仪征市)把一根5米长的木棍锯成同样长的小段,共锯了3次,每段占全长的_________,两段长_________米.17.(2008•仪征市)小强把一根长米的绳子对折,再对折后,沿着所有折痕剪开,每根绳子长_________米,每根绳子是总长度的_________.18.一个不为0的数除以一个真分数,商一定大于原数._________.(判断对错)19.小红小时走4千米,她每小时走_________千米,她走1千米平均用_________小时.20.有5千克水果糖,平均分成7份,每份是_________千克,每份占5千克的_________.21.一个数除以,相当于把这个数扩大10倍._________.(判断对错)22.水结成冰后,体积增加原来的十一分之一,冰化成水后,体积减少原来的_________.23.25dm是1m的_________;1.8吨的是_________千克.24.25比20多._________.25.甲数是30,比乙数少,乙数是_________.26.一个数除以,就是把这个数扩大6倍._________.27.甲数除以乙数(0除外),等于甲数乘以乙数的倒数._________.(判断对错)28.除以一个不为零的数,等于乘以这个数的倒数._________.(判断对错)29.五(1)班有男生25人,女生23人,男生占全班人数的._________.(判断对错)30.用200千克黄豆可以榨油26千克,平均1千克黄豆榨油_________千克,榨1千克油需要_________千克黄豆.参考答案与试题解析一.选择题(共8小题)1.25米比30米少(C)A.B.C.考点:分数除法.专题:分数和百分数.分析:先求出25米比30米少几米,然后用少的长度除以30米即可.解答:解:(30﹣25)÷30=5÷30=;答:25米比30米少.故选:C.点评:本题属于基本的分数除法应用题:求一个数是另一个数的几分之几,找出单位“1”,用除法求解.2.把5米长的绳子平均分成8份,每份的长是(C)A.B.米C.米D.考点:分数除法.分析:把5米长的绳子平均分成8份,求每份的长用除法.解答:解:5÷8=(米);答:每份的长是米点评:此题考查了分数的意义,把一个物体看作单位“1”,平均分作几份,每一份就占总数的几分之一.3.把10克盐放入100克水中,盐是盐水的(B)A.B.C.考点:分数除法.专题:分数百分数应用题.分析:先求出盐水的总重量是多少克,再用盐的重量除以盐水的总重量就是盐占盐水的几分之几,由此解答即可.解答:解:10÷(10+100)=10÷110=答:盐是盐水的.点评:此题属于分数除法应用题中的一个基本类型:求一个数是另一个数的几分之几.4.真分数除以真分数,商(C)A.>1 B.<1 C.不能确定考点:分数除法.专题:运算顺序及法则.分析:真分数都小于1,但是真分数除以真分数,商不能确定是否大于1还是小于1,可以举例说明.解答:解:比如:=<1;=2>1;=1=1;所以,真分数除以真分数,商可能大于1、也可能小于1、还可能等于1.点评:像这种判断选择题,往往利用举例说明的方法比较简单.5.一本书已看了全书的,则已看的页数比未看的页数少(C)A.B.C.D.考点:分数除法.分析:把全书的总页数看作单位“1”,已看的占,未看的占1﹣=;要求“已看的页数比未看的页数少几分之几”,被看做“1”的数变成了未看的页数,即占总数就被看做了“1”.因此得解.解答:解:1﹣=,﹣=,÷=×=;答:已看的页数比未看的页数少.点评:此题考查了分数除法,要分清哪个数量被看做单位“1”是解决此题的关键.6.千克的芝麻可榨千克油,每千克芝麻可榨油多少千克?正确列式是(A)A.÷B.÷C.×考点:分数除法.专题:文字叙述题.分析:求每千克芝麻可榨油多少千克,用油的质量除以芝麻的重量即可.解答:解:÷=(千克);答:每千克芝麻可榨油千克.点评:此题考查的是分数除法应用题,求1千克芝麻能榨油的数量,用油的千克数除以芝麻的千克数.7.一个数的一半是,这个数是(C)A.B.C.考点:分数除法.专题:运算顺序及法则.分析:把这个数看成单位“1”,它的一半也就是它的对应的数量是,由此用除法求出这个数.解答:解:÷=;答:这个数是.点评:本题先找出单位“1”,已知一个数的几分之几是多少,求这个数用除法.8.一个数的是,求这个数,应列式为(B)A.×B.÷C.+D.﹣考点:分数除法.专题:文字叙述题.分析:求这个数是多少,根据已知一个数的几分之几是多少,求这个数,用“÷”,解答即可.解答:解:÷=1;故选:B.二.填空题(共22小题)9.(2014•临川区模拟)里有6个,0.8里有80个0.01.考点:分数除法;小数除法.分析:求里有几个,0.8里有几个0.01,都用除法解答即可.解答:解:÷=×24=6;0.8÷0.01=80;答:里有6个,0.8里有80个0.01.点评:此题考查了分数除法和小数除法,除以一个分数等于乘这个分数的倒数;小数除法中被除数和除数同时扩大100倍,商不变.10.(2014•长沙模拟)甲数比乙数多,乙数比甲数少.考点:分数除法.专题:运算顺序及法则.分析:根据“甲数比乙数多”,知道是把乙数看做单位“1”,即甲数是乙数的(1+),进一步求出乙数比甲数少百分之几验证即可.解答:解:甲数是乙数的百分之几:1+=1,乙数比甲数少百分之几:(1﹣1)÷1=;故答案为:.点评:此题的两个百分数不是表示的具体的数,它们的单位“1”不同,找出单位“1”,根据题意,计算出正确的结果即可判断.11.(2013•毕节地区模拟)把2米长的铁丝平均截成5段,每段长米.×.(判断对错)考点:分数除法.专题:运算顺序及法则.分析:求每段长的米数,平均分的是具体的数量2米,求的是具体的数量;用除法计算.解答:解:2÷5=(米);答:每段长米;点评:解决此题关键是弄清求得是具体的数量还是分率,求具体的数量平均分的是具体的数量;求分率平均分的是单位“1”.12.(2013•黄冈模拟)将一根长5m的绳子平均分成6段,每段是这根绳子的,每段长米.考点:分数除法.分析:求每段长是这根绳子的几分之几,如果求的是分率,平均分的就是单位“1”;求每段长的米数,如果求的是具体的数量,平均分的是具体的数量5米;都用除法计算.解答:解:每段是这根绳子的:1÷6=,每段长的米数:5÷6=(米).答:每段是这根绳子的,每段长米.故答案为:,.点评:解决此题关键是弄清求得是分率还是具体的数量,求分率平均分的是单位“1”;求具体的数量平均分的是具体的数量.13.(2012•新疆模拟)甲数比乙数多,那乙数比甲数少.错误.(判断对错)考点:分数除法;分数的意义、读写及分类;分数大小的比较.分析:本题单位“1”不同,甲数比乙数多,是把乙数看作单位“1”,甲数是1+,即,那么乙数比甲数少(﹣1)÷,据此解答即可.解答:解:把乙数看作单位“1”,甲数是1+=,乙数比甲数少:(﹣1)÷=÷=;故答案为:错误.点评:解答本题要注意两个分数的单位“1”是不同的.14.(2011•北京)把7千克糖平均分装在9个袋子里,每袋是这些糖的,每袋重千克.考点:分数除法.分析:(1)把糖的总重量看成单位“1”根据分数的意义求出每份是总数量的几分之几;(2)根据除法的意义,用总重量除以分的份数就是每袋的重量.解答:解:(1)把全部的糖平均分装在9个袋子里,每袋是这些糖的;(2)7÷9=(千克);答:每袋是这些糖的,每袋重千克.点评:本题重在区分每份占总数的几分之几和每份的重量是多少,做到正确区分,选择合适的解题方法.15.(2012•翠屏区模拟)一个不为0的数除以一个分数,得到的商一定比这个数大.错误.考点:分数除法.分析:利用举反例的方法来进行判断,给这两个数赋值,并把这个分数写成一个假分数,计算出结果再判断.解答:解:设被除数是2,除数是那么:2=;<2,商小于被除数;故答案为:错误.点评:通过平常的计算我们可以总结规律:两个数的商与被除数数比较,(被除数和除数数都不为0),要看除数;如果除数大于1,则商小于被除数;如果除数小于1,则商大于除数;如果除数等于1,则商等于被除数;由此规律解决问题.16.(2010•仪征市)把一根5米长的木棍锯成同样长的小段,共锯了3次,每段占全长的,两段长米.考点:分数除法.分析:(1)因为段数=锯的次数+1,可算出段数,又因为锯的同样长,可求出每段占全长的多少.(2)两段是全长的多少,就是求5的.解答:解:(1)3+1=4(段),每段就是全长的;(2)(米);故答案为.点评:考查了锯木头问题和分数的意义,要注意段数=锯的次数+1.17.(2008•仪征市)小强把一根长米的绳子对折,再对折后,沿着所有折痕剪开,每根绳子长米,每根绳子是总长度的.考点:分数除法;分数的意义、读写及分类.分析:根据“把一根绳子对折再对折”,可知把这根绳子平均分成了4份;求每根绳子长的米数,平均分的是具体的数量米,表示把米平均分成4份,求得是具体的数量;求每根绳子是总长度的几分之几,平均分的是单位“1”,表示把“1”平均分成4份,求的是分率;都用除法计算.解答:解:每根绳子长的米数:÷4=×=(米);每根绳子是总长度的:1÷4=;答:每根绳子长米,每根绳子是总长度的.故答案为:,.点评:解决此题关键是弄清求得是具体的数量还是分率,求具体的数量平均分的是具体的数量;求分率平均分的是单位“1”;要注意:具体的数量要带单位名称,而分率不能带单位名称.18.一个不为0的数除以一个真分数,商一定大于原数.√.(判断对错)考点:分数除法.专题:运算顺序及法则.分析:因为真分数小于1,再根据商的变化规律可得:一个不为0的数除以一个真分数,商一定大于原数.解答:解:一个不为0的数除以一个真分数,商一定大于原数,这个说法是正确的;故答案为:√.点评:商的变化规律:两个非零的数相除,当除数大于1,商小于被除数;当除数小于1,商大于被除数;当除数等于1,商等于被除数.19.小红小时走4千米,她每小时走6千米,她走1千米平均用小时.考点:分数除法.分析:(1)根据速度=路程÷时间,小红走的路程是4千米,用的时间是小时,由此可求出速度.(2)根据时间=路程÷速度,小红走的路程是1千米,速度是每小时6千米,由此可求出时间.解答:解:(1)4(千米);(2)1÷6=(小时);故答案为:6,.点评:考查了路程、速度和时间三者之间的关系.20.有5千克水果糖,平均分成7份,每份是千克,每份占5千克的.考点:分数除法;分数的意义、读写及分类.专题:文字叙述题.分析:根据平均分除法,把5千克糖平均分成7份用除法,5千克除以7;根据分数的意义,把单位“1”平均分成7份,每份占.解答:解:5÷7=(千克)1÷7=答:每份是千克,每份占5千克的.故答案为:,.点评:本题主要是考查平均分和分数的意义.21.一个数除以,相当于把这个数扩大10倍.√.(判断对错)考点:分数除法.专题:运算顺序及法则.分析:根据分数的除法法则:一个分数除以另一个分数就是乘以这个分数的倒数.所以一个数除以也就是乘以的倒数,即乘以10.因此,一个数除以,相当于把这个数扩大10倍.解答:解:一个数除以,相当于把这个数扩大10倍是正确的.故答案为:√.点评:本题主要考查了分数除法法则:除以一个数就等于乘以这个数的倒数.22.水结成冰后,体积增加原来的十一分之一,冰化成水后,体积减少原来的.考点:分数除法.分析:设原来水的体积是1,的单位“1”就是水的体积,那么冰的体积就是水的1,冰化成水后的体积仍是1,用冰的体积减去水的体积再除以冰的体积即可.解答:解:设水的体积是1,则:冰的体积是1×(1+)=,化成水之后减少了:(﹣1)==;答:体积减少了.点评:解答此题的关键是分清两个单位“1”的区别,找清各自以谁为标准,再把数据设出,根据数量关系求解.23.25dm是1m的;1.8吨的是1200千克.考点:分数除法;分数乘法.分析:(1)先把1米化成10分米,然后用25分米除以10分米即可;(2)把1.8吨看成单位“1”,用乘法求出它的是多少吨,然后化成千克即可.解答:解:(1)1米=10分米;25÷10=;(2)1.8×=1.2(吨);1.2吨=1200千克.故答案为:,1200.点评:解答此题的关键是找出单位“1”,求单位“1”的百分之几用乘法;求一个数是另一个数的百分之几用除法.24.25比20多..考点:分数除法.分析:先求出25比20多几个,用减法,再求出多出的数占20的几分之几,用除法.解答:解:25﹣20=5,5÷20=.故答案为:.点评:此题考查了分数除法,在求解比谁多几分之几时,比谁就要除以谁,要记住.25.甲数是30,比乙数少,乙数是50.考点:分数除法.专题:文字叙述题.分析:把乙数看成单位“”,它的(1﹣)对应的数量是甲数30,由此用除法求出乙数.解答:解:30÷(1﹣)=30÷=50;答:乙数是50.点评:本题关键是找出单位“1”,已知一个数的几分之几是多少,求这个数用除法.26.一个数除以,就是把这个数扩大6倍.√.考点:分数除法.分析:一个数除以,就等于乘它的倒数,也就是乘6,就是把这个数扩大6倍.解答:解:一个数除以,就等于乘以它的倒数,也就是乘以6,就是把这个数扩大6倍.故答案为:√.点评:此题考查了分数除法,除以一个分数,就等于乘这个分数的倒数.27.甲数除以乙数(0除外),等于甲数乘以乙数的倒数.√.(判断对错)考点:分数除法.专题:运算顺序及法则.分析:根据分数除法的计算法则:甲数除以乙数(0除外)等于甲数乘乙数的倒数.据此判断即可.解答:解:分数除法的计算法则是:甲数除以乙数(0 除外)等于甲数乘乙数的倒数;故答案为:√.点评:此题考查的目的是理解掌握分数除法的计算法则.28.除以一个不为零的数,等于乘以这个数的倒数.√.(判断对错)考点:分数除法.专题:运算顺序及法则.分析:分数除法的计算法则是:甲数除以乙数(0除外),等于甲数乘乙数的倒数,据此判断.解答:解:根据分数除法的计算法则可得,“除以一个不为零的数,等于乘以这个数的倒数.”的说法是正确的;故答案为:√.点评:本题是分数除法的计算法则的识记,是基础题,注意:0没有倒数,0不能做除数.29.五(1)班有男生25人,女生23人,男生占全班人数的.√.(判断对错)考点:分数除法.专题:文字叙述题.分析:男生25人,女生23人,则全班有(25+23)=48人,根据求一个数是另一个数的几分之几,用除法求出男生人数占全班人数的几分之几,进而判断即可.解答:解:男生占全班人数的:25÷(23+25)=;答:男生占全班人数的.故答案为:√.点评:此题应根据求一个数是另一个数的几分之几,用除法解答,进而判断即可.30.用200千克黄豆可以榨油26千克,平均1千克黄豆榨油千克,榨1千克油需要千克黄豆.考点:分数除法.分析:(1)用榨出油的重量除以黄豆的重量就是平均1千克黄豆榨油多少千克;(2)用黄豆的重量除以油的重量就是榨1千克油需要多少千克的黄豆.解答:解:(1)26÷200=(千克);(2)200÷26=(千克);答:平均1千克黄豆榨油千克,榨1千克油需要千克黄豆..点评:本题注意区分两问的不同:求平均1千克黄豆榨油千克,是把油的重量平均分;求榨1千克油需要多少千克黄豆是把黄豆的重量平均分.。
分数除法讲义【精选】

课 题倒数与分数除法教 学 目 的1、了解倒数、分数除法的意义2、掌握计算方法3、会运用在实际问题中重 难 点重点:计算方法及实际问题中的运用 难点:实际问题中的运用教 学 内 容【知识点一】 :倒数1、倒数的意义:乘积为1的两个数互为倒数。
(1)、倒数是两个数的关系,它们互相依存,不能单独存在。
单独一个数不能称为倒数。
(必须说清谁是谁的倒数)(2)、判断两个数是否互为倒数的唯一标准是:两数相乘的积是否为“1”。
例如:a×b=1则a 、b 互为倒数。
2、求倒数的方法:①求分数的倒数:交换分子、分母的位置。
②求整数的倒数:整数分之一。
③求带分数的倒数:先化成假分数,再求倒数。
④求小数的倒数:先化成分数再求倒数。
3、1的倒数是它本身,因为1×1=10没有倒数,因为任何数乘0积都是0,且0不能作分母。
非零整数a 的倒数为a 1 ;分数 a b的倒数是ba 。
1、真分数的倒数是假分数,真分数的倒数大于1,也大于它本身。
假分数的倒数小于或等于1。
带分数的倒数小于1。
2、用倒数解决问题(1)用转化的方法解决倒数问题例题1:一个自然数与它的倒数的和是5.2,这个自然数是多少?小结:已知一个自然数与它的倒数的和,可以把这个和分成整数和纯小数(或真分数)两部分。
整数部分就是这个自然数,纯小数(或真分数)部分就是这个自然数的倒数。
1、用假设的方法比较数的大小 例题2:如果a ×43 = b ×53 = c ×37,且a ,b ,c 均不为0,把a ,b ,c 这三个数按从大到小的顺序排列。
(3): 用假设的方法解决倒数问题 例题3:两个连续自然数的倒数差是121,求这两个自然数。
小结:解决此类问题,可以假设其中一个自然数是a ,另一个为a+1,再根据题意中的数量关系求解【巩固练习二】1、83的倒数是( ),0.25和( )互为倒数。
2、21×( )=( )×718=1×( )=3×( )=13. 一个自然数与它的倒数的差是212221,这个数是多少?4.如果x ×74 = y ×92=z ×21,且x ,y ,z 均不为0 ,请按照从小到大的顺序排列这三个数。
第三章 分数除法(讲义)(含答案)

第三章 分数除法(讲义)➢ 知识点睛1. 倒数:乘积为1的两个数互为倒数。
特别的:0没有倒数。
2. 倒数是两个数的关系,它们互相依存,不能单独存在。
单独一个数不能称为倒数。
(必须说清谁是谁的倒数)3. 求分数的倒数:交换分子、分母的位置。
4. 求整数的倒数:整数分之1。
5. 求带分数的倒数:先化成假分数,再求倒数。
6. 求小数的倒数:先化成分数再求倒数。
7. 1的倒数是它本身,因为1×1=1。
0没有倒数,因为任何数乘0,积都是0,且0不能作分母。
8. 分数除法:除以一个数,相当于乘一个数的倒数。
9. 在分数四则混合运算中,整数的运算律仍旧适用。
➢ 精讲精练经典例题1计算并观察:3883⨯ 715157⨯ 12121⨯乘积为1的两个数互为 。
练一练写出下面数字的倒数:114 169 3587 154经典例题2 把一张纸的54平均分成2份,每份是这张纸的几分之几?练一练计算下面分数除法: 498÷4136÷131015÷1514103÷经典例题3计算:54851÷⨯ 653265÷÷1093265⨯⎪⎭⎫ ⎝⎛-练一练小明和爷爷一起去操场散步,小明走一圈需要8分钟,爷爷走一圈需要10分钟。
(1)如果两人同时同地出发,相背而行,多少分钟后相遇?(2)如果两人同时同地出发,同方向而行,多少分钟后小明超出爷爷一圈?经典例题4有一个分数,它的分母比分子多4,如果把分子、分母都加上9,得到的分数约5,这个分数是多少?分后是6经典例题5甲、乙、丙三人共同加工一批零件。
甲比乙多加工零件20个,丙加工的零件是乙加工零件的54,甲加工的零件是乙丙两人加工零件总数的65。
甲、乙、丙各加工零件多少个?【参考答案】经典例题1:1,1,1,倒数练一练:411,916,351,78,415 经典例题2:52 练一练:92,263,239,289经典例题3:2,23,203 练一练:940,40 经典例题4:1511经典例题5:甲:60,乙:40,丙:32。
【7A文】分数除法讲义+练习

第三单元分数除法第一部分:分数除法的计算法则课前准备:请说出下面各个数的倒数。
例1:幼儿园李老师把4个同样大的橙子分给小朋友。
(1)每人吃2个,可以分给几人?每人吃1个呢?解:4÷2=2(人)4÷1=4(人)(2)每人吃12个,可以分给几个人?144282÷=⨯=(人)例2:4米长的彩带,每23米剪一段,可以剪多少段?2344632÷=⨯=(段)通过前2个例子,我们看到:一个整数除以一个分数,相当于乘以这个分数的倒数例3:量杯里有45升果汁,平均分给2个小朋友喝,每人可以喝多少升?(升)通过这个例子,我们看到,一个分数除以一个整数,相当于乘以这个整数的倒数。
那么一个分数除以一个分数呢?请看下一个例题例4:小刚310小时走了35千米,那么他一个小时走了多少千米?3331022510531÷=⨯==(千米) 通过上面几道例题,我们可以得出分数除法的计算法则。
一个分数除以另一个分数,等于这个分数乘以另一个分数的倒数。
一个分数除以一个整数,等于这个分数乘以这个整数的倒数。
【练一练】 (1)计算2334÷=7899÷=93118÷= 714815÷=96147÷=12358÷= (2)一个数的58是112,这个数是多少?(3) 列式计算59是13的多少倍? 45乘一个数是310,这个数是多少? (4) 食堂运来240千克大米,第一天吃了总数的13,第二周吃的数量相当于第一周的89,第二周吃了多少千克大米?(5) 解方程129x =2536x =34105x ÷=2249x -=34245x +=(6) 能简算的就简算7115295115÷+⨯123325()714449-÷÷31313()81616+÷523527588--÷第二部分:认识“比”例题1:妈妈早晨准备了2杯果汁和3杯牛奶。
最新人教版六年级上册基础培优分数除法必考题专题讲义

第四讲:解决问题数的和倍、差倍问题已知两个数的和(或差)及这两个数的倍数关系,求这两个数。
方法一、和倍问题:单位1=和÷(1+倍数)另一个数=和-单位1差倍问题:单位1=和÷(1-倍数)另一个数=差+单位1方法二、列方程,设单位1为x方法三、转化为比,再计算例1.某单位四、五月份一共用电1680千瓦时,已知四月份的用电量是五月份的3/5。
五月份用电多少千瓦时?1、小利买了一只圆珠笔和一只钢笔,共用去了12元,圆珠笔的单价是钢笔的1/3。
圆珠笔和钢笔的单价各是多少元?2、两城相距112千米,甲、乙两车同时从两城相对开,经过4/5小时相遇,甲、乙两车的速度比是5:9,甲、乙两车每小时各行多少千米?3、一块长方形草地的周长是160cm,它的宽是长的3/5,这块草地的面积是多少?4、李奶奶和张奶奶一共捐款1200元,李奶奶捐的钱数是张奶奶的1/2,李奶奶和张奶奶各捐了多少元?工程问题工程问题的特点:一般工程问题都是,已知独做的工作时间(或合作的工作时间),求合作的时间(或独做的工作时间)数量关系:工作效率×工作时间=工作总量工作总量÷工作时间=工作效率工作总量÷工作效率=工作时间例1.一个蓄水池装有两个进水管,单开甲管10分钟可以将水池注满,单开乙管12分钟可以将水池注满。
如果同时打开两管,多少分钟可以将水池注满?1.往一个容积为600 m³的蓄水池里注水,4小时可以注满这个水池的。
如果要把这个水池全部注满水,一共需要几小时?2.工程队要修一条200 m的公路。
如果甲队单独修需要16天完成,乙队单独修需要20天完成。
现两队合修,10天能完成任务吗?3.修一批桌椅,甲单独修12天可以完成,乙的工作效率是甲的。
现由甲、乙全合修,多少天可以完成?4.一项工程甲队独做要40天完成,甲队工效是乙队的1/3 ,若两队合做,完成这项工程要多少天?5.一份稿件,甲每小时打这份稿件的1/4 ,乙单独打完这份稿件要4小时,如果两人合打这份稿件,几小时能完成?6.一项工程,甲、乙合作6天可以完全工程的,乙独做10天可以完成工程的。
(期末复习专题)分数除法(专项讲义)人教版六年级数学上册(知识梳理+典型例题+对应练习+答案)

(期末复习专题)分数除法(专项讲义)人教版六年级数学上册(知识梳理+典型例题+对应练习+答案)考点一、认识倒数1、乘积是1的两个数互为倒数。
2、倒数是指两个数之间的关系,相互依存,一个数不能叫倒数。
3、1的倒数是1,0没有倒数。
【例1】9的倒数是()。
8【解答】89。
【名师点睛】求一个数(0除外)的倒数,只要把这个数的分子、分母交换位置。
考点二、分数除法的计算分数除法计算法则:1、除以一个不等于0的数,等于乘这个数的倒数。
2、被除数÷除数=被除数×除数的倒数。
【例2】计算下面各题。
(1)1211÷18 =(2)310÷65=(3)815÷0.8=【解答】【名师点睛】除法转化成乘法时,被除数一定不能变,要将“÷”变成“×”,除数变成它的倒数。
考点三、分数的混合运算分数混合计算方法:1、同级运算,按照从左往右的顺序进行计算;2、没有括号的先乘、除后加、减;3、有括号的先算括号里面,再算括号外面。
【例3】计算下面各题。
(1)2514÷521×0.3(2) 12÷65÷213(3)815÷45+56×49(4)112÷(23-14)【例2】计算下面各题。
(1)÷18=(2)÷=(3)÷0.8=×=3×22÷=×1 3【解答】【例4】解方程。
(1) x +15x =130(2)14x ÷18=10 (3) 13x −19x =518(4)85x ÷25=56×310【例3】计算下面各题。
(1)÷×0.3(2)12÷÷=××10×=6512 ××522(3)÷+×(4)÷()×3++==÷(-)=÷=1=【解答】考点四、解决问题1、已知一个数的几分之几是多少,求这个数:已知量÷已知量占单位“1”的几分之几=单位“1”的量; 2、已知比一个数多(或少)几分之几的数是多少,求这个数: 已知量÷(1±几分之几)=单位“1”的量;【例4】解方程。
【应用题专项】第三单元 分数除法 小学数学六年级上册专项训练(知识梳理典例精讲专项训练)

第三单元分数除法(讲义)小学数学六年级上册专项训练(知识梳理+典例精讲+专项训练)1.倒数的意义。
乘积是1的两个数互为倒数。
2.求一个数的倒数的方法。
(1)求分数的倒数:将分数的分子与分母交换位置。
(2)求整数(0除外)的倒数:先把整数(0除外)看作分母是1 的分数,再交换分子、分母的位置。
1的倒数是1,0没有倒数。
(3)求小数的倒数:先把小数化成真分数或假分数,再交换分子、分母的位置。
3.分数除法的意义。
分数除法的意义与整数除法的意义相同,都是已知两个因数的积与其中一个因数,求另一个因数的运算。
4. 分数除法的计算方法。
除以一个不等于0的数,等于乘这个数的倒数。
5. 分数四则混合运算的运算顺序。
分数四则混合运算的运算顺序和整数四则混合运算的运算顺序相同。
含有两级运算的,要先算乘、除法,再算加、减法;只含有同级运算的,要按照从左到右的顺序依次计算;算式中带有括号的,要先算括号里面的,再算括号外面的。
6. 已知一个数的几分之几是多少,求这个数的问题的解法。
方法一:列方程解答,单位“1”的量(这个数)未知。
方法二:用算术法解答,已知量÷已知量占单位“1”的几分之几=单位“1”的量。
7.已知比一个数多(或少)几分之几的数是多少,求这个数的解题方法。
方法一:列方程解答,单位“1”的量(这个数)±单位“1”的量(这个数)×几分之几=已知量;单位“1”的量(这个数)×(1±几分之几)=已知量。
方法二:用算术法解答,已知量÷(1±几分之几)=单位“1”的量(这个数)。
8. 已知一个数是另一个数的几分之几及这两个数的和(或差),求这两个数分别是多少的问题的解法。
先找出单位“1”的量并设为x,用含有x的式子表示另一个量,再根据两个数的和(或差)列方程解答。
9. 工程问题。
设这项工程为一个具体数量或者“1”,根据“工作总量÷工作效率总和=工作时间总和”列式解答。
分数除法练习题【精选】

分数除法练习题【精选】分数除法是数学中非常重要的一部分,通过练习题可以帮助学生巩固这一知识点。
本文为大家精选了一些分数除法练习题,希望能对你的学习有所帮助。
练习题1:求下列分数的商:a) 3/4 ÷ 1/2b) 2/5 ÷ 3/4c) 7/8 ÷ 2/3d) 5/6 ÷ 1/3练习题2:计算下列分数的商,并将结果化简为最简形式:a) 2/3 ÷ 4/5b) 4/9 ÷ 3/7c) 7/8 ÷ 5/6d) 5/6 ÷ 2/3练习题3:计算下列分数的商,并将结果化简为最简形式:a) 2/3 ÷ 1/2b) 4/7 ÷ 3/5c) 3/4 ÷ 5/6d) 5/6 ÷ 2/3练习题4:求下列分数的商,并将结果化简为最简形式:a) 5/8 ÷ 1/4b) 3/5 ÷ 2/3c) 4/7 ÷ 3/8d) 7/9 ÷ 2/5练习题5:求下列分数的商,并将结果化简为最简形式:a) 1/2 ÷ 2/3b) 3/4 ÷ 4/5c) 5/6 ÷ 6/7d) 7/8 ÷ 8/9这些练习题涉及到了分数的除法运算,我们需要了解一些基本规则:规则1:两个分数相除,等于将被除数乘以倒数作为除数。
例如:a/b ÷ c/d = a/b × d/c。
规则2:将分子、分母两者的最大公约数约去,得到的新分数为最简形式。
现在,我们一起来解答这些题目吧!练习题1解答:a) 3/4 ÷ 1/2 = 3/4 × 2/1 = 6/4 = 3/2b) 2/5 ÷ 3/4 = 2/5 × 4/3 = 8/15c) 7/8 ÷ 2/3 = 7/8 × 3/2 = 21/16d) 5/6 ÷ 1/3 = 5/6 × 3/1 = 15/6 = 5/2练习题2解答:a) 2/3 ÷ 4/5 = 2/3 × 5/4 = 10/12 = 5/6b) 4/9 ÷ 3/7 = 4/9 × 7/3 = 28/27c) 7/8 ÷ 5/6 = 7/8 × 6/5 = 42/40 = 21/20d) 5/6 ÷ 2/3 = 5/6 × 3/2 = 15/12 = 5/4练习题3解答:a) 2/3 ÷ 1/2 = 2/3 × 2/1 = 4/3b) 4/7 ÷ 3/5 = 4/7 × 5/3 = 20/21c) 3/4 ÷ 5/6 = 3/4 × 6/5 = 18/20 = 9/10d) 5/6 ÷ 2/3 = 5/6 × 3/2 = 15/12 = 5/4练习题4解答:a) 5/8 ÷ 1/4 = 5/8 × 4/1 = 20/8 = 5/2b) 3/5 ÷ 2/3 = 3/5 × 3/2 = 9/10c) 4/7 ÷ 3/8 = 4/7 × 8/3 = 32/21d) 7/9 ÷ 2/5 = 7/9 × 5/2 = 35/18练习题5解答:a) 1/2 ÷ 2/3 = 1/2 × 3/2 = 3/4b) 3/4 ÷ 4/5 = 3/4 × 5/4 = 15/16c) 5/6 ÷ 6/7 = 5/6 × 7/6 = 35/36d) 7/8 ÷ 8/9 = 7/8 × 9/8 = 63/64通过以上练习题的解答,相信大家对分数除法有了更深入的了解。
分数除法 讲义
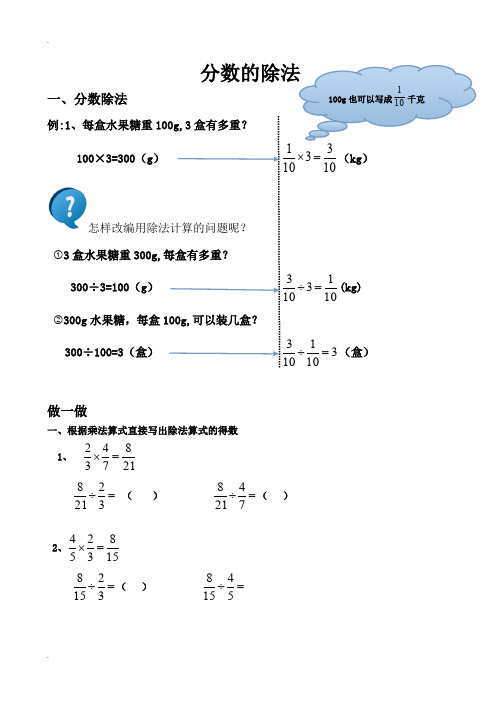
分数的除法一、分数除法例:1、每盒水果糖重100g,3盒有多重?100×3=300(g)1033101=⨯(kg)怎样改编用除法计算的问题呢?①3盒水果糖重300g,每盒有多重?300÷3=100(g)1013103=÷(kg)②300g水果糖,每盒100g,可以装几盒?300÷100=3(盒)3101103=÷(盒)做一做一、根据乘法算式直接写出除法算式的得数1、2187432=⨯=÷32218()=÷74218()2、1583254=⨯=÷32158()=÷54158100g也可以写成101千克2、把一张纸的54平均分成2份,每份是这张纸的几分之几?自己试着折一折,算一算。
=÷=÷524254=⨯=÷2154254 如果把这张纸的54平均分成3份,每份是这张纸的几分之几?=÷354根据上面的折纸实验和算式,你能发现什么规律?把54平均分成2份,就是把4个51平均分成两份,每份就是两个51,就是52把54 平均分成2份,每份就是54的21,也就是2154⨯3、小明32小时走2km,小红125小时走了65km 。
谁走得快些?小明平均每小时走:322÷想:先求31小时走了多少千米,也就是求2的21,即212⨯。
再求3个31小时走了多少千米,即3212⨯⨯。
32323212322=⨯=⨯⨯=÷(km )小红平均每小时走:)(25126512565km =⨯=÷答:小明走得快。
通过以上两个例子,你发现了什么?分数除法的计算法则:甲数除以乙数(0除外),等于甲数乘乙数的倒数。
为什么写成“512⨯” 怎么计算呢?画个图试试吧做一做一、用你发现的规律计算下面各题。
=÷3109=÷283=÷9824 54167÷二、直接写出得数。
《分数除法练习》课件

02
要避免分数除法的错误,首先需要理解分数除法的概念和运算
规则。
学生需要明确除法与乘法的区别,知道除法是将一个数分成相
03
等的若干份,而乘法是求一个数的若干倍。
避免错误的技巧和方法
技巧二:检查除数是否为0
在进行分数除法时,学生应始终确保除数不为0。
在每一步除法运算前,学生都应检查除数是否为0 ,避免出现除以0的错误。
如3/4米除以1/2等于多少米。
中等难度题目
稍复杂的分数除法计算
01
如(5/6)除以(2/3)等于多少。
带单位的分数除法计算
02
如(7/8)米除以(3/4)米等于多少米。
分数与小数之间的转换
03
如0.75除以(1/2)等于多少。
高难度题目
复杂分数除法计算
如(7/9)除以(5/6)等于多少。
带单位的复杂分数除法计算
避免错误的技巧和方法
01
02
03
技巧三:正确使用约分 技巧
在分数除法中,约分是 非常重要的步骤,可以 简化计算过程并提高准
确性。
学生应掌握约分的技巧 和方法,如最大公约数 、最小公倍数等,以便 在计算过程中正确地进
行约分。
易错题目的练习和解析
题目一
(3/4) ÷ (1/2) = ?
题目二
(4/3) ÷ 0 = ?
04
分数除法易错点解析
常见错误类型及解析
类型一:混淆除法与乘法 学生在进行分数除法时,容易将除法误认为是乘法,导致计算结果错误。
例如,将分数3/4除以1/2误认为是3/4乘以1/2,从而得出错误答案。
常见错误类型及解析
类型二:忽视除数不能为0
在进行分数除法时,学生常常忽视除数不能为的原则,导致出现除以0 的错误。
《分数除法》简便运算练习(讲义)

(一)导入新课(用时5分钟)
同学们,今天我们将要学习的是《分数除法》这一章节。在开始之前,我想先问大家一个问题:“你们在日常生活中是否遇到过需要将物品平均分配的情况?”(如分蛋糕等)这个问题与我们将要学习的内容密切相关。通过这个问题,我希望能够引起大家的兴趣和好奇心,让我们一同探索分数除法的奥秘。
在学生小组讨论环节,我发现有些学生在表达自己的观点时不够自信,甚至有些胆怯。我想,在今后的课堂中,我应该更加注重培养学生的表达能力和沟通技巧,让他们在讨论中更加积极主动。
最后,我会根据今天的课堂反馈,调整教学方法,力求在下一堂课中让每个学生都能更好地理解和应用分数除法。同时,我也会关注学生的学习效果,及时进行课后辅导,确保他们能够扎实掌握这一知识点。
-简便运算技巧的运用:部分学生可能难以掌握快速运算的方法,如乘以倒数、约分等。
-解决实际问题时,如何将问题转化为分数除法:模型。
-避免运算过程中的常见错误:如符号错误、约分不彻底、计算顺序混乱等。
举例:难点在于如何引导学生通过具体例题,理解分数除以分数时交叉相乘的原理,以及如何在实际问题中发现并运用分数除法的运算规则。此外,针对学生在运算过程中常见的错误,如分子分母颠倒、约分不准确等,需要设计专门的练习题进行针对性训练。
(三)实践活动(用时10分钟)
1.分组讨论:学生们将分成若干小组,每组讨论一个与分数除法相关的实际问题。
2.实验操作:为了加深理解,我们将进行一个简单的实验操作。这个操作将演示分数除法的基本原理。
3.成果展示:每个小组将向全班展示他们的讨论成果和实验操作的结果。
(四)学生小组讨论(用时10分钟)
1.讨论主题:学生将围绕“分数除法在实际生活中的应用”这一主题展开讨论。他们将被鼓励提出自己的观点和想法,并与其他小组成员进行交流。
五年级下册讲义 08讲 分数除法应用题(含答案、奥数板块)-精选

分数除法应用题【知识陈述】在解答分数应用题时,要通过分析数量关系,判断单位1、分率、对应量,熟悉三者之间的关系,正确列式解答(方程)。
已知一个数的几分之几是多少,求这个数,也就是求单位1,一般用分数除法或方程来解答。
对应的思想方法是解题时常用到的一种方法。
所谓“对应”,就是在两类事物之间建立某种联系,以实现未知向已知的转化。
1. 量率对应:解答分数应用题时,在确定单位“1”以后,一个具体数量总与一个具体分率相对应,抓住这种对应关系是解答分数应用题的关键。
2. 用除法的情况。
(1) 已知一个数的几分之几是多少,求这个数时,对应数量÷对应分率=单位“1”的量。
(2)求一个数是另一个数的几分之几。
对应量÷单位“1”的量=对应分率。
(3)平均分。
总数÷份数=每份数。
(4)包含除。
总数÷每份数=份数 3. 对应消去法:有些应用题,给出了两个或两个以上的未知数量间的关系,要求出这些未知的数量。
我们可以通过比较,分析对应的未知数量变化的情况,想办法消去一个未知量,从而求出最后问题。
【例题精讲】例1、四年级(3)班男生有30人,正好占全班的.这个班共有学生多少人?练习、超市运进一批水果,第一天运进320千克,第二天运进400千克,这两天运进的水果总量是现在超市水果总数的32,现在超市有多少千克水果?例2、商店运来500千克苹果,比运来的梨重,梨有多少千克?苹果比梨重多少千克?练习、一种彩电降价后是960元,这种彩电原价是多少元?例3、某小学学生中的38是男生,男生比女生少328人,女生占全校的几分之几?该小学共有学生多少人?练习、部队给养老院运苹果,第一次运来了全部的38,第二次运来了50千克,这时,已运来的恰好是没运来的57,还有多少千克苹果没有运来?例4、一根电线,第一次用去全长的41,第二次用去余下的51,这时还剩下108米,这根电线共长多少米?练习、工厂进了一批原料,第一周用去总数的52,第二周用去总数的94,这时用去的比剩下的多31吨,这批原料共有多少吨?例5、学校植树,第一天完成计划的83,第二天完成了计划的125,第三天植树55棵,结果超过计划的41,学校计划植树多少棵练习、服装厂计划两周生产一批服装,第一周完成计划的103,第二周完成计划的54,结果比计划多生产了200件,服装厂计划生产多少件服装?例6、甲数的23和乙数的14相等(甲乙两数均不为0),甲数是乙数的几分之几?乙数是甲数的几分之几?练习、小张邮票的52等于小王邮票的65,小张的邮票是小王的几分之几?小王的邮票是小张的几分之几?例7、一堆苹果,第一次运走83,第二次运走10千克, ,请问补充什么条件可以列式:)()(8311030-÷+?练习、一堆煤,第二次运走,第二次运走4吨, .求这堆煤的总吨数,列式是:(4+10)÷(1﹣),应补充的条件是( )【选讲】一列快车和一列慢车分别从甲乙两地同时相对开出,3时后相遇。
五年级下册讲义 08讲 分数除法应用题(含答案、奥数板块)

分数除法应用题【知识陈述】在解答分数应用题时,要通过分析数量关系,判断单位1、分率、对应量,熟悉三者之间的关系,正确列式解答(方程)。
已知一个数的几分之几是多少,求这个数,也就是求单位1,一般用分数除法或方程来解答。
对应的思想方法是解题时常用到的一种方法。
所谓“对应”,就是在两类事物之间建立某种联系,以实现未知向已知的转化。
1. 量率对应:解答分数应用题时,在确定单位“1”以后,一个具体数量总与一个具体分率相对应,抓住这种对应关系是解答分数应用题的关键。
2. 用除法的情况。
(1) 已知一个数的几分之几是多少,求这个数时,对应数量÷对应分率=单位“1”的量。
(2)求一个数是另一个数的几分之几。
对应量÷单位“1”的量=对应分率。
(3)平均分。
总数÷份数=每份数。
(4)包含除。
总数÷每份数=份数 3. 对应消去法:有些应用题,给出了两个或两个以上的未知数量间的关系,要求出这些未知的数量。
我们可以通过比较,分析对应的未知数量变化的情况,想办法消去一个未知量,从而求出最后问题。
【例题精讲】例1、四年级(3)班男生有30人,正好占全班的.这个班共有学生多少人?练习、超市运进一批水果,第一天运进320千克,第二天运进400千克,这两天运进的水果总量是现在超市水果总数的32,现在超市有多少千克水果?例2、商店运来500千克苹果,比运来的梨重,梨有多少千克?苹果比梨重多少千克?练习、一种彩电降价后是960元,这种彩电原价是多少元?例3、某小学学生中的38是男生,男生比女生少328人,女生占全校的几分之几?该小学共有学生多少人?练习、部队给养老院运苹果,第一次运来了全部的38,第二次运来了50千克,这时,已运来的恰好是没运来的57,还有多少千克苹果没有运来?例4、一根电线,第一次用去全长的41,第二次用去余下的51,这时还剩下108米,这根电线共长多少米?练习、工厂进了一批原料,第一周用去总数的52,第二周用去总数的94,这时用去的比剩下的多31吨,这批原料共有多少吨?例5、学校植树,第一天完成计划的83,第二天完成了计划的125,第三天植树55棵,结果超过计划的41,学校计划植树多少棵练习、服装厂计划两周生产一批服装,第一周完成计划的103,第二周完成计划的54,结果比计划多生产了200件,服装厂计划生产多少件服装?例6、甲数的23和乙数的14相等(甲乙两数均不为0),甲数是乙数的几分之几?乙数是甲数的几分之几?练习、小张邮票的52等于小王邮票的65,小张的邮票是小王的几分之几?小王的邮票是小张的几分之几?例7、一堆苹果,第一次运走83,第二次运走10千克, ,请问补充什么条件可以列式:)()(8311030-÷+?练习、一堆煤,第二次运走,第二次运走4吨, .求这堆煤的总吨数,列式是:(4+10)÷(1﹣),应补充的条件是( )【选讲】一列快车和一列慢车分别从甲乙两地同时相对开出,3时后相遇。
第5讲 分数除法-2022-2023学年五年级数学下册典题精讲专项讲义(北师大版)

第5讲分数除法-2022-2023学年五年级数学下册典题精讲专项讲义(北师大版)教学目标:1. 掌握分数除法的概念和方法;2. 能够灵活运用分数除法进行计算;3.能够在实际问题中运用分数除法进行解决。
教学重点:1. 分数除法的概念和方法;2. 小学题中常见的分数除法题型。
教学难点:1. 合理运用分数除法进行复杂计算;2. 在实际问题中运用分数除法解决问题。
教学方法:以讲解、练习、实例分析等多种教学方式相结合。
教学过程:一、导入1. 运用口算题目或计算的实例,把学生的思维引入分数除法的概念中。
例如:a ÷b = c,b不等于0,a、b、c都是数,并且c是用a除以b所得的商。
如果a和b都是整数,那么c也是整数,小学生们学过这种计算叫做“带余除法”。
那么如果a和b都是分数呢?我们可以将这个问题拆分成另外一个问题——把两个分数相除后是什么?这就引出了数学中的“分数除法”。
2. 用一些浅显易懂的例子来引入分数除法的概念。
例如:如果小明有9条毛毯,而小王有3条,那么我们就可以说小明有小王的3倍(9÷3=3),那么如果我们不知道小明和小王实际有多少毛毯,而只知道两个人各有几分之几呢?这个问题该怎么办呢?我们可以通过分数除法来解决这个问题。
二、分数除法的概念和方法我们知道,分数的基本运算有加、减、乘、除四种。
而分数除法就是指将两个分数相除,例如:Ⅱ.1. 基本概念1. 分数除法就是将两个分数相除,在运算结果中保留分数形式。
2. 分数除法的运算法则是:将除数倒数,即乘以倒数来进行分数除法。
Ⅱ.2. 基本方法我们在解决分数除法的题目时,需要掌握以下两种基本的方法:1. 直接除法法:直接按照分数除法的定义进行计算,例如:2. 倒数法:需要将除数倒数,即将除数的分子与分母调换位置,然后将除数乘以倒数,就得到了分数除法的结果。
例如:Ⅲ.小学题中常见的分数除法题型在小学数学题中,分数除法的题目比较常见,涉及到的形式也比较多,下面就给出一些常见的例子。
分数除法教案讲义及练习大全

4÷25 的积与其中一个因数,求另个一个因数的运算。
学生齐读。
2、巩固分数除法意义的练习:P28“做一做”3、学习分数除以整数的计算方法。
课件出示:教学例2(1)学生拿出课前准备好的纸,小组讨论操作,如何把这张纸的平均分成2份,并通过操作得出每份是这张纸的几分之几。
(2)小组汇报操作过程,得出:将一张纸的平均分成2份,每份是这张纸的。
(3)引导学生数形结合,对照不同的折法,说出两种不同的计算方法。
A 、÷2==,每份就是2个。
B 、÷2=×=,每份就是的。
(4)如果把这张纸的平均分成3份呢?让学生从上面两种方法中选择一种进行计算,通过操作对比,让学生发现第二种方法适用的范围更广。
2、学生总结:分数除以整数的计算方法。
引导学生观察÷2和÷3两个算式,概括出分数除545452545251545421525421545454课件演示:小时师:先画一条线段表示1小时走的路程,怎么样表示小时呢? 师:小时走了2km 怎样在图中表示?教师指出小时的部分。
师:这是几小时呢?又是多少千米?怎样求呢? 学生说说。
板书:2÷2=1(千米) 师:那全长就是多少千米? 学生说说。
板书:1×3=3(千米)师:先求小时走了多少千米,也就是求2个,算3232323131211小时走了?千米?2 km()×()=苹果的重量 学生完成后,师生共同检验。
二、新授 1、教学例1(1)解决第一个问题:小明的体重多少千克? 课件出示。
学生观察课件上的图画信息,并编成一道完整的题目。
课件出示。
小明的体内有水分28kg ,而他体内的水分约占体重的。
小明的体重是多少千克? 学生读题,理解题意,并分析重点句。
师生共同利用线段图进行理解。
学生结合线段图理解题意,分析题中的数量关系式,并写出等量关系式。
小明的体重×=体内水分的重量5454水分28千克 水分占体重的体重 ?千克学生独立完成。
最新苏教版六年级数学上册第三单元分数除法讲义与练习题

分数除法【知识要点】1、 分数除法的意义:分数除法的意义与整数除法的意义相同,都是已知两个因数的积,与其中的一个因数,求另一个因数的运算。
2、 分数除法的计算方法:(1)分数除以整数(0除外)等于分数乘这个整数的倒数。
(2)一个数除以分数,等于这个数乘分数的倒数。
3、商与被除数的大小关系:(1) 除数小于1时,商大于被除数(被除数不为0) (2) 除数大于1时,商小于被除数(被除数不为0) (3)除数等于1时,商等于被除数。
4、分数除法应用题 谁的几分之几(1)找出单位“1” 比谁多(少)几分之几 占谁的几分之几这里的谁就是单位“1”(2)已知单位“1”(标准量),一般用乘法标准量×对应分率=对应的量(3)未知单位“1”(未知标准量)求标准量,一般用除法对应的量÷对应分率=标准量【基础巩固】一、填空。
1、小花43时行走3千米,照这样计算,行走5千米要( )小时。
2、一堆煤重2021吨,21天烧完,每天烧( )吨,每天烧这堆煤的几分之几?( )3、( )千米的76是53千米。
43千克是109千克的( )。
4、把1652米长的电线平均剪成8段,求每段长是几米的算式是( )。
5、“一桶油的43重6千克”,把( )看作单位“1”,( )×43=( )6、“男生占全班人数的95”,把( )看作单位“1”,( )×95=( )7、“鸭只数的72等于鸡” 把( )看作单位“1”,( )×72=( )8、45是( )的95,107吨是( )吨的21, ( )是43平方米的31。
二、判断正误。
1、分数除法的意义与整数除法的意义相同。
( )2、当A 、B 、C 都不等于0时,若A ÷54=B ÷154=C ×141,则A >B >C 。
( )3、1吨煤用去14后,又运进14,还是1吨。
( )4、一个数除以真分数,商一定大于被除数。
《分数除法》(选择题篇四大题型)单元复习讲义(知识梳理+典例精讲+专项精练)六年级数学上册

第三单元分数除法单元复习讲义(讲义)六年级数学上册专项精练(知识梳理+典例精讲+专项精练)1、倒数的意义:乘积是1的两个数互为倒数。
2、倒数具备两个条件:一是两个数;二是乘积是1。
3、互为倒数的两个数的特点。
(1)如果两个数都是分数,那么两个分数的分子和分母正好颠倒了位置;(2)如果一个是整数,则另一个分数的分子是1,分母是这个整数。
4、求一个数的倒数的方法。
(1)求一个分数的倒数,把这个分数的分子、分母交换位置即可;(2)求小数的倒数,先把小数化成分数,再求倒数;(3)求非0整数的倒数,让这个整数作分母,分子是1。
5、注意事项:(1)1的倒数是1,等于它本身;(2)0没有倒数。
6、易错点:(1)易错点在于混淆倒数定义。
记住,乘积为1的两个数互为倒数,如5的倒数是15。
计算时,常错将分子分母颠倒而不求其积为1,如误将34的倒数写为43的相反数。
务必理解并准确应用倒数概念。
1、分数除以整数的计算方法。
(1)当一个分数被除以一个非零整数时,其结果等同于该分数乘以该整数的倒数。
在数学运算中,当遇到分子能够被某个整数整除的情况时,应采取以下步骤进行化简:将原分子除以该整数,并将所得的商作为新的分子,而分母则保持不变。
这一操作确保了分数的等价性,同时简化了其表达形式。
2、一个数除以分数。
(1)整数除以分数的计算方法:整数除以分数,用这个整数乘这个分数的倒数。
(2)分数除以分数的计算方法:分数除以分数,用被除数乘除数的倒数。
(3)分数除法的一般方法:一个数除以一个不等于0的数,等于乘这个数的倒数。
3、被除数与商的变化规律。
(1)除以大于 1 的数,商小于被除数:a÷b=c 当b>1时,c<a (a≠0);(2)除以小于 1 的数,商大于被除数:a÷b=c 当b<1时,c>a (a≠0,b≠0);(3)除以等于 1 的数,商等于被除数:a÷b=c 当b=1时,c=a。
4、易错点:分数除法时,易混淆除数与被除数位置,将分数除以整数误变为倒数相乘。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第三单元分数除法
第一部分:分数除法的计算法则
课前准备:请说出下面各个数的倒数。
3
9
10 幼儿园李老师把4
个同样大的橙子分给小朋友。
每人吃2个,可以分给几人?每人吃1个呢?
€ € C €
(人) (人)
2
3 4爲=4-=6
(段)
通过前2
个例子,我们看到:一个整数除以一个分数, 相当于乘以这个分数 的倒数
例2: 4米长的彩带每
1 2
米剪一段'可以剪多少段?
14 y 例1: 1
(2)
每人吃-个,可以分给几个人? 2
例3:量杯里有5升果汁,平均分给2
个小朋友喝,每人可以喝多少升?
通过这个例子,我们看到,一个分数除以一个整数,
相当于乘以这个整数的 倒数。
那么一个分数除以一个分数呢?请看下一个例题
3
3
例4
:小刚一小时走了 5千米'那么他一个小时走了多少千米?
^2 (千米)
5 10 5 3 1
通过上面几道例题,我们可以得出分数除法的计算法则。
一个分数除以另一个分数,等于这个分数乘以另一个分数的倒数。
一个分数除以一个整数,等于这个分数乘以这个整数的倒数
【练一练】
(1) 计算
11 8
9 .6
8 15
(2) —个数的I 是12,这个数是多少?
4-5
X 24-5
2-5
14 7
(3)列式计算
5是-的多少倍?
9 3
4乘一个数是—,这个数是多少?
5 10
(4)食堂运来240千克大米,第一天吃了总数的3,第二周吃的数量相当于第一周的9,第二周吃了多少千克大米?
(5)解方程
C 1 2x =-
3 . 4
一x =-
10 5 2
2 -4x
= 3 4 + 2x = 4 5
(6)能简算的就简算
7 亠11 .5 2 --- ■ ------- ~ -------- A.---- 9 5 11 5
3 . 3 . 25
_ - ―—)—-- 7 14 4 49
(3+乌斗12 8 16 16 2^2_^5
7 5 8 8
第二部分:认识“比”
例题1:妈妈早晨准备了2杯果汁和3杯牛奶。
请问:可以怎样表示这两个数量之间的关系?
运用我们学过的知识:可以从相差关系和倍数关系表示
牛奶比果汁多1杯,
果汁比牛奶少1杯档
果汁的杯数相当于牛奶的牛奶的杯数相当于
果汁的多。
这两个数量之间的关系还可以说成:
果汁和牛奶杯数的比是2比3 ;牛奶和果汁杯数的比是3比2。
其中2比3记作2:3; 3比2记作3:2。
“:”是比号,比号前面的数叫做比的前项,比号后面的数叫做比的后项。
例题2:走一段900米长的山路,小军用了15分,小伟用了20分。
分别计算他们的速度,填入下表。
速度=路程一时间,也可以用比来表示路程和时间的关系。
小军走的路程与时间的比是900: 15;
小伟走的路程与时间的比是900: 20。
请思考:两个数的比可以表示什么?
两个数的比表示两个数相除,比的前项除以后项所得的商叫做比值。
)=F)
从这题我们可以得出比,除法,分数的一些关系,见下表:
【练一练】
1、△△△0000
那么△与0的个数比是( ):( ),比值是( )
0与△的个数比是( ):( ),比值是( )
2、张祥买3本笔记本用了 10.5元,笔记本的总价和数量的比是( 值是(
3、11-6=(
4、看图填空
一张长方形方格纸被涂成了灰白相间的图案。
灰格与白格个数的比是 _________________ 白格与灰格个数的比是 _________________
5、在下面的方格图上,画出两个大小不同的长方形,使长方形的长与宽的比都
是 2: 10
【试一试】
3: 5=(
前项
后项 比值
除法 被除数 分数
分子
分数值
)。
),比
例题3:求出下面每个比的比值,并把比值相等的比填入等式。
4 :
5 1
6 : 20 50 : 40 40 : 50
):()
观察上面的等式,联系分数的基本性质想想,比会有什么性质?
比的前项和后项同时乘以或除以相同的数 (0除外),比值不变。
这就是 比
的基本性质。
应用比的性质,可以把一些比化成最简单的整数比。
⑵5
:3
6 4
【练一练】
一、认真思考,正确填写
氛公鸡有11只,母鸡的只数是公斜的春,母鸡有(
九比值是C 人
3. 把一根扌米的郭子平均分成4段,每段长和扌米的比是
■J J
是( 人比值是(
5*己知A :B=3:2,若肩苗山则卜( ):若A+B=15S 6. 把4: 5的前项乘5,要使比值不变「比的后项应加上<
后项减去12.要使比值不变,前项应(
7. ato A : B^3 : 2,若 A-150.则曲( );若 A+B-150,
氏 把3:5的前项加上翌使比值不变,后项应该加上( 如果把一个比的前顼乘Z S 项除以N 那么比值就(
4: 5= -- =)6'?(
)=
)(小数)
(1) 12: 18
(3) 1.8 : 0.09 (1) 12: 18= (12-6) (18-6) =2: 3,,,,,, 思考为什么除以 (2) )5:3
=(-X 12):(3
X 12H():(),,,,,思考为什么乘以
6 4 6 4
(3) 1.8 : 0.09= (1.8 X 100): (0.09 X 100) ,,,,思考为什
么乘以 6? 12? 100?
O 母鸡与公鸡
的只数的比是(
4.右图表示一个三角尺.Z2与Z3度数的比化成
最简单的整数比是(
比值是(
Z3与Z1度数的比比化成S 简单的整数比
则B=(
Q
氛右图是甲,乙.丙三个工程臥单独完成 同一项王程所需天数的统计图.
(1)甲、乙工作时间的比是牛乙单独 完成这项工程
用了(
)天。
C2)屮、丙的毎天工作量的比是(
10,从A 城到B 城,快车要6小时.慢车要8小时,快车
和慢车行完全程所需的
时间比是(
人快车与慢车的速度比是<
二.反复推敲.慎重选择。
口兔只数的沾当于灰兔只数的亍白兔和灰兔的只数比是(
A. 1: 4
B. 3* 4 Cx 3: 1
D. 4:
3
N 有甲、乙两袋大米.如果从甲袋中倒岀£给乙袋「两袋米就一样熏,原来甲"
」
乙两袋大米的熏量比是(
A. 5: 4
C> 5: 3 a
①桃树与梨树的比是4 : 3 @梨树是桃树的上 3
③桃树占两种果树的£
©梨树比桃树多丄
7 4
3.根据右图所示下面说法正确的是<
4、一个三角形三个内角度数的比是2 : 1 : 1,这个三角形叫是(
).
乩锐角三角形 C.等腰宜角三角形
D.等边
A.钝角三角形 三角
形
凤甲数除乙数*商是2,
A. 2 : 1
B.
甲数与乙数的最简整数比是C
1 :
2 C. 2 : 4
6,被减数与差的比是9: 5,那么减数与差的比是< 4 : 9 B. 9 : 4 G 4
: 5 A. C .
D .
三、耐心计算,仔细检査。
k
化简下面各比,并求出比值-(8分)
比25 : 10012・8 y' 15
0. 9 : 0.
36
丄吨:3了5千克
4
最简整数比
比值
2+递等式计算。
(每题3分.共9分)
4 21 2
5 亠 7
710 3 12 12
五.联系生活,解决问题。
U 一个长方形花圃,周长是册米,长和宽的比是5:4.a块花圃的面积是多少平方米7
2.大小两桶油,质量比是7: 3,如果从大桶中取出12千克油倒入小桶・则两桶中的油正好相等.两个桶中原来各有^^少油?
3. 一种长方体饼干盒子的棱长总和是216厘米,长.宽,寫
的比是4 ; 3 : 2.这个长方体的体积是多少立方厘米?
A X18-r-
3 4 3.如图,梯形的面积是48平方厘来,涂色部分的面积是多少?(4分)
4. 一种什锦糖是巧克力,水果糖,奶糖按照1 : 3 : 4配制而成口
(1)如果耍配制120千克这样什锦那么这三种耦各需多少千克?
5、某车间有140名职匸分成三个生产组.已知第一纽和第二组人数比是N 3,
第二组和第三组人数比是4: 5.这三个组各有多少人?
6.新生小学五,六年级共有学生450人,男,女生人数的比是5:4,男,女生
各有多少人?
了、一班和二班的人数比是创7.如果将一班的8名同学调去二班,那么一班和二班的人数
比是4: 5,原来两班各冇多少人?
1
4斗一=4X2=8 (人)
2。
