11-1 稳恒磁场
稳恒磁场

第十一章 稳恒磁场
如图所示,有一长为l , 半径为R的载流密绕直螺 线管,螺线管的总匝数为N,通有电流I. 设把螺线管 放在真空中,求管内轴线上一点处的磁感强度. o * p
R
x
dx
x
解 由圆形电流磁场公式
B
0 IR
2
2 2 3/ 2
( 2 x R)
第十一章 教学基本要求
第十一章 教学基本要求
s
s
B
B
dS
en
B
第十一章 稳恒磁场 磁通量:通过某一曲 面的磁感线数为通过此曲 面的磁通量.
B
s
Φ BS cos BS Φ B S B en S dΦ B dS dΦ BdS cos Φ s B dS
x
第十一章 教学基本要求
Id l
R
第十一章 稳恒磁场
r
x
o
r 2 2 2 r R x 0 I cosdl *p x B 2 l 4π r
dB
cos R
4π r 0 I cosdl dBx 2 4π r
dB
0 Idl
2
B
0 IR 2π R B dl 3 4π r 0 2 0 IR
1)若线圈有 N 匝
( 2 x R )2 2 N 0 IR
3
4)x R
B
0 IR
2x
3
2
, B
0 IS
2π x
3
第十一章 教学基本要求
第十一章 稳恒磁场
圆弧形电流在圆心处的磁场为什么?
I
大学物理 稳恒磁场

第十一章稳恒磁场磁场由运动电荷产生。
磁场与电场性质有对称性,学习中应注意对比.§11-1 基本磁现象磁性,磁力,磁现象;磁极,磁极指向性,N极,S极,同极相斥,异极相吸。
磁极不可分与磁单极。
一、电流的磁效应1819年,丹麦科学家奥斯特发现电流的磁效应;1820年,法国科学家安培发现磁场对电流的作用。
二、物质磁性的电本质磁性来自于运动电荷,磁场是电流的场。
注:1932年,英国物理学家狄拉克预言存在“磁单极”,至今科学家一直在努力寻找其存在的证据。
§11-2 磁场磁感强度一、磁场磁力通过磁场传递,磁场是又一个以场的形式存在的物质。
二、磁感强度磁感强度B 的定义:(1)规定小磁针在磁场中N 极的指向为该点磁感强度B 的方向。
若正电荷沿此方向运动,其所受磁力为零。
(2)正运动电荷沿与磁感强度B 垂直的方向运动时,其所受最大磁力F max 与电荷电量q 和运动速度大小v 的乘积的比值,规定为磁场中某点磁感强度的大小。
即:qvF B max=磁感强度B 是描写磁场性质的基本物理量。
若空间各点B 的大小和方向均相等,则该磁场为均匀磁场....;若空间各点B 的大小和方向均不随时间改变,称该磁场为稳恒磁场....。
磁感强度B 的单位:特斯拉(T)。
§11-3 毕奥-萨伐尔定律 一、毕-萨定律电流元: l Id电流在空间的磁场可看成是组成电流的所有电流元l Id 在空间产生元磁感强度的矢量和。
式中μ0:真空磁导率, μ0=4π×10-7NA 2 dB 的大小: 20sin 4rIdl dB θπμ=d B 的方向: d B 总是垂直于Id l 与r 组成的平面,并服从右手定则.一段有限长电流的磁场: ⎰⎰⨯==l l r r l Id B d B 304πμ二、应用1。
一段载流直导线的磁场 )cos (cos 42100θθπμ-=r IB 说明:(1)导线“无限长":002r I B πμ=(2)半“无限长”: 00004221r I r IB πμπμ==2.圆电流轴线上的磁场 磁偶极矩232220)(2x R R IB +=μ讨论:(1)圆心处的磁场:x = 0 RIB 20μ=;(2)半圆圆心处的磁场: RIR I B 422100μμ==(3)远场:x >>R ,引进新概念 磁偶极矩0n IS m =则: m xB 3012πμ=3.载流螺线管轴线上的磁场)cos (cos 2120ββμ-=nIB讨论:(1)“无限长”螺线管:nI B 0μ=(2)半“无限长”螺线管:nI B 021μ=例:求圆心处的B .§11-4 磁通量 磁场的高斯定理 一、磁感线作法类似电场线。
稳恒磁场

磁场 磁感应强度 基本磁现象1、通有电流的导线周围,小磁针会发生偏转。
2、磁铁附近的载流导线及载流线圈会受到力的作用。
3、载流导线之间或载流线圈之间有相互作用力。
4、电子射线束在磁场中路径发生偏转。
一切磁现象的根源是电流。
任何物质的分子中都存在有圆形电流,称为分子电流.分子电流相当于一个基元磁铁。
当物体不显示磁性时,各分子电流作无规则的排列, 它们对外界所产生的磁效应互相抵消。
在外磁场的作用下,与分子电流相当的基元磁铁将趋向于沿外磁场方向取向,从而使整个物体对外显示磁性。
磁感应强度磁现象中,电流与电流之间,电流与磁铁之间以及磁铁与磁铁之间的相互作用是通过一种叫磁场的特殊物质来传递的。
磁场对外的重要表现:1、磁场对进入场中的运动电荷或载流导体有磁力的作用;2、载流导体在磁场中移动时,磁场的作用力将对载流导体作功,表明磁场具有能量。
引入磁感应强度矢量B 来描述磁场的强弱和方向。
试验线圈(线度必须小,其引入不影响原有磁场的性质)的面积为 S ∆,线圈中电流为0I ,则定义试验线圈的磁矩为 n S I P m ∆0= 磁矩是矢量,其方向与线圈的法线方向一致,n 表示沿法线方向的单位矢量,法线与电流流向成右螺旋系。
(附图)线圈受到磁场作用的力矩(称为磁力矩)使试验线圈转到一定的位置而稳定平衡。
此时,线圈所受的磁力矩为零,此时线圈正法线所指的方向,定义为线圈所在处的磁场方向。
如果转动试验线圈,只要线圈稍偏离平衡位置,线圈所受磁力矩就不为零。
当试验线圈从平衡位置转过090时,线圈所受磁力矩为最大。
在磁场中给定点处,比值m P M max 仅与试验线圈所在位置有关,即只与试验线圈所在处的磁场性质有关。
规定磁感应强度矢量B 大小为m P M B max =磁场中某点处磁感应强度的方向与该点处试验线圈在稳定平衡位置时的法线方向相同;磁感应强度的量值等于具有单位磁矩的试验线圈所受到的最大磁力矩。
单位:磁感应强度的国际单位为特斯拉,简称特。
第十一章 电磁学 恒定磁场 Ma 2016

0 qnS d lv er dB 4 r2
d B 0 qv er B d N 4 r 2 方向根据右手螺旋法则, B 垂直 v 、 正, B 为 v r 的方向;q为负, B 与
q
+
r B
v
q-
q为 r组成的平面。 v r 相反。
μ0 I B (cos θ1 cos θ 2 ) 4πr0
0 π
2
I
无限长载流长直导线的磁场
θ1 θ2
μ0 I B 2πr0
注意用右手螺旋关系判断方向。 半无限长载流长直导线的磁场
1
r0
P
θ1 θ2
2 π
μ0 I B 4πr0
I
r0
P
大学物理 电磁学
2、载流圆线圈轴线上的磁场 真空中,半径为R的载流导线,通有电流I,称圆电流。求其 轴线上一点 P的磁感强度的方向和大小
1、5 点 : dB 0
7
6 5
Idl
R
×
× 3
3、7点 : dB
0 Idl 4 π R2
4
2、4、6、8 点 :
dB
0 Idl
4π R
2
sin 45
0
大学物理 电磁学
3. 毕—萨定律应用举例
dB 的方向均
沿x 轴负方向
(1) 载流长直导线的磁场
z
dz
解
2
dB
大学物理 电磁学
磁现象与电现象有没有联系?
静电场 ?
静止的电荷 运动的电荷
1820年奥斯特:发现电流的磁效应
N
电磁感应一章习题答案
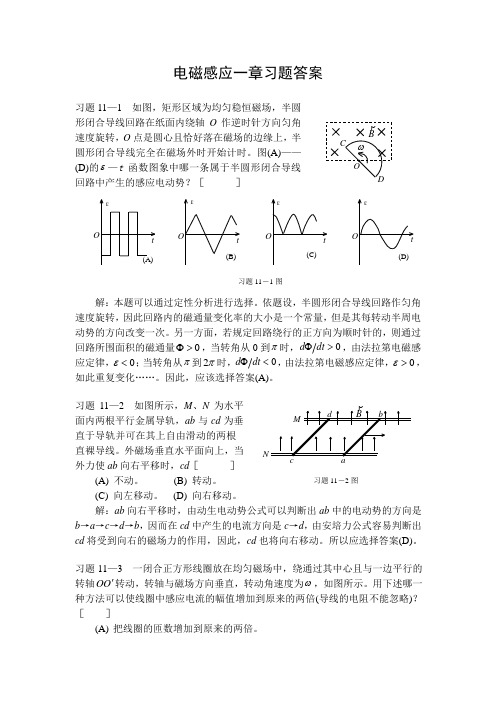
电磁感应一章习题答案习题11—1 如图,矩形区域为均匀稳恒磁场,半圆形闭合导线回路在纸面内绕轴O 作逆时针方向匀角速度旋转,O 点是圆心且恰好落在磁场的边缘上,半圆形闭合导线完全在磁场外时开始计时。
图(A)——(D)的ε—t 函数图象中哪一条属于半圆形闭合导线回路中产生的感应电动势?[ ]解:本题可以通过定性分析进行选择。
依题设,半圆形闭合导线回路作匀角速度旋转,因此回路内的磁通量变化率的大小是一个常量,但是其每转动半周电动势的方向改变一次。
另一方面,若规定回路绕行的正方向为顺时针的,则通过回路所围面积的磁通量0>Φ,当转角从0到π时,0>Φdt d ,由法拉第电磁感应定律,0<ε;当转角从π到π2时,0<Φdt d ,由法拉第电磁感应定律,0>ε,如此重复变化……。
因此,应该选择答案(A)。
习题11—2 如图所示,M 、N 为水平面内两根平行金属导轨,ab 与cd 为垂直于导轨并可在其上自由滑动的两根直裸导线。
外磁场垂直水平面向上,当外力使ab 向右平移时,cd [ ](A) 不动。
(B) 转动。
(C) 向左移动。
(D) 向右移动。
解:ab 向右平移时,由动生电动势公式可以判断出ab 中的电动势的方向是b →a →c →d →b ,因而在cd 中产生的电流方向是c →d ,由安培力公式容易判断出cd 将受到向右的磁场力的作用,因此,cd 也将向右移动。
所以应选择答案(D)。
习题11—3 一闭合正方形线圈放在均匀磁场中,绕通过其中心且与一边平行的转轴O O '转动,转轴与磁场方向垂直,转动角速度为ω,如图所示。
用下述哪一种方法可以使线圈中感应电流的幅值增加到原来的两倍(导线的电阻不能忽略)?[ ](A) 把线圈的匝数增加到原来的两倍。
习题11―1图t εO(A)tεO(B)tεO(C)tεO(D)abc d M NB ρ 习题11―2图(B) 把线圈的面积增加到原来的两倍,而形状不变。
大学物理——11-1磁感应强度B

电源电动势的方向:电源内部电势升高的方向; 或在电源内部从负极指向正极。
§11.1磁场 磁感应强度
一、基本磁现象
永磁体的性质:
(1)具有磁性,能吸引铁、 钴、镍等物质。 (2)具有磁极,分磁北极N和磁南极S。 (3)磁极之间存在相互作用,同性相斥,异性相吸。 (4)磁极不能单独存在。
司南勺
在磁极区域,磁性最强。
S
S
载流子:导体中宏观定向运动的带电粒子。
电流强度(I):单位时间内通过导体任一 横截面的电荷 。
dq I dt
3
单位:安培 1A 1 C s 1
6
1A 10 mA 10 μ A
恒定电流(直流电): 导体中通过任一截面的电流不随时间变化(I = 恒量)。 电流的方向:导体中正电荷的流向。
B
dF
dF
B
θ
Idl
三、安培力
电流元 Idl 置于磁感应强度为 B 的外磁场中时,
电流元所受的力为: 安培定律:
dF Idl B
安培定律:
一段电流元Idl在磁场中所受的力dF,其大小与电 流元Idl成正比,与电流元所在处的磁感应强度B成正 比,与电流元Idl和B的夹角的正弦成正比,即
dS
n
dI 大小: j j 速度方向上的单位矢量 d S d 对任意小面元 d S , I j d S j d S dS 对任意 dI I j d S j S 曲面S:
d S
P 处正电荷定向移动 j
三、电源和电动势
+
第11章 恒定电流的磁场
11.1 磁感应强度 B
稳恒磁场知识点复习

第11章 稳恒磁场

z
D
无限长载流长直导线的磁场 无限长载流长直导线的磁场. 载流长直导线的磁场
θ2
v B
B=
4 π r0
(cosθ 1 − cosθ 2 )
B=
I
o
µ0 I
2 π r0
θ1 → 0 θ2 → π
x
C
θ1
P y
无限长载流长直导线的磁场
B=
µ0I
2πr
I B
I
X
B
电流与磁感应 电流与磁感应强度成右螺旋关系 半无限长载流长直导线的磁场
=
I
2π R
v B
o
l
R
v v ∫ B ⋅ dl =
l
∫ 2πR
µ0 I
v dl
dl
v v µ0 I ∫l B ⋅ d l = 2 π R ∫l d l v v 设闭合回路 l 为圆形 ∫l B ⋅ dl = µ0 I 回路( 成右螺旋) 回路( l 与 I 成右螺旋)
I
o
v B
R
若回路绕向为顺时针时, 若回路绕向为顺时针时,则
z
带电粒子在磁场中沿其他方向运动时 F 垂直于 v 与特定直线所组成的平面 与特定直线所组成的平面. 当带电粒子在磁场中垂直于此特定直线运动 时受力最大. 时受力最大
F = Fmax = F⊥
Fmax ∝ qv
Fmax q , v 无关 qv 大小与
磁感应 的定义: 磁感应强度 B 的定义:当 正电荷垂直于 特定直线运动 时,受力 Fmax 将 Fmax ×v 方向 的方向. 定义为该点的 B 的方向
I I I
I S S N I N
磁通量 磁场的高斯定理
v ∆S B
大学物理学下册答案第11章-大学物理11章答案
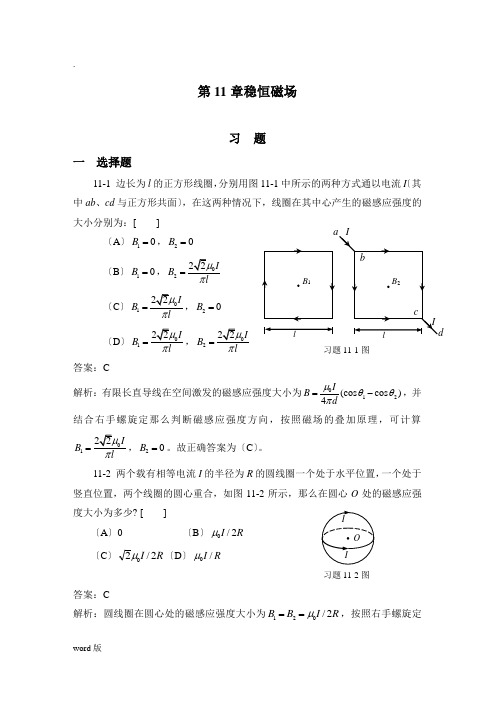
第11章稳恒磁场习 题一 选择题11-1 边长为l 的正方形线圈,分别用图11-1中所示的两种方式通以电流I 〔其中ab 、cd 与正方形共面〕,在这两种情况下,线圈在其中心产生的磁感应强度的大小分别为:[ ]〔A 〕10B =,20B = 〔B 〕10B =,02IB lπ= 〔C〕01IB lπ=,20B = 〔D〕01I B l π=,02IB lπ=答案:C解析:有限长直导线在空间激发的磁感应强度大小为012(cos cos )4IB dμθθπ=-,并结合右手螺旋定那么判断磁感应强度方向,按照磁场的叠加原理,可计算01IB lπ=,20B =。
故正确答案为〔C 〕。
11-2 两个载有相等电流I 的半径为R 的圆线圈一个处于水平位置,一个处于竖直位置,两个线圈的圆心重合,如图11-2所示,那么在圆心O 处的磁感应强度大小为多少? [ ]〔A 〕0 〔B 〕R I 2/0μ〔C 〕R I 2/20μ〔D 〕R I /0μ 答案:C解析:圆线圈在圆心处的磁感应强度大小为120/2B B I R μ==,按照右手螺旋定习题11-1图习题11-2图那么判断知1B 和2B 的方向相互垂直,依照磁场的矢量叠加原理,计算可得圆心O处的磁感应强度大小为0/2B I R =。
11-3 如图11-3所示,在均匀磁场B 中,有一个半径为R 的半球面S ,S 边线所在平面的单位法线矢量n 与磁感应强度B 的夹角为α,那么通过该半球面的磁通量的大小为[ ]〔A 〕B R 2π〔B 〕B R 22π〔C 〕2cos R B πα〔D 〕2sin R B πα 答案:C解析:通过半球面的磁感应线线必通过底面,因此2cos m B S R B παΦ=⋅=。
故正确答案为〔C 〕。
11-4 如图11-4所示,在无限长载流直导线附近作一球形闭合曲面S ,当曲面S 向长直导线靠近时,穿过曲面S 的磁通量ΦB 将如何变化?[]〔A 〕Φ增大,B 也增大〔B 〕Φ不变,B 也不变 〔C 〕Φ增大,B 不变〔D 〕Φ不变,B 增大 答案:D解析:根据磁场的高斯定理0SBdS Φ==⎰,通过闭合曲面S 的磁感应强度始终为0,保持不变。
第十一章真空中的恒定磁场(1)讲述

(3)当带电粒子沿与上述
特定方向垂直的方向运动时所
即: Fmax qv 受到的磁力最大(记为Fm ),
并且Fm与q v的比值是与q、v
Fmax qv
无关的确定值。
大小与 q,无v关
第十一章 真空中的恒定磁场
定
磁感应强度
B
:
反映空间某点的磁场大小和方向
义 大小: B Fmax qv
方向:小磁针平衡时N 极 的指向
第十一章 真空中的恒定磁场
例1 长直电流的磁场.
dB 方向均垂
直指向里
q2
Idl q r
Il
od
q1
解
dB
0
4π
Idl sinq
r2
B
dB
0I
4π
dl sinq
r2
l d cotq, r d / sinq
*P dB
dl d dq / sin2 q
B 0I q2 sinq dq 4 π d q1
第十一章 真空中的恒定磁场
第十一章 真空中的恒定磁场
静电荷 静电场
运动电荷 电场 磁场
稳恒电流 稳恒磁场
学习方法: 类比法
第十一章 真空中的恒定磁场
§11-1 磁感应强度 磁场的高斯定理
一、基本磁现象 (1) 天然磁铁吸引铁、钴、镍等物质。 (2) 条形磁铁两端磁性最强,称为磁极。
一只能够在水平面内自由转动的条形磁铁,平衡时总是顺
第十一章 真空中的恒定磁场
规定:通过垂直于磁感应线方向的单位面积的 磁感应线条数等于该点磁感应强度的大小。即
B dN
dN
dS
B
dN是穿过
dS
面的磁感应线条数。
大物稳恒磁场习题

= 4×10-5×1×0.5
= 2×10-5 Wb
(2) Φ´= B . S = BS cos 300
= 4×10-5×1×
3 2
= 3.46×10-5 Wb
Φ´´= 3.46×10-5 Wb
11-2 设一均匀磁场沿x 轴正方向,其磁 感应强度值B =1 Wb/m2。求:在下列情况 下,穿过面积为2m2的平面的磁通量。
=
NA m 0IA 2RA
=
10×10×4π×10-7
2×0.2
=31.4×10-5 T
BB
=
NB m 0IB 2RA
=
20×5×4π×10-7
2×0.1
=6.28×10-5 T
B = BA2 +BB2 =7.0×10-4 T
q
=
arc
tg
Ba BB
=
26.60
11-13 电流均匀地流过宽度为 b 的无限 长平面导体薄板,电流为 I ,沿板长方向流 动。求:
在薄板平面内, 距板的一边为 b 的 P 点处的磁感应强度;
I
b .P
b
结束
解:
dI
=
I b
dx
d B= 2mπ0dxI
=
2mπ0 Ib
dx x
B=
2mπ0 Ib
2 b
b
dx x
= 2mπ0Ib ln2
I
b .P
dx x
b
11-20 有一根很长的同轴电缆,由一圆 柱形导体和一同轴圆筒状导体组成,圆柱的
2πl
×4m
R 0I
=
82
π2
第33讲:稳恒磁场——磁场的基本概念,毕奥-萨伐尔定律

第33讲:稳恒磁场——磁场的基本概念,毕奥-萨伐尔定律内容:§11-1,§11-21.基本磁现象(15分钟)2.磁场,磁感应强度(20分钟)3.毕一萨定律及其应用(60分钟)4.小结(05分钟)要求:1.了解基本磁现象;认识电与磁之间的联系;2.理解磁场的基本概念,认识磁场的物质性;3.理解磁感应强度的物理意义;4.掌握毕一萨定律的物理意义,会用该定律求解简单的磁场分布问题。
重点与难点:1.磁感应强度的定义;2.毕一萨定律及其应用。
方法:结合中学的磁学知识,定性介绍电与磁的联系,重点讲述磁场的物质性及物理意义,着重讲述毕一萨定律的物理意义,并通过例题来说明毕一萨定律的应用,介绍解题方法与思路。
作业:问题:P172:2,3,4,6习题:P176:1,3,6,8预习:§11-3,§11-44)某些本来不显磁性的物质,在接近或接触磁铁后就有了磁性,称为磁化。
qvmax 磁场电 流运动电荷磁 铁电 流运动电荷磁 铁即以单位速率运动的单位正电荷所受到的磁力。
其方向为放在该点的小磁针平a k 2rk 204r π=304r=π2004r r l Id ϖϖϖ⨯=πμ ⎰304r π (cos 40π=r 204r π=204r π⎰第33讲稳恒磁场——磁场的基本概念,毕奥-萨伐尔定律()θθπactgactgz-=-=()θθπsinsinaa=-=(0244sinsincsc4πμπμθθθπμ==⎪⎭⎫⎝⎛⎰⎰aIaIadIa2rIπμ=4rIπμ=2244rrππ===r R,303044r r π==⎰()232203022x R r +==πR 20=302x π=。
πsin 420r =⎰πsin 420r()(⎰⎰⎰=0020204cos 4cos sec 4sin 4ππβππa aa r (04π=a(1)β角的定义:a π2=(方向可用右手螺旋法则判定)aπ40=πsin 420r=2=,因而204r π=⎰r πsin 420r=⎰==r r dl r r πππ303030202244sin 4 ()2/3220=(方向可用右手螺旋法则判定)方向:沿X轴正向R2=π220⋅=R32x=32xπ=()2/3222=π32Rπ=xxe3322ππ==问题:有一长为L ,半径为R 的载流密绕螺线管,总匝数为N ,管中电流为I ,()2/32202=π ()⎰2/32202π(0022022csc 2β=--R ==22)2/(Rl +=2200)2/(2cos 2Rl +==21μ=304r rl Id ⨯=πμ 304rrv qnSdl ⨯⋅=πμ 304r rv q dN B d ⨯=πμ= 2c E v ⨯=34rrq πε= SS IIdl1911年,俄国物理学家约飞最早提供实验验证。
大学物理 恒定磁场

11-1 恒定电流电流密度磁现象:我国是世界上最早发现和应用磁现象的国家之一,早在公元前300年久发现了磁铁矿石吸引铁的现象。
在11世纪,我国已制造出航海用的指南。
在1820年之前,人们对磁现象的研究仅局限于铁磁极间的相吸和排斥,而对磁与电两种现象的研究彼此独立,毫无关联。
1820年7月丹麦物理学家奥斯特发表了《电流对磁针作用的实验》,公布了他观察到的电流对磁针的作用,从此开创了磁电统一的新时代。
奥斯特的发现立即引起了法国数学家和物理学家安培的注意,他在短短的几个星期内对电流的磁效应作出了系列研究,发现不仅电流对磁针有作用,而且两个电流之间彼此也有作用,如图所示;位于磁铁附近的载流线圈也会受到力或力矩的作用而运动。
此外,他还发现若用铜线制成一个线圈,通电时其行为类似于一块磁铁。
这使他得出这样一个结论:天然磁性的产生也是由于磁体内部有电流流动。
每个磁性物质分子内部,都自然地包含一环形电流,称为分子电流,每个分子电流相当于一个极小的磁体,称为分子磁矩。
一般物体未被磁化时,单个分子磁矩取向杂乱无章,因而对外不显磁性;而在磁性物体内部,分子磁矩的取向至少未被完全抵消,因而导致磁铁之间有“磁力”相互作用。
1820年是人们对电磁现象的研究取得重大成果的一年。
人们发现,电荷的运动是一切磁现象的根源。
一方面,运动电荷在其周围空间激发磁场;另一方面,运动电荷在空间除受电场力作用之外,还受磁场力作用。
电磁现象是一个统一的整体,电学和磁学不再是两个分立的学科。
11-1 恒定电流电流密度如前所述,电荷的运动是一切磁现象的根源。
电荷的定向运动形成电流,称为传导电流;若电荷或宏观带电物体在空间作机械运动,形成的电流称为运流电流。
常见的电流是沿着一根导线流动的电流,其强弱用电流强度来描述,它等于单位时间通过某一截面的电量,方向与正电荷流动的方向相同,其数学表达式为dtdq I ,虽然我们规定了电流强度的方向,但电流强度I 是标量而不是矢量,因为电流的叠加服从代数加减法则,而不服从矢量叠加的平行四边形法则。
电磁感应一章习题答案

电磁感应一章习题答案习题11—1如图,矩形区域为均匀稳恒磁场,半圆形闭合导线回路在纸面内绕轴O 作逆时针方向匀角速度旋转,O 点是圆心且恰好落在磁场的边缘上,半圆形闭合导线完全在磁场外时开始计时。
图(A)——(D)的ε—t 函数图象中哪一条属于半圆形闭合导线回路中产生的感应电动势?[]解:本题可以通过定性分析进行选择。
依题设,半圆形闭合导线回路作匀角速度旋转,因此回路内的磁通量变化率的大小是一个常量,但是其每转动半周电动势的方向改变一次。
另一方面,若规定回路绕行的正方向为顺时针的,则通过回路所围面积的磁通量0>Φ,当转角从0到π时,0>Φdt d ,由法拉第电磁感应定律,0<ε;当转角从π到π2时,0<Φdt d ,由法拉第电磁感应定律,0>ε,如此重复变化……。
因此,应该选择答案(A)。
习题11—2如图所示,M 、N 为水平面内两根平行金属导轨,ab 与cd 为垂直于导轨并可在其上自由滑动的两根直裸导线。
外磁场垂直水平面向上,当外力使ab 向右平移时,cd [](A)不动。
(B)转动。
(C)向左移动。
(D)向右移动。
解:ab 向右平移时,由动生电动势公式可以判断出ab 中的电动势的方向是b →a →c →d →b ,因而在cd 中产生的电流方向是c →d ,由安培力公式容易判断出cd 将受到向右的磁场力的作用,因此,cd 也将向右移动。
所以应选择答案(D)。
习题11—3一闭合正方形线圈放在均匀磁场中,绕通过其中心且与一边平行的转轴O O '转动,转轴与磁场方向垂直,转动角速度为ω,如图所示。
用下述哪一种方法可以使线圈中感应电流的幅值增加到原来的两倍(导线的电阻不能忽略)?[](A)把线圈的匝数增加到原来的两倍。
OωBCD 习题11―1图tεO(A)tεO(B)tεO(C)tεO(D)ab c d M NB习题11―2图(B)把线圈的面积增加到原来的两倍,而形状不变。
稳恒磁场11如图11所示两根长直导线互相平行地放置

第十一章 稳恒磁场11-1 如图11-1 所示,两根长直导线互相平行地放置,导线中的电流大小相等,均为A I 10=方向相同,求图中M 、N 两点的磁感应强度B 的大小和方向(图中m r 020.00=)。
解:两导线在M 、N 点产生的磁感应强度如图11-1(a )所示。
在M 点,1B 和2B 大小相等方向相反,由场强叠加原理可知0B B B 21m =-=在N 点,两导线产生的磁感应强度大小为:002122''r IB B πμ==且21''B B ⊥,由场强叠加原理可得T r IB B N 4001100.12'2-⨯===πμ,方向水平向左。
11-2 已知地球北极磁场强度为B 的大小为T 5100.6-⨯。
如果想此地磁场是由地球赤道上一圆电流所激发的,此电流大小为多少?流向如何?解:设所求电流为I ,方向如图所示,因为圆形电流在距轴体上的磁感应强度为:232220)(2x R IR B +=μ对于北极点,R x =于是有:RIR R IR B 24)(20232220μμ=+=赤道上的电流强度为:A RBI 901073.124-⨯==μ11-3 如图11-3所示,有两根导线沿半径方向接触铁环的a 、b 两点,并与很远处的电源图11-1图11-2相接。
求环心O 的磁感应强度。
解:设圆环以acb 弧长1l ,其电流为1I ,而adb 弧长为2l ,电流为2I 。
因这两段弧可形成并联电路所以两端电压相等,于是有:2211R I R I =考虑环的截面积和电阻率是一样的,电阻与弧长成正比,所以上式改写为:2211L I L I =1l 弧:一电流在O 点产生的磁感应强度为:dl RI dB 21014πμ=,方向垂直纸面向里。
整个弧在O 点产生的磁感应强度为:210021011441R I dl R I dB B l πμπμ===⎰⎰,方向垂直纸面向里。
第十一章稳恒磁场

式的中 单K位为有比关例。系数,其值与介质的种dB类和选用
14
在国际单位制中, μ0称为真空磁导率,
K
0
0
4
/ 4P
10r7 Tθ
mId lA
I
1
故有:
dB的方向用右手螺旋法则确定:
右手弯曲的四指由Idl的方
向沿小于180°的θ角转向 r的方向,则伸直拇指的指 向就是dB 的方向。
5
一、磁感应强度
为了描述磁场中各点的磁场强弱和方向,引入磁 感应强度。用B表示,
定义
B Fm q0v
单位:特斯拉(T)。
比值B是一个与运动电荷的性质无关、仅与该点 磁场的性质有关的常量。
B为矢量,其方向用右手螺旋法则确定:
6
特斯拉
右手螺旋法则:
将右手拇指与其余四指垂直,先将四指的指向与 7 Fm方向相同,再使其向的v方向弯曲,这时拇指
大多数生物大分子是抗磁质,少数是顺磁质,极少呈铁磁质
43
三、超导体及其磁学特性
1、超导体 超导现象:当物质的温度下降到某一定值时, 该物质的电阻完全消失的现象称为超导现象。 超导性:物质失去电阻的性质叫超导性。 超导体:具有超导性的物质叫超导体。 超导体失去电阻的温度称为临界温度Tc, 可能成为超导体的物质是:①位于元素周期表 中部的金属元素(除一价金属、铁磁质、和抗 磁质)②许多化合物或合金。
磁感应线的特点:
I
I
通电螺线管的磁感应线
磁感应线是闭合的曲线,密集的地方磁场较
强,稀疏的地方磁场较弱。
9
1、磁通量
通过某曲面磁感应线的总数 称为通过该曲面的磁通量。
用Φ表示。
通过面积元dS的磁通量为:
11-1 稳恒磁场

一. 早期的磁现象
第十一章 稳恒磁场
天然磁石具有吸引铁, 天然磁石具有吸引铁,钴,镍的性质,称为磁性。而具有磁 镍的性质,称为磁性。 的物体称为磁体。 性 的物体称为磁体。 磁铁的两端磁性特别集中,磁性集中的区域称为磁极 磁铁的两端磁性特别集中 磁性集中的区域称为磁极 不可能把南,北 两极分开,单个磁极不存在 单个磁极不存在. 不可能把南 北 两极分开 单个磁极不存在 磁极之间有相互作用力,同性磁极互相排斥 同性磁极互相排斥,异性磁极互相吸引 磁极之间有相互作用力 同性磁极互相排斥 异性磁极互相吸引
F = Fmax = F⊥
Fmax ∝ qv
Fmax 大小与 q , v 无关 qv
11 – 1 磁场 磁感强度
第十一章 稳恒磁场 的定义: 磁感强度 B 的定义:当 正电荷垂直于零力 线运动 时,受力 Fmax ,将Fmax × v 方 将 向定义为该点的 磁感强度大小 的方向. B 的方向 Fmax B= qv
安培分子电流假说:一切磁现象都起源于电流,一切物 安培分子电流假说 一切磁现象都起源于电流 一切物
质的磁性都起源于构成物质的分子中存在的环形电流. 质的磁性都起源于构成物质的分子中存在的环形电流
电流 运动电荷
磁场 磁场
电流 运动电荷
11 – 1 磁场 磁感强度
磁感强度
第十一章 稳恒磁场
B的定义
带电粒子在磁场中运 动所受的力与运动方向有 关. 实验发现带电粒子在磁 场中沿某一特定直线方向运 动时不受力,此直线方向与 动时不受力, 电荷无关,由磁场自身的属性 电荷无关 由磁场自身的属性 决定,称为零力线 称为零力线--决定 称为零力线 B的方向
Fmax
稳恒磁场

Φ m = ∫∫ B ⋅ dS
S
孙秋华
Harbin Engineering University
3. 安培力(磁场对载流导线的作用力) 安培力(
F = ∫ Idl × B
4. 洛仑兹力(磁场对运动电荷的作用力) 洛仑兹力(
f = qv × B
5. 磁力矩(匀强磁场对载流线圈的作用力矩) 磁力矩(
M = Pm × B
6. 磁化强度(描述磁介质磁化强弱及方向的物理量) 磁化强度(
孙秋华
∑ Pm 顺磁质:M = ∆V 抗磁质:M = ∑ ∆Pm ∆V
Harbin Engineering University
二、基本定理和定律: 基本定理和定律: 1. 高斯定理: B ⋅ dS = 0 ∫∫
4、标出微元受到磁力矩的方向 标出微元受到磁力矩的方向 磁力矩 5、求出载流受到的磁力矩 求出载流受到的磁力矩
M=
孙秋华
ω
dpm dr r
∫0
R
1 Bπkωr 4 dr = BπkωR 5 5
M
B
Harbin Engineering University
6.已知空气中有一半径为 的无限长直圆柱金属导体,在圆 已知空气中有一半径为r的无限长直圆柱金属导体 已知空气中有一半径为 的无限长直圆柱金属导体, 柱体内挖一个直径为r/2的圆柱空洞 空洞侧面与oo'相切 的圆柱空洞, 相切, 柱体内挖一个直径为 的圆柱空洞 , 空洞侧面与 相切, 在未挖洞部分通以均匀电流I,方向沿oo'向下 向下, 在未挖洞部分通以均匀电流 ,方向沿 向下,求:有一 电子沿(如图所示)方向,以速率v运动到 运动到P点时所受的磁 电子沿(如图所示)方向,以速率 运动到 点时所受的磁 场力。 场力。 o
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第十一章 稳恒磁场 1、永磁体(四氧化三铁)的性质和相互作用 、永磁体(四氧化三铁)
)、南极 (1)分北极(N)、南极(S) )分北极( )、南极( ) (2)能吸铁、钴等 )能吸铁、 (3)磁铁之间同极相斥、异极相吸 )磁铁之间同极相斥、 2、实验:让两根直导线通有同向电流, 、实验:让两根直导线通有同向电流, 实验结果:是通有同向电流的两根直导线,( ,(向 实验结果:是通有同向电流的两根直导线,(向 内弯曲)即相互吸引。 内弯曲)即相互吸引。 问题:为什么通有同向电流的 问题: 两根直导线, 两根直导线,会相互吸引? 原因:电流(运动电荷)在其周 电流(运动电荷) 围激发一种物质、 围激发一种物质、它象磁铁一 样对磁针或运动电荷有作用力。 样对磁针或运动电荷有作用力。
v v v F = qv × B
0
←θ = 0
பைடு நூலகம்
Fmax ← θ = π 2
Fmax ∝ qv
Fmax v 的定义: 、 磁感强度 B 的定义: 1、磁感强度大小 B = qv
Fmax = 常数 (大小与 qv
q, v无关) 无关)
11 – 1 磁场 磁感强度
第十一章 稳恒磁场
v 2、 磁感强度 B 的方向:当 的方向: 、
正电荷垂直于 正电荷垂直于 特定直线运动
v v v Fmax ,将 Fmax × v 时,受力 v
也是放在该点的磁针 极 也是放在该点的磁针N极 该点的磁针 的方向
方向定义为该点的 的方向. 方向定义为该点的 B 的方向 定义
v Fmax
3、单位:特斯拉 、单位:
+
v v
q
v B
1(T ) = 1N/A ⋅ m
11 – 1 磁场 磁感强度
第十一章 稳恒磁场
洛伦兹力——运动电荷在磁场中受磁场力 运动电荷在磁场中受磁场力 洛伦兹力
F电
I
I
11 – 1 磁场 磁感强度
一 磁场 运动电荷 二 磁场
第十一章 稳恒磁场
运动电荷
v 磁感强度 B 的定义
y
v v v v
o
v F =0
+
v v v v
x
带电粒子在磁场中运 动所受的力与运动方向有 关. 实验发现带电粒子在 磁场中沿某一特定直线方 向(X)运动时不受力, )运动时不受力, 此直线方向与电荷无关. 此直线方向与电荷无关
z
11 – 1 磁场 磁感强度
第十一章 稳恒磁场 带电粒子在磁场中沿 v 其他方向运动时 , 总 F v 垂直于 是垂直于 v 与特定直线 所组成的平面. 所组成的平面 当带电粒子在磁场中 垂直于此特定直线( ) 垂直于此特定直线(X) 运动时受力最大. 运动时受力最大
v v v F = F⊥ = Fmax
