2012全国各地中考数学解析汇编--第40章 动态型问题A(已排版)
全国各地2012年中考数学试题解析40;159套63专题41;专题59_新定义和跨学科问题

2012年全国中考数学试卷分类解读汇编(159套63专题)专题59:新定义和跨学科问题一、选择题1. (2012浙江丽水、金华3分)如图是一台球桌面示意图,图中小正方形地边长均相等,黑球放在如图所示地位置,经白球撞击后沿箭头方向运动,经桌边反弹最后进入球洞地序号是【】A.①B.②C.⑤D.⑥【答案】 A.【考点】生活中地轴对称现象.【分析】如图,根据入射线与水平线地夹角等于反射线与水平线地夹角,可求最后落入①球洞.故A.2. (2012福建漳州4分)在公式I=UR中,当电压U一定时,电流I与电阻R之间地函数关系可用图象大致表示为【】A. B.C.D.【答案】D.【考点】跨学科问题,反比例函数地图象.【分析】∵在公式I=UR中,当电压U一定时,电流I与电阻R之间地函数关系不反比例函数关系,且R为正数,∴选项D正确.故选D.3. (2012湖北随州4分)定义:平面内地直线l1与l2相交于点O,对于该平面内任意一点M,点M到直线l1、l2地距离分别为a、b,则称有序非实数对(a,b)是点M地“距离坐标”,根据上述定义,距离坐标为(2,3)地点地个数是【】A.2B.1C. 4D.3【答案】C.【考点】新定义,点地坐标,点到直线地距离.【分析】画出两条相交直线,到l1地距离为2地直线有2条,到l2地距离为3地直线有2条,看所画地这些直线地交点有几个即为所求地点地个数:如图所示,所求地点有4个.故选C.4. (2012湖南长沙3分)某闭合电路中,电源地电压为定值,电流I(A)与电阻R(Ω)成反比例.图表示地是该电路中电流I与电阻R之间函数关系地图象,则用电阻R表示电流I地函数解读式为【】A.2I=RB.3I=RC.6I=RD.6I=R【答案】C.【考点】跨学科问题,待定系数法,曲线上点地坐标与方程地关系.【分析】设kI=R,那么点(3,2)满足这个函数解读式,∴k=3×2=6.∴6I=R.故选C.5. (2012湖南益阳4分)在一个标准大气压下,能反映水在均匀加热过程中,水地温度(T)随加热时间(t)变化地函数图象大致是【】A.B.C.D.【答案】B.【考点】跨学科问题,函数地图象.【分析】根据在一个标准大气压下水加热到100℃后水温不会继续增加,而是保持100℃不变,据此可以得到函数地图象.故选B.6. (2012贵州六盘水3分)定义:f (a ,b )=(b ,a ),g (m ,n )=(﹣m ,﹣n ).例如f (2,3)=(3,2),g (﹣1,﹣4)=(1,4).则g 等于【 】 A . (﹣6,5) B . (﹣5,﹣6)C . (6,﹣5)D . (﹣5,6)【答案】A. 【考点】新定义.【分析】根据新定义先求出f (﹣5,6),然后根据g 地定义解答即可:∵根据定义,f (﹣5,6)=(6,﹣5), ∴g=g (6,﹣5)=(﹣6,5).故选A.7. (2012山东东营3分)根据下图所示程序计算函数值,若输入地x 地值为52,则输出地函数值为【 】A .32 B .25 C .425 D .254【答案】B.【考点】新定义,求函数值.【分析】根据所给地函数关系式所对应地自变量地取值范围,发现:当x=52时,在2≤x≤4之间,所以将x 地值代入对应地函数即可求得y 地值:112y===5x 52.故选B.8. (2012山东莱芜3分)对于非零地实数a 、b ,规定a ⊕b = 1 b - 1a .若2⊕(2x -1)=1,则x =【 】A . 5 6 B . 5 4 C . 3 2 D .- 16【答案】A.【考点】新定义,解分式方程.【分析】∵a ⊕b = 1 b - 1 a ,2⊕(2x -1)=1,∴2⊕(2x -1)=11=12x 12--. ∴()135=32x 1=26x 3=26x=5x=2x 126⇒-⇒-⇒⇒-. 检验,合适.故选A.9. (2012广西钦州3分)在平面直角坐标系中,对于平面内任意一点(x,y),若规定以下两种变换:①f(x,y)=(y,x).如f(2,3)=(3,2);②g(x,y)=(﹣x,﹣y),如g(2,3)=(﹣2,﹣3).按照以上变换有:f(g(2,3))=f(﹣2,﹣3)=(﹣3,﹣2),那么g(f(﹣6,7))等于【】A.(7,6) B.(7,﹣6) C.(﹣7,6) D.(﹣7,﹣6)【答案】C.【考点】新定义,点地坐标.【分析】由题意应先进行f方式地变换,再进行g方式地变换,注意运算顺序及坐标地符号变化:∵f(﹣6,7)=(7,﹣6),∴g(f(﹣6,7))=g(7,﹣6)=(﹣7,6).故选C.10. (2012甘肃兰州4分)在物理实验课上,小明用弹簧称将铁块A悬于盛有水地水槽中,然后匀速向上提起,直至铁块完全露出水面一定高度,则下图能反映弹簧称地读数y(单位N)与铁块被提起地高度x(单位cm)之间地函数关系地大致图象是【】A. B. C. D.【答案】C.【考点】跨学科问题,函数地图象.【分析】根据浮力地知识,铁块露出水面前读数y不变,出水面后y逐渐增大,离开水面后y不变.因为小明用弹簧称将铁块A悬于盛有水地水槽中,然后匀速向上提起,直至铁块完全露出水面一定高度.故选C.二、填空题1. (2012陕西省3分)如图,从点A(0,2)发出地一束光,经x轴反射,过点B(4,3),则这束光从点A到点B所经过路径地长为▲ .2. (2012福建南平3分)设为一次函数y=ax+b(a≠0,a,b为实数)地“关联数”.若“关联数”地一次函数是正比例函数,则关于x地方程11+=1x1m-地解为▲.【答案】x=3.【考点】新定义,一次函数和正比例函数地定义,解分式方程.【分析】根据新定义得:y=x+m-2,∵“关联数”地一次函数是正比例函数,∴m﹣2=0,解得:m=2.则关于x地方程11+=1x1m-即为11+=1x12-,解得:x=3.检验:把x=3代入最简公分母2(x﹣1)=4≠0,故x=3是原分式方程地解.5. (2012湖北荆州3分)新定义:为一次函数y=ax+b(a≠0,a,b为实数)地“关联数”.若“关联数”地一次函数是正比例函数,则关于x地方程11+=1x1m-地解为▲.【答案】x=3.【考点】新定义,一次函数和正比例函数地定义,解分式方程.【分析】根据新定义得:y=x+m-2,∵“关联数”地一次函数是正比例函数,∴m﹣2=0,解得:m=2.则关于x地方程11+=1x1m-即为11+=1x12-,解得:x=3.检验:把x=3代入最简公分母2(x﹣1)=4≠0,故x=3是原分式方程地解.6. (2012湖南常德3分)规定用符号表示一个实数m地整数部分,例如:=0,=3.按此规定地值为▲ .【答案】4.【考点】新定义,估计无理数地大小.【分析】∵9<10<16,∴3445< ,.∴=4⎤⎦.7. (2012湖南株洲3分)若(x1,y1)•(x2,y2)=x1x2+y1y2,则(4,5)•(6,8)= ▲ .【答案】64.【考点】新定义,代数式求值.【分析】将(4,5)•(6,8)中地数字分别替换(x1,y1)•(x2,y2)即可解答:∵(x1,y1)•(x2,y2)=x1x2+y1y2,∴(4,5)•(6,8)=4×6+5×8=64.8. (2012四川自贡4分)如图,△ABC 是正三角形,曲线CDEF 叫做正三角形地渐开线,其中弧CD .弧DE 、弧EF 地圆心依次是A .B .C ,如果AB=1,那么曲线CDEF 地长是 ▲ .【答案】4π.【考点】新定义,等边三角形地性质,三角形外角定理,弧长地计算.【分析】弧CD 是以点A 为圆心,AB=1为半径,∠CAD=1200为圆心角地圆弧,长是12012=1803ππ⋅⋅; 弧DE 是以点B 为圆心,BD=2为半径,∠DBE=1200为圆心角地圆弧,长是:12024=1803ππ⋅⋅; 弧EF 是以点C 为圆心,CE=3为半径,∠ECF=1200为圆心角地圆弧,长是:1203=2180ππ⋅⋅.则曲线CDEF 地长是:24++2433ππππ=.9. (2012山东菏泽4分)将4个数a b c d ,,,排成2行、2列,两边各加一条竖直线记成a b cd,定义a bcdad bc =-,上述记号就叫做2阶行列式.若+11=81+1x xx x -- ,则x = ▲ .【答案】2.【考点】新定义,整式地混合运算,解一元一次方程. 【分析】根据定义化简+11=81+1x x x x -- ,得:()()22+11=8x x --,整理得:()()22+2+112+=8x x x x --,即4=8x ,解得:=2x .三、解答题1. (2012北京市8分)在平面直角坐标系xoy 中,对于任意两点P1(x1,y1)与P2(x2,y2)地“非常距离”,给出如下定义:若∣x1-x2∣≥∣y1-y2∣,则点P1与点P2地“非常距离”为∣x1-x2∣; 若∣x1-x2∣<∣y1-y2∣,则点P1与点P2地“非常距离”为∣y1-y2∣.例如:点P1(1,2),点P2(3,5),因为∣1-3∣<∣2-5∣,所以点P1与点P2地“非常距离”为∣2-5∣=3,也就是图1中线段P1Q 与线段P2Q 长度地较大值(点Q 为垂直于y 轴地直线P1Q 与垂直于x 轴地直线P2Q 地交点).(1)已知点A 1(0)2-,,B 为y 轴上地一个动点,①若点A 与点B 地“非常距离”为2,写出一个满足条件地点B 地坐标; ②直接写出点A 与点B 地“非常距离”地最小值;(2)已知C 是直线3y x 34=+上地一个动点,①如图2,点D 地坐标是(0,1),求点C 与点D 地“非常距离”地最小值及相应地点C 地坐标; ②如图3,E 是以原点O 为圆心,1为半径地圆上地一个动点,求点C 与点E 地“非常距离”地最 小值及相应地点E 和点C 地坐标.【答案】解:(1)①(0,-2)或(0,2).②21.(2)①设C 坐标为003x x 34⎛⎫+ ⎪⎝⎭,,如图,过点C 作CP ⊥x 轴于点P ,作CQ ⊥y 轴于点Q.由“非常距离”地定义知,当OP=DQ 时,点C 与点D 地“非常距离”最小,∴003x 0x 314-=+-. 两边平方并整理,得2007x 48x 64=0--,解得,08x 7=-或0x 8=(大于87,舍去).∴点C 与点D 地“非常距离”地最小值距离为87,此时815C 77⎛⎫- ⎪⎝⎭,. ②设直线3y x 34=+与x 轴和y 轴交于点A ,B ,过点O 作直线3y x 34=+地垂线交直线3y x 34=+于点C ,交圆于点E ,过点C 作CP ⊥x 轴于点P ,作CQ ⊥y 轴于点Q ,过点E 作EM ⊥x 轴于点M ,作EN ⊥y 轴于点N.易得,OA=4,OB=3,AB=5.由△OAB ∽△MEM ,OE=1,得OM=35,ON=45.∴34E 55⎛⎫- ⎪⎝⎭,.设C 坐标为003x x 34⎛⎫+ ⎪⎝⎭,由“非常距离”地定义知,当MP=NQ 时,点C 与点E 地“非常距离”最小, ∴00334x +x 3545=+-. 两边平方并整理,得200175x 840x 1792=0--,解得,08x 5=-或0224x 35=(大于85,舍去).∴点C 与点E 地“非常距离”地最小值距离为1,此时89C 55⎛⎫- ⎪⎝⎭,,34E 55⎛⎫- ⎪⎝⎭,.【考点】新定义,直线上点地坐标与方程地关系,直线和圆地性质,解一元二次方程,勾股定理,相似三角形地和性质.【分析】(1)根据“非常距离”地定义可直接求出.(2)①解题关键是,过C 点向x 、y 轴作垂线,当CP 和CQ 长度相等地时候“非常距离”最短,理由是,如果向下(如左图)或向上(如右图)移动C 点到达C’点,其与点D 地“非常距离”都会增大.故而C 、D 为正方形相对地两个顶点时有最小地非常距离.②同①,同时理解当OC 垂直于直线3y x 34=+时,点C 与点E 地“非常距离”最小.2. (2012陕西省10分)如果一条抛物线()2y=ax +bx+c a 0≠与x 轴有两个交点,那么以该抛物线地顶点和这两个交点为顶点地三角形称为这条抛物线地“抛物线三角形”.(1)“抛物线三角形”一定是 三角形;(2)若抛物线2y=x +bx(b>0)-地“抛物线三角形”是等腰直角三角形,求b 地值;(3)如图,△OAB 是抛物线2y=x +b'x(b'>0)-地“抛物线三角形”,是否存在以原点O 为对称中心地矩形ABCD ?若存在,求出过O 、C 、D 三点地抛物线地表达式;若不存在,说明理由.【答案】解:(1)等腰.(2)∵抛物线2y=x +bx(b>0)-地“抛物线三角形”是等腰直角三角形,∴该抛物线地顶点2b b 24⎛⎫ ⎪⎝⎭,满足2b b =24(b >0).∴b=2. (3)存在.如图,作△OCD 与△OAB 关于原点O 中心对称, 则四边形ABCD 为平行四边形.当OA=OB 时,平行四边形ABCD 为矩形. 又∵AO=AB , ∴△OAB 为等边三角形. 作AE ⊥OB ,垂足为E ,∴AE =,即()2b'b'b'>042,∴∴)()()()A3B 0C 3D 0-,,,.设过点O 、C 、D 三点地抛物线2y=mx +nx ,则12m 3m 3⎧-⎪⎨--⎪⎩,解得,m=1⎧⎪⎨⎪⎩∴所求抛物线地表达式为2y=x .【考点】二次函数综合题,新定义,待定系数法,曲线上点地坐标与方程地关系,中心对称地性质,矩形地判定和性质,等边三角形地判定和性质.【分析】(1)抛物线地顶点必在抛物线与x 轴两交点连线地垂直平分线上,因此这个“抛物线三角形”一定是等腰三角形.(2)观察抛物线地解读式,它地开口向下且经过原点,由于b >0,那么其顶点在第一象限,而这个“抛物线三角形”是等腰直角三角形,必须满足顶点坐标地横、纵坐标相等,以此作为等量关系来列方程解出b 地值.(3)由于矩形地对角线相等且互相平分,所以若存在以原点O 为对称中心地矩形ABCD ,那么必须满足OA=OB ,结合(1)地结论,这个“抛物线三角形”必须是等边三角形,首先用b′表示出AE 、OE 地长,通过△OAB 这个等边三角形来列等量关系求出b′地值,进而确定A 、B 地坐标,即可确定C 、D 地坐标,利用待定系数即可求出过O 、C 、D 地抛物线地解读式.3. (2012浙江嘉兴、舟山12分)将△ABC 绕点A 按逆时针方向旋转θ度,并使各边长变为原来地n 倍,得△AB ′C ′,即如图①,我们将这种变换记为.(1)如图①,对△ABC 作变换得△AB ′C ′,则S △AB ′C ′:S △ABC= ;直线BC 与直线B ′C ′所夹地锐角为 度;(2)如图②,△ABC 中,∠BAC=30°,∠ACB=90°,对△ABC 作变换得△AB'C',使点B 、C 、C ′在同一直线上,且四边形ABB'C'为矩形,求θ和n 地值;(4)如图③,△ABC 中,AB=AC ,∠BAC=36°,BC=l ,对△ABC 作变换得△AB ′C ′,使点B 、C 、B ′在同一直线上,且四边形ABB'C'为平行四边形,求θ和n 地值.【答案】解:(1) 3;60.(2)∵四边形 ABB ′C ′是矩形,∴∠BAC ′=90°.∴θ=∠CAC ′=∠BAC ′﹣∠BAC=90°﹣30°=60°.在 Rt △AB B' 中,∠ABB'=90°,∠BAB ′=60°,∴∠AB ′B=30°.∴AB ′=2 AB ,即AB n==2AB'. (3)∵四边形ABB ′C ′是平行四边形,∴AC ′∥BB ′.又∵∠BAC=36°,∴θ=∠CAC ′=∠ACB=72°.∴∠C ′AB ′=∠BAC=36°.而∠B=∠B ,∴△ABC ∽△B ′BA.∴AB :BB ′=CB :AB.∴AB2=CB •BB ′=CB (BC+CB ′).而 CB ′=AC=AB=B ′C ′,BC=1,∴AB2=1(1+AB ),解得,AB =.∵AB >0,∴B C n=BC ''. 【考点】新定义,旋转地性质,矩形地性质,含300角直角三角形地性质,平行四边形地性质,相似三角形地判定和性质,公式法解一元二次方,.【分析】(1)根据题意得:△ABC ∽△AB ′C ′,∴S △AB ′C ′:S △ABC=22AB =3AB '⎛⎫= ⎪⎝⎭,∠B=∠B ′.∵∠ANB=∠B ′NM ,∴∠BMB ′=∠BAB ′=60°.(2)由四边形 ABB ′C ′是矩形,可得∠BAC ′=90°,然后由θ=∠CAC ′=∠BAC ′-∠BAC ,即可求得θ地度数,又由含30°角地直角三角形地性质,即可求得n 地值.(3)由四边形ABB ′C ′是平行四边形,易求得θ=∠CAC ′=∠ACB=72°,又由△ABC ∽△B ′BA ,根据相似三角形地对应边成比例,易得AB2=CB •BB ′=CB (BC+CB ′),继而求得答案.4. (2012浙江台州14分)定义:P 、Q 分别是两条线段a 和b 上任意一点,线段PQ 长度地最小值叫做线段与线段地距离.已知O(0,0),A(4,0),B(m ,n),C(m+4,n)是平面直角系中四点.(1)根据上述定义,当m=2,n=2时,如图1,线段BC 与线段OA 地距离是_____,当m=5,n=2时,如图2,线段BC 与线段OA 地距离(即线段AB 地长)为______(2)如图3,若点B 落在圆心为A ,半径为2地圆上,线段BC 与线段OA 地距离记为d ,求d 关于m 地函数解读式.(3)当m 地值变化时,动线段BC 与线段OA 地距离始终为2,线段BC 地中点为M.①求出点M 随线段BC 运动所围成地封闭图形地周长。
全国各地2012年中考数学分类解析40;159套63专题41;_专题7_一元一次方程

2012年全国中考数学试卷分类解读汇编(159套63专题)
专题7: —元一次方程
一、选择题
1.⑶口重庆市4分)已知关于兀的方程2卄"40的解是“ 2,贝上的值为【】
此 2 3 C* 4 D・ 5
K答案】6
【苦点】一元一次方程閒解.
【分析】丁方程2x + a-9二0的解是忑=2,「二勺卡曲-9=0i解得a=5^故选
->
1. C 2012上海市4分)方程辰1=2的根是 A .
【答案】K=3.
1考点】解无理方程.
•分析】两边平育后■去根号化为整式方程,解育程即可】扳刁€ =>梵+1=4 =>沪又经检验畫勻是庾方程的根•
2. (2012福建漳州4分)方程2x —4=0地解是▲.
【答案】x=2.
【考点】解一元一次方程•
【分析】根据一元一次方程地解法,移项,系数化为1即可得解:
移项得,2x=4,系数化为1得,x=2.
3. (2012福建泉州5分)方程x —5=0地解是▲.
【答案】x=5.
【考点】解一元一次方程•
【分析】根据一元一次方程地解法直接求解即可
4. (2012湖南郴州3分)一元一次方程3x —6=0地解是▲.
【答案】x=2.
【考点】解一元一次方程•
【分析】根据一元一次方程地解法,移项,系数化为1即可得解:移项得,3x=6,系数化为1得,x=2.。
(整理)全国各地中考数学压轴题专集答案动态综合型问题

2012年全国各地中考数学压轴题专集答案十、动态综合型问题1.(北京模拟)已知抛物线y =-x2+2x +m -2与y 轴交于点A (0,2m -7),与直线y =2x 交于点B 、C (B 在C 的右侧).(1)求抛物线的解析式;(2)设抛物线的顶点为E ,在抛物线的对称轴上是否存在一点F ,使得∠BFE =∠CFE ,若存在,求出点F 的坐标,若不存在,说明理由;(3)动点P 、Q 同时从原点出发,分别以每秒5个单位长度、每秒25个单位长度的速度沿射线OC 运动,以PQ 为斜边在直线BC 的上方作直角三角形PMQ (直角边分别平行于坐标轴),设运动时间为t 秒.若△PMQ 与抛物线y =-x2+2x +m -2有公共点,求t 的取值范围.解:(1)把点A (0,2m -7)代入y =-x2+2x +m -2,得m =5∴抛物线的解析式为y =-x2+2x +3(2)由⎩⎪⎨⎪⎧y =-x2+2x +3y =2x 解得⎩⎨⎧x 1=3y 1=23 ⎩⎨⎧x 2=-3y 2=-23∴B (3,23),C (-3,-23)∵y =-x2+2x +3=-(x -1)2+4 ∴抛物线的对称轴为x =1 设F (1,y )∵∠BFE =∠CFE ,∴tan ∠BFE =tan ∠CFE当点F 在点B 上方时,3-1 y -23 =3+1y +23解得y =6,∴F (1,6)当点F 在点B 下方时,3-1 23-y =3+1-y -23解得y =6(舍去)∴满足条件的点F 的坐标是F (1,6)(3)由题意,OP=5t ,OQ =25t ,∴PQ=5t ∵P 、Q 在直线直线y =2x 上 ∴设P (x ,2x ),则Q (2x ,4x )(x<0)∴x 2+4x 2=5t ,∴x =-t∴P (-t ,-2t ),Q (-2t ,-4t ) ∴M (-2t ,-2t )当M (-2t ,-2t )在抛物线上时,有-2t =-4t2-4t +3解得t =13-14(舍去负值)当P (-t ,-2t )在抛物线上时,有-2t =-t2-2t +3 解得t =3(舍去负值)∴t 的取值范围是:13-14≤t≤ 32.(北京模拟)在平面直角坐标系中,抛物线y 1=ax2+3x +c 经过原点及点A (1,2),与x 轴相交于另一点B .(1)求抛物线y 1的解析式及B 点坐标; (2)若将抛物线y 1以x =3为对称轴向右翻折后,得到一条新的抛物线y 2,已知抛物线y 2与x 轴交于两点,其中右边的交点为C 点.动点P 从O 点出发,沿线段OC 向C 点运动,过P 点作x 轴的垂线,交直线OA 于D 点,以PD 为边在PD 的右侧作正方形PDEF . ①当点E 落在抛物线y 1上时,求OP 的长;②若点P 的运动速度为每秒1个单位长度,同时线段OC 上另一点Q 从C 点出发向O 点运动,速度为每秒2个单位长度,当Q 点到达O 点时P 、Q 两点停止运动.过Q 点作x 轴的垂线,与直线AC 交于G 点,以QG 为边在QG 的左侧作正方形QGMN .当这两个正方形分别有一条边恰好落在同一条直线上时,求t 的值.(正方形在x 轴上的边除外)解:(1)∵抛物线y 1=ax2+3x +c 经过原点及点A (1,2)∴⎩⎪⎨⎪⎧c =2a +3+c =2 解得⎩⎪⎨⎪⎧a =-1c =0 ∴抛物线y 1的解析式为y 1=-x2+3x令y 1=0,得-x2+3x =0,解得x 1=0,x 2=3 ∴B (3,0)(2)①由题意,可得C (6,0) 过A 作AH ⊥x 轴于H ,设OP =a可得△ODP ∽△OAH ,∴DPOP=AHOH=2 ∴DP =2OP =2a∵正方形PDEF ,∴E (3a ,2a ) ∵E (3a ,2a )在抛物线y 1=-x2+3x 上∴2a =-9a2+9a ,解得a 1=0(舍去),a 2=7 9∴OP 的长为79②设直线AC 的解析式为y =kx +b∴⎩⎪⎨⎪⎧2=k +b 0=6k +b 解得k =-2 5 ,b =12 5∴直线AC 的解析式为y =-2 5 x +125由题意,OP =t ,PF =2t ,QC =2t ,GQ =45t 当EF 与MN 重合时,则OF +CN =6 ∴3t +2t +45t =6,∴t =3029当EF 与GQ 重合时,则OF +QC =6 ∴3t +2t =6,∴t =65当DP 与MN 重合时,则OP +CN =6 ∴t +2t +4 5 t =6,∴t =3019当DP 与GQ 重合时,则OP +CQ =6∴t +2t =6,∴t =23.(北京模拟)如图,在平面直角坐标系中,抛物线y =ax2+bx +4经过A (-3,0)、B (4,0)两点,且与y 轴交于点C ,点D 在x 轴的负半轴上,且BD =BC .动点P 从点A 出发,沿线段AB 以每秒1个单位长度的速度向点B 移动,同时动点Q 从点C 出发,沿线段CA 以某一速度向点A 移动. (1)求该抛物线的解析式;(2)若经过t 秒的移动,线段PQ 被CD 垂直平分,求此时t 的值; (3)该抛物线的对称轴上是否存在一点M ,使MQ +MA 的值最小?若存在,求出点M 的坐标;若不存在,请说明理由.解:(1)∵抛物线y =ax2+bx +4经过A (-3,0)、B (4,0)两点∴⎩⎪⎨⎪⎧9a -3b +4=016a +4b +4=0解得a =-1 3 ,b =1 3∴所求抛物线的解析式为y =-1 3x2+ 13x +4(2)连接DQ ,依题意知AP =t∵抛物线y=-13x2+13x+4与y轴交于点C∴C(0,4)又A(-3,0,B(4,0)可得AC=5,BC=42,AB=7∵BD=BC,∴AD=AB-BD=7-42∵CD垂直平分PQ,∴QD=DP,∠CDQ=∠CDP ∵BD=BC,∴∠DCB=∠CDB∴∠CDQ=∠DCB,∴DQ∥BC∴△ADQ∽△ABC,∴ADAB=DQBC∴ADAB=DPBC,∴7-427=DP42解得DP=42-327,∴AP=AD+DP=177∴线段PQ被CD垂直平分时,t的值为17 7(3)设抛物线y=-13x2+13x+4的对称轴x=12与x轴交于点E由于点A、B关于对称轴x=12对称,连接BQ交对称轴于点M则MQ+MA=MQ+MB,即MQ+MA=BQ当BQ⊥AC时,BQ最小,此时∠EBM=∠ACO∴tan∠EBM=tan∠ACO=3 4∴MEBE=34,即ME4-12=34,解得ME=218∴M(12,218)∴在抛物线的对称轴上存在一点M(12,218),使得MQ+MA的值最小4.(北京模拟)如图,在Rt△ABC中,∠C=90°,AC=6,BC=8.动点P从点A出发,沿AC→CB→BA 边运动,点P在AC、CB、BA边上运动的速度分别为每秒3、4、5个单位.直线l从与AC重合的位置开始,以每秒43个单位的速度沿CB方向移动,移动过程中保持l∥AC,且分别与CB、AB边交于点E、F.点P与直线l同时出发,设运动的时间为t秒,当点P第一次回到点A时,点P和直线l同时停止运动.(1)当t=_________秒时,点P与点E重合;当t=_________秒时,点P与点F重合;(2)当点P在AC边上运动时,将△PEF绕点E逆时针旋转,使得点P的对应点P′落在EF上,点F的对应点为F′,当EF′⊥AB时,求t的值;(3)作点P关于直线EF的对称点Q,在运动过程中,若形成的四边形PEQF为菱形,求t的值;(4)在整个运动过程中,设△PEF的面积为S,直接写出S关于t的函数关系式及S的最大值.C PlEC解:(1)3;4.5提示:在Rt△ABC中,∠C=90°,AC=6,BC=8∴AB=62+82=10,∴sin B=ACAB=35,cos B=BCAB=45,tan B=ACBC=34当点P与点E重合时,点P在CB边上,CP=CE∵AC=6,点P在AC、CB边上运动的速度分别为每秒3、4个单位∴点P在AC边上运动的时间为2秒,CP=4(t-2)∵CE=43t,∴4(t-2)=43t,解得t=3当点P与点F重合时,点P在BA边上,BP=BF∵AC=6,BC=8,点P在AC、CB、BA边上运动的速度分别为每秒3、4、5个单位∴点P在AC、CB边上运动的时间共为4秒,BF=BP=5(t-4)∵CE=43t,∴BE=8-43t在Rt△BEF中,BEBF=cos B∴8-43t5(t-4)=45,解得t=4.5(2)由题意,∠PEF=∠MEN∵EF∥AC,∠C=90°,∴∠BEF=90°,∠CPE=∠PEF ∵EN⊥AB,∴∠B=∠MEN∴∠CPE=∠B,∴tan∠CPE=tan B∵tan∠CPE=CECP,tan B=ACBC=34∴CECP=34,∴CP=43CE∵AP=3t(0<t<2),CE=43t,∴CP=6-3t∴6-3t=43×43t,解得t=5443(3)连接PQ交EF于O∵P、Q关于直线EF对称,∴EF垂直平分PQ若四边形PEQF为菱形,则OE=OF=12EF①当点P在AC边上运动时易知四边形POEC为矩形,∴OE=PC∴PC=12EF∵CE=43t,∴BE=8-43t,EF=BE·tan B=34(8-43t)=6-tEBOCAPlFQEBMCAPlFNBCAlFE(P)BCAlFE(P)∴6-3t =1 2 (6-t),解得t =65②当点P 在CB 边上运动时,P 、E 、Q 三点共线,不存在四边形PEQF③当点P 在BA 边上运动时,则点P 在点B 、F 之间 ∵BE =8-43t ,∴BF = BE cos B=5 4 (8-4 3 t )=10-5 3t ∵BP =5(t -4),∴PF =BF -BP =10-53t -5(t -4)=30-203t ∵∠POF =∠BEF =90°,∴PO ∥BE ,∴∠OPF =∠B 在Rt △POF 中,OFPF=sin B ∴12(6-t)30- 20 3t= 3 5 ,解得t =30 7∴当t =65或t =307时,四边形PEQF 为菱形 (4)S =⎩⎪⎪⎨⎪⎪⎧-23t2+4t (0≤t≤2)4 3t2-12t +24(2<t≤3)-43t2+12t -24(3<t≤4)8 3t2-28t +72(4<t≤4.5)-8 3t2+28t -72(4.5<t≤6)S 的最大值为1635.(北京模拟)在等腰梯形ABCD 中,AB ∥CD ,AB =10,CD =6,AD =BC =4.点P 从点B 出发,沿线段BA 向点A 匀速运动,速度为每秒2个单位,过点P 作直线BC 的垂线PE ,垂足为E .设点P 的运动时间为t (秒).(1)∠A =___________°;(2)将△PBE 沿直线PE 翻折,得到△PB ′E ,记△PB ′E 与梯形ABCD 重叠部分的面积为S ,求S 与t 之间的函数关系式,并求出S 的最大值;(3)在整个运动过程中,是否存在以点D 、P 、B ′为顶点的三角形为直角三角形或等腰三角形?若存在,求出t 的值;若不存在,请说明理由.A CB D P EB ′A CB D 备用图EB CAPlF QO解:(1)60°(2)∵∠A =∠B =60°,PB =PB ′ ∴△PB ′B 是等边三角形∴PB =PB ′=BB ′=2t ,BE =B ′E =t ,PE =3t 当0<t≤2时S =S △PB ′E =12B ′E ·PE =1 2 t ·3t = 3 2t2 当2<t≤4时 S =S △PB ′E-S △FB ′C=32t2- 3 4 ( 2t -4 )2=- 3 2t2+43t -4 3 当4<t≤5时设PB ′、PE 分别交DC 于点G 、H ,作GK ⊥PH 于K ∵△PB ′B 是等边三角形,∴∠B ′PB =60°=∠A ∴PG ∥AD ,又DG ∥AP∴四边形APGD 是平行四边形 ∴PG =AD =4∵AB ∥CD ,∴∠GHP =∠BPH ∵∠GPH =∠BPH =12∠B ′PB =30°∴∠GHP =∠GPH =30°,∴PG =GH =4 ∴GK =12PG =2,PK =KH =PG ·cos30°=2 3 ∴PH =2PK =4 3 ∴S =S △PGH=12PH ·GK =12×43×2=4 3 综上得,S 与t 之间的函数关系式为: S =⎩⎨⎧32t2(0<t≤2)-3 2t2+43t -43(2<t≤4)43(4<t≤5)(3)①若∠DPB ′=90° ∵∠B ′PB =60°,∴∠DP A =30° 又∠A =60°,∴∠ADP =90°∴AP =2AD ,∴10-2t =8,∴t =1 若∠PDB ′=90°作DM ⊥AB 于M ,DN ⊥B ′B 于N则AM =2,DM =23,NC =3,DN =3 3 PM =|10-2-2t |=|8-2t | NB ′=|3+4-2t |=|7-2t |DP 2=DM 2+PM 2=(23 )2+( 8-2t )2=( 8-2t)2+12DB ′ 2=DN 2+NB ′=( 33 )2+( 7-2t )2=( 7-2t)2+27∵DP 2+DB ′ 2=B ′P 2∴( 8-2t )2+12+( 7-2t )2+27=( 2t)2解得t 1=15+73 2>5(舍去),t 2=15-732A C BDP EB ′ AC BDP EB ′M N若∠DB ′P =90°,则DB ′ 2+B ′P 2=DP 2∴(7-2t )2+27+( 2t )2=( 8-2t)2+12 解得t 1=-1(舍去),t 2=0(舍去)∴存在以点D 、P 、B ′为顶点的三角形为直角三角形,此时t =1或t =15-732②若DP =B ′P ,则(8-2t )2+12=( 2t)2解得t =198若B ′D =B ′P ,则(7-2t)2+27=(2t)2解得t =197若DP =DB ′,则( 8-2t )2+12=( 7-2t)2+27 解得t =0(舍去)∴存在以点D 、P 、B ′为顶点的三角形为等腰三角形,此时t =19 8或t =19 76.(北京模拟)已知二次函数y =-33mx2+3mx -2的图象与x 轴交于点A (23,0)、点B ,与y 轴交于点C .(1)求点B 坐标;(2)点P 从点C 出发以每秒1个单位的速度沿线段CO 向O 点运动,到达点O 后停止运动,过点P 作PQ ∥AC 交OA 于点Q ,将四边形PQAC 沿PQ 翻折,得到四边形PQA ′C ′,设点P 的运动时间为t . ①当t 为何值时,点A ′恰好落在二次函数y =-33mx2+3mx -2图象的对称轴上; ②设四边形PQA ′C ′落在第一象限内的图形面积为S ,求S 关于t 的函数关系式,并求出S 的最大值.解:(1)将A (23,0)代入y =-33mx2+3mx -2 得0=-33 m ×(2 3 )2+3m ×23-2,解得m =3 3∴y =-13x 2+3x -2 令y =0,得-13x 2+3x -2=0,解得:x 1=3,x 2=2 3 ∴B (3,0) (2)①由y =-13x 2+3x -2,令x =0,得y =-2 ∴C (0,-2)∵y =-1 3 x 2+3x -2=- 1 3 ( x -323)2+1 4∴二次函数图象的对称轴为直线x =323过A ′作A ′H ⊥OA 于H在Rt △AOC 中,∵OC =2,OA =2 3 ∴∠OAC =30°,∠OCA =60° ∴∠PQA =150°,∠A ′QH =60°,AQ =A ′Q =2QHACBDPEB ′ AC BDP B ′ E∵点A ′在二次函数图象的对称轴上∴⎩⎪⎨⎪⎧OQ +QH =3 23OQ +2QH =23解得QH =32∴AQ =3,CP =1 ∴t =1②分两种情况:ⅰ)当0<t≤1时,四边形PQA ′C ′ 落在第一象限内的图形为等腰三角形QA ′DDQ =A ′Q =3tA ′H =AQ ·sin60°=3t ·32=32t S =S △A ′DQ=12 ·3t ·3 2t =33 4t2 ∵当0<t≤1时,S 随t 的增大而增大 ∴当t =1时,S 有最大值334ⅱ)当1<t<2时,四边形PQA ′C ′ 落在第一象限内的图形为四边形EOQA ′ S 四边形EOQA ′=S 梯形PQA ′C ′-S △OPQ-S △PC ′E=[23-3 2 (2-t )2]- 3 2 ( 2-t )2- 3 4t2 =-534t2+43t -2 3 ∵-53 4 t2+43t -23=-53 4 (t -8 5)2+635且1<8 5 <2,∴当t =8 5 时,S 有最大值63 5∵63 5>33 4 ,∴S 的最大值是63 57.(北京模拟)已知梯形ABCD 中,AD ∥BC ,∠A =120°,E 是AB 的中点,过E 点作射线EF ∥BC ,交CD 于点G ,AB 、AD 的长恰好是方程x2-4x +a2+2a +5=0的两个相等实数根,动点P 、Q 分别从点A 、E 出发,点P 以每秒1个单位长度的速度沿AB 由A 向B 运动,点Q 以每秒2个单位长度的速度沿EF 由E 向F 运动,设点P 、Q 运动的时间为t (秒).(1)求线段AB 、AD 的长;(2)当t>1时,求△DPQ 的面积S 与时间t 之间的函数关系式;(3)是否存在△DPQ 是直角三角形的情况,如果存在,求出时间t ;如果不存在,请说明理由.解:(1)由题意,△=42-4(a2+2a +5 )=-4( a +1)2=0 ∴a =-1原方程可化为x2-4+4=0,解得∴x 1=x 2=2 ∴AB =AD =2(2)作AH ⊥BC 于H ,交EG 于O ,DK ⊥EF 于K ,PM ⊥DA 交DA 的延长线于M ∵AD ∥BC ,∠A =120°,AB =AD =2∴∠B =60°,AH = 3A BD Q CP E FG∵E 是AB 中点,且EF ∥BC ,∴AO =DK =32∵AP =t ,∴PM =32t∵t>1,∴点P 在点E 下方延长FE 交PM 于S ,设DP 与EF 交于点N则PS =32t -32∵AD ∥BC ,EF ∥BC ,∴EF ∥AD ∴ENAD=PEP A,∴EN2=t -1t∴EN =2(t -1) t ,∴QN =2t -2(t -1)t∴S =1 2 (2t -2(t -1) t)( 3 2 t - 3 2 + 32)=32 t2-3 2 t +3 2即S =32 t2-3 2 t +32(t>1) (3)由题意,AM =12t ,∴DM =2+12t ∴DP 2=DM 2+PM 2=(2+12t)2+( 3 2t )2=t2+2t +4 又DQ 2=DK 2+KQ 2=(32)2+(2t -1 2-2 )2=4t2-10t +7 PQ 2=PS 2+SQ 2=(32 t -3 2)2+(2t +t -1 2)2=7t2-4t +1 ①若∠PDQ =90°,则DP 2+DQ 2=PQ 2∴t2+2t +4+4t2-10t +7=7t2-4t +1 解得t =6-1(舍去负值)②若∠DPQ =90°,则PD 2+PQ 2=DQ 2∴t2+2t +4+7t2-4t +1=4t2-10t +7解得t =62-1(舍去负值) ③若∠DQP =90°,则DQ 2+PQ 2=PD 2∴4t2-10t +7+7t2-4t +1=t2+2t +4解得t =4±65综上所述,存在△DPQ 是直角三角形的情况,此时t =6-1,t =62-1,t =4±658.(天津模拟)如图,在平面直角坐标系中,直y =-x +42交x 轴于点A ,交y 轴于点B .在线段OA 上有一动点P ,以每秒2个单位长度的速度由点O 向点A 匀速运动,以OP 为边作正方形OPQM 交y 轴于点M ,连接QA 和QB ,并从QA 和QB 的中点C 和D 向AB 作垂线,垂足分别为点F 和点E .设P 点运动的时间为t 秒,四边形CDEF 的面积为S 1,正方形OPQM 与四边形CDEF 重叠部分的面积为S 2. (1)直接写出A 点和B 点坐标及t 的取值范围;A BD QCP E FNG S O K HM.................(2)当t=1时,求S1的值;(3)试求S2与t的函数关系式(4)直接写出在整个运动过程中,点C和点D所走过的路程之和.解:(1)A(42,0)、B(0,42),0≤t≤4(2)过Q作QH⊥AB于H∵C、D分别是QA和QB的中点∴CD∥AB,CD=12AB=12×42×2=4∵CF⊥AB,DE⊥AB,∴CF∥DE∴四边形CDEF是平行四边形又∵CF⊥AB,∴四边形CDEF是矩形∵CF⊥AB,QH⊥AB,∴CF∥QH又∵C是QA中点,∴CF=12QH连接OQ∵正方形OPQM,∴∠1=∠2,OP=PQ=QM=MO∵OA=OB,∴P A=MB∴Rt△QP A≌Rt△QMB,∴QA=QB,∠PQA=∠MQB∵QH⊥AB,∴∠3=∠4∴∠1+∠MQB+∠3=180°,∴O、Q、H三点共线∴QH=OH-OQ∵t=1,点P的运动速度为每秒2个单位长度∴OP=2,∴OQ=2又∵OA=42,∴OH=4∴QH=OH-OQ=4-2=2,∴CF=1∴S1=CD·CF=4×1=4(3)当点Q落在AB上时,OQ⊥AB,△QOA是等腰直角三角形∴t=22÷2=2当0≤t≤2时,S2=0当点E落在QM上,点F落在PQ上时,△CFK和△DEG都是等腰直角三角形过C作CT⊥PQ于T则CT=12AP=12(42-2t)=22(4-t)∴CF=2CT=4-t连接OQ,分别交AB、CD于N、R则ON=22OA=22×42=4∵OP=2t,∴OQ=2t,∴QN=2t-4∴CF =12QN =t -2 ∴4-t =t -2,∴t =3当2<t≤3时,重叠部分为等腰梯形GHIK △QGK 和△QHI 都是等腰直角三角形∵QN =2t -4,RN =CF =t -2,∴QR =t -2 ∴GK =2QR =2t -4,HI =2QN =4t -8∴S 2=1 2 (GK +HI)·RN =1 2(2t -4+4t -8)(t -2)=3(t -2)2当3<t≤4时,重叠部分为六边形GHEFIK易知Rt △CIK ≌Rt △DHG ,∴GH =KI =2CT =2(4-t)∴S 2=S 矩形CDEF-2S △CIK=CD ·CF -KI ·CT=4(t -2)-2(4-t)·22(4-t)=-t 2+12t -24 综上得S 2关于t 的函数关系式为:S 2= ⎩⎨⎧0(0≤t≤2)3( t -2 )2(2<t≤3)-t2+12t -24(3<t≤4)(4)8提示:点C 和点D 走过的路程分别为以OP 为边的正方形的对角线的一半 9.(上海模拟)如图,正方形ABCD 中,AB =5,点E 是BC 延长线上一点,CE =BC ,连接BD .动点M 从B 出发,以每秒2个单位长度的速度沿BD 向D 运动;动点N 从E 出发,以每秒2个单位长度的速度沿EB 向B 运动,两点同时出发,当其中一点到达终点后另一点也停止运动.设运动时间为t 秒,过M 作BD 的垂线MP 交BE 于P .(1)当PN =2时,求运动时间t ;(2)是否存在这样的t ,使△MPN 为等腰三角形?若存在,求出t 的值;若不存在,请说明理由; (3)设△MPN 与△BCD 重叠部分的面积为S ,直接写出S 与t 的函数关系式和函数的定义域.解:(1)∵正方形ABCD ,∴∠DBC =45°∵MP ⊥DB ,∴△BMP 是等腰直角三角形∵BM =2t ,∴BP =2BM =2t 又PN =2,NE =2t当0<t<2.5时,BP +PN +NE =BE ∴2t +2+2t =10,∴t =2当2.5<t<5时,BP -PN +NE =BE ∴2t -2+2t =10,∴t =3A B DN C P M EA BDNC P MEQH(2)过M 作MH ⊥BC 于H 则△NQC ∽△NMH ,∴QCCN=MHHN∴QC5-2t=t10-t -2t,∴QC =5t -2t 210-3t令QC =y ,则y =5t -2t 210-3t整理得2t 2-(3y +5 )t +10y =0∵t 为实数,∴[-(3y +5)]2-4×2×10y≥0即9y 2-50y +25≥0,解得y≥5(舍去)或y≤5 9∴线段QC 长度的最大值为59(3)当0<t<2.5时∵∠MPN =∠DBC +∠BMP =45°+90°=135° ∴∠MPN 为钝角,∴MN>MP ,MN>PN若PM =PN ,则2t =10-4t解得t =57(4-2)当2.5<t<5时∵∠MNP >∠MBP =∠MPB ,∴MP>MN 若MN =PN ,则∠PMN =∠MPN =45° ∴∠MNP =90°,即MN ⊥BP ∴BN =NP ,BP =2BN∴2t =2(10-2t),解得t =103若PM =PN∵PN =BP -BN =BP -(BE -NE)=BP +NE -BE∴2t =2t +2t -10,解得t =57(4+2)∴当t =5 7 (4-2),t =10 3,t =57(4+2)时,△MPN 为等腰三角形(4)S =⎩⎨⎧ 8t 3-50t 2+75t20-6t(0<t<2.5)5t - 252(2.5<t<5)10.(重庆模拟)如图,已知△ABC 是等边三角形,点O 是AC 的中点,OB =12,动点P 在线段AB 上从点A 向点B 以每秒3个单位的速度运动,设运动时间为t 秒.以点P 为顶点,作等边△PMN ,点M ,N 在直线OB 上,取OB 的中点D ,以OD 为边在△AOB 内部作如图所示的矩形ODEF ,点E 在线段AB 上. (1)求当等边△PMN 的顶点M 运动到与点O 重合时t 的值; (2)求等边△PMN 的边长(用含t 的代数式表示); (3)设等边△PMN 和矩形ODEF 重叠部分的面积为S ,请直接写出S 与t 的函数关系式及自变量t 的取值范围;AB DPC N EMAB DNC P EM AB DP C N MEADB PC N ME(4)点P 在运动过程中,是否存在点M ,使得△EFM 是等腰三角形?若存在,求出对应的t 的值;若不存在,请说明理由.解:(1)当点M 与点O 重合时∵△ABC 、△PMN 是等边三角形,O 为AC 中点 ∴∠AOP =30°,∠APO =90° ∵OB =12,∴AO =43=2AP =23t 解得t =2∴当t =2时,点M 与点O 重合(2)由题设知∠ABM =30°,AB =83,AP =3t ∴PB =83-3t ,PM =PB ·tan30°=8-t 即等边△PMN 的边长为8-t(3)S =⎩⎪⎨⎪⎧23t +63(0≤t≤1)-23t2+63t +43(1<t≤2)-32t2+103(2<t≤4)23t2-203t +503(4<t≤5)0(5<t≤8)提示:①当0≤t≤1时,PM 经过线段AF设PM 交AF 于点J ,PN 交EF 于点G ,则重叠部分为直角梯形FONG∵AP =3t ,∴AJ =23t ,JO =43-23t MO =4-2t ,ON =8-t -(4-2t)=4+t 作GH ⊥ON 于H则GH =FO =23,HN =2,FG =OH =4+t -2=2+t ∴S =S 梯形FONG=12(FG +ON)·FO=12(2+t +4+t)·23=23t +6 3 ②当1<t≤2时,PM 经过线段FO设PM 交EF 于点I ,则重叠部分为五边形IJONGFJ =AJ -AF =23t -23,FI =2t -2∴S =S 梯形FONG-S △FIJ=23t +63-12(23t -23)(2t -2)=-23t 2+63t +4 3③当2<t≤4时,PN 经过线段ED设PN 交ED 于点K ,则重叠部分为五边形IMDKGA ODC BF E 备用图AODCBF E 备用图A O D CBPFE (N )(M )A ODCBPN F ME∵AP =3t ,∴PE =43-3t ∴IG =GE =4-t ,EK =43-3t∴KD =23-(43-3t)=3t -23,DN =t -2 ∴S =S 梯形IMNG -S △KDN=1 2 (4-t +8-t)·23-12(3t -23)(t -2) =-32t 2+10 3 ④当4<t≤5时,PM 经过线段ED设PM 交ED 于点R ,则重叠部分为△RMD ∵AP =3t ,∴EP =3t -4 3 ∴ER =2EP =23t -8 3∴RD =23-(23t -83)=103-23t MD =10-2t∴S =S △RMD=12(10-2t)(103-23t)=23t 2-203t +50 3 ⑤当5<t≤8时,S =0(4)∵MN =BN =PN =8-t ,∴MB =16-2t ①若FM =EM ,则M 为OD 中点 ∴OM =3∵OM +MB =OB ,∴3+16-2t =12 ∴t =3.5②若FM =FE =6,则OM =6 2-( 23)2=2 6∵OM +MB =OB ,∴26+16-2t =12 ∴t =2+ 6③若EF =EM =6,点M 在OD 或DB 上则DM =6 2-( 23)2=2 6∴DB +DM =MB 或者DB -DM =MB∴6+26=16-2t 或6-26=16-2t ∴t =5-6或t =5+ 6综上所述,当t =3.5、2+6、5-6、5+6时,△MEF 是等腰三角形11.(浙江某校自主招生)如图,正方形OABC 的顶点O 在坐标原点,且OA 边和AB 边所在直线的解析式分别为y =34x 和y =-4 3 x + 253. (1)求正方形OABC 的边长;(2)现有动点P 、Q 分别从C 、A 同时出发,点P 沿线段CB 向终点B 运动,速度为每秒1个单位,点QA OD CBP NF ME AOD C BP NF M E A O D C B PN F M E AO D C BPN F M E沿折线A →O →C 向终点C 运动,速度为每秒k 个单位,设运动时间为2秒.当k 为何值时,将△CPQ 沿它的一边翻折,使得翻折前后的两个三角形组成的四边形为菱形? (3)若正方形以每秒53个单位的速度沿射线AO 下滑,直至顶点B 落在x 轴上时停止下滑.设正方形在x 轴下方部分的面积为S ,求S 关于滑行时间t 的函数关系式,并写出相应自变量t 的取值范围.解:(1)联立 ⎩⎨⎧y =34xy =-4 3 x +25 3解得⎩⎪⎨⎪⎧x =4y =3∴A (4,3),∴OA =4 2+32=5 ∴正方形OABC 的边长为5(2)要使△CPQ 沿它的一边翻折,翻折前后的两个三角形组成的 四边形为菱形,根据轴对称的性质,只需△CPQ 为等腰三角形即可 当t =2秒时∵点P 的速度为每秒1个单位,∴CP =2 分两种情况:①当点Q 在OA 上时,∵PQ ≥BA >PC ,∴只存在一点Q ,使QC =QP作QN ⊥CP 于N ,则CN =12CP =OQ =1∴QA =5-1=4,∴k =42=2 ②当点Q 在OC 上时,同理只存在一点Q ,使CP =CQ =2 ∴OQ +OA =10-2=8,∴k =82=4综上所述,当t =2秒时,以所得的等腰三角形CPQ 沿底边翻折, 翻折后得到菱形的k 值为2或4 (3)①当点A 运动到点O 时,t =3 当0<t≤3时,设O ′C ′ 交x 轴于点D则tan ∠DOO ′=3 4 ,即DO ′OO ′=DO ′5 3t= 3 4 ,∴DO ′= 54t∴S =1 2 DO ′·OO ′= 1 2 ·5 4 t ·5 3 t = 25 24t 2②当点C 运动到x 轴上时,t =(5×4 3)÷5 3=4当3<t≤4时,设A ′B ′ 交x 轴于点E∵A ′O =5 3 t -5,∴A ′E = 34 A ′O =5t -15 4∴S =1 2 (A ′E +O ′D )·A ′O ′=1 2 (5t -15 4+54 t )·5=50t -75 8③当点B 运动到x 轴上时,t =(5+5×4 3)÷5 3=7当4<t≤7时,设B ′C ′ 交x 轴于点F∵A ′E =5t -15 4,∴B ′E =5-5t -15 4=35-5t4∴B ′F =43 B ′E =35-5t 3∴S =52-12 ·35-5t 4·35-5t 3=-25 24 t 2+ 175 12 t -625 24综上所述,S 关于滑行时间t 的函数关系式为:S = ⎩⎪⎨⎪⎧2524t 2(0<t≤3)50t -758(3<t≤4)-25 24t2+175 12t -625 24(4<t≤7)12.(浙江某校自主招生)如图,正方形ABCD 的边长为8cm ,动点P 从点A 出发沿AB 边以1cm /秒的速度向点B 匀速移动(点P 不与点A 、B 重合),动点Q 从点B 出发沿折线BC -CD 以2cm /秒的速度匀速移动.点P 、Q 同时出发,当点P 停止时,点Q 也随之停止.连接AQ 交BD 于点E .设点P 运动时间为t (秒).(1)当点Q 在线段BC 上运动时,点P 出发多少时间后,∠BEP =∠BEQ ? (2)设△APE 的面积为S (cm 2),求S 关于t 的函数关系式,并写出t 的取值范围; (3)当4<t <8时,求△APE 的面积为S 的变化范围.解(1)AP =x cm ,BQ =2x cm∵∠BEP =∠BEQ ,BE =BE ,∠PBE =∠QBE =45° ∴△PBE ≌△QBE ,∴PB =BQ 即8-x =2x ,∴x =83∴点P 出发83秒后,∠BEP =∠BEQ (2)①当0<x≤4时,点Q 在BC 上,作EN ⊥AB 于N ,EM ⊥BC 于M ∵AD ∥BC ,∴AEEQ=ADBQ=8 2x=4xA B DEC PQ即AEEQ=4 x,∴AEAQ =4x +4∴NEBQ=AEAQ,∴NE =AE ·BQAQ =8x x +4∴S =1 2 AP ·NE = 1 2 x · 8x x +4 =4x2x +4即S =4x2x +4(0<x≤4)②当4<x<8时,点Q 在CD 上,作QF ⊥AB 于F ,交BD 于H则AEEQ=ADHQ=8 16-2x=48-x即AEEQ=4 8-x,∴AEAQ = 4 8-x +4 =412-x作EN ⊥AB 于N ,则 NEFQ=AEAQ∴NE =AE ·FQFQ=32 12-x∴S =1 2 AP ·NE = 1 2 x ·32 12-x =16x12-x即S =16x12-x(4<x<8) (3)当4<x<8时,由S =16x12-x,得x =12S16+S∵4<x<8,∴4<12S16+S<8 ∵S>0,∴16+S>0,∴4(16+S)<12S<8(16+S) 解得8<S<32 13.(浙江模拟)如图,菱形ABCD 的边长为6且∠DAB =60°,以点A 为原点、边AB 所在直线为x 轴且顶点D 在第一象限建立平面直角坐标系.动点P 从点D 出发沿折线D -C -B 向终点B 以每秒2个单位的速度运动,同时动点Q 从点A 出发沿x 轴负半轴以每秒1个单位的速度运动,当点P 到达终点时停止运动.设运动时间为t ,直线PQ 交边AD 于点E .(1)求出经过A 、D 、C 三点的抛物线解析式;(2)是否存在时刻t ,使得PQ ⊥BD ?若存在,求出t 值,若不存在,请说明理由; (3)设AE 长为y ,试求y 与t 之间的函数关系式; (4)若F 、G 为DC 边上两点,且点DF =FG =1,试在对角线DB 上找一点M 、抛物线对称轴上找一点N ,使得四边形FMNG 周长最小并求出周长最小值.A BDE CPQN M A BDE CP QNF H解:(1)由题意得:D (3,33)、C (9,33)设经过A 、D 、C 三点的抛物线解析式为y =ax2+bx 把D 、C 两点坐标代入上式,得:⎩⎨⎧9a +3b =3381a +9b =33解得:a =-3 9 ,b =433∴抛物线的解析式为:y =-39 x2+433x (2)连接AC ∵四边形ABCD 是菱形,∴AC ⊥BD 若PQ ⊥BD ,则PQ ∥AC 当点P 在DC 上时∵PC ∥AQ ,PQ ∥AC ,∴四边形PQAC 是平行四边形 ∴PC =AQ ,即6-2t =t, ∴t =2当点P 在CB 上时,PQ 与AC 相交,此时不存在符合要求的t 值 (3)①当点P 在DC 上,即0≤t≤3时 ∵DP ∥AQ ,∴△DEP ∽△AEQ∴ DE y= DP AQ = 2tt =2,∴y = 13AD =2②当点P 在CB 上,即3<t≤6时∵AE ∥BP ,∴△QEA ∽△QPB∴AEBP=QAQB,即y12-2t=t6+t∴y =12-2t6+t综上所述,y 与t 之间的函数关系式为: y =⎩⎪⎨⎪⎧2 (0≤t≤3) 12-2t6+t(3<t≤6)(4)作点F 关于直线BD 的对称点F ′,由菱形对称性知F ′ 在DA 上,且DF ′=DF =1作点G 关于抛物线对称轴的对称点G ′,易求DG ′=4 连接F ′G ′ 交DB 于点M 、交对称轴于点N ,则点M 、N过F ′ 作F ′H ⊥DG ′ 于H ,可得HD =1 2 ,F ′H= 3 2 ,HG ′=92∴F ′G ′=F ′H 2+HG ′ 2=21∴四边形FMNG 周长最小值为F ′G ′+FG =21+1 14.(浙江模拟)如图,直线y =-x +5和直线y =kx -4交于点C (3,m ),两直线分别交y 轴于点A 和点B ,一平行于y 轴的直线l 从点C 出发水平向左平移,速度为每秒1个单位,运动时间为t ,且分别交AC 、BC 于点P 、Q ,以PQ 为一边向左侧作正方形PQDE . (1)求m 和k 的值;(2)当t 为何值时,正方形的边DE 刚好在y 轴上?(3)当直线l 从点C 出发开始运动的同时,点M 也同时在线段AB 上由点A 向点B 以每秒4个单位的速度运动,问点M 从进入正方形PQDE 到离开正方形持续的时间有多长?解:(1)把C (3,m )代入y =-x +5得m =2 ∴C (3,2),代入y =kx -4得k =2(2)由题意,点P 横坐标为3-t当x =3-t 时,y =-x +5=t +2,∴P (3-t ,t +2) ∵PQ ∥y 轴,∴点Q 横坐标为3-t当x =3-t 时,y =2x -4=2-2t ,∴Q (3-t ,2-2t ) ∴PQ =t +2-(2-2t)=3t ∵正方形PQDE ,∴PQ =PE 当正方形的边DE 刚好在y 轴上时,3t =3-t ,∴t =3 4(3)∵直线y =-x +5交y 轴于点A ,∴A (0,5) ∴点M 坐标为(0,5-4t )当点M 和点P 的纵坐标相等时,5-4t =t +2,∴t =35∵3 5<3 4,∴点M 进入正方形PQDE 时,t =3 4当点M 和点Q 的纵坐标相等时,5-4t =2-2t ,∴t =3 2∴点M 从进入正方形PQDE 到离开正方形持续的时间为:t =32-3 4=3 415.(浙江模拟)如图,在平面直角坐标系中,O 为坐标原点,Rt △OAB 的直角边OA 在x 轴的正半轴上,点B 坐标为(3,1),以OB 所在直线为对称轴将△OAB 作轴对称变换得△OCB .动点P 从点O 出发,沿线段OA 向点A 运动,动点Q 从点C 出发,沿线段CO 向点O 运动.P 、Q 两点同时出发,速度都为每秒1个单位长度.设点P 运动的时间为t (秒).(1)求∠AOC 的度数;(2)记四边形BCQP 的面积为S (平方单位),求S 与t(3)设PQ 与OB 交于点M . ①当△OMQ 为等腰三角形时,求t的值.②探究线段OM 长度的最大值,说明理由.解:(1)∵点B坐标为(3,1),∴OA=3,AB=1∴在Rt△OAB中,tan∠AOB=ABOA=13=33∴∠AOB=30°∵将△OAB作轴对称变换得△OCB∴△OCB≌△OAB,∴∠COB=∠AOB=30°∴∠AOC=60°(2)∵OP=CQ=t,AB=1,OC=OA= 3 ∴AP=OQ=3-t∴S=2S△OAB-S△OPQ-S△P AB=OA·AB-12OP·OQ·sin∠AOC-12P A·AB=3×1-12×t×(3-t)×32-12×(3-t)×1=34t2-14t+32(3)①若△OMQ为等腰三角形,则可能有三种情况:(i)若OM=MQ,则∠MQO=∠MOQ=30°∵∠AOC=60°,∴∠OPQ=90°∴OP=12OQ,即t=12(3-t)解得:t=3 3(ii)若OM=OQ,则∠OMQ=∠OQM=75°∵∠AOC=60°,∴∠OPQ=45°过点Q作QD⊥OA于D,则QD=DP即32(3-t)=t-12(3-t)解得:t=1(iii)若MQ=OQ,则∠OMQ=∠MOQ=∠MOP 得PQ∥OA,显然不符合题意②分别过点P、Q作OB的垂线,垂足分别为E、F ∵OP=t,OQ=3-t,∠MOP=∠MOQ=30°∴S△OPQ=S△OPM+S△OOM=12OM·PE+12OM·QF=14OM·OP+14OM·OQ=14OM(OP+OQ)=14OM(t+3-t)=34OM过点Q作QG⊥OA于G则S△OPQ=12OP·QG=12OP·OQ·sin60°=34t(3-t)=-34(t2-3t)∴34OM=-34(t2-3t)∴OM=-(t2-3t)=-(t-32)2+34∴当t=32时,线段OM的长度取得最大值3416.(浙江模拟)已知直线y=43x+4与x轴、y轴分别相交于点A、B,点C从O点出发沿射线OA以每秒1个单位长度的速度匀速运动,同时点D从A点出发沿AB以每秒1个单位长度的速度向B点匀速运动,当点D到达B点时C、D都停止运动.点E是CD的中点,直线EF⊥CD交y轴于点F,点E′与E点关于y轴对称.点C、D的运动时间为t(秒).(1)当t=________秒时,点F经过原点O;(2)设四边形BDCO的面积为S,求S与t的函数关系式;(3)当直线EF与△AOB的一边垂直时,求t的值;(4)以CD为一边,在CD的右侧作菱形CDMN,其中DM∥x轴.当点N在直线E′F左侧时,直接写出菱形CDMN与△EFE′重叠部分为轴对称图形时t的取值范围.解:(1)5 2提示:∵直线y=43x+4与x轴、y轴分别相交于点A、B∴A(-3,0),B(0,4),∴AO=3,BO=4 ∴AB=AO2+BO2=32+42=5当点F经过原点时,连接OD由题意,EF是CD的垂直平分线∴OD=OC=t∵AD=t,∴AD=OD,∴∠DAO=∠DOA∵∠DBO+∠DAO=90°,∠DOB+∠DOA=90°∴∠DBO=∠DOB,∴OD=BD∴AD=BD,∴AD=12AB=52(2)∵AO=3,BO=4,AB=5∴sin∠BAO=BOAB=45,cos∠BAO=AOAB=35过D作DH⊥AC于H 当0≤t≤3时∵CO=t,AD=t,∴AC=3-t,DH=AD·sin∠BAO=4 5t∴S=S△ABO-S△ADC=12×3×4-12·(3-t)·45t=25t2-65t+6当3<t≤5时,AC=t-3∴S=S△ABO+S△ADC=12×3×4+12·(t-3)·45t=25t2-65t+6综合得S与t的函数关系式为:S=25t2-65t+6(0≤t≤5)(3)当EF⊥BO时∵EF⊥CD,∴CD∥BO,∴∠ACD=90°.................在Rt △ADC 中,ACAD=cos ∠BAO∴3-t t=3 5 ,∴t =158当EF ⊥AB 时∵EF ⊥CD ,∴直线CD 与直线AB 重合 ∴点C 与点A 重合,∴t =3 (4)t =5 4 或t =154提示:①当0<t<158则∠PEQ =∠MQE∵菱形CDMN ,∴CD ∥MN∴∠MQE =∠CEQ ,∴∠PEQ =∠CEQ ∵EF ⊥CD ,即∠CEF =90°,∴∠CEQ =∴∠ACD =∠CEQ =45°过D 作DH ⊥AC 于H ,则△DHC 是等腰直角三角形∴DH =HC ,∴4 5t =3-t -3 5 t ,∴t =54②当158<t<5,且重叠部分为等腰梯形EHNK 时 同理可得∠CHE =45° 连接DH∵EF 垂直平分CD ,∴CH =DH ,∠DHE =∠CHE =45° ∴∠DHC =90°,∴DH =45t 而CH =CO -HO =CO -(AO -AH)=t -(3-35t) ∴t -(3-3 5 t )=45 t ,∴t =15417.(浙江模拟)如图1,矩形ABCD 中,AB =21,AD =12,E 是CD 边上的一点,DE =16,M 是BC 边的中点,动点P 从点A 出发,沿边AB 以每秒1个单位长度的速度向终点B 运动.设动点P 的运动时间是t 秒.(1)求线段AE 的长;(2)当△ADE 与△PBM 相似时,求t 的值;(3)如图2,连接EP ,过点P 作PH ⊥AE 于H . ①当EP 平分四边形PMEH 的面积时,求t 的值;②以PE 为对称轴作线段BC 的轴对称图形B ′C ′,当线段B ′C ′ 与线段AE 有公共点时,写出t 的取值范围(直接写出答案).解:(1)∵ABCD 是矩形,∴∠D =90°∴AE =AD 2+DE 2=122+162=20 (2)∵∠D =∠B =90°∴△ADE 与△PBM 相似时,有两种情况:当∠DAE =∠PMB 时,有DEPB=ADBM即1621-t=126,解得t =13 当∠DAE =∠BPM 时,有DEBM=ADPB即166=1221-t,解得t =332(3)①由题意得:S △EHP=S △EMP ∵DC ∥AB ,∴∠DEA =∠HAP 又∵∠D =∠AHP =90°,∴△ADE ∽△PHA∴AHDE=PHAD=APAE,即AH16=PH12=t20∴AH =45t ,PH =3 5 t ,EH =20- 45t ∴S △EHP=1 2 ×3 5 t ×( 20- 45t)∵DC =21,DE =16,∴EC =5∴S △EMP=S 梯形EPBC-S △ECM-S △PBM=1 2 (5+21-t)×12-1 2 ×5×6-12×(21-t)×6 ∴1 2 ×3 5t ×(20-4 5 t )= 1 2 ( 5+21-t )×12- 1 2 ×5×6- 12×( 21-t)×6 解得t =75±5174∵0<t<21,∴t =75-5174②14011≤t≤20 提示:当点B ′ 落在线段AE 上时连接B ′P 、EB ,∵B ′C ′ 和BC 关于PE 对称 ∴B ′P =BP =21-t ,B ′E =BE =BC 2+EC 2=122+52=13D CE M P 图1 DC E MP H图2D CE BM备用图DA C E BMP HC ′B ′N DAC E B MPHDA C EBMP H。
全国各地2012年中考数学分类解析40;159套63专题41;专题60_代数几何综合

2012年全国中考数学试卷分类解读汇编(159套63专题)专题60:代数几何综合一、选择题1. (2012浙江义乌3分)一个正方形地面积是15,估计它地边长大小在【 】 A .2与3之间 B .3与4之间 C .4与5之间 D .5与6之间 【答案】B.【考点】算术平方根,估算无理数地大小.【分析】∵一个正方形地面积是15,∵9<15<16,∴3<4.故选B.2. (2012浙江杭州3分)已知抛物线()3y k x 1x k ⎛⎫=+ ⎪⎝⎭-与x 轴交于点A ,B ,与y 轴交于点C ,则能使△ABC 为等腰三角形地抛物线地条数是【 】 A .2 B .3 C .4 D .5 【答案】B.【考点】抛物线与x 轴地交点.【分析】根据抛物线地解读式可得C (0,﹣3),再表示出抛物线与x 轴地两个交点地横坐标,再根据ABC 是等腰三角形分三种情况讨论,求得k 地值,即可求出答案:根据题意,得C (0,﹣3). 令y=0,则()3k x 1x 0k ⎛⎫+= ⎪⎝⎭-,解得x=﹣1或x=3k . 设A 点地坐标为(﹣1,0),则B (3k,0), ①当AC=BC 时,OA=OB=1,B 点地坐标为(1,0),∴3k=1,k=3; ②当AC=AB 时,点B 在点A 地右面时,∵AC =B 1,0),∴31,k k ==③当AC=AB 时,点B 在点A 地左面时,B 0),∴3k k 10==. ∴能使△ABC 为等腰三角形地抛物线地条数是3条.故选B.3. (2012浙江湖州3分)如图,已知点A (4,0),O 为坐标原点,P 是线段OA 上任意一点(不含端点O ,A ),过P 、O 两点地二次函数y1和过P 、A 两点地二次函数y2地图象开口均向下,它们地顶点分别为B 、C ,射线OB 与AC 相交于点D .当OD=AD=3时,这两个二次函数地最大值之和等于【 】A .3 D .4 【答案】A.【考点】二次函数地性质,等腰三角形地性质,勾股定理,相似三角形地判定和性质. 【分析】过B 作BF ⊥OA 于F ,过D 作DE ⊥OA 于E ,过C 作CM ⊥OA 于M ,∵BF ⊥OA ,DE ⊥OA ,CM ⊥OA ,∴BF ∥DE ∥CM.∵OD=AD=3,DE ⊥OA ,∴OE=EA=12OA=2.由勾股定理得:设P (2x ,0),根据二次函数地对称性得出OF=PF=x , ∵BF ∥DE ∥CM ,∴△OBF ∽△ODE ,△ACM ∽△ADE.∴BF OF CM AMDE OE DE AE ==,x 2x 22-,解得:)2x BF CM 2-==,.∴故选A.4. (2012浙江嘉兴、舟山4分)已知△ABC 中,∠B 是∠A 地2倍,∠C 比∠A 大20°,则∠A 等于【 】 A . 40° B . 60°C . 80°D . 90°【答案】A.【考点】一元一次方程地应用(几何问题),三角形内角和定理.【分析】设∠A=x ,则∠B=2x ,∠C=x+20°,则x+2x+x+20°=180°,解得x=40°,即∠A=40°.故选A.5. (2012江苏苏州3分)已知在平面直角坐标系中放置了5个如图所示地正方形(用阴影表示),点B1在y 轴上,点C1、E1、E2、C2、E3、E4、C3在x 轴上.若正方形A1B1C1D1地边长为1,∠B1C1O=60°,B1C1∥B2C2∥B3C3,则点A3到x 轴地距离是【 】【答案】D.【考点】正方形地性质,平行地性质,三角形内角和定理,解直角三角形,锐角三角函数定义,特殊角地三角函数值.【分析】过小正方形地一个顶点W 作FQ ⊥x 轴于点Q ,过点A3F ⊥FQ 于点F ,∵正方形A1B1C1D1地边长为1,∠B1C1O=60°,B1C1∥B2C2∥B3C3,∴∠B3C3 E4=60°,∠D1C1E1=30°,∠E2B2C2=30°.∴D1E1=12D1C1=12. ∴D1E1=B2E2=12.∴222222B E 1cos30B C 2B C ︒===. 解得:. ∴∴343333B E cos30B C ︒=,解得:B3C3=13.∴WC3=13. 根据题意得出:∠WC3 Q=30°,∠C3 WQ=60°,∠A3 WF=30°,∴WQ=111=236⨯,FW=WA3•cos30°=13. ∴点A3到x 轴地距离为:FW+WQ=16故选D. 6. (2012湖南永州3分)下列说法正确地是【 】A B .32a a a a 0-⋅=≠()C .不等式2﹣x >1地解集为x >1D .当x >0时,反比例函数ky=x地函数值y 随自变量x 取值地增大而减小7. (2012湖南张家界3分)下列不是必然事件地是【 】 A . 角平分线上地点到角两边地距离相等 B . 三角形任意两边之和大于第三边 C . 面积相等地两个三角形全等 D . 三角形内心到三边距离相等 【答案】C.【考点】随机事件,必然事件.【分析】A .为必然事件,不符合题意;B .为必然事件,不符合题意;C .为不确定事件,面积相等地三角形不一定全等,符合题意;D .为必然事件,不符合题意.故选C.8. (2012四川资阳3分)下列计算或化简正确地是【 】A .235a +a =aB 3± D .11=x+1x 1--- 【答案】D.【考点】合并同类项,二次根式地化简,算术平方根,分式地基本性质.【分析】根据合并同类项和二次根式地化简地运算法则,算术平方根地概念和分式地基本性质逐一判断:A 、a2和a3不是同类项,不可以全并,此选项错误;BC ,此选项错误;D 、()111==x+1x 1x 1------,此选项正确. 故选D.9. (2012四川南充3分)下列计算正确地是【 】(A )x3+ x3=x6 (B )m2·m3=m6 (C )3-2=3 (D )14×7=72 【答案】D.【考点】合并同类项,同底数幂地乘法,二次根式地加减法,次根式地乘法. 【分析】对每一项分别进行解答,得出正确地结果,最后选出本题地答案即可:A 、x3+x3=2x3,故此选项错误;B 、m2•m3=m5,故此选项错误;C 、D ==. 故选D.10. (2012四川攀枝花3分)下列运算正确地是【 】A .2-B .3±C . (ab )2=ab2D . (﹣a2)3=a6【答案】A.【考点】立方根,算术平方根,幂地乘方与积地乘方.【分析】根据立方根,算术平方根,幂地乘方与积地乘方地知识,对各选项分析判断后利用排除法求解,即可求得答案:A 2-,故本选项正确;B ,故本选项错误;C .(ab )2=a2b2,故本选项错误;D .(﹣a2)3=﹣a6,故本选项错误.故选A.11. (2012四川泸州2分)已知三角形两边地长分别是3和6,第三边地长是方程x2 - 6x + 8 = 0地根,则这个三角形地周长等于【 】A 、13 B 、11C 、11 或13D 、12或15【答案】A.【考点】因式分解法解一元二次方程,三角形三边关系.【分析】首先由方程x2-6x +8=0,确定第三边地边长为2或4;其次考查2,3,6或4,3,6能否构成三角形,从而求出三角形地周长:解方程x2-6x +8=0,得:x1=2或x2=4.当第三边是2时,2+3<6,不能构成三角形,应舍去; 当第三边是4时,三角形地周长为4+3+6=13.故选A.12. (2012四川广元3分) 一组数据2,3,6,8,x 地众数是x ,其中x 又是不等式组240x 70x ->⎧⎨-<⎩地整数解,则这组数据地中位数可能是【 】A. 3B. 4C. 6D. 3或6【答案】D.【考点】一元一次不等式组地整数解,众数,中位数.【分析】先求出不等式组 2x-4>0x-7<0 地整数解,再根据众数、中位数地定义可求2x 40x 70><-⎧⎨-⎩①②, 解不等式①得x >2,解不等式②得x <7,∴不等式组地解为2<x <7. ∴不等式组地整数解为3,4,5,6.∵一组数据2、3、6、8、x 地众数是x ,∴x=3或6.如果x=3,排序后该组数据为2,3,3,6,8,则中位数为3; 如果x=6,排序后该组数据为2,3,6,6,8,则中位数为6.故选D.13. (2012辽宁本溪3分)已知一元二次方程x2-8x +15=0 地两个解恰好分别是等腰△ABC 地底边长和腰长,则△ABC 地周长为【 】:] A 、13 B 、11或13C 、11D 、12【答案】B.【考点】因式分解法解一元二次方程,等腰三角形地性质,三角形三边关系.【分析】∵x2-8x +15=0 ,∴(x -3)(x -5)=0.∴x -3=0或x -5=0,即x1=3,x2=5.∵一元二次方程x2-8x +15=0 地两个解恰好分别是等腰△ABC 地底边长和腰长, ∴当底边长和腰长分别为3和5时,3+3>5,∴△ABC 地周长为:3+3+5=11; ∴当底边长和腰长分别为5和3时,3+5>5,∴△ABC 地周长为:3+5+5=13. ∴△ABC 地周长为:11或13.故选B.14. (2012辽宁朝阳3分)如图,矩形ABCD 地对角线BD 经过坐标原点,矩形地边分别平行于坐标轴,点C 在反比例函数2k +4k+1y=x地图象上,若点A 地坐标为(-2,-3),则k 地值为【 】A.1B. -5C. 4D. 1或-5 【答案】D.【考点】矩形地性质,反比例函数图象上点地坐标特征.【分析】如图:∵四边形ABCD 、HBEO 、OECF 、GOFD 为矩形,又∵BO 为四边形HBEO 地对角线,OD 为四边形OGDF 地对角线, ∴BEO BHO OFD OGD CBD ADB S S S S S S ∆∆∆∆∆∆===,,. ∴CBD BEO OFD ADB BHO OGD S S S S S S ∆∆∆∆∆∆--=--. ∴CEOF HAGO S S 236==⨯=四形四形边边. ∴xy=k2+4k+1=6,解得,k=1或k=-5.故选D.15. (2012贵州黔西南4分)三角形地两边长分别为2和6,第三边是方程2x 10x+21=0--地解,则第三边地长为【 】(A )7 (B )3 (C )7或3 (D )无法确定【答案】A.【考点】因式分解法解一元二次方程,三角形三边关系.【分析】由2x 10x+21=0-因式分解得:(x -3)(x -7)=0,解得:x1=3,x2=7.∵三角形地第三边是2x 10x+21=0-地解,∴三角形地第三边为3或7. 当三角形第三边为3时,2+3<6,不能构成三角形,舍去; 当三角形第三边为7时,三角形三边分别为2,6,7,能构成三角形. ∴第三边地长为7.故选A.16. (2012贵州安顺3分)下列说法中正确地是【 】A .B . 函数地自变量地取值范围是x >﹣1C . 若点P (2,a )和点Q (b ,﹣3)关于x 轴对称,则a ﹣b 地值为1D . ﹣8地立方根是2【答案】C.【考点】无理数,函数自变量地取值范围,二次根式有意义地条件,关于x 轴对称地点地坐标,立方根.【分析】A 是有理数,故此选项错误;B 、函数地自变量地取值范围是x ≥﹣1,故此选项错误;C 、若点P (2,a )和点Q (b ,﹣3)关于x 轴对称,则b=2,a=3,故a ﹣b=3﹣2=1,故此选项正确;D 、﹣8地立方根式﹣2,故此选项错误. 故选C.17. (2012贵州黔东南4分)如图,矩形ABCD 中,AB=3,AD=1,AB 在数轴上,若以点A 为圆心,对角线AC 地长为半径作弧交数轴地正半轴于M ,则点M 地坐标为【 】A .(2,0)B 1,0 )C 1,0 )D 0) 【答案】C.【考点】实数与数轴,矩形地性质,勾股定理.【分析】在Rt △ABC 中利用勾股定理求出AC ,继而得出AM 地长,结合数轴地知识可得出点M 地坐标:由题意得,AC∴BM=AM ﹣ 3.又∵点B 地坐标为(2,0),∴点M ﹣1,0).故选C.18. (2012贵州黔西南4分)如图,⊙O 地半径为2,点A 地坐标为(2, ,直线AB 为⊙O 地切线,B 为切点,则B 点地坐标为【 】(A )85⎛⎫ ⎪⎪⎝⎭(B )()1 (C )49,55⎛⎫- ⎪⎝⎭ (D )(1,- 【答案】D.【考点】切线地判定和性质,坐标与图形性质,锐角三角函数定义,特殊角地三角函数值. 【分析】过点A 作AC ⊥x 轴于点C ,过点B 作BD ⊥x 轴于点D ,∵⊙O 地半径为2,点A 地坐标为(2, ,即OC=2.∴AC 是圆地切线. ∵OA=4,OC=2,∴∠AOC=60°.又∵直线AB 为⊙O 地切线,∴∠AOB=∠AOC=60°. ∴∠BOD=180°-∠AOB-∠AOC=60°.又∵OB=2,∴OD=1,B 点地坐标为(1,-.故选D.19. (2012山东济南3分)已知⊙O1和⊙O2地半径是一元二次方程x2-5x +6=0地两根,若圆心距O1O2=5,则⊙O1和⊙O2地位置关系是【 】A .外离 B .外切 C .相交 D .内切 【答案】B.【考点】一元二次方程根与系数地关系,圆与圆地位置关系.【分析】根据一元二次方程根与系数地关系,可知圆心距=两圆半径之和,再根据圆与圆地位置关系作出 判断,根据两圆地位置关系地判定:外切(两圆圆心距离等于两圆半径之和),内切(两圆圆心距离等于两圆半径之差),相离(两圆圆心距离大于两圆半径之和),相交(两圆圆心距离小于两圆半径之和大于两圆半径之差),内含(两圆圆心距离小于两圆半径之差).因此,∵⊙O1和⊙O2地半径是一元二次方程x2-5x +6=0地两根,∴两根之和=5=两圆半径之和. 又∵圆心距O1O2=5,∴两圆外切.故选B.20. (2012山东潍坊3分)已知两圆半径r1、r2分别是方程x2—7x+10=0地两根,两圆地圆心距为7,则两圆地位置关系是【 】. A .相交 B .内切 C .外切 D .外离 【答案】C.【考点】圆与圆地位置关系,因式分解法解一元二次方程.【分析】首先解方程x2—7x+10=0,求得两圆半径r1、r2地值,又由两圆地圆心距为7,根据两圆位置关系与圆心距d ,两圆半径r1、r2地数量关系间地联系即可得出两圆位置关系:∵()()212x 7x 100x 2x 50x 2x 5-+=⇒--=⇒==,,∴两圆半径r1、r2分别是2,5. ∵2+5=7,两圆地圆心距为7,∴两圆地位置关系是外切.故选C.21. (2012河北省3分)如图,两个正方形地面积分别为16,9,两阴影部分地面积分别为a ,b (a >b ),则(a -b )等于【 】A .7B .6C .5D .4 【答案】A.【考点】整式地加减.【分析】设重叠部分面积为c ,(a -b )可理解为(a +c )-(b +c ),即两个正方形面积地差,所以. A -b=(a +c )-(b +c )=16-9=7.故选A. 二、填空题1. (2012重庆市4分)将长度为8厘M 地木棍截成三段,每段长度均为整数厘M .如果截成地三段木棍长度分别相同算作同一种截法(如:5,2,1和1,5,2),那么截成地三段木棍能构成三角形地概率是 ▲ . 【答案】14. 【考点】三角形三边关系,概率公式.【分析】∵因为将长度为8厘M 地木棍截成三段,每段长度均为整数厘M ,共有4种情况,分别是1,2,5;1,3,4;2,3,3;4,2,2.其中能构成三角形地是:2,3,3一种情况.∴截成地三段木棍能构成三角形地概率是14. 2. (2012广东佛山3分)如图,边长为4 m 地正方形纸片剪出一个边长为m 地正方形之后,剩余部分可剪拼成一个矩形,若拼成地矩形一边长为4,则另一边长为 ▲【答案】2m +4.【考点】图形地变换,一元一次方程地应用(几何问题).【分析】根据拼成地矩形地面积等于大正方形地面积减去小正方形地面积,列式整理即可得解:设拼成地矩形地另一边长为x ,则4x=(m +4)2-m2=(m +4+m )(m +4-m )=8m +16,解得x=2m +4.3. (2012广东珠海4分)如图,矩形OABC 地顶点A 、C 分别在x 轴、y 轴正半轴上,B 点坐标为(3,2),OB 与AC 交于点P ,D 、E 、F 、G 分别是线段OP 、AP 、BP 、CP 地中点,则四边形DEFG 地周长为 ▲ .【答案】5.【考点】坐标与图形性质,矩形地性质,三角形中位线定理.【分析】根据题意,由B 点坐标知OA=BC=3,AB=OC=2;根据三角形中位线定理可求四边形DEFG 地各边长度,从而求周长:∵四边形OABC 是矩形,∴OA=BC ,AB=OC , BA ⊥OA ,BC ⊥OC. ∵B 点坐标为(3,2),∴OA=3,AB=2.∵D 、E 、F 、G 分别是线段OP 、AP 、BP 、CP 地中点,∴DE=GF=1.5; EF=DG=1. ∴四边形DEFG 地周长为 (1.5+1)×2=5.4. (2012浙江湖州4分)如图,将正△ABC 分割成m 个边长为1地小正三角形和一个黑色菱形,这个黑色菱形可分割成n 个边长为1地小三角形,若m 47n 25=,则△ABC 地边长是 ▲【答案】12.【考点】一元二次方程地应用(几何问题),菱形地性质,等边三角形地性质,锐角三角函数定义.【分析】设正△ABC 地边长为x ,2ABC 1S x 2∆=⋅=. ∵所分成地都是正三角形,∴根据锐角三角函数定义,可得黑色菱形地较长地对角线为,较短地对角线为1=x 12-⎝.∴黑色菱形地面积=()2113x 1x 2228⎛⎫-=- ⎪⎝⎭⎝.∴()()2223x 2m 4748=3n 25x 28--=-,整理得,11x2-144x +144=0. 解得112x 11=(不符合题意,舍去),x2=12. 所以,△ABC 地边长是12.5. (2012江苏镇江2分)如图,在平面直角坐标系x0y 中,直线AB 过点A (-4,0),B (0,4),⊙O 地半径为1(O 为坐标原点),点P 在直线AB 上,过点P 作⊙O 地一条切线PQ ,Q 为切点,则切线长PQ 地最小值为 ▲ .【考点】坐标和图形,切线地性质,矩形地判定和性质,垂直线段地性质,三角形边角关系,等腰直角三角形地判定和性质,勾股定理.【分析】如图,过点O 作OP1⊥AB ,过点P1作⊙O 地切线交⊙O 于点Q1,连接OQ ,OQ1. 当PQ ⊥AB 时,易得四边形P1PQO 是矩形,即PQ=P1O.∵P1 Q1是⊙O 地切线, ∴∠OQ1P1=900.∴在Rt △OP1Q1中,P1Q1<P1O ,∴P1Q1即是切线长PQ 地最小值. ∵A (-4,0),B (0,4),∴OA=OB=4.∴△OAB 是等腰直角三角形.∴△AOP1是等腰直角三角形. 根据勾股定理,得OP1= ∵⊙O 地半径为1,∴OQ1=1. 根据勾股定理,得.6. (2012江苏徐州2分)函数3y=x+x地图象如图所示,关于该函数,下列结论正确地是 ▲ (填序号).①函数图象是轴对称图形;②函数图象是中心对称图形;③当x>0时,函数有最小值;④点(1,4)在函数图象上;⑤当x <1或x >3时,y >4.【答案】②③④.【考点】函数地图象和性质,轴对称图形和中心对称图形,曲线上点地坐标与方程地关系. 【分析】根据图象作出判断:①函数图象不是轴对称图形.故结论①错误.②函数图象是中心对称图形,对称中心是坐标原点.故结论②正确.③∵当x>0时,23y=x+=x ,∴函数有最小值.故结论③正确. ④∵当x=1时,3y=1+=41.∴点(1,4)在函数图象上.故结论④正确. ⑤∵当x <0时,y <0,∴当x <1时,y 不大于4.故结论⑤错误. ∴结论正确地是②③④.7. (2012江苏宿迁3分)如图,已知P 是线段AB 地黄金分割点,且PA >PB.若S1表示以PA 为一边地正方形地面积,S2表示长是AB 、宽是PB 地矩形地面积,则S1 ▲ S2.(填“>”“=”“ <”)【答案】=.【考点】黄金分割点,二次根式化简.【分析】设AB=1,由P 是线段AB 地黄金分割点,且PA >PB ,根据黄金分割点地定义,,BP=1=.∴211S S 1====⎝⎭∴S1=S2. 8. (2012江苏盐城3分)已知1O 与2O 地半径分别是方程2430x x -+=地两根,且12O O t 2=+,若这两个圆相切,则t = ▲ . 【答案】2或0.【考点】圆与圆地位置关系,因式分解法解一元二次方程.【分析】先解方程求出⊙O1、⊙O2地半径,再分两圆外切和两圆内切两种情况列出关于t 地方程讨论求解:∵⊙O1、⊙O2地半径分别是方程2430x x -+=地两根,解得⊙O1、⊙O2地半径分别是1和3.①当两圆外切时,圆心距O1O2=t+2=1+3=4,解得t=2; ②当两圆内切时,圆心距O1O2=t+2=3-1=2,解得t=0. ∴t 为2或0.9. (2012湖北黄石3分)如图所示,已知A 点从点(1,0)出发,以每秒1个单位长地速度沿着x 轴 地正方向运动,经过t 秒后,以O 、A 为顶点作菱形OABC ,使B 、C 点都在第一象限内,且∠AOC=600,又以P (0,4)为圆心,PC 为半径地圆恰好与OA 所在直线相切,则t= ▲ .【答案】1.【考点】切线地性质,坐标与图形性质,菱形地性质,锐角三角函数定义,特殊角地三角函数值. 【分析】∵已知A 点从(1,0)点出发,以每秒1个单位长地速度沿着x 轴地正方向运动,∴经过t 秒后,∴OA=1+t.,∵四边形OABC 是菱形,∴OC=1+t.,当⊙P 与OA ,即与x 轴相切时,如图所示,则切点为O ,此时PC=OP.过点P 作PE ⊥OC ,垂足为点E. ∴OE=CE=12OC ,即OE=12(1+t ). 在Rt △OPE中,OP=4,∠OPE=900-∠AOC=30°,∴OE=OP•cos30°=11t 2+=∴t 1=.∴当PC 为半径地圆恰好与OA 所在直线相切时,t 1=.10. (2012湖北荆州3分)如图(1)所示,E 为矩形ABCD 地边AD 上一点,动点P 、Q 同时从点B 出发,点P 沿折线BE ﹣ED ﹣DC 运动到点C 时停止,点Q 沿BC 运动到点C 时停止,它们运动地速度都是1cm/秒.设P 、Q 同发t 秒时,△BPQ 地面积为ycm2.已知y 与t 地函数关系图象如图(2)(曲线OM 为抛物线地一部分),则下列结论:①AD=BE=5;②cos ∠ABE=;③当0<t ≤5时,22y= t 5;④当29t 4=秒时,△ABE ∽△QBP ;其中正确地结论是 ▲ (填序号).【答案】①③④.【考点】动点问题地函数图象,矩形地性质,勾股定理,锐角三角函数定义,相似三角形地判定和性质. 【分析】根据图(2)可知,当点P 到达点E 时点Q 到达点C ,∵点P 、Q 地运动地速度都是1cm/秒,∴BC=BE=5.∴AD=BE=5.故结论①正确. 又∵从M 到N 地变化是2,∴ED=2.∴AE=AD ﹣ED=5﹣2=3.在Rt △ABE 中,, ∴AB 4cos ABE==BE 5∠.故结论②错误. 过点P 作PF ⊥BC 于点F ,∵AD ∥BC ,∴∠AEB=∠PBF ,∴sin ∠PBF=sin ∠AEB=AB 4=BE 5. ∴PF=PBsin ∠PBF=45t. ∴当0<t ≤5时,21142y=BQ PF=t t= t 2255⋅⋅⋅⋅.故结论③正确.当29t 4=秒时,点P 在CD 上, 此时,PD=294-BE -ED=29152=44--,PQ=CD -PD=4-115=44.∵AB 4BQ 54==15AE 3PQ 34= ,,∴AB BQ =AE PQ . 又∵∠A=∠Q=90°,∴△ABE ∽△QBP.故结论④正确. 综上所述,正确地有①③④.11. (2012湖北武汉3分)如图,点A 在双曲线y =kx地第一象限地那一支上,AB 垂直于x 轴与点B ,点C 在x 轴正半轴上,且OC =2AB ,点E 在线段AC 上,且AE =3EC ,点D 为OB 地中点,若△ADE 地面积为3,则k 地值为 ▲ .【答案】163. 【考点】反比例函数综合题,曲线上点地坐标与方程地关系,相似三角形地判定和性质,同底三角形面积地计算,梯形中位线地性质.【分析】如图,连接DC ,∵AE=3EC ,△ADE 地面积为3,∴△CDE 地面积为1. ∴△ADC 地面积为4. ∵点A 在双曲线y =kx地第一象限地那一支上, ∴设A 点坐标为(kx x,). ∵OC =2AB ,∴OC=2x .∵点D 为OB 地中点,∴△ADC 地面积为梯形BOCA 面积地一半,∴梯形BOCA 地面积为8. ∴梯形BIEA 地面积=()11k x+2x y 3x =822x⋅=⋅⋅,解得16k=3.12. (2012湖北武汉3分)在平面直角坐标系中,点A 地坐标为(3,0),点B 为y 轴正半轴上地一点,点C 是第一象限内一点,且AC =2.设tan ∠BOC =m ,则m 地取值范围是 ▲ .【答案】m ≥【考点】锐角三角函数定义,勾股定理,一元二次方程根地判别式. 【分析】如图,设C 点坐标为(x y ,).∵tan ∠BOC =m ,∴EC x==m CD y,即x=my . ∵A 地坐标为(3,0),∴DA=3x -.又∵AC =2.∴由勾股定理,得()223x +y =4-, 即()223my +y =4-,整理得()221+m y 6my+5=0- 由()()222=6m 41+m 5=16m 200∆-⋅⋅-≥得25m 4≥.∵tan ∠BOC =m >0,∴m ≥13. (2012四川德阳3分) 有下列计算:①(m2)3=m62a 1-,③m6÷m2=m3, ④1565027=÷⨯,⑤31448332122=+-,其中正确地运算有 ▲ . 【答案】①④⑤.【考点】幂地乘方,同底数幂地除法,二次根式地性质与化简,二次根式地四则运算. 【分析】∵(m2)3=m2×3=m6,∴①正确;2a 1=-,∴②错误; ∵m6÷m2=m4,∴③错误;,∴④正确;∵⑤正确. ∴正确地运算有:①④⑤.14. (2012四川巴中3分)已知a 、b 、c 是△ABC 三边地长,且满足关系式a b 0-=, 则△ABC 地形状为 ▲ 【答案】等腰直角三角形.【考点】非负数地性质,算术平方根,非负数地性质,勾股定理地逆定理,等腰直角三角形地判定.【分析】∵a b 0-=,∴c2-a2-b2=0,且a -b=0.由c2-a2-b2=0得c2=a2+b2,∴根据勾股定理地逆定理,得△ABC 为直角三角形. 又由a -b=0得a=b ,∴△ABC 为等腰直角三角形.15. (2012四川内江6分)已知A (1,5),B (3,-1)两点,在x 轴上取一点M ,使AM -BN 取得最大值时,则M 地坐标为 ▲ 【答案】(72,0). 【考点】一次函数综合题,线段中垂线地性质,三角形三边关系,关于x 轴对称地点地坐标,待定系数法,直线上点地坐标与方程地关系,解二元一次方程组.【分析】如图,作点B 关于x 轴地对称点B′,连接AB′并延长与x 轴地交点,即为所求地M 点.此时AM -BM=AM -B′M=AB′.不妨在x 轴上任取一个另一点M′,连接M′A 、M′B 、M′B . 则M′A -M′B=M′A -M′B′<AB′(三角形两边之差小于第三边). ∴M′A -M′B <AM-BM ,即此时AM -BM 最大. ∵B′是B (3,-1)关于x 轴地对称点,∴B′(3,1).设直线AB′解读式为y=kx+b ,把A (1,5)和B′(3,1)代入得:k b 5 3k b 1+=⎧⎨+=⎩,解得 k 2b 7=-⎧⎨=⎩.∴直线AB′解读式为y=-2x+7. 令y=0,解得x=72 .∴M 点坐标为(72,0). 16. (2012四川资阳3分)如图,O 为矩形ABCD 地中心,M 为BC 边上一点,N 为DC 边上一点,ON ⊥OM ,若AB =6,AD =4,设OM =x ,ON =y ,则y 与x 地函数关系式为 ▲ .【答案】y=23x. 【考点】矩形地性质,相似三角形地判定和性质.【分析】如图,作OF ⊥BC 于F ,OE ⊥CD 于E ,∵ABCD 为矩形,∴∠C=90°.∵OF ⊥BC ,OE ⊥CD ,∴∠EOF=90°.∴∠EON+∠FON=90°. ∵ON ⊥OM ,∴∠EON=∠FOM.∴△OEN ∽△OFM. ∴OE ONOF OM=. ∵O 为矩形ABCD 地中心,∴OE AD 42OF AB 63===.∴ON 2=OM 3 ,即y=23x.17. (2012四川自贡4分)正方形ABCD 地边长为1cm ,M 、N 分别是BC .CD 上两个动点,且始终保持AM ⊥MN ,当BM= ▲ cm 时,四边形ABCN 地面积最大,最大面积为 ▲ cm2.【答案】12,58. 【考点】正方形地性质,相似三角形地判定和性质,二次函数地最值. 【分析】设BM=xcm ,则MC=1﹣xcm ,∵∠AMN=90°,∠AMB+∠NMC=90°,∠NMC+∠MNC=90°,∴∠AMB=90°﹣∠NMC=∠MNC.∴△ABM ∽△MCN ,∴AB BM MC CN =,即1x1x CN=-,解得CN=x (1﹣x ). ∴22ABCN 1111115S 1[1x 1x ]x x x 2222228=⨯⨯+-=-++=--+四形()()边.∵12-<0,∴当x=12cm 时,S 四边形ABCN 最大,最大值是58cm2.18. (2012辽宁朝阳3分)下列说法中正确地序号有 ▲ .①在Rt △ABC 中,∠C=900,CD 为AB 边上地中线,且CD=2,则AB=4; ②八边形地内角和度数为10800; ③2、3、4、3这组数据地方差为0.5; ④分式方程13x 1=x x -地解为2x=3;⑤已知菱形地一个内角为600,一条对角线为,则另一对角线为2. 【答案】①②③④.【考点】直角三角形斜边上中线地性质,多边形内角和定理,方差,解分式方程,菱形地性质,等边三角形地判定,勾股定理.【分析】①∵在Rt △ABC 中,∠C=90°,CD 为AB 边上地中线,且CD=2,∴根据直角三角形斜边上中线等于斜边一半地性质,得AB=2CD=4.∴①正确. ②∵八边形地内角和度数是(8-2)×180°=1080°.∴②正确. ③∵2、3、4、3地平均数是()12+3+4+3=34, ∴2、3、4、3地方差是22221[23334333]0.54-+-+-+-=()()()().∴③正确.④∵由13x 1=x x -去分母得:1=3x -1,解得:x=23.经检验x=23是原方程地解.∴④正确. ⑤∵四边形ABCD 是菱形,∴AC ⊥BD ,AO=OC ,OD=OB ,AB=AD.∵∠BAD=60°,∴△ABD 是等边三角形.∴AB=AD=BD ,AB=BD=2BO. 分为两种情况:当BD=时,AO=3,AC=6.当AC=BO=1,BD=2. ∴另一对角线为2或6.∴⑤错误. 故答案为:①②③④.19. (2012贵州黔南5分)如图,四边形ABCD 是矩形,A ,B 两点在x 轴地正半轴上,C ,D 两点在抛物线2y x 6x =-+上,设OA=m (0<m <3),矩形ABCD 地周长为l ,则l 与m 地函数解读式为 ▲ .【答案】2l 2m 8m 12=-++.【考点】矩形地性质,待定系数法,曲线上点地坐标与方程地关系.【分析】求l 与m 地函数解读式就是把m 当作已知量,求l ,先求AD ,它地长就是D 点地纵坐标,再把D 点纵坐标代入函数解读式求C 点横坐标,C 点横坐标与D 点横坐标地差就是线段CD 地长,用l=2(AD+AB ),建立函数关系式: 把x=m 代入抛物线2y x 6x =-+中,得AD=2m 6m -+,把y=2m 6m -+代入抛物线2y x 6x =-+中,得22m 6m x 6x -+=-+,解得x1=m ,x2=6-m. ∴C 地横坐标是6-m.∴AB=6-m -m=6-2m.∴矩形地周长是22l 2m 6m 262m 2m 8m 12=-++-=-++()().20. (2012山东济宁3分)在△ABC 中,若∠A 、∠B 满足|cosA ﹣12|+(sinB 2=0,则∠C=▲ .【答案】75°.【考点】非负数地性质,绝对值,偶次方,特殊角地三角函数值,三角形内角和定理.【分析】∵|cosA ﹣12|+(sinB ﹣22=0,∴cosA ﹣12=0,sinB ﹣2∴cosA=12,∴∠A=60°,∠B=45°.∴∠C=180°﹣∠A ﹣∠B=180°﹣60°﹣45°=75°.21. (2012广西北海3分)如图,点A 地坐标为(-1,0),点B 在直线y =2x -4上运动,当线段AB最短时,点B 地坐标是 ▲ .【答案】(7655-,). 【考点】直线上点地坐标与方程地关系,垂直线段最短地性质,相似三角形地判定和性质.【分析】如图,由题意,根据垂直线段最短地性质,当线段AB 最短时点B 地位置B1,有AB1⊥BD. 过点B1作B1E 垂直x 轴于点E.由点C 、D 在直线y =2x -4可得,C (2,0),D (0,-4)设点B1(x ,2x -4),则E (x ,0).由A (-1,0),得AE= x +1,EB1=∣2x -4∣=4-2x ,CO=2,DO=4.易得△AB1E ∽△DCO ,∴AE EB DO CO =,即x+142x42-=. 解得76x 2x 4=55=-- ,.∴B1(7655- ,).∴当线段AB 最短时,点B 地坐标是(7655- ,).三、解答题1. (2012海南省13分)如图,顶点为P (4,-4)地二次函数图象经过原点(0,0),点A 在该图象上,OA 交其对称轴l 于点M ,点M 、N 关于点P 对称,连接AN 、ON (1)求该二次函数地关系式.(2)若点A 地坐标是(6,-3),求△ANO 地面积.(3)当点A 在对称轴l 右侧地二次函数图象上运动,请解答下列问题: ①证明:∠ANM=∠ONM②△ANO 能否为直角三角形?如果能,请求出所有符合条件地点A 地坐标,如果不能,请说明理由.【答案】解:(1)∵二次函数图象地顶点为P (4,-4),∴设二次函数地关系式为()2y=a x 44--. 又∵二次函数图象经过原点(0,0),∴()20=a 044--,解得1a=4. ∴二次函数地关系式为()21y=x 444--,即21y=x 2x 4-. (2)设直线OA 地解读式为y=kx ,将A (6,-3)代入得3=6k -,解得1k=2-. ∴直线OA 地解读式为1y=-x 2.把x=4代入1y=x 2-得y=2-.∴M (4,-2).又∵点M 、N 关于点P 对称,∴N (4,-6),MN=4. ∴ANO 1S 64122∆=⋅⋅=. (3)①证明:过点A 作AH ⊥l 于点H ,,l 与x 轴交于点D.则 设A (20001x x 2x 4- ,),则直线OA 地解读式为200001x 2x 14y=x=x 2x x 4-⎛⎫- ⎪⎝⎭.则M (04 x 8-,),N (04 x -,),H (20014x 2x 4- ,).∴OD=4,ND=0x ,HA=0x 4-,NH=2001x x 4-. ∴()()()00022000000004x 44x 4x 4OD 4HA4tan ONM=tan ANM===1ND x NH x x 4x x 4x +64x x 4---∠=∠==--- ,. ∴tan ONM=∠tan ANM ∠.∴∠ANM=∠ONM. ②能.理由如下:分三种情况讨论:情况1,若∠ONA 是直角,由①,得∠ANM=∠ONM=450,∴△AHN 是等腰直角三角形.∴HA=NH ,即20001x 4=x x 4--. 整理,得200x 8x +16=0-,解得0 x =4.∴此时,点A 与点P 重合.故此时不存在点A ,使∠ONA 是直角.情况2,若∠AON 是直角,则222O A +ON =AN .∵()222222222220000000011 O A =x +x 2x ON =4+x AN =x 4+x 2x +x 44⎛⎫⎛⎫--- ⎪ ⎪⎝⎭⎝⎭,, ,∴()222222220000000011 x +x 2x +4+x =x 4+x 2x +x 44⎛⎫⎛⎫--- ⎪ ⎪⎝⎭⎝⎭.整理,得32000x 8x 16x =0--,解得0x =0,0 x =4±. 舍去0x =0,0 x =4-l 左侧).当0 x 0y =4. ∴此时存在点A(44),使∠AON 是直角. 情况3,若∠NAO 是直角,则△AMN ∽△DMO ∽△DON ,∴MD ODOD ND=. ∵OD=4,MD=08x -,ND=0x ,∴008x 44x -=. 整理,得200x 8x +16=0-,解得0x =4. ∴此时,点A 与点P 重合.故此时不存在点A ,使∠ONA 是直角.综上所述,当点A 在对称轴l 右侧地二次函数图象上运动时,存在点A(44),使∠AON 是直角,即△ANO 为直角三角形.【考点】二次函数综合题,待定系数法,曲线上点地坐标与方程地关系,对称地性质,锐角三角函数定义,等腰直角三角形地判定和性质,勾股定理,相似三角形地判定和性质,解一元二次方程.【分析】(1)由二次函数图象地顶点为P (4,-4)和经过原点,设顶点式关系式,用待定系数法即可求.(2)求出直线OA 地解读式,从而得到点M 地坐标,根据对称性点N 坐标,从而求得MN 地长,从而求得△ANO 地面积. (3)①根据正切函数定义,分别求出∠ANM 和∠ONM 即可证明.②分∠ONA 是直角,∠AON 是直角,∠NAO 是直角三种情况讨论即可得出结论.当∠AON 是直角时,还可在Rt △OMNK 中用直角三角形斜边上地中线等于斜边地一半求解:∵OP=PN=PM ,∵ PN=0x -4 ,∴0x -4 .∴0 x2. (2012宁夏区10分)在矩形ABCD 中,AB=2,AD=3,P 是BC 上地任意一点(P 与B 、C 不重合),过点P 作AP ⊥PE ,垂足为P ,PE 交CD 于点E.(1)连接AE ,当△APE 与△ADE 全等时,求BP 地长;(2)若设BP 为x ,CE 为y ,试确定y 与x 地函数关系式.当x 取何值时,y 地值最大?最大值是多少? (3)若PE ∥BD ,试求出此时BP 地长.【答案】解:(1)∵△APE ≌△ADE ,∴AP=AD=3.在Rt △ABP 中,AB=2,∴(2)∵AP ⊥PE ,∴Rt △ABP ∽Rt △PCE.∴AB BPPC CE=,即2x 3x y =-.∴213y x x 22=-+. ∵2213139y x x (x )22228=-+=--+ ∴当3x 2=时,y 地值最大,最大值是98.(2)设BP=x, 由(2)得213CE x x 22=-+.∵PE ∥BD ,,∴△CPE ∽△CBD.∴CP CE CB CD=, 即213x x3x 2232-+-=, 化简得23x 13x 120-+=.解得14x 3=或2x 3=(不合题意,舍去). ∴当BP=43时, PE ∥BD.【考点】矩形地性质,全等三角形地性质,勾股定理,相似三角形地判定和性质,二次函数地最值,平行地性质,解一元二次方程.【分析】(1)由△APE ≌△ADE 可得AP=AD=3,在Rt △ABP 中,应用勾股定理即可求得BP 地长.(2)由AP ⊥PE ,得Rt △ABP ∽Rt △PCE ,根据相似三角形地对应边成比例可列式得y 与x 地函数关系式.化为顶点式即可求得当3x 2=时,y 地值最大,最大值是98.(3)由PE ∥BD ,得△CPE ∽△CBD ,根据相似三角形地对应边成比例可列式可求得BP 地长.3. (2012广东省9分)如图,抛物线213y=x x 922--与x 轴交于A 、B 两点,与y 轴交于点C ,连接BC 、AC .(1)求AB 和OC 地长;(2)点E 从点A 出发,沿x 轴向点B 运动(点E 与点A 、B 不重合),过点E 作直线l 平行BC ,交AC 于点D .设AE 地长为m ,△ADE 地面积为s ,求s 关于m 地函数关系式,并写出自变量m 地取值范围;(3)在(2)地条件下,连接CE ,求△CDE 面积地最大值;此时,求出以点E 为圆心,与BC 相切地圆地面积(结果保留π).【答案】解:(1)在213y=x x 922--中,令x=0,得y=-9,∴C (0,﹣9);令y=0,即213x x 9=022--,解得:x1=﹣3,x2=6,∴A (﹣3,0)、B (6,0). ∴AB=9,OC=9.(2)∵ED ∥BC ,∴△AED ∽△ABC ,∴2AED ABC S AE S AB ∆∆⎛⎫= ⎪⎝⎭,即:2s m 19992⎛⎫= ⎪⎝⎭⋅⋅. ∴s=12m2(0<m <9). (3)∵S △AEC=12AE •OC=92m ,S △AED=s=12m2,∴S △EDC=S △AEC ﹣S △AED。
2012年全国各地中考数学阅读理解型问题试题(附答案)

2012年全国各地中考数学阅读理解型问题试题(附答案)2012年全国各地中考数学解析汇编39 阅读理解型问题 21.(2012四川达州,21,8分)(8分)�の侍獗尘�若矩形的周长为1,则可求出该矩形面积的最大值.我们可以设矩形的一边长为,面积为,则与的函数关系式为:�0),利用函数的图象或通过配方均可求得该函数的最大值. 提出新问题若矩形的面积为1,则该矩形的周长有无最大值或最小值?若有,最大(小)值是多少?分析问题若设该矩形的一边长为,周长为,则与的函数关系式为:(�0),问题就转化为研究该函数的最大(小)值了. 解决问题借鉴我们已有的研究函数的经验,探索函数(�0)的最大(小)值.(1)实践操作:填写下表,并用描点法�せ�出函数(�0)的图象:(2)观察猜想:观察该函数的图象,猜想当 = 时,函数(�0)有最值(填“大”或“小”),是 . (3)推理论证:问题背景中提到,通过配方可求二次函数�0)的最大值,请你尝试通过配方求函数(�0)的最大(小)值,以证明你的猜想. 〔提示:当>0时,〕解析:对于(1)按照画函数图象的列表、描点、连线三步骤进行即可;对于(2),由结合图表可知有最小值为4;对于(3),可按照提示,用配方法来求出。
答案:(1) …………………………………………..(1分)………………………………………….(3分)(2)1、小、4………………………………………………………………………..(5分)�ィ�3)证明:………………………………………………(7分)�さ�时,的最小值是4 �ぜ� =1时,的最小值是4………………………………………………………..(8分)点评:本题以阅读理解型的形式,考查学生画函数图象的基本步骤及结合图表求函数最值的观察力,考察了学生的模仿能力、配方思想和类比的能力。
28.(2012江苏省淮安市,28,12分)阅读理解如题28-1图,△ABC 中,沿∠BAC的平分线AB1折叠,剪掉重叠部分;将余下部分沿∠B1A1C 的平分线A1B2折叠,剪掉重叠部分;将余下部分沿∠BnAnC的平分线AnBn+1折叠,点Bn与点C重合.无论折叠多少次,只要最后一次恰好重合,我们就称∠BAC是△ABC的好角.小丽展示了确定∠BAC是△ABC的好角的两种情形.情形一:如题28-2图,沿等腰三角形ABC顶角∠BAC的平分线AB1折叠,点B与点C重合;情形二:如题28-3图,沿△ABC的∠BAC的平分线AB1折叠,剪掉重叠部分;将余下的部分沿∠B1A1C的平分线 A1B2折叠,此时点B1与点C重合.探究发现(1)△ABC中,∠B=2∠C,经过两次折叠,∠BAC是不是△ABC的好角? .(填:“是”或“不是”). (2)小丽经过三次折叠发现了∠BAC是△ABC的好角,请探究∠B与∠C(不妨设∠B>∠C)之间的等量关系.根据以上内容猜想:若经过n次折叠∠BAC是△ABC 的好角,则∠B与∠C(不妨设∠B>∠C)之问的等量关系为.应用提升 (3)小丽找到一个三角形,三个角分别为15º,60º,l05º,发现60º和l05º的两个角都是此三角形的好角.请你完成,如果一个三角形的最小角是4º,试求出三角形另外两个角的度数,使该三角形的三个角均是此三角形的好角.【解析】(1)利用三角形外角的性质和折叠对称性即可解决;(2)根据第(1)问的结论继续探索;(3)利用“好角”的定义和三角形内角和列出方程解之.具体过程见以下解答.【答案】解: (1) 由折叠的性质知,∠B=∠AA1B1.因为∠AA1B1=∠A1B1C+∠C,而∠B=2∠C,所以∠A1B1C=∠C,就是说第二次折叠后∠A1B1C与∠C重合,因此∠BAC是△ABC的好角. (2)因为经过三次折叠∠BAC是△ABC的好角,所以第三次折叠的∠A2B2C=∠C.如图12-4所示. 图12-4 因为∠ABB1=∠AA1B1,∠AA1B1=∠A1B1C+∠C,又∠A1B1C=∠A1A2B2,∠A1A2B2=∠A2B2C+∠C,所以∠ABB1=∠A1B1C+∠C=∠A2B2C+∠C+∠C=3∠C.由上面的探索发现,若∠BAC是△ABC的好角,折叠一次重合,有∠B=∠C;折叠二次重合,有∠B=2∠C;折叠三次重合,有∠B=3∠C;…;由此可猜想若经过n次折叠∠BAC是△ABC的好角,则∠B=n∠C.(3)因为最小角是4º是△ABC的好角,根据好角定义,则可设另两角分别为4mº,4mnº(其中m、n都是正整数).由题意,得4m+4mn+4=180,所以m(n+1)=44.因为m、n都是正整数,所以m与n+1是44的整数因子,因此有:m=1,n+1=44;m=2,n+1=22;m=4,n+1=11;m=11,n+1=4;m=22,n+1=2.所以m=1,n=43;m=2,n=21;m=4,n=10;m=11,n=3;m=22,n=1.所以4m=4,4mn=172;4m=8,4mn=168;4m=16,4mn=160;4m=44,4mn=132;4m=88,4mn=88.所以该三角形的另外两个角的度数分别为:4º,172º;8º,168º;16º,160º;44º,132º;88º,88º.【点评】本题主要考查轴对称图形、等腰三角形、三角形形的内角和定理及因式分解等知识点的理解和掌握,本题是阅读理解题,解决本题的关键是读懂题意,理清题目中数字和字母的对应关系和运算规则,然后套用题目提供的对应关系解决问题,具有一定的区分度.23.(2012湖北咸宁,23,10分)如图1,矩形MNPQ中,点E,F,G,H分别在NP,PQ,QM,MN上,若,则称四边形EFGH为矩形MNPQ的反射四边形.图2,图3,图4中,四边形ABCD为矩形,且,.理解与作图:(1)在图2、图3中,点E,F分别在BC,CD边上,试利用正方形网格在图上作出矩形ABCD的反射四边形EFGH.计算与猜想:(2)求图2,图3中反射四边形EFGH的周长,并猜想矩形ABCD的反射四边形的周长是否为定值?启发与证明:(3)如图4,为了证明上述猜想,小华同学尝试延长GF交BC的延长线于M,试利用小华同学给我们的启发证明(2)中的猜想.【解析】(1)根据网格结构,作出相等的角得到反射四边形;(2)图2中,利用勾股定理求出EF=FG=GH=HE的长度,然后可得周长;图3中利用勾股定理求出EF=GH,FG=HE的长度,然后求出周长,得知四边形EFGH的周长是定值;(3)证法一:延长GH交CB的延长线于点N,再利用“角边角”证明Rt△FCE≌Rt△FCM,根据全等三角形对应边相等可得EF=MF,EC=MC,同理求出NH=EH,NB=EB,从而得到MN=2BC,再证明GM=GN,过点G作GK⊥BC于K,根据等腰三角形三线合一的性质求出MK= MN=8,再利用勾股定理求出GM的长度,然后可求出四边形EFGH的周长;证法二:利用“角边角”证明Rt△FCE≌Rt△FCM,根据全等三角形对应边相等可得EF=MF,EC=MC,再根据角的关系推出∠M=∠HEB,根据同位角相等,两直线平行可得HE∥GF,同理可证GH∥EF,所以四边形EFGH是平行四边形,过点G作GK⊥BC于K,根据边的关系推出MK=BC,再利用勾股定理列式求出GM的长度,然后可求出四边形EFGH的周长.【答案】(1)作图如下: 2分(2)解:在图2中,,∴四边形EFGH的周长为. 3分在图3中,,.∴四边形EFGH的周长为. 4分猜想:矩形ABCD的反射四边形的周长为定值. 5分(3)如图4,证法一:延长GH交CB 的延长线于点N.∵ ,,∴ .而,∴Rt△FCE≌Rt△FCM.∴ ,. 6分同理:,.∴ . 7分∵ ,,∴ .∴ . 8分过点G作GK⊥BC于K,则. 9分∴.∴四边形EFGH的周长为. 10分证法二:∵ ,,∴ .而,∴Rt△FCE≌Rt△FCM.∴ ,. 6分∵ ,,而,∴ .∴HE∥GF.同理:GH∥EF.∴四边形EFGH是平行四边形.∴ .而,∴Rt△FDG≌Rt△HBE.∴ .过点G作GK⊥BC 于K,则∴ .∴四边形EFGH的周长为.【点评】本题主要考查了应用与设计作图,全等三角形的判定与性质,勾股定理的应用,矩形的性质,读懂题意理解“反射四边形EFGH”特征是解题的关键.25.(2012贵州黔西南州,25,14分)问题:已知方程x2+x-1=0,求一个一元二次方程,使它的根分别是已知方程根的2倍.解:设所求方程的根为y,则y=2x,所以x=y2.把x=y2代入已知方程,得(y2)2+y2-1=0.化简,得:y2+2y-4=0.故所求方程为y2+2y-4=0.这种利用方程根的代换求新方程的方法,我们称为“换根法”.请用阅读材料提供的“换根法”求新方程(要求:把所求方程化成一般形式): (1)已知方程x2+x-2=0,求一个一元二次方程,使它的根分别是已知方程根的相反数. (2)已知关于x的一元二次方程ax2+bx+c=0(a≠0)有两个不等于零的实数根,求一个一元二次方程,使它的根分别是已知方程根的倒数.【解析】按照题目给出的范例,对于(1)的“根相反”,用“y=-x”作替换;对于(2)的“根是倒数”,用“y=1x”作替换,并且注意有“不等于零的实数根”的限制,要进行讨论.【答案】(1)设所求方程的根为y,则y=-x,所以x=-y.………………(2分) 把x=-y代入已知方程x2+x-2=0,得(-y)2+(-y)-2=0.………………(4分) 化简,得:y2-y-2=0.………………(6分) (2)设所求方程的根为y,则y=1x,所以x=1y.………………(8分) 把x=1y 代如方程ax2+bx+c=0得. a(1y)2+b•1y+c=0,………………(10分) 去分母,得,a+by+cy2=0.……………………(12分) 若c=0,有ax2+bx=0,于是方程ax2+bx+c=0有一个根为0,不符合题意.∴c≠0,故所求方程为cy2+by+a=0(c≠0).……………………(14分) 【点评】本题属于阅读理解题,读懂题意,理解题目讲述的方法的基础;在实际解题时,还要灵活运用题目提供的方法进行解题,实际上是数学中“转化”思想的运用.八、(本大题16分) 26.(2012贵州黔西南州,26,16分)如图11,在平面直角坐标系xoy中,已知抛物线经过点A(0,4),B(1,0),C(5,0)抛物线的对称轴l与x轴相交于点M. (1)求抛物线对应的函数解析式和对称轴. (2)设点P为抛物线(x>5)上的一点,若以A、O、M、P为顶点的四边形的四条边的长度为四个连续的正整数.请你直接写出点P的坐标. (3)连接AC,探索:在直线AC下方的抛物线上是否存在一点N,使△NAC的面积最大?若存在,请你求出N的坐标;若不存在,请说明理由.【解析】(1)已知抛物线上三点,用“待定系数法”确定解析式;(2)四边形AOMP中,AO=4,OM=3,过A作x轴的平行线交抛物线于P点,这个P点符合要求“四条边的长度为四个连续的正整数”;(3)使△NAC的面积最大,AC确定,需要N点离AC的距离最大,一种方法可以作平行于AC的直线,计算这条直线与抛物线只有一个交点时,这个交点即为N;另一种方法,过AC上任意一点作y轴的平行线交抛物线于N点,这样△NAC被分成两个三角形,建立函数解析式求最大值.【答案】(1)根据已知条件可设抛物线对应的函数解析式为y=a(x�D1)•(x�D5),………………(1分) 把点A(0,4)代入上式,得a=45.………………(2分) ∴y=45(x�D1)(x�D5)=45x2�D245x +4=�D45(x�D3)2�D165.………………(3分) ∴抛物线的对称轴是x=3.…………(4分) (2)点P的坐标为(6,4).………………(8分) (3)在直线AC下方的抛物线上存在点N,使△NAC的面积最大,由题意可设点N的坐标为(t,45t2�D245t+4)(0<t<5).………………(9分) 如图,过点N作NG∥y轴交AC于点G,连接AN、CN.由点A(0,4)和点C(5,0)可求出直线AC的解析式为:y=�D45x+4.………………(10分) 把x=t代入y=�D45x+4得y=�D45t+4,则G(t,�D45t+4).………………(11分) 此时NG=�D45t+4�D(45t2�D245t+4)=�D45t2+205t.………………(12分) ∴S△NAC=12NG•OC=12(-45t2+205t)×5 =�D2t2+10t=�D2(t-52)2+252.………………(13分) 又∵0<t<5,∴当t=52时,△CAN的面积最大,最大值为252 .………………(14分) t=52时,45 t2-245t+4=-3.………………(15分) ∴点N的坐标为(52,-3).……………………(16分) 【点评】本题是一道二次函数、一次函数、三角形的综合题,其中第(3)问也是一道具有难度的“存在性”探究问题.本题主要考查二次函数、一次函数的图象与性质的应用.专项十阅读理解题19. (2012山东省临沂市,19,3分)读一读:式子“1+2+3+4+ (100)表示从1开始的100个连续自然数的和,由于式子比较长,书写不方便,为了简便起见,我们将其表示为,这里“ ”是求和符号,通过以上材料的阅读,计算 = . 【解析】式子“1+2+3+4+……+100”的结果是,即 = ;又∵ ,,………,∴ = + +…+ =1- ,∴ = = + +…+ =1- = . 【答案】【点评】本题是一道找规律的题目,要求学生的通过观察,分析、归纳并发现其中的规律,并应用发现的规律解决问题.此题重点除首位两项外,其余各项相互抵消的规律.23. (2012浙江省嘉兴市,23,12分)将△ABC绕点A按逆时针方向旋转θ度,并使各边长变为原来的n倍,得△AB′ C′ ,即如图①,∠BAB′ =θ, ,我们将这种变换记为. (1)如图①,对△ABC作变换得△AB′ C′ ,则 : =_______;直线BC与直线B′C′所夹的锐角为_______度; (2)如图② ,△ABC中,∠BAC=30° ,∠ACB=90° ,对△ABC作变换得△AB′ C′ ,使点B、C、在同一直线上,且四边形ABB′C′为矩形,求θ和n的值; (3)如图③ ,△ABC中,AB=AC,∠BAC=36° ,B C=1,对△ABC作变换得△AB′C′ , 使点B、C、B′在同一直线上,且四边形ABB′C′为平行四边形,求θ和n的值. 【解析】(1) 由题意知, θ为旋转角, n为位似比.由变换和相似三角形的面积比等于相似比的平方,得 : = 3, 直线BC与直线B′C′所夹的锐角为60°; (2)由已知条件得θ=∠CAC′=∠BAC′-∠BAC=60°.由直角三角形中, 30°锐角所对的直角边等于斜边的一半得n==2. (3) 由已知条件得θ=∠CAC′=∠ACB=72°.再由两角对应相等,证得△ABC∽△B′B A,由相似三角形的性质求得n== . 【答案】(1) 3;60°. (2) ∵四边形ABB′C′是矩形,∴∠BAC′=90°. ∴θ=∠CAC′=∠BAC′-∠BAC=90°-30°=60°. 在Rt△ABB′中,∠ABB′=90°, ∠BAB′=60°, ∴n==2. (3) ∵四边形ABB′C′是平行四边形,∴AC′∥BB′,又∵∠BAC=36°∴θ=∠CAC′=∠ACB=72° ∴∠C′AB′=∠ABB′=∠BAC=36°,而∠B=∠B, ∴△ABC∽△B′BA,∴AB2=CB•B′B=CB•(BC+CB′), 而CB′=AC=AB=B′C′, BC=1, ∴AB2=1•(1+AB) ∴AB=,∵AB>0, ∴n== . 【点评】本题是一道阅读理解题.命题者首先定义了一种变换,要求考生根据这种定义解决相关的问题.读懂定义是解题的关键所在. 本题所涉及的知识点有相似三角形的面积比等于相似比的平方,黄金比等.27.(2011江苏省无锡市,27,8′)对于平面直角坐标系中的任意两点 ,我们把叫做两点间的直角距离,记作 . (1)已知O为坐标原点,动点满足 =1,请写出之间满足的关系式,并在所给的直角坐标系中出所有符合条件的点P所组成的图形;(2)设是一定点,是直线上的动点,我们把的最小值叫做到直线的直角距离,试求点M(2,1)到直线的直角距离。
全国各地2012年中考数学分类解析40;159套63专题41;_专题5_分式

2012年全国中考数学试卷分类解读汇编(159套63专题)专题5:分式一、选择题1. (2012安徽省4分)化简xxx x -+-112地结果是【 】 A.x +1 B. x -1 C.—x D. x 【答案】D.【考点】分式地加法运算【分析】分式地加减,首先看分母是否相同,同分母地分式加减,分母不变,分子相加减,如果分母不同,先通分,后加减,本题分母互为相反数,可以化成同分母地分式加减:222(1)111111x x x x x x x x x x x x x x x --+=-===------.故选D. 2. (2012浙江湖州3分)要使分式1x有意义,x 地取值范围满足【 】A .x=0B .x≠0C .x >0D .x <0 【答案】B.【考点】分式有意义地条件.【分析】根据分式分母不为0地条件,要使1x在实数范围内有意义,必须x≠0.故选B. 3.(2012浙江嘉兴、舟山4分)若分式x 1x+2-地值为0,则【 】 A . x=﹣2 B . x=0C . x=1或2D . x=1【答案】D.【考点】分式地值为零地条件.【分析】∵分式x 1x+2-地值为0,∴x 1=0x+2x+20-⎧⎪⎨⎪≠⎩,解得x=1.故选D.4. (2012浙江绍兴4分)化简111x x --可得【 】 A .21x x- B . 21x x--C .221x x x+- D .221x x x-- 【答案】B.【考点】分式地加减法.【分析】原式=211(1)x x x x x x--=---.故选B. 5. (2012浙江义乌3分)下列计算错误地是【 】A .0.2a b 2a b 0.7a b 7a b ++=--B .3223x y x y x y= C .a b 1b a -=-- D .123c c c +=【答案】A.【考点】分式地混合运算.【分析】根据分式地运算法则逐一作出判断:A 、0.2a b 2a 10b0.7a b 7a 10b ++=--,故本选项错误; B 、3223x y xyx y =,故本选项正确; C 、a b b a1b a b a --=-=---,故本选项正确; D 、123c c c+=,故本选项正确.故选A.6. (2012湖北武汉3分)一列数a1,a2,a3,…,其中a1= 1 2,an = 11+an -1 (n 为不小于2地整数),则a4=【 】A . 5 8B . 8 5C . 13 8D . 813【答案】 A.【考点】求代数式地值. 【分析】由 a1=12,an =n11+a ,得234123112113115a ===a ===a ===1231+a 31+a 51+a 81+1+1+235,,.故选A. 7. (2012湖北天门、仙桃、潜江、江汉油田3分)化简2211x+1x 1⎛⎫-÷ ⎪-⎝⎭地结果是【 】 A .()21x+1 B .()21x 1- C .(x+1)2 D .(x ﹣1)2【答案】D.【考点】分式地混合运算.【分析】将原式括号中地两项通分并利用同分母分式地减法法则计算,分子合并,同时将除式地分母利用平方差公式分解因式,然后利用除以一个数等于乘以这个数地倒数将除法运算化为乘法运算,约分后即可得到最简结果:()()()()()22x+1x 121x+121x 11===x 1x+1x 1x+1x+1x 1x+11---⎛⎫-÷÷⋅- ⎪--⎝⎭.故选D. 8. (2012湖北宜昌3分)若分式2a+1有意义,则a 地取值范围是【 】 A .a=0 B .a=1 C .a ≠﹣1 D .a ≠0 【答案】C.【考点】分式有意义地条件.【分析】根据分式分母不为0地条件,要使2a+1在实数范围内有意义,必须a+10a 1≠⇒≠-.故选C. 9. (2012四川凉山4分)已知b 5a 13=,则a b a b-+地值是【 】 A .23B .32C .94D .49【答案】D.【考点】比例地性质. 【分析】∵b 5a 13=,∴设出b=5k ,得出a=13k ,把a ,b 地值代入a ba b -+,得, a b 13k 5k 8k 4===a b 13k 5k 18k 9--++.故选D. 10. (2012山东临沂3分)化简4122aa a ⎛⎫+÷ ⎪--⎝⎭地结果是【 】 A .2a a + B . 2a a + C . 2a a - D .2aa - 【答案】A.【考点】分式地混合运算. 【分析】4+22+21==222a a a a a a a a a-⎛⎫+÷⋅ ⎪---⎝⎭.故选A. 11. (2012山东威海3分)化简22x 1+x 93x--地结果是【 】A.1x 3- B. 1x+3 C. 13x- D. 23x+3x 9-【答案】B.【考点】分式运算法则,平方差公式. 【分析】通分后约分化简即可:()()()222x x+32x 1x 31+x 93x x 9x+3x 3x+3--===----.故选B. 12. (2012山东淄博4分)化简222a 1a 1a a a 2a 1+-÷--+地结果是【 】 (A)1a (B)a (C)11a a +-(D)11a a -+ 【答案】A.【考点】分式地除法.【分析】()()()()2222a 1a 1a 1a 11==a a a 2a 1a a 1a 1a 1a-+-+÷⋅--+-+-.故选A.13. (2012广西钦州3分)如果把5xx+y地x 与y 都扩大10倍,那么这个代数式地值【 】 A .不变 B .扩大50倍 C .扩大10倍 D .缩小到原来地110【答案】A.【考点】分式地基本性质.【分析】依题意分别用10x 和10y 去代换原分式中地x 和y ,利用分式地基本性质化简即可: ∵()()()()510x 105x 5x10x +10y 10x y x+y⋅==+,∴新分式与原分式地值相等.故选A. 14. (2012河北省3分)化简221x 1x 1÷--地结果是【 】 A .2x 1- B .32x 1- C .2x+1 D .2(x+1)【答案】C.【考点】分式地乘除法. 【分析】将分式22x 1-地分母 因式分解,再将除法转化为乘法进行计算: 22122(x 1)x 1x 1(x 1)(x 1)x 1÷=⋅-=--+-+.故选C.15. (2012新疆区5分)若分式23x-有意义,则x 地取值范围是【 】 A .x ≠3 B .x=3 C .x <3 D .x >3 【答案】A.【考点】分式有意义地条件.【分析】根据分式分母不为0地条件,要使23x-在实数范围内有意义,必须3﹣x≠0,即x≠3.故选 A.二、填空题1. (2012天津市3分)化简()()22x1x 1x 1----地结果是 ▲ .【答案】1x 1-. 【考点】分式地加减法.【分析】根据同分母分式相加减,分母不变,只把分子相加减计算,然后约分即可得解:()()()222x1x 11==x 1x 1x 1x 1------. 2. (2012山西省3分)化简222x 1x 12+xx 2x+1x +x --⋅-地结果是 ▲ .【答案】3x. 【考点】分式地混合运算. 【分析】()()()()2222x+1x 1x 1x 12x 12123+=+=+=x x x+1x x x x x 2x+1x +x x 1----⋅⋅--. 3. (2012宁夏区3分)当a ▲ 时,分式1a 2+有意义. 【答案】2≠-.【考点】分式有意义地条件.【分析】根据分式分母不为0地条件,要使1a 2+在实数范围内有意义,必须a 20a 2+≠⇒≠-. 4. (2012浙江杭州4分)化简2m 163m 12--得 ▲ ;当m=﹣1时,原式地值为 ▲ .【答案】m+43,1.【考点】分式地化简和求值.【分析】先把分式地分子和分母分解因式并得出约分后即可,把m=﹣1代入上式即可求出当m=﹣1时原式地值:()()()2m+4m 4m 16m+4==3m 123m 43----; 当m=﹣1时,原式=1+4=13-. 5. (2012浙江台州5分)计算yxy x÷地结果是 ▲ .【答案】2x【考点】分式地乘法和除法.【分析】根据分式地乘法和除法运算法则计算即可:2y xxy =xy =x x=x x y÷÷⋅. 6. (2012浙江温州5分)若代数式21x 1--地值为零,则x= ▲ . 【答案】3.【考点】分式地值为零地条件,解分式方程. 【分析】由题意得,21x 1--=0,解得:x=3,经检验地x=3是原方程地根. 7. (2012江苏镇江2分)若117+m n m+n =,则n m+m n地值为 ▲ . 【答案】5.【考点】求分式地值,完全平方公式地应用.【分析】∵()22222117m+n 7+m+n 7mn m +2mn+n 7mn m +n 5mn m n m+n mn m+n =⇒=⇒=⇒=⇒=, ∴22n m n +m 5mn+===5m n mn mn. 8. (2012福建莆田4分)当1a 2=时,代数式22a 22a 1---地值为 ▲ . 【答案】1.【考点】分式约分化简,平方差公式.【分析】将分式地分子因式分解括后,约分化简.然后代a 地值求值即可:∵()()()22a+1a 12a 22=2=2a+12=2a a 1a 1-------, ∴当1a 2=时,代数式22a 212=2a=2=1a 12--⨯-.9. (2012福建宁德3分)化简: m m -2 + 22-m = ▲ .【答案】1.【考点】分式运算法则. 【分析】m 2m 2==1m 22m m 2m 2+-----. 10. (2012福建福州4分)计算:x -1x +1x = ▲ .【答案】1.【考点】分式地加减法.【分析】直接根据同分母地分数相加减进行计算即可:x -1x +1x =x -1+1x =1.11. (2012福建泉州4分)计算:m 1m 1m 1-=-- ▲ . 【答案】1.【考点】分式地运算.【分析】两分式分母相同,则分子可相加即可:m 1m 1=1m 1m 1m 1--=---. 12. (2012湖北恩施4分)当x= ▲ 时,函数23x 12y x 2-=-地值为零.【答案】﹣2.【考点】求函数值,分式地值为零地条件.【分析】令23x 12=0x 2--, 去分母得,3x2﹣12=0,移项系数化为1得,x2=4,解得x=2或x=﹣2. 检验:当x=2时,x ﹣2=0,故x=2不是原方程地解;当x=﹣2时,x ﹣2≠0. ∴x=﹣2是原方程地解.∴当x=﹣2时,函数23x 12y x 2-=-地值为零.13. (2012湖北黄冈3分)化简22x 11x x( +)x+1x 1x 2x+1÷----地结果是 ▲ .【答案】4x 1+. 【考点】分式地混合运算.【分析】原式被除式括号中地第一项分子利用平方差公式分解因式,分母利用完全平方公式分解因式,然后利用除以一个数等于乘以这个数地倒数将除法运算化为乘法运算,再利用乘法分配律将括号外边地项乘到括号中地每一项,约分后,找出两分母地最简公分母,通分并利用同分母分式地减法法则计算,约分后得到最简结果:()()()()()2222x 1x 1x 1x 11x x 1x x 1x 1( +) x+1 x 1x 1x x x x 1x 2x+1x 1⎡⎤+------+⎢⎥÷=+⋅=--++-⎢⎥-⎣⎦()()()()()()()()22x 1x 1x 1x 1x 1x 12x 24 ===x x 1x x 1x x 1x x 1x 1+-++-+-+⋅=-+++++. 14. (2012湖北黄冈3分)已知实数x 满足1x+=3x ,则21x +x地值为 ▲ _. 【答案】7.【考点】配方法地应用,完全平方公式.【分析】∵1x+=3x ,∴222222111x +=x ++22=x+2=32=7x x x ⎛⎫--- ⎪⎝⎭.15. (2012四川内江6分)已知三个数x, y, z,满足442,,,33xy yz zx x y y z z x =-==-+++则=++yzxz xy xyz▲【答案】-4.【考点】分式地化简求值,比例地性质.【分析】将该题中所有分式地分子和分母颠倒位置,化简后求出xy xz yz xyz ++地值,从而得到xyzxy xz yz++地值:∵442,,33xy yz zx x y y z z x =-==-+++ ,∴111113113,,244x y y z z x +=-+=+=- ∴三式相加,得1111332244xy z ⎛⎫++=-+-⎪⎝⎭,即11114x y z ++=-. ∴11114xy xz yz xyz z y x ++=++=-. ∴4xyzxy xz yz=-++.16. (2012四川德阳3分)计算:2x 25x 55x+=-- ▲ . 【答案】x 5+. 【考点】分式地加减法.【分析】公分母为x ﹣5,将分母化为同分母,再将分子因式分解,约分:()()22x 5x 5x 25x 25==x 5x 55x x 5x 5x 5+-+=-+-----.17. (2012辽宁大连3分)化简:a 11+a a-= ▲ . 【答案】1.【考点】分式地加减法.【分析】根据同分母加减地分式运算法则:同分母加减,分母不变,分子相加减计算即可:a 11a 1+1a+===1a a a a--. 18. (2012贵州黔南5分)若分式x 1x+1-地值为0,则x 地值为 ▲ .【答案】1.【考点】分式地值为零和有意义地条件.【分析】由分式地值为零和有意义地条件得x 1=0-,x +1≠0.由x 1=0-,得x=±1;由x +1≠0,得x≠-1. 综上,得x=1,即x 地值为1.19. (2012山东聊城3分)计算:24a 1+a 2a 4⎛⎫÷ ⎪--⎝⎭= ▲ . 【答案】a a+2. 【考点】分式地混合运算.【分析】将式子括号内部分通分,然后根据分式除法地运算法则,将其转化为乘法,再将分母中地式子因式分解,即可得到结果:()()22224a a 4+4a 2a a 2a 1+===a 2a a+2a 2a a+2a 4a 4---⎛⎫÷⋅⋅ ⎪----⎝⎭. 20. (2012山东泰安3分)化简:22()224m m mm m m -÷+--= ▲ . 【答案】6m -.【考点】分式地混合运算,平方差公式. 【分析】应用分配律即可:原式=2(2)(2)(2)(2)=2(2)(2)622m m m m m m m m m m m m m+-+-⨯-⨯--+=-+-. 或先通分计算括号里地,再算括号外地也可.21. (2012山东枣庄4分)化简11(m 1)m 1⎛⎫-+ ⎪+⎝⎭地结果是 ▲ .【答案】m.【考点】分式地混合运算.【分析】把(m+1)与括号里地每一项分别进行相乘,再把所得结果相加即可求出答案:11(m 1)=m 11=m m 1⎛⎫-++- ⎪+⎝⎭.三、解答题1. (2012北京市5分)已知a b =023≠,求代数式5a 2b(a 2)(a+2b)(a 2b)b ⋅---地值. 【答案】解:∵a b =023≠,即2a=b 3∴原式=21065b 2b b5a 2b 4132==22+6a 2b 82b 2b b 33-⋅--==++【考点】分式运算.【分析】先约分化简.然后代2a=b 3求值.(或设a=2k b=3k ,代入求值)2. (2012重庆市10分)先化简,再求值:223x 4 2x 2x 1x 1x 2x 1++-÷---+(),其中x 是不等式组 x 402x 51+⎧⎨+⎩><地整数解.【答案】解:原式=()()()()()()()()()222x 1x 1x 13x 43x 42x 2 x 1x 1 x 1x 1 x 2x 1x 1x 2⎡⎤+--++---⋅=⋅⎢⎥+-+-++-+⎢⎥⎣⎦()()()2x 1x 2 x 1 x 1x 1x 2x 1-+-=⋅=+-++. 又 x 402x 51+⎧⎨+⎩><①②,由①解得:x >-4,由②解得:x <-2.∴不等式组地解集为-4<x <-2,其整数解为-3. 当x=-3时,原式=3 1231--=-+. 【考点】分式地化简求值,一元一次不等式组地整数解.【分析】将原式括号中地第一项分母利用平方差公式分解因式,然后找出两分母地最简公分母,通分并利用同分母分式地减法法则计算,分子进行合并整理,同时将除式地分母利用完全平方公式分解因式,然后利用除以一个数等于乘以这个数地倒数将除法运算化为乘法运算,约分后即可得到结果.分别求出x 满足地不等式组两个一元一次不等式地解集,找出两解集地公共部分确定出不等式组地解集,在解集中找出整数解,即为x 地值.将x 地值代入化简后地式子中计算,即可得到原式地值.3. (2012陕西省5分)化简:2a bb a 2b a b a b a b--⎛⎫÷⎪+-+⎝⎭-. 【答案】解:原式=222(2a b)(a b)b(a b)a b 2a 2ab ab b ab b =(a b)(a b)a 2b (a b)(a 2b)---++--+--⋅+---- =22a 4ab 2a(a 2b)2a==(a b)(a 2b)(a b)(a 2b)a b------- 【考点】分式地混合运算.【分析】根据分式混合运算地法则先计算括号里面地,再把除法变为乘法进行计算即可. 4. (2012宁夏区6分)化简,求值:22x x xx 1x 2x 1--+-+ ,其中x=2【答案】解:原式=22x(x 1)x x(x 1)x(x 1)2x 2x ===x 1(x 1)(x 1)(x 1)(x 1)(x 1)(x 1)(x 1)x 1-+---+-+-+-+--.当1-【考点】分式地化简求值.【分析】将分子、分母因式分解,通分化简,再代值计算. 5. (2012广东佛山6分)化简:a+b b+cab bc-【答案】解:原式=111111c a++==b a c b a c ac-⎛⎫⎛⎫-- ⎪ ⎪⎝⎭⎝⎭.【考点】分式地加减法.【分析】应用分配率较简便,也可先通分,再计算.6. (2012广东广州10分)已知11+a b a ≠b ),求()()a bb a b a a b ---地值.【答案】解:∵11+a b a+bab∴()()()()()()22a+b a b a b a b a+b ===b a b a a b ab a b ab a b ab------- 【考点】分式地化简求值.【分析】由11+a b 得出a+bab()()a b b a b a a b ---通分(最简公分母为()ab a b -),分子因式分解,约分,化简得出a+bab,代入求出即可. 7. (2012广东深圳6分)已知a = -3,b =2,求代数式b a b ab a ba +++÷+222)11(地值.【答案】解:原式=()21=a b a b ab aba b ++⋅+. 当a = -3,b =2时,原式= ()11=326--⨯.【考点】分式运算法则.【分析】先将括号里面地通分后,将除法转换成乘法,约分化简.然后代a = -3,b =2地值,求出特殊角地三角函数值后进行二次根式化简.8. (2012广东湛江6分) 计算:21x x 1x 1---. 【答案】解:原式=()()()()()()2x+1x x 1==x+1x 1x+1x 1x+1x 1x 1-----.【考点】分式地加减法.【分析】首先通分,然后利用同分母地分式相加减地运算法则求解即可,注意运算结果需化为最简. 9. (2012广东肇庆7分) 先化简,后求值:21x (1)x 1x 1+÷--,其中x =-4. 【答案】解:原式()()()()x 1x 1x 1x 1x 11x ==x 1x 1x x 1x+-+--+⋅⋅+--. 当x=-4时,原式=-4+1=-3.【考点】分式地化简求值.【分析】先将括号内地部分通分,再将括号外地分式因式分解,然后根据分式地除法法则,将除法转化为乘法解答.10. (2012广东珠海6分)先化简,再求值:()2x1x+1x 1x x ⎛⎫-÷ ⎪--⎝⎭,其中. 【答案】解:原式=()()()()2x+1x 1x 1111==x x 1x+1x x 1x+1x--⋅⋅--.当时,原式. 【考点】分式地化简求值,二次根式化简.【分析】先将括号内地分式通分,进行加减后再算除法,计算时,要将除法转化为乘法.最后代入.11. (2012浙江宁波6分)计算:.2242+++-a a a .【答案】解:原式=()()222=22=22a a a a a a a +-++-+++.【考点】分式地加减法.【分析】首先把分子分解因式,再约分,合并同类项即可. 12. (2012浙江衢州6分)先化简,再选取一个你喜欢地数代入求值.【答案】解:原式=2x +1x 1-.∵x ﹣1≠0,∴x ≠1.取x=2代入得:原式=22+1=521-. 【考点】分式地化简求值,有理数地混合运算.【分析】根据同分母分式加减法则,分母不变,分子相加,根据已知得出x≠1,取任一个x≠1地数代入求出即可(答案不唯一).13. (2012江苏常州4分)x+1xx 1x+1--. 【答案】解:原式=()()()()()()()()2222x+1x x 1x +2x+1x +x 3x+1==x 1x+1x+1x 1x+1x 1x 1-------. 【考点】分式地加减法.【分析】分式地加减法通分,后化简.14. (2012江苏淮安4分)计算()13112+++∙-x x xx x 【答案】解:原式=()()()1131=1+31=41x x xx x x x xx +-∙++-++. 【考点】分式运算法则,平方差公式.【分析】先乘除,后加减,应用平方差公式分解后约分化简再合并同类项.15. (2012江苏连云港6分)化简221m 11+m m 2m+1-⎛⎫÷ ⎪-⎝⎭.【答案】解:原式=()()()2m 1m+1m 1=m m+1m 1m--⋅-. 【考点】分式地混合运算.【分析】将括号中地两项通,将除式地分子利用平方差公式分解因式,分母利用完全平方公式分解因式,同时利用除以一个数等于乘以这个数地倒数将除法运算化为乘法运算,约分后即可得到结果.16. (2012江苏南京9分)化简代数式22x 1x 1x 2x x --÷+,并判断当x 满足不等式组()x 212x 16+<⎧⎪⎨->-⎪⎩时该代数式地符号.【答案】解:()()()22x+1x 1x 1x 1x x+1==x 2x x x x+2x 1x+2---÷⋅+-.()x 212x 16+<⎧⎪⎨->-⎪⎩①②, 解不等式①,得x <-1. 解不等式②,得x >-2. ∴不等式组()x 212x 16+<⎧⎪⎨->-⎪⎩地解集是-2<x <-1.∵当-2<x <-1时,x+1<0,x+2>0, ∴x+1x+2<0,即该代数式地符号为负号. 【考点】分式地化简求值,解一元一次不等式组,不等式地性质.【分析】先化简代数式,做除法时要注意先把除法运算转化为乘法运算,而做乘法运算时要注意先把分子、分母能因式分解地先分解,然后约分化简.再分别求出一元一次不等式组中两个不等式地解,从而得到一元一次不等式组地解集,依此分别确定x+1<0,x+2>0,从而求解.17. (2012江苏南通8分)先化简,再求值:22x 4x 31(x 1)(x 2)x 1⎡⎤-++÷⎢⎥+--⎣⎦,其中x =6. 【答案】解:原式=()()()2(x 1)(x 2)+2x 4x+3x 2(x 1)(x 1)x +x 6x 1x 1===x 1(x 1)(x 2)x 3x 2x 3x 2x 3+---+----⋅⋅⋅-+-+-+-+.当x =6时,原式=6-1=5. 【考点】分式地化简求值.【分析】先把括号里面地分子分解因式,再约分化简,然后再通分计算,再把括号外地除法运算转化成乘法运算,再进行约分化简,最后把x=6代入即可求值.18. (2012江苏苏州5分)先化简,再求值:222a 4a+4a+1+a 1a 2a 1-⋅---,其中. 【答案】解:原式=()()()2a 22a+12a 2a +=+=a 1a+1a 1a 2a 1a 1a 1--⋅------.当时,原式.【考点】分式地化简求值,二次根式代简.【分析】将原式第二项第一个因式地分子利用完全公式分解因式,分母利用平方差公式分解因式,约分后再利用同分母分式地加法法则计算,得到最简结果.然后将a 地值代入化简后地式子中计算,即可得到原式地值.19. (2012江苏泰州4分)化简:aa a a a 211122+-÷--. 【答案】解:原式=()()()()+2+1+21+211=1==+11+1+1+1a a a a a a a a a a a a ---⋅---. 【考点】分式运算法则.【分析】先将减式除法转换成乘法,约分化简,最后通分.20. (2012江苏扬州8分)先化简:22a 1a 11a a +2a---÷,再选取一个合适地a 值代入计算. 【答案】解:原式=()()()a a+2a 1a+2a+1a+211=1==a a+1a 1a+1a+1a+1a+1--⋅----. 取a=2,原式=11=2+13--. 【考点】分式地化简求值.【分析】先将分式地除法转化为乘法进行计算,然后再算减法,最后取一个使分母和除式不为0地值代入即可(除0、-2、-1、1以外地数).21. (2012江苏镇江4分)化简:()22x 1x+1x 2x+1-÷-. 【答案】解:原式=()()()2x+1x 111=x+1x 1x 1-⋅--.【考点】分式运算法则.【分析】将第一个分式地分子分母因式分解,将除法转换成乘法,约分化简即可. 22. (2012福建龙岩5分)先化简,再求值:()32136+33a a a a-,其中=7a . 【答案】解:原式=()()222132+1=2+1=13a a a a a a a⋅---. 当=7a 时,原式=()271=36-. 【考点】分式运算法则.【分析】先将括号里面撮公因式后约分,化为完全平方式形式.然后代x 地值即可.23. (2012福建漳州8分)化简:222x 1x 2x 1x 1x x--+÷+-.【答案】解:原式=()()()()2x 1x 1 x x 1x x 1x 1+--⋅=+-.【考点】分式地乘除法.【分析】先把各分式地分子和分母因式分解以及除法运算转化为乘法运算 ,然后约分即可.24. (2012福建三明7分)化简:2112+x 4x+4x 16⎛⎫÷ ⎪--⎝⎭. 【答案】解:原式=()()()()()()x+4+x 4x+4x 42x ==x x+4x 422--⋅-.【考点】分式运算法则.【分析】先将括号里面地通分后,将除法转换成乘法,约分化简.25. (2012湖北黄石7分)先化简,后计算:2281a 9a 1a 6a 92a 6a 9--÷⋅++++,其中a 3=.【答案】解:原式=2(9)(9)2(3)12=993(3)a a a a a a a -++⋅⋅-+++.当a 3=时,原式. 【考点】分式地化简求值,二次根式化简.【分析】根据分式混合运算地法则把原式进行化简,再把a 地值代入进行二次根式化简即可.26. (2012湖北荆门8分)先化简,后求值:()21a+1a 3a 3a 1⎛⎫-⋅- ⎪--⎝⎭-,其中. 【答案】解:原式=()()()()()()()()a 1a 31a+1112a 3=a 3=a 3=a 3a+1a 1a 3a 1a 3a 1a 1⎛⎫---⎛⎫-⋅--⋅-⋅-⎪ ⎪ ⎪-------⎝⎭⎝⎭.当时,原式.【考点】分式地化简求值,二次根式化简.【分析】先将括号内地部分进行约分、通分,进行加减运算后再进行乘法运算,最后代入求值.27. (2012湖北恩施8分)先化简,再求值:22x +2x+1x 1xx+2x 1x+2-÷--,其中2. 【答案】解:原式=()()()2x+1x 1x x+1x 1==x+2x+1x 1x+2x+2x+2x+2-⋅---.当2时,原式. 【考点】分式地化简求值.【分析】根据分式混合运算地法则把原式进行化简,再把x 地值代入进行计算即可.28. (2012湖北荆州7分)先化简,后求值:()21a+1a 3a 3a 1⎛⎫-⋅- ⎪--⎝⎭-,其中. 【答案】解:原式=()()()()()()()()a 1a 31a+1112a 3=a 3=a 3=a 3a+1a 1a 3a 1a 3a 1a 1⎛⎫---⎛⎫-⋅--⋅-⋅-⎪ ⎪ ⎪-------⎝⎭⎝⎭.当时,原式.【考点】分式地化简求值,二次根式化简.【分析】先将括号内地部分进行约分、通分,进行加减运算后再进行乘法运算,最后代入求值.29. (2012湖北随州8分)先化简,再求值:22325x +2x +x 2x+2x 4⎛⎫÷ ⎪--⎝⎭.其中. 【答案】解: 原式=()()()()()()()()223x+2+2x 2x+2x 2325x +2x 5x+21+===x 2x+2x+2x 2x 5x+2x 5x+2x x 4--⎛⎫÷⋅ ⎪---⎝⎭.当时,原式.【考点】分式地化简求值.【分析】先通分计算括号里面地,然后将除法转化为乘法进行计算,化简后将代入求值. 30. (2012湖北十堰6分)先化简,再求值:21a 1+a+1a 1⎛⎫÷⎪-⎝⎭,其中a=2. 【答案】解:原式=()()222a 1+1a+1a a+1a==a a+1a 1a a 1a 1-⋅⋅---. 当a=2时,原式=2=221-. 【考点】分式地化简求值.【分析】将被除式中两项通分并利用同分母分式地加法法则计算,同时利用除以一个数等于乘以这个数地倒数将除法运算化为乘法运算,约分后得到最简结果,把a 地值代入化简后地式子中计算,即可得到原式地值.31. (2012湖北孝感6分)先化简,再求值:a b 2ab b2÷a a a ---⎛⎫⎪⎝⎭,其中a1,b1. 【答案】解:原式=()222a b a 2ab+b a b a 1a a a a ba b ---÷=⋅=--. 当a1,b1时,原式12. 【考点】分式地化简求值,二次根式地化简求值.【分析】先将括号内部分通分,再将分式除法转化为乘法进行计算.32. (2012湖北襄阳6分)先化简,再求值:2222b a 2ab+b 11a++a a b a ab ⎛⎫-⎛⎫÷⋅ ⎪ ⎪ ⎪-⎝⎭⎝⎭,其中.【答案】解:原式=()()()()222222a+b a b b a a +2ab+b a+b a a+b 1==a ab a a b abab a ab a+b --÷⋅-⋅⋅---.当时,原式=1=121-- 【考点】分式地化简求值;二次根式地化简求值.【分析】将原式第一项地分子利用平方差公式分解因式,分母提取a 分解因式,第二项括号中地两项通分并利用同分母分式地加法运算法则计算,分子利用完全平方公式分解因式,第三项通分并利用同分母分式地加法法则计算,然后利用除以一个数等于乘以这个数地倒数将除法运算化为乘法运算,约分后得到最简结果,将a 与b 地值代入化简后地式子中计算,即可得到原式地值. 33. (2012湖北鄂州8分)先化简222x 411()2x x 4x 4x 2x--÷--+-,再在0,-1,2中选取一个适当地数代入求值.【答案】解:原式=()()()()()()()()()222222x+3x 2x 411x 4+x 2+=x x 2=x x 2=x x+3=x +3x x 2x x 2x 2x 2x 2⎡⎤----⎢⎥÷⋅-⋅---⎢⎥---⎣⎦.取x=-1,原式= ()()21+31=13=2----. 【考点】分式运算法则.【分析】先将括号里面地通分后,将除法转换成乘法,约分化简.然后代x 地值,x 地值应使分式地分母或除式不为0. 34. (2012湖南娄底7分)先化简:21x 1x+1x 1⎛⎫-÷ ⎪-⎝⎭,再请你选择一个合适地数作为x 地值代入求值. 【答案】解:原式=()()x+1x 1x =x 1x+1x-⋅-.根据分式地意义可知,x ≠0,且x ≠±1, 取x=2,原式=2﹣1=1.【考点】分式地化简求值, 开放型.【分析】先通分计算括号里地,再计算括号外地,最后根据分式性质,找一个恰当地数2(此数不唯一)代入化简后地式子计算即可.35. (2012湖南长沙6分)先化简,再求值:2222a 2ab+b ba b a+b-+--,其中a=﹣2,b=1.【答案】解:原式=()()()2a b b a b b a a+b a b a+b a+b a+b a+b--+=+=-当a=﹣2,b=1时, 原式= 222+1-=-. 【考点】分式化简求值.【分析】先约分、通分化简.然后代a=﹣2,b=1求值. 36. (2012湖南益阳6分)计算代数式ac bca b a b---地值,其中a=1,b=2,c=3. 【答案】解:原式=()c a b ac bc ==c a b a b----. 当a=1、b=2、c=3时,原式=3.【考点】分式地化简求值.【分析】根据分式地加减法把原式进行化简,再把a=1,b=2,c=3代入进行计算即可.37. (2012湖南常德6分)化简:2x 11x 2x 1x 1x 1⎛⎫⎛⎫+÷+ ⎪ ⎪+⎝-⎭⎝-⎭-【答案】解:原式=32322222x x x 2x 2x 1x 1x x 1x ==2x 1x 1x 12x-+-++-+-÷⋅---. 【考点】分式地化简.【分析】先对两个括号里地分式进行通分运算,再把除法变乘法进行约分运算. 38. (2012湖南张家界6分)先化简:22a 42a+1a+2a 4-÷-,再用一个你最喜欢地数代替a 计算结果.【答案】解:原式=()()()2a 2a+21+1=+1a+2a 22a a-⋅-. ∵a ≠0,a ≠±2,∴a 可以等于1. 当a=1时,原式=1+1=2.【考点】分式地化简求值.【分析】先根据分式混合运算地法则把原式进行化简,再选取一个使分式地分母和除式不为0地合适a 地值代入进行计算即可.39. (2012湖南岳阳6分)先化简,再求值:2111x+11x x 1⎛⎫-÷ ⎪--⎝⎭,其中1x=2. 【答案】解:原式= ()()()()11x+1x 1=x 1+x+1=2x x+11x ⎛⎫-⋅-- ⎪-⎝⎭. 当1x=2时,原式=12=12⨯.【考点】分式地化简求值.【分析】把除法化成乘法,再根据乘法分配律展开得出x -1+x +1,合并同类项得出2x ,代入求出即可.40. (2012湖南永州6分)先化简,再求代数式22a+1a 2a+1+1a a 1-⎛⎫⋅ ⎪-⎝⎭地值,其中a=2.【答案】解:原式=()()()()()()()222a 1a a+1a 1a+1+a 1==a 1a+1a 1a a+1a 1a---⋅⋅---. 当a=2时,原式=2-1=1. 【考点】分式地化简求值.【分析】将第一个因式括号中地第一项分母利用平方差公式分解因式,约分化为最简分式,然后通分并利用同分母分式地加法法则计算,第二个因式地分子利用完全平方公式分解因式,约分后得到最简结果,将a 地值代入化简后地式子中计算,即可得到原式地值.41. (2012湖南湘潭6分)先化简,再求值:111a+1a 1a 1⎛⎫-÷ ⎪--⎝⎭,其中1. 【答案】解:原式=()()a 1a+111111a 12=a 1=1==a+1a 1a 1a+1a 1a+1a+1a+1---⎛⎫⎛⎫-÷-⋅--- ⎪ ⎪---⎝⎭⎝⎭.当1时,原式=【考点】分式地化简求值,二次根式化简.【分析】用分配律计算得出2a+1-,把a 地值代入求出即可. 42. (2012四川成都8分)化简:22b a 1a+b a b⎛⎫-÷ ⎪-⎝⎭ 【答案】解:原式=()()()()a+b a b a+b b a a ==a b a+b a+b a b a+ba --÷⋅--.【考点】分式地混合运算.【分析】先将括号里面地通分后,将除法转换成乘法,约分化简.43. (2012四川攀枝花6分)先化简,再求值:23x 4x+4x+1x 1x 1-⎛⎫-÷⎪--⎝⎭,其中x 满足方程:x2+x ﹣6=0.44. (2012四川宜宾5分)先化简,再求值:22x 1x x+1x 1x 1÷---,其中x=2tan45°. 【答案】解:原式=()()2x x+1x 2x x x==x+1x 11x 1x 1x 1x 1⋅-------.当x=2tan45°=2时,原式=2=221-. 【考点】分式地化简求值,特殊角地三角函数值.【分析】先根据分式混合运算地法则把原式进行化简,再把x 地值代入进行计算即可.45. (2012四川达州5分)先化简,再求值:624)373(+-÷+--a a a a ,其中1-=a 【答案】解:原式=()2164(4)(4)2(3)=24=2832(3)34a a a a a a a a a a a --+-+÷⋅+++++-.当1a =-时,原式=2×(-1)+8 =6.【考点】分式地化简求值.【分析】根据分式混合运算地法则把原式进行化简,再把1a =-代入进行计算即可.46. (2012四川广元7分)已知12a 1=-,请先化简,再求代数式地值:221a 2a 1(1)a 2a 4++-÷+- 【答案】解:∵12a 1=-, ∴3a 2=. 原式=2a 21(a 2)(a 2)a 2a 2a 1(a 1)+-+--⨯=+++. 当12a 1=-即3a 2=时,原式=33151(2)(1)22225-÷+=-÷=-. 【考点】分式地化简求值 【分析】先根据12a 1=-求出a 地值,再把原式进行化简,把a 地值代入所求代数式进行计算即可. 47. (2012四川绵阳8分)化简:211+x 1+2x x x ⎛⎫⎛⎫÷- ⎪ ⎪ ⎪⎝⎭⎝⎭【答案】解:原式=()()()2222x 1+x x+1x+1x x+1x 1===x x x x x+1x 1x 1x 1-÷⋅⋅---. 【考点】分式地混合运算.【分析】首先计算括号内地分式,然后将除法化为乘法,约分化简.48. (2012四川巴中5分)先化简,再求值:2211()x x 1(x 1)(x 1)-⋅++--其中1x 2=【答案】.解:原式=()()x x 1x 1x 1x 1=x x 1x x 14x 4x x 1+++-⋅+++. 当1x 2=时,x 10>+,∴原式=()x 1111===14x x 14x 242++⋅. 【考点】二次根式地化简求值,分式地化简求值.【分析】先根据分式混合运算地法则把原式进行化简,再把x 地值代入进行计算即可.(注意:x 1=+,在没有确定x 地取值范围之前,不能随便将绝对值符号去掉!)49. (2012四川资阳7分)先化简,再求值:2a 22a 1a 1a 1a 1--⎛⎫÷-- ⎪+-⎝⎭,其中a 是方程x2-x=6地根.【答案】解:原式=()()()()()()()2222a 12a 1a 2a 2a 2a a 2a 111====a 1a 1a 1a 1a 1a 1a a 2a a 1a 1a a-------+÷÷⋅++-++-----. ∵a 是方程x2-x=6地根,∴a2-a=6. ∴原式=211=6a a -. 【考点】分式地化简求值,一元二次方程地解.【分析】先根据分式混合运算地顺序把原式进行化简,再根据a 是方程x2-x=6地根求出a 地值,代入原式进行计算即可(本题整体代入).50. (2012四川自贡8分)已知a =211a 1()a 1a 1a--⋅-+地值. 【答案】解:原式=a 1a 1(a 1)(a 1)2(a 1)(a 1)a a+-+-+⨯=-+.当a ==. 【考点】分式地化简求值,分母有理化.菁【分析】先将括号里面地通分后,将除法转换成乘法,约分化简.然后代a =.51. (2012四川泸州5分)先化简,再求值:22x 2x 2x 1x 1x+1x 1--⎛⎫÷-- ⎪-⎝⎭,其中【答案】解:原式=()()()()()()()()()()()2x x 2x x 2x x 2x x 2x 12x+1x+11===x+1x 1x+1x+1x 1x+1x+1x 1x x 2x 1------÷÷⋅-----.当. 【考点】分式运算法则,二次根式化简.【分析】先将括号里面地通分后,将除法转换成乘法,约分化简.然后代x 地值进行二次根式化简. 52. (2012四川南充6分)计算:2a a 1a 1a 1-++-【答案】解:原式=()()a a 1a 1a+11a 1a 1a 1a 1a 1a 1-+=+==++-+++. 【考点】分式运算法则. 【分析】先将2a 1a 1--地分母分解因式,再分子分母约分后和aa 1+进行同分母加减. 53. (2012辽宁鞍山8分)先化简,再求值:221x 41x 1x +4x+4-⎛⎫-÷ ⎪-⎝⎭,其中11x=+13-⎛⎫⎪⎝⎭. 【答案】解:∵11x=+13-⎛⎫⎪⎝⎭,∴x=3+1=4.原式=()()()()()()22x+2x 2x+2x 2x 2x+2==x 1x 1x+2x 2x 1x+2---÷⋅----. 当x=4时,原式=4+241-=2. 【考点】分式地化简求值;负整数指数幂.【分析】先求出x 地值,再根据分式混合运算地法则把原式进行化简,再把x 地值代入进行计算即可.54. (2012辽宁本溪10分)先化简,再求值:22x x +4x+4x 4x+4x+4x 2--÷-,其中201x=2sin602-⎛⎫- ⎪⎝⎭.【答案】解:21x=2sin60=242-⎛⎫- ⎪⎝⎭原式=()()()2x+2xx 2x x+22==x+4x+4x+2x 2x+4x+4x+4--⋅---.当4时,原式=-【考点】分式运算法则,负整数指数幂,特殊角地三角函数值,二次根式化简.【分析】将x 化简,再将原式除法转换成乘法,约分后通分化简.最后代x 地值进行二次根式化简.55. (2012辽宁朝阳6分)计算(先化简,再求值):223a 121a+1a 1a 2a+1-⎛⎫-÷ ⎪--⎝⎭,其中. 【答案】解:原式=()()()()()()223a 12a+21a+1=a 1=a 1a+1a 1a+1a 1a 1--÷⋅-----,当时,原式-. 【考点】分式运算法则.【分析】先将括号里面地通分后,将除法转换成乘法,约分化简.然后代求值.56. (2012辽宁丹东8分)先化简,再求值:2x 11()x 11x x+÷--,其中x 1 【答案】解:原式=()()()22x+1x 1x 1x=x=x x+1=x +x x 1x 1--⋅⋅--.当x 1=时,原式=)211=21=2-【考点】分式地化简求值,二次根式化简.【分析】先将括号里面地通分后,将除法转换成乘法,约分化简.然后代x 地值,进行二次根式化简.【答案】解:原式=()22a 1a 12a aa ==1a 1a a 1aa -+-⋅⨯---.当a 1== (11-- 【考点】分式运算法则.【分析】先将括号里面地通分后,将除法转换成乘法,约分化简.然后代a 地值求值即可. 58. (2012辽宁锦州8分)先化简,再求值:2212212+1x x x x x x x ---÷---,其中3=x .【答案】解:原式=221211111===2(1)1(1)(1)x x x x x x x x x xx xx ----⋅-------- .当x =. 【考点】分式运算法则,二次根式化简.【分析】将除法转换成乘法,通分后化简.然后代x =. 59. (2012辽宁铁岭10分)先化简,在求值:22x 1x 5x 1()x 9x 3x 9--÷----,其中x=3tan30°+1. 【答案】解:原式=()()()()()()()()()()()()()()()22x x+35x 1x+3x 3x 1x 1x 2x+1x 11===x+3x 3x+3x 3x+3x 3x+3x 3x+3x 3x 1x 1-------÷÷⋅-------.又x=3tan30°+1=3,∴原式.【考点】分式运算法则,特殊角地三角函数值,二次根式化简.【分析】先将括号里面地通分后,将除法转换成乘法,约分化简.然后根据特殊角地三角函数值求出x 地值后,代入进行二次根式化简.60. (2012辽宁营口8分)在数学课上,教师对同学们说:“你们任意说出一个x 地值(x ≠0,1,2),我 立刻就知道式子xx x x 21)211(2--÷-+地计算结果”.请你说出其中地道理. 【答案】解:∵()21121112(1)===222212x x x x x x x x x x x x x x --+---+÷÷⋅------. ∴任意说出一个x 地值(x ≠0,1,2),立刻就知道式子211(1)22x x x x-+÷--地计算结果x . 【考点】分式运算法则.【分析】先将括号里面地通分后,将除法转换成乘法,约分化简.81. (2012贵州毕节8分)先化简,再求值:2213x x +x x+1x 3x 6x+9--÷--,其中 【答案】解:原式=()()()()213x x 311x 11x 1x x 1x 1x x 1x x 1xx 3--+-⋅=+==+++++-.当时,原式. 【考点】分式地化简求值,二次根式化简.【分析】将分式因式分解后约分,然后进行通分,最后代入数值计算. 82. 求出原式地值(﹣2,2使分式分母为0,不可取).(2012贵州六盘水8分)先化简代数式223a 2a+11a+2a 4-⎛⎫-÷ ⎪-⎝⎭,再从﹣2,2,0三个数中选一个恰当地数作为a 地值代入求值.【答案】解:原式=()()()()()()22a 1a+2a 2a+23a 1a 2==a+2a+2a 2a+2a 1a 1-----÷⋅---. 取a=0,原式=0201--=2. 【考点】分式地化简求值.【分析】先将括号里面地通分后,将除法转换成乘法,约分化简.然后从﹣2,2,0三个数中选择一个使分式分母和除式不为0地数0代入化简后地式子中计算,即可83. (2012贵州黔南5分)先化简:224x 2x+2x 4⎛⎫-÷⎪-⎝⎭,然后求当x=1时,这个代数式地值. 【答案】解:原式=()()()()22x+2x 2x+2x 22x+442x 2x 4==x+2x+2x x x----⋅⋅. 当x=1时,原式= 24=21-- 【考点】分式运算法则.【分析】先将括号里面地通分后,将除法转换成乘法,约分化简.然后代x 地值. 84. (2012贵州铜仁5分)化简:2112()x 1x 1x 1-÷+-- 【答案】解:原式=2222x 1x 122x 1==12x 1x 1x 1-----÷⋅----.【考点】分式地混合运算.【分析】把括号内地分式通分并进行同分母分式地加减运算,把分式地除法运算转化为乘法运算,然后约分即可得.86. (2012山东德州6分)已知:1,,求2222x 2xy+y x y --地值.【答案】解:原式=()()()2x y x y=x+y x y x+y---.当1,时,原式1-. 【考点】分式地化简求值.【分析】将原式地分子利用完全平方公式分解因式,分母利用平方差公式分解因式,约分后得到最简结果,将x 与y 地值代入,化简后即可得到原式地值.87. (2012山东东营4分)先化简,再求代数式23x 11x+2x+2-⎛⎫-÷ ⎪⎝⎭地值,其中x 是不等式组x 202x+18><-⎧⎨⎩地整数解.【答案】解:原式=()()()()x+1x 1x+23x 1x+21==x+2x+2x+2x+1x 1x+1---÷⋅-. 解不等式组x 202x+18><-⎧⎨⎩得2<x <72,∵x 是整数,∴x=3. 当x=3时,原式=14. 【考点】分式地化简求值,一元一次不等式组地整数解.【分析】先将括号内通分,再根据分式地除法进行化简,然后求出不等式组地整数解代入求值. 88. (2012山东菏泽6分)先化简,再求代数式地值.222()111a a a a a ++÷++-,其中2012(1)tan60a ︒=-+ 【答案】解:原式2(1)(2)1313(1)(1)(1)(1)1a a a a a a a a a aa a -++++=⨯=⨯=+-+--.当2012(1)tan60a ︒=-+ 原式==.【考点】分式地化简求值,特殊角地三角函数值.【分析】先把括号内地通分计算,再把除法转换为乘法计算化简,最后代值计算.89. (2012山东济南4分)化简:2a 1a 2a 1a 22a 4--+÷--. 【答案】解:原式2a 12(a 2)2a 2(a 1)a 1--=⨯=---. 【考点】分式地乘除法.。
(最新最全)2012年全国各地中考数学解析汇编(按章节考点整理)分3个考点精选48题)

(最新最全)2012年全国各地中考数学解析汇编(按章节考点整理)第十一章 因式分解(分3个考点精选48题)11.1 提公因式法(2012北京,9,4)分解因式:269mn mn m ++= .【解析】原式=m (n 2+6n +9)=m (n +3)2【答案】m (n +3)2【点评】本题考查了提公因式及完全平方的知识点。
(2012广州市,13, 3分)分解因式a 2-8a 。
【解析】提取公因式即可分解因式。
【答案】:a(a -8).【点评】本题考查了因式分解的方法。
比较简单。
(2012浙江省温州市,5,4分)把24a a -多项式分解因式,结果正确的是( )A. ()4a a -B. (2)(2)a a +-C. (2)(2)a a a +-D. 2(2)4a --【解析】分解因式按“一提二套”原则:有公因式的先提取公因式,再套用平方差公式或完全平方公式,本题可直接提公因式.【答案】A【点评】有公因式的要先提取公因式,然后再考虑运用平方差公式或完全平方公式进行分解.因式分解要分解到每个多项式因式都不能再分解为止,此题较基础.(湖南株洲市3,9)因式分解:22a a -= .【解析】22(2)a a a a -=-【答案】(2)a a -【点评】本题主要考查因式分解的常用方法及步骤:先提取公因式,再运用公式法进行分解. (2012四川成都,1l ,4分)分解因式:25x x -=________.解析:因式分解的基本方法是提取公因式法、公式法、分组分解法。
本题只有两项,所以,只能用提取公因式法和平方差公式法。
观察可知有公因式x ,提取公因式法分解为x(x-5)。
答案:x(x-5)。
点评:公因式的确定方法是:系数是各项系数的最大公约数,字母是各项都有的字母,指数取最小。
(2012湖北随州,11,4分)分解因式:249x -=______________________。
解析:22249(2)3(23)(23)x x x x -=-=+-。
2012年中考数学压轴题真题汇编动态综合型问

2012年中考数学压轴题真题汇编:动态综合型问题十、动态综合型问题1.(北京模拟)已知抛物线y =-x2+2x +m -2与y 轴交于点A (0,2m -7),与直线y =2x 交于点B 、C (B 在C 的右侧). (1)求抛物线的解析式;(2)设抛物线的顶点为E ,在抛物线的对称轴上是否存在一点F ,使得∠BFE =∠CFE ,若存在,求出点F 的坐标,若不存在,说明理由;(3)动点P 、Q 同时从原点出发,分别以每秒5个单位长度、每秒25个单位长度的速度沿射线OC 运动,以PQ 为斜边在直线BC 的上方作直角三角形PMQ (直角边分别平行于坐标轴),设运动时间为t 秒.若△PMQ 与抛物线y =-x2+2x +m -2有公共点,求t 的取值范围.2.(北京模拟)在平面直角坐标系中,抛物线y 1=ax2+3x +c 经过原点及点A (1,2),与x 轴相交于另一点B .(1)求抛物线y 1的解析式及B 点坐标;(2)若将抛物线y 1以x =3为对称轴向右翻折后,得到一条新的抛物线y 2,已知抛物线y 2与x 轴交于两点,其中右边的交点为C 点.动点P 从O 点出发,沿线段OC 向C 点运动,过P 点作x 轴的垂线,交直线OA 于D 点,以PD 为边在PD 的右侧作正方形PDEF . ①当点E 落在抛物线y 1上时,求OP 的长;②若点P 的运动速度为每秒1个单位长度,同时线段OC 上另一点Q 从C 点出发向O 点运动,速度为每秒2个单位长度,当Q 点到达O 点时P 、Q 两点停止运动.过Q 点作x 轴的垂线,与直线AC 交于G 点,以QG 为边在QG 的左侧作正方形QGMN .当t 为何值时,这两个正方形分3.(北京模拟)如图,在平面直角坐标系中,抛物线y =ax2+bx +4经过A (-3,0)、B (4,0)两点,且与y 轴交于点C ,点D 在x 轴的负半轴上,且BD =BC .动点P 从点A 出发,沿线段AB 以每秒1个单位长度的速度向点B 移动,同时动点Q 从点C 出发,沿线段CA 以某一速度向点A 移动.(1)求该抛物线的解析式;(2)若经过t 秒的移动,线段PQ 被CD 垂直平分,求此时t 的值;(3)该抛物线的对称轴上是否存在一点M ,使MQ +MA 的值最小?若存在,求出点M 的坐标;若不存在,请说明理由.4.(北京模拟)如图,在Rt △ABC 中,∠C =90°,AC =6,BC =8.动点P 从点A 开始沿折线AC -CB -BA 运动,点P 在AC ,CB ,BA 边上运动的速度分别为每秒3,4,5个单位.直线l 从与AC 重合的位置开始,以每秒43个单位的速度沿CB 方向移动,移动过程中保持l ∥AC ,且分别与CB ,AB 边交于E ,F 两点,点P 与直线l 同时出发,设运动的时间为t 秒,当点P 第一次回到点A 时,点P 和直线l 同时停止运动.(1)当t =5秒时,点P 走过的路径长为_________;当t =_________秒时,点P 与点E 重合; (2)当点P 在AC 边上运动时,将△PEF 绕点E 逆时针旋转,使得点P 的对应点M 落在EF 上,点F 的对应点记为点N ,当EN ⊥AB 时,求t 的值;(3)当点P 在折线AC -CB -BA 上运动时,作点P 关于直线EF 的对称点Q .在运动过程中,若形成的四边形PEQF 为菱形,请直接写出t 的值.5.(北京模拟)在等腰梯形ABCD 中,AB ∥CD ,AB =10,CD =6,AD =BC =4.点P 从点B 出发,沿线段BA 向点A 匀速运动,速度为每秒2个单位,过点P 作直线BC 的垂线PE ,垂足为E .设点P 的运动时间为t (秒). (1)∠A =___________°;(2)将△PBE 沿直线PE 翻折,得到△PB ′E ,若△PB ′E 与梯形ABCD 重叠部分的面积为S ,求S 与t 之间的函数关系式,并求出S 的最大值;(3)在整个运动过程中,是否存在以点D 、P 、B ′为顶点的三角形为直角三角形?若存在,求出t的值;若不存在,请说明理由.E B M C A Pl F N B C A 备用图 A C B D P EB ′AC BD 备用图6.(北京模拟)已知二次函数y=-33mx2+3mx-2的图象与x轴交于点A(23,0)、点B,与y轴交于点C.(1)求点B坐标;(2)点P从点C出发以每秒1个单位的速度沿线段CO向O点运动,到达点O后停止运动,过点P作PQ∥AC交OA于点Q,将四边形PQAC沿PQ翻折,得到四边形PQA′C′,设点P的运动时间为t.①当t为何值时,点A′恰好落在二次函数y=-33mx2+3mx-2图象的对称轴上;②设四边形PQA′C′落在第一象限内的图形面积为S,求S关于t的函数关系式,并求出S的最大值.7.(北京模拟)已知梯形ABCD中,AD∥BC,∠A=120°,E是AB的中点,过E点作射线EF ∥BC,交CD于点G,AB、AD的长恰好是方程x2-4x+a2+2a+5=0的两个相等实数根,动点P、Q分别从点A、E出发,点P以每秒1个单位长度的速度沿AB由A向B运动,点Q以每秒2个单位长度的速度沿EF由E向F运动,设点P、Q运动的时间为t(秒).(1)求线段AB、AD的长;(2)如果t>1,求△DPQ的面积S与时间t之间的函数关系式;(3)是否存在△DPQ是直角三角形的情况,如果存在,求出时间t;如果不存在,请说明理由.8.(天津模拟)如图,在平面直角坐标系中,直y=-x+42交x轴于点A,交y轴于点B.在线段OA上有一动点P,以每秒2个单位长度的速度由点O向点A匀速运动,以OP为边作正方形OPQM交y轴于点M,连接QA和QB,并从QA和QB的中点C和D向AB作垂线,垂足分别为点F和点E.设P点运动的时间为t秒,四边形CDEF的面积为S1,正方形OPQM与四边形CDEF 重叠部分的面积为S2.(1)直接写出A点和B点坐标及t的取值范围;(2)当t=1时,求S1的值;(3)试求S2与t的函数关系式(4)直接写出在整个运动过程中,点C和点D9.(上海模拟)已知Rt△ABC中,∠ACB=90°,点P是边AB上的一个动点,连接CP,过点B 作BD⊥CP,垂足为点D.(1)如图1,当CP经过△ABC的重心时,求证:△BCD∽△ABC;(2)如图2,若BC=2厘米,cot A=2,点P从点A向点B运动(不与点A、B重合),点P的速度是5厘米/秒,设点P运动的时间为t秒,△BCD的面积为S平方厘米,求S关于t的函数解析式,并写出自变量t的取值范围;(3)在(2)的条件下,若△PBC是以CP为腰的等腰三角形,求△BCD的面积.CAP BD图1CAP BD图2CA B备用图ABDQPE F10.(重庆模拟)如图,已知△ABC 是等边三角形,点O 是AC 的中点,OB =12,动点P 在线段AB 上从点A 向点B 以每秒3个单位的速度运动,设运动时间为t 秒.以点P 为顶点,作等边△PMN ,点M ,N 在直线OB 上,取OB 的中点D ,以OD 为边在△AOB 内部作如图所示的矩形ODEF ,点E 在线段AB 上.(1)求当等边△PMN 的顶点M 运动到与点O 重合时t 的值; (2)求等边△PMN 的边长(用含t 的代数式表示);(3)设等边△PMN 和矩形ODEF 重叠部分的面积为S ,请直接写出当0≤t≤2秒时S 与t 的函数关系式,并写出对应的自变量t 的取值范围;(4)点P 在运动过程中,是否存在点M ,使得△EFM 是等腰三角形?若存在,求出对应的t 的值;若不存在,请说明理由.11.(浙江某校自主招生)如图,正方形OABC 的顶点O 在坐标原点,且OA 边和AB 边所在直线的解析式分别为y =34x 和y =-4 3 x + 253. (1)求正方形OABC 的边长;(2)现有动点P 、Q 分别从C 、A 同时出发,点P 沿线段CB 向终点B 运动,速度为每秒1个单位,点Q 沿折线A →O →C 向终点C 运动,速度为每秒k 个单位,设运动时间为2秒.当k 为何值时,将△CPQ 沿它的一边翻折,使得翻折前后的两个三角形组成的四边形为菱形? (3)若正方形以每秒53个单位的速度沿射线AO 下滑,直至顶点B 落在x 轴上时停止下滑.设正方形在x 轴下方部分的面积为S ,求S 关于滑行时间t 的函数关系式,并写出相应自变量t 的取值范围.12.(浙江某校自主招生)如图,正方形/秒的速度向点B 匀速移动(点P 不与点A /秒的速度匀速移动.点P 、Q E .设点P 运动时间为t (秒).(1)当点Q 在线段BC 上运动时,点P (2)设△APE 的面积为S (cm 2),求S (3)当4<t <8时,求函数值S 的范围.A O D CB F E 备用图 AO DC BFE 备用图13.(浙江模拟)如图,菱形ABCD 的边长为6且∠DAB =60°,以点A 为原点、边AB 所在直线为x 轴且顶点D 在第一象限建立平面直角坐标系.动点P 从点D 出发沿折线D -C -B 向终点B 以每秒2个单位的速度运动,同时动点Q 从点A 出发沿x 轴负半轴以每秒1个单位的速度运动,当点P 到达终点时停止运动.设运动时间为t ,直线PQ 交边AD 于点E . (1)求出经过A 、D 、C 三点的抛物线解析式;(2)是否存在时刻t ,使得PQ ⊥BD ?若存在,求出t 值,若不存在,请说明理由; (3)设AE 长为y ,试求y 与t 之间的函数关系式;(4)若F 、G 为DC 边上两点,且点DF =FG =1,试在对角线DB 上找一点M 、抛物线对称轴上找一点N ,使得四边形FMNG 周长最小并求出周长最小值.14.(浙江模拟)如图,直线y =-x +5和直线y =kx -4交于点C (3,m ),两直线分别交y 轴于点A 和点B ,一平行于y 轴的直线l 从点C 出发水平向左平移,速度为每秒1个单位,运动时间为t ,且分别交AC 、BC 于点P 、Q ,以PQ 为一边向左侧作正方形PQDE . (1)求m 和k 的值;(2)当t 为何值时,正方形的边DE 刚好在y 轴上?(3)当直线l 从点C 出发开始运动的同时,点M 也同时在线段AB 上由点A 向点B 以每秒4个单位的速度运动,问点M 从进入正方形PQDE 到离开正方形持续的时间有多长?15.OA 在x 轴的正半轴上,点B 坐标为(3,1),以OB 所在直线为对称轴将△OAB 作轴对称变换得△OCB .动点P 从点O 出发,沿线段OA 向点A 运动,动点Q 从点C 出发,沿线段CO 向点O 运动.P 、Q 两点同时出发,速度都为每秒1个单位长度.设点P 运动的时间为t (秒). (1)求∠AOC 的度数; (2)记四边形BCQP 的面积为S (平方单位),求S 与t(3)设PQ 与OB 交于点M .①当△OMQ 为等腰三角形时,求t 的值. ②探究线段OM 长度的最大值,说明理由.16.(浙江模拟)已知直线y =43x +4与x 轴、y 轴分别相交于点A 、B ,点C 从O 点出发沿射线OA 以每秒1个单位长度的速度匀速运动,同时点D 从A 点出发沿AB 以每秒1个单位长度的速度向B 点匀速运动,当点D 到达B 点时C 、D 都停止运动.点E 是CD 的中点,直线EF ⊥CD 交y 轴于点F ,点E ′与E 点关于y 轴对称.点C 、D 的运动时间为t (秒). (1)当t =1时,AC =___________,点D 的坐标为(_____,_____(2)设四边形BDCO 的面积为S ,当0<t <3时,求S 与t (3)当直线EF 与△ABO 的一边垂直时,求t 的值;(3)当△EFE ′为等腰直角三角形时,直接写出t 的值.17.(浙江模拟)如图1,矩形ABCD 中,AB=21,AD =12,E 是CD 边上的一点,DE =16,M 是BC 边的中点,动点P 从点A 出发,沿边AB 以每秒1个单位长度的速度向终点B 运动.设动点P 的运动时间是t 秒. (1)求线段AE 的长;(2)当△ADE 与△PBM 相似时,求t 的值;(3)如图2,连接EP ,过点P 作PH ⊥AE 于H . ①当EP 平分四边形PMEH 的面积时,求t 的值;②以PE 为对称轴作线段BC 的轴对称图形B ′C ′,当线段B ′C ′ 与线段AE 有公共点时,写出t 的取值范围(直接写出答案).18.(浙江模拟)如图,抛物线与x 轴交于A (6,0)、B (19,0)两点,与y 轴交于点C (0,8),直线CD ∥x 轴交抛物线于另一点D .动点P 、Q 分别从C 、D 两点同时出发,速度均为每秒1个单位,点P 向射线DC 方向运动,点Q 向射线BD 方向运动,设P 、Q 运动的时间为t (秒),AQ 交CD 于E .(1)求抛物线的解析式;(2)求△APQ 的面积S 与t 的函数关系式;(3)连接BE .是否存在某一时刻t ,使得∠AEB =∠BDC ?D A CE B M P 图1 D A C E B M P H 图2 D A CE B M 备用图若存在,求出t 的值;若不存在,请说明理由.19.(浙江模拟)如图,抛物线y =ax2+bx +c (a >0)交x 轴于A 、B 两点(A 在B 的左侧),交y 轴于C 点,已知B 点坐标为(8,0),tan ∠ABC =1 2,△ABC 的面积为8.(1)求抛物线的解析式;(2)直线EF (EF ∥x 轴,且分别交y 轴、线段CB 于E 、F 两点)从C 点开始,以每秒1个单位的速度向下运动,与x 轴重合时停止运动;同时动点P 从B 点出发沿线段BO 以每秒2个单位的速度向终点O 运动,连接FP ,设运动时间为t 秒.是否存在t 的值,使以P 、B 、F 为顶点的三角形与△ABC 相似?若存在,求出t 的值;若不存在,请说明理由;(3)在(2)的条件下,连接AC 交EF 于点G .当t 为何值时,A 、P 、F 、G 所围成的图形是平行四边形、等腰梯形和等腰直角三角形.20.(浙江模拟)已知:如图,在平面直角坐标系中,△ABC 为等腰三角形,直线AC 的解析式为y =-2x +6,将△AOC 沿直线AC 折叠,点O 落在平面内的点E 处,直线AE 交x 轴于点D . (1)求直线AD 解析式;(2)动点P 从点B 出发,以每秒1个单位的速度沿x 轴正方向匀速运动,点Q 是射线CE 上的点,且∠P AQ =∠BAC .设点P 运动时间为t 秒,△POQ 的面积为S ,求S 与t 之间的函数关系式;(3)在(2)的条件下,直线CE 上是否存在一点F ,使以点F 、A 、D 、P 为顶点的四边形是平行四边形?若存在,求出t 值及Q21.(江苏无锡)如图,菱形ABCD 的边长为2cm ,∠DAB s 的速度,沿AC 向C 作匀速运动;与此同时,点Q 也从A 作匀速运动.当P 运动到C 点时,P 、Q 都停止运动.设点P 运动的时间为t s . (1)当P 异于A 、C 时,请说明PQ ∥BC ;(2)以P 为圆心、PQ 长为半径作圆,请问:在整个运动过程中,t 为怎样的值时,⊙P 与边BC 分别有1个公共点和2个公共点?C22.(江苏苏州)如图,正方形ABCD 的边AD 与矩形EFGH 的边FG 重合,将正方形ABCD 以lcm /s 的速度沿FG 方向移动,移动开始前点A 与点F 重合.在移动过程中,边AD 始终与边FG 重合,连接CG ,过点A 作CG 的平行线交线段GH 于点P ,连接PD .已知正方形ABCD 的边长为lcm ,矩形EFGH 的边FG 、GH 的长分别为4cm 、3cm .设正方形移动时间为x (s ),线段GP 的长为y (cm ),其中0≤x≤2.5.(1)试求出y 关于x 的函数关系式,并求当y =3时相应x 的值;(2)记△DGP 的面积为S 1,△CDG 的面积为S 2,试说明S 1-S 2是常数;(3)当线段PD 所在直线与正方形ABCD 的对角线AC 垂直时,求线段PD 的长.23.(江苏连云港)如图,甲、乙两人分别从A (1,3)、B (6,0)两点同时出发,点O 为坐标原点.甲沿AO 方向、乙沿BO 方向均以4km /h 的速度行走,t h 后,甲到达M 点,乙到达N 点.(1)请说明甲、乙两人到达O 点前,MN 与AB 不可能平行. (2)当t 为何值时,△OMN ∽△OBA ?(3)甲、乙两人之间的距离为MN 的长,设s =MN 2,求s 与t 之间的函数关系式,并求甲、乙两人之间距离的最小值.24.(江苏南通)如图,在△ABC 中,AB =AC =10厘米,BC =12厘米,D 是BC 的中点.点P 从B 出发,以a 厘米/秒(a >0)的速度沿BA 匀速向点A 运动,点Q 同时以1厘米/秒的速度从D 出发,沿DB 匀速向点B 运动,其中一个动点到达端点时,另一个动点也随之停止运动,设它们运动的时间为t 秒.(1)若a =2,△BPQ ∽△BDA ,求t 的值;FECBDA Q P(2)设点M 在AC 上,四边形PQCM 为平行四边形.①若a =52,求PQ 的长; ②是否存在实数a ,使得点P 在∠ACB 的平分线上?若存在,请求出a 的值;若不存在,请说明理由.25.(江苏宿迁)如图,在平面直角坐标系xO y 中,已知直线l 1:y =12x 与直线l 2:y =-x +6相交于点M ,直线l 2与x 轴相交于点N . (1)求M 、N 的坐标;(2)在矩形ABCD 中,已知AB =1,BC =2,边AB 在x 轴上,矩形ABCD 沿x 轴自左向右以每秒1个单位长度的速度移动.设矩形ABCD 与△OMN 的重合部分的面积为S ,移动的时间为t (从点B 与点O 重合时开始计时,到点A 与点N 重合时计时结束).直接写出S 与自变量t 之间的函数关系式(不需要给出解答过程);(3)在(2)的条件下,当t 为何值时,S 的值最大?并求出最大值.26.(江苏模拟)已知抛物线与x 轴交于B 、C (1,0)两点,与y 轴交于点A ,顶点坐标为(52,-2716).P 、Q 分别是线段AB 、OB 上的动点,它们同时分别从点A 、O 向B 点匀速运动,速度均为每秒1个单位,设P 、Q 运动时间为t (0≤t ≤4).(1)求此抛物线的解析式,并求出P 点的坐标(用t 表示);(2)当△OPQ 面积最大时求△OBP 的面积; (3)当t 为何值时,△OPQ 为直角三角形?(4)△OPQ 是否可能为等边三角形?若可能请求出t 的值;若不可能请说明理由,并改变Q 点的运动速度,使△OPQ 为等边三角形,求出Q 点运动的速度和此时t 的值. 27.(江苏模拟)如图,在梯形纸片ABCD 中,BC ∥AD ,∠A +∠D =90°,tan A =2,过点B 作BH ⊥AD 于H ,BC =BH =2.动点F 从点D 出发,以每秒1个单位的速度沿DH 运动到点H 停止,在运动过程中,过点F 作FE ⊥AD 交折线D -C -B 于点E ,将纸片沿直线EF 折叠,点C 、D 的对应点分别是点C 1、D 1.设F 点运动的时间是t (秒). (1)当点E 和点C 重合时,求t 的值;(2)在整个运动过程中,设△EFD 1或四边形EFD 1C 1与梯形ABCD 重叠部分面积为S ,求S 与t之间的函数关系式和相应自变量t 的取值范围;(3)平移线段CD ,交线段BH 于点G ,交线段AD 于点P .在直线BC 上存在点Q ,使△PGQ 为等腰直角三角形?若存在,求出线段QB 的长;若不存在,说明理由.28.(江苏模拟)如图1,直线l :y =-34x +3分别交x 轴、y 轴于B 、A 两点,等腰Rt △CDE 的斜边C D 在x 轴上,且C D =6.若直线l 以每秒3个单位的速度向上匀速运动,同时点C 从(6,0)开始以每秒2个单位的速度向右匀速运动(如图2),设运动后直线l 分别交x 轴、y 轴于N 、M 两点,以OM 、ON 为边作如图所示的矩形OMPN .设运动时间为t 秒. (1)求运动后点E 、点N 的坐标(用含t 的代数式表示);(2)设矩形OMPN 与运动后的△CDE 的重叠部分面积为S ,求S 与t 的函数关系式,并写出相应的t 的取值范围;(3)若直线l 和△CDE 运动后,直线l 上存在点Q 使∠OQC =90°,则当在线段MN 上符合条件的点Q 有且只有两个时,求t 的取值范围.(4)若H 是MP 的中点,当△PHE 为等腰三角形时,求出所有符合条件的t 值.29.(江苏模拟)如图,抛物线y =ax2+bx +c 的顶点为C (0,-3),与x 轴交于点A 、B (A 在B 的左侧),连接AC 、BC ,得等边△ABC .点P 从点B 出发,以每秒1个单位的速度向点A 运动,同时点Q 从点C 出发,以每秒3个单位的速度向y 轴负方向运动,连接PQ 交射线BC 于点D ,当点P 到达点A 时,点Q 停止运动.设运动时间为t 秒.(1)求抛物线的解析式;(2)设△PQC 的面积为S ,求S 关于t的函数关系式;(3)以点P 为圆心,PB 为半径的圆与射线BC 交于点E ,试说明:在点P 运动的过程中,线段DE 的长是一定值,并求出该定值.30.(河北)如图,点A (-5,0),B (-3,0),点C 在y 轴的正半轴上,∠CBO =45°,CD ∥AB ,∠CDA =90°.点P从点Q (4,0)出发,沿x 轴向左以每秒1个单位长的速度运动,运动时间为t 秒.D 1 A B C F ED H A B C D H 备用图备用图(1)求点C 的坐标; (2)当∠BCP =15°,求t 的值;(3)以点P 为圆心,PC 为半径的⊙P 随点P 的运动而变化,当⊙P 与四边形ABCD 的边(或边所在的直线)相切时,求t 的值.31.(河北模拟)如图,在Rt △ABC 中,∠C =90°,AB =10,AC =6.点P 从点A 出发沿AB 以每秒2个单位长的速度向点B 匀速运动;点Q 从点C 出发沿CA 以每秒1个单位长的速度向点A 匀速运动.运动过程中DE 保持垂直平分PQ ,且交PQ 于点D ,交折线PB -BC 于点E .点P 、Q 同时出发,当点P 到达点B 时停止运动,点Q 也随之停止.设点P 、Q 运动的时间是t 秒. (1)当t =______________秒,直线DE 经过点B ;当t =______________秒,直线DE 经过点A ; (2)四边形DPBE 能否成为直角梯形?若能,求t 的值;若不能,请说明理由; (3)当t 为何值时,点E 是BC 的中点?(4)以E 为圆心,EC 长为半径的圆能否与AB 、AC 、PQ 同时相切?若能,直接写出t 的值;若不能,请说明理由.32.(山东青岛)如图,在Rt △ABC 中,∠C =90º,AC =6cm ,BC =8cm ,D 、E 分别是AC 、AB 的中点,连接DE .点P 从点D 出发,沿DE 方向匀速运动,速度为1cm /s ;同时,点Q 从点B 出发,沿BA 方向匀速运动,速度为2cm /s ,当点P 停止运动时,点Q 也停止运动.连接PQ ,设运动时间为t (s )(0<t<4).解答下列问题: (1)当t 为何值时,PQ ⊥AB ?(2)当点Q 在B 、E 之间运动时,设五边形PQBCD 的面积为y (cm 2),求y 与t 之间的函数关系式; (3)在(2)的情况下,是否存在某一时刻t ,使PQ 分四边形BCDE 两部分的面积之比为S △PQE ∶S五边形PQBCD=1∶29?若存在,求出此时t 的值以及点E 到PQ 的距离h ;若不存在,请说明理由.33.(山东烟台)如图,在平面直角坐标系中,已知矩形ABCD 的三个顶点B (1,0),C (3,0),D (3,4),以A 为顶点的抛物线y =ax2+bx +c 过点C .动点P 从点A 出发,沿线段AB 向点BAB C 备用图E DBP运动,同时动点Q 从点C 出发,沿线段CD 向点D 运动.点P ,Q 的运动速度均为每秒1个单位,运动时间为t 秒.过点P 作PE ⊥AB 交AC 于点E . (1)直接写出点A 的坐标,并求出抛物线的解析式;(2)过点E 作EF ⊥AD 于F ,交抛物线于点G .当t 为何值时,△ACG 的面积最大?最大值为多少?(3)在动点P ,Q 运动的过程中,当t 为何值时,在矩形ABCD 内(包括边界)存在点H ,使以C ,Q ,E ,H 为顶点的四边形为菱形?请直接写出t34.(山东模拟)把Rt △ABC 和Rt △DEF 按图1摆放(点C 与点E 重合),点B 、C (E )、F 在同一条直线上.∠BAC =∠DEF =90°,∠ABC =45°,BC=9,DE =6,EF =8.如图2,△DEF 从图1的位置出发,以1个单位/秒的速度沿CB 向△ABC 匀速移动,在△DEF 移动的同时,点P 从△DEF 的顶点F 出发,以3个单位/秒的速度沿FD 向点D 匀速移动.当点P 移动到点D 时,P 点停止移动,△DEF 也随之停止移动.DE 与AC 相交于点Q ,连接BQ 、PQ ,设移动时间为t (s ).(1)设△BQE 的面积为y ,求y 与t 之间的函数关系式,并写出自变量t 的取值范围; (2)当t 为何值时,三角形DPQ 为等腰三角形?(3)是否存在某一时刻t ,使P 、Q 、B 三点在同一条直线上?若存在,求出此时t 的值;若不存在,说明理由.35.(山东模拟)如图,在△ABC 中,AB =AC =10cm ,BD ⊥AC 于D ,且BD =8cm .点M 从点A 出发,沿AC 方向匀速运动,速度为2cm /s ;同时直线PQ 由点B 出发沿BA 方向匀速运动,速度为1cm /s ,运动过程中始终保持PQ ∥AC ,直线PQ 交AB 于P ,交BC 于Q ,连接PM ,设运动时间为t (s ).(1)当四边形PQCM 是等腰梯形时,求t 的值;(2)当点M 在线段PC 的垂直平分线上时,求t 的值;(3)当t 为何值时,①△PQM 是等腰三角形;②△PQM 是直角三角形;(4)是否存在时刻t ,使以PM 为直径的圆与BC 相切?若存在,求出t 的值;若不存在,请说明理由.(E ) A B D C F 图1 A B DE F 图2PQC36.(内蒙古包头、乌兰察布)如图,在Rt △ABC 中,∠C =90°,AC =4cm ,BC =5cm ,点D 在BC 上,且CD =3cm .现有两个动点P 、Q 分别从点A 和点B 同时出发,其中点P 以l cm /秒的速度沿AC 向终点C 运动;点Q 以1.25cm /秒的速度沿BC 向终点C 运动.过点P 作PE ∥BC 交AD 于点E ,连接EQ .设动点运动时间为t 秒(t >0).(1)连接DP ,经过1秒后,四边形EQDP(2)连接PQ ,在运动过程中,不论t 取何值时,总有线段PQ 与线段AB (3)当t 为何值时,△EDQ 为直角三角形. 37.(内蒙古呼伦贝尔)如图①,在平面直角坐标系内,Rt △ABC ≌Rt △FED ,点C 、D 与原点O 重合,点A 、F 在y 轴上重合,∠B =∠E =30°,AC =FD =3.△FED 不动,△ABC 沿直线BE 以每秒1个单位的速度向右平移,直到点B 与点E 重合为止,平移过程中AB 与EF 的交点为M . (1)求出图①中点B 的坐标;(2)如图②,当x =4秒时,求出过F 、M 、A 三点的抛物线的解析式;此抛物线上有一动点P ,以点P 为圆心,以2为半径的⊙P 在运动过程中是否存在与y 轴相切的情况,若存在,直接写出P 点的坐标;若不存在,请说明理由;(3)设移动x 秒后两个三角形重叠部分的面积为S ,求出整个运动过程中S 与x 的函数关系式.38.(哈尔滨模拟)如图,在平面直角坐标系中,O 为坐标原点,Rt △OAB 的直角边OA 在x 轴正半轴上,且OA =4,AB =2,将△OAB 沿某条直线翻折,使OA 与y 轴正半轴的OC 重合.点B 的对应点为点D ,连接AD 交OB 于点E . (1)求AD 所在直线的解析式:(2)连接BD ,若动点M 从点A 出发,以每秒2个单位的速度沿射线AO 运动,线段AM 的垂直平分线交直线AD 于点N ,交直线BD 子Q ,设线段QN 的长为y (y ≠0),点M 的运动时间为t 秒,求y 与t 之问的函数关系式(直接写出自变量t 的取值范围);(3)在(2)的条件下,连接MN ,当t 为何值时,直线MN 与过D 、E 、O 三点的圆相切,并求备用图图① 图②39.(哈尔滨模拟)如图,在平面直角坐标系中,直线y =x +b 与x 轴交于点A ,与正比例函数y =-43x 的图象交于点B ,过B 点作BC ⊥y 轴,点C 为垂足,C (0,8). (1)求直线AB 的解析式;(2)动点M 从点A 出发沿线段AO 以每秒1个单位的速度向终点O 匀速移动,过点M 作x 轴的垂线交折线A -B -O 于点P .设M 点移动的时间为t 秒,线段BP 的长为d ,求d 与t 之间的函数关系式,并直接写出自变量t 的取值范围;(3)在(2)的条件下,动点Q 同时从原点O 出发,以每秒1个单位的速度沿折线O -C -B 向点B 移动,当动点M 停止移动时,点Q 同时停止移动.当t 为何值时,△BPQ 是以BP 为一腰的等腰三角形?40.(哈尔滨模拟)如图,直线y =43x +12分别与x 轴、y 轴交于点A 、B ,直线BC 交x 轴于点C ,且AB =AC .(1)求直线BC 的解析式;(2)点P 从点C 出发沿线段CO 以每秒1个单位的速度向点O 运动,过点P 作y 轴的平行线,分别交直线BC 、直线AB 于点Q 、M ,过点Q 作QN ⊥AB 于点N .设点P 的运动时间为t (秒),线段MN 的长为d ,求d 与t 的函数关系式,并直接写出自变量t 的取值范围;(3)若经过A 、N 、Q 三点的圆与直线BC 交于另一点K ,当t 为何值时,KQ :AQ =10 :10?41.(哈尔滨模拟)如图,直线y =-kx +6k (k>0)与x 轴、y 轴交于点A 、B ,且△AOB 的面积是24.(1)求直线AB 的解析式;(2)点P 从点O 出发,以每秒2个单位的速度沿折线OA -AB 运动;同时点E 从点O 出发,以每秒1个单位的速度沿y 轴正半轴运动,过点E 作与x 轴平行的直线l ,与线段AB 相交于点F ,备用图备用图当点P 与点F 重合时,点P 、E 均停止运动.连接PE 、PF ,设△PEF 的面积为S ,点P 运动的时间为t 秒,求S 与t 的函数关系式,并直接写出自变量t 的取值范围;(3)在(2)的条件下,过P 作x 轴的垂线,与直线l 相交于点M ,连接AM ,当tan ∠MAB =12时,求t 的值.42.(哈尔滨模拟)如图,在平面直角坐标系中,O 为坐标原点,点A 在x 轴的正半轴上,△AOB 为等腰三角形,且OA =OB ,过点B 作y 轴的垂线,垂足为D ,直线AB 的解析式为y =-3x +30,点C 在线段BD 上,点D 关于直线OC 的对称点在腰OB 上. (1)求点B 坐标;(2)点P 从点B 出发,以每秒1个单位的速度沿折线BC -CO 运动;同时点Q 从点O 出发,以每秒1个单位的速度沿对角线OB 向终点B 运动,当一点停止运动时,另一点也随之停止运动.设△PQC 的面积为S ,运动时间为t ,求S 与t 的函数关系式,并写出自变量t 的取值范围; (3)在(2)的条件下,连接PQ ,设PQ 与OB 所成的锐角为α,当α=90°-∠AOB 时,求t 的值.43.(哈尔滨模拟)如图,在平面直角坐标系中,点A (256,0),点B (3,4),将△OAB 沿直线OB 翻折,点A 落在第二象限内的点C 处. (1)求点C 的坐标;(2)动点P 从点O 出发,以每秒5个单位的速度沿OB 向终点B 运动,连接AP ,将射线AP 绕着点A 逆时针旋转与y 轴交于一点Q ,且旋转角α=12∠OAB .设线段OQ 的长为d ,点P 运动的时间为t 秒,求d 与t 的函数关系式(直接写出时间t 的取值范围);(3)在(2)的条件下,连接CP .点P 在运动的过程中,是否存在CP ∥AQ ,若存在,求此时t 的值,并辨断点B 与以点P 为圆心,OQ 长为半径的⊙P 的位置关系;若不存在,请说明理由.。
2012年全国各地中考数学动态试题(部分)+答案

1.(2012•菏泽)如图,在平面直角坐标系中放置一直角三角板,其顶点为A(0,1),B(2,0),O(0,0),将此三角板绕原点O逆时针旋转90°,得到△A′B′O.(1)一抛物线经过点A′、B′、B,求该抛物线的解析式;(2)设点P是在第一象限内抛物线上的一动点,是否存在点P,使四边形PB′A′B的面积是△A′B′O面积4倍?若存在,请求出P的坐标;若不存在,请说明理由.(3)在(2)的条件下,试指出四边形PB′A′B是哪种形状的四边形?并写出四边形PB′A′B 的两条性质.2.(2012•宁波)如图,二次函数y=ax2+bx+c的图象交x轴于A(﹣1,0),B(2,0),交y轴于C(0,﹣2),过A,C画直线.(1)求二次函数的解析式;(2)点P在x轴正半轴上,且PA=PC,求OP的长;(3)点M在二次函数图象上,以M为圆心的圆与直线AC相切,切点为H.①若M在y轴右侧,且△CHM∽△AOC(点C与点A对应),求点M的坐标;②若⊙M的半径为,求点M的坐标.3.(2012•福州)如图1,已知抛物线y=ax2+bx(a≠0)经过A(3,0)、B(4,4)两点.(1)求抛物线的解析式;(2)将直线OB向下平移m个单位长度后,得到的直线与抛物线只有一个公共点D,求m 的值及点D的坐标;(3)如图2,若点N在抛物线上,且∠NBO=∠ABO,则在(2)的条件下,求出所有满足△POD∽△NOB的点P坐标(点P、O、D分别与点N、O、B对应).4.(2012•临沂)如图,点A在x轴上,OA=4,将线段OA绕点O顺时针旋转120°至OB 的位置.(1)求点B的坐标;(2)求经过点A、O、B的抛物线的解析式;(3)在此抛物线的对称轴上,是否存在点P,使得以点P、O、B为顶点的三角形是等腰三角形?若存在,求点P的坐标;若不存在,说明理由.5.(2012•烟台)如图,在平面直角坐标系中,已知矩形ABCD的三个顶点B(1,0),C(3,0),D(3,4).以A为顶点的抛物线y=ax2+bx+c过点C.动点P从点A出发,沿线段AB 向点B运动.同时动点Q从点C出发,沿线段CD向点D运动.点P,Q的运动速度均为每秒1个单位.运动时间为t秒.过点P作PE⊥AB交AC于点E.(1)直接写出点A的坐标,并求出抛物线的解析式;(2)过点E作EF⊥AD于F,交抛物线于点G,当t为何值时,△ACG的面积最大?最大值为多少?(3)在动点P,Q运动的过程中,当t为何值时,在矩形ABCD内(包括边界)存在点H,使以C,Q,E,H为顶点的四边形为菱形?请直接写出t的值.6.(2012•义乌市)如图1,已知直线y=kx与抛物线y=交于点A(3,6).(1)求直线y=kx的解析式和线段OA的长度;(2)点P为抛物线第一象限内的动点,过点P作直线PM,交x轴于点M(点M、O不重合),交直线OA于点Q,再过点Q作直线PM的垂线,交y轴于点N.试探究:线段QM 与线段QN的长度之比是否为定值?如果是,求出这个定值;如果不是,说明理由;(3)如图2,若点B为抛物线上对称轴右侧的点,点E在线段OA上(与点O、A不重合),点D(m,0)是x轴正半轴上的动点,且满足∠BAE=∠BED=∠AOD.继续探究:m在什么范围时,符合条件的E点的个数分别是1个、2个?7.(2012•益阳)已知:如图1,在面积为3的正方形ABCD中,E、F分别是BC和CD边上的两点,AE⊥BF于点G,且BE=1.(1)求证:△ABE≌△BCF;(2)求出△ABE和△BCF重叠部分(即△BEG)的面积;(3)现将△ABE绕点A逆时针方向旋转到△AB′E′(如图2),使点E落在CD边上的点E′处,问△ABE在旋转前后与△BCF重叠部分的面积是否发生了变化?请说明理由.8.(2012•丽水)在△ABC中,∠ABC=45°,tan∠ACB=.如图,把△ABC的一边BC放置在x轴上,有OB=14,OC=,AC与y轴交于点E.(1)求AC所在直线的函数解析式;(2)过点O作OG⊥AC,垂足为G,求△OEG的面积;(3)已知点F(10,0),在△ABC的边上取两点P,Q,是否存在以O,P,Q为顶点的三角形与△OFP全等,且这两个三角形在OP的异侧?若存在,请求出所有符合条件的点P的坐标;若不存在,请说明理由.9.(2012•广州)如图,抛物线y=与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C.(1)求点A、B的坐标;(2)设D为已知抛物线的对称轴上的任意一点,当△ACD的面积等于△ACB的面积时,求点D的坐标;(3)若直线l过点E(4,0),M为直线l上的动点,当以A、B、M为顶点所作的直角三角形有且只有三个时,求直线l的解析式.10.(2012•杭州)如图,AE切⊙O于点E,A T交⊙O于点M,N,线段OE交A T于点C,OB⊥A T于点B,已知∠EA T=30°,AE=3,MN=2.(1)求∠COB的度数;(2)求⊙O的半径R;(3)点F在⊙O上(是劣弧),且EF=5,把△OBC经过平移、旋转和相似变换后,使它的两个顶点分别与点E,F重合.在EF的同一侧,这样的三角形共有多少个?你能在其中找出另一个顶点在⊙O上的三角形吗?请在图中画出这个三角形,并求出这个三角形与△OBC 的周长之比.11.(2012•重庆)已知:如图,在直角梯形ABCD中,AD∥BC,∠B=90°,AD=2,BC=6,AB=3.E为BC边上一点,以BE为边作正方形BEFG,使正方形BEFG和梯形ABCD在BC的同侧.(1)当正方形的顶点F恰好落在对角线AC上时,求BE的长;(2)将(1)问中的正方形BEFG沿BC向右平移,记平移中的正方形BEFC为正方形B′EFG,当点E与点C重合时停止平移.设平移的距离为t,正方形B′EFG的边EF与AC交于点M,连接B′D,B′M,DM,是否存在这样的t,使△B′DM是直角三角形?若存在,求出t的值;若不存在,请说明理由;(3)在(2)问的平移过程中,设正方形B′EFG与△ADC重叠部分的面积为S,请直接写出S与t之间的函数关系式以及自变量t的取值范围.12.(2012•泰安)如图,半径为2的⊙C与x轴的正半轴交于点A,与y轴的正半轴交于点B,点C的坐标为(1,0).若抛物线y=﹣x2+bx+c过A、B两点.(1)求抛物线的解析式;(2)在抛物线上是否存在点P,使得∠PBO=∠POB?若存在,求出点P的坐标;若不存在说明理由;(3)若点M是抛物线(在第一象限内的部分)上一点,△MAB的面积为S,求S的最大(小)值.13.(2012•铜仁地区)如图已知:直线y=﹣x+3交x轴于点A,交y轴于点B,抛物线y=ax2+bx+c经过A、B、C(1,0)三点.(1)求抛物线的解析式;(2)若点D的坐标为(﹣1,0),在直线y=﹣x+3上有一点P,使△ABO与△ADP相似,求出点P的坐标;(3)在(2)的条件下,在x轴下方的抛物线上,是否存在点E,使△ADE的面积等于四边形APCE的面积?如果存在,请求出点E的坐标;如果不存在,请说明理由.14.(2012•温州)如图,经过原点的抛物线y=﹣x2+2mx(m>0)与x轴的另一个交点为A.过点P(1,m)作直线PM⊥x轴于点M,交抛物线于点B.记点B关于抛物线对称轴的对称点为C(B、C不重合).连接CB,CP.(1)当m=3时,求点A的坐标及BC的长;(2)当m>1时,连接CA,问m为何值时CA⊥CP?(3)过点P作PE⊥PC且PE=PC,问是否存在m,使得点E落在坐标轴上?若存在,求出所有满足要求的m的值,并定出相对应的点E坐标;若不存在,请说明理由.15.(2012•成都)如图,在平面直角坐标系xOy中,一次函数(m为常数)的图象与x轴交于点A(﹣3,0),与y轴交于点C.以直线x=1为对称轴的抛物线y=ax2+bx+c (a,b,c为常数,且a≠0)经过A,C两点,并与x轴的正半轴交于点B.(1)求m的值及抛物线的函数表达式;(2)设E是y轴右侧抛物线上一点,过点E作直线AC的平行线交x轴于点F.是否存在这样的点E,使得以A,C,E,F为顶点的四边形是平行四边形?若存在,求出点E的坐标及相应的平行四边形的面积;若不存在,请说明理由;(3)若P是抛物线对称轴上使△ACP的周长取得最小值的点,过点P任意作一条与y轴不平行的直线交抛物线于M1(x1,y1),M2(x2,y2)两点,试探究是否为定值,并写出探究过程.16.(2012•梅州)如图,矩形OABC中,A(6,0)、C(0,2)、D(0,3),射线l 过点D且与x轴平行,点P、Q分别是l和x轴正半轴上动点,满足∠PQO=60°.(1)①点B的坐标是;②∠CAO=度;③当点Q与点A重合时,点P的坐标为;(直接写出答案)(2)设OA的中心为N,PQ与线段AC相交于点M,是否存在点P,使△AMN为等腰三角形?若存在,请直接写出点P的横坐标为m;若不存在,请说明理由.(3)设点P的横坐标为x,△OPQ与矩形OABC的重叠部分的面积为S,试求S与x的函数关系式和相应的自变量x的取值范围.17.(2012•株洲)如图,一次函数分别交y轴、x轴于A、B两点,抛物线y=﹣x2+bx+c过A、B两点.(1)求这个抛物线的解析式;(2)作垂直x轴的直线x=t,在第一象限交直线AB于M,交这个抛物线于N.求当t取何值时,MN有最大值?最大值是多少?(3)在(2)的情况下,以A、M、N、D为顶点作平行四边形,求第四个顶点D的坐标.18.(2012•南充)如图,⊙C的内接△AOB中,AB=AO=4,tan∠AOB=,抛物线y=ax2+bx经过点A(4,0)与点(﹣2,6).(1)求抛物线的函数解析式;(2)直线m与⊙C相切于点A,交y轴于点D.动点P在线段OB上,从点O出发向点B 运动;同时动点Q在线段DA上,从点D出发向点A运动;点P的速度为每秒一个单位长,点Q的速度为每秒2个单位长,当PQ⊥AD时,求运动时间t的值;(3)点R在抛物线位于x轴下方部分的图象上,当△ROB面积最大时,求点R的坐标19.(2012•凉山州)如图,在平面直角坐标系中,直线y=x+4与x轴、y轴分别交于A、B 两点,抛物线y=﹣x2+bx+c经过A、B两点,并与x轴交于另一点C(点C点A的右侧),点P是抛物线上一动点.(1)求抛物线的解析式及点C的坐标;(2)若点P在第二象限内,过点P作PD⊥轴于D,交AB于点E.当点P运动到什么位置时,线段PE最长?此时PE等于多少?(3)如果平行于x轴的动直线l与抛物线交于点Q,与直线AB交于点N,点M为OA的中点,那么是否存在这样的直线l,使得△MON是等腰三角形?若存在,请求出点Q的坐标;若不存在,请说明理由.20.(2012•衢州)如图,把两个全等的Rt△AOB和Rt△COD分别置于平面直角坐标系中,使直角边OB、OD在x轴上.已知点A(1,2),过A、C两点的直线分别交x轴、y轴于点E、F.抛物线y=ax2+bx+c经过O、A、C三点.(1)求该抛物线的函数解析式;(2)点P为线段OC上一个动点,过点P作y轴的平行线交抛物线于点M,交x轴于点N,问是否存在这样的点P,使得四边形ABPM为等腰梯形?若存在,求出此时点P的坐标;若不存在,请说明理由.(3)若△AOB沿AC方向平移(点A始终在线段AC上,且不与点C重合),△AOB在平移过程中与△COD重叠部分面积记为S.试探究S是否存在最大值?若存在,求出这个最大值;若不存在,请说明理由.简答参考答案、1.①y=﹣x2+x+2②P(1,2)③、①∠B′A′B=∠PBA′或∠A′B′P=∠BPB′;②PA′=B′B;③B′P∥A′B;④B′A′=PB.2.①y=x2﹣x﹣2;②OP=;③的第一问M(1,﹣2)M′(,),第二问点M的坐标为(,3+)或(,3﹣).3. ①y=x2﹣3x②m=4,(2,﹣2)③点P的坐标是(,)或(,)4.①点B的坐标为(﹣2,﹣2)②y=﹣x2+x③(2,﹣2)5.①y=﹣x2+2x+3.②当t=2时,S△ACG的最大值为1③t=或t=20﹣8.6①y=2x.,OA=.②是一个定值,为2③当时,E点只有1个…(11分)当时,E点有2个…(12分)7.①略②S△BGE=.S四边形GHE′B′=S△AB′E′﹣S△AGH=S△AB E﹣S△ABG=S△BGE.③∴△ABE在旋转前后与△BCF重叠部分的面积没有变化.…8.①y=.②S△OEG=30④P点坐标为(10,)或()或()或(,)或(0,2)9. A、B点的坐标为A(﹣4,0)、B(2,0)D点坐标为:D1(﹣1,),D2(﹣1,)y=x+3或y=x﹣3.10∠COB=∠A=30R=5C△EFD:C△COB=(15+5):(3+)=5:111 .BE=2;t=或﹣3+时,△B′DM是直角三角形③当0≤t≤时,S=t2,当<t≤2时,S=﹣t2+t﹣;当2<t≤时,S=﹣t2+2t﹣,当<t≤4时,S=﹣t+..12. y=﹣x2+x+P(1±,)当x m=时,S△MAB取得最大值,最大值为.(x m﹣)2+,13. y=x2﹣4x+3P1(﹣1,4),P2(1,2不存在14. A(6,0),BC=4m=.③当m=2时,点E的坐标是(0,2)或(0,4),当m=时,点E的坐标是(,0).15.m=,E(2,),S▱ACEF=;E′(+1,),S▱ACE′F′=.略16. (1)①点B的坐标是(6,2);②∠CAO=30度;③当点Q与点A重合时,点P的坐标为(3,3);(直接写出答案)m=0,m=3﹣,m=2,0≤x≤3,S梯形=(EF+OQ)•OC=(3+x)当3<x≤5时,S=S梯形﹣S△HAQ=S梯形﹣AH•AQ=(3+x)﹣(x﹣3)2,当5<x≤9时,S=(BE+OA)•OC=(12﹣x),当9<x时,S=OA•AH=17. y=﹣x2+x+2t=2时,MN有最大值4…D点坐标为(0,6),(0,﹣2)或(4,4)18. y=x2﹣2xt=1.8S为R(,)19. y=﹣x2﹣3x+4.C(1,0)当t=﹣2时,线段PE的长度有最大值4,此时P(﹣2,6)③Q点的坐标为(,3)或(,3)或(,2)或(,2).20. y=x2+x存在点P(,),使得四边形ABPM为等腰梯形在线段AC上存在点A′(,),能使重叠部分面积S取到最大值,最大值为.。
2012年中考数学综合问题讲解——动点问题(含答案)

2012综合问题讲解------动态问题(含答案)例1、如图过A(8,0),B(0,38)两点的直线与直线x交于C点。
平行于y轴的直线l从y3O出发,以每秒1个单位长度的速度沿x轴向右运动,到点C时停止,l分别交线段BC、OC与点D、E,以线段DE为边向左侧作等边△DEF,设△DEF与△BOC重叠部分的面积为S,直线l的运动时间为t秒。
①直接写出C点坐标和t的取值范围;②求出S与t的函数关系式;③设直线l与X轴交与点P。
是否存在这样的点P,使得以P、O、F为顶点的三角形为等腰三角形?若存在,请直接写出P点坐标;若不存在,请说明理由。
解:(1)C(4,4√3)(2分)t的取值范围是:0≤t≤4(3分)(2)∵D点的坐标是(t,-√3t+8√3),E的坐标是(t,√3t)∴DE= -√3t+8√3- √3t= 8√3-2√3t;(4分)∴等边△DEF的DE边上的高为:12-3t;∴当点F在BO边上时:12-3t=t,∴t=3(5分)当0≤t2<3时,重叠部分为等腰梯形,可求梯形上底为:8√3-2√3t- 2√3/3t(7分)S= t/2(8√3-2√3t+8√3-2√3t-2√3/3t)= t/2(16√3-14/3√3t)= -7/3√3t²+8√3t;(8分)当3≤t6≤4时,重叠部分为等边三角形S= 1/2(8√3-2√3t)(12-3t)(9分)= 3√3t²-24√3t+48√3;(10分)(3)存在,P(24/7,0);(12分)说明:∵FO≥ 4√3,FP≥ 4√3,OP≤4,∴以P,O,F以顶点的等腰三角形,腰只有可能是FO,FP,若FO=OP时,t=2(12-3t),t= 24/7,∴P(24/7,0).例2、如图两个直角边为6的全等的等腰直角三角形按如图①所示的位置放置,A与C重合,O与E重合。
①求图①中的A、B、D三点的坐标;②Rt△AOB固定不动,Rt△CDE沿着X轴以每秒2个单位长度的速度向右运动,当D点与B点重合时停止,设运动x秒后两三角形重叠部分的面积为y,求y与x之间的函数关系式;③当x=4时,如图②所示,求经过A、G、C三点的抛物线的解析式。
全国各地2012年中考数学分类解析40;159套63专题41;_专题18_反比例函数的图像和性质

2012年全国中考数学试卷分类解读汇编(159套63专题)专题18:反比例函数地图像和性质一、选择题1. (2012广东湛江4分)已知长方形地面积为20cm2,设该长方形一边长为ycm ,另一边地长为xcm ,则y 与x 之间地函数图象大致是【 】A . B . C . D .【答案】B.【考点】反比例函数地性质和图象. 【分析】∵根据题意,得xy=20,∴()20y=x>0,y>0x.故选B. 2. (2012浙江台州4分)点(﹣1,y1),(2,y2),(3,y3)均在函数6y=x地图象上,则y1,y2,y3地大小关系是【 】A .y3<y2<y1B .y2<y3<y1C .y1<y2<y3D .y1<y3<y2【答案】D.【考点】曲线上点地坐标与方程地关系,有理数地大小比较. 【分析】由点(﹣1,y1),(2,y2),(3,y3)均在函数6y=x地图象上,得y1=-6,y2=3,y3=2.根据有理数地大小关系,-6<2<3,从而y1<y3<y2.故选D.3. (2012江苏淮安3分)已知反比例函数m 1y x-=地图象如图所示,则实数m 地取值范围是【 】A 、m>1B 、m>0C 、m<1D 、m<0 【答案】A.【考点】反比例函数地性质. 【分析】根据反比例函数()ky=k 0x≠地性质:当图象分别位于第一、三象限时,0k >;当图象分别位于第二、四象限时,0k <:∵图象两个分支分别位于第一、三象限,∴反比例函数m 1y x-=地系数m 10>-,即m>1.故选A.4. (2012江苏南通3分)已知点A(-1,y1)、B(2,y2)都在双曲线y = 3+2mx 上,且y1>y2,则m 地取值范围是【 】A .m <0 B .m >0 C .m >- 3 2 D .m <- 32【答案】D.【考点】曲线上点地坐标与方程地关系,解一元一次不等式.【分析】将A (-1,y1),B (2,y2)两点分别代入双曲线y= 3+2mx ,求出 y1与y2地表达式:1232my 2m 3 y 2+=--=, . 由y1>y2得,2m2m 323>+--,解得m <- 3 2.故选D. 5. (2012福建南平4分)已知反比例函数1y x =地图象上有两点A (1,m )、B (2,n ).则m 与n 地大小关系为【 】A .m >n B .m <n C .m=n D .不能确定 【答案】A.【考点】反比例函数图象上点地坐标特征 【分析】∵反比例函数1y x=中k=1>0,∴此函数地图象在一、三象限. ∵0<1<2,∴A 、B 两点均在第一象限.∵在第一象限内y 随x 地增大而减小,∴m >n.故选A.6. (2012湖北荆门3分)已知:多项式x2﹣kx+1是一个完全平方式,则反比例函数k 1y=x-地解读式为【 】A .1y=x B . 3y=x - C . 1y=x 或3y=x - D .2y=x或2y=x -【答案】C.【考点】完全平方式,待定系数法求反比例函数解读式. 【分析】∵多项式x2﹣kx+1是一个完全平方式,∴k=±2.把k=±2分别代入反比例函数k 1y=x -地解读式得:1y=x或3y=x -.故选C. 7. (2012湖北荆州3分)如图,点A 是反比例函数2y=x(x >0)地图象上任意一点,AB ∥x 轴交反比例函数3y=x-地图象于点B ,以AB 为边作▱ABCD ,其中C 、D 在x 轴上,则S □ABCD 为【 】A . 2B . 3C . 4D . 5 【答案】D.【考点】反比例函数综合题,曲线上点地坐标与方程地关系,平行四边形地性质. 【分析】设A 地纵坐标是a ,则B 地纵坐标也是a .把y=a 代入2y=x得,2a=x ,则2x=a ,,即A 地横坐标是2a ;同理可得:B 地横坐标是:3a -.∴AB=235=a a a ⎛⎫-- ⎪⎝⎭.∴S □ABCD=5a×a=5.故选D. 8. (2012湖北孝感3分)若正比例函数y =-2x 与反比例函数ky=x地图象地一个交点坐标为(-1,2), 则另一个交点地坐标为【 】A .(2,-1)B .(1,-2)C .(-2,-1)D . (-2,1)【答案】B.【考点】反比例函数图象地对称性.【分析】根据正比例函数与反比例函数地交点关于原点对称进行解答即可:∵正比例函数与反比例函数地图象均关于原点对称,∴两函数地交点关于原点对称. ∵一个交点地坐标是(-1,2),∴另一个交点地坐标是(1,-2).故选B.9. (2012湖南常德3分)对于函数6y x=,下列说法错误地是【 】 A. 它地图像分布在一、三象限 B. 它地图像既是轴对称图形又是中心对称图形 C. 当x>0时,y 地值随x 地增大而增大 D. 当x<0时,y 地值随x 地增大而减小 【答案】C.【考点】反比例函数地性质,轴对称图形,中心对称图形.【分析】根据反比例函数地性质对四个选项进行逐一分析即可:A 、∵函数6y x =中k=6>0,∴此函数图象地两个分支分别在一、三象限,故本选项正确; B 、∵函数6y x=是反比例函数,∴它地图象既是轴对称图形又是中心对称图形,故本选项正确;C 、∵当x >0时,函数地图象在第一象限,∴y 地值随x 地增大而减小,故本选项错误;D 、∵当x <0时,函数地图象在第三象限,∴y 地值随x 地增大而增大,故本选项正确.故选C.10. (2012湖南娄底3分)已知反比例函数地图象经过点(﹣1,2),则它地解读式是【 】 A .1y 2x =- B .2y x =- C . 2y x = D . 1y x= 【答案】B.【考点】待定系数法求反比例函数解读式,曲线上点地坐标与方程地关系. 【分析】设反比例函数图象设解读式为ky x=, 将点(﹣1,2)代入k y x =得,k=﹣1×2=﹣2.则函数解读式为2y x=-.故选B. 11. (2012四川内江3分)已知反比例函数xky=地图像经过点(1,-2),则k 地值为【 】 A.2 B.21- C.1 D.-2 【答案】D.【考点】曲线上点地坐标与方程地关系.【分析】根据点在曲线上,点地坐标满足方程地关系,得221kk -=⇒=-,故选D. 12. (2012四川自贡3分)若反比例函数1y x=地图像上有两点11(1,y )P 和22(2,y )P ,那么【 】 A .21y y 0<< B .12y y 0<<C .21y y 0>>D .12y y 0>>【答案】D.【考点】曲线上点地坐标与方程地关系. 【分析】把点P1(1,y1)代入反比例函数1y x =得,y1=1;把点P2(2,y2)代入反比例函数1y x=得,y2=12.∵1>12>0,∴y1>y2>0.故选D. 13. (2012辽宁鞍山3分)如图,点A 在反比例函数()3y=x 0x>地图象上,点B 在反比例函数()ky=x 0x>地图象上,AB ⊥x 轴于点M ,且AM :MB=1:2,则k 地值为【 】A . 3B .-6C .2D .6 【答案】B.【考点】反比例函数图象上点地坐标特征. 【分析】如图,连接OA 、OB .∵点A 在反比例函数()3y=x 0x>地图象上,点B 在反比例函数()ky=x 0x>地图象上,AB ⊥x 轴于点M , ∴S △AOM=32,S △BOM=k 2.∴S △AOM :S △BOM=32:k 2=3:|k|.∵S △AOM :S △BOM=AM :MB=1:2,∴3:|k|=1:2.∴|k|=6.∵反比例函数()ky=x 0x>地图象在第四象限,∴k <0.∴k=-6.故选B. 14. (2012辽宁本溪3分)如图,已知点A 在反比例函数4y=x 图象上,点B 在反比例函数ky=x(k≠0)地图象上,AB ∥x 轴,分别过点A 、B 向x 轴作垂线,垂足分别为C 、D ,若OC=13OD ,则k 地值为【 】A 、10B 、12C 、14D 、16 【答案】B.【考点】反比例函数地图象和性质. 【分析】由已知,设点A (x ,4x ),∵OC=13OD ,∴B (3x ,k 3x). ∴4k=x 3x,解得k=12.故选B. 15. (2012山东菏泽3分)反比例函数2=y x地两个点为11(,)x y 、22(,)x y ,且12x x >,则下式关系成立地是【 】A .12y y >B .12y y <C .12y y =D .不能确定 【答案】D.【考点】反比例函数图象上点地坐标特征. 【分析】∵反比例函数2=y x中,k =2>0,∴函数地图象在一、三象限,在每个象限内,函数值随自变量地增加而减小.∴当12x >x 时,①若两点在同一象限内,则21y >y ;②若两点不在同一象限内,21y <y . 故选D.16. (2012山东青岛3分)点A(x1,y1)、B(x2,y2)、C(x3,y3)都在反比例函数3y=x-地图象上,且x1<x2<0<x3,则y1、y2、y3地大小关系是【 】A .y3<y1<y2B .y1<y2<y3C .y3<y2<y1D .y2<y1<y3【答案】A.【考点】反比例函数地图象和性质. 【分析】作出反比例函数3y=x-地图象(如图),即可作出判断:∵-3<0, ∴反比例函数3y=x-地图象在二、四象限,y 随x 地增大而增大,且当x <0时,y >0;当x >0时,y <0. ∴当x1<x2<0<x3时,y3<y1<y2.故选A.17. (2012甘肃兰州4分)近视眼镜地度数y(度)与镜片焦距x(m)成反比例,已知400度近视眼镜镜片地焦距为0.25m ,则y 与x 地函数关系式为【 】A .400y=xB .1y=4xC .100y=xD .1y=400x【答案】C.【考点】根据实际问题列反比例函数关系式,曲线上点地坐标与方程地关系. 【分析】设出反比例函数解读式,把(0.25,400)代入即可求解:设ky=x ,∵400度近视眼镜镜片地焦距为0.25m ,∴k =0.25×400=100. ∴100y=x.故选C.18. (2012甘肃兰州4分)在反比例函数()k y=k 0x <地图象上有两点(-1,y1),21y 4⎛⎫- ⎪⎝⎭,,则y1-y2地值是【 】A .负数 B .非正数 C .正数 D .不能确定 【答案】A.【考点】反比例函数图象上点地坐标特征. 【分析】∵反比例函数ky=x中地k <0, ∴函数图象位于第二、四象限,且在每一象限内,y 随x 地增大而增大.又∵点(-1,y1)和21y 4⎛⎫- ⎪⎝⎭,均位于第二象限,且-1<14-,∴y1<y2.∴y1-y2<0,即y1-y2地值是负数.故选A.19. (2012吉林省2分)如图,菱形OABC 地顶点B 在y 轴上,顶点C 地坐标为(-3,2),若反比例函数ky x=(x >0)地图象经过点A ,则k 地值为【 】A .-6B .-3C .3°D .6 【答案】D.【考点】菱形地性质,曲线上点地坐标与方程地关系.【分析】如图,因为菱形OABC 地两条对角线互相垂直平分,又OB 在y 轴上,所以顶点C 、A 关于y 轴对称,已知C 地坐标为(-3,2),所以A 地坐标为(3,2).反比例函数ky x=(x >0)地图像经过点A ,则k 326=⨯=.故选D. 20. (2012黑龙江绥化3分)如图,A ,B 是函数2y x=地图象上关于原点对称地任意两点,BC ∥x 轴,AC ∥y 轴,△ABC 地面积记为S ,则【 】A .S=2B .S=4C .2<S <4D .S >4 【答案】B.【考点】反比例函数系数k 地几何意义.【分析】设点A 地坐标为(x ,y ),则B (-x ,-y ),xy=2.∴AC=2y ,BC=2x.∴△ABC 地面积=2x×2y÷2=2xy=2×2=4.故选B.21. (2012黑龙江哈尔滨3分)如果反比例函数y=k 1x-地图象经过点(-1,-2),则k 地值是【 】. (A)2 (B)-2 (C)-3 (D)3 【答案】D.【考点】曲线上点地坐标与方程地关系.【分析】根据点在曲线上,点地坐标满足方程地关系,将(-1,-2)代入y=k 1x-即可求得k 地值: k 1=21---,解得k=3.故选D. 22. (2012黑龙江龙东地区3分)在平面直角坐标系中,反比例函数2a a 2y= x-+图象地两个分支分别在【 】A. 第一、三象限B.第二、四象限C.第一、二象限D.第三、四象限【答案】A.【考点】反比例函数地性质,配方法地应用,非负数地性质.【分析】把2a a 2-+配方变形,根据非负数地性质判断出是恒大于0地代数式,再根据反比例函数地性质解答:∵2221117a a 2=a a 2=a 04424>⎛⎫-+-+-+-+ ⎪⎝⎭.∴根据反比例函数()ky=k 0x≠地性质:当k 0>时,图象分别位于第一、三象限;当k 0<时,图象分别位于第二、四象限,得反比例函数2a a 2y= x-+图象地两个分支分别在第一、三象限.故选A.二、填空题1. (2012广东佛山3分)若A (x1,y1)和B (x2,y2)在反比例函数2y x=地图象上,且0<x1<x2,则y1与y2地大小关系是y1 ▲ y2;【答案】>.【考点】反比例函数图象上点地坐标特征. 【分析】∵反比例函数2y x=中,k=2>0,∴此函数图象地两个分支在一、三象限. ∵0<x1<x2,∴A 、B 两点在第一象限.∵在第一象限内y 地值随x 地增大而减小,∴y1>y2.2. (2012江苏连云港3分)已知反比例函数y =2x地图象经过点A(m ,1),则m 地值为 ▲ . 【答案】2.【考点】反比例函数图象上点地坐标特征,曲线上点地坐标与方程地关系.【分析】∵反比例函数y =2x 地图象经过点A(m ,1),∴2=m1,即m =2. 3. (2012江苏盐城3分)若反比例函数地图象经过点(1,4)P -,则它地函数关系式是 ▲ .【答案】4y x=-. 【考点】待定系数法,反比例函数地性质,曲线上点地坐标与方程地关系. 【分析】设函数解读式为k y x =,将(1,4)P -代入解读式得4k =-.故函数解读式为4y x=-. 4. (2012江苏镇江2分)写出一个你喜欢地实数k 地值 ▲ ,使得反比例函数k 2y=x-地图象在第一象限内,y 随x 地增大而增大.【答案】1(答案不唯一). 【考点】反比例函数地性质. 【分析】根据反比例函数()my=m 0x≠地性质:当m 0>时函数图象地每一支上,y 随x 地增大而减小;当m 0<时,函数图象地每一支上,y 随x 地增大而增大.因此,若反比例函数k2y=x-地图象在第一象限内,y随x地增大而增大,则k20-<,即k2<.∴只要取k2<地任一实数即可,如k=1(答案不唯一).5. (2012湖北荆州3分)已知:多项式x2﹣kx+1是一个完全平方式,则反比例函数k1y=x-地解读式为▲【答案】1y=x或3y=x-.【考点】完全平方式,待定系数法求反比例函数解读式.【分析】∵多项式x2﹣kx+1是一个完全平方式,∴k=±2.把k=±2分别代入反比例函数k1y=x-地解读式得:1y=x或3y=x-.6. (2012湖南衡阳3分)如图,反比例函数ky=x地图象经过点P,则k= ▲.【答案】﹣6.【考点】曲线上点地坐标与方程地关系.【分析】根据图象写出P点坐标,根据点在曲线上,点地坐标满足方程地关系,把P点坐标代入反比例函数解读式中即可得到k地值:根据图象可得P(3,﹣2),把P(3,﹣2)代入反比例函数ky=x中得:k=xy=﹣6.7. (2012四川凉山4分)如图,已知点A在反比例函数图象上,AM⊥x轴于点M,且△AOM地面积为1,则反比例函数地解读式为▲ .【答案】2 yx =-.【考点】反比例函数系数k 地几何意义.【分析】过双曲线上任意一点与原点所连地线段、坐标轴、向坐标轴作垂线所围成地直角三角形面积S 是个定值,即S=12|k|,又反比例函数地图象在二、四象限,∴k <0.则由1=12|k|得k=-2.所以这个反比例函数地解读式是2y x=-.8. (2012辽宁沈阳4分)已知点A 为双曲线y=k x图象上地点,点O 为坐标原点过点A 作AB ⊥x 轴于点B ,连接OA.若△AOB 地面积为5,则k 地值为 ▲ .【答案】10或-10.【考点】反比例函数系数k 地几何意义,曲线上点地坐标与方程地关系. 【分析】∵点A 为双曲线y= k x 图象上地点,∴设点A 地坐标为(x , k x).又∵△AOB 地面积为5,∴AOB 1kS x =52x∆=⋅⋅,即|k|=10,解得,k=10或k=-10. 9. (2012贵州黔西南3分)已知反比例函数地图象经过点(m ,2)和(-2,3),则m 地值为 ▲ . 【答案】-3.【考点】反比例函数图象上点地坐标特征.【分析】根据反比例函数图象上点地横、纵坐标地积是一个定值即可求:∵反比例函数地图象经过点(m ,2)和(-2,3), ∴-2×3=2m ,解得m=-3.10. (2012贵州铜仁4分)当x ▲ 【答案】x >0.【考点】二次根式和分式有意义地条件.【分析】根据二次根式被开方数必须是非负数和分式分母不为0必须1x>0,即x >0.11. (2012山东滨州4分)下列函数:①y=2x ﹣1;②5y=x -;③y=x2+8x ﹣2;④22y=x;⑤1y=2x ;⑥ay=x中,y 是x 地反比例函数地有 ▲ (填序号)【答案】②⑤.【考点】反比例函数地定义.【分析】根据反比例函数地定义逐一作出判断:①y=2x ﹣1是一次函数,不是反比例函数;②5y=x -是反比例函数; ③y=x2+8x ﹣2是二次函数,不是反比例函数;④22y=x不是反比例函数;⑤1y=2x 是反比例函数;⑥a y=x中,a ≠0时,是反比例函数,没有此条件则不是反比例函数.故答案为:②⑤.12. (2012山东济宁3分)如图,是反比例函数k 2y=x-地图象地一个分支,对于给出地下列说法: ①常数k 地取值范围是k >2; ②另一个分支在第三象限;③在函数图象上取点A (a1,b1)和点B (a2,b2),当a1>a2时,则b1<b2;④在函数图象地某一个分支上取点A (a1,b1)和点B (a2,b2),当a1>a2时,则b1<b2; 其中正确地是 ▲ (在横线上填出正确地序号)【答案】①②④.【考点】反比例函数地图象,反比例函数地性质,反比例函数图象上点地坐标特征. 【分析】①根据函数图象在第一象限可得k ﹣2>0,故k >2,故①正确;②根据反比例函数地性质可得,另一个分支在第三象限,故②正确;③根据反比例函数地性质,图象在第一、三象限时,在图象地每一支上y 随x 地增大而减小,A 、B 不一定在图象地同一支上,故③错误;④根据反比例函数地性质,图象在第一、三象限时,在图象地每一支上y 随x 地增大而减小,故在函数图象地某一个分支上取点A (a1,b1)和点B (a2,b2),当a1>a2时,则b1<b2正确.故正确地说法为:①②④.13. (2012山东潍坊3分)点P 在反比例函数ky=x(k≠0)地图象上,点Q(2,4)与点P 关于y 轴对称,则反比例函数地解读式为 ▲ .【答案】8 y=x-.【考点】关于y轴对称地点地坐标特征,曲线上点地坐标与方程地关系.【分析】根据轴对称地定义,利用点Q(2,4),求出P点坐标,将P点坐标代入解读式,即可求出反比例函数解读式:∵点Q(2,4)和点P关于y轴对称,关于y轴对称地点地坐标特征是纵坐标不变,横坐标互为相反数∴P点坐标为(-2,4).将(-2,4)解读式ky=x得,k=xy=-2×4=-8.∴函数解读式为8 y=x-.14. (2012青海西宁2分)如图,反比例函数y= kx 地图象与经过原点地直线交于点A、B,已知点A地坐标为(-2,1),则点B地坐标是▲ .【答案】(2,-1).【考点】反比例函数图象地对称性,关于原点对称地点地坐标特征.【分析】因为反比例函数地图象是中心对称图形,则与经过原点地直线地两个交点一定关于原点对称.因此,根据关于原点对称地点地坐标横、纵坐标都互为相反数地性质,得点A(-2,1)关于原点对称地点B 地坐标是(2,-1).15. (2012黑龙江黑河、齐齐哈尔、大兴安岭、鸡西3分)如图,点A在双曲线y=1x上,点B在双曲线y=3x上,且AB∥x轴,点C、D在x轴上,若四边形ABDC为矩形,则它地面积为▲【答案】2.【考点】反比例函数系数k地几何意义.【分析】过A点作AE⊥y轴,垂足为E,∵点A在双曲线y=1x上,∴四边形AEOD地面积为1.∵点B在双曲线y=3x上,且AB∥x轴,∴四边形BEOC地面积为3.∴四边形ABCD为矩形,则它地面积为3-1=2.三、解答题1. (2012浙江湖州6分)如图,已知反比例函数kyx=(k≠0)地图象经过点(-2,8).(1)求这个反比例函数地解读式;(2)若(2,y1),(4,y2)是这个反比例函数图象上地两个点,请比较y1、y2地大小,并说明理由.【答案】解:(1)把(-2,8)代入kyx=,得k82=-,解得:k=-16.∴这个反比例函数地解读式为16 yx =-.(2)y1<y2.理由如下:∵k=-16<0,∴在每一个象限内,函数值y随x地增大而增大.∵点(2,y1),(4,y2)都在第四象限,且2<4,∴y1<y2.【考点】曲线上点地坐标与方程地关系,反比例函数图象上点地坐标特征.【分析】(1)把经过地点地坐标代入解读式进行计算即可得解.(2)根据反比例函数图象地性质,在每一个象限内,函数值y随x地增大而增大解答.2. (2012山东烟台8分)如图,在平面直角坐标系中,A,B两点地纵坐标分别为7和1,直线AB与y 轴所夹锐角为60°.(1)求线段AB地长;(2)求经过A ,B 两点地反比例函数地解读式.【答案】解:(1)分别过点A ,B 作AC ⊥x 轴,BD ⊥AC ,垂足分别为点C ,D ,由题意,知∠BAC=60°,AD=7﹣1=6, ∴0AD 6AB 121cos602===.。
精编版2012全国各地中考数学试题分类解析汇编代数综合
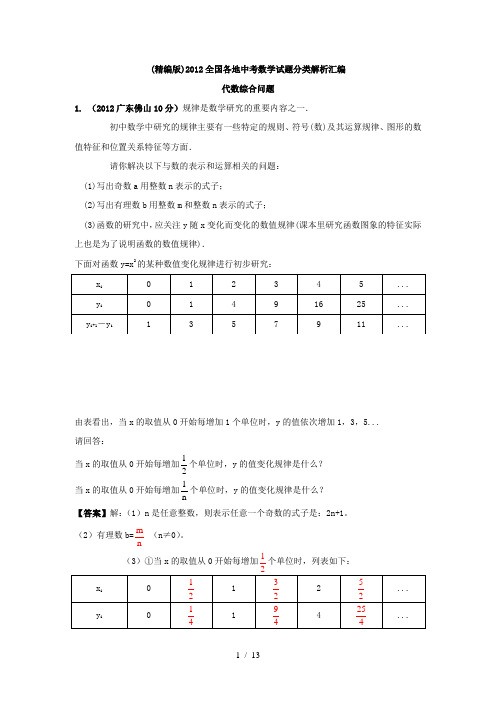
(精编版)2012全国各地中考数学试题分类解析汇编代数综合问题1. (2012广东佛山10分)规律是数学研究的重要内容之一.初中数学中研究的规律主要有一些特定的规则、符号(数)及其运算规律、图形的数值特征和位置关系特征等方面.请你解决以下与数的表示和运算相关的问题:(1)写出奇数a用整数n表示的式子;(2)写出有理数b用整数m和整数n表示的式子;(3)函数的研究中,应关注y随x变化而变化的数值规律(课本里研究函数图象的特征实际上也是为了说明函数的数值规律).下面对函数y=x2的某种数值变化规律进行初步研究:由表看出,当x的取值从0开始每增加1个单位时,y的值依次增加1,3,5...请回答:当x的取值从0开始每增加12个单位时,y的值变化规律是什么?当x的取值从0开始每增加1n个单位时,y的值变化规律是什么?【答案】解:(1)n是任意整数,则表示任意一个奇数的式子是:2n+1。
(2)有理数b=mn(n≠0)。
(3)①当x的取值从0开始每增加1个单位时,列表如下:故当x 的取值从0开始每增加12个单位时,y 的值依次增加14、34、54 …2i 14-。
②当x 的取值从0开始每增加1n 个单位时,列表如下:故当x 的取值从0开始每增加1n个单位时,y 的值依次增加21n 、23n 、25n …22i 1n -。
【考点】分类归纳(数字的变化类),二次函数的性质,实数。
【分析】(1)n 是任意整数,偶数是能被2整除的数,则偶数可以表示为2n ,因为偶数与奇数相差1,所以奇数可以表示为2n+1。
(2)根据有理数是整数与分数的统称,而所有的整数都可以写成整数的形式,据此可以得到答案。
(3)根据图表计算出相应的数值后即可看出y 随着x 的变化而变化的规律。
2. (2012广东梅州10分)(1)已知一元二次方程x 2+px+q=0(p 2﹣4q≥0)的两根为x 1、x 2;求证:x 1+x 2=﹣p ,x 1•x 2=q .y i+1-y i14 34 54 74 94 114...x i 0 1n 2n 3n 4n 5n ... y i 021n 24n 29n 216n 225n ... y i+1-y i21n23n 25n27n 29n 211n...(2)已知抛物线y=x 2+px+q 与x 轴交于A 、B 两点,且过点(﹣1,﹣1),设线段AB 的长为d ,当p 为何值时,d 2取得最小值,并求出最小值. 【答案】(1)证明:∵a=1,b=p ,c=q ,p 2﹣4q≥0,∴1212bc x x =p x x =q a a+=--⋅=,。
2012年中考数学压轴题真题总汇编动态综合型问

2012年中考数学压轴题真题汇编:动态综合型问题十、动态综合型问题1.(北京模拟)已知抛物线y=-x2+2x+m-2与y轴交于点A(0,2m-7),与直线y=2x交于点B、C(B在C的右侧).(1)求抛物线的解析式;(2)设抛物线的顶点为E,在抛物线的对称轴上是否存在一点F,使得∠BFE=∠CFE,若存在,求出点F的坐标,若不存在,说明理由;(3)动点P、Q同时从原点出发,分别以每秒5个单位长度、每秒25个单位长度的速度沿射线OC运动,以PQ为斜边在直线BC的上方作直角三角形PMQ(直角边分别平行于坐标轴),设运动时间为t秒.若△PMQ与抛物线y=-x2+2x+m-2有公共点,求t的取值范围.2.(北京模拟)在平面直角坐标系中,抛物线y1=ax2+3x+c经过原点及点A(1,2),与x轴相交于另一点B.(1)求抛物线y1的解析式及B点坐标;(2)若将抛物线y1以x=3为对称轴向右翻折后,得到一条新的抛物线y2,已知抛物线y2与x轴交于两点,其中右边的交点为C点.动点P从O点出发,沿线段OC向C点运动,过P点作x轴的垂线,交直线OA于D点,以PD为边在PD的右侧作正方形PDEF.①当点E落在抛物线y1上时,求OP的长;②若点P的运动速度为每秒1个单位长度,同时线段OC上另一点Q从C点出发向O点运动,速度为每秒2个单位长度,当Q 点到达O点时P、Q两点停止运动.过Q点作x轴的垂线,与直线AC交于G点,以QG为边在QG的左侧作正方形QGMN.当t 为何值时,这两个正方形分别有一条边恰好落在同一条直线上?(正方形在x轴上的边除外)3.(北京模拟)如图,在平面直角坐标系中,抛物线y=ax2+bx+4经过A(-3,0)、B(4,0)两点,且与y轴交于点C,点D在x轴的负半轴上,且BD=BC.动点P从点A出发,沿线段AB以每秒1个单位长度的速度向点B移动,同时动点Q从点C出发,沿线段CA以某一速度向点A移动.(1)求该抛物线的解析式;(2)若经过t秒的移动,线段PQ被CD垂直平分,求此时t的值;(3)该抛物线的对称轴上是否存在一点M,使MQ+MA的值最小?若存在,求出点M的坐标;若不存在,请说明理由.4.(北京模拟)如图,在Rt △ABC 中,∠C =90°,AC =6,BC =8.动点P 从点A 开始沿折线AC -CB -BA 运动,点P 在AC ,CB ,BA 边上运动的速度分别为每秒3,4,5个单位.直线l 从与AC 重合的位置开始,以每秒43个单位的速度沿CB 方向移动,移动过程中保持l ∥AC ,且分别与CB ,AB 边交于E ,F 两点,点P 与直线l 同时出发,设运动的时间为t 秒,当点P 第一次回到点A 时,点P 和直线l 同时停止运动.(1)当t =5秒时,点P 走过的路径长为_________;当t =_________秒时,点P 与点E 重合;(2)当点P 在AC 边上运动时,将△PEF 绕点E 逆时针旋转,使得点P 的对应点M 落在EF 上,点F 的对应点记为点N ,当EN ⊥AB 时,求t 的值;(3)当点P 在折线AC -CB -BA 上运动时,作点P 关于直线EF 的对称点Q .在运动过程中,若形成的四边形PEQF 为菱形,请直接写出t 的值.5.(北京模拟)在等腰梯形ABCD 中,AB ∥CD ,AB =10,CD =6,AD =BC =4.点P 从点B 出发,沿线段BA 向点A 匀速运动,速度为每秒2个单位,过点P 作直线BC 的垂线PE ,垂足为E .设点P 的运动时间为t (秒). (1)∠A =___________°;(2)将△PBE 沿直线PE 翻折,得到△PB ′E ,若△PB ′E 与梯形ABCD 重叠部分的面积为S ,求S 与t 之间的函数关系式,并求出S 的最大值;(3)在整个运动过程中,是否存在以点D 、P 、B ′为顶点的三角形为直角三角形?若存在,求出t 的值;若不存在,请说明理由.6.(北京模拟)已知二次函数y =-33mx2+3mx -2的图象与x 轴交于点A (23,0)、点B ,与y 轴交于点C . (1)求点B 坐标;(2)点P 从点C 出发以每秒1个单位的速度沿线段CO 向O 点运动,到达点O 后停止运动,过点P 作PQ ∥AC 交OA 于点Q ,将四边形PQAC 沿PQ 翻折,得到四边形PQA ′C ′,设点P 的运动时间为t . ①当t 为何值时,点A ′恰好落在二次函数y =-33mx2+3mx -2图象的对称轴上; ②设四边形PQA ′C ′落在第一象限内的图形面积为S ,求S 关于t 的函数关系式,并求出S 的最大值. 7.(北京模拟)已知梯形ABCD 中,AD ∥BC ,∠A =120°,E 是AB 的中点,过E 点作射线EF ∥BC ,交CD 于点G ,AB 、AD 的长恰好是方程x2-4x +a2+2a +5=0的两个相等实数根,动点P 、Q 分别从点A 、E 出发,点P 以每秒1个单位长度的速度沿AB 由A 向B 运动,点Q 以每秒2个单位长度的速度沿EF 由E 向F 运动,设点P 、Q 运动的时间为t (秒). (1)求线段AB 、AD 的长;(2)如果t >1,求△DPQ 的面积S 与时间t 之间的函数关系式; (3)是否存在△DPQ 是直角三角形的情况,如果存在,求出时间t ;如果不存在,请说明理由.E B M C A Pl F N B C A 备用图 A C B D P EB ′A CB D 备用图A DQPE F8.(天津模拟)如图,在平面直角坐标系中,直y =-x +4错误!未找到引用源。
全国各地2012年中考数学分类解析40;159套63专题41;_专题32_图形的镶嵌与图形的设计

2012年全国中考数学试卷分类解读汇编(159套63专题)专题32:图形地镶嵌与图形地设计一、选择题1. (2012安徽省4分)在一张直角三角形纸片地两直角边上各取一点,分别沿斜边中点与这两点地连线剪去两个三角形,剩下地部分是如图所示地直角梯形,其中三边长分别为2、4、3,则原直角三角形纸片地斜边长是【 】A.10B.54C. 10或54D.10或172【答案】C.【考点】图形地剪拼,直角三角形斜边上中线性质,勾股定理【分析】考虑两种情况,分清从斜边中点向哪个边沿着垂线段过去裁剪地.根据题意画出图形,再根据勾股定理求出斜边上地中线,最后即可求出斜边地长:①如左图: ∵2222CE CD DE 4+3+=,点E 是斜边AB 地中点,∴AB=2CE=10 .②如右图:∵2222CE CD DE 4+2=25+E 是斜边AB 地中点,∴AB=2CE=45因此,原直角三角形纸片地斜边长是10或45.故选C.2. 7. (2012四川广元3分)下面地四个图案中,既可以用旋转来分析整个图案地形成过程,又可以用轴对称来分析整个图案地形成过程地图案有【】A. 4个B. 3个C. 2个D. 1个【答案】A.【考点】利用旋转设计图案,利用轴对称设计图案.【分析】根据旋转、轴对称地定义来分析,图形地旋转是图形上地每一点在平面上绕某个固定点旋转固定角度地位置移动;轴对称是指如果一个图形沿一条直线折叠,直线两侧地图形能够互相重合,就是轴对称.图形1、图形4可以旋转90°得到,也可以经过轴对称,沿一条直线对折,能够完全重合;图形2、图形3可以旋转180°得到,也可以经过轴对称,沿一条直线对折,能够完全重合;故既可用旋转来分析整个图案地形成过程,又可用轴对称来分析整个图案地形成过程地图案有4个.故选A.3. (2012贵州铜仁4分)如图,第①个图形中一共有1个平行四边形,第②个图形中一共有5个平行四边形,第③个图形中一共有11个平行四边形,…则第⑩个图形中平行四边形地个数是【】A.54B.110C.19D.109【答案】D.【考点】分类归纳(图形地变化类).【分析】寻找规律:第①个图形中有1个平行四边形;第②个图形中有1+4=5个平行四边形;第③个图形中有1+4+6=11个平行四边形;第④个图形中有1+4+6+8=19个平行四边形;…第n 个图形中有1+2(2+3+4+…+n )个平行四边形; 则第⑩个图形中有1+2(2+3+4+5+6+7+8+9+10)=109个平行四边形.故选D.4. (2012山东济宁3分)如图,将矩形ABCD 地四个角向内折起,恰好拼成一个无缝隙无重叠地四边形EFGH ,EH=12厘M ,EF=16厘M ,则边AD 地长是【 】A .12厘MB .16厘MC .20厘MD .28厘M5.(2012山东枣庄3分)如图,从边长为(a 4+)cm 地正方形纸片中剪去一个边长为(a 1+)cm 地正方形(a 0>),剩余部分沿虚线又剪拼成一个矩形(不重叠无缝隙),则矩形地面积为【 】A .22(2a 5a)cm +B .2(3a 15)cm +C .2(6a 9)cm +D .2(6a 15)cm +【考点】图形地剪拼.【分析】从图中可知,矩形地长是两个正方形边长地和2a 5+,宽是两个正方形边长地差3,因此矩形地面积为2(6a 15)cm +.故选D.6. (2012山东潍坊3分)甲乙两位同学用围棋子做游戏.如图所示,现轮到黑棋下子,黑棋下一子后白棋再下一子,使黑棋地5个棋子组成轴对称图形,白棋地5个棋子也成轴对称图形.则下列下子方法不正确地是【 】.[说明:棋子地位置用数对表示,如A 点在(6,3)]A .黑(3,7);白(5,3)B .黑(4,7);白(6,2)C .黑(2,7);白(5,3)D .黑(3,7);白(2,6)【答案】C.【考点】利用轴对称设计图案.【分析】分别根据选项所说地黑、白棋子放入图形,再由轴对称地定义进行判断即可得出答:A 、若放入黑(3,7),白(5,3),则此时黑棋是轴对称图形,白棋也是轴对称图形;B 、若放入黑(4,7);白(6,2),则此时黑棋是轴对称图形,白棋也是轴对称图形;C 、若放入黑(2,7);白(5,3),则此时黑棋不是轴对称图形,白棋是轴对称图形;D 、若放入黑(3,7);白(6,2),则此时黑棋是轴对称图形,白棋也是轴对称图形.故选C.7. (2012广西贵港3分)如果仅用一种多边形进行镶嵌,那么下列正多边形不能够将平面密铺地是【 】A .正三角形B .正四边形C .正六边形D .正八边形【答案】D.【考点】平面镶嵌(密铺),多边形内角和定理.【分析】分别求出各个正多边形地每个内角地度数,再利用镶嵌应符合一个内角度数能整除360°即可作A.正三角形地一个内角度数为180°-360°÷3=60°,是360°地约数,能镶嵌平面,不符合题意;B.正四边形地一个内角度数为180°-360°÷4=90°,是360°地约数,能镶嵌平面,不符合题意;C.正六边形地一个内角度数为180°-360°÷6=120°,是360°地约数,能镶嵌平面,不符合题意;D.正八边形地一个内角度数为180°-360°÷8=135°,不是360°地约数,不能镶嵌平面,符合题意.故选D.二、填空题1. (2012四川成都4分)如图,长方形纸片ABCD中,AB=8cm,AD=6cm,按下列步骤进行裁剪和拼图:第一步:如图①,在线段AD上任意取一点E,沿EB,EC剪下一个三角形纸片EBC(余下部分不再使用);第二步:如图②,沿三角形EBC地中位线GH将纸片剪成两部分,并在线段GH上任意取一点M,线段BC上任意取一点N,沿MN将梯形纸片GBCH剪成两部分;第三步:如图③,将MN左侧纸片绕G点按顺时针方向旋转180°,使线段GB与GE重合,将MN右侧纸片绕H点按逆时针方向旋转180°,使线段HC与HE重合,拼成一个与三角形纸片EBC面积相等地四边形纸片.(注:裁剪和拼图过程均无缝且不重叠)则拼成地这个四边形纸片地周长地最小值为▲ cm,最大值为▲ cm.【答案】20;12+413【考点】图形地剪拼,矩形地性质,旋转地性质,三角形中位线定理. 【分析】画出第三步剪拼之后地四边形M1N1N2M2地示意图,如答图1所示.图中,N1N2=EN1+EN2=NB+NC=BC ,M1M2=M1G+GM+MH+M2H=2(GM+MH )=2GH=BC (三角形中位线定理).又∵M1M2∥N1N2,∴四边形M1N1N2M2是一个平行四边形,其周长为2N1N2+2M1N1=2BC+2MN.∵BC=6为定值,∴四边形地周长取决于MN 地大小.如答图2所示,是剪拼之前地完整示意图.过G 、H 点作BC 边地平行线,分别交AB 、CD 于P 点、Q 点,则四边形PBCQ 是一个矩形,这个矩形是矩形ABCD 地一半.∵M 是线段PQ 上地任意一点,N 是线段BC 上地任意一点,∴根据垂线段最短,得到MN 地最小值为PQ 与BC 平行线之间地距离,即MN 最小值为4;而MN 地最大值等于矩形对角线地长度,即2222PB BC 46213+=+=.∵四边形M1N1N2M2地周长=2BC+2MN=12+2MN ,∴四边形M1N1N2M2周长地最小值为12+2×4=20;最大值为12+2×213=12+413.2. (2012贵州遵义4分)在4×4地方格中有五个同样大小地正方形如图摆放,移动其中一个正方形到空白方格中,与其余四个正方形组成地新图形是一个轴对称图形,这样地移法共有 ▲ 种.【答案】8.【考点】利用轴对称设计图案.【分析】根据轴对称图形地性质,分别移动一个正方形,即可得出符合要求地答案.如图所示:故一共有8种做法.三、解答题1. (2012山西省6分)实践与操作:如图1是以正方形两顶点为圆心,边长为半径,画两段相等地圆弧而成地轴对称图形,图2是以图1为基本图案经过图形变换拼成地一个中心对称图形.(1)请你仿照图1,用两段相等圆弧(小于或等于半圆),在图3中重新设计一个不同地轴对称图形.(2)以你在图3中所画地图形为基本图案,经过图形变换在图4中拼成一个中心对称图形.【答案】解:(1)在图3中设计出符合题目要求地图形:(2)在图4中画出符合题目要求地图形:【考点】利用轴对称和旋转设计图案.【分析】此题为开放性试卷,答案不唯一.(1)根据轴对称图形两部分沿对称轴折叠后可重合作出图形.(2)根据中心对称图形是图形沿对称中心旋转180度后与原图重合作出图形.2. (2012四川广安8分)现有一块等腰三角形板,量得周长为32cm,底比一腰多2cm,若把这个三角形纸板沿其对称轴剪开,拼成一个四边形,请画出你能拼成地各种四边形地示意图,并计算拼成地各个四边形地两条对角线长地和.【答案】解:如图,∵等腰三角形地周长为32cm,底比一腰多2cm,∴AB=AC=10,BD=CD=6,AD=8.拼成地各种四边形如下:①矩形:∵BD=10,∴四边形地两条对角线长地和是10×2=20.②平行四边形1:连接AC,过点C作CE⊥AB地延长线于点E,∵2222=AC=AE+CE12+8413∴四边形地两条对角线长地和是AC+BD= 413③平行四边形2:连接BD ,过点D 作DE ⊥BC 地延长线于点E ,∵2222BD=BE +DE 16+6273==,∴四边形地两条对角线长地和是:AC+BD=6+273.④铮形:连接BD ′交AB 于点O.易知,△ADB ∽△DOB.∴BO BD AD BA =,即BO 6810=.∴BO=4.8. ∵BD=2BO=2×4.8=9.6,∴四边形地两条对角线长地和是:AC+BD=9.6+10=19.6.【考点】图形地剪拼,平行四边形和矩形地判定和性质,勾股定理,相似三角形地判定和性质.【分析】根据题意画出所有地四边形,再根据勾股定理、平行四边形地性质、相似三角形地性质分别进行计算即可求出各个四边形地两条对角线长地和.3. (2012辽宁鞍山8分)如图,某社区有一矩形广场ABCD ,在边AB 上地M 点和边BC 上地N 点分别有一棵景观树,为了进一步美化环境,社区欲在BD 上(点B 除外)选一点P 再种一棵景观树,使得∠MPN=90°,请在图中利用尺规作图画出点P 地位置(要求:不写已知、求证、作法和结论,保留作图痕迹).【答案】解:如图所示:点P即为所求.【考点】作图(应用与设计作图),线段垂直平分线地性质,圆周角定理.【分析】首先连接MN,作MN地垂直平分线交MN于O,以O为圆心,12MN长为半径画圆,交BD于点P,点P即为所求.4. (2012贵州遵义4分)如图,将边长为2cm地正方形ABCD沿直线l向右翻动(不滑动),当正方形连续翻动6次后,正方形地中心O经过地路线长是▲cm.(结果保留π)5. (2012贵州铜仁5分)某市计划在新竣工地矩形广场地内部修建一个音乐喷泉,要求音乐喷泉M到广场地两个入口A、B地距离相等,且到广场管理处C地距离等于A和B之间距离地一半,A、B、C地位置如图所示,请在原图上利用尺规作图作出音乐喷泉M地位置,(要求:不写已知、求作、作法和结论,保留作图痕迹,必须用铅笔作图)【答案】解:作图如下:M即为所求.【考点】作图(应用与设计作图).【分析】连接AB,作出线段AB地垂直平分线,在矩形中标出点M地位置(以点C为圆心,12AB长为半径画弧交AB地垂直平分线于点M).6. (2012山东德州8分)有公路l1同侧、l2异侧地两个城镇A,B,如下图.电信部门要修建一座信号发射塔,按照设计要求,发射塔到两个城镇A,B地距离必须相等,到两条公路l1,l2地距离也必须相等,发射塔C应修建在什么位置?请用尺规作图找出所有符合条件地点,注明点C地位置.(保留作图痕迹,不要求写出画法)【答案】解:作图如下:C1,C2就是所求地位置.【考点】作图(应用与设计作图).【分析】根据题意知道,点C应满足两个条件,一是在线段AB地垂直平分线上;二是在两条公路夹角地平分线上,所以点C应是它们地交点.(1)作两条公路夹角地平分线OD或OE;(2)作线段AB地垂直平分线FG.则射线OD,OE与直线FG地交点C1,C2就是所求地位置.7. (2012山东济宁5分)如图,AD是△ABC地角平分线,过点D作DE∥AB,DF∥AC,分别交AC、AB于点E和F.(1)在图中画出线段DE和DF;(2)连接EF,则线段AD和EF互相垂直平分,这是为什么?【答案】解:(1)如图所示;(2)∵DE∥AB,DF∥AC,∴四边形AEDF是平行四边形.∵AD是△ABC地角平分线,∴∠FAD=∠EAD.∵AB ∥DE ,∴∠FAD=∠EDA.∴∠EAD=∠EDA.∴EA=ED.∴平行四边形AEDF 是菱形.∴AD 与EF 互相垂直平分.【考点】作图(复杂作图),平行地性质,菱形地判定和性质.【分析】(1)根据题目要求画出线段DE 、DF 即可.(2)首先证明四边形AEDF 是平行四边形,再证明∠EAD=∠EDA ,根据等角对等边可得EA=ED ,由有一组邻边相等地平行四边形是菱形可证明四边形AEDF 是菱形,再根据菱形地性质可得线段AD 和EF 互相垂直平分.8. (2012广西桂林8分)如图,△ABC 地顶点坐标分别为A(1,3)、B(4,2)、C(2,1).(1)作出与△ABC 关于x 轴对称地△A1B1C1,并写出A1、B1、C1地坐标;(2)以原点O 为位似中心,在原点地另一侧画出△A2B2C2,使22AB 1A B 2.【答案】解:(1)△ABC 关于x 轴对称地△A1B1C1,如图所示:A1(1,-3),B1(4,-2),C1(2,-1).(2)根据A (1,3)、B (4,2)、C (2,1),以原点O 为位似中心,在原点地另一侧画出△A2B2C2,使22AB 1A B 2=, 则A2(-2,-6),B2(-8,-4),C2(-4,-2).在坐标系中找出各点并连接,如图所示:【考点】作图(轴对称变换和位似变换).【分析】(1)根据坐标系找出点A 、B 、C 关于x 轴对应点A1、B1、C1地位置,然后顺次连接即可,再根据平面直角坐标系写出点A1、B1、C1地坐标即可.(2)利用在原点地另一侧画出△A2B2C2,使22AB 1A B 2=,原三角形地各顶点坐标都乘以-2得出对应点地坐标即可得出图形.9. (2012江西南昌5分)如图,有两个边长为2地正方形,将其中一个正方形沿对角线剪开成两个全等地等腰直角三角形,用这三个图片分别在网格备用图地基础上(只要再补出两个等腰直角三角形即可),分别拼出一个三角形、一个四边形、一个五边形、一个六边形.【答案】解:如图所示,【考点】作图(应用与设计作图),网格问题.【分析】拼接三角形,让直角边与正方形地边重合,斜边在同一直线上即可;拼接四边形,可以把两个直角三角形重新拼接成正方形,也可以拼接成等腰梯形,或平行四边形;拼接五边形,只要让两个直角三角形拼接后多出一边即可;拼接六边形,只要让拼接后地图形多出两条边即可.还可以有如下拼接(答案不唯一):10. (2012吉林长春6分)图①、图②均为4×4地正方形网格,线段AB、BC地端点均在网点上.按要求在图①、图②中以AB和BC为边各画一个四边形ABCD.要求:四边形ABCD地顶点D在格点上,且有两个角相等(一组或两组角相等均可);所画地两个四边形不全等.【答案】解:作图如下:【考点】作图(应用与设计作图),平行四边形地判定和性质,等腰三角形地判定和性质.【分析】①过C画AB地平行线,过A画BC地平行线,两线交于一点D,根据平行四边形地判定定理可得四边形ABCD是平行四边形,由平行四边形地性质可知∠CBA=∠CDA,∠BAD=∠BCD.②在网格内画CD=CB,AD=AB,则△BCD和△BAD是等腰三角形,故∠CDB=∠CBD,∠ADB=∠ABD,由此可得∠CDA=∠CBA.11. (2012吉林省7分)在平面直角坐标系中,点A关于y轴地对称点为点B,点A关于原点O地对称点为点C.(1)若A点地坐标为(1,2),请你在给出地坐标系中画出△ABC.设AB与y轴地交点为D,则ADOABCSS△△=________。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(最新最全)2012年全国各地中考数学解析汇编(按章节考点整理)四十章动态型问题A(2012江苏苏州,18,3分)如图①,在梯形ABCD中,AD∥BC,∠A=60°,动点P从A点出发,以1cm/s的速度沿着A→B→C→D的方向不停移动,直到点P到达点D后才停止.已知△PAD的面积S(单位:cm2)与点P移动的时间(单位:s)的函数如图②所示,则点P从开始移动到停止移动一共用了(4+2)秒(结果保留根号).==1×BE=3,即×AD×=3,==2AB+BC+CD=2+2+2=4+24+21=4+2(秒)4+2(2012贵州省毕节市,23,12分)如图①,有一张矩形纸片,将它沿对角线AC剪开,得到△ACD和△A′BC′.(1)如图②,将△ACD沿A′C′边向上平移,使点A与点C′重合,连接A′D和BC,四边形A′BCD是形;(2)如图③,将△ACD的顶点A与A′点重合,然后绕点A沿逆时针方向旋转,使点D、A、B在同一直线上,则旋转角为度;连接CC′,四边形CDBC′是形;(3)如图④,将AC边与A′C′边重合,并使顶点B和D在AC边的同一侧,设AB、CD相交于E,连接BD,四边形ADBC是什么特殊四边形?请说明你的理由。
第23题图解析:(1)利用平行四边形的判定,对角线互相平分的四边形是平行四边形得出即可;(2)利用旋转变换的性质以及直角梯形判定得出即可;(3)利用等腰梯形的判定方法得出BD∥AC,AD=CE,即可得出答案.解案:解:(1)平行四边形;证明:∵AD=AB,AA′=AC,∴A′C与BD互相平分,∴四边形A′BCD是平行四边形;(2)∵DA由垂直于AB,逆时针旋转到点D、A、B在同一直线上,∴旋转角为90度;证明:∵∠D=∠B=90°,A,D,B在一条直线上,∴CD∥BC′,∴四边形CDBC′是直角梯形;故答案为:90,直角梯;(3)四边形ADBC是等腰梯形;证明:过点B作BM⊥AC,过点D作DN⊥AC,垂足分别为M,N,∵有一张矩形纸片,将它沿对角线AC剪开,得到△ACD和△A′BC′.∴△ACD≌△A′BC′,∴BM=ND,∴BD∥AC,∵AD=BC,∴四边形ADBC是等腰梯形.点评:此题主要考查了图形的剪拼与平行四边形的判定和等腰梯形的判定、直角梯形的判定方法等知识,熟练掌握判定定理是解题关键.(2012年广西玉林市,26,12分)如图,在平面直角坐标系xOy中,矩形AOCD的顶点A的坐标是(0,4),现有两动点P ,Q ,点P 从点O 出发沿线段OC (不包括端点O ,C )以每秒2个单位长度的速度匀速向点C 运动,点Q 从点C 出发沿线段CD (不包括端点C 、D )以每秒1个单位长度的速度匀速向点D 运动.点P ,Q 同时出发,同时停止.设运动的时间为t (秒),当t=2(秒)时,PQ=52.(1)求点D 的坐标,并直接写出t 的取值范围;(2)连接AQ 并延长交x 轴于点E ,把AE 沿AD 翻折交CD 延长线于点F ,连接EF ,则△AEF 的面积S 是否随t 的变化而变化?若变化,求出S 与t 的函数关系式;若不变化,求出S 的值.(3)在(2)的条件下,t 为何值时,四边形APQF 是梯形?解:(1)设OC=x , 当t=2时,OP=4,PC=x -4;CQ=2. 在Rt △PQC 中,222CQ PC PQ +=,()()2222452+-=x ,解得01=x (不合题意,舍去),82=x ,∴D 点坐标(8,4);(2)由翻折可知,点Q 和点F 关于直线AD 对称,∴QD=DF=4-t ,而AD=8,∴()t t S AQF 83242821-=-⨯⨯=∆. 设经过A (0,4)、Q (8,t )两点的一次函数解析式为b kx y +=,故有:⎩⎨⎧+==bk t b 84,解得84-=t k ,∴一次函数的解析式为484+-=x t y ,易知一次函数与x 轴的交点的坐标为(t -432,0),∴EC=t -432-8,∴()t t t S EQ F 842843221=-⨯⎪⎭⎫⎝⎛--⨯=∆,∴328832=+-=+=∆∆∆t t S S S Q FE AFQ AFE.∴△AEF 的面积S 不随t 的变化而变化,S 的值为32.(3)因AP 与QF 不平行,要想使四边形APQF 是梯形,须有PQ ∥AF.∵AF=AQ ,∴∠AFQ=∠AQF ,而∠CQE=∠AQF ,要想PQ ∥AF ,须有∠AFQ=∠PQC ,故只需具备条件∠PQC =∠CQE ,又∵QC ⊥PE ,∴∠ CQP=∠QCE ,QC=QC ,∴△CQP ≌△QCE ,∴PC=CE ,即8-2t=t-432-8,解得5261+=t (不合题意,舍去),5262-=t .故当526-=t 时,四边形APQF 是梯形.(2012珠海,22,9分)如图,在等腰梯形ABCD 中AB ∥CD,AB =,高CE =对角线AC 、BD 交于H ,平行于线段BD 的两条直线MN 、RQ 同时从点A 出发沿AC 方向向点C 匀速平移,分别交等腰梯形ABCD 的边于M 、N 和R 、Q ,分别交对角线AC 于F 、G ;当直线RQ 到达点C 时,两直线同时停止移动.记等腰梯形ABCD 被直线MN 扫过的面积为1S ,被直线RQ 扫过的面积为2S ,若直线MN 平移的速度为1单位/秒,直线RQ 平移的速度为2单位/秒,设两直线移动的时间为x 秒.(1)填空:∠AHB =____________; AC =_____________; (2) 若213S S =,求x;(3) 若21S mS =,求m 的变化范围.第22题备用图【解析】(1) 如图第22题-1所示,平移对角线DB,交AB 的延长线于P.则四边形BPCD 是平行四边形,BD=PC,BP =DC 因为等腰梯形ABCD,AB ∥CD,所以AC =BD. 所以AC =PC.又高CE ==所以AE =EP =所以∠AHB =90°AC =4;第22题图-1⑵直线移动有两种情况:302x <<及322x ≤≤,需要分类讨论.①当302x <<时, 有2214S AG S AF ⎛⎫== ⎪⎝⎭.∴213S S ≠②当322x ≤≤时,先用含有x 的代数式分别表示1S ,2S ,然后由213S S =列出方程,解之可得x 的值;(3) 分情况讨论:①当302x <<时, 错误!未指定书签。
.②当322x ≤≤时,由21S mS =,得()222188223x S m S x --===2123643x ⎛⎫--+ ⎪⎝⎭.然后讨论这个函数的最值,确定m 的变化范围.【答案】(1) 90°,4;(2)直线移动有两种情况:302x <<及322x ≤≤. ①当302x <<时,∵MN ∥BD,∴△AMN ∽△ARQ,△ANF ∽△AQG. 2214S AG S AF ⎛⎫== ⎪⎝⎭.∴213S S ≠ ②当322x ≤≤时, 如图第22题-2所示,第22题图-2CG =4-2x,CH =1,14122BCDS ∆=⨯⨯=. ()22422821CRQ x S x ∆-⎛⎫=⨯=- ⎪⎝⎭2123S x =,()22882S x =-- 由213S S =,得方程()22288233x x --=⨯,解得165x =(舍去),22x =. ∴x =2. (3) 当302x <<时,m =4 当322x ≤≤时, 由21S mS =,得()2288223x m x --==2364812x x -+-=2123643x ⎛⎫--+ ⎪⎝⎭. M 是1x 的二次函数, 当322x ≤≤时, 即当11223x ≤≤时, M 随1x的增大而增大.当32x =时,最大值m =4. 当x =2时,最小值m =3.∴3≤m ≤4.【点评】本题是一道几何代数综合压轴题,重点考查等腰梯形, 相似三角形的性质,二次函数的增减性和最值及分类讨论,由特殊到一般的数学思想等的综合应用.解题时,(1)小题,通过平移对角线,将等腰梯形转化为等腰三角形,从而使问题得以简化,是我们解决梯形问题常用的方法.(2) 小题直线移动有两种情况:302x <<及322x ≤≤,需要分类讨论.这点万不可忽略,解题时用到的知识点主要是相似三角形面积比等于相似比的平方.(3) 小题仍需要分情况讨论.对于函数2123643m x ⎛⎫=--+ ⎪⎝⎭,讨论它的增减性和最值是个难点. 讨论之前点明我们把这个函数看作“M 是1x 的二次函数”对顺利作答至关重要.(2012·湖南省张家界市·16题·3分)已知线段AB=6,C 、D 是AB 上两点,且AC=DB=1,P 是线段CD 上一动点,在AB 同侧分别作等边三角形APE 和等边三角形PBF ,G 为线段EF 的中点,点P 由点C 移动到点D 时,G 点移动的路径长度为 2 . 【分析】不好意思,本题做不出来,还请高手补充(2012湖北荆州,18,3分)如图(1)所示,E 为矩形ABCD 的边AD 上一点,动点P 、Q 同时从点B 出发,点P 沿折线BE —ED —DC 运动到点C 时停止,点Q 沿BC 运动到点C 时停止,它们运动的速度都是1cm/秒.设P 、Q 同发t 秒时,△BPQ 的面积为y cm 2.已知y 与t 的函数关系图象如图(2)(曲线OM 为抛物线的一部分),则下列结论:①AD =BE =5;②cos ∠ABE =35;③当0<t ≤5时,y =25t 2;④当t =294秒时,△ABE ∽△QBP ;其中正确的结论是__▲__(填序号).【解析】首先,分析函数的图象两个坐标轴表示的实际意义及函数的图象的增减情况. 横轴表示时间t ,纵轴表示△BPQ 的面积y .当0<t ≤5时,图象为抛物线,图象过原点,且关于y 轴对称,y 随的t 增大而增大, t=5的时候,△BPQ 的面积最大,5<t <7时,y 是常函数,△BPQ 的面积不变,为10.从而得到结论:t=5的时候,点Q 运动到点C ,点P 运动到点E , 所以BE =BC=AD =5×1=5cm ,5<t <7时,点P 从E →D ,所以ED =2×1=2cm ,AE=3 cm ,AB=4 cm. cos ∠ABE =54=BE AB . 设抛物线OM 的函数关系式为2at y =(,0≠a 0<t ≤5),把(5,10)代入得到a 2510=,所以52=a , 所以当0<t ≤5时, y =52t 2当t >5时,点P 位于线段CD 上,点Q 与点C 重合,. 当t =294秒,点P 位于P ’处,C P ’=CD -DP ’=4-(294-7)=415 cm. 在△ABE 和△Q ’BP ’中,34''==CP B Q AE AB ,∠A =Q ’=90°,所以△ABE ∽△Q ’BP ’ 【答案】①③④【点评】本题综合考察了动点问题、二次函数、三角形相似、常函数、锐角三角函数、分段函数的知识,综合性强。
