九年级数学下册第六章二次函数的图像与性质导学案(4)(无答案) 苏科版

合集下载

苏科版九年级数学下册《二次函数的图像和性质(4)》导学案-新版

5.2二次函数的图像和性质（4）学习目标：1．会用描点法画函数y＝a(x＋m)2＋k（a≠0）的图像；2．会用平移变换解释函数y＝a(x＋m)2＋k与函数y＝ax2＋k、y＝a(x＋m)2、y＝ax2（a≠0）的图像之间的关系；3．会用配方法确定二次函数图像的顶点坐标、对称轴，根据对称性列表、描点、画图，并确定函数的最大值或者最小值；4．进一步体会数学研究问题由具体到抽象、特殊到一般的思想方法．学习过程：【创设情境】复习：你知道函数y＝x2＋2的图像与y＝x2的图像有什么关系？函数y＝(x＋3)2的图像和y＝x2的图像有什么关系？猜想：函数y＝(x＋3)2＋2与y＝x2有什么关系？【新知探究】问题1.画函数y＝x2、y＝(x＋3)2和y＝(x＋3)2＋2的图像．1．填表：2．画图：在直角坐标系中，描点画出函数y＝x2、y＝(x＋3)2和y＝(x＋3)2＋2的图像；3．观察：（1）你能说出函数y＝(x＋3)2＋2的图像的形状吗？（2）函数y＝(x＋3)2＋2的图像与函数y＝(x＋3)2和y＝x2的图像有什么联系？（3）根据图像，你能得出函数y＝(x＋3)2＋2图像的性质吗？4．思考：函数y＝x2＋2x＋3的图像是抛物线吗？它与函数y＝(x＋1)2＋2有何关系？总结与归纳:(1)函数y＝a (x＋m)2＋k的图像与y＝ax2（a≠0）的图像有什么关系？(2) 函数y＝a(x＋m)2＋k（a≠0）有什么性质？问题2.你能将函数y＝－x2－4x－5转化为y＝a(x＋m)2＋k的形式吗？并画出它的图像，指出它的开口方向、顶点坐标、对称轴、最大（小）值．问题3.如何将二次函数y＝ax2＋bx＋c转化为y＝a(x＋m)2＋k（a≠0）的形式？总结与归纳:（1）二次函数y＝ax2＋bx＋c（a≠0）转化为y＝a(x＋m)2＋k的形式是什么？（2）你能得到函数y＝ax2＋bx＋c（a≠0）的哪些性质？【拓展延伸】问题4.已知，抛物线2=-+的顶点坐标是（2，2），且抛物线经过点（0，1）。

九年级数学下册第六章二次函数的图像与性质导学案苏科版

6.2.1二次函数的图像与性质⑸班级姓名【学习目标】1.会用描点法画二次函数c bx ax y ++=2的图像，掌握它的性质. 2.渗透数形结合思想. 【课前自习】1. 根据()k h x a y ++=2的图像和性质填表：函数图像a开口对称轴顶点增减性 ()k h x a y ++=2向上当x 时，y 随x的增大而减少. 当0>x时，y 随x的增大而 .0<a当x 时，y 随x的增大而减少. 当x 时，y 随x 的增大而 .2.抛物线()1222++=x y 的开口向，对称轴是；顶点坐标是，说明当x = 时，y 有最值是；无论x 取任何实数，y 的取值范围是 . 3.抛物线()1322---=x y 的开口向，对称轴是；顶点坐标是，说明当x = 时，y 有最值是；无论x 取任何实数，y 的取值范围是 . 4.抛物线()31212-+-=x y 与抛物线关于x 轴成轴对称；抛物线()31212-+-=x y 与抛物线关于y 轴成轴对称. 5.()k h x a y ++=2被我们称为二次函数的式.【课堂助学】教师评价家长签字xyOxyO一、探索归纳：1.问题：你能直接说出函数222++=x x y 的图像的对称轴和顶点坐标吗？ 2.你有办法解决问题①吗？222++=x x y 的对称轴是，顶点坐标是 .3.像这样我们可以把一个一般形式的二次函数用的方法转化为式，从而直接得到它的图像性质.练习1.用配方法把下列二次函数化成顶点式：①222+-=x x y ②232++=x x y ③c bx ax y ++=24.归纳：二次函数的一般形式c bx ax y ++=2可以被整理成顶点式：，说明它的对称轴是，顶点坐标公式是 .练习2.用公式法把下列二次函数化成顶点式：①4322+-=x x y ②232++-=x x y ③x x y 22--=二、典型例题：例1、用描点法画出12212-+=x x y 的图像. ⑴用法求顶点坐标： ⑵列表：顶点坐标填在x… ……⑶在下列平面直角坐标系中描出表中各点，并把这些点连成平滑的曲线：⑷观察图像，该抛物线与y 轴交与点，与x 轴有个交点.12212-+=x x y xy O 1-1-2-3-4-5234512-1-2例2、已知抛物线c x x y +-=42的顶点A 在直线14--=x y 上，求抛物线的顶点坐标.【课堂检测】1.用配方法把下列二次函数化成顶点式：①232+-=x x y ②242++=x x y2.用公式法把下列二次函数化成顶点式：①4322-+-=x x y ②2212+-=x x y3.用描点法画出322-+=x x y 的图像. ⑴用法求顶点坐标： ⑵列表：⑷观察左图：①抛物线与y 轴交点坐标是； ②抛物线与x 轴交点坐标是；③当=x 时，0=y ； ④它的对称轴是； ⑤当x 时，y 随x 的增大而减小.【课外作业】x… … 322-+=x x y …x yO 1-1-2-3-423412345-1-2-3-41.用配方法把下列二次函数化成顶点式：①252+-=x x y ②322-+=x x y2.用公式法把下列二次函数化成顶点式： ①322-+-=x x y ②x x y -=2213.抛物线y= 3x 2+2x 的图像开口向，顶点坐标是，说明当x= 时， y 有最值是 .4.函数y=-2x 2+8x+8的对称轴是，当x 时，y 随x 的增大而增大.5.用描点法画出23212+--=x x y 的图像. ⑴用法求顶点坐标： ⑵列表： ⑶在下列平面直角坐标系中描出表中各点，并把这些点连成平滑的曲线：⑷观察上图：①抛物线与y 轴交点坐标是；抛物线与x 轴交点坐标是； ②当=x 时，0=y ； ③它的对称轴是； ④当x 时，y 随x 的增大而减小.x… … …教师评价家长签字23212+--=x x y xy O 1-1234-2-3-4-5512-1-2-3。

苏科版九年级下册5.2《二次函数的图像和性质4》教案设计

（a≠0）可以转化为 y＝a(x＋ 4ac－b2 ，探讨
b 2a
)2＋
4ac－b2 4a
；由此可知，
4a b 和 4ac－b2 在
二次函数 y＝ax2＋bx＋（c a≠0） 2a
4a
的图像是抛物线，顶点坐标为二次函数 y＝ ax2
（- b ， 4ac－b2 ），对称轴是＋bx＋c（a≠0）
y＝x2 的图像有什么关系？
函数 y＝ax（2 a≠0）图像的关系，学习新知识的欲
猜想：函数 y＝(x＋3)2＋2 与 y＝x2 有什为本节课学习打下基础．
望．
么关系？
活动一：画图与观察
1．按照列表、描点、连线
学生有了上
画函数 y＝x2、y＝(x＋3)2 和 y＝(x＋3)2 的过程画函数图像．
学生相互交
思考：（1）函数 y＝a(x＋m)2＋k 的图像师生共同总结出结论：
流、补充，逐步完
与 y＝ax2（a≠0）的图像有什么关系？
（1）函数 y＝a(x＋m)2＋k 善函数 y＝ a(x＋
（2）函数 y＝a(x＋m)2＋k（a≠0）有什的图像可以看成由函数 y＝ax2 m)2＋k 的性质，函
3 的图像是抛物线．
抛物线；并通过观
y＝(x＋3)2 和 y＝(x＋3)2＋2 的图像； 3．观察：
察得到函数 y＝(x ＋1)2＋2 的性质．
（1）你能说出函数 y＝(x＋3)2＋2 的图像
通过配方将
的形状吗？
二次函数一般式 y
（2）函数 y＝(x＋3)2＋2 的图像与函数 y ＝(x＋3)2 和 y＝x2 的图像有什么联系？
2a
4a
图像和性质中的

九年级数学下册第六章二次函数导学案(无答案)

6.1二次函数班级姓名【学习目标】1.使学生理解二次函数的概念.2.使学生能够根据实际问题列出二次函数关系式，了解如何确定自变量的取值范围. 【课前自习】1.我们学过的函数有函数和函数.2.一次函数的关系式是y = （）；特别，当时，一次函数就是正比例函数y = .3.反比例函数的关系式是y = ( ).4.一元二次方程的一般形式是：（），其中是二次项，是一次项，是常数项，是一次项系数，是二次项系数.5.若关于x 方程013)1(12=++++x x k k是一元二次方程，则k = .6.圆的面积公式是：S = ，可以看成是关于的函数，其中是自变量，是因变量，根据实际r 的取值范围是 .【课堂助学】一、情境导入：1．一粒石子投入水中，激起的波纹不断向外扩展.扩展的圆的面积S 与半径r 之间的函数关系式是 .2．用16米长的篱笆围成长方形的生物园饲养小兔,怎样围可使小兔的活动范围最大? 在这个问题中，可设长方形生物园的长为x 米，则宽为米，如果将面积记为y 平方米，那么y 与x 之间的函数关系式为y = ，整理为y = . 3．要给边长为x 米的正方形房间铺设地板，已知某种地板的价格为每平方米240元，踢脚线的价格为每米30元，如果其他费用为1000元，门宽0.8米，那么总费用y 为多少元？在这个问题中,地板的费用与有关,为元,踢脚线的费用与有关,为元.其他费用固定不变为元,所以总费用教师评价家长签字y （元）与x （m ）之间的函数关系式是y = ，整理为y = .二、探究归纳： 1.上述函数关系式有哪些共同之处？它们与一次函数、反比例函数关系式有什么不同？2.一般地，我们把形如：y = ( )的函数称为二次函数.其中是自变量，是因变量，这是关于函数.3.一般地，二次函数c bx ax y ++=2中自变量x 的取值范围是 .但在实际问题中，他们的取值范围往往有所限制，你能说出上述三个问题中自变量的取值范围吗？① ② ③ 三、典型例题：例1、判断下列函数是否为二次函数.如果是，写出其中a 、b 、c 的值. ①231x y -=( ) ②)5(-=x x y ( ) ③ ( )④23)2(3x x x y +-=( ) ⑤ ( ) ⑥652++=x x y ( )⑦1224-+=x x y ( ) ⑧c bx ax y ++=2( )例2、当k 为何值时，函数1)1(2+-=+kk x k y 为二次函数？例3、用一根长为40cm 的铁丝围成一个半径为r 的扇形，求扇形的面积S 与它的半径r 之间的函数关系式．这个函数是二次函数吗？请写出半径r 的取值范围．例4、已知二次函数2ax y =，当x =3时，y = -5，当y =51-时，求x 的值．12321+-=x x y 21xy =【课堂检测】1.判断下列函数是否为二次函数.如果是，写出它的二次项系数、一次项系数、常数项.①232x y -=( )②323x x y +=( )③y = ( )④y = ( )2.写出下列函数关系式：⑴多边形的对角线的条数d 与边数n 之间的函数关系式。

苏科版数学九年级下册5.2《二次函数的图象和性质》(第4课时)讲教学设计

苏科版数学九年级下册5.2《二次函数的图象和性质》（第4课时）讲教学设计一. 教材分析苏科版数学九年级下册5.2《二次函数的图象和性质》（第4课时）的内容主要包括：二次函数的图象特点、二次函数的性质以及二次函数图象与系数的关系。

通过本节课的学习，使学生掌握二次函数的图象和性质，能够熟练运用二次函数的图象和性质解决实际问题。

二. 学情分析学生在学习本节课之前，已经掌握了二次函数的定义、标准式以及顶点式，对二次函数的基本概念有了初步的了解。

但学生对二次函数的图象和性质的认识尚浅，需要通过本节课的学习，进一步深化对二次函数的理解。

三. 教学目标1.知识与技能：使学生掌握二次函数的图象特点、二次函数的性质以及二次函数图象与系数的关系。

2.过程与方法：通过观察、分析、归纳等方法，引导学生发现二次函数的图象和性质，培养学生的观察能力和逻辑思维能力。

3.情感态度价值观：激发学生对数学的兴趣，培养学生的探索精神，使学生感受到数学在生活中的重要性。

四. 教学重难点1.重点：二次函数的图象特点、二次函数的性质以及二次函数图象与系数的关系。

2.难点：二次函数图象与系数的关系的推导和理解。

五. 教学方法1.采用问题驱动法，引导学生主动探究二次函数的图象和性质。

2.利用多媒体课件，直观展示二次函数的图象，增强学生的直观感受。

3.采用合作学习法，让学生在小组讨论中，共同探讨二次函数的图象和性质。

4.运用归纳总结法，引导学生发现二次函数的图象和性质的规律。

六. 教学准备1.多媒体课件：制作二次函数的图象和性质的课件，包括图片、动画等。

2.教学素材：准备一些关于二次函数的图象和性质的例题和练习题。

3.学生活动材料：准备一些卡片，用于小组讨论和展示。

七. 教学过程1.导入（5分钟）利用多媒体课件，展示一些二次函数的图象，如y=x²、y=x²-1、y=2x²-3x+1等，引导学生观察这些图象的特点，激发学生的学习兴趣。

苏科版数学九年级下册5.2《二次函数的图象和性质》教学设计4)

苏科版数学九年级下册5.2《二次函数的图象和性质》教学设计4）一. 教材分析苏科版数学九年级下册5.2《二次函数的图象和性质》是本节课的主要内容。

教材从学生已有的知识出发，通过观察、实验、探究等活动，引导学生认识二次函数的图象和性质，从而加深对二次函数的理解。

本节课的内容对于学生来说是比较抽象的，需要通过大量的实践活动来理解和掌握。

二. 学情分析学生在学习本节课之前，已经学习了二次函数的定义和标准式，对于二次函数有一定的了解。

但是，对于二次函数的图象和性质，大部分学生可能会感到比较抽象和难以理解。

因此，在教学过程中，需要引导学生通过观察、实验、探究等活动，来理解和掌握二次函数的图象和性质。

三. 教学目标1.理解二次函数的图象和性质，能够熟练地运用二次函数的图象和性质解决实际问题。

2.培养学生的观察能力、实验能力和探究能力。

3.提高学生对数学的兴趣和信心。

四. 教学重难点1.二次函数的图象和性质的理解和掌握。

2.如何运用二次函数的图象和性质解决实际问题。

五. 教学方法1.观察法：引导学生观察二次函数的图象，从而理解二次函数的性质。

2.实验法：让学生通过实际操作，探究二次函数的性质。

3.探究法：引导学生通过问题探究，深入理解二次函数的图象和性质。

4.讲解法：对于一些难以理解的概念和性质，采用讲解法进行解释。

六. 教学准备1.PPT课件：制作相关的PPT课件，以便于教学。

2.练习题：准备一些相关的练习题，以便于巩固所学知识。

3.教学工具：准备一些教学工具，如黑板、粉笔等。

七. 教学过程1.导入（5分钟）通过一个实际问题，引入二次函数的图象和性质。

例如：一个抛物线形的水池，求水池的深度。

2.呈现（10分钟）利用PPT课件，呈现二次函数的图象和性质。

通过观察和讲解，让学生理解二次函数的图象和性质。

3.操练（10分钟）让学生通过实际操作，探究二次函数的性质。

可以让学生用尺子和圆规，画出二次函数的图象，并观察其性质。

苏科版九年级数学(下)教案5.2二次函数图像和性质(4)

课题: §5.1二次函数教学目标：1.掌握二次函数2222m ))(+=+==++=x a y k ax y ax y k m x a y （、、与的图像的位置关系；2、会用配方法确定二次函数c bx ax y ++=2图象的顶点坐标、对称轴和函数的最值，会用列表描点法画函数k m x a y ++=2)(的图象．教学重点：通过配方法画二次函数y=ax 2+bx+c 的图象、确定其开口方向、顶点坐标、对称轴以及函数的最值问题教学难点：用配方法确定二次函数的顶点坐标和对称轴教学程序设计：一、情境创设上节课，我们发现了 2ax y =与 k ax y +=2， 2)(m x a y +=的图象之间的关系，那么你认为形如k m x a y ++=2)(的图象会是什么呢？形如 c bx ax y ++=2的图易用又是什么呢？它们有什么性质？生2：补充回答设计意图：展示上节课的探究内容，让学生进入这个数学活动，意图是引领学生从点坐标的数量变化、图形的位置变化着手，用运动变化的观点来分析解决问题二、探索活动抛物线2)1(2--=x y 的性质3．讨论c bx ax y ++=2的图象性质师生活动设计：师：展示同一坐标系中 2x y =与21）（+=x y 212++=）（x y 的图象，出示这个问题。

生：思考并解决。

活动一：探索二次函数 k m x a y ++=2)(的图象和性质。

1．在直角坐标系把2x y =的图象沿X 轴左向移动1个单位，再沿y 轴向上移动2 个单位，画出这条新的抛物线。

2．写出这条抛物线的解析式。

3．抛物线2)1(2++=x y 的性质。

活动二：探索c bx ax y ++=2的图象及其性质。

1．讨论322++=x x y 的图象及性质。

2．运用配方法，找一找c bx ax y ++=2的顶点坐标公式和对称轴。

生10：补充或纠正回答生7：（增减性方面）设计意图：活动一中：学生已有左加右减上加下减的平移规律，知道平移前后仅仅是顶点和对称轴的位置变化，容易归纳出形如k m x a y ++=2)(的图象性质。

苏科版九年级数学第六章《二次函数》全章导学案

《6.1 二次函数》导学案学习目标：1.经历对实际问题情境分析确定二次函数表达式的过程，体会二次函数意义；2.了解二次函数关系式，会确定二次函数关系式中各项的系数。

一、知识准备：1.设在一个变化过程中有两个变量x 和y ，如果对于x 的每一个值， y 都有唯一的值与它对应，那么就说y 是x 的，x 叫做。

2.我们已经学过的函数有：一次函数、反比例函数，其中的图像是直线，的图像是双曲线。

我们得到它们图像的方法和步骤是：① ；② ；③ 。

3. 形如___________y =，（）的函数是一次函数，当______0=时，它是函数，图像是经过的直线；形如k y x=，（）的函数是函数，它的表达式还可以写成：① 、② 二、提出问题（展示交流）：1．一粒石子投入水中，激起的波纹不断向外扩展，扩大的圆的面积S 与半径r 之间的函数关系式是。

2．用16m 长的篱笆围成长方形圈养小兔，圈的面积y(㎡)与长方形的长x(m)之间的函数关系式为。

3．要给一个边长为x (m)的正方形实验室铺设地板，已知某种地板的价格为每平方米240元，踢脚线价格为每米30元，如果其它费用为1000元，那么总费用y （元）与x （m ）之间的函数关系式是。

三、归纳提高（讨论归纳）：观察上述函数函数关系有哪些共同之处？它们与一次函数、反比例函数的关系式有什么不同？。

一般地，形如，（，且）的函数为二次函数。

其中x 是自变量，函数。

四、例题精讲（小组讨论交流）：例1 函数y=（m ＋2）x22-m ＋2x －1是二次函数，则m= ．点拨：从二次函数的定义出发:看二次项的系数和次数确定m 的取值例2．下列函数中是二次函数的有（）①y=x ＋x 1；②y=3（x －1）2＋2；③y=（x ＋3）2－2x 2；④y=21x＋x ．A ．1个B ．2个C ．3个D ．4个例3、写出下列各函数关系，并判断它们是什么类型的函数．⑴圆的面积y （cm 2）与它的周长x （cm ）之间的函数关系；⑵某种储蓄的年利率是1.98%，存入10000元本金，若不计利息税，求本息和y （元）与所存年数x 之间的函数关系；⑶菱形的两条对角线的和为26cm ，求菱形的面积S （cm 2）与一对角线长x （cm ）之间的函数关系五、课堂训练1．下列函数中，二次函数是（） A ．y=6x 2＋1 B ．y=6x ＋1 C ．y=x 6＋1 D ．y=26x ＋12．函数y=（m －n ）x 2＋mx ＋n 是二次函数的条件是（） A ．m 、n 为常数，且m ≠0 B ．m 、n 为常数，且m ≠n C ．m 、n 为常数，且n ≠0D ．m 、n 可以为任何常数3．半径为3的圆，如果半径增加2x ，则面积S 与x 之间的函数表达式为（） AS=2π（x ＋3）2B.S=9π＋xC.S=4πx 2＋12x ＋9 D S=4πx 2＋12πx ＋9π4.下列函数关系中,满足二次函数关系的是( )A.圆的周长与圆的半径之间的关系;B.在弹性限度内,弹簧的长度与所挂物体质量的关系;C.圆柱的高一定时,圆柱的体积与底面半径的关系;D.距离一定时,汽车行驶的速度与时间之间的关系.5.已知菱形的一条对角线长为a ，另一条对角线为它的3倍，用表达式表示出菱形的面积S 与对角线a 的关系_________．6.若一个边长为x cm 的无盖．．正方体形纸盒的表面积为y cm 2，则___________y =，其中x 的取值范围是。

江苏省沭阳县怀文中学九年级数学下册 6.2二次函数的图象和性质第四课时导学案(无答案) 苏科版

6.2二次函数的图象和性质第四课时班级：学号：姓名：学习目标：1．会用描点法画出二次函数的图象；2．知道抛物线的对称轴与顶点坐标．学习过程：一、自主探究1．函数、与及其图象间的相互关系3．请说出以下二次函数的图象、对称轴、顶点坐标、开口方向、增减性、最大（小）值．二、自主合作在同一直角坐标系内，用描点法画出二次函数2x y =，()21+=x y ()212++=x y 的图象，并指出它们的开口方向，对称轴及顶点坐标．三、自主展示在同一直角坐标系内，用描点法画出函数y=－12 x 2,y=－ 12 x 2-1, y=－ 12（x ＋1）2, y=－12(x+1)2－1的的图象，并指出它们的开口方向，对称轴及顶点坐标． 1．抛物线y=－12 (x+1)2－1是由抛物线y=－12x 2-1怎样移动得到的？ 2.抛物线y=－12 (x+1)2－1是由抛物线y=－12（x ＋1）2怎样移动得到的？ 3.抛物线y=－12 (x+1)2－1是由抛物线y=－12x 2怎样移动得到的？归纳：一般地，抛物线y=a(x-h)2+k 与y=ax 2形状相同，位置不同。

把抛物线y=ax 2向上（下）向左（右）平移，可以得到抛物线y=a(x-h)2+k ．平移的方向、距离要根据h,k 的值来决定. 抛物线y=a(x-h)2+k 有如下特点：（１）当a>0时，开口向上，当x ＞h 时，y 随x 的增大而增大；当x ＜h 时，y 随x 的增大而减小；当a<0时，开口向下，当x ＜h 时，y 随x 的增大而增大；当x ＞h 时，y 随x 的增大而减小；（２）对称轴是直线x=h ；（３）顶点坐标是（h ，k ）．四、自主拓展1．把抛物线y=x 2沿x 轴向平移个单位，再沿y 轴向平移个单位可得到抛物线y=(x －2)2+4.2．抛物线y=－5(x －1)2－3的顶点坐标是，对称轴是，开口向．3．二次函数y=2(x －12)2＋3,当x 时，y 随x 的增大而增大；当x 时，y 随x 的增大而减小；当x= 时，函数可取最值．4．当m= 时，抛物线y=（m ＋1）x m m 2＋9开口向下，对称轴是．在对称轴左侧，y 随x 的增大而；在对称轴右侧，y 随x 的增大而． 5.写出下列抛物线的开口方向、对称轴及顶点．（1）y=2(x ＋3)2＋5 （2）y=－3(x －1)2－20 （3）y= 4(x －3)2＋7 （4）y=－5(x＋2)2－66．把抛物线y=x 2＋bx ＋c 向右平移3个单位，在向下平移2个单位，所得图象的解析式是y=x 2－3x ＋5,求b,c 的值．7．已知抛物线y=a(x －t －1)2＋t 2 ( a,t 是常数，a ≠0，t ≠0 )的顶点是A.（1）判断点A 是否在抛物线y=x 2－2x ＋1上，为什么？（2）如果抛物线y= a(x －t －1)2＋t 2经过点B(B 为抛物线y=x 2-2x ＋1的顶点)①求a 的值；②这条抛物线与x 轴的两个交点和它的顶点A 能否构成直角三角形？若能，求出t 的值；若不能，请说明理由．。

九年级数学下册第六章求二次函数的关系式导学案 (无答案)苏科版

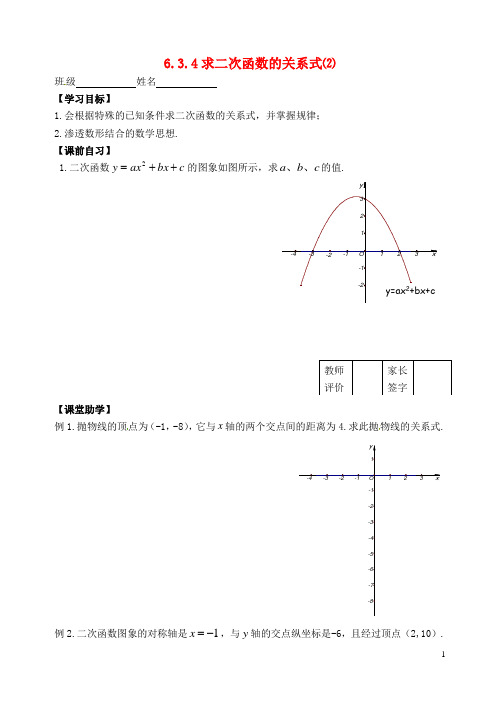
6.3.4求二次函数的关系式⑵班级姓名【学习目标】1.会根据特殊的已知条件求二次函数的关系式，并掌握规律；2.渗透数形结合的数学思想. 【课前自习】1.二次函数c bx ax y ++=2的图象如图所示，求c b a 、、的值.【课堂助学】例1.抛物线的顶点为（-1，-8），它与x 轴的两个交点间的距离为4.求此抛物线的关系式.例2.二次函数图象的对称轴是1-=x ，与y 轴的交点纵坐标是-6，且经过顶点（2,10）.求此二次函数的关系式.【拓展提升】二次函数c bx ax y ++=2的图象与x 轴交与A 、B 两点，与y 轴交C 点，A 点坐标为（-3,0）、B 点坐标为（1,0），且△ABC 的面积为6，求该二次函数的关系式.【课堂检测】1.抛物线与x 交与点A(-1,0)、B （-6,0），则线段AB= .2.二次函数c bx x y ++=2的对称轴是直线1=x ，则b = .3.函数c bx x y ++=2经过(-2,0)、(3,0)两点，则这个函数的关系式是b = ，c = . 4.已知二次函数c bx ax y ++=2，当3=x 时，函数取得最大值10，且它的图象在x 轴上截得的线段长为4，求c b a 、、的值.5.抛物线c bx x y ++=2与x 轴只有一个交点，坐标为（-2.，0）.求抛物线的解析式.【课后作业】1.已知二次函数当2=x 时，y 的最值是6，该抛物线可设为 .2.二次函数c bx x y ++=2经过点（0，-3）、（1,0），则该函数关系式是 .3.抛物线c bx x y ++=2经过点（1,0）、（-3,0），则关系式是： .4.抛物线bx ax y +=2在x 轴截得的线段长为4，且经过点（1，3），则该函数关系式是： .5.中考真题：（2010 江苏镇江）运算求解（本小题10分）已知二次函数m x x y ++=22的图象C 1与x 轴有且只有一个公共点. ⑴求C 1的顶点坐标；⑵将C 1向下平移若干个单位后，得抛物线C 2，如果C 2与x 轴的一个交点为A （—3，0），求C 2的函数关系式，并求C 2与x 轴的另一个交点坐标；⑶若n y y C y Q y n P 求实数且上的两点是,,),2(),,(21121>的取值范围.6.如图，二次函数2y x ax b =++的图象与x 轴交于1(,0)2A -,(2,0)B 两点，且与y 轴交于点C .⑴求该抛物线的解析式，并判断ABC ∆的形状；⑵在x 轴上方的抛物线上有一点D ,且以A C D B 、、、四点为顶点的四边形是等腰梯形，请直接写出D 点的坐标为 .★⑶在此抛物线上是否存在点P ,使得以A C B P 、、、四点为顶点的四边形是直角梯形？若存在，求出P 点的坐标；若不存在，说明理由.。

九年级数学下册第六章二次函数与一元二次方程导学案(无答案) 苏科版

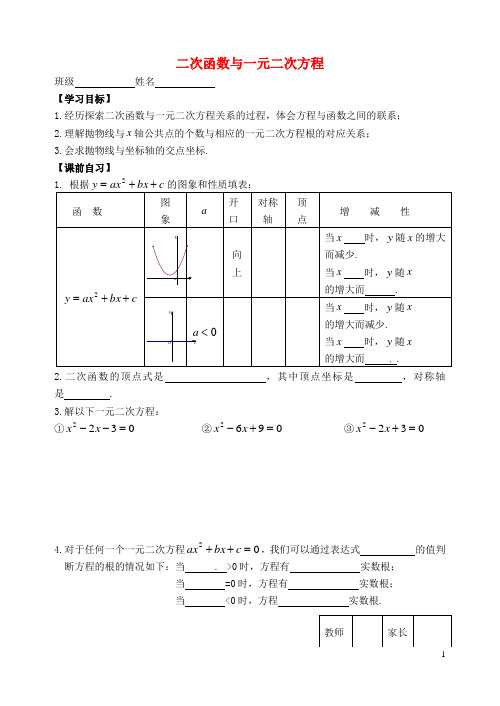
二次函数与一元二次方程班级姓名【学习目标】1.经历探索二次函数与一元二次方程关系的过程，体会方程与函数之间的联系；2.理解抛物线与x 轴公共点的个数与相应的一元二次方程根的对应关系；3.会求抛物线与坐标轴的交点坐标. 【课前自习】1. 根据c bx ax y ++=2的图象和性质填表：函数图象a开口对称轴顶点增减性 c bx ax y ++=2向上当x 时，y 随x 的增大而减少.当x 时，y 随x 的增大而 .0<a当x 时，y 随x的增大而减少. 当x 时，y 随x 的增大而 .2.二次函数的顶点式是，其中顶点坐标是，对称轴是 .3.解以下一元二次方程：①0322=--x x ②0962=+-x x ③0322=+-x x4.对于任何一个一元二次方程02=++c bx ax ，我们可以通过表达式的值判断方程的根的情况如下：当 >0时，方程有实数根；当 =0时，方程有实数根；当 <0时，方程实数根.教师家长xyOxyOxy( , )( , )Oxy( , )xy【课堂助学】一、探索归纳：1.观察二次函数的图象，写出它们与x 轴、y 轴的交点坐标：函数 322--=x x y962+-=x x y322+-=x x y图象交点与x 轴交点坐标是与x 轴交点坐标是与x 轴与y 轴交点坐标是与y 轴交点坐标是与y 轴交点坐标是2.比照《课前自习》第3题各方程的解，你发现什么？3.归纳：⑴一元二次方程02=++c bx ax 的实数根就是对应的二次函数c bx ax y ++=2与x 轴交点的 .⑵二次函数与一元二次方程的关系如下：（一元二次方程的实数根记为21x x 、）二次函数c bx ax y ++=2与一元二次方程02=++c bx ax与x 轴有个交点 ⇔ac b 42- 0，方程有的实数根是 .与x 轴有个交点这个交点是点⇔ac b 42- 0，方程有的实数根是 .与x 轴有个交点 ⇔ ac b 42- 0，方程实数根. ⑶二次函数c bx ax y ++=2与y 轴交点坐标是 .练习.判断以下函数的图象与x 轴是否有公共点，有几个公共点，并说明理由. ⑴x x y -=2； ⑵962-+-=x x y ⑶11632++=x x y评价签字xyy=x -6x+9Oxyy=x -2x-3Oxyy=x -2x+3O二、典型例题：例1、已知二次函数342+-=x x y .求该抛物线的图象与坐标轴的交点坐标.归纳：⑴求抛物线c bx ax y ++=2与x 轴的交点坐标只要令，转化为求对应方程的解；假设对应方程的实数根为21x x 、，那么抛物线与x 轴的交点坐标是，特别当21x x =时，这个交点就是抛物线的 .⑵求抛物线c bx ax y ++=2与y 轴的交点坐标只要令，该交点坐标是 . 这也是求任意函数的图象与坐标轴交点坐标的一般方法.【课堂检测】1.抛物线22x x y --=与x 轴的交点坐标是，与y 轴的交点坐标是 .2.抛物线c bx ax y ++=2的图象都在x 轴的下方，那么函数值y 的取值范围是 .3.抛物线c bx ax y ++=2与x 轴只有一个交点（-3，0），那么它的顶点坐标是 . 4. 假设抛物线42++=bx x y 与x 轴只有1个交点，求b 的值.5. 求抛物线822--=x x y 与x 轴的交点之间的距离.【拓展提升】利用以下平面直角坐标系求例①中抛物线342+-=x x y 与坐标轴的交点围成的 △ABC 的周长和面积.yC y=x 2-4x+3抛物线上是否存在点D ，令△ABD 与△ABC 面积相等，如果有，请写出D 点坐标. 【课外作业】1.判断以下函数的图象与x 轴是否有公共点，有几个公共点，并说明理由. ①252+-=x x y ②122-+-=x x y ③322-+-=x x y2.二次函数的图象与一元二次方程的根的关系如下：抛物线与x 轴有个公共点⇔ac b 42- 0，方程有实数根；抛物线与x 轴有个公共点⇔ac b 42- 0，方程有实数根；抛物线与x 轴有个公共点⇔ac b 42- 0，方程实数根.3.抛物线c bx ax y ++=2的图象都在x 轴的上方，那么函数值y 的取值范围是 .4.假设抛物线92+-=bx x y 与x 轴只有1个交点，那么b = . 5.抛物线c bx ax y ++=2的顶点是（3，0），那么它与x 轴有个交点. 6.已知二次函数1032--=x x y .⑴求该抛物线的图象与坐标轴的交点坐标. ⑵求抛物线与x 轴的交点之间的距离.。

九年级数学下册《6.2 二次函数的图象和性质》教案4 苏科版

2、二次函数 +k的开口方向，对称轴，顶点坐标
观察：
它们的开口方向都向，对称轴分为、、，顶点坐标分为、、．
请同学们完成填空，并观察三个图象之间的关系．
教
学
过
程
程序和内容
师生活动个性化设计
课堂训练
1、抛物线的开口，顶点坐标是，对称轴是；当x＝时，y有最值为；在对称轴左侧，即当x时，y随x的增大而，在对称轴右侧，即当x时，y随x的增大而.
教
学
过
程
程序和内容
师生活动个性化设计
探索你能说出函数 +k（a、h、k是常数，a≠0）的图象的开口方向、对称轴和顶点坐标吗？
小组总结（知识梳理）
1、二次函数的图象的变化规律：
二次函数的图象的上下平移，只影响二次函数 +k中k的值；左右平移，只影响h的值，抛物线的形状不变，所以平移时，可根据顶点坐标的改变，确定平移前、后的函数关系式及平移的路径．此外，图象的平移与平移的顺序无关．
2、你能否在这个直角坐标系中，再画出函数的图像？
小组合作
二次函数图象的变化规律：左加右减，上加下减
例1．在同一直角坐标系中，画出下列函数的图象．
，，，并指出它们的开口方向、对称轴和顶点坐标．
解（1）列表：略（2）描点：
（3）连线，画出这三个函数的图象
3、你能否指出抛物线的开口方向，对称轴，顶点坐标？
5.若把函数的图象分别向下、向左移动2个单位，则得到的函数解析式为。
小结及反馈：
6.把二次函数y=x2－4 x+5化成 y=(x—h)2+k的形式：y=。
7.一条抛物线的形状、开口方向与抛物线相同，对称轴和抛物线相同，且顶点纵坐标为0，求此抛物线的解析式.

九年级数学下册 62 二次函数的图象和性质教案(4) 苏科版教案

二次函数的图象和性质（4）
主备人用案人授课时间月日总第课时课题课型新授课
教学目标1．会用描点法画出二次函数的图像；2．知道抛物线的对称轴与顶点坐标；
重点会画形如的二次函数的图像难点
的二次函数
的顶点坐标和对称轴
教法及教具讲练结合三角板
教学过程
教学内容个案调整
教师主导活动学生主体活动
教学过程:
一、情景创设
1、复习
函数、与及其图象间的相互
关系
二、新授
1、请你在同一直角坐标系内，画出函数
的图像，并指出它们的开口
方向，对称轴及顶点坐标．
2、你能否在这个直角坐标系中，再画出函数的图
像？
3、你能否指出抛物线的开口方向，对称轴，顶点
坐标？将在上面练习中三条抛物线的性质填入所列的有中，如下表：
抛物线开口方向对称轴顶点坐标
教
学
过
教学内容个案调整
教师主导活动学生主体活动
三、练习
1、我们已知抛物线的开口方向是由二次函数中的a
的值决定的，你能通过上表中的特征，试着总结出抛物线的对称轴和
顶点坐标是由什么决定的吗？
2、抛物线
有什么关系？
3、它们的位置有什么关系？
①抛物线是由抛物线怎样移动得到的？
②抛物线是由抛物线怎样移动得到的？
③抛物线是由抛物线怎样移动得
到的？
程
④抛物线是由抛物线怎样移动得
到的？
⑤抛物线是由抛物线怎样移动得到
的？
四、总结、扩展
一般的二次函数，都可以变形成的形式，其中：1．a能决定什么？怎样决定的？
2．它的对称轴是什么？顶点坐标是什么？。

九年级数学下册 5.2 二次函数的图象与性质(4)教案 (新版)苏科版-(新版)苏科版初中九年级下册

二次函数的图像与性质
课题
§二次函数的图像与性质（4）
教学时间
教学目标：
1.会用描点法画出二次函数y ＝a (x ＋h )2
＋k 的图象；
2.能结合图像确定抛物线y ＝a (x ＋h )2
＋k 的开口方向、对称轴与顶点坐标
及其性质；
3.比较抛物线y ＝a (x ＋h )2
＋k 与2
y ax =关系，培养观察、分析、总结的能力.
教学重点：
画出形如y ＝a (x ＋h )2
＋k 的二次函数的图象，能指出开口方向，对称轴，
顶点坐标；理解函数y ＝a (x ＋h )2
＋k 与2
y ax = 及其图象间的相互关系.
教学难点：
画出形如y ＝a (x ＋h )2
＋k 的二次函数的图象，能指出开口方向，对称轴，
顶点坐标；理解函数y ＝a (x ＋h )2
＋k 与2
y ax = 及其图象间的相互关系.
教学方法：自主探究合作交流讲练结合教学媒体：电子白板【教学过程】：一.【情境创设】
回顾二次函数y ＝ax 2
+k 、y ＝a (x ＋h )2
（a ≠0）的图像和性质二.【问题探究】
问题1、（1）在同一坐标系中画出二次函数221x y =，21
(2)2
y x =-，21
(2)22
y x =-+的图象．
（2）在同一坐标系下画出二次函数22
1x y -=，12
12--=x y ，
1)1(2
1
2-+-=x y 的图象。

复备栏。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

6.2.1二次函数的图像与性质⑸
班级姓名【学习目标】
1.会用描点法画二次函数c bx ax y ++=2
的图像，掌握它的性质. 2.渗透数形结合思想. 【课前自习】
2
2.抛物线122++=x y 的开口向，对称轴是；顶点坐标
是，
说明当x = 时，y 有最值是；无论x 取任何实数，y 的取值范围是 . 3.抛物线()1322
---=x y 的开口向，对称轴是；顶点坐标
是，
说明当x = 时，y 有最值是；无论x 取任何实数，y 的取值范围是 . 4.抛物线()312
1
2-+-=x y 与抛物线关于x 轴成轴对称；
抛物线()312
1
2-+-
=x y 与抛物线关于y 轴成轴对称. 5.()k h x a y ++=2
被我们称为二次函数的式.
【课堂助学】
一、探索归纳：
1.问题：你能直接说出函数222
++=x x y 的图像的对称轴和顶点坐标吗？ 2.你有办法解决问题①吗？
222++=x x y 的对称轴是，顶点坐标是 .
3.像这样我们可以把一个一般形式的二次函数用的方法转化为式，从而直接得到它的图像性质.
练习1.用配方法把下列二次函数化成顶点式：
①222
+-=x x y ②232
++=x x y ③c bx ax y ++=2
4.归纳：二次函数的一般形式c bx ax y ++=2
可以被整理成顶点式：，说明它的对称轴是，顶点坐标公式是 .
练习2.用公式法把下列二次函数化成顶点式：
①4322
+-=x x y ②232
++-=x x y ③x x y 22
--=
二、典型例题：例1、用描点法画出122
12
-+=
x x y 的图像. ⑴用
⑶在下列平面直角坐标系中描出表中各点，并把这些点连成平滑的曲线：
⑷观察图像，该抛物线与y 轴交与点，与x 轴有个交点.
例2、已知抛物线c x x y +-=42
的顶点A 在直线14--=x y 上，求抛物线的顶点坐标.
【课堂检测】
1.用配方法把下列二次函数化成顶点式：
①232
+-=x x y ②242
++=x x y
2.用公式法把下列二次函数化成顶点式：
①4322-+-=x x y ②22
12
+-=x x y
3.用描点法画出322
-+=x x y 的图像. ⑴用法求顶点坐标： ⑵列表：
①抛物线与y 轴交点坐标
是；
②抛物线与
x
轴交点坐标
是；
③当=x 时，0=y ； ④它的对称轴是； ⑤当x 时，y 随x 的增大而减小.
【课外作业】
1.用配方法把下列二次函数化成顶点式：
①252+-=x x y ②322
-+=x x y
2.用公式法把下列二次函数化成顶点式： ①322
-+-=x x y ②x x y -=2
2
1
3.抛物线y= 3x 2
+2x 的图像开口向，顶点坐标是，说明当x= 时， y 有最值是 .
4.函数y=-2x 2+8x+8的对称轴是，当x 时，y 随x 的增大而增大.
5.用描点法画出2
3
212+--
=x x y 的图像. ⑴用法求顶点坐标： ⑵列表： ⑶在下列平面直角坐标系中描出表中各点，并把这些点连成平滑的曲线：
①抛物线与y 轴交点坐标是；抛物线与x 轴交点坐标是； ②当=x 时，0=y ； ③它的对称轴是； ④当x 时，y 随x 的增大而减小.。