电工第2章 正弦交流电路
合集下载
电工学-正弦交流电路
O
f 而对直流所呈现的容抗趋于无穷大，故
XL 与 f 的关系 可视为开路。
2.3.3 电容元件的交流电路
1. 电压电流关系 i
+
u
C
–
i
u Um sint i Im sin( t 90 )
+j •
u
I
波 形O 图
电流超前电压 90 电压与电流大小关系 电压与电流相量式
t
U XCI U jXC I
2.1 正弦电压与电流 I, U
直流电路在稳定状态下电流、电压的大
小和方向是不随时间变化的，如图所示。
正弦电压和电流是按正弦规律周期性
变化的，其波形如图示。
O u, i
t
电路图上所标的方向是指它们的参考
方向，即代表正半周的方向。
负半周时，由于的参考方向与实际方
+
向相反，所以为负值。
实
i
O i
t
际 方
第 2 章 正弦交流电路
在生产和生活中普遍应用正弦交流电，特别是三相电路应 用更为广泛。
正弦交流电路是指含有正弦电源(激励)而且电路各部分所 产生的电压和电流(响应)均按正弦规律变化的电路。
本章将介绍交流电路的一些基本概念、基本理论和基本分 析方法，为后面学习交流电机、电器及电子技术打下基础。
本章还将讨论三相交流电路和非正弦周期电压和电流。 交流电路具有用直流电路的概念无法理解和无法分析的物 理现象，因此在学习时注意建立交流的概念，以免引起错误。
•
UL
为正
时电路 中电压 电流相 量图
•
• UL UC
•
U
•
UR
•
UC
的大小和正负由
电工电子技术-第2章 正弦交流电路
区别与一般复数，相量的头顶上一般加符号“·”。 例：正弦量i=14.1sin(ωt+36.9°)A的最大值相量表示为：
•
I m = 14.1∠36.9°A
其有效值相量为：I• = 10∠36.9°A
由于一个电路中各正弦量都是同频率的，所以相量只需 对应正弦量的两要素即可。即模值对应正弦量的最大值或 有效值，幅角对应正弦量的初相。
i u u、i 即时对应！ R
电流、电压的瞬时值表达式
设 i Im sin t u、i 同相！
则 u ImR sin t Um sin t
u、i最大值或有效值之间符
合欧姆定律的数量关系。
Um ImR
或
U IR
•
相量关系式
•
I
U
U0
U
0 I0
RRR
相量图
U
I
（2）电阻元件上的功率关系
3
C -4
D
D 3 j4 第四象限 D 5 arctan 4
3
上式中的j 称为旋转因子，一个复数乘以j相当于在复
平面上逆时针旋转90°；除以j相当于在复平面上顺时针
旋转90°。
※数学课程中旋转因子是用i表示的，电学中为了区别 于电流而改为j。
正弦量的相量表示法
与正弦量相对应的复数形式的电压和电流称为相量。为
乘、除时用极坐标形式比较方便。
在复数运算当中，一定要根据复数所在象
限正确写出幅角的值。如：
+j
B4
A
A 3 j4 第一象限 A 553.1arctan 4 3
B 3 j4 第二象限 B 5180 arctan 4
-3 0
3
+1
3
•
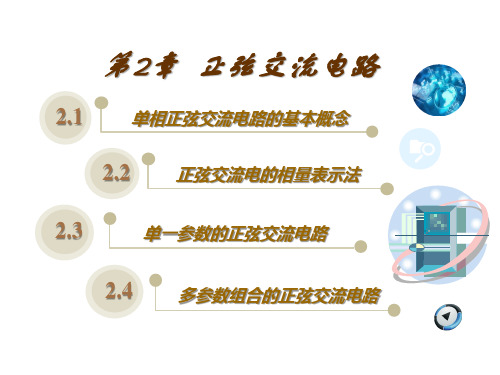
I m = 14.1∠36.9°A
其有效值相量为：I• = 10∠36.9°A
由于一个电路中各正弦量都是同频率的，所以相量只需 对应正弦量的两要素即可。即模值对应正弦量的最大值或 有效值，幅角对应正弦量的初相。
i u u、i 即时对应！ R
电流、电压的瞬时值表达式
设 i Im sin t u、i 同相！
则 u ImR sin t Um sin t
u、i最大值或有效值之间符
合欧姆定律的数量关系。
Um ImR
或
U IR
•
相量关系式
•
I
U
U0
U
0 I0
RRR
相量图
U
I
（2）电阻元件上的功率关系
3
C -4
D
D 3 j4 第四象限 D 5 arctan 4
3
上式中的j 称为旋转因子，一个复数乘以j相当于在复
平面上逆时针旋转90°；除以j相当于在复平面上顺时针
旋转90°。
※数学课程中旋转因子是用i表示的，电学中为了区别 于电流而改为j。
正弦量的相量表示法
与正弦量相对应的复数形式的电压和电流称为相量。为
乘、除时用极坐标形式比较方便。
在复数运算当中，一定要根据复数所在象
限正确写出幅角的值。如：
+j
B4
A
A 3 j4 第一象限 A 553.1arctan 4 3
B 3 j4 第二象限 B 5180 arctan 4
-3 0
3
+1
3
电工电子技术第2章
第2章 正弦交流电路
在交流电路中，因各电流和电压多 +j A 为同一频率的正弦量，故可用有向线段 b r 来表示正弦量的最大值(有效值) Im 、 ψ Um(I、U)和初相ψ ，称为正弦量的相量。 O a +1 在正弦量的大写字母上打“•”表示，如 图2-5 有向线段的表示正弦量 幅值电流、电压相量用 I m、 m表示，有 U • U 效值电流、电压相量用 I 、 表示。将电 U • 路中各电压、电流的相量画在同一坐标 φ I ψ 中，这样的图形称为相量图。 ψ 同频率的u和i可用图2-6相量图表示。 图2-6 u和i的相量图 即 超前 Iφ°，I或 U滞后φ°。 U
第2章 正弦交流电路
2.1
正弦交流电的基本概念
正弦交流电压和电流的大小和方向都按正弦规律 作周期性变化，波形如图2-1a。
u U m s in ( t u ) i I m s in ( t i )
(2-1)
为便于分析，在电路中电压参考方向用“+”、“–” 标出，电流参考方向用实线箭头表示；电压、电流实 际方向用虚线箭头表示如图2-1b、c所示
第2章 正弦交流电路
u Im O φ Ψu Ψi i Um
u
i
t
T
图2-2 u和i相位不等的正弦量波形图
当φ=0º 时，称u、I同相；当φ=180º 时，称u比i反相； 当φ=±90º 时，称u与i正交 。 u i u i
u i
ui
u
i
t
u
i
O a) 同相
t O
b) 反相
O c)正交
t
图2-3 正弦量的同相、反相和正交
第2章 正弦交流电路
中南大学电工学第2章正弦交流电路_02
例3 电路如图所示，图中各仪表均为交流电流表，其读数是 电路如图所示，图中各仪表均为交流电流表， 电流表的有效值。已知A 的读数为8A 8A， 的读数为60A 60A， 电流表的有效值。已知A1的读数为8A，A2的读数为60A，A3的 读数为66A 求电流表A 66A。 的读数，并画出相量图。 读数为66A。求电流表A和A4的读数，并画出相量图。 I4 I 解：由于电路为并联电 A A4 A3 路，则可设 I3 + A1 A2 US= US 0 V 1 US I1 I j L ω R j L 2 ω 则由已知条件得 I1= 8 0 A， 2= 60 -90 A，I3= 66 90 A ， I ， 根据KCL有 有 根据 I4= I2+I3= 60 -90 +66 90 =6 90 A I= I1+I4= 8 0 +6 90 =10 36.9 A 故表A的读数为 的读数为6A。 故表 的读数为10A，表A4的读数为 。 的读数为 ， 的读数为 相量图如图。 相量图如图。 I2 I2 I4 I I1 US I3
▲额定视在功率 额定视在功率 SN = UN IN —— 额定容量 ▲有功功率守恒 有功功率守恒: 有功功率守恒 P = ∑Pi =∑ Ui Ii cosϕ i ▲无功功率守恒 无功功率守恒: 无功功率守恒 Q = ∑Q i = ∑ Ui Ii sinϕ i ▲视在功率不守恒 视在功率不守恒: 视在功率不守恒 S ≠∑S i =∑ Ui Ii
& I 1 = 10 90 ° A = j10 A & & & I = I 1 + I 2 = 10 0 ° A
& & U L = I ( j10 )V = j100 V
电工第2章 正弦交流电路
函数(cos)。 1.正弦量数学表达式
图2-2 正弦交流电波形图
2.1 正弦交流电量及基本概念
(1)最大值 又称为幅值，是正弦量的最大值，用带右下标m的大写 字母表示，如Im、Um、Em分别表示正弦电流、正弦电压、正弦电动 势的最大值。 (2)角频率ω 在单位时间内正弦量所经历的电角度，用ω表示，其单 位为弧度每秒(rad/s)。正弦交流电变化一次所需的时间，称为周期T， 其单位为秒（s），正弦量在单位时间内变化的次数，称为频率f， 其单位为赫[兹](Hz)。
图2-9 纯电阻电路
2.3 单一参数元件的正弦交流电路
(2) 有效值关系 由电流与电压的幅值关系Im= Um /R，两端同除 以 ，可得它们的有效值关系为U=IR (3) 相量关系 因为电流i和电压u均为同频率的正弦量。 相量形式为 2.电阻元件的功率 (1) 瞬时功率 在关联参考方向下，电阻元件的 瞬时功率(用小写字母p表示)：
图2-4 两正弦量的同相与反相
2.1 正弦交流电量及基本概念
例2.1 已知正弦量u=220sin(314t + 30°)V， 试求正弦量的三要素、有效值及变化周期。 解：对照式(2-1)，可知三要素：
2.1 正弦交流电量及基本概念
例2.2 已知正弦电压u和正弦电流i1、i2的瞬时表达式为u = 310sin(ωt -45°)V，，i2=28.2sin(ωt +45°)A，试以电压u为参考量重新写出u和 电流i1、i2的瞬时值表达式。 解：以电压u为参考量， 则电压u的表达式为 由于i1、i2与u的相位差为
2.2 正弦交流电的相量表示方法
2.2.2 正弦量的相量表示法 正弦量和相量是一一对应关系（注意：正弦量和相量不是相等
关系！）。在复平面中，例如相量可用长度为 ，与实轴正向的夹 角为ψ的矢量表示。这种表示相量的图形称为相量图。如图2-7所示
图2-2 正弦交流电波形图
2.1 正弦交流电量及基本概念
(1)最大值 又称为幅值，是正弦量的最大值，用带右下标m的大写 字母表示，如Im、Um、Em分别表示正弦电流、正弦电压、正弦电动 势的最大值。 (2)角频率ω 在单位时间内正弦量所经历的电角度，用ω表示，其单 位为弧度每秒(rad/s)。正弦交流电变化一次所需的时间，称为周期T， 其单位为秒（s），正弦量在单位时间内变化的次数，称为频率f， 其单位为赫[兹](Hz)。
图2-9 纯电阻电路
2.3 单一参数元件的正弦交流电路
(2) 有效值关系 由电流与电压的幅值关系Im= Um /R，两端同除 以 ，可得它们的有效值关系为U=IR (3) 相量关系 因为电流i和电压u均为同频率的正弦量。 相量形式为 2.电阻元件的功率 (1) 瞬时功率 在关联参考方向下，电阻元件的 瞬时功率(用小写字母p表示)：
图2-4 两正弦量的同相与反相
2.1 正弦交流电量及基本概念
例2.1 已知正弦量u=220sin(314t + 30°)V， 试求正弦量的三要素、有效值及变化周期。 解：对照式(2-1)，可知三要素：
2.1 正弦交流电量及基本概念
例2.2 已知正弦电压u和正弦电流i1、i2的瞬时表达式为u = 310sin(ωt -45°)V，，i2=28.2sin(ωt +45°)A，试以电压u为参考量重新写出u和 电流i1、i2的瞬时值表达式。 解：以电压u为参考量， 则电压u的表达式为 由于i1、i2与u的相位差为
2.2 正弦交流电的相量表示方法
2.2.2 正弦量的相量表示法 正弦量和相量是一一对应关系（注意：正弦量和相量不是相等
关系！）。在复平面中，例如相量可用长度为 ，与实轴正向的夹 角为ψ的矢量表示。这种表示相量的图形称为相量图。如图2-7所示
04电工(第2章交流2RLC串联电路,交流电路分析,功率因数提高)
消耗有功功率为： P PR UI cos
当U、P 一定时 cos
I
供电线路功耗
希望将cos 提高
供电局一般要求用户的cos >0.85 ，否则受处罚
常用电路的功率因数
纯电阻电路
纯电感电路或 纯电容电路
cos 1 ( 0) cos 0 ( 90)
R-L-C串联电路
电动机 空载 满载
0 cos 1
第4讲
第2章 正弦交流电路
2.4 正弦交流电路的分析计算 2.5 正弦交流电路的功率
清华大学电机系电工学教研室 唐庆玉编
海南风光
本课内容
第2章 正弦交流电路
2.1 正弦电压与电流 2.1.1正弦量的参考方向和电源模型 2.1.1 周期、频率和角频率 2.1.2 相位、初相位和相位差 2.1.3 最大值和有效值
例3（教材例2.20）
已知： R1 、R2、R3 、R4 、L、C、u、i、，求支路电流i1、 i2 、i3 。
A
A
R1 i1 R2 i2 R3 i3 R4
R1
I1 R2
I2 R3
I3 R4
u
+
L
+ C uS
相量模型
i
-
U
-
+
+
jX L
jX
US
C-
I
B
B
结点电位法
U I
VA 1
R1 1
1
R1 R2 jX L R3 jX C
i 2I sint
u 2U sin(t )
UIZ
Z
R2
X
2 L
i
+
+
电路 第二章 正弦交流电路(1)
11
所以交流电的有效值就是与它热效应相等的直流电的数值， 它们之间的关系由焦耳－楞次定律确定。为了区别，交流电 流、电压和电动势的有效值分别用大写字母I、U、E表示。 设正弦电流i＝Imsin(ωt+ψ)，通过计算可知，正弦电流的有 效值是其最大值的1/√2倍，如图2—9(c)所示，即 I＝Im/√2 ＝0.707Im (2—9) 同理，正弦电压和电动势的有效值分别为 U＝Um/√2 ; E＝Um/√2 在工程上，主要使用有效值，今后不加特别声明，交流电 的大小均指有效值。从交流电流表和电压表上读取的数值也 是有效值。电气设备所标明的交流电压、电流数值也都是有 效值。可以证明有效值为正弦量在一个周期内的方均根值， 即它不随时间变化，因此，和最大值比较，有效值更为实用。
15
相量也可以用复平面上的有向线段来表示。如图所示。这种 用来表示相量的图形，叫相量图，相量图与力学和物理学中 的向量图相似。但是，相量表示的是随时间作正弦变动的函 数，而向量指的是力、电 场强度等空间向量。 2 因为实际工程中，常采用正弦量的有效值，而且最大值与 有效值之间有着固定的 2关系，所以有效值相量应用较多。 它等于最大值相量除以 2 ，即 U=Um/ 2 同理 I＝Im/ 2
上式表明，为了保证电动势的频率稳定，必须保 持发电机转速稳定。 周期T、频率f及角频率ω反映了正弦量随时间作 ω 周期性交变的快慢。各国在电力工业上所用交流 电的频率都规定了各自的标准。我国和有些国家 电力工业的标准频率为50Hz，称为工频。一般我 们讲交流电时，如果不加说明，指的就是50Hz的 工频。还有一些国家工频采用60Hz。
采用适当的磁极形状，使电枢表面的磁感应强度B 沿圆周按正弦规律分布，如图 (a)所示。由于铁芯 的磁导率远大于空气的磁导率，故磁力线的方向 与铁芯表面垂直。在磁极之间的分界面O～O',B＝ 0，称为磁中性面。在磁极的轴线上，磁感应强度 具有最大值Bm 。设线圈的一条有效边AA'(切割磁 力线的部分)和转轴所组成的平面，与磁中性面的 夹角为α，则AA'边所处位置的磁感应强度为(见图 2—2) B＝Bmsinα 当电枢被原动机拖动，在磁场中以逆时 针方向作 等速旋转时，电枢线圈有效 边因切 割磁力线而产生感 应电动势。其表达式为 e＝Emsinωt (2—1)
所以交流电的有效值就是与它热效应相等的直流电的数值， 它们之间的关系由焦耳－楞次定律确定。为了区别，交流电 流、电压和电动势的有效值分别用大写字母I、U、E表示。 设正弦电流i＝Imsin(ωt+ψ)，通过计算可知，正弦电流的有 效值是其最大值的1/√2倍，如图2—9(c)所示，即 I＝Im/√2 ＝0.707Im (2—9) 同理，正弦电压和电动势的有效值分别为 U＝Um/√2 ; E＝Um/√2 在工程上，主要使用有效值，今后不加特别声明，交流电 的大小均指有效值。从交流电流表和电压表上读取的数值也 是有效值。电气设备所标明的交流电压、电流数值也都是有 效值。可以证明有效值为正弦量在一个周期内的方均根值， 即它不随时间变化，因此，和最大值比较，有效值更为实用。
15
相量也可以用复平面上的有向线段来表示。如图所示。这种 用来表示相量的图形，叫相量图，相量图与力学和物理学中 的向量图相似。但是，相量表示的是随时间作正弦变动的函 数，而向量指的是力、电 场强度等空间向量。 2 因为实际工程中，常采用正弦量的有效值，而且最大值与 有效值之间有着固定的 2关系，所以有效值相量应用较多。 它等于最大值相量除以 2 ，即 U=Um/ 2 同理 I＝Im/ 2
上式表明，为了保证电动势的频率稳定，必须保 持发电机转速稳定。 周期T、频率f及角频率ω反映了正弦量随时间作 ω 周期性交变的快慢。各国在电力工业上所用交流 电的频率都规定了各自的标准。我国和有些国家 电力工业的标准频率为50Hz，称为工频。一般我 们讲交流电时，如果不加说明，指的就是50Hz的 工频。还有一些国家工频采用60Hz。
采用适当的磁极形状，使电枢表面的磁感应强度B 沿圆周按正弦规律分布，如图 (a)所示。由于铁芯 的磁导率远大于空气的磁导率，故磁力线的方向 与铁芯表面垂直。在磁极之间的分界面O～O',B＝ 0，称为磁中性面。在磁极的轴线上，磁感应强度 具有最大值Bm 。设线圈的一条有效边AA'(切割磁 力线的部分)和转轴所组成的平面，与磁中性面的 夹角为α，则AA'边所处位置的磁感应强度为(见图 2—2) B＝Bmsinα 当电枢被原动机拖动，在磁场中以逆时 针方向作 等速旋转时，电枢线圈有效 边因切 割磁力线而产生感 应电动势。其表达式为 e＝Emsinωt (2—1)
《电工与电子技术基础》第2章正弦交流电路习题解答
（2） I = I1 − I 2 = 8 + 6 （A）
（3） I =
I12
+
I
2 2
=
82 + 62 = 10 （A）
（4）设 I1 = 8/ 0° （A）则 I2 = 6/ 60° （A）
I = I1 + I2 = 8/ 0° + 6/ 60° = 12.2/ 25.3° （A）
I = 12.2 （A）
已知它们的电压分别为
u1
=
60
sin
⎛ ⎜⎝
314t
−
π 6
⎞ ⎟⎠
V， u2
=
80
sin
⎛ ⎜⎝
314t
+
π 3
⎞ ⎟⎠
V，求总电压
u
的瞬时值
表达式，并说明 u、u1、u2 三者的相位关系。
解：(1)最大值为 10（V），角频率为 100 π rad/s，初相角为-60°。 （2）U1m = 60/− 30° （V）U2m = 80/ 60° （V） 则Um = U1m + U2m = 60/− 30° + 80/ 60° = 100/ 23.1° （V） u = 100sin(314t + 23.1°) （V）u 滞后 u2，而超前 u1。
U R = IR
U = U R + UC
U
2
=
U
2 R
+
U
2 C
U = I X C
所以 （1）、（2）、（3）、（5）、（7）、（8）均是错的，（4）、（6）是对的。
2.13 题 2.13 图所示正弦交流电路中，已知 U=100V，UR=60V，试用相量图求电压 UL。
（3） I =
I12
+
I
2 2
=
82 + 62 = 10 （A）
（4）设 I1 = 8/ 0° （A）则 I2 = 6/ 60° （A）
I = I1 + I2 = 8/ 0° + 6/ 60° = 12.2/ 25.3° （A）
I = 12.2 （A）
已知它们的电压分别为
u1
=
60
sin
⎛ ⎜⎝
314t
−
π 6
⎞ ⎟⎠
V， u2
=
80
sin
⎛ ⎜⎝
314t
+
π 3
⎞ ⎟⎠
V，求总电压
u
的瞬时值
表达式，并说明 u、u1、u2 三者的相位关系。
解：(1)最大值为 10（V），角频率为 100 π rad/s，初相角为-60°。 （2）U1m = 60/− 30° （V）U2m = 80/ 60° （V） 则Um = U1m + U2m = 60/− 30° + 80/ 60° = 100/ 23.1° （V） u = 100sin(314t + 23.1°) （V）u 滞后 u2，而超前 u1。
U R = IR
U = U R + UC
U
2
=
U
2 R
+
U
2 C
U = I X C
所以 （1）、（2）、（3）、（5）、（7）、（8）均是错的，（4）、（6）是对的。
2.13 题 2.13 图所示正弦交流电路中，已知 U=100V，UR=60V，试用相量图求电压 UL。
电工学 第二章正弦交流电路
e = Em sin (wt + j e )
(1-2)
. 一、正弦量的三要素
二、同频率正弦量的相位差
三、正弦量的有效值
(1-3)
一、正弦量的三要素
i = Im sin (wt + j ) i
Im
j
wt Im：电流幅值（最大值）
三要素
w： 角频率（弧度/秒）
.
U Z = I
j = j u - ji
结论：Ｚ的模为电路总电压和总电流有效值之比， 而Ｚ的幅角则为总电压和总电流的相位差。
(1-46)
Z 和电路性质的关系
Z = R+ j (XL－ XC )
阻抗角
j = ju－ ji = arctg
(1-39)
以电流为 参考量时
正 误 判 断
在电阻电路中：
瞬时值
有效值
U I= R
？
U i= R
？
u ？ i = R
(1-40)
正 误 判 断
在电感电路中：
u i= XL
？
U I= ωL
u i= ωL
？
？
& U = XL & I
U = jω L I
？
？
(1-41)
第四节
RLC串、并联电路及功率因数的提高 一、RLC串联的正弦交流电路
& I U=&R
& I & U
(1-25)
相量图
总结功率关系
因为：
i= Im sinwt u =Ri=R Im sinwt p=u·=R·2=u2/R i i
小写，瞬时值功率
所以：
i
u
wt
(1-2)
. 一、正弦量的三要素
二、同频率正弦量的相位差
三、正弦量的有效值
(1-3)
一、正弦量的三要素
i = Im sin (wt + j ) i
Im
j
wt Im：电流幅值（最大值）
三要素
w： 角频率（弧度/秒）
.
U Z = I
j = j u - ji
结论：Ｚ的模为电路总电压和总电流有效值之比， 而Ｚ的幅角则为总电压和总电流的相位差。
(1-46)
Z 和电路性质的关系
Z = R+ j (XL－ XC )
阻抗角
j = ju－ ji = arctg
(1-39)
以电流为 参考量时
正 误 判 断
在电阻电路中：
瞬时值
有效值
U I= R
？
U i= R
？
u ？ i = R
(1-40)
正 误 判 断
在电感电路中：
u i= XL
？
U I= ωL
u i= ωL
？
？
& U = XL & I
U = jω L I
？
？
(1-41)
第四节
RLC串、并联电路及功率因数的提高 一、RLC串联的正弦交流电路
& I U=&R
& I & U
(1-25)
相量图
总结功率关系
因为：
i= Im sinwt u =Ri=R Im sinwt p=u·=R·2=u2/R i i
小写，瞬时值功率
所以：
i
u
wt
《电工学》教案02正弦交流电路
7. 掌握三相四线制供电系统中单相及三相负载的正确联接方法，理解中线的作用；
8. 掌握对称三相电路电压、电流及功率的计算。
2.1 正弦电压与电流
1. 正弦电流及其三要素
随时间按正弦规律变化的电流称为正弦电流，同样地有正弦电压等。这些按正弦规律变
化的物理量统称为正弦量。
设图 2.1 中通过元件的电流 i 是正弦电流，其参考方向如图所示。正弦电流的一般表达
式为：
i (t)= I m sin(ωt+ψ)
图 2.1 电路元件
图 2.2 正弦电流波形图
它表示电流 i 是时间 t 的正弦函数，不同的时间有不同的量值，称为瞬时值，用小写字
母表示。电流 i 的时间函数曲线如图 2.2 所示，称为波形图。
I m 为正弦电流的最大值（幅值），即正弦量的振幅，用大写字母加下标 m 表示正弦量 的最大值，例如 I m 、U m 、 Em 等,它反映了正弦量变化的幅度。( t +ψ)随时间变化，称
少角度或时间，以角度表示时为ψ1-ψ2，若以时间表示，则为(ψ1-ψ2)/ω。如果两个正弦 电流的相位差为 12 = ，则称这两个正弦量为反相。如果 12 = 2 ，则称这两个正弦量为正
交。
图 2.4 正弦量的相位关系
3. 有效值
周期电流 i 流过电阻 R 在一个周期所产生的能量与直流电流 I 流过电阻 R 在时间 T 内所
从以上分析可知：
（1） 电感两端的电压与电流同频率；
（2） 电感两端的电压在相位上超前电流 90°；
（3） 电感两端的电压与电流有效值(或最大值)之比为 L。
令
X L = L =2 f L
X L 称为感抗，它用来表示电感元件对电流阻碍作用的一个物理量。它与角频率成正比。
电工电子技术及应用第2章
需要强调的是，相量只表示正弦量，并不等于正
弦量；只有同频率的正弦量其相量才能相互运算，
才能画在同一个复平面上。
画在同一个复平面上表示相量的图称为相量图。
相量与正弦量的关系
U U
对应关系
Umsin( t )
不相等！！
例2-9
已知正弦电压、电流为 u 220 2 sin(t π )V，
i
+ +
R
i
us
u
π
2π
o
t
T
a)
b)
图2-1
Байду номын сангаас 一、正弦量的三要素
1.振幅值（最大值） 正弦量在任一时刻的值称为瞬 时值，用小写字母表示， 如
u
i、 u
, 分别表示电流及
u1 u2
电压的瞬时值。正弦量瞬时值
中的最大值称为振幅值也叫最 大值或峰值，用大写字母加下
o
Um2
Um1
t
图2-2
标m表示，如Im、Um , 分别表
6.55 j2.45 6.99 159.5
A B 685 11 130 0.52 j5.98 (7.07 j8.43)
7.59 j14.41 16.2962.2
例2-8
已知复数 A 4 j3 B 3 j4 ，求AB和A/B。
起点不同，正弦量的初相不同，因此初相与计时
起点的选择有关。我们规定初相|ψ |不超过π 弧 度，即-π ≤ψ ≤π 。图2-3所示是不同初相时的 几种正弦电流的波形图。
在选定参考方向下，已知正弦量的解析 式为 i 10sin( 314t 240 )A 。试求正弦量的 振幅、频率、周期、角频率和初相。
弦量；只有同频率的正弦量其相量才能相互运算，
才能画在同一个复平面上。
画在同一个复平面上表示相量的图称为相量图。
相量与正弦量的关系
U U
对应关系
Umsin( t )
不相等！！
例2-9
已知正弦电压、电流为 u 220 2 sin(t π )V，
i
+ +
R
i
us
u
π
2π
o
t
T
a)
b)
图2-1
Байду номын сангаас 一、正弦量的三要素
1.振幅值（最大值） 正弦量在任一时刻的值称为瞬 时值，用小写字母表示， 如
u
i、 u
, 分别表示电流及
u1 u2
电压的瞬时值。正弦量瞬时值
中的最大值称为振幅值也叫最 大值或峰值，用大写字母加下
o
Um2
Um1
t
图2-2
标m表示，如Im、Um , 分别表
6.55 j2.45 6.99 159.5
A B 685 11 130 0.52 j5.98 (7.07 j8.43)
7.59 j14.41 16.2962.2
例2-8
已知复数 A 4 j3 B 3 j4 ，求AB和A/B。
起点不同，正弦量的初相不同，因此初相与计时
起点的选择有关。我们规定初相|ψ |不超过π 弧 度，即-π ≤ψ ≤π 。图2-3所示是不同初相时的 几种正弦电流的波形图。
在选定参考方向下，已知正弦量的解析 式为 i 10sin( 314t 240 )A 。试求正弦量的 振幅、频率、周期、角频率和初相。
电工电子学-第二讲(正弦交流电路)
解：(1) X L L 106 6 103 6 kΩ
XC
1
C
106
1 0.001 106
1
kΩ
Z R j(X L X C ) 5 j(6 1) 5 245 kΩ
z 0 ，电路呈感性。
由 u 5 2 sin106tV ，得电压相量为：
| Z | R2 X 2
R | Z | cosz
z
arctg
X R
X | Z | sinz
Z
U I
Uu I i
U I
( u
i ) z
0
电压超前电流，感性
| Z | U Um I Im
z u i
z 0 电压滞后电流，容性
z 0 电压电流同相，阻性
dt
I jCU
iC
将U U u 、I Ii 代入上式，得：
I i jCU u CU ( u 90)
+ u － (a) 电容元件
I CU
I
θi
U
i u 90
或
U
j
1
C
I
jX CI
θu
(b) 相量图
容抗：XC=1/ωC，与频率成反比。
复数的四则运算： 设两复数为： A a1 ja2 a1
B b1 jb2 b2 (1)相等。若a1=b1，a2=b2，则A=B。 (2)加减运算：
A B (a1 b1) j(a2 b2 ) (3)乘除运算：
A B ae j1 be j 2 abe j(1 2 ) ab(1 2 )
《电工电子技术》 第2章
电工电子技术
第2章 正弦交流电路
2.1正弦交流电的基本概念 2.2同频率正弦量的相加和相减 2.3交流电路中的电阻、电容与电感 2.4电阻、电感的串联电路 2.5电阻、电感、电容串联电路及串联谐振 2.6感性负载的功率因数补偿 2.7三相交流电路 2.8三相负载的连接
第 2 章正弦交流电路
2.1正弦交流电的基本概念
电阻在直流电路与交流电路中作用相同， 起着限制电流
的作用，并把取用的电能转换成热能。
由于交流电路中电流、电压、电动势的大小和方向随时 间变化，因而分析和计算交流电路时，必须在电路中给电流、 电压、电动势标定一个正方向。同一电路中电压和电流的正 方向应标定一致（如图 2 - 11）。若在某一瞬时电流为正值，
上），其它正弦量仅按它们和参考量的相位关系画出， 便可 直接按矢量计算法进行。
另外，由于交流电路中通常只计算有效值， 而不计算瞬
时值，因而计算过程更简单。 例 2.5 已知i1=2 sin(ωt+30°) A，i2=4 sin(ωt-45°) A , 求i=i1+i2
解
相位差φ1,2=30°-(-45°)=75°,
则表示此时电流的实际方向与标定方向一致； 反之， 当电流
图 2 - 11交流电方向的设定
一、纯电阻电路 1. 电阻电路中的电流 将电阻R接入如图 2 - 12（a）所示的交流电路， 设交流 电压为 u=Umsinωt, 则R中电流的瞬时值为
这表明， 在正弦电压作用下， 电阻中通过的电流是一 个相同频率的正弦电流，而且与电阻两端电压同相位。画出 矢量图如图 2 - 12(b) 电流最大值为
图 2 - 1交流发电机
B=Bm sinα 当铁心以角速度ω旋转时， 线圈绕组切割磁力线， 产生 e= BLv 式中： e——绕组中的感应电动势（V B——磁感应强度(T(特［斯拉］), 1 T=1 Wb/m2) ； l——绕组的有效长度（m (2 - 1)
第2章 正弦交流电路
2.1正弦交流电的基本概念 2.2同频率正弦量的相加和相减 2.3交流电路中的电阻、电容与电感 2.4电阻、电感的串联电路 2.5电阻、电感、电容串联电路及串联谐振 2.6感性负载的功率因数补偿 2.7三相交流电路 2.8三相负载的连接
第 2 章正弦交流电路
2.1正弦交流电的基本概念
电阻在直流电路与交流电路中作用相同， 起着限制电流
的作用，并把取用的电能转换成热能。
由于交流电路中电流、电压、电动势的大小和方向随时 间变化，因而分析和计算交流电路时，必须在电路中给电流、 电压、电动势标定一个正方向。同一电路中电压和电流的正 方向应标定一致（如图 2 - 11）。若在某一瞬时电流为正值，
上），其它正弦量仅按它们和参考量的相位关系画出， 便可 直接按矢量计算法进行。
另外，由于交流电路中通常只计算有效值， 而不计算瞬
时值，因而计算过程更简单。 例 2.5 已知i1=2 sin(ωt+30°) A，i2=4 sin(ωt-45°) A , 求i=i1+i2
解
相位差φ1,2=30°-(-45°)=75°,
则表示此时电流的实际方向与标定方向一致； 反之， 当电流
图 2 - 11交流电方向的设定
一、纯电阻电路 1. 电阻电路中的电流 将电阻R接入如图 2 - 12（a）所示的交流电路， 设交流 电压为 u=Umsinωt, 则R中电流的瞬时值为
这表明， 在正弦电压作用下， 电阻中通过的电流是一 个相同频率的正弦电流，而且与电阻两端电压同相位。画出 矢量图如图 2 - 12(b) 电流最大值为
图 2 - 1交流发电机
B=Bm sinα 当铁心以角速度ω旋转时， 线圈绕组切割磁力线， 产生 e= BLv 式中： e——绕组中的感应电动势（V B——磁感应强度(T(特［斯拉］), 1 T=1 Wb/m2) ； l——绕组的有效长度（m (2 - 1)
电工学第2章正弦交流电路PPT课件
p=ui=Um sin(ωt+90°) Imsinωt
=UmIm cosωtsinωt =UIsin2ωt
电感元件的功率波形
上式表明， 电感元件的瞬时功率是一个幅值为UI 并以2ω的角频率随时间而变化的正弦量。瞬时功率 的变化曲线如右图所示。
26
当p>0时，表明电感元件吸收能量并作负载 使用，即将电能转换成磁场能量储存起来；
1. 相位角（或相位）——（ωt +ψi） 2. 初相位——t=0时的相位角，即ωt +ψi|t=0＝ψi
初相位不同，正弦波的起始点不同，如下图所 示。
(a)ψi＝0
(b)ψi＞0
(c)ψi<0
由于正弦量是周期性变化量，其值经2π后又重复，所
以一般取主值，| ψi |≤π。
8
2.1.3 初相位
在一个正弦交流电路中， 电压u和电流i的频率是相同的， 但初相位却可以不同。设：
19
在电阻元件的交流电路中，电压u与电流i 相 位相同、频率相同。其波形图、相量图如下所示：
根据 i=Imsinωt ；u=iR=ImRsinωt
可知电压幅值: Um=Im R；
U=I R
如果用相量来表 示电压与电流的
•
•
U
•
Um
•
R
或
••
U IR
关系，则有： I I m
20
瞬时功率：p=ui= Umsinωt Imsinωt=UmImsin²ωt
③指数形式可改写为极坐标形式：
A=r
三种复数式可以互相转换。复数的加减运 算可用直角坐标式；复数的乘除运算用指数形 式或极坐标形式则比较方便。
13
e e 例如: 设A1= a1+jb1 ＝r1 j 1 ；A2= a2+jb2 ＝r2 j 2
《电工电子技术》——正弦交流电路
dt
dt
Im sin(wt 90)
1 电压与电流之间的频率关系 电容元件两端的端电压与电流是同频率的正弦电量。
2 电压与电流之间的数值关系
最大值
Im
wCU m
Um 1 /(wC )
有效值
I wCU U U 1/(wC) X c
X c 等于电压有效值与电流有效值之比，单位为欧[姆]，称为容 抗。
计算过程请参考书本，相量图为：
2.3单一参数交流电路
2.3.1单一电阻元件正弦交流电路 一、单一电阻元件正弦交流电路电压与电流之间的关系
i
u
R
i u U m sin(wt u )
R
R
2U R
sin(wt
u
)
单一电阻元件正弦交流电路电压与电流之间有如下几种关系：
1 电压与电流之间的频率关系 在单一电阻电路中，通过电阻元件的电流与其两端电压是 同频率的正弦电量。
I Ie j i I i
I 为有效值
二、相量图
在复数平面上，用几何图形表示正弦量的相量的图，称为相 量图。
已知正弦电压： 相应的电压相量为
u 220 2 sin(wt 45)
U 22045
已知正弦电流： 相应的电流相量为：
i 8 2 sin(wt 30)
字母 T 表示，单位是秒（s）。正弦量在1秒时间内重复变化的
周期数称为频率，用小写字母 f 表示，单位为赫兹（Hz），如 果1秒钟内变化一个周期，频率是1Hz。周期与频率互为倒数关 系：
f 1 T
在我国，发电厂提供的交流电的频率为50Hz，其周期 T 0.02， 这一频率称为工业标准频率，也称工频。
电工学I(电路与电子技术)[第二章正弦交流电路]山东大学期末考试知识点复习
![电工学I(电路与电子技术)[第二章正弦交流电路]山东大学期末考试知识点复习](https://img.taocdn.com/s3/m/d0cf1af2941ea76e58fa0445.png)
第二章正弦交流电路2．1．1 正弦量的三要素及表示方法(1)正弦交流电路：如果在线性电路中施加正弦激励(正弦交流电压源或正弦交流电流源)，则电路中的所有响应在电路达到稳态时，也都是与激励同频率的正弦量，这样的电路称为正弦交流电路。
(2)正弦交流电压或正弦交流电流等物理量统称为正弦量，它们的特征表现在变化的快慢、大小及初值3个方面，分别由频率(或周期)、幅值(或有效值)和初相位来确定。
所以称频率、幅值(或有效值)和初相位为正弦量的三要素。
(3)因为正弦量具有3个要素，它们完全可以表达对应的正弦量的特点和共性。
所以，只要能够反映出正弦的三要素，就可以找到多种表示正弦量的方法，其常见的表示方法如下。
①三角函数表示法和正弦波形图示法，比如正弦电压u=U m sin(ωt+φ)，其正弦波形如图2．1所示，但是正弦量的这两种表示方法都不利于计算。
②旋转矢量表示法，由于复平面上一个逆时针方向旋转的复数能够反映出正弦量的3个要素，因此可用来表示正弦量。
③相量及相量图表示法，由于正弦交流电路中的激励和响应均为同频率的正弦量，故可在已知频率的情况下，只研究幅值和初相位的问题。
这样，不仅可以用旋转矢量表示正弦量，而且也能把正弦量表示成复数(该复数与一个正弦量对应，称为相量)。
图2．1所示正弦电压的幅值相量和有效值相量分别为2．1．2 电路基本定律的相量形式将正弦量用相量表示有利于简化电路的分析和计算，其中电路分析的基本定律在频域中也是成立的，即为表2．1的电路基本定律的相量形式。
当用相量来表示正弦电压与电流，用复阻抗来表示电阻、电感和电容时，正弦交流电路的分析与计算也就类似于直流电路，复阻抗的串并联等效、支路电流法、叠加定理和戴维宁定理等分析方法均可应用。
为了研究复杂正弦交流电路中激励与响应之间的关系，以及研究电路中能量的转换与功率问题，就必须首先掌握单一参数(电阻、电感、电容)元件在正弦交流电路中的特性(见表2．2)，以作为分析复杂正弦交流电路的基础。
电工学第二章 正弦交流电
电流超前电压 90 u i u i ωt O 90°
O
ωt
电压与电流同相 u i u i O
ψ1 ψ 2 0
ψ 1 ψ 2 180
电压与电流反相 u i u i O
ωt
ωt
注意: ① 两同频率的正弦量之间的相位差为常数， 与计时的选择起点无关,仅取决于两者的初相位。
i
O
i1
i2
t
② 不同频率的正弦量比较无意义。
例1
已知：
幅度：
i sin 1000 t 30 A
I 1 2 0 . 707 A
I m 1A
频率：
1000 rad/s
f
2
1000 2
159 Hz
初相位：
30
例2:
i1 I m1 sin t 90 i2 I m2 sin t 90
小写
u i O p
2
i u
ωt p
p ui
U m I m sin ω t
1 2 U m I m (1 cos 2 ω t )
O
ω t
结论: p 0
（耗能元件）,且随时间变化。
(2) 平均功率(有功功率)P 瞬时功率在一个周期内的平均值
P
大写
i
+
1 T 1
0
T 0
p dt
I 2 11 60 A
I I1 I 2 12.7 30A 11 60A
12.7( cos 30 j sin 30 )A 11( cos 60 j sin 60 )A
O
ωt
电压与电流同相 u i u i O
ψ1 ψ 2 0
ψ 1 ψ 2 180
电压与电流反相 u i u i O
ωt
ωt
注意: ① 两同频率的正弦量之间的相位差为常数， 与计时的选择起点无关,仅取决于两者的初相位。
i
O
i1
i2
t
② 不同频率的正弦量比较无意义。
例1
已知：
幅度：
i sin 1000 t 30 A
I 1 2 0 . 707 A
I m 1A
频率：
1000 rad/s
f
2
1000 2
159 Hz
初相位：
30
例2:
i1 I m1 sin t 90 i2 I m2 sin t 90
小写
u i O p
2
i u
ωt p
p ui
U m I m sin ω t
1 2 U m I m (1 cos 2 ω t )
O
ω t
结论: p 0
（耗能元件）,且随时间变化。
(2) 平均功率(有功功率)P 瞬时功率在一个周期内的平均值
P
大写
i
+
1 T 1
0
T 0
p dt
I 2 11 60 A
I I1 I 2 12.7 30A 11 60A
12.7( cos 30 j sin 30 )A 11( cos 60 j sin 60 )A
【精品】J__《电工电子技术基础》电子教案_电工电子技术课件_第2章 正弦交流电路
第3页
电感元件上电压、电流的有效值关系为：
U=LI=2πf LI=IXL
其中：
XL=2πf L=ωL称为电感元件的电抗，简称感抗。 感抗反映了电感元件对正弦交流电流的阻碍作用；
感抗的单位与电阻相同，也是欧姆【Ω】。
感抗与哪些 因素有关？
XL与频率成正比；与电感量L成正比
直流下频率f =0，所以XL=0。L 相当于短路。
平均功率用大写 ！
例
“220V、100W”和“220V、40W”灯泡的电阻？ U2 2202 解： R100 484 P 100 U2 2202 R40 1210 P 40 显然，在相同电压下，负载的电阻与功率成反比。
第3页
2.3.2 电感元件
1. 电感元件上的电压、电流关系
耐压为220V的电容 器，能否用在180V 的正弦交流电源上 ？
U=180V，则Um≈255V
255V>220V 不能用在180V正弦电源上！
u
何谓反相？ 同相？相位 正交？超前 ？滞后？
u1
u2
u3
u4
ωt
u1与u2反相； u1与u4同相；u3与u4正交； u3超前u490°；u3滞后u290°。
第3页
p<0
2. 平均功率（有功功率）P
P=0，电感元件不耗能。 3. 无功功率Q
U Q ULI I X L XL
2
2
Q反映了电感元件与电源之间能量交换的规模。
问题与讨论 1. 电源电压不变，当电路的频率变化时， 通过电感元件的电流发生变化吗？
f 变化时XL随之变化，导致电流i 变化。
则 p ic u I Cm cost U m sint
电感元件上电压、电流的有效值关系为：
U=LI=2πf LI=IXL
其中：
XL=2πf L=ωL称为电感元件的电抗，简称感抗。 感抗反映了电感元件对正弦交流电流的阻碍作用；
感抗的单位与电阻相同，也是欧姆【Ω】。
感抗与哪些 因素有关？
XL与频率成正比；与电感量L成正比
直流下频率f =0，所以XL=0。L 相当于短路。
平均功率用大写 ！
例
“220V、100W”和“220V、40W”灯泡的电阻？ U2 2202 解： R100 484 P 100 U2 2202 R40 1210 P 40 显然，在相同电压下，负载的电阻与功率成反比。
第3页
2.3.2 电感元件
1. 电感元件上的电压、电流关系
耐压为220V的电容 器，能否用在180V 的正弦交流电源上 ？
U=180V，则Um≈255V
255V>220V 不能用在180V正弦电源上！
u
何谓反相？ 同相？相位 正交？超前 ？滞后？
u1
u2
u3
u4
ωt
u1与u2反相； u1与u4同相；u3与u4正交； u3超前u490°；u3滞后u290°。
第3页
p<0
2. 平均功率（有功功率）P
P=0，电感元件不耗能。 3. 无功功率Q
U Q ULI I X L XL
2
2
Q反映了电感元件与电源之间能量交换的规模。
问题与讨论 1. 电源电压不变，当电路的频率变化时， 通过电感元件的电流发生变化吗？
f 变化时XL随之变化，导致电流i 变化。
则 p ic u I Cm cost U m sint
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
如图 2 -1 所示的发电机，当转子以等速旋转时， 绕组中 感应出的正弦交变电动势的波形如图 2 - 2 所示。图中横轴表 示时间，纵轴表示电动势大小。图形反映出感生电动势在转 子旋转过程中随时间变化的规律。下面介绍图 2 - 2 所示正弦 交流电的物理量。
Em
e T
O
t
q
图 2 - 2正弦交流波形图
有效值： 正弦交流电的瞬时值是随时间变化的， 计量时 用正弦交流电的有效值来表示。交流电表的指示值和交流电 器上标示的电流、 电压数值一般都是有效值。在工程应用中 常用有效值表示幅度。标准电压220V，也是指供电电压的有 上一页 下一页 效值。
有 效 值 概 念
交流电流 i通过电阻R在 一个周期T内产生的热量 与一直流电流I通过同一 电阻在同一时间T内产生 的热量相等，则称I的数 值为i的有效值
上一页 下一页
例如， 已知
i1 I m1 sin t
i2 I m 2 sin t 2
1
i1
2
i2
t
1
则 i1和 i2的相位差为
(t 1 ) (t 2 ) 1 2
两个同频率正弦量的相位差 = 初相差
上一页 下一页
i
R
热效应相当
T
0I
i R dt I RT
2
2
R
通电时间相等
交流 图2 .4
直流
则有
I
1 T
T
0
i dt
1 I 时， T
2
（均方根值）
当 i I m sin t
T
0
I sintdt
2 m
2 Im T
T
0
1 (1 cos 2t )dt 2
可得
Im I 2
S
1(b)）。若用α表示气隙中某点和轴线构成的平面与中
(a)
(b)
性面的夹角，则该点的磁感应强度为 B=Bm sinα
图2 .1
当铁心以角速度ω旋转时， 线圈绕组切割磁力线， 产生感 应电动势，其大小是
e= Blv
(2 - 1)
式中： e — 绕组中的感应电动势（V）； B — 磁感应强度(T(特)［斯拉］), 1 T=1 Wb/m2)；
>0
(t φ1 ) (t φ2 ) 1 2
两个同频率的正弦交流电的相位差 若φ1-φ2＞0, 称“i1超前于i2‖;
=0 <0 = ±180°
若φ1-φ2＜0, 称“i1滞后于i2‖；
若φ1-φ2=0，称“i1和i2同相位”；
若相位差φ1-φ2=±180°, 则称“i1和i2反相位”。
必须指出，在比较两个正弦交流电之间的相位时， 两正弦
量一定要同频率才有意义。否则随时间不同，两正弦量之间的
相位差是一个变量，这就没有意义了。
上一页 下一页
同 相 位
2 1
两种正弦信号的相位关系波形图 i2 1 2 i1 t i1 与 i2 同相
i2
相 位 领 先
相 位 落 后 反 相 位
u u1 u 2 2U 1 sin t 1 2U 2 sin t 2 2U sin t
幅度、相位变化 频率不变
结论:
因角频率（）不变，所以在讨论同频率正弦波时， 可不考虑 ，主要研究幅度与初相位的变化。
上一页 下一页
例
已知：
e=Blv=Bmsin（ωt+φ0）lv 或 e=Emsin（ωt+φ0） (2 - 2)
式中Em =Bm lv，称作感应电动势最大值。当线圈ab边转 到N极中心时，绕组中感应电动势最大，为 Em；线圈再转 180°， ab边对准S极中心时，绕组中感应电动势为-Em
上一页 下一页
二、表示正弦交流电特征的物理量(三要素)
i u
O
ωt
O 90°
ωt
电压与电流同相 u i u i O
ψ1 ψ2 0
ψ1 ψ2 180
电压与电流反相 u i u i O
ωt
ωt
上一页 下一页
同频率正弦波运算后，频率不变。
例如:
u1 u2
2U1 sin t 1 2U 2 sin t 2
上一页 下一页
一、交流电的产生
获得交流电的方法有多种，但大多数交流电是由交流发电
机产生的。 图 2 - 1（a）为一最简单的交流发电机， 标有N、S的为两 个静止磁极。 磁极间放置一个可以绕轴旋转的铁心， 铁心上绕 有线圈a、b、b′、 a′，线圈两端分别与两个铜质滑环相连。滑
环经过电刷与外电路相连。
果横轴用角度刻度，当角度变到π/2时，电动势达到最大值， 当角度变到π时，电动势变为零值（图 2 - 3）。这个角度不表 示任何空间角度，只是用来描述正弦交流电的变化规律， 所 以把这种角度叫电角度。 每秒钟经过的电角度叫角频率， 用ω表示。 式(2 - 2)中的ω 即是角频率。
e e=Emsin(t+q) Em
该用电器最高耐压低于电源电压的最大值，所 以不能用。
上一页 下一页
3. 正弦交流电的相位和相位差
1） 相位 正弦交变电动势e=Em sin(ωt+φ0)，它的瞬时值随着电度 (ωt+φ0)而变化。电角度(ωt+φ0)叫做正弦交流电的相位。 例 如图 2 - 5（a）所示的发电机，若在电机铁心上放置两个夹 角为φ0、匝数相同的线圈AX和BY, 当转子如图示方向转动时， 这两个线圈中的感生电动势分别是： 这两个正弦交 eA Em sin t 变电动势的最大值 eB Em sin(t φ0 ) 相同， 频率相同， 但相位不同: eA的 相位是ωt，eB的相 图2 .5 位是（ωt+φ0）。
显然，角频率与频率、 周期之间 有如下的关系：
1 f T
2 2 f T
上一页 下一页
小常识
* 电网频率： 中国 50 Hz
美国 、日本 60 Hz * 有线通讯频率：300 - 5000 Hz
* 无线通讯频率： 30 kHz - 3³104 MHz
上一页 下一页
2. 瞬时值、 最大值、 有效值
2 Im Im 0.707I m 2 2
I m 2I 有效值电量必须大写，如： U、 I
上一页 下一页
当
i I m sin t
时，
有
Im I 2
i可写为：
同理:
i= 2 I sin(t+)
u= Um sin(t+) u = 2 U sin(t+)
i
t
正弦交流电的优越性：
便于传输；
便于运用；
有利于电器设备的运行；
上一页 下一页
正弦交流电的正方向
正弦交流电也要规定正方向,表示电压或电流的瞬时方向
i
u
R
i
实际方向和假设方向一致
t
用小写字母表示 交流瞬时值
实际方向和假设方向相反
交流电路进行计算时，首先要规定物理量 的正方向，然后才能用数字表达式来描述。
e eB eA N
B q A
Z
Y
O
2
t
S
q
(a)
(b)
上一页 下一页
2） 初相 当t=0 时的相位称为初相位或初相角。。 以上述eA、eB为例，eA的初相是0, eB的初相是φ0。 3） 相位差
两个同频率的正弦交流电的相位之差叫相位差。 相位差表示两正弦量到达最大值的先后差距。
π 2 ω 2πf T
O 2
t
图2
q
图 2- 3用电角度表示正弦交流电
上一页 下一页
i
t
T
综上，描述变化周期的几种方法
1. 周期 T： 变化一周所需的时间 2. 频率 f ： 每秒变化的次数 3. 角频率 ω ： 每秒变化的弧度 单位：秒，毫秒.. 单位：赫兹，千赫兹 ... 单位：弧度/秒
上一页 下一页
交流电的概念
如果电流或电压每经过一定时间 （T ）就重复变 化一次，则此种电流 、电压称为周期性交流电流或 电压。如正弦波、方波、三角波、锯齿波 等。 记做： u(t) = u(t + T )
u t
T
u t
T
上一页 下一页
正弦交流电路
在电路中电动势的大小和方向随时间按正弦规
律变化，由此产生的电流、电压大小和方向也是正 弦的，这样的电路称为正弦交流电路。
l — 绕组的有效长度（m）；
v — 绕组切割磁力线的速度（m/s）。
上一页 下一页
假定计时开始时， 绕组所在位置与中性面的夹角为φ0， 经t秒后，它们之间的夹角则变为α=ωt+φ0，对应绕组切割磁 场的磁感应强度为B=Bmsinα=Bmsin（ωt+φ0） 将上式代入式（2 - 1）就得到绕组中感应电动势随时间 变化的规律， 即
瞬时值： 交流电在变化过程中， 每一时刻的值都不同， 该值称为瞬时值。瞬时值是时间的函数，只有具体指出在哪 一时刻，才能求出确切的数值和方向。瞬时值规定用小写字 母表示。例如图 2 - 3 中的电动势，其瞬时值为 幅值必须大写, e=Em sin(ωt+φ0) 下标加 m。
最大值： 正弦交流电波形图上的最大幅值便是交流电的 最大值（图 2 - 3）。它表示在一周内， 数值最大的瞬时值。 最大值规定用大写字母加脚标m表示，例如Im、Em、Um等。
b N
a e a′ b′ e
N
O O′
S