涉及2-卫星系统的一类几何不等式
高中数学第二章几何重要的不等式212一般形式的柯西不等式课件北师大版选修4

取到.
第23页
题型三 柯西不等式的综合应用 例 4 (2015·福建)已知 a>0,b>0,c>0,函数 f(x)=|x+a|+|x -b|+c 的最小值为 4. (1)求 a+b+c 的值; (2)求14a2+19b2+c2 的最小值.
第24页
【解析】 (1)因为 f(x)=|x+a|+|x-b|+c≥|(x+a)-(x-b)| +c=|a+b|+c,
第11页
思考题 1 若 x,y,z∈R+,且 x2+y2+z2=1,求证:0<xy +yz+zx≤1.
【证明】 (x2+y2+z2)(y2+z2+x2)≥(xy+yz+zx)2,即 1≥(xy +yz+zx)2,又 x,y,z∈R+,∴0<xy+yz+zx≤1.
第12页
题型二 利用柯西不等式求最值 例 2 设 2x+3y+5z=29,求函数 u= 2x+1+ 3y+4+ 5z+6的最大值. 【思路】 由题目可获取以下主要信息:①已知变量 x,y,z 之间的关系符合特定条件;②所求式子中含有根式.解答本题的关 键是去掉根号,并且利用好特定条件.
第6页
3.柯西不等式的两个变式 (1)当 ai∈R,bi>0(i=1,2,…,n),∑i=n1 abi2i ≥(∑i∑i=n=n11abi)i 2,当且 仅当 bi=λai 时等号成立. (2)设 ai,bi 同号且不为 0(i=1,2,…,n),则i∑=n1 baii≥(∑i∑=in=n11aaibi)i 2, 当且仅当 bi=λai 时,等号成立.
第9页
≥(
a· b
b+
b· c
c+
c· a
a)2
=(a+b+c)2,
即(ab2+bc2+ca2)(a+b+c)≥(a+b+c)2.
【国家自然科学基金】_迭代线性矩阵不等式_基金支持热词逐年推荐_【万方软件创新助手】_20140729
推荐指数 4 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
2013年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 阵不等式(lmi) 滚动时域 markov跳变系统 静态输出反馈控制 镇定 锥补线性化 迭代线性矩阵不等式 跳变模态 跟踪控制 自动控制技术 系统辨识 稳态误差系数 目标跟踪 混沌 模糊广义系统 有限记忆控制 时滞相关准则 时滞依赖 时滞 无偏条件 广域阻尼控制 容偏估计 多指标约束 同步 反馈增益 双线性矩阵不等式 协调控制 凸多面体不确定性 关联稳定 保性能控制 不确定离散时滞系统 不确定t-s模糊系统 h_∞扰动抑制水平
科研热词 线性矩阵不等式 迭代线性矩阵不等式 离散系统 状态饱和 鲁棒稳定 鲁棒控制 马尔可夫过程 间歇过程 迭代学习控制 超线性收敛性 线性矩阵不等式(lmi) 离散线性系统 广义投影梯度 奇异系统 多时滞 单调收敛 分布式 全局收敛性 估计器 二次型迭代学习控制 不等式约束优化 不确定线性系统 sqp算法 s-procedure qp-free算法 h∞控制
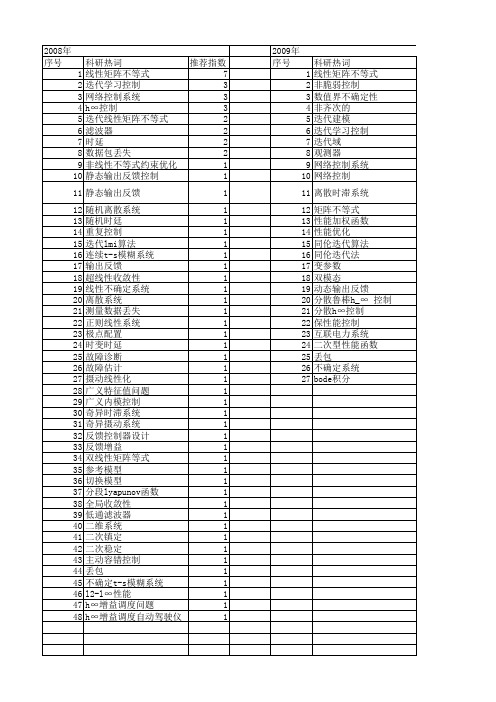
2009年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27
科研热词 线性矩阵不等式 非脆弱控制 数值界不确定性 非齐次的 迭代建模 迭代学习控制 迭代域 观测器 网络控制系统 网络控制 离散时滞系统 矩阵不等式 性能加权函数 性能优化 同伦迭代算法 同伦迭代法 变参数 双模态 动态输出反馈 分散鲁棒h_∞ 控制 分散h∞控制 保性能控制 互联电力系统 二次型性能函数 丢包 不确定系统 bode积分
现代控制理论

现代控制理论⾮线性动态系统的稳定性和鲁棒控制理论研究上世纪50年代,Kallman成功的将状态空间法引⼊到系统控制理论中,从⽽标志着现代控制理论研究的开始。
现代控制理论的研究对象是系统的数学模型,它根据⼈们对系统的性能要求,通过对被控对象进⾏模型分析来设计系统的控制律,从⽽保证闭环系统具有期望的性能。
其中,线性系统理论已经形成⼀套完整的理论体系。
过去⼈们常⽤线性系统理论来处理很多⼯程问题,并在⼀定范围内取得了⽐较满意的效果。
然⽽,这种处理⽅法是以忽略系统中的动态⾮线性因素为代价的。
实际中很多物理系统都具有固有的动态⾮线性特性,如库仑摩擦、饱和、死区、滞环等,这些⾮线性动态⾮线性特性的存在常常使系统的控制性能下降,甚⾄变得不稳定。
这就使得利⽤线性系统理论处理⾮线性动态系统⾯临巨⼤的困难。
此外,在控制系统运⾏过程中,环境的变化或者元件的⽼化,以及外界⼲扰等不确定因素也会造成系统实际参数和标称值之间出现较⼤差别。
因此,基于标称数学模型所设计的控制律⼀般很难达到期望的性能指标,甚⾄会使系统不稳定。
综上所述,研究不确定条件下⾮线性动态系统的鲁棒稳定性及鲁棒控制间题具有重要的理论意义和迫切的实际需要。
⾮线性动态系统是指按确定性规律随时间演化的系统,⼜称动⼒学系统,其理论来源于经典⼒学,⼀般由微分⽅程来描述。
美国数学家Birkhoff[1]发展了法国数学家Poincare在天体⼒学和微分⽅程定性理论⽅⾯的研究,奠定了动态系统理论的基础。
在实际动态系统中,对象往往受到各种各样的不确定的影响,所以其数学模型⼀般不可能精确得到。
因此,我们只能⽤近似的标称数学模型来描述被控对象,并据此来设计控制系统,动态系统鲁棒控制由此产⽣。
所谓鲁棒性就是指系统预期⾮线性动态系统的稳定性和鲁棒控制理论研究的设计品质不因不确定性的存在⽽遭到破坏的特性,鲁棒控制是⾮线性动态系统控制理论研究的⼀个⾮常重要的分⽀。
现代控制理论的发展促进了对动态系统的研究,使它的应⽤从经典⼒学扩⼤到⼀般意义下的系统。
联系两个高维单形的几何不等式定理

(
\ a
`
,
卫
儿
-
`
.
< j毯
n
”
`
才
<
.
`
+ n
l
其、 (v
十 1
1
”
v (2
.
`
)普 2)
》
(
(n +
`
l ) (n
Z
十
一 4)
l
浩
l
,` ( V V ,`
“ <杯
1
多
乏
。
.
;
,
((
1`
. , 、
+
1
考<
万
.
`
.
+
l
.
一
摊
Z
a
:
,
万
` <护
.
口 十
l
,
〔 石
.
乏
二 、 , 。 “
a
加
一 Za 仃 )
安徽教育学院学报 自然 科学版
年第
期 总挤期ຫໍສະໝຸດ 联 系 两 个 高 维 单 形 的 几 何 不 等 式 定 理
杨世国
摘要
、
不
e 等 式 被认 为 是 欧 氏 平 面 上 最 重 要 的 几 何 不 等 式 之 一 e 张景中 杨
,
,
、
路 苏化 明 以 不 同 形 式 将 它 推 广 到 高 维 空 间 建 立 了 维
十
:
气 召
认
-
-
二
r
口
,
乳
声
a
L
各种常用不等式汇总

各种常用不等式汇总文章目录•一、一般不等式•o1、一元二次不等式o2、正弦余弦不等式o3、均值不等式o4、绝对值不等式o5、排序不等式o6、权方和不等式•二、人名不等式•o1、柯西不等式o2、卡尔松不等式o3、琴声不等式o4、杨氏不等式o5、赫尔德不等式o6、闵可夫斯基不等式o7、伯努利不等式一、一般不等式经常会用到的不等式一般有前面三个是下面均值不等式的特殊情况。
一般情况下a=b时,才取到等号1、一元二次不等式首先回顾一下一元二次方程的求根公式一元二次不等式的解以及图像2、正弦余弦不等式3、均值不等式均值不等式中一般包含四个公式:调和平均数公式、算数平均数公式、平方平均数公式、几何平均数公式,下面一一介绍。
•调和平均数又称倒数平均数,是总体各统计变量倒数的算术平均数的倒数。
调和平均数是平均数的一种。
但统计调和平均数,与数学调和平均数不同,它是变量倒数的算术平均数的倒数。
由于它是根据变量的倒数计算的,所以又称倒数平均数。
调和平均数也有简单调和平均数和加权调和平均数两种。
•算术平均数又称均值,是统计学中最基本、最常用的一种平均指标,分为简单算术平均数、加权算术平均数。
它主要适用于数值型数据,不适用于品质数据。
根据表现形式的不同,算术平均数有不同的计算形式和计算公式。
•一组数据的平方的平均数的算术平方根。
英文缩写为RMS。
它是2次方的广义平均数的表达式,也可称为2次幂平均数。
英文名一般缩写成RMS。
•几何平均数是n个变量值连乘积的n次方根,分为简单几何平均数与加权几何平均数。
1)几何平均数受极端值的影响较算术平均数小;2)如果变量值有负值,计算出的几何平均数就会成为负数或虚数;3)它仅适用于具有等比或近似等比关系的数据;4)几何平均数的对数是各变量值对数的算术平均数。
它们的公式如下:调和平均数≤ 几何平均数≤ 算术平均数≤ 平方平均数(方均根)4、绝对值不等式5、排序不等式反序和≤乱序和≤顺序和6、权方和不等式权方和不等式是一个数学中重要的不等式。
几何平均不等式

几何平均不等式几何平均不等式(英文名称:TheArithmetic-GeometricInequality)是指一类数学不等式。
这类不等式中,两个数的几何平均值大于或等于这两个数的算术平均值。
几何平均不等式也被称之为乘积平均不等式或分母平均不等式。
几何平均不等式是1775年以英国数学家Joseph Louis Lagrange 的名字命名的,他发明了这一数学不等式。
几何平均不等式的基本形式是:(a1x1 + a2x2 + a3x3 ++ anxn)^2 (a1x1^2 + a2x2^2 + a3x3^2 ++ anxn^2)其中,a1, a2, ..., an是实数和正数,x1, x2, ..., xn是实数。
上式可以推广到n个不同的正数,即:(a1^(1/n) * a2^(1/n) * * an^(1/n))^n (a1 + a2 + + an) / n 而且,当实数x1, x2, ..., xn大于0时,几何平均不等式可以表示为:x1 * x2 * * xn (x1 + x2 + + xn) / n因此,几何平均不等式可以简单地表示为:几何平均值术平均值。
几何平均不等式的应用非常广泛,它主要用于解决实际问题中的数学积分和概率统计相关的问题。
例如,考虑一个自由市场中的公司A和公司B,每家公司都想获得最高的投资回报。
假设公司A和公司B分别在投资100万元后得出的投资回报分别为200000和500000。
如果两家公司将各自的投资资金合并起来,即将A公司的100万元和B公司的100万元合并起来投资,A/B公司可以获得最高的投资回报吗?在这种情况下,可以使用几何平均不等式来解答这个问题。
具体地说,A/B公司的投资回报分别为200000元和500000元,因此可以推出:(200000 * 500000)^(1/2) (200000 + 500000) / 2 进一步计算,可得:1000000 375000因此,可以得出结论:A/B公司将各自的投资资金合并起来投资,可以获得更高的投资回报。
E~n中两个几何不等式的改进

∑ 口 ≤ n 12 ; +) R
利用[ ] 7 中不等式
≤丽
引理 3 对 中 维单形 , 有
‘
(
便得 不 等式 ( ) 易知 ( )中等 号成 立 当且仅 当 为 正则单 形 。 5 , 5
(+ ) n 1
耳a ( [ i ≥
等号成立当且仅当 为正则单形 。
l ≤ 《c
() 2 4
由(4 式和(4 式 , 2) 1 ) 可得定理 2 证明过程中的等号成立当且仅 当 n , 维单形 为正则单形。 由于 ≥ 1所以本文的结论实质上推广 了 维 E l 不等式 , , ue r 同时本文 的两个定 理也 改进 了文
lr t
[0 1 ]中的两个 结果 。 参考 文献 :
F nlr—Ha w g r 等式 : is e d ie 不 a +b +c ≥ 4 +( 口一6 +( ) b—c +( ) c一口 )
当且仅 当三角形 A C为正三角形时等号成立。 B
由于 ≥ 1所 以本 文 的定理 1 n维 欧 氏空 间 中 Fn1r—H d ie 不 等式 进行 了加 强 。 , 对 ise awgr hi "
VOI1 . . 7 NO 3
第 l 第 3期 7卷
中两 个 几 何 不 等 式 的改 进
陈 士龙
( 安徽广播影视职业技术学 院 基础教学部 , 安徽 合肥 2 0 1 ) 30 1
摘
要 :应用几何不 等式理论和解析 的方法, 研究 了 维 欧 氏空 间中 n维单形 的 Fn lr—H d ie 不 等式和 维 is e a wg r
本文约定 中 n 维单形 的顶点集为 r= { . :…, } A, , A ( A =12 …, ,, n+1 , ) 它的体积为 I , ,
2019_2020学年高中数学第二章几何重要的不等式2_1_1简单形式的柯西不等式课件北师大版选修4_5

第1页
§1 柯西不等式 1.1 简单形式的柯西不等式
第2页
知识探究
第3页
简单形式的栖西不等式
第4页
1.柯西不等式三种形式的关系 根据向量的意义及其坐标表示不难发现简单形式的柯西不等 式及简单形式的三角不等式均可看作是柯西不等式的向量形式 的坐标表示条件 (1)代数形式中当且仅当ad=bc时取等号. (2)向量形式中当α=kβ或β=0时取等号. (3)三角形式中当P1(x1,y1),P2(x2,y2),O(0,0)三点共线且 P1,P2在原点O两旁时取等号. 3.简单形式的柯西不等式的变式 (1) a2+b2· c2+d2≥|ac+bd|. (2) a2+b2· c2+d2≥|ac|+|bd|. (3) a2+b2· c2+d2≥ac+bd.
第17页
思考题 2 已知 θ 为锐角,a,b∈R+, 求证:(a+b)2≤coas22θ+sinb22θ.
第18页
【证明】 设 m=(coasθ,sinbθ),n=(cosθ,sinθ), |a+b|=cosaθ·cosθ+sinbθ·sinθ =|m·n|≤|m|·|n| = (coasθ)2+(sinbθ)2·1 = coas22θ+sinb22θ, ∴(a+b)2≤coas22θ+sinb22θ.
第15页
【证明】 设 m=( ax, by),n=( a, b), 则|ax+by|=|m·n|≤|m|·|n| = ( ax)2+( by)2· ( a)2+( b)2 = ax2+by2· a+b= ax2+by2. ∴(ax+by)2≤ax2+by2.
第16页
探究 2 使用向量形式的柯西不等式时要注意向量模的计算 公式|α|= x2+y2对数学式子变形的影响.
几何模型之二图形中的最短距离定值及不等式问题

学生: 科目: 数 学 教师: 谭 前 富知识框架在平面几何问题中,当某几何元素在给定条件变动时,求某几何量(如线段的长度、图形的面积、角的度数)的最大值或最小值问题,称为最值问题。
最值问题的解决方法通常有两种: (1) 应用几何性质:① 三角形的三边关系:两边之和大于第三边,两边之差小于第三边; ② 两点间线段最短;③ 连结直线外一点和直线上各点的所有线段中,垂线段最短; ④ 定圆中的所有弦中,直径最长。
⑵运用代数证法:① 运用配方法求二次三项式的最值; ② 运用一元二次方程根的判别式。
【例题精讲】一. 最短路径和几何不等式问题: 考查知识点----:“两点之间线段最短”,“两边之和大于第三边”,“斜边大于直角边”,“垂线段最短”,“点关于线对称”,“线段的平移”。
原型----“饮马问题”,“造桥选址问题”。
考的较多的还是“饮马问题”,出题背景变式有角、三角形、菱形、矩形、正方形、梯形、圆、坐标轴、抛物线等。
最短路径和几何不等式问题的两种基本模型----:Ⅰ、归于函数模型:即利用一次函数的增减性和二次函数的对称性及增减性,确定某范围内函数的最大或最小值Ⅱ、归于几何模型,这类模型又分为两种情况:(1)归于“两点之间的连线中,线段最短”。
凡属于求“变动的两线段之和的最小值”时,大都应用这一模型。
(2)归于“三角形两边之差小于第三边”凡属于求“变动的两线段之差的最大值”时,大都应用这一模型。
解题总思路----找点关于线的对称点实现“折”转“直”,较难的会出现“三折线”转“直”等变式问题考查。
二.最短距离中的数形结合:例:求代数式9)12(422+-++x x 的最小值.课 题几何模型之二:图形中的最短距离、定值及不等式问题教学内容三.立体几何中的最短路径问题:(1)台阶问题 如图,是一个三级台阶,它的每一级的长、宽和高分别等于5cm ,3cm 和1cm ,A 和B 是这个台阶的两个相对的端点,A 点上有一只蚂蚁,想到B 点去吃可口的食物.请你想一想,这只蚂蚁从A 点出发,沿着台阶面爬到B 点,最短线路是多少?(2)圆柱问题 有一圆形油罐底面圆的周长为24m ,高为6m ,一只老鼠从距底面1m 的A 处爬行到对角B 处吃食物,它爬行的最短路线长为多少?变式1:有一圆柱形油罐,已知油罐周长是12m ,高AB 是5m ,要从点A 处开始绕油罐一周建造梯子,正好到达A 点的正上方B 处,问梯子最短有多长?变式2: 桌上有一个圆柱形玻璃杯(无盖),高为12厘米,底面周长18厘米,在杯口内壁离杯口3厘米的A 处有一滴蜜糖,一只小虫从桌上爬至杯子外壁,当它正好爬至蜜糖相对方向离桌面3厘米的B 处时,突然发现了蜜糖。
2020年四川省成都市中考数学试卷及答案

2020成都中考数学答案与解析A 卷(共100分) 第I 卷(选择题,共30分)一.选择题(本大题共10个小题,每小题3分,共30分,每小题均有四个选项,其中只有一项符合题目要求,答案涂在答题卡上) 1.-2的绝对值是( )A.-2B.1C.2D.21 2.如图所示的几何体是由四个大小相同的小立方块搭成,其左视图是( )3.2020年6月23日,北斗三号最后一颗全球组网卫星在西昌卫星发射中心成功发射并顺利进入预定轨道,它的稳定运行标志着全球四大卫星导航系统之一的中国北斗卫星导航系统全面建成.该卫星距离地面约为36000千米,将数据36000用科学记数法表示为( ) A.3.6×103 B.3.6×104 C.3.6×105 D.36×1044.在平面直角坐标系中,将点P (3,2)向下平移2个单位长度得到的点的坐标是( ) A.(3,0) B.(1,2) C.(5,2) D.(3,4)5.下列计算正确的是( )A.ab b a 523=+B.623a a a =⋅C.2623)(b a b a =- D.332b a b a =÷6.成都市国家历史文化名城,区域内的都江堰、武侯祠、杜甫草堂、金沙遗址、青羊宫都有深厚的文化底蕴.某班同学分组到以上五个地方进行研学旅行,人数分别为:12,5,11,5,7(单位:人)这组数据的众数和中位数分别是( )A.5人,7人B.5人,11人C.5人,12人D.7人,11人 7.如图,在△ABC 中,按以下步骤作图:△分别以点B 和C 为圆心,以大于21BC 的长为半径作弧,两弧相交于点M 和N ;△作直线MN 交AC 于点D.若AC=6,AD=2,则BD 的长为( )A.2B.3C.4D.68.已知2=x 是分式方程113=--+x x x k 的解,那么实数k 的值为( ) A.3 B.4 C.5 D.69.如图,直线1l △2l △3l ,直线AC 和DF 被321,,l l l 所截,AB=5,BC=6,EF=4,则DE 的长为( )A.2B.3C.4D.31010.关于二次函数822-+=x x y ,下列说法正确的是( ) A.图象的对称轴在y 轴的左侧 B.图象与y 轴的交点坐标为(0,8) C.图象与x 轴的交点坐标为(-2,0)和(4,0)D.y 的最小值为-9第II 卷(非选择题,共70分)二、填空题(本大题共4个小题,每小题4分,共16分,答案写在答题卡上) 11.分解因式:=+x x 32.12.一次函数2)12(+-=x m y 的值随x 值得增大而增大,则常数m 的取值范围为 .13.如图,A ,B ,C 是△O 上的三个点,△AOB=50°,△B=55°,则△A 的度数为 .14.《九章算术》是我国古代一部著名的算书,它的出现标志着中国古代数学形成了完整的体系.其中卷八方程[七]中记载:“今有牛五、羊二,直金十两.牛二、羊五直金八两.牛羊各直金几何?”题目大意是:5头牛、2只羊共值金10两.2头牛、5只羊共值金8两.每头牛、每只羊各值金多少两?设1头牛值金x 两,1只羊值金y 两,则可列方程组为 . 三.解答题(本大题共6个小题,共54分,解答过程写在答题卡上) 15.(本小题满分12分,每题6分)(1)计算:9|32|)21(60sin 22--++︒-. (2)解不等式组:⎪⎩⎪⎨⎧->++≥-②,1312①,2)1(4x x x x16.(本小题满分6分) 先化简,再求值923112-+÷+-x x x )(,其中23+=x .17.(本小题满分8分)2021年,成都将举办世界大学生运动会,这是在中国西部第一次举办的世界综合性运动会,目前,运动会相关准备工作正在有序进行,比赛项目已经确定.某校体育社团随机抽查了部分同学在田径、跳水、篮球、游泳四种比赛项目中选择一种观看的意愿,并根据调查结果绘制成了如下两幅不完整的统计图. 根据以上信息,解答下列问题(1)这次被调查的同学共有 人;(2)扇形统计图中“篮球”对应的扇形圆心角的度数为 ;(3)现拟从甲、乙、丙、丁四人中任选两名同学担任大运会的志愿者,请利用画树状图或列表的方法,求恰好选中甲、乙两位同学的概率.18.(本小题满分8分)成都“339”电视塔作为成都市的地标建筑之一,现已成为外地游客到成都旅游打卡的网红地.如图,为测量电视塔观景台A处的高度,某数学兴趣小组在电视塔附近一建筑物楼顶D处测得塔A处的仰角韦45°,塔底部B处的俯角韦22°.已知建筑物的高CD约为61米,请计算观景台的高AB的值.(结果精确到1米;参考数据:sin22°≈0.37,cos22°≈0.93,tan22°≈0.40).19.(本小题满分10分)在平面直角坐标系xOy 中,反比例函数)0(>=x xmy 的图象经过点A (3,4),过点A 的直线b kx y +=与x 轴、y 轴分别交于C B ,两点.(1)求反比例函数的表达式;(2)若△AOB 的面积为△BOC 的面积的2倍,求此直线的函数表达式.20.(本小题满分10分)如图,在△ABC 的边BC 上取一点O ,O 为圆心,OC 为半径画△O,△O 与边AB 相切于点D ,AC=AD ,连接OA 交△O 于点E ,连接CE ,并延长交线段AB 于点F. (1)求证:AC 是△O 的切线; (2)若AB=10,4tan 3B =,求△O 的半径; (3)若F 是AB 的中点,试探究BD+CE 与AF 的数量关系B 卷(共50分)一.填空题(本题共5个小题,每小题4分,共20分,答案写在答题卡上) 21.已知73a b =-,则代数式2269a ab b ++的值为 . 22.关于x 的一元二次方程232402x x m -+-=有实数根,则实数m 的取值范围是 . 23.如图,六边形ABCDEF 是正六边形 111111F E D C B FA 叫做“正六边形的渐开线”,1FA 、11A B 、11B C 、11C D 、11D E 、11E F , 的圆心依次按A ,B ,C ,D ,E ,F 循环,且每段弧所对的圆心角均为正六边形的一个外角.当AB=1时,曲线111111F E D C B FA 的长度是 .24.在平面直角坐标系xOy 中,已知直线(0)y mx m =>与双曲线4y x=交于A ,C 两点(点A 在第一象限),直线(0)y nx n =<与双曲线1y x=-交于B ,D 两点.当这两条直线互相垂直,且四边形ABCD 的周长为时,点A 的坐标为 .25.如图,在矩形ABCD中,AB=4,BC=3,E,F分别为AB,CD边的中点.动点P从点E 出发沿EA向点A运动,同时,动点Q从点F出发沿FC向点C运动,连接PQ,过点B作BH△PQ于点H,连接DH.若点P的速度是点Q的速度的2倍,在点P从点E运动至点A 的过程中,线段PQ长度的最大值为,线段DH长度的最小值为.二.解答题(本大题共3个小题,共30分,解答过程写在答题卡上)26.(本小题满分8分)在“新冠”疫情期间,全国人民“众志成城,同心抗疫”,某商家决定将一个月获得的利润全部捐赠给社区用于抗疫.已知商家购进一批产品,成本价为10元/件,拟采取线上和线下两种方式进行销售.调查发现,线下的月销量y(单位:件)与线下售价x(单位:元/件,x≤<)满足一次函数的关系,部分数据如下表:1224(1)求y与x的函数关系式;(2)若线上售价始终比线下每件便宜2元,且线上的月销量固定为400件.试问:当x为多少时,线上和线下月利润总和达到最大?并求出此时的最大利润.27.(本小题满分10分)在矩形ABCD 的CD 边上取一点E ,将△BCE 沿BE 翻折,使点C 恰好落在AD 边上点F 处. (1)如图1,若BC=2BA ,求△CBE 的度数;(2)如图2,当AB=2,且AF·FD=10时,求BC 的长;(3)如图3,延长EF ,与△ABF 的角平分线交于点M ,BM 交AD 于点N ,当NF=AN+FD时,求AB BC的值.28.(本小题满分12分)在平面直角坐标系xOy 中,已知抛物线2y ax bx c =++与x 轴交于(1,0),(4,0)A B - 两点,与y 轴交于点(0,2)C -. (1)求抛物线的函数表达式;(2)如图1,点D 为第四象限抛物线上一点,连接AD ,BC 交于点E ,连接BD ,记△BDE的面积为1S ,△ABE 的面积为2S ,求12S S 的最大值; (3)如图2,连接AC ,BC ,过点O 作直线l △BC ,点P 、Q 分别为直线l和抛物线上的点,试探究:在第一象限是否存在这样的点P,Q,使△PQB△△CAB.若存在,请求出所有符合条件的点P的坐标;若不存在,请说明理由.2020成都中考数学参考答案与解析A卷(共100分)第I卷(选择题,共30分)一.选择题(本大题共10个小题,每小题3分,共30分,每小题均有四个选项,其中只有一项符合题目要求,答案涂在答题卡上) 1.-2的绝对值是( )A.-2B.1C.2D.21【解析】根据负数的绝对值是它的相反数可知,答案为C2.如图所示的几何体是由四个大小相同的小立方块搭成,其左视图是( )【解析】根据左视图为从左往右观看几何体,故应选D3.2020年6月23日,北斗三号最后一颗全球组网卫星在西昌卫星发射中心成功发射并顺利进入预定轨道,它的稳定运行标志着全球四大卫星导航系统之一的中国北斗卫星导航系统全面建成.该卫星距离地面约为36000千米,将数据36000用科学记数法表示为( ) A.3.6×103 B.3.6×104 C.3.6×105 D.36×104 【解析】科学记数法为10Na ⨯,其中1||10a ≤<可得答案为B4.在平面直角坐标系中,将点P (3,2)向下平移2个单位长度得到的点的坐标是( ) A.(3,0) B.(1,2) C.(5,2) D.(3,4) 【解析】点的平移规律为左减右加,上加下减,所以答案为A5.下列计算正确的是( )A.ab b a 523=+B.623a a a =⋅C.2623)(b a b a =- D.332b a b a =÷【解析】A 选项3a 和2b 不是同类项,不能直接相加,B 选项,同底指数幂相乘,底数不变,指数应相加,所以正确结果为5a ,D 选项应是3ab ,故正确答案为C6.成都市国家历史文化名城,区域内的都江堰、武侯祠、杜甫草堂、金沙遗址、青羊宫都有深厚的文化底蕴.某班同学分组到以上五个地方进行研学旅行,人数分别为:12,5,11,5,7(单位:人)这组数据的众数和中位数分别是( )A.5人,7人B.5人,11人C.5人,12人D.7人,11人【解析】将数据按从小到大顺序排列号为5,5,7,11,12,所以众数是5,中位数是7,故答案为A7.如图,在△ABC 中,按以下步骤作图:△分别以点B 和C 为圆心,以大于21BC 的长为半径作弧,两弧相交于点M 和N ;△作直线MN 交AC 于点D.若AC=6,AD=2,则BD 的长为( )A.2B.3C.4D.6【解析】由题意可得,按步骤作图的结果是:DN 为线段BC 的垂直平分线,△DC=BD ,又△AC=6,AD=2,△CD=BD=4,故选C 8.已知2=x 是分式方程113=--+x x x k 的解,那么实数k 的值为( ) A.3 B.4 C.5 D.6 【解析】将2x =代入分式方程,得11221k -+=-得3k =,故选A 9.如图,直线1l △2l △3l ,直线AC 和DF 被321,,l l l 所截,AB=5,BC=6,EF=4,则DE 的长为( )A.2B.3C.4D.310【解析】由平行线分线段成比例564x =,得201063x ==,故选D 10.关于二次函数822-+=x x y ,下列说法正确的是( ) A.图象的对称轴在y 轴的左侧 B.图象与y 轴的交点坐标为(0,8) C.图象与x 轴的交点坐标为(-2,0)和(4,0) D.y 的最小值为-9【解析】对称轴为直线1x =-在y 轴的左侧,故A 选项错误,图象与y 轴的交点为(0,8)-,故选项B 错误,2280x x +-=的解为122,4x x ==-,△228y x x =+-与x 轴交点坐标为(2,0)和(-4,0),故选项C 错误,D 选项配方可得2(1)9y x =+-,所以y 的最小值为-9,故答案为D第II 卷(非选择题,共70分)二、填空题(本大题共4个小题,每小题4分,共16分,答案写在答题卡上) 11.分解因式:=+x x 32.【解析】提公因式即可得到答案,故答案为(3)x x +12.一次函数2)12(+-=x m y 的值随x 值得增大而增大,则常数m 的取值范围为 .【解析】由一次函数y kx b =+的增减性可知,y 随x 的增大而增大时,0k >,所以210m ->,解之得12m >,△本题答案为12m > 13.如图,A ,B ,C 是△O 上的三个点,△AOB=50°,△B=55°,则△A 的度数为 .【解析】△OB=OC=r ,△△B=△OCB=55°,△△BOC=180°-△B -△OCB=70°,△△AOC=△AOB+△BOC=50°+70°=120°,△OA=OC ,△△OAC=△OCA=30°,本题答案为30° 14.《九章算术》是我国古代一部著名的算书,它的出现标志着中国古代数学形成了完整的体系.其中卷八方程[七]中记载:“今有牛五、羊二,直金十两.牛二、羊五直金八两.牛羊各直金几何?”题目大意是:5头牛、2只羊共值金10两.2头牛、5只羊共值金8两.每头牛、每只羊各值金多少两?设1头牛值金x 两,1只羊值金y 两,则可列方程组为 .【解析】依题意可得5210258x y x y +=⎧⎨+=⎩三.解答题(本大题共6个小题,共54分,解答过程写在答题卡上) 15.(本小题满分12分,每题6分)(1)计算:9|32|)21(60sin 22--++︒-. (2)解不等式组:⎪⎩⎪⎨⎧->++≥-②,1312①,2)1(4x x x x【解析】(1)2122312()2⨯++-; (2)解不等式△得2x ≥;解不等式△得4x <423+=3 ; 所以不等式组的解集为24x ≤< 16.(本小题满分6分)先化简,再求值923112-+÷+-x x x )(,其中23+=x . 【解析】原式=2(3)(3)332x x x x x x ++-⋅=-++将3x =+3x - 17.(本小题满分8分)2021年,成都将举办世界大学生运动会,这是在中国西部第一次举办的世界综合性运动会,目前,运动会相关准备工作正在有序进行,比赛项目已经确定.某校体育社团随机抽查了部分同学在田径、跳水、篮球、游泳四种比赛项目中选择一种观看的意愿,并根据调查结果绘制成了如下两幅不完整的统计图. 根据以上信息,解答下列问题(4)这次被调查的同学共有 人;(5)扇形统计图中“篮球”对应的扇形圆心角的度数为 ;(6)现拟从甲、乙、丙、丁四人中任选两名同学担任大运会的志愿者,请利用画树状图或列表的方法,求恰好选中甲、乙两位同学的概率.【解析】(1)根据条形统计图和扇形统计图得到“跳水”项目有54人,所占比例为30%,所以被调查的总人数为5430%180÷=人(2)由扇形统计图可得“篮球”项目所占比例为130%15%20%35%---=,所以篮球项目对应的扇形圆心角的度数为36035%126︒⨯=︒ (3)列表可得由表格可得,甲,乙,丙,丁四人中任选两名同学担任大运会志愿者总的情况有12种,恰好是甲,乙两位同学的情况有2种,∴恰好选中甲、乙两位同学的概率为21 12618.(本小题满分8分)成都“339”电视塔作为成都市的地标建筑之一,现已成为外地游客到成都旅游打卡的网红地.如图,为测量电视塔观景台A处的高度,某数学兴趣小组在电视塔附近一建筑物楼顶D处测得塔A处的仰角韦45°,塔底部B处的俯角韦22°.已知建筑物的高CD约为61米,请计算观景台的高AB的值.(结果精确到1米;参考数据:sin22°≈0.37,cos22°≈0.93,tan22°≈0.40).【解析】过D作DE⊥AB于E在Rt△BDE中tan∠BDE=BE DE∴61152.5tan 200.4BE DE ===︒米∵△ADE 是等腰直角三角形, ∴AE=DE=152.5米,∵∠DCB=∠CBE=∠BED=90° ∴四边形BCDE 是矩形 ∴DC=BE=61米∴AB=AE+BE=213.5米≈214米 答:观景台AB 的高度约为214米. 19.(本小题满分10分)在平面直角坐标系xOy 中,反比例函数)0(>=x xmy 的图象经过点A (3,4),过点A 的直线b kx y +=与x 轴、y 轴分别交于C B ,两点.(1)求反比例函数的表达式;(2)若△AOB 的面积为△BOC 的面积的2倍,求此直线的函数表达式.【解析】(1)将A (3,4)代入m y x =得12m =,∴反比例函数的表达式为12y x= (2)当直线y kx b =+与x 轴负半轴交于B ,与y 轴正半轴交于C∵△AOB 的面积是△BOC 的面积的2倍∴BOC AOC S S ∆∆=,∴C 是AB 的中点又∵C 在y 轴上,∴0C x =∴02A BC x x x +==,即3B A x x =-=- ∴(3,0)B -,将B (-3,0)、A (3,4)代入直线y kx b =+得3430k b k b +=⎧⎨-+=⎩,解之得232k b ⎧=⎪⎨⎪=⎩,∴直线解析式为223y x =+当直线y kx b =+与x 轴正半轴交于B ,与y 轴负半轴交于C∵△AOB 的面积是△BOC 的面积的2倍 而11||,||22AOB A BOC C S OB y S OB y ∆∆==,∴|2||A C y y =,且0,4c A y y <= ∴2c y =-,∴(0,2)C -,将A (3,4),C (0,-2)代入直线可得342k b b +=⎧⎨=-⎩,∴22k b =⎧⎨=-⎩,此时直线的解析式为22y x =-综上所述:直线的函数表达式为223y x =+或22y x =- 20.(本小题满分10分)如图,在△ABC 的边BC 上取一点O ,O 为圆心,OC 为半径画△O,△O 与边AB 相切于点D ,AC=AD ,连接OA 交△O 于点E ,连接CE ,并延长交线段AB 于点F. (1)求证:AC 是△O 的切线; (2)若AB=10,4tan 3B =,求△O 的半径; (3)若F 是AB 的中点,试探究BD+CE 与AF 的数量关系【解析】(1)证明:连接OD ,∵△O 与AB 相切,∴∠ADO=90° 在△AOC 和△AOD 中,AC AD AO AO CO DO =⎧⎪=⎨⎪=⎩∴△AOC ≌△AOD (SSS ),∴∠ADO=∠ACO=90°,∴OC ⊥AC ∵OC 为△O 的半径,∴AC 是△O 的切线. (2)设OD=4x ,∵在Rt △OBD 中,4tan 3OD B DB ==,∴3BD x =,∴5OB x =,∴BC=OB+OC=9x 在Rt △ACB 中,4tan 3AC B CB ==,∴49123AC x x =⋅=,∴15AB x ==又∵AB=10,∴1510x =,∴23x =,∴843r x ==,即△O 的半径是83(3)探究关系结果:AF BD CE =+,理由如下:连接ED ,CD ,∵AC ,AD 为△O 的切线,∴AO 平分∠COD 和∠CAD ,∴∠COE=∠DOE 且∠COE 及∠DOE 均为圆心角,∴CE=DE ,∴∠ECD=∠EDC. 在△OCE 和△ODE 中,OC ODOE OE CE DE =⎧⎪=⎨⎪=⎩∴△OCE ≌△ODE (SSS ),∴∠CEO=∠DEO 设∠CAO=α,∠CEO=β∵AC=AD ,且OA 平分∠CAD ,∴OA ⊥CD ,∴∠CAO+∠ACD=90°,又∵∠ACD+∠OCD=90°,∴∠OCD=α ∴∠ECD=βα-,又∵∠AEF 和∠CEO 互为对顶角,∴∠AEF=∠CEO=β 在Rt △ACB 中,因为C 是斜边AB 中点,∴BF=AF=CF ,∴∠CAF=∠ACF=2α ∵∠CEO 为△ACE 的外角,∴∠CEO=∠CAO+∠ACF ,∴3βα=∴∠ECD=2βαα-=,又∵∠FED 是△CED 的外角,∴∠FED=∠ECD+∠EDC=4α∵∠EFD 是△AEF 的外角,∴∠EFD=∠OAD+∠AEF=4αβα+=,∴∠FED=∠EFD ,∴DE=DF ,∴EC=ED=FD 又∵BF=BD+DF ,且BF=AF ,DF=CE ,∴AF=BD+CEB 卷(共50分)一.填空题(本题共5个小题,每小题4分,共20分,答案写在答题卡上) 21.已知73a b =-,则代数式2269a ab b ++的值为 .【解析】222237,69(3)749a b a ab b a b +=++=+==22.关于x 的一元二次方程232402x x m -+-=有实数根,则实数m 的取值范围是 . 【解析】一元二次方程有实根,所以判别式△≥0,所以23(4)42()02m --⨯-≥,解之得72m ≤,∴此题答案为72m ≤ 23.如图,六边形ABCDEF 是正六边形 111111F E D C B FA 叫做“正六边形的渐开线”,1FA 、11A B 、11B C 、11C D 、11D E 、11E F , 的圆心依次按A ,B ,C ,D ,E ,F 循环,且每段弧所对的圆心角均为正六边形的一个外角.当AB=1时,曲线111111F E D C B FA 的长度是 .【解析】曲线111111FA B C D E F 是由两段圆心角为60°,半径不同的扇形弧长组成.其长度为六段弧长之和,所以6016026036046056067180180180180180180πππππππ︒⋅︒⋅︒⋅︒⋅︒⋅︒⋅+++++=︒︒︒︒︒︒故答案为:7π24.在平面直角坐标系xOy 中,已知直线(0)y mx m =>与双曲线4y x=交于A ,C 两点(点A 在第一象限),直线(0)y nx n =<与双曲线1y x=-交于B ,D 两点.当这两条直线互相垂直,且四边形ABCD 的周长为时,点A 的坐标为 .【解析】由于正比例函数和反比例函数均关于坐标原点中心对称,所以四边形中A 、C 关于O 对称,B 、D 关于O 中心对称,所以对角线AC 、BD 被坐标原点平分,即四边形ABCD是平行四边形,当AC ⊥BD 时,可得四边形ABCD 为菱形.由四边形周长为边形边长2AD =,将直线y mx =代入反比例函数4y x =得24x m =,∴A x =,代入反比例函数得A y =AC ⊥BD ,∴1mn =-,即1n m =-,将直线1y x m=-代入反比例函数1yx =-得2x m =,∴D x =D y =,∴D ∴22414,OA m OD m m m =+=+,在Rt △AOD 中,222AD OA OD =+,∴52552m m +=整理得(21)(2)0m m --=,∴12m =或2,当12m =时,A ,当2m =时,A ,∴A 的坐标为或25.如图,在矩形ABCD 中,AB=4,BC=3,E ,F 分别为AB ,CD 边的中点.动点P 从点E 出发沿EA 向点A 运动,同时,动点Q 从点F 出发沿FC 向点C 运动,连接PQ ,过点B 作BH△PQ 于点H ,连接DH.若点P 的速度是点Q 的速度的2倍,在点P 从点E 运动至点A 的过程中,线段PQ 长度的最大值为 ,线段DH 长度的最小值为 .【解析】∵P 由E 往A 运动,Q 由F 往C 运动,且点P 的速度是点Q 的速度的2倍,所以当P 与A 重合时,Q 在FC 中点时,线段PQ 取得最大值,过Q 作QN ⊥AB 于N ,则AN=QN=3,此时线段2322=+=QN AN PQ ,连接DE ,HE ,则1322=+=AE AD DE ,所以HE DE DH -≥,当D 、H 、E 三点共线时DH 取得最小值,此时HE=2,故DH 最小值为213-二.解答题(本大题共3个小题,共30分,解答过程写在答题卡上) 26.(本小题满分8分)在“新冠”疫情期间,全国人民“众志成城,同心抗疫”,某商家决定将一个月获得的利润全部捐赠给社区用于抗疫.已知商家购进一批产品,成本价为10元/件,拟采取线上和线下两种方式进行销售.调查发现,线下的月销量y (单位:件)与线下售价x (单位:元/件,1224x ≤<)满足一次函数的关系,部分数据如下表:(3)求y 与x 的函数关系式;(4)若线上售价始终比线下每件便宜2元,且线上的月销量固定为400件.试问:当x 为多少时,线上和线下月利润总和达到最大?并求出此时的最大利润.【解析】(1)设一次函数的函数关系式为)0(≠+=k b kx y ,将1200,12==y x 代入函数得120012=+b k ,将1100,13==y x 代入函数得110013=+b k ,解方程组⎩⎨⎧=+=+110013120012b k b k 得⎩⎨⎧=-=2400100b k ,∴一次函数的函数关系式为2400100+-=x y(2)设商家线上和线下的月利润总和为w 元,由题意可得)10()102(400-+--=x y x w将2400100+-=x y 代入可得7300)19(1002+--=x w ,∴当线下售价定为19元/件时,月利润总和最大,此时最大利润是7300元27.(本小题满分10分)在矩形ABCD 的CD 边上取一点E ,将△BCE 沿BE 翻折,使点C 恰好落在AD 边上点F 处. (1)如图1,若BC=2BA ,求△CBE 的度数;(2)如图2,当AB=2,且AF·FD=10时,求BC 的长;(3)如图3,延长EF ,与△ABF 的角平分线交于点M ,BM 交AD 于点N ,当NF=AN+FD 时,求ABBC的值.【解析】(1)由翻折可得BC=BF ,∠EBF=∠CBE ,∵BC=2BA∴在Rt △ABF 中,sin ∠AFB=21=BF AB ,∴∠AFB=30° ∵在矩形ABCD 中,AD ∥BC ,∴∠AFB=∠CBF=30°∴∠CBE=21∠CBF=15° (2)在矩形ABCD 中,有∠A=∠D=∠C=90°,由翻折性质可知∠C=∠BFE=90°. ∵在Rt △ABF 中,有∠AFB+∠ABF=90°,根据平角定义可得∠AFB+∠BFE+∠EFD=180°∴∠ABF=∠EFD ,又∵∠A=∠D=90°,∴△FAB ∽△EDF∴DFABED EA =,∴DF FA ED AB ⋅=⋅,∵10=⋅FD AF ,AB=5,解得ED=2 CE=CD -ED=5-2=3,由翻折性质可知EF=CE=3,在Rt △EFD 中,522=-=DE EF DF ;∵10=⋅FD AF ,∴52=AF ,∴53552=+=+=FD AF AD由矩形ABCD 性质可得,BC=AD=53 (3)作NG ⊥BF 于G ,在△FNG 和△FBA 中⎩⎨⎧︒=∠=∠∠=∠90BAF NGF BFA NFG ∴△FNG ∽△FBA ,∴BF NFBA NG FA FG ==, ∵NF=AN+FD 且NF+AN+FD=AD ,∴2NF=AD ,即21=AD NF ∵AD=BC ,BC=BF ,∴21=BF NF ,∴21=FA GF 设x AN NF ==,1,则x FD -=1,x AF +=1,∴2===BF BC AD ,∴21+=x GF ∵BM 平分∠ABF ,N 在BM 上,且NA ⊥AB ,NG ⊥BF ,∴NA=NG=x 在Rt △NGF 中,222NF GF NG =+,∴2221)21(=++x x ,整理可得03252=-+x x 解得53=x ,负值舍掉,∴54=GF ,∴56=BG 在Rt △BAN 和Rt △BGN 中⎩⎨⎧==BN BN NGAN ,∴Rt △BAN ≌Rt △BGN (HL ),∴56==BG BA ,∴53256==BC AB28.(本小题满分12分)在平面直角坐标系xOy 中,已知抛物线2y ax bx c =++与x 轴交于(1,0),(4,0)A B - 两点,与y 轴交于点(0,2)C -. (2)求抛物线的函数表达式;(2)如图1,点D 为第四象限抛物线上一点,连接AD ,BC 交于点E ,连接BD ,记△BDE的面积为1S ,△ABE 的面积为2S ,求12S S 的最大值; (3)如图2,连接AC ,BC ,过点O 作直线l △BC ,点P 、Q 分别为直线l 和抛物线上的点,试探究:在第一象限是否存在这样的点P ,Q ,使△PQB△△CAB.若存在,请求出所有符合条件的点P 的坐标;若不存在,请说明理由.【解析】(1)将)2,0(),0,4(),0,1(--C B A 分别代入c bx ax y ++=2可得,204160⎪⎩⎪⎨⎧-==++=+-c c b a c b a 解之得⎪⎪⎪⎩⎪⎪⎪⎨⎧-=-==22321c b a ,∴二次函数的解析式为223212--=x x y(2)设直线BC 的解析式为q px y +=,将)2,0(),0,4(-C B 代入直线可得⎩⎨⎧-==+204q q p ,解得⎪⎩⎪⎨⎧-==221q p ,∴直线BC 的表达式为:221-=x y 过点D 作DG ⊥x 轴于点G ,交BC 于点F ,过点A 作AK ⊥x 轴交BC 的延长线于点K .可得AK DF AE DE S S S S ABE BDE ===∆∆21,∵1-==K A x x ,∴25-=K y ,即线段25=AK 设点)22321,(2--m m m D ,则可得m m DF 2212+-=. 从而可得m m S S 5451221+-==54)2(512+--m ,当2=m 时,21S S 有最大值54(3)符合条件的点P 的坐标为)934,968(或)5413,54126(++,∵l ∥BC 且l 过原点O ,∴直线l 的表达式为x y 21=,设点P 的坐标为)2,(m m ①当点P 在直线BQ 的右侧时,如图,过P 作y 轴的平行线交x 轴于N ,过Q 作QM ⊥PN 于M.∵△PQB ∽△CAB ,∴∠BPQ=∠BCA在Rt △AOC 中,522=+=OC AO AC ,在Rt △BOC 中,5222=+=OB OC BC∵AB=5,∴222AB BC AC =+,即∠ACB=90°∴∠BPQ=90°,∴∠MPQ+∠BPN=90°,∵∠BPN+∠PBN=90°,∴∠PBN=∠QPM ∴△QPM ∽△PBN ,∴PNQM BN PM PB QP == 又∵△PQB ∽△CAB ,∴21525===CB CA PB QP ∴21==PN QM BN PM ,∵2,4mPN m NB =-=, ∴4,221mQM m PM =-=, ∴2,43-=+==-=m PM y y m QM x x p Q P Q ,∴)2,43(-m m Q ∵Q 在抛物线上,∴24323)43(21)2(2-⋅-=-m m m ,且4>m ,∴27272=m ∴此时P 的坐标为)934,968(②当点P 在直线BQ 左侧时.由①的方法可得点Q 的坐标为)2,45(m ,此时P 点坐标为)5413,54126(++。
一类几何不等式的推广

I ≤
即
~ 3 — 4 — 睾 — 二仁. — ≤ ~ <.完 2兀 ‘ ‘ 证 Ⅱ
定理2 得出的结论与问题 1 中的结论相比, 形
式变化很大, 因此, 以下再 给出与问题 1 更类似 的结论. 定理 3 对任意 a 、c 、b ∈R+ 都有 ,
1
4 第三种推广 . 问题 1 提出的是平方关 系, 那么对于 3 次方, 4 次方, . … 是否也有类似的结论呢? 引理 1 设 a 、b∈R+, a +b a -6 则 n≥ n 1+
nn . 6 一1
’ 2 +) 成. . ( … 立 完 a a< 一 兰 证 l篇 ++ …
a
证: 参看文 [ 第35 3 6 页。 】
则 ≤ <
-
, 口_ 6 c , 当 =
3 ≤
< 1 ,
定理 5 设 △ JC中三边长分别为a b , E } 、 、C
不等式是数学研 究的重要 内容, 含有几何元
礼口 +n +… +0) 0 +a +… +0) ( } ; 2 ≥( 1 2 。 ,
素( 线段、角、面积等) 的不等式称为几何不等
式. 几何不等式涉及的 内容丰富, 处理 问题的方
毗若等篇
法与技巧灵活多变. …提出下列问题 文
问题 1 设 AAB C中三边长分别为 0 b , 、 、c
02 01+ n2 03+ … + n2 n 0
=n(1 3 2 +n +… +0) ; n n >n,
nn0l十 nn02十 … + nn0n一1
再 鬈譬蒂<,证( 6 证 { 即 2+ + n。 2
C)<( 口+b ), +c 即证以 +b +C 2<2b a+
2c c. b c (+C >b,c 0 b+2a 由a +b =b a ) b+c = c +n >C,n b (+b >0 , ( ) 。 c +a =ac ) 6
卫星几何关系对定位精度的影响

卫星几何位置与定位精度之间的关系1卫星几何关系对定位精度的影响假设s 表示从地心到卫星的向量,u 代表从地心到用户位置的向量,用 r 表示从用户到卫星的偏移向量,则r 与s,u 之间的关系是:r= s-u (1)距离||r||可通过测量GPS 接收机接收的卫星信号的时间延迟获得,这种式获得的距离||r||称为伪距,因为时间延迟中包含有GPS 接收机与系统时的偏差。
假设第j 颗卫星与GPS 接收机之间的伪距用jρ表示,则jρ可用式 ( 2 )表示:bj j ct ||u -s ||+=ρ (2)式中,c 表示光速,bt 是GP S 接收机与系统时的偏差,||u -s ||j 表示第颗j 颗卫与用户之间的真距。
如果用),,(u u u z y x 和),,(j j j z y x 分别表示用户和第j 颗卫星的三维位置坐标,则jρ可表示为:bu j u j u j j ct z z y y x x +-+-+-=222)()()(ρj=1,2,3,4 (3)用),,(^^^u u u z y x 表示在用户实际位置附近的某位置,可以对式(3)在),,(^^^u u u z y x 附近展开成Taylor 级数,并且忽略高次项,这样就完成了对式(3)的线性化。
bu z u y u x ct z a y a x a j j j -∆+∆+∆==∆^j j j -ρρρ (4)像jρ一样,^jρ 表示在用户附近),,(^^^u u u z y x 到卫星的伪距。
这里,^uu u ζζζ-=∆^^juj r a j ζζζ-=, z y x ,,=ζ (5)2^2^^2^^)()()(u j u j u j j z z y y x x r -+-+-=可以把式(5)写成紧凑的矩阵形式:⎪⎪⎪⎪⎪⎭⎫ ⎝⎛∆-∆∆∆⎪⎪⎪⎪⎪⎭⎫ ⎝⎛≈⎪⎪⎪⎪⎪⎭⎫ ⎝⎛∆∆∆∆=∆b u u u z y x z y x z y x z y x t c z y x a a a a a a a a a a a a 11114443332221114321ρρρρρ (6)或者写成更简洁的形式:x H ∆≈∆ρ(7)矩阵H 有时称为视度矩阵, 它是一个nx4矩阵,z ≥ 4。
闵可夫斯基不等式二维形式

闵可夫斯基不等式二维形式摘要:一、闵可夫斯基不等式的简介1.闵可夫斯基不等式的基本概念2.二维形式的闵可夫斯基不等式二、闵可夫斯基不等式在二维形式下的具体应用1.二维形式的闵可夫斯基不等式的推导过程2.二维形式的闵可夫斯基不等式的几何意义3.二维形式的闵可夫斯基不等式的实际应用三、总结与展望1.二维形式的闵可夫斯基不等式的重要性2.闵可夫斯基不等式在其他领域的应用3.对二维形式的闵可夫斯基不等式未来研究的展望正文:闵可夫斯基不等式是数学领域中一个非常重要的不等式,它广泛应用于概率论、统计学、图像处理、通信理论等多个领域。
在二维形式下,闵可夫斯基不等具有其独特的性质和应用价值。
一、闵可夫斯基不等式的简介闵可夫斯基不等式是由德国数学家赫尔曼·闵可夫斯基在1909 年提出的,其基本形式是:对于任意的实数a1, a2, ..., an 和b1, b2, ..., bn,有(a1^2 + a2^2 + ...+ an^2)(b1^2 + b2^2 + ...+ bn^2) >= (a1b1 + a2b2 + ...+anbn)^2。
在二维形式下,闵可夫斯基不等式可以表示为:设二维随机变量(X, Y) 的联合概率密度函数为f(x, y),边缘概率密度函数分别为f_X(x) 和f_Y(y),则对于任意的实数a 和b,有E[aX + bY]^2 <= (a^2 + b^2)E[X^2 +Y^2],其中E[·] 表示期望。
二、闵可夫斯基不等式在二维形式下的具体应用1.二维形式的闵可夫斯基不等式的推导过程根据二维随机变量的定义,我们可以得到E[X] = ∫xf_X(x)dx,E[Y] =∫yf_Y(y)dy,E[XY] = ∫x∫yf(x, y)dxdy。
然后,根据概率论中的柯西- 施瓦茨不等式,我们可以得到E[aX + bY]^2 <= (a^2 + b^2)E[X^2 + Y^2]。
基本不等式的几何前提条件

基本不等式的几何前提条件
基本不等式的几何前提条件通常涉及到图形的性质和关系。
以下是一些常见的基本不等式的几何前提条件:
1. 三角形不等式:
- 对于任意三角形ABC,任意两边之和大于第三边。
- \(AB + BC > AC\)
- \(AC + BC > AB\)
- \(AB + AC > BC\)
2. 角的性质:
- 两条平行线被一条横切线截断,对应角相等。
- 同位角、内错角等性质。
3. 平行线和角的关系:
- 被平行线截取的同位角相等。
- 被平行线截取的内错角互补。
4. 相似三角形的性质:
- 如果两个三角形的对应角相等,则这两个三角形相似。
- 如果两个三角形的对应边成比例,则这两个三角形相似。
5. 圆的性质:
- 圆内角等于其半径所对应的弧的角度。
- 圆周角等于360度(或\(2\pi\) 弧度)。
6. 多边形的内角和:
- 一个n边形的内角和等于\((n-2) \times 180^\circ\) 或\((n-2) \times \pi\) 弧度。
这些几何前提条件在解决问题时非常有用,特别是在证明几何命题或解决与几何形状有关的不等式问题时。
浅析高中数学课程内容主线 精选教育文档

浅析高中数学课程内容主线华罗庚在《大哉数学之为用》中叙述数学为“宇宙之大、粒子之微、火箭之速、化工之巧、地球之变、生物之谜、日用之繁”等各方面的应用。
数学应用的广泛性使得数学应用在数学课程中的地位越发的重要。
2011年数学课程标准:“为了适应时代发展对人才培养的需要,数学课程还要特别注重发展学生的应用意识和创新意识。
”注重高中数学应用,分析高中课程内容主线--数学应用,对高中数学应用内容教学有重要作用。
高中数学应用主线把高中数学课程所涉及到的数学应用内容有机地紧密联系起来。
抓住应用主线所构成的知识网,就可以更好的把握高中数学课程中的数学应用内容,了解实质,提高教学和学习的效率。
一、数学应用的含义数学应用对发展学生应用意识具有重大意义。
数学应用指用数学的知识与思想方法去解决生产、生活乃至学习中的各种实际问题的过程,它包括数式的运算、推理、分析、制表、绘图、估计、符号变换、优化方案等诸多方面。
数学应用主要体现在两个方面:一是数学的内部应用,即运用已有的数学知识和数学思想方法解决新的数学问题;二是数学在社会生活和生产中的应用。
二、高中数学应用教学现状数学来源于生活,又运用于生活。
我国数学教学中,比较突出的一个问题是忽视数学的应用,忽视数学与其他学科以及与日常生活的联系,忽视培养学生的应用意识,学生的数学应用能力普遍偏低。
据调查发现现在高中数学应用教学现状如下:1.学生对数学应用价值认识不足。
有的学生仅仅把数学学科当作一个考试科目。
为的是取得好成绩,却忽视了数学的应用价值。
2.解决实际问题时存在障碍,比如,学生在运用已学过的数学思想、方法解决问题方面、在生活语言与数学语言的转化上存在一定的困难。
3.部分老师认为高中课程内容多,时间紧,高考中的比重不大,不强调数学应用。
培养学生数学应用意识不强,开展数学应用意识教学意识淡薄,在教学中不注意联系生活实际体现数学的应用价值。
在教学过程中忽视了教学内容在应用主线中的地位与作用。
2022年山东省菏泽市中考数学真题 (解析版)

【解析】
【分析】先按分式混合运算法则化简分式,再把已知变形为a2-2a=15,整体代入即可.
【详解】解:
=
=a(a-2)
=a2-2a,
∵a2-2a-15=0,
∴a2-2a=15,
∴原式=15.
故答案为:15.
【点睛】本题考查分式化简求值,熟练掌握分式混合运算法则是解题的关键.
14.如图,在第一象限内的直线 上取点 ,使 ,以 为边作等边 ,交 轴于点 ;过点 作 轴的垂线交直线 于点 ,以 为边作等边 ,交 轴于点 ;过点 作 轴的垂线交直线 于点 ,以 为边作等边 ,交 轴于点 ;……,依次类推,则点 的横坐标为_______.
4.如图所示,将一矩形纸片沿AB折叠,已知 ,则 ()
A 48°B.66°C.72°D.78°
【答案】C
【解析】
【分析】由折叠及矩形的性质可得 ,再根据平行线的性质求出 ,根据周角的定义求解即可.
【详解】∵将一矩形纸片沿AB折叠,
∴ ,
,
,
,
,
故选:C.
【点睛】本题考查了矩形的性质,折叠的性质及平行线的性质,熟练掌握知识点是解题的关键.
A.1B. C. D.2
【答案】C
【解析】
【分析】连接AF,则AF的长就是AM+FM的最小值,证明△ABC是等边三角形,AF是高线,利用三角函数即可求解.
【详解】解:连接AF,则AF的长就是AM+FM的最小值.
∵四边形ABCD是菱形,
∴AB=BC,
又∵∠ABC=60°,
∴△ABC是等边三角形,
∵
∴F是BC的中点,
三、解答题(本题共78分,把解答或证明过程写在答题卡的相应区域内,写在其他区域不得分.)
Wirtinger不等式的一个几何应用_赵亮

Li Lj Ai · Aj = Li Lj
Ai Aj ,
(3.4)
即 A2 ij ≥ Ai Aj . 当 Ki 与 Kj 位似时等号显然成立, 而要使 (3.2) 式中的等号成立, (3.3) 式和 (3.4) 式中的等号必须同时成立, 则由引理存在常数 a, b, 使 p (φ) pj (φ) i − = a cos φ + b sin φ, Li Lj (3.5) Lj Li Ai = Aj . Li Lj 即
888
数
学
杂
志
Vol. 31
若 C 为凸闭曲线, 设 C 的支持函数为 p = p(θ), 则 p = −X · n, 由 t = (− sin θ, cos θ), 则曲线 C 的周长与面积还可以表示为
2π 2π
(2.3)
n = (− cos θ, − sin θ).
(2.4)
L =
C
ds =
0
C
∗
dt = κn, ds
dn = −κt. ds
(2.1)
ds,
A=−
1 2
X · nds.
C
(2.2)
收稿日期: 2010-05-17 接收日期: 2010-09-29 基金项目:国家自然科学基金资助 (10971167). 作者简介: 赵亮 (1985–), 男, 山东临沂, 硕士, 研究方向: 积分几何. E–mail: feigewang1985@.
2π
(p2 − p 2 )dθ
0 2π 2 (p2 j − pj )dθ + 0 0 2π
1 2π 2 1 (pi − pi2 )dθ + = 2 0 2 = Ai + Aj + 2Aij ,
wirtinger不等式在几何中的应用

wirtinger不等式在几何中的应用Wirtinger不等式在几何中的应用引言:Wirtinger不等式是一种重要的数学不等式,它在几何中有着广泛的应用。
本文将探讨Wirtinger不等式在几何中的应用,并以具体的例子加以说明。
一、Wirtinger不等式的定义和基本性质Wirtinger不等式是指对于任意实数x和y,有以下不等式成立:(x-y)^2 ≥ 0该不等式的证明相对简单,可以通过展开式来证明。
Wirtinger不等式的基本性质包括:1. 不等式成立的充分必要条件是x=y;2. 不等式两边同时开平方后得到的不等式也成立;3. 不等式两边同时乘以一个正数后得到的不等式也成立;4. 不等式两边同时乘以一个负数后得到的不等式方向相反。
二、Wirtinger不等式在几何中的应用举例1. 证明平行四边形对角线相等设ABCD是一个平行四边形,我们需要证明对角线AC和BD相等。
根据平行四边形的性质,我们可以得到向量AB=CD,以及向量AD=BC。
根据向量的模长定义,我们可以得到AB的模长等于CD的模长,即|AB|=|CD|,同样地,AD的模长等于BC的模长,即|AD|=|BC|。
现在我们将不等式(x-y)^2 ≥ 0应用到向量的模长上,即(|AB|-|CD|)^2 ≥ 0和(|AD|-|BC|)^2 ≥ 0。
根据Wirtinger不等式的性质3,我们可以得到|AB|^2-2|AB||CD|+|CD|^2 ≥ 0和|AD|^2-2|AD||BC|+|BC|^2 ≥ 0。
由于|AB|=|CD|和|AD|=|BC|,所以|AB|^2=|CD|^2和|AD|^2=|BC|^2,将它们代入不等式中,得到|AB|^2+|CD|^2-2|AB||CD| ≥ 0和|AD|^2+|BC|^2-2|AD||BC| ≥ 0。
进一步化简可得(|AB|-|CD|)^2 ≥ 0和(|AD|-|BC|)^2 ≥ 0,由此可知|AB|-|CD|≥0和|AD|-|BC|≥0,即|AB|≥|CD|和|AD|≥|BC|。
球面上Wirtinger不等式的一个几何应用

球面上Wirtinger不等式的一个几何应用马磊;李妮【摘要】In this paper, we investigate some quermassintegrals inequalities which have been obtained by Fradelizi, Giannopoulos and Meyer, via the Wirtinger inequality on sphere-space. Further,we give a simple proof of this inequality for the case k = n-2.%利用球面上的Wirtinger不等式研究由Fradelizi,Giannopoulos和Meyer得到一组关于均质积分的不等式,对于这细小等式中k=n-2的情形给出了一种简单的证明.【期刊名称】《湖北民族学院学报(自然科学版)》【年(卷),期】2012(000)004【总页数】4页(P376-379)【关键词】凸体;混合体积;均质积分;Wirtinger不等式【作者】马磊;李妮【作者单位】广东石油化工学院师范学院,广东茂名525200;建始县第一中学,湖北建始445300【正文语种】中文【中图分类】O186.5经典Brunn-minkowski理论起源于1887年H.Brunn的论文和H.Minkowski开创性工作的实质部分,1934年Bonnesen和Fenchel的著名论著收集了己经出版的结果,R.Schneider的专著[1]是一部最近出版的优秀的参考书.Brunn-minkowski理论是Euclidean空间中向量的Minkowski线性组合和体积结合的产物,其精髓是结合体积的记号和基本的Brunn-minkowski不等式.它己成为凸性理论的中心,其应用涉及到物理学、医学、信息工程和数学的各个分支.特别地,凸体混合体积的不等式在Brunn-minkowski理论[2-4]中起到了关键性的作用. 2002年,Giannopoulos,Hartzoulaki和Paouris证明了一组关于凸体混合体积的Aleksandrov-fenche[5]型的不等式,2003年Fradelizi,Giannopoulos 和Meyer对这组不等式作了进一步的发展,得到了一组与均质积分相关的不等式[6].本文将从调和分析的角度对Fradelizi,Giannopoulos和Meyer得到的不等式给出一个简单的证明.设 x=(x1,x2,…,xn)(xi>0,i=1,2,…,n)为 n 维正实向量的全体,为k阶初等对称的数,并规定E0(K)=1.设 x,y 为正实向量,Marcus-lopes[7]证明了如下的不等式:设A,B是正定对称矩阵,Ak,Bk分别表示从矩阵A,B中删除第k行与第k列的矩阵.Bergstrom[8]得到了不等式:对于上述不等式,man猜想在混合体积理论是否也存在类似于式(1)和式(2)的不等式:这里的Vk(K),Vk(L)分别表示Rn中凸体 K,L的k阶混合体积.在不等式(3)中,如果K是Rn中任意凸体,L是Rn中的单位球,Giannopoulos、Hartzoulaki和 Paouris[5]证明了不等式(3)是正确的.当K,L为Rn中的凸体时,Fradelizi,Giannopoulos和Meyer证明了关于均质积分仅对 k=n-2,n-1 时是正确的[6],即:这里Wk(K),Wk(L)分别表示Rn中凸体 K,L的k阶均质积分.关于对偶的结合体积与对偶的均质积分李小燕与冷岗松[9]也得到了类似的结果.由于 Wn-1(K)是线性的且Wn(K)为单位球的体积,因此不等式(4)对于k=n-1的情形是显然的.本文主要利用球面上的Wirtinger不等式,研究了不等式 (4)中对于k=n-2的情形,即如下定理.定理1 设K,L为Rn中两个C2光滑凸体,则有如下不等式成立:等号成立当且仅当K与L位似.1 预备知识设Kn是欧式空间Rn中的紧致凸集族,B是Rn中的单位球.Kn中所有包含空内点的凸集叫做凸体,记作:Kn0,凸体M⊂Rn的体积记作:V(M).对于 K,L∈Kn0,Minkowski加法定义为:K+L={x+y:x ∈K,y∈L},K∈Kn0与常数λ∈R的乘积定义为:λK={λx:x∈K}.则Minkowski-steiner公式可表示为:其中t≥ 0,且:叫做 K 与 L的混合体积.特别地,V0(K,L)=V(K),Vn(K,L)=V(L),Vi(K,L)=Vn-1(L,K).特别地,当L=B时式(5)可变为经典的Steiner公式:其中:称为凸体K的第i阶均质积分.特别地,nW1(K)为K的表面积,Wn(K)=V(B)=ωn为n维单位球 B的体积,(K)=(2/ωn)Wn-1(K)是凸体 K的平均宽度.设K⊆Knt,K的支撑函数hK(u)定义为Sn→R的如下的数:hK(u)=max{u· x:x∈K},u∈Sn-1.这里u·x表示Rn中u和x的内积.由支撑函数的定义可知其满足以下性质:h(K+tB)(u)=hK(u)+t,∀t∈R+,h(K+L)(u)=hK(u)+hL(u),h(λK)(u)= λhK(u),∀λ≥ 0,h(K)(u+v)≤hK(u)+hK(v).设 K,L⊆K0n,B 为单位球,如果记,则 V(K,L)可由 K,L 的支撑的数 hK(u),hL(u)表示出来[10]:其中:▽o为球面Sn-1上的梯度算子,dσ(u)为球面微元.特别地,由式(8)可知:因此:2 Wirtinger不等式的应用引理1[10](Sn-1上的Wirtinger不等式) 设F为Rn中定义在球面Sn-1上的C2光滑的数,若:则:其中:dσ(u)为球面做元,▽oF(u)为F(u)球面上的梯度算子.等号成立当且仅当F(u)为一次球面调和函数.证明由于F(u)为Sn-1上的C2光滑函数,设F(u)的调和展开式为:由式(9),可知 Q0=0,所以因为:,所以:即:定理2 设K,L分别是Rn中任意两个C2类的光滑凸体,则有如下不等式成立:等号成立当且仅当K与L位似.证明令,根据引理1以及式(6)和式(7)可知 :等号成立是一次球面调和函数,即K与L位似.由于:由不等式(10)可得:即:由等式(8)可知即:注记事实上,对不等式(20)的右边应用不等式,立刻可以得到 Aleksandrov-fenchel型的不等式 V2(K,L)≥Wn-2(K)Wn-2(L).特别地,当L=B时可以得到一个关于均质积分不等式Wn-1(K)2-ωnWn-2(K)≥0.参考文献:[1] Schneider R,Weil W.Zonoids and related topics,Convexity and Its Applications[M].Basel:Birkhäuser,1983:296-317.[2] Burago Y D,Zalgaller V A.Geometric inequalities[M].Berlin:Springer-Verlag,1988.[3] Stanley R P.Two combinatorial applications of the Aleksandrov-Fenchel inequalities[J].J Combin Theory,1981,31A:56-65.[4] Santalo L A.Integral Geometry and Geometric Probability[M].Addison Wesley Publishing Company,1976.[5] Giannopoulos A,Hartzoulaki M,Paouris G.On a local version of the Aleksandrov-Fenchel inequality for the quermassintegrals of a convexbody[J].Proc Amer Math Soc,2002,130:2403-2412.[6] Fradelizi M,Giannopoulos A,Meyer M.Some inequalities about mixed volumes[J].Israel Journal of Math,2003,135:157-179.[7] Beckenbach E F,Bellman R.Inequalities[M].Berlin:Springer-Verlag,1971.[8] Bergstrom H.A triangle inequality for matrices[J].Den Elfte Skandinaviske Matematikerkongress.Trond-heim,1949.Oslo Johan Grundt Tanums Forlag,1952.[9] Li X Y,Leng G S.Some inequalities about dual mixed volumes of star bodies[J].Acta Mathematica Scientia,2005,25B(3):505-510.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
r) p s d s
( Vp≤一2 . )有心 2 一卫星 系统 . , , ,} S P r, B z 在空 间科学 中的背景是 : 点 P视为地球 ( ”f 可将
中心 , A, 为地球的 两颗具有相 同的运动轨道和相 同的运动 线速 度的卫星 , 点 B视 曲线 r为卫星运动 的轨道 , : r
0 Vt ( , ) , ( ∈ a b ) 则称 曲线 r为 光滑 曲线
了 ( )=了 ( ) 为光滑 的 Jra 闭 曲线, a b) o n d 并且
D( r)为 凸区域 如果
l n l
()实数 2 i 为给 定 常数 , 0< 2< 且
二
;
(i i )A, B ∈r,B=了 ( + 2 , B, 一 r t )
一
=
r(^+l A t B)1( B∈r, r( ) vA, t t) > .
B∈R A ≠ B, 用 l B l 示直 线段 A , 则 表 A B的
1 .
由弧 长 的计算 公式 我们 有 ,
长度 , l B l 即 =l A
定 义 11 设 曲线 r: =一 t ( s b . 7 r( ) as t )
1 引 言 和 主 要 结 果
我们 要 用 到 如 下 记 号 : 为 实 数 集 ; 为 R m( m 2 维 实数空 间 ; ) Z为 整数 集 ; 为空 集 ; 若
,
l 是 存在 的 . l r 本文 约定 : 滑 曲线 的参 数 t 自 光 为 然参 数 L ] 即 3 , t =t A 口 ^+l r( B)l ,
维普资讯
第 2 卷 第3 6 期 2 0年 9 07 月
Ju n l fC e guU i es t (a ua c e c dt o ) o r a hn d n v r iy N tr l in eE i in o S
成 都大学 学报( 自然科 学版)
一
=
r( 一2 ; t ) 沿 着 曲 线
(i i )用 ( B ) 从点 B运 动至点 B 时
光 滑 曲线 r: ’ r() n t b 的长 度 r: ’ t( )
收 稿 E期 :20 l 07—0 1 . 5— 4
射 线 A 的轨迹 区域 M 当动点 A在 曲线 r上连 续运
基 金 项 目 :国 家 自然 科 学 基 金 (0703 ,四 川省 教 育 厅 自然 科 学 基 金 (05 2 1 资 助 项 目 1117 ) 20 A 0 )
=
d P,B) 示地球 中心到 直线 A ( A 表 B的距 离, 它是有心 2一卫星 系统的一种基本几何量 .
文献标识码 : A
关键 词 : 一卫 星 系统 ; ra 2 J dn闭 曲线 ; o 区域 ; 一凸 函数 S
中 图 分 类 号 : 16 10 7 .3 0 7 0 8 .; 14 1 ; 18
Jra odn曲线定 理 任 意 Jra odn闭曲线将 平 面 分成 两个 区域 它们 都 以该 曲线 为 边界 . 中一 个 其 为有界 区域 , 为该 Jra 曲线 的 内部 , 一 个 称 odn闭 另 为无界 区域 , 为该 Jra 闭 曲线 的外 部 . 称 odn 定 义 12 设 曲线 r: :一 t ( . 了 r( ) 口< t b < ) 为 zm 2 维 实数 空 间 上 的一条 连续 曲线 ( ) 如 果一 t::d r()d 连 续 , 且 lr()l r() — t/£ 并 — t >
一
:
r( 的点一 t) 为 曲线 r的重 点 ; t) r( 称 没有重
点 的连 续 曲线 叫简 单 曲线 ; 简 单 曲线 r 满足 7 若 ( ):一 b , 称 曲线 r为 简单 闭 曲线 . 中的 口 r( )则
简单 闭曲线 称为 Jra 曲线 . odn闭 以于 J ra od n闭曲线 , 我们 有 下面 的 :
l (B l J lr() tv , r . A ) :l — £ l ( B∈ ) r d A
设 曲线 r为 中的光滑 的 简单 闭 曲线 . 我们 用 F( B)表 示 以 , 为 端 点 的 简 单 曲线 , A B 且 F( B)c r, B ∈ F( B ,它 的 长 度 记 为 l A A, A) F( B)l 特 别 地 ,简 单 闭 曲 线 r 的 长 度 记 为 A ,
l 1Jra 曲线 r 所 围成 的 区域记 为 D( , . d n闭 r o r) 区域 D( r)的面 积记 为 l r)1 D( 定 义 13 设 曲线 r: =一 t ( t b . 7 r( ) a ,
为 m( 2 维 实数空 间 上 的一 条连续 曲线 . m ) 对于 满足 a < t b as 2 b t ≠ t, 。 t) 1< , t s ,1 2 r(1
V_ . 6 o 2 No. 1 3
S p 2 0 e . 0 7
文章编号:04—52 (0 7 0 —0 9 —0 10 4 2 2 O )3 19 8
涉 及 2一卫星 系统 的 一 类 几 何 不 等 式
文 家金
( 成都大学 信息科 学与技 术学院 ,四川 成 都 60 0 ) 116
摘 要 : 定义 了无心 2 一卫星 系统 S ’r A B z 和有心 2 ‘ { , , ,} 一卫星 系统 S ’P r A B z, 适当的假 设下, ‘ { , , , ,}在
借 于 超 论 立 涉 有 2 卫 系 .tr ,z 一 几 不 式( 助 优 理 建 了 及 心 一 星 统S ,B} 类 何 等 : (P ,的 ”,
