1立体几何易错题集
立体几何易错题精选(部分解析).

立体几何易错题精选(部分解析)16.已知三棱锥P-
ABC的三条侧棱PA、PB、PC两两垂直,D是底面三角形内一点,且∠DPA=450,∠DPB=600,则∠DPC=_____
答案:600
点评:以PD为对角线构造长方体,问题转化为对角线PD与棱PC的夹角,利用co s2450+cos2600+cos2α=1得α=600,构造模型问题能力弱。
29.点P在直径为2的球面上,过P作两两垂直的三条弦,若其中一条弦长是另一条弦长的2倍,则这三条弦长之和为最大值是
正确答案:
错误原因:找不到解题思路
20.自半径为R的球面上一点P引球的两两垂直的弦PA、PB、PC,则
=_____。
正解:,可将PA,PB,PC看成是球内接矩形的三度,则应是矩形对角线的平方,即球直径的平方。
误解:没有考虑到球内接矩形,直接运算,易造成计算错误。
25.异面直线a ,
b所成的角为,过空间一定点P,作直线L,使L与a ,b
所成的角均为,这样的直线L有条。
答案:三条
错解:一条
错因:没有能借助于平面衬托,思考问题欠严谨。
过P作
确定一平面,画相交所成角的
平分线m、g,过m,
g分别作平面的垂面,则在中易找到所求直线共有3条。
立体几何易错大汇聚

立体几何易错大汇聚【高考动向】立体几何考试题是体现高考“稳中求变”罪贴切的一部分,重点考查“直线与平面性质”是稳的一方面,变的方面主要体现在:在填空题方面,陆续出现了多选、多填的形式,改变了填空题形式单一的弊端,拓宽了填空题的考查功能。
近几年高考题中又出现了开放性的填空题,重点考查探索、分析和解决问题的能力,解答题由单纯的直线与平面的证明题的变为以多面体为载体的多角度考查的试题,表现为计算中有证明、证明中有计算的新特点。
高考中立体几何试题侧重于对线线、线面、面面等各种位置关系的考查,一般以特殊的多面体为载体 ,将点、线、面融合在一起,考查内部位置关系,计算各种角、距离、面积、体积等。
解答题中以小步设问的方式,各问之间既独立成题,又有相互联系;既有平行与垂直等位置关系的证明,又有角、距离、体积等的计算,突出对空间概念、空间想象能力和逻辑思维、逻辑表达能力的考查,对于线线、线面、面面的各种位置关系,平行与垂直是特殊的两种,它们之间的推理与论证是高考的重点。
近年来高考题常立足于棱柱、棱锥、正方体及长方体,对于给定的一个特殊几何体,利用隐含的点、线、面的关系建立适当的空间直角坐标系,借助空间向量把抽象推理向计算型推理转变。
【知识死角】一、概念理解错误解立体几何问题时,常见一些对基本概念或公式及定理的考查。
如对各种空间角、空间距离的考查,对各种多面体的定义及性质的考查,对几何体体积的考查等,因此在解题过程中,概念或范围不清、公式错用是常见的解题失误。
例1、已知二面角βα--l 的大小为060,m ,n 为异面直线,且βα⊥⊥n m ,,则m , n 所成的角【 】A 、030B 、060C 、090D 、0120错解:如图,设α⊥m 于A ,过m 的点P 引n 的平行线交β于B ,设平面PAB 与l 交于O 点,连结AO 、BO ,由βα⊥⊥n m ,可知面⊥l 面PAB ,所以BO l AO l ⊥⊥,,所以AOB ∠是二面角的平面角,所以AOB ∠=060,可得APB ∠=0120,则m ,n 所成的角为0120,故选D.剖析:错解中很明显没有弄清异面直线所成的角的范围。
高三数学易错立体几何多选题 易错题难题自检题学能测试试题
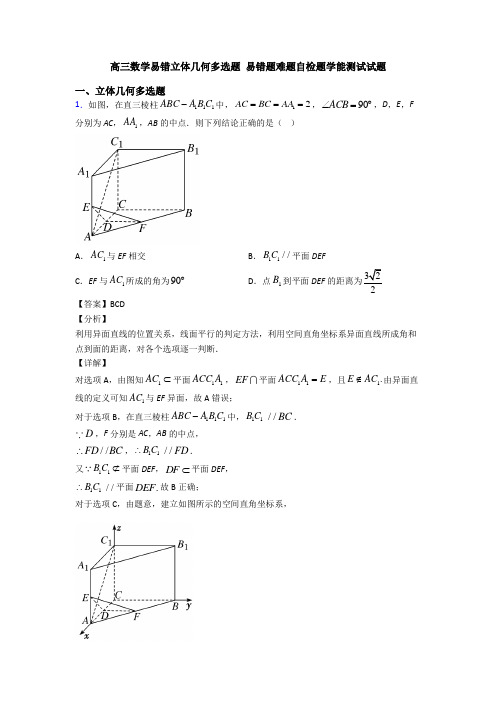
高三数学易错立体几何多选题 易错题难题自检题学能测试试题一、立体几何多选题1.如图,在直三棱柱111ABC A B C -中,12AC BC AA ===,90ACB ∠=︒,D ,E ,F分别为AC ,1AA ,AB 的中点.则下列结论正确的是( )A .1AC 与EF 相交B .11//BC 平面DEF C .EF 与1AC 所成的角为90︒D .点1B 到平面DEF 的距离为322【答案】BCD 【分析】利用异面直线的位置关系,线面平行的判定方法,利用空间直角坐标系异面直线所成角和点到面的距离,对各个选项逐一判断. 【详解】对选项A ,由图知1AC ⊂平面11ACC A ,EF 平面11ACC A E =,且1.E AC ∉由异面直线的定义可知1AC 与EF 异面,故A 错误;对于选项B ,在直三棱柱111ABC A B C -中,11B C //BC .D ,F 分别是AC ,AB 的中点, //∴FD BC ,11B C ∴ //FD .又11B C ⊄平面DEF ,DF ⊂平面DEF ,11B C ∴ //平面.DEF 故B 正确;对于选项C ,由题意,建立如图所示的空间直角坐标系,则(0C ,0,0),(2A ,0,0),(0B ,2,0),1(2A ,0,2),1(0B ,2,2),1(0C ,0,2),(1D ,0,0),(2E ,0,1),(1F ,1,0).(1EF ∴=-,1,1)-,1(2AC =-,0,2). 1·2020EF AC =+-=,1EF AC ∴⊥,1EF AC ∴⊥. EF 与1AC 所成的角为90︒,故C 正确;对于选项D ,设向量(n x =,y ,)z 是平面DEF 的一个法向量. (1DE =,0,1),(0DF =,1,0), ∴由n DE n DF ⎧⊥⎨⊥⎩,,,即·0·0n DE n DF ⎧=⎨=⎩,,,得00.x z y +=⎧⎨=⎩,取1x =,则1z =-,(1n ∴=,0,1)-, 设点1B 到平面DEF 的距离为d . 又1(1DB =-,2,2),1·102DB n d n-+∴===, ∴点1B 到平面DEF 的距离为2,故D 正确.故选:BCD 【点睛】本题主要考查异面直线的位置关系,线面平行的判定,异面直线所成角以及点到面的距离,还考查思维能力及综合分析能力,属难题.2.在三棱柱111ABC A B C -中,ABC ∆是边长为( )A .直线1A C 与直线1BB 之间距离的最大值为3B .若1A 在底面ABC 上的投影恰为ABC ∆的中心,则直线1AA 与底面所成角为60︒ C .若三棱柱的侧棱垂直于底面,则异面直线AB 与1A C 所成的角为30D .若三棱柱的侧棱垂直于底面,则其外接球表面积为64π【答案】AD 【分析】建立空间直角坐标系,用向量法求解. 【详解】如图示,以A 为原点,AC 为y 轴正方向,Ax 为x 轴正方向,过A 点垂直于面ABC 的向上方向为z 轴正方向建系,则()()()0,0,0,3,0,0,23,0,A B C 设()()()100010001000,,,3,3,,,23,,A x y z B x y z C x y z ++所以()()()1000100011,23,,,,,3,3,0,AC x y z BB x y z A B =---== 对于A:设n 为直线1A C 与直线1BB 的公垂线的方向向量,则有:11·0·0AC n BB n ⎧=⎪⎨=⎪⎩,即()()0000002300x x y y zz x x y y zz ⎧-+-=⎪⎨++=⎪⎩解得:()00,0n z x =- 设直线1A C 与直线1BB 之间距离为d ,则22011222200009||||z A B nd d x z n x z ===++ 22009x d ≥∴≤,即3d ≤,故A 正确;对于B :若1A 在底面ABC 上的投影恰为ABC ∆的中心,则(13,211A 底面法向量()(10,0,1,1,3,211m AA ==,设直线 1AA 与底面所成角为θ,则:121133sin |cos ,|143AA n θ===⨯,故B 错误; 对于C : 三棱柱的侧棱垂直于底面时,则(((1110,0,43,3,43,0,23,43,A B C则()(13,3,0,3,43,AB AC ==-设异面直线AB 与1A C 所成的角为θ,则1115cos |cos ,|||10||||23215AB AC AB AC AB AC θ====⨯,故C 错误;对于D :若三棱柱的侧棱垂直于底面时,外接球的球心O 为上下底面中心DD 1连线的中点,所以外接球的半径()222324R =+=,所以2464S R ππ==.故D 正确故选:AD 【点睛】向量法解决立体几何问题的关键: (1)建立合适的坐标系; (2)把要用到的向量正确表示; (3)利用向量法证明或计算.3.在棱长为1的正方体1111ABCD A B C D -中,P 为底面ABCD 内(含边界)一点.( ) A .若13A P P 点有且只有一个 B .若12A P ,则点P 的轨迹是一段圆弧 C .若1//A P 平面11B D C ,则1A P 2D .若12A P 且1//A P 平面11B DC ,则平面11A PC 截正方体外接球所得截面的面积为23π【答案】ABD 【分析】选项A ,B 可利用球的截面小圆的半径来判断;由平面1//A BD 平面11B D C ,知满足1//A P 平面11B D C 的点P 在BD 上,1A P 2P 与B 或D 重合,利用12sin 60A P r =︒,求出6r =,进而求出面积.对A 选项,如下图:由13A P =,知点P 在以1A 为球心,半径为3的球上,又因为P 在底面ABCD 内(含边界),底面截球可得一个小圆,由1A A ⊥底面ABCD ,知点P 的轨迹是在底面上以A 为圆心的小圆圆弧,半径为22112r A P A A =-=,则只有唯一一点C满足,故A 正确;对B 选项,同理可得点P 在以A 为圆心,半径为22111r A P A A =-=的小圆圆弧上,在底面ABCD 内(含边界)中,可得点P 轨迹为四分之一圆弧BD .故B 正确;对C 选项,移动点P 可得两相交的动直线与平面11B D C 平行,则点P 必在过1A 且与平面11B D C 平行的平面内,由平面1//A BD 平面11B D C ,知满足1//A P 平面11B D C 的点P 在BD上,则1A P 长的最大值为12A B =,则C 不正确; 对选项D ,由以上推理可知,点P 既在以A 为圆心,半径为1的小圆圆弧上,又在线段BD 上,即与B 或D 重合,不妨取点B ,则平面11A PC 截正方体外接球所得截面为11A BC 的外接圆,利用2126622,,sin 60333A B r r S r ππ==∴=∴==︒.故D 正确.故选:ABD(1)平面截球所得截面为圆面,且满足222=R r d +(其中R 为球半径,r 为小圆半径,d 为球心到小圆距离);(2)过定点A 的动直线平行一平面α,则这些动直线都在过A 且与α平行的平面内.4.如图,已知正方体1ABCD ABC D -的棱长为a ,E 是棱CD 上的动点.则下列结论中正确的有( )A .11EB AD ⊥B .二面角11E A B A --的大小为4π C .三棱锥11A B D E -体积的最小值为313a D .1//D E 平面11A B BA 【答案】ABD 【分析】连接1A D 、1B C ,则易证1AD ⊥平面11A DCB ,1EB ⊂平面11A DCB ,则由线面垂直的性质定理可以判断选项A 正确;二面角11E A B A --的平面角为1DA A ∠,易知14DA A π∠=,则可判断选项B 正确;用等体积法,将求三棱锥11A B D E -的体积转化为求三棱锥11E AB D -的体积,当点E 与D 重合时,三棱锥11E AB D -的体积最小,此时的值为316a ,则选项C 错误;易知平面11//D DCC 平面11A B BA ,而1D E ⊂平面11D DCC ,则根据面面平行的性质定理可得1//D E 平面11A B BA ,可判断选项D 正确. 【详解】选项A ,连接1A D 、1B C ,则由正方体1ABCD ABC D -可知,11A D AD ⊥,111A B AD ⊥,1111A DA B A =,则1AD ⊥平面11A DCB ,又因为1EB ⊂平面11A DCB ,所以11EB AD ⊥,选项A 正确; 选项B ,因为11//DE A B ,则二面角11E A B A --即为二面角11D A B A --, 由正方体1ABCD ABC D -可知,11A B ⊥平面1DA A , 则1DA A ∠为二面角11D A B A --的平面角,且14DA A π∠=,所以选项B 正确;选项C ,设点E 到平面11AB D 的距离为d , 则11111113A B D E E AB D AB D V V S d --==⋅,连接1C D 、1C B ,易证平面1//BDC 平面11AB D ,则在棱CD 上,点D 到平面11AB D 的距离最短, 即点E 与D 重合时,三棱锥11A B D E -的体积最小, 由正方体1ABCD ABC D -知11A B ⊥平面1ADD , 所以1111123111113326D AB D B ADDADD a V V S A B a a --==⋅=⋅⋅=, 则选项C 错误;选项D ,由正方体1ABCD ABC D -知,平面11//CC D D 平面11A B BA ,且1D E ⊂平面11CC D D , 则由面面平行的性质定理可知1//D E 平面11A B BA ,则选项D 正确. 故选:ABD. 【点睛】关键点点睛:本题对于选项C 的判断中,利用等体积法求三棱锥的体积是解题的关键.5.如图,正方体1111ABCD A B C D -的棱长为3,线段11B D 上有两个动点,E F ,且1EF =,以下结论正确的有( )A .AC BE ⊥B .异面直线,AE BF 所成的角为定值C .点A 到平面BEF 的距离为定值D .三棱锥A BEF -的体积是定值 【答案】ACD 【详解】由AC BD ⊥,1AC DD ⊥可证AC ⊥平面11D DBB ,从而AC BE ⊥,故A 正确; 取特例,当E 与1D 重合时,F 是F ',AE 即1AD ,1AD 平行1BC ,异面直线,AE BF '所成的角是1C BF '∠,当F 与1B 重合时,E 是E ',BF 即1BB ,异面直线,AE BF '所成的角是1A AE '∠,可知1C BF '∠与1A AE '∠不相等,故异面直线,AE BF 所成的角不是定值,故B 错误;连结BD 交AC 于O ,又AC ⊥平面11D DBB ,点A 到平面11BDD B 的距离是2AO ,也即点A 到平面BEF 的距离是22,故C 正确; 2=2AO 为三棱锥A BEF -的高,又1111224BEF S =⨯⨯=△,故三棱锥A BEF -的体积为112234224⨯⨯=为定值,D 正确. 故选:ACD 【点睛】求空间中点到平面的距离常见方法为: (1)定义法:直接作平面的垂线,求垂线;(2)等体积法:不作垂线,通过等体积法间接求点到面的距离; (3)向量法:计算斜线在平面的法向量上的投影即可.6.在长方体1111ABCD A B C D -中,AB =12AD AA ==,P 、Q 、R 分别是AB 、1BB 、1A C 上的动点,下列结论正确的是( )A .对于任意给定的点P ,存在点Q 使得1D P CQ ⊥B .对于任意给定的点Q ,存在点R 使得1D R CQ ⊥C .当1AR A C ⊥时,1ARD R ⊥D .当113AC A R =时,1//D R 平面1BDC 【答案】ABCD 【分析】本题先建立空间直角坐标系,再运用空间向量在立体几何中的应用逐一判断即可. 【详解】如图所示,建立空间直角坐标系,设(2,,0)P a,0a ⎡∈⎣,(2,)Q b ,[]0,2b ∈,设11A R AC λ=,得到(22,,22)R λλ--,[]0,1λ∈. 1(2,,2)D P a =-,(2,0,)CQ b =,142D P CQ b ⋅=-,当2b =时,1D P CQ ⊥,A 正确;1(22,2)D R λλ=--,12(22)2D R CQ b λλ⋅=--,取22bλ=+时,1D R CQ ⊥,B 正确;1AR A C ⊥,则1(2,22)(2)412440AR AC λλλλλ⋅=--⋅--=+-+=,解得:15λ=,此时12282(,)(,)0555555AR D R ---⋅=⋅=,1AR D R ⊥,C 正确;113AC A R =,则44(,)333R,142(,)333D R =-,设平面1BDC 的法向量为(,,)n x y z =,则100n BD n DC ⎧⋅=⎪⎨⋅=⎪⎩,解得(3,n =-,故10n D R ⋅=,故1//D R 平面1BDC ,D 正确.故选:ABCD.【点睛】本题考查了空间向量在立体几何中的应用,是偏难题.7.如图四棱锥P ABCD -,平面PAD ⊥平面ABCD ,侧面PAD 是边长为26的正三角形,底面ABCD 为矩形,23CD =,点Q 是PD 的中点,则下列结论正确的是( )A .CQ ⊥平面PADB .PC 与平面AQC 所成角的余弦值为223C .三棱锥B ACQ -的体积为62D .四棱锥Q ABCD -外接球的内接正四面体的表面积为3【答案】BD 【分析】取AD 的中点O ,BC 的中点E ,连接,OE OP ,则由已知可得OP ⊥平面 ABCD ,而底面ABCD 为矩形,所以以O 为坐标原点,分别以,,OD OE OP 所在的直线为x 轴,y 轴 ,z 轴,建立空间直角坐标系,利用空间向量依次求解即可. 【详解】解:取AD 的中点O ,BC 的中点E ,连接,OE OP , 因为三角形PAD 为等边三角形,所以OP AD ⊥, 因为平面PAD ⊥平面ABCD ,所以OP ⊥平面 ABCD , 因为AD OE ⊥,所以,,OD OE OP 两两垂直,所以,如下图,以O 为坐标原点,分别以,,OD OE OP 所在的直线为x 轴,y 轴 ,z 轴, 建立空间直角坐标系,则(0,0,0),(6,0,0),(6,0,0)O D A ,(0,0,32),6,23,0),(6,23,0)P C B ,因为点Q是PD的中点,所以Q,平面PAD的一个法向量为(0,1,0)m =,6(2QC=-,显然m与QC不共线,所以CQ与平面PAD不垂直,所以A不正确;3632(6,23,32),(,0,),(26,2PC AQ AC=-==,设平面AQC的法向量为(,,)n x y z=,则362260n AQ x zn AC⎧⋅=+=⎪⎨⎪⋅=+=⎩,令=1x ,则y z==,所以(1,2,n=-,设PC与平面AQC所成角为θ,则21sin36n PCn PCθ⋅===,所以cos3θ=,所以B正确;三棱锥B ACQ-的体积为1132B ACQ Q ABC ABCV V S OP--==⋅1116322=⨯⨯⨯=,所以C不正确;设四棱锥Q ABCD-外接球的球心为)M a,则MQ MD=,所以222222a a⎛++-=++⎝⎭⎝⎭,解得0a=,即M为矩形ABCD对角线的交点,所以四棱锥Q ABCD-外接球的半径为3,设四棱锥Q ABCD-外接球的内接正四面体的棱长为x,将四面体拓展成正方体,其中正四面体棱为正方体面的对角线,x,所以22362x⎛⎫=⎪⎪⎝⎭,得224x=,所以正四面体的表面积为234243x ⨯=,所以D 正确. 故选:BD【点睛】此题考查线面垂直,线面角,棱锥的体积,棱锥的外接球等知识,综合性强,考查了计算能力,属于较难题.8.如图,在正方体ABCD ﹣A 1B 1C 1D 1中,点P 在线段B 1C 上运动,则( )A .直线BD 1⊥平面A 1C 1DB .三棱锥P ﹣A 1C 1D 的体积为定值C .异面直线AP 与A 1D 所成角的取值范用是[45°,90°]D .直线C 1P 与平面A 1C 1D 6 【答案】ABD【分析】在A 中,推导出A 1C 1⊥BD 1,DC 1⊥BD 1,从而直线BD 1⊥平面A 1C 1D ;在B 中,由B 1C ∥平面 A 1C 1D ,得到P 到平面A 1C 1D 的距离为定值,再由△A 1C 1D 的面积是定值,从而三棱锥P ﹣A 1C 1D 的体积为定值;在C 中,异面直线AP 与A 1D 所成角的取值范用是[60°,90°];在D 中,以D 为原点,DA 为x 轴,DC 为y 轴,DD 1为z 轴,建立空间直角坐标系,利用向量法能求出直线C1P与平面A1C1D 所成角的正弦值的最大值为63.【详解】解:在A中,∵A1C1⊥B1D1,A1C1⊥BB1,B1D1∩BB1=B1,∴A1C1⊥平面BB1D1,∴A1C1⊥BD1,同理,DC1⊥BD1,∵A1C1∩DC1=C1,∴直线BD1⊥平面A1C1D,故A正确;在B中,∵A1D∥B1C,A1D⊂平面A1C1D,B1C⊄平面A1C1D,∴B1C∥平面A1C1D,∵点P在线段B1C上运动,∴P到平面A1C1D的距离为定值,又△A1C1D的面积是定值,∴三棱锥P﹣A1C1D的体积为定值,故B正确;在C中,异面直线AP与A1D所成角的取值范用是[60°,90°],故C错误;在D中,以D为原点,DA为x轴,DC为y轴,DD1为z轴,建立空间直角坐标系,设正方体ABCD﹣A1B1C1D1中棱长为1,P(a,1,a),则D(0,0,0),A1(1,0,1),C1(0,1,1),1DA=(1,0,1),1DC=(0,1,1),1C P=(a,0,a﹣1),设平面A1C1D的法向量(),,n x y z=,则11n DA x zn DC y z⎧⋅=+=⎪⎨⋅=+=⎪⎩,取x=1,得1,1,1n,∴直线C1P与平面A1C1D所成角的正弦值为:11||||||C P nC P n⋅⋅=22(1)3a a+-⋅=21132()22a⋅-+,∴当a=12时,直线C1P与平面A1C1D所成角的正弦值的最大值为6,故D正确.故选:ABD.【点睛】求直线与平面所成的角的一般步骤:(1)、①找直线与平面所成的角,即通过找直线在平面上的射影来完成;②计算,要把直线与平面所成的角转化到一个三角形中求解;(2)、用空间向量坐标公式求解.。
详解十五道高中立体几何典型易错题

例1 设有四个命题:①底面是矩形的平行六面体是长方体;②棱长都相等的直四棱柱是正方体;③有两条侧棱都垂直于底面一边的平行六面体是直平行六面体;④对角线相等的平行六面体是直平行六面体.其中真命题的个数是( )A .1B .2C .3D .4分析:命题①是假命题.因为底面是矩形的直平行六面体才是长方体.底面是矩形,侧棱不垂直于底面,这样的四棱柱仍是斜平行六面体;命题②是假命题.底面是菱形,底面边长与棱长相等的直四棱柱不是正方体; 命题③是假命题.因为有两条侧棱垂直于义面一边不能推出侧棱与底面垂直. 命题④是真命题,如图所示,平行六面体1111-D C B A ABCD 中所有对角线相等,对角面11BDD B 是平行四边形,对角线D B BD 11=,所以四边形11BDD B 是矩形,即BD BB ⊥1,同理四边形11ACC A 是矩形,所以AC AA ⊥1,由11//BB AA 知⊥1BB 底面ABCD ,即该平行六面体是直平行六面体.故选A .说明:解这类选择题的关键在于理清各种棱柱之间的联系与区别,要紧扣底面形状及侧棱与底面的位置关系来解题.下面我们列表来说明平行四边形与平行六面体的性质的“类比”,由此,我们可以发现立体几何与平面几何许多知识是可以进行类比的.见表表例2 如图,正四棱柱1111-D C B A ABCD 中,对角线81=BD ,1BD 与侧面C C BB 11所成角为 30,求:(1)1BD 与底面ABCD 所成角;(2)异面直线1BD 与AD 所成角;(3)正四棱柱的全面积.分析:正四棱柱是一种特殊的长方体,它的两底面ABCD 、1111D C B A 是正方形,长方体中有比较多的线面垂直关系,而线面垂直关系往往是解决立体几何问题的关键条件.题中无论是已知线面成角,还是求线面成角,都要把它们转化为具体的角,落实线面成角,先要找线面垂直关系.异面直线1BD 与AD 所成角通过11//D A AD ,落实为具体的B D A 11∠.正四棱柱各个面都是矩形,求面积只要用矩形面积公式. 解:(1)在正四棱柱C A 1中,∵⊥11C D 面C C BB 11,∴11BC D ∠是B D 1与侧面C C BB 11所成角,即 3011=∠BC D .∵ 81=BD ,∴ 411=C D ,341=BC ,∵ 1111D C B A 是正方形,∴41111==C D C B ,⊥D D 1平面ABCD ,∴ BD D 1∠是B D 1与底面ABCD 所成角,在Rt △DB D 1中,2411==D B BD ,81=BD , ∴22cos 11==∠BD BD BD D ,∴ 451=∠BD D , 即1BD 与底面ABCD 所成角为 45.(2)∵11//D A AD ,∴B D A 11∠是1BD 与AD 所成角(或补角).∵⊥11A D 平面B B AA 11,∴ B A A D 111⊥,Rt △B D A 11中,411=D A ,81=BD , ∴21cos 11=∠B D A ,∴ 6011=∠B D A ,即异面直线AD 与1BD 所成角为 60.(3)Rt △11C BB 中,411=C B ,341=BC .∴ 241=BB ,∴ ()()12232244244442+=⨯+⨯+⨯=全S .说明:长方体是一种特殊的棱柱,充分感受其中丰富的线面垂直、线线垂直关系是灵活解题的关键,各种垂直关系是解决立体几何中证明和计算的重要条件.典型例题三例3 如图,已知长方体1111-D C B A ABCD 中,棱长51=AA ,12=AB ,求直线11C B 与平面11BCD A 的距离.分析:求直线到平面的距离,首先要找直线上的点到平面的垂线,而找平面的垂线的一个很有用的思路是,找平面内一条直线与某一平面垂直,这里我们不难看出,长方体中有⊥CB 平面11BB AA ,这样,只要作B A H B 11⊥,又有CB H B ⊥1,得到⊥H B 1平面11A BC D . 解:长方体1AC 中,有⊥BC 平面11BB AA ,过1B 作B A H B 11⊥于H ,又有H B BC1⊥,∴ ⊥H B 1平11A BCD ,即H B 1是11C B 到平面11BCD A 的距离.在Rt △11A BB 中,由已知可得,51=BB ,1211=B A ,∴ 131=B A ,∴13601=H B . 即H B 1是11C B 到平面11BCD A 的距离为1360. 说明:长方体中有棱与面的线面垂直关系,正方体除此之外,还有对角线与对角面的线面垂直关系,比如,求正方体1AC 中,11C A 与面BD C 1所成角.这里,要找11C A 与BD C 1所成角,必须找1A 到平面BD C 1的垂线,因为⊥BD 面C C AA 11,在对角面1AC 内,过1A 作11OC H A ⊥于H ,则H A BD 1⊥,所以⊥H A 1面BD C 1,可以得到O C A 11∠为11C A 与面BD C 1所成角,在对角面C C AA 11中可计算2arctan 11=∠O C A .典型例题四例4 如图,已知直三棱柱1111-D C B A ABCD 中,AC AB =,F 为侧棱1BB 上一点,a BC BF 2==,a FB =1.(1)若D 为BC 的中点,E 为AD 上不同于A 、D 的任一点,求证:1FC EF ⊥;(2)若a B A 311=,求1FC 与平面B B AA 11所成角的大小. 分析:E 点在AD 上变化,EF 为平面ADF 内变化的一组相交直线(都过定点F ),要证明F C 1与EF 垂直,必有⊥F C 1平面ADF .求1FC 与平面11A ABB 所成角的关键是找1C 到面11A ABB 的垂线,从而落实线面成角,直三棱柱中,侧棱⊥1AA 平面111C B A 给找点1C 到面1AB 的垂线创造了方便的条件.解:(1)∵AC AB =,且D 是BC 的中点,∴BC AD ⊥,又∵ 直三棱柱中⊥1BB 平面ABC ,∴1BB AD ⊥,∴ ⊥AD 平面C C BB 11,∴F C AD 1⊥.在矩形C C BB 11中,a BC BF 2==,a F B =1, ∴a DF 5=,a FC 51=,a DC 101=,∴21212DC FC DF =+,∴ 901=∠DFC ,即DF FC ⊥1,∴⊥1FC 平面ADF ,∴EF FC ⊥1.(2)过1C 作111B A H C ⊥于H ,∵⊥1AA 平面C B A 11,∴H C AA 11⊥,∴⊥H C 1平面B B AA 11,连接FH ,FH C 1∠是F C 1与平面1AB 所成角.在等腰△ABC 中,a AC AB 3==,a BC 2=,∴a AD 22=,在等腰△111C B A 中,由面积相等可得,a a H C 22231⨯=⨯, ∴a H C 3241=,又a F C 51=, 在Rt △HF C 1中,15104sin 1=∠FH C , ∴15104arcsin1=∠FH C , 即F C 1与平面1AB 所成角为15104arcsin . 说明:由于点E 在AD 上变化,给思考增加了难度,但仔细思考,它又提供了解题的突破口,使得线线垂直成为了1CF 与一组直线垂直.本题的证明还有一个可行的思路,虽然E 在AD 上变化,但是由于⊥AD 平面C C BB 11,所以E 点在平面1BC 上的射影是定点D ,EF 在平面1BC 上射影为定直线DF ,使用三垂线定理,可由DF F C ⊥1,直接证明EF F C ⊥1.三垂线定理是转化空间线线垂直为平面内线线垂直的一个有力工具,再看一个例子,正方体1AC 中,O 是底面ABCD的中心,E 是11B A 上动点,F 是1DD 中点,求AF 与OE 所成角.我们取AD 中点G ,虽然E 点变化,但OE 在面1AD 上射影为定直线G A 1,在正方形D D AA 11中,易证AF B A ⊥1,所以,OE AF ⊥,即AF 与OE 所成角为 90.典型例题五例5 如图,正三棱柱111-C B A ABC 的底面边长为4,侧棱长为a ,过BC的截面与底面成 30的二面角,分别就(1)3=a ;(2)1=a 计算截面的面积.分析:要求出截面的面积,首先必须确定截面的形状,截面与底面成 30的二面角,如果a 较大,此时截面是三角形;但是如果a 较小,此时截面与侧棱不交,而与上底面相交,截面为梯形.解:截面与侧棱1AA 所在直线交于D 点,取BC 中点E ,连AE 、DE ,△ABC 是等边三角形,∴BC AE ⊥,∵⊥1AA 平面ABC ,∴BC DE ⊥.∴DEA ∠为截面与底面所成二面角的平面角,∴ 30=∠DEA .∵等边△ABC 边长为4,∴32=AE .在Rt △DAE 中,2tan =∠=DEA AE DA .(1)当3=a 时,D 点在侧棱1AA 上,截面为△BCD ,在Rt △DAE 中,422=+=AE AD DE , ∴8442121=⨯⨯=⋅=∆DE BC S BCD . (2)当1=a 时,D 点在1AA 延长线上,截面为梯形BCMN ,∵2=AD ,11=AA ∴MN 是△DBC 的中位线, ∴684343=⨯==∆DBC BCMN S S 梯形. 说明:涉及多面体的截面问题,都要经过先确定截面形状,再解决问题的过程,本例通过改变侧棱长而改变了截面形状,我们也可以通过确定侧棱长,改变截面与底面成角而改变截面形状.典型例题六例6 斜三棱柱111-C B A ABC 中,平面⊥C C AA 11底面ABC ,2=BC ,32=AC ,90=∠ABC ,C A AA 11⊥,且C A AA 11=.(1)求1AA 与平面ABC 所成角;(2)求平面11ABB A 与平面ABC 所成二面角的大小;(3)求侧棱1BB 到侧面C C AA 11的距离.分析:按照一般思路,首先转化条件中的面面垂直关系,由C A A A 11=,取AC 的中点D ,连D A 1,则有AC D A ⊥1,从而有⊥D A 1平面ABC ,在此基础上,A A 1与底面所成角以及平面11ABB A 与底面所成二面角都能方便地找到,同时⊥D A 1底面ABC 也为寻找B 点到面C C AA 11的垂线创造了条件.解:(1)取AC 的中点D ,连接D A 1,∵C A A A 11=,∴AC D A ⊥1,∵平面⊥C C AA 11底面ABC ,∴⊥D A 1底面ABC ,∴AC A 1∠为A A 1与底面ABC 所成角.∵C A AA 11=且C A AA 11⊥,∴ 451=∠AC A .(2)取AB 中点E ,则BC DE //,∵ 90=∠ABC ,∴AB CB ⊥,∴AB DE ⊥.连E A 1,∵⊥D A 1底面ABC ,∴E A 1在平面ABC 上射影为DE ,∴AB E A ⊥1,∴ED A 1∠为侧面B A 1与底面ABC 所成二面角的平面角. 在等腰Rt △AC A 1中,32=AC ,∴31=D A .在Rt △ABC 中,2=BC ,∴1=DE .在Rt △DE A 1中,3tan 11==∠DED A ED A , ∴ 601=∠ED A ,即侧面B B AA 11与底面ABC 所成二面角的大小为 60.(3)过B 作AC BH ⊥于H ,∵⊥D A 1底面ABC ,∴BH D A ⊥1,∴⊥BH 平面C C AA 11,在Rt △ABC 中,32=AC ,2=BC ,∴22=AB , ∴632=⋅=AD BC AB BH ,即1BB 到平面C C AA 11的距离为632. 说明:简单的多面体是研究空间线面关系的载体,而线面垂直关系又是各种关系中最重要的关系,立体几何中的证明与计算往往都与线面垂直发生联系,所以在几何体中发现并使用线面垂直关系往往是解题的关键.典型例题七例7 斜三棱柱111-C B A ABC 的底面△ABC 是直角三角形, 90=∠C ,cm 2=BC ,1B 在底面上的射影D 恰好是BC 的中点,侧棱与底面成 60角,侧面B B AA 11与侧面C C BB 11所成角为 30,求斜棱柱的侧面积与体积.分析:1B 在底面ABC 上射影D 为BC 中点,提供了线面垂直⊥D B 1平面ABC ,另外又有 90=∠C ,即BC AC ⊥,又可以得到⊥AC 平面C C BB 11,利用这两个线面垂直关系,可以方便地找到条件中的线面角以及二面角的平面角.解:∵1B 在底面ABC 上,射影D 为BC 中点.∴⊥D B 1平面ABC .∴BD B 1∠为侧棱B B 1与底面ABC 所成角,即 601=∠BD B ,∵ 90=∠C ,即BC AC ⊥,又D B AC 1⊥,∴⊥AC 平面C C BB 11,过A 作B B AE 1⊥于E ,连接CE ,则B B CE 1⊥. ∴AEC ∠是侧面B B AA 11与侧面B B CC 11所成二面角的平面角,∴ 30=∠AEC ,在直角△CEB 中,∵ 60=∠CEB ,2=BC ,∴3=CE ,在直角△ACE 中,∵ 30=∠CEA ,3=CE ,∴130tan == EC AC ,22==AC AE ,在直角△DB B 1中, 601=∠BD B ,121==BC BD , ∴221==BD BB ,360sin 11== BB D B .∴侧面积为111AA AC BB AE BB CE S ⋅+⋅+⋅=侧()()()2cm 3322332123+=⨯+=⨯++=. 体积为311cm 33212121=⨯⨯⨯=⋅⋅=⋅=∆D B BC AC D B S V ABC .说明:本例中△ACE 是斜棱柱的一个截面,而且有侧棱与该截面垂直,这个截面称为斜棱柱的直截面,我们可以用这个截面把斜棱柱分成两部分,并且用这两部分拼凑在一个以该截面为底面的直棱柱,斜棱柱的侧面积等于该截面周长乘以侧棱长,体积为该截面面积乘以侧棱长.典型例题八例8 如图所示,在平行六面体1111D C B A ABCD -中,已知a AD AB 2==,a AA =1,又︒=∠=∠=∠6011AB A DAB AD A .(1)求证:1AA ⊥截面C D B 11;(2)求对角面11ACC A 的面积.分析:(1)由题设易证111D B AA ⊥,再只需证C B AA 11⊥,即证11CD CC ⊥.而由对称性知,若C B CC 11⊥,则11CD CC ⊥,故不必证111D B AA ⊥.(2)关键在于求对角面的高.证明:(1)∵a AD C B 211==,a A A CC ==11,︒=∠=∠60111AD A C C B ,∴在C C B 11∆中,由余弦定理,得2213a C B =.再由勾股定理的逆定理,得C B C C 11⊥.同理可证:11CD C C ⊥.∴C C 1⊥平面C D B 11.又A A C C 11//,∴1AA ⊥平面C D B 11.解:(2)∵AD AB =,∴平行四边形ABCD 为菱形.AC 为BAD ∠的平分线. 作O A 1∴⊥平面AC 于O ,由AB A AD A 11∠=∠,知AC O ∈.作AB M A ⊥1于M ,连OM ,则AB OM ⊥. 在AM A Rt 1∆中,a A A AM 2160cos 1=︒⋅=, 在AOM Rt ∆中,330sec a AM AO =︒⋅=.在AO A Rt 1∆中,a AO A A O A 322211=-=. 又在ABC ∆中,由余弦定理,得a AC 32=. ∴212211a O A AC S ACC A =⋅=.说明:本题解答中用到了教材习题中的一个结论——经过一个角的顶点引这个角所在平面的斜线.如果斜线和这个角两边的夹角相等,那么斜线在平面上的射影是这个角的平分线所在的直线.另外,还有一个值得注意的结论就是:如果一个角所在平面外一点到角的两边所在直线的距离相等,那么这一点在平面上的射影在这个角的平分线所在的直线上.典型例题九例9 如图所示,已知:直三棱柱111C B A ABC -中,︒=∠90ACB ,︒=∠30BAC ,1=BC ,61=AA ,M 是1CC 的中点.求证:M A AB 11⊥.分析:根据条件,正三棱柱形状和大小及M 点的位置都是确定的,故可通过计算求出M A 1与1AB 两异面直线所成的角.因为C C C B 111⊥,1111C A C B ⊥,所以11C B ⊥侧面C C AA 11.1AC 是斜线1AB 在平面C C AA 11的射影,设1AC 与M A 1的交点为D ,只需证得︒=∠901MDC 即可.证明:∵C C C B 111⊥,1111C A C B ⊥,C C 1与11C A 交于点1C ,∴11C B ⊥面C C AA 11.∵M 为1CC 的中点,∴262111==C C MC . 在111B C A Rt ∆中,︒=∠30111C A B ,∴221111==C B B A ,311=C A .在M C A Rt 11∆中, ()22332622211211=+⎪⎪⎭⎫ ⎝⎛=+=C A MC M A . 在11C AA Rt ∆中,33622211211=+=+=C A AA AC . 又1MDC ∆∽DA A 1∆且21=MC AA ∶, ∴22122331311=⨯==M A MD , 13313111=⨯==AC D C . 在1MDC ∆中,23122122212=+⎪⎭⎫ ⎝⎛=+D C MD , 2326221=⎪⎪⎭⎫ ⎝⎛=M C , ∴︒=∠901DM C ,11AC M A ⊥,∴11AB M A ⊥.说明:证明两直线垂直,应用三垂线定理或逆定理是重要方法之一.证明过程中的有关计算要求快捷准确,不可忽视.本题证明两异面直线垂直,也可用异面直线所成的角,在侧面C C AA 11的一侧或上方一个与之全等的矩形,平移M A 1或1AB ,确定两异面直线所成的角,然后在有关三角形中通过计算可获得证明.典型例题十例10 长方体的全面积为11,十二条棱长度之和为24,求这个长方体的一条对角线长.分析:要求长方体对角线长,只要求长方体的一个顶点上的三条棱的长即可. 解:设此长方体的长、宽、高分别为x 、y 、z ,对角线长为l ,则由题意得:⎩⎨⎧=++=++②①24)(411)(2z y x zx yz xy由②得:6=++z y x ,从而由长方体对角线性质得:5116)(2)(22222=-=++-++=++=zx yz xy z y x z y x l .∴长方体一条对角线长为5.说明:(1)本题考查长方体的有关概念和计算,以及代数式的恒等变形能力.在求解过程中,并不需要把x 、y 、z 单个都求出来,而要由方程组的①②从整体上导出222z y x ++,这需要同学们掌握一些代数变形的技巧,需要有灵活性.(2)本题采用了整体性思维的处理方法,所谓整体性思维就是在探究数学问题时,应研究问题的整体形式,整体结构或对问题的数的特征、形的特征、结构特征作出整体性处理.整体思维的含义很广,根据问题的具体要求,需对代数式作整体变换,或整体代入,也可以对图形作出整体处理.典型例题十一例11 如图,长方体1111D C B A ABCD -中,a AB =,b BC =,c BB =1,并且0>>>c b a .求沿着长方体的表面自A 到1C 的最短线路的长.分析:解本题可将长方体表面展开,可利用在平面内两点间的线段长是两点间的最短距离来解答.解:将长方体相邻两个展开有下列三种可能,如图.三个图形甲、乙、丙中1AC 的长分别为:ab c b a c b a 2)(22222+++=++bc c b a c b a 2)(22222+++=++ac c b a b c a 2)(22222+++=++∵0>>>c b a ,∴0>>>bc ab ab . 故最短线路的长为bc c b a 2222+++.说明:(1)防止只画出一个图形就下结论,或者以为长方体的对角线2221c b a AC ++=是最短线路.(2)解答多面体表面上两点间,最短线路问题,一般地都是将多面体表面展开,转化为求平面内两点间线段长.典型例题十二例12 设直平行六面体的底面是菱形,经下底面的一边及与它相对的上义面的一边的截面与底面成︒60的二面角,面积为Q ,求直平行六面体的全面积.分析:如图,由于⊥'DD 面AC .作出截面与底面所成的二面角的平面角HD D '∠后,因DH D Rt '∆中︒=∠60'HD D ,可分别求出D D '、DH 和H D '的值.又上下底面的边长是相等的,便可进一步求出全面积.解:设平行六面体为''''D C B A ABCD -,过D 作AB DH ⊥,H 为垂足,连结H D '.∵⊥'DD 平面ABCD ,∴AB H D ⊥',︒=∠60'HD D , ∴H D D D ''23=,H D DH '21=. 又在菱形ABCD 中,有CD BC AB AD ===,∴截面''D ABC 的面积为:Q AB H D S =⋅='1.侧面''DCC D 的面积为:Q AB H D AB D D DC D D S 2323'''2=⋅=⋅=⋅= 底面ABCD 的面积为:Q AB H D AB DH S 2121'3=⋅=⋅=. 所以Q S S S )132(2432+=+=全.典型例题十三例13 设有三个命题:甲:底面是平行四边形的四棱柱是平行六面体;乙:底面是矩形的平行六面体是长方体;丙:直四棱柱是直平行六面体.以上命题中,真命题的个数是( ).A .0B .1C .2D .3解:甲命题是真命题,因为它就是平行六面体的定义;乙命题不是真命题,因为平行六面体的侧棱不一定垂直于底面;丙命题也不是真命题,因为四棱柱的底面不一定是平行四边形.∴应选B .说明:要认真搞清平行六面体、直平行六面体、长方体等特殊四棱柱的有关概念及性质.典型例题十四例14 如图,ABC C B A -111是直三棱柱,︒=∠90BCA ,点1D 、1F 分别是11B A 、11C A 的中点.若1CC CA BC ==,则1BD 与1AF 所成角的余弦值是( ).A .1030B .21 C .1530 D .1015 解:可将异面直线所成角转化为相交直线的角,取BC 的中点E ,并连结1EF 、EA .∵11F D BC 21BE =, ∴11//BD EF ,∴A EF 1∠是1BD 与1AF 所成角.设a BC 2=,则a CC 21=,a CA 2=.∴a AB 22=,a AF 51=,a AE 5=,a D B B B BD EF 62112111=+==. ∴1030652)5()6()5(2cos 22211221211=⨯⨯-+=⨯⨯-+=∠a a a a a EF AF AE EF AF A EF ∴应选A .说明:本题主要考查棱柱的性质,以及两条异面直线所成的角、勾股定理、余弦定理等内容:对运算能力和空间想象能力也有较高的要求.典型例题十五例15 如图,已知ABC C B A -111是正三棱柱,D 是AC 的中点.(1)证明://1AB 平面1DBC ;(2)假设11BC AB ⊥,求以1BC 为棱,1DBC 与1CBC 为面的二面角α的度数.(1)证明:∵ABC C B A -111是正三棱柱,∴四边形11BCC B 是矩形.连结C B 1交1BC 于E ,则E 是C B 1的中点.连结DE .∵D 、E 分别是AC 、C B 1的中点,∴1//AB DE .又⊄1AB 平面1DBC ,⊂DE 平面1DBC ,.∴//1AB 平面1DBC .(2)解:作BC DF ⊥于F ,则⊥DF 平面C C BB 11,连结EF 则EF 是ED 在平面C C BB 11上的射影.∵11BC AB ⊥又ED AB //1.∴1BC ED ⊥.根据三垂线定理的逆定理,得1BC EF ⊥.从而DEF ∠是二面角C BC D --1的平面角,即α=∠DEF ,设1=AC ,则21=DC ∵ABC ∆是正三角形,∴在DCF Rt ∆中,有4360sin =︒=DC DF ,4160cos =︒=DC CF 取BC 的中点G ,∵EC EB =,∴BC EG ⊥.在BEF Rt ∆中,FG BF EF ⋅=2 而43=-=FC BC BF ,41=GF , ∴41432⋅=EF ,∴43=EF , ∴在DEF Rt ∆中,14343tan ===∠EF DF DEF . ∴︒=∠45DEF ,即︒=45α.从而所求二面角的大小为︒45.说明:(1)纵观近十年高考题,其中解答题大多都是以多面体进行专利权查,解答此类题,有些同学往往忽略或忘记了多面体的性质,从而解题时,思维受阻.今后要引以为戒.(2)本题考查空间的线面关系,正棱柱的概念和性质,空间想象能力、逻辑思维能力和运算能力.本题涉及到的知识面宽,有一定的深度,但入手不难,逐渐加深;逻辑推理和几何计算交织为一体;正三棱柱放倒,与课本习题不同,加强了对空间想象能力的考查;在解答过程中,必须添加适当的辅助线,不仅考查了识图,而且考查了作图.本题是一道综合性试题,较深入和全面地考查了各种数学能力,正确解答本题,要求同学们有较高的数学素质.。
错题宝典高考复习易错题分类《立体几何》易错题1830

错题宝典高考复习易错题分类《立体几何》易错题测试题 2019.9 1,给出下列四个命题:(1)各侧面都是正方形的棱柱一定是正棱柱(2)若一个简单多面体的各顶点都有三条棱,则其顶点数V ,面数F 满足的关系式为2F-V=4(3)若直线L ⊥平面α,L ∥平面β,则α⊥β(4)命题“异面直线a,b 不垂直,则过a 的任一平面和b 都不垂直”的否定,其中,正确的命题是()A 、(2)(3) B、(1)(4) C 、(1)(2)(3) D 、(2)(3)(4)2,1. 有一棱长为a 的正方体骨架,其内放置一气球,使其充气且尽可能地大(仍保持为球的形状),则气球表面积的最大值为__________. 3,一个广告气球某一时刻被一束平行光线投射到水平地面上的影子是一个椭圆,椭圆的离心率为,则该时刻这平行光线对于水平平面的入射角为________。
4,已知正三棱柱底面边长是10,高是12,过底面一边AB ,作与底面ABC 成角的截面面积是___________________。
5,过球面上两已知点可以作的大圆个数是_________个。
6,判断题:若两个平面互相垂直,过其中一个平面内一点作它们的交线32e 111ABCA B C 060的垂线,则此直线垂直于另一个平面。
7,平面外有两点A,B ,它们与平面的距离分别为a,b ,线段AB 上有一点P ,且AP:PB=m:n ,则点P 到平面的距离为_________________.8,点AB 到平面距离距离分别为12,20,若斜线AB 与成的角,则AB 的长等于_____.9,与空间四边形ABCD 四个顶点距离相等的平面共有______个。
10,在棱长为1的正方体ABCD--A 1B 1C 1D 1中,若G 、E 分别为BB 1,C 1D 1的中点,点F 是正方形ADD 1A 1的中心,则四边形BGEF 在正方体六个面上的射影图形面积的最大值为________。
高中数学127个立体几何易错题精选

2011年高考考前复习资料—高中数学立体几何部分错题精选一、选择题:1.(石庄中学)设ABCD 是空间四边形,E ,F 分别是AB ,CD 的中点,则BC AD EF ,,满足( )A 共线B 共面C 不共面D 可作为空间基向量 正确答案:B 错因:学生把向量看为直线。
2.(石庄中学)在正方体ABCD-A 1B 1C 1D 1,O 是底面ABCD 的中心,M 、N 分别是棱DD 1、D 1C 1的中点,则直线OM( )A 是AC 和MN 的公垂线B 垂直于AC 但不垂直于MN C 垂直于MN ,但不垂直于ACD 与AC 、MN 都不垂直正确答案:A 错因:学生观察能力较差,找不出三垂线定理中的射影。
3.(石庄中学)已知平面α∥平面β,直线L ⊂平面α,点P ∈直线L,平面α、β间的距离为8,则在β内到点P 的距离为10,且到L 的距离为9的点的轨迹是( )A 一个圆B 四个点C 两条直线D 两个点正确答案:B 错因:学生对点线距离、线线距离、面面距离的关系不能灵活掌握。
4.(石庄中学)正方体ABCD-A 1B 1C 1D 1中,点P 在侧面BCC 1B 1及其边界上运动,并且总保持A P ⊥BD 1,则动点P 的轨迹( )A 线段B 1C B BB 1的中点与CC 1中点连成的线段 C 线段BC 1D CB 中点与B 1C 1中点连成的线段正确答案:A 错因:学生观察能力较差,对三垂线定理逆定理不能灵活应用。
5. (石庄中学)下列命题中:① 若向量a 、b 与空间任意向量不能构成基底,则a ∥b 。
② 若a ∥b , b ∥c ,则c ∥a .③ 若 OA 、OB 、OC 是空间一个基底,且 OD =31OA +31 OB +31OC ,则A 、B 、C 、D 四点共面。
④ 若向量 a + b , b + c , c + a 是空间一个基底,则 a 、 b 、 c 也是空间的一个基底。
其中正确的命题有( )个。
高三数学易错立体几何多选题 易错题提高题学能测试试卷

高三数学易错立体几何多选题 易错题提高题学能测试试卷一、立体几何多选题1.在正三棱柱111ABC A B C -中,AC =11CC =,点D 为BC 中点,则以下结论正确的是( ) A .111122A D AB AC AA =+-B .三棱锥11D ABC -的体积为6C .1AB BC ⊥且1//AB 平面11AC DD .ABC 内到直线AC 、1BB 的距离相等的点的轨迹为抛物线的一部分 【答案】ABD 【分析】A .根据空间向量的加减运算进行计算并判断;B .根据1111D ABC A DB C V V --=,然后计算出对应三棱锥的高AD 和底面积11DB C S,由此求解出三棱锥的体积;C .先假设1AB BC ⊥,然后推出矛盾;取AB 中点E ,根据四点共面判断1AB //平面11AC D 是否成立;D .将问题转化为“ABC 内到直线AC 和点B 的距离相等的点”的轨迹,然后利用抛物线的定义进行判断. 【详解】A .()11111111222A D A A AD AD AA AB AC AA AB AC AA =+=-=+-=+-,故正确; B .1111D AB C A DB C V V --=,因为D 为BC 中点且AB AC =,所以AD BC ⊥, 又因为1BB ⊥平面ABC ,所以1BB AD ⊥且1BB BC B =,所以AD ⊥平面11DB C ,又因为AD ===11111122DB C S BB B C =⨯⨯=,所以1111111133226D AB C A DB C DB C V V AD S --==⨯⨯=⋅=,故正确;C .假设1AB BC ⊥成立,又因为1BB ⊥平面ABC ,所以1BB BC ⊥且111BB AB B =,所以BC ⊥平面1ABB ,所以BC AB ⊥,显然与几何体为正三棱柱矛盾,所以1AB BC ⊥不成立;取AB 中点E ,连接11,,ED EA AB ,如下图所示:因为,D E 为,BC AB 中点,所以//DE AC ,且11//AC A C ,所以11//DE AC ,所以11,,,D E A C 四点共面,又因为1A E 与1AB 相交,所以1AB //平面11AC D 显然不成立,故错误;D .“ABC 内到直线AC 、1BB 的距离相等的点”即为“ABC 内到直线AC 和点B 的距离相等的点”,根据抛物线的定义可知满足要求的点的轨迹为抛物线的一部分,故正确; 故选:ABD. 【点睛】方法点睛:求解空间中三棱锥的体积的常用方法:(1)公式法:直接得到三棱锥的高和底面积,然后用公式进行计算;(2)等体积法:待求三棱锥的高和底面积不易求出,采用替换顶点位置的方法,使其求解高和底面积更容易,由此求解出三棱锥的体积.2.如图所示,正三角形ABC中,D,E分别为边AB,AC的中点,其中AB=8,把△ADE 沿着DE翻折至A'DE位置,使得二面角A'-DE-B为60°,则下列选项中正确的是()A.点A'到平面BCED的距离为3B.直线A'D与直线CE所成的角的余弦值为5 8C.A'D⊥BDD.四棱锥A'-BCED237【答案】ABD【分析】作AM⊥DE,交DE于M,延长AM交BC于N,连接A'M,A'N.利用线面垂直的判定定理判定CD⊥平面A'MN,利用面面垂直的判定定理与性质定理得到'A到平面面BCED的高A'H,并根据二面角的平面角,在直角三角形中计算求得A'H的值,从而判定A;根据异面直线所成角的定义找到∠A'DN就是直线A'D与CE所成的角,利用余弦定理计算即可判定B;利用勾股定理检验可以否定C;先证明底面的外接圆的圆心为N,在利用外接球的球心的性质进行得到四棱锥A'-BCED的外接球的球心为O,则ON⊥平面BCED,且OA'=OC,经过计算求解可得半径从而判定D.【详解】如图所示,作AM⊥DE,交DE于M,延长AM交BC于N,连接A'M,A'N.则A'M⊥DE,MN⊥DE, ,∵'A M∩MN=M,∴CD⊥平面A'MN,又∵CD⊂平面ABDC,∴平面A'MN⊥平面ABDC,在平面A'MN中作A'H⊥MN,则A'H⊥平面BCED,∵二面角A'-DE-B为60°,∴∠A'EF=60°,∵正三角形ABC中,AB=8,∴AN=43∴A'M3,∴A'H=A'M sin60°=3,故A正确;连接DN,易得DN‖EC,DN=EC=4,∠A'DN就是直线A'D与CE所成的角,DN=DA'=4,A'N=A'M3,cos∠A'DN=22441252448+-=⨯⨯,故B正确;A'D=DB=4,22121627A N BN+=+=',∴222A D DB A B '≠'+,∴A'D 与BD 不垂直,故C 错误’ 易得NB =NC =ND =NG =4,∴N 为底面梯形BCED 的外接圆的圆心, 设四棱锥A'-BCED 的外接球的球心为O ,则ON ⊥平面BCED ,且OA'=OC , 若O 在平面BCED 上方,入图①所示:设ON =x ,外接球的半径为R ,过O 作A'H 的垂线,垂足为P , 则HP =x ,易得()()22222433x x R +=-+=,解得23x =-,舍去; 故O 在平面BCED 下方,如图②所示:设ON =x ,外接球的半径为R ,过O 作A'H 的垂线,垂足为P , 则HP =x ,易得()()22222433x x R +=++=, 解得23x =, ∴244371699R ⨯=+=,237R ∴=,故D 正确. 故选:ABD .【点睛】本题考查立体几何中的折叠问题,涉及二面角问题,异面直线所成的角,用到线面、面面垂直的判定与性质及外接球的球心的性质和有关计算,余弦定理等,属综合性较强的题目,关键是利用线面垂直,面面垂直的判定和性质进行空间关系和结构的判定,注意球心在四棱锥的底面上方和下方的讨论与验证.3.如图,一个结晶体的形状为平行六面体1111ABCD A B C D -,其中,以顶点A 为端点的三条棱长都等于1,且它们彼此的夹角都是60,下列说法中正确的是( )A .()()2212AA AB ADAC ++=B .1A 在底面ABCD 上的射影是线段BD 的中点C .1AA 与平面ABCD 所成角大于45 D .1BD 与AC 6 【答案】AC 【分析】对A ,分别计算()21++AA AB AD 和2AC ,进行判断;对B ,设BD 中点为O ,连接1A O ,假设1A 在底面ABCD 上的射影是线段BD 的中点,应得10⋅=O AB A ,计算10⋅≠O AB A ,即可判断1A 在底面ABCD 上的射影不是线段BD 的中点;对C ,计算11,,A A AC AC ,根据勾股定理逆定理判断得11⊥A A AC ,1AA 与平面ABCD 所成角为1A AC ∠,再计算1tan ∠A AC ;对D ,计算1,AC BD 以及1BD AC ⋅,再利用向量的夹角公式代入计算夹角的余弦值. 【详解】对A ,由题意,11111cos602⋅=⋅=⋅=⨯⨯=AA AB AA AD AD AB ,所以()2222111112*********++=+++⋅+⋅+⋅=+++⨯⨯=AA AB ADAA AB AD AA AB AB AD AA AD ,AC AB AD =+,所以()222221113=+=+⋅+=++=AC AB ADAB AB AD AD ,所以()()22126++==AA AB AD AC ,故A 正确;对B ,设BD 中点为O ,连接1A O ,1111111222=+=+=++AO A A AO A A AC A A AD AB ,若1A 在底面ABCD 上的射影是线段BD 的中点,则1A O ⊥平面ABCD ,则应10⋅=O AB A ,又因为21111111111110222222224⎛⎫⋅=++⋅=-⋅+⋅+=-+⨯+=≠⎪⎝⎭O AB A A AD AB AB AA AB AD AB AB A ,故B 错误;对D ,11,BD AD AA AB AC AB AD =+-=+,所以()()2211=2,=3=+-=+AD A B A AB AC AB AD D ,()()2211111⋅=+-⋅+=⋅++⋅+⋅--⋅=AC AD AA AB AB AD AD AB AD AA AB AA AD ABAB AD BD ,1116cos ,23⋅<>===⋅B AC D BD BD AC AC,故D 不正确;对C ,112==AC BD ,在1A AC 中,111,2,3===A A AC AC ,所以22211+=A A AC AC ,所以11⊥A A AC ,所以1AA 与平面ABCD 所成角为1A AC ∠,又1tan 21∠=>A AC ,即145∠>A AC ,故C 正确;故选:AC【点睛】方法点睛:用向量方法解决立体几何问题,需要树立“基底”意识,利用基向量进行线性运算,要理解空间向量概念、性质、运算,注意和平面向量类比;同时对于立体几何中角的计算问题,往往可以利用空间向量法,利用向量的夹角公式求解.4.如图,直三棱柱11,ABC A B C -,ABC 为等腰直角三角形,AB BC ⊥,且12AC AA ==,E ,F 分别是AC ,11A C 的中点,D ,M 分别是1AA ,1BB 上的两个动点,则( )A .FM 与BD 一定是异面直线B .三棱锥D MEF -的体积为定值14C .直线11B C 与BD 所成角为2π D .若D 为1AA 中点,则四棱锥1D BB FE -55【答案】CD 【分析】A 当特殊情况M 与B 重合有FM 与BD 相交且共面;B 根据线面垂直、面面垂直判定可证面1BEFB ⊥面11ACC A ,可知EMFS、D 到面1BEFB 的距离,可求D EMF V -;C 根据线面垂直的判定及性质即可确定11B C 与BD 所成角;D 由面面垂直、勾股、矩形性质等确定外接球半径,进而求体积,即可判断各项的正误. 【详解】A :当M 与B 重合时,FM 与BD 相交且共面,错误; B :由题意知:BE AC ⊥,AC EF ⊥且BEEF E =,则AC ⊥面1BEFB ,又AC ⊂面11ACC A ,面1BEFB ⋂面11ACC A EF =,所以面1BEFB ⊥面11ACC A ,又1121122EMFSEF BE =⋅⋅=⨯⨯=,D 到面1BEFB 的距离为1h =,所以1133D EMF EMFV h S-=⋅⋅=,错误; C :由AB BC ⊥,1BC B B ⊥,1B BAB B =,所以BC ⊥面11ABB A ,又11//BC B C ,即11B C ⊥面11ABB A ,而BD ⊂面11ABB A ,则11BD B C ⊥,正确;D :由B 中,面1BEFB ⊥面11ACC A ,即面DEF ⊥面1BEFB ,则D 到面1BEFB 的距离为1h =,又D 为1AA 中点,若1,BF EB 交点为O ,G 为EF 中点,连接,,OG GD OD ,则OG GD ⊥,故2252OD OG GD =+=,由矩形的性质知:15OB OE OF OB ====令四棱锥1D BB FE -的外接球半径为R ,则52R =,所以四棱锥1D BB FE -的外接球体积为35435V R π==,正确. 故选:CD. 【点睛】关键点点睛:利用线面、面面关系确定几何体的高,结合棱锥体积公式求体积,根据线面垂直、勾股定理及矩形性质确定外接球半径,结合球体体积公式求体积.5.在长方体1111ABCD A B C D -中,23AB =12AD AA ==,P 、Q 、R 分别是AB 、1BB 、1A C 上的动点,下列结论正确的是( )A .对于任意给定的点P ,存在点Q 使得1D P CQ ⊥B .对于任意给定的点Q ,存在点R 使得1D R CQ ⊥C .当1AR A C ⊥时,1ARD R ⊥D .当113AC A R =时,1//D R 平面1BDC 【答案】ABCD 【分析】本题先建立空间直角坐标系,再运用空间向量在立体几何中的应用逐一判断即可. 【详解】如图所示,建立空间直角坐标系,设(2,,0)P a ,023a ⎡⎤∈⎣⎦,,(2,23,)Q b ,[]0,2b ∈,设11A R AC λ=,得到(22,3,22)R λλλ--,[]0,1λ∈. 1(2,,2)D P a =-,(2,0,)CQ b =,142D P CQ b ⋅=-,当2b =时,1D P CQ ⊥,A 正确;1(22,23,2)D R λλλ=--,12(22)2D R CQ b λλ⋅=--,取22bλ=+时,1D R CQ ⊥,B 正确;1AR A C ⊥,则1(2,23,22)(2,23,2)412440AR AC λλλλλλ⋅=--⋅--=+-+=,解得:15λ=,此时122328232(,,)(,,)0555555AR D R ---⋅=⋅=,1AR D R ⊥,C 正确;113AC A R =,则4234(,,)333R ,14232(,,)333D R =-,设平面1BDC 的法向量为(,,)n x y z =,则100n BD n DC ⎧⋅=⎪⎨⋅=⎪⎩,解得(3,1,3)n =-,故10n D R ⋅=,故1//D R 平面1BDC ,D 正确.故选:ABCD.【点睛】本题考查了空间向量在立体几何中的应用,是偏难题.6.如图四棱锥P ABCD -,平面PAD ⊥平面ABCD ,侧面PAD 是边长为26的正三角形,底面ABCD 为矩形,23CD =,点Q 是PD 的中点,则下列结论正确的是( )A .CQ ⊥平面PADB .PC 与平面AQC 所成角的余弦值为223C .三棱锥B ACQ -的体积为62D .四棱锥Q ABCD -外接球的内接正四面体的表面积为3【答案】BD 【分析】取AD 的中点O ,BC 的中点E ,连接,OE OP ,则由已知可得OP ⊥平面 ABCD ,而底面ABCD 为矩形,所以以O 为坐标原点,分别以,,OD OE OP 所在的直线为x 轴,y 轴 ,z 轴,建立空间直角坐标系,利用空间向量依次求解即可. 【详解】解:取AD 的中点O ,BC 的中点E ,连接,OE OP , 因为三角形PAD 为等边三角形,所以OP AD ⊥, 因为平面PAD ⊥平面ABCD ,所以OP ⊥平面 ABCD , 因为AD OE ⊥,所以,,OD OE OP 两两垂直,所以,如下图,以O 为坐标原点,分别以,,OD OE OP 所在的直线为x 轴,y 轴 ,z 轴,建立空间直角坐标系,则(0,0,0),(O D A ,(P C B ,因为点Q 是PD的中点,所以)2Q , 平面PAD 的一个法向量为(0,1,0)m =,6(QC =,显然 m 与QC 不共线, 所以CQ 与平面PAD 不垂直,所以A 不正确;3632(6,23,32),(,0,),(26,22PC AQ AC =-==, 设平面AQC 的法向量为(,,)n x y z =,则3602260n AQ x zn AC ⎧⋅=+=⎪⎨⎪⋅=+=⎩,令=1x ,则y z ==, 所以(1,2,n =-, 设PC 与平面AQC 所成角为θ,则21sin 36n PC n PCθ⋅===, 所以cos 3θ=,所以B 正确; 三棱锥B ACQ -的体积为1132BACQ Q ABC ABCV V SOP --==⋅ 1116322=⨯⨯⨯=,所以C 不正确;设四棱锥Q ABCD -外接球的球心为(0,3,)M a ,则MQ MD =, 所以()()()2222226323632a a ⎛⎫⎛⎫++-=++ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭,解得0a =,即(0,3,0)M 为矩形ABCD 对角线的交点,所以四棱锥Q ABCD -外接球的半径为3,设四棱锥Q ABCD -外接球的内接正四面体的棱长为x ,将四面体拓展成正方体,其中正四面体棱为正方体面的对角线,故正方体的棱长为22x ,所以22236x ⎛⎫= ⎪ ⎪⎝⎭,得224x =, 所以正四面体的表面积为2342434x ⨯=,所以D 正确. 故选:BD【点睛】此题考查线面垂直,线面角,棱锥的体积,棱锥的外接球等知识,综合性强,考查了计算能力,属于较难题.7.如果一个棱锥的底面是正方形,且顶点在底面内的射影是底面的中心,那么这样的棱锥叫正四棱锥.若一正四棱锥的体积为18,则该正四棱锥的侧面积最小时,以下结论正确的是( ).A .棱的高与底边长的比为22B .侧棱与底面所成的角为4π C 2D .侧棱与底面所成的角为3π 【答案】AB【分析】设四棱锥S ABCD -的高为h ,底面边长为a ,由21183V a h ==得254h a =,然后可得侧面积为242108a a+,运用导数可求出当32a =时侧面积取得最小值,此时3h =,然后求出棱锥的高与底面边长的比和SAO ∠即可选出答案.【详解】设四棱锥S ABCD -的高为h ,底面边长为a可得21183V a h ==,即254h a= 所以其侧面积为2222244215410842244a a a h a a a⋅⋅+=+=+令()242108f a a a =+,则()23321084f a a a ⨯'=- 令()233210840f a a a ⨯'=-=得32a = 当(0,32a ∈时()0f a '<,()f a 单调递减 当()32,a ∈+∞时()0f a '>,()f a 单调递增 所以当32a =时()f a 取得最小值,即四棱锥的侧面积最小此时3h =2,故A 正确,C 错误 侧棱与底面所成的角为SAO ∠,由3h =,32a =可得3AO =所以4SAO π∠=,故B 正确,D 错误故选:AB【点睛】本题考查的知识点有空间几何体的体积和表面积、线面角及利用导数求最值,属于综合题.8.如图,矩形ABCD 中,M 为BC 的中点,将ABM 沿直线AM 翻折成1AB M ,连结1B D ,N 为1B D 的中点,则在翻折过程中,下列说法中所有正确的是( )A .存在某个位置,使得CN AB ⊥B .翻折过程中,CN 的长是定值C .若AB BM =,则1AM BD ⊥D .若1AB BM ==,当三棱锥1B AMD -的体积最大时,三棱锥1B AMD -的外接球的表面积是4π【答案】BD【分析】对于选项A ,取AD 中点E ,取1AB 中点K ,连结KN ,BK ,通过假设CN AB ⊥,推出AB ⊥平面BCNK ,得到AB BK ⊥,则22AK AB BK AB =+>,即可判断; 对于选项B ,在判断A 的图基础上,连结EC 交MD 于点F ,连结NF ,易得1NEC MAB ∠=∠,由余弦定理,求得CN 为定值即可;对于选项C ,取AM 中点O ,1B O ,DO ,由线面平行的性质定理导出矛盾,即可判断; 对于选项D ,易知当平面1AB M 与平面AMD 垂直时,三棱锥1B AMD -的体积最大,说明此时AD 中点E 为外接球球心即可.【详解】如图1,取AD 中点E ,取1AB 中点K ,连结EC 交MD 于点F ,连结NF ,KN ,BK ,则易知1//NE AB ,1//NF B M ,//EF AM ,//KN AD ,112NE AB =,EC AM = 由翻折可知,1MAB MAB ∠=∠,1AB AB =, 对于选项A ,易得//KN BC ,则K 、N 、C 、B 四点共面,由题可知AB BC ⊥,若CN AB ⊥,可得AB ⊥平面BCNK ,故AB BK ⊥,则22AK AB BK AB =+>,不可能,故A 错误;对于选项B ,易得1NEC MAB ∠=∠,在NEC 中,由余弦定理得222cos CN CE NE NE CE NEC =+-⋅⋅∠, 整理得222212422AB AB AB CN AM AM BC AB AM =+-⋅⋅=+, 故CN 为定值,故B 正确;如图2,取AD 中点E ,取AM 中点O ,连结1B E ,OE ,1B O ,DO ,,对于选项C ,由AB BM =得1B O AM ⊥,若1AM B D ⊥,易得AM ⊥平面1B OD ,故有AM OD ⊥,从而AD MD =,显然不可能,故C 错误;对于选项D ,由题易知当平面1AB M 与平面AMD 垂直时,三棱锥B 1﹣AMD 的体积最大,此时1B O ⊥平面AMD ,则1B O OE ⊥,由1AB BM ==,易求得122BO =,2DM =22221122122B E OB OE ⎛⎫⎛⎫=+=+= ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭,因此1EB EA ED EM ===,E 为三棱锥1B AMD -的外接球球心,此外接球半径为1,表面积为4π,故D 正确.故选:BD.【点睛】本题主要考查了立体几何中的翻折问题以及空间图形的位置关系,考查了空间想象能力,属于较难题.。
立体几何易错题集

立体几何复习易做易错题选如皋市教育局教研室一、选择题:1.(石庄中学)设ABCD 是空间四边形,E ,F 分别是AB ,CD 的中点,则,,满足( )A 共线B 共面C 不共面D 可作为空间基向量正确答案:B 错因:学生把向量看为直线。
2.(石庄中学)在正方体ABCD-A 1B 1C 1D 1,O 是底面ABCD 的中心,M 、N 分别是棱DD 1、D 1C 1的中点,则直线OM( )A 是AC 和MN 的公垂线B 垂直于AC 但不垂直于MNC 垂直于MN ,但不垂直于ACD 与AC 、MN 都不垂直正确答案:A 错因:学生观察能力较差,找不出三垂线定理中的射影。
3.(石庄中学)已知平面α∥平面β,直线L ⊂平面α,点P ∈直线L,平面α、β间的距离为8,则在β内到点P 的距离为10,且到L 的距离为9的点的轨迹是( )A 一个圆B 四个点C 两条直线D 两个点正确答案:B 错因:学生对点线距离、线线距离、面面距离的关系不能灵活掌握。
4.(石庄中学)正方体ABCD-A 1B 1C 1D 1中,点P 在侧面BCC 1B 1及其边界上运动,并且总保持A P ⊥BD 1,则动点P 的轨迹( )A 线段B 1C B BB 1的中点与CC 1中点连成的线段C 线段BC 1D CB 中点与B 1C 1中点连成的线段正确答案:A 错因:学生观察能力较差,对三垂线定理逆定理不能灵活应用。
5. (石庄中学)下列命题中:① 若向量a 、b 与空间任意向量不能构成基底,则a ∥b 。
② 若a ∥b , b ∥c ,则c ∥a .③ 若 OA 、OB 、OC 是空间一个基底,且 OD =31OA +31 OB +31OC ,则A 、B 、C 、D 四点共面。
④ 若向量 a + b , b + c , c + a 是空间一个基底,则 a 、 b 、 c 也是空间的一个基底。
其中正确的命题有( )个。
A 1B 2C 3D 4正确答案:C 错因:学生对空间向量的基本概念理解不够深刻。
高三数学易错立体几何多选题 易错题学能测试

高三数学易错立体几何多选题 易错题学能测试一、立体几何多选题1.已知正方体1111 ABCD A B C D -的棱长为2,M 为1DD 的中点,N 为正方形ABCD 所在平面内一动点,则下列命题正确的有( )A .若2MN =,则MN 的中点的轨迹所围成图形的面积为πB .若N 到直线1BB 与直线DC 的距离相等,则N 的轨迹为抛物线C .若1D N 与AB 所成的角为3π,则N 的轨迹为双曲线 D .若MN 与平面ABCD 所成的角为3π,则N 的轨迹为椭圆【答案】BC 【分析】对于A ,连接MN ,ND ,DP ,得到直角MDN △,且P 为斜边MN 的中点,所以1PD =,进而得到P 点的轨迹为球面的一部分,即可判断选项A 错误;对于B ,可知1NB BB ⊥,即NB 是点N 到直线1BB 的距离,在平面ABCD 中,点N 到定点B 的距离与到定直线DC 的距离相等,利用抛物线定义知B 正确;对于C ,建立空间直角坐标系,设(,,0)N x y ,利用空间向量求夹角知122121cos3224D N AB y x y D N ABπ⋅===⨯++⋅,化简可知N 的轨迹为双曲线;对于D ,MN 与平面ABCD 所成的角为3MND π∠=,3ND =,可知N 的轨迹是以D 为圆心,33为半径的圆周; 【详解】对于A ,如图所示,设P 为MN 的中点,连接MN ,ND ,DP ,由正方体性质知MDN △为直角三角形,且P 为MN 的中点,2MN =,根据直角三角形斜边上的中线为斜边的一半,知MDN △不管怎么变化,始终有1PD =,即P 点的轨迹与正方体的面围城的几何体是一个以D 为球心,1为半径的球的18,其面积214182S ππ=⨯⨯=,故A 错误;对于B ,由正方体性质知,1BB ⊥平面ABCD 由线面垂直的性质定理知1NB BB ⊥,即NB 是点N 到直线1BB 的距离,在平面ABCD 中,点N 到定点B 的距离与到定直线DC 的距离相等,所以点N 的轨迹是以点B 为焦点,直线DC 为准线的抛物线,故B 正确; 对于C ,如图以D 为直角坐标系原点,建立空间直角坐标系,(,,0)N x y ,1(0,0,2)D ,(0,2,0)A ,(2,2,0)B ,则1(,,2)D N x y =-,(0,2,0)AB =,利用空间向量求夹角知122121cos3224D N AB y x y D N ABπ⋅===⨯++⋅,化简整理得:2234y x -=,即221443y x -=,所以N 的轨迹为双曲线,故C 正确;对于D ,由正方体性质知,MN 与平面ABCD 所成的角为MND ∠,即3MND π∠=,在直角MDN △中,3ND =,即N 的轨迹是以D 3D 错误; 故选:BC 【点睛】关键点睛:本题考查立体几何与解析几何的综合,解题的关键是抓住解析几何几种特殊曲线的定义,考查学生的逻辑推理能力,转化与划归能力与运算求解能力,属于难题.2.在正方体1111ABCD A B C D -中,M 、N 分别是棱AB 、1CC 的中点,1MB P 的顶点P 在棱1CC 与棱11C D 上运动,有以下四个命题正确命题的序号是( )A .平面1MB P 1ND ⊥ B .平面1MB P ⊥平面11ND AC .1MB P 在底面ABCD 上的射影图形的面积为定值 D .1MB P 在侧面11D C CD 上射影图形是三角形 【答案】BC 【分析】取N 与P 重合,结合勾股定理可判断A 选项的正误;利用面面垂直的判定定理可判断B 选项的正误;分点P 在棱1CC 、11C D 上运动两种情况讨论,利用三角形的面积公式可判断C 选项的正误;取点P 与点1C 重合,判断1MB P 在侧面11D C CD 上射影图形形状,可判断D 选项的正误. 【详解】对于A 选项,设正方体1111ABCD A B C D -的棱长为2,如下图所示:当点P 与点N 重合时, 若1ND ⊥平面1MB P ,1B N ⊂平面1MB P ,则11ND B N ⊥,由勾股定理可得2211115D N C N C D =+=,同理可得15B N =1122B D =2221111B N D N B D ∴+≠,则1ND 与1B N 不垂直,假设不成立,A 选项错误;对于B 选项,取1BB 的中点E ,连接1A E 、EN ,在正方体1111ABCD A B C D -中,11//BB CC ,且E 、N 分别为1BB 、1CC 的中点, 则11//B E C N 且11B E C N =,所以,四边形11B ENC 为平行四边形,则11//EN B C 且11EN B C =,1111//A D B C 且1111A D B C =,所以,11//A D EN 且11A D EN =,所以,四边形11A END 为平行四边形,所以,11//A E D N ,111A B BB =,1B E BM =,11190A B E B BM ∠=∠=,所以,111Rt A B E Rt B BM ≅△△,所以,111B A E BB M ∠=∠,所以,111111190A EB BB M A EB B A E ∠+∠=∠+∠=,190B FE ∴∠=,所以,11B M A E ⊥,11A D ⊥平面11AA B B ,1B M ⊂平面11AA B B ,111B M A D ∴⊥, 1111A D A E A =,11A D 、1A E ⊂平面11ND A ,1MB ∴⊥平面11ND A ,1MB ⊂平面1MB P ,所以,平面1MB P ⊥平面11ND A ,B 选项正确;对于C 选项,设正方体1111ABCD A B C D -的棱长为a .若点P 在棱1CC 上运动时,1MB P 在底面ABCD 上的射影为MBC △, 此时,射影图形的面积为21224MBCa a S a =⋅=△; 若点P 在棱11C D 上运动时,设点P 在底面ABCD 上的射影点为G ,则G CD ∈, 且点G 到AB 的距离为a ,1MB 在底面ABCD 内的射影为MB ,则1MB P 在底面ABCD 内的射影为MBG △,且21224MBGa a S a =⋅⋅=△.综上所述,1MB P 在底面ABCD 内的射影图形的面积为定值,C 选项正确; 对于D 选项,当点P 与1C 重合时,P 、1B 两点在平面11D C CD 上的射影重合, 此时,1MB P 在侧面11D C CD 上的射影不构成三角形,D 选项错误. 故选:BC. 【点睛】方法点睛:证明面面垂直常用的方法: (1)面面垂直的定义; (2)面面垂直的判定定理.在证明面面垂直时,一般假设面面垂直成立,然后利用面面垂直转化为线面垂直,即为所证的线面垂直,组织论据证明即可.3.已知四面体ABCD 的所有棱长均为2,则下列结论正确的是( ) A .异面直线AC 与BD 所成角为60︒ B .点A 到平面BCD 的距离为263C .四面体ABCD 6πD .动点P 在平面BCD 上,且AP 与AC 所成角为60︒,则点P 的轨迹是椭圆 【答案】BC 【分析】在正四面体中通过线面垂直可证得AC ⊥BD ,通过计算可验证BC,通过轨迹法可求得P 的轨迹为双曲线方程即可得D 错误. 【详解】取BD 中点E ,连接,AE CE ,可得BD ⊥面ACE ,则AC ⊥BD ,故A 错误;在四面体ABCD 中,过点A 作AF ⊥面BCD 于点F ,则F 为为底面正三角形BCD 的重心,因为所有棱长均为2,22263AF AB BF =-=即点A 到平面BCD 26,故B 正确;设O 为正四面体的中心则OF 为内切球的半径,OA 我外接球的半径, 因为11433A BCD BCD BCD V S AF S OF -=⋅=⨯⋅△△,所以4AF OF =,即6=6OF AO =,, 所以四面体ABCD 的外接球体积3344633V R OA πππ===,故C 正确; 建系如图:26230,0,,0,,0A C ⎛⎫⎛⎫⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭,设(,,0)P x y ,则262326,,0,,333AP x y AC →→⎛⎫⎛⎫=-=- ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭,因为cos 60AP AC AP AC →→→→⋅=,所以222324812241393972y x y +=++⨯+⨯, 即222388=33y x y +++,平方化简可得:22323400399y x y ----,可知点P 的轨迹为双曲线,故D 错误. 故选:BC .【点睛】方法点睛:立体几何中动点轨迹的求解问题,解决此类问题可采用空间向量法,利用空间向量法表示出已知的角度或距离的等量关系,从而得到轨迹方程.4.正方体1111ABCD A B C D -中,E 是棱1DD 的中点,F 在侧面11CDD C 上运动,且满足1//B F 平面1A BE .以下命题正确的有( )A .侧面11CDD C 上存在点F ,使得11B F CD ⊥ B .直线1B F 与直线BC 所成角可能为30︒C .平面1A BE 与平面11CDD C 所成锐二面角的正切值为2D .设正方体棱长为1,则过点E ,F ,A 5 【答案】AC 【分析】取11C D 中点M ,1CC 中点N ,连接11,,B M B N MN ,易证得平面1//B MN 平面1A BE ,可得点F 的运动轨迹为线段MN .取MN 的中点F ,根据等腰三角形的性质得1B F MN ⊥,即有11B F CD ⊥,A 正确;当点F 与点M 或点N 重合时,直线1B F 与直线BC 所成角最大,可判断B 错误;根据平面1//B MN 平面1A BE ,11B FC ∠即为平面1B MN 与平面11CDD C 所成的锐二面角,计算可知C 正确;【详解】取11C D 中点M ,1CC 中点N ,连接11,,B M B N MN ,则易证得11//B N A E ,1//MN A B ,从而平面1//B MN 平面1A BE ,所以点F 的运动轨迹为线段MN .取MN 的中点F ,因为1B MN △是等腰三角形,所以1B F MN ⊥,又因为1//MN CD ,所以11B F CD ⊥,故A 正确;设正方体的棱长为a ,当点F 与点M 或点N 重合时,直线1B F 与直线BC 所成角最大,此时11tan C B F ∠=1tan 3023︒<=,所以B 错误; 平面1//B MN 平面1A BE ,取F 为MN 的中点,则1MN C F ⊥,1MN B F ⊥,∴11B FC ∠即为平面1B MN 与平面11CDD C 所成的锐二面角,11111tan B C B FC C F∠==22C 正确;因为当F 为1C E 与MN 的交点时,截面为菱形1AGC E (G 为1BB 的交点),面积为62D 错误.故选:AC.【点睛】本题主要考查线面角,二面角,截面面积的求解,空间几何中的轨迹问题,意在考查学生的直观想象能力和数学运算能力,综合性较强,属于较难题.5.已知正方体1111ABCD A B C D -棱长为2,如图,M 为1CC 上的动点,AM ⊥平面α.下面说法正确的是()A .直线AB 与平面α所成角的正弦值范围为322⎣⎦B .点M 与点1C 重合时,平面α截正方体所得的截面,其面积越大,周长就越大 C .点M 为1CC 的中点时,若平面α经过点B ,则平面α截正方体所得截面图形是等腰梯形D .已知N 为1DD 中点,当AM MN +的和最小时,M 为1CC 的中点 【答案】AC 【分析】以点D 为坐标原点,DA 、DC 、1DD 所在直线分别为x 、y 、z 轴建立空间直角坐标系D xyz -,利用空间向量法可判断A 选项的正误;证明出1AC ⊥平面1A BD ,分别取棱11A D 、11A B 、1BB 、BC 、CD 、1DD 的中点E 、F 、Q 、N 、G 、H ,比较1A BD 和六边形EFQNGH 的周长和面积的大小,可判断B 选项的正误;利用空间向量法找出平面α与棱11A D 、11A B 的交点E 、F ,判断四边形BDEF 的形状可判断C 选项的正误;将矩形11ACC A 与矩形11CC D D 延展为一个平面,利用A 、M 、N 三点共线得知AM MN +最短,利用平行线分线段成比例定理求得MC ,可判断D 选项的正误. 【详解】对于A 选项,以点D 为坐标原点,DA 、DC 、1DD 所在直线分别为x 、y 、z 轴建立空间直角坐标系D xyz -,则点()2,0,0A 、()2,2,0B 、设点()()0,2,02M a a ≤≤,AM ⊥平面α,则AM 为平面α的一个法向量,且()2,2,AM a =-,()0,2,0AB =, 2232cos ,,32288AB AM AB AM AB AMa a ⋅<>===⎢⋅⨯++⎣⎦, 所以,直线AB 与平面α所成角的正弦值范围为322⎣⎦,A 选项正确; 对于B 选项,当M 与1CC 重合时,连接1A D 、BD 、1A B 、AC , 在正方体1111ABCD A B C D -中,1CC ⊥平面ABCD ,BD ⊂平面ABCD ,1BD CC ∴⊥,四边形ABCD 是正方形,则BD AC ⊥,1CC AC C =,BD ∴⊥平面1ACC ,1AC ⊂平面1ACC ,1AC BD ∴⊥,同理可证11AC A D ⊥, 1A D BD D ⋂=,1AC ∴⊥平面1A BD ,易知1A BD 是边长为22(12322234A BD S =⨯=△为22362=.设E 、F 、Q 、N 、G 、H 分别为棱11A D 、11A B 、1BB 、BC 、CD 、1DD 的中点,易知六边形EFQNGH 是边长为2的正六边形,且平面//EFQNGH 平面1A BD , 正六边形EFQNGH 的周长为62,面积为()236233⨯⨯=,则1A BD 的面积小于正六边形EFQNGH 的面积,它们的周长相等,B 选项错误; 对于C 选项,设平面α交棱11A D 于点(),0,2E b ,点()0,2,1M ,()2,2,1AM =-,AM ⊥平面α,DE ⊂平面α,AM DE ∴⊥,即220AM DE b ⋅=-+=,得1b =,()1,0,2E ∴,所以,点E 为棱11A D 的中点,同理可知,点F 为棱11A B 的中点,则()2,1,2F ,()1,1,0EF =,而()2,2,0DB =,12EF DB ∴=,//EF DB ∴且EF DB ≠, 由空间中两点间的距离公式可得2222015DE =++=()()()2222212205BF =-+-+-=,DE BF ∴=,所以,四边形BDEF 为等腰梯形,C 选项正确;对于D 选项,将矩形11ACC A 与矩形11CC D D 延展为一个平面,如下图所示:若AM MN +最短,则A 、M 、N 三点共线,11//CC DD ,2222222MC AC DN AD ∴===+, 11222MC CC =≠,所以,点M 不是棱1CC 的中点,D 选项错误.故选:AC. 【点睛】本题考查线面角正弦值的取值范围,同时也考查了平面截正方体的截面问题以及折线段长的最小值问题,考查空间想象能力与计算能力,属于难题.6.在长方体1111ABCD A B C D -中,23AB =12AD AA ==,,,P Q R 分别是11,,AB BB AC 上的动点,下列结论正确的是( ) A .对于任意给定的点P ,存在点Q 使得1D P CQ ⊥ B .对于任意给定的点Q ,存在点R 使得1D R CQ ⊥ C .当1AR A C ⊥时,1AR D R ⊥D .当113AC A R =时,1//D R 平面1BDC 【答案】ABD 【分析】如图所示建立空间直角坐标系,计算142D P CQ b ⋅=-,()12222D R CQ b λλ⋅=--,134AR D R ⋅=-,10D R n ⋅=,得到答案.【详解】如图所示,建立空间直角坐标系,设()2,,0P a ,0,23a ⎡∈⎣,()2,23,Q b ,[]0,2b ∈,设11A R AC λ=,得到()22,23,22R λλλ--,[]0,1λ∈. ()12,,2P a D -=,()2,0,CQ b =,142D P CQ b ⋅=-,当2b =时,1D P CQ ⊥,A 正确;()122,23,2D R λλλ=--,()12222D R CQ b λλ⋅=--,取22bλ=+时,1D R CQ ⊥,B 正确; 1AR A C ⊥,则()()12,23,222,23,2212440AR AC λλλλλλ⋅=--⋅--=-+-+=, 14λ=,此时11333313,,,,022224AR D R ⎛⎫⎛⎫⋅=-⋅-=-≠ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭,C 错误; 113AC A R =,则4234,,33R ⎛⎫ ⎪ ⎪⎝⎭,14232,,33D R ⎛⎫=- ⎪ ⎪⎝⎭,设平面1BDC 的法向量为(),,n x y z =,则100n BD n DC ⎧⋅=⎪⎨⋅=⎪⎩,解得()3,1,3n =-,故10D R n ⋅=,故1//D R 平面1BDC ,D 正确. 故选:ABD .【点睛】本题考查了空间中的线线垂直,线面平行,意在考查学生的计算能力和空间想象能力,推断能力.7.如图,点O 是正四面体P ABC -底面ABC 的中心,过点O 的直线交AC ,BC 于点M ,N ,S 是棱PC 上的点,平面SMN 与棱PA 的延长线相交于点Q ,与棱PB 的延长线相交于点R ,则( )A .若//MN 平面PAB ,则//AB RQ B .存在点S 与直线MN ,使PC ⊥平面SRQC .存在点S 与直线MN ,使()0PS PQ PR ⋅+= D .111PQPRPS++是常数【答案】ABD 【分析】对于选项A ,根据线面平行的性质定理,进行推理判断即可;对于选项B ,当直线MN 平行于直线AB , 13SC PC =时,通过线面垂直的判定定理,证明此时PC ⊥平面SRQ ,即可证明,存在点S 与直线MN ,使PC ⊥平面SRQ ;对于选项C ,假设存在点S 与直线MN ,使()0PS PQ PR ⋅+=,利用线面垂直的判定定理可证得PC ⊥平面PAB ,此时通过反证法说明矛盾性,即可判断; 对于选项D ,利用S PQR O PSR O PSQ O PQR V V V V ----=++,即可求得111PQPRPS++是常数.【详解】 对于选项A , 若//MN 平面PAB ,平面SMN 与棱PA 的延长线相交于点Q ,与棱PB 的延长线相交于点R ,∴平面SMN 平面PAB =RQ ,又MN ⊂平面SMN ,//MN 平面PAB ,∴//MN RQ ,点O 在面ABC 上,过点O 的直线交AC ,BC 于点M ,N ,∴MN ⊂平面ABC ,又//MN 平面PAB ,平面ABC平面PAB AB =,∴//MN AB , ∴//AB RQ ,故A 正确; 对于选项B ,当直线MN 平行于直线AB ,S 为线段PC 上靠近C 的三等分点,即13SC PC =, 此时PC ⊥平面SRQ ,以下给出证明: 在正四面体P ABC -中,设各棱长为a ,∴ABC ,PBC ,PAC △,PAB △均为正三角形,点O 为ABC 的中心,//MN AB ,∴由正三角形中的性质,易得23CN CM a ==, 在CNS 中,23CN a =,13SC a =,3SCN π∠=,∴由余弦定理得,3SN a ==, ∴222249SC SN a CN +==,则SN PC ⊥, 同理,SM PC ⊥,又SM SN S =,SM ⊂平面SRQ ,SN ⊂平面SRQ ,∴PC ⊥平面SRQ ,∴存在点S 与直线MN ,使PC ⊥平面SRQ ,故B 正确; 对于选项C ,假设存在点S 与直线MN ,使()0PS PQ PR ⋅+=, 设QR 中点为K ,则2PQ PR PK +=,∴PS PK ⊥,即PC PK ⊥,()cos cos 0PC AB PC PB PA PC PB CPB PC PA CPA ⋅=⋅-=⋅∠-⋅∠=,∴PC AB ⊥,又易知AB 与PK 为相交直线,AB 与PK 均在平面PQR 上,∴PC ⊥平面PQR ,即PC ⊥平面PAB ,与正四面体P ABC -相矛盾,所以假设不成立, 故C 错误; 对于选项D ,易知点O 到面PBC ,面PAC ,面PAB 的距离相等,记为d , 记PC 与平面PAB 所处角的平面角为α,α为常数,则sin α也为常数, 则点S 到PQR 的距离为sin PS α,又13sin 234PQRSPQ PR PQ PR π=⋅=⋅ ∴()()1133sin sin sin 33412S PQR PQRV PS S PS PQ PR PQ PR PS ααα-=⋅=⋅⋅=⋅⋅, 又13sin 234PSRSPS PR PS PR π=⋅=⋅, 13sin 234PSQS PS PQ PS PQ π=⋅=⋅, 13sin 234PQRSPQ PR PQ PR π=⋅=⋅, ()312S PQR O PSR O PSQ O PQR V V V V d PS PR PS PQ PQ PR ----=++=⋅+⋅+⋅, ∴()33sin 1212PQ PR PS d PS PR PS PQ PQ PR α⋅⋅=⋅+⋅+⋅, ∴111sin d PQPRPSα++=为常数,故D 正确. 故选:ABD. 【点睛】本题考查了线面平行的性质定理、线面垂直的判定定理,考查了三棱锥体积的计算,考查了向量的运算,考查了转化能力与探究能力,属于较难题.8.如图,正三棱柱11ABC A B C -中,11BC AB ⊥、点D 为AC 中点,点E 为四边形11BCC B 内(包含边界)的动点则以下结论正确的是( )A .()1112DA A A B A BC =-+ B .若//DE 平面11ABB A ,则动点E 的轨迹的长度等于22ACC .异面直线AD 与1BCD .若点E 到平面11ACC AEB ,则动点E 的轨迹为抛物线的一部分 【答案】BCD 【分析】根据空间向量的加减法运算以及通过建立空间直角坐标系求解,逐项判断,进而可得到本题答案. 【详解】解析:对于选项A ,()1112AD A A B A BC =-+,选项A 错误; 对于选项B ,过点D 作1AA 的平行线交11A C 于点1D .以D 为坐标原点,1DA DB DD ,,分别为,,x y z 轴的正方向建立空间直角坐标系Oxyz .设棱柱底面边长为a ,侧棱长为b ,则002aA ⎛⎫ ⎪⎝⎭,,,00B ⎛⎫ ⎪ ⎪⎝⎭,,10B b ⎛⎫ ⎪ ⎪⎝⎭,,102a C b ⎛⎫- ⎪⎝⎭,,,所以12a BC b ⎛⎫=- ⎪ ⎪⎝⎭,,,12a AB b ⎛⎫=- ⎪ ⎪⎝⎭,. ∵11BC AB ⊥,∴110BC AB ⋅=,即222022a a b ⎛⎫⎛⎫--+= ⎪ ⎪ ⎪⎝⎭⎝⎭,解得2b a =. 因为//DE 平面11ABB A ,则动点E的轨迹的长度等于1BB =.选项B 正确. 对于选项C ,在选项A 的基础上,002a A ⎛⎫⎪⎝⎭,,,00B ⎛⎫ ⎪ ⎪⎝⎭,,()0,0,0D ,1022a C a ⎛⎫- ⎪ ⎪⎝⎭,,,所以002a DA ⎛⎫= ⎪⎝⎭,,,1222a BC a ⎛⎫=- ⎪ ⎪⎝⎭,-,,因为2111cos ,||||aBC DA BC DA BC DA a ⎛⎫- ⎪⋅<>===1,BC DA 所成角C 正确. 对于选项D ,设点E 在底面ABC 的射影为1E ,作1E F 垂直于AC ,垂足为F ,若点E 到平面11ACC A 的距离等于32EB ,即有312E F EB =,又因为在1CE F ∆中,311E F E C =,得1EB E C =,其中1E C 等于点E 到直线1CC 的距离,故点E 满足抛物线的定义,另外点E 为四边形11BCC B 内(包含边界)的动点,所以动点E 的轨迹为抛物线的一部分,故D 正确.故选:BCD 【点睛】本题主要考查立体几何与空间向量的综合应用问题,其中涉及到抛物线定义的应用.。
立体几何多选题 易错题难题专项训练学能测试试卷

立体几何多选题 易错题难题专项训练学能测试试卷一、立体几何多选题1.如图①,矩形ABCD 的边2BC =,设AB x =,0x >,三角形BCM 为等边三角形,沿BC 将三角形BCM 折起,构成四棱锥M ABCD -如图②,则下列说法正确的有( )A .若T 为BC 中点,则在线段MC 上存在点P ,使得//PD 平面MATB .当)3,2x ∈时,则在翻折过程中,不存在某个位置满足平面MAD ⊥平面ABCDC .若使点M 在平面ABCD 内的射影落在线段AD 上,则此时该四棱锥的体积最大值为1 D .若1x =,且当点M 在平面ABCD 内的射影点H 落在线段AD 上时,三棱锥M HAB -6322++【答案】BCD 【分析】对于A ,延长AT 与DC 的延长线交于点N ,此时,DP 与MN 必有交点; 对于B ,取AD 的中点H ,表示出2223MH MT HT x --,验证当)3,2x ∈时,无解即可; 对于C ,利用体积公式21233V x x =⨯⨯-,借助基本不等式求最值即可; 对于D ,要求外接球半径与内切球半径,找外接圆的圆心,又内接圆半径为2323r =++【详解】对于A ,如图,延长AT 与DC 的延长线交于点N ,则面ATM ⋂面()MDC N MN =.此时,DP 与MN 必有交点,则DP 与面ATM 相交,故A 错误; 对于B ,取AD 的中点H ,连接MH ,则MH AD ⊥.若面MAD ⊥面ABCD ,则有2223MH MT HT x =-=- 当)3,2x ∈时,无解,所以在翻折过程中,不存在某个位置满足平面MAD ⊥平面ABCD故B 正确;对于C ,由题可知,此时面MAD ⊥面ABCD ,由B 可知,(3x ∈,所以()22222221223232331333232x x V x x x x ⎛⎫+-⎛⎫=⨯⨯-=-≤== ⎪ ⎪⎝⎭⎝⎭当且仅当223x x =-,即6x =时等号成立.故C 正确; 对于D ,由题可知,此时面MAD ⊥面ABCD ,且2MH =因为AHB ,MHB 都是直角三角形,所以M ABH -底面外接圆的圆心是中点,所以1R =,由等体积法,可求得内接圆半径为2323r =++,故61322R r ++=,故D 正确.故选:BCD . 【点睛】本题从多个角度深度考查了立体几何的相关内容,注意辅助线的作法,以及求内接圆半径的公式、基本不等式、构造函数等核心思想.2.已知正方体1111 ABCD A B C D -的棱长为2,M 为1DD 的中点,N 为正方形ABCD 所在平面内一动点,则下列命题正确的有( )A .若2MN =,则MN 的中点的轨迹所围成图形的面积为πB .若N 到直线1BB 与直线DC 的距离相等,则N 的轨迹为抛物线C .若1D N 与AB 所成的角为3π,则N 的轨迹为双曲线 D .若MN 与平面ABCD 所成的角为3π,则N 的轨迹为椭圆【答案】BC 【分析】对于A ,连接MN ,ND ,DP ,得到直角MDN △,且P 为斜边MN 的中点,所以1PD =,进而得到P 点的轨迹为球面的一部分,即可判断选项A 错误;对于B ,可知1NB BB ⊥,即NB 是点N 到直线1BB 的距离,在平面ABCD 中,点N 到定点B 的距离与到定直线DC 的距离相等,利用抛物线定义知B 正确;对于C ,建立空间直角坐标系,设(,,0)N x y ,利用空间向量求夹角知122121cos3224D N AB y x y D N ABπ⋅===⨯++⋅,化简可知N 的轨迹为双曲线;对于D ,MN 与平面ABCD 所成的角为3MND π∠=,3ND =,可知N 的轨迹是以D 为圆心,33为半径的圆周; 【详解】对于A ,如图所示,设P 为MN 的中点,连接MN ,ND ,DP ,由正方体性质知MDN △为直角三角形,且P 为MN 的中点,2MN =,根据直角三角形斜边上的中线为斜边的一半,知MDN △不管怎么变化,始终有1PD =,即P 点的轨迹与正方体的面围城的几何体是一个以D 为球心,1为半径的球的18,其面积214182S ππ=⨯⨯=,故A 错误;对于B ,由正方体性质知,1BB ⊥平面ABCD 由线面垂直的性质定理知1NB BB ⊥,即NB 是点N 到直线1BB 的距离,在平面ABCD 中,点N 到定点B 的距离与到定直线DC 的距离相等,所以点N 的轨迹是以点B 为焦点,直线DC 为准线的抛物线,故B 正确; 对于C ,如图以D 为直角坐标系原点,建立空间直角坐标系,(,,0)N x y ,1(0,0,2)D ,(0,2,0)A ,(2,2,0)B ,则1(,,2)D N x y =-,(0,2,0)AB =,利用空间向量求夹角知122121cos3224D N AB y x y D N ABπ⋅===⨯++⋅,化简整理得:2234y x -=,即221443y x -=,所以N 的轨迹为双曲线,故C 正确;对于D ,由正方体性质知,MN 与平面ABCD 所成的角为MND ∠,即3MND π∠=,在直角MDN △中,3ND =,即N 的轨迹是以D 为圆心,3为半径的圆周,故D 错误; 故选:BC 【点睛】关键点睛:本题考查立体几何与解析几何的综合,解题的关键是抓住解析几何几种特殊曲线的定义,考查学生的逻辑推理能力,转化与划归能力与运算求解能力,属于难题.3.如图,已知正方体1ABCD ABC D -的棱长为a ,E 是棱CD 上的动点.则下列结论中正确的有( )A .11EB AD ⊥B .二面角11E A B A --的大小为4πC .三棱锥11A BDE -体积的最小值为313a D .1//D E 平面11A B BA 【答案】ABD 【分析】连接1A D 、1B C ,则易证1AD ⊥平面11A DCB ,1EB ⊂平面11A DCB ,则由线面垂直的性质定理可以判断选项A 正确;二面角11E A B A --的平面角为1DA A ∠,易知14DA A π∠=,则可判断选项B 正确;用等体积法,将求三棱锥11A B D E -的体积转化为求三棱锥11E AB D -的体积,当点E 与D 重合时,三棱锥11E AB D -的体积最小,此时的值为316a ,则选项C 错误;易知平面11//D DCC 平面11A B BA ,而1D E ⊂平面11D DCC ,则根据面面平行的性质定理可得1//D E 平面11A B BA ,可判断选项D 正确. 【详解】选项A ,连接1A D 、1B C ,则由正方体1ABCD ABC D -可知,11A D AD ⊥,111A B AD ⊥,1111A DA B A =,则1AD ⊥平面11A DCB ,又因为1EB ⊂平面11A DCB ,所以11EB AD ⊥,选项A 正确; 选项B ,因为11//DE A B ,则二面角11E A B A --即为二面角11D A B A --, 由正方体1ABCD ABC D -可知,11A B ⊥平面1DA A , 则1DA A ∠为二面角11D A B A --的平面角,且14DA A π∠=,所以选项B 正确;选项C ,设点E 到平面11AB D 的距离为d , 则11111113A B D E E AB D AB D V V S d --==⋅,连接1C D 、1C B ,易证平面1//BDC 平面11AB D ,则在棱CD 上,点D 到平面11AB D 的距离最短, 即点E 与D 重合时,三棱锥11A B D E -的体积最小, 由正方体1ABCD ABC D -知11A B ⊥平面1ADD ,所以1111123111113326D AB D B ADDADD a V V S A B a a --==⋅=⋅⋅=, 则选项C 错误;选项D ,由正方体1ABCD ABC D -知,平面11//CC D D 平面11A B BA ,且1D E ⊂平面11CC D D , 则由面面平行的性质定理可知1//D E 平面11A B BA ,则选项D 正确. 故选:ABD. 【点睛】关键点点睛:本题对于选项C 的判断中,利用等体积法求三棱锥的体积是解题的关键.4.已知四面体ABCD 的所有棱长均为2,则下列结论正确的是( ) A .异面直线AC 与BD 所成角为60︒B .点A 到平面BCDC .四面体ABCDD .动点P 在平面BCD 上,且AP 与AC 所成角为60︒,则点P 的轨迹是椭圆 【答案】BC 【分析】在正四面体中通过线面垂直可证得AC ⊥BD ,通过计算可验证BC,通过轨迹法可求得P 的轨迹为双曲线方程即可得D 错误. 【详解】取BD 中点E ,连接,AE CE ,可得BD ⊥面ACE ,则AC ⊥BD ,故A 错误;在四面体ABCD 中,过点A 作AF ⊥面BCD 于点F ,则F 为为底面正三角形BCD 的重心,因为所有棱长均为2,AF ==即点A 到平面BCD 的距离为3,故B 正确;设O 为正四面体的中心则OF 为内切球的半径,OA 我外接球的半径, 因为11433A BCD BCD BCD V S AF S OF -=⋅=⨯⋅△△,所以4AF OF =,即OF AO =所以四面体ABCD 的外接球体积334433V R OA ππ===,故C 正确;建系如图:0,0,,0,,033A C ⎛⎛⎫⎪ ⎪⎝⎭⎝⎭,设(,,0)P x y ,则262326,,0,,AP x y AC →→⎛⎫⎛⎫=-=- ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭,因为cos 60AP AC AP AC →→→→⋅=,所以222324812241393972y x y +=++⨯+⨯, 即222388=33y x y +++,平方化简可得:22323400399y x y ----,可知点P 的轨迹为双曲线,故D 错误. 故选:BC .【点睛】方法点睛:立体几何中动点轨迹的求解问题,解决此类问题可采用空间向量法,利用空间向量法表示出已知的角度或距离的等量关系,从而得到轨迹方程.5.在直角梯形ABCD 中,2ABC BCD π∠=∠=,1AB BC ==,2DC =,E 为DC 中点,现将ADE 沿AE 折起,得到一个四棱锥D ABCE -,则下列命题正确的有( ) A .在ADE 沿AE 折起的过程中,四棱锥D ABCE -体积的最大值为13B .在ADE 沿AE 折起的过程中,异面直线AD 与BC 所成的角恒为4π C .在ADE 沿AE 折起的过程中,二面角A EC D --的大小为45︒D .在四棱锥D ABCE -中,当D 在EC 上的射影恰好为EC 的中点F 时,DB 与平面ABCE 所成的角的正切为155【答案】ABD 【分析】对于A ,四棱锥D ABCE -的底面面积是固定值,要使得体积最大,需要平面DAE ⊥平面ABCE ,此时DE CE ⊥,可求得1133D ABCE ABCE V S DE -=⋅=可判断A ;对于B ,在ADE 沿AE 折起的过程中,//AE BC ,所以异面直线AD 与AE 所成的角即为AD 与BC所成角,由翻折前可知4DAE π∠=可判断B ;对于C ,利用线面垂直的判定定理,结合翻折前可知AE ⊥平面DEC ,又AE ⊂平面ABCE ,所以平面DEC ⊥平面ABCE ,即二面角A EC D --的在大小为2π判断C ;对于D ,利用线面垂直的判定定理可知DF ⊥平面ABCE ,所以DBF ∠为直线DB 与平面ABCE 所成的角,在直角DFB △中,15tan DF DBF BF ∠==,可判断D 正确;【详解】对于A ,ADE 沿AE 折起得到四棱锥D ABCE -,由四棱锥底面面积是固定值,要使得体积最大,需要四棱锥的高最大,即平面DAE ⊥平面ABCE ,此时DE CE ⊥,由已知得1DE =,则111111333D ABCE ABCE V S DE -=⋅=⨯⨯⨯=,故A 正确; 对于B ,在ADE 沿AE 折起的过程中,//AE BC ,所以异面直线AD 与AE 所成的角即为AD 与BC 所成角,又1AB BC ==,2DC =,E 为DC 中点,可知4DAE π∠=,即异面直线AD 与BC 所成的角恒为4π,故B 正确; 对于C ,由翻折前知,,AE EC AE ED ⊥⊥,且ECED E =,则AE ⊥平面DEC ,又AE ⊂平面ABCE ,所以平面DEC ⊥平面ABCE ,即二面角A EC D --的大小为2π,故C 错误; 对于D ,如图连接,DF BF ,由C 选项知,AE ⊥平面DEC ,又DF ⊂平面DEC ,则AE DF ⊥,又由已知得EC DF ⊥,且EC AE E ⋂=,则DF ⊥平面ABCE ,所以DBF ∠为直线DB 与平面ABCE 所成的角,在直角DFB △中,222222113122152tan 5511122DE CE DFDBF BFBC CE ⎛⎫⎛⎫-- ⎪⎪⎝⎭⎝⎭∠=====⎛⎫⎛⎫++ ⎪ ⎪⎝⎭⎝⎭,所以DB 与平面ABCE 所成的角的正切为15,故D 正确; 故选:ABD 【点睛】关键点睛:本题考查立体几何综合问题,求体积,求线线角,线面角,面面角,解题的关键要熟悉几种角的定义,通过平移法找到线线角,通过证垂直找到线面角和面面角,再结合三角形求出角,考查了学生的逻辑推理能力,转化能力与运算求解能力,属于难题.6.如图,矩形ABCD 中, 22AB AD ==,E 为边AB 的中点.将ADE 沿直线DE 翻折成1A DE △(点1A 不落在底面BCDE 内),若M 在线段1A C 上(点M 与1A ,C 不重合),则在ADE 翻转过程中,以下命题正确的是( )A .存在某个位置,使1DE A C ⊥B .存在点M ,使得BM ⊥平面1A DC 成立 C .存在点M ,使得//MB 平面1A DE 成立D .四棱锥1A BCDE -体积最大值为24【答案】CD 【分析】利用反证法可得A 、B 错误,取M 为1A C 的中点,取1A D 的中点为I ,连接,MI IE ,可证明//MB 平面1A DE ,当平面1A DE ⊥平面BCDE 时,四棱锥1A BCDE -体积最大值,利用公式可求得此时体积为24. 【详解】如图(1),取DE 的中点为F ,连接1,A F CF ,则45CDF ∠=︒,22DF =,故212254222222CF =+-⨯⨯=, 故222DC DF CF ≠+即2CFD π∠≠.若1CA DE ⊥,因为11,A D A E DF FE ==,故1A F DE ⊥,而111A F A C A ⋂=, 故DE ⊥平面1A FC ,因为CF ⊂平面1A FC ,故DE CF ⊥,矛盾,故A 错. 若BM ⊥平面1A DC ,因为DC ⊂平面1A DC ,故BM DC ⊥,因为DC CB ⊥,BM CB B ⋂=,故CD ⊥平面1A CB ,因为1AC ⊂平面1A CB ,故1CD A C ⊥,但1A D CD <,矛盾,故B 错. 当平面1A DE ⊥平面BCDE 时,四棱锥1A BCDE -体积最大值,由前述证明可知1A F DE ⊥,而平面1A DE 平面BCDE DE =,1A F ⊂平面1A DE ,故1A F ⊥平面BCDE ,因为1A DE △为等腰直角三角形,111A D A E ==,故122A F =, 又四边形BCDE 的面积为13211122⨯-⨯⨯=, 故此时体积为13223224⨯⨯=D 正确. 对于C ,如图(2),取M 为1A C 的中点,取1A D 的中点为I ,连接,MI IE ,则1//,2IM CD IM CD =,而1//,2BE CD BE CD =, 故//,IM BE IM BE =即四边形IEBM 为平行四边形,故//IE BM ,因为IE ⊂平面1A DE ,BM ⊄平面1A DE ,故//MB 平面1A DE , 故C 正确.故选:CD.【点睛】本题考查立体几何中的折叠问题,注意对于折叠后点线面的位置的判断,若命题的不成立,往往需要利用反证法来处理,本题属于难题.7.如图,已知P 为棱长为1的正方体对角线1BD 上的一点,且()()10,1BP BD λλ=,下面结论中正确结论的有( )A .11A D C P ⊥;B .当1A P PD +取最小值时,23λ=; C .若()0,1λ∈,则7,312APC ππ⎛⎫∠∈ ⎪⎝⎭; D .若P 为1BD 的中点,四棱锥11P AA D D -的外接球表面积为94π. 【答案】ABD【分析】 以D 为坐标原点建立如图空间直角坐标系,利用向量关系可判断ABC ;根据几何体外接球关系建立方程求出球半径即可判断D.【详解】以D 为坐标原点建立如图空间直角坐标系,则()1,1,0B ,()10,0,1D ,设(),,P x y z ,()()10,1BP BD λλ=,1BP BD λ∴=,即()()1,1,1,1,1x y z λ--=--,则可解得()1,1,P λλλ--,对A ,()()()111,0,1,0,0,0,0,1,1A D C ,()11,0,1A D ∴=--,()11,,1C P λλλ=---,则()()()()11110110A D C P λλλ⋅=-⨯-+⨯-+-⨯-=,则11A D C P ⊥,故A 正确;对B ,()()()()()2222221111111A P PD λλλλλλ+=--+-+--+-+222223422333λλλ⎛⎫=-+=-+ ⎪⎝⎭ 则当23λ=时,1A P PD +取最小值,故B 正确; 对C ,()()1,0,0,0,1,0A C ,(),1,PA λλλ∴=--,()1,,PC λλλ=--,则222321cos 1321321PA PC APC PA PC λλλλλλ⋅-∠===--+-+⋅, 01λ<<,则2232123λλ≤-+<,则2111123212λλ-≤-<-+, 即11cos 22APC -≤∠<,则2,33APC ππ⎛⎤∠∈ ⎥⎝⎦,故C 错误; 对于D ,当P 为1BD 中点时,四棱锥11P AA D D -为正四棱锥,设平面11AA D D 的中心为O ,四棱锥11P AA D D -的外接球半径为R ,所以222122R R ⎛⎫-+= ⎪⎝⎭⎝⎭,解得34R =,故四棱锥11P AA D D -的外接球表面积为94π,所以D 正确. 故选:ABD.【点睛】 关键点睛:本题考查空间相关量的计算,解题的关键是建立空间直角坐标系,利用向量建立关系进行计算.8.半正多面体(semiregularsolid )亦称“阿基米德多面体”,是由边数不全相同的正多边形围成的多面体,体现了数学的对称美.二十四等边体就是一种半正多面体,是由正方体切截而成的,它由八个正三角形和六个正方形构成(如图所示),若它的所有棱长都为2,则( )A .BF ⊥平面EABB .该二十四等边体的体积为203C .该二十四等边体外接球的表面积为8πD .PN 与平面EBFN 所成角的正弦值为22【答案】BCD【分析】 A 用反证法判断;B 先补齐八个角成正方体,再计算体积判断;C 先找到球心与半径,再计算表面积判断;D 先找到直线与平面所成角,再求正弦值判断.【详解】解:对于A ,假设A 对,即BF ⊥平面EAB ,于是BF AB ⊥,90ABF ∠=︒,但六边形ABFPQH 为正六边形,120ABF ∠=︒,矛盾,所以A 错;对于B ,补齐八个角构成棱长为2的正方体,则该二十四等边体的体积为3112028111323-⋅⋅⋅⋅⋅=,所以B 对;对于C ,取正方形ACPM 对角线交点O ,即为该二十四等边体外接球的球心, 其半径为2R =,其表面积为248R ππ=,所以C 对;对于D ,因为PN 在平面EBFN 内射影为NS ,所以PN 与平面EBFN 所成角即为PNS ∠,其正弦值为22PS PN ==,所以D 对. 故选:BCD .【点睛】本题考查了正方体的性质,考查了直线与平面所成角问题,考查了球的体积与表面积计算问题.。
高考复习易做易错题精选立体几何全国通用.

高考复习易做易错题精选立体几何、选择题:(石庄中学)设ABCD 是空间四边形,E ,F 分别是AB ,CD 的中点,贝U EF,AD,BC 满足()A 共线B 共面C 不共面D 可作为空间基向量 正确答案:B 错因:学生把向量看为直线。
(石庄中学)在正方体 ABCD-A i B i C i D i ,0是底面ABCD 的中心,M 、N 分别是棱DD 1、D 1C 1的中点,则直线OM ()保持AP 丄BD i ,则动点P 的轨迹(正确答案:A错因:学生观察能力较差,对三垂线定理逆定理不能灵活应用。
(石庄中学)下列命题中:1. 2. A 是AC 和MN 的公垂线C 垂直于MN ,但不垂直于 AC 正确答案:A 错因:学生观察能力较差, B 垂直于AC 但不垂直于MND 与AC 、MN 都不垂直 找不出三垂线定理中的射影。
3. (石庄中学)已知平面//平面 ,直线 L 平面,点P 直线L,平面间的距离为8, 则在 内到点P 的距离为10,且到L 的距离为9的点的轨迹是()A 一个圆B 四个点C 两条直线 正确答案:B 错因:学生对点线距离、线线距离、面面距离的关系不能灵活掌握。
四个点D 两个点 4. (石庄中学)正方体 ABCD-A i B i C i D i 中,点P 在侧面BCC 1B 1及其边界上运动,并且总A 线段B 1C BB 1的中点与CC i 中点连成的线段 C 线段BC 1CB 中点与B i C i 中点连成的线段5. 若向量a 、b 与空间任意向量不能构成基底,则 a // b 。
若 a // b , b // c ,贝 U c // a . 若 OA 、 OB 、 --- * ------------------------------------ 1 ----- 1O C 是空间一个基底,且OD =3 OA +1--- 1 ---------OB + - OC ,则 A 、B 、C 、3D 四点共面。
人教版立体几何多选题单元 易错题质量专项训练试题

人教版立体几何多选题单元 易错题质量专项训练试题一、立体几何多选题1.如图①,矩形ABCD 的边2BC =,设AB x =,0x >,三角形BCM 为等边三角形,沿BC 将三角形BCM 折起,构成四棱锥M ABCD -如图②,则下列说法正确的有( )A .若T 为BC 中点,则在线段MC 上存在点P ,使得//PD 平面MATB .当)3,2x ∈时,则在翻折过程中,不存在某个位置满足平面MAD ⊥平面ABCDC .若使点M 在平面ABCD 内的射影落在线段AD 上,则此时该四棱锥的体积最大值为1 D .若1x =,且当点M 在平面ABCD 内的射影点H 落在线段AD 上时,三棱锥M HAB -6322++【答案】BCD 【分析】对于A ,延长AT 与DC 的延长线交于点N ,此时,DP 与MN 必有交点; 对于B ,取AD 的中点H ,表示出2223MH MT HT x --,验证当)3,2x ∈时,无解即可; 对于C ,利用体积公式21233V x x =⨯⨯-,借助基本不等式求最值即可; 对于D ,要求外接球半径与内切球半径,找外接圆的圆心,又内接圆半径为2323r =++【详解】对于A ,如图,延长AT 与DC 的延长线交于点N ,则面ATM ⋂面()MDC N MN =.此时,DP 与MN 必有交点,则DP 与面ATM 相交,故A 错误; 对于B ,取AD 的中点H ,连接MH ,则MH AD ⊥.若面MAD ⊥面ABCD ,则有2223MH MT HT x =-=- 当)3,2x ∈时,无解,所以在翻折过程中,不存在某个位置满足平面MAD ⊥平面ABCD故B 正确;对于C ,由题可知,此时面MAD ⊥面ABCD ,由B 可知,(3x ∈,所以()22222221223232331333232x x V x x x x ⎛⎫+-⎛⎫=⨯⨯-=-≤== ⎪ ⎪⎝⎭⎝⎭当且仅当223x x =-,即6x =时等号成立.故C 正确; 对于D ,由题可知,此时面MAD ⊥面ABCD ,且2MH =因为AHB ,MHB 都是直角三角形,所以M ABH -底面外接圆的圆心是中点,所以1R =,由等体积法,可求得内接圆半径为2323r =++,故61322R r ++=,故D 正确.故选:BCD . 【点睛】本题从多个角度深度考查了立体几何的相关内容,注意辅助线的作法,以及求内接圆半径的公式、基本不等式、构造函数等核心思想.2.如图,在直三棱柱111ABC A B C -中,12AC BC AA ===,90ACB ∠=︒,D ,E ,F 分别为AC ,1AA ,AB 的中点.则下列结论正确的是( )A .1AC 与EF 相交B .11//BC 平面DEF C .EF 与1AC 所成的角为90︒D .点1B 到平面DEF 的距离为322【答案】BCD 【分析】利用异面直线的位置关系,线面平行的判定方法,利用空间直角坐标系异面直线所成角和点到面的距离,对各个选项逐一判断. 【详解】对选项A ,由图知1AC ⊂平面11ACC A ,EF平面11ACC A E =,且1.E AC ∉由异面直线的定义可知1AC 与EF 异面,故A 错误;对于选项B ,在直三棱柱111ABC A B C -中,11B C //BC .D ,F 分别是AC ,AB 的中点, //∴FD BC ,11B C ∴ //FD .又11B C ⊄平面DEF ,DF ⊂平面DEF ,11B C ∴ //平面.DEF 故B 正确;对于选项C ,由题意,建立如图所示的空间直角坐标系,则(0C ,0,0),(2A ,0,0),(0B ,2,0),1(2A ,0,2),1(0B ,2,2),1(0C ,0,2),(1D ,0,0),(2E ,0,1),(1F ,1,0).(1EF ∴=-,1,1)-,1(2AC =-,0,2). 1·2020EF AC =+-=,1EF AC ∴⊥,1EF AC ∴⊥. EF 与1AC 所成的角为90︒,故C 正确;对于选项D ,设向量(n x =,y ,)z 是平面DEF 的一个法向量. (1DE =,0,1),(0DF =,1,0), ∴由n DE n DF ⎧⊥⎨⊥⎩,,,即·0·0n DE n DF ⎧=⎨=⎩,,,得00.x z y +=⎧⎨=⎩,取1x =,则1z =-,(1n ∴=,0,1)-, 设点1B 到平面DEF 的距离为d . 又1(1DB =-,2,2),1·1023222DB n d n-+-∴===, ∴点1B 到平面DEF 的距离为322,故D 正确.故选:BCD 【点睛】本题主要考查异面直线的位置关系,线面平行的判定,异面直线所成角以及点到面的距离,还考查思维能力及综合分析能力,属难题.3.在正方体1111ABCD A B C D -中,M 、N 分别是棱AB 、1CC 的中点,1MB P 的顶点P 在棱1CC 与棱11C D 上运动,有以下四个命题正确命题的序号是( )A .平面1MB P 1ND ⊥ B .平面1MB P ⊥平面11ND AC .1MB P 在底面ABCD 上的射影图形的面积为定值 D .1MB P 在侧面11D C CD 上射影图形是三角形 【答案】BC 【分析】取N 与P 重合,结合勾股定理可判断A 选项的正误;利用面面垂直的判定定理可判断B 选项的正误;分点P 在棱1CC 、11C D 上运动两种情况讨论,利用三角形的面积公式可判断C 选项的正误;取点P 与点1C 重合,判断1MB P 在侧面11D C CD 上射影图形形状,可判断D 选项的正误. 【详解】对于A 选项,设正方体1111ABCD A B C D -的棱长为2,如下图所示:当点P 与点N 重合时, 若1ND ⊥平面1MB P ,1B N ⊂平面1MB P ,则11ND B N ⊥,由勾股定理可得2211115D N C N C D =+=,同理可得15B N =,1122B D =,2221111B N D N B D ∴+≠,则1ND 与1B N 不垂直,假设不成立,A 选项错误;对于B 选项,取1BB 的中点E ,连接1A E 、EN ,在正方体1111ABCD A B C D -中,11//BB CC ,且E 、N 分别为1BB 、1CC 的中点, 则11//B E C N 且11B E C N =,所以,四边形11B ENC 为平行四边形,则11//EN B C 且11EN B C =,1111//A D B C 且1111A D B C =,所以,11//A D EN 且11A D EN =,所以,四边形11A END 为平行四边形,所以,11//A E D N ,111A B BB =,1B E BM =,11190A B E B BM ∠=∠=,所以,111Rt A B E Rt B BM ≅△△,所以,111B A E BB M ∠=∠,所以,111111190A EB BB M A EB B A E ∠+∠=∠+∠=,190B FE ∴∠=,所以,11B M A E ⊥,11A D ⊥平面11AA B B ,1B M ⊂平面11AA B B ,111B M A D ∴⊥, 1111A D A E A =,11A D 、1A E ⊂平面11ND A ,1MB ∴⊥平面11ND A ,1MB ⊂平面1MB P ,所以,平面1MB P ⊥平面11ND A ,B 选项正确;对于C 选项,设正方体1111ABCD A B C D -的棱长为a .若点P 在棱1CC 上运动时,1MB P 在底面ABCD 上的射影为MBC △, 此时,射影图形的面积为21224MBCa a S a =⋅=△;若点P 在棱11C D 上运动时,设点P 在底面ABCD 上的射影点为G ,则G CD ∈, 且点G 到AB 的距离为a ,1MB 在底面ABCD 内的射影为MB ,则1MB P 在底面ABCD 内的射影为MBG △,且21224MBGa a S a =⋅⋅=△.综上所述,1MB P 在底面ABCD 内的射影图形的面积为定值,C 选项正确; 对于D 选项,当点P 与1C 重合时,P 、1B 两点在平面11D C CD 上的射影重合, 此时,1MB P 在侧面11D C CD 上的射影不构成三角形,D 选项错误. 故选:BC. 【点睛】方法点睛:证明面面垂直常用的方法: (1)面面垂直的定义; (2)面面垂直的判定定理.在证明面面垂直时,一般假设面面垂直成立,然后利用面面垂直转化为线面垂直,即为所证的线面垂直,组织论据证明即可.4.在三棱锥M ABC -中,下列命题正确的是( )A .若1233AD AB AC =+,则3BC BD = B .若G 为ABC 的重心,则111333MG MA MB MC =++C .若0MA BC ⋅=,0MC AB ⋅=,则0MB AC ⋅=D .若三棱锥M ABC -的棱长都为2,P ,Q 分别为MA ,BC 中点,则2PQ = 【答案】BC 【分析】作出三棱锥M ABC -直观图,在每个三角形中利用向量的线性运算可得. 【详解】对于A ,由已知12322233AD AB AC AD AC AB AD AC AB AD =+⇒=+⇒-=-,即2CD DB =,则32BD BD DC BC =+=,故A 错误; 对于B ,由G 为ABC 的重心,得0GA GB GC ++=,又MG MA AG =+,MG MB BG =+,MG MC CG =+,3MA MB MC MG ∴++=,即111333MG MA MB MC =++,故B 正确;对于C ,若0MA BC ⋅=,0MC AB ⋅=,则0MC MA BC AB ⋅+⋅=,即()00MA BC AC CB MA BC AC C MC C M B M C ⋅++=⇒⋅++⋅⋅=⋅()00MA BC A MC MC MC MC C BC MA BC AC ⋅⋅⋅⇒⋅+-=⇒-+=⋅()000MC M CA BC AC AC CB AC CB AC C MC ⇒+=⇒+=⇒+=⋅⋅⋅⋅⋅,即0MB AC ⋅=,故C 正确;对于D ,111()()222PQ MQ MP MB MC MA MB MC MA ∴=-=+-=+- ()21122PQ MB MC MA MB MC MA ∴=+-=+-,又()2222222MB MC MA MB MC MA MB MC MB MA MC MA+-=+++⋅-⋅-⋅2221112222222222228222=+++⨯⨯⨯-⨯⨯⨯-⨯⨯⨯=,1822PQ ∴==,故D 错误. 故选:BC 【点睛】关键点睛:本题考查向量的运算,用已知向量表示某一向量的三个关键点: (1)用已知向量来表示某一向量,一定要结合图形,以图形为指导是解题的关键.(2)要正确理解向量加法、减法与数乘运算的几何意义,如首尾相接的若干向量之和,等于由起始向量的始点指向末尾向量的终点的向量. (3)在立体几何中三角形法则、平行四边形法则仍然成立.5.正方体1111ABCD A B C D -中,E 是棱1DD 的中点,F 在侧面11CDD C 上运动,且满足1//B F 平面1A BE .以下命题正确的有( )A .侧面11CDD C 上存在点F ,使得11B F CD ⊥ B .直线1B F 与直线BC 所成角可能为30︒C .平面1A BE 与平面11CDD C 所成锐二面角的正切值为2D .设正方体棱长为1,则过点E ,F ,A 5 【答案】AC 【分析】取11C D 中点M ,1CC 中点N ,连接11,,B M B N MN ,易证得平面1//B MN 平面1A BE ,可得点F 的运动轨迹为线段MN .取MN 的中点F ,根据等腰三角形的性质得1B F MN ⊥,即有11B F CD ⊥,A 正确;当点F 与点M 或点N 重合时,直线1B F 与直线BC 所成角最大,可判断B 错误;根据平面1//B MN 平面1A BE ,11B FC ∠即为平面1B MN 与平面11CDD C 所成的锐二面角,计算可知C 正确;【详解】取11C D 中点M ,1CC 中点N ,连接11,,B M B N MN ,则易证得11//B N A E ,1//MN A B ,从而平面1//B MN 平面1A BE ,所以点F 的运动轨迹为线段MN .取MN 的中点F ,因为1B MN △是等腰三角形,所以1B F MN ⊥,又因为1//MN CD ,所以11B F CD ⊥,故A 正确;设正方体的棱长为a ,当点F 与点M 或点N 重合时,直线1B F 与直线BC 所成角最大,此时11tan C B F ∠=1tan 3023︒<=,所以B 错误; 平面1//B MN 平面1A BE ,取F 为MN 的中点,则1MN C F ⊥,1MN B F ⊥,∴11B FC ∠即为平面1B MN 与平面11CDD C 所成的锐二面角,11111tan B C B FC C F ∠==22,所以C 正确;因为当F 为1C E 与MN 的交点时,截面为菱形1AGC E (G 为1BB 的交点),面积为62,故D 错误. 故选:AC.【点睛】本题主要考查线面角,二面角,截面面积的求解,空间几何中的轨迹问题,意在考查学生的直观想象能力和数学运算能力,综合性较强,属于较难题.6.如图,点E 为正方形ABCD 边CD 上异于点C ,D 的动点,将ADE 沿AE 翻折成SAE △,在翻折过程中,下列说法正确的是( )A .存在点E 和某一翻折位置,使得SB SE ⊥ B .存在点E 和某一翻折位置,使得//AE 平面SBCC .存在点E 和某一翻折位置,使得直线SB 与平面ABC 所成的角为45°D .存在点E 和某一翻折位置,使得二面角S AB C --的大小为60° 【答案】ACD 【分析】依次判断每个选项:当SE CE ⊥时,⊥SE SB ,A 正确,//AE 平面SBC ,则//AE CB ,这与已知矛盾,故B 错误,取二面角D AE B --的平面角为α,取4=AD ,计算得到2cos 3α=,C 正确,取二面角D AE B --的平面角为60︒,计算得到5tan 5θ=,故D 正确,得到答案.当SE CE ⊥时,SE AB ⊥,SE SA ⊥,故SE ⊥平面SAB ,故⊥SE SB ,A 正确; 若//AE 平面SBC ,因AE ⊂平面ABC ,平面ABC 平面SBC BC =,则//AE CB ,这与已知矛盾,故B 错误;如图所示:DF AE ⊥交BC 于F ,交AE 于G ,S 在平面ABCE 的投影O 在GF 上, 连接BO ,故SBO ∠为直线SB 与平面ABC 所成的角,取二面角D AE B --的平面角为α,取4=AD ,3DE =,故5AE DF ==,1CE BF ==,125DG =,12cos 5OG α=,故只需满足12sin 5SO OB α==, 在OFB △中,根据余弦定理:2221213121312sin 1cos 2cos cos 55555OFB ααα⎛⎫⎛⎫⎛⎫=+---∠ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭,解得2cos 3α=,故C 正确; 过O 作OMAB ⊥交AB 于M ,则SMO ∠为二面角S AB C --的平面角,取二面角D AE B --的平面角为60︒,故只需满足22DG GO OM ==,设OAG OAM θ∠=∠=,84ππθ<<,则22DAG πθ∠=-,tan tan 22DG OGAG πθθ==⎛⎫- ⎪⎝⎭,化简得到2tan tan 21θθ=,解得5tan θ=,验证满足,故D 正确; 故选:ACD .【点睛】本题考查了线线垂直,线面平行,线面夹角,二面角,意在考查学生的计算能力,推断能力和空间想象能力.7.如图,已知矩形ABCD 中,2AB AD =,E 为边AB 的中点,将ADE ∆沿直线DE 翻折成1A DE ∆,若M 为线段1A C 的中点,则ADE ∆在翻折过程中,下列说法正确的是A .线段BM 的长是定值B .存在某个位置,使1DE AC ⊥ C .点M 的运动轨迹是一个圆D .存在某个位置,使MB ⊥平面1A DE 【答案】AC 【分析】取CD 中点F ,连接BF ,MF ,根据面面平行的判定定理可得平面//BMF 平面1A DE ,由面面平行的性质定理可知//BM 平面1A DE ,可判断D ;在BFM ∆中,利用余弦定理可求得BM a =为定值,可判断A 和C ;假设1DE A C ⊥,由线面垂直的判定定理可得DE ⊥平面1A CE ,由线面垂直的性质定理可知1DE A E ⊥,与11DA A E ⊥矛盾,可判断B . 【详解】解:取CD 的中点F ,连接BF ,MF ,∵M ,F 分别为1A C 、CD 中点, ∴1MF A D ∥,∵1A D ⊂平面1A DE ,MF ⊄平面1A DE , ∴MF 平面1A DE , ∵DF BE ∥且DF BE =, ∴四边形BEDF 为平行四边形, ∴BFDE ,∵DE ⊂平面1A DE ,BF ⊄平面1A DE , ∴BF ∥平面1A DE , 又BFMF F =,BF 、MF ⊂平面BMF ,∴平面//BMF 平面1A DE , ∵BM ⊂平面BMF ,∴BM ∥平面1A DE ,即D 错误,设22AB AD a ==,则112MF A D a ==,BF DE ==,145A DE MFB ︒∠=∠=,∴BM a ==,即BM 为定值,所以A 正确,∴点M 的轨迹是以B 为圆心,a 为半径的圆,即C 正确, ∵DE CE ==,2CD AB a ==,∴222DE CE CD +=,∴DE CE ⊥, 设1DE A C ⊥,∵1A C 、CE ⊂平面1A CE ,1AC CE C =,∴DE ⊥平面1A CE , ∵1A E ⊂平面1A CE ,∴1DE A E ⊥,与11DA A E ⊥矛盾, 所以假设不成立,即B 错误. 故选:AC . 【点睛】本题考查立体几何中的翻折问题,涉及到线段长度的求解、直线与平面位置关系的判定、点的轨迹的求解、反证法的应用等知识点,考查学生的空间立体感和推理论证能力.8.已知正四棱柱1111ABCD A B C D -的底面边长为2,侧棱11AA =,P 为上底面1111D C B A 上的动点,给出下列四个结论中正确结论为( )A .若3PD =,则满足条件的P 点有且只有一个B .若PD =,则点P 的轨迹是一段圆弧C .若PD ∥平面1ACB ,则DP 长的最小值为2D .若PD ∥平面1ACB ,且PD =,则平面BDP 截正四棱柱1111ABCD A B C D -的外接球所得平面图形的面积为94π【答案】ABD 【分析】若3PD =,由于P 与1B 重合时3PD =,此时P 点唯一;()13PD =,,则1PD =P 的轨迹是一段圆弧;当P 为11A C 中点时,DP 有最小值为=断C ;平面BDP 截正四棱柱1111ABCD A B C D -的外接球所得平面图形为外接球的大圆,其半径为32=,可得D . 【详解】 如图:∵正四棱柱1111ABCD A B C D -的底面边长为2, ∴1122B D =,又侧棱11AA =, ∴()2212213DB =+=,则P 与1B 重合时3PD =,此时P 点唯一,故A 正确;∵()313PD =∈,,11DD =,则12PD =,即点P 的轨迹是一段圆弧,故B 正确; 连接1DA ,1DC ,可得平面11//A DC 平面1ACB ,则当P 为11A C 中点时,DP 有最小值为()22213+=,故C 错误;由C 知,平面BDP 即为平面11BDD B ,平面BDP 截正四棱柱1111ABCD A B C D -的外接球所得平面图形为外接球的大圆,其半径为2221322122++=,面积为94π,故D 正确. 故选:ABD . 【点睛】本题考查了立体几何综合,考查了学生空间想象,逻辑推理,转化划归,数学运算的能力,属于较难题.9.如图,正三棱柱11ABC A B C -中,11BC AB ⊥、点D 为AC 中点,点E 为四边形11BCC B 内(包含边界)的动点则以下结论正确的是( )A .()1112DA A A B A BC =-+B .若//DE 平面11ABB A ,则动点E的轨迹的长度等于2AC C .异面直线AD 与1BC ,所成角的余弦值为6D .若点E 到平面11ACC A 的距离等于2EB ,则动点E 的轨迹为抛物线的一部分 【答案】BCD 【分析】根据空间向量的加减法运算以及通过建立空间直角坐标系求解,逐项判断,进而可得到本题答案. 【详解】解析:对于选项A ,()1112AD A A B A BC =-+,选项A 错误; 对于选项B ,过点D 作1AA 的平行线交11A C 于点1D .以D 为坐标原点,1DA DB DD ,,分别为,,x y z 轴的正方向建立空间直角坐标系Oxyz .设棱柱底面边长为a ,侧棱长为b ,则002aA ⎛⎫ ⎪⎝⎭,,,002B a ⎛⎫ ⎪ ⎪⎝⎭,,,102B a b ⎛⎫ ⎪ ⎪⎝⎭,,,102a C b⎛⎫- ⎪⎝⎭,,,所以122a BC a b ⎛⎫=-- ⎪ ⎪⎝⎭,,,122a AB a b ⎛⎫=- ⎪ ⎪⎝⎭,,. ∵11BC AB ⊥,∴110BC AB ⋅=,即22202a b ⎫⎛⎫--+=⎪ ⎪⎪⎝⎭⎝⎭,解得b =. 因为//DE 平面11ABB A ,则动点E 的轨迹的长度等于1BB =.选项B 正确. 对于选项C ,在选项A 的基础上,002a A ⎛⎫⎪⎝⎭,,,002B a ⎛⎫ ⎪ ⎪⎝⎭,,,()0,0,0D ,1022a C a ⎛⎫- ⎪ ⎪⎝⎭,,,所以002a DA ⎛⎫= ⎪⎝⎭,,,122a BC a ⎛⎫=- ⎪ ⎪⎝⎭,,因为2111cos ,6||||a BC DA BC DA BC DA a ⎛⎫- ⎪⋅<>===-,所以异面直线1,BC DA 所成角的余弦值为6,选项C 正确. 对于选项D ,设点E 在底面ABC 的射影为1E ,作1E F 垂直于AC ,垂足为F ,若点E 到平面11ACC A 的距离等于3EB ,即有31E F EB =,又因为在1CE F ∆中,311E F E C =,得1EB E C =,其中1E C 等于点E 到直线1CC 的距离,故点E 满足抛物线的定义,另外点E 为四边形11BCC B 内(包含边界)的动点,所以动点E 的轨迹为抛物线的一部分,故D 正确.故选:BCD 【点睛】本题主要考查立体几何与空间向量的综合应用问题,其中涉及到抛物线定义的应用.10.如图所示,正方体ABCD A B C D ''''-的棱长为1,E ,F 分别是棱AA ',CC '的中点,过直线EF 的平面分别与棱BB ',DD '交于点M ,N ,以下四个命题中正确的是( )A .0MN EF ⋅=B .ME NE =C .四边形MENF 的面积最小值与最大值之比为2:3D .四棱锥A MENF -与多面体ABCD EMFN -体积之比为1:3 【答案】ABD 【分析】证明EF ⊥平面BDD B '',进而得EF MN ⊥,即可得A 选项正确;证明四边形MENF 为菱形即可得B 选项正确;由菱形性质得四边形MENF 的面积12S MN EF =⋅,再分别讨论MN 的最大值与最小值即可;根据割补法求解体积即可. 【详解】对于A 选项,如图,连接BD ,B D '',MN .由题易得EF BD ⊥,EFBB '⊥,BD BB B '⋂=,所以EF ⊥平面BDD B '',又MN ⊂平面BDD B '',所以EF MN ⊥,因此0MN EF ⋅=,故A 正确.对于B 选项,由正方体性质得:平面''//BCC B 平面''ADD A ,平面''BCC B 平面EMFN MF =,平面''ADD A 平面EMFN EN =, 所以//MF EN ,同理得//ME NF ,又EF MN ⊥,所以四边形MENF 为菱形, 因此ME NE =,故B 正确.对于C 选项,由B 易得四边形MENF 的面积12S MN EF =⋅, 所以当点M ,N 分别为BB ',DD '的中点时,四边形MENF 的面积S 最小,此时MN EF ==,即面积S 的最小值为1;当点M ,N 分别与点B (或点B '),D (或D )重合时,四边形MENF 的面积S 最大,此时MN =,即面积S 的最大值为2所以四边形MENF 的面积最小值与最大值之比为2C 不正确. 对于D 选项,四棱锥A MENF -的体积11113346M AEF N AEF AEF V V V DB S --=+=⋅==△; 因为E ,F 分别是AA ',CC '的中点,所以BM D N '=,DN B M '=,于是被截面MENF 平分的两个多面体是完全相同的,则它们的体积也是相同的,因此多面体ABCD EMFN -的体积21122ABCD A B C D V V ''''-==正方体,所以四棱锥A MENF -与多面体ABCD EMFN -体积之比为1:3,故D 正确. 故选:ABD .【点睛】本题考查立体几何与向量的综合、截面面积的最值、几何体的体积,考查空间思维能力与运算求解能力,是中档题.本题解题的关键在于证明四边形MENF 为菱形,利用割补法将四棱锥A MENF -的体积转化为三棱锥M AEF - 和N AEF -的体积之和,将多面体ABCD EMFN -的体积转化为正方体的体积的一半求解.。
立体几何多选题 易错题难题测试基础卷试卷

立体几何多选题 易错题难题测试基础卷试卷一、立体几何多选题1.在三棱柱111ABC A B C -中,ABC ∆是边长为23的等边三角形,侧棱长为43,则( )A .直线1A C 与直线1BB 之间距离的最大值为3B .若1A 在底面ABC 上的投影恰为ABC ∆的中心,则直线1AA 与底面所成角为60︒ C .若三棱柱的侧棱垂直于底面,则异面直线AB 与1A C 所成的角为30D .若三棱柱的侧棱垂直于底面,则其外接球表面积为64π 【答案】AD 【分析】建立空间直角坐标系,用向量法求解. 【详解】如图示,以A 为原点,AC 为y 轴正方向,Ax 为x 轴正方向,过A 点垂直于面ABC 的向上方向为z 轴正方向建系,则()()()0,0,0,3,0,0,23,0,A B C 设()()()100010001000,,,3,3,,,23,,A x y z B x y z C x y z ++所以()()()1000100011,23,,,,,3,3,0,AC x y z BB x y z A B =---== 对于A:设n 为直线1A C 与直线1BB 的公垂线的方向向量,则有:11·0·0AC n BB n ⎧=⎪⎨=⎪⎩,即()()0000002300x x y y zz x x y y zz ⎧-+-=⎪⎨++=⎪⎩解得:()00,0n z x =- 设直线1A C 与直线1BB 之间距离为d ,则22011222200009||||z A B nd d x z n x z ===++ 22009x d ≥∴≤,即3d ≤,故A 正确;对于B :若1A 在底面ABC 上的投影恰为ABC ∆的中心,则()11,3,211A 底面法向量()()10,0,1,1,3,211m AA ==,设直线 1AA 与底面所成角为θ,则:121133sin |cos ,|6143AA n θ===⨯,故B 错误; 对于C : 三棱柱的侧棱垂直于底面时,则()()()1110,0,43,3,3,43,0,23,43,A B C则()()13,3,0,0,23,43,AB AC ==-设异面直线AB 与1A C 所成的角为θ,则1115cos |cos ,|||||||23215AB AC AB AC AB AC θ====⨯,故C 错误;对于D :若三棱柱的侧棱垂直于底面时,外接球的球心O 为上下底面中心DD 1连线的中点,所以外接球的半径()222324R =+=,所以2464S R ππ==.故D 正确故选:AD 【点睛】向量法解决立体几何问题的关键: (1)建立合适的坐标系; (2)把要用到的向量正确表示; (3)利用向量法证明或计算.2.已知球O 为正方体1111ABCD A B C D -的内切球,平面11A C B 截球O 的面积为24π,下列命题中正确的有( )A .异面直线AC 与1BC 所成的角为60°B .1BD ⊥平面11AC B C .球O 的表面积为36πD .三棱锥111B AC B -的体积为288 【答案】AD 【分析】连接11A C ,1A B ,通过平移将AC 与1BC 所成角转化为11A C 与1BC 所成角可判断A ;通过反证法证明B ;由已知平面11A C B 截球O 的面积为24π求出正方体棱长,进而求出内切球的表面积可判断C ;利用等体积法可求得三棱锥111B AC B -的体积可判断D. 【详解】对于A ,连接11A C ,1A B ,由正方体1111ABCD A B C D -,可知11//A C AC ,11AC B ∴∠为异面直线AC 与1BC 所成的角,设正方体边长为a,则1111AC A B BC ==,由等边三角形知1160A C B ∠=,即异面直线AC 与1BC 所成的角为60,故A 正确; 对于B ,假设1BD ⊥平面11A C B ,又1A B ⊂平面11A C B ,则11BD B A ⊥,设正方体边长为a ,则11A D a =,1A B =,1BD =,由勾股定理知111A D B A ⊥,与假设矛盾,假设不成立,故1BD 不垂直于平面11A C B ,故B 错误; 对于C ,设正方体边长为a,则11AC =,内切球半径为2a,设内切球的球心O 在面11A C B 上的投影为O ',由等边三角形性质可知O '为等边11A C B △的重心,则11123233O A AC a ='=⨯=,又12OA a =,∴球心O 到面11A C B 的距离6a ==,又球心与截面圆心的连线垂直于截面,∴6a =,又截面圆的面积2246S a ππ⎛⎫= ⎪ ⎪⎝⎭=,解得12a =,则内切球半径为6,内切球表面积214644S ππ==⨯,故C 错误;对于D ,由等体积法知111111111111212122812383B A C B B A C B A C B V V S a --==⨯⨯=⨯⨯=,故D 正确; 故选:AD【点睛】关键点点睛:本题考查了正方体和它的内切球的几何结构特征,关键是想象出截面图的形状,从而求出正方体的棱长,进而求出内切球的表面积及三棱锥的体积,考查了空间想象能力,数形结合的思想,属于较难题.3.如图,一个结晶体的形状为平行六面体1111ABCD A B C D -,其中,以顶点A 为端点的三条棱长都等于1,且它们彼此的夹角都是60,下列说法中正确的是( )A .()()2212AA AB ADAC ++=B .1A 在底面ABCD 上的射影是线段BD 的中点C .1AA 与平面ABCD 所成角大于45 D .1BD 与AC 6 【答案】AC 【分析】对A ,分别计算()21++AA AB AD 和2AC ,进行判断;对B ,设BD 中点为O ,连接1A O ,假设1A 在底面ABCD 上的射影是线段BD 的中点,应得10⋅=O AB A ,计算10⋅≠O AB A ,即可判断1A 在底面ABCD 上的射影不是线段BD 的中点;对C ,计算11,,A A AC AC ,根据勾股定理逆定理判断得11⊥A A AC ,1AA 与平面ABCD 所成角为1A AC ∠,再计算1tan ∠A AC ;对D ,计算1,AC BD 以及1BD AC ⋅,再利用向量的夹角公式代入计算夹角的余弦值.【详解】对A ,由题意,11111cos602⋅=⋅=⋅=⨯⨯=AA AB AA AD AD AB ,所以()2222111112221113262++=+++⋅+⋅+⋅=+++⨯⨯=AA AB ADAA AB AD AA AB AB AD AA AD ,AC AB AD =+,所以()222221113=+=+⋅+=++=AC AB ADAB AB AD AD ,所以()()22126++==AA AB AD AC ,故A 正确;对B ,设BD 中点为O ,连接1A O ,1111111222=+=+=++AO A A AO A A AC A A AD AB ,若1A 在底面ABCD 上的射影是线段BD 的中点,则1A O ⊥平面ABCD ,则应10⋅=O AB A ,又因为21111111111110222222224⎛⎫⋅=++⋅=-⋅+⋅+=-+⨯+=≠ ⎪⎝⎭O AB A A AD AB AB AA AB AD AB AB A ,故B 错误;对D ,11,BD AD AA AB AC AB AD =+-=+,所以()()2211=2,=3=+-=+AD A B A AB AC AB AD D ,()()2211111⋅=+-⋅+=⋅++⋅+⋅--⋅=AC AD AA AB AB AD AD AB AD AA AB AA AD ABAB AD BD ,1116cos ,23⋅<>===⋅B AC D BD BD AC AC,故D 不正确;对C ,112==AC BD ,在1A AC 中,111,2,3===A A AC AC ,所以22211+=A A AC AC ,所以11⊥A A AC ,所以1AA 与平面ABCD 所成角为1A AC ∠,又1tan 21∠=>A AC ,即145∠>A AC ,故C 正确;故选:AC【点睛】方法点睛:用向量方法解决立体几何问题,需要树立“基底”意识,利用基向量进行线性运算,要理解空间向量概念、性质、运算,注意和平面向量类比;同时对于立体几何中角的计算问题,往往可以利用空间向量法,利用向量的夹角公式求解.4.在直角梯形ABCD 中,2ABC BCD π∠=∠=,1AB BC ==,2DC =,E 为DC 中点,现将ADE 沿AE 折起,得到一个四棱锥D ABCE -,则下列命题正确的有( ) A .在ADE 沿AE 折起的过程中,四棱锥D ABCE -体积的最大值为13B .在ADE 沿AE 折起的过程中,异面直线AD 与BC 所成的角恒为4π C .在ADE 沿AE 折起的过程中,二面角A EC D --的大小为45︒D .在四棱锥D ABCE -中,当D 在EC 上的射影恰好为EC 的中点F 时,DB 与平面ABCE 所成的角的正切为15 【答案】ABD 【分析】对于A ,四棱锥D ABCE -的底面面积是固定值,要使得体积最大,需要平面DAE ⊥平面ABCE ,此时DE CE ⊥,可求得1133D ABCE ABCE V S DE -=⋅=可判断A ;对于B ,在ADE 沿AE 折起的过程中,//AE BC ,所以异面直线AD 与AE 所成的角即为AD 与BC所成角,由翻折前可知4DAE π∠=可判断B ;对于C ,利用线面垂直的判定定理,结合翻折前可知AE ⊥平面DEC ,又AE ⊂平面ABCE ,所以平面DEC ⊥平面ABCE ,即二面角A EC D --的在大小为2π判断C ;对于D ,利用线面垂直的判定定理可知DF ⊥平面ABCE ,所以DBF ∠为直线DB 与平面ABCE 所成的角,在直角DFB △中,15tan 5DF DBF BF ∠==,可判断D 正确;【详解】对于A ,ADE 沿AE 折起得到四棱锥D ABCE -,由四棱锥底面面积是固定值,要使得体积最大,需要四棱锥的高最大,即平面DAE ⊥平面ABCE ,此时DE CE ⊥,由已知得1DE =,则111111333D ABCE ABCE V S DE -=⋅=⨯⨯⨯=,故A 正确; 对于B ,在ADE 沿AE 折起的过程中,//AE BC ,所以异面直线AD 与AE 所成的角即为AD 与BC 所成角,又1AB BC ==,2DC =,E 为DC 中点,可知4DAE π∠=,即异面直线AD 与BC 所成的角恒为4π,故B 正确; 对于C ,由翻折前知,,AE EC AE ED ⊥⊥,且ECED E =,则AE ⊥平面DEC ,又AE ⊂平面ABCE ,所以平面DEC ⊥平面ABCE ,即二面角A EC D --的大小为2π,故C 错误; 对于D ,如图连接,DF BF ,由C 选项知,AE ⊥平面DEC ,又DF ⊂平面DEC ,则AE DF ⊥,又由已知得EC DF ⊥,且EC AE E ⋂=,则DF ⊥平面ABCE ,所以DBF ∠为直线DB 与平面ABCE 所成的角,在直角DFB △中,tan DFDBF BF∠=====DB 与平面ABCE所成的角的正切为5,故D 正确; 故选:ABD 【点睛】关键点睛:本题考查立体几何综合问题,求体积,求线线角,线面角,面面角,解题的关键要熟悉几种角的定义,通过平移法找到线线角,通过证垂直找到线面角和面面角,再结合三角形求出角,考查了学生的逻辑推理能力,转化能力与运算求解能力,属于难题.5.已知正方体1111ABCD A B C D -的棱长为2,点O 为11A D 的中点,若以O为半径的球面与正方体1111ABCD A B C D -的棱有四个交点E ,F ,G ,H ,则下列结论正确的是( )A .11//A D 平面EFGHB .1AC ⊥平面EFGHC .11A B 与平面EFGH 所成的角的大小为45°D .平面EFGH 将正方体1111ABCD A B C D -分成两部分的体积的比为1:7 【答案】ACD 【分析】如图,计算可得,,,E F G H 分别为所在棱的中点,利用空间中点线面的位置关系的判断方法可判断A 、B 的正确与否,计算出直线AB 与平面EFGH 所成的角为45︒后可得C 正确,而几何体BHE CGF -为三棱柱,利用公式可求其体积,从而可判断D 正确与否. 【详解】如图,连接OA ,则2115OA AA =+=,故棱1111,,,A A A D D D AD 与球面没有交点.同理,棱111111,,A B B C C D 与球面没有交点. 因为棱11A D 与棱BC 之间的距离为26>BC 与球面没有交点.因为正方体的棱长为2,而26<球面与正方体1111ABCD A B C D -的棱有四个交点E ,F ,G ,H , 所以棱11,,,AB CD C C B B 与球面各有一个交点, 如图各记为,,,E F G H .因为OAE △为直角三角形,故22651AE OE OA -=-=,故E 为棱AB 的中点. 同理,,F G H 分别为棱11,,CD C C B B 的中点.由正方形ABCD 、,E F 为所在棱的中点可得//EF BC , 同理//GH BC ,故//EF GH ,故,,,E F G H 共面. 由正方体1111ABCD A B C D -可得11//A D BC ,故11//A D EF因为11A D ⊄平面EFGH ,EF ⊂平面EFGH ,故11//A D 平面EFGH ,故A 正确. 因为在直角三角1BA C 中,122A B =2BC = ,190A BC ∠=︒, 1A C 与BC 不垂直,故1A C 与GH 不垂直,故1A C ⊥平面EFGH 不成立,故B 错误.由正方体1111ABCD A B C D -可得BC ⊥平面11AA B B ,而1A B ⊂平面11AA B B , 所以1BC A B ⊥,所以1EF A B ⊥在正方形11AA B B 中,因为,E H 分别为1,AB BB 的中点,故1EH A B ⊥, 因为EFEH E =,故1A B ⊥平面EFGH ,所以BEH ∠为直线AB 与平面EFGH 所成的角,而45BEH ∠=︒, 故直线AB 与平面EFGH 所成的角为45︒,因为11//AB A B ,故11A B 与平面EFGH 所成的角的大小为45°.故C 正确. 因为,,,E F G H 分别为所在棱的中点,故几何体BHE CGF -为三棱柱, 其体积为111212⨯⨯⨯=,而正方体的体积为8, 故平面EFGH 将正方体1111ABCD A B C D -分成两部分的体积的比为1:7,故D 正确. 故选:ACD. 【点睛】本题考查空间中线面位置的判断、空间角的计算和体积的计算,注意根据球的半径确定哪些棱与球面有交点,本题属于中档题.6.如图,已知矩形ABCD 中,2AB AD =,E 为边AB 的中点,将ADE ∆沿直线DE 翻折成1A DE ∆,若M 为线段1A C 的中点,则ADE ∆在翻折过程中,下列说法正确的是( )A .线段BM 的长是定值B .存在某个位置,使1DE AC ⊥ C .点M 的运动轨迹是一个圆D .存在某个位置,使MB ⊥平面1A DE 【答案】AC 【分析】取CD 中点F ,连接BF ,MF ,根据面面平行的判定定理可得平面//BMF 平面1A DE ,由面面平行的性质定理可知//BM 平面1A DE ,可判断D ;在BFM ∆中,利用余弦定理可求得BM a =为定值,可判断A 和C ;假设1DE A C ⊥,由线面垂直的判定定理可得DE ⊥平面1A CE ,由线面垂直的性质定理可知1DE A E ⊥,与11DA A E ⊥矛盾,可判断B . 【详解】解:取CD 的中点F ,连接BF ,MF ,∵M ,F 分别为1A C 、CD 中点,∴1MF A D ∥,∵1A D ⊂平面1A DE ,MF ⊄平面1A DE , ∴MF 平面1A DE , ∵DF BE ∥且DF BE =, ∴四边形BEDF 为平行四边形, ∴BFDE ,∵DE ⊂平面1A DE ,BF ⊄平面1A DE , ∴BF ∥平面1A DE , 又BFMF F =,BF 、MF ⊂平面BMF ,∴平面//BMF 平面1A DE , ∵BM ⊂平面BMF , ∴BM ∥平面1A DE ,即D 错误,设22AB AD a ==,则112MF A D a ==,BF DE ==,145A DE MFB ︒∠=∠=,∴BM a ==,即BM 为定值,所以A 正确,∴点M 的轨迹是以B 为圆心,a 为半径的圆,即C 正确, ∵DE CE ==,2CD AB a ==,∴222DE CE CD +=,∴DE CE ⊥, 设1DE A C ⊥,∵1A C 、CE ⊂平面1A CE ,1AC CE C =,∴DE ⊥平面1A CE , ∵1A E ⊂平面1A CE ,∴1DE A E ⊥,与11DA A E ⊥矛盾, 所以假设不成立,即B 错误. 故选:AC . 【点睛】本题考查立体几何中的翻折问题,涉及到线段长度的求解、直线与平面位置关系的判定、点的轨迹的求解、反证法的应用等知识点,考查学生的空间立体感和推理论证能力.7.如图,1111ABCD A B C D -为正方体,下列结论中正确的是( )A .11A C ⊥平面11BB D DB .1BD ⊥平面1ACBC .1BD 与底面11BCC B 2D .过点1A 与异面直线AD 与1CB 成60角的直线有2条【答案】ABD【分析】由直线与平面垂直的判定判断A 与B ;求解1BD 与底面11BCC B 所成角的正切值判断C ;利用空间向量法可判断D .【详解】对于A 选项,如图,在正方体1111ABCD A B C D -中,1BB ⊥平面1111D C B A ,11A C ⊂平面1111D C B A ,则111BB A C ⊥,由于四边形1111D C B A 为正方形,则1111AC B D ⊥, 1111BB B D B =,因此,11A C ⊥平面11BB D D ,故A 正确;对于B 选项,在正方体1111ABCD A B C D -中,1DD ⊥平面ABCD ,AC ⊂平面ABCD ,1AC DD ∴⊥,因为四边形ABCD 为正方形,所以,AC BD ⊥,1D DD BD =,AC ∴⊥平面11BB D D ,1BD ⊂平面11BB D D ,1AC BD ∴⊥,同理可得11BD B C ⊥, 1ACB C C =,1BD ∴⊥平面1ACB ,故B 正确; 对于C 选项,由11C D ⊥平面11BCC B ,得11C BD ∠为1BD 与平面11BCC B 所成角, 且111112tan 2C D C BD BC ∠==,故C 错误; 对于D 选项,以点D 为坐标原点,DA 、DC 、1DD 所在直线分别为x 、y 、z 轴建立如下图所示的空间直角坐标系,设正方体的棱长为1,则()1,0,0A 、()0,0,0D 、()0,1,0C 、()11,1,1B ,()1,0,0DA =,()11,0,1CB =,设过点1A 且与直线DA 、1CB 所成角的直线的方向向量为()1,,m y z =, 则221cos ,21DA mDA m DA m y z ⋅<>===⋅++, 1122111cos ,221CB m z CB m CB m y z ⋅+<>===⋅⋅++, 整理可得2222341y z y z z ⎧+=⎨=++⎩,消去y 并整理得2210z z +-=,解得12z =-12z =-由已知可得3z ≤,所以,12z =-+22y =±因此,过点1A 与异面直线AD 与1CB 成60角的直线有2条,D 选项正确.故选:ABD.【点睛】方法点睛:证明线面垂直的方法:一是线面垂直的判定定理;二是利用面面垂直的性质定理;三是平行线法(若两条平行线中一条垂直于这个平面,则另一条也垂直于这个平面),解题时,注意线线、线面与面面关系的相互转化;另外,在证明线线垂直时,要注意题中隐含的垂直关系,如等腰三角形的底边上的高、中线和顶角的角平分线三线合一、矩形的内角、直径所对的圆周角、菱形的对角线互相垂直、直角三角形(或给出线段长度,经计算满足勾股定理)、直角梯形等等.8.如图,已知P 为棱长为1的正方体对角线1BD 上的一点,且()()10,1BP BD λλ=,下面结论中正确结论的有( )A .11A D C P ⊥;B .当1A P PD +取最小值时,23λ=;C .若()0,1λ∈,则7,312APC ππ⎛⎫∠∈ ⎪⎝⎭; D .若P 为1BD 的中点,四棱锥11P AA D D -的外接球表面积为94π. 【答案】ABD【分析】以D 为坐标原点建立如图空间直角坐标系,利用向量关系可判断ABC ;根据几何体外接球关系建立方程求出球半径即可判断D.【详解】以D 为坐标原点建立如图空间直角坐标系,则()1,1,0B ,()10,0,1D ,设(),,P x y z ,()()10,1BP BD λλ=,1BP BD λ∴=,即()()1,1,1,1,1x y z λ--=--,则可解得()1,1,P λλλ--,对A ,()()()111,0,1,0,0,0,0,1,1A D C ,()11,0,1A D ∴=--,()11,,1C P λλλ=---,则()()()()11110110A D C P λλλ⋅=-⨯-+⨯-+-⨯-=,则11A D C P ⊥,故A 正确;对B ,1A P PD +=== 则当23λ=时,1A P PD +取最小值,故B 正确; 对C ,()()1,0,0,0,1,0A C ,(),1,PA λλλ∴=--,()1,,PC λλλ=--,则222321cos 1321321PA PC APC PA PC λλλλλλ⋅-∠===--+-+⋅, 01λ<<,则2232123λλ≤-+<,则2111123212λλ-≤-<-+, 即11cos 22APC -≤∠<,则2,33APC ππ⎛⎤∠∈ ⎥⎝⎦,故C 错误; 对于D ,当P 为1BD 中点时,四棱锥11P AA D D -为正四棱锥,设平面11AA D D 的中心为O ,四棱锥11P AA D D -的外接球半径为R ,所以222122R R ⎛⎛⎫-+= ⎪ ⎝⎭⎝⎭,解得34R =, 故四棱锥11P AA D D -的外接球表面积为94π,所以D 正确. 故选:ABD.【点睛】 关键点睛:本题考查空间相关量的计算,解题的关键是建立空间直角坐标系,利用向量建立关系进行计算.。
高三数学易错立体几何多选题 易错题综合模拟测评检测试题

高三数学易错立体几何多选题 易错题综合模拟测评检测试题一、立体几何多选题1.如图,在棱长为2的正方体ABCD A B C D ''''-中,M 为BC 边的中点,下列结论正确的有( )A .AM 与DB ''10 B .过三点A 、M 、D 的正方体ABCD A BCD ''''-的截面面积为92C .四面体A C BD ''的内切球的表面积为3π D .正方体ABCD A B C D ''''-中,点P 在底面A B C D ''''(所在的平面)上运动并且使MAC PAC ''∠=∠,那么点P 的轨迹是椭圆 【答案】AB 【分析】构建空间直角坐标系,由异面直线方向向量的夹角cos ,||||AM D B AM D B AM D B ''⋅''<>=''为AM 与D B ''所成角的余弦值判断A 的正误;同样设(,,0)P x y 结合向量夹角的坐标表示,2221543x y =++⨯P 的轨迹知D 的正误;由立方体的截面为梯形,分别求,,,MN AD AM D N '',进而得到梯形的高即可求面积,判断B 的正误;由四面体的体积与内切球半径及侧面面积的关系求内切球半径r ,进而求内切球表面积,判断C 的正误. 【详解】A :构建如下图所示的空间直角坐标系:则有:(0,0,2),(1,2,2),(0,2,0),(2,0,0)A M B D '', ∴(1,2,0),(2,2,0)AM D B ''==-,10cos ,10||||58AM D B AM D B AM D B ''⋅''<>===''⨯,故正确.B :若N 为CC '的中点,连接MN ,则有//MN AD ',如下图示,∴梯形AMND’为过三点A 、M 、D 的正方体ABCD A B C D ''''-的截面, 而2,2,5MN AD AM D N ''====322, ∴梯形的面积为132932222S =⨯=,故正确. C :如下图知:四面体A C BD ''的体积为正方体体积减去四个直棱锥的体积,∴118848323V =-⨯⨯⨯=,而四面体的棱长都为22,有表面积为142222sin 8323S π=⨯⨯⨯⨯=,∴若其内切圆半径为r ,则有188333r ⨯⋅=,即33r =,所以内切球的表面积为2443r ππ=.故错误. D :正方体ABCD A B C D ''''-中,点P 在底面A B C D ''''(所在的平面)上运动且MAC PAC ''∠=∠,即P 的轨迹为面A B C D ''''截以AM 、AP 为母线,AC’为轴的圆锥体侧面所得曲线,如下图曲线GPK ,构建如下空间直角坐标系,232(0,0,2),(2),(0,22,0)22A M C '-,若(,,0)P x y ,则232(,,0),(0,22,2),(,,2)22AM AC AP x y '=-=-=-,∴15cos ||||512AMAC MAC AM AC '⋅'∠==='⨯,2222cos ||||43AP AC y PAC AP AC x y '⋅+'∠=='++⨯,即222215543y x y +=++⨯,整理得22(102)9216(0)y x y +-=>,即轨迹为双曲线的一支,故错误.故选:AB 【点睛】关键点点睛:应用向量的坐标表示求异面直线的夹角,并结合等角的余弦值相等及向量数量积的坐标表示求动点的轨迹,综合立方体的性质求截面面积,分割几何体应用等体积法求内切球半径,进而求内切球的表面积.2.如图,直三棱柱11,ABC A B C -,ABC 为等腰直角三角形,AB BC ⊥,且12AC AA ==,E ,F 分别是AC ,11A C 的中点,D ,M 分别是1AA ,1BB 上的两个动点,则( )A .FM 与BD 一定是异面直线B .三棱锥D MEF -的体积为定值14C .直线11B C 与BD 所成角为2π D .若D 为1AA 中点,则四棱锥1D BB FE -的外接球体积为556π 【答案】CD 【分析】A 当特殊情况M 与B 重合有FM 与BD 相交且共面;B 根据线面垂直、面面垂直判定可证面1BEFB ⊥面11ACC A ,可知EMFS、D 到面1BEFB 的距离,可求D EMF V -;C 根据线面垂直的判定及性质即可确定11B C 与BD 所成角;D 由面面垂直、勾股、矩形性质等确定外接球半径,进而求体积,即可判断各项的正误. 【详解】A :当M 与B 重合时,FM 与BD 相交且共面,错误; B :由题意知:BE AC ⊥,AC EF ⊥且BEEF E =,则AC ⊥面1BEFB ,又AC ⊂面11ACC A ,面1BEFB ⋂面11ACC A EF =,所以面1BEFB ⊥面11ACC A ,又1121122EMFSEF BE =⋅⋅=⨯⨯=,D 到面1BEFB 的距离为1h =,所以1133D EMF EMFV h S-=⋅⋅=,错误; C :由AB BC ⊥,1BC B B ⊥,1B BAB B =,所以BC ⊥面11ABB A ,又11//BC B C ,即11B C ⊥面11ABB A ,而BD ⊂面11ABB A ,则11BD B C ⊥,正确;D :由B 中,面1BEFB ⊥面11ACC A ,即面DEF ⊥面1BEFB ,则D 到面1BEFB 的距离为1h =,又D 为1AA 中点,若1,BF EB 交点为O ,G 为EF 中点,连接,,OG GD OD ,则OG GD ⊥,故225OD OG GD =+=,由矩形的性质知:152OB OE OF OB ====,令四棱锥1D BB FE -的外接球半径为R ,则5R =,所以四棱锥1D BB FE -的外接球体积为35435V R ππ==,正确. 故选:CD. 【点睛】关键点点睛:利用线面、面面关系确定几何体的高,结合棱锥体积公式求体积,根据线面垂直、勾股定理及矩形性质确定外接球半径,结合球体体积公式求体积.3.在三棱锥M ABC -中,下列命题正确的是( )A .若1233AD AB AC =+,则3BC BD = B .若G 为ABC 的重心,则111333MG MA MB MC =++C .若0MA BC ⋅=,0MC AB ⋅=,则0MB AC ⋅=D .若三棱锥M ABC -的棱长都为2,P ,Q 分别为MA ,BC 中点,则2PQ = 【答案】BC 【分析】作出三棱锥M ABC -直观图,在每个三角形中利用向量的线性运算可得. 【详解】对于A ,由已知12322233AD AB AC AD AC AB AD AC AB AD =+⇒=+⇒-=-,即2CD DB =,则32BD BD DC BC =+=,故A 错误; 对于B ,由G 为ABC 的重心,得0GA GB GC ++=,又MG MA AG =+,MG MB BG =+,MG MC CG =+,3MA MB MC MG ∴++=,即111333MG MA MB MC =++,故B 正确;对于C ,若0MA BC ⋅=,0MC AB ⋅=,则0MC MA BC AB ⋅+⋅=,即()00MA BC AC CB MA BC AC C MC C M B M C ⋅++=⇒⋅++⋅⋅=⋅()00MA BC A MC MC MC MC C BC MA BC AC ⋅⋅⋅⇒⋅+-=⇒-+=⋅()000MC M CA BC AC AC CB AC CB AC C MC ⇒+=⇒+=⇒+=⋅⋅⋅⋅⋅,即0MB AC ⋅=,故C 正确;对于D ,111()()222PQ MQ MP MB MC MA MB MC MA ∴=-=+-=+- ()21122PQ MB MC MA MB MC MA ∴=+-=+-,又()2222222MB MC MA MB MC MA MB MC MB MA MC MA+-=+++⋅-⋅-⋅2221112222222222228222=+++⨯⨯⨯-⨯⨯⨯-⨯⨯⨯=,1822PQ ∴==,故D 错误. 故选:BC 【点睛】关键点睛:本题考查向量的运算,用已知向量表示某一向量的三个关键点: (1)用已知向量来表示某一向量,一定要结合图形,以图形为指导是解题的关键.(2)要正确理解向量加法、减法与数乘运算的几何意义,如首尾相接的若干向量之和,等于由起始向量的始点指向末尾向量的终点的向量. (3)在立体几何中三角形法则、平行四边形法则仍然成立.4.如图,正方体1111ABCD A B C D -的棱长为3,线段11B D 上有两个动点,E F ,且1EF =,以下结论正确的有( )A .AC BE ⊥B .异面直线,AE BF 所成的角为定值C .点A 到平面BEF 的距离为定值D .三棱锥A BEF -的体积是定值 【答案】ACD 【详解】由AC BD ⊥,1AC DD ⊥可证AC ⊥平面11D DBB ,从而AC BE ⊥,故A 正确; 取特例,当E 与1D 重合时,F 是F ',AE 即1AD ,1AD 平行1BC ,异面直线,AE BF '所成的角是1C BF '∠,当F 与1B 重合时,E 是E ',BF 即1BB ,异面直线,AE BF '所成的角是1A AE '∠,可知1C BF '∠与1A AE '∠不相等,故异面直线,AE BF 所成的角不是定值,故B 错误;连结BD 交AC 于O ,又AC ⊥平面11D DBB ,点A 到平面11BDD B 的距离是2=AO ,也即点A 到平面BEF 的距离是22,故C 正确; 2=AO 为三棱锥A BEF -的高,又1111224BEFS =⨯⨯=△,故三棱锥A BEF -的体积为112234224⨯⨯=为定值,D 正确. 故选:ACD 【点睛】求空间中点到平面的距离常见方法为: (1)定义法:直接作平面的垂线,求垂线;(2)等体积法:不作垂线,通过等体积法间接求点到面的距离; (3)向量法:计算斜线在平面的法向量上的投影即可.5.如图,线段AB 为圆O 的直径,点E ,F 在圆O 上,//EF AB ,矩形ABCD 所在平面和圆O 所在平面垂直,且2AB =,1EF AD ==,则下述正确的是( )A .//OF 平面BCEB .BF ⊥平面ADFC .点A 到平面CDFE 的距离为7D .三棱锥C BEF - 【答案】ABC 【分析】由1EF OB ==,//EF OB ,易证//OF 平面BCE ,A 正确;B , 由所矩形ABCD 所在平面和圆O 所在平面垂直, 易证AD ⊥平面ABEF ,所以AD BF ⊥,由线段AB 为圆O 的直径,所以BF FA ⊥,易证故B 正确.C ,由C DAF A CDF V V --=可求点A 到平面CDFE ,C 正确.D ,确定线段DB 的中点M 是三棱锥C BEF -外接球心,进一步可求其体积,可判断D 错误. 【详解】解:1EF OB ==,//EF OB ,四边形OFEB 为平行四边形,所以//OF BE ,OF ⊄平面BCE ,BE ⊂平面BCE ,所以//OF 平面BCE ,故A 正确.线段AB 为圆O 的直径,所以BF FA ⊥,矩形ABCD 所在平面和圆O 所在平面垂直,平面ABCD 平面ABEF AB =,AD ⊂平面ABCD ,所以AD ⊥平面ABEF ,BF ⊂平面ABEF ,所以AD BF ⊥ AD ⊂平面ADF ,AF ⊂平面ADF ,AD AF A =, 所以BF ⊥平面ADF ,故B 正确.1OF OE EF ===,OFE △是正三角形,所以1EF BE AF ===, //DA BC ,所以BC ⊥平面ABEF ,BC BF ⊥,BF =2CF ==,DF ===2AB CD ==,CDF 是等腰三角形,CDF 的边DF 上的高2==,122CDF S =⨯=△ //DA BC ,AD ⊂平面ADF ,BC ⊄平面ADF ,//BC 平面ADF ,点C 到平面ADF 的距离为BF = 111122DAF S =⨯⨯=△,C DAF A CDF V V --=,设点A 到平面CDFE 的距离为h ,1133ADF CFD S FB S h ⨯⨯=⨯⨯△△,111733232h ⨯⨯=⨯⨯, 所以217h =,故C 正确. 取DB 的中点M ,则//MO AD ,12MO =,所以MO ⊥平面CDFE ,所以215122ME MF MB MC ⎛⎫====+= ⎪⎝⎭所以M 是三棱锥C BEF -外接球的球心,其半径5, 三棱锥C BEF -外接球的体积为33445553326V r πππ⎛⎫==⨯= ⎪ ⎪⎝⎭,故D 错误, 故选:ABC. 【点睛】综合考查线面平行与垂直的判断,求点面距离以及三棱锥的外接球的体积求法,难题.6.如图,正方体1111ABCD A B C D -的棱长为1,线段11B D 上有两个动点E ,F ,且22EF =.则下列结论正确的是( )A .三棱锥A BEF -的体积为定值B .当E 向1D 运动时,二面角A EF B --逐渐变小C .EF 在平面11ABB A 内的射影长为12D .当E 与1D 重合时,异面直线AE 与BF 所成的角为π4【答案】AC【分析】对选项分别作图,研究计算可得.【详解】选项A:连接BD ,由正方体性质知11BDD B 是矩形,1112212224BEF S EF BB ∆∴=⋅=⨯⨯= 连接AO 交BD 于点O由正方体性质知AO ⊥平面11BDD B ,所以,AO 是点A 到平面11BDD B 的距离,即22AO = 11221334212A BEF BEF V S AO -∆∴=⨯=⨯⨯= A BEF V -∴是定值.选项B:连接11A C 与11B D 交于点M ,连接11,AD AB ,由正方体性质知11AD AB =,M 是11B D 中点,AM EF ∴⊥ ,又1BB EF ⊥,11//BB AAA EFB ∴--的大小即为AM 与1AA 所成的角,在直角三角形1AA M 中,12tan 2MAA ∠=为定值. 选项C:如图,作1111,,,FH A B EG A B ET EG ⊥⊥⊥在直角三角形EFT 中,221cos 45222FT EF =⨯=⨯= 12HG FT ∴== 选项D:当E 与1D 重合时,F 与M 重合,连接AC 与BD 交于点R ,连接1D R ,1//D R BM 异面直线AE 与BF 所成的角,即为异面直线1AD 与1D R 所成的角,在三角形1AD R 中,22111132,2AD D R MB BB M B ===+=2AR = 由余弦定理得13cos AD R ∠=故选:AC【点睛】本题考查空间几何体性质问题.求解思路:关键是弄清(1)点的变化,点与点的重合及点的位置变化;(2)线的变化,应注意其位置关系的变化;(3)长度、角度等几何度量的变化.求空间几何体体积的思路:若所给定的几何体是柱体、锥体或台体等规则几何体,则可直接利用公式进行求解.其中,求三棱锥的体积常用等体积转换法;若所给定的几何体是不规则几何体,则将不规则的几何体通过分割或补形转化为规则几何体,再利用公式求解.7.在边长为2的等边三角形ABC 中,点,D E 分别是边,AC AB 上的点,满足//DE BC 且AD AC λ=,(()01λ∈,),将ADE 沿直线DE 折到A DE '△的位置.在翻折过程中,下列结论不成立的是( )A .在边A E '上存在点F ,使得在翻折过程中,满足//BF 平面A CD 'B .存在102λ∈⎛⎫ ⎪⎝⎭,,使得在翻折过程中的某个位置,满足平面A BC '⊥平面BCDE C .若12λ=,当二面角A DE B '--为直二面角时,||104A B '= D .在翻折过程中,四棱锥A BCDE '-体积的最大值记为()fλ,()f λ的最大值为23【答案】ABC【分析】 对于A.在边A E '上点F ,在A D '上取一点N ,使得//FN ED ,在ED 上取一点H ,使得//NH EF ,作//HG BE 交BC 于点G ,即可判断出结论.对于B ,102λ∈⎛⎫ ⎪⎝⎭,,在翻折过程中,点A '在底面BCDE 的射影不可能在交线BC 上,即可判断出结论.对于C ,12λ=,当二面角A DE B '--为直二面角时,取ED 的中点M ,可得AM ⊥平面BCDE .可得22A B AM BM '=+,结合余弦定理即可得出.对于D.在翻折过程中,取平面AED ⊥平面BCDE ,四棱锥A BCDE '-体积()3133BCDE f S λλλλ=⋅⋅=-,()01λ∈,,利用导数研究函数的单调性即可得出. 【详解】对于A.在边A E '上点F ,在A D '上取一点N ,使得//FN ED ,在ED 上取一点H ,使得//NH EF ,作//HG BE 交BC 于点G ,如图所示,则可得FN 平行且等于BG ,即四边形BGNF 为平行四边形,∴//NG BE ,而GN 始终与平面ACD 相交,因此在边A E '上不存在点F ,使得在翻折过程中,满足//BF 平面A CD ',A 不正确.对于B ,102λ∈⎛⎫ ⎪⎝⎭,,在翻折过程中,点A '在底面BCDE 的射影不可能在交线BC 上,因此不满足平面A BC '⊥平面BCDE ,因此B 不正确.对于C.12λ=,当二面角A DE B '--为直二面角时,取ED 的中点M ,如图所示:可得AM ⊥平面BCDE ,则22223111010()1()21cos12022224A B AM BM '=+=++-⨯⨯⨯︒=≠,因此C 不正确;对于D.在翻折过程中,取平面AED ⊥平面BCDE ,四棱锥A BCDE '-体积()3133BCDE f S λλλλ=⋅⋅=-,()01λ∈,,()213f λλ'=-,可得3λ=时,函数()f λ取得最大值()31231339f λ⎛⎫=-= ⎪⎝⎭,因此D 正确. 综上所述,不成立的为ABC.故选:ABC.【点睛】本题考查了利用运动的观点理解空间线面面面位置关系、四棱锥的体积计算公式、余弦定理、利用导数研究函数的单调性极值与最值,考查了推理能力空间想象能力与计算能力,属于难题.8.如图,1111ABCD A B C D -为正方体,下列结论中正确的是( )A .11A C ⊥平面11BB D DB .1BD ⊥平面1ACBC .1BD 与底面11BCC B 所成角的正切值是2D .过点1A 与异面直线AD 与1CB 成60角的直线有2条【答案】ABD【分析】由直线与平面垂直的判定判断A 与B ;求解1BD 与底面11BCC B 所成角的正切值判断C ;利用空间向量法可判断D .【详解】 对于A 选项,如图,在正方体1111ABCD A B C D -中,1BB ⊥平面1111D C B A ,11A C ⊂平面1111D C B A ,则111BB A C ⊥,由于四边形1111D C B A 为正方形,则1111AC B D ⊥, 1111BB B D B =,因此,11A C ⊥平面11BB D D ,故A 正确;对于B 选项,在正方体1111ABCD A B C D -中,1DD ⊥平面ABCD ,AC ⊂平面ABCD ,1AC DD ∴⊥,因为四边形ABCD 为正方形,所以,AC BD ⊥,1D DD BD =,AC ∴⊥平面11BB D D , 1BD ⊂平面11BB D D ,1AC BD ∴⊥,同理可得11BD B C ⊥,1AC B C C =,1BD ∴⊥平面1ACB ,故B 正确; 对于C 选项,由11C D ⊥平面11BCC B ,得11C BD ∠为1BD 与平面11BCC B 所成角, 且111112tan 2C D C BD BC ∠==,故C 错误; 对于D 选项,以点D 为坐标原点,DA 、DC 、1DD 所在直线分别为x 、y 、z 轴建立如下图所示的空间直角坐标系,设正方体的棱长为1,则()1,0,0A 、()0,0,0D 、()0,1,0C 、()11,1,1B ,()1,0,0DA =,()11,0,1CB =,设过点1A 且与直线DA 、1CB 所成角的直线的方向向量为()1,,m y z =,则1cos ,2DA mDA m DA m y ⋅<>===⋅, 1111cos ,22CB m CB mCB m ⋅<>===⋅, 整理可得2222341y z y z z ⎧+=⎨=++⎩,消去y 并整理得2210z z +-=,解得1z =-1z =-由已知可得z ≤,所以,1z =-+y =因此,过点1A 与异面直线AD 与1CB 成60角的直线有2条,D 选项正确.故选:ABD.【点睛】方法点睛:证明线面垂直的方法:一是线面垂直的判定定理;二是利用面面垂直的性质定理;三是平行线法(若两条平行线中一条垂直于这个平面,则另一条也垂直于这个平面),解题时,注意线线、线面与面面关系的相互转化;另外,在证明线线垂直时,要注意题中隐含的垂直关系,如等腰三角形的底边上的高、中线和顶角的角平分线三线合一、矩形的内角、直径所对的圆周角、菱形的对角线互相垂直、直角三角形(或给出线段长度,经计算满足勾股定理)、直角梯形等等.。
高三数学易错立体几何多选题 易错题难题提优专项训练试卷

高三数学易错立体几何多选题 易错题难题提优专项训练试卷一、立体几何多选题1.如图,直三棱柱11,ABC A B C -,ABC 为等腰直角三角形,AB BC ⊥,且12AC AA ==,E ,F 分别是AC ,11A C 的中点,D ,M 分别是1AA ,1BB 上的两个动点,则( )A .FM 与BD 一定是异面直线B .三棱锥D MEF -的体积为定值14C .直线11B C 与BD 所成角为2π D .若D 为1AA 中点,则四棱锥1D BB FE -55【答案】CD 【分析】A 当特殊情况M 与B 重合有FM 与BD 相交且共面;B 根据线面垂直、面面垂直判定可证面1BEFB ⊥面11ACC A ,可知EMFS、D 到面1BEFB 的距离,可求D EMF V -;C 根据线面垂直的判定及性质即可确定11B C 与BD 所成角;D 由面面垂直、勾股、矩形性质等确定外接球半径,进而求体积,即可判断各项的正误. 【详解】A :当M 与B 重合时,FM 与BD 相交且共面,错误; B :由题意知:BE AC ⊥,AC EF ⊥且BEEF E =,则AC ⊥面1BEFB ,又AC ⊂面11ACC A ,面1BEFB ⋂面11ACC A EF =,所以面1BEFB ⊥面11ACC A ,又1121122EMFSEF BE =⋅⋅=⨯⨯=,D 到面1BEFB 的距离为1h =,所以1133D EMF EMFV h S-=⋅⋅=,错误; C :由AB BC ⊥,1BC B B ⊥,1B BAB B =,所以BC ⊥面11ABB A ,又11//BC B C ,即11B C ⊥面11ABB A ,而BD ⊂面11ABB A ,则11BD B C ⊥,正确;D :由B 中,面1BEFB ⊥面11ACC A ,即面DEF ⊥面1BEFB ,则D 到面1BEFB 的距离为1h =,又D 为1AA 中点,若1,BF EB 交点为O ,G 为EF 中点,连接,,OG GD OD ,则OG GD ⊥,故2252OD OG GD =+=,由矩形的性质知:152OB OE OF OB ====,令四棱锥1D BB FE -的外接球半径为R ,则5R =,所以四棱锥1D BB FE -的外接球体积为35435V R ππ==,正确. 故选:CD. 【点睛】关键点点睛:利用线面、面面关系确定几何体的高,结合棱锥体积公式求体积,根据线面垂直、勾股定理及矩形性质确定外接球半径,结合球体体积公式求体积.2.如图,已知正方体1ABCD ABC D -的棱长为a ,E 是棱CD 上的动点.则下列结论中正确的有( )A .11EB AD ⊥B .二面角11E A B A --的大小为4πC .三棱锥11A BDE -体积的最小值为313a D .1//D E 平面11A B BA【答案】ABD 【分析】连接1A D 、1B C ,则易证1AD ⊥平面11A DCB ,1EB ⊂平面11A DCB ,则由线面垂直的性质定理可以判断选项A 正确;二面角11E A B A --的平面角为1DA A ∠,易知14DA A π∠=,则可判断选项B 正确;用等体积法,将求三棱锥11A B D E -的体积转化为求三棱锥11E AB D -的体积,当点E 与D 重合时,三棱锥11E AB D -的体积最小,此时的值为316a ,则选项C 错误;易知平面11//D DCC 平面11A B BA ,而1D E ⊂平面11D DCC ,则根据面面平行的性质定理可得1//D E 平面11A B BA ,可判断选项D 正确. 【详解】选项A ,连接1A D 、1B C ,则由正方体1ABCD ABC D -可知,11A D AD ⊥,111A B AD ⊥,1111A DA B A =,则1AD ⊥平面11A DCB ,又因为1EB ⊂平面11A DCB ,所以11EB AD ⊥,选项A 正确; 选项B ,因为11//DE A B ,则二面角11E A B A --即为二面角11D A B A --, 由正方体1ABCD ABC D -可知,11A B ⊥平面1DA A , 则1DA A ∠为二面角11D A B A --的平面角,且14DA A π∠=,所以选项B 正确;选项C ,设点E 到平面11AB D 的距离为d , 则11111113A B D E E AB D AB D V V S d --==⋅,连接1C D 、1C B ,易证平面1//BDC 平面11AB D ,则在棱CD 上,点D 到平面11AB D 的距离最短, 即点E 与D 重合时,三棱锥11A B D E -的体积最小, 由正方体1ABCD ABC D -知11A B ⊥平面1ADD , 所以1111123111113326D AB D B ADDADD a V V S A B a a --==⋅=⋅⋅=, 则选项C 错误;选项D ,由正方体1ABCD ABC D -知,平面11//CC D D 平面11A B BA ,且1D E ⊂平面11CC D D , 则由面面平行的性质定理可知1//D E 平面11A B BA ,则选项D 正确. 故选:ABD. 【点睛】关键点点睛:本题对于选项C 的判断中,利用等体积法求三棱锥的体积是解题的关键.3.在直角梯形ABCD 中,2ABC BCD π∠=∠=,1AB BC ==,2DC =,E 为DC 中点,现将ADE 沿AE 折起,得到一个四棱锥D ABCE -,则下列命题正确的有( ) A .在ADE 沿AE 折起的过程中,四棱锥D ABCE -体积的最大值为13B .在ADE 沿AE 折起的过程中,异面直线AD 与BC 所成的角恒为4π C .在ADE 沿AE 折起的过程中,二面角A EC D --的大小为45︒D .在四棱锥D ABCE -中,当D 在EC 上的射影恰好为EC 的中点F 时,DB 与平面ABCE【答案】ABD 【分析】对于A ,四棱锥D ABCE -的底面面积是固定值,要使得体积最大,需要平面DAE ⊥平面ABCE ,此时DE CE ⊥,可求得1133D ABCE ABCE V S DE -=⋅=可判断A ;对于B ,在ADE 沿AE 折起的过程中,//AE BC ,所以异面直线AD 与AE 所成的角即为AD 与BC所成角,由翻折前可知4DAE π∠=可判断B ;对于C ,利用线面垂直的判定定理,结合翻折前可知AE ⊥平面DEC ,又AE ⊂平面ABCE ,所以平面DEC ⊥平面ABCE ,即二面角A EC D --的在大小为2π判断C ;对于D ,利用线面垂直的判定定理可知DF ⊥平面ABCE ,所以DBF ∠为直线DB 与平面ABCE 所成的角,在直角DFB △中,15tanDF DBF BF ∠==,可判断D 正确;【详解】对于A ,ADE 沿AE 折起得到四棱锥D ABCE -,由四棱锥底面面积是固定值,要使得体积最大,需要四棱锥的高最大,即平面DAE ⊥平面ABCE ,此时DE CE ⊥,由已知得1DE =,则111111333D ABCE ABCE V S DE -=⋅=⨯⨯⨯=,故A 正确; 对于B ,在ADE 沿AE 折起的过程中,//AE BC ,所以异面直线AD 与AE 所成的角即为AD 与BC 所成角,又1AB BC ==,2DC =,E 为DC 中点,可知4DAE π∠=,即异面直线AD 与BC 所成的角恒为4π,故B 正确; 对于C ,由翻折前知,,AE EC AE ED ⊥⊥,且ECED E =,则AE ⊥平面DEC ,又AE ⊂平面ABCE ,所以平面DEC ⊥平面ABCE ,即二面角A EC D --的大小为2π,故C 错误; 对于D ,如图连接,DF BF ,由C 选项知,AE ⊥平面DEC ,又DF ⊂平面DEC ,则AE DF ⊥,又由已知得EC DF ⊥,且EC AE E ⋂=,则DF ⊥平面ABCE ,所以DBF ∠为直线DB 与平面ABCE 所成的角,在直角DFB △中,222222113122152tan 5511122DE CE DFDBF BFBC CE ⎛⎫⎛⎫-- ⎪⎪⎝⎭⎝⎭∠=====⎛⎫⎛⎫++ ⎪ ⎪⎝⎭⎝⎭,所以DB 与平面ABCE 15D 正确; 故选:ABD 【点睛】关键点睛:本题考查立体几何综合问题,求体积,求线线角,线面角,面面角,解题的关键要熟悉几种角的定义,通过平移法找到线线角,通过证垂直找到线面角和面面角,再结合三角形求出角,考查了学生的逻辑推理能力,转化能力与运算求解能力,属于难题.4.如图,正方体1111ABCD A B C D -的棱长为3,线段11B D 上有两个动点,E F ,且1EF =,以下结论正确的有( )A .AC BE ⊥B .异面直线,AE BF 所成的角为定值C .点A 到平面BEF 的距离为定值D .三棱锥A BEF -的体积是定值 【答案】ACD 【详解】由AC BD ⊥,1AC DD ⊥可证AC ⊥平面11D DBB ,从而AC BE ⊥,故A 正确; 取特例,当E 与1D 重合时,F 是F ',AE 即1AD ,1AD 平行1BC ,异面直线,AE BF '所成的角是1C BF '∠,当F 与1B 重合时,E 是E ',BF 即1BB ,异面直线,AE BF '所成的角是1A AE '∠,可知1C BF '∠与1A AE '∠不相等,故异面直线,AE BF 所成的角不是定值,故B 错误;连结BD 交AC 于O ,又AC ⊥平面11D DBB ,点A 到平面11BDD B 的距离是2AO ,也即点A 到平面BEF 的距离是22,故C 正确; 2AO 为三棱锥A BEF -的高,又1111224BEF S =⨯⨯=△,故三棱锥A BEF -的体积为112234224⨯⨯=为定值,D 正确. 故选:ACD 【点睛】求空间中点到平面的距离常见方法为: (1)定义法:直接作平面的垂线,求垂线;(2)等体积法:不作垂线,通过等体积法间接求点到面的距离; (3)向量法:计算斜线在平面的法向量上的投影即可.5.如图,点E 为正方形ABCD 边CD 上异于点C ,D 的动点,将ADE 沿AE 翻折成SAE △,在翻折过程中,下列说法正确的是( )A .存在点E 和某一翻折位置,使得SB SE ⊥ B .存在点E 和某一翻折位置,使得//AE 平面SBCC .存在点E 和某一翻折位置,使得直线SB 与平面ABC 所成的角为45°D .存在点E 和某一翻折位置,使得二面角S AB C --的大小为60° 【答案】ACD 【分析】依次判断每个选项:当SE CE ⊥时,⊥SE SB ,A 正确,//AE 平面SBC ,则//AE CB ,这与已知矛盾,故B 错误,取二面角D AE B --的平面角为α,取4=AD ,计算得到2cos 3α=,C 正确,取二面角D AE B --的平面角为60︒,计算得到5tan θ=,故D 正确,得到答案. 【详解】当SE CE ⊥时,SE AB ⊥,SE SA ⊥,故SE ⊥平面SAB ,故⊥SE SB ,A 正确;若//AE 平面SBC ,因AE ⊂平面ABC ,平面ABC 平面SBC BC =,则//AE CB ,这与已知矛盾,故B 错误;如图所示:DF AE ⊥交BC 于F ,交AE 于G ,S 在平面ABCE 的投影O 在GF 上, 连接BO ,故SBO ∠为直线SB 与平面ABC 所成的角,取二面角D AE B --的平面角为α,取4=AD ,3DE =,故5AE DF ==,1CE BF ==,125DG =,12cos 5OG α=,故只需满足12sin 5SO OB α==, 在OFB △中,根据余弦定理:2221213121312sin 1cos 2cos cos 55555OFB ααα⎛⎫⎛⎫⎛⎫=+---∠ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭,解得2cos 3α=,故C 正确; 过O 作OMAB ⊥交AB 于M ,则SMO ∠为二面角S AB C --的平面角,取二面角D AE B --的平面角为60︒,故只需满足22DG GO OM ==, 设OAG OAM θ∠=∠=,84ππθ<<,则22DAG πθ∠=-,tan tan 22DG OGAG πθθ==⎛⎫- ⎪⎝⎭,化简得到2tan tan 21θθ=,解得5tan 5θ=,验证满足,故D 正确; 故选:ACD .【点睛】本题考查了线线垂直,线面平行,线面夹角,二面角,意在考查学生的计算能力,推断能力和空间想象能力.6.在正方体1111ABCD A B C D -中,如图,,M N 分别是正方形ABCD ,11BCC B 的中心.则下列结论正确的是( )A .平面1D MN 与11BC 的交点是11B C 的中点 B .平面1D MN 与BC 的交点是BC 的三点分点 C .平面1D MN 与AD 的交点是AD 的三等分点 D .平面1D MN 将正方体分成两部分的体积比为1∶1 【答案】BC 【分析】取BC 的中点E ,延长DE ,1D N ,并交于点F ,连FM 并延长分别交,BC AD 于,P Q ,连1,D Q PN 并延长交11B C 与H ,平面四边形1D HPQ 为所求的截面,进而求出,,P Q H 在各边的位置,利用割补法求出多面体11QPHD C CD 的体积,即可求出结论.【详解】如图,取BC 的中点E ,延长DE ,1D N ,并交于点F , 连接FM 并延长,设FM BC P ⋂=,FM AD Q ⋂=, 连接PN 并延长交11B C 于点H .连接1D Q ,1D H ,则平面四边形1D HPQ 就是平面1D MN 与正方体的截面,如图所示.111111////,22NE CC DD NE CC DD ==,NE ∴为1DD F ∆的中位线,E ∴为DF 中点,连BF , ,,90DCE FBE BF DC AB FBE DCE ∴∆≅∆==∠=∠=︒, ,,A B F ∴三点共线,取AB 中点S ,连MS ,则12//,,23BP FB MS BP MS BC MS FS =∴==, 22111,33236BP MS BC BC PE BC ∴==⨯=∴=, E 为DF 中点,11//,233PE DQ DQ PE BC AD ∴===N 分别是正方形11BCC B 的中心,11113C H BP C B ∴==所以点P 是线段BC 靠近点B 的三等分点, 点Q 是线段AD 靠近点D 的三等分点, 点H 是线段11B C 靠近点1C 的三等分点. 做出线段BC 的另一个三等分点P ', 做出线段11A D 靠近1D 的三等分点G ,连接QP ',HP ',QG ,GH ,1H QPP Q GHD V V '--=, 所以111113QPHD C CD QPHQ DCC D V V V -==多面体长方体正方体 从而平面1D MN 将正方体分成两部分体积比为2∶1. 故选:BC.【点睛】本题考查直线与平面的交点及多面体的体积,确定出平面与正方体的交线是解题的关键,考查直观想象、逻辑推理能力,属于较难题.7.已知正四棱柱1111ABCD A B C D -的底面边长为2,侧棱11AA =,P 为上底面1111D C B A 上的动点,给出下列四个结论中正确结论为( )A .若3PD =,则满足条件的P 点有且只有一个B .若3PD =,则点P 的轨迹是一段圆弧C .若PD ∥平面1ACB ,则DP 长的最小值为2D .若PD ∥平面1ACB ,且3PD =,则平面BDP 截正四棱柱1111ABCD A B C D -的外接球所得平面图形的面积为94π 【答案】ABD 【分析】若3PD =,由于P 与1B 重合时3PD =,此时P 点唯一;()313PD =∈,,则12PD =,即点P 的轨迹是一段圆弧;当P 为11A C 中点时,DP 有最小值为3=,可判断C ;平面BDP 截正四棱柱1111ABCD A B C D -的外接球所得平面图形为外接球的大圆,其半径为32=,可得D . 【详解】 如图:∵正四棱柱1111ABCD A B C D -的底面边长为2, ∴1122B D =11AA =,∴()2212213DB =+=,则P 与1B 重合时3PD =,此时P 点唯一,故A 正确; ∵()313PD =∈,,11DD =,则12PD =,即点P 的轨迹是一段圆弧,故B 正确; 连接1DA ,1DC ,可得平面11//A DC 平面1ACB ,则当P 为11A C 中点时,DP 有最小值为()22213+=,故C 错误;由C 知,平面BDP 即为平面11BDD B ,平面BDP 截正四棱柱1111ABCD A B C D -的外接球所得平面图形为外接球的大圆,其半径为2221322122++=,面积为94π,故D 正确.故选:ABD .【点睛】本题考查了立体几何综合,考查了学生空间想象,逻辑推理,转化划归,数学运算的能力,属于较难题.8.如图所示,正方体ABCD A B C D ''''-的棱长为1,E ,F 分别是棱AA ',CC '的中点,过直线EF 的平面分别与棱BB ',DD '交于点M ,N ,以下四个命题中正确的是( )A .0MN EF ⋅=B .ME NE =C .四边形MENF 的面积最小值与最大值之比为2:3D .四棱锥A MENF -与多面体ABCD EMFN -体积之比为1:3【答案】ABD【分析】证明EF ⊥平面BDD B '',进而得EF MN ⊥,即可得A 选项正确;证明四边形MENF 为菱形即可得B 选项正确;由菱形性质得四边形MENF 的面积12S MN EF =⋅,再分别讨论MN 的最大值与最小值即可;根据割补法求解体积即可.【详解】对于A 选项,如图,连接BD ,B D '',MN .由题易得EF BD ⊥,EF BB '⊥,BD BB B '⋂=,所以EF ⊥平面BDD B '',又MN ⊂平面BDD B '',所以EF MN ⊥,因此0MN EF ⋅=,故A 正确.对于B 选项,由正方体性质得:平面''//BCC B 平面''ADD A ,平面''BCC B 平面EMFN MF =,平面''ADD A 平面EMFN EN =, 所以//MF EN ,同理得//ME NF ,又EF MN ⊥,所以四边形MENF 为菱形, 因此ME NE =,故B 正确.对于C 选项,由B 易得四边形MENF 的面积12S MN EF =⋅, 所以当点M ,N 分别为BB ',DD '的中点时,四边形MENF 的面积S 最小,此时MN EF ==,即面积S 的最小值为1; 当点M ,N 分别与点B (或点B '),D (或D )重合时,四边形MENF 的面积S 最大,此时MN =,即面积S所以四边形MENF 的面积最小值与最大值之比为2C 不正确.对于D 选项,四棱锥A MENF -的体积11113346M AEF N AEF AEF V V V DB S --=+=⋅==△; 因为E ,F 分别是AA ',CC '的中点,所以BM D N '=,DN B M '=,于是被截面MENF 平分的两个多面体是完全相同的,则它们的体积也是相同的,因此多面体ABCD EMFN -的体积21122ABCD A B C D V V ''''-==正方体, 所以四棱锥A MENF -与多面体ABCD EMFN -体积之比为1:3,故D 正确. 故选:ABD .【点睛】本题考查立体几何与向量的综合、截面面积的最值、几何体的体积,考查空间思维能力与运算求解能力,是中档题.本题解题的关键在于证明四边形MENF 为菱形,利用割补法将四棱锥A MENF -的体积转化为三棱锥M AEF - 和N AEF -的体积之和,将多面体ABCD EMFN -的体积转化为正方体的体积的一半求解.。
高三数学易错立体几何多选题 易错题难题质量专项训练试卷

高三数学易错立体几何多选题 易错题难题质量专项训练试卷一、立体几何多选题1.如图,在边长为4的正方形ABCD 中,点E 、F 分别在边AB 、BC 上(不含端点)且BE BF =,将AED ,DCF 分别沿DE ,DF 折起,使A 、C 两点重合于点1A ,则下列结论正确的有( ).A .1A D EF ⊥B .当12BE BF BC ==时,三棱锥1A F DE -6π C .当14BE BF BC ==时,三棱锥1A F DE -217 D .当14BE BF BC ==时,点1A 到平面DEF 的距离为177【答案】ACD 【分析】A 选项:证明1A D ⊥面1A EF ,得1A D EF ⊥;B 选项:当122BE BF BC ===时,三棱锥1A EFD -的三条侧棱111,,A D A E A F 两两相互垂直,利用分隔补形法求三棱锥1A EFD -的外接球体积; C 选项:利用等体积法求三棱锥1A EFD -的体积; D 选项:利用等体积法求出点1A 到平面DEF 的距离. 【详解】 A 选项:正方形ABCD,AD AE DC FC ∴⊥⊥由折叠的性质可知:1111,A D A E A D A F ⊥⊥ 又111A E A F A ⋂=1A D ∴⊥面1A EF又EF ⊂面1A EF ,1A D EF ∴⊥;故A 正确.B 选项:当122BE BF BC ===时,112,22A E A F EF ===在1A EF 中,22211A E A F EF +=,则11A E A F ⊥由A 选项可知,1111,A D A E A D A F ⊥⊥∴三棱锥1A EFD -的三条侧棱111,,A D A E A F 两两相互垂直,把三棱锥1A EFD -=, 三棱锥1A EFD -,体积为334433R ππ==,故B 错误C 选项:当114BE BF BC ===时,113,A E A F EF ===在1A EF中,22222211111338cos 22339A E A F EF EA F A E A F+-+-∠===⋅⨯⨯,1sin 9EA F ∠=则111111sin 332292A EFSA E A F EA F =⋅⋅∠=⨯⨯⨯=111111433A EFD D A EF A EF V V SA D --∴==⋅⋅==故C 正确;D 选项:设点1A 到平面EFD 的距离为h ,则 在EFD △中,2222225524cos 225525DE DF EF EDF DE DF +-+-∠===⋅⨯⨯, 7sin 25EDF ∠=则1177sin 5522252EFDSDE DF EDF =⋅⋅∠=⨯⨯⨯=11173323A EFD DEFV Sh h -∴=⋅⋅=⨯⨯=即7h =故D 正确; 故选:ACD 【点睛】方法点睛:求三棱锥的体积时要注意三棱锥的每个面都可以作为底面,例如三棱锥的三条侧棱两两垂直,我们就选择其中的一个侧面作为底面,另一条侧棱作为高来求体积.2.在三棱柱111ABC A B C -中,ABC ∆是边长为( )A .直线1A C 与直线1BB 之间距离的最大值为3B .若1A 在底面ABC 上的投影恰为ABC ∆的中心,则直线1AA 与底面所成角为60︒ C .若三棱柱的侧棱垂直于底面,则异面直线AB 与1A C 所成的角为30D .若三棱柱的侧棱垂直于底面,则其外接球表面积为64π 【答案】AD 【分析】建立空间直角坐标系,用向量法求解. 【详解】如图示,以A 为原点,AC 为y 轴正方向,Ax 为x 轴正方向,过A 点垂直于面ABC 的向上方向为z 轴正方向建系,则()()()0,0,0,3,0,0,23,0,A B C 设()()()100010001000,,,3,3,,,23,,A x y z B x y z C x y z ++所以()()()1000100011,23,,,,,3,3,0,AC x y z BB x y z A B =---== 对于A:设n 为直线1A C 与直线1BB 的公垂线的方向向量,则有:11·0·0AC n BB n ⎧=⎪⎨=⎪⎩,即()()0000002300x x y y zz x x y y zz ⎧-+-=⎪⎨++=⎪⎩解得:()00,0n z x =- 设直线1A C 与直线1BB 之间距离为d ,则22011222200009||||z A B nd d x z n x z ===++ 22009x d ≥∴≤,即3d ≤,故A 正确;对于B :若1A 在底面ABC 上的投影恰为ABC ∆的中心,则(13,211A 底面法向量()(10,0,1,1,3,211m AA ==,设直线 1AA 与底面所成角为θ,则:121133sin |cos ,|143AA n θ===⨯,故B 错误;对于C : 三棱柱的侧棱垂直于底面时,则()()()1110,0,43,3,3,43,0,23,43,A B C则()()13,3,0,0,23,43,AB AC ==-设异面直线AB 与1A C 所成的角为θ,则1115cos |cos ,|||10||||23215AB AC AB AC AB AC θ====⨯,故C 错误;对于D :若三棱柱的侧棱垂直于底面时,外接球的球心O 为上下底面中心DD 1连线的中点,所以外接球的半径()222324R =+=,所以2464S R ππ==.故D 正确故选:AD 【点睛】向量法解决立体几何问题的关键: (1)建立合适的坐标系; (2)把要用到的向量正确表示; (3)利用向量法证明或计算.3.如图,在棱长为2的正方体ABCD A B C D ''''-中,M 为BC 边的中点,下列结论正确的有( )A .AM 与DB ''所成角的余弦值为1010B .过三点A 、M 、D 的正方体ABCD A BCD ''''-的截面面积为92C .四面体A C BD ''的内切球的表面积为3π D .正方体ABCD A B C D ''''-中,点P 在底面A B C D ''''(所在的平面)上运动并且使MAC PAC ''∠=∠,那么点P 的轨迹是椭圆 【答案】AB 【分析】构建空间直角坐标系,由异面直线方向向量的夹角cos ,||||AM D B AM D B AM D B ''⋅''<>=''为AM 与D B ''所成角的余弦值判断A 的正误;同样设(,,0)P x y 结合向量夹角的坐标表示,且由等角的余弦值相等可得22221543y x y +=++⨯,进而判断P 的轨迹知D 的正误;由立方体的截面为梯形,分别求,,,MN AD AM D N '',进而得到梯形的高即可求面积,判断B 的正误;由四面体的体积与内切球半径及侧面面积的关系求内切球半径r ,进而求内切球表面积,判断C 的正误. 【详解】A :构建如下图所示的空间直角坐标系:则有:(0,0,2),(1,2,2),(0,2,0),(2,0,0)A M B D '', ∴(1,2,0),(2,2,0)AM D B ''==-,10cos ,10||||58AM D B AM D B AM D B ''⋅''<>===''⨯,故正确.B :若N 为CC '的中点,连接MN ,则有//MN AD ',如下图示,∴梯形AMND’为过三点A 、M 、D 的正方体ABCD A B C D ''''-的截面, 而2,22,5MN AD AM D N ''====,可得梯形的高为322, ∴梯形的面积为13293222S =⨯⨯=,故正确. C :如下图知:四面体A C BD ''的体积为正方体体积减去四个直棱锥的体积,∴118848323V =-⨯⨯⨯=,而四面体的棱长都为22142222sin 8323S π=⨯⨯=,∴若其内切圆半径为r ,则有188333r ⨯=,即3r =2443r ππ=.故错误. D :正方体ABCD A B C D ''''-中,点P 在底面A B C D ''''(所在的平面)上运动且MAC PAC ''∠=∠,即P 的轨迹为面A B C D ''''截以AM 、AP 为母线,AC’为轴的圆锥体侧面所得曲线,如下图曲线GPK ,构建如下空间直角坐标系,232 (0,0,2),(,,2),(0,22,0)22A M C'-,若(,,0)P x y,则232(,,0),(0,22,2),(,,2)22AM AC AP x y'=-=-=-,∴15cos||||512AM ACMACAM AC'⋅'∠==='⨯222cos||||43AP ACPACAP AC x y'⋅'∠=='++⨯22215543x y=++⨯,整理得22(102)9216(0)y x y+-=>,即轨迹为双曲线的一支,故错误.故选:AB【点睛】关键点点睛:应用向量的坐标表示求异面直线的夹角,并结合等角的余弦值相等及向量数量积的坐标表示求动点的轨迹,综合立方体的性质求截面面积,分割几何体应用等体积法求内切球半径,进而求内切球的表面积.4.在长方体1111ABCD A B C D-中,4AB BC==,18AA=,点P在线段11A C上,M为AB 的中点,则( ) A .BD ⊥平面PACB .当P 为11AC 的中点时,四棱锥P ABCD -外接球半径为72C .三棱锥A PCD -体积为定值D .过点M 作长方体1111ABCD A B C D -的外接球截面,所得截面圆的面积的最小值为4π 【答案】ACD 【分析】利用线面垂直的判定定理可判断A 选项的正误;判断出四棱锥P ABCD -为正四棱锥,求出该四棱锥的外接球半径,可判断B 选项的正误;利用等体积法可判断C 选项的正误;计算出截面圆半径的最小值,求出截面圆面积的最小值,可判断D 选项的正误. 【详解】对于A 选项,因为AB BC =,所以,矩形ABCD 为正方形,所以,BD AC ⊥, 在长方体1111ABCD A B C D -中,1AA ⊥底面ABCD ,BD ⊂平面ABCD ,1BD AA ∴⊥,1AC AA A ⋂=,AC 、1AA ⊂平面PAC ,所以,BD ⊥平面PAC ,A 选项正确;对于B 选项,当点P 为11A C 的中点时,PA ===同理可得PB PC PD ===因为四边形ABCD 为正方形,所以,四棱锥P ABCD -为正四棱锥, 取AC 的中点N ,则PN 平面ABCD ,且四棱锥P ABCD -的外接球球心在直线PN上,设该四棱锥的外接球半径为R ,由几何关系可得222PN R AN R -+=, 即2288R R -+=,解得92R =,B 选项错误; 对于C 选项,2114822ACDSAD CD =⋅=⨯=, 三棱锥P ACD -的高为18AA =,因此,116433A PCD P ACD ACD V V S AA --==⋅=△,C 选项正确;对于D 选项,设长方体1111ABCD A B C D -的外接球球心为E ,则E 为1BD 的中点, 连接EN 、MN ,则1142EN DD ==,122MN AD ==, E 、N 分别为1BD 、BD 的中点,则1//EN DD , 1DD ⊥平面ABCD ,EN ∴⊥平面ABCD ,MN ⊂平面ABCD ,EN MN ∴⊥,EM ∴==过点M 作长方体1111ABCD A B C D -的外接球截面为平面α,点E 到平面α的距离为d ,直线EM 与平面α所成的角为θ,则sin 25sin 25d EM θθ==≤, 当且仅当2πθ=时,等号成立,长方体1111ABCD A B C D -的外接球半径为222126AB AD AA R ++'==,所以,截面圆的半径()()222226252r R d '=-≥-=,因此,截面圆面积的最小值为4π,D 选项正确.故选:ACD. 【点睛】方法点睛:求空间多面体的外接球半径的常用方法:①补形法:侧面为直角三角形,或正四面体,或对棱二面角均相等的模型,可以还原到正方体或长方体中去求解;②利用球的性质:几何体中在不同面均对直角的棱必然是球大圆直径,也即球的直径; ③定义法:到各个顶点距离均相等的点为外接球的球心,借助有特殊性底面的外接圆圆心,找其垂线,则球心一定在垂线上,再根据带其他顶点距离也是半径,列关系求解即可.5.已知正方体1111ABCD A B C D -的棱长为2,点O 为11A D 的中点,若以O 6为半径的球面与正方体1111ABCD A B C D -的棱有四个交点E ,F ,G ,H ,则下列结论正确的是( )A .11//A D 平面EFGHB .1AC ⊥平面EFGHC .11A B 与平面EFGH 所成的角的大小为45°D .平面EFGH 将正方体1111ABCD A B C D -分成两部分的体积的比为1:7 【答案】ACD 【分析】如图,计算可得,,,E F G H 分别为所在棱的中点,利用空间中点线面的位置关系的判断方法可判断A 、B 的正确与否,计算出直线AB 与平面EFGH 所成的角为45︒后可得C 正确,而几何体BHE CGF -为三棱柱,利用公式可求其体积,从而可判断D 正确与否. 【详解】如图,连接OA ,则2115OA AA =+=,故棱1111,,,A A A D D D AD 与球面没有交点.同理,棱111111,,A B B C C D 与球面没有交点. 因为棱11A D 与棱BC 之间的距离为26>BC 与球面没有交点.因为正方体的棱长为2,而26<球面与正方体1111ABCD A B C D -的棱有四个交点E ,F ,G ,H , 所以棱11,,,AB CD C C B B 与球面各有一个交点, 如图各记为,,,E F G H .因为OAE △为直角三角形,故22651AE OE OA -=-=,故E 为棱AB 的中点. 同理,,F G H 分别为棱11,,CD C C B B 的中点.由正方形ABCD 、,E F 为所在棱的中点可得//EF BC , 同理//GH BC ,故//EF GH ,故,,,E F G H 共面. 由正方体1111ABCD A B C D -可得11//A D BC ,故11//A D EF因为11A D ⊄平面EFGH ,EF ⊂平面EFGH ,故11//A D 平面EFGH ,故A 正确. 因为在直角三角1BA C 中,122A B =2BC = ,190A BC ∠=︒, 1A C 与BC 不垂直,故1A C 与GH 不垂直,故1A C ⊥平面EFGH 不成立,故B 错误.由正方体1111ABCD A B C D -可得BC ⊥平面11AA B B ,而1A B ⊂平面11AA B B , 所以1BC A B ⊥,所以1EF A B ⊥在正方形11AA B B 中,因为,E H 分别为1,AB BB 的中点,故1EH A B ⊥,因为EF EH E =,故1A B ⊥平面EFGH ,所以BEH ∠为直线AB 与平面EFGH 所成的角,而45BEH ∠=︒,故直线AB 与平面EFGH 所成的角为45︒,因为11//AB A B ,故11A B 与平面EFGH 所成的角的大小为45°.故C 正确.因为,,,E F G H 分别为所在棱的中点,故几何体BHE CGF -为三棱柱, 其体积为111212⨯⨯⨯=,而正方体的体积为8, 故平面EFGH 将正方体1111ABCD A B C D -分成两部分的体积的比为1:7,故D 正确. 故选:ACD.【点睛】本题考查空间中线面位置的判断、空间角的计算和体积的计算,注意根据球的半径确定哪些棱与球面有交点,本题属于中档题.6.如图,矩形ABCD 中, 22AB AD ==,E 为边AB 的中点.将ADE 沿直线DE 翻折成1A DE △(点1A 不落在底面BCDE 内),若M 在线段1A C 上(点M 与1A ,C 不重合),则在ADE 翻转过程中,以下命题正确的是( )A .存在某个位置,使1DE A C ⊥B .存在点M ,使得BM ⊥平面1A DC 成立C .存在点M ,使得//MB 平面1A DE 成立D .四棱锥1A BCDE -体积最大值为24【答案】CD【分析】利用反证法可得A 、B 错误,取M 为1A C 的中点,取1A D 的中点为I ,连接,MI IE ,可证明//MB 平面1A DE ,当平面1A DE ⊥平面BCDE 时,四棱锥1A BCDE -体积最大值,利用公式可求得此时体积为24. 【详解】如图(1),取DE 的中点为F ,连接1,A F CF ,则45CDF ∠=︒,22DF =,故212254222222CF =+-⨯⨯=, 故222DC DF CF ≠+即2CFD π∠≠.若1CA DE ⊥,因为11,A D A E DF FE ==,故1A F DE ⊥,而111A F A C A ⋂=, 故DE ⊥平面1A FC ,因为CF ⊂平面1A FC ,故DE CF ⊥,矛盾,故A 错. 若BM ⊥平面1A DC ,因为DC ⊂平面1A DC ,故BM DC ⊥,因为DC CB ⊥,BM CB B ⋂=,故CD ⊥平面1A CB ,因为1AC ⊂平面1A CB ,故1CD A C ⊥,但1A D CD <,矛盾,故B 错. 当平面1A DE ⊥平面BCDE 时,四棱锥1A BCDE -体积最大值,由前述证明可知1A F DE ⊥,而平面1A DE 平面BCDE DE =,1A F ⊂平面1A DE ,故1A F ⊥平面BCDE ,因为1A DE △为等腰直角三角形,111A D A E ==,故122A F =, 又四边形BCDE 的面积为13211122⨯-⨯⨯=, 故此时体积为13223224⨯⨯=D 正确. 对于C ,如图(2),取M 为1A C 的中点,取1A D 的中点为I ,连接,MI IE ,则1//,2IM CD IM CD =,而1//,2BE CD BE CD =, 故//,IM BE IM BE =即四边形IEBM 为平行四边形,故//IE BM ,因为IE ⊂平面1A DE ,BM ⊄平面1A DE ,故//MB 平面1A DE , 故C 正确.故选:CD.【点睛】本题考查立体几何中的折叠问题,注意对于折叠后点线面的位置的判断,若命题的不成立,往往需要利用反证法来处理,本题属于难题.7.如图,1111ABCD A B C D -为正方体,下列结论中正确的是( )A .11A C ⊥平面11BB D DB .1BD ⊥平面1ACBC .1BD 与底面11BCC B 2D .过点1A 与异面直线AD 与1CB 成60角的直线有2条【答案】ABD【分析】由直线与平面垂直的判定判断A 与B ;求解1BD 与底面11BCC B 所成角的正切值判断C ;利用空间向量法可判断D .【详解】对于A 选项,如图,在正方体1111ABCD A B C D -中,1BB ⊥平面1111D C B A ,11A C ⊂平面1111D C B A ,则111BB A C ⊥,由于四边形1111D C B A 为正方形,则1111AC B D ⊥,1111BB B D B =,因此,11A C ⊥平面11BB D D ,故A 正确;对于B 选项,在正方体1111ABCD A B C D -中,1DD ⊥平面ABCD ,AC ⊂平面ABCD ,1AC DD ∴⊥,因为四边形ABCD 为正方形,所以,AC BD ⊥,1D DD BD =,AC ∴⊥平面11BB D D ,1BD ⊂平面11BB D D ,1AC BD ∴⊥,同理可得11BD B C ⊥, 1ACB C C =,1BD ∴⊥平面1ACB ,故B 正确; 对于C 选项,由11C D ⊥平面11BCC B ,得11C BD ∠为1BD 与平面11BCC B 所成角, 且111112tan 2C D C BD BC ∠==,故C 错误; 对于D 选项,以点D 为坐标原点,DA 、DC 、1DD 所在直线分别为x 、y 、z 轴建立如下图所示的空间直角坐标系,设正方体的棱长为1,则()1,0,0A 、()0,0,0D 、()0,1,0C 、()11,1,1B ,()1,0,0DA =,()11,0,1CB =,设过点1A 且与直线DA 、1CB 所成角的直线的方向向量为()1,,m y z =, 则221cos ,21DA mDA m DA m y z ⋅<>===⋅++, 1122111cos ,221CB m z CB m CB m y z ⋅+<>===⋅⋅++, 整理可得2222341y z y z z ⎧+=⎨=++⎩,消去y 并整理得2210z z +-=,解得12z =-12z =-由已知可得3z ≤,所以,12z =-+22y =±因此,过点1A 与异面直线AD 与1CB 成60角的直线有2条,D 选项正确.故选:ABD.【点睛】方法点睛:证明线面垂直的方法:一是线面垂直的判定定理;二是利用面面垂直的性质定理;三是平行线法(若两条平行线中一条垂直于这个平面,则另一条也垂直于这个平面),解题时,注意线线、线面与面面关系的相互转化;另外,在证明线线垂直时,要注意题中隐含的垂直关系,如等腰三角形的底边上的高、中线和顶角的角平分线三线合一、矩形的内角、直径所对的圆周角、菱形的对角线互相垂直、直角三角形(或给出线段长度,经计算满足勾股定理)、直角梯形等等.8.半正多面体(semiregularsolid)亦称“阿基米德多面体”,是由边数不全相同的正多边形围成的多面体,体现了数学的对称美.二十四等边体就是一种半正多面体,是由正方体切截而成的,它由八个正三角形和六个正方形构成(如图所示),若它的所有棱长都为2,则()A.BF⊥平面EABB.该二十四等边体的体积为20 3C.该二十四等边体外接球的表面积为8πD.PN与平面EBFN所成角的正弦值为2 2【答案】BCD【分析】A用反证法判断;B先补齐八个角成正方体,再计算体积判断;C先找到球心与半径,再计算表面积判断;D先找到直线与平面所成角,再求正弦值判断.【详解】解:对于A,假设A对,即BF⊥平面EAB,于是BF AB⊥,90ABF∠=︒,但六边形ABFPQH为正六边形,120ABF∠=︒,矛盾,所以A错;对于B ,补齐八个角构成棱长为2的正方体, 则该二十四等边体的体积为3112028111323-⋅⋅⋅⋅⋅=, 所以B 对;对于C ,取正方形ACPM 对角线交点O ,即为该二十四等边体外接球的球心,其半径为2R =,其表面积为248R ππ=,所以C 对;对于D ,因为PN 在平面EBFN 内射影为NS ,所以PN 与平面EBFN 所成角即为PNS ∠,其正弦值为222PS PN ==,所以D 对. 故选:BCD .【点睛】本题考查了正方体的性质,考查了直线与平面所成角问题,考查了球的体积与表面积计算问题.。
高三数学精选立体几何多选题 易错题质量专项训练试题

高三数学精选立体几何多选题 易错题质量专项训练试题一、立体几何多选题1.在棱长为1的正方体1111ABCD A B C D -中,P 为底面ABCD 内(含边界)一点.( ) A .若13A P =,则满足条件的P 点有且只有一个 B .若12A P =,则点P 的轨迹是一段圆弧 C .若1//A P 平面11B DC ,则1A P 长的最小值为2D .若12A P =且1//A P 平面11B DC ,则平面11A PC 截正方体外接球所得截面的面积为23π 【答案】ABD【分析】选项A ,B 可利用球的截面小圆的半径来判断;由平面1//A BD 平面11B D C ,知满足1//A P 平面11B D C 的点P 在BD 上,1A P 长的最大值为2;结合以上条件点P 与B 或D 重合,利用12sin 60A P r =︒,求出63r =,进而求出面积. 【详解】对A 选项,如下图:由13A P =,知点P 在以1A 为球心,半径为3的球上,又因为P 在底面ABCD 内(含边界),底面截球可得一个小圆,由1A A ⊥底面ABCD ,知点P 的轨迹是在底面上以A 为圆心的小圆圆弧,半径为22112r A P A A =-=,则只有唯一一点C满足,故A 正确;对B 选项,同理可得点P 在以A 为圆心,半径为22111r A P A A =-=的小圆圆弧上,在底面ABCD 内(含边界)中,可得点P 轨迹为四分之一圆弧BD .故B 正确;对C 选项,移动点P 可得两相交的动直线与平面11B D C 平行,则点P 必在过1A 且与平面11B D C 平行的平面内,由平面1//A BD 平面11B D C ,知满足1//A P 平面11B D C 的点P 在BD上,则1A P 长的最大值为12A B =,则C 不正确; 对选项D ,由以上推理可知,点P 既在以A 为圆心,半径为1的小圆圆弧上,又在线段BD 上,即与B 或D 重合,不妨取点B ,则平面11A PC 截正方体外接球所得截面为11A BC 的外接圆,利用2126622,,sin 60333A B r r S r ππ==∴=∴==︒.故D 正确.故选:ABD【点睛】(1)平面截球所得截面为圆面,且满足222=R r d +(其中R 为球半径,r 为小圆半径,d 为球心到小圆距离);(2)过定点A 的动直线平行一平面α,则这些动直线都在过A 且与α平行的平面内.2.在正方体1111ABCD A B C D -中,M 、N 分别是棱AB 、1CC 的中点,1MB P 的顶点P 在棱1CC 与棱11C D 上运动,有以下四个命题正确命题的序号是( )A .平面1MB P 1ND ⊥B .平面1MB P ⊥平面11ND AC .1MB P 在底面ABCD 上的射影图形的面积为定值D .1MB P 在侧面11D C CD 上射影图形是三角形【答案】BC【分析】取N 与P 重合,结合勾股定理可判断A 选项的正误;利用面面垂直的判定定理可判断B选项的正误;分点P 在棱1CC 、11C D 上运动两种情况讨论,利用三角形的面积公式可判断C 选项的正误;取点P 与点1C 重合,判断1MB P 在侧面11D C CD 上射影图形形状,可判断D 选项的正误.【详解】对于A 选项,设正方体1111ABCD A B C D -的棱长为2,如下图所示:当点P 与点N 重合时,若1ND ⊥平面1MB P ,1B N ⊂平面1MB P ,则11ND B N ⊥, 由勾股定理可得2211115D N C N C D =+=,同理可得15B N =,1122B D =, 2221111B N D N B D ∴+≠,则1ND 与1B N 不垂直,假设不成立,A 选项错误;对于B 选项,取1BB 的中点E ,连接1A E 、EN ,在正方体1111ABCD A B C D -中,11//BB CC ,且E 、N 分别为1BB 、1CC 的中点,则11//B E C N 且11B E C N =,所以,四边形11B ENC 为平行四边形,则11//EN B C 且11EN B C =,1111//A D B C 且1111A D B C =,所以,11//A D EN 且11A D EN =,所以,四边形11A END 为平行四边形,所以,11//A E D N ,111A B BB =,1B E BM =,11190A B E B BM ∠=∠=,所以,111Rt A B E Rt B BM ≅△△,所以,111B A E BB M ∠=∠,所以,111111190A EB BB M A EB B A E ∠+∠=∠+∠=, 190B FE ∴∠=,所以,11B M A E ⊥,11A D ⊥平面11AA B B ,1B M ⊂平面11AA B B ,111B M A D ∴⊥,1111A D A E A =,11A D 、1A E ⊂平面11ND A ,1MB ∴⊥平面11ND A ,1MB ⊂平面1MB P ,所以,平面1MB P ⊥平面11ND A ,B 选项正确;对于C 选项,设正方体1111ABCD A B C D -的棱长为a .若点P 在棱1CC 上运动时,1MB P 在底面ABCD 上的射影为MBC △, 此时,射影图形的面积为21224MBC a a S a =⋅=△; 若点P 在棱11C D 上运动时,设点P 在底面ABCD 上的射影点为G ,则G CD ∈, 且点G 到AB 的距离为a ,1MB 在底面ABCD 内的射影为MB ,则1MB P 在底面ABCD 内的射影为MBG △, 且21224MBG a a S a =⋅⋅=△.综上所述,1MB P 在底面ABCD 内的射影图形的面积为定值,C 选项正确;对于D 选项,当点P 与1C 重合时,P 、1B 两点在平面11D C CD 上的射影重合, 此时,1MB P 在侧面11D C CD 上的射影不构成三角形,D 选项错误.故选:BC.【点睛】方法点睛:证明面面垂直常用的方法:(1)面面垂直的定义;(2)面面垂直的判定定理.在证明面面垂直时,一般假设面面垂直成立,然后利用面面垂直转化为线面垂直,即为所证的线面垂直,组织论据证明即可.3.如图,正方体1111ABCD A B C D -的棱长为3,点E ,F 分别在1CC ,1BB 上,12C E EC →→=,12BF FB →→=.动点M 在侧面11ADD A 内(包含边界)运动,且满足直线//BM 平面1D EF ,则( )A .过1D ,E ,F 的平面截正方体所得截面为等腰梯形B .三棱锥1D EFM -的体积为定值C .动点M 10D .过B ,E ,M 的平面截正方体所得截面面积的最小值为10【答案】BCD【分析】由题做出过1D ,E ,F 的平面截正方体所得截面为梯形1D EFN ,进而计算即可排除A 选项;根据//BM 平面1D EF ,由等体积转化法得1111D EFM M D EF B D EF D BEF V V V V ----===即可得B 选项正确;取1AA 靠近1A 点的三等分点H , 1DD 靠近D 点的三等分点I ,易知M 的轨迹为线段HI 10,故C 选项正确;过M 点做BE 的平行线交1AA 于P ,交1DD 于O ,连接,BP OE ,易知过B ,E ,M 的平面截正方体所得截面即为平行四边形BPOE ,进而得当H 位于点I 时,截面面积最小,为四边形ABEI 的面积,且面积为310S AB BE =⋅=【详解】解:对于A 选项,如图,取BF 中点G ,连接1A G ,由点E ,F 分别在1CC ,1BB 上,12C E EC →→=,12BF FB →→=,故四边形11A D EG 为平行四边形,故11//AG D E ,由于在11A B G △,F 为1B G 中点,当N 为11A B 中点时,有11////NF A G D E ,故过1D ,E ,F 的平面截正方体所得截面为梯形1D EFN ,此时22133532D N ⎛⎫=+= ⎪⎝⎭,223110EF =+=,故梯形1D EFN 不是等腰梯形,故A 选项错误;对于B 选项,三棱锥1D EFM -的体积等于三棱锥1M D EF -的体积,由于//BM 平面1D EF ,故三棱锥1M D EF -的体积等于三棱锥1B D EF -的体积,三棱锥1B D EF -的体积等于三棱锥1D BEF -的体积,而三棱锥1D BEF -的体积为定值,故B 选项正确; 对于C 选项,取1AA 靠近1A 点的三等分点H , 1DD 靠近D 点的三等分点I ,易知1////HB AG NF ,1//BI D F ,由于1,HI BI I NF D F F ==,故平面//BHI 平面1D EF ,故M 的轨迹为线段HI ,其长度为10,故C 选项正确;对于D 选项,过M 点做BE 的平行线交1AA 于P ,交1DD 于O ,连接,BP OE ,则过B ,E ,M 的平面截正方体所得截面即为平行四边形BPOE ,易知当H 位于点I 时,平行四边形BPOE 边BP 最小,且为AB ,此时截面平行四边形BPOE 的面积最小,为四边形ABEI 的面积,且面积为310S AB BE =⋅=,故D 选项正确;故选:BCD【点睛】本题解题的关键在于根据题意,依次做出过1D ,E ,F 的平面截正方体所得截面为梯形1D EFN ,过B ,E ,M 的平面截正方体所得截面即为平行四边形BPOE ,进而讨论AD 选项,通过//BM 平面1D EF ,并结合等体积转化法得1111D EFM M D EF B D EF D BEF V V V V ----===知B 选项正确,通过构造面面平行得M 的轨迹为线段HI ,进而讨论C 选项,考查回归转化思想和空间思维能力,是中档题.4.在直角梯形ABCD 中,2ABC BCD π∠=∠=,1AB BC ==,2DC =,E 为DC 中点,现将ADE 沿AE 折起,得到一个四棱锥D ABCE -,则下列命题正确的有( ) A .在ADE 沿AE 折起的过程中,四棱锥D ABCE -体积的最大值为13 B .在ADE 沿AE 折起的过程中,异面直线AD 与BC 所成的角恒为4π C .在ADE 沿AE 折起的过程中,二面角A EC D --的大小为45︒D .在四棱锥D ABCE -中,当D 在EC 上的射影恰好为EC 的中点F 时,DB 与平面ABCE 所成的角的正切为15 【答案】ABD【分析】对于A ,四棱锥D ABCE -的底面面积是固定值,要使得体积最大,需要平面DAE ⊥平面ABCE ,此时DE CE ⊥,可求得1133D ABCE ABCE V S DE -=⋅=可判断A ;对于B ,在ADE 沿AE 折起的过程中,//AE BC ,所以异面直线AD 与AE 所成的角即为AD 与BC 所成角,由翻折前可知4DAE π∠=可判断B ;对于C ,利用线面垂直的判定定理,结合翻折前可知AE ⊥平面DEC ,又AE ⊂平面ABCE ,所以平面DEC ⊥平面ABCE ,即二面角A EC D --的在大小为2π判断C ;对于D ,利用线面垂直的判定定理可知DF ⊥平面ABCE ,所以DBF ∠为直线DB 与平面ABCE 所成的角,在直角DFB △中,15tan 5DF DBF BF ∠==,可判断D 正确;【详解】对于A ,ADE 沿AE 折起得到四棱锥D ABCE -,由四棱锥底面面积是固定值,要使得体积最大,需要四棱锥的高最大,即平面DAE ⊥平面ABCE ,此时DE CE ⊥,由已知得1DE =,则111111333D ABCE ABCE V S DE -=⋅=⨯⨯⨯=,故A 正确; 对于B ,在ADE 沿AE 折起的过程中,//AE BC ,所以异面直线AD 与AE 所成的角即为AD 与BC 所成角,又1AB BC ==,2DC =,E 为DC 中点,可知4DAE π∠=,即异面直线AD 与BC 所成的角恒为4π,故B 正确; 对于C ,由翻折前知,,AE EC AE ED ⊥⊥,且EC ED E =,则AE ⊥平面DEC ,又AE ⊂平面ABCE ,所以平面DEC ⊥平面ABCE ,即二面角A EC D --的大小为2π,故C 错误; 对于D ,如图连接,DF BF ,由C 选项知,AE ⊥平面DEC ,又DF ⊂平面DEC ,则AE DF ⊥,又由已知得EC DF ⊥,且EC AE E ⋂=,则DF ⊥平面ABCE ,所以DBF ∠为直线DB 与平面ABCE 所成的角,在直角DFB △中,tan DF DBF BF ∠=====DB 与平面ABCE所成的角的正切为5,故D 正确; 故选:ABD【点睛】 关键点睛:本题考查立体几何综合问题,求体积,求线线角,线面角,面面角,解题的关键要熟悉几种角的定义,通过平移法找到线线角,通过证垂直找到线面角和面面角,再结合三角形求出角,考查了学生的逻辑推理能力,转化能力与运算求解能力,属于难题.5.已知正方体1111ABCD A B C D -的棱长为2,点O 为11A D 的中点,若以O为半径的球面与正方体1111ABCD A B C D -的棱有四个交点E ,F ,G ,H ,则下列结论正确的是( )A .11//A D 平面EFGHB .1AC ⊥平面EFGHC .11A B 与平面EFGH 所成的角的大小为45°D .平面EFGH 将正方体1111ABCD A B C D -分成两部分的体积的比为1:7【答案】ACD【分析】如图,计算可得,,,E F G H 分别为所在棱的中点,利用空间中点线面的位置关系的判断方法可判断A 、B 的正确与否,计算出直线AB 与平面EFGH 所成的角为45︒后可得C 正确,而几何体BHE CGF -为三棱柱,利用公式可求其体积,从而可判断D 正确与否.【详解】如图,连接OA ,则2115OA AA =+=,故棱1111,,,A A A D D D AD 与球面没有交点. 同理,棱111111,,A B B C C D 与球面没有交点.因为棱11A D 与棱BC 之间的距离为26>BC 与球面没有交点. 因为正方体的棱长为2,而26<球面与正方体1111ABCD A B C D -的棱有四个交点E ,F ,G ,H ,所以棱11,,,AB CD C C B B 与球面各有一个交点, 如图各记为,,,E F G H .因为OAE △为直角三角形,故22651AE OE OA -=-=,故E 为棱AB 的中点. 同理,,F G H 分别为棱11,,CD C C B B 的中点.由正方形ABCD 、,E F 为所在棱的中点可得//EF BC ,同理//GH BC ,故//EF GH ,故,,,E F G H 共面.由正方体1111ABCD A B C D -可得11//A D BC ,故11//A D EF因为11A D ⊄平面EFGH ,EF ⊂平面EFGH ,故11//A D 平面EFGH ,故A 正确.因为在直角三角1BA C 中,122A B =2BC = ,190A BC ∠=︒, 1A C 与BC 不垂直,故1A C 与GH 不垂直,故1A C ⊥平面EFGH 不成立,故B 错误. 由正方体1111ABCD A B C D -可得BC ⊥平面11AA B B ,而1A B ⊂平面11AA B B , 所以1BC A B ⊥,所以1EF A B ⊥在正方形11AA B B 中,因为,E H 分别为1,AB BB 的中点,故1EH A B ⊥,因为EF EH E =,故1A B ⊥平面EFGH ,所以BEH ∠为直线AB 与平面EFGH 所成的角,而45BEH ∠=︒,故直线AB 与平面EFGH 所成的角为45︒,因为11//AB A B ,故11A B 与平面EFGH 所成的角的大小为45°.故C 正确.因为,,,E F G H 分别为所在棱的中点,故几何体BHE CGF -为三棱柱, 其体积为111212⨯⨯⨯=,而正方体的体积为8, 故平面EFGH 将正方体1111ABCD A B C D -分成两部分的体积的比为1:7,故D 正确. 故选:ACD.【点睛】本题考查空间中线面位置的判断、空间角的计算和体积的计算,注意根据球的半径确定哪些棱与球面有交点,本题属于中档题.6.M ,N 分别为菱形ABCD 的边BC ,CD 的中点,将菱形沿对角线AC 折起,使点D 不在平面ABC 内,则在翻折过程中,下列结论正确的有( )A .MN ∥平面ABDB .异面直线AC 与MN 所成的角为定值C .在二面角D AC B --逐渐变小的过程中,三棱锥D ABC -外接球的半径先变小后变大D .若存在某个位置,使得直线AD 与直线BC 垂直,则ABC ∠的取值范围是0,2π⎛⎫ ⎪⎝⎭ 【答案】ABD【分析】利用线面平行的判定即可判断选项A ;利用线面垂直的判定求出异面直线AC 与MN 所成的角即可判断选项B ;借助极限状态,当平面DAC 与平面ABC 重合时,三棱锥D ABC -外接球即是以ABC ∆外接圆圆心为球心,外接圆的半径为球的半径,当二面角D AC B --逐渐变大时,利用空间想象能力进行分析即可判断选项C;过A 作AH BC ⊥,垂足为H ,分ABC ∠为锐角、直角、钝角三种情况分别进行分析判断即可判断选项D.【详解】对于选项A:因为M ,N 分别为菱形ABCD 的边BC ,CD 的中点,所以MN 为BCD ∆的中位线,所以//MN BD ,因为MN ⊄平面ABD ,BD ⊂平面ABD ,所以MN ∥平面ABD ,故选项A 正确;对于选项B :取AC 的中点O ,连接,DO BO ,作图如下:则,AC DO AC BO ⊥⊥,BO DO O =,由线面垂直的判定知,AC ⊥平面BOD ,所以AC BD ⊥,因为//MN BD ,所以AC MN ⊥,即异面直线AC 与MN 所成的角为定值90,故选项B 正确;对于选项C:借助极限状态,当平面DAC 与平面ABC 重合时,三棱锥D ABC -外接球即是以ABC ∆外接圆圆心为球心,外接圆的半径为球的半径,当二面角D AC B --逐渐变大时,球心离开平面ABC ,但是球心在底面的投影仍然是ABC ∆外接圆圆心,故二面角D AC B --逐渐变小的过程中,三棱锥D ABC -外接球的半径不可能先变小后变大, 故选项C 错误;对于选项D:过A 作AH BC ⊥,垂足为H ,若ABC ∠为锐角,H 在线段BC 上;若ABC ∠为直角,H 与B 重合;若ABC ∠为钝角,H 在线段BC 的延长线上;若存在某个位置,使得直线AD 与直线BC 垂直,因为AH BC ⊥,所以CB ⊥平面AHD ,由线面垂直的性质知,CB HD ⊥,若ABC ∠为直角,H 与B 重合,所以CB BD ⊥,在CBD ∆中,因为CB CD =, 所以CB BD ⊥不可能成立,即ABC ∠为直角不可能成立;若ABC ∠为钝角,H 在线段BC 的延长线上,则在原平面图菱形ABCD 中,DCB ∠为锐角,由于立体图中DB DO OB <+,所以立体图中DCB ∠一定比原平面图中更小,,所以DCB ∠为锐角,CB HD ⊥,故点H 在线段BC 与H 在线段BC 的延长线上矛盾,因此ABC ∠不可能为钝角;综上可知,ABC ∠的取值范围是0,2π⎛⎫ ⎪⎝⎭.故选项D 正确; 故选:ABD【点睛】本题考查异面垂直、线面平行与线面垂直的判定、多面体的外接球问题;考查空间想象能力和逻辑推理能力;借助极限状态和反证法思想的运用是求解本题的关键;属于综合型强、难度大型试题.7.如图,已知P 为棱长为1的正方体对角线1BD 上的一点,且()()10,1BP BD λλ=,下面结论中正确结论的有( )A .11A D C P ⊥;B .当1A P PD +取最小值时,23λ=;C .若()0,1λ∈,则7,312APC ππ⎛⎫∠∈ ⎪⎝⎭; D .若P 为1BD 的中点,四棱锥11P AA D D -的外接球表面积为94π. 【答案】ABD【分析】以D 为坐标原点建立如图空间直角坐标系,利用向量关系可判断ABC ;根据几何体外接球关系建立方程求出球半径即可判断D.【详解】以D 为坐标原点建立如图空间直角坐标系,则()1,1,0B ,()10,0,1D ,设(),,P x y z ,()()10,1BP BD λλ=,1BP BD λ∴=,即()()1,1,1,1,1x y z λ--=--,则可解得()1,1,P λλλ--,对A ,()()()111,0,1,0,0,0,0,1,1A D C ,()11,0,1A D ∴=--,()11,,1C P λλλ=---,则()()()()11110110A D C P λλλ⋅=-⨯-+⨯-+-⨯-=,则11A D C P ⊥,故A 正确;对B ,1A P PD +=== 则当23λ=时,1A P PD +取最小值,故B 正确; 对C ,()()1,0,0,0,1,0A C ,(),1,PA λλλ∴=--,()1,,PC λλλ=--,则222321cos 1321321PA PC APC PA PC λλλλλλ⋅-∠===--+-+⋅, 01λ<<,则2232123λλ≤-+<,则2111123212λλ-≤-<-+, 即11cos 22APC -≤∠<,则2,33APC ππ⎛⎤∠∈ ⎥⎝⎦,故C 错误; 对于D ,当P 为1BD 中点时,四棱锥11P AA D D -为正四棱锥,设平面11AA D D 的中心为O ,四棱锥11P AA D D -的外接球半径为R ,所以222122R R ⎛⎛⎫-+= ⎪ ⎝⎭⎝⎭,解得34R =, 故四棱锥11P AA D D -的外接球表面积为94π,所以D 正确. 故选:ABD.【点睛】 关键点睛:本题考查空间相关量的计算,解题的关键是建立空间直角坐标系,利用向量建立关系进行计算.8.半正多面体(semiregularsolid )亦称“阿基米德多面体”,是由边数不全相同的正多边形围成的多面体,体现了数学的对称美.二十四等边体就是一种半正多面体,是由正方体切截而成的,它由八个正三角形和六个正方形构成(如图所示),若它的所有棱长都为)A .BF ⊥平面EABB .该二十四等边体的体积为203C .该二十四等边体外接球的表面积为8πD .PN 与平面EBFN 2 【答案】BCD【分析】 A 用反证法判断;B 先补齐八个角成正方体,再计算体积判断;C 先找到球心与半径,再计算表面积判断;D 先找到直线与平面所成角,再求正弦值判断.【详解】解:对于A ,假设A 对,即BF ⊥平面EAB ,于是BF AB ⊥,90ABF ∠=︒,但六边形ABFPQH 为正六边形,120ABF ∠=︒,矛盾,所以A 错;对于B ,补齐八个角构成棱长为2的正方体, 则该二十四等边体的体积为3112028111323-⋅⋅⋅⋅⋅=, 所以B 对;对于C ,取正方形ACPM 对角线交点O ,即为该二十四等边体外接球的球心, 其半径为2R =248R ππ=,所以C 对;对于D ,因为PN 在平面EBFN 内射影为NS ,所以PN 与平面EBFN 所成角即为PNS ∠, 其正弦值为22PS PN =,所以D 对. 故选:BCD .【点睛】本题考查了正方体的性质,考查了直线与平面所成角问题,考查了球的体积与表面积计算问题.。
高三数学易错立体几何多选题 易错题难题专题强化试卷学能测试

高三数学易错立体几何多选题 易错题难题专题强化试卷学能测试一、立体几何多选题1.如图①,矩形ABCD 的边2BC =,设AB x =,0x >,三角形BCM 为等边三角形,沿BC 将三角形BCM 折起,构成四棱锥M ABCD -如图②,则下列说法正确的有( )A .若T 为BC 中点,则在线段MC 上存在点P ,使得//PD 平面MATB .当)3,2x ∈时,则在翻折过程中,不存在某个位置满足平面MAD ⊥平面ABCD C .若使点M 在平面ABCD 内的射影落在线段AD 上,则此时该四棱锥的体积最大值为1 D .若1x =,且当点M 在平面ABCD 内的射影点H 落在线段AD 上时,三棱锥M HAB -6322++【答案】BCD【分析】 对于A ,延长AT 与DC 的延长线交于点N ,此时,DP 与MN 必有交点;对于B ,取AD 的中点H ,表示出2223MH MT HT x --,验证当)3,2x ∈时,无解即可;对于C ,利用体积公式21233V x x =⨯⨯-,借助基本不等式求最值即可; 对于D ,要求外接球半径与内切球半径,找外接圆的圆心,又内接圆半径为2323r =++ 【详解】对于A ,如图,延长AT 与DC 的延长线交于点N ,则面ATM ⋂面()MDC N MN =.此时,DP 与MN 必有交点,则DP 与面ATM 相交,故A 错误;对于B ,取AD 的中点H ,连接MH ,则MH AD ⊥.若面MAD ⊥面ABCD ,则有2223MH MT HT x =-=- 当)3,2x ∈时,无解,所以在翻折过程中,不存在某个位置满足平面MAD ⊥平面ABCD故B 正确;对于C ,由题可知,此时面MAD ⊥面ABCD ,由B 可知,(3x ∈, 所以()22222221223232331333232x x V x x x x ⎛⎫+-⎛⎫=⨯⨯-=-≤== ⎪ ⎪⎝⎭⎝⎭ 当且仅当223x x =-,即6x =时等号成立.故C 正确; 对于D ,由题可知,此时面MAD ⊥面ABCD ,且2MH =因为AHB ,MHB 都是直角三角形,所以M ABH -底面外接圆的圆心是中点,所以1R =, 由等体积法,可求得内接圆半径为2323r =++,故61322R r +=,故D 正确. 故选:BCD .【点睛】本题从多个角度深度考查了立体几何的相关内容,注意辅助线的作法,以及求内接圆半径的公式、基本不等式、构造函数等核心思想.2.在正三棱柱111ABC A B C -中,2AC =11CC =,点D 为BC 中点,则以下结论正确的是( )A .111122A D AB AC AA =+- B .三棱锥11D AB C -3C .1AB BC ⊥且1//AB 平面11AC DD .ABC 内到直线AC 、1BB 的距离相等的点的轨迹为抛物线的一部分【答案】ABD【分析】A .根据空间向量的加减运算进行计算并判断;B .根据1111D ABC A DB C V V --=,然后计算出对应三棱锥的高AD 和底面积11DB C S ,由此求解出三棱锥的体积;C .先假设1AB BC ⊥,然后推出矛盾;取AB 中点E ,根据四点共面判断1AB //平面11AC D 是否成立;D .将问题转化为“ABC 内到直线AC 和点B 的距离相等的点”的轨迹,然后利用抛物线的定义进行判断.【详解】A .()11111111222A D A A AD AD AA AB AC AA AB AC AA =+=-=+-=+-,故正确;B .1111D ABC A DB C V V --=,因为D 为BC 中点且AB AC =,所以AD BC ⊥,又因为1BB ⊥平面ABC ,所以1BB AD ⊥且1BB BC B =,所以AD ⊥平面11DB C , 又因为36322AD BD BC ===,111111222DB C S BB B C =⨯⨯=, 所以11111111623332D AB C A DB C DB C V V AD S --==⨯⨯=⋅⋅=,故正确;C .假设1AB BC ⊥成立,又因为1BB ⊥平面ABC ,所以1BB BC ⊥且111BB AB B =, 所以BC ⊥平面1ABB ,所以BC AB ⊥,显然与几何体为正三棱柱矛盾,所以1AB BC ⊥不成立;取AB 中点E ,连接11,,ED EA AB ,如下图所示:因为,D E 为,BC AB 中点,所以//DE AC ,且11//AC A C ,所以11//DE AC ,所以11,,,D E A C 四点共面,又因为1A E 与1AB 相交,所以1AB //平面11AC D 显然不成立,故错误;D .“ABC 内到直线AC 、1BB 的距离相等的点”即为“ABC 内到直线AC 和点B 的距离相等的点”,根据抛物线的定义可知满足要求的点的轨迹为抛物线的一部分,故正确;故选:ABD.【点睛】方法点睛:求解空间中三棱锥的体积的常用方法:(1)公式法:直接得到三棱锥的高和底面积,然后用公式进行计算;(2)等体积法:待求三棱锥的高和底面积不易求出,采用替换顶点位置的方法,使其求解高和底面积更容易,由此求解出三棱锥的体积.3.在正方体1111ABCD A B C D -中,M 、N 分别是棱AB 、1CC 的中点,1MB P 的顶点P 在棱1CC 与棱11C D 上运动,有以下四个命题正确命题的序号是( )A .平面1MB P 1ND ⊥B .平面1MB P ⊥平面11ND AC .1MB P 在底面ABCD 上的射影图形的面积为定值D .1MB P 在侧面11D C CD 上射影图形是三角形【答案】BC【分析】取N 与P 重合,结合勾股定理可判断A 选项的正误;利用面面垂直的判定定理可判断B 选项的正误;分点P 在棱1CC 、11C D 上运动两种情况讨论,利用三角形的面积公式可判断C 选项的正误;取点P 与点1C 重合,判断1MB P 在侧面11D C CD 上射影图形形状,可判断D 选项的正误.【详解】对于A 选项,设正方体1111ABCD A B C D -的棱长为2,如下图所示:当点P 与点N 重合时,若1ND ⊥平面1MB P ,1B N ⊂平面1MB P ,则11ND B N ⊥,由勾股定理可得2211115D N C N C D =+=,同理可得15B N =,1122B D =, 2221111B N D N B D ∴+≠,则1ND 与1B N 不垂直,假设不成立,A 选项错误;对于B 选项,取1BB 的中点E ,连接1A E 、EN ,在正方体1111ABCD A B C D -中,11//BB CC ,且E 、N 分别为1BB 、1CC 的中点, 则11//B E C N 且11B E C N =,所以,四边形11B ENC 为平行四边形,则11//EN B C 且11EN B C =,1111//A D B C 且1111A D B C =,所以,11//A D EN 且11A D EN =,所以,四边形11A END 为平行四边形,所以,11//A E D N ,111A B BB =,1B E BM =,11190A B E B BM ∠=∠=,所以,111Rt A B E Rt B BM ≅△△,所以,111B A E BB M ∠=∠,所以,111111190A EB BB M A EB B A E ∠+∠=∠+∠=, 190B FE ∴∠=,所以,11B M A E ⊥,11A D ⊥平面11AA B B ,1B M ⊂平面11AA B B ,111B M A D ∴⊥,1111A D A E A =,11A D 、1A E ⊂平面11ND A ,1MB ∴⊥平面11ND A ,1MB ⊂平面1MB P ,所以,平面1MB P ⊥平面11ND A ,B 选项正确;对于C 选项,设正方体1111ABCD A B C D -的棱长为a .若点P 在棱1CC 上运动时,1MB P 在底面ABCD 上的射影为MBC △,此时,射影图形的面积为21224MBC a a S a =⋅=△; 若点P 在棱11C D 上运动时,设点P 在底面ABCD 上的射影点为G ,则G CD ∈, 且点G 到AB 的距离为a ,1MB 在底面ABCD 内的射影为MB ,则1MB P 在底面ABCD 内的射影为MBG △, 且21224MBG a a S a =⋅⋅=△.综上所述,1MB P 在底面ABCD 内的射影图形的面积为定值,C 选项正确; 对于D 选项,当点P 与1C 重合时,P 、1B 两点在平面11D C CD 上的射影重合, 此时,1MB P 在侧面11D C CD 上的射影不构成三角形,D 选项错误.故选:BC.【点睛】方法点睛:证明面面垂直常用的方法:(1)面面垂直的定义;(2)面面垂直的判定定理.在证明面面垂直时,一般假设面面垂直成立,然后利用面面垂直转化为线面垂直,即为所证的线面垂直,组织论据证明即可.4.如图,正方体1111ABCD A B C D -的棱长为3,点E ,F 分别在1CC ,1BB 上,12C E EC →→=,12BF FB →→=.动点M 在侧面11ADD A 内(包含边界)运动,且满足直线//BM 平面1D EF ,则( )A .过1D ,E ,F 的平面截正方体所得截面为等腰梯形B .三棱锥1D EFM -的体积为定值C .动点MD .过B ,E ,M 的平面截正方体所得截面面积的最小值为【答案】BCD【分析】由题做出过1D ,E ,F 的平面截正方体所得截面为梯形1D EFN ,进而计算即可排除A 选项;根据//BM 平面1D EF ,由等体积转化法得1111D EFM M D EF B D EF D BEF V V V V ----===即可得B 选项正确;取1AA 靠近1A 点的三等分点H , 1DD 靠近D 点的三等分点I ,易知M 的轨迹为线段HI ,故C 选项正确;过M 点做BE 的平行线交1AA 于P ,交1DD 于O ,连接,BP OE ,易知过B ,E ,M 的平面截正方体所得截面即为平行四边形BPOE ,进而得当H 位于点I 时,截面面积最小,为四边形ABEI 的面积,且面积为S AB BE =⋅=【详解】解:对于A 选项,如图,取BF 中点G ,连接1A G ,由点E ,F 分别在1CC ,1BB 上,12C E EC →→=,12BF FB →→=,故四边形11A D EG 为平行四边形,故11//AG D E ,由于在11A B G △,F 为1B G 中点,当N 为11A B 中点时,有11////NF A G D E ,故过1D ,E ,F 的平面截正方体所得截面为梯形1D EFN ,此时1D N ==,EF ==1D EFN 不是等腰梯形,故A 选项错误;对于B 选项,三棱锥1D EFM -的体积等于三棱锥1M D EF -的体积,由于//BM 平面1D EF ,故三棱锥1M D EF -的体积等于三棱锥1B D EF -的体积,三棱锥1B D EF -的体积等于三棱锥1D BEF -的体积,而三棱锥1D BEF -的体积为定值,故B 选项正确; 对于C 选项,取1AA 靠近1A 点的三等分点H , 1DD 靠近D 点的三等分点I ,易知1////HB AG NF ,1//BI D F ,由于1,HI BI I NF D F F ==,故平面//BHI 平面1D EF ,故M 的轨迹为线段HI ,故C 选项正确;对于D 选项,过M 点做BE 的平行线交1AA 于P ,交1DD 于O ,连接,BP OE ,则过B ,E ,M 的平面截正方体所得截面即为平行四边形BPOE ,易知当H 位于点I 时,平行四边形BPOE 边BP 最小,且为AB ,此时截面平行四边形BPOE 的面积最小,为四边形ABEI 的面积,且面积为S AB BE =⋅=D 选项正确;故选:BCD【点睛】本题解题的关键在于根据题意,依次做出过1D ,E ,F 的平面截正方体所得截面为梯形1D EFN ,过B ,E ,M 的平面截正方体所得截面即为平行四边形BPOE ,进而讨论AD 选项,通过//BM 平面1D EF ,并结合等体积转化法得1111D EFM M D EF B D EF D BEF V V V V ----===知B 选项正确,通过构造面面平行得M 的轨迹为线段HI ,进而讨论C 选项,考查回归转化思想和空间思维能力,是中档题.5.在三棱锥M ABC -中,下列命题正确的是( )A .若1233AD AB AC =+,则3BC BD = B .若G 为ABC 的重心,则111333MG MA MB MC =++ C .若0MA BC ⋅=,0MC AB ⋅=,则0MB AC ⋅=D .若三棱锥M ABC -的棱长都为2,P ,Q 分别为MA ,BC 中点,则2PQ =【答案】BC【分析】作出三棱锥M ABC -直观图,在每个三角形中利用向量的线性运算可得.【详解】对于A ,由已知12322233AD AB AC AD AC AB AD AC AB AD =+⇒=+⇒-=-,即2CD DB =,则32BD BD DC BC =+=,故A 错误; 对于B ,由G 为ABC 的重心,得0GA GB GC ++=,又MG MA AG =+,MG MB BG =+,MG MC CG =+,3MA MB MC MG ∴++=,即111333MG MA MB MC =++,故B 正确; 对于C ,若0MA BC ⋅=,0MC AB ⋅=,则0MC MA BC AB ⋅+⋅=,即()00MA BC AC CB MA BC AC C MC C M B M C ⋅++=⇒⋅++⋅⋅=⋅()00MA BC A MC MC MC MC C BC MA BC AC ⋅⋅⋅⇒⋅+-=⇒-+=⋅()000MC M CA BC AC AC CB AC CB AC C MC ⇒+=⇒+=⇒+=⋅⋅⋅⋅⋅,即0MB AC ⋅=,故C 正确;对于D ,111()()222PQ MQ MP MB MC MA MB MC MA ∴=-=+-=+- ()21122PQ MB MC MA MB MC MA ∴=+-=+-,又()2222222MB MC MA MB MC MA MB MC MB MA MC MA +-=+++⋅-⋅-⋅2221112222222222228222=+++⨯⨯⨯-⨯⨯⨯-⨯⨯⨯=,1822PQ ∴==,故D 错误.故选:BC【点睛】关键点睛:本题考查向量的运算,用已知向量表示某一向量的三个关键点:(1)用已知向量来表示某一向量,一定要结合图形,以图形为指导是解题的关键.(2)要正确理解向量加法、减法与数乘运算的几何意义,如首尾相接的若干向量之和,等于由起始向量的始点指向末尾向量的终点的向量. (3)在立体几何中三角形法则、平行四边形法则仍然成立.6.在长方体1111ABCD A B C D -中,AB =12AD AA ==,P 、Q 、R 分别是AB 、1BB 、1A C 上的动点,下列结论正确的是( )A .对于任意给定的点P ,存在点Q 使得1D P CQ ⊥B .对于任意给定的点Q ,存在点R 使得1D R CQ ⊥C .当1AR A C ⊥时,1ARD R ⊥D .当113AC A R =时,1//D R 平面1BDC 【答案】ABCD 【分析】本题先建立空间直角坐标系,再运用空间向量在立体几何中的应用逐一判断即可. 【详解】如图所示,建立空间直角坐标系,设(2,,0)P a,0a ⎡∈⎣,(2,)Q b ,[]0,2b ∈,设11A R AC λ=,得到(22,,22)R λλ--,[]0,1λ∈. 1(2,,2)D P a =-,(2,0,)CQ b =,142D P CQ b ⋅=-,当2b =时,1D P CQ ⊥,A 正确;1(22,2)D R λλ=--,12(22)2D R CQ b λλ⋅=--,取22bλ=+时,1D R CQ ⊥,B 正确;1AR A C ⊥,则1(2,22)(2)412440AR AC λλλλλ⋅=--⋅--=+-+=,解得:15λ=,此时12282(,)(,)0555555AR D R ---⋅=⋅=,1AR D R ⊥,C 正确;113AC A R =,则44(,)333R,142(,)333D R =-,设平面1BDC 的法向量为(,,)n x y z =,则100n BD n DC ⎧⋅=⎪⎨⋅=⎪⎩,解得(3,n =-,故10n D R ⋅=,故1//D R 平面1BDC ,D 正确.故选:ABCD.【点睛】本题考查了空间向量在立体几何中的应用,是偏难题.7.如图,线段AB 为圆O 的直径,点E ,F 在圆O 上,//EF AB ,矩形ABCD 所在平面和圆O 所在平面垂直,且2AB =,1EF AD ==,则下述正确的是( )A .//OF 平面BCEB .BF ⊥平面ADFC .点A 到平面CDFE 的距离为217D .三棱锥C BEF -5π 【答案】ABC 【分析】由1EF OB ==,//EF OB ,易证//OF 平面BCE ,A 正确;B , 由所矩形ABCD 所在平面和圆O 所在平面垂直, 易证AD ⊥平面ABEF ,所以AD BF ⊥,由线段AB 为圆O 的直径,所以BF FA ⊥,易证故B 正确.C ,由C DAF A CDF V V --=可求点A 到平面CDFE 21,C 正确. D ,确定线段DB 的中点M 是三棱锥C BEF -外接球心,进一步可求其体积,可判断D 错误. 【详解】解:1EF OB ==,//EF OB ,四边形OFEB 为平行四边形,所以//OF BE ,OF ⊄平面BCE ,BE ⊂平面BCE ,所以//OF 平面BCE ,故A 正确.线段AB 为圆O 的直径,所以BF FA ⊥,矩形ABCD 所在平面和圆O 所在平面垂直,平面ABCD 平面ABEF AB =,AD ⊂平面ABCD ,所以AD ⊥平面ABEF ,BF ⊂平面ABEF ,所以AD BF ⊥ AD ⊂平面ADF ,AF ⊂平面ADF ,AD AF A =, 所以BF ⊥平面ADF ,故B 正确.1OF OE EF ===,OFE △是正三角形,所以1EF BE AF ===, //DA BC ,所以BC ⊥平面ABEF ,BC BF ⊥,3BF =,22312CF CB BF =+=+=,22112DF DA AF =+=+=,2AB CD ==,CDF 是等腰三角形,CDF 的边DF 上的高22222142222DF CF ⎛⎫⎛⎫-=-= ⎪ ⎪ ⎪⎝⎭⎝⎭, 11472222CDF S =⨯⨯=△, //DA BC ,AD ⊂平面ADF ,BC ⊄平面ADF , //BC 平面ADF ,点C 到平面ADF 的距离为3BF =, 111122DAF S =⨯⨯=△,C DAF A CDF V V --=,设点A 到平面CDFE 的距离为h ,1133ADF CFD S FB S h ⨯⨯=⨯⨯△△,111733232h ⨯⨯=⨯⨯, 所以217h =,故C 正确. 取DB 的中点M ,则//MO AD ,12MO =,所以MO ⊥平面CDFE ,所以21512ME MF MB MC ⎛⎫====+= ⎪⎝⎭所以M 是三棱锥C BEF -5,三棱锥C BEF -外接球的体积为33445553326V r πππ⎛⎫==⨯= ⎪ ⎪⎝⎭,故D 错误, 故选:ABC. 【点睛】综合考查线面平行与垂直的判断,求点面距离以及三棱锥的外接球的体积求法,难题.8.如图,已知P 为棱长为1的正方体对角线1BD 上的一点,且()()10,1BP BD λλ=,下面结论中正确结论的有( )A .11A D C P ⊥;B .当1A P PD +取最小值时,23λ=; C .若()0,1λ∈,则7,312APC ππ⎛⎫∠∈⎪⎝⎭; D .若P 为1BD 的中点,四棱锥11P AA D D -的外接球表面积为94π. 【答案】ABD 【分析】以D 为坐标原点建立如图空间直角坐标系,利用向量关系可判断ABC ;根据几何体外接球关系建立方程求出球半径即可判断D. 【详解】以D 为坐标原点建立如图空间直角坐标系,则()1,1,0B ,()10,0,1D ,设(),,P x y z ,()()10,1BP BD λλ=,1BP BD λ∴=,即()()1,1,1,1,1x y z λ--=--,则可解得()1,1,P λλλ--, 对A ,()()()111,0,1,0,0,0,0,1,1A D C ,()11,0,1A D ∴=--,()11,,1C P λλλ=---,则()()()()11110110A D C P λλλ⋅=-⨯-+⨯-+-⨯-=,则11A D C P ⊥,故A 正确;对B ,1A P PD +===则当23λ=时,1A P PD +取最小值,故B 正确; 对C ,()()1,0,0,0,1,0A C ,(),1,PA λλλ∴=--,()1,,PC λλλ=--,则222321cos 1321321PA PCAPC PA PC λλλλλλ⋅-∠===--+-+⋅,01λ<<,则2232123λλ≤-+<,则2111123212λλ-≤-<-+, 即11cos 22APC -≤∠<,则2,33APC ππ⎛⎤∠∈ ⎥⎝⎦,故C 错误;对于D ,当P 为1BD 中点时,四棱锥11P AA D D -为正四棱锥,设平面11AA D D 的中心为O ,四棱锥11P AA D D -的外接球半径为R ,所以222122R R ⎛⎛⎫-+= ⎪ ⎝⎭⎝⎭,解得34R =, 故四棱锥11P AA D D -的外接球表面积为94π,所以D 正确. 故选:ABD. 【点睛】关键点睛:本题考查空间相关量的计算,解题的关键是建立空间直角坐标系,利用向量建立关系进行计算.。
高三数学易错立体几何多选题 易错题自检题学能测试试卷

高三数学易错立体几何多选题 易错题自检题学能测试试卷一、立体几何多选题1.如图①,矩形ABCD 的边2BC =,设AB x =,0x >,三角形BCM 为等边三角形,沿BC 将三角形BCM 折起,构成四棱锥M ABCD -如图②,则下列说法正确的有( )A .若T 为BC 中点,则在线段MC 上存在点P ,使得//PD 平面MATB .当)3,2x ∈时,则在翻折过程中,不存在某个位置满足平面MAD ⊥平面ABCDC .若使点M 在平面ABCD 内的射影落在线段AD 上,则此时该四棱锥的体积最大值为1 D .若1x =,且当点M 在平面ABCD 内的射影点H 落在线段AD 上时,三棱锥M HAB -6322++【答案】BCD 【分析】对于A ,延长AT 与DC 的延长线交于点N ,此时,DP 与MN 必有交点; 对于B ,取AD 的中点H ,表示出2223MH MT HT x --,验证当)3,2x ∈时,无解即可; 对于C ,利用体积公式21233V x x =⨯⨯-,借助基本不等式求最值即可; 对于D ,要求外接球半径与内切球半径,找外接圆的圆心,又内接圆半径为2323r =++【详解】对于A ,如图,延长AT 与DC 的延长线交于点N ,则面ATM ⋂面()MDC N MN =.此时,DP 与MN 必有交点,则DP 与面ATM 相交,故A 错误; 对于B ,取AD 的中点H ,连接MH ,则MH AD ⊥.若面MAD ⊥面ABCD ,则有2223MH MT HT x =-=- 当)3,2x ∈时,无解,所以在翻折过程中,不存在某个位置满足平面MAD ⊥平面ABCD故B 正确;对于C ,由题可知,此时面MAD ⊥面ABCD ,由B 可知,(3x ∈,所以()22222221223232331333232x x V x x x x ⎛⎫+-⎛⎫=⨯⨯-=-≤== ⎪ ⎪⎝⎭⎝⎭当且仅当223x x =-,即6x =时等号成立.故C 正确; 对于D ,由题可知,此时面MAD ⊥面ABCD ,且2MH =因为AHB ,MHB 都是直角三角形,所以M ABH -底面外接圆的圆心是中点,所以1R =,由等体积法,可求得内接圆半径为2323r =++,故61322R r +=,故D 正确.故选:BCD . 【点睛】本题从多个角度深度考查了立体几何的相关内容,注意辅助线的作法,以及求内接圆半径的公式、基本不等式、构造函数等核心思想.2.已知三棱锥A BCD -的三条侧棱AB ,AC ,AD 两两垂直,其长度分别为a ,b ,c .点A 在底面BCD 内的射影为O ,点A ,B ,C ,D 所对面的面积分别为A S ,B S ,C S ,D S .在下列所给的命题中,正确的有( ) A .2A BCO D S SS ⋅=; B .3333A B C D S S S S <++;C .若三条侧棱与底面所成的角分别为1α,1β,1γ,则222111sin sin sin 1αβγ++=;D .若点M 是面BCD 内一个动点,且AM 与三条侧棱所成的角分别为2α,2β,2γ,则22cos α+2222cos cos 1βγ+=.【答案】ACD 【分析】由Rt O OA '与Rt O AD '相似,得边长关系,进而判断A 正确;当M 与O 重合时,注意线面角与线线角的关系,即可得C 正确;构造长方体,建立直角坐标系,代入夹角公式计算可得D 正确;代入特殊值,可得B 错误. 【详解】由三棱锥A BCD -的三条侧棱AB ,AC ,AD 两两垂直,则将三棱锥A BCD -补成长方体ABFC DGHE -,连接DO 并延长交BC 于O ', 则AO BC ⊥.对A :由Rt O OA '与Rt O AD '相似,则2O A O O O D '''=⨯ 又12A S BC O D '=⋅,12BCOS BC O O '=⋅, 22221124D S BC O A BC O A ⎛⎫''=⋅=⋅ ⎪⎝⎭所以2A BCOD S SS ⋅=,故A 正确.对B :当1a b c ===时,33318B C D S S S ===,则33338B C D S S S ++=,而332333322288A S ⎛⎫=⨯⨯=> ⎪ ⎪⎝⎭,此时3333A B C D S S S S >++,故B 不正确. 对D :分别以AB ,AC ,AD 为x ,y ,z 轴,建立空间直角坐标系. 设(),,M x y z ,则(),,AM x y z =,222AM x y z =++,(),0,0AB a =,()0,,0AC b =,()0,0,AD c =所以222222222cos cos cos AM AB AM AC AM AD AM ABAM ACAM ADαβγ⎛⎫⎛⎫⎛⎫⋅⋅⋅++=++ ⎪ ⎪ ⎪ ⎪⎪⎪⋅⋅⋅⎝⎭⎝⎭⎝⎭2222221x y z AMAMAM=++=,所以D 正确.对C :当M 与O 重合时,AO ⊥面BCD ,由D 有222222cos cos cos 1αβγ++=,由各侧棱与底面所成角与侧棱与所AO 成角互为余角,可得C 正确. 故选:ACD.【点睛】关键点睛:本题考查空间线面角、线线角、面积关系的问题,计算角的问题关键是建立空间直角坐标系,写出点的坐标,利用数量积的公式代入计算,解决这道题目还要结合线面角与线线角的关系判断.3.在直角梯形ABCD 中,2ABC BCD π∠=∠=,1AB BC ==,2DC =,E 为DC 中点,现将ADE 沿AE 折起,得到一个四棱锥D ABCE -,则下列命题正确的有( ) A .在ADE 沿AE 折起的过程中,四棱锥D ABCE -体积的最大值为13B .在ADE 沿AE 折起的过程中,异面直线AD 与BC 所成的角恒为4π C .在ADE 沿AE 折起的过程中,二面角A EC D --的大小为45︒D .在四棱锥D ABCE -中,当D 在EC 上的射影恰好为EC 的中点F 时,DB 与平面ABCE 所成的角的正切为15 【答案】ABD 【分析】对于A ,四棱锥D ABCE -的底面面积是固定值,要使得体积最大,需要平面DAE ⊥平面ABCE ,此时DE CE ⊥,可求得1133D ABCE ABCE V S DE -=⋅=可判断A ;对于B ,在ADE 沿AE 折起的过程中,//AE BC ,所以异面直线AD 与AE 所成的角即为AD 与BC所成角,由翻折前可知4DAE π∠=可判断B ;对于C ,利用线面垂直的判定定理,结合翻折前可知AE ⊥平面DEC ,又AE ⊂平面ABCE ,所以平面DEC ⊥平面ABCE ,即二面角A EC D --的在大小为2π判断C ;对于D ,利用线面垂直的判定定理可知DF ⊥平面ABCE ,所以DBF ∠为直线DB 与平面ABCE 所成的角,在直角DFB △中,15tan 5DF DBF BF ∠==,可判断D 正确;【详解】对于A ,ADE 沿AE 折起得到四棱锥D ABCE -,由四棱锥底面面积是固定值,要使得体积最大,需要四棱锥的高最大,即平面DAE ⊥平面ABCE ,此时DE CE ⊥,由已知得1DE =,则111111333D ABCE ABCE V S DE -=⋅=⨯⨯⨯=,故A 正确; 对于B ,在ADE 沿AE 折起的过程中,//AE BC ,所以异面直线AD 与AE 所成的角即为AD 与BC 所成角,又1AB BC ==,2DC =,E 为DC 中点,可知4DAE π∠=,即异面直线AD 与BC 所成的角恒为4π,故B 正确; 对于C ,由翻折前知,,AE EC AE ED ⊥⊥,且ECED E =,则AE ⊥平面DEC ,又AE ⊂平面ABCE ,所以平面DEC ⊥平面ABCE ,即二面角A EC D --的大小为2π,故C 错误; 对于D ,如图连接,DF BF ,由C 选项知,AE ⊥平面DEC ,又DF ⊂平面DEC ,则AE DF ⊥,又由已知得EC DF ⊥,且EC AE E ⋂=,则DF ⊥平面ABCE ,所以DBF ∠为直线DB 与平面ABCE 所成的角,在直角DFB △中,tan 5DFDBF BF∠=====,所以DB 与平面ABCE所成的角的正切为5,故D 正确; 故选:ABD 【点睛】关键点睛:本题考查立体几何综合问题,求体积,求线线角,线面角,面面角,解题的关键要熟悉几种角的定义,通过平移法找到线线角,通过证垂直找到线面角和面面角,再结合三角形求出角,考查了学生的逻辑推理能力,转化能力与运算求解能力,属于难题.4.如图,矩形ABCD 中, 22AB AD ==,E 为边AB 的中点.将ADE 沿直线DE 翻折成1A DE △(点1A 不落在底面BCDE 内),若M 在线段1A C 上(点M 与1A ,C 不重合),则在ADE 翻转过程中,以下命题正确的是( )A .存在某个位置,使1DE A C ⊥B .存在点M ,使得BM ⊥平面1A DC 成立 C .存在点M ,使得//MB 平面1A DE 成立D .四棱锥1A BCDE -体积最大值为24【答案】CD 【分析】利用反证法可得A 、B 错误,取M 为1A C 的中点,取1A D 的中点为I ,连接,MI IE ,可证明//MB 平面1A DE ,当平面1A DE ⊥平面BCDE 时,四棱锥1A BCDE -体积最大值,利用公式可求得此时体积为24. 【详解】如图(1),取DE 的中点为F ,连接1,A F CF , 则45CDF ∠=︒,22DF =,故212254222222CF =+-⨯⨯=,故222DC DF CF ≠+即2CFD π∠≠.若1CA DE ⊥,因为11,A D A E DF FE ==,故1A F DE ⊥,而111A F A C A ⋂=, 故DE ⊥平面1A FC ,因为CF ⊂平面1A FC ,故DE CF ⊥,矛盾,故A 错. 若BM ⊥平面1A DC ,因为DC ⊂平面1A DC ,故BM DC ⊥, 因为DC CB ⊥,BM CB B ⋂=,故CD ⊥平面1A CB ,因为1AC ⊂平面1A CB ,故1CD A C ⊥,但1A D CD <,矛盾,故B 错. 当平面1A DE ⊥平面BCDE 时,四棱锥1A BCDE -体积最大值, 由前述证明可知1A F DE ⊥,而平面1A DE平面BCDE DE =,1A F ⊂平面1A DE ,故1A F ⊥平面BCDE ,因为1A DE △为等腰直角三角形,111A D A E ==,故122A F =, 又四边形BCDE 的面积为13211122⨯-⨯⨯=, 故此时体积为13223224⨯⨯=,故D 正确. 对于C ,如图(2),取M 为1A C 的中点,取1A D 的中点为I ,连接,MI IE ,则1//,2IM CD IM CD =,而1//,2BE CD BE CD =, 故//,IM BE IM BE =即四边形IEBM 为平行四边形,故//IE BM ,因为IE ⊂平面1A DE ,BM ⊄平面1A DE ,故//MB 平面1A DE , 故C 正确. 故选:CD.【点睛】本题考查立体几何中的折叠问题,注意对于折叠后点线面的位置的判断,若命题的不成立,往往需要利用反证法来处理,本题属于难题.5.如图,线段AB 为圆O 的直径,点E ,F 在圆O 上,//EF AB ,矩形ABCD 所在平面和圆O 所在平面垂直,且2AB =,1EF AD ==,则下述正确的是( )A .//OF 平面BCEB .BF ⊥平面ADFC .点A 到平面CDFE 的距离为217D .三棱锥C BEF -5π 【答案】ABC 【分析】由1EF OB ==,//EF OB ,易证//OF 平面BCE ,A 正确;B , 由所矩形ABCD 所在平面和圆O 所在平面垂直, 易证AD ⊥平面ABEF ,所以AD BF ⊥,由线段AB 为圆O 的直径,所以BF FA ⊥,易证故B 正确.C ,由C DAF A CDF V V --=可求点A 到平面CDFE 21,C 正确. D ,确定线段DB 的中点M 是三棱锥C BEF -外接球心,进一步可求其体积,可判断D 错误. 【详解】解:1EF OB ==,//EF OB ,四边形OFEB 为平行四边形,所以//OF BE ,OF ⊄平面BCE ,BE ⊂平面BCE ,所以//OF 平面BCE ,故A 正确.线段AB 为圆O 的直径,所以BF FA ⊥,矩形ABCD 所在平面和圆O 所在平面垂直,平面ABCD 平面ABEF AB =,AD ⊂平面ABCD ,所以AD ⊥平面ABEF ,BF ⊂平面ABEF ,所以AD BF ⊥ AD ⊂平面ADF ,AF ⊂平面ADF ,AD AF A =, 所以BF ⊥平面ADF ,故B 正确.1OF OE EF ===,OFE △是正三角形,所以1EF BE AF ===, //DA BC ,所以BC ⊥平面ABEF ,BC BF ⊥,3BF =22312CF CB BF +=+=,22112DF DA AF =+=+=2AB CD ==,CDF 是等腰三角形,CDF 的边DF 上的高22222142222DF CF ⎛⎫⎛⎫-=-= ⎪ ⎪ ⎪⎝⎭⎝⎭, 11472222CDF S =⨯⨯=△, //DA BC ,AD ⊂平面ADF ,BC ⊄平面ADF , //BC 平面ADF ,点C 到平面ADF 的距离为3BF =, 111122DAF S =⨯⨯=△,C DAF A CDF V V --=,设点A 到平面CDFE 的距离为h ,1133ADF CFD S FB S h ⨯⨯=⨯⨯△△,111733232h ⨯⨯=⨯⨯, 所以21h =,故C 正确. 取DB 的中点M ,则//MO AD ,12MO =,所以MO ⊥平面CDFE ,所以215122ME MF MB MC ⎛⎫====+= ⎪⎝⎭所以M 是三棱锥C BEF -5, 三棱锥C BEF -外接球的体积为33445553326V r ππ⎛==⨯= ⎝⎭,故D 错误, 故选:ABC. 【点睛】综合考查线面平行与垂直的判断,求点面距离以及三棱锥的外接球的体积求法,难题.6.如图所示,在长方体1111ABCD A B C D -中,11,2,AB BC AA P ===是1A B 上的一动点,则下列选项正确的是( )A .DP 35B .DP 5C .1AP PC +6D .1AP PC +的最小值为1705【答案】AD【分析】 DP 的最小值,即求1DA B △底边1A B 上的高即可;旋转11A BC 所在平面到平面11ABB A ,1AP PC +的最小值转化为求AC '即可.【详解】求DP 的最小值,即求1DA B △底边1A B 上的高,易知115,2A B A D BD ===,所以1A B 边上的高为355h =111,AC BC ,得11A BC ,以1A B 所在直线为轴,将11A BC 所在平面旋转到平面11ABB A ,设点1C 的新位置为C ',连接AC ',则AC '即为所求的最小值,易知11122,2,cos 10AA AC AAC ''==∠=-, 所以217042222()105AC '=+-⨯⨯⨯-=. 故选:AD.【点睛】 本题考查利用旋转求解线段最小值问题.求解翻折、旋转问题的关键是弄清原有的性质变化与否, (1)点的变化,点与点的重合及点的位置变化;(2)线的变化,翻折、旋转前后应注意其位置关系的变化;(3)长度、角度等几何度量的变化.7.M ,N 分别为菱形ABCD 的边BC ,CD 的中点,将菱形沿对角线AC 折起,使点D 不在平面ABC 内,则在翻折过程中,下列结论正确的有( )A .MN ∥平面ABDB .异面直线AC 与MN 所成的角为定值C .在二面角D AC B --逐渐变小的过程中,三棱锥D ABC -外接球的半径先变小后变大D .若存在某个位置,使得直线AD 与直线BC 垂直,则ABC ∠的取值范围是0,2π⎛⎫ ⎪⎝⎭【答案】ABD【分析】利用线面平行的判定即可判断选项A ;利用线面垂直的判定求出异面直线AC 与MN 所成的角即可判断选项B ;借助极限状态,当平面DAC 与平面ABC 重合时,三棱锥D ABC -外接球即是以ABC ∆外接圆圆心为球心,外接圆的半径为球的半径,当二面角D AC B --逐渐变大时,利用空间想象能力进行分析即可判断选项C;过A 作AH BC ⊥,垂足为H ,分ABC ∠为锐角、直角、钝角三种情况分别进行分析判断即可判断选项D.【详解】对于选项A:因为M ,N 分别为菱形ABCD 的边BC ,CD 的中点,所以MN 为BCD ∆的中位线,所以//MN BD ,因为MN ⊄平面ABD ,BD ⊂平面ABD ,所以MN ∥平面ABD ,故选项A 正确;对于选项B :取AC 的中点O ,连接,DO BO ,作图如下:则,AC DO AC BO ⊥⊥,BO DO O =,由线面垂直的判定知,AC ⊥平面BOD ,所以AC BD ⊥,因为//MN BD ,所以AC MN ⊥,即异面直线AC 与MN 所成的角为定值90,故选项B 正确;对于选项C:借助极限状态,当平面DAC 与平面ABC 重合时,三棱锥D ABC -外接球即是以ABC ∆外接圆圆心为球心,外接圆的半径为球的半径,当二面角D AC B --逐渐变大时,球心离开平面ABC ,但是球心在底面的投影仍然是ABC ∆外接圆圆心,故二面角D AC B --逐渐变小的过程中,三棱锥D ABC -外接球的半径不可能先变小后变大, 故选项C 错误;对于选项D:过A 作AH BC ⊥,垂足为H ,若ABC ∠为锐角,H 在线段BC 上;若ABC ∠为直角,H 与B 重合;若ABC ∠为钝角,H 在线段BC 的延长线上;若存在某个位置,使得直线AD 与直线BC 垂直,因为AH BC ⊥,所以CB ⊥平面AHD ,由线面垂直的性质知,CB HD ⊥,若ABC ∠为直角,H 与B 重合,所以CB BD ⊥,在CBD ∆中,因为CB CD =, 所以CB BD ⊥不可能成立,即ABC ∠为直角不可能成立;若ABC ∠为钝角,H 在线段BC 的延长线上,则在原平面图菱形ABCD 中,DCB ∠为锐角,由于立体图中DB DO OB <+,所以立体图中DCB ∠一定比原平面图中更小,,所以DCB ∠为锐角,CB HD ⊥,故点H 在线段BC 与H 在线段BC 的延长线上矛盾,因此ABC ∠不可能为钝角;综上可知,ABC ∠的取值范围是0,2π⎛⎫ ⎪⎝⎭.故选项D 正确; 故选:ABD【点睛】本题考查异面垂直、线面平行与线面垂直的判定、多面体的外接球问题;考查空间想象能力和逻辑推理能力;借助极限状态和反证法思想的运用是求解本题的关键;属于综合型强、难度大型试题.8.已知正四棱柱1111ABCD A B C D -的底面边长为2,侧棱11AA =,P 为上底面1111D C B A 上的动点,给出下列四个结论中正确结论为( )A .若3PD =,则满足条件的P 点有且只有一个B .若PD =,则点P 的轨迹是一段圆弧C .若PD ∥平面1ACB ,则DP 长的最小值为2D .若PD ∥平面1ACB ,且PD =,则平面BDP 截正四棱柱1111ABCD A B C D -的外接球所得平面图形的面积为94π 【答案】ABD【分析】若3PD =,由于P 与1B 重合时3PD =,此时P 点唯一;()13PD =,,则1PD =P 的轨迹是一段圆弧;当P 为11A C 中点时,DP 有最小值为=断C ;平面BDP 截正四棱柱1111ABCD A B C D -的外接球所得平面图形为外接球的大圆,其半径为32=,可得D . 【详解】如图:∵正四棱柱1111ABCD A B C D -的底面边长为2,∴1122B D =11AA =, ∴()2212213DB =+=,则P 与1B 重合时3PD =,此时P 点唯一,故A 正确; ∵()313PD =,,11DD =,则12PD P 的轨迹是一段圆弧,故B 正确; 连接1DA ,1DC ,可得平面11//A DC 平面1ACB ,则当P 为11A C 中点时,DP 有最小值为()22213+=C 错误;由C 知,平面BDP 即为平面11BDD B ,平面BDP 截正四棱柱1111ABCD A B C D -的外接2221322122++=,面积为94π,故D 正确.故选:ABD .【点睛】本题考查了立体几何综合,考查了学生空间想象,逻辑推理,转化划归,数学运算的能力,属于较难题.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一、选择题:1.设ABCD 是空间四边形,E ,F 分别是AB ,CD 的中点,则,,满足( )A.共线B.共面C.不共面D.可作为空间基向量 正确答案:B 错因:学生把向量看为直线。
2.在正方体1111ABCD A B C D -,O 是底面ABCD 的中心,M 、N 分别是棱1DD 、11D C 的中点, 则直线OM ( )A.是AC 和MN 的公垂线B.垂直于AC 但不垂直于MNC.垂直于MN ,但不垂直于ACD.与AC 、MN 都不垂直正确答案:A 错因:学生观察能力较差,找不出三垂线定理中的射影。
3.已知平面α∥平面β,直线l ⊂平面α,点P ∈直线l ,平面α、β间的距离为8,则在β内到 点P 的距离为10,且到l 的距离为9的点的轨迹是( )A.一个圆B.四个点C.两条直线D.两个点正确答案:B 错因:学生对点线距离、线线距离、面面距离的关系不能灵活掌握。
4.正方体1111ABCD A B C D -中,点P 在侧面11BCC B 及其边界上运动, 并且总保持1AP BD ⊥,则动点P 的轨迹( )A.线段1B CB.1BB 的中点与1CC 中点连成的线段C.线段1BCD.CB 中点与11B C 中点连成的线段 正确答案:A 错因:学生观察能力较差,对三垂线定理逆定理不能灵活应用. 5. 下列命题中:① 若向量a 、b 与空间任意向量不能构成基底,则a ∥b . ② 若a ∥b , b ∥c ,则c ∥a .③ 若、、是空间一个基底,且=31+31+31,则A 、B 、C 、D 四点共面.④ 若向量 + ,+ ,+ 是空间一个基底,则、、也是空间的一个基底。
其中 正确的命题有( )个. A.1 B.2 C.3 D.4 正确答案:C 错因:学生对空间向量的基本概念理解不够深刻.6.给出下列命题:①分别和两条异面直线AB 、CD 同时相交的两条直线AC 、BD 一定是异面直线; ②同时与两条异面直线垂直的两直线不一定平行; ③斜线b 在面α内的射影为c ,直线a c ⊥,则a b ⊥; ④有三个角为直角的四边形是矩形,其中真命题是( ) 正确答案:① 错误原因:空间观念不明确,三垂线定理概念不清 7.已知一个正四面体和一个正八面体的棱长相等,把它们拼接起来,使一个表面重合,所得多面体的面数有( ) A.7 B.8 C.9 D.10 正确答案:A 错误原因:48210+-= 8.下列正方体或正四面体中,P 、Q 、R 、S 分别是所在棱的中点,这四个点不共面的一个图是( )D C B A正确答案:D 错误原因:空间观点不强.9. a 和b 为异面直线,则过a 与b 垂直的平面( )A.有且只有一个B.一个面或无数个C.可能不存在D.可能有无数个 正确答案:C 错误原因:过a 与b 垂直的夹平面条件不清.立体几何易错题集锦10.给出下列四个命题:(1)各侧面在都是正方形的棱柱一定是正棱柱.(2)若一个简单多面体的各顶点都有3条棱,则其顶点数V 、面数F 满足的关系式为24F V -= (3)若直线l ⊥平面α,l ∥平面β,则α⊥β. (4)命题“异面直线a 、b 不垂直,则过a 的任一平面与b 都不垂直”的否定. 其中正确的命题是( ) A.(2)(3) B.(1)(4) C.(1)(2)(3) D.(2)(3)(4)正确答案:A11.如图,ABC ∆是简易遮阳棚,A ,B 是南北方向上两个定点,正东方向射出的太阳光线与地面成40 角,为了使遮阴影面ABD 面积最大,遮阳棚 ABC 与地面所成的角应为( )A.75B.60C.50D.45正确答案:C12.一直线与直二面角的两个面所成的角分别为α、β, 则αβ+满足( )A.90αβ+<B.90αβ+≤C.90αβ+≥D.90αβ+≥答案:B 点评:易误选A . 错因:忽视直线与二面角棱垂直的情况.13.在正方体1AC 中,过它的任意两条棱作平面,则能作得与1A B 成30 角的平面的个数为( ) A.2个 B.4个 C.6个 D.8个 答案:B 点评:易瞎猜. 6个面不合,6个对角面中有4个面适合条件.14.ABC ∆的BC 边上的高线为AD ,BD a =,CD b =,将ABC ∆沿AD 折成大小为θ的二面角B ADC --,若ba=θcos ,则三棱锥A BCD -的侧面三角形ABC 是( )A.锐角三角形B.钝角三角形C.直角三角形D.形状与a 、b 的值有关的三角形 答案:C 点评:将平面图形折成空间图形后线面位置关系理不清,易瞎猜.15.设a 、b 、c 表示三条直线,βα,表示两个平面,则下列命题中逆命题不成立的是( )A.α⊥c ,若β⊥c ,则βα//B.α⊂b ,α∉c ,若α//c ,则c b //C.β⊂b ,若β⊥b ,则αβ⊥D.β⊂b ,c 是α在β内的射影,若c b ⊥,则α⊥b 正解:C . C 的逆命题是β⊂b ,若αβ⊥,则a b ⊥显然不成立. 误解:选B . 源于对C 是α在β内的射影理不清.16.α和β是两个不重合的平面,在下列条件中可判定平面α和β平行的是( )A.α和β都垂直于平面B.α内不共线的三点到β的距离相等C.m l ,是α平面内的直线且ββ//,//m lD.m l ,是两条异面直线且ββαα//,//,//,//l m m l 正解:D 对于βα,,A 可平行也可相交;对于B 三个点可在β平面同侧或异侧;对于ml C ,,在平面α内可平行,可相交.对于D 正确证明如下:过直线m l ,分别作平面与平面βα,相交,设交线分别为11,m l 与22,m l ,由已知βα//,//l l 得21//,//l l l l ,从而21//l l ,则β//1l ,同理β//1m ,βα//∴。
误解:B 往往只考虑距离相等,不考虑两侧.17.一个盛满水的三棱锥容器,不久发现三条侧棱上各有一个小洞D 、E 、F ,且知:SD DA =::2:1SE EB CF FS ==,若仍用这个容器盛水,则最多可盛原来水的A.2923 B.2719 C.3130 D.2723 正解:D . 当平面EFD 处于水平位置时,容器盛水最多2121sin 31sin 313131h ASB SB SA h DSE SE SD h S h S V V SAB SDE SABC SDE F ⋅∠⋅⋅⋅⋅∠⋅⋅⋅=⋅⋅=∴∆∆--DCB AA27431323221=⋅⋅=⋅⋅=h h SB SE SA SD 最多可盛原来水得1-2723274= 误解:A 、B 、C . 由过D 或E 作面ABC 得平行面,所截体计算而得. 18.球的半径是R ,距球心4R 处有一光源,光源能照到的地方用平面去截取,则截面的最大面积是( )A.2R π B.21615R π C.2169R π D.221R π 正解:B . 如图,在Rt OPA ∆中,AB OP ⊥于B则2OA OB OP =⋅即24R OB R =⋅14OB R ∴= 又22221516AB OA OB R =-=∴以AB 为半径的圆的面积为21516R误解:审题不清,不求截面积,而求球冠面积.19.已知AB 是异面直线的公垂线段,2AB =,且a 与b 成 30角,在直线a 上取4AP =,则点P 到直线b 的距离是( )A.22B.4C.142D.22或142正解:A . 过B 作//BB a ',在BB '上截取BP AP '=,连结PP ',过P '作P Q '⊥b 连结PQ ,∴PP '⊥由BB '和b 所确定的平面,∴PP '⊥b∴PQ 即为所求.在Rt PQP ∆'中,2PP AB '==,P Q BP ''=,sin 'sin30P BQ AP ∠=2= ∴PQ误解:D . 认为点P 可以在点A 的两侧.本题应是由图解题.20.若平面α外的直线a 与平面α所成的角为θ,则θ的取值范围是( )A.)2,0(πB.)2,0[πC.]2,0(πD.]2,0[π错解:C .直线在平面α外应包括直线与平面平行的情况,此时直线a 与平面α所成的角为0正解:D21.如果,a b 是异面直线,P 是不在,a b 上的任意一点,下列四个结论:(1)过P 一定可作直线l 与,a b 都相交;(2)过P 一定可作直线l 与,a b 都垂直;(3)过P 一定可作平面α与,a b 都平行;(4)过P 一定可作直线l 与,a b 都平行,其中正确的结论有( )A 、0个B 、1个C 、2个D 、3个 答案:B 错解:C 认为(1)(3)对; D 认为(1)(2)(3)对错因:认为(2)错误的同学,对空间两条直线垂直理解不深刻,认为作的直线应该与,a b 都垂直相交;而认为(1)(3)对的同学,是因为设能借助于两个平行平面衬托从而对问题的分析欠严密。
22.空间四边形中,互相垂直的边最多有( )A 、1对B 、2对C 、3对D 、4对答案:C 错解:D 错因:误将空间四边形理解成四面体,对“空间四边形”理解不深刻。
23.底面是正三角形,且每个侧面是等腰三角形的三棱锥是A 、一定是正三棱锥B 、一定是正四面体C 、不是斜三棱锥D 、可能是斜三棱锥 正确答案:(D )错因:此是正三棱锥的性质,但很多学生凭感觉认为如果侧面是等腰三角形,则侧棱长相等,所以一定是正三棱锥,事实上,只须考察一个正三角形绕其一边抬起后所构成的三棱锥就知道应选DA24.给出下列四个命题:(1)各侧面都是正方形的棱柱一定是正棱柱 (2)若一个简单多面体的各顶点都有三条棱,则其顶点数V ,面数F 满足的关系式为24F V -= (3)若直线l ⊥平面α,l ∥平面β,则⊥αβ (4)命题“异面直线,a b 不垂直,则过a 的任一平面和b 都不垂直”的否定, 则正确的命题是( ) A 、(2)(3) B 、(1)(4) C 、(1)(2)(3) D 、(2)(3)(4)正确答案:(A ) 错误原因:易认为命题(1)正确二填空题:1. 有一棱长为a 的正方体骨架,其内放置一气球,使其充气且尽可能地大(仍保持为球的形状),则气球表面积的最大值为__________.错解:学生认为球最大时为正方体的内切球,所以球的直径为a ,球的表面积为2a π。
这里学生未能弄清正方体骨架是一个空架子,球最大时与正方体的各棱相切,直径应为,所以正确答案为:22a π。
2. 一个广告气球某一时刻被一束平行光线投射到水平地面上的影子是一个椭圆,椭圆的离心率为e =________。
