江苏省扬州市宝应县七年级数学下学期期末试卷(含解析)
江苏省扬州市2023年七年级数学下册第二学期期末试卷【含答案】

七年级扬州市2023年七年级数学下册第二学期期末试卷数学试卷(满分:150分 测试时间:120分钟)一、选择题(本大题共8小题,每小题3分,共24分,请将正确选项前的字母代号填涂在答.题卡相应位置......上) 1.对于-21的运算结果正确的是( )A .-2B .21C .-21 D .22. 下列计算结果正确的是 ( )A. =x x 26()5153B. -=-x x ()4123C. =x x 22()362D. -=x x [] 473)(3.若a <b ,则下列不等式一定成立的是( ) A .a b <1 B .ba>1 C .a -b <0 D .ab <0 4.下列命题中,是假命题的是( )A .同位角相等,两直线平行B .三条线段可以组成一个三角形C .在同一平面内,平行于同一条直线的两条直线平行D .对顶角相等 5.如果一个多边形的内角和是外角和的3倍,那么这个多边形是( )A.八边形B.九边形C.十边形D.十二边形6如图,在△ABC 与△DEF 中,已知=AB DE ,∠=∠A D ,再添加一个条件才能使△ABC≌△DEF ,下列不能添加的条件是( )A .∠=∠B E B .=BC EF C .∠=∠C FD .=AC DF7. 若不等式组有解,则实数a 的取值范围是( ) A .a <﹣36B .a ≤﹣36C .a >﹣36D . a ≥﹣368. 一个正方形和两个等边三角形的位置如图,若∠3=50°,则∠1+∠2=( )A .90°B .100°C .130°D .180°BACDEF二、填空题(本大题共有10小题,每小题3分,共30分,请把答案直接填写在答题卡相应.....位置..上) 9.某种生物细胞的直径约为0.00056米,用科学记数法表示为______米.10.若a >0,且a x=2,a y=3,则ax ﹣2y=11.已知,4=+t s 则t t s 822+-= .12.若3a b +=,2ab =,则22a b +=________.13.如图,已知AB∥CD,直线EF 分别交AB 、CD 于E 、F ,ED 平分∠BEF,若∠1=72°,则∠2= °.14.命题:对顶角相等,其逆命题为_______________________.15.若x 、y 满足0)1(12=++++-y x y x ,则=-22y x .16.已知方程组⎩⎨⎧=+=-04by ax by ax 的解为⎩⎨⎧==12y x ,则2a+3b 的值为__ _.17. 三个同学对问题“若方程组111222a x b y c a x b y c +=⎧⎨+=⎩的解是23x y =⎧⎨=⎩,求方程组111222435435a x b y c a x b y c +=⎧⎨+=⎩ 的解.”提出各自的想法,甲说:“这个题目好象条件不够,不能求解”;乙说:“它们的系数有一定的规律,可以试试”;丙说:“能不能把第二个方程组的两个方程的两边都除以5.通过换元替代的方法来解决”.参考他们的讨论,你认为这个题目的解应该是 . 18.如图,在△ABC 中,E 是BC 上的一点,EC=2BE ,点D 是AC 的中点,设△ABC 、△ADF 、△BEF的面积分别S 、S 1、S 2,且S=36,则S 1﹣S 2=三、解答题(本大题共有10小题,共96分.请在答题卡指定区域内作答,解答时应写出必要的文字说明、证明过程或演算步骤) 19.(本题满分8分)计算: (1)(π﹣2013)0﹣()﹣2+|﹣4| (2)(x +1)2﹣(x +2)(x ﹣2).20.(本题满分8分)因式分解(1)﹣2x 2+4x ﹣2 (2)a 3﹣4ab 2;21.(本题满分8分)解方程组或不等式组(1)⎩⎨⎧-=+=-74723y x y x (2)22.(本题满分8分)已知,关于x ,y 的方程组的解满足x <y <0.(1)求a 的取值范围; (2)化简|a|﹣|a+3|.23.(本题满分10分)小明在网上预订了全国运动会开幕式和闭幕式两种门票共10张,其中开幕式门票每张700元,闭幕式门票每张550元.(1)若小明订票总共花费5800元,问小明预定了开幕式和闭幕式的门票各多少张? (2)若小明订票用了不到6100元(不含6100元),则开幕式门票最多有几张?24.(本题满分10分)如图,在:①AB ∥CD ;②AD ∥BC ;③∠A =∠C 中,请你选取其中的两个作为条件,另一个作为结论,写出一个正确命题,并证明其正确性.选取的条件是_______,结论是_______.(填写序号) 证明:GHEDCBA 25.(本题满分10分)如图,已知AB⊥AD,AC⊥AE,AB=AD ,AC=AE ,BC 交AD 于点G ,AC 与DE 交于点H . 求证:(1)△ABC≌△ADE;(2)BC⊥DE.26.(本题满分10分)阅读理解:解方程组⎪⎪⎩⎪⎪⎨⎧=-=+1412723yxy x 时,如果设n y m x ==1,1,则原方程组可变形为关于m 、n的方程组⎩⎨⎧=-=+142723n m n m 。
扬州七年级下册数学期末试卷测试卷(解析版)

扬州七年级下册数学期末试卷测试卷(解析版)一、解答题1.已知AB //CD .(1)如图1,E 为AB ,CD 之间一点,连接BE ,DE ,得到∠BED .求证:∠BED =∠B +∠D ;(2)如图,连接AD ,BC ,BF 平分∠ABC ,DF 平分∠ADC ,且BF ,DF 所在的直线交于点F .①如图2,当点B 在点A 的左侧时,若∠ABC =50°,∠ADC =60°,求∠BFD 的度数. ②如图3,当点B 在点A 的右侧时,设∠ABC =α,∠ADC =β,请你求出∠BFD 的度数.(用含有α,β的式子表示)2.如图,已知直线12//l l ,点A B 、在直线1l 上,点C D 、在直线2l 上,点C 在点D 的右侧,()80,2,ADC ABC n BE ∠=︒∠=︒平分,ABC DE ∠平分ADC ∠,直线BE DE 、交于点E .(1)若20n =时,则BED ∠=___________;(2)试求出BED ∠的度数(用含n 的代数式表示);(3)将线段BC 向右平行移动,其他条件不变,请画出相应图形,并直接写出BED ∠的度数.(用含n 的代数式表示)3.如图,已知AM //BN ,点P 是射线AM 上一动点(与点A 不重合),BC BD 、分别平分ABP ∠和PBN ∠,分别交射线AM 于点,C D .(1)当60A ∠=︒时,ABN ∠的度数是_______;(2)当A x ∠=︒,求CBD ∠的度数(用x 的代数式表示);(3)当点P 运动时,ADB ∠与APB ∠的度数之比是否随点P 的运动而发生变化?若不变化,请求出这个比值;若变化,请写出变化规律.(4)当点P 运动到使ACB ABD =∠∠时,请直接写出14DBN A +∠∠的度数.4.已知,如图1,射线PE 分别与直线AB ,CD 相交于E 、F 两点,∠PFD 的平分线与直线AB 相交于点M ,射线PM 交CD 于点N ,设∠PFM =α°,∠EMF =β°,且(40﹣2α)2+|β﹣20|=0(1)α= ,β= ;直线AB 与CD 的位置关系是 ;(2)如图2,若点G 、H 分别在射线MA 和线段MF 上,且∠MGH =∠PNF ,试找出∠FMN 与∠GHF 之间存在的数量关系,并证明你的结论;(3)若将图中的射线PM 绕着端点P 逆时针方向旋转(如图3),分别与AB 、CD 相交于点M 1和点N 1时,作∠PM 1B 的角平分线M 1Q 与射线FM 相交于点Q ,问在旋转的过程中1FPN Q∠∠的值是否改变?若不变,请求出其值;若变化,请说明理由. 5.汛期即将来临,防汛指挥部在某水域一危险地带两岸各安置了一探照灯,便于夜间查看河水及两岸河堤的情况.如图1,灯A 射出的光束自AM 顺时针旋转至AN 便立即回转,灯B 射出的光束自BP 顺时针旋转至BQ 便立即回转,两灯不停交叉照射巡视.若灯A 射出的光束转动的速度是a ︒/秒,灯B 射出的光束转动的速度是b ︒/秒,且a 、b 满足20)34(a b a b -++-=.假定这一带水域两岸河堤是平行的,即//PQ MN ,且45BAN ∠=︒.(1)求a 、b 的值;(2)如图2,两灯同时转动,在灯A 射出的光束到达AN 之前,若两灯射出的光束交于点C ,过C 作CD AC ⊥交PQ 于点D ,若20BCD ∠=︒,求BAC ∠的度数;(3)若灯B 射线先转动30秒,灯A 射出的光束才开始转动,在灯B 射出的光束到达BQ 之前,A 灯转动几秒,两灯的光束互相平行?二、解答题6.已知//a b ,直角ABC 的边与直线a 分别相交于O 、G 两点,与直线b 分别交于E ,F 点,且90ACB ∠=︒.(1)将直角ABC 如图1位置摆放,如果56AOG ∠=︒,则CEF ∠=________; (2)将直角ABC 如图2位置摆放,N 为AC 上一点,180NEF CEF ∠+∠=︒,请写出NEF ∠与AOG ∠之间的等量关系,并说明理由;(3)将直角ABC 如图3位置摆放,若135GOC ∠=︒,延长AC 交直线b 于点Q ,点P 是射线GF 上一动点,探究,POQ OPQ ∠∠与PQF ∠的数量关系,请直接写出结论. 7.如图1,//AB CD ,E 是AB 、CD 之间的一点.(1)判定BAE ∠,CDE ∠与AED ∠之间的数量关系,并证明你的结论;(2)如图2,若BAE ∠、CDE ∠的两条平分线交于点F .直接写出AFD ∠与AED ∠之间的数量关系;(3)将图2中的射线DC 沿DE 翻折交AF 于点G 得图3,若AGD ∠的余角等于2E ∠的补角,求BAE ∠的大小.8.如图1,O 为直线AB 上一点,过点O 作射线,30OC AOC ︒∠=,将一直角三角板(30M ︒∠=)的直角顶点放在点O 处,一边ON 在射线OA 上,另一边OM 与OC 都在直线AB 的上方,将图1中的三角板绕点O 以每秒3°的速度沿顺时针方向旋转一周.(1)几秒后ON 与OC 重合?(2)如图2,经过t 秒后,//MN AB ,求此时t 的值.(3)若三角板在转动的同时,射线OC 也绕O 点以每秒6°的速度沿顺时针方向旋转一周,那么经过多长时间OC 与OM 重合?请画图并说明理由.(4)在(3)的条件下,求经过多长时间OC 平分MOB ∠?请画图并说明理由. 9.已知两条直线l 1,l 2,l 1∥l 2,点A ,B 在直线l 1上,点A 在点B 的左边,点C ,D 在直线l 2上,且满足115ADC ABC ∠=∠=o .(1)如图①,求证:AD ∥BC ;(2)点M ,N 在线段CD 上,点M 在点N 的左边且满足MAC BAC ∠=∠,且AN 平分∠CAD ;(Ⅰ)如图②,当30ACD ∠=o 时,求∠DAM 的度数; (Ⅱ)如图③,当8CAD MAN ∠=∠时,求∠ACD 的度数. 10.问题情境(1)如图1,已知//AB CD ,125PBA ︒∠=,155PCD ︒∠=,求BPC ∠的度数.佩佩同学的思路:过点P 作PG//AB ,进而//PG CD ,由平行线的性质来求BPC ∠,求得BPC ∠=________. 问题迁移(2)图2.图3均是由一块三角板和一把直尺拼成的图形,三角板的两直角边与直尺的两边重合,90ACB ︒∠=,//DF CG ,AB 与FD 相交于点E ,有一动点P 在边BC 上运动,连接PE ,PA ,记PED α∠=∠,PAC β∠=∠.①如图2,当点P 在C ,D 两点之间运动时,请直接写出AOE ∠与α∠,β∠之间的数量关系;②如图3,当点P 在B ,D 两点之间运动时,APE ∠与α∠,β∠之间有何数量关系?请判断并说明理由;拓展延伸(3)当点P 在C ,D 两点之间运动时,若PED ∠,PAC ∠的角平分线EN ,AN 相交于点N ,请直接写出ANE ∠与α∠,β∠之间的数量关系.三、解答题11.小明在学习过程中,对教材中的一个有趣问题做如下探究:(习题回顾)已知:如图1,在ABC 中,90ACB ∠=︒,AE 是角平分线,CD 是高,AE 、CD 相交于点F .求证:CFE CEF ∠=∠;(变式思考)如图2,在ABC 中,90ACB ∠=︒,CD 是AB 边上的高,若ABC 的外角BAG ∠的平分线交CD 的延长线于点F ,其反向延长线与BC 边的延长线交于点E ,则CFE ∠与CEF ∠还相等吗?说明理由;(探究延伸)如图3,在ABC 中,AB 上存在一点D ,使得ACD B ∠=∠,BAC ∠的平分线AE 交CD 于点F .ABC 的外角BAG ∠的平分线所在直线MN 与BC 的延长线交于点M .直接写出M ∠与CFE ∠的数量关系.12.如图,已知直线a ∥b ,∠ABC =100°,BD 平分∠ABC 交直线a 于点D ,线段EF 在线段AB 的左侧,线段EF 沿射线AD 的方向平移,在平移的过程中BD 所在的直线与EF 所在的直线交于点P .问∠1的度数与∠EPB 的度数又怎样的关系?(特殊化)(1)当∠1=40°,交点P 在直线a 、直线b 之间,求∠EPB 的度数;(2)当∠1=70°,求∠EPB 的度数;(一般化)(3)当∠1=n°,求∠EPB 的度数(直接用含n 的代数式表示).13.问题情境:如图1,AB ∥CD ,∠PAB=130°,∠PCD=120°.求∠APC 度数. 小明的思路是:如图2,过P 作PE ∥AB ,通过平行线性质,可得∠APC=50°+60°=110°.问题迁移:(1)如图3,AD ∥BC ,点P 在射线OM 上运动,当点P 在A 、B 两点之间运动时,∠ADP=∠α,∠BCP=∠β.∠CPD 、∠α、∠β之间有何数量关系?请说明理由; (2)在(1)的条件下,如果点P 在A 、B 两点外侧运动时(点P 与点A 、B 、O 三点不重合),请你直接写出∠CPD 、∠α、∠β间的数量关系.14.如果三角形的两个内角α与β满足290αβ+=︒,那么我们称这样的三角形是“准互余三角形”.(1)如图1,在Rt ABC 中,90ACB ∠=︒,BD 是ABC 的角平分线,求证:ABD △是“准互余三角形”;(2)关于“准互余三角形”,有下列说法:①在ABC 中,若100A ∠=︒,70B ∠=︒,10C ∠=︒,则ABC 是“准互余三角形”; ②若ABC 是“准互余三角形”,90C ∠>︒,60A ∠=︒,则20B ∠=︒; ③“准互余三角形”一定是钝角三角形.其中正确的结论是___________(填写所有正确说法的序号);(3)如图2,B ,C 为直线l 上两点,点A 在直线l 外,且50ABC ∠=︒.若P 是直线l 上一点,且ABP △是“准互余三角形”,请直接写出APB ∠的度数. 15.如图1,已知AB ∥CD ,BE 平分∠ABD ,DE 平分∠BDC . (1)求证:∠BED =90°;(2)如图2,延长BE 交CD 于点H ,点F 为线段EH 上一动点,∠EDF =α,∠ABF 的角平分线与∠CDF 的角平分线DG 交于点G ,试用含α的式子表示∠BGD 的大小;(3)如图3,延长BE 交CD 于点H ,点F 为线段EH 上一动点,∠EBM 的角平分线与∠FDN 的角平分线交于点G ,探究∠BGD 与∠BFD 之间的数量关系,请直接写出结论: .【参考答案】一、解答题1.(1)见解析;(2)55°;(3) 【分析】(1)根据平行线的判定定理与性质定理解答即可;(2)①如图2,过点作,当点在点的左侧时,根据,,根据平行线的性质及角平分线的定义即可求的度数; ②如图解析:(1)见解析;(2)55°;(3)1118022αβ︒-+【分析】(1)根据平行线的判定定理与性质定理解答即可;(2)①如图2,过点F 作//FE AB ,当点B 在点A 的左侧时,根据50ABC ∠=︒,60ADC ∠=︒,根据平行线的性质及角平分线的定义即可求BFD ∠的度数;②如图3,过点F 作//EF AB ,当点B 在点A 的右侧时,ABC α∠=,ADC β∠=,根据平行线的性质及角平分线的定义即可求出BFD ∠的度数. 【详解】解:(1)如图1,过点E 作//EF AB ,则有BEF B ∠=∠,//AB CD ,//EF CD ∴,FED D ∴∠=∠,BED BEF FED B D ∴∠=∠+∠=∠+∠;(2)①如图2,过点F 作//FE AB ,有BFE FBA ∠=∠.//AB CD ,//EF CD ∴.EFD FDC ∴∠=∠.BFE EFD FBA FDC ∴∠+∠=∠+∠.即BFD FBA FDC ∠=∠+∠, BF 平分ABC ∠,DF 平分ADC ∠,1252FBA ABC ∴∠=∠=︒,1302FDC ADC ∠=∠=︒,55BFD FBA FDC ∴∠=∠+∠=︒.答:BFD ∠的度数为55︒; ②如图3,过点F 作//FE AB ,有180BFE FBA ∠+∠=︒.180BFE FBA ∴∠=︒-∠,//AB CD ,//EF CD ∴.EFD FDC ∴∠=∠.180BFE EFD FBA FDC ∴∠+∠=︒-∠+∠.即180BFD FBA FDC ∠=︒-∠+∠,BF 平分ABC ∠,DF 平分ADC ∠,1122FBA ABC α∴∠=∠=,1122FDC ADC β∠=∠=,1118018022BFD FBA FDC αβ∴∠=︒-∠+∠=︒-+.答:BFD ∠的度数为1118022αβ︒-+.【点睛】本题考查了平行线的判定与性质,解决本题的关键是熟练掌握平行线的判定与性质.2.(1)60°;(2)n°+40°;(3)n°+40°或n°-40°或220°-n° 【分析】(1)过点E作EF∥AB,然后根据两直线平行内错角相等,即可求∠BED的度数;(2)同(1)中方法求解解析:(1)60°;(2)n°+40°;(3)n°+40°或n°-40°或220°-n°【分析】(1)过点E作EF∥AB,然后根据两直线平行内错角相等,即可求∠BED的度数;(2)同(1)中方法求解即可;(3)分当点B在点A左侧和当点B在点A右侧,再分三种情况,讨论,分别过点E作EF∥AB,由角平分线的定义,平行线的性质,以及角的和差计算即可.【详解】解:(1)当n=20时,∠ABC=40°,过E作EF∥AB,则EF∥CD,∴∠BEF=∠ABE,∠DEF=∠CDE,∵BE平分∠ABC,DE平分∠ADC,∴∠BEF=∠ABE=20°,∠DEF=∠CDE=40°,∴∠BED=∠BEF+∠DEF=60°;(2)同(1)可知:∠BEF=∠ABE=n°,∠DEF=∠CDE=40°,∴∠BED=∠BEF+∠DEF=n°+40°;(3)当点B在点A左侧时,由(2)可知:∠BED=n°+40°;当点B在点A右侧时,如图所示,过点E作EF∥AB,∵BE平分∠ABC,DE平分∠ADC,∠ABC=2n°,∠ADC=80°,∴∠ABE=12∠ABC=n°,∠CDG=12∠ADC=40°,∵AB∥CD∥EF,∴∠BEF=∠ABE=n°,∠CDG=∠DEF=40°,∴∠BED=∠BEF-∠DEF=n°-40°;如图所示,过点E作EF∥AB,∵BE平分∠ABC,DE平分∠ADC,∠ABC=2n°,∠ADC=80°,∴∠ABE=12∠ABC=n°,∠CDG=12∠ADC=40°,∵AB∥CD∥EF,∴∠BEF=180°-∠ABE=180°-n°,∠CDE=∠DEF=40°,∴∠BED=∠BEF+∠DEF=180°-n°+40°=220°-n°;如图所示,过点E作EF∥AB,∵BE平分∠ABC,DE平分∠ADC,∠ABC=n°,∠ADC=70°,∴∠ABG=12∠ABC=n°,∠CDE=12∠ADC=40°,∵AB∥CD∥EF,∴∠BEF=∠ABG=n°,∠CDE=∠DEF=40°,∴∠BED=∠BEF-∠DEF=n°-40°;综上所述,∠BED的度数为n°+40°或n°-40°或220°-n°.【点睛】此题考查了平行线的判定与性质,以及角平分线的定义,正确应用平行线的性质得出各角之间关系是解题关键.3.(1)120°;(2)90°-x°;(3)不变,;(4)45°【分析】(1)由平行线的性质:两直线平行同旁内角互补可得;(2)由平行线的性质可得∠ABN=180°-x°,根据角平分线的定义知∠解析:(1)120°;(2)90°-12x°;(3)不变,12;(4)45°【分析】(1)由平行线的性质:两直线平行同旁内角互补可得;(2)由平行线的性质可得∠ABN=180°-x°,根据角平分线的定义知∠ABP=2∠CBP、∠PBN=2∠DBP,可得2∠CBP+2∠DBP=180°-x°,即∠CBD=∠CBP+∠DBP=90°-12x°;(3)由AM∥BN得∠APB=∠PBN、∠ADB=∠DBN,根据BD平分∠PBN知∠PBN=2∠DBN,从而可得∠APB:∠ADB=2:1;(4)由AM∥BN得∠ACB=∠CBN,当∠ACB=∠ABD时有∠CBN=∠ABD,得∠ABC+∠CBD=∠CBD+∠DBN,即∠ABC=∠DBN,根据角平分线的定义可得∠ABP=∠PBN=12∠ABN=2∠DBN,由平行线的性质可得12∠A+12∠ABN=90°,即可得出答案.【详解】解:(1)∵AM∥BN,∠A=60°,∴∠A+∠ABN=180°,∴∠ABN=120°;(2)∵AM∥BN,∴∠ABN+∠A=180°,∴∠ABN=180°-x°,∴∠ABP+∠PBN=180°-x°,∵BC平分∠ABP,BD平分∠PBN,∴∠ABP=2∠CBP,∠PBN=2∠DBP,∴2∠CBP+2∠DBP=180°-x°,∴∠CBD=∠CBP+∠DBP=12(180°-x°)=90°-12x°;(3)不变,∠ADB:∠APB=12.∵AM∥BN,∴∠APB=∠PBN,∠ADB=∠DBN,∵BD平分∠PBN,∴∠PBN=2∠DBN,∴∠APB:∠ADB=2:1,∴∠ADB:∠APB=12;(4)∵AM∥BN,∴∠ACB=∠CBN,当∠ACB=∠ABD时,则有∠CBN=∠ABD,∴∠ABC+∠CBD=∠CBD+∠DBN,∴∠ABC=∠DBN,∵BC 平分∠ABP ,BD 平分∠PBN ,∴∠ABP =2∠ABC ,∠PBN =2∠DBN ,∴∠ABP =∠PBN =2∠DBN =12∠ABN ,∵AM ∥BN ,∴∠A +∠ABN =180°, ∴12∠A +12∠ABN =90°, ∴12∠A +2∠DBN =90°, ∴14∠A +∠DBN =12(12∠A +2∠DBN )=45°. 【点睛】本题主要考查平行线的性质和角平分线的定义,熟练掌握平行线的性质是解题的关键. 4.(1)20,20,;(2);(3)的值不变,【分析】(1)根据,即可计算和的值,再根据内错角相等可证;(2)先根据内错角相等证,再根据同旁内角互补和等量代换得出;(3)作的平分线交的延长线于解析:(1)20,20,//AB CD ;(2)180FMN GHF ∠+∠=︒;(3)1FPN Q∠∠的值不变,12FPN Q =∠∠ 【分析】(1)根据2(402)|20|0αβ-+-=,即可计算α和β的值,再根据内错角相等可证//AB CD ; (2)先根据内错角相等证//GH PN ,再根据同旁内角互补和等量代换得出180FMN GHF ∠+∠=︒;(3)作1PEM ∠的平分线交1M Q 的延长线于R ,先根据同位角相等证//ER FQ ,得1FQM R =∠∠,设PER REB x ==∠∠,11PM R RM B y ==∠∠,得出12EPM R ∠=∠,即可得12FPN Q=∠∠. 【详解】解:(1)2(402)|20|0αβ-+-=,4020α∴-=,200β-=,20αβ∴==,20PFM MFN ∴∠=∠=︒,20EMF ∠=︒,EMF MFN ∴∠=∠,//AB CD ∴;故答案为:20、20,//AB CD ;(2)180FMN GHF ∠+∠=︒;理由:由(1)得//AB CD ,MNF PME ∴∠=∠,MGH MNF ∠=∠,PME MGH ∴∠=∠,//GH PN ∴,GHM FMN ∴∠=∠,180GHF GHM ∠+∠=︒,180FMN GHF ∴∠+∠=︒;(3)1FPN Q ∠∠的值不变,12FPN Q=∠∠; 理由:如图3中,作1PEM ∠的平分线交1M Q 的延长线于R ,//AB CD ,1PEM PFN ∴∠=∠,112PER PEM ∠=∠,12PFQ PFN =∠∠, PER PFQ ∴∠=∠,//ER FQ ∴,1FQM R ∴∠=∠,设PER REB x ==∠∠,11PM R RM B y ==∠∠,则有:122y x R y x EPM =+∠⎧⎨=+∠⎩, 可得12EPM R ∠=∠,112EPM FQM ∴∠=∠,∴112EPM FQM ∠=∠. 【点睛】本题主要考查平行线的判定与性质,熟练掌握内错角相等证平行,平行线同旁内角互补等知识是解题的关键.5.(1),;(2)30°;(3)15秒或82.5秒【分析】(1)解出式子即可;(2)根据,用含t 的式子表示出,根据(2)中给出的条件得出方程式 ,求出 t 的值,进而求出的度数;(3)根据灯B 的解析:(1)3a =,1b =;(2)30°;(3)15秒或82.5秒【分析】(1)解出式子()2340a b a b -++-=即可;(2)根据//PQ MN ,用含t 的式子表示出BCA ∠,根据(2)中给出的条件得出方程式 ()()9090180229020⎡⎤∠=︒-∠=︒-︒-︒=︒-︒=︒⎣⎦BCD BCA t t ,求出 t 的值,进而求出BAC ∠的度数;(3)根据灯B 的要求,t <150,在这个时间段内A 可以转3次,分情况讨论.【详解】解:(1)2|3|(4)0a b a b -++-=.又|3|0a b -≥,2(4)0a b +-≥.3a ∴=,1b =;(2)设A 灯转动时间为t 秒,如图,作//CE PQ ,而//,PQ MN////,PQ CE MN ∴1803ACE CAN t ∴∠=∠=︒-︒,BCE CBD t ∠=∠=︒,()()18031802∴∠=∠+∠=︒+︒-︒=︒-︒BCA CBD CAN t t t ,90ACD ∠=︒,[]9090180(2)(2)9020∴∠=︒-∠=︒-︒-︒=︒-︒=︒BCD BCA t t ,55∴=t()1803∠=︒-︒CAN t ,()()451803313516513530∴∠=︒-︒-︒=︒-︒=︒-︒=︒⎡⎤⎣⎦BAC t t(3)设A 灯转动t 秒,两灯的光束互相平行.依题意得0150t <<①当060t <<时,两河岸平行,所以()233t ∠=∠=︒ 两光线平行,所以2130t ∠=∠=+︒所以,13∠=∠即:330=+t t ,解得15t =;②当60120t <<时,两光束平行,所以()2330t ∠=∠=+︒两河岸平行,所以12180∠+∠=︒13180t ∠=-︒所以,318030180-++=t t ,解得82.5t =;③当120150t <<时,图大概如①所示336030t t -=+,解得195150t =>(不合题意)综上所述,当15t =秒或82.5秒时,两灯的光束互相平行.【点睛】这道题考察的是平行线的性质和一元一次方程的应用.根据平行线的性质找到对应角列出方程是解题的关键.二、解答题6.(1)146°;(2)∠AOG+∠NEF=90°;(3)见解析【分析】(1)作CP//a ,则CP//a//b ,根据平行线的性质求解.(2)作CP//a ,由平行线的性质及等量代换得∠AOG+∠N解析:(1)146°;(2)∠AOG +∠NEF =90°;(3)见解析【分析】(1)作CP //a ,则CP //a //b ,根据平行线的性质求解.(2)作CP //a ,由平行线的性质及等量代换得∠AOG +∠NEF =∠ACP +∠PCB =90°.(3)分类讨论点P在线段GF上或线段GF延长线上两种情况,过点P作a,b的平行线求解.【详解】解:(1)如图,作CP//a,∵a//b,CP//a,∴CP//a//b,∴∠AOG=∠ACP=56°,∠BCP+∠CEF=180°,∴∠BCP=180°-∠CEF,∵∠ACP+∠BCP=90°,∴∠AOG+180°-∠CEF=90°,∴∠CEF=180°-90°+∠AOG=146°.(2)∠AOG+∠NEF=90°.理由如下:如图,作CP//a,则CP//a//b,∴∠AOG=∠ACP,∠BCP+∠CEF=180°,∵∠NEF+∠CEF=180°,∴∠BCP=∠NEF,∵∠ACP+∠BCP=90°,∴∠AOG+∠NEF=90°.(3)如图,当点P在GF上时,作PN//a,连接PQ,OP,则PN//a//b,∴∠GOP=∠OPN,∠PQF=∠NPQ,∴∠OPQ =∠OPN +∠NPQ =∠GOP +∠PQF ,∵∠GOC =∠GOP +∠POQ =135°,∴∠GOP =135°-∠POQ ,∴∠OPQ =135°-∠POQ +∠PQF .如图,当点P 在GF 延长线上时,作PN //a ,连接PQ ,OP ,则PN //a //b ,∴∠GOP =∠OPN ,∠PQF =∠NPQ ,∵∠OPN =∠OPQ +∠QPN ,∴∠GOP =∠OPQ +∠PQF ,∴135°-∠POQ =∠OPQ +∠PQF .【点睛】本题考查平行线的性质的应用,解题关键是熟练掌握平行线的性质,通过添加辅助线及分类讨论的方法求解.7.(1),见解析;(2);(3)60°【分析】(1)作EF//AB ,如图1,则EF//CD ,利用平行线的性质得∠1=∠BAE ,∠2=∠CDE ,从而得到∠BAE +∠CDE =∠AED ;(2)如图2,解析:(1)BAE CDE AED ∠+∠=∠,见解析;(2)12AFD AED ∠=∠;(3)60° 【分析】(1)作EF //AB ,如图1,则EF //CD ,利用平行线的性质得∠1=∠BAE ,∠2=∠CDE ,从而得到∠BAE +∠CDE =∠AED ;(2)如图2,由(1)的结论得∠AFD =∠BAF +∠CDF ,根据角平分线的定义得到∠BAF =12∠BAE ,∠CDF =12∠CDE ,则∠AFD =12(∠BAE +∠CDE ),加上(1)的结论得到∠AFD =12∠AED ;(3)由(1)的结论得∠AGD =∠BAF +∠CDG ,利用折叠性质得∠CDG =4∠CDF ,再利用等量代换得到∠AGD =2∠AED -32∠BAE ,加上90°-∠AGD =180°-2∠AED ,从而可计算出∠BAE 的度数.【详解】解:(1)BAE CDE AED ∠+∠=∠理由如下:作//EF AB ,如图1,//AB CD ,//EF CD ∴.1BAE ∴∠=∠,2CDE ∠=∠,BAE CDE AED ∴∠+∠=∠;(2)如图2,由(1)的结论得AFD BAF CDF ∠=∠+∠,BAE ∠、CDE ∠的两条平分线交于点F ,12BAF BAE ∴∠=∠,12CDF CDE ∠=∠, 1()2AFD BAE CDE ∴∠=∠+∠, BAE CDE AED ∠+∠=∠,12AFD AED ∴∠=∠; (3)由(1)的结论得AGD BAF CDG ∠=∠+∠,而射线DC 沿DE 翻折交AF 于点G ,4CDG CDF ∴∠=∠,11422()22AGD BAF CDF BAE CDE BAE AED BAE ∴∠=∠+∠=∠+∠=∠+∠-∠= 322AED BAE ∠-∠, 901802AGD AED ︒-∠=︒-∠,390218022AED BAE AED ∴︒-∠+∠=︒-∠, 60BAE ∴∠=︒.【点睛】本题考查了平行线性质:两直线平行,同位角相等;两直线平行,同旁内角互补;两直线平行,内错角相等.8.(1)10秒;(2)20秒;(3)20秒,画图见解析;(4)秒,画图见解析【分析】(1)用角的度数除以转动速度即可得;(2)求出∠AON=60°,结合旋转速度可得时间t ;(3)设∠AON=3解析:(1)10秒;(2)20秒;(3)20秒,画图见解析;(4)703秒,画图见解析【分析】(1)用角的度数除以转动速度即可得;(2)求出∠AON=60°,结合旋转速度可得时间t;(3)设∠AON=3t,则∠AOC=30°+6t,由题意列出方程,解方程即可;(4)根据转动速度关系和OC平分∠MOB,由题意列出方程,解方程即可.【详解】解:(1)∵30÷3=10,∴10秒后ON与OC重合;(2)∵MN∥AB∴∠BOM=∠M=30°,∵∠AON+∠BOM=90°,∴∠AON=60°,∴t=60÷3=20∴经过t秒后,MN∥AB,t=20秒.(3)如图3所示:∵∠AON+∠BOM=90°,∠BOC=∠BOM,∵三角板绕点O以每秒3°的速度,射线OC也绕O点以每秒6°的速度旋转,设∠AON=3t,则∠AOC=30°+6t,∵OC与OM重合,∵∠AOC+∠BOC=180°,可得:(30°+6t)+(90°-3t)=180°,解得:t=20秒;即经过20秒时间OC与OM重合;(4)如图4所示:∵∠AON+∠BOM=90°,∠BOC=∠COM,∵三角板绕点O以每秒3°的速度,射线OC也绕O点以每秒6°的速度旋转,设∠AON=3t,∠AOC=30°+6t,∵∠BOM+∠AON=90°,∴∠BOC=∠COM=12∠BOM=12(90°-3t ),由题意得:180°-(30°+6t )=12( 90°-3t ), 解得:t=703秒, 即经过703秒OC 平分∠MOB . 【点睛】 此题考查了平行线的判定与性质,角的计算以及方程的应用,关键是应该认真审题并仔细观察图形,找到各个量之间的关系求出角的度数是解题的关键.9.(1)证明见解析;(2)(Ⅰ);(Ⅱ).【分析】(1)先根据平行线的性质可得,再根据角的和差可得,然后根据平行线的判定即可得证;(2)(Ⅰ)先根据平行线的性质可得,从而可得,再根据角的和差可得 解析:(1)证明见解析;(2)(Ⅰ)5DAM ∠=︒;(Ⅱ)25ACD ∠=︒.【分析】(1)先根据平行线的性质可得65BAD ∠=︒,再根据角的和差可得180BAD ABC ∠+∠=︒,然后根据平行线的判定即可得证;(2)(Ⅰ)先根据平行线的性质可得30BAC ACD ∠=∠=︒,从而可得30MAC ∠=︒,再根据角的和差可得35DAC ∠=︒,然后根据DAM DAC MAC ∠=∠-∠即可得;(Ⅱ)设MAN x ∠=,从而可得8CAD x ∠=,先根据角平分线的定义可得142CAN CAD x ∠=∠=,再根据角的和差可得5BAC MAC x ∠=∠=,然后根据65CAD BAC BAD ∠+∠=∠=︒建立方程可求出x 的值,从而可得BAC ∠的度数,最后根据平行线的性质即可得.【详解】(1)12//,115l l ADC ∠=︒,18065BAD ADC ∴∠=︒-∠=︒,又115ABC ∠=︒,180BAD ABC ∴∠+∠=︒,//AD BC ∴;(2)(Ⅰ)12//,30l l ACD ∠=︒,30BAC ACD ∴∠=∠=︒,MAC BAC ∠=∠,30MAC ∴∠=︒,由(1)已得:65BAD ∠=︒,35DAC BAD BAC ∴∠=∠-∠=︒,35305DAM DAC MAC ∴∠=∠-∠=︒-︒=︒;(Ⅱ)设MAN x ∠=,则8CAD x ∠=, AN 平分CAD ∠,142CAN CAD x ∴∠=∠=, 5MAC CAN MAN x ∴∠=∠+∠=,MAC BAC ∠=∠,5BAC x ∴∠=,由(1)已得:65BAD ∠=︒,65CAD BAC BAD ∴∠+∠=∠=︒,即8565x x +=︒,解得5x =︒,525BAC x ∴∠==︒,又12//l l ,25ACD BAC ∴∠=∠=︒.【点睛】本题考查了平行线的判定与性质、角的和差、角平分线的定义、一元一次方程的几何应用等知识点,熟练掌握平行线的判定与性质是解题关键.10.(1);(2)①,②,理由见解析;(3)【分析】(1)过点作,则,由平行线的性质可得的度数;(2)①过点作的平行线,依据平行线的性质可得与,之间的数量关系; ②过作,依据平行线的性质可得,,即解析:(1)80︒;(2)①APE αβ∠=∠+∠,②APE βα∠=∠-∠,理由见解析;(3)1()2ANE αβ∠=∠+∠ 【分析】(1)过点P 作//PG AB ,则//PG CD ,由平行线的性质可得BPC ∠的度数;(2)①过点P 作FD 的平行线,依据平行线的性质可得APE ∠与α∠,β∠之间的数量关系;②过P 作//PQ DF ,依据平行线的性质可得QPA β∠=∠,QPE α∠=∠,即可得到APE APQ EPQ βα∠=∠-∠=∠-∠;(3)过P 和N 分别作FD 的平行线,依据平行线的性质以及角平分线的定义,即可得到ANE ∠与α∠,β∠之间的数量关系为1()2ANE αβ∠=∠+∠. 【详解】解:(1)如图1,过点P 作//PG AB ,则//PG CD ,由平行线的性质可得180B BPG ︒∠+∠=,180C CPG ︒∠+∠=,又∵125PBA ︒∠=,155PCD ︒∠=,∴36012515580BPC ︒︒︒︒∠=--=,故答案为:80︒;(2)①如图2,APE ∠与α∠,β∠之间的数量关系为APE αβ∠=∠+∠;过点P 作PM ∥FD ,则PM ∥FD ∥CG ,∵PM ∥FD ,∴∠1=∠α,∵PM ∥CG ,∴∠2=∠β,∴∠1+∠2=∠α+∠β,即:APE αβ∠=∠+∠,②如图,APE ∠与α∠,β∠之间的数量关系为APE βα∠=∠-∠;理由:过P 作//PQ DF ,∵//DF CG ,∴//PQ CG ,∴QPA β∠=∠,QPE α∠=∠,∴APE APQ EPQ βα∠=∠-∠=∠-∠;(3)如图,由①可知,∠N=∠3+∠4,∵EN 平分∠DEP ,AN 平分∠PAC ,∴∠3=12∠α,∠4=12∠β, ∴1()2ANE αβ∠=∠+∠,∴ANE ∠与α∠,β∠之间的数量关系为1()2ANE αβ∠=∠+∠. 【点睛】本题主要考查了平行线的性质,解决问题的关键是过拐点作平行线,利用平行线的性质得出结论.三、解答题11.[习题回顾]证明见解析;[变式思考] 相等,证明见解析;[探究延伸] ∠M+∠CFE=90°,证明见解析.【分析】[习题回顾]根据同角的余角相等可证明∠B=∠ACD ,再根据三角形的外角的性质即可解析:[习题回顾]证明见解析;[变式思考] 相等,证明见解析;[探究延伸]∠M+∠CFE=90°,证明见解析.【分析】[习题回顾]根据同角的余角相等可证明∠B=∠ACD ,再根据三角形的外角的性质即可证明;[变式思考]根据角平分线的定义和对顶角相等可得∠CAE=∠DAF 、再根据直角三角形的性质和等角的余角相等即可得出CFE ∠=CEF ∠;[探究延伸]根据角平分线的定义可得∠EAN=90°,根据直角三角形两锐角互余可得∠M+∠CEF=90°,再根据三角形外角的性质可得∠CEF=∠CFE ,由此可证∠M+∠CFE=90°.【详解】[习题回顾]证明:∵∠ACB=90°,CD 是高,∴∠B+∠CAB=90°,∠ACD+∠CAB=90°,∴∠B=∠ACD ,∵AE 是角平分线,∴∠CAF=∠DAF ,∵∠CFE=∠CAF+∠ACD ,∠CEF=∠DAF+∠B ,∴∠CEF=∠CFE ;[变式思考]相等,理由如下:证明:∵AF 为∠BAG 的角平分线,∴∠GAF=∠DAF ,∵∠CAE=∠GAF ,∴∠CAE=∠DAF ,∵CD 为AB 边上的高,∠ACB=90°,∴∠ADC=90°,∴∠ADF=∠ACE=90°,∴∠DAF+∠F=90°,∠E+∠CAE=90°,∴∠CEF=∠CFE;[探究延伸]∠M+∠CFE=90°,证明:∵C、A、G三点共线 AE、AN为角平分线,∴∠EAN=90°,又∵∠GAN=∠CAM,∴∠M+∠CEF=90°,∵∠CEF=∠EAB+∠B,∠CFE=∠EAC+∠ACD,∠ACD=∠B,∴∠CEF=∠CFE,∴∠M+∠CFE=90°.【点睛】本题考查三角形的外角的性质,直角三角形两锐角互余,角平分线的有关证明,等角或同角的余角相等.在本题中用的比较多的是利用等角或同角的余角相等证明角相等和三角形一个外角等于与它不相邻的两个内角之和,理解并掌握是解决此题的关键.12.(1)∠EPB=170°;(2)①当交点P在直线b的下方时:∠EPB=20°,②当交点P在直线a,b之间时:∠EPB=160°,③当交点P在直线a的上方时:∠EPB=∠1﹣50°=20°;(3)①当解析:(1)∠EPB=170°;(2)①当交点P在直线b的下方时:∠EPB=20°,②当交点P在直线a,b之间时:∠EPB=160°,③当交点P在直线a的上方时:∠EPB=∠1﹣50°=20°;(3)①当交点P在直线a,b之间时:∠EPB=180°﹣|n°﹣50°|;②当交点P在直线a上方或直线b下方时:∠EPB=|n°﹣50°|.【分析】(1)利用外角和角平分线的性质直接可求解;(2)分三种情况讨论:①当交点P在直线b的下方时;②当交点P在直线a,b之间时;③当交点P在直线a的上方时;分别画出图形求解;(3)结合(2)的探究,分两种情况得到结论:①当交点P在直线a,b之间时;②当交点P在直线a上方或直线b下方时;【详解】解:(1)∵BD平分∠ABC,∠ABC=50°,∴∠ABD=∠DBC=12∵∠EPB是△PFB的外角,∴∠EPB=∠PFB+∠PBF=∠1+(180°﹣50°)=170°;(2)①当交点P在直线b的下方时:∠EPB=∠1﹣50°=20°;②当交点P在直线a,b之间时:∠EPB=50°+(180°﹣∠1)=160°;③当交点P在直线a的上方时:∠EPB=∠1﹣50°=20°;(3)①当交点P在直线a,b之间时:∠EPB=180°﹣|n°﹣50°|;②当交点P在直线a上方或直线b下方时:∠EPB=|n°﹣50°|;【点睛】考查知识点:平行线的性质;三角形外角性质.根据动点P的位置,分类画图,结合图形求解是解决本题的关键.数形结合思想的运用是解题的突破口.13.(1),理由见解析;(2)当点P在B、O两点之间时,;当点P在射线AM上时,.【分析】(1)过P作PE∥AD交CD于E,推出AD∥PE∥BC,根据平行线的性质得出∠α=∠DPE,∠β=∠C∠=∠+∠,理由见解析;解析:(1)CPDαβ∠=∠-∠;(2)当点P在B、O两点之间时,CPDαβ∠=∠-∠.当点P在射线AM上时,CPDβα【分析】(1)过P作PE∥AD交CD于E,推出AD∥PE∥BC,根据平行线的性质得出∠α=∠DPE,∠β=∠CPE,即可得出答案;(2)分两种情况:①点P在A、M两点之间,②点P在B、O两点之间,分别画出图形,根据平行线的性质得出∠α=∠DPE,∠β=∠CPE,即可得出结论.【详解】解:(1)∠CPD=∠α+∠β,理由如下:如图,过P作PE∥AD交CD于E.∵AD∥BC,∴AD∥PE∥BC,∴∠α=∠DPE,∠β=∠CPE,∴∠CPD=∠DPE+∠CPE=∠α+∠β.(2)当点P在A、M两点之间时,∠CPD=∠β-∠α.理由:如图,过P作PE∥AD交CD于E.∵AD∥BC,∴AD∥PE∥BC,∴∠α=∠DPE,∠β=∠CPE,∴∠CPD=∠CPE-∠DPE=∠β-∠α;当点P在B、O两点之间时,∠CPD=∠α-∠β.理由:如图,过P作PE∥AD交CD于E.∵AD∥BC,∴AD∥PE∥BC,∴∠α=∠DPE,∠β=∠CPE,∴∠CPD=∠DPE-∠CPE=∠α-∠β.【点睛】本题考查了平行线的性质的运用,主要考核了学生的推理能力,解决问题的关键是作平行线构造内错角,利用平行线的性质进行推导.解题时注意:问题(2)也可以运用三角形外角性质来解决.14.(1)见解析;(2)①③;(3)∠APB的度数是10°或20°或40°或110°【分析】(1)由和是的角平分线,证明即可;(2)根据“准互余三角形”的定义逐个判断即可;(3)根据“准互余三角解析:(1)见解析;(2)①③;(3)∠APB 的度数是10°或20°或40°或110°【分析】(1)由90ABC A ∠+∠=︒和BD 是ABC 的角平分线,证明290ABD A ∠+∠=︒即可; (2)根据“准互余三角形”的定义逐个判断即可;(3)根据“准互余三角形”的定义,分类讨论:①2∠A +∠ABC =90°;②∠A +2∠APB =90°;③2∠APB +∠ABC =90°;④2∠A +∠APB =90°,由三角形内角和定理和外角的性质结合“准互余三角形”的定义,即可求出答案.【详解】(1)证明:∵在Rt ABC 中,90ACB ∠=︒,∴90ABC A ∠+∠=︒,∵BD 是ABC ∠的角平分线,∴2ABC ABD ∠=∠,∴290ABD A ∠+∠=︒,∴ABD △是“准互余三角形”;(2)①∵70,10B C ∠=︒∠=︒,∴290B C ∠+∠=︒,∴ABC 是“准互余三角形”,故①正确;②∵60A ∠=︒, 20B ∠=︒,∴210090A B ∠+∠=︒≠︒,∴ABC 不是“准互余三角形”,故②错误;③设三角形的三个内角分别为,,αβγ,且αβγ<<,∵三角形是“准互余三角形”,∴290αβ+=︒或290αβ+=︒,∴90αβ+<︒,∴180()90γαβ=︒-+>︒,∴“准互余三角形”一定是钝角三角形,故③正确;综上所述,①③正确,故答案为:①③;(3)∠APB 的度数是10°或20°或40°或110°;如图①,当2∠A+∠ABC=90°时,△ABP是“准直角三角形”,∵∠ABC=50°,∴∠A=20°,∴∠APB=110°;如图②,当∠A+2∠APB=90°时,△ABP是“准直角三角形”,∵∠ABC=50°,∴∠A+∠APB=50°,∴∠APB=40°;如图③,当2∠APB+∠ABC=90°时,△ABP是“准直角三角形”,∵∠ABC=50°,∴∠APB=20°;如图④,当2∠A+∠APB=90°时,△ABP是“准直角三角形”,∵∠ABC=50°,∴∠A+∠APB=50°,所以∠A=40°,所以∠APB=10°;综上,∠APB的度数是10°或20°或40°或110°时,ABP△是“准互余三角形”.【点睛】本题是三角形综合题,考查了三角形内角和定理,三角形的外角的性质,解题关键是理解题意,根据三角形内角和定理和三角形的外角的性质,结合新定义进行求解.15.(1)见解析;(2)∠BGD=;(3)2∠BGD+∠BFD=360°.【分析】(1)根据角平分线的性质求出∠EBD+∠EDB=(∠ABD+∠BDC),根据平行线的性质∠ABD+∠BDC=180°解析:(1)见解析;(2)∠BGD=902a︒-;(3)2∠BGD+∠BFD=360°.【分析】(1)根据角平分线的性质求出∠EBD+∠EDB=12(∠ABD+∠BDC),根据平行线的性质∠ABD+∠BDC=180°,从而根据∠BED=180°﹣(∠EBD+∠EDB)即可得到答案;(2)过点G作GP∥AB,根据AB∥CD,得到GP∥AB∥CD,从而得到∠BGD=∠BGP+∠PGD=∠ABG+∠CDG,然后根据∠EBD+∠EDB=90°,∠ABD+∠BDC=180°,得到∠ABE+∠EDC=90°,即∠ABE+α+∠FDC=90°,再利用角平分线的定义求出2∠ABG+2∠CDG=90°﹣α即可得到答案;(3)过点F、G分别作FM∥AB、GM∥AB,从而得到AB∥GM∥FN∥CD,得到∠BGD=∠BGM+∠DGM=∠4+∠6,根据BG平分∠FBP,DG平分∠FDQ,∠4=12∠FBP=12(180°﹣∠3),∠6=12∠FDQ=12(180°﹣∠5),即可求解.【详解】解:(1)证明:∵BE平分∠ABD,∴∠EBD=12∠ABD,∵DE平分∠BDC,∴∠EDB=12∠BDC,∴∠EBD+∠EDB=12(∠ABD+∠BDC),∵AB∥CD,∴∠ABD+∠BDC=180°,∴∠EBD+∠EDB=90°,∴∠BED=180°﹣(∠EBD+∠EDB)=90°.(2)解:如图2,由(1)知:∠EBD+∠EDB=90°,又∵∠ABD+∠BDC=180°,∴∠ABE+∠EDC=90°,即∠ABE+α+∠FDC=90°,∵BG平分∠ABE,DG平分∠CDF,∴∠ABE=2∠ABG,∠CDF=2∠CDG,∴2∠ABG+2∠CDG=90°﹣α,过点G作GP∥AB,∵AB∥CD,∴GP∥AB∥CD∴∠ABG=∠BGP,∠PGD=∠CDG,∴∠BGD=∠BGP+∠PGD=∠ABG+∠CDG=902α-;(3)如图,过点F、G分别作FN∥AB、GM∥AB,∵AB∥CD,∴AB∥GM∥FN∥CD,∴∠3=∠BFN,∠5=∠DFN,∠4=∠BGM,∠6=∠DGM,∴∠BFD=∠BFN+∠DFN=∠3+∠5,∠BGD=∠BGM+∠DGM=∠4+∠6,∵BG平分∠FBP,DG平分∠FDQ,∴∠4=12∠FBP=12(180°﹣∠3),∠6=12∠FDQ=12(180°﹣∠5),∴∠BFD+∠BGD=∠3+∠5+∠4+∠6,=∠3+∠5+12(180°﹣∠3)+12(180°﹣∠5),=180°+12(∠3+∠5),=180°+12∠BFD,整理得:2∠BGD+∠BFD=360°.【点睛】本题主要考查了平行线的性质与判定,角平分线的性质和三角形内角和定理,解题的关键在于能够熟练掌握相关知识进行求解.。
江苏省扬州市宝应县2019-2020学年七年级(下)期末考试数学试卷 解析版

2019-2020学年江苏省扬州市宝应县七年级(下)期末数学试卷一.选择题(本大题共有8小题,每小题3分,共24分.在每小题所给出的四个选项中,恰有一项是符合题目要求的,请将正确选项前的字母代号填涂在答题卡相应位置上)1.(3分)下列运算中,正确的是()A.(a2)3=a5B.(a+2b)2=a2+2ab+4b2C.a5÷a2=a3(a≠0)D.a(a+1)=a2+12.(3分)如图,a∥b,若∠1=110°,则∠2的度数是()A.110°B.80°C.70°D.60°3.(3分)在△ABC中,若一个内角等于另两个内角的差,则这个三角形必定是()A.锐角三角形B.直角三角形C.钝角三角形D.以上三个都是4.(3分)若a>b.则依据不等式的基本性质下列变形不正确的是()A.3﹣2a>3﹣2b B.4+a>4+bC.ac2>bc2(c≠0)D.﹣a<﹣b5.(3分)若方程mx+ny=6的两个解是,,则m,n的值为()A.4,2B.2,4C.﹣4,﹣2D.﹣2,﹣4 6.(3分)判断命题“如果n<1,那么n2﹣2<0”是假命题,只需举出一个反例.反例中的n可以为()A.B.0C.﹣1D.﹣27.(3分)如图,一块直角三角尺的一个顶点落在直尺的一边上,若∠2=25°,则∠1的度数为()A.45°B.55°C.65°D.75°8.(3分)小明网购了一本《好玩的数学》,同学们想知道书的价格,小明让他们猜.甲说:“至少12元.”乙说“至多10元.”丙说“至多8元.”小明说:“你们三个人都说错了.”则这本书的价格x(元)所在的范围为()A.8<x<10B.9<x<11C.8<x<12D.10<x<12二、填空题(本大题共有10小题,每小题3分,共30分.不需写出解答过程,请把答案直接填写在答题卡相应位t上)9.(3分)成人每天维生素D的摄入量约为0.0000046克.数据“0.0000046”用科学记数法表示为.10.(3分)一个多边形的每一个内角为150°,那么这个多边形是边形.11.(3分)命题:“如果|a|=|b|,那么a=b”的逆命题是:(填“真命题”或“假命题”).12.(3分)一个等腰三角形的两边长分别是2cm和3cm,则它的周长是cm.13.(3分)如图,公园管理处在一块长是40m,宽是20m的草坪绿地中间修一条宽度均为2m的弯道便捷通道,则剩余草坪绿地的面积是m2.14.(3分)如图,在五边形ABCDE中,AE∥BC,则∠C+∠D+∠E=.15.(3分)若3m=2,9n=10,则3m﹣2n=.16.(3分)不等式组的解集为x>2,则a的取值范围是.17.(3分)若关于x、y的二元一次方程组,的解是,则关于a、b的二元一次方程组的解是.18.(3分)定义:如果一个数的平方等于﹣1,记为i2=﹣1,这个数i叫做虚数单位,把形如a+bi(a、b为实数)的数叫做复数,其中a叫这个复数的实部,b叫这个复数的虚部.它的加、减、乘法运算与整式的加、减、乘法运算类似.例如:(4+i)+(6﹣2i)=(4+6)+(1﹣2)i=10﹣i;(2﹣i)(3+i)=6﹣3i+2i﹣i2=6﹣i﹣(﹣1)=7﹣i;(2+i)2=4+4i+i2=4+4i﹣1=3+4i.根据以上信息,完成下面计算:(2+i)(1﹣2i)+(2﹣i)2=.三、解答题(本大题共有9小题,共96分.请在答题卡指定区域内作答,解答时应写出必要的文字说明、证明过程或演算步骤)19.(8分)计算::(1)(m2)4﹣4m6•m2+(3m4)2;(2)(x﹣3)2﹣x(x﹣6).20.(8分)因式分解:(1)m2(x+y)﹣n2(x+y);(2)x4﹣2x2+1.21.(8分)(1)解方程组:;(2)解不等式﹣4<﹣,并把它的解集在数轴上表示出来.22.(8分)先化简,再求值:(x﹣y)2﹣(﹣x+2y)(﹣x﹣2y),其中x,y满足方程组.23.(10分)如图,在△ABC中,点D、E分别在BC、AB上,且EF∥AD,∠1+∠2=180°.(1)试猜想∠2与∠BAD的关系,并说明理由;(2)若DG平分∠ADC,求证:DG∥AB.24.(10分)已知关于x,y的二元一次方程组.(1)若满足方程x﹣2y=k,请求出此时这个方程组的解;(2)若该方程组的解满足x>y,求k的取值范围.25.(10分)对于任意的有理数a、b、c、d,我们规定=ad﹣bc,例如:=(﹣2)×5﹣(﹣4)×3=2.据这一规定,解下列问题:(1)化简;(2)若x同时满足≤1,<3x,求x的取值范围.26.(10分)在数学学习里,我们常常用作差法比较两个数(或代数式)的大小.具体地说:若a﹣b>0,则a>b;若a﹣b=0,则a=b:若a﹣b<0,则a<b.(1)已知a=n2,b=2n﹣1,n是不等于1的任意有理数,试运用作差法比较a、b的大小;(2)若M=(2a+b)(a﹣2b),N=(a+3b)(a﹣2b),试运用作差法比较M、N的大小.27.(12分)为响应国家“足球进校园”的号召,某校购买了50个A类足球和25个B类足球共花费7500元,已知购买一个B类足球比购买一个A类足球多花30元.(1)求购买一个A类足球和一个B类足球各需多少元?(2)通过全校师生的共同努力,今年该校被评为“足球特色学校”,学校计划用不超过4800元的经费再次购买A类足球和B类足球共50个,若单价不变,则本次至少可以购买多少个A类足球?28.(12分)(1)如图1,AD平分∠BAC,AE⊥BC,∠B=30°,∠C=70°.①∠BAC=°,∠DAE=°;②如图2.若把“AE⊥BC”变成“点F在AD的延长线上,FE⊥BC”,其它条件不变,求∠DFE的度数;(2)如图3,AD平分∠BAC,AE平分∠BEC,∠C﹣∠B=40°,求∠DAE的度数.2019-2020学年江苏省扬州市宝应县七年级(下)期末数学试卷参考答案与试题解析一.选择题(本大题共有8小题,每小题3分,共24分.在每小题所给出的四个选项中,恰有一项是符合题目要求的,请将正确选项前的字母代号填涂在答题卡相应位置上)1.(3分)下列运算中,正确的是()A.(a2)3=a5B.(a+2b)2=a2+2ab+4b2C.a5÷a2=a3(a≠0)D.a(a+1)=a2+1【分析】直接利用整式的混合运算进而结合完全平方公式计算得出答案.【解答】解:A、(a2)3=a6,故此选项错误;B、(a+2b)2=a2+4ab+4b2,故此选项错误;C、a5÷a2=a3(a≠0),正确;D、a(a+1)=a2+a,故此选项错误;故选:C.2.(3分)如图,a∥b,若∠1=110°,则∠2的度数是()A.110°B.80°C.70°D.60°【分析】根据两直线平行,同位角相等,即可求得∠3的度数,进而得出∠2的度数.【解答】解:∵a∥b,∴∠1=∠3=110°.∵∠2+∠3=180°,∴∠2=180°﹣∠3=70°,故选:C.3.(3分)在△ABC中,若一个内角等于另两个内角的差,则这个三角形必定是()A.锐角三角形B.直角三角形C.钝角三角形D.以上三个都是【分析】根据三角形的内角和可求解△ABC的一内角为90°,进而可判断三角形的形状.【解答】解:设∠A=∠B﹣∠C,则∠A+∠C=∠B,∵∠A+∠C+∠B=180°,∴∠B=90°,∴△ABC为直角三角形,故选:B.4.(3分)若a>b.则依据不等式的基本性质下列变形不正确的是()A.3﹣2a>3﹣2b B.4+a>4+bC.ac2>bc2(c≠0)D.﹣a<﹣b【分析】利用不等式的性质对各选项进行判断.【解答】解:∵a>b,∴3﹣2a<3﹣2b,4+a>4+b,ac2>bc2(c≠0),﹣a<﹣b.故选:A.5.(3分)若方程mx+ny=6的两个解是,,则m,n的值为()A.4,2B.2,4C.﹣4,﹣2D.﹣2,﹣4【分析】将x与y的两对值代入方程计算即可求出m与n的值.【解答】解:将,分别代入mx+ny=6中,得:,①+②得:3m=12,即m=4,将m=4代入①得:n=2,故选:A.6.(3分)判断命题“如果n<1,那么n2﹣2<0”是假命题,只需举出一个反例.反例中的n可以为()A.B.0C.﹣1D.﹣2【分析】根据实数的大小比较法则、乘方法则解答.【解答】解:﹣2<1,(﹣2)2﹣2>0,∴当n=﹣2时,“如果n<1,那么n2﹣2<0”是假命题,故选:D.7.(3分)如图,一块直角三角尺的一个顶点落在直尺的一边上,若∠2=25°,则∠1的度数为()A.45°B.55°C.65°D.75°【分析】根据平行线的性质和直角三角形的性质,可以得到∠1的度数,本题得以解决.【解答】解:过直角顶点作长边的平行线,如右图所示,则∠2=∠3,∠1=∠4,∵∠2=25°,∴∠3=25°,∵∠3+∠4=90°,∴∠4=65°,∴∠1=65°,故选:C.8.(3分)小明网购了一本《好玩的数学》,同学们想知道书的价格,小明让他们猜.甲说:“至少12元.”乙说“至多10元.”丙说“至多8元.”小明说:“你们三个人都说错了.”则这本书的价格x(元)所在的范围为()A.8<x<10B.9<x<11C.8<x<12D.10<x<12【分析】根据题意得出不等式组解答即可.【解答】解:根据题意可得:,∵三个人都说错了,∴这本书的价格x(元)所在的范围为10<x<12.故选:D.二、填空题(本大题共有10小题,每小题3分,共30分.不需写出解答过程,请把答案直接填写在答题卡相应位t上)9.(3分)成人每天维生素D的摄入量约为0.0000046克.数据“0.0000046”用科学记数法表示为 4.6×10﹣6.【分析】利用科学记数法的知识即可解答.【解答】解:0.0000046=4.6×10﹣6.故答案为:4.6×10﹣6.10.(3分)一个多边形的每一个内角为150°,那么这个多边形是十二边形.【分析】设多边形的边数为n,根据多边形的内角和定理:180°•(n﹣2)可得180°•(n ﹣2)=150°•n,再解方程求解即可.【解答】解:设多边形的边数为n,由题意可得:180•(n﹣2)=150•n,解得n=12.故答案为:十二.11.(3分)命题:“如果|a|=|b|,那么a=b”的逆命题是:真命题(填“真命题”或“假命题”).【分析】分析是否为真命题,需要分别分析各题设是否能推出结论,可得答案.【解答】解:“如果|a|=|b|,那么a=b”的逆命题是“如果a=b,那么|a|=|b|”,为真命题,故答案为:真命题.12.(3分)一个等腰三角形的两边长分别是2cm和3cm,则它的周长是8或7cm.【分析】题目给出等腰三角形有两条边长为2cm和3cm,而没有明确腰、底分别是多少,所以要进行讨论,还要应用三角形的三边关系验证能否组成三角形.【解答】解:分两种情况:当三边是2,3,3时,能构成三角形,则周长是8;当三边是2,2,3时,能构成三角形,则周长是7.所以等腰三角形的周长为8cm或7cm.故答案为8cm或7cm.13.(3分)如图,公园管理处在一块长是40m,宽是20m的草坪绿地中间修一条宽度均为2m的弯道便捷通道,则剩余草坪绿地的面积是760m2.【分析】利用总面积减去便捷通道的面积即可.【解答】解:剩余草坪绿地的面积是:40×20﹣20×2=760(m2),故答案为:760.14.(3分)如图,在五边形ABCDE中,AE∥BC,则∠C+∠D+∠E=360°.【分析】首先过点D作DF∥AE,交AB于点F,由AE∥BC,可证得AE∥DF∥BC,然后由两直线平行,同旁内角互补,证得∠A+∠B=180°,∠E+∠EDF=180°,∠CDF+∠C=180°,继而证得结论.【解答】过点D作DF∥AE,交AB于点F,∵AE∥BC,∴AE∥DF∥BC,∴∠A+∠B=180°,∠E+∠EDF=180°,∠CDF+∠C=180°,∴∠C+∠CDE+∠E=360°,故答案为360°.15.(3分)若3m=2,9n=10,则3m﹣2n=.【分析】直接利用同底数幂的除法运算法则、幂的乘方运算法则将原式变形得出答案.【解答】解:∵3m=2,9n=10=32n,∴3m﹣2n=3m÷32n=2÷10=.故答案为:.16.(3分)不等式组的解集为x>2,则a的取值范围是a≤2.【分析】根据不等式组的公共解集即可确定a的取值范围.【解答】解:由不等式组的解集为x>2,可得a≤2.故答案为:a≤217.(3分)若关于x、y的二元一次方程组,的解是,则关于a、b的二元一次方程组的解是.【分析】根据已知得出关于a,b的方程组进而得出答案.【解答】解:∵关于x、y的二元一次方程组,的解是,∴方程组中,解得:.故答案为:.18.(3分)定义:如果一个数的平方等于﹣1,记为i2=﹣1,这个数i叫做虚数单位,把形如a+bi(a、b为实数)的数叫做复数,其中a叫这个复数的实部,b叫这个复数的虚部.它的加、减、乘法运算与整式的加、减、乘法运算类似.例如:(4+i)+(6﹣2i)=(4+6)+(1﹣2)i=10﹣i;(2﹣i)(3+i)=6﹣3i+2i﹣i2=6﹣i﹣(﹣1)=7﹣i;(2+i)2=4+4i+i2=4+4i﹣1=3+4i.根据以上信息,完成下面计算:(2+i)(1﹣2i)+(2﹣i)2=7﹣7i.【分析】直接利用已知结合多项式乘多项式以及完全平方公式化简,进而得出答案.【解答】解:(2+i)(1﹣2i)+(2﹣i)2=2﹣4i+i﹣2i2+4+i2﹣4i=6﹣i2﹣7i=6﹣(﹣1)﹣7i=7﹣7i.故答案为:7﹣7i.三、解答题(本大题共有9小题,共96分.请在答题卡指定区域内作答,解答时应写出必要的文字说明、证明过程或演算步骤)19.(8分)计算::(1)(m2)4﹣4m6•m2+(3m4)2;(2)(x﹣3)2﹣x(x﹣6).【分析】(1)首先利用幂的乘方、积的乘方的性质、单项式乘以单项式计算法则进行计算,然后再算加减即可;(2)先利用完全平方公式和单项式乘以多项式计算法则进行计算,然后再合并同类项即可.【解答】解:(1)原式=m8﹣4m8+9m8=6m8;(2)原式=x2﹣6x+9﹣x2+6x=9.20.(8分)因式分解:(1)m2(x+y)﹣n2(x+y);(2)x4﹣2x2+1.【分析】(1)原式提取公因式,再利用平方差公式分解即可;(2)原式利用完全平方公式,以及平方差公式分解即可.【解答】解:(1)原式=(x+y)(m2﹣n2)=(x+y)(m+n)(m﹣n);(2)原式=(x2﹣1)2=(x+1)2(x﹣1)2.21.(8分)(1)解方程组:;(2)解不等式﹣4<﹣,并把它的解集在数轴上表示出来.【分析】(1)方程组利用加减消元法求出解即可;(2)不等式去分母,去括号,移项,合并同类项,把x系数化为1,求出解集,表示在数轴上即可.【解答】解:(1),②﹣①×2得:x=6,把x=6代入①得:y=﹣3,则方程组的解为;(2)去分母得:2(2x﹣1)﹣24<﹣3(x+4),去括号得:4x﹣2﹣24<﹣3x﹣12,移项得:4x+3x<2+24﹣12,合并得:7x<14,解得:x<2,表示在数轴上,如图所示:22.(8分)先化简,再求值:(x﹣y)2﹣(﹣x+2y)(﹣x﹣2y),其中x,y满足方程组.【分析】先算乘法,再合并同类项,最后求出方程组的解代入,即可求出答案.【解答】解:原式=x2﹣2xy+y2﹣(x2﹣4y2)=x2﹣2xy+y2﹣x2+4y2=﹣2xy+5y2.解方程组得:,当x=﹣1,y=时,原式=﹣2xy+5y2=﹣2×(﹣1)×+5×()2=.23.(10分)如图,在△ABC中,点D、E分别在BC、AB上,且EF∥AD,∠1+∠2=180°.(1)试猜想∠2与∠BAD的关系,并说明理由;(2)若DG平分∠ADC,求证:DG∥AB.【分析】(1)由平行线的性质和∠1+∠2=180°,可推出∠2与∠BAD的关系;(2)由(1)的结论和DG平分∠ADC,可得∠ADG与∠BAD的关系,利用平行线的判定得结论.【解答】证明:(1)∠2与∠BAD相等.理由:∵EF∥AD,∴∠1+∠BAD=180°.∵∠1+∠2=180°.∴∠2=∠BAD.(2)∵DG平分∠ADC,∴∠2=∠ADG.由(1)知∠2=∠BAD,∴∠ADG=∠BAD.∴DG∥AB.24.(10分)已知关于x,y的二元一次方程组.(1)若满足方程x﹣2y=k,请求出此时这个方程组的解;(2)若该方程组的解满足x>y,求k的取值范围.【分析】(1)把x与y的值代入已知方程求出k的值,进而求出方程组的解即可;(2)表示出方程组的解,根据x>y,求出k的范围即可.【解答】解:(1)把代入x﹣2y=k得:k=3+4=7,方程组为,①﹣②×2得:y=﹣9,把y=﹣9代入①得:x=﹣11,则方程组的解为;(2),①﹣②得:x﹣y=5﹣k,∵x>y,即x﹣y>0,∴5﹣k>0,解得:k<5.25.(10分)对于任意的有理数a、b、c、d,我们规定=ad﹣bc,例如:=(﹣2)×5﹣(﹣4)×3=2.据这一规定,解下列问题:(1)化简;(2)若x同时满足≤1,<3x,求x的取值范围.【分析】(1)根据题意列式,然后再计算乘法,后算加减即可;(2)根据题意列出不等式组,再解不等式组确定解集即可.【解答】解:(1)原式=(x+2y)(x﹣2y)﹣(2x+y)2=x2﹣4y2﹣(4x2+4xy+y2)=x2﹣4y2﹣4x2﹣4xy﹣y2=﹣3x2﹣5y2﹣4xy;(2)∵≤1,<3x,∴,解不等式①得:x≤2,解不等式②得:x>,∴<x≤2.26.(10分)在数学学习里,我们常常用作差法比较两个数(或代数式)的大小.具体地说:若a﹣b>0,则a>b;若a﹣b=0,则a=b:若a﹣b<0,则a<b.(1)已知a=n2,b=2n﹣1,n是不等于1的任意有理数,试运用作差法比较a、b的大小;(2)若M=(2a+b)(a﹣2b),N=(a+3b)(a﹣2b),试运用作差法比较M、N的大小.【分析】(1)根据偶次方的非负性得到(n﹣1)2>0,根据不等式的性质解答;(2)根据偶次方的非负性得到(a﹣2b)2≥0,根据不等式的性质解答.【解答】解:(1)∵a=n2,b=2n﹣1,∴a﹣b=n2﹣(2n﹣1)=n2﹣2n+1=(n﹣1)2,∵n是不等于1的任意有理数,∴(n﹣1)2>0,∴a>b;(2)∵M=(2a+b)(a﹣2b),N=(a+3b)(a﹣2b),∴M﹣N=(2a+b)(a﹣2b)﹣(a+3b)(a﹣2b)=2a2﹣4ab+ab﹣2b2﹣a2+2ab﹣3ab+6b2=a2﹣4ab+4b2=(a﹣2b)2,∵(a﹣2b)2≥0,∴M≥N.27.(12分)为响应国家“足球进校园”的号召,某校购买了50个A类足球和25个B类足球共花费7500元,已知购买一个B类足球比购买一个A类足球多花30元.(1)求购买一个A类足球和一个B类足球各需多少元?(2)通过全校师生的共同努力,今年该校被评为“足球特色学校”,学校计划用不超过4800元的经费再次购买A类足球和B类足球共50个,若单价不变,则本次至少可以购买多少个A类足球?【分析】(1)设购买一个A类足球需要x元,购买一个B类足球需要y元,根据“购买50个A类足球和25个B类足球共花费7500元,购买一个B类足球比购买一个A类足球多花30元”,即可得出关于x,y的二元一次方程组,解之即可得出结论;(2)设购买m个A类足球,则购买(50﹣m)个B类足球,根据总价=单价×数量结合总费用不超过4800元,即可得出关于m的一元一次不等式,解之取其中的最小值即可得出结论.【解答】解:(1)设购买一个A类足球需要x元,购买一个B类足球需要y元,依题意,得:,解得:.答:购买一个A类足球需要90元,购买一个B类足球需要120元.(2)设购买m个A类足球,则购买(50﹣m)个B类足球,依题意,得:90m+120(50﹣m)≤4800,解得:m≥40.答:本次至少可以购买40个A类足球.28.(12分)(1)如图1,AD平分∠BAC,AE⊥BC,∠B=30°,∠C=70°.①∠BAC=80°,∠DAE=20°;②如图2.若把“AE⊥BC”变成“点F在AD的延长线上,FE⊥BC”,其它条件不变,求∠DFE的度数;(2)如图3,AD平分∠BAC,AE平分∠BEC,∠C﹣∠B=40°,求∠DAE的度数.【分析】(1)①利用三角形内角和定理求出∠BAC,再求出∠CAD,∠CAE即可解决问题.②想办法求出∠ADC即可解决问题.(2)利用三角形内角和定理以及角平分线的定义构建关系式解决问题即可.【解答】解:(1)①∵∠B=30°,∠C=70°,∴∠BAC=180°﹣(30°+70°)=80°,∵AD平分∠ABC,∴∠CAD=∠BAC=40°,∵AE⊥BC,∴∠AEC=90°,∴∠CAE=90°﹣70°=20°,∴∠DAE=∠CAD﹣∠CAD=20°.故答案为80,20.②∵∠ADC=180°﹣∠CAD﹣∠C=180°﹣40°﹣70°=70°,∴∠FDE=∠ADC=70°,∵FE⊥BC,∴∠FED=90°,∴∠DFE=90°﹣∠FDE=20°.(3)∵AD平分∠ABC,∴∠BAD=∠CAD,∵AE平分∠BEC,∴∠AEB=∠AEC,∵∠C+∠CAE+∠AEC=180°,∠B+∠BAE+∠AEB=180°,∴∠C+∠CAE=∠B+∠BAE,∵∠CAE=∠CAD﹣∠DAE,∠BAE=∠BAD+∠DAE,∴∠C+∠CAD﹣∠DAE=∠B+∠BAD+∠DAE,∴2∠DAE=∠C﹣∠B=40°,∴∠DAE=20°.。
江苏省扬州市宝应县2019-2020学年七年级(下)期末考试数学试卷 解析版

2019-2020学年江苏省扬州市宝应县七年级(下)期末数学试卷一.选择题(本大题共有8小题,每小题3分,共24分.在每小题所给出的四个选项中,恰有一项是符合题目要求的,请将正确选项前的字母代号填涂在答题卡相应位置上)1.(3分)下列运算中,正确的是()A.(a2)3=a5B.(a+2b)2=a2+2ab+4b2C.a5÷a2=a3(a≠0)D.a(a+1)=a2+12.(3分)如图,a∥b,若∠1=110°,则∠2的度数是()A.110°B.80°C.70°D.60°3.(3分)在△ABC中,若一个内角等于另两个内角的差,则这个三角形必定是()A.锐角三角形B.直角三角形C.钝角三角形D.以上三个都是4.(3分)若a>b.则依据不等式的基本性质下列变形不正确的是()A.3﹣2a>3﹣2b B.4+a>4+bC.ac2>bc2(c≠0)D.﹣a<﹣b5.(3分)若方程mx+ny=6的两个解是,,则m,n的值为()A.4,2B.2,4C.﹣4,﹣2D.﹣2,﹣4 6.(3分)判断命题“如果n<1,那么n2﹣2<0”是假命题,只需举出一个反例.反例中的n可以为()A.B.0C.﹣1D.﹣27.(3分)如图,一块直角三角尺的一个顶点落在直尺的一边上,若∠2=25°,则∠1的度数为()A.45°B.55°C.65°D.75°8.(3分)小明网购了一本《好玩的数学》,同学们想知道书的价格,小明让他们猜.甲说:“至少12元.”乙说“至多10元.”丙说“至多8元.”小明说:“你们三个人都说错了.”则这本书的价格x(元)所在的范围为()A.8<x<10B.9<x<11C.8<x<12D.10<x<12二、填空题(本大题共有10小题,每小题3分,共30分.不需写出解答过程,请把答案直接填写在答题卡相应位t上)9.(3分)成人每天维生素D的摄入量约为0.0000046克.数据“0.0000046”用科学记数法表示为.10.(3分)一个多边形的每一个内角为150°,那么这个多边形是边形.11.(3分)命题:“如果|a|=|b|,那么a=b”的逆命题是:(填“真命题”或“假命题”).12.(3分)一个等腰三角形的两边长分别是2cm和3cm,则它的周长是cm.13.(3分)如图,公园管理处在一块长是40m,宽是20m的草坪绿地中间修一条宽度均为2m的弯道便捷通道,则剩余草坪绿地的面积是m2.14.(3分)如图,在五边形ABCDE中,AE∥BC,则∠C+∠D+∠E=.15.(3分)若3m=2,9n=10,则3m﹣2n=.16.(3分)不等式组的解集为x>2,则a的取值范围是.17.(3分)若关于x、y的二元一次方程组,的解是,则关于a、b的二元一次方程组的解是.18.(3分)定义:如果一个数的平方等于﹣1,记为i2=﹣1,这个数i叫做虚数单位,把形如a+bi(a、b为实数)的数叫做复数,其中a叫这个复数的实部,b叫这个复数的虚部.它的加、减、乘法运算与整式的加、减、乘法运算类似.例如:(4+i)+(6﹣2i)=(4+6)+(1﹣2)i=10﹣i;(2﹣i)(3+i)=6﹣3i+2i﹣i2=6﹣i﹣(﹣1)=7﹣i;(2+i)2=4+4i+i2=4+4i﹣1=3+4i.根据以上信息,完成下面计算:(2+i)(1﹣2i)+(2﹣i)2=.三、解答题(本大题共有9小题,共96分.请在答题卡指定区域内作答,解答时应写出必要的文字说明、证明过程或演算步骤)19.(8分)计算::(1)(m2)4﹣4m6•m2+(3m4)2;(2)(x﹣3)2﹣x(x﹣6).20.(8分)因式分解:(1)m2(x+y)﹣n2(x+y);(2)x4﹣2x2+1.21.(8分)(1)解方程组:;(2)解不等式﹣4<﹣,并把它的解集在数轴上表示出来.22.(8分)先化简,再求值:(x﹣y)2﹣(﹣x+2y)(﹣x﹣2y),其中x,y满足方程组.23.(10分)如图,在△ABC中,点D、E分别在BC、AB上,且EF∥AD,∠1+∠2=180°.(1)试猜想∠2与∠BAD的关系,并说明理由;(2)若DG平分∠ADC,求证:DG∥AB.24.(10分)已知关于x,y的二元一次方程组.(1)若满足方程x﹣2y=k,请求出此时这个方程组的解;(2)若该方程组的解满足x>y,求k的取值范围.25.(10分)对于任意的有理数a、b、c、d,我们规定=ad﹣bc,例如:=(﹣2)×5﹣(﹣4)×3=2.据这一规定,解下列问题:(1)化简;(2)若x同时满足≤1,<3x,求x的取值范围.26.(10分)在数学学习里,我们常常用作差法比较两个数(或代数式)的大小.具体地说:若a﹣b>0,则a>b;若a﹣b=0,则a=b:若a﹣b<0,则a<b.(1)已知a=n2,b=2n﹣1,n是不等于1的任意有理数,试运用作差法比较a、b的大小;(2)若M=(2a+b)(a﹣2b),N=(a+3b)(a﹣2b),试运用作差法比较M、N的大小.27.(12分)为响应国家“足球进校园”的号召,某校购买了50个A类足球和25个B类足球共花费7500元,已知购买一个B类足球比购买一个A类足球多花30元.(1)求购买一个A类足球和一个B类足球各需多少元?(2)通过全校师生的共同努力,今年该校被评为“足球特色学校”,学校计划用不超过4800元的经费再次购买A类足球和B类足球共50个,若单价不变,则本次至少可以购买多少个A类足球?28.(12分)(1)如图1,AD平分∠BAC,AE⊥BC,∠B=30°,∠C=70°.①∠BAC=°,∠DAE=°;②如图2.若把“AE⊥BC”变成“点F在AD的延长线上,FE⊥BC”,其它条件不变,求∠DFE的度数;(2)如图3,AD平分∠BAC,AE平分∠BEC,∠C﹣∠B=40°,求∠DAE的度数.2019-2020学年江苏省扬州市宝应县七年级(下)期末数学试卷参考答案与试题解析一.选择题(本大题共有8小题,每小题3分,共24分.在每小题所给出的四个选项中,恰有一项是符合题目要求的,请将正确选项前的字母代号填涂在答题卡相应位置上)1.(3分)下列运算中,正确的是()A.(a2)3=a5B.(a+2b)2=a2+2ab+4b2C.a5÷a2=a3(a≠0)D.a(a+1)=a2+1【分析】直接利用整式的混合运算进而结合完全平方公式计算得出答案.【解答】解:A、(a2)3=a6,故此选项错误;B、(a+2b)2=a2+4ab+4b2,故此选项错误;C、a5÷a2=a3(a≠0),正确;D、a(a+1)=a2+a,故此选项错误;故选:C.2.(3分)如图,a∥b,若∠1=110°,则∠2的度数是()A.110°B.80°C.70°D.60°【分析】根据两直线平行,同位角相等,即可求得∠3的度数,进而得出∠2的度数.【解答】解:∵a∥b,∴∠1=∠3=110°.∵∠2+∠3=180°,∴∠2=180°﹣∠3=70°,故选:C.3.(3分)在△ABC中,若一个内角等于另两个内角的差,则这个三角形必定是()A.锐角三角形B.直角三角形C.钝角三角形D.以上三个都是【分析】根据三角形的内角和可求解△ABC的一内角为90°,进而可判断三角形的形状.【解答】解:设∠A=∠B﹣∠C,则∠A+∠C=∠B,∵∠A+∠C+∠B=180°,∴∠B=90°,∴△ABC为直角三角形,故选:B.4.(3分)若a>b.则依据不等式的基本性质下列变形不正确的是()A.3﹣2a>3﹣2b B.4+a>4+bC.ac2>bc2(c≠0)D.﹣a<﹣b【分析】利用不等式的性质对各选项进行判断.【解答】解:∵a>b,∴3﹣2a<3﹣2b,4+a>4+b,ac2>bc2(c≠0),﹣a<﹣b.故选:A.5.(3分)若方程mx+ny=6的两个解是,,则m,n的值为()A.4,2B.2,4C.﹣4,﹣2D.﹣2,﹣4【分析】将x与y的两对值代入方程计算即可求出m与n的值.【解答】解:将,分别代入mx+ny=6中,得:,①+②得:3m=12,即m=4,将m=4代入①得:n=2,故选:A.6.(3分)判断命题“如果n<1,那么n2﹣2<0”是假命题,只需举出一个反例.反例中的n可以为()A.B.0C.﹣1D.﹣2【分析】根据实数的大小比较法则、乘方法则解答.【解答】解:﹣2<1,(﹣2)2﹣2>0,∴当n=﹣2时,“如果n<1,那么n2﹣2<0”是假命题,故选:D.7.(3分)如图,一块直角三角尺的一个顶点落在直尺的一边上,若∠2=25°,则∠1的度数为()A.45°B.55°C.65°D.75°【分析】根据平行线的性质和直角三角形的性质,可以得到∠1的度数,本题得以解决.【解答】解:过直角顶点作长边的平行线,如右图所示,则∠2=∠3,∠1=∠4,∵∠2=25°,∴∠3=25°,∵∠3+∠4=90°,∴∠4=65°,∴∠1=65°,故选:C.8.(3分)小明网购了一本《好玩的数学》,同学们想知道书的价格,小明让他们猜.甲说:“至少12元.”乙说“至多10元.”丙说“至多8元.”小明说:“你们三个人都说错了.”则这本书的价格x(元)所在的范围为()A.8<x<10B.9<x<11C.8<x<12D.10<x<12【分析】根据题意得出不等式组解答即可.【解答】解:根据题意可得:,∵三个人都说错了,∴这本书的价格x(元)所在的范围为10<x<12.故选:D.二、填空题(本大题共有10小题,每小题3分,共30分.不需写出解答过程,请把答案直接填写在答题卡相应位t上)9.(3分)成人每天维生素D的摄入量约为0.0000046克.数据“0.0000046”用科学记数法表示为 4.6×10﹣6.【分析】利用科学记数法的知识即可解答.【解答】解:0.0000046=4.6×10﹣6.故答案为:4.6×10﹣6.10.(3分)一个多边形的每一个内角为150°,那么这个多边形是十二边形.【分析】设多边形的边数为n,根据多边形的内角和定理:180°•(n﹣2)可得180°•(n ﹣2)=150°•n,再解方程求解即可.【解答】解:设多边形的边数为n,由题意可得:180•(n﹣2)=150•n,解得n=12.故答案为:十二.11.(3分)命题:“如果|a|=|b|,那么a=b”的逆命题是:真命题(填“真命题”或“假命题”).【分析】分析是否为真命题,需要分别分析各题设是否能推出结论,可得答案.【解答】解:“如果|a|=|b|,那么a=b”的逆命题是“如果a=b,那么|a|=|b|”,为真命题,故答案为:真命题.12.(3分)一个等腰三角形的两边长分别是2cm和3cm,则它的周长是8或7cm.【分析】题目给出等腰三角形有两条边长为2cm和3cm,而没有明确腰、底分别是多少,所以要进行讨论,还要应用三角形的三边关系验证能否组成三角形.【解答】解:分两种情况:当三边是2,3,3时,能构成三角形,则周长是8;当三边是2,2,3时,能构成三角形,则周长是7.所以等腰三角形的周长为8cm或7cm.故答案为8cm或7cm.13.(3分)如图,公园管理处在一块长是40m,宽是20m的草坪绿地中间修一条宽度均为2m的弯道便捷通道,则剩余草坪绿地的面积是760m2.【分析】利用总面积减去便捷通道的面积即可.【解答】解:剩余草坪绿地的面积是:40×20﹣20×2=760(m2),故答案为:760.14.(3分)如图,在五边形ABCDE中,AE∥BC,则∠C+∠D+∠E=360°.【分析】首先过点D作DF∥AE,交AB于点F,由AE∥BC,可证得AE∥DF∥BC,然后由两直线平行,同旁内角互补,证得∠A+∠B=180°,∠E+∠EDF=180°,∠CDF+∠C=180°,继而证得结论.【解答】过点D作DF∥AE,交AB于点F,∵AE∥BC,∴AE∥DF∥BC,∴∠A+∠B=180°,∠E+∠EDF=180°,∠CDF+∠C=180°,∴∠C+∠CDE+∠E=360°,故答案为360°.15.(3分)若3m=2,9n=10,则3m﹣2n=.【分析】直接利用同底数幂的除法运算法则、幂的乘方运算法则将原式变形得出答案.【解答】解:∵3m=2,9n=10=32n,∴3m﹣2n=3m÷32n=2÷10=.故答案为:.16.(3分)不等式组的解集为x>2,则a的取值范围是a≤2.【分析】根据不等式组的公共解集即可确定a的取值范围.【解答】解:由不等式组的解集为x>2,可得a≤2.故答案为:a≤217.(3分)若关于x、y的二元一次方程组,的解是,则关于a、b的二元一次方程组的解是.【分析】根据已知得出关于a,b的方程组进而得出答案.【解答】解:∵关于x、y的二元一次方程组,的解是,∴方程组中,解得:.故答案为:.18.(3分)定义:如果一个数的平方等于﹣1,记为i2=﹣1,这个数i叫做虚数单位,把形如a+bi(a、b为实数)的数叫做复数,其中a叫这个复数的实部,b叫这个复数的虚部.它的加、减、乘法运算与整式的加、减、乘法运算类似.例如:(4+i)+(6﹣2i)=(4+6)+(1﹣2)i=10﹣i;(2﹣i)(3+i)=6﹣3i+2i﹣i2=6﹣i﹣(﹣1)=7﹣i;(2+i)2=4+4i+i2=4+4i﹣1=3+4i.根据以上信息,完成下面计算:(2+i)(1﹣2i)+(2﹣i)2=7﹣7i.【分析】直接利用已知结合多项式乘多项式以及完全平方公式化简,进而得出答案.【解答】解:(2+i)(1﹣2i)+(2﹣i)2=2﹣4i+i﹣2i2+4+i2﹣4i=6﹣i2﹣7i=6﹣(﹣1)﹣7i=7﹣7i.故答案为:7﹣7i.三、解答题(本大题共有9小题,共96分.请在答题卡指定区域内作答,解答时应写出必要的文字说明、证明过程或演算步骤)19.(8分)计算::(1)(m2)4﹣4m6•m2+(3m4)2;(2)(x﹣3)2﹣x(x﹣6).【分析】(1)首先利用幂的乘方、积的乘方的性质、单项式乘以单项式计算法则进行计算,然后再算加减即可;(2)先利用完全平方公式和单项式乘以多项式计算法则进行计算,然后再合并同类项即可.【解答】解:(1)原式=m8﹣4m8+9m8=6m8;(2)原式=x2﹣6x+9﹣x2+6x=9.20.(8分)因式分解:(1)m2(x+y)﹣n2(x+y);(2)x4﹣2x2+1.【分析】(1)原式提取公因式,再利用平方差公式分解即可;(2)原式利用完全平方公式,以及平方差公式分解即可.【解答】解:(1)原式=(x+y)(m2﹣n2)=(x+y)(m+n)(m﹣n);(2)原式=(x2﹣1)2=(x+1)2(x﹣1)2.21.(8分)(1)解方程组:;(2)解不等式﹣4<﹣,并把它的解集在数轴上表示出来.【分析】(1)方程组利用加减消元法求出解即可;(2)不等式去分母,去括号,移项,合并同类项,把x系数化为1,求出解集,表示在数轴上即可.【解答】解:(1),②﹣①×2得:x=6,把x=6代入①得:y=﹣3,则方程组的解为;(2)去分母得:2(2x﹣1)﹣24<﹣3(x+4),去括号得:4x﹣2﹣24<﹣3x﹣12,移项得:4x+3x<2+24﹣12,合并得:7x<14,解得:x<2,表示在数轴上,如图所示:22.(8分)先化简,再求值:(x﹣y)2﹣(﹣x+2y)(﹣x﹣2y),其中x,y满足方程组.【分析】先算乘法,再合并同类项,最后求出方程组的解代入,即可求出答案.【解答】解:原式=x2﹣2xy+y2﹣(x2﹣4y2)=x2﹣2xy+y2﹣x2+4y2=﹣2xy+5y2.解方程组得:,当x=﹣1,y=时,原式=﹣2xy+5y2=﹣2×(﹣1)×+5×()2=.23.(10分)如图,在△ABC中,点D、E分别在BC、AB上,且EF∥AD,∠1+∠2=180°.(1)试猜想∠2与∠BAD的关系,并说明理由;(2)若DG平分∠ADC,求证:DG∥AB.【分析】(1)由平行线的性质和∠1+∠2=180°,可推出∠2与∠BAD的关系;(2)由(1)的结论和DG平分∠ADC,可得∠ADG与∠BAD的关系,利用平行线的判定得结论.【解答】证明:(1)∠2与∠BAD相等.理由:∵EF∥AD,∴∠1+∠BAD=180°.∵∠1+∠2=180°.∴∠2=∠BAD.(2)∵DG平分∠ADC,∴∠2=∠ADG.由(1)知∠2=∠BAD,∴∠ADG=∠BAD.∴DG∥AB.24.(10分)已知关于x,y的二元一次方程组.(1)若满足方程x﹣2y=k,请求出此时这个方程组的解;(2)若该方程组的解满足x>y,求k的取值范围.【分析】(1)把x与y的值代入已知方程求出k的值,进而求出方程组的解即可;(2)表示出方程组的解,根据x>y,求出k的范围即可.【解答】解:(1)把代入x﹣2y=k得:k=3+4=7,方程组为,①﹣②×2得:y=﹣9,把y=﹣9代入①得:x=﹣11,则方程组的解为;(2),①﹣②得:x﹣y=5﹣k,∵x>y,即x﹣y>0,∴5﹣k>0,解得:k<5.25.(10分)对于任意的有理数a、b、c、d,我们规定=ad﹣bc,例如:=(﹣2)×5﹣(﹣4)×3=2.据这一规定,解下列问题:(1)化简;(2)若x同时满足≤1,<3x,求x的取值范围.【分析】(1)根据题意列式,然后再计算乘法,后算加减即可;(2)根据题意列出不等式组,再解不等式组确定解集即可.【解答】解:(1)原式=(x+2y)(x﹣2y)﹣(2x+y)2=x2﹣4y2﹣(4x2+4xy+y2)=x2﹣4y2﹣4x2﹣4xy﹣y2=﹣3x2﹣5y2﹣4xy;(2)∵≤1,<3x,∴,解不等式①得:x≤2,解不等式②得:x>,∴<x≤2.26.(10分)在数学学习里,我们常常用作差法比较两个数(或代数式)的大小.具体地说:若a﹣b>0,则a>b;若a﹣b=0,则a=b:若a﹣b<0,则a<b.(1)已知a=n2,b=2n﹣1,n是不等于1的任意有理数,试运用作差法比较a、b的大小;(2)若M=(2a+b)(a﹣2b),N=(a+3b)(a﹣2b),试运用作差法比较M、N的大小.【分析】(1)根据偶次方的非负性得到(n﹣1)2>0,根据不等式的性质解答;(2)根据偶次方的非负性得到(a﹣2b)2≥0,根据不等式的性质解答.【解答】解:(1)∵a=n2,b=2n﹣1,∴a﹣b=n2﹣(2n﹣1)=n2﹣2n+1=(n﹣1)2,∵n是不等于1的任意有理数,∴(n﹣1)2>0,∴a>b;(2)∵M=(2a+b)(a﹣2b),N=(a+3b)(a﹣2b),∴M﹣N=(2a+b)(a﹣2b)﹣(a+3b)(a﹣2b)=2a2﹣4ab+ab﹣2b2﹣a2+2ab﹣3ab+6b2=a2﹣4ab+4b2=(a﹣2b)2,∵(a﹣2b)2≥0,∴M≥N.27.(12分)为响应国家“足球进校园”的号召,某校购买了50个A类足球和25个B类足球共花费7500元,已知购买一个B类足球比购买一个A类足球多花30元.(1)求购买一个A类足球和一个B类足球各需多少元?(2)通过全校师生的共同努力,今年该校被评为“足球特色学校”,学校计划用不超过4800元的经费再次购买A类足球和B类足球共50个,若单价不变,则本次至少可以购买多少个A类足球?【分析】(1)设购买一个A类足球需要x元,购买一个B类足球需要y元,根据“购买50个A类足球和25个B类足球共花费7500元,购买一个B类足球比购买一个A类足球多花30元”,即可得出关于x,y的二元一次方程组,解之即可得出结论;(2)设购买m个A类足球,则购买(50﹣m)个B类足球,根据总价=单价×数量结合总费用不超过4800元,即可得出关于m的一元一次不等式,解之取其中的最小值即可得出结论.【解答】解:(1)设购买一个A类足球需要x元,购买一个B类足球需要y元,依题意,得:,解得:.答:购买一个A类足球需要90元,购买一个B类足球需要120元.(2)设购买m个A类足球,则购买(50﹣m)个B类足球,依题意,得:90m+120(50﹣m)≤4800,解得:m≥40.答:本次至少可以购买40个A类足球.28.(12分)(1)如图1,AD平分∠BAC,AE⊥BC,∠B=30°,∠C=70°.①∠BAC=80°,∠DAE=20°;②如图2.若把“AE⊥BC”变成“点F在AD的延长线上,FE⊥BC”,其它条件不变,求∠DFE的度数;(2)如图3,AD平分∠BAC,AE平分∠BEC,∠C﹣∠B=40°,求∠DAE的度数.【分析】(1)①利用三角形内角和定理求出∠BAC,再求出∠CAD,∠CAE即可解决问题.②想办法求出∠ADC即可解决问题.(2)利用三角形内角和定理以及角平分线的定义构建关系式解决问题即可.【解答】解:(1)①∵∠B=30°,∠C=70°,∴∠BAC=180°﹣(30°+70°)=80°,∵AD平分∠ABC,∴∠CAD=∠BAC=40°,∵AE⊥BC,∴∠AEC=90°,∴∠CAE=90°﹣70°=20°,∴∠DAE=∠CAD﹣∠CAD=20°.故答案为80,20.②∵∠ADC=180°﹣∠CAD﹣∠C=180°﹣40°﹣70°=70°,∴∠FDE=∠ADC=70°,∵FE⊥BC,∴∠FED=90°,∴∠DFE=90°﹣∠FDE=20°.(3)∵AD平分∠ABC,∴∠BAD=∠CAD,∵AE平分∠BEC,∴∠AEB=∠AEC,∵∠C+∠CAE+∠AEC=180°,∠B+∠BAE+∠AEB=180°,∴∠C+∠CAE=∠B+∠BAE,∵∠CAE=∠CAD﹣∠DAE,∠BAE=∠BAD+∠DAE,∴∠C+∠CAD﹣∠DAE=∠B+∠BAD+∠DAE,∴2∠DAE=∠C﹣∠B=40°,∴∠DAE=20°.。
D_2017-2018学年江苏省扬州市宝应县七年级(下)期末数学试卷(解析版)

【解析】
第 8 页,共 21 页
解:4-3<x<4+3, 则 1<x<7. 故选:D. 根据三角形的三边关系:三角形第三边的长度应是大于两边的差而小于两边 的和,这样就可求出第三边长的范围. 本题考查了三角形的三边关系,已知三角形的两边,则第三边的范围是:大于 已知的两边的差,而小于两边的和.
D. −2 ≤ ������ < 2
二、填空题(本大题共 10 小题,共 30.0 分)
9. 人体血液由血浆和血细胞组成,血细胞包括红细胞和白细胞和血小板三类细胞, 科学家测得红细胞直径约为 0.00077cm,将 0.00077 用科学记数法表示为______.
10. 一个多边形的内角和是外角和的 4 倍,则此多边形的边数是______.
2.【答案】B
【解析】
解:A、∵∠1=∠2,∴AB∥CD,正确; B、∵∠2=∠E,∴AD∥BE,错误; C、∵∠B+∠E=180°,∴AB∥CD,正确; D、∵∠BAF=∠C,∴AB∥CD,正确; 故选:B. 根据平行线的判定定理对各选项进行逐一判断即可. 本题考查的是平行线的判定,熟知平行线的判定定理是解答此题的关键.平 行线的判定定理 1:同位角相等,两直线平行.定理 2:两条直线被第三条所内 错角相等,两直线平行.定理 3:同旁内角互补,两直线平行.
8.【答案】A
【解析】
第 10 页,共 21 页
解:∵x=4 是不等式 mx-3m+2≤0 的解, ∴4m-3m+2≤0, 解得:m≤-2, ∵x=2 不是这个不等式的解, ∴2m-3m+2>0, 解得:m<2, ∴m≤-2, 故选:A.
根据 x=4 是不等式 mx-3m+2≤0 的解,且 x=2 不是这个不等式的解,列出不等 式,求出解集,即可解答. 本题考查了不等式的解集,解决本题的关键是根据 x=4 是不等式 mx-
七年级下册扬州数学期末试卷测试卷(解析版)

七年级下册扬州数学期末试卷测试卷(解析版)一、选择题1.“49的平方根是7±”的表达式正确的是() A .497±=± B .497=C .497=±D .497±=2.下列现象中是平移的是( )A .将一张纸对折B .电梯的上下移动C .摩天轮的运动D .翻开书的封面3.下列各点中,在第三象限的点是( ) A .()2,4B .()2,4-C .()2,4-D .()2,4--4.下列给出四个命题:①如果两个角相等,那么它们是对顶角;②如果两个角互为邻补角,那么它们的平分线互相垂直;③如果两条直线垂直于同一条直线,那么这两条直线平行;④如果两条直线平行于同一条直线,那么这两条直线平行.其中为假命题的是( ) A .① B .①②C .①③D .①②③④5.如图所示,//CD AB ,OE 平分∠AOD ,80EOF ∠=︒,60D ∠=︒,则∠BOF 为( )A .35︒B .40︒C .25︒D .20︒ 6.若325.36 2.938=,3253.6 6.329=,则325360000=( )A .632.9B .293.8C .2938D .63297.如图,直线AB ∥CD ,BE 平分∠ABD ,若∠DBE =20°,∠DEB =80°,求∠CDE 的度数是( )A .50°B .60°C .70°D .80°8.已知点0(E x ,)o y ,点2(F x ,2)y ,点1(M x ,1)y 是线段EF 的中点,则0212x x x +=,0212y y y +=.在平面直角坐标系中有三个点A (1,1-),B (1-,1-),C (0,1),点P (0,2)关于点A 的对称点1P (即P ,A ,1P 三点共线,且1)PA P A =,1P 关于点B 的对称点2P ,2P 关于点C 的对称点3P ,⋯按此规律继续以A ,B ,C 三点为对称点重复前面的操作.依次得到点4P ,5P ,6P ⋯,则点2015P 的坐标是( )A .(0,0)B .(0,2)C .(2,4-)D .(4-,2)二、填空题9.2(4)-的算术平方根为__________10.点(,1)a 关于x 轴的对称点的坐标为(5,)b ,则+a b 的值是______.11.如图,△ABC 中∠BAC =60°,将△ACD 沿AD 折叠,使得点C 落在AB 上的点C ′处,连接C ′D 与C ′C ,∠ACB 的角平分线交AD 于点E ;如果BC ′=DC ′;那么下列结论:①∠1=∠2;②AD 垂直平分C ′C ;③∠B =3∠BCC ′;④DC ∥EC ;其中正确的是:________;(只填写序号)12.如图,把一块三角板的直角顶点放在一直尺的一边上,若∠1=50°,则∠2的度数为_____.13.如图,将长方形纸片ABCD 折叠,使点D 与点B 重合,点C 落在点C ’处,折痕为EF ,若∠ABE =30°,则∠EFC ’的度数为____________.14.“⊗”定义新运算:对于任意的有理数a 和b ,都有21a b b ⊗=+.例如:2955126⊗=+=.当m 为有理数时,则(3)m m ⊗⊗等于________.15.已知ABC ∆的面积为16,其中两个顶点的坐标分别是()()7,0,1,0A B -,顶点C 在y 轴上,那么点C 的坐标为 ____________16.在平面直角坐标系xoy 中,对于点(,)P x y 我们把(1,1)P y x -++叫做点P 的伴随点,已知1A 的伴随点为2A ,点2A 的伴随点为3A ,点3A 的伴随点为4A ,这样依次得到123,,,n A A A A ⋯,若点1A 的坐标为(3,1),则点2021A 的坐标为_______三、解答题17.计算:(1)3840.04---(2)23(2)279-+-18.求下列各式中实数的x值.(1)25x2﹣36=0(2)|x+2|=π19.填充证明过程和理由.如图,已知∠B+∠BCD=180°,∠B=∠D.求证:∠E=∠DFE.证明:∵∠B+∠BCD=180°(已知),∴AB∥CD().∴∠B=().又∵∠B=∠D(已知),∴∠D=∠.∴AD∥BE().∴∠E=∠DFE().20.如图,在平面直角坐标系中,三角形ABC经过平移得到三角形A1B1C1,结合图形,完成下列问题:(1)三角形ABC先向左平移个单位,再向平移个单位得到三角形A1B1C1.(2)三角形ABC内有一点P(x,y),则在三角形A1B1C1内部的对应点P1的坐标是.(3)三角形ABC的面积是.21.阅读下面的文字,解答问题22的小数部分我们不可能全部21221,将这个数减去其整数部分,差就是小数部分.又例如:4<7<9,即2<7<3, ∴7的整数部分为2,小数部分为(7﹣2)请解答:(1)57整数部分是 ,小数部分是 .(2)如果11的小数部分为a ,7的整数部分为b ,求|a ﹣b |+11的值. (3)已知:9+5=x +y ,其中x 是整数,且0<y <1,求x ﹣y 的相反数.二十二、解答题22.如图,用两个面积为2200cm 的小正方形拼成一个大的正方形. (1)则大正方形的边长是___________;(2)若沿着大正方形边的方向裁出一个长方形,能否使裁出的长方形纸片的长宽之比为5:4,且面积为2360cm ?二十三、解答题23.已知,//AE BD ,A D ∠=∠. (1)如图1,求证://AB CD ;(2)如图2,作BAE ∠的平分线交CD 于点F ,点G 为AB 上一点,连接FG ,若CFG ∠的平分线交线段AG 于点H ,连接AC ,若ACE BAC BGM ∠=∠+∠,过点H 作HM FH ⊥交FG 的延长线于点M ,且3518E AFH ∠-∠=︒,求EAF GMH ∠+∠的度数.24.已知//a b ,直角ABC 的边与直线a 分别相交于O 、G 两点,与直线b 分别交于E ,F 点,且90ACB ∠=︒.(1)将直角ABC 如图1位置摆放,如果56AOG ∠=︒,则CEF ∠=________; (2)将直角ABC 如图2位置摆放,N 为AC 上一点,180NEF CEF ∠+∠=︒,请写出NEF ∠与AOG ∠之间的等量关系,并说明理由;(3)将直角ABC 如图3位置摆放,若135GOC ∠=︒,延长AC 交直线b 于点Q ,点P 是射线GF 上一动点,探究,POQ OPQ ∠∠与PQF ∠的数量关系,请直接写出结论. 25.小明在学习过程中,对教材中的一个有趣问题做如下探究:(习题回顾)已知:如图1,在ABC 中,90ACB ∠=︒,AE 是角平分线,CD 是高,AE 、CD 相交于点F .求证:CFE CEF ∠=∠;(变式思考)如图2,在ABC 中,90ACB ∠=︒,CD 是AB 边上的高,若ABC 的外角BAG ∠的平分线交CD 的延长线于点F ,其反向延长线与BC 边的延长线交于点E ,则CFE ∠与CEF ∠还相等吗?说明理由;(探究延伸)如图3,在ABC 中,AB 上存在一点D ,使得ACD B ∠=∠,BAC ∠的平分线AE 交CD 于点F .ABC 的外角BAG ∠的平分线所在直线MN 与BC 的延长线交于点M .直接写出M ∠与CFE ∠的数量关系.26.如图,直线m 与直线n 互相垂直,垂足为O 、A 、B 两点同时从点O 出发,点A 沿直线m 向左运动,点B 沿直线n 向上运动.(1)若∠BAO 和∠ABO 的平分线相交于点Q ,在点A ,B 的运动过程中,∠AQB 的大小是否会发生变化?若不发生变化,请求出其值,若发生变化,请说明理由.(2)若AP 是∠BAO 的邻补角的平分线,BP 是∠ABO 的邻补角的平分线,AP 、BP 相交于点P ,AQ 的延长线交PB 的延长线于点C ,在点A ,B 的运动过程中,∠P 和∠C 的大小是否会发生变化?若不发生变化,请求出∠P 和∠C 的度数;若发生变化,请说明理由.【参考答案】一、选择题 1.A 解析:A 【分析】根据平方根的表示方法,即可得到答案. 【详解】解:“49的平方根是7±”表示为:497±=±. 故选A . 【点睛】本题主要考查平方根的表示法,掌握正数a 的平方根表示为a2.B 【分析】根据平移的概念,依次判断即可得到答案; 【详解】解:根据平移的概念:把一个图形整体沿某一的方向移动,这种图形的平行移动,叫做平移变换,简称平移,判断: A 、将一张纸对折,不符合平移定解析:B 【分析】根据平移的概念,依次判断即可得到答案; 【详解】解:根据平移的概念:把一个图形整体沿某一的方向移动,这种图形的平行移动,叫做平移变换,简称平移,判断:A 、将一张纸对折,不符合平移定义,故本选项错误;B 、电梯的上下移动,符合平移的定义,故本选项正确;C 、摩天轮的运动,不符合平移定义,故本选项错误;D 、翻开的封面,不符合平移的定义,故本选项错误. 故选B . 【点睛】本题考查平移的概念,在平面内,把一个图形整体沿某一的方向移动,这种图形的平行移动,叫做平移变换,简称平移.3.D 【分析】应先判断点在第三象限内点的坐标的符号特点,进而找相应坐标. 【详解】解:∵第三象限的点的横坐标是负数,纵坐标也是负数, ∴结合选项符合第三象限的点是(-2,-4). 故选:D . 【点睛】本题主要考查了点在第三象限内点的坐标的符号特点.四个象限的符号特点分别是:第一象限(+,+);第二象限(-,+);第三象限(-,-);第四象限(+,-). 4.C 【分析】根据两个相等的角不一定是对顶角对①进行判定,根据邻补角与角平分线的性质对②进行判断,根据在同一平面内,两条直线垂直于同一条直线,那么这两条直线平行对③进行判断,根据平行线的判定对④进行判断. 【详解】解:①如果两个角相等,那么它们不一定是对顶角,选项说法错误,符合题意; ②如果两个角互为邻补角,那么它们的平分线互相垂直,选项说法正确,不符合题意; ③在同一平面内,如果两条直线垂直于同一条直线,那么这两条直线平行,选项说法错误,符合题意;④如果两条直线平行于同一条直线,那么这两条直线平行,选项说法正确,不符合题意; 故选:C . 【点睛】本题考查了命题与定理:命题的“真”“假”是就命题的内容而言.任何一个命题非真即假.要说明一个命题的正确性,一般需要推理、论证,而判断一个命题是假命题,只需举出一个反例即可. 5.B 【分析】由平行线的性质和角平分线的定义,求出60BOD D ∠=∠=︒,20DOF ∠=︒,然后即可求出∠BOF 的度数. 【详解】解:∵//CD AB ,60D ∠=︒∴60BOD D ∠=∠=︒,18060120AOD ∠=︒-︒=︒, ∵OE 平分∠AOD , ∴1120602DOE ∠=⨯︒=︒,∴806020DOF EOF DOE ∠=∠-∠=︒-︒=︒; ∴602040BOF BOD DOF ∠=∠-∠=︒-︒=︒; 故选:B .【点睛】本题考查了平行线的性质,角平分线的定义,以及角的和差关系,解题的关键是熟练掌握所学的知识,正确的求出角的度数. 6.B 【分析】把3632536000025.3610=⨯,再利用立方根的性质化简即可得到答案. 【详解】解: 325.36 2.938=,∴ 3632536000025.3610=⨯362325.3610 2.93810293.8.=⨯=⨯= 故选:.B 【点睛】本题考查的是立方根的含义,立方根的性质,熟练立方根的含义与性质是解题的关键. 7.B 【分析】延长DE ,交AB 于点F ,根据角平分线的定义以及已知条件可得20EBF ∠=︒,由三角形的外角性质可求EFB ∠,最后由平行线的性质即可求解. 【详解】延长DE ,交AB 于点F ,BE 平分∠ABD ,20DBE ∠=︒,20EBF DBE ∴∠=∠=︒,DEB DFB EBF ∠=∠+∠,∠DEB =80°,802060EFB DEB EBF ∴∠=∠-∠=︒-︒=︒,//AB CD ,60CDE EFB ∴∠=∠=︒, 故选B . 【点睛】本题考查了角平分线的定义,平行线的性质,三角形的外角性质,掌握以上知识是解题的关键.8.A 【分析】首先利用题目所给公式求出的坐标,然后利用公式求出对称点的坐标,依此类推即可求出的坐标;由的坐标和的坐标相同,即坐标以6为周期循环,利用这个规律即可求出点的坐标 【详解】 解:设, ∵,解析:A 【分析】首先利用题目所给公式求出1P 的坐标,然后利用公式求出对称点2P 的坐标,依此类推即可求出7P 的坐标;由7P 的坐标和1P 的坐标相同,即坐标以6为周期循环,利用这个规律即可求出点2015P 的坐标 【详解】解:设()1P xy ,, ∵()1,1A -,()0,2P ,且A 是1PP 的中点, ∴021122x y ++==-,,解得:2y 4x ==-,, ∴()124P -, 同理可得:()()()()()()234567424022000224P P P P P P ----,,,,,,,,,,,, ∴每6个点一个循环, ∵201533656=∴点2015P 的坐标是()500P , 故选A 【点睛】此题考查了平面直角坐标系中坐标规律的探索,读懂题目,利用题目所给公式是解题的关键,利用公式求出几个点的坐标,找到循环规律,利用这个规律即可求出.二、填空题 9.4 【分析】先利用平方的意义求出值,再利用算术平方根的概念求解即可. 【详解】=16,16的算术平方根是4 故答案为4. 【点睛】本题考查算术平方根的定义,难度低,属于基础题,注意算术平方根与解析:4 【分析】先利用平方的意义求出值,再利用算术平方根的概念求解即可.【详解】2=16,16的算术平方根是4(4)故答案为4.【点睛】本题考查算术平方根的定义,难度低,属于基础题,注意算术平方根与平方根的区别. 10.4【分析】根据横坐标不变,纵坐标相反,确定a,b的值,计算即可.【详解】∵点关于轴的对称点的坐标为,∴a=5,b= -1,∴a+b= 5-1=4,故答案为:4.【点睛】本题考查了坐解析:4【分析】根据横坐标不变,纵坐标相反,确定a,b的值,计算即可.【详解】∵点(,1)a关于x轴的对称点的坐标为(5,)b,∴a=5,b= -1,∴a+b= 5-1=4,故答案为:4.【点睛】本题考查了坐标系中轴对称问题,熟练掌握轴对称的坐标变化特点是解题的关键.11.①②④【分析】根据折叠的全等性质,垂直平分线的性质,平行线的判定定理,外角的性质等判断即可【详解】解:如图,∵△ACD沿AD折叠,使得点C落在AB上的点C′处,∴∠1=∠2,A=AC,DC解析:①②④【分析】根据折叠的全等性质,垂直平分线的性质,平行线的判定定理,外角的性质等判断即可【详解】解:如图,∵△ACD沿AD折叠,使得点C落在AB上的点C′处,∴∠1=∠2,A C '=AC ,DC =D C ',∴AD 垂直平分C ′C ;∴①,②都正确;∵B C '=D C ', DC =D C ',∴B C '=D C '= DC ,∴∠3=∠B ,∠4=∠5,∴∠3=∠4+∠5=2∠5即∠B =2∠BC C ';∴③错误;根据折叠的性质,得∠ACD =∠A C 'D =∠B +∠3=2∠3,∵∠ACB 的角平分线交AD 于点E ,∴2(∠6+∠5)=2∠B ,653,∴∠+∠=∠∴3,DCE ∴∠=∠∴D C '∥EC∴④正确;故答案为:①②④.【点睛】本题考查了折叠的性质,平行线的判定,外角的性质,线段垂直平分线的性质,熟练掌握各种基本性质是解题的关键.12.40°【分析】利用平行线的性质求出∠3即可解决问题.【详解】解:∵直尺的两边互相平行,∴∠1=∠3=50°,∵∠2+∠3=90°,∴∠2=90°﹣∠3=40°,故答案为:40°.解析:40°【分析】利用平行线的性质求出∠3即可解决问题.【详解】解:∵直尺的两边互相平行,∴∠1=∠3=50°,∵∠2+∠3=90°,∴∠2=90°﹣∠3=40°,故答案为:40°.【点睛】本题考查了平行线的性质,直角三角形两锐角互余等知识,解题的关键是灵活运用所学知识解决问题.13.120【分析】由折叠的性质知:∠EBC′、∠BC′F都是直角,因此BE∥C′F,那么∠EFC′和∠BEF 互补,欲求∠EFC′的度数,需先求出∠BEF的度数;根据折叠的性质知∠BEF=∠DEF,而解析:120【分析】由折叠的性质知:∠EBC′、∠BC′F都是直角,因此BE∥C′F,那么∠EFC′和∠BEF互补,欲求∠EFC′的度数,需先求出∠BEF的度数;根据折叠的性质知∠BEF=∠DEF,而∠AEB的度数可在Rt△ABE中求得,由此可求出∠BEF的度数,即可得解.【详解】解:Rt△ABE中,∠ABE=30°,∴∠AEB=60°;由折叠的性质知:∠BEF=∠DEF;而∠BED=180°-∠AEB=120°,∴∠BEF=60°;由折叠的性质知:∠EBC′=∠D=∠BC′F=∠C=90°,∴BE∥C′F,∴∠EFC′=180°-∠BEF=120°.故答案为:120.【点睛】本题考查图形的翻折变换以及平行线的性质的运用,解题过程中应注意折叠是一种对称变换,它属于轴对称,根据轴对称的性质,折叠前后图形的形状和大小不变.14.101【分析】根据“”的定义进行运算即可求解.【详解】解:=== =101.故答案为:101.【点睛】本题考查了新定义运算,理解新定义的法则是解题关键.解析:101【分析】根据“⊗”的定义进行运算即可求解.【详解】解:(3)m m ⊗⊗=2(31)m ⊗+=10m ⊗=2101+ =101.故答案为:101.【点睛】本题考查了新定义运算,理解新定义的法则是解题关键.15.或【分析】已知,可知AB=8,已知的面积为,即可求出OC 长,得到C 点坐标.【详解】∵∴AB=8∵的面积为∴=16∴OC=4∴点的坐标为(0,4)或(0,-4)故答案为:(0,4)解析:(0,4)或(0,4) -【分析】已知()()7,0,1,0A B -,可知AB=8,已知ABC ∆的面积为16,即可求出OC 长,得到C 点坐标.【详解】∵()()7,0,1,0A B -∴AB=8∵ABC ∆的面积为16∴12AB OC⨯⨯=16∴OC=4∴点C的坐标为(0,4)或(0,-4)故答案为:(0,4)或(0,-4)【点睛】本题考查了直角坐标系中坐标的性质,已知两点坐标可得出两点间距离长度,如果此两点在坐标轴上,求解距离很简单,如果不在坐标轴上,可通过两点间距离公式求解.16.【分析】根据“伴随点”的定义依次求出各点,不难发现,每4个点为一个循环组依次循环,用2021除以4,根据商和余数的情况确定点A2021的坐标即可.【详解】解:∵A1的坐标为(3,1),∴A解析:()3,1【分析】根据“伴随点”的定义依次求出各点,不难发现,每4个点为一个循环组依次循环,用2021除以4,根据商和余数的情况确定点A2021的坐标即可.【详解】解:∵A1的坐标为(3,1),∴A2(0,4),A3(−3,1),A4(0,−2),A5(3,1),…,依此类推,每4个点为一个循环组依次循环,∵2021÷4=505…1,∴2021A的坐标与A1的坐标相同,为(3,1).故答案是:(3,1).【点睛】考查点的坐标规律,读懂题目信息,理解“伴随点”的定义并求出每4个点为一个循环组依次循环是解题的关键.三、解答题17.(1);(2).【分析】直接利用立方根以及算术平方根的定义化简得出答案.【详解】(1)(2)【点睛】此题主要考查了实数运算,正确化简各数是解题关键.解析:(1) 4.2-;(2)2.【分析】直接利用立方根以及算术平方根的定义化简得出答案.【详解】(1220.2=---4.2=-(2233=+-2=【点睛】此题主要考查了实数运算,正确化简各数是解题关键.18.(1)x=±;(2)x=﹣2﹣π或x=﹣2+π【分析】(1)先移项,再将两边都除以25,再开平方即可求解;(2)根据绝对值的性质即可求解.【详解】解:(1)25x2﹣36=0,25x2=解析:(1)x=±65;(2)x=﹣2﹣π或x=﹣2+π【分析】(1)先移项,再将两边都除以25,再开平方即可求解;(2)根据绝对值的性质即可求解.【详解】解:(1)25x2﹣36=0,25x2=36,x2=36 25,x=±65;(2)|x+2|=π,x+2=±π,x=﹣2﹣π或x=﹣2+π.【点睛】本题主要考查了绝对值及平方根,注意一个正数的平方根有两个,它们互为相反数.19.同旁内角互补,两直线平行;∠DCE;两直线平行,同位角相等;DCE;内错角相等,两直线平行;两直线平行,内错角相等【分析】根据平行线的判定得出AB∥CD,根据平行线的性质得出∠B=∠DCE,求出解析:同旁内角互补,两直线平行;∠DCE;两直线平行,同位角相等;DCE;内错角相等,两直线平行;两直线平行,内错角相等【分析】根据平行线的判定得出AB∥CD,根据平行线的性质得出∠B=∠DCE,求出∠DCE=∠D,根据平行线的判定得出AD∥BE,根据平行线的性质得出即可.【详解】证明:∵∠B+∠BCD=180°(已知),∴AB∥CD(同旁内角互补,两直线平行),∴∠B=∠DCE(两直线平行,同位角相等),又∵∠B=∠D(已知),∴∠D=∠DCE(等量代换),∴AD∥BE(内错角相等,两直线平行),∴∠E=∠DFE(两直线平行,内错角相等).故答案为:同旁内角互补,两直线平行;∠DCE;两直线平行,同位角相等;DCE;内错角相等,两直线平行;两直线平行,内错角相等.【点睛】本题主要考查平行线的判定和性质,掌握同旁内角互补,两直线平行;内错角相等,两直线平行;两直线平行,内错角相等是解题的关键.20.(1)5,下,4;(2)(,);(3)7.【分析】(1)根据题图直接判断即可;(2)由平移的性质:上加下减,左减右加解答即可;(3)利用分割法求出三角形的面积即可.【详解】解:(1)根据题图y-);(3)7.解析:(1)5,下,4;(2)(5x-,4【分析】(1)根据题图直接判断即可;(2)由平移的性质:上加下减,左减右加解答即可;(3)利用分割法求出三角形的面积即可.【详解】解:(1)根据题图可知,三角形ABC先向左平移5个单位,再向下平移4个单位得到三角形A1B1C1;故答案是:5,下,4;(2)由平移的性质:上加下减,左减右加可知,三角形ABC内有一点P(x,y),则在y-),三角形A1B1C1内部的对应点P1的坐标是(5x-,4y-);故答案是:(5x-,4(3)11144142423162437222ABC S =⨯-⨯⨯-⨯⨯-⨯⨯=---=, 故答案是:7.【点睛】本题考查作图:平移变换,三角形的面积等知识,熟练掌握基本知识,学会用分割法求三角形的面积是解题的关键.21.(1)7;-7;(2)5;(3)13-.【分析】(1)估算出的范围,即可得出答案;(2)分别确定出a 、b 的值,代入原式计算即可求出值;(3)根据题意确定出等式左边的整数部分得出y 的值,进而求解析:(1)7;(2)5;(3)【分析】(1(2)分别确定出a 、b 的值,代入原式计算即可求出值;(3)根据题意确定出等式左边的整数部分得出y 的值,进而求出y 的值,即可求出所求.【详解】解:(1)∵78, ∴7.故答案为:7.(2)∵34, ∴3a ,∵23,∴b =2∴=5(3)∵23∴11<12,∵,其中x 是整数,且0﹤y <1,∴x =11,y =,∴x-y ==【点睛】本题考查的是无理数的小数部分和整数部分及其运算.估算无理数的整数部分是解题关键.二十二、解答题22.(1);(2)不能剪出长宽之比为5:4,且面积为的大长方形,理由详见解析【分析】(1)根据已知得到大正方形的面积为400,求出算术平方根即为大正方形的边长;(2)设长方形纸片的长为,宽为,根据解析:(1)20cm ;(2)不能剪出长宽之比为5:4,且面积为2360cm 的大长方形,理由详见解析【分析】(1)根据已知得到大正方形的面积为4002cm ,求出算术平方根即为大正方形的边长;(2)设长方形纸片的长为5xcm ,宽为4xcm ,根据面积列得54360x x ⋅=,求出x =得到520x =>,由此判断不能裁出符合条件的大正方形.【详解】(1)∵用两个面积为2200cm 的小正方形拼成一个大的正方形,∴大正方形的面积为4002cm ,∴20cm =故答案为:20cm ;(2)设长方形纸片的长为5xcm ,宽为4xcm ,54360x x ⋅=,解得:x520x =,答:不能剪出长宽之比为5:4,且面积为2360cm 的大长方形.【点睛】此题考查利用算术平方根解决实际问题,利用平方根解方程,正确理解题意是解题的关键. 二十三、解答题23.(1)见解析;(2)【分析】(1)根据平行线的性质得出,再根据等量代换可得,最后根据平行线的判定即可得证;(2)过点E 作,延长DC 至Q ,过点M 作,根据平行线的性质及等量代换可得出,再根据平角的解析:(1)见解析;(2)72︒【分析】(1)根据平行线的性质得出180A B ∠+∠=︒,再根据等量代换可得180B D ∠+∠=︒,最后根据平行线的判定即可得证;(2)过点E 作//EP CD ,延长DC 至Q ,过点M 作//MN AB ,根据平行线的性质及等量代换可得出ECQ BGM DFG ∠=∠=∠,再根据平角的含义得出ECF CFG ∠=∠,然后根据平行线的性质及角平分线的定义可推出,BHF CFH CFA FAB ∠=∠∠=∠;设,FAB CFH αβ∠=∠=,根据角的和差可得出2AEC AFH ∠=∠,结合已知条件35180AEC AFH ∠-∠=︒可求得18AFH ∠=︒,最后根据垂线的含义及平行线的性质,即可得出答案.【详解】(1)证明://AE BD180A B ∴∠+∠=︒A D ∠=∠180B D ∴∠+∠=︒//AB CD ∴;(2)过点E 作//EP CD ,延长DC 至Q ,过点M 作//MN AB//AB CDQCA CAB ∴∠=∠,BGM DFG ∠=∠,CFH BHF ∠=∠,CFA FAG ∠=ACE BAC BGM ∠=∠+∠ECQ QCA BAC BGM ∴∠+∠=∠+∠ECQ BGM DFG ∴∠=∠=∠180,180ECQ ECD DFG CFG ∠+=︒∠+=︒ECF CFG ∴∠=∠//AB CD//AB EP ∴,PEA EAB PEC ECF ∴∠=∠∠=∠AEC PEC PEA ∠=∠-∠AEC ECF EAB ∴∠=∠-∠ECF AEC EAB ∴∠=∠+∠AF 平分BAE ∠12EAF FAB EAB ∴∠=∠=∠ FH 平分CFG ∠12CFH HFG CFG ∴∠=∠=∠ //CD AB,BHF CFH CFA FAB ∴∠=∠∠=∠设,FAB CFH αβ∠=∠=AFH CFH CFA CFH FAB ∠=∠-∠=∠-∠AFH βα∴∠=-,BHF CFH β∠=∠=222ECF AFH AEC EAB AFH AEC β∴∠+∠=∠+∠+∠=∠+22ECF AFH E BHF ∴∠+∠=∠+∠2AEC AFH ∴∠=∠35180AEC AFH ∠-∠=︒18AFH ∴∠=︒FH HM ⊥90FHM ∴∠=︒90GHM β∴∠=︒-180CFM NMF ∠+∠=︒90HMB HMN β∴∠=∠=︒-EAF FAB ∠=∠18EAF CFA CFH AFH β∴∠=∠=∠-∠=-︒189072EAF GMH ββ∴∠+∠=-︒+︒-=︒72EAF GMH ∴∠+∠=︒.【点睛】本题考查了平行线的判定及性质,角平分线的定义,能灵活根据平行线的性质和判定进行推理是解此题的关键.24.(1)146°;(2)∠AOG+∠NEF=90°;(3)见解析【分析】(1)作CP//a ,则CP//a//b ,根据平行线的性质求解.(2)作CP//a ,由平行线的性质及等量代换得∠AOG+∠N解析:(1)146°;(2)∠AOG +∠NEF =90°;(3)见解析【分析】(1)作CP //a ,则CP //a //b ,根据平行线的性质求解.(2)作CP //a ,由平行线的性质及等量代换得∠AOG +∠NEF =∠ACP +∠PCB =90°.(3)分类讨论点P 在线段GF 上或线段GF 延长线上两种情况,过点P 作a ,b 的平行线求解.【详解】解:(1)如图,作CP//a,∵a//b,CP//a,∴CP//a//b,∴∠AOG=∠ACP=56°,∠BCP+∠CEF=180°,∴∠BCP=180°-∠CEF,∵∠ACP+∠BCP=90°,∴∠AOG+180°-∠CEF=90°,∴∠CEF=180°-90°+∠AOG=146°.(2)∠AOG+∠NEF=90°.理由如下:如图,作CP//a,则CP//a//b,∴∠AOG=∠ACP,∠BCP+∠CEF=180°,∵∠NEF+∠CEF=180°,∴∠BCP=∠NEF,∵∠ACP+∠BCP=90°,∴∠AOG+∠NEF=90°.(3)如图,当点P在GF上时,作PN//a,连接PQ,OP,则PN//a//b,∴∠GOP=∠OPN,∠PQF=∠NPQ,∴∠OPQ=∠OPN+∠NPQ=∠GOP+∠PQF,∵∠GOC=∠GOP+∠POQ=135°,∴∠GOP=135°-∠POQ,∴∠OPQ =135°-∠POQ +∠PQF .如图,当点P 在GF 延长线上时,作PN //a ,连接PQ ,OP ,则PN //a //b ,∴∠GOP =∠OPN ,∠PQF =∠NPQ ,∵∠OPN =∠OPQ +∠QPN ,∴∠GOP =∠OPQ +∠PQF ,∴135°-∠POQ =∠OPQ +∠PQF .【点睛】本题考查平行线的性质的应用,解题关键是熟练掌握平行线的性质,通过添加辅助线及分类讨论的方法求解.25.[习题回顾]证明见解析;[变式思考] 相等,证明见解析;[探究延伸] ∠M+∠CFE=90°,证明见解析.【分析】[习题回顾]根据同角的余角相等可证明∠B=∠ACD ,再根据三角形的外角的性质即可解析:[习题回顾]证明见解析;[变式思考] 相等,证明见解析;[探究延伸]∠M+∠CFE=90°,证明见解析.【分析】[习题回顾]根据同角的余角相等可证明∠B=∠ACD ,再根据三角形的外角的性质即可证明;[变式思考]根据角平分线的定义和对顶角相等可得∠CAE=∠DAF 、再根据直角三角形的性质和等角的余角相等即可得出CFE ∠=CEF ∠;[探究延伸]根据角平分线的定义可得∠EAN=90°,根据直角三角形两锐角互余可得∠M+∠CEF=90°,再根据三角形外角的性质可得∠CEF=∠CFE ,由此可证∠M+∠CFE=90°.【详解】[习题回顾]证明:∵∠ACB=90°,CD 是高,∴∠B+∠CAB=90°,∠ACD+∠CAB=90°,∴∠B=∠ACD ,∵AE 是角平分线,∴∠CAF=∠DAF ,∵∠CFE=∠CAF+∠ACD ,∠CEF=∠DAF+∠B ,∴∠CEF=∠CFE ;[变式思考]相等,理由如下:证明:∵AF 为∠BAG 的角平分线,∴∠GAF=∠DAF,∵∠CAE=∠GAF,∴∠CAE=∠DAF,∵CD为AB边上的高,∠ACB=90°,∴∠ADC=90°,∴∠ADF=∠ACE=90°,∴∠DAF+∠F=90°,∠E+∠CAE=90°,∴∠CEF=∠CFE;[探究延伸]∠M+∠CFE=90°,证明:∵C、A、G三点共线 AE、AN为角平分线,∴∠EAN=90°,又∵∠GAN=∠CAM,∴∠M+∠CEF=90°,∵∠CEF=∠EAB+∠B,∠CFE=∠EAC+∠ACD,∠ACD=∠B,∴∠CEF=∠CFE,∴∠M+∠CFE=90°.【点睛】本题考查三角形的外角的性质,直角三角形两锐角互余,角平分线的有关证明,等角或同角的余角相等.在本题中用的比较多的是利用等角或同角的余角相等证明角相等和三角形一个外角等于与它不相邻的两个内角之和,理解并掌握是解决此题的关键.26.(1)∠AQB的大小不发生变化,∠AQB=135°;(2)∠P和∠C的大小不变,∠P=45°,∠C=45°.【分析】第(1)题因垂直可求出∠ABO与∠BAO的和,由角平分线和角的和差可求出∠BA 解析:(1)∠AQB的大小不发生变化,∠AQB=135°;(2)∠P和∠C的大小不变,∠P=45°,∠C=45°.【分析】第(1)题因垂直可求出∠ABO与∠BAO的和,由角平分线和角的和差可求出∠BAQ与∠ABQ 的和,最后在△ABQ中,根据三角形的内角各定理可求∠AQB的大小.第(2)题求∠P的大小,用邻补角、角平分线、平角、直角和三角形内角和定理等知识求解.【详解】解:(1)∠AQB的大小不发生变化,如图1所示,其原因如下:∵m⊥n,∴∠AOB=90°,∵在△ABO中,∠AOB+∠ABO+∠BAO=180°,∴∠ABO+∠BAO=90°,又∵AQ、BQ分别是∠BAO和∠ABO的角平分线,∴∠BAQ=12∠BAC,∠ABQ=12∠ABO,∴∠BAQ+∠ABQ=12 (∠ABO+∠BAO)=190452⨯=又∵在△ABQ中,∠BAQ+∠ABQ+∠AQB=180°,∴∠AQB=180°﹣45°=135°.(2)如图2所示:①∠P的大小不发生变化,其原因如下:∵∠ABF+∠ABO=180°,∠EAB+∠BAO=180°∠BAQ+∠ABQ=90°,∴∠ABF+∠EAB=360°﹣90°=270°,又∵AP、BP分别是∠BAE和∠ABP的角平分线,∴∠PAB=12∠EAB,∠PBA=12∠ABF,∴∠PAB+∠PBA=12 (∠EAB+∠ABF)=12×270°=135°,又∵在△PAB中,∠P+∠PAB+∠PBA=180°,∴∠P=180°﹣135°=45°.②∠C的大小不变,其原因如下:∵∠AQB=135°,∠AQB+∠BQC=180°,∴∠BQC=180°﹣135°,又∵∠FBO=∠OBQ+∠QBA+∠ABP+∠PBF=180°∠ABQ=∠QBO=1∠ABO,∠PBA=∠PBF=∠ABF,2∴∠PBQ=∠ABQ+∠PBA=90°,又∵∠PBC=∠PBQ+∠CBQ=180°,∴∠QBC=180°﹣90°=90°.又∵∠QBC+∠C+∠BQC=180°,∴∠C=180°﹣90°﹣45°=45°【点睛】本题考查三角形内角和定理,垂直,角平分线,平角,直角和角的和差等知识点,同时,也是一个以静求动的一个点型题目,有益于培养学生的思维几何综合题.。
2017-2018学年江苏省扬州市宝应县七年级(下)期末数学试卷(解析版)

2017-2018学年江苏省扬州市宝应县七年级(下)期末数学试卷(解析版)2017-2018学年江苏省扬州市宝应县七年级(下)期末数学试卷学校:___________姓名:___________班级:___________考号:___________一、选择题(本大题共8小题,共24.0分)1.下列运算中,正确的是()A. B.C. D.2.如图,下列条件不能判定AB∥CD的是()A.B.C.D.3.已知一个三角形的两条边分别是3cm、4cm,则第三条边长度可以是()A. 1cmB. 10cmC. 7cmD. 5cm4.下列多项式不能用公式法因式分解的是()A. B. C. D.5.如图,一副直角三角板按如图所示放置,若AB∥DF,则∠AGD的度数为()A.B.C.D.6.根据如图提供的信息,小红去商店买一只水瓶和一只杯子应付()A. 30元B. 32元C. 31元D. 34元7.下列命题:(1)如果a>0,b<0,那么a+b<0;(2)如果两个数的绝对值相等,那么这两个数相等;(3)对顶角相等;(4)同位角相等.其中,真命题的个数是()A. 1B. 2C. 3D. 48.已知x=4是不等式mx-3m+2≤0的解,且x=2不是这个不等式的解,则实数m的取值范围为()A. B. C. D.二、填空题(本大题共10小题,共30.0分)9.人体血液由血浆和血细胞组成,血细胞包括红细胞和白细胞和血小板三类细胞,科学家测得红细胞直径约为0.00077cm,将0.00077用科学记数法表示为______.11.如图是某公园里一处矩形风景欣赏区ABCD,长AB=50米,宽BC=30米,为方便游人观赏,公园特意修建了如图所示的小路(图中非阴影部分),小路的宽均为1米,那么小明沿着小路的中间出口A到出口B所走的路线(图中虚线)长为______米.12.如图,线段AC、BD相交于点E,连结AB、CD,若∠A=98°,∠B=25°,∠C=50°,则∠D=______°.13.已知若a-b=8,则代数式a2-b2-16b的值为______.14.如图,AD是△AB C的高,已知∠1=∠B,∠C=70°.则∠BAC=______°.15.写出命题“内错角相等”的逆命题______.16.如图,点D、E、F、G、H分别是△ABC的边上一点,将△ABC三个角分别沿DE、HG、EF翻折,三个顶点均落在△ABC内点O处,则∠1+∠2为______°.17.滴滴快车是一种便捷的出行工具,计价规则如表:计费项目里程费时长费远途费单价 1.8元/公里0.3元/分钟0.8元/公里注:车费由里程费、时长费、远途费三部分构成,其中里程费按行车的实际里程计算;时长费按行车的实际时间计算;远途费的收取方式为:行车里程7公里以内(含7公里)不收远途费,超过7公里的,超出部分每公里收0.8元.小王与小张各自乘坐滴滴快车,行车里程分别为6公里与8.5公里.如果下车时两人所付车费相同,那么这两辆滴滴快车的行车时间相差______.18.已知x1、x2、x3、…、x n中每一个数值只能取-2、0、-1中的一个,且满足x1+x2+…+x n=-19,x12+x22+…+x n2=37,则x13+x23+…+x n3=______.三、计算题(本大题共3小题,共28.0分)19.计算:(1)()-2+π0+(-5)2018?(-)2017;(2)(3+4y)(4y-3)-(x-4y)2.20.已知二元一次方程x+2y=-5.当x取什么值时,y的值是大于-1的负数?21.为迎接省运会,宝应县绿化部门计划购买甲、乙两种树苗共计n棵对体育休闲公园及周边道路进行绿化,有关甲、乙两种树苗的信息如表所示.甲种树苗乙种树苗单价(元/棵)6090成活率92%96%(1)当n=500时,如果购买甲、乙两种树苗共用33000元,那么甲、乙两种树苗各买了多少棵?(2)实际购买这两种树苗的总费用恰好为33000元,其中甲种树苗买了m棵.①写出m与n满足的关系式;②要使这批树苗的成活率不低于95%,求m的最大值.四、解答题(本大题共7小题,共68.0分)22.因式分解:(1)(x+3)2-16;(2)x4-18x2+81.23.小明和小红同解同一个方程组时,小红不慎将一滴墨水滴在了题目上使得方程组的系数看不清了,显示如下,同桌的小明说:“我正确的求出这个方程组的解为”,而小红说:“我求出的解是,于是小红检查后发现,这是她看错了方程组中第二个方程中x的系数所致”,请你根据他们的对话,24.如图,一个四边形纸片ABCD,∠B=∠D,把纸片按如图所示折叠,使点B落在AD边上的B′点,AE是折痕.(1)试判断B′E与DC的位置关系;(2)如果∠C=140°,求∠AEB的度数.25.已知关于x、y的二元一次方程组.(1)若m=1,求方程组的解;(2)若方程组的解中,x的值为正数,y的值为正数,求m的范围.26.已知:如图1,在△ABC中,CD是高,若∠A=∠DCB.(1)试说明∠ACB=90°;(2)如图2,若AE是角平分线,AE、CD相交于点F.求证:∠CFE=∠CEF.27.我们知道,对于一个图形,通过两种不同的方法计算它的面积,可以得到一个数学等式.例如图1可以得到(a+2b)(a+b)=a2+3ab+2b2.请解答下列问题:(1)写出图2中所表示的数学等式;(2)利用(1)中所得到的结论,解决下面的问题:已知a+b+c=12,ab+bc+ac=47,求a2+b2+c2的值;(3)小明同学又用x张边长为a的正方形,y张边长为b的正方形,z张边长为a、b的长方形纸片拼出了一个面积为(25a+8b)(17a+44b)长方形,求x+y+z的值.28.(1)如图1,AB∥CD,点E是在AB、CD之间,且在BD的左侧平面区域内一点,连结BE、DE.求证:∠E=∠ABE+∠CDE.(2)如图2,在(1)的条件下,作出∠EBD和∠EDB的平分线,两线交于点F,猜想∠F、∠ABE、∠CDE之间的关系,并证明你的猜想.(3)如图3,在(1)的条件下,作出∠EBD的平分线和△EDB的外角平分线,两线交于点G,猜想∠G、∠ABE、∠CDE之间的关系,并证明你的猜想.答案和解析1.【答案】D【解析】解:A、a2?a3=a5,故此选项错误;B、(-a)6÷a3=a3,故此选项错误;C、3a2b?5ab4c=15a3b5c,故此选项错误;D、(2a2b)3=8a6b3,正确.故选:D.直接利用单项式乘以单项式以及同底数幂的乘法运算法则和积的乘方运算法则分别计算得出答案.此题主要考查了单项式乘以单项式以及同底数幂的乘法运算和积的乘方运算,正确掌握运算法则是解题关键.2.【答案】B【解析】解:A、∵∠1=∠2,∴AB∥CD,正确;B、∵∠2=∠E,∴AD∥BE,错误;C、∵∠B+∠E=180°,∴AB∥CD,正确;D、∵∠BAF=∠C,∴AB∥CD,正确;故选:B.根据平行线的判定定理对各选项进行逐一判断即可.本题考查的是平行线的判定,熟知平行线的判定定理是解答此题的关键.平行线的判定定理1:同位角相等,两直线平行.定理2:两条直线被第三条所内错角相等,两直线平行.定理3:同旁内角互补,两直线平行.3.【答案】D【解析】解:4-3<x<4+3,则1<x<7.故选:D.的和,这样就可求出第三边长的范围.本题考查了三角形的三边关系,已知三角形的两边,则第三边的范围是:大于已知的两边的差,而小于两边的和.4.【答案】C【解析】解:A、a2-8a+16=(a-4)2,故此选项不合题意;B、a2+a+=(a+)2,故此选项不合题意;C、a2+9无法分解因式,故此选项符合题意;D、a2-4=(a-2)(a+2),故此选项不合题意;故选:C.直接利用完全平方公式以及平方差公式分别分解因式得出答案.此题主要考查了公式法分解因式,正确应用公式是解题关键.5.【答案】B【解析】解:∵AB∥DF,∴∠D=∠AHG=45°,又∵∠A=30°,∴∠AGD=∠A+∠AHG=75°,故选:B.依据AB∥DF,即可得到∠D=∠AHG=45°,再根据三角形外角性质,即可得到∠AGD=∠A+∠AHG=75°.本题主要考查了平行线的性质,解题时注意:两直线平行,内错角相等.6.【答案】C【解析】解:设购买一只水瓶需要x元,购买一只杯子需要y元,根据题意得:,(①+②)÷3,得:x+y=31.故选:C.设购买一只水瓶需要x元,购买一只杯子需要y元,根据给定的两种购买方案论.本题考查了二元一次方程组的应用,找准等量关系,正确列出二元一次方程组是解题的关键.7.【答案】A【解析】解:(1)如果a>0,b<0,那么a+b不一定<0是假命题;(2)如果两个数的绝对值相等,那么这两个数相等或互为相反数是假命题;(3)对顶角相等是真命题;(4)两直线平行,同位角相等,是假命题;故选:A.利用不等式,绝对值及对顶角和同位角判定即可.本题考查了命题与定理:判断一件事情的语句,叫做命题.许多命题都是由题设和结论两部分组成,题设是已知事项,结论是由已知事项推出的事项,一个命题可以写成“如果…那么…”形式.有些命题的正确性是用推理证实的,这样的真命题叫做定理.8.【答案】A【解析】解:∵x=4是不等式mx-3m+2≤0的解,∴4m-3m+2≤0,解得:m≤-2,∵x=2不是这个不等式的解,∴2m-3m+2>0,解得:m<2,∴m≤-2,故选:A.根据x=4是不等式mx-3m+2≤0的解,且x=2不是这个不等式的解,列出不等式,求出解集,即可解答.本题考查了不等式的解集,解决本题的关键是根据x=4是不等式mx-3m+2≤0的解,且x=2不是这个不等式的解,列出不等式,从而求出m的取值范围.9.【答案】7.7×10-4【解析】解:将0.00077用科学记数法表示为7.7×10-4.故答案为:7.7×10-4.绝对值小于1的正数也可以利用科学记数法表示,一般形式为a×10-n,与较大数的科学记数法不同的是其所使用的是负指数幂,指数由原数左边起第一个不为零的数字前面的0的个数所决定.本题考查用科学记数法表示较小的数,一般形式为a×10-n,其中1≤|a|<10,n 为由原数左边起第一个不为零的数字前面的0的个数所决定.10.【答案】10【解析】解:设边数为n,则(n-2)?180°=4×360°,解得:n=10.则多边形的边数是10.任何多边形的外角和是360度,内角和是外角和的4倍,则内角和是4×360度.n边形的内角和是(n-2)?180°,如果已知多边形的内角和,就可以得到一个关于边数的方程,解方程就可以求出多边形的边数.已知多边形的内角和求边数,可以转化为方程的问题来解决.11.【答案】108【解析】解:利用已知可以得出此图形可以分为横向与纵向分析,横向距离等于AB,纵向距离等于(AD-1)×2,∴图是某公园里一处矩形风景欣赏区ABCD,长AB=50米,宽BC=30米,为50+(30-1)×2=108米,故答案为:108.根据已知可以得出此图形可以分为横向与纵向分析,横向距离等于AB,纵向距离等于(AD-1)×2,求出即可.此题主要考查了生活中的平移现象,根据已知得出所走路径是解决问题的关键.12.【答案】73【解析】解:在△ABE中,∠A=98°,∠B=25°,∴∠AEB=180°-∠A-∠B=57°,∴∠DEC=∠AEB=57°,在△CDE中,∠C=50°,∴∠D=180°-∠C-∠DEC=73°,故答案为:73.利用三角形的内角和定理和对顶角即可得出结论.此题主要考查了三角形的内角和定理和对顶角的性质,熟记三角形的内角和定理是解本题的关键.13.【答案】64【解析】解:∵a-b=8,∴原式=(a+b)(a-b)-16b=8a+8b-16b=8a-8b=8(a-b)=64,故答案为:64原式前两项利用平方差公式化简,将a-b的值代入计算即可求出值.此题考查了完全平方公式,熟练掌握完全平方公式是解本题的关键.14.【答案】65【解析】解:∵AD是△ABC的高,∴∠1=∠B=45°,又∵∠C=70°,∴∠BAC=180°-45°-70°=65°,故答案为:65.依据AD是△ABC的高,即可得到∠1=∠B=45°,再根据三角形内角和定理,即可得到∠BAC的度数.本题主要考查了三角形内角和定理的运用,解题时注意:三角形内角和是180°.15.【答案】如果两个角相等,那么这两个角是内错角.【解析】解:其逆命题为:如果两个角相等,那么这两个角是内错角.将原命题的条件与结论互换就得到其逆命题了.此题主要考查学生对逆命题的理解及运用能力.16.【答案】180【解析】解:由折叠的性质得:∠A=∠DOE,∠B=∠GOH,∠C=∠EOF,∵∠A+∠B+∠C=180°,∴∠DOE+∠GOH+∠EOF=180°,∴∠1+∠2=360°-180°=180°,故答案为;180.根据折叠的性质得:∠A=∠DOE,∠B=∠GOH,∠C=∠EOF,中间以O的顶点的周角为360°,和三角形内角和定理可得结论.本题考查了三角形内角和定理和折叠的性质,熟练掌握折叠前后的两个角相等是关键.17.【答案】19分钟【解析】解:设小王的行车时间为x分钟,小张的行车时间为y分钟,依题可得:1.8×6+0.3x=1.8×8.5+0.3y+0.8×(8.5-7),10.8+0.3x=16.5+0.3y,0.3(x-y)=5.7,x-y=19.故这两辆滴滴快车的行车时间相差19分钟.故答案是:19分钟.设小王的行车时间为x分钟,小张的行车时间为y分钟,根据题意列出小王和小张车费的代数式,两者相等,计算可得出时间差.考查了二元一次方程的应用,解题的关键是仔细审题,确定已知量和未知量,找出它们之间的等量关系.18.【答案】-73【解析】解:设有p个x取-1,q个x取-2,有,解得,所以原式=1×(-1)3+9×(-2)3=-73.先设有p个x取1,q个x取-2,根据x1+x2+…+x n=-17,x12+x22+…+x n2=37可得出关于p,q的二元一次方程组,求出p,q的值,再把p,q及x的值代入x13+x23+…+x n3求解.本题考查的是解二元一次方程组,根据题意列出关于p、q的二元一次方程组是解答此题的关键19.【答案】解:(1)原式=100+1+5×(-5×)2017=100+1+5-1=105;(2)原式=16y2-9-x2+8xy-16y2=8xy-9-x2.【解析】(1)原式利用零指数幂、负整数指数幂法则,积的乘方逆运算计算即可求出值;(2)原式利用平方差公式,以及完全平方公式计算即可求出值.此题考查了平方差公式,完全平方公式,以及实数的运算,熟练掌握运算法则及公式是解本题的关键.20.【答案】解:∵x+2y=-5.∴y=-x-,而-1<y<0,∴-1<-x-<0,解得-5<x<-3,∴当-5<x<-3时,y的值是大于-1的负数.【解析】先用x表示y,从而得到-1<-x-<0,然后解不等式组即可.本题考查了解一元一次不等式:根据不等式的性质解一元一次不等式,掌握解一元一次不等式的步骤.21.【答案】解:(1)设甲种树苗买了x棵,则乙种树苗买了(500-x)棵,60x+90(500-x)=33000,答:甲、乙两种树苗各买了400棵,100棵;(2)①甲种树苗买了m棵,则乙种树苗买了(n-m)棵,60m+90(n-m)=33000,化简,得m=3n-1100,即m与n满足的关系式是m=3n-1100;②由题意可得,m×92%+(n-m)×96%≥95%n,∵m=3n-1100,∴n=,∴92%m+96%(-m)≥95%?,解得,m≤100,答:m的最大值是100.【解析】(1)根据题意可以列出相应的一元一次方程,从而可以解答本题;(2)①根据题意可以得到m与n关系式;②根据题意可以得到关于m的不等式,从而可以求得m的取值范围,进而求得m的最大值.本题考查一元一次不等式的应用、函数关系式,解答本题的关键是明确题意,找出所求问题需要的条件,利用函数和不等式的性质解答.22.【答案】解:(1)(x+3)2-16=(x+3+4)(x+3-4)=(x+7)(x-1);(2)x4-18x2+81=(x2-9)2=(x-3)2(x+3)2.【解析】(1)直接利用平方差公式分解因式进而得出答案;(2)直接利用完全平方公式以及平方差公式分解因式进而得出答案.此题主要考查了运用公式法分解因式,正确应用公式是解题关键.23.【答案】解:设原方程组为,解得:c=-2,把和代入①得:,解得:a=4,b=5,即原方程组为.【解析】设原方程组为,把代入②,求出c,把和代入①,得出方程组,求出a、b的值,即可得出答案.本题考查了二元一次方程组的解和解二元一次方程组,能够根据题意得出方程或方程组是解此题的关键.24.【答案】解:(1)结论:B′E∥CD理由:由翻折可知,∠B=∠AB′E,∵∠B=∠D,∴∠AB′E=′D,∴B′E∥CD.(2)∵B′E∥CD,∴∠B′EC+∠C=180°,∵∠C=140°,∴∠B′EC=40°,∴∠AEB=∠AEB′=(180°-40°)=70°.【解析】(1)利用翻折不变性只要证明∠AB′E=∠D即可;(2)利用平行线的性质,求出∠B′EC即可解决问题;本题考查翻折变换、平行线的性质和判定等知识,解题的关键是学会利用翻折不变性解决问题,属于中考常考题型.25.【答案】解:(1)把m=1代入方程组,得,解这个方程组得(2)由②,得x=5-m-2y③把③代入①,得整理,得y=把y=代入③,得x=∵x的值为正数,y的值为正数,∴ >>解得-9<m<【解析】(1)把m=1代入方程组,求解即可;(2)用含m的代数式表示出x、y,根据x的值为正数,y的值为正数,得关于m 的一元一次不等式组,求解即可.本题考查了二元一次方程组及解法、一元一次不等式组及解法.会用代入法或加减法解二元一次方程组是解决本题的关键.26.【答案】解:(1)∵在△ABC中,CD是高,∠A=∠DCB,∴∠CDA=90°,∴∠A+∠ACD=90°,∴∠DCB+∠ACD=90°,∴∠ACB=90°;(2)证明:∵AE是角平分线,∴∠CAE+∠BAE,∵∠FDA=90°,∠ACE=90°,∴∠DAF+∠AFD=90°,∠CAE+∠CEA=90°,∴∠AFD=∠CEA,∵∠AFD=∠CFE,∴∠CFE=∠CEA,即∠CFE=∠CEF.【解析】(1)根据题意可以求得∠BCD+∠ACD的度数,从而可以解答本题;(2)根据题意和(1)中的结论,直角三角形中两个锐角互余和对顶角相等,可以求得结论成立.本题考查三角形内角和,解答本题的关键是明确题意,找出所求问题需要的条件,利用数形结合的思想解答.27.【答案】解:(1)正方形的面积可表示为=(a+b+c)2;正方形的面积=各个矩形的面积之和=a2+b2+c2+2ab+2bc+2ca,∴(a+b+c)2=a2+b2+c2+2ab+2bc+2ca.(2)由(1)可知:a2+b2+c2=(a+b+c)2-2(ab+bc+ca)=122-47×2=50.(3)∵长方形的面积=xa2+yb2+zab=(25a+8b)(17a+44b)=425a2+1236ab+352b2,∴x=425,y=352,z=1236∴x+y+z=2013.【解析】(1)直接求得正方形的面积,然后再根据正方形的面积=各矩形的面积之和求解即可;(2)将a+b+c=12,ab+bc+ac=47代入(1)中得到的关系式,然后进行计算即可;(3)长方形的面积xa2+yb2+zab=(25a+8b)(17a+44b),然后运算多项式乘多项式法则求得(25a+8b)(17a+44b)的结果,从而得到x、y、z的值,代入即可求解.本题考查的是多项式乘多项式、因式分解的应用,利用面积法列出等式是解题的关键.28.【答案】解:(1)如图,过点E作EH∥AB,∴∠BEH=∠ABE,∵EH∥AB,CD∥AB,∴EH∥CD,∴∠DEH=∠CDE,∴∠BED=∠BEH+∠DEH=∠ABE+∠CDE;(2)2∠F-(∠ABE+∠CDE)=180°,理由:由(1)知,∠BED=∠ABE+∠CDE,∵∠EDB+∠EBD+∠BED=180°,∴∠EBD+∠EDB=180°-∠BED=180°-(∠ABE+∠CDE),∵BF,DF分别是∠DBE,∠BDE的平分线,∴∠EBD=2∠DBF,∠EDB=2∠BDF,∴2∠DBF+2∠BDF=180°-(∠ABE+∠CDE),在△BDF中,∠F=180°-(∠DBF+∠BDF)=180°-[90°-(∠ABE+∠CDE)]=90°+(∠ABE+∠CDE),即:2∠F-(∠ABE+∠CDE)=180°;(3)2∠G=∠ABE+∠CDE,理由:如图3,由(1)知,∠BED=∠ABE+∠CDE,∵BG是∠EBD的平分线,∴∠DBE=2∠DBG,∵DG是∠EDP的平分线,∴∠EDP=2∠GDP,∴∠BED=∠EDP-∠DBE=2∠GDP-2∠DBG=2(∠GDP-∠DBG),∴∠GDP-∠DBG=∠BED=(∠ABE+∠CDE)∴∠G=∠GDP-∠DBG=(∠ABE+∠CDE),∴2∠G=∠ABE+∠CDE.【解析】(1)利用平行线的性质即可得出结论;(2)先判断出∠EBD+∠EDB=180°-(∠ABE+∠CDE),进而得出∠DBF+∠BDF=90°-(∠ABE+∠CDE),最后用三角形的内角和即可得出结论;(3)先由(1)知,∠BED=∠ABE+∠CDE,再利用角平分线的意义和三角形外角的性质即可得出结论.此题主要考查了平行线的性质,三角形的内角和定理,三角形的外角的性质,判断出∠BED=∠EDP-∠DBE是解本题的关键.。
2019-2020学年扬州市宝应县七年级(下)期末数学试卷(含答案解析)
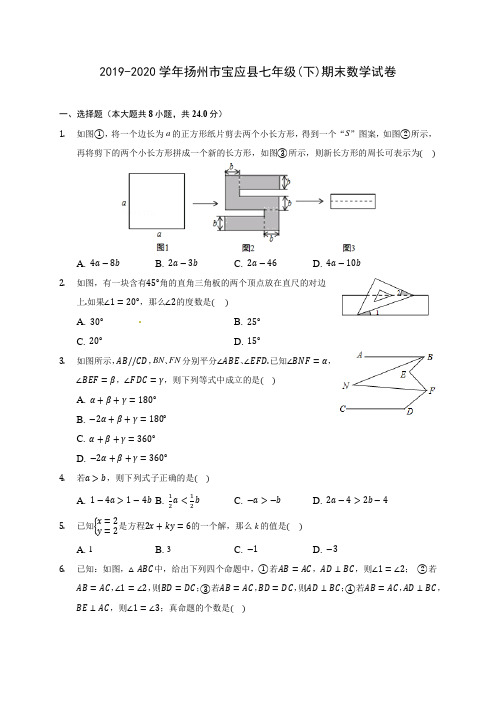
2019-2020学年扬州市宝应县七年级(下)期末数学试卷一、选择题(本大题共8小题,共24.0分)1. 如图①,将一个边长为a 的正方形纸片剪去两个小长方形,得到一个“S ”图案,如图②所示,再将剪下的两个小长方形拼成一个新的长方形,如图③所示,则新长方形的周长可表示为( )A. 4a −8bB. 2a −3bC. 2a −46D. 4a −10b 2. 如图,有一块含有45°角的直角三角板的两个顶点放在直尺的对边上.如果∠1=20°,那么∠2的度数是( )A. 30°B. 25°C. 20°D. 15° 3. 如图所示,AB//CD ,BN 、FN 分别平分∠ABE 、∠EFD.已知∠BNF =α,∠BEF =β,∠FDC =γ,则下列等式中成立的是( )A. α+β+γ=180°B. −2α+β+γ=180°C. α+β+γ=360°D. −2α+β+γ=360°4. 若a >b ,则下列式子正确的是( )A. 1−4a >1−4bB. 12a <12bC. −a >−bD. 2a −4>2b −4 5. 已知{x =2y =2是方程2x +ky =6的一个解,那么k 的值是( ) A. 1B. 3C. −1D. −3 6. 已知:如图,△ABC 中,给出下列四个命题中,①若AB =AC ,AD ⊥BC ,则∠1=∠2; ②若AB =AC ,∠1=∠2,则BD =DC ;③若AB =AC ,BD =DC ,则AD ⊥BC ;④若AB =AC ,AD ⊥BC ,BE ⊥AC ,则∠1=∠3;真命题的个数是( )A. 1个B. 2个C. 3个D. 4个7.如图,a//b,∠1=70°,则∠2等于()A. 20°B. 35°C. 70°D. 110°8.如图是测量一颗玻璃球体积的过程:①将300ml的水倒进一个容量为500ml的杯子中;②将四颗相同的玻璃球放入水中,结果水没有满;③再加一颗同样的玻璃球放入水中,结果水满且溢出.根据以上过程,推测这样一颗玻璃球的体积在()A. 20cm3以上,30cm3以下B. 30cm3以上,40cm3以下C. 40cm3以上,50cm3以下D. 50cm3以上,60cm3以下二、填空题(本大题共10小题,共30.0分)9.某种细菌的直径为0.000123,用科学记数法表示为______.10.如图所示,把两个大小完全一样的矩形拼成“L”形图案,则∠FAC=度,∠FCA=度.11.命题:“任意两个奇数之和是偶数”的逆命题是______命题.(填“真”或“假”)12. 如图,已知AB =A 1B ,A 1C =A 1A 2,A 2D =A 2A 3,A 3E =A 3A 4,∠B =20°,则∠A 4=______度.13. 平移变换不仅与几何图形紧密联系,在汉字中也存在着平移现象,如“圭”“品”等,请你开动脑筋,写出至少三个可由平移变换得到的汉字: ; 14. 如图,抛物线y =14p x 2(p >0),点F(0,p),直线l :y =−p ,已知抛物线上的点到点F 的距离与到直线l 的距离相等,过点F 的直线与抛物线交于A ,B 两点,AA 1⊥l ,BB 1⊥l ,垂足分别为A 1、B 1,连接A 1F ,B 1F ,A 1O ,B 1O.若A 1F =a ,B 1F =b 、则△A 1OB 1的面积=______.(只用a ,b 表示).15. 若a m =3,3n =5,则a mn = .16. 如果(m +3)x >2m +6的解集为x <2,则m 的取值范围是______.17. 已知关于x ,y 的方程组{3x +y =3a x +3y =−a的解满足x +y >0,则a 的取值范围是______ . 18. 已知有理数a ,b 满足a −b √2=(1+√2)2,则a =______,b =______.三、解答题(本大题共10小题,共96.0分)19. 计算:(−5a 3)2+(−3a 2)2⋅(−a 2)20. 把下列各式因式分解(1)x 3−x ;(2)x 2(a −b)+y 2(b −a)21. 解方程组{x −y =4①3x +y =8②.22. (1)计算:(−0.25)2015⋅(−4)2016⋅(1−0.5632)0(2)先化简,再求值:[(x +2y)(x −2y)−(x +4y)2]÷4y ,其中x =5,y =2.23. 如图,已知A 、B 、C 、D 是正方形网格纸上的四个格点,根据要求在网格中画图并标注相关字母.①画线段AB ;②画射线CA 、直线AD ;③过点B 画AD 的平行线BE ;④过点D 画AC 的垂线,垂足为F .24. 解方程组{x +2y =23x −4y =−24.25. 先化简,再求值:(a −b)2+b(3a −b)−a 2,其中a =−1,b =4.26. 问题提出:我们知道,等式具有性质:(1)等式两边同时加或减同一个代数式,所得结果仍是等式;(2)等式两边同时乘同一个数或除以同一个不为0的数,所得结果仍是等式.那么任意一个三阶幻方是否也有类似的性质?问题探究:为了探究上述问题,我们不妨从简单的三阶幻方①入手;探究一如图②,九个数2,3,4,5,6,7,8,9,10已填到方格中,显然每行、每列、每条对角线上的三个数之和都相等,构成了一个三阶幻方②,所以构成三阶幻方①的九个数同时加1,所得到的九个数仍可构成一个三阶幻方.如图③,九个数−2,−1,0,1,2,3,4,5,6已填到方格中,显然每行、每列、每条对角线上的三个数之和都相等,构成了一个三阶幻方③,所以构成三阶幻方①的九个数同时减3,所得到的九个数仍可构成一个三阶幻方.请把九个数0.5,1.5,2.5,3.5,4.5,5.5,6.5,7.5,8.5填到图④的方格中,使得每行、每列、每条对角线上的三个数之和都相等,构成了一个三阶幻方④,所以构成三阶幻方①的九个数同时减0.5,所得到的九个数仍可构成一个三阶幻方.(1)根据探究一可得任意三阶幻方的性质(1):______.探究二:如图⑤,九个数3,6,9,12,15,18,21,24,27已填到方格中,显然每行、每列、每条对角线上的三个数之和都相等,构成了一个三阶幻方⑤.所以构成三阶幻方①的九个数同时乘3,所得到的九个数仍可构成一个三阶幻方.如图⑥,九个数0.5,1,1.5,2,2.5,3,3.5,4,4.5已填到方格中,显然每行、每列、每条对角线上的三个数之和都相等,构成了一个三阶幻方⑥.所以构成三阶幻方①的九个数同时除以2,所得到的九个数仍可构成一个三阶幻方.请把九个数−4,−8,−12,−16,−20,−24,−28,−32,−36填到图⑦的方格中,使得每行、每列、每条对角线上的三个数之和都相等,构成了一个三阶幻方⑦.所以构成三阶幻方①的九个数同时乘−4,所得到的九个数仍可构成一个三阶幻方.(2)根据探究二可得任意三阶幻方的性质(2):______.性质应用:6,8,10,12,14,16,18,20,22这九个数能否构成三阶幻方?请在图8中用三阶幻方的性质进行说明.27.穿楼而过的轻轨、《千与千寻》现实版洪崖洞、空中巴士长江索道……,“3D魔幻城”吸引着海量游客前来重庆打卡.2018年的清明节和“五一”节,洪崖洞入围全球旅游热门目的地榜单,排名仅次于故宫.位于洪崖洞的重庆知名火锅小天鹅火锅在节日期间每天也人满为患,其中鸳鸯火锅和红汤火锅最受游客青睐.在清明节期间,前来就餐选择鸳鸯火锅和红汤火锅的游客共有2200名,鸳鸯火锅和红汤火锅的人均消费分别为130元和120元.(1)清明节期间,若选择红汤火锅的人数不超过鸳鸯火锅人数的1.5倍.求至少有多少人选择鸳鸯火锅?(2)“五一”节期间,因天气渐热的原因,前来就餐的游客人数有所下降,与(1)问中选择鸳鸯火锅的人数最少时相比,选择两种火锅的人数均下降了a%;人均消费与清明节期间相比均有所上升,a%,最终“五一”节期间两其中鸳鸯火锅的人均消费上涨了a%,红汤火锅的人均消费上涨了32种火锅的总销售额与(1)问中选择鸳鸯火锅的人数最少时的两种火锅的总销售额持平,求a的值.28.如图,在△ABC中,∠B=∠C,D是BC边上一点,且FD⊥BC于D,DE⊥AB于E,∠AFD=140°,求∠EDF的度数.【答案与解析】1.答案:A解析:解:根据题意得:新矩形的长为a−b,宽为a−3b,则新矩形周长为2(a−b+a−3b)=2(2a−4b)=4a−8b,故选:A.根据图形表示出新矩形的长与宽,即可确定出周长.此题考查了整式的加减,熟练掌握运算法则是解本题的关键.2.答案:B解析:本题主要考查了两直线平行,内错角相等的性质,需要注意隐含条件,直尺的对边平行,等腰直角三角板的锐角是45°的利用.本题主要利用两直线平行,同位角相等作答,即可得到结论.解:根据题意可知,两直线平行,同位角相等,∴∠1=∠3,∵∠3+∠2=45°,∴∠1+∠2=45°∵∠1=20°,∴∠2=25°.故选B.3.答案:B解析:解:如图所示:作EM//AB,FK//DC,延长FE交NB于点H,∵EM//AB,FK//DC,AB//CD,∴∠ABE=∠BEM,∠MEF=∠EFK,∠KFD+∠CDF=180°,∴∠ABE +∠EFK =∠BEM +∠MEF =β,∠KFD =180°−γ,∴∠ABE +∠EFD =β+180°−γ,∵BN 、FN 分别平分∠ABE 、∠EFD ,∴∠NBE +∠NFE =β+180°−γ2,∵∠BNF +∠NFE =∠BHE ,∴∠BHE +∠HBE +∠HEB =∠BNF +∠EFN +∠HBE +∠BEH=α+β+180°−γ2+180°−β=180°,∴整理得:−2α+β+γ=180°.故选:B .直接利用平行线的性质结合三角形内角和定理以及三角形外角的性质分析得出答案.此题主要考查了平行线的性质以及三角形内角和定理等知识,正确应用平行线的性质转化角的关系是解题关键.4.答案:D解析:解:A 、由a >b ,可得:−4a <−4b ,可得:1−4a <1−4b ,故A 错误;B 、由a >b ,可得:12a >12b ,故B 错误;C 、由a >b ,可得:−a <−b ,故C 错误;D 、由a >b ,可得:2a >2b ,可得:2a −4>2b −4,故D 正确;故选:D .根据不等式的性质找到变形正确的选项即可.考查不等式性质的应用;用到的知识点为:不等式的两边加上或减去同一个数或式子,不等号的方向不变;乘以或除以同一个的正数,不等号的方向不变;乘以或除以同一个的负数,不等号的方向改变. 5.答案:A解析:解:将{x =2y =2代入方程2x +ky =6,得 4+2k =6,解得k =1,故选:A .根据方程的解满足方程,可得关于k 的方程,根据解方程,可得答案.本题考查了二元一次方程的解,利用方程解满足方程得出关于k的方程是解题关键.6.答案:D解析:[分析]根据等腰三角形的三线合一证明即可.本题考查的是命题的真假判断,等腰三角形的性质,掌握等腰三角形的三线合一是解题的关键.[详解]解:∵AB=AC,AD⊥BC,∴∠1=∠2,①是真命题;∵AB=AC,∠1=∠2,∴BD=DC,②是真命题;∵AB=AC,BD=DC,∴AD⊥BC,③是真命题;∵AD⊥BC,BE⊥AC,∴∠2+∠C=90°,∠3+∠C=90°,∴∠2=∠3,∵AB=AC,AD⊥BC,∴∠1=∠2,∴∠1=∠3,④是真命题,故选D.7.答案:C解析:解:∵a//b,∠1=70°,∴∠3=∠1=70°,∴∠2=∠1=70°,故选:C.先根据平行线的性质得出∠3的度数,再根据对顶角相等求解.本题主要考查了平行线的性质的运用,解题时注意:两直线平行,同位角相等.8.答案:C解析:解:因为把5颗玻璃球放入水中,结果水满溢出,所以5颗玻璃球的体积最少是:500−300=200(cm3),一颗玻璃球的体积最少是:200÷5=40(cm3),因此推得这样一颗玻璃球的体积在40cm3以上,50cm3以下.故选:C.要求每颗玻璃球的体积在哪一个范围内,根据题意,先求出5颗玻璃球的体积最少是多少,5颗玻璃球的体积最少是(500−300)cm3,进而推测这样一颗玻璃球的体积的范围即可.此题考查了探索某些实物体积的测量方法,本题关键是明白:杯子里水上升的体积就是5颗玻璃球的体积,进而得解.9.答案:1.23×10−4解析:解:0.000123=1.23×10−4.故答案为1.23×10−4.绝对值小于1的正数也可以利用科学记数法表示,一般形式为a×10−n,与较大数的科学记数法不同的是其所使用的是负指数幂,指数由原数左边起第一个不为零的数字前面的0的个数所决定.本题考查用科学记数法表示较小的数,一般形式为a×10−n,其中1≤|a|<10,n为由原数左边起第一个不为零的数字前面的0的个数所决定.10.答案:90;45解析:试题分析:两个大小完全一样的矩形拼成“L”形图案所构成的△AFG≌△CAB,所以AF=AC,∠FAC=90°,∠FCA=45度.由已知△AFG≌△CAB,∴∠AFG=∠CAB,∵∠AFG+∠FAG=90°,∴∠CAB+∠FAG=90°,∴∠FAC=90°.=45°.∴∠FCA=(180°−90°)×12故答案为90,45.11.答案:假解析:解:命题:“任意两个奇数之和是偶数”的逆命题是偶数是两个奇数之和,错误,为假命题,故答案为:假.写出原命题的逆命题后判断正误即可.考查了命题与定理的知识,解题的关键是了解如何写出一个命题的逆命题,难度不大.12.答案:10解析:本题考查了三角形内角和定理,三角形外角与内角的关系及等腰三角形的性质的综合运用.充分利用外角找着∠BA1A与∠A4的关系是正确解答本题的关键.由∠B=20°根据三角形内角和公式可求得∠BA1A的度数,再根据等腰三角形的性质及三角形外角的性质找∠BA1A与∠A4的关系即可解答.解:∵AB=A1B,∠B=20°,∴∠A=∠BA1A=12×(180°−∠B)=12×(180°−20°)=80°∵A1C=A1A2,A2D=A2A3,A3E=A3A4∴∠A1CD=∠A1A2C,∵∠BA1A是△A1A2C的外角,∴∠BA1A=2∠CA2A1=4∠DA3A2=8A4∴∠A4=10°.故填10.13.答案:晶、森、从解析:本题考查生活中的平移,解题的关键是理解平移的定义,属于中考常考题型.根据平移的基本性质,写出的汉字只需由两或三个完全相同的部分组成即可.根据题意,由两或三个完全相同的部分组成的汉字即可,所以可以有:晶、森、从等.14.答案:ab4解析:解:∵AA1=AF,B1B=BF,∴∠AFA1=∠AA1F,∠BFB1=∠BB1F,∵AA1⊥l,BB1⊥l,∴AA1//BB1,∴∠BAA1+∠ABB1=180°,∴180°−2∠AFA1+180°−2∠BFB1=180°,∴∠AFA1+∠BFB1=90°,∴∠A1FB1=90°,∴△A 1OB 1的面积=12△A 1FB 1的面积=14ab ;故答案为14ab .利用AA 1⊥l ,BB 1⊥l 可得AA 1//BB 1,证明∠AFA 1+∠BFB 1=90°,确定△∠A 1FB 1是直角三角形,则可求△A 1OB 1的面积=12△A 1FB 1的面积=14ab ;本题考查二次函数的图象及性质,平行线的性质;能够通过垂直与平行得到△∠A 1FB 1是直角三角形是解题的关键. 15.答案:5解析:试题分析:根据幂的乘方,底数不变指数相乘解答.∵a m =3,3n =5,∴(a m )n =3n =5.故答案为:5.16.答案:m <−3解析:解:∵(m +3)x >2m +6的解集为x <2,∴m +3<0,解得m <−3,故答案为:m <−3.根据不等式的基本性质3可得m +3<0,解之可得.本题考查的是解一元一次不等式组,正确求出每一个不等式解集是基础,熟知“同大取大;同小取小;大小小大中间找;大大小小找不到”的原则是解答此题的关键.17.答案:a >0解析:解:{3x +y =3a①x +3y =−a②,①+②得,4(x +y)=2a ,即x +y =a 2, ∵x +y >0,∴a 2>0,解得a >0.故答案为:a >0.直接把两式相加得出x +y 的值,再由x +y >0即可得出a 的取值范围.本题考查的是解一元一次不等式,熟知不等式的基本性质是解答此题的关键. 18.答案:3 −2解析:解:已知等式整理得:a −b √2=3+2√2,可得a =3,b =−2,故答案为:3,−2已知等式右边利用完全平方公式化简,再利用多项式相等的条件求出a 与b 的值即可.此题考查了实数的运算,熟练掌握运算法则是解本题的关键.19.答案:解:(−5a 3)2+(−3a 2)2⋅(−a 2)=25a 6+9a 4⋅(−a 2)=25a 6−9a 6=16a 6.解析:根据积的乘方、幂的乘方和同底数幂的乘法可以解答本题.本题考查整式的混合运算,解答本题的关键是明确整式的化简的方法.20.答案:解:(1)x 3−x =x(x 2−1)=x(x +1)(x −1);(2)x 2(a −b)+y 2(b −a)=(a −b)(x 2−y 2)=(a −b)(x +y)(x −y).解析:(1)首先提取公因式x ,再利用平方差公式分解因式即可;(2)首先提取公因式(a −b),再利用平方差公式分解因式即可.此题主要考查了公式法以及提取公因式法分解因式,熟练利用公式法分解因式是解题关键. 21.答案:解:{x −y =4①3x +y =8②, ①+②得4x =12,解得x =3,将x =3代入①得3−y =4,解得y =−1.故原方程组的解是{x =3y =−1. 解析:由加减消元法即可求解.本题考查的是二元一次方程组的基本解法,本题属于基础题,比较简单.22.答案:解:(1)原式=[(−0.25)×(−4)]2015×(−4)×1=−4;(2)[(x +2y)(x −2y)−(x +4y)2]÷4y=[x 2−4y 2−x 2−8xy −16y 2]÷4y=(−20y 2−8xy)÷4y=−5y −2x ,当x =5,y =2时,原式=−5×2−2×5=−20.解析:(1)先根据积的乘方、零指数幂进行计算,再求出即可;(2)先算乘法,再合并同类项,算除法,最后代入求出即可.本题考查了整式的混合运算和零指数幂的应用,能灵活运用法则进行化简是解此题的关键. 23.答案:解:如图所示:①线段AB 即为所求作的图形;②射线CA 、直线AD 即为所求作的图形;③过点B 画AD 的平行线BE 即为所求;④过点D 画AC 的垂线,垂足为F ,DF 为所求作的图形.解析:①在网格线上画线段AB 即可;②以点C 为端点画射线CA ,再画直线AD 即可;③借助网格线画直线AD 的平行线BE 即可;④根据网格3×3格对角线与1×1格对角线互相垂直即可画出DF .本题考查了应用与设计作图,解决本题的关键是根据平行线的判定、网格线准确画图.要理解题意,弄清问题中对所作图形的要求,结合对应几何图形的性质和基本作图的方法作图.24.答案:解:{x +2y =2①3x −4y =−24②, ①×2+②得:5x =−20,解得:x =−4,把x =−4代入①得:y =12,则方程组的解为{x =−4y =12. 解析:方程组利用加减消元法求出解即可.此题考查了解二元一次方程组,利用了消元的思想,消元的方法有:代入消元法与加减消元法. 25.答案:解:原式=a 2−2ab +b 2+3ab −b 2−a 2=ab ,当a=−1,b=4时,原式=−4.解析:原式利用完全平方公式,单项式乘以多项式法则计算,去括号合并得到最简结果,把a与b 的值代入计算即可求出值.此题考查了整式的混合运算−化简求值,熟练掌握运算法则是解本题的关键.26.答案:(1)构成三阶幻方的九个数,每个数同时加或减同一个数,所得到的九个数仍能构成三阶幻方;(2)构成三阶幻方的九个数,每个数同时乘同一个数或除以同一个不为0的数,所得到的九个数仍能构成三阶幻方;性质应用:6,8,10,12,14,16,18,20,22这九个数能构成三阶幻方;先将三阶幻方的九个数1,2,3,4,5,6,7,8,9,每个数都乘2,得2,4,6,8,10,12,14,16,18,根据三阶幻方性质②,2,4,6,8,10,12,14,16,18能构成三阶幻方.再将2,4,6,8,10,12,14,16,18,每个数都加4得6,8,10,12,14,16,18,20,22,根据三阶幻方性质①,6,8,10,12,14,16,18,20,22能构成三阶幻方.所以,6,8,10,12,14,16,18,20,22这九个数能构成三阶幻方,如图⑧,解析:解:(1)如图④,由题意知,三阶幻方的性质(1)构成三阶幻方的九个数,每个数同时加或减同一个数,所得到的九个数仍能构成三阶幻方.故答案为:构成三阶幻方的九个数,每个数同时加或减同一个数,所得到的九个数仍能构成三阶幻方;(2)如图⑦,由题意得:三阶幻方的性质(2)构成三阶幻方的九个数,每个数同时乘同一个数或除以同一个不为0的数,所得到的九个数仍能构成三阶幻方.故答案为:构成三阶幻方的九个数,每个数同时乘同一个数或除以同一个不为0的数,所得到的九个数仍能构成三阶幻方.性质应用见答案.(1)根据图②、③的作法将九个数同时减0.5填到图④中相应位置,类比等式性质得出规律即可;(2)根据图⑤、⑥的作法将九个数同时乘−4填到图⑦相应位置,可类比等式的性质得出规律;将1,2,3,4,5,6,7,8,9这9个数先乘以2、再加上4即可得出结论.本题主要考查数字的变化类,理解题意类比等式的性质是解题的关键.6,8,10,12,14,16,18,20,2227.答案:解:(1)设有x人选择鸳鸯火锅,则有(2200−x)人选择红汤火锅,根据题意得:2200−x≤1.5x,解得:x≥880.答:至少有880人选择鸳鸯火锅.a%)=(2)根据题意得:880(1−a%)×130(1+a%)+(2200−880)(1−a%)×120(1+32880×130+(2200−880)×120,令m=a%,整理,得:40m2−9m=0,,解得:m1=0,m2=940∴a1=0(舍去),a2=45.2答:a的值为45.2解析:(1)设有x人选择鸳鸯火锅,则有(2200−x)人选择红汤火锅,根据选择红汤火锅的人数不超过鸳鸯火锅人数的1.5倍.即可得出关于x的一元一次不等式,解之取其中的最小值即可得出结论;(2)根据“五一”节期间两种火锅的总销售额与(1)问中选择鸳鸯火锅的人数最少时的两种火锅的总销售额持平,即可得出关于a的一元二次方程,解之取其正值即可得出结论.本题考查了一元二次方程的应用以及一元一次不等式的应用,解题的关键是:(1)根据各数量间的关系,正确列出一元一次不等式;(2)找准等量关系,正确列出一元二次方程.28.答案:解:∵DF⊥BC,DE⊥AB,∴∠FDC=∠FDB=∠DEB=90°,又∵∠B=∠C,∴∠EDB=∠DFC,∵∠AFD=140°,∴∠EDB=∠DFC=40°,∴∠EDF=90°−∠EDB=50°.解析:由于DF⊥BC,DE⊥AB,所以∠FDC=∠FDB=∠DEB=90°,又因为△ABC中,∠B=∠C,所以∠EDB=∠DFC,因为∠AFD=140°,所以∠EDB=∠DFC=40°,所以∠EDF=90°−∠EDB= 50°.本题考查了等腰三角形的性质;利用三角形的内角和定理求解角的度数是正确解答本题的关键.。
2022-2023学年江苏省扬州市宝应县七年级(下)期末数学试卷
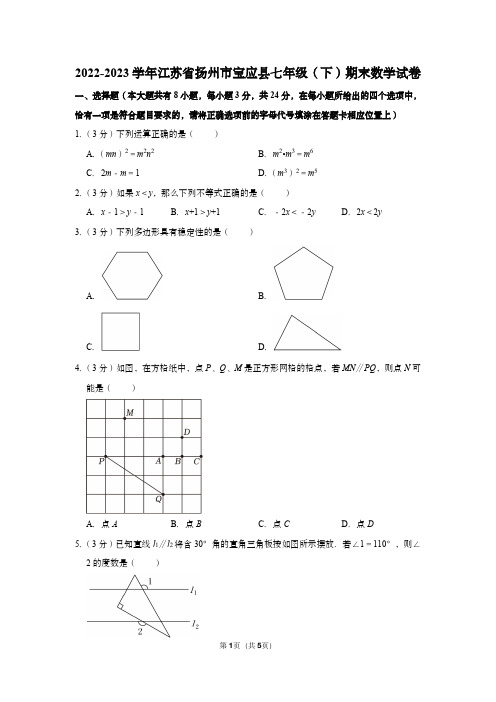
2022-2023学年江苏省扬州市宝应县七年级(下)期末数学试卷一、选择题(本大题共有8小题,每小题3分,共24分,在每小题所给出的四个选项中,恰有一项是符合题目要求的,请将正确选项前的字母代号填涂在答题卡相应位置上)1.(3分)下列运算正确的是()A.(mn)2=m2n2B.m2•m3=m6C.2m﹣m=1D.(m3)2=m52.(3分)如果x<y,那么下列不等式正确的是()A.x﹣1>y﹣1B.x+1>y+1C.﹣2x<﹣2y D.2x<2y3.(3分)下列多边形具有稳定性的是()A.B.C.D.4.(3分)如图,在方格纸中,点P、Q、M是正方形网格的格点,若MN∥PQ,则点N可能是()A.点A B.点B C.点C D.点D5.(3分)已知直线l1∥l2将含30°角的直角三角板按如图所示摆放.若∠1=110°,则∠2的度数是()A.120°B.130°C.140°D.150°6.(3分)下列因式分解正确的是()A.ax+ay=a(x+y)+1B.3a+3b=3(a+b)C.a2+4a+4=(a+4)2D.a2﹣b2=(a﹣b)27.(3分)我国古代《算法统宗》里有这样一首诗:“我问开店李三公,众客都来到店中,一房七客多七客,一房九客一房空.”诗中后面两句的意思是:如果一间客房住7人,那么有7人无房可住;如果一间客房住9人,那么就空出一间客房,若设该店有客房x间,房客y人,则列出关于x、y的二元一次方程组正确的是()A.B.C.D.8.(3分)关于x的不等式组有且只有三个整数解,则a的最大值是()A.3B.4C.5D.6二、填空题(本大题共有10小题,每小题3分,共30分,不需写出解答过程,请把答案直接填写在答题卡相应位置上)9.(3分)科学家在实验室中检测出某种病毒的直径约为0.000000103米,该直径用科学记数法表示为米.10.(3分)因式分解:x2y+xy2=.11.(3分)请写出命题“如果a>b,那么b﹣a<0”的逆命题:.12.(3分)已知x+y=4,x﹣y=6,则x2﹣y2=.13.(3分)一个多边形的每一个内角都是140°,则这个多边形是边形.14.(3分)已知等腰三角形两边长分别为3cm和5cm,则等腰三角形的周长为cm.15.(3分)如图,直线a∥b,点C、A分别在直线a、b上,AC⊥BC,若∠1=50°,则∠2的度数为.16.(3分)如图,将△ABC沿直线BC方向平移后得到△DEF,已知BC=5,EC=2,则平移的距离是.17.(3分)一个盒子里有若干个大小相同的白球和红球,从中摸到1个红球得4分,摸到1个白球得3分,王俊凯同学摸到了x个红球,y个白球,共得32分,如果把他摸到的一组红球和白球的数量表示为(x,y)的形式,那么(x,y)为.18.(3分)如图,长方形ABCD的周长为8,分别以长方形的一条长和一条宽为边向外作两个正方形,且这两个正方形的面积和为10,则长方形ABCD的面积是.三、解答题(本大题共有9小题,共96分.请在答题卡指定区域内作答,解答时应写出必要的文字说明、证明过程或演算步骤)19.(8分)计算:(1)(﹣3)101×(﹣)100﹣(π﹣3)0+(﹣)﹣2;(2)(3a2)2﹣a2•2a2+(﹣2a3)2÷a2;20.(8分)(1)解方程组:;(2)解不等式:.21.(8分)已知3x2﹣2x﹣3=0,求(x﹣1)2+x(x+)的值.22.(8分)整式的值为P.(1)当m=2时,求P的值;(2)若P的取值范围如图所示,求m的非正整数值.23.(10分)如图,直线a∥b,且直线a、b被直线c、d所截.(1)求证:∠1=∠2;(2)若∠1+∠3=180°,试判断直线c与直线d的位置关系,并说明理由.24.(10分)如图1,将长为2a+3,宽为2a的大长方形分割成四个完全相同的直角三角形,拼成“赵爽弦图”(如图),得到大小两个正方形.(1)用关于a的代数式表示图1中大长方形的面积;(2)求图2中小正方形的面积是多少(结果要化简)?25.(10分)如图,BD是△ABC的角平分线,DE∥BC,交AB于点E.(1)求证:∠EBD=∠EDB;(2)若∠A=72°,∠C=58°,求∠CDB的度数.26.(10分)在解二元一次方程组时,我们常常也会采用了一种“整体代入消元”的方法将二元一次方程组转化为一元一次方程求解,比如,解方程组,首先将方程②变形得4x+10y+y=5,即2(2x+5y)+y=5…③,其次把方程①代入③得:2×3+y=5,即y=﹣1,最后把y=﹣1代入方程①,得x=4,所以方程组的解为,请你解决以下问题:(1)你能否尝试用“整体代入消元”的方法解方程组;(2)已知x、y满足方程组.①求xy的值;②求出这个方程组的所有整数解.27.(12分)为实现区域教育均衡发展,某市计划对A、B两类薄弱学校全部进行改造,根据预算,共需资金2000万元.改造一所A类学校和两所B类学校共需资金210万元;改造两所A类学校和一所B类学校共需资金180万元.(1)改造一所A类学校和一所B类学校所需的资金分别是多少万元?(2)若该市的A类学校不超过16所,则B类学校至少有多少所?28.(12分)如图,四边形ABCD中,AD∥BC,∠BDC=∠BCD,DE⊥DC交AB于E.(1)求证:DE平分∠ADB;(2)若∠ABD的平分线与CD的延长线交于F,设∠F=α,①若α=50°,求∠A的值;②若∠F<∠ABC,试确定α的取值范围.。
2019-2020学年扬州市宝应县七年级下学期期末数学试卷

2019-2020学年扬州市宝应县七年级下学期期末数学试卷一、选择题(本大题共8小题,共24.0分)1. 下列计算中,正确的是( )A. (x +3)2=x 2+9B. a 3÷a =a 2C. 6a −3=3aD. 20−2−1=2 2. 若两条平行线被第三条直线所截,则一对内错角的角平分线互相 ( )A. 垂直B. 平行C. 重合D. 相交 3. 如图,直线l 1//l 2,以直线l 2上的点A 为圆心,适当长为半径画弧,分别交直线l 2、l 1于点B 、C ,连接AC 、BC ,若∠ABC =70°,则∠1=( )A. 40°B. 20°C. 60°D. 70°4. 如果a <b ,那么下列结论一定正确的是( )A. a −3>b −3B. 3−a >3−bC. ac 2<bc 2D. 2a 2<2b 2 5. 已知下列命题:①若a b >1,则a >b ;②等边三角形的三个内角都相等;③若a >0,b >0,则ab >0;④直角三角形中30°的角所对的直角边等于斜边的一半.其中原命题与逆命题均为真命题的有( )A. ①②B. ②③C. ③④D. ②④ 6. 第35届全国中学生物理竞赛全国决赛于10月27日在上海举行,并于10月31日落下帷幕,重庆代表队所有参赛同学均获得奖牌,重庆一中在此次物理竞赛中取得优异成绩,入围决赛的学生均获得奖牌,已知重庆一中入围决赛人数比重庆代表队人数的一半少1人,重庆代表队的人数比重庆一中入围决赛人数多8人,若设重庆一中入围决赛人数为x 人,重庆代表队为y 人,可列方程组( )A. {2x +1=y x +8=yB. {x =12y −1x +8=yC. {x +1=12y x −8=yD. {2x +2=yx −8=y 7. 下列计算中,正确的是( )A. a ⋅a 2=a 2B. (a +1)2=a 2+1C. (ab)2=ab 2D. (−a)3=−a 38. 用反证法证明命题“在四边形中至少有一个内角不大于90°”时,首先应假设( )A. 每个内角都小于90°B. 每个内角都大于90°C. 没有一个内角大于90°D. 每个内角都等于90° 二、填空题(本大题共10小题,共30.0分)9. 我国自行研制的探月工程“嫦娥三号”在西昌点火升空,准确入轨,并在月球软着陆成功.月球离地球有380000千米,把这个数据用科学记数法表示为______千米.10. 一个多边形的内角和等于540°,那么这个多边形为 边形.11. 下列命题中逆命题成立的有______(填序号).①同旁内角互补,两直线平行;②如果两个角是直角,那么它们相等;③全等三角形的对应边相等;④如果两个实数相等,那么它们的平方相等.12. 如图,平移△ABC 可得到△DEF ,如果∠C =60°,AE =7cm ,AB =4cm ,那么∠F = ______ 度,DB = ______ cm .13. 已知{x =1y =2是二元一次方程mx −y =−1的一个解,则m =______. 14. 如图,∠A =70°,O 是AB 上一点,直线OD 与AB 所夹的∠B0D =78°,要使OD//AC ,直线OD 绕点O 按逆时针方向至少旋转______.15. 如图,在一个大圆盘中有4个相同的小圆盘,已知大、小圆盘的半径R ,r 都是整数,阴影部分的面积为5πcm 2,则R +r =______.16.把一张正方形纸条按下图所示折叠后,若得到∠AOB′=70°,则∠B′OG=.17.一次方程组的解满足2x+y≤2,则t的取值范围为18.不等式组{x+2>03−2x<1的解集为______ .三、计算题(本大题共3小题,共24.0分)19.先化简,再求值:(−2a2+5+4a)−(5a+4−2a2),其中a=−2.20.分解因式①3a3−18a2+27a②x2+4xy+4y2−2x−4y−321.解不等式组,并把解集在数轴上表示出来.{2x+1≥0 x+53−x2>1.四、解答题(本大题共7小题,共72.0分)22.(1)计算:(−1)3+(2012−√2)0−(12)−2;(2)用简便方法计算:20172−2023×2011.23.(1)如图①,在△ABC中,P是△ABC内任意一点,∠BPC与∠A有怎样的大小关系?证明你的结论。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2015-2016学年江苏省扬州市宝应县七年级(下)期末数学试卷一、选择题(本题共8小题,每小题3分,共24分)1.下列运算正确的()A.a3﹣a2=a B.a2•a3=a6C.(a3)2=a6D.(3a)3=9a32.如图,直线l1∥l2∥l3,等边△ABC的顶点B、C分别在直线l2、l3上,若边BC与直线l3的夹角∠1=25°,则边AB与直线l1的夹角∠2=()A.25° B.30° C.35° D.45°3.下列命题是真命题的是()A.内错角相等B.如果a2=b2,那么a3=b3C.三角形的一个外角大于任何一个内角D.平行于同一直线的两条直线平行4.己知(x﹣y)2=49,xy=2,则x2+y2的值为()A.53 B.45 C.47 D.515.已知是方程组的解,则a+2b的值为()A.4 B.5 C.6 D.76.关于x的不等式x﹣b>0恰有两个负整数解,则b的取值范围是()A.﹣3<b<﹣2 B.﹣3<b≤﹣2 C.﹣3≤b≤﹣2 D.﹣3≤b<﹣27.如图,三角形ABC被分成三角形BEF和四边形AEFC两部分,BE=3,BF=4,FC=5,AE=6,那么三角形BEF面积和四边形AEFC面积的比是()A.4:23 B.4:25 C.5:26 D.1:68.7张如图1的长为a,宽为b(a>b)的小长方形纸片,按图2的方式不重叠地放在矩形ABCD内,未被覆盖的部分(两个矩形)用阴影表示.设左上角与右下角的阴影部分的面积的差为S,当BC的长度变化时,按照同样的放置方式,S始终保持不变,则a,b满足()A.a= b B.a=3b C.a= b D.a=4b二、填空题(本题共10小题,每小题3分,共30分,请将正确答案填写在答题卡上)9.一种花粉颗粒的直径约为0.0000065米,将0.0000065用科学记数法表示为.10.计算:3a3•a2﹣2a7÷a2= .11.一个n边形的内角和是1260°,那么n= .12.若代数式x2+(a﹣1)x+16是一个完全平方式,则a= .13.若a+3b﹣2=0,则3a•27b= .14.将一副三角板如图放置.若AE∥BC,则∠AFD= °.15.水仙花是漳州市花,如图,在长为14m,宽为10m的长方形展厅,划出三个形状、大小完全一样的小长方形摆放水仙花,则每个小长方形的周长为m.16.定义运算“*”,规定x*y=ax2+by,其中a、b为常数,且1*2=5,2*1=6,则2*3= .17.已知0≤x≤1,若x﹣2y=6,则y的最小值是.18.如图,在四边形ABCD中,∠DAB的角平分线与∠ABC的外角平分线相交于点P,且∠D+∠C=240°,则∠P= °.三、解答题(本题共10小题,共96分)19.(8分)计算:(1)(π﹣3)0+(﹣)﹣2+32016×()1008(2)(x﹣2)2﹣(x+2)(x﹣2)20.(8分)因式分解:(1)3x2y﹣18xy2+27y3(2)x2(x﹣2)+(2﹣x)21.(8分)先化简,再求值.(a+b)(a﹣b)+b(a+2b)﹣b2,其中a=1,b=﹣2.22.(8分)解不等式组:.23.(10分)将一副三角板拼成如图所示的图形,过点C作CF平分∠DCE交DE于点F.(1)求证:CF∥AB;(2)求∠DFC的度数.24.(10分)如图,四边形ABCD中,∠A=∠C=90°,BE平分∠ABC交CD于E,DF平分∠ADC交AB于F.(1)若∠ABC=60°,则∠ADC= °,∠AFD= °;(2)BE与DF平行吗?试说明理由.25.(10分)已知方程组的解满足x为非正数,y为负数.(1)求m的取值范围;(2)化简:|m﹣3|﹣|m+2|;(3)在m的取值范围内,当m为何整数时,不等式2mx+x<2m+1的解为x>1.26.(10分)(1)填空21﹣20=2(),22﹣21=2(),23﹣22=2()…(2)探索(1)中式子的规律,试写出第n个等式,并说明第n个等式成立;(3)运用上述规律计算:20﹣21﹣22﹣…﹣22014+22015.27.(12分)“二广”高速在益阳境内的建设正在紧张地进行,现有大量的沙石需要运输.“益安”车队有载重量为8吨、10吨的卡车共12辆,全部车辆运输一次能运输110吨沙石.(1)求“益安”车队载重量为8吨、10吨的卡车各有多少辆?(2)随着工程的进展,“益安”车队需要一次运输沙石165吨以上,为了完成任务,准备新增购这两种卡车共6辆,车队有多少种购买方案,请你一一写出.28.(12分)已知△ABC中,∠ABC=∠ACB,D为线段CB上一点(不与C、B重合),点E为射线CA上一点,∠ADE=∠AED.设∠BAD=α,∠CDE=β.(1)如图(1),①若∠BAC=42°,∠DAE=30°,则α=,β=.②写出α与β的数量关系,并说明理由;(2)如图(2),当E点在CA的延长线上时,其它条件不变,写出α与β的数量关系,并说明理由.2015-2016学年江苏省扬州市宝应县七年级(下)期末数学试卷参考答案与试题解析一、选择题(本题共8小题,每小题3分,共24分)1.下列运算正确的()A.a3﹣a2=a B.a2•a3=a6C.(a3)2=a6D.(3a)3=9a3【考点】幂的乘方与积的乘方;合并同类项;同底数幂的乘法.【分析】根据同底数幂的乘法、幂的乘方与积的乘方法则,分别进行各选项的判断即可.【解答】解:A、a3与a2不是同类项,不能直接合并,故本选项错误;B、a2•a3=a5,原式计算错误,故本选项错误;C、(a3)2=a6,计算正确,故本选项正确;D、(3a)3=27a3,原式计算错误,故本选项错误;故选C.【点评】本题考查了同底数幂的乘法、幂的乘方与积的乘方,解答本题的关键是掌握各部分的运算法则.2.如图,直线l1∥l2∥l3,等边△ABC的顶点B、C分别在直线l2、l3上,若边BC与直线l3的夹角∠1=25°,则边AB与直线l1的夹角∠2=()A.25° B.30° C.35° D.45°【考点】平行线的性质;等边三角形的性质.【分析】先根据∠1=25°得出∠3的度数,再由△ABC是等边三角形得出∠4的度数,根据平行线的性质即可得出结论.【解答】解:∵直线l1∥l2∥l3,∠1=25°,∴∠1=∠3=25°.∵△ABC是等边三角形,∴∠ABC=60°,∴∠4=60°﹣25°=35°,∴∠2=∠4=35°.故选C.【点评】本题考查的是平行线的性质,用到的知识点为:两直线平行,内错角相等.3.下列命题是真命题的是()A.内错角相等B.如果a2=b2,那么a3=b3C.三角形的一个外角大于任何一个内角D.平行于同一直线的两条直线平行【考点】命题与定理.【分析】根据平行线的性质对A、D进行判断;根据平方根的定义对B进行判断;根据三角形外角性质对C进行判断.【解答】解:A、两直线平行,内错角相等,所以A选项错误;B、如果a2=b2,那么a3=b3或a3=﹣b3,所以B选项错误;C、三角形的一个外角大于任何一个不相邻的一个内角,所以C选项错误;D、平行于同一直线的两条直线平行,所以D选项正确.故选D.【点评】本题考查了命题与定理:判断一件事情的语句,叫做命题.许多命题都是由题设和结论两部分组成,题设是已知事项,结论是由已知事项推出的事项,一个命题可以写成“如果…那么…”形式.有些命题的正确性是用推理证实的,这样的真命题叫做定理.4.己知(x﹣y)2=49,xy=2,则x2+y2的值为()A.53 B.45 C.47 D.51【考点】完全平方公式.【分析】原式利用完全平方公式变形,将已知等式代入计算即可求出值.【解答】解:∵(x﹣y)2=49,xy=12,∴x2+y2=(x﹣y)2+2xy=49+4=53.故选:A.【点评】此题考查了完全平方公式,熟练掌握完全平方公式是解本题的关键.5.已知是方程组的解,则a+2b的值为()A.4 B.5 C.6 D.7【考点】二元一次方程组的解.【分析】首先把方程组的解代入方程组,得到一个关于a,b的方程组,即可求得代数式的值.【解答】解:把代入方程组,可得:,解得:,则a+2b=7,故选D【点评】本题主要考查了方程组的解的定义:能使方程组中每个方程的左右两边相等的未知数的值即是方程组的解.6.关于x的不等式x﹣b>0恰有两个负整数解,则b的取值范围是()A.﹣3<b<﹣2 B.﹣3<b≤﹣2 C.﹣3≤b≤﹣2 D.﹣3≤b<﹣2【考点】一元一次不等式的整数解.【分析】表示出已知不等式的解集,根据负整数解只有﹣1,﹣2,确定出b的范围即可.【解答】解:不等式x﹣b>0,解得:x>b,∵不等式的负整数解只有两个负整数解,∴﹣3≤b<﹣2故选D.【点评】此题考查了一元一次不等式的整数解,弄清题意是解本题的关键.7.如图,三角形ABC被分成三角形BEF和四边形AEFC两部分,BE=3,BF=4,FC=5,AE=6,那么三角形BEF面积和四边形AEFC面积的比是()A.4:23 B.4:25 C.5:26 D.1:6【考点】三角形的面积.【分析】连接AF,根据△BEF的边BE上的高和△ABF边AB上的高相等,推出=,推出S△BEF=S△ABF,同理得出S△ABF=S△ABC,推出S△BEF=S△ABC,即可得出答案.【解答】解:连接AF,∵BE=3,AE=6,∴AB=9,∵△BEF的边BE上的高和△ABF边AB上的高相等,∴=,即S△BEF=S△ABF,同理BF=4,CF=5,BC=9,得出S△ABF=S△ABC,推出S△BEF=S△ABC,∴S△BEF:S四边形AEFC=4:23,故选A【点评】本题考查了面积与等积变形的应用,主要考查学生能否灵活运用等高的三角形的面积比等于对应边之比.8.7张如图1的长为a,宽为b(a>b)的小长方形纸片,按图2的方式不重叠地放在矩形ABCD内,未被覆盖的部分(两个矩形)用阴影表示.设左上角与右下角的阴影部分的面积的差为S,当BC的长度变化时,按照同样的放置方式,S始终保持不变,则a,b满足()A.a= b B.a=3b C.a= b D.a=4b【考点】整式的混合运算.【分析】表示出左上角与右下角部分的面积,求出之差,根据差与BC无关即可求出a与b 的关系式.【解答】解:左上角阴影部分的长为AE,宽为AF=3b,右下角阴影部分的长为PC,宽为a,∵AD=BC,即AE+ED=AE+a,BC=BP+PC=4b+PC,∴AE+a=4b+PC,即AE﹣PC=4b﹣a,∴阴影部分面积之差S=AE•AF﹣PC•CG=3bAE﹣aPC=3b(PC+4b﹣a)﹣aPC=(3b﹣a)PC+12b2﹣3ab,则3b﹣a=0,即a=3b.解法二:既然BC是变化的,当点P与点C重合开始,然后BC向右伸展,设向右伸展长度为X,左上阴影增加的是3bX,右下阴影增加的是aX,因为S不变,∴增加的面积相等,∴3bX=aX,∴a=3b.故选:B.【点评】此题考查了整式的混合运算的应用,弄清题意是解本题的关键.二、填空题(本题共10小题,每小题3分,共30分,请将正确答案填写在答题卡上)9.一种花粉颗粒的直径约为0.0000065米,将0.0000065用科学记数法表示为 6.5×10﹣6.【考点】科学记数法—表示较小的数.【分析】根据科学记数法和负整数指数的意义求解.【解答】解:0.0000065=6.5×10﹣6.故答案为6.5×10﹣6.【点评】本题考查了科学记数法﹣表示较小的数:用a×10n(1≤a<10,n为负整数)表示较小的数.10.计算:3a3•a2﹣2a7÷a2= a5.【考点】整式的混合运算.【分析】根据整式的混合运算顺序,首先计算乘法和除法,然后计算减法,即可求出算式3a3•a2﹣2a7÷a2的值是多少.【解答】解:3a3•a2﹣2a7÷a2=3a5﹣2a5=a5故答案为:a5.【点评】(1)此题主要考查了整式的混合运算,要熟练掌握,解答此题的关键是要明确:有乘方、乘除的混合运算中,要按照先乘方后乘除的顺序运算,其运算顺序和有理数的混合运算顺序相似.(2)此题还考查了同底数幂的乘法法则:同底数幂相乘,底数不变,指数相加,要熟练掌握,解答此题的关键是要明确:①底数必须相同;②按照运算性质,只有相乘时才是底数不变,指数相加.(3)此题还考查了同底数幂的除法法则:同底数幂相除,底数不变,指数相减,要熟练掌握,解答此题的关键是要明确:①底数a≠0,因为0不能做除数;②单独的一个字母,其指数是1,而不是0;③应用同底数幂除法的法则时,底数a可是单项式,也可以是多项式,但必须明确底数是什么,指数是什么.11.一个n边形的内角和是1260°,那么n= 9 .【考点】多边形内角与外角.【分析】根据多边形的内角和公式:(n﹣2).180 (n≥3)且n为整数)可得方程:(n ﹣2)×180=1260,再解方程即可.【解答】解:由题意得:(n﹣2)×180=1260,解得:n=9,故答案为:9.【点评】此题主要考查了多边形的内角和公式,关键是掌握内角和公式.12.若代数式x2+(a﹣1)x+16是一个完全平方式,则a= 9或﹣7 .【考点】完全平方式.【分析】利用完全平方公式的结构特征判断即可得到a的值.【解答】解:∵x2+(a﹣1)x+16是一个完全平方式,∴a﹣1=±8,解得:a=9或﹣7,故答案为:9或﹣7【点评】此题考查了完全平方式,熟练掌握完全平方公式是解本题的关键.13.若a+3b﹣2=0,则3a•27b= 9 .【考点】幂的乘方与积的乘方;同底数幂的乘法.【分析】根据幂的乘方运算以及同底数幂的乘法运算法则得出即可.【解答】解:∵a+3b﹣2=0,∴a+3b=2,则3a•27b=3a×33b=3a+3b=32=9.故答案为:9【点评】此题主要考查了幂的乘方与同底数幂的乘法运算,熟练掌握运算法则是解题关键.14.将一副三角板如图放置.若AE∥BC,则∠AFD= 75 °.【考点】平行线的性质.【分析】本题主要利用两直线平行,同旁内角互补及三角板的特征进行做题.【解答】解:因为AE∥BC,∠B=60°,所以∠BAE=180°﹣60°=120°;因为两角重叠,则∠DAF=90°+45°﹣120°=15°,∠AFD=90°﹣15°=75°.故∠AFD的度数是75度.【点评】根据三角板的特殊角和平行线的性质解答.要用到:两直线平行,同旁内角互补.15.水仙花是漳州市花,如图,在长为14m,宽为10m的长方形展厅,划出三个形状、大小完全一样的小长方形摆放水仙花,则每个小长方形的周长为16 m.【考点】二元一次方程组的应用.【分析】设小长方形的长为x m,宽为y m,由图可知,长方形展厅的长是(2x+y)m,宽为(x+2y)m,由此列出方程组求得长、宽,进一步解决问题.【解答】解:设小长方形的长为x m,宽为y m,由图可得解得x+y=8,∴每个小长方形的周长为8×2=16m.故答案为:16.【点评】此题考查二元一次方程组的运用,看清图意,正确利用图意列出方程组解决问题.16.定义运算“*”,规定x*y=ax2+by,其中a、b为常数,且1*2=5,2*1=6,则2*3= 10 .【考点】解二元一次方程组.【分析】已知等式利用新定义化简,求出a与b的值,即可求出所求式子的值.【解答】解:根据题中的新定义化简已知等式得:,解得:a=1,b=2,则2*3=4a+3b=4+6=10,故答案为:10.【点评】此题考查了解二元一次方程组,弄清题中的新定义是解本题的关键.17.已知0≤x≤1,若x﹣2y=6,则y的最小值是﹣3 .【考点】一次函数的性质.【分析】先把原式化为一次函数的形式,再判断出函数的增减性,根据0≤x≤1即可得出结论.【解答】解:∵函数x﹣2y=6可化为y=﹣3,∴此函数是增函数,∵0≤x≤1,∴当x=0时,y有最小值,y最小=﹣3.故答案为:﹣3.【点评】本题考查的是一次函数的性质,熟知一次函数的增减性是解答此题的关键.18.如图,在四边形ABCD中,∠DAB的角平分线与∠ABC的外角平分线相交于点P,且∠D+∠C=240°,则∠P= 30 °.【考点】三角形内角和定理;多边形内角与外角.【分析】利用四边形内角和是360°可以求得∠DAB+∠ABC=120°.然后由角平分线的性质,邻补角的定义求得∠PAB+∠ABP=∠DAB+∠ABC+(180°﹣∠ABC)=90°+(∠DAB+∠ABC)的度数,所以根据△ABP的内角和定理求得∠P的度数即可.【解答】解:如图,∵∠D+∠C=240°,∠DAB+∠ABC+∠C+∠D=360°,∴∠DAB+∠ABC=120°.又∵∠DAB的角平分线与∠ABC的外角平分线相交于点P,∴∠PAB+∠ABP=∠DAB+∠ABC+(180°﹣∠ABC)=90°+(∠DAB+∠ABC)=150°,∴∠P=180°﹣(∠PAB+∠ABP)=30°.故答案是:30.【点评】本题考查了三角形内角和定理、多边形的内角与外角.熟知“四边形的内角和是360°”是解题的关键.三、解答题(本题共10小题,共96分)19.计算:(1)(π﹣3)0+(﹣)﹣2+32016×()1008(2)(x﹣2)2﹣(x+2)(x﹣2)【考点】整式的混合运算;零指数幂;负整数指数幂.【分析】(1)根据零指数幂、负整数指数幂、幂的乘方可以解答本题;(2)根据完全平方公式和平方差公式可以解答本题.【解答】解:(1)(π﹣3)0+(﹣)﹣2+32016×()1008=1+4+32016×=1+4+1=6;(2)(x﹣2)2﹣(x+2)(x﹣2)=(x﹣2)[(x﹣2)﹣(x+2)]=(x﹣2)(x﹣2﹣x﹣2)=(x﹣2)×(﹣4)=﹣4x+8.【点评】本题考查零指数幂、负整数指数幂、整式的混合运算,解题的关键是明确它们各自的计算方法.20.因式分解:(1)3x2y﹣18xy2+27y3(2)x2(x﹣2)+(2﹣x)【考点】提公因式法与公式法的综合运用.【分析】(1)原式提取公因式,再利用完全平方公式分解即可;(2)原式变形后,提取公因式,再利用平方差公式分解即可.【解答】解:(1)原式=3y(x2﹣6xy+9y2)=3y(x﹣3y)2;(2)原式=x2(x﹣2)﹣(x﹣2)=(x﹣2)(x2﹣1)=(x﹣2)(x+1)(x﹣1).【点评】此题考查了提公因式法与公式法的综合运用,熟练掌握因式分解的方法是解本题的关键.21.先化简,再求值.(a+b)(a﹣b)+b(a+2b)﹣b2,其中a=1,b=﹣2.【考点】整式的混合运算—化简求值.【分析】先利用平方差公式和整式的乘法计算,再合并化简,最后代入求得数值即可.【解答】解:原式=a2﹣b2+ab+2b2﹣b2=a2+ab,当a=1,b=﹣2时原式=1+(﹣2)=﹣1.【点评】此题考查代数式求值,注意先利用整式的乘法化简,再代入求得数值.22.解不等式组:.【考点】解一元一次不等式组.【分析】分别求出各不等式的解集,再求出其公共解集即可.【解答】解:,由①得,x>,由②得,x<2,故不等式组的解集为:<x<2.【点评】本题考查的是解一元一次不等式组,熟知“同大取大;同小取小;大小小大中间找;大大小小找不到”的原则是解答此题的关键.23.(10分)(2013•邵阳)将一副三角板拼成如图所示的图形,过点C作CF平分∠DCE 交DE于点F.(1)求证:CF∥AB;(2)求∠DFC的度数.【考点】平行线的判定;角平分线的定义;三角形内角和定理.【分析】(1)首先根据角平分线的性质可得∠1=45°,再有∠3=45°,再根据内错角相等两直线平行可判定出AB∥CF;(2)利用三角形内角和定理进行计算即可.【解答】(1)证明:∵CF平分∠DCE,∴∠1=∠2=∠DCE,∵∠DCE=90°,∴∠1=45°,∵∠3=45°,∴∠1=∠3,∴AB∥CF(内错角相等,两直线平行);(2)∵∠D=30°,∠1=45°,∴∠DFC=180°﹣30°﹣45°=105°.【点评】此题主要考查了平行线的判定,以及三角形内角和定理,关键是掌握内错角相等,两直线平行.24.(10分)(2016春•宝应县期末)如图,四边形ABCD中,∠A=∠C=90°,BE平分∠ABC 交CD于E,DF平分∠ADC交AB于F.(1)若∠ABC=60°,则∠ADC= 120 °,∠AFD= 30 °;(2)BE与DF平行吗?试说明理由.【考点】平行线的判定与性质.【分析】(1)根据四边形内角和为360°可计算出∠ADC=120°,再根据角平分线定义得到∠FDA=ADC=60°,然后利用互余可计算出∠AFD=30°;(2)先根据BE平分∠ABC交CD于E得∠ABE=∠ABC=30°,而∠AFD=30°则∠ABE=∠AFD,于是可根据平行线的判定方法得到BE∥DF.【解答】解:(1)∵∠A=∠C=90°,∠ABC=60°,∴∠ADC=360°﹣∠A﹣∠C﹣∠ABC=120°,∵DF平分∠ADC交AB于F,∴∠FDA=ADC=60°,∴∠AFD=90°﹣∠ADF=30°;故答案为120,30;(2)BE∥DF.理由如下:∵BE平分∠ABC交CD于E,∴∠ABE=∠ABC=×60°=30°,∵∠AFD=30°;∴∠ABE=∠AFD,∴BE∥DF.【点评】本题考查了平行线的判定与性质:同位角相等,两直线平行;内错角相等,两直线平行;两直线平行,同位角相等.25.(10分)(2016春•雁江区期末)已知方程组的解满足x为非正数,y 为负数.(1)求m的取值范围;(2)化简:|m﹣3|﹣|m+2|;(3)在m的取值范围内,当m为何整数时,不等式2mx+x<2m+1的解为x>1.【考点】不等式的解集;解二元一次方程组.【分析】首先对方程组进行化简,根据方程的解满足x为非正数,y为负数,就可以得出m 的范围,然后再化简(2),最后求得m的值.【解答】解:(1)解原方程组得:,∵x≤0,y<0,∴,解得﹣2<m≤3;(2)|m﹣3|﹣|m+2|=3﹣m﹣m﹣2=1﹣2m;(3)解不等式2mx+x<2m+1得,(2m+1)x<2m+1,∵x>1,∴2m+1<0,∴m<﹣,∴﹣2<m<﹣,∴m=﹣1.【点评】主要考查了一元一次不等式组解集的求法,其简便求法就是用口诀求解.求不等式组解集的口诀:同大取大,同小取小,大小小大中间找,大大小小找不到(无解).26.(10分)(2016春•宝应县期末)(1)填空21﹣20=2(),22﹣21=2(),23﹣22=2()…(2)探索(1)中式子的规律,试写出第n个等式,并说明第n个等式成立;(3)运用上述规律计算:20﹣21﹣22﹣…﹣22014+22015.【考点】规律型:数字的变化类.【分析】(1)根据幂的运算方法,可得21﹣20=2﹣1=1=20,22﹣21=4﹣2=2=21,23﹣22=8﹣4=4=22,据此解答即可.(2)根据(1)中式子的规律,可得2n﹣2n﹣1=2n﹣1;然后根据幂的运算方法,证明第n个等式成立即可.(3)根据2n﹣2n﹣1=2n﹣1,求出算式20﹣21﹣22﹣…﹣22014+22015的值是多少即可.【解答】解:(1)21﹣20=2﹣1=1=20,22﹣21=4﹣2=2=21,23﹣22=8﹣4=4=22.(2)∵21﹣20=20,22﹣21=21,23﹣22=22,∴2n﹣2n﹣1=2n﹣1;证明:∵2n﹣2n﹣1=2×2n﹣1﹣2n﹣1=2n﹣1×(2﹣1)=2n﹣1,∴2n﹣2n﹣1=2n﹣1成立.(3)20﹣21﹣22﹣…﹣22014+22015=22015﹣22014﹣22013﹣…﹣21+20=22014﹣22013﹣…﹣21+20=22013﹣22012﹣…﹣21+20=…=22﹣21+20=21+20=2+1=3故答案为:0、1、2.【点评】此题主要考查了探寻数列规律问题,认真观察、仔细思考,善用联想是解决这类问题的方法,注意观察总结规律,并能正确的应用规律,解答此题的关键是判断出:2n﹣2n﹣1=2n ﹣1成立.27.(12分)(2013•益阳)“二广”高速在益阳境内的建设正在紧张地进行,现有大量的沙石需要运输.“益安”车队有载重量为8吨、10吨的卡车共12辆,全部车辆运输一次能运输110吨沙石.(1)求“益安”车队载重量为8吨、10吨的卡车各有多少辆?(2)随着工程的进展,“益安”车队需要一次运输沙石165吨以上,为了完成任务,准备新增购这两种卡车共6辆,车队有多少种购买方案,请你一一写出.【考点】一元一次不等式的应用;二元一次方程组的应用.【分析】(1)根据“‘益安’车队有载重量为8吨、10吨的卡车共12辆,全部车辆运输一次能运输110吨沙石”分别得出等式组成方程组,求出即可;(2)利用“‘益安’车队需要一次运输沙石165吨以上”得出不等式求出购买方案即可.【解答】解:(1)设“益安”车队载重量为8吨、10吨的卡车分别有x辆、y辆,根据题意得:,解之得:.答:“益安”车队载重量为8吨的卡车有5辆,10吨的卡车有7辆;(2)设载重量为8吨的卡车增加了z辆,依题意得:8(5+z)+10(7+6﹣z)>165,解之得:z<,∵z≥0且为整数,∴z=0,1,2;∴6﹣z=6,5,4.∴车队共有3种购车方案:①载重量为8吨的卡车购买1辆,10吨的卡车购买5辆;②载重量为8吨的卡车购买2辆,10吨的卡车购买4辆;③载重量为8吨的卡车不购买,10吨的卡车购买6辆.【点评】此题主要考查了二元一次方程组的应用以及不等式的应用,根据已知得出正确的不等式关系是解题关键.28.(12分)(2016春•宝应县期末)已知△ABC中,∠ABC=∠ACB,D为线段CB上一点(不与C、B重合),点E为射线CA上一点,∠ADE=∠AED.设∠BAD=α,∠CDE=β.(1)如图(1),①若∠BAC=42°,∠DAE=30°,则α=12°,β=6°.②写出α与β的数量关系,并说明理由;(2)如图(2),当E点在CA的延长线上时,其它条件不变,写出α与β的数量关系,并说明理由.【考点】三角形综合题.【分析】(1)①直接求α的度数,根据三角形的内角和与等腰三角形的性质求∠ACB和∠AED的度数,再根据外角定理求出β的度数;②α=2β,理由是:设∠BAC=x°,∠DAE=y°,则α=x°﹣y°,同理求出∠ACB=和∠AED=,利用外角定理得:β=∠AED﹣∠ACB,代入可得结论;(2)如图(2),2β=180°+α,理由是:设∠BAC=x°,∠DAE=y°,根据图形先表示α=x°﹣(180°﹣y°)=x°﹣180°+y°,同理得∠ACB和∠AED的度数,在△EDC中利用外角定理列式可得结论.【解答】解:(1)如图(1),①∵∠BAC=42°,∠ACB=∠ABC,∴∠ABC=∠ACB==69°,∵∠DAE=30°,∠ADE=∠AED,∴∠ADE=∠AED=75°,∵∠AED是△DEC的一个外角,∴∠AED=∠EDC+∠ACB,∴∠EDC=∠AED﹣∠ACB=75°﹣69°=6°,即β=6°,α=∠BAC﹣∠DAE=42°﹣30°=12°;故答案为:12°,6°;②α=2β,理由是:设∠BAC=x°,∠DAE=y°,则α=x°﹣y°,∵∠ACB=∠ABC,∴∠ACB=,∵∠ADE=∠AED,∴∠AED=,∴β=∠AED﹣∠ACB=﹣==,∴α=2β;(2)如图(2),2β=180°+α,理由是:设∠BAC=x°,∠DAE=y°,α=x°﹣(180°﹣y°)=x°﹣180°+y°,∵∠ACB=∠ABC,∴∠ACB=,∵∠ADE=∠AED,∴∠AED=,∴∠EDB是△EDC的一个外角,∴∠EDB=∠AED+∠ACB,∴180°﹣β=+,2β=x°+y°,2β=180°+α.【点评】本题是三角形的综合题,难度适中,考查了三角形的内角和、等腰三角形的性质、外角定理;本题的解题思路为:①先表示两个等腰三角形两个底角的度数,②利用外角定理列式,将α、β代入即可.。
