必修2综合测试题

合集下载

高中生物综合测试卷(含解析)新人教版必修2-新人教版高中必修2生物试题

综合测试卷一、选择题(每小题2分，共60分)1．孟德尔遗传规律包括分离定律和自由组合定律。

下列相关叙述正确的是( )A．自由组合定律是以分离定律为基础的B．分离定律不能用于分析两对等位基因的遗传C．自由组合定律也能用于分析一对等位基因的遗传D．基因的分离发生在配子形成的过程中，基因的自由组合发生在合子形成的过程中答案 A2．在豌豆杂交实验中，紫花和白花由一对等位基因控制，紫花植株与白花植株杂交，F2中紫花和白花的比为787∶277，出现该比值的根本原因是( )A．F1产生配子时，显性基因和隐性基因彼此分离且比例为1∶1B．雌雄配子的结合是随机的C．显性遗传因子对隐性遗传因子有显性作用D．F1自交，后代出现性状分离答案 A解析F2中紫花∶白花＝787∶277≈3∶1，说明这对相对性状的遗传遵循分离定律，根本原因是F1产生配子时，显性基因和隐性基因彼此分离且比例为1∶1。

3．果蝇的灰身(A)与黑身(a)、大脉翅(B)与小脉翅(b)是两对相对性状，相关基因位于常染色体上且独立遗传。

灰身大脉翅的雌蝇和灰身小脉翅的雄蝇杂交，子代中47只为灰身大脉翅，49支为灰身小脉翅，17只为黑身大脉翅，15只为黑身小脉翅。

下列说法错误的是( ) A．亲本中雌雄果蝇的基因型分别为AaBb和AabbB．亲本雌蝇产生卵的基因组成种类数为4种C．子代中表现型为灰身大脉翅个体的基因型有4种D．子代中灰身小脉翅雌雄个体相互交配的子代中会出现黑身小脉翅个体答案 C解析灰身大脉翅(A_B_)雌蝇和灰身小脉翅(A_bb)雄蝇杂交，后代灰身∶黑身＝3∶1，大脉翅∶小脉翅＝1∶1，因此可推断亲本中雌雄果蝇的基因型分别为AaBb和Aabb，A正确；亲本雌蝇的基因型为AaBb，因此它可产生基因组成为AB、Ab、aB和ab4种类型的卵细胞，B 正确；由于亲本的基因型为AaBb和Aabb，所以它们的后代中灰身A_大脉翅B_的基因型有AABb、AaBb两种基因型，C错误；子代中灰身小脉翅雌雄果蝇的基因型均为AAbb和Aabb，因此这些个体相互交配，后代中会出现aabb黑身小脉翅的个体，D正确。

高中化学必修一必修二综合测试题和解答

高中化学必修一必修二综合测试题和解答专业技术资料分享：高中化学必修一/必修二综合测试题本文为高中化学综合测试题，时间为90分钟，总分为100分。

单项选择题：1.“垃圾是放错了位置的资源”。

生活中废弃的铁锅、铝制易拉罐、铜导线等可以归为一类加以回收，它们属于金属或合金。

2.近日，一批湖南大米中重金属元素镉超标事件被媒体广泛报道。

下列有关镉(Cd)的说法正确的是：原子序数为48.3.下列物质水解的最终产物中含有葡萄糖的是淀粉。

4.可以用来鉴别甲烷和乙烯两种气体的试剂是溴水。

5.下列可用排水法收集的气体是NH3.6.常温下，将铜片投入到稀盐酸中，会产生气体。

7.有NaCl、MgCl2、A1C13三种溶液，只用一种试剂就可以把它们鉴别开来，这种试剂是氨水。

8.下列物质既含离子键又含共价键的是CaCl2.9.在无色透明的强酸性溶液中，能大量共存的一组离子是Cu、SO4ˉ、NO3ˉ+2.10.下列反应的离子方程式书写正确的是铁溶于盐酸中：Fe + 2H+ == Fe2+ + H2↑。

11.下列有机物互为同分异构体的是正丁烷和异丁烷。

本文为高中化学综合测试题，涉及多个知识点，包括化学元素、化学反应、有机物等。

通过选择题的形式，考察学生对这些知识点的掌握情况。

12.下列有机物的说法中错误的是：A。

CH4和Cl2反应可生成CCl4.B。

石油的主要成分是碳氢化合物。

C。

苯能使酸性KMnO4溶液褪色。

D。

乙醇能与金属钠反应。

13.下列有关表示正确的是：A。

CH4的比例模型：四个氢原子围绕着一个碳原子。

B。

HCl的电子式：H:Cl。

C。

S的结构示意图：S。

D。

Fe2(SO4)3的电离方程式：Fe2(SO4)3 → 2Fe3+ + 3SO42-。

14.下列有关离子(或物质)的检验及结论正确的是：A。

用一束光照射区别氢氧化铁胶体和氯化铁溶液，都会出现XXX现象。

B。

向无色溶液中加入BaCl2溶液有白色沉淀出现，则溶液中一定含有SO42-。

高一数学必修测试题及答案

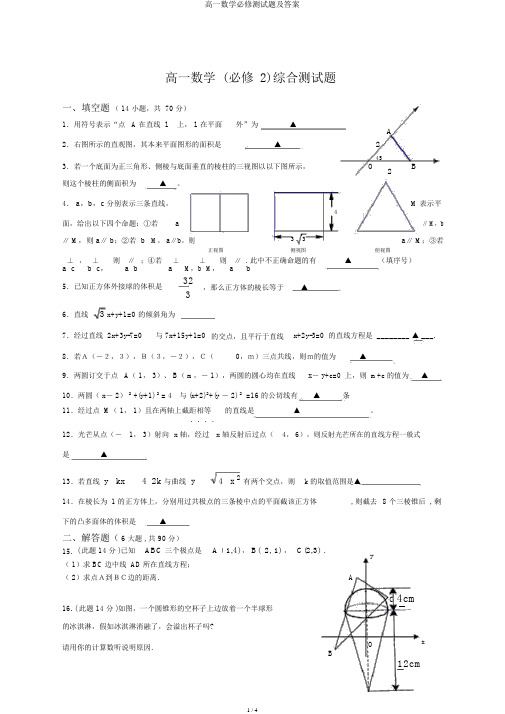
高一数学 (必修 2)综合测试题一、填空题（ 14 小题，共 70 分）1．用符号表示“点 A 在直线l上， l在平面外”为▲A 2．右图所示的直观图，其本来平面图形的面积是▲23．若一个底面为正三角形、侧棱与底面垂直的棱柱的三视图以以下图所示，O 45B2则这个棱柱的侧面积为▲。

4．a，b，c分别表示三条直线，4M表示平面，给出以下四个命题：①若a∥ M，b ∥ M，则 a∥ b；②若 b M， a∥b，则33a∥ M；③若正视图侧视图俯视图⊥，⊥则∥；④若⊥⊥M，则a∥ . 此中不正确命题的有▲（填序号）a cb c， a b a M，b b5．已知正方体外接球的体积是32，那么正方体的棱长等于▲36．直线 3 x+y+1=0的倾斜角为7．经过直线 2x+3y-7=0与 7x+15y+1=0的交点，且平行于直线x+2y-3=0 的直线方程是 ________ ▲ ___. 8．若Ａ（－２，３），Ｂ（３，－２），Ｃ（0，ｍ）三点共线，则ｍ的值为▲9．两圆订交于点 A（ 1， 3）、 B（ m，－ 1），两圆的圆心均在直线x－ y+c=0上，则 m+c的值为▲10．两圆（ x― 2）2 +(y+1) 2 = 4与 (x+2)2+(y ― 2) 2 =16 的公切线有▲条11．经过点 M（ 1， 1）且在两轴上截距相等的直线是▲。

．．．．12．光芒从点（―1， 3）射向x 轴，经过x 轴反射后过点（4， 6），则反射光芒所在的直线方程一般式是▲13．若直线y kx 4 2k 与曲线y4x 2有两个交点，则k 的取值范围是▲14．在棱长为 1 的正方体上，分别用过共极点的三条棱中点的平面截该正方体, 则截去8 个三棱锥后 , 剩下的凸多面体的体积是▲二、解答题（ 6 大题 , 共 90 分）15.( 此题 14 分 )已知ABC 三个极点是 A (1,4)， B( 2, 1) ，C(2,3)．y（ 1）求 BC边中线 AD所在直线方程；（ 2）求点Ａ到ＢＣ边的距离．AC 4cm16.( 此题 14 分 )如图，一个圆锥形的空杯子上边放着一个半球形的冰淇淋，假如冰淇淋消融了，会溢出杯子吗?请用你的计算数听说明原因．O xB12cm17． (本 15 分 )如， ABCD是正方形， O是正方形的中心，PO 底面 ABCD， E 是 PC的中点．P求：（ 1）PA∥平面 BDE；（2）平面 PAC 平面 BDE．18． (本15 分 )已知直 l 点P（1，1），并与直 l 1：x E－ y+3=0 和l2：2x+y － 6=0 分交于点A、B，若段 AB 被点 P 平分，求：（Ⅰ）直l 的方程；D C （Ⅱ）以 O心且被l 截得的弦8 5的的方程．O5A B19．( 本16 分) 已知数a足 0<a<2，直l1：ax－ 2y－ 2a+4=0 和l2：2x+a2y－ 2a2－ 4=0 与两坐成一个四形。

高中化学必修二综合测试题及解答

高中化学必修二综合测试题时间90分钟，总分100分。

一、选择题〔共25题，每题2分，共50分〕1．海水是巨大的化学资源库，以下有关海水综合利用说法正确的选项是()。

A．海水的淡化，只需经过化学变化就可以得到B．海水蒸发制海盐的过程中只发生了化学变化C．从海水中可以得到NaCl，电解熔融NaCl可制备金属NaD．利用海水、铝、空气的航标灯的原理是将电能转化为化学能2．32He可以作为核聚变材料。

以下关于32He的表达中，正确的选项是( )。

A．质子数为2 B．电子数为3C．中子数为2 D．质量数为23．目前世界上最重要的气态化石燃料是( )。

A．水煤气B．一氧化碳C．天然气D．氢气4．以下物质中，属于天然有机高分子化合物的是( )。

A．葡萄糖B．蔗糖C．淀粉D．油脂5．鉴别某种白色织物是否是蚕丝制品，可选用的方法是( )。

A．滴加盐酸B．滴加浓硫酸C．滴加氢氧化钠溶液D．滴加浓硝酸6．卤族元素随着原子序数的增大，以下递变规律正确的选项是( )。

A．单质熔、沸点逐渐降低B．单质的氧化性逐渐增强C．原子半径逐渐增大D．气态氢化物稳定性逐渐增强7．以下金属中，通常采用热复原法冶炼的是( )。

A．Na B．Al C．Fe D．Ag 8．以下关于甲烷分子结构的表达中，正确的选项是( )。

A．甲烷分子中C、H原子间是离子键B．甲烷分子的空间结构是正方体C．甲烷的结构式为CH4D．甲烷分子中4个碳氢键完全相同9．运用元素周期律分析以下推断，其中错误的选项是()。

A．铍是一种轻金属，它的氧化物的水化物可能具有两性B ．砹单质是一种有色固体，砹化氢很不稳定C ．硫酸锶难溶于水D ．硒化氢(H 2Se )是无色、有毒、比H 2S 稳定的气体 10．废电池必须进行集中处理的首要原因是( )。

A ．充电后可再使用B ．回收利用石墨电极和金属材料C ．防止电池中汞、镉和铅等重金属离子污染土壤和水源D ．防止电池中的电解质溶液腐蚀其他物品11．山梨酸(CH 3—CH ＝CH —CH ＝CH —COOH )是一种常用的食品防腐剂。

2022年高中数学选择性必修第二册综合测试卷

2022年高中数学选择性必修第二册综合测评(满分:150分;时间:120分钟)一、单项选择题(本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.已知等差数列{a n}的公差d≠0,且a3+a6+a9=18,若a n=6,则n为()A.12B.8C.6D.42.已知函数f(x)=aln x+2,f'(e)=2,则a的值为()A.-1B.1C.2eD.e23.在等比数列{a n}中,a2+a3=1,a4+a5=2,则a6+a7=()A.2B.2√2C.4D.4√24.我国古代数学名著《九章算术》中有如下问题:“今有女子善织,日自倍,五日织五尺,问日织几何?”意思是:“一女子善于织布,每天织出的布都是前一天的2倍,已知她5天共织布5尺,问这女子每天分别织布多少?”根据上述已知条件,该女子第3天所织布的尺数为()A.1031B.2031C.54D.525.在等差数列{a n}中,首项a1>0,公差d≠0,前n项和为S n(n∈N*),且满足S3=S15,则S n 的最大项为()A.S7B.S8C.S9D.S106.已知函数f(x)=e-x(cos x+sin x),记f'(x)是f(x)的导函数,将满足f'(x)=0的所有正数x从小到大排成数列{x n},n∈N*,则f(x n)=()A.(-1)n e-(n+1)πB.(-1)n+1e-nπC.(-1)n e-nπD.(-1)n+1e-(n+1)π7.设奇函数f(x)在R 上存在导函数f'(x),且在(0,+∞)上f'(x)<x 2,若f(1-m)-f(m)≥13[(1-m)3-m 3],则实数m 的取值范围为( )A.[-12,12]B.(-∞,-12]∪[12,+∞)C.(-∞,-12]D.[12,+∞)8.已知定义在R 上的函数y=f(x)满足:函数y=f(x-1)的图象关于直线x=1对称,且当x ∈(-∞,0)时,有f(x)+xf'(x)<0(f'(x)是函数f(x)的导函数)成立.若a=(sin 12)·f (sin 12),b=(ln 2)·f(ln 2),c=(log 1214)·f (log 1214),则a,b,c 的大小关系是(深度解析)A.a>b>cB.b>a>cC.c>a>bD.a>c>b二、多项选择题(本大题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求,全部选对的得5分,部分选对的得3分,有选错的得0分)9.设等差数列{a n }的首项为a 1,公差为d,其前n 项和为S n ,已知S 16>0,S 17<0,则下列结论正确的是( ) A.a 1>0,d<0 B.a 8+a 9>0C.S 8与S 9均为S n 的最大值D.a 9<010.已知函数f(x)=e x -ln x-2,则下列说法正确的是( ) A. f(x)有且仅有一个极值点 B. f(x)有零点C.若f(x)的极小值点为x 0,则0< f(x 0)<12D.若f(x)的极小值点为x 0,则12< f(x 0)<111.已知数列{a n}为等差数列,a1=1,且a2,a4,a8是一个等比数列中的相邻三项,记b n=a n q a n(q≠0,1),则{b n}的前n项和S n可以是()A.nB.nqC.q+nq n+1-nq n-q n(1-q)D.q+nq n+2-nq n+1-q n+1 (1-q)212.已知f(x)=e x·x3,则下列结论正确的是()A.f(x)在R上单调递增B.f(log52)<f(e-12)<f(lnπ)C.方程f(x)=-1有实数根D.存在实数k,使得方程f(x)=kx有4个实数根三、填空题(本大题共4小题,每小题5分,共20分.将答案填在题中横线上)13.在等差数列{a n}中,已知a3=4,a6=10,则a10-a7=.14.已知数列{a n}的前n项和为S n,若a1=1,a n+1=3S n(n∈N*),则a6=.15.已知函数f(x)=xg(x),曲线y=f(x)在点(1,f(1))处的切线方程是x-y-1=0,则曲线y=g(x)在点(1,g(1))处的切线方程是.16.已知函数f(x)=(4-x2)(x2+ax+b)的图象关于直线x=1对称,则a+b=,f(x)的最大值为.(第一空2分,第二空3分)四、解答题(本大题共6小题,共70分.解答应写出必要的文字说明、证明过程或演算步骤)17.(本小题满分10分)在等差数列{a n}中,a2=3,a5=6.(1)求数列{a n}的通项公式;(2)设b n=1,求数列{b n}的前n项和S n.a n a n+118.(本小题满分12分)已知函数f(x)=e x(x-1)-1e a x2,a<0.2(1)求曲线y=f(x)在点(0,f(0))处的切线方程;(2)求函数f(x)的极小值;(3)求函数f(x)的零点个数.}的前n项19.(本小题满分12分)已知数列{a n}是首项为正数的等差数列,数列{1a n a n+1.和为n2n+1(1)求数列{a n}的通项公式;(2)设b n=(a n+1)·2a n,求数列{b n}的前n项和T n.20.(本小题满分12分)某公司一下属企业从事某种高科技产品的生产.该企业第一年年初有资金2000万元,将其投入生产,到当年年底资金增长了50%.预计以后每年资金年增长率与第一年的相同.公司要求企业从第一年开始,每年年底上缴资金d万元,并将剩余资金全部投入下一年生产.设第n年年底企业上缴资金后的剩余资金为a n 万元.(1)用d表示a1,a2,并写出a n+1与a n的关系式;(2)若公司希望经过m(m≥3)年使企业的剩余资金为4000万元,试确定企业每年上缴资金d的值(用m表示).21.(本小题满分12分)如图,有一块半径为20米,圆心角∠AOB=2π3的扇形展示台,该展示台分为四个区域:三角形OCD,弓形CMD,扇形AOC 和扇形BOD(其中∠AOC=∠BOD).某次菊花展依次在这四个区域摆放:泥金香、紫龙卧雪、朱砂红霜、朱砂红霜.预计这三种菊花展示带来的日效益分别是:泥金香50元/米2,紫龙卧雪30元/米2,朱砂红霜40元/米2.(1)设∠COD=θ,试建立日效益总量y 关于θ的函数关系式; (2)试探求θ为何值时,日效益总量达到最大值.22.(本小题满分12分)已知函数f(x)=ln(2x+a)(x>0,a>0),曲线y=f(x)在点(1,f(1))处的切线在y 轴上的截距为ln 3-23.(1)求a 的值;(2)讨论函数g(x)=f(x)-2x(x>0)和h(x)=f(x)-2x 2x+1(x>0)的单调性;(3)设a 1=25,a n+1=f(a n ),求证:5−2n+12<1a n-2<0(n ≥2).答案全解全析一、单项选择题1.C 由a 3+a 6+a 9=18,得3a 6=18,∴a 6=6,又a n =6,∴a n =a 6,又d ≠0,∴{a n }为单调数列,∴n=6.故选C. 2.C 由f(x)=aln x+2得, f'(x)=ax ,∴f'(e)=ae=2,解得a=2e.故选C.3.C 设等比数列{a n }的公比为q,则a 4+a 5a 2+a 3=a 2q 2+a 3q 2a 2+a 3=q 2=2, ∴a 6+a 7=a 4q 2+a 5q 2=(a 4+a 5)q 2=2×2=4. 故选C.4.B 设该女子每天分别织布的尺数构成数列{a n },则数列{a n }为等比数列,设其首项为a 1,公比为q,前n 项和为S n .则q=2,S 5=5, ∴5=a 1(1-25)1−2,解得a 1=531,∴a 3=531×22=2031.故选B.5.C 由S 3=S 15得,a 4+a 5+…+a 15=0, ∴6(a 9+a 10)=0,即a 9+a 10=0. 又a 1>0,∴a 9>0,a 10<0, ∴S n 的最大项为S 9.故选C.6.C f'(x)=-e -x (cos x+sin x)+e -x (-sin x+cos x)=-2e -x sin x.令f'(x)=0,得-2e -x sin x=0,解得x=kπ,k ∈Z,从而x n =nπ,n ∈N *, f(x n )=(-1)n e -nπ.因为f(x n+1)f(x n )=-e -π,所以数列{f(x n )}是公比为-e -π的等比数列,其首项f(x 1)=(-1)1e -π=-e -π.其通项公式为f(x n )=(-1)n e -nπ,故选C.7.D 由f(1-m)-f(m)≥13[(1-m)3-m 3]得, f(1-m)-13(1-m)3≥f(m)-13m 3,构造函数g(x)=f(x)-13x 3,则g'(x)=f'(x)-x 2<0.故g(x)在(0,+∞)上单调递减,由函数f(x)为奇函数可得g(x)为奇函数,故g(x)在R 上单调递减, 因此原不等式可化为1-m ≤m,解得m ≥12,故选D.8.A 由函数y=f(x-1)的图象关于直线x=1对称知,f(x)是偶函数,设g(x)=x ·f(x),则g(x)是奇函数,且当x<0时,g'(x)=f(x)+x ·f'(x)<0,即g(x)是减函数,∴当x>0时,g(x)也是减函数.又0<sin 12<12<ln 2<lo g 1214=2,∴g (sin 12)>g(ln 2)>g (log 1214).即(sin 12)f (sin 12)>(ln 2)f(ln 2)>(log 1214)f (log 1214). ∴a>b>c. 故选A.解题模板构造函数,利用单调性解决比较大小的问题中,掌握一些基本的大小关系可帮助解题,如本题中,当0<x<π2时,sin x<x,ln 2>ln √e =12等.二、多项选择题 9.ABD ∵S 16=16(a 1+a 16)2>0,∴a 8+a 9=a 1+a 16>0,∴B 正确. 又S 17=17(a 1+a 17)2=17a 9<0,∴a 9<0,∴a 8>0,∴d=a 9-a 8<0,∴a 1>0,∴A 、D 正确.易知S 8是S n 的最大值,S 9不是S n 的最大值,∴C 错误.故选ABD.10.AC 由题意得, f(x)的定义域为(0,+∞),且f'(x)=e x -1x,设h(x)=f'(x),则h'(x)=e x +1x>0,∴h(x)在(0,+∞)上单调递增, 又h (12)=e 12-2=√e -2<0,h(1)=e 1-1>0,∴h(x)存在唯一零点,设为x 0, 当0<x<x 0时, f'(x)<0, f(x)单调递减, 当x>x 0时, f'(x)>0, f(x)单调递增, ∴f(x)有唯一极小值点x 0,∴A 正确. 令f'(x 0)=e x 0-1x 0=0,得e x 0=1x 0,∴x 0=ln 1x 0=-ln x 0.∴f(x 0)=e x 0-ln x 0-2=1x 0+x 0-2≥2√1x 0·x 0-2=0(当且仅当x 0=1时等号成立),又12<x 0<1,∴f(x 0)>0,即[f(x)]min >0, ∴f(x)无零点,∴B 错误. 由f(x 0)=1x 0+x 0-2,12<x 0<1,可设g(x)=1x+x-2,则g'(x)=-1x+1.当12<x<1时,g'(x)<0,∴g(x)在(12,1)上单调递减.∴g(1)<g(x)<g (12),即0<f(x 0)<12, ∴C 正确,D 错误.故选AC.11.BD 设等差数列{a n }的公差为d,由题意得a 42=a 2a 8,即(1+3d)2=(1+d)(1+7d),∴d 2-d=0,解得d=0或d=1. 当d=0时,a n =a 1=1, ∴b n =a n q a n =q,∴{b n }的前n 项和为nq,B 正确. 当d=1时,a n =n, ∴b n =n ·q n (q ≠0,1). ∴S n =1×q+2×q 2+…+nq n ,∴qS n =1×q 2+…+(n-1)q n +n ·q n+1, ∴(1-q)S n =q+q 2+…+q n-nq n+1=q(1-q n)1−q-nqn+1=q -qn+1+nq n+2-nq n+11−q.又q ≠1,∴S n =q+nq n+2-nq n+1-q n+1(1-q)2,D 正确.故选BD.12.BCD f(x)=e x ·x 3, ∴f'(x)=e x (x 3+3x 2). 令f'(x)=0,得x=0或x=-3. 当x<-3时, f'(x)<0, f(x)单调递减, 当x>-3时, f'(x)≥0, f(x)单调递增,A 错误. 又0<log 52<12<e -12<1<ln π,∴f(log 52)< f(e -12)< f(ln π),B 正确. ∵f(0)=0, f(-3)=e -3·(-3)3=-(3e)3<-1,∴f(x)=-1有实数根,C 正确. 设f(x)=kx,显然x=0是方程的根, 当x ≠0时,k=f(x)x=e x ·x 2,设g(x)=e x ·x 2,则g'(x)=x(x+2)e x ,令g'(x)=0,得x=0或x=-2.当x 发生变化时,g'(x),g(x)的变化情况如下表:x (-∞,-2) -2 (-2,0) 0 (0,+∞) g'(x) + 0 - 0 + g(x)↗4e 2↘↗画出y=g(x)的大致图象,如图,∴当0<k<4e2时,g(x)=k 有3个实数根,∴D 正确.故选BCD.三、填空题 13.答案 6解析设等差数列{a n }的公差为d.则3d=a 6-a 3=6,解得d=2. 所以a 10-a 7=3d=6. 14.答案 768解析由a n+1=3S n ,得S n+1-S n =3S n ,即S n+1=4S n ,又S 1=a 1=1,所以数列{S n }是首项为1,公比为4的等比数列,所以S n =4n -1,所以a 6=S 6-S 5=45-44=3×44=768. 15.答案 x-y-1=0解析 ∵f(x)=xg(x),∴f'(x)=g(x)+xg'(x).∵曲线y=f(x)在(1, f(1))处的切线方程是x-y-1=0, ∴{1−f(1)-1=0,f'(1)=1,∴{f(1)=0,f'(1)=1.∴{f(1)=1×g(1)=0,f'(1)=g(1)+1×g'(1)=1,解得{g(1)=0,g'(1)=1.则曲线y=g(x)在(1,g(1))处的切线方程为y-0=1×(x-1),即x-y-1=0, 即切线方程为x-y-1=0. 16.答案 -4;16解析由4-x 2=0可得x=2或x=-2,即2,-2是函数f(x)的零点,∵f(x)=(4-x 2)(x 2+ax+b)的图象关于直线x=1对称,且(2,0),(-2,0)关于x=1对称的点分别为(0,0),(4,0),∴0,4也是函数f(x)的零点, ∴0,4是x 2+ax+b=0的根,∴b=0,a=-4,∴a+b=-4, ∴f(x)=(4-x 2)(x 2-4x),∴f'(x)=-4(x-1)(x 2-2x-4), 令f'(x)=0,得x=1或x=1-√5或x=1+√5.当x>1+√5或1-√5<x<1, f'(x)<0, f(x)单调递减, 当1<x<1+√5或x<1-√5时, f'(x)>0, f(x)单调递增.又当x →∞时, f(x)<0, f(1+√5)=f(1-√5)=16,∴f(x)的最大值为16. 四、解答题17.解析 (1)设等差数列{a n }的首项为a 1,公差为d. ∵a 2=3,a 5=6,∴{a 1+d =3,a 1+4d =6,解得{a 1=2,d =1,(2分) ∴a n =a 1+(n-1)d=n+1.(4分) (2)由(1)知a n =n+1,∴b n =1a n a n+1=1(n+1)(n+2)=1n+1-1n+2,(6分)∴S n =b 1+b 2+…+b n =12-13+13-14+…+1n+1-1n+2(8分)=12-1n+2=n2(n+2).(10分)18.解析 (1)由已知得, f(x)的定义域为R, f'(x)=e x (x-1)+e x -e a x=x(e x -e a ), f'(0)=0. 又f(0)=-1,∴切点坐标为(0,-1).∴曲线y=f(x)在点(0,-1)处的切线方程为y=-1.(4分) (2)由(1)知f'(x)=x(e x -e a ). 令f'(x)=0,得x=0或x=a(a<0).当x 发生变化时, f'(x), f(x)的变化情况如下表:x (-∞,a) a (a,0) 0 (0,+∞) f'(x) + 0 - 0 + f(x)↗极大值↘极小值↗∴f(x)在(-∞,a),(0,+∞)上单调递增,在(a,0)上单调递减.∴f(x)在x=0处取得极小值,且极小值为f(0)=-1.(8分)(3)由(2)知f(x)的极大值为f(a)=e a (a-1)-12e a a 2=(a -1-12a 2)e a <0(a<0),f(0)=-1<0, f(2)=e 2-2e a . ∵a<0,∴0<e a <1,∴f(2)>0. ∴函数f(x)的零点个数为1.(12分)19.解析 (1)设等差数列{a n }的首项为a 1,公差为d, 令n=1,得1a 1a 2=13,所以a 1a 2=3.①(1分) 令n=2,得1a 1a 2+1a 2a 3=25,所以a 2a 3=15.②(3分)由①②得a 1=1,d=2,所以a n =2n-1.(5分) (2)由(1)知b n =2n ·22n-1=n ·4n , 所以T n =1·41+2·42+…+n ·4n ,所以4T n =1·42+…+(n-1)·4n +n ·4n+1,(7分) 两式相减,得-3T n =41+42+…+4n -n ·4n+1(9分) =4(1−4n )1−4-n ·4n+1=1−3n 3·4n+1-43,(11分)所以T n =3n -19·4n+1+49=4+(3n -1)·4n+19.(12分)20.解析 (1)由题意得a 1=2 000(1+50%)-d=3 000-d,a 2=a 1(1+50%)-d=32a 1-d=4 500-52d,(2分)a n+1=a n (1+50%)-d=32a n -d.(5分)(2)由(1)得a n =32a n-1-d=32·(32a n -2-d)-d=(32)2·a n-2-32d-d=…=(32)n -1a 1-d1+32+(32)2+…+(32)n -2,(7分)整理得a n =(32)n -1(3 000-d)-2d ·[(32)n -1-1]=(32)n -1(3 000-3d)+2d.(9分)由题意知a m =4 000,所以(32)m -1(3 000-3d)+2d=4 000,解得d=[(32)m -2]×1 000(32)m -1=1 000(3m -2m+1)3m -2m.(11分)故该企业每年上缴资金d 的值为1 000(3m -2m+1)3m -2m万元时,经过m(m ≥3)年企业的剩余资金为4 000万元.(12分) 21.解析 (1)依题意得,∠AOC=2π3-θ2=π3-θ2,(2分)则y=12×(π3-θ2)×202×40×2+12×202×sin θ×50+12×θ×202-12×202×sin θ×30 =16 000×(π3-θ2)+10 000sin θ+6 000θ-6 000sin θ =16 000π3+4 000sin θ-2 000θ,0<θ<2π3.(6分)(2)由(1)得,y'=4 000cos θ-2 000, 令y'=0,得cos θ=12,又0<θ<2π3,所以θ=π3,(8分)当0<θ<π3时,y'>0,当π3<θ<2π3时,y'<0,(10分)所以θ=π3是函数的极大值点,且唯一;所以当θ=π3时,日效益总量达到最大值.(12分)22.解析 (1)由f(x)=ln(2x+a), 得f'(x)=22x+a,因此f'(1)=22+a.(1分)又因为f(1)=ln(2+a),所以曲线y=f(x)在点(1, f(1)处的切线方程为y-ln(2+a)=22+a(x-1),即y=22+ax+ln(2+a)-22+a.(2分)由题意得,ln(2+a)-22+a=ln 3-23,易得a=1,符合上式.(3分) 令φ(a)=ln(2+a)-22+a(a>0),则φ'(a)=12+a +2(2+a)>0,所以φ(a)为单调递增函数,故a=1是唯一解.(4分) (2)由(1)可知,g(x)=ln(2x+1)-2x(x>0),h(x)=ln(2x+1)-2x 2x+1(x>0),则g'(x)=22x+1-2=-4x2x+1<0,所以g(x)=f(x)-2x(x>0)为单调递减函数.(6分) 因为h'(x)=22x+1-2(2x+1)=4x(2x+1)>0,所以h(x)=f(x)-2x 2x+1(x>0)为单调递增函数.(8分)(3)证明:由a 1=25,a n+1=f(a n )=ln(2a n +1),易得a n >0.所以5−2n+12<1a n-2等价于a n <2n5.(9分)由(2)可知,g(x)=f(x)-2x=ln(2x+1)-2x 在(0,+∞)上为单调递减函数. 因此,当x>0时,g(x)<g(0)=0,即f(x)<2x. 令x=a n-1(n ≥2),得f(a n-1)<2a n-1, 即a n <2a n-1.因此,当n ≥2时,a n <2a n-1<22a n-2<…<2n-1·a 1=2n5.所以5−2n+12<1a n-2成立.(10分)下面证明:1a n-2<0.由(2)可知,h(x)=f(x)-2x2x+1=ln(2x+1)-2x2x+1在(0,+∞)上为单调递增函数,因此,当x>0时,h(x)>h(0)=0, 即f(x)>2x 2x+1>0.因此1f(x)<12x+1,即1f(x)-2<12(1x-2). 令x=a n-1(n ≥2), 得1f(a n -1)-2<12(1an -1-2),即1a n-2<12(1an -1-2).当n=2时,1a n-2=1a 2-2=1f(a 1)-2=1f(25)-2=1ln1.8-2.因为ln 1.8>ln √3>ln √e =12,所以1ln1.8-2<0,所以1a 2-2<0.(11分)所以,当n ≥3时,1a n-2<12(1an -1-2)<12(1an -2-2)<…<12(1a 2-2)<0.所以,当n ≥2时,1a n-2<0成立. 综上所述,当n ≥2时,5−2n+12n<1a n-2<0成立.(12分)。

必修2综合测试

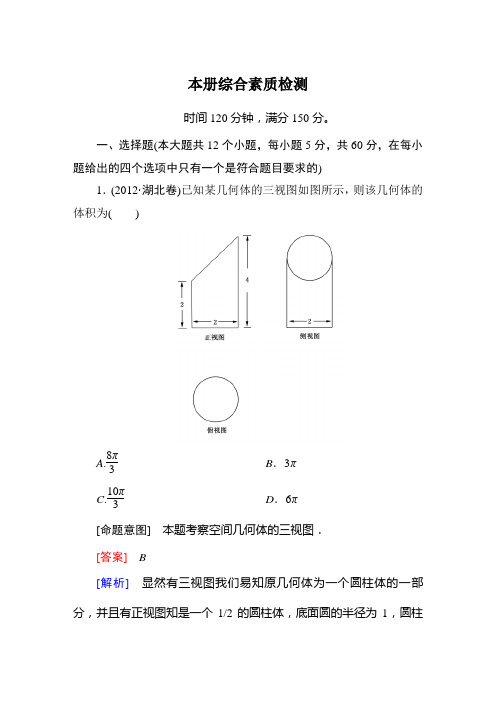
本册综合素质检测时间120分钟，满分150分。

一、选择题(本大题共12个小题，每小题5分，共60分，在每小题给出的四个选项中只有一个是符合题目要求的)1．(2012·湖北卷)已知某几何体的三视图如图所示，则该几何体的体积为( )A .8π3 B ．3π C .10π3D ．6π[命题意图] 本题考察空间几何体的三视图． [答案] B[解析] 显然有三视图我们易知原几何体为一个圆柱体的一部分，并且有正视图知是一个1/2的圆柱体，底面圆的半径为1，圆柱体的高为6，则知所求几何体体积为原体积的一半为3π.选B .2．已知正方体外接球的体积是323π，那么正方体的棱长等于( ) A ．2 2 B .223 C .423 D .433[答案] D[解析] 设正方体的棱长为a ，球的半径为R ，则43πR 3＝323π，∴R ＝2.又∵3a ＝2R ＝4，∴a ＝433.3．直线x －2y ＋1＝0关于直线x ＝1对称的直线方程是( ) A ．x ＋2y －1＝0 B ．2x ＋y －1＝0 C ．2x ＋y －3＝0 D ．x ＋2y －3＝0 [答案] D[解析] 在所求直线上任取一点P(x ，y)，则点P 关于直线x ＝1的对称点为P ′(2－x ，y)，且P ′在直线x －2y ＋1＝0上，即2－x －2y ＋1＝0，整理得x ＋2y －3＝0，故选D .4．在空间直角坐标系中，O 为坐标原点，设A(12，12，12)，B(12，12，0)，C(13，13，13)，则( )A ．OA ⊥AB B ．AB ⊥AC C ．AC ⊥BCD ．OB ⊥OC [答案] C[解析] |AB|＝12，|AC|＝36，|BC|＝66，因为|AC|2＋|BC|2＝|AB|2，所以AC ⊥BC.5．若P(2，－1)为圆(x －1)2＋y 2＝25的弦AB 的中点，则直线AB的方程为()A．x－y－3＝0 B．2x＋y－3＝0C．x＋y－1＝0 D．2x－y－5＝0[答案]A[解析]设圆(x－1)2＋y2＝25的圆心为C(1,0)，则AB⊥CP，∵k CP＝－1，∴k AB＝1，∴y＋1＝x－2，即x－y－3＝0，故选A.6．已知m，n是两条不同直线，α，β，γ是三个不同平面，下列命题中正确的是()A．若m∥α，n∥α，则m∥nB．若α⊥γ，β⊥γ，则α∥βC．若m∥α，m∥β，则α∥βD．若m⊥α，n⊥α，则m∥n[答案]D[解析]A中还可能m，n相交或异面，所以A不正确；B、C中还可能α，β相交，所以B、C不正确．很明显D正确．7．如图，在长方体ABCD－A1B1C1D1中，M，N分别是棱BB1，B1C1的中点，若∠CMN＝90°，则异面直线AD1和DM所成角为()A．30°B．45°C．60°D．90°[答案]D[解析]因为MN⊥DC，MN⊥MC，所以MN⊥平面DCM.所以MN⊥DM.因为MN∥AD1，所以AD1⊥DM.8．(2012－2013·山东济宁模拟)已知直线l过点(－2,0)，当直线l 与圆x2＋y2＝2x有两个交点时，其斜率k的取值范围是() A．(－22，22) B．(－2，2)C．(－24，24) D．(－18，18)[答案]C[解析]设直线l的斜率为k，则l的方程为y＝k(x＋2)，即kx－y＋2k＝0，由于l与圆x2＋y2＝2x有两个交点，则需满足圆心到直线的距离d＝|3k|k2＋1＜1，解得－24＜k＜24.9．在三棱柱ABC－A1B1C1中，各棱长相等，侧棱垂直于底面，点D是侧面BB1C1C的中心，则AD与平面BB1C1C所成角的大小是()A．30°B．45°C．60°D．90°[答案]C[解析]过A作AE⊥BC于点E，则易知AE⊥面BB1C1C，则∠ADE即为所求，又tan∠ADE＝AEDE＝3，故∠ADE＝60°.故选C.10．过点M(－2,4)作圆C：(x－2)2＋(y－1)2＝25的切线l，且直线l1：ax＋3y＋2a＝0与l平行，则l1与l间的距离是()A .85B .25C .285D .125[答案] D[解析] 因为点M(－2,4)在圆C 上，所以切线l 的方程为(－2－2)(x －2)＋(4－1)(y －1)＝25，即4x －3y ＋20＝0.因为直线l 与直线l 1平行，所以－a 3＝43，即a ＝－4，所以直线l 1的方程是－4x ＋3y －8＝0，即4x －3y ＋8＝0.所以直线l 1与直线l 间的距离为|20－8|42＋(－3)2＝125.故选D .11．点P(4，－2)与圆x 2＋y 2＝4上任一点连线的中点轨迹方程是( )A ．(x －2)2＋(y ＋1)2＝1B ．(x －2)2＋(y －1)2＝4C ．(x －4)2＋(y －2)2＝1D ．(x －2)2＋(y －1)2＝1 [答案] A[解析] 设圆上任意一点为(x 1，y 1)，中点为(x ，y)，则⎩⎨⎧x ＝x 1＋42y ＝y 1－22，⎩⎪⎨⎪⎧x 1＝2x －4y 1＝2y ＋2，代入x 2＋y 2＝4，得(2x －4)2＋(2y ＋2)2＝4，化简得(x －2)2＋(y ＋1)2＝1.12．设P(x ，y)是圆x 2＋(y ＋4)2＝4上任意一点，则(x －1)2＋(y －1)2的最小值为( ) A .26＋2 B .26－2 C ．5 D ．6[答案] B[解析] 如图，设A(1,1)，(x －1)2＋(y －1)2 ＝|PA|，则|PA|的最小值为|AC|－r ＝26－2.三、填空题(本大题共4小题，每小题5分，共20分)13．顺次连结A(1,0)，B(1,4)，C(3,4)，D(5,0)所得到的四边形绕y 轴旋转一周，所得旋转体的体积是________．[答案] 184π3[解析] 所得旋转体的上底、下底分别为3,5，高为4的圆台，去掉一个半径为1，高为4的圆柱．V 台＝13(9π＋9π×25π＋25π)×4＝196π3，V 柱＝4π，则V ＝V 台－V 柱＝184π3.14．经过点P(1,2)的直线，且使A(2,3)，B(0，－5)到它的距离相等的直线方程为________．[答案] 4x －y －2＝0或x ＝1[解析] x ＝1显然符合条件；当A(2,3)，B(0，－5)在所求直线同侧时，所求直线与AB 平行，∵k AB ＝4，∴y －2＝4(x －1)，即4x －y －2＝0.15．圆x 2＋y 2＋Dx ＋Ey ＋F ＝0关于直线l 1：x －y ＋4＝0与直线l 2：x ＋3y ＝0都对称，则D ＝________，E ＝________.[答案] 6 －2[解析] 由题设知直线l 1，l 2的交点为已知圆的圆心．由⎩⎪⎨⎪⎧ x －y ＋4＝0，x ＋3y ＝0，得⎩⎪⎨⎪⎧x ＝－3，y ＝1，所以－D 2＝－3，D ＝6，－E2＝1，E ＝－2.16．已知圆C 过点(1,0)，且圆心在x 轴的正半轴上，直线l ：y ＝x －1被圆C 所截得的弦长为22，则过圆心且与直线l 垂直的直线的方程为________．[答案] x ＋y －3＝0 [解析] 设圆心(a,0)(a ＞0)， ∴(|a －1|2)2＋(2)2＝|a －1|2.∴a ＝3.∴圆心(3,0)．∴所求直线方程为x ＋y －3＝0.四、解答题(本大题共6小题，共70分，解答应写出文字说明，证明过程或演算步骤)17．(本小题满分10分)(2011·课标全国高考，文18)如图，四棱锥P －ABCD 中，底面ABCD 为平行四边形，∠DAB ＝60°，AB ＝2AD ，PD ⊥底面ABCD.(1)证明PA⊥BD；(2)设PD＝AD＝1，求棱锥D－PBC的高．[解析](1)证明：因为∠DAB＝60°，AB＝2AD，由余弦定理得BD＝3AD.从而BD2＋AD2＝AB2，故BD⊥AD.又PD⊥底面ABCD，可得BD⊥PD.所以BD⊥平面PAD.故PA⊥BD.(2)如图，作DE⊥PB，垂足为E.已知PD⊥底面ABCD，则PD⊥BC.由(1)知BD⊥AD，又BC ∥AD ，所以BC ⊥BD. 故BC ⊥平面PBD ，所以BC ⊥DE. 则DE ⊥平面PBC.由题设知PD ＝1，则BD ＝3，PB ＝2. 根据DE·PB ＝PD·BD ，得DE ＝32，即棱锥D －PBC 的高为32.18．(本小题满分12分)如图，矩形ABCD 的两条对角线相交于点M(2,0)，AB 边所在直线的方程为x －3y －6＝0，点T(－1,1)在AD 边所在直线上．(1)求AD 边所在直线的方程； (2)求矩形ABCD 外接圆的方程．[解析] (1)因为AB 边所在直线的方程为x －3y －6＝0，且AD 与AB 垂直，所以直线AD 的斜率为－3.又因为点T(－1,1)在直线AD 上，所以AD 边所在直线的方程为y －1＝－3(x ＋1)，即3x ＋y ＋2＝0.(2)由⎩⎪⎨⎪⎧x －3y －6＝03x ＋y ＋2＝0，解得点A 的坐标为(0，－2)．因为矩形ABCD两条对角线的交点为M(2,0)，所以M 为矩形ABCD 外接圆的圆心．又r ＝|AM|＝(2－0)2＋(0＋2)2＝2 2.所以矩形ABCD 外接圆的方程为(x －2)2＋y 2＝8.19．(本小题满分12分)已知圆的半径为10，圆心在直线y ＝2x 上，圆被直线x －y ＝0截得的弦长为42，求圆的方程．[解析] 方法一：设圆的方程是(x －a)2＋(y －b)2＝10.因为圆心在直线y ＝2x 上，所以b ＝2a. ①解方程组⎩⎪⎨⎪⎧x －y ＝0，(x －a )2＋(y －b )2＝10，得2x 2－2(a ＋b)x ＋a 2＋b 2－10＝0，所以x 1＋x 2＝a ＋b ，x 1·x 2＝a 2＋b 2－102. 由弦长公式得2·(a ＋b )2－2(a 2＋b 2－10) ＝42，化简得(a －b)2＝4. ②解①②组成的方程组，得a ＝2，b ＝4，或a ＝－2，b ＝－4.故所求圆的方程是(x －2)2＋(y －4)2＝10，或(x ＋2)2＋(y ＋4)2＝10.方法二：设圆的方程为(x －a)2＋(y －b)2＝10，则圆心为(a ，b)，半径r ＝10，圆心(a ，b)到直线x －y ＝0的距离d ＝|a －b|2.由弦长、弦心距、半径组成的直角三角形得d 2＋(422)2＝r 2，即(a －b )22＋8＝10，所以(a －b)2＝4.又因为b ＝2a ，所以a ＝2，b ＝4，或a＝－2，b＝－4.故所求圆的方程是(x－2)2＋(y－4)2＝10，或(x＋2)2＋(y＋4)2＝10.20．(本小题满分12分)(2012·山东卷)如图，几何体E－ABCD是四棱锥，△ABD为正三角形，CB＝CD，EC⊥BD.(1)求证：BE＝DE；(2)若∠BCD＝120°，M为线段AE的中点，求证：DM∥平面BEC.[解析](1)设BD中点为O，连接OC，OE，则由BC＝CD知，CO⊥BD，又已知CE ⊥BD ，所以BD ⊥平面OCE.所以BD ⊥OE ，即OE 是BD 的垂直平分线，所以BE ＝DE.(2)取AB 中点N ，连接MN ，DN ，∵M 是AE 的中点，∴MN ∥BE ，∵△ABD 是等边三角形，∴DN ⊥AB.由∠BCD ＝120°知，∠CBD ＝30°，所以∠ABC ＝60°＋30°＝90°，即BC ⊥AB ，所以ND ∥BC ，所以平面MND ∥平面BEC ，故DM ∥平面BEC.21．(本小题满分12分)在平面直角坐标系xOy 中，已知圆C 1：(x －4)2＋(y －5)2＝4和圆C 2：(x ＋3)2＋(y －1)2＝4.(1)若直线l 1过点A(2,0)，且与圆C 1相切，求直线l 1的方程；(2)直线l 2的方程是x ＝52，证明：直线l 1上存在点P ，满足过P 的无穷多对互相垂直的直线l 3和l 4，它们分别与圆C 1和圆C 2相交，且直线l 3被圆C 1截得的弦长与直线l 4被圆C 2截得的弦长相等．[解析] (1)若直线斜率不存在，x ＝2符合题意；当直线l 1的斜率存在时，设直线l 1的方程为y ＝k(x －2)，即kx －y －2k ＝0，由条件得|4k －5－2k|k 2＋1＝2，解得k ＝2120，所以直线l 1的方程为x ＝2或y ＝2120(x －2)，即x ＝2或21x －20y －42＝0.(2)由题意知，直线l 3，l 4的斜率存在，设直线l 3的斜率为k ，则直线l 4的斜率为－1k ，设点P 坐标为(52，n)，互相垂直的直线l 3，l 4的方程分别为：y －n＝k(x －52)，y －n ＝－1k (x －52)，即kx －y ＋n －52k ＝0，－1k x －y ＋n ＋52k ＝0，根据直线l 3被圆C 1截得的弦长与直线l 4被圆C 2截得的弦长相等，两圆半径相等．由垂径定理得：圆心C 1到直线l 3与圆心C 2到直线l 4的距离相等．故有⎪⎪⎪⎪⎪⎪4k －5＋n －52k k 2＋1＝⎪⎪⎪⎪⎪⎪3k －1＋n ＋52k 1k 2＋1，化简得(52－n)k ＝212－n 或(12＋n)k ＝－n －12＝－(12＋n)．关于k 的方程有无穷多解，有12＋n ＝0，即n ＝－12，即直线l 2上满足条件的点P 是存在的，坐标是(52，－12)．22．(本小题满分12分)(2013·全国高考卷Ⅱ文科18题)如图已知三棱柱ABC －A 1B 1C 1中，D 、E 分别是AB 、BB 1的中点．(1)证明：BC1∥面A1CD1；(2)设AA1＝AC＝CB＝2，AB＝22，求三棱锥C－A1DE的体积．[解析](1)连结AC1交A1C于点F，则F为AC1的中点，又D是AB中点，连结DF，则BC1∥DF，因为DF⊂平面A1CD，BC1⊄平面A1CD，所以BC1∥平面A1CD.(2)因为ABC－A1B1C1是直三棱柱，所以AA1⊥CD，由已知AC ＝CB，D为AB中点，所以，CD⊥AB，又AA1∩AB＝A，于是CD⊥平面ABB1A1，由AA1＝AC＝CB＝2，AB＝22得，∠ACB＝90°，CD＝2，A1D＝6，DE＝3，A1E＝3，故A1D2＋DE2＝A1E2，即DE⊥A1D，所以VC－A1DE＝13×12×6×3×2＝1.。

高中数学必修一必修二综合测试题(含答案)

Q PC'B'A'C BA高中数学必修一必修二综合测试题（时间90分钟，满分150分）姓名___________________ 总分：________________ 一、选择题（本大题共10小题，每小题5分，共50分） 1．下面四个命题：①分别在两个平面内的两直线是异面直线；②若两个平面平行，则其中一个平面内的任何一条直线必平行于另一个平面； ③如果一个平面内的两条直线平行于另一个平面，则这两个平面平行；④如果一个平面内的任何一条直线都平行于另一个平面，则这两个平面平行．其中正确的命题是( )A ．①②B ．②④C ．①③D ．②③ 2．过点(1,3)P -且垂直于直线032=+-y x 的直线方程为（） A ．012=-+y x B ．052=-+y x C ．052=-+y x D ．072=+-y x 3．圆(x －1)2＋y 2＝1的圆心到直线y ＝33x 的距离是( )A ．12B ．32 C ．1 D ．34．设0<a <1，函数f (x )＝log a (a 2x －2a x －2)，则使f (x )<0的x 的取值范围是( )A ．(－∞，0)B ．(0，＋∞)C ．(－∞，log a 3)D ．(log a 3，＋∞)5．设y1＝40.9，y2＝80.48，y3＝(12)-1.5，则( )A ．y3>y1>y2B ．y2>y1>y3C ．y1>y2>y3D ．y1>y3>y26．圆x 2＋y 2－2x ＋4y －20＝0截直线5x －12y ＋c ＝0所得的弦长为8，则c 的值是( ) A ．10 B ．10或－68 C ．5或－34 D ．－68 7．已知0,0ab bc <<，则直线ax by c +=通过（）A ．第一、二、三象限B ．第一、二、四象限C ．第一、三、四象限D ．第二、三、四象限8．正方体ABCD —A 1B 1C 1D 1中，E 、F 分别是AA 1与CC 1的中点，则直线ED 与D 1F 所成角的大小是（）A ．15B ．13 C ．12D 39. 在三棱柱111ABC A B C -中，各棱长相等，侧掕垂直于底面，点D 是侧面11BB C C 的中心，则AD 与平面11BB C C 所成角的大小是 ( )A ．30B ．45C ．60D ．9010．如图:直三棱柱ABC —A 1B 1C 1的体积为V ，点P 、Q 分别在侧棱AA 1 和 CC 1上，AP=C 1Q ，则四棱锥B —APQC 的体积为( ) A ．2V B ．3V C ．4V D ．5V（10题）二、填空题（本大题共4小题，每小题5分，共20分）11．函数f (x )＝⎩⎪⎨⎪⎧log 12x ，x ≥12x ，x <1的值域为________．12．两圆221x y +=和22(4)()25x y a ++-=相切，则实数a 的值为13．已知集合U ＝{2,3,6,8}，A ＝{2,3}，B ＝{2,6,8}，则(∁U A )∩B ＝________.14.过点A (4,0)的直线l 与圆(x －2)2＋y 2＝1有公共点，则直线l 斜率的取值范围为三、解答题（本大题共6小题，共80分）15．(本小题满分10分)如图，在三棱柱ABC －A 1B 1C 1中，△ABC 与△A 1B 1C 1都为正三角形且AA 1⊥面ABC ，F 、F 1分别是AC ，A 1C 1的中点．求证：(1)平面AB 1F 1∥平面C 1BF ； (2)平面AB 1F 1⊥平面ACC 1A 1.（17题）16．(本小题满分12分)(1)定义在(－1,1)上的奇函数f (x )为减函数，且f (1－a )＋f (1－a 2)>0，求实数a 的取值范围．(2)定义在[－2,2]上的偶函数g (x )，当x ≥0时，g (x )为减函数，若g (1－m )<g (m )成立，求m 的取值范围．17．(本小题满分12分)如图，DC⊥平面ABC，EB∥DC，AC＝BC＝EB＝2DC＝2，∠ACB＝120°，P，Q分别为AE，AB的中点．（1）证明：PQ∥平面ACD；（2）求AD与平面ABE所成角的正弦值（17题）18．(本小题满分15分)已知圆C1：x2+y2－2x－4y+m=0，（1）求实数m的取值范围；（2）若直线l：x+2y－4=0与圆C相交于M、N两点，且OM⊥ON，求m的值。

人教版高中英语必修二综合测试卷

必修2综合测试卷测试时间：100分钟本卷总分：150分第一部分听力(共两节，满分30分)第一节(共5小题；每小题1.5分，满分7.5分)听下面5段对话。

每段对话后有一个小题，从题中所给的A、B、C三个选项中选出最佳选项，并标在试卷的相应位置。

听完每段对话后，你都有10秒钟的时间来回答有关小题和阅读下一小题。

每段对话仅读一遍。

1．Why didn't the man visit the Great Wall?A．He was ill.B．He had no time.C．He didn't know the way to it.2．What do you know from the conversation?A．The man had to work over time.B．Henry failed to meet the man.C．The man had a traffic accident.3．What is the woman going to do next?A．Pick up her boyfriend somewhere.B．Go to the cinema.C．Meet her boyfriend at a park.4．What is the man doing?A．Playing in the rain.B．Watching a football match.C．Listening to the radio.5．What can't European children do on the Internet?A．Play computer games.B．Listen to music.C．Make films.第二节(共15小题；每小题1.5分，满分22.5分)听下面5段对话或独白。

每段对话或独白后有几个小题，从题中所给的A、B、C三个选项中选出最佳选项，并标在试卷的相应位置。

高一数学必修一必修二综合测试题(有答案)

高一数学《必修1》《必修2》综合测试题一、选择题（共12小题；每小题5分，共60分）1. 已知全集R U =，集合}32{≤≤-=x x A ，}41{>-<=x x x B 或，则()B C A U ⋃（）A.{}42≤≤-x xB.}43{≥≤x x x 或C.}12{-<≤-x xD.}31{≤≤-x x2. 过点(1,0)且与直线x －2y －2＝0垂直的直线方程是( )A ．x －2y －1＝0B ．x －2y ＋1＝0C ．2x ＋y －2＝0D ．x ＋2y －1＝03. 圆台的一个底面圆周长是另一个底面圆周长的3倍，母线长为3，圆台的侧面积为84π，则圆台较小底面圆的半径为( )A ．3B ．5C ．6D ．74. 已知圆C ：x 2：y 2：4y ：0，直线l 过点P (0,1)，则 ( )A. l 与C 相交B. l 与C 相切C. l 与C 相离D. 以上三个选项均有可能5. 一个几何体的三视图如图所示（单位：m ），则该几何体的体积为（）3mA.π2B.38πC.π3D. 310π6. 已知，则函数的图象不经过（）A. 第一象限B. 第二象限C. 第三象限D. 第四象限7. 若直线2x y -=被圆22()4x a y -+=所截得的弦长为22,则实数a 的值为（） A. 0或4 B. 1或3 C. 2-或6 D. 1-或3 8. 在三棱柱ABCA 1B 1C 1中，各棱长相等，侧棱垂直于底面，点D 是侧面BB 1C 1C 的中心，则AD 与平面BB 1C 1C 所成角的大小是( ) A ．30° B ．45° C ．60° D ．90° 9. 若幂函数)(x f y =是经过点)33,3(，则此函数在定义域上是 ( ) A ．偶函数 B ．奇函数 C ．增函数 D ．减函数 10. 一个多面体的三视图如图所示，则该多面体的表面积为 A.321+ B.318+ C.18 D.21 11.若定义在R 上的偶函数()x f 满足)()2(x f x f =+，且当[]1,0∈x 时，x x f y x x f 3log )(,)(-==则函数的零点个数是（） A ．6个 B ．4个 C ．3个 D ．2个 12. 已知A(3,1)，B(－1,2)，若：ACB 的平分线方程为y ＝x ＋1，则AC 所在的直线方程为( ) A ．y ＝2x ＋4 B ．y ＝12x －3 C ．x －2y －1＝0 D ．3x ＋y ＋1＝001,1a b <<<-x y a b =+二、填空题（共4小题，每小题5分，共20分）13. 若直线1x y +=与圆222(0)x y r r +=>相切，则实数r 的值等于________.14. 在平面直角坐标系中，正三角形ABC 的边BC 所在直线的斜率是0，则AC ，AB 所在直线的斜率之和为________．15. 函数ax x y 22--=()10≤≤x 的最大值是2a ，则实数a 的取值范围是________ ．16.若圆C :x 2+y 2−2ax +b =0上存在两个不同的点A ,B 关于直线x −3y −2=0对称,其中b ∈N ,则圆C 的面积最大时,b = ．三、解答题（共6小题，共70分．解答时应写出必要的文字说明、证明过程或演算步骤）17. (10分)已知f (x )是定义在R 上的奇函数，当x ≥0时，f (x )＝2x －1.(1)求f (3)＋f (－1)；(2)求f (x )的解析式.18. (12分)如图，在三棱锥P ABC 中，PC ⊥底面ABC ，AB ⊥BC ，D ，E 分别是AB ，PB 的中点.(1)求证：DE ∥平面PAC ；(2)求证：AB ⊥PB ．19．(12分)直线l 1过点A (0,1)，l 2过点B (5,0)，如果l 1∥l 2且l 1与l 2的距离为5，求l 1，l 2的方程． 20.（12分）已知圆22:2240C x y mx ny ++++=，直线:10l x my -+=相交于A ：B 两点．：1）若交点为(1,2)A ，求m 及n 的值．：2）若直线l 过点(2,3)：60ACB ∠=︒，求22m n +的值． 21.（12分）已知直线:(1)(23)60m a x a y a -++-+=，:230n x y -+=. （1）当0a =时，直线l 过m 与n 的交点，且它在两坐标轴上的截距相反，求直线l 的方程；（2）若坐标原点O 到直线m 的距离为5，判断m 与n 的位置关系. 22.（12分）(1)圆C 与直线2x ＋y －5＝0切于点(2,1)，且与直线2x ＋y ＋15＝0也相切，求圆C 的方程． (2)已知圆C 和y 轴相切，圆心C 在直线x －3y ＝0上，且被直线y ＝x 截得的弦长为27，求圆C 的方程.高一数学答案一、选择题（共12小题；每小题5分，共60分）. 题号 1 2 3 4 5 6 7 8 9 10 11 12 答案 A C D A B A A C D A B C二、填空题：本大题共4小题，每小题5分，共20分，把答案填在题中横线上13.22 14.0 15.[－1,0] 16.0三、解答题（本大题共6小题，共70分）17.解：(1)∵f (x )是奇函数，∴f (3)＋f (－1)＝f (3)－f (1)＝23－1－2＋1＝6. .................4分(2)设x ＜0，则－x ＞0，∴f (－x )＝2－x －1，∵f (x )为奇函数，∴f (x )＝－f (－x )＝－2－x ＋1，.................8分∴f (x )＝⎩⎪⎨⎪⎧ 2x －1，x ≥0，－2－x ＋1，x ＜0. ........................10分18. 解 (1)证明：因为D ，E 分别是AB ，PB 的中点，所以DE ∥PA.又因为PA ⊂平面PAC ，DE ⊄平面PAC ，所以DE ∥平面PAC. .................6分(2)证明：因为PC ⊥底面ABC ，AB ⊂底面ABC ，所以PC ⊥AB.又因为AB ⊥BC ，PC ∩BC ＝C ，所以AB ⊥平面PBC ，又因为PB ⊂平面PBC ，所以AB ⊥PB. .................6分19．解: 若直线l 1，l 2的斜率都不存在，则l 1的方程为x ＝0，l 2的方程为x ＝5，此时l 1，l 2之间距离为5，符合题意；.................3分若l 1，l 2的斜率均存在，设直线的斜率为k ，由斜截式方程得直线l 1的方程为y ＝kx ＋1，即kx －y ＋1＝0，.................6分由点斜式可得直线l 2的方程为y ＝k (x －5)，即kx －y －5k ＝0，在直线l 1上取点A (0,1)，则点A 到直线l 2的距离d ＝|1＋5k |1＋k2＝5，∴25k 2＋10k ＋1＝25k 2＋25，∴k ＝125. ∴l 1的方程为12x －5y ＋5＝0，l 2的方程为12x －5y －60＝0. .................10分综上知，满足条件的直线方程为l 1：x ＝0，l 2：x ＝5或l 1：12x －5y ＋5＝0，l 2：12x －5y －60＝0. .......12分20.【解析】试题分析：（1）将点()1,2A 代入直线和圆方程，可解得1m =，114n =-．（2）将点()2,3代入直线方程得1m =．又由已知可判断ACB V 是等边三角形．所以有圆心到直线10x y -+=的距离233322d r n ==-，代入解得29n =，从而2210m n +=．试题解析：：1）将点()1,2A 代入直线10x my -+=：∴1210m -+=，解出1m =：再将()1,2A 代入圆2221240x y x ny ++⨯++=： ∴22122440n ++++=，解得114n =-： ∴1m =：114n =-：：2）将点()2,3代入直线10x my -+=：∴2310m -+=，解出1m =：又∵在ACB V 中，CA CB =且60ACB ∠=︒：∴ACB V 是等边三角形．∵圆()()222221230x x y ny nn ++++++-=：即()()22213x y n n +++=-：圆心()1,n --，半径23r n =-：其中圆心到直线10x y -+=的距离222113332211n d r n -++===-+：代入解出29n =：∴2210m n +=：21．（12分）【详解】试题分析：（1）联立360230.x y x y -++=⎧⎨-+=⎩，解得m 与n 的交点为（-21，-9），当直线l 过原点时，直线l 的方程为370x y -=；当直线l 不过原点时，设l 的方程为1x y b b+=-，将（-21，-9）代入得12b =-，解得所求直线方程（2）设原点O 到直线m 的距离为d ，则()()2265123a d a a -+==-++，解得：14a =-或73a =-，分情况根据斜率关系判断两直线的位置关系;试题解析：解：（1）联立360230.x y x y -++=⎧⎨-+=⎩，解得21,9,x y =-⎧⎨=-⎩即m 与n 的交点为（-21，-9）. 当直线l 过原点时，直线l 的方程为370x y -=；当直线l 不过原点时，设l 的方程为1x y b b+=-，将（-21，-9）代入得12b =-，所以直线l 的方程为120x y -+=，故满足条件的直线l 方程为370x y -=或120x y -+=.（2）设原点O 到直线m 的距离为d ，则()()2265123a d a a -+==-++，解得：14a =-或73a =-，当14a =-时，直线m 的方程为250x y --=，此时//m n ；当73a =-时，直线m 的方程为250x y +-=，此时m n ⊥.22.解： (1)设圆C 的方程为(x －a )2＋(y －b )2＝r 2.∵两切线2x ＋y －5＝0与2x ＋y ＋15＝0平行，∴2r ＝|15－(－5)|22＋12＝45，∴r ＝25， ∴|2a ＋b ＋15|22＋1＝r ＝25，即|2a ＋b ＋15|＝10①|2a ＋b －5|22＋1＝r ＝25，即|2a ＋b －5|＝10② 又∵过圆心和切点的直线与过切点的切线垂直，∴b －1a －2＝12③ 由①②③解得⎩⎨⎧ a ＝－2，b ＝－1.∴所求圆C 的方程为(x ＋2)2＋(y ＋1)2＝20.(2)设圆心坐标为(3m ，m )．∵圆C 和y 轴相切，得圆的半径为3|m |，∴圆心到直线y ＝x 的距离为|2m |2＝2|m |.由半径、弦心距、半弦长的关系得9m 2＝7＋2m 2，∴m ＝±1，∴所求圆C 的方程为(x －3)2＋(y －1)2＝9或(x ＋3)2＋(y ＋1)2＝9.。

必修2综合测试题(有答案)

必修2综合测试题考试时间：120分钟试卷满分：120分一、选择题:大题共10小题，每小题4，共40分，在每小题给出的四个选项中，只有一项是符合题目要求的.1．点(1，－1)到直线01=+-y x 的距离是A ．21 B ．23 C ．22 D ．223 2．过点(1，0)且与直线022=--y x 平行的直线方程是A ．012=--y xB ．012=+-y xC ．022=-+y xD ．012=-+y x3．下列直线中与直线012=++y x 垂直的一条是A ．012=--y xB ．012=+-y xC ．012=++y xD ．0121=-+y x 4．右图的正方体1111D C B A ABCD －中,异面直线B A 1与11D B 所成的角是 A.︒30 B.︒45 C.︒60 D.︒905．圆A : 012422=++++y x y x 与圆B : 016222=+-+y x y x －的位置关系是A ．相交B ．相离C ．相切D ．内含6．如图(1)、(2)、(3)、(4)为四个几何体的三视图，根据三视图可以判断这四个几何体依次分别为A ．三棱台、三棱柱、圆锥、圆台B ．三棱台、三棱锥、圆锥、圆台C ．三棱柱、四棱锥、圆锥、圆台D ．三棱柱、三棱台、圆锥、圆台7．下列命题中错误的是：A ．如果α⊥β，那么α内一定存在直线平行于平面β；B ．如果α⊥β，那么α内所有直线都垂直于平面β；C ．如果平面α不垂直平面β，那么α内一定不存在直线垂直于平面β；D ．如果α⊥γ，β⊥γ，α∩β＝l,那么l ⊥γ.8．在同一直角坐标系中，表示直线ax y =与a x y +=正确的是A B C D9．如图,直三棱柱111C B A ABC -的体积为V ，点P 、Q 分别在侧棱1AA 和1CC 上，Q C AP 11=，则四棱锥APQC B -的体积为A ．2V B ．3V C ．4V D ．5V10．在棱长均为2的四棱锥ABCD P -中，底面ABCD 是正方形，点E 为PC 的中点，则下列命题正确的是A ．BE ∥平面PAD ，且BE 到平面PAD 的距离为3;B ．BE ∥平面P AD ，且BE 到平面PAD 的距离为362; C ．BE 与平面P AD 不平行，且BE 与平面PAD 所成的角大于︒30; D ．BE 与平面PAD 不平行，且BE 与平面PAD 所成的角小于︒30.二、填空题: 本大题共7小题，每小题3分，共21分. 11、若直线08)3(1=-++=-my x m y x 与直线平行，则=m ▲ .12.已知一个空间几何体的三视图如图所示,其中正视图、侧视图都是由半圆和矩形组成,根据图中标出的尺寸,计算这个几何体的表面积是_▲_____.13.空间四个点P 、A 、B 、C 在同一球面上，PC PB PA 、、两两垂直，且a PC PB PA ===，那么这个球面的面积是 ▲ ．14.已知二面角α—l —β为︒60，若平面α内有一点A 到平面β的距离为，那么A 在平面β内的射影B 到平面α的距离为▲ .15.如图长方体中，32==AD AB ，21=CC ，则二面角PABC D E(第10题) ABCDA 1B 1C 1D1（4）（3）（1）（2）C BD C --1的大小为 ▲16．若圆C : 02422=++-+m y x y x 与y 轴交于A ，B 两点，且︒=∠90ACB ，则实数m 的值为_____▲_____．17．过圆C : 012222=+-+y x y x －外一点P 向圆引切线PT ，T 是切点，且｜｜＝｜｜PO PT (O是坐标原点)，当｜｜PT 最小时，点P 的坐标为____▲______．三、解答题:本大题共5小题，共59分.解答应写出文字说明，证明过程或演算步骤. 18．（本题满分11分）已知点A （1，0），B （5，2），(Ⅰ)求直线AB 的方程；(Ⅱ)若ABC ∆是以AB 为斜边的等腰直角三角形，求顶点C 的坐标.19．（本题满分12分）如图，在四边形ABCD 中，︒=∠90DAB ，︒=∠135ADC ，5=AB ，22=CD ，2=AD ，求四边形ABCD 绕AD 旋转一周所成几何体的表面积S 和体积V.20．（本题满分12分）已知圆C ：03232y x 22=+--+y x ，过原点O 作直线与圆C 相切，设切点分别为A 和B.(Ⅰ)求切线OA 和OB 的方程； (Ⅱ)求AOB ∆的面积．21.（本题满分12分）如图，在直三棱柱111ABC A BC -(侧棱垂直于底面的棱柱)中，E,F 分别是11A B,AC 的中点，点ABC ∠︒＝90，1AB AA BC ==.求证：(Ⅰ)EF ∥平面ABC ；(Ⅱ)平面1A EF ⊥平面1B EF ；(Ⅲ)求二面角1B BC E －－的正切值.22. （本题满分12分）已知在△ABC 中，)48(，A ，)2,6(-B ，点C 在直线x y 2-=上. (Ⅰ)若△ABC 的面积为5，求点C 的坐标；(Ⅱ)若直线x y 2-=正好是C ∠的内角平分线所在直线的方程，(ⅰ) 求ABC ∆外接圆O '的方程；(ⅱ)过)12(，－－P 作相互垂直的两条直线21,l l ，求直线21,l l 被圆O '所截得弦长之和的最大值.ABCA B 1C 1EF19．（本小题满分12分）必修2综合测试题答题卷一、选择题：本大题共10小题，每小题4分，共40分．二、填空题：本大题共7小题，每小题3分，共21分．11.12.13.14..15.16. 17.三、解答题：本大题共5小题，共59分．解答应写出文字说明、证明过程或演算步骤．18．（本小题满分11分）20．（本小题满分12分）21．（本小题满分12分）22．（本小题满分12分）AB CAB1C1EF参考答案：选择题：DABCC CBCBD 填空题：11.23－ 12.π11 13.23a π 14.23 15.︒30 16.－3 17.)41,41( 解答题：18.（Ⅰ）012=--y x （Ⅱ）)3,2(),1,4(C C - 19. ππ2460+=S ，π3148=V 20.（Ⅰ）x y y 3,0==，（Ⅱ）343=S 21.（Ⅲ）222.（Ⅰ）)310,35(),2,1(--C C （Ⅱ）（ⅰ）50)3()1(22=-+-y x （ⅱ）610。

必修一必修二测试题(综合卷)

必修一必修二测试题（综合卷）一：选择题1、若{}21A x x ==，{}2230B x x x =--=，则A B = （）Ａ．{}3 Ｂ．{}1 Ｃ．∅ Ｄ．{}1- 2、下列函数中是同一函数的是 ( )A 1y =与0y x =B y x =与log a x y a =C 122x x y +=-与2x y =D y =y x =3. 已知0>>b a ，则3,3,4a b a 的大小关系是（）A ．334a b a >>B ．343b a a <<C ． 334b a a <<D ． 343a a b <<4.函数log (3)1a y x =++的图象过定点（）A.（1，2）B.（2，1）C.（-2，1）D.（-1，1）5．设()338x f x x =+-, 用二分法求方程3380(1,2)x x x +-=∈在内近似解的过程中, 计算得到(1)0,(1.5)0,(1.25)0,f f f <>< 则方程的根落在区间（）．A ．（1，1.25）B ．（1.25，1.5）C ．（1.5，2）D ．不能确定6.在x 轴上的截距为2且倾斜角为135°的直线方程为：（）Ａ. ｙ＝－ｘ＋２Ｂ. ｙ＝－ｘ－２Ｃ. ｙ＝ｘ＋２Ｄ. ｙ＝ｘ－２7、点(1,2)到直线0x y a -+=的距离为2，则a 的值为（）Ａ．2-或2 Ｂ．12或32Ｃ．2或0 Ｄ．2-或0 8．如果函数f (x )＝x 2＋2(a －1)x ＋2在区间(－∞，4]上是减函数，那么实数a 的取值范围是( )A ．[－3，＋∞）B ．（－∞，－3]C ．（－∞，5]D ．[3，＋∞）9．如图，空间四边形ABCD 中，E F G H ，，，分别为A B B C C D D ，，，的中点，对角线BD DA ⊥，BD CD ⊥，则四边形EFGH 为（）Ａ．正方形Ｂ．菱形Ｃ．梯形Ｄ．矩形9．()log (1)x a f x a x =++在[0,1]上的最大值与最小值和为a ，则a的值为（）A ．14B ．12C ．2D ．411 ．若2log 0a <,1()12b>,则 A.1a >,0b > B.1a >,0b < C. 01a <<, 0b > D. 01a <<, 0b <12、设,a b 是两条直线，α、β是两个平面，则下列命题中错误．．的是（） A.若,a a αβ⊥⊥，则//αβ B.若,a b αα⊥⊥，则//a bC.若,a b αα⊂⊥则 a b ⊥D.若//,a b αα⊂则//a b二：填空题13.已知函数2log (0)()3(0)x x x f x x >⎧=⎨≤⎩，则1[()]4f f 的值是______________. 14. 如果一个几何体的三视图如右图所示（单位长度：cm ），则此几何体的表面积是 .15. 若直线03)1(:1=--+y a ax l 与直线02)32()1(:2=-++-y a x a l 互相垂直，则a 的值是____________________三：解答题16．在四棱锥P ABCD ABCD PA ABCD E PC -⊥中，底面是正方形，侧棱底面，点在上运动，问（1）：不管点E 在什么位置，是否总有“EBD PAC ⊥平面平面” 成立（2）当点E 位于PC 的什么位置时，有PA||平面EBD 。

人教版高中化学必修2期末综合测试卷I(含答案解析版)

人教版高中化学必修2期末综合测试卷I一、单选题(共15小题)1.下列关于“甲烷燃烧”的叙述中错误的是()A．甲烷在空气中燃烧时火焰呈淡蓝色B．甲烷燃烧一定只生成二氧化碳和水C．甲烷燃烧放出大量的热，常用作气体燃料D．点燃甲烷前要先检验其纯度2.下列关于化学反应速率的说法中，不正确的是()A．化学反应速率是衡量化学反应进行快慢程度的物理量B．化学反应速率通常用生成或消耗某物质的质量的多少来表示C．在同一个反应中，各物质的反应速率之比等于化学方程式中的化学计量数之比D．化学反应速率的常用单位有mol·L－1·s－1和mol·L－1·min－13.在下列说法中，可以说明恒温恒容密闭容器中的反应：P(g)＋Q(g)R(g)＋S(g)已达到平衡状态的是()A．反应容器内压强不随时间变化B． P和S的生成速率相等C．容器内P、Q、R、S的物质的量浓度之比为1∶1∶1∶1D．反应容器内气体的总物质的量不随时间变化4.下列关于卤素单质的说法不正确的是()A．它们都具有颜色B．从F2到I2其熔点逐渐降低C．它们都易溶于有机溶剂D．相同状况下从F2到I2其密度逐渐增大5.下列说法正确的是()A．只含有共价键的物质属于共价化合物B．共价化合物中一定不含离子键C．含有离子键的物质肯定含金属元素D．离子化合物中一定不含共价键6.垃圾处理无害化、减量化和资源化逐渐被人们所认识。

垃圾的分类收集是实现上述理念的重要措施。

某垃圾箱上贴有如图所示的标志，向此垃圾箱中丢弃的垃圾应是()A．危险垃圾B．可回收垃圾C．有害垃圾D．其他垃圾7.化学时刻影响着我们的生活，它在工农业生产和日常生活中起到了非常重要的作用。

下列说法中正确的是()A．使用一些新型的可降解的塑料可减少“白色污染”B．蛋白质、糖类、油脂、维生素是人体必须的营养素，应尽可能多吃C．熟石灰可以改良酸性土壤，而且能和硫酸铵混合使用D．为了减少水体的污染，农业上禁止使用农药和化肥8.两种气态烷烃的混合物，在标准状况下其密度为1.03 g·L－1，则关于该混合物组成的说法正确的是()A．一定有甲烷B．一定有乙烷C．不可能是甲烷和乙烷的混合物D．可能是乙烷和丙烷的混合物9.两种微粒的核外电子数相同，核电荷数不同。

必修2综合模块测试 1(人教B版必修2)

必修二模块测试1一、填空题：本大题共14小题，每小题5分，共计70分．请把答案填写在答题卡相应位置上．．．．．．．．． 1.“{1,1,0},210x x ∀∈-+>”是 ▲ 命题.（填写“真”或“假”） 2. 若平面α与平面β相交于直线l ，直线m 与直线l 相交于点P ，则直线m 与平面α的公共点的个数可能为 ▲ . 3. 直线1y =+的倾斜角大小为▲ .4. 若点B 是(1,3,4)A -关于坐标平面xOz 的对称点，则AB = ▲ .5. 过(0,4),(2,0)-两点的直线的方程的一般式为 ▲ .6. 已知圆C 的圆心坐标为(2,3)-，一条直径的两个端点分别在x 轴和y 轴上，则圆C 的标准方程为 ▲ .7. “(0)0f =”是“函数()f x 是R 上的奇函数”的 ▲ 条件.（填写“充分不必要”、“必要不充分”、“充要”、“既不充分也不必要”）8. 空间三条直线,,a b c .下列正确命题的序号是 ▲ . ①若,a c b c ⊥⊥，则//a b ； ②若//,a b //b c ，则//a c ；③过空间一点P 有且只有一条直线与直线a 成60°角； ④与两条异面直线,a b 都垂直的直线有无数条. 9. 与直线210x y +-=切于点(1,0)A ，且经过点(2,3)B -的圆的方程为▲ .10. 下列命题正确．．的序号是 ▲ ．（其中,l m 表示直线，,,αβγ表示平面）①若,,,l m l m αβαβ⊥⊥⊥⊥则； ②若,,,l m l m αβαβ⊥⊂⊂⊥则； ③若,//,αγβγαβ⊥⊥则； ④若//,,,l m l m αβαβ⊥⊂⊥则.11. 已知点(1,3)A 和点(5,2)B 分别在直线320x y a ++=的两侧，则实数a 的取值范围为 ▲ .12. 正方体1111ABCD A B C D -的棱长为a ，若过AC 作平面1//D B α，则截面三角形的面积为 ▲ .13. 在三棱锥S ABC -中，侧棱SA 、SB 、SC 两两垂直且长度均为a ，点H 在BC 上，且SH BC ⊥，则sin HAS ∠的值为▲ .14. 若△ABC 的一个顶点(3,1)A -，,B C ∠∠的平分线分别为0,x y x ==，则直线BC 的方程为 ▲ .二、解答题：本大题共6小题，共计90分．请在答题卡指定区域．．．．．．．内作答，解答时应写出文字说明、证明过程或演算步骤． 15.（本题满分14分）已知直线1:80l mx y n ++=和2:210l x my +-=. （1）若1l 和2l 相交于点(,1)P m -，求m 、n 的值；（2）若12//l l ，求m 、n 的值；（3）若点(0,1)Q 到直线2l 的距离为1，求m 的值.如图，已知一个圆锥的底面半径为R ，高为h ，在其中有一个高为x 的内接圆柱（其中,R h 均为常数）.（1）当23x h 时，求内接圆柱上方的圆锥的体积V ；（2）当x 为何值时，这个内接圆柱的侧面积最大？并求出其最大值。

综合测试卷2-统编版高中政治选择性必修二

2021—2022学年高二政治统编版选择性必修2综合测试卷2第Ⅰ卷一、选择题(本大题共16题，每在每题列出的四个选项中，只有一项是最符合题目要求的。

) 1．近期，国家网信办对公众大量使用的部分App进行检测，共发现84款App存在过度索权、超范围索取、非法获取个人信息等问题。

对此，网信办要求App运营者在规定时间内完成整改，逾期未完成的将依法予以处置。

上述材料告诉我们（）①自然人的个人信息与隐私权均受法律保护①公民需增强权利意识，维护自身的身份权①APP运营者应依法经营，严禁收集个人信息①政府依法行政，依法维护自然人的民事权利A．①①B．①①C．①①D．①①2．民法基本原则是民事主体从事民事活动和司法机关审理民事案件时应当遵循的基本准则。

下列属于民法典规定的民法基本原则的是（）①按劳分配原则①等价有偿原则①平等原则①绿色原则A．①①B．①①C．①①D．①①3．2018年3月6日，甲研制出一种市场上从未销售过的新产品向国家专利局申请发明专利。

2018年8月6日获得专利权并公告。

2019年4月，乙独立研发相同产品，立即组织生产并销售，2019年10月，甲发现乙的销售行为后向法院起诉，下列选项正确的有（）①任何人使用该产品均侵犯甲的专利权①乙虽然独立研发该产品，但仍侵犯了甲的专利权①甲成为专利权人的时间节点是2018年8月6日①2028年3月6日之后任何人均可无偿使用甲的发明A．①①B．①①C．①①D．①①4．农民甲翻修房屋，多盖了两间，占用了邻居乙的宅基地，乙诉请法院保护。

甲的行为侵犯了乙对宅基地的（）A．所有权B．用益物权C．担保物权D．承包经营权5．某房地产公司在推销商品房时印发了大量宣传广告，称出售的商品房依山傍水、小区内绿化率达60%、一户一梯等。

小嘉被广告吸引，签订了购房合同。

交房后，小嘉发现广告中的多数条件并未兑现，于是要求退房。

对此，下列说法正确的是（）①商业广告既不是合同，也不是合同条款，小嘉不能以此要求退房①本案中商业广告中的内容具体确定，具有要约的效力，商家应承担违约责任①该合同的客体是房地产公司给付商品房及小嘉支付价款的行为①该合同的客体是合同标的的商品房A．①①B．①①C．①①D．①①6．下列情形中，在当事人之间产生合同法律关系的是（）A．甲拾得乙遗失的一块表B．甲邀请乙一起去看球赛，乙有事没有赴约C．暑假期间，甲将一台电脑存放在乙家D．甲的鱼塘中的鱼跳人乙的鱼塘7．某啤酒厂因使用啤酒瓶不当，造成消费者在饮用时被炸伤。