云南省文山市南鹰学校2013-2014学年九年级数学上学期9月月考试卷

合集下载

云南初三初中数学月考试卷带答案解析

云南初三初中数学月考试卷班级:___________ 姓名：___________ 分数：___________一、选择题1.下列标志中，可以看作是中心对称图形的是（）2.下列事件是不确定事件的是（）A．水中捞月B．守株待兔C．风吹草动D．瓮中捉鳖3.在平面直角坐标系中，将二次函数y=2x2的图象向上平移2个单位，所得图象的解析式为（）A．y=2x2-2B．y=2x2+2C．y=2（x-2）2D．y=2（x+2）24.已知x=2是关于x的方程的一个解，则2a-1的值是（）A．3B．4C．5D．65.某超市1月份的营业额为200万元，3月份的营业额为600万元，如果平均每月增长率为x，根据题意列出方程为（）A．200（1+x）2=600B．200+200x=600C．200+200×2x=600D．200[1+（1+x）+（1+x）2]=6006.如图，BD为⊙O的直径，∠A=30°，则∠CBD的度数为（）A．30°B．60°C．80°D．120°7.图中实线部分是半径为9m的两条等弧组成的游泳池．若每条弧所在的圆都经过另一个圆的圆心，则游泳池的周长为（）A．12πm B．18πm C．20πm D．24πm8.二次函数y=ax2+bx+c的图象如图所示，则下列关系式不正确的是（）A．a＜0B．abc＞0C．a+b+c＞0D．b2-4ac＞0二、填空题1.2x 2-x-1=0的二次项系数是，一次项系数是，常数项是．2.平面直角坐标系中，一点P （-2，3）关于原点的对称点P′的坐标是．3.已知一元二次方程：x 2-3x-1=0的两个根分别是x 1、x 2，则x 12x 2+x 1x 22= ．4.已知抛物线y=ax 2+bx+c （a ＞0）的对称轴为直线x=1，且经过点（-1，y 1），（2，y 2），试比较y 1和y 2的大小：y 1 y 2．5.如图，分别以四边形ABCD 的四个顶点为圆心，以3为半径画弧，则图中四个阴影部分面积和为．6.将点A （-3，0）绕原点顺时针旋转90°，得到点B ，则点B 的坐标为．7.如图，某公园的一座石拱桥是圆弧形（劣弧），其跨度为24米，拱的半径为13米，则拱高CD 为米．三、解答题1.解方程：（1）2x 2+x-3=0（用公式法）（2）（x-1）（x+3）=12．2.如图，在Rt △OAB 中，∠OAB=90°，OA=AB=6，将△OAB 绕点O 沿逆时针方向旋转90°得到△OA 1B 1．（1）线段OA 1的长是，∠AOB 1的度数是；（2）连接AA 1，求证：四边形OAA 1B 1是平行四边形；（3）求四边形OAA 1B 1的面积． 3.如图，△ABC 中，∠C=90°，BC=7cm ，AC=5，点P 从B 点出发，沿BC 方向以2m/s 的速度移动，点Q 从C出发，沿CA 方向以1m/s 的速度移动．（1）若P 、Q 同时分别从B 、C 出发，那么几秒后，△PCQ 的面积等于4？（2）若P 、Q 同时分别从B 、C 出发，那么几秒后，PQ 的长度等于5？（3）△PCQ 的面积何时最大，最大面积是多少？4.不透明的口袋里装有白、黄、蓝三种颜色的乒乓球（除颜色外其余都相同），其中白球有2个，黄球有1个，现从中任意摸出一个是白球的概率为．（1）试求袋中蓝球的个数；（2）第一次任意摸一个球（不放回），第二次再摸一个球，请用画树状图或列表格法，求两次摸到都是白球的概率．5.一种进价为每件40元的T恤，若销售单价为60元，则每周可卖出300件，为提高利益，就对该T恤进行涨价销售，经过调查发现，每涨价1元，每周要少卖出10件，请确定该T恤涨价后每周销售利润y（元）与销售单价x（元）之间的函数关系式，并求出销售单价定为多少元时，每周的销售利润最大？6.如图，抛物线y=-x2-2x+3 的图象与x轴交于A、B两点（点A在点B的左边），与y轴交于点C，点D为抛物线的顶点．（1）求A、B、C的坐标；（2）设点H是第二象限内抛物线上的一点，且△HAB的面积是6，求点H的坐标；（3）点M为线段AB上一点（点M不与点A、B重合），过点M作x轴的垂线，与直线AC交于点E，与抛物线交于点P，过点P作PQ∥AB交抛物线于点Q，过点Q作QN⊥x轴于点N．若点P在点Q左边，当矩形PQMN 的周长最大时，求△AEM的面积．云南初三初中数学月考试卷答案及解析一、选择题1.下列标志中，可以看作是中心对称图形的是（）【答案】D.【解析】试题解析：A、不是中心对称图形，故本选项错误；B、不是中心对称图形，故本选项错误；C、不是中心对称图形，故本选项错误；D、是中心对称图形，故本选项正确；故选D．【考点】中心对称图形.2.下列事件是不确定事件的是（）A．水中捞月B．守株待兔C．风吹草动D．瓮中捉鳖【答案】B.【解析】试题解析：：A．水中捞月是不可能事件，B．守株待兔是不确定事件，C．风吹草动是必然事件，D．瓮中捉鳖是必然事件，故选B．【考点】随机事件.3.在平面直角坐标系中，将二次函数y=2x2的图象向上平移2个单位，所得图象的解析式为（）A．y=2x2-2B．y=2x2+2C．y=2（x-2）2D．y=2（x+2）2【解析】试题解析：二次函数y=2x2的图象向上平移2个单位，得y=2x2+2．故选B．【考点】二次函数图象与几何变换.4.已知x=2是关于x的方程的一个解，则2a-1的值是（）A．3B．4C．5D．6【答案】C.【解析】试题解析：∵x=2是关于x的方程的一个解，∴×22-2a=0，即6-2a=0，则2a=6，∴2a-1=6-1=5．故选C．【考点】一元二次方程的解.5.某超市1月份的营业额为200万元，3月份的营业额为600万元，如果平均每月增长率为x，根据题意列出方程为（）A．200（1+x）2=600B．200+200x=600C．200+200×2x=600D．200[1+（1+x）+（1+x）2]=600【答案】A.【解析】试题解析：设平均每月的增长率为x，200（1+x）2=600．故选A．【考点】一元二次方程的应用.6.如图，BD为⊙O的直径，∠A=30°，则∠CBD的度数为（）A．30°B．60°C．80°D．120°【答案】B.【解析】试题解析：∵BD为⊙O的直径，∴∠BCD=90°，∵∠D=∠A=30°，∴∠CBD=90°-∠D=60°．故选B．【考点】圆周角定理.7.图中实线部分是半径为9m的两条等弧组成的游泳池．若每条弧所在的圆都经过另一个圆的圆心，则游泳池的周长为（）A．12πm B．18πm C．20πm D．24πm【解析】试题解析：．故选D ．【考点】弧长的计算.8.二次函数y=ax 2+bx+c 的图象如图所示，则下列关系式不正确的是（）A ．a ＜0B ．abc ＞0C ．a+b+c ＞0D ．b 2-4ac ＞0【答案】C.【解析】试题解析：∵抛物线开口向下， ∴a ＜0，∵抛物线与y 轴交于正半轴， ∴c ＞0，∵对称轴在y 轴左边，-＜0，∴b ＜0，abc ＞0，∵抛物线与x 轴有两个交点， ∴b 2-4ac ＞0，当x=1时，y ＜0， ∴a+b+c ＜0．故选C ．【考点】二次函数图象与性质.二、填空题1.2x 2-x-1=0的二次项系数是，一次项系数是，常数项是．【答案】2，-，-1.【解析】试题解析：根据一元二次方程的定义得：2x 2-x-1=0的二次项系数是2，一次项系数是-，常数项是-1．【考点】一元二次方程的定义.2.平面直角坐标系中，一点P （-2，3）关于原点的对称点P′的坐标是．【答案】（2，-3）【解析】试题解析：根据中心对称的性质，得点P （-2，-3）关于原点对称点P′的坐标是（2，-3）．【考点】点的坐标.3.已知一元二次方程：x 2-3x-1=0的两个根分别是x 1、x 2，则x 12x 2+x 1x 22= ．【答案】-3.【解析】试题解析：根据题意得x 1+x 2=3，x 1x 2=-1，所以x 12x 2+x 1x 22=x 1x 2（x 1+x 2）=-1×3=-3．【考点】一元二次方程根与系数的关系.4.已知抛物线y=ax 2+bx+c （a ＞0）的对称轴为直线x=1，且经过点（-1，y 1），（2，y 2），试比较y 1和y 2的大小：y 1 y 2．【答案】＞.【解析】试题解析：∵二次函数y=ax 2+bx+c 的图象的对称轴为直线x=1，而1-（-1）=2，2-1=1，∴点（-1，y 1）离对称轴的距离比点（2，y 2）要远， ∴y 1＞y 2．【考点】二次函数图象与性质.5.如图，分别以四边形ABCD 的四个顶点为圆心，以3为半径画弧，则图中四个阴影部分面积和为．【答案】9π.【解析】试题解析：∵四个扇形的圆心角的和等于四边形ABCD 的内角和，即为（4-2）180°=360°， ∴阴影部分面积之和==9π．【考点】弧长的计算.6.将点A （-3，0）绕原点顺时针旋转90°，得到点B ，则点B 的坐标为．【答案】（0，3）【解析】试题解析：∵点A （-3，0）， ∴点A 在x 轴负半轴上，且OA=3， ∵将点A （-3，0）绕原点顺时针旋转90°，得到点B ，∴点B 在y 轴正半轴上，且OB=3，∴点B 的坐标为：（0，3）．【考点】旋转的性质.7.如图，某公园的一座石拱桥是圆弧形（劣弧），其跨度为24米，拱的半径为13米，则拱高CD 为米．【答案】8.【解析】试题解析：因为跨度AB=24m ，拱所在圆半径为13m ，延长CD 到O ，使得OC=OA ，则O 为圆心，则AD=AB=12（米），则OA=13米，在Rt △AOD 中，DO==5，进而得拱高CD=CO-DO=13-5=8米．【考点】1.垂径定理；2.勾股定理.三、解答题1.解方程：（1）2x 2+x-3=0（用公式法）（2）（x-1）（x+3）=12．【答案】（1），；（2）x 1=-5，x 2=3.【解析】（1）直接运用公式法求解即可；（2）先把原方程转化为一元二次方程的一般形式，再运用因式分解法求解即可. 试题解析：（1）2x 2+x-3=0（用公式法） ∵a=2，b=1，c=-3 b 2-4ac=25＞0∴，；（2）化为一般形式，得：x 2+2x-15=0 （x+5）（x-3）=0（x+5）=0或（x-3）=0∴x 1=-5，x 2=3．【考点】1.解一元二次方程—公式法；2.解一元二次方程—因式分解法.2.如图，在Rt △OAB 中，∠OAB=90°，OA=AB=6，将△OAB 绕点O 沿逆时针方向旋转90°得到△OA 1B 1．（1）线段OA 1的长是，∠AOB 1的度数是；（2）连接AA 1，求证：四边形OAA 1B 1是平行四边形；（3）求四边形OAA 1B 1的面积．【答案】（1）6；135°；（2）证明见解析；（3）36. 【解析】（1）图形在旋转过程中，边长和角的度数不变；（2）可证明OA ∥A 1B 1且相等，即可证明四边形OAA 1B 1是平行四边形；（3）平行四边形的面积=底×高=OA×OA 1．试题解析：（1）因为，∠OAB=90°，OA=AB ，所以，△OAB 为等腰直角三角形，即∠AOB=45°，根据旋转的性质，对应点到旋转中心的距离相等，即OA 1=OA=6，对应角∠A 1OB 1=∠AOB=45°，旋转角∠AOA 1=90°，所以，∠AOB 1的度数是90°+45°=135°．（2）∵∠AOA 1=∠OA 1B 1=90°， ∴OA ∥A 1B 1，又∵OA=AB=A 1B 1，∴四边形OAA 1B 1是平行四边形．（3）▱OAA 1B 1的面积=6×6=36．【考点】1.旋转的性质；2.平行四边形的判定．3.如图，△ABC 中，∠C=90°，BC=7cm ，AC=5，点P 从B 点出发，沿BC 方向以2m/s 的速度移动，点Q 从C 出发，沿CA 方向以1m/s 的速度移动．（1）若P 、Q 同时分别从B 、C 出发，那么几秒后，△PCQ 的面积等于4？（2）若P 、Q 同时分别从B 、C 出发，那么几秒后，PQ 的长度等于5？（3）△PCQ 的面积何时最大，最大面积是多少？【答案】（1）、秒；（2）秒；（3）当t=时△PCQ 的面积最大，最大面积为．【解析】（1）分别表示出线段CP 和线段CQ 的长，利用三角形的面积公式列出方程求解即可；（2）表示出线段CP 和CQ 后利用勾股定理列出方程求解即可；（3）列出△PCQ 的面积关于t 的函数解析式，配方可得最大值．试题解析：（1）设t 秒后△PCQ 的面积等于4，根据题意得：CQ=t ，BP=2t ，则CP=7-2t ，CQ×CP=×t （7-2t ）=4，整理，得：t 1=，t 2=，故若P 、Q 同时分别从B 、C 出发，那么、秒后，△PCQ 的面积等于4；（2）若PQ 的长度等于5，则PC 2+QC 2=PQ 2，即：（7-2t ）2+t 2=25，整理，得：5t 2-28t+24=0，解得：t 1=，t 2=，∵CP=7-2t≥0，即t≤3.5，∴t=＞3.5，舍去，故那么秒后，PQ的长度等于5；（3）由（1）知△PCQ的面积S=×t（7-2t）=-（t-）2+，当t=时，S取得最大值，最大值为，故当t=时△PCQ的面积最大，最大面积为．【考点】一元二次方程的应用；二次函数的应用．4.不透明的口袋里装有白、黄、蓝三种颜色的乒乓球（除颜色外其余都相同），其中白球有2个，黄球有1个，现从中任意摸出一个是白球的概率为．（1）试求袋中蓝球的个数；（2）第一次任意摸一个球（不放回），第二次再摸一个球，请用画树状图或列表格法，求两次摸到都是白球的概率．【答案】（1）1；（2）.【解析】（1）直接利用概率公式，结合摸出一个球是白球的概率为求出答案；（2）采用列表法或树状图法，解题时要注意是放回实验还是不放回实验．试题解析：（1）设蓝球个数为x个，则由题意得，解得：x=1，答：蓝球有1个；（2）故两次摸到都是白球的概率=．【考点】1.列表法与树状图法；2.概率公式．5.一种进价为每件40元的T恤，若销售单价为60元，则每周可卖出300件，为提高利益，就对该T恤进行涨价销售，经过调查发现，每涨价1元，每周要少卖出10件，请确定该T恤涨价后每周销售利润y（元）与销售单价x（元）之间的函数关系式，并求出销售单价定为多少元时，每周的销售利润最大？【答案】销售单价定为65元时，每周的销售利润最大．【解析】用每件的利润乘以销售量即可得到每周销售利润，即y=（x-40）[300-20（x-60）]，再把解析式整理为一般式，然后根据二次函数的性质确定销售单价定为多少元时，每周的销售利润最大．试题解析：根据题意得y=（x-40）[300-10（x-60）]=-10x2+1300x-36000，∵x-60≥0且300-10（x-60）≥0，∴60≤x≤90，∵a=-10＜0，而抛物线的对称轴为直线x=65，即当x＞65时，y随x的增大而减小，而60≤x≤90，∴当x=65时，y的值最大，即销售单价定为65元时，每周的销售利润最大．【考点】二次函数的应用.6.如图，抛物线y=-x2-2x+3 的图象与x轴交于A、B两点（点A在点B的左边），与y轴交于点C，点D为抛物线的顶点．（1）求A、B、C的坐标；（2）设点H是第二象限内抛物线上的一点，且△HAB的面积是6，求点H的坐标；（3）点M为线段AB上一点（点M不与点A、B重合），过点M作x轴的垂线，与直线AC交于点E，与抛物线交于点P，过点P作PQ∥AB交抛物线于点Q，过点Q作QN⊥x轴于点N．若点P在点Q左边，当矩形PQMN 的周长最大时，求△AEM的面积．【答案】（1）A（-3，0），B（1，0），C（0，3）；（2）H（-2，3）；（3）．【解析】（1）通过解析式即可得出C点坐标，令y=0，解方程得出方程的解，即可求得A、B的坐标．（2）根据AB的长和三角形面积求得H的纵坐标为3，代入解析式即可求得横坐标；（3）设M点横坐标为m，则PM=-m2-2m+3，MN=（-m-1）×2=-2m-2，矩形PMNQ的周长d=-2m2-8m+2，将-2m2-8m+2配方，根据二次函数的性质，即可得出m的值，然后求得直线AC的解析式，把x=m代入可以求得三角形的边长，从而求得三角形的面积．试题解析：（1）由抛物线y=-x2-2x+3可知，C（0，3），令y=0，则0=-x2-2x+3，解得x=-3或x=1，∴A（-3，0），B（1，0）．（2）∵A（-3，0），B（1，0）．∴AB=4，∵△HAB的面积是6，点H是第二象限内抛物线上的一点，∴H的纵坐标为3，把y=3代入y=-x2-2x+3得3=-x2-2x+3，解得x1=0，x2=-2，∴H（-2，3）；（3）由抛物线y=-x2-2x+3可知，对称轴为x=-1，设M点的横坐标为m，则PM=-m2-2m+3，MN=（-m-1）×2=-2m-2，∴矩形PMNQ的周长=2（PM+MN）=（-m2-2m+3-2m-2）×2=-2m2-8m+2=-2（m+2）2+10，∴当m=-2时矩形的周长最大．∵A（-3，0），C（0，3），设直线AC解析式为y=kx+b，则解得：，∴解析式y=x+3，当x=-2时，则E（-2，1），∴EM=1，AM=1，∴S=×AM×EM=．【考点】二次函数综合题．。

2013-2014初三上学期学业水平考试初三数学(含答案)

2013-2014初三上学期学业水平考试数学试题注意事项：1．本试题分第Ⅰ卷和第Ⅱ卷两部分，第Ⅰ卷共3页，满45分；第Ⅱ卷共7页，满分75分.本试题共10页，满分120分，考试时间为120分钟．2．答卷前，考生务必将自己的姓名、准考证号、考试科目涂写在答题卡上，并同时将考点、姓名、准考证号、座号填写在试卷的密封线内．3．第Ⅰ卷为选择题，每小题选出答案后，用2B 铅笔把答题卡上对应题目的正确答案标号涂黑.如需改动，用橡皮擦干净后，再选涂其他答案，答案写在试卷上无效． 4．考试期间，一律不得使用计算器；考试结束，应将本试卷和答题卡一并交回．第Ⅰ卷（选择题共45分）一、选择题（本大题共15个小题，每小题3分，共45分．在每小题给出的四个选项中，只有一项是符合题目要求的）1．一个等腰三角形的顶角是40°，则它的底角是（）A ．40°B ．50°C ．60°D ．70° 2．方程 x (x +3)= 0的根是（） A ．x =0B ．x =-3C ．x 1=0，x 2 =3D ．x 1=0，x 2 =-33．下列函数中，属于反比例函数的是（） A ．2xy =B ．12y x=C ．23y x =+D ．223y x =+4．下面四幅图是两个物体不同时刻在太阳光下的影子，按照时间的先后顺序正确的是（）A. A →B →C →DB. D →B →C →AC. C →D →A →BD. A →C →B →D北东5．在Rt △ABC 中，∠C=90°，a =4，b =3，则cosA 的值是（） A ．54 B ．35C ．43 D ．456．二次函数223y x x =-+顶点坐标是（）A ．（-1，-2）B ．（1，2）C ．（-1，2）D ．（0，2）7．如图，一飞镖游戏板，其中每个小正方形的大小相等，则随意投掷一个飞镖，击中黑色区域的概率是（）A ．38 B ．12 C ．14 D ．138. 与如图所示的三视图对应的几何体是( )9．下列命题中，不正确．．．的是（） A ．对角线相等的平行四边形是矩形．B ．有一个角为60°的等腰三角形是等边三角形．C ．直角三角形斜边上的高等于斜边的一半．D ．正方形的两条对角线相等且互相垂直平分．10. 已知点A( -2 ,y 1 ) , ( -1 ,y 2 ) , ( 3 ,y 3 )都在反比例函数xy 4=的图象上,则 ( )A. y 1＜y 2＜y 3B. y 3＜y 2＜y 1C. y 3 ＜y 1＜y 2D. y 2＜y 1＜y 311．若关于x 的一元二次方程0962=+-x kx 有两个不相等的实数根，则k 的取值范围是( )A. 1k <B. 0k =/C. 10k k <=/且D. 1k >12. 如右图,在□ABCD 中,EF ∥AB,GH ∥AD,EF 与GH 交于点O,则图中的平行四边形的个数共有（）A. 7个B. 8个C. 9个D. 10个13．如图，在△ABC 中，AB=a ，AC=b ，BC 边上的垂直平分线DE 交BC ，BA 分别于点D ，E ，则△AEC 的周长等于（）A. a+bB.a-bC.2a+bD.a+2b14.图1是一个边长为1的等边三角形和一个菱形的组合图形，菱形边长为等边三角形边长的一半，以此为基本单位，可以拼成一个形状相同但尺寸更大的图形（如图2），依此规律继续拼下去（如图3），……，则第n 个图形的周长是( )A.2nB.4nC.12n + D.22n +15.已知x y z ，，为实数，且满足253x y z +-=，25x y z --=-，则222x y z ++的最小值为( ).A.111 B. 0 C. 5 D. 5411OGHFEC BAD图1图2图3……F EDC A2011年初三上学期学业水平考试数学试题第Ⅱ卷（非选择题共75分）注意事项：1.第Ⅱ卷共6页．用蓝、黑钢笔或圆珠笔直接答在考试卷上．二、填空题（本大题共6个小题，每小题3分，共18分．把答案填在题中横线上） 16．已知反比例函数xky =的图象经过点P(一l ，2)，则这个函数的图象位于_____________17．甲、乙两楼相距20m ，甲楼高20 m ，自甲楼顶看乙楼楼顶，仰角为60º，则乙楼的高为。

云南省2024-2025学年九年级上学期九月份月考模拟测试数学试题

云南省2024-2025学年九年级上学期九月份月考模拟测试数学试题一、单选题1．下列方程是关于x 的一元二次方程的是（）A ．20ax bx c ++=B ．212x x +=C ．31x x y +=-D ．()()23121x x +=+2．对于一元二次方程2213x x +=，下列说法错误的是（）A ．二次项系数是2B ．一次项系数是3x -C ．常数项是1D ．1x =是它的一个根3．如果关于x 的一元二次方程20ax bx c ++=满足240a b c -+=，那么我们称这个方程为“阿凡达”方程．已知20ax bx c ++=是“阿凡达”方程，且有两个相等的实数根，则下列结论正确的是（）A ．a b =B ．a c =C ．b c =D ．4b c a =-= 4．一元二次方程2650x x -+=配方可变形为（）A ．()234-=xB ．()2314x +=C ．()2314x -=D ．()234x += 5．将一元二次方程2850x x --=化成2()x a b +=（a ，b 为常数）的形式，则a ，b 的值分别是（）A ．4-，21B ．4-，11C ．4，21D ．8-，69 6．关于x 的一元二次方程2420kx x +-=有实数根，则k 的取值范围是（） A ．2k ≥- B ．2k >-且0k ≠ C ．2k ≥-且0k ≠ D ．2k ≤- 7．对于抛物线23y x =-，下列说法不正确．．．的是（） A ．图象开口向下 B ．y 随x 的增大而减小C ．顶点坐标为()0,0 D ．对称轴为y 轴 8．某农机厂四月份生产零件50万个，第二季度共生产零件182万个．设该厂第二季度平均每月的增长率为x ，那么x 满足的方程是（）A ．()251182x +=B ．()()250501501182x x ++++=C ．()()2501501182x x +++=D ．()50501182x ++=9．若二次函数2y ax =的图像经过点(3,2)P -，则该图像必经过点（）A ．(2,3)B ．(2,3)--C ．(3,2)D ．(3,2)-10．如图，用一段长为18 米的篱笆围成一个一边靠墙（墙长不限）的矩形花园，设该矩形花园的一边长为(m)x ，另一边的长为(m)y ，矩形的面积为2(m )S ．当x 在一定范围内变化时，y 与x ，S 与x 满足的函数关系分别是（）A ．一次函数关系，二次函数关系B ．正例函数关系，二次函数关系C ．二次函数关系，正例函数关系D ．二次函数关系，一次函数关系 11．对于二次函数()21y x =--的图象，下列说法不正确的是（）A ．开口向下B ．对称轴是直线x =1C ．当x =1时，y 有最大值0D ．当x <1时，y 随x 的增大而减小12．若()()()1232,,1,,2,A y B y C y -是抛物线()221y x a =-+上的三点，则123,,y y y 为的大小关系为（）A ．123y y y >>B ．132y y y >>C ．321y y y >>D ．312y y y >> 13．关于x 的方程()2222230x x x x +++-=，则2x x +的值是（）A ．3-B ．1C ．3-或1D ．3或1-14．若关于x 的一元二次方程220(0)ax bx a ++=≠有一根为2024x =，则一元二次方程2(2)22a x bx b -+-=-必有一根为（）A ．2024B ．2025C ．2026D ．202715．对于一元二次方程()200ax bx c a ++=≠，下列说法：①若a c b +=，则240b ac -≥；②若方程20ax c +=有两个不相等的实根，则方程20ax bx c ++=必有两个不相等的实根；③若x c =是方程20ax bx c ++=的一个根，则一定有10ac b ++=成立；④若0x x =是一元二次方程20ax bx c ++=的根，则()22042b ac ax b -=+其中正确的（）A ．只有①②④B ．只有①②③C ．只有②③④D ．只有①②二、填空题16．若||(2)23m y m x x =-++是关于x 的二次函数，则m 的值是．17．抛物线()232y x =---的顶点坐标是．18．如图，在一块长30m ，宽20m 的矩形花园基地上修建两横一纵三条等宽的道路，剩余空地种植花苗，若种植花苗的面积为2522m ，则道路的宽为 m ．19．二次函数2(0)y ax bx c a =++≠的图像如图所示，下列说法：①20a b +=；②当13x -≤≤时，0y <；③若()()1122,,,x y x y 在函数图像上，当12x x <时，12y y <；④0a b c -+=；⑤420a b c -+<，其中正确的有（填写正确的序号）．三、解答题20．解下列方程：(1)230x x -=；(2)210x x +-=；(3)244x x -=；(4)2560x x -+=．21．探究二次函数22(3)1y x =--及其图象的性质，请填空：①图象的开口方向是；②图象的对称轴为直线；③图象与y 轴的交点坐标为；④当x = 时，函数y 有最小值，最小值为．22．（换元法）解方程：22232380x x x x ----=（）（）解：设23x x y -=则原方程可化为2280y y --=解得：1224y y =-=，当2y =-时，232x x -=-，解得1221x x ==，当4y =时，234x x -=，解得1241x x ==-，∴原方程的根是12342141x x x x ====-，，，，根据以上材料，请解方程：(1)2222352340x x x x -+-+=（）（）． (2)2263503x x x x-++=- 23．已知关于x 的一元二次方程x 2﹣（m +3）x +3m ＝0．(1)求证：无论m 取任何实数，方程总有实数根；(2)若等腰三角形的其中一边为4，另两边是这个方程的两根，求m 的值．24．如图，有长为18米的篱笆，一面利用墙（墙的最大可用长度为10m ），围成中间隔有一道篱笆的长方形花圃．设花圃的宽AB 为x 米，面积为2m S ．(1)求S 与x 的函数关系式，并写出x 的取值范围；(2)如果要围成面积为224m 的花圃，AB 的长是多少米？25．自2023年1月以来，甲流便肆虐横行，成为当前主流流行疾病．某一小区有1位住户不小心感染了甲流，由于甲流传播感染非常快，小区经过两轮传染后共有121人患了甲流．(1)每轮感染中平均一个人传染几人？(2)如果按照这样的传播速度，经过三轮传染后累计是否超过1500人患了甲流？ 26．如图，抛物线的顶点为C (1，9)，与x 轴交于A ，B (4，0)两点．(1)求抛物线的解析式；(2)抛物线与y 轴交点为D ，求BCD S △．27．栖霞某旅游景点的超市以每件45元的价格购进某款果都吉祥物摆件，以每件69元的价格出售．经统计，4月份的销售量为192件，6月份的销售量为300件．(1)求该款吉祥物摆件4月份到6月份销售量的月平均增长率；(2)从7月份起，超市决定采用降价促销的方式回馈游客，经试验，发现该吉祥物摆件每降价1元，月销售量就会增加20件．当该吉祥物摆件售价为多少元时，月销售利润达7200元？。

云南初三初中数学月考试卷带答案解析

云南初三初中数学月考试卷班级:___________ 姓名：___________ 分数：___________一、选择题1.方程：①；②；③；④中一元二次方程是（）A ．①和②B ．②和③C ．③和④D ．①和③2.用配方法解方程，配方后的方程是（）A ．B ．C ．D ．3.关于x 的一元二次方程有一个根为0，则a 的值是（）A ．±1B ．－1C ．1D ．04.如果一元二次方程x 2-2－3=0的两根为x 1、x 2，则x 12x 2＋x 1x 22的值等于（） A ．-6 B ．6 C ．-5D ．55.不能判定四边形ABCD 是平行四边形的条件是（） A ．∠A=∠C ∠B=∠D B ．AB ∥CD AD="BC" C ．AB ∥CD ∠A=∠C D ．AB ∥CD AB=CD6.如果顺次连接一个四边形各边中点所得新的四边形是菱形，那么对这个四边形的形状描述最准确的是（） A ．矩形 B ．等腰梯形 C ．菱形 D ．对角线相等的四边形7.已知等腰三角形的腰长、底边长分别是一元二次方程x 2-7x ＋10=0的两根，则该等腰三角形的周长是（） A ．9或12 B ．9 C ．12 D ．218.下列命题中，不正确的是（）A ．顺次连结菱形各边中点所得的四边形是矩形。

B ．有一个角是直角的菱形是正方形。

C ．对角线相等且垂直的四边形是正方形。

D ．有一个角是60°的等腰三角形是等边三角形。

二、填空题1.方程（x+5）（x-7）=-26，化成一般形式是，其二次项的系数和一次项系数的和是。

2.为解决群众看病难的问题，一种药品连续两次降价，每盒的价格由原来的60元降至48．6元，则平均每次降价的百分率为 _______ ．3.如图所示，某小区规划在一个长为40 m 、宽为26 m 的矩形场地ABCD 上修建三条同样宽的甬路，使其中两条与AB 平行，另一条与AD 平行，其余部分种草．若使每一块草坪的面积为144 m 2，求甬路的宽度．若设甬路的宽度为x m，则x满足的方程为．4.已知平行四边形ABCD中，∠A -∠B = 30°，则∠C = ________。

2013-2014学年度九年级第一学期数学质量检测试题

2013-2014学年度九年级第一学期数学质量检测试题一、选一选（本大题共10小题，每小题3分，共30分）．1、如图，在△ABC 中，∠C=90°，AB=13，BC=5，则cosA 的值是（）A ．135 B. 1312 C.125 D. 5132、已知1是关于x 的一元二次方程（m-1）x 2+x+1=0的一个根，则m 的值是（） A. 1 B. 0 C. -1 D. 无法确定3、（河南中考）在平面直角坐标系中，将抛物线y =x 24先向右平移2个单位，再向上平移2个单位，得到的抛物线的表达式是（） A.y =(x +2)2+2B.y =(x 2)2 2C.y =(x 2)2+2D.y =(x +2)2 24、抛物线y=x 2-2x+1的顶点坐标是（）A.（-1，0） B.（1，0） C.（-2，1） D.（2，-1）5、已知反比例函数xy 1=，下列结论中不正确的是（）A.图象经过点（-1，-1）B.图象在第一、三象限C.当1>x 时，10<<yD.当0<x 时，y 随着x 的增大而增大 6、已知下列命题：①对角线互相平分的四边形是平行四边形；②等腰梯形的对角线相等； ③对角线互相垂直的四边形是菱形；④内错角相等．其中假命题有（） A.1个 B.2个 C.3个 D.4个7、由一些相同的小立方块搭成的几何体的三视图如图所示，则搭成该几何体的小立方块有（） A.3块 B.4块 C.6块 D.9块8、如图，P （x ，y ）是反比例函数xy 3=的图象在第一象限分支上的一个动点，PA ⊥x 轴于点A ，PB ⊥y 轴于点B ，随着自变量x 的增大，矩形OAPB 的面积（）A.增大B.减小C.不变D.无法确定9、在中华经典美文阅读中，小明同学发现自己的一本书的宽与长之比为黄金比．已知这本书的长为20cm ，则它的宽约为（） A. 12.36cm B. 13.6cm C. 32.36cm D. 7.64cm10、函数2-=ax y （0≠a ）与2ax y =（0≠a ）在同一平面直角坐标系中的图象可能是（）A. B. C. D.二、填空（本大题共5小题，每小题3分，共15分．请你把答案填在横线的上方）．11、方程022=-x 的根是．12、将二次函数3)2(2+-=x y 的图象向右平移2个单位，再向下平移2个单位，所得二次函数的解析式为．13、为了估计不透明的袋子里装有多少白球，先从袋中摸出10个球都做上标记，然后放回袋中去，充分摇匀后再摸出10个球，发现其中有一个球有标记，那么你估计袋中大约有个白球．14、如图，在梯形ABCD 中，AB ∥DC ，∠ADC 的平分线与∠BCD 的平分线的交点E 恰在AB 上．若AD=7cm ，BC=8cm ，则AB 的长度是 cm ．15、观察下列有序整数对：（1，1）．（1，2），（2，1）．（1，3），（2，2），（3，1）（1，4），（2，3），（3，2），（4，1）．（1，5），（2，4），（3，3），（4，2），（5，1）． …它们是按一定规律排列的，依照此规律，第10行从左到右第5个整数对是．三、用心做一做（本大题共3小题，每小题7分，共21分）16、（1）计算：︒---+30sin 2)1(4)3-(20110π （2）解一元二次方程0432=-+x x17、如图，现有m 、n 两堵墙，两个同学分别在A 处和B 处，请问小明在哪个区域内活动才不会被这两个同学发现（画图用阴影表示）．解：18、（2011•株洲）某水果批发商场经销一种高档水果，如果每千克盈利10元，每天可售出500kg ，经市场调查发现，在进货价不变的情况下，每涨价1元，日销售量将减少20kg ，现该商场要保证每天盈利6000元，同时又要使顾客得到实惠，那么每千克应涨价多少元？四、（本大题共2小题，每小题7分，共14分）．19、有红、黄两个盒子，红盒子中装有编号分别为1、2、3、5的四个红球，黄盒子中装有编号为1、2、3的三个黄球．甲、乙两人玩摸球游戏，游戏规则为：甲从红盒子中每次摸出一个小球，乙从黄盒子中每次摸出一个小球，若两球编号之和为奇数，则甲胜，否则乙胜．（1）试用列表或画树状图的方法，求甲获胜的概率；（2）请问这个游戏规则对甲、乙双方公平吗？若公平，请说明理由；若不公平，试改动红盒子中的一个小球的编号，使游戏规则公平．解：20、我市某中学开展以“三创一办”为中心，以“校园文明”为主题的手抄报比赛，同学们积极参与，参赛同学每人交了一份得意作品，所有参赛作品均获奖，奖项分为一等奖、二等奖、三等奖和优秀奖，将获奖结果绘制成如下两幅统计图．请你根据图中所给信息解答下列问题：（1）一等奖所占的百分比是．（2）在此次比赛中，一共收到多少份参赛作品？请将条形统计图补充完整；（3）各奖项获奖学生分别有多少人？解：五、（本大题共3小题，每小题8分，共24分）．21、（本题满分8分）为解决楼房之间的挡光问题，某地区规定：两幢楼房间的距离至少为40米，中午12时不能挡光.如图，某旧楼的一楼窗台高1米，要在此楼正南方40米处再建一幢新楼.已知该地区冬天中午12时阳光从正南方照射，并且光线与水平线的夹角最小为30°，在不违反规定的情况下，请问新建楼房最高多少米？（结果保留准确值）22、（本题满分8分）如图，在一正方形ABCD 中，E 为对角线AC 上一点，连接EB 、ED ，（1）求证：△BEC≌△DEC：（2）延长BE 交AD 于点F ，若∠DEB=140°．求∠AFE 的度数．解：23、（本题满分8分）国家发改委公布的《商品房销售明码标价规定》，从2011年5月1日起商品房销售实行一套一标价．商品房销售价格明码标价后，可以自行降价、打折销售，但涨价必须重新申报．某市某楼盘准备以每平方米5000元的均价对外销售，由于新政策的出台，购房者持币观望．为了加快资金周转，房地产开发商对价格两次下调后，决定以每平方米4050元的均价开盘销售．（1）求平均每次下调的百分率；（2）某人准备以开盘均价购买一套100平方米的房子，开发商还给予以下两种优惠方案以供选择： ①打9.8折销售；②不打折，送两年物业管理费，物业管理费是每平方米每月1.5元．请问哪种方案更优惠？解：六、灵（本大题共2小题，每小题8分，共16分）．24、（本题满分8分）如图，在平面直角坐标系xOy 中，一次函数()0y kx b k =+≠的图象与反比例函数()0my m x=≠的图象交于二、四象限内的A B 、两点，与x 轴交于C 点，点B 的坐标为()6n ，，线段5OA =，E 为x 轴负半轴上一点，且4sin 5AOE ∠=．（1）求该反比例函数和一次函数的解析式；（2）求AOC △的面积．水平线 ABCD 30°新楼 1米40米旧楼（26）题AE O CBxy （第24题图）25.（8分）炮弹的运行轨道若不计空气阻力是一条抛物线．现测得我军大炮A与射击目标B的水平距离为600 m，炮弹运行的最大高度为1 200 m.（1）求此抛物线的表达式．（2）若在A、B之间距离A点500 m处有一高350 m的障碍物，计算炮弹能否越过障碍物.友情提示：范文可能无法思考和涵盖全面，供参考!最好找专业人士起草或审核后使用，感谢您的下载！。

云南初三初中数学月考试卷带答案解析

云南初三初中数学月考试卷班级:___________ 姓名：___________ 分数：___________一、选择题1.下列图形中，可以看作是中心对称图形的是（）A．B．C．D．2.如图，在⊙O中，∠ABC=50°，则∠AOC等于（）A．50°B．80°C．90°D．100°3.有5张大小、背面都相同的扑克牌，正面上的数字分别是4，5，6，7，8．若将这5张牌背面朝上洗匀后，从中任意抽取1张，那么这张牌正面上的数字为偶数的概率是（）A．B．C．D．4.用配方法解一元二次方程x2＋4x﹣5＝0，此方程可变形为（）A．（x＋2）2＝9B．（x﹣2）2＝9C．（x＋2）2＝1D．（x﹣2）2＝15.已知关于的方程的一个根为，则实数的值为（）A．2B．﹣1C．1D．﹣26.若将抛物线y＝x2向右平2个单位，再向上平移3个单位，则所得抛物线的表达式为（）A．y＝（x＋2）2＋3B．y＝（x－2）2＋3．C．y＝（x＋2）2－3D．y＝（x－2）2－37.如图，CD是⊙O的直径，弦AB⊥CD于E，连接BC、BD，下列结论中不一定正确的是（）A．AE=BE B． = C．OE=DE D．∠DBC=90°8.某旅游景点三月份共接待游客25万人次，五月份共接待游客64万人次，设每月的平均增长率为，则可列方程为（）A．B．C．D．二、填空题1.抛物线的顶点坐标为．2.二次函数，开口方向向，当时，y 随x 的增大而_______．3.一只不透明的袋子中装有1个白球和3个红球，这些球除颜色外都相同，搅匀后从中任意摸出1个球，则摸出红球的概率为．4.如图，⊙O 是△ABC 的外接圆，连结OA 、OB ，若∠AOB=70°，则∠ACB 的度数为．5.如图，⊙O 的直径CD 垂直弦AB 于点E ，且CE=4，DE=16，则AB 的长为．6.已知一个布袋里装有2个红球，3个白球和若干个黄球，这些球除颜色外其余都相同．若从该布袋里任意摸出1个球，是红球的概率为，则黄球有个．7.如图，已知圆心角∠AOB 的度数为100°,则圆周角∠ACB 的度数是．三、解答题1.（10分）解方程（1）（2）x 2﹣5x ﹣6="0"2.（10分）确定下列抛物线的开口方向、对称轴和顶点坐标（1）（2）3.（6分）将分别标有数学2，3，5的三张质地，大小完全一样的卡片背面朝上放在桌面上，（1）随机抽取一张，求抽到奇数的概率；（2）随机抽取一张作为个位上的数字（不放回），再抽取一张作为十位上的数字，能组成哪些两位数？并求出抽取到的两位数恰好是35的概率．4.（8分）如图，在平面直角坐标系中，已知点B （4，2），BA ⊥x 轴于A ．（1）画出将△OAB 绕原点逆时针旋转90°后所得的△OA 1B 1，并写出点A 1、B 1的坐标；（2）作△OAB 关于原点O 的中心对称图形，写出对称点、的坐标．5.（7分）如图，小华和小丽两人玩游戏，她们准备了A 、B 两个分别被平均分成三个、四个扇形的转盘．游戏规则：小华转动A盘、小丽转动B盘．转动过程中，指针保持不动，如果指针恰好指在分割线上，则重转一次，直到指针指向一个数字所在的区域为止．两个转盘停止后指针所指区域内的数字之和小于6，小华获胜．指针所指区域内的数字之和大于6，小丽获胜．（1）用树状图或列表法求小华、小丽获胜的概率；（2）这个游戏规则对双方公平吗？请判断并说明理由．6.（7分）已知AB是⊙O的直径，弦CD⊥AB，垂足为P，（1）若半径为5，CD＝8，求OP及BD的长度．（2）若,求的度数．7.（7分）如图，在一面靠墙的空地上用长为24米的篱笆围成中间隔有两道篱笆的长方形花圃，设花圃的宽AB 为x米，面积为y平方米．（1）求y与x之间的函数关系式（2）当x取何值时所围成的花圃的面积最大？最大面积是多少？云南初三初中数学月考试卷答案及解析一、选择题1.下列图形中，可以看作是中心对称图形的是（）A．B．C．D．【答案】B【解析】根据中心对称图形的定义：把一个图形绕某一点旋转180°，如果旋转后的图形能够与原来的图形重合，那么这个图形就叫做中心对称图形进行解答．第一个图形，第三个图形和第四个图形都不是中心对称图形，故选：B．【考点】中心对称图形2.如图，在⊙O中，∠ABC=50°，则∠AOC等于（）A．50°B．80°C．90°D．100°【答案】D【解析】∵∠ABC=50°，∴∠AOC=2∠ABC=100°．故选D．【考点】圆周角定理3.有5张大小、背面都相同的扑克牌，正面上的数字分别是4，5，6，7，8．若将这5张牌背面朝上洗匀后，从中任意抽取1张，那么这张牌正面上的数字为偶数的概率是（）A．B．C．D．【答案】B【解析】∵有5张大小、背面都相同的扑克牌，正面上的数字分别是4，5，6，7，8．其中偶数为：4，6，8，∴从中任意抽取1张，那么这张牌正面上的数字为偶数的是：．故选：B．【考点】概率公式4.用配方法解一元二次方程x2＋4x﹣5＝0，此方程可变形为（）A．（x＋2）2＝9B．（x﹣2）2＝9C．（x＋2）2＝1D．（x﹣2）2＝1【答案】A【解析】x2+4x﹣5=0，x2+4x=5，x2+4x+22=5+22，（x+2）2=9，故选A．【考点】配方法解一元二次方程5.已知关于的方程的一个根为，则实数的值为（）A．2B．﹣1C．1D．﹣2【答案】C【解析】一元二次方程的根就是一元二次方程的解，就是能够使方程左右两边相等的未知数的值．即用这个数代替未知数所得式子仍然成立．因为x=3是原方程的根，所以将x=3代入原方程，即32 k﹣3k﹣6=0成立，解得k=1．故选：C．【考点】一元二次方程的解6.若将抛物线y＝x2向右平2个单位，再向上平移3个单位，则所得抛物线的表达式为（）A．y＝（x＋2）2＋3B．y＝（x－2）2＋3．C．y＝（x＋2）2－3D．y＝（x－2）2－3【答案】B【解析】将抛物线y=x2向右平移2个单位可得y=（x﹣2）2，再向上平移3个单位可得y=（x﹣2）2+3，故选：B．【考点】二次函数图象与几何变换7.如图，CD是⊙O的直径，弦AB⊥CD于E，连接BC、BD，下列结论中不一定正确的是（）A．AE=BE B． = C．OE=DE D．∠DBC=90°【答案】C【解析】∵CD⊥AB，∴AE=BE，=，∵CD是⊙O的直径，∴∠DBC=90°，不能得出OE=DE．故选：C．【考点】垂径定理8.某旅游景点三月份共接待游客25万人次，五月份共接待游客64万人次，设每月的平均增长率为，则可列方程为（）A．B．C．D．【答案】A【解析】设每月的平均增长率为x，依题意得25（1+x）2=64；故选A．【考点】一元二次方程二、填空题1.抛物线的顶点坐标为．【答案】（﹣1，2）．【解析】∵抛物线，∴抛物线的顶点坐标为：（﹣1，2）．故答案为：（﹣1，2）．【考点】二次函数的性质2.二次函数，开口方向向，当时，y随x的增大而_______．【答案】下，减小．【解析】∵二次函数二次项系数a=﹣，∴开口方向向下，顶点坐标为（﹣2，﹣2），当x≥﹣2时，函数y随着x的增大而减小．故答案为：下，减小．【考点】二次函数的性质3.一只不透明的袋子中装有1个白球和3个红球，这些球除颜色外都相同，搅匀后从中任意摸出1个球，则摸出红球的概率为．【答案】【解析】∵一只不透明的袋子中装有1个白球和3个红球，这些球除颜色外都相同，∴搅匀后从中任意摸出1个球，则摸出红球的概率为：=．故答案为：【考点】概率公式4.如图，⊙O 是△ABC 的外接圆，连结OA 、OB ，若∠AOB=70°，则∠ACB 的度数为．【答案】35° 【解析】根据圆周角定理：∠AOB=70°，则∠ACB=35°【考点】圆周角定理5.如图，⊙O 的直径CD 垂直弦AB 于点E ，且CE=4，DE=16，则AB 的长为．【答案】16【解析】∵CE=4，DE=16，∴OB=10， ∴OE=6， ∵AB ⊥CD ， ∴在△OBE 中，得BE=8， ∴AB=2BE=16．【考点】垂径定理6.已知一个布袋里装有2个红球，3个白球和若干个黄球，这些球除颜色外其余都相同．若从该布袋里任意摸出1个球，是红球的概率为，则黄球有个．【答案】1【解析】设有a 个黄球，根据题意得：=，解得：a=1，经检验，a=1是原分式方程的解，∴a=1．【考点】概率公式7.如图，已知圆心角∠AOB 的度数为100°,则圆周角∠ACB 的度数是．【答案】130°【解析】∵∠AOB=100°∴∠D=∠AOB=50°∴∠ACB=180°﹣∠D=130°．【考点】圆周角定理三、解答题1.（10分）解方程（1）（2）x 2﹣5x ﹣6="0"【答案】（1）（2）x 1=6，x 2=-1【解析】先把方程化为一般式，再计算出判别式的值，然后利用求根公式解方程．试题解析：（1）2x 2+5x-1=0△=52-4×2×（-1）=33x=所以（2）x 2﹣5x ﹣6=0（x-6）（x+1）=0x 1=6，x 2=-1【考点】解一元二次方程2.（10分）确定下列抛物线的开口方向、对称轴和顶点坐标（1）（2）【答案】（1）开口向上，对称轴x=2, 顶点（2，-3）；（2）开口向下，对称轴x= -2 顶点（-2，-1）．【解析】可以将函数化为顶点坐标式，即y=a （x ﹣h ）2+k ，或者直接代入公式也可求出．试题解析：（1）y=2x 2﹣8x+5=2（x ﹣2）2﹣3，开口向上，对称轴x=2, 顶点（2，-3）；（2）y=﹣x 2﹣4x -5=﹣（x+2）2-1，开口向下，对称轴x= -2 顶点（-2，-1）．【考点】二次函数的性质3.（6分）将分别标有数学2，3，5的三张质地，大小完全一样的卡片背面朝上放在桌面上，（1）随机抽取一张，求抽到奇数的概率；（2）随机抽取一张作为个位上的数字（不放回），再抽取一张作为十位上的数字，能组成哪些两位数？并求出抽取到的两位数恰好是35的概率．【答案】（1）抽到奇数的概率P=；（2）恰好为35的概率为．【解析】（1）先求出这组数中奇数的个数，再利用概率公式解答即可；（2）根据题意列举出能组成的数的个数及35的个数，再利用概率公式解答．试题解析：（1）根据题意可得：有三张卡片，奇数只有“3和5”一张，故抽到奇数的概率P=；（2）根据题意可得：随机抽取一张作为个位上的数字（不放回），再抽取一张作为十位上的数字，共能组成6个不同的两位数：32，52，23，53，25，35．其中恰好为35的概率为．【考点】概率公式4.（8分）如图，在平面直角坐标系中，已知点B （4，2），BA ⊥x 轴于A ．（1）画出将△OAB 绕原点逆时针旋转90°后所得的△OA 1B 1，并写出点A 1、B 1的坐标；（2）作△OAB 关于原点O 的中心对称图形，写出对称点、的坐标．【答案】（1）A 1、B 1的坐标分别为（﹣2，4）（﹣2，0）；（2）点B 2、A 2的坐标分别为（﹣4，﹣2）、（﹣4，0）．【解析】（1）将点B 绕原点逆时针方向旋转90°可理解为把Rt △OAB 绕原点逆时针方向旋转90°，画图后即可得到A 1、B 1点坐标；（2）根据关于原点对称的坐标特征求解．试题解析：（1）如图，A 1、B 1的坐标分别为（﹣2，4）（﹣2，0）；（2）如图：点B 2、A 2的坐标分别为（﹣4，﹣2）、（﹣4，0）．【考点】旋转5.（7分）如图，小华和小丽两人玩游戏，她们准备了A 、B 两个分别被平均分成三个、四个扇形的转盘．游戏规则：小华转动A 盘、小丽转动B 盘．转动过程中，指针保持不动，如果指针恰好指在分割线上，则重转一次，直到指针指向一个数字所在的区域为止．两个转盘停止后指针所指区域内的数字之和小于6，小华获胜．指针所指区域内的数字之和大于6，小丽获胜．（1）用树状图或列表法求小华、小丽获胜的概率；（2）这个游戏规则对双方公平吗？请判断并说明理由．【答案】（1）P （小华获胜）=，P （小丽获胜）=；（2）游戏规则对双方不公平．【解析】（1）首先根据题意列出表格，然后由表格即可求得所有等可能的结果与小华、小丽获胜的情况，再利用概率公式即可求得答案；（2）比较小华、小丽获胜的概率的大小，即可知这个游戏规则对双方公平试题解析：（1）列表如下：∵共有12种等可能的结果，小华获胜的有6种情况、小丽获胜的有3情况， ∴P （小华获胜）==，P （小丽获胜）==；（2）这个游戏规则对双方不公平，∵P（小华获胜）＞P（小丽获胜），∴游戏规则对双方不公平．【考点】游戏公平性6.（7分）已知AB是⊙O的直径，弦CD⊥AB，垂足为P，（1）若半径为5，CD＝8，求OP及BD的长度．（2）若,求的度数．【答案】（1）OP=3，BD=；（2）∠B=20°【解析】（1）根据垂径定理直接求出OP，再求BD即可；（2）连接OD，根据圆周角定理可得=试题解析：（1）∵CD＝8，∴CP=4，∵CP=4，半径为5，∴OP=，∵OP=3，半径为5，∴PB=8，∵PB=8，PD=4，∴BD=；（2）连接OD，∴∠AOD=∠AOC=40°，∵∠B=∠AOD，∴∠B=20°【考点】1.垂径定理2.勾股定理3.圆周角定理7.（7分）如图，在一面靠墙的空地上用长为24米的篱笆围成中间隔有两道篱笆的长方形花圃，设花圃的宽AB 为x米，面积为y平方米．（1）求y与x之间的函数关系式（2）当x取何值时所围成的花圃的面积最大？最大面积是多少？【答案】（1）S=﹣4x2+24x；=36平方米（2）当x=3m时，S最大值【解析】（1）求出S=AB×BC代入即可；（2）把解析式化成顶点式，再利用二次函数增减性即可得到答案．试题解析：（1）设花圃的宽AB为x米，则BC=（24﹣4x）m，根据题意得出：S=x（24﹣4x）=﹣4x2+24x；（2）S=﹣4x2+24x=﹣4（x2﹣6x）=﹣4（x﹣3）2+36，∴当x=3m时，S=36平方米最大值【考点】二次函数的应用。

云南初三初中数学月考试卷带答案解析

云南初三初中数学月考试卷班级:___________ 姓名：___________ 分数：___________一、填空题1.代数式有意义，则x的取值范围是．2.曲靖市计划从2013年到2016年新增林地面积253万亩，253万亩用科学记数法表示正确的是_________亩.3.如图，已知△ABC为直角三角形，∠C=90°，若沿图中虚线剪去∠C，则∠1+∠2等于________．4.若点（a，b）在一次函数y=2x﹣3上，则代数式3b﹣6a+8的值是__________．5.如图，正六边形ABCDEF的边长为2，则对角线AE的长是______________．6.如图，动点P在平面直角坐标系中按图中箭头所示方向运动，第1次从原点运动到点（1, 2），第2次接着运动到点（2, 0），第3次接着运动到点（3, 1），…，按这样的运动规律，经过第2016次运动后，动点P的坐标是_______________.7.如图，该几何体的俯视图是（）A．B．C．D．二、单选题1.－的倒数是（）A．B．C．D．2.下列运算正确的是（）A．3x-2x=1B．C．D．3.不等式组的整数解的个数是（）A．3B．4C．5D．无数个4.如图，在△ABC中，分别以点A和点B为圆心，大于的长为半径画弧，两弧相交于点M,N，作直线MN交BC 于点D，连接AD若△ABC 的周长为21，AB=7，则△ADC的周长为（）A．28B．24C．18.5D．145.关于x的一元二次方程2x2－(a－1)x+a=0的两个实数根互为相反数，则a的值是（）A．a = -1B．a = 0C．a = 1D．a = 26.已知：如图，四边形ABCD是⊙O的内接正方形，点P是劣弧上不同于点C的任意一点，则cos∠BPC的值是（）A．B．C．1D．7.如图，已知双曲线经过直角三角形OAB斜边OA的中点D，且与直角边AB相交于点C．若点A的坐标为（, 4），则△AOC的面积为（）A. 15B. 12C. 9D. 6三、解答题1.计算：2.先化简，再求值：，其中.3.如图，在正方形方格中，的顶点都在格点上，结合所给的平面直角坐标系解答下列问题：（1）将向右平移4个单位长度，再向上平移3个单位长度，画出平移后的；（2）将绕点C顺时针旋转90°，画出旋转后的；（3）求出、所在直线的函数解析式.4.某市教育主管部门为了解学生的作业量情况，随机抽取了几所中学八年级的部分学生进行了一次调查，并根据收集到的信息进行了统计，绘制了下面两幅尚不完整的统计图．请你根据统计图、表中所提供的信息解答下列问题：（1）本次共抽取了名学生进行调查；（2）x= ，y= ，补全条形统计图；（3）若这几所中学八年级的学生共有3200人，请估计做作业时间在2小时以上的学生人数是多少？（4）由图表可知，这次被调查的八年级学生的作业时间的中位数一定落在1.5小时—2小时这一时段内，你认为这种判断正确吗？（不需要说明理由）5.如图，在四边形ABCD中，AB=AD，CB=CD，AC与BD相交于O点，OC=OA，若E是CD上任意一点，连接BE交AC于点F，连接DF．（1）证明：△CBF≌△CDF；（2）若AC=2，BD=2，求四边形ABCD的周长。

云南省文山市南鹰学校2013年9月九年级上月考数学试卷

文山南鹰学校九年级上学期数学九月月考试卷总分：100分考试时间：100分钟学号学生姓名分数一、选择题(每小题3分，共30分)1、两个直角三角形全等的条件是（）A 、一锐角对应相等B 、两锐角对应相等C 、一条边对应相等D 、两条边对应相等 2、如图，由∠1=∠2，BC=DC ，AC=EC ，得△ABC ≌△EDC 的根据是（） A 、SAS B 、ASA C 、AAS D 、SSS3、等腰三角形底边长为7，一腰上的中线把其周长分成两部分的差为3，则腰长是（） A 、4 B 、10 C 、4或10 D 、以上答案都不对4、如图，EA ⊥AB ，BC ⊥AB ，EA=AB=2BC ，D 为AB 中点，有以下结论：(1)DE=AC ；(2)DE ⊥AC ；(3)∠CAB=30°；(4)∠EAF=∠ADE 。

其中结论正确的是（） A 、(1)，(3) B 、(2)，(3) C 、(3)，(4) D 、(1)，(2)，(4)5、如图，△ABC 中，∠ACB=90°，BA 的垂直平分线交CB 边于D ，若AB=10，AC=5，则图中等于60°的角的个数为（） A 、2 B 、3 C 、4 D 、5(第2题图) (第4题图) (第5题图)6、设M 表示直角三角形，N 表示等腰三角形，P 表示等边三角形，Q 表示等腰直角三角形，则下列四个图中，能表示他们之间关系的是（）7、如图，△ABC 中，∠C=90°，AC=BC ，AD 平分∠CAB 交BC 于点D ，DE ⊥AB ，垂足为E ，且AB=6cm ，则△DEB 的周长为（） A 、4cm B 、6cm C 、8 cm D 、10cm8、如图，△ABC 中，AB=AC ，点D 在AC 边上，且BD=BC=AD ，则∠A 的度数为（） A 、30° B 、36° C 、45° D 、70°9、如图，已知AC 平分∠PAQ ，点B ，B ′分别在边AP ，AQ 上，如果添加一个条件，即可推出AB=AB ′，那么该条件不可以是（）A 、BB ′⊥AC B 、BC=B ′C C 、∠ACB=∠ACB ′D 、∠ABC=∠AB ′C(第7题图) (第8题图) (第9题图) (第10题图)10、如图，△ABC 中，AD ⊥BC 于D ，BE ⊥AC 于E ，AD 与BE 相交于F ，若BF=AC ，则∠ABC 的大小是（）A 、40°B 、45°C 、50°D 、60°二、填空题(每小题2分，共14分)11、如果等腰三角形的一个底角是80°，那么顶角是度.12、如图，点F 、C 在线段BE 上，且∠1=∠2，BC=EF ，若要使△ABC ≌△DEF ，则还须补充一个条件(第12题图) (第13题图) (第15题图)13、如图，点D 在AB 上，点E 在AC 上，CD 与BE 相交于点O ，且AD=AE ，AB=AC 。

2013～2014学年(上)九年级第三次月考

2013～2014学年（上）九年级第三次月考数学试题（完卷时间：120分钟满分：150分）一、选择题（本大题共10小题，每小题4分，共40分．） 1．下列根式是二次根式的是：（）A ．xB ．18C ．314D ．10-2．下列方程是一元二次方程的是：（）A ．65322+=-+x x xB ．02=++c bx ax C ．4424322--=+x x x D ．0393=+-x x3．下列事件中必然发生的是：（）A ．明天一定会下雨。

B ．两个负数的和是正数。

C. 地球上，抛出的铁球最后总往下落D ．任意选择某个电视频道,正在播放动画片4．抛物线3)3(52+-=x y 的顶点坐标是：（）A ．（－3，3）B ．（3，3）C ．（3，－3）D ．（―3，―3）5．一元二次方程0752=+-x x 根的情况是：（）A ．只有一个实数根B ．有两个相等的实数根C ．有两个不相等的实数根 D. 没有实数根6．已知：A 点坐标是（－2，5），B 点是A 点关于原点对称点，则B 点坐标是（） A ．（2，－5） B ．（―2，―5） C ．（2，5） D ．（－2，5）7．已知⊙1O 的半径是4cm ,⊙2O 的半径是2cm ,21O O ＝6cm ,则⊙1O 和⊙2O 的位置关系是（）A ．内切B ．外切C ．相交D ．内含8．下列图形中既是中心对称图形，又是轴对称图形的是：（）A ．正三角形B ．平行四边形C ．等腰梯形D ．矩形9．在半径为r 的圆中，圆内接正六边形的边长为（）A . r B. 2r C. 3r D. 2r 10．高速公路的隧道和桥梁最多．如图是一个隧道的横截面，若它的形状是以O 为圆心的圆的一部分，路面AB =12米，净高CD =9米，则此圆的半径OA =（）A .212米 B. 213米 C.214米 D.215米二、填空题（本大题共8小题，每小题3分，共24分） 11．二次根式x -3有意思则x ______. 12．如图，∠BAC=35°则∠BOC=______°. 13．抛物线3)1(522+--=x y 是由抛物线252x y -=先向_____平移个单位长度，再向平移3个单位长度得到. 14．如图，⊙O 外一点P 向⊙O 引两条切线PA ，PB 与⊙O 相切于点A 、B ，且PA=PB=10cm ；线段CD 与⊙O 相切于点M 。

人教版九年级上册数学月考试卷(含答案解析)

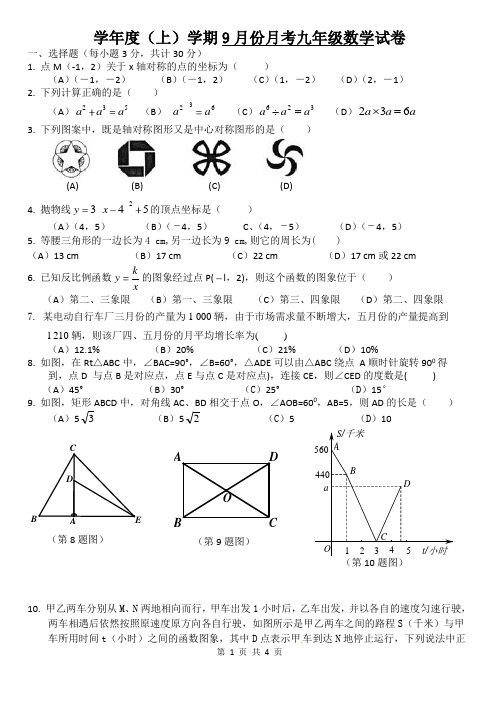
t/小时S/千米a 44056054321D C B A O 学年度（上）学期9月份月考九年级数学试卷一、选择题（每小题3分，共计30分）1. 点M （-1，2）关于x 轴对称的点的坐标为（）（A ）（－1，－2）（B ）（－1，2）（C ）（1，－2）（D ）（2，－1）2. 下列计算正确的是（）（A ）235a a a （B ）326a a （C ）326a a a =÷ （D ）a a a 632=⨯3. 下列图案中，既是轴对称图形又是中心对称图形的是（）4. 抛物线2345y x 的顶点坐标是（）（A ）（4，5）（B ）（4，5） C 、（4，5）（D ）（4，5）5. 等腰三角形的一边长为4 cm,另一边长为9 cm,则它的周长为( )（A ）13 cm （B ）17 cm （C ）22 cm （D ）17 cm 或22 cm6. 已知反比例函数k y x的图象经过点P(l ，2)，则这个函数的图象位于（）（A ）第二、三象限（B ）第一、三象限（C ）第三、四象限（D ）第二、四象限7. 某电动自行车厂三月份的产量为1 000辆，由于市场需求量不断增大，五月份的产量提高到 l 210辆，则该厂四、五月份的月平均增长率为( )（A ）12.1% （B ）20% （C ）21% （D ）10%8. 如图，在Rt △ABC 中，∠BAC=90°，∠B=60°，△ADE 可以由△ABC 绕点 A 顺时针旋转900得到，点D 与点B 是对应点，点E 与点C 是对应点)，连接CE ，则∠CED 的度数是( )（A ）45° （B ）30° （C ）25° （D ）15°9. 如图，矩形ABCD 中，对角线AC 、BD 相交于点O ，∠AOB=600，AB=5，则AD 的长是（）（A ）53 （B ）52 （C ）5 （D ）1010. 甲乙两车分别从M 、N 两地相向而行，甲车出发1小时后，乙车出发，并以各自的速度匀速行驶，两车相遇后依然按照原速度原方向各自行驶，如图所示是甲乙两车之间的路程S （千米）与甲车所用时间t （小时）之间的函数图象，其中D 点表示甲车到达N 地停止运行，下列说法中正(A) (B) (C) (D) E D A C （第8题图） O C D AB （第9题图）（第10题图）确的是（）（A ）M 、N 两地的路程是1000千米；（B ）甲到N 地的时间为4.6小时；（C ）甲车的速度是120千米/小时；（D ）甲乙两车相遇时乙车行驶了440千米.二、填空题（每小题3分，共计30分）11. 将2 580 000用科学记数法表示为．12. 函数12y x 的自变量x 的取值范围是． 13. 计算：82= . 14. 分解因式：322_____________x xx . 15. 抛物线223y x bx 的对称轴是直线1x ，则b 的值为 .16. 如图，CD 为⊙O 的直径，AB ⊥CD 于E ，DE =8cm ，CE =2cm ，则AB = cm.17.不等式组⎩⎨⎧-≤--14352x x ＞的解集是 .18. 如图，在⊙O 中，圆心角∠BOC=60°，则圆周角∠BAC 的度数为度.19. 在ΔABC 中，若AB=34,AC=4，∠B=30°，则ABC S ∆= .20. 如图，△ABC ，AB=AC ，∠BAC=90°，点D 为BC 上一点，CE ⊥BC ，连接AD 、DE ，若CE=BD ，DE=4，则AD 的长为 .三、解答题(其中21-22题各7分．23-24题各8分．25-27题各l0分．共计60分)21. 先化简，再求值：2211121x x x x x -⎛⎫-÷ ⎪+++⎝⎭，其中x=12+.22. 如图，图1和图2都是7×4正方形网格，每个小正方形的边长是1，请按要求画出下列图形，所画图形的各个顶点均在所给小正方形的顶点上.(1)在图1中画出一个等腰直角△ABC ；（第16题图） O C B A (第18题图) (第20题图)(2)在图2中画出一个钝角△ABD，使△ABD的面积是3.ABAB图1 图223. 某中学为了丰富校园文化生活.校学生会决定举办演讲、歌唱、绘画、舞蹈四项比赛，要求每位学生都参加.且只能参加一项比赛.围绕“你参赛的项目是什么?(只写一项)”的问题，校学生会在全校范围内随机抽取部分学生进行问卷调查.将调查问卷适当整理后绘制成如图所示的不完整的条形统计图.其中参加舞蹈比赛的人数与参加歌唱比赛的人数之比为1:3，请你根据以上信息回答下列问题：（1）通过计算补全条形统计图；（2）在这次调查中，一共抽取了多少名学生?（3）如果全校有680名学生，请你估计这680名学生中参加演讲比赛的学生有多少名?24. 已知：BD是△ABC的角平分线，点E，F分别在BC，AB上，且DE∥AB，BE=AF.（1）如图1，求证：四边形ADEF是平行四边形；（2）如图2，若AB=AC，∠A=36°，不添加辅助线，请你直接写出与DE相等的所有线段（AF除外）.25.哈尔滨地铁“二号线”正在进行修建，现有大量的残土需要运输.某车队有载重量为8吨、10吨的卡车共12台，全部车辆运输一次可以运输110吨残土.GFEDAB C图1图2(1)求该车队有载重量8吨、10吨的卡车各多少辆？(2)随着工程的进展，该车队需要一次运输残土不低于165吨，为了完成任务，该车队准备再新购进这两种卡车共6辆，则最多购进载重量为8吨的卡车多少辆？26. 如图，在⊙O 中，AB 、CE 是直径，BD ⊥CE 于G ，交⊙O 于点D ，连接CD 、CB.（1）如图1，求证：∠DCO=90°-21∠COB ；（2）如图2，连接BE ，过点G 作BE 的垂线分别交BE 、AB 、CD 于点F 、H 、M ，求证：MC=MD ；（3）在（2）的条件下，连接AC 交MF 于点N ，若MN=1，NH=4，求CG 的长.（第26题图1）（第26题图2）（第26题图3）27. 已知：如图，抛物线y=-x 2+bx+c 与x 轴负半轴交于点A ，与x 轴正半轴交于点B ，与y 轴正半轴交于点C ，OA=3，O B=1，点M 为点A 关于y 轴的对称点.（1）求抛物线的解析式；（2）点P 为第三象限抛物线上一点，连接PM 、PA ，设点P 的横坐标为t ，△PAM 的面积为S ，求S 与t 的函数关系式；（3）在（2）的条件下，PM 交y 轴于点N ，过点A 作PM 的垂线交过点C 与x 轴平行的直线于点G ，若ON ∶CG=1∶4，求点P 的坐标.答案一、ABCAC DDDAC二、11、2.58×106 12、x ≠2 13、23 14、-x(x+1)2 15、-4 16、817、x ≥5 18、30 19、34或38 20、22三、21、（7分）原式=2211=-x 22、(1)（3分） (2)（4分）23、(1)30%；（2分）(2)100－30－35－5=30，补图略；（3分）(3)(5÷100)×2000=100人（3分）24、(1)（4分）EB=ED=AF ，ED ∥AF∴四边形ADEF 为平行四边形；(2)（4分）CD 、BE 、BG 、FG25、(1)（4分）设89吨卡车有x 辆8x+10(12－x)=110解得：x=5，∴12－x=7；(2)（4分）设购进载重量8吨a 辆8(a+5)+10(6+7－a)≥165a≤2.5∵a 为整数，∴a 的最大值为226、（1）略（2）略（3）AC ∥BE ，△CNG ≌△BFH,设GN=x ，CE=x+1，BC=2x+2=FN=x+4,x=2 CN=22,CG=3227、（1）322+--=x x y （2）963S 2-+=x x （3）过点A 作CG 的垂线，垂足为E ，四边形CEAO 为正方形 △AGE ≌△MNO ，ON=EG ，CE=3ON=3，N （0，-1）直线MP 解析式为131-=x y ，⎪⎩⎪⎨⎧+--=-=321312x x y x y 解得 P （6193-7-，18193-25-） D。

云南省文山市南鹰学校2013年9月八年级上月考数学试卷.doc

学校班级姓名文山南鹰学校八年级上学期数学九月月考试卷总分：100分考试时间：100分钟学号学生姓名分数一、选择题（每题3分，共30分）题号 1 2 3 4 5 6 7 8 9 10 答案1.如图（1），带阴影的长方形面积是A ．9 cm 2B ．24 cm 2C ．45 cm 2D ．51 cm 22. 三角形各边长度的如下，其中不是直角三角形的是（）A ． 3，4，5B ． 6，8，10C ．5，11，12D ．15，8，17 3. 在0.458，•2.4，2π，4.0，3001.0-，71这几个数中无理数有（）个．A.4B.3C.2D.1 4. 25的平方根是（）A 、5B 、-5C 、±5D 、5± 5. 下列说法错误的是（）A. 1的平方根是±1B. –1的立方根是－1C. 2是2的平方根D. –3是2)3(-的平方根 6. 下列各式中，正确的是（）A ．()222-=- B ．()932=- C ．39±= D ．39±=±7.如果一个数的平方根是这个数本身，那么这个数是( ) A 、0 、1 B 、0、1- C 、0、1± D 、08. 三角形的三边长为a 、b 、c 满足()ab c b a 222+=+,则这个三角形是 ( )CBAA.等边三角形;B.钝角三角形;C.直角三角形;D.锐角三角形. 9. 若9,422==b a ，且0>ab ，则b a -的值为（）A ． 5±B ． 1±C ． 5D ． 1- 10.要使二次根式x 有意义，那么X 的取值（）A.X>0B.X ≤0C.X<0D.X ≥0 二、填空题（每题3分，共24分）11. 在⊿ABC 中，∠C=90°，若a=5,b=12,则c =_______.12. 36的平方根是；64的立方根是；3 -2的绝对值是。

2013-2014学年度第一学期期末考试九年级数学试卷(2021年整理)

2013-2014学年度第一学期期末考试九年级数学试卷(word版可编辑修改) 编辑整理：尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（2013-2014学年度第一学期期末考试九年级数学试卷(word版可编辑修改)）的内容能够给您的工作和学习带来便利。

同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。

本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为2013-2014学年度第一学期期末考试九年级数学试卷(word版可编辑修改)的全部内容。

2013~2014学年度第一学期期末抽测九年级数学试题本试卷分卷Ⅰ(1至2页)和卷Ⅱ（3至8页）两部分．全卷满分120分，考试时间90分钟.卷Ⅰ一、选择题(本大题共有8小题,每小题3分，共24分．请将正确选项前的字母代号填写在第3页相应的答题栏内，在卷Ⅰ上答题无效)1．两圆的半径分别为3和4，圆心距为7,则这两圆的位置关系为A ．相交B ．内含C ．内切D ．外切 2．如图,OA 、OB 是⊙O 的两条半径，且OA ⊥OB ，点C 在⊙O 上,则∠ACB 的度数为 A ．45° B ．35° C ．25° D ．20°3．如图，AB 是⊙O 的直径，弦CD ⊥AB ，垂足为E ,如果AB ＝20，CD ＝16．那么线段OE 的长为A ．4B ．5C ．6D ．84．如果将抛物线2=y x 向上平移1个单位，那么所得抛物线对应的函数关系式是A ．21=+y xB ．21=-y xC ．2(1)=+y xD ．2(1)=-y x5．菱形具有而矩形不一定具有的性质是A ．对角线相等B ．对角线互相垂直C ．对角线互相平分D ．对角互补6．若圆锥的轴截面为等边三角形，则称此圆锥为正圆锥．正圆锥侧面展开图的圆心角是 A ．90° B ．120°C ．150°D ．180°（第2题）（第3题）7．根据下列表格的对应值：可得方程2530+-=x x 一个解x 的范围是A ．0＜x ＜0。

2013—2014学年度九年级第一学期九月月考数学试卷

2013—2014学年度九年级第一学期九月月考数学试卷一、选择题(每小题4分,共40分) 题号 1 2 3 45 6 7 8 9 10 答案1. 如图中，既是中心对称又是轴对称的图案是（）.A B C D 2. 如图，△OAB 绕点O 逆时针旋转80°到△OCD 的位置，已知∠AOB ＝45°，则∠AOD 等于（）Ａ．55° Ｂ．45° Ｃ．40° Ｄ．35°3.如图,将正方形图案绕中心O 旋转180°后,得到的图案是 ( )4.下列命题中的真命题是 ( ) (A)全等的两个图形是中心对称图形. (B)关于中心对称的两个图形全等. (C)中心对称图形都是轴对称图形. (D)轴对称图形都是中心对称图形.5.有以下图形:平行四边形、矩形、等腰三角形、线段、菱形,其中既是轴对称图形又是中心对称图形的有( ) (A)5个. (B)4个. (C)3个. (D)2个 6．如图，如果正方形ABCD 旋转后能与正方形CDEF 重合，那么图形所在平面内可作旋转中心的点共有（）A ．1 个B ．2 个C ．3 个D ．4个7．从生产的一批螺钉中抽取1000个进行质量检查，结果发现有5个是次品，那么从中任取1个是次品概率约为（）．A B C DA ．11000 B ．1200C ．12D ．158．下列说法正确的是（）Ａ．为了了解我市今夏冰淇淋的质量，应采用普查的调查方式Ｂ．想了解一个同学5次数学考试成绩的稳定程度，只需关注该生这5次数学考试成绩的中位数Ｃ．随意翻到一本书的某页，这页的页码是偶数，这一事件是随机事件Ｄ．某种彩票中奖的概率是1%，买100张该种彩票一定会中奖9．不透明的口袋里装有白、黄、蓝三种颜色的乒乓球（除颜色外都相同），其中黄球有2 个，蓝球有3个.现从中任意摸出一个是蓝球的概率是31，则口袋里白球有（）Ａ．5个Ｂ．4个Ｃ．3个Ｄ．2个10．有一枚质地均匀的正六面体骰子，骰子六个面上分别刻有1，2，3，4，5，6的数字，随机地抛掷一次，落在桌面后，朝上一面的数字为奇数的概率为（） A.12 B. 13 C. 14 D. 16二、填空(每小题4分,共32分)11、任意掷一枚均匀硬币两次，两次都是同一面朝上的概率是___ 12.如图,△ABC ,△ACD ,△ADE 是三个全等的正三角形,那么△ABC 绕着顶点A 沿逆时针方向旋转______度,才能与△ADE 完全重合.13、小明、小刚、小亮三人正在做游戏，现在要从他们三人中选出一人去帮王奶奶干活，则小明被选中的概率为__ ___, 小明未被选中的概率为______ 。