CHAP10排序lhj
chap10(文件)

3、 reat 函数 Turbo C不允许用open函数建立新文件,而提 供一个 creat 函数用来建立新文件。调用格式: creat(文件名, 打开方式); 若建立成功,该函数返回一个正整数(文件号),否则 返回–1。 4、 read 函数 调用格式: read(fd, buf, count); read函数的作用是从正整数fd代表的非缓冲文件中 读出count个字节的信息到buf指向的缓冲区中。读 出成功,read函数返回值为读出的字节数,遇文件 结束,read函数返回值为0,否则为–1。
fseek(fp,100L,0); fseek(fp,50L,1); fseek(fd,–10L,1);
/* 将指针移到离文件头100个字节处 */ /* 将指针移到离当前位置50个字节处*/ /* 将指针从当前位置倒退10个字节 */
fseek(fp,–10L,2);
/* 将指针移到文件末倒数10个字节处*/
文件的打开模式
r 以只读方式打开一个文本文件 w 以只写方式打开一个文本文件 a 以追加方式打开一个文本文件 r+ 以读/写方式打开一个文本文件
w+ 以读/写方式建立一个新的文本文件 a+ 以读/写方式打开一个文本文件
rb 以只读方式打开一个二进制文件 wb 以只写方式打开一个二进制文件 ab 以追加方式打开一个二进制文件 rb+ 以读/写方式打开一个二进制文件 wb+ 以读/写方式建立一个新的二进制文件 ab+ 以读/写方式打开一个二进制文件
二、 文件类型指针 “文件指针”是缓冲文件系统中的一个重要概念。 在C系统的头文件stdio.h中定义了一个名叫FILE(注意 大写!)的结构体类型(其成员反映了对文件进行输入/输 出操作时的有关信息): typedef struct { short level; /* 缓冲区饱和程度 */ unsigned flage; /* 文件状态标志 */ char fd; /* 文件号 */ unsigned char hold; /* 无缓冲区取消字符输入 */ short bsize; /* 缓冲区大小, 缺省值512 */ unsigned char *buffer; /* 缓冲区 */ unsigned char *curp; /* 当前活动指针 */ unsigned istemp; /* 草稿文件标识 */ short token; /* 作正确性检验 */ }FILE ;
十大排序算法原理

十大排序算法原理排序算法是计算机科学中最基本的算法之一,它可以将一组无序的数据按照一定的规则进行排列,使得数据更加有序,方便后续的处理。
在计算机科学中,有许多种排序算法,其中比较经典的有十大排序算法,它们分别是冒泡排序、选择排序、插入排序、希尔排序、归并排序、快速排序、堆排序、计数排序、桶排序和基数排序。
1. 冒泡排序冒泡排序是一种简单的排序算法,它的基本思想是从头到尾依次比较相邻的两个元素,如果前一个元素比后一个元素大,则交换它们的位置。
这样一趟下来,最大的元素就被排到了最后面。
然后再对剩下的元素进行同样的操作,直到所有元素都被排好序为止。
2. 选择排序选择排序是一种简单的排序算法,它的基本思想是从待排序的数据中选择最小的元素,将其放到已排序的数据的末尾。
然后再从剩余的数据中选择最小的元素,放到已排序的数据的末尾。
依次类推,直到所有的数据都被排序完毕。
3. 插入排序插入排序是一种简单的排序算法,它的基本思想是将待排序的数据分为已排序和未排序两部分,每次从未排序的数据中取出一个元素,插入到已排序的数据中的合适位置。
插入的过程中,需要将已排序的数据中比插入元素大的元素向后移动一位,为插入元素腾出位置。
4. 希尔排序希尔排序是一种改进的插入排序算法,它的基本思想是将待排序的数据分成若干个子序列,对每个子序列进行插入排序,然后再将所有子序列合并成一个序列。
希尔排序的特点是可以先对距离较远的元素进行比较和交换,从而减少比较和交换的次数,提高排序的效率。
5. 归并排序归并排序是一种分治算法,它的基本思想是将待排序的数据分成两个子序列,对每个子序列进行排序,然后将两个子序列合并成一个有序序列。
归并排序的特点是稳定、效率高,但需要额外的存储空间。
6. 快速排序快速排序是一种分治算法,它的基本思想是选择一个基准元素,将待排序的数据分成两个子序列,一个子序列中的元素都比基准元素小,另一个子序列中的元素都比基准元素大。
十进制数的大小比较与排序知识点总结

十进制数的大小比较与排序知识点总结在数学的世界里,十进制数是我们最常见和最常用的数制。
理解十进制数的大小比较和排序是非常基础且重要的知识。
首先,让我们来明确一下什么是十进制数。
十进制数就是由 0、1、2、3、4、5、6、7、8、9 这十个数字组成,采用“逢十进一”的进位规则。
那么,如何比较两个十进制数的大小呢?这需要我们从数位的高低开始看起。
就像我们比较两个多位数,先比较最高位(也就是最左边的数字)。
如果最高位上的数字不同,那么数字大的那个数就大。
例如,比较 543 和 87,因为 8 大于 5,所以 87 大于 543 。
但如果最高位上的数字相同,那我们就接着比较次高位(也就是从左往右数的第二个数字)。
比如 543 和 521 ,最高位都是 5 ,接着比较次高位,4 大于 2 ,所以 543 大于 521 。
如果次高位也相同,那就继续比较下一位,以此类推,直到比较出大小为止。
在比较小数的时候,我们先比较整数部分,整数部分大的那个数就大。
如果整数部分相同,就比较小数部分。
从小数点后的第一位开始比较,数字大的那个数就大。
如果第一位相同,就比较第二位,依此类推。
例如,比较 35 和 28 ,因为 3 大于 2 ,所以 35 大于 28 。
再比如,比较 256 和 251 ,整数部分都是 2 相同,接着比较小数部分第一位, 5 也相同,再比较小数部分第二位, 6 大于 1 ,所以 256 大于 251 。
接下来,我们说一说十进制数的排序。
排序就是将一组十进制数按照从小到大或者从大到小的顺序排列起来。
当我们要将一组整数进行从小到大排序时,可以采用多种方法。
比如冒泡排序法,它的基本思想是:从数组的第一个元素开始,依次比较相邻的两个元素,如果顺序不对,就进行交换,直到把最大的数“冒”到数组的末尾。
然后对剩下的元素重复这个过程,直到整个数组都排好序。
还有选择排序法,它先在未排序序列中找到最小(大)元素,存放到排序序列的起始位置,然后,再从剩余未排序元素中继续寻找最小(大)元素,然后放到已排序序列的末尾。
chap_10 排序

二趟排序: 二趟排序: 13 4 48 38 27 49 55 65 97 76 取d3=1 13 三趟分组: 三趟分组: 4 48 38 27 49 55 65 97 76
三趟排序: 三趟排序: 13 27 38 48 49 55 65 76 97 4
8
希尔排序特点
子序列的构成不是简单的“逐段分割” 子序列的构成不是简单的“逐段分割”,而是将 相隔某个增量的记录组成一个子序列 希尔排序可提高排序速度, 希尔排序可提高排序速度,因为
2
3.排序的数据类型描述 排序的数据类型描述 在以后讨论排序时,待排序记录的数据类型统一描述如下 待排序记录的数据类型统一描述如下: 在以后讨论排序时 待排序记录的数据类型统一描述如下 typedef struct{ #define MAXSIZE 20 //r[0]闲置或用作哨兵单元 闲置或用作哨兵单元 typedef int KeyType; RedType R[MAXSIZE+1]; typedef struct{ int length; //顺序表长度 顺序表长度 KeyType key; //关键字项 关键字项 }SqList; InfoType otherinfo; //其它数据项 其它数据项 } RedType; 10.2 插入排序 一.直接插入排序 直接插入排序 基本思想:把一个记录插入到已排好序的有序表中 从而得到 基本思想 把一个记录插入到已排好序的有序表中,从而得到 把一个记录插入到已排好序的有序表中 一个新的记录数增1 一个新的记录数增 的有序表
6
希尔排序(缩小增量法 希尔排序 缩小增量法) 缩小增量法
排序过程:先取一个正整数 排序过程:先取一个正整数d1<n,把 , 所有相隔d1的记录放一组, 所有相隔 的记录放一组,组内进行直接插 的记录放一组 入排序;然后取 入排序;然后取d2<d1,重复上述分组和 , 排序操作;直至di=1, 排序操作;直至di=1,即所有记录放进一 个组中排序为止
十大排序算法总结

十大排序算法总结在计算机科学领域,排序算法是一个非常重要的研究方向。
排序算法可以帮助我们更快速、更有效率地处理大量数据。
在本文中,我们将介绍十大常见的排序算法,包括冒泡排序、选择排序、插入排序、希尔排序、归并排序、快速排序、堆排序、计数排序、桶排序、基数排序。
1. 冒泡排序冒泡排序是一种基本的排序算法。
它重复地遍历待排序的序列,一次比较两个元素,如果它们的顺序错误就交换位置,直到整个序列有序为止。
冒泡排序的时间复杂度为O(n^2),空间复杂度为O(1)。
2. 选择排序选择排序是一种简单直观的排序算法。
它的工作原理是:首先在未排序的序列中找到最小元素,然后将其放到序列的起始位置;接着从剩余未排序的元素中继续寻找最小的元素,然后放到已排序序列的末尾。
选择排序的时间复杂度为O(n^2),空间复杂度为O(1)。
3. 插入排序插入排序是一种基本的排序算法。
它的工作原理是:将一个元素插入到已经排好序的序列中,使得插入后的序列仍然有序。
插入排序的时间复杂度为O(n^2),空间复杂度为O(1)。
4. 希尔排序希尔排序是一种改进版的插入排序。
它通过比较距离较远的元素,可以快速地将大元素向右移动,从而减少后续排序的比较次数。
希尔排序的时间复杂度为O(nlogn),空间复杂度为O(1)。
5. 归并排序归并排序是一种分治算法。
它将待排序的序列分成若干个子序列,每个子序列都是有序的。
然后再将有序的子序列合并成最终的有序序列。
归并排序的时间复杂度为O(nlogn),空间复杂度为O(n)。
6. 快速排序快速排序是一种基于分治思想的排序算法。
它通过不断地将序列分成两个部分,将较小的元素移动到左边、较大的元素移动到右边,最终将整个序列排好序。
快速排序的时间复杂度为O(nlogn),空间复杂度为O(nlogn)。
7. 堆排序堆排序是一种基于堆的排序算法。
它将待排序的序列看成一棵完全二叉树,每个节点的值都不大于其父节点的值。
然后将最大值不断地从堆中取出,放到已排序序列的末尾。
c数据结构chapt10

16
08
21
25
49
25*
16
08
21
25
49
25*
16
08
21
16
1
08 2
25* 3
25 4
49 5
i=2
Gap = 2
0
21
16
08
25*
25
49
21
16
08
25*
25
49
08
16
21
25*
25
49
08
16
1
21 2
25* 3
25 4
49 5
i=3
Gap = 1
0
08
16
21
25*
25
49
i=5
16
21
25
25*
49 08 08
0
1
2
3
4
5
temp
完成
08 0 i=4 j=3 21 i=4 j=2 0
16
1
21 2
25 3
25* 4
49 5
i = 4 时的排序过程
25
1
25*
2
49 3
16 16 4 49 08 08 5 16 temp
21
25
16 25* 49 2 3
16
0
1
4
5
⑶ 希尔排序法是不稳定的。
void ShellSort(RecType R[],int n) /*希尔排序算法*/ { int i,j,d;RecType temp; d=n/2; /*d取初值n/2*/ while (d>0) { for (i=d;i<n;i++) /*将R[d..n-1]分别插入各组当前有序区*/ { j=i-d; while (j>=0 && R[j].key>R[j+d].key) { temp=R[j]; /*R[j]与R[j+d]交换*/ 希尔排序的时间复 R[j]=R[j+d];R[j+d]=temp; 杂度随d值取法的 j=j-d; 不同而不同,但d } 值的取法并无定式 } 。需保证最后一个 d=d/2; /*递减增量d*/ 增量必须为1。 } }
十大排序算法

⼗⼤排序算法算法之排序排序算法基本上是我们⽆论是在项⽬中还是在⾯试中都会遇到的问题,加上最近在看《算法》这本书,所以就准备好好的将排序算法整理⼀下。
所有排序算法都是基于 Java 实现,为了简单,只使⽤了int类型,从⼩到⼤排序基本排序⾼效的排序各⼤排序的时间测试如何选择排序排序之基本排序算法准备阶段:有⼀个交换位置的函数exc/*** 交换a数组中i和j的位置* @param a 需要交换的数组* @param i 位置* @param j 位置*/public static void exc(int a[],int i,int j){// 当他们相等的时候就没必要进⾏交换if(a[i] != a[j]){a[i] ^= a[j];a[j] ^= a[i];a[i] ^= a[j];}}基本排序算法主要是分为插⼊排序,选择排序,冒泡排序和梳排序。
选择排序原理:选择排序的原理很简单,就是从需要排序的数据中选择最⼩的(从⼩到⼤排序),然后放在第⼀个,选择第⼆⼩的放在第⼆个……代码:/*** 选择排序* @param a 进⾏排序的数组*/public static int[] selectionSort(int a[]){int min;for(int i=0;i<a.length;i++){min = i;// 这个for循环是为了找出最⼩的值for (int j = i+1; j < a.length; j++) {if(a[min]>a[j]){min = j;}}/** 如果第⼀个取出的元素不是最⼩值,就进⾏交换* 意思就是:如果取出的元素就是最⼩值,那么就没有必要进⾏交换了 */if(min != i){// 进⾏交换exc(a, i, min);}}return a;}选择排序的动画演⽰img假如数组的长度是N,则时间复杂度:进⾏⽐较的次数:(N-1)+(N-2)+……+1 = N(N-1)/2进⾏交换的次数:N特点:(稳定)1. 运⾏时间与输⼊⽆关。
数据结构(C语言版CHAP10

分组方法:选定一增量d,将间隔为d的记录作为一组 例 待排记录 49 38 65 97 76 13 27 49 55 04 d=5 d=3 49 13 13 13 04 38 27 27 04 13 65 49 49 49 27 97 55 55 38 38 76 04 04 27 49 13 27 49 49 38 65 49 38 65 49 55 65 49 55 65 55 97 97 97 76 04 76 76 76 97
10.1
概 述
排序也是数据处理中经常使用的一种操作.例 高考考生信息管理 系统提供了将考生按总分排序,按单科排序的功能; 1 排序定义 设R1 R2 R3 … Rn 是n个记录,k1,k2, k3 … kn为它们的关键字,排序 就是将记录按关键字递增(或递减)的次序排列起来. 2 分类 按记录的存放位置分类有 内排序:待排记录放在内存 外排序:待排记录放在外存 按排序原则分类(内排序) 插入排序 交换排7,76,13,27,49 是待排序列
稳性排序的应用: 例 股票交易系统 考虑一种股票交易(清华紫光)) 1)顾客输入:股东帐号,股票代码,申购价格,数量,股票交易系统 将用户申购请求插入申购队列队尾; 2)股票交易系统按如下原则交易: A)申购价高者先成交 B)申购价相同者按申购时间先后顺序成交 结束 第 5 页
76 38 49 65 97 76 13 27 49
L.r[5]复制为哨兵 0 1 2 3 4 5 6 7 8 9
76 38 49 65 97 97 13 27 49
L.r[0].key < L.r[4].key, L.r[4]记录后移 L.r[0].key≥ L.r[3].key 找到插入位置 插入! 0 1 2 3 4 5 6 7 8 9
经典十大排序算法

经典⼗⼤排序算法前⾔排序种类繁多,⼤致可以分为两⼤类:⽐较类排序:属于⾮线性时间排序,时间复杂度不能突破下界O(nlogn);⾮⽐较类排序:能达到线性时间O(n),不是通过⽐较来排序,有基数排序、计数排序、桶排序。
了解⼀个概念:排序的稳定性稳定是指相同⼤⼩的元素多次排序能保证其先后顺序保持不变。
假设有⼀些学⽣的信息,我们先根据他们的姓名进⾏排序,然后我们还想根据班级再进⾏排序,如果这时使⽤的时不稳定的排序算法,那么第⼀次的排序结果可能会被打乱,这样的场景需要使⽤稳定的算法。
堆排序、快速排序、希尔排序、选择排序是不稳定的排序算法,⽽冒泡排序、插⼊排序、归并排序、基数排序是稳定的排序算法。
1、冒泡排序⼤多数⼈学编程接触的第⼀种排序,名称很形象。
每次遍历排出⼀个最⼤的元素,将⼀个最⼤的⽓泡冒出⽔⾯。
时间复杂度:平均:O(n2);最好:O(n);最坏:O(n2)空间复杂度:O(1)public static void bubbleSort(int[] arr) {/*** 总共⾛len-1趟即可,每趟排出⼀个最⼤值放在最后*/for (int i = 0; i < arr.length - 1; i++) {for (int j = 0; j < arr.length - i - 1; j++) {if (arr[j] > arr[j + 1]) {int tp = arr[j];arr[j] = arr[j + 1];arr[j + 1] = tp;}}}}2、选择排序最直观易理解的排序算法,每次排出⼀个最⼩的元素。
也是最稳定的算法,时间复杂度稳定为O(n^2)。
需要⼀个变量记录每次遍历最⼩元素的位置。
时间复杂度:O(n2)空间复杂度:O(1)public static void selectSort(int[] arr){int n = arr.length;for (int i = 0; i < n; i++) {int maxIdx = 0;for(int j = 1; j < n - i; j++){if(arr[maxIdx] < arr[j]){maxIdx = j;}}int tp = arr[maxIdx];arr[maxIdx] = arr[n - 1 - i];arr[n - 1 - i] = tp;}}3、插⼊排序⼀种直观的排序算法,从第⼆个元素开始,每次往前⾯遍历找到⾃⼰该在的位置。
十进制数的大小比较与排序知识点总结

十进制数的大小比较与排序知识点总结在十进制数的大小比较与排序知识点总结方面,我们将从以下几个方面进行讨论:十进制数的大小比较原理、大小比较的常用方法、十进制数的排序方法以及在实际应用中的相关知识点。
一、十进制数的大小比较原理十进制数的大小比较是根据每个数位的权值来进行判断的。
通常,我们将十进制数从左到右依次排列,权值由大到小递减。
比较两个十进制数大小时,先比较最高位,如果相等,则继续比较下一位,直到有某一位不相等为止。
如此便可确定两个数的大小关系。
二、大小比较的常用方法1. 左对齐比较法:将两个数按照位数对齐,比较每一位的大小,直到有某一位不相等为止。
例如,比较数123和456时,可以将123改写为123000,然后进行逐位比较。
2. 加零比较法:通过在位数较少的数的高位加零,实现两个数位数相等后再进行比较。
例如,比较数123和456时,可以将123改写为0123,然后进行逐位比较。
3. 倒序排列比较法:将两个数的数位顺序颠倒后再进行比较。
例如,比较数123和456时,将它们改写为321和654,然后进行逐位比较。
三、十进制数的排序方法在实际应用中,我们经常需要对一组十进制数进行排序。
下面介绍两种常用的排序方法:1. 冒泡排序:冒泡排序是一种简单直观的排序方法。
它通过比较相邻两个数的大小,将较大的数向后移动,较小的数向前移动,从而实现数列的排序。
冒泡排序的步骤如下:- 从数列的第一个数开始,依次比较相邻两个数的大小,如果前者大于后者,则交换它们的位置。
- 继续比较下一对相邻的数,重复上述操作,直到将最大的数移到数列的最后一位。
- 对除最后一个数以外的所有数重复上述步骤,直到排序完成。
2. 快速排序:快速排序是一种高效的排序算法,它通过选择一个基准数,根据该数将原数列分成两部分,一部分为小于基准数的数,另一部分为大于基准数的数,然后对这两部分分别进行递归排序,最终将数列有序化。
快速排序的步骤如下:- 选择一个基准数,将数列分成左右两个部分。
拓扑排序简单的例子

拓扑排序简单的例子拓扑排序是一种对有向无环图(Directed Acyclic Graph, DAG)进行排序的方法,它可以帮助我们确定图中所有节点的线性顺序。
拓扑排序在实际应用中非常有用,例如任务调度、编译顺序等场景。
下面将从不同的角度给出10个简单的拓扑排序的例子,以展示其用途和特点。
标题1:拓扑排序概述拓扑排序是一种对有向无环图进行排序的方法,它可以帮助我们确定图中所有节点的线性顺序。
拓扑排序的基本原理是通过不断删除入度为0的节点,直到所有节点都被删除或没有入度为0的节点为止。
拓扑排序可以应用于各种实际场景,例如任务调度、编译顺序等。
标题2:任务调度的拓扑排序在任务调度中,我们需要确定任务的执行顺序,以保证所有任务都能按照正确的顺序运行。
拓扑排序可以帮助我们解决这个问题。
例如,假设有一组任务,它们之间存在依赖关系,我们可以使用拓扑排序确定它们的执行顺序,从而保证任务能够按照正确的顺序完成。
标题3:编译顺序的拓扑排序在编译过程中,我们需要确定源代码文件的编译顺序,以保证所有文件都能正确地被编译。
拓扑排序可以帮助我们解决这个问题。
例如,假设有一组源代码文件,它们之间存在依赖关系,我们可以使用拓扑排序确定它们的编译顺序,从而保证文件能够按照正确的顺序被编译。
标题4:拓扑排序的应用举例除了任务调度和编译顺序外,拓扑排序还可以应用于其他许多场景。
例如,在学校的课程安排中,拓扑排序可以帮助我们确定课程的学习顺序。
在软件工程中,拓扑排序可以用于解决模块的依赖关系。
在交通规划中,拓扑排序可以用于确定道路的修建顺序。
总之,拓扑排序在各个领域都有重要的应用。
标题5:拓扑排序的算法步骤拓扑排序的算法步骤如下:1. 找到图中入度为0的节点,将其加入结果集中。
2. 删除该节点以及与其相连的边。
3. 重复步骤1和步骤2,直到所有节点都被删除。
4. 如果还有剩余的节点没有被删除,则说明图中存在环,无法进行拓扑排序。
标题6:用邻接表表示图在拓扑排序中,我们通常使用邻接表来表示图。
Chaper10_排序

排序算法的效率分析
与许多算法一样,对各种排序算法性能的评价主要从 两个方面来考虑,一是时间性能;二是空间性能。 1. 时间复杂度分析
排序算法的时间复杂度可用排序过程 中记录之间关键字的比较次数与记录的移
动次数来衡量。
2.空间复杂度分析
排序算法的空间复杂度是指算法在执行时所需的附加存 储空间,也就是用来临时存储数据的内存使用情况。
即使得式(8-1)的序列成为一个按关键字有序的序列
{R
p1,R p2
,…,Rpn}
(8-3)
这个将原有表中任意顺序的记录变成一个按关键字有 序排列的过程称为排序。
2.排序分类 增排序和减排序:
如果排序的结果是按关键字从小到大的 次序排列的,就是增排序,否则就是减 排序。
稳定排序和不稳定排序 内部排序与外部排序:
待排序的顺序表类型的类型定义如下: typedef int KeyType //定义关键字类型 typedef struct dataType { keytype key; //记录类型 //关键字项
elemtype otherelement;
}RecType;
//其他数据项
10.2 插入排序
插入排序的基本思想是:每次将一个待排序的记录,
堆排序方法:是由J. Williams和Floyd提出的一种改进 方法,它在选择当前最小关键字记录的同时,还保存了 本次排序过程所产生的比较信息。
不断从待排记录序列中选出关键字最小的记录插入已排
序记录序列的后面,直到n个记录全部插入已排序记录 序列中。 主要介绍两种选择排序方法: 简单选择排序
堆排序。
10.4 选择排序
10.4.1 简单选择排序 简单选择排序(Simple Selection Sort)也称直接选择 排序,是选择排序中最简单直观的一种方法。 其基本操作思想: (1)每次从待排记录序列中选出关键字最小的记录; (2)将它与待排记录序列第一位置的记录交换后,再将 其“插入”已排序记录序列(初始为空);
十进制数的大小比较与排序知识点总结

十进制数的大小比较与排序知识点总结在数学的世界中,十进制数的大小比较与排序是非常基础且重要的知识。
无论是在日常生活中的简单计算,还是在复杂的科学研究和工程应用中,我们都离不开对十进制数大小的准确判断和有序排列。
十进制数,是我们最为熟悉和常用的计数方式。
它由 0、1、2、3、4、5、6、7、8、9 这十个数字组成,通过不同的位置表示不同的数值大小。
例如,数字 123,其中 1 在百位,表示 1 个百;2 在十位,表示2 个十;3 在个位,表示 3 个一。
那么,如何比较两个十进制数的大小呢?首先,我们从最高位开始比较。
如果最高位上的数字不同,那么数字大的那个数就大。
比如,比较 256 和 189,256 的最高位是 2,189 的最高位是 1,因为 2 大于 1,所以 256 大于 189。
如果最高位上的数字相同,那就比较次高位上的数字,以此类推。
例如,比较 582 和 537,最高位都是 5,接着比较次高位,8 大于 3,所以 582 大于 537。
当我们要对多个十进制数进行排序时,常见的方法有冒泡排序、选择排序和插入排序等。
冒泡排序的基本思想是,依次比较相邻的两个数,如果顺序不对则进行交换,并一直重复这样的操作,直到没有要交换的数据为止。
举个例子,对数组{5, 2, 8, 1, 4} 进行冒泡排序。
首先比较 5 和 2,因为 5 大于 2,所以交换它们的位置,数组变成{2, 5, 8, 1, 4}。
然后比较 5 和 8,因为 5 小于 8,位置不变。
接着比较 8 和 1,交换位置,数组变成{2, 5, 1, 8, 4}。
再比较 8 和 4,交换位置,数组变成{2, 5, 1, 4, 8}。
经过一轮比较,最大的数 8 已经“浮”到了最后。
接着对剩下的{2, 5, 1, 4} 重复上述过程,最终得到有序数组{1, 2, 4, 5, 8}。
选择排序则是每次从待排序的数据元素中选出最小(或最大)的一个元素,存放在序列的起始位置,然后再从剩余未排序元素中继续寻找最小(大)元素,然后放到已排序序列的末尾。
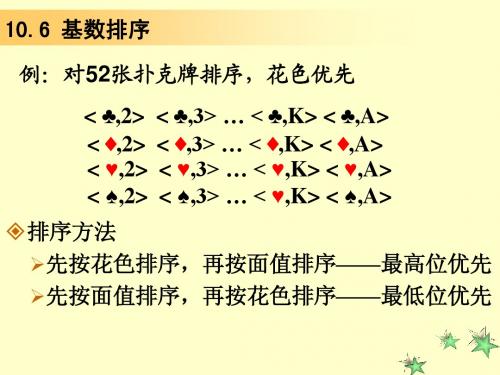
排序(2010)-基数
O(nlog2n) O(nlog2n) O(nlog2n)
归并排序 O(nlog2n) O(nlog2n) O(nlog2n) 基数排序 O(d(n+r)) O(d(n+r)) O(d(n+r))
排序算法小结 几点说明 1. 几种简单的排序算法(1、2、3)的最好时间复 几种简单的排序算法( 、 、 ) 杂度都为O(n). 说明算法的输入在接近有序时的 杂度都为 效率比较高。 效率比较高。 2. 三种平均时间复杂度为O(nlog2n)的算法中 三种平均时间复杂度为O(nlog n)的算法中 快速排序的平均效率高 的平均效率高, 快速排序的平均效率高,但是最坏时间复杂 度为O(n2),且空间复杂度为 度为 ,且空间复杂度为O(log2n) 堆排序的最坏时间复杂度为 的最坏时间复杂度为O(nlog2n),且空 堆排序的最坏时间复杂度为 , 间复杂度仅为O(1) 间复杂度仅为 归并排序的最坏时间复杂度也为 的最坏时间复杂度也为O(nlog2n), 归并排序的最坏时间复杂度也为 , 而且是稳定算法,但是空间复杂度为O(n) 而且是稳定算法,但是空间复杂度为
e
0 0
0 0
0 0
L.bitnum L.recnum
2 8
L.r 0
key next
4 9 8 1 9 3 3 2 6 1 5 5 2 5 1 2 2 0 5 0 0 0 0 6 0
分配
1 2 3 4 5 6 7 8
f
0 1 2 3 4 5 6 7 8 9 4 8 7 1 0 1 2 3 4 5 6 7 8 9
3 1
6 1
L.bitnum L.recnum
2 8
L.r 0
key next
4 9 8 1 9 3 3 2 6 1 5 5 2 5 1 2 2 0 7 4 6 8 1 5 3
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
10.1 概述
10.2 插入类排序
10.3 交换类排序
10.4 选择排序 10.5 归并排序 10.6 基数排序 10.7 各种排序方法的综合比较
2
10.1 概 述
10.1.1 排序的定义
10.1.2 比较的标准 10.1.3 排序的分类
10.1.4 基本操作 10.1.5 内部排序的方法
3
10.1.1 排序的概念
n
( n 4)( n 1) (i 1) 2 i 2
n
24
平均时间复杂度:O(n2) (2)空间复杂度 需要一个记录的辅助空间r(0)。 (3)稳定性 稳定 特点:简单、容易实现,适用于待 排序记录基本有序或待排序记录较 小时。
25
10.2.2 折半插入排序
1.基本思想:因为 R[1..i-1] 是一个按
6
10.1.2 比较的标准
空间复杂度 时间复杂度 稳定性 排序过后能使值相同的数据保
稳定性
持原顺序中的相对位臵 32
32
49
27
56
49
49
49
27
56
不稳定性
排序过后不能使值相同的数据 保持原顺序中的相对位臵
7
10.1.3 排序的分类
将欲处理的数据整个存放到内部存 储器中排序,数据可被随机存取 内部排序
30
9.2.3希尔排序(又称缩小增量排序)
1.基本思想
把待排序的数据元素分成若干个小组, 对同一小组内的数据元素用直接插入法排 序;小组的个数逐次缩小;当完成了所有 数据元素都在一个组内的排序后排序过程
结束。
31
例如:
56 65 34
14 25
25 87 77 87 12 38 23 65 56 46 14 77 92
1 15 24 6 17 5 1 1 15 6 6 15 17 5 5 24
1
15
6
17
5
24
17 24
假设L.length=n,则总共比较Байду номын сангаас2次
40
改进算法
void bubblf_sort(SqList &L) {//自小至大有序 for(i=1;i<=L.length-1;++i) for(j=1;j<L.length-i;++j) //n-i已经有序 if(L.r[j+1].key<L.r[j].key)) L.r[j] ←→L.r[j+1] }//bubblf_sort
low high low high m m m high
L.r[high+1] = L.r[0]; // 插入
27
2. 算法实现 void BiInsertionSort ( SqList &L ) {
for ( i=2; i<=L.length; ++i ) { L.r[0] = L.r[i]; // 将 L.r[i] 暂存到 L.r[0]
2.算法实现
for ( i=2; i<=L.length; ++i ) if (L.r[i].key < L.r[i-1].key) { L.r[0] = L.r[i]; // 复制为监视哨 for ( j=i-1; L.r[0].key < L.r[j].key; -- j ) L.r[j+1] = L.r[j]; // 记录后移 L.r[j+1] = L.r[0]; } } // InsertSort // 插入到正确位臵
1.排序(sorting)
是计算机内经常进行的一种操作, 其目的是将一组“无序”的记录序列调 整为“有序”的记录序列。
例如:
成绩表;奖学金评定综合分。
4
2.数据表 (datalist): 它是待排序数据
对象的有限集合。 3.主关键字(key): 数据对象有多个属性 域, 即多个数据成员组成, 其中有一个 属性域可用来区分对象, 作为排序 依据,称为关键字。也称为排序码。
20
(2)对于在查找过程中找到的那些关 键字不小于R[i].key的记录,并在查找 的同时实现记录向后移动;
for (j=i-1; R[0].key<R[j].key; --j); R[j+1] = R[j]
(3)上述循环结束后可以直接进行“插 入”。 L.r[j+1] = L.r[0];
21
void InsertionSort ( SqList &L ) { // 对顺序表 L 作直接插入排序
插入式排序 交换式排序 选择式排序 归并排序 基数排序
借助外部的辅助存储器(比如:硬 盘),由于数据是存在外存中,故 数据不可随机被存取 外部排序
8
10.1.4 排序基本操作
(1)比较两个排序码的大小; (2)改变指向记录的指针或移动记录 本身。 注意: 第(2)种基本操作的实现依赖于待排序 记录的存储方式。 所以排序的时间开销可用算法执行中的 数据比较次数与数据移动次数来衡量。
希尔排序(基于逐趟缩小增量)
17
10.2.1 直接插入排序
1.算法的实现要点
利用 “顺序查找”实现 “在R[1..i-1]
中查找R[i]的插入位臵”。
18
例如:
i=1
( 49) 38 65 97 76 13 27
i=2 38 (38 49) 65 97 76 13 27
i=3 65 (38 49 65) 97 76 13 27 i=4 97 (38 49 65 97) 76 13 27 i=5 76 (38 49 65 76 97) 13 27 i=6 13 (13 38 49 65 76 97) 27 76 27 i=7 27 (13 38 27 49 38 65 49 76 65 97) 97 j j j j j j (13 27 38 49 65 76 97) 排序结果:
13
10.2 插 入 排 序
14
一趟直接插入排序的基本思想:
有序序列R[1..i-1] R[i] 无序序列 R[i..n]
将无序子序列中的一个或
几个记录“插入”到有序
序列中,从而增加记录的
有序子序列的长度。
有序序列R[1..i]
无序序列 R[i+1..n]15
实现“一趟插入排序”可分三步进行:
22
3.性能分析
直接插入排序的基本操作有两个:
“比较”序列中两个关键字的大 小; “移动”记录。
23
(1)时间复杂度 ①最好的情况(关键字正序) “比较”的次数: “移动”的次数:
1 n 1
i 2
n
0
“移动”的次数:
②最坏的情况(关键字逆序) “比较”的次数:
( n 4)( n 1) (i 1) 2 i 2
1.在R[1..i-1]中查找R[i]的插入位臵;
R[1..j].key R[i].key < R[j+1..i-1].key
2.将R[j+1..i-1]中的所有记录均后移
一个位臵;
3.将R[i] 插入(复制)到R[j+1]的位臵上。
16
不同的具体实现方法导致不同的算法描述
直接插入排序(基于顺序查找) 折半插入排序(基于折半查找)
1 1 15 15 24 6 6 17 17 5 5 24 1 1 15 6 6 15 17 5 5 24 17 24
注意第i趟比较了n-i次,则可以有效的减少比较次数 比较的总的次数是1+2+…+n-1=n(n-1)/2
10.3 交换类排序
通过“交换”无序序列中的记录从 而得到其中关键字最小或最大的记录, 并将它加入到有序子序列中,以此方法
增加记录的有序子序列的长度。
冒泡排序
快速排序
37
10.3.1 冒泡排序
1.基本思想 (1)依次比较相邻两个数据元素的大小, 若逆序则交换两个数据元素,否则不交换。 (2)当完成一趟交换以后,最大的元素 将会出现在数据序列的最后一个位臵。 (3)重复以上过程,直到待排序序列中 没有逆序为止。
11
存储方式
3. 地址连续的一组存储单元,另设一个 指示各个记录存储位臵的地址向量,在 排序过程中不移动记录本身,而移动地 址向量中的地址,在排序之后再按照地 址向量中的值调整记录的存储位臵-- 地址排序
12
#define MAXSIZE 20 // 待排顺序表最大长度 待排记录的数据类型定义如下 : typedef int KeyType; // 关键字类型为整数类型 typedef struct { KeyType key; // 关键字项 InfoType otherinfo; // 其它数据项 } RedType; // 记录类型 typedef struct { RedType r[MAXSIZE+1]; // r[0]闲臵 int length; // 顺序表长度 } SqList; // 顺序表类型
//在 L.r[1..i-1]中折半查找插入位臵;
for ( j=i-1; j>=high+1; --j ) L.r[j+1] = L.r[j]; // 记录后移 L.r[high+1] = L.r[0]; // 插入 } // for } // BInsertSort
28
//在 L.r[1..i-1]中折半查找插入位臵(是否完 善?) low = 1; high = i-1; while (low<=high) { m = (low+high)/2;
// 折半
if (L.r[0].key < L.r[m].key)
