福建省宁德市2018年5月初中毕业班质量检测数学试题(纯word版)
宁德市初中毕业班质量检测及答案

宁德市初中毕业班质量检测及答案WTD standardization office【WTD 5AB- WTDK 08- WTD 2C】2018年宁德市初中毕业班质量检测数 学 试 题本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,第Ⅰ卷1至2页,第Ⅱ卷3至5页.满分150分. 注意事项:1.答题前,考生务必在试题卷、答题卡规定位置填写本人准考证号、姓名等信息.考生要认真核对答题卡上粘贴的条形码的“准考证号、姓名”与考生本人准考证号,姓名是否一致.2.选择题每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑.如需改动,用橡皮擦干净后,再选涂其他答案标号.非选择题答案用毫米黑色签字笔在答题卡上相应位置书写作答,在试题卷上答题无效.3.作图可先使用2B 铅笔画出,确定后必须毫米黑色签字笔描黑. 4.考试结束,考生必须将试题卷和答题卡一并交回.第 Ⅰ 卷一、选择题:本题共10小题,每小题4分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的. 1.2018-的值是A .12018B .2018C .12018-D .2018-2.如图,若a ∥b ,∠1=58°,则∠2的度数是A .58°B .112°C .122°D .142°3.下列事件是必然事件的是A .2018年5月15日宁德市的天气是晴天B .从一副扑克中任意抽出一张是黑桃C .在一个三角形中,任意两边之和大于第三边D .打开电视,正在播广告a b第2题图214.由6个大小相同的小正方体拼成的几何体如图所示,则下列说法正确的是 A .主视图的面积最大 B .左视图的面积最大 C .俯视图的面积最大 D .三种视图的面积相等5.不等式组10,10≤>x x -⎧⎨+⎩的解集在数轴上表示正确的是6.在平面直角坐标系中,A ,B ,C ,D ,M ,N 的位置如图所示,若点M 的坐标为(-2 ,0), N 的坐标为(2 ,0),则在第二象限内的点是 A .A 点 B .B 点C .C 点D .D 点7.在“创文明城,迎省运会”合唱比赛中,10位评委给某队的评分如下表所示,则下列说法正确的是 A .中位 C .众数和18.如图,将△OA=4,∠A .∠BDO =60° B .∠BOC =25° C .OC=4D .BD=49.某校为进一步开展“阳光体育”活动,购买了一批篮球和足球.已知购买足球数量是篮球的2倍,购买足球用了4 000元,购买篮球用了2 800元,篮球单价比足球贵16元.若可列方程40002800162x x=-表示题中的等量关系,则方程中x 表示的是 A .足球的单价 B .篮球的单价 C .足球的数量D .篮球的数量C1 0 D第4题图B 1 0 A第8题图第6题图MNA B D CCFEDA BA 1 010.如图,已知等腰△ABC ,AB=BC ,D 是AC 上一点,线段BE 与BA 关于直线BD 对称,射线CE 交射线BD 于点F ,连接AE ,AF .则下列关系正确的是 A .180∠∠AFE ABE +=︒ B .12∠∠AEF ABC = C .180∠∠AEC ABC +=︒D .∠∠AEB ACB =第 Ⅱ 卷注意事项:1.用毫米黑色签字笔在答题卡上相应位置书写作答,在试题卷上作答,答案无效.2.作图可先使用2B 铅笔画出,确定后必须毫米黑色签字笔描黑. 二、填空题:本题共6小题,每小题4分,共24分.11.2017年10月18日,中国共产党第十九次全国代表大会在北京隆重召开.从全国近89 400 000党员中产生的2 300名代表参加了此次盛会.将数据89 400 000用科学记数法表示为 . 12.因式分解:222a -= .13.小明同学在计算一个多边形的内角和时,由于粗心少算了一个内角,结果得到的总和是800°,则少算了这个内角的度数为 .14. 已知一次函数23(0)y kx k k =++≠,不论k 为何值,该函数的图像都经过点A ,则点A 的坐标为 .15.小丽计算数据方差时,使用公式2222221(5)(8)(13)(14)(15)5S x x x x x ⎡⎤=-+-+-+-+-⎣⎦,则公式中x = .16.如图,点A ,D 在反比例函数(0)my m x=<点B ,C 在反比例函数(0)ny n x=>的图像上.若AB ∥CD ∥x 轴,AC ∥y 轴,且AB =4,AC =3,CD =2则n = .第16题图第10题图三、解答题:本题共9小题,共86分.17.(本题满分8分)计算:14cos302-︒+18.(本题满分8分)如图,在△ABC 中, D ,E 分别是AB ,AC 的中点,△ABC 的角平分线AG 交DE 于点F ,若∠ABC =70°,∠BAC =54°,求∠19.(本题满分8如期举行,某校组织一辆A 型车可坐5辆.学校至少要租用B 型车多少辆?20.(本题满分8分)某中学为推动“时刻听党话 永远跟党走”校园主题教育活动,计划开展四项活动:A:党史演讲比赛,B :党史手抄报比赛,C :党史知识竞赛,D :红色歌咏比赛.校团委对学生最喜欢的一项活动进行调查,随机抽取了部分学生,并将调查结果绘制成图1,图2两幅不完整的统计图.请结合图中信息解答下列问题:(1(2(31名女生,21.(本题满分8分)如图,已知矩形ABCD ,E (1)如图1,若F 是BC 上一点,在AD ,CD 上分别截取DH =BF ,DG =BE .求证:四边形EFGH 是平行四边形;(2)如图2,利用尺规分别在BC ,CD ,AD 上确定点F ,G ,H ,使得四边形EFGH 是特殊的平行四边形.(提示:①保留作图痕迹,不写作法;②只需作出一种情况即可)22.(本题满分10分)若正整数a ,b ,c b ,c 为一组和谐整数.(1)判断2,3,6是否是一组和谐整数,并说明理由;图ADF H B EG C 图2图1(2)已知x ,y ,z (其中x y z <≤)是一组和谐整数,且1x m =+,3y m =+,用含m 的代数式表示z ,并求当24z =时m 的值.23.(本题满分10分)如图,在△ABC 中,∠ACB =90°,O 是AB 上一点,以OA 为半径的⊙O 与BC 相切于点D ,与AB 交于点E ,连接ED 并延长交AC 的延长线于点F . (1)求证:AE =AF ;(2)若DE =3,sin ∠BDE =13,求AC 的长.24.(本题满分13分)如图1,在△ABC 中,∠BAC =90°,AB =AC =4,D 是BC 上一个动点,连接AD ,以AD 为边向右侧作等腰直角△ADE ,其中∠ADE =90°. (1)如图2,G ,H 分别是边AB ,BC 的中点,连接DG ,AH ,EH .求证:△AGD ∽△AHE ;(2)如图3,连接BE ,直接写出当BD 为何值时,△ABE 是等腰三角形; (3)在点D 从点B 向点C 运动过程中,求△ABE 周长的最小值.25.(本题满分13分)已知抛物线22(y axax c a =-+< (1)当a =-1,m =0时,求抛物线的顶点坐标;(2)若P (t ,n )为该抛物线上一点,且n <m t 的取值范围;(3)如图,直线:(0)l y kx c k =+<交抛物线于B ,两点,点Q (x ,y )是抛物线上点B ,C 个动点,作QD ⊥x 轴交直线 l 于点D ,作QE ⊥y 轴于点E ,连接DE .设∠QED=?x 2≤≤4时,? 恰好满足°°30≤≤60β,求a 的值.2018年宁德市初中毕业班质量检测数学试题参考答案及评分标准⑴本解答给出了一种或几种解法供参考,如果考生的解法与本解答不同,可参照本答案的评分标准的精神进行评分.B图1 ABC D E图2 ABC D G H⑵对解答题,当考生的解答在某一步出现错误时,如果后续部分的解答未改变该题的立意,可酌情给分.⑶解答右端所注分数表示考生正确作完该步应得的累加分数. ⑷评分只给整数分,选择题和填空题均不给中间分. 一、选择题:(本大题有10小题,每小题4分,满分40分) 1.B 2.C 3.C 4.A 5.D 6.A 7.B 8.D 9.D 10.B 二、填空题:(本大题有6小题,每小题4分,满分24分)11.78.9410⨯ 12.2(1)(1)a a +- 13.100 14.(-2,3) 15.11 16.83三、解答题(本大题共9小题,共86分.请在答题卡...的相应位置作答) 17.(本题满分8分)解:原式= 142+-························································ 6分 =12··································································· 8分18.(本题满分8分)证明:∵∠BAC =54°,AG 平分∠BAC ,∴∠BAG =12∠BAC =27°. ················ 2分 ∴∠BGA =180 °-∠ABC -∠ BAG =83° · 4分 又∵点D ,E 分别是AB ,AC 的中点, ∴DE ∥BC . ································· 6分 ∴∠AFD =∠BGA =83°. ··················· 8分19.(本题满分8分)解: 设租用B 型车x 辆,则租用A 型车(5-x )辆,根据题意,得 ·· 1分 2820(5)115≥x x +-. ···························································· 5分解得 158≥x . ·································································· 7分因为x 为整数,所以x 的最小值是2.答:学校至少租用了2辆B 型车. ············································ 8分 20.(本题满分8分)(1)40; ·········································································· 2分 (2)图略 ·········································································· 4分CFEDBAG(3)列表如下: ··································································· 6分一名女生的结果有6种,所以抽到一名男生和一名女生的概率是612,即12. 8分21.(本题满分8分)(1)证明:∵四边形ABCD 是矩形, ∴AD =BC ,AB=CD ,∠A =∠B =∠C =∠D =90°,∵DG =BE ,DH =BF ,∴△GDH≌△EBF . ············ 2分 ∴GH = EF .∵AD =BC ,AB =CD ,DH =BF ,DG =BE , ∴AD -DH =BC -BF ,AB -BE =CD -DG . 即AH =CF ,AE =CG .∴△AEH ≌△CGF . ·················· 4分 ∴EH =GF .∴四边形EFGH 是平行四边形. · 5分 (2)作图如下:作法一:作菱形(如图2) ························································ 7分 ∴四边形EFGH 就是所求作的特殊平行四边形. ························· 8分 作法二:作矩形(如图3,图4) ············································ 7分∴·· 8分22(1)····················· 1分 ADFHBE GC图∵111362+=,满足和谐整数的定义,∴2,3,6是和谐整数. ··················································· 4分(2) 解:∵x y z <≤, 依题意,得 111yzx+=.∵1x m =+,3y m =+, ∴11111213(1)(3)zxym m m m =-=-=++++.∴(1)(3)2m m z ++=. ···························································· 7分 ∵24z =,∴(1)(3)242m m ++=. 解得 59,m m ==-. ························································· 9分 ∵x 是正整数,∴5m =. ····································································· 10分23.(本题满分10分)解:(1)证明:连接OD .∵ OD =OE ,∴∠ODE =∠OED .······················ 1分∵直线BC 为⊙O 的切线, ∴OD ⊥BC .∴∠ODB =90°.··························· 2分 ∵∠ACB =90°,∴OD ∥AC . ······························ 3分∴∠ODE =∠F .∴∠OED =∠F . ·········································4分 ∴AE =AF . ················································5分 (2)连接AD . ∵AE 是⊙O 的直径∴∠ADE =90°. ··········································6分 ∵AE =AF ,B图1∴DF =DE =3. ∵∠ACB =90°.∴∠DAF +∠F =90°,∠CDF +∠F =90°, ∴∠DAF =∠CDF =∠BDE . ·········· 7分 在Rt △ADF 中,1sin sin 3∠DF DAF BDE AF ==∠=, ∴39AF DF ==. ························· 8分 在Rt △CDF 中,1sin sin 3∠CF CDF BDE DF ==∠=, ∴113CF DF ==. ························· 9分∴AC =AF -CF =8. ······················· 10分 24.(本题满分13分)解:(1)由题意知△ABC 和△ADE∴∠B =∠DAE =45°.∵G 为AB 中点,H 为BC 中点, ∴AH ⊥BC .∴∠BAH =45°=∠DAE .∴∠GAD =∠HAE . ····················· 1分 在等腰直角△BAH 和等腰直角△DAE 中,AH AB ==,AE .∴AH AE AGAD=. ····························· 3分∴△AGD ∽△AHE . ···················· 4分(2)当BD =0△ABE 是等腰三角形. ····················· 8分(注:给出0和12分) (3)解法一:当点D 与点B 重合时,点E 的位置记为点M .此时,∠ABM =∠BAC =90°,∠AMB =∠BAM =45°,BM = AB = AC .B图1图2∴四边形ABMC 是正方形. ∴∠BMC =90°,∴∠AMC =∠BMC -∠AMB =45°,9分 ∵∠BAM =∠DAE =45°, ∴∠BAD =∠MAE ,在等腰直角△BAM 和等腰直角△DAE中,AM =,AE .∴AM AE ABAD=.∴△ABD ∽△AME . ∴∠AME =∠ABD =45°∴点E 在射线MC 上. ·········10分作点B 关于直线MC 的对称点N ,连接AN 交MC 于点E ′, ∵BE +AE =NE +AE ≥AN =NE ′+AE ′=∴△ABE ′就是所求周长最小的△在Rt △ABN 中,∵AB =4,BN =2BM =2AB =8, ∴AN =AN =∴△ABE 周长最小值为4AB AN +=+ ············································· 13分 解法二:取BC 的中点H ,连接AH , 同解法一证△ACE ∽△AHD . ∴∠ACE=∠AHD=90°.∴点E 在过点C 且垂直于AC 的直线上,记为直线l . ··········· 10分 点A 关于直线l 的对称点M ,连接BM 交直线l 于点E ′, 同解法一,△ABE ′就是所求周长最小的△ABE .∴△ABE 周长最小值为4AB BM +=+. ··························· 13分25.(本题满分13分) 解:(1)当a =-1,m =0时,22y x x c =-++,A 点的坐标为(3,0),图2BACDE ′ MNE∴-9+6+c =0.解得 c =3. ····································································· 2分 ∴抛物线的表达式为223y x x =-++. 即2(1)4y x =--+.∴抛物线的顶点坐标为(1,4). ······································ 4分 (2)∵22y ax ax c =-+的对称轴为直线212ax a-==-, ······················· 5分 ∴点A 关于对称轴的对称点为(-1,m ). ··························· 6分 ∵0<a ,∴当1<x ,y 随x 的增大而增大; 当1>x ,y 随x 的增大而减小. 又∵n <m ,∴当点P 在对称轴左边时,t <-1; 当点P 在对称轴右边时,t >3.综上所述:t 的取值范围为t <-1或t >3.····························· 8分(3)∵点Q (x ,y )在抛物线上,∴22y ax ax c =-+.又∵QD ⊥x 轴交直线 :(0)l y kx c k =+<于点∴D 点的坐标为(x ,kx+c ).又∵点Q 是抛物线上点B ,C ∴222()(2)QD ax ax c kx c ax a k x =-+-+=-+ ············································· 10分 ∵QE =x , ∴在Rt △QED 中,2(2)tan 2QD ax a k x ax a k QE x-+===--β. ································ 11分∴tan β是关于x 的一次函数, ∵a <0,∴tan β随着x 的增大而减小.又∵当x 2≤≤4时,β恰好满足°°30≤≤60β,且tan β随着β的增大而增大, ∴当x=2时,β=60°;当x=4时,β=30°.∴2242a a k a a k ⎧--=⎪⎨--=⎪⎩解得k a ⎧=⎪⎨=⎪⎩∴a =. ·································································· 13分。
208年宁德市初中毕业班质量检测及答案

2018年宁德市初中毕业班质量检测数 学 试 题本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,第Ⅰ卷1至2页,第Ⅱ卷3至5页.满分150分. 注意事项:1.答题前,考生务必在试题卷、答题卡规定位置填写本人准考证号、姓名等信息.考生要认真核对答题卡上粘贴的条形码的“准考证号、姓名”与考生本人准考证号,姓名是否一致.2.选择题每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑.如需改动,用橡皮擦干净后,再选涂其他答案标号.非选择题答案用0.5毫米黑色签字笔在答题卡上相应位置书写作答,在试题卷上答题无效.3.作图可先使用2B 铅笔画出,确定后必须0.5毫米黑色签字笔描黑. 4.考试结束,考生必须将试题卷和答题卡一并交回.第 Ⅰ 卷一、选择题:本题共10小题,每小题4分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的. 1.2018-的值是A .12018B .2018C .12018-D .2018-2.如图,若a ∥b ,∠1=58°,则∠2的度数是A .58°B .112°C .122°D .142°3.下列事件是必然事件的是A .2018年5月15日宁德市的天气是晴天B .从一副扑克中任意抽出一张是黑桃C .在一个三角形中,任意两边之和大于第三边D .打开电视,正在播广告4.由6个大小相同的小正方体拼成的几何体如图所示,则下列说法正确的是正面ab第2题图21A .主视图的面积最大B .左视图的面积最大C .俯视图的面积最大D .三种视图的面积相等5.不等式组10,10≤>x x -⎧⎨+⎩的解集在数轴上表示正确的是6.在平面直角坐标系中,A ,B ,C ,D ,M ,N 的位置如图所示,若点M 的坐标为(-2 ,0), N 的坐标为(2 ,0),则在第二象限内的点是 A .A 点 B .B 点C .C 点D .D 点7.在“创文明城,迎省运会”合唱比赛中,10位评委给某队的评分如下表所示,则下列说法正确的是A .中位数是9.4分B .中位数是9.35分C .众数是3和1D .众数是9.4分8.如图,将△OAB 绕O 点逆时针旋转60°得到△OCD ,若OA=4,∠AOB =35°,则下列结论错误的是 A .∠BDO =60° B .∠BOC =25° C .OC=4D .BD=49.某校为进一步开展“阳光体育”活动,购买了一批篮球和足球.已知购买足球数量是篮球的2倍,购买足球用了4 000元,购买篮球用了2 800元,篮球单价比足球贵16元.若可列方程40002800162x x=-表示题中的等量关系,则方程中x 表示的是 A .足球的单价 B .篮球的单价C .足球的数量D .篮球的数量10.如图,已知等腰△ABC ,AB=BC ,D 是AC 上一点,线段BE 与BA 关于直线BD 对称,射线CE 交射线BD 于点F ,连接AE ,AF .则下列关系正确的是成绩(分) 9.2 9.3 9.4 9.59.6 人数32311C 1 2 3-1 0 -2 D1 2 3-1 0 -2 第4题图B 1 2 3-1 0 -2 DCBAO第8题图第6题图MN A BD CCFE D ABA 1 2 3-1 0 -2A .180∠∠AFE ABE +=︒B .12∠∠AEF ABC =C .180∠∠AEC ABC +=︒D .∠∠AEB ACB =第 Ⅱ 卷注意事项:1.用0.5毫米黑色签字笔在答题卡上相应位置书写作答,在试题卷上作答,答案无效. 2.作图可先使用2B 铅笔画出,确定后必须0.5毫米黑色签字笔描黑. 二、填空题:本题共6小题,每小题4分,共24分.11.2017年10月18日,中国共产党第十九次全国代表大会在北京隆重召开.从全国近89 400 000党员中产生的2 300名代表参加了此次盛会.将数据89 400 000用科学记数法表示为 .12.因式分解:222a -= .13.小明同学在计算一个多边形的内角和时,由于粗心少算了一个内角,结果得到的总和是800°,则少算了这个内角的度数为 .14. 已知一次函数23(0)y kx k k =++≠,不论k 为何值,该函数的图像都经过点A ,则点A 的坐标为 .15.小丽计算数据方差时,使用公式2222221(5)(8)(13)(14)(15)5S x x x x x ⎡⎤=-+-+-+-+-⎣⎦,则公式中x = . 16.如图,点A ,D 在反比例函数(0)my m x=<的图像上,点B ,C 在反比例函数(0)ny n x=>的图像上.若AB ∥CD ∥x 轴,AC ∥y 轴,且AB =4,AC =3,CD =2,则n = .三、解答题:本题共9小题,共86分.17.(本题满分8分)计算:14cos30212-︒+-.18.(本题满分8分)如图,在△ABC 中, D ,E 分别是AB ,AC 的中点,△ABC 的角平分线AG 交DE 于点F ,若∠ABC =70°,∠BAC =54°,求∠AFD 的度数.CFEDBAGxyOBAC D第16题图第10题图19.(本题满分8分)首届数字中国建设峰会于4月22日至24日在福州海峡国际会展中心如期举行,某校组织115位师生去会展中心参观,决定租用A ,B 两种型号的旅游车.已知一辆A 型车可坐20人,一辆B 型车可坐28人,经测算学校需要租用这两种型号的旅游车共5辆.学校至少要租用B 型车多少辆?20.(本题满分8分)某中学为推动“时刻听党话 永远跟党走”校园主题教育活动,计划开展四项活动:A :党史演讲比赛,B :党史手抄报比赛,C :党史知识竞赛,D :红色歌咏比赛.校团委对学生最喜欢的一项活动进行调查,随机抽取了部分学生,并将调查结果绘制成图1,图2两幅不完整的统计图.请结合图中信息解答下列问题:(1)本次共调查了 名学生; (2)将图1的统计图补充完整;(3)已知在被调查的最喜欢“党史知识竞赛”项目的4个学生中只有1名女生,现从这4名学生中任意抽取2名学生参加该项目比赛,请用画树状图或列表的方法,求出恰好抽到一名男生一名女生的概率.21.(本题满分8分)如图,已知矩形ABCD ,E 是AB 上一点.(1)如图1,若F 是BC 上一点,在AD ,CD 上分别截取DH =BF ,DG =BE .求证:四边形EFGH 是平行四边形;(2)如图2,利用尺规分别在BC ,CD ,AD 上确定点F ,G ,H ,使得四边形EFGH是特殊的平行四边形.(提示:①保留作图痕迹,不写作法;②只需作出一种情况即可)ADFHBEGC CDB AEA 15%BC10%D 35%图2图1活动项人数/人AB CD4 6 8 10 12 14 16 222.(本题满分10分)若正整数a ,b ,c 满足111a b c+=,则称正整数a ,b ,c 为一组和谐整数.(1)判断2,3,6是否是一组和谐整数,并说明理由;(2)已知x ,y ,z (其中x y z <≤)是一组和谐整数,且1x m =+,3y m =+,用含m 的代数式表示z ,并求当24z =时m 的值.23.(本题满分10分)如图,在△ABC 中,∠ACB =90°,O 是AB 上一点,以OA 为半径的⊙O 与BC 相切于点D ,与AB 交于点E ,连接ED 并延长交AC 的延长线于点F .(1)求证:AE =AF ;(2)若DE =3,sin ∠BDE =13,求AC 的长.24.(本题满分13分)如图1,在△ABC 中,∠BAC =90°,AB =AC =4,D 是BC 上一个动点,连接AD ,以AD 为边向右侧作等腰直角△ADE ,其中∠ADE =90°. (1)如图2,G ,H 分别是边AB ,BC 的中点,连接DG ,AH ,EH .求证:△AGD ∽△AHE ;(2)如图3,连接BE ,直接写出当BD 为何值时,△ABE 是等腰三角形; (3)在点D 从点B 向点C 运动过程中,求△ABE 周长的最小值.25.(本题满分13分)已知抛物线22(0)y ax ax c a =-+<的图像过点A (3,m ).(1)当a =-1,m =0时,求抛物线的顶点坐标; (2)若P (t ,n )为该抛物线上一点,且n <m ,求t 的取值范围;(3)如图,直线:(0)l y kx c k =+<交抛物线于B ,C 两F AE CDBO图1 ABCDE图2图3ABCDEABCDEGH图1图2ED QC Bxy O点,点Q (x ,y )是抛物线上点B ,C 之间的一个动点,作QD ⊥x 轴交直线 l 于点D ,作QE ⊥y 轴于点E ,连接DE .设∠QED=β,当x 2≤≤4时,β 恰好满足°°30≤≤60β,求a 的值. 2018年宁德市初中毕业班质量检测数学试题参考答案及评分标准⑴本解答给出了一种或几种解法供参考,如果考生的解法与本解答不同,可参照本答案的评分标准的精神进行评分.⑵对解答题,当考生的解答在某一步出现错误时,如果后续部分的解答未改变该题的立意,可酌情给分.⑶解答右端所注分数表示考生正确作完该步应得的累加分数. ⑷评分只给整数分,选择题和填空题均不给中间分.一、选择题:(本大题有10小题,每小题4分,满分40分)1.B 2.C 3.C 4.A 5.D 6.A 7.B 8.D 9.D 10.B 二、填空题:(本大题有6小题,每小题4分,满分24分)11.78.9410⨯ 12.2(1)(1)a a +- 13.100 14.(-2,3) 15.11 16.83三、解答题(本大题共9小题,共86分.请在答题卡...的相应位置作答) 17.(本题满分8分)解:原式= 3142322⨯+- ····················· 6分 =12························ 8分 18.(本题满分8分)证明:∵∠BAC =54°,AG 平分∠BAC ,∴∠BAG =12∠BAC =27°. ········ 2分 ∴∠BGA =180 °-∠ABC -∠ BAG =83° ·· 4分 又∵点D ,E 分别是AB ,AC 的中点,∴DE ∥BC . ·············· 6分 ∴∠AFD =∠BGA =83°. ········· 8分 19.(本题满分8分)解: 设租用B 型车x 辆,则租用A 型车(5-x )辆,根据题意,得 ····· 1分 2820(5)115≥x x +-. ····················· 5分CFEDBAG解得 158≥x . ························· 7分因为x 为整数,所以x 的最小值是2.答:学校至少租用了2辆B 型车. ··················· 8分 20.(本题满分8分)(1)40; ···························· 2分 (2)图略 ···························· 4分 (3)列表如下: ·························· 6分男 男男女男 (男,男) (男,男) (男,女)男 (男,男)(男,男) (男,女)男 (男,男) (男,男)(男,女)女(女,男) (女,男) (女,男)总共有12种结果,每种结果出现的可能性相同,其中恰好抽到一名男生和一名女生的结果有6种,所以抽到一名男生和一名女生的概率是612,即12. ·· 8分 21.(本题满分8分)(1)证明:∵四边形ABCD 是矩形,∴AD =BC ,AB =CD ,∠A =∠B =∠C =∠D =90°, ∵DG =BE ,DH =BF ,∴△GDH ≌△EBF . ····· 2分 ∴GH = EF .∵AD =BC ,AB =CD ,DH =BF ,DG =BE , ∴AD -DH =BC -BF ,AB -BE =CD -DG . 即AH =CF ,AE =CG .∴△AEH ≌△CGF . ········ 4分 ∴EH =GF .∴四边形EFGH 是平行四边形. ··· 5分 (2)作图如下:作法一:作菱形(如图2) ····················· 7分 ∴四边形EFGH 就是所求作的特殊平行四边形. ············· 8分 作法二:作矩形(如图3,图4) ·················· 7分CDBAE 图2GH FADFHB EGC图1G H F CDBAE GHFCDBA E∴四边形EFGH 就是所求作的特殊平行四边形. ············ 8分 22.(本题满分10分)(1)是 ······························· 1分理由如下:∵111362+=,满足和谐整数的定义,∴2,3,6是和谐整数. ····················· 4分(2) 解:∵x y z <≤,依题意,得 111yzx+=.∵1x m =+,3y m =+,∴11111213(1)(3)z x y m m m m =-=-=++++.∴(1)(3)2m m z ++=. ······················ 7分∵24z =,∴(1)(3)242m m ++=.解得 59,m m ==-. ······················ 9分 ∵x 是正整数,∴5m =. ·························· 10分23.(本题满分10分)解:(1)证明:连接OD .∵ OD =OE ,∴∠ODE =∠OED . ·········· 1分∵直线BC 为⊙O 的切线, ∴OD ⊥BC .∴∠ODB =90°. ··········· 2分 ∵∠ACB =90°,∴OD ∥AC . ············ 3分∴∠ODE =∠F .F AE CDBO图1图3图4∴∠OED =∠F . ················· 4分 ∴AE =AF . ··················· 5分(2)连接AD .∵AE 是⊙O 的直径∴∠ADE =90°. ················· 6分 ∵AE =AF , ∴DF =DE =3. ∵∠ACB =90°.∴∠DAF +∠F =90°,∠CDF +∠F =90°, ∴∠DAF =∠CDF =∠BDE . ······· 7分 在Rt △ADF 中,1sin sin 3∠DF DAF BDE AF ==∠=, ∴39AF DF ==. ········· 8分 在Rt △CDF 中,1sin sin 3∠CF CDF BDE DF ==∠=, ∴113CF DF ==. ········· 9分∴AC =AF -CF =8. ··········· 10分 24.(本题满分13分)解:(1)由题意知△ABC 和△ADE 都是等腰直角三角形, ∴∠B =∠DAE =45°.∵G 为AB 中点,H 为BC 中点, ∴AH ⊥BC .∴∠BAH =45°=∠DAE .∴∠GAD =∠HAE . ·········· 1分 在等腰直角△BAH 和等腰直角△DAE 中, 222AH AB AG ==,2AE AD =.∴AH AE AG AD =. ··········· 3分 ∴△AGD ∽△AHE . ·········· 4分(2)当BD =0或2或22时,△ABE 是等腰三角形. ··········· 8分(注:给出0和22各得1分,给出2得2分)F AE CDBO图1AB CDEGH图2(3)解法一:当点D 与点B 重合时,点E 的位置记为点M .此时,∠ABM =∠BAC =90°,∠AMB =∠BAM =45°,BM = AB = AC .∴四边形ABMC 是正方形. ∴∠BMC =90°,∴∠AMC =∠BMC -∠AMB =45°, ··· 9分 ∵∠BAM =∠DAE =45°, ∴∠BAD =∠MAE ,在等腰直角△BAM 和等腰直角△DAE 中, 2AM AB =,2AE AD =.∴AM AE AB AD =.∴△ABD ∽△AME . ∴∠AME =∠ABD =45°∴点E 在射线MC 上. ····· 10分作点B 关于直线MC 的对称点N ,连接AN 交MC 于点E ′, ∵BE +AE =NE +AE ≥AN =NE ′+AE ′=BE ′+AE ′, ∴△ABE ′就是所求周长最小的△ABE . 在Rt △ABN 中,∵AB =4,BN =2BM =2AB =8, ∴AN =2245AN AB BN =+=.∴△ABE 周长最小值为445AB AN +=+. ················· 13分 解法二:取BC 的中点H ,连接AH , 同解法一证△ACE ∽△AHD . ∴∠ACE=∠AHD=90°.∴点E 在过点C 且垂直于AC 的直线上,记为直线l . ······· 10分 点A 关于直线l 的对称点M ,连接BM 交直线l 于点E ′, 同解法一,△ABE ′就是所求周长最小的△ABE .∴△ABE 周长最小值为445AB BM +=+. ··········· 13分25.(本题满分13分) 解:(1)当a =-1,m =0时,22y x x c =-++,A 点的坐标为(3,0),图2BACDE ′ MNE 图3BACDE ′MEH∴-9+6+c =0.解得 c =3. ··························· 2分 ∴抛物线的表达式为223y x x =-++.即2(1)4y x =--+.∴抛物线的顶点坐标为(1,4). ················· 4分(2)∵22y ax ax c =-+的对称轴为直线212a x a-==-, ·········· 5分 ∴点A 关于对称轴的对称点为(-1,m ). ············· 6分 ∵0<a ,∴当1<x ,y 随x 的增大而增大; 当1>x ,y 随x 的增大而减小.又∵n <m ,∴当点P 在对称轴左边时,t <-1;当点P 在对称轴右边时,t >3.综上所述:t 的取值范围为t <-1或t >3. ············· 8分 (3)∵点Q (x ,y )在抛物线上,∴22y ax ax c =-+.又∵QD ⊥x 轴交直线 :(0)l y kx c k =+<于点D ,∴D 点的坐标为(x ,kx+c ).又∵点Q 是抛物线上点B ,C 之间的一个动点,∴222()(2)QD ax ax c kx c ax a k x =-+-+=-+.················· 10分∵QE =x ,∴在Rt △QED 中,2(2)tan 2QD ax a k x ax a k QE x -+===--β. ············ 11分 ∴tan β是关于x 的一次函数,∵a <0,∴tan β随着x 的增大而减小.又∵当x 2≤≤4时,β恰好满足°°30≤≤60β,且tan β随着β的增大而增大, ∴当x=2时,β=60°;当x=4时,β=30°.E D QC B x y O∴2233 423,.a a ka a k⎧--=⎪⎨--=⎪⎩解得333,. ka⎧=-⎪⎨=-⎪⎩∴33a=-.·························13分。
福建省宁德市2018-2019学年度九年级上数学期末质量检测试卷

宁德市2018-2019学年度第一学期期末九年级质量检测数学本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,第Ⅰ卷1至2页,第Ⅱ卷3至6页.满分150分.注意事项:1.答题前,考生务必在试题卷、答题卡规定位置填写本人准考证号、姓名等信息.考生要认真核对答题卡上粘贴的条形码的“准考证号、姓名”与考生本人准考证号、姓名是否一致.2.选择题每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑.如需改动,用橡皮擦干净后,再选涂其他答案标号.非选择题答案用0.5毫米黑色签字笔在答题卡上相应位置书写作答,在试题卷上答题无效.3.作图可先使用2B 铅笔画出,确定后必须用0.5毫米黑色签字笔描黑.4.考试结束,考生必须将试题卷和答题卡一并交回.第Ⅰ卷一、选择题:本题共10小题,每小题4分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知25a b =,则a bb +的值为A .25B .35C .23D .752.已知∠A 为锐角,若sin A =12,则∠A 的度数为A .30°B .45°C .60°D .75°3.已知一个几何体如图所示,则该几何体的左视图是AB C D4.一元二次方程2+20x x =的根的情况是A .有两个相等的实数根B .有两个不相等的实数根C .只有一个实数根D .没有实数根第3题图正方向5.为了估计抛掷同一枚啤酒瓶盖落地后凸面向上的概率,小明做了大量重复试验.经过统计得到凸面向上的次数为420次,凸面向下的次数为580次,由此可估计抛掷这枚啤酒瓶盖落地后凸面向上的概率约为A .0.42B .0.50C .0.58D .0.726.如图,网格中的两个三角形是位似图形,它们的位似中心是A .点AB .点BC .点CD .点D7.已知Rt △ABC ,∠C =90°,若∠A >∠B ,则下列选项正确的是A .sin A <sinB B .cos A <cos BC .tan A <tan BD .sin A <cos A8.如图,在△ABC 中,点D ,E ,F 分别是AB ,BC ,AC 的中点,则下列四个判断中不一定正确的是A .四边形ADEF 一定是平行四边形B .若∠B +∠C =90°,则四边形ADEF 是矩形C .若四边形ADEF 是菱形,则△ABC 是等边三角形D .若四边形ADEF 是正方形,则△ABC 是等腰直角三角形9.已知20y ax bx c a =++ ≠()的部分图象如图所示,若x 1,x 2是一元二次方程20ax bx c ++= 的两个根,且12x x <,则下列说法正确的是A .2x 4<<5B .112x <<C .240b ac -<D .122x x +=10.下列每个“田”字中的数据都按相同的规律排列,其最后一个“田”字中a 的值为A .7B .8C .9D .10第8题图13252431035417a b c82......A DE B CF 第9题图第6题图第Ⅱ卷注意事项:1.用0.5毫米黑色签字笔在答题卡上相应位置书写作答,在试题卷上答题无效.2.作图可先用2B 铅笔画出,确定后必须用0.5毫米黑色签字笔描黑.二、填空题:本题共6小题,每小题4分,共24分.11.广场上一个大型艺术字板块在地上的投影如图所示,则该投影属于.(填写“平行投影”或“中心投影”)12.若=3x 是方程260x kx --=的一个解,则方程的另一个解是.13.已知四边形ABCD 与四边形EFGH 相似,相似比为23,若四边形ABCD 的面积为36cm 2,则四边形EFGH 的面积为cm 2.14.在Rt △ABC 中,∠C =90°,若tan A =25,则tan B =.15.已知二次函数的图象与抛物线223y x =-+的开口大小、方向完全相同,且顶点坐标为(2,-1),则该二次函数的表达式为.16.如图,已知直线l :103y x b b =-+ (<)与x ,y 轴分别交于A ,B 两点,以AB 为边在直线l 的上方作正方形ABCD ,反比例函数11k y x =和22ky x=的图象分别过点C和点D .若13k =,则2k 的值为.三、解答题:本题有9小题,共86分.17.(本题满分7分)解方程:2410x x -+=.18.(本题满分7分)如图,已知△ADE ∽△ABC ,且AD =6,AE =4,AB =12,求CD 的长.第16题图ADEBC第11题图某商场在促销活动中规定,顾客每消费100元就能获得一次抽奖机会.为了活跃气氛,设计了两个抽奖方案:方案一:转动转盘A 一次,转出红色可领取一份奖品;方案二:转动转盘B 两次,两次都转出红色可领取一份奖品.(两个转盘都被平均分成3份)如果你获得一次抽奖机会,你会选择哪个方案?请用相关的数学知识说明理由.20.(本题满分8分)利用所给的图形证明:一个顶点到它所对的两边距离相等的平行四边形是菱形.(写出已知、求证并加以证明)已知:求证:证明:21.(本题满分10分)已知二次函数222y x x =++与反比例函数ky x=(0k ≠)的图象都经过点A (1,m ).(1)求反比例函数的表达式;(2)当二次函数与反比例函数的值都随x 的增大而减小时,求x 的取值范围.22.(本题满分10分)小颖根据网络图片,制作了一个如图1所示的手机支架,图2是该支架的侧面示意图.已知靠板AB 的倾角∠ABC =68°,支撑板CD 与靠板AB 的夹角∠AEC =87°,插孔E 与端点B 之间的线段BE =3cm ,若支撑板上DE 部分的长为2cm ,求支撑板CD 的长.(结果精确到0.1cm )温馨提示:°sin 680.927≈,°cos680.375≈,°tan 68 2.475≈,°sin 710.946≈,°cos710.326≈,°tan 71 2.904≈.AD EBCFABDCE 图2图1转盘A蓝120°红蓝转盘B蓝红120°红某地特产槟榔芋深受欢迎,某商场以7元/千克收购了3000千克优质槟榔芋,若现在马上出售,每千克可获得利润3元.根据市场调查发现,近段时间内槟榔芋的售价每天上涨0.2元/千克,为了获得更大利润,商家决定先贮藏一段时间后再出售.根据以往经验,这批槟榔芋的贮藏时间不宜超过100天,在贮藏过程中平均每天损耗约10千克.(1)若商家将这批槟榔芋贮藏x 天后一次性出售,请完成下列表格:每千克槟榔芋售价(单位:元)可供出售的槟榔芋重量(单位:千克)现在出售3000x 天后出售(2)将这批槟榔芋贮藏多少天后一次性出售最终可获得总利润29000元?24.(本题满分13分)如图,矩形ABCD 中,BC =10,AB =7,点P 在CD 边上运动,将矩形ABCD 沿BP 折叠,使点C 落在直线AD 上方的点G 处,BG ,PG 分别交边AD 于点M ,N .(1)求证:△ABM ∽△DNP ;(2)当点G 与边CD 的距离为5时,求CP 的长;(3)连接MC ,在点P 的运动过程中,是否存在某一点P ,使得△BCM 是等腰三角形?若存在,请用尺规在作图区内的矩形中作出所有可能的△BGP ,并标出相应的字母;若不存在,请说明理由.A CBD A CBD A CBD图2图1图3ACB D GMNP如图,已知抛物线23(0)y ax bx a =++≠与x 轴交于点A (-4,0),B (6,0)两点,与y 轴交于点C .若G 是该抛物线上A ,C 之间的一个动点,过点G 作直线GD ∥x 轴,交抛物线于点D ,过点D ,G 分别作x 轴的垂线,垂足分别为E ,F ,得到矩形DEFG .(1)求该抛物线的表达式;(2)当点G 与点C 重合时,求矩形DEFG 的面积;(3)若直线BC 分别交DG ,DE 于点M ,N ,求△DMN 面积的最大值.AG D FExy BC MNO。
福建省宁德市2018届高三第二次(5月)质量检测数学(理)试卷及答案

2018届宁德市普通高中毕业班第二次质量检查试卷理 科 数 学本试卷分第I 卷和第II 卷两部分.第I 卷1至2页,第II 卷3至5页,满分150分.第I 卷一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的. 1.复数i1iz =+的共轭复数z 在复平面内对应的点位于 A .第一象限 B .第二象限 345C .第三象限 D .第四象限2.已知集合}{1A x x =≥-,1,2x B y y x A ⎧⎫⎪⎪⎛⎫==∈⎨⎬ ⎪⎝⎭⎪⎪⎭⎩,则A B =IA .}{12x x -≤≤B .}{2x x ≥C .}{02x x <≤ D .∅3.某几何体的三视图如图所示,若该几何体的体积为2,则图中x 的值为 A .1 BCD4.设,x y 满足约束条件12324x y x ≤-≤⎧⎨≤≤⎩,,则目标函数2z x y =-的最大值为A .72 B .92 C .132D .152 5.将函数1sin()24y x π=+图象上各点的横坐标缩小为原来的12(纵坐标不变),得到函数()y f x =的图象,则函数()4y f x 3π=+的一个单调递增区间是 A .(,0)2π-B .(0,)2πC .(,)2ππD .3(,2)2ππ俯视图侧视图正视图6.在如图所示的正方形中随机投掷10000个点,则落入由曲线C(曲线C 为正态分布(2,1)N 的密度曲线)与直线0,x =1x = 及0y =围成的封闭区域内点的个数的估计值为 (附:若X2(,)N μσ,则()0.6826P X μσμσ-<<+=,(22)0.9544P X μσμσ-<<+=,(33)0.9974P X μσμσ-<<+=)A .2718B .1359C .430D .2157. 已知F 是抛物线2:2(0)C y px p =>的焦点,P 是C 上的一点,Q 是C 的准线上一点.若ΔPQF是边长为2的等边三角形,则该抛物线的方程为A .28y x =B .26y x =C .24y x =D .22y x = 8.已知锐角,αβ满足sin 2cos αα=,1cos()7αβ+=,则cos β的值为 A .1314 B .1114CD9.已知O 是坐标原点,12,F F 分别是双曲线C :22221x y a b-=(0a >,0b >)的左、右焦点,过左焦点1F 作斜率为12的直线,与其中一条渐近线相交于点A .若2||||OA OF =,则双曲线C 的离心率e 等于 A .54B .53CD .210.世界著名的百鸡问题是由南北朝时期数学家张丘建撰写的《张丘建算经》中的一个问题:鸡翁一,值钱五,鸡母一,值钱三,鸡雏三,值钱一.百钱买百鸡,问鸡翁母雏各几何?张丘建是数学史上解决不定方程解的第一人.用现代方程思想,可设,,x y z 分别为鸡翁、鸡母、鸡雏的数量,则不定方程为53100,3100.z x y x y z ⎧++=⎪⎨⎪++=⎩如图是体现张丘建求解该问题思想的框图,则方框中①,②应填入的是 A .3?t <,257y t =- B .3?t ≤,257y t =- C .5?t <,255y t =- D .5?t ≤,255y t =- 11.底面边长为6的正三棱锥的内切球半径为1,则其外接球的表面积为A .49πB .36πC .25πD .16π12.设函数()ln()f x x k =+,()e 1x g x =-.若12()()f x g x =,且12x x -有极小值1-,则实数k 的值是 A .1- B .2-C .0D .22018届宁德市普通高中毕业班第二次质量检查试卷理 科 数 学第II 卷注意事项:用0.5毫米黑色签字笔在答题卡上书写作答. 在试题卷上作答,答案无效.本卷包括必考题和选考题两部分.第13~21题为必考题,每个试题考生都必须做答.第22、23题为选考题,考生根据要求做答.二、填空题:本大题共4小题,每小题5分. 13.边长为2的正三角形ABC 中,12AD DC =,则BD AC ⋅=___________. 14.()22344(1)x x x -++的展开式中,3x 的系数是___________.(用数字填写答案)15.B 村庄在A 村庄正西10km ,C 村庄在B 村庄正北3km .现在要修一条从A 村庄到C 村庄的公路,沿从A 村庄到B 村庄的方向线路报价是800万元/km ,沿其他线路报价是1000万元/km ,那么修建公路最省的费用是___________万元. 16.在ABC ∆中,D 为边BC 上的点,且满足2DAC π∠=,1sin 3BAD ∠=.若13ABD ADC S S ∆∆=, 则C ∠的余弦值为___________.三、解答题:本大题共6小题,满分70分.解答须写出文字说明、证明过程和演算步骤. 17.(12分)已知数列{}n a 的前n 项和为n S ,12a =,132n n S a +=-. (1)求数列{}n a 的通项公式;(2)设2log n n b a =,若4(1)n n n c b b =+,求证:123n c c c +++<.18.(12分)为响应绿色出行,某市在推出“共享单车”后,又推出“新能源分时租赁汽车”.其中一款新能源分时租赁汽车,每次租车收费的标准由两部分组成:①根据行驶里程数按1元/公里计费;②行驶时间不超过40分时,按0.12元/分计费;超过40分时,超出部分按0.20元/分计费.已知张先生家离上班地点15公里,每天租用该款汽车上、下班各一次.由于堵车、红绿灯等因素,每次路上开车花费的时间t (分)是一个随机变量.现统计了50次路上开车花费时间,在各时间段内的频数分布情况如下表所示:将各时间段发生的频率视为概率,每次路上开车花费的时间视为用车时间,范围为(]20,60分. (1)写出张先生一次租车费用y (元)与用车时间t (分)的函数关系式;(2)若张先生一次开车时间不超过40分为“路段畅通”,设ξ表示3次租用新能源分时租赁汽车中“路段畅通”的次数,求ξ的分布列和期望;(3)若公司每月给1000元的车补,请估计张先生每月(按22天计算)的车补是否足够上、下班租用新能源分时租赁汽车?并说明理由.(同一时段,用该区间的中点值作代表)19.(12分)如图,四棱锥P ABCD -中,底面ABCD 为梯形,//AB DC ,112BC DC AB ===. O 是AB 的中点,PO ⊥底面ABCD .O 在平面PAD 上的正投影为点H ,延长PH 交AD 于点E . (1)求证: E 为AD 中点;(2)若90ABC ∠=,PA BC 上确定一点G ,使得HG //平面PAB ,并求出OG 与面PCD 所成角的正弦值.20.(12分)已知椭圆2222:1(0)x y M a b a b+=>>的左、右顶点分别为,A B ,上、下顶点分别为,C D .OHED CBAP若四边形ADBC 的面积为4,且恰与圆224:5O x y +=相切. (1)求椭圆M 的方程;(2) 已知直线l 与圆O 相切,交椭圆M 于点,P Q ,且点,A B 在直线l 的两侧.设APQ ∆的面积为1S ,BPQ ∆的面积为2S ,求12S S -的取值范围.21.(12分)已知函数221()()ln ()2f x x x x ax a =++∈R ,曲线()y f x =在1x =处的切线与直线210x y +-=垂直.(1)求a 的值,并求()f x 的单调区间;(2)若λ是整数,当0x >时,总有2211()(3)ln 24f x x x x x λλ-+->+,求λ的最大值.请考生在第22、23题中任选一题做答,如果多做,则按所做的第一题记分.做答时请写清题号. 22.[选修4―4:坐标系与参数方程](10分)在直角坐标系xOy 中,以坐标原点O 为极点,x 轴正半轴为极轴建立极坐标系,曲线1C 的极坐标方程为2(4cos )4r ρρθ-=-,曲线2C 的参数方程为4cos ,sin x y θθ⎧=+⎪⎨=⎪⎩(θ为参数).(1)求曲线1C 的直角坐标方程和曲线2C 的极坐标方程;(2)当r 变化时,设1,C 2C 的交点M 的轨迹为3C .若过原点O ,倾斜角为3π的直线l 与曲线3C 交于点,A B ,求OA OB -的值.23.[选修4—5:不等式选讲](10分)已知实数x , y 满足1x y +=.(1)解关于x 的不等式225x x y -++≤;(2)若,0x y >,证明:2211119x y ⎛⎫⎛⎫--≥ ⎪ ⎪ ⎪⎝⎭⎝⎭2018年宁德市普通高中毕业班质量检查数学(理科)试题参考答案及评分标准说明:一、本解答指出了每题要考查的主要知识和能力,并给出了一种或几种解法供参考,如果考生的解法与本解法不同,可根据试题的主要考查内容比照评分标准指定相应的评分细则.二、对计算题,当考生的解答在某一部分解答未改变该题的内容和难度,可视影响的程度决定后继部分的给分,但不得超过该部分正确解答应给分数的一半;如果后继部分的解答有较严重的错误,就不再给分.三、解答右端所注分数,表示考生正确做到这一步应得的累加分数. 四、只给整数分数,选择题和填空题不给中间分.一、选择题:本题考查基础知识和基本运算,每小题5分,满分60分. 1.D 2.C 3.A 4.D 5.C 6.B 7.D 8.C 9.B 10.B 11.A 12.D二、填空题:本题考查基础知识和基本运算,每小题5分,满分20分.13.23- 14.8 15.9800 16三、解答题:本大题共6小题,满分70分,解答须写出文字说明、证明过程和演算步骤.17.本小题主要考查数列及数列求和等基础知识,考查运算求解能力,考查函数与方程思想、化归与转化思想等,满分12分. 解:(1)由题设132n n S a +=-, 当2n ≥时,132n n S a -=-,两式相减得13n n n a a a +=-,即14n n a a += . …………………2分又1a =2,1232a a =-,可得28a =, ∴214a a =. ………………………………3分 ∴数列{}n a 构成首项为2,公比为4的等比数列,∴121242n n n a --=⨯=. ………………………………5分 (没有验证214a a =扣一分)(2)∵212log 221n n b n -==-,………………………………6分442(1)(21)2(21)n n n c b b n n n n===+-⋅-⋅(*n ∈N ), ………………7分∴2n ≥时,22111(21)(22)(1)1n c n n n n n n n n=<==--⋅-⋅-⋅- , ………9分∴1231111112()()()12231n c c c c n n ++++≤+-+-++-- …………10分13n=- ………………………………11分3<. ………………………………12分解法二:(1)同解法一;(2)∵212log 221n n b n -==-,………………………………6分442(1)(21)2(21)n n n c b b n n n n===+-⋅-⋅(*n ∈N ), ………………7分 ∵2n ≥时,211n n -≥+,∴22112()(21)(1)1n c n n n n n n =≤=--⋅+⋅+ , ………9分 ∴123111122()()23+1n c c c c n n ⎡⎤++++≤+-++-⎢⎥⎣⎦…………10分 112221n ⎛⎫=+- ⎪+⎝⎭………………………………11分3<. ………………………………12分解法三:(1)同解法一;(2)∵212log 221n n b n -==-,………………………………6分442(1)(21)2(21)n n n c b b n n n n===+-⋅-⋅(*n ∈N ), ………………7分∴2n ≥时,22112()(21)(1)1n c n n n n n n=≤=--⋅-⋅- , ………8分∴1231234511112()()561n c c c c c c c c c n n ⎡⎤++++≤+++++-++-⎢⎥-⎣⎦…………10分 1212112231514455n ⎛⎫=+++++- ⎪⎝⎭ (1)1分619223630n<+-<. ………………………………12分18.本小题主要考查频率分布表、平均数、随机变量的分布列及数学期望等基础知识,考查运算求解能力、数据处理能力、应用意识,考查分类与整合思想、必然与或然思想、化归与转化思想.满分12分. 解法一:(1)当2040t <≤时,0.1215y t =+ ………………………………1分 当4060t <≤时,.y t t=⨯+-. ………………………………2分得:0.1215,2040,0.211.8,4060t t y t t +<≤⎧=⎨+<≤⎩………………………………3分(2)张先生租用一次新能源分时租赁汽车,为“路段畅通”的概率2182505P +==……4分 ξ可取0,1,2,3.03032327(0)55125P C ξ⎛⎫⎛⎫=== ⎪ ⎪⎝⎭⎝⎭,2132354(1)55125P C ξ⎛⎫⎛⎫=== ⎪⎪⎝⎭⎝⎭ 2232336(2)55125P C ξ⎛⎫⎛⎫=== ⎪ ⎪⎝⎭⎝⎭,3033238(3)55125P C ξ⎛⎫⎛⎫=== ⎪ ⎪⎝⎭⎝⎭ ξ的分布列为……………7分27543680123 1.2125125125125E ξ=⨯+⨯+⨯+⨯= ……………………………8分 或依题意2(3,)5B ξ,23 1.25E ξ=⨯= ……………………………8分(3)张先生租用一次新能源分时租赁汽车上下班,平均用车时间21820102535455542.650505050t =⨯+⨯+⨯+⨯=(分钟),……………10分 每次上下班租车的费用约为0.242.611.820.32⨯+=(元). ……………11分 一个月上下班租车费用约为20.32222894.081000⨯⨯=<,估计张先生每月的车补够上下班租用新能源分时租赁汽车用. ………………12分解法二:(1)(2)同解法一; (3)张先生租用一次新能源分时租赁汽车上下班,平均租车价格为2182010(150.1225)(150.1235)(11.80.245)(11.80.255)20.51250505050+⨯⨯++⨯⨯++⨯⨯++⨯⨯=(元)……………10分一个月上下班租车费用约为20.512222902.5281000⨯⨯=<……………11分估计张先生每月的车补够上下班租用新能源分时租赁汽车用. ………………12分19.本小题主要考查空间直线与直线、直线与平面的位置关系及直线与平面所成的角等基础知识,考查空间想象能力、推理论证能力、运算求解能力,考查化归与转化思想等.满分12分. 解法一:(1)连结OE .2,AB O =是AB 的中点,1CD =, OB CD ∴=,//AB CD ,∴ 四边形BCDO 是平行四边形, 1OD ∴=.………………1分OHEDCBAPPO ⊥平面ABCD ,AD ⊂平面ABCD , PO AD ∴⊥,………………2分 O 在平面PAD 的正投影为H , OH ∴⊥平面PAD ,OH AD ∴⊥.………………3分又OH PO O =,AD ∴⊥平面POE ,AD OE ∴⊥,………………4分 又1AO OD ==,E ∴是AD 的中点. ………………5分 (2)90ABC ∠=,//OD BC ,OD AB ∴⊥,OP ⊥平面ABCD ,∴以O 为原点,,,OD OB OP 分别为,,x y z 轴的正方向建立空间直角坐标系O xyz -,………………6分(0,0,0)O ∴,(0,0,1)P ,(1,1,0)C ,(1,0,0)D ,2PA =OP AB ⊥,1PO ∴OA OD OP ∴==,∴H ∴是ADP ∆的的外心,AD PD AP ==H ∴是ADP ∆的的重心,OH OP PH ∴=+23OP PE =+111(,,)333=-.………………8分设BG BC λ=,(,1,0)OG BC OB λλ∴=+=,141(,,)333GH OH OG λ∴=-=--,又(1,0,0)OD =是平面PAB 的一个法向量,且//HG 平面PAB , 0GH OD ∴⋅=,103λ∴-=,解得13λ=,1(,1,0)3OG ∴=,………………9分设(,,)n x y z =是平面PCD 的法向量,(1,0,1)PD =-,(0,1,0)CD =-,0,0,n PD n CD ⎧⋅=⎪∴⎨⋅=⎪⎩即0,0,x z y -=⎧⎨=⎩ 取1,x =则1,0z y ==,(1,0,1)n ∴=.………………11分cos ,||||n PGn PG n PG ⋅∴<>=⋅1==, ∴直线OG 与平面PCD 所成角的正弦值为.………………12分 解法二:(1)同解法一;(2)过H 作HM EO ⊥,交EO 于点M ,过点M 作//GM AB ,分别交,OD BC 于,Q G ,则//HG 平面PAB ,………………6分 证明如下://,MG AB AB ⊂平面,PAB MG ⊄平面PAB ,//MG ∴平面PABPO ⊥平面ABCD ,EO ⊂平面ABCD ,PO EO ∴⊥, ∴在平面POD 中,//PO MH ,PO ⊂平面,PAB HM ⊄平面PAB , //MH ∴平面PABMG MH M =,∴平面//MHG 平面PABGH ⊂平面MHG ,//HG ∴平面PAB .………………7分,OM PH OM ME HE =∴=, 1,3BG OQ ∴===………………8分 在OD 上取一点N ,使23ON =, CN OG ∴=,………………9分 作NT PD ⊥于T ,连结CT .∵,CD OD ⊥,CD OP OD OP O ⊥=,CD ∴⊥平面POD , NT CD ∴⊥,PD CD D =, NT ∴⊥平面PCD ,NCT ∴∠就是OG 与平面PCD 所成的角.………………10分DN DPNT PO =,NT ∴, (11)分 sinNT OTN CN ∴∠===, 即直线OG 与平面PCD (12)分解法三:(1)同解法一.(2)过E 作//EQ AB ,交BC 于点Q ,连结PQ ,过H 作//HM EQ 交PQ 于点M ,TNQ PAB CD E HOMG过点M 作//GM PB ,交BC 于G ,连结HG , 则//HG 平面PAB ,………………6分 证明如下://,MG PB PB ⊂平面,PAB MG ⊄平面PAB ,//MG ∴平面PAB同理://MH 平面PABMG MH M =,∴平面//MHG 平面PAB .GH ⊂平面MHG ,//HG ∴平面PAB ,………………7分 2BG PM PH GQ MQ HE∴===, E 是AD 的中点,∴Q 是BC 的中点,1133BG BC ∴==,………………8分取PD 的中点N ,连结ON ,再连结OG 并延长交DC 的延长线于点T ,连结NT , OP OD =,N 是PD 中点, ON PD ∴⊥,OB OD ⊥,,OB OP OD OP D ⊥=,OB ∴⊥平面POD OB ON ∴⊥,//OB CD ,ON CD ∴⊥,PD CD D =, ON ∴⊥平面PCD , OTN ∴∠就是OG 与平面PCD 所成的角.BG OBGC CT=, 2CT ∴=,OT ∴12ON DP ==………………11分sin ON OTN OT ∴∠===即直线OG 与平面PCD ………………12分20.本题主要考查直线、椭圆、直线与椭圆的位置关系等基础知识,考查运算求解能力、推理论证能力,考查函数与方程思想、化归与转化思想,考查考生分析问题和解决问题的能力,满分12分. 解法一:(1)根据题意,可得:1224,21122a b ab ⎧⨯⨯=⎪⎪⎨⎪=⎪⎩即2,ab =⎧………………………………………………………2分 TNG MQ OHE DCB AP解得2,1.a b =⎧⎨=⎩………………………………………………………4分∴椭圆M 的方程为2214x y +=.………………………………………………………5分(2)设:l x my n =+,(2,2)n ∈-,直线l 与圆O 相切,得=,即224(1)5m n +=,………………………………6分 从而[)20,4m ∈.又1121(2)2S n y y =+-,2121(2)2S n y y =--,∴1212121(2)(2)2S S n n y y n y y -=⨯--+⋅-=⋅-.………………………………7分将直线l 的方程与椭圆方程联立得222(4)240m y mny n +++-=,显然0∆>.设11(,)P x y∴12y y -=∴12S S -=85, 当20m =时,1285S S -=;………………………………10分当2(0,4)m ∈时,122S S -==, (11)分且1285S S ->.综上,128,25S S ⎡⎫-∈⎪⎢⎣⎭.………………………………12分解法二:(1)同解法一;(2)当直线l的斜率不存在时,由对称性,不妨设:l x =,此时直线l与椭圆的交点为,12182)(225S S ⎡⎤-=-=⎢⎥⎣⎦. 直线l 的斜率存在时,设:l y kx b =+,由直线l 与圆O 相切,得=224(1)5k b +=.又点,A B 在直线l 的两侧,∴(2)(2)0k b k b +-+<,2240b k -<,∴224(1)405k k +-<,解得12k >或12k <-.点,A B 分别到直线l 的距离为1d =2d =将直线l 的方程与椭圆方程联立得222(14)8440k x kbx b +++-=,显然0∆>.设11(,)P x y ,22(,)Q x y ,得122814kbx x k +=-+,21224414b x x k -⋅=+.…………………………………7分∴12PQ x =-=………………………8分∴121212S S d d AB -=-⋅=b =b =2=,且1285S S ->.综上,128,25S S ⎡⎫-∈⎪⎢⎣⎭.…………………………………………………………………………12分21.本小题主要考查导数的几何意义、导数及其应用、不等式等基础知识,考查推理论证能力、运算求解能力、创新意识等,考查函数与方程思想、化归与转化思想、分类与整合思想、数形结合思想等.满分12分.解法一: (1)函数()f x 的定义域是(0,)+∞,1()(1)ln (2)12f x x x a x '=++++,……………………………………………………………1分依题意可得, (1)1f '=, 12122a ∴++=,14a ∴= .……………………………………………………………………2分 ()(1)ln (1)f x x x x '∴=+++=(1)(ln 1)x x ++令()0f x '=,即(1)(ln 1)0x x ++=,10,x x >∴=,……………………………………3分 ()f x ∴的单调递增区间是1(,)e +∞,单调递减区间为1(0,)e .………………………………5分(2)由(Ⅰ)可知, 2211()()ln 24f x x x x x =++,2211()(3)ln 24f x x x x x λλ∴-+->+ln 31x x x x λ-⇔>+,………………………………6分 设ln 3()1x x xh x x -=+, ∴只要min ()h x λ>,……………………………………………7分2(1ln 3)(1)(ln 3)()(1)+-+--'=+x x x x x h x x22ln (1)x xx -+=+,…………………………………………………………………8分令()2ln u x x x =-+, 1()10u x x'∴=+> ()u x ∴在(0,)+∞上为单调递增函数, (1)10u =-<, (2)ln 20=>u∴存在0(1,2)x ∈,使0()0u x =,……………………………………………………9分当0(,)x x ∈+∞时,()0u x >,即()0h x '>, 当0(0,)x x ∈时,()0u x <,即()0h x '<, ()h x ∴在0x x =时取最小值,且000min 0ln 3()1-=+x x x h x x ,………………………………10分又0()0u x =, 00ln 2x x ∴=-, 000min 00(2)3()1--∴==-+x x x h x x x ,……………………………………………………11分00(1,2),(2,1)x x ∈∴-∈--又min ()h x λ<,max 2Z λλ∈∴=-. …………………………………………………………………12分解法二:(1)同解法一.(2)由(1)可知, 2211()()ln 24f x x x x x =++2211()(3)ln 24f x x x x λλ∴-+->+ln 30x x x x λλ⇔--->.…………………………6分 设()ln 3g x x x x x λλ=---,∴只要min ()0g x >,………………………………………7分 则()1ln 3g x x λ'=+--ln 2x λ=--令()0g x '=,则ln 2x λ=+,2x e λ+∴=.…………………………………………………8分 当2(0,)x e λ+∈时,()0g x '<,()g x 单调递减;当2(,)x e λ+∈+∞时,()0g x '>,()g x 单调递增,2min ()()g x g e λ+∴=222(2)3e e e λλλλλλ+++=+---2e λλ+=--.…………………………9分设2()h e λλλ+=--,则()h λ在R 上单调递减,………………………………………10分 (1)10,(2)120h e h -=-+<-=-+>,………………………………………………11分 0(2,1)λ∴∃∈--,使0()0h λ=,max 2Z λλ∈∴=- . …………………………………………………………………12分22.选修44-;坐标系与参数方程本小题考查直线和圆的极坐标方程、参数方程等基础知识,考查运算求解能力,考查数形结合思想、化归与转化思想等. 满分10分. 解法一:(1)由1C :2(4cos )4r ρρθ-=-, 得224cos 4r ρρθ-+=,即222440x y x r +-+-=, ………………………………………………………2分 曲线2C 化为一般方程为:222(4)3x y r -+=,即2228163x y x r +-+=,………4分 化为极坐标方程为:228cos 1630r ρρθ-+-=.………………………………5分(2)由224cos 4r ρρθ-+=及228cos 1630r ρρθ-+-=,消去2r ,得曲线3C 的极坐标方程为22cos 20()ρρθρ--=∈R . …………………………………………………7分将θπ=3代入曲线3C 的极坐标方程,可得220ρρ--=,…………………8分 故121ρρ+=,1220ρρ=-<,…………………………………………………9分 故121OA OB ρρ-=+=.…………………………………………………10分 (或由220ρρ--=得0)1)(2(=+-ρρ得1,221-==ρρ,…………………9分 故211-=-=OA OB …………………………………………………10分) 解法二:(1)同解法一;(2)由22244x y x r +-+=及2228163x y x r +-+=,消去2r ,得曲线3C 的直角坐标方程为2222x y x +-=. ………………………………………………………………7分设直线l的参数方程为1,2x t y ⎧=⎪⎪⎨⎪=⎪⎩(t 为参数),………………………………8分与2222x y x +-=联立得2213244t t t +-=,即220t t --=,………………………………………………………………9分故121t t +=,1220t t =-<,∴121OA OB t t -=+=.……………………………………………………10分 (或由220t t --=得,,0)1)(2(=+-t t 得1,221-==t t ,∴211-=-=OA OB .……………………………………………………10分)23.选修45-:不等式选讲本小题考查绝对值不等式、基本不等式的解法与性质等基础知识,考查运算求解能力、推理论证能力,考查分类与整合思想、化归与转化思想等. 满分10分. 解法一:(1)1,x y +=|2||1|5x x ∴-++≤,………………………………………1分当2x ≥时,原不等式化为215x -≤,解得3x ≤,∴23x ≤≤;………………………………………………2分 当12x -≤<时,原不等式化为215x x -++≤,∴12x -≤<;………………………………………………3分 当1x <-时,原不等式化为215x -+≤,解得2x ≥-,∴21x -≤<-;………………………………………………4分 综上,不等式的解集为{}23x x -≤≤..……………………5分 (2)1,x y +=且0,0x y >>,2222222211()()(1)(1)x y x x y y x y x y +-+-∴--=⋅……………7分222222xy y xy x x y ++=⋅222222()()y y x x x x y y=++225x y y x=++………………………………8分59≥=. 当且仅当12x y ==时,取“=”. ………………………………10分 解法二:(1)同解法一;(2)1,x y +=且0,0x y >>,2222221111(1)(1)x y x y x y --∴--=⋅………………………………6分 22(1)(1)(1)(1)x x y y x y +-+-=⋅22(1)(1)x y y x x y ++=⋅………………………………7分 1x y xyxy+++=………………………………8分21xy =+2219()2x y ≥+=+当且仅当12x y ==时,取“=”. ………………………………10分。
福建省福州市2018年初中毕业班质量检测数学试卷(WORD版-含答案)

##省##市2018年初中毕业班质量检测数学试卷本试卷分第Ⅰ卷〔选择题〕和第Ⅱ卷〔非选择题〕两部分,第Ⅰ卷1至2页,第Ⅱ卷3至5页,满分150分.注意事项:1.答题前,考生务必在试题卷、答题卡规定位置填写本人##号、##等信息.考生要认真核对答题卡上粘贴的条形码的"##号、##〞与考生本人##号、##是否一致.2.选择题每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其他答案标号.非选择题答案用0.5毫米黑色墨水签字笔在答题卡上相应位置书写作答,在试题卷上答题无效.3.作图可先使用2B 铅笔画出,确定后必须用0.5毫米黑色墨水签字笔描黑.4.考试结束后,考生必须将试题卷和答题卡一并交回.第Ⅰ卷一、选择题:本题共10小题,每小题4分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.〔1〕-3的绝对值是〔A 〕13 〔B 〕13- 〔C 〕-3 〔D 〕3〔2〕如图是五个大小相同的正方体组成的几何体,这个几何体的俯视图是〔A 〕 〔B 〕 〔C 〕 〔D 〕〔3〕中国倡导的"一带一路〞建设将促进我国与世界各国的互利合作.根据规划,"一带一路〞地区覆盖总人口约为4400000000人,将4400000000用科学记数法表示,其结果是〔A 〕44108 〔B 〕4.4109〔C 〕4.4108 〔D 〕4.41010 〔4〕如图,数轴上M ,N ,P ,Q 四点中,〔A 〕M〔B 〕N 〔C 〕P〔D 〕Q 〔5〕下列计算正确的是〔A 〕8a -a =8〔B 〕<-a >4=a 4 〔C 〕a 3a 2=a 6〔D 〕<a -b >2=a 2-b 2 〔6〕下列几何图形不.是中心对称图形的是 从正面看 0 1 2 M QN P〔A〕平行四边形〔B〕正方形〔C〕正五边形〔D〕正六边形〔7〕如图,AD是半圆O的直径,AD=12,B,C是半圆O上两点.若AB BC CD==,则图中阴影部分的面积是〔A〕6π〔B〕12π〔C〕18π〔D〕24π〔8〕如图,正方形网格中,每个小正方形的边长均为1个单位长度.A,B在格点上,现将线段AB向下平移m个单位长度,再向左平移n个单位长度,得到线段A′B′,连接AA′,BB′.若四边形AA′B′B是正方形,则m+n的值是〔A〕3 〔B〕4〔C〕5 〔D〕6〔9〕若数据x1,x2,…,x n的众数为a,方差为b,则数据x1+2,x2+2,…,x n+2的众数,方差分别是〔A〕a,b〔B〕a,b+2〔C〕a+2,b〔D〕a+2,b+2〔10〕在平面直角坐标系xOy中,A〔0,2〕,B〔m,m-2〕,则AB+OB的最小值是〔A〕〔B〕4〔C〕〔D〕2 第Ⅱ卷注意事项:1.用0.5毫米黑色墨水签字笔在答题卡上相应位置书写作答,在试题卷上作答,答案无效.2.作图可先用2B铅笔画出,确定后必须用0.5毫米黑色墨水签字笔描黑.二、填空题:本题共6小题,每小题4分,共24分.〔11〕2-1=.〔12〕若∠α=40°,则∠α的补角是°.〔13〕不等式2x+1≥3的解集是.〔14〕一个不透明的袋子中有3个白球和2个黑球,这些球除颜色外完全相同.从袋子中随机摸出1个球,这个球是白球的概率是.〔15〕如图,矩形ABCD中,E是BC上一点,将△ABE沿AE折叠,得到△AFE.若F恰好是CD的中点,则ADAB 的值是.DAECBF〔16〕如图,直线y 1=43-x 与双曲线y 2=k x交于A ,B 两点,点C 在x 轴上,连接AC ,BC .若∠ACB =90°,△ABC 的面积为10,则k 的值是.三、解答题:本题共9小题,共86分.解答应写出文字说明、证明过程或演算步骤. 〔17〕〔本小题满分8分〕先化简,再求值:2212(1)11x x x x -+-÷++,其中x=1+.〔18〕〔本小题满分8分〕 如图,点B ,F ,C ,E 在一条直线上,AB ∥DE ,AC ∥DF 且AC =DF ,求证:AB =DE . 〔19〕〔本小题满分8分〕如图,在Rt △ABC 中,∠C =90°,∠B =54°,AD 是△ABC 的角平分线.求作AB 的垂直平分线MN 交AD 于点E ,连接BE ;并证明DE =DB .〔要求:尺规作图,保留作图痕迹,不写作法〕 〔20〕〔本小题满分8分〕我国古代数学著作《九章算术》的"方程〞一章里,一次方程组是由算筹布置而成的.如图1,图中各行从左到右列出的算筹数分别表示未知数x ,y 的系数与相应的常数项,把图1所示的算筹图用我们现在所熟悉的方程组的形式表述出来,就是41061134x y x y +=⎧⎨+=⎩.,请你根据图2所示的算筹图,列出方程组,并求解.〔21〕如图,于点P 〔22〕已知y 与性质进行探究.〔Ⅰ〕如图,在平面直角坐标系xOy 中,描出了上表中各对对应值为坐标的点.根据描出的点,画出该函数的图象;A CB D A E B F C〔23〕〔本小题满分10分〕李先生从家到公司上班,可以乘坐20路或66路公交车.他在乘坐这两路车时,对所需的时间分别做了20次统计,并绘制如下统计图:请根据以上信息,解答下列问题.〔Ⅰ〕完成右表中〔ⅰ〕,〔ⅱ〕的数据: 〔Ⅱ〕李先生从家到公司,除乘车时间外,另需10分钟〔含等车,步行等〕.该公司规定每天8点上班,16点下班. 〔ⅰ〕某日李先生7点20分从家里出发,乘坐哪路车合适?并说明理由;〔ⅱ〕公司出于人文关怀,允许每个员工每个月迟到两次.若李先生每天同一时刻从家里出发,则每天最迟几点出发合适?并说明理由.〔每月的上班天数按22天计〕〔24〕〔本小题满分12分〕已知菱形ABCD ,E 是BC 边上一点,连接AE 交BD 于点F .〔Ⅰ〕如图1,当E 是BC 中点时,求证:AF =2EF ;〔Ⅱ〕如图2,连接CF ,若AB =5,BD =8,当△CEF 为直角三角形时,求BE 的长;〔Ⅲ〕如图3,当∠ABC =90°时,过点C 作CG ⊥AE 交AE 的延长线于点G ,连接DG ,若BE =BF ,求tan ∠BDG 的值.图1 图2图3〔25〕〔本小题满分14分〕如图,抛物线y =ax 2+bx 〔a >0,b <0〕交x 轴于O ,A 两点,顶点为〔Ⅰ〕直接写出A ,B 两点的坐标〔用含a ,b 的代数式表示〕; 〔Ⅱ〕直线y =kx +m 〔k >0〕过点B ,且与抛物线交于另一点D 与点A 不重合〕,交y 轴于点C .过点D 作DE ⊥x 轴于点AB ,CE ,求证:CE ∥AB ;〔Ⅲ〕在〔Ⅱ〕的条件下,连接OB ,当∠OBA =≤k ,的取值X 围.参考答案 次数/min路公交 路公交 B A D C E F B A D C E F。
2018年5月份福建省宁德市高三毕业班第二次综合质量检查试卷理科数学试题

2018届宁德市普通高中毕业班第二次质量检查试卷理 科 数 学本试卷分第I 卷和第II 卷两部分.第I 卷1至2页,第II 卷3至5页,满分150分. 考生注意:1.答题前,考生务必将自己的姓名、准考号填写在答题卡上.考生要认真核对答题卡上粘贴的“姓名、准考证号、考试科目”与考生本人准考证号、姓名是否一致.2.第I 卷每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其他答案标号.第II 卷用0.5毫米的黑色墨水签字笔在答题卡上书写作答.若在试题卷上作答,答案无效.3.考试结束,监考员将试题卷和答题卡一并交回 .第I 卷一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的. 1.复数i1iz =+的共轭复数z 在复平面内对应的点位于 A.第一象限 B.第二象限 345C.第三象限 D.第四象限2.已知集合}{1A x x =≥-,1,2x B y y x A ⎧⎫⎪⎪⎛⎫==∈⎨⎬ ⎪⎝⎭⎪⎪⎭⎩,则A B =IA.}{12x x -≤≤B.}{2x x ≥C.}{02x x <≤ D.∅3.某几何体的三视图如图所示,若该几何体的体积为2,则图中x 的值为 A.14.设,x y 满足约束条件12324x y x ≤-≤⎧⎨≤≤⎩,,则目标函数2z x y =-的最大值为俯视图侧视图正视图A.72 B.92C.132 D.1525.将函数1sin()24y x π=+图象上各点的横坐标缩小为原来的12(纵坐标不变),得到函数()y f x =的图象,则函数()4y f x 3π=+的一个单调递增区间是 A.(,0)2π-B.(0,)2πC.(,)2ππD.3(,2)2ππ6.在如图所示的正方形中随机投掷10000个点,则落入由曲线C(曲线C 为正态分布(2,1)N 的密度曲线)与直线0,x =1x = 及0y =围成的封闭区域内点的个数的估计值为(附:若X 2(,)N μσ,则()0.6826P X μσμσ-<<+=,(22)0.9544P X μσμσ-<<+=,(33)0.9974P X μσμσ-<<+=)A.2718B.1359C.430D.2157. 已知F 是抛物线2:2(0)C y px p =>的焦点,P 是C 上的一点,Q 是C 的准线上一点.若ΔPQF 是边长为2的等边三角形,则该抛物线的方程为A.28y x =B.26y x =C.24y x =D.22y x =8.已知锐角,αβ满足sin 2cos αα=,1cos()7αβ+=,则cos β的值为A.1314B.11149.已知O 是坐标原点,12,F F 分别是双曲线C :22221x y a b -=(0a >,0b >)的左、右焦点,过左焦点1F 作斜率为12的直线,与其中一条渐近线相交于点A .若2||||OA OF =,则双曲线C 的离心率e 等于A.54B.53D.210.世界著名的百鸡问题是由南北朝时期数学家张丘建撰写的《张丘建算经》中的一个问题:鸡翁一,值钱五,鸡母一,值钱三,鸡雏三,值钱一.百钱买百鸡,问鸡翁母雏各几何?张丘建是数学史上解决不定方程解的第一人.用现代方程思想,可设,,x y z 分别为鸡翁、鸡母、鸡雏的数量,则不定方程为53100,3100.z x y x y z ⎧++=⎪⎨⎪++=⎩如图是体现张丘建求解该问题思想的框图,则方框中①,②应填入的是A.3?t <,257y t =-B.3?t ≤,257y t =-C.5?t <,255y t =-D.5?t ≤,255y t =- 11.底面边长为6的正三棱锥的内切球半径为1,则其外接球的表面积为A.49πB.36πC.25πD.16π12.设函数()ln()f x x k =+,()e 1x g x =-.若12()()f x g x =,且12x x -有极小值1-,则实数k 的值是 A.1-B.2-C.0D.22018届宁德市普通高中毕业班第二次质量检查试卷理 科 数 学第II 卷注意事项:用0.5毫米黑色签字笔在答题卡上书写作答. 在试题卷上作答,答案无效.本卷包括必考题和选考题两部分.第13~21题为必考题,每个试题考生都必须做答.第22、23题为选考题,考生根据要求做答. 二、填空题:本大题共4小题,每小题5分. 13.边长为2的正三角形ABC 中,12AD DC =,则BD AC ⋅=___________. 14.()22344(1)x x x -++的展开式中,3x 的系数是___________.(用数字填写答案)15.B 村庄在A 村庄正西10km,C 村庄在B 村庄正北3km.现在要修一条从A 村庄到C村庄的公路,沿从A 村庄到B 村庄的方向线路报价是800万元/km,沿其他线路报价是1000万元/km,那么修建公路最省的费用是___________万元. 16.在ABC ∆中,D 为边BC 上的点,且满足2DAC π∠=,1sin 3BAD ∠=.若13ABD ADC S S ∆∆=, 则C ∠的余弦值为___________.三、解答题:本大题共6小题,满分70分.解答须写出文字说明、证明过程和演算步骤. 17.(12分)已知数列{}n a 的前n 项和为n S ,12a =,132n n S a +=-. (1)求数列{}n a 的通项公式; (2)设2log n n b a =,若4(1)n n n c b b =+,求证:123n c c c +++<.18.(12分)为响应绿色出行,某市在推出“共享单车”后,又推出“新能源分时租赁汽车”.其中一款新能源分时租赁汽车,每次租车收费的标准由两部分组成:①根据行驶里程数按 1元/公里计费;②行驶时间不超过40分时,按0.12元/分计费;超过40分时,超出部分按0.20元/分计费.已知张先生家离上班地点15公里,每天租用该款汽车上、下班各一次.由于堵车、红绿灯等因素,每次路上开车花费的时间t (分)是一个随机变量.现统计了50次路上开车花费时间,在各时间段内的频数分布情况如下表所示:将各时间段发生的频率视为概率每次路上开车花费的时间视为用车时间范围为(]20,60错误!未找到引用源。
2018年宁德初中数学质检试题

2018年宁德市初中毕业班质量检测数学试题本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,第Ⅰ卷1至2页,第Ⅱ卷3至5页.满分150分.注意事项:1.答题前,考生务必在试题卷、答题卡规定位置填写本人准考证号、姓名等信息.考生要认真核对答题卡上粘贴的条形码的“准考证号、姓名”与考生本人准考证号,姓名是否一致.2.选择题每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑.如需改动,用橡皮擦干净后,再选涂其他答案标号.非选择题答案用0.5毫米黑色签字笔在答题卡上相应位置书写作答,在试题卷上答题无效.3.作图可先使用2B铅笔画出,确定后必须0.5毫米黑色签字笔描黑.4.考试结束,考生必须将试题卷和答题卡一并交回.第Ⅰ卷一、选择题:本题共10小题,每小题4分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.2018-的值是A.12018B.2018C.12018-D.2018-2.如图,若a∥b,∠1=58°,则∠2的度数是A.58°B.112°C.122°D.142°3.下列事件是必然事件的是A.2018年5月15日宁德市的天气是晴天B.从一副扑克中任意抽出一张是黑桃C.在一个三角形中,任意两边之和大于第三边D.打开电视,正在播广告4.由6个大小相同的小正方体拼成的几何体如图所示,则下列说法正确的是A.主视图的面积最大B.左视图的面积最大C.俯视图的面积最大D.三种视图的面积相等正面第4题图ab 第2题图21数学试题第 1 页共 7 页数学试题 第 2 页 共 7 页5.不等式组10,10≤>x x -⎧⎨+⎩的解集在数轴上表示正确的是6.在平面直角坐标系中,A ,B ,C ,D ,M ,N 的位置如图所示,若点M 的坐标为(-2 ,0), N 的坐标为(2 ,0),则在第二象限内的点是 A .A 点 B .B 点C .C 点D .D 点7.在“创文明城,迎省运会”合唱比赛中,10位评委给某队的评分如下表所示,则下列说法正确的是A .中位数是9.4分B .中位数是9.35分C .众数是3和1D .众数是9.4分8.如图,将△OAB 绕O 点逆时针旋转60°得到△OCD ,若OA=4,∠AOB =35°,则下列结论错误的是 A .∠BDO =60° B .∠BOC =25° C .OC=4D .BD=49.某校为进一步开展“阳光体育”活动,购买了一批篮球和足球.已知购买足球数量是篮球的2倍,购买足球用了4 000元,购买篮球用了2 800元,篮球单价比足球贵16元.若可列方程40002800162x x=-表示题中的等量关系,则方程中x 表示的是 A .足球的单价 B .篮球的单价C .足球的数量D .篮球的数量10.如图,已知等腰△ABC ,AB=BC ,D 是AC 上一点,线段BE 与BA 关于直线BD 对称,射线CE 交射线BD 于点F ,连接AE ,AF .则下列关系正确的是 A .180∠∠AFE ABE +=︒ B .12∠∠AEF ABC =C .180∠∠AEC ABC +=︒D .∠∠AEB ACB =成绩(分) 9.2 9.3 9.4 9.59.6 人数32311C 1 2 3-1 0 -2 D1 2 3-1 0 -2 B 1 2 3-1 0 -2 DCBAO第8题图第6题图MN A BD C第10题图CFE DABA 1 2 3-1 0 -2数学试题 第 3 页 共 7 页第 Ⅱ 卷注意事项:1.用0.5毫米黑色签字笔在答题卡上相应位置书写作答,在试题卷上作答,答案无效. 2.作图可先使用2B 铅笔画出,确定后必须0.5毫米黑色签字笔描黑. 二、填空题:本题共6小题,每小题4分,共24分.11.2017年10月18日,中国共产党第十九次全国代表大会在北京隆重召开.从全国近89 400 000党员中产生的2 300名代表参加了此次盛会.将数据89 400 000用科学记数法表示为 .12.因式分解:222a -= .13.小明同学在计算一个多边形的内角和时,由于粗心少算了一个内角,结果得到的总和是800°,则少算了这个内角的度数为 .14. 已知一次函数23(0)y kx k k =++≠,不论k 为何值,该函数的图像都经过点A ,则点A 的坐标为 .15.小丽计算数据方差时,使用公式2222221(5)(8)(13)(14)(15)5S x x x x x ⎡⎤=-+-+-+-+-⎣⎦,则公式中x = . 16.如图,点A ,D 在反比例函数(0)my m x=<的图像上,点B ,C 在反比例函数(0)ny n x=>的图像上.若AB ∥CD ∥x 轴,AC ∥y 轴,且AB =4,AC =3,CD =2,则n = .三、解答题:本题共9小题,共86分.17.(本题满分8分)计算:14cos30212-︒+-.18.(本题满分8分)如图,在△ABC 中, D ,E 分别是AB ,AC 的中点,△ABC 的角平分线AG 交DE 于点F ,若∠ABC =70°,∠BAC =54°,求∠AFD 的度数.CFEDBAGxyOBAC D第16题图数学试题 第 4 页 共 7 页19.(本题满分8分)首届数字中国建设峰会于4月22日至24日在福州海峡国际会展中心如期举行,某校组织115位师生去会展中心参观,决定租用A ,B 两种型号的旅游车.已知一辆A 型车可坐20人,一辆B 型车可坐28人,经测算学校需要租用这两种型号的旅游车共5辆.学校至少要租用B 型车多少辆?20.(本题满分8分)某中学为推动“时刻听党话 永远跟党走”校园主题教育活动,计划开展四项活动:A :党史演讲比赛,B :党史手抄报比赛,C :党史知识竞赛,D :红色歌咏比赛.校团委对学生最喜欢的一项活动进行调查,随机抽取了部分学生,并将调查结果绘制成图1,图2两幅不完整的统计图.请结合图中信息解答下列问题:(1)本次共调查了 名学生; (2)将图1的统计图补充完整;(3)已知在被调查的最喜欢“党史知识竞赛”项目的4个学生中只有1名女生,现从这4名学生中任意抽取2名学生参加该项目比赛,请用画树状图或列表的方法,求出恰好抽到一名男生一名女生的概率.A 15%BC10%D 35%图2图1活动项人数/人AB CD4 6 8 10 12 14 16 2数学试题 第 5 页 共 7 页21.(本题满分8分)如图,已知矩形ABCD ,E 是AB 上一点.(1)如图1,若F 是BC 上一点,在AD ,CD 上分别截取DH =BF ,DG =BE .求证:四边形EFGH 是平行四边形;(2)如图2,利用尺规分别在BC ,CD ,AD 上确定点F ,G ,H ,使得四边形EFGH是特殊的平行四边形.(提示:①保留作图痕迹,不写作法;②只需作出一种情况即可)22.(本题满分10分)若正整数a ,b ,c 满足111a b c+=,则称正整数a ,b ,c 为一组和谐整数.(1)判断2,3,6是否是一组和谐整数,并说明理由;(2)已知x ,y ,z (其中x y z <≤)是一组和谐整数,且1x m =+,3y m =+,用 含m 的代数式表示z ,并求当24z =时m 的值.23.(本题满分10分)如图,在△ABC 中,∠ACB =90°,O 是AB 上一点,以OA 为半径的⊙O 与BC 相切于点D ,与AB 交于点E ,连接ED 并延长交AC 的延长线于点F .(1)求证:AE =AF ;(2)若DE =3,sin ∠BDE =13,求AC 的长.F AE CDBO图1ADFHBEGC图2CDBAE数学试题 第 6 页 共 7 页24.(本题满分13分)如图1,在△ABC 中,∠BAC =90°,AB =AC =4,D 是BC 上一个动点,连接AD ,以AD 为边向右侧作等腰直角△ADE ,其中∠ADE =90°. (1)如图2,G ,H 分别是边AB ,BC 的中点,连接DG ,AH ,EH .求证:△AGD ∽△AHE ;(2)如图3,连接BE ,直接写出当BD 为何值时,△ABE 是等腰三角形; (3)在点D 从点B 向点C 运动过程中,求△ABE 周长的最小值.图1ABCDE图2图3ABCDEABCDEGH数学试题 第 7 页 共 7 页25.(本题满分13分)已知抛物线22(0)y ax ax c a =-+<的图像过点A (3,m ).(1)当a =-1,m =0时,求抛物线的顶点坐标; (2)若P (t ,n )为该抛物线上一点,且n <m ,求t 的取值范围;(3)如图,直线:(0)l y kx c k =+<交抛物线于B ,C 两点,点Q (x ,y )是抛物线上点B ,C 之间的一个动点,作QD ⊥x 轴交直线 l 于点D ,作QE ⊥y 轴于点E ,连接DE .设∠QED=β,当x 2≤≤4时,β 恰好满足°°30≤≤60β,求a 的值.EDQC Bxy O。
2018年宁德初中数学质检答案6稿

1 2018年宁德市初中毕业班质量检测数学试题参考答案及评分标准⑴本解答给出了一种或几种解法供参考,如果考生的解法与本解答不同,可参照本答案的评分标准的精神进行评分.⑵对解答题,当考生的解答在某一步出现错误时,如果后续部分的解答未改变该题的立意,可酌情给分. ⑶解答右端所注分数表示考生正确作完该步应得的累加分数. ⑷评分只给整数分,选择题和填空题均不给中间分. 一、选择题:(本大题有10小题,每小题4分,满分40分)1.B 2.C 3.C 4.A 5.D 6.A 7.B 8.D 9.D 10.B 二、填空题:(本大题有6小题,每小题4分,满分24分)11.78.9410⨯ 12.2(1)(1)a a +- 13.100 14.(-2,3) 15.11 16.83三、解答题(本大题共9小题,共86分.请在答题卡...的相应位置作答) 17.(本题满分8分)解:原式= 3142322⨯+- ··································································· 6分 =12············································································ 8分 18.(本题满分8分) 证明:∵∠BAC =54°,AG 平分∠BAC ,∴∠BAG =12∠BAC =27°. ······················· 2分 ∴∠BGA =180 °-∠ABC -∠ BAG =83° ········ 4分 又∵点D ,E 分别是AB ,AC 的中点,∴DE ∥BC . ········································· 6分 ∴∠AFD =∠BGA =83°. ·························· 8分 19.(本题满分8分)解: 设租用B 型车x 辆,则租用A 型车(5-x )辆,根据题意,得 ················ 1分 2820(5)11≥x x +-. ·································································· 5分解得 158≥x . ·············································································· 7分因为x 为整数,所以x 的最小值是2.答:学校至少租用了2辆B 型车.··························································· 8分 20.(本题满分8分)(1)40; ······················································································ 2分 (2)图略 ······················································································ 4分 (3)列表如下: ·················································································· 6分CFEDBAG2 男 男 男 女男 (男,男) (男,男) (男,女)男 (男,男)(男,男) (男,女)男 (男,男) (男,男)(男,女)女(女,男) (女,男) (女,男)总共有12种结果,每种结果出现的可能性相同,其中恰好抽到一名男生和一名女生的结果有6种,所以抽到一名男生和一名女生的概率是612,即12. ··································· 8分 21.(本题满分8分)(1)证明:∵四边形ABCD 是矩形,∴AD =BC ,AB =CD ,∠A =∠B =∠C =∠D =90°, ∵DG =BE ,DH =BF ,∴△GDH ≌△EBF . ·············· 2分 ∴GH = EF .∵AD =BC ,AB =CD ,DH =BF ,DG =BE , ∴AD -DH =BC -BF ,AB -BE =CD -DG . 即AH =CF ,AE =CG .∴△AEH ≌△CGF . ························ 4分 ∴EH =GF .∴四边形EFGH 是平行四边形. ········· 5分 (2)作图如下:作法一:作菱形(如图2) ···································································· 7分 ∴四边形EFGH 就是所求作的特殊平行四边形. ······································· 8分 作法二:作矩形(如图3,图4) ························································ 7分∴四边形EFGH 就是所求作的特殊平行四边形. ······································ 8分 22.(本题满分10分)(1)是 ······························································································· 1分理由如下:∵111362+=,满足和谐整数的定义,∴2,3,6是和谐整数. ·································································· 4分(2) 解:∵x y z <≤,CDBAE 图2GHFA DFH BEGC图1GH FC DBAE GHF C DBA E 图3图43 依题意,得 111y z x+=.∵1x m =+,3y m =+,∴11111213(1)(3)z x y m m m m =-=-=++++.∴(1)(3)2m m z ++=.······································································ 7分∵24z =,∴(1)(3)242m m ++=.解得 59,m m ==-. ····································································· 9分 ∵x 是正整数,∴5m =. ·················································································· 10分23.(本题满分10分)解:(1)证明:连接OD .∵ OD =OE ,∴∠ODE =∠OED . ······························ 1分∵直线BC 为⊙O 的切线, ∴OD ⊥BC .∴∠ODB =90°. ··································· 2分 ∵∠ACB =90°,∴OD ∥AC . ····································· 3分∴∠ODE =∠F .∴∠OED =∠F . ··················································· 4分 ∴AE =AF . ·························································· 5分(2)连接AD .∵AE 是⊙O 的直径∴∠ADE =90°. ···················································· 6分 ∵AE =AF , ∴DF =DE =3. ∵∠ACB =90°.∴∠DAF +∠F =90°,∠CDF +∠F =90°, ∴∠DAF =∠CDF =∠BDE . ·················· 7分 在Rt △ADF 中,1sin sin 3∠DF DAF BDE AF ==∠=, ∴39AF DF ==. ······························· 8分 在Rt △CDF 中,F AE CDBOF AE CDBO图14 1sin sin 3∠CF CDF BDE DF ==∠=, ∴113CF DF ==. ······························· 9分∴AC =AF -CF =8. ································ 10分 24.(本题满分13分)解:(1)由题意知△ABC 和△ADE 都是等腰直角三角形, ∴∠B =∠DAE =45°.∵G 为AB 中点,H 为BC 中点, ∴AH ⊥BC .∴∠BAH =45°=∠DAE .∴∠GAD =∠HAE .······························ 1分 在等腰直角△BAH 和等腰直角△DAE 中,222AH AB AG ==,2AE AD =.∴AH AE AG AD =. ···································· 3分 ∴△AGD ∽△AHE . ····························· 4分(2)当BD =0或2或22时,△ABE 是等腰三角形. ································ 8分(注:给出0和22各得1分,给出2得2分) (3)解法一:当点D 与点B 重合时,点E 的位置记为点M .此时,∠ABM =∠BAC =90°,∠AMB =∠BAM =45°,BM = AB = AC .∴四边形ABMC 是正方形. ∴∠BMC =90°,∴∠AMC =∠BMC -∠AMB =45°, ······ 9分 ∵∠BAM =∠DAE =45°, ∴∠BAD =∠MAE ,在等腰直角△BAM 和等腰直角△DAE 中, 2AM AB =,2AE AD =.∴AM AE AB AD =.∴△ABD ∽△AME . ∴∠AME =∠ABD =45°∴点E 在射线MC 上. ················· 10分作点B 关于直线MC 的对称点N ,连接AN 交MC 于点E ′, ∵BE +AE =NE +AE ≥AN =NE ′+AE ′=BE ′+AE ′, ∴△ABE ′就是所求周长最小的△ABE .图2图1ABCDEGHB ACDE ′ MNE 图3BACDE ′E H 图25 在Rt △ABN 中,∵AB =4,BN =2BM =2AB =8, ∴AN =2245AN AB BN =+=.∴△ABE 周长最小值为445AB AN +=+.····················································· 13分 解法二:取BC 的中点H ,连接AH , 同解法一证△ACE ∽△AHD . ∴∠ACE=∠AHD=90°.∴点E 在过点C 且垂直于AC 的直线上,记为直线l . ························· 10分 点A 关于直线l 的对称点M ,连接BM 交直线l 于点E ′, 同解法一,△ABE ′就是所求周长最小的△ABE .∴△ABE 周长最小值为445AB BM +=+. ····································· 13分25.(本题满分13分) 解:(1)当a =-1,m =0时,22y x x c =-++,A 点的坐标为(3,0), ∴-9+6+c =0.解得 c =3. ··················································································· 2分 ∴抛物线的表达式为223y x x =-++. 即2(1)4y x =--+.∴抛物线的顶点坐标为(1,4). ······················································ 4分 (2)∵22y ax ax c =-+的对称轴为直线212ax a-==-, ································· 5分 ∴点A 关于对称轴的对称点为(-1,m ). ··········································· 6分 ∵0<a ,∴当1<x ,y 随x 的增大而增大; 当1>x ,y 随x 的增大而减小. 又∵n <m ,∴当点P 在对称轴左边时,t <-1; 当点P 在对称轴右边时,t >3.综上所述:t 的取值范围为t <-1或t >3. ··········································· 8分(3)∵点Q (x ,y )在抛物线上,∴22y ax ax c =-+.又∵QD ⊥x 轴交直线 :(0)l y kx c k =+<于点D , ∴D 点的坐标为(x ,kx+c ).又∵点Q 是抛物线上点B ,C 之间的一个动点, ∴222()(2)QD ax ax c kx c ax a k x =-+-+=-+. ····················································· 10分ED QC Bxy O6 ∵QE =x ,∴在Rt △QED 中,2(2)tan 2QD ax a k xax a k QE x-+===--β. ········································ 11分∴tan β是关于x 的一次函数, ∵a <0,∴tan β随着x 的增大而减小.又∵当x 2≤≤4时,β恰好满足°°30≤≤60β,且tan β随着β的增大而增大,∴当x=2时,β=60°;当x=4时,β=30°. ∴2233423,.a a k a a k ⎧--=⎪⎨--=⎪⎩解得 333,.k a ⎧=-⎪⎨=-⎪⎩∴33a =-. ·············································································· 13分。
2018年宁德初中数学质检及标准答案
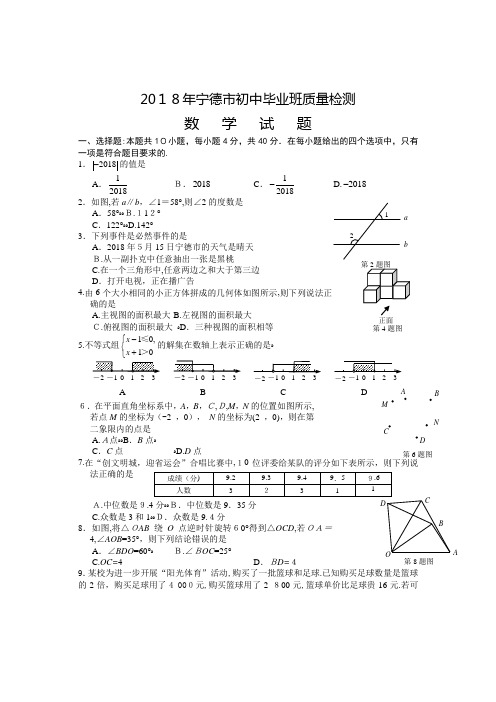
2018年宁德市初中毕业班质量检测数 学 试 题一、选择题:本题共10小题,每小题4分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.2018-的值是A .12018 B.2018 C .12018- D.2018- 2.如图,若a ∥b ,∠1=58°,则∠2的度数是A .58°ﻩﻩB.112° C .122°ﻩﻩD.142°3.下列事件是必然事件的是 A .2018年5月15日宁德市的天气是晴天B.从一副扑克中任意抽出一张是黑桃 C.在一个三角形中,任意两边之和大于第三边 D .打开电视,正在播广告4.由6个大小相同的小正方体拼成的几何体如图所示,则下列说法正确的是A.主视图的面积最大B.左视图的面积最大 C.俯视图的面积最大 ﻩD .三种视图的面积相等 5.不等式组10,10≤>x x -⎧⎨+⎩的解集在数轴上表示正确的是ﻩ6.在平面直角坐标系中,A ,B ,C,D,M ,N 的位置如图所示,若点M 的坐标为(-2 ,0), N 的坐标为(2 ,0),则在第二象限内的点是 A.A点ﻩﻩB .B 点ﻩ C .C 点 ﻩD.D 点 7.在“创文明城,迎省运会”合唱比赛中,10位评委给某队的评分如下表所示,则下列说法正确的是 A.中位数是9.4分ﻩﻩB.中位数是9.35分C.众数是3和1ﻩﻩD.众数是9.4分 8.如图,将△OAB 绕O 点逆时针旋转60°得到△OCD ,若OA=4,∠AOB =35°,则下列结论错误的是A .∠BDO =60°ﻩ B.∠BOC =25° C.OC=4 D .BD=49.某校为进一步开展“阳光体育”活动,购买了一批篮球和足球.已知购买足球数量是篮球的2倍,购买足球用了4 000元,购买篮球用了2 800元,篮球单价比足球贵16元.若可C D 正面 第4题图B 1 -1 0 DC B A O 第8题图 第6题图 M N A B DC a b 2 1 A 1 -1 0列方程40002800162x x=-表示题中的等量关系,则方程中x 表示的是 A.足球的单价 B.篮球的单价C .足球的数量 ﻩD.篮球的数量 10.如图,已知等腰△ABC,AB =BC ,D 是AC 上一点,线段B E与BA 关于直线BD对称,射线C E交射线BD 于点F ,连接AE ,AF .则下列关系正确的是 A .180∠∠AFE ABE +=︒ﻩB.12∠∠AEF ABC = C.180∠∠AEC ABC +=︒ﻩD.∠∠AEB ACB =二、填空题:本题共6小题,每小题4分,共24分.11.2017年10月18日,中国共产党第十九次全国代表大会在北京隆重召开.从全国近89400 000党员中产生的2 300名代表参加了此次盛会.将数据89 400 000用科学记数法表示为 .12.因式分解:222a -= .13.小明同学在计算一个多边形的内角和时,由于粗心少算了一个内角,结果得到的总和是800°,则少算了这个内角的度数为 .14. 已知一次函数23(0)y kx k k =++≠,不论k为何值,该函数的图像都经过点A ,则点A 的坐标为 .15.小丽计算数据方差时,使用公式2222221(5)(8)(13)(14)(15)5S x x x x x ⎡⎤=-+-+-+-+-⎣,则公式中x = .16.如图,点A ,D在反比例函数(0)m y m x =<的图像上,点B ,C 在反比例函数(0)n y n x=>的图像上.若AB ∥CD ∥x 轴,AC ∥y轴,且AB =4,A C=3,CD =2,则n= .三、解答题:本题共9小题,共86分.17.(本题满分8分)计算:14cos302-︒+18.(本题满分8分)如图,在△ABC 中, D ,E 分别是AB ,AC 的中点,△ABC的角平分线AG 交DE 于点F,若∠A BC =70°,∠BA C=54°,求∠AFD 的度数.19.(本题满分8分)首届数字中国建设峰会于4月22日至24日在福州海峡国际会展中心如期举行,某校组织115位师生去会展中心参观,决定租用A,B 两种型号的旅游车.已知一辆A 型车可坐20人,一辆B型车可坐28人,经测算学校需要租用这两种 C F E D B A G 第16题图 第10题图 C F E DA B。
福建省宁德市2018年普通高中毕业班(5月)质量检测数学(文)试卷(扫描版)

2018届宁德市普通高中毕业班第二次质量检查数学(文科)试题参考答案及评分标准
评分说明:
1、本解答指出了每题要考查的主要知识和能力,并给出了一种或几种解法供参考,如果考生的解法与本解法不同,可根据试题的主要考查内容比照评分标准指定相应的评分细则.
2、对计算题,当考生的解答在某一步出现错误时,如果后继部分的解答未改变该题的内容和难度,可视影响的程度决定后继部分的给分,但不得超过该部分正确解答应给分数的一半;如果后继部分的解答有较严重的错误,就不再给分.
3、解答右端所注分数,表示考生正确做到这一步应得的累加分数.
4、只给整数分数,选择题和填空题不给中间分.
一、选择题:本题考查基础知识和基本运算,每小题5分,满分60分.
1.C
2. A
3. B
4. D
5.B
6.C
7. B 8. A 9. C 10. B 11. D 12.C
二、填空题:本题考查基础知识和基本运算,每小题5分,满分20分.。
2018年福建省宁德市5月普通高中毕业班质量试卷理科数

2018年宁德市普通高中毕业班第二次质量检查数学(理科)试卷本试卷分第I 卷(选择题)和第II 卷(非选择题),第II 卷第(21)题为选考题,其它题为必考题.满分150分,考试时间120分钟. 注意事项:1.答题前,考生先将自己的姓名、准考证号填写在答题卡上. 2.考生作答时,将答案答在答题卡上.请按照题号在各题的答题区域(黑色线框)内作答,超出答题区域书写的答案无效.在草稿纸、试题卷上答题无效.3.选择题答案使用2B 铅笔填涂,如需改动,用橡皮擦干净后,再选涂其他答案标号;非选择题答案使用0.5毫米的黑色中性(签字)笔或碳素笔书写,字体工整、笔迹清楚.4.保持答题卡卡面清楚,不折叠、不破损.考试结束后,将本试卷和答题卡一并交回. 参考公式:第I 卷(选择题 共50分),,(n x x ++-一、选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的. 1.若向量a (3,)m =,b (2,1)=-,//a b ,则实数m 的值为A .32- B . 32C .2D .62.若集合{|21}xA x =>,集合{|lg 0}B x x =>,则“x A ∈”是“x B ∈”的A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件3.已知等比数列{}n a 的第5项是二项式41x x ⎛⎫+ ⎪⎝⎭展开式的常数项,则37a a ⋅=A . 6B . 18C .244.若函数2()1f x ax bx =++是定义在[1--则该函数的最大值为 A .5 B .4 C .5的整数i 的最大值为A .3B .4C .6.已知某市两次数学测试的成绩1ξ2正态分布11(90,86)N ξ和22(93,79)N ξ,则以下结论正确的是A .第一次测试的平均分比第二次测试的平均分要高,也比第二次成绩稳定B .第一次测试的平均分比第二次测试的平均分要高,但不如第二次成绩稳定C .第二次测试的平均分比第一次测试的平均分要高,也比第一次成绩稳定D .第二次测试的平均分比第一次测试的平均分要高,但不如第一次成绩稳定7.已知双曲线2222:1(0,0)x y C a b a b-=>>的左、右焦点分别为12,F F ,过点1F 作直线l x ⊥轴交双曲线C 的渐近线于点,A B .若以AB 为直径的圆恰过点2F ,则该双曲线的离心率为A..2 D8.某单位安排甲、乙、丙三人在某月1日至12日值班,每人4天.甲说:我在1日和3日都有值班; 乙说:我在8日和9日都有值班;丙说:我们三人各自值班的日期之和相等.据此可判断丙必定值班的日期是A . 2日和5日B . 5日和6日C . 6日和11日D . 2日和11日9.若关于x 的方程320()x x x a a --+=∈R1x ,2x ,3x ,且满足123x x x ≤≤,则1x A .2- B .1- C .13- D 10.如图所示为某几何体的正视图和侧视图,则该几何体体积的所有可能取值的集合是侧视图正视图A .12,33⎧⎫⎨⎬⎩⎭B .12,,336π⎧⎫⎨⎬⎩⎭C .1233VV ⎧⎫≤≤⎨⎬⎩⎭ D .203V V ⎧⎫<≤⎨⎬⎩⎭第II 卷 (非选择题共100分)二、填空题:本大题共5小题,每小题4分,共20分.把答案填在答题卡相应位置.11.复数1i iz +=(i 为虚数单位)在复平面上对应的点到原点的距离为__________.12.设a 是抛掷一枚骰子得到的点数,则方程20xax a ++=有两个不等实根的概率 为 . 13.若关于x ,y的不等式组 0,,10x y x kx y ≥⎧⎪≥⎨⎪-+≥⎩表示的平面区域是一个直角三角形,则k 的值为 . 14.若在圆22:()4C xy a +-=上有且仅有两个点到原点O 的距离为1,则实数a 的取值范围是 .15的ABC ∆中,3A π∠=.若点D 为BC 边上的一点,且满足2CD DB =,则当AD 取最小时,BD 的长为 . 三、解答题:本大题共6小题,满分80分.解答须写出文字说明、证明过程和演算步骤. 16.(本小题满分13分)将射线1(0)7y x x =≥绕着原点逆时针旋转4π后所得的射线经过点(cos sin )A θθ,.(Ⅰ)求点A 的坐标;(Ⅱ)若向量(sin 2,2cos )x θ=m ,(3sin ,2cos2)x θ=n ,求函数()f x ⋅=m n ,[0,2x π∈]的值域.17.(本小题满分13分)某校为选拔参加“央视猜灯谜大赛”的队员,在校内组织猜灯谜竞赛.规定:第一阶段知识测试成绩不小于160分的学生进入第二阶段比赛.现有200名学生参加知识测试,并将所有测试成绩绘制成如下所示的频率分布直方图.(Ⅰ)估算这200名学生测试成绩的中位数,并求进入第二阶段比赛的学生人数;(Ⅱ)将进入第二阶段的学生分成若干队进行比赛.现甲、乙两队在比赛中均已获得120分,进入最后抢答阶段.抢答规则:抢到的队每次需猜3条谜语,猜对1条得20分,猜错1条扣20分.根据经验,甲队猜对每条谜语的概率均为34,乙队猜对前两条的概率均为45,猜对第3条的概率为12.若这两队抢到答题的机会均等,您做为场外观众想支持这两队中的优胜队,会把支持票投给哪队?18. (本小题满分13分)如图,在四棱柱1111ABCD A B C D -中,底面ABCD 是矩形,且22AD CD ==,12AA =,13A AD π∠=.若O 为AD 的中点,且1CD AO ⊥. (Ⅰ)求证:1AO ⊥平面ABCD ;(Ⅱ)线段BC 上是否存在一点P ,使得二面角1D A A P --为6π?若存在,求出BP 的长;不存在,说明理由.19. (本小题满分13分)已知点(0,1)F ,直线1:1l y =-,直线21ll ⊥于P ,连结PF ,作线段PF 的垂直平分线交直线2l 于点H .设点H 的轨迹为曲线Γ. (Ⅰ)求曲线Γ的方程;(Ⅱ)过点P 作曲线Γ的两条切线,切点分别为,C D ,Bya1(ⅰ)求证:直线CD 过定点;(ⅱ)若(1,1)P -,过点P 作动直线l 交曲线Γ于点,A B ,直线CD 交l 于是否为定值?若是,求出该定值;不是,说20.(本小题满分14分)已知函数2()e()xf x x ax -=+在点(0,(0))f 处的切线斜率为2.(Ⅰ)求实数a 的值;(Ⅱ)设3()(eg x x x t t =---∈R )(),若()()g x f x ≥对[0,1]x ∈恒成立,求t 的取值范围;(Ⅲ)已知数列{}na 满足11a=,11(1)n n a a n +=+,求证:当2,n n ≥∈N 时11213()()()62e n a a a f f f n n n n -⎛⎫+++<⋅+ ⎪⎝⎭xyO(e 为自然对数的底数,e 2.71828≈).21.本题有(1)、(2)、(3)三个选答题,每题7分,请考生任选2题作答,满分14分.如果多做,则按所做的前两题记分.作答时,先用2B 铅笔在答题卡上把所选题目对应的题号涂黑,并将所选题号填入括号中.(1)(本小题满分7分)选修4—2:矩阵与变换在平面直角坐标系中,矩阵M 对应的变换将平面上任意一点(,)P x y 变换为点(2,3)P x y x '+.(Ⅰ)求矩阵M 的逆矩阵1M -; (Ⅱ)求曲线410x y +-=在矩阵M 的变换作用后得到的曲线C '的方程.(2)(本小题满分7分)选修4-4:坐标系与参数方程 已知极坐标系的极点在直角坐标系的原点,极轴与x 轴的正半轴重合,直线l的参数方程为2x y ⎧=+⎪⎪⎨⎪=⎪⎩(t 为参数), 圆C 的极坐标方程为222sin()1(0)4r r ρρθπ+++=>.(Ⅰ)求直线l 的普通方程和圆C 的直角坐标方程;(Ⅱ)若圆C 上的点到直线l 的最大距离为3,求r 的值.(3)(本小题满分7分)选修4—5:不等式选讲 已知函数()|5||3|f x x x =-+-. (Ⅰ)求函数()f x 的最小值m ; (Ⅱ)若正实数,a b 满足11ab+2212m a b +≥.2018年宁德市普通高中毕业班质量检查 数学(理科)试题参考答案及评分标准说明:一、本解答指出了每题要考查的主要知识和能力,并给出了一种或几种解法供参考,如果考生的解法与本解法不同,可根据试题的主要考查内容比照评分标准指定相应的评分细则.二、对计算题,当考生的解答在某一部分解答未改变该题的内容和难度,可视影响的程度决定后继部分的给分,但不得超过该部分正确解答应给分数的一半;如果后继部分的解答有较严重的错误,就不再给分.三、解答右端所注分数,表示考生正确做到这一步应得的累加分数.四、只给整数分数,选择题和填空题不给中间分.一、选择题:本题考查基础知识和基本运算,每小题5分,满分50分. 1.A 2.B 3.D 4.A 5.B 6.C 7.D 8.C 9.B10.D二、填空题:本题考查基础知识和基本运算,每小题4分,满分20分.11.1313.1-或0 14.(3,1)(1,3)-- 15三、解答题:本大题共6小题,满分80分,解答须写出文字说明、证明过程和演算步骤. 16.本题考查三角函数、平面向量等基础知识,考查运算求解能力,考查函数与方程的思想、数形结合的思想,满分13分. 解: (Ⅰ)设射线1(0)7y x x =≥的倾斜角为α,则1tan 7α=,(0,)2απ∈. (1)分∴1147tan tan()143117θα+π=+==-⨯,……………………………………………4分∴由22sin cos 1,sin 4,cos 3θθθθ⎧=⎪⎨=⎪⎩+解得4sin ,53cos .5θθ⎧=⎪⎪⎨⎪=⎪⎩……………………………………………6分∴点A 的坐标为3455⎛⎫⎪⎝⎭,.…………………………………………………………7分 (Ⅱ)()3sin sin 22cos 2cos2f x x x θθ⋅+⋅=……………………………………8分1212sin 2cos255x x =+).4x π=+…………………………………………………10分由[0,2x π∈],可得2[,]444x ππ5π+∈,∴sin(2)[4x π+∈,………………………………………………………12分 ∴函数()f x 的值域为12[5-.……………………………………………13分17.本小题主要考查概率、概率与统计等基础知识,考查推理论证能力、数据处理能力、运算求解能力及应用意识,考查或然与必然的思想,满分13分. 解法一:(Ⅰ)设测试成绩的中位数为x ,由频率分布直方图得, (0.00150.019)20(140)0.0250.5x +⨯+-⨯=,解得:143.6x =.……………………………2分 ∴测试成绩中位数为143.6.进入第二阶段的学生人数为200×(0.003+0.0015)×20=18人.…………………4分(Ⅱ)设最后抢答阶段甲、乙两队猜对灯谜的条数分别为ξ、η,则3(3,)4B ξ,……………………………5分∴39344E ξ=⨯=.……………………………6分∴最后抢答阶段甲队得分的期望为99[(3)]203044--⨯=,………………………8分∵2111(0)5250P η⎛⎫==⨯= ⎪⎝⎭,2411119(1)25525250P η⎛⎫==⨯⨯⨯+⨯=⎪⎝⎭, 24141112(2)25255225P η⎛⎫==⨯+⨯⨯⨯= ⎪⎝⎭,24116(3)5250P η⎛⎫==⨯= ⎪⎝⎭,∴9121621012350255010E η=+⨯+⨯+⨯=, …………………………………………10分∴最后抢答阶段乙队得分的期望为2121[(3)]20241010--⨯=.……………………12分∴1203012024+>+,∴支持票投给甲队..……………………………13分 解法二:(Ⅰ)同解法一. ……………………………4分 (Ⅱ)设最后抢答阶段甲队获得的分数为ξ, 则ξ所有可能的取值为60-,20-,20,60.331(60)1464P ξ⎛⎫=-=-= ⎪⎝⎭, 213339(20)14464P C ξ⎛⎫=-=-=⎪⎝⎭, 3233327(20)14464P C ξ⎛⎫⎛⎫==-= ⎪⎪⎝⎭⎝⎭,3327(60)464P ξ⎛⎫=== ⎪⎝⎭.∴19276020206030646464E ξ=-⨯-⨯+⨯+=.……………………………8分设最后抢答阶段乙队获得的分数为η,则η所有可能的取值为60-,20-,20,60.∵2111(60)5250P η⎛⎫=-=⨯= ⎪⎝⎭,2411119(20)25525250P η⎛⎫=-=⨯⨯⨯+⨯=⎪⎝⎭,24141112(20)25255225P η⎛⎫==⨯+⨯⨯⨯= ⎪⎝⎭,24116(60)5250P η⎛⎫==⨯=⎪⎝⎭, ∴191216602020602450502550E η=-⨯-⨯+⨯+⨯=,……………………………12分∵1203012024+>+,∴支持票投给甲队.…………………………………………13分18.本小题主要考查直线与平面的位置关系,二面角的大小等基础知识,考查空间想象能力、推理论证能力和运算求解能力,考查函数与方程思想、化归与转化思想、数形结合思想,满分13分. (Ⅰ)证明:∵13A AD π∠=,且12AA =,1AO =,∴1A O =…………………………………………2分∴22211AO AD AA +=∴1AO AD ⊥.…………………………………………3分 又1CD AO ⊥,且CD AD D =,∴1AO ⊥平面ABCD .…………………………………………5分(Ⅱ)解:过O 作//Ox AB ,以OO xyz -(如图),则(0,1,0)A -,1A 设(1,,0)([1,1])P m m ∈-,平面1A AP ∵1(0,1AA =,(1,1,0)AP m =+,Ba1a且1110,(1)0.AA y AP x m y ⋅⋅⎧=+=⎪⎨=++=⎪⎩n n 取1z =,得1n=1),m +. (8)分又1AO ⊥平面ABCD ,且1AO ⊂平面11A ADD , ∴平面11A ADD ⊥平面ABCD .又CD AD ⊥,且平面11A ADD 平面ABCD AD =∴CD ⊥平面11A ADD .不妨设平面11A ADD 的法向量为2n =(1,0,0).………………………10分由题意得12cos,=n n ,……………………12分解得1m =或3m =-(舍去). ∴当BP的长为2时,二面角1D A A P--的值为6π.………………………13分19.本题主要考查直线、抛物线、直线与抛物线的位置关系等基础知识,考查运算求解能力、推理论证能力,考查函数与方程思想、化归与转化思想,考查考生分析问题和解决问题的能力,满分13分. 解法一: (Ⅰ)由题意可知,HF HP=,∴点H到点(0,1)F 的距离与到直线1:1l y =-的距离相等,……………………………2分∴点H 的轨迹是以点(0,1)F 为焦点, 直线1:1l y =-为准线的抛物线,………………3分 ∴点H 的轨迹方程为24xy =. (4)分(Ⅱ)(ⅰ)证明:设0(,1)P x -,切点(,),(,)CC D D C xy D x y .由214y x =,得12y x '=.∴直线01:1()2CPC y xx x +=-,…………………………………………5分又PC 过点C ,214CC y x =, ∴2001111()222CC C C C y x x x x x x +=-=-, ∴1122C C C y y x x +=-,即01102C C x x y -+=.…………………………………………6分同理01102D D xx y -+=,∴直线CD的方程为01102xx y -+=,…………………………………………7分∴直线CD 过定点(0,1).…………………………………………8分 (ⅱ)由(Ⅱ)(ⅰ)得,直线CD 的方程为1102x y -+=.设:1(1)l y k x +=-, 与方程1102x y -+=联立,求得4221Q kx k +=-.……………………………………9分设(,),(,)AA B B A xy B x y ,联立1(1)y k x +=-与24x y =,得24440x kx k -++=,由根与系数的关系,得4,44A B A B x x k x x k +=⋅=+.…………………………………………10分∵1,1,1QA B xx x ---同号,∴11PQ PQPQ PAPB PA PB ⎛⎫+=+⎪ ⎪⎝⎭11111Q A B x x x ⎛⎫=-+⎪⎪--⎭ ()11111Q A B x x x ⎛⎫=-⋅+ ⎪--⎝⎭…………………………………………11分()()24212111A B A B x x k k x x +-+⎛⎫=-⋅ ⎪---⎝⎭ 5422215k k -=⋅=-, ∴PQ PQ PAPB+为定值,定值为2.…………………………………………13分 解法二: (Ⅰ)设(,)H x y ,由题意可知, HF HP=,1y =+, (2)分∴化简得24xy =,∴点H 的轨迹方程为24x y =. (4)分(Ⅱ)(ⅰ)证明:设切点(,),(,)CC D D C x y D x y ,直线CD 的方程为y kx t =+.联立y kx t =+与24xy =得2440x kx t --=,由根与系数的关系,得4,4C D C D x x k x x t +=⋅=-.…………………………………………5分由214y x =,得12y x '=.∴直线1:()2CC C PC y yx x x -=-,又214C C y x =,所以211:24CC PC y xx x =-. 同理211:24D D PD y xx x =-.…………………………………………6分联立两直线方程,解得1y t =-=-,∴1t =,即直线CD 过定点(0,1).…………………………………………8分(ⅱ)由(Ⅱ)(ⅰ),解得11()22CD xx k =+=,∴12k =,∴直线CD 的方程为1102x y -+=.以下同解法一.20.本题考查函数、导数等基础知识,考查推理论证能力和运算求解能力,考查函数与方程的思想、化归与转化的思想、数形结合的思想,考查运用数学知识分析和解决问题的能力,满分14分. 解: (Ⅰ)22()e ()e (2)e (2)xx x f x x ax x a x ax x a ---'=-+++=-+--,…………………1分由(0)()2f a '=--=,得2a =.…………………………………………3分 (Ⅱ)2()e(2)xf x x x -=+.由()()g x f x ≥,得23()e(2)exx x t x x ----≥+,[0,1]x ∈.当0x =时,该不等式成立; (4)分当(0,1]x ∈,不等式3e(2)exx t x --++≥+对(0,1]x ∈恒成立,即max3e(2)e xt x x -⎡⎤≥++-⎢⎥⎣⎦. (5)分设3()e(2)exh x x x -=++-,(0,1]x ∈, ()e (2)e 1e (1)1x x x h x x x ---'=-+++=-++,()e (1)e e 0x x xh x x x ---''⎡⎤=--++=⋅>⎣⎦, ∴()h x '在(0,1]单调递增, ∴()(0)0h x h ''>=, ∴()h x 在(0,1]单调递增, …………………………………………………………7分 ∴max33()(1)11e eh x h ==+-=,∴1.t ≥………………………………………………………………………………8分 (Ⅲ)∵11(1)n n a a n+=+, ∴11n nan a n++=,又11a =, ∴2n ≥时,321121231121n nn a a a na a n a a a n -=⋅⋅⋅⋅=⋅⋅⋅⋅=-,对1n =也成立, ∴nan =. (10)分∵当[0,1]x ∈时,2()e(2)0xf x x -'=-->,∴()f x 在[0,1]上单调递增,且()(0)0f x f ≥=.又∵1()i f nn⋅(11,)i n i ≤≤-∈N 表示长为()i f n,宽为1n的小矩形的面积,∴11()()i n i nif f x dx n n +⋅<⎰(11,)i n i ≤≤-∈N , ∴1112011121()()()()()()()n a a a n f f f f f f f x dx n n nn n n nn --⎡⎤⎡⎤+++=+++<⎢⎥⎢⎥⎣⎦⎣⎦⎰.…… 12分又由(Ⅱ),取1t =,得23()()(1)ef xg x x x ≤=-++,∴1132100011313()()(1)32e 62ef x dxg x dx x x ≤=-++=+⎰⎰,∴112113()()()62en f f f n n n n -⎡⎤+++<+⎢⎥⎣⎦, ∴11213()()()62e n a a af f f n n nn -⎛⎫+++<⋅+ ⎪⎝⎭.…………………………………………14分21.(1)本题主要考查矩阵与变换等基础知识,考查运算求解能力及化归与转化思想.满分7分.解:(Ⅰ)设点(),P x y 在矩阵M 对应的变换作用下所得的点为(,)P x y ''',则2,3,x x y y x '=+⎧⎨'=⎩即2130x x y y '⎛⎫⎛⎫⎛⎫= ⎪⎪⎪'⎝⎭⎝⎭⎝⎭,∴2130M ⎛⎫=⎪⎝⎭.…………………………………………1分又det()3M =-, ∴1103213M-⎛⎫- ⎪⎪= ⎪-- ⎪⎝⎭.…………………………………………3分(Ⅱ)设点(),A x y 在矩阵M 对应的变换作用下所得的点为(,)A x y ''',则1103213x x x M y y y -⎛⎫- ⎪''⎛⎫⎛⎫⎛⎫ ⎪== ⎪ ⎪⎪'' ⎪⎝⎭⎝⎭⎝⎭-- ⎪⎝⎭, 即1,32,3x y y x y ⎧'=-⎪⎪⎨⎪''=--⎪⎩…………………………………………5分∴代入410x y +-=,得241033y x y '⎛⎫''----= ⎪⎝⎭,即变换后的曲线方程为210x y ++=.…………………………7分 (2)本题主要考查直线的参数方程及极坐标方程等基础知识,考查运算求解能力及化归与转化思想.满分7分. 解:(Ⅰ)直线l的直角坐标方程为x y +=2分圆C的直角坐标方程为222(((0)x y r r +++=>.………………………… 4分(Ⅱ)∵圆心(C ,半径为r ,………………………………………5分圆心C到直线x y +=的距离为2d ,………………………6分又∵圆C 上的点到直线l 的最大距离为3,即3d r +=, ∴321r =-=.………………………………………7分(3)本题主要考查绝对值不等式和均值不等式等基础知识,考查运算求解能力,考查化归与转化思想.满分7分. 解:(Ⅰ)∵()|5||3|532f x x x x x =-+-≥-+-=, (2)分当且仅当[3,5]x ∈时取最小值2,……………………3分2m ∴=. (4)分(Ⅱ)22222121()[1](13a b a ++≥⨯+=,222123()2a b ∴+⨯≥, ∴22122a b +≥.…………………………………………7分。
【数学答案】2018福州5月初三质检考试

E A
N
如图,MN 就是所求作的线段 AB 的垂直平分线,点 E 就是所求作的点,线段 BE 就 是所要连接的线段. ·········································································· 4 分 证明:在 Rt△ABC 中,∠C = 90°,∠CBA = 54°, ∴∠CAB = 90° − ∠CBA = 36°. ···················································· 5 分 ∵AD 是△ABC 的角平分线, ∴∠BAD = 1 ∠CAB = 18°. ······················································· 6 分 2 ∵点 E 在 AB 的垂直平分线上, ∴EA = EB, ∴∠EBA = ∠EAB = 18°, ∴∠DEB = ∠EBA + ∠EAB = 36°,∠DBE = ∠CBA − ∠EBA = 36°, ∴∠DEB = ∠DBE, ································································· 7 分 ∴DE = DB. ··········································································· 8 分 注:作图 3 分,垂直平分线画对得 2 分,连接 BE 得 1 分;结论 1 分(结论不全面 不给分) .
注:方程写对一个得 2 分,未知数解对一个得 2 分.
数学试题答案及评分参考 第 2 页(共 7 页)
(21)证法一:连接 AC. ··········································································· 1 分 = CB , ∵ CB ∴∠COB = 2∠CAB. ····························································· 2 分 ∵∠COB = 2∠PCB, ∴∠CAB = ∠PCB. ······························································· 3 分 ∵OA = OC, C ∴∠OAC = ∠OCA, ∴∠OCA = ∠PCB. ································ 4 分 A B P O ∵AB 是⊙O 的直径, ∴∠ACB = 90°, ····································· 5 分 ∴∠OCA + ∠OCB = 90°, ∴∠PCB + ∠OCB = 90°, 即∠OCP = 90°, ··································································· 6 分 ∴OC⊥CP. ········································································ 7 分 ∵OC 是⊙O 的半径, ∴PC 是⊙O 的切线. ···························································· 8 分 证法二:过点 O 作 OD⊥BC 于 D,则∠ODC = 90°, ································ 1 分 ∴∠OCD + ∠COD = 90°. ······················································ 2 分 ∵OB = OC, C ∴OD 平分∠COB, D ∴∠COB = 2∠COD. ······························ 3 分 A B P O ∵∠COB = 2∠PCB, ∴∠COD = ∠PCB, ································ 4 分 ∴∠PCB + ∠OCD = 90°, 即∠OCP = 90°, ··································································· 6 分 ∴OC⊥CP. ········································································ 7 分 ∵OC 是⊙O 的半径, ∴PC 是⊙O 的切线. ···························································· 8 分 证法三:设∠PCB = x°, ····································································· 1 分 则∠COB = 2x°. ··································································· 2 分 ∵OB = OC, C ∴∠OCB = 180° − 2 x° = 90° − x°,··············· 4 分 2 A B P O ∴∠OCP = ∠OCB + ∠PCB = 90° − x° + x° = 90°, ··················· 6 分 ∴OC⊥PC. ·········································· 7 分 ∵OC 是⊙O 的半径, ∴PC 是⊙O 的切线. ···························································· 8 分
最新-福建省宁德市2018届高三数学5月质量检查试题(201

2018年宁德市普通高中毕业班第二次质量检查数学(文科)试卷本试卷分第I 卷(选择题)和第Ⅱ卷(非选择题)两部分.本卷满分150分,考试时间120分钟. 注意事项:1.答题前,考生先将自己的姓名、准考证号填写在答题卡上.2.考生作答时,将答案答在答题卡上.请按照题号在各题的答题区域(黑色线框)内作答,超出答题区域书写的答案无效.在草稿纸、试题卷上答题无效.3.选择题答案使用2B 铅笔填涂,如需改动,用橡皮擦干净后,再选涂其他答案标号;非选择题答案使用0.5毫米的黑色中性(签字)笔或碳素笔书写,字体工整、笔迹清楚.4.保持答题卡卡面清楚,不折叠、不破损.考试结束后,将本试卷和答题卡一并交回.第I 卷(选择题 共60分)一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知全集,U =R 集合{}1,2,3A =,{}3,4,5B =,下图中阴影部分所表示的集合为A .{}3 B .{}1,2 C .{}4,5 D .{}1,2,3,4,5 2.复数2()i z m m m =++(m ∈R ,i 为虚数单位)是纯虚数,则实数m 的值为A .0或1-B .0C .1-D .1 3.“1a =”是“直线10ax y ++=与0ax y -=互相垂直”的A .充分而不必要条件B .必要而不充分条件C .充要条件D .既不充分也不必要条件 4.右图中几何体为正方体的一部分,则以下图形不可能...图之一的是,,(n x x ++-A .B .C .D .5.已知函数32 0,()2 0,x x f x x x x ⎧-≤⎪=⎨+>⎪⎩若()8f a =,则a =A .2-B .2C .2±D .2或4-6.已知,m n 是不重合的直线,,αβ是不重合的平面,则下列命题正确的是A .若,//m n αα⊂,则//m nB .若//,//m m αβ,则//αβC .若,m m αβ⊥⊥,则//αβD .若,//n m n αβ=,则//m α且//m β 7.阅读如图所示的程序框图,运行相应的程序 则输出的结果是A. B .0C 8.在区间[1,6]上随机取一实数x ,使得2[2,4]x ∈A .16 B .15 C .13D .259.函数()sin ()f x x x x =-∈R 的部分图像可能是A .B .C .D .10.设二元一次不等式组2,1,220,y x x y ≤⎧⎪≤⎨⎪+-≥⎩所表示的平面区域为M ,O 为坐标原点,P M ∈,则OP 的取值范围是 A . B . C . D .2] 11. 已知函数()sin()(0,)2f x A x ωϕωϕπ=+><,y =)(x f的部分图像如右图,则()2f π=A .B .1-C .D .12-12. 已知,A B 为单位圆O 上的点,点P 在劣弧AB 上(不包括端点),且3AOB π∠=,OP xOA yOB =+,则下列结论不恒成立....的是A .2223x y +≥B .x y +≤C .11x y +≤.13xy ≤第Ⅱ卷(非选择题 共90分)二、填空题:本大题共4小题,每小题4分,共16分.把答案填写在答题卡的相应位置.13.已知平面向量(1)(22)x ==-,,,a b ,若//a b ,则实数x 的值为 . 14.为调查学生的身高与饮食习惯的关系,某中学将高三同学的身高(单位:厘米)数据绘制成频率分布 直方图(如图).现采用分层抽样的方法从中选取40 名进行调查,则身高在[160,170]内的学生中应选取的 人数为 .15.若抛物线28y x =的焦点到双曲线22221(0,0)x y a b a b-=>>则双曲线的离心率为 .16.定义“sh 2x x e e x --=,x ∈R ”为双曲正弦函数,“ch 2x xe e x -+=,x ∈R ”为双曲余弦函数,它们与正、余弦函数有某些类似的性质,如:sh()sh ch ch sh x y x y x y +=⋅+⋅、22(ch )(sh )1x x -=等.请你再写出一个类似的性质:ch()x y += .三、解答题:本大题共6小题,共74分,解答应写出文字说明、证明过程或演算步骤. 17.(本小题满分12分)已知等差数列{}n a 中,23a = ,4618a a +=. (Ⅰ)求数列{}n a 的通项公式;(Ⅱ)若数列{}n b 满足:12n n b b +=,并且15b a =,试求数列{}n b 的前n 项和n S . 18.(本小题满分12分)ABC ∆中,已知3BC =,3A π∠=,设B x ∠=,ABC ∆的周长为()f x . (Ⅰ)求()f x 的表达式;(Ⅱ)当x 为何值时()f x 最大,并求出()f x 的最大值.19.(本小题满分12分)(Ⅰ)设y 关于x 的回归直线方程为ˆˆybx a =+.现根据表中数据已经正确计算出了b 的值为1.6,试求a 的值,并估计该厂6月份的产量(计算结果精确到1).(Ⅱ)质检部门发现该厂1月份生产的游艇存在质量问题,要求厂家召回;现有一旅游公司曾向该厂购买了今年前两个月....生产的游艇2艘,求该旅游公司有游艇被召回的概率.20.(本小题满分12分)如图,三棱柱111ABC A B C -中,1AA ⊥平面ABC ,D 、E 分别为11A B 、1AA 的中点,点F在棱AB 上,且14AF AB =.(Ⅰ)求证://EF 平面1BDC ;(Ⅱ)在棱AC 上是否存在一个点G ,使得平面EFG 将 三棱柱分割成的两部分体积之比为1:15,若存在,指出 点G 的位置;若不存在,说明理由. 21.(本小题满分12分)已知函数()21)ln f x ax a x b =--+(. (Ⅰ)若()f x 在点((1,(1))f )处的切线方程为y x =,求实数a b 、的值;A 1A(Ⅱ)当12a >时,研究()f x 的单调性; (Ⅲ)当1a =时,()f x 在区间1(,)e e上恰有一个零点,求实数b 的取值范围.22.(本小题满分14分)平面直角坐标系中,已知圆O :221x y +=过椭圆Γ:22221(0)x y a b a b+=>>的右焦点F 和上顶点.(Ⅰ) 求椭圆Γ的方程;(Ⅱ)设A 为圆O 上任意一点,连结OA 并延长到B,使OB ,过点B 作x 轴的垂线l ,再过点A 作l 的垂线,垂足为C ,求证:点C 在椭圆Γ上;(Ⅲ)过点F 的直线交椭圆于,M N 两点,过点M 作直线2x =的垂线,垂足为P ,试问直线PN 是否恒过定点,若是,求出定点的坐标;若不是,说明理由.2018年宁德市普通高中毕业班质量检查 数学(文科)试题参考答案及评分标准说明:一、本解答指出了每题要考察的主要知识和能力,并给出了一种或几种解法供参考,x如果考生的解法与本解法不同,可根据试题的主要考察内容比照评分标准指定相应的评分细则。
〖中考零距离-新课标〗2018年福建省初中毕业生学业质量测查数学试题及答案解析

2018年福建省初中学业质量测查(第二次)数 学 试 题(试卷满分:150分;考试时间:120分钟)友情提示:请认真作答,把答案准确地填写在答题卡上学校 姓名 考生号一、选择题(每小题3分,共21分)每小题有四个答案,其中有且只有一个答案是正确的,请在答题卡上相应题目的答题区域内作答,答对的得3分,答错或不答的一律得0分. 1.化简4的结果是( )A .2B .2C .-2D .±22.下列计算错误..的是( ) A .6a + 2a =8a B .a – (a – 3) =3 C .a 2÷a 2 = 0D .a –1·a 2 = a3. 下列四个平面图形中,三棱锥的表面展开图的是( )A .B .C .D . 4.学校团委组织“阳光助残”捐款活动,九年级一班学生捐款情况如下表:捐款金额(元)5102050人数(人) 10 13 12 15 则该班学生捐款金额的中位数是( )A .13B .12C .10D .20 5.下列事件发生属于不可能事件的是( ) A .射击运动员只射击1次,就命中靶心B .画一个三角形,使其三边的长分别为8cm ,6cm ,2cmC .任取一个实数x ,都有|x |≥0D .抛掷一枚质地均匀且六个面分别刻有1到6的点数的正方体骰子,朝上一面的点数为6 6.如图,⊙O 的直径CD 垂直弦AB 于点E ,且CE =2,DE =8,则AB 的长为( ) A .8 B. 6 C. 4 D. 27.已知Rt △ABC 中,∠C =90°,AC =3,BC =4,AD 平分∠BAC ,则点B 到AD 的距离是( ) A .23 B .2 C .5 D .13136E B D O CA (第6题图) (第7题图)二、填空题(每小题4分,共40分)在答题卡上相应题目的答题区域内作答. 8.若70A ︒∠=,则A ∠的余角是 度.9.我国第一艘航母“辽宁舰”的最大排水量为68000吨,用科学记数法表示这个数据是 吨. 10.计算:2-x x +x-22= . 11.分解因式:xy 2 – 9x = .12.如图,点O 是正五边形ABCDE 的中心,则∠BAO 的度数为 .13. 如图,在△ABC 中,两条中线BE ,CD 相交于点O ,则S △DOE :S △DCE = . 14.若关于x 的方程x 2+(k -2)x -k2=0的两根互为相反数,则k = .15.如果圆锥的底面周长....为2πcm ,侧面展开后所得的扇形的圆心角是120º,则该圆锥的侧面积是 cm 2.(结果保留π)16.如图,已知四边形ABCD 是矩形,把矩形沿直线AC 折叠,点B 落在点E 处,连结DE .若DE :AC =3:5,则ABAD的值为 . 17.如图,在平面直角坐标系xoy 中,直线:l 3y kx k =-(0k <)与x 、y 轴的正半轴分别交于点A 、B ,动点D (异于点A 、B ) 在线段AB 上,DC ⊥x 轴于C .(1)不论k 取任何负数,直线l 总经过一个定点,写出该定点的坐标为 ;(2)当点C 的横坐标为2时,在x 轴上存在点P ,使得PB ⊥PD ,则k 的取值范围为 . 三、解答题(共89分)在答题卡上相应题目的答题区域内作答. 18.(9分)计算:232(2)2sin 60---+-(2π-1)0.19.(9分)先化简,再求值:2x (x +1)+(x ﹣1)2,其中x =23.(第17题图)20.(9分)如图,已知四边形ABCD 是菱形,DE ⊥AB 于E ,DF ⊥BC 于F .求证:△ADE ≌△CDF .21.(9分)某校开展“中国梦•泉州梦•我的梦”主题教育系列活动,设有征文、独唱、绘画、手抄报四个项目,该校共有800人次参加活动.下面是该校根据参加人次绘制的两幅不完整的统计图,请根据图中提供的信息,解答下面的问题.(1)此次有 名同学参加绘画活动,扇形统计图中“独唱”部分的圆心角是 度.请你把条形统计图补充完整.(2)经研究,决定拨给各项目活动经费,标准是:征文、独唱、绘画、手抄报每人次分别为10元、12元、15元、12元,请你帮学校计算开展本次活动共需多少经费? 22.(9分)有三张正面分别写有数字﹣2,﹣1,1的卡片,它们的背面完全相同,将这三张卡片的背面朝上洗匀后随机抽取一张,以其正面的数字作为x 的值,放回卡片洗匀,再从三张卡片中随机抽取一张,以其正面的数字作为y 的值,两次结果记为(x ,y ). (1)用树状图或列表法表示(x ,y )所有可能出现的结果;(2)求使分式y x yyx xy x -+--2223有意义的(x ,y )出现的概率;(第20题图)23.(9分)如图,在平面直角坐标系xoy 中,抛物线12-+=bx ax y 经过点A (2,﹣1),它的对称轴与x 轴相交于点B . (1)求点B 的坐标; (2)如果直线y =x +1与抛物线的对称轴交于点C , 与抛物线在对称轴右侧交于点D ,且∠BDC =∠ACB ,求此抛物线的表达式.24.(9分)某公司采购某商品60箱销往甲乙两地,已知某商品在甲地销售平均每箱的利润1y (百元)与销售数量x (箱)的关系为⎪⎪⎩⎪⎪⎨⎧<≤+-≤<+=)6020(5.7401),200(51011x x x x y 在乙地销售平均每箱的利2y (百元)与销售数量t (箱)的关系为⎪⎩⎪⎨⎧<≤+-≤<=)6030(8151),300(62t t t y(1)将y 2转换为以x 为自变量的函数,则y 2= ;(2)设某商品获得总利润W (百元),当在甲地销售量x (箱)的范围是0<x ≤20时,求W 与x的关系式;(总利润=在甲地销售利润+在乙地销售利润)(3)经测算,在20<x ≤30的范围内,可以获得最大总利润,求这个最大总利润,并求出此时x的值.25.(12分)如图,在平面直角坐标xoy 内,函数y =xm(x >0,m 是常数)的图象经过A (1,4),B (a ,b ),其中a >1.过点A 作x 轴垂线,垂足为C ,过点B 作y 轴垂线,垂足为D ,连结AD ,DC ,CB .(1)求m 的值;(2)求证:DC ∥AB ;(3)当AD =BC 时,求直线AB 的函数表达式.(第23题图).26.(14分)如图,矩形ABCD的边AB=3,AD=4,点E从点A出发,沿射线AD移动,以CE为直径作圆O,点F为圆O与射线BD的公共点,连结EF、CF,过点E作EG⊥EF,EG 与圆O相交于点G,连结CG.(1)求证:四边形EFCG是矩形;(2)求tan∠CEG的值;(3)当圆O与射线BD相切时,点E停止移动,在点E移动的过程中,求四边形EFCG面积的取值范围;(第26题图)数学试题参考答案及评分标准说明:(一)考生的正确解法与“参考答案”不同时,可参照“参考答案及评分标准”的精神进行评分. (二)如解答的某一步出现错误,这一错误没有改变后续部分的考查目的,可酌情给分,但原则上不超过后面应得的分数的二分之一;如属严重的概念性错误,就不给分.(三)以下解答各行右端所注分数表示正确做完该步应得的累计分数. 一、选择题(每小题3分,共21分)1.B2.C3.B4.D5.B6.A7.C 二、填空题(每小题4分,共40分)8. 20; 9. 46.810⨯; 10. 1; 11. (3)(y 3)x y +-; 12. 54°; 13. 1:3;14. 2; 15. 3π; 16. 12; 17.(1)(3,0); (2)303k -≤<. 三、解答题(共89分) 18.(本小题9分)解:原式23431=--+- ……………………(8分) 3=- ……………………(9分)19.(本小题9分)解:原式=2x 2+2x +x 2﹣2x +1,……………………(6分)=3x 2+1……………………(7分)当x =2时,原式=3×(2)2+1………………(8分)=37.……………………(9分)20.(本小题9分)解:∵四边形ABCD 是菱形, ∴AD =CD ;∠A =∠C ,……………………(6分) 又∵DE ⊥AB 于E ,DF ⊥BC 于F,∴∠AED =∠CFD =90°; ……………………(8分) 在△ADE 和△CDF 中,∠A =∠C ,∠AED =∠CFD , AD =CD ; ∴△ADE ≌△CDF .……………………(9分) 21.(本小题9分) 解:(1)200,36.……………………(4分) 画图如图:……………………(6分)(2)根据题意得:296×10+80×12+200×15+224×12=9608(元)答:开展本次活动共需9608元经费. ……………………(9分)22.(本小题9分) 解:(1)列表如下:-2 -1 1 -2 (-2,-2) (-2,-1) (-2,1) -1 (-1,-2) (-1,-1) (-1,1) 1 (1,-2) (1,-1) (1,1)……………………(5分)(2)由上表可知,所有等可能的情况共有9种,……………………(6分)∵使分式yx yy x xy x -+--2223有意义,∴x ≠y 且x ≠-y;……………………(7分) ∴满足条件的点有4种,…………………(8分) 则P=49.………………(9分) (树状图略)23.(本小题9分)解:(1)∵抛物线经过点A (2,-1),∴ 4a +2b -1=-1,即 b =-2a ,………………(1分)∵ -2b a =-22a a-=1,………………(2分) ∴点B 的坐标是(1,0). ………………(3分)(2)(解法1)如图2所示.由(1)得,抛物线的对称轴是x =1,可得直线y =x +1与x 轴的交点为E (-1,0), 与抛物线的对称轴的交点C (1,2),∴BE =BC =2, ∴△EBC 是等腰直角三角形;…………(4分) 连结AB ,则∠ABC =∠BCD =135 º,且AB =2; 又∵∠BDC =∠ACB ,∴△ABC ∽△BCD .∴AB BCBC CD=,∴2BCAB CD =∙;………………(5分) 过D 作DH ⊥BC 于H ,则CH =HD ,设点D 的坐标为(m ,m +1), 在Rt △CHD 中,∵m >1, CH =HD =m -1,∴CD =2HD =21(m )-∴22=2×21(m )- , 解得m =3,………………(5分) ∴点D (3,4),………………(7分)把D (3,4)坐标代入抛物线y =ax 2-2ax -1得9a -6a -1=4,解得a =53.………………(8分) ∴此抛物线的表达式为y =53x 2-103x -1.………………(9分)(解法2)如图3所示.由(1)得,抛物线的对称轴是x =1,(图2)可得直线y =x +1与x 轴、y 轴的交点为E (-1,0), F (0,1),与抛物线的对称轴的交点C (1,2), ∴BE =BC ,BE ⊥BC ,∴△EBC 是等腰直角三角形.………………(4分) 连结BF ,则BF ⊥EC ,且BF =2;过A 作AG ⊥BC 于G ,则∠DFB =∠CGA =90º, 又∵∠BDF =∠ACG ,∴△BDF ∽△ACG . ∴BD BFAC AG = ∴2213BD +=21 ∴BD =25.………………(5分)过D 作DH ⊥BC 于H ,设点D 的坐标为(m ,m +1),在Rt △BDH 中,BH 2+HD 2=BD 2, ∴(m +1)2+(m -1)2=20,解得m =±3(负数不合题意,舍去),∴点D (3,4)………………(7分) 把D (3,4)坐标代入抛物线y =ax 2-2ax -1得9a -6a -1=4, 解得a =53.………………(8分) ∴此抛物线的表达式为y =53x 2-103x -1.………………(9分)24.(本小题9分)解:(1)⎪⎩⎪⎨⎧<≤≤<+=)6030(6),300(41512x x x y ……………………(2分)(2)综合⎪⎪⎩⎪⎪⎨⎧<≤+-≤<+=)6020(5.7401),200(51011x x x x y 和(1)中 y 2,当对应的x 范围是0<x ≤20 时,W 1=(110x +5)x +(115x +4)(60-x )……………………(4分) =130x 2+5x +240;……………………(6分) (3)当20<x ≤30 时,W 2=(-140x +75)x +(115x +4)(60-x )……………………(7分) =-11120x 2+75x +240……………………8分 (图3)∵x =-2b a =45011>30,∴W 在20<x ≤30随x 增大而增大 ∴当x =30时,W 2取得最大值为832.5(百元).……………………………(9分) 25.(本小题12分) 解:(1)∵函数xmy =(x >0,m 是常数)图象经过)4,1(A ∴4=m ……………………(2分)(2)(解法1) 设AC BD ,交于点E ,则在Rt △AEB 中,tan ∠EAB =1;444BE a aAE a-==- 在Rt △CED 中,tan ∠ECD =1;44DE aCE a==……………………(5分)∴;EAB ECD ∠=∠……………………(6分) ∴AB DC //.……………………(7分)(解法2)设AC BD ,交于点E ,根据题意,可得B 点的坐标为)4,(aa ,D 点的坐标为)4,0(a ,E 点的坐标为)4,1(a ……………………(3分),a AE 44-=,4;CE a =1,1;EB a ED =-=……………………(4分)∴441;4AE a a CEa-==-∴1-==a ED EB CE AE ……………………(5分) 又∵;AEB CED ∠=∠ ∴△AEB ∽△CED ∴;EAB ECD ∠=∠……………………(6分) ∴AB DC //.……………………(7分)(3)(解法1)∵AB DC // ∴当BC AD =时,有两种情况:①当BC AD //时,由中心对称的性质得:BE =DE ,则11=-a ,得2=a . ∴点B 的坐标是(2,2).……………………(8分)设直线AB 的函数表达式为b kx y +=,分别把点B A ,的坐标代入,得⎩⎨⎧+=+=b k b k 22,4 解得⎩⎨⎧=-=.6,2b k∴直线AB 的函数表达式是.62+-=x y ……………………(9分) ②当AD 与BC 所在直线不平行时,由轴对称的性质得: AC BD =, ∴4=a ,∴点B 的坐标是(4,1).……………………(10分) 设直线AB 的函数表达式为b kx y +=,分别把点B A ,的坐标代入,得⎩⎨⎧+=+=.41,4b k b k 解得⎩⎨⎧=-=5,1b k∴直线AB 的函数表达式是.5+-=x y ……………………(11分)综上所述,所求直线AB 的函数表达式是62+-=x y 或.5+-=x y ……………(12分) (解法2)当BC AD =时,AD 2=BC 2.在Rt △AED 中,222DE AE AD += ; 在Rt △BEC 中,222CE BE BC +=∴222244(4)1(1)(),a aa-+=-+……………………(8分)整理得:32216320,a a a ---= ∴ (2)(4)(4)0a a a -+-= ∴244a a a ==-=或或,∴24a a ==或……………………(9分)① 当2=a 时,点B 的坐标是(2,2).设直线AB 的函数表达式为b kx y +=,分别把点B A ,的坐标代入,得⎩⎨⎧+=+=b k b k 22,4 解得⎩⎨⎧=-=.6,2b k∴直线AB 的函数解析式是62+-=x y .……………………(10分) ②当4=a 时,点B 的坐标是(4,1).设直线AB 的函数解析式为b kx y +=,分别把点B A ,的坐标代入,得⎩⎨⎧+=+=.41,4b k b k 解得⎩⎨⎧=-=5,1b k∴直线AB 的函数表达式是.5+-=x y ……………………(11分)综上所述,所求直线AB 的函数表达式是62+-=x y 或.5+-=x y ……………(12分)26.(本小题14分)解:(1)证明:∵CE为⊙O的直径,∴∠CFE=∠CGE=90°.……………………(1分)∵EG⊥EF,∴∠FEG=90°.∴∠CFE=∠CGE=∠FEG=90°.……………………(2分)∴四边形EFCG是矩形.……………………(3分)(2)由(1)知四边形EFCG是矩形.∴CF∥EG,∴∠CEG=∠ECF,∵∠ECF=∠EDF,∴∠CEG=∠EDF,……………………(4分)在Rt△ABD中,AB=3,AD=4,∴tan34ABBDAAD∠==,……………………(5分)∴tan∠CEG= 34;……………………(6分)(3)∵四边形EFCG是矩形,∴FC∥EG.∴∠FCE=∠CEG.∴tan∠FCE=tan∠CEG=3 4∵∠CFE=90°,∴EF=34CF, ……………………(7分)∴S矩形EFCG=234CF;……………………(8分)连结OD,如图2①,∵∠GDC=∠CEG,∠FCE=∠FDE,∴∠GDC=∠FDE.∵∠FDE+∠CDB=90°,∴∠GDC+∠CDB=90°.∴∠GDB=90°……………………(9分)(Ⅰ)当点E在点A(E′)处时,点F在点B(F′)处,点G在点D(G′)处,如图2①所示.此时,CF=CB=4.……………(10分)(Ⅱ)当点F在点D(F″)处时,直径F″G″⊥BD,如图2②所示,此时⊙O与射线BD相切,CF=CD=3.……………(11分)(Ⅲ)当CF⊥BD时,CF最小,如图2③所示.S△BCD=12BC×CD=12BD×CF,∴4×3=5×CF∴CF=125.……………(12分)∴125≤CF≤4.……………(13分)∵S矩形EFCG=234CF,∴34×(125)2≤S矩形EFCG≤34×42.∴10825≤S矩形EFCG≤12.……………(14分)。
福建省宁德市2018届普通高中毕业班5月质量检查文科数学试卷Word版含解析

福建省宁德市2018届普通高中毕业班5月质量检查文科数学试卷本试卷分第I 卷和第II 卷两部分.第I 卷1至3页,第II 卷4至6页,满分150分. 考生注意:1.答题前,考生务必将自己的准考证号、姓名填写在答题卡上.考生要认真核对答题卡上粘贴的“准考证号、姓名、考试科目”与考生本人准考证号、姓名是否一致.2.第I 卷每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其他答案标号.第II 卷用0.5毫米的黑色墨水签字笔在答题卡上书写作答.若在试题卷上作答,答案无效.3.考试结束,监考员将试题卷和答题卡一并交回.第I 卷一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的. (1)已知复数z 满足z i iz 3-=+,则z =(A )12i + (B )12i - (C )22i + (D )22i - (2)已知集合{}1,0,1,2A =-,{}220B x x x =--≤,则x A ∈是x B ∈的(A )充分不必要条件 (B )必要不充分条件(C )充要条件 (D )既不充分也不必要条件 (3)右图中的程序框图表示求三个实数,,a b c 中最大数的算法,那么在空白的判断框中,应该填入(A )a x > (B )b x >(C )c x < (D )c x >(4)已知3sin ,,52θθπ⎛⎫=∈π ⎪⎝⎭,则tan()4θπ+=(A )7- (B )7(C )17- (D )17(5)已知双曲线222:1(0)4x y C b b-=>的焦点到渐近线的距离为3,则C 的离心率为(A (B (C )32 (D )52(6)函数2()()ax bf x x c -=-的图象如图所示,则下列结论成立的是(A )0,0,0a b c >>> (B )0,0,0a b c <<>O正视图俯视图侧视图(C )0,0,0a b c >>< (D )0,0,0a b c <>>(7)某几何体的三视图如右图所示,则此几何体的体积等于(A )4 (B )12(C )24 (D )30(8)已知函数21,0,()1,0,x x f x x x ⎧+≤=⎨-+>⎩ 若113221(log ),(2),(3)3a f b f c f -===,则(A )a b c >> (B )c b a >> (C )a c b >> (D )b c a >> (9)已知函数()sin(2)2f x x π=-,下列结论错误..的是 (A )()f x 的最小正周期为π(B )()f x 在区间0,2π⎡⎤⎢⎥⎣⎦上是增函数(C )()f x 的图象关于点3,04π⎛⎫-⎪⎝⎭对称 (D )()f x 的图象关于直线54x π=对称 (10)过点(1,1)M 的直线与椭圆22143x y +=交于,A B 两点,且点M 平分弦AB ,则直线AB 的方程为(A )4370x y +-= (B )3470x y +-= (C )3410x y -+= (D )4310x y --=(11)边长为2的两个等边ABD ∆,CBD ∆所在的平面互相垂直,则四面体ABCD 的外接球的表面积为(A (B )6π (C )203π(D )16π(12)已知方程23ln 02x ax -+=有4个不同的实数根,则实数a 的取值范围是(A )2e 0,2⎛⎫ ⎪⎝⎭ (B )2e 0,2⎛⎤ ⎥⎝⎦ (C )2e 0,3⎛⎫ ⎪⎝⎭ (D )2e 0,3⎛⎤ ⎥⎝⎦福建省宁德市2018届普通高中毕业班5月质量检查文科数学试卷第II 卷注意事项:第II 卷共3页,须用黑色签字笔在答题卡上书写作答.若在试卷上作答,答案无效.本卷包括必考题和选考题两部分.第13题~第21题为必考题,每个试题考生都必须做答.第22题~第24题为选考题,考生根据要求做答.二、填空题:本大题共4小题,每小题5分.(13)某单位有420名职工,现采用系统抽样方法抽取21人做问卷调查,将420人按1,2,…,420随机编号,则抽取的21人中,编号落入区间[]281,420的人数为 . (14)在ABC ∆中,3,4AB AC ==,M 是边BC 的中点,则AM BC ⋅=.(15)不等式组2,6,20x x y x y ≥⎧⎪+≥⎨⎪-≤⎩所表示的平面区域为Ω,若直线10ax y a -++=与Ω有公共点,则实数a 的取值范围是 .(16)在ABC ∆中,角,,A B C 所对的边分别为,,a b c ,22,2,44A C c a b ===-,则a = . 三、解答题:解答须写出文字说明、证明过程和演算步骤. (17)(本小题满分12分)已知递增等差数列{}n a 的前n 项和为n S ,11a =,且2441,1,a a S ++成等比数列. (Ⅰ)求数列{}n a 的通项公式; (Ⅱ)设112n n n n na ab a a ++=+-,求数列{}n b 的前n 项和n T .(18)(本小题满分12分)某校为了解本校学生在校小卖部的月消费情况,随机抽取了60名学生进行统计.得到如下样本频数记月消费金额不低于300元为“高消费”,已知在样本中随机抽取1人,抽到是男生“高消费”的概率为16.(Ⅰ)从月消费金额不低于400元的学生中随机抽取2人,求至少有1人月消费金额不低于500元的概率;(Ⅱ)请将下面的22⨯列联表补充完整,并判断是否有90%的把握认为“高消费”与“男女性别”有关,说明理由.下面的临界值表仅供参考:7.879(参考公式:22()()()()()n ad bcKa b c d a c b d-=++++,其中n a b c d=+++)(19)(本小题满分12分)在四棱锥P ABCD-中,,ABC ACD∆∆都为等腰直角三角形,90ABC ACD︒∠=∠=,E为PA的中点.(Ⅰ)求证://BE平面PCD;(Ⅱ)若PAC∆是边长为2的等边三角形,PB=求三棱锥P BEC-的体积.DCEBAP(20)(本小题满分12分)已知抛物线Γ:22(0)x py p =>上一点(4,)P m 到焦点F 的距离为54m .(Ⅰ)求Γ的方程;(Ⅱ)过点(0,2)C 的直线交Γ于,A B 两点,以AB 为直径的圆交y 轴于,M N 两点,证明:OM ON ⋅为定值.(21)(本小题满分12分)已知函数()(1)e x f x x k =--.(Ⅰ)当0x >时,求()f x 的单调区间和极值; (Ⅱ)若12x x ≠,且12()()f x f x =,证明:122x x k +<.请考生在第22、23题中任选一题做答,如果多做,则按所做的第一题记分.做答时请写清题号. (22)(本小题满分10分)选修4—4:坐标系与参数方程在平面直角坐标系xOy 中,已知曲线6cos ,:3sin x C y αα=⎧⎨=⎩(α为参数),以坐标原点O 为极 点,x 轴的非负半轴为极轴建立极坐标系.(Ⅰ)求曲线C 的极坐标方程;(Ⅱ)若点,A B 为曲线C 上的两点,且OA OB ⊥,求OA OB ⋅的最小值. (23)(本小题满分10分)选修4—5:不等式选讲已知函数()21f x x x a =+--(0)a >.(Ⅰ)当1a =时,求不等式()f x x ≤的解集;(Ⅱ)当12x ≤-时,不等式2()230f x t t +++≥对任意t ∈R 恒成立,求实数a 的取值范围.福建省宁德市2018届普通高中毕业班5月质量检查文科数学试卷 参考答案及评分标准说明:一、本解答指出了每题要考察的主要知识和能力,并给出了一种或几种解法供参考,如果考生的解法与本解法不同,可根据试题的主要考察内容比照评分标准指定相应的评分细则。
2018年福建省宁德市中考数学试卷及答案

2018年宁德市初中毕业、升学考试数 学 试 题(全卷共6页,三大题,共26小题;满分150分;考试时间120分钟)友情提示:所有答案都必须填涂在答题卡上,答在本试卷上无效.参考公式:抛物线()02≠++=a c bx ax y 的顶点坐标为 ⎪⎪⎭⎫⎝⎛--a b ac a b 4422,,对称轴 a b x 2-=. 一、选择题(共10小题,每小题4分,满分40分;每小题只有一个正确的选项,请在答题卡的相应位置填涂) 1.-3的绝对值是( )A .3B .-3C .13D .13-2.未来三年,国家将投入8500亿元用于缓解群众“看病难,看病贵”问题.将8500亿元用科学记数法表示为( )A .0.85×104亿元B .8.5×103亿元C .8.5×104亿元D .85×102亿元 3.在如图所示的四个汽车标志图案中,能用平移变换来分析其形成过程的图案是( )A .B .C .D . 4.下列运算正确的是( )A .651a a -=B .235()a a = C .632a a a ÷= D .532a a a =⋅5.如图所示几何体的左视图是( )A. B. C. D.第5题图6.不等式组1024x x ->⎧⎨<⎩的解集是( )A .x >1B .x <2C .1<x <2D .无解 7.如图,已知直线AB 、CD 相交于点O ,OE 平分∠COB , 若∠EOB =55º,则∠BOD 的度数是( )A .35ºB .55ºC .70ºD .110º8.为配合世界地质公园申报,闽东某景区管理部门随机调查了1000名游客,其中有800人对景区表示满意.对于这次调查以下说法正确的是( )A .若随机访问一位游客,则该游客表示满意的概率约为0.8B .到景区的所有游客中,只有800名游客表示满意C .若随机访问10位游客,则一定有8位游客表示满意D .本次调查采用的方式是普查9.如图,直线AB 与⊙O 相切于点A ,⊙O 的半径为2,若∠OBA = 30°,则OB 的长为( )A. B .4C. D .210.图(1)表示一个正五棱柱形状的高大建筑物,图(2)是它的俯视图.小健站在地面观察该建筑物,当他在图(2)中的阴影部分所表示的区域活动时,能同时看到建筑物的三个侧面,图中∠MPN 的度数为( )A .30ºB .36ºC .45ºD .72º二、填空题(共8小题,每小题3分,满分24分.请将答案用黑色签字笔填入答题卡的相应位置)11.实数a b ,在数轴上对应点的位置如图所示, 则a b .(填“>”、“<”或“=”)12.如图,AB 是⊙O 的直径,AC 是弦,若∠ACO = 32°,则∠COB 的度数等于 .13.在本赛季NBA 比赛中,姚明最后六场的得分情况如下:17、15、21、28、12、19,这组数据的极差为 .BECO DA第7题图BAOA B第9题图图(1)第10题图图(2)b第11题图14.方程042=-x x 的解是______________.15.如图,△ABC 与△DEF 是位似图形,位似比为2∶3,已知AB =4,则DE 的长为 ____.16.张老师带领x 名学生到某动物园参观,已知成人票每张10元,学生票每张5元,设门票的总费用为y 元,则y = .17.小华为参加毕业晚会演出,准备制作一顶圆锥形纸帽,如图所示,纸帽的底面半径为9cm ,母线长为30cm ,制作这个纸帽至少需要纸板的面积至少为 cm 2.(结果保留π)18.如图,已知点A 、B 在双曲线xky =(x >0)上,AC ⊥x 轴于点C ,BD ⊥y 轴于点D ,AC 与BD 交于点P ,P 是AC 的中点,若△ABP 的面积为3,则k = . 三、解答题(满分86分.请将解答过程填入答题卡的相应位置.作图或添辅助线用铅笔画完,需用水笔再描黑)19.(每小题8分,满分16分)(1)计算:︒-+60cos 2200990 (2)解分式方程:14143=-+--xx x 20.(本题满分8分)如图:点A 、D 、B 、E 在同一直线上,AD =BE ,AC =DF ,AC ∥DF ,请从图中找出一个与∠E 相等的角,并加以证明.(不再添加其他的字母与线段)21.(本题满分8分)某刊物报道:“2018年12月15日,两岸海上直航、空中直航和直接通邮启动,‘大三通’基本实现.‘大三通’最直接好处是省时间和省成本,据测算,空运平均每航次可节省4小时,海运平均每航次可节省22小时,以两岸每年往来合计500万人次计算,则共可为民众节省2900万小时……”根据文中信息,求每年采用空运和海运往来两岸的人员各有多少万人次.AFEDCB第18题图第15题图CODEF A B22.(本题满分8分)为应对全球经济危机,中国政府投资40000亿元人民币以拉动内需, 5月21日国家发改委公布了40000亿元投资构成.具体内容如下:单位:亿元请你根据统计图表中所提供的信息,完成下列问题: (1)在统计表中,投向“铁路等重大基础设施建设和城市电网改造”的资金测算是 亿元,投向“汶川地震灾后恢复重建”的资金测算是 亿元; (2)在扇形统计图中,“卫生、教育等社会事业发展”部分所占的百分数是 ,“节能减排和生态建设工程”部分所占的百分数是; (3)统计表“资金测算”栏目下的七个数据中,中位数是 亿元,众数是 亿元; (4)在扇形统计图中,“廉租住房等保障性住房”部分所占的圆心角为 度. 23.(本题满分10分)某大学计划为新生配备如图(1)所示的折叠椅.图(2)是折叠椅撑开后的侧面示意图,其中椅腿AB 和CD 的长相等,O 是它们的中点.为使折叠椅既舒适又牢固,厂家将撑开后的折叠椅高度设计为32cm ,∠DOB =100°,那么椅腿的长AB 和篷布面的宽AD 各应设计为多少cm ?(结果精确到0.1cm )图(1) B 图(2) 消息来源于:廉租住房等 保障性住房农村民生工程和基础设施铁路等重大基础设施建设和城市电网改造卫生、教育等社会事业发展自主创新和产业结构调整 节能减排和生态建设工程汶川地震灾后恢复重建A B24.(本题满分10分)在学习“轴对称现象”内容时,王老师让同学们寻找身边的轴对称图形,小明有一副三角尺和一个量角器(如图所示).(1; (2)请用这三个图形中的两个..(只须画出一种);(3)小红也有同样的一副三角尺和一个量角器.若他们分别从自己这三件文具中随机取出一件,则可以拼成一个轴对称图案的概率是多少?(请画树状图或列表计算)25.(本题满分13分)如图(1),已知正方形ABCD 在直线MN 的上方,BC 在直线MN 上,E 是BC 上一点,以AE 为边在直线MN 的上方作正方形AEFG . (1)连接GD ,求证:△ADG ≌△ABE ;(4分)(2)连接FC ,观察并猜测∠FCN 的度数,并说明理由;(4分) (3)如图(2),将图(1)中正方形ABCD 改为矩形ABCD ,AB =a ,BC =b (a 、b 为常数),E 是线段BC 上一动点(不含端点B 、C ),以AE 为边在直线MN 的上方作矩形AEFG ,使顶点G 恰好落在射线CD 上.判断当点E 由B 向C 运动时,∠FCN 的大小是否总保持不变,若∠FCN 的大小不变,请用含a 、b 的代数式表示tan ∠FCN 的值;若∠FCN 的大小发生改变,请举例说明.(5分)NM B E A CDF G图(1)图(2)M BE A CDF GN26.(本题满分13分)如图,已知抛物线C 1:()522-+=x a y 的顶点为P ,与x 轴相交于A 、B 两点(点A 在点B 的左边),点B 的横坐标是1.(1)求P 点坐标及a 的值;(4分)(2)如图(1),抛物线C 2与抛物线C 1关于x 轴对称,将抛物线C 2向右平移,平移后的抛物线记为C 3,C 3的顶点为M ,当点P 、M 关于点B 成中心对称时,求C 3的解析式;(4分)(3)如图(2),点Q 是x 轴正半轴上一点,将抛物线C 1绕点Q 旋转180°后得到抛物线C 4.抛物线C 4的顶点为N ,与x 轴相交于E 、F 两点(点E 在点F 的左边),当以点P 、N 、F 为顶点的三角形是直角三角形时,求点Q 的坐标.(5分)2018年宁德市初中毕业、升学考试 数学试题参考答案及评分标准(1)本解答给出了一种或几种解法供参考,如果考生的解法与本解答不同,可参照本答案的评分标准的精神进行评分.(2)对解答题,当考生的解答在某一步出现错误时,如果后续部分的解答未改变该题的立意,可酌情给分,但原则上不超过后面应得的分数的一半;如果有较严重的错误,就不给分.(3)解答右端所注分数表示考生正确作完该步应得的累加分数. (4)评分只给整数分,选择题和填空题均不给中间分. 一.选择题;(本大题共有10小题,每小题4分,共40分)1.A ;2.B ; 3.D ; 4.D ; 5.C ; 6.C 7.C 8.A 9.B 10.B 二.填空题:(本大题共有8小题,每小题3分,共24分)11.>; 13.16; 15.6; 17.270π; 12.64º; 14.x 1=0, x 2=4; 16.5 x +10; 18.12; 三.解答题:(本大题有8题,共86分)19.(本题满分16分)(1)解: 原式=3+1-1 ………………6分=3 ………………8分 (2)解:方程两边同乘以x -4,得3-x -1=x -4 ……………3分解这个方程,得x =3 ……………6分 检验:当x ==3时,x -4=-1≠0 ……7分∴ x =3是原方程的解 ………………8分20.(本题满分8分)解法1:图中∠CBA =∠E ……1分 证明:∵AD =BE∴AD +DB =BE +DB 即AB =DE …3分 ∵AC ∥DF ∴∠A =∠FDE …5分 又∵AC =DF∴△ABC ≌△DEF ……7分 ∴∠CBA =∠E ……8分解法2:图中∠FCB =∠E ………1分 证明:∵AC =DF ,AC ∥DF∴四边形ADFC 是平行四边形 ………3分 ∴CF ∥AD ,CF =AD ………5分 ∵AD =BE ∴CF =BE ,CF ∥BE ∴四边形BEFC 是平行四边形 ………7分 ∴∠FCB =∠E ………8分 21.(本题满分8分)解:设每年采用空运往来的有x 万人次,海运往来的有y 万人次,依题意得 …1分⎩⎨⎧x +y =5004x +22y =2900……5分 解得 ⎩⎨⎧x =450 y =50……7分答:每年采用空运往来的有450万人次,海运往来的有50万人次. ……8分 22.(本题满分8分) 解:(1)15000,10000; …………2分 (2)3.75%,5.25% …………4分(3)3700,3700; …………6分 (4)36; …………8分23.(本题满分10分)解法1:连接AC ,BDA F E D C B∵OA=OB=OC=OB∴四边形ACBD 为矩形∵∠DOB=100º, ∴∠ABC=50º ……2分 由已知得AC=32在Rt △ABC 中,sin ∠ABC=ABAC∴AB=ABC AC ∠sin =︒50sin 32≈41.8(cm ) …6分tan ∠ABC=BC AC ,∴BC=ABC AC ∠tan =︒50tan 32≈26.9 (cm )∴AD=BC =26.9 (cm ) 答:椅腿AB 的长为41.8cm ,篷布面的宽AD 为26.9cm . ……10分 解法2:作O E ⊥AD 于E.∵OA=OB=OC=OD, ∠AOD=∠BOC ∴△AOD ≌△BOC∵∠DOB =100º, ∴∠OAD =50º (2)∴OE =3221⨯=16在Rt △AOE 中,sin ∠OAE =AO OE∴AO =OAE OE ∠sin = ︒50sin 16≈20.89 ∴AB =2AO ≈41.8(cm ) ……6分tan ∠OAE =AEOE ,AE=OAE OE ∠tan =︒50tan 16≈13.43 ∴AD =2 AE ≈26.9(cm ) 答:椅腿AB 的长为41.8cm ,篷布面的宽AD 为26.9cm . ……10分 24.(本题满分10分) 解:(1)B ,C ……本小题2分,答错不得分(2)画图正确得2;等(3或…开始ABCA B C A B C A B C (A ,A ) (A ,B ) (A ,C ) (B ,A ) (B ,B ) (B ,C ) (C ,A ) (C ,B ) (C ,C ) …4分图(2)一共有9种结果,每种结果出现的可能性是相同的.而其中能恰好拼成轴对称图形的结果有五种,分别是(A ,A ) 、(B ,B )、(C ,C)、(B ,C )、(C ,B ),所以两件文具可以拼成一个轴对称图案的概率是59. …………6分25.(本题满分13分)解:(1)∵四边形ABCD 和四边形AEFG 是正方形∴AB =AD ,AE =AG ,∠BAD =∠EAG =90º∴∠BAE +∠EAD =∠DAG +∠EAD ∴∠BAE =∠DAG∴△ BAE ≌△DAG …………4分(2)∠FCN =45º …………5分理由是:作FH ⊥MN 于H ∵∠AEF =∠ABE =90º ∴∠BAE +∠AEB =90º,∠FEH +∠AEB =90º ∴∠FEH =∠BAE又∵AE =EF ,∠EHF =∠EBA =90º∴△EFH ≌△ABE …………7分 ∴FH =BE ,EH =AB =BC ,∴CH =BE =FH∵∠FHC =90º,∴∠FCH =45º …………8分(3)当点E 由B 向C 运动时,∠FCN 的大小总保持不变,…………9分 理由是:作FH ⊥MN 于H 由已知可得∠EAG =∠BAD =∠AEF =90º 结合(1)(2)得∠FEH =∠BAE =∠DAG又∵G 在射线CD 上∠GDA =∠EHF =∠EBA =90º∴△EFH ≌△GAD ,△EFH ∽△ABE ……11分∴EH =AD =BC =b ,∴CH =BE ,∴EH AB =FH BE =FH CH ∴在Rt △FEH 中,tan ∠FCN =FH CH =EH AB =ba…………13分∴当点E 由B 向C 运动时,∠FCN 的大小总保持不变,tan ∠FCN =ba26.(本题满分13分)解:(1)由抛物线C 1:()522-+=x a y 得 顶点P 的为(-2,-5) ………2分∵点B (1,0)在抛物线C 1上∴()52102-+=a 解得,a =59 ………4分(2)连接PM ,作PH ⊥x 轴于H ,作MG ⊥x 轴于∵点P 、M 关于点B 成中心对称 ∴PM 过点B ,且PB =MB ∴△PBH ≌△MBG∴MG =PH =5,BG =BH =3∴顶点M 的坐标为(4,5) ………6分抛物线C 2由C 1关于x 轴对称得到,抛物线C 3由C 2平移得到∴抛物线C 3的表达式为()54952+--=x y ………8分(3)∵抛物线C 4由C 1绕点x 轴上的点Q 旋转180°得到∴顶点N 、P 关于点Q 成中心对称 由(2)得点N 的纵坐标为5M B E A C N DF G 图(1) HM B E A C N D F G 图(2)H设点N 坐标为(m ,5)作PH ⊥x 轴于H ,作NG ⊥x 轴于G 作PK ⊥NG 于K ∵旋转中心Q 在x 轴上∴EF =AB =2BH =6 ∴FG =3,点F 坐标为(m +3,0) H 坐标为(2,0),K 坐标为(m ,-5),根据勾股定理得 PN 2=NK 2+PK 2=m 2+4m +104PF 2=PH 2+HF 2=m 2+10m +50 NF 2=52+32=34 ………10分①当∠PNF =90º时,PN 2+ NF 2=PF 2,解得m =443,∴Q 点坐标为(193,0)②当∠PFN =90º时,PF 2+ NF 2=PN 2,解得m =103,∴Q 点坐标为(23,0)③∵PN >NK =10>NF ,∴∠NPF ≠90º综上所得,当Q 点坐标为(193,0)或(23,0)时,以点P 、N 、F 为顶点的三角形是直角三角形. ………13分。
福建省宁德市2018年初中毕业班质量检测数学试题

2018年宁德市初中毕业班质量检测数学试题本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,第Ⅰ卷1至2页,第Ⅱ卷3至5页.满分150分.注意事项:1.答题前,考生务必在试题卷、答题卡规定位置填写本人准考证号、姓名等信息.考生要认真核对答题卡上粘贴的条形码的“准考证号、姓名”与考生本人准考证号,姓名是否一致.2.选择题每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑.如需改动,用橡皮擦干净后,再选涂其他答案标号.非选择题答案用0.5毫米黑色签字笔在答题卡上相应位置书写作答,在试题卷上答题无效.3.作图可先使用2B铅笔画出,确定后必须0.5毫米黑色签字笔描黑.4.考试结束,考生必须将试题卷和答题卡一并交回.第Ⅰ卷一、选择题:本题共10小题,每小题4分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.2018-的值是A.12018B.2018C.12018-D.2018-2.如图,若a∥b,∠1=58°,则∠2的度数是A.58°B.112°C.122°D.142°3.下列事件是必然事件的是A.2018年5月15日宁德市的天气是晴天B.从一副扑克中任意抽出一张是黑桃C.在一个三角形中,任意两边之和大于第三边D.打开电视,正在播广告4.由6个大小相同的小正方体拼成的几何体如图所示,则下列说法正确的是A.主视图的面积最大B.左视图的面积最大C.俯视图的面积最大D.三种视图的面积相等正面第4题图ab 第2题图215.不等式组10,10≤>x x -⎧⎨+⎩的解集在数轴上表示正确的是6.在平面直角坐标系中,A ,B ,C ,D ,M ,N 的位置如图所示,若点M 的坐标为(-2 ,0), N 的坐标为(2 ,0),则在第二象限内的点是 A .A 点 B .B 点C .C 点D .D 点7.在“创文明城,迎省运会”合唱比赛中,10位评委给某队的评分如下表所示,则下列说法正确的是A .中位数是9.4分B .中位数是9.35分C .众数是3和1D .众数是9.4分8.如图,将△OAB 绕O 点逆时针旋转60°得到△OCD ,若OA=4,∠AOB =35°,则下列结论错误的是 A .∠BDO =60° B .∠BOC =25° C .OC=4D .BD=49.某校为进一步开展“阳光体育”活动,购买了一批篮球和足球.已知购买足球数量是篮球的2倍,购买足球用了4 000元,购买篮球用了2 800元,篮球单价比足球贵16元.若可列方程40002800162x x=-表示题中的等量关系,则方程中x 表示的是 A .足球的单价 B .篮球的单价C .足球的数量D .篮球的数量10.如图,已知等腰△ABC ,AB=BC ,D 是AC 上一点,线段BE 与BA 关于直线BD 对称,射线CE 交射线BD 于点F ,连接AE ,AF .则下列关系正确的是 A .180∠∠AFE ABE +=︒ B .12∠∠AEF ABC =C .180∠∠AEC ABC +=︒D .∠∠AEB ACB =成绩(分) 9.2 9.3 9.4 9.59.6 人数32311C 1 2 3-1 0 -2 D1 2 3-1 0 -2 B 1 2 3-1 0 -2 DCBAO第8题图第6题图MN A BD C第10题图CFE DABA 1 2 3-1 0 -2第 Ⅱ 卷注意事项:1.用0.5毫米黑色签字笔在答题卡上相应位置书写作答,在试题卷上作答,答案无效. 2.作图可先使用2B 铅笔画出,确定后必须0.5毫米黑色签字笔描黑. 二、填空题:本题共6小题,每小题4分,共24分.11.2017年10月18日,中国共产党第十九次全国代表大会在北京隆重召开.从全国近89 400 000党员中产生的2 300名代表参加了此次盛会.将数据89 400 000用科学记数法表示为 .12.因式分解:222a -= .13.小明同学在计算一个多边形的内角和时,由于粗心少算了一个内角,结果得到的总和是800°,则少算了这个内角的度数为 .14. 已知一次函数23(0)y kx k k =++≠,不论k 为何值,该函数的图像都经过点A ,则点A 的坐标为 .15.小丽计算数据方差时,使用公式2222221(5)(8)(13)(14)(15)5S x x x x x ⎡⎤=-+-+-+-+-⎣⎦,则公式中x = . 16.如图,点A ,D 在反比例函数(0)my m x=<的图像上,点B ,C 在反比例函数(0)ny n x=>的图像上.若AB ∥CD ∥x 轴,AC ∥y 轴,且AB =4,AC =3,CD =2,则n = .三、解答题:本题共9小题,共86分.17.(本题满分8分)计算:14cos30212-︒+-.18.(本题满分8分)如图,在△ABC 中, D ,E 分别是AB ,AC 的中点,△ABC 的角平分线AG 交DE 于点F ,若∠ABC =70°,∠BAC =54°,求∠AFD 的度数.CFEDBAGxyOBAC D第16题图19.(本题满分8分)首届数字中国建设峰会于4月22日至24日在福州海峡国际会展中心如期举行,某校组织115位师生去会展中心参观,决定租用A ,B 两种型号的旅游车.已知一辆A 型车可坐20人,一辆B 型车可坐28人,经测算学校需要租用这两种型号的旅游车共5辆.学校至少要租用B 型车多少辆?20.(本题满分8分)某中学为推动“时刻听党话 永远跟党走”校园主题教育活动,计划开展四项活动:A :党史演讲比赛,B :党史手抄报比赛,C :党史知识竞赛,D :红色歌咏比赛.校团委对学生最喜欢的一项活动进行调查,随机抽取了部分学生,并将调查结果绘制成图1,图2两幅不完整的统计图.请结合图中信息解答下列问题:(1)本次共调查了 名学生; (2)将图1的统计图补充完整;(3)已知在被调查的最喜欢“党史知识竞赛”项目的4个学生中只有1名女生,现从这4名学生中任意抽取2名学生参加该项目比赛,请用画树状图或列表的方法,求出恰好抽到一名男生一名女生的概率.21.(本题满分8分)如图,已知矩形ABCD ,E 是AB 上一点.(1)如图1,若F 是BC 上一点,在AD ,CD 上分别截取DH =BF ,DG =BE .求证:四边形EFGH 是平行四边形;(2)如图2,利用尺规分别在BC ,CD ,AD 上确定点F ,G ,H ,使得四边形EFGH是特殊的平行四边形.(提示:①保留作图痕迹,不写作法;②只需作出一种情况即可)图1ADFHBEGC图2CDBAEA 15%BC10%D 35%图2图1活动项人数/人AB CD4 6 8 10 12 14 16 222.(本题满分10分)若正整数a ,b ,c 满足111a b c+=,则称正整数a ,b ,c 为一组和谐整数.(1)判断2,3,6是否是一组和谐整数,并说明理由;(2)已知x ,y ,z (其中x y z <≤)是一组和谐整数,且1x m =+,3y m =+,用含m 的代数式表示z ,并求当24z =时m 的值.23.(本题满分10分)如图,在△ABC 中,∠ACB =90°,O 是AB 上一点,以OA 为半径的⊙O 与BC 相切于点D ,与AB 交于点E ,连接ED 并延长交AC 的延长线于点F .(1)求证:AE =AF ;(2)若DE =3,sin ∠BDE =13,求AC 的长.24.(本题满分13分)如图1,在△ABC 中,∠BAC =90°,AB =AC =4,D 是BC 上一个动点,连接AD ,以AD 为边向右侧作等腰直角△ADE ,其中∠ADE =90°. (1)如图2,G ,H 分别是边AB ,BC 的中点,连接DG ,AH ,EH .求证:△AGD ∽△AHE ;(2)如图3,连接BE ,直接写出当BD 为何值时,△ABE 是等腰三角形; (3)在点D 从点B 向点C 运动过程中,求△ABE 周长的最小值.25.(本题满分13分)已知抛物线22(0)y ax ax c a =-+<的图像过点A (3,m ).(1)当a =-1,m =0时,求抛物线的顶点坐标; (2)若P (t ,n )为该抛物线上一点,且n <m ,求t 的取值范围;(3)如图,直线:(0)l y kx c k =+<交抛物线于B ,C 两点,点Q (x ,y )是抛物线上点B ,C 之间的一个动点,作QD ⊥x 轴交直线 l 于点D ,作QE ⊥y 轴于点E ,连接DE .设∠QED=β,当x 2≤≤4时,β 恰好满足°°30≤≤60β,求a 的值. F AE CDBO图1ABCDE图2图3ABCDEABCDEGHEDQC Bxy O。
福建省宁德市2018届初中数学5月毕业班质量检测试题(pdf)

16 14 12 10
8 6 4 2
0
A B C D 活动项
图1
C
D
10%
35%
A
B
15%
图2
(1)本次共调查了
名学生;
(2)将图 1 的统计图补充完整;
(3)已知在被调查的最喜欢“党史知识竞赛”项目的 4 个学生中只有 1 名女生,现
从这 4 名学生中任意抽取 2 名学生参加该项目比赛,请用画树状图或列表的方
A 的坐标为
.
15.小丽计算数据方差时,使用公式
S2
1 5
(5
x)2
(8
x)2
(13
x)2
(14
x)2
(15
x)2
,
则公式中 x =
.
16.如图,点 A,D 在反比例函数 y m (m 0) 的图像上,点 B, x
C 在反比例函数 y n (n 0) 的图像上.若 AB∥CD∥x 轴, x
AC∥y 轴,且 AB=4,AC=3,CD=2,则 n=
正面 第 4 题图
-2 -1 0 1 2 3
A
-2 -1 0 1 2 3
B
-2 -1 0 1 2 3
C
6.在平面直角坐标系中,A,B,C,D,M,N 的位置如图所 示,若点 M 的坐标为(-2 ,0), N 的坐标为(2 ,0),
数学试题 第 1 页 共 6 页
-2 -1 0 1 2 3
D
A
B
M
N C
法,求出恰好抽到一名男生一名女生的概率.
21.(本题满分 8 分)如图,已知矩形 ABCD,E 是 AB 上一点.
(1)如图 1,若 F 是 BC 上一点,在 AD,CD 上分别截取 DH=BF,DG=BE.
福建省宁德市2018届高三第二次(5月)质量检测数学(理)试卷及答案

2018届宁德市普通高中毕业班第二次质量检查试卷理 科 数 学本试卷分第I 卷和第II 卷两部分.第I 卷1至2页,第II 卷3至5页,满分150分. 考生注意:1.答题前,考生务必将自己的姓名、准考号填写在答题卡上.考生要认真核对答题卡上粘贴的“姓名、准考证号、考试科目”与考生本人准考证号、姓名是否一致.2.第I 卷每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其他答案标号.第II 卷用0.5毫米的黑色墨水签字笔在答题卡上书写作答.若在试题卷上作答,答案无效.3.考试结束,监考员将试题卷和答题卡一并交回 .第I 卷一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的. 1.复数i1iz =+的共轭复数z 在复平面内对应的点位于 A .第一象限 B .第二象限 345C .第三象限 D .第四象限2.已知集合}{1A x x =≥-,1,2x B y y x A ⎧⎫⎪⎪⎛⎫==∈⎨⎬ ⎪⎝⎭⎪⎪⎭⎩,则A B =IA .}{12x x -≤≤B .}{2x x ≥ C .}{02x x <≤ D .∅3.某几何体的三视图如图所示,若该几何体的体积为2,则图中x 的值为 A .1 BCD4.设,x y 满足约束条件12324x y x ≤-≤⎧⎨≤≤⎩,,则目标函数2z x y =-的最大值为A .72 B .92 C .132D .152俯视图正视图5.将函数1sin()24y x π=+图象上各点的横坐标缩小为原来的12(纵坐标不变),得到函数()y f x =的图象,则函数()4y f x 3π=+的一个单调递增区间是 A .(,0)2π-B .(0,)2πC .(,)2ππD .3(,2)2ππ6.在如图所示的正方形中随机投掷10000个点,则落入由曲线C(曲线C 为正态分布(2,1)N 的密度曲线)与直线0,x =1x = 及0y =围成的封闭区域内点的个数的估计值为(附:若X :2(,)N μσ,则()0.6826P X μσμσ-<<+=,(22)0.9544P X μσμσ-<<+=,(33)0.9974P X μσμσ-<<+=)A .2718B .1359C .430D .2157. 已知F 是抛物线2:2(0)C y px p =>的焦点,P 是C 上的一点,Q 是C 的准线上一点.若ΔPQF是边长为2的等边三角形,则该抛物线的方程为A .28y x =B .26y x =C .24y x =D .22y x = 8.已知锐角,αβ满足sin2cos αα=,1cos()7αβ+=,则cos β的值为 A .1314 B .1114CD9.已知O 是坐标原点,12,F F 分别是双曲线C :22221x y a b-=(0a >,0b >)的左、右焦点,过左焦点1F 作斜率为12的直线,与其中一条渐近线相交于点A .若2||||OA OF =,则双曲线C 的离心率e 等于 A .54B .53CD .210.世界著名的百鸡问题是由南北朝时期数学家张丘建撰写的《张丘建算经》中的一个问题:鸡翁一,值钱五,鸡母一,值钱三,鸡雏三,值钱一.百钱买百鸡,问鸡翁母雏各几何?张丘建是数学史上解决不定方程解的第一人.用现代方程思想,可设,,x y z分别为鸡翁、鸡母、鸡雏的数量,则不定方程为53100,3100.z x y x y z ⎧++=⎪⎨⎪++=⎩如图是体现张丘建求解该问题思想的框图,则方框中①,②应填入的是A .3?t <,257y t =-B .3?t ≤,257y t =-C .5?t <,255y t =-D .5?t ≤,255y t =- 11.底面边长为6的正三棱锥的内切球半径为1,则其外接球的表面积为A .49πB .36πC .25πD .16π12.设函数()ln()f x x k =+,()e 1x g x =-.若12()()f x g x =,且12x x -有极小值1-,则实数k 的值是 A .1- B .2-C .0D .22018届宁德市普通高中毕业班第二次质量检查试卷理 科 数 学第II 卷注意事项:用0.5毫米黑色签字笔在答题卡上书写作答. 在试题卷上作答,答案无效.本卷包括必考题和选考题两部分.第13~21题为必考题,每个试题考生都必须做答.第22、23题为选考题,考生根据要求做答.二、填空题:本大题共4小题,每小题5分.13.边长为2的正三角形ABC 中,12AD DC =u u u v u u u v,则BD AC ⋅=u u u v u u u v ___________.14.()22344(1)x x x -++的展开式中,3x 的系数是___________.(用数字填写答案)15.B 村庄在A 村庄正西10km ,C 村庄在B 村庄正北3km .现在要修一条从A 村庄到C 村庄的公路,沿从A 村庄到B 村庄的方向线路报价是800万元/km ,沿其他线路报价是1000万元/km ,那么修建公路最省的费用是___________万元. 16.在ABC ∆中,D 为边BC 上的点,且满足2DAC π∠=,1sin 3BAD ∠=.若13ABD ADC S S ∆∆=, 则C ∠的余弦值为___________.三、解答题:本大题共6小题,满分70分.解答须写出文字说明、证明过程和演算步骤. 17.(12分)已知数列{}n a 的前n 项和为n S ,12a =,132n n S a +=-. (1)求数列{}n a 的通项公式; (2)设2log n n b a =,若4(1)n n n c b b =+,求证:123n c c c +++<L .18.(12分)为响应绿色出行,某市在推出“共享单车”后,又推出“新能源分时租赁汽车”.其中一款新能源分时租赁汽车,每次租车收费的标准由两部分组成:①根据行驶里程数按1元/公里计费;②行驶时间不超过40分时,按0.12元/分计费;超过40分时,超出部分按0.20元/分计费.已知张先生家离上班地点15公里,每天租用该款汽车上、下班各一次.由于堵车、红绿灯等因素,每次路上开车花费的时间t (分)是一个随机变量.现统计了50次路上开车花费时间,在各时间段内的频数分布情况如下表所示:将各时间段发生的频率视为概率,每次路上开车花费的时间视为用车时间,范围为(]20,60分. (1)写出张先生一次租车费用y (元)与用车时间t (分)的函数关系式;(2)若张先生一次开车时间不超过40分为“路段畅通”,设ξ表示3次租用新能源分时租赁汽车中“路段畅通”的次数,求ξ的分布列和期望;(3)若公司每月给1000元的车补,请估计张先生每月(按22天计算)的车补是否足够上、下班租用新能源分时租赁汽车?并说明理由.(同一时段,用该区间的中点值作代表)19.(12分)如图,四棱锥P ABCD -中,底面ABCD 为梯形,//AB DC ,112BC DC AB ===.O 是AB 的中点,PO ⊥底面ABCD .O 在平面PAD 上的正投影为点H ,延长PH 交AD 于点E . (1)求证: E 为AD 中点;(2)若90ABC ∠=o,PA BC 上确定一点G ,使得HG //平面PAB ,并求出OG 与面PCD 所成角的正弦值.20.(12分)已知椭圆2222:1(0)x y M a b a b+=>>的左、右顶点分别为,A B ,上、下顶点分别为,C D .若四边形ADBC 的面积为4,且恰与圆224:5O x y +=相切.(1)求椭圆M 的方程;(2) 已知直线l 与圆O 相切,交椭圆M 于点,P Q ,且点,A B 在直线l 的两侧.设APQ ∆的面积为1S ,BPQ ∆的面积为2S ,求12S S -的取值范围.21.(12分)已知函数221()()ln ()2f x x x x ax a =++∈R ,曲线()y f x =在1x =处的切线与直线210x y +-=垂直.(1)求a 的值,并求()f x 的单调区间;(2)若λ是整数,当0x >时,总有2211()(3)ln 24f x x x x x λλ-+->+,求λ的最大值.请考生在第22、23题中任选一题做答,如果多做,则按所做的第一题记分.做答时请写清题号. 22.[选修4―4:坐标系与参数方程](10分)在直角坐标系xOy 中,以坐标原点O 为极点,x 轴正半轴为极轴建立极坐标系,曲线1C 的极坐标方程为2(4cos )4r ρρθ-=-,曲线2C的参数方程为4cos ,sin x y θθ⎧=⎪⎨=⎪⎩(θ为参数).(1)求曲线1C 的直角坐标方程和曲线2C 的极坐标方程;(2)当r 变化时,设1,C 2C 的交点M 的轨迹为3C .若过原点O ,倾斜角为3π的直线l 与曲线3C 交于点,A B ,求OA OB -的值.OHED CBAP23.[选修4—5:不等式选讲](10分)已知实数x , y 满足1x y +=.(1)解关于x 的不等式225x x y -++≤;(2)若,0x y >,证明:2211119x y ⎛⎫⎛⎫--≥ ⎪ ⎪ ⎪⎝⎭⎝⎭2018年宁德市普通高中毕业班质量检查数学(理科)试题参考答案及评分标准说明:一、本解答指出了每题要考查的主要知识和能力,并给出了一种或几种解法供参考,如果考生的解法与本解法不同,可根据试题的主要考查内容比照评分标准指定相应的评分细则.二、对计算题,当考生的解答在某一部分解答未改变该题的内容和难度,可视影响的程度决定后继部分的给分,但不得超过该部分正确解答应给分数的一半;如果后继部分的解答有较严重的错误,就不再给分.三、解答右端所注分数,表示考生正确做到这一步应得的累加分数. 四、只给整数分数,选择题和填空题不给中间分.一、选择题:本题考查基础知识和基本运算,每小题5分,满分60分. 1.D 2.C 3.A 4.D 5.C 6.B 7.D 8.C 9.B 10.B 11.A 12.D二、填空题:本题考查基础知识和基本运算,每小题5分,满分20分.13.23- 14.8 15.9800 16三、解答题:本大题共6小题,满分70分,解答须写出文字说明、证明过程和演算步骤.17.本小题主要考查数列及数列求和等基础知识,考查运算求解能力,考查函数与方程思想、化归与转化思想等,满分12分. 解:(1)由题设132n n S a +=-, 当2n ≥时,132n n S a -=-,两式相减得13n n n a a a +=-,即14n n a a += . …………………2分又1a =2,1232a a =-,可得28a =, ∴214a a =. ………………………………3分 ∴数列{}n a 构成首项为2,公比为4的等比数列,∴121242n n n a --=⨯=. ………………………………5分(没有验证214a a =扣一分)(2)∵212log 221n n b n -==-,………………………………6分442(1)(21)2(21)n n n c b b n n n n===+-⋅-⋅(*n ∈N ), ………………7分 ∴2n ≥时,22111(21)(22)(1)1n c n n n n n n n n=<==--⋅-⋅-⋅- , ………9分∴1231111112()()()12231n c c c c n n ++++≤+-+-++--L L …………10分13n=- ………………………………11分3<. ………………………………12分解法二:(1)同解法一;(2)∵212log 221n n b n -==-,………………………………6分442(1)(21)2(21)n n n c b b n n n n===+-⋅-⋅(*n ∈N ), ………………7分 ∵2n ≥时,211n n -≥+,∴22112()(21)(1)1n c n n n n n n =≤=--⋅+⋅+ , ………9分∴123111122()()23+1n c c c c nn ⎡⎤++++≤+-++-⎢⎥⎣⎦L L …………10分 112221n ⎛⎫=+- ⎪+⎝⎭………………………………11分3<. ………………………………12分解法三:(1)同解法一;(2)∵212log 221n n b n -==-,………………………………6分442(1)(21)2(21)n n n c b b n n n n===+-⋅-⋅(*n ∈N ), ………………7分 ∴2n ≥时,22112()(21)(1)1n c n n n n n n=≤=--⋅-⋅- , ………8分∴1231234511112()()561n c c c c c c c c c n n ⎡⎤++++≤+++++-++-⎢⎥-⎣⎦L L …………10分 1212112231514455n ⎛⎫=+++++- ⎪⎝⎭ (1)1分619223630n<+-<. ………………………………12分18.本小题主要考查频率分布表、平均数、随机变量的分布列及数学期望等基础知识,考查运算求解能力、数据处理能力、应用意识,考查分类与整合思想、必然与或然思想、化归与转化思想.满分12分. 解法一:(1)当2040t <≤时,0.1215y t =+ ………………………………1分 当4060t <≤时,0.12400.20(40)150.211.8y t t =⨯+-+=+. ………………………………2分得:0.1215,2040,0.211.8,4060t t y t t +<≤⎧=⎨+<≤⎩………………………………3分(2)张先生租用一次新能源分时租赁汽车,为“路段畅通”的概率2182505P +==……4分 ξ可取0,1,2,3.03032327(0)55125P C ξ⎛⎫⎛⎫=== ⎪ ⎪⎝⎭⎝⎭,2132354(1)55125P C ξ⎛⎫⎛⎫=== ⎪⎪⎝⎭⎝⎭ 2232336(2)55125P C ξ⎛⎫⎛⎫=== ⎪ ⎪⎝⎭⎝⎭,333238(3)55125P C ξ⎛⎫⎛⎫=== ⎪ ⎪⎝⎭⎝⎭ ξ的分布列为……………7分27543680123 1.2125125125125E ξ=⨯+⨯+⨯+⨯= ……………………………8分 或依题意2(3,)5B ξ:,23 1.25E ξ=⨯= ……………………………8分(3)张先生租用一次新能源分时租赁汽车上下班,平均用车时间21820102535455542.650505050t =⨯+⨯+⨯+⨯=(分钟),……………10分 每次上下班租车的费用约为0.242.611.820.32⨯+=(元). ……………11分 一个月上下班租车费用约为20.32222894.081000⨯⨯=<,估计张先生每月的车补够上下班租用新能源分时租赁汽车用. ………………12分解法二:(1)(2)同解法一;(3)张先生租用一次新能源分时租赁汽车上下班,平均租车价格为2182010(150.1225)(150.1235)(11.80.245)(11.80.255)20.51250505050+⨯⨯++⨯⨯++⨯⨯++⨯⨯=(元)……………10分一个月上下班租车费用约为20.512222902.5281000⨯⨯=<……………11分估计张先生每月的车补够上下班租用新能源分时租赁汽车用. ………………12分19.本小题主要考查空间直线与直线、直线与平面的位置关系及直线与平面所成的角等基础知识,考查空间想象能力、推理论证能力、运算求解能力,考查化归与转化思想等.满分12分. 解法一:(1)连结OE .2,AB O =Q 是AB 的中点,1CD =, OB CD ∴=,//AB CD Q ,∴ 四边形BCDO 是平行四边形, 1OD ∴=.………………1分PO ⊥Q 平面ABCD ,AD ⊂平面ABCD , PO AD ∴⊥,………………2分 O Q 在平面PAD 的正投影为H , OH ∴⊥平面PAD ,OH AD ∴⊥.………………3分 又OH PO O =Q I ,AD ∴⊥平面POE ,AD OE ∴⊥,………………4分 又1AO OD ==Q ,E ∴是AD 的中点. ………………5分 (2)90ABC ∠=o Q ,//OD BC ,OD AB ∴⊥,OP ⊥Q 平面ABCD ,∴以O 为原点,,,OD OB OP u u u v u u u v u u u v分别为,,x y z 轴的正方向建立空间直角坐标系O xyz -,………………6分(0,0,0)O ∴,(0,0,1)P ,(1,1,0)C ,(1,0,0)D ,PA Q OP AB ⊥,1PO ∴=OA OD OP ∴==,∴H ∴是ADP ∆的的外心,AD PD AP ==QH ∴是ADP ∆的的重心, OH OP PH ∴=+u u u v u u u v u u u v 23OP PE =+u u u v u u u v 111(,,)333=-.………………8分设BG BC λ=u u u v u u u v ,(,1,0)OG BC OB λλ∴=+=u u u v u u u v u u u v ,141(,,)333GH OH OG λ∴=-=--u u u v u u u v u u u v ,OHEDCBAP又(1,0,0)OD =u u u vQ 是平面PAB 的一个法向量,且//HG 平面PAB , 0GH OD ∴⋅=u u u v u u u v,13λ∴-=,解得13λ=,1(,1,0)3OG ∴=u u u v ,………………9分 设(,,)n x y z =v是平面PCD 的法向量, (1,0,1)PD =-u u u v Q ,(0,1,0)CD =-u u u v,0,0,n PD n CD ⎧⋅=⎪∴⎨⋅=⎪⎩u u u v v u u u vv 即0,0,x z y -=⎧⎨=⎩ 取1,x =则1,0z y ==,(1,0,1)n ∴=v.………………11分 cos ,||||n PG n PG n PG ⋅∴<>=⋅u u u v v u u u v vu u uvv 1==, ∴直线OG 与平面PCD.………………12分 解法二:(1)同解法一;(2)过H 作HM EO ⊥,交EO 于点M ,过点M 作//GM AB ,分别交,OD BC 于,Q G ,则//HG 平面PAB ,………………6分 证明如下://,MG AB AB ⊂Q 平面,PAB MG ⊄平面PAB , //MG ∴平面PABQ PO ⊥平面ABCD ,EO ⊂平面ABCD ,PO EO ∴⊥, ∴在平面POD 中,//PO MH ,PO ⊂Q 平面,PAB HM ⊄平面PAB , //MH ∴平面PABMG MH M =Q I ,∴平面//MHG 平面PABGH ⊂Q 平面MHG ,//HG ∴平面PAB .………………7分,OM PH OM ME HE =∴Q ,1,3BG OQ ∴===………………8分 在OD 上取一点N ,使23ON =,CN OG ∴==………………9分 作NT PD ⊥于T ,连结CT .∵,CD OD ⊥,CD OP OD OP O ⊥=I , CD ∴⊥平面POD , NT CD ∴⊥,TNQ PAB CD E HOMGPD CD D =Q I , NT ∴⊥平面PCD ,NCT ∴∠就是OG 与平面PCD 所成的角. ………………10分DN DPNT PO =Q ,NT ∴,………………11分sin NT OTN CN ∴∠===, 即直线OG 与平面PCD.………………12分解法三:(1)同解法一.(2)过E 作//EQ AB ,交BC 于点Q ,连结PQ ,过H 作//HM EQ 交PQ 于点M , 过点M 作//GM PB ,交BC 于G ,连结HG , 则//HG 平面PAB ,………………6分 证明如下://,MG PB PB ⊂Q 平面,PAB MG ⊄平面PAB , //MG ∴平面PAB 同理://MH 平面PABMG MH M =Q I ,∴平面//MHG 平面PAB .GH ⊂Q 平面MHG ,//HG ∴平面PAB ,………………7分 2BG PM PH GQ MQ HE∴===, Q E 是AD 的中点,∴Q 是BC 的中点,1133BG BC ∴==,………………8分取PD 的中点N ,连结ON ,再连结OG 并延长交DC 的延长线于点T ,连结NT , OP OD =Q ,N 是PD 中点,ON PD ∴⊥,Q OB OD ⊥,,OB OP OD OP D ⊥=I , OB ∴⊥平面POD OB ON ∴⊥,//OB CD Q ,ON CD ∴⊥,PD CD D =Q I , ON ∴⊥平面PCD , OTN ∴∠就是OG 与平面PCD 所成的角.BG OBGC CT=Q, 2CT ∴=,OT ∴=.12ON DP =Q ………………11分TNG MQ OHE DCB APsinONOTNOT∴∠==即直线OG与平面PCD (12)分20.本题主要考查直线、椭圆、直线与椭圆的位置关系等基础知识,考查运算求解能力、推理论证能力,考查函数与方程思想、化归与转化思想,考查考生分析问题和解决问题的能力,满分12分.解法一:(1)根据题意,可得:1224,21122a bab⎧⨯⨯=⎪⎪⎨⎪=⎪⎩即2,ab=⎧=………………………………………………………2分解得2,1.ab=⎧⎨=⎩………………………………………………………4分∴椭圆M的方程为2214xy+=.………………………………………………………5分(2)设:l x my n=+,(2,2)n∈-,直线l与圆O相切,得=,即224(1)5mn+=,………………………………6分从而[)20,4m∈.又1121(2)2S n y y=+-,2121(2)2S n y y=--,∴1212121(2)(2)2S S n n y y n y y-=⨯--+⋅-=⋅-.………………………………7分将直线l的方程与椭圆方程联立得222(4)240m y mny n+++-=,显然0∆>.设11(,)P x y∴12y y-=∴12S S-=85, 当20m =时,1285S S -=;………………………………10分当2(0,4)m ∈时,122S S -=<, (11)分且1285S S ->.综上,128,25S S ⎡⎫-∈⎪⎢⎣⎭.………………………………12分解法二:(1)同解法一;(2)当直线l的斜率不存在时,由对称性,不妨设:l x =,此时直线l与椭圆的交点为,12182)(225S S ⎡⎤-=+--=⎢⎥⎣⎦. 直线l 的斜率存在时,设:l y kx b =+,由直线l 与圆O 相切,得=,即224(1)5k b +=. 又点,A B 在直线l 的两侧,∴(2)(2)0k b k b +-+<,2240b k -<,∴224(1)405k k +-<,解得12k >或12k <-.点,A B 分别到直线l 的距离为1d =2d =将直线l 的方程与椭圆方程联立得222(14)8440k x kbx b +++-=, 显然0∆>.设11(,)P x y ,22(,)Q x y ,得122814kbx x k +=-+,21224414b x x k -⋅=+.…………………………………7分∴12PQ x=-=.………………………8分∴121212S S d d AB-=-⋅=b=b===2==,且1285S S->.综上,128,25S S⎡⎫-∈⎪⎢⎣⎭.…………………………………………………………………………12分21.本小题主要考查导数的几何意义、导数及其应用、不等式等基础知识,考查推理论证能力、运算求解能力、创新意识等,考查函数与方程思想、化归与转化思想、分类与整合思想、数形结合思想等.满分12分.解法一: (1)函数()f x的定义域是(0,)+∞,1()(1)ln(2)12f x x x a x'=++++,……………………………………………………………1分依题意可得,(1)1f'=,12122a∴++=,14a∴=.……………………………………………………………………2分()(1)ln(1)f x x x x'∴=+++=(1)(ln1)x x++令()0f x'=,即(1)(ln1)0x x++=,10,x x>∴=Q,……………………………………3分()f x∴的单调递增区间是1(,)e+∞,单调递减区间为1(0,)e.………………………………5分(2)由(Ⅰ)可知,2211()()ln24f x x x x x=++,2211()(3)ln24f x x x x xλλ∴-+->+ln31x x xxλ-⇔>+,………………………………6分设ln3()1x x xh xx-=+,∴只要min()h xλ>,……………………………………………7分2(1ln 3)(1)(ln 3)()(1)+-+--'=+x x x x x h x x22ln (1)x xx -+=+,…………………………………………………………………8分令()2ln u x x x =-+, 1()10u x x'∴=+> ()u x ∴在(0,)+∞上为单调递增函数,(1)10u =-<Q , (2)ln 20=>u∴存在0(1,2)x ∈,使0()0u x =,……………………………………………………9分当0(,)x x ∈+∞时,()0u x >,即()0h x '>, 当0(0,)x x ∈时,()0u x <,即()0h x '<, ()h x ∴在0x x =时取最小值,且000min 0ln 3()1-=+x x x h x x ,………………………………10分又0()0u x =Q , 00ln 2x x ∴=-, 000min 00(2)3()1--∴==-+x x x h x x x ,……………………………………………………11分00(1,2),(2,1)x x ∈∴-∈--Q又min ()h x λ<Q ,max 2Z λλ∈∴=-Q . …………………………………………………………………12分解法二:(1)同解法一.(2)由(1)可知, 2211()()ln 24f x x x x x =++2211()(3)ln 24f x x x x λλ∴-+->+ln 30x x x x λλ⇔--->.…………………………6分 设()ln 3g x x x x x λλ=---,∴只要min ()0g x >,………………………………………7分 则()1ln 3g x x λ'=+--ln 2x λ=--令()0g x '=,则ln 2x λ=+,2x e λ+∴=.…………………………………………………8分 当2(0,)x e λ+∈时,()0g x '<,()g x 单调递减;当2(,)x e λ+∈+∞时,()0g x '>,()g x 单调递增,2min ()()g x g e λ+∴=222(2)3e e e λλλλλλ+++=+---2e λλ+=--.…………………………9分 设2()h e λλλ+=--,则()h λ在R 上单调递减,………………………………………10分 (1)10,(2)120h e h -=-+<-=-+>Q ,………………………………………………11分0(2,1)λ∴∃∈--,使0()0h λ=,max 2Z λλ∈∴=-Q . …………………………………………………………………12分22.选修44-;坐标系与参数方程本小题考查直线和圆的极坐标方程、参数方程等基础知识,考查运算求解能力,考查数形结合思想、化归与转化思想等. 满分10分. 解法一:(1)由1C :2(4cos )4r ρρθ-=-, 得224cos 4r ρρθ-+=,即222440x y x r +-+-=, ………………………………………………………2分 曲线2C 化为一般方程为:222(4)3x y r -+=,即2228163x y x r +-+=,………4分 化为极坐标方程为:228cos 1630r ρρθ-+-=.………………………………5分(2)由224cos 4r ρρθ-+=及228cos 1630r ρρθ-+-=,消去2r ,得曲线3C 的极坐标方程为22cos 20()ρρθρ--=∈R . …………………………………………………7分将θπ=3代入曲线3C 的极坐标方程,可得220ρρ--=,…………………8分 故121ρρ+=,1220ρρ=-<,…………………………………………………9分 故121OA OB ρρ-=+=.…………………………………………………10分 (或由220ρρ--=得0)1)(2(=+-ρρ得1,221-==ρρ,…………………9分 故211-=-=OA OB …………………………………………………10分) 解法二:(1)同解法一;(2)由22244x y x r +-+=及2228163x y x r +-+=,消去2r ,得曲线3C 的直角坐标方程为2222x y x +-=. ………………………………………………………………7分 设直线l的参数方程为1,2x t y ⎧=⎪⎪⎨⎪=⎪⎩(t 为参数),………………………………8分与2222x y x +-=联立得2213244t t t +-=,即220t t --=,………………………………………………………………9分故121t t +=,1220t t =-<,∴121OA OB t t -=+=.……………………………………………………10分 (或由220t t --=得,,0)1)(2(=+-t t 得1,221-==t t ,∴211-=-=OA OB .……………………………………………………10分)23.选修45-:不等式选讲本小题考查绝对值不等式、基本不等式的解法与性质等基础知识,考查运算求解能力、推理论证能力,考查分类与整合思想、化归与转化思想等. 满分10分. 解法一:(1)1,x y +=Q|2||1|5x x ∴-++≤,………………………………………1分当2x ≥时,原不等式化为215x -≤,解得3x ≤,∴23x ≤≤;………………………………………………2分 当12x -≤<时,原不等式化为215x x -++≤,∴12x -≤<;………………………………………………3分 当1x <-时,原不等式化为215x -+≤,解得2x ≥-,∴21x -≤<-;………………………………………………4分 综上,不等式的解集为{}23x x -≤≤..……………………5分 (2)1,x y +=Q 且0,0x y >>,2222222211()()(1)(1)x y x x y y x y x y+-+-∴--=⋅……………7分 222222xy y xy x x y ++=⋅222222()()y y x x x x y y=++225x y y x =++………………………………8分59≥=. 当且仅当12x y ==时,取“=”. ………………………………10分 解法二:(1)同解法一;(2)1,x y +=Q 且0,0x y >>,2222221111(1)(1)x y x y x y--∴--=⋅………………………………6分 22(1)(1)(1)(1)x x y y x y +-+-=⋅22(1)(1)x y y xx y ++=⋅………………………………7分 1x y xyxy +++=………………………………8分21xy =+2219()2x y ≥+=+ 当且仅当12x y ==时,取“=”. ………………………………10分。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
宁德市2018年5月初中毕业班质量检测数学试题本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,第Ⅰ卷1至2页,第Ⅱ卷3至5页.满分150分.注意事项:1.答题前,考生务必在试题卷、答题卡规定位置填写本人准考证号、姓名等信息.考生要认真核对答题卡上粘贴的条形码的“准考证号、姓名”与考生本人准考证号,姓名是否一致.2.选择题每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑.如需改动,用橡皮擦干净后,再选涂其他答案标号.非选择题答案用0.5毫米黑色签字笔在答题卡上相应位置书写作答,在试题卷上答题无效.3.作图可先使用2B铅笔画出,确定后必须0.5毫米黑色签字笔描黑.4.考试结束,考生必须将试题卷和答题卡一并交回.第Ⅰ卷一、选择题:本题共10小题,每小题4分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.2018-的值是A.12018B.2018C.12018-D.2018-2.如图,若a∥b,∠1=58°,则∠2的度数是A.58°B.112°C.122°D.142°3.下列事件是必然事件的是A.2018年5月15日宁德市的天气是晴天B.从一副扑克中任意抽出一张是黑桃C.在一个三角形中,任意两边之和大于第三边D.打开电视,正在播广告4.由6个大小相同的小正方体拼成的几何体如图所示,则下列说法正确的是A.主视图的面积最大B.左视图的面积最大C.俯视图的面积最大D.三种视图的面积相等5.不等式组10,10≤>xx-⎧⎨+⎩的解集在数轴上表示正确的是C1-10D正面第4题图B1-10ab第2题图21A 1-106.在平面直角坐标系中,A ,B ,C ,D ,M ,N 的位置如图所示,若点M 的坐标为(-2 ,0), N 的坐标为(2 ,0),则在第二象限内的点是 A .A 点 B .B 点C .C 点D .D 点7.在“创文明城,迎省运会”合唱比赛中,10位评委给某队的评分如下表所示,则下列说法正确的是A .中位数是9.4分B .中位数是9.35分C .众数是3和1D .众数是9.4分8.如图,将△OAB 绕O 点逆时针旋转60°得到△OCD ,若OA=4,∠AOB =35°,则下列结论错误的是 A .∠BDO =60° B .∠BOC =25° C .OC=4D .BD=49.某校为进一步开展“阳光体育”活动,购买了一批篮球和足球.已知购买足球数量是篮球的2倍,购买足球用了4 000元,购买篮球用了2 800元,篮球单价比足球贵16元.若可列方程40002800162x x=-表示题中的等量关系,则方程中x 表示的是 A .足球的单价 B .篮球的单价C .足球的数量D .篮球的数量10.如图,已知等腰△ABC ,AB=BC ,D 是AC 上一点,线段BE 与BA 关于直线BD 对称,射线CE 交射线BD 于点F ,连接AE ,AF .则下列关系正确的是A .180∠∠AFE ABE +=︒B .12∠∠AEF ABC =C .180∠∠AEC ABC +=︒D .∠∠AEB ACB =第 Ⅱ 卷注意事项:DCBAO第8题图第6题图 MNABD C第10题图CFE DAB1.用0.5毫米黑色签字笔在答题卡上相应位置书写作答,在试题卷上作答,答案无效.2.作图可先使用2B 铅笔画出,确定后必须0.5毫米黑色签字笔描黑. 二、填空题:本题共6小题,每小题4分,共24分.11.2017年10月18日,中国共产党第十九次全国代表大会在北京隆重召开.从全国近89 400 000党员中产生的2 300名代表参加了此次盛会.将数据89 400 000用科学记数法表示为 .12.因式分解:222a -= .13.小明同学在计算一个多边形的内角和时,由于粗心少算了一个内角,结果得到的总和是800°,则少算了这个内角的度数为 .14. 已知一次函数23(0)y kx k k =++≠,不论k 为何值,该函数的图像都经过点A ,则点A 的坐标为 .15.小丽计算数据方差时,使用公式2222221(5)(8)(13)(14)(15)5S x x x x x ⎡⎤=-+-+-+-+-⎣⎦,则公式中= .16.如图,点A ,D 在反比例函数(0)my m x=<的图像上,点B ,C 在反比例函数(0)ny n x=>的图像上.若AB ∥CD ∥x 轴,AC ∥y 轴,且AB =4,AC =3,CD =2,则n = .三、解答题:本题共9小题,共86分.17.(本题满分8分)计算:14cos302-︒+-18.(本题满分8分)如图,在△ABC 中, D ,E 分别是AB ,AC 的中点,△ABC 的角平分线AG 交DE 于点F ,若∠ABC =70°,∠BAC =54°,求∠AFD 的度数.19.(本题满分8分)首届数字中国建设峰会于4月22日至24日在福州海峡国际会展中心如期举行,某校组织115位师生去会展中心参观,决定租用A ,B 两种CFEDBAG型号的旅游车.已知一辆A 型车可坐20人,一辆B 型车可坐28人,经测算学校需要租用这两种型号的旅游车共5辆.学校至少要租用B 型车多少辆?20.(本题满分8分)某中学为推动“时刻听党话 永远跟党走”校园主题教育活动,计划开展四项活动:A :党史演讲比赛,B :党史手抄报比赛,C :党史知识竞赛,D :红色歌咏比赛.校团委对学生最喜欢的一项活动进行调查,随机抽取了部分学生,并将调查结果绘制成图1,图2两幅不完整的统计图.请结合图中信息解答下列问题:(1)本次共调查了 名学生; (2)将图1的统计图补充完整;(3)已知在被调查的最喜欢“党史知识竞赛”项目的4个学生中只有1名女生,现从这4名学生中任意抽取2名学生参加该项目比赛,请用画树状图或列表的方法,求出恰好抽到一名男生一名女生的概率.21.(本题满分8分)如图,已知矩形ABCD ,E 是AB 上一点.(1)如图1,若F 是BC 上一点,在AD ,CD 上分别截取DH =BF ,DG =BE .求证:四边形EFGH 是平行四边形;(2)如图2,利用尺规分别在BC ,CD ,AD 上确定点F ,G ,H ,使得四边形EFGH 是特殊的平行四边形.(提示:①保留作图痕迹,不写作法;②只需作出一种情况即可)22.(本题满分10分)若正整数a ,b ,c 满足111a b c+=,则称正整数a ,b ,c 为一组和图1ADFHEG图2图2图1项谐整数.(1)判断2,3,6是否是一组和谐整数,并说明理由;(2)已知x ,y ,z (其中x y z <≤)是一组和谐整数,且1x m =+,3y m =+,用含m 的代数式表示z ,并求当24z =时m 的值.23.(本题满分10分)如图,在△ABC 中,∠ACB =90°,O 是AB 上一点,以OA 为半径的⊙O 与BC 相切于点D ,与AB 交于点E ,连接ED 并延长交AC 的延长线于点F .(1)求证:AE =AF ;(2)若DE =3,sin∠BDE =13,求AC 的长.24.(本题满分13分)如图1,在△ABC 中,∠BAC =90°,AB =AC =4,D 是BC 上一个动点,连接AD ,以AD 为边向右侧作等腰直角△ADE ,其中∠ADE =90°. (1)如图2,G ,H 分别是边AB ,BC 的中点,连接DG ,AH ,EH .求证:△AGD ∽△AHE ;(2)如图3,连接BE ,直接写出当BD 为何值时,△ABE 是等腰三角形; (3)在点D 从点B 向点C 运动过程中,求△ABE 周长的最小值.25.(本题满分13分)已知抛物线22(0)y ax ax c a =-+<的图像过点A (3,m ).(1)当a =-1,m =0时,求抛物线的顶点坐标; (2)若P (t ,n )为该抛物线上一点,且n <m ,求t 的取值范围;(3)如图,直线:(0)l y kx c k =+<交抛物线于B ,C 两点,点Q (x ,y )是抛物线上点B ,C 之间的一个动点,作QD ⊥x 轴交直线 l 于点D ,作QE ⊥y 轴于点E ,连接DE .设∠QED=β,当x 2≤≤4时,β 恰好满足°°30≤≤60β,求a 的值.2018年宁德市初中毕业班质量检测B图1 ABCD图2图3ABCDABCDGH数学试题参考答案及评分标准⑴本解答给出了一种或几种解法供参考,如果考生的解法与本解答不同,可参照本答案的评分标准的精神进行评分.⑵对解答题,当考生的解答在某一步出现错误时,如果后续部分的解答未改变该题的立意,可酌情给分.⑶解答右端所注分数表示考生正确作完该步应得的累加分数. ⑷评分只给整数分,选择题和填空题均不给中间分.一、选择题:(本大题有10小题,每小题4分,满分40分)1.B 2.C 3.C 4.A 5.D 6.A 7.B 8.D 9.D 10.B 二、填空题:(本大题有6小题,每小题4分,满分24分)11.78.9410⨯ 12.2(1)(1)a a +- 13.100 14.(-2,3) 15.11 16.83三、解答题(本大题共9小题,共86分.请在答题卡...的相应位置作答) 17.(本题满分8分)解:原式= 142- ····················· 6分 =12························ 8分 18.(本题满分8分)证明:∵∠BAC =54°,AG 平分∠BAC ,∴∠BAG =12∠BAC =27°. ········ 2分 ∴∠BGA =180 °-∠ABC -∠ BAG =83° ·· 4分 又∵点D ,E 分别是AB ,AC 的中点,∴DE ∥BC . ·············· 6分 ∴∠AFD =∠BGA =83°. ········· 8分 19.(本题满分8分)解: 设租用B 型车x 辆,则租用A 型车(5-x )辆,根据题意,得 ····· 1分 2820(5)115≥x x +-. ····················· 5分解得 158≥x . ························· 7分因为x 为整数,所以x 的最小值是2.答:学校至少租用了2辆B 型车. ··················· 8分 20.(本题满分8分)(1)40; ···························· 2分CFEDBA(2)图略 ···························· 4分 (3)列表如下: ·························· 6分女生的结果有6种,所以抽到一名男生和一名女生的概率是612,即12. ·· 8分 21.(本题满分8分)(1)证明:∵四边形ABCD 是矩形,∴AD =BC ,AB =CD ,∠A =∠B =∠C =∠D =90°, ∵DG =BE ,DH =BF ,∴△GDH ≌△EBF .····· 2分 ∴GH = EF .∵AD =BC ,AB =CD ,DH =BF ,DG =BE , ∴AD -DH =BC -BF ,AB -BE =CD -DG . 即AH=CF ,AE =CG .∴△AEH ≌△CGF . ········ 4分 ∴EH =GF .∴四边形EFGH 是平行四边形. ···5分 (2)作图如下:作法一:作菱形(如图2) ····················· 7分 ∴四边形EFGH 就是所求作的特殊平行四边形. ············· 8分 作法二:作矩形(如图3,图4) ·················· 7分∴四边形EFGH 就是所求作的特殊平行四边形. ············ 8分 22.(本题满分10分)ADFHBEGC图3(1)是 ······························· 1分理由如下:∵111362+=,满足和谐整数的定义,∴2,3,6是和谐整数. ····················· 4分(2) 解:∵x y z <≤,依题意,得 111yzx+=.∵1x m =+,3y m =+,∴11111213(1)(3)z x y m m m m =-=-=++++.∴(1)(3)2m m z ++=. ······················ 7分∵24z =,∴(1)(3)242m m ++=.解得 59,m m ==-. ······················ 9分 ∵x 是正整数,∴5m =. ·························· 10分23.(本题满分10分)解:(1)证明:连接OD .∵ OD =OE ,∴∠ODE =∠OED . ·········· 1分∵直线BC 为⊙O 的切线, ∴OD ⊥BC .∴∠ODB =90°. ··········· 2分 ∵∠ACB =90°,∴OD ∥AC . ············ 3分∴∠ODE =∠F .∴∠OED =∠F . ················· 4分 ∴AE =AF . ··················· 5分(2)连接AD .∵AE 是⊙O 的直径∴∠ADE =90°. ················· 6分 ∵AE =AF ,B图1∴DF =DE =3. ∵∠ACB =90°.∴∠DAF +∠F =90°,∠CDF +∠F =90°, ∴∠DAF =∠CDF =∠BDE . ······· 7分 在Rt△ADF 中,1sin sin 3∠DF DAF BDE AF ==∠=, ∴39AF DF ==. ········· 8分 在Rt△CDF 中,1sin sin 3∠CF CDF BDE DF ==∠=, ∴113CF DF ==. ········· 9分∴AC =AF -CF =8. ··········· 10分 24.(本题满分13分)解:(1)由题意知△ABC 和△ADE∴∠B =∠DAE =45°.∵G 为AB 中点,H 为BC 中点, ∴AH ⊥BC .∴∠BAH =45°=∠DAE .∴∠GAD =∠HAE . ·········· 1分 在等腰直角△BAH 和等腰直角△DAE 中, AH AB =,AE =.∴AH AE AG AD =. ··········· 3分 ∴△AGD ∽△AHE . ·········· 4分(2)当BD =0△ABE 是等腰三角形. ··········· 8分(注:给出0和1得2分) (3)解法一:当点D 与点B 重合时,点E 的位置记为点M .此时,∠ABM =∠BAC =90°,∠AMB =∠BAM =45°,BM = AB = AC .∴四边形ABMC 是正方形. ∴∠BMC =90°,∴∠AMC =∠BMC -∠AMB =45°, ··· 9分B图1BACDE ′E图2∵∠BAM =∠DAE =45°, ∴∠BAD =∠MAE ,在等腰直角△BAM 和等腰直角△DAE 中,AM =,AE =.∴AM AE AB AD =.∴△ABD ∽△AME . ∴∠AME =∠ABD =45°∴点E 在射线MC 上. ····· 10分作点B 关于直线MC 的对称点N ,连接AN 交MC 于点E ′, ∵BE +AE =NE +AE ≥AN =NE ′+AE ′=BE ′+AE′, ∴△ABE ′就是所求周长最小的△ABE . 在Rt△ABN 中,∵AB =4,BN =2BM =2AB =8, ∴AN =AN ==∴△ABE 周长最小值为4AB AN +=+. ················· 13分 解法二:取BC 的中点H ,连接AH , 同解法一证△ACE ∽△AHD . ∴∠ACE=∠AHD=90°.∴点E 在过点C 且垂直于AC 的直线上,记为直线l . ······· 10分 点A 关于直线l 的对称点M ,连接BM 交直线l 于点E ′, 同解法一,△ABE ′就是所求周长最小的△ABE .∴△ABE 周长最小值为4AB BM +=+. ··········· 13分25.(本题满分13分) 解:(1)当a =-1,m =0时,22y x x c =-++,A 点的坐标为(3,0),∴-9+6+c =0.解得 c =3. ··························· 2分 ∴抛物线的表达式为223y x x =-++. 即2(1)4y x =--+.∴抛物线的顶点坐标为(1,4). ················· 4分图2图3BACDE ′MEH(2)∵22y ax ax c =-+的对称轴为直线212a x a-==-, ·········· 5分 ∴点A 关于对称轴的对称点为(-1,m ). ············· 6分 ∵0<a ,∴当1<x ,y 随x 的增大而增大; 当1>x ,y 随x 的增大而减小.又∵n <m ,∴当点P 在对称轴左边时,t <-1;当点P 在对称轴右边时,t >3.综上所述:t 的取值范围为t <-1或t >3. ············· 8分 (3)∵点Q (x ,y )在抛物线上,∴22y ax ax c =-+.又∵QD ⊥x 轴交直线 :(0)l y kx c k =+<于点D ,∴D 点的坐标为(x ,kx+c ).又∵点Q 是抛物线上点B ,C 之间的一个动点,∴222()(2)QD ax ax c kx c ax a k x =-+-+=-+.················· 10分∵QE =x ,∴在Rt △QED 中,2(2)tan 2QD ax a k x ax a k QE x -+===--β. ············ 11分 ∴tan β是关于x 的一次函数,∵a <0,∴tan β随着x 的增大而减小.又∵当x 2≤≤4时,β恰好满足°°30≤≤60β,且tan β随着β的增大而增大, ∴当x=2时,β=60°;当x=4时,β=30°.∴2242a a k a a k ⎧--=⎪⎨--=⎪⎩解得 k a ⎧=⎪⎨=⎪⎩∴a =. ························· 13分。
