北京市2012届高三数学文科仿真模拟卷8
2012年北京市高考数学试卷(文科)答案与解析

2012年北京市高考数学试卷(文科)参考答案与试题解析一、选择题共8小题,每小题5分,共40分,在每小题给出的四个选项中,选出符合题目要求的一项.1.(5分)(2012•北京)已知集合A={x∈R|3x+2>0},B={x∈R|(x+1)(x﹣3)>0},则A∩B=()A.(﹣∞,﹣1)B.(﹣1,)C.﹙,3﹚D.(3,+∞)考点:一元二次不等式的解法;交集及其运算.专题:集合.分析:求出集合B,然后直接求解A∩B.解答:解:因为B={x∈R|(x+1)(x﹣3)>0﹜={x|x<﹣1或x>3},又集合A={x∈R|3x+2>0﹜={x|x},所以A∩B={x|x}∩{x|x<﹣1或x>3}={x|x>3},故选:D.点评:本题考查一元二次不等式的解法,交集及其运算,考查计算能力.2.(5分)(2012•北京)在复平面内,复数对应的点的坐标为()A.(1,3)B.(3,1)C.(﹣1,3)D.(3,﹣1)考点:复数代数形式的乘除运算;复数的代数表示法及其几何意义.专题:数系的扩充和复数.分析:由==1+3i,能求出在复平面内,复数对应的点的坐标.解答:解:∵===1+3i,∴在复平面内,复数对应的点的坐标为(1,3),故选A.点评:本题考查复数的代数形式的乘积运算,是基础题.解题时要认真审题,注意复数的几何意义的求法.3.(5分)(2012•北京)设不等式组,表示的平面区域为D,在区域D内随机取一个点,则此点到坐标原点的距离大于2的概率是()A.B.C.D.考点:二元一次不等式(组)与平面区域;几何概型.专题:概率与统计.分析:本题属于几何概型,利用“测度”求概率,本例的测度即为区域的面积,故只要求出题中两个区域:由不等式组表示的区域和到原点的距离大于2的点构成的区域的面积后再求它们的比值即可.解答:解:其构成的区域D如图所示的边长为2的正方形,面积为S1=4,满足到原点的距离大于2所表示的平面区域是以原点为圆心,以2为半径的圆外部,面积为=4﹣π,∴在区域D内随机取一个点,则此点到坐标原点的距离大于2的概率P=故选:D.点评:本题考查几何概型,几何概型的概率的值是通过长度、面积、和体积、的比值得到,本题是通过两个图形的面积之比得到概率的值.4.(5分)(2012•北京)执行如图所示的程序框图,输出的S值为()A.2B.4C.8D.16考点:循环结构.专题:算法和程序框图.分析:列出循环过程中S与K的数值,不满足判断框的条件即可结束循环.解答:解:第1次判断后S=1,k=1,第2次判断后S=2,k=2,第3次判断后S=8,k=3,第4次判断后3<3,不满足判断框的条件,结束循环,输出结果:8.故选C.点评:本题考查循环框图的应用,注意判断框的条件的应用,考查计算能力.5.(5分)(2012•北京)函数f(x)=的零点个数为()A.0B.1C.2D.3考点:根的存在性及根的个数判断.专题:函数的性质及应用.分析:先判断函数的单调性,由于在定义域上两个增函数的和仍为增函数,故函数f(x)为单调增函数,而f(0)<0,f()>0由零点存在性定理可判断此函数仅有一个零点解答:解:函数f(x)的定义域为[0,+∞)∵y=在定义域上为增函数,y=﹣在定义域上为增函数∴函数f(x)=在定义域上为增函数而f(0)=﹣1<0,f(1)=>0故函数f(x)=的零点个数为1个故选B点评:本题主要考查了函数零点的判断方法,零点存在性定理的意义和运用,函数单调性的判断和意义,属基础题6.(5分)(2012•北京)已知{a n}为等比数列,下面结论中正确的是()A.a1+a3≥2a2B.a12+a32≥2a22C.若a1=a3,则a1=a2D.若a3>a1,则a4>a2考点:等比数列的性质.专题:等差数列与等比数列.分析:a1+a3=,当且仅当a2,q同为正时,a1+a3≥2a2成立;,所以;若a1=a3,则a1=a1q2,从而可知a1=a2或a1=﹣a2;若a3>a1,则a1q2>a1,而a4﹣a2=a1q(q2﹣1),其正负由q的符号确定,故可得结论.解答:解:设等比数列的公比为q,则a1+a3=,当且仅当a2,q同为正时,a1+a3≥2a2成立,故A不正确;,∴,故B正确;若a1=a3,则a1=a1q2,∴q2=1,∴q=±1,∴a1=a2或a1=﹣a2,故C不正确;若a3>a1,则a1q2>a1,∴a4﹣a2=a1q(q2﹣1),其正负由q的符号确定,故D不正确故选B.点评:本题主要考查了等比数列的性质.属基础题.7.(5分)(2012•北京)某三棱锥的三视图如图所示,该三棱锥的表面积是()A.28+6B.30+6C.56+12D.60+12考点:由三视图求面积、体积.专题:立体几何.分析:通过三视图复原的几何体的形状,利用三视图的数据求出几何体的表面积即可.解答:解:三视图复原的几何体是底面为直角边长为4和5的三角形,一个侧面垂直底面的等腰三角形,高为4,底边长为5,如图,所以S底==10,S后=,S右==10,S左==6.几何体的表面积为:S=S底+S后+S右+S左=30+6.故选:B.点评:本题考查三视图与几何体的关系,注意表面积的求法,考查空间想象能力计算能力.8.(5分)(2012•北京)某棵果树前n年的总产量S n与n之间的关系如图所示.从目前记录的结果看,前m年的年平均产量最高,则m的值为()A.5B.7C.9D.11考点:函数的图象与图象变化;函数的表示方法.专题:函数的性质及应用.分析:由已知中图象表示某棵果树前n年的总产量S与n之间的关系,可分析出平均产量的几何意义为原点与该点边线的斜率,结合图象可得答案.解答:解:若果树前n年的总产量S与n在图中对应P(S,n)点则前n年的年平均产量即为直线OP的斜率由图易得当n=9时,直线OP的斜率最大即前9年的年平均产量最高,故选C点评:本题以函数的图象与图象变化为载体考查了斜率的几何意义,其中正确分析出平均产量的几何意义是解答本题的关键.二、填空题共6小题,每小题5分,共30分.9.(5分)(2012•北京)直线y=x被圆x2+(y﹣2)2=4截得的弦长为.考点:直线与圆相交的性质.专题:直线与圆.分析:确定圆的圆心坐标与半径,求得圆心到直线y=x的距离,利用垂径定理构造直角三角形,即可求得弦长.解答:解:圆x2+(y﹣2)2=4的圆心坐标为(0,2),半径为2∵圆心到直线y=x的距离为∴直线y=x被圆x2+(y﹣2)2=4截得的弦长为2=故答案为:点评:本题考查直线与圆相交,考查圆的弦长,解题的关键是求得圆心到直线y=x的距离,利用垂径定理构造直角三角形求得弦长.10.(5分)(2012•北京)已知{a n}为等差数列,S n为其前n项和,若a1=,S2=a3,则a2= 1,S n=.考点:等差数列的前n项和;等差数列的通项公式.专题:等差数列与等比数列.分析:根据等差数列的性质可求出公差,从而可求出第二项,以及等差数列的前n项和.解答:解:根据{a n}为等差数列,S2=a1+a2=a3=+a2;∴d=a3﹣a2=∴a2=+=1S n==故答案为:1,点评:本题主要考查了等差数列的前n项和,以及等差数列的通项公式,属于容易题.11.(5分)(2012•北京)在△ABC中,若a=3,b=,,则∠C的大小为.考点:正弦定理.专题:解三角形.分析:利用正弦定理=,可求得∠B,从而可得∠C的大小.解答:解:∵△ABC中,a=3,b=,,∴由正弦定理=得:=,∴sin∠B=.又b<a,∴∠B<∠A=.∴∠B=.∴∠C=π﹣﹣=.故答案为:.点评:本题考查正弦定理,求得∠B是关键,易错点在于忽视“△中大变对大角,小边对小角”结论的应用,属于基础题.12.(5分)(2012•北京)已知函数f(x)=lgx,若f(ab)=1,则f(a2)+f(b2)=2.考点:对数的运算性质.专题:函数的性质及应用.分析:由函数f(x)=lgx,f(ab)=lg(ab)=1,知f(a2)+f(b2)=lga2+lgb2=2lg(ab).由此能求出结果.解答:解:∵函数f(x)=lgx,f(ab)=lg(ab)=1,f(a2)+f(b2)=lga2+lgb2=lg(ab)2=2lg(ab)=2.故答案为:2.点评:本题考查对数的运算性质,是基础题.解题时要认真审题,仔细解答.13.(5分)(2012•北京)己知正方形ABCD的边长为1,点E是AB边上的动点.则的值为1.考点:平面向量数量积的运算.专题:平面向量及应用.分析:直接利用向量转化,求出数量积即可.解答:解:因为====1.故答案为:1点评:本题考查平面向量数量积的应用,考查计算能力.14.(5分)(2012•北京)已知f(x)=m(x﹣2m)(x+m+3),g(x)=2x﹣2.若∀x∈R,f (x)<0或g(x)<0,则m的取值范围是(﹣4,0).考点:复合命题的真假;全称命题.专题:简易逻辑.分析:由于g(x)=2x﹣2≥0时,x≥1,根据题意有f(x)=m(x﹣2m)(x+m+3)<0在x >1时成立,根据二次函数的性质可求解答:解:∵g(x)=2x﹣2,当x≥1时,g(x)≥0,又∵∀x∈R,f(x)<0或g(x)<0∴此时f(x)=m(x﹣2m)(x+m+3)<0在x≥1时恒成立则由二次函数的性质可知开口只能向下,且二次函数与x轴交点都在(1,0)的左面则∴﹣4<m<0故答案为:(﹣4,0)点评:本题主要考查了全称命题与特称命题的成立,指数函数与二次函数性质的应用是解答本题的关键三、解答题共6小题,共80分,解答应写出文字说明,演算步骤或证明过程.15.(13分)(2012•北京)已知函数f(x)=.(1)求f(x)的定义域及最小正周期;(2)求f(x)的单调递减区间.考点:三角函数中的恒等变换应用;正弦函数的定义域和值域;复合三角函数的单调性.专题:三角函数的图像与性质.分析:(1)由sinx≠0可得x≠kπ(k∈Z),将f(x)化为f(x)=sin(2x﹣)﹣1即可求其最小正周期;(2)由(1)得f(x)=sin(2x﹣)﹣1,再由2kπ+≤2x﹣≤2kπ+,x≠kπ(k∈Z)即可求f(x)的单调递减区间.解答:解:(1)由sinx≠0得x≠kπ(k∈Z),故求f(x)的定义域为{x|x≠kπ,k∈Z}.∵f(x)==2cosx(sinx﹣cosx)=sin2x﹣cos2x﹣1=sin(2x﹣)﹣1∴f(x)的最小正周期T==π.(2)∵函数y=sinx的单调递减区间为[2kπ+,2kπ+](k∈Z)∴由2kπ+≤2x﹣≤2kπ+,x≠kπ(k∈Z)得kπ+≤x≤kπ+,(k∈Z)∴f(x)的单调递减区间为:[kπ+,kπ+](k∈Z)点评:本题考查三角函数中的恒等变换应用,着重考查正弦函数的单调性,注重辅助角公式的考察应用,求得f(x=sin(2x﹣)﹣1是关键,属于中档题.16.(14分)(2012•北京)如图1,在Rt△ABC中,∠C=90°,D,E分别为AC,AB的中点,点F为线段CD上的一点,将△ADE沿DE折起到△A1DE的位置,使A1F⊥CD,如图2.(1)求证:DE∥平面A1CB;(2)求证:A1F⊥BE;(3)线段A1B上是否存在点Q,使A1C⊥平面DEQ?说明理由.考点:直线与平面垂直的性质;直线与平面平行的判定;直线与平面垂直的判定.专题:空间位置关系与距离;立体几何.分析:(1)D,E分别为AC,AB的中点,易证DE∥平面A1CB;(2)由题意可证DE⊥平面A1DC,从而有DE⊥A1F,又A1F⊥CD,可证A1F⊥平面BCDE,问题解决;(3)取A1C,A1B的中点P,Q,则PQ∥BC,平面DEQ即为平面DEP,由DE⊥平面,P是等腰三角形DA1C底边A1C的中点,可证A1C⊥平面DEP,从而A1C⊥平面DEQ.解答:解:(1)∵D,E分别为AC,AB的中点,∴DE∥BC,又DE⊄平面A1CB,∴DE∥平面A1CB.(2)由已知得AC⊥BC且DE∥BC,∴DE⊥AC,∴DE⊥A1D,又DE⊥CD,∴DE⊥平面A1DC,而A1F⊂平面A1DC,∴DE⊥A1F,又A1F⊥CD,∴A1F⊥平面BCDE,∴A1F⊥BE.(3)线段A1B上存在点Q,使A1C⊥平面DEQ.理由如下:如图,分别取A1C,A1B的中点P,Q,则PQ∥BC.∵DE∥BC,∴DE∥PQ.∴平面DEQ即为平面DEP.由(Ⅱ)知DE⊥平面A1DC,∴DE⊥A1C,又∵P是等腰三角形DA1C底边A1C的中点,∴A1C⊥DP,∴A1C⊥平面DEP,从而A1C⊥平面DEQ,故线段A1B上存在点Q,使A1C⊥平面DEQ.点评:本题考查直线与平面平行的判定,直线与平面垂直的判定与性质,考查学生的分析推理证明与逻辑思维能力,综合性强,属于难题.17.(13分)(2012•北京)近年来,某市为促进生活垃圾的分类处理,将生活垃圾分为厨余垃圾、可回收物和其他垃圾三类,并分别设置了相应的垃圾箱,为调查居民生活垃圾分类投放情况,先随机抽取了该市三类垃圾箱总计1000吨生活垃圾,数据统计如下(单位:吨); “厨余垃圾”箱 “可回收物”箱 “其他垃圾”箱 厨余垃圾 400 100 100可回收物 30 240 30其他垃圾 20 20 60(1)试估计厨余垃圾投放正确的概率;(2)试估计生活垃圾投放错误的概率;(3)假设厨余垃圾在“厨余垃圾”箱、“可回收物”箱、“其他垃圾”箱的投放量分别为a ,b ,c ,其中a >0,a+b+c=600.当数据a ,b ,c 的方差s 2最大时,写出a ,b ,c 的值(结论不要求证明),并求此时s 2的值.(求:S 2=[++…+],其中为数据x 1,x 2,…,x n 的平均数)考点:模拟方法估计概率;极差、方差与标准差.专题:概率与统计.分析: (1)厨余垃圾600吨,投放到“厨余垃圾”箱400吨,故可求厨余垃圾投放正确的概率; (2)生活垃圾投放错误有200+60+20+20=300,故可求生活垃圾投放错误的概率;(3)计算方差可得=,因此有当a=600,b=0,c=0时,有s 2=80000.解答: 解:(1)由题意可知:厨余垃圾600吨,投放到“厨余垃圾”箱400吨,故厨余垃圾投放正确的概率为;(2)由题意可知:生活垃圾投放错误有200+60+20+20=300,故生活垃圾投放错误的概率为;(3)由题意可知:∵a+b+c=600,∴a ,b ,c 的平均数为200 ∴=,∵(a+b+c )2=a 2+b 2+c 2+2ab+2bc+2ac ≥a 2+b 2+c 2,因此有当a=600,b=0,c=0时,有s 2=80000. 点评:本题考查概率知识的运用,考查学生的阅读能力,属于中档题.18.(13分)(2012•北京)已知函数f (x )=ax 2+1(a >0),g (x )=x 3+bx .(1)若曲线y=f (x )与曲线y=g (x )在它们的交点(1,c )处有公共切线,求a ,b 的值;(2)当a=3,b=﹣9时,函数f(x)+g(x)在区间[k,2]上的最大值为28,求k的取值范围.考点:利用导数求闭区间上函数的最值;利用导数研究曲线上某点切线方程.专题:导数的综合应用.分析:(1)根据曲线y=f(x)与曲线y=g(x)在它们的交点(1,c)处具有公共切线,可知切点处的函数值相等,切点处的斜率相等,故可求a、b的值;(2)当a=3,b=﹣9时,设h(x)=f(x)+g(x)=x3+3x2﹣9x+1,求导函数,确定函数的极值点,进而可得k≤﹣3时,函数h(x)在区间[k,2]上的最大值为h(﹣3)=28;﹣3<k<2时,函数h(x)在区间[k,2]上的最大值小于28,由此可得结论.解答:解:(1)f(x)=ax2+1(a>0),则f′(x)=2ax,k1=2a,g(x)=x3+bx,则g′(x)=3x2+b,k2=3+b,由(1,c)为公共切点,可得:2a=3+b ①又f(1)=a+1,g(1)=1+b,∴a+1=1+b,即a=b,代入①式,可得:a=3,b=3.(2)当a=3,b=﹣9时,设h(x)=f(x)+g(x)=x3+3x2﹣9x+1则h′(x)=3x2+6x﹣9,令h'(x)=0,解得:x1=﹣3,x2=1;∴k≤﹣3时,函数h(x)在(﹣∞,﹣3)上单调增,在(﹣3,1]上单调减,(1,2)上单调增,所以在区间[k,2]上的最大值为h(﹣3)=28﹣3<k<2时,函数h(x)在区间[k,2]上的最大值小于28所以k的取值范围是(﹣∞,﹣3]点评:本题考查导数知识的运用,考查导数的几何意义,考查函数的单调性与最值,解题的关键是正确求出导函数.19.(14分)(2012•北京)已知椭圆C:+=1(a>b>0)的一个顶点为A(2,0),离心率为,直线y=k(x﹣1)与椭圆C交于不同的两点M,N,(Ⅰ)求椭圆C的方程;(Ⅱ)当△AMN的面积为时,求k的值.考点:直线与圆锥曲线的综合问题;椭圆的标准方程.专题:圆锥曲线的定义、性质与方程.分析:(Ⅰ)根据椭圆一个顶点为A (2,0),离心率为,可建立方程组,从而可求椭圆C的方程;(Ⅱ)直线y=k(x﹣1)与椭圆C联立,消元可得(1+2k2)x2﹣4k2x+2k2﹣4=0,从而可求|MN|,A(2,0)到直线y=k(x﹣1)的距离,利用△AMN的面积为,可求k的值.解答:解:(Ⅰ)∵椭圆一个顶点为A (2,0),离心率为,∴∴b=∴椭圆C的方程为;(Ⅱ)直线y=k(x﹣1)与椭圆C联立,消元可得(1+2k2)x2﹣4k2x+2k2﹣4=0设M(x1,y1),N(x2,y2),则x1+x2=,∴|MN|==∵A(2,0)到直线y=k(x﹣1)的距离为∴△AMN的面积S=∵△AMN的面积为,∴∴k=±1.点评:本题考查椭圆的标准方程,考查直线与椭圆的位置关系,考查三角形面积的计算,解题的关键是正确求出|MN|.20.(13分)(2012•北京)设A是如下形式的2行3列的数表,a b cd e f满足性质P:a,b,c,d,e,f∈[﹣1,1],且a+b+c+d+e+f=0.记r i(A)为A的第i行各数之和(i=1,2),C j(A)为A的第j列各数之和(j=1,2,3);记k(A)为|r1(A)|,|r2(A)|,|c1(A)|,|c2(A)|,|c3(A)|中的最小值.(1)对如下数表A,求k(A)的值1 1 ﹣0.80.1 ﹣0.3 ﹣1(2)设数表A形如1 1 ﹣1﹣2dd d ﹣1其中﹣1≤d≤0.求k(A)的最大值;(Ⅲ)对所有满足性质P的2行3列的数表A,求k(A)的最大值.考点:进行简单的演绎推理.专题:推理和证明.分析:(1)根据r i(A)为A的第i行各数之和(i=1,2),C j(A)为A的第j列各数之和(j=1,2,3);记k(A)为|r1(A)|,|r2(A)|,|c1(A)|,|c2(A)|,|c3(A)|中的最小值可求出所求;(2)k(A)的定义可求出k(A)=1+d,然后根据d的取值范围可求出所求;(III)任意改变A三维行次序或列次序,或把A中的每个数换成它的相反数,所得数表A*仍满足性质P,并且k(A)=k(A*)因此,不防设r1(A)≥0,c1(A)≥0,c2(A)≥0,然后利用不等式的性质可知3k(A)≤r1(A)+c1(A)+c2(A),从而求出k(A)的最大值.解答:解:(1)因为r1(A)=1.2,r2(A)=﹣1.2,c1(A)=1.1,c2(A)=0.7,c3(A)=﹣1.8,所以k(A)=0.7(2)r1(A)=1﹣2d,r2(A)=﹣1+2d,c1(A)=c2(A)=1+d,c3(A)=﹣2﹣2d 因为﹣1≤d≤0,所以|r1(A)|=|r2(A)|≥1+d≥0,|c3(A)|≥1+d≥0所以k(A)=1+d≤1当d=0时,k(A)取得最大值1(III)任给满足性质P的数表A(如下所示)a b cd e f任意改变A三维行次序或列次序,或把A中的每个数换成它的相反数,所得数表A*仍满足性质P,并且k(A)=k(A*)因此,不防设r1(A)≥0,c1(A)≥0,c2(A)≥0,由k(A)的定义知,k(A)≤r1(A),k(A)≤c1(A),k(A)≤c2(A),从而3k(A)≤r1(A)+c1(A)+c2(A)=(a+b+c)+(a+d)+(b+e)=(a+b+c+d+e+f)+(a+b﹣f)=a+b﹣f≤3所以k(A)≤1由(2)可知,存在满足性质P的数表A使k(A)=1,故k(A)的最大值为1.点评:本题主要考查了进行简单的演绎推理,同时分析问题的能力以及不等式性质的应用,同时考查了转化的思想,属于中档题.。
北京市2012届高三数学文科仿真模拟卷1.pdf

北京市2012届高三数学文科仿真模拟卷1 选择题(本大题共8小题,每小题5分,共40分,在每小题给出的四个选项中,只有一项是符合题目要求的) 1.设集合,,则等于 A B C D 2.已知,,,当∥时,实数等于 A B 0 C D 3.设是两条不同的直线,是三个不同的平面,则下列命题正确的是A 若,则B 若,则C 若,则D 若,则 4.已知等比数列中,各项都是正数,且成等差数列,则等于 A B C D 5.设抛物线的焦点与椭圆的右焦点重合,则p的值为,A -4B 4C - 8D 8 6. a=0是函数为奇函数的 A 充分但不必要条件 B必要但不充分条件 C 充要条件 D 既不充分也不必要条件 7.已知点的坐标满足条件,那么点P到直线的距离的最小值为 A B C 2 D 1 8.已知定义在区间上的函数的图像关于直线对称,当时,,如果关于的方程有解,记所有解的和为S, 则S不可能为 A B C D 二.填空题(本大题共6小题,每小题5分,共30分) 9.在复平面内,复数对应的点的坐标为________________________. 10. 在两个袋内,分别装着写有0,1,2,3,4,5六个数字的6张卡片,今从每个袋中任取一张卡片,则两数之和等于5的概率为______________________. 11.在△ABC中,若b=1,c=,,则a=________,________________. 12.如图是一个正三棱柱的三视图,若三棱柱的体积是,则____________________. 13.某棉纺厂为了解一批棉花的质量,从中随机抽测100根棉花纤维的长度(棉花纤维的长度是棉花质量 的重要指标)。
所得数据均在区间中,其频率分布直方图如图所示,由图中数据可知_______, 在抽测的100根中,棉花纤维的长度在内的有__________根。
14.给定集合A,若对于任意,有,且,则称集合A为闭集合,给出如下三个结论: ①集合为闭集合; ②集合为闭集合; ③若集合为闭集合,则为闭集合; 其中正确结论的序号是________________________. 三.解答题(本大题共6小题,共80分. 解答应写出文字说明,演算步骤或证明过程.) 15. (本小题满分13分) 已知函数, 求函数的最小正周期; (2)求f(x)在区间上的最小值及f(x)取最小值时x的值。
北京市通州区2012届高三上学期文科数学期末摸底考试及答案

北京市通州区2012届高三上学期期末摸底考试数学(文科)试卷2012年1月本试卷分第I 卷和第II 卷两部分,第I 卷第1至2页,第II 卷2至4页,共150分.考试时间长120分钟.考生务必将答案答在答题卡上,在试题卷上作答无效.考试结束后,将本试题卷和答题卡一并交回.第Ⅰ卷 (选择题 共40分)一、本大题共8个小题,每小题5分,共40分.在每小题列出的四个选项中,选出符合题目要求的一项.把正确答案选项的标号填涂在答题卡上. 1.已知集合{} |10A x x =-<,{} |02B x x ≤=<,那么A B 等于A .{}1x x <- B .{}2x x >C .{} |01x x ≤<D .{}|12x x <<2.复数11ii-+等于 A .1- B .i - C .1 D .i3.已知向量()1,2=-a ,(),4m =b ,且//a b ,那么2-a b 等于A .()4,0B .()0,4C .()4,8-D .()4,8-4.已知数列{n a } 是等差数列,且121a a +=,511a =,那么数列{n a }的前5项的和5S 等于A .22B .25C .30D .355.已知,a b ∈R ,那么“1122log log a b >”是 “a b <”的 A .充分不必要条件 B .必要不充分条件 C .充要条件 D .既不充分也不必要条件6.如右图,设A ,B 两点在河的两岸,一测量者在A 的同侧,在所在的河岸边选定一点C ,测出AC 的距离为50m ,45ACB ∠=︒,105CAB ∠=︒后,就可以计算出A ,B 两点的距离为(其中2 1.414=⋅⋅⋅,3 1.732=⋅⋅⋅,精确到0.1)A .70.7mB .78.7mC .86.6mD .90.6m7.过圆()()22125x y -++=上一点()3,1M -的切线方程是 A .270x y +-= B .250x y +-= C .210x y +-=D .250x y --=8.当()3,4x ∈时,不等式()()2log 230a x x -+-<恒成立,则实数a 的取值范围是 A .10,2⎛⎤ ⎥⎝⎦ B .1,12⎡⎫⎪⎢⎣⎭C .(]1,2D .[)2,+∞第Ⅱ卷 (非选择题 共110分)二、填空题:本大题共6个小题,每小题5分,共30分. 把答案填在答题卡相应的位置上. 9.观察下列式子:213122+<,221151233++<,222111712344+++<,… ,根据以上式子可以猜想:2221111232012++++< _________________.10.如图,已知图中的三个直角三角形是一个几何体的三视图,那么这个几何体的体积等于________________.11.某程序框图如图所示,该程序运行后,输出的x 值是______________.12.已知不等式组 3,1,30,x y x y x +⎧⎪--⎨⎪-⎩≥≥≤ 那么2z x y =+的最小值是________________.13.已知双曲线的一个焦点与抛物线218x y =-的焦点相同,且双曲线的离心率是2,那么双曲线的渐近线方程是___________________.开 始n =n +1x =2x +1n ≤3输出x 结束是否 n =1,x =1(第11题图)(第10题图)14.下面四个命题:①已知函数(),0,,0,x x f x x x ⎧⎪=⎨-<⎪⎩≥ 且()()44f a f +=,那么4a =-;②一组数据18,21,19,a ,22的平均数是20,那么这组数据的方差是2;③要得到函数sin 23y x π⎛⎫=+⎪⎝⎭的图象,只要将sin 2y x =的图象向左平移3π单位; ④已知奇函数()f x 在(0,)+∞为增函数,且(1)0f -=,则不等式()0f x <的解集{}1x x <-.其中正确的是__________________.三、解答题:本大题共6个小题,共80分.解答题写出文字说明,演算步骤或证明过程. 15.(本小题共13分)已知函数()2sin 22cos 1f x x x =+-.(Ⅰ)求函数()f x 的最小正周期和最大值; (Ⅱ)求函数()f x 在区间3,44ππ⎡⎤⎢⎥⎣⎦上的最大值和最小值.16.(本小题共13分)如图,四边形ABCD 是矩形,BC ⊥平面ABE ,F 是CE 上一点,BF ⊥平面ACE ,点M ,N 分别是CE ,DE 的中点.(Ⅰ)求证://MN 平面ABE ; (Ⅱ)求证:AE BE ⊥.17.(本小题共13分)已知甲袋中有1只白球,2只红球;乙袋中有2只白球,2只红球,现从两袋中各取一球. (Ⅰ)两球颜色相同的概率; (Ⅱ)至少有一个白球的概率.18.(本小题共13分)已知函数()ln .f x ax x =-(Ⅰ)若曲线()y f x =在点()()1,1f 处的切线与直线10x y -+=平行,求a 的值; (Ⅱ)求()f x 的单调区间.19.(本小题共14分)已知数列{}n a 中,1a a =,22a =,n S 是数列{}n a 的前n 项和,且()123n n S n a a =+,n N *∈.(Ⅰ)求a 的值;(Ⅱ)求数列{}n a 的通项公式;(Ⅲ)若()()1221,82,n n n n b n a a++=⎧⎪=⎨⎪⋅⎩≥ n T 是数列{}n b 的前n 项和,求n T . 20.(本小题共14分)已知椭圆C :22221(0)x y a b a b+=>>的焦点分别是1F ,2F ,点31,2M ⎛⎫⎪ ⎪⎝⎭在椭圆上,且124MF MF +=. (Ⅰ)求椭圆C 的标准方程;(Ⅱ)若直线l :()0,0y kx t k t =+≠>与椭圆C :22221x y a b+=交于A ,B 两点,点P 满足0AP BP += ,点Q 的坐标是30,2⎛⎫⎪⎝⎭,设直线PQ 的斜率是1k ,且12k k ⋅=,求实数t 的取值范围.(考生务必将答案答在答题卡上,在实体卷上作答无效)摸底考试文科参考答案2012、1 一、选择题1. C 2. B 3 C 4. B 5. A 6. A 7. B 8. B二、填空题 9.4023201210.10 11.15 12.3 13.3y x =± 14.② 三、解答题15.解:(Ⅰ)因为()2sin 22cos 1f x x x =+-,所以()sin 2cos 2f x x x =+2sin 24x π⎛⎫=+ ⎪⎝⎭. ……………………….. 3分所以2.2πωπ== ………………………….. 5分 又因为1sin 214x π⎛⎫-≤+≤ ⎪⎝⎭, 所以()22f x -≤≤.所以函数()f x 的最小正周期是π;最大值是2. …………………….. 7分 (Ⅱ)由(Ⅰ)知()f x 2sin 24x π⎛⎫=+ ⎪⎝⎭.因为344x ππ≤≤, 所以372444x πππ≤+≤. 所以当3244x ππ+=,即4x π=时,函数()f x 有最大值是1;当3242x ππ+=,即58x π=时,函数()f x 有最小值是2-.所以函数()f x 在区间3,44ππ⎡⎤⎢⎥⎣⎦上的最大值是1,最小值是2-. ……………….. 13分 16.(Ⅰ)证明:∵点M ,N 分别是CE ,DE 的中点,∴MN 是CDE ∆的中位线. ∴//.MN CD∵四边形ABCD 是矩形, ∴//.CD AB ∴//.MN AB∵AB ⊂平面ABE ,MN ⊄平面ABE ,∴//MN 平面ABE . ……………………….. 6分 (Ⅱ)证明:∵BF ⊥平面ACE ,AE ⊂平面ACE , ∴.BF AE ⊥∵BC ⊥平面ABE ,AE ⊂平面ACE , ∴.BC AE ⊥∵BF BC B = ,BF ⊂平面BCE ,BC ⊂平面BCE , ∴AE ⊥平面BCE .∴.AE BE ⊥ ……………….. 13分17. 解:设甲袋中1只白球记为1a ,2只红球记为12,b b ;乙袋中2只白球记为23,a a ,2只红球记为34,b b .所以“从两袋中各取一球”包含基本事件()12,a a ,()13,a a ,()13,a b ,()14,a b ,()12,b a ,()13,b a ,()13,b b ,()14,b b ,()22,b a ,()23,b a ,()23,b b ,()24,b b 共有12种.……………….. 4分 (Ⅰ)设A 表示“从两袋中各取一球,两球颜色相同”,所以事件B 包含基本事件()12,a a ,()13,a a , ()13,b b ,()14,b b , ()23,b b ,()24,b b 共有6种. 所以()61.122P A == ……………………….. 8分 (Ⅱ)设B 表示“从两袋中各取一球,至少有一个白球”,所以事件A 包含基本事件()12,a a ,()13,a a ,()13,a b ,()14,a b ,()12,b a ,()13,b a ,()22,b a ,()23,b a 共有8种.所以()82.123P B == …………………….. 13分18.解:(Ⅰ)因为()ln f x ax x =-, 所以()1.f x a x'=-因为曲线()y f x =在点()()1,1f 处的切线与直线10x y -+=平行, 所以切线的斜率 1.k = 所以()11f '=,即1 1.a -=所以 2.a = ………………….. 4分 (Ⅱ)因为函数()f x 的定义域是()0,+∞,且()11ax f x a x x-'=-=, …………………….. 6分 ①当0a ≤时,()0f x '<,所以()f x 在()0,+∞上是减函数. …………………….. 8分 ②当0a >时,令()0f x '=,1.x a= 所以当10,a a ⎛⎫∈ ⎪⎝⎭时,()0f x '<,()f x 在10,a ⎛⎫ ⎪⎝⎭上是减函数; ……………….. 10分 当1,a a ⎛⎫∈+∞⎪⎝⎭时,()0f x '>,()f x 在1,a ⎛⎫+∞ ⎪⎝⎭上是增函数. ………………….. 12分 所以当0a ≤时,()f x 的递减区间是()0,+∞; 当0a >时,()f x 的递减区间是10,a ⎛⎫ ⎪⎝⎭,()f x 的递增区间是1,a ⎛⎫+∞ ⎪⎝⎭. …………….. 13分 19.解:(Ⅰ)因为()123n n S n a a =+,11S a a ==,所以0.a = ………….. 3分(Ⅱ)由(Ⅰ)可知 2nn na S =, 所以()111.2n n n a S +++=所以()1111.22n n n n n n a na a S S ++++=-=-所以()11.n n n a na +-= 所以当2n ≥时,1.1n n a na n +=- 所以11n n a n a n +=-112n n a n a n --=-,,⋅⋅⋅,3221a a =, 所以12.n a n a += 所以()21n a n =-,2n ≥. 因为10a a ==满足上式,所以()21n a n =-,n N *∈. …………….. 8分(Ⅲ)当2n ≥时,()()82112.22111n b n n n n n n ⎛⎫===- ⎪⋅+++⎝⎭…………….. 10分又12b =, 所以12n n T b b b =++⋅⋅⋅+ 1111222231n n ⎛⎫⎛⎫=+-+⋅⋅⋅+-⎪ ⎪+⎝⎭⎝⎭……………….. 12分 112221n ⎛⎫=+- ⎪+⎝⎭311n n +=+ 所以31.1n n T n +=+ ………….. 14分20.解:(Ⅰ)因为点31,2M ⎛⎫ ⎪ ⎪⎝⎭在椭圆C :()222210x y a b a b +=>>上,且124MF MF +=,所以221314a b +=,2 4.a = 所以24a =,21.b =所以椭圆C 的标准方程是22 1.4x y += ………………………….. 3分(Ⅱ)联立方程组22,1,4y kx t x y =+⎧⎪⎨+=⎪⎩ 消去y ,得()()222148410.k x ktx t +++-= 所以()()222264161410k t kt∆=-+->, ………………………….. 4分即2214.k t +> ① ………………………….. 5分 设()()1122,,,A x y B x y ,所以1228.14ktx x k-+=+ ………………………….. 6分 因为0AP BP +=所以点P 是AB 的中点,设(),P P P x y , 所以2414p kt x k -=+,21.14p Py kx t k =+=+ ………………………….. 8分 因为点Q 的坐标是30,2⎛⎫ ⎪⎝⎭,直线PQ 的斜率是1k ,所以()21323142.8P P y t k k x kt--+==- …………………….. 10分 因为12k k ⋅=,所以()22314 2.8t k k kt-+⋅=-所以2146.k t += ② ………………………….. 12分所以由①,②式,可得 26.t t > 所以0 6.t <<所以实数t 的取值范围是0 6.t << ………………………….. 14分。
北京市各区2012届高三第一学期文科数学期末试卷汇编

北京市昌平区2012届高三上学期期末考试试题(数学文)北京市朝阳区2012届高三上学期期末考试试题(数学文)北京市东城区2012届高三上学期期末教学统一检测(数学文)北京市房山区2012届高三上学期期末统测数学(文)试题北京市丰台区2012届高三上学期期末考试试题(数学文)北京市海淀区2012届高三上学期期末考试试题(数学文)北京市石景山区2012届高三上学期期末考试数学(文)试卷北京市西城区2012届高三上学期期末考试试题(数学文)2012年2月昌平区2011-2012学年第一学期高三年级期末质量抽测数 学 试 卷(文科) 2012 .1考生注意事项:1.本试卷共6页,分第Ⅰ卷选择题和第Ⅱ卷非选择题两部分,满分150分,考试时间 120分钟.2.答题前,考生务必将学校、班级、考试编号填写清楚.答题卡上第一部分(选择题)必须用2B 铅笔作答,第二部分(非选择题)必须用黑色字迹的签字笔作答,作图时可以使用2B 铅笔.3.修改时,选择题用塑料橡皮擦干净,不得使用涂改液.请保持卡面整洁,不要折叠、折皱、破损.不得在答题卡上作任何标记.4.请按照题号顺序在各题目的答题区域内作答,未在对应的答题区域作答或超出答题区域的作答均不得分. 第Ⅰ卷(选择题 共40分)一、选择题(本大题共8小题,每小题5分,共40分.在每小题列出的四个选项中,选出符合题目要求的一项.)1.设全集}7,5,3,1{=U ,集合}7,3,1{},5,3{==B A ,则()U A B ð等于A .{5}B .{3,5}C .{1,5,7}D .Φ2.21i -等于A . 22i -B .1i -C .iD .1i +3.“x y >”是“22x y>”的A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件4.从3名男同学,2名女同学中任选2人参加体能测试,则选到的2名同学中至少有一名男同学的概率是A .910B .45C .25D .125.若某空间几何体的三视图如图所示,则该 几何体的体积是 A .2 B .4 C .6. D .8 6. 某程序框图如图所示,则输出的S =A .120B . 57C .56D . 267.某类产品按工艺共分10个档次,最低档次产品每件利润为8元.主视俯视同样工时,可以生产最低档产品60件,每提高一个档次将少生产3件产品.则获得利润最大时生产产品的档次是A.第7档次B.第8档次C.第9档次D.第10档次8. 一圆形纸片的圆心为点O ,点Q 是圆内异于O 点的一定点,点A 是圆周上一点.把纸片折叠使点A 与Q 重合,然后展平纸片,折痕与OA 交于P 点.当点A 运动时点P 的轨迹是 A .圆 B .椭圆 C . 双曲线 D .抛物线第Ⅱ卷(非选择题 共110分)填空题(本大题共6小题,每小题5分,共30分).9.已知函数x x y cos sin = ,则函数的最小正周期是 .10.已知向量(2,1)=a ,10⋅=a b , 7+=a b ,则=b .11.某工厂对一批产品进行了抽样检测,右图是根据抽样检测后的 产品净重(单位:克)数据绘制的频率分布直方图,其中产品净重的范围是[96,106],样本数据分组为[96,98),[98,100),[100,102),[102,104),[104,106] .已知样本中产品净重小于100克的个数是48,则a =___________ ;样本中净重在[98,104)的产品的个数是__________ .12. 已知双曲线122=-y m x 的右焦点恰好是抛物线x y 82=的焦点,则m = .13. 已知D是由不等式组0,0,x y x -≥⎧⎪⎨+≥⎪⎩所确定的平面区域,则圆224x y +=在区域D 内的弧长为_____________;该弧上的点到直线320x y ++=的距离的最大值等于__________ .14.设函数)(x f 的定义域为R ,若存在与x 无关的正常数M ,使|||)(|x M x f ≤对一切实数x 均成立,a则称)(x f 为有界泛函.在函数①x x f 5)(-=,②x x f 2sin )(=,③xx f )21()(=,④x x x f cos )(=中,属于有界泛函的有__________(填上所有正确的序号) .三、解答题(本大题共6小题,共80分.解答应写出文字说明,证明过程或演算步骤.) 15.(本小题满分13分)在ABC ∆中,AA A cos cos 2cos 212-=.(I )求角A 的大小;(II )若3a =,sin 2sin B C =,求ABCS ∆.16.(本小题满分13分) 已知数列}{n a 是等差数列,22, 1063==a a ,数列}{n b 的前n 项和是nS ,且131=+n n b S .(I )求数列}{n a 的通项公式;(II )求证:数列}{n b 是等比数列;17.(本小题满分14分)如图在四棱锥P ABCD -中,底面ABCD 是正方形,ABCD PA 底面⊥,垂足为点A ,2==AB PA ,点M ,N 分别是PD ,PB 的中点.(I )求证:ACM PB 平面// ; (II )求证:⊥MN 平面PAC ;(III )求四面体A MBC -的体积.18.(本小题满分13分)已知函数ax x x x f ++=1ln )((a 为实数).(I )当0=a 时, 求)(x f 的最小值;(II )若)(x f 在),2[+∞上是单调函数,求a 的取值范围.19.(本小题满分14分)已知椭圆C 的中心在原点,左焦点为(,离心率为23.设直线l 与椭圆C 有且只有一个公共点P ,记点P 在第一象限时直线l 与x 轴、y 轴的交点分别为B A 、,且向量+=.求: (I )椭圆C 的方程;(II )||的最小值及此时直线l 的方程.20. (本小题满分13分)M 是具有以下性质的函数()f x 的全体:对于任意s ,0t >,都有()0f s >,()0f t >,且()()()f s f t f s t +<+.(I )试判断函数12()log (1)f x x =+,2()21x f x =-是否属于M ?(II )证明:对于任意的0x >,0(x m m +>∈R 且0)m ≠都有[()()]0m f x m f x +->;(III )证明:对于任意给定的正数1s >,存在正数t ,当0x t <≤时,()f x s <.昌平区2011-2012学年第一学期高三年级期末质量抽测 数学(文科)试卷参考答案及评分标准 2012.1一、选择题(本大题共8小题,每小题5分,共40分.)二、填空题(本大题共6小题,每小题5分,共30分.) 9.π 10. 26 11. 0.125;120 12. 313. 65π;5102+14. ① ② ④三、解答题(本大题共6小题,共80分)15.(本小题满分13分)解:(I )由已知得:AA A cos cos )1cos 2(2122-=-,……2分.21cos =∴A ……4分 π<<A 0 ,.3π=∴A …………6分(II )由C c B b sin sin = 可得:2sin sin ==c bC B ………7分∴ c b 2= …………8分214942cos 222222=-+=-+=c c c bc a c b A ………10分 解得:32b , 3==c ………11分2332333221sin 21=⨯⨯⨯==A bc S . ……13分16(本小题满分13分)解:(1)由已知⎩⎨⎧=+=+.225,10211d a d a 解得 .4,21==d a.244)1(2-=⨯-+=∴n n a n ………………6分(2)由于nn b S 311-=, ① 令n =1,得.31111b b -= 解得431=b ,当2≥n 时,11311---=n n b S ② -②得n n n b b b 31311-=- , 141-=∴n n b b 又0431≠=b ,.411=∴-n n b b ∴数列}{n b 是以43为首项,41为公比的等比数列.……………………13分17.(本小题满分14分)证明:(I )连接O BD AC MN MO MC AM BD AC = 且,,,,,,的中点分别是点BD PD M O ,, ACM PB PB MO 平面⊄∴,//∴ACM PB 平面//. …… 4分(II) ABCD PA 平面⊥ ,ABCD BD 平面⊂BD PA ⊥∴是正方形底面ABCDBD AC ⊥∴又A AC PA =⋂ PAC BD 平面⊥∴ ……7分在中PBD ∆,点M ,N 分别是PD ,PB 的中点.∴BD MN //PAC MN 平面⊥∴. …… 9分(III )由h S V V ABC ABC M MBC A ⋅⋅==∆--31 ……11分PAh 21= ……12分 32212131=⋅⋅⋅⋅⋅=∴-PA AD AB V MBC A . ……14分18.(本小题满分13分)解:(Ⅰ) 由题意可知:0>x ……1分当0=a 时21)(x x x f -=' …….2分当10<<x 时,0)(<'x f 当1>x 时,0)(>'x f ……..4分故1)1()(m in ==f x f . …….5分(Ⅱ) 由222111)(x x ax a x x x f -+=+-='① 由题意可知0=a 时,21)(x x x f -=',在),2[+∞时,0)(>'x f 符合要求 …….7分② 当0<a 时,令1)(2-+=x ax x g 故此时)(x f 在),2[+∞上只能是单调递减0)2(≤'f 即04124≤-+a 解得41-≤a …….9分 当0>a 时,)(x f 在),2[+∞上只能是单调递增 0)2(≥'f 即,04124≥-+a 得41-≥a 故0>a …….11分综上),0[]41,(+∞⋃--∞∈a …….13分19. (本小题满分14分) 解:(Ⅰ)由题意可知3=c ,23==a c e ,所以2=a ,于是12=b ,由于焦点在x 轴上,故C 椭圆的方程为2214x y += ………………………………5分(Ⅱ)设直线l 的方程为:m kx y +=)0(<k ,),0(),0,(m B k mA -⎪⎩⎪⎨⎧=++=,14,22y x m kx y 消去y 得:012)41(222=-+++m kmx x k …………………7分直线l 与曲线C 有且只有一个公共点,0)1)(41(42222=-+-=∆m k m k即1422+=k m ① …………………… 9分 ∵OB OA OM +=222||m k m OM +=∴② ……………………11分将①式代入②得:||3OM ==当且仅当22-=k 时,等号成立,故min ||3OM =,此时直线方程为:03222=-+y x . …………………14分20(本小题满分13分)(Ⅰ)由题意可知,0)(,0)(,0)(,0)(2211>>>>t f s f t f s f 若)1(log )1(log )1(log 222++<+++t s t s 成立 则1)1)(1(++<++t s t s 即0<st与已知任意s ,0t >即0>st 相矛盾,故M x f ∉)(1; ……2分 若12222-<-++ts ts成立 则01222<--++ts t s即0)21)(12(<--t s s ,0t > 021,12<->∴t s 即0)21)(12(<--ts 成立 …..4分故M x f ∈)(2.综上,M x f ∉)(1,M x f ∈)(2. ……5分(II) 当0>m 时,)()()()(x f m f x f m x f >+>+ 0)()(>-+∴x f m x f 当0<m 时,)()()()()(m x f m f m x f m m x f x f +>-++>-+=0)()(<-+∴x f m x f故0)]()([ >-+x f m x f m . ……9分(III) 据(II ))上为增函数在(∞+.0)(x f ,且必有)(2)2(x f x f >(*) ①若s f <)1(,令1=t ,则t x ≤<0时 s x f <)(;②若,)1(s f >则存在*N ∈k ,使t f k 12)1(=<由(*)式可得s f f f kk k <<<<<-1)1(21)21(21)21(1即当s x f t x <≤<)(0时, 综①、②命题得证。
2012届高三摸底考试文科数学试题

2012届高三摸底考试数学试题(文科)本卷分选择题非选择题两部分,共4页,满分150分.考试用时间120分钟. 注意事项:1. 考生务必将自己的姓名、班级、学校用蓝、黑墨水钢笔签字笔写在答题卷上;2. 选择题、填空题每小题得出答案后,请将答案填写在答题卷相应指定位置上。
答在试题卷上不得分;3.考试结束,考生只需将答题卷交回. 4. 参考公式:球体的体积公式343V r π=,其中r 是球体的半径. 一、选择题(本大题共10小题,每小题5分,满分50分.在每小题给出的四个选项中,只有一项是符合题目要求的) 1.函数y =)A .(),1-∞B .(],1-∞C .()1,+∞D .[)1,+∞ 2.复数2ii -(i 为虚数单位)等于( ) A. 12i -- B. 12i -+C. 12i -D. 12i +3.已知命题2:,210p x R x ∀∈+>,则( ) A .2:,210p x R x ⌝∃∈+≤ B .2:,210p x R x ⌝∀∈+≤C .2:,210p x R x ⌝∃∈+<D .2:,210p x R x ⌝∀∈+<4.圆1)3()1(22=++-y x 的一条切线方程是( )A .0x y -=B .0x y +=C .0x =D .0y = 5.不等式32x x -+<0的解集为( ) A .{}23x x -<< B .{}2x x <- C .{}23x x x <->或 D .{}3x x > 6.若平面向量(1,2)=-a 与b 的夹角是180°,且||=b b 等于( ) A .(6,3)- B .(3,6)- C .(6,3)- D .(3,6)-7.设变量x 、y 满足线性约束条件⎪⎩⎪⎨⎧≤--≥-≥+3213y x y x y x ,则目标函数y x z 32+=的最小值为( ).A 6 .B 7 .C 8 .D 23(图3)8.一个几何体的三视图如图1所示,其中俯视图与左视图均为半径是1的圆,则这个几何体的体积是( ) A .43π B .π C .23π D .3π9. 执行图2中的程序框图,若0.8p =,则输出的n =( ) A .2 B .3 C .4 D . 5 10.对函数()sin f x x x =,现有下列命题:①函数()f x 是偶函数;②函数()f x 的最小正周期是2π;③点(,0)π是函数()f x 的图象的一个对称中心;④函数()f x 在区间0,2π⎡⎤⎢⎥⎣⎦上单调递增,在区间,02π⎡⎤-⎢⎥⎣⎦上单调递减。
2012年北京市海淀区高三二模文科数学含答案纯word版-推荐下载

(16)(本小题满分 13 分)
在一次“知识竞赛”活动中,有 A1, A2 , B, C 四道题,其中 A1, A2 为难度相同的容易题, B 为中档 题, C 为较难题. 现甲、乙两位同学均需从四道题目中随机抽取一题作答.
(Ⅰ)求甲、乙两位同学所选的题目难度相同的概率; (Ⅱ)求甲所选题目的难度大于乙所选题目的难度的概率.
A, B 两点,点 O 是坐标原点. 给出三个命题:① PA = PB ;② OAB 的面积为定值;③曲线 C 上存
在两点 M , N ,使得 OMN 为等腰直角三角形.其中真命题的个数是
(A)1
(B)2 (C)3 (D)0
二、填空题:本大题共6小题,每小题5分,共30分,把答案填在题中横线上.
(9)复数
(10)已知双曲线
z
=
1+ i3
i
x2 a2
,则
-
z
=
.
y2 = 1的渐近线方程是 y = ± 2x ,那么此双曲线的离心率为 b2
(11)在 ABC 中,若 ÐA = 120° , c = 6 , ABC 的面积为 9 3 ,则 a =
(12)在面积为 1 的正方形 ABCD 内部随机取一点 P ,则 PAB 的面积大于等于 1 的概率是
海淀区高 三年级第 二学期期 末练习
数 学(文科)
2012.05 一、选择题:本大题共 8 小题,每小题 5 分,共 40 分.在每小题给出的四个选项中,只有一项是符合题目
要求的.
(1)函数 y = - x2 + 1,- 1£ x < 2 的值域是
(A) (- 3, 0]
(2)已知命题 p : $x Î
值点是
;函数 f (x) 的值域是
2012年高考文科数学北京卷及答案

数学试卷 第1页(共18页)数学试卷 第2页(共18页)数学试卷 第3页(共18页)绝密★启用前2012年普通高等学校招生全国统一考试(北京卷)数学(文科)本试卷共6页,150分.考试时长120分钟.考试生务必将答案答在答题卡上,在试卷上作答无效.考试结束后,将本试卷和答题卡一并交回.第一部分(选择题 共40分)一、选择题共8小题,每小题5分,共40分.在每小题列出的四个选项中,选出符合题目要求的一项.1. 已知集合{320}A x x =∈+>R |,{|(1)(3)0}B x x x =∈+->R ,则A B =( )A . (,1)-∞-B . 2(1,)3-- C . 2(,3)3-D . (3,)+∞2. 在复平面内,复数10i3i+对应的点的坐标为 ( )A . (1,3)B . (3,1)C .(1,3)-D . (3,1)-3. 设不等式组02,02x y ⎧⎨⎩≤≤≤≤表示的平面区域为D .在区域D 内随机取一个点,则此点到坐标原点的距离大于2的概率是( )A . π4 B . π22-C .π6D .4π4- 4. 执行如图所示的程序框图,输出的S 值为 ( )A . 2B . 4C . 8D . 16 5. 函数121()()2x f x x =-的零点个数为( )A . 0B . 1C . 2D . 3 6. 已知{}n a 为等比数列.下面结论中正确的是( )A . 1322a a a +≥B . 2221322a a a +≥C . 若13a a =,则12a a =D . 若31a a >,则42a a >7. 某三棱锥的三视图如图所示,该三棱锥的表面积是( )A .28+ B .30+C .56+D .60+8. 某棵果树前n 年的总产量n S 与n 之间的关系如图所示.从目前记录的结果看,前m 年的年平均产量最高,m 的值为( )A . 5B . 7C . 9D . 11第二部分(非选择题 共110分)二、填空题共6小题,每小题5分,共30分.9. 直线y x =被圆22(2)4x y +-=截得的弦长为________. 10. 已知{}n a 为等差数列,n S 为其前n 项和.若112a =,23S a =,则2a =________;=n S ________.11. 在ABC △中,若3a =,b =,π3A ∠=,则C ∠的大小为________. 12. 已知函数()lg f x x =,若()1f ab =,则22()()f a f b +=________.13. 已知正方形ABCD 的边长为1,点E 是AB 边上的动点,则 DE CB 的值为________;DE DC 的最大值为________.14. 已知()(2)(3)f x m x m x m =-++,()22x g x =-.若x ∀∈R ,()0f x <或()0g x <,则m的取值范围是________.三、解答题共6小题,共80分.解答应写出文字说明,演算步骤或证明过程.15.(本小题共13分) 已知函数(sin cos )sin 2()sin x x xf x x-=.(Ⅰ)求()f x 的定义域及最小正周期; (Ⅱ)求()f x 的单调递减区间.16.(本小题共14分)俯视图侧(左)视图正(主)视图434姓名________________ 准考证号_____________--------在--------------------此--------------------卷--------------------上--------------------答--------------------题--------------------无--------------------效--------数学试卷 第4页(共18页)数学试卷 第5页(共18页) 数学试卷 第6页(共18页)如图1,在Rt ABC △中,90C ∠=,D ,E 分别为AC ,AB 的中点,点F 为线段CD 上的一点.将ADE △沿DE 折起到1A DE △的位置,使1A F CD ⊥,如图2.(Ⅰ)求证:DE ∥平面1ACB ; (Ⅱ)求证:1A F BE ⊥;(Ⅲ)线段1A B 上是否存在点Q ,使1A C ⊥平面DEQ ?说明理由.17.(本小题共13分)近年来,某市为了促进生活垃圾的分类处理,将生活垃圾分为厨余垃圾、可回收物和其他垃圾三类,并分别设置了相应的垃圾箱.为调查居民生活垃圾分类投放情况,现随机抽取了该市三类垃圾箱中总计1 000吨生活垃圾,数据统计如下(单位:吨):(Ⅰ)试估计厨余垃圾投放正确的概率; (Ⅱ)试估计生活垃圾投放错误的概率;(Ⅲ)假设厨余垃圾在“厨余垃圾”箱、“可回收物”箱、“其他垃圾”箱的投放量分别为a ,b ,c ,其中0a >,600a b c ++=.当数据a ,b ,c 的方差2s 最大时,写出a ,b ,c 的值 (结论不要求证明),并求此时2s 的值.(求:2222121[()()()]n s x x x x x x n=-+-++-,其中x 为数据1x ,2x ,,n x 的平均数)18.(本小题共13分)已知函数2()1(0)f x ax a =+>,3()g x x bx =+.(Ⅰ)若曲线()y f x =与曲线()y g x =在它们的交点(1,)c 处具有公共切线,求a ,b 的值; (Ⅱ)当3a =,9b =-时,若函数()()f x g x +在区间[,2]k 上的最大值为28,求k 的取值范围.19.(本小题共14分)已知椭圆C :22221(0)x y a b a b+=>>的一个顶点为(2,0)A ,直线(1)y k x =-与椭圆C 交于不同的两点M,N . (Ⅰ)求椭圆C 的方程; (Ⅱ)当AMN ∆时,求k 的值.20.(本小题共13分)设A 是如下形式的2行3列的数表,满足性质P :,,,,,[1,1]a b c d e f ∈-,且0a b c d e f +++++=.记()i r A 为A 的第i 行各数之和(1,2)i =,()j c A 为A 的第j 列各数之和(1,2,3)j =;记()k A 为1|()|r A ,2|()|r A ,1|()|c A ,2|()|c A ,3|()|c A 中的最小值.(Ⅰ)对如下数表A ,求()k A 的值;(Ⅱ)设数表A 形如其中10d -≤≤.求()k A 的最大值;(Ⅲ)对所有满足性质P 的2行3列的数表A ,求()k A 的最大值.D FDE BCA 1F CB 图2图1数学试卷 第7页(共18页)数学试卷 第8页(共18页) 数学试卷 第9页(共18页)2012年普通高等学校招生全国统一考试(北京卷)数学(文科)答案解析{|1A B x x x x ⎧⎫=<-⎨⎬⎩⎭【提示】求出集合,然后直接求解AB 。
北京市顺义区2012届高三二模文科数学
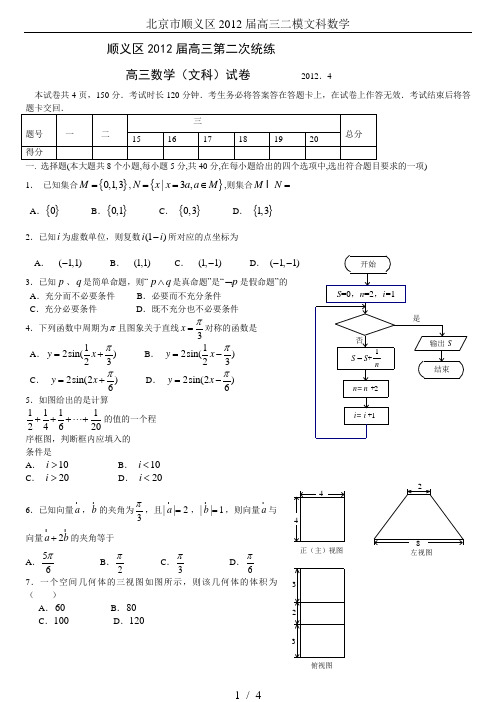
n= n +2S =0,n =2,i =1i= i +1S = S +1n输出 S 开始结束是否顺义区2012届高三第二次统练高三数学(文科)试卷 2012.4本试卷共4页,150分.考试时长120分钟.考生务必将答案答在答题卡上,在试卷上作答无效.考试结束后将答题卡交回. 题号 一 二三 总分 15 16 17 18 19 20 得分一. 选择题(本大题共8个小题,每小题5分,共40分,在每小题给出的四个选项中,选出符合题目要求的一项) 1. 已知集合{}0,1,3M =,{}|3,N x x a a M ==∈,则集合M N =I A .{}0 B .{}0,1 C . {}0,3 D . {}1,3 2.已知i 为虚数单位,则复数(1)i i -所对应的点坐标为A . (1,1)-B . (1,1)C . (1,1)-D . (1,1)-- 3.已知p 、q 是简单命题,则“p q ∧是真命题”是“p ⌝是假命题”的 A .充分而不必要条件 B .必要而不充分条件 C .充分必要条件 D .既不充分也不必要条件 4.下列函数中周期为π且图象关于直线3x π=对称的函数是A .12sin()23y x π=+B . 12sin()23y x π=-C . 2sin(2)6y x π=+D . 2sin(2)6y x π=-5.如图给出的是计算111124620+++⋅⋅⋅+的值的一个程 序框图,判断框内应填入的 条件是A . 10i >B . 10i <C . 20i >D . 20i < 6.已知向量a ,b 的夹角为3π,且||2a =,||1b =,则向量a 与向量2a b +的夹角等于A .56πB .2πC .3πD .6π7.一个空间几何体的三视图如图所示,则该几何体的体积为 ( )A .60B .80C .100D .120俯视图左视图正(主)视图82323448.已知全集为,U P U Ø,定义集合P 的特征函数为1,,()0,.P U x P f x x P ∈⎧⎪=⎨∈⎪⎩ð,对于A U Ø, B U Ø,给出下列四个结论:① 对x U ∀∈,有()()1UA Af x f x +=ð;② 对x U ∀∈,若A B Ø,则()()A B f x f x ≤; ③ 对x U ∀∈,有()()()A B A B f x f x f x =⋅I ; ④ 对x U ∀∈,有()()()ABA B f x f x f x =+.其中,正确结论的序号是A . ①②④B . ②③④C . ②③D . ①②③二.填空题(本大题共6个小题,每小题5分,共30分,把答案填在答题卡上) 9.已知点()3,4P -在角α的终边上,则sin α=_____________. 10.随机抽取100名学生,测得他们的身高(单位cm )按照区间[)[)[)[)[)[)155,160,160,165,165,170,170,175,175,180,180,185分组,得到样本身高的频率分布直方图(如图).则频率分布 直方图中的x 值为__________;若将身高在[)[)[)170,175,175,180,180,185区间内的学生依次记为,,A B C 三组,用分层抽样的方法从这 三组中抽取6人,则从,,A B C 三组中依次抽 取的人数为______________.11.以双曲线2244x y -=的中心为顶点,右焦点为焦点的抛物线方程为_________.12.如果实数x 、y 满足条件101010x y y x y -+≥⎧⎪+≥⎨⎪++≤⎩,则11y x --的最小值为___________;最大值为 .13.函数11y x =-的图象与函数2cos 2y x π=(46)x -≤≤的图象所有交点的横坐标之和等于 ______ . 14. 已知集合2012{|22}A x x a a a ==+⨯+⨯,其中{0,1,2}(0,1,2)i a i ∈=,且20a ≠,则集合A 中所有元素之和是_____________;从集合A 中任取两元素,m n ,则随机事件“||3m n -≥”的概率是_____________.三.解答题(本大题共6小题,共80分,解答应写出文字说明、证明过程或演算步骤). 15.(本小题共13分)已知向量(2cos,1)2x m =,(cos ,1)2xn =-,()x R ∈,设函数()f x m n =⋅. (Ⅰ)求函数()f x 的值域;(Ⅱ)已知锐角ABC V 的三个内角分别为A 、B 、C ,若53(),()135f A f B ==,求()f C 的值.16. (本小题共13分)如图四棱锥P ABCD -中,底面A B C D 是平行四边形,090ACB ∠=,PA ⊥平面ABCD ,1PA BC ==,2AB =,F是BC 的中点.(Ⅰ)求证:DA ⊥平面PAC ;(Ⅱ)试在线段PD 上确定一点G ,使CG ∥平面PAF ,并求三棱锥A -CDG 的体积.17.(本小题共13分)设数列{}n a 是公比为正数的等比数列,13,a =3229a a =+ (Ⅰ)求数列{}n a 的通项公式;(Ⅱ)设3132333log log log log n n b a a a a =+++⋅⋅⋅+,求数列1n b ⎧⎫⎨⎬⎩⎭的前n 项和n S .ADCFPB18.(本小题共14分)已知函数2()(1)2ln ,f x a x x =-+()2g x ax =,其中1a > (Ⅰ)求曲线()y f x =在(1,(1))f 处的切线方程; (Ⅱ)设函数()()()h x f x g x =-,求()h x 的单调区间. 19.(本小题共14分)已知椭圆:G 12222=+b y a x )0(>>b a 的离心率22e =,点(1,0)F 为椭圆的右焦点.(Ⅰ)求椭圆G 的方程;(Ⅱ)过右焦点F 作斜率为k 的直线l 与椭圆G 交于M 、N 两点,若在x 轴上存在着动点(,0)P m ,使得以,PM PN 为邻边的平行四边形是菱形,试求出m 的取值范围.20. (本小题共13分)对于定义域为A 的函数)(x f ,如果任意的A x x ∈21,,当21x x <时,都有()()21x f x f <,则称函数()x f 是A 上的严格增函数;函数()k f 是定义在*N 上,函数值也在*N 中的严格增函数,并且满足条件()()k k f f 3=.(Ⅰ)判断函数)(32)3(N x f xx∈⨯=是否是N 上的严格增函数; (Ⅱ)证明:)(3)3(k f k f =;(Ⅲ)是否存在正整数k ,使得2012)(=k f ,若存在求出k 值;若不存在请说明理由.。
2012北京高考文科数学试题(详细答案)

2012北京高考文科数学试题(详细答案)第一部分(选择题共40分)一、选择题共8小题,每小题5分,共40分,在每小题给出的四个选项中,选出符合题目要求的一项。
(1)已知集合,,则(A)(B)(C)(D)(2)在复平面内,复数对应的点的坐标为(A)(B)(C)(D)(3)设不等式组表示的平面区域为,在区域内随机取一个点,则此点到坐标原点的距离大于2的概率是(A)(B)(C)(D)(4)执行如图所示的程序框图,输出的值为(A)2(B)4(C)8(D)16(5)函数的零点个数为(A)0 (B)1 (C)2 (D)3(6)已知为等比数列,下面结论中正确的是(A)(B)(C)若,则(D)若,则(7)某三棱锥的三视图如图所示,该三棱锥的表面积是(A)(B)(C)(D)(8)某棵果树前年的总产量与之间的关系如图所示,从目前记录的结果看,前年的年平均产量最高,的值为(A)5(B)7(C)9(D)11第二部分(非选择题共110分)二、填空题共6小题,每小题5分,共30分。
(9)直线被圆截得的弦长为__________。
(10)已知为等差数列,为其前项和,若,,则____________,_________________。
(11)在中,若,,,则的大小为_________。
(12)已知函数,若,则_____________。
(13)已知正方形的边长为,点是边上的动点,则的值为_______;的最大值为_______。
(14)已知,。
若,或,则的取值范围是_________。
三、解答题共6小题,共80分,解答应写出文字说明,演算步骤或证明过程。
(15)(本小题共13分)已知函数。
(Ⅰ)求的定义域及最小正周期;(Ⅱ)求的单调递减区间。
(16)(本小题共14分)如图1,在中,,分别为的中点,点为线段上的一点,将沿折起到的位置,使,如图2。
(Ⅰ)求证:平面;(Ⅱ)求证:;(Ⅲ)线段上是否存在点,使平面?说明理由。
(17)(本小题共13分)近年来,某市为了促进生活垃圾的分类处理,将生活垃圾分为厨余垃圾、可回收物和其他垃圾三类,并分别设置了相应的垃圾箱,为调查居民生活垃圾分类投放情况,现随机抽取了该市三类垃圾箱中总计1000吨生活垃圾,数据统计如下(单位:吨):“厨余垃圾”箱“可回收物”箱“其他垃圾”箱厨余垃圾400 100 100可回收物30 240 30其他垃圾20 20 60(Ⅰ)试估计厨余垃圾投放正确的概率;(Ⅱ)试估计生活垃圾投放错误的概率;(Ⅲ)假设厨余垃圾在“厨余垃圾”箱、“可回收物”箱、“其他垃圾”箱的投放量分别为,其中,。
北京市2012届高三数学文科仿真模拟卷4.pdf

北京市2012届高三数学文科仿真模拟卷4 第一部分(选择题 共40分) 一、选择题:本大题共8小题,每小题5分,共40分.全集,,则=(A) (B) (C) (D) (2)设,那么“”是“ ”的 (A)必要不充分条件 (B)充分不必要条件 (C)充分必要条件(D)既不充分又不必要条件 (3)已知,,则=(A) (B)-1 (C) (D) (4)双曲线的焦点到渐近线的距离为 (A)2 (B)3 (C)4 (D)5 (5)三棱柱的侧棱与底面垂直,且底面是边长为2的等边三角形.若三棱柱 的正视图(如图所示)的面积为8,则侧视图的面积为 (A) 8 (B) 4 (C) (D) (6)连续抛两枚骰子分别得到的点数是,,则向量与向量垂直的概率是 (A) (B) (C) (D) (7)已知函数,则,,的大小关系是 (A) (B) (C) (D) (8)已知点是的中位线上任意一点,且. 设,,,的面积分别为,,,, 记,,,定义.当取最大值时,则等于 (A) (B) (C) (D) 第二部分(非选择题 共110分) 二、填空题:本大题共6小题,每小题5分,共30分.把答案填在题中横线上. (9)设为虚数单位,复数满足,则 . (10)已知向量,的夹角为,,,若,则实数 的值为 . (11)如图,一艘船上午8:00在A处测得灯塔S在它的北偏东30°处,之后它继续沿正北方向匀速航行,上午8:30到达B处,此时又测得灯塔S在它的北偏东75°处,且与它相距n mile,则此船的航行速度是 n mile/h. (12)右边程序框图的程序执行后输出的结果是 . (13)某射击运动员在一组射击训练中共次平均数为: 则的最小值是 ; 若圆C:与区域有公共点,则实数的取值范围是 . 三、解答题:本大题共6小题,共80分.解答应写出文字说明,演算步骤或证明过程. (15)(本小题满分13分) 已知函数. (Ⅰ)求函数的最小正周期及值域; (Ⅱ)求的单调递增区间. (16)(本小题满分13分) 设是一个公差为的等差数列,,,成等比数列. (Ⅰ)求数列的通项公式; (Ⅱ)数列满足,求(用含的式子表示). (17)(本小题满分13分) 在长方形中,,,分别是,的中点(如左图).将此长方形沿对折,使平面平面(如右图),已知,分别是,的中点. (Ⅰ)求证:∥平面; (Ⅱ)求证:平面平面; (Ⅲ)求三棱锥的体积. (18)(本小题满分13分) 已知函数,. (Ⅰ)求函数的单调区间; (Ⅱ)当时,都有成立,求实数的取值范围. (19)(本小题满分14分) 已知椭圆经过点,离心率为. (Ⅰ)求椭圆的方程; (Ⅱ)过点的直线与椭圆交于不同的两点,,设直线和直线的斜率分别为和,求证:为定值. (20)(本小题满分14分) 对于整数,存在唯一一对整数和,使得,. 特别地,当时,称能整除,记作,已知. (Ⅰ)存在,使得,试求,的值; (Ⅱ)若,(指集合B 中的元素的个数),且存在,,,则称B为“谐和集”.请写出一个含有元素7的“谐和集”和一个含有元素8的非“谐和集”,并求最大的,使含的集合有12个元素的任意子集为“谐和集”,并说明理由. 参考答案 1. C 【解析】分别把两个集合表示为,所以, 2. B【解析】 当时成立,若,则出现和两种情形。
北京2012高考预测试卷 数学(文)试题.pdf

北京2012届高考预测试卷数学文试题 第卷为选择题,共分;第卷为非选择题共分。
满分100分,考试时间为0分钟。
第卷(选择题,共60分) 一、本题共12小题,每小题5分,共60分,在每小题给出的四个选项中只有一个选项是符合题目要求的. 1.已知集合,集合,则( ) A.B.C.D. 2.是虚数单位,则等于( ) A.B.C.D. 3.一个几何体的三视图如图所示,则该几何体的体积为( ) A.2 B.1C.D. 3.的前n项和为,则下列命题: (1)若数列是递增数列,则数列也是递增数列; (2)数列是递增数列的充要条件是数列的各项均为正数; (3)若是等差数列(公差),则的充要条件是 (4)若是等比数列,则的充要条件是 其中,正确命题的个数是( ) A.0个B.1个C.2个D.3个 5. 6.已知:命题:“是的充分必要条件”;命题:“”.则下列命题正确的是 A.命题“”是真命题 B.命题“(┐)”是真命题 C.命题“(┐)”是真命题 D.命题“(┐)(┐)”是真命题 7.,则直线( ) A.一定平行B.一定相交 C.一定是异面直线 D.一定垂直 8. 的图象大致是( ) 9.如图所示的方格纸中有定点,则( ) A. B. C. D. 10.设的最大值为( ) A. 80 B. C. 25 D. 11.若双曲线的左、右顶点分别为A、B,点P是第一象限内双曲线上的点。
若直线PA、PB的倾斜角分别为α,β,且,那么α的值是( ) A.B.C.D.12.若实数满足,则称是函数的一个次不动点.设函数与函数(其中为自然对数的底数)的所有次不动点之和为,则( ) A. B. C. D. 第卷(非选择题,共90分) 二、填空题:本大题共4小题,每小题4分,共16分,把答案填在题中横线上。
1已知与之间的部分对应关系如下表: 1112131415……则和满足的一个关系式是.中,已知分别为,,所对的边,为的面积.若向量满足,则=. 15.在<的概率为 16、已知,。
2012年高考终极仿真模拟试题数学文(北京卷).pdf

20.2.1正比例函数 2006 年7月12日,我国著名运动员刘翔在瑞士洛桑的田径110米栏的决赛中,以12.88秒的成绩打破了尘封13年的世界纪录,为我们中华民族争得了荣誉. (1)刘翔大约每秒钟跑多少米呢? (2)刘翔奔跑的路程s(单位:米)与奔跑时间t(单位:秒)之间有什么关系? (3)在前5秒,刘翔跑了多少米? 新课导入 分析:(1)刘翔大约每秒钟跑 110÷12.88=8.54(米). (2)假设刘翔每秒奔跑的路程为8.54米,那么他奔跑的路程s(单位:米)就是其奔跑时间t(单位:秒)的函数,函数解析式为 s=8.54t (0≤t ≤12.88). (3)刘翔在前5秒奔跑的路程,大约是t=5时函数s=8.54t 的值,即 s=8.54×5=42.7(米). 写出下列问题中的函数关系式 (1)圆的周长 随半径r变化的关系; (2)每个练习本的厚度为0.5cm,一些练习本 叠在一起的总厚度 h随练习本的本数n变化 的关系; (3)冷冻一个0℃的物体,使它每分下降2℃, 物体的温度T(单位:℃)随冷冻时间t变化 的关系(单位:分) (3)h=0.5n (4)T=-2t 这些函数有什么共同点? 这些函数都是常数与自变量的乘积的形式。
(2)T=-2t (1)l=2πr (3)h=0.5n (4) s=8.54t(0≤t ≤12.88) 一般地,形如y=kx(k是常数,k≠0)的函数,叫做正比例函数,其中k叫做比例系数. 思考 为什么强调k是常数, k≠0呢? y=k x (k≠0的常数) 比例系数 自变量 X的正比例函数 注: 正比例函数y=kx(k≠0) 的结构特征 ①k≠0 ②x的次数是1 1.下列函数是否是正比例函数?比例系数是 多少? 是,比例系数k=8. 不是. 不是. 是,比例系数k=. 练一练 (5)y=2x-1 不是. 应用新知 例1 (1)若y=5x3m-2是正比例函数,m= 。
2012年北京市石景山区高三一模文科数学含答案纯word版

2012年石景山区高三统一测试数学(文科)第Ⅰ卷 选择题一、选择题:本大题共8个小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的. 1.设集合}032|{2<--=x x x M ,{|220}N x x =->,则N M 等于( )A .(1,1)-B .(1,3) C .(0,1) D .(1,0)-2.在复平面内,复数21ii-+对应的点位于( ) A .第一象限B . 第二象限C .第三象限D .第四象限3.函数1sin()y x π=+-的图象( )4.设n m ,是两条不同的直线,γβα,,是三个不同的平面,下列命题正确的是( )A .αα//,//,//n m n m 则若B .βαγβγα//,,则若⊥⊥C .n m n m //,//,//则若ααD .n m n m ⊥⊥则若,//,αα5.执行右面的框图,若输入的N 是6, 则输出p 的值是( )A .120B .720C .1440D .50406.直线5x y +=和圆22: x 40O y y +-= 的位置关系是( )A .相离B .相切C .相交不过圆心D .相交过圆心A .关于2x π=对称 B .关于y 轴对称 C .关于原点对称 D .关于x π=对称7.某几何体的三视图如图所示,则它的体积是( )A.83+B.83+C.83+ D .3238.如图,已知平面l αβ=,A 、B 是l 上的两个点,C 、D 在平面β内,且,,DA CB αα⊥⊥ 4AD =,6,8AB BC ==,在平面α上有一个 动点P ,使得APD BPC ∠=∠,则PAB ∆面积 的最大值是()A .239 B .536 C .12 D .24αAC BDP β第Ⅱ卷 非选择题二、填空题:本大题共6个小题,每小题5分,共30分.9.设向量(cos ,1),(1,3cos )a b θθ==,且b a//,则θ2cos = .10.等差数列{}n a 前9项的和等于前4项的和.若0,141=+=k a a a ,则k =________.11. 已知点(,)P x y 的坐标满足条件4,,1.x y y x y +≤⎧⎪≤⎨⎪≥⎩点O 为坐标原点,那么PO 的最小值等于______,最大值等于_____.12.在区间[]9,0上随机取一实数x ,则该实数x 满足不等式21log 2x ≤≤的概率为 .13.设函数,1,()2,1x x a x f x x -+<⎧=⎨≥⎩的最小值为2,则实数a 的取值范围是 .14.集合{}{},|),(,,|),(a y x y x M R y R x y x U <+=∈∈={},)(|),(x f y y x P == 现给出下列函数:①xa y =,②x y a log =,③()sin y x a =+,④cos y ax =,若10<<a 时,恒有,P M C P U = 则所有满足条件的函数)(x f 的编号是 .三、解答题:本大题共6个小题,共80分.应写出文字说明,证明过程或演算步骤. 15.(本小题满分13分)在ABC ∆中,角A ,B ,C 所对应的边分别为a ,b ,c ,且C b B c a cos cos )2(=-. (Ⅰ)求角B 的大小; (Ⅱ)若2,4==a A π,求ABC ∆的面积.16.(本小题满分13分)我区高三期末统一测试中某校的数学成绩分组统计如下表:(Ⅰ)求出表中m 、n 、M 、N 的值,并根据表中所给数据在下面给出的坐标系中画出频率分布直方图;(Ⅱ)若我区参加本次考试的学生有600人,试估计这次测试中我区成绩 在90分以上的人数;(Ⅲ)若该校教师拟从分数不超过60的学生中选取2人进行个案分析,求 被选中2人分数不超过30分的概率.17 .(本小题满分13分)如图所示,在正方体1111ABCD A B C D -中,E 是棱1DD 的中点. (Ⅰ)证明:平面11ADC B ⊥平面1A BE ;(Ⅱ)在棱11D C 上是否存在一点F , 使F B 1//平面BE A 1?证明你的结论.18.(本小题满分14分)已知函数2()2ln f x x a x =+.(Ⅰ)若函数()f x 的图象在(2,(2))f 处的切线斜率为1,求实数a 的值;E A BCDB 1A 1 D 1 C 1(Ⅱ)求函数()f x 的单调区间; (Ⅲ)若函数2()()g x f x x=+在[1,2]上是减函数,求实数a 的取值范围.19.(本小题满分14分)已知椭圆12222=+by a x (0>>b a 1,短轴长为.(Ⅰ)求椭圆的方程;(Ⅱ)过左焦点F 的直线与椭圆分别交于A 、B 两点,若线段AB , 求直线AB 的方程.20.(本小题满分13分)若数列}{n A 满足21n n A A =+,则称数列}{n A 为“平方递推数列”.已知数列}{n a 中,21=a ,点(1,+n n a a )在函数x x x f 22)(2+=的图像上,其中n 为正整数.(Ⅰ)证明数列}1{2+n a 是“平方递推数列”,且数列)}1{lg(2+n a 为等比数列; (Ⅱ)设(1)中“平方递推数列”的前n 项之积为n T ,即)12)12)(12(21+++=n n a a a T ( ,求数列}{n a 的通项及n T 关于n 的表达式;(Ⅲ)记21log n n a n b T += ,求数列{}n b 的前n 项和n S .2012年石景山区高三统一测试高三数学(文科)参考答案一、选择题:本大题共8个小题,每小题5分,共40分.二、填空题:本大题共6个小题,每小题5分,共30分.注:两空的题第1个空3分,第2个空2分.三、解答题:本大题共6个小题,共80分.应写出文字说明,证明过程或演算步骤. 15.(本小题满分13分)解:(Ⅰ)∵ C b B c a cos cos )2(=-,由正弦定理,得∴ C B B C A cos sin cos )sin sin 2(=-. …………2分∴ A C B C B B C B A sin )sin(cos sin cos sin cos sin 2=+=+=,………4分 ∵ ()π,0∈A , ∴0sin ≠A ∴ 21cos =B . 又∵ π<<B 0 , ∴ 3π=B . …………6分 (Ⅱ)由正弦定理BbA a sin sin =,得622232=⨯=b …………8分,43A B ππ==426sin +=∴C …………11分2334266221s i n 21+=+⨯⨯⨯==∴C ab s . …………13分16.(本小题满分13分) 解:(I )由频率分布表得31000.03M ==, …………1分 所以100(333715)42m =-+++=, …………2分420.42100n ==,0.030.030.370.420.151N =++++=. …………3分…………5分 (Ⅱ)由题意知,全区90分以上学生估计为4215600342100+⨯=人.………7分 (III )设考试成绩在(]0,30内的3人分别为A 、B 、C ;考试成绩在(]30,60内的3人分别为a 、b 、c ,从不超过60分的6人中,任意抽取2人的结果有: (A ,B),(A ,C),(A ,a),(A ,b),(A ,c), (B ,C),(B ,a),(B ,b),(B ,c),(C ,a),(C ,b),(C ,c),(a ,b),(a ,c),(b ,c)共有15个. …………10分 设抽取的2人的分数均不大于30分为事件D .则事件D 含有3个结果: (A ,B),(A ,C) ,(B ,C) …………11分∴31()155P D == .…………13分 17.(本小题满分13分)解: (Ⅰ)证明:因为多面体1111D C B A ABCD -为正方体, 所以1111B C A ⊥面ABB ;因为111A B A ⊂面ABB ,所以111B C A ⊥B . …………2分又因为11A AB ⊥B ,1111B C AB B ⋂=,所以111DC A A B ⊥B 面.…………4分 因为11A A ⊂B 面BE ,所以平面11ADC B ⊥平面1A BE . …………6分 (Ⅱ)当点F 为11D C 中点时,可使F B 1//平面BE A 1. …………7分 以下证明之:易知:EF //112C D ,且EF 11=2C D , …………9分 设11AB A B O ⋂=,则1B O //112C D 且1B O 11=2C D , 所以EF //1B O 且EF 1=B O ,所以四边形1B OEF 为平行四边形. 所以1B F //OE . …………11分 又因为11B F A BE ⊄面,1OE A BE ⊂面.所以F B 1//面BE A 1 …………13分18.(本小题满分14分)解:(Ⅰ)2222'()2a x a f x x x x+=+= …………1分 由已知'(2)1f =,解得3a =-. …………3分(II )函数()f x 的定义域为(0,)+∞.E F A BCD B 1A 1 D 1C 1(1)当0a ≥时, '()0f x >,()f x 的单调递增区间为(0,)+∞;……5分(2)当0a <时'()f x =.当x 变化时,'(),()f x f x 的变化情况如下:由上表可知,函数()f x 的单调递减区间是;单调递增区间是)+∞. …………8分 (II )由22()2ln g x x a x x =++得222'()2ag x x x x=-++,…………9分 由已知函数()g x 为[1,2]上的单调减函数,则'()0g x ≤在[1,2]上恒成立,即22220ax x x -++≤在[1,2]上恒成立. 即21a x x≤-在[1,2]上恒成立. …………11分令21()h x x x =-,在[1,2]上2211'()2(2)0h x x x x x=--=-+<,所以()h x 在[1,2]为减函数. min 7()(2)2h x h ==-,所以72a ≤-. …………14分19.(本小题满分14分)解:解:(Ⅰ)由题意,2221a cb a bc ⎧-=⎪⎪=⎨⎪=+⎪⎩解得1a c ==.即:椭圆方程为.12322=+y x ------------4分(Ⅱ)当直线AB 与x轴垂直时,AB =,此时AOB S ∆= -----------6分 当直线AB 与x 轴不垂直时,设直线AB 的方程为:)1(+=x k y , 代入消去y 得:2222(23)6(36)0k x k x k +++-= .设1122(,),(,)A x y B x y ,则212221226233623k x x k k x x k ⎧-+=⎪⎪+⎨-⎪=⎪+⎩ -----------8分所以221)23k AB k +=+ , ------------11分由222AB k k =⇒=⇒= ------------13分所以直线0AB l y -=或0AB l y +=. ---------14分20.(本小题满分13分)解:(I )因为2221122,212(22)1(21)++=++=++=+n n n n n n n a a a a a a a所以数列}1{2+n a 是“平方递推数列” . --------2分由以上结论21lg(21)lg(21)2lg(21)n n n a a a ++=+=+ ,所以数列)}1{lg(2+n a 为首项是lg5公比为2的等比数列 . --------4分(II )11121lg(21)[lg(21)]22lg5lg5---+=+⨯==n n n n a a ,11221215,(51)2--+==-n n n n a a .--------6分1l g l g (21)l g (21)(21)l g 5nn n T aa =++++=-,215nn T -=.--------9分(III )11lg (21)lg512lg(21)2lg52---===-+n n n n n n T b a ,11222n n S n -=-+. --------13分[注:若有其它解法,请酌情给分]。
北京市西城区2012届高三第一次模拟考试文科数学试题.pdf

北京市西城区2012年高三一模试卷 数 学(文科) 2012.4 第Ⅰ卷(选择题 共40分) 一、题共8小题,每小题5分,共40分在每小题列出的四个选项中,选出符合题目要求的一项,,那么()(A)(B)(C)(D) 2.执行如图所示的程序框图,若输入,则输出的 值为( ) (A) (B) (C) (D) 3.若,,,则下列结论正确的是( )(A)(B)(C)(D) 4.如图,在复平面内,复数,对应的向量分别是 ,,则复数对应的点位于( )(A)第一象限(B)第二象限(C)第三象限(D)第四象限 5.已知正六棱柱的底面边长和侧棱长均为,其三视图 中的俯视图如图所示,则其左视图的面积是( )(A)(B)(C)(D)6.若实数,满足条件 则的最大值为()(A)(B)(C)(D)7.设等比数列的前项和为.则“”是“”的( )(A)充分而不必要条件(B)必要而不充分条件(C)充要条件(D)既不充分又不必要条件8.已知集合,其中,且 .则中所有元素之和是( )(A)(B)(C)(D) 第Ⅱ卷(非选择题 共110分) 二、填空题共6小题,每小题5分,共30分,.若,则实数_____. 10. 某年级名学生在一次百米测试中,成绩全部介于秒 与秒之间.将测试结果分成组:,, ,,,得到如图所示的频率分 布直方图.如果从左到右的个小矩形的面积之比为 ,那么成绩在的学生人数是_____. 11. 函数的最小正周期为_____. 12. 圆的圆心到直线的距离是_____. 13. 已知函数 则的零点是_____;的值域是_____.14. 如图,已知抛物线及两点和,其中.过,分别作轴的垂线,交抛物线于,两点,直线与轴交于点,此时就称, 确定了.依此类推,可由,确定,.记,. 给出下列三个结论: ① 数列是递减数列; ② 对,; ③ 若,,则. 其中,所有正确结论的序号是_____. 三、15.(本小题满分13分) 在△中,已知. (); (),△的面积是,求. 16.(本小题满分13分) 某校高一年级开设研究性学习课程,()班和()班报名参加的人数分别是和.现用分层抽样的方法,从中抽取若干名学生组成研究性学习小组,已知从()班抽取了名同学. ()()次交流活动,每次随机抽取小组中名同学发言.求次发言的学生恰好来自不同班级的概率. 17.(本小题满分14分) 如图,矩形中,,.,分别在线段和上,∥,将矩形沿折起.记折起后的矩形为,且平面平面. ()∥平面; (),求证:; (Ⅲ)求四面体体积的最大值. 已知椭圆的离心率为,一个焦点为. (Ⅰ)求椭圆的方程; (Ⅱ)设直线交椭圆于,两点,若点,都在以点为圆心的圆上,求的值. 19.(本小题满分13分) 如图,抛物线与轴交于两点,点在抛物线上(点在第一象限),∥.记,梯形面积为. (Ⅰ)求面积以为自变量的函数式; (Ⅱ)若,其中为常数,且,求的最大值. 20.(本小题满分13分) 对于数列,定义“变换”:将数列变换成数列,其中,且.这种“变换”记作.继续对数列进行“变换”,得到数列,依此类推,当得到的数列各项均为时变换结束. (Ⅰ)试问经过不断的“变换”能否结束?若能,请依次写出经过“变换”得到的各数列;若不能,说明理由; (Ⅱ)设,.若,且的各项之和为. ()求,; ()若数列再经过次“变换”得到的数列各项之和最小,求的最小值,并说明理由. 北京市西城区2012年高三一模试卷 数学(文科)参考答案及评分标准 2012.4 一、选择题:本大题共8小题,每小题5分,共40分.1. C;2. D ;3. D;4. B;5. A;6. B;7. C;8. C . 二、填空题:本大题共6小题,每小题5分,共30分. 9. ; 10. ; 11. ; 12. ; 13. 和,; 14. ① ② ③. 注:13题第一问2分,第二问3分; 14题少选1个序号给2分. 三、解答题:本大题共6小题,共80分.若考生的解法与本解答不同,正确者可参照评分标准给分. 15.(本小题满分13分) (Ⅰ)解:由,得. ………………3分 所以原式化为. ………………4分 因为,所以 , 所以 . ………………6分 因为, 所以 . ………………7分 (Ⅱ)解:由余弦定理, 得 . ………9分 因为 ,, 所以 . ………………11分 因为 , 所以 . ………………13分 16.(本小题满分13分) ())班抽取的人数为, 依题意得 ,所以, 研究性学习小组的人数为. ………………5分 ())班的人为,()班的人为. 次交流活动中,每次随机抽取名同学发言的基本事件为: ,,,,, ,,,,, ,,,,, ,,,,, ,,,,,共种. ………………9分 次发言的学生恰好来自不同班级的基本事件为: ,,,,,,,,, ,,,共种. ………………12分 所以次发言的学生恰好来自不同班级的概率为. ………………13分 (Ⅰ)证明:因为四边形,都是矩形, 所以 ∥∥,. 所以 四边形是平行四边形,……………2分 所以 ∥, ………………3分 因为 平面, 所以 ∥平面. ………………4分 (Ⅱ)证明:连接,设. 因为平面平面,且, 所以 平面, ………………5分 所以 . ………………6分 又 , 所以四边形为正方形,所以 .……………7分 所以 平面, ………………8分 所以 . ………………9分 (Ⅲ)解:设,则,其中. 由(Ⅰ)得平面, 所以四面体的体积为.………………11分 所以 . ………………13分 当且仅当,即时,四面体的体积最大. ………………14分 18.(本小题满分14分) (Ⅰ)解:设椭圆的半焦距为,则. ………………1分 由, 得 , 从而. ………………4分 所以,椭圆的方程为. ………………5分 (Ⅱ)解:设. 将直线的方程代入椭圆的方程, 消去得 . ………………7分 由,得,且.……9分 设线段的中点为,则,.………10分由点,都在以点为圆心的圆上,得, ………………11分 即 , 解得 ,符合题意. ………………13分 所以 . ………………14分 19.(本小题满分13分) (Ⅰ)解:依题意,点的横坐标为,点的纵坐标为. ……………1分 点的横坐标满足方程,解得,舍去.…………2分 所以.…4分 由点在第一象限,得. 所以关于的函数式为 ,. ………………5分 (Ⅱ)解:由 及,得. ………………6分 记, 则. ………………8分 令,得. ………………9分 ① 若,即时,与的变化情况如下: 极大值所以,当时,取得最大值,且最大值为. ………………11分 ② 若,即时,恒成立, 所以,的最大值为. ………………13分 综上,时,的最大值为;时,的最大值为. 20.(本小题满分13分) (Ⅰ)解:数列不能结束,各数列依次为;;;;;…. 以下重复出现,所以不会出现所有项均为的情形. ………………3分 (Ⅱ)解:()因为的各项之和为,且, 所以为的最大项, 所以最大,即,或. ………………5分 由,得,即,故.………7分 当时,同理可得 ,. ………………8分 ()方法一:由,则经过次“变换”得到的数列分别为:;;;;;. 由此可见,经过次“变换”后得到的数列也是形如“”的数列,与数列“结构”完全相同,但最大项减少12. 因为, 所以,数列经过次“变换”后得到的数列为. 接下来经过“变换”后得到的数列分别为:;;;;; ;,…… 从以上分析可知,以后重复出现,所以数列各项和不会更小. 所以经过次“变换”得到的数列各项和最小,的最小值为. ………………13分 方法二:若一个数列有三项,且最小项为,较大两项相差,则称此数列与数列 “结构相同”. 若数列的三项为,则无论其顺序如何,经过“变换”得到的数列的三项为(不考虑顺序) . 所以与结构相同的数列经过“变换”得到的数列也与结构相同,除外其余各项减少,各项和减少. 因此,数列经过次“变换”一定得到各项为 (不考虑顺序)的数列. 通过列举,不难发现各项为的数列,无论顺序如何,经过“变换”得到的数列会重复出现,各项和不再减少. 所以,至少通过次“变换”,得到的数列各项和最小,故的最小值为. ………………13分 北京利德智达文化发展有限公司。
2012年北京市高考压轴卷 文科数学试题

2012年普通高校招生考试 数学(文)(北京卷)本试卷共5页,150分.考试时间长120分钟.考生务必将答案答在答题卡上,在试卷上作答无效.考试结束后,将本试卷和答题卡一并交回.第一部分(选择题 共40分)一、选择题共8小题,每小题5分,共40分.在每小题列出的四个选项中,选出符合题目要求的一项. 1.已知集合1{1,10,}10A =,{|lg ,}B y y x x A ==∈,则A B = A.1{}10B. {10}C. {1}D. ∅2.复数11z i=+在复平面的对应的点位于 (A) 第一象限 (B)第二象限 (C)第三象限 (D)第四象限3.设,a b ∈R ,若||0b a ->,则下列不等式中正确的是(A)0a b ->(B)0a b +>(C)220a b ->(D)330a b +<4.函数()sin x f x e x =的图象在点(0,(0))f 处的切线的倾斜角为 (A) 0 (B)4π (C) 1 (D)325.若某程序框图如图所示,则输出的P 的值是(A)21 (B)26 (C)30 (D)556.已知命题p :函数12x y a +=-恒过(1,2)点;命题q :若函数(1)f x -为偶函数,则()f x 的图像关于直线1x =对称,则下列命题为真命题的是A.p q ∧B.p q ⌝∧⌝C.p q ⌝∧D.p q ∧⌝7.如图,三棱锥V ABC -底面为正三角形,侧面VAC 与底面垂直且VA VC =,已知其主视图的面积为23,则其左视图的面积为8.函数y =能成为该数列的公比的数是( )A .34B C D 第二部分 (非选择题 共110分)二、填空题共6小题,每小题5分,共30分. 9.若函数()sin()f x x ϕ=+是偶函数,则tan 2ϕ=10.已知(1,)a k =- ,(4,2)b =-且a b + 与a 垂直,则k 的值为__________.11.抛物线22y px =与直线20x y a ++=交于A B 、两点,其中点A 的坐标为(1,2),设抛物线的焦点为F ,则FA FB +的值等于12.若集合12,n A A A 满足12n A A A A = ,则称12,n A A A 为集合A 的一种拆分.已知:①当12123{,,}A A a a a = 时,有33种拆分; ②当1231234{,,,}A A A a a a a = 时,有47种拆分;③当123412345{,,,}A A A A a a a a a = ,时,有515种拆分; ……由以上结论,推测出一般结论:当121231{,,,}n n A A A a a a a += 有_____________种拆分.13.已知函数()f x 满足(1)()f x f x +=-,且()f x 是偶函数,当[0,1]x ∈时,2()f x x =,若在区间[1,3]-内,函数()()g x f x kx k =--有4个零点,则实数k 的取值范围是14.下面给出的四个命题中:①以抛物线y 2=4x 的焦点为圆心,且过坐标原点的圆的方程为22(1)1x y -+=;②若2m =-,则直线(2)10m x my +++=与直线(2)(2)30m x m y -++-=相互垂直; ③命题“R x ∈∃,使得0432=++x x ”的否定是“R x ∈∀,都有0432≠++x x ”;④将函数x y 2sin =的图象向右平移3π个单位,得到函数sin(2)6y x π=-的图象。
北京市密云县2012年高中模拟试卷及答案(文数)含答案

2012年密云县高三模拟考试数学(文科)、选择题:本大题共 8小题,每小题5分,满分40分•在每小题给出的四个选项中,只 有一项是符合题目要求的.21•设集合M {x|x 1}, P {x|x 1},则下列关系中正确的是C . 1A • M=PB.M UP=P2.函数y cosx 的一个单调递增区间为C.M U P=M3.已知向量aB .0, C .D .M n P =PD • ,21,1 , b2, n ,若agD ,则 n4.已知等比数列a n 的前三项依次为则a n25.抛物线y 4x 上一点M 至憔点的距离为A . 1B . 2C . 36 .如图1所示,是关于闰年的流程,则以下年份是闰年的为 A . 2012年 B . 2010 年 C . 2100 年 D . 1998年x 2,7.设变量x , y 满足约束条件y x,则目标函数z 2x y 的最小值为3,则点M 的横坐标x D . 4输小//输出:于長国甲/ /眷出‘棗倒年/1 1&给出定义:若m x m (其中m为整数),则m叫做离实数x最近的整数,2 2记作x = m.在此基础上给出下列关于函数f(x) x x的四个命题:1①函数y= f (x)的定义域为R,值域为0,-;2k②函数y= f (x)的图像关于直线x - ( k Z )对称;2③函数y= f (x)是周期函数,最小正周期为 1 ;1 1④函数y= f (x)在-,-上是增函数.2 2其中正确的命题的个数为A . 1 B.2 C. 3 D. 4二、填空题:本大题共6小题,每小题5分,满分30分. 9 .某校对全校男女学生共样本•已知女生抽了设复数z满足iz 10.1600名进行健康调查,选用分层抽样法抽取一个容量为95人,则该校的女生人数应是_________ 人.i,贝y z __________ .200的11.x2已知双曲线 -41的离心率为2,则实数m12.如图2所示,函数y f (x)的图象在点P处的切线方程是13.已知8,则f 5是平面, m , n是直线,给出下列命题①若m,则②若m,m P , n P ,则③如果m,n ,m、n是异面直线,那么相交.④若I// m,且,则n// 且n// 其中正确命题的有(填命题序号) ①④14 •规定一种运算:a a, abb, ab,例如:1b 2=1 ,3 2=2,则函数f (x) sinx cosxx的值域为三、解答题:本大题共6小题,满分80分•解答须写出文字说明、证明过程和演算步骤.15. (本小题满分12分)1 在厶ABC中,角A, B,C所对的边分别为a,b,c,已知a2 , c 3, cosB -.4(I)求b的值;(II)求sin C的值.16. (本小题满分13分)某高校在2011年的自主招生考试成绩中随机抽取100名学生的笔试成绩,按成绩分组:第 1 组[75,80),第 2 组[80,85),第 3 组[85,90),第 4 组[90,95),第 5 组[95,100], 得到的频率分布直方图如图所示.(I )分别求第3, 4, 5组的频率;(II )若该校决定在笔试成绩高的第3,4,5组中用分层抽样的方法抽取6名学生进入第二轮面试,求第3, 4, 5组每组各抽取多少名学生进入第二轮面试?(川)在(I)的前提下,学校决定在这6名学生中随机抽取2名学生接受甲考官的面试,求第4组至少有一名学生被甲考官面试的概率.频率17. (本小题满分14分)女口图,在长方体ABCD A1B1C1D1中,点E在棱CC1的延长线上,且1 CC1C1E BC AB 1.2(I )求证:D1E //平面ACB1;(n )求证:平面D1B1E 平面DCB1;(川)求四面体D1 B1AC的体积.A B1 设函数f(x) —X32ax23a2x 1, 0 a 1.3(I)求函数f (x)的极大值;(II)若x 1 a,1 a时,恒有a f (x) a成立(其中f x是函数f x的导函数),试确定实数a的取值范围.已知曲线上任意一点P到两个定点R, .3,0和F2 .3,0的距离之和为4. (I)求曲线的方程;(II)设过0, 2的直线I与曲线交于C、D两点,且OO C OD 0 ( O为坐标原点),求直线I的方程.2,已知数列a n中,a i 2, a23,其前n项和&满足& i S n 1 2& 1 ( n * n N *).(I)求数列a n的通项公式;(II)设b n 4n ( 1)n 1 2a n(为非零整数,n N*),试确定的值,使得对任意n N *,都有b n 1 b n 成立.2012年密云县高三模拟测试数学(文科)试题参考答案及评分标准9. 76010. 1 2i 11. 1212. 3;— 113.①④14. [ 1,]2三、解答题:本大题共 6小题,满分80分•解答须写出文字说明、证明过程和演算步骤. 15.(本小题满分12分)解:(I )由余弦定理, b 2 a 2 c 2 2accosB , ............................................................ 2分1得 b 2 22 322 2 310, .................................................................... 4 分4b .10 . ............................................................................................................. 6 分16.解:(I )由题意,第3组的频率为0.06 50.3 ,(II )方法1:由余弦定理,得 cosC2 , 2 2a b c 2ab4 10 9 迈 ...........................2 2 10 8 '•/ C 是ABC 的内角,二 sin C • 1 cos 2 C3,6 8 1方法2:v cosB ,且B 是ABC 的内角,4sin B ■. 1 cos 2 B根据正弦定理,b c sin B sin C得 sin Ccsin B b15—4 103-6 8 .8分10分12分8分10分12分3分第4组的频率为0.04 5 0.2 , 第5组的频率为0.02 5 0.1 .(n )第3组的人数为0.3 100 30 , 第4组的人数为0.2 100 20 , 第5组的人数为0.1 100 10 •因为第3 , 4 , 5组共有60名学生,所以利用分层抽样的方法在 60名学生中抽取6名学生,每组抽取的人数分别为:第3组: 3060 6 3 , 第4组:20 6 2,60第5组:10 6 1.60所以第3,4,5组分别抽取3人,2人,1人. ...................... 8分 (川)设第3组的3名学生为A , A 2 , A 3,第4组的2名学生为B 1, B 2 , 第5组的1名学生为C 1 • 则从六名学生中抽两名学生有:(A 1,A 2),(A 1 ,A 3),( A 1 ,B 1 ),(A 1,B 2),(A 1,C 1),(A 2,A 3),( A 2 , B 1),( A 2,B 2 ),(A 2 ,C 1 ),(A 3, BJ,(A 3,B 2),( A 3,G),(B 1, B 2),( B 1 ,C 1 ),(B2C),共15种可能.其中第4组的2名学生为B 1, B 2至少有一名学生入选的有:(A 1, B 1 ),( A 1, B 2),( A 2, B 1 ),( A 2, B 2),(A 3, BJ,( B 1,B 2),( A 3, B 2),( B 1,CJ,( B2G),共 9种可能,93所以第4组至少有一名学生被甲考官面试的概率为....... 13分15 517.解:(I)证明:连AD 1四边形AB i ED i 是平行四边形2分由长方体的特征可知:CD 平面 B i BCE平面D i B i E 平面DCB i (川)四面体D i B i AC 的体积i i 2 i i 2 4 3 2i8.(本小题满分i4分)••• f (x)的单调递增区间为(a,3a);i a —时,i3• f (x)在区间i a,i a 内是单调递减.AD 1//BC 1//B 1E则 D 1E//AB 1 又AB i 平面AB i C , D i E 平面AB i C D i E //平面 ACB i (n) 由已知得B i C 2 B i E 2 4 CE 2则 B 1E B 1C6分E5分i而B i E 平面B 1 BCE ,则 CD B i E B i E 平面 DCB i又B i E平面D 1B 1E10分VABCD A i B i C i D i iV A A i^D i V B ACB iV C B 1C i D i V D ACD ii4分解:(I ): f (x)x 2 4ax 3a 2,当f (x)0时,得3a ; 当 f (x) 0时,得x a 或x 3a ;f (x)的单调递减区间为(,a)和(3a,故当x 3a 时,f (x)有极大值,其极大值为x 2 4ax 3a 2x 2aa 2a ,此时,a9分19.(本小题满分14分)解:(I )根据椭圆的定义,可知动点 M 的轨迹为椭圆, .......................... 1分其中a 2,c 3, 则b a 2 c 21 . ............................. ............. 2分2所以动点M 的轨迹方程为—y 21 . ........................................................ 4分4(2)当直线l 的斜率不存在时,不满足题意............................... 5分 当直线l 的斜率存在时,设直线l 的方程为y kx 2,设C (x-i , y-i ) , D(x 2, y 2), uur uuur••• OC OD 0,二 x-j x 2 y-j y 2 0 . ............................................................. 7 分••• y 1 kx 1 2, y 2 kx ?2,2y 1y 2 k x-i x 2 2k (为 x 2) 4 .2•- (1 k )X 1X 2 2k(X 1 X 2) 4 0 .................................. ① ............................................................................ 9 分2X21 由方程组4 71,y kx 2.得 1 4k 2 x 2 16kx 12 0. .......................................................................... 11 分f (x)f 1-a8 a 28a 2 2a 16a 1, f(x) minf 1+a 2a 1.6a 1 a, a.当13a 1时, f (x )f 2amaxf (x)2a a,2a 1 a, 8a 2 6a 1此时,7 .,17 16综上可知, 实数a.716a 1, 1 3'帀7 .17 1611分13分a 的取值范围为丄,71731614分二 a n n 1 . ....................................................................................................................... 4 分 (II )•「a nn 1 ,• b n 4n ( 1)n12n1,要使 b n 1 b n 恒成立,•- 01 04n1 4n 1 n 2n 2 1 n 1 2n 1 0 恒成立,•- 3 4n 31 n 1 2n 1 0恒成立,n 1n 1•- 1 2 恒成立. ................................................ 6分(i) 当n 为奇数时,即2n 1恒成立, ............................... 7分当且仅当n 1时,2n 1有最小值为1, •1 . .......................................................... 9 分(ii)当n 为偶数时,即......................... 2n 1恒成立, 10分则 x 1 x 216k 1 4k 2,x 1 x 2代入①,得12121 4k 216k ’ 门2 4 0.4k 22k 1 即 k 2 4, 解得,k13分所以,直线 I 的方程是 y 2x 2x14分20. 解:(本小题满分 13 分) (I )由已知, S n 1 S n S n S n 12,n N ),即 a n 1 a n ),且 a 2•••数列a n2为首项,公差为1的等差数列.当且仅当n 2时,2n 1有最大值2 ,• 2 . ....................................................................................................... 12 分即2 1,又为非零整数,则 1 .综上所述,存在1,使得对任意n N*,都有b n 1 b n. ............................................................. 13分。
2012年高考数学 最新密破仿真模拟卷 第8周测试(学生测试版)

2012年高考数学 最新密破仿真模拟卷本试卷分第Ⅰ卷和第Ⅱ卷两部分,共4页,满分150分,考试用时120分钟,考试结束后,将本试卷和答题卡一并交回.注意事项:1. 答题前,考生务必用0.5毫米的黑色签字笔将自己的姓名、座号、准考证号、县区和科类填写在自己的答题卡和试卷规定的位置上.2. 第Ⅰ卷每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑;如需改动,用橡皮擦干净后,再选涂其他答案标号。
答案不能答在试卷上。
3. 第Ⅱ卷必须用0.5毫米黑色签字笔作答,答案必须写在答题卡各题目指定区域内相应的位置,不能写在试卷上;如需改动,先划掉原来的答案,然后再写上新的答案;不能使用涂改液、胶带纸、修正带。
不按以上要求作答的答案无效。
4.填空题请直接填写答案,解答题应写出文字说明、证明过程或演算步骤. 参考公式:柱体的体积公式:v sh =,其中s 表示柱体的底面积,h 表示柱体的高. 圆柱的侧面积公式:s cl =,其中c 是圆柱的底面周长,l 是圆柱的母线长. 球的体积公式V=34R 3π, 其中R 是球的半径. 球的表面积公式:S=4πR 2,其中R 是球的半径.用最小二乘法求线性回归方程系数公式1221ˆˆˆ,ni ii n i i x y nx ybay bx x nx==-⋅==--∑∑ . 如果事件A B 、互斥,那么()()()P A B P A P B +=+.第1卷(共60分)一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的。
1复数231i i -⎛⎫= ⎪+⎝⎭(A )34i -- (B )34i -+ (C )34i - (D )34i +2.命题p :若0a b ⋅<,则a 与b 的夹角为钝角。
命题q :定义域为R 的函数()f x 在(,0)-∞及(0,)+∞上都是增函数,则()f x 在(,)-∞+∞上是增函数。
下列说法正确的是( )A .“p 或q ”是真命题B .“p 且q ”是假命题C .“p ⌝”为假命题D .“q ⌝”为假命题3 .若函数32()22f x x x x =+--的一个正数零点附近的函数值用二分法计算,其参考数据如下:(1)2f =-(1.5)0.625f = (1.25)0.984f =- (1.375)0.260f =-(1.4375)0.162f =(1.40625)0.054f =-那么方程32220x x x +--=的一个近似根(精确到0.1)为( )(A)1.2 (B)1.3 (C)1.4 (D) 1.54.已知4cos ,(,),52πααπ=-∈则tan()4πα+等于( ) A.17-B.-7C.17D.7 5.(文)已知y =12sin2x +sin x ,则y ′是 ( )A.仅有最小值的奇函数B.既有最大值又有最小值的偶函数C.仅有最大值的偶函数D.非奇非偶函数5.(理)由曲线y=x 2,y=x 3围成的封闭图形面积为 ( )A.112B. 14C. 13D. 7126.若3sin α+cos α=0,则21cos sin 2αα+的值为 ( )A.103B.53C.23D.-27.已知函数则不等式f(x)>0的解的区间是 ( )A.(0,1)B.(-1,0)∪(0,1)C.(-1,1)D.(-∞,-1)∪(1,+∞)8.设2z x y =+,式中变量,x y 满足条件4624x y x y ≤+≤⎧⎨≤-≤⎩求z 的最大值和最小值A.11,7B.-7,-9C.11,6D.7,19. 过点P (0,1)且和A (3,3),B (5,-1)的距离相等的直线方程是 ( ) A .y =1B .2x +y -1=0C .y =1或2x +y -1=0D .2x +y -1=0或2x +y +1=010.设函数f (x )=-x 2+4x 在[m ,n ]上的值域是[-5,4],则m +n 的取值所组成的集合为 ( )A .[0,6]B .[-1,1]C .[1,5]D .[1,7]11.将正方体ABCD -A 1B 1C 1D 1截去四个角后得到一个四面体BDA 1C 1,这个四面体的体积是原正方体体积的 ( ) A.12 B.13 C.23 D.1412. 圆心在抛物线y 2=2x (y >0)上,并且与抛物线的准线及x 轴都相切的圆的方程是( )A .x 2+y 2-x -2y +1=0B .x 2+y 2+x -2y +1=0C .x 2+y 2-x -2y -14=0D .x 2+y 2-x -2y +14=0第II 卷(共90分)二、填空题:本大题共4小题,每小题4分,共16分.13.将容量为n 的样本中的数据分成6组,绘制频率分布直方图.若第一组至第六组数据的频率之比为2∶3∶4∶6∶4∶1,且前三组数据频数之和等于27,则n= .14.某管理部门用问卷调查的方式对当地10 000名中学生开展了“阳光冬季长跑”活动情况调查,x (单位:米)表示平均每天参加长跑的里程,现按长跑里程分下列四种情况进行统计:①0~1 000米;②1 000~2 000米;③2 000~3 000米;④3 000米以上,下图是此次调查中数据统计过程的算法框图,已知输出的结果是6 800,则平均每天参加长跑不超过2 000米的学生的频率是 .15.在△ABC 中,|BC|=4,且BC 落在x 轴上,BC 中点为坐标原点,如果sin C-sin B=12sin A,则顶点A 的轨迹方程是 .16. 方程2-x +x 2=3的实数解的个数为__ __.三、解答题:本大题共6小题,共74分. 17。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
北京市2012届高三数学文科仿真模拟卷8第Ⅰ卷一.选择题:本大题共8小题,每小题5分,共40分.在每小题列出的四个选项中,只有一项是符合题目要求的.选出符合题目要求的一项填在机读卡上. 1.设{}B x A x x B A ∉∈=-且,若{}3,4,5,2,1=A ,{}9,7,5,3=B ,则B A -等于( ) (A) {},9,7,5,4,3,2,1 (B) {}4,2,1 (C) {}9,7,4,2,1 (D) {}5,3 2.在复平面内,复数2)31(12i i---对应的点位于( ) (A) 第一象限 (B) 第二象限 (C) 第三象限 (D) 第四象限3.在等差数列{}n a 中,若76543=++++a a a a a ) (A) 45 (B) 90 (C) 180 (D)300 4.在区间⎥⎦⎤⎢⎣⎡-2,2ππ上随机取一个x ,x sin )(A)31 (B) π2 (C) 21 (D) 325.设函数6ln 2)(-+=x x x f 的零点为m ,则m 的所在区间为( ) (A) ()1,0 (B) ()2,1 (C) ()3,2 (D) )4,3( 6x 2的图像( )向左平移2π个单位长度 向左平移4π个单位长度7b ,则)()(c b c a+⋅+的最小值为( )(D) 2-8)0,)0,10(2F ,M 是此双曲线上一点,若021=⋅MF MF 2,则该双曲线的方程是( )(A) 1922=-y x (B) 1922=-y x (C) 17322=-y x (D) 13722=-y x第Ⅱ卷(非选择题,共110分)二.填空题:本大题共6小题,每小题5分,共30分.9.某程序的框图如图所示,则执行该程序,输出的结果=a _______.10则这个几何体的侧面积为11.某班50名学生在一次百米测试中,成绩全部介于13秒与18秒之间,将测试结果 绘制成频率分布直方图(如图),若成绩介于 14秒与16秒之间认为是良好,则该班在这次 测试中成绩良好的人数为_______.12.若实数y x ,满足⎪⎩⎪⎨⎧≥++≤-≥+-020022y x y x y x ,则yx z 22+=的最大值为_______,最小值为______.13.已知两条直线m ,n ,两个平面α,β,给出下面四个命题:①m ∥n ,αα⊥⇒⊥n m ;②α∥β,α⊂m ,⇒⊂βn m ∥n ; ③m ∥n ,m ∥α⇒n ∥α;④α∥β,m ∥n , βα⊥⇒⊥n m .其中正确命题的序号是____________.14.A 点从原点出发,每步走一个单位,方向为向上或向右,则走三步时,所有可能终点的横坐标的和为_________;走n 步时,所有可能终点的横坐标的和为_________.三.解答题:本大题共6小题,共80分.解答应写出文字说明,证明过程或演算步骤.15.(本小题13分)已知向量)23,(sin x a = ,)1,(cos -=x b(1)当a ∥b时,求x x 2sin cos 22-的值; (2)求b b a x f ⋅+=)()(在⎥⎦⎤⎢⎣⎡-0,2π上的值域.16.(本小题12分)袋中有大小、形状相同的红、黑球各两个,现依次不放回地随机取3次,每次取一个球.(1)试问:一共有多少种不同的结果,请列出所有可能的结果;(2)若摸到红球时得2分,摸到黑球时得1分,求3次摸球所得总分为5的概率. 17.(本小题13分)如图,在四棱锥ABCD -P 中, 底面ABCD 是矩形,侧棱PD ⊥底面ABCD ,DC PD =,E 是PC 的中点,作EF ⊥PB 交PB 于点F . (1)证明:PA ∥平面EDB ; (2)证明:PB ⊥平面EFD .18.(本小题14分)已知函数)(1031)(23R x x ax x x f ∈+-=. (1)若3=a ,点P 为曲线)(x f y =上的一个动点,求以点P 为切点的切线斜率取最小值时的切线方程;(2)若函数)(x f y =在),0(+∞上为单调增函数,试求a 的取值范围.19.(本小题14分)椭圆12222=+by a x )0(>>b a 的一个顶点为A )3,0(,离心率54=e(1)求椭圆方程;(2)若直线3-=kx y : 与椭圆交于不同的两点N M ,,且满足=,0=⋅,求直线 的方程.20.(本小题14分)已知数列{}n a 为等差数列,53=a ,137=a ,数列{}n b 的前n 项和为n S ,且有12-=n n b S(1)求{}n a 、{}n b 的通项公式;(2)若n n n b a c =,{}n c 的前n 项和为n T ,求n T ; (3)试比较n T 与n n S a 的大小,并说明理由.参考答案选择题1.B 2.A 3.C 4.A 5.C 6.D 7.B 8.A 填空题9.127 10.π2 11.27 12.64 ; 81 13.①④ 14.6 ; 2)1(+n n 注:两空的题目,第一个空2分,第二个空3分 解答题15.解:(1)∵a ∥b,∴0sin cos 23=+x x , ∴23tan-=x ,∴cos sin cos sin 2cos 22sin cos 22222=+-=-x x x x x x x (2)∵)21,cos (sin x x b a +=+ ,∴2sin(22)()(=⋅+=b b a x f∵02≤≤-x π,∴243π+≤-x …10分 …12分 . …13分(红黑黑)(黑红黑)(黑黑红)…6分 (2)记“3次摸球所得总分为5”为事件A. 事件A 包含的基本事件为:(红红黑)(红黑红)(黑红红) 由(1)可知,基本事件总数为6 ∴事件A 的概率2163)(==A P . …12分17.证明:(1)连结AC 交BD 与O ,连结EO .∵底面ABCD 是正方形, ∴点O 是AC 的中点. 又∵E 是PC 的中点∴在△PAC 中,EO 为中位线∴PA ∥EO . …3分 而EO ⊂平面EDB ,PA ⊄平面EDB ,∴PA ∥平面EDB . …6分 (2)由PD ⊥底面ABCD ,得PD ⊥BC . ∵底面ABCD 是正方形, ∴DC ⊥BC ,∴BC ⊥平面PDC . 而DE ⊂平面PDC ,∴BC ⊥DE .① …8分 ∵DC PD =,E 是PC 的中点,∴△PDC 是等腰三角形, DE ⊥PC .② …10分 由①和②得DE ⊥平面PBC . 而PB ⊂平面PBC ,∴DE ⊥PB . …12分 又EF ⊥PB 且DE EF =E , ∴PB ⊥平面EFD . …13分 18.解:(1)设切线的斜率为k ,则1)3(106)(22+-=+-='x x x x f , …2分 显然当3=x 时切线斜率取最小值1,又12)3(=f , …4分 ∴所求切线方程为312-=-x y ,即09=+-y x 。
…6分 (2)102)(2+-='ax x x f . …8分∵)(x f y =在),0(+∞∈x 为单调递增函数即对任意的),0(+∞∈x ,恒有0)(≥'x f , …10分 即0102)(2≥+-='ax x x f .∴xx x x a 522102+=+≤, …12分而1052≥+xx ,当且仅当10=x 时,等号成立,19.解:(1)依题意,有⎪⎪⎩⎪⎪⎨⎧+====222543cb a ac e b ,解得⎩⎨⎧==35b a …3分∴椭圆方程为192522=+y x . …5分(2)∵=,0=⋅,∴MN AP ⊥,且P 是线段MN 的中点, …7分由⎪⎩⎪⎨⎧=+-=1925322y x kx y 消去y 并整理得, 0150)925(22=-+kx x k . …9分 设),(11y x M 、),(22y x N 、),(y x P 则925150221+=+k kx x ,∴9257520+k k x…11分 k k k k k k AP 25182592575392527222--=+-+-= 1-=⋅k ,解得 57±=k (此时满足判别式0>∆) …13分 ∴直线 的方程为357-±=x y . …14分 20.解:(1)∵{}n a 是等差数列,且53=a ,137=a ,设公差为d 。
∴⎩⎨⎧=+=+1365211d a d a , 解得⎩⎨⎧==211d a∴12)1(21-=-+=n n a n (*∈N n ) …2分 在{}n b 中,∵12-=n n b S 当1=n 时,1211-=b b ,∴11=b当2≥n 时,由12-=n n b S 及1211-=--n n b S 可得 122--=n n n b b b ,∴12-=n n b b ∴{}n b 是首项为1公比为2的等比数列∴12-=n n b (*∈N n ) …4分(2)12)12(-⋅-==n n n n n b a c122)12(25231-⋅-++⋅+⋅+=n n n T ① n n n n n T 2)12(2)32(2523212132⋅-+⋅-++⋅+⋅+⋅=- ② ①-②得 n n n n T 2)12(222222112⋅--⋅++⋅+⋅+=--n n 2)12(⋅--n n 2)1⋅-*) …8分 (3))12)(1--n n n n n 122)12(32)32(-+⋅--+⋅-=n n n nn)21(22222nnn n -+=⋅-+= …9分令)1(21)(≥-+=x x x f x ,则2ln 21)(xx f -='∵)(x f '在[)+∞,1是减函数,又04ln 12ln 21)1(<-=-='f ∴1≥x 时,0)(<'x f∴1≥x 时,)(x f 是减函数. 又0211)1(=-+=f ∴1≥x 时,0)(≤x f∴1≥x 时,021≤-+x x …13分 ∴*∈N n 时,021≤-+n n∴*∈N n 时,n n n S a T ≤ …14分。
