四年级暑期讲义(第3讲)

合集下载

第3讲和差倍问题+讲义

第3讲和差倍问题【知识点汇总】一、解题方法：画线段图在解决和差倍问题时，线段图法是最常用的方法，一般选取较少的数量画成一段，再按照题目条件中所给的数量关系画出其他量的长度，再设法通过条件求出一段所代表的数量即可。

具体步骤如下：（1）先画一倍量（2）再画多倍量（3）左端对齐（4）右端比较（5）大括号表示和二、和倍问题（1）和倍问题就是条件中给出了和的关系和倍数关系的问题。

（2）解题方法：画线段图，找到“总量”和“1”段之间的关系，设法求出“1”段所代表的数量。

（3）一倍量=和÷（倍数+1）二、差倍问题（1）差倍问题就是条件中给出了差的关系和倍数关系的问题。

（2）解题方法：画线段图，找到“差量”和“1”段之间的关系，设法求出“1”段所代表的数量。

（3）一倍量=差÷（倍数－1）四、非整倍数的情况“几倍多几”就把多的减去，“几倍少几”就把少的添上。

五、和差问题（1）和差问题就是条件中给出了和的关系和差的关系的问题。

（2）大数=（和＋差）÷2小数=（和－差）÷2（1）纺织厂有职工480人，其中女职工人数是男职工人数的3倍。

请问：男、女职工各有几人？（2）学校买来乒乓球和篮球共78个，乒乓球的数量比篮球的4倍还多3个。

请问：学校一共买了几个乒乓球？（3）果园中梨树和苹果树共有67棵，梨树比苹果树的2倍少2棵。

请问：苹果树有多少棵？（1）学校合唱团成员中，女生人数是男生的3倍，而且女生比男生多80人。

请问：合唱团里男生和女生各有多少人？（2）甲、乙两筐苹果重量原来相等，现在从甲筐拿出12千克苹果放入乙筐，结果乙筐苹果的重量就比甲筐的3倍少2千克。

两筐苹果原来各有多少千克？【例3】（1）小明和小华一共有4014张。

请问：小华有几张积分卡？（2）登月行动地面控制室的成员由两组专家组成，两组共有专家125名。

原来第一组人太多，所以从第一组调了20人到第二组，即使这样第一组仍比第二组多5名。

人教版四年级数学下册第3讲运算定律 - (1)知识梳理及巩固练习

第3讲运算定律加法交换律两个数相加，交换加数的位置和不变加法结合律三个数相加，先把前两个数相加，或者先把后两个数相加，和不变加法运算定律a+b=b+a(a+b)+c=a+(b+c )一个数连续减去两个数，可以用这个数减去两个减数的和，即a-b-c=a-(b+c )减法的运算性质及简算在连减运算中，任意交换减数的位置，差不变，即a-b-c=a-c-b乘法交换律两个数相乘，交换两个因数的位置，积不变乘法分配律三个数相乘，先乘前两个数，或者先乘后两个数，积不变乘法运算定律乘法结合律a×b=b×a(a×b)×c=a×(b×c )两个数的和与一个数相乘，可以先把它们与这个数分别相乘(a+b)×c=a×c+b×c在连除法中，如果除数的积正好是整十、整百或整千……的数，那么可以应用除法的运算性质a÷b÷c=a÷(b×c)进行简便计算除法的运算性质及简算两个数相除，如果除数分解成的因数恰好与被除数成倍数关系，那么可以运用a÷(b×c)=a÷b÷c进行简便计算知识梳理知识点一：加法运算定律+＝+ a+b=b+a）++（）(a+b)+c=a+(b+c)减法的运算性质及简算－－＝－a－b－c＝a－c－b＝－－）a－b－c＝a－（ b + c）知识点二：乘法运算定律两个因数交换位置，积不变，这叫做乘法交换律。

a×b＝b×a三个数相乘，先乘前两个数或者先乘后两个数，积不变。

叫做乘法结合律。

（a×b）×c=a×(b×c)两个数的和与一个数相乘，可以先把它们与这个数分别相乘，再相加。

叫做乘法分配律。

(a＋b)×c=a×c＋b×c除法的运算性质及简算1. 一个数连续除以两个数，等于这个数除以这两个数的积。

四年级下册数学讲义奥数导引第3讲：格点与割补

一、掌握格点多边形面积的计算方法，以及这些方法的推广和拓展．二、分割法，正所谓“大事化小”，把不规则的大图形化为规则的小图形，来进行计算．三、添补法，则正好相反，是“以小见大”，把不规则图形周围添上规则的小图形，使总面积便于计算．四、遇在图形中进行适当的分割拼补，把不规则的形状拼成规则形状，也是常见的方法．五、公式法:在最小的正方形面积为1的图形中：21=÷+−正方形格点多边形面积边界格点数内部格点数．在最小正三角形面积为1的图形中：22=+×−三角形格点多边形面积边界格点数内部格点数．六、对于很多非格点图形的面积计算，分割和添补的方法依然适用．知识精讲第三讲格点与割补【例1】图17-27中每个小正方形的边长为1厘米，阴影部分的面积是多少平方厘米？【例2】如图17-28，平面上有16个点，相邻两点间隔为1厘米，在每个点都钉上钉子，形成4行4列的正方形钉阵．现在有许多皮筋，请问：可以套出多少种不同面积的三角形？（面积相同但形状不同的三角形算一种）图17‐28图17‐27例题解析【例3】已知大的正六边形面积是72平方厘米，按图17-29中不同方式切割（切割点均为等分点），形成的阴影部分面积各是多少平方厘米？【例4】图17-30为一个边长为2厘米的正方形，分别连接顶点与对应边中点．围成的阴影部分的面积为多少平方厘米？【例5】如图17-31所示，已知一个四边形的两条边的长度和三个角的度数，这个四边形的面积是多少平方厘米？（单位：厘米）图17‐3111图17‐3011图17‐29【例6】如图17-32所示，这个多边形六条边的长度分别是1，2，3，4，5，7．问：这个图形的面积最大可能是多少？【例7】如图17-33，有一个80100×的长方形网格，它的四个顶点分别为A，B，C，D．已知图中每一个小方格的面积都是1，请选出一个合适的格点P，使得三角形P AC的面积尽可能小（不能等于0），那么这个最小的面积是多少？【例8】正12边形的边长为1厘米，阴影部分都是正三角形（边长也为1厘米），如图17-34．那么空白部分面积等于多少平方厘米？图17‐34A BCD图17‐33图17‐32。

第3讲(学生)一次函数的图象和性质讲义

第3讲(学生)一次函数的图象和性质讲义编辑整理：尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（第3讲(学生)一次函数的图象和性质讲义）的内容能够给您的工作和学习带来便利。

同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。

本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为第3讲(学生)一次函数的图象和性质讲义的全部内容。

第3讲一次函数的图象和性质(1)学习目标：学会用图表描述变量的变化规律，会准确地画出函数图象，结合函数图象，能体会出函数的变化情况学习重点：函数的图象学习难点：函数图象的画法学习过程引入:信息1：下图是一张心电图，信息2：下图是自动测温仪记录的图象,他反映了北京的春季某天气温T如何随时间的变化二变化，你从图象中得到了什么信息？问题：正方形的边长x与面积S的函数关系为S=x2，你能想到更直观地表示S与x 的关系的方法吗？一般地,对于一个函数，如果把自变量与函数的每对对应诃子分别作为点的横、纵坐标，那么坐标平面内由这些点组成的图形,就是这个函数的图象(graph）.•已经知道了形如y=•kx•（k•是常数， k ≠0 )的函数，•叫做正比例函数，其中k 叫做比例系数．那么正比例函数的图象有什么特征呢？范例：例1．画出下列正比例函数的图象，并进行比较,寻找两个函数图象的相同点与不同点，考虑两个函数的变化规律．1．y=2x 2．y=—2x2．y=列表表示几组对应值：y3．两个图象的共同点:都是经过原点的直线．不同点：函数y=2x 的图象从左向右呈上升状态，即随着x 的增大y 也增大；经过第一、三象限．函数y=—2x 的图象从左向右呈下降状态，即随x 增大y 反而减小；•经过第二、四象限． 1比较可以看出：两个图象都是经过原点的直线．函数y=x•的图象从左向右上升,经过一、三象限,即随x增大y也增大;函数y=—x•的图象从左向右下降，经过二、四象限，即随x增大y反而减小．归纳：正比例函数图象的规律：正比例函数y=kx（k是常数，k≠0）的图象是一条经过原点的直线．•当x〉0时,图象经过一、三象限，从左向右上升，即随x的增大y也增大；当k〈0时，•图象经过二、四象限，从左向右下降,即随x增大y反而减小．正是由于正比例函数y=kx（k是常数，k≠0）的图象是一条直线,•我们可以称它为直线y=kx．思考：经过原点与点（1，k)的直线是哪个函数的图象？画正比例函数的图象时，•怎样画最简单?为什么?经过原点与点（1，k）的直线是函数y=kx的图象．画正比例函数图象时，只需在原点外再确定一个点，即找出一组满足函数关系式的对应数值即可，如（1，k)．因为两点可以确定一条直线．Ⅲ．练习用你认为最简单的方法画出下列函数图象:1．y=x 2．y=-3x练习1、某函数具有下面的性质：（1）．它的图象是经过原点的一条直线．（2）．y随x增大反而减小．121232请你举出一个满足上述条件的函数,写出解析式，画出图象．2。

人教版小学四年级上册秋季数学讲义专项强化练习《第3讲无法超越的差距》题目+答案

第3讲无法超越的差距例题练习题例1今年墨莫的年龄是10岁，小高的年龄是13岁．8年后毛毛的年龄正好是墨莫、小高年龄差的7倍．请问：今年毛毛的年龄是多少？练1今年卡莉娅比萱萱大4岁，6年后小花的年龄与卡莉娅、萱萱年龄差的和是20岁．请问：今年小花的年龄是多少？例25年前飞飞与他爸爸的年龄差是24岁，今年爸爸的年龄是飞飞的4倍，请问：今年飞飞和爸爸的年龄分别是多少？练210年前小高和爸爸的年龄差是28岁，今年爸爸的年龄是小高的3倍，请问：今年小高和爸爸的年龄分别是多少？例3今年丁丁10岁，他父亲38岁，请问：多少年后，父亲年龄是丁丁的2倍？多少年前，父亲年龄是丁丁的5倍？练3今年小白10岁，小黑22岁，请问：多少年前，小黑年龄是小白的3倍？多少年前，小黑年龄是小白的4倍？例4今年小高和爸爸的年龄和是40岁．4年后，爸爸的年龄是小高的3倍．请问：小高今年的年龄是多少？练4今年阿宝和老李的年龄和是70岁．5年前，老李的年龄是阿宝年龄的4倍．请问：阿宝今年的年龄是多少？挑战极限1今年，叔叔的年龄是阿呆的2倍，且叔叔的年龄比阿呆的大18岁．请问：多少年前叔叔的年龄是阿呆年龄的3倍？自我巩固1．今年小明爸爸、妈妈的年龄差是12岁，2年后小明的年龄与爸爸、妈妈的年龄差一样大．那么今年小明的年龄是___________岁．2．3年前大明爸爸、妈妈的年龄差是12岁，4年后大明的年龄与爸爸、妈妈的年龄差一样大．那么今年大明的年龄是___________岁．3．今年毛毛9岁，瓜瓜17岁．那么当毛毛15岁时，瓜瓜___________岁．4．2年前爸爸比儿子大36岁，今年爸爸的年龄是儿子的5倍，那么今年儿子___________岁．5．5年前妈妈比儿子大24岁，5年后妈妈的年龄是儿子的3倍，那么今年妈妈___________岁．6．父亲今年比儿子大32岁，2年后，父亲的年龄是儿子的5倍，那么今年儿子___________岁．7．6年前姐姐比弟弟大10岁，10年前，姐姐的年龄是弟弟的3倍，那么今年姐姐___________岁．8．今年六六8岁，妈妈32岁，那么___________年后，妈妈的年龄是六六的3倍．9．今年阿瓜和爸爸的年龄和是34岁．5年后，爸爸的年龄是阿瓜的3倍．那么阿瓜今年___________岁．10．5年前阿呆和爸爸的年龄和是31岁．2年后爸爸的年龄是阿呆的4倍．那么阿呆今年___________岁．课堂落实1．今年小高爸爸、妈妈的年龄差是3岁，10年后小高的年龄与爸爸、妈妈年龄差的和是21岁．那么今年小高___________岁．2．11年前阿呆和他叔叔的年龄差是26岁，今年叔叔的年龄是阿呆的3倍．那么今年阿呆___________岁．3．今年墨莫14岁，墨爸爸40岁，那么___________年后墨爸爸的年龄是墨莫的2倍．4．今年斯斯22岁，斯斯爸爸47岁，那么___________年前斯斯爸爸的年龄是斯斯的6倍．5．父子两人今年的年龄之和是58岁，4年前，爸爸的年龄是儿子年龄的4倍．那么爸爸现在的年龄是___________岁．第3讲无法超越的差距·参考答案例题练习题答案例1 【答案】13岁【解析】两人的年龄差不变，是13-10＝3（岁），8年后毛毛的年龄是小高、墨莫年龄差的7倍，也就是3×7＝21（岁）.所以今年毛毛21-8＝13（岁）.练1 【答案】10岁【解析】卡莉娅、萱萱的年龄差不变，6年后小花的年龄与卡莉娅、萱萱年龄差的和是20岁，6年后小花的年龄是20-4＝16（岁）.所以今年小花16-6＝10（岁）例2 【答案】飞飞8岁；爸爸32岁【解析】飞飞和爸爸年龄差24岁，根据年龄差不变的性质，今年爸爸年龄是飞飞的4倍，设飞飞年龄为“1”，爸爸年龄为“4”，差为“3”，“1”即24÷3＝8（岁），此时爸爸年龄为4×8＝32（岁），则当飞飞8岁，爸爸32岁时，爸爸年龄是飞飞的4倍.练2 【答案】小高14岁；爸爸42岁【解析】小高和爸爸年龄差28岁，根据年龄差不变的性质，今年爸爸年龄是小高3倍，设小高年龄为“1”，爸爸年龄为“3”，差值为“2”，即28岁，则当小高14岁，爸爸42岁时，爸爸年龄是小高的3倍.例3 【答案】18年后；3年前【解析】丁丁和父亲年龄差28岁，根据年龄差不变的性质，当父亲年龄是丁丁的2倍时，设丁丁为“1”，父亲年龄为“2”，差值为“1”，即28岁，则当丁丁28岁，父亲56岁时，父亲的年龄是丁丁的2倍，这是在18年后；同理，当父亲年龄是丁丁的5倍时，设丁丁年龄为“1”，父亲年龄为“5”，差值为“4”，即28岁，则“1”为7岁，丁丁为7岁，那是在3年前.练3 【答案】4年前；6年前【解析】小白和小黑的年龄差是12岁，根据年龄差不变的性质，当小黑年龄是小白的3倍时，设小白年龄为“1”，小黑年龄为“3”，差值为“2”，即12岁，则“1”为6岁，小白6岁，这是在4年前；同理，当小黑年龄是小白的4倍时，设小白年龄为“1”，小黑年龄为“4”，差值为“3”，即12岁，则“1”为4岁，小白为4岁，那是在6年前例4 【答案】8岁【解析】4年后，小高和爸爸的年龄都增加了4岁，即一共增加了8岁，此时小高和爸爸的年龄和是48岁，爸爸的年龄是小高的3倍，设小高年龄为“1”，爸爸年龄为“3”，和为“4”即“1”是48÷4＝12（岁），小高四年后的年龄是12岁，今年是8岁.练4 【答案】17岁【解析】5年前，阿宝和老李的年龄都减少了5岁，即一共减少了10岁，此时阿宝和老李的年龄和是60岁，老李的年龄是阿宝的4倍，设阿宝年龄为“1”，老李年龄为“4”，和为“5”即“1”是60÷5＝12（岁），阿宝五年前的年龄是12岁，今年是17岁.挑战极限1 【答案】9年前【解析】叔叔和阿呆的年龄差是18岁，设今年阿呆年龄为“1”，叔叔年龄为“2”，差值为“1”，即18岁，今年阿呆18岁，叔叔36岁.如果叔叔的年龄是阿呆年龄的3倍，设此时阿呆年龄为“1”，叔叔年龄为“3”，差值为“2”，即18岁，则“1”为9岁，也就是阿呆9岁，叔叔27岁时，叔叔年龄是阿呆的3倍，即9年前.自我巩固答案1 【答案】10【解析】小明爸爸、妈妈的年龄差不变，2年后小明的年龄与爸爸、妈妈的年龄差一样大，也就是12岁.所以今年小明12-2＝10（岁）.2 【答案】8【解析】大明爸爸、妈妈的年龄差不变，4年后大明爸爸、妈妈的年龄差与3年前一样大，也就是12岁.所以今年大明12-4＝8（岁）.3 【答案】23【解析】两人年龄差17-9＝8（岁），当毛毛15岁时，瓜瓜15+8＝23（岁）.4 【答案】9【解析】爸爸和儿子年龄差36岁，根据年龄差不变的性质，今年爸爸的年龄是儿子的5倍，则儿子的年龄是36÷(5-1)＝9（岁）.5 【答案】31【解析】妈妈和儿子年龄差24岁，根据年龄差不变的性质，5年后妈妈的年龄是儿子的3倍，则5年后妈妈的年龄是24÷(3-1)×3＝36（岁），今年妈妈的年龄是36-5＝31（岁）6 【答案】6【解析】父亲和儿子年龄差32岁，根据年龄差不变的性质，当父亲年龄是儿子的5倍时，设儿子年龄为“1”，父亲年龄为“5”，差值为“4”，即32岁，则当儿子8岁，父亲40岁时，父亲年龄是儿子的5倍，这是在2年后，所以今年儿子8-2＝6（岁）7 【答案】25【解析】姐姐和弟弟年龄差10岁，根据年龄差不变的性质，当姐姐年龄是弟弟的3倍时，设弟弟的年龄为“1”，姐姐的年龄为“3”，差值为“2”，即10岁，则当弟弟5岁时，姐姐15岁时，姐姐年龄是弟弟的3倍，这是在10年前，所以今年姐姐15+10＝25（岁）8 【答案】4【解析】两人年龄差是24岁.年龄是3倍时，设六六的年龄是“1”，妈妈是“3”，“1”是24÷(3-1)＝12（岁），即六六12岁，是在12-8＝4(年)后.9 【答案】6【解析】5年后，阿瓜和爸爸的年龄都增加了5岁，即一共增加了10岁，此时阿瓜和爸爸的年龄和是44岁，爸爸的年龄是阿瓜的3倍，设阿瓜年龄为“1”，爸爸年龄为“3”，和为“4”即“1”是44÷4＝11（岁），阿瓜五年后的年龄是11岁，今年是6岁.10 【答案】7【解析】5年前到2年后，阿呆和爸爸的年龄都增加了7岁，即一共增加了14岁，此时阿呆和爸爸的年龄和是45岁，爸爸的年龄是阿呆的4倍，设阿呆年龄为“1”，爸爸年龄为“4”，和为“5”，即“1”是45÷5＝9（岁），阿呆两年后的年龄是9岁，今年是7岁.课堂落实答案1 【答案】82 【答案】133 【答案】124 【答案】175 【答案】44。

四年级暑期讲义第三讲.小数的除法

【例题精讲】例1．4.7÷0.8的商和余数分别是（）。

A. 5和0.7B. 5和7C. 0.5和0.7D. 0.5和7例2．计算：．【课堂练习】1．0.00……045÷0.00……09=__________100个0 101个02．1÷6的商精确到百分位是__________知识点三（商的近似数）【知识梳理】1．求商的近似数的方法：（1）先看要保留几位小数；（2）然后除到比需要保留的小数位数多一位；（3）再将最后一位“四舍五入”。

【注意】（1）求商的近似数时应该用“≈”连接；（2）求得的商的近似数末尾的0不能去掉。

【例题精讲】例1．一批货物75吨，已经运了6次，还剩41.4吨，平均每次运了多少吨？剩下的还要运几次？（结果保留整数）知识点五（有限小数和无限小数）【知识梳理】1．小数的分类：（1）按整数部分分类：；（2）按小数位数分类：。

【例题精讲】例1．在3.8288888，5.666...，0.35，0.00202...，2.75，3.2727...中，，是有限小数的是( )，是循环小数的数( )【课堂练习】1．2.235235……的循环节是（）A. 2.235B. 2.35C. 235D. 2353知识点二（用计算器探索规律）【知识梳理】1．用计算器探索规律的方法：用计算器计算——观察、发现规律——根据规律写出得数。

【例题精讲】例1．用计算器计算前3题,直接写出后3题的得数:1234.5679×9 =1234.5679×18=2.1÷3≈0.3 。

（）3. 5.6除以一个小数，所得的商必定大于5.6。

（）4.循环小数都是无限小数。

（）5.小数除法的意义与整数除法的意义相同。

（）三、快乐。

1. 比0.17大，比0.19小的小数有（）个。

A．１ B．9 C．无数2. 8.995保留两位小数约是（）。

A．8.00 B．9.00 C．8.993. 下列算式中结果大于１的是（）。

四年级数学暑假讲义学生版

目录第1讲大数的认识初步 (3)第2讲大数的认识进阶 (15)第3讲图形的计数 (44)第4讲角的认识和度量 (53)第5讲三位数乘两位数初步 (62)第6讲除数是一位数的竖式谜 (69)第7讲暑假闯关 (78)He Is a Bus DriverHe is a bus driver. He drives a school bus. He drives the bus five days a week. He drives the bus in the morning. He drives it in the afternoon. He picks up kids near their homes. He takes them to school. He picks them up at school. He takes them home.第1讲大数的认识初步1.掌握亿以上数的读法和写法。

2.结合题目要求组成符合要求的大数。

一. 数位顺序表数位顺序表:数级、数位和计数单位三部分组成。

每相邻两个计数单位之间的进率都是十,这种计数的方法叫做十进制计数法。

例：把下面数字分级。

897589229 100008776358736500000 87265872588同步练习1.把下面数字分级。

30017600 150609000 23478598322.选择（1）一个整数,它的最高位是十亿位.这个数是( )位数。

A.八B.九C.十D.十一（2）万、十万、百万、千万……这些都是( )。

A.数位B.位数C.计数单位（3）一个九位数,它的最高位是( )。

A. 千万B.亿C.亿位3.判断正误（1）个位、十位、百位、千位都是个级的计数单位( )。

A.正确B.错误（2）两个计数单位之间的进率是十( )。

A.正确B.错误2.填空（1）数位顺序表:由( )、( )和( )。

（2）从个位起,每( )个数位是一级,个级包括( )、( )、( )、( ),万级包括( )、( )、( )、( ),亿级包括( )、( )、( )、( )。

四年级下第3讲《多人多次相遇与追及》教学课件

极限挑战
mathematics
例题5：A、B两城相距48千米，甲、乙、丙三人分别以每小时4千米、2千米、2千米的速度行走；甲、乙两人从A城，丙从B城同时出发，相向而行；请问：出发多长时间后，甲正好在乙和丙的中点？分析：速度分别是4、2、2，那么我们可以把三人的路程分别设为几份呢？请试着画出线
例题4：甲、乙、丙三人走路，甲每分钟走60米，乙每分钟走50米，丙每分钟走40米；如果甲从A地，乙和丙从B地同时出发相向而行，甲和乙相遇后，过了15分钟又与丙相遇；求 A、B两地间的距离为多少米? 分析：请自己画出详细的线段图，好好分析一下，还能像前面两个例题那样一段一段计
算吗？如果不能，该怎么办呢？
分析，看看哪个过程是可以计算的?
A地叮叮
咚咚
B地铛铛
例题讲解
mathematics
练习2：小春、小秋两人从A地出发，小夏则从B地同时出发，相向而行；小春的速度为每小时60千米，小夏的速度为每小时40千米，出发3小时后，小春与小夏相遇，又过了1小时，小秋也与小夏相遇，请问：小秋的速度是多少?
例题讲解
mathematics
练习4：刘备、关羽、张飞三人，刘备每分钟走40米，关羽每分钟走60米，张飞每分钟走50 米；如果刘备从A地，关羽和张飞从B地同时出发相向而行，刘备和关羽相遇后，过了10分钟又与张飞相遇，求A、B两地间的距离为多少米?
例题讲解
mathematics
上面几道例题的运动过程是一样的，在这样的运动过程里面，会有两次相遇运动和一次追及运动；在这个运动过程中有一段路程既是路程和又是路程差，需要同学们格外注意. 接下来我们来看一下和速度倍数相关的行程问题，大家想象一下，如果甲、乙两人的同时出发同向前进，甲的速度是乙的3倍，那么5分钟后，甲的路程是乙的几倍？ 30分钟后，甲的路程又是乙的几倍？2个小时后，甲的路程又是乙的几倍？其实上述问题的答案都是3倍，不管时间过了多久，只要甲、乙两人的时间相同，他们路程的倍数关系就等于速度的倍数关系.

【引流课讲义】四年级第3讲-数形规律

第3讲数形规律1.常见的数列：等差数列:相邻两项的差相等.比如0、2、4、6、8、10……等比数列:相邻两项的比值相同.比如2、4、8、16、32、64……兔子数列:前两项的和等于后项.比如1、1、2、3、5、8、13……山顶数列:先按等差数列递增,再按等差数列递减.比如1、2、3、4、5、4、3、2、12.算式找规律：口诀：照葫芦画瓢3.图形中的规律通常给出前几幅图形,通过观察图形的数量与各个图形所在的序数的对应关系,找出第n个图形的结构,常用的方法为:求差法、列表法、分割法。

知识点1：常见的数列1.找规律填数字（1）1, 4, 9, 16, 25, ( ), ( )（2）1, 1, 2, 3, 5, 8, 13, ( ), ( )（3）2, 6, 12, 20, 30, ( ), ( )2.找规律填数字（1）5, 9, 13, 17, ( ), ( )（2）5, 15, 45, 135, ( ), ( )3.找规律（1）2、6、10、14、18、22、26、（）；（2）0.5、1.6、2.7、3.8、4.9、6、（）；（3）0、2、2、4、6、10、16、26、（）；（4）1、2、4、8、16、32、64、（）；（5）70、71、72、61、74、51、76、41、（）、（）；（6）1、8、27、64、125、（）；（7）1、6、16、31、51、76、（）；（8）1、4、5、9、14、23、37、60、（）；（9）67、66777、66677777、66667777777、（）；（10）7.7、77.07、777.007、7777.0007、（）。

5.下面图形是按规律排列的，根据规律可以判断第125个图形是（），前125个图形中这个图形共有（）个。

知识点2：算式找规律1.算式中的规律1+3=1+3+5=1+3+5+7=1+3+5+7+…+97+99=2.观察下面的几个算式:1+2+1=41+2+3+2+1=91+2+3+4+3+2+1=161+2+3+4+5+4+3+2+1=25 …根据你所发现的规律,请你直接写出下面式子的结果:1+2+3+…+99+100+99+…+3+2+1=( )知识点3：图形找规律1.如图，如果正方形每个端点各摆一个花盆，20个正方形端点可摆放多少个花盆？2.用边长为1cm的小正方形搭如下的塔状图形，则第10次所搭图形的周长是3.观察下面的点阵图规律,第9个点阵图中有( )个点。

第03讲基本直线型面积公式(教师版)-三升四暑期数学奥数培优讲义

一、基本直线形面积计算公式（四上）第3讲基本直线型面积公式四年级暑期知识点熟练掌握各种图形面积公式，梯形和三角形的面积公式最后一定要除以2.理解每个图形的高是什么，会做高.一、长方形、正方形1、如下图，有一块长方形田地被分成了五小块，分别栽种了茄子、黄瓜、豆角、莴笋和苦瓜．其中栽种茄子的面积是16平方米，栽种黄瓜的面积是28平方米，栽种豆角的面积是32平方米，栽种莴笋的面积是72平方米，而且左上角栽种茄子的田地恰好是一个正方形．请问：剩下的栽种苦瓜的田地面积是多少？【答案】116【解析】课堂例题方法精讲7222814428116×−=−=．2、（金帆四年级春季）如图有九个小长方形，其中编号为1，2，3，4，5的5个小长方形的面积分别为2，4，6，8，10平方米，求6号长方形的面积．【答案】15【解析】根据已知面积相互间的倍数关系可将各块面积求出，如图所示．二、三角形求面积3、如下图所示，两个正方形并排放在一起，大正方形的边长是8厘米，小正方形的边长是6厘米．请问：阴影三角形的面积是多少？【答案】42平方厘米【解析】×÷=．阴影三角形的底是6，高是14，所以阴影三角形的面积是6142424、如图，小正方形的边长为6厘米，大正方形的边长为11厘米，请问：图中阴影部分的面积？【答案】15平方厘米【解析】阴影三角形的第是6，高是5，所以面积是15．5、如图，把两个正方形拼在一起，小正方形的边长是5厘米，大正方形的边长是7厘米．请问：阴影部分的面积是多少？【答案】12平方厘米【解析】×÷+×÷=．将阴影部分分成左右两个三角形，根据三角形面积公式25227212三、平行四边形6、下图是由两个边长分别为4和7的正方形拼成的，请求出阴影平行四边形的面积．【答案】【解析】平行四边形的底是4高是11，所以面积是44．7、如下图所示，两个边长10厘米的正方形相互错开3厘米，那么图中阴影平行四边形的面积是多少？【答案】91平方厘米【解析】×=．阴影部分是平行四边形，面积是137918、图中，平行四边形的面积是24，大正方形的边长是8，小正方形的面积是________．【答案】9【解析】平行四边形的面积等于底乘高，平行四边形的高就是大正方形的边长，底是小正方形的边长，所以小正方形的边长是2483×=．÷=，所以小正方形的面积是3399、如图，两个一样的长方形相互错开2厘米拼在一起，长方形的长是10厘米，宽是4厘米，请问：图中阴影平行四边形的面积是多少？【答案】64平方厘米【解析】阴影平行四边形的底是8高是8，所以面积是64．四、梯形10、一个正方形和一个长方形按下图的方式排放，已知正方形的面积是49平方厘米，长方形的长为11厘米，宽为8厘米，那么阴影部分的面积是多少？【答案】30平方厘米【解析】正方形的边长是7，阴影部分是一个梯形，说以阴影部分的面积是()() 87117230 +×−÷=．11、如图，两个正方形按如图方式放在一起，小正方形的边长为3厘米，大正方形的面积是49平方厘米．请问：阴影部分的面积是多少？【答案】50【解析】梯形的面积是()()3737250+×+÷=．12、如图，ABCD 是直角梯形，△AEC 和△EBD 都是等腰直角三角形，已知梯形高为20，那么梯形的面积是______（改自2010年4月18日考试真题）【答案】200 【解析】上下两个三角形均为等腰直角三角形，由此可知梯形上下底之和即为梯形的高，故梯形面积为20202200×÷=．13、如图所示，平行四边形的一边长为15厘米，这条边上的高为6厘米，一条线段将此平行四边形分成了两部分，它们的面积相差18平方厘米．请问：其中梯形的上底是多少厘米？【答案】3厘米【解析】如下图所示，从线段的顶点做边的平行线，把梯形又分成了一个三角形和一个小平行四边形，分割出的三角形显然和原来的三角形面积相等．那么最左边的小平行四边形的面积就是多出来的18平方厘米，又其高为6厘米，它的底边长又正好是所需求的梯形的上底长．所以，梯形的上底长为1863÷=厘米．1、如图，有一块长方形田地被分成了四小块，分别栽种了冬瓜、西瓜、南瓜、黄瓜，其中冬瓜地的面积是24平方米，西瓜地的面积是36平方米，南瓜地的面积是18平方米，而且左下角西瓜地恰好是一个正方形．请问：剩下的黄瓜地的面积是多少？【答案】12平方米【解析】24212÷=平方米．2、如图，大正方形里有一个小正方形还有一个阴影平行四边形．如果大正方形的边长是20厘米，小正方形的边长是8厘米．那么阴影平行四边形的面积是多少？【答案】144平方厘米【解析】第是12高是12，所以面积是144．3、右图是由两个边长分别为4和6的正方形拼成的，请求出阴影三角形的面积． 36 1824随堂练习【答案】30【解析】阴影三角形的第是6高是10，所以面积是30．4、如下图，大正方形的边长是8厘米，小正方形的边长是6厘米．请问：图中的阴影图形的面积是多少平方厘米？【答案】14平方厘米【解析】根据梯形面积公式()()6886214+×−÷=．1、在下面的三角形中，以AB 为底作高，正确的是__________．课后作业【答案】C【解析】C，从这条边的对应的顶点做高．2、如图，大正方形被分成三块区域．左上角的正方形面积为4，右上角的长方形面积为6，那么大正方形的面积是__________．【答案】25【解析】左上角正方形的边长是2，所以面积为6的长方形的长是3，所以大正方形的边长是5，大正方形的面积是25．3、下图中，大正方形的面积是64，小正方形的面积是36．那么平行四边形的面积是__________．【答案】48【解析】×=．小正方形的边长是6，大正方形的边长是8，阴影部分的面积四68484、下图是边长为8和6的两个正方形拼成的，根据图中所示的线段长度，阴影三角形的面积是_________.【答案】24【解析】阴影三角形的底是6，高是8，所以面积是24．5、如图，两个正方形并排放在一起，小正方形的面积是81平方厘米，大正方形的面积是169平方厘米．那么阴影梯形的面积是___________平方厘米．【答案】242平方厘米【解析】小正方形的边长是9，大正方形的边长是13，所以图中梯形的上底是9，下底是13，高是22，说以面积是242．6、（金帆四年级春季）如图，平行四边形ABCD的边BC长10cm，直角三角形BCE的直角边EC长8cm，已知两块阴影部分的面积和比△EFG的面积大10cm2，求CF的长．【答案】5cm【解析】同时加上BCFG可知，梯形ABCD面积比△BCE面积大10cm2．直角三角形BCE的面积为2×÷=，108240cm故()+÷．4010105CF cm。

四年级下册语文讲义-培优专题讲练(人教部编版)第3讲：写景文章阅读+景物描写方法(教师版)

3
【例题精讲】
例 1.文段选读（一）（28 分）
春天的阳光特别的温暖，天地间的万物都苏醒过来了。天刚亮，树林里就传出了鸟儿的欢叫声。傍晚，
青蛙都从冬眠中走了出来，在田野里叫个不停。昆虫们都纷纷地行动起来了。
春来了，花园里的花开得更加（娇矫）艳。山上山下的桃花，千树万枝就像火焰一般地怒放了。
小区里弯弯曲曲的小路旁，也开出了野花，小野菊也一丛丛由草堆里攒出头来，有白的、有红的、有黄的、
向我耳语着：快去看啊，大江复活了！它扯着我的衣襟向江岸奔去。我和人们一起站在江岸上，我被眼前的
景象惊呆了，只见整个大江的（坚、艰）冰崩溃了。被禁锢了一冬的大江奔腾着，汹涌着，以它那不可抗拒
的力量推开了坚冰，呼叫着，撞击着。一块块巨大的冰排，被江水推动着，山一样地竖了起来，又摔倒下
去，发出咔嚓咔嚓的声响，溅起一片片雪白的浪花。滚滚的春潮把坚冰击溃了，淹没了，迫使它（训、驯）
A、奔腾汹涌
B、不可抗拒
C、山崩地裂
5、第四自然段中，春水告诉大地一个什么消息呢？（3 分）
文段选读（一）
1、春来了（意思答对便可）
2、不正确的字：矫秆穿毫
3、若隐若现十全十美无缘无故
白花花金灿灿
黑乎乎
4、柔软鲜花盛开色彩鲜艳南来北往或精神饱满细姨茂盛青青人山人海
5、花园小草树木火车站
（1）北方的二月，春天在进攻，冬天在撤退。
从第二自然段中哪些词语可以看出“春天在进攻，冬天在撤退”？请抄写在下面（写三至四个）。（3
分）
（2）风从窗缝里挤了进来，激动地向我耳语着：快去看啊，大江复活了！它扯着我的衣襟向江岸奔去。（3 分） “挤”和“扯”这两个词表现了什么？这个句子运用了怎样的修辞手法？

四升五暑期奥数培优讲义——5-03-加减巧算4-讲义-教师

第3讲加减巧算【学习目标】1、掌握加法中的速算技巧；2、熟悉整数、小数、分数在计算时的联系。

【知识梳理】1、加减法或者乘除法中的巧算：（1）移数凑整法：（2）借数凑整法：（3）拆数凑整法：（4）找“基准数”法：（5）分组凑整法。

2、等差数列：（1）等差数列的和＝（首项＋末项）×项数÷2（2）末项＝首项＋公差×（项数－1）（3）项数＝（末项－首项）÷公差＋13、公式计算：（1）1+2+3+……+n=（1+n）n÷2（2）1+3+5+……+（2n-1）=n²（3）1+2+3+……+(n-1)+n+（n-1）+（n-2）+……+3+2+1=n²【典例精析】【例1】用简便方法计算下面各题：（1）866-201 （2）3568－（199＋568）（3）3842﹣1567﹣433﹣842 =866-200-1 =3568-568-200+1 =3842-842-（1567+433） =665 =2801 =1000【趁热打铁-1】用简便方法计算下面各题：（1）30.1-19.9 （2）356.45-（19.9+56.45）（3）564.65-45.54-54.46-64.65 =30.1-20+0.1 =356.45-56.45-20+0.1 =564.65-64.65-（45.54+54.46） =10.2 =280.1 =400【例2】怎样简便就怎样计算。

（1）9+99+999+9999+99999 （2）8+18+28+38+48+58+68+78+88+98 =10+100+1000+10000+100000-5 =10+20+30+40+50+60+70+80+90+100-20=111105 =530【趁热打铁-2】怎样简便就怎样计算。

（1）0.9+9.9+99.9+999.9+9999.9 （2）1991+199.1+19.91+1.991 =1+10+100+1000+10000-0.5 =2000+200+20+2-9.999=11110.5 =2212.001【例3】计算：60+65+59+58+57+62+61+60+55+64=60×10+5-1-2-3+2+1-5+4=601【趁热打铁-3】计算：59.8+60.1+59.5+58.4+60.2+60.5+59.9+59.7+61.6+60.9=60×10-0.2+0.1-0.5-1.6+0.2+0.5-0.1-0.3+1.6+0.9=600.6【例4】计算：1234+2345+3456+4567+5678+6789=(1+2+…+6)×1000+(2+3+…+7)×100+(3+4+…+8)×10+(4+5+…+9)×1=21×1000+27×100+33×10+39×1=21000+2700+330+39=24069【趁热打铁-4】计算：12.34+23.45+34.56+45.67+56.78+67.89+78.91+89.12+91.23 =(1+2+…+9)×10+(1+2+…+9)×1+(1+2+…+9)×0.1+(1+2+…+9)×0.01=45×11.11=499.95【例5】计算：2000-111-89-112-88-113-87-114-86-115-85-116-84=2000-(111+89)-(112+88)-(113+87)-(114+86)-(115+85)-(116+84) =2000-200×6=800【趁热打铁-5】计算：0.0625+0.125+0.1875+0.25+0.3125+0.375+0.4375+0.5+0.875+0.625+0.6875+0.75+0.8125 =(0.0625+0.4375)+(0.1875+0.8125)+(0.25+0.75)+(0.3125+0.6875)+(0.375+0.625)+(0.125+0.875)+0.5=0.5+1+1+1+1+1+0.5=6【例6】计算：2+4+6+8+…+98+100=（2+100）×50÷2=2550【趁热打铁-6】计算：1.001+1.005+1.009+1.013+…+1.197．=(1.001+1.197)×50÷2=2.198×50÷2=54.95【例7】一个等差数列的第1项是4.1,公差是3.1,其中最后一项是50.6,求所有项的和。

四年级暑期数学思维训练讲

例题 1
计算下面各题：
（1）3＋6＋ 9＋12＋15＋18＋21＋24＋27＋30
（2）41＋37＋33＋29＋25＋21＋17＋13＋ 9＋5＋1
练习 1
计算： 6＋11＋16＋21＋26＋31＋36＋41＋ 46
例题 2 计算下列各题：
（1） 5＋ 11＋ 17＋⋯＋ 77＋ 83
（2）82＋ 77＋72＋⋯＋ 12＋7
作业
1.一个等差数列共有 10 项，每一项都比它的前一项大 2，并且末项为 75，那么首项是多少？
2.一个等差数列共有 10 项，每一项都比它的前一项小 2，并且末项为 75，那么首项是多少？ 3．一个等差数列首项为 13，第 9 项为 29，那么这个等差数列的公差等于多少？第 20 项等于多少？
9 块小长方形蛋糕的周长总和为多少厘米？
100
例题 2
如下图，是有 6 个相同的等腰直角三角形拼成的图形，求这个图形的面积（单位：分米）
练习 2
如下图，是由 12 个相同的等腰直角三角形拼成的，这个图形的面积是多少（单位：厘米）？
例题 3
如图，已知大正方形的边长比小正方形多 4 厘米，大正方形的面积比小正方形多 96平方厘米。求：大正方形和小正方形的面积各是多少？
例题 1
如图，用一个边长是 4厘米的正方形和 4个一样大的小长方形，一起拼成一个边长是 20 厘米的大长方形，请问小长方形的长和宽分别是多少厘米？
练习 1
如图，用 4 个完全相同的长方形拼成了一个长是 20 厘米的长方形，请问小长方形的长和宽分别是多少厘米？
例题 2
如图，把长为 2 厘米、宽为 1 厘米的 6个长方形摆成 3 层，那么摆成的图形周长是多少厘米？

数学四年级第3讲还原问题与年龄问题(教师版+学生版,含详细解析)

第3讲还原问题与年龄问题内容概述学会用逆推法求解还原问题，处理多个对象时可采用列表的形式，在年龄问题中，通常采用和差倍问题的分析方法，有时需注意任意两人的年龄差保持不变。

典型问题兴趣篇1. 某数加上6，再乘以6，再减去6，再除以6，其结果等于6，则这个数是多少？答案：这个数是1 倒推法解决此问题。

详解：+6 x6 -6 ÷662. 有一个人非常喜欢喝酒，他每经过一个酒店都要买酒喝. 这个人出门带了一个酒葫芦，看到一个酒店就把酒葫芦中的酒加一倍，然后喝下8两酒，这天他一共遇到3家酒店，在最后一家酒店喝完酒后，葫芦里的酒刚好喝完. 问：原来酒葫芦里有多少两酒？答案：7两酒。

详解：每经过一个酒店，葫芦里酒的数量就先乘2，再减8，利用倒推法，我们反过来应该先加8，再除以2.那么到第3家酒店之前葫芦里应该有（0+8）÷2=4两酒，他在到第2家酒店之前候应该有（4+8）÷2=6两酒，所以他原来的酒葫芦应该有（6+8）÷2=7两酒。

（0+8）÷2=4（两）（4+8）÷2=6（两）（6+8）÷2=7（两）3. 某人发现了一条魔道，下面有一个存钱的小箱子，当他从魔道走过去的时候，箱子里的一些钱会飞到人的身上使人身上的钱增加一倍，这人很高兴；当他从魔道走回来时，身上的钱会飞到箱子里，使箱子里的钱增加一倍；这人一连走了3个来回后，箱子里的钱和人身上的钱都是64枚一元的硬币，那么原来这人身上有多少元？箱子里有多少元？答案：原来这个人身上有43元，箱子里有85元。

详解：4. 三棵树上共有48只鸟. 后来，第一棵树上有一半的鸟飞到了第二棵树上；之后，第二棵树上又有与第三棵树同样数目的鸟飞到了第三棵树上；最后，第三棵树上又有10只鸟飞到了第一棵树上，此时三棵树上的鸟一样多. 问：一开始三棵树上各有几只鸟？答案：第一棵树上有12，第二棵23，第三棵13 详解：5. 1997年张伯伯45岁，小方9岁，在哪一年张伯伯的年龄是小方年龄的4倍？答案：小方12岁那年。

暑假讲义小学数学教案

暑假讲义小学数学教案
主题：小学数学暑假讲义
时间：暑假期间
对象：小学生
一、教学目标：
1. 让学生在暑假期间保持数学学习的习惯；
2. 复习巩固小学数学基础知识；
3. 提高学生的数学解题能力。

二、教学内容：
1. 复习小学各个年级的数学知识点，包括数学加减乘除、面积体积、分数小数等；
2. 给学生提供一些数学练习题，让他们在暑假期间进行练习。

三、教学步骤：
1. 提醒学生在暑假期间要保持良好的学习习惯，每天抽出一定时间复习数学知识；
2. 按照学生不同年级的情况，给予他们相应的练习题；
3. 每周定期检查学生的练习情况，帮助他们解决遇到的问题。

四、教学方法：
1. 以讲解和示范的方式复习数学知识；
2. 给予学生练习题，并鼓励他们自主完成；
3. 在学生解题过程中，及时纠正错误，指导正确。

五、教学评价：
1. 根据学生的练习情况和表现给予及时的评价和反馈；
2. 对学生有进步的地方给予肯定和奖励，对有不足的地方给予指导和帮助。

六、教学反思：
1. 教学过程中发现问题及时调整教学方法、内容，以提高教学效果；
2. 对学生的学习情况及时进行评估，制定下一步的教学计划。

第3讲四年级数学周期问题教案

广|精锐1对1哈传北大用菩创立lSMART 北京大学精锐教育客索^啥探北大■智削立战映合作伙伴精锐教育学科教师辅导讲义学员编号：年级：课时数: 学员姓名：辅导科目：学科教师：授课 "、一~~,、…,,…--…类型 T 一般周期问题 C 较复杂的周期问题 T 能力提升授课日期时段教学内容回顾上次课的知识。

1、倍数问题应用题包括哪几种类型？（和差问题，和倍问题、差倍问题）每一类应用题的特征分别是什么？2、这几种类型的应用题的解题方法分别是什么？试举例说明?3 T 犍【专题导入】在日常生活中，有一些现象按照一定的规律不断重复出现，例如，人的生肖、每周的七天等等。

我们把这种特殊的规律性问题称为周期问题。

解答周期问题的关键是找规律，找出周期。

确定周期后，用总量除以周期，如果正好有整数个周期，结果为周期里的最后一个；如果比整数个周期多n 个，那么为下个周期里的第 n 个；如果不是从第一个开始循环，可以从总量里减掉不是特球的个数后，再继续算。

nn亶翳北京大学木吉钳.教令救日器is窗北大鼻葬知立战BS合作伙伴一般周期问题一、专题精讲例题1：2001年10月1日是星期一，问10月25日是星期几？分析：我们知道，每个星期有7天，也就是说以7天为一个周期不断地重复。

那么从10月1日到10月25日经过了25—1=24 （天）。

因此用除法算式解答。

解：（1）、从10月1日到10月25日有：25-1=24 （天）（2）、24天里有多少个星期余多少天？24+7=3（个星期）……3 （天）（说明24天中包含3个星期还多3天，最后一天起，再过3天就应是星期四）答：10月25日是星期四。

例2:你能找出下面每组图形的排列规律吗？根据发现的规律，算出每组第20个图形分别是什么。

（1）……（2）……分析与解答：第（1）题排列规律是“口△”两个图形重复出现，20+2=10,即“口△”重复出现10次，所以第20个图形是4。

3三升四年级数学暑假讲义第3讲：大数的认识(一)(含解析)

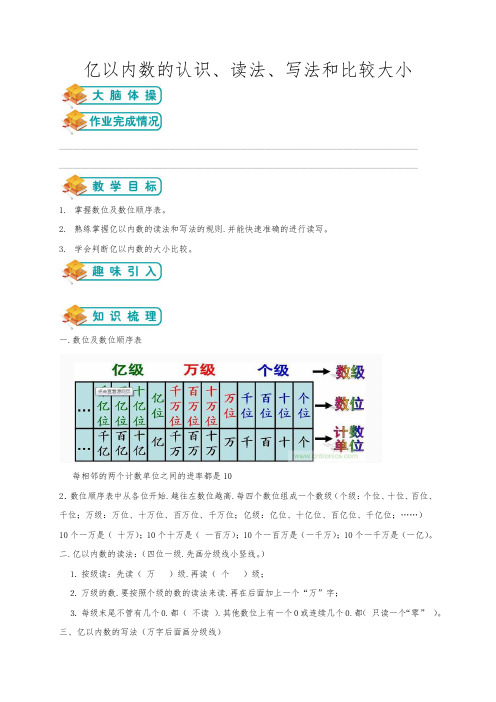
亿以内数的认识、读法、写法和比较大小____________________________________________________________________________________________________________________________________________________________________1.掌握数位及数位顺序表。

2.熟练掌握亿以内数的读法和写法的规则.并能快速准确的进行读写。

3.学会判断亿以内数的大小比较。

一.数位及数位顺序表每相邻的两个计数单位之间的进率都是102．数位顺序表中从各位开始.越往左数位越高.每四个数位组成一个数级（个级：个位、十位、百位、千位；万级：万位、十万位、百万位、千万位；亿级：亿位、十亿位、百亿位、千亿位；……）10个一万是（十万）；10个十万是（一百万）；10个一百万是（一千万）；10个一千万是（一亿）。

二.亿以内数的读法：（四位一级.先画分级线小竖线。

）⒈按级读：先读（万）级.再读（个）级；⒉万级的数.要按照个级的数的读法来读.再在后面加上一个“万”字；⒊每级末尾不管有几个0.都（不读）.其他数位上有一个0或连续几个0.都（只读一个“零”）。

三、亿以内数的写法（万字后面画分级线）⒈ 按级写：先写万级.再写个级；⒉ 哪个数为上一个单位也没有.就在那个数位上写＿0＿＿。

四、亿以内的数的大小比较1．位数不同的两个数.位数多的那个数就＿大＿＿。

2. 位数相同的两个数.从最高为比起.最高位上的数大的那个数就＿大＿＿.如果最高位上的数相同.就比较下一个数位上的数。

题目类型一：数位顺序的掌握例1、一个数由4个百万、7个十万和5个十组成.这个数是（）。

练习1.(1) 从个位起.第( )位是万位.第（）位是亿位。

(2) 万位的右面一位是（）位.左面一位是（）位。

练习2．写出由下面各数组成的数。