MATLAB与数学实验讲义
MATLAB实验讲义_2013版

MATLAB 操作环境、MATLAB 数值计算一、实验目的1、熟悉MATLAB 操作界面;2、掌握MATLAB 基本操作和简单语句函数的输入;3、掌握变量的创建及数据类型间转换;4、掌握矩阵和数组运算,可利用MATLAB 进行基本数值计算;5、掌握多项式的创建和基本运算。
二、实验内容(一)MATLAB 操作环境1、常用窗口及操作方法2、MATLAB 初步应用(1)计算b a b a y ++⨯=,其中43==b a 的值。
(2)绘制正、余弦曲线。
X=0:0.2:2*piY1=sin(x);y2=cos(x);plot(x,y1,x,y2)(3)计算5323645sin + 和5323630cos + 的值。
>> (sin(0.25*pi)+sqrt(36))/32^(1/5)ans =3.3536>> (cos(pi/6)+sqrt(36))/32^(1/5)ans =3.43303、变量的创建和类型转换创建一个5维魔方阵A ,并将其转换成无符号16位整型数组B 。
察看两个变量的详细信息。
4、创建一结构数组Stu ,包含ID 、name 、score 三个域,并输入3个同学的记录信息,并查看第2个记录的信息。
>> A=magic(5),B=uint16(A),whos A BA =17 24 1 8 1523 5 7 14 164 6 13 20 2210 12 19 21 311 18 25 2 9B =17 24 1 8 1523 5 7 14 164 6 13 20 2210 12 19 21 311 18 25 2 9Name Size Bytes ClassA 5x5 200 double arrayB 5x5 50 uint16 arrayGrand total is 50 elements using 250 bytes(二)MATLAB数值计算1、矩阵创建(1)直接输入法A=[1 2 3 4; 5 6 7 8](2)用矩阵编辑器创建复杂矩阵(3)创建特殊矩阵:要求创建随机矩阵、全0矩阵。
数学实验课件--MATLAB简介

数组(向量和矩阵)及其 运算
学习如何在MATLAB中创建和操 作向量、矩阵及其运算符号。
控制语句和函数
探索MATLAB中的条件语句和循 环语句的使用,以及自定义函 数的编写。
三、MATLAB图形用户界面
1
MATLAB图形用户界面的基本元素
了解MATLAB图形用户界面的常见元素,如按钮、文本框和图形显示区。
数学实验课件--MATLAB简 介
MATLAB是一种强大的数学计算软件,广泛应用于科学、工程和金融领域。本 课件将介绍MATLAB的基本概念、语言基础、图形用户界面、特殊工具箱、应 用实例以及相关资源。
一、MATLAB基本概念
什么是MATLAB?
MATLAB是一种高级数学计算 软件,具有强大的数据分析 和可视化功能。
2
创建图形用户界面
学习如何使用MATLAB的GUI设计工具创建自定义的交互式界面。
图像处理和交互式数据可视化的方法。
四、MATLAB特殊工具箱
统计工具箱
了解如何使用MATLAB的统计 工具箱进行数据分析和统计 建模。
信号处理工具箱
学习使用MATLAB的信号处理 工具箱进行信号滤波、谱分 析和音频处理等操作。
MATLAB的特点和优势
MATLAB具有易于学习、功能 丰富、速度快、内存管理优 秀等特点。
MATLAB能够解决哪些 问题?
MATLAB可以用于数值计算、 数据分析、图像处理、模拟 和仿真等各种问题。
二、MATLAB语言基础
MATLAB变量和运算
了解MATLAB中的变量定义和基 本运算符号。掌握变量的赋值 和算术运算。
MATLAB社区资源
加入MATLAB的技术社区,与其他MATLAB用户分享经验和解决问题。
数学实验讲义1
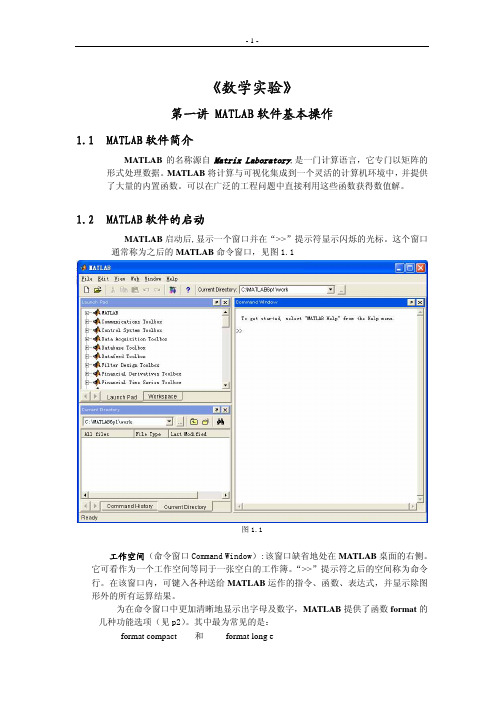
表 1.9.1 limit 函数的用法
表达式
函数格式
备注
lim x→a f (x) lim x→a− f (x) lim x→a+ f (x) lim x→a f (x)
limit(f, x, a) limit(f, x, a, ’left’) limit(f, x, a, ’right’) limit(f, a)
format long
15 位数字表示
3.14159265358979
format short e 5 位科学记数表示
3.1416e+00
format long e 15 位科学记数表示
3.14159265358979e+00
format short g 从 format short 和 format short e 中自动选最佳记述方式 3.1416
ans =
-1/12
(2) lim x→2
x−2 x2x-2)/(x^2-4),x,2)
ans =
1/4
(3) lim x→+∞
(1 +
t )4x 2x
>> syms x t
>> limit((1+t/(2*x))^(4*x),x,inf)
-1-
《数学实验》
第一讲 MATLAB 软件基本操作
1.1 MATLAB 软件简介
MATLAB 的名称源自 Matrix Laboratory,是一门计算语言,它专门以矩阵的 形式处理数据。MATLAB 将计算与可视化集成到一个灵活的计算机环境中,并提供 了大量的内置函数。可以在广泛的工程问题中直接利用这些函数获得数值解。
MATLAB数学实验讲义-经典

例1. 发射角为450的抛射曲线绘制
v0=515;alpha=45*pi/180; T=2*v0*sin(alpha)/9.8; t= T(0:16) /16;
%计算飞行时间 %飞行时刻
x=v0 *t *cos(alpha);
%计算航点
y=v0 *t *sin(alpha) -0.5*9.8*t.^2;
例14.汽车紧急刹车问题数据拟合实验
V 20 25 30 35 40 45 50 55 60 65 70
T 20 28 41 53 72 93 118 149 182 221 266
V表示刹车时汽车行驶速度(英里/小时),T表示刹车 后汽车滑行距离(英尺)
v=[20 25 30 35 40 45 50 55 60 65 70]*1.609; T=[20 28 41 53 72 93 118 149 182 221 266]*.3048; P2=polyfit(v,T,2);T2=polyval(P2,v); R2=sum((T-T2).^2) figure(2),plot(v,T,'*',v,T2) P3=polyfit(v,T,3);T3=polyval(P3,v); R3=sum((T-T3).^2) figure(3),plot(v,T,'*',v,T3)
f=inline('exp(-0.2*x).*sin(0.5*x)'); t=(0:20)*pi/10; theta=t;r=f(t); x=t'*ones(size(t)); y=r'*cos(theta); z=r'*sin(theta); mesh(x,y,z) colormap([0 0 0]) axis off view(-17,54)
数学实验 第2章 MATLAB数值运算

软
件
篇
数学实验
软
例2.5 向量的点积和叉积运算.
>> A = [4 -2 1];
>> B = [1 -1 3];
>> C=dot(A,B)
%向量A和B的点积
C=
9
>> D = cross(A,B) %向量A和B的叉积
D=
-5 -11 -2
件
篇
澡身浴德 修业及时
澡身浴德 修业及时
2.2 矩阵及其运算
① x(n)
表示向量中的第n个元素
② x(n1:n2)
表示向量中的第n1至n2个元素
例2.3 向量元素的引用、修改和扩展.
>> x=1:2:5
x=
1
3
5
件
篇
数学实验
软
>> x(2)=6
%修改第2个元素为6
x=
1
6
>> x(5)=7
%增加第5个分量,第4个分量没有赋值,自动设为0
x=
1
6
5
0
7
>> x([1,end])
2
.
= ( , , . . . , )
或
1 2
.
.
叫做 n 维向量,向量的第 i 个分量称为 .
件
篇
数学实验
软
2.1.1 向量的创建
MATLAB中向量可以由以下方法创建:
(1)元素输入法
在命令行窗口中直接输入,向量元素用“[ ]”括起来,元素之间用空格、逗号或分
号分隔.用空格和逗号分隔生成行向量,用分号分隔生成列向量.
数学实验MATLAB第五章

学习方法与建议
学习方法
通过理论学习和实践操作相结合的方式,深入理解MATLAB高级编程技术的原 理和应用。
建议
在学习本章之前,读者应该已经具备一定的MATLAB基础知识和编程经验。同 时,建议读者在学习过程中多进行实践操作,通过编写代码来加深对知识点的 理解和掌握。
02 MATLAB基础知识回顾
数学实验matlab第五章
目 录
• 第五章概述 • MATLAB基础知识回顾 • 数组与矩阵操作 • 数值计算与数据分析 • 程序设计与优化 • 综合应用与案例分析
01 第五章概述
章节内容与目标
内容
介绍MATLAB中的高级编程技术 ,包括脚本和函数编程、数据结 构和算法、面向对象编程等。
目标
通过学习本章,读者应该能够熟 练掌握MATLAB的高级编程技术 ,并能够灵活运用这些技术解决 复杂的数学问题。
运算符与函数
运算符
详细讲解MATLAB中的运算符, 包括算术运算符、关系运算符、 逻辑运算符等。同时介绍运算符
的优先级和结合性。
函数
阐述函数的概念,以及如何在 MATLAB中定义和使用函数。同时 介绍函数的输入和输出参数,以及 函数的返回值。
常用函数
介绍MATLAB中常用的函数,包括 数学函数、字符串处理函数、文件 操作函数等。同时给出函数的语法 和使用示例。
矩阵的乘法
按照矩阵乘法的规则进行运算 ,结果矩阵的维数可能发生变
化。
矩阵的转置
将矩阵的行和列互换,得到转 置矩阵。
矩阵的逆
对于方阵,若其逆矩阵存在, 则可以通过特定的运算求得逆
矩阵。
数组与矩阵的应用举例
线性方程组求解
数据分析与处理
Matlab与数学实验

>>5+sin(7) ↙
ans=
3117/551
>>format long↙
>>5+sin(7) ↙
ans=
5.65698659871879
-5-
第三节 变量
一、变量
Matlab 中参与计算的数据需要存放在一个储存空间中,每个储存空间都给 予一个名称,就是变量的名称。
Matlab 中变量的命名规则是: (1)变量名必须是不含空格的单个词; (2)变量名区分大小写; (3)变量名最多不超过 19 个字符; (4)变量名必须以字母打头; (5)变量名中不允许使用标点符号; (6)不要使用内部函数名。 变量赋值格式:
-6-
四、标点符号
标点符号需要在英文状态下输入,常见的有
,
命令分隔符号,显示的结果
;
命令分隔符号,不显示的结果
%
它后面为注释文字
…
续行符号(使用时前面加空格)
( ) 运算优先级
例 1 >>a=20;b=3;c=a+b,d=a*b↙
运行结果:
c=
23
d=
60
例 2 交换两个变量的取值
>>a=1;b=2;
sqrt(x) log(x)
log10(x)
max(x) sign(x) fix(x) gcd(x,y)
lcm(x,y)
asin(x)
开平方
自然对数
以 10 为 底 的数
最大值 符号函数 取整 整数 x,y 的最大公因 数 整数 x,y 的最小公倍 数 反正弦函数
cos(x)
tan(x)
sinh(x) cosh(x) tanh(x) real(z) abs(z) angle(z)
数学建模与数学实验第2讲 MATLAB入门

MATLAB入门
一、变 量 与 函 数 二、数 三、 矩 组 阵
四、 MATLAB编程 五、 实 验 作 业
一、变 量 与 函 数
1. 变量
MATLAB中变量的命名规则是:
(1)变量名必须是不含空格的单个词;
(2)变量名区分大小写;
(3)变量名最多不超过19个字符;
(4)变量名必须以字母打头,之后可以是
a./b= [a1/b1,a2/b2,…,an/bn] a.\b=[b1/a1,b2/a2,…,bn/an] a.^b=[a1^b1,a2^b2,…,an^bn] MATLAB(shuzu4)
返回
三、 矩
阵
1. 矩阵的建立
逗号或空格用于分隔某一行的元素,分号用于区分不
同的行. 除了分号,在输入矩阵时,按Enter键也表示开始
果时,返回空矩阵,空矩阵的大小为零
d=eye(m,n) 产生一个m行n列的单位矩阵
MATLAB(matrix1)
2. 矩阵中元素的操作
(1)矩阵A的第r行:A(r,:) (2)矩阵A的第r列:A(:,r) (3)依次提取矩阵A的每一列,将A拉伸为一个列向量:A(:) (4)取矩阵A的第i1~i2行、第j1~j2列构成新矩阵:A(i1:i2, j1:j2) (5)以逆序提取矩阵A的第i1~i2行,构成新矩阵:A(i2:-1: i1,:) (6)以逆序提取矩阵A的第j1~j2列,构成新矩阵:A(:,j2:-1: j1) (7)删除A的第i1~i2行,构成新矩阵:A(i1:i2,:)=[] (8)删除A的第j1~j2列,构成新矩阵:A(:,j1:j2)=[] (9)将矩阵A和B拼接成新矩阵:[A B];[A;B] MATLAB(matrix2)
M文件建立方法:1. 在MATLAB中,点:File→New → M-file 2. 在编辑窗口中输入程序内容 3. 点File → Save,存盘,M文件名必须 与函数名一致.
基于matlab的数学实验-高等数学中的若干问题1

基于MATLAB的数学实验——高等数学中的若干问题(一)§1.1数列及其极限1.1.1引言极限(Limit )是高等数学中应用最普遍的基本概念之一,因而,正确地理解和把握极限的概念是非常重要的,借助于直观的想象和解释,不仅可以帮助我们理解和把握这一表述抽象的数学定义,而且对利用极限定义的其他数学概念如微分(Differential)、积分(Integral)和无穷级数的敛散性(Convergence and Divergence of Infinite Series)等重要概念的理解也是有帮助的。
1.1.2数列的收敛与发散例1.1让我们首先考察如下的数列:xnnn=+sin()12,n=12,, (1.1)如果我们把xn 看成是沿x轴运动的点P在t n=时刻所处的位置,那么容易看出(也容易证明),随着时间t→+∞,动点P趋近于原点0。
这个事实可借助于软件MATLAB直观地观察到,应用如下程序sequence01.m:%CONVERGENCE AND LIMIT OF SEQUENCEk=700;n=1:3:k;x=sin(n)./(10+n);e=input('Input epsilon, Please: epsilon=')t=e\10;for m=1:t;if m>1/e;N=mbreakendendplot(n,x)hold ontitle('CONVERGENCE AND LIMIT OF SEQUENCE')gtext('xn = sin(n)/(10+n)')QQ:121681692Email:*****************可得到图1.1:用上述程序还可以对任意给定的ε>0,求出N,使得当n N>时,满足不等式:xn -<0ε。
此外,我们还可以使用MATLAB程序文件seqnummovie1.m和seqnummovie2.m演示动点P趋近于原点0的动态过程。
第1章 MATLAB数学实验与建模基础知识

第1章MATLAB数学实验与建模基础知识首先介绍三个概念:数学实验、数学建模、MATLAB软件。
数学实验是以问题为载体,应用数学知识建立数学模型,以计算机为手段,以数学软件为工具,以学生为主体,通过实验解决实际问题。
数学实验是数学模型方法的初步实践,而数学模型方法是用数学模型解决实际问题的一般数学方法,它是根据实际问题的特点和要求,做出合理的假设,使问题简化,并进行抽象概括建立数学模型,然后研究求解所建立的数学模型的方法与算法,利用数学软件求解数学模型,最后将所得的结果运用到实践中。
当需要从定量的角度分析和研究一个实际问题时,人们就要在深入调查研究、了解对象信息、作出简化假设、分析内在规律等工作的基础上,用数学的符号和语言,把它表述为数学式子,也就是数学模型,然后用通过计算得到的模型结果来解释实际问题,并接受实际的检验。
这个建立数学模型的全过程就称为数学建模。
MATLAB是由美国MathWorks公司发布的主要面对科学计算、可视化以及交互式程序设计的高科技计算环境。
它将数值分析、矩阵计算、科学数据可视化以及非线性动态系统的建模和仿真等诸多强大功能集成在一个易于使用的视窗环境中,为科学研究、工程设计以及必须进行有效数值计算的众多科学领域提供了一种全面的解决方案,并在很大程度上摆脱了传统非交互式程序设计语言(如C、FORTRAN语言)的编辑模式,代表了当今国际科学计算软件的先进水平。
1.1MATLAB概述MATLAB和Mathematica、Maple、MathCAD并称为四大数学软件。
在数学类科技应用软件中,MA TLAB在数值计算方面首屈一指,它可以进行矩阵运算、绘制函数和数据、实现算法、创建用户界面、连接其他编程语言的程序等,主要应用于工程计算、控制设计、信号处理与通信、图像处理、信号检测、金融建模设计与分析等领域。
MATLAB的基本数据单位是矩阵,它的指令表达式与数学、工程中常用的形式十分相似,故用MATLAB来解决问题要比用C、FORTRAN等语言完成相同的事情简捷得多,并且MA TLAB也吸收了Maple等软件的优点,使MATLAB成为一个强大的数学软件。
matlab.数学问题与数学实验

应用数学思想的目的
在生活中,我们已经自觉不自觉地使用了最 优化的数学思想,目的可能是最省钱,或者 是最省时间,或者是其他目的,总之,是对 我们最有利。
模型与数学模型
什么是模型 模型是对现实原型的一种抽象或模仿。这种 抽象或模仿要抓住原型的本质,抛弃原型中 的次要因素。从这个意义上讲,模型既反映 原型,又不等于原型,或者说,它是原型的 一种近似。 例如,地球仪是地球的模型,一个人的塑像 是这个人的模型。
第二章 初等数学方法建模
现实世界中有很多问题,它的机理较简单, 用静态、线性或逻辑的方法即可建立模型, 使用初等的数学方法即可求解,我们称之为 初等数学模型。本章主要介绍有关自然数, 比例关系,状态转移等建模例子,这些问题 的巧妙的分析处理方法,可使读者达到举一 反三,开拓思路,提高分析 解决实际问题 的能力。
分析:关键是对棋盘进行黑白着色,使得相邻的两 个方格有不同的颜色;用一块骨牌覆盖两个方格, 必是盖住颜色不同的方格。我们计算一下黑白着色 棋盘的黑格,白格个数,分别为21 和19 ;因此 不同能用 20块骨牌盖住这张残缺的棋盘。 用奇偶校验法,我们可以把黑色方格看成奇数方格, 白色方格看成偶数方格;因为奇偶个数不同,所以 不能进行奇偶配对,故题中要求的作法是不可能实 现的。
状态转移问题
人、狗、鸡、米问题
人、狗、鸡、米均要过河,船上除 人划船外,最 多还能运载一物,而人不在场时,狗要吃鸡,鸡要 吃米,问人,狗、鸡、米应如和过河? 分析:假设人、狗、鸡、米要从河的南岸到河的北 岸,由题意,在过河的过程中,两岸的状态要满足 一定条件,所以该问题为有条件的状态转移问题。
1.允许状态集合 我们用( w, x, y, z ), w, x, y, z=0 或 1 ,表示南岸的状 态,例如( 1, 1, 1, 1)表示它们都在南岸,( 0,1 ,1 ,0 ) 表示狗,鸡在南岸,人,米在北岸;很显然有些状态是允许的, 有些状态是不允许的,用穷举法可列出全部10 个允许状态向 量,(1, 1, 1, 1) (1, 1, 1, 0) (1, 1, 0, 1) (1, 0, 1, 1) (1, 0, 1, 0) (0, 0, 0, 0) (0, 0, 0, 1) (0, 0, 1, 0) (0, 1, 0, 0) (0, 1, 0, 1) 我们将上述10 个可取状态向量组成的集合记为S ,称 S为允 许状态集合
数学实验--MATLAB简介PPT课件

一,课程绪论
1,数学实验课程的主要内容 数学实验是近年来国内外高校所开设的一门新课 程,因为较能适应时代的需要深受同学们的欢迎。 类似的课程在研究生阶段,甚至一些中学也纷纷 开设。关于该课程准确的界定没有统一的说法, 一般认为可以是通过借助计算机以及相关软件对 已有的数学结论的验证和探索,这部分可以看成 和其他的实验一样;另一个方面可以看成将数学 的有关知识和实际问题结合,利用计算机进行求 解分析。
“;”“,”“…”的作用
1) 表达式后面跟分号“;”,将不
显示结果; 2) 跟‘,’或不跟任何符号,将显 示表达式的计算结果; 3) 当一个表达式没写完就需换行时, 应在该行末尾键入‘…’之后再回 车换行。(但若行末是‘.’时,应键入 ‘....’)。 34
三.数组和函数——矩阵的创建
3) 一维数组的操作 键入:x=pi*(0:0.1:1); y=sin(x)
三.数组和函数——矩阵的创建
1) 直接定义 键入:A=[1 2 3;4 5 6] 输出:A= 123 456
2) 一维数组的简单构造:
x=0 : 0.1 : 1
% 从0到1, 增量为0.1。
x=linspace(0, pi, 11) % 11个从0到pi的
等间隔数.
33
三.数组和函数——矩阵的创建
2
一,课程绪论
前一种界定可以看成是狭义的,后一种界定包 括非常的广泛,也可以认为是数学的应用,相关 的课程比如有数学模型等。我们课程的内容应该 属于后一种界定。
当然由于学时的限制,主要以下面的几个方面 进行讲解:方程求解,微分方程,数据处理(插 值和拟合),最优化方法。
数学软件是进行数学实验的基本平台,我们的 实验主要依靠matlab进行,可以是直接调用该软 件的函数,也可能是通过软件进行编程解决问题。
Matlab软件与基础数学实验(讲义16k)2
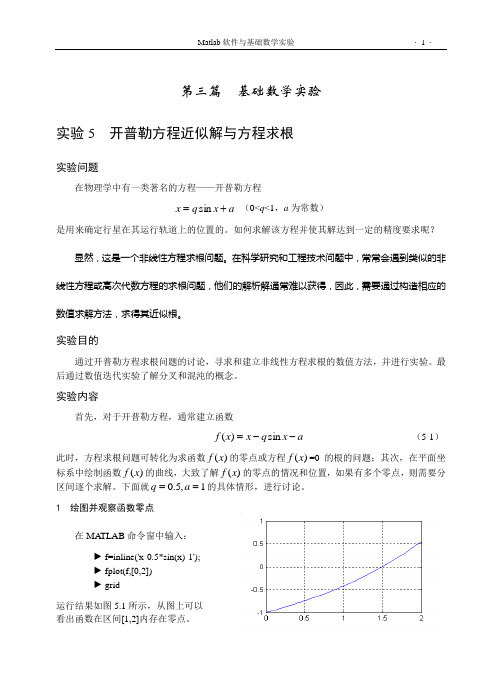
第三篇 基础数学实验实验5 开普勒方程近似解与方程求根实验问题在物理学中有一类著名的方程——开普勒方程a x q x +=sin (0<q <1,a 为常数)是用来确定行星在其运行轨道上的位置的。
如何求解该方程并使其解达到一定的精度要求呢? 显然,这是一个非线性方程求根问题。
在科学研究和工程技术问题中,常常会遇到类似的非线性方程或高次代数方程的求根问题,他们的解析解通常难以获得,因此,需要通过构造相应的数值求解方法,求得其近似根。
实验目的通过开普勒方程求根问题的讨论,寻求和建立非线性方程求根的数值方法,并进行实验。
最后通过数值迭代实验了解分叉和混沌的概念。
实验内容首先,对于开普勒方程,通常建立函数a x q x x f --=sin )( (5-1) 此时,方程求根问题可转化为求函数)(x f 的零点或方程)(x f =0的根的问题;其次,在平面坐标系中绘制函数)(x f 的曲线,大致了解)(x f 的零点的情况和位置,如果有多个零点,则需要分区间逐个求解。
下面就1,5.0==a q 的具体情形,进行讨论。
1 绘图并观察函数零点在MA TLAB 命令窗中输入:► f=inline('x-0.5*sin(x)-1'); ► fplot(f,[0,2]) ► grid运行结果如图5.1所示,从图上可以 看出函数在区间[1,2]内存在零点。
图5.1 函数f(x)=x-0.5*sin(x )-1的图形2 利用MATLAB 中fzero 命令求解在MA TLAB 命令窗中输入:► f=inline(' x-0.5*sin(x)-1'); %建立函数1sin 5.0)(--=x x x f ► c=fzero(f,[1,2]) %求函数)(x f 在[1,2]内的零点c 运行结果为:◄ Zero found in the interval: [1, 2]. ◄ c = 1.4987 或输入:► c=fzero(f,1) %求函数)(x f 在1附近的零点c 运行结果为:◄ Zero found in the interval: [0.98, 1.82]. ◄ c = 1.4987显然, fzero 命令用起来简单易行,但从科学的态度出发,我们应该充分了解“隐藏”在该命令背后的原理、算法以及实现过程。
MATLAB实验讲义

MATLAB实验讲义目录实验大纲 (2)实验一/二 MATLAB的基础操作 (3)实验三 MATLAB运算基础(一) (3)实验四 MATLAB运算基础(二) (4)实验五循环结构程序设计(一) (5)实验六循环结构程序设计(二) (5)实验七 MATLAB的绘图操作(一) (6)实验八 MATLAB的绘图操作(二) (7)实验九函数和文件(一) (7)实验十函数和文件(二) (7)实验十一线性代数中的数值计算问题 (8)实验十二 MATLAB函数库的运用(一) (9)实验十三 MATLAB函数库的运用(二) (10)《MATLAB》课程实验教学大纲课程名称:MATLAB(MATLAB)课程编号:16072327课程性质:选修实验总学时:27实验室名称:电子设计自动化一、课程简介:本课程是电气工程及其自动化、自动化、电力工程与管理专业本科生的学科基础选修课,它在线性代数、信号分析和处理、控制系统设计和仿真等方面有着广泛的应用。
主要是学习MATLAB的语法规则、基本命令和使用环境,使学生掌握MATLAB的基本命令和基本程序设计方法,提高使用该语言的应用能力,具有使用MATLAB语言编程和调试的能力,以便为后续多门课程使用该语言奠定必要的基础。
二、课程实验目的与要求:1.基本掌握MATLAB在线帮助功能的使用、熟悉MATLAB运行环境和MATLAB语言的主要特点,掌握MATLAB语言的基本语法规则及基本操作命令的使用,学会M文件的建立和使用方法以及应用MATLAB实现二维和三维图形的绘制方法,具有使用MATLAB语言编程和调试的能力。
2.初步掌握MATLAB在电路和信号与系统中的应用。
3.能根据需要选学参考书,查阅手册,通过独立思考,深入钻研有关问题,学会自己独立分析问题、解决问题,具有一定的创新能力。
三、主要仪器设备及台(套)数:计算机50台、MATLAB软件五、主要参考书目:1.《MATLAB及在电子信息课程中的应用》陈怀琛、杨吉斌编著,电子工业出版社,2002年1版2.《MATLAB7.0编程基础》王家文、王皓、刘海等;机械工业出版社,2005年7月3.《MATLAB教程——基于6.x版本》张志涌、徐彦琴等;北京航空航天大学出版,2001年4月出版实验一/二 MATLAB的基础操作一、实验目的1、掌握MATLAB的启动和退出。
第6章 MATLAB数学实验

第6章 MATLAB数学实验没有大胆的猜测,就做不出伟大的发现。
——牛顿MATLAB是Matrix Laboratory的缩写,是一个集数值计算、图形处理、符号运算、文字处理、数学建模、实时控制、动态仿真和信号处理等功能为一体的数学应用软件,而且该系统的基本数据结构是矩阵,又具有数量巨大的内部函数库和多个工具箱,使得该系统迅速普及到个领域,尤其在大学校园里,许多学生借助它来学习大学数学和计算方法等课程,并用它做数值计算和图形处理等工作。
下面介绍它的基本功能,并用它做与线性代数相关的数学实验。
在正确完成安装MATLAB软件之后,直接双击系统桌面上的MATLAB图标,启动MATLAB,进入MATLAB默认的用户主界面,界面有3个主要的窗口:命令窗口(Commend Window),当前目录窗口(Current Directory),工作间管理窗口(Workspace)。
如图6.1所示。
图6.1命令窗口是和MATLAB编译器连接的主要窗口,“>>”为运算提示符,表示MTALAB 处于准备状态,当在提示符后输入一段正确的运算式时,只需按Enter键,命令窗口中就会直接显示运算结果。
如图6.2所示。
图6.2数据的默认格式为五位有效数字,可用format命令改变输出格式。
Help是获取帮助的命令,在它之后应该跟一个主题词。
例如,help format,系统就会对format的用法提供说明,因此它对初学者是非常有用的。
当需要编写比较复杂的程序时,就需要用到M文件,而只需要将所有命令按顺序放到一个扩展名.m的文本文件下,每次运行只需输入该M文件的文件名即可。
下面介绍MATLAB程序设计中常用的程序控制语句和命令。
●顺序结构是最简单的程序结构,在编写程序后,系统将按照程序的物理位置顺序执行。
●选择语句。
在编写程序时,往往需要根据一定的条件来执行不同的语句,此时,需要使用分支语句来控制程序的进程,通常使用if-else-end结构来实现这种控制。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
目录第一部分MATLAB 入门 (1)第一讲变量与函数 (1)一、变量与函数 (1)第二讲数组与矩阵 (3)一、数组 (3)二、矩阵 (4)第三讲M文件与程序设计初步 (6)一、M文件的特点与形式 (6)二. 命令式M文件 (7)三. 函数式M文件 (7)四、控制流 (8)第四讲图形处理功能 (10)一、二维图形 (11)二、三维图形 (18)第二部分Matlab与数学实验 (19)第五讲插值 (19)一、一维插值 (19)二、二维插值 (25)第六讲拟合 (27)一、线性最小二乘拟合 (27)二、非线性最小二乘拟合 (29)二、非线性最小二乘拟合 (33)第七讲数值积分与数值微分 (35)一数值积分 (35)二、数值微分 (39)第八讲常微分方程数值解 (40)一、微分方程的解析解 (40)二、常微分方程数值解 (41)三、用Matlab软件求常微分方程的数值解 (42)四、实例1:导弹追踪问题 (43)第九讲线性方程组的数值解法 (47)一、直接解法 (47)二、迭代解法 (48)第一部分MATLAB 入门第一讲变量与函数1.MATLAB作为线性系统的一种分析和仿真工具,是理工科大学生应该掌握的技术工具,它作为一种编程语言和可视化工具,可解决工程、科学计算和数学学科中许多问题. 2.MATLAB建立在向量、数组和矩阵的基础上,使用方便,人机界面直观,输出结果可视化。
3.矩阵是MA TLAB的核心4.MATLAB的进入与运行方式(两种)一、变量与函数1、变量MATLAB中变量的命名规则是:(1)变量名必须是不含空格的单个词;(2)变量名区分大小写;(3)变量名最多不超过19个字符;(4)变量名必须以字母打头,之后可以是任意字母、数字或下划线,变量名中不允许使用标点符号.特殊变量表2、数学运算符号及标点符号(1)MATLAB的每条命令后,若为逗号或无标点符号,则显示命令的结果;若命令后为分号,则禁止显示结果. (2)“%” 后面所有文字为注释.(3)“...”表示续行.3、数学函数第二讲数组与矩阵一、数组1、创建简单的数组x=[a b c d e f ]创建包含指定元素的行向量x=first:last创建从first开始,加1计数,到last结束的行向量x=first:increment:last创建从first开始,加increment计数,last结束的行向量x=linspace(first,last,n)创建从first开始,到last结束,有n个元素的行向量x=logspace(first,last,n)创建从first开始,到last结束,有n个元素的对数分隔行向量.2、数组元素的访问(1)访问一个元素:x(i)表示访问数组x的第i个元素.(2)访问一块元素:x(a :b :c)表示访问数组x的从第a个元素开始,以步长为b到第c个元素(但不超过c),b可以为负数,b缺损时为1.(3)直接使用元素编址序号. x([a b c d]) 表示提取数组x的第a、b、c、d个元素构成一个新的数组[x(a) x(b) x(c) x(d)].3、数组的方向前面例子中的数组都是一行数列,是行方向分布的. 称之为行向量. 数组也可以是列向量,它的数组操作和运算与行向量是一样的,唯一的区别是结果以列形式显示.产生列向量有两种方法:直接产生例c=[1;2;3;4]转置产生例b=[1 2 3 4]; c=b‟说明:以空格或逗号分隔的元素指定的是不同列的元素,而以分号分隔的元素指定了不同行的元素.4、数组的运算(1)标量-数组运算数组对标量的加、减、乘、除、乘方是数组的每个元素对该标量施加相应的加、减、乘、除、乘方运算.设:a=[a1,a2,…,an], c=标量则:a+c=[a1+c,a2+c,…,an+c]a.*c=[a1*c,a2*c,…,an*c]a./c= [a1/c,a2/c,…,an/c](右除)a.\c= [c/a1,c/a2,…,c/an] (左除)a.^c= [a1^c,a2^c,…,an^c]c.^a= [c^a1,c^a2,…,c^an]当两个数组有相同维数时,加、减、乘、除、幂运算可按元素对元素方式进行的,不同大小或维数的数组是不能进行运算的.设:a=[a1,a2,…,an], b=[b1,b2,…,bn]则:a+b= [a1+b1,a2+b2,…,an+bn]a.*b= [a1*b1,a2*b2,…,an*bn]a./b= [a1/b1,a2/b2,…,an/bn]a.\b=[b1/a1,b2/a2,…,bn/an]a.^b=[a1^b1,a2^b2,…,an^bn]二、矩阵1、矩阵的建立逗号或空格用于分隔某一行的元素,分号用于区分不同的行. 除了分号,在输入矩阵时,按Enter键也表示开始一新行. 输入矩阵时,严格要求所有行有相同的列.例m=[1 2 3 4 ;5 6 7 8;9 10 11 12]p=[1 1 1 12 2 2 23 3 3 3]特殊矩阵的建立:a=[ ] 产生一个空矩阵,当对一项操作无结果时,返回空矩阵,空矩阵的大小为零.b=zeros(m,n) 产生一个m行、n列的零矩阵c=ones(m,n) 产生一个m行、n列的元素全为1的矩阵d=eye(m,n) 产生一个m行、n列的单位矩阵2、矩阵中元素的操作(1)矩阵A的第r行:A(r,:)(2)矩阵A的第r列:A(:,r)(3)依次提取矩阵A的每一列,将A拉伸为一个列向量:A(:)(4)取矩阵A的第i1~i2行、第j1~j2列构成新矩阵:A(i1:i2, j1:j2)(5)以逆序提取矩阵A的第i1~i2行,构成新矩阵:A(i2:-1:i1,:)(6)以逆序提取矩阵A的第j1~j2列,构成新矩阵:A(:, j2:-1:j1)(7)删除A的第i1~i2行,构成新矩阵:A(i1:i2,:)=[ ](8)删除A的第j1~j2列,构成新矩阵:A(:,j1:j2)=[ ](9)将矩阵A和B拼接成新矩阵:[A B];[A;B]3、矩阵的运算同标量-数组运算。
(2)矩阵-矩阵运算[1] 元素对元素的运算,同数组-数组运算。
[2]矩阵运算:矩阵加法:A+B矩阵乘法:A*B方阵的行列式:det(A)方阵的逆:inv(A)方阵的特征值与特征向量:[V,D]=eig[A]关系与逻辑运算1、关系操作符2、逻辑运算符第三讲M文件与程序设计初步一、M文件的特点与形式要说明M文件的特点,就得从MATLAB本身说起。
MATLAB实质上是一种解释性语言,就MATLAB(matlab.exe)本身来说,它并不能做任何事情,它就像DOS操作系统的一样,本身没有实现功能而只对用户发出的指令起到解释执行的作用。
像前面介绍过的命令行式的操作一样,命令先送到MATLAB系统内解释,再运行得到结果。
这样就给用户提供了最大的方便。
用户可以把所要实现的指令罗列编制成文件,再统一送入MATLAB系统中解释运行,这就是M文件。
只不过此文件必须以m为扩展名,MA TLAB 系统才能识别。
也就是说,M文件其实是一个像命令集一样的ASCII(纯文本)码文件。
因此M文件语法简单,调试容易,人机交互性强。
用户可以便用任何字处理软件对其进行编写和修改。
正是M文件的这个特点造就了MATLAB强大的可开发性和可扩展性,Mathworks 公司推出的一系列工具箱就是明证。
而正是有了这些工具箱,MATLAB才能被广泛地应用于信号处理、神经网络、鲁棒控制、系统识别、控制系统、实时工作系统、图形处理、光谱分析、模型预测、模糊逻辑、数字信号处理、定点设置、金融管理、小波分析、地图工具、交流通信、模型处理、LMI控制、概率统计、样条处理、工程规划、非线性控制设计、QFT控制设计、NAG等各个领域。
对个人用户来说,还可以利用M文件来建造和扩充属于自己的“库”。
因此,一个不了解M文件,没有掌握M文件的MATLAB使用者不能称其为一个真正的MATLAB用户。
由于商用的MA TLAB软件用C/C++语言编写而成。
因此,M文件的语法与C语言十分相似。
对广大的C语言爱好者来说,M文件的编写是相当容易的。
M文件有两种形式,命令式(Script)和函数式(Function).两者相同之处在于它们都是以m作为扩展名的文本文件,不进入命令窗口,而是由文本编辑器来创建的外部文本文件。
命令式M文件就是命令行的简单叠加,MATLAB会自动按顺序执行文件中的命令,与批处理文件类似,在MA TLAB命令窗口直接输入此文件的文件名,MA TLAB可逐一执行在此文件内的所有命令,和在命令窗口中逐行输入这些命令一样。
这样就解决了用户在命令窗中运行许多命令的麻烦;还可以避免用户做许多重复性的工作。
函数式M文件主要用以解决参数传递和函数调用的问题,它的第一句以function语句为引导。
另外,值得注意的是,命令式M文件在运行过程中可以调用MATLAB工作域内所有的数据,而且,所产生的所有变量均为全局变量。
也就是说,这些变量一旦生成,就一直保存在工作空间中,直到执行clear 或quit时为止。
在函数式M文件中的变量除特别声明外,均为局部变量。
因为MATLAB是一种解释性语言,所以即使在某个或某些函数中存在语法错误,但如果没执行到该语句时可能就不会发现该错误,这在一个成功的程序设计中是不能容许的。
要查出某目录中所有的M函数语法错误,首先应该用cd 命令进入该目录,然后运行pcode * 命令进行伪代码转换。
因为该命令会将MATLAB 函数转换成伪代码,而在转换过程中该程序将自动翻译每一条语句,所以一旦发现有语法错误,将会停止翻译,给出错误信息。
改正了该语法错误后,再重新执行pcode 命令,直到没有错误为止。
至少这样会保证目录下所有的程序不含有语法错误。
一个M文件首次被调用时,MATLAB将首先对该M文件进行语法分析。
并把生成的相应内部伪代码(P码)存放在内存中。
此后当再次调用该M文件时,将直接运行该文件在内存中的P码文件而不会对原码文件重复进行语法分析。
P码文件和原码文件具有相同的文件名,但其扩展名为“.p”,并且其运行速度要高于原码文件,但对于规模不大的文件,用户一般察觉不到这种速度上的优势。
P码文件不是只有当M文件被调用时才生成,也可被预先生成。
二. 命令式M文件由于命令式M文件的运行相当于在命令窗口中逐行输入并运行命令,因此,在编制此类文件时,只需把所要执行的命令按行编辑到指定的文件中,且变量不需要预先定义,也不存在文件名对应问题。
例:假设当前目录下有一个命令M文件:%solver.m%used to solve A*x=b%where A=[-1.5 1 2;3 -1 1;-1 3 5],b=[2.5;5;8].A=[-1.5 1 2;3 -1 1;-1 3 5];b=[2.5;5;8];x=A\b在命令窗口中执行solver命令,即可得到方程组的解。
