九年级数学下册32直棱柱、圆锥的侧面展开图圆锥的侧面展开图问题素材湘教版

合集下载

湘教版九年级数学下册课件：3.2 直棱柱、圆锥的侧面展开图(共29张PPT)

A．(30＋5 29)π m2 C．(30＋5 21)π m2
B．40π m2 D．55π m2
【解析】设底面圆的半径为 R，则πR2＝25π，解
得 R＝5，圆锥的母线长＝ 22＋52＝ 29，∴圆锥的侧面
积＝π×5× 29＝5 29π，圆柱的侧面积＝2π×5×3 ＝30π，∴需要毛毡的面积＝(30＋5 29)π m2.
得：3π 4 ＝2πr，
∴r＝38 .∴h＝
12－382＝
55 8
cm.
15. 如图，在正方形网格图中建立一直角坐标系，一条圆弧经过网格点 A，B，C，请在网格中进行下列操作：
(1)请在图中确定该圆弧所在圆心 D 点的位置，D 点坐标为；
(2)连接 AD，CD，求⊙D 的半径及扇形 DAC 的圆心角度数；
(1)求扇形 CEF 的面积； (2)用扇形 CEF 做成圆锥的侧面，求圆锥的高．
解：(1)连接 CG， ∴CG⊥AB， ∵∠B＝45°， BC＝ 2，∴CG＝1， ∴S 扇 CEF＝135·36π0·12＝38π；
(2)设圆锥的底面半径为 r，
E︵F的弧长＝135×18π0 ×1＝3π 4 ，由题意，
图① A．面 CDHE C．面 ABFG
图② B．面 BCEF D．面 ADHG
•9、要学生做的事，教职员躬亲共做；要学生学的知识，教职员躬亲共学；要学生守的规则，教职员躬亲共守。2021/9/82021/9/8Wednesday, September 08, 2021 •10、阅读一切好书如同和过去最杰出的人谈话。2021/9/82021/9/82021/9/89/8/2021 6:01:46 PM •11、只有让学生不把全部时间都用在学习上，而留下许多自由支配的时间，他才能顺利地学习……（这）是教育过程的逻辑。2021/9/82021/9/82021/9/8Sep-218-Sep-21 •12、要记住，你不仅是教课的教师，也是学生的教育者，生活的导师和道德的引路人。2021/9/82021/9/82021/9/8Wednesday, September 08, 2021

湘教版九下数学3.2 直棱柱、圆锥的侧面展开图

（1）侧棱不垂直于底的棱柱叫做斜棱柱. 我
们
只
斜棱柱
直棱柱
研究直棱
柱
（2）侧棱垂直于底的棱柱叫做直棱柱.
推进新课
展开展开
五棱柱
展开
六棱柱
展开
棱柱的侧面展开图是一个矩形，矩形的宽等于棱柱的侧棱长，矩形的长等于棱柱底面的周长.
圆锥的侧面展开图又是什么图形呢？
我们把连接圆锥的顶点S和底面圆上任一点的连线SA，SB 等叫做圆锥的母线.
第3章投影与视图
3.2 直棱柱、圆锥的侧面展开图
湘教版九年级下册
新课导入
棱柱的分类
根据棱柱底面多边形的边数，棱柱的底面可以是三角形、四边形、五边形……把这样的棱柱分别叫做三棱柱、四棱柱、五棱柱.
三棱柱
四棱柱五棱柱
棱柱的每个面都是多边形，棱柱是多面体.
棱柱的分类按侧棱与底面是否垂直可分为：
a _-_2_,b _-_7_,c __1__
2 c 7 -1 b
a
2.下列的三幅平面图是三棱柱的表面展开图的有（甲、乙）.
甲
乙
丙
3.如图，长方体的长为15cm，宽为10cm，高为20cm，点B到点C的距离为5cm，一只蚂蚁如果要沿着长方体的表面从A点爬到B点，需要爬行的最短距离是多少？
典例赏析
AD=AB
例2：如图所示的扇形中，半径R=10，圆心角θ=144°用这个扇形围成一个圆锥的侧面.求这个圆锥的底面半径r.
A
C
O
B
2×3.14×10×144°÷360°=25.12 25.12÷3.14÷2=4
随堂演练
1.如图是一个立方体纸盒的展开图，使展开图沿虚线折叠成正方体后相对面上的两个数互为相反数,求:

九下第3章投影与视图3-2直棱柱圆锥的侧面展开图新版湘教版

感悟新知
知1－练
(1)一共有多少条棱？长度分别是多少？解：一共有 18 条棱，其中有 6 条侧棱，其长度都为 6 cm，其余的棱都等于底面边长，其长度都为 3 cm.
感悟新知
知1－练
(2)一共有多少个面？它们分别是什么形状？哪些面的形状一定相同？解：一共有 8 个面，其中 2 个底面都为六边形，这 2 个底面的形状完全相同，6 个侧面都为矩形，这 6 个侧面的形状完全相同 .
感悟新知
知2－讲
(2) 直棱柱的侧面展开图是一个矩形，这个矩形的长是直棱柱的底面周长，宽是直棱柱的侧棱长(高) .
感悟新知
特别提醒沿直棱柱表面不同的棱剪开，可得
到不同组合方式的表面展开图 . 以直三棱柱为例，如图 3.2-4 所示，①②③依次为沿不同的棱剪开而得到的直三棱柱的表面展开图 .
锥的底面圆半径或高 .
感悟新知
知3－练
解题秘方：紧扣两个等量关系解题：一是圆锥的母线长与展开后所得扇形的半径相等；二是圆锥的底面圆的周长与展开后接 BC， AO. ∵∠ BAC=90°，知3－练
∴
BC
是直径，即
BC=2.
∴
OA=
1 2
感悟新知
知识点 3 圆锥
1. 与圆锥有关的概念 (1) 圆锥：如图 3.2-6 所示的立体图形称为圆
锥，圆锥是由一个底面和一个侧面围成的图形 . 圆锥可以看作一个直角三角形绕它的一条直角边所在的直线旋转一周所形成的图形 . 这条直线叫作圆锥的轴 .
知3－讲
感悟新知
知3－讲
(2)圆锥的高：圆锥的底面是一个圆，连接顶点与底面圆心的线段叫作圆锥的高 .
知2－讲
感悟新知

湘教版九年级数学下册《3.2直棱柱、圆锥的侧面展开图》公开课精品课件

考点讲练
考点一平行投影及其相关计算
例1 某校墙边有两根木杆． (1)某一时刻甲木杆在阳光下的影子如图所示，你能画出乙木杆的影子吗？(用线段表示影子) (2)在图中，当乙木杆移动到什么位置时，其影子刚好不落在墙上？ (3)在你所画的图中有相似三角形吗？为什么？
【解析】所要画出的乙木杆的影子与甲木杆形成的影子是同一时刻，根据同一时刻两物体的高度比等于其影长的比，同时，在同一时刻太阳光线是互相平行的，平行移动乙杆，使乙杆顶端的影长恰好抵达墙角．
相等 2.这个扇形的半径与圆锥中的哪一条线段相等？
母线 3.圆锥的高、母线以及底面半径之间有什么关系？
母线2=高2+半径2
要点归纳
概念对比
r
扇形
l n r
180
l
侧面展开图
lh r
o
C 2 r
✓其侧面展开图扇形的半径=母线的长l ✓侧面展开图扇形的弧长=底面周长 2r ✓母线、高及底面半径间的关系 l2=h2+r2
15π(cm2 )
l h
S全=S侧+S底
15π 9π
A
O
B 24π(cm2 )
r
8.如图,圆锥的底面半径为1,母线长为6,一只蚂蚁要从底
面圆周上一点B出发,沿圆锥侧面爬行一圈再回到点B,问
它爬行的最短路线是多少?
解:设圆锥的侧面展开图为扇形ABB’, ∠BAB’=n°
连接BB’,即为蚂蚁爬行的最短路线
（2）∵DG∥AC，
∴∠G=∠C，
∴Rt△ABC∽△RtDEG，
∴
A D
B E

BC EG
，即 1 .6 2 .4 DE 16

湘教版九年级下册数学：3.2 直棱柱、圆锥的侧面展开图(共16张PPT)

S侧= ?
“鱼米之乡的江南”农家艺术展开展在即，咱们武冈想到用常见的斗笠表面包一层印有宣封楼等武冈特色事物的画纸（接缝忽略不计），一是参展，二是作为城市名片。
请问扇形画纸面积多大？
迷你：底面半径5cm,母线长20cm
R
中号：底面半径16cm
A
B
所用画纸半径为20cm
大号：底面半径20cm,高为15cm
S
h
A
O
B
·
前置练习
1、扇形的弧长计算公式是__________ ，面积公式是__________。
2、已知扇形的半径为4厘米，圆心角是 1200，则此扇形的弧长是________，面积是________。
3、已知扇形圆心角是1200，弧长为 10∏厘米，则扇形半径为________。
小结与反思
知
实
美
识
践
感
设计者包好画纸后，决定在迷你型的斗笠加一条象征丰收的黄色装饰带（从A点出发，绕圆锥表面一圈回到A点）
装饰带最短需要多长？
迷你：底面半径5cm,母线长20cm
R
A
B
“挑战升级”
中点 C A
若最“终鱼米确之定乡的的方江案南”为农：家黄艺色术装展开饰展在带即从，A咱点们出武发冈，想到绕用圆常锥hu表见面的，斗笠在表面画作母如包纸为线图（一城S所接层市A示缝的印名忽）有片终略。宣点不封计C楼）处等，结武一束冈是（特参色示展事，意物二图的是
请问画纸面积多大？
知识补充: 圆锥的母线和圆锥的
高有什么关系？
S
h
A
O
B
思考：
1.圆锥侧面展开图扇形的弧长与底面圆的周长有什么联系？

湘教版九年级数学下册第三章《3.2直棱柱、圆锥的侧面展开图(第1课时)》公开课课件

什么关系？
做一做
1.制作圆锥并计算其相关的量. （1）在纸上画一个半径为6 cm，圆心角为216°的扇形. （2）将这个扇形剪下来，按图37-36所示围成一个圆锥. （3）指出这个圆锥的母线长，并求圆锥的高和底面的半
径（粘合部分忽略不计）.
216°
S
A
OB
做一做
2. 图3-3是四个几何体的平面展开图，请用纸分别复制下来，猜想下列展开图可折成什么立体图形，实际动手折一下，并指出围成的几何体的形状.
练习
下列各图是几何体的平面展开图，猜想下列展开图可折成什么立体图形，并指出围成的几何体的形状.
11、一个好的教师，是一个懂得心理学和教育学的人。2021/7/302021/7/302021/7/30Jul-2130-Jul-21
12、要记住，你不仅是教课的教师，也是学生的教育者，生活的导师和道德的引路人。2021/7/302021/7/302021/7/30Friday, July 30, 2021
13、He who seize the right moment, is the right man.谁把握机遇，谁就心想事成。2021/7/302021/7/302021/7/302021/7/307/30/2021
14、谁要是自己还没有发展月30日星期五2021/7/302021/7/302021/7/30
观察与思考
底面
侧棱侧面
底面
图3-1
图3-2
观察与思考
1.这个棱柱有几个侧面？每个侧面是什么形状的？ 2.这个棱柱的上、下底面的形状一样吗？他们各有几条边？ 3.侧面的个数与底面图形的边数有什么关系？ 4.这个棱柱有几条侧棱？它们的长度之间有什么关系？ 5.侧面展开图的长和宽分别与棱柱底面的周长和侧棱长有

《直棱柱、圆锥的侧面展开图》PPT课件(湘教版)

湘教·九年级下册
直棱柱、圆锥的侧面展开图
新课导入
长方体有几个面，几条棱，上下面与侧面有什么位置关系，竖着的棱有上、下面有什么位置关系？
新课导入
观察图中的立体图形，它们的形状有什么共同特点？直棱柱
都是直四棱柱
直三棱柱直四棱柱直棱柱的特征：
直五棱柱
直六棱柱
（1）有两个面互相平行，称它们为底面；（2）其余各个面均为矩形，称它们为侧面；（3）侧棱（指两个侧面的公共边）垂直于底面.
S=（2.5+2+1.5）×3=18
直棱柱侧面展开图
圆锥侧面展开图
2
答：这张扇形纸板的面积是240π cm2.
1.某个立体图形的侧面展开图如图所示，它的底面是正三
角形，那么这个立体图形是( A ) 【教材P103页】 (A)三棱柱 (B)四棱柱 (C)三棱锥
2.如图为一直三棱柱，试画出它的侧面展开图，并求侧面展开图的面积. 【教材P103页】
3
2.5图。
母线高
O
A
例2 如图小刚用一张半径为24cm的扇形纸板做一个圆锥形帽子(接缝忽略不计)，如果做成的圆锥形帽子的底面半径为 10cm，那么这张扇形纸板的面积S是多少？【教材P103页】
解扇形的弧长（即底面圆周长）为
l=2×π×10=20π（cm） S= 1 ×20π×24=240π（cm2）
探索新知
收集几个直棱柱模型，再把侧面沿一条侧棱剪开，它们的侧面能否展开成平面图形，是矩形吗？
直棱柱的侧面沿着一条侧棱剪开，可以展开成平面图形，称为直棱柱的侧面展开图。
直棱柱的侧面展开图是一个矩形，这个矩形的长是直棱柱的底面周长，宽是直棱柱的侧棱长。
例1 一个食品包装盒的侧面展开图如图所示，它的底面是边长为2的正六边形，这个包装盒是什么形状的几何体？试根据已知数据求出它的侧面积.【教材P102页】

九年级数学下册 3.2 直棱柱、圆锥的侧面展开图直棱柱的表面展开图素材 (新版)湘教版

直棱柱的表面展开图立方体是常见的特殊的直四棱柱，下面我们以它为代表来复习直棱柱的表面展开图.一、知识要点1. 立方体的表面展开图(1)概念:将立方体沿某些棱剪开，且使六个面连在一起，然后铺平，这样展开后的平面图形称为立方体的表面展开图.(2)类型:立方体的表面展开图共有11种不同的情形，可归纳为4种基本类型. ① 1—4—1型，如图(1)～(6)，包括下列6种情形:(6)(5)(4)(3)(2)(1)说明:(a)每个图形都由三行组成，从上到下每行分别有1个，4个，1个小正方形； (b)以图(1)为基准，将第1行或第3行的小正方形左右平移即可得图(2)～(6)；(c)若两个图形可通过轴对称变换得到的，就认为是同一种情形，如图(甲)与图(乙)所示.② 1—3—2型，如图(7)～(9)，包括下列3种情形:(9)(8)(7)说明:每个图形都由三行组成，从上到下每行分别有1个，3个，2个小正方形； ③2—2—2型，如图(10)，只有1种情形.说明:这个图形由三行组成，从上到下每行都有2个小正方形；(乙)(甲)(10)(11)④3—0—3型，如图(11)，只有1种情形.说明:这个图形可看作由三行组成，从上到下每行分别有3个，0个，3个小正方形，这样便于统一编写、记忆它们的型号.(3)注意点:①展开图的面与面之间必须以棱相连接，不能以顶点相连接；②行与行之间，不能同时有两对或两对以上的小正方形具有公共边；③有下列情形之一者，肯定不是立方体的表面展开图:(a)小正方形的个数不足6个或超过6 个; (b)行数是1行或超过3行(经旋转变换的图形除外)；(c)图中包含“田”字型部份；(d)整个图形呈“L”字型.2.直棱柱的侧面展开图直棱柱的侧面展开图是由若干个长方形或正方形组合而成的，整个图形是一个长方形或正方形.3.直棱柱的表面积与侧面积计算直棱柱的表面积与侧面积，实质上就是利用长方形或正方形的面积公式进行面积计算.二、典例赏析例1 如图是某些多面体的平面展开图，说出这些多面体的名称.解:因为图(1)是由6个正方形组成的多面体的平面展开图，所以它是立方体；图(2)是由2个直角三角形，3个长方形组成的多面体的平面展开图，所以它是直三棱柱.析解:(1)根据平面展开图中所给图形的形状，先判断几何体的底面是什么图形，从而确定是哪一种多面体.(2) 如图，图(1)可看作由上述“1—3—2型”的基本图形(8)旋转变换而得.例2 如图是一个几何体的三视图，主视图与左视图是大小相同的长方形，俯视图是等边三角形.(1) 任意画出它的一种表面展开图；(2)若长方形的长为10cm,等边三角形的边长为4cm,求这个几何体的表面积. 解:(1) 如图是该几何体的一种表面展开图.(2)这个几何体的表面积为3×(10×4)+)24421(222-⨯⨯⨯ =120+83(cm 2). 析解:整个图形是一个不规则的图形，不能直接利用公式来计算，可用分割法把它转化为规则图形的面积来计算.例3 如图甲，有一个棱长为10cm 的立方体盒子，在盒子底部A 处有一只蚂蚁，欲吃顶点C 1处的一粒熟米.问蚂蚁应沿什么路径爬行，才能在最短的间内吃到这粒熟米?求出蚂蚁爬行的最短路径长.解：如图乙，它是立方体盒子沿侧棱展开的平面图形之一. 观察图形，根据“两点之间，线段最短”，可知蚂蚁沿线段AC 1爬行的路径最短，所用时间最短.在Rt △AB 1C 1中，AB 1=20cm ，B 1C 1=10cm.由勾股定理得AC 12=AB 12+B 1C 12=202+102=400+100=500,∴AC 1=105(cm). 因此，蚂蚁沿着路径AC 1爬行，才能在最短的时间内吃到熟米，最短路径长为105cm. 析解：因为蚂蚁必须沿着立方体盒子的侧面爬行，所以要想在最短时间内吃到熟米，必须选择最短的路径.此时A 、C 1两点不在同一个面内，须将它展开转化为平面图形来解决.图乙是立方体盒子沿侧棱展开的平面图形之一.观察图形可知，蚂蚁沿线段AC 1爬行的路径最短，所用时间最短.。

九年级数学下册3.2直棱柱、圆锥的侧面展开图圆锥的侧面展开图问题素材湘教版(new)

圆锥的侧面展开图问题解决圆锥问题的关键是明确圆锥的侧面展开图各元素与圆锥各元素的关系——圆锥的侧面展开图是扇形，扇形的半径是圆锥的母线，弧长是圆锥的底面圆的周长．问题往往涉及圆锥的母线长、圆锥的高以及底面半径之间的关系，勾股定理则是架起三元素间的桥梁．如图1，设圆锥的底面半径为r ,母线AB 的长为l ,高为h ，则r 2+h 2=l 2,圆锥的侧面展开图是扇形ACD ，该扇形的半径为l ，设扇形ACD 的圆心角是θ，则扇形的弧CD 的长=2πr =180l θπ,圆锥的侧面积为S 侧=12×2πr ×l =πrl ．一、计算圆锥的侧面积例1 （邵阳）如图2所示的圆锥主视图是一个等边三角形，边长为2，则这外圆锥的侧面积为______（结果保留π）．分析：依题意，圆锥主视图是一个等边三角形，所以圆锥的母线长为2，底面半径为1，可以直接代入公式求得．解:依题意，r=1,l =2，所以S 侧=π×1×2=2π．二、求圆锥的母线长例2 （桂林）已知圆锥的侧面积为8πcm 2, 侧面展开图的圆心角为45°，则该圆锥的母线长为（）．(A)64cm （B)8cm （C)22cm （D ）24cm 分析:圆锥的侧面积即其侧面展开图扇形的面积，由扇形的面积公式可求出圆锥的母线长(侧面展开图扇形的半径即为圆锥的母线长）．解:由2360n l S π=扇形,即2360n l π＝8π，解得l ＝8(cm ）．故应选（B ）．三、计算圆锥的底面半径例3 （日照）将直径为60cm 的圆形铁皮，做成三个相同的圆锥容器的侧面（不浪费材料，不计接缝处的材料损耗），那么每个圆锥容器的底面半径为( )．（A ）10cm （B)30cm （C ）40cm （D ）300cm分析:依题意，将直径为60cm 的圆形铁皮分割成三个大小相等的扇形，这三个扇形即三个相同的圆锥容器的侧面展开图．根据“侧面展开图扇形的弧长是圆锥的底面圆的周长”图1 图2可求每个圆锥容器的底面半径．解：直径为60cm 的圆形铁皮的周长为60πcm ，故将该铁皮分割成三个大小相等的扇形的弧长为20πcm ．设圆锥的底面半径为r ,则2πr ＝20π，解得r ＝10．故应选(A ）．四、计算圆锥的高例4 （鸡西)如图3,小明想用图中所示的扇形纸片围成一个圆锥，已知扇形的半径为5cm ，弧长是6πcm ，那么围成的圆锥的高度是 cm ．分析：借助图1分析，知在r 2+h 2=l 2中，欲求h ，需知道r ，l ，显然这里l ＝5 cm ，故只需再求出r ．解:设圆锥的底面半径为r ，则2πr ＝6π，解得r ＝3．所以h 2=l 2－ r 2＝52－32，所以h ＝4（cm ）．五、计算侧面展开图中扇形圆心角的度数例5 （成都）若一个圆锥的底面圆的周长是4πcm ，母线长是6cm ,则该圆锥的侧面展开图的圆心角的度数是（）．（A ）40° (B ）80° （C ）120° （D ）150°分析：设圆锥展开图的圆心角为n °，根据弧长公式可求出侧面展开图扇形的弧长为180n l π,再根据“侧面展开图扇形的弧长是圆锥的底面圆的周长"列方程可解．解：设圆锥展开图的圆心角为n °，则4π=6180n π．解得n ＝120．所以选（C ）．六、最短路径问题例6 （青岛）如图4是一个用来盛爆米花的圆锥形纸杯,纸杯开口圆的直径EF 长为10cm ．母线OE （OF )长为10cm ．在母线OF 上的点A 处有一块爆米花残渣，且FA ＝2cm ,一只蚂蚁从杯口的点E 处沿圆锥表面爬行到A 点．则此蚂蚁爬行的最短距离为 cm ．分析:由于小蚂蚁只能在圆锥侧面上爬行，所以我们可考虑把圆锥侧面展开，将问题转化为平面图形解决.将圆锥沿母线OEO B A 图3 5cm 图5ＡＦＥＯ图4剪开，如图7所示的展开图,根据“两点之间线段最短"，知EA 即为最短路径．解：设圆锥侧面展开后扇形的圆心角为n °，因为底面的周长等于展开后扇形的弧长，所以180n OE π⋅＝π EF ，即10180n π⋅＝10π,解得n °＝180°．此圆锥的侧面展开图为扇形（如图5），在Rt △AEO 中， OA ＝OF －AF ＝8（cm ），尊敬的读者：本文由我和我的同事在百忙中收集整编出来，本文档在发布之前我们对内容进行仔细校对，但是难免会有不尽如人意之处，如有疏漏之处请指正，希望本文能为您解开疑惑,引发思考。

湘教版九年级数学下册3.2直棱柱、圆锥的侧面展开图课件

母线高
图 3-16
新知讲解
例2 如图3-17，小刚用一张半径为24cm的扇形纸板做一个圆锥形帽子(接缝忽略不计)，如果做成的圆锥形帽子的底面半径为 10cm，那么这张扇形纸板的面积S是多少？
图3-17
新知讲解
分析圆锥形帽子的底面周长就是扇形的弧长. 解扇形的弧长（即底面圆周长）为 l=2×π×10=20π（cm）. 所以扇形纸板的面积 S=12×20π×24=240π（cm2）.
宽
图3-11
新知讲解
直棱柱侧面展开图的特点： n棱柱，侧面展开图是由n个小矩形组成面积：底面周长×高.
都是矩形宽
图3-11
新知讲解
例1 一个食品包装盒的侧面展开图如图所示，它的底面是边长为2的正六边形，这个包装盒是什么形状的几何体？试根据已知数据求出它的侧面积.
图3-12
新知讲解
解根据图示可知该包装盒的侧面是矩形，又已知上、下底面是正六边形，因此这个几何体是正六棱柱（如图3-13所示）. 由已知数据可知它的底面周长为2×6=12，因此它的侧面积为12×6=72.
图3-17
新知讲解
总结
直棱柱的侧面展开图是一个矩形，这个矩形的长是直棱柱的底面周长，宽是直棱柱的侧棱长（高）；圆锥的侧面展开图是一个扇形.这个扇形的半径是圆锥的母线长，弧长是圆锥的底面圆的周长.
课堂练习
1.如图是一个粉笔盒的表面展开图，若字母A表示粉笔盒的上盖， B表示侧面，则底面在表面展开图中的位置是( C )
A. ①
B. ② C. ③ D. ④
课堂练习
解：根据题意可得，还原为原来的长方体。若字母A表示粉笔盒的上盖，B表示侧面，则底面在表面展开图中的位置是③．故选：C．

九年级数学下册3.2直棱柱、圆锥的侧面展开图习题湘教版

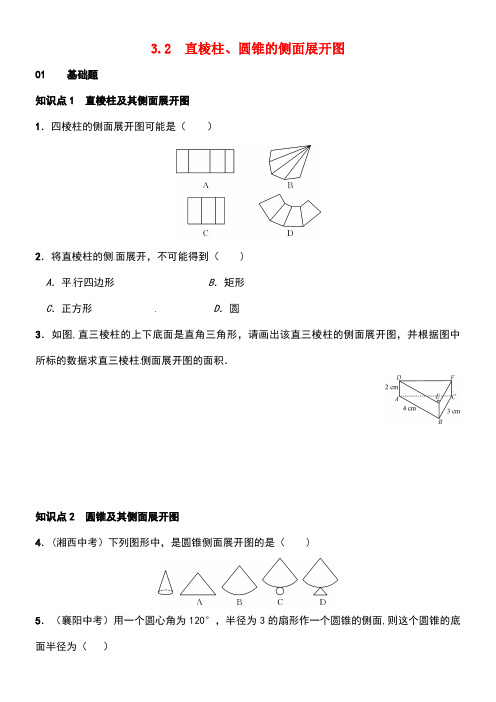
3.2 直棱柱、圆锥的侧面展开图01 基础题知识点1 直棱柱及其侧面展开图1．四棱柱的侧面展开图可能是（）2．将直棱柱的侧面展开，不可能得到（ )A．平行四边形B．矩形C．正方形D．圆3．如图,直三棱柱的上下底面是直角三角形，请画出该直三棱柱的侧面展开图，并根据图中所标的数据求直三棱柱侧面展开图的面积．知识点2 圆锥及其侧面展开图4．(湘西中考）下列图形中，是圆锥侧面展开图的是（ )5．（襄阳中考）用一个圆心角为120°，半径为3的扇形作一个圆锥的侧面,则这个圆锥的底面半径为（）A。

错误!B．1 C.错误!D．26．(常德中考）一个圆锥的底面半径为 1 cm，母线长为 2 cm，则该圆锥的侧面积是____________cm2(结果保留π)．7．如图，沿一条母线将圆锥侧面剪开并展平，得到一个扇形,若圆锥底面圆的半径r＝2 cm，扇形的圆心角θ＝120°，则该圆锥的母线长l为________cm.8．已知圆锥的侧面展开图是一个半径为12 cm,弧长为12πcm的扇形,求这个圆锥的侧面积及高．02中档题9．(荆门中考)若圆锥的侧面展开图为半圆，则该圆锥的母线l与底面半径r的关系是（ ) A．l＝2r B．l＝3rC．l＝r D．l＝错误!r10．(昆明中考）如图，从直径为4 cm的圆形纸片中，剪出一个圆心角为90°的扇形OAB,且点A，B在圆周上，把它围成一个圆锥，则圆锥的底面圆的半径是____________cm.11．一个底面为正方形的直棱柱的侧面展开图是边长为12的正方形，则它的表面积为____________．12．将一个底面半径为6 cm，母线长为15 cm的圆锥形纸筒沿一条母线剪开并展平，求所得的侧面展开图的圆心角度数．13．已知一个直四棱柱的底面是边长为5 cm的正方形,侧棱长都是8 cm,回答下列问题：(1)将这个直四棱柱的侧面展开成一个平面图形，这个图形是什么形状？面积是多少？(2）这个直四棱柱的体积是多少?14．在△ABC中，AB＝错误!,AC＝错误!，BC＝1.(1）求证：∠A≠30°；（2)将△ABC绕BC所在直线旋转一周,求所得几何体的表面积．03综合题15．已知一个底面为菱形的直棱柱，高为10 cm，体积为150 cm3。