组合图形面积(2)练习题及答案
苏教版五年级数学上册《组合图形的面积计算》专项练习题

《组合图形的面积计算》习题
一、基础题
(一)填空题
1
面积公式(字母)
图形名称面积
公式(文字)
平行四边形
三角形
梯形
长方形
正方形
2计算组合图形的面积,一般通过_____或_____的方法,把它转化成基本图形后进行计算.
(二)判断题
1.一个三角形底长8厘米,高5厘米,它的面积是40平方厘米。
()
2.任意两个三角形都可以拼成一个平行四边形。
()
3.任意一个梯形都能分成两个一样的平行四边形。
()
4.下面三个三角形的面积都相等。
()
5.如果两个三角形的形状不同,它们面积一定不相等。
()
二、综合题
1.如图的两个正方形,边长分别为8厘米和4厘米,那么阴影部分的面积是_____平方厘米.
2.
1
三、提高题
在一块梯形的地上有一个长方形的花园,其余的是草地(如图).草地的面积是多少?。
北师大版小学数学五年级上册《组合图形的面积》单元检测(2)

《组合图形的面积》单元检测(2)―、填一填。
(第3题4分,其余每空1分,共31分)1.在括号里填上合适的面积单位。
(1)游泳池的占地面积约是5000()。
(2)天安门广场的面积约是44()。
(3)颐和园的占地面积是2.908()。
(4)我的手掌面积约是1()。
(5)数学书封面的面积约是500()。
2.在括号里填上合适的数。
5平方千米=()公顷 7000公顷=()平方千米0.28公顷=()平方米 4900000平方米=()平方千米4平方千米=()平方米=()公顷600公顷=()平方米=()平方千米3.将下面的面积按从大到小的顺序排列。
7.05公顷 75000平方米 0.705平方千米 7公顷50平方米()4.图①的面积等于()的面积()()的面积。
图②的面积等于()的面积()()的面积。
5.每个小方格的面积表示1cm2。
面积约是()cm2面积约是()cm2面积约是()cm26.(1)每个小方格的面积是1平方厘米,估计上图中树叶的面积约是()平方厘米。
(2)如果右图中的这棵树有50000片这样的叶子,那么这棵树所有树叶的总面积约是()平方米。
(3)有阳光时,大约每25平方米的树叶能在一天内释放足够一个人呼吸所需的氧气。
右图中的这棵树在有阳光时,一天释放的氧气约能满足()人呼吸的需要。
(结果保留整数)7.两个完全一样的直角梯形正好拼成一个正方形,每个梯形的上底是10厘米,下底是20厘米,拼成的正方形的面积是()平方厘米。
8.如右图,将四条长20厘米、宽5厘米的长方形纸条垂直相交编织,平放在桌面上,桌面被盖住的面积是()平方厘米。
二、判一判。
(每题1分,共5分)1.面积是1公顷的土地一定是边长为100米的正方形。
()2.在5000平方厘米、40平方米、1公顷中,最小的是5000平方厘米。
()3.在一块面积是6公顷的坡地上种树,每棵树占地2平方米,这块地可种树3000棵。
()4.下面图形的面积是。
()5.右图中平行四边形的面积是48cm²,A是平行四边形底边的中点,则阴影部分的面积是12cm²。
《组合图形的面积》练习题(含答案)

3(4)
解:2.5×1.5+(2.5+4)×(8-3-1.5)÷2+4×3=27.125(平方分米)
4
解:10×(52-10-14-16)÷2=60(平方厘米)
5
解:2×2+(5-2)×6=22(平方米)
6பைடு நூலகம்
解:大正方形面积为:22×22=484(平方厘米)
7.如图所示,一个平行四边形背分成A.B两被封,A的面积比B的面积打40平方米,A的上底是若干?
B
A
8米
【参考答案】
1
解:
A
B D
C
2
解:48÷8×3÷2=9(平方分米)
3(1)
解:8×6+(8+12)×3÷2=78(平方分米)
3(2)
解:(14+12)×6÷2+12×6÷2=114(平方分米)
3(3)
4.如图所示,梯形的周长是52厘米,求暗影部分的面积.
10
14
16
5.校园里有一块花园,(如图所示),算出它的面积.(单位:米)
6 2
2
5
6.大小正方形如图放置,暗影部分为重叠部分,求空白部分面积.(单位:厘米)
15
7
7
22
7.有一块地盘如图所示,你能用几种办法求出它的面积?(单位:米)
12
15
8
22
小正方形面积为:15×15=225(平方厘米)
暗影部分面积为:7×7=49(平方厘米)
空白部分的面积为:484+225-2×49=611(平方厘米)
7
解:办法一:
《组合图形的面积》压轴题大全 北师大版数学五年级上册 (2)
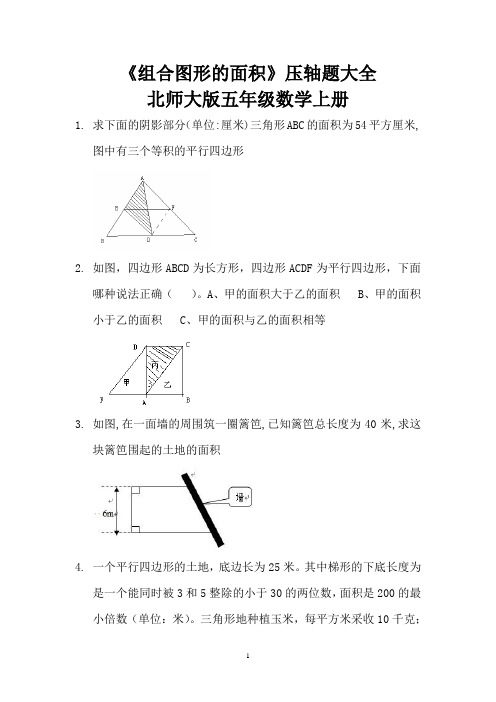
《组合图形的面积》压轴题大全北师大版五年级数学上册1. 求下面的阴影部分(单位:厘米)三角形ABC的面积为54平方厘米,图中有三个等积的平行四边形2. 如图,四边形ABCD为长方形,四边形ACDF为平行四边形,下面哪种说法正确()。
A、甲的面积大于乙的面积 B、甲的面积小于乙的面积 C、甲的面积与乙的面积相等3. 如图,在一面墙的周围筑一圈篱笆,已知篱笆总长度为40米,求这块篱笆围起的土地的面积4. 一个平行四边形的土地,底边长为25米。
其中梯形的下底长度为是一个能同时被3和5整除的小于30的两位数,面积是200的最小倍数(单位:米)。
三角形地种植玉米,每平方米采收10千克;问:这块三角形地可收入玉米多少千克?5. 公园里有一块面积是180平方米的三角形绿地(如下图),底长24米。
绿地扩展,把底延长8米,高不变。
(1)请在下图上画出扩展后的三角形绿地。
(只需画出示意图)(2)列式计算出扩展后三角形绿地的总面积。
6. 图中阴影部分的面积与空白部分的面积相比较,它们()(1)相等②不相等③无法比较7. 长方形ABCD被ED分成两部分,阴影部分的面积比空白部分大20平方厘米,AD=10厘米。
CD=8厘米。
求阴影部分的面积。
8. 如右图,三角形面积是24平方厘米,平行四边形的面积是()平方厘米,平行四边形与梯形面积的最简整数比是(),平行四边形面积比梯形少(),三角形面积比平行四边形少()%,梯形面积比三角形面积多()%,三角形面积是梯形面积的(—)9. 王大爷在自家墙外围成一个菜园(如下图),他测得篱笆的总长是22米,其中一条边是8米,你能求菜园的面积吗?10. 下图,梯形面积为60平方厘米,上底是下底的2倍,已知梯形的高5厘米,求阴影部分的面积。
11. 右图梯形中,阴影部分面积是150平方厘米,求梯形面积。
12. 有一个正方形和一个有阴影的三角形重叠在一起,(如图)已知正方形的面积比三角形的面积大25平方厘米,求图中a的长度。
人教版小学五年级上册数学课时练第6单元《组合图形的面积》 试卷试题含答案(2)

课时练第6单元多边形的面积组合图形的面积一、填空题1.一个正方形的边长增加2厘米,面积增加了20平方厘米,扩大后正方形的面积是__________平方厘米.2.求不规则图形的面积,一般利用__________和__________的方法,将不规则图形转化成__________.3.把两个边长都是4厘米的正方形拼成一个长方形,这个长方形的周长是__________厘米;面积是__________平方厘米.4.如图是用边长1厘米的小正方形拼成的,它的周长是__________厘米,面积是__________平方厘米。
5.如图的阴影部分是__________形,它的底是小正方形的__________,它的高是__________.二、单选题6.如图,图中阴影部分的面积是()cm2。
A.12B.16C.18D.367.如图是刘大伯家的一面墙。
若砌这面墙每平方米用砖185块,一共需要用()块砖。
A.7400B.6350C.59208.计算如图组合图形的面积,下面四幅图中,可以列式为“30×12+(9+30)×(20﹣12)÷2”的是()A.B.C.D.9.两个完全一样的直角三角形重叠一部分(如图),形成两个梯形A、B,这两个梯形的面积的大小关系是()A.梯形A的面积大B.梯形B的面积大C.它们的面积相等D.无法确定10.下面组合图形的面积是()平方米。
A.216B.380C.596D.164 11.如图所示:甲和乙是完全一样的两个长方形,两幅图的阴影面积相比,下列说法正确的是()A.甲>乙B.甲<乙C.甲=乙D.无法确定三、判断题12.面积相等的图形,形状一定相同.()13.在梯形中,阴影①的面积与阴影②的面积相等。
()14.不规则图形用单位方格纸测面积,单位越小测得结果越准确。
()15.任何一个梯形都可以分成两个等高的三角形.()16.任何两个三角形都可以拼成一个四边形.()17.平行四边形的面积大于梯形面积.()四、计算题18.梯形的面积是39平方分米,求阴影部分的面积。
五年级数学上册《组合图形的面积》测试卷及答案-北师大版

五年级数学上册《组合图形的面积》测试卷及答案-北师大版一.选择题(共8小题)1.如图,边长相等的两个正方形中,画了甲、乙两个三角形(用阴影表示),它们的面积相比()A.甲的面积大B.乙的面积大C.相等2.点A是长方形内任意一点,阴影部分的总面积与空白部分总面积比较,哪个的面积较大?A.阴影部分面积大B.空白部分面积大C.一样大D.无法确定3.图中每个小方格的面积是1cm2.请你估计一下,这个脚印的面积约是()A.45B.35C.254.下面图形中涂色部分面积与其它不同的一个是()5.中心广场的占地面积约为5公顷,()个中心广场的面积约为1平方千米.A.2 B.20 C.2006.丫丫家的面积有110平方分米.她家所在的小区有300平方千米.丫丫最喜欢楼下的游乐场了,它有10公顷那么大呢.这段话里有()处错误.A.1 B.2 C.37.“6平方千米〇601公顷”,比较大小,在〇里应填的符号是()A.>B.<C.=D.×8.如图:树叶的面积约是()(每个小方格的面积是1cm2)A.15cm2~25cm2B.35cm2~45cm2C.55cm2~65cm2二.填空题(共8小题)9.如图是一个不规则的土地,估测一下,它的面积大约是平方米.10.如图,平行四边形中,阴影部分的面积是36.5dm2,平行四边形的面积是平方分米.11.右图平行四边形的面积是25平方厘米,阴影部分的面积是平方厘米.12.如果1平方米能站9人,那么1公顷能站人,1平方千米能站人.13.260000000平方米=公顷=平方千米800平方千米=公顷=平方米14.如下图所示,平行四边形的面积是28cm2,阴影部分的面积是cm2.15.如图中这片树叶的面积约是cm2.16.如图是一个平行四边形被分成了三个三角形,涂色图形的面积是40cm2,没涂色的三角形的面积是cm2.三.判断题(共5小题)17.200个50平方米的教室面积是1公顷.(判断对错)18.100个1角的硬币大约重1千克.(判断对错)19.一张床的周长估计是2米.(判断对错)20.计算的面积,只能把它分成一个正方形和一个三角形来计算.(判断对错)21.如图中阴影部分的面积是14平方厘米.(判断对错)四.计算题(共2小题)22.求下面组合图形的面积.(单位:dm)23.如图,阴影部分是两个正方形,周长分别为12厘米和32厘米.求空白部分的总面积是多少平方厘米?五.操作题(共2小题)24.先估计下面图形的面积,再用1平方厘米的正方形学具量一量,填在括号里.25.分割组合图形(不计算):你有哪几种分割方法便于计算其面积,请画出分割示意图.六.应用题(共6小题)26.某街心广场有一块地(如图所示),李叔叔要在这块地上铺满草坪.(1)他需要购买多少平方米草皮?(2)如果每平方米草皮需要68元,请你估计一下,李叔叔要带多少元钱才能一次性把草皮买够?请写出你的估计过程.27.王大伯从平行四边形菜地中划出一块三角形地种西红柿,其余地方种黄瓜(如图),这块黄瓜地的面积是多少平方米?28.一个果园形状如图,一棵果树占地5m2,这个果园一共可以种多少棵树?29.李阿姨家有一块菜地,(如图)这块菜地的面积有多少平方米?30.王村有一块梯形果园,村里进行道路规划时,有一条公路穿过了这个果园.这个果园的实际面积是多少平方米?31.下面三个大正方形的边长都是32厘米,先计算每个正方形中一个小方格的面积,再估计出荷叶的面积.你觉得哪幅图估计得最接近实际面积?参考答案一.选择题(共8小题)1.解:两个阴影三角形的底等于正方形的边长,三角形的高也等于正方形的边长,因此两个三角形等底等高,所以面积相等;故选:C.2.解:阴影部分两个三角形的高等于长方形宽,底等于长方形的长,空白部分两个三角形的高等于长方形的长,底等于长方形的宽,所以阴影部分的面积与空白部分的面积相等。
五年级数学上册《组合图形的面积》练习题

五年级数学上册《组合图形的面积》练习题
1、计算下列图形的面积。
(6+8)×5÷2+8×4÷2=51(cm²)
10×4+10×3=70(cm²)
12×5÷2+12×4÷2=54(cm²)
2、如图,一块平行四边形的菜地,中间有一个正方形池塘,这块菜地的实际面积是多少平方米?
50×44-2×2=2196(平方米)
答:这块菜地的实际面积是2196平方米。
3、已知平行四边形的面积是192dm²,求阴影部分的面积。
192÷16=12(dm)
(16-7)×12÷2=54(dm²)
答:阴影部分的面积为54dm²。
4、如图,校园里有一块花圃,算出它的面积。
(单位:米)
1+2+1=4(米)
4×4-1×1×4=12(平方米)
答:花圃的面积为12平方米。
5、下图是由4个相同的直角三角形拼成的一个大正方形,直角三角形的两条直角边的长度分别是3cm 和4cm。
求大正形的面积。
4-3=1(cm)4×3÷2×4+1×1=25(cm²)
答:大正形的面积为25cm²。
人教版小学五年级数学上学期第六单元《组合图形的面积》同步检测题及答案(含两套题)
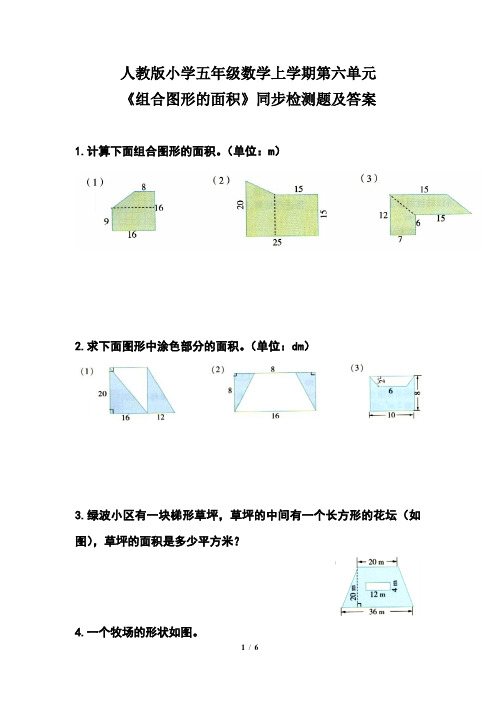
人教版小学五年级数学上学期第六单元《组合图形的面积》同步检测题及答案1.计算下面组合图形的面积。
(单位:m)2.求下面图形中涂色部分的面积。
(单位:dm)3.绿波小区有一块梯形草坪,草坪的中间有一个长方形的花坛(如图),草坪的面积是多少平方米?4.一个牧场的形状如图。
5.剪纸艺术受到大家的喜爱,聪聪也非常喜欢剪纸,如图是聪聪用一张边长是6 cm的正方形纸剪下的一个大写字母“Y”,请你帮聪聪计算一下它的面积。
参考答案1.(l)(8+16)×(16-9)÷2=84(m²)16×9=144(m²) 84+144=228(m²)(2)(15+20)×(25-15)÷2=175(m²) 15×15=225(m²)175+225=4000(m²)(3)(6+12)×7÷2=63(m²)12-6=6(m)15×6=90(m²)90+63=153(m²)2.(1)16×20÷2=160(dm²) 12×20÷2=120(dm²) 160+120=280(dm²)(2)16×8=128(dm²)(8+16)×8÷2=96(dm²) 128-96=32(dm²)(3)10×8=80(dm²)(6+10)×2÷2=16(dm²) 80-16=64(dm²)3.(20+36)×20÷2=560(m²)12×4=48(m²)560-48=512(m²)答:草坪的面积是512平方米。
4.230-150=80(m)(30+220)×80÷2=l0000(m²)(180+220)×150÷2=30000(m²)10000+30000=40000(m²)40000平方米=4公顷答:这个牧场的面积是40000平方米,合4公顷。
五年级上-组合图形面积(二)

聚成教育2015年五年级数学上讲义第十四讲组合图形的面积(二)练习1【题目】:如图,长方形ABCD中,AB﹦8厘米,BC﹦15厘米,E是BC的中点,F是CD的中点,连结BD、AF、AE,把下图分成六块,阴影部分的总面积是多少?【解析】:如下图,连接GC、HC。
因为E是BC的中点,F是CD的中点,所以△GBE与△GCE面积相等,△HCF与△HDF面积相等。
因为△AGH与△CGH同底等高,所以这两个三角形的面积也相等。
因为E、F分别是DC、BC的中点,所以△ABE与△ADF的面积和正好等于长方形ABCD 面积的一半;△ABD的面积也是长方形ABCD面积的一半;等量减等量差相等,所以△AGH的面积就等于△GBE与△HDF的面积和。
又因为△AGH与△CGH面积相等,所以△GBE与△HDF的面积和等于△BCD面积的三分之一:8×15÷2÷3﹦20(平方厘米)。
所以阴影部分面积为:20×2﹦40(平方厘米)。
【题目】:如图,三角形ABO的面积是9平方厘米,线段BO的长度是OD的3倍,梯形ABCD的面积是多少平方厘米?【解析】:因为△ABC与△DBC等底等高,面积相等,且等量减等量差相等,所以△DOC的面积就等于△ABO的面积,也是9平方厘米。
又因为线段BO的长度是OD的3倍,则△ABO的面积是△ADO的3倍;△BOC的面积是△DO C的3倍。
所以△ADO的面积是:9÷3﹦3(平方厘米)△BOC的面积是:9×3﹦27(平方厘米)梯形ABCD的面积为:9×2+3+27﹦48(平方厘米)。
练习2【题目】:如图,四边形ACEH是梯形,ACEG是平行四边形,ABGH是正方形,CDFG是长方形。
已知AC=8厘米,HE=13厘米,求三角形CDE和三角形GFE的面积之和。
【解析】:平行四边形AGEC中,GE=AC=8厘米。
则正方形边长,BG=HG=13-8=5(厘米)。
北师大版五年级数学上册--第六单元 组合图形的面积习题(按章节)(含答案)

第六章6.1《组合图形的面积》习题一、基础题1.把下面各个图形分成已学过的图形,请你在图上画一画。
2.填一填。
二、综合题1.求下面图形的面积(单位:m )。
你能想出几种方法。
102、求下面图形的面积。
(单位:cm )15 30 40 20 106 4 3 32 20 153.计算下面图形中阴影部分的面积。
30dm12dm25dm6.2《公顷、平方千米》习题一、基础题1.常用的面积单位有()、()、()。
2.边长是()的正方形,它的面积是1平方米。
3.35000平方米=()公顷 0.45公顷=()平方米 0.32平方千米=()公顷15265平方米=()公顷 320平方分米=()平方米 45公顷=()平方千米4.填上适当的单位名称。
(1)一个人工湖的湖面面积是2.8万()。
(2)我国领土面积大约是960万()。
(3)鱼池的占地面积是2500()。
(4)小华身高140()。
5.在()里填上“>”“<”“=”。
5公顷()50平方米 400平方米()4公顷 3平方米()30平方分米1.6米()16厘米 9平方千米()90公顷 200公顷()1平方千米12平方千米()68公顷 10平方分米()1000平方厘米 6公顷()60000平方米二、综合题1.一块长方形水稻田长250米,宽40米,面积是()公顷。
A.1 B.10 C.100002.一块占地2公顷的果园中,种了5000棵果树,平均每棵树占地()平方米。
A.400 B.4000 C.40 D.4三、提高题1.青青草原有一块长方形的草场,长是300米,宽是200米,如果能养6000只羊,平均每公顷草地能养多少只羊?2、一块占地2公顷的长方形果园,长250米,宽是多少米?6.3《成长的脚印》习题一、基础题1.请你估计一下方格纸上图形的面积。
(每个小正方形的边生是1厘米)2.请你数一数方格纸上的图形占了多少个格子。
()()()二、综合题1.下面分别是两片树叶的平面图(每个小方格表示1平方厘米,不满整格的按半格计算),请你填一填。
组合图形的面积的练习题

组合图形的面积的练习题组合图形的面积的练习题组合图形是数学中一个重要的概念,它由多个简单的图形组合而成。
在解决组合图形的面积问题时,我们需要将图形拆分成简单的几何形状,计算每个形状的面积,然后将它们相加得到最终的结果。
下面,我将为大家提供一些组合图形的面积练习题,希望能够帮助大家更好地理解和掌握这一概念。
练习题一:矩形与半圆的组合图形给定一个长为10cm,宽为5cm的矩形,矩形的上边界与下边界上分别有一个半径为5cm的半圆,求整个组合图形的面积。
解答:首先,我们可以将这个组合图形分成三个部分:矩形的面积、上半圆的面积和下半圆的面积。
矩形的面积可以通过长度乘以宽度得到,即10cm × 5cm = 50cm²。
半圆的面积可以通过半径的平方乘以π再除以2得到,即(5cm)² × π ÷ 2 ≈ 39.27cm²。
由于上半圆和下半圆的半径相等,所以它们的面积也相等。
因此,整个组合图形的面积等于矩形的面积加上两个半圆的面积,即50cm² + 2 × 39.27cm² ≈ 128.54cm²。
练习题二:长方形与三角形的组合图形给定一个长为8cm,宽为6cm的长方形,长方形的左边界上有一个底边长为6cm,高为4cm的等腰直角三角形,求整个组合图形的面积。
解答:同样地,我们可以将这个组合图形分成两个部分:长方形的面积和三角形的面积。
长方形的面积可以通过长度乘以宽度得到,即8cm × 6cm = 48cm²。
三角形的面积可以通过底边乘以高再除以2得到,即6cm × 4cm ÷ 2 = 12cm²。
因此,整个组合图形的面积等于长方形的面积加上三角形的面积,即48cm² +12cm² = 60cm²。
练习题三:正方形与半圆的组合图形给定一个边长为10cm的正方形,正方形的左边界上有一个半径为10cm的半圆,求整个组合图形的面积。
人教版小学数学组合图形的面积 (经典例题含答案)

班级小组姓名成绩(满分120)一、组合图形的面积(一)组合图形的面积计算(共4小题,每题3分,共计12分)例1.求下面图形的面积。
(单位:cm)32×10÷2+32×203×4÷2+(5+10)×5÷210×12-(4+8)×2÷2=160+640=6+37.5=120-12=800(cm²)=43.5(cm²)=108(cm²)例1.变式1.先回答问题,再计算图形的面积。
(单位:cm)(1)组合图形的面积=(长方形)面积+(三角形)面积36×24+24×21÷2=1116(平方厘米)(2)52阴影部分的面积=(梯形)面积-(三角形)面积(30+52)×28÷2-30×28÷2=728(cm²)例1.变式2.计算下面图形的面积,你能用不同的计算方法吗?5×2.5+(3+5)×(5-2.5)÷2=5×2.5+8×2.5÷2=12.5+10=22.5(平方米)5×3+(2.5+5)×(5-3)÷2=5×3+7.5×2÷2=15+7.5=22.5(平方米)例1.变式3.如图,左边阴影部分的面积是60平方厘米。
求右边空白部分(梯形)的面积。
(单位:厘米)60×2÷8=15(厘米)(16+16+8)×15÷2=40×15÷2=300(平方厘米)答:空白部分的面积是300平方厘米.(二)组合图形的面积计算(共4小题,每题3分,共计12分)例2.计算下列组合图形的面积。
(单位:cm)(8.5+15)×13÷2-8.5×4÷2=135.75(cm²)例2.变式1.解决问题。
【期末专项复习】北师大版小学五年级上册数学《组合图形的面积 》期末专项强化突破卷(二)含答案
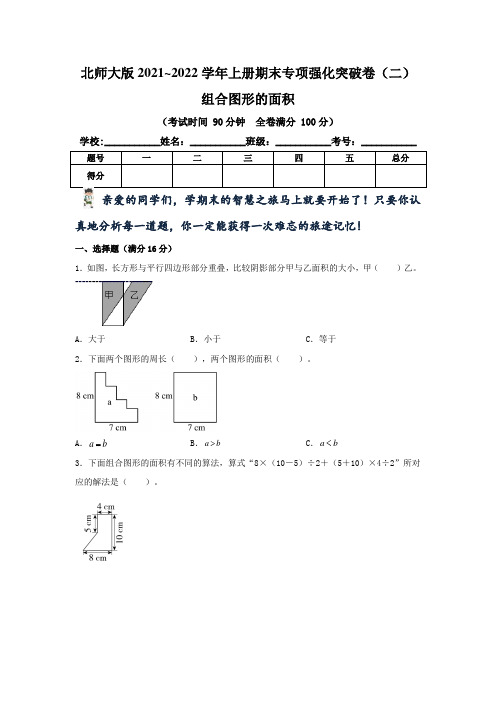
北师大版2021~2022学年上册期末专项强化突破卷(二)组合图形的面积(考试时间 90分钟 全卷满分 100分) 学校:___________姓名:___________班级:___________考号:___________ 题号一 二 三 四 五 总分 得分 亲爱的同学们,学期末的智慧之旅马上就要开始了!只要你认真地分析每一道题,你一定能获得一次难忘的旅途记忆!一、选择题(满分16分)1.如图,长方形与平行四边形部分重叠,比较阴影部分甲与乙面积的大小,甲( )乙。
A .大于B .小于C .等于2.下面两个图形的周长( ),两个图形的面积( )。
A .a b =B .a b >C .a b <3.下面组合图形的面积有不同的算法,算式“8×(10-5)÷2+(5+10)×4÷2”所对应的解法是( )。
A.B.C.D.4.下面三个图形中,()的面积最大(每个□代表1平方厘米)。
A.B.C.5.如下图,每个小正方形的面积是2cm2,涂色部分的面积是()cm2。
A.32 B.24 C.20 D.10时6.下图阴影部分的面积是()2cm。
(每个方格边长为1cm的正方形)A.24 B.25 C.24.57.如图是一个不规则的四边形,已知AC=12厘米,BD=16厘米,这个四边形的面积是()平方厘米.A.192 B.96 C.48 D.无法计算8.新华小学的占地面积大约是6()。
A.公顷B.平方米C.平方干米二、填空题(满分16分)9.0.78公顷=(________)平方米 7070平方千米=(________)公顷7时=(________)天 13分米=(________)千米10.在括号里填上合适的单位名称。
(1)做一道口算题约用2(________)。
(2)公交车从宁阳到泰安大约用70(________)。
(3)教室黑板面的周长约是9(________)。
小学五年级数学---组合图形的面积知识点及练习题(含答案)

小学五年级数学---组合图形的面积知识点及练习题(含答案)有几个简单的图形拼出来的图形,我们把它们叫做组合图形。
计算组合图形的面积的方法是多种多样的。
一般运用的方法是“分割法”和“添补法”。
分割法,即将这个图形分割成几个基本的图形。
分割图形越简洁,其解题的方法也将越简单,同时又要考虑分割的图形与所给条件的关系。
添补法,即通过补上一个简单的图形,使整个图形变成一个大的规则图形。
运用所学的知识,解决生活中组合图形的实际问题。
能正确估计不规则图形面积的大小。
能用数格子的方法,计算不规则图形的面积。
估计、计算不规则图形面积的内容主要是以方格图作为北京进行估计与计算的,所以借助方格图能帮助建立估计与计算不规则图形面积的方法。
01习题带答案02突破练习1. 在一个直角三角形铁皮上剪下一块正方形,剩下两个三角形,已知AD=3cm,DB=4cm,两个三角形面积和是多少?2. 已知平行四边表的面积是28平方厘米,求阴影部分的面积。
3. 下图中甲和乙都是正方形,求阴影部分的面积。
(单位:厘米)4. 求图中阴影部分的面积。
(单位:厘米)5. 一个长方形的草坪,宽是14厘米,中间有两个人行道。
求草坪的面积。
(单位:厘米)6. 下面的梯形中,阴影部分面积是150平方厘米,求梯形的面积。
7. 求图中阴影部分的面积。
单位:厘米8. 正方形ABCD的边长是12厘米,已知DE是EC长度的2倍,求:(1)三角形DEF的面积。
(2)CF的长。
9. 梯形ABCD的面积是45平方厘米,高6厘米。
三角AED的面积是5平方厘米,BC=10厘米,求阴影部分的面积。
10. 正方形ABCD的面积是100平方厘米,AE=8厘米,CF=6厘米,求阴影部分的面积。
11. 如下图,是一块长方形草地,长方形的长是16米,宽是10米,中间有两条宽2米的道路,一条是长方形,一条是平行四边形,那么有草部分(阴影部分)的面积有多大?12. 如图,一个三角形的底长5米,如果底延长1米,那么面积就增加2平方米。
六年级数学组合图形的面积试题答案及解析

六年级数学组合图形的面积试题答案及解析1.我们开始提到的“乡村小屋”的面积是多少?【答案】18【解析】图形内部格点数;图形边界上的格点数;根据毕克定理,则(单位面积).2.两个边长相等的正方形各被分成25个大小相同的小方格.现将这两个正方形的一部分重叠起来,若左上角的阴影部分(块状)面积为,右下角的阴影部分(线状)面积为,求大正方形的面积.【答案】19【解析】块状部分与线状部分之间的部分称为D,则D与前者共14个方格,与后者共17个方格,因此每个方格的面积是大正方形的面积为.3.如图,平行四边形,,,,,平行四边形的面积是,求平行四边形与四边形的面积比.【答案】1/18【解析】连接、.根据共角定理∵在和中,与互补,∴.又,所以.同理可得,,.所以.所以.4.如图,有三个正方形的顶点、、恰好在同一条直线上,其中正方形的边长为10厘米,求阴影部分的面积.【答案】100【解析】对于这种几个正方形并排放在一起的图形,一般可以连接正方形同方向的对角线,连得的这些对角线互相都是平行的,从而可以利用面积比例模型进行面积的转化.如右图所示,连接、、,则,根据几何五大模型中的面积比例模型,可得,,所以阴影部分的面积就等于正方形的面积,即为平方厘米.5.如图,与均为正方形,三角形的面积为6平方厘米,图中阴影部分的面积为多少?【答案】6【解析】如图,连接,比较与,由于,,即与的底与高分别相等,所以与的面积相等,那么阴影部分面积与的面积相等,为6平方厘米.6.在边长为6厘米的正方形内任取一点,将正方形的一组对边二等分,另一组对边三等分,分别与点连接,求阴影部分面积.【答案】15【解析】(法1)特殊点法.由于是正方形内部任意一点,可采用特殊点法,假设点与点重合,则阴影部分变为如上中图所示,图中的两个阴影三角形的面积分别占正方形面积的和,所以阴影部分的面积为平方厘米.(法2)连接、.由于与的面积之和等于正方形面积的一半,所以上、下两个阴影三角形的面积之和等于正方形面积的,同理可知左、右两个阴影三角形的面积之和等于正方形面积的,所以阴影部分的面积为平方厘米.7.右图中,和是两个正方形,和相交于,已知等于的三分之一,三角形的面积等于6平方厘米,求五边形的面积.【答案】49.5【解析】连接、,由于与平行,可知四边形构成一个梯形.由于面积为6平方厘米,且等于的三分之一,所以等于的,根据梯形蝴蝶定理或相似三角形性质,可知的面积为12平方厘米,的面积为6平方厘米,的面积为3平方厘米.那么正方形的面积为平方厘米,所以其边长为6厘米.又的面积为平方厘米,所以(厘米),即正方形的边长为3厘米.那么,五边形的面积为:(平方厘米).8.如图,长方形的面积是2平方厘米,,是的中点.阴影部分的面积是多少平方厘米?【答案】【解析】如下图,连接,、的面积相等,设为平方厘米;、的面积相等,设为平方厘米,那么的面积为平方厘米.,.所以有.比较②、①式,②式左边比①式左边多,②式右边比①式右边大0.5,有,即,.而阴影部分面积为平方厘米.9.如图,与均为正方形,三角形的面积为6平方厘米,图中阴影部分的面积为多少.【答案】6【解析】如图,连接,比较与,由于,,即与的底与高分别相等,所以与的面积相等,那么阴影部分面积与的面积相等,为6平方厘米.10.如图,是梯形的一条对角线,线段与平行,与相交于点.已知三角形的面积比三角形的面积大平方米,并且.求梯形的面积.【答案】28【解析】连接.根据差不变原理可知三角形的面积比三角形大4平方米,而三角形与三角形面积相等,因此也与三角形面积相等,从而三角形的面积比三角形的大4平方米.但,所以三角形的面积是三角形的,从而三角形的面积是(平方米),梯形的面积为:(平方米).11.如图,已知,,,,线段将图形分成两部分,左边部分面积是38,右边部分面积是65,求三角形的面积.【答案】40【解析】连接,.根据题意可知,;;所以,,,,,于是:;;可得.故三角形的面积是40.12.如图,长方形的面积是36,是的三等分点,,则阴影部分的面积为多少?【答案】2.7【解析】如图,连接.根据蝴蝶定理,,所以;,所以.又,,所以阴影部分面积为:.13.如图,如果长方形的面积是平方厘米,那么四边形的面积是多少平方厘米?【答案】32.5【解析】如图,过、、、分别作长方形的各边的平行线.易知交成中间的阴影正方形的边长为厘米,面积等于平方厘米.设、、、的面积之和为,四边形的面积等于,则,解得(平方厘米).14.已知正方形的边长为10,,,则?【答案】53【解析】如图,作于,于.则四边形分为4个直角三角形和中间的一个长方形,其中的4个直角三角形分别与四边形周围的4个三角形相等,所以它们的面积和相等,而中间的小长方形的面积为,所以.15.如下图,长方形和长方形拼成了长方形,长方形的长是20,宽是12,则它内部阴影部分的面积是多少.【答案】120【解析】根据面积比例模型可知阴影部分面积等于长方形面积的一半,为.16.长方形的面积为36,、、为各边中点,为边上任意一点,问阴影部分面积是多少?【答案】13.5【解析】解法一:寻找可利用的条件,连接、,如下图:可得:、、,而即;而,.所以阴影部分的面积是:解法二:特殊点法.找的特殊点,把点与点重合,那么图形就可变成右图:这样阴影部分的面积就是的面积,根据鸟头定理,则有:.17.在长方形内部有一点,形成等腰的面积为16,等腰的面积占长方形面积的,那么阴影的面积是多少?【答案】3.5【解析】先算出长方形面积,再用其一半减去的面积(长方形面积的),再减去的面积,即可求出的面积.根据模型可知,所以,又与的面积相等,它们的面积和等于长方形面积的一半,所以的面积等于长方形面积的,所以.18.在边长为6厘米的正方形内任取一点,将正方形的一组对边二等分,另一组对边三等分,分别与点连接,求阴影部分的面积.【答案】15【解析】(法1)特殊点法.由于是正方形内部任意一点,可采用特殊点法,假设点与点重合,则阴影部分变为如上图所示,图中的两个阴影三角形的面积分别占正方形面积的和,所以阴影部分的面积为平方厘米.(法2)连接、.由于与的面积之和等于正方形面积的一半,所以上、下两个阴影三角形的面积之和等于正方形面积的,同理可知左、右两个阴影三角形的面积之和等于正方形面积的,所以阴影部分的面积为平方厘米.19.如图所示,长方形内的阴影部分的面积之和为70,,,四边形的面积为多少?【答案】10【解析】利用图形中的包含关系可以先求出三角形、和四边形的面积之和,以及三角形和的面积之和,进而求出四边形的面积.由于长方形的面积为,所以三角形的面积为,所以三角形和的面积之和为;又三角形、和四边形的面积之和为,所以四边形的面积为.另解:从整体上来看,四边形的面积三角形面积三角形面积白色部分的面积,而三角形面积三角形面积为长方形面积的一半,即60,白色部分的面积等于长方形面积减去阴影部分的面积,即,所以四边形的面积为.20.如图,长方形的面积是36,是的三等分点,,求阴影部分的面积.【答案】2.7【解析】如图,连接.根据蝴蝶定理,,所以;,所以.又,,所以阴影部分面积为:.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第2课时组合图形面积(2)
基础作业
不夯实基础,难建成高楼。
1. 下面各个图形可以分成哪些已学过的图形?
2. 为感谢市人民医院的医生,某病人准备制作一面锦旗,规格如图,制作这面锦旗需要多少布料?
3. 求下面图形中阴影部分的面积。
(单位:厘米)
4. 科技小组制作飞机模型,机翼的平面图是由两个完全一样的梯形组成的。
它的面积是多少?
综合提升
重点难点,一网打尽。
5. 学校操场有一个如下图的正方形的花坛,边长为20 m,在花坛的四周有一条宽1 m的小路(阴影部分),小路的面积是多少平方米?
6. 下图为一面墙,砌这面墙每平方米需要50块砖,那么砌这面墙共需要多少块砖?
拓展探究
举一反三,应用创新,方能一显身手。
7. 有一条小路穿过一平行四边形麦地(如下图),这块麦地的播种面积是多少平方米?
8. 平行四边形的面积是440平方厘米,求梯形的面积。
第2课时
1.略
2. 1200 cm2
3. 2132平方厘米42平方厘米
4.33180㎜ 2
5. 84平方米
6. 825块
7. 1290平方米
8. 440÷22=20(厘米)(15+22)×20÷2=370(平方厘米)。
