上海市“光明链”三校运动会成功举办
《职业院校数字校园建设规范》

《职业院校数字校园建设规范》教育部2015年1月目录前言 (3)1引言 (4)2总体要求 (5)2.1意义与作用 (5)2.2目标与原则 (6)2.3内容与组成 (7)2.4组织结构与体系 (8)2.5实施过程 (13)3师生发展 (16)3.1数字校园与师生发展 (16)3.2学生发展 (16)3.3教师发展 (17)4数字资源 (20)4.1数字资源的分类 (20)4.2数字资源的来源 (20)4.3数字资源建设与应用的原则与要求 (20)4.4通用性基础资源 (21)4.5仿真实训资源 (21)4.6数字化场馆资源 (23)4.7数字图书馆资源 (24)5应用服务 (26)5.1应用服务的类型 (26)5.2应用服务的提供方式 (26)5.3应用服务的总体要求 (26)5.4应用服务的集成 (27)5.5决策支持应用服务 (28)5.6网络教学服务 (28)5.7实习实训教学服务 (29)5.8产教融合服务 (29)5.9工场实时教学服务 (30)5.10校企共享信息服务 (30)5.11远程职业培训服务 (31)5.12教学资源管理与共享服务 (31)5.13教学管理服务 (33)5.14学生管理服务 (33)5.15教科研管理服务 (34)5.16人力资源管理服务 (34)5.17办公自动化服务 (35)5.18财务管理服务 (35)5.19设备资产管理服务 (35)5.20学校后勤服务 (36)5.21校园一卡通服务 (36)6基础设施 (38)6.1基础设施的组成 (38)6.2校园网络 (38)6.3数据中心 (39)6.4网络信息服务 (40)6.5网络管理与网络安全 (40)6.6多媒体教室 (43)6.7仿真实训系统环境 (45)6.8数字广播与网络电视系统 (47)6.9数字安防系统 (48)7附录 (51)7.1规范性引用文件 (51)7.2术语与缩略语 (52)前言为了顺应全球教育信息化发展的潮流,促进信息技术与职业教育教学的深度融合,贯彻全国职业教育工作会议精神,落实教育部《教育信息化十年发展规划(2011-2020年)》关于“加强教育信息化标准规范制定和应用推广”的要求,规范职业院校数字校园的实施,推动职业教育信息化良性发展,特制订《职业院校数字校园建设规范》。
上海市教育委员会、上海市体育局关于做好2024年本市高中阶段学校招收优秀体育学生工作的通知

上海市教育委员会、上海市体育局关于做好2024年本市高中阶段学校招收优秀体育学生工作的通知文章属性•【制定机关】上海市教育委员会,上海市体育局•【公布日期】2024.03.07•【字号】沪教委体〔2024〕4号•【施行日期】2024.03.07•【效力等级】地方规范性文件•【时效性】现行有效•【主题分类】文化、新闻出版、广播影视、体育其他规定正文上海市教育委员会、上海市体育局关于做好2024年本市高中阶段学校招收优秀体育学生工作的通知沪教委体〔2024〕4号各区教育局、体育局,各委属高中学校:为全面贯彻国家和本市关于加强新时代体教融合和学校体育工作有关精神,进一步深化本市学校体育工作改革发展,按照《上海市人民政府办公厅关于加强本市中小学体育艺术工作的指导意见》(沪府办规〔2019〕10号)、《上海市教育委员会关于印发〈上海市高中阶段学校招生录取改革实施办法〉的通知》(沪教委规〔2021〕2号)等要求,根据2024年本市高中阶段学校招生考试总体安排,现就做好2024年本市高中阶段学校招收优秀体育学生工作有关要求通知如下:一、工作目标围绕全面育人目标,进一步健全本市优秀体育学生培养体系,完善高中阶段学校招生录取运行机制和管理体制,统一程序、统一标准,严格规范操作,强化过程管理,确保公开、公平、公正,保证中招工作平稳有序进行,促进中小学运动队高水平建设发展,更好地发挥示范引领和辐射带动效应,培养德智体美劳全面发展的社会主义建设者和接班人。
二、组织管理本市高中阶段学校招收优秀体育学生计划的编制、招生办法的制定和实施,按市、区两级行政部门的管理职责和工作程序进行。
(一)市教育、体育行政部门负责编制市级优秀体育学生招生计划和制定录取办法,并对各区优秀体育学生招收工作进行指导和协调。
(二)各区教育、体育行政部门负责结合本地区经济社会发展实际情况,根据教育和体育发展规划及资源配置状况等,制定本区优秀体育学生招生计划和招生录取办法。
校园运动会的新闻稿精选6篇

校园运动会的新闻稿精选6篇(实用版)编制人:__________________审核人:__________________审批人:__________________编制单位:__________________编制时间:____年____月____日序言下载提示:该文档是本店铺精心编制而成的,希望大家下载后,能够帮助大家解决实际问题。
文档下载后可定制修改,请根据实际需要进行调整和使用,谢谢!并且,本店铺为大家提供各种类型的实用范文,如工作总结、策划方案、演讲致辞、报告大全、合同协议、条据书信、党团资料、教学资料、作文大全、其他范文等等,想了解不同范文格式和写法,敬请关注!Download tips: This document is carefully compiled by this editor. I hope that after you download it, it can help you solve practical problems. The document can be customized and modified after downloading, please adjust and use it according to actual needs, thank you!In addition, this shop provides various types of practical sample essays for everyone, such as work summary, planning plan, speeches, reports, contracts and agreements, articles and letters, party and group materials, teaching materials, essays, other sample essays, etc. Please pay attention to the different formats and writing methods of the model essay!校园运动会的新闻稿精选6篇现今社会公众的追求意识不断提升,我们用到新闻稿的地方越来越多,新闻稿是公司/机构/政府/学校等单位发送予传媒的通信渠道,用来公布有新闻价值的消息。
2023上海超级杯短道速滑时间定了

2023上海超级杯短道速滑时间定了2023上海超级杯短道速滑时间定了比赛时间:2023年10月3日-5日比赛地点:浦发银行东方体育中心海上王冠体育馆上海市浦东新区泳耀路300号交通指南:地铁11号线;地铁6号线;地铁8号线6号口出短道速滑比赛装备冰刀短道速滑的冰刀与长道速滑的冰刀虽然从外观上看有较大的区别,但其结构却是基本相同的。
短道速滑的赛道有许多弯道、倾斜角度大。
一场比赛的选手人数较多,比赛时选手躲闪的次数多,滑跑的速度快,这就要求冰刀能够适应比赛的特点。
和普通冰刀相比,短道速滑的冰刀更高更短,弧度更大,这种设计使得转弯更流畅;刀托是可移动的,滑跑时选手可自行调节刀刃的位置。
冰刀管必须是封闭的,刀根必须是圆弧形。
最小半径为10毫米。
刀管最少有两点固定在鞋上,没有可动的部分。
冰鞋短道速滑的冰鞋与长道速滑的冰鞋比较相似,不过它的鞋腰更高,鞋底、前鞋帮、后跟两侧都是硬性材质,其他部位为皮制。
这样冰鞋更具稳定性,滑跑时的力量更大。
防切割训练比赛服由于经常在比赛中发生运动员受伤的事件,因此在经过多年的观察后,国际滑联研究认为,短道速滑运动员高危险区域包括颈部、腹股部、腋部、臀部、下臂、手部、膝盖。
所以国际滑联从2003年7月1日起,要求所有运动员在参加比赛的时候,必须要身穿防切割服,以保护自己的安全。
头盔短道速滑选手使用硬塑料头盔来保护自己,以免遭撞击所致的伤害。
短道速滑安全头盔应符合现行的ASTM标准。
头盔必须有一个规则的形状不能有突起。
短道速滑比赛背手原因在滑冰比赛的时候,运动员把双手背在背后主要是为了减少空气阻力,好滑的更快。
滑冰运动很多人以为是从国外传进来的,但其实中国在古代就已经有了滑冰运动。
不过那时候不叫滑冰,叫做冰嬉。
早在宋朝,就已经有了滑冰运动的相关记载,到了清朝,滑冰已经成为了人们非常喜爱的民间运动。
而且经常还出现了冰球运动,是我国北方民间非常传统的一项体育活动在山西部分地区也非常流行。
运动会方阵口号有哪些

贵州省第十届运动会(THE 10TH GAMES OF GUIZHOU PROVINCE),简称“省十运会”,由贵州 省人民政府主办,遵义市人民政府、贵州省体育局承办,于2018年8月8日-8月18日在遵义市举 办。
运动会方阵口号有哪些
2011年12月,“方阵体”在上迅速走红。“方阵体”的格式采用的是运动会时播音员解说词的写 作格式,因为朗朗上口和万人皆知的特点,受到友的热捧。
具体如下: 基础医学院:百年同济,生生不息,基础医学,再创佳绩。 机械学院:自强不息,团队精神,快速反应,尽职尽责。 建规学院:建我体魄,规我人生,建规建规,众望所归。 经济学院:魅力经院,激情无限,超越自我,勇往直前。 控制:华大骄子,飞扬控制,龙行天下,控制争先。 啦啦队口号:远程远程,心想事成。 生科院:二十二载,唯志唯勤,生命之光,闪耀中华。
贵州省第十届运动会竞技体育组设置20个大项377个小项,共10个代表团3038名运动员参赛,教 练员、领队647人,裁判员971人;群众体育组设置31个大项168个小项,共14个代表团2632名运 动员参赛,教练员、领队790人,裁判员785人,是历届省运会中规格最高、规模最大的一届综合 性体育盛会。
广西壮族自治区第十四届运动会是在广西壮族自治区举办的运动会。
“活力相伴,健康相随!”11月21日,金秋时节,阳光明媚,上海交大迎来了第45届运动会。校 园里充满了欢声笑语,光明体育场内彩旗招展。本届运动会首次采取师生同场合作竞技的方式, 力求展示交大师生团结进取、创建一流的精神追求。
谢谢观看
国内外大型网球赛事

国内外大型网球赛事一、网球四大公开赛 (2)1. 澳洲公开赛(USTRALIAN OPEN) (2)2. 法国公开赛(FRENCH OPEN) (3)3. 温布敦公开赛(WIMBLEDON TENNIS CHAMPIONSHIPS) (4)4. 美国公开赛(U.S. OPEN) (7)二、三大网球团体赛 (8)1、台维斯杯网球赛简介(Davis Cup) (8)2、霍普曼杯(Hopman Cup)简介 (9)3、联合会杯(Fed Cup)网球赛 (10)三、ATP大师杯赛 (10)四、大师系列赛 (11)五、国内大型网球赛事 (13)中国网球公开赛( China Open) (13)CTA全国网球俱乐部联赛 (15)中国网球大奖赛 (16)2006国际女子网球系列赛 (17)2006年DUNLOP&《网球》杂志杯业余网球赛 (19)雪佛兰业余网球大赛 (19)上海网球123推广计划 (20)中国业余网球公开赛 (21)中国大学生网球联赛 (22)年终业余网球大师杯 (22)国际男子"永丰杯"网球巡回赛 (23)"水井坊杯"中国大城市业余网球团体赛(简称CTC) (23)2006中网网球擂台争霸战 (24)六、地区网球赛事 (25)PTA北京大学网球联赛 (25)Wilson杯罗兰时尚网球赛 (25)2005 Wilson杯内蒙古业余网球公开赛 (25)2005红人杯业余网球赛 (27)2005“新民晚报”杯上海市大学生网球联赛 (27)2006 “威能杯”百家社区网球公开赛 (28)首届省港澳"新年鸿杯"网球团体赛 (29)“新年鸿杯”2006广东城际网球邀请赛 (29)“鹰牌花旗参杯”上海精英网球公开赛 (30)"李宁"打造北京青少年网球品牌赛事 (31)一、网球四大公开赛四大公开赛,又称为大满贯赛,是所有的职业正式网球比赛中奖金最多、积分最多、地位最高的比赛,也是所有网球选手最想拿到的冠军。
2012年上海市学生阳关体育大联赛 跳踢拍竞赛规程
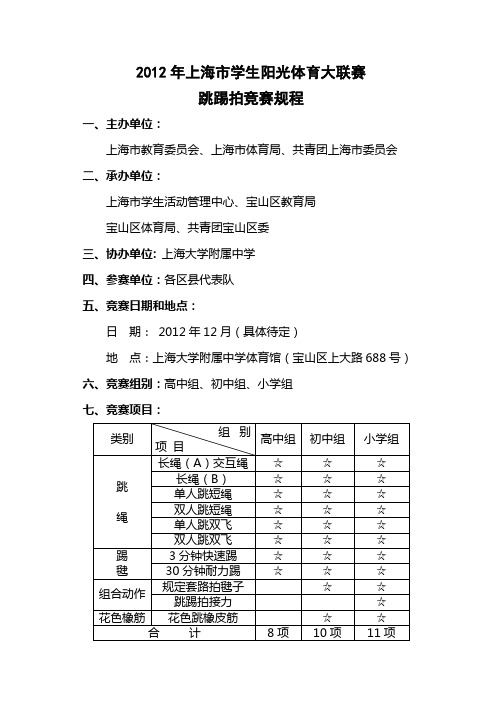
2012年上海市学生阳光体育大联赛跳踢拍竞赛规程一、主办单位:上海市教育委员会、上海市体育局、共青团上海市委员会二、承办单位:上海市学生活动管理中心、宝山区教育局宝山区体育局、共青团宝山区委三、协办单位: 上海大学附属中学四、参赛单位:各区县代表队五、竞赛日期和地点:日期: 2012年12月(具体待定)地点:上海大学附属中学体育馆(宝山区上大路688号)六、竞赛组别:高中组、初中组、小学组七、竞赛项目:八、参赛办法:(一)各区县组队参加比赛。
1、长绳(A)(B):高中、初中、小学各报1队,每队12人(6男6女,其中1男1女为摇绳);2、单、双人跳短绳:高中、初中、小学组男女各报1队,每队2人;3、单、双人跳双飞:高中、初中、小学组男女各报1队,每队2人;5、3分钟快速踢毽:高中、小学组可报男女各1队,每队2人;初中组可报男女各1队,每队3人;6、30分钟耐力踢毽:高中、初中、小学男女各报2人;7、规定套路拍毽子:初中、小学各报1队,每队男女各3人;8、跳踢拍组合接力:小学报1个队,每队男女各3人;9、花色跳橡筋:初中、小学各报1队,每队16人(男女不限)。
(二)运动员不得跨组别参加比赛,参赛运动员一律凭社保学籍卡参加比赛,无学籍卡者一律不得参赛。
(三)各区县设总领队、总教练各1人,各组别由参赛学校指派各项目教练员。
(四)运动员保险等费用由各区县自行负责。
九、竞赛办法:(一)长绳(A式):3分钟交互“8”字长绳:(附视频)每队12名队员参赛(6男6女其中1男1女摇绳),预备时绳子处于静止状态,比赛开始后两名同学左右手同时各摇一绳,10名运动员在间距3.00米的长绳中依次按“8”字线连续跳,但绳子中间必须保留2人,即第1人进绳跳3只后出绳,第2人等第1人跳2只后立即进绳,以后按序进行。
除第1人跳时允许有l人外,其余在绳内均应有2人。
中途失误可继续比赛。
摇绳者脚踏线为犯规,将取消成绩;(二)长绳(B式):齐心同步跳长绳,时间2分钟,每队1男1女摇绳,10名队员集体跳长绳,绳子在队员脚下受阻为失误,中途失误可继续比赛,摇绳者必须在听到发令后才能摇绳,比赛中途摇绳者不能更换,但可以换手,两摇绳者站位距离为7米。
上海市体育局关于第三届上海杯象棋大师公开赛组织架构的批复

上海市体育局关于第三届上海杯象棋大师公开赛组织
架构的批复
文章属性
•【制定机关】上海市体育局
•【公布日期】2023.07.26
•【字号】沪体赛〔2023〕120号
•【施行日期】2023.07.26
•【效力等级】地方规范性文件
•【时效性】现行有效
•【主题分类】体育
正文
上海市体育局关于第三届上海杯象棋大师公开赛组织架构的
批复
沪体赛〔2023〕120号
上海市棋牌运动管理中心:
“关于第三届上海杯象棋大师公开赛组织架构的请示”收悉。
经研究,同意赛事组织结构。
请做好竞赛组织、场地保障、接待服务和宣传推广等工作,确保安全顺利办赛。
特此批复。
上海市体育局
2023年7月26日。
三校联动实施方案及措施

三校联动实施方案及措施为了进一步提高三校联动的工作效率和协同性,我们制定了以下实施方案及措施,以期能够更好地推动三校联动工作的开展。
一、加强沟通协调1.建立三校联动工作小组,由各校相关负责人组成,定期召开联席会议,及时沟通交流,协商解决工作中的问题。
2.建立联动工作交流平台,利用微信群、邮件、电话等多种方式进行信息沟通,确保信息畅通。
二、统一规划部署1.制定三校联动工作年度计划,明确工作目标、任务分工和时间节点,确保各项工作有序推进。
2.统一制定相关工作制度和规范,明确各校在联动工作中的职责和权限,建立健全工作机制。
三、资源共享1.建立三校资源共享平台,包括教学资源、人力资源、物资设备等,实现资源共享、优势互补。
2.加强教师培训和交流,定期举办联动工作经验交流会,促进教学理念和方法的交流与碰撞。
四、加强监督考核1.建立三校联动工作考核评估机制,对各项工作进行定期评估,发现问题及时纠正,推动工作不断向前发展。
2.加强对工作进展情况的监督,及时发现并解决工作中的矛盾和问题,确保联动工作的顺利推进。
五、宣传推广1.利用各自校园网站、校报、微信公众号等宣传媒介,积极宣传三校联动工作的成果和亮点,提升工作的知名度和影响力。
2.加强与社会各界的交流与合作,扩大三校联动工作的社会影响力,争取更多的支持和资源。
六、持续改进1.建立三校联动工作改进机制,定期开展工作评估,总结经验,找准问题,不断改进工作方法和措施。
2.鼓励广大师生积极参与三校联动工作,提出建设性意见和建议,共同推动工作的不断完善和发展。
以上就是我们制定的三校联动实施方案及措施,希望能够得到各校领导和广大师生的支持与配合,共同推动三校联动工作取得更大的成绩,为教育教学事业的发展贡献力量。
深圳外国语学校(集团)龙华高中部2024-2025学年高三上学期第一次月考数学试卷(含答案)

深圳外国语学校(集团)龙华高中部2025届高三年级第一次月考 数学试卷本试卷共4页,19小题,满分150分.考试用时120分钟. 注意事项:1.答卷前,考生务必用黑色字迹钢笔或签字笔将自己的姓名、考生号、考场号和座位号填写在答题卡上.用2B 铅笔将试卷类型(A )填涂在答题卡相应位置上.将条形码横贴在答题卡右上角“条形码粘贴处”.2.作答选择题时,选出每小题答案后,用2B 铅笔把答题卡上对应题目选项的答案信息点涂黑;如需改动,用橡皮擦干净后,再选涂其他答案,答案不能答在试卷上.3.非选择题必须用黑色字迹钢笔或签字笔作答,答案必须写在答题卡各题目指定区域内相应位置上;如需改动,先划掉原来的答案,然后再写上新的答案;不准使用铅笔和涂改液.不按以上要求作答的答案无效.4.考生必须保持答题卡的整洁.考试结束后,将试卷和答题卡一并交回. 一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.设集合{}30xAx ex =−<,{}1,0,1,2B =−,则集合A B = ( )A .{}1,2−B .{}1,1,2−C .{}1,2D .{}12.已知2i 1iz−=−+,则z =( ) A .1i +B .1i −C .3i −D .3i + 3.已知向量(,1)a x = ,(2,1)b =− ,若()(2)a b a b +⊥−,则实数x =( )A .2B .12−C .2−或4D .44.已知3sin 24θ=−,则1tan tan θθ+=( )A .43B .12−C .83D .83−5.已知圆锥的底面半径为2,高为4,有一个半径为1的圆柱内接于此圆锥,则该圆柱的侧面积是( )A .πB .2πC .3πD .4π6.已知函数()122,0,,0,x x f x x x ≤= > 则下列说法正确的是( )A .()f x 是R 上的增函数B .()f x 的值域为[)0,∞+C .“14x >”是“()12f x >”的充要条件D .若关于x 的方程()f x a =恰有一个实根,则1a >7.已知函数π()sin(2)2f x x ϕϕ=+< 满足ππ43f f = ,若()f x 在区间π,2t上恰有3个零点,则实数t 的取值范围为( )A .25π37π,2424B .25π49π,2424C .37π49π,2424D .37π49π,24248.已知函数()y f x =具有以下的性质:对于任意实数a 和b ,都有()()()()2f a b f a b f a f b ++−=⋅,则以下选项中,不可能是()1f 值的是( ) A .2− B .1− C .0 D .1二、选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.9.若随机变量()2~0,X N σ,()()f x P X x =≤,则( )A .()()1f x f x −=− B .()()22f x f x =C .()()()210P X x f x x <=−> D .若()121x f f x +> −,则113x << 10.已知三次函数()325(0)f x x bx b =++<有极小值点2x =,则下列说法中正确的有( )A .3b =−B .函数()f x 有三个零点C .函数()f x 的对称中心为(1,3D .过()1,1−可以作两条直线与()y f x =的图象相切11.数学中有许多形状优美,寓意美好的曲线,曲线22|:1|C x y x y +=+就是其中之一(如图).给出下列四个结论,其中正确结论是( )A .图形关于y 轴对称B .曲线C 恰好经过6个整点(即横、纵坐标均为整数的点)C .曲线C 的点D .曲线C 所围成的“心形”区域的面积大于3 三、填空题:本题共3小题,每小题5分,共15分.12.已知12,F F 为椭圆2222:1(0)C b b x a a y +>>=的两个焦点,P 为椭圆C 上一点,且12PF F △的周长为6,面C 的离心率为 .13.已知函数32(),()f x x x g x x a =−=+,曲线()y f x =在点(1,(1))f −−处的切线也是曲线()y g x =的切线.则a 的值是14.有一道楼梯共10阶,小王同学要登上这道楼梯,登楼梯时每步随机选择一步一阶或一步两阶,小王同学7步登完楼梯的概率为 .四、解答题:本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.15.(13分)如图,一智能扫地机器人在A 处发现位于它正西方向的B 处和北偏东30°方向上的C 处分别有需要清扫的垃圾,红外线感应测量发现机器人到B 的距离比到C 的距离少0.4m ,于是选择沿A →B →C 路线清扫.已知智能扫地机器人的直线行走速度为0.2m /s ,忽略机器人吸入垃圾及在B 处旋转所用时间,10s 完成了清扫任务.(1)求B 、C 两处垃圾之间的距离;(2)求智能扫地机器人此次清扫行走路线的夹角B 的余弦值.16.(15分)已知双曲线2222:1(0,0)x y C a b a b −=>>的焦点与椭圆2215x y +=的焦点重合,其渐近线方程为y x =. (1)求双曲线C 的方程;(2)若,A B 为双曲线C 上的两点且不关于原点对称,直线1:3l y x =过AB 的中点,求直线AB 的斜率.17.(15分)如图,在四棱锥B ACDE -中,正方形ACDE 所在平面与正ABC 所在平面垂直,M N ,分别为BC AE ,的中点,F 在棱CD 上.(1)证明://MN 平面BDE .(2)已知2AB =,点M 到AF 求三棱锥C AFM -的体积.18.(17分)蓝莓种植技术获得突破性进展,喷洒A 型营养药有--定的改良蓝莓植株基因的作用,能使蓝莓果的产量和营养价值获得较大提升.某基地每次喷洒A 型营养药后,可以使植株中的80%获得基因改良,经过三次喷洒后没有改良基因的植株将会被淘汰,重新种植新的植株. (1)经过三次喷洒后,从该基地的所有植株中随机检测一株,求-株植株能获得基因改良的概率;(2)从该基地多个种植区域随机选取一个,记为甲区域,在甲区域第一次喷洒A 型营养药后,对全部N 株植株检测发现有162株获得了基因改良,请求出甲区域种植总数N 的最大可能值;(3)该基地喷洒三次A 型营养药后,对植株进行分组检测,以淘汰改良失败的植株,每组n 株(50)n ≤,一株检测费为10元,n 株混合后的检测费用为8n +元,若混合后检测出有未改良成功的,还需逐一检测,求n 的估计值,使每株检测的平均费用最小,并求出最小值.(结果精确到0.1元)附:当0.01a <,50n ≤时,()11nna a ≈++,*n N ∈.19.(17分)“函数()x ϕ的图象关于点(),m n 对称”的充要条件是“对于函数()x ϕ定义域内的任意x ,都有()(2)2x m x n ϕϕ+−=,若函数()f x 的图象关于点()12,对称,且当[]01x ∈,时,2()1f x x ax a =−++ (1)求(0)(2)f f +的值; (2)设函数4()2xg x x=− ①证明函数()g x 的图象关于点(2,4)−称;②若对任意[]10,2x ∈,总存在22,13x∈−,使得()()12f x g x =成立,求实数a 的取值范围.数学参考答案:1.D【详解】解:将B 中元素分别代入30x e x −<,只有1符合,则{}1A B ∩=. 故选:D. 2.B 【详解】2i 21i 1i 1izz z −=−⇒−=−⇒=++, 所以1i z =−. 故选:B . 3.C【详解】由题设(2,0)a b x +=+ ,2(4,3)a b x −=−, 所以()(2)(2)(4)0a b a b x x +⋅−=+−=,可得x =2−或4.故选:C 4.D【详解】3sin 22sin cos 4θθθ==− ,3sin cos 8θθ∴=−,221sin cos sin cos 18tan 3tan cos sin sin cos 38θθθθθθθθθθ+∴+=+===−−. 故选:D. 5.D【详解】如图,设圆柱的高为h ,由题意可得142h =,所以2h =,从而圆柱的侧面积2124S ππ=××=侧,故选:D.6.D【详解】对于A ,当0x =时,102210=>,所以()f x 不是R 上的增函数,所以A 错误, 对于B ,当0x ≤时,021x <≤,当0x >时,120x >, 所以()f x 的值域为(0,)+∞,所以B 错误, 对于C ,当0x ≤时,由()12f x >,得122x >,解得10−<≤x ,当0x >时,由()12f x >,得1212x >,解得14x >,综上,由()12f x >,得10−<≤x ,或14x >,所以“14x >”是“()12f x >”的充分不必要条件,所以C 错误,对于D ,()f x 的图象如图所示,由图可知当1a >时,直线y a =与()y f x =图象只有一个交点, 即关于x 的方程()f x a =恰有一个实根,所以D 正确, 故选:D 7.C【详解】由题意可知,()f x 的最小正周期2ππ2T ==, 因为πππ34124T−=<,可知ππ7π34224x +=为()f x 的一条对称轴, 所以()f x 在7π24x =之后的零点依次为7π13π24424T +=,7π325π24424T +=,7π537π24424T +=,7π749π24424T +=,…, 若()f x 在区间π,2t上恰有3个零点,所以37π49π2424t ≤<. 故选:C. 8.A【详解】因为函数()y f x =对于任意实数a 和b ,都有()()()()2f a b f a b f a f b ++−=⋅,所以令0a b ==,有()()()()00200f f f f +=⋅,即()()20[01]0f f −=,所以()00f =或()01f =;令2x a b ==,x 为任意实数,有()()0222x x f x f f f +=⋅ ,即()()2022x x f x f f f⋅−; 因为022x x f f⋅≥,所以()()0f x f ≥−,当()00f =时,()0f x ≥;当()01f =时,()1f x ≥−; 所以()f x 的值不可能是2−, 故选:A. 9.ACD【详解】对于A ,随机变量()2~0,X N σ满足正态分布,且0µ=,故()()()()1f x P X x P X x f x −=≤−=≥=−,故A 正确; 对于B ,当0x =时,()()()(),20212201,f x P X f x P X =≤=≤== 此时()()22f x f x ≠,故B 错误;对于C ,()()()20P X x P x X x P X x <=−<<=<<()()12212f x f x=−=−,故C 正确;对于D ,()()f x P X x =≤,故()f x 单调递增,故()121x f f x +> −,即121x x +>−, 解得113x <<,故D 正确. 故选:ACD 10.ACD【详解】()232f x x bx ′=+, 因为函数()325(0)f x x bx b =++<有极小值点2x =,所以()21240f b ′=+=,解得3b =−,所以()3235f x x x =−+,()236f x x x ′=−, 当2x >或0x <时,()0f x '>,当02x <<时,()0f x ′<, 所以函数()f x 在()(),0,2,−∞+∞上单调递增,在()0,2上单调递减,所以()()()()05,21f x f f x f ====极大值极小值, 又()215f −=− 所以函数()f x 仅有1个在区间()2,0−上的零点,故A 正确,故B 错误;对于C ,由()()3223535f x x x x x =−+=−+,得()()()()()()2211113511356f x f x x x x x ++−=++−++−−−+=, 所以函数()f x 的图象关于()1,3对称,故C 正确;对于D ,设切点为()32000,35x x x −+,则()200036f x x x =−′, 故切线方程为()()()320020003365y x x x x x x −−+−−=,又过点()1,1−,所以()()()3200200315163x x xx x −−−+=−−,整理得300320x x −−=,即()()200120x x +−=, 解得01x =−或02x =,所以过()1,1−可以作两条直线与()y f x =的图象相切,故D 正确. 故选:ACD.11.ABD【详解】对于A ,将x 换成x −方程不变,所以图形关于y 轴对称,故A 正确; 对于B ,当0x =时,代入可得21y =,解得1y =±,即曲线经过点(0,1),(0,1)−,当0x >时,方程变换为2210y xy x −+−=,由224(1)0x x ∆=−−≥,解得x ∈ ,所以x 只能取整数1,当1x =时,20y y −=,解得0y =或1y =,即曲线经过(1,0),(1,1), 根据对称性可得曲线还经过(1,0),(1,1)−−,故曲线一共经过6个整点,故B 正确;对于C ,当0x >时,由221x y xy +=+可得222212x y x y xy ++−=≤,(当x y =时取等号),222x y ∴+≤,C 上y称性可得:曲线C ,故C 错误;对于D ,如图所示,在x 轴上图形的面积大于矩形ABCD 的面积:1122S =×=,x 轴下方的面积大于等腰三角形ABE 的面积:212112S =××=,所以曲线C 所围成的“心形”区域的面积大于213+=,故D 正确; 故选:ABD12.12/0.5【详解】依题意,12PF F △的周长为226a c +=,所以123,a c PF F +=面积的最大值为122c b bc ××又222a b c =+,整理得2223(3)c c c−=+,即2(1)(21)0c c −+=,解得1,2,===c a b C 的离心率为12,故答案为:12 13.3【详解】由题意知,(1)1(1)0f −=−−−=,2()31x f x ′=−,(1)312f ′−=−=, 则()y f x =在点()1,0−处的切线方程为2(1)y x =+, 即22y x =+,设该切线与()g x 切于点()00,()x g x , 其中()2g x x ′=,则00()22g x x ′==,解得01x =, 将01x =代入切线方程,得2124y =×+=, 则(1)14g a =+=,解得3a =; 故答案为:3 14.3589【详解】解:由题意可分为5步、6步、7步、8步、9步、10步共6种情况,①5步:即5步两阶,有551C =种;②6步:即4步两阶与2步一阶,有2615C =种;③7步:即3步两阶与4步一阶,有3735C =种;④8步:即2步两阶与6步一阶,有2828C =种;⑤9步:即1步两阶与8步一阶,有199C =种;⑥10步:即10步一阶,有10101C =种;综上可得一共有89种情况,满足7步登完楼梯的有35种; 故7步登完楼梯的概率为3589故答案为:358915.(1)()1.4m (2)1114【详解】(1)由题意得0.2102AB BC +=×=,设BC x =,02x <<,则2AB x =−,20.4 2.4AC x x =−+=−,由题意得9030120A=°+°=°. 在ABC 中,由余弦定理得222cos 2AB AC BC A AB AC+−=× ()()222(2)(2.4)122 2.42x x x x x −+−−==−×−×−, 解得 1.4x =或5.2(舍去), ∴()1.4m BC =(2)由(1)知62 1.0.4AB =−=, 2.4 1.41AC =−=, 1.4BC =. ∴2222220.6 1.4111cos 220.6 1.414AB BC AC B AB BC +−+−===⋅××. 16.(1)2213x y −= (2)1 【详解】(1)椭圆2215x y +=的焦点为()2,0±,故224a b +=,由双曲线的渐近线为y =,故b a =1,b a ==故双曲线方程为:2213x y −=. (2)设()()1122,,,A x y B x y ,AB 的中点为M ,因为M 在直线1:3l y x =,故13M M y x =, 而121231y x −=,222231y x −=()()12120y y y y −+=, 故()()121203M M x x x y y y −−−=, 由题设可知AB 的中点不为原点,故0M M x y ≠,所以121213M M y y xx x y −==−, 故直线AB 的斜率为1.此时12:33M M M AB y x x x x x =−+=−, 由222333M x y x x y =− −=可得222333M x x x −−= ,整理得到:22424303M M x x x x −++=, 当222416Δ168324033M M M x x x =−+=−>即M x <M x >即当M x <M x >AB 存在且斜率为1. 17.(1)证明见解析;(2)【详解】(1)取CD 中点G ,连接NG ,MG,G M 为,CD BC 中点 //GM BD ∴又BD ⊂平面BDE ,GM ⊄平面BDE //GM ∴平面BDE四边形ACDE 为正方形,,N G 为,AE CD 中点 //NG DE ∴又NG ⊂平面BDE ,NG ⊄平面BDE //NG ∴平面BDEGM NG G = ,,GM NG ⊂平面MNG ∴平面//MNG 平面BDE又MN ⊂平面MNG //MN ∴平面BDE(2)ABC ∆ 为正三角形,M 为BC 中点 AM BC ∴⊥平面ACDE ⊥平面ABC ,CD AC ⊥,平面ACDE 平面ABC AC =,CD ⊂平面ACDE CD 平面ABC ,又AM ⊂平面ABC AM CD ∴⊥又BC CD C ∩=,,BC CD ⊂平面BCD AM ∴⊥平面BCD FM ⊂ 平面BCD AM MF ∴⊥设CF a =,则AF =MF =,AM =AF AM MF ∴=⋅=1a =11111332C AFM A FCM FCM V V S AM −−∆∴==⋅=×××=18.(1)0.992(2)202株(3)10n =,2.6元 【详解】(1)记事件A =“该基地的植株经过三次喷洒后,随机检测一株植株能获得基因改良”,所以2()0.80.20.80.20.80.992P A =+×+×=,(2)因为植株经过一次喷洒后基因改良的概率为0.8,经过一次喷洒后基因改良的株数k 服从二项分布,()C 0.80.2k k N k N P N k −⋅==,0,1,2,,k N = 当162k <时,()1620Pk == 当162k ≥时,设162162162(162)C 0.80.2N N P k −==⋅ 若162N =时,则()()162161P k P k =<=若162N >时,则16216216216216216111621621621621621631C 0.80.2C 0.80.2C 0.80.2C 0.80.2N N N N N N NN −−+−−− ≥ ≥ ,所以0.8161.20.8162N N ≥ ≤ , 解得201.5202.5N ≤≤,又*N N ∈,所以202N = 所以甲区域种植总数N 的最大可能值为202株. (3)设每组n 株(50)n ≤的总费用为X 元,则X 的取值为8n +,118n + 所以 X8n + 118n +P 0.992n 10.992n −所以()(8)0.992(118)(10.992)n n E X n n =+++− (8)0.992(118)(10.992)n nn n n+++−= 所以()811100.992n E X n n=−×+ 因为()0.99210.00810.008n n n =−≈− 所以()810.081 2.6E X n n n =++≥+=(当且仅当10n =时等号成立) 所以当以10个每组时,检测成本最低,每株2.6元.19.(1)4【详解】(1)由题意可得,()(2)224f x f x +−=×=,令0x =,可得(0)(2)4f f +=. (2)①由4()2x g x x=−,(,2)(2,)x ∈−∞+∞ , 44(4)()(4)22(4)x x g x g x x x −+−=+−−−416422x x x x−−−−8162x x −=−8=−2(4)=×−, 所以函数()g x 的图象关于点(2,4)−对称.②4()2x g x x =−842x =−+−,函数在2,13 − 上单调递增,所以[]()1,4g x ∈−, 不妨设()f x 在[]0,2上的值域为A ,则[]1,4A ⊆−,因为[]01x ∈,时,2()1f x x ax a =−++, 所以(1)2f =,即函数()f x 的图象过对称中心()12,, (i )当02a ≤时,即0a ≤,函数()f x 在[]0,1上单调递增, 由对称性可知,()f x 在[]1,2上单调递增,所以()f x 在[]0,2上单调递增,由(0)1f a =+,(0)(2)4f f +=,所以(2)3f a =−,所以[]1,3A a a =+−, 由[]1,4A ⊆−,可得114313a a a a +≥− ≥− +≤−,解得10a −≤≤; (ii )当012a <<时,即02a <<,函数()f x 在0,2a上单调递减,()f x 在,12a 上单调递增,由对称性可知,()f x 在1,22a − 上单调递增,()f x 在2,22a −上单调递减, 所以()f x 在0,2a 上单调递减,在,222a a − 上单调递增,在2,22a − 上单调递减, 结合对称性可得,[](2),(0)A f f = 或(),(2)22a a A f f =− , 因为02a <<,所以(0)1(1,3)f a =+∈,(2)3(1,3)f a =−∈, 易知2()1(1,2)24a a f a =−++∈,又()(2)422a a f f +−=,所以(2)(2,3)2a f −∈, 所以当02a <<时,[]1,4A ⊆−成立; (iii )当12a ≥时,即2a ≥时,函数()f x 在[]0,1上单调递减, 由对称性可知,()f x 在[]1,2上单调递减,所以函数()f x 在[]0,2上单调递减,又(0)1f a =+,(2)3f a =−,则[]3,1A a a =−+,由[]1,4A ⊆−得, 311431a a a a −≥− +≤ −≤+,解得23a ≤≤. 综上可知,实数a 的取值范围为[]1,3−.。
阳光体育 健康成长 - 上海市光明初级中学

5班、余家淋1501 江焕1502 孙梦1503 邓维嘉1504 谢毅1505 厉霞1506
李鑫1507 刘佳宁1508 陈松松1509 徐兰1510 徐振1511 安德卫1512
穆甲已1513 陈玲玲1514 6班、周超宇1601 宋祖浩1602 刘欣怡1603 涂琰琰1604 陈宇 1605 邓海洋1606
1211 许洁1212 王佳雯1213 张京程1214 谢申1215 范诗敏1216
3班、杨正浩1301 张童1302 俞婧1303 孙婧1304 张云翔1305 顾兴源1306
余琳1307 贺禕灵1308 朱尚麟1309 耿泽源1310 郭姣妍1311 胡斯妍1312
周世昊1313 胡珺璐1314 龚玲燕1315 4班、 刘海齐1401 李木恒1402 高晚栗1403 熊维妮1404 戎承诺 1405 宋庆庆1406
27、高一(1) 28、高三(8)
2012年“光明教育链”秋季田径运动会竞赛日程
径赛
8:30
小学30M 女子50M
预决赛
12组
预赛
90人
14组
8:45
男子50M
预赛
92人
14组
8:50
25*2往返接力 预决赛
2组
9:00
女子50M
决赛
8人
4组
9:10
男子50M
决赛
8人
4组
9:20
女子丁组400M霓红 向贤祥
王玉
2、光明初中年级组学生组织管理岗位安排(现场 调度:张烨)
年级
年级学生管理
年级学生运动项目 引导教师
2024上海市星光计划大赛职业英语

2024上海市星光计划大赛职业英语The 2024 Shanghai Starlight Program Professional English CompetitionIntroductionThe 2024 Shanghai Starlight Program Professional English Competition is an annual event that aims to promote English proficiency and language skills among professionals in Shanghai. The competition is open to individuals working in various industries, including finance, technology, healthcare, education, and more. Participants will have the opportunity to showcase their English language abilities, compete in challenging language tasks, and network with other professionals in the city.Competition FormatThe competition consists of several rounds, including a written test, a presentation round, and a group discussion round. In the written test, participants will be tested on their grammar, vocabulary, reading comprehension, and writing skills. The presentation round requires participants to give a short presentation on a given topic in English, demonstrating their speaking and presentation skills. The group discussion round involves participants discussing a specific topic with a group oftheir peers, showcasing their ability to communicate effectively and collaborate with others.Benefits of ParticipatingParticipating in the 2024 Shanghai Starlight Program Professional English Competition offers a range of benefits for professionals in Shanghai. Firstly, it provides a platform for individuals to improve their English language skills and gain confidence in using English in a professional setting. Additionally, the competition offers networking opportunities, allowing participants to connect with other professionals in their field and expand their professional network. Finally, the competition serves as a valuable experience that can enhance participants' resumes and career prospects.PrizesParticipants in the 2024 Shanghai Starlight Program Professional English Competition have the chance to win a variety of prizes, including cash prizes, scholarships for language courses, and opportunities for career advancement. Winners will be selected based on their performance in the various rounds of the competition, as well as their overall language proficiency and communication skills. Prizes will be awarded at a ceremonyfollowing the conclusion of the competition, where participants will be recognized for their achievements.ConclusionThe 2024 Shanghai Starlight Program Professional English Competition is a prestigious event that provides professionals in Shanghai with the opportunity to showcase their English language skills, network with other professionals, and win valuable prizes. By participating in the competition, individuals can improve their language proficiency, gain confidence in using English in a professional context, and enhance their career prospects. Don't miss the chance to participate in this exciting event and take your English skills to the next level!。
三校联盟共建实施方案

三校联盟共建实施方案为了促进高校之间的交流与合作,提高教育教学质量,三校联盟决定共建实施方案,旨在加强三校之间的合作,共同推动教育事业的发展。
本实施方案将从以下几个方面展开。
一、合作领域。
三校联盟将在教学科研、师资培训、学术交流、学生实习就业等方面展开合作。
在教学科研方面,三校将共同开展科研项目,组织学术讲座,推动教师之间的学术交流与合作;在师资培训方面,三校将共同举办教师培训班,提高教师教学水平;在学术交流方面,三校将定期举办学术交流会议,促进学术成果的分享与交流;在学生实习就业方面,三校将共同开展实习基地建设,为学生提供更多的实习机会,促进学生就业。
二、资源共享。
三校联盟将建立资源共享机制,共享教学资源、科研设施、图书馆资源等。
在教学资源共享方面,三校将共同建设教学资源库,共享优质教学资源,提高教学质量;在科研设施共享方面,三校将共同建设科研平台,共享科研设施,提高科研水平;在图书馆资源共享方面,三校将建立图书馆资源互借制度,共享图书馆馆藏资源,提高图书馆利用率。
三、学科交叉。
三校联盟将推动学科交叉,拓宽学科发展空间。
三校将共同开设跨学科课程,鼓励学生跨学科学习,提高学生综合素质;三校将共同开展学科交叉研究,促进学科间的交流与融合,提高学科发展水平;三校将共同建设学科交叉平台,促进学科交叉合作,推动学科交叉发展。
四、成果评价。
三校联盟将建立成果评价机制,定期对合作成果进行评价。
通过对合作项目的成果进行评价,及时总结经验,发现问题,不断完善合作机制,提高合作效益。
同时,也可以借鉴其他高校的成功经验,促进合作的不断深化与发展。
五、风险应对。
在合作过程中,可能会面临各种风险与挑战,三校联盟将建立风险应对机制,及时应对各种风险。
同时,也将加强沟通与协调,共同解决合作中的问题,确保合作取得良好效果。
六、合作机制。
三校联盟将建立合作机制,明确合作的具体方式与步骤。
通过建立合作机制,明确合作的具体内容与责任,提高合作的效率与效果。
上海市文绮中学2025届高三三校联考物理试题试卷

上海市文绮中学2025届高三三校联考物理试题试卷注意事项:1.答题前,考生先将自己的姓名、准考证号码填写清楚,将条形码准确粘贴在条形码区域内。
2.答题时请按要求用笔。
3.请按照题号顺序在答题卡各题目的答题区域内作答,超出答题区域书写的答案无效;在草稿纸、试卷上答题无效。
4.作图可先使用铅笔画出,确定后必须用黑色字迹的签字笔描黑。
5.保持卡面清洁,不要折暴、不要弄破、弄皱,不准使用涂改液、修正带、刮纸刀。
一、单项选择题:本题共6小题,每小题4分,共24分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1、氢原子的能级图如图所示。
用氢原子从n =4能级跃迁到n =1能级辐射的光照射逸出功为6.34eV 的金属铂,下列说法正确的是( )A .产生的光电子的最大初动能为6.41eVB .产生的光电子的最大初动能为12.75eVC .氢原子从n =2能级向n =1能级跃迁时辐射的光不能使金属铂发生光电效应D .氢原子从n =6能级向n =2能级跃迁时辐射的光也能使金属铂发生光电效应2、我国计划在2030年之前制造出可水平起飞、水平着陆并且可以多次重复使用的空天飞机。
假设一航天员乘坐空天飞机着陆某星球后,由该星球表面以大小为v 0的速度竖直向上抛出一物体,经时间t 后物体落回抛出点。
已知该星球的半径为R ,该星球没有大气层,也不自转。
则该星球的第一宇宙速度大小为( )A 02v R tB 0v R tC 02v R tD 02v Rt t3、在空间P 点以初速度v 0水平抛出一个小球,小球运动到空中A 点时,速度与水平方向的夹角为60°,若在P 点抛出的初速度方向不变,大小变为02v ,结果小球运动到空中B 点时速度与水平方向的夹角也为60°,不计空气阻力,则下列说法正确的是A .PB 长是PA 长的2倍B .PB 长是PA 长的4倍C .PA 与水平方向的夹角小于PB 与水平方向的夹角D .PA 与水平方向的夹角大于PB 与水平方向的夹角4、如图所示,虚线所围矩形区域abcd 内充满磁感应强度为B 、方向垂直纸面向外的匀强磁场。
三校联动实施方案及措施

三校联动实施方案及措施
为了更好地推进教育教学改革,提高教学质量,我们三校决定进行
联动实施方案及措施,以共同促进学校教育的发展。
一、联动实施方案
1. 教学资源共享:三校可以通过建立教学资源共享平台,共享优质
教学资源,包括教案、教学设计、教学视频等,以丰富教学内容,
提高教学质量。
2. 教师交流合作:三校可以定期举办教师交流活动,开展教学观摩、教学研讨等活动,促进教师之间的交流与合作,提高教学水平。
3. 学生交流互动:三校可以组织学生交流活动,包括学科竞赛、文
化交流等,促进学生之间的交流互动,拓宽学生的视野,提高学生
综合素质。
二、联动实施措施
1. 建立联动工作小组:每所学校成立由教学主管领导和骨干教师组
成的联动工作小组,负责具体的联动工作安排和实施。
2. 制定联动计划:联动工作小组制定每学期的联动计划,包括教学资源共享安排、教师交流活动安排、学生交流活动安排等。
3. 定期评估总结:每学期结束后,联动工作小组对联动实施情况进行评估总结,发现问题及时调整和改进联动方案和措施。
4. 宣传推广联动成果:通过学校网站、校园广播、校园电视台等媒介,宣传推广三校联动的成果和效果,鼓励更多的教师和学生参与到联动活动中来。
5. 加强管理保障:学校领导要高度重视三校联动工作,加强对联动工作的组织领导和管理保障,确保联动工作的顺利实施。
通过三校联动实施方案及措施,我们相信可以更好地促进学校教育的发展,提高教学质量,为学生的全面发展和成长提供更好的教育环境和条件。
让我们携手合作,共同推动教育事业的蓬勃发展!。
DJI Mavic Mini 2 无人驾驶遥控器说明书

52
14,922
107-1 8,079 4,083 1,378 214 1,431 185 157
55
15,582
-4-
4 of 206
學年期
106-2 106-1 105-2 105-1
日間學制
學士 碩士 博士
7,807 8,085 7,759 8,028
3,844 3,956 3,785 3,926
五、108 學年度第 1 學期教師延遲繳交學士班成績,計有 6 科,成績筆數 85
筆,較前一學期(107 學年度第 2 學期)增加 69 筆。近年成績延遲繳交
情形如下:
學年期別 108-1 107-2 107-1 106-2 106-1 105-2 105-1
教師人數 6 2 7 3 4 7 3
科目數 6 2 9 3 6 9 6
上人數統計如下:
學年期 105-1 105-2 106-1 106-2 107-1 107-2 108-1
人數
265
313
290
268
287
276
266
七、109 學年度轉系、雙主修、輔系作業刻正進行中,依行事曆所訂於 5 月 25
日公告申請結果,近年錄取人數及錄取率如下:
二、108 學年度第 1 學期休學人數共計 2,266 人,近年休學人數如下:
學年期
108-1 107-2 107-1 106-2 106-1 105-2 105-1
日間學制
學士
358 335 353 323 331 291 283
碩士
961 881 937 870 906 861 909
博士
425 418 432 414 419 410 445
上海市体育局、市体育总会关于给予获得第一届全国智力运动会体育道德风尚奖的队伍及运动员嘉奖的通知-

上海市体育局、市体育总会关于给予获得第一届全国智力运动会体育道德风尚奖的队伍及运动员嘉奖的通知正文:---------------------------------------------------------------------------------------------------------------------------------------------------- 上海市体育局、市体育总会关于给予获得第一届全国智力运动会体育道德风尚奖的队伍及运动员嘉奖的通知第一届全国智力运动会上海市代表团各项目运动队:第一届全国智力运动会已于11月12日至23日在四川省成都市圆满落幕。
在本届智运会上,上海代表团共参加了围棋、象棋、国际象棋、桥牌、五子棋、国际跳棋全部六个项目的比赛。
经过全体教练员、运动员的共同努力,上海代表团以9枚金牌、10枚银牌、8枚铜牌的优异成绩,名列智运会金牌榜首位,充分展现了上海人民团结奋斗、勇于拼搏、追求卓越的精神风貌。
上海代表团荣获大会颁发的“体育道德风尚奖”,上海象棋队、国际跳棋队、桥牌队3个运动队,以及胡荣华、刘沛、沈之远、曹佳杰、顾婉卿、庄则军、陈怡毅7名运动员分别荣获各赛区竞委会颁发的体育道德风尚奖,取得了运动成绩和精神文明双丰收。
为树立榜样,弘扬先进,上海市体育局、上海市体育总会决定对荣获智运会各赛区竞委会“体育道德风尚奖”的运动队和运动员予以嘉奖。
希望市体育局系统各单位,以及运动员、教练员向上述获得嘉奖的单位和个人学习,大力弘扬中华体育精神和奥林匹克精神,戒骄戒躁,不断进取,为促进上海体育事业蓬勃发展,增强城市综合竞争力,加快上海“四个中心”和现代化建设而不懈努力。
特此通知。
上海市体育局上海市体育总会二○○九年十二月三十一日——结束——。
上海市第三女子中学2024-2025学年高三上学期9月月考数学试题 (无答案)

2025届市三女中高三年级上学期月考一、填空题(1-6每小题4分,7-12每小题5分,共54分)1、复数(是虚数单位)的实部是______2、不等式的解集为______3、若,且为第四象限角,则的值是______4、的二项展开式中的系数为______5、记等差数列的前项和为,若,,则______6、已知向量,的夹角为,且,,则______7,若其侧面展开图为一个半圆,则该圆锥的侧面积为______8、若,都是正实数,且,则的最大值为______9、在空间直角坐标系中,若平面的一个法向量,则点到平面的距离为______10、某市高考新政规定每位学生在物理、化学、生物、历史、政治、地理中选择三门作为等级考试科目,则甲、乙两位学生等级考试科目恰有一门相同的不同选择共有______种(用数字作答)11、已知,是双曲线:的左、右焦点,点是双曲线上的任意一点(不是顶点),过作的角平分线的垂线,垂足为,线段的延长线交于点,是坐标原点,若,则双曲线的渐近线方程为______12、已知函数,若对任意的,都存在,使得,则实数的取值范围为______二、选择题(13-14每小题4分,15-16每小题5分,共18分)13、已知且,则下列不等式恒成立的是( )A. B. C. D.14、若方程表示双曲线,则此双曲线的虚轴长等于( )2i 1i+i 15x +<5sin 13α=-αtan α()42x -x {}n a n n S 30a =6714a a +=7S =a b 60︒3a = 3b = a b += x y 123y x +=y x O xyz -OMQ ()2,1,2n =- ()1,1,4P -OMQ 1F 2F Γ()222210,0x y a b a b-=>>M Γ1F 12F MF ∠N 1F N 2MF Q O 126F F ON =Γ()800x x f x xx a x ⎧-<⎪=⎨⎪-≥⎩[)12,x ∈+∞[]22,1x ∈--()()12f x f x a ⋅≥a x y z >>0x y z ++=xy yz>xz yz >xy xz >x y z y >2244x ky k +=A. B.15、函数的图像可能为( )A. B. C. D.16、函数,零点的个数不可能是( )A.12个 B.13个C.14个D.15个三、解答题(共78分)17、(共14分)如图,在长方体中,是上一点,已知,,,;(1)求直线与平面所成角;(2)求点到平面的距离;18、(共14分)已知向量,,且;(1)求函数在上的单调递减区间;(2)已知的三个内角分别为,,,其对应边分别为,,,若有,,求面积的最大值;19、(共14分)如图所示,边长为2(百米)的正方形区域是某绿地公园的一个局部,环线是修建的健身步道(不计宽度),其中弯道段是抛物线的一段,该抛物线的对称轴与平行,端点是该抛物线的顶点且为的中点,端点在上,且长为0.5(百米);建立适当的平面直角坐标系,解决下列问题:(1)求弯道段所确定的函数的表达式;()21x y x e =-()1sin 2f x x =-[],40x t t ∈+1111ABCD A B C D -M 1BB 2BM =3CD =4AD =15AA =1AC ABCD A 1A MC 11,sin222m x x ⎛⎫=+ ⎪ ⎪⎝⎭()(),1n f x =- m n ⊥ ()f x []0,πx ∈ABC △A B C a b c π112f A ⎛⎫-= ⎪⎝⎭BC =ABC △ABCD AEFCDA EF AD E AB F BC FB EF ()y f x =(2)绿发管理部门欲在弯道段上选取一点安装监控设备,使得点处监测段的张角()最大,求点的坐标;20、(18分)已知函数;(1)求证:函数是上的减函数;(2)已知函数的图像存在对称中心的充要条件是的图像关于原点中心对称;判断函数的图像是否存在对称中心,若存在,求出该对称中心的坐标;若不存在,说明理由;(3)若对任意,都存在及实数,使得,求实数的最大值;21、(18分)已知椭圆:的长轴长为,直线与椭圆有两个不同的交点;(1)求椭圆的方程;(2)若直线的方程为,椭圆上的点关于直线的对称点(与不重合)在椭圆上,求的值;(3)设,直线与椭圆的另一个交点为,直线与椭圆的另一个交点为,若点,和点三点共线,求直线的斜率的值;EF P P CD CPD ∠P ()()121x f x x =∈+R ()f x R ()f x (),a b ()()g x f x a b =+-()f x []11,x n ∈231,2x ⎡⎤∈⎢⎥⎣⎦m ()()11211f mx f x x -+=n Γ()222210x y a b a b +=>>l Γ,A B Γl y x t =+31,22M ⎛⎫- ⎪⎝⎭l N M Γt ()2,0P -PA ΓC PB ΓD C D 71,42Q ⎛⎫- ⎪⎝⎭l k。
上海杨思高级中学2021-2022学年高一物理联考试题含解析

上海杨思高级中学2021-2022学年高一物理联考试题含解析一、选择题:本题共5小题,每小题3分,共计15分.每小题只有一个选项符合题意1. 下列关于加速度的说法中,正确的是()A、加速度就是物体增加的速度B、物体速度为零时,加速度必为零C、物体速度变化越小,加速度越小D、物体速度变化越快,加速度越大参考答案:D2. 下列关于物理学史实的描述,错误的是A.牛顿发现了万有引力定律,揭示了天体运行的规律与地上物体运动的规律具有内在的一致性,成功地实现了天上力学与地上力学的统一B.开普勒发现了行星的运动规律,为人们解决行星运动学问题提供了依据,澄清了多年来人们对天体运动的神秘、模糊的认识C.人们通过望远镜发现了天王星,海王星和冥王星也是通过望远镜发现的,而不是预言后再观测到的D.德国物理学家亥姆霍兹概括和总结了自然界中最重要、最普遍的规律之一——能量守恒定律参考答案:C3. 下图是物理教材中的一幅漫画,以下对图片的解释合理的是()A.甲小孩用较小的水平推力推不动木箱,是因为木箱受到地面的摩擦力大于小孩推力的缘故B.乙小孩用较大的水平推力仍推不动木箱,此时一定是小孩推力与地面对木箱摩擦力的大小相等C.丙小孩用更大的水平推力推木箱,木箱才开始滑动,之后小孩失去支撑而摔跤D.以上三种说法中只有C是正确的参考答案:BC4. 如图所示水平放置的两个用相同材料制成的轮P和Q靠摩擦传动,两轮的半径R∶r =2∶1。
当主动轮Q匀速转动时,在Q轮边缘上放置的小木块恰能相对静止在Q轮边缘上,此时Q轮转动的角速度为ω1,木块的向心加速度为a1;若改变转速,把小木块放在P轮边缘也恰能相对p轮静止,此时Q轮转动的角速度为ω2,木块的向心加速度为a2,则( )A. B.C. D.参考答案:AC5. 如图所示,小物体A与水平圆盘保持相对静止,跟着圆盘一起做匀速圆周运动,则A的受力情况是( )A.受重力、支持力B.受重力、支持力和指向圆心的摩擦力C.重力、支持力、向心力、摩擦力D.以上均不正确参考答案:B二、填空题:本题共8小题,每小题2分,共计16分6. 为了测量子弹射出枪口的速度,两人用如图所示的装置进行测量,重木板用细线悬于高处,甲同学持枪在距板水平距离50m的地方射击,枪口水平并瞄准木板的中心O,乙同学用剪刀剪断细线后,甲立即开枪,设甲同学的反应时间为0.1s (即剪断细线到子弹射出的时间),结果木板上的弹孔在O点正上方的A点,测得OA距离为20cm,则子弹离开枪口的速度为_________m/s。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
庆祝“光明链”成立十周年暨三校秋季运动会成功举行
9月29日上午,为庆祝“光明链”成立十周年,光明初中、光明中学、光明小学在源深体育场隆重举办了“光明链”三校秋季田径运动会。
黄浦区副区长程霄玉亲率区教育局、政协、体育局等各部门相关领导出席了开幕式。
程副区长向“光明链”三位校长授予火炬,三位校长再分别向各自学校的光明学子传递火炬,由此拉开了本次庆典的序幕。
随后,江伟鸣副局长致开幕辞,王伟鸣局长宣布运动会正式开始,五彩缤纷的气球瞬时腾空而起,飘散在体育场的上空,展示着“光明链”成立十周年的成功与辉煌。
在入场仪式中,我校学生舞动着五彩啦啦球,激情洋溢的跳着青春健美操出场,并高喊“励志勤学,全面发展”的口号,赢得了全场阵阵热烈掌声,展现了光初学子的风采。
为了更好的把三校运动员“链”起来,此次运动会首次把运动员分为:甲组(高二、高三)、乙组(初三、高一)、丙组(初一、初二)、丁组(五年级、预备班)和低年级组(小学一到四年级)。
在随后进行的各项赛事中,同学们大显身手,奋勇拼搏。
尤其在压轴比赛的4x100米,我校初三男、女联队都击败了高中组的八支队伍,勇夺乙组男、女冠军。
尤其是初三(2)班黎鑫怡同学更是夺得了乙组女子50、800米的二个单项冠军。
自“光明链”成立以来,三校始终坚持教育创新的理念,加强建设教育现代化,不断提高教学水平,并树立“健康第一”的指导思想。
此次运动会的成功召开必将进一步推动了三校体育活动的蓬勃开展和交流融合,让光明学子们真正成为德、智、体、美全面发展的优秀人才。
