高中数学必修5__第二章《数列》复习知识点总结与练习(一)
高中数学必修5(人教A版)第二章数列2.3知识点总结含同步练习及答案

{ a = 7, 或 { a = 7, d = 4, d = −4.
因为数列{an }为单调递增的数列,所以 d > 0.因此
{ a = 7, d = 4.
所以
an = 4n − 1.
在等差数列{an }中,前 n 项和为 S n : (1)a2 = 1 ,a4 = 5 ,求数列{an }的前 5 项和 S 5 ; (2)S 5 = 25,a8 = 15 ,求 a21 . 解:(1)因为 {an }为等差数列,所以 a2 + a4 = 2a3 = 6 ,即 a3 = 3 .所以
S5 =
(2)设首项为 a1 ,公差为 d ,则
5(a1 + a5 ) 5 × 2a3 = = 15. 2 2
5×4 ⎧ d = 25, S 5 = 5a1 + ⎨ 2 ⎩ a8 = a1 + 7d = 15. { a1 = 1, d = 2.
解方程组,得
所以a21 = a1 + 20d = 41 . 在等差数列 {an } 中,a1 = 25 ,S 17 = S 9 ,求前 n 项 和 S n 的最大值. 解:因为 a1 = 25 ,S 17 = S 9 ,所以
四、课后作业
(查看更多本章节同步练习题,请到快乐学)
1. 在等差数列 {an } 中,已知 a5 + a7 = 10,S n 是数列 {an } 的前 n 项和,则 S 11 = ( A.45
答案: C 解析:
)
B.50
C.55
D.60
S 11 =
10 a1 + a11 a + a7 × 11 = 5 × 11 = × 11 = 55. 2 2 2 )
25 × 17 +
人教版高中数学必修五《数列》基础知识要点总结知识分享

3 、判断等差 (比)数列的 方法
4、等差(比) 数列的通项 公式
5、性质 1
① ????- ????-1 = ?? ② 2????= ????-1 + ????+1(??≥ 2) ③ ????= ???+? ??
① ????= ??1 + (??- 1)?? ② ????= ???? + ( ??- ??) ?? ③ ????= ???+? ??,其中 ??、 ??是常数 在等差数列 {????} 中,若已知 ????与 ????, 其中 ??,??∈??? ,则该数列的公差 ??= ????-????。
在等比数列 {????}中,若 ??+ ??= ??+ ?? ( ??,??,?,? ??∈???),则 ???? ?????= ????? ???。?
特别地,等比数列 {????} 中,若 2?? = ??+ ?(???,??,??∈???),则 ???2? = ????????。?
只供学习与交流
若 {????} 和 {????} 分别是公比为 ??和 ??的等
比数列,
则数列
{????
?????}
,{
????}
????
仍是等
比数列,它们的公比分别为 ???,? ??。
??
9、等差(比) 数列的单调 性
①若 ??> 0,则 {????}为递增数列; ②若 ??< 0,则 {????}为递减数列; ③若 ??= 0,则 {????}为常数列。
此文档仅供收集于网络,如有侵权请联系网站删除
第二章 《数列》基础知识小结
一、数列的概念与表示方法
1、数列的概念 2、数列的通项 公式
高中数学必修5(人教B版)第二章数列2.4知识点总结含同步练习题及答案

四、课后作业
(查看更多本章节同步练习题,请到快乐学)
1. 数列 1, 3, 7, 15, ⋯ 的通项公式 an 等于 ( A.2 n
答案: C
)
C.2 n − 1 D.2 n−1
B.2 n + 1
2. 已知 a1 = 1 , an+1 = 第 66 项是 ( 6a n + 1 1 1 B. C. 391 390
答案: A
1 ) ,则 an = ( n
)
C.2 + n ln n
B.2 + (n − 1) ln n D.1 + n + ln n
高考不提分,赔付1万元,关注快乐学了解详情。
an ,等式两边同时取倒数,得 2an + 1 an+1 1 =
an ,求数列{an }的通项公式. 2an + 1 2an + 1 1 = + 2, an an
所以
an+1
故数列{
1
−
1 = 2. an
1 1 }为等差数列,首项 = 1 ,公差 d = 2.所以 an a1 1 = 1 + (n − 1) × 2 = 2n − 1, an
因此数列{an }的通项公式为
an =
1 . 2n − 1
已知数列{an }中,a1 = 2 ,an+1 = 2an + 3 × 2 n ,求数列{an }的通项公式. 解:因为 an+1 = 2an + 3 × 2 n ,等式两边同时除以 2 n+1 ,得
an+1 2 n+1
所以
=
2an + 3 × 2 n 2 n+1
最新高中数学必修5__第二章《数列》复习知识点总结与练习(一)
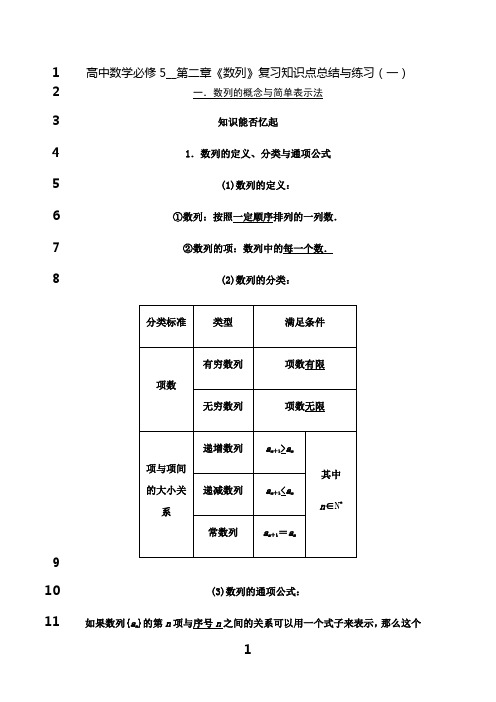
1高中数学必修5__第二章《数列》复习知识点总结与练习(一)2一.数列的概念与简单表示法3知识能否忆起41.数列的定义、分类与通项公式5(1)数列的定义:6①数列:按照一定顺序排列的一列数.7②数列的项:数列中的每一个数.8(2)数列的分类:910(3)数列的通项公式:11如果数列{a n}的第n项与序号n之间的关系可以用一个式子来表示,那么这个公式叫做这个数列的通项公式.12 2.数列的递推公式13 如果已知数列{a n }的首项(或前几项),且任一项a n 与它的前一项a n -1(n ≥2)(或14 前几项)间的关系可用一个公式来表示,那么这个公式叫数列的递推公式.15 1.对数列概念的理解16 (1)数列是按一定“顺序”排列的一列数,一个数列不仅与构成它的“数”有17 关,而且还与这些“数”的排列顺序有关,这有别于集合中元素的无序性.因18 此,若组成两个数列的数相同而排列次序不同,那么它们就是不同的两个数列. 19 (2)数列中的数可以重复出现,而集合中的元素不能重复出现,这也是数列与20 数集的区别.21 2.数列的函数特征22 数列是一个定义域为正整数集N *(或它的有限子集{1,2,3,…,n })的特殊函23 数,数列的通项公式也就是相应的函数解析式,即f (n )=a n (n ∈N *).24 25 3.考点26 (一)由数列的前几项求数列的通项公式27 [例1] (2012·天津南开中学月考)下列公式可作为数列{a n }:28 1,2,1,2,1,2,…的通项公式的是( )29 A .a n =1 B .a n =-1n +1230C .a n =2-⎪⎪⎪⎪⎪⎪sin n π2 D .a n =-1n -1+3231[自主解答] 由a n =2-⎪⎪⎪⎪⎪⎪sin n π2可得a 1=1,a 2=2, 32 a 3=1,a 4=2,…. 33 [答案] C 34 由题悟法35 1.根据数列的前几项求它的一个通项公式,要注意观察每一项的特点,观察36 出项与n 之间的关系、规律,可使用添项、通分、分割等办法,转化为一些常37 见数列的通项公式来求.对于正负符号变化,可用(-1)n 或(-1)n +1来调整. 38 2.根据数列的前几项写出数列的一个通项公式是不完全归纳法,它蕴含着39 “从特殊到一般”的思想40 以题试法41 写出下面数列的一个通项公式. 42 (1)3,5,7,9,…; 43 (2)12,34,78,1516,3132,…; 44 (3)3,33,333,3 333,…; 45 (4)-1,32,-13,34,-15,36,….46 解:(1)各项减去1后为正偶数,所以a n =2n +1.47 (2)每一项的分子比分母少1,而分母组成数列21,22,23,24,…,所以a n =2n -12n .48(3)将数列各项改写为93,993,9993,99993,…,分母都是3,而分子分别是1049 -1,102-1,103-1,104-1,….50 所以a n =13(10n -1).51 (4)奇数项为负,偶数项为正,故通项公式的符号为(-1)n ;各项绝对值的分52 母组成数列1,2,3,4,…;而各项绝对值的分子组成的数列中,奇数项为1,偶53 数项为3,即奇数项为2-1,偶数项为2+1,54 所以a n =(-1)n·2+-1nn,也可写为55a n=⎩⎪⎨⎪⎧-1n ,n 为正奇数,3n ,n 为正偶数.56(二)由a n 与S n 的关系求通项a n57 已知数列{a n }的前n 项和S n ,求数列的通项公式,其求解过程分为三步: 58 (1)先利用a 1=S 1求出a 1;59 (2)用n -1替换S n 中的n 得到一个新的关系,利用a n =S n -S n -1(n ≥2)便可求60 出当n ≥2时a n 的表达式;61 (3)对n =1时的结果进行检验,看是否符合n ≥2时a n 的表达式,如果符合,62 则可以把数列的通项公式合写;如果不符合,则应该分n =1与n ≥2两段来写. 63 [例2] 已知数列{a n }的前n 项和S n ,根据下列条件分别求它们的通项a n . 64 (1)S n =2n 2+3n ;(2)S n =3n +1.65[自主解答] (1)由题可知,当n =1时,a 1=S 1=2×12+3×1=5, 66 当n ≥2时,a n =S n -S n -1=(2n 2+3n )-[2(n -1)2+3(n -1)]=4n +1. 67 当n =1时,4×1+1=5=a 1,故a n =4n +1. 68 (2)当n =1时,a 1=S 1=3+1=4, 69 当n ≥2时,70 a n =S n -S n -1=(3n +1)-(3n -1+1)=2×3n -1. 71 当n =1时,2×31-1=2≠a 1, 72 故a n =⎩⎨⎧4, n =1,2×3n -1, n ≥2.73以题试法74 (2012·聊城模拟)已知数列{a n }的前n 项和为S n ,且S n =nn +1,则1a 5=( )75A.56B.65 76C.130D .3077解析:选D 当n ≥2时,a n =S n -S n -1=nn +1-n -1n =1n n +1,则a 5=15×678 =130. 79 (三)数列的性质80 [例3] 已知数列{a n }的通项公式为a n =n 2-21n +20.81(1)n 为何值时,a n 有最小值?并求出最小值; 82 (2)n 为何值时,该数列的前n 项和最小?83 [自主解答] (1)因为a n =n 2-21n +20=⎝⎛⎭⎪⎫n -2122-3614,可知对称轴方程为n84 =212=10.5.又因n ∈N *,故n =10或n =11时,a n 有最小值,其最小值为112-85 21×11+20=-90.86 (2)设数列的前n 项和最小,则有a n ≤0,由n 2-21n +20≤0,解得1≤n ≤20,87 故数列{a n }从第21项开始为正数,所以该数列的前19或20项和最小. 88 由题悟法89 1.数列中项的最值的求法90 根据数列与函数之间的对应关系,构造相应的函数a n =f (n ),利用求解函数91 最值的方法求解,但要注意自变量的取值.92 2.前n 项和最值的求法93 (1)先求出数列的前n 项和S n ,根据S n 的表达式求解最值;94 (2)根据数列的通项公式,若a m ≥0,且a m +1<0,则S m 最大;若a m ≤0,且a m +1>0,95 则S m 最小,这样便可直接利用各项的符号确定最值. 96 以题试法97 3.(2012·江西七校联考)数列{a n }的通项a n =nn 2+90,则数列{a n }中的最大值98 是( )99 A .310B .19100C.119D.1060101解析:选C a n =1n+90n,由基本不等式得,1n+90n≤1290,由于n∈N*,易知102当n=9或10时,a n=119最大.103二.等差数列及其前n项和104知识能否忆起105一、等差数列的有关概念1061.定义:如果一个数列从第2项起,每一项与它的前一项的差都等于同一个107常数,那么这个数列就叫做等差数列.符号表示为a n+1-a n=d(n∈N*,d为常数).1082.等差中项:数列a,A,b成等差数列的充要条件是A=a+b2,其中A叫做109a,b的等差中项.110二、等差数列的有关公式1111.通项公式:a n=a1+(n-1)d. 1122.前n项和公式:S n=na1+n n-12d=a1+a n n2.113三、等差数列的性质1141.若m,n,p,q∈N*,且m+n=p+q,{a n}为等差数列,则a m+a n=a p+a q. 1152.在等差数列{a n}中,a k,a2k,a3k,a4k,…仍为等差数列,公差为kd.1163.若{a n}为等差数列,则S n,S2n-S n,S3n-S2n,…仍为等差数列,公差为n2d. 1174.等差数列的增减性:d>0时为递增数列,且当a1<0时前n项和S n有最小值.d<0 118时为递减数列,且当a1>0时前n项和S n有最大值.1195.等差数列{a n}的首项是a1,公差为d.若其前n项之和可以写成S n=An2+Bn,120则A=d2,B=a1-d2,当d≠0时它表示二次函数,数列{a n}的前n项和S n=An2+121Bn是{an }成等差数列的充要条件.1221.与前n项和有关的三类问题123(1)知三求二:已知a1、d、n、a n、S n中的任意三个,即可求得其余两个,这124体现了方程思想.125(2)S n=d2n2+⎝⎛⎭⎪⎫a1-d2n=An2+Bn⇒d=2A.126(3)利用二次函数的图象确定S n的最值时,最高点的纵坐标不一定是最大值,127最低点的纵坐标不一定是最小值.1282.设元与解题的技巧129已知三个或四个数组成等差数列的一类问题,要善于设元,若奇数个数成等130差数列且和为定值时,可设为…,a-2d,a-d,a,a+d,a+2d,…;131若偶数个数成等差数列且和为定值时,可设为…,a-3d,a-d,a+d,a+1323d,…,其余各项再依据等差数列的定义进行对称设元.133134考点135等差数列的判断与证明136[例1] 在数列{a n}中,a1=-3,a n=2a n-1+2n+3(n≥2,且n∈N*).137(1)求a2,a3的值;138(2)设b n=an+32n(n∈N*),证明:{b n}是等差数列.139[自主解答] (1)∵a1=-3,a n=2a n-1+2n+3(n≥2,且n∈N*),∴a2=2a1+14022+3=1,a3=2a2+23+3=13.141(2)证明:对于任意n∈N*,142∵b n+1-b n=an+1+32n+1-an+32n=12n+1[(a n+1-2a n)-3]=12n+1[(2n+1+3)-3]=1,143∴数列{b n}是首项为a1+32=-3+32=0,公差为1的等差数列.144由题悟法1451.证明{a n}为等差数列的方法:146(1)用定义证明:a n-a n-1=d(d为常数,n≥2)⇔{a n}为等差数列;147(2)用等差中项证明:2a n+1=a n+a n+2⇔{a n}为等差数列;148(3)通项法:a n为n的一次函数⇔{a n}为等差数列;149(4)前n项和法:S n=An2+Bn或S n=n a1+a n2.1502.用定义证明等差数列时,常采用的两个式子a n+1-a n=d和a n-a n-1=d,但151它们的意义不同,后者必须加上“n≥2”,否则n=1时,a0无定义.152以题试法1531.已知数列{a n}的前n项和S n是n的二次函数,且a1=-2,a2=2,S3=6. 154(1)求S n ;155 (2)证明:数列{a n }是等差数列. 156 解:(1)设S n =An 2+Bn +C (A ≠0),157则⎩⎨⎧-2=A +B +C ,0=4A +2B +C ,6=9A +3B +C ,158解得A =2,B =-4,C =0.故S n =2n 2-4n . 159 (2)证明:∵当n =1时,a 1=S 1=-2.160 当n ≥2时,a n =S n -S n -1=2n 2-4n -[2(n -1)2-4(n -1)]=4n -6. 161 ∴a n =4n -6(n ∈N *).a n +1-a n =4, 162 ∴数列{a n }是等差数列. 163 等差数列的基本运算 164165 典题导入166 [例2] (2012·重庆高考)已知{a n }为等差数列,且a 1+a 3=8,a 2+a 4=12. 167 (1)求{a n }的通项公式;168 (2)记{a n }的前n 项和为S n ,若a 1,a k ,S k +2成等比数列,求正整数k 的值. 169 [自主解答] (1)设数列{a n }的公差为d ,由题意知 170 ⎩⎨⎧2a 1+2d =8,2a 1+4d =12,解得⎩⎨⎧a 1=2,d =2.171所以a n =a 1+(n -1)d =2+2(n -1)=2n .172 (2)由(1)可得S n =n a 1+a n2=n 2+2n2=n (n +1).173 因为a 1,a k ,S k +2成等比数列,所以a 2k =a 1S k +2. 174 从而(2k )2=2(k +2)(k +3),即k 2-5k -6=0, 175 解得k =6或k =-1(舍去),因此k =6.176 由题悟法177 1.等差数列的通项公式a n =a 1+(n -1)d 及前n 项和公式S n =n a 1+a n2=178na 1+n n -12d ,共涉及五个量a 1,a n ,d ,n ,S n ,知其中三个就能求另外两个,179 体现了方程的思想.180 2.数列的通项公式和前n 项和公式在解题中起到变量代换作用,而a 1和d 是181 等差数列的两个基本量,用它们表示已知和未知是常用方法.182 以题试法183 2.(1)在等差数列中,已知a 6=10,S 5=5,则S 8=________.184 (2)设等差数列{a n }的前n 项和为S n ,若S 412-S 39=1,则公差为________.185 解析:(1)∵a 6=10,S 5=5, 186 ∴⎩⎨⎧a 1+5d =10,5a 1+10d =5.187解方程组得⎩⎨⎧a 1=-5,d =3.188 则S 8=8a 1+28d =8×(-5)+28×3=44.189 (2)依题意得S 4=4a 1+4×32d =4a 1+6d ,S 3=3a 1+3×22d =3a 1+3d ,于是有190 4a 1+6d 12-3a 1+3d9=1,由此解得d =6,即公差为6. 191 答案:(1)44 (2)6 192 等差数列的性质193194 典题导入195 [例3] (1)等差数列{a n }中,若a 1+a 4+a 7=39,a 3+a 6+a 9=27,则前9项和196 S 9等于( )197 A .66 B .99 198 C .144D .297199 (2)(2012·天津模拟)设等差数列{a n }的前n 项和S n ,若S 4=8,S 8=20,则a 11200 +a 12+a 13+a 14=( )201 A .18 B .17 202 C .16D .15203 [自主解答] (1)由等差数列的性质及a 1+a 4+a 7=39,可得3a 4=39,所以a 4204 =13.同理,由a 3+a 6+a 9=27,可得a 6=9.205所以S9=9a1+a92=9a4+a62=99.206(2)设{a n}的公差为d,则a5+a6+a7+a8=S8-S4=12,(a5+a6+a7+a8)-S4=20716d,解得d=14,a11+a12+a13+a14=S4+40d=18.208[答案] (1)B (2)A209由题悟法2101.等差数列的性质是等差数列的定义、通项公式以及前n项和公式等基础知211识的推广与变形,熟练掌握和灵活应用这些性质可以有效、方便、快捷地解决212许多等差数列问题.2132.应用等差数列的性质解答问题的关键是寻找项的序号之间的关系.214以题试法2153.(1)(2012·江西高考)设数列{a n},{b n}都是等差数列,若a1+b1=7,a3+216b3=21,则a5+b5=________.217(2)(2012·海淀期末)若数列{a n}满足:a1=19,a n+1=a n-3(n∈N*),则数列218{a n}的前n项和数值最大时,n的值为( )219A.6 B.7220C.8 D.9221解析:(1)设两等差数列组成的和数列为{c n},由题意知新数列仍为等差数列222且c1=7,c3=21,则c5=2c3-c1=2×21-7=35.223(2)∵a n+1-a n=-3,∴数列{a n}是以19为首项,-3为公差的等差数列,∴224a n =19+(n -1)×(-3)=22-3n .设前k 项和最大,则有⎩⎨⎧a k ≥0,a k +1≤0,即225 ⎩⎨⎧22-3k ≥0,22-3k +1≤0,226解得193≤k ≤223.∵k ∈N *,∴k =7.故满足条件的n 的值为7.227 答案:(1)35 (2)B228 三.等比数列及其前n 项和229230 [知识能否忆起]231 1.等比数列的有关概念 232 (1)定义:233 如果一个数列从第2项起,每一项与它的前一项的比等于同一个常数(不为234 零),那么这个数列就叫做等比数列.这个常数叫做等比数列的公比,通常用字235 母q 表示,定义的表达式为a n +1a n=q (n ∈N *,q 为非零常数). 236 (2)等比中项:237 如果a 、G 、b 成等比数列,那么G 叫做a 与b 的等比中项.即:G 是a 与b 的238 等比中项⇔a ,G ,b 成等比数列⇒G 2=ab .239 2.等比数列的有关公式 240 (1)通项公式:a n =a 1q n -1.241(2)前n 项和公式:S n=⎩⎨⎧na 1,q =1,a 11-q n1-q=a 1-a nq1-q ,q ≠1.242243 3.等比数列{a n }的常用性质244 (1)在等比数列{a n }中,若m +n =p +q =2r (m ,n ,p ,q ,r ∈N *),则a m ·a n =245a p ·a q =a 2r . 246 特别地,a 1a n =a 2a n -1=a 3a n -2=….247 (2)在公比为q 的等比数列{a n }中,数列a m ,a m +k ,a m +2k ,a m +3k ,…仍是等比数248 列,公比为q k ;249 数列S m ,S 2m -S m ,S 3m -S 2m ,…仍是等比数列(此时q ≠-1);250 a n =a m q n -m . 251 1.等比数列的特征252 (1)从等比数列的定义看,等比数列的任意项都是非零的,公比q 也是非零常253 数.254 (2)由a n +1=qa n ,q ≠0并不能立即断言{a n }为等比数列,还要验证a 1≠0. 255 2.等比数列的前n 项和S n256 (1)等比数列的前n 项和S n 是用错位相减法求得的,注意这种思想方法在数列257 求和中的运用.258 (2)在运用等比数列的前n 项和公式时,必须注意对q =1与q ≠1分类讨论,259 防止因忽略q =1这一特殊情形导致解题失误260考点261 等比数列的判定与证明262263 典题导入264 [例1] 已知数列{a n }的前n 项和为S n ,且a n +S n =n . 265 (1)设c n =a n -1,求证:{c n }是等比数列; 266 (2)求数列{a n }的通项公式.267 [自主解答] (1)证明:∵a n +S n =n ,① 268 ∴a n +1+S n +1=n +1.② 269 ②-①得a n +1-a n +a n +1=1, 270 ∴2a n +1=a n +1,∴2(a n +1-1)=a n -1,271 ∴a n +1-1a n -1=12. 272 ∵首项c 1=a 1-1,又a 1+a 1=1,273 ∴a 1=12,c 1=-12.274又c n =a n -1,故{c n }是以-12为首项,12为公比的等比数列.275(2)由(1)可知c n =⎝ ⎛⎭⎪⎫-12·⎝ ⎛⎭⎪⎫12n -1=-⎝ ⎛⎭⎪⎫12n ,276∴a n =c n +1=1-⎝ ⎛⎭⎪⎫12n.277278 在本例条件下,若数列{b n }满足b 1=a 1,b n =a n -a n -1(n ≥2),证明{b n }是等比279 数列.280 证明:∵由(2)知a n =1-⎝ ⎛⎭⎪⎫12n,281 ∴当n ≥2时,b n =a n -a n -1 282 =1-⎝ ⎛⎭⎪⎫12n -⎣⎢⎡⎦⎥⎤1-⎝ ⎛⎭⎪⎫12n -1283=⎝ ⎛⎭⎪⎫12n -1-⎝ ⎛⎭⎪⎫12n =⎝ ⎛⎭⎪⎫12n. 284又b 1=a 1=12也符合上式,∴b n =⎝ ⎛⎭⎪⎫12n .285∵b n +1b n =12,∴数列{b n }是等比数列. 286287 由题悟法288 等比数列的判定方法289 (1)定义法:若a n +1a n =q (q 为非零常数,n ∈N *)或a na n -1=q (q 为非零常数且n ≥2,290n ∈N *),则{a n }是等比数列. 291 (2)等比中项法:若数列{a n }中,a n ≠0且a 2n +1=a n ·a n +2(n ∈N *),则数列{a n }292是等比数列.293(3)通项公式法:若数列通项公式可写成a n=c·q n(c,q均是不为0的常数,294n∈N*),则{an }是等比数列.295以题试法2961.(2012·沈阳模拟)已知函数f(x)=log a x,且所有项为正数的无穷数列{a n} 297满足log a a n+1-log a a n=2,则数列{a n}( )298A.一定是等比数列299B.一定是等差数列300C.既是等差数列又是等比数列301D.既不是等差数列又不是等比数列302解析:选A 由log a a n+1-log a a n=2,得log a an+1an=2=log a a2,故an+1an=a2.又a>0303且a≠1,所以数列{a n}为等比数列.304等比数列的基本运算305306典题导入307[例2] {an }为等比数列,求下列各值:308(1)a6-a4=24,a3a5=64,求an;309(2)已知a2·a8=36,a3+a7=15,求公比q.310解:(1)设数列{an }的公比为q,311由题意得⎩⎨⎧a 6-a 4=a 1q3q 2-1=24, ①a 3a 5=a 1q32=64. ②312 由②得a 1q 3=±8,313 将a 1q 3=-8代入①中,得q 2=-2(舍去). 314 将a 1q 3=8代入①中,得q 2=4,q =±2. 315 当q =2时,a 1=1,∴a n =a 1q n -1=2n -1.316 当q =-2时,a 1=-1,∴a n =a 1q n -1=-(-2)n -1. 317 ∴a n =2n -1或a n =-(-2)n -1.318 (2)∵a 2·a 8=36=a 3·a 7,而a 3+a 7=15, 319 ∴⎩⎨⎧a 3=3,a 7=12或⎩⎨⎧a 3=12,a 7=3.320∴q 4=a 7a 3=4或14.321∴q =±2或q =±22. 322323 由题悟法324 1.等比数列基本量的运算是等比数列中的一类基本问题,数列中有五个量a 1,325n ,q ,a n ,S n ,一般可以“知三求二”,通过列方程(组)可迎刃而解. 326 2.在使用等比数列的前n 项和公式时,应根据公比q 的情况进行分类讨论,327 切不可忽视q 的取值而盲目用求和公式.328以题试法3292.(2012·山西适应性训练)已知数列{a n}是公差不为零的等差数列,a1=2,330且a2,a4,a8成等比数列.331(1)求数列{a n}的通项公式;332(2)求数列{3a n}的前n项和.333解:(1)设等差数列{a n}的公差为d(d≠0).334因为a2,a4,a8成等比数列,335所以(2+3d)2=(2+d)·(2+7d),336解得d=2.337所以a n=2n(n∈N*).338(2)由(1)知3a n=32n,设数列{3a n}的前n项和为S n,339则S n=32+34+…+32n=91-9n1-9=98(9n-1).340等比数列的性质341342典题导入343[例3] (1)(2012·威海模拟)在由正数组成的等比数列{a n}中,若a3a4a5=3π,344则sin(log3a1+log3a2+…+log3a7)的值为( )345A.12B.32346C .1D .-32347 (2)设等比数列{a n }的前n 项和为S n ,若S 6∶S 3=1∶2,则S 9∶S 3等于( ) 348 A .1∶2 B .2∶3 349 C .3∶4D .1∶3350 [自主解答] (1)因为a 3a 4a 5=3π=a 34,所以a 4=3π3. 351 log 3a 1+log 3a 2+…+log 3a 7 352 =log 3(a 1a 2…a 7)=log 3a 74353 =7log 33π3=7π3, 354故sin(log 3a 1+log 3a 2+…+log 3a 7)=32. 355 (2)由等比数列的性质:S 3,S 6-S 3,S 9-S 6仍成等比数列,于是(S 6-S 3)2=S 3·(S 9356 -S 6),357 将S 6=12S 3代入得S 9S 3=34.358 [答案] (1)B (2)C359 由题悟法360 等比数列与等差数列在定义上只有“一字之差”,它们的通项公式和性质有361 许多相似之处,其中等差数列中的“和”“倍数”可以与等比数列中的362 “积”“幂”相类比.关注它们之间的异同有助于我们从整体上把握,同时也363有利于类比思想的推广.对于等差数列项的和或等比数列项的积的运算,若能364 关注通项公式a n =f (n )的下标n 的大小关系,可简化题目的运算.365 以题试法366 3.(1)(2012·新课标全国卷)已知{a n }为等比数列,a 4+a 7=2,a 5a 6=-8,则367a 1+a 10=( )368 A .7 B .5 369 C .-5D .-7370 (2)(2012·成都模拟)已知{a n }是等比数列,a 2=2,a 5=14,则a 1a 2+a 2a 3+…371 +a n a n +1=( ) 372 A .16(1-4-n )B .16(1-2-n ) 373 C.323(1-4-n )D.323(1-2-n ) 374 解析:(1)选D 法一:375 由题意得⎩⎨⎧a 4+a 7=a 1q 3+a 1q 6=2,a 5a 6=a 1q 4×a 1q 5=a 21q 9=-8,376解得⎩⎨⎧q 3=-2,a 1=1或⎩⎨⎧q 3=-12,a 1=-8,377故a 1+a 10=a 1(1+q 9)=-7. 378 法二:由⎩⎨⎧a 4+a 7=2,a 5a 6=a 4a 7=-8,解得⎩⎨⎧a 4=-2,a 7=4或⎩⎨⎧a 4=4,a 7=-2.379则⎩⎨⎧q 3=-2,a 1=1或⎩⎨⎧q 3=-12,a 1=-8,故a 1+a 10=a 1(1+q 9)=-7.380(2)选C ∵a 2=2,a 5=14,∴a 1=4,q =12,a n a n +1=⎝ ⎛⎭⎪⎫122n -5.381故a 1a 2+a 2a 3+…+a n a n +1=8⎝⎛⎭⎪⎫1-14n 1-14=323(1-4-n ).382练习题383 1.(教材习题改编)数列1,23,35,47,59…的一个通项公式是 ( )384A .a n =n2n +1 B .a n =n 2n -1 385C .a n =n2n -3D .a n =n 2n +3386 答案:B387 2.设数列{a n }的前n 项和S n =n 2,则a 8的值为( ) 388 A .15 B .16 389 C .49D .64390 解析:选A a 8=S 8-S 7=64-49=15.391 3.已知数列{a n }的通项公式为a n =nn +1,则这个数列是( )392 A .递增数列 B .递减数列393C .常数列D .摆动数列394 解析:选A a n+1-a n =n +1n +2-nn +1=n +12-n n +2n +1n +2=395 1n +1n +2>0.3964.(教材习题改编)已知数列{a n }的通项公式是a n =⎩⎨⎧2·3n -1n 为偶数,2n -5n 为奇数,397 则a 4·a 3=________.398 解析:a 4·a 3=2×33·(2×3-5)=54. 399 答案:54400 5.已知数列{a n }的通项公式为a n =pn +q n ,且a 2=32,401a 4=32,则a 8=________.402解析:由已知得⎩⎪⎨⎪⎧2p +q 2=32,4p +q 4=32,解得⎩⎨⎧p =14,q =2.403则a n =14n +2n ,故a 8=94.404答案:94405 1.(2012·福建高考)等差数列{a n }中,a 1+a 5=10,a 4=7,则数列{a n }的公差406 为( )407A .1B .2 408C .3D .4409 解析:选B 法一:设等差数列{a n }的公差为d ,由题意得⎩⎨⎧2a 1+4d =10,a 1+3d =7.410解得⎩⎨⎧a 1=1,d =2.故d =2.411 法二:∵在等差数列{a n }中,a 1+a 5=2a 3=10,∴a 3=5. 412 又a 4=7,∴公差d =7-5=2.413 2.(教材习题改编)在等差数列{a n }中,a 2+a 6=3π2,则sin ⎝⎛⎭⎪⎫2a 4-π3=( )414A.32B.12 415C .-32D .-12416解析:选D ∵a 2+a 6=3π2,∴2a 4=3π2. 417∴sin ⎝ ⎛⎭⎪⎫2a 4-π3=sin ⎝⎛⎭⎪⎫3π2-π3=-cos π3=-12. 418 3.(2012·辽宁高考)在等差数列{a n }中,已知a 4+a 8=16,则该数列前11项419 和S 11=( )420 A .58B .88421 C .143D .176422解析:选B S 11=11a 1+a 112=11a 4+a 82=88.423 4.在数列{a n }中,若a 1=1,a n +1=a n +2(n ≥1),则该数列的通项a n =________. 424 解析:由a n +1=a n +2知{a n }为等差数列其公差为2. 425 故a n =1+(n -1)×2=2n -1. 426 答案:2n -1427 5.(2012·北京高考)已知{a n }为等差数列,S n 为其前n 项和,若a 1=12,S 2=428a 3,则a 2=________,S n =________. 429 解析:设{a n }的公差为d ,430 由S 2=a 3知,a 1+a 2=a 3,即2a 1+d =a 1+2d , 431 又a 1=12,所以d =12,故a 2=a 1+d =1,432S n =na 1+12n (n -1)d =12n +12(n 2-n )×12433=14n 2+14n . 434答案:1 14n 2+14n435 1.(2011·江西高考){a n }为等差数列,公差d =-2,S n 为其前n 项和.若S 10436 =S 11,则a 1=( )437 A .18 B .20438C .22D .24439 解析:选 B 由S 10=S 11,得a 11=S 11-S 10=0,a 1=a 11+(1-11)d =0+(-440 10)×(-2)=20.441 2.(2012·广州调研)等差数列{a n }的前n 项和为S n ,已知a 5=8,S 3=6,则442 S 10-S 7的值是( ) 443 A .24 B .48 444 C .60D .72445 解析:选B 设等差数列{a n }的公差为d ,由题意可得⎩⎨⎧a 5=a 1+4d =8,S 3=3a 1+3d =6,解446 得⎩⎨⎧a 1=0,d =2,则S 10-S 7=a 8+a 9+a 10=3a 1+24d =48.447 3.(2013·东北三校联考)等差数列{a n }中,a 5+a 6=4,则448 log 2(2a 1·2a 2·…·2a 10)=( )449 A .10 B .20 450 C .40D .2+log 25451 解析:选B 依题意得,a 1+a 2+a 3+…+a 10=10a 1+a 102=5(a 5+a 6)=20,452 因此有log 2(2a 1·2a 2·…·2a 10)=a 1+a 2+a 3+…+a 10=20.453 4.(2012·海淀期末)已知数列{a n }满足:a 1=1,a n >0,a 2n +1-a 2n =1(n ∈N *),454 那么使a n <5成立的n 的最大值为( )455 A .4B .5 456C .24D .25457解析:选C ∵a 2n +1-a 2n =1,∴数列{a 2n }是以a 21=1为首项,1为公差的等差数458 列.∴a 2n =1+(n -1)=n .又a n >0,∴a n =n .∵a n <5,∴n <5.即n <25.故n 的459 最大值为24.460 5.已知等差数列{a n }的前n 项和为S n ,并且S 10>0,S 11<0,若S n ≤S k 对n ∈N *461 恒成立,则正整数k 的值为( )462 A .5 B .6 463 C .4D .7464 解析:选A 由S 10>0,S 11<0知a 1>0,d <0,并且a 1+a 11<0,即a 6<0,又a 5+a 6>0,465 所以a 5>0,即数列的前5项都为正数,第5项之后的都为负数,所以S 5最大,466 则k =5.467 6.数列{a n }的首项为3,{b n }为等差数列且b n =a n +1-a n (n ∈N *).若b 3=-2,468 b 10=12,则a 8=( ) 469 A .0 B .3 470 C .8D .11471 解析:选B 因为{b n }是等差数列,且b 3=-2,b 10=12,472 故公差d =12--210-3=2.于是b 1=-6,473 且b n =2n -8(n ∈N *),即a n +1-a n =2n -8.474 所以a 8=a 7+6=a 6+4+6=a 5+2+4+6=…=a 1+(-6)+(-4)+(-2)+0475 +2+4+6=3.476 7.(2012·广东高考)已知递增的等差数列{a n }满足a 1=1,a 3=a 22-4,则a n477=________.478 解析:设等差数列公差为d ,∵由a 3=a 22-4,得1+2d =(1+d )2-4,解得d 2479 =4,即d =±2.由于该数列为递增数列,故d =2.480 ∴a n =1+(n -1)×2=2n -1. 481 答案:2n -1482 8.已知数列{a n }为等差数列,S n 为其前n 项和,a 7-a 5=4,a 11=21,S k =9,483 则k =________.484 解析:a 7-a 5=2d =4,则d =2.a 1=a 11-10d =21-20=1,485 S k =k +k k -12×2=k 2=9.又k ∈N *,故k =3.486 答案:3487 9.设等差数列{a n },{b n }的前n 项和分别为S n ,T n ,若对任意自然数n 都有S nT n488 =2n -34n -3,则a 9b 5+b 7+a 3b 8+b 4的值为________. 489 解析:∵{a n },{b n }为等差数列,490 ∴a 9b 5+b 7+a 3b 8+b 4=a 92b 6+a 32b 6=a 9+a 32b 6=a 6b 6. 491∵S 11T 11=a 1+a 11b 1+b 11=2a 62b 6=2×11-34×11-3=1941,∴a 6b 6=1941. 492答案:1941493 10.(2011·福建高考)已知等差数列{a n }中,a 1=1,a 3=-3.494(1)求数列{a n }的通项公式;495 (2)若数列{a n }的前k 项和S k =-35,求k 的值. 496 解:(1)设等差数列{a n }的公差为d ,则a n =a 1+(n -1)d . 497 由a 1=1,a 3=-3,可得1+2d =-3,解得d =-2. 498 从而a n =1+(n -1)×(-2)=3-2n . 499 (2)由(1)可知a n =3-2n ,500 所以S n =n [1+3-2n ]2=2n -n 2.501 由S k =-35,可得2k -k 2=-35, 502 即k 2-2k -35=0,解得k =7或k =-5. 503 又k ∈N *,故k =7.504 11.设数列{a n }的前n 项积为T n ,T n =1-a n ,505 (1)证明⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫1T n 是等差数列;506(2)求数列⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫a n T n 的前n 项和S n .507解:(1)证明:由T n =1-a n 得,当n ≥2时,T n =1-T nT n -1, 508两边同除以T n 得1T n -1T n -1=1.509 ∵T 1=1-a 1=a 1,510故a 1=12,1T 1=1a 1=2.511∴⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫1T n 是首项为2,公差为1的等差数列.512(2)由(1)知1T n =n +1,则T n =1n +1,513从而a n =1-T n =nn +1.故a nT n=n .514∴数列⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫a n T n 是首项为1,公差为1的等差数列.515∴S n =n n +12.516 12.已知在等差数列{a n }中,a 1=31,S n 是它的前n 项和,S 10=S 22. 517 (1)求S n ;518 (2)这个数列的前多少项的和最大,并求出这个最大值. 519 解:(1)∵S 10=a 1+a 2+…+a 10,520 S 22=a 1+a 2+…+a 22,又S 10=S 22, 521 ∴a 11+a 12+…+a 22=0, 522 即12a 11+a 222=0,故a 11+a 22=2a 1+31d =0.523 又∵a 1=31,∴d =-2,524 ∴S n =na 1+n n -12d =31n -n (n -1)=32n -n 2.525(2)法一:由(1)知S n =32n -n 2,526 故当n =16时,S n 有最大值,S n 的最大值是256. 527 法二:由S n =32n -n 2=n (32-n ),欲使S n 有最大值, 528 应有1<n <32,从而S n ≤⎝⎛⎭⎪⎫n +32-n 22=256, 529 当且仅当n =32-n ,即n =16时,S n 有最大值256.530 1.(教材习题改编)等比数列{a n }中,a 4=4,则a 2·a 6等于( ) 531 A .4 B .8 532 C .16D .32533 解析:选C a 2·a 6=a 24=16.534 2.已知等比数列{a n }的前三项依次为a -1,a +1,a +4,则a n =( ) 535 A .4·⎝ ⎛⎭⎪⎫32nB .4·⎝ ⎛⎭⎪⎫23n536C .4·⎝ ⎛⎭⎪⎫32n -1D .4·⎝ ⎛⎭⎪⎫23n -1537 解析:选C (a +1)2=(a -1)(a +4)⇒a =5,538 a 1=4,q =32,故a n =4·⎝ ⎛⎭⎪⎫32n -1.539 3.已知等比数列{a n }满足a 1+a 2=3,a 2+a 3=6,则a 7=( ) 540 A .64B .81541 C .128D .243542解析:选A q =a 2+a 3a 1+a 2=2, 543 故a 1+a 1q =3⇒a 1=1,a 7=1×27-1=64.544 4.(2011·北京高考)在等比数列{a n }中,若a 1=12,a 4=4,则公比q =________;545a 1+a 2+…+a n =________.546 解析:a 4=a 1q 3,得4=12q 3,解得q =2,a 1+a 2+…+a n =121-2n 1-2=2n -1-12.547答案:2 2n -1-12548 5.(2012·新课标全国卷)等比数列{a n }的前n 项和为S n ,若S 3+3S 2=0,则549 公比q =________.550 解析:∵S 3+3S 2=0,∴a 1+a 2+a 3+3(a 1+a 2)=0, 551 ∴a 1(4+4q +q 2)=0. 552 ∵a 1≠0,∴q =-2. 553 答案:-2554 1.设数列{a n }是等比数列,前n 项和为S n ,若S 3=3a 3,则公比q 为( ) 555 A .-12B .1556C .-12或1D.14557 解析:选C 当q =1时,满足S 3=3a 1=3a 3.558当q ≠1时,S 3=a 11-q 31-q =a 1(1+q +q 2)=3a 1q 2,559解得q =-12,综上q =-12或q =1.560 2.(2012·东城模拟)设数列{a n }满足:2a n =a n +1(a n ≠0)(n ∈N *),且前n 项和561 为S n ,则S 4a 2的值为( )562A.152 B.154563 C .4D .2564解析:选A 由题意知,数列{a n }是以2为公比的等比数列,故S 4a 2=a 11-241-2a 1×2565 =152. 566 3.(2012·安徽高考)公比为2的等比数列{a n }的各项都是正数,且a 3a 11=16,567 则log 2a 10=( )568 A .4 B .5 569 C .6D .7570 解析:选B ∵a 3·a 11=16,∴a 27=16. 571 又∵等比数列{a n }的各项都是正数,∴a 7=4. 572 又∵a 10=a 7q 3=4×23=25,∴log 2a 10=5.573 4.已知数列{a n },则“a n ,a n +1,a n +2(n ∈N *)成等比数列”是“a 2n +1=a n a n +2”574 的( )575A .充分不必要条件B .必要不充分条件 576C .充要条件D .既不充分也不必要条件577 解析:选A 显然,n ∈N *,a n ,a n +1,a n +2成等比数列,则a 2n +1=a n a n +2,反之,578 则不一定成立,举反例,如数列为1,0,0,0,…579 5.(2013·太原模拟)各项均为正数的等比数列{a n }的前n 项和为S n ,若S n =2,580S 3n =14,则S 4n 等于( ) 581 A .80 B .30 582 C .26D .16583 解析:选B 设S 2n =a ,S 4n =b ,由等比数列的性质知: 584 2(14-a )=(a -2)2,解得a =6或a =-4(舍去), 585 同理(6-2)(b -14)=(14-6)2,所以b =S 4n =30.586 6.已知方程(x 2-mx +2)(x 2-nx +2)=0的四个根组成以12为首项的等比数列,587 则m n=( )588A.32B.32或23589C.23D .以上都不对590 解析:选B 设a ,b ,c ,d 是方程(x 2-mx +2)(x 2-nx +2)=0的四个根,不591 妨设a <c <d <b ,则a ·b =c ·d =2,a =12,故b =4,根据等比数列的性质,得到592c=1,d=2,则m=a+b=92,n=c+d=3,或m=c+d=3,n=a+b=92,则mn=5933 2或mn=23.5947.已知各项不为0的等差数列{a n},满足2a3-a27+2a11=0,数列{b n}是等比595数列,且b7=a7,则b6b8=________.596解析:由题意可知,b6b8=b27=a27=2(a3+a11)=4a7,597∵a7≠0,∴a7=4,∴b6b8=16.598答案:165998.(2012·江西高考)等比数列{a n}的前n项和为S n,公比不为1.若a1=1,600则对任意的n∈N*,都有a n+2+a n+1-2a n=0,则S5=________.601解析:由题意知a3+a2-2a1=0,设公比为q,则a1(q2+q-2)=0.由q2+q-6022=0解得q=-2或q=1(舍去),则S5=a11-q51-q=1--253=11.603答案:116049.(2012·西城期末)已知{a n}是公比为2的等比数列,若a3-a1=6,则a1=605________;1a21+1a22+…+1a2n=________.606解析:∵{a n}是公比为2的等比数列,且a3-a1=6,∴4a1-a1=6,即a1=2,607故a n=a12n-1=2n,∴1an=⎝⎛⎭⎪⎫12n,1a2n=⎝⎛⎭⎪⎫14n,即数列⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫1a2n是首项为14,公比为14的等比608数列,609∴1a 21+1a 22+…+1a 2n =14⎝ ⎛⎭⎪⎫1-14n 1-14=13⎝ ⎛⎭⎪⎫1-14n . 610答案:2 13⎝ ⎛⎭⎪⎫1-14n 611 10.设数列{a n }的前n 项和为S n ,a 1=1,且数列{S n }是以2为公比的等比数列. 612 (1)求数列{a n }的通项公式; 613 (2)求a 1+a 3+…+a 2n +1.614 解:(1)∵S 1=a 1=1,且数列{S n }是以2为公比的等比数列,∴S n =2n -1, 615 又当n ≥2时,a n =S n -S n -1=2n -2(2-1)=2n -2. 616 ∴a n =⎩⎨⎧1,n =1,2n -2,n ≥2.617 (2)a 3,a 5,…,a 2n +1是以2为首项,以4为公比的等比数列,618 ∴a 3+a 5+…+a 2n +1=21-4n 1-4=24n -13.619∴a 1+a 3+…+a 2n +1=1+24n -13=22n +1+13.620 11.设数列{a n }的前n 项和为S n ,其中a n ≠0,a 1为常数,且-a 1,S n ,a n +1成621 等差数列.622 (1)求{a n }的通项公式;623 (2)设b n =1-S n ,问:是否存在a 1,使数列{b n }为等比数列?若存在,求出a 1624 的值;若不存在,请说明理由.625解:(1)依题意,得2S n =a n +1-a 1. 626 当n ≥2时,有⎩⎨⎧2S n =a n +1-a 1,2S n -1=a n -a 1.627 两式相减,得a n +1=3a n (n ≥2). 628 又因为a 2=2S 1+a 1=3a 1,a n ≠0,629 所以数列{a n }是首项为a 1,公比为3的等比数列. 630 因此,a n =a 1·3n -1(n ∈N *).631 (2)因为S n =a 11-3n1-3=12a 1·3n -12a 1, 632b n =1-S n =1+12a 1-12a 1·3n .633要使{b n }为等比数列,当且仅当1+12a 1=0,即a 1=-2.634 所以存在a 1=-2,使数列{b n }为等比数列.635 12. (2012·山东高考)已知等差数列{a n }的前5项和为105,且a 10=2a 5. 636 (1)求数列{a n }的通项公式;637 (2)对任意m ∈N *,将数列{a n }中不大于72m 的项的个数记为b m .求数列{b m }的前638m 项和S m . 639 解:(1)设数列{a n }的公差为d ,前n 项和为T n , 640 由T 5=105,a 10=2a 5,641得⎩⎨⎧5a 1+5×5-12d =105,a 1+9d =2a 1+4d ,642解得a 1=7,d =7.643 因此a n =a 1+(n -1)d =7+7(n -1)=7n (n ∈N *). 644 (2)对m ∈N *,若a n =7n ≤72m ,则n ≤72m -1. 645 因此b m =72m -1.646 所以数列{b m }是首项为7,公比为49的等比数列,647 故S m =b 11-q m 1-q =7×1-49m 1-49=7×72m -148=72m +1-748.648649650。
高中数学必修5 第二章 数列 知识整理

第二章 数列2.1 数列1.数列(1)数列的概念按照一定次序排列的一列数称为数列。
数列中的每一个数都叫做这个数列的项,各项依次叫做这个数列的第1项(或首项),第2项,…,第n 项,…,所以,数列的一般形式可以写成:123,,,,,n a a a a ……,简记为{}n a 。
其中数列{}n a 的第n 项n a 也叫做数列的通项。
注意:①数列中每一项都和它的序号有关,排在第一位的数称为这个数列的第1项(通常也叫做首项),排在第二位的数称为这个数列的第2项,…,排在第n 位的数称为这个数列的第n 项。
所以,数列的一般形式可以写成123,,,,n a a a a …,简记为{}n a 。
如:数列1,2,3,4,…,可以简记为{n}。
②数列中的数是按一定次序排列的。
因此,如果组成两个数列的数相同而排列次序不同,那么它们就不是相同的数列。
如:数列1,2,3,4,5与5,4,3,2,1是不同的数列。
③数列的定义中,并没有规定数列中的数必须不同。
因此,同一个数在数列中可以重复出现。
如:1,1,1,1,1,1,---…;2,2,2,2,2,…等。
④{}n a 与n a 是不同的概念。
{}n a 表示数列123,,,,,n a a a a ……,而n a 仅表示数列{}n a的第n 项。
⑤从映射函数的观点看,数列可以看做是一个定义域为正整数N +(或它的有限子集{1,2,3,,}n …)的数与自变量从小到大依次取值时对应的一列函数值,这里的函数是一种特殊函数:它的自变量只能取正整数,由于数列的值是函数值,序号是自变量,数列的通项公式也就是相应函数的解析式。
可以将序号为横坐标,相应的像为纵坐标,通过描点画图来表示一个数列,从数列的图像表示可以直观的看出数列的变化情况。
(2)数列的分类①按照数列的项数的多少可分为:有穷数列与无穷数列。
项数有限的数列叫有穷数列,项数无限的数列叫无穷数列。
②按照数列的每一项随序号变化的情况可分为:递增数列、递减数列、常数列、摆动数列。
人教版数学高二必修五第二章《数列》知识整合

一、等差数列1.定义:a n+1-a n=d(n∈N*)或a n-a n-1=d(n∈N*,n≥2).2.通项公式:a n=a1+(n-1)d(n∈N*).3.如果数列{a n}的通项公式是a n=An+B(A、B是与n无关的常数),那么数列{a n}一定是等差数列.4.等差数列前n项和公式:S n=n(a1+a n)2,S n=na1+n(n-1)2d.5.如果数列{a n}的通项公式是S n=An2+Bn(A、B是与n无关的常数),那么数列{a n}一定是等差数列.6.a、b、c成等差数列{a n}⇔b为a、c的等差中项⇔2b=a+c.7.在等差数列{a n}中,a n=a m+(n-m)d(n∈N*).8.在等差数列{a n}中,由m+n=p+q⇒a m+a n=a p+a q,若m+n=2p⇒a m+a n=2a p.9.在等差数列{a n}中,S k,S2k-S k,S3k-S2k构成等差数列⇔2(S2k-S k )=S k+( S3k-S2k).10.已知{a n} 、{b n}为等差数列,则{a n-c},{ca n},{a n+b n},{a n+kb n}(其中c为常数,k∈N*)仍是等差数列.11.已知{a n} 为等差数列,若k1,k2,k3,…,k n为等差数列,则ak1,ak2,ak3,…,ak n仍是等差数列.12.若三个数成等差数列,则设这三个数为a-d,a,a+d,可简化计算.13.证明等差数列的两种方法.(1)定义:a n+1-a n=d(n∈N*).(2)等差中项2a n=a n-1+a n+1(n∈N*,n≥2).二、等比数列1.定义:a n+1a n=q(n∈N*)或a na n-1=q(n∈N*,n≥2).2.通项公式:a n =a 1q n -1(n ∈N *).3.等比数列前n 项和:S n =a 1-a n q 1-q =a 1(1-q n )1-q(q ≠1);S n =na 1(q =1).4.a ,b ,c 成等比数列⇒b 为a 、c 的等比中项⇒b 2=ac .5.在等比数列{a n }中,a n =a m ×q n -m (n ∈N *).6.在等比数列{a n }中,由m +n =p +q ⇒a m a n =a p a q ,若m +n =2p ⇒a m a n =a 2p .7.在等比数列{a n }中,S k ,S 2k -S k ,S 3k -S 2k 构成等比数列⇔( S 2k -S k )2=S k (S 3k -S 2k )(S k ≠0).8.已知{a n } 、{b n }为等比数列,则{ca n },{a n b n },⎩⎨⎧⎭⎬⎫a n b n (其中c 为不为0的常数,k ∈N *)仍是等比数列.9.已知{a n } 为等比数列,若k 1,k 2,k 3,…,k n 为等差数列,则ak 1,ak 2,ak 3,…,ak n 仍是等比数列.10.若三个数成等比数列,则设这三个数为a q,a ,aq ,可简化计算. 11.证明等比数列的两种方法.(1)利用定义:a n +1a n =q 或a n a n -1=q (n ∈N *,n ≥2). (2)等比中项:a 2n =a n -1a n +1(n ∈N *,n ≥2).三、通项公式的求法数列的通项公式是数列的重要内容之一,它把数列各项的性质集于一身.常用的求通项的方法有观察法、公式法、累加法、累乘法、前n 项和作差法、辅助数列法.累加法:数列的基本形式为a n +1-a n =f (n )(n ∈N *)的解析式,而f (1)+f (2)+……+f (n )的和可求出.累乘法:数列的基本形式为a n +1a n=f (n )(n ∈N *)的解析关系,而f (1)·f (2)·…·f (n )的积可求出.前n 项和作差法:利用a n =⎩⎪⎨⎪⎧S 1(n =1),S n -S n -1(n ≥2),能合则合. 待定系数法:数列有形如a n +1=ka n +b (k ≠1)的关系,可用待定系数法求得(a n +t )为等比数列,再求得a n .四、特殊数列的前n 项和利用等差、等比数列求和公式是最基本最重要的方法.数列的求和除记住一些公式外,还应注重对通项公式的分析与整理,根据其特征求和,常用的方法技巧有分组求和法、倒序相加法、错位相减法、裂项相消法等.分组求和法:有一类数列,既不是等差数列,也不是等比数列,但如果将这类数列适当拆开,可分为几个等差、等比或常见的数列,那么就可以分别求和,再将其合并即可.倒序相加法:这是在推导等差数列的前n 项和公式时所用的方法,就是将一个数列倒过来排列(反序),再把它与原数列相加,就可以得到n 个a 1+a n .错位相减法:这是在推导等比数列的前n 项和公式时所用的方法,这种方法主要用于求数列{a n ·b n }的前n 项和,其中{a n }、{b n }分别是等差和等比数列.裂项相消法:这是分解与组合思想在数列求和中的具体应用.裂项法的实质是将数列中的每项(通项)分解,然后重新组合,使之能消去一些项,最终达到求和的目的.题型1 求数列的通项公式(一)观察法就是观察数列的特征,横向看各项之间的关系结构,纵向看各项与项数n 的内在联系,从而归纳出数列的通项公式.例1 数列114,329,5316,7425,…的通项公式为( ) A .a n =(2n -1)·n (n +1)2B .a n =(2n -1)+n (n +1)2C .a n =(2n +1)+n (n +1)2D .a n =4n +1(n +1)2解析:114=1+14,329=3+29,5316=5+316,…, ∴a n =(2n -1)+n (n +1)2. 答案:B(二)公式法等差数列与等比数列是两种常见且重要的数列,所谓公式法就是先分析后项与前项的差或比是否符合等差、等比数列的定义,然后用等差、等比数列的通项公式表示它.例2 已知数列{a n }为无穷数列,若a n -1+a n +1=2a n (n ≥2且n ∈N *),且a 2=4,a 6=8,求通项a n .解析:∵a n -1+a n +1=2a n ,∴a n -1,a n ,a n +1成等差数列.又∵n ≥2且n ∈N *,∴数列{a n }为等差数列,设首项为a 1,公差为d .由⎩⎨⎧a 2=4,a 6=8,可得⎩⎨⎧a 1=3,d =1,∴通项a n =3+(n -1)×1=n +2.(三)利用a n 与S n 的关系前n 项和关系式有两种形式:一种是S n 与n 的关系式,记为S n =f (n ),它可由公式a n =⎩⎨⎧S 1,n =1,S n -S n -1,n ≥2直接求出通项a n ,但要注意n =1与n ≥2两种情况能否统一;另一种是S n 与a n 的关系式,记为f (a n ,S n )=0,求它的通项公式a n .例3 已知数列{a n }的前n 项和为S n ,且a n =5S n -3,求数列{a n }的通项公式.解析:当n =1时,∵a 1=5a 1-3,∴a 1=34, 当n ≥2时,∵a n =5S n -3,∴a n -1=5S n -1-3,∴a n -a n -1=5(S n -S n -1).即a n -a n -1=5a n ,a n a n -1=-14, ∴{a n }是首项a 1=34,公比q =-14的等比数列. ∴a n =a 1q n -1=34⎝ ⎛⎭⎪⎫-14n -1(n ∈N *). (四)累加法、累乘法有些数列,虽然不是等差数列或等比数列,但是它的后项与前项的差或商具有一定的规律性,这时,可考虑利用累加或累乘法,结合等差、等比数列的知识解决.例4 (1)已知a 1=1,a n +1a n =n +2n,求a n ; (2)已知数列{a n }中,a 1=1,a n =a n -1+n (n ≥2),求数列{a n }的通项公式.解析:(1)当n ≥2时,a n =a 1·a 2a 1·a 3a 2·…·a n a n -1=1×31×42×53×…×n +1n -1=n (n +1)2. 而a 1=1也适合上式.故{a n }的通项公式a n =12n (n +1)(n ∈N *). (2)∵a n =a n -1+n (n ≥2),∴a 2-a 1=2,a 3-a 2=3,a 4-a 3=4,a 5-a 4=5,…,a n -a n -1=n .将这n -1个等式两边分别相加得a n -a 1=2+3+…+n ,∴a n =1+2+3+…+n =n (n +1)2(n ≥2). 当n =1时,a 1=1×(1+1)2=1成立. ∴a n =n (n +1)2(n ∈N *). (五)构造法有些数列直观上不符合以上各种形式,这时,可对其结构进行适当变形,以利于使用以上各类方法.形如已知a 1,a n +1=pa n +q (p 、q 为常数)形式均可用构造等比数列法,即a n +1+x =p (a n +x ),{a n +x }为等比数列,或a n +2-a n +1=p (a n +1-a n ),{a n +1-a n }为等比数列.例 5 设数列{a n }是首项为1的正项数列,且a n +1-a n +a n +1·a n =0(n ∈N *),求{a n }的通项.解析:∵a n +1-a n +a n +1·a n =0.∴1a n +1-1a n=1. 又1a 1=1,∴⎩⎨⎧⎭⎬⎫1a n 是首项为1,公差为1的等差数列, 故1a n =n ,∴a n =1n(n ∈N *). 若数列{a n }满足a 1=1,a n +1=12a n +1,求a n .分析:根据递推公式求出前几项,再观察规律,猜想通项公式,有时比较困难.可变换递推公式,利用构造等差或等比数列的技巧,从而求通项公式.解析:方法一 ∵a n +1=12a n +1, ∴a n +2=12a n +1+1, 两式相减得:a n +2-a n +1=12(a n +1-a n ), 令b n =a n +1-a n (n =1,2,3,…),则b 1=a 2-a 1=32-1=12,b n +1=12b n , ∴数列{b n }是以12为首项,12为公比的等比数列. ∴a n =a 1+(a 2-a 1)+(a 3-a 2)+…+(a n -a n -1)=a 1+b 1+b 2+…+b n -1=1+12⎣⎢⎢⎡⎦⎥⎥⎤1-⎝ ⎛⎭⎪⎫12n -11-12=2-⎝ ⎛⎭⎪⎫12n -1(n ∈N *). 方法二 设a n +1-A =12(a n -A ), 则a n +1=12a n -12A +A , 根据a n +1=12a n +1可得:-12A +A =1,即A =2, ∴a n +1-2=12(a n -2).令b n =a n -2,则b 1=a 1-2=-1,b n +1=12b n , ∴数列{b n }是以-1为首项,12为公比的等比数列. ∵b n =b 1·q n -1=(-1)·⎝ ⎛⎭⎪⎫12n -1, ∴a n =2+b n =2-⎝ ⎛⎭⎪⎫12n -1(n ∈N *). 题型2 数列求和的方法数列中求前n 项和是数列运算的重要内容,高考题中涉及此部分与通项的综合问题,对于等差数列与等比数列可依据公式求其和,对于某些具有特殊结构的非等差、等比数列可转化为利用等差或等比数列前n 项和公式能求和的形式,常用方法有公式法、分组法、裂项法、错位相减法等.要对通项进行深入研究,找出规律,确定恰当的解题方法.例7 等差数列{a n }中,a 1=3,公差d =2,S n 为前n 项和,求1S 1+1S 2+…+1S n. 解析:∵等差数列{a n }的首项a 1=3,公差d =2,∴前n 项和S n =na 1+n (n -1)2d =3n +n (n -1)2×2 =n 2+2n(n ∈N *),∴1S n =1n 2+2n =1n (n +2)=12⎝ ⎛⎭⎪⎪⎫1n -1n +2, ∴1S 1+1S 2+…+1S n=12[(1-13)+(12-14)+(13-15)+…+(1n -1-1n +1)+(1n -1n +2)]=34-2n +32(n +1)(n +2). 例8 设数列{a n }满足a 1+3a 2+32a 3+…+3n -1a n =n 3(n ∈N *). (1)求数列{a n }的通项;(2)设b n =na n ,求数列{b n }的前n 项和S n .解析:(1)∵a 1+3a 2+32a 3+…+3n -1a n =n 3,①∴当n ≥2时,a 1+3a 2+32a 3+…+3n -2a n -1=n -13,②由①-②得3n -1a n =13,∴a n =13n ,在①中,令n =1,得a 1=13,∴数列{a n }的通项公式a n =13n (n ∈N *).(2)∵b n =na n =n ·3n ,∴S n =3+2×32+3×33+…+n ×3n ,③∴3S n =32+2×33+3×34+…+n ×3n +1.④由④-③得2S n =n ×3n +1-(3+32+33+…+3n )=n ×3n +1-3(1-3n)1-3,∴S n =(2n -1)×3n +14+34. 题型3 数列的应用问题例9 (2013·广东卷)设数列{a n }的前n 项和为S n .已知a 1=1,2S n n=a n +1-13n 2-n -23,n ∈N *. (1)求a 2的值;(2)求数列{a n }的通项公式.(3)证明:对一切正整数n ,有1a 1+1a 2+…+1a n <74. (1)解析:依题意,2S 1=a 2-13-1-23,又S 1=a 1=1,所以a 2=4. (2)解析:当n ≥2时,2S n =na n +1-13n 3-n 2-23n , 2S n -1=(n -1)a n -13(n -1)3-(n -1)2-23(n -1), 两式相减得2a n =na n +1-(n -1)a n -13(3n 2-3n +1)-(2n -1)-23, 整理得(n +1)a n =na n +1-n (n +1),即a n +1n +1-a n n=1,又a 22-a 11=1, 故数列⎩⎨⎧⎭⎬⎫a n n 是首项为a 11=1,公差为1的等差数列,所以a n n =1+(n -1)×1=n ,当n =1时,上式显然成立.所以a n =n 2(n ∈N *).(3)证明:当n =1时,1a 1=1<74;当n =2时,1a 1+1a 2=1+14=54<74; 当n ≥3时,1a n =1n 2<1(n -1)n =1n -1-1n, 此时,1a 1+1a 2+…+1a n =1+14+132+142+…+1n 2<1+14+⎝ ⎛⎭⎪⎫12-13+⎝ ⎛⎭⎪⎫13-14+…+⎝ ⎛⎭⎪⎪⎫1n -1-1n =1+14+12-1n =74-1n <74, 综上,对一切正整数n ,有1a 1+1a 2+…+1a n <74. 例10 夏季高山上的温度从山脚起,每升高100 m ,降低0.7 ℃,已知山顶处的温度是14.8 ℃,山脚处的温度是26 ℃,问此山相对于山脚处的高度是多少?解析:∵每升高100 m 温度降低0.7 ℃,∴该处温度的变化是一个等差数列问题.设山脚温度为首项a 1=26,山顶温度为末项a n =14.8,∴26+(n -1)(-0.7)=14.8,解得n =17.此山的高度为(17-1)×100=1 600(m).故此山相对于山脚处的高度是1 600 m.。
必修五数学第二章知识点

必修五数学第二章知识点必修五数学第二章知识点11、数列概念①数列是一种特殊的函数。
其特殊性主要表现在其定义域和值域上。
数列可以看作一个定义域为正整数集Nx或其有限子集{1,2,3,…,n}的函数,其中的{1,2,3,…,n}不能省略。
②用函数的观点认识数列是重要的思想方法,一般情况下函数有三种表示方法,数列也不例外,通常也有三种表示方法:a、列表法;b、图像法;c、解析法。
其中解析法包括以通项公式给出数列和以递推公式给出数列。
③函数不一定有解析式,同样数列也并非都有通项公式。
等差数列1、等差数列通项公式an=a1+(n—1)dn=1时a1=S1n≥2时an=Sn—Sn—1an=kn+b(k,b为常数)推导过程:an=dn+a1—d令d=k,a1—d=b 则得到an=kn+b2、等差中项由三个数a,A,b组成的等差数列可以堪称最简单的等差数列。
这时,A叫做a与b的等差中项(arithmeticmean)。
有关系:A=(a+b)÷23、前n项和倒序相加法推导前n项和公式:Sn=a1+a2+a3+·····+an=a1+(a1+d)+(a1+2d)+······+[a1+(n—1)d]①Sn=an+an—1+an—2+······+a1=an+(an—d)+(an—2d)+······+[an—(n—1)d]②由①+②得2Sn=(a1+an)+(a1+an)+······+(a1+an)(n 个)=n(a1+an)∴Sn=n(a1+an)÷2等差数列的前n项和等于首末两项的和与项数乘积的一半:Sn=n(a1+an)÷2=na1+n(n—1)d÷2Sn=dn2÷2+n(a1—d÷2)亦可得a1=2sn÷n—an=[sn—n(n—1)d÷2]÷nan=2sn÷n—a1有趣的是S2n—1=(2n—1)an,S2n+1=(2n+1)an+14、等差数列性质一、任意两项am,an的关系为:an=am+(n—m)d它可以看作等差数列广义的通项公式。
高中数学必修五-知识点总结【经典】

第二章:数列知识要点一、数列的概念1、数列的概念:一般地,按一定次序排列成一列数叫做数列,数列中的每一个数叫做这个数列的项,数列的一般形式可以写成,简记为数列,其中第一项也成为首项;是数列的第项,也叫做数列的通项.数列可看作是定义域为正整数集(或它的子集)的函数,当自变量从小到大取值时,该函数对应的一列函数值就是这个数列.2、数列的分类:按数列中项的多数分为:(1)有穷数列:数列中的项为有限个,即项数有限;(2)无穷数列:数列中的项为无限个,即项数无限.3、通项公式:如果数列的第项与项数之间的函数关系可以用一个式子表示成,那么这个式子就叫做这个数列的通项公式,数列的通项公式就是相应函数的解析式.4、数列的函数特征:一般地,一个数列,如果从第二项起,每一项都大于它前面的一项,即,那么这个数列叫做递增数列;如果从第二项起,每一项都小于它前面的一项,即,那么这个数列叫做递减数列;如果数列的各项都相等,那么这个数列叫做常数列.5、递推公式:某些数列相邻的两项(或几项)有关系,这个关系用一个公式来表示,叫做递推公式.二、等差数列1、等差数列的概念:123,,,,,n a a a a{}1n a n N *{}na n ()n a f n ={}n a 1n n a a +>1n n a a +<{}n a如果一个数列从第二项起,每一项与前一项的差是同一个常数,那么这个数列久叫做等差数列,这个常数叫做等差数列的公差.即(常数),这也是证明或判断一个数列是否为等差数列的依据.2、等差数列的通项公式:设等差数列的首项为,公差为,则通项公式为:.3、等差中项:(1)若成等差数列,则叫做与的等差中项,且;(2)若数列为等差数列,则成等差数列,即是与的等差中项,且;反之若数列满足,则数列是等差数列.4、等差数列的性质:(1)等差数列中,若则,若则;(2)若数列和均为等差数列,则数列也为等差数列;(3)等差数列的公差为,则为递增数列,为递减数列,为常数列.5、等差数列的前n 项和:(1)数列的前n 项和=;(2)数列的通项与前n 项和的关系:(3)设等差数列的首项为公差为,则前n 项和6、等差数列前n 和的性质:(1)等差数列中,连续m 项的和仍组成等差数列,即,仍为等差数列(即成等差数列);(2)等差数列的前n 项和当时,可看作关于n 的二次函数,且不含常数项;1n n a a d +-={}n a 1a d ()()()11,n m a a n d a n m d n m N +=+-=+-∈、a b、、A a b =2a A +12,,n n n a a a ++1n +a 2n a +21=2n n n a a a +++{}n{}n a (),m n p q m n p q N ++=+∈、、、m n pq a a a a +=+2m n p =,2m n p a a a +={a }n b {}n n a b ±{}n a d >{}0n a <⇔d =nS {}n a n S ()1231,n n a a a a a n N -++++++∈ {}n a n S 11,1.,2n n n n a S S n -=⎧=⎨-≥⎩{}n 1,a d ()()111=.22n n n a a n n S na d +-=+{}n a 12122,,m m m m a a a a a a ++++++++ 21223m m a a a +++++ 232,,,m m m m m S S S S S -- {}na ()2111==,222n n n d d S na d n a n -⎛⎫++- ⎪⎝⎭0d ≠n S(3)若等差数列共有2n+1(奇数)项,则若等差数列共有2n (偶数)项,则7、等差数列前n 项和的最值问题:设等差数列的首项为公差为,则(1)(即首正递减)时,有最大值且的最大值为所有非负数项之和;(2)(即首负递增)时,有最小值且的最小值为所有非正数项之和.三、等比数列1、等比数列的概念:如果一个数列从第二项起,每一项与前一项的比是同一个不为零的常数,那么这个数列就叫做等比数列,这个常数叫做等比数列的公比,公比通常用字母表示().即,这也是证明或判断一个数列是否为等比数列的依据.2、等比数列的通项公式:设等比数列的首项为,公比为,则通项公式为:.3、等比中项:(1)若成等比数列,则叫做与的等比中项,且;(2)若数列为等比数列,则成等比数列,即是与的等比中项,且;反之若数列满足,则数列是等比数列.4、等比数列的性质:(1)等比数列中,若则,若则;(2)若数列和均为等比数列,则数列也为等比数列;(3)等比数列的首项为,公比为,则为递增数列,为递减数列,为常数列.5、等比数列的前n 项和:(1)数列的前n 项和=;(2)数列的通项与前n 项和的关系:()11==,n S n S S a S n ++-奇奇偶偶中间项且{}n a 1==.n n S a S S nd S a +-偶奇偶奇且n S {}n 1,a d 100a d ><且n S 100a d <>且n S q 0q ≠()1n na q q a +=为非零常数{}n a 1a q ()11,,n n m n m a a q a q n m n m N --+==≥∈、a b、、A a b 2=A ab 12,,n n n a a a ++1n +2n a +212=n n a a ++⋅{}n a {}n a (),m n p q m n p q N ++=+∈、、、m n p q a a a a ⋅=⋅2m n p +=,2m n pa a a ⋅={a }nb {}n n a b ⋅{}na 1a q 1100101a a q q ><⎧⎧⎨><<⎩或{}1100011n a a a q q ><⎧⇔⎨⎨<<>⎩⎩或{}1n q a =⇔{}na n S ()1231,n n a a a a a n N -++++++∈ {}n a n 11,1.,2n n n S n a S S n -=⎧=⎨-≥⎩(3)设等比数列的首项为,公比为,则由等比数列的通项公式及前n 项和公式可知,已知中任意三个,便可建方程组求出另外两个.6、等比数列的前n 项和性质:设等比数列中,首项为,公比为,则(1)连续m 项的和仍组成等比数列,即,仍为等比数列(即成等差数列);(2)当时,,设,则.四、递推数列求通项的方法总结1、递推数列的概念:一般地,把数列的若干连续项之间的关系叫做递推关系,把表达递推关系的式子叫做递推公式,而把由递推公式和初始条件给出的数列叫做递推数列.2、两个恒等式:对于任意的数列恒有:(1)(2)3、递推数列的类型以及求通项方法总结:类型一(公式法):已知(即)求,用作差法:类型二(累加法):已知:数列的首项,且,求.给递推公式中的n 依次取1,2,3,……,n-1,可得到下面n-1个式子:利用公式可得:{}n a 1a ()0q q ≠()11,1.1,11nn na q S a q q q =⎧⎪=-⎨≠⎪-⎩1,,,,n n a q n a S {}n a 1a ()0q q ≠12122,,m m m m a a a a a a ++++++++ 21223m m a a a +++++ 23,,,m m m m m S S S S S -- 1q ≠()()11111111111111n nn n n a q a a a a a S q q q q q q q q q -==⋅-=-⋅=⋅-------11a t q =-n n S tqt =-{}n a ()()()()12132431n n n a a a a a a a a a a -=+-+-+-++- ()23411231,0,n n n n a a a aa a a n N a a a a +-=⨯⨯⨯⨯⨯≠∈ S 12()na a a f n +++= n a {11,(1),(2)n n n S n a S S n -==-≥{}na 1a ()()1,n n a a f n n N ++-=∈n a 通项()()1,n n a a f n n N ++-=∈()()()()21324311,2,3,,1.n n a a f a a f a a f a a f n --=-=-=-=- ()()()()12132431n n n a a a a a a a a a a -=+-+-+-++- ()()()()11231.n a a f f f f n =+++++-类型三(累乘法):已知:数列的首项,且,求.给递推公式中的n 一次取1,2,3,……,n-1,可得到下面n-1个式子:利用公式可得:类型四(构造法):形如、(为常数)的递推数列都可以用待定系数法转化为公比为的等比数列后,再求。
高中数学必修五第二章数列知识复习.doc

【知识复习】1、相关概念:②数列的通项公式:如杲数列{a n}的第n项為与n Z间的关系可以用一个公式来表示,这个公式就叫做数列的通项公式。
③数列的递推公式:如果己知数列{弭的第一项(或前n项,口任一项気与它的前一项时(或前n项)间的关系可以用一个式子来表示,那么这个公式就叫做这个数列的递推公式。
④若数列{a」的前n项和为h则2、等差与等比数列等差数列等比数列如果一个数列从第2项起,每一项与它的前一如果一个数列从第2项起,每一项与它的前一项的项的并等于同一个常数,这个数列就叫做等丼比等于同一个常数,这个数列就叫做等比数列。
即定义数列。
即a-anFd,公差d可为正数、负数和零色-%:q,公比q是一个不等于零的常数。
通项公式爲F+S_l)d (来源:定义,迭加,迭代)a n=a m+(n-m)d(证明)a n = a}q n~x (% H 0, a H °)= 0捫叽北0, q H 0)(定义迭乘,迭代)若“ A, b成等差数列,那么A叫做a与b的若a,G, b成等比数列,那么G叫做a与b的等比中项等差中项,lLA~a + b中项, H G2=abo (a, b 是同号)2心+Q”)S/ 2na x(q = l)前n项S n ―W) (E)和或S〃 5 -(错位相减)2 (倒序和加)(1)⑷+% =°2 +勺1 =…二% +匕-冲=…(1) W = a屮' =…=a#十' =…(2)m + 兀=p + q(m,n,p,q w NJ(2)m + n = p + q{m.n.p.q e N+)o 几 +久=ci a to Qg•么— ci.. 5性质m n p q m j? n p q(3)若{aj为等差数列,则a n, a2n, a和也为(3)若{aj为等比数列,则縮a2n, asn也为等比等差数列数列。
(4)若{an}为等差数列,则Sn,S2n-S n,S3n-S2n(4)若{aj为等比数列,则Sn,S2n-S n, S3n-S2n也也为等斧数列为等比数列。
必修五第二章数列归纳总结

必修五第二章数列归纳总结一、数列1.数列的定义数列是按一定次序排成的一列数,从函数观点看,数列是定义域为正整数集(或它的有限子集)的函数f (n ),当自变量n 从1开始依次取正整数时所对应的一列函数值f (1),f (2),…,f (n ),….通常用an 代替f (n ).于是数列的一般形式为a 1,a 2,…,an ,…,简记为{an }.一、数列1.数列的定义数列是按一定次序排成的一列数,从函数观点看,数列是定义域为正整数集(或它的有限子集)的函数f (n ),当自变量n 从1开始依次取正整数时所对应的一列函数值f (1),f (2),…,f (n ),….通常用an 代替f (n ).于是数列的一般形式为a 1,a 2,…,an ,…,简记为{an }.3.a n 与S n 的关系设S n =a 1+a 2+a 3+…+a n ,则a n =⎩⎪⎨⎪⎧S 1 (n =1),S n -S n -1(n ≥2). 二、等差数列1.等差数列的定义如果一个数列从第二项起,每一项与它的前一项的差都等于同一个常数,这样的数列叫做等差数列.2.等差中项如果三数a 、A 、b 成等差数列,则A 叫做a 和b 的等差中项,∴A =a +b 2. 3.(1)通项公式a n =a 1+(n -1)d .推导方法:累加法a n =(a n -a n -1)+(a n -1-a n -2)+…+(a 2-a 1)+a 1.(2)前n 项和公式S n =n (a 1+a n )2=na 1+n (n -1)2d . 推导方法:倒序相加法.4.用函数观点认识等差数列(1)a n =nd +(a 1-d )是n 的一次函数.(2)S n =d 2n 2+(a 1-d 2)n ,是关于n 的常数项为零的二次函数. 5.等差数列的判定方法(1)定义法:an +1-an =d (常数)(n ∈N *)⇔{an }是等差数列;(2)中项公式法:2an +1=an +an +2(n ∈N *)⇔{an }是等差数列;(3)通项公式法:an =kn +b (k ,b 是常数)(n ∈N *)⇔{an }是等差数列;(4)前n 项和公式法:Sn =An 2+Bn (A 、B 是常数)(n ∈N *)⇔{an }是等差数列.(5){a n }是等差数列⇔{S n n}是等差数列 6.等差数列的性质(1)下标和与项的和的关系在等差数列中,若p +q =m +n ,则有ap +aq =am +an ;若2m =p +q ,则有2am =ap +aq ,(p ,q ,m ,n ∈N*).(2)任意两项的关系在等差数列{a n }中,m 、n ∈N *,则a m -a n =(m -n )d 或a m =a n +(m -n )d 或a m -a n m -n=d . (3)在等差数列中,等距离取出若干项也构成一个等差数列,即an ,an +m ,an +2m ,…为等差数列,公差为md .等差数列的依次n 项的和也构成一个等差数列,即Sn ,S 2n -Sn ,S 3n -S 2n ,……为等差数列,公差为n 2d .即下标成等差的项成等差数列,下标和成等差的具有相同构成规律的项的和成等差数列.(4)设等差数列{an }的公差为d ,那么d >0⇔{an }是递增数列;d <0⇔{an }是递减数列;d =0⇔{an }是常数数列.(5)①数列{λa n +b }仍为等差数列,公差为λd .若{b n },{a n }都是等差数列,则{a n ±b n }仍为等差数列,{λ1a n +λ2b n }(λ1,λ2为常数)也是等差数列.②项数为n 的等差数列中,n 为奇数时,设m =n +12,则S 奇-S 偶=a m ,S 奇S 偶=n +1n -1,S n=na 中=na m .n 为偶数时,S 偶-S 奇=n 2d . ③若{a n }与{b n }为等差数列,且前n 项和分别为S n 与S ′n ,则a m b m =S 2m -1S ′2m -1. ④等差数列{a n }中,若a n =m ,a m =n (m ≠n ),则a m +n =0.⑤若数列{a n }的前p 项和为S p =q ,前q 项和为S q =p (p ≠q ),则S p +q =-(p +q ). ⑥若数列{a n }的前n 项和为S n ,S p =S q (p ≠q ),则S p +q =0.三、等比数列1.等比数列的定义一般地,如果一个数列从第2项起,每一项与它的前一项的比等于同一个常数,这个数列就叫做等比数列.2.等比中项如果三个数a 、G 、b 成等比数列,那么G 叫做a 和b 的等比中项,即G 2=ab .3.等比数列的通项公式a n =a 1·q n -1(n ∈N *).推导方法:累乘法:a n a n -1·a n -1a n -2……a 3a 2·a 2a 1=q n -1. 4.等比数列的前n 项和当q =1时,S n =na 1,当q ≠1时.S n =a 1(1-q n )1-q =a 1-a n q 1-q. 推导方法:乘公比、错位相减法.5.等比数列的判定方法(1)an +1=anq (q 是不为0的常数,n ∈N *,an ≠0)⇔{an }是等比数列.(2)an =cqn -1(c ,q 均是不为0的常数,n ∈N *)⇔{an }是等比数列.(3)an +12=an ·an +2(an ≠0,n ∈N *)⇔{an }是等比数列.(4)Sn =A ·qn -A (A 、q 为常数且A ≠0,q ≠0,1)⇔{an }是公比不为1的等比数列.6.等比数列的主要性质(1)下标和与项的积的关系在等比数列{an }中,若m 、n 、p 、q ∈N *且m +n =p +q ,则am ·an =ap ·aq .特别地,若2m =p +q ,则ap ·aq =am 2;a 1an =a 2an -1=a 3an -2=….(2)任意两项的关系若{a n }为等比数列,则a m a n=q m -n 或a m =a n ·q m -n (m 、n ∈N *). (3)等间隔的k 项和(或积)仍成等比数列.例如:{a n }是等比数列,则①a 1,a 3,a 5,…,a 2n -1;②a 1+a 2,a 2+a 3,a 3+a 4,…;③a 1a 2,a 2a 3,a 3a 4,…;④a 1+a 2,a 3+a 4,a 5+a 6……均成等比数列.(4)等比数列{a n }的单调性当⎩⎨⎧ a 1>0q >1,或⎩⎨⎧ a 1<00<q <1时,{a n }为递增数列;当⎩⎨⎧ a 1>00<q <1或⎩⎨⎧ a 1<0q >1时,{a n }为递减数列. (5)①{a n }是等比数列⇒{c ·a n }是等比数列(c ≠0).②{a n }、{b n }均为等比数列⇒{a n ·b n }、{a n b n}仍是等比数列. ③若{a n }是等比数列,则{a n 2}、{a n }(a n >0)、{1a n}、{|a n |}均为等比数列. ④非零常数列既是等差数列,也是等比数列.⑤若{an }是等差数列,则{ba n }是等比数列.若{an }是正项等比数列,则{lg a n }是等差数列.误区警示1.数列与数集应予区别,数列中的数排列有序,数集中的元素无序;数列中的数可重复出现,数集中的元素互异.2.并不是每一个数列都有通项公式,给出前n 项时,写出的通项公式可以不止一个.3.已知{a n }的前n 项和S n 求a n 时,用a n =⎩⎪⎨⎪⎧ S 1 (n =1)S n -S n -1(n ≥2)求解应注意分类讨论. a n =S n -S n -1是在n ≥2条件下求出的,应检验a 1是否适合.如果适合,则合写在一块,如果不适合,则分段表示.千万注意用a n =S n -S n -1判断数列{a n }是否为等差(或等比)数列时,不要忘记验证a 1是否满足.如:S n =n 2+n 时,{a n }是等差数列.S n =n 2+n +1时,{a n }不是等差数列.S n =2n -1时,{a n }是等比数列.S n =2n +1时,{a n }不是等比数列.4.在讨论等差数列{an }的前n 项和Sn 的最值时,不要忽视n 是整数的条件及含0项的情形.如:在等差数列{an }中,已知a 1=20,前n 项和为S n ,且如S 10=S 15,求当n 取何值时,S n 有最大值,并求出它的最大值.取最大值的应为S 12和S 13.5.G 是a 、b 的等比中项⇒/⇐/ G =ab .6.在应用等比数列的前n 项和公式时,一定要对q =1与q ≠1进行分类讨论.7.等比数列中隐含着各项不为零、公比不为零,项与公比的符号有着密切的联系,解题时应特别注意.。
(推荐)人教版高一数学必修5-第二章数列总结

人教版高一数学必修5第二章数列总结1、数列的基本概念(1)定义:按照一定的次序排列的一列数叫做数列.(2)通项公式:如果数列{a n }的第n 项a n 与n 之间的函数关系可以用一个公式表示,这个公式就叫做这个数列的通项公式.(3)递推公式:如果已知数列{a n }的第一项(或前几项),且任何一项a n 与它前一项a n -1(或前几项)间的关系可用一个公式来表示,那么这个公式就叫做这个数列的递推公式. 通项公式与递推公式,是给出一个数列的两种主要方法.2、主要公式(1)通项公式a n 与前n 项和公式S n 间的关系:a n =⎩⎪⎨⎪⎧S 1 n =1S n -S n -1 n ≥2. (2)等差数列 a n =a 1+(n -1)d =a m +(n -m )d . S n =12n (a 1+a n ),S n =na 1+12n (n -1)d .A =a +b 2(等差中项). (3)等比数列a n =a 1q n -1,a n =a m ·q n -m . S n =⎩⎪⎨⎪⎧ na 1 q =1a 1-a n q 1-q=a 11-q n 1-q q ≠1.G =±ab (等比中项).3.主要性质(1)若m +n =p +q (m 、n 、p 、q ∈N *),在等差数列{a n }中有:a m +a n =a p +a q ;在等比数列{a n }中有:a m ·a n =a p ·a q .(2)等差(比)数列依次k 项之和仍然成等差(比).专题一 数列的通项公式的求法1.观察法 根据下面数列的前几项,写出数列的一个通项公式.(1)1,1,57,715,931,…; 2.定义法等差数列{a n }是递增数列,前n 项和为S n ,且 a 1,a 3,a 9成等比数列,S 5=a 25.求数列{a n }的通项公式.3.前n 项和法(1)已知数列{a n }的前n 项和S n =n 2+3n +1,求通项 a n ;(2)已知数列{a n}的前n项和S n=2n+2,求通项a n. 4.累加法已知{a n}中,a1=1,且a n+1-a n=3n(n∈N*),求通项a n. 5.累乘法已知数列{a n },a 1=13,前n 项和S n 与a n 的关系是S n =n (2n -1)a n ,求通项a n . 6.辅助数列法已知数列{a n }满足a 1=1,a n +1=3a n +2(n ∈N *).求数列{a n }的通项公式.7.倒数法已知数列{a n }中,a 1=1,a n +1=a n a n +1(n ∈N *).求通项a n . 专题二 数列的前n 项和的求法1.分组转化求和法如果一个数列的每一项是由几个独立的项组合而成,并且各独立项也可组成等差或等比数列,则该数列的前n 项和可考虑拆项后利用公式求解.求和:S n =112+214+318+…+(n +12n ). 2.裂项求和法对于裂项后明显有能够相消的项的一类数列,在求和时常用“裂项法”,分式的求和多利用此法.可用待定系数法对通项公式进行拆项,相消时应注意消去项的规律,即消去哪些项,保留哪些项,常见的拆项公式有:(1)1n n +k =1k ·(1n -1n +k); (2)若{a n }为等差数列,公差为d ,则1a n ·a n +1=1d (1a n -1a n +1); (3)1n +1+n =n +1-n 等.3.错位相减法若数列{a n }为等差数列,数列{b n }是等比数列,由这两个数列的对应项乘积组成的新数列为{a n b n },当求该数列的前n 项的和时,常常采用将{a n b n }的各项乘以等比数列{b n }的公比q ,然后错位一项与{a n b n }的同次项对应相减,即可转化为特殊数列的求和,所以这种数列求和的方法称为错位相减法.已知数列{a n }中,a 1=3,点(a n ,a n +1)在直线y =x +2上.(1)求数列{a n }的通项公式;(2)若b n =a n ·3n ,求数列{b n }的前n 项和T n .4.分段求和法如果一个数列是由各自具有不同特点的两段构成,则可考虑利用分段求和.已知数列{a n }的前n 项和为S n ,且a n +S n =1(n ∈N *).(1)求数列{a n }的通项公式;(2)若数列{b n }满足b n =3+log 4a n ,设T n =|b 1|+|b 2|+…+|b n |,求T n .附注:常用结论1)1+2+3+...+n =2) 1+3+5+...+(2n-1) =3)三、等差、等比数列的对比(1)判断数列的常用方法看数列是不是等差数列有以下三种方法:①②2()③(为常数).看数列是不是等比数列有以下四种方法:①②(,)③(为非零常数).④正数列{}成等比的充要条件是数列{}()成等比数列.(2)等差数列与等比数列对比小结:等差数列等比数列定义公式1.2.1.2.性质1.,称为与的等差中项2.若(、、、1.,称为与的等比中项2.若(、、、),则),则3.,,成等差数列4. 3.,,成等比数列4. ,(3)在等差数列{}中,有关Sn 的最值问题:1),时,有最大值;,时,有最小值;2)最值的求法:①若已知,可用二次函数最值的求法();②若已知,则最值时的值()可如下确定或。
必修5 第二章 数列 期末复习(知识点及题型全)

必修5 第二章《 数 列 》期末复习制卷:王小凤 学生姓名【知识梳理】一.等差数列与等比数列二.数列通项公式的求法1.根据n S ,利用公式11(1)(1)n n n S n a S S n -=⎧⎪=⎨->⎪⎩求通项n a 。
注.已知n S 求n a ,应分1=n 及2≥n 两步,最后验证1a 是否满足后面的n a .2.根据数列的递推关系,叠加法、累乘法求通项n a ,其要点是: (1)121321()()()n n n a a a a a a a a -=+-+-++-L ;(2)321121(2)n n n a a a a a n a a a -=⋅⋅⋅⋅≥L 3.构造新的等差、等比数列,转化法求通项n a 。
三.数列求和1.利用等差、等比数列的公式求和; 2.分组求和法;3.错位相减求和,适用于由一个等差数列和一个等比数列对应项乘积组成的数列; 4.裂项相消求和,它的基本思想是设法将数列的每一项拆成两项(裂项),并使它们在相加时除了首尾各有一项或少数几项外,其余各项都能前后相消.常见裂项公式:(1)1111()()n n k k n n k =-++ (2)11()n k n kn k n =+-++5.倒序相加法求和。
四.n S 的最值问题:在等差数列{}n a 中,有关n S 的最值问题——常用邻项变号法求解:(1)当0,01<>d a 时,满足⎩⎨⎧≤≥+001m m a a 的项数m 使得mS 取最大值.(2)当 0,01><d a 时,满足⎩⎨⎧≥≤+001m m a a 的项数m 使得mS 取最小值。
【考点题型】考点一:通项公式、递推公式的基本应用1.下列四个数中,哪一个是数列{(1)n n +}中的一项( ) A .380 B .39 C .35 D .232.已知数列{}n a ,13a =,26a =,且21n n n a a a ++=-,则数列的第五项为( ) A .6 B .3- C .12- D .6-等差数列 等比数列定义1n n a a d --=(2n ≥)通项公式 d n a a n )1(1-+=,(),()n m a a n m d n m =+->, 中项如果,,a A b 成等差数列,那么A 叫做a 与b 的等差中项,且2a bA +=.三个数成等差数列的设法: .如果,,a G b 成等比数列,那么G 叫做a 与b 的等比中项,且 三个数成等比数列的设法:aq,a ,aq 前n 项和 1()2n n n a a S +=或1(1)2n n n S na d -=+当1q =时:n S = 当1q ≠时:n S =性质若q p n m +=+,则 m n p q a a a a +=+;若2m p q =+,则 *(,,,)p q n m N ∈若q p n m +=+,则2*2,,(,,,)m p q m p q a a a p q n m N =+=⋅∈若则有n S 、2n n S S -、32n n S S -为等差数列n S 、2n n S S -、32n n S S -为等比数列 函数思想 看数列12221()()22n n a dn a d An B d ds n a n An Bn =+-=+=+-=+111(1)11nn n n n n a a q Aq qa as q A Aq q q q===-=-≠--判定方法(1)定义法:证明)(*1N n a a n n ∈-+为一个常数; (2)等差中项:证明*11(2N n a a a n n n∈+=+-,)2≥n(3)通项公式:(,n a kn b k b =+为常数)(*N∈n )(4)2ns An Bn =+(,A B 为常数)(∈*n N )(1)定义法:证明)(*1N n a a nn ∈+为一个常数(2)中项:证明21nn a a -=*1(,2)n a n N n +⋅∈≥ (3)通项公式:(,nn a cq c q =均是不为0常数)(4)n ns Aq =A -(,A q 为常数,≠≠A 0,q 0,1)考点二:等差、等比数列的基本运算3.若等差数列{}n a 的前三项依次为1a -、1a +、23a +,则2011是这个数列的( ) A .第1006项B .第1007项C .第1008项D .第1009项4.已知等差数列{}n a 满足244a a +=,3510a a +=,则它的前10项的和10S =( ) A .138B .135C .95D .235.在等比数列}{n a 中,,8,1641=-=a a 则=7a ( )A .4-B .4±C .2-D .2±6.已知,,,a b c d 是公比为2的等比数列,则dc ba ++22= ( ) A .1 B .21 C .41 D .817.在等比数列{}n a 中,485756=-=+a a a a ,则10S 等于( ) A .1023 B .1024 C .511 D .5128.等差数列{}n a 的公差不为零,首项1a =1,2a 是1a 和5a 的等比中项,则数列的前10项之和是( )A .90B .100C .145D .1909.在3和9之间插入两个正数,使前三个数成等比数列,后三个数成等差数列,则二数之和为( )A .2113B .1114C .2110 D .21910.已知某等差数列共有10项,其奇数项之和为15,偶数项之和为30,则其公差为( )A .5B .4C .3D . 2考点三:等差、等比数列的性质的应用11.已知{}n a 是等差数列,且2381148a a a a +++=,则67a a += ( ) A .12 B .16 C .20 D .2412.已知等差数列{}n a 满足1231010a a a a ++++=L ,则有( ) A .11010a a +> B .21000a a +< C.3990a a += D .5151a = 13.设{}n a 是公差为正数的等差数列,若12315a a a ++=,12380a a a =,则111213a a a ++=( ) A .120 B .105 C .90 D .75 14.等差数列{}n a 中,1590S =,则8a = ( )A .3B .4C .6D .1215.若一等差数列前四项的和为124,后四项的和为156,又各项的和为350,则此数列共有 ( ) A .10项 B .11项 C .12项 D .13项16.等比数列{}n a 中,0n a >,965=a a ,则313233310log log log log a a a a +++⋅⋅⋅+=( ) A .12 B .10 C .8 D .32log 5+ 17.等差数列{}n a 中,121015a a a +++=L ,11122020a a a +++=L ,则212230a a a +++=L ( )A .15B .25C .35D .4518.已知等比数列前10项的和为10,前20项的和为30,那么前30项的和为( ) A .60 B .70 C .90 D .126考点四:等差、等比数列的实际应用19.夏季高山上温度从山脚起每升高100米,降低0.7℃,已知山顶的温度是14.1℃,山脚的温度是26℃,则山的相对高度是( )A .1500B . 1600C .1700D .180020.某种细菌培养过程中,每半小时分裂一次(一次分裂为两个),经过4小时,这种细菌由1个可繁殖成( )个.A .64B .128C .256D .51221.一套共7册的书计划每2年出一册,若各册书的出版年份数之和为13979,则出齐这套书的年份是( )A .1997B . 1999C .2001D .2003考点五:等差数列前n 项和的最值22.等差数列{n a }中,39||||,a a =公差0,d <那么使前n 项和n S 最大的n 值为( ) A .5 B .6 C .5 或6 D .6或723.数列{a n }是首项为23,公差为整数的等差数列,且第六项为正,第七项为负. (1)求数列的公差d ; (2)求前n 项和S n 的最大值.考点六:数列的通项公式的求解24.已知数列{}n a 满足1n n a a n +=+,11=a ,求n a .25.已知数列{}n a 的前n 项和n n S 23+=,求n a .考点七:等差、等比数列的证明数列求和26.已知数列{a n }是首项为a 且公比不等于1的等比数列,S n 为其前n 项和,a 1,2a 7,3a 4成等差数列,求证:12S 3,S 6,S 12-S 6成等比数列.27.在数列{}n a 中,11a =,122n n n a a +=+. (Ⅰ)设12nn n a b -=.证明:数列{}n b 是等差数列; (提示:利用等差数列定义证明) (Ⅱ)求数列{}n a 的前n 项和n S . (提示:错项相减求和)28.等差数列{}n a 的各项均为正数,13a =,前n 项和为n S ,{}n b 为等比数列, 11b =,且2264,b S = 33960b S =.(1)求n a 与n b ; (2)求和:12111nS S S +++L .(提示:裂项相消求和) (注:将第26—28题解题过程写在试卷背面 )。
高三人教版必修五数学第二章知识点:数列的概念与简单表示法知识点总结

高三人教版必修五数学第二章知识点:数列的概念与简单表示法知识点总结伟大的数学家华罗庚曾经说过:“宇宙之大、粒子之微、火箭之速、化工之巧、地球之变、生活之迷、日月之繁,无处不用数学。
小编准备了高三人教版必修五数学第二章知识点,希望你喜欢。
1.数列的定义按一定次序排列的一列数叫做数列,数列中的每一个数都叫做数列的项.(1)从数列定义可以看出,数列的数是按一定次序排列的,如果组成数列的数相同而排列次序不同,那么它们就不是同一数列,例如数列1,2,3,4,5与数列5,4,3,2,1是不同的数列.(2)在数列的定义中并没有规定数列中的数必须不同,因此,在同一数列中可以出现多个相同的数字,如:-1的1次幂,2次幂,3次幂,4次幂,…构成数列:-1,1,-1,1,….(4)数列的项与它的项数是不同的,数列的项是指这个数列中的某一个确定的数,是一个函数值,也就是相当于f(n),而项数是指这个数在数列中的位置序号,它是自变量的值,相当于f(n)中的n.(5)次序对于数列来讲是十分重要的,有几个相同的数,由于它们的排列次序不同,构成的数列就不是一个相同的数列,显然数列与数集有本质的区别.如:2,3,4,5,6这5个数按不同的次序排列时,就会得到不同的数列,而{2,3,4,5,6}中元素不论按怎样的次序排列都是同一个集合.2.数列的分类(1)根据数列的项数多少可以对数列进行分类,分为有穷数列和无穷数列.在写数列时,对于有穷数列,要把末项写出,例如数列1,3,5,7,9,…,2n-1表示有穷数列,如果把数列写成1,3,5,7,9,…或1,3,5,7,9,…,2n-1,…,它就表示无穷数列.(2)按照项与项之间的大小关系或数列的增减性可以分为以下几类:递增数列、递减数列、摆动数列、常数列.3.数列的通项公式数列是按一定次序排列的一列数,其内涵的本质属性是确定这一列数的规律,这个规律通常是用式子f(n)来表示的,这两个通项公式形式上虽然不同,但表示同一个数列,正像每个函数关系不都能用解析式表达出来一样,也不是每个数列都能写出它的通项公式;有的数列虽然有通项公式,但在形式上,又不一定是唯一的,仅仅知道一个数列前面的有限项,无其他说明,数列是不能确定的,通项公式更非唯一.如:数列1,2,3,4,…,由公式写出的后续项就不一样了,因此,通项公式的归纳不仅要看它的前几项,更要依据数列的构成规律,多观察分析,真正找到数列的内在规律,由数列前几项写出其通项公式,没有通用的方法可循.再强调对于数列通项公式的理解注意以下几点:(1)数列的通项公式实际上是一个以正整数集N_或它的有限子集{1,2,…,n}为定义域的函数的表达式.(2)如果知道了数列的通项公式,那么依次用1,2,3,…去替代公式中的n就可以求出这个数列的各项;同时,用数列的通项公式也可判断某数是否是某数列中的一项,如果是的话,是第几项.(3)如所有的函数关系不一定都有解析式一样,并不是所有的数列都有通项公式.如2的不足近似值,精确到1,0.1,0.01,0.001,0.000 1,…所构成的数列1,1.4,1.41,1.414,1.414 2,…就没有通项公式.(4)有的数列的通项公式,形式上不一定是唯一的,正如举例中的:(5)有些数列,只给出它的前几项,并没有给出它的构成规律,那么仅由前面几项归纳出的数列通项公式并不唯一.4.数列的图象对于数列4,5,6,7,8,9,10每一项的序号与这一项有下面的对应关系:序号:1 2 3 4 5 6 7项: 4 5 6 7 8 9 10这就是说,上面可以看成是一个序号集合到另一个数的集合的映射.因此,从映射、函数的观点看,数列可以看作是一个定义域为正整集N_(或它的有限子集{1,2,3,…,n})的函数,当自变量从小到大依次取值时,对应的一列函数值.这里的函数是一种特殊的函数,它的自变量只能取正整数.由于数列的项是函数值,序号是自变量,数列的通项公式也就是相应函数和解析式.数列是一种特殊的函数,数列是可以用图象直观地表示的.数列用图象来表示,可以以序号为横坐标,相应的项为纵坐标,描点画图来表示一个数列,在画图时,为方便起见,在平面直角坐标系两条坐标轴上取的单位长度可以不同,从数列的图象表示可以直观地看出数列的变化情况,但不精确. 把数列与函数比较,数列是特殊的函数,特殊在定义域是正整数集或由以1为首的有限连续正整数组成的集合,其图象是无限个或有限个孤立的点.5.递推数列一堆钢管,共堆放了七层,自上而下各层的钢管数构成一个数列:4,5,6,7,8,9,10.①数列①还可以用如下方法给出:自上而下第一层的钢管数是4,以下每一层的钢管数都比上层的钢管数多1高三人教版必修五数学第二章知识点就为大家介绍到这里,希望对你有所帮助。
数学必修5第二章数列知识梳理

数列知识总结2、数列通项公式的求法: (1)定义法:①等差数列:d n a a n)1(1-+=; ②等比数列:11-=n n q a a .(2)公式法:⎩⎨⎧≥--==)2(1)1(1n S S n S a n n n(3)用递推公式求数列通项公式解题方法: ①累加法:形如已知1a ,且)(1n f a a n n +=+()(n f 可求积),用:112211)()()(a a a a a a a a n n n n n +-++-+-=--- 累加来求通项公式n a 。
②累乘法:形如已知1a ,且)(1n f a a n n=-()(n f 可求积),用: 112211a a a a a a a a n n n n n ⋅⋅⋅⋅=--- 累乘来求通项公式n a 。
③构造法(辅助数列): 形如)1,0(1≠≠+=+p pq q pa a n n 转化为:)(1λλ+=++n n a p a (λ为待定系数),1-=p qλ;形如)1,0)((1≠≠+=+p p n f pa a n n 转化为:))(()1(1n g a p n g a n n +=+++,)1()()(+-⋅=n g n g p n f ;形如n n n q pa a +=+1或11+++=n n n n da ca a a 的形式;3、数列前n 项和的求法:(1)公式法:①等差数列:()12n nn a a S +=()112n n na d -=+ )(*N n ∈;②等比数列:⎪⎩⎪⎨⎧≠--=--==).1(11)1(,)1(111q q q a a qq a q na S n nn (2)分组求和法:形如n n nb ac +=,可以分别对数列}{n a 和}{n b 进行求和;(3)倒序相加法:如果数列}{n a 具有n k k n cb a a =+-或k n k n a a a a -++=+11,可以用倒序相加法进行求和;。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高中数学必修5__第二章《数列》复习知识点总结及练习(一)一.数列的概念及简单表示法知识能否忆起1.数列的定义、分类及通项公式(1)数列的定义:①数列:按照一定顺序排列的一列数.②数列的项:数列中的每一个数.(2)数列的分类:(3)数列的通项公式:如果数列{a n}的第n项及序号n之间的关系可以用一个式子来表示,那么这个公式叫做这个数列的通项公式.2.数列的递推公式如果已知数列{a n}的首项(或前几项),且任一项a n及它的前一项a n-1(n≥2)(或前几项)间的关系可用一个公式来表示,那么这个公式叫数列的递推公式.1.对数列概念的理解(1)数列是按一定“顺序”排列的一列数,一个数列不仅及构成它的“数”有关,而且还及这些“数”的排列顺序有关,这有别于集合中元素的无序性.因此,若组成两个数列的数相同而排列次序不同,那么它们就是不同的两个数列.(2)数列中的数可以重复出现,而集合中的元素不能重复出现,这也是数列及数集的区别.2.数列的函数特征数列是一个定义域为正整数集N *(或它的有限子集{1,2,3,…,n })的特殊函数,数列的通项公式也就是相应的函数解析式,即f (n )=a n (n ∈N *).3.考点(一)由数列的前几项求数列的通项公式[例1] (2012·天津南开中学月考)下列公式可作为数列{a n }:1,2,1,2,1,2,…的通项公式的是( )A .a n =1B .a n =-1n+12C .a n =2-⎪⎪⎪⎪⎪⎪⎪⎪sin n π2 D .a n =-1n -1+32[自主解答] 由a n =2-⎪⎪⎪⎪⎪⎪⎪⎪sin n π2可得a 1=1,a 2=2,a 3=1,a 4=2,….[答案] C 由题悟法1.根据数列的前几项求它的一个通项公式,要注意观察每一项的特点,观察出项及n 之间的关系、规律,可使用添项、通分、分割等办法,转化为一些常见数列的通项公式来求.对于正负符号变化,可用(-1)n或(-1)n +1来调整.2.根据数列的前几项写出数列的一个通项公式是不完全归纳法,它蕴含着“从特殊到一般”的思想以题试法写出下面数列的一个通项公式. (1)3,5,7,9,…;(2)12,34,78,1516,3132,…;(3)3,33,333,3 333,…;(4)-1,32,-13,34,-15,36,….解:(1)各项减去1后为正偶数,所以a n =2n +1.(2)每一项的分子比分母少1,而分母组成数列21,22,23,24,…,所以a n =2n-12n .(3)将数列各项改写为93,993,9993,99993,…,分母都是3,而分子分别是10-1,102-1,103-1,104-1,….所以a n =13(10n-1).(4)奇数项为负,偶数项为正,故通项公式的符号为(-1)n;各项绝对值的分母组成数列1,2,3,4,…;而各项绝对值的分子组成的数列中,奇数项为1,偶数项为3,即奇数项为2-1,偶数项为2+1,所以a n =(-1)n·2+-1nn,也可写为a n=⎩⎪⎨⎪⎧-1n ,n 为正奇数,3n ,n 为正偶数.(二)由a n 及S n 的关系求通项a n已知数列{a n }的前n 项和S n ,求数列的通项公式,其求解过程分为三步:(1)先利用a 1=S 1求出a 1;(2)用n -1替换S n 中的n 得到一个新的关系,利用a n =S n -S n -1(n ≥2)便可求出当n ≥2时a n 的表达式;(3)对n =1时的结果进行检验,看是否符合n ≥2时a n 的表达式,如果符合,则可以把数列的通项公式合写;如果不符合,则应该分n =1及n ≥2两段来写.[例2] 已知数列{a n }的前n 项和S n ,根据下列条件分别求它们的通项a n .(1)S n =2n 2+3n ;(2)S n =3n+1.[自主解答] (1)由题可知,当n =1时,a 1=S 1=2×12+3×1=5,当n ≥2时,a n =S n -S n -1=(2n 2+3n )-[2(n -1)2+3(n -1)]=4n +1.当n =1时,4×1+1=5=a 1,故a n =4n +1.(2)当n =1时,a 1=S 1=3+1=4, 当n ≥2时,a n =S n -S n -1=(3n +1)-(3n -1+1)=2×3n -1.当n =1时,2×31-1=2≠a 1,故a n =⎩⎪⎨⎪⎧4, n =1,2×3n -1, n ≥2.以题试法(2012·聊城模拟)已知数列{a n }的前n 项和为S n ,且S n =nn +1,则1a 5=( )A.56B.65 C.130D .30 解析:选D 当n ≥2时,a n =S n -S n -1=nn +1-n -1n =1n n +1,则a 5=15×6=130.(三)数列的性质[例3] 已知数列{a n }的通项公式为a n =n 2-21n +20. (1)n 为何值时,a n 有最小值?并求出最小值; (2)n 为何值时,该数列的前n 项和最小? [自主解答] (1)因为a n =n2-21n +20=⎝ ⎛⎭⎪⎪⎫n -2122-3614,可知对称轴方程为n =212=10.5.又因n ∈N *,故n =10或n =11时,a n 有最小值,其最小值为112-21×11+20=-90.(2)设数列的前n 项和最小,则有a n ≤0,由n 2-21n +20≤0,解得1≤n ≤20,故数列{a n }从第21项开始为正数,所以该数列的前19或20项和最小. 由题悟法1.数列中项的最值的求法根据数列及函数之间的对应关系,构造相应的函数a n =f (n ),利用求解函数最值的方法求解,但要注意自变量的取值.2.前n 项和最值的求法(1)先求出数列的前n 项和S n ,根据S n 的表达式求解最值; (2)根据数列的通项公式,若a m ≥0,且a m +1<0,则S m 最大;若a m ≤0,且a m +1>0,则S m 最小,这样便可直接利用各项的符号确定最值. 以题试法3.(2012·江西七校联考)数列{a n }的通项a n =nn 2+90,则数列{a n }中的最大值是( )A .310B .19 C.119 D.1060解析:选C a n =1n +90n ,由基本不等式得,1n +90n≤1290,由于n ∈N *,易知当n =9或10时,a n =119最大.二.等差数列及其前n 项和 知识能否忆起一、等差数列的有关概念1.定义:如果一个数列从第2项起,每一项及它的前一项的差都等于同一个常数,那么这个数列就叫做等差数列.符号表示为a n +1-a n =d (n ∈N *,d 为常数).2.等差中项:数列a ,A ,b 成等差数列的充要条件是A =a +b2,其中A 叫做a ,b 的等差中项.二、等差数列的有关公式1.通项公式:a n =a 1+(n -1)d . 2.前n 项和公式:S n =na 1+n n -12d =a 1+a n n2.三、等差数列的性质1.若m ,n ,p ,q ∈N *,且m +n =p +q ,{a n }为等差数列,则a m +a n =a p +a q .2.在等差数列{a n }中,a k ,a 2k ,a 3k ,a 4k ,…仍为等差数列,公差为kd .3.若{a n }为等差数列,则S n ,S 2n -S n ,S 3n -S 2n ,…仍为等差数列,公差为n 2d .4.等差数列的增减性:d >0时为递增数列,且当a 1<0时前n 项和S n 有最小值.d <0时为递减数列,且当a 1>0时前n 项和S n 有最大值.5.等差数列{a n }的首项是a 1,公差为d .若其前n 项之和可以写成S n =An 2+Bn ,则A =d 2,B =a 1-d2,当d ≠0时它表示二次函数,数列{a n }的前n 项和S n =An 2+Bn 是{a n }成等差数列的充要条件.1.及前n 项和有关的三类问题(1)知三求二:已知a 1、d 、n 、a n 、S n 中的任意三个,即可求得其余两个,这体现了方程思想.(2)S n =d2n2+⎝⎛⎭⎪⎪⎫a 1-d 2n =An 2+Bn ⇒d =2A . (3)利用二次函数的图象确定S n 的最值时,最高点的纵坐标不一定是最大值,最低点的纵坐标不一定是最小值.2.设元及解题的技巧已知三个或四个数组成等差数列的一类问题,要善于设元,若奇数个数成等差数列且和为定值时,可设为…,a -2d ,a -d ,a ,a +d ,a +2d ,…;若偶数个数成等差数列且和为定值时,可设为…,a -3d ,a -d ,a +d ,a +3d ,…,其余各项再依据等差数列的定义进行对称设元.考点等差数列的判断及证明[例1] 在数列{a n }中,a 1=-3,a n =2a n -1+2n+3(n ≥2,且n ∈N *).(1)求a 2,a 3的值;(2)设b n =a n +32n(n ∈N *),证明:{b n }是等差数列.[自主解答] (1)∵a 1=-3,a n =2a n -1+2n+3(n ≥2,且n ∈N *),∴a 2=2a 1+22+3=1,a 3=2a 2+23+3=13.(2)证明:对于任意n ∈N *, ∵b n +1-b n =a n +1+32n +1-a n +32n=12n +1[(a n +1-2a n )-3]=12n +1[(2n +1+3)-3]=1,∴数列{b n }是首项为a 1+32=-3+32=0,公差为1的等差数列.由题悟法1.证明{a n }为等差数列的方法:(1)用定义证明:a n -a n -1=d (d 为常数,n ≥2)⇔{a n }为等差数列;(2)用等差中项证明:2a n +1=a n +a n +2⇔{a n }为等差数列; (3)通项法:a n 为n 的一次函数⇔{a n }为等差数列; (4)前n 项和法:S n =An 2+Bn 或S n =n a 1+a n2.2.用定义证明等差数列时,常采用的两个式子a n +1-a n =d 和a n -a n -1=d ,但它们的意义不同,后者必须加上“n ≥2”,否则n =1时,a 0无定义.以题试法1.已知数列{a n }的前n 项和S n 是n 的二次函数,且a 1=-2,a 2=2,S 3=6.(1)求S n ;(2)证明:数列{a n }是等差数列. 解:(1)设S n =An 2+Bn +C (A ≠0), 则⎩⎪⎨⎪⎧-2=A +B +C ,0=4A +2B +C ,6=9A +3B +C ,解得A =2,B =-4,C =0.故S n =2n 2-4n . (2)证明:∵当n =1时,a 1=S 1=-2.当n ≥2时,a n =S n -S n -1=2n 2-4n -[2(n -1)2-4(n -1)]=4n -6.∴a n =4n -6(n ∈N *).a n +1-a n =4, ∴数列{a n }是等差数列. 等差数列的基本运算典题导入[例2] (2012·重庆高考)已知{a n }为等差数列,且a 1+a 3=8,a 2+a 4=12.(1)求{a n }的通项公式;(2)记{a n }的前n 项和为S n ,若a 1,a k ,S k +2成等比数列,求正整数k 的值.[自主解答] (1)设数列{a n }的公差为d ,由题意知⎩⎪⎨⎪⎧2a 1+2d =8,2a 1+4d =12,解得⎩⎪⎨⎪⎧a 1=2,d =2.所以a n =a 1+(n -1)d =2+2(n -1)=2n .(2)由(1)可得S n =n a 1+a n2=n 2+2n2=n (n +1). 因为a 1,a k ,S k +2成等比数列,所以a 2k =a 1S k +2.从而(2k )2=2(k +2)(k +3),即k 2-5k -6=0,解得k =6或k =-1(舍去),因此k =6.由题悟法1.等差数列的通项公式a n =a 1+(n -1)d 及前n 项和公式S n =n a 1+a n2=na 1+n n -12d ,共涉及五个量a 1,a n ,d ,n ,S n ,知其中三个就能求另外两个,体现了方程的思想.2.数列的通项公式和前n 项和公式在解题中起到变量代换作用,而a 1和d 是等差数列的两个基本量,用它们表示已知和未知是常用方法.以题试法2.(1)在等差数列中,已知a 6=10,S 5=5,则S 8=________.(2)设等差数列{a n }的前n 项和为S n ,若S 412-S 39=1,则公差为________.解析:(1)∵a 6=10,S 5=5,∴⎩⎪⎨⎪⎧ a 1+5d =10,5a 1+10d =5.解方程组得⎩⎪⎨⎪⎧ a 1=-5,d =3.则S 8=8a 1+28d =8×(-5)+28×3=44.(2)依题意得S 4=4a 1+4×32d =4a 1+6d ,S 3=3a 1+3×22d =3a 1+3d ,于是有4a 1+6d 12-3a 1+3d 9=1,由此解得d =6,即公差为6.答案:(1)44 (2)6等差数列的性质典题导入[例3] (1)等差数列{a n }中,若a 1+a 4+a 7=39,a 3+a 6+a 9=27,则前9项和S 9等于( )A .66B .99C .144D .297(2)(2012·天津模拟)设等差数列{a n }的前n 项和S n ,若S 4=8,S 8=20,则a 11+a 12+a 13+a 14=( )A .18B .17C .16D .15[自主解答] (1)由等差数列的性质及a 1+a 4+a 7=39,可得3a 4=39,所以a 4=13.同理,由a 3+a 6+a 9=27,可得a 6=9.所以S 9=9a 1+a 92=9a 4+a 62=99.(2)设{a n }的公差为d ,则a 5+a 6+a 7+a 8=S 8-S 4=12,(a 5+a 6+a 7+a 8)-S 4=16d ,解得d =14,a 11+a 12+a 13+a 14=S 4+40d =18.[答案] (1)B (2)A由题悟法1.等差数列的性质是等差数列的定义、通项公式以及前n 项和公式等基础知识的推广及变形,熟练掌握和灵活应用这些性质可以有效、方便、快捷地解决许多等差数列问题.2.应用等差数列的性质解答问题的关键是寻找项的序号之间的关系.以题试法3.(1)(2012·江西高考)设数列{a n },{b n }都是等差数列,若a 1+b 1=7,a 3+b 3=21,则a 5+b 5=________.(2)(2012·海淀期末)若数列{a n }满足:a 1=19,a n +1=a n -3(n ∈N *),则数列{a n }的前n 项和数值最大时,n 的值为( )A .6B .7C .8D .9解析:(1)设两等差数列组成的和数列为{c n },由题意知新数列仍为等差数列且c 1=7,c 3=21,则c 5=2c 3-c 1=2×21-7=35.(2)∵a n +1-a n =-3,∴数列{a n }是以19为首项,-3为公差的等差数列,∴a n =19+(n -1)×(-3)=22-3n .设前k 项和最大,则有⎩⎪⎨⎪⎧ a k ≥0,a k +1≤0,即⎩⎪⎨⎪⎧ 22-3k ≥0,22-3k +1≤0,解得193≤k ≤223.∵k ∈N *,∴k =7.故满足条件的n 的值为7. 答案:(1)35 (2)B三.等比数列及其前n 项和 [知识能否忆起]1.等比数列的有关概念(1)定义:如果一个数列从第2项起,每一项及它的前一项的比等于同一个常数(不为零),那么这个数列就叫做等比数列.这个常数叫做等比数列的公比,通常用字母q 表示,定义的表达式为a n +1a n=q (n ∈N *,q 为非零常数).(2)等比中项:如果a 、G 、b 成等比数列,那么G 叫做a 及b 的等比中项.即:G 是a 及b 的等比中项⇔a ,G ,b 成等比数列⇒G 2=ab .2.等比数列的有关公式(1)通项公式:a n =a 1q n -1.(2)前n 项和公式:S n =⎩⎪⎨⎪⎧ na 1,q =1,a 11-q n 1-q=a 1-a n q 1-q ,q ≠1.3.等比数列{a n }的常用性质(1)在等比数列{a n }中,若m +n =p +q =2r (m ,n ,p ,q ,r ∈N *),则a m ·a n =a p ·a q =a 2r .特别地,a 1a n =a 2a n -1=a 3a n -2=….(2)在公比为q 的等比数列{a n }中,数列a m ,a m +k ,a m +2k ,a m +3k ,…仍是等比数列,公比为q k ;数列S m,S2m-S m,S3m-S2m,…仍是等比数列(此时q≠-1);a n=a m q n-m.1.等比数列的特征(1)从等比数列的定义看,等比数列的任意项都是非零的,公比q也是非零常数.(2)由a n+1=qa n,q≠0并不能立即断言{a n}为等比数列,还要验证a1≠0.2.等比数列的前n项和S n(1)等比数列的前n项和S n是用错位相减法求得的,注意这种思想方法在数列求和中的运用.(2)在运用等比数列的前n项和公式时,必须注意对q=1及q≠1分类讨论,防止因忽略q=1这一特殊情形导致解题失误考点等比数列的判定及证明典题导入[例1] 已知数列{a n}的前n项和为S n,且a n+S n=n.(1)设c n=a n-1,求证:{c n}是等比数列;(2)求数列{a n}的通项公式.[自主解答] (1)证明:∵a n+S n=n,①∴a n+1+S n+1=n+1.②②-①得a n+1-a n+a n+1=1,∴2a n+1=a n+1,∴2(a n+1-1)=a n-1,∴a n +1-1a n -1=12. ∵首项c 1=a 1-1,又a 1+a 1=1,∴a 1=12,c 1=-12. 又c n =a n -1,故{c n }是以-12为首项,12为公比的等比数列. (2)由(1)可知c n =⎝ ⎛⎭⎪⎪⎫-12·⎝ ⎛⎭⎪⎪⎫12n -1=-⎝ ⎛⎭⎪⎪⎫12n , ∴a n =c n +1=1-⎝ ⎛⎭⎪⎪⎫12n .在本例条件下,若数列{b n }满足b 1=a 1,b n =a n -a n -1(n ≥2),证明{b n }是等比数列.证明:∵由(2)知a n =1-⎝ ⎛⎭⎪⎪⎫12n , ∴当n ≥2时,b n =a n -a n -1=1-⎝ ⎛⎭⎪⎪⎫12n -⎣⎢⎢⎡⎦⎥⎥⎤1-⎝ ⎛⎭⎪⎪⎫12n -1 =⎝ ⎛⎭⎪⎪⎫12n -1-⎝ ⎛⎭⎪⎪⎫12n =⎝ ⎛⎭⎪⎪⎫12n . 又b 1=a 1=12也符合上式,∴b n =⎝ ⎛⎭⎪⎪⎫12n . ∵b n +1b n =12,∴数列{b n }是等比数列.由题悟法等比数列的判定方法(1)定义法:若a n +1a n =q (q 为非零常数,n ∈N *)或a n a n -1=q (q 为非零常数且n ≥2,n ∈N *),则{a n }是等比数列.(2)等比中项法:若数列{a n }中,a n ≠0且a 2n +1=a n ·a n +2(n ∈N *),则数列{a n }是等比数列.(3)通项公式法:若数列通项公式可写成a n =c ·q n(c ,q 均是不为0的常数,n ∈N *),则{a n }是等比数列.以题试法1. (2012·沈阳模拟)已知函数f (x )=log a x ,且所有项为正数的无穷数列{a n }满足log a a n +1-log a a n =2,则数列{a n }( )A .一定是等比数列B .一定是等差数列C .既是等差数列又是等比数列D .既不是等差数列又不是等比数列 解析:选A 由log a a n +1-log a a n =2,得log a a n +1a n=2=log a a 2,故a n +1a n=a 2.又a >0且a ≠1,所以数列{a n }为等比数列. 等比数列的基本运算典题导入[例2] {a n }为等比数列,求下列各值:(1)a 6-a 4=24,a 3a 5=64,求a n ;(2)已知a 2·a 8=36,a 3+a 7=15,求公比q.解:(1)设数列{a n }的公比为q ,由题意得⎩⎪⎨⎪⎧ a 6-a 4=a 1q 3q 2-1=24, ①a 3a 5=a 1q 32=64. ②由②得a 1q 3=±8,将a 1q 3=-8代入①中,得q 2=-2(舍去).将a 1q 3=8代入①中,得q 2=4,q =±2.当q =2时,a 1=1,∴a n =a 1q n -1=2n -1.当q =-2时,a 1=-1,∴a n =a 1qn -1=-(-2)n -1. ∴a n =2n -1或a n =-(-2)n -1. (2)∵a 2·a 8=36=a 3·a 7,而a 3+a 7=15,∴⎩⎪⎨⎪⎧ a 3=3,a 7=12或⎩⎪⎨⎪⎧ a 3=12,a 7=3. ∴q 4=a 7a 3=4或14. ∴q =±2或q =±22.由题悟法1.等比数列基本量的运算是等比数列中的一类基本问题,数列中有五个量a 1,n ,q ,a n ,S n ,一般可以“知三求二”,通过列方程(组)可迎刃而解.2.在使用等比数列的前n 项和公式时,应根据公比q 的情况进行分类讨论,切不可忽视q 的取值而盲目用求和公式.以题试法2.(2012·山西适应性训练)已知数列{a n }是公差不为零的等差数列,a 1=2,且a 2,a 4,a 8成等比数列.(1)求数列{a n }的通项公式;(2)求数列{3a n }的前n 项和.解:(1)设等差数列{a n }的公差为d (d ≠0).因为a 2,a 4,a 8成等比数列,所以(2+3d )2=(2+d )·(2+7d ),解得d =2.所以a n =2n (n ∈N *).(2)由(1)知3a n =32n ,设数列{3a n }的前n 项和为S n ,则S n =32+34+…+32n =91-9n 1-9=98(9n -1). 等比数列的性质典题导入[例3] (1)(2012·威海模拟)在由正数组成的等比数列{a n }中,若a 3a 4a 5=3π,则sin(log 3a 1+log 3a 2+…+log 3a 7)的值为( )A.12 B .32C .1D .-32(2)设等比数列{a n }的前n 项和为S n ,若S 6∶S 3=1∶2,则S 9∶S 3等于( )A .1∶2B .2∶3C .3∶4D .1∶3[自主解答] (1)因为a 3a 4a 5=3π=a 34,所以a 4=3π3. log 3a 1+log 3a 2+…+log 3a 7=log 3(a 1a 2…a 7)=log 3a 74=7log 33π3=7π3, 故sin(log 3a 1+log 3a 2+…+log 3a 7)=32. (2)由等比数列的性质:S 3,S 6-S 3,S 9-S 6仍成等比数列,于是(S 6-S 3)2=S 3·(S 9-S 6),将S 6=12S 3代入得S 9S 3=34. [答案] (1)B (2)C由题悟法等比数列及等差数列在定义上只有“一字之差”,它们的通项公式和性质有许多相似之处,其中等差数列中的“和”“倍数”可以及等比数列中的“积”“幂”相类比.关注它们之间的异同有助于我们从整体上把握,同时也有利于类比思想的推广.对于等差数列项的和或等比数列项的积的运算,若能关注通项公式a n =f (n )的下标n 的大小关系,可简化题目的运算.以题试法3.(1)(2012·新课标全国卷)已知{a n }为等比数列,a 4+a 7=2,a 5a 6=-8,则a 1+a 10=( )A .7B .5C .-5D .-7(2)(2012·成都模拟)已知{a n }是等比数列,a 2=2,a 5=14,则a 1a 2+a 2a 3+…+a n a n +1=( )A .16(1-4-n )B .16(1-2-n )C.323(1-4-n )D.323(1-2-n ) 解析:(1)选D 法一:由题意得⎩⎪⎨⎪⎧ a 4+a 7=a 1q 3+a 1q 6=2,a 5a 6=a 1q 4×a 1q 5=a 21q 9=-8,解得⎩⎪⎨⎪⎧ q 3=-2,a 1=1或⎩⎪⎨⎪⎧ q 3=-12,a 1=-8,故a 1+a 10=a 1(1+q 9)=-7.法二:由⎩⎪⎨⎪⎧ a 4+a 7=2,a 5a 6=a 4a 7=-8,解得⎩⎪⎨⎪⎧a 4=-2,a 7=4或⎩⎪⎨⎪⎧ a 4=4,a 7=-2.则⎩⎪⎨⎪⎧ q 3=-2,a 1=1或⎩⎪⎨⎪⎧ q 3=-12,a 1=-8,故a 1+a 10=a 1(1+q 9)=-7.(2)选C ∵a 2=2,a 5=14,∴a 1=4,q =12,a n a n +1=⎝ ⎛⎭⎪⎪⎫122n -5.故a 1a 2+a 2a 3+…+a n a n +1=8⎝ ⎛⎭⎪⎪⎫1-14n 1-14=323(1-4-n ). 练习题1.(教材习题改编)数列1,23,35,47,59…的一个通项公式是 ( )A .a n =n 2n +1B .a n =n 2n -1C .a n =n 2n -3D .a n =n 2n +3答案:B2.设数列{a n }的前n 项和S n =n 2,则a 8的值为( )A .15B .16C .49D .64解析:选A a 8=S 8-S 7=64-49=15.3.已知数列{a n }的通项公式为a n =nn +1,则这个数列是( )A .递增数列B .递减数列C .常数列D .摆动数列解析:选A a n +1-a n =n +1n +2-n n +1=n +12-n n +2n +1n +2=1n +1n +2>0.4.(教材习题改编)已知数列{a n }的通项公式是a n =⎩⎪⎨⎪⎧2·3n -1n 为偶数,2n -5n 为奇数,则a 4·a 3=________. 解析:a 4·a 3=2×33·(2×3-5)=54.答案:545.已知数列{a n }的通项公式为a n =pn +q n ,且a 2=32, a 4=32,则a 8=________. 解析:由已知得⎩⎪⎨⎪⎧ 2p +q 2=32,4p +q 4=32,解得⎩⎪⎨⎪⎧ p =14,q =2.则a n =14n +2n ,故a 8=94. 答案:94 1.(2012·福建高考)等差数列{a n }中,a 1+a 5=10,a 4=7,则数列{a n }的公差为( )A .1B .2C .3D .4解析:选 B 法一:设等差数列{a n }的公差为d ,由题意得⎩⎪⎨⎪⎧ 2a 1+4d =10,a 1+3d =7.解得⎩⎪⎨⎪⎧ a 1=1,d =2.故d =2.法二:∵在等差数列{a n }中,a 1+a 5=2a 3=10,∴a 3=5. 又a 4=7,∴公差d =7-5=2.2.(教材习题改编)在等差数列{a n }中,a 2+a 6=3π2,则sin ⎝ ⎛⎭⎪⎪⎫2a 4-π3=( )A.32B.12C .-32D .-12解析:选D ∵a 2+a 6=3π2,∴2a 4=3π2. ∴sin ⎝ ⎛⎭⎪⎪⎫2a 4-π3=sin ⎝⎛⎭⎪⎪⎫3π2-π3=-cos π3=-12. 3.(2012·辽宁高考)在等差数列{a n }中,已知a 4+a 8=16,则该数列前11项和S 11=( )A .58B .88C .143D .176解析:选B S 11=11a 1+a 112=11a 4+a 82=88.4.在数列{a n }中,若a 1=1,a n +1=a n +2(n ≥1),则该数列的通项a n =________.解析:由a n +1=a n +2知{a n }为等差数列其公差为2. 故a n =1+(n -1)×2=2n -1.答案:2n -15.(2012·北京高考)已知{a n }为等差数列,S n 为其前n 项和,若a 1=12,S 2=a 3,则a 2=________,S n =________. 解析:设{a n }的公差为d ,由S 2=a 3知,a 1+a 2=a 3,即2a 1+d =a 1+2d ,又a 1=12,所以d =12,故a 2=a 1+d =1, S n =na 1+12n (n -1)d =12n +12(n 2-n )×12=14n 2+14n . 答案:1 14n 2+14n 1.(2011·江西高考){a n }为等差数列,公差d =-2,S n 为其前n 项和.若S 10=S 11,则a 1=( )A .18B .20C .22D .24解析:选B 由S 10=S 11,得a 11=S 11-S 10=0,a 1=a 11+(1-11)d =0+(-10)×(-2)=20.2.(2012·广州调研)等差数列{a n }的前n 项和为S n ,已知a 5=8,S 3=6,则S 10-S 7的值是( )A .24B .48C .60D .72解析:选B 设等差数列{a n }的公差为d ,由题意可得⎩⎪⎨⎪⎧ a 5=a 1+4d =8,S 3=3a 1+3d =6,解得⎩⎪⎨⎪⎧ a 1=0,d =2,则S 10-S 7=a 8+a 9+a 10=3a 1+24d =48.3.(2013·东北三校联考)等差数列{a n }中,a 5+a 6=4,则log 2(2a 1·2a 2·…·2a 10)=( )A .10B .20C .40D .2+log 25解析:选B 依题意得,a 1+a 2+a 3+…+a 10=10a 1+a 102=5(a 5+a 6)=20,因此有log 2(2a 1·2a 2·…·2a 10)=a 1+a 2+a 3+…+a 10=20.4.(2012·海淀期末)已知数列{a n }满足:a 1=1,a n >0,a 2n +1-a 2n =1(n ∈N *),那么使a n <5成立的n 的最大值为( ) A .4 B .5C .24D .25解析:选C ∵a 2n +1-a 2n =1,∴数列{a 2n }是以a 21=1为首项,1为公差的等差数列.∴a 2n =1+(n -1)=n .又a n >0,∴a n =n .∵a n <5,∴n <5.即n <25.故n 的最大值为24.5.已知等差数列{a n }的前n 项和为S n ,并且S 10>0,S 11<0,若S n ≤S k 对n ∈N *恒成立,则正整数k 的值为( )A .5B .6C .4D .7解析:选A 由S 10>0,S 11<0知a 1>0,d <0,并且a 1+a 11<0,即a 6<0,又a 5+a 6>0,所以a 5>0,即数列的前5项都为正数,第5项之后的都为负数,所以S 5最大,则k =5.6.数列{a n }的首项为3,{b n }为等差数列且b n =a n +1-a n (n ∈N *).若b 3=-2,b 10=12,则a 8=( )A .0B .3C .8D .11解析:选B 因为{b n }是等差数列,且b 3=-2,b 10=12,故公差d =12--210-3=2.于是b 1=-6, 且b n =2n -8(n ∈N *),即a n +1-a n =2n -8.所以a 8=a 7+6=a 6+4+6=a 5+2+4+6=…=a 1+(-6)+(-4)+(-2)+0+2+4+6=3.7.(2012·广东高考)已知递增的等差数列{a n }满足a 1=1,a 3=a 22-4,则a n =________.解析:设等差数列公差为d ,∵由a 3=a 22-4,得1+2d =(1+d )2-4,解得d 2=4,即d =±2.由于该数列为递增数列,故d =2.∴a n =1+(n -1)×2=2n -1.答案:2n -18.已知数列{a n }为等差数列,S n 为其前n 项和,a 7-a 5=4,a 11=21,S k =9,则k =________.解析:a 7-a 5=2d =4,则d =2.a 1=a 11-10d =21-20=1, S k =k +k k -12×2=k 2=9.又k ∈N *,故k =3. 答案:39.设等差数列{a n },{b n }的前n 项和分别为S n ,T n ,若对任意自然数n 都有S n T n =2n -34n -3,则a 9b 5+b 7+a 3b 8+b 4的值为________.解析:∵{a n },{b n }为等差数列, ∴a 9b 5+b 7+a 3b 8+b 4=a 92b 6+a 32b 6=a 9+a 32b 6=a 6b 6. ∵S 11T 11=a 1+a 11b 1+b 11=2a 62b 6=2×11-34×11-3=1941,∴a 6b 6=1941. 答案:194110.(2011·福建高考)已知等差数列{a n }中,a 1=1,a 3=-3.(1)求数列{a n }的通项公式;(2)若数列{a n }的前k 项和S k =-35,求k 的值. 解:(1)设等差数列{a n }的公差为d ,则a n =a 1+(n -1)d . 由a 1=1,a 3=-3,可得1+2d =-3,解得d =-2. 从而a n =1+(n -1)×(-2)=3-2n .(2)由(1)可知a n =3-2n ,所以S n =n [1+3-2n ]2=2n -n 2. 由S k =-35,可得2k -k 2=-35,即k 2-2k -35=0,解得k =7或k =-5.又k ∈N *,故k =7.11.设数列{a n }的前n 项积为T n ,T n =1-a n ,(1)证明⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫1T n 是等差数列; (2)求数列⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫a n T n 的前n 项和S n .解:(1)证明:由T n =1-a n 得,当n ≥2时,T n =1-T n T n -1,两边同除以T n 得1T n -1T n -1=1.∵T 1=1-a 1=a 1,故a 1=12,1T 1=1a 1=2.∴⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫1T n 是首项为2,公差为1的等差数列.(2)由(1)知1T n =n +1,则T n =1n +1,从而a n =1-T n =n n +1.故a nT n=n .∴数列⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫a n T n 是首项为1,公差为1的等差数列.∴S n =n n +12.12.已知在等差数列{a n }中,a 1=31,S n 是它的前n 项和,S 10=S 22.(1)求S n ;(2)这个数列的前多少项的和最大,并求出这个最大值. 解:(1)∵S 10=a 1+a 2+…+a 10,S 22=a 1+a 2+…+a 22,又S 10=S 22,∴a 11+a 12+…+a 22=0,即12a 11+a 222=0,故a 11+a 22=2a 1+31d =0.又∵a 1=31,∴d =-2,∴S n =na 1+n n -12d =31n -n (n -1)=32n -n 2.(2)法一:由(1)知S n =32n -n 2,故当n =16时,S n 有最大值,S n 的最大值是256. 法二:由S n =32n -n 2=n (32-n ),欲使S n 有最大值, 应有1<n <32,从而S n ≤⎝ ⎛⎭⎪⎪⎫n +32-n 22=256, 当且仅当n =32-n ,即n =16时,S n 有最大值256.1.(教材习题改编)等比数列{a n }中,a 4=4,则a 2·a 6等于( )A .4B .8C .16D .32解析:选C a 2·a 6=a 24=16.2.已知等比数列{a n }的前三项依次为a -1,a +1,a +4,则a n =( )A .4·⎝ ⎛⎭⎪⎪⎫32n B .4·⎝ ⎛⎭⎪⎪⎫23n C .4·⎝ ⎛⎭⎪⎪⎫32n -1D .4·⎝ ⎛⎭⎪⎪⎫23n -1 解析:选C (a +1)2=(a -1)(a +4)⇒a =5,a 1=4,q =32,故a n =4·⎝ ⎛⎭⎪⎪⎫32n -1. 3.已知等比数列{a n }满足a 1+a 2=3,a 2+a 3=6,则a 7=( )A .64B .81C .128D .243解析:选A q =a 2+a 3a 1+a 2=2,故a 1+a 1q =3⇒a 1=1,a 7=1×27-1=64.4.(2011·北京高考)在等比数列{a n }中,若a 1=12,a 4=4,则公比q =________;a 1+a 2+…+a n =________.解析:a 4=a 1q 3,得4=12q 3,解得q =2,a 1+a 2+…+a n =121-2n1-2=2n -1-12. 答案:2 2n -1-125.(2012·新课标全国卷)等比数列{a n }的前n 项和为S n ,若S 3+3S 2=0,则公比q =________.解析:∵S 3+3S 2=0,∴a 1+a 2+a 3+3(a 1+a 2)=0, ∴a 1(4+4q +q 2)=0. ∵a 1≠0,∴q =-2. 答案:-21.设数列{a n }是等比数列,前n 项和为S n ,若S 3=3a 3,则公比q 为( )A .-12 B .1C .-12或1 D.14解析:选C 当q =1时,满足S 3=3a 1=3a 3.当q ≠1时,S 3=a 11-q 31-q=a 1(1+q +q 2)=3a 1q 2,解得q =-12,综上q =-12或q =1.2.(2012·东城模拟)设数列{a n }满足:2a n =a n +1(a n ≠0)(n ∈N *),且前n 项和为S n ,则S 4a 2的值为( )A.152B.154C .4D .2解析:选A 由题意知,数列{a n }是以2为公比的等比数列,故S 4a 2=a 11-241-2a 1×2=152.3.(2012·安徽高考)公比为2的等比数列{a n }的各项都是正数,且a 3a 11=16,则log 2a 10=( )A .4B .5C .6D .7解析:选B ∵a 3·a 11=16,∴a 27=16. 又∵等比数列{a n }的各项都是正数,∴a 7=4. 又∵a 10=a 7q 3=4×23=25,∴log 2a 10=5.4.已知数列{a n },则“a n ,a n +1,a n +2(n ∈N *)成等比数列”是“a 2n +1=a n a n +2”的( )A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件解析:选A 显然,n ∈N *,a n ,a n +1,a n +2成等比数列,则a 2n +1=a n a n +2,反之,则不一定成立,举反例,如数列为1,0,0,0,…5.(2013·太原模拟)各项均为正数的等比数列{a n }的前n 项和为S n ,若S n =2,S 3n =14,则S 4n 等于( )A .80B .30C .26D .16解析:选B 设S 2n =a ,S 4n =b ,由等比数列的性质知: 2(14-a )=(a -2)2,解得a =6或a =-4(舍去), 同理(6-2)(b -14)=(14-6)2,所以b =S 4n =30.6.已知方程(x 2-mx +2)(x 2-nx +2)=0的四个根组成以12为首项的等比数列,则mn=( )A.32B.32或23C.23D .以上都不对 解析:选B 设a ,b ,c ,d 是方程(x 2-mx +2)(x 2-nx +2)=0的四个根,不妨设a <c <d <b ,则a ·b =c ·d =2,a =12,故b=4,根据等比数列的性质,得到c =1,d =2,则m =a +b =92,n =c +d =3,或m =c +d =3,n =a +b =92,则m n =32或m n =23.7.已知各项不为0的等差数列{a n },满足2a 3-a 27+2a 11=0,数列{b n }是等比数列,且b 7=a 7,则b 6b 8=________.解析:由题意可知,b 6b 8=b 27=a 27=2(a 3+a 11)=4a 7,∵a 7≠0,∴a 7=4,∴b 6b 8=16. 答案:168.(2012·江西高考)等比数列{a n }的前n 项和为S n ,公比不为1.若a 1=1,则对任意的n ∈N *,都有a n +2+a n +1-2a n =0,则S 5=________.解析:由题意知a 3+a 2-2a 1=0,设公比为q ,则a 1(q 2+q -2)=0.由q 2+q -2=0解得q =-2或q =1(舍去),则S 5=a 11-q 51-q =1--253=11.答案:119.(2012·西城期末)已知{a n }是公比为2的等比数列,若a 3-a 1=6,则a 1=________;1a 21+1a 22+…+1a 2n=________.解析:∵{a n }是公比为2的等比数列,且a 3-a 1=6,∴4a 1-a 1=6,即a 1=2,故a n =a 12n -1=2n,∴1a n =⎝ ⎛⎭⎪⎪⎫12n ,1a 2n =⎝ ⎛⎭⎪⎪⎫14n,即数列⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫1a 2n 是首项为14,公比为14的等比数列,∴1a 21+1a 22+…+1a 2n =14⎝ ⎛⎭⎪⎪⎫1-14n1-14=13⎝⎛⎭⎪⎪⎫1-14n . 答案:2 13⎝⎛⎭⎪⎪⎫1-14n10.设数列{a n }的前n 项和为S n ,a 1=1,且数列{S n }是以2为公比的等比数列.(1)求数列{a n }的通项公式; (2)求a 1+a 3+…+a 2n +1.解:(1)∵S 1=a 1=1,且数列{S n }是以2为公比的等比数列,∴S n =2n -1,又当n ≥2时,a n =S n -S n -1=2n -2(2-1)=2n -2.∴a n =⎩⎪⎨⎪⎧1,n =1,2n -2,n ≥2.(2)a 3,a 5,…,a 2n +1是以2为首项,以4为公比的等比数列, ∴a 3+a 5+…+a 2n +1=21-4n1-4=24n-13.∴a 1+a 3+…+a 2n +1=1+24n-13=22n +1+13.11.设数列{a n }的前n 项和为S n ,其中a n ≠0,a 1为常数,且-a 1,S n ,a n +1成等差数列.(1)求{a n }的通项公式;(2)设b n =1-S n ,问:是否存在a 1,使数列{b n }为等比数列?若存在,求出a 1的值;若不存在,请说明理由.解:(1)依题意,得2S n =a n +1-a 1. 当n ≥2时,有⎩⎪⎨⎪⎧2S n =a n +1-a 1,2S n -1=a n -a 1.两式相减,得a n +1=3a n (n ≥2). 又因为a 2=2S 1+a 1=3a 1,a n ≠0,所以数列{a n }是首项为a 1,公比为3的等比数列. 因此,a n =a 1·3n -1(n ∈N *).(2)因为S n =a 11-3n1-3=12a 1·3n-12a 1,b n =1-S n =1+12a 1-12a 1·3n .要使{b n }为等比数列,当且仅当1+12a 1=0,即a 1=-2.所以存在a 1=-2,使数列{b n }为等比数列.12. (2012·山东高考)已知等差数列{a n }的前5项和为105,且a 10=2a 5.(1)求数列{a n }的通项公式;(2)对任意m ∈N *,将数列{a n }中不大于72m的项的个数记为b m .求数列{b m }的前m 项和S m .解:(1)设数列{a n }的公差为d ,前n 项和为T n , 由T 5=105,a 10=2a 5,得⎩⎪⎨⎪⎧5a 1+5×5-12d =105,a 1+9d =2a 1+4d ,解得a 1=7,d =7.因此a n =a 1+(n -1)d =7+7(n -1)=7n (n ∈N *). (2)对m ∈N *,若a n =7n ≤72m,则n ≤72m -1.因此b m =72m -1.所以数列{b m }是首项为7,公比为49的等比数列,故S m =b 11-q m 1-q=7×1-49m1-49=7×72m-148=72m+1-7.48。
