江苏省苏北四市2011届高三第三次调研考试物理试题

合集下载

江苏省苏北四市2012届高三第三次模拟考试物理试题

江苏苏北四市（徐、淮、连、宿）2012届高三5月第三次质量检测物理试题一、单项选择题：本题共5小题，每小题3分，共计15分．每小题选项符合题意．只有一个．．．．1．牛顿的三大运动定律构成了物理学和工程学的基础.它的推出、地球引力的发现和微积分的创立使得牛顿成为过去一千多年中最杰出的科学巨人之一。

下列说法中正确的是A．牛顿第一定律是牛顿第二定律的一种特例B．牛顿第二定律在非惯性系中不成立C．两物体之间的作用力和反作用力是一对平衡力D．为纪念牛顿，人们把“力”定为基本物理量，其基本单位为“牛顿”2．某驾培中心训练场有一段圆弧形坡道如图所示,将同一辆车物后停放在a点和b点。

下述分析和比较正确的是A．车在a点受坡道的支持力大于在b点受的支持力B．车在a点受坡道的摩擦力大于在b点受的摩擦力C．车在a点受到的合外力大于在b点受的合外力D．车在a点受到重力的下滑分力大于在b 点受到重力的下滑分力3．我国正在建设中的“北斗"卫星导航系统将由5颗地球同步卫星和30颗非同步卫星组成.已知有两颗同步轨道卫星A、B分别定点于赤道上东经80°和140°的上空，轨道半径为r。

则关于A、B两颗卫星，下列说法中正确的是A．两卫星内的物体都处于平衡状态B．两卫星运动的线速度相同C．这两颗卫星的信号可覆盖整个地球表面D．两卫星的间距是固定的,大小为r4．两个等量异种电荷位于正方体的两个顶点a 和f上,如图所示。

在此正方体的顶点间移动一正试探电荷，以下说法中正确的是A．电场中b点和d点的电场强度相同B．电场中b点和e点电势相等C．试探电荷在c点和h点受力大小相等,方向相同D．试探电荷从c点移到h点电场力做功为零5．如图所示，两光滑平等长直导轨，水平放置在磁感应强度为B的匀强磁场中，磁场与导轨所在平面垂直。

已知金属棒MN能沿导轨自由滑动，导轨一端跨接一个定值电阻R，金属棒与导轨电阻不计。

金属棒在恒力F作用下从静止开始沿导轨向右运动，在以后过程中,能正确表示金属棒速度v、加速度a、感应电动势E以及通过电阻R的电量q随时间t变化错误的是．．二、多项选择题：本题共4小题,每小题4分，共计16分．每小题有多个选项符合题意．全部选对的得4分，选对但不全的得2分，错选或不答得0分．6．如图所示为一质点从静止开始运动的加速度－时间变化的图像,关于该质点的运动，下列说法中正确的是A．质点在起点附近往复运动B．质点始终在起点一侧往复运动C．质点在第6s末的速度大小是4m/sD．质点在前4s内的位移为07．霍尔元件是一种基于霍尔将就的磁传感器，已发展成一个品种多样的磁传感器产品族，得到广泛应用。

苏、锡、常、镇四市2011届高三调研测试(一)(物理)

苏州市 2011 届高三调研测试（一）物理 2011 . 3注意事项：考生在答题前请认真阅读本注意事项 1 ．本试卷包含选择题和非选择题两部分．考生答题全部答在答题卡上，答在本试卷上无效．本次考试时间为 100 分钟，满分值为 120 分． 2 ．答题前，请务必将自己的姓名、准考证号（考试号）用书写黑色字迹的 0 . 5 毫米签字笔填写在答题卡上，并用 2B 铅笔将对应的数字标号涂黑． 3 ．答选择题必须用 2B 铅笔把答题卡上对应题目的答案标号涂黑．如需改动，请用橡皮擦干净后，再选涂其它答案．答非选择题必须用书写黑色字迹的 0 . 5 毫米签字笔写在答题卡上的指定位置，在其它位置答题一律无效． 4 ．如有作图需要，可用 2B 铅笔作答，并请加黑加粗画清楚．G 一、单项选择题：本大题共 5 小题，每小题 3 分，共计 15 分．每小题只有一个选项符合题意1 ．有研究发现，轿车的加速度变化情况将影响乘客的舒适度：即加速度变化得越慢，乘坐轿车的人就会感到越舒适；加速度变化得越快，乘坐轿车的人就会感到越不舒适．若引入一个新物理量来表示加速度变化的快慢，则该物理量的单位是( A ) m / s ( B ) m / s 2( C ) m / s 3( D ) m 2/ s2 ．将两个分别带有电荷量-2Q 和+5Q 的相同金属小球 A 、 B 分别固定在相距为r 的两处（均可视为点电荷），它们间库仑力的大小为 F ．现将第三个与 A 、 B 两小球完全相同的不带电小球 C 先后与A 、 B 相互接触后拿走， A 、 B 间距离保持不变，则两球间库仑力的大小为 ( A ) F ( B ）51F ( c ）F109 ( D ）F 413 ．小球从空中某处从静止开始自由下落，与水平地面碰撞后上升到空中某一高度处，此过程中小球速度随时间变化的关系如图所示，则( A ）在下落和上升两个过程中，小球的加速度不同 ( B ）小球开始下落处离地面的高度为 o . 8m ( C ）整个过程中小球的位移为 1 . 0m( D ）整个过程中小球的平均速度大小为2m/s4 ．阴极射线示波管的聚焦电场是由电极 A 1、 A2 形成，实线为电场线，虚线为等势线， Z 轴为该电场的中心轴线，P 、 Q 、 R 为一个从左侧进入聚焦电场的电子运动轨迹上的三点，则( A ）电极 A 1的电势高于电极 A 2的电势( B ）电场中 Q 点的电场强度小于 R 点的电场强度 ( C ）电子在P 点处的动能大于在 Q 点处的动能 ( D ）电子从P 至 R 的运动过程中，电场力对它一直做正功5 ．图中 L 是绕在铁芯上的线圈，它与电阻 R 、 R 0、开关和电池 E 构成闭合回路．开关 S1 和 S2 开始都处在断开状态．设在 t = 0 时刻，接通开关 Sl ，经过一段时间，在 t = t1时刻，再接通开关 S2 ，则能较准确表示电阻 R 两端的电势差U ab 随时间 t 变化的图线是二、多项选择题：本大题共 4 小题，每小题 4 分，共计 16 分．每小题有多个选项符合题意．全部选对的得 4 分，选对但不全的得 2 分，错选或不答的得 0 分．6 ．如图所示，质量均为 m 的小球 A 、 B 用两根不可伸长的轻绳连接后悬挂于O 点，在外力F 的作用下，小球 A 、 B 处于静止状态．若要使两小球处于静止状态且悬线OA 与竖直方向的夹角保持 300不变，则外力 F 的大小 ( A ）可能为mg33 ( B ）可能为mg25( c ）可能为mg2 ( D ）可能为 mg7 ．如图（ l ）所示，理想变压器原、副线圈的匝数比为 20 : 1 , Rl = 10Ω . , R2= 20 Ω。

苏北四市2011届高三年级第三次调研考试

苏北四市2011届高三年级第三次调研考试数学Ⅰ一、填空题：本大题共14小题，每小题5分，共计70分．请把答案填写在答题卡相应位．．．．．．置上．．． 1．复数(1i)i z =-(i 为虚数单位)的共轭复数为 ▲ ．2．在空间直角坐标系O xyz -中，点(4,3,7)P -关于坐标平面yOz 的对称点的坐标为 ▲ ．3．已知函数22,0,(),0x x x f x ax bx x ⎧+=⎨+>⎩≤为奇函数，则a b += ▲ ．4．在某个容量为300的样本的频率分布直方图中，共有9个小长方形，若中间一个小长方形的面积等于其他8个小长方形面积和的15，则中间一组的频数为 ▲ .5．如图是一个算法的程序框图，其输出的结果是 ▲ ．6．若1cos 3α=，则cos(2)sin()sin()tan(3)2ααααπ-⋅π+π+⋅π-的值为 ▲ ．7．数列{}n a 满足11()2n n a a n *++=∈N ,112a =-,n S 是{}n a 的前n 项和,则2011S ＝ ▲ .8．若()0,3m ∈，则直线(2)(3)30m x m y ++--=与x 轴、y 轴围成的三角形的面积小于98的概率为 ▲ ．(第5题)9．若中心在原点、焦点在坐标轴上的双曲线的一条渐近线方程为30x y +=，则此双曲线的离心率为 ▲ ．10．已知二次函数2()()f x ax x c x =-+∈R 的值域为[0,)+∞，则22c a a c+++的最小值为 ▲ ．11．已知点,,,P A B C 是球O 表面上的四个点，且,,PA PB PC 两两成60 角，1P A P B P C ===cm ，则球的表面积为 ▲ 2cm ．12．如图，过点(5,4)P 作直线l 与圆22:25O x y +=交于,A B 两点，若2PA =，则直线l 的方程为 ▲ ．13.如图，在△ABC 和△AEF 中，B 是EF 的中点，AB =EF =1，2CA CB ==，若2AB AE AC AF ⋅+⋅=，则EF 与BC 的夹角等于 ▲ ． 14.若关于x 的方程43210x ax ax ax ++++=有实数根，则实数a 的取值范围为 ▲ ．二、解答题: 本大题共6小题，共计90分．请在答题卡指定的区域．．．．．．．．内作答，解答时应写出文字说明、求证过程或演算步骤． 15.(本小题满分14分)已知函数22()sin ()cos ()sin cos 63f x x x x x ππ=-+-+⋅，x ∈R .(1) 求()f x 的最大值及取得最大值时的x 的值；(2) 求()f x 在[0,]π上的单调增区间.FC(第13题)EB A(第12题)16. (本小题满分14分)在直角梯形ABCD 中，AB ∥CD ，24AB BC ==，3CD =，E 为AB 中点，过E 作EF CD ⊥,垂足为F ，如（图一），将此梯形沿EF 折成一个直二面角A EF C --，如（图二）.(1)求证：BF ∥平面ACD ； (2)求多面体ADFCBE 的体积.17. (本小题满分14分)在平面直角坐标系xOy 中，已知圆B ：22(1)16x y -+=与点(1,0)A -,P 为圆B 上的动点，线段PA 的垂直平分线交直线PB 于点R ，点R 的轨迹记为曲线C ． (1) 求曲线C 的方程；（2）曲线C 与x 轴正半轴交点记为Q ，过原点O 且不与x 轴重合的直线与曲线C 的交点记为,M N ，连接,QM QN ,分别交直线x t =（t 为常数，且2t ≠）于点,E F ，设,E F 的纵坐标分别为12,y y ，求12y y ⋅的值（用t 表示）.(第17题)(第16题)(图一) BCD E FA (图二)BACFDE18．(本小题满分16分)如图，某新建小区有一片边长为1(单位：百米)的正方形剩余地块ABCD ，中间部分MNK 是一片池塘，池塘的边缘曲线段MN 为函数29y x =12()33x ≤≤的图象，另外的边缘是平行于正方形两边的直线段．为了美化该地块，计划修一条穿越该地块的直路l （宽度不计），直路l 与曲线段MN 相切（切点记为P ），并把该地块分为两部分．记点P 到边AD 距离为t ，()f t 表示该地块在直路 l 左下部分的面积．（1）求()f t 的解析式；（2）求面积()S f t =的最大值．19．(本小题满分16分)设函数2()ln f x x a x =-与1()g x x a=1x =于点,A B ，且曲线()y f x =在点A 处的切线与曲线()y g x =在点B 处的切线平行（斜率相等）．（1）求函数()f x ,()g x 的表达式；（2）当1a >时，求函数()()()h x f x g x =-的最小值；（3）当1a <时，不等式()()f x m g x ⋅≥在11,42x ⎡⎤∈⎢⎥⎣⎦上恒成立，求实数m 的取值范围．20. (本小题满分16分)已知各项均为正数的等比数列{}n a 的公比为q ，且102q <<. （1）在数列{}n a 中是否存在三项，使其成等差数列？说明理由；(2)若11a =，且对任意正整数k ，12()k k k a a a ++-+仍是该数列中的某一项. (i)求公比q ；(ii)若1log 1)n n a b +=-，12n n S b b b =+++ ，12n n T S S S =+++ ,试用2011S 表示2011T .(第18题)徐州市2011届高三年级第三次调研考试数学Ⅰ答案及评分标准一、填空题：1． 1i - 2．(4,3,7)-- 3．0 4．50 5．16 6．13 7．502 8．23 910．10 11．32π 12．4y =或4091640x y --= 13.3π 14. [)2,2,3⎛⎤-∞-+∞ ⎥⎝⎦二、解答题:15. (1)1cos(2)1cos(2)133()sin 2222x x f x x π2π--+-=++………………………………2分 11(sin 2cos2)2x x =+-)14x π=-+，………………………………4分当2242x k ππ-=π+，即3,8x k k π=π+∈Z 时，……………………………………6分()f x1.………………………………………………………………8分 (2)由222242k x k ππππ--π+≤≤，即3,88k x k k πππ-π+∈Z ≤≤，又因为0x π≤≤，所以所求()f x 的增区间为3[0,],[,π]88π7π.……………………14分16.（1）连接EC ，交BF 于点O ，取AC 中点P ，连接,PO PD ，可得PO ∥AE ，且12PO AE =，而DF ∥AE ，且12DF AE =，所以DF ∥PO ，且DF PO =，所以四边形DPOF 为平行四边形，所以FO ∥PD ，即BF ∥PD ，又PD ⊂平面ACD ，BF ⊄平面ACD ，所以BF ∥平面ACD .……………………………………………8分(2)二面角A EF C --为直二面角，且AE EF ⊥，所以AE ⊥平面BCFE ，又BC ⊂平面BCFE ，所以AE BC ⊥，又BC BE ⊥，BE AE E = ，所以BC ⊥平面AEB ，所以BC 是三棱锥C ABE -的高，同理可证CF 是四棱锥C AEFD -的高，……………………………………………10分B C F D E A OP所以多面体ADFCBE 的体积111110222(12)2232323C ABE C AEFD V V V --=+=⨯⨯⨯⨯+⨯+⨯⨯=.………………14分17. (1)连接RA ，由题意得，RA RP =，4RP RB +=，所以42RA RB AB +=>=，…………………………………………………………2分由椭圆定义得，点R 的轨迹方程是22143x y +=.……………………………………4分 (2)设M 00(,)x y ，则00(,)N x y --，,QM QN 的斜率分别为,QM QN k k ，则002QM y k x =-，002NQ y k x =+，………………………………………………………6分所以直线QM 的方程为00(2)2y y x x =--，直线QN 的方程00(2)2y y x x =-+，…8分令(2)x t t =≠，则001200(2),(2)22y y y t y t x x =-=--+，……………………………10分又因为00(,)x y 在椭圆2200143x y +=，所以2200334y x =-，所以222022********(3)(2)34(2)(2)444x t y y y t t x x --⋅=-==----，其中t 为常数.……14分 18.（1）因为29y x=，所以229y x '=-，所以过点P 的切线方程为222()99y x t t t -=--，即22499y x t t=-+，…………2分令0x =，得49y t=，令0y =，得2x t =.所以切线与x 轴交点(2,0)E t ，切线与y 轴交点4(0,)9F t .………………………4分①当21,41,912,33t tt ⎧⎪⎪⎪⎨⎪⎪⎪⎩≤≤≤≤即4192t ≤≤时，切线左下方的区域为一直角三角形，所以144()2299f t t t =⨯⨯=.…………………………………………………………6分②当21,41,912,33t tt ⎧⎪>⎪⎪⎨⎪⎪⎪⎩≤≤≤ 即1223t <≤时，切线左下方的区域为一直角梯形， 22144241()()12999t t f t t t t --=+⋅=，……………………………………………………8分 ③当21,41,912,33t tt ⎧⎪⎪⎪>⎨⎪⎪⎪⎩≤≤≤即1439t <≤时,切线左下方的区域为一直角梯形, 所以221499()(2)12224t t f t t t t -=+⋅=-. 综上229142,,439441(),,9924112,.923t t t f t t t t t ⎧-<⎪⎪⎪=⎨⎪-⎪<⎪⎩≤≤≤≤……………………………………………………10分 (2)当1439t <≤时, 29()24f t t t =- 29444()4999t =--+<，……………………………12分当1223t <≤时, 241()9t f t t -=21144(2)999t =--+<，………………………………14分所以max 49S =．…………………………………………………………………………16分19．（1）由2()ln f x x a x =-，得22()x a f x x-'=，………………………………………2分由1()g x x a ='()g x =．又由题意可得(1)(1)f g ''=，即222a a a --=，故2a =，或12a =．………………………………………………4分所以当2a =时，2()2ln f x x x =-,1()2g x x =；当12a =时，21()ln 2f x x x =-，()2g x x =6分（2）当1a >时，21()()()2ln 2h x f x g x x x x =-=--212(1)(1)'()22x x h x x x x -+=--+=1)=⎣⎦，………………………………………8分由0x >0>，故当(0,1)x ∈时，()0h x '<,()h x 递减，当(1,)x ∈+∞时，()0h x '>,()h x 递增, 所以函数()h x 的最小值为13(1)12ln1122h =--+=．…………………10分（3）12a =，21()ln 2f x x x =-,()2g x x =当11[,)42x ∈时, 21()ln 2f x x x =-,2141'()2022x f x x x x -=-=<， ()f x 在1142⎡⎤⎢⎥⎣⎦，上为减函数，111()()ln 20242f x f =+>≥，………………………12分当11[,)42x ∈时，()2g x x ='()20g x ==>，()g x 在1142⎡⎤⎢⎥⎣⎦，上为增函数，1()()12g x g =-≤，且1()()04g x g =≥．……14分要使不等式()()f x m g x ⋅≥在11,42x ⎡⎤∈⎢⎥⎣⎦上恒成立，当14x =时，m 为任意实数；当11(,]42x ∈时，()()f x m g x ≤，而min1()()21()()2f f xg x g ⎡⎤==⎢⎥⎣⎦.所以m .……………………………………………………………16分20.⑴由条件知：11-=n n q a a ，102q <<，01>a ，所以数列{}n a 是递减数列，若有k a ，m a ，n a ()k m n <<成等差数列，则中项不可能是k a （最大），也不可能是n a （最小），………………………………2分若 k n k m n k m q q a a a --+=⇔+=122，（*）由221m k q q -<≤, 11>+-k h q ，知(* )式不成立，故k a ，m a ，n a 不可能成等差数列. ………………………………………………4分 ⑵(i)方法一： ⎥⎦⎤⎢⎣⎡++-=--=----++45)21()1(21121121q q a q q q a a a a k k k k k ，……6分由)1,41(45)21(2∈++-q 知， 121k k k k k a a a a a ++---<<< ，且>>>--++++3221k k k k k a a a a a … ，………………………………………………8分所以121+++=--k k k k a a a a ，即0122=-+q q ，所以12-=q ，………………………………………………………………………10分方法二：设12k k k m a a a a ++--=，则21m k q q q ---=，…………………………………6分由211,14q q ⎛⎫--∈ ⎪⎝⎭知1m k -=，即1m k =+， ……………………………………8分以下同方法一. …………………………………………………………………………10分 (ii) nb n 1=，………………………………………………………………………………12分方法一：nS n 131211++++= ，)131211()31211()211(1n T n +++++++++++=n n n n n n )1(3221--++-+-+= )1433221()131211(nn n n -++++-++++=)]11()411()311()211[(nnS n -++-+-+--=)]13121()1[(n n nS n +++---=)]131211([nn nS n ++++--=n n S n nS +-=(1)n n S n =+-，所以2011201120122011T S =-.…………………………………………………16分方法二：11111312111++=++++++=+n S n n S n n 所以 1(1)(1)1n n n S n S ++-+=，所以1(1)1n n n n S nS S ++-=+， 12112+=-S S S ， 123223+=-S S S ， … … 1)1(1+=-++n n n S nS S n ，累加得n T S S n n n +=-++11)1(，所以1(1)1(1)(1)()1n n n n n T n S n n S n n S b n +=+--=+-=++--1(1)()11n n S n n =++--+ (1)n n S n =+-，所以2011201120122011T S =-. ……………………………………………………16分徐州市2011届高三年级第三调研考试数学Ⅱ（附加题）21．【选做题】在下面A 、B 、C 、D 四个小题中只能选做两题，每小题10分，共20分． A ．选修4－1：几何证明选讲如图所示，圆O 的两弦AB 和CD 交于点E ，EF ∥CB ，EF 交AD 的延长线于点F ，FG 切圆O 于点G ．（1）求证：△DFE ∽△EFA ；（2）如果1FG =，求EF 的长．B ．选修4—2 矩阵与变换设M 是把坐标平面上点的横坐标不变、纵坐标沿y 轴方向伸长为原来5倍的伸压变换．（1）求直线4101x y -=在M 作用下的方程；（2）求M 的特征值与特征向量．(第21—A 题)C ．选修4－4：坐标系与参数方程已知极坐标系的极点与直角坐标系的原点重合，极轴与x 轴的正半轴重合．若曲线1C 的方程为2=8sin 15ρρθ-，曲线 2C的方程为,x y αα⎧=⎪⎨=⎪⎩（α为参数）．（1）将1C 的方程化为直角坐标方程；（2）若2C 上的点Q 对应的参数为34απ=，P 为1C 上的动点，求PQ 的最小值． D ．选修4—5：不等式选讲设函数()11f x x x =-++，若不等式2()a b a b a f x +--⋅≤对任意,a b ∈R 且0a ≠恒成立，求实数x 的范围． 22．（本小题满分10分）如图，在直三棱柱111ABC A B C -中，3AC =,4BC =，5=AB ，14AA =．(1)设AD AB λ= ,异面直线1AC 与CD 所成角的余弦值为925，求λ的值；(2)若点D 是AB 的中点，求二面角1D CB B --的余弦值．23．（本小题满分10分）在0，1，2，3，…，9这十个自然数中，任取3个不同的数字．（1）求组成的三位数中是3的倍数的有多少个？（2）将取出的三个数字按从小到大的顺序排列，设ξ为三个数字中相邻自然数的组数（例如：若取出的三个数字为0,1,2，则相邻的组为0,1和1,2，此时ξ的值是2），求随机变量ξ的分布列及其数学期望E ξ．(第22题)BAC A 1D B 1C 1徐州市2011届高三年级第三次调研考试数学Ⅱ（附加题）答案及评分标准21．【选做题】A ．选修4－1：几何证明选讲(1)因为EF ∥CB ，所以BCE FED ∠=∠，又BAD BCD ∠=∠，所以BAD FED ∠=∠，又EFD EFD ∠=∠，所以△DEF ∽△EFA ．……………………………………6分（2）由（1）得，EF FDFA EF=，2EF FA FD =⋅．因为FG 是切线，所以2FG FD FA =⋅，所以1EF FG ==．…………………10分B ．选修4—2：矩阵与变换（1）1005⎡⎤=⎢⎥⎣⎦M ．………………………………………………………………………2分设(,)x y ''是所求曲线上的任一点，1005x x y y '⎡⎤⎡⎤⎡⎤=⎢⎥⎢⎥⎢⎥'⎣⎦⎣⎦⎣⎦，所以,5,x x y y '=⎧⎨'=⎩所以,1,5x x y y '=⎧⎪⎨'=⎪⎩代入4101x y -=得，421x y ''-=，所以所求曲线的方程为124=-y x ．……………………………………………4分（2）矩阵M 的特征多项式1()(1)(5)005f λλλλλ-==--=-，所以M 的特征值为5,121==λλ．………………………………………………6分当11=λ时，由111λ=M αα，得特征向量110⎡⎤=⎢⎥⎣⎦α；当52=λ时，由222λ=M αα，得特征向量201⎡⎤=⎢⎥⎣⎦α．………………………10分C ．选修4－4：坐标系与参数方程（1）228150x y y +-+=．…………………………………………………………4分（2）当34απ=时，得(2,1)Q -，点Q 到1C ，所以PQ 1．………………………………………………10分D ．选修4—5：不等式选讲由2()a b a bf x a +--≥，对任意的,a b ∈R ，且0a ≠恒成立，而223a b a ba b a b+--++-=≤，()3f x ≥，即113x x -++≥，解得32x -≤，或32x ≥，所以x 的范围为33,22x x x ⎧⎫-⎨⎬⎩⎭≤或≥． …………10分22．(1)以1,,CA CB CC 分别为x y z ,,因为3AC =,4BC =，14AA =，所以(300)A ，，， (0,4,0)B ，(000)C ，，，1(0,0,4)C =，所以1(3,0,4)AC =-，因为AD AB λ= ，所以点(33,4,0)D λλ-+，所以(33,4,0)CD λλ=-+，因为异面直线1AC 与CD 所成角的余弦值为925，所以 19|cos ,|25AC CD <>==，解得12λ=．……………4分 (2)由（1）得1(044)B ，，，因为 D 是AB 的中点，所以3(20)2D ，，，所以3(20)2CD = ，，，1(044)CB = ，，，平面11CBB C 的法向量 1n (1,0,0)=，设平面1DB C 的一个法向量2000(,,)x y z =n ，则1n ，2n 的夹角（或其补角）的大小就是二面角1D CB B --的大小,由2210,0,CD CB ⎧⋅=⎪⎨⋅=⎪⎩ n n 得0000320,2440,x y y z ⎧+=⎪⎨⎪+=⎩令04x =，则03y =-，03z =，所以2n (4,3,3)=-， 12122cos ||||⋅<>==⋅，n n n n n n ，所以二面角1D B C B --． …………………………………10分 23.（1）要想组成的三位数能被3整除，把0,1,2,3，…，9这十个自然数中分为三组：0,3,6,9；1,4,7；2,5,8．若每组中各取一个数，含0，共有1112332236=C C C A 种；若每组中各取一个数不含0，共有11133333=162C C C A 种；若从每组中各取三个数，共有322233223=30A +C A A 种.所以组成的三位数能被3整除，共有36+162+30=228种.………………………6分（2）随机变量ξ0,1,2所以ξ的数学期望为77130121515155E ξ=⨯+⨯+⨯=.……………………………10分。

苏北四市高三第三次调研考试物理试题

江苏省苏北四市2011-2012学年度高三年级第三次调研测试物理试题2012.3.30注意：本试卷满分120分，考试时间100分钟。

将答案写在答题卡上，写在试卷上不得分。

一、单项选择题：本题共5小题，每小题3分，满分15分。

每小题只有一个选项符合题意。

1．如图所示，物体A用轻质细绳与圆环B连接，圆环套在固定竖直杆MN上，用一水平力F作用在绳上的O点，整个装置处于静止状态。

现将O方向的夹角增大。

下列说法正确的是A．水平力F逐渐增大B．O点能到达与圆环B等高处C．杆对圆环B的摩擦力增大D．杆对圆环B的弹力不变2．某导体置于电场后周围的电场分布情况如图所示，图中虚线表示电场线，实线表示等势面，A、B、C为电场中的三个点。

下列说法错．误．的是A．A点的电场强度小于B点的电场强度B．A点的电势高于B点的电势C．将负电荷从A点移到B点，电场力做正功D．将正电荷从A点移到C点，电场力做功为零3．2012年2月25日我国成功地将第十一颗北斗导航卫星送入太空预定轨道—地球静止轨道，使之成为地球同步卫星。

关于该卫星下列说法正确的是A．相对于地面静止，离地面高度为在R～4 R（R为地球半径）之间的任意值B．运行速度大于7.9km/sC．角速度大于静止在地球赤道上物体的角速度D．向心加速度大于静止在地球赤道上物体的向心加速度4．如图所示，矩形线圈abcd与可变电容器C、理想电流表A组成闭合电路。

线圈在有界匀强磁场中绕垂直于磁场的bc边匀速转动，转动的角速度ω=100π rad/s。

线圈的匝数N=100，边长ab=0.2m、ad=0.4m，电阻不计。

磁场只分布在bc边的左侧，磁感应强度大小B=162T。

电容器放电时间不计。

下列说法正确的是A．该线圈产生的交流电动势峰值为50 VB．该线圈产生的交流电动势有效值为C．电容器的耐压值至少为50VD．电容器的电容C变大时，电流表的示数变小5．“蹦极”是一项刺激的极限运动，运动员将一端固定的长弹性绳绑在踝关节处，从几十米高处跳下。

4月苏北四市第三次联考

苏北四市（连云港、徐州、淮安、宿迁）2011届高三年级第二次调研考试数学试题 2011年3月31日试卷 Ⅰ一、填空题：本大题共14小题，每小题5分，共70分． 1.若iia -+1（i 是虚数单位）是是实数，则实数a 的值是 . 2.已知集合{}{},02,12<-=>=x x x B x x A 则=⋃B A .3.为了解某校教师使用多媒体进行教学的情况，从该校200名授课教师中随机抽取20名教师，调查了他们上学期使用多媒体进行教学的次数，结果用茎叶图表示如下：据此可估计该校上学期200名教师中，使用多媒体进行教学次数在[]30,15内的人数为 .4.在如图所示的流程图中，输出的结果是 .5.若以连续掷两次骰子得到的点数n m ,分别为点P 的横、纵坐标，则点P 在圆1622=+y x 内的概率为 .6.在约束条件⎪⎩⎪⎨⎧≥-≤≤≤≤122010x y y x 下，则22)1(y x +-的最小值为 .7.一个匀速旋转的摩天轮每12分钟旋转一周，最低点距地面2米，最高点距地面18米，P 是摩天轮轮周上的一个定点，从P 在摩天轮最低点好似开始计时，则16分钟后P 点距地面的高度为 .8.已知集合{}{},0),(,1),(222>≤+=≤+=r r y x y x B y x y x A 若点A y x ∈),(是点B y x ∈),(的必要条件，则r 的最大值是 .9.已知点),2,0(A 抛物线)0(22>=p px y 的焦点为F ,准线为l ，线段FA 交抛物线与点B ,过B 作l 的垂线，垂足为M ,若,MF AM ⊥则=p .10.若函数,0,20,2)(⎪⎩⎪⎨⎧<-<=-x x x f xx 则函数))((x f f y =的值域是 . 11.如图所示，在直三棱柱111C B A ABC -中，2,4,1===⊥CC BC AC BC AC ,若用平行于三棱柱111C B A ABC -的某一侧面的平面去截此三棱柱，使得到的两个几B112.已知椭圆B A y x ,,12422=+是其左、右顶点，动点M 满足AB MB ⊥,连接AM 交椭圆于点P ，在x 轴上有异于点B A ,的定点Q ,以MP 为直径的圆经过直线MQ BP ,的交点，则点Q 的坐标为 .13.在ABC ∆中，过中线AD 中点E 任作一直线分别交AC AB ,于N M ,两点，设)0(,≠==xy y x ，则y x +4的最小值是 .14.如图是一个数表，第1行依次写着从小到大的正整数，然后把每行相邻的两个数的和写在这两个数正中间的下方，得到下一行，数表从上到下与从左到右均为无限项，则这个数表中的第13行第10个数为 .二、解答题：本大题共6小题,共90分,解答应写出文字说明,证明过程或演算步骤.15.如图，在平面直角坐标系xoy 中，点A 在x 轴正半轴上，直线AB 的倾斜角为43π，2=OB 设θ=∠AOB ,)43,2(ππθ∈.(1)用θ表示;OA (2)求⋅的最小值.16.如图，已知四面ABCD 的四个面均为锐角三角形，E 、F 、G 、H 分别为边DA CD BC AB ,,,上的点，//BD 平面,EFGH 且FG EF =.(1)求证：//HG 平面ABC ;(2)请在面ABD 内过点E 作一条线段垂直于AC ,并给出证明.B17.如图，已知位于y 轴左侧的圆C 与y 轴相切与点)1,0(，且被x 轴分成的两段弧之长比为1:2，过点),0(t H 的直线l 与圆C 相交于M 、N 两点，且以MN 为直径的圆恰好经过坐标原点O . (1)求圆C 的方程；(2)当1=t 时，求出直线l 的方程； (3)求直线OM 的斜率k 的取值范围.18.心理学家研究某位学生的学习情况发现：若这位学生刚学完的知识存留量记为1，则x 天后的存留量441+=x y ；若在)4(>t t 天时进行第一次复习，则此时知识存留量比未复习情况下增加一倍（复习时间忽略不计），其后存储量2y 随时间变化的曲线恰为直线的一部分，其斜率为),0()4(2<+a t a存留量随时间变化的曲线如图所示.当进行第一次复习后的存留量与不复习的存留量相差最大时，则称此时此刻为“二次复习最佳时机点”.（1）若5,1=-=t a ，求“二次最佳时机点”；（2）若出现了“二次复习最佳时机点”，求a 的取值范围.(天)19.已知各项均为正数的等差数列{}n a 的公差d 不等于0，设k a a a ,3,1是公比q 的等比数列{}n b 的前三项. (1)若2,71==a k .（ⅰ）求数列{}n n b a 的前n 项和n T ；（ⅱ）将数列{}n a 中与{}n b 相同的项去掉，剩下的项依次构成新的数列{}n c ，设其前n 项和为n S ，求),2(23211212*----∈≥⋅+-N n n S n n n n 的值；（2）若存在*∈>N m k m ,使得m k a a a a ,,,31成等比数列，求证：k 为奇数.20. 已知波函数R a ax x x f x x x x f x ax x f ∈+=++=+=,221)(,ln 953461)(,ln )(22212. (1) 求证：函数)(x f 在点))(,(e f e 处的切线恒过定点，并求出定点坐标； (2) 若)()(2x f x f <在区间),1(+∞上恒成立，求a 的取值范围； (3) 当32=a 时，求证：在区间),1(+∞上，满足)()()(21x f x g x f <<恒成立的函数)(x g 有无穷多个.苏北四市（连云港、徐州、淮安、宿迁）2011届高三年级第三次调研考试数学试题试卷 Ⅱ21.【选做题】在下面A,B,C,D 四个小题中只能选做两题，每小题10分，共20分. A.选修4—1：几何证明选讲如图，过圆O 外一点M 作圆的切线，切点为A ,过A 作OM AP ⊥于P . (1) 求证：2OA OP OM =⋅;(2) N 为线段AP 上一点，直线NB 垂直直线ON ,且交圆O 于B 点.过B 点的切线交直线ON 于K ,求证：90=∠OKM .B.选修4—2：矩阵与变换已知矩阵⎢⎣⎡=c M 1 ⎥⎦⎤2b 有特征值41=λ及对应的一个特征向量⎥⎦⎤⎢⎣⎡=321e . （1）求矩阵M ;（2）求曲线148522=++y xy x 在M 的作用下的新曲线方程.C.选修4—4：坐标系与参数方程已知极坐标系的极点与直角坐标系的原点重合，极轴与x 轴的正半轴重合.若直线l 的极坐标方程为23)4s in(=-πθρ.（1）把直线l 的极坐标方程化为直角坐标系方程；（2）已知P 为椭圆1916:22=+y x C 上一点，求P 到直线l 的距离的最大值.D.选修4—5：不等式选讲z y x ,,)()()()(2222333y x z z x y z y x z y x +++++≥++22．（本小题满分10分）如图，已知三棱柱111C B A ABC -的侧面与底面垂直，,,11AC AB AC AB AA ⊥===P N M ,,分别是111,,B A BC CC 的中点.(1)求证：AM PN ⊥;(2)若直线MB 与平面PMN 所成的角为θ，求θsin 的值. 23．（本小题满分10分）已知数列{}n a 中，对于任意n n n a a a N n 34,3-=∈*.（1）求证：若,1>n a 则11>+n a ；（2）若存在正整数m ，使得1=m a ，求证：（ⅰ）1≤m a ；（ⅱ）1132cos -=m k a π（其中Z k ∈）(参考公式：αααcos 3cos 43cos 3-=).苏北四市（连云港、徐州、淮安、宿迁）2011届高三年级第三次调研考试数学参考答案及评分标准一、填空题： 1．1-； 2．}{x x >；3．100； 4. 60； 5．92； 67．14； 8．2； 9； 10．11(1,)(,1)22-- ； 11．24； 12．(0,0)； 13．94； 14．162（或者65536）．二、解答题:15. (1)在△ABC 中，因为2OB =，θπθπππ-=--=∠=∠434,4ABO BAO ，，由正弦定理，得sin sin4OB OA ABOp =Ð，……………………………………3分 3sin()4OAp q -，所以 3sin()4OA p q =-. ……………6分注：仅写出正弦定理，得3分. 若用直线AB 方程求得2(sin cos)OA q q =+或)4OA πθ=+也得分.(2)由(1)得3||||cos sin()cos 4OA OBOA OB p q q q ?鬃-?uu r uu u ruu r uu u r ，…………………8分2(sin 2cos2)2θθ=++)24θπ=++， …………………10分因为3(,),24p p q Î所以572(,)444p p pq +?，所以当3242p p q +=，即58pq =时，OA OB ×uu r uu u r 的最小值为2-14分16. （1）因为BD //平面EFGH ，BDC EFGH FG =平面平面，所以BD //FG ．同理BD //EH ，又因为EH FG =，所以四边形EFGH 为平行四边形，所以HG //EF ，又HG ABC ⊄平面，所以HGABC 平面． ……………………………………………………6分（2）在ABC 平面内过点E 作EP AC ⊥，且交AC 于P 点，在ACD 平面内过点P 作PQ AC ⊥，且交AD 于Q 点，连结EQ ，则EQ 即为所求线段．………………………………………………10分证明如下：EP AC AC EPQ PQ AC EQ AC EQ EPQ EP PQ P ⊥⎫⇒⊥⎫⎪⊥⇒⊥⎬⎬⊂⎭⎪=⎭平面平面…………………………………14分17解：（1）因为位于y 轴左侧的圆C 与y 轴相切于点(0,1)，所以圆心C 在直线1y =上，设圆C 与x 轴的交点分别为A 、B ，由圆C 被x 轴分成的两段弧长之比为21:，得23ACB π∠=，所以2CA CB ==，圆心C 的坐标为(2,1)-，所以圆C 的方程为：22(2)(1)4x y ++-=． ………………………………4分（2）当1t =时，由题意知直线l 的斜率存在，设直线l 方程为1y mx =+，由221(2)(1)4y mx x y =+⎧⎨++-=⎩得01x y =⎧⎨=⎩或22241411x m m m y m -⎧=⎪⎪+⎨-+⎪=⎪+⎩，不妨令222441(,),(0,1)11m m M N m m --+++，因为以MN 为直径的圆恰好经过(0,0)O ，所以2222244141(,)(0,1)0111m m m m OM ON m m m m --+-+⋅=⋅==+++，解得2m =，所以所求直线l方程为(21y x =+或(21y x =+．………………………………10分（3）设直线MO 的方程为y kx =，2，解之得34k ≤，同理得，134k-≤，解之得43k ≤-或>0k ．由（2）知，=0k 也满足题意．所以k 的取值范围是43(,][0,]34-∞-． ………………………………………14分18. 设第一次复习后的存留量与不复习的存留量之差为y ，由题意知，228()(4)(4)4a y x t t t t =-+>++ ………………………………2分所以21284()(4)(4)44a y y y x t t t t x =-=-+->+++ ……………………4分(1) 当1,5a t =-=时，184(5)y x -=-+-(4)41x -+=-+≤1-+5=，当且仅当 14x = 时取等号，所以“二次复习最佳时机点”为第14天． ………………10分 (2) 284()(4)44a y x t t t x =-+-+++22(4)48(4)(4)44(4)a x a t t x t t -++=--+-++++≤84at --+， …………………………………………14分当且仅当4)4(244)4()4(2-+-=+=++-t ax x t x a 即时取等号，由题意t t a>-+-4)4(2，所以 40a -<<． ………………16分注：使用求导方法可以得到相应得分.19．⑴ 因为7k =，所以137,,a a a 成等比数列，又{}n a 是公差0d ≠的等差数列，所以()()211126a d a a d +=+，整理得12a d =，又12a =，所以1d =， 112b a ==，32111122a b a d q b a a +====，所以()11111,2n n n n a a n d n b b q -=+-=+=⨯=， ……………………………4分 ①用错位相减法或其它方法可求得{}n n a b 的前n 项和为12n n T n +=⨯； ………6分② 因为新的数列{}n c 的前21n n --项和为数列{}n a 的前21n -项的和减去数列{}n b 前n 项的和，所以121(21)(22)2(21)(21)(21)221n n n n n n n S ----+-=-=---.所以211212321n n n n S -----+⋅=-． ………………………10分 ⑵ 由d k a a d a ))1(()2(1121-+=+，整理得)5(412-=k d a d ，因为0≠d ，所以4)5(1-=k a d ，所以3111232a a d k q a a +-===. 因为存在m ＞k,m ∈N *使得13,,,k m a a a a 成等比数列，所以313123⎪⎭⎫⎝⎛-==k a q a a m ， ………………………………………………12分又在正项等差数列{a n }中，4)5)(1()1(111--+=-+=k m a a d m a a m ， ……13分所以3111234)5)(1(⎪⎭⎫⎝⎛-=--+k a k m a a ，又因为01>a ，所以有[]324(1)(5)(3)m k k +--=-， …………………………………14分因为[]24(1)(5)m k +--是偶数，所以3(3)k -也是偶数，即3-k 为偶数，所以k 为奇数. ……………………………………16分20. (1)因为1()2f x ax x '=+ ，所以()f x 在点(e,(e))f 处的切线的斜率为12k ae e=+，所以()f x 在点(,())e f e 处的切线方程为21(2)()1y ae x e ae e=+-++ ，……2分整理得11(2)()22e y ae x e -=+-，所以切线恒过定点1(,)22e ． ………4分(2) 令x ax x a x f x f x p ln 2)21()()()(22+--=-=<0，对(1,)x ∈+∞恒成立，因为21(21)21(1)[(21)1]()(21)2a x ax x a x p x a x a x x x--+---'=--+== （*）………………………………………………………………6分令()0p x '=，得极值点1x 1=，2121x a =-， ①当112a <<时，有1x x 12=>，即1a 21<<时，在（2x ，+∞）上有()0p x '>，此时)(x p 在区间2(,)x +∞上是增函数，并且在该区间上有)(x p ∈2((),)p x +∞，不合题意；②当1a ≥时，有211x x <=，同理可知，)(x p 在区间(1,)+∞上，有)(x p ∈((1),)p +∞，也不合题意； …………………………………………… 8分③当12a ≤时，有210a -≤，此时在区间(1,)+∞上恒有()0p x '<，从而)(x p 在区间(1,)+∞上是减函数；要使0)(<x p 在此区间上恒成立，只须满足021)1(≤--=a p 12a ⇒≥-，所以1122a -≤≤．综上可知a 的范围是11,22⎡⎤-⎢⎥⎣⎦． ……………………………………………12分 (3)当23a =时，221214514()ln ,()63923f x x x x f x x x =++=+记22115()()ln ,(1,)39y f x f x x x x =-=-∈+∞．因为225650x x y -'=-=>，所以21()()y f x f x =-在(1,)+∞上为增函数，所以21211()()(1)(1)3f x f x f f ->-=， ………………………………14分设11()(),(01)3R x f x λλ=+<<, 则12()()()f x R x f x <<, 所以在区间()1,+∞上，满足12()()()f x g x f x <<恒成立的函数()g x 有无穷多个． ………………………………………………………………16分数学附加题答案与评分标准21．A 选修4-l ：几何证明选讲证明：（1）因为MA 是圆O 的切线，所以OA AM ⊥，又因为AP OM ⊥．在Rt OAM △中，由射影定理知，2OA OM OP =．…………4分（2）因为BK 是圆O 的切线，BN OK ⊥，同（1），有2OB ON OK =，又OB OA =，所以OP OM ON OK =，即ON OMOP OK=，又NOP MOK =∠∠，所以ONP OMK △∽△，故90OKM OPN ==∠∠． …………………………10分 B ．选修4—2 矩阵与变换解：（1）由已知1283122b c ⎡⎤⎡⎤⎡⎤=⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦，即238,2612b c +=+=，2,3b c ==，所以1232M ⎡⎤=⎢⎥⎣⎦; …………………………4分（2）设曲线上任一点P (,)x y ，P 在M 作用下对应点///(,)P x y ，则//1232x x y y ⎡⎤⎡⎤⎡⎤=⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦即{//232x x y y x y=+=+，解之得////234y x x x y y ⎛-= - =⎝，代入225841x xy y ++=得222x y ''+=，即曲线225841x xy y ++=在M 的作用下的新曲线的方程是222x y +=．………10分C ．选修4-4：坐标系与参数方程解：（1）直线l的极坐标方程sin 4ρθπ⎛⎫-= ⎪⎝⎭sin cos θθ-=即sin cos 6ρθρθ-=，所以直线l 的直角坐标方程为60x y -+=； ……………4分（2）P 为椭圆221169x y C +=:上一点，设(4cos 3sin )P αα,，其中[02)α∈π,，则P 到直线l的距离d ==4cos 5ϕ=所以当cos()1αϕ+=时，d………………………………10分 D ．选修4－5：不等式选讲因为2220x y xy +≥≥，所以()()()3322x y x y x xy y xy x y +=+-+≥+， ………………………………4分同理()33y z yz y z +≥+,()33z x zx z x +≥+三式相加即可得()()()()3332x y z xy x y yz y z zx z x ++≥+++++ 又因为()()()()()()222xy x y yz y z zx z x x y z y x z z x y +++++=+++++所以()()()()3332222x y z x y z y x z z x y ++≥+++++ ………………10分 22．解：（1）建立如图所示直角坐标系，则(0,0,0)A ,(1,0,0)B ,(0,1,0)C ,1(0,0,1)A ,1(1,0,1)B ,1(0,1,1)C , 1(,0,1)2P ,1(0,1,)2M ,11(,,0)22N ,1(0,,1)2=-,AM 1(0,1,)2=, 因为⋅11001(1)022=⨯+⨯+-⨯=,所以AM PN ⊥． (4)（2）设平面PMN 的一个法向量为1111(,,)n x y z =,1(0,,1)2NP =-,111(,,)222NM =-,则1100n NP n NM ⎧⋅=⎪⎨⋅=⎪⎩⇒1111110,21110.222y z x y z ⎧-+=⎪⎪⎨⎪-++=⎪⎩令12y =，得11z =，13x =所以1(3,2,1)n =． …………………………………………………6分又1(1,1,)2MB =--，所以1112sin 342||||2n MB n MB θ⋅===⨯． ……………………10分23．证明：⑴因为1n a >，3143n n n a a a +=-所以2311143(43)1n n n n n a a a a a +++=-=->． ……………………2分 ⑵① 假设11a >，则232111143(43)1a a a a a =-=->若1k a >，则2311143(43)1k k k k ka a a a a +++=-=->．所以当1||1a >时，有*||1()n a n N >∈，这与已知1m a =矛盾，所以11a ≤. ………………………………………………………6分 ②由①可知，存在θ，使得1cos a θ=．则324cos 3cos cos3a θθθ=-=假设 n k =时，有1cos3n n a θ-=即1cos3k k a θ-=则()()33111434cos33cos3cos3k k k k k k a a a θθθ--+=-=-=所以对任意*n N ∈,1cos3n n a θ-=，则1cos3m m a θ-==1，132m k θπ-=，其中k Z ∈即123m k πθ-=，所以112cos 3m k a π-= (其中k 为整数). ……………………………10分。

苏北四市高三第三次质量检测

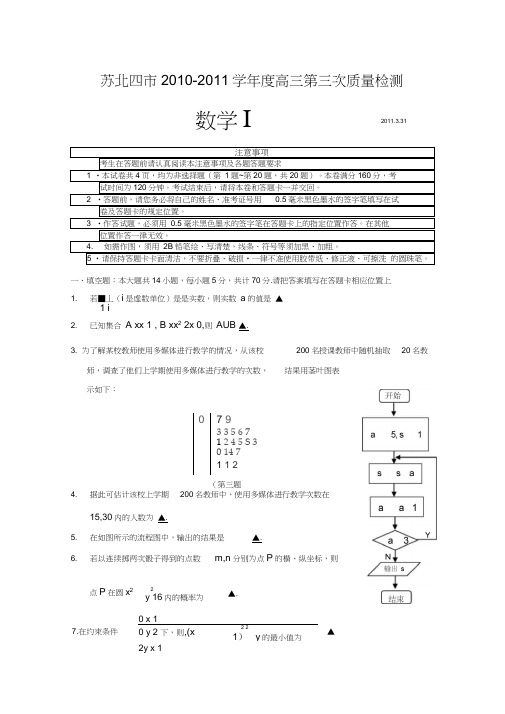
苏北四市2010-2011学年度高三第三次质量检测数学I注意事项考生在答题前请认真阅读本注意事项及各题答题要求1 •本试卷共4页，均为非选择题（第 1题~第20题，共20题）。

本卷满分160分，考试时间为120分钟。

考试结束后，请将本卷和答题卡一并交回。

2 •答题前，请您务必将自己的姓名、准考证号用 0.5毫米黑色墨水的签字笔填写在试卷及答题卡的规定位置。

3 •作答试题，必须用 0.5毫米黑色墨水的签字笔在答题卡上的指定位置作答。

在其他位置作答一律无效。

4. 如需作图，须用 2B 铅笔绘、写清楚，线条、符号等须加黑、加粗。

5 •请保持答题卡卡面清洁，不要折叠、破损•一律不准使用胶带纸、修正液、可擦洗的圆珠笔。

一、填空题：本大题共14小题，每小题5分，共计70分.请把答案填写在答题卡相应位置上 1. 若■丄（i 是虚数单位）是是实数，则实数 a 的值是 ▲1 i2.已知集合 A xx 1 , B xx 2 2x 0,则 AUB ▲.3. 为了解某校教师使用多媒体进行教学的情况，从该校师，调查了他们上学期使用多媒体进行教学的次数，结果用茎叶图表示如下：4.据此可估计该校上学期 200名教师中，使用多媒体进行教学次数在15,30内的人数为 ▲.5. 在如图所示的流程图中，输出的结果是 ▲.6.若以连续掷两次骰子得到的点数m,n 分别为点P 的横、纵坐标，则0 7 93 3 5 6 7 1 245 S 30 14 71 1 2点P 在圆x 22y 16内的概率为 ▲.0 x 17.在约束条件0 y 2 下，则,(x2 21） y 的最小值为▲2y x 12011.3.31200名授课教师中随机抽取 20名教（第三题图）8. 一个匀速旋转的摩天轮每 12分钟旋转一周，最低点距地面2米，最高点距地面18米，P从P 在摩天轮最低点好似开始计时，则16分钟后P 点距地面的高度为 ▲体能够拼接成长方体，则长方体表面积的最小值为于点P ，在x 轴上有异于点代B 的定点Q ,以MP 为直径的圆经过直线 BP, MQ 的交点, 则点Q 的坐标为 ▲.14. 在 ABC 中，过中线AD 中点E 任作一直线分别交ABAC 于M, N 两点，设AM xAB,AN yAC(xy 0)，则 4x y 的最小值是—▲.15. 如图是一个数表，第 1行依次写着从小到大的正整数，然后把每行相邻的两个数的和写在这两个数正中间的下方，得到下一行，数表从上到下与从左到右均为无限项，则这个数表中的第13行第10个数为 ▲.12 3 4 5 6 7 (3)5 7 9 11 13 …… 8 12 16 20 24 …… 20 23 36 44 ................... 48 64 80 ...............是摩天轮轮周上的一个定点, 9.已知集合A (x, y)|xy 1 ,B (x, y2 2 2x y r r 0 ,若点(x, y) A 是点10. 11. 12.(x, y) B 的必要条件，则已知点A(0,2),抛物线y过B 作I 的垂线, 若函数f (x)AC BC, AC 垂足为2x ,x 2x ABC r 的最大值是 ▲2 px(p 0)的焦点为F ,准线为I ，线段FA 交抛物线与点B ,M ,若 AM MF ,则 p _▲则函数y,x 0'4,BC CC 1 2 ,f( f (x))的值域柱 ABC A 1B 1C 1 中平行于三棱 A 1B 1C 1的某一侧面的平面去截此三棱柱,使得到的两个几何13.2 2已知椭圆24乡MB 是其左、右顶点，动点M 满足MB AB ,连接AM 交椭圆C 1柱解答题：本大题共6小题，共计90分.请在答题卡指定的区域内作答，解答时应写出文字说明、求证过程或演算步骤15. (本小题共14分)如图，在平面直角坐标系xoy中，点A在x轴正半轴上,3直线AB的倾斜角为，0B16.17.3设AOB , (―二).2 4(1)用表示0A;⑵求OA 0B的最小值.(本小题共14分)如图，已知四面体ABCD的四个面均为锐角三角形, E、F、G、H分别为边AB,BC,CD,DA上的点，BD //平面EFGH ,且EH FG .(1) 求证：HG//平面ABC;(2) 请在面ABD内过点E作一条线段垂直于给出证明.(本小题共14 分)如图，已知位于y轴左侧的圆C与y轴相切与点(0,1)，且被x轴分成的两段弧之长比为2:1,过点H(0,t)的直线l与圆C相交于M、N两点,且以MN为直径的圆恰好经过坐标原点O.(1)求圆C的方程；⑵当t 1时，求出直线l的方程；(3)求直线OM的斜率k的取值范围.18. (本小题共16分)心理学家研究某位学生的学习情况发现：若这位学生刚学完的知识存留量记为1，则x天4后的存留量％；若在t(t 4)天时进行第一次复习，则此时知识存留量比未复习x 4情况下增加一倍(复习时间忽略不计) ，其后存储量y2随时间变化的曲线恰为直线的一部分，其斜率为一(a 0),存留量随时间变化的曲线如(t 4)图所示.当进行第一次复习后的存留量与不复习的存留量相差最大时，则称此时此刻为“二次复习最佳时机点”.(1)若a 1,t 5，求“二次最佳时机点”；(2)若出现了“二次复习最佳时机点”，求a的取值范围19. (本小题共16分)已知各项均为正数的等差数列a n的公差d不等于0,设a1,a3,a k是公比q的等比数列b n的前三项.(1)若k 7,a12.(i)求数列a n b n的前n项和T n；(ii)将数列a n中与b n 中相同的项去掉，剩下的项依次构成新的数列c n，设其前n 项和为S n,求S2n n 1 22n 13 2n1( n 2,n N)的值；(2)若存在m k, m N使得a1,a3,a k,a m成等比数列，求证：k为奇数.20. (本小题共16分)1 4 5 1 o已知函数f(x) ax2ln x, f1 (x) x2x ln x, f2(x) x22ax,a R.6 3 9 2(1)求证：函数f (x)在点(e, f (e))处的切线恒过定点，并求出定点坐标；(2)若f(x) f2(x)在区间(1,)上恒成立，求a的取值范围；2(3)当a 时，求证：在区间(1,)上，满足f1(x) g(x) f2(x)恒成立的函数g(x)3有无穷多个苏北四市2010-2011学年度高三第三次质量检测数学H (附加题)注意事项考生在答题前请认真阅读本注意事项及各题答题要求1 •本试卷共2页，均为非选择题(第 21题~第23题)。

江苏苏北四市2011届高三第一次调研考试物理试题(word版)

江苏省苏北四市2011届高三调研抽测考试物理试题 2010.10.22注意：本试卷满分120分，考试时间100分钟．请将答案填写在答题卡上，直接写在试卷上不得分．一、单项选择题：本题共5小题，每小题3分，共15分．每小题只有一个选项符合题意． 1．在第十一届全运会男子举重56公斤级比赛中，龙清泉以302公斤的总成绩获得冠军，并以169公斤超该级别挺举世界纪录。

如图所示，设龙清泉所举杠铃的总重为G ，杠铃平衡时每只手臂与竖直线所成的夹角为30°，则他每只手臂承受的张力为 A ．2GB ．G 33C ．23GD ．G2．某电场的电场线分布如图所示，下列说法正确的是 A ．a 点的电势高于b 点的电势 B ．c 点的电场强度大于d 点的电场强度C ．若将一正试探电荷由a 点移到b 点，电场力做负功D ．若将一负试探电荷由c 点移到d 点，电势能增加 3．一轻质弹簧一端固定在竖直墙壁上，另一自由端位于O 点，现用一滑块将弹簧的自由端（与滑块未拴接）从O 点压自 A O t OAtOBtO DtOCa b cd4．如图，L 是直流电阻为零、自感系数很大的线圈，A 和B 是两个相同的小灯泡，某时刻闭合开关S ，通过A 、B 两灯泡中的电流IA 、IB 随时间t 变化的图象，正确的是5．如图所示，一物体从斜面上高为h 处的A 点由静止滑下，滑至斜面底端B 时，因与水平面碰撞仅保留了水平分速度而进入水平轨道，在水平面上滑行一段距离后停在C 点，测得A 、C 两点间的水平距离为xA ．x h >μ B ．x h<μ C ．x h=μD ．无法确定二、多项选择题：本题共4小题，每小题4分，共16分．每题有多个选项符合题意，全部选对的得4分，选对但不全的得2分，错选或不答的得0分．6．如图甲所示，理想变压器原、副线圈的匝数比为10︰1，电阻R=22Ω，各电表均为理想电表。

原线圈输入电压的变化规律如图乙所示。

苏北四市高三年级第三次模拟考试(物理)详细解答过程

苏北四市高三年级第三次模拟考试1. C 解析：用整体法研究，竖直方向上受整体重力和杆对圆环B 的摩擦力，所以摩擦力大小不变；水平方向上受人的拉力、杆对圆环B 的弹力，弹力大小与人的拉力大小相等；再以O 点为研究对象，它所受的合力为零，随着细绳与竖直方向夹角的增大，拉力变大；由于物块A 有重力，绳OB 不可能水平．2. A 解析：由图中电场线方向可知，B 点电势比A 点低，所以负电荷从A 到B 电场力做负功；图中A 、C 在同一条等势线上(整个导体为等势体)，其间移动电荷电场力不做功；B 点的电场线明显比A 点密集，场强比A 点大．只有选项A 说法错误，选A.3. B 解析：因其为同步卫星，所以周期与地球自转周期相等，角速度与地球相同；由向心加速度a ＝ω2r 可知，卫星的向心加速度大于静止在地球赤道上物体的向心加速度；同步卫星的高度为确定值，约为地球半径的6倍；由G Mm r 2＝m v 2r 有v ＝GM r，随着高度的增加，运行速率减小，小于第一宇宙速度7.9 km/s.4. D 解析：图示位置线圈的磁通量最大、电动势为0，转过90°、270°时的电动势最大，E m ＝nBSω＝50 2 V ，A 、C 两个选项错误；电容器的电容变大时，对交流的阻碍作用减小，电流变大；交流的有效值由电流的热效应计算，502R ×T 2＋0＝U 2R×T ，求得U ＝25 2 V ．选项D 正确．5. D 解析：题中给出了力F 随时间t 的关系图线，由于弹性绳中弹力F 与伸长量x 遵循胡克定律——线性关系，所以图线也是弹性绳的形变量x 与时间t 的关系图线，图线上任一点的切线的斜率即为位移的变化率——速度，t 2、t 4两个时刻运动员的速度最大加速度为0，弹性绳的拉力等于运动员的总重力；t 3时刻拉力最大、形变量最大、速度为0、加速度最大；t 4时刻运动员具有向上的最大速度；t 1～t 2时间内运动员向下加速运动，处于失重状态；t 2～t 4时间内运动员先向下运动再向上运动，机械能先减小后增大．6. BC 解析：船头始终与河岸垂直时渡河时间最短，t ＝6004s ＝150 s ；船离岸400 m 时，离近岸为200 m ，由图知水流速度为2 m/s ，船的合速度为2 5 m/s ；在航行的全过程中，水流速度先增大，后变小，合速度的方向不可能保持不变，船的轨迹一定为曲线．选项BC 正确．7. BD 解析：S 接c 时，实际上只是利用了两组副线圈中的一组，其输出电压是确定值2n 2U m 2n 1；当滑动触头P 向下移动时，电阻变大，电流变小，变压器的输入、输出功率都变小，当P 向上移动时，变压器的输入、输出功率都变大；当S 接b 时，输出电压为0.8. BD 解析：金属棒与轨道间的压力大小等于金属所受的安培力，N ＝Bdkt ，所以有mg －μBdkt ＝ma ，金属棒的加速度a ＝g －μBdk mt ，所以A 、B 图象中B 图正确；速度图象的斜率表示加速度，图象D 正确．选项BD 正确．9. AC 解析：设甲、乙两滑块被弹开时的速率均为v 1，如果v 1>v 0，则两滑块一开始就做匀减速运动，我们试着作出两滑块和皮带的速度图象如图所示．如果在图中t 1时刻之前两滑块就离开了皮带，则两滑块落在两侧，离开时的速度大小相等，落点距释放点的水平位移大小相等；如果滑块甲在t 1～t 2之间的某个时刻离开皮带，则乙已做匀速运动，且速率大于甲的速率，两者位移不等；若在t 2之前滑块甲未能离开皮带，则甲必在t 3之后离开，且甲、乙必落在同一侧，同一点．如果v 1<v 0，则释放后甲做匀减速运动，乙做匀加速运动，速度图象如图所示，如果滑块甲在图中t 2之前能离开皮带，则两滑块一定分落两侧，位移大小不等；若滑块甲在图中t 2之前不能离开皮带，则两滑块一定落在同一侧，且速率一定相等，位移大小也一定相等．综合以上分析，选项AC 正确．10. (1) L t(3分) (2) 如图(纵坐标1分，图象2分) (3) 16mv 2A (2分)解析：(1) 因为L 很小，所以杆通过光电门时的平均速度作为瞬时速度，v A ＝L t. (2) 结合表格数据进行分析和猜想，应作v 2h 图象，所作图像如上图所示．(3) 由杆转动过程中机械能守恒可知，当杆的末端下降高度h 时，E k ＝mg h 2；而由所作的图象可知，v 2A ＝30h ，所以E k ＝16mv 2A . 11. (1) 如图(2分) A 2 (2分)(2) E ＝1b (2分) r ＝k b(2分) 电压表的分流(2分) 解析：由于滑动变阻器阻值只有40 Ω，而待测电阻阻值约为2 k Ω，所以应该采用分压式电路；通过R 0的电流小于2 mA ，应选电流表A 2.所连线路图如上图所示．(2) 根据闭合电路欧姆定律有E ＝U ＋Ir ＝U ＋U R 2r ，整理得1U ＝r E ·1R 2＋1E，结合图象，E ＝1b ，r ＝k b.造成这一误差的主要原因是电压表的分流作用． 12A. (1) BD(4分)(2) 吸收 260 J(每空2分)(3) 4×1025(4分)解析：(1) 晶体具有各向异性；由于表面张力的作用，自由液滴都有将表面积收为最小的趋势；布朗运动是颗粒的运动，但反映了周边分子的运动规律；两个相邻的分子间距离为r 0时，它们间的分子引力和分子斥力大小相等，分子力表现为0.选项BD 正确．(2) 由热力学第一定律ΔU ＝Q ＋W 可知，沿abc 变化内能增加了220 J ，同理，沿adc 变化内能也增加220 J ，所以吸收热量260 J.(3) 由体积和摩尔体积换算物质的量，所以N ＝ρV M×N A ，代入数值得N ＝4×1025. 12B. (1) BD (4分) (2) 先到达后壁短(每空2分)(3) α＝45°(2分) C ＝45°(2分)解析：(1) 质点A 、C 平衡位置间的距离为半波长；若M 向下振动，则波向右传播，极短时间后波形如虚线所示；在粗糙平面上的振动为阻尼振动；单摆回复力来源于小球重力在轨迹切线方向上的分力，F ＝mgsin θ＝－mg x l ＝－mg lx. (2) 地面观察者观察到光先到达后壁，车厢长度变短，高度不变．(3) ∵ sin αsin30°＝n ＝ 2.∴ α＝45°，∵ sinC ＝1n ，∴ C ＝45°. 12C. (1) ABD (4分) (2) 10 9.5×10－8(每空2分)(3) 2 m/s(4分)解析：(1) 衍射现象是波的特有属性；由动量守恒定律可知，α粒子的大角度偏转，说明原子的质量绝大部分集中在很小范围内；根据玻尔理论，原子的能级是不连续的，电子的轨道半径也是不连续的；光电效应说明了光子有能量，而且光子的能量是不连续的，具有粒子性．(2) 用能量为13.06 eV 的光子照射基态氢原子，可使其跃迁到－0.54 eV 的第5能级，可发射10种不同波长的光；其中最短波长对应着能量最大的光子，E ＝hν＝h c λ，所以λ＝hc E＝6.63×10－34×3×10813.06×1.6×10－19m ＝9.5×10－8m. (3) 根据动量守恒定律m 1v 1＋m 2v 2＝ m 1v 1′＋m 2v 2′，代入数据计算得v 2′＝2 m/s.13. (15分)解：(1) 设物体上升到h 1＝1 m 处的速度为v 1，由图乙知mgh 1＋12mv 21＝12 解得 v 1＝2 m/s(2分)(2) 由图乙知，物体上升到h 1＝1 m 后机械能守恒，即撤去拉力F ，物体仅在重力作用下先匀减速上升，至最高点后再自由下落．设向上减速时间为t 1，自由下落时间为t 2对减速上升阶段有0－v 1＝－gt 1 解得 t 1＝0.2 s(1分)减速上升距离Δh ＝v 12t 1＝0.2 m(1分) 自由下落阶段有h 1＋Δh ＝12gt 22 解得t 2＝65s(2分) 即有 t ＝t 1＋t 2＝6＋15s(1分) (3) 对F 作用下物体的运动过程，由能量守恒有F ·Δh ＝ΔE(1分)由图象可得，物体上升h 1＝1 m 的过程中所受拉力F ＝12 N(1分)物体向上做匀加速直线运动，设上升至h 2＝0.25 m 时的速度为v 2，加速度为a 由牛顿第二定律有F －mg ＝ma(1分)由运动学公式有v 22＝2ah 2(1分)瞬时功率P ＝Fv 2(1分)解得 P ＝12 W(1分)14. (16分)解：(1) 设质子从左侧O 1点射入的速度为v 0，极板长为L在复合场中匀速运动：q U 2R＝qv 0B(2分) 在电场中做类平抛运动：L －2R ＝v 0t R ＝12qE mt 2(2分) 又L ＝v 0t 0(1分)撤去磁场，仅受电场力，有R ＝12qE m ⎝⎛⎭⎫t 022(1分) 解得t ＝t 02 L ＝4R v 0＝4R t 0 U ＝8R 2B t 0(2分) (2) 质子从极板间飞出时的沿电场方向分速度大小v y ＝qE m t ＝2R t ＝v 0(1分) 从极板间飞出时的速度大小v ＝v 20＋v 2y ＝2v 0＝42R t 0(1分)(3) 设质子在磁场中做圆周运动的轨道半径为r ，质子恰好从上极板左边缘飞出时速度的偏转角为α，由几何关系可知β＝π－α＝45°，r ＋ 2 r ＝R (2分)因为R ＝12qE m ⎝⎛⎭⎫t 022，所以qE m ＝qv 0B m ＝8R t 20(1分) 根据向心力公式qvB ＝m v 2r ，解得 v ＝2（2－1）R t 0(2分) 所以，质子两板左侧间飞出的条件为0<v<2（2－1）R t 0(1分) 15. (16分)解：(1) 设线框下边离开磁场时做匀速直线运动的速度为v 0，则E ＝BLv 0 I ＝E RF A ＝BIL ＝B 2L 2v 0R(2分) 由平衡条件F A ＝B 2L 2v 0R＝mgsin θ(2 分) 可解得v 0＝mgRsin θB 2L 2＝1 m/s(1 分) (2) 从线框刚离开磁场区域到小球刚运动到电场的下边界，由动能定理－qEL ＋mgsin θ×2 L ＝0－12mv 20(3分)可求得 E ＝6×106 N/C(2分)(3) 设经足够长时间后，小球运动的最低点到电场上边界的距离为x, 线框最终不会再进入磁场，即运动的最高点是线框的上边与磁场的下边界重合．由动能定理qEx －mgsin θ(L ＋x)＝0(4分)可得x ＝1617m(2分)。

江苏省苏北四市2011届高三第三次调研考试(物理)

学必求其心得，业必贵于专精OA D hm江苏省苏北四市2011届高三第三次调研考试物理试题 2011。

4.1．一、单项选择题：本题共5小题，每小题3分，共15分．每小题只有一个选项符合题意．1．在杂技表演中，猴子沿竖直杆向上做初速度为零、加速度为a 的匀加速运动，同时人顶着直杆以速度0v 水平匀速移动，经过时间t ，猴子沿杆向上移动的高度为h ，人顶杆沿水平地面移动的距离为x ，如图所示。

关于猴子的运动情况，下列说法中正确的是A ．相对地面的运动轨迹为直线B ．相对地面做变加速曲线运动C ．t 时刻猴子对地速度的大小为at v +0D ．t 时间内猴子对地的位移大小为22h x +2．风洞是进行空气动力学实验的一种主要设备。

某兴趣小组为了检验一飞机模型的性能，对该模型进行了模拟风洞实验，该实验的示意图如图，其中AB 代表飞机模型的截面，OL 为飞机模型的牵引绳。

已知飞机模型重为G ,风向水平，当牵引绳水平时,飞机模型恰好静止在空中，此时飞机模型截面与水平面的夹角为θ，则作用于飞机模型上的风力大小为A ．θcos GB ．G cos θC ．θsin G D ．G sin θ3．真空中有一半径为r 0的带电金属球壳，通过其球心的一直线上各点的电势φ分布如图，r 表示该直线上某点到球心的距离，r 1、r 2分别是该直线上A 、B 两点离球心的距离。

下列说法中正确的是A ．A 点的电势低于B 点的电势 B ．A 点的电场强度方向由A 指向BC ．A 点的电场强度小于B 点的电场强度D ．正电荷沿直线从A 移到B 的过程中，电场力做负功 4．如图，在一直立的光滑管内放置一劲度系数为k 的轻质弹簧，管口上方O 点与弹簧上端初位置A 的距离为h ,一质量为m 的小球从O 点由静止下落，压缩弹簧至最低点D ,弹簧始终处于弹性限度内,不计空气阻力.小球自O 点下落到最低点D 的过程中,下列说法中正确的是 A ．小球最大速度的位置随h 的变化而变化 B ．小球的最大速度与h 无关r O φφ0r 0 r 1 r 2风向 A B L O θx h学必求其心得，业必贵于专精压缩量与h 成正比5．闭合矩形导线框abcd 固定在匀强磁场中，磁场的方向与导线框所在平面垂直，磁感应强度B 随时间t 变化的规律如图所示。

苏北市第三次调研考试(答案)

苏北四市2009届高三第三次调研考试物理答案一、二、选择题：1~5小题每小题3分，6~9每小题4分，共31分．1．D 2．C 3．A 4．Ｄ 5．B 6．AC 7．CD 8．BC 9．AD三、简答题：本题分必做题（第10、11题）和选做题（第12题）两部分，共计42分．10．⑴小车所受合外力大小等于(或约等于)mg ……(2分)⑵两光电门之间的距离（或“小车由光电门1运动至光电门2所用时间”）…………………(2分) 2221222122)(t xt t t d - （或“2121)(t xt t t d -”）………(2分) ⑶如右图…………………………………………(2分) ⑷木板倾角偏小（或“平衡摩擦力不足”或“末完全平衡摩擦力”）……………………………(2分)11．⑴①③……………………………………………(2分) ⑵作图（2分） 1.45（±0.02）(1分) 0.75（±0.02）(1分⑶偏小(1分) 偏小(1分) 12．A.⑴BD (4分) ⑵减小(2分) 减小(2分) ⑶Q Sh p Pt --0…………………………………… (4分)B.⑴BD (4分) ⑵ ①y ＝5cos2πt (2分) 110cm (2分) ⑶ ①45°(2分) ②不能…………(2分)C ．⑴AB (4分) ⑵ 2432110)2(,n 3c m m m m --- (4分) ⑶0.025(2分) 相同…………(2分)13．⑴以10个小球整体为研究对象，由力的平衡条件可得 m gF10tan =θ…………………………（2分）得10tan F mg θ=…………………………………………………………………………………（2分）⑵以1号球为研究对象，根据机械能守恒定律可得 221mv mgh =………………………………（2分）解得gh v 2=………………………………………………………………………………………（2分）⑶撤去水平外力F 后，以10个小球整体为研究对象，利用机械能守恒定律可得218110(sin )1022r mg h m v θ+=⋅⋅ （2分）得 v =（1分）以1号球为研究对象，由动能定理得 212mgh W mv +=……………………………………（2分）得9sin W mgr θ=…………………………………………………………………………………（2分）14．⑴小球受力如图所示 qE=mgcotα…（2分） E=3mg/q ……………………………（2分）⑵设小球在D 点速度为v D ，在水平方向由牛顿第二定律得：qE =ma x ………………（1分） 22D x v d a =………………………………………………（2分）小球在D 点离开水平面的条件是： qv D B =mg ……………………………………………（1分）得：d =22263Bq gm …………………………………………………………………………………（2分）⑶当速度方向与电场力和重力合力方向垂直时，速度最大，……………………（1分）则：R v m mg B qv mm 2030sin =-……（2分）R = kh ………………………………（1分）mgBqv mv h m m22-=…………………（2分）15．⑴设匀速直线运动的速度为v 0， ef 有效切割长度为l ，则电流：rBv rl Blv I 3300==，由于v 0不变，所以I 不变。

苏北四市2011届高三第三次调研考试

苏北四市2011届高三第三次调研考试一、填空题：本大题共14小题，每小题5分，共70分． 1.若iia -+1（i 是虚数单位）是是实数，则实数a 的值是 . 2.已知集合{}{},02,12<-=>=x x x B x x A 则=⋃B A .3.为了解某校教师使用多媒体进行教学的情况，从该校200名授课教师中随机抽取20名教师，调查了他们上学期使用多媒体进行教学的次数，结果用茎叶图表示如下：据此可估计该校上学期200名教师中，使用多媒体进行教学次数在[]30,15内的人数为 .4.在如图所示的流程图中，输出的结果是 .5.若以连续掷两次骰子得到的点数n m ,分别为点P 的横、纵坐标，则点P 在圆1622=+y x 内的概率为 .6.在约束条件⎪⎩⎪⎨⎧≥-≤≤≤≤122010x y y x 下，则22)1(y x +-的最小值为 .7.一个匀速旋转的摩天轮每12分钟旋转一周，最低点距地面2米，最高点距地面18米，P 是摩天轮轮周上的一个定点，从P 在摩天轮最低点好似开始计时，则16分钟后P 点距地面的高度为 .8.已知集合{}{},0),(,1),(222>≤+=≤+=r r y x y x B y x y x A 若点A y x ∈),(是点B y x ∈),(的必要条件，则r 的最大值是 .9.已知点),2,0(A 抛物线)0(22>=p px y 的焦点为F ,准线为l ，线段FA 交抛物线与点B ,过B 作l 的垂线，垂足为M ,若,MF AM ⊥则=p .10.若函数,0,20,2)(⎪⎩⎪⎨⎧<-<=-x x x f xx 则函数))((x f f y =的值域是 . 11.如图所示，在直三棱柱111C B A ABC -中，2,4,1===⊥CC BC AC BC AC ,若用平行于三棱柱111C B A ABC -的某一侧面的平面去截此三棱柱，使得到的两个几何体能够拼接成长方体，则长方体表面积的最小值为 .12.已知椭圆B A y x ,,12422=+是其左、右顶点，动点M 满足AB MB ⊥,连接AM 交椭圆于点P ，在x 轴上有异于点B A ,的定点Q ,以MP 为直径的圆经过直线MQ BP ,的交点，则点Q 的坐标为 .13.在ABC ∆中，过中线AD 中点E 任作一直线分别交AC AB ,于N M ,两点，设)0(,≠==xy AC y AN AB x AM ，则y x +4的最小值是 .14.如图是一个数表，第1行依次写着从小到大的正整数，然后把每行相邻的两个数的和写在这两个数正中间的下方，得到下一行，数表从上到下与从左到右均为无限项，则这个数表中的第13行第10个数为 .二、解答题：本大题共6小题,共90分,解答应写出文字说明,证明过程或演算步骤.15.如图，在平面直角坐标系xo y 中，点A 在x 轴正半轴上，直线AB 的倾斜角为43π，2=OB 设θ=∠AOB ,)43,2(ππθ∈.(1)用θ表示;OA (2)求OB OA ⋅的最小值.16.如图，已知四面ABCD 的四个面均为锐角三角形，E 、F 、G 、H 分别为边DA CD BC AB ,,,上的点，//BD 平面,EFGH 且FG EF =.(1)求证：//HG 平面ABC ;(2)请在面ABD 内过点E 作一条线段垂直于AC ,并给出证明.17.如图，已知位于y 轴左侧的圆C 与y 轴相切与点)1,0(，且被x 轴分成的两段弧之长比为1:2，过点),0(t H 的直线l 与圆C 相交于M 、N 两点，且以MN 为直径的圆恰好经过坐标原点O . (1)求圆C 的方程；(2)当1=t 时，求出直线l 的方程； (3)求直线OM 的斜率k 的取值范围.18.心理学家研究某位学生的学习情况发现：若这位学生刚学完的知识存留量记为1，则x 天后的存留量441+=x y ；若在)4(>t t 天时进行第一次复习，则此时知识存留量比未复习情况下增加一倍（复习时间忽略不计），其后存储量2y 随时间变化的曲线恰为直线的一部分，其斜率为),0()4(2<+a t a存留量随时间变化的曲线如图所示.当进行第一次复习后的存留量与不复习的存留量相差最大时，则称此时此刻为“二次复习最佳时机点”.（1）若5,1=-=t a ，求“二次最佳时机点”；（2）若出现了“二次复习最佳时机点”，求a 的取值范围.19.已知各项均为正数的等差数列{}n a 的公差d 不等于0，设k a a a ,3,1是公比q 的等比数列{}n b 的前三项. (1)若2,71==a k .（ⅰ）求数列{}n n b a 的前n 项和n T ；（ⅱ）将数列{}n a 中与{}n b 相同的项去掉，剩下的项依次构成新的数列{}n c ，设其前n 项和为n S ，求),2(23211212*----∈≥⋅+-N n n S n n n n 的值；（2）若存在*∈>N m k m ,使得m k a a a a ,,,31成等比数列，求证：k 为奇数.20. 已知波函数R a ax x x f x x x x f x ax x f ∈+=++=+=,221)(,ln 953461)(,ln )(22212.(1) 求证：函数)(x f 在点))(,(e f e 处的切线恒过定点，并求出定点坐标； (2) 若)()(2x f x f <在区间),1(+∞上恒成立，求a 的取值范围； (3) 当32=a 时，求证：在区间),1(+∞上，满足)()()(21x f x g x f <<恒成立的函数)(x g 有无穷多个.苏北四市（连云港、徐州、淮安、宿迁）2011届高三年级第三次调研考试数学试题试卷 ⅡB.选修4—2：矩阵与变换已知矩阵⎢⎣⎡=cM 1⎥⎦⎤2b 有特征值41=λ及对应的一个特征向量⎥⎦⎤⎢⎣⎡=321e . （1）求矩阵M ;（2）求曲线148522=++y xy x 在M 的作用下的新曲线方程.C.选修4—4：坐标系与参数方程已知极坐标系的极点与直角坐标系的原点重合，极轴与x 轴的正半轴重合.若直线l 的极坐标方程为23)4s in (=-πθρ.（1）把直线l 的极坐标方程化为直角坐标系方程；（2）已知P 为椭圆1916:22=+y x C 上一点，求P 到直线l 的距离的最大值. 22．（本小题满分10分）如图，已知三棱柱111C B A ABC -的侧面与底面垂直，,,11AC AB AC AB AA ⊥===P N M ,,分别是111,,B A BC CC 的中点.(1)求证：AM PN ⊥;(2)若直线MB 与平面PMN 所成的角为θ，求θsin 的值.23．（本小题满分10分）已知数列{}n a 中，对于任意n n n a a a N n 34,3-=∈*.（1）求证：若,1>n a 则11>+n a ；（2）若存在正整数m ，使得1=m a ，求证：（ⅰ）1≤m a ；（ⅱ）1132cos -=m k a π（其中Z k ∈）(参考公式：αααcos 3cos 43cos 3-=).苏北四市2011届高三第三次调研考试一、填空题： 1．1-； 2．}{x x >；3．100； 4. 60； 5．92； 6．57．14； 89； 10．11(1,)(,1)22-- ； 11．24； 12．(0,0)； 13．94； 14．162（或者65536）．二、解答题:15. (1)在△ABC 中，因为2OB =，θπθπππ-=--=∠=∠434,4ABO BAO ，，由正弦定理，得sin sin4OB OA ABOp =Ð，……………………………………3分3sin()42OAp q =-，所以3sin()4OA p q =-. ……………6分 (2)由(1)得3||||cos sin()cos 4OA OB OA OB pq q q ?鬃- uu r uu u r uu r uu u r ，…………………8分2(sin 2cos2)2θθ=++)24θπ=++， …………………10分因为3(,),24p p q Î所以572(,)444p p pq + ，所以当3242p pq +=，即为2.5π时，OA OB ×uu r uu u r的最小值为2-14分16. （1）因为BD //平面EFGH ，BDC EFGH FG = 平面平面，所以BD //FG ．同理BD //EH ，又因为EH FG =，所以四边形EFGH 为平行四边形，所以HG //EF ，又HG ABC ⊄平面，所以HG ABC 平面． ……………………………………………………6分（2）在ABC 平面内过点E 作EP AC ⊥，且交AC 于P 点，在ACD 平面内过点P 作PQ AC ⊥，且交AD 于Q 点，连结EQ ，则EQ 即为所求线段．………………………………………………10分证明如下：EP AC AC EPQ PQ AC EQ AC EQ EPQ EP PQ P ⊥⎫⇒⊥⎫⎪⊥⇒⊥⎬⎬⊂⎭⎪=⎭平面平面…………………………………14分17解：（1）因为位于y 轴左侧的圆C 与y 轴相切于点(0,1)，所以圆心C 在直线1y =上，设圆C 与x 轴的交点分别为A 、B ，由圆C 被x 轴分成的两段弧长之比为21:，得23ACB π∠=，所以2CA CB ==，圆心C 的坐标为(2,1)-，所以圆C 的方程为：22(2)(1)4x y ++-=． ………………………………4分（2）当1t =时，由题意知直线l 的斜率存在，设直线l 方程为1y mx =+，由221(2)(1)4y mx x y =+⎧⎨++-=⎩得01x y =⎧⎨=⎩或22241411x m m m y m -⎧=⎪⎪+⎨-+⎪=⎪+⎩，不妨令222441(,),(0,1)11m m M N m m --+++，因为以MN 为直径的圆恰好经过(0,0)O ，所以2222244141(,)(0,1)0111m m m m OM ON m m m m --+-+⋅=⋅==+++ ，解得2m =±l方程为(21y x =+或(21y x =+．………………………………10分（3）设直线MO 的方程为y kx =，2，解之得34k ≤，同理得，134k -≤，解之得43k ≤-或>0k ．由（2）知，=0k 也满足题意．所以k 的取值范围是43(,][0,]34-∞- ． ………………………………………14分18. 设第一次复习后的存留量与不复习的存留量之差为y ，由题意知，228()(4)(4)4a y x t t t t =-+>++ ………………………………2分所以21284()(4)(4)44a y y y x t t t t x =-=-+->+++ ……………………4分 (1) 当1,5a t =-=时，2184(5)(54)544y x x -=-+-+++(4)41814x x -+=-++≤1-59=，当且仅当 14x = 时取等号，所以“二次复习最佳时机点”为第14天． ………………10分 (2) 284()(4)44a y x t t t x =-+-+++22(4)48(4)(4)44(4)a x a t t x t t -++=--+-++++≤84at --+， …………………………………………14分当且仅当4)4(244)4()4(2-+-=+=++-t ax x t x a 即时取等号，由题意t t a>-+-4)4(2，所以 40a -<<． ………………16分19．⑴ 因为7k =，所以137,,a a a 成等比数列，又{}n a 是公差0d ≠的等差数列，所以()()211126a d a a d +=+，整理得12a d =，又12a =，所以1d =， 112b a ==，32111122a b a d q b a a +====，所以()11111,2n n n n a a n d n b b q -=+-=+=⨯=， ……………………………4分 ①用错位相减法或其它方法可求得{}n n a b 的前n 项和为12n n T n +=⨯； ………6分② 因为新的数列{}n c 的前21n n --项和为数列{}n a 的前21n -项的和减去数列{}n b 前n 项的和，所以121(21)(22)2(21)(21)(21)221n n n n n n n S ----+-=-=---.所以211212321n n n n S -----+⋅=-． ………………………10分 ⑵ 由d k a a d a ))1(()2(1121-+=+，整理得)5(412-=k d a d ，因为0≠d ，所以4)5(1-=k a d ，所以3111232a a d k q a a +-===.因为存在m ＞k,m ∈N *使得13,,,k m a a a a 成等比数列，所以313123⎪⎭⎫ ⎝⎛-==k a q a a m ， ………………………………………………12分又在正项等差数列{a n }中，4)5)(1()1(111--+=-+=k m a a d m a a m ， ……13分所以3111234)5)(1(⎪⎭⎫⎝⎛-=--+k a k m a a ，又因为01>a ，所以有[]324(1)(5)(3)m k k +--=-， …………………………………14分因为[]24(1)(5)m k +--是偶数，所以3(3)k -也是偶数，即3-k 为偶数，所以k 为奇数. ……………………………………16分20. (1)因为1()2f x ax x '=+ ，所以()f x 在点(e,(e))f 处的切线的斜率为12k ae e=+，所以()f x 在点(,())e f e 处的切线方程为21(2)()1y ae x e ae e=+-++ ，……2分整理得11(2)()22e y ae x e -=+-，所以切线恒过定点1(,)22e ． ………4分(2) 令x ax x a x f x f x p ln 2)21()()()(22+--=-=<0，对(1,)x ∈+∞恒成立，因为21(21)21(1)[(21)1]()(21)2a x ax x a x p x a x a x x x--+---'=--+== （*）………………………………………………………………6分令()0p x '=，得极值点1x 1=，2121x a =-， ①当112a <<时，有1x x 12=>，即1a 21<<时，在（2x ，+∞）上有()0p x '>，此时)(x p 在区间2(,)x +∞上是增函数，并且在该区间上有)(x p ∈2((),)p x +∞，不合题意；②当1a ≥时，有211x x <=，同理可知，)(x p 在区间(1,)+∞上，有)(x p ∈((1),)p +∞，也不合题意； …………………………………………… 8分③当12a ≤时，有210a -≤，此时在区间(1,)+∞上恒有()0p x '<，从而)(x p 在区间(1,)+∞上是减函数；要使0)(<x p 在此区间上恒成立，只须满足021)1(≤--=a p 12a ⇒≥-，所以1122a -≤≤．综上可知a 的范围是11,22⎡⎤-⎢⎥⎣⎦． ……………………………………………12分(3)当23a =时，221214514()ln ,()63923f x x x x f x x x =++=+记22115()()ln ,(1,)39y f x f x x x x =-=-∈+∞．因为225650399x x y x x-'=-=>，所以21()()y f x f x =-在(1,)+∞上为增函数，所以21211()()(1)(1)3f x f x f f ->-=， ………………………………14分设11()(),(01)3R x f x λλ=+<<, 则12()()()f x R x f x <<, 所以在区间()1,+∞上，满足12()()()f x g x f x <<恒成立的函数()g x 有无穷多个． ………………………………………………………………16分数学附加题答案与评分标准B ．选修4—2 矩阵与变换解：（1）由已知1283122b c ⎡⎤⎡⎤⎡⎤=⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦，即238,2612b c +=+=，2,3b c ==，所以1232M ⎡⎤=⎢⎥⎣⎦; …………………………4分（2）设曲线上任一点P (,)x y ，P 在M 作用下对应点///(,)P x y ，则//1232x x y y ⎡⎤⎡⎤⎡⎤=⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦即{//232x x y y x y=+=+，解之得////234y x x x y y ⎛-= - =⎝，代入225841x xy y ++=得222x y ''+=，即曲线225841x xy y ++=在M 的作用下的新曲线的方程是222x y +=．………10分C ．选修4-4：坐标系与参数方程解：（1）直线l的极坐标方程sin 4ρθπ⎛⎫-= ⎪⎝⎭sin cos θθ=，即sin cos 6ρθρθ-=，所以直线l 的直角坐标方程为60x y -+=； ……………4分（2）P 为椭圆221169x y C +=:上一点，设(4cos 3sin )P αα,，其中[02)α∈π,，则P 到直线l的距离d =，其中4cos 5ϕ=所以当cos()1αϕ+=时，d………………………………10分 22．解：（1）建立如图所示直角坐标系，则(0,0,0)A ,(1,0,0)B ,(0,1,0)C ,1(0,0,1)A ,1(1,0,1)B ,1(0,1,1)C , 1(,0,1)2P ,1(0,1,)2M ,11(,,0)22N ,1(0,,1)2=-,1(0,1,)2=, 因为⋅11001(1)022=⨯+⨯+-⨯=,所以AM PN ⊥． (4)（2）设平面PMN 的一个法向量为1111(,,)n x y z =,1(0,,1)2NP =- ,111(,,)222NM =- ,则1100n NP n NM ⎧⋅=⎪⎨⋅=⎪⎩ ⇒1111110,21110.222y z x y z ⎧-+=⎪⎪⎨⎪-++=⎪⎩ 令12y =，得11z =，13x =所以1(3,2,1)n =． …………………………………………………6分又1(1,1,)2MB =-- ，所以1112sin ||||2n MB n MB θ⋅===⨯……………………10分23．证明：⑴因为1n a >，3143n n n a a a +=-所以2311143(43)1n n n n n a a a a a +++=-=->． ……………………2分 ⑵① 假设11a >，则232111143(43)1a a a a a =-=-> 若1k a >，则2311143(43)1k k k k ka a a a a +++=-=->．所以当1||1a >时，有*||1()n a n N >∈，这与已知1m a =矛盾，所以11a ≤. ………………………………………………………6分 ②由①可知，存在θ，使得1cos a θ=．则324cos 3cos cos3a θθθ=-= 假设 n k =时，有1cos3n n a θ-=即1cos3k k a θ-=则()()33111434cos33cos3cos3k k k k k k a a a θθθ--+=-=-=所以对任意*n N ∈,1cos3n n a θ-=，则1cos3m m a θ-==1，132m k θπ-=，其中k Z ∈ 即123m k πθ-=，所以112cos 3m k a π-= (其中k 为整数). ……………………………10分。

2011江苏高考各市最新模拟试题-苏州市2011届高三调研测试试卷及答案

2011江苏高考各市最新模拟试题-苏州市2011届高三调研测试试卷及答案苏州市2011届高三调研测试试卷本试卷总分160分。

考生作答时，将答案答在答题卡上，在本试卷上答题无效。

注意事项：1、答题前，考生务必将自己的姓名、考试号填写在答题卡上。

2、答题时使用0、5毫米黑色中性（签字）笔或碳素笔书写，字体工整、笔迹清楚。

3、请按照题号在答题卡上各题的答题区域（黑色线框）内作答，超出答题区域书写的答案无效。

一、语言文字运用（15分）1、下列词语中加点的字，每对读音都不相同的一组是（3分）A、粮囤/囤积居奇露底/抛头露面参悟/斗转参横B、成见/图穷匕见朝政/朝晖夕阴惩艾/自怨自艾C、埋怨/埋没人才着数/棋高一着校官/犯而不校D、勒令/悬崖勒马蹊跷/独辟蹊径呼吁/长吁短叹2、下列各句中，加点的成语使用恰当的一句是（3分）A、城市建设的盲点地区，由于管理不力，垃圾堆2得像小山，令人叹为观止，那里的环境必须尽快加以整治。

B、一年一度在苏州博览中心举办的电博会，聚集了全国各地各种各样的电子新产品，真可谓浩如烟海，应有尽有。

C、中国改革开放以来坚持“韬光养晦，有所作为”的策略，大力发展经济，综合国力逐渐增强，在国际事务中发挥了越来越重要的作用。

D、亚运会在广州召开，广州各主要运动场馆的门票炙手可热，有的场馆甚至到了一票难求的地步。

3、阅读下面的文字，用两个四字短语概括“三季人”的特点，同时用不超过25个字的句子概括孔子对待“三季人”的态度和方法。

（5分）一个人到孔子家拜访，孔子的门生拦住了他，问他有什么事。

那人说：我想问问先生，一年到底有几季？孔子门生回答说一年当然有四季。

那个人反驳说，不对，一年有三季。

两个人就争论起来，各不相让，最后两个人打赌，当面向孔子请教，如果谁输了，就向对方磕头。

孔子听了两位的争论之后说，一年三季。

那个人很是得意，就让孔子的门生给他磕头。

34方贤豪交益广，往来赠答，岁久盈箧。

会国难频仍，余倡大义于江东，凡从前雕虫之技，散亡几尽矣。

2010-2023历年江苏省苏北四市高三第三次质量检测物理试卷(带解析)

2010-2023历年江苏省苏北四市高三第三次质量检测物理试卷（带解析）第1卷一.参考题库(共20题)1.如图所示，光滑斜面固定在水平地面上，匀强电场平行于斜面下，弹簧另一端固定，滑块处于静止状态。

现给滑块一个沿斜面向下的初速度，滑块最远能到达P点。

在些过程中A．滑块的动能一定减小B．弹簧的弹性势能一定增大C．滑块电势能的改变量一定小于重力与弹簧弹力做功的代数和D．滑块机械能的改变量等于电场力与弹簧弹力做功的代数和2.（8分）某课外小组为探测一遥控电动小车的额定功率，进行了如下实验：A．用天平测出电动小车的质量为0.6 kg；B．将一长直导轨水平放在实验桌上，电动小车、纸带和打点计时器按如图甲所示安装；C．接通打点计时器(其打点时间间隔为0.02 s)；D．启动电动小车使其以额定功率加速运动，达到最大速度一段时间后关闭小车电源，待小车静止时再关闭打点计时器(在整个过程中小车所受的阻力可以认为是恒定的)。

在上述过程中，得到一条记录纸带，图中O点是打点计时器打的起点，请分析本实验并回答下列问题。

（1）该电动小车运动的最大速度为____________m／s；（2）关闭电源后小车的加速度大小为___________m／s2；（3）该电动小车运动过程中所受的阻力大小为_________N；（4）该电动小车的额定功率为__________W。

3.牛顿的三大运动定律构成了物理学和工程学的基础。

它的推出、地球引力的发现和微积分的创立使得牛顿成为过去一千多年中最杰出的科学巨人之一。

下列说法中正确的是A．牛顿第一定律是牛顿第二定律的一种特例B．牛顿第二定律在非惯性系中不成立C．两物体之间的作用力和反作用力是一对平衡力D．为纪念牛顿，人们把“力”定为基本物理量，其基本单位为“牛顿”4.两个等量异种电荷位于正方体的两个顶点a和f上，如图所示。

在此正方体的顶点间移动一正试探电荷，以下说法中正确的是A．电场中b点和d点的电场强度相同B．电场中b点和e点电势相等C．试探电荷在c点和h点受力大小相等，方向相同D．试探电荷从c点移到h点电场力做功为零5.（10分）某学习小组研究用碳丝做成的电阻导电规律。

2019—2020学年度苏北四市高三第三次调研考试高中物理

2019—2020学年度苏北四市高三第三次调研考试高中物理物理试卷一、单项选择题：此题共5小题，每题3分，共15分．每题只有一个选项符合题意．1．学习物理除了知识的学习外，还要领会并把握处理物理咨询题的思想与方法，如下图是我们学习过的几个实验，其中研究物理咨询题的思想与方法相同的是A．〔1〕〔2〕B．〔2〕〔3〕C．〔3〕〔4〕D．〔1〕〔4〕2．如以下图为使用汽车安全带的报警电路．S为汽车启动开关，闭合时代表汽车启动．R T 代表安全带拉力传感器，驾驶员系好安全带时其电阻变大．要求只有当驾驶员启动汽车且安全带未使用时，蜂鸣器才能报警．那么在图中虚线框内应接入的元件是A．〝非〞门B．〝或〞门C．〝与〞门D．〝与非〞门3．如以下图所示，ACB是一光滑的、足够长的、固定在竖直平面内的〝∧〞形框架，其中CA、CB边与竖直方向的夹角均为θ．P、Q两个轻质小环分不套在CA、CB上，两根细绳的一端分不系在P、Q环上，另一端和一绳套系在一起，结点为O．将质量为m的钩码挂在绳套上，OP、OQ两根细绳拉直后的长度分不用l1、l2表示，假设l1 : l2 = 2 : 3，那么两绳受到的拉力之比F1 : F2等于A．1︰1 B．2︰3 C．3︰2 D．4︰94．将一只苹果斜向上抛出，苹果在空中依次飞过三个完全相同的窗户1、2、3．图中曲线为苹果在空中运行的轨迹．假设不计空气阻力的阻碍，以下讲法正确的选项是A．苹果通过第1个窗户所用的时刻最长B．苹果通过第3个窗户的平均速度最大C．苹果通过第1个窗户重力做的功最大D．苹果通过第3个窗户重力的平均功率最小5．如以下图所示，A、B、C、D、E、F为匀强电场中一个边长为10cm的正六边形的六个顶点，A、B、C三点电势分不为1.0V、2.0V、3.0V，正六边形所在平面与电场线平行．以下讲法中错误的选项是A．通过CD和AF的直线应为电场中的两条等势线B．匀强电场的场强大小为10V/mC．匀强电场的场强方向为由C指向AD．将一个电子由E点移到D点，电子的电势能将减少1.6×10－19J二、多项选择题：此题共4小题，每题4分，共16分．每题有多个选项符合题意，全部选对的得4分，选对但不全的得2分，错选或不答的得0分．6．为纪念伽利略将望远镜用于天文观测400周年，2018年被定为以〝探究我的宇宙〞为主题的国际天文年．我国发射的〝嫦娥一号〞卫星绕月球通过一年多的运行，完成了既定任务，于2009年3月1日16时13分成功撞月．如图为〝嫦娥一号〞卫星撞月的模拟图，卫星在操纵点1开始进入撞月轨道．假设卫星绕月球作圆周运动的轨道半径为R ，周期为T ，引力常量为G ．依照题中信息，以下讲法正确的选项是A ．能够求出月球的质量B ．能够求出月球对〝嫦娥一号〞卫星的引力C ．〝嫦娥一号〞卫星在操纵点1处应减速D ．〝嫦娥一号〞在地面的发射速度大于11.2km/s7．如下图为一理想变压器，原、副线圈的匝数比为n ．原线圈接电压为u=U 0sin ωt 的正弦交流电，输出端接有一个交流电流表和一个电动机，电动机的线圈电阻为R ．当输入端接通电源后，电动机带动一质量为m 的重物匀速上升，现在电流表的示数为I ，重力加速度为g ，以下讲法正确的选项是A ．电动机两端电压为IRB ．原线圈中的电流为nIC ．电动机消耗的电功率为n IU 20D ．重物匀速上升的速度为nmg nIR U I 2)2(08．如下图，匀强电场水平向右，虚线右边空间存在着方向水平、垂直纸面向里的匀强磁场，虚线左边有一固定的光滑水平杆，杆右端恰好与虚线重合．有一电荷量为q 、质量为m 的小球套在杆上并从杆左端由静止开释，带电小球离开杆的右端进入正交电、磁场后，开始一小段时刻内，小球A．可能做匀速直线运动B．一定做变加速曲线运动C．重力势能可能减小D．电势能可能增加9．如以下图甲所示，水平抛出的物体，抵达斜面上端P处时速度恰好沿着斜面方向，紧贴斜面PQ无摩擦滑下；图乙为物体沿x方向和y方向运动的位移-时刻图象及速度-时刻图象，其中可能正确的选项是三、简答题：此题分必做题〔第10、11题〕和选做题〔第12题〕两部分，共计42分．请将解答填在答题卡相应的位置．10．〔10分〕光电计时器是一种研究物体运动情形的常见仪器．当有物体从光电门通过时，光电计时器就能够显示物体的挡光时刻．现利用如图甲所示装置探究物体的加速度与合外力、质量关系，其NQ是水平桌面，PQ是一端带有滑轮的长木板，1、2是固定在木板上的两个光电门〔与之连接的两个光电计时器没有画出〕．小车内固定着用于挡光的窄片K，测得其宽度为d，让小车从木板的顶端滑下，光电门各自连接的计时器显示窄片K的挡光时刻分不为t1和t2．〔1〕该实验中，在改变小车的质量M或沙桶的总质量m时，保持M >>m，如此做的目的是；〔2〕为了运算出小车的加速度，除了测量d、t1和t2之外，还需要测量，假设上述测量量用x表示，那么用这些物理量运算加速度的表达式为a = ；〔3〕某位同学通过测量、运算得到如下表数据，请在图乙中作出小车加速度与所受合外力的关系图像．组不 1 2 3 4 5 6 7M/kg 0.58 0.58 0.58 0.58 0.58 0.58 0.58F/N 0.10 0.15 0.20 0.25 0.30 0.35 0.40a/m·s-20.13 0.17 0.26 0.34 0.43 0.51 0.59〔4〕由图象能够看出，该实验存在着较大的误差，产生误差的要紧缘故是：．11．〔8分〕如图甲所示为一黑箱装置，盒内有电源、电阻等元件，a、b为黑箱的两个输出端．〔1〕为了探测黑箱，某同学进行了以下几步测量：①用多用电表的电阻档测量a、b间的电阻；②用多用电表的电压档测量a、b间的输出电压；③用多用电表的电流档测量a、b间的输出电流．你认为以上测量中不妥的有：〔填序号〕．〔2〕含有电源的黑箱相当于一个〝等效电源〞，a、b是等效电源的两极．为了测定那个等效电源的电动势和内阻，该同学设计了如图乙所示的电路，调剂变阻器的阻值，记录下电压表和电流表的示数，并在方格纸上建立了U-I坐标，依照实验数据画出了坐标点，如图丙所示．请你完成U-I图线，并由图线求出等效电源的电动势E = V，内阻r = Ω．〔3〕由于电压表和电流表内阻的阻碍不可忽略，那么采纳此测量电路所测得的电动势与实际值相比，测得的内阻与实际值相比〔填〝偏大〞、〝偏小〞或〝相同〞〕．12．选做题〔请从A、B和C三小题中选定两小题作答，并在答题卡上把所选题目对应字母后的方框涂满涂黑．如都作答那么按A、B两小题评分．〕A．〔选修模块3-3〕〔12分〕〔1〕〔4分〕以下讲法中正确的选项是A．布朗运动的剧烈程度与温度有关，因此布朗运动也叫做热运动B．彩色液晶显示屏是应用液晶在不同电场中对不同颜色的光吸取强度不同制成的C．能量耗散讲明能量在不断减少D．热力学第二定律也能够表述为：气体向真空的自由膨胀是不可逆的〔2〕〔4分〕将剩有半杯热水的玻璃杯盖子旋紧后通过一段时刻，假设玻璃杯盖子不漏气，那么杯内水蒸汽饱和气压〔填〝增大〞、〝减小〞或〝不变〞〕，杯内气体压强〔填〝增大〞、〝减小〞或〝不变〞〕．〔3〕〔4分〕如图气缸放置在水平地面上，缸内封闭一定质量的理想气体，活塞横截面积为S，外界大气压强为p0，气缸内电热丝热功率为P，测得通电时刻t内活塞缓慢向左移动距离为h，气缸向外界放出热量为Q，不计活塞与气缸之间的摩擦，那么在时刻t内缸内气体内能的变化量为．B．〔选修模块3-4〕〔12分〕〔1〕〔4分〕以下讲法中正确的选项是A．光的偏振现象讲明光是一种纵波B．相对论认为空间和时刻与物质的运动状态有关C．麦克斯韦预言并用实验验证了电磁波的存在D．在光的双缝干涉实验中，假设仅将入射光由绿光变为红光，那么条纹间距变宽〔2〕〔4分〕如以下图所示是一列沿x轴正方向传播的简谐横波在t = 0时刻的波形图，波的传播速度v = 2m/s．试回答以下咨询题：①写出x = 0.5 m 处的质点做简谐运动的表达式： cm ；②x = 0.5m 处质点在0～5.5s 内通过的路程为 cm ．〔3〕〔4分〕直角玻璃三棱镜的截面如下图，一条光线从AB 面入射，ab 为其折射光线，ab 与AB 面的夹角α= 60°．这种玻璃的折射率n =2，那么：①这条光线在AB 面上的的入射角为；②图中光线ab 〔填〝能〞或〝不能〞〕从AC 面折射出去．C ．〔选修模块3-5〕〔12分〕〔1〕〔4分〕以下四幅图涉及到不同的物理知识，其中讲法正确的选项是A ．图甲：普朗克通过研究黑体辐射提出能量子的概念，成为量子力学的奠基人之一B ．图乙：玻尔理论指出氢原子能级是分立的，因此原子发射光子的频率也是不连续的C ．图丙：卢瑟福通过分析α粒子散射实验结果，发觉了质子和中子D ．图丁：依照电子束通过铝箔后的衍射图样，能够讲明电子具有粒子性〔2〕〔4分〕目前核电站是利用核裂变产生的庞大能量来发电的。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

淮安市2011届高三第三次调研考试物理试题 2011.4.1注意：本试卷满分120分，考试时间100分钟．请将答案填写在答题卡上，直接写在试卷上不得分．一、单项选择题：本题共5小题，每小题3分，共15分．每小题只有一个选项符合题意． 1．在杂技表演中，猴子沿竖直杆向上做初速度为零、加速度为a 的匀加速运动，同时人顶着直杆以速度0v 水平匀速移动，经过时间t ，猴子沿杆向上移动的高度为h ，人顶杆沿水平地面移动的距离为x ，如图所示。

关于猴子的运动情况，下列说法中正确的是 A ．相对地面的运动轨迹为直线B ．相对地面做变加速曲线运动C ．t 时刻猴子对地速度的大小为at v +0D ．t 时间内猴子对地的位移大小为22h x +2．风洞是进行空气动力学实验的一种主要设备。

某兴趣小组为了检验一飞机模型的性能，对该模型进行了模拟风洞实验，该实验的示意图如图，其中AB 代表飞机模型的截面，OL 为飞机模型的牵引绳。

已知飞机模型重为G ，风向水平，当牵引绳水平时，飞机模型恰好静止在空中，此时飞机模型截面与水平面的夹角为θ，则作用于飞机模型上的风力大小为 A ．θcos GB ．G cos θC ．θsin GD ．G sin θ3．真空中有一半径为r 0的带电金属球壳，通过其球心的一直线上各点的电势φ分布如图，r 表示该直线上某点到球心的距离，r 1、r 2分别是该直线上A 、B 两点离球心的距离。

下列说法中正确的是A ．A 点的电势低于B 点的电势B ．A 点的电场强度方向由A 指向BC ．A 点的电场强度小于B 点的电场强度D ．正电荷沿直线从A 移到B 的过程中，电场力做负功4．如图，在一直立的光滑管内放置一劲度系数为k 的轻质弹簧，管口上方O 点与弹簧上端初位置A 的距离为h ，一质量为m 的小球从O 点由静止下落，压缩弹簧至最低点D ，φ012B弹簧始终处于弹性限度内，不计空气阻力。

小球自O点下落到最低点D的过程中，下列说法中正确的是A．小球最大速度的位置随h的变化而变化B．小球的最大速度与h无关C．小球的最大加速度大于重力加速度D．弹簧的最大压缩量与h成正比5．闭合矩形导线框abcd固定在匀强磁场中，磁场的方向与导线框所在平面垂直，磁感应强度B随时间t变化的规律如图所示。

规定垂直纸面向里为磁场的正方向，abcda的方向为线框中感应电流的正方向，水平向右为安培力的正方向。

关于线框中的电流i与ad边所受的安培力F随时间t变化的图象，下列正确的是二、多项选择题：本题共4小题，每小题4分，共计16分．每小题有多个选项符合题意，全部选对的得4分，选对但不全的得2分，错选或不答得0分．6．我国将于今年下半年发射目标飞行器“天宫一号”，若“天宫一号”能在离地面约300km 高的圆轨道上正常运行，两月后再发射“神舟八号”飞船并与其进行对接试验。

下列说法中正确的是A．“天宫一号”的发射速度应大于第二宇宙速度B．对接前，“神舟八号”欲追上“天宫一号”，必须在同一轨道上点火加速C．对接时，“神舟八号”与“天宫一号”的加速度相等D．对接后，“天宫一号”的速度小于第一宇宙速度7．如图是医用回旋加速器示意图，其核心部分是两个D形金属盒，两金属盒置于匀强磁场中，并分别与高频电源相连。

现分别加速氘核（H21）和氦核（He42）。

下列说法中正确的是A．它们的最大速度相同B．它们的最大动能相同C．它们在D形盒中运动的周期相同D．仅增大高频电源的频率可增大粒子的最大动能线束D型盒离子源高频电源真空室B-Ba b d cF0F0 -II I-I8．如图甲所示的电路中，理想变压器原、副线圈匝数比为5︰l ，原线圈接入图乙所示的电压，副线圈接火灾报警系统 (报警器未画出)，电压表和电流表均为理想电表，R 0为定值电阻，R 为半导体热敏电阻，其阻值随温度的升高而减小。

下列说法中正确的是A ．图乙中电压的有效值为1102VB ．电压表的示数为44VC ．R 处出现火警时电流表示数增大D ．R 处出现火警时电阻R 0消耗的电功率增大 9．低碳、环保是未来汽车的发展方向。

某汽车研发机构在汽车的车轮上安装了小型发电机，将减速时的部分动能转化并储存在蓄电池中，以达到节能的目的。

某次测试中，汽车以额定功率行驶一段距离后关闭发动机，测出了汽车动能E k 与位移x 的关系图象如图，其中①是关闭储能装置时的关系图线，②是开启储能装置时的关系图线。

已知汽车的质量为1000kg ，设汽车运动过程中所受地面阻力恒定，空气阻力不计。

根据图象所给的信息可求出 A ．汽车行驶过程中所受地面的阻力为1000N B ．汽车的额定功率为80kWC ．汽车加速运动的时间为22.5sD ．汽车开启储能装置后向蓄电池提供的电能为5×105J 三、简答题：本题分必做题（第10、11题）和选做题（第12题）两部分，共计42分．请将解答填在答题卡相应的位置．【必做题】10．（8分）某研究性学习小组利用气垫导轨验证机械能守恒定律，实验装置如图甲所示。

在气垫导轨上相隔一定距离的两处安装两个光电传感器A 、B ，滑块P 上固定一遮光条，若光线被遮光条遮挡，光电传感器会输出高电压，两光电传感器采集数据后与计算机相连。

滑块在细线的牵引下向左加速运动，遮光条经过光电传感器A 、B 时，通过计算机可以得到如图乙所示的电压U 随时间t 变化的图象。

⑴实验前，接通气源，将滑块（不挂钩码）置于气垫导轨上，轻推滑块，当图乙中的 Δt 1 ▲ Δt 2（选填“＞”、“=”或“＜”）时，说明气垫导轨已经水平。

⑵用螺旋测微器测遮光条宽度d ，测量结果如图丙所示，则d = ▲ mm 。

220甲乙m) 12乙甲4045 05 05丙⑶滑块P 用细线跨过气垫导轨左端的定滑轮与质量为m 的钩码Q 相连，将滑块P 由图甲所示位置释放，通过计算机得到的图象如图乙所示，若Δt 1、Δt 2和d 已知，要验证滑块和砝码组成的系统机械能是否守恒，还应测出 ▲ 和 ▲ （写出物理量的名称及符号）。

⑷若上述物理量间满足关系式 ▲ ，则表明在上述过程中，滑块和砝码组成的系统机械能守恒。

11．（10分）现有以下器材：电流表A （量程0.6A 、内阻Ar =0.5Ω），电阻箱R （量程99.99Ω），待测电阻R x ，直流电源（电动势E 和内阻r 待测），单刀单掷开关S 1，单刀双掷开关S 2，带铁夹的导线若干。

某探究实验小组设计如图甲所示的实验电路，用来测定待测电阻的阻值R x 、直流电源的电动势E 和内阻r 。

⑴按图甲所示的电路，将图乙所示的实物连线补画完整⑵测量电阻R x 的阻值①将开关S 1闭合、开关S 2接a ，读出电流表的示数I 1②保持开关S 1闭合，将开关S 2接b ，调节电阻箱R 的阻值，使得电流表的示数也为I 1，此时电阻箱的阻值R = 4.00Ω，则R x = ▲ Ω ⑶测电源的电动势E 和内阻r将开关S 1闭合、开关S 2接b ，调节电阻箱R 的阻值，记下电流表的示数I ，得到若干组 R 、I 的数据（见下表），请在图丙所示的坐标纸上作出I1-R 的图象，并根据图象求得电动势E = ▲ V ，内阻r = ▲ ΩΩ甲R xa bS 2S 1E rR乙12．【选做题】（请从A 、B 和C 三小题中选定两小题作答，并在答题卡相应的答题区域内作答，如都作答则按A 、B 两小题评分） A ．（选修模块3-3）（12分）⑴如图，固定的导热气缸内用活塞密封一定质量的理想气体，气缸置于温度不变的环境中。

现用力使活塞缓慢地向上移动，密闭气体的状态发生了变化。

下列图象中p 、V 和U 分别表示该气体的压强、体积和内能，k E 表示该气体分子的平均动能，n 表示单位体积内气体的分子数，a 、d 为双曲线，b 、c 为直线。

能正确反映上述过程的是 ▲⑵2010年诺贝尔物理学奖授予安德烈·海姆和康斯坦丁·诺沃肖洛夫，以表彰他们在石墨烯材料方面的卓越研究。

他们通过透明胶带对石墨进行反复的粘贴与撕开使得石墨片的厚度逐渐减小，最终寻找到了厚度只有0.34nm 的石墨烯，是碳的二维结构。

如图所示为石墨、石墨烯的微观结构，根据以上信息和已学知识判断，下列说法中正确的是 ▲A ．石墨是晶体，石墨烯是非晶体B ．石墨是单质，石墨烯是化合物C ．石墨、石墨烯与金刚石都是晶体D ．他们是通过物理变化的方法获得石墨烯的⑶为保证驾乘人员的安全，轿车中设有安全气囊。

轿车在发生一定强度的碰撞时，利用叠氮化钠（NaN 3）爆炸产生气体(假设都是N 2)充入气囊。

若氮气充入后安全气囊的容积V =56L ，囊中氮气密度ρ=2.5kg/m 3，已知氮气摩尔质量M =2.8×10-2kg/mol ，阿伏加德罗常数N A =6.02×1023mol -1，试估算囊中氮气分子的总个数N （结果保留一位有效数字）。

B ．（选修模块3-4）（12分） ⑴下列说法中正确的是 ▲A ．当某列声波产生多普勒效应时，相应声源的振动频率一定发生变化B ．狭义相对论指出：电磁相互作用在真空中的传播速度c 是自然界中速度的极限C ．家用微波炉的工作应用了一种电磁波，而军用雷达的工作应用了一种脉冲超声波D ．大豆色拉油中的气泡看起来特别明亮，是因为光从气泡射向油时，一部分光在界面上发生了全反射的缘故石墨的微观结构石墨烯的微观结构AV BCaD(2)图甲为某一简谐横波在t =0时刻的波动图象，P 为其传播方向上的一个质点，图乙为质点P 的振动图象。

根据图象可知：波的传播速度为 ▲ m/s ，波沿x 轴的 ▲ 方向传播（选填“正”或 “负”），质点P 振动12s 所通过的路程为 ▲ m 。

⑶如图ABC 为等腰三棱镜的横截面，已知顶角A 为60°，图中EF ∥BC ，一束光线在AB 边上的入射角为45°，真空中的光速为c 。

试求光在该种介质中的折射率n 及传播速度v 。

C ．（选修模块3-5）（12分）⑴下列相互作用的过程中，可以认为系统动量守恒的是 ▲⑵北京时间2011年3月11日在日本海域发生强烈地震，强震引发了福岛核电站危机。

下列关于核裂变和核辐射的方程中书写正确的是 ▲ A ．n 10Kr Ba n U 1923614156123592++→+B ．He U Pu 422359223994+→C ．eBa Cs 011375613755-+→D ．e Xe I 011315413153-+→⑶已知中子的质量n m ，质子的质量p m ，α粒子的质量αm ，真空中的光速为c 。

求α粒子的比结合能。

-5乙m甲滑轮男孩推滑轮女孩子弹击穿地上面粉袋的瞬间太空人在舱外发射子弹公路上运动的汽车发生碰撞 A B C D四、计算题：本题共3小题，共计47分．解答时请写出必要的文字说明、方程式和重要的演算步骤，只写出最后答案的不能得分．有数值计算的题，答案中必须明确写出数值和单位．13．（15分）如图，顶角为90°的光滑金属导轨MON固定在水平面上，导轨MO、NO的长度相等，M、N两点间的距离l＝2m，整个装置处于磁感应强度大小B＝0.5T、方向竖直向下的匀强磁场中。