圆柱和圆锥单元整理和复习要点
人教版六年级下册数学 圆柱与圆锥整理和复习

40
(单位:厘米)
增加两个长方形的面, 长等于圆柱的高,宽等 于底面直径。
滚、刷、切、削、熔……
切割前后的表面积 增加了,体积不变
。
滚、刷、切、削、熔……
把圆柱削成最大的圆锥,需要削去多少?
50
问题1:怎么削才算是最大的圆锥?
问题2:削成的圆锥与圆柱有什么关系?
2
3.14×(40÷2)2×50×
选择 一个有盖的圆柱形铁桶。 1、求这个铁桶的占地面积,是求( A. 容积 B. 底面积 C. 表面积
B) D. 体积
2、做这样一个铁桶用多少铁皮,是求( C ) A. 容积 B. 底面积 C. 表面积 D. 体积
3、这个铁桶能装多少水,是求( A ) A. 容积 B. 底面积 C. 表面积 D. 体积
0.5m 1m 4.5m ——
314dm3 2.198m3 6280cm3 10.048dm3 1.1775m3
3.妈妈给小雨的塑料壶做了一个布套(如图)小雨每天上学带一壶水。 (1)至少用了多少布料? (2)小雨在学校一天喝1.5L的水,这壶水够喝吗?(水壶的厚度忽略不 计。)
分析:求所用布料就是求水壶的表面积,求能装多少水 即求水壶的体积。
答:旋转一周后围成的立体图形的体积是301.44cm3。
3.一个圆柱形鱼缸,底面直径是40cm,高是25cm,里面盛了一 些水,把一个底面半径为10cm的圆锥放入鱼缸中(圆锥全部浸 入水中),鱼缸中的水面升高了2cm。这个圆锥的高是多少?
水面升高的那部分圆柱的体积就是
放入水中的圆锥的体积。
2cm
V 锥 = V 柱=3.14×(40÷2)2×2 =3.14×800 =2512(cm3)
3.一个圆柱形鱼缸,底面直径是40cm,高是25cm,里面盛了一 些水,把一个底面半径为10cm的圆锥放入鱼缸中(圆锥全部浸 入水中),鱼缸中的水面升高了2cm。这个圆锥的高是多少?
(完整版)圆柱和圆锥知识点总结

长方体里削出最大的圆柱、圆锥:圆柱、圆锥底面直径等于宽(宽﹥高),圆柱、圆锥高等于长方体高。
4.浸物体积问题(排水法测不规则物体的体积):水面上升部分的体积就是浸
入水中物品的体积,等于盛水容器的底面积乘上升的高度。
也就是变化的水的体积。
主要类型:①盛满水,浸物溢水;②浸物水面上升;③取物水面下降。
5.等体积转换问题:圆锥体沙堆铺路;长方体钢材熔铸成圆柱或圆锥;橡皮泥
改变形状;圆柱中的溶液倒入圆锥……都是体积不变的问题。
解决此类问题,最好列出体积相等公式,再代入数据进行计算。
六年级数学下册圆柱与圆锥知识点总结(全面)

圆柱与圆锥一.圆柱1、圆柱的形成:圆柱是以长方形的一边为轴旋转而得到的;圆柱也可以由长方形卷曲而得到。
2、圆柱各部分的名称:圆柱的的两个圆面叫做底面(又分上底和下底);周围的面叫做侧面;两个底面之间的距离叫做高(高有无数条他们的数值是相等的)。
3、圆柱的侧面展开图:A、沿着高展开,展开图形是长方形,长方形的长等于圆柱底面的周长,长方形的宽等于圆柱的高,当底面周长和高相等时(h=2πR),侧面沿高展开后是一个正方形,展开图形为正方形。
B、不沿着高展开,展开图形是平行四边形或不规则图形。
C、无论如何展开都得不到梯形.侧面积=底面周长×高S侧=Ch=πd×h=2πr×h4、圆柱的表面积:圆柱表面的面积,叫做这个圆柱的表面积。
圆柱的表面积=2×底面积+侧面积,即S表=S侧+S底×2=2πr×h+2×πr2(实际中,使用的材料都要比计算的结果多一些,因此,要保留数的时候,都要用进一法)圆柱的体积:圆柱所占空间的大小,叫做这个圆柱的体积。
圆柱切拼成近似的长方体,分的份数越多,拼成的图形越接近长方体。
长方体的底面积等于圆柱的底面积,长方体的高等于圆柱的高。
长方体的体积=底面积×高圆柱体积=底面积×高V柱=S h=πr2hh=V柱÷S=V柱÷(πr2)S=V柱÷h5、圆柱的切割:A.横切:切面是圆,表面积增加2倍底面积,即S增=2πr2B.竖切(过直径):切面是长方形(如果h=2R,切面为正方形),该长方形的长是圆柱的高,宽是圆柱的底面直径,表面积增加两个长方形的面积,即S增=4rh考试常见题型:A.已知圆柱的底面积和高,求圆柱的侧面积,表面积,体积,底面周长B.已知圆柱的底面周长和高,求圆柱的侧面积,表面积,体积,底面积C.已知圆柱的底面周长和体积,求圆柱的侧面积,表面积,高,底面积D.已知圆柱的底面面积和高,求圆柱的侧面积,表面积,体积E.已知圆柱的侧面积和高,求圆柱的底面半径,表面积,体积,底面积以上几种常见题型的解题方法,通常是求出圆柱的底面半径和高,再根据圆柱的相关计算公式进行计算。
完整版)六年级下册圆柱和圆锥知识点

完整版)六年级下册圆柱和圆锥知识点文章已经没有格式错误和明显有问题的段落了,但可以对每段话进行小幅度改写,如下:第一单元圆柱和圆锥知识点一、圆柱的特征:圆柱有两个底面、一个侧面和无数条高。
其底面为大小相同的圆形。
圆柱的侧面展开后可以得到长方形、正方形或平行四边形,与圆柱有密切关系。
例如,长方形的长等于圆柱的底面周长,长方形的宽等于圆柱的高,长方形的面积等于圆柱的侧面积。
当圆柱的底面周长和高相等时,其侧面展开图为正方形。
二、圆锥的特征:圆锥有一个圆形底面和一个扇形侧面,只有一条高。
圆锥的高是从圆锥顶点到底面圆心的距离。
三、基本公式:在求圆柱表面积、圆柱和圆锥的体积时,需要先复圆的半径计算公式。
已知直径求半径为r=d÷2,已知周长求半径为r=c÷π÷2.圆柱的底面积为πr²,侧面积为底面周长×高,即S侧=Ch=πdh=2πrh,圆柱的表面积为侧面积加上底面积的两倍。
圆柱的体积为底面积乘以高,即V圆柱=Sh=πr²h。
圆锥的体积为底面积乘以高再除以3,即V圆锥=1/3Sh=1/3πr²h。
四、单位换算:在长度单位换算中,相邻两个长度单位之间的进率是10,1千米等于1000米,1米等于10分米,1分米等于10厘米,1厘米等于10毫米。
在面积单位换算中,相邻两个面积单位之间的进率是100,1平方千米等于100公顷,1公顷等于平方米,1平方米等于100平方分米,1平方分米等于100平方厘米,1平方厘米等于100平方毫米。
在体积单位换算中,相邻两个体积单位之间的进率是1000,1立方米等于1000升,1升等于1立方分米,1立方分米等于1000立方厘米,1立方厘米等于1毫升。
在单位换算中,大单位化为小单位使用乘法,小单位化为大单位使用除法。
(完整版)圆柱与圆锥知识点总结
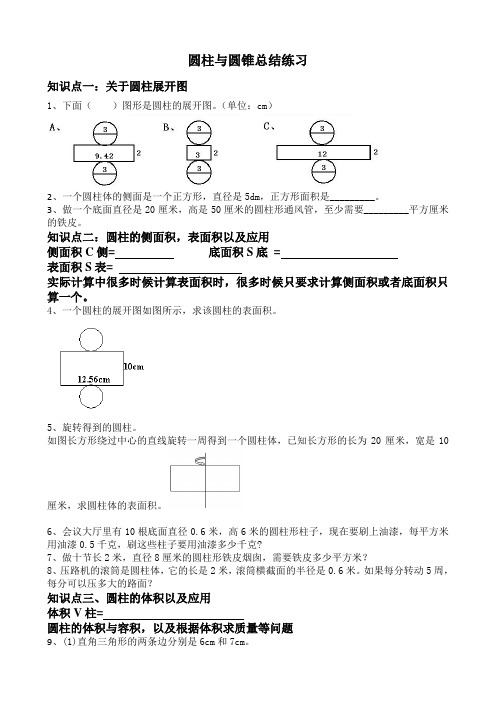
圆柱与圆锥总结练习知识点一:关于圆柱展开图1、下面()图形是圆柱的展开图。
(单位:cm)2、一个圆柱体的侧面是一个正方形,直径是5dm,正方形面积是_________。
3、做一个底面直径是20厘米,高是50厘米的圆柱形通风管,至少需要_________平方厘米的铁皮。
知识点二:圆柱的侧面积,表面积以及应用侧面积C侧= 底面积S底=表面积S表=实际计算中很多时候计算表面积时,很多时候只要求计算侧面积或者底面积只算一个。
4、一个圆柱的展开图如图所示,求该圆柱的表面积。
5、旋转得到的圆柱。
如图长方形绕过中心的直线旋转一周得到一个圆柱体,已知长方形的长为20厘米,宽是10厘米,求圆柱体的表面积。
6、会议大厅里有10根底面直径0.6米,高6米的圆柱形柱子,现在要刷上油漆,每平方米用油漆0.5千克,刷这些柱子要用油漆多少千克?7、做十节长2米,直径8厘米的圆柱形铁皮烟囱,需要铁皮多少平方米?8、压路机的滚筒是圆柱体,它的长是2米,滚筒横截面的半径是0.6米。
如果每分转动5周,每分可以压多大的路面?知识点三、圆柱的体积以及应用体积V柱=圆柱的体积与容积,以及根据体积求质量等问题9、(1)直角三角形的两条边分别是6cm和7cm。
(2)长方形的长是10厘米,宽是5厘米,绕过中点的直线旋转一圈。
知识点四、圆锥的体积以及应用体积V柱=圆锥的体积与容积,以及根据体积求质量等问题10、一个圆锥体的体积是15.7立方分米,底面积是3.14平方分米,它的高有多少分米?知识点五、圆柱圆锥体积之间的关系,底面积,体积比的问题①如果圆柱与圆锥等底等高,圆柱的体积是圆锥的②如果圆柱与圆锥体积相等,高相等,则圆锥的底面积是圆柱的③如果圆柱与圆锥体积相等,底面积相等,则圆锥的高是圆柱的11、一个圆柱体橡皮泥,底面积是12平方厘米,高4厘米,把它捏成:(1)底面积不变的圆锥,圆锥的高是多少?(2)高不变的圆锥,圆锥的底面积是多少?(3)底面积是8平方厘米的圆锥,高是多少?12、一个圆柱形容器的底面半径是4分米,高6分米,里面盛满水,把水倒在棱长是8分米的正方体容器内,水深是多少分米?13、有一段钢可做一个底面直径8厘米,高9厘米的圆锥形零件.如果把它改制成高是12厘米的圆柱形零件,零件的底面积是多少平方厘米?知识点六、体积单位,表面积单位之间的互换,以及常见立体图形的体积表面积问题表面积单位:平方厘米平方分米平方米(进率是10*10=100)体积单位:立方厘米立方分米立方米(进率是10*10*10=1000)表面积是所有表面的面积的总和,算出各个面的面积求和即可长方形面积= 正方形面积= 三角形面积=平行四边形面积= 梯形面积=体积:所有立体图形的体积都可以用底面积×高求解,各个立体图形也有自己的体积公式。
圆柱和圆锥整理复习总结

THANK FOR YOU WATCHING
演讲人姓名
演讲时间
把一堆高5米,底面直径是6米的圆锥形小麦堆放入底面积是12.56平方米的圆柱粮仓内,至少要装多高?
将一个底面半径是4分米,高是6分米的圆柱木料削成一个最大的圆锥,至少要削去多少立方分米的木料?
一、求圆柱的表面积。(单位:厘米)
(1)侧面积:3.14×10×2=62.8(平方厘米) (2)底面积: 3.14 ×(10÷2)2=78.5 (平方厘米) (3)表面积;62.8+78.5×2=219.8(平方厘米)
二、计算下列图形的体积:单位(厘米)
5
2
3.14×2 ×5 =12.56 ×5 =62.8(立方厘米)
整 理 复 习
圆柱和圆锥
圆柱体 圆锥体 两个完全相同的圆形底面 ;一个曲形侧面,打开是个长方形;有无数条高。 尖顶;底面是个圆;侧面是一个曲面;只有一条高。
图形
名称
特征
底面周长×高
侧面积+底面积×2
侧面积=
表面积=
体积=
底面积×高
V=sh
V= sh
体积=底面积×高×
10
2
2
S=50.24厘米2
12
.
50.24×12× =50.24×4 = 200.96(立方厘米)
三、我会判断。
圆柱的体积是圆锥体积的3倍。( ) (2)一个圆柱的体积是60立方厘米,和它等 底等高的圆锥体积是20立方厘米。( ) (3)把一段圆柱形的木料削成一个最大的圆 锥,削去的部分是原体积的 。( ) 一个圆柱和一个圆锥底面积相等,体积也相等,已知圆柱的高是15厘米,圆锥的高是5厘米。( )
c
c
A
人教版六年级数学下册第三单元《圆柱与圆锥》知识点汇总

人教版六年级下册第三单元《圆柱与圆锥》知识点汇总一、圆柱的认识1、圆柱的形成:(1)圆柱是以长方形的一边为轴旋转而得到的。
两种情况:○1若以长方形的长边为轴旋转而得到的圆柱,长方形的长等于圆柱的高,宽等于圆柱的底面半径。
○2若以长方形的宽边为轴旋转而得的圆柱,长方形的宽等于圆柱的高,长等于圆柱的底面半径。
(2)圆柱也可以由长方形卷曲而得到。
两种情况:○1以长方形的长为底面周长,宽为高。
○2以长方形的宽为底面周长,长为高。
其中,第一种方式得到的圆柱体体积较大。
2、圆柱的高、底面和侧面定义(1)圆柱的高:圆柱的两个底面之间的距离叫做高。
圆柱有无数条高,他们的数值是相等的。
(2)圆柱的底面:圆柱的上、下两个面叫做底面。
(3)圆柱的侧面:圆柱周围的面(上、下底面除外)叫做侧面。
3、圆柱的特征:圆柱是由两个大小相等的圆形底面(上底面、下底面)和一个侧面围成的。
圆柱高的特征:圆柱有无数条高,每条高的长度都相等。
圆柱底面的特征:圆柱的底面是完全相等的两个圆。
圆柱侧面的特征:圆柱的侧面是一个曲面。
圆柱的侧面展开图可能是长方形或正方形,也可能是平行四边形,不可能是梯形。
4、圆柱的切割:(1)横切:切面是圆,切成n段,需要n-1次,增加2×(n-1)个底面积。
如:切成3段,需要3-1=2次,增加2×(3-1)=4个底面积。
(2)竖切(过高过直径):切面是长方形(如果h=2r,切面为正方形),该长方形的长是圆柱的高,宽是圆柱的底面直径,表面积增加两个长方形的面积,即:S增=4rh。
5、圆柱的侧面展开图:(1)如果沿着高展开,展开的图形是长方形;如果高等于底面周长,则展开的图形为正方形。
(2)如果不沿着高展开,展开图形是平行四边形或不规图形。
(3)圆柱无论怎么展开都不可能得到梯形。
二、圆柱的表面积1、圆柱的表面积:圆柱是由两个大小相等的圆形底面(上底面、下底面)和一个侧面围成的,所以圆柱的表面积=底面面积×2+侧面面积。
六年级数学下册第三单元知识点整理汇总(圆柱和圆锥)

六年级数学下册第三单元知识点整理汇总(圆柱和圆锥)一、圆柱1、圆柱的形成:圆柱是以长方形的一边为轴旋转而得的。
圆柱也可以由长方形卷曲而得到。
两种方式:1.以长方形的长为底面周长,宽为高;2.以长方形的宽为底面周长,长为高。
其中,第一种方式得到的圆柱体体积较大。
2、圆柱的高是两个底面之间的距离,一个圆柱有无数条高,他们的数值是相等的3、圆柱的特征:(1)底面的特征:圆柱的底面是完全相等的两个圆。
(2)侧面的特征:圆柱的侧面是一个曲面。
(3)高的特征:圆柱有无数条高4、圆柱的切割:①横切:切面是圆,表面积增加2倍底面积,即S增=2πr²②竖切(过直径):切面是长方形(如果h=2R,切面为正方形),该长方形的长是圆柱的高,宽是圆柱的底面直径,表面积增加两个长方形的面积,即S增=4rh5、圆柱的侧面展开图:①沿着高展开,展开图形是长方形,如果h=2πr,则展开图形为正方形②不沿着高展开,展开图形是平行四边形或不规则图形③无论怎么展开都得不到梯形6、圆柱的相关计算公式:底面积:S底=πr²底面周长:C底=πd=2πr侧面积:S侧=2πrh表面积:S表=2S底+S侧=2πr²+2πrh体积:V柱=πr²h考试常见题型:①已知圆柱的底面积和高,求圆柱的侧面积,表面积,体积,底面周长②已知圆柱的底面周长和高,求圆柱的侧面积,表面积,体积,底面积③已知圆柱的底面周长和体积,求圆柱的侧面积,表面积,高,底面积④已知圆柱的底面面积和高,求圆柱的侧面积,表面积,体积⑤已知圆柱的侧面积和高,求圆柱的底面半径,表面积,体积,底面积以上几种常见题型的解题方法,通常是求出圆柱的底面半径和高,再根据圆柱的相关计算公式进行计算无盖水桶的表面积=侧面积+一个底面积油桶的表面积=侧面积+两个底面积烟囱通风管的表面积=侧面积只求侧面积:灯罩、排水管、漆柱、通风管、压路机、卫生纸中轴、薯片盒包装侧面积+一个底面积:玻璃杯、水桶、笔筒、帽子、游泳池侧面积+两个底面积:油桶、米桶、罐桶类二、圆锥1、圆锥的形成:圆锥是以直角三角形的一直角边为轴旋转而得到的。
圆柱和圆锥的整理与复习.

圆柱的特征:
1 有两个底面:
、
面积相等
2 一个侧面:
、
宽= 高
宽
长=底面周长
长
圆锥的特征:
h
侧面展开
扇形
圆形
底面
从圆锥的顶点到底面圆心的 距离叫做圆锥的高。
图形
名称
特征
举例
两个底面是完全相同的两 桥墩、门 圆柱体 个圆;侧面是一个曲面,展开 厅柱子… 是个长方形;有无数条高。 尖顶;底面是个圆;侧面是 沙堆、圣 圆锥体 一个曲面,展开是个扇形;只 诞帽子… 有一条高。
侧面积= 底面周长×高
表面积= 侧面积+底面积× 2
体积= 底面积×高
V=Sh 体积= 底面积×高÷3 V=Sh÷3
20厘米
15 厘 米
一、圆柱和圆锥的关系
1.等底等高时,圆柱的体积是圆锥的( )
圆锥的体积是圆柱的( ) 圆柱的体积比圆锥多( )
圆锥的体积比圆柱少( )
圆柱和圆锥的体积比( )
三、走进生活
1.冬天护林工人给圆柱形的 树干的下端涂防蛀涂料,那么 粉刷树干的面积是指( B ).
A.底面积
C.表面积
B.侧面积
D.体积
2.下雨时,给打谷场上的圆锥形谷堆盖上 塑料防雨布,所需防雨布的最小面积是指 圆锥的( C )
A. 表面积
B.体积
C. 侧面积
3.甲乙两人分别利用一张长20厘米, 宽15厘米的纸用两种不同的方法围成 一个圆柱体(接头处不重叠),那么 围成的圆柱( B )。 A.高一定相等
(1)求可装水多少升,就是求什么? (2)玻璃杯是什么形状的?如何计算玻璃杯 的容积? (3)你认为计算过程中要注意什么?
(完整版)六年级下册第二单元《圆柱与圆锥》知识点整理

六年级下册第二单元《圆柱与圆锥》知识点整理第二单元:圆柱与圆锥一.圆柱、圆柱的形成:圆柱是以长方形的一边为轴旋转而得到的;圆柱也可以由长方形卷曲而得到。
2、圆柱各部分的名称:圆柱的的两个圆面叫做底面(又分上底和下底);周围的面叫做侧面;两个底面之间的距离叫做高(高有无数条他们的数值是相等的)。
3、圆柱的侧面展开图:a沿着高展开,展开图形是长方形,长方形的长等于圆柱底面的周长,长方形的宽等于圆柱的高,当底面周长和高相等时(h=2πR),侧面沿高展开后是一个正方形,展开图形为正方形。
b.不沿着高展开,展开图形是平行四边形或不规则图形。
c.无论如何展开都得不到梯形.侧面积=底面周长×高S侧=ch=πd×h=2πr×h4、圆柱的表面积:圆柱表面的面积,叫做这个圆柱的表面积。
圆柱的表面积=2×底面积+侧面积,即S表=S侧+S底×2=2πr×h+2×πr2(实际中,使用的材料都要比计算的结果多一些,因此,要保留数的时候,都要用进一法)圆柱的体积:圆柱所占空间的大小,叫做这个圆柱的体积。
圆柱切拼成近似的长方体,分的份数越多,拼成的图形越接近长方体。
长方体的底面积等于圆柱的底面积,长方体的高等于圆柱的高。
长方体的体积=底面积×高圆柱体积=底面积×高V柱=Sh=πr2hh=V柱÷S=V柱÷S=V柱÷h5、.圆柱的切割:a.横切:切面是圆,表面积增加2倍底面积,即S增=2πr2b.竖切(过直径):切面是长方形(如果h=2R,切面为正方形),该长方形的长是圆柱的高,宽是圆柱的底面直径,表面积增加两个长方形的面积,即S增=4rh考试常见题型:a已知圆柱的底面积和高,求圆柱的侧面积,表面积,体积,底面周长b已知圆柱的底面周长和高,求圆柱的侧面积,表面积,体积,底面积c已知圆柱的底面周长和体积,求圆柱的侧面积,表面积,高,底面积d已知圆柱的底面面积和高,求圆柱的侧面积,表面积,体积e已知圆柱的侧面积和高,求圆柱的底面半径,表面积,体积,底面积以上几种常见题型的解题方法,通常是求出圆柱的底面半径和高,再根据圆柱的相关计算公式进行计算。
苏科版数学六年级下册圆柱与圆锥单元复习知识梳理与总结

学科教师辅导教案授课类型圆柱和圆锥教学目标1、认识圆柱和圆锥的特点2、掌握圆锥的体积以及圆柱的体积和表面积的应用星级★★★★进门测1、小欣统计了六年级某次数学测试的成绩,制成了如图所示的两个不完整的统计图.(1)扇形统计图用整个圆表示六年级某次数学测试的总人数.(填“单位1“以外的答案)(2)成绩为的人数占了测试总人数的12,所在扇形的圆心角是.(3)对照两个统计图的数据,可求出六年级一共有人参加了本次测试.(4)把如图所示的两个统计图分别补充完整.2.下面的数据,()适合用折线统计图表示.A.本年级各班人数B.一年内气温的变化情况C.女生人数占全校人数的百分之几3.如图,用一张长165.6厘米的铁皮,剪下一个最大的圆作为圆柱的底面,剩下的部分围在底面上做成一个无盖的铁皮水桶,算一算这个铁皮水桶的容积是多少?(铁皮厚度不计, 取3.14)知识梳理根据书本上的实验可以得到结论:等底等高的圆柱和圆锥,圆柱的体积是圆锥的 3 倍,或者说圆锥的体积是圆柱的三分之一。
用字母表示为V 圆柱=3V 圆锥或者V 圆锥=1/3V 圆柱。
相关公式:只需要在圆柱的相关公式前面乘以三分之一。
①已知半径和高,V 圆锥=________________②已知直径和高,V 圆锥=_________________③已知周长和高,V 圆锥=__________________知识点六:圆柱和圆锥的横截面理解掌握:★圆柱横截面的分割方法:①按底面的直径分割,这样分割的横截面是长方形或者是正方形,如果横截面是正方形说明圆柱的底面直径和高相等。
②按平行于底面分割,这样分割的横截面是圆。
圆锥横截面的分割方法:①按圆锥的高分割,这样分割的横截面是等腰三角形。
②按平行于底面分割,这样分割的横截面是圆。
精讲精练考点1:圆柱的特征例1、用塑料绳捆扎一个圆柱形的蛋糕盒(如图),打结处正好是底面圆心,打结用去绳长32厘米.扎这个盒子至少用去塑料绳多少厘米?举一反三1.下面的平面图形分别绕虚线旋转一周会形成圆柱的是()A.B.C.D.2.李师傅先选好了一个直径是30厘米的圆形铁板做桶底.然后从下面三块铁板中选择一块做桶身.第块比较合适.3.用塑料绳捆扎一个圆柱形的蛋糕盒(如图),打结处正好是底面圆心,打结用去绳长15厘米.扎这个盒子至少用去塑料绳多少厘米?考点2:圆锥的特征例2.一个圆锥的底面周长是18.84厘米,高是4厘米.从圆锥的顶点沿着高将它切成两半后,表面积比原来的圆锥增加了多少平方厘米?举一反三1.以一个等腰直角三角形的一条直角边为轴,旋转一周生成的图形是圆锥.如果这个等腰直角三角形的一条直角边的长是10厘米,那么生成图形的高是厘米,底面积是平方厘米.2.从纸上剪下一个半径是30厘米、圆心角是120度的扇形,用这个扇形做一个圆锥的侧面,另外再配一个底面,这个底面的直径是厘米.3.在正方形铁皮上剪下一个圆形和扇形,恰好围成一个圆锥形(如图).如果圆的半径为r,扇形的半径为R;那么圆的半径占扇形半径的%.考点3:圆柱的侧面积、表面积和体积例3.如图是个圆柱体,求它的侧面积、表面积和体积(单位:)cm举一反三1.计算如图所示的圆柱的侧面积和体积(单位:)cm(1)如图,圆柱的侧面积是多少?(2)如图,圆柱的体积是多少?2.计算如图图形的体积和表面积.(单位:)cm3.计算空心钢管的表面积(所有与空气接触的面)(单位:厘米)例4.求如图的表面积和体积.(单位:)dm举一反三1.求如图的体积(单位:厘米)2.求下面图形的表面积和体积.3.在一个底面积是16平方厘米的正方体铸铁中,以相对的两个面为底,挖出一个最大的圆柱体.求剩下的铸铁的表面积是多少平方厘米.( 取3.14)例5.一个圆柱,如果高减少2厘米,表面积就减少25.12平方厘米,体积减少15.这个圆柱原来的体积是多少立方厘米?举一反三1.一个底面积是15平方厘米的玻璃杯中装有高3厘米的水.现把一个底面半径是1厘米、高5厘米的圆柱形铁块垂直放入玻璃杯水中,问水面升高了多少厘米(圆周率取3)2.一个圆柱高8厘米,如果它的高增加2厘米,那么它的表面积增加25.12平方厘米,求原来圆柱的表面积是多少平方厘米?3.一个正方体的木块,它的棱长总和是240厘米,在这个正方体木块里削一个最大的圆柱,这个圆柱的体积是多少立方厘米?(画出草图)考点4:圆锥的体积例6.一个直角三角形的三条边分别是3厘米、4厘米、5厘米,以一条直角边为轴旋转一周可以形成一个什么图形?体积最大是多少立方厘米?举一反三1.如图为一个棱长6分米的正方体,以正方体的底面向内挖去一个最大的圆锥体,求剩下的体积是原正方体体积的百分之几?2.红星广场有一个圆锥形玻璃罩,底面周长31.4米,高15米,这个玻璃罩的容积是多少立方米?(玻璃厚度忽略不计)3.一个圆锥形沙堆,底面积是28.26平方米,高是2.5米.用这堆沙在10米宽的公路上铺2厘米厚的路面,能铺多少米?考点5:组合图形的体积例7.如图是一种钢制的配件(图中数据单位:)cm请计算它的表面积和体积.举一反三1.一个零件,如图,求它的体积.( 取3)2.求图中图1图2的体积.3.如图,将三个高都是1米,底面半径分别是1.5米、1米、0.5米的3个圆柱体组成一个物体.①求这个物体的体积?②求这个物体的表面积?例8.求体积.(单位:)cm举一反三1.如图所示,直角三角形三条边分别长为3厘米、4厘米、5厘米.求绕斜边旋转一周后所形成的物体体积.2.一囤小麦,上面是圆锥形,下面是圆柱形.如图所示.(1)这个麦囤约有多少立方米的小麦?(得数保留整数)(2)如果每立方米小麦大约重735千克,小麦的出粉率是85%,这些小麦能磨出面粉多少千克?3.这只工具箱的下半部是棱长为20cm的正方体,上半部分是圆柱体的一半.这只箱子的体积是多少?(单位:厘米)考点6:体积的等积变形例9.如图,一个酒瓶里面深24厘米,底面内径是16厘米,瓶里酒高15厘米.把酒瓶塞紧后,使其瓶口向下倒立,这时酒高19厘米,酒瓶容积是多少毫升?举一反三1.一个酸奶瓶(如图),它的瓶身呈圆柱形(不包括瓶颈),容积是32.4立方厘米.当瓶子正放时,瓶内酸奶高为8厘米,瓶子倒放时,空余部分高为2厘米.请你算一算,瓶内酸奶体积是多少立方厘米?2.为了测量一个如图形状的酒瓶容积,一位同学先向酒瓶倒入了一些水,塞上瓶盖,量得了一些数据,再将酒瓶旋转过来又量得一些数据.你能帮他算一下酒瓶的容积吗?(单位:厘米)3.刘华测量一个瓶子的容积,测得瓶子的底面直径12厘米,然后给瓶子内盛入一些水,正放时水高20厘米,倒放时水高25厘米,瓶子深30厘米.你能根据这些信息求出瓶子的容积吗?。
人教新课标版六年级数学下册第三单元《圆柱与圆锥》核心考点梳理(共26张PPT)

圆锥的体 积公式
圆锥体积 公式运用
ห้องสมุดไป่ตู้
知识梳理
圆柱
1、圆柱的形成:圆柱是以长方形的一边为轴旋转而得的。 2、圆柱也可以由长方形卷曲而得到。 两种方式: 1.以长方形的长为底面周长,宽为高; 2.以长方形的宽为底面周长,长为高。其中,第一种方式得到的圆柱体体积较大。 3.圆柱的高是两个底面之间的距离,一个圆柱有无数条高,他们的数值是相等的。
5mm=0.5cm 3.14×(0.5÷2)2×2=0.3925(cm3)=0.3925(mL)
120÷0.3925÷2≈152(天)
答:这支牙膏最多能用152天。
课堂小结
这节课你有什么收获?
这节课我们对圆柱与圆锥这一章做了整理和复 习,先自主回顾了本章主要内容,然后在问题解决 中复习应用了所学知识。接着通过一些练习来巩固 技能。最后补充完善了知识网络图。
(1)3.14×(10÷2)2×2+3.14×10×20=785(cm2)
(2)3.14×(10÷2)2×20=1570(cm3) 1570cm3=1.57L>1.5L
答:(1)至少用了785cm2的布料。 (2)这壶水够喝。
3.有块正方体的木块,它的棱长是4dm。把这 块木料加工成一个最大的圆柱,求这个圆柱的体积。
思考:每一个问题都涉及哪些方面的知识?
2.妈妈给小雨的塑料水壶做了一个 布套,小雨每条上学带一壶水。 (1)至少用了多少布料? (2)小雨在学校喝1.5L水,这壶水够 喝吗?(水壶的厚度忽略不计。)
提问: ①要想求用了多少布料,就是要求什么?
②你需要求哪些面的面积? (两个底面和侧面)
2.妈妈给小雨的塑料水壶做了一个 布套,小雨每条上学带一壶水。 (1)至少用了多少布料? (2)小雨在学校喝1.5L水,这壶水够 喝吗?
六年级下册圆柱和圆锥知识点

第一单元圆柱和圆锥知识点
一、圆柱的特征:
有2个底面,1个侧面,无数条高。
大小相同
圆柱的侧面展开:长方形或正方形或平行四边形。
(说出与圆柱的关系)
当圆柱的底面周长和高相等的时候,它的侧面展开图就是一个正方形.
二、圆锥的特征
有1个是圆形的底面,1个是扇形的侧面,只有1条高.
圆锥的高:从圆锥的顶点到底面圆心的距离叫做高。
三、基本公式
求圆柱表面积、圆柱、圆锥的体积的时候,先复习下圆的半径求法:已知直径求半径~~r=d÷2 已知周长求半径~~r=c÷π÷2
字母公式S底=πr2
字母公式S侧=Ch=πdh=2πrh
字母公式V圆柱=Sh=πr2h
字母公式V圆锥=1/3Sh=1/3πr2h 四、单位换算:大单位化小单位用乘法(乘进率),小单位化大单
位用除法(除以进率)
长度单位换算:相邻两个长度单位之间的进率是10
1千米=1000米 1米=10分米
1分米=10厘米 1米=100厘米
1厘米=10毫米
面积单位换算:相邻两个面积单位之间的进率是100
1平方千米=100公顷1公顷=10000平方米
1平方米=100平方分米=10000平方厘米
1平方分米=100平方厘米
1平方厘米=100平方毫米
体(容)积单位换算:相邻两个体积单位之间的进率是1000 1立方米=1000立方分米=1000000立方厘米
1立方分米=1000立方厘米
1立方分米=1升 1立方厘米=1毫升
1立方米=1000升
重量单位换算
1吨=1000千克 1千克=1000克。
圆柱与圆锥圆锥整理和复习精编

面积的公式,可以得出答案。
03
圆柱和圆锥的关系问题
例如,一个圆柱和一个圆锥的底面半径相同,圆柱的高是圆锥的高的2
倍。求两者的体积之比。可以通过建立数学模型,运用公式解决这个问
题。
05
复习方法和建议
系统复习,掌握知识脉络
01
02
03
复习笔记和课本
经常回顾课堂笔记和数学 课本,熟悉圆柱与圆锥的 基本概念和公式。
圆锥的表面积计算
圆锥的表面积包括底面圆和侧面扇形 的面积。
侧面扇形的面积公式为:θr²/2(其 中θ为侧面展开后的中心角,r为底面 圆的半径)。
底面圆的面积公式为:πr²(其中r为 底面圆的半径)。
圆锥表面积的计算公式为:底面圆面 积 + 侧面扇形面积。
圆锥的体积计算
圆锥的体积可以通过底面积和高 来计算。
题目中可能存在隐藏的条件或限制条件,如果忽略这些条件,可能导致错误。因此,在解题时需要认 真读题,并注意题目中的限制条件。
经典例题解析和解题技巧分享
01
圆柱的体积问题
例如,求半径为3cm的圆柱的体积。通过运用圆柱体积的公式,可以得
出答案。
02
圆锥的表面积问题
例如,求底面半径为4cm,高为5cm的圆锥的表面积。通过运用圆锥表
圆锥的体积公式为:V = (1/3)πr²h(其中r为底面圆的半
径,h为圆锥的高)。
当圆锥的底面积和高度不同时, 需要先通过底面积和高度的关系 求出等效半径,再使用上述公圆锥形屋顶可以有效地利用空间,并且能够让雨雪等自 然物质顺畅地滑落。
圆锥形冰淇淋筒可以方便地握持,并且能够让冰淇淋均 匀地融化。
圆柱
用于各种容器、管道、建筑物等,如水桶、管道、柱子、灯罩等。
(背诵)圆柱和圆锥知识点归纳总结
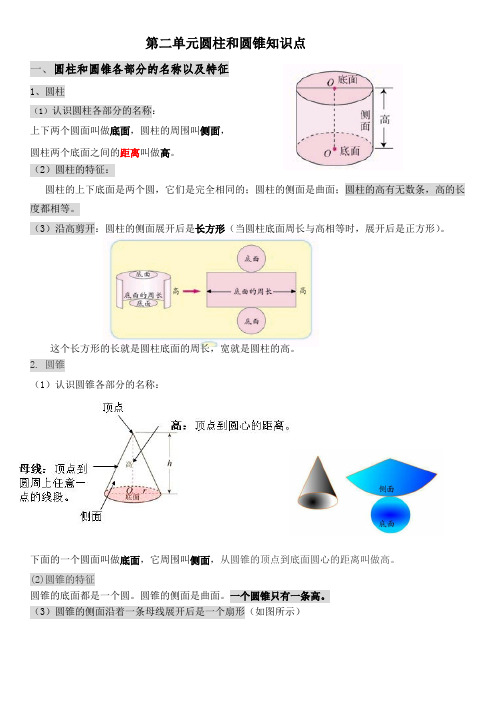
第二单元圆柱和圆锥知识点一、圆柱和圆锥各部分的名称以及特征1、圆柱(1)认识圆柱各部分的名称:上下两个圆面叫做底面,圆柱的周围叫侧面,圆柱两个底面之间的距离叫做高。
(2)圆柱的特征:圆柱的上下底面是两个圆,它们是完全相同的;圆柱的侧面是曲面;圆柱的高有无数条,高的长度都相等。
(3)沿高剪开:圆柱的侧面展开后是长方形(当圆柱底面周长与高相等时,展开后是正方形)。
这个长方形的长就是圆柱底面的周长,宽就是圆柱的高。
2. 圆锥(1)认识圆锥各部分的名称:下面的一个圆面叫做底面,它周围叫侧面,从圆锥的顶点到底面圆心的距离叫做高。
(2)圆锥的特征圆锥的底面都是一个圆。
圆锥的侧面是曲面。
一个圆锥只有一条高。
(3)圆锥的侧面沿着一条母线展开后是一个扇形(如图所示)二、基本公式1、圆的知识直径 d = 2 r半径r = d÷2圆的周长: 已知直径求周长 C =πd 逆推公式有:已知周长求直径: d = C÷π已知半径求周长C=2πr 已知周长求半径: r = C÷π÷2 圆的面积: 已知半径求面积S=πr2已知直径求面积先求半径r =d÷2 再求面积S=πr2已知周长求面积先求半径r =C÷π÷2 再求面积S=πr22、圆柱的表面积:圆柱的表面积=圆柱的侧面积+圆柱的底面积×2S表= S侧+ 2S底(三个面) S表= 2πr (r+ h)(二个面) S表= πr h (r+2 h)(一个面) S侧 = 2πr h把圆柱侧面沿高展开,得到一个长方形(或正方形),长方形的长是圆柱的底面周长,长方形的宽是圆柱的高。
圆柱的侧面积=底面周长×高S侧= C hS侧 = πd hS侧 = 2πr h如果圆柱的侧面展开是一个正方形,那么这个圆柱的高和底面周长相等。
3 、圆柱的体积圆柱的体积=底面积×高V圆= S hV圆= πr2 h逆推公式有:圆柱的高=圆柱的体积÷底面积H = V圆÷ S圆柱的底面积=圆柱的体积÷高S = V圆÷ h4 、半个圆柱的表面积= 圆柱表面积÷25、圆锥的体积圆锥的体积=底面积×高×13V锥=31Sh V锥=31πr2 h逆推公式有:圆锥的高=圆锥的体积×3÷底面积h=V锥×3÷Sh=V锥×3÷π÷r2圆锥的底面积=圆锥的体积×3÷高S= V锥×3 ÷h5、等底等高的圆柱和圆锥,圆柱体积是圆锥体积的3倍。
圆柱圆锥知识点归纳

圆柱圆锥知识点归纳第一单元知识归纳与梳理一、面的旋转1、点、线、面、体之间的关系为:点的运动形成线;线的运动形成面;面的旋转形成体。
2、圆柱的特征:1) 圆柱的两个底面是完全相同的两个圆。
2) 两个底面间的距离称为圆柱的高。
3) 圆柱有无数条高,且高的长度都相等。
3、圆锥的特征:1) 圆锥的底面是一个圆。
2) 圆锥的侧面是一个曲面,侧面展开是一个扇形。
3) 圆锥的顶点到底面的距离叫圆锥的高,圆锥只有一条高。
二、圆柱的表面积1、表面积指物体露在外面的面的面积。
2、完整圆柱的表面积包括一个侧面和两个底面。
3、圆柱的表面积计算:1) 侧面积:沿圆柱的高剪开,圆柱的侧面展开图是一个长方形(或正方形)。
(如果不是沿高剪开,有可能还会是平行四边形或其他不规则图形)2) 圆柱的侧面积=底面周长×高,用字母表示为:S侧=ch3) 圆柱的侧面积公式的应用:1) 已知底面周长和高,求侧面积,可运用公式:S侧=ch2) 已知底面直径和高,求侧面积,可运用公式:S侧=πdh3) 已知底面半径和高,求侧面积,可运用公式:S侧=2πrh4、圆柱表面积的计算方法:如果用S侧表示一个圆柱的侧面积,S底表示底面积,d表示底面直径,r表示底面半径,h表示高,那么这个圆柱的表面积为:1) S表=S侧+2S底或 S表=S侧+S底或 S表=S侧5、圆柱表面积的计算方法的特殊应用:1) 圆柱的表面积只包括侧面积和一个底面积的,例如无盖水桶等圆柱形物体。
2) 圆柱的表面积只包括侧面积的,例如烟囱、油管等圆柱形物体。
6、已知侧面积求c、h、s表1) h=s侧÷c2) 求s表三、圆柱的体积1、圆柱的体积是一个圆柱所占空间的大小。
2、圆柱体积的推导过程:把圆柱沿高切开,可以拼成一个近似的长方体,圆柱的底面积是长方体的底面积,圆柱的高是长方体的高,因为长方体的体积=底面积×高,所以圆柱的体积=底面积×高3、圆柱的体积=底面积×高。
西师大版六年级数学下册第2单元 圆柱和圆锥 知识点汇总

第2单元总结
智慧小锦囊
易错集锦
易错点1:圆柱形实物的表面积计算。
误区点拨:
(1)理不清要计算一个底面积、两个底面积还是不计算底面积。
(2)在计算圆柱形物体的表面积时,要联想该物体在生活中的具体形态是由哪些基本图形组成的。
一般情况下,计算通风管、烟囱的用料面积、压路机压路的面积和油漆廊柱的面积时,只计算侧面积;计算油桶的表面积时,计算侧面积加上两个底面积。
如果题目中给出了具体的说明,则按照题意去解答。
易错点2:圆锥的体积计算。
误区点拨:
(1)在计算圆锥体积时,漏乘13。
(2)圆锥的体积是利用圆柱的体积公式推导出来的,等底等高的圆锥的体积是圆柱体积的13 ,因为圆柱的体积公式是V=Sh ,所以圆锥的体积公式是V =13Sh 。
