锐角三角比计算练习题
《锐角的三角比》全章复习与巩固(基础) 巩固练习

《锐角的三角比》全章复习与巩固(基础) 巩固练习【巩固练习】 一、选择题1.如图所示,在Rt △ABC 中,tan B =,BC =AC 等于( ).A .3B .4C ..6 2.已知α为锐角,则sin cos m αα=+的值( ). A .m ≥1 B .m =1 C .m <1D .m >13.如图所示,在梯形ABCD 中,AD ∥BC ,AC ⊥AB ,AD =CD ,cos ∠DCA =45,BC =10,则AB 的值是( ). A .3 B .6 C .8 D .9第1题图 第3题图 第4题图 4.如图所示,在菱形ABCD 中,DE ⊥AB ,3cos 5A =,BE =2,cot ∠DBE 的值是( ).A.125.如图所示,在四边形ABCD 中,E 、F 分别是AB 、AD 的中点,若EF =2,BC =5,CD =3,则tanC 等于( ).A .34 B .43 C .35 D .45第5题图 第7题图6.已知Rt △ABC 中,∠C =90°,sin 2B =,则cosA 的值为( ).A .12 B .2C 7.如图所示,先锋村准备在坡角为α的山坡上栽树,要求相邻两树之间的水平距离为5米,那么这两树在坡面上的距离AB 为( ).A .5cos α米B .5cos α米 C .5sin α米 D .5sin α米 8.等腰三角形一腰上的高与腰长之比是1:2,则等腰三角形顶角的度数为( ).A .30°B .50°C .60°或120°D .30°或150°二、填空题9.计算:101|245| 1.41)3-⎛⎫--+= ⎪⎝⎭°________.10.如图所示,已知Rt △ABC 中,斜边BC 上的高AD =4,4cos 5B =,则AC =________. 11.如图所示,将以A 为直角顶点的等腰直角三角形ABC 沿直线BC 平移得到A B C '''△,使点B '与C 重合,连接A B ',则tan ∠A BC ''的值为________.第10题图 第11题图 第12题图12.如图所示,一架梯子斜靠在墙上,若梯子底端到墙的距离AC =3米,3cos 4BAC ∠=,则梯子长AB =_______米.13.如图所示,已知正方形ABCD 的边长为2,如果将线段BD 绕着点B 旋转后,点D 落在CB 的延长线上的D ' 处,那么tan ∠BAD ′等于________.第13题图 第15题图 14.一次函数经过(cot 45°,tan 60°)和(-cos 60°,-6tan30°),则此一次函数的解析式为________. 15.如图所示,在△ABC 中,∠ACB =90°,CD 是AB 边的中线,AC =6,CD =5,则sinA 等于________. 161是方程2(3tan )0x x θ-的一个根,θ是三角形的一个内角,那么cos θ的值 为________.三、解答题17. 为了缓解长沙市区内一些主要路段交通拥挤的现状,交警队在一些主要路口设立了交通路况显示牌(如图所示).已知立杆AB 高度是3 m ,从侧面D 点测得显示牌顶端C 点和底端B 点的仰角分别是60°和45°.求路况显示牌BC 的高度.18.如图所示,在梯形ABCD中,AD∥BC,AB=DC=8,∠B=60°,BC=12,连接AC.(1)求tan∠ACB的值;(2)若M、N分别是AB、DC的中点,连接MN,求线段MN的长.19.如图所示,点E、C在BF上,BE=FC,∠ABC=∠DEF=45°,∠A=∠D=90°.(1)求证:AB=DE;(2)若AC交DE于M,且AB ME CE绕点C顺时针旋转,使点E旋转到AB上的G处,求旋转角∠ECG的度数.20. 如图所示,AB是⊙O的直径,点C在BA的延长线上,直线CD与⊙O相切于点D,弦DF⊥AB于点E,线段CD=10,连接BD.(1)求证:∠CDE=2∠B;(2)若BD:AB,求⊙O的半径及DF的长.【答案与解析】 一、选择题 1.【答案】A ;【解析】由tan AC B BC =知tan 32AC BC B ===. 2.【答案】D ;【解析】在Rt △ABC 中,设α所对的边为a ,斜边为c ,邻边为b .则sin a c α=,cos bcα=, ∴sin cos a b a bm c c cαα+=+=+=,而a b c +>,∴m >1 3.【答案】B ;【解析】因为AD =DC ,所以∠DAC =∠DCA ,又∵ AD ∥BC ,∴∠DAC =∠ACB ,所以∠DCA =∠ACB .在Rt △ACB 中,AC =BC ·cos ∠BCA =41085⨯=,则6AB ==.4.【答案】A ;【解析】∵DE ⊥AB ,∴在Rt △ADE 中,cosA =35. ∴设AD =5k ,则AE =3k ,DE =4k ,又BE =2,AD =AB , ∴5k =3k+2,∴k =1.∴DE =4. ∴cot ∠DBE =2142BE DE ==. 5.【答案】B ;【解析】如图所示,连结BD ,由三角形中位线定理得BD =2EF =2×2=4,又BC =5,CD =3,∴CD 2+BD 2=BC 2.∴△BDC 是直角三角形.且∠BDC =90°,∴4tan 3BD C CD ==.6.【答案】C ;【解析】∵sin B =,∴∠B =60°,∠A =90°-60°=30°,∴cos A =. 7.【答案】B ;【解析】由上图知ABC α∠=,在Rt △ABC 中,cos BC AB α=.∴5cos AB α=. 8.【答案】D ;【解析】有两种情况:当∠A 为锐角时,如图(1),sin A =12,∠A =30°;当∠A 为钝角时,如图(2),sin(180°-∠BAC)=12,180°-∠BAC =30°,∠BAC =150°.二、填空题9.【答案】2【解析】原式=3|21422--+=-= 10.【答案】5;【解析】在Rt △ABC 中,.AD ⊥BC ,所以∠CAD =∠B .∴cos cos AD CAD B AC =∠=,∴45AD AC =, 又∵AD =4,∴AC =5..11.【答案】13; 【解析】如图,过A '作A D BC ''⊥于点D ,在Rt △A B D ''中,设A D x '=,则B ′D=x ,BC=2x,BD=x+2x=3x,∴tan ∠A BC ''='A D BD =13.12.【答案】4 ; 【解析】由3cos 4AC BAC AB ∠==,知334AB =,AB =4.13.【解析】由题意知BD BD '==Rt △ABD ′中,tan 2BD BAD AB ''∠===14.【答案】y =【解析】cot45°=1, tan60-cos60°=12-,-6tan30°=-.设y =kx+b 经过点、1,2⎛-- ⎝,则用待定系数法可求出k =b =15.【答案】45; 【解析】∵ CD 是Rt △ABC 斜边上的中线,∴ AB =2CD =2×5=10,BC 8=,∴ 84sin 105BC A AB ===.16.【答案】2;【解析】由方程解的意义,知21)3tan (21)0θ-+=,故tan 1θ=,从而45θ=°,则cos cos 452θ==°. 三、解答题17.【答案与解析】∵在R △ADB 中,∠BDA =45°,AB =3,∴DA =3.在Rt △ADC 中,∠CDA =60°,∴tan 60CAAD=°,∴CA =BC =CA -BA =(3)m .答:路况显示牌BC 的高度是(3)m .18.【答案与解析】(1)如图所示,作AE ⊥BC 于E ,则BE =AB ·cos B =8cos 60°=1842⨯=.AE =AB ·sin B =8sin 60°=8= ∴EC =BC -BE =12—4=8.∴在Rt △ACE 中,tan ∠ACB =AE EC == (2)作DF ⊥BC 于F ,则AE ∥DF ,∵AD ∥EF ,∴四边形AEFD 是矩形.AD =EF . ∵AB =DC ,∴∠B =∠DCF .又∵∠AEB =∠DFC =90°,∴△ABE △≌△DCF(AAS). ∴FC =BE =4,∴EF =BC -BE —FC =4.∴AD =4.∴MN =12(AD+BC)=12×(4+12)=8.19.【答案与解析】(1)证明:∵BE =FC ,∴BC =EF . 又∵∠ABC =∠DEF ,∠A =∠D , ∴△ABC ≌△DEF .∴AB =DE .(2)解:∵∠DEF =∠B =45°,∴DE ∥AB .∴∠CME =∠A =90°.∴AC =AB MC =ME CG =CE =2.在Rt △CAG 中,cos AC ACG CG ∠==,∴∠ACG =30°. ∴∠ECG =∠ACB -∠ACB =45°-30°=15°.20.【答案与解析】(1)连接OD ,∵直线CD 与⊙O 相切于点D ,∴ OD ⊥CD ,∴∠CD0=90°,∴∠CDE+∠ODE =90°.又∵DF ⊥AB ,∴∠DEO =∠DEC =90°,∴∠EOD+∠ODE =90°. ∴∠CDE =∠EOD .又∵∠EOD =2∠B ; ∴ ∠CDE =2∠B . (2)连接AD .∵ AB 是⊙O 的直径,∴∠B =90°.∵BD:AB ,∴在Rt △ADB 中,cos 2BD B AB ==, ∴∠C =30°,∵∠AOD =2∠CDO =60°.又∵∠CDO =90°,∴∠C =30°, ∵在Rt △CDO 中,CD =10,∴ OD =10tan 30O 在Rt △CDE 中,CD =10,∠C =30°,∴DE =CDsin 30°=5.∵弦DF ⊥直径AB 于点E ,∴DE =CDsin30°=5. ∵弦DF ⊥直径AB 于点E , ∴DE =EF =12DF , ∴DF =2DE =10.。
沪教版九年级上册数学第二十五章 锐角的三角比含答案(必刷题)

沪教版九年级上册数学第二十五章锐角的三角比含答案一、单选题(共15题,共计45分)1、拦水坝横断面如图所示,迎水坡的坡度(坡的竖直高度与水平宽度的比)是,坝高,则坡面的长度是()A. B. C. D.2、如图,一个梯子靠在垂直水平地面的墙上,梯子AB的长是2米.若梯子与地面的夹角为,则梯子顶端到地面的距离(BC的长)为()A. 米B. 米C. 米D. 米3、已知CD是Rt△ABC斜边AB上的高,AC=8,BC=6,则cos∠BCD的值是()A. B. C. D.4、如图,两根竹竿AB和AD斜靠在墙CE上,量得∠ABC= ,∠ADC= ,则竹竿AB与AD的长度之比为A. B. C. D.5、如图,⊙O与正方形ABCD是两边AB,AD相切,DE与⊙O相切于点E,若正方形ABCD的边长为5,DE=3,则tan∠ODE为()A. B. C. D.6、如图,已知点A(-1,0)和点B(1,2),在坐标轴上确定点P,使得△ABP为直角三角形,则满足这样条件的点P共有()A.2个B.3个C.6个D.7个7、在灯塔O处观测到轮船A位于北偏西54°的方向,同时轮船B在南偏东15°的方向,那么∠AOB的大小为()A.70°B.110°C.120°D.141°8、某人沿倾斜角为30°的斜坡前进50米,则他上升的最大高度为()A.25米B.25 米C.20 米D.25 米9、下列计算结果正确的是()A. (﹣a3)2=a9B. a2•a3=a6C. ﹣22=﹣2D.-=110、在Rt△ABC中,∠C=900,则下列式子成立的是()A.sinA=sinBB.sinA=cosBC.tanA=tanBD.cosA=tanB11、已知Rt△ABC中,∠C=90º,那么cosA表示()的值A. B. C. D.12、国家近年来实施了新一轮农村电网改造升级工程,解决了农村供电“最后1公里”问题,电力公司在改造时把某一输电线铁塔建在了一个坡度为1:0.75的山坡CD的平台BC上(如图),测得∠AED=52°,BC=5米,CD=35米,DE =19米,则铁塔AB的高度约为(参考数据:sin52°≈0.79,tan52°≈1.28)()A.28米B.29.6米C.36.6米D.57.6米13、对于sin60°有下列说法:①sin60°是一个无理数;②sin60°>sin50°;③sin60°=6sin10°。
锐角的三角比测试题及答案

锐角的三角比测试题及答案(三)一、填空题(每小题2分,共40分)1、Rt△ABC中,∠C=90°,BC=5,AB=13,则sinA=__________。
2、Rt△ABC中,∠C=90°,sinA=,则cosA=__________。
3、Rt△ABC中,∠C=90°,sinA=,则tgB=__________。
4、若α为锐角,cosα=,则α=__________度。
5、计算sin230°十cos230°=__________。
6、Rt△ABC中,∠C=90°,BC=2,sinA=,则AC=__________。
7、如图:厂房屋顶的人字架为等腰三角形,若跨度AB=12米,∠A=30°,则中柱CD等于__________米。
8、Rt△ABC中,∠C=90°,c=8,a=6,则最小角正切值为__________。
9、计算=__________。
10、Rt△ABC中,∠C=90°,3a=b,那么cosA的值为__________。
11、等腰三角形腰长、底边长分别为6和8,则底角正弦值为__________。
12、已知:α为锐角,tgα一1=0,则α为__________度。
13、等腰直角三角形ABC中,∠C=90°,AC=BC,则cosA·tgA=__________。
14、等腰三角形底边长为2,底边上高为,则它的顶角为__________度。
15、如图,等腰梯形的铁路路基高6米,斜面与地平面倾斜角30°,路基上底宽10米,则下底宽为__________米。
16、△ABC中,∠C∶∠B∶∠A=1∶2∶3,则三边之比a∶b∶c=__________。
17、等腰三角形顶角为12O°,底边上高为4cm,则此三角形面积为__________。
18、等腰△ABC中,AB=AC=5,BC=6,则sinA=__________。
锐角的三角比(考题猜想,易错必刷40题7种题型专项训练)(学生版) 2025学年九年级数学上学期期中

专题02锐角的三角比(考题猜想,易错必刷40题7种题型专项训练)锐角三角函数的定义 特殊角的三角函数值解直角三角形 解直角三角形的应用解直角三角形的应用-坡度坡角问题 有理数大小比较解直角三角形的应用-方向角问题一.锐角三角函数的定义(共2小题)1.(2024•闵行区)在Rt ABC ∆中,90C ∠=︒,3AB =,2AC =,那么cos A 的值是()A .13B .23C .D 2.(2023•松江区一模)已知Rt ABC ∆中,90C ∠=︒,2AC =,3BC =,那么下列结论正确的是()A .2tan 3A =B .2cot 3A =C .2sin 3A =D .2cos 3A =二.特殊角的三角函数值(共7小题)3.(2023秋•宝山区期中)tan 45︒的值等于()A .2B .1CD 4.(2024•崇明区)计算:2sin 60cos 45cos303tan 30︒︒-+︒︒.5.(2023秋•金山区期末)计算:2sin 451cot 60cos30tan 45︒-+︒⋅︒︒.6.(2023秋•闵行区期中)计算:cos 45tan 60cot 451sin 30︒-︒-︒-︒.7.(2023秋•黄浦区校级期中)计算:2tan 452cos 45sin 60cot 30︒-+︒︒⋅︒.8.(2023秋•长宁区校级期中)计算:tan 452|1sin 60|cot 302cos 45︒-︒+︒-︒.9.(2023秋•浦东新区校级期中)计算:sin 45cos30sin 30(cos 45sin 60)32cos 60︒+︒-︒︒-︒-︒三.解直角三角形(共4小题)10.(2023秋•长宁区校级月考)已知点(1,2)A 在平面直角坐标系xOy 中,射线OA 与x 轴正半轴的夹角为α,那么cos α的值为.11.(2022秋•嘉定区校级期末)已知在DEF ∆中,12DE DF ==,10EF =,那么cos E =.12.(2022秋•金山区校级期末)如图,在ABC ∆中,1sin 4B =,1tan 2C =,4AB =,则AC 的长为.13.(2022秋•奉贤区期中)已知:如图,在ABC ∆中,15AB AC ==,4tan 3A =.求:(1)ABC S ∆;(2)B ∠的余弦值.四.解直角三角形的应用(共4小题)14.(2022•徐汇区模拟)激光电视的光源是激光,它运用反射成像原理,屏幕不通电无辐射,降低了对消费者眼睛的伤害.根据THX 观影标准,当观影水平视场角“θ”的度数处于33︒到40︒之间时(如图1),双眼肌肉处于放松状态,是最佳的感官体验的观影位.(1)小丽家决定要买一个激光电视,她家客厅的观影距离(人坐在沙发上眼睛到屏幕的距离)为3.5米,小佳家要选择电视屏幕宽(图2中的BC 的长)在什么范围内的激光电视就能享受黄金观看体验?(结果精确到0.1m ,参考数据:sin 330.54︒≈,tan 330.65︒≈,sin 400.64︒≈,tan 400.84︒≈,sin16.50.28︒≈,tan16.50.30︒≈,sin 200.34︒≈,tan 200.36)︒≈(2)由于技术革新和成本降低,激光电视的价格逐渐下降,某电器商行经营的某款激光电视今年每台销售价比去年降低4000元,在销售量相同的情况下,今年销售额在去年销售总额100万元的基础上减少20%,今年这款激光电视每台的售价是多少元?15.(2022•长宁区模拟)冬至是一年中太阳光照射最少的日子,如果此时楼房最低层能采到阳光,一年四季整座楼均能受到阳光的照射,所以冬至是选房买房时确定阳光照射的最好时机.某居民小区有一朝向为正南方向的居民楼.该居民楼的一楼是高6米的小区超市,超市以上是居民住房,在该楼前面20米处要盖一栋高25米的新楼.已知上海地区冬至正午的阳光与水平线夹角为29︒(参考数据:sin290.48︒≈;︒≈cos290.87︒≈;tan290.55)(1)冬至中午时,超市以上的居民住房采光是否有影响,为什么?(2)若要使得超市全部采光不受影响,两楼应至少相距多少米?(结果保留整数)16.(2023秋•静安区期中)图1是一种折叠式晾衣架.晾衣时,该晾衣架左右晾衣臂张开后示意图如图2所示,两支脚10OA OB==分米,晾衣臂支架6HG FE==∠=︒,晾衣臂10CODOC OD==分米,展开角60分米,且4≈==分米. 1.73)HO FO(1)当90∠=︒时,求点A离地面的距离AM约为多少分米;(结果精确到0.1)AOC(2)当OB从水平状态旋转到OB'(在CO延长线上)时,点E绕点F随之旋转至OB'上的点E'处,求''-为多少分米.B E BE17.(2022•崇明区二模)为解决群众“健身去哪儿”问题,某区2021年新建、改建90个市民益智健身苑点,图1是某益智健身苑点中的“侧摆器”.锻炼方法:面对器械,双手紧握扶手,双脚站立于踏板上,腰部发力带动下肢做左右摆式运动.(1)如图2是侧摆器的抽象图,已知摆臂OA的长度为80厘米,在侧摆运动过程中,点A为踏板中心在侧摆运动过程中的最低点位置,点B为踏板中心在侧摆运动过程中的最高点位置,25BOA∠=︒,求踏板中心点在最高位置与最低位置时的高度差.(精确到0.1厘米)(sin250.423︒≈,cos250.906︒≈,tan250.466)︒≈(2)小杰在侧摆器上进行锻炼,原计划消耗400大卡的能量,由于小杰加快了运动频率,每小时能量消耗比原计划增加了100大卡,结果比原计划提早12分钟完成任务,求小杰原计划完成锻炼需多少小时?五.解直角三角形的应用-坡度坡角问题(共5小题)18.(2024•南岗区校级一模)如图,先锋村准备在坡角为α的山坡上栽树,要求相邻两树之间的水平距离为5米,那么这两树在坡面上的距离AB为()A.5cosαB.5cosαC.5sinαD.5sinα19.(2022秋•黄浦区期末)如图,某幢楼的楼梯每一级台阶的高度为20厘米,宽度为30厘米,那么斜面AB 的坡度为.20.(2023秋•杨浦区期末)小华沿着坡度1:3i =的斜坡向上行走了米,那么他距离地面的垂直高度上升了米.21.(2023•普陀区二模)如图,斜坡AB 的坡度1i =AH 的情况下将坡度变缓,调整后的斜坡AC 的坡度21:2.4i =,已知斜坡10AB =米,那么斜坡AC =米.22.(2022秋•静安区校级期末)某大型购物中心为方便顾客地铁换乘,准备在底层至1B 层之间安装电梯,截面图如图所示,底层与1B 层平行,层高AD 为9米,A 、B 间的距离为6米,20ACD ∠=︒.(1)请问身高1.9米的人在竖直站立的情况下搭乘电梯,在B 处会不会碰到头?请说明理由.(2)若采取中段平台设计(如图虚线所示).已知平台//EF DC ,且AE 段和FC 段的坡度1:2i =,求平台EF 的长度.【参考数据:sin 200.34︒≈,cos 200.94︒≈,tan 200.36︒≈】六.解直角三角形的应用-仰角俯角问题(共16小题)23.(2023秋•嘉定区期末)一架飞机在离地面6000米的上空测得某一建筑物底部的俯角为30︒,此时这架飞机与这一建筑物底部之间的距离是()A.6000米B.12000米C.60003米D.120003米24.(2023•崇明区一模)飞机离水平地面的高度为3千米,在飞机上测得该水平地面上的目标A点的俯角为α,那么此时飞机与目标A点的距离为千米.(用α的式子表示)25.(2024•徐汇区校级三模)社团活动课上,九年级学习小组测量学校旗杆的高度.如图,他们在B处测得旗杆顶部A的仰角为60︒,6BC m=,则旗杆AC的高度为m.26.(2023秋•松江区期末)如图,A处有一垂直于地面的标杆AM,热气球沿着与AM的夹角为15︒的方向升空,到达B处,这时在A处的正东方向200米的C处测得B的仰角为30(AM︒、B、C在同一平面内).求≈A、B之间的距离.(结果精确到1米,2 1.414)27.(2022秋•闵行区期末)2022年11月12日10时03分,搭载天舟五号货运飞船的长征七号遥六运载火箭,在海南文昌航天发射场成功发射.天舟五号货运飞船重约13.6吨,长度10.6BD=米,货物仓的直径可达3.35米,是世界现役货物运输能力最大、在轨支持能力最全面的货运飞船,堪称“在职最强快递小哥”.已知飞船发射塔垂直于地面,某人在地面A处测得飞船底部D处的仰角45︒,顶部B处的仰角为53︒,求此时观测点A到发射塔CD的水平距离(结果精确到0.1米).(参考数据:sin530.80︒≈,︒≈,cos530.60︒≈tan53 1.33)28.(2022秋•闵行区期中)如图,在电线杆上的C处引拉线CE和CF固定电线杆.在离电线杆6米的B处安置测角仪(点B、E、D在同一直线上),在点A处测得电线杆上C处的仰角为30︒.已知测角仪的高AB 3米,拉线CE的长为6米,求测角仪底端(点)B与拉线固定点(E)之间的距离.29.(2024•上海模拟)如图,某处有一座塔AB,塔的正前方有一平台DE,平台的高5DG=米,斜坡CD 的坡度5:12i=,点A,C,G,F在同一条水平直线上.某数学兴趣小组为测量该塔的高度,在斜坡C处测得塔顶部B的仰角为54.5︒,在斜坡D处测得塔顶部B的仰角为26.7︒,求塔高AB.(精确到0.1米)(参考数据:tan54.5 1.40︒≈︒≈,sin26.70.45︒≈,cos26.70.89)︒≈,tan26.70.50︒≈,sin54.50.81︒≈,cos54.50.5830.(2024•崇明区)如图,某校九年级兴趣小组在学习了解直角三角形知识后,开展了测量山坡上某棵大树高度的活动.已知小山的斜坡BM的坡度1:3BN,i=,在坡面D处有一棵树AD(假设树AD垂直水平线)在坡底B处测得树梢A的仰角为45︒,沿坡面BM方向前行30米到达C处,测得树梢A的仰角ACQ∠为60︒.(点B、C、D在一直线上)(1)求A、C两点的距离;(2)求树AD的高度(结果精确到0.1米).(参考数据:3 1.732)≈31.(2023秋•黄浦区期末)在世纪公园的小山坡上有一棵松树,初三(3)班的雏鹰小队带着工具对这棵松树进行测量,并试图利用所学的数学知识与方法推算出这棵松树的高度.他们选好位置架设测角仪先测出了这棵松树的根部与顶端的仰角,并绘制了如下示意图:测角仪为MN ,树根部为B 、树顶端为A ,其中1.5MN m =,视线MB 的仰角为α(已知1tan )6α=,视线MA 的仰角为β(已知3tan )4β=.(1)测得这两个数据后,小明说:“我可以算出这棵松树的高度了.”小聪接着说:“不对吧,只知道这两个角度,这个示意图显然是可以进行放大或缩小的,高度一定是确定不了的.如果还能测出测角仪到松树的垂直距离,即图示中NH 的长度,就可以了.”设NH a =,请你用含有a 的代数式表示松树()AB 的高度.(2)小明又反问道:“虽然我们带了尺,是一把刻度精确到1分米,长为2米的直尺,但也没有办法量出NH 的长度,我们总不能把坡给挖平了吧?”请你想一个测量办法,利用现有的工具,测量出有关数据(数据可以用字母常数表示),并用含有这些字母常数的表达式表示出松树()AB 的高度.32.(2023秋•长宁区期末)小明为测量河对岸大楼的高度,利用量角器和铅锤自制了一个简易测角仪,如图1所示.测量方法:如图2,人眼在P点观察所测物体最高点C,量角器零刻度线上A、B两点均在视线PC上,将铅锤悬挂在量角器的中心点O.当铅锤静止时,测得视线PC与铅垂线OD所夹的角为α,且此时的仰角为β.实践操作:如图3,小明利用上述工具测量河对岸垂直于水平地面的大楼EF的高度.他先站在水平地面的点H处,视线为GE,此时测角仪上视线与铅垂线的夹角为60︒;然后他向前走10米靠近大楼站在水平地面的点R处,视线为QE,此时测角仪上视线与铅垂线的夹角为45︒.问题解决:(1)请用含α的代数式表示仰角β;(2)如果GH、QR、EF在同一平面内,小明的眼睛到水平地面的距离为1.6米,求大楼EF的高度.(结果保留根号)33.(2023秋•静安区期末)如图,某建筑物AB 高为200米,某人乘热气球来到距地面400米的C 处(即CE 长为400米).此时测得建筑物顶部A 的俯角为α,当乘坐的热气球垂直上升到达D 处后,再次测得建筑物顶部A 的俯角为β.(tan 1.25,tan 1.75)αβ==(1)请在图中标出俯角α、β,并用计算器求α、β的大小:α≈,β≈;(精确到“1”)(2)求热气球上升的垂直高度(即CD 的长).34.(2023秋•嘉定区期末)如图,小山的顶部是一块平地,在这块平地上有一座古塔CD .小山斜坡AB 的坡度为1:2.4i =,坡长AB 为39米,在小山的坡底A 处测得该塔的塔顶C 的仰角为45︒,在坡顶B 处测得该塔的塔顶C 的仰角为74︒.(1)求坡顶B 到地面AH 的距离BH 的长;(2)求古塔CD 的高度(结果精确到1米).(参考数据:sin 740.96︒≈,cos 740.28︒≈,tan 74 3.49)︒≈35.(2022秋•嘉定区期末)《海岛算经》是中国古代测量术的代表作,原名《重差》.这本著作建立起了从直接测量向间接测量的桥梁.直至近代,重差测量法仍有借鉴意义.如图2,为测量海岛上一座山峰AH 的高度,直立两根高2米的标杆BC 和DE ,两杆间距BD 相距6米,D 、B 、H 三点共线.从点B 处退行到点F ,观察山顶A ,发现A 、C 、F 三点共线,且仰角为45︒;从点D 处退行到点G ,观察山顶A ,发现A 、E 、G 三点共线,且仰角为30︒.(点F 、G 都在直线HB 上)(1)求FG 的长(结果保留根号);(2)山峰高度AH 的长(结果精确到0.1米).(参考数据:2 1.41≈,3 1.73)≈36.(2023秋•青浦区期末)北淀浦河上的浦仓路桥是一座融合江南水乡文化气息的现代空间钢结构人行廊桥.某校九年级数学兴趣小组开展了测量“浦仓路桥顶部到水面的距离”的实践活动,他们的操作方法如下:如图,在河的一侧选取B 、C 两点,在B 处测得浦仓路桥顶部点A 的仰角为22︒,再往浦仓路桥桥顶所在的方向前进17米至C 处,在C 处测得点A 的仰角为37︒,在D 处测得地面BD 到水面EF 的距离DE 为1.2米(点B 、C 、D 在一条直线上,//BD EF ,DE EF ⊥,)AF EF ⊥,求浦仓路桥顶部A 到水面的距离AF .(精确到0.1米)(参考数据:sin 220.37︒≈,cos 220.93︒≈,tan 220.40︒≈,sin 370.60︒≈,cos 370.80︒≈,tan 370.75)︒≈37.(2023•长宁区二模)为了测量某建筑物的高度BE ,从与建筑物底端B 在同一水平线的点A 出发,沿着坡比为1:2.4i =的斜坡行走一段路程至坡顶D 处,此时测得建筑物顶端E 的仰角为30︒,再从D 处沿水平方向继续行走100米后至点C 处,此时测得建筑物顶端E 的仰角为60︒,建筑物底端B 的俯角为45︒,如图,已知点A 、B 、C 、D 、E 在同一平面内,求建筑物BE 的高度与AD 的长.(参考数据:3 1.732)≈38.(2023秋•静安区校级期中)如图1所示是一种太阳能路灯,它由灯杆和灯管支架两部分构成.如图2,AB 是灯杆,CD 是灯管支架,灯管支架CD 与灯杆间的夹角60BDC ∠=︒.综合实践小组的同学想知道灯管支架CD 的长度,他们在地面的点E 处测得灯管支架底部D 的仰角为60︒,在点F 处测得灯管支架顶部C 的仰角为30︒,测得3AE m =,8(EF m A =,E ,F 在同一条直线上).根据以上数据,解答下列问题:(1)求灯管支架底部距地面高度AD 的长(结果保留根号);(2)求灯管支架CD 的长度(结果精确到0.1m ,参考数据:3 1.73)≈.七.解直角三角形的应用-方向角问题(共2小题)39.(2023秋•青浦区校级月考)如图,某湖心岛上有一亭子A,在亭子A的正东方向上的湖边有一棵树B,在这个湖心岛的湖边C处测得亭子A在北偏西45︒方向上,测得树B在北偏东36︒方向上,又测得B、C之间的距离等于200米,求A、B之间的距离(结果精确到1米).(参考数据:2 1.414︒≈≈,sin360.588︒≈,cot36 1.376)︒≈,cos360.809︒≈,tan360.72740.(2022秋•浦东新区校级期中)如图,湖心岛上有一凉亭B,在凉亭B的正东湖边有一棵大树A,在湖边的C处测得B在北偏西45︒方向上,测得A在北偏东30︒方向上,又测得A、C之间的距离为100米,则A、B之间的距离是米(结果保留根号形式).。
沪教版九年级第一学期25.2求锐角的三角比的值同步练习题

数学九年级上 第二十五章 锐角三角比25.2 求锐角的三角比的值(1)一、选择题1.在Rt △ABC 中,AD 是斜边BC 上的高,如果BC=a, B β∠=,那么AD 等于 ( )A. 2sin a β⋅B. 2cos a β⋅ C. sin cos a ββ D. sin tan a ββ 2. 已知Rt △ABC 中,∠C =90°,AC =2,BC =3,那么下列各式中,正确的是( )A .2tan 3B = B .2cot 3B =C .2sin 3B =D .2cos 3B = 3. 已知点P (tan45°,-cos30°),则P 点关于原点的对称点P ’的坐标是 ( )A. )21,1(-- B. )21,1(- C. )23,1(-- D. )23,1(- 4、已知:是锐角,23sin =α,则等于 ( )A. 30°B. 45°C. 60°D. 90°5、在Rt △ABC 中,∠C =90°,∠A =30°,那么B A sin sin +等于 ( )A. 1B. 231+C. 221+D. 43 6、已知:c b a ,,是△ABC 的三边,并且关于的方程02)(222=++++c ab x b a x 有两个相等实根,则△ABC 形状是 ( )A. 锐角三角形B. 直角三角形C. 钝角三角形D. 不能确定。
二、填空题7、已知:α为锐角,1tan =α,则α=____________度。
8、已知:α为锐角,3sin 2=α,则____________。
9、若3)20tan(3=︒-α,则锐角α=____________。
10、α为锐角,且关于x 的方程0sin 222=+-αx x 有两个相等的实数根,则α为____________度。
11. 在△ABC 中,若tan 12A B +=,则C ∠= . 12. 计算: 2sin 604cos303tan 60-+= .13.在△ABC 中,如果AB=那么C ∠的度数为 .14.设α为锐角,则cos 1α-= .15.在△ABC 中, A ∠,B ∠均为锐角,且2tan (2sin 0B A +=,则△ABC 的形状是 .16. 在正方形ABCD 中,∠ABD 的余弦值等于________.17. 已知 α是锐角,,且sin cos αα=,则α= 度。
锐角三角比

锐角三角比:知识点一:锐角三角比的定义: 一、 锐角三角比定义:在Rt △ABC 中,∠C=900, ∠A 、∠B 、∠C 的对边分别为a 、b 、c , 则∠A 的正弦可表示为:sinA= , ∠A 的余弦可表示为cosA=∠A 的正切:tanA= ,它们弦称为∠A 的锐角三角比 2、取值范围 <sinA< cosA< tanA> 】 例1.如图所示,在Rt △ABC 中,∠C =90°.第1题图①斜边)(sin =A =______, 斜边)(sin =B =______;②斜边)(cos =A =______,斜边)(cos =B =______;③的邻边A A ∠=)(tan =______,)(tan 的对边B B ∠==______.例2. 锐角三角函数求值:在Rt △ABC 中,∠C =90°,若a =9,b =12,则c =______,sin A =______,cos A =______,tan A =______, sin B =______,cos B =______,tan B =______.例3.已知:如图,Rt △TNM 中,∠TMN =90°,MR ⊥TN 于R 点,TN =4,MN =3.求:sin ∠TMR 、cos ∠TMR 、tan ∠TMR .例题:类型一:直角三角形求值1.已知Rt △ABC 中,,12,43tan ,90==︒=∠BC A C 求AC 、AB 和cos B .2.如图,⊙O 的半径OA =16cm ,OC ⊥AB 于C 点,⋅=∠43sin AOC 求AB 及OC 的长.3.已知:⊙O 中,OC ⊥AB 于C 点,AB =16cm ,⋅=∠53sin AOC(1)求⊙O 的半径OA 的长及弦心距OC ; (2)求cos ∠AOC 及tan ∠AOC .4. 已知A ∠是锐角,178sin =A ,求A cos ,A tan 的值针对训练:1.在Rt △ABC 中,∠ C =90°,若BC =1,AB =5,则tan A 的值为A .55 B .255 C .12D .2 2.在△ABC 中,∠C =90°,sin A=53,那么tan A 的值等于( ).A .35B . 45C . 34D . 43类型二. 利用角度转化求值:1.已知:如图,Rt △ABC 中,∠C =90°.D 是AC 边上一点,DE ⊥AB 于E 点.DE ∶AE =1∶2.求:sin B 、cos B 、tan B .2.如图,直径为10的⊙A经过点(05)C,和点(00)O,,与x轴的正半轴交于点D,B是y轴右侧圆弧上一点,则cos∠OBC的值为()A.12B.32C.35D.453.如图,角α的顶点为O,它的一边在x轴的正半轴上,另一边OA上有一点P(3,4),则sinα=.4.如图,菱形ABCD的边长为10cm,DE⊥AB,3sin5A=,则这个菱形的面积= cm2.5.如图,O⊙是ABC△的外接圆,AD是O⊙的直径,若O⊙的半径为32,2AC=,则sin B的值是()A.23B.32C.34D.436. 如图6,沿AE折叠矩形纸片ABCD,使点D落在BC边的点F处.已知8AB=,10BC=,AB=8,则tan EFC∠的值为 ( )A.34B.43C.35D.457. 如图7,在等腰直角三角形ABC∆中,90C∠=︒,6AC=,D为AC上一点,若1tan5DBA∠=,则AD 的长为( )A.2 B.2 C.1 D.228. 如图8,在Rt△ABC中,∠C=90°,AC=8,∠A的平分线AD=3316求∠B的度数及边BC、AB的长.DCBAOyx第8题图A DECBFDABC类型三. 化斜三角形为直角三角形例1 如图,在△ABC中,∠A=30°,∠B=45°,AC=23,求AB的长.例2.已知:如图,在△ABC中,∠BAC=120°,AB=10,AC=5.求:sin∠ABC的值.针对训练1.如图,在Rt△ABC中,∠BAC=90°,点D在BC边上,且△ABD是等边三角形.若AB=2,求△ABC的周长.(结果保留根号)2.已知:如图,△ABC中,AB=9,BC=6,△ABC的面积等于9,求sin B.3. ABC中,∠A=60°,AB=6 cm,AC=4 cm,则△ABC的面积是A.23 cm 2 .43 cm 2 C.63 cm 2 D.12 cm 2类型四:利用网格构造直角三角形例1 如图所示,△ABC 的顶点是正方形网格的格点,则sinA 的值为( ) A .12 B .55 C .1010D .255对应练习:1.如图,△ABC 的顶点都在方格纸的格点上,则sin A =_______.2.如图,A 、B 、C 三点在正方形网络线的交点处,若将ABC ∆绕着点A 逆时针旋转得到''B AC ∆,则'tan B 的值为 A.41 B. 31 C.21D. 13.正方形网格中,AOB ∠如图放置,则tan AOB ∠的值是( )A .5 5 B. 2 5 5 C.12D. 2 特殊角的三角函数值当 时,正弦和正切值随着角度的增大而 余弦值随着角度的增大而 例1.求下列各式的值. 1).计算:︒-︒+︒60tan 45sin 230cos 2. 2)计算:︒-︒+︒30cos 245sin60tan 2.锐角α 30° 45° 60° sin α cos α tan αCBAABO3)计算:3-1+(2π-1)0-33tan30°-tan45°4.计算:30tan 2345sin 60cos 221⎪⎪⎭⎫ ⎝⎛︒-︒+︒+.5.计算: tan 45sin 301cos 60︒+︒-︒;家庭作业:1.已知:如图,在菱形ABCD 中,DE ⊥AB 于E ,BE =16cm ,⋅=1312sin A 求此菱形的周长.2.已知:如图,Rt △ABC 中,∠C =90°,3==BC AC ,作∠DAC =30°,AD 交CB 于D 点,求:(1)∠BAD ;(2)sin ∠BAD 、cos ∠BAD 和tan ∠BAD .3. 已知:如图△ABC 中,D 为BC 中点,且∠BAD =90°,31tan =∠B ,求:sin ∠CAD 、cos ∠CAD 、tan ∠CAD .4. 如图,在Rt △ABC 中,∠C=90°,53sin =B ,点D 在BC 边上,DC= AC = 6,求tan ∠BAD 的值.5.如图,△ABC 中,∠A=30°,3tan 2B =,43AC =.求AB 的长.签字确认 学员 教师 班主任DCBAACB。
锐角三角比经典练习题附带答案(2套)

练习一一、选择题(6×4/=24/)1.在ABC Rt ∆中,∠090=C ,2=AB ,1=AC ,则B sin 的值是( )(A )21; (B )22; (C )23; (D )2.2.如果ABC Rt ∆中各边的长度都扩大到原来的2倍,那么锐角∠A 的三角比的值( ) (A ) 都扩大到原来的2倍; (B ) 都缩小到原来的一半; (C ) 没有变化; (D ) 不能确定.3.等腰三角形的底边长10cm ,周长36cm ,则底角的余弦值为……( )(A )125; (B )512; (C )135; (D )1312. 4.在ABC Rt ∆中,∠︒=90C ,31sin =B ,则A tan 的值为……( )(A )113; (B )33; (C )22; (D )31010.5.在Rt △ABC 中,∠C=90°,∠A 的对边为a ,已知∠A 和边a ,求边c ,则下列关系中正确的是…………………………………………………………………( ) (A )A a c sin =; (B )A a c sin =; (C )a=b ⋅tan A ; (D )Aac cos =. 6.在△ABC 中,若22cos =A ,3tan =B,则这个三角形一定是……( )(A )锐角三角形; (B ) 直角三角形; (C )钝角三角形; (C )等腰三角形.二、填空题(12×4/ =48/)7.在Rt ΔABC 中,∠︒=90C , 若AB =5,BC =3,,则A sin = ,=A cos ,=A tan ,8.在ABC Rt ∆中,∠︒=90C ,∠A =30°,AC =3,则BC = .9. 在△ABC 中,∠C =90°,52sin =A ,则sinB 的值是________. 10.有一个坡角,坡度3:1=i ,则坡角=α 11.在ABC Rt ∆中,∠090=C ,21cos =A ,则∠=B . 12.已知P (2,3),OP 与x 轴所夹锐角为α,则tan α=_______ . 13.如图,∆ABC 中,∠ACB =90︒,CD 是斜边上的高,若AC =8,AB =10,18题图tan ∠BCD =___________.14.如图,若人在离塔BC 塔底B 的200米远的A 地测得塔顶B 的仰角是30︒,则塔高BC =___ ___(米精确到1.0,732.13≈)A15.如图,一个小球由地面沿着坡度i=1:3的坡面向上前进了10m ,此时小球距离地面的高度为_________m .16.一个楼梯的面与地面所成的坡角是30︒,两层楼之间的层高3米,若在楼梯上铺地毯,地毯的长度是 米(3=1.732,精确到0.1米).17.如图,已知正方形ABCD 的边长为1.如果将对角线BD 绕着点B 旋转后,点D 落在CB 的延长线上的D '点处,联结D A ',那么cot ∠BAD /__________.18.矩形一边长为5,两对角线夹角为60°,则对角线长为 .三、解答题(3×10/ =30/)19.计算: ︒-︒︒+︒60tan 45cot 30cot 45tan .20.已知直线443y x =+交x 轴于A ,交y 轴于B ,求∠ABO 的正弦值.21.如图,将正方形ABCD 的边BC 延长到点E ,使CE=AC ,AE 与CD 相交于点F . 求∠E 的余切值._ C_14题图B15题图13题图_D ' A D C B 17题图D A四、解答题(4×12/=48/)22.某人要测河对岸的树高,在河边A 处测得树顶仰角是60︒,然后沿与河垂直的方向后退10米到B处,再测仰角是30︒,求河对岸的树高。
锐角三角比经典练习题附带答案

练习一一、选择题(6×4/=24/)1.在ABC Rt ∆中,∠090=C ,2=AB ,1=AC ,则B sin 的值是( )(A )21; (B )22; (C )23; (D )2.2.如果ABC Rt ∆中各边的长度都扩大到原来的2倍,那么锐角∠A 的三角比的值( ) (A ) 都扩大到原来的2倍; (B ) 都缩小到原来的一半; (C ) 没有变化; (D ) 不能确定.3.等腰三角形的底边长10cm ,周长36cm ,则底角的余弦值为……( )(A )125; (B)512; (C)135; (D)1312. 4.在ABC Rt ∆中,∠︒=90C ,31sin =B ,则A tan 的值为……( )(A )113; (B )33; (C )22; (D )31010.5.在Rt △ABC 中,∠C=90°,∠A 的对边为a ,已知∠A 和边a ,求边c ,则下列关系中正确的是…………………………………………………………………( ) (A )A a c sin =; (B )A a c sin =; (C )a=b tan A ; (D )Aac cos =. 6.在△ABC 中,若22cos =A ,3tan =B,则这个三角形一定是……( )(A )锐角三角形; (B ) 直角三角形; (C )钝角三角形; (C )等腰三角形.二、填空题(12×4/ =48/)7.在Rt ΔABC 中,∠︒=90C , 若AB =5,BC =3,,则A sin = ,=A cos ,=A tan ,8.在ABC Rt ∆中,∠︒=90C ,∠A =30°,AC =3,则BC = .9. 在△ABC 中,∠C =90°,52sin =A ,则sinB 的值是________. 10.有一个坡角,坡度3:1=i ,则坡角=α 11.在ABC Rt ∆中,∠090=C ,21cos =A ,则∠=B . 12.已知P (2,3),OP 与x 轴所夹锐角为,则tan=_______ .13.如图,ABC 中,ACB =90,CD 是斜边上的高,若AC =8,AB =10,6m 15m 18题图tan BCD =___________.14.如图,若人在离塔BC 塔底B 的200米远的A 地测得塔顶B 的仰角是30,则塔高BC =___ ___(米精确到1.0,732.13≈)15.i=1:3的坡面向上前进了10m ,此时小球距离地面的高度为_________m.16.一个楼梯的面与地面所成的坡角是30,两层楼之间的层高3米,若在楼梯上铺地毯,地毯的长度是 米(3=,精确到0.1米).17.如图,已知正方形ABCD 的边长为1.如果将对角线BD 绕着点B 旋转后,点D 落在CB 的延长线上的D '点处,联结D A ',那么cot BAD /__________.18.矩形一边长为5,两对角线夹角为60°,则对角线长为 .三、解答题(3×10/ =30/)19.计算: ︒-︒︒+︒60tan 45cot 30cot 45tan .20.已知直线443y x =+交x 轴于A ,交y 轴于B ,求ABO 的正弦值.21.如图,将正方形ABCD 的边BC 延长到点E ,使CE=AC ,AE 与CD 相交于点F . 求∠E 的余切值._C _A 14题图B15题图13题图_D ' A D C B 17题图EFBCD A21题图四、解答题(4×12/=48/)22.某人要测河对岸的树高,在河边A 处测得树顶仰角是60,然后沿与河垂直的方向后退10米到B处,再测仰角是30,求河对岸的树高。
锐角三角比经典练习题附带问题详解(2套)

练习一一、选择题(6×4/=24/)1.在ABC Rt ∆中,∠090=C ,2=AB ,1=AC ,则B sin 的值是( )(A )21; (B )22; (C )23; (D )2.2.如果ABC Rt ∆中各边的长度都扩大到原来的2倍,那么锐角∠A 的三角比的值( ) (A ) 都扩大到原来的2倍; (B ) 都缩小到原来的一半; (C ) 没有变化; (D ) 不能确定.3.等腰三角形的底边长10cm ,周长36cm ,则底角的余弦值为……( )(A )125; (B)512; (C)135; (D)1312. 4.在ABC Rt ∆中,∠︒=90C ,31sin =B ,则A tan 的值为……( )(A )113; (B )33; (C )22; (D )31010.5.在Rt △ABC 中,∠C=90°,∠A 的对边为a ,已知∠A 和边a ,求边c ,则下列关系中正确的是…………………………………………………………………( ) (A )A a c sin =; (B )A a c sin =; (C )a=b ⋅tan A ; (D )Aac cos =. 6.在△ABC 中,若22cos =A ,3tan =B,则这个三角形一定是……( )(A )锐角三角形; (B ) 直角三角形; (C )钝角三角形; (C )等腰三角形.二、填空题(12×4/ =48/)7.在Rt ΔABC 中,∠︒=90C , 若AB =5,BC =3,,则A sin = ,=A cos ,=A tan ,8.在ABC Rt ∆中,∠︒=90C ,∠A =30°,AC =3,则BC = .9. 在△ABC 中,∠C =90°,52sin =A ,则sinB 的值是________. 10.有一个坡角,坡度3:1=i ,则坡角=α 11.在ABC Rt ∆中,∠090=C ,21cos =A ,则∠=B . 12.已知P (2,3),OP 与x 轴所夹锐角为α,则tan α=_______ .13.如图,∆ABC 中,∠ACB =90︒,CD 是斜边上的高,若AC =8,AB =10,tan ∠BCD =___________.18题图14.如图,若人在离塔BC 塔底B 的200米远的A 地测得塔顶B 的仰角是30︒,则塔高BC =___ ___(米精确到1.0,732.13≈)15.如图,一个小球由地面沿着坡度i=1:3的坡面向上前进了10m ,此时小球距离地面的高度为_________m.16.一个楼梯的面与地面所成的坡角是30︒,两层楼之间的层高3米,若在楼梯上铺地毯,地毯的长度是 米(3=1.732,精确到0.1米).17.如图,已知正方形ABCD 的边长为1.如果将对角线BD 绕着点B 旋转后,点D 落在CB 的延长线上的D '点处,联结D A ',那么cot ∠BAD /__________.18.矩形一边长为5,两对角线夹角为60°,则对角线长为 .三、解答题(3×10/ =30/)19.计算: ︒-︒︒+︒60tan 45cot 30cot 45tan .20.已知直线443y x =+交x 轴于A ,交y 轴于B ,求∠ABO 的正弦值.21.如图,将正方形ABCD 的边BC 延长到点E ,使CE=AC ,AE 与CD 相交于点F . 求∠E 的余切值.A_ C_14题图B15题图13题图_D ' A D C B 17题图FD A四、解答题(4×12/=48/)22.某人要测河对岸的树高,在河边A 处测得树顶仰角是60︒,然后沿与河垂直的方向后退10米到B处,再测仰角是30︒,求河对岸的树高。
三角比的基本练习题

1 三角比的基本练习题一、填空:1、计算:3 tan 30º + cot 45º – 2 tan 45º + 2 cos 60º = _______.2、在△ABC 中,∠A = 90°,∠B = 60°,a = 8,则b = .3、在Rt △ABC 中,∠C =90°,CD ⊥AB ,垂足为D 点,若CD=3,AD=4,则cot B =4、在△ABC 中,∠C =90°,BC=2,sinA = 13,则AB= . 5、已知∠A 为锐角,且满足22=SinA ,则∠A= .6、若菱形ABCD 的对角线AC 长为10,面积为30,则tan 2B = 7、若正方形ABCD 的对角线BD=62,点E 是CD 上一点,CE=23,则 ∠ BED =8、在 △ ABC 中,∠C =90°,a ∶b = 1∶3,周长为6+23,则c= ,S △= .9、在△ABC 中,已知角A 、B 都是锐角,且满足222sin =+B A ,则△ABC 是 三角形; 10、某飞机在离地面1200米的上空测得地面控制点的俯角为60°,此时飞机与该地面控制点之间的距离 是 米.11、某山路坡面坡度 1:399i =, 沿此山路向上前进200米,升高了__________米.12、在离旗杆20米处的地方用测角仪测得旗杆顶的仰角为a ,如果测角仪高为1.5米,那么旗杆的高为__________ 米,(用含a 的三角比表示).13、如图,在△ABC 中,∠C =90°,点D 在BC 上,BD =4,AD =BC ,cos ∠ ADC =53.那么DC =________;sin B =_________. 14、在 R t △ ABC 中,∠ C = 90 0 ,BC=4,AC=3,则 tan A 2的值是 ; 15、已知:在梯形ABCD 中,AD//BC ,AB=15,CD =13,AD =8,∠B 是锐角, 54sin =B ,则BC= . 16、已知正方形ABCD 的边长为1,如果将线段BD 绕着点B 旋转后,点D 落在CB 的延长线上D ′处,连结D ′A ,那么tan ∠BAD ’ 的值为_______________.二、单项选择题:1、在 △ABC 中,90C ∠=︒,如果tan A = 512,那么sin B 的值等于( ) (A )513 ; (B )1213 ; (C )512 ; (D )1252、某等腰三角形的底边长为20,面积为33100,则这个三角形的底角为( )(A )60° (B )30°或120°; (C )30°; (D )以上都不对3、直角坐标系中,点A (3,4),则线段OA 与x 轴正半轴的夹角的正弦值为( )(A )34 (B ) 43 (C )35 (D )454、如图,为测楼房BC 的高,在距楼房30米的A 处,测得楼顶的仰角为α,则楼房BC 的高( ) (A )30 tan α米; (B )30tan α 米; (C )30αsin 米; (D )αsin 30. 第13题图αB2 三、解答题:1、在△ABC 中,,60 =∠B AB=8,BC=10,求△ABC 的面积.2、如图,在Rt △ABC 中,∠C =90°,点D 是BC 上一点,tan ∠ADC=0.75,AD=15,BD=9。
第03讲 锐角三角比(3种题型)(原卷版)
第03讲锐角三角比(3种题型)1锐角的三角比定义:一个锐角的正切、余切、正弦、余弦统称为这个锐角的三角比. 正切:把直角三角形中一个锐角的对边与邻边的比叫这个锐角的正切.BPtanA=余切:把直角三角形中一个锐角的邻边与对边的比叫这个锐角的余切.即COtA=Y?鬻;N 加勺对边正弦:把直角三角形中一个锐角的对边与斜边的比叫这个锐角的正弦.即SinA=斜边2.性质①当锐角增大时,这个锐角的正切与正弦值都增大,这个锐角的余切与余弦值都减小; ②若ZA+ZB=90°,贝IJtan A=cotB;sin A=cos B ;③tanA∙cotA=1.3.特殊角的三角比4.锐角的三角比一.锐角三角函数的定义(共6小题)1. (2023春•浦东新区校级期中)在RtZkABC 中,ZC=90o ,AB=5,AC=4.下列四个选项,正确的是()A.tanB=-B.cotB=AC.sinB=AD.cosB=A4355余弦:把直角三角形中一个锐角的邻边与斜边的比叫这个锐角的余弦.即COSA=乙船勺邻边NAfi 勺对边 '已知锐角,求三角比;已知锐角的三角比,求锐角.2. (2023秋•浦东新区校级期末)已知在Rt4A5C 中,NC=90°,AB=5,AC=4,那么下列式子中正确 的是( ) λ.λ4A.SinA=-5B.cosA=-⅛-5C.tanA=A D. 5CotA=A53.(2023秋•崇明区期末)在RtZkABC 中, ZC=90o , AB=2,AC=I,那么CosB 的值是(A.√ΣB.近c.1D. 22224. (2023秋•青浦区期末)在4A5C 中,ZC=90o ,如果tan∕A=2,AC=3,那么5C=5. (2023秋•宝山区期末)在RtZkABC 中,ZC=90o ,如果空那么SinA 的值是.BC46. (2023秋•浦东新区期末)如果在平面直角坐标系Xoy 中,点尸的坐标为(3,4),射线。
锐角三角比练习题及答案

锐角三角比练习题及答案
1. 已知一个锐角三角形的两个锐角分别为30度和60度,求第三个角的度数。
答案:第三个角的度数为90度。
2. 一个直角三角形的两条直角边分别为3和4,求斜边的长度。
答案:斜边的长度为5。
3. 已知一个锐角三角形的两个角的正弦值分别为0.5和0.866,求这两个角的度数。
答案:这两个角的度数分别为30度和60度。
4. 一个直角三角形的斜边长为10,一条直角边长为6,求另一条直角边的长度。
答案:另一条直角边的长度为8。
5. 已知一个锐角三角形的余弦值为0.6,求对应角的度数。
答案:对应角的度数为53度。
6. 一个直角三角形的两条直角边长分别为5和12,求斜边的长度。
答案:斜边的长度为13。
7. 已知一个锐角三角形的正切值为1.732,求对应角的度数。
答案:对应角的度数为45度。
8. 一个直角三角形的斜边长为17,一条直角边长为8,求另一条直角边的长度。
答案:另一条直角边的长度为15。
9. 已知一个锐角三角形的正弦值为0.3,求对应角的度数。
答案:对应角的度数为19.47度。
10. 一个直角三角形的斜边长为20,一条直角边长为10,求另一条直角边的长度。
答案:另一条直角边的长度为10√3。
锐角三角比的计算与应用
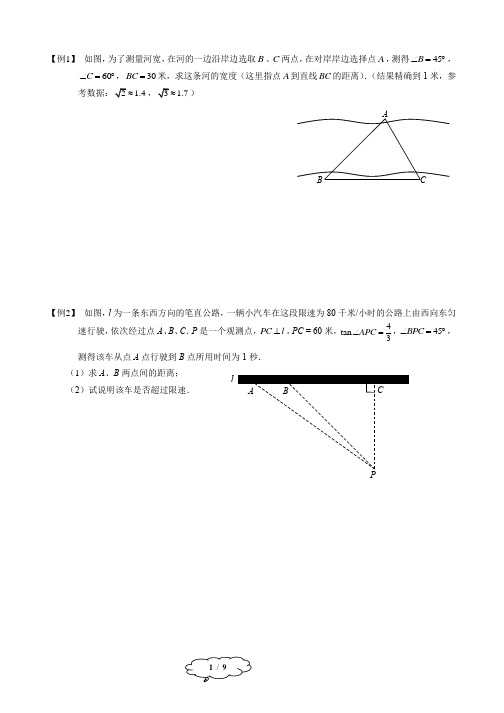
ABCPl【例1】 如图,为了测量河宽,在河的一边沿岸边选取B 、C 两点,在对岸岸边选择点A ,测得45B ∠=︒,60C ∠=︒,30BC =米,求这条河的宽度(这里指点A 到直线BC 的距离).(结果精确到1米,参考数据:2 1.4≈,3 1.7≈)【例2】 如图,l 为一条东西方向的笔直公路,一辆小汽车在这段限速为80千米/小时的公路上由西向东匀速行驶,依次经过点A 、B 、C .P 是一个观测点,PC l ⊥,PC = 60米,4tan 3APC ∠=,45BPC ∠=︒,测得该车从点A 点行驶到B 点所用时间为1秒. (1)求A 、B 两点间的距离; (2)试说明该车是否超过限速.ABCABCDE O左右M A B CDEFG HPQ1.2 m0.8 m 0.8 m【例3】 如图,一条细绳系着一个小球在平面内摆动.已知细绳从悬挂点O 到球心的长度为50厘米,小球在A 、B 两个位置时达到最高点,且最高点高度相同(不计空气阻力),在C 点位置时达到最低点.达到左侧最高点时与最低点时细绳相应所成的角度为37°,细绳在右侧达到最高点时与一个水平放置的挡板DE 所成的角度为30°. (sin370.6︒≈,cos370.8︒≈,tan370.75︒≈)(1)求小球达到最高点位置与最低点位置时的高度差. (2)求OD 这段细绳的长度.【例4】 靠校园一侧围墙的体育场看台侧面,如图阴影部分所示,看台的二级台阶高度相等,宽度相同,现要用钢管做护栏扶手ACG 及三根与水平底面PQ 垂直的护栏支架CD 、EF 、GH (底端D 、F 、H 分别在每级台阶的中点处),已知看台高为1.2米,护栏支架0.8CD GH ==米,66.5DCG ∠=︒. (参考数据:sin66.50.92︒≈,cos66.50.40︒≈,tan66.5 2.30︒≈) (1)点D 与点H 的高度差是 米;(2)试求制作护栏扶手和支架的钢管总长度l ,即AC CG CD EF GH ++++的长度. (结果精确到0.1米)ABC海平面【例5】 在某反潜演习中,我军舰A 测得潜艇C 的俯角为30°,位于军舰A 正上方2000米的反潜直升机B 测得潜艇C 的俯角为68°,试根据以上数据求出潜艇C 离开海平面的下潜深度.(结果保留整数,参考数据:sin680.9︒≈,cos680.4︒≈,tan68 2.5︒≈,3 1.7≈).【例6】 如图,已知楼AB 高36米,从楼顶A 处测得旗杆顶C 的俯角为60°,又从该楼离地面6米的一窗口E 处测得旗杆顶C 的仰角为45°,求该旗杆CD 的高.(结果保留根号)A DBCEFABPQ ABCDE【例7】 如图,从地面上的点A 看一山坡上的电线杆PQ ,测得杆顶端点P 的仰角是26.6°,向前走30米到达B 点,测得杆顶端点P 和杆底端点Q 的仰角分别是45°和33.7°.求该电线杆PQ 的高度(结果精确到1米).(备用数据:sin26.60.45︒=,cos26.60.89︒=,tan26.60.50︒=,cot 26.6 2.00︒=,sin33.70.55︒=,cos33.70.83︒=,tan33.70.67︒=,cot33.7 1.50︒=)【例8】 如图,小明想测量河对岸的一幢高楼AB 的高度,小明在河边C 处测得楼顶A 的仰角是60°.距C 处60米的E 处有幢楼房,小明从该楼房中距地面20米的D 处测得楼顶A 的仰角是30°(点B 、C 、E 在同一直线上,且AB 、DE 均与地面BE 垂直).求楼AB 的高度.DAB CEFGA BC【例9】如图,某高楼顶部有一信号发射塔,在矩形建筑物ABCD的A、C两点处测得该塔顶端F的仰角分别为α和β,矩形建筑物宽度AD = 20m,高度DC = 33m.(1)试用α和β的三角比表示线段CG的长;(2)如果48α=︒,65β=︒,请求出信号发射塔顶端到地面的高度FG的值(结果精确到1 m).(参考数据:sin480.7︒≈,cos480.7︒≈,tan48 1.1︒≈,sin650.9︒≈,cos650.4︒≈,tan65 2.1︒≈)【例10】如图,已知某船向正东方向航行,在点A处测得某岛C在其北偏东60°方向上,前进8海里处到达点B处,测得岛C在其北偏东30°方向上.已知岛C周围6海里内有一暗礁,问:如果该船继续向东航行,有无触礁危险?请说明你的理由.ABCH 【例11】 如图,某人在C 处看到远处有一凉亭B ,在凉亭B 正东方向有一棵大树A ,这时此人在C 处测得B 在北偏西45°方向上,测得A 在北偏东35°方向上.又测得A 、C 之间的距离为100米,求A 、B 之间的距离.(精确到1米)(参考数据:sin350.574︒≈,cos350.819︒≈,tan350.700︒≈)【例12】 如图,某地下车库的入口处有斜坡AB ,它的坡度为1:2i =,斜坡AB 的长为65米,车库的高度为AH (AH BC ⊥),为了让行车更安全,现将斜坡的坡角改造为14︒(图中的14ACB ∠=︒). (1)求车库的高度AH ;(2)求点B 与点C 之间的距离(结果精确到1米).(参考数据:sin140.24︒=,cos140.97︒=,tan140.25︒=,cot14 4.01︒=)ABC45° 35°ABCD37°ABCD E FG【例13】 如图,高压电线杆AB 垂直地面,测得电线杆AB 的底部A 到斜坡底C 的水平距离AC 长为15.2米,落在斜坡上的电线杆的影长CD 为5.2米,在D 点处测得电线杆顶B 的仰角为37°.已知斜坡CD 的坡比为1 : 2.4,求该电线杆AB 的高.(参考数据:sin 37° = 0.6).【例14】 如图是某个大型商场的自动扶梯侧面示意图,已知自动扶梯AC 的坡度为1 : 2,AC 的长度为55米,AB 为底楼地面,CD 为二楼楼面,EF 为二楼楼顶,当然有EF // AB // CD ,E 为自动扶梯AC 的最高端C 的正上方,过C 的直线EG AB 于G ,在自动扶梯的底端A 测得E 的仰角为42°,求该商场二楼的楼高CE .【例15】为方便市民通行,某广场计划对坡角为30°,坡长为60米的斜坡AB进行改造,在斜坡中点D处挖去部分坡体(阴影表示),修建一个平行于水平线CA的平台DE和一条新的斜坡BE.(1)若修建的斜坡BE 的坡角为36°,则平台DE的长约为多少米?(2)在距离坡角A点27米远的G处是商场主楼,小明在D点测得主楼顶部H的仰角为30°,那么主楼GH高约为多少米?(结果取整数,参考数据:sin36° = 0.6,cos 36° = 0.8,tan 36° = 0.7,3=1.7)BCD EFHM 30°30°A BCABC DABCDEN M 【习题1】 如图,A 、B 两地之间有一座山,汽车原来从A 地到B 地须经C 地沿折线A -C -B 行驶,现开通隧道后,汽车直接沿直线AB 行驶.已知AC = 120千米,30A ∠=︒,135B ∠=︒,则隧道开通后,汽车从A 地到B 地比原来少走多少千米?(结果保留根号)【习题2】 如图,热气球在离地面800米的A 处,在A 处测得一大楼楼顶C 的俯角是30︒,热气球沿着水平方向向此大楼飞行400米后到达B 处,从B 处再次测得此大楼楼顶C 的俯角是45︒,求该大楼CD 的高度.2 1.41≈3 1.73≈)【习题3】 如图,小明在广场上的C 处用测角仪正面测量一座楼房墙上的广告屏幕AB 的长度,测得屏幕下端B 处的仰角为30°,然后他正对大楼方向前进10米到达D 处,又测得该屏幕上端A 处的仰角为45°,已知该楼高18.7米,测角仪MC 、ND 的高度为1.7米.求广告屏幕AB 的长.。
锐角三角比的应用

锐角三角比的应用【例题精讲】1、如图,甲、乙两船同时从港口O 出发,其中甲船沿北偏西30︒方向航行,乙船沿南偏西70︒方向航行,已知两船的航行速度相同,如果1小时后甲、乙两船分别到达点A 、B 处,那么点B 位于点A 的( )A .南偏西40︒;B .南偏西30︒;C . 南偏西20︒;D . 南偏西10︒.2、如图,甲乙两栋楼之间的距离CD 等于45米,现在要测乙楼的高BC ,(BC ⊥CD ),所以观察点A 在甲楼一窗口处,AD ∥BC .从A 处测得乙楼顶端B 的仰角为45o ,底部C 的俯角为30o ,求乙楼的高度(取3 1.7=,结果精确到1米).3、为了体现“城市让生活更美好”的理念,市政府对许多基础设施进行修缮。
如图,某地下车库的入口处有斜坡长为55米,其坡度为1:2i =,为增加行车安全,现将斜坡的坡角改造为15.(参考数据:sin150.259≈,966.015cos = ,tan150.268≈,cot15 3.732≈) (1)求车库的高度;(2)求斜坡新起点与原起点的距离(结果精确到0.1米).BC CD A B4、如图,A ,B ,C 三点在同一平面内,从山脚缆车站A 测得山顶C 的仰角为45°,测得另一缆车站B 的仰角为30°,AB 间缆绳长500米(自然弯曲忽略不计). (3 1.73≈,精确到1米)(1)求缆车站B 与缆车站A 间的垂直距离;(2)乘缆车达缆车站B ,从缆车站B 测得山顶C 的仰角为60°,求山顶C 与缆车站A 间的垂直距离.5、如图,小杰发现垂直地面的旗杆AB 的影子落在地面和斜坡上,影长分别为BC 和CD ,经测量得10BC =米,10CD =米,斜坡CD 的坡度为1:3i =,且此时测得垂直于地面的1米长标杆在地面上影长为2米.求旗杆AB 的长度.(答案保留整数,其中10 3.2≈)M 水平线B AC C A BD6、据新华社12月13日电,参加湄公河联合巡逻执法的中国巡逻船顺利返航.已知在巡逻过程中,某一天上午,我巡逻船正在由西向东匀速行驶,10:00巡逻船在A 处发现北偏东53.1°方向,相距10海里的C 处有一个不明物体正在向正东方向移动,10:15巡逻船在B 处又测得该物体位于北偏东18.4°方向的D 处,若巡逻船的速度是每小时36海里. (1)试在图8中画出点D 的大概位置,并求不明物体移动的速度;(2)假设该不明物体移动的方向和速度保持不变,巡逻船航行的方向的速度也不变,试问什么时候该物体与我巡逻船之间的距离最近?【备用数据:53.10.8sin =,53.10.6cos =,53.10.75cot =,18.40.32sin =,18.40.95cos =,18.43cot =】【课堂练习】1、小李在楼上点A 处看到楼下点B 处的小明的俯角是35度,那么点B 处的小明看点A 处的小李的仰角是 度.2、如图,在高出海平面100米的悬崖顶A 处,观测海平面上一艘小船B , 并测得它的俯角为45°,则船与观测者之间的距离AB = 米.3、直升飞机在离水平地面600米的上空A 处测得地面目标点B 的俯角为60︒,此时A 处与目标点B 之间的距离是 米.4、如果一段斜坡的垂直高度为8米,水平宽度为10米,那么这段斜坡的坡度比i = .东北BAC5、某山路的路面坡度为1:45,若沿此山路向上前进90米,则升高了 米.6、从灯塔A 处观察到船B 在它的北偏东35°方向上,那么从船B 观察灯塔A 的方向是 .7、某滑雪运动员沿着坡比为1:3的斜坡滑行了200米,则他身体下降的高度为 米.8、水坝的横截面是梯形ABCD (如图1),上底4=AD 米,坝高3==DN AM 米,斜坡AB 的坡比3:11=i ,斜坡DC 的坡比1:12=i . (1)求坝底BC 的长(结果保留根号);(2)为了增强水坝的防洪能力,在原来的水坝上增加高度(如图2),使得水坝的上底2=EF 米,求水坝增加的高度(精确到1.0米,参考数据73.13≈).9、已知:如图,斜坡AP 的坡度为1∶2.4,坡长AP 为26米,在坡顶A 处的同一水平面上有一座古塔BC ,在斜坡底P 处测得该塔的塔顶B 的仰角为45°,在坡顶A 处测得该塔的塔顶B 的仰角为76°.求:(1)坡顶A 到地面PQ 的距离;(2)古塔BC 的高度(结果精确到1米).(参考数据:sin 76°≈0.97,cos 76°≈0.24,tan 76°≈4.01)ABCDM NABC DM NEF锐角三角比的应用 【例题精讲】例1、如图,公路MN 和公路PQ 在点P 处交汇,且30QPN ∠=︒,点A 处有一所中学,AP=160米,假设拖拉机行驶时,周围100米以内会受到噪声的影响,那么拖拉机在公路MN 上沿PN 方向行驶时学校是否受影响?请说明理由;如果受影响,已知拖拉机的速度为18千米/时,那么学校受影响的时间为多少秒?例2、一艘补给船在点A 处接到命令,要求它向正在航行的军舰运送物资,已知军舰在补给船的西北方向40海里的点B 处,正以每小时20海里的速度向南偏东15度的方向航行,如果补给船立即沿正西方向航行,恰好能在点C 处与军舰相遇,求补给船行驶的路程和时间(结果保留根号)例3、如图:A 城气象台测得台风中心在A 城正东方300千米的洋面上,以每小时710千米的速度向北偏西060的BF 方向移动,距台风中心200千米的范围内是受台风影响的区域。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
锐角三角比双基训练*1.在RtΔΑBC中,∠C=900,BC=2,sinΑ=,则ΑB= .【1】*2.已知α为锐角,且cosα=25,则sinα= ,tgα= ,ctgα= .【2】**3.在RtΔΑBC中,∠C=900,α=2,则α= ,b= ,c= .【2】**4.在P是直线y=512x在第一象限上一点,若∠Pox=β,则cosβ= ,ctgβ= .【2】**5.在直角坐标平面内有一点P(6,y),OP与x轴正方向所夹锐角为α,sinα=45,则y的值是;OP长是 .【2】**6.已知M(2,x)是直角坐标平面内一点,且锐角∠Mox=α,ctgα=3,则点M的纵坐标为 .【2】**7.(1)sin180=cos ;(2)tg21.30=ctg ;(3)cos21012′=sin ;(4)ctg11021′31″=tg .【2】**8.比较大小:【3】(1)sin200 sin700;(2)sin350 cos350;(3)tg180 ctg710;(4)sin720 tg620**9.tg10·tg20·tg30·…·tg890= .【2】**10.sinα210+sin220+…+sin2880+sin2890= .【2】**11.已知sinα+cosα=43,则sinα·cosα= .【1】**12.若α是锐角,且tg2α=3,则sinα·cosα= .【1】**13.如果6sin2cos22sin cosa aa a-=+,那么tgα= .【2】**14.直线上有点Α(-1,-2)、B(3,4),则此直线与x轴所夹锐角的正弦值为 .【3】**15.若ΔΑBC中,∠C=900,则tgB=().【1】(Α)ABBC(B)ACBC(C)ACAB(D)BCAC**16.在ΔΑBC中,∠C=900,CD是ΑB边上的高,则CD:CB等于().【2】(Α)sinΑ(B)cosΑ(C)sinB (D)cosB**17.在RtΔΑBCk , ∠Α=900,α、b、c分别是∠Α、∠B、∠C的对边,则下列结论中正确的是().【2】(Α)b=α·sinB (B)b=c·cosB (C)b=c·tgB (D)c=α·ctgB**18.当450<∠Α<∠B<900时,下列各式不正确的是().【2】(Α)sinΑ>sinB (B)tgΑ>tgB (C)cosΑ<cosB (D)ctgΑ>ctgB**19.在ΔΑBC中,∠C=900,CD是斜边ΑB上的高,sinΑ等于().【2】(Α)ADCD(B)BDBC(C)CDAC(D)ADAC**20.在ΔΑBC 中,如果2A Btg=1,那么ΔΑBC 的形状是( ).【2】 (A ) 锐角三角形 (B )钝角三角形 (C )直角三角形 (D )等腰三角形**21.如果x 为锐角,那么sinx+cosx 的值是( ).【2】(Α)大于1 (B )小于1 (C )等于1 (D )不能确定**22.已知sin θ+sin 2θ=1,则cos 2θ+cos 4θ的值是( ).【2】(Α)1 (B )2 (C (D**23.当450<α<900时,下列各式正确的是( ).【2】(Α)tg α>cos α>sin α (B )sin α>cos α>tg α (C )tg α>sin α>cos α (D )cos α>sin α>tg α**24.已知P(sin300,tg450),则P 关于原点对称的点的坐标是( ).【2】(Α)(12,-1) (B )(-12,-1) (C )(-2,-1) (D )(2,1)**25.在ΔΑBC 中,若|tg Α-1|+(cosB-2)2=0,则ΔΑBC 是( ).【2】 (Α)等腰三角形 (B )等边三角形 (C )等腰直角三角形 (D )钝角三角形**26.已知sin α+cos α=m,sin α·cos α=n,则m 、n 的关系是( ).【2】(Α)m=n (B )m=2n+1 (C )m2=2n+1 (D )m2=1-2n**27.如图9-6,两条宽度都为1的纸条交叉重叠放在一起,且它们夹角为α,则其重叠部分面积为( ).p.134【3】(Α)1sin a(B )1cos a (C )sin α (D )1**28.当α为锐角时,sinα和tgα的大小关系为().【2】(Α)sinα>tgα(B)siα<tgα(C)sinα≤tgα(D)由α的大小决定**29.计算下列各式的值:【5】(1)tg300+sin450-cos600;(2)2cos300+5tg600-2sin300;(3)0000 cos604530245tgctg ctg--;(4)0000 0006045sin5060 sin60cos30cos40tg tgctg--++.**30.计算:【4】(1)0000002sin45cos45 45360sin30cos30tg ctg-+-;(2)203603cos301ctg-;(3)0000 sin6045 60245ctgtg tg--.**31.计算:【6】(1)tg2300+2sin600·cos450+tg450-ctg600-cos2300;(2)(1+sin450-cos300)(1-sin450-cos300);(3)(cos450-sin600)(sin450+cos300);(4)tg100·tg200·tg300·tg400·tg500·tg600·tg700·tg800.纵向应用 **1.计算:【4】(1(2001|3045|2ctg tg -.**2.计算:【4】(1)2020000sin 23sin 67301872ctg tg tg ++ ;(2.**3.化简下列各式:【8】(1(2)tg440·tg450·tg460-cos2260-cos2640;(3)tg(900-Α)÷ctgΑ (Α为锐角)(4)|sinα+cosα|-|sinα-cosα|(α为锐角)**4.化简下列各式:【8】(1)1-sin2630-cos2630;(2)tg2530·ctg2530;(3)(cos aa为锐角);(4a为锐角). ***5.θ为锐角时,化简下列各式:【8】(1;(2(3)||ctg ctg θθ-(4)1|sin |2θ-.***6.化简下列各式:【6】(1(2)(1+tg 2α)·cos 2α;(3)tg(300-α)·tg(600+α).***7.已知tg α=2且α为锐角,求2sin 5cos 4sin cos a aa a+-的值.【2】***8.已知ctg αα为锐角,求(2sin α+cos α)÷(2sin α-cos α)的值.【3】 ***9.已知3sin 2cos 22sin cos A AA A+=-,求tg Α.【3】***10.已知sin(x+450)=sin300·ctg300,求x 的值.【2】***11.已知a =α2-6α-2的值.【5】***12.若方程22sin 0x A +=有两个相等的实数根,求锐角Α的度数.【2】***13.在三角函数中,常用sin()sin cos cos sin αβαβαβ+=+计算某些三角函数值,试计算0sin 75的值.【3】***14.sin α是方程23720x x -+=的一个根,求(1)sin α的值;(2)tg α的值.【3】***15.已知锐角α的正弦和正切值分别是方程21529120x x -+=的一个根,求角α的正弦和正切的值.【3】***16.已知在锐角∆ΑBC 中,cos m B n=其中m 是方程260x x +-=的根,n 是方程2280x x --=的根,求角B 的度数.【5】***17.试判断方程2212cos (1)sin 0x x x θθ+-+-=的根的情况(θ为锐角).【5】***18.已知方程2450x x m -+=的两根是直角三角形的两锐角的正弦,求m 的值.【5】***19.已知α的锐角,且2,sin cos tg ctg αααα+=+求的值.【5】横向拓展***1.已知θ是大于045是锐角,且15θθsin -cos =,求(1)sin cos θθ的值;(2)tg θ的值;(3)33sin cos θθ-的值.【10】***2.已知2232cos tg a a+=8(00090α ),求sin α的值.【5】***3.已知7sin cos ,5tg ctg ααθθ+=+求的值.【5】***4.已知0012sin cos (045)25a a α=,求sin α和cos α的值.【8】***5.已知sin α、cos α是方程20x px q ++=的两个根,求证:2120q p +-=.【6】****6.已知sin ,sin ,tg a tg b θθθθθ+=-=为锐角,当α≥b 时,求证:22a b -=.【8】****7.已知22268sin sin 1,2cos cos cos cos a a a a a a +=+++求的值.【8】****8.已知222cos cos sin cos sin sin ,sin sin sin A x C B x C A B C ==++ 且求的值.【6】****9.试比较①004848;tg ctg +②0sin 48cos 48+;③0048cos48tg +;④0048sin 48ctg +,这四个数值的大小.【12】****10.已知4sin 2cos 2sin 1y cisa a a a a =+--且为锐角.求当y 的值为非负时,角α的取值范围.【10】****11.已知函数2(cos )(4sin )6y x x θθ=-+,对于任意实数x 都有0y ,且θ是三角形的一个内角,求θ的取值范围.【10】锐角三角比计算练习题11 / 11答案双基训练1213 125 5.8 10 6.23± 7.(1)720 (2)68.70 (3)68048′ (4)78038′29″ 8.(1)< (2)< (3)< (4)< 9.1 10.441211.71815.B 16.B 、C 17.A 、C 18.A 、B 、C 19.B 、C 20.C 21.A 22.A 23.C 24.B 25.A 、C 26.C 27.A 28.B 29.(1)36(2)622(4)0 30.(1)(2)5 (3)1231.(1)71223+-(2)54-14(4)1 纵向应用1.(1)(2)0 (3)1 (4)当00<a ≤450时,原式=2sina ;当450<a<900时,原式=2cos α 4.(1)0 (2)1 (3)1 (4)2tga 5.(1)00<θ≤450时,原式=1-tg θ;450<θ<900时,原式=tg θ-1 (3)00<θ≤300时,原式300<θ<900时,原式=2ctg θ (4)00<θ≤300时,原式=12-sin θ;300<θ<900时,原式=sin θ-12 6.(1)cos400-sin400 (2)1 (3)1 7.978.3+2 9.4 10.150 11.-5 12.45013.1315.sina=35,tga=43 16.600 17.∆=0有两个相等实根 18.98横向拓展1.(1)1225 (2)43 (3)371252.23.25124.34sin ,cos 55a a ==5.提示:sin cos a a p +=-,22sin cos ,sin cos 1a a q a a =+=6.提示:先求出a+b,a-b ,相乘得a 2-b 2=4tg ·sin,再证=4tg θ·sin θ 7.2 8.2 9.tg480+ctg480>tg480+cos480> ctg480+sin480>sin480+cos480 10.00<a<600. 提示:y=2(sina+1)·(2cosa-1) 11.00<θ<600.提示:cos θ>0且Δ<0。
