第6章 定位导航误差
定位误差的分析与计算

定位误差的分析与计算一、定位误差的概念和原因定位误差是指定位系统测量结果与真实位置之间的差异或偏差。
在现代生活中,定位系统广泛应用于导航系统、无人驾驶、无人飞行器等领域,而定位误差对于系统的准确性和可靠性至关重要。
1.信号传播误差:这是由于信号在传播过程中受到大气中的影响,如电离层、大气湿度等所产生的误差。
这种误差对于GPS系统尤为明显,导致多径效应、钟差误差等。
2.接收机误差:接收机的硬件和软件系统可能存在不同程度的误差。
硬件方面,接收机的时钟精度、天线阻抗匹配等问题都可能导致定位误差。
软件方面,接收机的算法、数据处理等也可能引入误差。
3.观测误差:观测误差是指由于测量设备的精度或不完善性所导致的误差。
例如,测量设备的精度限制了对信号强度、TOA(Time of Arrival)等参数的准确测量。
4.环境因素:环境因素也是定位误差产生的原因之一、比如,建筑物、树木、走廊等物体会对信号传播产生阻碍和衍射,从而影响接收机的测量结果。
5.多径效应:多径效应是指信号传播过程中,信号除了直射到达接收机外,还经历了反射,导致信号的多个传播路径同时到达接收机。
多径效应会产生明显的信号干扰和测量误差。
二、定位误差的计算方法1.位置误差计算:位置误差是指实际测量位置与真实位置之间的距离差异。
一种常见的计算方法是通过比较GPS测量点与参考点之间的差异来计算位置误差。
通过收集多个测量点的数据,可以使用最小二乘法进行曲线拟合,从而计算出测量点与真实位置之间的距离差异。
2.时间误差计算:时间误差是指实际测量时间与真实时间之间的差异。
在GPS系统中,时间误差主要由于卫星钟的钟差所引起。
通过GPS接收机接收到的卫星信号的时间戳和GPS接收机内部的时间戳之间的差异,可以计算出时间误差。
4.误差修正算法:为了减小定位误差,可以使用一些误差修正算法来对测量结果进行修正。
一种常见的方法是差分GPS技术,通过使用两个或多个接收机接收同一卫星信号,对测量结果进行差分处理,从而减小定位误差。
卫星导航系统的定位误差分析方法

卫星导航系统的定位误差分析方法导航定位是现代科技中的一项重要技术,卫星导航系统是其中最常用和最准确的一种方法。
然而,由于各种因素的影响,导航定位结果不可避免地会存在一定的误差。
因此,对卫星导航系统的定位误差进行准确的分析和评估,对于了解其性能和改进算法具有重要意义。
卫星导航系统的定位误差来源于多个方面,主要包括卫星、接收机、大气层、地球自转等因素。
针对不同的误差来源,有不同的分析方法和修正技术。
首先,卫星导航系统的定位误差源于卫星的位置不确定性。
卫星的位置误差是导致定位误差的主要因素之一。
因此,在定位误差分析中,需要考虑卫星轨道的误差、钟差的误差以及卫星运动引起的各项误差。
针对这些误差,各个导航系统会采用不同的修正算法,如差分定位、精密星历、卫星轨道的插值等。
这些算法可以有效地降低卫星位置误差,从而提高导航定位的准确性。
其次,接收机本身的误差也会对导航定位结果产生影响。
接收机的硬件设计和信号处理算法的不同,可能导致接收机定位误差的差异。
为了准确评估接收机的定位误差,需要进行接收机性能测试和精度分析。
这可以通过与参考点的比较测试、信号质量分析、多路径误差补偿等方法来实现。
通过对接收机的性能进行评估,可以进一步明确接收机的误差来源,并采取相应的措施进行修正。
此外,大气层的影响也是导航定位误差的一个重要来源。
大气层会对无线电波信号的传播速度和路径产生影响,从而引入定位误差。
针对这一问题,可以通过多普勒频率的变化、电离层延迟等效应进行修正。
此外,大气层中的水汽含量、温度和空气密度等因素也会对导航定位结果产生影响。
因此,在定位误差分析中,需要考虑大气层的变化和模型,以便更准确地估计定位误差。
最后,地球自转也会对卫星导航系统的定位误差产生影响。
地球的自转会不断改变接收机所处的观测点的位置,从而导致起伏、切线偏差等误差。
为了准确分析定位误差,需要考虑地球自转对导航系统的影响,并进行相应的修正。
通常,通过使用地球模型、对卫星轨道和速度进行预测,可以对定位误差进行有效地补偿。
卫星导航定位系统中误差分析与控制

卫星导航定位系统中误差分析与控制卫星导航定位系统是我们日常生活中使用频率较高的一种定位技术,被广泛应用于车载导航、船舶航行、空中导航等领域。
但是由于各种因素的影响,卫星导航定位系统的定位精度可能会受到一定误差的影响。
本文将对卫星导航定位系统中的误差进行分析,并提供一些控制误差的方法。
一、卫星导航定位系统中的误差1.环境误差太阳活动、大气状况等自然环境因素都会对卫星导航定位系统造成一定的干扰。
太阳活动导致的电离层扰动,大气层中的对流层差异等都会对定位精度造成一定的影响。
2.多路径误差指卫星导航信号在传输过程中,因为反射、折射等多种因素的影响,导致信号到达接收设备的时间与实际信号到达时间不一致,从而影响定位精度。
3.接收机误差接收机的性能不同、制造、校准水平的差异都会导致定位精度上存在误差。
例如,接收机的时钟稳定性、多路径抑制能力等都是影响定位精度的重要因素。
4.卫星误差由于卫星运行的轨道可能会受到地球引力、大气拖力等因素的影响,造成卫星的位置偏差,从而影响定位精度。
二、误差的控制方法1.差分定位差分定位是一种有效的误差控制方法。
它通过同时接收信号的两个接收站,对比两个站点接收到的卫星信号差异,然后将两个站点之间的差异加入位置求解中,以消除误差。
2.概率误差控制在卫星导航定位系统中,由于各种误差因素的影响,定位误差一定程度上具有随机性。
因此,概率误差控制可以通过多次定位测量,得到位置分布的误差范围和信度范围等信息,从而有效控制误差。
3.接收机校准接收机本身的性能差异会导致定位精度的差异,因此接收机的校准非常重要。
常见的校准方法包括时钟校准、接收机信号校准等,可以有效降低接收机对定位精度的影响。
4.多路径抑制技术多路径误差是卫星导航定位系统中最常见的误差之一,因此多路径抑制技术是非常重要的。
常见的多路径抑制技术包括基于信号组合的抑制方法、空间抑制技术等,能够有效控制多路径误差,提高定位精度。
总之,卫星导航定位系统中的误差是定位精度的主要影响因素之一。
第6章GPS测量的误差来源及减弱措施

误差影响定位精度10-30 m接收机天线相位中心的偏移和变化消除或消弱各种误差影响的方法①•模型改正法–原理:利用模型计算出误差影响的大小,直接对观测值进行修正–适用情况:对误差的特性、机制及产生原因有较深刻了解,能建立理论或经验公式–所针对的误差源•相对论效应•电离层延迟•对流层延迟•卫星钟差–限制:有些误差难以模型化改正后的观测值=原始观测值+模型改正•求差法–原理:通过观测值间一定方式的相互求差,消去或消弱求差观测值中所包含的相同或相似的误差影响–适用情况:误差具有较强的空间、时间或其它类型的相关性。
–所针对的误差源•电离层延迟•对流层延迟•卫星轨道误差•…–限制:空间相关性将随着测站间距离的增加而减弱消除或消弱各种误差影响的方法②消除或消弱各种误差影响的方法③•参数法–原理:采用参数估计的方法,将系统性偏差求定出来–适用情况:几乎适用于任何的情况–限制:不能同时将所有影响均作为参数来估计消除或消弱各种误差影响的方法④•回避法–原理:选择合适的观测地点,避开易产生误差的环境;采用特殊的观测方法;采用特殊的硬件设备,消除或减弱误差的影响–适用情况:对误差产生的条件及原因有所了解;具有特殊的设备。
–所针对的误差源•电磁波干扰•多路径效应–限制:无法完全避免误差的影响,具有一定的盲目性6.1 GPS测量误差分类及对距离测量的影响与信号传播有关的误差与卫星有关的误差与接收机有关的误差其它误差•对流层折射•电离层折射•多路径效应•星历误差•卫星钟差•相对论效应•接收机钟差•位置误差•天线相位中心的偏差及变化•各通道间的信号延迟误差•地球潮汐1.5-15m1.5-15m1.5-5m1. m6.2 与信号传播有关的误差电离层折射对流层折射多路径误差电离层中的气体分子由于大气折射效应)利用电离层改正)(2cos P T t P-π∑3ϕαDC =5ns T P =14hαn 和βn :由导航tropion N δρδρλ++- 6.2.2对流层折射▪离地面高度40km 以下的大气层,是一种非电离大气层。
定位误差的概念

定位误差的概念
定位误差是指在测量或定位过程中,实际位置与所期望位置之间的差异。
它是衡量定位准确性的一种指标,通常用于描述测量设备、导航系统或定位技术的精度。
定位误差的来源可以是多样的。
其中一些可能包括测量设备的精度限制、信号干扰、环境条件的变化以及算法或模型的假设或简化等。
这些因素都可能导致定位结果与真实位置之间产生差异。
为了理解和减少定位误差,可以采取一些技巧和方法。
一种常见的方法是使用多个独立的测量或定位系统,通过将它们的结果进行组合,来提高准确性和鲁棒性。
此外,校准和校正测量设备也是减小误差的重要步骤,可以通过与已知位置或基准进行比较来确定误差。
定位误差在许多领域中都有应用。
例如,在导航和地理信息系统中,准确的定位是关键,可以帮助人们找到目的地、规划路线、测绘地理特征等。
在无人驾驶汽车、航空航天和机器人技术等领域,准确的定位也是实现自主导航和操作的关键因素。
第6章定位导航误差

置信椭圆的长短半轴,分别表示二维位置坐标分量的标准差(如经度的σλ和 纬度的σφ)。
7
6.1.1 均方根差(2/2)
注意:许多中外文献所述“精度”多为一倍标准差(lσ),且用“距离
;
精度( (a3c)c接ur收acy误)表差示:一信个号量接观收测机值所与产其生真的值测接量近误或差一。致的程度,常 以误差( error)予以表述。GNSS系统精度为用GNSS信号所测定的 载体在航点位与载体实际点位之差。
6
6.1.1 均方根差(1/2)
一倍标准差(lσ)的概率值:68.3%; 二倍标准差(2σ)的概率值:95.5%; 三倍标准差(3σ)的概率值:99. 796。 ➢均方根差的探测概率:
2DRMS
2 DRMS
2
2
2
1/2
8
6.1.2 圆概率误差(1/2)
在导航领域,圆概率误差(CEP,circular error probable)被广泛应 用。 当概率为50%时,圆概率误差定义为:
CEP 0.59
当概率为95%时,则有:
CEP95 CEP 2.08 1.2272
GPS导航定位精度,用伪噪声码测量时分为: ➢ 标准定位服务(SPS)精度(民用精度); ➢ 精密定位服务(PPS)精度(军用精度);
15
6.1.5 GPS定位的精度(2/2)
注意:随着GPS导航定位测量模式不同,精度也随之变化。
16
内容提要
§6.1 卫星导航定位的精度、误差与偏差 §6.2 卫星导航定位的误差 §6.3 GPS卫星几何布局和精度因子
定位误差
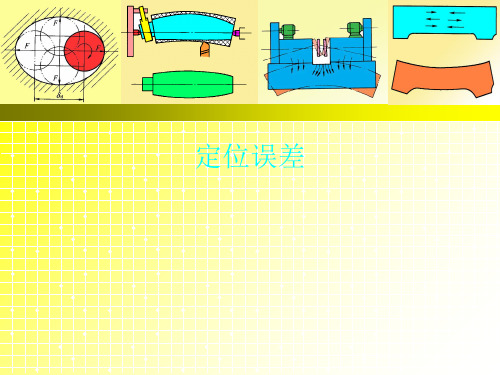
解: 定位基准与工序基准重合 ΔB=0 定位基准O的变动方向与 加工尺寸39±0.04方向间的夹 角为30°
定位误差计算实例6
例6:如下图所示,求加工尺 寸A的定位误差。 解:(1)定位基准为底面, 工序基准为圆孔中心线O ,定 位基准与工序基准不重合。 ΔΒ=0.2mm 工序基准O的变动方向与加工 尺寸的方向间夹角为45º ,则: ΔΒ=0.2×cos45º =0.1414mm (2)平面定位ΔY=0 (3)ΔD=ΔΒ=0.1414mm
16
(2)工件以圆孔定位 2)水平放置时(单边接触)
定 位 误 差 的 概 念 与 计 算
17
(2)工件以圆孔在圆柱销(心轴)上定位
定 位 误 差 的 概 念 与 计 算
D d D d m ax m i n m i n m ax O O OO OO Y 1 2 1 2 2 2
定位误差计算实例7
解: (1)对称度的工序 基准是Φ12H8的轴线,定 位基准是工件 Φ80±0.05mm的轴线, 两者不重合, ΔΒ=0.02mm
3)工件以外圆在V形块上定位
定 位 Td 误 Y 差 2 sin 2 的 概 如在加工尺寸方向上与垂直方向有一夹角β,则 念 在加工尺寸方向上的基准位移误差为 与 计 Td Y cos 算
2sin 2
V形块的对中性好,所以沿其水平方向的位移量为零。 如工件的加工尺寸方向与垂直方向相同,则在加 工尺寸方向上的基准位移误差为:
解:(1)A1的定位误差 1)工序基准是圆柱轴线,定位基准也是圆柱轴线, 两者重合,ΔB1 =0。 2)以圆柱面在的V形块上定位时, Td Y1 2 sin 2
定位误差计算实例4
卫星导航系统中的定位误差分析与纠正方法

卫星导航系统中的定位误差分析与纠正方法卫星导航系统是一种基于卫星和接收机的无线电导航系统,可为用户提供位置信息和时间信息。
目前世界上最著名的卫星导航系统是GPS系统。
卫星导航系统广泛应用于航空、航海、汽车等领域,但定位误差一直是制约卫星导航系统精度的主要因素之一。
因此,有效的定位误差分析和纠正方法对于提高卫星导航系统的精度具有重要意义。
一、定位误差的来源在实际应用中,定位误差的来源主要包括以下几个方面:1.多径效应:在卫星导航中,信号从卫星到接收机会经过大气层、地面及建筑物等障碍物的反射,形成多条路径,导致信号到达接收机时时间不同,从而影响信号的接收强度和相位,引起定位误差。
2.大气延迟:卫星信号在传播至地面接收机过程中,会和大气层中的水汽、离子层等物质发生作用,形成信号的延迟和衍射,造成定位误差。
3.时钟误差:由于卫星时钟和接收机时钟存在差异,导致信号的到达时间和时间标准存在误差,引起定位误差。
4.卫星轨道误差:卫星的轨道参数可能存在变化,导致卫星位置计算的误差,进而影响到距离计算和定位精度。
二、定位误差分析方法为了解决卫星导航系统中的定位误差问题,需要对误差源进行定位误差分析。
常用的定位误差分析方法包括以下几种:1.测量方法:通过测量不同地点的接收机接收到相同卫星的时间和位置,验证不同地点的定位误差,并对误差进行分析。
2.数据处理方法:用多条卫星信号计算一个接收机的位置,在数据处理时通过加权、差分、平均等方法消除干扰信号,提高数据质量,减小定位误差。
3.数学模型方法:通过数学建模描述误差的产生过程,并用模型对误差进行分析和预测。
三、定位误差纠正方法为了改善卫星导航系统的定位精度,需要对定位误差进行纠正,常用的纠正方法包括以下几种:1.差分方法:通过使用同时接收同一组卫星数据的两个接收机进行差分计算,除去通用误差项,提高单个接收机的定位精度。
2.观测矩阵法:利用卫星信号和接收机位置观测数据,建立观测矩阵,最小二乘法求解参数,实现对定位误差的纠正。
第6章 卫星导航系统误差分析

②测站附近不应有高层建筑物,观测时测站附近也不要
停放汽车; ③测站不宜选在山坡、山谷和盆地中。
与卫星有关的误差
与卫星有关的误差
卫星星历误差
卫星钟的钟误差
相对论效应
与卫星有关的误差
星历误差
由星历所给出的卫星位置与实际位置之差
报告位置 ( x, y , z )
卫星
实际位置 ( x, y, z )
Ws WT 1 1 f 2 f0 2 f0 ( ) 2 c c R r
其中, 3.986005 1014 m3 / s 2 若地面的地心距R近似取6378km,卫星的地心距近似取26560km,则
f 2 5.284 1010 f 0
对GPS 卫星而言,广义相对论效应的影响比狭义相对论效应的 影响要大得多,且符号相反。总的相对论效应影响:
对单点定位的影响 星历误差在接收机至卫星方向上影响测站坐标和接收 机钟改正数。与卫星的几何图形有关。 对相对定位的影响 星历误差对相对定位的影响一般采用下列公式估算:
b 基线长度 db 卫星误差引起的基误差
db ds b
卫星至测站的距离
ds 星历误差 ds 卫星星历相对误差
轨道误差对不同长度的基线影响
轨道误差 基线长度 基线误差(ppm) 基线误差(mm)
2.5m 2.5m 2.5m 2.5m
1km 10km 100km 1000km
0.1ppm 0.1ppm 0.1ppm 0.1ppm
0.1mm 1mm 10mm 100mm
0.5m 0.5m 0.5m 0.5m
考虑到GPS卫星的平均运动速度Vs=3874m/s和真空中的光速 c=299792458m/s,则
卫星导航定位系统中的误差分析与校正

卫星导航定位系统中的误差分析与校正卫星导航定位系统是一种广泛应用于航空、航海、军事、交通、测绘等领域的技术。
它利用全球定位系统(GPS)和其他卫星导航系统,通过接收多个卫星信号来确定位置、速度和时间信息。
然而,由于各种因素的影响,卫星导航定位系统在实际应用中会出现一定的误差。
因此,在实际使用卫星导航定位系统时,需要对误差进行分析和校正,以提高定位的精度和准确性。
首先,我们来分析卫星导航定位系统中可能出现的误差来源。
主要的误差来源可以分为以下几类:1.卫星误差:卫星本身的位置和时钟精度可能存在误差。
这些误差可能是由于卫星运动的不确定性、卫星时钟的不稳定性等造成的。
卫星误差的大小会直接影响到定位的准确性。
2.接收机误差:接收机的硬件和算法也可能引入误差。
例如,接收机的天线可能会受到天线阴影、多径效应等因素的影响,导致接收到的信号失真。
此外,接收机的算法也可能存在一定的误差。
3.大气误差:大气层对于卫星信号的传播会引起信号的传播速度变化和折射效应,从而产生定位误差。
大气误差的大小与天气条件、地理位置等因素有关。
4.多路径误差:多路径效应是指卫星信号在到达接收机时经过多个路径传播,导致接收到的信号中存在多个信号的叠加。
这会引入额外的误差,特别是在城市等有高楼大厦的地区。
了解了卫星导航定位系统中可能出现的误差来源,接下来我们来讨论误差的分析和校正方法。
1.数据处理与滤波:在定位系统中,经常使用最小二乘法等方法对接收到的原始数据进行处理和滤波。
可以使用多项式拟合等方法来估计卫星位置和时钟误差,进而进行误差校正。
2.差分定位:差分定位是一种常用的误差校正方法。
它通过同时接收基准站和移动站的信号,利用基准站提供的已知位置信息,对接收到的信号进行差分处理,进而校正定位误差。
3.电离层校正:电离层是大气层中带电粒子的层,对卫星信号的传播会产生一定影响。
可以使用电离层数据和模型来校正电离层引起的定位误差。
4.多路径抑制:多路径效应是导致定位误差的一个重要原因。
第六章定位误差
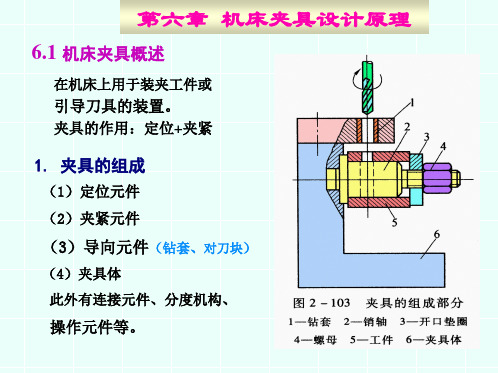
6.2.3.1 定位误差的组成(来源) 定位误差包括基准不重合误差和基准位置误差
1)基准不重合误差△jb——定位基准与工序基准不一致所引起的定
位误差。
其大小等于工序基准相对于定位基准在加工尺寸方向上的最大变动量(公差)。
一次安装加工两孔A和B,孔B在X方向定位基准C与设计基
准A不重合,基准不重合误差为联系尺寸22的公差0.2
dw jbjw jw
6.2.3.2 常见定位方法的定位误差计算 (3)工件以内孔表面定位时的定位误差
根据工件装夹时心轴放置位置的不同,可分为如下两种情况:
① 心轴垂直放置(图6.22(a))改错
6.2.3.2 常见定位方法的定位误差计算 (3)工件以内孔表面定位时的定位误差
① 心轴垂直放置(图6.22(a))
+
Td 2
1 sinα2
-
d 2
=
Td 2
1 sinα2 - 1
(2)工件以外圆柱面定位时的定位误差
工件在V形块上定位
④ 定位误差分析:
a) 定位误差Δdw 随工件误差Td 的增大而增大; b) 定位误差Δdw 随V形块夹角α 增大而减小,但稳定性变差;
c) 定位误差Δdw 与工序尺寸标注方式有关,Δdw2 >Δdw1 > Δdw3 d) 水平方向定位误差Δdw =0
总 T
△总——各种因素产生的误差总和;
T——工件被加工尺寸的公差。
6.2.3 定位误差
本章只考虑定位误差对加工精度的影响。
上式可写成:
dwT
△dw——定位误差; ω——除定位误差外,其它因素所引起的误差总和。
定位误差概念
定位误差——由于工件在夹具上(或机床上)定位不准确而
《GPS导航与应用》GPS的误差源 ppt课件

偏差 2 .1 2.0 4.0 0.5 1.0 0.5 5.1 5.1
1-sigma 误差,单位 m 随机误差 0.0 0.7 0.5 0.5 1.0 0.2 1.4 0.4 12.8 10.2
总误差 2.1 2.1 4.0 0.7 1.4 0.5 5.3 5.1
ppt课件
41
GPS测量误差的大小②
ppt课件
34
应对多路径误差的方法①
• 观测上
– 选择合适的观测地点,避开易产生多路径的环 境
易发生多路径的环境
ppt课件
35
应对多路径误差的方法②
• 硬件上
– 采用抗多路径误差的仪器设备
• 抗多路径的天线:带抑径板或抑径圈的天线,极化 天线
• 抗多路径的接收机:窄相关技术MEDLL(Multipath Estimating Delay Lock Loop)等
ppt课件
36
抗多路径效应的天线
应对多路径误差的方法③
• 数据处理上
– 加权 – 参数法 – 滤波法 – 信号分析法 – 模板法 –…
ppt课件
37
第8节 其他误差
ppt课件
38
其他误差源
• 引力延迟 • 地球自转改正 • 地球固体潮改正 • 天线相位中心偏差及变化改正 • 相位回旋
•…
ppt课件
– 对GPS信号来说,电离层是色散介质,对流层是非色散 介质
ppt课件
20
电离层延迟
ppt课件
21
电离层延迟
• 电离层延迟与下列因素有关
– 信号频率 – 信号传播途径上的总电子含量(TEC)
电离层
TEC
柱 体 底 面 积 为1 m 2
导航测量定位误差分析课件

基于模型改正的方法
坐标系转换
将导航坐标系转换为地理坐标系,消除坐标系转换误差,提高定位精度。
高程修正
考虑地球重力场模型误差,建立高程修正模型,对高程数据进行修正,提高定位精度。
06 实验与分析
数据采集与处理
01
02
03
原始数据
收集与导航测量相关的原 始数据,包括但不限于 GPS轨迹、传感器读数、 图像数据等。
仿真实验与结果分析
利用采集的数据进行仿真实验,并对实验结果进行分析。 通过对比分析实际数据和仿真结果,可以评估误差模型的 准确性和有效性。
导航测量定位误差修正与优化
05
方法研究
基于滤波的方法
卡尔曼滤波
利用系统的运动方程和观测方程,通过迭代方式求解最优估计值,适用于动态 系统的定位误差修正。
粒子滤波
详细介绍了当前导航测量技术的发展情况,包括卫星 导航系统、惯性导航系统、组合导航系统等。
定位误差分析
对各种导航测量技术的定位误差进行了深入分析,包括误差 来源、误差传播、误差建模等。
定位误差补偿
讨论了如何对导航测量技术的定位误差进行补偿, 包括硬件补偿、软件补偿、组合补偿等。
未来发展趋势
展望了导航测量技术的发展趋势,包括高精度定位、多源融合、 人工智能等。
导航测量定位误差分 析课件
目录
• 引言 • 导航测量定位技术概述 • 导航测量定位误差来源及影响分析 • 导航测量定位误差建模与仿真分析
目录
• 导航测量定位误差修正与优化方法 研究
• 实验与分析 • 结论与展望
01
引言
背景介绍
01
介绍导航测量定位技术在各种领 域(如航空、航海、陆地导航等 )的重要应用。
第6章 定位导航误差

精度( accuracy)表示一个量观测值与其真值接近或一致的程度, 常以误差( error)予以表述。GNSS系统精度为用GNSS信号所测定 的载体在航点位与载体实际点位之差。
2014-12-12 哈尔滨工业大学 电子与信息工程学院 5
6.1.1 均方根差(1/2)
一倍标准差(lσ)的概率值:68.3%; 二倍标准差(2σ)的概率值:95.5%; 三倍标准差(3σ)的概率值:99. 796。 均方根差的探测概率: 置信椭圆(confidence ellipse,二维定位); 置信椭球(confidence ellipsoid,三维定位);
在GPS卫星导航定位测量中,不仅存在测量误差(error),而 且存在偏差(bias)。 例如:GPS卫星时钟导致两个不同而相关的概念:卫星时钟偏差 和卫星时钟误差。 星钟偏差:每一颗GPS卫星时钟相对于GPS时间系统的差值, 表示为
ts a0 a1 t toc a2 t toc
• 狭义相对论
– 原理:时间膨胀。钟的频率与其运动速度有关。 – 对GPS卫星钟的影响:
若卫星在地心惯性坐标系中的运动速度为Vs,则在地面频率为f 的钟 若安置到卫星上,其频率f s 将变为: Vs 2 1 2 Vs 2 f s f [1 ( ) ] f (1 2 ) c 2c 即两者的频率差f s 为 Vs 2 f s f s f 2 f 2c 考虑到GPS 卫星的平均运动速度Vs 3874 m s 和真空中的光速c 299792458 m s ,则 f s 0.835 1010 f
卫星定位导航原理与应用
哈尔滨工业大学通信技术研究所
韩帅
1
第六章 定位导航误差
2
卫星导航-定位误差_图文

精度与衡量
估值:
残差 :
(即平均值) (即观测值与估值之差)
精度与衡量
观测成果的精度
真值的统计学公式: 真误差:
( i =1,2,…,n )
当观测值为离散抽样值时:
精度与衡量
当 N 为有限值时,则 和 为估计值。 方差
中误差、标准差、 均方根差
精度与衡量
如果真值事先不知道,则观测成果的精度为:
假设有 n 个观测值,其均值为:
均方根值( 也叫RMS )为 :
精度与衡量
极限误差
#
区间
概率
极限误差
1
(-σ,+ σ )
68.3%
σ
2
( - 2σ,+ 2 σ ) 95.5%
2σ
3
(- 3σ,+ 3 σ )
99.7%
3σ
极限误差
极限误差
极限误差
1 σ = 68.3% 2 σ = 95.5% 3 σ = 99.7%
§ 干温、湿温、气压 § 干温、相对湿度、气压 § 普通仪器:通风干湿温度表、空盒气压计 § 自动化的电子仪器 Ø 不同模型所算出的高度角30 以上方向的延迟差 异不大。
对流层模型改正的误差分析
Ø 模型误差 § 模型本身的误差
Ø 气象元素误差
§ 量测误差
•
仪器误差
•
读数误差
§ 测站气象元素的代表性误差
Ø 双频改正
§ 方法:利用双频观测值直接计算出延迟改正或组 成无电离层延迟的组合观测量 § 效果:改正效果最好
Ø 实测模型改正
§ 方法:利用实际观测所得到的离散的电离层延迟 (或电子含量),建立模型(如内插) § 效果:改正效果较好
第六章GPS测量定位误差

相对论效应对卫星钟的影响(2/3)
❖广义相对论 –原理:钟的频率与其所处的重力位有关 –对GPS卫星钟的影响:
若卫星所在处的为 重Ws力 ,位 地面测站处的为 重WT力 ,位
则同一台钟放在与 卫放 星在 上地面上时将 钟的 频差 率异 f2为:
f2
Wsc2WT
f
c2
f
(1 1) Rr
其中3.9860015014m3 s2,若地面处的地 R近心似距取 637k8m,
在时刻t时,在卫星钟读数上上加改正数tr , tr (t) F e AsinE(t)
课本上为:
F
2 1 2
c2
4.4428076331010 s
m1 2
因而,实际卫星钟的正改t(t)应为
tr(t) 22 es9 iE ( n 0 t)
因为:
F A 2290
tL1(t) a0 a1 (t toc) a2 (t toc)2 tr TGD
实测星历(精密星历)
实测星历(精密星历)是根据实测资料进行事后处理而 直接得出的星历,精度较高。这种星历用于进行精密定位 的事后处理,对于提高精密定位精度,减少观测时间和作 业费用等具有重要作用,还可以使数据处理较为简便。由 于这种星历要在观测后一段时间(例如1~2个星期)才能 得到,所以对导航和实时定位无任何意义。
仔细分析误差对观测值或平差结果的影响,安排 适当的观测纲要和数据处理方法(如同步观测,相 对定位等),利用误差在观测值之间的相关性或在 定位结果之间的相关性,通过求差来消除或削弱其 影响的方法称为求差法。
例如,当两站对同一卫星进行同步观测时,观测值中 都包含了共同的卫星钟误差,将观测值在接收机间求差即 可消除此项误差。同样,一台接收机对多颗卫星进行同步 观测时,将观测值在卫星间求差即可消除接收机钟误差的 影响。 又如,目前广播星历的误差可达数十米,这种误差属于起 算数据的误差,并不影响观测值,不能通过观测值相减来消 除。利用相距不太远的两个测站上的同步观测值进行相对定 位时,由于两站至卫星的几何图形十分相似,因而星历误差 对两站坐标的影响也很相似。利用这种相关性在求坐标差时 就能把共同的坐标误差消除掉。其残余误差(即星历误差对 相对定位的影响)一般可用下列经验公式估算: b=b*s/。
卫星导航系统定位误差评价方案

卫星导航系统定位误差评价方案导航是现代社会不可或缺的一项技术,而卫星导航系统是导航技术中最为先进和精确的一种。
然而,在使用卫星导航系统进行定位时,由于各种因素的影响,定位误差是不可避免的。
因此,为了评估卫星导航系统的定位误差,需要制定一个科学合理的评价方案。
首先,为了评估卫星导航系统的定位误差,需要确定评估的指标。
常用的指标包括定位精度、定位稳定性和定位可靠性等。
定位精度是指实际定位结果与真实位置之间的误差大小;定位稳定性是指在一段时间内定位结果的稳定性和一致性;定位可靠性是指在各种条件下系统定位的可靠性和正确性。
通过分析这些指标,可以全面评估卫星导航系统的定位误差。
其次,为了评估卫星导航系统的定位误差,需要收集实际的定位数据。
可以通过在不同地理位置、不同时间段进行实地测试或者使用模拟器进行仿真实验的方式收集数据。
同时,需要保证收集到的数据具有代表性,可以覆盖不同的环境条件和使用场景,以提高评估的准确性和可靠性。
然后,为了评估卫星导航系统的定位误差,需要建立合适的评估模型。
评估模型可以基于统计方法、数学模型和机器学习等技术进行构建。
其中,统计方法可以通过分析定位数据的均值、方差、标准差等指标来评估定位误差;数学模型可以通过建立定位误差的数学模型,利用数学推导和分析来评估定位误差;机器学习可以通过训练数据集来构建模型,利用机器学习算法预测定位误差。
根据具体的应用场景和需求,选择合适的评估模型进行定位误差评估。
最后,为了评估卫星导航系统的定位误差,需要进行实际的评估和验证。
通过将评估模型应用于实际的定位数据,对定位误差进行评估和验证。
可以与真实位置进行对比,计算实际定位结果与真实位置之间的误差,并对评估结果进行统计分析和可视化展示。
通过评估和验证的结果,可以得出卫星导航系统的定位误差情况,为后续的改进和优化提供参考。
总之,卫星导航系统的定位误差评价方案需要确定评估指标、收集定位数据、建立评估模型以及进行实际的评估和验证。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
ts a0 a1 t toc a2 t toc
精度( accuracy)表示一个量观测值与其真值接近或一致的程度, 常以误差( error)予以表述。GNSS系统精度为用GNSS信号所测定 的载体在航点位与载体实际点位之差。
2014-12-12 哈尔滨工业大学 电子与信息工程学院 5
6.1.1 均方根差(1/2)
一倍标准差(lσ)的概率值:68.3%; 二倍标准差(2σ)的概率值:95.5%; 三倍标准差(3σ)的概率值:99. 796。 均方根差的探测概率: 置信椭圆(confidence ellipse,二维定位); 置信椭球(confidence ellipsoid,三维定位);
2
2 1/2
距离均方根差( DRMS),也称:圆径向误差(circular radial error) 或均方位置误差(MSPE,mean squared position error) 注意:也可采用“双倍距离均方根差”(2DRMS,twice distance root mean square error),即
4
6.1 GPS卫星导航定位的误差简介
被动式测距原理: 测量来自GPS卫星的导航定位信号的传播时延,测得 接收天线相位中心和卫星发射天线相位中心间的距离 (站星距离),将它和GPS卫星在轨位置联合解算出 用户的三维坐标。 GPS卫星导航定位误差: (1)卫星误差:信号自身误差及人为的SA误差; (2)传播误差:信号从卫星传播到用户接收天线的传播误差; (3)接收误差:信号接收机所产生的测量误差。
• 与传播途径有关的误差
– 电离层延迟 – 对流层延迟 – 多路径效应
• 与接收设备有关的误差
– 接收机天线相位中心的偏移和变化 – 接收机钟差 – 接收机内部噪声
GPS测量误差的性质①
• 偶然误差
– 内容
• 卫星信号发生部分的随机噪声 • 接收机信号接收处理部分的随机噪声 • 其它外部某些具有随机特征的影响
– 限制:有些误差难以模型化
消除或消弱各种误差影响的方法②
• 求差法
– 原理:通过观测值间一定方式的相互求差,消去或消弱 求差观测值中所包含的相同或相似的误差影响 – 适用情况:误差具有较强的空间、时间或其它类型的相 关性。 – 所针对的误差源
• • • • 电离层延迟 对流层延迟 卫星轨道误差 …
结论:在广义相对论效应作用下,卫星上钟的频率将变快
相对论效应对卫星钟的影响③
• 相对论效应对卫星钟的影响
– 狭义相对论+广义相对论
在狭义相对论效应和广 面 上时总的变化量 f为 : f f1 f 2 4.449 1010 f
2 DRMS 2 DRMS 2
2
2014-12-12 哈尔滨工业大学 电子与信息工程学院
2 1/2
7
6.1.2 圆概率误差(1/2)
在导航领域,圆概率误差(CEP,circular error probable)被广泛应 用。 当概率为50%时,圆概率误差定义为:
消除或消弱各种误差影响的方法①
• 模型改正法
– 原理:利用模型计算出误差影响的大小,直接对观测值 进行修正 – 适用情况:对误差的特性、机制及产生原因有较深刻了 解,能建立理论或经验公式 – 所针对的误差源
• • • • 相对论效应 电离层延迟 对流层延迟 卫星钟差
改正后的观测值=原始观测值+模型改正
SEP 0.51 h
球概率误差(SEP)是在以天线真实位置为球心的球内,偏离球 心概率为50%的三维点位精度分布度量。
2014-12-12 哈尔滨工业大学 电子与信息工程学院 9
6.1.3 RMS与CEP关系(1/2)
2014-12-12
哈尔滨工业大学 电子与信息工程学院
6.1.4 偏差 (2/2)
GPS数据处理时,依据GPS卫星导航电文第一数据块提供的时 钟多项式的A系数,按上列公式计算出时钟偏差(对于Block II/IIA卫星为1ms左右,其相应距离为300km),以此将每颗卫 星的时间(ts)换算成统一的GPS时间。
GPS卫星导航电文提供计算时钟偏差的A系数,不能真实地代 表GPS导航定位测量时的时钟多项式系数(1ns时间误差相应于 30cm距离误差);星钟误差是A系数代表性误差的综合影响。 注意:电离层/对流层效应对GPS卫星测量的影响,也存在着 “偏差”和“误差”两个不同而相关的概念。 “偏差”为电离层/对流层效应导致的附加时延改正(几米至 100余米,视GPS卫星高度角大小而定); “误差”是附加时延改正的非真实性和非实径性而引起的。
卫星定位导航原理与应用
哈尔滨工业大学通信技术研究所
韩帅
1
第六章 定位导航误差
2
内容提要
§6.1 卫星导航定位的精度、误差与偏差 §6.2 卫星导航定位的误差 §6.3 GPS卫星几何布局和精度因子
3
内容提要
§6.1 卫星导航定位的精度、误差与偏差 §6.2 卫星导航定位的误差 §6.3 GPS卫星几何布局和精度因子
ts a0 a1 ts toc a2 ts toc
相对论效应
• 狭义相对论效应 • 广义相对论效应
狭义相对论和广义相对论
• 狭义相对论
– 1905 – 运动将使时间、空间和物质的质量发生变化
• 广义相对论
– 1915 – 将相对论与引力论进行了统一
相对论效应对卫星钟的影响①
解决相对论效应对卫星钟影响的方法
• 方法(分两步):首先考虑假定卫星轨道为 圆轨道的情况;然后考虑卫星轨道为椭圆轨 道的情况。
– 第一步:
在地面上调低将要搭载 到卫星上去的钟的频率 ,调低后的频率为 10.23MHz (1 4.4491010 ) 10.2299999954 5MHz
– 第二步:
tEin 2e a sin E 2 C0
卫星星历误差
卫星星历(轨道)误差
• 定义 由卫星星历给出的卫星在空间的位置与卫星 的实际位置之差称为卫星星历误差。
广播星历(预报星历)的精度 (无SA) 20~30米 (有SA) 100米 精密星历(后处理星历)的精度 可达1厘米
CEP 0.59
当概率为95%时,则有:
CEP95 CEP 2.08 1.2272
(CEP)95,也记“R95",表示概率为95%的二维点位精度。 当概率为99%时,则有:
CEP99 CEP 2.58 1.5222
2
2014-12-12
a0 ---相对于GSP时系的时间偏差(钟差); a1 ---相对于实际频率的偏差系数(钟速); a2 ---卫星时钟的频率漂移系数(钟速变化率,即钟漂); toc --- GPS卫星导航电文第一数据块的参考时元; t --- GPS导航定位的观测时元。
哈尔滨工业大学 电子与信息工程学院 12
• 狭义相对论
– 原理:时间膨胀。钟的频率与其运动速度有关。 – 对GPS卫星钟的影响:
若卫星在地心惯性坐标系中的运动速度为Vs,则在地面频率为f 的钟 若安置到卫星上,其频率f s 将变为: Vs 2 1 2 Vs 2 f s f [1 ( ) ] f (1 2 ) c 2c 即两者的频率差f s 为 Vs 2 f s f s f 2 f 2c 考虑到GPS 卫星的平均运动速度Vs 3874 m s 和真空中的光速c 299792458 m s ,则 f s 0.835 1010 f
置信椭圆
置信椭圆的长短半轴,分别表示二维位置坐标分量的标准差(如经度 的σλ和纬度的σφ)。
2014-12-12
哈尔滨工业大学 电子与信息工程学院
6
6.1.1 均方根差(2/2)
注意:许多中外文献所述“精度”多为一倍标准差(lσ),且用“距离 均方根差 (DRMS) ”表示二维定位精度,即
DRMS
– 特点
• 随机 • 量级小 – 毫米级
GPS测量误差的性质②
• 系统误差(偏差 - Bias)
– 内容
• 其它具有某种系统性特征的误差
– 特点
• 具有某种系统性特征 • 量级大 – 最大可达数百米
GPS测量误差的大小①
• SPS(无SA)
误差来源 星历数据 卫星钟 电离层 对流层 多路径 接收机观测 用户等效距离误差 (UERE), rms 滤波后的 UERE , rms 1-sigma 垂直误差 – VDOP = 2.5 1-sigma 水平误差 – HDOP = 2.0 1-sigma 误差,单位 m 偏差 2 .1 2.0 4.0 0.5 1.0 0.5 5.1 5.1 随机误差 0.0 0.7 0.5 0.5 1.0 0.2 1.4 0.4 12.8 10.2 总误差 2.1 2.1 4.0 0.7 1.4 0.5 5.3 5.1
– 结论:在狭义相对论效应作用下,卫星上钟的频率将变 慢
相对论效应对卫星钟的影响②
• 广义相对论
– 原理:钟的频率与其所处的重力位有关 – 对GPS卫星钟的影响:
若卫星所在处的重力位 为Ws,地面测站处的重力位 为WT, 则同一台钟放在卫星上 与放在地面上时钟频率 将的差异f 2为: Ws WT 1 1 f 2 f 2 f ( ) 2 c c R r 其中 3.986005 1014 m3 s 2 ,若地面处的地心距 R近似取6378 km, 卫星的地心距近似取 26560 km,则 f 2 5.2841010 f
