数列中的“类比”错误例说

数列中的“类比”错误例说
江西省永丰中学 刘 忠
（本文发表于《起跑线》2004年第10期）
数学的高度抽象性与形式化(数学化)的特点, 决定了学生在学习数学时, 如果要真正理解、掌握进而领悟数学中的精神和方法，就必须经历一个“再创造”的过程. 因此，教师在教学中要营造诸如类比等学习环境，引导学生主动参与到认识事物的实践
中去，从而提高数学能力，形成数学思想.
所谓类比，就是根据两种事物在某些特征上的相似
作出它们或然性的推理，其结论是否正确还有待证明. 在“数列”的学习中, 我们可以通过类比, 由函数的有关结论和解决函数问题的方法得到数列的有关结论和
解决数列问题的方法，还可由等差数列的有关结论得到等比数列的有关结论等.由于类比所
得推理是或然性的, 因此, 在这一章的学习中学生就容易出现错误了,现举例说明.
一、从函数到数列的类比
例1 ①设函数f(n)=n 2
+λn, n [)+∞∈,1, 若f(n)是增函数, 求实数λ的取值范围; ②设数列{a n }的通项a n =n 2
+λn, n *,
N ∈, 若{a n }是增数列, 求实数λ的取值范围. 解① f '
(n)=2n+λ, ∵f(n) 在[)+∞,1内是增函数, ∴2n+λ>0, 即λ>－2n 在[)
+∞,1内恒成立, ∴λ>－2.
② 法1 f '
(n)=2n+λ,∵ f(n)在N*内是增函数, ∴2n+λ>0即λ>－2n 在n ∈N *
时恒成立, ∴λ>－2.
法 2 1+n a －a n =(n+1)2
+2
()1(n n -+λ+λn)=2n+1+λ>0, ∴)12(+->n λ在
n *
N ∈时恒成立, λ∴>－3. 评析 解②的方法1是类比解①得到的, 所得结果与方法2所得结果不同. 哪个正确呢?
方法2所得结果是正确的. 事实上, 由λ>-2n 恒成立得到的λ>-2说明的是n a 在[)∞+,1上是增函数，而n a 在N *上是增函数，不要求在[)∞
+,1上是增函数. 如以上问题中2
5
=λ－时，
n 2
5
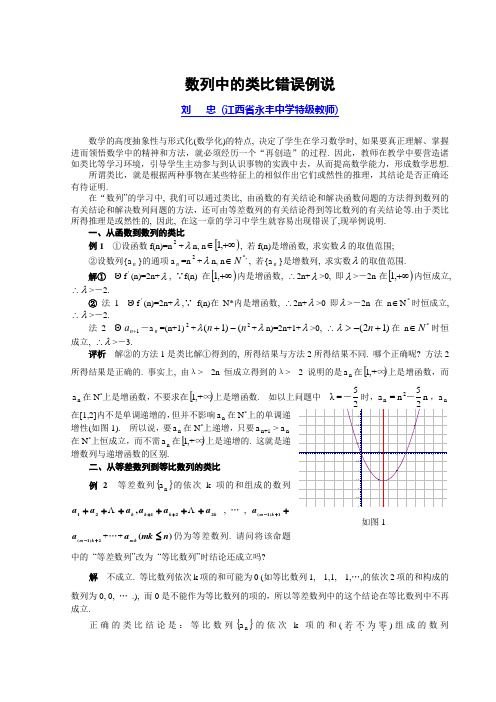
n =a 2n －，n a 在[1,2]内不是单调递增的，但并不影响n a 在N *上的单调递增性(如图1).
所以说，要n a 在N *上递增，只要n 1+n a >a 在N *上恒成立，而不需n a 在[)∞
+,1上是递增的.
这就是递增数列与递增函数的区别.
二、从等差数列到等比数列的类比 例
2
等差数列
{}
n a 的依次k 项的和组成的数列
k k k k a a a a a a 22121,++++++++ ,…,++-1)1(k m a 2)1(+-k m a +…+)(n mk a mk ≤仍为等差
数列. 请问将该命题中的 “等差数列”改为 “等比数列”时结论还成立吗?
解 不成立. 等比数列依次k 项的和可能为0 (如等比数列1,-1,1,-1,…,的依次2项的和构成的数列为0, 0, … .), 而0是不能作为等比数列的项的，所以等差数列中的这个结论在等比数列中不再成立.
正确的类比结论是：等比数列{}n a 的依次k 项的和(若不为零．．．．)组成的数列
k 22+k 1+k k 21a ++a +a ,a ++a +a ,…,++-1)1(k m a 2)1(+-k m a +…+)(n mk a mk ≤仍为等比
数列.
例 3 四个数成等差数列, 这四个数可设为d a d a d a d a 3,,,3++--. 若四个数成等比数列, 请问这四个数能设为313,,,aq aq aq aq --吗?
解 不能. 因为313,,,aq aq aq aq --四个数构成公比为2q 的等比数列, 因此这四个数同号, 而实际上四个成等比数列的数未必同号.
正确的类比结论是：若四个同号．．的数成等比数列, 则这四个同号的数可设为
313,,,aq aq aq aq --.
例4 等差数列{}n a 中,若)(,k n B a A a k n k n >==+-, 则2
B
A a n +=(A 、
B 的算术平均数). 等比数列{}n a 中：(1)若)(,k n B a A a k n k n >==+-,则AB a n =(A 、B 的几何平均数)
吗? (2)若)2(,22k n B a A a k n k n >==+-,则AB a n ±=吗?
解 (1)不等.设等比数列{}n a 的公比为q,则
k q A
B
2=,∴A B q k ±=,∴AB A
B
A q a a k k n n ±=±
=⋅=-)(. (2)不等. ∵
k q A
B
4=,∴A
B
q k =2, ∴A
B
A q a a k k n n ⋅==-22.(实际上n a 与A 同号). 由以上的解题过程不难得到正确的类比结论.
“类比法”是数学学习中应该掌握的方法. 函数的有关结论和解决函数问题的方法可类比到数列中去; 等差数列中的许多方法和结论也可类比到等比数列中, 但在类比过程中要谨防错误(如以上几例). 这就要求我们在“数列”学习的过程中既要注意函数与数列、等差数列和等比数列的共性, 还要注意它们的个性.。