第五章 立体(32)
合集下载
医学有机化学--第五章立体异构
Br Cl
Cl
CC
Cl
H
Br
(E)-1，2-二氯-1-溴乙烯 顺-1，2-二氯-1-溴乙烯
2020/3/2
9
H C
H3C
CH3 C CH3 CH
CH3
H3C C
H
CH3 C CH3 CH
CH3
(E)-3, 4-二甲基-2-戊烯 顺-3, 4-二甲基-2-戊烯
(Z)-3, 4-二甲基-2-戊烯 反-3, 4-二甲基-2-戊烯
1、确定C*abcd分子，优先顺序a>b>c>d;
2、若最小基d在垂直方向，ab c顺时针时为R 构型；
反之，为S构型。
3、若最小基d在水平方向，ab c顺时针时为 S构型；
反之，为R构型。
a
Rc
b
a dc
d
b
2020/3/2
S
a
a
bc
cd
32
d
b
乳酸
OH COOH CH3 H
COOH
（一）命名法法则： 针对 C*abcd分子
1、根据次序规则，排列成序：a>b>c>d; 2、把最小的d基团放在最远，其它三个朝向自己；
3、观察abc顺序,若呈顺时针为R-构型；呈逆时针
为S-构型。
a
a
2020/3/2
d
b
c
d
c b
a b c顺时针 a b c逆时针
R-构型
S-构型
31
（二）由费歇尔投影式确定R/S构型的方法
CH3
2020/3/2
6
③当取代基为不饱和基团时，则把双键、三键原子 看成是它以两个或三个单键与相同的原子相连。
立体化学基础
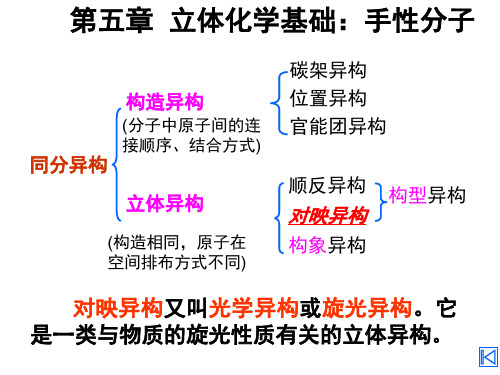
Cl大 HOCH2
Cl
键上，纸面 走向与实际
CH2Cl 走 向 相 同 ，
S-2,3-二氯丙醇
R-2,3-二氯丙醇
顺时针为R型， 逆时针为S型。
直接根据Fischer投影式命名的简便方法介绍
Problem 6: Give the names of the following compounds。(by R/S nomenclature)
有相等的距离。实物与镜像的关系叫对映关系。
镜面
实物与镜像
若实物与其镜像能够完全重合，则实物与镜像所 代表的两个分子为同一个分子。
OH
OH
CH H
CH3
HC H
CH3
OOHH
HH
CC HH 所有基团都重合 CCHH3 3
乙醇分子模型的重叠操作
对于某些分子，两个互为实物与镜像关系的分 子不能重合，如乳酸。
CO2H
CO2H
CO2H
NH2
NH2
H CH3
NH2 H
CH3 H
CO2H
CH3
H
NH2
CH3
即：固定*C上某个基团，其它三基团顺序轮换，不 改变其构型。
Problem 3: 下列Fischer式是否表示同一化合物？
COOH
CH2OH
H
OH
HO
H
--
CH2OH
COOH
镜 像
1
2
关
旋转180℃后可重叠
丙酸分子 的对称面
分子的对称面 具有对称面的分子为非手性分子
四、判断对映体的方法
1、看分子和它的镜像能不能重合。如果 不能重合，就具有对映异构现象。
2、寻找对称面和对称中心。如果分子没 有对称因素（对称面和对称中心），就 具有对映异构现象。
5.2三视图(教案)
4.培养学生的团队协作能力：通过小组合作完成三视图的绘制任务，培养学生沟通、协作、共同解决问题的能力，增强集体荣誉感。
三、教学难点与重点
1.教学重点
-理解三视图的概念：正视图、侧视图、俯视图的定义及其在空间中的位置关系。
-掌握三视图的绘制方法：如何从立体图形中提取信息，准确地绘制出三视图。
-能够识别三视图所表示的立体图形：通过三视图反推出立体图形的形状和结构。
四、教学流程
（一）导入新课（用时5分钟）
同学们，今天我们将要学习的是“5.2三视图”这一章节。在开始之前，我想先问大家一个问题：“你们在日常生活中是否遇到过需要从不同角度观察物体的情况？”比如，当我们看到一个立方体，从正面看和从侧面看，它的形状会有什么不同？这个问题与我们将要学习的内容密切相关。通过这个问题，我希望能够引起大家的兴趣和好奇心，让我们一同探索三视图的奥秘。
二、核心素养目标
1.培养学生的空间观念：通过学习三视图，使学生能够更好地观察和理解立体图形，提高空间想象力，形成对空间物体和图形的认识。
2.提升学生的几何直观能力：通过绘制和分析三视图，培养学生从不同角度观察问题、解决问题的能力，增强几何直观。
3.培养学生的逻辑思维和推理能力：在分析、绘制三视图的过程中，引导学生运用几何知识进行逻辑推理，提高解决问题的能力。
五、教学反思
在今天的教学中，我发现学生们对三视图的概念和绘制方法的理解程度有所不同。有的学生能够迅速抓住关键，而有的学生在理解上还存在一些障碍。我意识到，对于这部分学生，我需要采用更直观、更生动的教学方法来帮助他们。
在导入新课环节，通过提问的方式引发学生的思考，这是一个很好的开始。但在讲授理论部分，我发现有的学生似乎对抽象的概念感到困惑。下次，我可以尝试结合更多的实物模型或图片来进行讲解，让学生能够直观地感受到三视图与实际物体之间的联系。
三、教学难点与重点
1.教学重点
-理解三视图的概念：正视图、侧视图、俯视图的定义及其在空间中的位置关系。
-掌握三视图的绘制方法：如何从立体图形中提取信息，准确地绘制出三视图。
-能够识别三视图所表示的立体图形：通过三视图反推出立体图形的形状和结构。
四、教学流程
（一）导入新课（用时5分钟）
同学们，今天我们将要学习的是“5.2三视图”这一章节。在开始之前，我想先问大家一个问题：“你们在日常生活中是否遇到过需要从不同角度观察物体的情况？”比如，当我们看到一个立方体，从正面看和从侧面看，它的形状会有什么不同？这个问题与我们将要学习的内容密切相关。通过这个问题，我希望能够引起大家的兴趣和好奇心，让我们一同探索三视图的奥秘。
二、核心素养目标
1.培养学生的空间观念：通过学习三视图，使学生能够更好地观察和理解立体图形，提高空间想象力，形成对空间物体和图形的认识。
2.提升学生的几何直观能力：通过绘制和分析三视图，培养学生从不同角度观察问题、解决问题的能力，增强几何直观。
3.培养学生的逻辑思维和推理能力：在分析、绘制三视图的过程中，引导学生运用几何知识进行逻辑推理，提高解决问题的能力。
五、教学反思
在今天的教学中，我发现学生们对三视图的概念和绘制方法的理解程度有所不同。有的学生能够迅速抓住关键，而有的学生在理解上还存在一些障碍。我意识到，对于这部分学生，我需要采用更直观、更生动的教学方法来帮助他们。
在导入新课环节，通过提问的方式引发学生的思考，这是一个很好的开始。但在讲授理论部分，我发现有的学生似乎对抽象的概念感到困惑。下次，我可以尝试结合更多的实物模型或图片来进行讲解，让学生能够直观地感受到三视图与实际物体之间的联系。
立体构成 第五章
5 第一节 多面体的分类
第一节 立体构成观念的建立
一、正多面体
1.正四面体 正四面体是由四个相同的正三角形的面封闭而成形体。
正四面体包括四个正三角形平面、六条棱边和四个棱角，每 个面有三条边，每个顶点汇聚了三条棱。
5 第一节 多面体的分类
图5-3 正四面体
图5-4 正四面体展开图
5 第一节 多面体的分类
5 第一节 多面体的分类
第一节 立体构成观念的建立
二、半正多面体
1.十四面体 十四面体是由正六面体，即正方体在其相邻棱边中点之
间的相互连线为切线，切掉其顶角所形成一个多面体。从十 四面体的展开图可看出，十四面体是由正方形和正三角形结 合围成的空间造型。
5 第一节 多面体的分类
图5-13 十四面体形成示意图 图5-14 十四面体 图5-15 十四面体展开图
5 第一节 多面体的分类
第一节 立体构成观念的建立
二、半正多面体
2.三十二面体 三十二面体是由十二个正五边形和二十个正六边形组合
而成的，其展开图相对复杂一些。三十二面体由正二十面体 变化而来。
5 第一节 多面体的分类
图5-16 足球 图5-17 三十二面体 图5-18 三十二面体展开图
5 多面体构成
第一节 立体构成观念的建立
一、正多面体
4.正十二面体 正十二面体由十二个正五边形平面构成。正十二面体包
括十二个正五边形平面、三十条棱边和二十个棱角顶点，每 个面有五条边，每个顶点有三条棱。
5 第一节 多面体的分类
图-9 正十二面体
图5-10正十二面体展开图
5 第一节 多面体的分类
第一节 立体构成观念的建立
第二节 多面体变化构成
机械制图第五章部分答案
一般位置点： P平面与外环面的交 P点平面与内环面的交 点
判别可见性，连线
16
P33 5-5（3）作 出组合回转体截交 线的正面投影。
17
P34 5-6（1）作 出组合回转体截交 线的正面投影。
18
P34 5-6（2） 完成球体被水平 面P、两个侧平 面Q和两个侧垂 面S截切后的三 面投影。
19
5
P30 5-2(2)作出1/4环体的水平投影，以及它表面上A、B、C点的三面投影
(a)’ c’
b’
(a) ’’
c’’
b’’
a
(b) (c)
6
b’’
c’’
（b’） a’
P30 5-2(3)作出
组合回转体的水平
投影，以及它表面
c’
上A、B、C点的三
c
面投影
a’’
b
单击此处输入你的正文
7
P31 5-3 （1） 已
11
P32 5-4（3）完成圆柱体 被截后的三面投影。
12
P32 5-4（4）完成圆锥体 被截后的三面投影。
13
P32 5-4（4）完成球体体 被截后的三面投影。
14
P33 5-5（2）作出正平面P与 圆环截交线的正面投影。
15
平面与圆环相交 作图步骤：
特殊位置点： 水平面转向线上的点 最高点、最低点 中间点
P29 5-1（1）作出六棱柱的水平投影，以及它表面上A、B、C点的三面 投影。
a b’ ’
c’
b’ ’
a ’ ’
c
’’
b
a
(c)
1
CONTENTS
目录
(a’)
c’
a
判别可见性，连线
16
P33 5-5（3）作 出组合回转体截交 线的正面投影。
17
P34 5-6（1）作 出组合回转体截交 线的正面投影。
18
P34 5-6（2） 完成球体被水平 面P、两个侧平 面Q和两个侧垂 面S截切后的三 面投影。
19
5
P30 5-2(2)作出1/4环体的水平投影，以及它表面上A、B、C点的三面投影
(a)’ c’
b’
(a) ’’
c’’
b’’
a
(b) (c)
6
b’’
c’’
（b’） a’
P30 5-2(3)作出
组合回转体的水平
投影，以及它表面
c’
上A、B、C点的三
c
面投影
a’’
b
单击此处输入你的正文
7
P31 5-3 （1） 已
11
P32 5-4（3）完成圆柱体 被截后的三面投影。
12
P32 5-4（4）完成圆锥体 被截后的三面投影。
13
P32 5-4（4）完成球体体 被截后的三面投影。
14
P33 5-5（2）作出正平面P与 圆环截交线的正面投影。
15
平面与圆环相交 作图步骤：
特殊位置点： 水平面转向线上的点 最高点、最低点 中间点
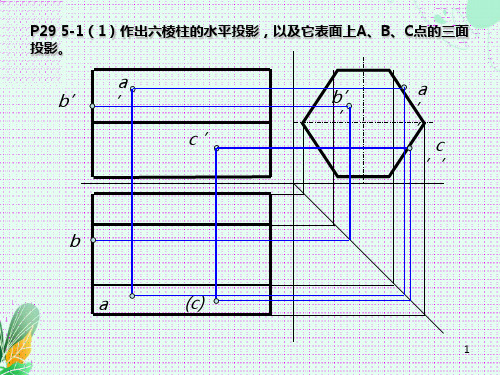
P29 5-1（1）作出六棱柱的水平投影，以及它表面上A、B、C点的三面 投影。
a b’ ’
c’
b’ ’
a ’ ’
c
’’
b
a
(c)
1
CONTENTS
目录
(a’)
c’
a
工程制图第五章立体的投影
投影的分类
01
02
03
正投影
光线与投影面垂直，物体 的投影与原物体形状、大 小一致。
斜投影
光线与投影面形成一定角 度，物体的投影与原物体 形状、大小可能存在差异。
中心投影
光线通过一点投影到投影 面上，物体的投影与原物 体形状、大小可能存在较 大差异。
投影法在工程中的应用
建筑设计
通过正投影法绘制建筑物 的平面图、立面图和剖面 图，以表达建筑物的外观 和内部结构。
圆锥体的投影
1 2
圆锥体的投影特性
圆锥体在三面投影体系中分别形成圆、椭圆和抛 物线。
圆锥体的三视图
主视图、俯视图和左视图。
3
圆锥体投影的作图方法
根据圆锥体的轴线位置，确定其在三面投影体系 中的位置，然后根据投影规律画出其三视图。
曲面立体投影的作图方法
曲面立体投影的作图步骤
曲面立体投影的应用
首先确定曲面立体的形状和尺寸，然 后根据其在三面投影体系中的位置， 按照投影规律画出其三视图。
曲面立体投影在工程制图、建筑设计、 机械制造等领域有着广泛的应用，是 工程技术人员必须掌握的基本技能之 一。
曲面立体投影的注意事项
在作图过程中，需要注意曲面的曲率、 方向和投影角度等因素，以确保绘制 的图形准确无误。
04 组合体的投影
组合体的构成方式
叠加型
由基本几何体按一定方式叠加而成，各基本体之间相 对位置关系明确。
对于截断立体和相贯立体，尺寸标注更为复杂。需要明确截断和相贯的位置，以及各个部分的大小。这涉及到对立体结构的 深入理解，以确保标注的尺寸能够准确反映立体的实际结构和形状。
Hale Waihona Puke 组合体的尺寸标注全面反映组合体的结构和功能
立体构成第5章
(2) 从视觉传达的速度来讲，色比形快，色彩是人的感官第 一印象。从视觉流程看，在色彩到形态的过程中，色彩优 先于形态作用于人的视觉。
(3) 色彩与形态是一个不可分割的整体，色附于形，形也存 于色，“皮之不存，毛将焉附”，形是离不开色的。
25
二、色彩与色调
1．物体本色的利用
2．人工色的运用
色彩对形体的表现可分为强烈的表现、中性的表现和 隐性的表现。
35
二、联想与意境
案例分析：
如图5-67～图5-70所示，“艺术来源于生活(自然) 而高于生活”，其中的奥妙便是你如何把自然形态 艺术化，使其显现出某种美的特征。
36
二、联想与意境
案例分析：
如图5-71～图5-75所示，抽象的几何形态带来的联 想意境，其实也离不开人的生活经历和情感认同。
37
本章小结
多样与统一是指不同的形态有机地体现在一件 作品中，在统一中求多样，在多样中求统一， 没有多样只有统一则单调乏味，只有多样而无 统一则会造成杂乱无章。
多样与统一是相辅相成的，多样与统一实际上 就是讲究秩序美。
11
二、多样与统一
案例分析：
如图5-15和图5-16所示，多样与统一是艺术设计时 经常面临的问题，除了秩序的统一以外，色彩、材 质的统一也可以使形态产生协调。
立体的色彩设计关键是把握好主导色，即色调。
形体表面的不同肌理会给人带来不同的色彩感觉，由 于肌理对色光的吸收、反射和透射的不同，形体表面 肌理的变化也会造成表面的明暗变化。即使是相同的 形体、相同的材料用同一种色彩表现，由于材质表面 的肌理不同，也会产生不同的色彩效果。
26
二、色彩与色调
案例分析：
2 第五章 立体构成的形式法则与要素
(3) 色彩与形态是一个不可分割的整体，色附于形，形也存 于色，“皮之不存，毛将焉附”，形是离不开色的。
25
二、色彩与色调
1．物体本色的利用
2．人工色的运用
色彩对形体的表现可分为强烈的表现、中性的表现和 隐性的表现。
35
二、联想与意境
案例分析：
如图5-67～图5-70所示，“艺术来源于生活(自然) 而高于生活”，其中的奥妙便是你如何把自然形态 艺术化，使其显现出某种美的特征。
36
二、联想与意境
案例分析：
如图5-71～图5-75所示，抽象的几何形态带来的联 想意境，其实也离不开人的生活经历和情感认同。
37
本章小结
多样与统一是指不同的形态有机地体现在一件 作品中，在统一中求多样，在多样中求统一， 没有多样只有统一则单调乏味，只有多样而无 统一则会造成杂乱无章。
多样与统一是相辅相成的，多样与统一实际上 就是讲究秩序美。
11
二、多样与统一
案例分析：
如图5-15和图5-16所示，多样与统一是艺术设计时 经常面临的问题，除了秩序的统一以外，色彩、材 质的统一也可以使形态产生协调。
立体的色彩设计关键是把握好主导色，即色调。
形体表面的不同肌理会给人带来不同的色彩感觉，由 于肌理对色光的吸收、反射和透射的不同，形体表面 肌理的变化也会造成表面的明暗变化。即使是相同的 形体、相同的材料用同一种色彩表现，由于材质表面 的肌理不同，也会产生不同的色彩效果。
26
二、色彩与色调
案例分析：
2 第五章 立体构成的形式法则与要素
建筑图学课件---第五章-立体的阴影(平面立体)只是分享
五棱柱的阴影(2)
A
F
E
B
C
D
阳面
七棱柱的阴影
DE
I
BCF A
阴面
GH
1.判断阴线为 ABCDEFGHIJ 2.求阴线的顶点的落影
3.连接各影线
4.给阴面和落影上色
二、 棱锥的阴影
1. 棱锥的变化引起阴影的变化 2. 判别立体（ a ）的阴阳面 3. 判别立体（ b）的阴阳面 4. 判别立体（ c）的阴阳面 5. 判别立体（ d）的阴阳面
位于H面且靠在V面上的长方体
为了作图清晰， 可将投影分开画
左右组合的长方体的落影
上下组合的长方体的落影
D A
CE B
l1=l2 如果l1>l2或者 l1<l2呢？
正三棱柱的落影
A
C
B
E D
五棱柱的阴影(1)
1.判断阴线为 ABCDEF 2.求阴线的顶点B、 C、D、E的落影 3.连接各影线 4.给阴面和落影上 色
（b）
（c）
（d）
棱锥的侧棱面不是特殊位置 那么棱锥的阴线该如何求？ 平面，阴阳面不能直接判断
三棱锥的阴影
三棱锥的阴影
2. 判别立体（ a ）的阴阳面
s'
先作出棱锥的落 a' b' e' c' d' 影，再根据影线 来判断阴线
Eh Ah
SHEH和SHDH 处于最外轮廓
Sh
，成为影线,
那么SE和SD
1. 棱锥的变化引起阴影的变化
s' d'
a' b' e' c'
s' d'
a' b' e' c'
第5章立体化学基础
CH3
CH3
H
OH
异丙醇
H
OH
H CH3
OH
2,32,3-丁二醇
CH3
H
CH3
H
CH3
CH3
H
1,11,1-二氯乙烷
H
顺-1,2-二甲基环丙烷 二甲基环丙烷
四、判断对映体的方法
1. 最直接的方法是建造一个分子及其镜像的模型。 最直接的方法是建造一个分子及其镜像的模型。 如果两者能重合，说明分子无手性， 如果两者能重合，说明分子无手性，没有对映异构现 象；如果两者不能重合，则为手性分子，有对映异构 如果两者不能重合，则为手性分子， 现象，存在对映体。 现象，存在对映体。 2. 考察分子有无对称面。如果分子有对称面， 考察分子有无对称面 如果分子有对称面， 对称面。 则该分子与其镜像就能重合，没有对映异构现象。 则该分子与其镜像就能重合，没有对映异构现象。 3. 大多数情况下，可根据分子中是否存在手性碳 大多数情况下，可根据分子中是否存在手性碳 原子(或手性中心 来判断分子是否有手性。 原子 或手性中心) 来判断分子是否有手性。 或手性中心
COOH COO H
CO OH H HO C CH 3
H OH CH 3 CH 3 OH H
COO H C H3 C H OH
-
二者的关系：互为镜象（实物与镜象关系， 二者的关系：互为镜象（实物与镜象关系，或 者说左、右手关系）。二者无论如何也不能完全重 者说左、右手关系）。二者无论如何也不能完全重 ）。 叠。这种呈物体与镜像关系，彼此又不能重叠的性 这种呈物体与镜像关系， 呈物体与镜像关系 质称为手性。 质称为手性。
COOH COOH
H OH CH3 CH3 OH
H
高中物理必修二第五章《抛体运动》测试卷(含答案解析)(32)
一、选择题1．在杂技表演中，猴子沿竖直杆向上做初速度为零、加速度为a 的匀加速运动，同时人顶着直杆以速度v 0水平匀速移动，经过时间t ，猴子沿杆向上移动的高度为h ，人顶杆沿水平地面移动的距离为x ，如图所示，关于猴子的运动情况，下列说法中正确的是（ ）A ．相对地面的运动轨迹为直线B ．相对地面做匀加速曲线运动C ．t 时刻，猴子对地面的速度大小为0v at +D ．t 时间内，猴子对地面的位移大小为x h +2．已知小船在静水中的速度是河水流速的2倍，设河水匀速流动，小河两条河岸互相平行，若小船渡过小河的最短时间为t ，则小船以最短位移过河需要的时间为（ ） A ．2t B ．3t C ．233t D ．332t 3．一水平抛出的小球落到一倾角为θ的斜面上时，其速度方向与斜面垂直，运动轨迹如图中虚线所示，小球在竖直方向下落的距离与在水平方向通过的距离之比为（ ）A ．1tan θB ．tan θC ． 12tan θD ．2tan θ 4．如图所示，做匀速直线运动的小车A 通过一根绕过定滑轮的长绳吊起一重物B ，设重物和小车速度的大小分别为B v 、A v ，则（ ）A ．AB v v <B ．A B v v >C ．重物B 匀速上升D ．绳的拉力小于B 的重力5．如图所示，相距l 的两小球A 、B 位于同一高度h （l 、h 均为定值）。
将A 、B 同时沿水平方向抛出。
A 、B 与地面碰撞前后，水平分速度不变，竖直分速度大小不变、方向相反。
不计空气阻力及小球与地面碰撞的时间，则（ ）A ．若A 向右、B 向左抛出，A 、B 不一定会发生相撞B ．若A 向右、B 向左抛出，A 、B 一定不会在h 高度发生相撞C ．若A 、B 都向右抛出A 、B 必然相撞D ．若A 、B 都向右抛出A 、B 可能在h 高处相撞6．如图所示，在倾角为37°足够长的斜面顶端处，一小球以与斜面成30°角的初速度v 抛出，小球最终落在斜面上。
立体及其交线
C B A 利用积聚性先求出水平投影
4.圆柱面上的曲线
a’ c’
注意求出特殊位 置的点（A、C） ----特殊点 利用积聚性 先求出侧面投影
曲线投影的求法是先求出线段上一系列点的投影； 然后，再将这些点的投影依次光滑地连接起来。
二、圆锥体的投影
圆锥的形成
1.圆锥体的组成 由圆锥面和底圆组成。
S
1’ a’
b’ c’ c c”
1” a”
a锥被截切后的水平投影和侧面投影
1’
1”
2’ 3’(4’)
4”
3”
y
4 1
3
y
2
[例题5] 求立体切割后的投影
6 6 5 4 1 2
（5 ）
1
4
2
（3）
3
Ⅵ Ⅴ 3 5
1 2 6
Ⅳ Ⅲ Ⅰ Ⅱ
4
第二节 曲面立体的投影
3.具体的作图步骤
4.截交线上的特殊点
极限点 转向点
特征点 结合点
一、 平面与圆柱相交
矩形
圆
椭圆
一、 平面与圆柱相交
截平面垂直于圆 柱轴线，截交线 为垂直于轴线的
截平面平行于圆 柱轴线，截交线 为 平行于轴线的
截平面倾斜于圆 柱轴线，截交线为
椭圆
圆
两条直线
[例1] 求圆柱被截切后的侧面投影
棱柱体
棱锥体
平面立体侧表面的交线称为棱线 若平面立体所有棱线互相平行，称为棱柱 若平面立体所有棱线交于一点，称为棱锥
平面立体的投影 是平面立体各表面投影的集合 ----由直线段组成的封闭图形。
1 棱柱的投影
1. 六棱柱
由两个底面 和六个侧棱面组
成。侧棱面与侧
工程制图 第5章 立体表面交线的投影
用以截切物体的平面。 截平面 :用以截切物体的平面。 截平面与物体表面的交线。 截交线 :截平面与物体表面的交线。 因截平面的截切，在物体上形成的平面。 截断面 :因截平面的截切，在物体上形成的平面。
讨论的问题： 讨论的问题：截交线的分析和作图 。
一、平面截切的基本形式
截断面 截交线
截平面
截交线与截断面
3’ 2’ 1’ 5” 4” (4’) (5’) 3” 2” 1”
（2）再求一般点。 再求一般点。 （3）依次光滑连接各点。 依次光滑连接各点。
5 4 3 2 1
平面与圆锥相交
已知立体的正面投影，试完成H、 两面 例5 已知立体的正面投影，试完成 、W两面 投影
1’ (2)’ (8)’ (4)’ 3’ 2” 4” 3” 1”
平面截切圆锥有四种情况，如图所示。
平面与圆锥相交
如图所示，圆锥被正垂面截切， 例1 如图所示，圆锥被正垂面截切，求出截 交线的另外两个投影。 交线的另外两个投影。
此种截交线为一椭圆。 由于圆锥前后对称，故椭圆 也前后对称。椭圆的长轴为 截平面与圆锥前后对称面的 交线——正平线，椭圆的短 轴是垂直与长轴的正垂线。
确定截交线 的投影特性
3. 截交线的形状
截交线的形 怎样确定截交线 的投影形状？ 状是怎样的？ 的投影形状？ 状是怎样的？
（1）分析截平面与立体的相对位置以确 定截交线形状。 定截交线形状。 截交线多边形的边数= 截交线多边形的边数=截平面截到的棱面数 （2）分析截平面与投影面的相对位置以确 定截交线的投影形状。 定截交线的投影形状。
二、平面立体截交线的画图
4
求截交线的两种方法： ⒈ 求截交线的两种方法：
棱线法: 棱线法 求各棱线与截平面的交点 棱面法: 棱面法:求各棱面与截平面的交线
工程制图第5章 基本立体
(连线之间须判别可见性）。 （4）检查整理完成全图
二、 立体表面上取线作图
''
'
图示已知三棱柱棱 面 上 的 折 线 MKN 的 正 面 投 影 m′k′n′, 求 该 线 的 H、W 面 投 影。作图过程是：
先作出垂直面 ABB1A1 上 点 M 的 水 平 投 影 m， 再 由 m′ 和 m 求 作 m″。 同 理 由 n′ 作 n， 再 作 出 n″。 因为分界点K在棱线 上，所以直接求出
立体表面已知线上取点（一）
C A
立体表面已知线上取点（二）
2'
2"
2
2
立
b’
b’’
体
表
(a’)
(a’’)
面
已
知
线
a
上
取
点
b
三
（二）立体表面特殊位置面上取点
作图要点
• 应首先找到点所在的特殊位置平面 （投影面平行面或垂直面）的各面 投影，然后，在该面的各面投影上 找点的各面投影。
• 作图时应先作出特殊位置平面的积 聚性投影上点的投影，然后再做点 的另外一个投影。
第五章 基本立体
第一节 基本立体的投影
第二节 基本立体表面的点和线
内容提要：在工程制图中，通常把棱柱、棱锥、圆
柱、圆锥、圆球、圆环等立体称为基本立体（也称 常见基本体），各种工程形体都可看作是由基本立 体（或其变化体）组成的。学习基本立体及其表面 点和线作图方法是解决复杂形体问题的基础。
基本体
基本几何体通常分为两类：
回转体的形成
a) 立体图
母线？ 导线？ 素线？ 纬圆？ 转向线？
回转体的形成及投影
回转轴线 上底圆
二、 立体表面上取线作图
''
'
图示已知三棱柱棱 面 上 的 折 线 MKN 的 正 面 投 影 m′k′n′, 求 该 线 的 H、W 面 投 影。作图过程是：
先作出垂直面 ABB1A1 上 点 M 的 水 平 投 影 m， 再 由 m′ 和 m 求 作 m″。 同 理 由 n′ 作 n， 再 作 出 n″。 因为分界点K在棱线 上，所以直接求出
立体表面已知线上取点（一）
C A
立体表面已知线上取点（二）
2'
2"
2
2
立
b’
b’’
体
表
(a’)
(a’’)
面
已
知
线
a
上
取
点
b
三
（二）立体表面特殊位置面上取点
作图要点
• 应首先找到点所在的特殊位置平面 （投影面平行面或垂直面）的各面 投影，然后，在该面的各面投影上 找点的各面投影。
• 作图时应先作出特殊位置平面的积 聚性投影上点的投影，然后再做点 的另外一个投影。
第五章 基本立体
第一节 基本立体的投影
第二节 基本立体表面的点和线
内容提要：在工程制图中，通常把棱柱、棱锥、圆
柱、圆锥、圆球、圆环等立体称为基本立体（也称 常见基本体），各种工程形体都可看作是由基本立 体（或其变化体）组成的。学习基本立体及其表面 点和线作图方法是解决复杂形体问题的基础。
基本体
基本几何体通常分为两类：
回转体的形成
a) 立体图
母线？ 导线？ 素线？ 纬圆？ 转向线？
回转体的形成及投影
回转轴线 上底圆
《立体构成》(整理)
出版稿件摄质量章第一章计算机辅助室内设计的基本原理节第一节计算机辅助设计与。
小节一、室内设计的。
小标题1．小要点要求：（1）正文中小点①正文计算机辅助室内设计的基本原理计算机辅助室内设计的基本原理计算机辅助室内设计的基本原理计算机辅助室内设计的基本原理计算机辅助室内设计的基本原理立体构成（工业设计基础课程教材）（草稿）目录概述 (1)第一节构成的概念及其分类 (1)一、构成的起源 (1)二、“构成”的定义 (1)三、构成的分类 (2)第二节立体构成的概念 (2)第三节《立体构成》的教学目的 (3)第四节立体构成的特征 (4)一、无框架 (4)二、力感 (4)三、有光影 (4)四、“四次元”性（亦可谓“四维”性） (4)第五节立体构成与设计 (5)第一章立体构成的要素 (6)第一节立体的本质 (6)第二节实体与虚体 (6)一、实体的种类 (7)二、虚体的种类 (7)第三节形态与形态要素 (8)一、形态的分类 (8)二、形态的基本要素 (9)第四节立体构成的美学原则 (12)一、主次与重点 (12)二、比例与尺度 (12)三、稳定与均衡 (13)五、节奏与韵律 (14)第二章立体构成的材料 (16)第一节材料的种类 (16)一、主要用于主体的材料 (16)二、主要用于辅助的材料 (17)三、主要用于连接的材料 (17)第二节材料的加工方法 (17)一、减切加工 (17)二、连接加工 (17)三、变形加工 (18)四、材料的后处理 (18)第三章面材构成 (19)第一节从平面到半立体的构成 (19)第二节面材的立体构成 (22)一、面材的插接构成 (22)二、面材的曲面构成： (22)三、面材的仿生构成 (24)第四章线材的立体构型 (26)第一节认识线材 (26)一、线材 (26)二、线材的种类 (26)三、线材在立体造型中的重要作用 (27)第二节线材的立体构型 (27)一、软质线材的立体构型 (27)第五章体（块材）的立体构成 (30)第一节块材的种类 (30)一、角块（体） (30)二、方块（体） (30)三、球块（体） (30)第二节块材的构成 (31)一、块材的部位变化 (31)二、块材的组合构成 (32)第六章综合立体构成 (34)第一节形体的综合 (34)一、线、框组合 (34)二、线与面组合 (34)三、线与块的组合 (34)四、面与块的组合 (35)第二节材料的综合 (35)一、硬质综合 (35)二、软质综合 (35)三、异材综合 (36)第三节空间的综合 (36)一、空间维度的组合 (36)二、静动空间的组合 (36)三、环面空间的组合 (36)第七章立体构成在设计中的应用 (37)主要参考文献 (38)概述第一节构成的概念及其分类一、构成的起源“构成”一词来源于德国包豪斯设计学院，它是指一种基本的设计思维方法。
《第5章 立体表面的相贯线》
内外表 面相交
第一页 上一页
两内表 面相交
下一页 最后页 目 录 结 束
2.两立体相交的种类
两曲面立 体相交
曲面与平面 立体面相交
两平面立 体相交
第一页
上一页
下一页
最后页
目 录
结 束
二、相贯线的性质
1.共有性——相贯线是两立体表面的共有线。 2.封闭性——相贯线一般是封闭的空间折线(通 常由直线和曲线组成)或空间曲线。
分析与作图： B圆 C圆 面 与 C 圆 柱 B、 柱 顶柱 交 线 的 已 A、C圆柱交线的已 交线为侧垂线 知投影有积聚性，用 近似画法作主视图
第一页 上一页 下一页 最后页 目 录 结 束
七、三体相交 首先应分析每个局部相邻两立体的相交形 式，然后再进行相贯线的分析与作图。 例题6：补全三圆柱体相交后的主、俯视图。
表面相切
第一页 上一页 下一页 最后页 目 录 结 束
例题10：求多体相贯的相贯线投影。
完成相贯线投影
第一页
上一页
下一页
最后页
目 录
结 束
本章结束
第一页
上一页
下一页
最后页
目 录
结 束
第一页 上一页 下一页 最后页 目 录 结 束
例1：求作两正交圆柱体相贯线投影。
作图步骤： 分析： 光滑连接各投影点 作一般点： 作特殊点： 大圆柱侧投影积聚为圆， 小圆柱水平投影积聚为圆， 相贯线为积聚在此圆上的 相贯线的投影积聚在此圆 一段圆弧 上
第一页 上一页 下一页 最后页 目 录 结 束
例1：求作两正交圆柱体相贯线投影。
作图步骤： 完成投影
第一页
上一页
下一页
最后页
有机化学PPT第五章 立体化学基础课件
凡是连有4个不同的原子或基团的碳原子称为手 性碳原子, 也可称为手性中心。
南京医科大学康达学院化学教研室 有机化学
南京医科大学康达学院 博学至精 明德至善
含有一个手性碳原子的化合物，在空间有2种不同构
型, 它们彼此构成一对对映体。
CH3C* HCOOH
COOH
OH
乳酸
HO C H
CH3
COOH H C OH
CH3
有一个手性碳的化合物必定 是手性化合物，只有一对对映体。
南京医科大学康达学院化学教研室 有机化学
南京医科大学康达学院 博学至精 明德至善
问题：下列化合物哪些含手性碳原子？
1. CH2Cl2
2. CHCl3 3.CH3CHClCH2CH3
4. CH3-CH-CH2CH3 CH2CH3
H
6.
CH3 7.
南京医科大学康达学院化学教研室 有机化学
南京医科大学康达学院 博学至精 明德至善
第一节 手性分子和对映体
一、手 性
观察自己的双手, 左手与右手有什么联系和区别？
南京医科大学康达学院化学教研室 有机化学
南京医科大学康达学院 博学至精 明德至善
左右手互为镜像与实物关系(称为对映关 系)，彼此又不能重合的现象称为手性。
H
2 COOH
H3C3 1Cl
H 1OH
2 CH2CH3
3CH3
竖，顺，R南-京型医科大学康达学院化学教横研室，有逆机化，学 R-型
南京医科大学康达学院 博学至精 明德至善
课堂练习：根据Fischer投影式命名。
2
CO2H
H
OH 1
3 CH3 R-(-)-乳酸
HOCH2 3
南京医科大学康达学院化学教研室 有机化学
南京医科大学康达学院 博学至精 明德至善
含有一个手性碳原子的化合物，在空间有2种不同构
型, 它们彼此构成一对对映体。
CH3C* HCOOH
COOH
OH
乳酸
HO C H
CH3
COOH H C OH
CH3
有一个手性碳的化合物必定 是手性化合物，只有一对对映体。
南京医科大学康达学院化学教研室 有机化学
南京医科大学康达学院 博学至精 明德至善
问题：下列化合物哪些含手性碳原子？
1. CH2Cl2
2. CHCl3 3.CH3CHClCH2CH3
4. CH3-CH-CH2CH3 CH2CH3
H
6.
CH3 7.
南京医科大学康达学院化学教研室 有机化学
南京医科大学康达学院 博学至精 明德至善
第一节 手性分子和对映体
一、手 性
观察自己的双手, 左手与右手有什么联系和区别？
南京医科大学康达学院化学教研室 有机化学
南京医科大学康达学院 博学至精 明德至善
左右手互为镜像与实物关系(称为对映关 系)，彼此又不能重合的现象称为手性。
H
2 COOH
H3C3 1Cl
H 1OH
2 CH2CH3
3CH3
竖，顺，R南-京型医科大学康达学院化学教横研室，有逆机化，学 R-型
南京医科大学康达学院 博学至精 明德至善
课堂练习：根据Fischer投影式命名。
2
CO2H
H
OH 1
3 CH3 R-(-)-乳酸
HOCH2 3
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
重庆交通大学画法几何及工程制图
8
圆柱投影图
作图步骤： 画轴线
画底面和顶面的投影 画转向线 正面转向线 侧面转向线
2012-8-4
重庆交通大学画法几何及工程制图
9
圆柱投影图分析
底面——水平面 顶面——水平面 圆柱面 前半个圆柱面 后半个圆柱面 左半个圆柱面 右半个圆柱面 转向线 正面转向线 侧面转向线
第五章
5.1
立体（Solid）
立体的投影（The orthographic projection of solid ）
5.1.1 根据已知立体作投影图
5.1.1.1 平面立体的投影 1、棱柱 2、棱锥
5.1.1.2 曲面立体的投影 1、圆柱 2、圆锥 3、球 4、圆环
5.1.2 根据已知条件作立体投影图
投影，
以及它 表面上
A、B、
C点的 三面投
b
影
(a)
c
重庆交通大学画法几何及工程制图 27
2012-8-4
5.2
5.2.1 一般性质
1、共线、共点性质
2、封闭性质
平面与立体相交
截交线
截断面
3、截交线的形状决定于立体 表面的形状和截平面与立体 的相对位置。 截平面
2012-8-4
重庆交通大学画法几何及工程制图
重庆交通大学画法几何及工程制图
44
平面与球相交——例2
影面投影是椭圆
作图步骤：
当截断面垂直于某投影面时，在另外两个投
特殊位置点 最前、最后点 (椭圆长轴端点)
一般位置点 连线
2012-8-4
重庆交通大学画法几何及工程制图
45
5.3 平面立体与曲面立体相交
5.3.1 一般性质
两相交的立体称相贯体，两立体的交线称相贯线。
2012-8-4
重庆交通大学画法几何及工程制图
13
圆锥投影图分析
底面：水平面 锥顶: 圆锥面： 前半个圆锥面 后半个圆锥面 左半个圆锥面 右半个圆锥面
2012-8-4
重庆交通大学画法几何及工程制图
14
圆锥表面上取点——特殊位置点
2012-8-4
重庆交通大学画法几何及工程制图
15
圆锥表面上取点——辅助圆法
34
（1）平面与圆柱相交——例1 截交线为直线
y
2012-8-4
重庆交通大学画法几何及工程制图
y
35
平面与圆柱相交——例2
2
截交线为椭圆 椭圆（截交线）作图步骤
2
3 （4 ） a 1
b
4
b
a
1. 求特殊点Ⅰ、Ⅱ、Ⅲ 、Ⅳ。 b 3 2. 求一般点A、B。 3. 光滑且顺次地连接各 1 a 点，整理轮廓线。
a
4
b
Ⅳ
2
Ⅱ Ⅲ
1 a 3 b
Ⅰ
2012-8-4
重庆交通大学画法几何及工程制图
36
（2）平面与圆锥相交——例1
截交线为圆
2012-8-4
重庆交通大学画法几何及工程制图
37
平面与圆锥相交——例2
作图步骤：
求特殊位置点
截交线为椭圆
转向线上的点I、II (最低、最左和最高、最右点) 最前、最后点IV、V 求一般位置点III 判可见性、连线、描深 截交线为椭圆，可仅求出长短轴端点
5.1.2.1 根据已知条件作平面立体的投影
5.1.2.2 根据已知条件作曲面立体的投影
2012-8-4 重庆交通大学画法几何及工程制图 1
正棱柱图例：
五棱柱
六棱柱
四棱柱 (长方体)
2012-8-4
三棱柱
重庆交通大学画法几何及工程制图
2
正棱锥图例
六棱锥
四棱锥
2012-8-4
三棱锥
重庆交通大学画法几何及工程制图
(c) a b
重庆交通大学画法几何及工程制图
2012-8-4
62
b’
b’’ a’ a’’
5-2(1)
(c’)
c’’
(c) b a
2012-8-4
重庆交通大学画法几何及工程制图
63
5-4(1)
2012-8-4
重庆交通大学画法几何及工程制图
64
5-4(2)
2012-8-4
重庆交通大学画法几何及工程制图
2012-8-4 重庆交通大学画法几何及工程制图 41
平面与圆柱相交——例4
求冲模切刀的截交线 y
直线
y
椭圆
2012-8-4 重庆交通大学画法几何及工程制图 42
2012-8-4
重庆交通大学画法几何及工程制图
43
（3）平面与球相交——例1
的投影为圆
当截断面平行于某投影面时，在该投影面
2012-8-4
65
2012-8-4
重庆交通大学画法几何及工程制图
66
右 后 左
2012-8-4
前
重庆交通大学画法几何及工程制图 10
例 已知属于圆柱面上的点A、B、C 的一个投影，求另外两面投影。
2012-8-4
重庆交通大学画法几何及工程制图
11
2、圆锥
2012-8-4
重庆交通大学画法几何及工程制图
12
圆锥投影图 作图步骤： 画轴线 画底面的投影 画锥顶 画最大轮廓线（转向 线） 画正面最大轮廓线 （转向线） 画侧面最大轮 廓（转向线）
1’’ 2’’
a’’
s’’
c ’’
b’’
3’’
a
1 (4)
s
(b) c
2 (3)
重庆交通大学画法几何及工程制图 60
2012-8-4
5-1(3)
a’ c’ c ’’ a’’
b’
c a
b’’
(b)
2012-8-4
重庆交通大学画法几何及工程制图
61
5-1(4)
b’’ a’’ c’’
a’ (c )’
b’
已知圆环面上的点A、B 的一个投影，求它们的另一个投影。
2012-8-4
重庆交通大学画法几何及工程制图
25
(a)’ c’
(a’’)
c’’
b’
b’’
a
(b) (c)
2012-8-4
重庆交通大学画法几何及工程制图
26
P30 52(3)作 出组合 回转体 的水平
(b’)
c’ a’
b’’ a’’
c’’
1、两共锥顶的锥体或轴线平行的柱体，相贯线为直线
2012-8-4
重庆交通大学画法几何及工程制图
50
2、回转体与圆球体相交、球心在回转体轴上，相贯线为圆
2012-8-4
重庆交通大学画法几何及工程制图
51
3、相贯线为平面曲线
2012-8-4
重庆交通大学画法几何及工程制图
52
4、两轴线正交圆柱相贯线的趋势
重庆交通大学画法几何及工程制图
19
圆球表面上取点——特殊位置点
2012-8-4
重庆交通大学画法几何及工程制图
20
已知属于圆球面的点K 的水平投影，求其另外两面投影 ——辅助圆法
2012-8-4
重庆交通大学画法几何及工程制图
21
4、圆环
2012-8-4
重庆交通大学画法几何及工程制图
22
圆环的投影：
28
5.2.2 作图方法 1、平面与平面立体相交 例： 三棱锥被正垂面所截，求截交线。
2012-8-4
重庆交通大学画法几何及工程制图
29
2012-8-4
重庆交通大学画法几何及工程制图
30
完成带切口的三棱锥的投影
s'
4' 1'
a' 2'(3‘) 3'' b' c' c'' 1'' a'' 2'' b''
B
b
2012-8-4 重庆交通大学画法几何及工程制图 6
棱锥表面取点（面上取点的方法）
s'
s"
m
(n )
(n)
1'
a' a 1 m 2' s b' n c' c
m
a"(c")
b"
2
b
2012-8-4
辅助直线法
重庆交通大学画法几何及工程制图
7
5.1.1.2曲面立体的投影 1、圆柱
2012-8-4
2012-8-4
重庆交通大学画法几何及工程制图
16
圆锥表面上取点——辅助素线法
2012-8-4
重庆交通大学画法几何及工程制图
17
3、球
2012-8-4
重庆交通大学画法几何及工程制图
18
圆球投影图分析
正面最大轮廓线A （转向线）
侧面最大轮廓线B（转 向线）
水平面最大轮廓线C （转向线）
2012-8-4
3 五棱锥
5.1.1.1平面立体的投影
1、五棱柱
2012-8-4
重庆交通大学画法几何及工程制图
4
五棱柱投影图
作图步骤： 画底面和顶面的投影 画五条棱线的投影
判别可见性
例：棱柱表面取点
2012-8-4
重庆交通大学画法几何及工程制图
5
2、三棱锥
s' s"
S
C
a' a s
b'
c'
c
a"(c")
b"