第十三章_拉普拉斯变换_Green电路13
合集下载
《电路》第十三章 拉普拉斯变换
S
12
3.积分性质
设： [ f (t)] = F (s)
则：
∫t
[ 0−
f
(t)dt] =
1 F(s) s
证：令
∫t
[ 0−
f (t)dt] =
φ( s )
[ f (t)] =
⎡ ⎢⎣
d dt
∫t 0−
f
(t
)dt
⎤ ⎥⎦
F(s) =
sφ(s) −
∫t 0−
f (t)dt
t =0−
应用微分性质
∴ φ(s) = F (s) s
注 f (t − t0) = 0 当 t < t0
[ ] ∫ 证：
f(t - t0 )
=
∞ 0−
f (t − t0 )e−stdt
∫=
f (t − t )e e dt ∞
f (t) = δ (t)
∫ F (s) =
[δ (t)] =
∞ 0−
δ
(
t
)e
−
st
dt
∫=
δ0+
0−
(
t
)e − st dt
= e−s0 = 1
(3)指数函数的象函数
f ( t ) = eat
[ ] ∫ F( s ) =
e at
=
e e dt ∞ at −st
0−
= − 1 e−(s−a)t s−a
1
− jω
−
S
1⎤
+ jω ⎥⎦
=
ω S2 +ω2
9
2. 微分性质ቤተ መጻሕፍቲ ባይዱ
若： [ f ( t ) ] = F ( S )
13.1 拉普拉斯变换的定义
用符号L-1 [ ]表示对方括号里的复变函数作 表示对方括号里的复变函数作 拉氏反变换 反变换。 拉氏反变换。
−st
L [F(s)] =
−1
∫ 2π j
1
c+ j∞
c− j∞
F(s)e ds
st
三、运算法
F(s) = ∫ f (t)e dt
0−Байду номын сангаас
∞
−st
函数， 积分的结果不再是 t 的函数，而是复变量 s 的函数。 的函数。 所以拉氏变换是把一个时间域的函数f(t)变 所以拉氏变换是把一个时间域的函数 变 域内的复变函数F(s)。 换到 s 域内的复变函数 。 称为复频率。 变量 s 称为复频率。 应用拉氏变换法进行电路分析称为电路的一 种复频域分析方法，又称为运算法 运算法。 种复频域分析方法，又称为运算法。 定义中拉氏变换的积分从t=0-开始，可以计 开始， 定义中拉氏变换的积分从 开始 包含的冲激， 及t=0时f(t)包含的冲激，从而给计算存在冲激函数 时 包含的冲激 从而给计算存在冲激函数 电压和电流的电路带来方便。 电压和电流的电路带来方便。
∞
1 L[e ] = s −a
at
F(s) = L[ f (t)] = ∫ eate−stdt
0−
1 −(s−a)t =− e s −a 0−
∞
1 = s −a
二、拉普拉斯变换的定义
1、拉普拉斯变换（拉氏变换） 、拉普拉斯变换（拉氏变换） 一个定义在[0， 区间的函数 区间的函数f(t)， 一个定义在 ，∞)区间的函数 ，它的拉普 拉斯变换式F(s)定义为 拉斯变换式 定义为
F(s) = ∫ f (t)e dt
0−
∞
−st
−st
L [F(s)] =
−1
∫ 2π j
1
c+ j∞
c− j∞
F(s)e ds
st
三、运算法
F(s) = ∫ f (t)e dt
0−Байду номын сангаас
∞
−st
函数， 积分的结果不再是 t 的函数，而是复变量 s 的函数。 的函数。 所以拉氏变换是把一个时间域的函数f(t)变 所以拉氏变换是把一个时间域的函数 变 域内的复变函数F(s)。 换到 s 域内的复变函数 。 称为复频率。 变量 s 称为复频率。 应用拉氏变换法进行电路分析称为电路的一 种复频域分析方法，又称为运算法 运算法。 种复频域分析方法，又称为运算法。 定义中拉氏变换的积分从t=0-开始，可以计 开始， 定义中拉氏变换的积分从 开始 包含的冲激， 及t=0时f(t)包含的冲激，从而给计算存在冲激函数 时 包含的冲激 从而给计算存在冲激函数 电压和电流的电路带来方便。 电压和电流的电路带来方便。
∞
1 L[e ] = s −a
at
F(s) = L[ f (t)] = ∫ eate−stdt
0−
1 −(s−a)t =− e s −a 0−
∞
1 = s −a
二、拉普拉斯变换的定义
1、拉普拉斯变换（拉氏变换） 、拉普拉斯变换（拉氏变换） 一个定义在[0， 区间的函数 区间的函数f(t)， 一个定义在 ，∞)区间的函数 ，它的拉普 拉斯变换式F(s)定义为 拉斯变换式 定义为
F(s) = ∫ f (t)e dt
0−
∞
−st
第十三章 拉普拉斯变换
拉普拉斯反变换的计算较复杂，一般多采用部分分式展开的 方法间接求得。 设F(s)可以表示为如下的有理分式，m 和n 为正整数，且 n ≥m 。
N ( s ) a0 s m + a1s m −1 + L + am F ( s) = = D( s ) b0 s n + b1s n −1 + L + bn
∞
−
F (s) f (ξ )dξ ] = s
e-stdt，
利用∫ udv = uv − ∫ vdu
则： 0 [(
1 − st ∴ du = f (t )dv，v = − e s
− st ∞
∫ ∫
= (∫
t
t
0−
f (ξ )dξ )e − st dt ] = ( ∫
t
0−
0−
e f (ξ )dξ ) −s
16
例：13-7
s+3 求：F(s) = 2 的原函数f (t ) s + 2s + 5
17
3、D(s)=0 具有q阶重根p1 ， 其余为单根p2、 p3、
K11 K2 则：F ( s ) = + +L+ +( + L) 2 q s − p1 ( s − p1 ) ( s − p1 ) s − p2
则 f(t)的拉氏变换F(s)总是存在。 本书涉及的f(t)均满足上述条件
1 c + j∞ 拉普拉斯反变换的定义： f (t ) = F ( s )e st ds 2πj ∫c − j∞
式中，M , c为正的有限常数
−1
用 [ ]表示对中括号中的时域函数作拉氏变换 用 [ ]表示对中括号中的复变函数作拉氏反变换 例如：F(s)= [f(t)]=
电路十拉普拉斯变换
（1）根据换路前电路的工作状态，计算电感电流初始值 和电容电压初始值 ；
（2）作出换路以后复频域的等效电路，即运算电路（注意附加电源的值和方向）；
（3）应用线性网络一般分析方法（结点法、回路法、支路法、电路定理、等效变换等）列写运算形式的电路方程，求出响应的象函数 或 等；
（4）用部分分式展开法对象函数取反变换，求出时域响应 或 等。
2．正确地画出复频域等效电路模型。注意附加电源的大小和方向，注意一些常见信号的象函数的记忆。
3．正确地计算出响应的象函数。在求解象函数时，由于复频率 是以符号形式存在，在复频域求解响应的过程有时比较繁琐，这是该方法的不足之处。
13．3典型例题
13．3．1拉普拉斯变换的定义及性质
例13-1已知 如图13-1所示，求其拉氏变换的象函数。
本题中周期为 ，于是得到
例13-4求 的拉氏变换式。
解题指导：任意函数与 的乘积的象函数的求解可利用拉普拉斯变换的频移特性。
解应用频移特性，先求
所以：
13．3．2拉普拉斯反变换
例13-5已知下列象函数 。导：仅含有两个单实根的情况。
（2）解题指导：包含了两个重根的情况。
13．2重点、难点分析
13．2．1本章重点
拉普拉斯变换的核心问题是把以 为变量的时间函数 与以复频率 为变量的复变函数 联系起来，也就是把时域问题通过数学变换后成为频域问题，把时间函数的线性常系数微分方程化为复变函数的代数方程，在求出待求的复变函数后，再作相反的变换，就得到待求的时间函数。所以，本章重点为：
为一对共轭复数，设 ， ，
则
13．1．4线性动态电路的拉氏变换分析法——运算法（即复频域分析法）
1．元件的伏安关系及运算电路如表13-2所示附表13-2。
（2）作出换路以后复频域的等效电路，即运算电路（注意附加电源的值和方向）；
（3）应用线性网络一般分析方法（结点法、回路法、支路法、电路定理、等效变换等）列写运算形式的电路方程，求出响应的象函数 或 等；
（4）用部分分式展开法对象函数取反变换，求出时域响应 或 等。
2．正确地画出复频域等效电路模型。注意附加电源的大小和方向，注意一些常见信号的象函数的记忆。
3．正确地计算出响应的象函数。在求解象函数时，由于复频率 是以符号形式存在，在复频域求解响应的过程有时比较繁琐，这是该方法的不足之处。
13．3典型例题
13．3．1拉普拉斯变换的定义及性质
例13-1已知 如图13-1所示，求其拉氏变换的象函数。
本题中周期为 ，于是得到
例13-4求 的拉氏变换式。
解题指导：任意函数与 的乘积的象函数的求解可利用拉普拉斯变换的频移特性。
解应用频移特性，先求
所以：
13．3．2拉普拉斯反变换
例13-5已知下列象函数 。导：仅含有两个单实根的情况。
（2）解题指导：包含了两个重根的情况。
13．2重点、难点分析
13．2．1本章重点
拉普拉斯变换的核心问题是把以 为变量的时间函数 与以复频率 为变量的复变函数 联系起来，也就是把时域问题通过数学变换后成为频域问题，把时间函数的线性常系数微分方程化为复变函数的代数方程，在求出待求的复变函数后，再作相反的变换，就得到待求的时间函数。所以，本章重点为：
为一对共轭复数，设 ， ，
则
13．1．4线性动态电路的拉氏变换分析法——运算法（即复频域分析法）
1．元件的伏安关系及运算电路如表13-2所示附表13-2。
第13章 拉普拉斯变换
k2 s2
k3 s5
0 .1 s
0 .5 s2
0 .6 s5
k 1 sF ( s )
s0
1 25
0 .1
k1
2s 1 3s 14s 10
2 s0
1 10
0 .1
k 2 ( s 2 ) F ( s ) s 2
2( 2) 1 2 ( 2 5)
I2(s) + sL2
+ i1
u1 –
u 1 L1
M
L1 L2
i2
+
u2 –
+ –
+ – + –
+
L2i2(0-)
U2(s)
–
Mi1(0-)
+
–
d i1 dt d i2 dt
M
d i2 dt
U 1 ( s ) sL 1 I 1 ( s ) L1 i 1 ( 0 ) sMI 2 ( s ) Mi 2 ( 0 ) U 2 ( s ) sL 2 I 2 ( s ) L 2 i 2 ( 0 ) sMI 1 ( s ) Mi 1 ( 0 )
本章重点：
1. 运算形式的电路定律和元件约束
2. 用运算法分析线性电路
§13－1 拉普拉斯变换的定义
一、定义
F 双边拉氏变换：( s ) F 单边拉氏变换：( s ) 1 f (t ) 拉氏反变换： 2 j
f (t ) e
0
c j
c j
把傅氏变换的 j s j F f ( t ) e dt 记作 ( s ) L [ f ( t )] 正变换 1 F ( s ) e ds 记作 f ( t ) L [ F ( s )] 反变换
电路第十三章 拉普拉斯变换
目录
§13—1 拉普拉斯变换的定义 §13—2 拉普拉斯变换的基本性质 §13—3 拉普拉斯反变换的部分分式展开 §13—4 运算电路 §13—5 应用拉普拉斯变换法分析线性电路
本章作业
13—1(2)(4)(6)(8)、13—2(1)(3)、 13—3(2)(4)、13—4、13—12、 12—16、12—18
例： δ(t) R C uC
求：uc(t)的冲击响应 duc 1 解： C + uc=δ(t) dt R 等式两边进行拉普拉斯变换
duc 1 L[C dt ]+L[ R uc]=L[δ(t)] 1 sCUC(s) –Cuc(0–)+ UC(s)=1 R 1 1 1 UC(s)= 1 1 = C s+ RC sC+ R
t 1 1 1 –τ uc(t)=L–1[ C 1 ]= C e s+ RC
1 (sC+ )UC(s)=1 R 进行拉氏反变换
三、(时域)积分性质 设：L[f(t)]=F(s) F(s) 则：L[ ∫ f(ξ)d(ξ)]= s 0–
t
积分性质的意义在于把时域中原函数的积分运算 转换为复频域中象函数除以s的代数运算。 d t f(ξ)d(ξ)=f(t) 证： dt ∫ 0– 两边进行拉氏变换 根据导数性质 d t f(ξ)d(ξ) ]=L[f(t)] L[ ∫ dt 0–
原函数f(t)
Aδ(t) Aε(t) Ae–αt 1–e–αt sin(ωt) cos(ωt) sin(ωt+ϕ) cos(ωt+ϕ) e–αtsin(ωt)
常用函数的拉氏变换表 象函数F(s) 原函数f(t)
A A/s A s+α α s(s+α) ω s2+ω2 s s2+ω2 ssinϕ+ωcosϕ s2+ω2 scosϕ+ωsinϕ s2+ω2 ω (s+α)2+ω2 e–αtcos(ωt) te–αt t sinh(αt) cosh(αt) (1–αt)e–αt 1 2 2 t 1 tn n！ 1 tne–αt n！
13第十三章拉普拉斯变换
1 ( s 1)
2 t
3
( s 1)
t
2
f (t ) 3e
2 te
0 .5 t e
3t
小结： 1.由F(S)求f(t) 的步骤 1.) n =m 时将F(S)化成真分式
F (S ) C0 P(S ) D(S )
2.)求真分式分母的根，确定分解单元 3.)求各部分分式的系数 4.)对每个部分分式和多项式逐项求拉氏反变换 。
2 t
(t ) 7e
(t )
例
求 F (s) s
2s 1
3
7s
2
10 s
的 原 函 数 f ( t )。
解：令D(s)=0，则 s1 = 0，s2=－2，s3=－5
D ( s ) 3 s 14 s 10
2
K1
N (s) D ( s )
s s1
3
s p1
则： f (t ) K1e 当为n阶重根：
Kn
K 2te
d
( n 1) ( n 1)
p1t
1 2
K 3t e
n
2
p1t
1
(n 1)! ds
(s p )
1
F ( s)
s p1
例： 2 S ( S 1)
S 4
K1 S
K 21 ( S 1)
L[ (t )]
0
(t )e
St
dt
0 0
(t )e
St
dt
0 0
电路 第十三章 拉普拉斯变换
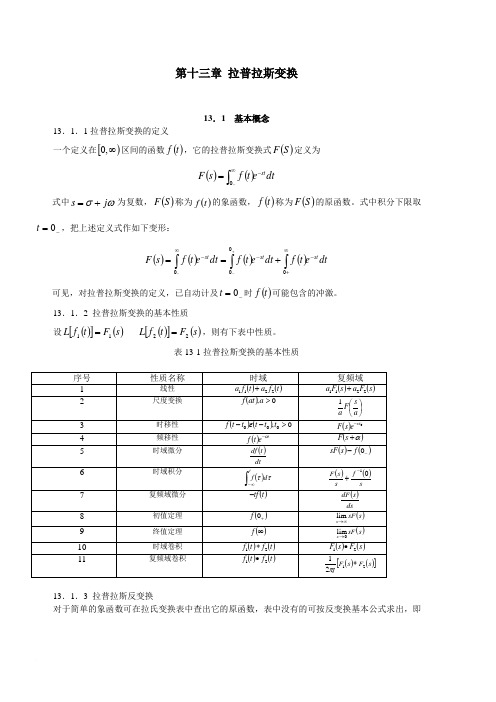
第十三章 拉普拉斯变换13．1 基本概念13．1．1拉普拉斯变换的定义一个定义在[)∞,0区间的函数()t f ，它的拉普拉斯变换式()S F 定义为()()dt e t f s F st -∞⎰-=0式中ωσj s +=为复数，()S F 称为()t f 的象函数，()t f 称为()S F 的原函数。
式中积分下限取-=0t ，把上述定义式作如下变形：()()()()dt e t f dt e t f dt e t f s F st stst-∞+--∞⎰⎰⎰+==+--0000可见，对拉普拉斯变换的定义，已自动计及-=0t 时()t f 可能包含的冲激。
13．1．2 拉普拉斯变换的基本性质设()[]()s F t f L 11= ()[]()s F t f L 22=，则有下表中性质。
表13-1拉普拉斯变换的基本性质13．1．3 拉普拉斯反变换对于简单的象函数可在拉氏变换表中查出它的原函数，表中没有的可按反变换基本公式求出，即()()[]()ds e s F js F L t f stj c j c ⎰∞+∞--==π211，但此式涉及到计算一个复变函数的积分，一般比较复杂。
电路响应的象函数通常可表示为两个实系数的s 的多项式之比，即s 的一个有理分式()()()nn n mm m b s b s b a s a s a s D s N s F ++++++==-- 110110 式中m 和n 为正整数，且m n ≥。
若m n =时，先将其化简成真分式，然后用部分分式展开，将复杂变换式分解为许多简单变换式之和，然后分别查表即可求得原函数。
1．()0=s D 具有n 个单实根时()iini p s K s F -=∑=1式中：()()i p s i i s F p s K =-=|则 ()()[]t p ni i ie K s F Lt f ∑=-==112．()0=s D 具有重根时设()0=s D 除了m 个重根外，其它均为单根，共有n 个根。
电路分析第十三章-拉普拉斯变换
⑵ 在t充分大时， f (t) 满足不等式
f (t) ≤ Me ct
其中M和c 都是实常数，即f(t)为指数级函数。
∫ 则 F (s) = ∞ f (t)e−st dt 0− 在σ > c 的范围内存在。
西南交通大学
证明条件⑵：
∫ 若 ∞ f (t)e−st dt 收敛， 则 L[ f (t)] 也收敛。 0−
)
−
Eε (t
−
t0
)
F (s)
=
L
[
f
(t)] =
E t0
⋅
1 s2
−
E t0
⋅
1 s2
e − st0
−
E
1 e−st0 s
=
E s 2t0
[1− (1+
st0 )e−st0 ]
西南交通大学
3、复频域位移 f (t) ↔ F (s)
f (t)e−αt ↔ F (s + α)
∫ 证明：L [ f (t)e−αt ] = ∞ f (t)e−αte−st dt 0− ∫= ∞ f (t)e−(s+α)t dt = F (s + α) 0−
同理
L[
cosω0t ⋅ε (t)
]=
s
s2 + ω02
5、幂函数tn ，n为正整数
L [ tn
]=
n! s n+1
L[
t
]=
1 s2
西南交通大学
4、幂指数信号 tn n为正整数
L ∫ [t n ] =
∞ 0−
t
en −st
dt
| ∫ =
− tn s
e − st
∞ 0−
f (t) ≤ Me ct
其中M和c 都是实常数，即f(t)为指数级函数。
∫ 则 F (s) = ∞ f (t)e−st dt 0− 在σ > c 的范围内存在。
西南交通大学
证明条件⑵：
∫ 若 ∞ f (t)e−st dt 收敛， 则 L[ f (t)] 也收敛。 0−
)
−
Eε (t
−
t0
)
F (s)
=
L
[
f
(t)] =
E t0
⋅
1 s2
−
E t0
⋅
1 s2
e − st0
−
E
1 e−st0 s
=
E s 2t0
[1− (1+
st0 )e−st0 ]
西南交通大学
3、复频域位移 f (t) ↔ F (s)
f (t)e−αt ↔ F (s + α)
∫ 证明：L [ f (t)e−αt ] = ∞ f (t)e−αte−st dt 0− ∫= ∞ f (t)e−(s+α)t dt = F (s + α) 0−
同理
L[
cosω0t ⋅ε (t)
]=
s
s2 + ω02
5、幂函数tn ，n为正整数
L [ tn
]=
n! s n+1
L[
t
]=
1 s2
西南交通大学
4、幂指数信号 tn n为正整数
L ∫ [t n ] =
∞ 0−
t
en −st
dt
| ∫ =
− tn s
e − st
∞ 0−
第十三章拉普拉斯变换
4、时域位移定理
L f t F S ,
L f t F S ,
L[ f (t t0 ) 1(t t0 )] F ( S )e St0
5、初值定理与终值定理
f (0 ) lim f (t ) lim SF ( S )
S j
f(t)：原函数；F(S)：f(t)在S域中的象函数。
拉普拉斯反变换：
f (t ) [ F ( S )]
1
1 2 j
j
j
F ( S )e St dS
13.2 拉氏变换的性质
13-2拉氏变换的性质
1、线性定理
L f1 t F1 S , L f 2 t F2 S : L af1 t bf 2 t aL f1 t bL f 2 t aF1 S bF2 S
2、微分定理
L f t F S
df SF ( S ) f (0 ) dt
3、积分定理
L f t F S ,
t F S L f t dt 0 S
13.2 拉氏变换的性质
]
0
e
t St
e
dt
0
e( S )t dt
0
1 ( S )t e S
0
1 S
2、常数
1 [1(t )] 1 t e st dt e st 0 S
1 S
3、正弦函数
[ 1 jt 1 1 1 (e e jt )] ( ) 2 2j 2 j S j S j S 2
13-1拉普拉斯变换
第十三章拉普拉斯变换经典法．．．——根据电路列出微分方程然后进行求解来求解动态电路响应的方法。
也叫时域解法．．．．（求解时间函数方程）。
优点：物理概念清楚，便于理解。
但是这种方法对于求解二阶以上的复杂电路，很困难。
即使是一阶电路，当激励为常数、正弦函数与冲击函数时，应用三要素法进行时域分析是方便的，但当激励为指数函数、斜坡函数、特别是任意函数式，时域分析也是很麻烦的。
在正弦稳态分析中，采用向量法后，将时域中的微积分运算转化成了频域中的代数运算，使运算十分简单。
向量分析是一种变换。
在暂态分析中，能否也建立这种类似的变换?拉普拉斯变换（简称拉氏变换）线性定常电路的拉氏变换分析与向量分析十分相似，用拉氏变换求解动态电路，先将时域函数通过拉氏变换变成复频域（S域）函数，并画出S域电路，在S域电路中确定响应后，经过拉氏反变换得到时域响应。
这种分析法不用求特解、通解、及确定积分常数，所得结果就是全响应。
拉氏变换将时域中的微积分方程变成S域中的代数方程。
因为拉氏变换分析要经过求拉氏变换和反变换两次运算（变换），所以也称为运算法．．．。
运算法是一种通过数学变换间接求解动态电路的简捷方法。
应当指出，拉氏变换求解动态电路，只适用于线性，非时变的电路，不适用于时变及非线性电路。
§15-1 拉普拉斯变换的定义一、 拉氏变换的定义先定义一个复数 ωδj s +=其中δ是使函数)(t f 在区间（0－，∞）内积分收敛而选定的一个常数；ω是角频率，是变量；s 是复变量。
δ、ω、s 的单位都是1/秒。
复变量s 也称为广义频率，或复频率。
1、 拉氏正变换的定义定义在（0－，∞）内的时间函数)(t f （)(t f 代表电路中的激励，或响应），与因子ste-相乘，构成一个新的函数st e t f -)(，再在（0－，∞）内对t 积分，该积分称为单边拉普拉斯（Laplace ）正变换，简称拉氏变换。
⎰∞--== 0 )()()]([dt e t f s F t f L st式中 ωδj s +=为复数（复频率变量）上式对t 求定积分后，变成了复变量s 的函数，所以记作)(s F 。
第十三章拉普拉斯变换
t f (ξ )dξ e − st dt 所以 ∫ ∫ 0− 0−
∞
t f (ξ )dξ e = ∫ 0− −s t f (ξ )dξ e = ∫ 0− −s
− st ∞
− ∫ f (t )e − st dt
0−
∞ ∞
其中，当t<t0时，f (t-t0)=0。令τ=t-t0
ℓ[ f (t − t 0 )] = ∫ f (t − t 0 )e dt = ∫ f (t − t 0 )e − st dt
0− ∞ t0 − st ∞
= ∫ f (τ )e
0−
− s (τ + t 0 )
dτ = e
− st 0
∫
0−
−t
( s − pi ) n 的因 3、如果D(s)=0具有重根，则应含 ( s − pi )3的因式，p1为 式。现设D(s)中含有
即
N (s) Ki = (i = 1、、 …、n) 2 3、 D′( s) s = pi
确定了各待定系数后，相应的原函数为
f (t ) = ℓ [ F ( s)] = ∑ K i e
−1 i =1 n pi t
N ( pi ) pit =∑ e i =1 D′( pi )
n
例13-6
解 因为
2s + 1 求 F ( s) = s 3 + 7 s 2 + 10s
ω = 2 s +ω2
(2)ℓ[ K (1 − e −αt )] = ℓ[ K ] − ℓ[ Ke −αt ] K K = − s s +α Kα = s( s + α )
由此可见，根据拉氏变换的线性性质， 求函数乘以常数的象函数以及求几个函数 相加减的结果的象函数时，可以先求各函 数的象函数再进行计算。
第十三章 拉氏变换分析线性电路
K1 K2 N1 ( s) s α jω s α jω D1 ( s )
2 若D( s) 0有共轭复根
K1,K2也是一对共轭复根
设K1 K e
jθ
K2 K e
( α jω ) t
-jθ
f (t ) ( K1e( α jω) t K 2e( α jω) t ) f1 (t )
F (s)
sin(t )
1 j t j t 2 j ( e e )
1 1 1 S j S j 2 2j S 2
2. 微分性质
若： f (t ) F ( S )
则
例 解
df ( t ) dt sF ( s ) f (0 )
求 : f (t ) t ( t )的象函数
[tε( t )]
[ 0 ε( t )dt ]
ห้องสมุดไป่ตู้
11 ss
4.延迟性质
设：
注
例
[ f ( t )] F ( s )
则：
[ f ( t t0 )] e
st0
F ( s)
f ( t t0 ) 0 当 t t0
求矩形脉冲的象函数
方法2
求极限的方法
i
i 1、 、 、n 23
N ( s )( s pi ) ki lim s p D( s ) ' N ( s )( s pi ) N ( s ) N ( pi ) lim ' ' s p D ( pi ) D ( s)
i
i
4s 5 求F ( s ) 2 的原函数 例 s 5s 6 4s 5 K1 K2 解法1 F ( s) 2 s 5s 6 s2 s3 4s 5 4s 5 K2 7 K1 3 s 3 S 2 s2 s3 N ( p1 ) 4 s 5 解法2 K1 ' 3 s 2 D ( p1 ) 2 s 5
2 若D( s) 0有共轭复根
K1,K2也是一对共轭复根
设K1 K e
jθ
K2 K e
( α jω ) t
-jθ
f (t ) ( K1e( α jω) t K 2e( α jω) t ) f1 (t )
F (s)
sin(t )
1 j t j t 2 j ( e e )
1 1 1 S j S j 2 2j S 2
2. 微分性质
若： f (t ) F ( S )
则
例 解
df ( t ) dt sF ( s ) f (0 )
求 : f (t ) t ( t )的象函数
[tε( t )]
[ 0 ε( t )dt ]
ห้องสมุดไป่ตู้
11 ss
4.延迟性质
设：
注
例
[ f ( t )] F ( s )
则：
[ f ( t t0 )] e
st0
F ( s)
f ( t t0 ) 0 当 t t0
求矩形脉冲的象函数
方法2
求极限的方法
i
i 1、 、 、n 23
N ( s )( s pi ) ki lim s p D( s ) ' N ( s )( s pi ) N ( s ) N ( pi ) lim ' ' s p D ( pi ) D ( s)
i
i
4s 5 求F ( s ) 2 的原函数 例 s 5s 6 4s 5 K1 K2 解法1 F ( s) 2 s 5s 6 s2 s3 4s 5 4s 5 K2 7 K1 3 s 3 S 2 s2 s3 N ( p1 ) 4 s 5 解法2 K1 ' 3 s 2 D ( p1 ) 2 s 5
电路 第十三章拉普拉斯变换
[t ε(t )]
n
dn 1 = (−1)n n ( ) ds s
n! = ( n+1 ) s
求: f (t ) = te−at的象函数
[te
−αt
d 1 1 )= =− ( ] ds s + α (s + α)2
3.积分性质 3.积分性质
[∫ −
0
t
t
1 f (t)dt] = F(s) s
应用微分性质
4s + 5 K1 = s+3
解法2 解法2
4s + 5 3 K2 = S=−2 = − s=−3 = 7 s+2 N( p1 ) 4s + 5 K1 = ' 3 = s=−2 = − D ( p1 ) 2s + 5
N( p2 ) 4s + 5 K2 = ' = s=−3 = 7 D (p2 ) 2s + 5
第13章 拉普拉斯变换 13章
重点 (1) 拉普拉斯变换的基本原理和性质 (2) 掌握用拉普拉斯变换分析线性电 路的方法和步骤 (3) 电路的时域分析变换到频域分析 的原理
13.1 拉普拉斯变换的定义
1. 关于变换
例
1
熟悉的变换 对数变换
C=A× B
2 相量法
lg C = lg A + lg B
把乘法运算变换为加法运算
(
情变换
微分方程) 微分方程
引 入 变 换 拉普拉斯变换
(
方程) 方程
3. 拉氏变换的定义 已知时域函数 定义: 定义
f (t) t ∈[0, ∞)
+∞ 0
F(s) = ∫ − f (t)e−st dt
第十三章 拉普拉斯变换法
一﹑线性性质： 线性性质： 设 L[ f 1 (t )] = F 1 ( s )， L[ f 2 (t )] =
a和b为两个任意实常数， 为两个任意实常数，则
F ( s ),
2
2
L[ a
例1.
f ( t ) + b f ( t )] = a F ( s ) + b F ( s )
1 2 1
f ( t ) = A (1 −
j 26 . 6
× e (− 1 −
j 2 )t
= 0 . 559 e − t ⋅ e j (2 t − 26 . 6 ) + 0 . 559 e − t ⋅ e − j (2 t − 26 . 6 ) = 2 × 0 . 559 e − t cos 2 t − 26 . 6 = 1 . 118 e − t cos 2 t − 26 . 6
t ε
L[ f (t − t0 )] = e
F (S )
页
华东理工大学 上 页 下
13.3 拉普拉斯反变换的部分分式展开
用拉氏变换求解线性电路的时域响应时， 用拉氏变换求解线性电路的时域响应时，需要把 求得的响应的拉氏变换式反变换为时间函数。 求得的响应的拉氏变换式反变换为时间函数。 由象函数求原函数的方法： 由象函数求原函数的方法： (1)利用公式
三﹑积分性质： 积分性质：
1 若 L [ f ( t )] = F ( s ), 则有 L [ ∫0 f ( t ) dt ] = F ( s ) s
t
说明： 说明：拉普拉斯变换将时域中的积分运算变成了复频域中 算子s与象函数的除法运算。 与象函数的除法运算。 华东理工大学 上 页 下
页
证明： 证明：
t
a和b为两个任意实常数， 为两个任意实常数，则
F ( s ),
2
2
L[ a
例1.
f ( t ) + b f ( t )] = a F ( s ) + b F ( s )
1 2 1
f ( t ) = A (1 −
j 26 . 6
× e (− 1 −
j 2 )t
= 0 . 559 e − t ⋅ e j (2 t − 26 . 6 ) + 0 . 559 e − t ⋅ e − j (2 t − 26 . 6 ) = 2 × 0 . 559 e − t cos 2 t − 26 . 6 = 1 . 118 e − t cos 2 t − 26 . 6
t ε
L[ f (t − t0 )] = e
F (S )
页
华东理工大学 上 页 下
13.3 拉普拉斯反变换的部分分式展开
用拉氏变换求解线性电路的时域响应时， 用拉氏变换求解线性电路的时域响应时，需要把 求得的响应的拉氏变换式反变换为时间函数。 求得的响应的拉氏变换式反变换为时间函数。 由象函数求原函数的方法： 由象函数求原函数的方法： (1)利用公式
三﹑积分性质： 积分性质：
1 若 L [ f ( t )] = F ( s ), 则有 L [ ∫0 f ( t ) dt ] = F ( s ) s
t
说明： 说明：拉普拉斯变换将时域中的积分运算变成了复频域中 算子s与象函数的除法运算。 与象函数的除法运算。 华东理工大学 上 页 下
页
证明： 证明：
t
电路课件(邱关源)13第十三章拉斯变换
t
f ( t ) = t = ∫0 ε( ξ)dξ
1 L[ε(t)] = s
1 1 1 L[ f (t)] = × = 2 s s s
4. 延迟性质
若 则
L[ f ( t )] = F ( s ) − st L[ f ( t − t0 )] = e F ( s )
0
函 原 数f(t) 数
函 象 数F 数 (s)
i
i
N ( pi ) N ( pi ) ki = ( s − pi ) = ' D( pi ) D ( pi )
k1 k2 kn F ( s) = + + ⋅⋅⋅ + s − p1 s − p2 s − pn
f ( t ) = L [ F ( s )]
−1
= k1e + k2e
p1t
p2 t
+ ⋅ ⋅ ⋅ + kn e
= ∫0 - ε( t − T ) × e
=e
− sT ∞ ' 0-
− αt
∞
− st
∞
− s ( t −T )
× e d (t − T )
− sT
∫ ε( t ) × e dt
−1
− st
'
'
1 -sT = e s
1 − sT ε( t − T ) ⇔ e s
1 -sT L [ e ] = ε( t − T ) s
m
m −1
2、 D(s)=0 有共轭复根。 、 有共轭复根。 D(s)=0有复根，则必须成对出现，为共轭复根。 有复根，则必须成对出现，为共轭复根。 有复根 有一对共轭复根： 设D(s)=0有一对共轭复根： 有一对共轭复根
f ( t ) = t = ∫0 ε( ξ)dξ
1 L[ε(t)] = s
1 1 1 L[ f (t)] = × = 2 s s s
4. 延迟性质
若 则
L[ f ( t )] = F ( s ) − st L[ f ( t − t0 )] = e F ( s )
0
函 原 数f(t) 数
函 象 数F 数 (s)
i
i
N ( pi ) N ( pi ) ki = ( s − pi ) = ' D( pi ) D ( pi )
k1 k2 kn F ( s) = + + ⋅⋅⋅ + s − p1 s − p2 s − pn
f ( t ) = L [ F ( s )]
−1
= k1e + k2e
p1t
p2 t
+ ⋅ ⋅ ⋅ + kn e
= ∫0 - ε( t − T ) × e
=e
− sT ∞ ' 0-
− αt
∞
− st
∞
− s ( t −T )
× e d (t − T )
− sT
∫ ε( t ) × e dt
−1
− st
'
'
1 -sT = e s
1 − sT ε( t − T ) ⇔ e s
1 -sT L [ e ] = ε( t − T ) s
m
m −1
2、 D(s)=0 有共轭复根。 、 有共轭复根。 D(s)=0有复根，则必须成对出现，为共轭复根。 有复根，则必须成对出现，为共轭复根。 有复根 有一对共轭复根： 设D(s)=0有一对共轭复根： 有一对共轭复根
第十三章 拉普拉斯变换电路
相量法(频 域分析法) 谐波分析 法(频域分 析法)
列解相量为 变量的线性 代数方程 列解相量为 变量的线性 代数方程
相量变换 变量频域形式的 KVL、KCL和VCR 激励的傅立叶级数 展开
任意激励 动态电路
？
？
？
13.1 拉普拉斯变换的定义
一.积分变换法 采用经典法列解微分方程去分析动态电路时，必须知道变 量及其各阶导数(直至n-1阶)在t=0+时刻的值，即变量的初始 条件。而电路中给定的初始状态是各电感电流和电容电压在 t=0+时刻的值，从这些值求得所需变量的初始条件工作量很大 ，也很困难，高阶动态电路中尤为突出。 积分变换法是通过积分变化，把已知的时域函数变换为频 域函数，从而把时域的微分方程化为频域函数的代数方程。求出 函数的频域解后，再做反变换，返回时域，求出满足电路初始条 件的原微分方程的时域解，而不需要确定变量的初始条件，即积 分常数。拉普拉斯变换和傅立叶变都是积分变换，但拉普拉斯变 换比傅立叶变换有更广泛的适用性，所以拉普拉斯变换法是求解 任意激励下高阶线性动态电路的有效而重要的方法之一。
二.傅立叶变换 周期函数如果连续或在一个周期内只有有限个第一类 间断点和有限个极值点，它能展开成收敛的傅立叶级数。即 周期函数可表示为成谐波关系的正弦函数的加权和。
f (t ) a0 (ak cos k1t bk sin k1t ) ＝A0 Akm cos(k1t k )
例13－2
二.微分性质
若L f t =F ( s )，则 L f ' t sF ( s ) f (0 )
例13－3 三.积分性质
t f t dt F ( s) 若L f t =F (s)，则 L 0 s
电路第十三章拉普拉斯变换
电路第十三章拉普拉斯变换第十三章拉普拉斯变换内容提要本章介绍拉普拉斯变换法在线性电路分析中的应用。
主要内容有：拉普拉斯变换的定义，拉普拉斯变换与电路分析有关的一些基本性质，求拉普拉斯反变换的部分分式法(分解定理),还将介绍KCL和KVL的运算形式，运算阻抗，运算导纳及运算电路，并通过实例说明它们在电路分析中的应用。
目录§13—1拉普拉斯变换的定义§13—2拉普拉斯变换的基本性质§13—3拉普拉斯反变换的部分分式展开§13—4运算电路§13—5应用拉普拉斯变换法分析线性电路本章作业13—1(2)(4)(6)(8)、13—2(1)(3)、13—3(2)(4)、13—4、13—12、12—16、12—18§13—1拉普拉斯变换的定义拉普拉斯变换是一种数学变换。
定义：F()=∫f(t)e–tdt0–∞S=σ+jω拉普拉斯正变换1σ+j∞F()etdf(t)=拉普拉斯反变换2πj∫σ–j∞拉氏正变换f(t)拉氏反变换F()=L[f(t)]原函数一一对应象函数f(t)=L–1[F()]F()简写符号例：计算下列原函数的象函数；1.f(t)=ε(t)2.f(t)=δ(t)∞0–3.f(t)=e–αtε(t)4.f(t)=tε(t)解：F()=∫f(t)e–tdt1.F()=L[ε(t)]=∫∞0–ε(t)e–tdt=∫0∞–e–tdt=0+1–t–e1=0–∞∞2.F()=L[δ(t)]=∫δ(t)e–tdt=∫δ(t)dt=10–0–∞3.F()=L[e–αtε(t)]=∫∞∞0–e–αte–tdt=1e–(α+)t–α+∞0–1=α+0–124.F()=L[tε(t)]=∫=–1[te–t0–同理：F()=L[tnε(t)]=n!n+1te–tdt–∫∞0–e–tdt]=§13—2拉普拉斯变换的基本性质一、线性性质若：L[f1(t)]=F1()L[f2(t)]=F2()则：L[A1f1(t)+A2f2(t)]=A1F1()+A2F2()证：L[A1f1(t)+A2f2(t)]=∫[A1f1(t)+A2f2(t)]e–tdt0–∞=∫A1f1(t)e–tdt+∫0A2f2(t)e–tdt0––∞∞=A1∫0f1(t)e–tdt+A2∫f2(t)e–tdt–∞∞0–=A1F1()+A2F2()例：计算下列原函数的象函数；1、常数U解：1、L[U]=L[Uε(t)]=U2、L[A(1–e–αt)]=L[A]–L[Ae–αt]=3、L[inωt]=L[1ejωt–2j11–=2j–jωαAA–A+α=(+α)2、A(1–e–αt)3、inωt1–jωte]2jω112j+jω=2+ω2同理：L[coωt]=22+ω二、(时域)微分性质设：L[f(t)]=F()则：L[f′(t)]=F()–f(0–)证：L[f′(t)]=∫∞df(t)0–dte–tdt=∫e–tdf(t)0–∞=e–tf(t)∞0––∫f(t)(–)e–tdt∞0–0–∞=–f(0–)+∫f(t)e–tdt=F()–f(0–)导数性质的意义在于把原函数求导数的运算转换为象函数乘以再减去初始值的代数运算。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
上页
下页
返回
66
拉普拉斯变换
一个定义在[ 0，∞ ) 区间的函数ƒ(t)，它的 拉普拉斯变换式F(s)定义为 F ( s ) = ∫ − f ( t )e − st dt
0 ∞
(13-1)
式中s=σ +jω 为复数，F(s)称为ƒ(t)的象函数、 ƒ(t)称为F(s)的原函数。拉普拉斯变换简称拉氏 变换。F(s) 可用符号L[ ƒ(t) ]表示. 式（13-1）表明拉氏变换是一种积分变换。
式中 c为正的有限常数。用符号L -1[F(s)]表示对 方括号里的复变函数作拉氏反变换。
哈尔滨理工大学 王竹萍
PDF 文件使用 "pdfFactory Pro" 试用版本创建
上页
下页
返回 9
常用函数的拉氏变换表
原函数 f(t) 象函数 F(s) 原函数 f(t) 象函数 F(s) ω A Aδ(t) sin(ωt) s2 + ω 2 ω A Aε(t) e-αtsin(ωt) 2 2 ( α ) ω s + + s s A 2 2 cos(ωt) Ae-αt s + ω s +α 1 s +α 1 n −αt t e -αtcos(ωt) n +1 e (s + α ) ( s + α )2 + ω 2 n!
uC (0 -) 1 RI ( s ) + sLI ( s ) − Li (0- ) + I ( s) + = U S ( s) sC s uC (0- ) 1 R + sL + I ( s ) = U S ( s ) + Li (0- ) − sC s
哈尔滨理工大学 王竹萍
哈尔滨理工大学 王竹萍
PDF 文件使用 "pdfFactory Pro" 试用版本创建
上页
下页
返回 15
思考 思考
i (t ) ª
已知uS(t) 求i(t) 。 uR(t) + -
根据KVL, KVL 有 + + R uR(t)+uL(t)+uC(t) =uS(t), t ≥0 uS(t) u ( t ) L L C di 1 t - u (t)+ Ri + L + ∫0- i (ξ )dξ + uC (0- ) = uS ( t ) C dt C 两边取拉氏变换
哈尔滨理工大学 王竹萍
PDF 文件使用 "pdfFactory Pro" 试用版本创建
上页
下页
返回 13
3.积分性质 函数ƒ(t)的象函数与其积分 ∫0 f (ξ )dξ 的象函数 − 之间有如下关系: 若L [ƒ(t)] = F(s), 则 F ( s) L [ ∫ f (ξ )dξ ] = s
PDF 文件使用 "pdfFactory Pro" 试用版本创建
Pierre Simon Laplace( Laplace 1749-1827), a French astronomer and
拉 普 拉 斯
上页 下页 返回 2
Historical Profiles
上页
下页
返回
44
已知uS(t), 求t>0时，i(t) 。
思考 思考
u (t ) + R + + R uS(t) uL(t) L C - u (t)+ i (t ) ª
C
S(t=0)
t>0时，根据KVL, KVL 有 uR(t)+uL(t)+uC(t) =uS(t), t ≥0 di 1 t Ri + L + ∫0- i (ξ )dξ + uC (0- ) = uS ( t ) dt C 以上属于高阶微分方程的求解问题。
哈尔滨理工大学 王竹萍
PDF 文件使用 "pdfFactory Pro" 试用版本创建
上页
下页
返回 12
2.微分性质 df ( t ) 函数ƒ(t)的象函数与其导数 f ′( t ) = 的象函数 dt 之间有如下关系: 若 L [ƒ(t)] = F(s), 则 df ( t ) L [ f ′( t )] = L [ ] = sF ( s ) − f (0- ) dt
哈尔滨理工大学 王竹萍
PDF 文件使用 "pdfFactory Pro" 试用版本创建
上页
下页
返回 10
§13-2 拉普拉斯变换的基本性质
Proerties of the th Laplace Transform 1.线性性质 2.微分性质 3.积分性质 4.延迟性质
哈尔滨理工大学 王竹萍
PDF 文件使用 "pdfFactory Pro" 试用版本创建 上页下页Fra bibliotek返回 7
ƒ(t) 的拉氏变换F(s)存在条件是该式右边的积 分为有限值, 故e-st 称为收敛因子。对于一个函数ƒ(t)， 如果存在正的有限值常数M和 c, 使得对于所有 t 满足 条件 |ƒ(t)|≤M ect 则 ƒ(t) 的拉氏变换式F(s)总存在，因为总可以找到 一个合适的 s 值,使式（13-1）中的积分为有限值。假 设本章涉及的ƒ(t)都满足此条件。拉氏变换是把一个 时间域的函数ƒ(t)变换到 s 域内的复变函数F(s)。变量 s 称为复频率。应用拉氏变换法进行电路分析称为电 路的一种复频域分析方法，又称为运算法。
第十三章
§13-1 §13-2 §13-3 §13-4 §13-5
拉普拉斯变换
拉普拉斯变换的定义 拉普拉斯变换的基本性质 拉普拉斯反变换的部分分式展开 运算电路 应用拉普拉斯变换法分析线性电路
哈尔滨理工大学 王竹萍
PDF 文件使用 "pdfFactory Pro" 试用版本创建
哈尔滨理工大学 王竹萍
PDF 文件使用 "pdfFactory Pro" 试用版本创建
上页
下页
返回 8
拉普拉斯反变换
如果F(s)已知，要求出与它对应的原函数ƒ(t)，由 F(s)到ƒ(t)的变换称为，它定义为 1 c + j∞ st f (t ) = F s e ds ( ) ∫ 2πj c − j∞ (13-2)
上页
下页
返回 1
Historical Profiles
mathematician, first presented the transform that bears his name and its applications to differential equations in 1779. B Born of humble origins in Beaumont-en- Auge, Normandy, France, Laplace became a professor of mathematics at the age of 20. His mathematical abilities inspired the famous mathematicain Simeon Poisson, who called Laplace the Isaac Newton of France. He made important contributions in potential theory, probability theory, astronomy, and celestial mechanics. He was widely known for his work, Traite de Mecanique Celeste(Celestial Mechanics), which supplemented the work of Newton on astronomy. The Laplace transform, the subject of this chapter, is named after him. 哈尔滨理工大学 王竹萍
哈尔滨理工大学 王竹萍
PDF 文件使用 "pdfFactory Pro" 试用版本创建
上页
下页
11 返回 11
本节仅介绍与分析线性电路有关的一些拉普拉斯 变换的基本性质。 1.线性性质 设ƒ1(t)和ƒ2(t)是两个任意的时间函数，它们的象函 数分别为F1(s)和F2(s)，A1和A2是两个任意实常数，则 L [A1ƒ1(t) +A2ƒ2(t)] = A1L [ƒ1(t)] + A2L [ƒ2(t)] = A1F1(s) + A2F2(s) L [A1ƒ1(t) +A2ƒ2(t)] = A1F1(s) + A2F2(s)
t 0− t
哈尔滨理工大学 王竹萍
PDF 文件使用 "pdfFactory Pro" 试用版本创建
上页
下页
返回 14
4.延迟性质 函数ƒ(t)的象函数与其延迟函数ƒ(t-t0)的象函数之 间有如下关系: 若 L [ƒ(t)] = F(s) , L [ƒ(t-t0)]=e-st0F(s)
PDF 文件使用 "pdfFactory Pro" 试用版本创建
上页
下页
返回 16
UR(s) + + R i (t ) uR(t) + sL + ª UL(s) U ( s ) 1 S u ( 0 ) + C - Li(0-) + R uS(t) uL(t) sC - s + L C - u (t)+ - UC(s) + C uC (0 -) 1 RI ( s ) + sLI ( s ) − Li (0- ) + I ( s) + = U S ( s) sC s uC (0- ) 1 R + sL + I ( s ) = U S ( s ) + Li (0 -) − sC s uC (0- ) U S ( s ) + Li (0 -) − −1 s i ( t ) = L [ I ( s )] I ( s) = 1 R + sL + 上页 下页 返回 17 sC 哈尔滨理工大学 王竹萍