Fuzzy Logic Based Modified...(IJISA-V8-N5-7)
基于模糊的多发烧症状分类器诊断模型(IJITCS-V9-N10-2)

I.J. Information Technology and Computer Science, 2017, 10, 13-28Published Online October 2017 in MECS (/)DOI: 10.5815/ijitcs.2017.10.02Fuzzy Based Multi-Fever Symptom ClassifierDiagnosis ModelIghoyota Ben Ajenaghughrure and Dr. P. SujathaVels University, Department of computer science, Chennai, 600117, IndiaIghoyotaben@, suja.research@Dr. Maureen I. AkazueDelta State University, Department of Computer Science, Abraka, 330106, NigeriaAkazuem@Received: 08 November 2016; Accepted: 31 August 2017; Published: 08 October 2017Abstract—Fever has different causes and types, but with similar symptoms. Therefore, making fever diagnosis with human physiological symptoms more complicated. This research project delves into the design of a web based expert multi-fever diagnosis system using a novel fuzzy symptom classifier with human self-observed physiological symptoms. Considering malaria, Lassa, dengue, typhoid and yellow fever. The fuzzy-symptom classifier has two stages. Fist stage is fever type confirmation using common fever symptoms, leading to five major fuzzy rules and the second phase is determining the level of infection (severe or mild) of the confirmed type of fever using unique fever symptoms. Furthermore, Case studies during the system implementation yielded data collected from 50 patients of having different types of fever. The analysis clearly shows the effectiveness and accuracy in the system performance through false result elimination. In addition, acceptability of the system was investigated through structured questionnaire administered to same 50 patients. This result clearly indicates that the system is well accepted, by users and considered fairly easy to use, time and cost saving.Index Terms—Fuzzy classifier, fever diagnosis, multi fever, expert fever diagnosis.I.I NTRODUCTIONFever is a change in the human body temperature, both minimum and maximum [4],[5]. During this condition, a sufferer generally experiences cold and muscle seizure [3], resulting to alteration of body temperature regulation system producing more heat in a bid to sustain normal body temperature, which when restored, leads to excessive sweating[25]. Although there is discrepancy in the normal human temperature [1],[2], but fever occurs in body temperature between the range 41 to 42 °C (105.8 to 107.6 °F)[5].The causes of fever varies from infectious to non-infectious diseases, but the case of body temperature changes also referred to as hypothermia is completely different[7]. Since it is not a result of either causative above. Treatment of both fever and hyperthermia to reduce or subside its presence is not necessary[6],[24], but a direct treatment of its associated symptoms such as muscle pains, headache etc is considered more useful[8], using common drug such as paracetamol to more intensive care methodology, depending on the severity of the sufferers health status[8],[9]. Being a common symptom of most health problem, fever is accountable for approximately 30% of children healthcare-centers visit [6] and dominates up to 75% of critically ill adults [10].The common types of fever widely reported with scientifically available medication includes malaria, dengue, typhoid, Lassa, and yellow fever. These has great similarities in sympt om’s irrespective of carriers, infection type(bacteria, virus etc) and treatment. This relationship between various types of fever symptoms, makes diagnosis of fever with human physiological symptoms is difficult, for example symptoms of Lassa is very hard to differentiate from those of malaria, yellow, dengue and typhoid fever [11],[12]. In addition to the high cost associated with acquiring wet lab fever diagnosis service, lack of medical expert availability and accessibility, has prompted the development of computer aided expert fever diagnosis systems for diagnosing single or multiple types of fever. Unfortunately, the existing computer based expert fever diagnosis systems do not take symptoms relationship into consideration, which has significant impact on the accuracy of the fever diagnosis results they produce. To overcome this challenge, a fuzzy-based multi-fever symptom classifier for fever diagnosis implemented as a web system for accessibility is proposed and designed in this research. The fuzzy-based multi-fever symptom classifier put into consideration all the various types of fever related symptoms, and accurately determine the type fever and level of infection (mild/acute) a patient is suffering from, based on user input of physiological symptoms. The implemented fuzzy-based multi-fever symptoms classifier is known as e-fever portal. Fuzzy technique derived from artificial intelligence was specifically chosen, because of its longstanding successful applicationin health related application. This research only considers the use of human physiological symptoms to diagnose fever. In addition, it does not take into account a critically ill patient who cannot speak, walk e.tc. Furthermore, it does not serve as a total replacement for expert medical practitioners, but as an assistive solution to fever diagnosis. Finally our study solely encompasses five types of fever (malaria, dengue, yellow, Lassa and typhoid).This research paper is divided into seven sections. The first section is an introductory overview of the research paper, while the second is review of related literature. The third section is a comparative study between existing fever diagnosis system and the proposed fuzzy based multi-fever symptom classifier diagnosis system. Furthermore, the fourth section encompasses the design of the fuzzy based multi-fever symptom classifier and the e-fever web application architecture. The fifth section is the implementation and acceptability data analysis of the proposed system. The sixth section is conclusion based on findings from the system implementation.II.R ELATED W ORKSThe application of artificial intelligence techniques in fever diagnosis towards optimizing diagnostics results accuracy has been adopted by several researcher amongst which includes: (1) [26], which developed a system named diagnosis portal for human disease diagnosis based on human physiological symptom. The system did not focus on fever diagnosis, but exhibited the applicability and importance of fuzzy logic in medical diagnosis. Disease such as sleep apnea, irritable bowel syndrome, and attention deficit hyperactivity disorder. This project further proved and support the long growing research in application of fuzzy in medical diagnosis. (2) In addition, [27] carried out an in-depth review on the applications of fuzzy logic in expert medical diagnosis systems, as an important technique useful in expert medical system. Through in-depth review on existing fuzzy expert medical diagnosis system. Their result shows significant success and adaption of artificial intelligence technique in expert computer aided medical diagnosis systems. (3) Furthermore, to enhance the accuracy of artificial intelligent based expert medical diagnosis system, [28] developed a genetic algorithm to enhance optimum performance of neuro-fuzzy systems used for diagnosis of typhoid. This is to ensure accuracy of result, which in an ordinary neuron fuzzy based typhoid fever diagnosis system, is computed with errors. This is an advancement on the performance of typhoid fever diagnosis systems based on neuro-fuzzy , but its applicability on other fever types was not considered, as well as symptoms interrelationship among different fever types was not also considered in the neurofuzzy system.(4) A computer aided malaria fever diagnosis system was developed using the rough set theory machine learning technique, implemented as a web based application [20]. While the correctness of the result of the training and testing data are 100% and 94% being promising solution. It lack the consideration of various fever symptoms relationships which could hinder the correctness of malaria fever diagnosis in the case of multiple infection [20]. (5) Furthermore, [21] developed a web based multi-fever diagnosis system based on simple if-then rules for diagnosing malaria, dengue, typhoid, Lassa, Hay, pee-ebstein, leptospirosisscarlet and rheumatic fever. Quiet an integrated novel system, but the result will be prone to error due to the lack of the various types of fever symptoms relationships consideration. Although it promises to speedup medical diagnosis and treatment administration time. (6) Also, [22] proposed a fuzzy logic based malaria fever diagnosis system, using UML simulation, with the sole aim of speeding up the diagnosis process, time and reducing embodiment on medical professionals. Although quiet promising due to the optimistic success shown by fuzzy application in medical diagnosis this system lacks implementation. (7) In addition, [23] developed a malaria fever diagnosis system incorporating intelligence and expertise using fuzzy logic. The results of these systems reviewed so far seem accurate and perfect solution for timely and effective diagnosis of malaria, if only malaria fever symptoms are reported by patients and are not similarly to other types of fever general symptoms, which is not possible. Hence rendering the results from existing system in question of accuracy since malaria fever share some common symptoms with other types of fever.Most Computer aided expert fever diagnosis systems developed by researchers so far are broadly classified into two categories as either multi or single fever diagnosis system. S. Govinda et al [29] developed a ruled based expert multi fever diagnosis system that diagnoses dengue, malaria and typhoid fever using fuzzy logic. The result is the type of fever, its level of infection (severe or mild), and recommended food and drugs. This system fail to consider the interlink between types of fever through symptoms similarity, hence the diagnosis results accuracy cannot be ascertain in this context. Furthermore, [19] developed a fuzzy based malaria and dengue fever diagnosis system. The system was developed using MATLAB fuzzy toolbox GUI. This novel system, diagnoses malaria and dengue fever effectively, but lack consideration of interrelationship of symptoms, making the result of this system uncertain in terms of validity. While single fever diagnosis systems, as seen in [14], which developed a clinical machine learning based expert typhoid fever diagnosis system,. Although the result from this research seem promising , as a computer based typhoid fever diagnosis system with implementation and therapy, but it fails to put into account the symptoms relationship between typhoid and other fever types, which when considered renders the diagnosis rule developed here invalid as some will lead to other fever types. Also, [15] developed a non-invasive cost effective adaptive neuron fuzzy based dengue fever patient risk level diagnosis system, to diagnose dengue fever accurately and determine the risk level of a patient. In order to avoid unwanted hospitalization and its associated cost. Although the system seem effective, but solelyconcentrated on dengue fever and its symptoms alone, hence making its diagnosis results accuracy subject to wet lab test, due to its non-inclusion of system relationship. In addition, [16] developed a web-based expert system to diagnose dengue fever. This system enables easy access to diagnosis and self-diagnosis of dengue fever from normal fever. Quit novel, but its results lack the credibility, as the project did not consider symptom relationship, which has great impact on the diagnosis result. Furthermore, [17] developed a fuzzy logic based expert typhoid fever diagnosis system. The system is a web application to enable accessibility. Unfortunately, the system still did not consider symptoms relationship, which renders the validity of the system diagnosis result uncertain. In addition, [18] developed a fuzzy expert system for management of malaria. Although quit novel, the system did not also consider symptoms relationships among the various types of fever, hence, leaving the results from the system uncertain, in terms of validity and accuracy, despite the practical approach towards real life data collection .in addition to the fact that it only considered malaria fever symptoms. Hence, the proposed fuzzy-based multi-fever symptom classifier is a novel method that promises to optimize the accuracy of multi-fever diagnosis.III.C OMPARATIVE A NALYSIS OF E XISTING ANDP ROPOSED E XPERT F EVER D IAGNOSIS S YSTEMSThe table1 shows analysis comparing some existing expert fever diagnosis system, using indicators such as single or multiple fever diagnosis capability, inclusion of artificial intelligence technique, therapy recommendation, symptom relationship from numerous types of fever well successful in medical diagnosis application, symptom relationship and implementation. The numbers 29, 14, 15, 16, 17, 18, 19, 20, 21, 22, and 23 are references for articles containing the respective expert fever diagnosis systems under review for comparison.We can clearly see that not all-existing system considered the impact of fevers symptoms relationship, as an important factor during fever diagnosis using human physiological symptom, which can affect the diagnosis result negatively.Table 1. Comparative analysis of existing expert fever diagnosis systems and our proposed fever diagnosis system 29, 14, 15,16, 17, 18, 19, 20, 21, 22, and 23Furthermore, the authors of [29], [19] and [21] research work attempted diagnosing multiple fever in their system using artificial intelligence technique. While the authors of [15], [16], [17], [18], [19], [20], [21], [22] and [23] designed a single fever diagnosis system. To further support the importance of artificial intelligence technique in medical diagnosis, the systems developed by authors in [29], [14],[15], [16], [18], [19], [20], [21], [22], and [23] all utilized artificial intelligence technique. Furthermore, we can infer that only our proposed system has multi-fevers symptoms relationship considered, hence making it not just a novel system, but necessary for effective diagnosis of fever as a result of the complication involved in physiological symptoms based diagnosis of fever.IV.I MULTI-F EVER S YMPTOM R ELATIONSHIPAn indepth study was conducted on malaria, dengue, Lassa, yellow and typhoid fever symptoms to identify common symptoms. During which, literature review and interview were used as the technique for collecting information about these types of fever. The results reveal symptoms relationship between malaria, dengue Lassa, yellow and typhoid fever. These common symptoms were classified as general symptoms, while symptoms unique to each type of fever were classified as unique. It can be inferred that fever is the most common symptom of all the five types of fever under study. Followed by headache and vomiting, that is common to four. Next common symptoms are conjunctiva, nausea, abdominal pain, diarrhea, malaise, and muscular pains, which are common to only three types of fever randomly permuted. Finally severe hepatitis, shivering/chills, cough, and mucosal bleeding are the less common symptoms, but found in any two type of fever under study. All other symptoms are unique to a particular fever, or common to two or three types respectively.Table 2. Fever symptom relationshipV.D ESIGN O F F UZZY B ASED M ULTI-F EVER D IAGNOSISS YMPTOM C LASSIFIERAs depicted in table2 above, its is obvious that there are similarities in symptoms among various types of fever, hence rendering fever diagnosis more difficult with physiological signs. Therefore, the fuzzy based multi-fever symptoms classifier for accurate diagnosis proposed in this study is designed in this section as shown in the fig1. The fuzzy based multi-fever symptom classifier consists of three major stages. At the first stage, each input symptom is classified as general symptom and unique symptom in order of entry. The general symptoms input are arranged as the first sets of input variables of the fuzzy model. These will determine the type of fever a patient is suffering from. While the unique symptoms are used to determine the level of infection of the confirmed type of fever. The second stage is a further classification of the symptoms as mild or severe, to determine the level of infection of the confirmed type of fever using membership function and rule. The third level is the inference engine of the fuzzy based symptom classifier that comprises several rules to determine the output of the fuzzy classifier. The finally stage is the output stage, which gives two results the type of fever confirmed and the level of infection. Hence, the fuzzy based classifier is a multi-input and multi-output fuzzy model. Where all the five types of fever symptoms serves as input to the fuzzy system, and two types of output corresponding to fever types confirmed and the level of infection of the confirmed type of fever(severe or mild) are produced.Fig.1. Proposed model of fuzzy based multi-fever ymptom classifier for e-fever portalA. Fuzzy system components ∙Input:The fuzzy based multi-fever symptom classifier Model for the e-fever portal inputs variables are the symptoms responses from users. These responses are classified into the following fuzzy linguistics variables and their corresponding values as recorded table3.Table 3. Fuzzy based multi-fever symptom classifier model for e-feverportal input variables linguistics and numerical valuesThese values for the linguistics variable are mapped to all the symptoms in table2. The general and unique symptom classification is silent but very important to the diagnosis process through the arrangement of the system input variable; therefore, all first few inputs are general symptoms, while the last sets of inputs are unique symptoms. Similarly, in the e-fever portal implementation of the fuzzy classifier, patients respond to general symptoms questions before unique symptoms related question.The triangular membership (MF) is used which Is specified by the three parameters {a,b,c} for each membership function x = (mild, severe), denoted mathematically asFever symptom (A:a,b,c) = max(min(,1x a c xb c b----),0) [13] (1)Where parameters a,b,c determines the x coordinates of the three corners of the underlying triangular membership function.∙ Fuzzy inference engine/system:This is the brain and Intelligence of the fuzzy based multi-fever symptom classifier for the e-fever portal. it takes the premise as input and produces different consequences as output. The premise here are the symptoms, which are represented with numerical values and the consequence here, is the type of fever confirmed and the level of infection. Hence, the inference engine is referred to as the fuzzy inference system, mainly consisting of the fuzzy RULE, which is described in detail belowRules: the fuzzy system rules, first confirms the type of fever, and then confirm the level of infection consequently. Following table2 analysis, we can clearly infer that Fever, Headache, Vomiting, Nausea, Abdominal pains are the most common symptoms among the five types of fever under study. Hence, our fuzzy rule uses these five symptoms to confirm the type of fever infection, before further investigation into the level of infection of the confirmed type of fever is done. The first five rules confirms the various types of fever without level of infection known, next an in-depth analysis base on further user responses to symptoms, reveals the level of infection.∙ If fever =yes and headache=yes and vomiting=yes,and nausea=yes and abdominal pain=yes then fever type = yellow fever and level of infection = unknown∙ If fever =yes and headache=yes and vomiting=yes,and nausea=yes and abdominal pain=no and others = no then fever type = malaria fever and level of infection = unknown∙ If fever =yes and headache=yes and vomiting=yes,and nausea=no and abdominal pain=yes and others =no then fever type = dengue fever and level of infection = unknown∙ If fever =yes and headache=yes and vomiting=no,and nausea=no and abdominal pain=no and others = no then fever type = typhoid fever and level of infection = unknown∙If fever =yes and headache=no and vomiting=yes, and nausea=yes and abdominal pain=no others = no then fever type =Lassa fever and level of infection = unknown B. Fever Type Confirmation And Infection Level Detection Technique:Symptoms already hold numerical values classifying them as either mild or severe symptoms, as seen in table3 for all symptom in table2. Hence determining the type of infection, and the level of infection, can be done by summing up all the symptoms numerical values, for each patient response during diagnosis. Mathematically expressed below:F x = M symptom + S symptom (2)M symptom = 1nSV∑ (3)S symptom = 1n SV ∑ (4)Where SV is symptom corresponding numeric value for each class of symptom.M symptom is the sum of all the numerical values corresponding to general symptoms for confirming the type of fever that are responded to by patient during diagnosis.S symptom is the sum of all the numerical values corresponding to unique symptoms for confirming the type of fever that are responded to by patient during diagnosis.Y= all symptoms values (i).i= number of symptoms.Where x = any fever (malaria, dengue, Lassa, yellow, typhoid) confirmed and the level of infection C. Expert System Design:The proposed e-fever portal implementing the novel fuzzy classifier designed comprises of two modules. The first module is an educational module, consisting of additional five-sub module. Each education modules contains information relevant to each of the five types of fever under study, their causes, symptoms and few precautionary measures. While the second module is the diagnosis module implementing the fuzzy based classifier designed in this research project as a two state system, corresponding to two more sub module, the first diagnosis sub module confirms the type of fever, using the general symptoms. In addition, the last diagnosis module determines the level of infection of the confirmed type of fever ∙Education module :This module consists of detailed information about the various types of fever. it is subdivided into five modules, each of which consist of detailed information about thevarious types of fever (lassa, dengue, malaria, typhoid and yellow fever) . Such as, symptoms, history, geographical location infected, treatments and general advices ∙Diagnosis Module:This is the module where patient self-diagnose themselves to identify the type of fever they are suffering from, through inputted selfFig.2. E –fever portal architectureDiagnosis flow chart of the e-fever portal: fig3 depicts the typical flowchart of the e-fever portal. It consists of two stages. Firstly begins with fever symptom, if a response this question is ―NO‖, then there is no point proceeding further, as the user is currently not suffering from fever. Else, it continues to ascertain the type of fever the patient is suffering from, before advancing to the second stage to identify the level of infection using unique symptoms of the confirmed type of feverFig.3. Fuzzy based integrated expert fever diagnosis system FlowchartVI.D ATA A NALYSISData were collected from several fever patients with medial records cards from government and privately operated health centers. A total of 50 participants were exposed to the e-fever portal. 28% were female and 72% male, with an average age of 25years. Their response to the symptoms questions were recorded automatically into the system database. As presented in table4. The collected data were analyzed using descriptive statistic technique (bar char, pie chart histogram etc) for the sole purpose of clarity and better interpretation of the results.Table 4. Sample data of various fever patientsA. General Symptoms Confrimation Of Fever Type Applying eq(3) to the general symptoms entries(first five rows) in table4 above, the results is presented graphically in fig4 below. We can clearly see the demarcation between the various types of fever confirmed (malaria, dengue, typhoid, lass and yellow fever), as each patients in each group of fever type have same general symptoms value. Also, a group with higher general symptom value includes all symptoms of other fever types with lower general symptom value.. For example, the symptoms difference between p1 to p10, and p11 to p19 are symptoms not reported by patients p1 to p10 but are reported by p11 to p19 patients who also reported symptoms of p1 to p10 as well. Similarly, p1 to p10 patients has reported all symptoms reported by p20 to p30 patients and some extra symptoms not reported by p20 to p30 patients. In addition, p31 to p42 patients has reported more symptoms than p43 to p50 patients but p31 to p42 patients also reported all symptoms reported by p43 to p50 patients as well. Furthermore, p1 to p10 patients has reported slightly few symptoms than p43 to p50 patients, although p43 to p50 patients all reported symptoms reported by p1 to p10 patients as well. Hence, increasing the accuracy of fever type diagnosis with physiological symptoms.Fig.4. General symptoms summation and the type of fever confirmedFurthermore, an extension of the general symptom analysis, applying eq(3) is presented in fig4 below, showing all the confirmed types of fever. Here, dengueand yellow fever infected patients is nine (9) each, malaria, and typhoid infected patients is 11 patients each, and Lassa fever infected patients is 10.Fig.5. Type of fever confirmed with number of patients.B. Unique Symptoms Confirmation Of Level Of Infection Furthermore, an analysis on the confirmed type of fever to determine their level of infection using unique symptoms reported by patients and applying eq(4). The summary of all unique symptoms reported by all fifty patients are analyzed in the bar-chart FIG6 below, to better visualize the unique symptoms patterns. The graph clearly pictures a vast variation in the unique symptoms reported by all patients irrespective of the type of fever confirmed. For example patients p1, p19, p20, and p43 did not report any other symptoms, irrespective of the type fever confirmed Hence further supporting the variation of level of infection among patients of the same type of fever and different type types of fever as either severe or mild.Applyign eq(3) to table4 above, for each patient, the summation of general symptom reported is obtained and presented graphically in fig4. Clealry we can see that each group of patients has equal number of general symptom reported value, that distinugish each of the types of fever under study. Furthermore, the type of fever confirmed for each group in fig4 is presented in fig5 . Therefore, confirming malaria and typhoid fever being the highest with 11 patient ptients each. While lassa fever had 10 patients and the The laeast was dengue and yelow fever with 9 patients each.Furthermore, Applying eq(4) to table4 above, the totalunique symptoms values of unique symptoms reported by each patient after corresponding to the type of fever confirmed above is obtained and graphically presented in fig6 . It can be observed that, though at fever type confirmation stage in fig4&5 above, all patients has the same general symptom total value for each types of fever confirmed clearly dinstinuishing the various types of fever, but the reverse is the case in confirming the level of infection. Clearly we observe visually the unequal total unique symptom values in fig6 , which is an evidence to the variation to the level of infection of the confirmed type of fever for each patient, further supported by the variation in the number of unique symptoms reported by each patients.Furthermore applying eq(2) to table4 is a combination of the result from applying eq(3) and eq(4) to table4 above, which is also equivalent to the combination of fig4 and fig6. This outcome is the total integrated diagnosis result for each patient with confirmed type of fever infection and level of infection, which is represented in fig7. We can clearly observe great variation between patient symptoms values infig6 and fig7, which further implies that the level of infection has to do with the number of severe and mild symptoms irrespective to general or unique symptom classification since this only helps in stepwise diagnosis. A patient may have higher total symptom value but will be in mild state because he/she has not reported occurrence of any additional。
Fuzzy Logic and Systems

Fuzzy Logic and SystemsFuzzy logic and systems have become increasingly important in various fields, including engineering, artificial intelligence, and decision-making processes.This approach allows for the modeling of vague and uncertain information, which is often encountered in real-world scenarios. Fuzzy logic provides a framework for dealing with imprecision and ambiguity, offering a more flexible and realistic way to represent and process data. From an engineering perspective, fuzzy logic has been widely applied in control systems. Unlike traditional binary logic, whichonly deals with true or false values, fuzzy logic allows for the representation of partial truths. This is particularly useful in control systems where inputs and outputs may not always be clearly defined. By using fuzzy logic, engineers can create more robust and adaptive control systems that can handle imprecise input data and respond in a more human-like manner. In the realm of artificial intelligence, fuzzy logic plays a crucial role in mimicking human reasoning. Human thinking is often characterized by its fuzziness, as people make decisions basedon vague and incomplete information. Fuzzy logic enables AI systems to emulatethis aspect of human cognition, allowing them to make more human-like decisions in uncertain and complex environments. This has significant implications for applications such as natural language processing, image recognition, and expert systems. Moreover, fuzzy logic has also found its way into decision-making processes, where it offers a more natural and intuitive approach to handling uncertainty. In fields such as economics, finance, and risk management, decision-makers often have to deal with imprecise and conflicting information. Fuzzy logic provides a means to model and analyze this uncertainty, enabling decision-makersto make more informed and nuanced choices. On the other hand, some critics argue that fuzzy logic may introduce unnecessary complexity and subjectivity into systems. They contend that traditional binary logic is often sufficient for many applications and that the introduction of fuzziness may lead to less transparent and more difficult-to-understand systems. Additionally, there are concerns about the potential misuse of fuzzy logic, particularly in safety-critical systems where precision and determinism are paramount. Despite these criticisms, it is clearthat fuzzy logic and systems have made significant contributions to various fields.The ability to handle imprecise and uncertain information is a crucial aspect of real-world problem-solving, and fuzzy logic provides a valuable tool for addressing this challenge. As technology continues to advance, the role of fuzzy logic is likely to expand, offering new ways to model and understand the complexities of the world around us.。
关于fuzzy logic的简述(英文)

My Understanding about Fuzzy LogicWhen it comes to fuzzy logic, there are different kinds of definitions and understanding about this concept. However, in essence, I think,these definitions and understanding are similar. Because the fuzzy is based on the uncertainty of abstract thinking and concept, as well as the imprecise nature of things. As my understanding of fuzzy logic is superficial, so I have to use a relatively perfect definition to express my thought.In narrow sense: Fuzzy logic is a logical system, which is an extension of multi-valued logic.In a wider sense: Fuzzy logic (FL) is almost synonymous with the theory of fuzzy sets, a theory which relates to classes of objects with unsharp boundaries in which membership is a matter of degree.----- by Mahesh Todkar Fuzzy logic is not the unclear logic. Actually, it is founded on the fuzzy set, which was put forward by Pro. Zadeh in 1965. Then Zadeh developed fuzzy logic as a way of processing data. Instead of requiring a data element to be either a member or non-member of a set, he introduced the idea of partial set membership.Fuzzy logic is a method between the symbolic reasoning of traditional artificial intelligence and numerical computing theory of the conventional control. It does not rely on the model, it uses linguistic variables to represent the abstract variables and uses rules for fuzzy reasoning and processing. Moreover, it is also featured in its recognition of the intermediate transitional between true value ( True ) and false value ( False ).Hence, the most essential concept for fuzzy logic is the membership function, which defines how each point in the input space is mapped to a membership value between 0 and 1. The membership function is denoted by μ and also called as degree of membership or membership grade or degree of truth of proposal. There are many types of membership functions, like Piece-wise linear functions, Gaussian distribution function, Sigmoid curve and Singleton Membership Function etc.In addition, we should pay the major attention to the fuzzy inference, which is the process of formulating the mapping from a given input to an output using fuzzy logic.It involves Membership Functions (MF), Logical Operators and If-Then Rules. The MF is mentioned above, so an introduction about Logical Operators and If-Then Rules will be presented as followed.Fuzzy Logic Operators are used to write logic combinations between fuzzy notions.As for Zadeh operators, its definitions are :1)Intersection: μ(A AND B) = MIN(μ(A), μ(B))2)Union: μ(A OR B) = MAX(μ(A), μ(B))3)Negation: μ(NOT A) = 1 -μ(A)Fuzzy If-Then Rules are the statements used to formulate the conditional statements that comprise fuzzy logic. For example:if x is A then y is Bwhere,A &B – Linguistic values x – Element of Fuzzy set X y – Element of Fuzzy set YIn above example,Antecedent (or Premise)– if part of rule (i.e. x is A)Consequent (or Conclusion) – then part of rule (i.e. y is B)Here, interpreting if-then rule is a three–part process:1) Fuzzify input:Resolve all fuzzy statements in the antecedent to a degree of membership between 0 and 1.2) Apply fuzzy logic operator to multiple part antecedents:If there are multiple parts to the antecedent, apply fuzzy logic operators and resolve the antecedent to a single number between 0 and 1.3) Apply implication method:The output fuzzy sets for each rule are aggregated into a single output fuzzy set. Then the resulting output fuzzy set is defuzzified, or resolved to a single number.In general, from my perspective, compared with conventional binary logic, fuzzy logic is a breakthrough for the classification of things. To some degree, fuzzy logic makes the uncertainty and imprecision clearer. Though the membership functions vary from person to person, which indicates that fuzzy logic is subjective, its advantages are explicit. Just asMr. Hu Baoqing(from Wuhan University) notes that Benefits of Fuzzy Mathematics are:①The ability to model highly complex business problems②Improved cognitive modeling of expert system③The ability to model systems involving multiple experts④Reduced model complexity⑤Improved handling of uncertainty and possibilities……。
Fuzzy logic-based evidence fusion tool for network

专利名称:Fuzzy logic-based evidence fusion tool for network analysis发明人:Michael D. Smith,Allen R. Bonde, Jr.,Gregory J. Catherine,Rosemarie Napolitano,Diane M.Wolfe申请号:US08/437732申请日:19950509公开号:US05787235A公开日:19980728专利内容由知识产权出版社提供摘要:A fuzzy-logic-based evidence fusion tool for predicting function levels of a switch in a telecommunications network. Confidence factors related to the geographical location and to the physical characteristics of the switch are acquired and mapped into fuzzy membership values. The membership values activate a set of fuzzy evidence fusion rules at each function level, and a degree of truth for each rule is inferred. A defuzzification scheme combines the degree of truth of each rule into a single combined confidence factor for each function level. Finally, the maximum combined confidence factor for each rule is determined, and the switch function level corresponding to that confidence factor is assigned to the switch.申请人:GTE GOVERNMENT SYSTEMS CORPORATION代理人:Leonard C. Suchyta更多信息请下载全文后查看。
Fuzzy Logic and Systems

Fuzzy Logic and SystemsFuzzy logic is a fascinating concept that has revolutionized the way we approach decision-making and problem-solving in various fields, includingartificial intelligence, control systems, and pattern recognition. Unlike traditional binary logic, which relies on crisp values of true or false, fuzzy logic allows for a more nuanced approach by incorporating degrees of truth between 0 and 1. This flexibility enables us to capture and process complex, uncertain, and imprecise information more effectively, mirroring the way humans think and make decisions. One of the key advantages of fuzzy logic is its ability to handle ambiguity and vagueness, which are inherent in many real-world problems. By allowing for degrees of truth and membership functions, fuzzy logic can model and reason with uncertain and incomplete information in a more natural and intuitive way. This is particularly useful in situations where precise measurements orclear-cut boundaries are difficult to define, such as in medical diagnosis, financial forecasting, or linguistic analysis. In the realm of artificial intelligence, fuzzy logic plays a crucial role in mimicking human reasoning and decision-making processes. By incorporating fuzzy sets, fuzzy rules, and fuzzy inference systems, AI systems can effectively deal with uncertain and imprecise data, leading to more robust and adaptive solutions. This is evident in applications such as autonomous vehicles, where fuzzy logic helps navigate complex and dynamic environments by making decisions based on fuzzy rules and fuzzycontrol actions. Moreover, fuzzy logic has found widespread use in control systems, where it offers a more flexible and robust alternative to traditional control techniques. By using fuzzy sets to represent linguistic variables and fuzzy rules to define control strategies, fuzzy logic controllers can adapt and respond to changing conditions in real-time, leading to improved performance and stability. This is particularly valuable in systems that operate in uncertain or unpredictable environments, such as industrial processes, robotics, or power systems. From a practical standpoint, fuzzy logic provides a powerful tool for modeling and simulating complex systems that exhibit non-linear and uncertain behavior. By capturing the inherent fuzziness and imprecision in the system's inputs and outputs, fuzzy logic can generate accurate and reliable predictions,enabling better decision-making and control. This is crucial in fields such as engineering, economics, and social sciences, where traditional mathematical models may fall short in capturing the complexity and variability of real-world phenomena. In conclusion, fuzzy logic represents a significant advancement in the field of artificial intelligence and control systems, offering a more flexible and adaptive approach to handling uncertain and imprecise information. By allowing for degreesof truth and membership functions, fuzzy logic enables us to model and reason with complex systems in a more natural and intuitive way, mirroring human reasoning processes. As we continue to explore and harness the power of fuzzy logic, we can expect to see further advancements in AI, robotics, and other fields that rely on intelligent decision-making and control.。
LOGIC AND FUZZY SYSTEM Fuzzy Analogy of Linear Systems

LOGIC AND FUZZY SYSTEMLESSON 14:SYSTEMS OF FUZZY LINEAR EQUATIONSFuzzy Analogy of Linear SystemsAbstract: In this start up study fuzzy logic theory is incorporated into modelling of linearsystems whose parameters and variables subject to uncertainty.The major intention is to try to understand the complicated mathematical background and therefore the principles and formulations can be properly interpreted into transparent engineering implementation. Two examples are selected to illustrate the fuzzy analogy of linear systems to accommodate uncertainties due to imprecise measurements or lack of complete information.Key words: Fuzzy numbers, convex fuzzy sets, fuzzy analogy,and implementation algorithms.The main advantage of fuzzy models is their ability to describe expert knowledge in a descriptive, human like way, in the form of simple rules using linguistic variables. The theory of fuzzy sets (Zimmermann 2000) allows the existence of uncertainty to vagueness (or fuzziness) rather than due to randomness. When using fuzzy sets, accuracy is traded for complexity – fuzzy logic models do not need an accurate definition for many systems (in terms of the parameters). This results in a natural reduction in number of variables and states for an ad hoc system structure.Simultaneous linear equations play a major role in representing various systems in natural science, engineering, and social domain. Since in many applications at least some of the system’s parameters and measurements are represented byexpert experience in terms of fuzzy rather than crisp numbers, it is immensely important to develop mathematical models and numerical procedures that would appropriately deal with those general fuzzy terms.One of the major applications using fuzzy number arithmetics is treating those linear systems, which their parameters are entirely or partially represented by fuzzy numbers. A general model for solving a n fuzzy linear system whosecoefficients matrix is crisp and the right-hand side column is an arbitrary fuzzy number vector, which use the embedding method and replace the original linear fuzzy systemcrisp linear system with a matrix Swhich may be singular if A be nonsingular.The following contents are organised with five major sections.In section 2 some fundamental concepts and definitions are selected from classical fuzzy logic theory for treating fuzzy linear systems. In Section 3 fuzzy analogy method is presented to lay a basis for translating linear equations into their fuzzycounterparts. In Section 4 fuzzy solutions are described. InSection 5 two examples are used to demonstrate the algorithms.In section 6 the conclusions are drawn.2. PreliminariesAn arbitrary fuzzy number can be described with an ordered pair of functions where1. is a bounded left continuous non-decreasing functionover [0,1].2. is a bounded left continuous non-increasing function over [0,1].3.A crisp number a is simply representedbyDefinition 1 : Consider a nxnlinear system of equations= + · · · + +(2.1) may be expressed in a vector form(2.2)Expression (2.2) can be used as a Fuzzy Linear Equation (FLE),while . n x n matrix, and, ( are fuzzy vector, so called system transfermatrix, input, and output respectively in classical system notations.Let P denote the product and g be a mapping, which is The Extension Principle (Dubois 1980) states that g can be extended to five tuples (A, B, C, D, E)which are all fuzzy subsets ofas follows:Where sup is taken over allDefinition 2: A fuzzy set A of X is called convex if thefollowing relation holds:for any . A is said to be normalised if there exists an x such that A (x ) = 1. Theany. A is said to be normalised if thereexists an x such that A (x ) = 1. The a-level of a fuzzy subset A denoted by, if defined byA fuzzy set A can be shown to be convex if and only if its a cuts are intervals for all . Fuzzy set A can be defined by its acuts,wheredenotes the characteristic function of the setLOGIC AND FUZZY SYSTEMDefinition 3 Fuzzy number A is called a number of the R L .type if its membership functionhas the following form:where L and R are continuous non-increasing functions, defined on ), strictly decreasing to zero in those subintervals of the interval ) , in which they are positive, and fulfilling the condition The parameters a and â are non-negative real numbers.3. Fuzzy AnalogyIf X is the set of real numbers, by a fuzzy number x N , this means a fuzzy subset of X where •, if and only if y = x.•is continuous.• is convex.•vanishes at infinity..denotes the degree of belief that the value of x is infact y. Consider a class of functional equations of the formwhere f is unknown, may be either addition or multiplication of real numbers. (3.1) may be put in a generalformwhereis a function relating the unknownquantities stands for andstands forLet denote the degree of belief that x equals to y . Using extension principle (Dubois 1980), (3.2) can be expressed in thefuzzy formwhere the sup is taken over all y 1and y2 for whichAccording to Nguyen (1978), (3.3) and (3.1) may be the implies as following For the alevels are equalis a closed and bounded interval. Hence,,where are the left endpointand the right endpoint respectively associated with the a level of the fuzzy number w . If F is non-decreasing in its argument and Fis continuous, then it givesMoreover solutions to (3.5) and (3.6), say functions H 1and H2, respectively, are continuous and no-decreasing. ThusSo, the solution of (3.3) is given bywhere H 1 and H 2 are the solutions of (3.5) and (3.6),respectively. According to (3.3), the solution of (3.8) may alsobe represented bywhere the sup is taken over allis thecharacteristic function over the interval4. Fuzzy Solutions A solution tto (2.1) one should recall that forarbitrary fuzzy numbers and realnumber k ,•x = yif and only if•Definition 4: A fuzzy number vector givenby is called a solution ofthe FSLE ifConsider the ith equation of the system (2.1)it hasFrom (2.4) two crisp linear systems for all i that there can be extended to. crisp linear system as follows:LOGIC AND FUZZY SYSTEMThus FLE (2.1) is extended to a crisp (2.5) where A= S 2 + S 1.(4.5) can be write as follows:where the matrix S is nonsingular if and only if the matrices A=S1+S2 and S1-S2 are both non-singular.Definition 5: Let denote the unique solution of SX = Y . The fuzzy number vectoris defined byis called the fuzzy solution of SX = Y . Ifare all triangular fuzzy numbers thenand U is called a strongfuzzy solution. Otherwise, U is a weak fuzzy solution.In the general, the structure of S implies thatand thatWhere B contains the positive entries of A , C the absolute values of the negative entries of A , and A=B-C If linear system are fuzzy variables, for the inputsdenotes the degree of,inputThesolution of linear system are givenIf linear system are fuzzy coefficients and fuzzy variables, whichis in system (2.1)are fuzzy numbers, denotes the degree ofcoefficients and variable respectively.where so the solution of systemsAX = Yis5. Examples and SimulationsTwo examples were selected to demonstrate the understanding of the fuzzy of analogy of linear systems.Example 1:Consider a simple linear system B AX Y + = withfuzzy output and input variablesFig.1 shows a fuzzy line, which denotes what a line looks like with a fuzzy input.Example 2 :Consider a two inputs & single output fuzzy system with fuzzy outputsY = AX + B(5.3)Where .The extended 4 x 4 . matrix isThe fuzzy solution isFig.2 shows that variables x 1and x 2 are determined by the output y which is the ácut, when y = 1, an accurate value for thesolution can be obtained.LOGIC AND FUZZY SYSTEM6. ConclusionsIn this paper a general model structure is presented for solving of linear equations (systems) with fuzzy variables andparameters. With this structure, a fuzzy system with a matrix Ais transformed into a crisp linear system S . The system is then solved with crisp variables and parameters and thesolution vector is either a strong fuzzy solution or a weak fuzzy solution. Solutions of linear fuzzy equations have been well addressed in mathematics. However it is still a long distance to arrive in engineering field for applications. This study has attempted to bridge the two domains. Additionally fuzzy analogy of nonlinear systems is a new area and will be studied as the expansion of linear systems.References1.Zimmermann, H.J., Fuzzy Set Theory-and Its Applications,3rd Edition, Kluwer Academic Publishers, Dordrecht, 2000.2.Wang, L.X., Adaptive Fuzzy Systems and Control, New Jersey 07632, 1999.3.Klir, G.J., Folger, T.A., Fuzzy Sets, Uncerainty andInformation, Prentice-Hall, Englewood, Cli.s, NJ, 1988.4.Dubois, D., and Prade, H., Fuzzy Sets and Systems: Theory and Applications, Academic Press, New York, 1980.5.Deeba, E., On a fuzzy difference equation. IEEE Trans.Fuzzy Systems 3(3):469-472, 1995.6.Deeba, E., On a fuzzy logistic difference equation.Differential Equations Dynam. Systems 4(2):149-156, 19967.Deschrijver, G., On the relationship between someextensions of fuzzy set theory, Fuzzy Sets and Systems 133:227-235, 2003.8.Friedman, M., Fuzzy Linear Systems, Fuzzy Sets and Systems 96(2): 201-209, 1998.9.Soliman, S.A., Fuzzy linear parameter estimation algorithms:a new formulation, International Journal of Electrical Power & Energy Systems 24(5): 415-420, 200210.Nguyen, H.T., A note on the extension principle for fuzzy sets, J. Math. Anl. 64(2): 369-380, 1978Notes。
Fuzzy Logic and Neural Networks

Fuzzy Logic and Neural Networks Fuzzy logic and neural networks are two powerful tools in the field ofartificial intelligence that have revolutionized the way we approach complex problems. Fuzzy logic is a form of reasoning that deals with uncertainty and imprecision, allowing for more flexible decision-making in situations where traditional binary logic may fall short. On the other hand, neural networks are a type of machine learning algorithm inspired by the way the human brain works, capable of learning complex patterns and relationships in data. One of the key advantages of fuzzy logic is its ability to handle vague and ambiguous information, which is often present in real-world scenarios. For example, in a system that controls the temperature of a room, fuzzy logic can be used to adjust the temperature based on inputs such as "too hot" or "a little chilly," rather than precise numerical values. This flexibility makes fuzzy logic particularly usefulin applications where human judgment and intuition play a significant role.Neural networks, on the other hand, excel at tasks that involve patternrecognition and classification. By training a neural network on a large dataset,it can learn to recognize complex patterns in the data and make predictions or decisions based on those patterns. This makes neural networks well-suited fortasks such as image recognition, speech recognition, and natural language processing. When it comes to combining fuzzy logic and neural networks, researchers have found that the two approaches complement each other well. Fuzzy logic can be used to handle the uncertainty and imprecision in the inputs to a neural network, providing a more robust and flexible system overall. For example,in a medical diagnosis system, fuzzy logic can be used to interpret vague symptoms from a patient, which can then be fed into a neural network to make a moreaccurate diagnosis. Overall, the combination of fuzzy logic and neural networks has the potential to create more intelligent and adaptive systems that can handlea wide range of complex tasks. By leveraging the strengths of both approaches, researchers can develop AI systems that are better able to cope with the uncertainties and complexities of the real world. As we continue to push the boundaries of artificial intelligence, the synergy between fuzzy logic and neuralnetworks will undoubtedly play a crucial role in shaping the future of intelligent systems.。
Fuzzy Logic and Neural Networks

Fuzzy Logic and Neural Networks Fuzzy logic and neural networks are two important concepts in the field of artificial intelligence and machine learning. Both of these technologies havetheir own strengths and weaknesses, and they are often used in combination to create more powerful and efficient systems. In this response, we will explore the basics of fuzzy logic and neural networks, their applications, and the potential challenges and limitations associated with each. Fuzzy logic is a form of multi-valued logic that deals with reasoning that is approximate rather than fixed and exact. It is an extension of traditional binary logic that allows for the representation of vague or imprecise information. Fuzzy logic is particularly useful in situations where there is uncertainty or ambiguity, as it allows for the modeling of complex systems with incomplete or uncertain data. One of the key advantages of fuzzy logic is its ability to handle linguistic terms and subjective concepts, making it well-suited for applications in natural language processing, control systems, and decision-making processes. On the other hand, neural networks are a set of algorithms, modeled loosely after the human brain, that are designed to recognize patterns. They interpret sensory data through a kind of machine perception, labeling or clustering raw input. Neural networks are widely used in image and speech recognition, medical diagnosis, financial forecasting, and many other applications where complex patterns need to be analyzed. One of the main advantages of neural networks is their ability to learn from data, which allows them to improve their performance over time and adapt to changing environments. When it comes to applications, both fuzzy logic and neural networks have a wide range of uses across different industries. Fuzzy logic is commonly applied in control systems, such as in automotive systems, household appliances, and industrial processes. It is also used in consumer electronics, such as digital cameras and camcorders, to improve image quality and reduce noise. On the other hand, neural networks are widely used in fields such as finance, healthcare, marketing, and customer service, where they are employed for tasks such as fraud detection, patient diagnosis, recommendation systems, and sentiment analysis. Despite their numerous applications and advantages, both fuzzy logic and neural networks have their own set of challenges and limitations. Fuzzy logic systems canbe difficult to design and interpret, as they often rely on expert knowledge and linguistic rules that may be hard to formalize. Additionally, fuzzy logic systems can be computationally expensive, especially when dealing with large amounts of data. On the other hand, neural networks are known for their black box nature, meaning that it can be difficult to understand how they arrive at a particular decision or prediction. This lack of interpretability can be a significant barrier in domains where transparency and accountability are crucial, such as in healthcare and finance. In conclusion, fuzzy logic and neural networks are powerful tools in the field of artificial intelligence and machine learning, each with its own unique strengths and weaknesses. While fuzzy logic excels in handling uncertainty and imprecise information, neural networks are adept at pattern recognition and learning from data. By combining these two technologies, researchers and engineers can create more robust and versatile systems that can tackle a wide range of complex problems. However, it is important to be mindful of the challenges and limitations associated with each of these technologies, and to continue exploring ways to improve their performance and applicability in real-world scenarios.。
功能点的A型-2模糊逻辑框架(IJISA-V5-N3-8)

I.J. Intelligent Systems and Applications, 2013, 03, 74-82Published Online February 2013 in MECS (/)DOI: 10.5815/ijisa.2013.03.08A Type-2 Fuzzy Logic Based Framework forFunction PointsAnupama KaushikDept. of IT, Maharaja Surajmal Institute of Technology, GGSIP University, Delhi, Indiaanupama@msit.inA.K. SoniDept. of IT, School of Engineering and Technology, Sharda University, Greater Noida, Indiaak.soni@sharda.ac.inRachna SoniDept. of Computer Science and Applications, DAV College, Yamuna Nagar, Haryana, Indiasonirachna67@Abstract —Software effort estimation is very crucial in software project planning. Accurate software estimation is very critical for a project success. There are many software prediction models and all of them utilize software size as a key factor to estimate effort. Function Points size metric is a popular method for estimating and measuring the size of application software based on the functionality of the software from the user‘s point of view. While there is a great advancement in software development, the weight values assigned to count standard FP remains the same. In this paper the concepts of calibrating the function point weights using Type-2 fuzzy logic framework is provided whose aim is to estimate a more accurate software size for various software applications and to improve the effort estimation of software projects. Evaluation experiments have shown the framework to be promising.Index Terms —Project management, Software Effort Estimation, Type-2 Fuzzy Logic System, Function Point AnalysisI.IntroductionSoftware development has become an important activity for many modern organizations. Software engineers have become more and more concerned about accurately predicting the cost and quality of software product under development. Consequently, many models for estimating software cost have been proposed such as Constructive Cost Model(COCOMO) [1],Constructive Cost Model II (COCOMO II) [2], Software Life Cycle Management (SLIM) [3] etc. These models identify key contributors to effort and use historical organizational projects data to generate a set of mathematical formulae that relates these contributors to effort. Such a set of mathematical formulae are often referred to as parametric model because alternative scenarios can be defined by changing the assumed values of a set of fixed coefficients (parameters) [4]. All these models use the software size as the major determinant of effort. Function Points is an ideal software size metric to estimate cost since it can be used in the early development phase, such as requirement, measures the software functional size from user‘s view, and is programming language independent [5].Today the scenario of software industry has changed from what it has many years ago. Now-a-days the object oriented paradigm has incorporated into the software development which leads to the creation of object oriented function points [6]. All the traditional cost estimation models are limited by their inability to cope with vagueness and imprecision in the early stages of the software life cycle. So, a number of soft computing approaches like fuzzy logic (FL), artificial neural networks (ANN), evolutionary computation (EC) etc. are incorporated to make rational decisions in an environment of uncertainty and vagueness. The first realization of the fuzziness of several aspects of COCOMO was that of Fei and Liu [7] called F-COCOMO. Jack Ryder [8] investigated the application of fuzzy modelling techniques to COCOMO and the Function Points models, respectively. Venkatachalam [9] investigated the application of artificial neural network (ANN) to software cost estimation. Many researchers have applied the evolutionary computation approach towards cost estimation [10, 11].1.1 Background and related workOsias de Souza Lima Junior et al. [12] have worked on trapezoidal fuzzy numbers to model function point analysis for the development and enhancement projectassessment. Ho Leung [13] has presented a case study for evaluation of function points. Finnie et al. [14] provided the combination of machine learning approach with FP. They compared the three approaches i.e. regression analysis, artificial neural networks and case based reasoning using FP as an estimate of software size. The authors observed that both artificial neural networks and case based reasoning performed well on the given dataset in contrast to regression analysis. They concluded that case based reasoning is appealing because of its similarity to the expert judgement approach and for its potential in supporting human judgement. Al-Hajri et al. [15] establish a new FP weight system using artificial neural network. Lima et al. [16] proposed the concepts and properties from fuzzy set theory to extend FP analysis into a fuzzy FP analysis and the calibration was done using a small database comprised of legacy systems developed mainly in Natural 2, Microsoft Access and Microsoft Visual Basic. Yau and Tsoi [17] introduced a fuzzified FP analysis model to help software size estimators to express their judgement and use fuzzy B-spline membership function to derive their assessment values. The weak point of their work is that they use limited in-house software to validate the model. Abran and Robillard‘s empirical study [18] demonstrates the clear relationship between FPA‘s primary component and work-effort. Kralj et al. [19] identified the function point analysis method deficiency of upper boundaries in the rating complexity process and proposed an improved FPA method. Wei Xia et al. [20] proposed a Neuro-Fuzzy calibration approach for function point complexity weights. Their model provided an equation between Unadjusted Function Points and work effort which is used to train the neural network and estimated the effort. Moataz A. Ahmed and Zeeshan Muzaffar [4] provided an effort prediction framework that is based on type-2 fuzzy logic to allow handling imprecision and uncertainty present in the effort prediction. Mohd. Sadiq et al. [21] developed two different linear regression models using fuzzy function point and non fuzzy function point in order to predict the software project effort.The above researches have concluded that the combination of soft computing approaches and the traditional cost estimation models yields a more accurate prediction of software costs and effort. All the earlier work on software cost estimation using fuzzy logic incorporated type-1 or type-2 fuzzy framework for effort prediction. This paper proposes an improved FPA method by calibrating the function point‘s weight using type-2 fuzzy logic framework.1.2 Function Point Analysis: A short description Function point analysis is a process used to calculate the software size from the user‘s point of view, i.e. on the basis of what the user requests and receives in return from the system. Allan J Albrecht [22] of IBM proposed Function Point Count (FPC) as a size measure in the late 1970s. Albrecht had taken up the task of arriving at size measures of software systems to compute a productivity measure that could be used across programming languages and development technologies. The current promoter of Albrecht‘s function point model is the International Function Point User‘s Group (IFPUG). IFPUG evolves the FPA method and periodically releases the Counting Practices Manual for consistent counting of function points across different organizations. In FPA, a system is decomposed into five functional units: Internal Logical Files (ILF), External Interface Files (EIF), External Inputs (EI), External Outputs (EO) and External Inquiry (EQ). These functional units are categorized into data functional units and transactional function units. All the functions do not provide the same functionality to the user. Hence, the function points contributed by each function varies depending upon the type of function (ILF, EIF, EI, EO or EQ) and complexity (Simple, Average or Complex) of the function. The data functions complexity is based on the number of Data Element Types (DET) and number of Record Element Types (RET). The transactional functions are classified according to the number of file types referenced (FTRs) and the number of DETs. The complexity matrix for all the five components is given in Table 1, Table 2 and Table 3. Table 4 illustrates how each function component is then assigned a weight according to its complexity.The actual calculation process of FPA is accomplished in three stages: (i) determine the unadjusted function points (UFP); (ii) calculate the value adjustment factor (VAF); (iii) calculate the final adjusted function points.The Unadjusted Function Points (UFP) is calculated using ―(1)‖, where W ij are the complexity weights and Z ij are the counts for each function component.∑∑ (1) The second stage, calculating the value adjustment factor (VAF), is derived from the sum of the degree of influence (DI) of the 14 general system characteristics (GSCs). The DI of each one of these characteristics ranges from 0 to 5 as follows: (i) 0 – no influence; (ii) 1 –incidental influence; (iii) 2 –moderate influence; (iv) 3 – average influence; (v) 4 – significant influence; and (vi) 5 – strong influence.The general characteristics of a system are: (i) data communications; (ii) distributed data processing; (iii) performance; (iv) heavily used configuration; (v) transaction rate; (vi) online data entry; (vii) end-user efficiency; (viii) on-line update; (ix) complex processing; (x) reusability; (xi) installation ease; (xii) operational ease; (xiii) multiple sites; and (xiv) facilitate change. VAF is then computed using ―(2)‖:∑ (2)x i is the Degree of Influence (DI) rating of each GSC. Finally, the adjusted function points are calculated as given in ―(3)‖.(3)Table 1: Complexity Matrix of ILF/EIFTable 2: Complexity Matrix of EITable 3: Complexity Matrix of EO/EQTable 4: Functional Units with weighting factorsII.Type 2 Fuzzy Logic SystemsFuzzy Logic is a methodology to solve problems which are too complex to be understood quantitatively. It is based on fuzzy set theory and introduced in 1965 by Prof. Zadeh in the paper fuzzy sets [23]. It is a theory of classes with unsharp boundaries, and considered as an extension of the classical set theory [24]. The membership µA(x) of an element x of a classical set A, as subset of the universe X, is defined by:µA(x) = {That is, x is a member of set A (µA (x) = 1) or not (µA (x) = 0). The classical sets where the membership value is either zero or one are referred to as crisp sets. Fuzzy sets allow partial membership. A fuzzy set A is defined by giving a reference set X, called the universe and a mapping;µA : X []called the membership function of the fuzzy set A µA(x), for x X is interpreted as the degree of membership of x in the fuzzy set A. A membership function is a curve that defines how each point in the input space is mapped to a membership value between 0 and 1. The higher the membership x has in the fuzzy set A, the more true that x is A. The membership functions (MFs) may be triangular, trapezoidal, Gaussian, parabolic etc.Fuzzy logic allows variables to take on qualitative values which are words. When qualitative values are used, these degrees may be managed by specific inferential procedures. Just as in fuzzy set theory the set membership values can range (inclusively) between 0 and 1, in fuzzy logic the degree of truth of a statement can range between 0 and 1 and is not constrained to the two truth values {true, false} as in classic predicate logic.Fuzzy Logic System (FLS) is the name given to any system that has a direct relationship with fuzzy concepts. The most popular fuzzy logic systems in the literature may be classified into three types [25]: pure fuzzy logic systems, Takagi and Sugeno‘s fuzzy system and fuzzy logic system with fuzzifier and defuzzifier also known as Mamdani system. As most of the engineering applications use crisp data as input and produce crisp data as output, the Mamdani system [26] is the most widely used one where the fuzzifier maps crisp inputs into fuzzy sets and the defuzzifier maps fuzzy sets into crisp outputs.Zadeh [27], proposed more sophisticated kinds of fuzzy sets, called type-2 fuzzy sets (T2FSs). A type-2 fuzzy set lets us incorporate uncertainty about the membership function into fuzzy set theory. In order to symbolically distinguish between a type-1 fuzzy set and a type-2 fuzzy set, a tilde symbol is put over the symbol for the fuzzy set; so, A denotes a type-1 fuzzy set, whereas à denotes the comparable type-2 fuzzy set. Mendel and Liang [28, 29] characterized T2FSs using the concept of footprint of uncertainty (FOU), and upper and lower MFs. To depict the concept, let us consider type-1 gauss MF shown in ―Fig. 1‖.As can be seen from the figure type-1 gaussian membership function is constrained to be in between 0 and 1 for all x X, and is a two dimensional function. These types of membership don‘t carry any uncertainty. There exists a clear membership value for every input data point.If the Gaussian function in ―Fig.1‖ is blurred ―Fig. 2‖can be obtained. The FOU represents the bounded region obtained by blurring the boundaries of type-1 MF. The upper and lower MFs represent the upper and lower boundaries of the FOU, respectively. In this case, for a specific input value, there is no longer a single certain value of membership; instead the MF takes on values wherever the vertical line intersects the blur. Those values do not have to be all weighted the same; hence, an amplitude distribution can be assigned to those points. Doing this for all input values x, a three dimensional MF is created, which is a type-2 MF. In this, the first two dimensions allow handlingimprecision via modelling the degree of membership of x; while the third dimension allows handling uncertainty via modelling the amplitude distribution of the degree of membership of x. Here also, like in type-1 MFs the degree of membership along the second dimension and the amplitude distribution values along the third dimension is always in the interval [0, 1]. Clearly, if the blur disappears; then a type-2 MF reduces to a type-1 MF.A general architecture of type-2 fuzzy logic system (T2FL) as proposed by Mendel is depicted in ―Fig. 3‖.Fig. 1: A Gaussian Type-1 membership functionFig. 2: A Gaussian Type-2 membership functionFig. 3: A typical type-2 fuzzy logic system [29]Table 5: Example on FP complexity classificationT2FL systems contain five components –rules, fuzzifier, inference engine, type reducer, and defuzzifier. Rules are the heart of a T2FL system, and may be provided by experts or can be extracted from numerical data. These rules can be expressed as a collection of IF-THEN statements. The IF part of a rule is its antecedent, and the THEN part of the rule is its consequent. Fuzzy sets are associated with terms that appear in the antecedents or consequents of rules, and with inputs to and output of the T2FL system. The inference engine combines rules and gives mapping from input type-2 fuzzy sets to output type-2 fuzzy set. The fuzzifier converts inputs into their fuzzy representation. The defuzzifier converts the output of the inference engine into crisp output. The type reducer transforms the type-2 fuzzy output set into type-1 fuzzy set to be processed by the defuzzifier. A T2FL system is very similar to a T1FL system; the major difference being that the output processing block of T1FL system is just a defuzzifier while the output processing block of a T2FL system contains the type reducer as well. III.Problem Description and AnalysisIn cost estimation process, the primary input is the software size and the secondary inputs are the various cost drivers. There is a significant relationship between the software size and cost. There are mainly two types of software size metrics: lines of code (LOC) and Function Point (FP). Size estimation is best done when there is complete information about the system; but this is not available till the system is actually built. The challenge for the estimator is therefore to arrive at a reasonable estimate of the size of the system with partial information.LOC is usually not available until the coding phase, so FP has gained popularity because it can be used at an earlier stage of software development.In our work, we are using type-2 based fuzzy logic approach to calibrate the function point weight values which provides an improvement in the software size estimation process. There are 15 parameters in the FP complexity weight system to calibrate. These parameters are low, average and high values of External Inputs, External Outputs, Internal Logical Files, External Interface Files and External Inquiries respectively. A fuzzy based approach is chosen since it can capture human‘s judgement with ease and instead of giving an exact number to all 15 function points parameters we can define fuzzy linguistic terms and assign a fuzzy set within numeric range. This provides an ability to cope up with the vagueness and imprecision present in the earlier stages of software development.In Function Point Analysis (FPA) method each component is classified to a complexity level determined by the number of its associated files such as DET, RET or FTR as given in Table 4. If we determine the FPA complexity of a particular software application, in some cases it may not correctly reflect the complexity for its components.Table 5 shows a software project with three EIF‘s A, B and C. According to the complexity matrix, A and B are classified as having the same complexity and are assigned the same weight value of 10. However, A has 19 more DET than B and is certainly more complex. But both of them are assigned the same complexity. Also, EIF C is having only one DET less than EIF B and it is classified as average and assigned a weight value of 7. From the above example it is concluded that there is a huge scope of improvement in the FPA complexity classification. Processing the number of FP component associated files such as DET, RET and FTR using fuzzy logic can provide an exact complexity degree.IV.Fuzzy Logic calibration to improve FPAType-2 fuzzy inference system is developed for all the five FPA components (ILF, EIF, EI, EO, EQ) using the Mamdani approach. We define three new linguistic terms: small, medium and large, to express the inputs qualitatively. Also we use linguistic terms: simple, average and complex for the output. To fuzzify the inputs and outputs, we define fuzzy sets to represent the linguistic terms [30]. The fuzzy membership grade is captured through the membership functions of each fuzzy set. The inputs and outputs are represented using gaussian igaussstype2 membership which is represented in ―Fig. 4‖. It has certain mean m, and an uncertain standard deviation that takes on values in [σ1, σ2]. The shaded area represents the FOU. Using interval type-2 Gaussian MF‘s makes it easier to build T2FL systems since the mathematics behind the corresponding inferential procedures and training algorithms are less complicated [29]. ―Fig.5 (a)‖and ―Fig.5 (b)‖ shows how the inputs of EIF are assigned the membership functions and represented using linguistic variables of fuzzy sets. ―Fig. 6‖ depicts the output of EIF using membership functions. After representing the inputs and output of EIF using membership functions nine fuzzy rules are defined using rule editor based on the original complexity matrices and illustrated in Table 6. Each rule has two parts in its antecedent linked with an ‗AND‘ operatorand one part in its consequence. These fuzzy rules define the connection between the input and output fuzzy variables. A fuzzy rule has the form: IF <Antecedent> THEN <Consequent>, where antecedent is a compound fuzzy logic expression of one or more simple fuzzy expressions connected with fuzzy operators; and the consequent is an expression that assigns fuzzy values to output variables. The inference system evaluates all the rules of the rule base and combines the weights of the consequents of all relevantrules in one fuzzy set using the aggregate operation. Finally, the output fuzzy set is defuzzified to a crisp single number.Fig. 4: FOU for Gaussian MFFig. 5 (a): Input fuzzy set DET for EIFFig. 5 (b): Input fuzzy set RET for EIFFig. 6: Output fuzzy set Complexity for EIFTable 6: Truth table of fuzzy logic rule setFig. 7: Type-2 Fuzzy Inference process of Function Points Model Table 7: Calibration using type-2 fuzzy logicAn example of the complete fuzzy inference process is shown in ―Fig. 7‖. Input values are set to DET 51 and RET 5. These are represented using the antecedent part of the fuzzy rules. Finally, the consequent part isdefuzzified and the output is achieved as a single value of 7.63.A fuzzy logic system for each FPA element (ILF, EIF, EI, EO, EQ) is constructed. A fuzzy complexity measurement system that takes into account all five Unadjusted Function Points function components is built after the fuzzy logic system for each function component is established as shown in ―Fig. 8‖. The calibrated values for EIF A, EIF B and EIF C is listed in Table 7 and it is found that these calibrated weight values are more convincing than the original weight values.Fig. 8: Fuzzy complexity measurement system for Type-2 Fuzzyfunction points modelTable 8: Calculation of t2UFFP and UFP for ILFV.Experimental Methodology and ResultsWe have conducted some experiments to develop a type-2 fuzzy system for function points analysis using our framework as depicted in ―Fig. 8‖. Our model has been implemented in Matlab(R2008a). As it is the case with validating any prediction model, real industrial data necessary to use our framework to develop and tune the parameters of prediction models were not available. To get around this data scarcity problem for the sake of showing the validity of our framework for the industry where organizations have their own data available, we generated artificial datasets consisting of 20 projects. A complexity calculation for all the five components for each project is done using the type-2 fuzzy framework. The Tables (8, 9, 10, 11, 12) lists the complexity values for all the five components for the first project using type-2 fuzzy framework (t2UFFP) and conventional method i.e.UFP.Using ―(1)‖ total unadjusted function points from the type-2 technique and the conventional technique is calculated and listed in Table 13. It is found that the type-2 technique is at par than the conventional technique.Table 9: Calculation of t2UFFP and UFP for EIFTable 10: Calculation of t2UFFP and UFP for EITable 11: Calculation of t2UFFP and UFP for EOTable 12: Calculation of t2UFFP and UFP for EQTable 13: Comparison of t2UFFP and UFPTable 14: Comparison of type-2 fuzzy FP and conventional FPIn order to compute the value of the conventional function point and type-2 fuzzy function point, we have treated all the 14 general system characteristics as average. Using ―(2)‖and ―(3)‖VAF and FPA is calculated and listed in Table 14.From the above results it is concluded that the calibrated function points using type-2 fuzzy yields better results than conventional function points.VI.ConclusionsFP as a software size metric is an important topic in the software engineering domain. The use of type2 fuzzy logic to calibrate FP weight values further improves the estimation of FP. This in turn will improve the cost estimation process of software projects. Empirical evaluation has shown that T2FL is promising. But there are potentials for improvements when the framework is deployed in practice. As all the experiments were conducted using artificial datasets, a need to evaluate the prediction performance of the framework on real data still persists. Some future work can be directed towards developing inferential procedures using various other membership functions present in type-2 fuzzy systems. This work can also be extended using Neuro Fuzzy approach. AcknowledgementThe authors would like to thank the anonymous reviewers for their careful reading of this paper and for their helpful comments.References[1] B.W. Boehm. Software Engineering Economics.Prentice Hall, Englewood Cliffs, NJ, 1981.[2] B. Boehm, B. Clark, E. Horowitz, R. Madachy, R.Shelby, C. Westland. Cost models for future software life cycle processes: COCOMO 2.0.Annals of Software Engineering, 1995.[3]L.H. Putnam. A general empirical solution to themacro software sizing and estimation problem.IEEE Transactions on Software Engineering, vol.4, 1978, pp 345-361.[4]Moataz A. Ahmed, Zeeshan Muzaffar. Handlingimprecision and uncertainty in software development effort prediction: A type-2 fuzzylogic based framework. Information and Software Technology Journal. vol. 51, 2009, pp. 640-654. [5]Function Point Counting Practices Manual, fourthedition, International Function Point Users Group, 2004.[6]G. Antoniol, C. Lokan, G. Caldiera, R. Fiutem. Afunction point like measure for object oriented software. Empirical Software Engineering. vol. 4, 1999, pp. 263-287.[7]Fei. Z, X. Liu. f-COCOMO-Fuzzy ConstructiveCost Model in Software Engineering. Proceedings of IEEE International Conference on Fuzzy System. IEEE Press, New York, 1992, pp. 331-337.[8]J. Ryder. Fuzzy Modeling of Software EffortPrediction. Proceedings of IEEE Information Technology Conference. Syracuse, NY, 1998. [9] A.R. Venkatachalam. Software Cost Estimationusing artificial neural networks. Proceedings of the International Joint Conference on Neural Networks, 1993, pp. 987-990.[10]K.K. Shukla. Neuro-genetic Prediction ofSoftware Development Effort. Journal of Information and Software Technology, Elsevier.vol. 42, 2000, pp. 701-713.[11]Alaa.F.Sheta. An Estimation of the COCOMOmodel parameters using the genetic algorithms for the NASA project parameters. Journal of Computer Science, vol. 2, 2006, pp.118 -123. [12]Osias de Souza Lima Junior, Pedro PorfirioMuniaz Parias, Arnaldo Dias Belchior. A fuzzy model for function point analysis to development and enhancement project assessement. CLEI Electronic Journal, vol. 5, 1999, pp. 1-14.[13]Ho Leung, TSOI. To evaluate the function pointanalysis: A case study. International Journal of computer, Internet and management vol. 13, 2005, pp. 31-40.[14]G.R. Finnie, G.E. Wittig, J.M. Desharnais. Acomparison of software effort estimation techniques: using function points with neural networks, case-based reasoning and regression models. Journal of Systems Software, Elsevier.vol. 39, 1977, pp. 281-289.[15]M.A. Al-Hajri, A.A.A Ghani, M.S. Sulaiman,M.H. Selamat. Modification of standard function point complexity weights system. Journal of Systems and Software, Elsevier,vol. 74, 2005, pp.195-206.[16]O.S. Lima, P.F.M. Farias, A.D. Belchior. Fuzzymodeling for function point analysis. Software Quality Journal, vol. 11, 2003, pp. 149-166. [17]C. Yau, H. L. Tsoi. Modelling the probabilisticbehavior of function point analysis. Journal ofInformation and Software Technology, Elsevier.vol. 40, 1998, pp. 59-68.[18]A. Abran, P. Robillard. Function Points Analysis:An empirical study of its measurement processes.IEEE Transactions on Software Engineering, vol.22, 1996, pp.895-910.[19]T. Kralj, I. Rozman, M. Hericko, A. Zivkovic.Improved standard FPA method- resolving problems with upper boundaries in the rating complexity process. Journal of Systems and Software, Elsevier, vol. 77, 2005, pp. 81-90. [20]Wei Xia, Luiz Fernando Capretz, Danny Ho,Faheem Ahmed. A new calibration for function point complexity weights. Journal of Information and Software Technology, Elsevier. vol. 50, 2008 pp.670-683.[21]Mohd. Sadiq, Farhana Mariyam, Aleem Ali,Shadab Khan, Pradeep Tripathi. Prediction of Software Project Effort using Fuzzy Logic.Proceedings of IEEE International Conference on Fuzzy System, 2011, pp. 353-358.[22]A. Albrecht. Measuring application developmentproductivity. Proceedings of the Joint SHARE/GUIDE/IBM Application Development Symposium, 1979, pp. 83-92.[23] L. A. Zadeh. Fuzzy Sets. Information and Control,vol. 8, 1965, pp. 338-353.[24]M. Wasif Nisar, Yong-Ji Wang, Manzoor Elahi.Software Development Effort Estimation using Fuzzy Logic – A Survey. Fifth International Conference on Fuzzy Systems and Knowledge Discovery, 2008, pp 421-427.[25]L. Wang. Adaptive Fuzzy System and Control:Design and Stability Analysis. Prentice Hall, Inc., Englewood Cliffs, NJ 07632, 1994.[26]E.H. Mamdani. Applications of fuzzy algorithmsfor simple dynamic plant. Proceedings of IEEE, vol. 121, 1974, pp. 1585-1588.[27]L. A. Zadeh. The Concept of a Linguistic Variableand Its Application to Approximate Reasoning–1. Information Sciences, vol. 8, 1975, pp. 199-249.[28]J.M. Mendel, Q. Liang. Pictorial comparison ofType-1 and Type-2 fuzzy logic systems.Proceedings of IASTED International Conference on Intelligent Systems and Control, Santa Barbara, CA, October 1999.[29]J.M. Mendel. Uncertain Rule-Based Fuzzy LogicSystems, Prentice Hall, Upper Saddle River, NJ 07458, 2001.[30]E.H. Mamdani. Application of fuzzy logic toapproximate reasoning using linguistic synthesis.IEEE transactions on computers, vol. 26, 1977, pp.1182-1191. Anupama Kaushik is an Assistant Professor at Maharaja Surajmal Institute of Technology, New Delhi, India. Her research area includes Software Engineering, Object Oriented Software Engineering and Soft Computing.Dr. A.K Soni has done his Ph.D. and M.S.(Computer Science) both from Bowling Green State University in Ohio, USA . He is the Professor and Head, Department of Information Technology, Sharda University, Greater Noida, India. His research area includes Software Engineering, Datamining, Database Management Systems and Object Oriented Systems.Dr. Rachna Soni did her M. Phil from IIT Roorkee and Ph.D. from Kururukshetra University, Kurukshetra. She is the Associate Professor and Head, Dept. of Computer Science and Applications, D.A.V. College, Yamunanagar, India. Her area of interest includes Software Risk Management, Project Management, Requirement Engineering, Simulation and Component based Software Engineering.。
Fuzzy Logic - IT Knowledge Base - home模糊逻辑知识库-家-它-精选文档31页

• For this reason, Fuzzy Logic has been compared to the human decision making process.
• Conventional Logic (and computing systems for that matter) are by nature related to the Boolean Conditions (true/false).
Fastest
[ 0.75 – 1.00 ]
FUZZY LOGIC REPRESENTATION CONT.
Slowest
Slow
Fast
float speed; get the speed if ((speed >= 0.0)&&(speed < 0.25)) { // speed is slowest } else if ((speed >= 0.25)&&(speed < 0.5)) { // speed is slow } else if ((speed >= 0.5)&&(speed < 0.75)) { // speed is fast } else // speed >= 0.75 && speed < 1.0 { // speed is fastest }
• Fuzzy logic calculates the shades of gray between black/white and true/false.
• Fuzzy logic is a super set of conventional (or Boolean) logic and contains similarities and differences with Boolean logic.
Fuzzy Logic and Systems

Fuzzy Logic and SystemsFuzzy logic and systems are a fascinating area of study that bridges the gap between traditional binary logic and the vagueness of human reasoning. This field has gained significant attention in recent years due to its ability to handle uncertainty and imprecision in a way that mimics human decision-making processes. Fuzzy logic allows for a more nuanced approach to problem-solving by assigning degrees of truth to statements rather than simply labeling them as true or false. This flexibility is particularly useful in situations where exact values are difficult to determine or where the boundaries between categories are blurred. One of the key advantages of fuzzy logic is its ability to handle complex systems with multiple variables and inputs. Traditional logic often struggles to cope with the intricacies of real-world problems, which may involve a multitude of factors that interact in non-linear ways. Fuzzy logic, on the other hand, excels in situations where the relationships between variables are not well-defined or where there is a high degree of uncertainty. By allowing for degrees of truth and membership functions, fuzzy logic can capture the nuances of these complex systems and provide more accurate and robust solutions. Another important aspect of fuzzy logic is its ability to model human reasoning and decision-making processes. Humans are inherently fuzzy creatures, prone to ambiguity, vagueness, and uncertainty in their thinking. Fuzzy logic mirrors this cognitive style by allowing for shades of gray in its reasoning, rather than the black-and-white distinctions of traditional logic. This makes fuzzy logic particularly well-suited for applications that involve human judgment or subjective criteria, such as expert systems, decision support systems, and artificial intelligence. Inaddition to its theoretical advantages, fuzzy logic has also found practical applications in a wide range of fields, including control systems, pattern recognition, image processing, and data analysis. Fuzzy logic controllers, for example, are widely used in industrial automation and robotics to handle complex control tasks that traditional controllers struggle with. Fuzzy systems have also been applied to medical diagnosis, financial forecasting, and natural language processing, demonstrating their versatility and effectiveness in real-world applications. Despite its many strengths, fuzzy logic is not without itslimitations and criticisms. Some researchers argue that fuzzy logic can be overly complex and difficult to interpret, particularly when dealing with systems with a large number of variables or fuzzy rules. Others question the validity of fuzzylogic as a formal system of reasoning, pointing to its reliance on heuristic methods and lack of a solid mathematical foundation. These criticisms highlightthe need for further research and development in the field of fuzzy logic to address these challenges and improve its applicability in a wider range of domains. In conclusion, fuzzy logic and systems offer a powerful and flexible approach to handling uncertainty and imprecision in decision-making processes. By allowing for degrees of truth and membership functions, fuzzy logic can model complex systems more accurately and capture the nuances of human reasoning. While there are valid criticisms of fuzzy logic, its practical applications and theoretical advantages make it a valuable tool for a wide range of fields. As research in this area continues to evolve, we can expect to see even more innovative applications offuzzy logic in the future, further solidifying its position as a key technologyfor handling uncertainty in a complex world.。
FuzzyLogicandFuzzyAlgorithms:模糊逻辑和模糊算法

Fuzzy Logic and FuzzyAlgorithmsCISC871/491Md Anwarul Azim(10036952)Presentation OutlineFuzzy control systemFuzzy Traffic controllerModeling and SimulationHardware DesignConclusion2Figure from Prof. Emil M. Petriu, University of Ottawa6Basic Structure of ControllerDEFUZZIFIER –It extracts a crisp value from a fuzzy set.·Smallest of Maximum.·Largest of Maximum.·Centroid of area.·Bisector of Area·Mean of maximum.FUZZIFIERFuzzifier takes the crisp inputs to a fuzzy controller and converts them into fuzzy inputs.FUZZY RULE BASE (Knowledge base)It consists of fuzzy IF-THEN rules that form the heart of a fuzzy inference system. A fuzzy rule base is comprised of canonical fuzzy IF-THEN rules of the form IF x1 is A1(l) and ... and xn is An (l)THEN y is B(l), where l = 1, 2, ...,M. Should have Completeness, Consistency, Continuity..FUZZY INFERENCE ENGINEFuzzy Inference Engine makes use of fuzzy logic principles to combine the fuzzy IF-THEN rules. Composition based inference (Max/Min,Max/Product)and individual-rule based inference (Mamdani). Other methods like Tsukamoto, Takagi Sugeno Kang (TSK)7“Fuzzy Control”Kevin M. Passino and Stephen Yurkovichhttp://if.kaist.ac.kr/lecture/cs670/textbook/ Fuzzy Traffic controller--Most traffic has fixed cycle controllers that need manual changes to --One of the desirable features of traffic controllers is to dynamically effect the change of signal phase durations--This problem can be solved by use of fuzzy traffic controllers whichadaptively at an intersection.12 /help/toolbox/fuzzy/fp243dup9.html13 /watch?v=hFWGToL-NHw/products/simulink/demos.htmlModeling using Simulink(Cont.)14 /watch?v=hFWGToL-NHw/products/simulink/demos.html15Case Study 2 (Extra)17。
适用于轴承故障诊断的数据增强算法

2021577轴承故障诊断在制造业的故障预测和健康管理中起着十分重要的作用。
除了传统的故障诊断方法以外,学者们将改进过的机器学习[1-4]和深度学习算法[5-8]应用于故障诊断领域,其诊断效率与准确率得到了较大的提高。
在大部分应用中,这些算法有两个共同点[9]:第一、根据经验风险最小化原则(Empirical Risk Minimization,ERM)[10]训练故障诊断模型。
第二、使用此原则训练的诊断模型的性能优劣主要取决于所使用的训练样本的数量和质量。
但在工业应用中,数据集中正负样本的比例不平衡:故障数据包含着区分类别的有用信息,但是所占比例较少。
此外由于机器的载荷、转轴转速等工况的不同,所记录的数据并不服从ERM原则中的独立同分布假设。
这两点使得ERM原则不适用于训练工业实际场景中的故障诊断模型,并且文献[11]表明使用ERM原则训练的模型无法拥有较好的泛化性能。
数据增强算法是邻域风险最小化原则[12](Vicinal Risk Minimization,VRM)的实现方式之一,能够缓解ERM原则所带来的问题。
在VRM中通过先验知识来构建每个训练样本周围的领域区域,然后可从训练样本的领域分布中获取额外的模拟样本来扩充数据集。
例如,对于图像分类来说,通过将一个图片的领域定义为其经过平移、旋转、翻转、裁剪等变化之后的集合。
但与机器学习/深度学习中的数据不同,故障诊断中的数据(例如轴承故障诊断中的振动信号)具有明显的物理意义和机理特征,适用于机器视觉的数据增强方法可能导致物理意义的改变。
因此,本文从信号处理和信号分析的角度出发,设计了一种适用于轴承故障诊断中振动信号的数据增强方法。
适用于轴承故障诊断的数据增强算法林荣来,汤冰影,陈明同济大学机械与能源工程学院,上海201804摘要:针对在轴承故障诊断中存在的故障数据较少、数据所属工况较多的问题,提出了一种基于阶次跟踪的数据增强算法。
该算法利用阶次跟踪中的角域不变性,对原始振动信号进行时域重采样从而生成模拟信号,随后重新计算信号的幅值来抵消时域重采样以及环境噪声对原始信号能量的影响,最后使用随机零填充来保证信号在变化过程中采样长度不变。
Fuzzy logic based system and method for informatio

专利名称:Fuzzy logic based system and method forinformation processing with uncertain inputdata发明人:Chidambar Ganesh申请号:US09246208申请日:19990120公开号:US06282526B1公开日:20010828专利内容由知识产权出版社提供专利附图:摘要:A fuzzy logic information processing system and method are disclosed that may be used not only with known or definite data input but also with uncertain data input. Theuncertain data input may be represented by a set of values wherein the possibility of any particular or specific value within the set being the true or accurate value is uncertain. The preferred embodiment of the system provides for an extensor to extend or map a representation of the uncertain data into at least one additional dimension related to dimensions of a set of rules used for making fuzzy logic inferences. The set of rules may be provided effectively in a mapped or graphed form. The set of rules and uncertain data are combined, for instance by locating intersection regions, to produce an output set that may be also be described as a map or plot. In a presently preferred embodiment the uncertain inputs and rules are represented mathematically or symbolically and then operated on to produce an output set. A projector then projects the output set to the desired output dimension as an output for the system. The system output may then be used for control purposes such as, for example only, a combat control system to provide a tactical picture, decision aid, presets for a guidance system, or the like.申请人:THE UNITED STATES OF AMERICA AS REPRESENTED BY THE SECRETARY OF THE NAVY代理人:Michael J. McGowan,Michael F. Oglo,Prithvi C. Lall更多信息请下载全文后查看。
Fuzzy logic based control
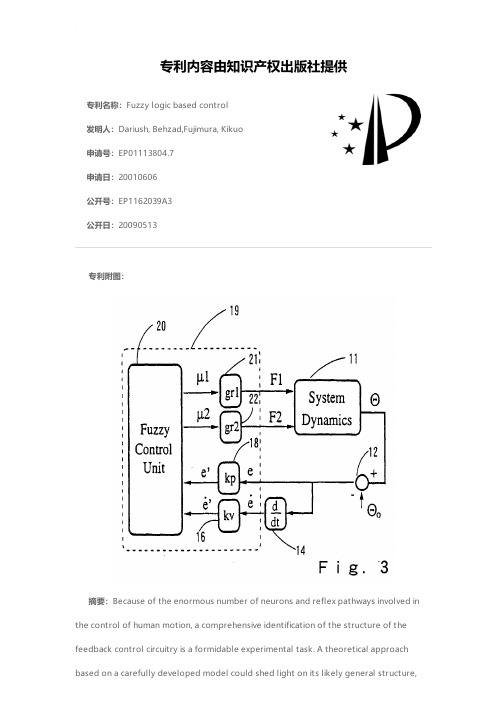
专利名称:Fuzzy logic based control发明人:Dariush, Behzad,Fujimura, Kikuo申请号:EP01113804.7申请日:20010606公开号:EP1162039A3公开日:20090513专利内容由知识产权出版社提供专利附图:摘要:Because of the enormous number of neurons and reflex pathways involved in the control of human motion, a comprehensive identification of the structure of the feedback control circuitry is a formidable experimental task. A theoretical approach based on a carefully developed model could shed light on its likely general structure,thereby providing guidance to experimenters. A fuzzy logic based control strategy for modeling the human postural dynamics is proposed. In particular, a fuzzy controller (1) is presented to coordinate the movement of a three segment sagittal human model to achieve upright posture. The actuation mechanism of the system consists of six muscle like actuators which are co-activated to modulate the stiffness at the joints. Simulation results are presented to illustrate the underlying principles.申请人:HONDA GIKEN KOGYO KABUSHIKI KAISHA地址:1-1, Minami-Aoyama 2-chome Minato-ku, Tokyo JP国籍:JP代理机构:Rupp, Christian更多信息请下载全文后查看。
人工智能边境设计以及特定地区的管理改善人与人之间的关系(IJISA-V5-N9-7)

I. Introduction
Who benefits and/or profits from these waterfronts Performances and their use values? Not surprisingly,
An analysis of any waterfront city is incomplete without first including a brief background to the development of waterfront cities in general. During the early to mid 1900's, waterfront's downtown population
Mohammad Mohsen Farhadi Department of Civil Engineering, Islamic Azad University Yasouj Branch, Iran
E-mail: fatemeh_farhadi_designer@
Abstract— Tourist attraction was used to achieve a stable waterfront, while the fuzzy-logic added intelligence to the select strategy through an automatic selection of the tourist attraction coefficient. This paper examines the relationship between heritage sites, waterfronts, and relationships between people in present-day in urban culture. Urban waterfronts are important and special assets and that, when redeveloped, they often contribute to healthy traditional communities. Waterfronts can serve as a unifying force in a city or town and can be, and often are, a force for community enrichment. Further, vibrant communities are essential for environmental, economic and social advancement. There are several strategy specific principles as a way to improve of usage from particular places and waterfront city. Select and design the best strategy play important role to tourist attraction. Fuzzy logic inference system is used to select the best methodology and based on this research and fuzzy logic method, striped methodology is used to have a best performance.
Fuzzy Logic and Neural Networks

Fuzzy Logic and Neural Networks Fuzzy logic and neural networks are two important concepts in the field of artificial intelligence and machine learning. Both have their own unique characteristics and applications, and they have been widely used in various fields such as control systems, pattern recognition, and decision-making. However, they also have their own limitations and challenges that need to be addressed. In this response, I will discuss the fundamentals of fuzzy logic and neural networks,their applications, and the challenges associated with their implementation. Fuzzy logic is a form of multi-valued logic that deals with reasoning that is approximate rather than fixed and exact. It is based on the idea that things can be partially true, rather than simply true or false. This makes it a powerful tool for dealing with uncertainty and imprecision, which are common in real-world decision-making processes. Fuzzy logic has been successfully applied in various fields such as control systems, image processing, and decision support systems. One of the key advantages of fuzzy logic is its ability to model complex, non-linear systems with a relatively simple set of rules. This makes it particularly useful in situations where traditional binary logic may not be suitable. On the other hand, neural networks are a set of algorithms, modeled loosely after the human brain, that are designed to recognize patterns. They interpret sensory data through a kind of machine perception, labeling or clustering raw input. Neural networks have been widely used in applications such as image and speech recognition, medical diagnosis, and financial forecasting. One of the key advantages of neural networks is their ability to learn from data, which makes them suitable for tasks that are too complex or difficult to be programmed using traditional rule-based algorithms. However, neural networks also have their limitations, such as the need for large amounts of data for training, and the lack of transparency in the decision-making process. In recent years, there has been a growing interest in combining fuzzy logic and neural networks to take advantage of their complementary strengths. This has led to the development of neuro-fuzzy systems, which integrate the learning capabilities of neural networks with the reasoning capabilities of fuzzy logic. Neuro-fuzzy systems have been successfully applied in various fields such as forecasting, control systems, and decisionsupport. One of the key advantages of neuro-fuzzy systems is their ability to handle complex, uncertain, and imprecise information in a more effective way than either fuzzy logic or neural networks alone. Despite the many advantages of fuzzy logic, neural networks, and neuro-fuzzy systems, there are also several challenges associated with their implementation. One of the main challenges is the interpretability of the models. Fuzzy logic and neural networks are often considered as "black box" models, meaning that it is difficult to understand how they arrive at a particular decision. This lack of transparency can be a significant barrier to their adoption, especially in applications where accountability and trust are important. Another challenge is the need for large amounts of data for training neural networks, which can be difficult to obtain in some applications. Additionally, designing effective neuro-fuzzy systems requires a deep understanding of both fuzzy logic and neural networks, which can be a significant barrier for practitioners. In conclusion, fuzzy logic, neural networks, and neuro-fuzzy systems are important tools in the field of artificial intelligence and machine learning. They have been successfully applied in a wide range of applications, and they have the potential to address complex, uncertain, and imprecise problems. However, there are also several challenges associated with their implementation, such as the lack of interpretability and the need for large amounts of training data. Addressing these challenges will be crucial for the widespread adoption of these techniques in real-world applications.。
Fuzzy Logic and Neural Networks

Fuzzy Logic and Neural Networks Fuzzy logic and neural networks are two powerful tools in the field ofartificial intelligence that have revolutionized the way we approach complex problems. Fuzzy logic is a form of reasoning that deals with uncertainty and imprecision, allowing for more flexible decision-making in situations where traditional binary logic falls short. On the other hand, neural networks are a type of machine learning algorithm inspired by the way the human brain processes information, enabling computers to learn from data and make decisions without being explicitly programmed. One of the key advantages of fuzzy logic is its ability to handle vague and ambiguous information, which is common in real-world scenarios. For example, in a system that controls the temperature of a room, fuzzy logic can account for factors like "slightly warm" or "very cold" instead of just "hot" or "cold." This flexibility allows for more nuanced decision-making and can lead to better outcomes in complex systems where precise rules are difficult to define. Neural networks, on the other hand, excel at tasks that involve pattern recognition and nonlinear relationships in data. By simulating the interconnected neurons in the brain, neural networks can learn from large amounts of data and make predictions or classifications with high accuracy. This makes themparticularly well-suited for tasks like image recognition, speech recognition, and natural language processing. In recent years, there has been a growing interest in combining fuzzy logic and neural networks to take advantage of the strengths of both approaches. This hybrid approach, known as neuro-fuzzy systems, aims to leverage the interpretability of fuzzy logic with the learning capabilities of neural networks. By combining fuzzy rules with neural network models, neuro-fuzzy systems can capture complex relationships in data while still providing transparent and understandable reasoning. One of the main challenges in developing neuro-fuzzy systems is finding the right balance between the fuzzy rules and the neural network model. Too many fuzzy rules can lead to a complex and computationally expensive system, while too few rules may not capture the full complexity of the problem. Additionally, training a neuro-fuzzy system requires a large amount of data and computational resources, which can be a barrier for some applications. Despite these challenges, neuro-fuzzy systems have beensuccessfully applied in a wide range of fields, including control systems, forecasting, and decision support. For example, in the field of robotics, neuro-fuzzy systems have been used to improve the accuracy and efficiency of robot control algorithms. In healthcare, neuro-fuzzy systems have been applied to medical diagnosis and treatment planning, helping doctors make more informed decisions based on patient data. Overall, the combination of fuzzy logic and neural networks offers a powerful approach to solving complex problems inartificial intelligence. By leveraging the strengths of both techniques, neuro-fuzzy systems can provide a more robust and interpretable solution to a wide range of real-world challenges. As research in this area continues to advance, we can expect to see even more innovative applications of neuro-fuzzy systems in the future.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
I.J. Intelligent Systems and Applications, 2016, 5, 49-54Published Online May 2016 in MECS (/)DOI: 10.5815/ijisa.2016.05.07Fuzzy Logic Based Modified Adaptive Modulation Implementation for Performance Enhancement in OFDM SystemsKuldeep SinghGuru Nanak Dev University Regional Campus Fattu Dhinga, Kapurthala, Punjab, India-14606E-mail: kuldeepsinghbrar87@Abstract—Adaptive modulation is one of the recent technologies used to improve future communication systems. Many adaptive modulation techniques have been developed for the improving the performance of Orthogonal Frequency Division Multiplexing (OFDM) system in terms of high data rates and error free delivery of data. But uncertain nature of wireless channel reduces the performance of OFDM system with fixed modulation techniques. In this paper, modified adaptive modulation technique has been proposed which adapts to the nature of communication channel based upon present modulation order, code rate, BER and SNR characterizing uncertain nature of communication channel by using a Fuzzy Inference System which further enhances the performance of OFDM systems in terms of high transmission data rate and error free delivery of data. Index Terms—Adaptive Modulation, Bit Error Rate (BER), Coding Rate, Fuzzy Inference System (FIS), Orthogonal Frequency Division Multiplexing (OFDM), Signal to Noise Ratio (SNR).I.I NTRODUCTIONOrthogonal Frequency Division Multiplexing System (OFDM) is a multiple-carrier trans mission technique, which divides the higher spectrum into many s mall carriers, i.e. it divide the wideband frequency channel into a number of parallel narrowband sub channel s, and each low-rate data carriers are transmitted over different sub channels. Orthogonal Frequency Division Multiplexing technique (OFDM) is basically a combination of both modulation and multiplexing techniques. It is considered to be a special case of Frequency Division Multiplexing (FDM), in which multiple user access is achieved by dividing the available bandwidth into several channels which are allocated to different users [1]. However; Orthogonal Frequency Division Multiplexing System (OFDM) uses the available bandwidth spectrum very efficiently by spacing different communication channels as closer as possible. This efficient spectrum allocation can be achieved by making all available carriers orthogonal to one another, so the interference between the closely spaced carriers is removed. In an OFDM signal each carrier has a very narrow bandwidth, thus output symbol rate is low. This fact of low symbol rate results the OFDM signal having a high tolerance towards the multipath delay spread. The main reasons to use OFDM are to enhance the strength against narrowband interference and frequency selective fading. In a distinct carrier system, a distinct fade or interference can cause the whole link to fail. On the other hand, in a multicarrier system, only a small fraction of the subcarriers will be affected [2]. OFDM also overcomes the problems with both TDMA and FDMA. In FDMA many carriers are spaced from each other in that way the signals can be received using any conventional filters and demodulators. In such that receivers guard bands are placed between carriers which lowers the spectrum efficiency. In OFDM sub carriers are orthogonal to one another so the signal can be received without intercarrier interference. OFDM efficiently use the spectrum by allowing over-lapping of carriers.OFDM also removes the ISI through use of a cyclic prefix (CP).OFDM provides protection against impulsive parasitic noise and co-channel interference .OFDM is less responsive to sample timing offsets as compared to single carrier systems [3].In this paper, a modified adaptive modulation technique has been implemented using Fuzzy Inference System which makes OFDM system adaptive to communication channel. This Fuzzy system takes into consideration input parameters such as Present modulation, Coding Rate, SNR and BER and gives better modulation order among others so as to enhance the overall performance of OFDM system in terms of efficient, fast and error free delivery of data.II.R ELATED W ORKK. Seshadri Sastry et al. [4] discover the OFDM system with adaptive modulation by using fuzzy logic interface (FIS) which improves system capacity by maintaining good error performance. Adaptive modulation systems by using ordinary hardware decision circuits are ineffective to decide or to change modulation order according to given conditions. So, by using fuzzy logic in the decision making interface which makes the system more efficient.Atta-ur-Rahman et al. [5] implement a method whichenhance capacity of system in Rayleigh fading channel where the Genetic Algorithm (GA) with FRBS based Adaptive allocation performs better than water filling (WF) with FRBS based adaptive resource allocation. Harivikram et al. [6] investigated OFDM system with adaptive modulation and coding rate performs very well than normal OFDM system i.e. without adaptive modulation and coding rate and it also maintains the bit error rate and spectrum efficiency of the OFDM system. Faezah et al. [3]have been investigated adaptive transmission scheme for OFDM, which results the adaptive transmission scheme is better than the fixed transmission system. Adaptation algorithm helps to improve the throughput performance with considerable BER performance.K. Seshadri Sastryet al. [7] implement a method by using Fuzzy Logic Interface and Non-Data-Aided SNR estimation which results adaptive modulation for OFDM system increases performance of system by maintaining channel conditions, bit error rate and capacity efficiently . Qureshi et al. [8] proposed an adaptive modulation and coding scheme by using Fuzzy Rule Base System (FRBS), where product codes are used with M- QAM which increases the data rate in an OFDM system with a fixed bit error rate and transmit power for each subcarrier. Atta-ur-Rahman Fuzzy et al. [9] proposed a Rule Based System based adaptive modulation with coding scheme which shows that FRBS is more powerful in terms of throughput and bit error rate.Khem Kumar et al. [10] proposed a method of an adaptive modulated OFDM system by using fuzzy Inference system (FIS) which results the Bit Error Rate and modulation order of QAM techniques of the system performs better than the fixed system because of its adaptive nature.Parminder Kaur et al. [14] presented that OFDM system provides the high spectral efficiency, high data rate, but further by using neuro-fuzzy approach and machine learning approach, the quality of service (QoS), data rate, Signal to Noise Ratio (SNR), Bit Error Rate (BER), Inter Symbol Interference (ISI), fading and capacity of the system can be improved.In this research paper, efforts are made to enhance the performance of OFDM system in terms of transmission speed and error free delivery of data by proposing a Fuzzy logic based modified adaptive modulation system based upon present modulation, code rate and parameters representing uncertain nature of communication channel such as SNR and BER at given time.III.F UZZY I NFERENCE S YSTEMFuzzy system suitable for tasks involving logic has been proposed as an addition to classical formal logic. They were first developed in set theory. The “fuzzy set” has been employed to expand classical sets, which are characterised by some margins. This addition allows a degree of flexibility for each object which belongs to a particular set. This quality is realized by membership functions which give fuzzy sets the capacity of modeling linguistic, fuzzy expression [11]. Fuzzy logic is considered to be a novel way for developing reasoning and decision making models by handling imprecise information, in which truth can assume a value between 0 and 1. This information is referred to as fuzziness: so, fuzziness does not come from randomness, but it comes from the uncertain and imprecise nature of conceptual thoughts and concepts. Fuzzy reasoning realizes a form of reasoning that, by using particular mathematical inferences which provides conclusions based on a set of fuzzy IF-THEN rules. Fuzzy logic is a suitable technique of describing the behaviour of systems which are either too complex or too unclear to be agreeable to precise mathematical analysis. Classical systems cannot deal withimprecise or imperfect information, because they do not provide any means of representing vague propositions and this is not having any provisions which can make an inference from such uncertain propositions. Fuzzy logic system is based upon IF-THEN rules and can be characterised in terms of their primary constituents: fuzzification, rule base, inference, and defuzzification. A generalized Fuzzy Inference System is shown in figure 1 [12], [13].Fig.1. Fuzzy Inference SystemFuzzy logic based Fuzzy Inference System is a powerful system which helps in decision making based upon input parameters. In this research paper, this fuzzy system has been taken into consideration for deciding best modulation technique which suits the most in uncertain and continuously changing communication channel and gives better performance for error free delivery of data.IV.P ROPOSED S CHEMEIn this paper, authors have proposed a scheme of modified adaptive OFDM modulation system based on fuzzy inference system (FIS), in which modulation order is changed according to the values of signal to noise ratio, bit error rate, exiting modulation order and coding rate. OFDM model work in two parts modulation and demodulation, Incoming bits are pass through in different stages of modulation process then after passing through channel, these channel pass the output to fuzzy logic interface, fuzzy box co mpare the present order of modulation which is coming from OFDM channel and change it according to the values of SNR and BER (Figure.2). Fuzzy Inference System work with some set of rules and output of this system controls both modulation and demodulation of the OFDM system toimprove the overall efficiency of the system.Fig.2. Fuzzy Inference System based OFDM SystemV. S IMULATIONS AND R ESULTSFuzzy Inference system is modeled in Fuzzy Inference system editor of Fuzzy Logic toolbox in MATLA B. This Fuzzy Inference system consists of four input functions: SNR, BER, Present Modulation and Code Rate and one output function Best Modulation. Every input and output function have different membership function. Fuzzy System is implemented by using Fuzzy logic tool of MATLAB 2009b in window 7 with i5 processor. FIS can be created by using either Sugeno or Mamdani types of fuzzy tool .But here we use mamdani type of FIS. Table 1 show the parameters with their values which are used to create Fuzzy Inference System (FIS).Table 1. Parameters of FIS with Their ValuesFig.3. Fuzzy Inference SystemMembership functions of different Input and Output parameters are described as follows:∙Membership functions of input SNR are low, medium, and high with the range of 0 to 30 dB (Figure 4).∙Membershipfunctions of input BER are low, medium, high with range of 10-5 to 1bits/s/Hz (Figure 5)∙Membership functions of input present modulation areQPSK,4QAM,8QAM,16QAM,32QAM,64QAM,128QAM,256QAM,512QAM (Figure 6)∙ Membership functions of input Code rate are 1/4,1/3,1/2 (Figure 7)∙Membership functions of output best modulation are BPSL, QPSK, 4QAM, 8QAM, 16QAM, 32QAM, 64QAM, 128QAM, 256QAM, 512QAM, 1024QAM (Figure 8).Fig.4. Membership Functions of SNRFig.5. Membership Functions of BERFig.6. Membership Functions of Present ModulationFig.7. Membership Functions of Code Rate Fig.8. Membership Functions of Best ModulationFig.9. Rule viewers of Fuzzy Inference SystemFig.10. Rules of Fuzzy Inference SystemIn this system IF-Then rules are used to make decision about best modulation technique. The rule are set in Fuzzy inference system (FIS) .When the Signal to Noise Ratio (SNR) or Modulation order of present signal is low then the output modulation order decreases by order 1, but if Signal to Noise Ratio (SNR) or Modulation order of present signal is high, then the output modulation order increases by order 1.Now if Signal to Noise Ratio (SNR) or Modulation order of present signal is medium then the output modulation order will remains same. If SNR is High, BER is Low, Present Modulation is 4 QAM and Code Rate is 1/4 then Best Modulation is 8 QAM”.The Rule viewer of FIS gives the better description of all fuzzy logic set of rule (Figure 10). Figure11 shows different surface views of FIS. These surface views gives degree of correlation among all input variables for a particularNow the validation of data is done by using MATLA B 2009b and results are shown in table 2 given below.Table 2. Validation of DataFig.11. Different Surface Views of FISFig.12. Different Surface Views of FISFinally, in this research work, Fuzzy Inference system has been designed by taking into consideration present modulation, code rate , SNR and BER which reveals the nature of communication channel . This Fuzzy system gives best modulation technique as output which is most suitable for OFDM system for a given communication channel at a particular time. As a result of this, this implementation of modifiedadaptivemodulation usingfuzzy logic system enhances the performance of OFDM system to great extent in terms of error free and high speed delivery of data.VI.C ONCLUSIONThe proposed approach of modified adaptive modulation based on Fuzzy Inference System enhances the performance of an OFDM system. In this approach, Fuzzy Inference System uses present Modulation, SNR, BER and Coding Rater as input parameters and gives best modulation as output which is then feedback to modulator and demodulator of OFDM system to improve overall efficiency of the system. As fixed modulation system works on some fixed conditions, but modified adaptive modulation of OFDM by using FIS gives the better performance and improves the capacity of the system by getting adaptive to environment of communication channel. So, Fuzzy logic system is a technique which helps to make the OFDM system adaptive in nature, that it can choose a better modulation order with coding rate according to the value of SNR and BER and enhances the performance of OFDM system in terms of fast and error free delivery of data.R EFERENCES[1]Hara, S., & Prasad, R., “Multicarrier techniques for 4Gmobile communications”,Artech House, 2003.[2]Li, Ye Geoffrey, and Gordon L. Stuber. “Orthogonalfrequency division multiplexing for wireless communications”. Springer, 2006.[3]Faezah, J., and K. Sabira. “Adaptive Modulation forOFDM Systems”International Journal of Communication Networks & Information Security 1.2, 2009.[4]K. Seshadri Sastry and Dr.M.S.Prasad Babu. “AdaptiveModulation for OFDM system using Fuzzy logic interface”, IEEE ICSESS, 368-371, 2010.[5]Atta-ur-Rahman, Ijaz Mansoor Qureshi, and AqdasNaveed Malik, “Adaptive Resource Allocation in OFDM Systems Using GA and Fuzzy Rule Base System”. World Applied Sciences Journal18.6, 836-844, 2012.[6]Harivikram, T. S., et al. “Adaptive Modulation andCoding Rate for OFDM Systems”. International Journal of Emerging Technology and Advanced Engineering. Vol.3, Issue 2, 250-255, 2013.[7]K. Seshadri Sastry and Dr.M.S.Prasad Babu. “Fuzzy logicbased Adaptive Modulation Using Non Data Aided SNR Estimation for OFDM system”. International Journal of Engineering Science and Technology, Vol. 2(6), 2384-2392, 2010.[8]Qureshi, Ijaz Mansoor, and M. Zeeshan Muzaffar.“Adaptive Coding and Modulation for OFDM S ystems using Product Codes and Fuzzy Rule Base System”.International Journal of Computer Applications 35.4, 2011.[9]Atta-ur-Rahman, Ijaz Mansoor Qureshi, and AqdasNaveed Malik. “A Fuzzy Rule Base Assisted Adaptive Coding and Modulation Scheme for OFDM Systems”. J.Basic. Appl. Sci. Res., 2(5)4843-4853, 2012..[10]Khem Kumar Nagar, Kanchan Sharma. “Adaptive OFDMImplementation Using Fuzzy Inference System”International Journal of Advanced Research in Computer Science and Software Engineering, Volume 3, Issue 7, 2013.[11]Seetha Subramanian, Mohanavalli, and Sheila Anand.“Fuzzy system to authenticate assisted living patients in their home environment” Journal of Computer Science9.5, 2013.[12]Klir, George J., and Bo Yuan. Fuzzy sets and fuzzy logic.Vol. 4. New Jersey: Prentice Hall, 1995[13]Ross, Timothy J., Fuzzy logic with engineeringapplications. John Wiley & Sons, 2009.[14]Parminder Kaur, Kuldeep Singh, Hardeep Kaur.“Performance analysis of MIMO-OFDM system in 4g technologies: A Review”. International Journal of Mathematical and Engineering sciences, 2014.Authors’ ProfilesKuldeep Singh received his B. techdegree in Electronics & CommunicationEngineering from Punjab TechnicalUniversity, Jalandhar, Punjab, India in2009 & Master’s degree in Electronics &Communication Engineering from PanjabUniversity, Chandigarh, India in 2011. Heis working as assistant professor in GuruNanak Dev University Regional Campus Fattu Dhinga, Kapurthala, Punjab, India. His areas of interest include Wireless Communications, Machine Learning Techniques etc. He has published 25 research paper in various national & International conferences and International Journals.How to cite this paper: Kuldeep Singh, "Fuzzy Logic Based Modified Adaptive Modulation Implementation for Performance Enhancement in OFDM Systems", International Journal of Intelligent Systems and Applications (IJISA), Vol.8, No.5, pp.49-54, 2016. DOI: 10.5815/ijisa.2016.05.07。
