图的深度和广度
深度优先算法和广度优先算法的时间复杂度

深度优先算法和广度优先算法的时间复杂度深度优先算法和广度优先算法是在图论中常见的两种搜索算法,它们在解决各种问题时都有很重要的作用。
本文将以深入浅出的方式从时间复杂度的角度对这两种算法进行全面评估,并探讨它们在实际应用中的优劣势。
1. 深度优先算法的时间复杂度深度优先算法是一种用于遍历或搜索树或图的算法。
它从图中的某个顶点出发,沿着一条路径一直走到底,直到不能再前进为止,然后回溯到上一个节点,尝试走其他的路径,直到所有路径都被走过为止。
深度优先算法的时间复杂度与图的深度有关。
在最坏情况下,深度优先算法的时间复杂度为O(V+E),其中V表示顶点的数量,E表示边的数量。
2. 广度优先算法的时间复杂度广度优先算法也是一种用于遍历或搜索树或图的算法。
与深度优先算法不同的是,广度优先算法是从图的某个顶点出发,首先访问这个顶点的所有邻接节点,然后再依次访问这些节点的邻接节点,依次类推。
广度优先算法的时间复杂度与图中边的数量有关。
在最坏情况下,广度优先算法的时间复杂度为O(V+E)。
3. 深度优先算法与广度优先算法的比较从时间复杂度的角度来看,深度优先算法和广度优先算法在最坏情况下都是O(V+E),并没有明显的差异。
但从实际运行情况来看,深度优先算法和广度优先算法的性能差异是显而易见的。
在一般情况下,广度优先算法要比深度优先算法快,因为广度优先算法的搜索速度更快,且能够更快地找到最短路径。
4. 个人观点和理解在实际应用中,选择深度优先算法还是广度优先算法取决于具体的问题。
如果要找到两个节点之间的最短路径,那么广度优先算法是更好的选择;而如果要搜索整个图,那么深度优先算法可能是更好的选择。
要根据具体的问题来选择合适的算法。
5. 总结和回顾本文从时间复杂度的角度对深度优先算法和广度优先算法进行了全面评估,探讨了它们的优劣势和实际应用中的选择。
通过对两种算法的时间复杂度进行比较,可以更全面、深刻和灵活地理解深度优先算法和广度优先算法的特点和适用场景。
第15讲图的遍历

V6
V8
V8
V7
V5 深度优先生成树
V8 V1
V2
V3
V4 V5 V6 V7
V8 广度优先生成树
27
例A
B
CD E
F
GH
I
K
J
L
M
A
D
G
LCF
KI E
H M
JB
深度优先生成森林
28
二、图的连通性问题
▪1、生成树和生成森林
▪ 说明
G
▪ 一个图可以有许多棵不同的生成树
KI
▪ 所有生成树具有以下共同特点:
g.NextAdjVex(v, w))
{
if (g.GetTag(w) == UNVISITED)
{
g.SetTag(w, VISITED);
g.GetElem(w, e);
Visit(e);
q.InQueue(w);
}
}}}
24
一、图的遍历 两种遍历的比较
V0
V1 V4
V0
V1 V4
V3
V2 V5
16
一、图的遍历
广度优先遍历序列?入队序列?出队序列?
V1
V2
V3
V1
V4
V5 V6
V7
V8
遍历序列: V1
17
一、图的遍历
广度优先遍历序列?入队序列?出队序列?
V1
V2
V3
V2 V3
V4
V5 V6
V7
V8
遍历序列: V1 V2 V3
18
一、图的遍历
广度优先遍历序列?入队序列?出队序列?
V1
V2
第7章图的深度和广度优先搜索遍历算法
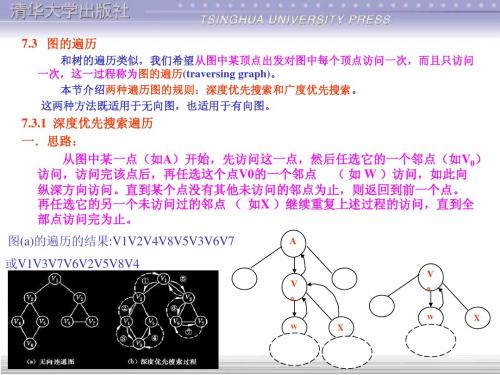
和树的遍历类似,我们希望从图中某顶点出发对图中每个顶点访问一次,而且只访问 一次,这一过程称为图的遍历(traversing graph)。 本节介绍两种遍历图的规则:深度优先搜索和广度优先搜索。 这两种方法既适用于无向图,也适用于有向图。
7.3.1 深度优先搜索遍历 一.思路: 从图中某一点(如A)开始,先访问这一点,然后任选它的一个邻点(如V0) 访问,访问完该点后,再任选这个点V0的一个邻点 ( 如 W )访问,如此向 纵深方向访问。直到某个点没有其他未访问的邻点为止,则返回到前一个点。 再任选它的另一个未访问过的邻点 ( 如X )继续重复上述过程的访问,直到全 部点访问完为止。 图(a)的遍历的结果:V1V2V4V8V5V3V6V7 或V1V3V7V6V2V5V8V4
p
v0 w x v 1
V
0
v 2
V
0
typedef struct {VEXNODE adjlist[MAXLEN]; // 邻接链表表头向量 int vexnum, arcnum; // 顶点数和边数 int kind; // 图的类型 }ADJGRAPH;
W W
X
X
7.3.2 广度优先搜索遍历 一.思路:
V
0
A V
0
W W
XXΒιβλιοθήκη 二.深度优先搜索算法的文字描述: 算法中设一数组visited,表示顶点是否访问过的标志。数组长度为 图的顶点数,初值均置为0,表示顶点均未被访问,当Vi被访问过,即 将visitsd对应分量置为1。将该数组设为全局变量。 { 确定从G中某一顶点V0出发,访问V0; visited[V0] = 1; 找出G中V0的第一个邻接顶点->w; while (w存在) do { if visited[w] == 0 继续进行深度优先搜索; 找出G中V0的下一个邻接顶点->w;} }
dfs和bfs算法

dfs和bfs算法深度优先搜索(DFS)和广度优先搜索(BFS)是图论中常用的两种搜索算法,也是许多算法题中的基础算法。
本文将从什么是图、什么是搜索算法开始介绍DFS、BFS的基本原理以及应用场景。
一、图的概念图是由节点集合以及它们之间连线所组成的数据结构。
图分为有向图和无向图两种,有向图中的边具有一定的方向性,而无向图中的边是没有方向的。
二、DFS(深度优先搜索)深度优先搜索从一个点开始,根据规定的遍历方式始终向着深度方向搜索下去,直到到达目标节点或者无法继续搜索为止。
具体实现可以用递归或者非递归的方式进行。
1、深度优先搜索的框架def dfs(v,visited,graph):visited[v] = True #将节点v标记为已经被访问#遍历v的所有连接节点for w in graph[v]:if not visited[w]:dfs(w,visited,graph)2、深度优先搜索的应用DFS常用来解决最长路径问题、拓扑排序问题以及判断图是否存在环。
三、BFS(广度优先搜索)广度优先搜索是从一个点开始,逐层扩散的搜索方式。
具体实现可以用队列实现。
1、广度优先搜索的框架def bfs(start,graph):visited = [False] * len(graph) #标记所有节点为未访问queue = [start] #队列存储已经访问过的节点visited[start] = True #起始点被标记为已经访问过while queue:v = queue.pop(0) #弹出队列首节点#遍历该节点的所有连接节点for w in graph[v]:if not visited[w]:visited[w] = True #标记该节点已经被访问queue.append(w) #加入队列2、广度优先搜索的应用BFS常用来解决最短路径问题,如迷宫问题、网络路由问题等。
四、DFS和BFS的区别DFS从一个节点开始,向下深度优先搜索,不断往下搜索直到无路可走才返回,因此将搜索过的节点用栈来存储。
图的概念

V3
//第一行给给出边数和顶点数:n,m 。n和m的值均小于100 //第二行到n+1行,每一个行2个数,分别表示边的起点,终点。 //如 3,3 // 1 2 // 2 3 // 3 1 /*以邻接矩阵来存储。 #include <iostream> using namespace std; bool juzhen[101][101]; int main() { int m,n; cin>>m>>n; int a,b; for(int i=0;i<m;i++) { cin>>a>>b; juzhen[a][b]=1;// juzhen[b][a]=1; } }
如何用计算机来存储图的信息,这是图的存储结构 要解决的问题。 第一种:边集数组表示法。 定义一个结构体,存储边的起点和终点。 Struct bian { int s;//边的起点 int e;//边的终点 int v;//边的权值 } 然后定义一个该结构体的数组,存储图中所有的边。
第二种:邻接矩阵表示法。矩阵即二维数组。 设G=(V,E)是一个n阶图,顶点为 (V0,V1,……Vn-1).则可以定义一个n阶矩 阵arr[n][n]。即n行n列的二维数组。如果存 在边(Vi,Vj),则矩阵中arr[i][j]=1,否则 arr[i][j]=0.
这是著名的柯尼斯堡七桥问题。在一段时间内都没 有人能够给出正确答案。后来,欧拉证明了此题 是无解的。从而,引出了著名的“欧拉问题”或 “图的一笔画问题”。欧拉得出的结论是: 1.如果一个图中没有奇点,则该图可以从起点 出发经过所有边一次,再回到起点。 2.如果一个图中有且只有两个奇点,则该图可 以一个奇点出发,经过所有边一次,到达另一个 奇点。 欧拉开启了人们研究图的历史。
广度优先和深度优先的例子

广度优先和深度优先的例子广度优先搜索(BFS)和深度优先搜索(DFS)是图遍历中常用的两种算法。
它们在解决许多问题时都能提供有效的解决方案。
本文将分别介绍广度优先搜索和深度优先搜索,并给出各自的应用例子。
一、广度优先搜索(BFS)广度优先搜索是一种遍历或搜索图的算法,它从起始节点开始,逐层扩展,先访问起始节点的所有邻居节点,再依次访问其邻居节点的邻居节点,直到遍历完所有节点或找到目标节点。
例子1:迷宫问题假设有一个迷宫,迷宫中有多个房间,每个房间有四个相邻的房间:上、下、左、右。
现在我们需要找到从起始房间到目标房间的最短路径。
可以使用广度优先搜索算法来解决这个问题。
例子2:社交网络中的好友推荐在社交网络中,我们希望给用户推荐可能认识的新朋友。
可以使用广度优先搜索算法从用户的好友列表开始,逐层扩展,找到可能认识的新朋友。
例子3:网页爬虫网页爬虫是搜索引擎抓取网页的重要工具。
爬虫可以使用广度优先搜索算法从一个网页开始,逐层扩展,找到所有相关的网页并进行抓取。
例子4:图的最短路径在图中,我们希望找到两个节点之间的最短路径。
可以使用广度优先搜索算法从起始节点开始,逐层扩展,直到找到目标节点。
例子5:推荐系统在推荐系统中,我们希望给用户推荐可能感兴趣的物品。
可以使用广度优先搜索算法从用户喜欢的物品开始,逐层扩展,找到可能感兴趣的其他物品。
二、深度优先搜索(DFS)深度优先搜索是一种遍历或搜索图的算法,它从起始节点开始,沿着一条路径一直走到底,直到不能再继续下去为止,然后回溯到上一个节点,继续探索其他路径。
例子1:二叉树的遍历在二叉树中,深度优先搜索算法可以用来实现前序遍历、中序遍历和后序遍历。
通过深度优先搜索算法,我们可以按照不同的遍历顺序找到二叉树中所有节点。
例子2:回溯算法回溯算法是一种通过深度优先搜索的方式,在问题的解空间中搜索所有可能的解的算法。
回溯算法常用于解决组合问题、排列问题和子集问题。
例子3:拓扑排序拓扑排序是一种对有向无环图(DAG)进行排序的算法。
图的搜索与应用实验报告(附源码)(word文档良心出品)

哈尔滨工业大学计算机科学与技术学院实验报告课程名称:数据结构与算法课程类型:必修实验项目名称:图的搜索与应用实验题目:图的深度和广度搜索与拓扑排序设计成绩报告成绩指导老师一、实验目的1.掌握图的邻接表的存储形式。
2.熟练掌握图的搜索策略,包括深度优先搜索与广度优先搜索算法。
3.掌握有向图的拓扑排序的方法。
二、实验要求及实验环境实验要求:1.以邻接表的形式存储图。
2.给出图的深度优先搜索算法与广度优先搜索算法。
3.应用搜索算法求出有向图的拓扑排序。
实验环境:寝室+机房+编程软件(NetBeans IDE 6.9.1)。
三、设计思想(本程序中的用到的所有数据类型的定义,主程序的流程图及各程序模块之间的调用关系)数据类型定义:template <class T>class Node {//定义边public:int adjvex;//定义顶点所对应的序号Node *next;//指向下一顶点的指针int weight;//边的权重};template <class T>class Vnode {public:T vertex;Node<T> *firstedge;};template <class T>class Algraph {public:Vnode<T> adjlist[Max];int n;int e;int mark[Max];int Indegree[Max];};template<class T>class Function {public://创建有向图邻接表void CreatNalgraph(Algraph<T>*G);//创建无向图邻接表void CreatAlgraph(Algraph<T> *G);//深度优先递归搜索void DFSM(Algraph<T>*G, int i);void DFS(Algraph<T>* G);//广度优先搜索void BFS(Algraph<T>* G);void BFSM(Algraph<T>* G, int i);//有向图的拓扑排序void Topsort(Algraph<T>*G);/得到某个顶点内容所对应的数组序号int Judge(Algraph<T>* G, T name); };主程序流程图:程序开始调用关系:主函数调用五个函数 CreatNalgraph(G)//创建有向图 DFS(G) //深度优先搜索 BFS(G) //广度优先搜索 Topsort(G) //有向图拓扑排序 CreatAlgraph(G) //创建无向图其中 CreatNalgraph(G) 调用Judge(Algraph<T>* G, T name)函数;DFS(G)调用DFSM(Algraph<T>* G , int i)函数;BFS(G) 调用BFSM(Algraph<T>* G, int k)函数;CreatAlgraph(G) 调选择图的类型无向图有向图深 度 优 先 搜 索广度优先搜索 深 度 优 先 搜 索 广度优先搜索拓 扑 排 序程序结束用Judge(Algraph<T>* G, T name)函数。
图的各种算法(深度、广度等)

vex next 4 p
3
2 ^
2
^
5
5 5 4 3 2 1 0 ^
^
4 ^
top
4
输出序列:6 1
1 2 3 4 5 6
in link 0 2 ^ 1 0 2 0
vex next 4 p
3
2 ^
2
^
5
5 5 4 3 2 1 0 ^
^
4 ^
top 4
输出序列:6 1
1 2 3 4 5 6
in link 0 2 ^ 1 0 2 0
c a g b h f d e
a
b h c d g f
e
在算法中需要用定量的描述替代定性的概念
没有前驱的顶点 入度为零的顶点 删除顶点及以它为尾的弧 弧头顶点的入度减1
算法实现
以邻接表作存储结构 把邻接表中所有入度为0的顶点进栈 栈非空时,输出栈顶元素Vj并退栈;在邻接表中查找 Vj的直接后继Vk,把Vk的入度减1;若Vk的入度为0 则进栈 重复上述操作直至栈空为止。若栈空时输出的顶点个 数不是n,则有向图有环;否则,拓扑排序完毕
^
4
^
top
输出序列:6 1 3 2 4
1 2 3 4 5 6
in link 0 0 ^ 0 0 0 0
vex next 4
3
2 ^
2
^
5
5 5 4 3 2 1 0 ^ p
^
4
^topBiblioteka 5输出序列:6 1 3 2 4
1 2 3 4 5 6
in link 0 0 ^ 0 0 0 0
vex next 4
w2 w1 V w7 w6 w3
深度遍历和广度遍历例题

深度遍历和广度遍历例题深度遍历(Depth-First Search,DFS)和广度遍历(Breadth-First Search,BFS)是图遍历算法中常用的两种方法。
下面我将为你提供一个例题,并从多个角度进行全面的回答。
例题,给定一个无向图,使用深度遍历和广度遍历两种方法遍历该图,并输出遍历的结果。
首先,我们需要明确一下图的表示方式。
常用的图表示方法有邻接矩阵和邻接表,这里我们选择使用邻接表表示图。
假设我们有如下无向图:A./ \。
B---C.\ /。
D.邻接表表示如下:A: B, C.B: A, C, D.C: A, B, D.D: B, C.接下来,我们来进行深度遍历。
深度遍历的基本思想是从起始节点开始,尽可能深地访问每个节点,直到无法继续深入为止,然后回溯到上一个节点,继续访问其他未访问的节点。
从节点A开始进行深度遍历,访问顺序为A-B-C-D。
具体步骤如下:1. 将节点A标记为已访问。
2. 访问与节点A相邻的未被访问的节点,即节点B和节点C。
3. 选择其中一个节点(这里选择节点B),将其标记为已访问,并继续深度遍历该节点。
4. 对节点B进行相同的操作,访问与节点B相邻的未被访问的节点,即节点A、节点C和节点D。
5. 选择其中一个节点(这里选择节点C),将其标记为已访问,并继续深度遍历该节点。
6. 对节点C进行相同的操作,访问与节点C相邻的未被访问的节点,即节点A、节点B和节点D。
7. 选择其中一个节点(这里选择节点D),将其标记为已访问,并继续深度遍历该节点。
8. 由于节点D没有未被访问的相邻节点,回溯到节点C。
9. 由于节点C也没有未被访问的相邻节点,回溯到节点B。
10. 由于节点B还有一个未被访问的相邻节点(节点A),将其标记为已访问,并继续深度遍历该节点。
11. 由于节点A没有未被访问的相邻节点,回溯到节点B。
12. 由于节点B没有未被访问的相邻节点,回溯到节点A。
13. 完成深度遍历。
【算法】广度优先算法和深度优先算法

【算法】⼴度优先算法和深度优先算法⼴度(BFS)和深度(DFS)优先算法这俩个算法是图论⾥⾯⾮常重要的两个遍历的⽅法。
下⾯⼀个例⼦迷宫计算,如下图解释:所谓⼴度,就是⼀层⼀层的,向下遍历,层层堵截,看下⾯这幅图,我们如果要是⼴度优先遍历的话,我们的结果是V1 V2 V3 V4 V5 V6 V7 V8。
⼴度优先搜索的思想: ①访问顶点vi ; ②访问vi 的所有未被访问的邻接点w1 ,w2 , …wk ; ③依次从这些邻接点(在步骤②中访问的顶点)出发,访问它们的所有未被访问的邻接点; 依此类推,直到图中所有访问过的顶点的邻接点都被访问; 说明: 为实现③,需要保存在步骤②中访问的顶点,⽽且访问这些顶点的邻接点的顺序为:先保存的顶点,其邻接点先被访问。
这⾥我们就想到了⽤标准模板库中的queue队列来实现这种先进现出的服务。
步骤: 1.将V1加⼊队列,取出V1,并标记为true(即已经访问),将其邻接点加进⼊队列,则 <—[V2 V3] 2.取出V2,并标记为true(即已经访问),将其未访问过的邻接点加进⼊队列,则 <—[V3 V4 V5]3.取出V3,并标记为true(即已经访问),将其未访问过的邻接点加进⼊队列,则 <—[V4 V5 V6 V7]4.取出V4,并标记为true(即已经访问),将其未访问过的邻接点加进⼊队列,则 <—[V5 V6 V7 V8]5.取出V5,并标记为true(即已经访问),因为其邻接点已经加⼊队列,则 <—[V6 V7 V8]6.取出V6,并标记为true(即已经访问),将其未访问过的邻接点加进⼊队列,则 <—[V7 V8]7.取出V7,并标记为true(即已经访问),将其未访问过的邻接点加进⼊队列,则 <—[V8]8.取出V8,并标记为true(即已经访问),将其未访问过的邻接点加进⼊队列,则 <—[]区别:深度优先遍历:对每⼀个可能的分⽀路径深⼊到不能再深⼊为⽌,⽽且每个结点只能访问⼀次。
广度优先算法,深度优先算法

广度优先算法,深度优先算法
广度优先算法(BFS)和深度优先算法(DFS)是两种常用的图遍历算法。
广度优先算法(BFS)从图的起始节点开始,先访问其所有直接邻居节点,然后再访问邻居节点的邻居节点,以此类推,直到访问到图中所有可达节点。
深度优先算法(DFS)从图的起始节点开始,首先访问其一个邻居节点,然后再依次递归地访问该邻居节点的邻居节点,直到访问到某个节点的所有邻居节点为止,然后再回退到上一个节点,继续访问其他未被访问的邻居节点。
两种算法的主要区别在于遍历的顺序和使用的数据结构。
BFS通常使用队列(Queue)来实现,通过先进先出的原则保证节点的访问顺序。
DFS通常使用栈(Stack)或递归来实现,通过先进后出的原则进行节点的访问。
广度优先算法适用于寻找最近的目标节点或在无权图中查找路径等问题。
深度优先算法适用于判断图中是否存在特定节点或搜索图中的所有路径等问题。
需要注意的是,在有环图中,深度优先算法有可能陷入死循环,需要额外的处理来避免重复访问节点。
深度优先和广度优先算法

深度优先和广度优先算法深度优先和广度优先算法深度优先遍历和广度优先遍历是两种常用的图遍历算法。
它们的策略不同,各有优缺点,可以在不同的场景中使用。
一、深度优先遍历深度优先遍历(Depth First Search,DFS)是一种搜索算法,它从一个顶点开始遍历,尽可能深地搜索图中的每一个可能的路径,直到找到所有的路径。
该算法使用栈来实现。
1. 算法描述深度优先遍历的过程可以描述为:- 访问起始顶点v,并标记为已访问; - 从v的未被访问的邻接顶点开始深度优先遍历,直到所有的邻接顶点都被访问过或不存在未访问的邻接顶点; - 如果图中还有未被访问的顶点,则从这些顶点中任选一个,重复步骤1。
2. 算法实现深度优先遍历算法可以使用递归或者栈来实现。
以下是使用栈实现深度优先遍历的示例代码:``` void DFS(Graph g, int v, bool[] visited) { visited[v] = true; printf("%d ", v);for (int w : g.adj(v)) { if(!visited[w]) { DFS(g, w,visited); } } } ```3. 算法分析深度优先遍历的时间复杂度为O(V+E),其中V是顶点数,E是边数。
由于该算法使用栈来实现,因此空间复杂度为O(V)。
二、广度优先遍历广度优先遍历(Breadth First Search,BFS)是一种搜索算法,它从一个顶点开始遍历,逐步扩展到它的邻接顶点,直到找到所有的路径。
该算法使用队列来实现。
1. 算法描述广度优先遍历的过程可以描述为:- 访问起始顶点v,并标记为已访问; - 将v的所有未被访问的邻接顶点加入队列中; - 从队列头取出一个顶点w,并标记为已访问; - 将w的所有未被访问的邻接顶点加入队列中; - 如果队列不为空,则重复步骤3。
2. 算法实现广度优先遍历算法可以使用队列来实现。
图的遍历深度优先遍历和广度优先遍历

4
5
f
^
对应的邻接表
终点2作为下次的始点, 由于1点已访问过,跳过, 找到4,记标识,送输出, 4有作为新的始点重复上 述过程
1 2 4
5
输出数组 resu
3.邻接表深度优先遍历的实现
template <class TElem, class TEdgeElem>long DFS2(TGraphNodeAL<TElem, TEdgeElem> *nodes,long n,long v0, char *visited, long *resu,long &top) {//深度优先遍历用邻接表表示的图。nodes是邻接表的头数组,n 为结点个数(编号为0~n)。 //v0为遍历的起点。返回实际遍历到的结点的数目。 //visited是访问标志数组,调用本函数前,应为其分配空间并初 始化为全0(未访问) //resu为一维数组,用于存放所遍历到的结点的编号,调用本函 数前,应为其分配空间 long nNodes, i; TGraphEdgeAL<TEdgeElem> *p; nNodes=1;
1 2
4
图 20-1有向图
5
3
1 2 3 4 5
1 0 1 0 1 0
2 1 0 0 0 0
3 0 0 0 0 0
4 0 1 0 0 0
5 1 0 1 0 0
1 2 3 4 5
1 1 0 1 1
1 2 4 5
所示图的邻接矩阵g
访问标识数组 visited
输出数组 resu
例如从1点深度优先遍历,先把1设置访问标志,并置入输出数组resu,然后从邻接 矩阵的第一行,扫描各列,找到最近的邻接点2,将其设置访问标志,并进入输出数 组,接着从邻接矩阵的2行扫描,找到第一个构成边的点是1,检查访问标识数组, 发现1已经访问过,跳过,找第二个构成边 的点4,设置访问标识,进入输出数组, 再从邻接矩阵的第4行扫描,寻找构成边的点,除1外在无其他点,返回2行,继续 寻找,也无新点,返回1,找到5,将5置访问标志,进入输出数组,1行再无其他新 点,遍历结束,返回遍历元素个数为4 。
深度优先搜索和广度优先搜索

深度优先搜索和广度优先搜索深度优先搜索(DFS)和广度优先搜索(BFS)是图论中常用的两种搜索算法。
它们是解决许多与图相关的问题的重要工具。
本文将着重介绍深度优先搜索和广度优先搜索的原理、应用场景以及优缺点。
一、深度优先搜索(DFS)深度优先搜索是一种先序遍历二叉树的思想。
从图的一个顶点出发,递归地访问与该顶点相邻的顶点,直到无法再继续前进为止,然后回溯到前一个顶点,继续访问其未被访问的邻接顶点,直到遍历完整个图。
深度优先搜索的基本思想可用以下步骤总结:1. 选择一个初始顶点;2. 访问该顶点,并标记为已访问;3. 递归访问该顶点的邻接顶点,直到所有邻接顶点均被访问过。
深度优先搜索的应用场景较为广泛。
在寻找连通分量、解决迷宫问题、查找拓扑排序等问题中,深度优先搜索都能够发挥重要作用。
它的主要优点是容易实现,缺点是可能进入无限循环。
二、广度优先搜索(BFS)广度优先搜索是一种逐层访问的思想。
从图的一个顶点出发,先访问该顶点,然后依次访问与该顶点邻接且未被访问的顶点,直到遍历完整个图。
广度优先搜索的基本思想可用以下步骤总结:1. 选择一个初始顶点;2. 访问该顶点,并标记为已访问;3. 将该顶点的所有邻接顶点加入一个队列;4. 从队列中依次取出一个顶点,并访问该顶点的邻接顶点,标记为已访问;5. 重复步骤4,直到队列为空。
广度优先搜索的应用场景也非常广泛。
在求最短路径、社交网络分析、网络爬虫等方面都可以使用广度优先搜索算法。
它的主要优点是可以找到最短路径,缺点是需要使用队列数据结构。
三、DFS与BFS的比较深度优先搜索和广度优先搜索各自有着不同的优缺点,适用于不同的场景。
深度优先搜索的优点是在空间复杂度较低的情况下找到解,但可能陷入无限循环,搜索路径不一定是最短的。
广度优先搜索能找到最短路径,但需要保存所有搜索过的节点,空间复杂度较高。
需要根据实际问题选择合适的搜索算法,例如在求最短路径问题中,广度优先搜索更加合适;而在解决连通分量问题时,深度优先搜索更为适用。
深度优先遍历算法和广度优先遍历算法实验小结

深度优先遍历算法和广度优先遍历算法实验小结一、引言在计算机科学领域,图的遍历是一种基本的算法操作。
深度优先遍历算法(Depth First Search,DFS)和广度优先遍历算法(Breadth First Search,BFS)是两种常用的图遍历算法。
它们在解决图的连通性和可达性等问题上具有重要的应用价值。
本文将从理论基础、算法原理、实验设计和实验结果等方面对深度优先遍历算法和广度优先遍历算法进行实验小结。
二、深度优先遍历算法深度优先遍历算法是一种用于遍历或搜索树或图的算法。
该算法从图的某个顶点开始遍历,沿着一条路径一直向前直到不能再继续前进为止,然后退回到上一个节点,尝试下一个节点,直到遍历完整个图。
深度优先遍历算法通常使用栈来实现。
以下是深度优先遍历算法的伪代码:1. 创建一个栈并将起始节点压入栈中2. 将起始节点标记为已访问3. 当栈不为空时,执行以下步骤:a. 弹出栈顶节点,并访问该节点b. 将该节点尚未访问的邻居节点压入栈中,并标记为已访问4. 重复步骤3,直到栈为空三、广度优先遍历算法广度优先遍历算法是一种用于遍历或搜索树或图的算法。
该算法从图的某个顶点开始遍历,先访问起始节点的所有相邻节点,然后再依次访问这些相邻节点的相邻节点,依次类推,直到遍历完整个图。
广度优先遍历算法通常使用队列来实现。
以下是广度优先遍历算法的伪代码:1. 创建一个队列并将起始节点入队2. 将起始节点标记为已访问3. 当队列不为空时,执行以下步骤:a. 出队一个节点,并访问该节点b. 将该节点尚未访问的邻居节点入队,并标记为已访问4. 重复步骤3,直到队列为空四、实验设计本次实验旨在通过编程实现深度优先遍历算法和广度优先遍历算法,并通过对比它们在不同图结构下的遍历效果,验证其算法的正确性和有效性。
具体实验设计如下:1. 实验工具:使用Python编程语言实现深度优先遍历算法和广度优先遍历算法2. 实验数据:设计多组图结构数据,包括树、稠密图、稀疏图等3. 实验环境:在相同的硬件环境下运行实验程序,确保实验结果的可比性4. 实验步骤:编写程序实现深度优先遍历算法和广度优先遍历算法,进行多次实验并记录实验结果5. 实验指标:记录每种算法的遍历路径、遍历时间和空间复杂度等指标,进行对比分析五、实验结果在不同图结构下,经过多次实验,分别记录了深度优先遍历算法和广度优先遍历算法的实验结果。
数据结构与算法(13):深度优先搜索和广度优先搜索
2.2.2 有向图的广广度优先搜索
下面面以“有向图”为例例,来对广广度优先搜索进行行行演示。还是以上面面的图G2为例例进行行行说明。
第1步:访问A。 第2步:访问B。 第3步:依次访问C,E,F。 在访问了了B之后,接下来访问B的出边的另一一个顶点,即C,E,F。前 面面已经说过,在本文文实现中,顶点ABCDEFG按照顺序存储的,因此会先访问C,再依次访 问E,F。 第4步:依次访问D,G。 在访问完C,E,F之后,再依次访问它们的出边的另一一个顶点。还是按 照C,E,F的顺序访问,C的已经全部访问过了了,那么就只剩下E,F;先访问E的邻接点D,再访 问F的邻接点G。
if(mVexs[i]==ch)
return i;
return -1;
}
/* * 读取一一个输入入字符
*/
private char readChar() {
char ch='0';
do {
try {
ch = (char)System.in.read();
} catch (IOException e) {
数据结构与算法(13):深度优先搜索和 广广度优先搜索
BFS和DFS是两种十十分重要的搜索算法,BFS适合查找最优解,DFS适合查找是否存在解(或者说 能找到任意一一个可行行行解)。用用这两种算法即可以解决大大部分树和图的问题。
一一、深度优先搜索(DFS)
1.1 介绍
图的深度优先搜索(Depth First Search),和树的先序遍历比比较类似。 它的思想:假设初始状态是图中所有顶点均未被访问,则从某个顶点V出发,首首先访问该顶点, 然后依次从它的各个未被访问的邻接点出发深度优先搜索遍历图,直至至图中所有和V有路路径相通 的顶点都被访问到。若此时尚有其他顶点未被访问到,则另选一一个未被访问的顶点作起始点,重 复上述过程,直至至图中所有顶点都被访问到为止止。 显然,深度优先搜索是一一个递归的过程。
深度遍历和广度遍历例题

深度遍历和广度遍历例题【实用版】目录1.深度遍历和广度遍历的定义与特点2.深度遍历和广度遍历的实现方法与算法3.深度遍历和广度遍历的应用场景与优缺点比较4.深度遍历和广度遍历的例题解析正文一、深度遍历和广度遍历的定义与特点深度遍历,简称 DFS(Depth First Search),是一种遍历图的算法。
它的特点是优先访问顶点,然后逐层访问相邻顶点,遇到死路时回溯。
深度遍历不需要记录所有节点,占用空间较小,但时间复杂度相对较高。
广度遍历,简称 BFS(Breadth First Search),是另一种遍历图的算法。
它的特点是逐层访问顶点,每层访问完所有相邻顶点后,再访问下一层的顶点。
广度遍历需要记录所有节点,占用空间较大,但时间复杂度相对较低。
二、深度遍历和广度遍历的实现方法与算法1.深度遍历算法:从出发点开始,沿着一条路径一直向前,遇到死路时回溯。
可以用递归或栈实现。
2.广度遍历算法:从出发点开始,逐层访问所有相邻顶点,然后继续访问下一层的顶点。
可以用队列实现。
三、深度遍历和广度遍历的应用场景与优缺点比较1.深度遍历:适用于寻找某个目标节点是否存在,或寻找从出发点到目标节点的一条路径。
优点是空间占用小,缺点是时间复杂度高,可能会出现重复访问。
2.广度遍历:适用于寻找从出发点到目标节点的最短路径,或遍历整个图。
优点是时间复杂度低,缺点是空间占用大,可能会出现重复访问。
四、深度遍历和广度遍历的例题解析例题:有一个无向图,共有 5 个顶点,分别标号为 1、2、3、4、5。
边有 5 条,分别是 (1, 2),(1, 3),(2, 4),(3, 4),(3, 5)。
从顶点1 开始,采用深度遍历和广度遍历,分别列出遍历过程。
1.深度遍历:- 从顶点 1 开始,访问顶点 2、3。
- 从顶点 3 开始,访问顶点 4、5。
- 顶点 5 没有其他相邻顶点,回溯到顶点 3。
- 从顶点 3 开始,回溯到顶点 2。
- 从顶点 2 开始,回溯到顶点 1,结束。
深度优先搜索和广度优先搜索的比较和应用场景

深度优先搜索和广度优先搜索的比较和应用场景在计算机科学中,深度优先搜索(DFS)和广度优先搜索(BFS)是两种常用的图搜索算法。
它们在解决许多问题时都能够发挥重要作用,但在不同的情况下具有不同的优势和适用性。
本文将对深度优先搜索和广度优先搜索进行比较和分析,并讨论它们在不同应用场景中的使用。
一、深度优先搜索(DFS)深度优先搜索是一种通过遍历图的深度节点来查找目标节点的算法。
它的基本思想是从起始节点开始,依次遍历该节点的相邻节点,直到到达目标节点或者无法继续搜索为止。
如果当前节点有未被访问的相邻节点,则选择其中一个作为下一个节点继续进行深度搜索;如果当前节点没有未被访问的相邻节点,则回溯到上一个节点,并选择其未被访问的相邻节点进行搜索。
深度优先搜索的主要优势是其在搜索树的深度方向上进行,能够快速达到目标节点。
它通常使用递归或栈数据结构来实现,代码实现相对简单。
深度优先搜索适用于以下情况:1. 图中的路径问题:深度优先搜索能够在图中找到一条路径是否存在。
2. 拓扑排序问题:深度优先搜索能够对有向无环图进行拓扑排序,找到图中节点的一个线性排序。
3. 连通性问题:深度优先搜索能够判断图中的连通分量数量以及它们的具体节点组合。
二、广度优先搜索(BFS)广度优先搜索是一种通过遍历图的广度节点来查找目标节点的算法。
它的基本思想是从起始节点开始,先遍历起始节点的所有相邻节点,然后再遍历相邻节点的相邻节点,以此类推,直到到达目标节点或者无法继续搜索为止。
广度优先搜索通常使用队列数据结构来实现。
广度优先搜索的主要优势是其在搜索树的广度方向上进行,能够逐层地搜索目标节点所在的路径。
它逐层扩展搜索,直到找到目标节点或者遍历完整个图。
广度优先搜索适用于以下情况:1. 最短路径问题:广度优先搜索能够在无权图中找到起始节点到目标节点的最短路径。
2. 网络分析问题:广度优先搜索能够在图中查找节点的邻居节点、度数或者群组。
三、深度优先搜索和广度优先搜索的比较深度优先搜索和广度优先搜索在以下方面有所不同:1. 搜索顺序:深度优先搜索按照深度优先的顺序进行搜索,而广度优先搜索按照广度优先的顺序进行搜索。
深度优先算法与广度优先算法

深度优先算法与广度优先算法
深度优先算法和广度优先算法是两种常用的图遍历算法。
它们都是基
于图的遍历来搜索图中的所有节点,并且都是基于图中节点之间的关
联性来进行搜索操作的。
首先来说深度优先算法。
深度优先算法即从一条边开始遍历,如果遇
到死路则返回上一个节点,继续从它的下一条边继续遍历。
整个搜索
的过程是以深度为优先,直到遍历所有的节点为止。
深度优先算法使
用的是栈数据结构,先访问的节点会被后访问的节点所覆盖,直到遍
历到最深处,然后回死路走回上一个节点,继续访问它的下一个节点。
深度优先算法一般用于寻找迷宫或图中的某条路径等应用场景。
接下来是广度优先算法。
广度优先算法即在图中按照一层一层的方式
遍历所有的节点,直到遍历完为止。
广度优先算法使用的是队列数据
结构,先访问的节点会先被访问到,后访问的节点会被后访问的节点
所覆盖,确保按层次进行遍历。
广度优先算法一般用于求出图中所有
节点的最短路径等应用场景。
总结起来,深度优先算法和广度优先算法都有各自的优点和应用场景。
深度优先算法主要是在有解的情况下寻找具体的解,而广度优先算法
则是在寻找最短路径的情况下使用。
在具体应用时,可以根据实际情
况选择使用哪一种算法,或者结合两种算法的优点进行优化,以达到更好的搜索效果。
因此,深度优先算法和广度优先算法都是图遍历中经典而又经典的算法,能够应用于很多具体的场景中,为寻找路径和搜索解决方案等问题提供了很好的方法和实现手段。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
图的深度优先遍历和广度优先遍历Java实现收藏一图的基本概念及存储结构图G是由顶点的有穷集合,以及顶点之间的关系组成,顶点的集合记为V,顶点之间的关系构成边的集合EG=(V,E).说一条边从v1,连接到v2,那么有v1Ev2(E是V上的一个关系)《=》<v1,v2>↔E.图有有向图,无向图之分,无向图的一条边相当于有向图的中两条边,即如果无向图的顶点v1和v2之间有一条边,那么既有从v1连接到v2的边,也有从v2连接到v1的边,<v1,v2>↔E 并且<v2,v1>↔E,而有向图是严格区分方向的。
一般图的存储有两种方式1)相邻矩阵,用一个矩阵来保持边的情况,<v1,v2>↔E则Matrix[v1][v2]=Weight.2)邻接表,需要保存一个顺序存储的顶点表和每个顶点上的边的链接表。
这里的实现采用第二种方案,另外图又复杂图,简单图之分,复杂图可能在两点之间同一个方向有多条边,我们考虑的都是无环简单图,无环简单图是指顶点没有自己指向自己的边的简单图,即任取vi属于V => <vi,vi>不属于E并且没有重复边。
我们先给出图的ADT:package algorithms.graph;/*** The Graph ADT* @author yovn**/public interface Graph {//markpublic static interface Edge{public int getWeight();}int vertexesNum();int edgeNum();boolean isEdge(Edge edge);void setEdge(int from,int to, int weight);Edge firstEdge(int vertex);Edge nextEdge(Edge edge);int toVertex(Edge edge);int fromVertex(Edge edge);String getVertexLabel(int vertex);void assignLabels(String[] labels);void deepFirstTravel(GraphVisitor visitor);void breathFirstTravel(GraphVisitor visitor);}其中的方法大多数比较一目了然,其中1)Edge firstEdge(int vertex)返回指定节点的边的链表里存的第一条边2)Edge nextEdge(Edge edge),顺着边链表返回下一条边3)fromVertex,toVertex很简单返回该边的起始顶点和终结顶点4)getVertexLabel返回该定点对应的标号,assignLabels给所有顶点标上号GraphVisitor是一个很简单的接口:package algorithms.graph;/*** @author yovn*-*/public interface GraphVisitor {void visit(Graph g,int vertex);}OK,下面是该部分实现:package algorithms.graph;import java.util.Arrays;/*** @author yovn**/public class DefaultGraph implements Graph {private static class _Edge implements Edge{private static final _Edge NullEdge=new _Edge();int from;int to;int weight;_Edge nextEdge;private _Edge(){weight=Integer.MAX_V ALUE;}_Edge(int from, int to, int weight){this.from=from;this.to=to;this.weight=weight;}public int getWeight(){return weight;}}private static class _EdgeStaticQueue{_Edge first;_Edge last;}private int numVertexes;private String[] labels;private int numEdges;private _EdgeStaticQueue[] edgeQueues;//tag the specified vertex be visited or notprivate boolean[] visitTags;/****/public DefaultGraph(int numVertexes) {if(numVertexes<1){throw new IllegalArgumentException();}this.numVertexes=numVertexes;this.visitTags=new boolean[numVertexes];bels=new String[numVertexes];for(int i=0;i<numVertexes;i++){labels[i]=i+"";}this.edgeQueues=new _EdgeStaticQueue[numVertexes];for(int i=0;i<numVertexes;i++){edgeQueues[i]=new _EdgeStaticQueue();edgeQueues[i].first=edgeQueues[i].last=_Edge.NullEdge;}this.numEdges=0;}/* (non-Javadoc)* @see algorithms.graph.Graph#edgeNum()*/@Overridepublic int edgeNum() {return numEdges;}/* (non-Javadoc)* @see algorithms.graph.Graph#firstEdge(int)*/@Overridepublic Edge firstEdge(int vertex) {if(vertex>=numVertexes) throw new IllegalArgumentException();return edgeQueues[vertex].first;}/* (non-Javadoc)* @see algorithms.graph.Graph#isEdge(algorithms.graph.Graph.Edge)*/@Overridepublic boolean isEdge(Edge edge) {return (edge!=_Edge.NullEdge);}/* (non-Javadoc)* @see algorithms.graph.Graph#nextEdge(algorithms.graph.Graph.Edge)*/@Overridepublic Edge nextEdge(Edge edge) {return ((_Edge)edge).nextEdge;}/* (non-Javadoc)* @see algorithms.graph.Graph#vertexesNum()*/@Overridepublic int vertexesNum() {return numVertexes;}@Overridepublic int fromVertex(Edge edge) {return ((_Edge)edge).from;}@Overridepublic void setEdge(int from, int to, int weight) {//we don't allow ring existif(from<0||from>=numVertexes||to<0||to>=numVertexes||weight<0||from==to)throw newIllegalArgumentException();_Edge edge=new _Edge(from,to,weight);edge.nextEdge=_Edge.NullEdge;if(edgeQueues[from].first==_Edge.NullEdge)edgeQueues[from].first=edge;elseedgeQueues[from].last.nextEdge=edge;edgeQueues[from].last=edge;}@Overridepublic int toVertex(Edge edge) {return ((_Edge)edge).to;}@Overridepublic String getVertexLabel(int vertex) {return labels[vertex];}@Overridepublic void assignLabels(String[] labels) {System.arraycopy(labels, 0, bels, 0, labels.length);}//to be continue}二深度优先周游即从从某一点开始能继续往前就往前不能则回退到某一个还有边没访问的顶点,沿这条边看该边指向的点是否已访问,如果没有访问,那么从该指向的点继续操作。
那么什么时候结束呢,这里我们在图的ADT实现里加上一个标志数组。
该数组记录某一顶点是否已访问,如果找不到不到能继续往前访问的未访问点,则结束。
你可能会问,如果指定图不是连通图(既有2个以上的连通分量)呢?OK,解决这个问题,我们可以让每一个顶点都有机会从它开始周游。
下面看deepFirstTravel的实现:/* (non-Javadoc)* @see algorithms.graph.Graph#deepFirstTravel(algorithms.graph.GraphVisitor)*/@Overridepublic void deepFirstTravel(GraphVisitor visitor) {Arrays.fill(visitTags, false);//reset all visit tagsfor(int i=0;i<numVertexes;i++){if(!visitTags[i])do_DFS(i,visitor);}}private final void do_DFS(int v, GraphVisitor visitor) {//first visit this vertexvisitor.visit(this, v);visitTags[v]=true;//for each edge from this vertex, we do one time//and this for loop is very classical in all graph algorithmsfor(Edge e=firstEdge(v);isEdge(e);e=nextEdge(e)){if(!visitTags[toVertex(e)]){do_DFS(toVertex(e),visitor);}}}三广度优先周游广度优先周游从每个指定顶点开始,自顶向下一层一层的访问。
