计算机组成原理第2章 例题及参考答案
计算机组成原理第2章作业参考答案

第2章部分习题参考答案【2-9】某计算机字长为16位,简述下列几种情况下所能表示数值的范围。
解:(1)无符号整数;0≤X≤(216-1)(2)用原码表示定点小数;-(1-2-15)≤X≤ +(1-2-15)(3)用补码表示定点小数;-1 ≤X≤ +(1-2-15)最小:1.000000000000000最大:0.111111*********(4)用原码表示定点整数;-(215-1)≤X≤ +(215-1)(5)用补码表示定点整数。
-215≤X≤ +(215-1)最小:1000000000000000.最大:0111111111111111.【2-10】【2-11】某浮点数字长为12位,其中阶符为1位,阶码数值为3位,数符为1位,尾数数值为7位,阶码以2为底,阶码和尾数均用补码表示。
它所能表示的最大正数是多少?最小规格化正数是多少?绝对值最大的负数是多少?解:X最大正数 = (1-2-7)× 22^3-1 = (1-2-7) × 27X最小规格化正数 = 2-1× 2-2^3 = 2-9X绝对值最大负数 = -1 × 22^3-1 = -27= -128【2-12】【2-15】【2-16】试将 (-0.1101)2用IEEE短浮点数格式表示出来。
解:-0.1101 = -1.101*2-1符号位 = 1阶码-1的移码 = 01111111-1=01111110尾数 = 10100000000000000000000∴短浮点数代码为:1011 1111 0101 0000 0000 0000 0000 0000表示为十六进制的代码:BF500000H(4)+0.0解:短浮点数代码为:00000000000000000000000000000000 表示为十六进制的代码:00000000H【2-18】将下列IEEE短浮点数转换为十进制数(1)1(数符)1000000 1(阶码)1110000 00000000 00000000(尾数)解:计算出阶码真值:10000001 – 01111111 = 00000010尾数隐含了一个1以规格化二进制数形式写出此数:-1.111 * 22写成非规格化二进制数形式: -111.1转换成十进制数为:(-111.1)2 = (-7.5)10∴X = -7.5【2-22】已知下面数据块约定:横向校验、纵向校验均为奇校验,指出至少有多少位出错。
计算机组成原理第2章答案

第2章综合应用题参考答案1. 在CRC校验中。
已知生成多项式是G(x)=x4+x3+1。
要求写出信息1011001的CRC 校验码。
解:生成多项式G(x)=11001,为5位,校验余数取4位,按模2除法计算过程如下:110101011001 1011001000011001111101100101111011001011100110011010余数R(x)= 1010CRC校验码=1011001 10102. 双方采用CRC循环校验码进行通信,已知生成多项式为x4+x3+x+1,接收到码字为10111010011。
判断该信息有无错误。
解:依题意,生成多项式G(x)=11011,如果信息正确,则模2除法余数应为0110010111011 1011101001111011110001101111100110111111111011100结果余数R(x)= 100不为零所以结果有错。
3. 简述算术移位与逻辑移位的区别算术移位,符号位保持不变,右移用符号位填充,左移用0填充逻辑移位,不考虑符号位,左右移位,空出位都用0填充4.已知机器字长n=8位,X=-44,Y=-53,按补码计算X-Y=?解:[X]补=11010100,[Y]补=11001011,[-Y]补=00110101[X]补11010100[-Y]补+) 00110101000010015. 设机器字长为8位(含1位符号位)设A=9/64, B=-13/32,计算[A±B]补,并还原成真值。
解:A=9/16=1001/26=0.0010010 B=-13/32=1101/25=-0.0110100[A]补=0.0010010 [B]补=1.1001100 [-B]补= 0.0110100[A]补 0.0010010[B]补 +) 1.10011001.1011110[A+B]补=1.1011110 真值A+B =-0.0100010=-17/64[A]补 0.0010010[-B]补 +)0.01101000.1000110[A-B]补=0.1000110 真值A-B =0.1000110=35/646. X=-0.1110,Y=-0.1101,采用原码一位乘法运算求[Z]原=[X×Y]原=?解:[X]原=1.1110 [Y]原=1.1101符号单独处理:积Z的符号位Zs=1 1=0被乘数、乘数都取绝对值:即[|X|] =00.1110 [|Y|]]原=0.1101部分积单元清000.0000 1101+X 00.111000.1110右移1位 00.0111 0110 1+0 00.000000.0111右移1位 00.0011 1011 0+X 00.111001.0001右移1位 00.1000 1101 1+X 00.111001.0110右移1位00.1011 0110 1积的绝对值 |Z|=0.10110110[Z]原=Zs.10110110=0.101101107. 若X=-0.1101, Y=-0.1011,用布斯算法求[X.Y]补=?解:对于Both补码乘法,符号参与运算,被乘数采用双符号位,乘数采用单符号,在乘数最末增加一个0,每次看最低两位(式中画底线的数字):相同(00,或11)则加0,若为10,则加[-X]补,若为01,则加[X]补[X]补=1.0011 [-X]补=0.1101 [Y]补=1.010100.0000 101010+[-X]补 00.110100.1101右移1位 00.0110 110101+[X]补 11.001111.1001右移1位 11.1100 111010+[-X]补 00.110100.1001右移1位 00.0100 111101+[X]补 11.001111.0111右移1位 11.1011 111110+[-X]补 00.110100.1000 1111最后一步不移位积的补码 [Z]补=0.10001111真值 Z= 0.100011118. 设X=-15,Y=-13, 用原码阵列乘法器求乘积Z=X×Y=? 并用十进制乘法验证。
计算机组成原理习题与解答 第二章

第一节1.把下列各数化成二进制数和八进制数(二进制取3位小数,八进制取一位小数): 7+3/4,±3/64,73.5,725.9375,25.34答:7+3/4=111.110B; 7+3/4=7.6O; ±3/64=±0.000B; ±3/64=±0.0O; 73.5=.100B; 73. 5=111.4O;725.9375=.111B; 725.9375=1325.7O; 25.34=11001.011B; 25.34=31.3O2.把下列各数化成十进制数:101.10011B ,22.2O,AD.4H答:101.10011B=5.59375; 22.2O=18.25; AD.4H=173.253.完成下列二进制数运算:101.111+11.011,1001.10-110.01,101.11*11.01,/1101答:101.111+11.011=1001.01; 1001.10-110.01=11.01;101.11*11.01=10010.1011; /1101=11100.114.完成下列各十六进制数的运算:A39E+28DC,D5AB-7CE5,2BF*4C,C16E/3A答:A39E+28DC=CC7A; D5AB-7CE5=58C6; 2BF*4C=D014; C16E/3A=355.C25.先将15B*8E/2A中的十六进制数化成十进制数,再进行计算,最后再将结果化为十六进制数。
答:15BH*8EH/2AH=347*142/42=49274/42=1173.19=495.30AH6.试分别判断下列各组数据中哪个数据最大?哪个数据最小?(1) A=0.1001B,B=0.1001D,C=0.1001H(2) A=B,B=1001D,C=111H答:(1) A最大, C最小; (2) B最大, A最小;第二节1.写出下列各数的二进制原码和补码(最后两个用双字节): 0,96,-128,-38H,127,10 5,879H,-32768答:上述各数的原码依次为:(), , 无, , , , 11001, 无;上述各数的补码依次为:, , , , , , 11001, 00000;2.分别列出下述10进制数的16进制数、非压缩的BCD数、压缩的BCD数、ASCII数字串(用16进制形式写出):10, 64, 78, 81, 92, 100, 125, 255答:上述各数的16进制数依次为:AH,40H,4EH,51H,5CH,64H,7DH,FFH;上述各数的非压缩的BCD数依次为:0100H,0604H,0708H,0801H,0902H,H, H,H;上述各数的压缩的BCD数依次为:10H,64H,78H,81H,92H,0100H,0125H,0255H;上述各数的ASCII数字串依次为:3130H,3634H,3738H,3831H,3932H,H,H, H;3.用10进制数写出下列补码表示的机器数的真值:71H,1BH,80H,F8H,397DH,CF4 2H,9350H答:上述补码表示的各机器数的真值用10进制数分别表示为: +113,+27,-128,-8,+14717,-20670,-278284.若用一个字节来表示带符号数,判断下列各运算在机内进行时是否会产生溢出,写出判断过程。
组成原理2章答案

2.[x]补= a7. a6a5…a0解、(1)当a7= 0时,x≥0 此时x>-0.5则a0 = 0, a1→a6任意即可当a7= 1时,[x]补= =2-|x||x|=2- 1. a6a5…a0=1-0.a6a5…a0若要x>-0.5则|x |<0.5所以有1-0.a6a5…a0<0.50.a6a5…a0>0.50.a6a5…a0>0.100000即a7a6 = 11, a5→a0不全为0或至少有一个为13.字长32位浮点数,符号位1位,阶码8位,用移码表示,尾数23位,用补码表示,基为2(1)最大正数的二进制表示E = 11111111 e=E-27=01111111=+127Ms = 0, M = 11…1(全1)最大的数的二进制表示:+2+127×(1-2-23)(2) 最小负数的二进制数表示:E = 11111111Ms = 1, M = 00…0(全0)(注意:用10….0来表示尾数-1) 表示为:-2+127×1(3)最小正数的二进制表示:+2-128×2-23(4)最大负数的二进制表示: [+2-128×2-23, +2+127×(1-2-23)]∪[-2-128×2-23,-2+127×1] 4. (1)2270.011011 1.1011264-==⨯ X=(-1)s ×2E-127×1.M S=0阶码:E=127+e=127-2=125=01111101 (阶码用移码表示) 尾数:M=0.1011(2) 2270.011011 1.1011264--==-⨯ X=(-1)s ×2E-127×1.M S=1阶码:E=127+e=127-2=125=01111101 (阶码用移码表示) 尾数:M=0.1011 (用原码表示)结果没有溢出,x+y=-101116.(1)x = 11011 , y = - 11111[x]变补=0 0 1 1 0 1 1[-y]变补=0 0 1 1 1 1 1上溢(2)x = 0.10111 , y = 0.11011[x]变补=0 0 1 0 1 1 1[-y]变补=1 1 0 0 1 0 1无溢出(3)x = 11011 , y = - 10011[y]变补=0 0 1 0 0 1 1[x]变补=0 0 1 1 0 1 17.(1)原码阵列x = 11011, y = -11111符号位: x0⊕y0 = 0⊕1 = 1|x| = 11011, |y|= 11111[x*y]原=1. 1 1 0 1 0 0 0 1 0 1X*y=-0. 1 1 0 1 0 0 0 1 0 1带求补器的补码阵列[x]补= 0 11011, [y]补= 1 00001乘积符号位单独运算0⊕1=1尾数部分算前求补输出│X│=11011,│y│=111112n算后求补输出1.0010111011[X×Y]补=1.0010111011X×Y=-0.1101000101(2) 原码阵列x = -0.11111, y = -0.11011符号位: x0⊕y0 = 1⊕1 = 0[x]原= 11111, [y]原 = 11011[x×y]原 = 01101000101x×y =+0.1101000101带求补器的补码阵列[x]补= 1 00001, [y]补= 1 00101乘积符号位单独运算1⊕1=0尾数部分算前求补输出│X│=11111,│y│=110112n算后求补输出1 1 0 1 0 0 0 1 0 1[X×Y]补=0 1 1 0 1 0 0 0 1 0 1X×Y=+0.11010001019.假设两数均用补码表示,阶码采用双符号法,尾数采用单符号法(1) x = 2-011*0.100101, y = 2-010*(-0.011110)[x]浮= 11101, 0.100101[y]浮= 11110, 1.100010计算x+y①完成对阶Ex-Ey = Ex+(-Ey)= 11 ,101+00,010=11,111<0无溢出Ex-Ey的值为-1Ex向Ey靠M x右移1位,Ex+1M x=0.010010 (1)②尾数相加③规格化处理:M不是1.M的形式,尾数左移2位,阶码-2M= 1.010010 阶码E=E y+11 110= 11100④舍入处理:采用0舍1入法处理M=1.010010⑤判是否溢出:阶码符号为11 无溢出x+y= = - 0.101110×2-4计算x-y①完成对阶与x+y相同②尾数相减③规格化处理:M=0.110000 E=11 110④舍入处理:采用0舍1入法处理M=0.110001⑤判是否溢出:阶码符号为11 无溢出x-y= 0.110001×2-2(2) x = 2-101×(-0.010110), y = 2-100×0.010110[x]浮= 11 011,1.101010[y]浮= 11 100,0.010110计算x+y①完成对阶Ex-Ey = Ex+(-Ey)= 11 ,011+00,100=11,111<0 无溢出Ex-Ey的值为-1Ex向Ey靠M x右移1位,Ex+1M x=1.110101 (0)②尾数相加③规格化处理:M不是1.M的形式,尾数左移2位,阶码-2M= 0.101100 阶码E=E y+11 110= 11 100+11 110=11 010 ④舍入处理:采用0舍1入法处理M= 0.101100⑤判是否溢出:阶码符号为11 无溢出x+y= = +0.101100×2-6计算x-y①完成对阶与x+y相同②尾数相减③规格化处理:M=1.011111 E=11 100④舍入处理:采用0舍1入法处理M=1.011111⑤判是否溢出:阶码符号为11 无溢出x-y= -0.100001×2-4。
计算机组成原理第2章习题参考答案

= (1-2 )×2
5 31
-9
31
(3)绝对值最小负数:000000, 1.011111111; -(2 +2 )×2 。 (4)绝对值最大负数:111111, 1.000000000; -1×2 = -2 。
-2
2-18.某浮点数字长 32 位,格式如下。其中阶码部分 8 位,以 2 为底,移码表示;尾 数部分一共 24 位(含 1 位数符) ,补码表示。现有一浮点代码为(8C5A3E00)16,试写出它所 表示的十进制真值。 0 阶码 7 8 数符
2-3.已知下列数的原码表示,分别写出它们的补码表示:[X1] 原 =0.10100,[X2] 原 =1.10111。 [解] [X1]补=0.10100,[X2]补=1.01001 2-4.已知下列数的补码表示,分别写出它们的真值:[X1]补=0.10100,[X2]补=1.10111。 [解] X1=0.10100,X2=-0.01001 2-6. 设[X]原=1.A1A2A3A4A5A6, (1)若要 X > -1/2,A1~A6 要满足什么条件? (2)若要 -1/8 ≥ X ≥ -1/4,A1~A6 要满足什么条件? [解] (1) ∵-1/2=-0.100000, [-1/2]原=1.100000
故 X>-1/2 的条件是 1.A1A2A3A4A5A<1.100000 ∴A1=0 (2)∵-1/8=-0.001, [-1/8]原=1.001000,-1/4=-0.010, [-1/4]原=1.010000 故-1/8 ≥ X ≥ -1/4 的条件是 1.001000≤X≤1.010000 ∴ A1 ( A2 A3 A2 A3 A4 A5 A6 ) 1 可简化为 A1 ( A2 A3 A4 A5 A6 ) 1 2-7.设[X]补=1.A1A2A3A4A5A6, (1)若要 X > -1/2,A1~A6 要满足什么条件? (2)若要 -1/8 ≥ X ≥ -1/4,A1~A6 要满足什么条件? [解](1)∵ [-1/2]补=1.100000 ∴ X > -1/2 的条件是:1.A1A2A3A4A5A6 >1.100000 即 A1(A2+A3+A4+A5+A6)=1 (2)∵ [-1/8]补=1.111000 [-1/4]补=1.110000 ∴-1/8 ≥ X ≥ -1/4 的条件是: 1.A1A2A3A4A5A6 ≤1.111000 并且 1.A1A2A3A4A5A6≥1.110000 即 A1A2(A3 A4 A5 A6 + A3)=1 简化为:A1A2(A4 A5 A6 + A3)=1 2-9.某机字长 16 位,问在下列几种情况下所能表示数值的范围: (1)无符号整数 (2)用原码表示定点小数 (3)用补码表示定点小数 (4)用原码表示定点整数 (5)用补码表示定点整数 [解](1) 0≤X≤(2 -1) (2) -(1-2 )≤X≤(1-2 ) (3) -1≤X≤(1-2 ) (4) -(2 -1)≤X≤(2 -1) (5) -2 ≤X≤(2 -1) 2-10.某计算机字长为 32 位,试分别写出无符号整数和带符号整数(补码)的表示范围 (用十进制数表示) [解] 无符号整数的表示范围为:0~2 -1 带符号整数的补码的表示为:-2 ~2 -1 2-11.假设机器字长为 8 位,若机器数为 81H,当它分别代表原码、补码、反码和移码 时,等价的十进制整数是多少? [解]81H=10000001B, 若表示原码,其等价的十进制整数为-1;若表示补码,其等价的 十进制整数为-127;若表示反码,其等价的十进制整数为-126;若表示移码,其等价的十进 制整数为 1。 2-15.某浮点数字长 16 位,其中阶码部分 6 位(含一位阶符) ,移码表示,以 2 为底; 尾数部分 10 位(含 1 位数符,位于尾数最高位) ,补码表示,规格化。分别写出下列各题的
计算机组成原理(第四版)课后答案(第二章)

2.5 术语:存储元、存储单元、存储体、存储 单元地址,有何联系和区别?
存储元:存储一位二进制信息的基本单元电路。 存储单元:由若干存储元组成。一台机器的所有存储
单元长度相同,一般由8的整数倍个存储元构成。 存储体:是存储单元的集合,它由许多存储单元组成,
ห้องสมุดไป่ตู้用来存储大量的数据和程序。 存储器单元地址:计算机在存取数据时,以存储单元
访问; (4)固定存储器(ROM)中的任何一个单元不能随机访问. (5)一般情况下,ROM和RAM在存储体中是统一编址的. (6)由于半导体存储器加电后才能存储数据,断电后数
据就丢失了,因此,用EPROM做的存储器,加电后 必须重写原来的内容。
6
解:(1)F。主存是随机存储器,CPU访问任何单元的时 间都是相同的,同容量的大小没有关系。
2
2.2 存储器的带宽有何物理意义?存储器总线宽度为32 位,存取周期为250nS,这个存储器带宽是多少?
解:存储器的带宽是指每秒钟访问的二进制位的数目。 其物理意义是一个以存储器为中心的机器可以获取 的信息传输速度。 若存储周期为250ns,则工作速度=1/ 250ns , 所以,存储器带宽=工作速度×总线宽度 =1/250ns*32bit =1/250X10-9 × 32 bps =32X109 /250 bps =128X106 bps =128M bps
A15 D
A15 D
A15 D
A15 D
16片
.A14
.A14
.A14
16片64K×1 16片64K×1 16片64K×1
.A14
64K×1
A0
A0
A0
A0
10
2.9 2114是排列成64 x 64阵列的六管存储芯片,试 问组成4K x l6位的存储器,共需少片2114? 画出 逻辑框图。 解:Intel 2114芯片一片的容量为1Kx4位,要组成 4KXl6位的存储器,需要2114芯片 4K/l x l6/4=16(片)。 片内地址需要10根地址线,用A0~A9,片选需要2 位地址线,用A10~A11。
计算机组成原理第二章参考答案

第2章 参考答案2写出下列十进制数的原码、反码、补码和移码表示(用8位二进制数)。
如果是小数,则用定点小数表示;若为整数,则用定点整数表示。
其中MSB 是最高位(符号位),LSB 是最低位。
(1)-1 (2) -38/64 解:(1)-1=(-0000001)2 原码: 10000001反码: 11111110 补码: 11111111 移码: 01111111(2)-38/64=-0.59375=(-0.1001100)2或-38/64=-(32+4+2)*2-6=-(100110)*2-6=(-0.1001100)2 原码: 1.1001100反码: 1.0110011补码: 1.0110100移码: 0.0110100注:-1如果看成小数,那么只有补码和移码能表示得到,定点小数-1的补码为:1.0000000此例类似于8位定点整数的最小值-128补码为100000003 有一字长为32位的浮点数,符号位1位;阶码8位,用移码表示;尾数23位,用补码表示;基数为2.请写出:(1)最大数的二进制表示,(2)最小数的二进制表示,(3)规格化数所能表示的数的范围。
解:(题目没有指定格式的情况下,用一般表示法做)(1)最大数的二进制表示:0 11111111 11111111111111111111111 (2)最小数的二进制表示:1 11111111 00000000000000000000000(1) 7232112*2---() (2) 7211*2--()(3)规格化最大正数:0 11111111 111111111111111111111117232112*2---()规格化最小正数:0 00000000 100000000000000000000007122*2--规格化最大负数:1 00000000 011111111111111111111117123222*2----+()规格化最小负数:1 11111111 000000000000000000000007211*2--()规格化数的表示的数的范围为:7777211232122321[1*2,22*2][2*2,12)*2]----------+- ()()(下面补充IEEE 754的规格化浮点数表示范围:IEEE 754的尾数采用1.M 的形式,原码表示;阶e=E-127 (相对于一般表示法的e=E-128,人为的加了1);并且最大的阶(11111111)和最小的阶(00000000)用去作为特殊用途。
(完整版)计算机组成原理第2章例题及参考答案
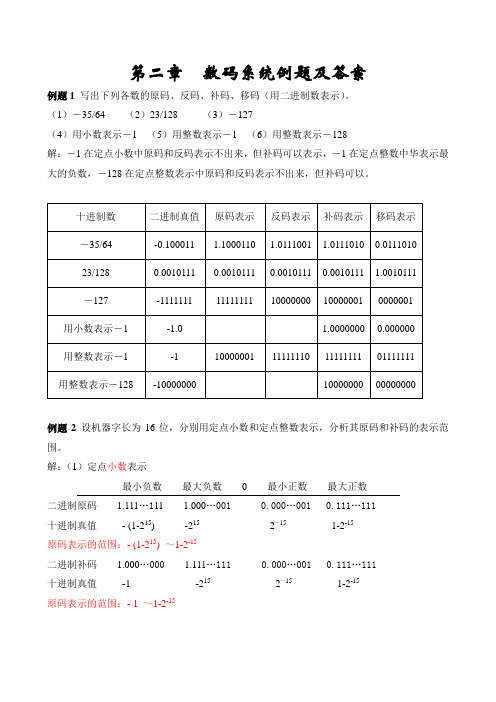
第二章数码系统例题及答案例题1写出下列各数的原码、反码、补码、移码(用二进制数表示)。
(1)-35/64 (2)23/128 (3)-127(4)用小数表示-1 (5)用整数表示-1 (6)用整数表示-128解:-1在定点小数中原码和反码表示不出来,但补码可以表示,-1在定点整数中华表示最大的负数,-128在定点整数表示中原码和反码表示不出来,但补码可以。
例题2设机器字长为16位,分别用定点小数和定点整数表示,分析其原码和补码的表示范围。
解:(1)定点小数表示最小负数最大负数0 最小正数最大正数二进制原码 1.111...111 1.000...001 0.000...001 0.111 (111)十进制真值- (1-215) -2152-151-2-15原码表示的范围:- (1-215) ~1-2-15二进制补码 1.000...000 1.111...111 0.000...001 0.111 (111)十进制真值-1 -2152-151-2-15原码表示的范围:- 1 ~1-2-15(2)定点整数表示最小负数最大负数0 最小正数最大正数二进制原码1111...111 1000...001 0000...001 0111 (111)十进制真值- (215-1) -1 +1 215-1原码表示的范围:- (215-1) ~215-1 [-32767 ~ +32767]二进制补码1000...0001111...111 0000...001 0111 (111)十进制真值-1 +1 215-1原码表示的范围:- 215~215-1 [-32768 ~ +32767]一、选择题1.下列数中最小的数为()。
A.(101001)2B.(52)8C.(101001)BCD D.(233)162.下列数中最大的数为()。
A.(10010101)2B.(227)8C.(96)16D.(143)53.在机器数中,()的零的表示形式是惟一的。
计算机组成原理第二章单元测试(含答案)

第二章单元测试
1、计算机中表示地址时使用
A、无符号数
B、原码
C、反码
D、补码
2、当-1 < x < 0时,[x]补=
A、2+x
B、2-x
C、1-x
D、2-2^-n+x
3、浮点数的表示范围和表示精确度分别取决于
A、阶码的位数和尾数的位数
B、尾数的位数和阶码的位数
C、阶码的编码和尾数的编码
D、机器字长和阶码的位数
4、设G(x) = 1011,某(7,4)码为K1K2K3K4K5K6K7,仅K7出错时进行CRC校验得到的余数为001,当仅K5出错时,进行CRC校验得到的余数为
A、100
B、010
C、011
D、110
5、假设寄存器为8位,用补码形式存储机器数,包括一位符号位,那么十进制数一25在寄存器中的十六进制形式表示为
A、E7H
B、67H
C、99H
D、E6H
6、如果某系统15*4=112成立,则系统采用的进制是
A、6
B、7
C、8
D、9
1。
计算机组成原理(肖铁军编)第二章习题及答案

导读:第二章运算方法和运算器练习,3.运算器虽有许多部件组成,11.现代计算机的运算器一般通过总线结构来组织,目的是位计算机提供判断条件,计算机按0处理,第二章运算方法和运算器练习一、填空题1.补码加减法中,(符号位)作为数的一部分参加运算,(符号位产生的进位)要丢掉。
2.为判断溢出,可采用双符号位补码,此时正数的符号用(00)表示,负数的符号用(11)表示。
3.采用双符号位的方法进行溢出检测时,若第二章运算方法和运算器练习一、填空题1. 补码加减法中,(符号位)作为数的一部分参加运算,(符号位产生的进位)要丢掉。
2. 为判断溢出,可采用双符号位补码,此时正数的符号用(00)表示,负数的符号用(11)表示。
3. 采用双符号位的方法进行溢出检测时,若运算结果中两个符号位(不相同),则表明发生了溢出。
若结果的符号位为(01),表示发生正溢出;若为(10),表示发生负溢出。
4. 采用单符号位进行溢出检测时,若加数与被加数符号相同,而运算结果的符号与操作数的符号(不一致),则表示溢出;当加数与被加数符号不同时,相加运算的结果(不会产生溢出)。
5. 利用数据的数值位最高位进位C和符号位进位Cf的状况来判断溢出,则其表达式为over=(C⊕Cf)。
6. 在减法运算中,正数减(负数)可能产生溢出,此时的溢出为(正)溢出;负数减(正数)可能产生溢出,此时的溢出为(负)溢出。
7. 补码一位乘法运算法则通过判断乘数最末位Yi和Yi-1的值决定下步操作,当YiYi-1=(10)时,执行部分积加【-x】补,再右移一位;当YiYi-1=(01)时,执行部分积加【x】补,再右移一位。
8. 浮点加减运算在(阶码运算溢出)情况下会发生溢出。
9. 原码一位乘法中,符号位与数值位(分开运算),运算结果的符号位等于(两操作数符号的异或值)。
10. 一个浮点数,当其补码尾数右移一位时,为使其值不变,阶码应该(加1)。
11. 左规的规则为:尾数(左移一位),阶码(减1)。
计算机组成原理二章答案

第2章作业参考答案1、(1) -35(=23)16 (2)127 (3)-127 (4)-1 [-35]原=10100011 [127]原=01111111 [-127]原=11111111 [-1]原=10000001 [-35]反=11011100 [127]反=01111111 [-127]反=10000000 [-1]反=11111110 [-35]补=11011101 [127]补=01111111 [-127]补=10000001 [-1]补=11111111 2当a 7=0时,x ≥0,满足x>-0.5的条件,即:若a 7=0,a 6~ a 0可取任意值 当a 7=1时,x<0,若要满足x>-0.5的条件,则由补码表示与其真值的关系,可知:7061524334251676022222221)2(1--------=*+*+*+*+*+*+*+-=*+-=∑a a a a a a a a x i i i 要使x>-0.5 ,所以要求a 6=1,并且a 5~a 0不能全部为0所以,要使x>-0.5,则要求a 7=0;或者a 7= a 6=1,并且a 5~a 0至少有一个为1 3、由题目要求可知,该浮点数的格式为:M(23位)不必存储符号位,只需存小数点后面的有效数值位即可。
(1)最大数的二进制表示为:0 11111111 1111……111(23个1) (2)最小数的二进制表示为:1 11111111 0000……000(23个0)(3)非IEEE754标准的补码表示的规格化数是指其最高有效位与符号位相反 故有:最大正数为:0 11111111 1111……111(23个1)=+(1-2-23)⨯2127 最小正数为:0 00000000 1000……000(22个0)=+0.5⨯2-128最大负数为:1 00000000 0111……111(22个1)=-(0.5+2-23)⨯2-128最小负数为:1 11111111 0000……000(23个0)=-1⨯2127所以其表示数的范围是:+0.5⨯2-128~+(1-2-23)⨯2127以及-1⨯2127~-(0.5+2-23)⨯2-1284、IEEE754标准32位浮点的规格化数为X=(-1)S⨯1.M⨯2E-127(1)27/6427/64=27⨯2-6=(11011)2⨯2-6=(1.1011)2⨯2-2所以S=0,E=e+127=125=(01111101)2,M=101132位的规格化浮点数为:00111110 11011000 00000000 00000000,即十六进制的(3ED80000)16 (2)-27/64-27/64=-(1.1011)2⨯2-2所以S=1,E=e+127=125=(01111101)2,M=101132位的规格化浮点数为:10111110 11011000 00000000 00000000,即十六进制的(BED80000)16 5、[x+y]补=[x]补+[y]补(1)x=11011,y=00011[x+y]补=0011011+0000011=0011110;没有溢出,x+y=11110(2)x=11011,y=-10101[x+y]补=0011011+1101011=0000110;0 0 1 1 0 1 1+ 1 1 0 1 0 1 10 00 0 1 1 0没有溢出,x+y=00110(3)x=-10110,y=-00001[x+y]补=1101010+1111111=1101001;没有溢出,x+y=-101116、[x-y]补=[x]补+[-y]补(1)x=11011,y=-11111[-y]补=0011111[x-y]补=0011011+0011111=0111010;0 0 1 1 0 1 1+ 0 0 1 1 1 1 10 1 1 1 0 1 0正溢出,x-y=+111010(2)x=10111,y=11011[-y]补=1100101[x-y]补=0010111+1100101=1111100;0 0 1 0 1 1 1+ 1 1 0 0 1 0 11 1 1 1 1 0 0没有溢出,x-y=-00100(3)x=11011,y=-10011[-y]补=0010011[x-y]补=0011011+0010011=0101110;正溢出,x-y=+101110 7、(1)x=11011,y=-11111用原码阵列乘法器1 1 0 1 1⨯ 1 1 1 1 11 1 0 1 11 1 0 1 11 1 0 1 11 1 0 1 11 1 0 1 11 1 0 1 0 0 0 1 0 1[x⨯y]符号=0⊕1=1所以[x⨯y]原=1 1101000101用直接补码阵列乘法器:[x]补=011011,[y]补=100001(0) 1 1 0 1 1⨯(1) 0 0 0 0 1(0) 1 1 0 1 1(0) 0 0 0 0 0(0) 0 0 0 0 0(0) 0 0 0 0 0(0) 0 0 0 0 00 (1) (1) (0) (1) (1)0 (1) (1) 0 (1) (1) 1 1 0 1 1将乘积中的符号位用负权表示,其他的负权位化为正权,得:[x⨯y]补=1 0010111011 (2) x=-11111,y=-11011用原码阵列乘法器1 1 1 1 1⨯ 1 1 0 1 11 1 1 1 11 1 1 1 10 0 0 0 01 1 1 1 11 1 1 1 11 1 0 1 0 0 0 1 0 1[x⨯y]符号=1⊕1=0所以[x⨯y]原=0 1101000101用直接补码阵列乘法器:[x]补=100001,[y]补=100101(1) 0 0 0 0 1 ⨯(1) 0 0 1 0 1(1) 0 0 0 0 1(0) 0 0 0 0 0(1) 0 0 0 0 1(0) 0 0 0 0 0(0) 0 0 0 0 01 (0) (0) (0) (0) (1)1 0 0 (1) (1) 0 0 0 1 0 1将乘积中的符号位用负权表示,其他的负权位化为正权,得:[x⨯y]=0 1101000101补8、(1) x=11000,y=-11111用原码阵列除法器计算,符号位单独处理,商的符号位=0⊕1=1设a=(|x|⨯2-5),b=(|y|⨯2-5),则a,b均为正的纯小数,且x÷y的数值=(a÷b);余数等于(a÷b)的余数乘以25下面用不恢复余数法的原码阵列除法器计算a÷b[a]补=[|x|⨯2-5]补=0.11000,[b]补=[|y|⨯2-5]补=0.11111,[-b]补=1.00001过程如下:0. 1 1 0 0 0+[-b]补 1. 0 0 0 0 11. 1 1 0 0 1 ——余数为负,商为01. 1 0 0 1 0 ——余数和商左移一位(0)+[b]补0. 1 1 1 1 10. 1 0 0 0 1 ——余数为正,商为11. 0 0 0 1 0 ——余数和商左移一位(01)+[-b]补 1. 0 0 0 0 10. 0 0 0 1 1 ——商为10. 0 0 1 1 0 ——(011)+[-b]补 1. 0 0 0 0 11. 0 0 1 1 1 ——商为00. 0 1 1 1 0 ——(0110)+[b]补0. 1 1 1 1 11. 0 1 1 0 1 ——商为00. 1 1 0 1 0 ——(01100)+[b]补0. 1 1 1 1 11. 1 1 0 0 1 ——商为0——(011000)即:a÷b的商为0.11000;余数为1.11001⨯2-5,因为1.11001为负数,加b处理为正数,1.11001+b=1.11001+0.11111=0.11000,所以a÷b的余数为0.11000⨯2-5所以,(x÷y)的商=-0.11000,原码为:1.11000;余数为0.11000(2) x=-01011,y=11001商的符号位=1⊕0=1设a=|x|⨯2-5,b=|y|⨯2-5,则a,b均为正的纯小数,且x÷y的数值=a÷b;余数等于(a÷b)的余数乘以25下面用不恢复余数法的原码阵列除法器计算a÷b[a]补=[|x|⨯2-5]补=0.01011,[b]补=[|y|⨯2-5]补=0.11001,[-b]补=1.00111过程如下:0. 0 1 0 1 1+[-b]补 1. 0 0 1 1 11. 1 0 0 1 0 ——余数为负,商为01. 0 0 1 0 0 ——余数和商左移一位(0)+[b]补0. 1 1 0 0 11. 1 1 1 0 1 ——余数为负,商为01. 1 1 0 1 0 ——余数和商左移一位(00)+[b]补0. 1 1 0 0 10. 1 0 0 1 1 ——商为11. 0 0 1 1 0 ——(001)+[-b]补 1. 0 0 1 1 10. 0 1 1 0 1 ——商为10. 1 1 0 1 0 ——(0011)+[-b]补 1. 0 0 1 1 10. 0 0 0 0 1 ——商为10. 0 0 0 1 0 ——(00111)+[-b]补 1. 0 0 1 1 11. 0 1 0 0 1 ——商为0——(001110)即:a÷b的商为0.01110;余数为1.01001⨯2-5,因为1.01001为负数,加b处理为正数,1.01001+b=1.01001+0.11001=0.00010,所以a÷b的余数为0.00010⨯2-5所以,(x÷y)的商=-0.01110,原码为:1.01110;余数为0.000109、(1)x=2-011⨯0.100101,y=2-010⨯(-0.011110)E X=-011,E y=-010,所以[E X]补=1101,[E y]补=1110M X=0.100101,M y=-0.011110,所以[M X]补=0.100101,[M y]补=1.100010 [x]浮=1101 0.100101,[y]浮=1110 1.100010E X<E y,E y-E X = E y+(-E X)=1110+0011=0001对阶后[x]浮=1110 0.010010(1),[y]浮=1110 1.100010对阶后的尾数相加:M X+M y=0.010010(1)+1.1000100. 0 1 0 0 1 0 (1)+ 1. 1 0 0 0 1 01. 1 1 0 1 0 0 (1)x+y=1.110100(1)⨯21110,化为规格化数(左移2位)为:x+y=1.010010⨯21100,即:x+y=-0.101110⨯2-4对阶后的位数相减:M X-M y=M X+(-M y)=0.010010(1)+0.0111100. 0 1 0 0 1 0 (1)+ 0. 0 1 1 1 1 00. 1 1 0 0 0 0 (1)x-y=0.110000(1)⨯21110,已经是规格化数,采用0舍1入法进行舍入处理:x-y=0.110001⨯21110,即:x-y=0.110001⨯2-2(2)x=2-101⨯(-0.010110),y=2-100⨯(0.010110) E X =-101,E y =-100,所以 [E X ]补=1011,[E y ]补=1100M X =-0.010110,M y =0.010110,所以[M X ]补=1.101010,[M y ]补=0.010110 [x]浮=1011 1.101010,[y]浮=1100 0.010110 E X <E y ,E y -E X = E y +(-E X )=1100+0101=0001对阶后[x]浮=1100 1.110101(0),[y]浮=1100 0.010110 对阶后的尾数相加:M X +M y =1.110101+0.010110 1. 1 1 0 1 0 1 + 0. 0 1 0 1 1 0 0. 0 0 1 0 1 1x+y=0.001011⨯21100,化为规格化数(左移2位)为:x+y=0.101100⨯21010,即: x+y=0.101100⨯2-6对阶后的位数相减:M X -M y =M X +(-M y )=1.110101+1.101010 1. 1 1 0 1 0 1 + 1. 1 0 1 0 1 0 1. 0 1 1 1 1 1x-y=1.011111⨯21100,已经是规格化数,所以 x-y=-0.100001⨯2-4 10、(1) ⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛-⨯⨯⎪⎭⎫ ⎝⎛⨯16921613243M x =110100.021*******4=⨯=-,Ex=0011 M y =100100.0210011694-=⨯-=--,Ey=0100Ex+Ey=0011+0100=0111[x ⨯y]符=0⊕1=1,乘积的数值=|M x |⨯|M y |: 0. 1 1 0 1 ⨯ 0. 1 0 0 1 0 1 1 0 1 0 0 0 0 0 0 0 0 0 0 0 1 1 0 10 0 0 0 0 0 0 1 1 1 0 1 0 1所以,x ⨯y =-0.01110101⨯20111,规格化处理(左移一位),并采用0舍1入法进行舍入:x ⨯y =-0.111011⨯20110 即:⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛-⨯⨯⎪⎭⎫ ⎝⎛⨯16921613243=-0.111011⨯26(2) ⎪⎭⎫ ⎝⎛⨯÷⎪⎭⎫ ⎝⎛⨯-161523213232将x 、y 化为规格化数: M x =011010.021********=⨯=-,Ex=1110M y =111100.02111116154=⨯=-,Ey=0011Ex-Ey=Ex+(-Ey)=1110+1101=1011[x ÷y]符=0⊕0=0,下面用加减交替法计算尾数M x ÷M y : [Mx]补=0.011010,[My]补=0.111100,[-My]补=1.0001000. 0 1 1 0 1 0+[-My]补 1. 0 0 0 1 0 01. 0 1 1 1 1 0 ——余数为负,商为00. 1 1 1 1 0 0 ——余数和商左移一位(0)+[My]补 0. 1 1 1 1 0 01. 1 1 1 0 0 0 ——余数为负,商为0 1. 1 1 0 0 0 0 ——余数和商左移一位(00) +[My]补 0. 1 1 1 1 0 00. 1 0 1 1 0 0 ——余数为正,商为11. 0 1 1 0 0 0 ——余数和商左移一位(001) +[-My]补 1. 0 0 0 1 0 00. 0 1 1 1 0 0 ——商为1 0. 1 1 1 0 0 0 ——(0011) +[-My]补 1. 0 0 0 1 0 01. 1 1 1 1 0 0 ——商为0 1. 1 1 1 0 0 0 ——(00110) +[My]补 0. 1 1 1 1 0 00. 1 1 0 1 0 0 ——商为1 1. 1 0 1 0 0 0 ——(001101) +[-My]补 1. 0 0 0 1 0 00. 1 0 1 1 0 0 ——商为1 1. 0 1 1 0 0 0 ——(0011011) +[-My]补 1. 0 0 0 1 0 00. 0 1 1 1 0 0 ——商为1——(00110111) Mx ÷My 的商为0.0110111,余数为0.011100⨯2-7,由于x 化为0.01101(Mx)是尾数右移2位才得到,所以x ÷y 真正的余数是0.011100⨯2-7再尾数左移2位,即0.011100⨯2-9=0.111000⨯2-10 所以,x ÷y 的商为:0.0110111⨯21011,规格化处理后为:0.110111⨯21010=0.110111⨯2-6,余数为0.111000⨯2-10 11、不考虑181ALU的函数发生器,而是从简单的全加器出发,则:若设4位的二进制数为A=A3A2A1A0,B=B3B2B1B0,并设G i=A i B i,P i=A i⊕B i,由全加器进位输出的逻辑函数C i+1=A i B i+C i(A i⊕B i)可知:(由于进位输出函数还可以写成C i+1=A i B i+C i(A i+B i),故P i=A i+B i也可)(1) 串行进位方式:C1=A0B0+C0(A0⊕B0)=G0+P0C0C2=A1B1+C1(A1⊕B1)=G1+P1C1C3=A2B2+C2(A2⊕B2)=G2+P2C2C4=A3B3+C3(A3⊕B3)=G3+P3C3(2) 并行进位方式:C1=G0+P0C0C2=G1+P1C1=G1+P1(G0+P0C0)=G1+P1G0+P1P0C0C3=G2+P2C2=G2+P2(G1+P1G0+P1P0C0)=G2+P2G1+P2P1G0+P2P1P0C0C4=G3+P3C3=G3+P3G2+P3P2G1+P3P2P1G0+P3P2P1P0C012、(1) -5-5=-(101)2=-(1.01)2⨯22所以S=1E=e+127=2+127=129=(81)16=(10000001)2M=(010 0000 0000 0000 0000 0000)2故浮点格式为:1 10000001 010 0000 0000 0000 0000 0000,用十六进制表示为:(C0A00000)16(2) -1.5-1.5=-(1.1)2=-(1.1)2⨯20所以S=1E=e+127=0+127= (7F)16=(01111111)2M=(100 0000 0000 0000 0000 0000)2故浮点格式为:1 01111111 100 0000 0000 0000 0000 0000,用十六进制表示为:(BFC00000)16 (3) 384384=(180)16=(1 1000 0000)2=(1.1)2⨯28所以S=0E=e+127=8+127=135= (87)16=(10000111)2M=(100 0000 0000 0000 0000 0000)2故浮点格式为:0 10000111 100 0000 0000 0000 0000 0000,用十六进制表示为:(43C00000)16 (4) 1/161/16= (1.0)2⨯2-4所以S=0E=e+127=-4+127= (7B)16=(01111011)2M=(000 0000 0000 0000 0000 0000)2故浮点格式为:0 01111011 000 0000 0000 0000 0000 0000,用十六进制表示为:(3D800000)16 (5) -1/32-1/32=-(1.0)2⨯2-5所以S=1E=e+127=-5+127= (7A)16=(01111010)2M=(000 0000 0000 0000 0000 0000)2故浮点格式为:1 01111010 000 0000 0000 0000 0000 0000,用十六进制表示为:(BD000000)16 13、(1) 1 10000011 110 0000 0000 0000 0000 0000S=1E=(83)16=131 e=E-127=131-127=41.M=(1.11)2所以,该浮点数为-(1.11)2⨯24=-(11100)2=-28(2) 0 01111110 101 0000 0000 0000 0000 0000S=0E=(7E)16=126 e=E-127=126-127=-11.M=(1.101)2所以,该浮点数为(1.101)2⨯2-1=(0.1101)2=0.812514、IEEE754标准中,32位二进制数仍然有232种不同的组合,但是由于在IEEE754标准中,阶码为全1并且尾数为非0的情况不表示一个数。
计算机组成原理》第章习题答案

第二章习题解答1.设机器数的字长8位(含1位符号位),分别写出下列各二进制数的原码、补码和反码:0,-0,0.1000,-0.1000,0.1111,-0.1111,1101,-1101。
解:2.写出下列各数的原码、补码和反码:7/16,4/16,1/16,±0,-7/16,-4/16,-1/16。
解:7/16=7*2-4=0.01114/16=4*2-4=0.01001/16=1*2-4=0.0001真值原码补码反码7/16 0.0111 0.0111 0.01114/16 0.0100 0.0100 0.01001/16 0.0001 0.0001 0.0001+0 O.0OOO O.0OOO O.0OOO-0 1.0OOO O.0OOO 1.1111-1/16 1.0OO1 1.1111 1.1110-4/16 1.0100 1.1100 1.1011-7/16 1.0111 1.1001 1.10003.已知下列数的原码表示,分别写出它们的补码表示:[X1]原=O.10100,[X2]原=l.10111。
解:[X1]补=0.10100,[X2]补=1.01001。
4.已知下列数的补码表示,分别写出它们的真值:[X1]补=O.10100,[X2]补=1.10111。
解: X1=O.10100, X2=-0.01001。
5.设一个二进制小数X≥0,表示成X=0.a1a2a3a4a5a6,其中a1~a6取“1”或“O”:(1)若要X>1/2,a1~a6要满足什么条件(2)若要X≥1/8,a1~a6要满足什么条件(3)若要1/4≥X>1/16,a1~a6要满足什么条件解:(1) X>1/2的代码为:0.100001~0.111111。
a1=1,a2+a3+a4+a5+a6=1。
(2) X≥1/8的代码为:0.001001~0.111111(1/8~63/64)a1+a2=0,a3=1或a1=0,a2=1,或a2=1(3)1/4≥X>1/16的代码为:0.000101~0.01000(5/64~1/4)a1+a2+a3 =0, a4=1,a5+a6=1 或a1+a2=0,a3=1 或a2=1,a1+a3+a4+a5+a6=06.设[X]原=1.a1a2a3a4a5a6(1)若要X>-1/2,a1~a6要满足什么条件(2)若要-1/8≥X≥-1/4,a1~a6要满足什么条件解:(1) X>-1/2的代码为:1.000001~1.011111(-1/64~-31/64)。
计算机组成原理第2章习题答案

第2章习题及解答2-2将下列十进制表示成二进制浮点规格化的数(尾数取12位,包括一位符号位;阶取4位,包括一位符号位),并写出它的原码、反码、补码三和阶移尾补四种码制形式;(1)7.75解:X=7.75=(111.11)2=0.11111×211[X]原=0011×0.[X]反=0011×0.[X]补=0011×0.[X]阶称,尾补=1011×0.(2) –3/64解:X=-3/64=(-11/26)2=(-0.00001)2=-0.11×2-100[X]原=1100×1.[X]反=1011×1.[X]补=1100×1.[X]阶称,尾补=0100×1.(3) 83.25解:X=-3/64=(.01)2=0.×2111[X]原=0111×0.[X]反=[X]补=[X]原[X]阶称,尾补=1111×0.(4) –0.3125解:X=(–0.3125)10=(-0.0101)2=-0.101×2-1[X]原=1001×1.[X]反=1110×1.[X]补=1111×1.[X]阶称,尾补=0111×1.2-4 已知x和y,用变形补码计算x+y,并对结果进行讨论。
(2) x=0.11101,y=-0.10100解:[X]补=00.11101, [Y]补=11.01100, [-Y]补=00.10100[X]补+ [Y]补=00.11101+11.01100=00.01001X+Y=0.01001[X]补- [Y]补=[X]补+ [-Y]补=00.11101+00.10100=01.10001X+Y 正溢(3) x=-0.10111,y=-0.11000解: [X]补=11.01001, [Y]补=11.01000, [-Y]补=00.11000[X]补+ [Y]补=11.01001+11.01000=11.10001X+Y=-.[X]补- [Y]补=[X]补+ [-Y]补=11.01001+00.11000=00.00001X-Y =0.000012-5 已知x和y,用变形补码计算x-y,并对结果进行讨论。
计算机组成原理第2章 部分习题答案

-7.2812510=-111.010012
然后移动小数点,使其在第1,2位之间 -111.01001=-1.1101001×22 e= 2
∵ e =E – 127
∴
S=1,E=2+127=129=1000,0001,M=1101001
最后得到32位浮点数的二进制存储格式为
1100 0000 1110 1001 0000 0000 0000 0000
第二章
习题解答
7.若浮点数 x 的IEEE754标准32位存储格式为(8FEFC000 )16,求其浮点数 的十进制值。 【解】: 将x展开成二进制: 1000 , 1111, 1110 ,1111 ,1100,0000,0000,0000 数符:1 阶码:0001,1111
尾数:110,1111,1100,0000,0000,0000
110011
商
q0=0 q1=1 q2=0 q3=1 q4=1
故得 商q=q0q1q2q3q4q5=010110, 余数r=r5r6r7r8r9r10=110011 所以 [x÷y]原=1. 10110,[余数]原=0.0000110011 即 x÷y=-0.10110,余数=0.0000110011
第 4页
第二章
习题解答
17. 已知x和y,用移码运算方法计算x-y,同时指出运算结果是否发生溢出。 (1) x=1011,y= - 0010
【解】 [x-y]移=[x]移+[-y]补 [x]移=11 1011=01 1011 [-y]补=00 0010 注意:移码最高符号位恒置为0参与运算。 01 1011
= (C0E90000)16
第 2页
第二章
习题解答
11. 已知x和y,用变形补码计算x+y ,同时指出结果是否溢出。 (1) x= 0.11011, y= -0.10101
《计算机组成原理》第2章习题答案

第二章习题解答1.设机器数的字长8位(含1位符号位),分别写出下列各二进制数的原码、补码和反码:0,-0,0.1000,-0.1000,0.1111,-0.1111,1101,-1101。
解:2.写出下列各数的原码、补码和反码:7/16,4/16,1/16,±0,-7/16,-4/16,-1/16。
解:7/16=7*2-4=0.01114/16=4*2-4=0.01001/16=1*2-4=0.0001真值原码补码反码7/16 0.0111 0.0111 0.01114/16 0.0100 0.0100 0.01001/16 0.0001 0.0001 0.0001+0 O.0OOO O.0OOO O.0OOO-0 1.0OOO O.0OOO 1.1111-1/16 1.0OO1 1.1111 1.1110-4/16 1.0100 1.1100 1.1011-7/16 1.0111 1.1001 1.10003.已知下列数的原码表示,分别写出它们的补码表示:[X1]原=O.10100,[X2]原=l.10111。
解:[X1]补=0.10100,[X2]补=1.01001。
4.已知下列数的补码表示,分别写出它们的真值:[X1]补=O.10100,[X2]补=1.10111。
解: X1=O.10100, X2=-0.01001。
5.设一个二进制小数X≥0,表示成X=0.a1a2a3a4a5a6,其中a1~a6取“1”或“O”:(1)若要X>1/2,a1~a6要满足什么条件?(2)若要X≥1/8,a1~a6要满足什么条件?(3)若要1/4≥X>1/16,a1~a6要满足什么条件?解:(1) X>1/2的代码为:0.100001~0.111111。
a1=1,a2+a3+a4+a5+a6=1。
(2) X≥1/8的代码为:0.001001~0.111111(1/8~63/64)a1+a2=0,a3=1或a1=0,a2=1,或a2=1(3)1/4≥X>1/16的代码为:0.000101~0.01000(5/64~1/4)a1+a2+a3 =0, a4=1,a5+a6=1 或a1+a2=0,a3=1 或a2=1,a1+a3+a4+a5+a6=06.设[X]原=1.a1a2a3a4a5a6(1)若要X>-1/2,a1~a6要满足什么条件?(2)若要-1/8≥X≥-1/4,a1~a6要满足什么条件?解:(1) X>-1/2的代码为:1.000001~1.011111(-1/64~-31/64)。
计算机组成原理逻辑运算

(7)
§1.2 基本逻辑关系
逻辑:指事物的前因和后果所遵循的规律 逻辑状态:逻辑“真”为“1”,逻辑“假”为 “0” 基本逻辑关系:与 ( and ) 或 (or ) 非 ( not ) 与逻辑:决定事件发生的各条件中,所有条件都 具备,事件才会发生(成立) 规定: A E B F 开关合为逻辑“1” 开关断为逻辑“0”
=1
提出A 反变量吸收
(38)
利 用 逻 辑 代 数 的 基 本 公 式
例2:F
AB A B BC B C
(AB A B ) (BC B C) AB A B(C C)
五、反演定理
德 • 摩根 (De • Morgan)定理:
AB A B
A B AB
可以用列真值表的方法证明:
A 0 0 1 1 B 0 1 0 1 AB 0 0 0 1
AB
A
1 1 0 0
B
AB
1 1 1 0
1 0 1 0
1 1 1 0
(24)
反演定理内容:将函数式 F 中所有的
A 0 0 0 0 1 1 1 1
B C 0 0 0 1 1 0 1 1 0 0 0 1 1 0 1 1
F 0 0 0 0 0 1 1 1
(28)
1.4.2 逻辑函数式
逻辑代数式:把逻辑函数的输入、输出关 系写成与、或、非等逻辑运算的组合 式。也称为逻辑函数式,通常采用 “与或”的形式。 例:
F ABC ABC ABC ABC ABC
利用卡诺图化简
卡诺图适用于输入变量为3、4个的逻辑代数式的 化简;化简过程比公式法简单直观。
(37)
利用逻辑代数的基本公式
计算机组成原理第二章参考答案

计算机组成原理第二章参考答案计算机组成原理第二章主要介绍了计算机的层次结构和性能指标。
以下是第二章的参考答案,详细介绍了计算机层次结构的各个层次和性能指标。
第二章:计算机的层次结构和性能指标1. 什么是计算机的层次结构?计算机的层次结构是指计算机系统中各个层次之间的相互关系和功能划分。
计算机的层次结构从上到下分为五个层次:应用层、操作系统层、汇编和机器语言层、微程序层和硬件层。
2. 请介绍计算机的五个层次结构。
- 应用层:计算机的最顶层,负责处理用户的应用程序和数据。
- 操作系统层:负责管理计算机系统的资源和控制计算机的运行。
- 汇编和机器语言层:负责将高级语言转化为机器语言,供计算机硬件执行。
- 微程序层:负责实现计算机指令的具体执行过程。
- 硬件层:计算机的最底层,包括处理器、内存、输入输出设备等硬件组件。
3. 什么是计算机的性能指标?计算机的性能指标是指衡量计算机性能优劣的指标,主要包括速度、存储容量、可靠性和成本四个方面。
4. 请介绍计算机的速度性能指标。
- 响应时间:指从用户发出请求到计算机给出响应的时间。
- 时钟周期:指计算机内部处理器的时钟周期时间。
- 主频:指处理器的时钟频率,单位为赫兹。
- MIPS:指每秒执行百万条指令数,是衡量计算机运算速度的指标。
5. 请介绍计算机的存储容量性能指标。
- 主存容量:指计算机中用于存储程序和数据的主存容量。
- 硬盘容量:指计算机中用于存储大容量数据的硬盘容量。
- 缓存容量:指计算机中用于提高数据访问速度的高速缓存容量。
6. 请介绍计算机的可靠性性能指标。
- 故障率:指计算机发生故障的概率。
- 可用性:指计算机正常工作的时间占总时间的比例。
- 容错能力:指计算机在部分组件故障时仍然可以正常工作的能力。
7. 请介绍计算机的成本性能指标。
- 硬件成本:指计算机硬件的购买和维护成本。
- 能耗成本:指计算机在运行过程中消耗的能源成本。
- 人工成本:指计算机的使用和维护所需的人力成本。
计算机组成原理第2章习题答案

1.设机器数的字长8位(含1位符号位),分别写出下列各二进制数的原码、补码和反码:0,-0,,,,,1101,-1101。
解:2.写出下列各数的原码、补码和反码:7/16,4/16,1/16,±0,-7/16,-4/16,-1/16。
解:7/16=7*2-4=4/16=4*2-4=1/16=1*2-4=真值原码补码反码7/164/161/16+0-0-1/16-4/16-7/163.已知下列数的原码表示,分别写出它们的补码表示:[X1]原=,[X2]原=。
解:[X1]补=,[X2]补=。
4.已知下列数的补码表示,分别写出它们的真值:[X1]补=,[X2]补=。
解: X1=, X2=。
5.设一个二进制小数X≥0,表示成X=,其中a1~a6取“1”或“O”:(1)若要X>1/2,a1~a6要满足什么条件?(2)若要X≥1/8,a1~a6要满足什么条件?(3)若要1/4≥X>1/16,a1~a6要满足什么条件?解:(1) X>1/2的代码为:~。
a1=1,a2+a3+a4+a5+a6=1。
(2) X≥1/8的代码为:~(1/8~63/64)a1+a2=0,a3=1或a1=0,a2=1,或a2=1(3)1/4≥X>1/16的代码为:~(5/64~1/4)a1+a2+a3 =0, a4=1,a5+a6=1 或a1+a2=0,a3=1 或a2=1,a1+a3+a4+a5+a6=0 6.设[X]原=(1)若要X>-1/2,a1~a6要满足什么条件?(2)若要-1/8≥X≥-1/4,a1~a6要满足什么条件?解:(1) X>-1/2的代码为:~(-1/64~-31/64)。
a1=0,a2+a3+a4+a5+a6=1。
(2) -1/8≥X≥-1/4的代码为:~(-1/8~-1/4)a1+a2 =0, a3=1或a2=1,a1+a3+a4+a5+a6=07.若上题中[X]原改为[X]补,结果如何?解:(1) X>-1/2的代码为:~(-31/64~-1/64)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第二章数码系统例题及答案例题1写出下列各数的原码、反码、补码、移码(用二进制数表示)。
(1)-35/64 (2)23/128 (3)-127(4)用小数表示-1 (5)用整数表示-1 (6)用整数表示-128解:-1在定点小数中原码和反码表示不出来,但补码可以表示,-1在定点整数中华表示最大的负数,-128在定点整数表示中原码和反码表示不出来,但补码可以。
例题2设机器字长为16位,分别用定点小数和定点整数表示,分析其原码和补码的表示范围。
解:(1)定点小数表示最小负数最大负数0 最小正数最大正数二进制原码 1.111...111 1.000...001 0.000...001 0.111 (111)十进制真值- (1-215) -2152-151-2-15原码表示的范围:- (1-215) ~1-2-15二进制补码 1.000...000 1.111...111 0.000...001 0.111 (111)十进制真值-1 -2152-151-2-15原码表示的范围:- 1 ~1-2-15(2)定点整数表示最小负数最大负数0 最小正数最大正数二进制原码1111...111 1000...001 0000...001 0111 (111)十进制真值- (215-1) -1 +1 215-1原码表示的范围:- (215-1) ~215-1 [-32767 ~ +32767]二进制补码1000...0001111...111 0000...001 0111 (111)十进制真值-1 +1 215-1原码表示的范围:- 215~215-1 [-32768 ~ +32767]一、选择题1.下列数中最小的数为()。
A.(101001)2B.(52)8C.(101001)BCD D.(233)162.下列数中最大的数为()。
A.(10010101)2B.(227)8C.(96)16D.(143)53.在机器数中,()的零的表示形式是惟一的。
A.原码B.补码C.反码D.原码和反码4.针对8位二进制数,下列说法中正确的是()。
A.-127的补码为10000000 B.-127的反码等于0的移码C.+1的移码等于-127的反码D.0的补码等于-1的反码5.一个8位二进制整数,采用补码表示,且由3个“1”和5个“0”组成,则最小值为()。
A.-127 B.-32 C.-125 D.-36.计算机系统中采用补码运算的目的是为了( )。
A.与手工运算方式保持一致B.提高运算速度C,简化计算机的设计D.提高运算的精度7.某机字长32位,采用定点小数表示,符号位为1位,尾数为31位,则可表示的最大正小数为( ),最小负小数为( )。
A,+(231-1) B.-(1-2-32) C.+(1-2-31)≈+1 D.-(1-2-31)≈-18.某机字长32位,采用定点整数(原码)表示,符号位为1位,尾数为31位,则可表示的最大正整数为(),最小负整数为()。
A.+(231-1) B.-(1-2-32) C.+(230-1) D.-(231-1)9.用n+1位字长(其中1位符号位)表示定点整数(原码)时,所能表示的数值范围是()。
A.0≤︱N︱≤2n+1-1 B.0≤︱N︱≤2n-1 C.0≤︱N︱≤2n-1-110.用n+1位字长(其中1位符号位)表示定点小数(原码)时,所能表示的数值范围是()。
A.0≤︱N︱≤1-2-(n+1)B.0≤︱N︱≤1-2-n C.0≤︱N︱≤1-2-n-1 11.定点8位字长的字,采用2的补码形式表示8位二进制整数,可表示的数范围为()。
A.-127~+127 B.-2-127~+2-127C.2-128~2+127D.-128~+12712.32位浮点数格式中,符号位为1位,阶码为8位,尾数为23位。
则它所能表示的最大规格化正数为()。
A.+(2-2-23)×2+127B.+(1-2-23)×2-127C.+(2-2-23)×2+255D.2+127-2-2313.64位浮点数格式中,符号位为1位,阶码为11位,尾数为52位。
则它所能表示的最小规格化负数为()。
A.-(2-2-52)×2-1023B.-(2-2-52)×2+1023C.-1×2-1024D.-(1-2-52)×2+204714.假定下列字符码中有奇偶校验位,但没有数据错误,采用偶校验的字符码是()。
A.11001011 B.11010110 C.11000001 D.1100100115.若某数z的真值为-0.1010,在计算机中该数表示为1.0110,则该数所用的编码方法是()码。
A.原B.补C.反D.移16.长度相同但格式不同的2种浮点数,假设前者阶码长、尾数短,后者阶码短、尾数长,其他规定均相同,则它们可表示的数的范围和精度为()。
A.两者可表示的数的范围和精度相同B.前者可表示的数的范围大但精度低C.后者可表示的数的范围大且精度高D.前者可表示的数的范围大且精度高17.某数在计算机中用8421BCD码表示为0111 1000 1001,其真值为()。
A.789 B.789H C.1929 D.1lll0001001B18.在浮点数原码运算时,判定结果为规格化数的条件是()。
A.阶的符号位与尾数的符号位不同B.尾数的符号位与最高数值位相同C.尾数的符号位与最高数值位不同D.尾数的最高数值位为119.若浮点数用补码表示,则判断运算结果是否为规格化数的方法是()。
A.阶符与数符相同B.阶符与数符相异C.数符与尾数小数点后第1位数字相异D.数符与尾数小数点后第1位数字相同答案:1.C 2.B 3.C 4.B 5.C 6.C 7.①C,②D 8.①A,②D 9.B 10.B 11.D 12.A 13.C 14.D 15.B 16.B 17.A 18.D 19.C二、计算题1.设机器字长16位,定点表示,尾数15位,数符1位,问:(1)定点原码整数表示时,最大正数是多少?最小负数是多少?(2)定点原码小数表示时,最大正数是多少?最小负数是多少?[解](1)定点原码整数表示:最小负数值=-(215-1)=-32767最小负整数表示:1111 1111 1111 1111最大正数值:(215-1)=+32767最大正整数表示:0111 1111 1111 1111(2)定点原码小数表示:最大正数值=(1-215)10=+0.1111 1111 111最小负数值=-(1—2-15)10=-0.111 1111 1112.机器字长32位,定点表示,尾数31位,数符1位,问:(1)定点原码整数表示时,最大正数是多少? 最小负数是多少?(2)定点原码小数表示时,最大正数是多少? 最小负数是多少?2.[解](1)定点原码整数表示时,最大正数值=(231-1)10最小负数值;-(231-1)10(2)定点原码小数表示时,最大正数值;(1-231)10 最小负数值:-(1-2-31)103.把十进制数X=(+128.75)×2-10写成浮点表示的机器数,阶码、尾数分别用原码、反码和补码表示。
设阶码4位,阶符1位,尾数15位,尾数符号1位。
3.[解]X=(+128.75)×2-10[X]原=1 0010 0 100000001100000[X]反=1 1101 0 100000001100000[X]补=1 1110 0 100000001100000阶阶数尾符码符数4.设机器字长为16位,浮点表示时,阶码5位,阶符1位,数符1位,尾数9位。
问:最大浮点数为多少? 最小浮点数为多少?4.[解] 最大浮点数=2+31×(1-2-9)最小浮点数=-2+31×(1-2-9)例题:某机采用使用浮点数格式的短浮点数数为“C2308000H”首,计算该浮点数的真值解:先将其展开为二进制数,并区分出三个字段的编码为:1,100,0010,0011,0000,1000,0000,0000,0000数阶尾符码数由于数符为1,该浮点数是一个负数。
阶码真值=10000100-011111ll=00000101尾数=1.0110,0001,0000,0000,0000,000于是该浮点数的真值为:-101100001×2+101=-101100.001=-54.125例②某机中现有浮点数为+74.75,将其变换成32位的短浮点数格式的过程如下:精选文库首先将其变换成二进制格式:+74.75=+1001100.1l表示成规格化二进制格式为:+1001100.1l=+1.00110011×2+110计算出阶码的移码为:110+01111111=10000101于是该浮点数的短浮点数格式应为:0100,0010,1001,1001,1000,0000,0000,0000=42998000H例如:①X=+0.1110110l×2-101则[X]原=1101,0.11101101[X]反=1010,0.11101101[X]补=10ll,0.1110110l②X=+0.1010110×2+010则[X]原=0010,0.1010110[X]反=0010,0.1010110[X]补=0010,0.1010110③X=-0.10101100×2+011则[X]原=0011,1.10101100[X]反=0011,1.010100ll[X]补=0011,1.01010100④X=-0.01010001×2-111则[X]原=1111,1.01010001[X]反=1000,1.10101110[X]补=1001,1.10101111。
