4.4角的比较
4.4角的比较

3、O 是直线 AB 上一点,∠AOC=53°,OD 平分∠BOC,求∠BOD 的度数?
D C B
A
O
五 自我提高 如图,∠AOB=90°,∠BOC=30°,OM 平分∠AOB,ON 平分∠BOC, ⑴求∠MON 的度数, ⑵若∠AOB=∠α ,若∠BOC=∠β (∠β 为锐角)其他条件不变,求∠MON 的度数。 (用含 α 、β 的式子表示) ⑶探究:从⑴⑵中你发现有什么规律?
2、如图,OB 是平角∠AOC 的角平分线,OD 平分∠BOC,求∠AOD 的度数。
B D
A
O
C
六.教学反思:
角的大小比较和角平分线的概念. 角的大小比较和角平分线的概念.
重点 难点
导学过程 一、学前准备: (1)海洋世界在大门的正东方向,你能说出它在大门的北偏东多少度吗? (2)虎豹园、猴山、大象馆分别在大门的北偏东(或南偏东) 多少度? (3)在图中连接各个景点与大门,并用适当方式表示各角。 (4)上面各个角中,哪些是锐角?哪些是钝角?哪些是直角?并指出它们 的大小关系。 猴山B
大象馆D
练习: 1、根据图形填空: (1) AOB AOC _____ ; (2) AOD AOB ____ ___ COD ; (3) AOC BOD AOB _____ .
B C
D O 第 2题
A
(5)知识目标: 1、理解角的大小比较意义;掌握直角、锐角、钝角的概念;掌握角平分线的概念. 2、会估计一个角的大小;会用叠合法和度量法进行角的大小比较;会区别直角、锐角和 钝角;会运用角平分线的性质解决一些角的计算问题. 德育目标: 体验生活中的几何知识,激发学生对生活的热爱;通过动脑、动手、动口、合作和探究, 启发学生的智慧,感受快乐数学,接受逻辑推理思维的熏陶.
北师大版七上 角的比较复习题3(含答案)-

4.4 角的比较 (C卷)(能力拔高训练题 40分 30分钟)一、探究题:(10分)1.已知∠AOB=90°,∠COD=90°,则∠AOD与∠BOC之间有什么关系?二、开放题:(10分)2.在0时与12时之间,钟面上的时针与分针在什么时候成30°的角? 请写出两个答案.三、竞赛题:(10分)3.(1)如图,已知∠AOB=90°,∠BOC=30°,OM平分∠AOC,ON平分∠BOC, 求∠MON的度数.(2)如果(1)中的∠AOB=α,其他条件不变,求∠MON的度数.(3)如果(1)中的∠BOC=β (β为锐角),其他条件不变,求∠MON的度数.(4)从(1)、(2)、(3)的结果中能得出什么结论?OC MABN四、趣味题:(10分)4.在抗日战争时期,一组游击队员奉命把A村的一批文物送往一个安全地带, 在A村的南偏东50°距离3千米处有一B村,他们从A村出发,以北偏东80°方向行军, 不知道走了多远以后,他们发现B村出现了烟火,于是决定先把文物就地埋藏起来,然后调转方向走了7千米的路程,直接赶到B村消灭了敌人,结束战斗后, 这组游击队员应到哪里去取文物呢?假如你在场,凭以上信息,你能估计文物藏在什么地方吗?答案:一、1.解:如答图(1),∠AOD+∠COB=∠AOC+∠COB+∠BOD+∠COB=∠AOB+∠COD=180°. 如图(2),∠AOD+∠BOC=360°-∠AOB-∠COD=180°. 如图(3),∠AOD=∠BOC.如图(4),∠AOD=∠BOC.(1)O C ADB(2)O CADB(3)CADB(4)O CADB二、2.1时和11时三、3.(1)解:∵OM 平分∠AOC,DN 平分∠BOC,∠AOB=90°, ∴∠MOC=12∠AOC, ∠NOC=12∠BOC,∴∠MON=∠MOC-∠NOC= 12∠AOC- 12∠BOC=12(∠AOC-∠BOC)=12∠AOB= 12×90°=45°(2)当∠AOC=α,其他条件不变时,∠MON= 12∠AOB=2;(3)当∠BOC=β,其他条件不变时,∠MON=12∠AOB=12×90°=45°(4)分析(1)、(2)、(3)的结果和(1)的解答过程可以看出:∠MON 的大小总等于∠AOB 的一半,而与锐角∠BOC 的大小变化无关. 四、4.解:由题意作答图.作法如下:(1)在平面上任找一点为A(村)(2)作出A 村的南偏东50°的方向线AM,在AM 上截取AB=3cm(以1cm 表示1千米) (3)作出A 村的北偏东80°的方向线AN(4)以B 点为圆心,以7cm 为半径作圆弧交AN 于C.(5)连结BC,量出C 点在B 点处的方向为北偏东62°,BC=7cm,则从B 处以北偏东62°的方向出发走7千米到达C 处,则C 处附近就为藏文物的地方.3cm7cm62︒50︒80︒北西南东CMA BN。
《角的比较》参考课件1

观察与思考:
① 使用叠合法比较角的大小必须注意哪些细节? ②角的大小与两边画出部分的长短是否相关?
【例
1】
根据下图,求解下列问题:
(1)比较∠AOB、∠AOC、∠AOD、∠AOE的大小,并指出 其中 的锐角、直角、钝角、平角. (2)写出∠AOB、∠AOC、∠BOC、 ∠AOE中某些角之间的两个等量 关系. (3)借助三角尺估测 图中各角的度数. C O D E A B
一个含150角的方法很多。请你画出其中两种不
同构成的示意图,并在图上作出必要的标注,
不写作法。
想一想:
用一副三角板可以画出哪些不同度数的角?
4.4 角的比较
想一想:
► 如何比较两条线段的长短? ► 如何比较两个角的大小呢?
A O B
A
O
B c
c
c
o
D
o
D
D
o
与比较线段的长短类似,如果直接观察难以判断,我们可以 用两种方法对角进行比较: 一种方法是用量角器量出它们的度数,在进行比较; 另一种方法是将两个角的定点及一条边重合,另一边放在重 合的同侧就可比较大小。
在方格纸上有三个角,试确定每个角的大小及各角之
间的等量关系.(直接作在课本上)
闯一闯:
(1) 如图,∠AOC和∠BOD都是直角。
①估测∠COB的度数;
②若∠DOC=28°,说出∠AOB的度数。
D A B O C
试一试:
一副三角板由一个等腰直角三角形和一个含
300角的直角三角形组成。利用这副三角板构成
角平分线
A B
C O D
∠AOE =2∠AOC =2∠COE 1 ∠AOC =∠COE = ∠AOE 2
4.4角的比较

上面各个角中,哪些是锐角?钝角?直角?并指出他
们的大小关系。
角的大小比较的主要方法:
•测量法 •重叠法:
B(D)
O
A(C)
(1) ∠AOB=∠COD
D
B
B
DLeabharlann OA(C) OA(C)
(2)
(3)
∠AOB<∠COD ∠AOB>∠COD
折一折:
B
•1 在纸上画一个角并剪下,将
它对折使其两边重合,折痕与
O
•角的动态定义:角可以看成是由一条射线绕着它 的端点旋转而成的。 角的分类:锐角、直角、钝角、平角、周角。
猴山B
•海洋世界在大门的正东方向, 大象馆D 你能说出它在大门的北偏东多
少度吗?
•虎豹园、猴山、大象馆分别在
大
海洋世界A
门 口
O
大门的北偏东(或南偏东)多
少度?
虎豹园C
•在图中连接各个景点与大门, 并用适当的方式表示各个角。
D
角两边所成的两个角的大小关
系怎样? 2. 角平 分线 定义 :从 一 个
角的顶点引出的一条射线, 把这个角分成两个相等的角, 这条射线叫这个角的平分线。
A
AOD=BOD AOB=2AOD (或AOB=2BOD) (或AODB=O12D=12AOBAOB)
拓展: 如何将一个角三等分、四等分?一个角的三等分
第四章 基本平面图形
4 角的比较
教学目标
❖知识目标:在现实情境中进一步丰富对角与锐角、 直角、钝角、平角、周角及其大小关系的认识。会比 较角的大小,能估计一个角的大小。在操作活动中认 识角的平分线,能画出一个角的平分线。
教学重点: 角的大小比较方法,角平分线的概念。
北师大版数学七年级上册4.4《角的比较》教案

北师大版数学七年级上册4.4《角的比较》教案一. 教材分析《角的比较》是北师大版数学七年级上册4.4节的内容,主要包括角的概念、分类和度量。
本节课通过引入角的比较,让学生理解角的大小不仅与边的长短有关,还与角的开口大小有关。
教材内容由浅入深,从基本概念到实际应用,使学生能够逐步掌握角的大小比较方法。
二. 学情分析学生在进入七年级前,已经学习了角的基本概念,如锐角、直角、钝角等。
他们对角的大小有一定的认识,但可能仅局限于边的长短。
通过本节课的学习,学生需要理解角的大小不仅与边的长短有关,还与角的开口大小有关。
此外,学生需要学会用量角器测量角的大小,并能进行角的比较。
三. 教学目标1.知识与技能:学生能够理解角的概念,掌握角的大小比较方法,会用量角器测量角的大小。
2.过程与方法:学生通过观察、操作、交流等活动,培养逻辑思维能力和解决问题的能力。
3.情感态度与价值观:学生培养对数学的兴趣,激发探究精神,培养合作意识。
四. 教学重难点1.教学重点:学生能够理解角的大小比较方法,会用量角器测量角的大小。
2.教学难点:学生能够灵活运用角的大小比较方法,解决实际问题。
五. 教学方法1.情境教学法:通过生活实例引入角的概念,激发学生学习兴趣。
2.启发式教学法:引导学生主动探究角的大小比较方法,培养学生的思维能力。
3.合作学习法:学生分组讨论,共同解决问题,培养学生的合作意识。
六. 教学准备1.教具:量角器、直尺、三角板等。
2.教学素材:课件、教学图片等。
七. 教学过程1.导入(5分钟)利用课件展示生活中常见的角,如钟表、自行车等,引导学生关注角的大小。
提问:你们认为角的大小与什么有关?2.呈现(10分钟)介绍角的概念,讲解角的大小比较方法。
通过示例,让学生明白角的大小不仅与边的长短有关,还与角的开口大小有关。
3.操练(10分钟)学生分组进行实践活动,使用量角器测量不同角的大小,并进行比较。
教师巡回指导,解答学生的疑问。
北师大版七年级数学上册《基本平面图形——角的比较》教学PPT课件(4篇)

角的大小的比较方法: (1)如果已知角是锐角、直角、钝角、平角、周角几类中不同 类的角,就可以直接由它们之间的关系比较出它们的大小; (2)可以通过量角器进行量度来比较角的大小; (3)可以根据各角在同一图中的位置关系比较角的大小.
角的平分线
活动:大家在练习本上画一个角,然后把角的两边 对折,展开以后你会发现折痕把角分成了两个角, 这两个角有什么关系呢,它们又和原来的角有着怎 样的等量关系?
4.4 角的比较
知识回顾 比较两条线段的长短的方法? 1、度量法:用刻度尺测量线段的长度的方法。 2、叠合法:将其中一条线段移到另一条线段 上作比较。
猜想:比较两个角的大小方法?
获取新知
问题:有一天学生张虎和王鹏各带了一把折扇(如图),下面是他们的 一段对话:
张:我的折扇大一些,所以我的折扇的角也大一些.
2
2
2
(2)结合(1)的结论可求出∠DOE的度数,从而求出∠BOE的度数
解:(1)因为OC平分∠AOD,
1 所以∠DOC= 2 ∠AOD.
因为OE平分∠BOD,
1
所以∠DOE= 2∠BOD.
所以∠COE=∠DOC+∠DOE=
1
(∠AOD+∠BOD)
= 1 ∠AOB= 1 ×130°=65°.
2
2
2
2. 已知,如图,∠AOB = 130°,∠AOD = 30°,∠BOC = 70° ,问:OC 是∠AOB 的平 分线吗?OD 是∠AOC 的平分线吗?
解: OC不是∠AOB 的平分线 OD是∠AOC 的平分线 B
C D
A O
3. 如图,直线 m 外有一定点 O,A 是 m 上的 一个动点,当点 A 从左向右运动时,观察∠α 和 ∠β 是如何变化的,∠α 和 ∠β 之间有关系吗?
第四章基本平面图形4.4角的比较

C
B O A
如图,OC平分∠AOD,∠BOD=2∠AOB.
若∠AOD=114°,求∠BOC的度数?
B C ∠BOD=2∠AOB ∴∠AOB=1/3∠AOD=38° ∵OC平分∠AOD O D ∴∠AOC=1/2∠AOD=57° (角平分线的定义)
数学·课标版(BS)
将一副三角板按图示方法放置(直角顶点重合) 则∠AOB+∠DOC= ____ 180° .
D A
┓
C
O
H
29
已知点O是直线AB上一点 ∠AOC=60°, OM、ON分别平分 ∠AOC、∠BOC, 求∠MON
C M A O B N
已知O为直线AB上一点,OE平分∠AOC,OF平分 ∠COB,求∠EOF的大小? 解: C ∵ OE平分 ∠ AOC,OF平分 ∠COB (已知) 1 ∴∠EOC= 2 ∠AOC, (角平分线的定义) ∠COF= 1 ∠COB F
75°、 90° 105°、120°、
135°、150°、 165°、180°
用一副学生用的三角板的内角 (其中一个三角板的内角是45°,45°,90°;另一 个是30°,60°,90°) 可以画出大于0°且小于等于150° 的不同角度的角共有(C )种. A.8 B.9 C.10 D.11
如图,∠AOC和∠BOD都是直角。
①∠COB和∠AOD有何关系?
②若∠DOC=28°,求∠AOB的度数。 ③若∠AOB=150°,求∠COD的度数。 ④图中相等的角是_________
D A B O C
如图,∠AOC和∠BOD都是直角。
(1)若∠DOC=28°,说出∠AOB的度数。 (2)找出图中相等的角。如果∠DOC≠28°,它 们还会相等吗? (3)若∠DOC变化,∠AOB 如何变化?
角的比较教学反思

4.4角的比较教学反思
本节课是教学内容是角的比较,而在这之前学生已经学习了角和比较线段的长短,也对线段的比较的研究有了经验,因此对于即将开始的角的比较,可以与线段的比较进行类比探索学习。
重点研究角的比较的方法,我课前让学生制作两个不同的角,在小组合作时,引导学生类比线段的比较,通过观察、操作、猜测、验证进一步研究角的比较,通过度量从数的方面比较形的大小,通过动手操作,让学生小组内总结,利用叠合法比较大小时的步骤。
通过折叠手中的角,引出角平分线以及角平分线的性质,并类比线段的中点的几何语言,描述角平分线的几何语言,多次让学生体会类比的思想。
初次熟悉课本,我将本节课重点研究两点:角的比较大小的方法与角平分线及其性质,认为两者是独立的,通过反复研读课本,研究教材,认真研究课本P119页做一做,设计的目的,即是对上面角的比较的再次巩固,又是从折叠感受叠合法比较角的大小同时,引出角平分线,让两者融为一体,在磨课中发现,学生对于做一做(3)在操作中可能会存在困难,我采取利用手中的透明袋,制作图形,让学生课堂动手折叠,很直观的观察出它们之间的关系,再利用PPT演示的形式,隐去多余的线段,引出角平分线。
对于如何上好本节课、本节课教学深度的把握,我依然存在疑惑和不足,期待各位评委老师的点拨与指正。
点评:
1.本节课教师语言清晰,表达准确,教态自然,课堂的教学思路清晰,环节过渡自然,重难点突出,过程的安排符合初中学生的认知规律,多媒体的使用充分得当,给学生留下了比较深刻的印象,是一堂清晰实在数
学课。
2.教师充分发挥学生主动学习,引导学生,经历知识的形成过程,学生动手,动脑,动口,学生参与度高,既调动了学生学习的积极性、主动性,又提高了学生合作交流的意识,充分体现了学生的主体地位,教师的主导地位。
2017年秋北师大版七年级数学上课堂内外课时练习4.4角的比较(PDF版)

6 ������ 如 图 , O B 是 ㊀ ∠A O C ㊀ 的 角 平 分 线, O C 是 øB O D=㊀4 5㊀ 度 .
A. 2 0 ʎ ㊀㊀㊀B. 2 5 ʎ ㊀㊀㊀C. 3 0 ʎ ㊀㊀㊀D. 7 0 ʎ
(D )
㊀ ∠A O D㊀ 的 角 平 分 线 , øA O D = ㊀6 0㊀ 度 ,
若 øA 则 2 ������ 如图所示 , O B=øC O D, B ������ø1<ø2 A ������ø1>ø2
C ������øB O C=øA O C
D ������øB O C>øA O C
, 分 线, 若ø 那 么 øA C O D =7 6 ʎ O D = ㊀1 5 2°㊀ ,
1 øA O B 2
(D )
从一 个 角 的 顶 点 出 发 , 把这个角分成㊀ 3 ������ 角平分线 : 相等的 ㊀ 两个角的 ㊀ 射 ㊀ 线 , 叫做这个角的角平分 线.
第 5 题图
则 øA 4 ������ 如 图 , O C 平 分 øA O B, O C= ㊀ ∠B O C㊀=㊀ 1 ㊀øA O B. 2
C ������ø1=ø2
D ������ø1 与 ø2 的大小关系不能确定
第 8 题图
㊀㊀㊀ 如图 , 填空 . 3.
第 2 题图 第 3 题图
1 (∠ ∴∠E O F = ∠E O C + ∠F O C= B O C+ 2 ∠A O C), ∵点 O 在直线A B 上,
( 1) øA O C = øA O B + ㊀ ∠B O C ㊀ = øA O D- ( ) 2 øB O C=øA O C+øB O D-㊀ ∠A O D㊀ . ㊀ ∠C O D㊀ .
, ∴∠B O C+ ∠A O C=1 8 0°
初中数学七年级上册《角的比较》

1. 在现实情境中,进一步丰富锐角、钝角、直角及大小的认识; 2. 学会比较角的大小,能估计一个角的大小;3. 在操作活动中认识角平分线,能画出一个角的平分线。
4. 认识度、分、秒,并会进行简单的换算。
【情感态度与价值观】1. 能通过角的测量、折叠等体验数、符号和图形是描述现实世界的重要手段。
2. 通过实际观察、操作体会角的大小,发展几何直觉。
3. 能用符号语言叙述角的大小关系,解决实际问题。
【重点与难点】1、角的大小的比较方法2、从图形中观察角的和、差关系。
【学习过程】一、预习导学1、 请同学们回忆,比较两条线段的大小关系有哪几种方法? (测量法和叠合法---类比联想,探索解决问题的方法)2、引导学生观看P148/图4-15并回答](1)请同学们把图中的五大景点中的任何两个之间都用线段连接。
(2)你能比较出这两个角的大小吗?你是怎样比较的?引导学生探讨出角的大小比较的一种方法———测量法。
3、 引导由学生动手操作探讨出叠合法的比较过程,若两个角能完全重合,说说这两个角的大小有何关系?4、角的分类二、例题讲解:例1 P148. 根据图4-16 ,求解下列问题:(1) 比较∠AOB 、∠AOC 、∠AOD 、∠AOE 的大小,并指出其中的锐角、直角、钝角、平角;(2) 写出∠AOB 、∠AOC 、∠BOC 、∠AOE 中某些角之间的两个等量关系。
例2、下面请大家各自在纸上任意画一个∠BOA ,再完成书上的做一做。
发现了什么?像刚才这条折痕,它是由角的顶点出发,把原来的角分成两个相等的角。
那么这条射线叫做 。
对这个定义的理解要注意以下几点:1.角平分线是一条射线,不是一条直线,也不是一条线段.它是由角的顶点出发的一条射线,这一点也很好理解,因为角的两边都是射线.2.当一个角有角平分线时,可以产生几个数学表达式.可写成 因为 OC 是∠AOB 的角平分线,所以 ∠AOB=2∠AOC=2∠COB , (1)⎪⎪⎪⎩⎪⎪⎪⎨⎧︒=∠︒=∠︒<∠<︒︒=∠︒<∠<︒3601801809090900ααααα周角:平角:钝角:直角:锐角:角的分类∠AOC=∠COB , (2)反过来,只要具备上述(1)、(2)、中的式子之一,就能得到OC 为∠AOB 的角平分线。
4.4角的比较
教案、学案一体化设计
投影显示:两个度数相差1度以内的角,不标明度数,只凭眼观察不能确定两个角的大小.
[板书] 1.4 角的比较
由学生熟知的三角板各角的比较入手,把学生带入比较角的大小的意境.但问题一转,出现了不标度数,观察又不能确定大小的角,当学生束手无策时,教师提出这就是我们要学习的新内容,调动学生的积极性,吸引其注意力.
1.角的比较
(1)叠合法
演示:移动,使其顶点与的顶点重合,一边和
请同学们观察的另一边
①与重合,等于,记作
②落在的内部,小于,记作
③落在的外部,大于,记作
,、.
,,把移到上,使它们的顶点重合,一边重合,会
你如何把移到才能保证
)在,是与的差,记作:
)在,是与的和,记作:
几何语言表示:是的平分线,(或
如何移到
教师根据学生回答小结:量角器可起移角的作用,测量的度数,然后以
边为作作一个角等于。
4.4角的比较

七年级第四章第四节角的比较课型:新授课教学目标:1.经历比较角的大小的研究过程,体会角的比较和线段的比较方法的一致性.2.会比较角的大小,能估计一个角的大小.3.理解角平分线的意义.教法与学法指导:本课利用了东沙河中学“三为主,六环节”课堂教学模式,采用自主探索,启发引导,合作交流展开教学,引导学生主动地进行观察、归纳、猜测和验证.学生已经掌握了线段的比较方法,在此基础上,学生通过类比的方法,探索、归纳角的比较方法,整个过程突出以学生为主体的探索性学习活动.重点:角的比较方法.难点:角平分线的意义及应用.课前准备:教师:多媒体课件,导学案.教学过程:一、创设情境,导入新课师:请大家回忆两个线段是如何比较大小的?生:用度量法和叠合法.师:怎样用叠合法比较线段的大小?生:将两条线段的一个端点重合,另一个端点落在重合端点的同一侧,看另一端点的位置来比较线段的长短.师:同学们说的很好,那对于两个角的大小我们又怎么比较呢,这就是我们今天要探究的内容.(板书:角的比较)设计意图:复习回顾旧知,同时利用线段的比较方法引入角的比较方法,并为角的比较方法做铺垫.二、目标展示师:看一下我们这节课的学习目标(多媒体展示)学习目标:1.会比较角的大小,能估计一个角的大小.2.理解角平分线的意义并会应用.设计意图:让学生了解本节课要学习的内容,激发学生的探究欲望.三、自主学习,合作探究探究活动一:比较角的大小师:如何比较下面两个角的大小呢? 请大家讨论归纳出比较的方法及相关步骤。
(多媒体展示)(学生利用导学案,独立思考6、7分钟之后小组讨论.) 师:哪位同学能说一说你是如何比较这两个角大小的. 生1:我是用量角器量出它们的度数,再比较的. 师:这就是度量法,还有其他方法吗?生2:我是把这两个角减下来,再放在一起比较的. 师:你能给大家演示,并讲解一下吗?生2:(上台演示并讲解)两个角的顶点和一边要重合,另一边要放在重合边的同侧,观察另一边的位置.如果这条边落在角的内部,则它比这个角小;如果落在角的外部,则它比这个角大;如果与另一边重合,则这两个角相等.师:很好,这种方法和我们以前学的那种方法很类似? 生:线段的比较方法中的叠合法. 师:在这里我们也称这种方法为叠合法.下面我就用多媒体演示一下如何用叠合法比较两个角的大小:首先确定∠ABC 的位置,然后使∠DEF 的顶点E 与∠ABC 的顶点BC 重合,边EF 与BC 重合,并使另一边ED 与BA 在重合边的同一侧;(1)如果DE 和AB 重合,那么∠ABC 等于∠DEF ,记作∠DEF =∠ABC . 如图(动画演示):(2)如果ED 落在∠ABC 内部,那么∠DEF 小于∠ABC ,记作∠DEF <∠ABC .如图(动画演示):BACEDFB AC (E )(F )(D )(3)如果ED 落在∠ABC 外部,那么∠DEF 大于∠ABC ,记作∠DEF >∠ABC .如图(动画演示):(教师板书:角的比较方法:1、度量法 2、叠合法 )设计意图:通过复习线段的比较方法,让学生通过类比的方法总结出角的比较方法.探究活动二:角的平分线(多媒体展示)根据图4-19求解下列问题:(1)比较∠AOB ,∠AOC ,∠AOD ,∠AOE 的大小,并指出其中的锐角、直角、钝角、平角.(2)试比较∠BOC 和∠DOE 的大小.(3)小亮通过折叠的方法,使OD 与OC 重合,OE 落在∠BOC 的内部,所以∠BOC 大于∠DOE .你能理解这种方法吗?(4)请在图中画出小亮的折痕OF ,∠DOF 与∠COF 有什么大小关系?(学生分组讨论完成)师:如图4-19,∠AOB ,∠AOC ,∠AOD ,∠AOE 分别是属于什么角,并比较它们的大小.生1:∠AOB 是锐角,∠AOC 是直角,∠AOD 是钝角,∠AOE 是平角,因为锐角<直角<钝角<平角,所以∠AOB <∠AOC <∠AOD <∠AOE .DB AC(E )(F ) (F )B AC DOEDCBA图4-19-1师:很好,哪位同学还有其他的方法比较这几个角的大小吗? 生2:可以用度量法.生3:可以用叠合法,因为这几个角的顶点O 及一边OA 重合,另一边都在重合边OA 的同侧,只需观察另一边的位置就可比较它们的大小。
陕西省宝鸡市渭滨区七年级数学上册 4.4 角的比较教案 (新版)北师大版

4.角的比较一、学生状况分析本节课是教材第四章的第四节,学生对点、线、角这些基本的几何元素已具有一定的认知水平,特别是经历了比较线段和度量角等数学活动后,探索图形性质的意识明显增强。
在此基础上对角作进一步的研究,无论是思想上还是方法上都具备良好的契机。
这节课的内容对学生认识空间与图形具有重要的作用。
进入数学新课程后,因教师理念的更新、多媒体的广泛使用以及受年龄特征和所用教材特点的影响,学生的学习习惯和基础水平与以往相比均有明显提高,主要表现在课堂上活跃大胆,具有较强的参与意识,特别是少数学生已能够有意识的将数学与生活联系起来,从他们充分列举实例来解释数学问题就可以说明这一点。
借助计算机演示和学生动手画图、度量、折叠,有利于学生理解和掌握三种角的比较方法。
二、教学任务分析角和线段一样都是几何中最基本的概念。
教材先研究了线段,分两个课时,分别研究了它的表示和比较,对于角的研究也同样安排两课时,分别研究了表示和比较。
本课时的教学内容是角的度量与比较,而在这之前学生已有了对线段的研究经验,因此对于即将开始的角的比较,可以与线段的比较进行类比。
当然角会有自己独特的性质,在研究中也要加以注意和总结。
教学中要始终遵循学生主动学习的原则,通过丰富的活动让学生经历数学知识的形成与应用过程,采用多媒体辅助教学拓展学生的思维,同时注重培养学生使用规范的数学语言进行交流。
在具体的教学中可以参照教科书创设的实际情景的意图,结合当地的实际(主要或标志性建筑的相对位置等)创设新的学生更为熟悉的情景。
根据以上分析,确定本节课的教学目标如下:1.经历比较角的大小的研究过程,体会角的大小比较和线段长短比较方法的一致性。
2.会比较角的大小,能估计一个角大小。
3.在操作活动中认识角的平分线,能画出一个角的平分线。
三、教学过程分析本节课由四个教学环节组成,它们是①回顾引入,类比学习②,观察思考③应用举例,理解概念④随堂练习,归纳拓展。
其具体内容与分析如下:第一环节①回顾引入,类比学习内容:回顾小学认识的各种角,我们来通过动画演示它们的形成过程,看看角的分类、角的大小比较是否存在其的必要性?那我们又应该怎样比较两个角的大小呢?前面学过的一些方法在这儿能否借鉴?目的:通过教材中的4个问题串,回顾上节课学习的角的度量、角表示的以及小学学习中关于锐角、钝角、直角的概念。
4.4 角的比较

第四章 基本平面图形4.4 角的比较一、选择题:1.在∠AOB 的内部任取一点C ,作射线OC ,则一定存在( )A .∠AOB >∠AOC B .∠AOC =∠BOCC .∠BOC >∠AOCD .∠AOC >∠BOC2.如图所示,已知O 是直线AB 上一点,∠1=40°,OD 平分∠BOC ,则∠2的度数是( )A .20°B .25°C .30°D .70°3.如图,点B ,O ,D 在同一直线上,若∠1=15°,∠2=105°,则∠AOC 的度数是( )A .75°B .90°C .105°D .125°第2题图 第3题图 第4题图4.如图所示,已知∠AOC =∠COD =∠BOD ,若∠COD =14°34′,则∠AOB 的度数是( ) A .28°68′ B .43°102′ C .43°2′ D .43°42′5.如图,下列条件中不能确定OC 平分∠AOB 的是( )A .∠AOC =∠BOCB .∠AOC =12∠AOB C .∠AOB =2∠BOC D .∠AOC +∠BOC =∠AOB6.如图,OC 是∠AOB 的平分线,∠BOD =14∠DOC ,∠BOD =10°,则∠AOD 的度数为( )A .50°B .60°C .70°D .80°7.如图,射线OB 、OC 将∠AOD 分成三部分,下列判断错误的是( )A .如果∠AOB =∠COD ,那么∠AOC =∠BODB .如果∠AOB >∠COD ,那么∠AOC >∠BODC .如果∠AOB <∠COD ,那么∠AOC <∠BODD .如果∠AOB =∠BOC ,那么∠AOC =∠BOD第5题图 第6题图 第7题图8.已知∠AOB =70°,以O 为端点作射线OC ,使∠AOC =42°,则∠BOC 的度数为( )A .28°B .112°C .28°或112°D .68°二、填空题:9.用“<”“=”或“>”填空:(1)若∠α=∠β,∠β=∠γ,则∠α ∠γ;(2)若∠1+∠2=70°,∠3+∠2=100°,则∠1 ∠3.10.用一副三角板拼角,能拼出的最小角(非0°)的大小是 °,能拼出的最大角(非平角)的大小是 .11.如图,∠AOB =∠COD =90°,∠AOD =140°,则∠BOC = .三、解答题:12.如图,OB是∠AOC的平分线,∠BOC=30°,∠COD=40°,求∠AOD的度数.13.如图,∠AOD=120°,∠2=2∠1=60°,求:(1)∠DOC的度数;(2)∠BOD的度数.14.如图,点O是直线AB上的一点,∠AOC=130°,OB平分∠COD,OE平分∠AOD,求∠AOE的度数.四、选做题:15.如图,∠AOB是直角,∠AOC=50°,ON是∠AOC的平分线,OM是∠BOC的平分线.(1)求∠MON的大小;(2)当锐角∠AOC的大小发生改变时,∠MON的大小也会发生改变吗,为什么?。
七年级数学上册教学课件《角的比较》

所以∠AOC=2x=2×40°=80°,
因为OD平分∠AOB,所以∠AOD=20°,
所以∠COD=∠AOC+∠AOD=80°+20°=100°.C
所以OC与∠AOB的平分线所成的角的度数为4°或100°.
探究新知 方法点拨
4.4 角的比较
涉及到角度的计算时,除常规的和差倍分计算外, 通常还需运用方程思想和分类讨论思想解决问题.
探究新知
4.4 角的比较
素养考点 3 利用角平分线求角的度数 例3 如图,OB 是∠AOC的平分线,OD是∠COE的平分线.
(1) 如果∠AOC=80°,那么∠BOC 是多少度?
解:因为 OB 平分∠AOC, ∠AOC=80°,
E
DC
B
所以∠BOC= 12∠AOC
=
1 2
×80°
O
A
=40°.
探究新知
A
所以∠AOC=2x=2×8°=16°.
因为OD平分∠AOB,所以∠AOD=20°,
所以∠COD=∠AOD-∠AOC=20°-16°=4°.
探究新知
4.4 角的比较
②如图,OC在∠AOB外部,OD平分∠AOB,
B
所以设∠AOC=2x,∠COB=3x,
D
因为∠AOB=40°,
O
A
所以3x-2x=40°,得x=40°,
提示:无图条件下要分情况讨论.
4.4 角的比较
B C
O
A
C
巩固练习
变式训练
4.4 角的比较
如图,借助一副三角尺可以画出15°和75°的角, 你还能画出哪些度数的角?
75°
15°
探究新知
素养考点 2 角的度数的计算
角的比较与补(余)角教学课件七年级数学上册教材配套(沪科版)

O
B (D)
A
4
角的倍数关系又怎么表示?
如果∠a是∠b的2倍,那么就记作∠a=2∠b
同时∠b就是∠a的
,记作∠b= ∠a
如果∠a是∠b的3倍,那么就记作∠a=4∠b
同时∠b就是∠a的 ,记作∠b= ∠a
根据图形填空。
AOB + ∠_______
2
两个角的差怎么计算?
C
A
O
B
O
D
2
两个角的差怎么计算?
C
当其中一个角∠AOB在另一个角∠COD
A
的内部时,它们的另两条边构成的角就是它
们的差,即:∠COA=∠COD-∠AOBOB (D)源自3两个角的和怎么计算?
C
A
O
B
O
D
3
两个角的和怎么计算?
C
当其中一个角∠AOB在另一个角∠COD
的外部时,它们的另两条边构成的角就是它
所以这个角是45°
“ THANKS
合作方:飞卢数学
”
第4章 直线与角
4.4 角的比较与补(余)角
1
怎么比较两个角的大小?
【1】叠合法
把两个角的顶点重合,一边也重合,另一边放在一侧来比较
1
怎么比较两个角的大小?
1
【2】度量法
2
用量角器量出两个角的度数,然后进行比较
∠1=27°,∠2=49°,所以∠1<∠2
注意:角的大小只跟角两边张开的程度有关,与其他因素无关
可以一个角在地球上, 一个角在火星上。
6
互余和互补是什么意思?
专题4.4 角-重难点题型(学生版)2022年七年级数学上册举一反三系列(人教版)
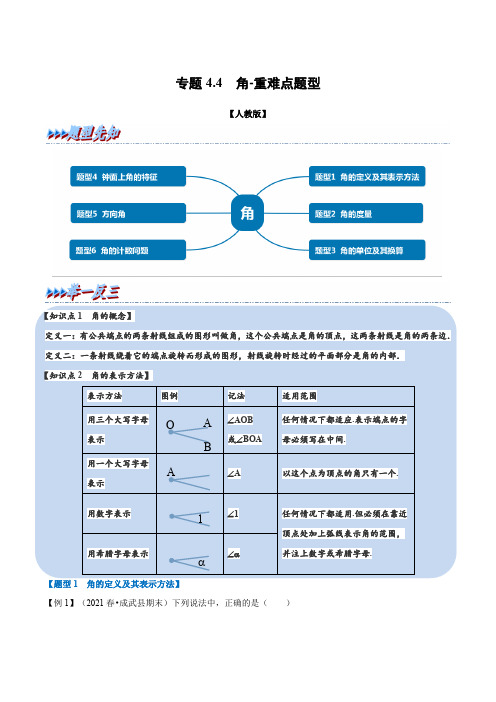
专题4.4 角-重难点题型【人教版】【题型1 角的定义及其表示方法】【例1】(2021春•成武县期末)下列说法中,正确的是()A.两条射线组成的图形叫做角B.有公共端点的两条线段组成的图形叫做角C.角可以看做是由一条射线绕着它的端点旋转而形成的图形D.角可以看做是由一条线段绕着它的端点旋转而形成的图形【变式1-1】(2021秋•成华区期中)如图,用适当的方法表示图中的角:锐角有,钝角有,直角有.【变式1-2】(2021春•潍坊期中)如图所示,下列说法错误的是()A.∠DAO可用∠DAC表示B.∠COB也可用∠O表示C.∠2也可用∠OBC表示D.∠CDB也可用∠1表示【变式1-3】(2021春•宁阳县期末)如图,下列各个图形中,能用∠1,∠AOB,∠O三种方法表示同一角的图形是()A.B.C.D.【题型2 角的度量】【例2】(2021秋•延边州期末)用量角器测量∠AOB的度数,操作正确的是()A.B.C.D.【变式2-1】(2021•石景山区二模)如图,用量角器度量∠AOB,可以读出∠AOB的度数为()A.30°B.60°C.120°D.150°【变式2-2】(2021春•长安区期末)如图,直线a,b相交于点O,将半圆形量角器的圆心与点O重合,发现表示60°的刻度与直线a重合,表示138°的刻度与直线b重合,则∠1=°.【变式2-3】(2021秋•通州区期末)射线OA,OB,OC,OD的位置如图所示,可以读出∠COB的度数为()A.50°B.40°C.70°D.90°【题型3 角的单位及其换算】 【例3】计算:(1)90°﹣36°12′15″; (2)32°17′53″+42°42′7″; (3)53°÷8.【变式3-1】(2021秋•溧水区期末)已知∠α=25°15′,∠β=25.15°,则∠α ∠β.(填“>”“<”或“=”号)【变式3-2】(2016秋•崇川区期末)计算72°34′÷2+18°33′×4= .【变式3-3】(2021秋•南开区期末)如图1是一个14的圆(∠AOB =90°),芳芳第一次在图1中画了一条线,将图1等分成2份,第二次又加了两条线,将图1等分成4份,第三次由加了四条线,将图1等分成8份,第四次又加了八条线,将图1等分成16份,如图2所示,则第n (n >1)次可将图1等分成 份,当n =5时,图1中的每份的角度是 (用度,分,秒表示)【题型4 钟面上角的特征】【例4】钟面上从2点到4点有几次时针与分针的夹角为60°?分别是几点几分?【变式4-1】(2021秋•北碚区期末)钟表在7点55分时,它的时针和分针所构成的角(小于平角)的度数是( ) A .122.5°B .117.5°C .87.5°D .92.5°【变式4-2】(2021春•静安区期末)早晨8:00以后,时钟的分针和时针第一次垂直的准确时间是( ) A .8点23113分 B .8点25分 C .8点27311分 D .9点整【变式4-3】(2021秋•武昌区期末)某同学晚上6点多钟开始做作业,他家墙上时钟的时针和分针的夹角是120°,他做完作业后还是6点多钟,且时针和分针的夹角还是120°,此同学做作业大约用了( ) A .40分钟 B .42分钟C .44分钟D .46分钟【题型5 方向角】【例5】(2021秋•沂水县期末)如图,A 地和B 地都是海上观测站,B 地在A 地正东方向,从A 地发现它的北偏东60°方向有一艘船C ,同时,从B 地发现船C 在它的北偏东30°方向,此时在C 船上观测A ,B 两地.下列说法正确的是( )A.A地在C船南偏西30°方向B.A地在C船北偏西60°方向C.B地在C船南偏西30°方向D.B地在C船北偏西60°方向【变式5-1】(2021•路南区三模)小丽在小华北偏东40°的方向,则小华在小丽的()A.南偏西50°B.北偏西50°C.南偏西40°D.北偏西40°【变式5-2】(2021秋•河东区期末)学校,电影院,公园在平面图上的标点分别是A,B,C,电影院在学校的正东方向,公园在学校的南偏西25°方向,那么平面图上的∠CAB等于()A.115°B.155°C.25°D.65°【变式5-3】(2021•河北模拟)对于题目:“如图1,已知A,B为两个海岛,点B在点A的正东方向,若灯塔C在海岛A北偏东65°的方向上,在海岛B北偏西35°的方向上,请画出灯塔C的位置.”甲、乙两人分别作出了如下解答:甲:先以A为参照点,作南偏东25°,再以B为参照点,作南偏西65°,画出图形如图2.乙:先以A为参照点,作东偏北25°,再以B为参照点,作西偏北55°,画出图形如图3.下列判断正确的是()A.甲的说法和画图都正确B.乙的说法正确,画图错误C.乙的说法和画图都正确D.甲乙的说法都错误【题型6 角的计数问题】【例6】(2021春•莱山区期末)如图,已知∠MON,在∠MON内画一条射线时,则图中共有3个角;在∠MON内画两条射线时,则图中共有6个角;在∠MON内画三条射线时,则图中共有10个角;…….按照此规律,在∠MON内画20条射线时,则图中角的个数是()A.190B.380C.231D.462【变式6-1】(2021秋•凤翔县期末)如图所示,小于平角的角有个.【变式6-2】(2021秋•惠山区校级期中)如图,图中共有12个小于平角的角,其中以A为顶点的角共有个,它们分别是.【变式6-3】(2021秋•腾冲县校级期末)如图所示,从一点O出发,引两条射线可以得到一个角,引三条射线可以得到三个角,引四条射线可以得到六个角,引五条射线可以得到十个角,如果从一点出发引n (n为大于等于2的整数)条射线,则会得到多少个角?如果n=8时,检验你所得的结论是否正确.。
4.4《角的比较》练习
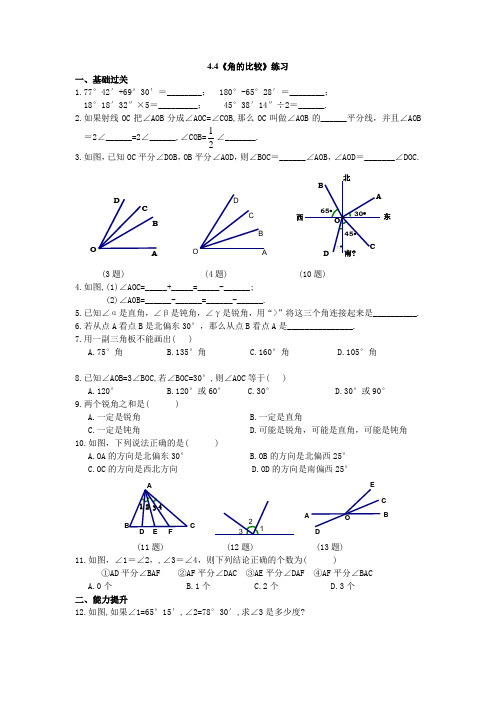
4.4《角的比较》练习一、基础过关1.77°42′+69°30′=________; 180°-65°28′=________; 18°18′32″×5=_________; 45°38′14″÷2=______.2.如果射线OC 把∠AOB 分成∠AOC=∠COB,那么OC 叫做∠AOB 的______平分线,并且∠AOB =2∠______=2∠______,∠COB=21∠_______. 3.如图,已知OC 平分∠DOB ,OB 平分∠AOD ,则∠BOC =______∠AOB ,∠AOD =_______∠DOC.OD C BAODC BA︒北西南东45︒65︒30︒ODCBA(3题) (4题) (10题) 4.如图,(1)∠AOC=_____+_____=_____-______;(2)∠AOB=______-______=______-______.5.已知∠α是直角,∠β是钝角,∠γ是锐角,用“>”将这三个角连接起来是__________.6.若从点A 看点B 是北偏东30°,那么从点B 看点A 是_______________.7.用一副三角板不能画出( )A.75°角B.135°角C.160°角D.105°角8.已知∠AOB=3∠BOC,若∠BOC=30°,则∠AOC 等于( )A.120°B.120°或60°C.30°D.30°或90° 9.两个锐角之和是( )A.一定是锐角B.一定是直角C.一定是钝角D.可能是锐角,可能是直角,可能是钝角 10.如图,下列说法正确的是( )A.OA 的方向是北偏东30°B.OB 的方向是北偏西25°C.OC 的方向是西北方向D.OD 的方向是南偏西25°FEDCBA 4321321COEDBA(11题) (12题) (13题)11.如图,∠1=∠2,,∠3=∠4,则下列结论正确的个数为( )①AD 平分∠BAF ②AF 平分∠DAC ③AE 平分∠DAF ④AF 平分∠BAC A.0个 B.1个 C.2个 D.3个 二、能力提升12.如图,如果∠1=65°15′,∠2=78°30′,求∠3是多少度?13.如图,已知直线AB 、CD 相交于O 点,∠AOE =130°,OC 是∠BOE 的平分线,求∠AOD.14.如图,∠AOB 是平角,OD 、OC 、OE 是三条射线,OD 是∠AOC 的平分线, 请你补充一个条件,使∠DOE=90°,并说明你的理由.EODCBA(14题)15.如图,AOB 为直线,OE 、OD 、OC 为射线,OC 平分∠BOD ,∠AOE ∶∠EOD =1∶3,∠AOD ―∠DOB=40°,求∠EOC 的度数.OE DC BA(15题)16.(1)如图,已知∠AOB=90°,∠BOC=30°,OM 平分∠AOC,ON 平分∠BOC, 求∠MON 的度数. (2)如果(1)中的∠AOB=α,其他条件不变,求∠MON 的度数.(3)如果(1)中的∠BOC=β (β为锐角),其他条件不变,求∠MON 的度数. (4)从(1)、(2)、(3)的结果中能得出什么结论?N MOCBA(16题)三、聚沙成塔数学小知识丹顶鹤总是成群结队迁飞,而且排成“人”字形.“人”字形的角度是110度.更精确地计算还表明“人”字形夹角的一半——即每边与鹤群前进方向的夹角为54度44分8秒!而金刚石结晶体的角度正好也是54度44分8秒!是巧合还是某种大自然的“默契”?。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
达标检测 反思目标
1. 如图,∠AOD-∠AOC=( D ) A.∠AOC B.∠BOC C.∠BOD D.∠COD
2.已知∠AOB=30°,又自∠AOB么∠BOC=( D ) A.10° B.40° C.70° D.10°或70°
3.如果∠1=4°18′,∠2=3°79′,∠3=4.4°,则 1<∠2<∠3 由小到 ∠1,∠2,∠3的大小顺序是∠ _____________.( 大排列)
(1)比较∠AOB, ∠AOC, ∠AOD, ∠AOE的 大小,并指出其中的锐角、直角、钝角、平角。 (2)比较∠BOC 和∠DOE的大小。
(3)小亮通过折叠的方法,使OD与OC重合,
B
A O E C
OE 落在∠BOC的内部,所以∠BOC大于∠DOE.
你能理解这种方法吗? (4)请在图中画出小亮折叠的折痕OF, ∠DOF与∠COF有什么大小关系?
1.度量法:用刻度尺测量线段的长度的方法。
2.叠合法:将其中一条线段移到另一条线段上作比较。
问题:如何比较两个角的大小?
创设情景 明确目标 你还记得怎样比较线段的长短吗?类似地,你能 比较角的大小吗?
观察图形上共有多少个角?在上述各角中哪些是 锐角?哪些是钝角?哪些是直角?并指出它们的 大小关系.
活动一:如何比较下列各组中两个角的大小?
活动一:展示点评
1.比较两个角的大小的方法: ①度量法:是用量角器量出它们的度数,再进 行比较; ②叠合法:是将两个角的顶点及一条边重合,另 一条边放在重合边的同侧就可以比较大小.
2.图(2)(3)中,你还有什么发现?
(2):∠AOB= ∠CO ′D+ ∠AOC (3):∠AOB= ∠CO ′D- ∠AOC
【展示点评】从一个角的顶点引出一条射线,把
这个角分成两个相等的角,这条射线叫做这个角 的平分线.例如OC平分∠AOB,其对应的几何语言 可表述为∠AOC=∠BOC(或∠AOB=2∠AOC或 1 1 ∠AOB=2∠BOC或∠AOC= ∠AOB或∠BOC = 2 2 ∠AOB).
1.如图,回答下列问题
4.4 角的比较
指阳中学 李艳辉
【学习目标】
1.运用类比的方法,学会比较两个角的大小; 2.理解角的平分线的概念,并能借助角的平分线的概念 解决问题; 3.理解两个角的和、差、倍、分的意义,会进行角的运算
【学习重点】角平分线的概念及其应用,角的计算.
【学习难点】角平分线的应用及角的计算.
回顾:比较两条线段的长短的方法
趣味三角板
A
借助三角尺画150、750的角。用一副三角尺,你 还能画哪些度数的角?试一试!
E ∠AEC=1350 300 450 B ∠ABC=750 C D
O
∠DOC=150
C
趣味三角板
A
A
B ∠ABC=1050
C
C
∠AOC=1200 E
O
G
F
∠EFG=1500
活动一:阅读教材内容,思考:教材对角平分线 是如何定义的?怎么表示一条射线平分已知角?
2. 我的困惑
达标检测 反思目标
4. 如图,OM是∠AOB的平分线,OP是∠MOB内的一条 射线,已知∠AOP比∠BOP大30°,则∠POM的度数 15° 是________.
第4题图
第5题图
5. 如图所示,∠AOB是平角,∠AOC=30°,∠BOD= 60°,OM,ON分别是∠AOC,∠BOD的平分线, ∠MON等于________ 135 度.
D
1.定义:从一个角的顶点出发引出的一条
射线,
把这个角分成两个相等的角,这条射
线叫做这
个角的平分线.
2.角平分线的几何表示:如图,OC平分
∠AOB,
则∠AOC=∠BOC=
∠AOB=
∠AOB(或
总结梳理 内化目标 1.课本知识
(1)角的比较: ①用量角器量出它们的度数,再进行比较; ②将两个角的顶点及一条边重合,另一条边放 在重合边的同侧就可以比较大小. (2)角的分类,小于平角的角按大小分成三类: 当一个角等于平角的一半时叫直角;大于零度角小于直 角的角叫锐角;大于直角小于平角的叫钝角. (3)从一个角的顶点引出的一条射线,把这个角 分成两个相等的角,这条射线叫做这个角的平分线.
