人大微积分课件7-6曲面及其方程
合集下载
高等数学-曲面及其方程
f y, x2 z2 0.
平面曲线绕某轴旋转，轴坐标变量不变， 而将曲线方程中的另一变量改写成该变量与 第三个变量的平方和的正负平方根。
例 5 直线L绕另一条与L相交的直线旋转一周，
所得旋转曲面叫圆锥面．两直线的交点叫圆锥面的
顶点，两直线的夹角
0
2
叫圆锥面的半顶
角．试建立顶点在坐标原点，旋转轴为z 轴，半顶
曲面及其方程
一、曲面方程的概念
曲面的实例： 水桶的表面、台灯的罩子面等． 曲面在空间解析几何中被看成是点的几何轨迹． 曲面方程的定义：
如果曲面S 与三元方程F ( x, y, z) 0有下述关系： （1）曲面S 上任一点的坐标都满足方程； （2）不在曲面S 上的点的坐标都不满足方程； 那么，方程F ( x, y, z) 0就叫做曲面S 的方程， 而曲面S 就叫做方程的图形．
思考题
指出下列方程在平面解析几何中和空 间解析几何中分别表示什么图形？
(1) x 2;
(2) x2 y2 4;
(3) y x 1.
思考题解答
方程
平面解析几何中 空间解析几何中
x2
平行于 y 轴的直线 平行于 yoz 面的平面
圆心在(0,0)，
x2 y2 4
半径为 2 的圆
以z 轴为中心轴的圆柱面
特殊地：球心在原点时方程为 x2 y2 z2 R2
例 2 求与原点O 及 M0 (2,3,4)的距离之比为1 : 2的
点的全体所组成的曲面方程.
解 设M ( x, y, z)是曲面上任一点，
根据题意有 | MO | 1 , | MM0 | 2
x2 y2 z2
1
,
x 22 y 32 z 42 2
空间直角坐标系中表示母线平行于z 轴的柱 面，其准线为xoy面上曲线C . （其他类推）
平面曲线绕某轴旋转，轴坐标变量不变， 而将曲线方程中的另一变量改写成该变量与 第三个变量的平方和的正负平方根。
例 5 直线L绕另一条与L相交的直线旋转一周，
所得旋转曲面叫圆锥面．两直线的交点叫圆锥面的
顶点，两直线的夹角
0
2
叫圆锥面的半顶
角．试建立顶点在坐标原点，旋转轴为z 轴，半顶
曲面及其方程
一、曲面方程的概念
曲面的实例： 水桶的表面、台灯的罩子面等． 曲面在空间解析几何中被看成是点的几何轨迹． 曲面方程的定义：
如果曲面S 与三元方程F ( x, y, z) 0有下述关系： （1）曲面S 上任一点的坐标都满足方程； （2）不在曲面S 上的点的坐标都不满足方程； 那么，方程F ( x, y, z) 0就叫做曲面S 的方程， 而曲面S 就叫做方程的图形．
思考题
指出下列方程在平面解析几何中和空 间解析几何中分别表示什么图形？
(1) x 2;
(2) x2 y2 4;
(3) y x 1.
思考题解答
方程
平面解析几何中 空间解析几何中
x2
平行于 y 轴的直线 平行于 yoz 面的平面
圆心在(0,0)，
x2 y2 4
半径为 2 的圆
以z 轴为中心轴的圆柱面
特殊地：球心在原点时方程为 x2 y2 z2 R2
例 2 求与原点O 及 M0 (2,3,4)的距离之比为1 : 2的
点的全体所组成的曲面方程.
解 设M ( x, y, z)是曲面上任一点，
根据题意有 | MO | 1 , | MM0 | 2
x2 y2 z2
1
,
x 22 y 32 z 42 2
空间直角坐标系中表示母线平行于z 轴的柱 面，其准线为xoy面上曲线C . （其他类推）
高等数学微积分曲率课件.
MM y 2 1 ( ) MM x s s( x) lim 1 ( y)2 x0 x
M M lim 1 x 0 M M
机动
目录
上页
下页
返回
结束
2 2 或 ds (dx) (d y ) ds 1 ( y) dx x x(t ) 若曲线由参数方程表示: y y (t ) 2
注意: 直线上任意点处的曲率为 0
机动 目录 上页 下页 返回 结束
例1. 求半径为R 的圆上任意点处的曲率 .
解: 如图所示 ,
s R
1 K lim s 0 s R
M s R M
可见: R 越小, 则K 越大 , 圆弧弯曲得越厉害 ;
R 越大, 则K 越小 , 圆弧弯曲得越小 .
处的曲率.
y
R B
o
l
1 3 y x 6 Rl
x
K
x 0
0;
K
x l
1 R
机动
目录
上页
下页
返回
结束
例3. 求椭圆 解: x a sin t ; y b cos t ; 故曲率为
在何处曲率最大?
x a cos t y b sin t
ab xy x y K 2 2 32 2 2 2 2 32 ( x y ) (a sin t b cos t )
机动
目录
上页
下页
返回
结束
曲率K 的计算公式 设曲线弧 y f ( x) 二阶可导, 则由
tan y ( 设
得
arctan y
d (arctan y) d x
高等数学6(6)曲面及其方程
p 0,q 0
21
特殊地 当p q时, 方程变为
x2 y2 z ( p 0)
旋转抛物面
2p 2p
x2 y2 z 2 p 2q
(由 xOz面上的抛物线 x2 2 pz 绕z轴旋转
而成的)
用平面 z z1 (z1 0)去截这曲面,截痕为圆.
x2
y2
2 pz1
z z1
当 z1变动时，这种圆 的中心都在 z 轴上.
特点是: 平方项有一个取负号,另两个取正号.
z z
O
x
yx
O
y
炼油厂、炼焦厂的冷却塔就是单叶双曲面
的形状.
24
x2 a2
y2 b2
z2 c2
1
单叶双曲面
z
类似地, 方程
x 2 a2
y2 b2
z2 c2
1
O
ax22
y2 b2
z2 c2
1
x
y
亦表示 单叶双曲面.
想一想 以上两方程的图形是与此图形 一样吗?
f ( y, x2 z2 ) 0
4
例3 直线L绕另一条与L相交的直线旋转一周
所得旋转曲面称为圆锥面. 两直线的交点称为
圆锥面的顶点, 两直线的夹角 (0 )称为
2 圆锥面的半顶角. 试建立顶点在坐标原点O, 旋
转轴为z轴,半顶角为 的圆锥面的方程.
解 yOz面上直线方程为 z
z
z y cot
z z1
当z1 0时,截痕退缩为原点;当z1 0时, 截痕不存在. 原点叫做椭圆抛物面的顶点.
19
x2 y2 z 2 p 2q
(2) 用坐标面 xOz( y 0)去截这曲面, 截痕为抛物线.
高等数学曲面方程画法ppt课件
l
沿曲线C平行于 z 轴的一切直线所形成的曲面称为圆 柱面. 其上所有点的坐标都满足此方程, 故在空间
x2 y2 R2
表示圆柱面
机动 目录 上页 下页 返回 结束
定义3. 平行定直线并沿定曲线 C 移动的直线 l 形成
的轨迹叫做柱面. C 叫做准线, l 叫做母线.
•
表示抛物柱面,
z
母线平行于 z 轴;
方程 G( y, z) 0 表示柱面,
母线 平行于 x 轴;
准线 yoz 面上的曲线 l2.
方程 H (z, x) 0 表示柱面,
母线 平行于 y 轴; 准线 xoz 面上的曲线 l3.
z
x l1
y z l2
x z l3
x
y y
机动 目录 上页 下页 返回 结束
四、二次曲面
三元二次方程
Ax2 By2 Cz 2 Dxy Eyx Fzx Gx Hy Iz J 0
( 必要时需作图 ).
机动 目录 上页 下页 返回 结束
例1. 求动点到定点
距离为 R 的轨迹
方程.
解: 设轨迹上动点为
依题意
即
(x x0 )2 ( y y0 )2 (z z0 )2 R
故所求方程为
(x x0 )2 ( y y0 )2 (z z0 )2 R2
z 特别,当M0在原点时,球面方程为
机动 目录 上页 下页 返回 结束
M (0, y, z)
y
两边平方
x
z2 a2( x2 y2 )
机动 目录 上页 下页 返回 结束
例4. 求坐标面 xoz 上的双曲线
分别绕 x
轴和 z 轴旋转一周所生成的旋转曲面方程.
高等数学曲面及其方程(课堂PPT)
x 2 y2 z 2 R2 (3)
7
例2 求到A (1,2,3),B(2,-1,4)两点距离相等的点的轨迹方程.
解： 设轨迹上的动点为M(x,y,z)
A• • M '源自有 MA MB即 x 1 2y2 2z3 2
•
•M
x 2 2 y 1 2 z 4 2
B•
整理得 2x6y2z70
即为所求点的轨迹方程. 线段AB 的垂直平分面.
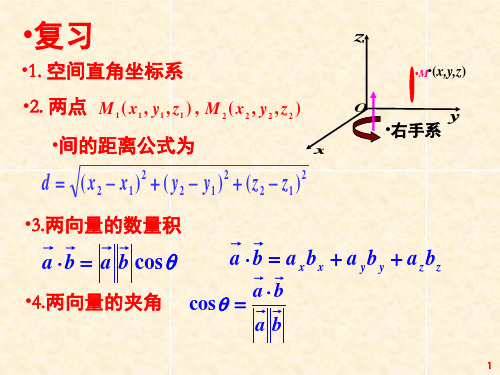
•复习
z
•1. 空间直角坐标系
•M•(x,y,z)
•2. 两点 M 1 ( x1 , y1 , z1 ) , M 2 ( x2 , y2 , z2 )
•间的距离公式为
x
d ( x2 x1)2 ( y2 y1)2 (z2 z1)2
O
y
•右手系
•3.两向量的数量积
a b a b cos
a b axbx a yby azbz
14
二、旋转曲面
定义：以一条平面曲 线绕其平面上的一条 直线旋转一周所成的 曲面称为旋转曲面。 这条曲线和定直线一 次称为旋转曲面的母 线和旋转轴。
15
二、旋转曲面
定义：以一条平面曲 线绕其平面上的一条 直线旋转一周所成的 曲面称为旋转曲面。 这条曲线和定直线一 次称为旋转曲面的母 线和旋转轴。
解 设轨迹上的动点为M(x,y,z)
z
则 M0M R
M x,y,z
•
即 xx 02 yy02 z z02R
x x0 2 y y0 2 z z0 2 R2 (2)
R M 0 x0 , •y0 , z0
就是以 M 0x0,y0,z0为球心 ,
o
y
半径为 R 的球面方程.
大学微积分课件
定积分应用举例
01
面积计算
利用定积分可以计算平面图形或 立体图形的面积，如曲线围成的 面积、旋转体体积等。
物理应用
02
03
经济应用
在物理学中，定积分可以用来计 算物体的质心、转动惯量等物理 量。
在经济学中，定积分可以用来计 算总收益、总成本等经济指标， 以及进行边际分析和弹性分析。
04
多元函数微积分学
微分概念与性质
阐述微分的概念，包括微分的定义、几何意义及物理意义，探讨微分的性质，如微分与导数的关系、微分的运算法则 等。
微分中值定理及其应用
介绍微分中值定理，包括罗尔定理、拉格朗日中值定理和柯西中值定理，并探讨它们在证明不等式、求 极限等方面的应用。
积分概念及性质
定积分概念与性质
引入定积分的概念，包括定积分的定义、几何意义及物理 意义，探讨定积分的性质，如可积性、积分区间可加性等 。
大学微积分课件
contents
目录
• 微积分基本概念 • 微分学基本原理 • 积分学基本原理 • 多元函数微积分学 • 无穷级数与微分方程初步 • 微积分在实际问题中应用举例
01
微积分基本概念
函数与极限
函数定义与性质
阐述函数的基本概念，包括定义 域、值域、对应关系等，并介绍 函数的性质，如单调性、奇偶性 、周期性等。
根据加速度函数和时间的关系，利用 二次积分可以计算物体在一段时间内 的位移。
03
求解功和能量
在力学中，功是力和位移的乘积，利 用定积分可以计算变力沿直线所做的 功；能量则是功的积累，通过定积分 可以求解物体的势能或动能。
在经济学问题中应用
计算总收益和总成本
在经济学中，总收益和总成本都 是价格或产量的函数，利用定积 分可以计算在一定价格或产量范 围内的总收益或总成本。
7-6曲面及其方程27249
问：方程
表示怎样的曲面？
说明: 如下形式的三元二次方程 ( A≠ 0 )
都可通过配方研究它的图形。 其图形可能是 一个球面 , 或点 , 或虚轨迹.
机动 目录 上页 下页 返回 结束
研究曲面的两个基本问题： （1）已知曲面作为点的轨迹时，求曲面方程．
（讨论旋转曲面） （2）已知坐标间的关系式，研究曲面形状．
x
用y = y1 截曲面
用x = x1 截曲面
0 y
机动 目录 上页 下页 返回 结束
双曲抛物面 （马鞍面）
x2 a2
y2 b2
z
z
截痕法
用z = z1 截曲面
x
用y = y1 截曲面
用x = x1 截曲面
0 y
.
机动 目录 上页 下页 返回 结束
双曲抛物面 （马鞍面）
x2 a2
y2 b2
0
单叶：
x2 a2
y2 b2
z2
c2
1
在平面上，双曲线有渐近线。
相仿，单叶双曲面和双叶双曲 面有渐进锥面。用z=h去截它们， 当|h|无限增大时， 双曲面的截口椭圆与它 x 的渐进锥面 的截口椭圆
任意接近，即：双曲面和
锥面任意接近。
z
o
y
机动 目录 上页 下页 返回 结束
单叶双曲面是直纹面
旋转椭球面
由椭圆
x2 a2
z2 c2
1
绕
z
轴旋转而成．
方程可写为
x2 a2
y2
z2 c2
1
(2) a b c,
x2 a2
高等数学-曲面及其方程44页PPT
高等数学-曲面及其方程
11、用道德的示范来造就一个人，显然比用法律来约束他更有价值。—— 希腊
12、法律是无私的，对谁都一视同仁。在每件事上，她都不徇私情。—— 托马斯
13、公正的法律限制不了好的自由，因为好人不会去做法律不允许的事 情。——弗劳德
14、法律是为了保护无辜而制定的。——爱略特 15、像房子一样，法律和法律都是相互依存的。——伯克
31、只有永远躺在泥坑里的人，才不会再掉进坑里。——黑格尔 32、希望的灯一旦熄灭，生活刹那间变成了一片黑暗。——普列姆昌形成天才的决定因素应该是勤奋。——郭沫若 35、学到很多东西的诀窍，就是一下子不要学很多。——洛克
11、用道德的示范来造就一个人，显然比用法律来约束他更有价值。—— 希腊
12、法律是无私的，对谁都一视同仁。在每件事上，她都不徇私情。—— 托马斯
13、公正的法律限制不了好的自由，因为好人不会去做法律不允许的事 情。——弗劳德
14、法律是为了保护无辜而制定的。——爱略特 15、像房子一样，法律和法律都是相互依存的。——伯克
31、只有永远躺在泥坑里的人，才不会再掉进坑里。——黑格尔 32、希望的灯一旦熄灭，生活刹那间变成了一片黑暗。——普列姆昌形成天才的决定因素应该是勤奋。——郭沫若 35、学到很多东西的诀窍，就是一下子不要学很多。——洛克
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
解
设 M ( x, y, z)是所求平面上任一点，
根据题意有 | MA | | MB |,
x 1 y 2 z 3
2 2
2
x 2 y 1 z 4 ,
2 2 2
化简得所求方程 2 x 6 y 2 z 7 0 .
x y
2
11 ) z x y
2
2
12 )
x
2
y
2
z
4
9
x a
2 2
y c
2 2
z c
2 2
1
2)抛物面(Paraboloids)
x
2
I) 椭圆抛物面 2p (Elliptic Paraboloids)
p=q时，成为旋转抛物面
y
2
Z
(p, q 同号）
2q
z
II)双曲抛物面（马鞍面）
(Hyperbolic Paraboloids)
x
2
y
2
y z 2 x 4 y 0表 示 怎 样 的 曲
2 2
2 2 2
解 原 方 程 可 化 为 ( x 1) ( y 2 ) z 5 所以原方程表示球心为( 1 , 2 , 0 ), 半径为 5 的球面.
x 2 y 2 z 2 2 Ax 2 By 2 Cz D 0 ： A 2 B 2 C 2 D 其特点为缺 ( x A) 当A 2 B A B B 2 xy 、 yz 、 zx 项.配方后化为 (y B) C B C C 2 2 2 (z C ) 2
1 c
x
半径随c 的增大而增 大 .
图形上不封顶，下封底．
以上几例表明研究空间曲面有两个基本问题： （1）已知曲面作为点的轨迹时，求曲面方程． （讨论旋转曲面） （2）已知坐标间的关系式，研究曲面形状． （讨论柱面、二次曲面）
二、旋转曲面
定义 以一条平面
曲线绕其平面上的 一条直线旋转一周 所成的曲面称为旋 转曲面. 这条定直线叫旋转 曲面的轴．
2 2 2
2 2
1分别绕 x 轴和z 轴；
y z
2 2
绕 x 轴旋转
c
2
2 2 2
1 1
绕 z 轴旋转
x y a
2
z c
旋 转 双 曲 面
y z 2 2 1 （ 2） 椭 圆 a 绕 y 轴和z 轴； c x 0 2 2 2 y x z 绕 y轴旋转 1 2 2 a c
注：设有三元二次方程
2 2
D 0 时，表示球心为 C 2 D 的球面 .
( A , B , C )，
半径为 当A 当A 2 2
2 2
2 2
D ＝ 0 时 ， 表示点球面. D 0 时，表示的轨迹称为虚 球面.
例 3 已 知 A ( 1 , 2 , 3 ) ， B ( 2 , 1 , 4 ) ， 求 线 段 AB 的 垂直平分面的方程.
2 2
1
b 2 x a
2
2
c 2 y b
2
椭圆柱面 // x 轴
1 双曲柱面 // z 轴
x 2 pz
抛物柱面 // y 轴
四、二次曲面 (Quadratic Surfaces)
1 定义：三元二次方程表示的曲面,称为二次曲 面。
如球面
x 1
2
y 2 z 3 4
2 2
绕 z 轴旋转
2
x y
2
2
a
2
z c
2 2
1
旋 转 椭 球 面
y 2 pz （ 3） 抛 物 线 绕z 轴； x 0
x y 2 pz
2 2
旋转抛物面
三、柱面
定义 平行于定直线并沿定曲线 C 移动的直线 L 所形成的曲面称为柱面. 这条定曲线 C 叫柱面的准线 ，动直线 L 叫 柱面的母线. 观察柱面的形 成过程:
例4 方程 z ( x 1 ) ( y 2 ) 1 的图形是怎样的？
2 2
解
根据题意有 z 1
用平面 z c 去截图形得圆：
2 2
z
( x 1) ( y 2 ) 1 c
(c 1)
c
o
y
当平面 z c 上下移动时， 得到一系列圆
圆 心 在 (1 , 2 , c ) ， 半 径 为
那 么 ， 方 程 F ( x , y , z ) 0 就 叫 做 曲 面S 的 方 程 ， 而曲面 S 就叫做方程的图形．
以下给出几例常见的曲面.
例 1 建 立 球 心 在 点 M 0 ( x0 , y0 , z0 ) 、 半 径 为
R的球面方程.
解
设 M ( x, y, z)是球面上任一点，
y b
2 2
z c
2 2
(Ellipsoids)
a
x
特殊情形：1）当a=b=c时，此时为球面
x y
2
2
z
2
a
2
2）当a=b时，此时为旋转曲面
x
2 2
y
2 2
z
2 2
1
a a c 3) 当a=c时，此时为旋转曲面
x a
2 2
y b
2 2
z a
2 2
1
4) 当c=b时，此时为旋转曲面
f y,
x z
2
2
0.
例 5
直 线 L 绕 另 一 条 与L 相 交 的 直 线 旋 转 一 周 ，
所得旋转曲面叫圆锥面．两直线的交点叫 圆锥面的 顶点，两直线的夹角 0 叫圆锥面的半顶 2 z 角．试建立顶点在坐标原点，旋转轴为 轴，半顶 角 为 的 圆 锥 面 方 程 ．
2 2
圆锥面、旋转曲面等
2、二次曲面的研究方法： (不能用描点法，而用截面法) 用平行于坐标面的平面去截曲面由所得截痕来 勾画曲面的大体形状。 1）对称性：关于坐标面，坐标轴 2）存在范围
z 3）曲面与坐标轴、坐标面的关系 4）曲面弯曲状况。 y
1
3、几种重要的二次曲面：
1）椭球面： x 2
2
2 2 2 2
2)
x
2
2
y
2
z 1
2
4
9
3)
x
2
2
y
2
z 1
2
4)
x
y
2
z 1
2
4
9
4
9
2 2
5) x
y
2
2x
2
6)z 6 x y
8)z
2
7)z 6 x y
2
4 x y
2
2
9 )2 z
x y
2
2
10 ) z 1
2
Z
(p, q 同号）
(0,0,0)
(P>0,q>0)
y
2p
2q
x
z
II)双曲抛物面（马鞍面）
x
2
y
2
Z
(p, q 同号）
2p
2q
o
x y
z
z xy
y
x
y x
3) 双曲面(Hyperboloids)
I)单叶双曲面(Hyperboloids of one sheet)
x
2 2
f ( y1 , z1 ) 0
将 z z1 ,
y1
f
x y
2
2 2
2
代入 f ( y1 , z1 ) 0
得方程
x y , z 0,
yoz 坐 标 面 上 的 已 知 曲 线 f ( y , z ) 0 绕 z 轴 旋 转
一周的旋转曲面方程.
同 理 ： yoz 坐 标 面 上 的 已 知 曲 线 f ( y , z ) 0 绕 y 轴旋转一周的旋转曲面方程为
播放
旋转过程中的特征：
z
如图 设 M ( x , y , z ),
(1 ) z z 1
（ 2） 点 M 到 z 轴 的 距 离
o
M M
d
1
( 0 , y1 , z1 )
f ( y, z ) 0
y
d
x y | y1 |
2 2
x
将 z z1 ,
y1
x y
2
2
代入
第六节 曲面及其方程
一 二 三 四 曲面方程的概念 旋转曲面 柱面 二次曲面
一、曲面方程的概念
曲面的实例： 水桶的表面、台灯的罩子面等． 曲面在空间解析几何中被看成是点的几何轨迹． 曲面方程的定义：
如果曲面 S 与三元方程 F ( x, y, z) 0 有下述关系：
（ 1）曲 面 S 上 任 一 点 的 坐 标 都 满 足 方 程 ； （2）不 在曲 面 S 上 的 点的 坐标 都不 满足 方程 ；
z
解
yoz 面 上 直 线 方 程 为
z y cot
M 1 ( 0 , y1 , z1 )
y
圆锥面方程
z x y cot
2 2
o
x x