水泵效率曲线拟合的Matlab_GUI设计

合集下载

Matlab中的曲线拟合方法

Matlab中的曲线拟合方法引言在科学与工程领域，数据拟合是一个重要的技术，可用于分析实验数据、预测未知的对应关系，并量化观察到的现象。

其中，曲线拟合是一种常见的数据拟合方法，而Matlab作为一种功能强大的科学计算软件，提供了多种曲线拟合工具和函数，方便用户进行数据分析和模型建立。

本文将对Matlab中的曲线拟合方法进行详细介绍和讨论。

一、线性拟合线性拟合是最简单且常见的曲线拟合方法，其基本思想是通过一条直线拟合数据点，找到最佳拟合直线的参数。

在Matlab中，可以使用polyfit函数实现线性拟合。

该函数接受两个输入参数，第一个参数为数据点的x坐标，第二个参数为数据点的y坐标。

返回结果为一个一次多项式拟合模型的参数。

例如，我们有一组实验测量数据如下：x = [1, 2, 3, 4, 5];y = [3, 5, 7, 9, 11];通过polyfit函数进行线性拟合：coeff = polyfit(x, y, 1);其中，1表示要拟合的多项式的次数，这里我们选择了一次多项式（直线）。

coeff即为拟合得到的直线的参数，可以通过polyval函数将参数代入直线方程，得到对应x的y值。

y_fit = polyval(coeff, x);接下来，我们可以使用plot函数将原始数据点和拟合曲线都绘制在同一张图上：figure;plot(x, y, 'o', 'MarkerSize', 10); % 绘制原始数据点hold on;plot(x, y_fit); % 绘制拟合曲线xlabel('x');ylabel('y');legend('原始数据点', '拟合曲线');通过观察图像，我们可以初步判断拟合的效果如何。

如果数据点较为分散，直线拟合效果可能较差。

在此情况下，可以考虑使用更高次的多项式进行拟合。

二、多项式拟合多项式拟合是一种常见的曲线拟合方法，其基本思想是通过一个一定次数的多项式函数来拟合数据点。

Matlab曲线拟合工具箱

Matlab曲线拟合工具箱一、单一变量的曲线逼近Matlab有一个功能强大的曲线拟合工具箱 cftool ，使用方便，能实现多种类型的线性、非线性曲线拟合。

下面结合我使用的Matlab R2007b 来简单介绍如何使用这个工具箱。

假设我们要拟合的函数形式是 y=A*x*x + B*x, 且A>0,B>0 。

1、在命令行输入数据：》x=[110.3323 148.7328 178.064 202.8258033 224.7105 244.5711 262.908 280.0447 296.204 311.5475]；》y=[5 10 15 20 25 30 35 40 45 50]；2、启动曲线拟合工具箱》cftool3、进入曲线拟合工具箱界面“Curve Fitting tool”（1）点击“Data”按钮，弹出“Data”窗口；（2）利用X data和Y data的下拉菜单读入数据x,y，可修改数据集名“Data set name”，然后点击“Create data set”按钮，退出“Data”窗口，返回工具箱界面，这时会自动画出数据集的曲线图；（3）点击“Fitting”按钮，弹出“Fitting”窗口；（4）点击“New fit”按钮，可修改拟合项目名称“Fit name”，通过“Data set”下拉菜单选择数据集，然后通过下拉菜单“Type of fit”选择拟合曲线的类型，工具箱提供的拟合类型有：Custom Equations：用户自定义的函数类型Exponential：指数逼近，有2种类型， a*exp(b*x) 、 a*exp(b*x) + c*exp(d*x)Fourier：傅立叶逼近，有7种类型，基础型是 a0 + a1*cos(x*w) + b1*sin(x*w)Gaussian：高斯逼近，有8种类型，基础型是a1*exp(-((x-b1)/c1)^2)Interpolant：插值逼近，有4种类型，linear、nearestneighbor、cubic spline、shape-preservingPolynomial：多形式逼近，有9种类型，linear ~、quadratic ~、cubic ~、4-9th degree ~Power：幂逼近，有2种类型，a*x^b 、a*x^b + cRational：有理数逼近，分子、分母共有的类型是linear ~、quadratic ~、cubic ~、4-5th degree ~；此外，分子还包括constant型Smoothing Spline：平滑逼近（翻译的不大恰当，不好意思）Sum of Sin Functions：正弦曲线逼近，有8种类型，基础型是a1*sin(b1*x + c1)Weibull：只有一种，a*b*x^(b-1)*exp(-a*x^b)选择好所需的拟合曲线类型及其子类型，并进行相关设置：——如果是非自定义的类型，根据实际需要点击“Fit options”按钮，设置拟合算法、修改待估计参数的上下限等参数；——如果选Custom Equations，点击“New”按钮，弹出自定义函数等式窗口，有“Linear Equations线性等式”和“General Equations构造等式”两种标签。

运用MATLAB实现单泵调速运行工况点求解

即：满足上式的的所有（H, Q）点互为相似工况，
各点对应的效率值相等
求解步骤：1）由给定工况点计算 k 值，作过 B 点的相似工况抛物线。H = k Q2 与转速 n1 下
特性曲线（H ~ Q）1 交与 C 点， C（HC, QC）与 B （HB, QB）为相似工况点。
比例律求出对应 B（HB, QB）工况点的转速值
对比第一类调速的结果可以看出，运用 MATLAB 模块不仅能实现第二类水泵调速运行的工况点球解，同时可已验证第一类调速结果的可靠性。
5、水泵调速运行连续运行和自我反馈的实现
水泵调速的连续性是建立在 MATLAB 快速计算的基础上，通过采集水泵出流量对比给定流量参数，不断调节电压频率进而以调节水泵的转速。水泵连续调速运行依赖于水泵两类调速运行之间的反馈，给定流量参数下通过第二类调速运行来模块求解出 nr1,再通过第一类调速运行求解出调速后流量 QK，对比 QK 和给定参数比较之间的偏差对 nr1 做出修整，从而使得电机能快速、精准的变频以实现水泵的调速运行。
39 卷第 1 期 [7] 关海奎. 单.三相汽油机组的设计，国防技术基础 2003 年第 5 期 37
结语运用 MATLAB 编译模块能快速精准的实现水泵的调速运行，有利于变频泵的
快速、连续、精准变频。水泵调速运行，大大的提高了设备的使用效率，同时满足了现在建筑内供水流量、水压变化复杂的情形，且节约能源促进低碳经济的发展。
参考文献
[1] 军奇. 柴油发电机组实用技术,机械工业出版社. 2006,7. 前言 [2] 张玉民戚伯云. 电磁学,科学出版社. 2007,2 254 [3] 金续曾. 三相异步电机使用与维修，科学出版社 2003,7 2 [4] 邓隐北邓江.新兴无刷三相同步发电机，电工技术.2000 年第 5 期 [5] 郭立正译自英国 Railway Gazette 列车照明三相发电机 May 3, 1963, 493 [6] 杜钦君. 三相半控桥式车用永磁发电装置的研究，微电机. 2006 年第

曲线拟合法的Matlab实现

曲线拟合法的Matlab实现曲线拟合在许多科学和工程领域中都有广泛应用，包括机器学习，数据科学，信号处理，控制工程等。

在Matlab中实现曲线拟合的方法有多种，其中最常用的是使用fit()函数。

以下是一个基本的示例，演示如何在Matlab中使用fit()函数进行曲线拟合。

我们需要一些数据。

假设我们有一组x和y数据点，我们想要在这些点上拟合一条曲线。

y = 3*x.^2 + 2*x + 1 + randn(size(x));fitresult = fit(x, y, 'poly1');在这里，'poly1'表示我们想要拟合一个一次多项式。

你可以使用'poly2'，'poly3'等来拟合更高次的多项式。

同样，你也可以使用其他类型的模型，如指数、对数、自定义函数等。

然后，我们可以使用plot()函数将原始数据和拟合曲线一起绘制出来。

在这里，'hold on'命令用于保持当前图像，这样我们就可以在同一个图形上绘制多条线了。

我们可以使用fitresult来获取拟合曲线的参数和其他信息。

例如：以上就是在Matlab中进行曲线拟合的基本步骤。

需要注意的是，对于复杂的实际问题，可能需要进行更复杂的模型选择和参数优化。

也可以使用其他工具如curve fitting toolbox进行更详细的分析和拟合。

最小二乘曲线拟合是一种数学统计方法，用于根据给定数据点拟合出一条曲线或曲面，使得该曲线或曲面最小化每个数据点到拟合曲线或曲面的平方误差之和。

这种方法广泛应用于数据分析和科学计算等领域。

本文将介绍最小二乘曲线拟合的基本原理和在Matlab中的实现方法。

假设有一组数据点 (x_i, y_i)，i=1,2,...,n，需要拟合出一条曲线y=f(x)。

最小二乘法要求曲线 f(x)最小化每个数据点到曲线的平方误差之和，即E = sum (f(x_i)-y_i)^2对曲线 f(x)进行求导，得到一元一次方程：f'(x)=sum(f(x)-y)*x-sum(f(x)-y)E = sum [(f'(x))^2] * x^2 - 2 * sum [f(x) * f'(x) * x] + 2 * sum [f(x)^2]令 E对 f'(x)的导数为零，可得到最小二乘曲线拟合的方程：sum [f'(x)^2] * x^2 - 2 * sum [f(x) * f'(x) * x] + 2 * n * f(x)^2 = 0在Matlab中，可以使用polyfit函数实现最小二乘曲线拟合。

Matlab在循环水泵性能曲线拟合中的应用

归系数Ａ和Ａ可按正规方程组求得，中ｎ４：其ｔ＞．
ｎｎｎ
．
真，用强大的图形功能对数值进行显示．
１循环水泵不同设置方案的特性曲
线拟合
１１单台循环水泵定速运行时的特性曲线拟合．
ｎ
ｅｅｔｏｅｅｔｄｐｍｐｓｉｖｒｔｅｍａｉｍｌｗａｅａｄａｏｄｔｅｗｏｋｐｉｔｉｕｆｔｆｃｆｓｌｃｅｕｓｏｅｈｘｍｕｆｏｒｔｎｖｉｈｒｏｎｓｏｔｏｈｅ
ｈｇｆｅｔｓｃｉｎ，ａｄｐｃｓｔｅｏｒｓｏｄｎｕｅａｔｒｅｕｉｇｔｅｈｒｃｅｉｔｃｉｈｅｆｃｅｔｏｎｄｅｉｔｈｃｒｅｐｎｉｇｃｒｓｆｅｄｃｎｈｃａａｔｒｓｉｖｃｒｅｙＭａｌｂｓｆｗａｅｕｓｂｔｏｔｒ．ｖａＫｅｏｄｓｔｉｕｔｐｙ；Ｍａｌｂ；ｃｒｕａｉｇｐｍｐ；ｃａａｔｒｓｉｕｅｙｗｒ：ｗａｎｍｌｉｌｔａｉｃｌｔｕｎｈｒｃｅｉｔｃｒｓｃｖ
Ｖ１３。ｏ２．．Ｎ３
Ｊｎ２０ｕ．０７
Ｍａａｔｂ在循环水泵性能曲线拟合中的应用ｌ
左行涛，蒙生，立群，焕岩朱丁庞
（哈尔滨工业大学市政环境工程学院，哈尔滨１０９）５００摘要：根据最小二乘法，对水泵的不同组合形式进行其性能曲线拟合，这样有利于设计人员在选取

matlab曲线拟合代码

matlab曲线拟合代码
在MATLAB中进行曲线拟合有多种方法，其中一种常用的方法是使用polyfit函数进行多项式拟合。

下面是一个简单的例子：
假设有一组数据点x和对应的y，我们想要对这些数据进行二次多项式拟合。

可以使用以下代码：
matlab.
x = [1, 2, 3, 4, 5];
y = [2, 3, 5, 7, 9];
p = polyfit(x, y, 2); % 进行二次多项式拟合，这里的2表示二次多项式。

x_fit = 1:0.1:5; % 生成拟合曲线的x坐标。

y_fit = polyval(p, x_fit); % 计算拟合曲线的y坐标。

plot(x, y, 'o', x_fit, y_fit); % 绘制原始数据点和拟合曲线。

legend('原始数据', '拟合曲线');
在这段代码中，我们首先定义了一组数据点x和y。

然后使用polyfit函数对这些数据进行二次多项式拟合，得到拟合的系数p。

接着生成拟合曲线的x坐标x_fit，并利用polyval函数计算对应
的y坐标y_fit。

最后使用plot函数将原始数据点和拟合曲线绘制
在同一张图上。

除了多项式拟合，MATLAB还提供了其他曲线拟合的函数和工具，比如使用fit函数进行各种类型的曲线拟合，或者使用regress函
数进行线性回归分析。

不同的拟合方法适用于不同类型的数据和拟
合需求，你可以根据具体情况选择合适的方法进行曲线拟合。

matlab自定义函数拟合曲线

matlab自定义函数拟合曲线（实用版）目录1.MATLAB 自定义函数的概述2.拟合曲线的简介3.MATLAB 自定义函数拟合曲线的步骤4.MATLAB 自定义函数拟合曲线的实例5.MATLAB 自定义函数拟合曲线的优点与局限性正文一、MATLAB 自定义函数的概述MATLAB（Matrix Laboratory）是一款广泛应用于科学计算、数据分析、可视化等领域的软件。

在 MATLAB 中，用户可以通过编写自定义函数（也称为脚本或剧本）来实现特定的功能。

自定义函数可以根据用户的需求进行定制，具有很高的灵活性和实用性。

二、拟合曲线的简介拟合曲线是指通过将一组数据点按照某种数学关系进行连接，得到一条光滑的曲线。

在 MATLAB 中，拟合曲线通常采用最小二乘法、多项式拟合等方法实现。

拟合曲线有助于更好地理解数据点的内在规律，为数据分析和预测提供参考。

三、MATLAB 自定义函数拟合曲线的步骤1.准备数据：首先需要收集一组数据点，这些数据点可以用 MATLAB 中的数组或表格表示。

2.编写自定义函数：根据拟合需求，编写 MATLAB 自定义函数。

例如，可以使用 polyfit 函数进行多项式拟合，使用 nlinfit 函数进行非线性最小二乘拟合等。

3.调用自定义函数：在 MATLAB 命令窗口或脚本中调用自定义函数，将数据点作为输入参数传递。

4.显示结果：使用 MATLAB 的绘图功能，将拟合后的曲线与原始数据点一同展示。

四、MATLAB 自定义函数拟合曲线的实例下面以多项式拟合为例，展示如何使用 MATLAB 自定义函数拟合曲线：1.准备数据：x = [1, 2, 3, 4, 5]; y = [2, 4, 5, 8, 10];2.编写自定义函数：function y_fit = polyfit_curve(x, y)% 多项式拟合n = length(x);y_fit = polyfit(x, y, 1);end3.调用自定义函数：y_fit = polyfit_curve(x, y);4.显示结果：plot(x, y, "o", x, y_fit, "-");五、MATLAB 自定义函数拟合曲线的优点与局限性优点：1.高度灵活：可以根据用户需求编写自定义函数，实现特定的拟合需求。

基于MATLAB的离心式水泵性能曲线绘制

基于MATLAB的离心式水泵性能曲线绘制
李明
【期刊名称】《天津城市建设学院学报》
【年(卷),期】2004(010)001
【摘要】离心式水泵性能的测定和曲线绘制工作无论是对生产厂家还是对用户都是很必要的,但又是很繁杂的.随着计算机技术的发展,数学正以其所特有的卓越能力进入到各个领域,从而使离心式水泵性能的测定和曲线绘制工作得以简化. MATLAB 的出现又使离心式水泵的性能曲线绘制达到了更加快速、准确、直观.
【总页数】3页(P59-61)
【作者】李明
【作者单位】辽宁工程技术大学,辽宁,阜新,123000
【正文语种】中文
【中图分类】TP391.7
【相关文献】
1.基于MATLAB的气动马达万有特性曲线绘制方法研究 [J], 曾鸣;王葆葆;张仕民;王文明
2.基于VB与Matlab的发动机外特性曲线绘制 [J], 王丽;迟永滨
3.基于matlab的双绕组变压器经济运行曲线绘制 [J], 陈小平
4.基于MATLAB的水平井井眼轨迹及响应曲线绘制 [J], 李宇腾;陈延军
5.MATLAB在离心式水泵性能曲线测定中的应用 [J], 孟凡英;范美霞
因版权原因，仅展示原文概要，查看原文内容请购买。

基于Matlab GUI的曲线拟合程序设计范例

基于Matlab GUI的曲线拟合程序设计范例1.TargetCase1：选择数据源——census，后台载入数据census.mat，提示用户输入多项式的幂n，输入n后，点击按钮“开始拟合”，后台对数据进行多项式拟合，并在绘图区域绘制原始数据散点图及拟合曲线。

Case2：选择数据源——trash，点击“开始拟合”，后台对数据进行指定类型拟合（即拟合成函数：f(t)=a∗cos(k∗t)∗exp(u∗t)），并在绘图区域绘制原始数据散点图及拟合曲线。

2.SolutionStep1，绘制GUI界面按下键盘上的组合键“Win+R”，弹出“运行”窗口，输入“Matlab”，回车，打开Matlab工作区。

在Matlab命令窗口输入“guide”，回车，启动GUI创建向导，修改存储路径，保存*.fig 文件。

Tip：如果要打开现有的GUI fig文件，可以在命令窗口输入“guide 你的文件目录及文件名”。

在GUI-Fig工作区，拖入相应控件（两个text，一个popupmenu，一个axes，一个edit 以及一个push button），双击控件，打开属性窗口，修改其属性。

（1）text1（2）text2设置字号15将“Enable”属性设成“off”——当选择“census”时，再通过程序将其修改为“on”String设置：（3）popupmenu字号：15String：（4）edit字号：18，Tag：times （为了方便程序中调用），删除“string”属性的内容（5）push button（6）拖入一个axes控件，用于画图，属性值默认Step2，修改回调函数（1）popupmenu在popupmenu上右击，选择“View Callbacks”——“Callback”，在弹出来的M 文件对应代码行，输入以下代码：option=get(handles.popupmenu1,'value'); %获得下拉菜单的值，当用户选择第一个选项时，value=1，选择第第二个选项时，value=2，以此类推switch optioncase 2 %当选择census时set(handles.text2,'Enable','on'); %显示text2文本框set(handles.times,'Enable','on'); %显示times输入框case 3 %当选择trash时set(handles.text2,'Enable','off'); %隐藏text2文本框set(handles.times,'Enable','off'); %隐藏times输入框end（2）pushbuttonoption=get(handles.popupmenu1,'value');switch optioncase 2load census; %载入census数据x=cdate;y=pop; %将数据源赋给x和ysx=(x-mean(x))./std(x); %将x标准化n=str2num(get(handles.times,'string')); %获取输入框的值，并转成数值A=polyfit(sx,y,n); %进行多项式拟合y1=polyval(A,sx); %多项式求值，求出拟合曲线上对应的点plot(x,y,'r*',x,y1); %绘制原始数据散点图，以及拟合曲线case 3x=[0 0.4 1.2 2 2.8 3.6 4.4]';y=[1 0.85 0.24 0.27 0.53 0.4 0.12]';syms t; %定义t为符号常量ft=fittype('a*cos(k*t)*exp(u*t)','indep',t,'coeff',{'a','k','u'}); %给定类型，t作为自变量，a,k,u为待定参数f=fit(x,y,ft) ; %确定待定参数，求出拟合函数y2=f(x); %求出拟合曲线上对应的点plot(x,y,'ro',x,y2); %绘制原始数据散点图，以及拟合曲线endStep3，至此，程序就初步完成了，接下来就交给你自己去完善了，发挥你的创造力吧！。

基于MATLAB的多角度水泵性能曲线的拟合

ｐｍｐｍｏｅｒｌｏｄｓｎｄａｈａｉ．ｒｔｅｖｌａｉｎｏｎｔｎｅｔｉｐｏｅａｈｓｍｅｏｓｓｌｕｄｌａｅａｓｅｉｅｔｔｅｓｍｅｔＭｅｈａｉｔｆｉｓｃ￣ｓｒｖｄｔｔｔｉｇｍｅｄｏａｈｔｄｉｉｙｈｍｐ
《．ｎｎＸａｄｎＰｍａｕａｔｅＣ．ＬｄＭｉｏＨｕａ，４４０，ｈｎ；ｉＨｕａｉｉｕｐＭｎｆｃｕｏ，ｔ，ｌｎｎ１４０ｉｎａｒｕＣａ２ｏｌｅｏｅｇｎｎｉｎｅｔｈａＵｉｒｉ，ＣｅｇｕＳｃｕ１０９Ｃｉ）．ｌｇｆｅｒａｄｅｖｒｍｎ，ｕｎｅｓｙｈｎｄｉａ６０３，ｈｎＣｅｎｙｏＸｉｖｔｈｎａ
ＦｉｔｎｆＭｕｔｖｅＰｕｔｉｇｏｌｉｉｗｍｐＰｅｆｒｎｅＣｕｖｓ－ｒｏｍａｃｒｅＢａｅｎＭＡＴＬＡＢｏｔｒｓｄｏＳｆｗａｅ
ＷｅＤｎ￣ｉｏｇ，－Ｘｅｎｕ咖
２１测试点数据的导入．
我们可以将试验的原始数据输入ＥＣＬ表格中并计算ＸＥ得到给定转速下各点的流量、扬程、轴功率的效率，并在ＭＴＡＡＬＢ中建立一个矩阵．利用简单的复制和粘贴就可将
ＥＣＬ表格中计算后的数据导入ＭＡｌＡＸＥｒＢ中的矩阵。表１＇Ｌ
ｏｅａｅ、ｈｒｕｓａｄｅａｔｕｅｉｒｐｌｄｐｒｔｄｓｏｔｔｎｘｃｉｄ，ｗｔｍｏｅａｐｉ．ｃｔｈｅ

使用MATLAB曲线拟合工具箱做曲线拟合(2013)

使用 MATLAB 曲线拟合工具箱做曲线拟合在实际的工程应用领域和经济应用领域中，人们往往通过实验或者观测得到一些数据，为了从这些数据中找到其内在的规律性，也就是求得自变量和因变量之间的近似函数关系表达式。

这类问题可以归结曲线拟合。

1．MATLAB 曲线拟合工具箱简介MATLAB 做曲线拟合可以通过内建函数或者拟合工具箱（Curve Fitting Toolbox ）。

这个工具箱集成了用MATLAB 建立的图形用户界面（GUIs ）和 M 文件函数。

利用这个工具箱可以进行参数拟合（当想找出回归系数以及他们背后的物理意义的时候就可以采用参数拟合），或者通过采用平滑样条或者其他各种插值方法进行参数拟合（当回归系数不具有物理意义并且不在意他们的时候，就采用非参数拟合）。

利用这个界面，可以快速地在简单易用的环境中实现许多基本的曲线拟合。

2．实际例子应用数学模型书上关于汽车刹车距离模型，建立的模型如下：2 1 d t v kv=+ 其中v 是汽车速度， 1 t 是反应时间，按大多数人平均取 0.75 秒，d 是刹车距离。

交通部门提供了一组刹车的距离实际数据如表1 所示（刹车距离括号内为最大值）。

表 1车速（英尺秒）29.3 44 58.7 73.3 88 102.7 1173 刹车距离（英尺） 42(44) 73.5(78) 116(124) 173(186) 248(268) 343(372) 464(506) 利用表 1 的数据，我们拟合在 MATLAB 的 command window 里输入：>>v=[29.3 44 58.7 73.3 88 102.7 117.3];>>d1=[42 73.5 116 173 248 343 464];>>cftool %cftool 是打开拟合工具箱的命令;则跳出曲线拟合工具箱的界面如图 1 所示，如果输入数据非常大，并且每次输入有困难，可以新建一个 M 文件，依次输入上述命令行，保存之后执行，同样可以进入曲线拟合工具箱界面。

matlab曲线拟合函数用法以及例子

matlab 曲线拟合函数⽤法以及例⼦⼯具/原料matlab 曲线拟合在运⾏MATLAB 编程进⾏数据的处理过程当中，我们常常⽤到matlab 曲线拟合，但是⼯具箱由于需要⼈⼯交互，得到的拟合结果，需要⼈⼯的去提取，再输⼊，所以，⼯具箱拟合结果⼗分不适合调⽤，以及继续下⾯的操作，所以我们需要⽤到matlab 曲线拟合函数,并且以最常⽤的多项式拟合函数为例作为matlab 曲线拟合例⼦，进⾏详细介绍。

MATLAB数据准备：关于MATLAB曲线拟合，我写了⼀系列的经验，为了相互统⼀，采⽤下⾯的数据：x=[0 0.3000 0.6000 0.9000 1.2000 1.5000 1.8000 2.1000 2.4000 2.7000 3.0000]y=[2.0000 2.3780 3.9440 7.3460 13.2320 22.2500 35.0480 52.2740 74.5760 102.6020 137.0000]由函数y=4*x^3+3*x^2+2 产⽣。

1函数命令拟合：MATLAB为我们提供了多项式拟合函数命令polyfit，下⾯我们就⽤这个函数命令进⾏拟合。

在MATLAB主窗⼝中输⼊y1=polyfit(x,y,3)，回车我们会看到下⾯结果：y1 =4.0000 3.0000 0.0000 2.00002函数的说明：y1=polyfit(x,y,N)，这⾥函数polyfit第⼀个参数传递的是拟合数据的⾃变量，第⼆个参数是因变量，第三个参数是拟合多项式的阶数，这个由我们给定。

如下图。

我们可以给定不同的N，运⽤不同的多项式进⾏拟合。

输出结果：在上⾯的例⼦中我们看到输出的结果是：y1 =4.0000 3.0000 0.0000 2.0000对照原始的函数y=4*x^3+3*x^2+2 ，我们可以看到，y1其实输出的是拟合函数的系数，并且由⾼次到低次由左到右输出。

3多项式阶数N的确定：这⾥有些⼈可能会有问题了，我们事先不知道要拟合的数据是⼏阶的，那么我们如何判断我们给定的拟合阶数N最终为多少呢？4matlab 曲线拟合结果调⽤及显⽰阶数确定⽅法⼀：这种⽅法是最常⽤的确定⽅法，⼀般情况下，我们拟合函数的⽬的，就是为了调⽤，所以在⽤函数拟合之前会⽤matlab曲线拟合⼯具箱进⾏拟合函数阶数的确定，由其确定拟合的阶数，然后我们⽤这个函数命令在其他地⽅进⾏⼗分⽅便地调⽤，这是最常⽤的做法。

matlab 曲线拟合器自定义方程

在MATLAB中，曲线拟合器是一个非常有用的工具，可以帮助我们根据实验数据拟合出一个最符合实际情况的数学模型。

而其中的自定义方程功能更是让我们能够根据具体问题的需要，灵活地定义自己的拟合模型，从而得到更加精确的结果。

让我们来了解一下什么是曲线拟合器。

曲线拟合器是一种数学工具，用于找到一条曲线，使其最大程度地拟合已知的数据点。

在MATLAB 中，曲线拟合器包括了各种不同的拟合方法，比如多项式拟合、指数拟合、对数拟合等。

通过这些方法，我们可以根据实验数据找到一个最佳的拟合曲线，从而可以做出一些预测或者推断。

接下来，让我们来具体看一下MATLAB中的自定义方程功能。

自定义方程功能是指，我们可以根据具体的问题需求，自己来定义拟合模型，而不是受限于预设的拟合方法。

这样一来，我们就可以更加灵活地应对各种不同的数据特征，得到更加准确的拟合结果。

举个例子来说，比如我们有一组实验数据，它们的变化规律并不是简单的多项式关系，而是一个复杂的非线性函数。

这时，如果我们能够使用自定义方程功能，就可以根据实际情况，构建一个更加符合数据特点的拟合模型，从而得到更加准确的结果。

在实际操作中，使用MATLAB的自定义方程功能并不复杂。

我们需要定义一个代表拟合模型的函数，然后将这个函数传递给拟合器进行拟合。

在定义函数的过程中，我们可以根据具体的问题需求，自由地选择函数的形式和参数，从而得到一个最适合实验数据的拟合模型。

MATLAB中的曲线拟合器和自定义方程功能为我们提供了一种强大的工具，能够帮助我们根据实际情况灵活地拟合数据，得到更加准确的模型。

通过这些工具，我们不仅能够更好地理解数据背后的规律，还可以做出更加准确的预测和推断。

个人观点上，我认为MATLAB中的曲线拟合器和自定义方程功能是非常有价值的工具。

在实际应用中，我们经常会遇到各种各样复杂的数据特征，而这些工具能够帮助我们更好地理解数据，做出更加准确的分析和预测。

通过灵活运用这些工具，我们可以更加深入地挖掘数据背后的规律，从而做出更加明智的决策。

探究水泵性能曲线在线拟合

关键词：水泵；性能曲线；抛物线回归；仿真模拟
在火力发电厂中，不同类型的水泵分别用于输送给水、凝结水、冷却水、疏水、润滑油等流体，是发电机组必须的重要辅助设备【１】。水泵的安全经济运行是保证整个电厂安全经济运行的关键因素之一，因此机组运行人员、专业技术人员及时方便的掌握水泵的运行特性非常必要。
ａ）＋ｋ（３）ｋ（１）＝ｅ－ｂ’ｋ（３）－ａ。ｋ（２）三、结果展示将有效样本库中的数据调用回程模
块进行计算，得出各转速下给水泵压力一流量特性曲线的回归系数。还原回归公式如下：
转速５１００ｒｐｍ时．Ｐ＝４Ｅ一０６Ｆ２—０．０１７Ｆ＋４６．７５转速４８００ｒｐｍ时．Ｐ＝５Ｅ一０６ｘ２—０．０２０Ｆ＋４４．８７转速４５００ｒｐｍ时．Ｐ＝７Ｅ一０６Ｆ２—０．０２０Ｆ＋３９．ቤተ መጻሕፍቲ ባይዱ５
转速３９００ｒｐｍ时．Ｐ…１Ｅ转速４２００ｒｐｍ时，Ｐ＝２Ｅ～０５Ｆ２—００４２Ｆ＋４５．６９０５ｘ２＋０．０２１ｘ＋１１．７０
转速３６００ｒｐｍ时尸＝一２Ｅ一０５Ｆ２＋０．０２９Ｆ＋６．０６６转速３３００ｒｐｍ时，Ｐ＝４Ｅ一０６Ｆ２—０．００９Ｆ＋１８．５３转速３０００ｒｐｍ时，Ｐ一１Ｅ一０５Ｆ２＋０．０１１Ｆ＋９．２８５根据回归公式，即可绘制出给水泵的压力一流量特性曲线，并在实时运行状态中标记当前运行点以作比较。四、结论此方法适用于火力发电厂与给水泵类似的重要辅机设备。包括各种水泵与风机的压力一流量特性曲线拟合。以图形方式直观展示设备实际特性曲线，并根据当前运行工况，帮助运行人员了解设备当前状态。值得推广。参考文献：［１］毛正孝，赵友君，泵与风机［Ｍ】．中国电力出版社．１９９９．
一糕瓣鬻鞲鋈
程序环境：Ｕｎｉｘ，广东亚仿科技股份有限公司科英仿真平台

用MATLAB作曲线拟合

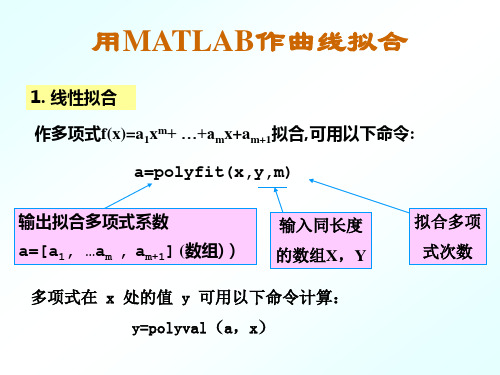
2. lsqnonlin 已知数据点：已知数据点： xdata=（xdata1，xdata2，…，xdatan） ydata=（ydata1，ydata2，…，ydatan） lsqnonlin用以求含参量x（向量）的向量值函数用以求含参量x 向量）用以求含参量 f(x)=(f (x),…,f f(x)=(f1(x),f2(x), ,fn(x))T
T 2 2
中的参量x 中的参量x，使得
2
f ( x) f ( x) = f1 ( x) + f 2 ( x) + ⋯ + f n ( x)
最小。最小。其中 fi（x）=f（x，xdatai，ydatai））（， =F(x,xdatai)-ydatai
输入格式为：输入格式为： 1） x=lsqnonlin（‘fun’，x0）； 2） x= lsqnonlin （‘fun’，x0，options）； 3） x= lsqnonlin （‘fun’，x0，options，‘grad’）； 4） [x，options]= lsqnonlin （‘fun’，x0，…）； 5） [x，options，funval]= lsqnonlin （‘fun’，说明：x= ，，）； x0，…）； lsqnonlin （‘fun’，x0，options）； fun是一个事先建立的是一个事先建立的定义函数f(x)的M-文件，文件，定义函数的文件自变量为x 自变量为选项见无迭代初值约束优化
n 2 i i
∑ ( F ( x, xdata ) − ydata )
i =1
最小
输入格式为: 输入格式为: (1) x = lsqcurvefit (‘fun’,x0,xdata,ydata); (2) x =lsqcurvefit (‘fun’,x0,xdata,ydata,options); (3) x = lsqcurvefit (‘fun’,x0,xdata,ydata,options,’grad’); (4) [x, options] = lsqcurvefit (‘fun’,x0,xdata,ydata,…); (5) [x, options,funval] = lsqcurvefit (‘fun’,x0,xdata,ydata,…); (6) [x, options,funval, Jacob] = lsqcurvefit (‘fun’,x0,xdata,ydata,…); 说明：x = lsqcurvefit (‘fun’,x0,xdata,ydata,options); fun是一个事先建立的是一个事先建立的定义函数F(x,xdata) 的定义函数 M-文件自变量为和文件文件自变量为x和 xdata 选项见无迭代初值已知数据点约束优化

水泵效率曲线拟合的Matlab-GUI设计

水泵效率曲线拟合的Matlab-GUI设计
胡大明;陈开谱;孙勇
【期刊名称】《中国农村水利水电》
【年(卷),期】2008()9
【摘要】介绍了在Matlab平台下开发图形用户界面GUI的方法和步骤。

利用Matlab强大的数值计算能力和数据可视化能力,以基于多项式的最小二乘法和B样条函数法为例进行图形用户界面的设计开发,演示了其常用控件的应用方法;把GUI 应用于水泵的效率曲线拟合,利用m文件的函数调用达到数据的输入和输出,实现了数据文件的读取,完成了图形的绘制,同时方便地实现了计算结果的形象输出;由于编程语言简单从而可以快速方便地进行计算,特别是矩阵的计算,与常规方法相比大大减少了工作量,简化了计算过程。

【总页数】3页(P93-94)
【关键词】水泵;效率;曲线拟合;Matlab图形用户界面
【作者】胡大明;陈开谱;孙勇
【作者单位】中水淮河工程有限公司;温州市水利电力勘测设计院;高邮水利局灌区管理处
【正文语种】中文
【中图分类】TV136
【相关文献】
1.热网中设置混水泵站和升压泵站时水泵特性曲线拟合方法探讨 [J], 廖嘉瑜
2.三棱镜色散曲线拟合的MATLAB-GUI设计 [J], 严达利;孙佩雄;寇晶
3.无堵塞泵中的持久效率浅析水泵效率及自清洁系统与水泵实际持续高效运行的关系 [J],
4.基于B样条的水泵效率特性曲线拟合方法 [J], 张林;于永海;姜晓明
5.大型水泵性能曲线拟合算法分析与实现 [J], 高伟恒
因版权原因，仅展示原文概要，查看原文内容请购买。

matlab数据拟合曲线

matlab数据拟合曲线
在Matlab中，可以通过拟合曲线方法来实现拟合数据。

拟合曲线就是根据数据构造出函数曲线，这条曲线可以描绘出数据之间的关系，从而推导出有用的信息。

Matlab的拟合曲线功能可以让用户快速拟合数据，使用简单。

首先，用户可以在Matlab中输入想要拟合的数据，然后使用拟合曲线命令，根据数据输入计算出复杂的统计模型或简单的函数模型，从而得到最佳的拟合曲线。

当拟合曲线得到时，用户可以在Matlab中绘制该曲线，把原始数据和最佳拟合曲线一起显示出来，用于比较分析和更加准确地描述数据之间的关系。

此外，用户还可以在Matlab中取得这条拟合曲线的相关信息，包括斜率、拟合误差、函数参数等。

基于MATLAB GUI技术的离心泵装置特性绘制软件二次开发

计算技术与自动化２０１０年９月２装置特性在石油产品的储存工程中，泵和管路一起组成一个输送系统。

在这个输送系统中，要遵循质量守恒和能量守恒这两个基本定律，即机器所排出的流量等于管路中的流量；单位质量流体所获得的能头等于流体沿管路输送所消耗的能头，这样才能稳定的工作。

泵和管路任何一方工况发生变化，都会引起整个系统工作参数的变化。

为此研究泵的装置特性对节能有重大意义。

装置特性，即将泵的扬程性能曲线Ｈ—Ｑ与管路特性ｈ—Ｑ画在一张图上，如图ｌ所示。

管路特性曲线的绘制主要依据管路特性曲线方程：ｈ—Ｈ。

＋姻２（１）式中管路特性系数五，它与管路长度、横截面积、各种阻力系数有关。

五＝（∑Ａ寺＋∑ｐ菱（２）式中Ａ——沿程阻力系数；卜局部阻力系数；Ｚ——管路长度，ｍ；ｄ——管路直径，ｍ，ｔ‘——管路内液体流速，“＝Ｑ／ｆ，ｍ／ｓｌ卜管路横截面积，ｍ２；Ｑ一管路中液体流量，ｍ３／ｓ；其中Ａ是流体的流速和管路特性的函数，可由摩擦因数Ａ与Ｒｅ和管壁相对粗糙度Ｕｄ的实验关系表查出。

而Ｒｅ可用下式计算：Ｒｅ—ａｕｐ（３）ｐ式中：Ｐ是流体密度，ｚ‘是流速，弘是流体黏度。

图１离心泵装王特性示意图３可视化界面设计Ｍａｔｌａｂ可视化界面的设计，一般有两种方法，一是直接通过编辑Ｍ脚本文件产生ＧＵＩ，二是通过Ｍａｔｌａｂ图形用户界面开发环境ＧＵＩＤＥ（Ｇｒａｐｈ—ｉｃａｌＵｓｅｒＩｎｔｅｒｆａｃｅＤｅｖｅｌｏｐｍｅｎｔＥｎｖｉｒｏｎｍｅｎｔ）来形成相应文件。

本篇只讲述在ＧＵＩＤＥ环境中利用控件实现可视化界面功能，不探讨直接通过编辑Ｍ脚本文件实现可视化界面的方法。

图形用户界面的外观设计一般采用可视化编程方式，其包括如下过程：（１）进入ＧＵＩ；（２）添加图形对象；（３）修改菜单属性；（４）修改图形对象属性；（５）编辑回调函数或命令；（６）另存为图形文件；（７）打开图形文件，对有关对象属性进行修改。

４基于ＭＡＴＬＡＢＧＵＩ技术的装置特性交互界面实现４．１图形用户界面的制作图形用户界面是指由窗口、光标、按钮、菜单、文字说明等对象构成一个用户界面。