4.4 三角函数的求值化简、和证明

合集下载

30师-三角函数的求值、化简与证明.

三角函数的求值、化简与证明编写教师：伍建明审稿教师：盛世红一、知识梳理1．在三角函数的求值、化简与证明中，除直接应用同角三角函数基本关系式、诱导公式、和、差、二倍角公式外，还要注意公式的变形形式：①，；②，；③，，.2．注意常用角的变形①，；②，；③.3．注意公式中1的妙用二、题型探究探究一：三角函数的求值问题例1已知,求的值.解：，∴ ，..例2在△中，，，求.解：，为锐角，.，，当为锐角时，，此时，；当为钝角时，，此时，，这与矛盾，不成立. 综上，.探究二：三角函数式的化简问题例3 化简.解：原式===.探究三：三角恒等式的证明例4已知求证：.证明：左边=，∵∴，∴.∴左边=，右边==左边，∴等式成立.三、方法提升化简、求值与证明就是对给定的三角函数式，通过适当的三角恒等变形，使之取较简单形式或求出值.三角恒等变形的实质是对角、函数名称及运算结构的转化，而转化的依据就是一系列的三角公式.因此，对一下三角公式在实现这种转化过程中的应用应有足够的了解：（1）同角三角函数基本关系-------------可实现函数名称的转化；（2）诱导公式及和、差角的三角函数-----------------可实现角的形式的转化；（3）倍角公式及其变形公式----------可实现三角函数式的升幂或降幂的转化，同时也可以完成角的形式的转化.四、反思感悟五、课时作业一、选择题1．的值为（ B ）（A）（B）（C）（D）2．化简的结果是（ A ）（A）（B）（C）（D）3．若（ C ）（A）（B）（C）-（D）4．已知函数，则（ B ）（A）（B）（C）（D）5．已知，那么（ C ）（A）（B）（C）（D）6．化简（ D ）（A）（B）（C）（D）7．已知，且，则（ D ）（A）（B）（C）（D）二、填空题8．.9．若，，则等于.10．已知，且，则的值是.11．在△中，已知，=，则的值为.三、解答题12．求值：.解：原式=.13.已知，，求的值.答案：.14．已知，，，求的值.解：∵ ，∴∵ ，∴，∴ ，∵ ，∴ ，又, ∴ ，∴ ，∴ ，∴ . ∴.。

三角函数求值与化简的三种常用方法

．．
化
成
鼻
參
＃參麝參
蘑
罄Ｉ张
菌子璇
＿
３＾（
Ｑｓｉ
ｎ
—
ｃｏｓ＾
）１２＇＝
—
２ｓｉｎＱ
？
４９
７
．
ｃｏ
ｓ
＾
＝
ｓ
ｉ
ｎ
〇
—
ｃｏ
ｓ夕
＝
。
Ｚｂｂ
评析由＋求出：
ｓｉｎ夕
ｃｏｓ夕
＾ｎｓｉ
？
ｃｏｓ６是解题的突破口。
，
ｓｉｎ夕ｃｏｓ０
０
，
ｓｉｎ夕
０
，
倒化简＋＋５
／
１
ｓｉｎ２
／ｎ２Ｉｓ —
ｉ
０
解易知＞：
ｓｉｎｌ
ｃｏｓ１。
故＋＋／ｌ
ｓｉｎ２
／Ｉ
—ｓΒιβλιοθήκη ｉｎ２＝
／＋＋（ｓｉｎ１
ｃｏｓｌ
）
２
／（
ｏｎｃｓｉ
种常用方法是：弦切互化法，和积转
换法
和
巧用“
” １
的
变
换法
。
下面举例
分析，供大家学习与参考。一、弦切互化法
例已知＋１
ｔａｎ（２０１９兀
？２
）＝
，

(完整版)三角函数化简求值证明技巧

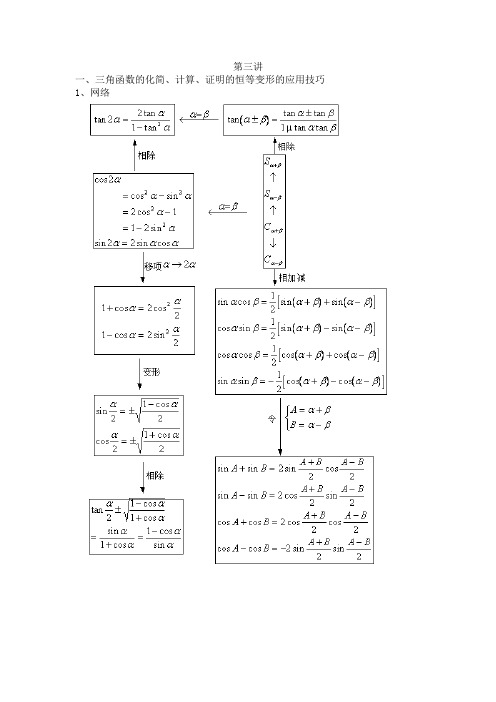
第三讲一、三角函数的化简、计算、证明的恒等变形的应用技巧1、网络2、三角函数变换的方法总结（1）变换函数名对于含同角的三角函数式，通常利用同角三角函数间的基本关系式及诱导公式，通过“切割化弦”，“切割互化”，“正余互化”等途径来减少或统一所需变换的式子中函数的种类，这就是变换函数名法．它实质上是“归一”思想，通过同一和化归以有利于问题的解决或发现解题途径。

【例1】已知θ同时满足和,且a、b 均不为0，求a、b的关系。

练习：已知sin（α＋β）＝，cos（α－β）＝，求的值。

2）变换角的形式对于含不同角的三角函数式，通常利用各种角之间的数值关系，将它们互相表示，改变原角的形式，从而运用有关的公式进行变形，这种方法主要是角的拆变．它应用广泛，方式灵活，如α可变为（α＋β）－β；2α可变为（α＋β）＋（α－β）；2α－β可变为（α－β）＋α；α／2可看作α／4的倍角；（45°＋α）可看成（90°＋2α）的半角等等。

【例2】求sin（θ＋75°）＋cos（θ＋45°）－cos（θ＋15°）的值。

练习已知，求的值【例3】已知sinα＝Ａsin（α＋β）（其中cosβ≠A），试证明：tan（α＋β）＝提示：sin[（α＋β）－β]＝Ａsin （α＋β）（3）以式代值利用特殊角的三角函数值以及含有1的三角公式，将原式中的1或其他特殊值用式子代换，往往有助于问题得到简便地解决。

这其中以“1”的变换为最常见且最灵活。

“1”可以看作是sin2x＋cos2x, sec2x－tan2x, csc2x －cot2x，tanxcotx, secxcosx, tan45°等，根据解题的需要，适时地将“1”作某种变形，常能获得较理想的解题方法。

【例4】化简：（4）和积互化积与和差的互化往往可以使问题得到解决，升幂和降次实际上就是和积互化的特殊情形。

这往往用到倍、半角公式。

三角函数式的化简和证明

简单的三角恒等变换——化简与证明学习目标：能正确地运用三角函数的有关公式进行三角函数式的求值，化简与恒等式的证明．学习重点：三角函数的有关公式的灵活应用和一些简单的变性技巧.学习过程一、知识清单1.证明了cos()a b -= ®cos()a b += ®cos()2p a -= ，cos()2p a += ®sin()a b += sin()a b -= ®tan()a b += ，tan()a b -= 2. cos (+)a b = ®cos 2a = = = sin()a b += ®sin 2a = tan()a b += ®tan 2a =3.倍角的相对性sin a = ，cos a = ，tan a =4.要掌握这些公式的推导和联系，用时注意公式的“正用”，“逆用”和“变用”.如：降幂扩角公式 2sin a = ；2cos a = ； 1cos a += ；1cos a -= ；1sin a += ；1sin a -= .5. 划一公式：sin cos a x b x += （其中tan f = ，f 所在象限由确定）.二、范例解析题型一三角函数式的化简和证明1.三角函数式的化简要求：通过对三角函数式的恒等变形使最后所得到的结果中：①所含函数和角的名称或种类最少；②各项的次数尽可能地低；③出现的项数最少； ④一般应使分母和根号不含三角函数式；⑤对能求出具体数值的，要求出值．2.三角变换的三项基本原则：（1）角的变换：划同角（角的拆分，配角和凑角，1的变换）；（2）函数名称的变换：划同名（正切划弦）；（3）幂指数的变换：划同次（升幂、降幂公式，同角公式）.例1化简下列各式； ②1sin 2cos 21sin 2cos 2a a a a+-=++ ； ③2sin 2cos 1cos 2a a a-=+ ； ④222cos 12tan()sin ()44a p p a a -=-+ ；例2 证明下列各式（从左到右或从右到左或左右开攻中间会师，一般化繁为简）①22tan 2sin 1tan 2a a a =+ ②221tan 2cos 1tan 2a a a -=+③sin 1cos tan21cos sin a a a a a -==+ ④[]1sin cos sin()sin()2a b a b a b =++-⑤sin sin 2sincos 22q f q f q f +-+=.三、课下练习：课本142P 2 ； 143P A 组 1, 2, 3, 4；B 组 1； 146P 8；147P 5.。

三角函数化简求值的技巧

三角函数化简与求值常用技巧
三角函数化简与求值常用技巧
三角函数在高考中通常以中低档题型出现,难度不大,但由于三角公式的特殊性,解题中往往也涉及一些小的变换技巧,如果处理得当,往往可以事半功倍,快速而准确地得到正确结论.通常情况下,三角变换应从“角度、函数、常数、次数、结构”等几方面着手解决.
一、三角变换,角为先锋三角函数作为一种特殊函数,其“角”的特殊性不容忽视,因此我们在三角函数恒等变换中,应该首先注意角的形式,从统一角的角度出发,往往能够达到事半功倍的效果.
【例 1】已知α、 β为锐角,cos α＝
3 5
,tan (α−β)＝−
1 3
,则
tan β＝(
)
A、
1 3
B、 3
【变式演练】已知 sin
x－π
4
＝3,则
sin
2x 的值为(
)
5
A．－ 7 25
B. 7 25
C. 9 25
D.16 25
【解析】法一、sin 2x＝cos(2x－ π )＝1－2sin2(x－ π )＝1－2×(3)2＝ 7 ,选 B.
2
4
5 25
法二、依题意得 2(sin x－cos x)＝3,1(sin x－cos x)2＝ 9 ,1－sin 2x＝18,sin 2x＝ 7 ,选
C、
9 13
D、
13 9
【例
1】已知α、 β为锐角,cos α＝
3 5
,tan (α−β)＝−
1 3
,则
tan β＝(
)
A、
1 3
B、 3
C、
9 13
D、
13 9
【分析】依题意,可求得 tan α＝

三角函数的化简与证明

第35课三角函数的化简与证明●考试目标主词填空1.三角函数式的化简要求及常规方法化简就是使式子最简,即:能求值的应求值；次数最低，项数最少，三角函数种类最少，将高级运算表为低级运算；化简的常规方法有：直用公式，逆用公式，变用公式，切割化弦，异名化同名，异角化同角，高次化低次.2.三角恒等式的证明常用的方法有:化繁为简，左右归一，变更等式，化异为同，异角化同角，异名化同名. 3.条件等式的证明认真解读条件与结论，发现已知条件和待定等式之间的关系，选择适当的途径和机会把条件等式用上去!●题型示例点津归纳【例1】化简下列各式 (1)⎪⎭⎫ ⎝⎛<<+-παπα2232cos 21212121; (2)42sin 42cos tan 5312sin 2cos 2tan 31--+--++x x xx x x ; (3)se c 2280°－3c s c 2280°.【解前点津】 (1)利用升次公式,去掉开方符号. (2)可使用换元化简，令t =t a n x . (3)化割为弦.【规范解答】 (1)∵αααπαπcos |cos |2cos 2121,223==+∴<<, 又∵2sin ,2sin |2sin |cos 2121,243ααααπαπ=∴==-∴<<原式. (2)令t =t a n x ,则原式=41811531121)1(231222222-+-+-+--+++-+t t t t tttt t t =x t t t t t t t t t t 2sec 212)1()1)(53()1)(51()1)(31()1()31(2222=-+=+++++-++∙+.(3)原式=csc 210°－3se c 210°=(csc10°+3sec10°)·(csc10°－3sec10°)=︒︒-︒∙︒+︒=︒︒︒-︒∙︒∙︒︒+︒20sin )1030sin()1030sin(1610cos 10sin 10sin 310cos 10cos 10sin 10sin 310cos 2=32cos20°.【解后归纳】切割化弦，巧用换元,都是常规方法.【例2】证明:cos 3α+sin 3α+cos 4α－sin 4α=2cos 24sin 4cos 2422ααπαπ∙⎪⎭⎫⎝⎛-∙⎪⎭⎫ ⎝⎛-.【解前点津】左右两边结构都较复杂，可同时化简，左、右归一.【规范解答】左边=(cos α+sin α)·(cos 2α－cos α·sin α+sin 2α)+(cos 2α+sin 2α)·(cos α+sin α)·(cos α－sin α)=(cos α+sin α)·(1－cos αsin α+cos α－sin α)=(cos α+sin α)·(1+cos α)(1－sin α)右边=2cos 122cos 1sin 4sin cos 4cos 24ααπαπαπ+∙⎪⎭⎫ ⎝⎛--∙⎪⎭⎫ ⎝⎛∙+∙)s i n (c o s αα+=·(1－sin α)·(1+cos α),∴左边=右边，等式成立. 【解后归纳】若被证明的等式两边都很复杂，则同时化简，双营齐下，是左、右归一的必然途径.【例3】若2t a n α=3t a n β,证明:t a n(α－β)=ββ2cos 52sin -.【解前点津】利用条件，用t a n β表示等式左边,而右边同样可用t a n β表示. 【规范解答】 ∵t a n α=23t a n β,∴t a n(α－β)=βαβαtan tan 1tan tan ∙+-=βββββ22tan 32tan tan 231tan tan 23+=+- 又∵βββββββββββ2222222tan 32tan )tan 1()tan 1(5tan 2tan 1tan 15)tan 1(tan 2cos 52sin +=--+=+--+=-∴t a n(α－β)=ββ2cos 52sin -.【解后归纳】将被证等式的两边都用t a n β表示，而不含t a n α,本质上是“消元法”，将多个变量的表达式，变为单个变量的表达式，往往要使用“消元”的方法.【例4】在△ABC 中,若sin 22A +sin 22B +sin 22C =cos 22B,求证:t a n312tan 2=∙C A . 【解前点津】因结论等式中不含B .故需设法消去已知等式中的B 角,可考虑使用三角形内角和定理.【规范解答】 ∵sin 22A +sin 22B +sin 22C =cos 22B,∴2sin 212cos 12cos 12BC A -=-+-. 又∵sin 2B =cos 2C A +,∴2sin 22B =21(cos A +cos C )⇒2cos 22C A + =cos 2C A +·cos ⇒-2C A 2cos2C A +=cos 2CA -. ∴2sin 2sin 2cos 2cos 2sin 2sin 2cos 2cos 2C A C A C A C A +=⎪⎭⎫ ⎝⎛-.∴.2cos 2cos 2sin 2sin3C A C A ∙=∙故312tan 2tan =∙C A . 【解后归纳】本题证明使用了降次公式，和差化积，三角形内角和定理，熟练使用公式与定理，是做论证题的一项基本功. ●对应训练分阶提升一、基础夯实1.若3(sin α+sin β)=cos β－cos α,α、β∈(0,π),则α－β等于 ( ) A.－32π B.－3π C.3πD.32π 2.化简:)tan(tan tan tan )tan(βααβαβα+∙--+的结果是 ( )A.t a n αB.t a n βC.t a n(α+β)D.t a n(α－β) 3.若t a n(α+β)=52,t a n 414=⎪⎭⎫ ⎝⎛-πβ,则t a n ⎪⎭⎫ ⎝⎛+4πα的值是 ( )A.1813 B.223 C.1213D.183 4.已知α+β=32π,则y =cos 2α+cos 2β的最大值为 ( )A.21 B.23C.43D.222+5.若α、β为锐角,sin α=552,sin(α+β)=53,则cos β等于 ( )A.552B.2552C.2552552或D.－2552 6.已知180°<α<270°,且sin(α+β)·cos β－cos(α+β)sin β=－54,则t a n 2α的值为 ( )A.3B.2C.－2D.－3 7.已知cos(α+β)·cos(α－β)=－32,则cos 2α+cos 2β的值为 ( ) A.－32 B.－31 C.31 D.328.已知α+β=3π,且α、β满足关系式:3(t a n α·t a n β+a )+t a n α=0,则t a n β= ( )A.3(1+a ) B.3(1－a ) C.33(1+a ) D. 33(1－a ) 9.若0<x <2π,则函数y =⎪⎭⎫ ⎝⎛-+2tan 2cot )2cos 1(x x x 取最大值时x 的值是 ( )A.4πB.8πC.6πD.12π10.若2523<<θππ,则θθsin 1sin 1--+可化简为 ( )A.2sin 2θB.－2sin 2θC.2cos 2θD.－2cos 2θ二、思维激活11.化简⎪⎭⎫ ⎝⎛+∙⎪⎭⎫ ⎝⎛+-απαπα4cos 4sin cos 212= .12.若θθθθcos 3sin cos sin 2-+=－5,则3cos2θ+sin2θ= .13.已知t a n θ=2,则⎪⎭⎫ ⎝⎛+--θπθθ4sin 21sin 2cos 22= . 14.已知:sin(α+β)=21,sin(α－β)=31,则log 5(t a n α·cot β)2= .三、能力提高15.已知cos θ－sin θ=2sin θ,求证:cos θ+sin θ=2cos θ.16.已知cos α=53,cos(α+β)=－135,且α、β都是锐角，求sin β值.17.求证:t a n A +cot A =Asin 2.18.在△ABC 中,sin A ,sin B ,sin C 成等差数列,求证:5cos A －4cos A ·cos C +5cos C =4.第6课三角函数的化简与证明习题解答1.D 和差化积:3·2sin 2tan2sin2sin22cos2βαβαβαβαβα-⇒-++=-+＝32323πβαπβα=-⇒=-⇒+. 2.B ∵tan β=tan ［(α+β)－α］=()[]()[]βαααβα+∙+-+tan tan 1tan tan 故原式=[]ββααββααβtan )tan(tan tan )tan(tan 1tan =+∙-+∙+∙.3.B tan ⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛--+=⎪⎭⎫ ⎝⎛+4)(tan 4πββαπα =4152141524tan )tan(14tan )tan(⨯+-=⎪⎭⎫ ⎝⎛-++⎪⎭⎫ ⎝⎛--+πββαπββα. 4.B y =21(1+cos2α)+21(1+cos2β)=1+21(cos2α+cos2β)=1+cos(α+β)·cos(α－β) =1－21cos(α－β)≤23.5.B cos β=cos ［(α+β)－α］=cos(α+β)·cos α+sin(α+β)·sin α=2552552535554=⨯+⨯⎪⎭⎫⎝⎛-.6.C 由条件知sin α=－542tan 12tan2542-=+⇒αα,解之:tan 2α=-2. 7.C 原式=21(1+cos2α)－21(1+cos2β)=21(cos2α+cos2β)=－sin(α+β)·sin(α－β),由条件:21(cos2α+cos2β)=31.8.A 由α+β=[]βαβαπtan tan 1)tan (tan 33∙-=⇒从方程组中消去tan α即得.9.A 分子=2cos 2x ,分母=x y x x x x xx x x x 2sin 21sin cos 22cos 2sin 2sin cos 2cos 2sin 2sin 2cos22==-=-故. 10.B 原式=2cos 2sin ,45243,2cos2sin2cos2sin θθπθπθθθθ>∴<<--+.11.分子－cos2α,分母=α2cos 21,故原式=－2. 12.由条件得:2tan 53tan 1tan 2=⇒-=-+θθθ,故3cos2α+3sin2θ=3·12149tan tan 2tan 1tan 12222-=++-=+++-θθθθ. 13.原式=⎪⎭⎫ ⎝⎛+⎪⎭⎫⎝⎛+=⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛-∙=⎪⎭⎫ ⎝⎛+-⎪⎭⎫ ⎝⎛-=⎪⎭⎫ ⎝⎛+-θπθπθπθππθπθθπθπθθ4sin 4cos 4sin 24sin 4cos 24sin 2sin 2sin 4sin 2sin cos . =2232121tan 1tan 14tan 1+-=+-=+-=⎪⎭⎫⎝⎛+θθθπ.14.∵tan α·cot β=βαtan tan . 由条件:()()23)tan (tan )tan (tan sin cos cos sin sin cos cos sin sin sin =-+=-+=-+βαβαβαβαβααβαβαβα,解之:4)5(log5log ,5tan tan 4525====故原式βα.15.∵cos θ－sin θ=2sin θ,∴cos θ=(2+1)sin θ,∴左边－右边=(1－2)cos θ+sin θ=(1－2)·(1+2)sin θ+sin θ=0,∴左边=右边. 16.由条件知:sin α=,54,sin(α+β)=⇒1312sin β=sin ［(α+β)－α］ =sin(α+β)·cos α－cos(α+β)·sin α=655654135531312=⨯⎪⎭⎫ ⎝⎛--⨯. 17.证明:∵sin2A ·(tan A +cot A )=A A 2tan 1tan 2+ (tan A +cot A )=AA 22tan 1)1(tan 2++=2,∴原等式成立.18.由条件:2sin B =sin A +sin C ⇒2sin(A +C )=sin A +sin C⇒2·2sin2C A +·cos 2C A + =2·sin 2C A +cos 2CA - ⇒2cos 2C A +=cos 2CA -,展开得: 2cos 2A cos 2C －2sin 2A sin 2C =cos 2A cos 2C +sin 2A sin 2C即cos 2A cos 2C =3sin 2A sin 2C ,∴tan 2A ·tan 2C =31.令x =tan 2A ,y =tan 2C则x ·y =31.故⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡⎪⎪⎪⎪⎭⎫ ⎝⎛+-∙⎪⎪⎪⎪⎭⎫ ⎝⎛+-+÷⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡+-++-=∙++2tan 12tan 12tan 12tan 112tan 12tan 12tan 12tan 1cos cos 1cos cos 22222222C C A A C C A A C A C A =5491191111111*********222222222=+-=+-=⎪⎪⎭⎫ ⎝⎛+-∙⎪⎪⎭⎫ ⎝⎛+-++-++-y x y x y y x x y y x x , ∴5(cos A +cos C )=4(1+cos A ·cos C )，即5cos A －4cos A ·cos C +5cos C =4.。

三角函数化简求值常用技巧

三角函数化简求值常用技巧三角函数式的化简和求值是高考考查的重点内容之一。

掌握化简和求值问题的解题规律和一些常用技巧，以优化我们的解题效果，做到事半功倍。

这也是解决三解函数问题的前提和出发点。

一、切割化弦例1、已知 )2(cot tan22≥=+m m x x ，求xx 4cos 14cos 3-+的值。

解： 24cos 14cos 34cos 1)4cos 3(24cos 12cos 444cos 1)2cos 1(484cos 12sin 48)4cos 1(812sin 2112sin 412sin 2112sin 41cos sin 2)cos (sin cos sin cos sin sin cos cos sin 2cot tan 2222222222222244222222m x x m x x x x x x x x x x x x x x x x x x x x x x x x x x x =-+∴=-+=-+=---=--=--=-=-+=+=+∴=+Θ 点评：由已知式与待求式的差异知，若选择“从已知到未知”，必定要“切切割化弦”；利用降幂公式实现已知与未知的统一。

二、统一配凑例2、已知2π＜β＜α＜43π,cos(α－β)=1312,sin(α+β)=－53,求sin2α的值. 解：注意到2α= (α－β)+(α+β)，于是可用配凑法求解。

∵2π＜β＜α＜43π,∴0＜α－β＜4π.π＜α+β＜43π, ∴sin(α－β)=.54)(sin 1)cos(,135)(cos 122-=+--=+=--βαβαβα ∴sin2α=sin ［(α－β)+(α+β)］=sin(α－β)cos(α+β)+cos(α－β)sin(α+β).6556)53(1312)54(135-=-⨯+-⨯=点评：本题以凑角的形式来实现未知与已知的统一，这是三角函数化简求值的常用技巧之一。

三、异角化同例3、已知cos(4π+x )=53，(1217π＜x ＜47π)，求x x x tan 1sin 22sin 2-+的值. 752853)54(257)4cos()4sin(2sin sin cos cos )cos (sin sin 2cos sin 1sin 2cos sin 2tan 1sin 22sin 54)4sin(,2435,471217.257)4(2cos 2sin ,53)4cos(:22=-⨯=++=-+=-+=-+-=+∴<+<∴<<=+-=∴=+x x x x x x x x x x x x x x x x x x x x x x x ππππππππππ又解Θ 点评：本题求解关键是将如何将已知条件中的角与目标关系式中的角统一起来。

【高考风向标】高考数学一轮复习第六章第6讲三角函数的求值、化简与证明课件文

设 φ(t)＝t＋4t ，由(1)知 t∈[1， 2]， ∴φ′(t)＝1－t42<0，即函数 φ(t)在区间[1， 2]上是减函数，其最小值为 φ( 2)＝ 2＋ 42＝3 2. 即 x＝π4时，函数 f(x)的最小值为 3 2. 【失误与防范】认清二次函数问题是解决问题的关键，例如：若 sinα＋cosα 是“一次”，则 sinαcosα 是“二次”；若 1＋k是“一次”，则 2k＋1 是“二次”等．
∵x∈0，2π，∴x＋π4∈π4，34π. ∴ 2sinx＋π4∈[1， 2]． ∴sinx＋cosx 的取值范围是[1， 2]． (2)设 t＝sinx＋cosx，则 t2＝(sinx＋cosx)2＝1＋2sinxcosx,2sinxcosx＝t2－1. 则 f(x)＝2ssiinnxxc＋oscxo＋sx5＝t2＋t 4＝t＋4t .
＝－2sicno2s05°0s°in70°＝－2sicno2s05°0c°os20°
＝－cossin5400°°＝－cocso5s05°0°＝－1.
切化弦和边角统一都是基本方法．关于三角形中的三角函数问题，边角的统一是问题的切入点，等式右边的分子分母均为 a，b，c 的二次齐次式，所以考虑使用余弦定理．
易错、易混、易漏 11．三角函数中的二次函数问题，忽视了自变量范围的研究例题：已知函数 f(x)＝2ssiinnxxc＋oscxo＋sx5，x∈0，2π.
(1)求 sinx＋cosx 的取值范围； (2)求函数 f(x)的最小值．
正解：(1)sinx＋cosx＝
2
22sinx＋
2
2
cosx
＝ 2cos4πsinx＋sinπ4cosx＝ 2sinx＋π4.
2．三角公式的三大作用 (1)三角函数式的化简． (2)三角函数式的求值． (3)三角函数式的证明． 3．求三角函数最值的常用方法 (1)配方法． (2)化为一个角的三角函数． (3)数形结合法． (4)换元法． (5)基本不等式法等．

三角函数的化简与求值

1．三角恒等变换的两原则（1）化繁为简：变复角为单角，变不同角为同角，化非同名函数为同名函数，化高次为低次，化多项式为单项式，化无理式为有理式。

（2）消除异差：消除已知与未知、条件与结论、左端与右端以及各项的次数、角、函数名称、结构式等方面的差异。

2．三角函数式的化简（1）化简要求①三角函数名称尽量少；②次数尽量低；③能求值的尽量求值； ④尽量使分母不含三角函数；⑤使被开方数不含三角函数．（2）化简思路对于和式，基本思路是降次、消项和逆用公式；对于三角分式，基本思路是分子与分母约分或逆用公式；对于二次根式，注意二倍角公式的逆用，另外，还可以用切割化弦、变量代换、角度归一等方法 (3)化简的方法弦切互化，异名化同名，异角化同角，降幂或升幂，和差化积，积化和差等。

3．三角恒等式的证明 (1)证明三角恒等式的方法观察等式两边的差异(角、函数、运算的差异)，从解决某一差异入手(同时消除其他差异)，确定从该等式的哪些证明(也可两边同时化简)，当从解决差异方面不易入手时，可采用转换命题法或用分析法等。

(2)证明三角条件等式的方法首先观察条件与结论的差异，从解决这一差异入手，确定从结论开始．通过变换，将已知表达式代入得出结论，或通过变换已知条件得出结论，如果这两种方法都证不出来，可采用分析法；如果已知条件含参数，可采用消去参数法；如果已知条件是连比的式子，可采用换元法等。

1. 三角函数的化简、计算、证明的恒等变形的基本思路是：一角二名三结构。

即首先观察角与角之间的关系，注意角的一些常用变式，角的变换是三角函数变换的核心！第二看函数名称之间的关系，通常“切化弦”；第三观察代数式的结构特点。

基本的技巧有:（1）巧变角（已知角与特殊角的变换、已知角与目标角的变换、角与其倍角的变换、两角与其和差角的变换. 如()()ααββαββ=+-=-+，2()()ααβαβ=++-，2()()αβαβα=+--，22αβαβ++=⋅，()()222αββααβ+=---等），如（1）已知2tan()5αβ+=，1tan()44πβ-=，那么tan()4πα+的值是_____ （答：322）；（2）已知02πβαπ<<<<，且129cos()βα-=-，223sin()αβ-=，求cos()αβ+的值（答：490729）；（3）已知,αβ为锐角，sin ,cos x y αβ==，3cos()5αβ+=-，则y 与x 的函数关系为______（答：43(1)55y x x =<<）(2)三角函数名互化(切化弦)，如（1）求值sin 50(13tan10)+（答：1）；（2）已知sin cos 21,tan()1cos 23αααβα=-=--，求tan(2)βα-的值（答：18）(3)公式变形使用（tan tan αβ±()()tan 1tan tan αβαβ=±。

三角函数化简题

2222
2|cos||cos|
22
∵0，∴0
∴原式cos．
22
，∴|cos|cos
22
，
§4.04三角函数的化简、求值与证明共7页,第3页
222(3cos4x)
例3．证明：（1）tanxcotx
1cos4x
sin(2AB)sinB
；（2）2cos()
AB
sinAsinA
．
证：（1）左边
224422222
右边，∴得证．
说明：由等式两边的差异知：若选择“从左证到右”，必定要“切化弦”；若“从右证到
左”，必定要用倍角公式．
（2）左边
sin[(AB)B]2cos(AB)sinA
sinA
sin(AB)cosAcos(AB)sinA
sinA
sin[(AB)A]sinB
sinAsinA
右边，∴得证．
课堂练习
1．若cos130a，则tan50
1cos1cossin1cos
()(1)
sinsincossin
2cos1cos1
(1)2cot(11)2csc
sincoscos
．
（3）原式
2
(2cos2cossin)(sincos)
22222
2(1cos)
2cos(cossin)(sincos)
22222
2
22cos
2
22
2cos(sincos)cos(cos)
1．三角函数式的化简：
三角函数式的化简常用方法是：异名函数化为同名三角函数，异角化为同角，异次化为
同次，切割化弦，特殊值与特殊角的三角函数互化．
2．三角恒等式的证明：
三角恒等式包括有条件的恒等式和无条件的恒等式．①无条件的等式证明的基本方法是

三角函数的化简求值

三角函数的化简求值一.主要公式:1．诱导公式：=-)sin(απ =-)c o s (απ =+)s i n (απ=+)cos(απ =-)s i n (α =-)cos(α=-)2sin(απ =-)2c o s (απ =+)2sin(απ =+)2c o s (απ2．和、差角公式： =+)sin(βα =-)s i n (βα ； =+)cos(βα =-)c o s (βα ； =+)tan(βα =-)t a n (βα ； 3．二倍角公式：=α2sin =α2c o s = = =α2tan ； 4．降幂公式： =2sin 2α=2c o s2α=2t a n2α；5．半角公式sin 2α= c o s 2α= t a n 2α= ；6．升幂公式：=+αcos 1 ，=-αcos 1 ；=+αsin 1 ，=-αsin 1 。

7．万能公式：=αsin =αcos =αtan ； 8．三角形ABC 中的相关公式：=+)sin(B A =+)cos(B A =+)t a n (B A =+2sinBA =+2cosB A =+2tan B A ； 9．常用公式结论：=+ααcot tan =ααcos sin =-α2sin 1 =+α2sin 1 =+βαtan tan =-βαt a n t a n ；sin 3α= cos3α= 1tan 1tan αα+=-10．辅助角公式：=+ααcos sin = =+ααcos 3sin ==+x b x a cos sin = 。

二、例题分析:例1已知02πβαπ<<<<，且129cos()βα-=-，223sin()αβ-=，求cos()αβ+的值.例2.已知0,1413)cos(,71cos 且=β-α=α<β<α<2π,(Ⅰ)求α2tan的值.(（Ⅱ）求β. ( π3β=)例3．已知51cos sin ,02=+<<-x x x π. （I ）求sin x －cos x 的值；（Ⅱ）求xx x x x x cot tan 2cos 2cos 2sin 22sin 322++-的值.例 4.是否存在锐角,αβ，使得①223παβ+=；②22tantan αβ=同时成立？若存在，求出,αβ；若不存在，说明理由。

高考数学难点突破_难点16__三角函数式的化简与求值

高考数学难点突破_难点16__三角函数式的化简与求值在高考数学中，三角函数式的化简与求值是一个很常见的难点。

在解决这一难点时，我们需要掌握一些基本的化简公式和常用的解题技巧。

首先，我们来回顾一下一些常见的三角函数化简公式：1.两角之和的三角函数公式：sin(A+B) = sinA·cosB + cosA·sinBcos(A+B) = cosA·cosB - sinA·sinBtan(A+B) = (tanA + tanB) / (1 - tanA·tanB)2.两角之差的三角函数公式：sin(A-B) = sinA·cosB - cosA·sinBcos(A-B) = cosA·cosB + sinA·sinBtan(A-B) = (tanA - tanB) / (1 + tanA·tanB)3.倍角的三角函数公式：sin2A = 2sinA·cosAcos2A = cos^2A - sin^2A = 2cos^2A - 1 = 1 - 2sin^2Atan2A = (2tanA) / (1 - tan^2A)4.半角的三角函数公式：sin(A/2) = ±√[(1 - cosA) / 2]cos(A/2) = ±√[(1 + cosA) / 2]tan(A/2) = ±√[(1 - cosA) / (1 + cosA)]（在这里需要根据A的范围来确定取正还是取负）掌握了这些基本的化简公式后，我们可以运用它们来解决一些常见的难点问题。

1.求三角函数值：高考中经常会出现需要求一些特定角度的三角函数值的问题。

我们可以通过套用基本的化简公式，将所给的角度化简到我们熟悉的角度（如30°，45°，60°等），然后代入公式求值即可。

例如，要求sin75° 的值，我们可以化简为sin(45°+30°)，然后套用两角之和的公式，得到sin45°·cos30° + cos45°·sin30°。

例析三角函数求值与化简的三种常用方法

题过程简单明了。
作者单位 :湖北省巴东县第三高级中学
(责任编辑郭正华)
16
三、巧用 “1”的变换法
例3
已
知
1+tanx 1-tanx
=5+2
6,则
1c -os sin 2x2x=
。
解
:由
1+tanx 1-tanx
=tan(45°+x
),可
得
tan(45°+x)=5+2 6。
1c -os sin 2x2x=1+ sic no(s 90 (9 °0+°2 +x2x ))
m
=
3。 2
(3)原
方
程
可
化
为
2x2
-(3+1)x+
3 2=
0,解
得
x1
=
23,x2
=
1 2
,所
以
ìïïsinθ= í
3, 2或
îïïcosθ=
1 2
ìïïcosθ= í
3, 2又
îïïsinθ=
1 2
。
因
为
x∈
(0,2π),所
以θ=
π 3
或θ=
π。 6
评析:已知 sinθ+cosθ,sinθ-cosθ, sinθcosθ 中的任何一个值,则另两个式子的值均可求出。
知识篇·知识结构与拓展高一使用 2020年4月
■张红梅
三角函数求值与化简的三种常用方法:
弦切互化法、和积转换法、巧用 “1”的变换法。
下面举例分析 ,供大家学习与参考。

§4.4同角三角函数的基本恒等式

§4.4 同角三角函数的基本恒等式预备知识∙恒等变形的知识∙证明恒等式的基本方法∙乘法公式重点∙同角三角函数的基本恒等式及其应用难点∙应用同角三角函数基本恒等式，结合常用的解题技巧，进行求值、化简和证明学习要求∙理解并熟记同角三角函数的基本恒等式∙能应用同角三角函数基本恒等式，结合常用的解题技巧,进行求值、化简和证明六个三角函数是在同一个直角三角形中定义出来的，即使推广到了任意角，仍然与三角形密切相关．同一个直角三角形的边角之间是存在一定关系的，反映在同一角的三角函数之间也必定存在一定的关系．本节的内容，就是揭示同角三角函数间的关系，并应用这些关系于求值、化简等问题中．1.同角三角函数的基本恒等式根据三角函数的定义，立即可以得到下列基本恒等式：倒数关系式sin α⋅csc α=1， cos α⋅sec α=1， tan α⋅cot α=1；商数关系式αααt a n c o s s i n =， αααcot sin cos =；从三角函数定义，经过简单推导，并应用勾股定理，又能得到平方关系式sin 2α+cos 2α=1； 1+tan 2α=sec 2α； 1+cot 2α =csc 2α．如从sin α=y , cos α=x ⇒ sin 2α+cos 2α=(y )2+(x )2=222r y x +=1(见图4-16)；又如1+tan 2α=1+(x y )2=222222)(x r x r x y x ==+= sec 2α．上述三种、八个关系，称为同角三角函数的基本恒等式．之所以称之为“恒等式”，是因为这些等式，对所有使出现在等式中的三角函数有意义的角α，都是成立的．同角三角函数的基本恒等式，是三角函数最重要的特性之一，今后经常应用，你必须熟记．2. 同角三角函数基本恒等式的应用(1)已知一个角的三角函数值，求同角的其余三角函数值应用同角三角函数的基本恒等式，只要知道了角α 的一个三角函数值和α 是哪个象限角，就能求出α 的其余三角函数值．例1 (1)已知cos α=53-，并且α 是第二象限角，求α 的其余三角函数值；(2)已知tan α =72，并且α是第三象限角，求α 的其余三角函数值； (3)已知sin α=-0.35，并且α 是第四象限角，求α的其余三角函数值(保留四个有效数字)；(4)已知tan α =-11.4，并且α 是第二象限角，求α的其余三角函数值(保留四个有效数字)．解 (1)由sin 2α+cos 2α=1，可得sin α=±α21cos -．因为α是第二象限角，sin α >0，所以sin α=α21cos -=2)53(1--=54；因为αααcos sin tan =，所以34tan 534-=-=α；再应用倒数关系，即得cot α=43tan 1-=α，csc α=45sin 1=α，sec=35cos 1-=α ▍ 注意，本题也可用几何方法来解．从cos α=53-，立即可以画出如图4-25那样的三角形，由此立即可以得到⎪sin α⎪,⎪tan α⎪，然后再根据α是第二象限角得到结果．(2)用几何解法．从tan α =72，立即可以画出如图 4-26那的三角形，由此立即可以得到 ⎪sin α⎪=532，⎪cos α⎪=537，因为α是第三象限角，sin α<0, cos α<0，所以 sin α =-532=-53532；cos α=-537=-53537；据倒数关系，又可得 cot α=27tan 1=α，csc α=253sin 1-=α，sec =753cos 1-=α ▍ (3)由平方关系sin 2α+cos 2α=1，可得cos α=±α21sin -；因为α是第四象限角，cos α>0，所以 cos α=α21sin -=2)35.0(1--≈0.9367；tan α=93670350..-=ααcos sin ≈-0.3737；据倒数关系cot α=-2.676, csc α=-2.857, sec α=1.068 ▍(4)由平方关系1+tan 2α=sec 2α及所在象限，可得sec α=22)4.11(1tan 1+=+α≈-11.4438；由倒数关系 cos α=αsec 1，得到 5 4 图4-25 53572图4-26cos α =αsec 1≈-4438111.≈-0.0874；再由平方关系sin 2α+cos 2α=1，并注意α是第二象限角，得到sin α=α21cos -=2)0874.0(1--≈0.9962；最后应用倒数关系得cot α=-0.08772, csc α=1.004 ▍从上面四个典型例子可见：知道了角α 的一个三角函数值和α 是哪个象限角，求α 的其余三角函数值的问题，可以有两种解法．第一种，若已知的三角函数值是以数字不大的分数形式给出的，或者虽然用小数形式给出，但化为分数后数字也不大，则用几何方法比较简单；否则用第二种方法，利用同角三角函数恒等式来解．用后一种方法时，在不同已知条件下，采用不同步骤：弦(平方关系)→弦→切，或切(平方关系)→割→弦．它的含义，表示若已知正弦(或余弦)，则总是先用sin 2α+cos 2α=1算出余弦 (或正弦)，然后算正切、余切；若已知正切(或余切)，则总是先用1+tan 2α=sec 2α (或1+cot 2α=csc 2α)算出正割(或余割)，然后用倒数关系算余弦(或正弦)．课内练习1(1)已知cos α=31，并且α 是第四象限角，求α 的其余三角函数值； (2)已知cot α =-72，并且α是第二象限角，求α的其余三角函数值；(3)已知cos α=-0.35，并且α 是第三象限角，求α的其余三角函数值(保留四个有效数字)；(4)已知cot α =2.4，并且α 是第三象限角，求α 的其余三角函数值(保留四个有效数字)．(2)化简三角函数式应用同角三角函数基本恒等式，可以把某些较繁的三角函数式予以简化. 例2 化简下列各式：(1)︒-10012sin ； (2)θθθsin cos -．解 (1)︒-10012sin =︒1002cos =| cos100︒|=- cos100︒ ▍ (2)1cot sin cos --θθθ=θθθθθθθθθθsin sin sin cos sin cos 1sin cos sin cos =--=-- ▍ 第(1)题使用了三角函数的平方关系，在这中间特别要注意，代数式开方、移到根式外面时，需要加绝对值符号．课内练习21. 化简下列各式：(1)θθθcot cos ++1； (2)︒-22012cos ． (3)证明三角恒等式应用同角三角函数的基本恒等式，可证明一些更复杂的同角三角函数的恒等式，这类问题，常称证明三角恒等式．例3 求证：(1)θcot tan +-θ=sin θ -cos θ； (2)tan 2α -sin 2α=tan 2α⋅sin 2α．证明 (1)左边=θθθθθθsin cos cos sin 11+-=θθθθθθθθcos sin sin cos cos sin +-22 =θθθθθθcos sin )cos sin )(cos sin (+-+=sin θ -cos θ=右边 ▍ (2)证法1左边=ααα222sin cos sin -=αααα2222cos cos sin sin ⋅- =ααααα24222cos sin cos )cos 1(sin =-=tan 2α⋅sin 2α=右边 ▍ 证法2tan 2α -sin 2α -tan 2α⋅sin 2α =tan 2α(1- sin 2α)-sin 2α=ααα222cos cos sin ⋅-sin 2α=sin 2α -sin 2α=0 所以左边=右边 ▍在证明三角函数恒等式中，经常使用的技巧之一,是所谓“化弦法”，意思是把正切、余切、正割、余割函数，应用商数关系或倒数关系，化为正弦、余弦函数，其目的，当然是为了减少等式中的三角函数的种类，而且，正弦和余弦函数还有一个平方关系sin 2α+co s 2α=1可用，这常常会给证明带来方便．课内练习31. 证明下列三角函数恒等式：(1)xx x x cos sin cot tan =++11； (2)(cos α-1)2+sin 2α=2-2cos α．下面我们介绍一个常用的技巧：三角函数的平方关系sin 2α+cos 2α=1是很有用的，恰当地应用它是三角函数解题的基本技巧之一．例4 已知sin α+co s α=21，求 (1)sin α⋅co s α； (2)sin 3α+cos 3α解 (1)对sin α+cos α=21 两边平方，得 sin 2α+2sin α⋅cos α+cos 2α=41，因为sin 2α+cos 2α=1，所以2sin α⋅cos α=-43，sin α⋅cos α=-83 ▍ (2)sin 3α+cos 3α =(sin α+cos α) (sin 2α-sin α⋅cos α+cos 2α)=21(1-sin α⋅cos α)=21(1+83)=1611 ▍ 课内练习41. 已知sin α+co s α=22，求 (1)sin α⋅cos α； (2)sin 3α+cos 3α．2. 已知α为第一象限角，且sin α⋅co s α=21，求sin α +co s α．课外习题A 组1. 根据下列条件，求角α的其它三角函数值：(1)sin α=-23，且α为第四象限角； (2)cos α=-23，且α为第三象限角； (3)tan α=-3，且α为第二象限角；(4)sin α=21(没有指定α的象限，应该讨论α可能的象限)． 2. 化简下列各式：(1)cos θ tan θ； (2)(1- sin x )(1+sin x )；(3)αα222112sin cos --； (4)sin α cos α (tan α+cot α)． 3. 证明下列三角函数恒等式：(1)sin 4α+sin 2α cos 2α+cos 2α=1； (2)sin 4α+cos 4α=1-2sin 2α cos 2α；(3)θcos sin tan tan 12=+θ．B 组1. 根据下列条件，求角α的其它三角函数值：(1)sin α=31，且α为第二象限角； (2)tan α=-2，且α为第四象限角； (3)cos α=32． 2. 已知sin α- cos α=2，求下列各式的值：(1)sin α⋅cos α； (2)sin 3α- cos 3α．3. 已知sin α=51，求下列各式的值： (1)5sin 2α+3cos 2α； (2)sin 4α+cos 4α．4. 已知cos α=54，求αα2211sin cos +． 5. 化简下列各式：(1)︒-31012cos ；(2)θθcot tan ++11；(3)θθθθcos sin sin cos +++11；(4)θθθsin cot cos ++1. 6. 证明下列三角函数恒等式：(1)θθθθθθcos sin )tan 1(cos )cot 1(sin 33+=+++； (2)222)cot 1tan 1(cot 1tan 1A A A A --=++； (3)αααα2222111cot cot cos sin -+=-．C 组1. 已知tan α=2，求下列各式的值：(1)cos 2α； (2)sin α cos α； (3)sin 2α -cos 2α； (4)ααααcos sin cos sin 253-+． 2. 已知tan α=3，π<α<23π，求cos α - sin α． 3. 化简ααααsin sin sin sin +---+1111，α≠k π+2π, k ∈Z ．。

4.4简单的三角恒等变换

方法总结:
典型例题及方法总结
典型例题及方法总结
考点二给值求值(角)
典例 2
2．给值求值： ①直接分析角的关系 ②化简或变形后分析角的关系
3.给值求角问题可以转化为给值求值问题Leabharlann 考点三三角恒等变换的简单应用
4.利用三角函数解决实际问题：(1) 引入角当变量； (2)建立函数模型；(3)求解模型。
1.三角函数的化简、求值、证明，要从分析角的关系、函归纳反思数名称、式子的结构入手。
总结
2. 利用三角函数解决实际问题：选择恰当的角作为变量是关键；
56 级实验部数学一轮复习研究表(二)
课时
知识点近 5 年考查次数掌握情况
简单的三角恒等变换三角恒等变换
研究人
日期
10.4
知识点要求
能运用上述公式进行简单的恒等变换(包括导出积化和差、和差化积、半角公式，但对这三组公式不要求记忆 . 典型例题: 考点一三角函数式化简典例 1 1. ①分析角的关系；②函数名的转化(切弦互化)；③ 根据式子的结构特征恰当选择和使用公式(正用、逆用、变形用)

2022届高三数学一轮复习三角函数之三角公式的化简与求值题型方法归纳

高考数学专题—三角函数（三角公式的化简与求值）高中阶段三角函数公式主要包括：同角三角公式、诱导公式、两角和差公式、二倍角公式、和差化积与积化和差关系式。

（1）同角三角公式—主要用于正弦、余弦、正切之间的计算与推导（2）诱导公式—将角的三角函数值推广到全体实数（3）两角和差与二倍角公式—研究不同角度之间的公式一、三角函数求值与化简必会的三种方法（常用）(1)弦切互化法:主要利用公式tan α=;形如,asin2x+bsin xcos x+ccos2x等类型可进行弦化切；(2)“1”的灵活代换法:1=sin2θ+cos2θ=(sinθ+cosθ)2-2sinθcosθ=tan等；(3)和积转换法:利用(sinθ±cosθ)2=1±2sinθcosθ,(sinθ+cosθ)2+(sinθ-cosθ)2=2的关系进行变形、转化.例1、【2020年高考全国Ⅰ卷理数】已知，且，则A．B．C．D．【答案】A【解析】，得，即，解得或（舍去），又.故选：A ．例2、cos 150−sin 150cos 150+sin 150=A,−√3 B,0 C√3 D,√33法一：利用两角和差公式，求出cos 150，sin 150因为cos 150=cos (450−300)=cos 450cos 30°−sin 450sin 300=√6+√24同理可得sin 150=√6−√24所以cos 15o −sin 150cos 150+sin 150=√6+√24−√6−√24√6+√24+√6−√24=√33故选D法二:利用利用同角的正弦与余弦平方和为1，求解。

因为sin 150>0，cos 150>0 所以令cos 150−sin 150cos 150+sin 150=t (t >0)t 2=cos 2150−2cos 150sin 150+sin 2150cos 2150+2cos 150sin 15°+sin 215°=1−sin 3001+sin 300=13故选D法三：利用平方差公式，将非特殊角转化为特殊角。

三角函数的化简、求值——诱导公式

三角函数的化简、求值——诱导公式
三角函数的化简和求值是解决三角函数问题中常见的任务，而诱导公式是一种常用的化简工具。

首先，让我们回顾一下三角函数的基本定义。

对于任意角θ，正弦函数sin(θ)定义为对边与斜边的比值，余弦函数cos(θ)定义为邻边与斜边的比值，而正切函数tan(θ)定义为对边与邻边的比值。

现在，让我们来讨论一下诱导公式。

诱导公式是指一组用于将一个角的三角函数表示为另一个角的三角函数的公式。

最常用的诱导公式包括：
1. 正弦函数的诱导公式，sin(α±β) = sinαcosβ ±
cosαsinβ。

2. 余弦函数的诱导公式，cos(α±β) = cosαcosβ ∓
sinαsinβ。

3. 正切函数的诱导公式，tan(α±β) = (tanα ± tanβ) / (1 ∓ tanαtanβ)。

这些诱导公式可以帮助我们化简复杂的三角函数表达式，或者求解包含多个角的三角函数表达式。

通过使用这些诱导公式，我们可以将一个角的三角函数表示为另一个角的三角函数，从而更容易地进行计算和分析。

当我们需要化简或求解涉及多个角的三角函数表达式时，诱导公式是非常有用的工具。

通过灵活运用这些公式，我们可以更加高效地解决各种三角函数相关的问题。

因此，熟练掌握诱导公式是学习和应用三角函数的重要一步。

三角函数的求值与化简

三角函数的求值与化简一三角函数式的化简与证明 1．两角和与差的三角函数公式 sin(α＋β)＝sin αcos β＋cos αsin β(S α＋β) sin(α－β)＝sin αcos β－cos αsin β.(S α－β) cos(α＋β)＝cos αcos β－sin αsin β；(C α＋β) cos(α－β)＝cos αcos β＋sin αsin β.(C α－β) tan (α＋β)＝tan α＋tan β1－tan αtan β；(T α＋β)tan (α－β)＝tan α－tan β1＋tan α·tan β(T α－β)2．二倍角公式sin 2α＝2sin αcos α；(S 2α)cos 2α＝cos 2α－sin 2α＝2cos 2α－1＝1－2sin 2α；(C 2α) tan 2α＝2tan α1－tan 2α.(T 2α)3．公式的变形与应用(1)两角和与差的正切公式的变形 tan α＋tan β＝tan (α＋β)/(1－tan αtan β)； tan α－tan β＝tan (α－β)/(1＋tan αtan β)． (2)升幂公式1＋cos α＝2cos 2α2；1－cos α＝2sin 2α2.(3)降幂公式 sin 2α＝1－cos 2α2；cos 2α＝1＋cos 2α2. (4)其他常用变形sin 2α＝2sin αcos αsin 2α＋cos 2α＝2tan α1＋tan 2α； cos 2α＝cos 2α－sin 2αcos 2α＋sin 2α＝1－tan 2α1＋tan 2α；1±sin α＝⎝⎛⎭⎫sin α2±cos α22； tan α2＝sin α1＋cos α＝1－cos αsin α.5．角的拆分与组合 (1)已知角表示未知角例如，2α＝(α＋β)＋(α－β)，2β＝(α＋β)－(α－β)， α＝(α＋β)－β＝(α－β)＋β， α＝⎝⎛⎭⎫π4＋α－π4＝⎝⎛⎭⎫α－π3＋π3. 例1化简：sin 2αsin 2β＋cos 2αcos 2β－12cos 2αcos 2β＝________.即时训练1化简：sin(θ＋75°)＋cos(θ＋45°)－3cos(θ＋15°)＝________.例24cos 50°－tan 40°＝( ) A.2B.2＋32C.3D.22－1 (2)已知cos ⎝⎛⎭⎫α－β2＝－513，sin ⎝⎛⎭⎫α2－β＝45且0<β<π2<α<π，则sin(α＋β)的值为________．即时训练2．(1)已知α为锐角，且sin α(1＋3tan 10°)＝1，则α的值为________． (2)已知α，β∈(0，π)，且tan (α－β)＝12，tan β＝－17，求2α－β的值．。