3.1.1 椭圆及其标准方程 课件(北师大选修2-1)
合集下载
3.1 椭圆 课件1 (北师大选修2-1)
小知识 与《几何原本》齐名的《圆锥曲线论》
公元前三世纪产生了具有完整体系的欧 几里得的《几何原本》。半个世纪以后,古 希腊的另一位数学家阿波罗尼斯又著《圆锥 曲线论》(8卷)—以其几乎将圆锥曲线的全 部性质网罗殆尽而名垂史册。 在解析几何之前的所有研究圆锥曲线的著 作中,没有一本达到象《圆锥曲线论》那样 对圆锥曲线研究得如此详尽的程度。 解析几何是由费尔马和笛卡尔分别创立的。 自从有了解析几何,圆锥曲线的研究才开辟 了新的纪元。
自学教材P28-29页例3之前内容,思考解答下列问题 (1)在椭圆标准方程中,x、y的取值范围分别是什么? 你是怎样探得的? (2)请结合椭圆标准方程确定椭圆的对称性。 (3)请结合图形说明什么是椭圆的顶点? y 若该椭圆的标准方程是 B2(0,b)
x2 y2 2 1(a b 0) 2 a b
A2(-a,0)
A1(a,0)
则它的顶点坐标分别是什么? (4)什么叫椭圆离心率?
o
B1(0,-b) (1)
x
思考:[1]离心率的取值范围是什么?
[2]离心率对椭圆形状有什么影响? y 离心率对椭圆形状的影响: 1)e 越接近 1,c 就越接近 o x ( a ),从而 b就接近( 0 ),椭 圆形状就越( 扁 )。 2)e 越接近 0,c 就越接近 ( 0 ),从而 b就越( a ), 椭圆就越圆( 圆 )。 3)当e =0时,a 与b有什么关系?此时椭圆变成什么 3)当e =0时,a =b,此时椭圆变成圆。 形状?
a ,0
(
),(0,
c,0)
b)
(
b ,0
),(0,
(0,
c)
a)
长半轴长为a,短半轴长为b.
a,b,c关系
3.1 椭圆 课件1 (北师大选修2-1)

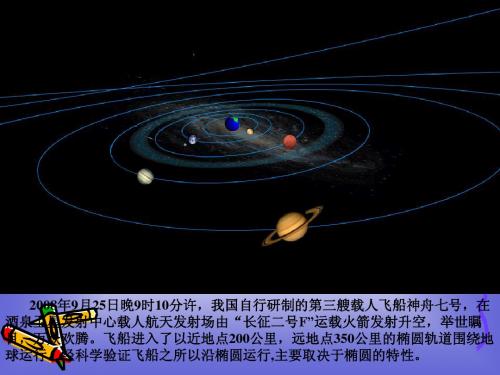
2008年9月25日晚9时10分许,我国自行研制的第三艘载人飞船神舟七号,在 酒泉卫星发射中心载人航天发射场由“长征二号F”运载火箭发射升空,举世瞩 目,万众欢腾。飞船进入了以近地点200公里,远地点350公里的椭圆轨道围绕地 球运行,经科学验证飞船之所以沿椭圆运行,主要取决于椭圆的特性。
活动一 尝试自学,探究新知
小知识 与《几何原本》齐名的《圆锥曲线论》
公元前三世纪产生了具有完整体系的欧 几里得的《几何原本》。半个世纪以后,古 希腊的另一位数学家阿波罗尼斯又著《圆锥 曲线论》(8卷)—以其几乎将圆锥曲线的全 部性质网罗殆尽而名垂史册。 在解析几何之前的所有研究圆锥曲线的著 作中,没有一本达到象《圆锥曲线论》那样 对圆锥曲线研究得如此详尽的程度。 解析几何是由费尔马和笛卡尔分别创立的。 自从有了解析几何,圆锥曲线的研究才开辟 了新的纪元。
a ,0
(
),(0,
c,0)
b)
(
b ,0
),(0,
(0,
c)
a)
长半轴长为a,短半轴长为b.
a,b,c关系
离 心 率
焦距为2c;
e c a
a2=b2+c2
推荐作业:
必做题:1 、 阅读教材p28-31页内容完成例5;2 、 课本第31页习题第3、4、6题 选做题:
课外练习 1、已知椭圆的长轴长是短轴长的2倍, 且椭圆过(-2,-4)点,求椭圆的标准方程. 2、已知椭圆的焦距、短轴长、长轴长成 等差数列,求该椭圆的离心率.
称中心。 四 [3]一个椭圆有_____个顶点,
椭圆与它的对称轴 顶点是___________________的交 点。 o
y x
想想、试试,你能行!
[4]对称轴与长轴、短轴的位置关系是
活动一 尝试自学,探究新知
小知识 与《几何原本》齐名的《圆锥曲线论》
公元前三世纪产生了具有完整体系的欧 几里得的《几何原本》。半个世纪以后,古 希腊的另一位数学家阿波罗尼斯又著《圆锥 曲线论》(8卷)—以其几乎将圆锥曲线的全 部性质网罗殆尽而名垂史册。 在解析几何之前的所有研究圆锥曲线的著 作中,没有一本达到象《圆锥曲线论》那样 对圆锥曲线研究得如此详尽的程度。 解析几何是由费尔马和笛卡尔分别创立的。 自从有了解析几何,圆锥曲线的研究才开辟 了新的纪元。
a ,0
(
),(0,
c,0)
b)
(
b ,0
),(0,
(0,
c)
a)
长半轴长为a,短半轴长为b.
a,b,c关系
离 心 率
焦距为2c;
e c a
a2=b2+c2
推荐作业:
必做题:1 、 阅读教材p28-31页内容完成例5;2 、 课本第31页习题第3、4、6题 选做题:
课外练习 1、已知椭圆的长轴长是短轴长的2倍, 且椭圆过(-2,-4)点,求椭圆的标准方程. 2、已知椭圆的焦距、短轴长、长轴长成 等差数列,求该椭圆的离心率.
称中心。 四 [3]一个椭圆有_____个顶点,
椭圆与它的对称轴 顶点是___________________的交 点。 o
y x
想想、试试,你能行!
[4]对称轴与长轴、短轴的位置关系是
3.1 椭圆 课件3 (北师大选修2-1)

探究交流二
LOGO
• 如何用几何图形解释? a ,b, c 在椭圆中分别表示 哪些线段的长? • 当a为定值时,椭圆形状的变化与c有怎样的关系?
交流结果 1.勾股定理...... 2.a不变c变大椭圆越扁 a不变c变小椭圆越圆
课堂小结:
1.椭圆的定义:
平面内与两个定点F1,F2的距离之和等于常 数(大于ΙF1F2Ι)的点的集合叫作椭圆,这两 个定点叫作椭圆的焦点,两焦点间的距离叫作 椭圆的焦距 .
课前预习情况汇报(2)
完成问题3和问题4
这是大家在学习推导椭圆的方程时应该注 意的2个问题 ①建立坐标系的问题. ②怎样消去方程总的根式.
求椭圆方程的步骤
建立坐标系
1 2 3
别忘了还 有⑤呢?
设点
列式
4
化简
注意:①②③④只说明了椭圆上点的坐标 满足方程,事实上我们还可以证明,方程 的“每一组解所对应的点都在椭圆上”。
椭圆的标准方程 焦点位置 在X轴
Y
F1
LOGO
在Y轴
Y
图 形
标准方程
F1
F2
X
F2
X
x2 y2 2 1 2 a b ( a b 0)
y2 x2 2 1 2 a b ( a b 0)
焦点坐标 F1(-c ,0 ),F2(c,0)
F1(0 ,c ),F2(0,-c)
2 2
a
探究结果
线段F1F2 • 设定义中的常数为 2a, 无轨迹 • 若ΙF1F2Ι = 2a,动点的轨迹是 椭圆
• 若ΙF1F2Ι > 2a,动点 试试: 已知F1(-4,0),F2(4,0),到F 1,F2 • 若ΙF1F2Ι < 2a,动点的轨迹是 两点的
高中数学第三章圆锥曲线与方程3.1椭圆3.1.1椭圆及其标准方程课件北师大版选修2_1

∴点
������2 ������2 A 的轨迹方程是 + =1(y ≠0). 25 16
探究一
探究二
探究三
探究四
反思感悟找出点A的轨迹满足|AB|+|AC|=10>6后,知A的轨迹是 椭圆,用定义法求出其方程,但要注意去掉不符合题意的点(5,0),(5,0).Βιβλιοθήκη 探究一探究二探究三
探究四
变式训练1过椭圆4x2+y2=1的一个焦点F1的直线与椭圆交于A,B 两点,F2是椭圆的另一个焦点,求△ABF2的周长. 解:根据题意画出图形如图所示, ∵A,B在椭圆4x2+y2=1上,a2=1, ∴2a=2. ∴|AF1|+|AF2|=2a=2, |BF1|+|BF2|=2a=2. ∴|AF1|+|BF1|+|AF2|+|BF2|=4, 即|AB|+|AF2|+|BF2|=4. ∴△ABF2的周长为4.
探究一
探究二
探究三
探究四
求椭圆的标准方程 【例2】 求适合下列条件的椭圆的标准方程: (1)两个焦点的坐标分别是(-4,0),(4,0),椭圆上任意一点P到两焦点 的距离的和等于10;
(2)两个焦点的坐标分别为(0,-2),(0,2),并且椭圆经过点 - , (3)经过两点(2,- √2), -1,
探究一
探究二
探究三
探究四
解:如图,建立平面直角坐标系,使x轴经过点B,C,原点O与BC的中 点重合. 由已知|AB|+|AC|+|BC|=16,|BC|=6,有|AB|+|AC|=10>6,即点A的 轨迹是椭圆,且2c=6,2a=16-6=10. ∴c=3,a=5,b2=52-32=16. 但当点A在直线BC上,即y=0时,A,B,C三点不能构成三角形,
数学第三章1.1椭圆及其标准方程课件(北师大版选修2-1)

25 9
(2)由于椭圆的焦点在 y 轴上, ∴设它的标准方程 为ya22+xb22= 1(a>b>0).
由于椭圆经过点 (0, 2)和 (1, 0),
∴
a42+b02= a02+b12=
11, ,∴ab22= =
4, 1.
故所求椭圆的标准 方程为y2+ x2= 1. 4
【名师点评】 本例中的解法体现了求椭圆 方程的一般方法,通过“定位”与“定量” 两个过程可求得所求椭圆的方程.
93
法二:由已知,设椭圆的方程是 Ax2+By2=1
(A>0, B>0, A≠ B),
故6A+B=1, ⇒ 3A+2B=1,
A=1, 9
B= 1, 3
即所求的椭圆的标 准方程是x2 +y2 = 1. 93
椭圆定义及标准方程的应用
已知椭例圆2的焦点是F1(-1,0),F2(1,0), P为椭圆上一点,且|F1F2|是|PF1|和|PF2|的等 差中项. (1)求椭圆的方程; (2)若点P在第二象限,且∠PF1F2=120°,求 △PF1F2的面积.
第三章 圆锥曲线与方程
•§1 椭 圆 •1.1 椭圆及其标准方程
学习导航
学习目标
重点难点 重点:椭圆的定义及其标准方程. 难点:椭圆的标准方程的推导过程.
新知初探思维启动
1.椭圆的定义 (1)椭圆的定义 平面内到两个定点F1,F2的距离之和等于常数 (大于|F1F2|)的点的集合叫作椭圆. 这两个定点F1,F2叫作椭圆的焦点,两个焦点 F1,F2间的距离叫作椭圆的焦距.
25 16
4.若方程xa22-ya2=1 表示焦点在 y 轴上的椭圆, 则 a 的取值范围是______. 解析:∵a2>0,xa22-ya2=1 即xa22+-y2a=1, ∴-a>a2,-1<a<0.
(2)由于椭圆的焦点在 y 轴上, ∴设它的标准方程 为ya22+xb22= 1(a>b>0).
由于椭圆经过点 (0, 2)和 (1, 0),
∴
a42+b02= a02+b12=
11, ,∴ab22= =
4, 1.
故所求椭圆的标准 方程为y2+ x2= 1. 4
【名师点评】 本例中的解法体现了求椭圆 方程的一般方法,通过“定位”与“定量” 两个过程可求得所求椭圆的方程.
93
法二:由已知,设椭圆的方程是 Ax2+By2=1
(A>0, B>0, A≠ B),
故6A+B=1, ⇒ 3A+2B=1,
A=1, 9
B= 1, 3
即所求的椭圆的标 准方程是x2 +y2 = 1. 93
椭圆定义及标准方程的应用
已知椭例圆2的焦点是F1(-1,0),F2(1,0), P为椭圆上一点,且|F1F2|是|PF1|和|PF2|的等 差中项. (1)求椭圆的方程; (2)若点P在第二象限,且∠PF1F2=120°,求 △PF1F2的面积.
第三章 圆锥曲线与方程
•§1 椭 圆 •1.1 椭圆及其标准方程
学习导航
学习目标
重点难点 重点:椭圆的定义及其标准方程. 难点:椭圆的标准方程的推导过程.
新知初探思维启动
1.椭圆的定义 (1)椭圆的定义 平面内到两个定点F1,F2的距离之和等于常数 (大于|F1F2|)的点的集合叫作椭圆. 这两个定点F1,F2叫作椭圆的焦点,两个焦点 F1,F2间的距离叫作椭圆的焦距.
25 16
4.若方程xa22-ya2=1 表示焦点在 y 轴上的椭圆, 则 a 的取值范围是______. 解析:∵a2>0,xa22-ya2=1 即xa22+-y2a=1, ∴-a>a2,-1<a<0.
3.1.1 椭圆及其标准方程 课件(北师大选修2-1)

提示:相同.
返回
问题2:这种游戏设计的原理是什么? 提示:椭圆的定义.椭圆上的点到两焦点距离之 和为定值. 问题3:在游戏中,选手所跑的路程能否等于两焦 点间的距离?为什么? 提示:不能.椭圆上的点到两焦点距离之和一定
大于两焦点间的距离.
返回
椭圆的定义
定义
焦点
平面内到两个定点F1,F2的 距离之和等于常数 (大于|F2|)的点的集合叫作椭圆 两个 定点 F1,F2叫作椭圆的焦点
返回
[例3]
(12分)已知圆B:(x+1)2+y2=16及点A(1,0),C
为圆B上任意一点,求AC的垂直平分线l与线段CB的交点P 的轨迹方程. [思路点拨] P为AC垂直平分线上的点,则|PA|=|PC|,
而BC为圆的半径,从而4=|PA|+|PB|,可得点P轨迹为以A、
B为焦点的椭圆.
返回
[精解详析]如图所示,连接AP,∵l垂直平分AC, ∴|AP|=|CP|. ∴|PB|+|PA|=|BP|+|PC|=4, ∴P点的轨迹是以A,B为焦点的椭圆. ∵2a=4,2c=|AB|=2, ∴a=2,c=1,b2=a2-c2=3. x2 y2 ∴点P的轨迹方程为 4 + 3 =1. (10分) (12分) (8分) (3分)
y2 x2 轴上时,方程为36+35=1.
答案:D 返回
2.已知椭圆C经过点A(2,3),且点F(2,0)为其右焦点,求 椭圆C的标准方程.
x2 y2 解:依题意,可设椭圆 C 的方程为a2+b2=1(a>b>0),且可 知左焦点为 F′(-2,0).
c=2, 从而有 2a=|AF|+|AF′|=3+5=8, c=2, 解得 a=4.
返回
4.平面内有一个动点M及两定点A,B.设p:|MA|+|MB|为
高中数学北师大版选修2-1 3.1.1.2椭圆及其标准方程习题课 课件(27张)

题型一
题型二
题型三
题型四
解:(方法一)由已知的椭圆方程为 ������2
+
������2 ������
2
= 1(������ > ������ >
4
������2 0), 由 9
+
������2 4
= 1 得c2 =5, ∴a2 -
b2 =5, ① 又点 Q(2,1)在椭圆上, 则 ������2 +
+
������2 ������2
= 1(������ > ������ > 0) 上任一点, 且∠
F1PF2=α,则△ PF1F2(常称为椭圆的焦点三角形)的面积有下面的一 般求法:
M 目标导航 Z 知识梳理 D典例透析 S随堂演练
UBIAODAOHANG HISHI SHULI IANLI TOUXI
= ������ 2tan
������ . 2
在选择题、填空题中可以直接使用此公式求椭圆焦点三角形 对于椭圆上的点 P , ∠F 1 PF 2 随着点 P 从长轴端点向短轴端点 的移动而变大, 当点 P 在短轴端点时, ∠F 1 PF2 最大.
M 目标导航 Z 知识梳理 D典例透析 S随堂演练
UBIAODAOHANG HISHI SHULI IANLI TOUXI
2.焦点三角形
如图所示,椭圆上一点P与椭圆的两焦点F1,F2构成的△F1PF2称 为焦点三角形,解关于椭圆中的焦点三角形问题时,要充分利用椭 圆的定义,解三角形中的正弦定理、余弦定理等知识.如△PF1F2的 面积问题,|PF1|· |PF2|的最值问题.
������2 若点 P(x 0,y 0)是椭圆 2 ������
高中数学 3.1第1课时椭圆及其标准方程课件 北师大版选修2-1

① 解得①②得-3<a<-1 或 a>1.
当 a>1 时,③不成立.当-3<a<-1 时,得 a<-2. 综上可得:a 的取值范围是-3<a<-2.
最值问题
F1 是x92+y52=1 的左焦点,P 是椭圆上的动点,A(1,1) 为定点,则|PA|+|PF1|的最小值为________________.
[解析] (1)∵椭圆的焦点在 x 轴上,所以设它的标准方程为ax22 +by22=1(a>b>0).
∵2a= 5+32+0+ 5-32+0=10,2c=6. ∴a=5,c=3, ∴b2=a2-c2=52-32=16. ∴所求椭圆的方程为:2x52 +1y62 =1.
(2)∵椭圆的焦点在 y 轴上,所以设它的标准方程为:ay22+bx22= 1(a>b>0).
3.已知△ABC 的顶点 B、C 在椭圆x32+y2=1 上,顶点 A 是
椭圆的一个焦点,且椭圆的另外一个焦点在 BC 边上,则△ABC
的周长是( )
A.2 3
B.6
C.4 3
D.12
[答案] C
[解析] 设椭圆的另一个焦点为 F(如图),
则 △ ABC 的 周 长 为 (|AB| + |BF|) + (|CA| + |CF|) = 2a + 2a =
∴-2c≤|PF1|-|PF2|≤2c, ∴2a-2c≤2|PF1|≤2a+2c,即 a-c≤|PF1|≤a+c
∴|PF1|的最大值为 a+c,最小值为 a-C.
[总结反思] 椭圆上到某一焦点的最远点与最近点分别是长 轴的两个端点,应掌握这一性质.
[总结反思] 椭圆的焦点在哪个坐标轴上主要看标准方程 中x2和y2项分母的大小,如果x2项的分母大于y2项的分母,则椭 圆的焦点在x轴上;反之,焦点在y轴上.由于本题中x2和y2项 分母的大小不确定,因此需要进行分类讨论.
3.1.1《椭圆及其标准方程》课件(北师大版选修2-1)

(2)因为m2+n2≥2mn,
所以2(m2+n2)≥m2+n2+2mn=(m+n)2.
4 故m2+n2≥ =8,当且仅当m=n=2时,等号成立. 2
2
所以|PF1|2+|PF2|2的最小值是8, 此时P位于短轴的端点处.
焦点.
由椭圆定义知
|AB|+|BM|+|AM|=|AN|+|BN|+|BM|+|AM| =|AN|+|AM|+|BN|+|BM| =2a+2a=4a=16.
x 2 y 2 的内部,则a的取值范围是 2.(5分)点A(a,1)在椭圆 + =1 4 2
(
)
(A)- 2 <a< 2
(C)-2<a<2
(B)a<- 2 或a> 2
【解析】
x 2 y2 1.(5分)已知点M( 7 ,0),椭圆 + =1与直线y=k(x+ 7 )交 16 9
于A,B两点,则△ABM的周长为(
(A)11 (B)10
)
(C)9 (D)16
【解析】选D.如图.
直线y=k(x+ 7 )恒过定点N(- 7 ,0).
x 2 y2 由椭圆方程 + =1知M( 7 ,0),N(- 7 ,0)恰好为椭圆的两 16 9
【解析】如图所示,由题意知, F1(- 3 ,0),F2( 3 ,0). 设|PF1|=m,|PF2|=n(m>0,n>0), 由椭圆的定义知m+n=4.
(1)根据均值不等式知mn≤ ( m+n ) 2= ( 4 )2 = 4,
2 2
高中数学北师大版选修2-1 3.1.2.1椭圆的简单性质 课件(30张)

= 1 的短轴长为6,∴a2= 25,b2=9. 答案 :D
M 目标导航 Z 知识梳理 D典例透析 S随堂演练
UBIAODAOHANG HISHI SHULI IANLI TOUXI
UITANGYANLIAN
【做一做 2】 若椭圆的焦距等于它的短轴长,则椭圆的离心率 为( )
1 2 A. B. C. 2 2
2D. 2
2 , 3
答案 :B 【做一做 3】 若椭圆以坐标轴为对称轴,离心率 e = 长轴长为 6, 则椭圆的方程为( )
������2 ������2 1或 + 36 20 ������2 ������2 ������2 ������2 A. + = 1B. + = 1 36 20 9 5 ������2 ������2 ������2 ������2 ������2 ������2 C. + = 1 或 + = 1D. + 9 5 5 9 20 36
������ , ������, ������, ������之间的关系为������2 ������ ������ ������
= ������2 − ������2,
������ ������
长轴与短轴的长短关系决定椭圆形状的变化. 椭圆的离心率������ = , 用������, ������表示为������ = 1������ 2 ������ ������ , 当 越小时, 椭圆越扁 , ������越大; 当 越大时 ������ ������ ������
1.对称性
������2 椭圆 2 ������
+
= 1 是以������轴、 ������轴为对称轴的轴对称图形 ,
高中数学 第三章 圆锥曲线与方程 3.1.1 椭圆及其标准

(4)对于椭圆xa22+by22=1(a>b>0),F1,F2 为其左、右焦 点.点 P 坐标为(x1,y1). ①当点 P 落在椭圆外时,|PF1|+|PF2|>2a;xa212+by212>1; ②当点 P 落在椭圆上时,|PF1|+|PF2|=2a,xa212+by212=1; ③当点 P 落在椭圆内时,|PF1|+|PF2|<2a,xa212+by212<1.
第三 章
圆锥曲线与方程
§1 椭 圆 1.1 椭圆及其标准方程
学课前预习学案
1.影视剧中常有这样的镜头:武士为了显示自 己的功夫超群及手中刀剑锋利,对准身边树桩 或毛竹,手起刀(剑)落,劈为两截,你知道截口 是什么形状吗? [提示] 椭圆或圆形
2.你能举出几个椭圆形的例子吗? [提示] 卫星轨道,镜子,会议桌等. 3.特殊的曲线都可以看作是满足特定的条件的动 点运动的轨迹.(1)圆是动点满足什么条件时形成 的轨迹?(2)线段的垂直平分线是动点满足什么条 件时的轨迹?
1.a=6,c=1 的椭圆的标准方程是( )
பைடு நூலகம்
A.3x62+3y52 =1
B.3y62 +3x52=1
C.3x62 +y52=1
D.以上都不对
解析: ∵a=6,c=1,∴b2=a2-c2=35 ∵椭圆的焦点在x轴,还是在y轴不确定. 答案: D
2.椭圆3x2+4y2=12的两个焦点之间的距离为
()
(2)椭圆的标准方程中,焦点的位置由分母的大小 来确定.如果x2的分母大,焦点就在x轴上;如 果y2的分母大,则焦点就在y轴上.简记为“焦点 位置看大小,焦点随着大的跑”.
(3)椭圆方程中,a 表示椭圆 上的点 M 到两焦点间距离的 和的一半,可借助图帮助记 忆,a、b、c(都是正数)恰构 成一个直角三角形的三条边, a 是斜边,所以 a>b,a>c,且 a2=b2+c2,其中 c 是焦距的一半,叫做半焦距.
3.1 第1课时 椭圆及其标准方程 课件(北师大版选修2-1)(1)

• [点评] 椭圆的焦点在哪个坐标轴上主要看标 准方程中x2和y2项分母的大小,如果x2项的分 母大于y2项的分母,则椭圆的焦点在x轴上; 反之,焦点在y轴上.由于本题中x2和y2项分 母的大小不确定,因此需要进行分类讨论.
2 2 x y 式. 统一形式为 mx2+ny2=1(m>0, n>0, m≠n)或m+ n =1(m>0,
n>0,m≠n).
• 4.观察椭圆的图形,发现椭圆有两条互相垂 直的对称轴,以这两条对称轴作为坐标系的 两轴建立平面直角坐标系,在方程的推导过 程中遇到了无理方程的化简,这类方程的化 简方法:(1)方程中只有一个根式时,需将它 单独留在方程的一侧,把其他项移到另一侧; (2)方程中有两个根式时,需将它们放在方程 的两侧,并使其中一侧只有一个根式.
x2 y2 3.焦点在 x 轴上的椭圆的标准方程为________________ a2+b2=1(a>b>0) , y2 x2 焦点在 y 轴上的椭圆的标准方程为________________ a2+b2=1(a>b>0) ,其中 a
a>b 与 b 的关系为_______. a2=b2+c2 4.椭圆的标准方程中,a、b、c 之间的关系是__________.
• 4.通过椭圆的标准方程的推导,使学生进一 步掌握求曲线方程的一般方法,并渗透数形 结合和等价转化的思想方法,提高运用坐标 法解决几何问题的能力. • 5.通过让学生大胆探索椭圆的定义和标准方 程,激发学生学习数学的积极性,培养学生 的学习兴趣和创新意识.
重点难点点拨
• 本节重点:椭圆的定义和椭圆标准方程的两 种形式. • 本节难点:椭圆标准方程的建立和推导.
思路方法技巧
• 椭圆的标准方程
高中数学北师大版选修2-1 3.1.1.1椭圆及其标准方程 课件(30张)

������2 或 ������ ������2 + ������
= 1(������ > 0, ������ > 0, ������≠n).
M 目标导航 Z 知识梳理 D典例透析 S随堂演练
UBIAODAOHANG HISHI SHULI IANLI TOUXI
UITANGYANLIAN
【做一做 2-1】 A.(±4,0) C.(± 3,0) 答案 :D
M 目标导航 Z 知识梳理 D典例透析 S随堂演练
UBIAODAOHANG HISHI SHULI IANLI TOUXI
UITANGYANLIAN
【做一做1】 命题甲:动点P到两个定点A,B的距离之和 |PA|+|PB|=2a(a>0,且a为常数),命题乙:P点的轨迹是椭圆,则命题甲 是命题乙的( ) A.充分不必要条件 B.必要不充分条件 C.充要条件 D.既不充分又不必要条件
M 目标导航 Z 知识梳理 D典例透析 S随堂演练
UBIAODAOHANG HISHI SHULI IANLI TOUXI
UITANGYANLIAN
解析:若P点的轨迹是椭圆,则一定有|PA|+|PB|=2a(a>0,且a为常 数 ). ∴甲是乙的必要条件. 反过来,若|PA|+|PB|=2a(a>0,且a为常数),是不能推出P点的轨迹 是椭圆的.这是因为,仅当2a>|AB|时,P点的轨迹才是椭圆;而当 2a=|AB|时,P点的轨迹是线段AB;当2a<|AB|时,P点无轨迹. ∴甲不是乙的充分条件. 故甲是乙的必要不充分条件. 答案:B
M 目标导航 Z 知识梳理 D典例透析 S随堂演练
UBIAODAOHANG HISHI SHULI IANLI TOUXI
= 1(������ > 0, ������ > 0, ������≠n).
M 目标导航 Z 知识梳理 D典例透析 S随堂演练
UBIAODAOHANG HISHI SHULI IANLI TOUXI
UITANGYANLIAN
【做一做 2-1】 A.(±4,0) C.(± 3,0) 答案 :D
M 目标导航 Z 知识梳理 D典例透析 S随堂演练
UBIAODAOHANG HISHI SHULI IANLI TOUXI
UITANGYANLIAN
【做一做1】 命题甲:动点P到两个定点A,B的距离之和 |PA|+|PB|=2a(a>0,且a为常数),命题乙:P点的轨迹是椭圆,则命题甲 是命题乙的( ) A.充分不必要条件 B.必要不充分条件 C.充要条件 D.既不充分又不必要条件
M 目标导航 Z 知识梳理 D典例透析 S随堂演练
UBIAODAOHANG HISHI SHULI IANLI TOUXI
UITANGYANLIAN
解析:若P点的轨迹是椭圆,则一定有|PA|+|PB|=2a(a>0,且a为常 数 ). ∴甲是乙的必要条件. 反过来,若|PA|+|PB|=2a(a>0,且a为常数),是不能推出P点的轨迹 是椭圆的.这是因为,仅当2a>|AB|时,P点的轨迹才是椭圆;而当 2a=|AB|时,P点的轨迹是线段AB;当2a<|AB|时,P点无轨迹. ∴甲不是乙的充分条件. 故甲是乙的必要不充分条件. 答案:B
M 目标导航 Z 知识梳理 D典例透析 S随堂演练
UBIAODAOHANG HISHI SHULI IANLI TOUXI
相关主题
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
返回
[一点通] 求椭圆标准方程的一般步骤为:
返回
1.若 a=6,b= 35,则椭圆的标准方程是 ( ) x2 y2 A.36+35=1 y2 x2 x2 y2 B. 6 + =1 或 6 + =1 35 35 x2 C.36+y2=1 x2 y2 y2 x2 D.36+35=1 或36+35=1 x2 y2 解析:椭圆的焦点在 x 轴上时,方程为36+35=1,在 y
返回
即|PF2|=4-|PF1|. 6 将②代入①解得|PF1|=5,
②
1 1 6 3 3 3 ∴S△ PF1F2=2|PF1|· 1F2|· 120° 2× × 2 = 5 . |F sin = 5 2× 3 因此所求△ PF1F2 的面积是5 3.
返回
[一点通]
椭圆上一点 P 与椭圆的两焦点 F1、F2 构成的
a2=15, 解得 2 b =5.
x2 y2 所以所求椭圆的方程为 + =1. 15 5
返回
y2 x2 ②当焦点在 y 轴上时,设椭圆的标准方程为 2+ 2=1(a a b >b>0).依题意有 -22 32 2 + 2 =1, b a 2 1 -2 3 a2+ b2 =1,
形问题的常用方法.
返回
点击下图进入“应用创新演练”
返回
返回
[例 2]
如图所示, 已知椭圆的方程
x2 y2 为 4 + 3 =1,若点 P 在椭圆上,F1,F2 为椭圆的两个焦点,且∠PF1F2=120° , 求△ PF1F2 的面积. [思路点拨] 因为∠PF1F2=120°,|F1F2|=2c,所以要
求S△PF1F2,只要求|PF1|即可.可由椭圆的定义|PF1|+|PF2| =2a,并结合余弦定理求解. 返回
返回
1.用待定系数法求椭圆的标准方程时,若已知焦点的位 置,可直接设出标准方程;若焦点位置不确定,1(A>0,B>0,A≠B)求解.
2.解决与椭圆有关的轨迹问题时,要注意检验所得到的 方程的解是否都在曲线上. 3.涉及椭圆的焦点三角形问题,可结合椭圆的定义列出 |PF1|+|PF2|=2a求解,因此回归定义是求解椭圆的焦点三角
y2 x2 轴上时,方程为36+35=1.
答案:D 返回
2.已知椭圆C经过点A(2,3),且点F(2,0)为其右焦点,求 椭圆C的标准方程.
x2 y2 解:依题意,可设椭圆 C 的方程为a2+b2=1(a>b>0),且可 知左焦点为 F′(-2,0).
c=2, 从而有 2a=|AF|+|AF′|=3+5=8, c=2, 解得 a=4.
解得 a2=4,b2=1.
返回
y2 x2 若焦点在 y 轴上,设椭圆方程为 a2+ b2 =1(a>b>0),同理
a2=1, 2 b =4,
这与 a>b 矛盾.
x2 2 故所求椭圆方程为 4 +y =1.
返回
法二:设椭圆的方程为 mx2+ny2=1(m>0,n>0,m≠n). 4m=1, 将 A,B 坐标代入得 3 m+4n=1, 1 m= , x2 2 4 解得 故所求椭圆方程为 4 +y =1. n=1,
焦距
集合语言
两焦点F1,F2间的 距离 叫作椭圆的焦距 P={M| |MF1|+|MF2|=2a, >|F |}
2
返回
在平面直角坐标系中,已知A(-2,0),B(2,0),C(0,2), D(0,-2). 问题1:若动点P满足|PA|+|PB|=6,则P点的轨迹方 程是什么? x2 y2 提示:9 + 5 =1. 问题2:若动点P满足|PC|+|PD|=6,则动点P的轨 迹方程是什么? y 2 x2 提示: 9 + 5 =1. 返回
[精解详析]
由已知 a=2,b= 3,
所以 c= a2-b2=1,|F1F2|=2c=2, 在△ PF1F2 中,由余弦定理得 |PF2|2=|PF1|2+|F1F2|2-2|PF1|· 1F2|· 120° |F cos , 即|PF2|2=|PF1|2+4+2|PF1|. 由椭圆定义,得|PF1|+|PF2|=4, ①
∴a+c=2b=4,即|AB|+|BC|=4, ∴点 B 到定点 A、C 的距离之和为定值 4,由椭圆定义知 B 点的轨迹为椭圆,其中 a′=2,c′=1. ∴b′2=3. 又∵A、B、C 三点共线时不能构成三角形, x2 y2 ∴顶点 B 的轨迹方程为 4 + 3 =1(y≠0).
返回
8.已知动圆M过定点A(-3,0),并且在定圆B:(x-3)2+y2
2.椭圆的标准方程有两种形式,若含x2项的分母大于
含y2项的分母,则椭圆的焦点在x轴上,反之焦点在y轴上.
返回
返回
[例 1]
写出适合下列条件的椭圆的标准方程:
(1)a=4,c=3,焦点在 y 轴上; (2)a+b=8,c=4; (3)经过点 A( 3,-2)和点 B(-2 3,1). [思路点拨] 求椭圆的标准方程时,要先判断焦
=|AF1|+|BF1|+|AF2|+|BF2|=4a=16.
答案:B 返回
x2 2 6.点 P 在椭圆 4 +y =1 上,且 PF1⊥PF2,求 S△ PF1F2. 解:∵点 P 在椭圆上∴|PF1|+|PF2|=4,
即|PF1|2+|PF2|2+2|PF1||PF2|=16, 又 PF1⊥PF2∴|PF1|2+|PF2|2=|F1F2|2=12, ∴|PF1||PF2|=2, 1 ∴S△ PF1F2=2|PF1||PF2|=1.
又 a2=b2+c2,所以 b2=12, x2 y2 故椭圆 C 的标准方程为16+12=1.
返回
3.求焦点在坐标轴上,且过点 A(2,0)和 准方程.
B1,
3 的椭圆的标 2
x2 y2 解: 法一: 若焦点在 x 轴上, 设椭圆方程为a2+b2=1(a>b>0), 4 a2=1, 依题意,有 12+ 3 2=1, a 4b
a2=5, 解得 2 b =15.
舍去,
x2 y2 故所求椭圆的方程为 + =1. 15 5
返回
法二:设所求椭圆的方程为 mx2+ny2=1(m>0,n>0, 且 m≠n). 1 3m+4n=1, m=15, 依题意有 解得 12m+n=1, n=1. 5 x2 y2 所以所求椭圆的方程为 + =1. 15 5
返回
4.平面内有一个动点M及两定点A,B.设p:|MA|+|MB|为
定值,q:点M的轨迹是以A,B为焦点的椭圆.那么(
A.p是q的充分不必要条件 B.p是q的必要不充分条件 C.p是q的充要条件 D.p既不是q的充分条件,又不是q的必要条件
)
解析:若|MA|+|MB|为定值,只有定值>|AB|时,点M轨迹
提示:相同.
返回
问题2:这种游戏设计的原理是什么? 提示:椭圆的定义.椭圆上的点到两焦点距离之 和为定值. 问题3:在游戏中,选手所跑的路程能否等于两焦 点间的距离?为什么? 提示:不能.椭圆上的点到两焦点距离之和一定
大于两焦点间的距离.
返回
椭圆的定义
定义
焦点
平面内到两个定点F1,F2的 距离之和等于常数 (大于|F2|)的点的集合叫作椭圆 两个 定点 F1,F2叫作椭圆的焦点
a+b=8, (2) 2 a -b2=16 a+b=8, ⇒ a-b=2 a+b=8, ⇒ a+ba-b=16 a=5, ⇒ b=3.
返回
x2 y2 y2 x2 ∴椭圆的标准方程为 + =1,或 + =1. 25 9 25 9 (3)法一:①当焦点在 x 轴上时,设椭圆的标准方程为 x2 y2 + =1(a>b>0). a2 b2 32 -22 2 + 2 =1, b a 依题意有 2 -2 3 1 a2 +b2=1,
返回
[例3]
(12分)已知圆B:(x+1)2+y2=16及点A(1,0),C
为圆B上任意一点,求AC的垂直平分线l与线段CB的交点P 的轨迹方程. [思路点拨] P为AC垂直平分线上的点,则|PA|=|PC|,
而BC为圆的半径,从而4=|PA|+|PB|,可得点P轨迹为以A、
B为焦点的椭圆.
返回
[精解详析]如图所示,连接AP,∵l垂直平分AC, ∴|AP|=|CP|. ∴|PB|+|PA|=|BP|+|PC|=4, ∴P点的轨迹是以A,B为焦点的椭圆. ∵2a=4,2c=|AB|=2, ∴a=2,c=1,b2=a2-c2=3. x2 y2 ∴点P的轨迹方程为 4 + 3 =1. (10分) (12分) (8分) (3分)
椭圆的标准方程 焦点在x轴上 标准方程 焦点坐标 a、b、c
x y a2+b2=1(a>b>0)
2 2
焦点在y轴上
y2 x2 a2+b2=1(a>b>0)
(±c,0) a2-b2=c2
(0,±c)
的关系
返回
1.平面内点M到两定点F1,F2的距离之和为常数2a, 当2a>|F1F2|时,点M的轨迹是椭圆; 当2a=|F1F2|时,点M的轨迹是一条线段F1F2; 当2a<|F1F2|时,点M的轨迹不存在.
=64的内部与其相内切,求动圆圆心M的轨迹方程.
解: 设动圆 M 和定圆 B 内切于点 C, 由|MA|=|MC|得|MA| +|MB|=|MC|+|MB|=|BC|=8,即动圆圆心 M 到两定点 A(-3,0),B(3,0)的距离之和等于定圆的半径, ∴动圆圆心 M 的轨迹是以 A、B 为焦点的椭圆, 且 2a=8,2c=6,b= a2-c2= 7, x2 y2 ∴M 的轨迹方程是16+ 7 =1.
返回
设计游戏时,要考虑游戏的公平性.某电视台少儿节目欲 设计如下游戏.规则是:参赛选手站在椭圆的一个焦点处,快 速跑到随机出现在椭圆上的某一点处,然后再跑向另一个焦点, 用时少者获胜.考验选手的反应能力与速度. 问题1:参赛选手要从椭圆的一焦点跑向椭圆上随机一点 再跑向椭圆的另一焦点,每个参赛选手所跑的路程相同吗?
