重叠问题

合集下载

重叠问题

重叠问题1、教室里每一组的人数同样多，小华的座位从前面数是第5个，从后面数是第2个，从左边数是第3个，从右边数是第6个，问：全班一共有多少人呢？2，小朋友排队去春游，排了很多队，每队人数都一样。

小虎的位置无论从前数还是后数，从左数还是从右数，都是在第6个，问：有多少个小朋友去春游呢？3，小华在上课的时候要用到一张50厘米长的纸条，但他只有两张长为30厘米，不剪断而把它们贴在一起，问：重叠的部分有几厘米？4，两块木板钉在一起长为180里面，中间重叠的部分为34厘米，已知其中一快木板长为120厘米，问：另外一块木板长多少厘米？5，小朋友参加兴趣小组，其中参加数学的有40人，参加英语的有32人，两项都参加的有12人，问：一共有多少个小朋友参加兴趣小组呢？6、学校文艺组的成员每人至少会演奏一种乐器，会拉二胡的有24人，会弹钢琴的有17人，两种都会的有8人，这个文艺组有多少人？姓名7、全班36个同学在一项测试中，做对第一题的有25人，做对第二题的有23人，两道题都做对的有15人，问两题都做错的有多少人？8、某校选出50名学生参加作文比赛和数学比赛，结果其中有3人两项比赛都获奖，有27人两项都没有获奖，已知作文比赛获奖的有14人，问数学比赛获奖的有多少人？9、三年（1）班有15人会游泳，有12人会骑自行车，有7人既会骑车又会游泳，有21人两者都不会，那么三年（1）班有多少人？10、有一个长方形和一个正方形，如图，放在桌上，那么这两个图形盖住桌面的面积是多少？11、两个正方形拼成一个图形，如下图，求这个图形的面积。

另：有10箱苹果，如果从每箱中都取出5千克，剩下的比原来的一半多25千克，原来每箱苹果有多少千克？重叠问题姓名1、教室里每一组的人数同样多，小华的座位从前面数是第5个，从后面数是第2个，从左边数是第3个，从右边数是第6个，问：全班一共有多少人呢？2，两块木板钉在一起长为180里面，中间重叠的部分为34厘米，已知其中一快木板长为120厘米，问：另外一块木板长多少厘米？3、学校文艺组的成员每人至少会演奏一种乐器，会拉二胡的有24人，会弹钢琴的有17人，两种都会的有8人，这个文艺组有多少人？4、三年（1）班有15人会游泳，有12人会骑自行车，有7人既会骑车又会游泳，有21人两者都不会，那么三年（1）班有多少人？5、两个正方形拼成一个图形，如下图，求这个图形的面积。

第20讲重叠问题(含解题思路和参考答案)

第20讲重叠问题（含解题思路与参考答案）一、解题方法1. 解答重叠问题，要用到数学中一个重要原理一一包含与排除原理，即当两个计数部分有重复包含时，为了不重复计算，应从他们的和中排除重复部分。

2. 解答重叠问题的应用题，必须从条入手进行认真的分析，有时还要画出图示，借助图形进行思考，找出哪些是重复的，重复了几次，明确要求的是哪一部分，从而找出解答方法。

3. 在数学中，我们经常用平面上封闭曲线的内部代表集合与集合之间的关系，这种图称为韦恩图(也叫文氏图)。

例题1.两块一样长的木板搭在一起共长160厘米，中间重叠部分是20厘米，如图，这两块木板各长多少厘米？解题思路：解题过程：把等长的两块木板的一端搭起来，搭在一起的长度就是重叠部分，重叠部分20厘米，所以这两块木板的总长度是160+20＝180（厘米），每块木板的长度是180÷2＝90（厘米）解：（160+20）÷2 ＝180÷2＝90（厘米）答：这两块木板各长90厘米。

巩固练习1. 把两根同样长的绳子的一端捆绑在一起，共长120厘米，两根绳子捆在一起的重叠部分长12厘米，原来两根绳子各长多少厘米？2. 两块一样长的红条幅缝在一起，变成一块长条幅，现在这两块条幅共长22米，中间重叠部分长6分米，原来两块条幅各长多少分米？3. 一根长80厘米的木棍，不小心被折成了长短不一的两段，现在把两段接起来，其中重叠部分长6厘米，两根木棍接起来后共长多少厘米？例题2.三(2)班同学排队做操，每行人数相同，亮亮的位置从左数起是第5个，从右数是第4个，从前数是第2个，从后数是第4个。

三(2)班共有多少人？解题思路：解题过程：根据题意画右图。

由图可看出：亮亮的位置从左数起是第5个，从右数是第4个，说明横有5+4－1＝8（个）人；从前数是第2个，从后数是第4个，说明竖行有2+4－1＝5（个）人。

所以二（3）班有8×5＝40（个）（说明：减“1”是因为亮亮重复数了一次）解：（5+4－1）×（2+4－1）＝8×5＝40（人）答：三（2）班共有40人。

重叠问题

42人象棋 21人
？人
围棋17人
42-10=32（名）
21+17-32=6（名）
都没参加10人
答：两种棋都会下的有6名同学。
学校乐器队招收了42名新学员，其中会拉小提琴的有25名，会弹电子琴的有22名，两项都不会的有3名。两项都会的有多少名？
三六班才艺赛
三六班有学生55人，参加学校绘画比赛的有20人，即参加绘画比赛又参加书法比赛的有12人，两项比赛都没参加的有14 人。参加书法比赛的有多少人？三六班
音乐 32人
10 人美术 30人
？人
32+30-10=52（人）答：三五班共有学生52人。
三五班定《数学报》的有32人，订《语文报》的有30人，两份报纸都定的有10人，全班每人至少订一种报纸，三五班有学生多少人？
共有学生55人，每人至少参加跳绳和踢毽子比赛中的一种，已知参加跳绳的有36人，参加踢毽子的有38人。两项比赛都参加的有几人？踢毽子38
55人
绘画 20人
12 人
书法？人
都没参加14人
55-14=41（人） 41-20+12=33（人）
答：参加书法比赛的有33人。
乐器兴趣小组有42人，其中会弹钢琴的有27人，即会弹钢琴又会弹古筝的有16人，两项都不会的只有1人。会弹古筝的有多少人？
两个妈妈和两个女儿去动物园，只买了三张票就进去了，这是为什么呢？
因为是姥姥、妈妈、女儿祖孙三代。
重叠问题：当把一些事物进行归纳分类后，有些事物是重复出现的，像这样的问题称为重叠问题。
重叠问题
例1.学校组织看文艺表演，东东的座位从左数起是第7个，从右数起是第10个，这一行座位有多少个？

重叠问题课件ppt

来验证假设的有效性。
诊断重叠问题的工具和方法
鱼骨图
用于展示问题产生的原因和影响，帮助团队全面了解问题的
各个方面。
5W分析法
通过对问题进行“为什么、是什么、在哪里、何时、谁”的分析，深入挖掘问题的根源。
流程图
用于梳理业务流程，发现流程中的瓶颈和问题。
数据分析
利用统计学和数据挖掘技术，对大量数据进行深入分析，发
现数据背后的规律和趋势。
重叠问题的根源分析
组织结构问题
组织结构不合理，导致部门间沟通不畅、职责
不明确。
流程问题
业务流程存在缺陷或不合理之处，导致工作效
率低下、资源浪费。
文化问题
企业文化不健康，缺乏团队协作精神、创新精
神。
人员素质问题
员工素质不高，缺乏必要的技能和知识，导致
工作质量低下。
2023
流程再造
对不合理流程进行重新设计，提高流程效率和效益。
信息化管理
利用信息技术手段，实现流程自动化和智能化。
资源整合
资源共享
实现资源在不同部门间的共享，提高资源利用效率。
集中采购
通过集中采购降低成本，提高采购效益。
内部市场
建立内部市场机制，促进资源优化配置和有效利用。
激励机制设计
目标管理
2023
重叠问题课件
REPORTING
2023
目录
• 引言 • 重叠问题的识别与诊断 • 解决重叠问题的策略 • 重叠问题的案例分析 • 总结与展望
2023
PART 01
引言
REPORTING
什么是重叠问题
重叠问题是指两个或多个物体或形状在空间上部分或全部重叠在一起的问题。

重叠问题

1、无重叠，求排队总数
小朋友排队玩滑梯，小花前面4个人，后面5个人，一共几个人？
小朋友排队玩滑梯，从前面数小花是第4，她后面有5个人，一共几个人？
小朋友排队坐车去旅行，小花前面有4个人，从后面数小花是第5个人，一共几个人？
2、有重叠，求排队总数
森林里举行赛跑比赛，兔子从前面排第3，从后面排第6，一共有几只小动物参加比赛？
3、已知排队总数，无重叠
小明有8辆车，从左向右排成一排，他从左边数排第4，他的后面还有几辆车？
他从右边数排第3，他的前面还有几辆车？
4、已知排队总数，有重叠
小动物们排队分果果，一共有10只小动物，花栗鼠从前数排在第七个，从后面数他排在第几个？
小动物们排队分果果，一共有10只小动物，小兔子从后面数排在第5个，从前面数他是排在第几个呢？
5、已知排队总数，求位置
一群小动物们排队去河边玩耍，一共有（）小动物，从左面数排在第3位的是谁（），从后面数排在第4个的是（），小金鱼排在第（）位，长颈鹿排在第（）位。

、。

第20讲重叠问题含解题思路和参考答案

第20讲重叠问题仁解题思路与参考答案）一、解题方法1 .解答重叠问题，要用到数学中一个重要原理一一包含与排除原理，即当两个计数部分有重复包含时，为了不重复计算，应从他们的和中排除重复部分。

2 .解答重叠问题的应用题，必须从条入手进行认真的分析，有时还要画出图示，借助图形进行思考，找出哪些是重复的，重复了几次，明确要求的是哪一部分，从而找出解答方法。

3 .在数学中，我们经常用平面上封闭曲线的内部代表集合与集合之间的关系，这种图称为韦恩图（也叫文氏图）。

例题1.两块一样长的木板搭在一起共长160厘米，中间重叠部分是20厘米，如图，这两块木板各长多少厘米?解题思路: 把等长的两块木板的一端搭起来，搭在一起的长度就是重叠部分，重叠部分20 厘米，所以这两块木板的总长度是160+20 = 180 （厘米），每块木板的长度是180-2 =90 （厘米）答：这两块木板各长90厘米。

巩固练习1.把两根同样长的绳子的一端捆绑在一起，共长120厘米，两根绳子捆在一起的重叠部分长12厘米，原来两根绳子各长多少厘米？4 .两块一样长的红条幅缝在一起，变成一块长条幅，现在这两块条幅共长 22米，中间重叠部分长6分米，原来两块条幅各长多少分米？5 . 一根长80厘米的木棍，不小心被折成了长短不一的两段，现在把两段接起来，其中重叠部分长6厘米，两根木棍接起来后共长多少厘米？解题过程:解：（160+20）-2= 180-2 =90 （厘米）例题2.三（2）班同学排队做操，每行人数相同，亮亮的位置从左数起是第5 个，巩固练习1.同学们排队表演节目，每行人数同样多，小林的位置从左数是第6个，从右数是第1个，从前数是第3个，从后数狮第2个。

表演的同学共有多少人？2 .小红在一张方格纸上练字，它每行、每列写的同样多，“国"字的位置从上是第4个，从下数第5个，从左数、右数都是第3个。

小红一共写了多少个字？3 .同学们排队做操，每行、每列人数同样多，小兰的位置无论从前数，从后数，从左数、从右数都是第5个，做操的共有多少人？例题3.三（4）班有学生48人，写完语文作业的有23人，写完数学作业的有 29巩固练习1.三(1)班有60人，每人都参加了航模或书法课外兴趣小组，参加航模小组的有34人，参加书法小组的有40人。

二年级数学重叠问题

二年级数学重叠问题一、知识点讲解1. 重叠问题的概念在数学中，重叠问题是指有部分元素在不同的集合中重复出现的情况。

例如，同学们参加语文小组和数学小组，有一些同学既参加了语文小组又参加了数学小组，这就是重叠部分。

2. 解决重叠问题的方法常用的方法是画韦恩图（集合图）来直观地表示各个集合以及它们之间的重叠关系。

另外，也可以通过计算来解决，计算时要注意避免重复计算重叠部分。

例如：计算参加两个小组的总人数时，如果直接把参加语文小组的人数和参加数学小组的人数相加，就会把既参加语文小组又参加数学小组（重叠部分）的人数多计算一次，所以需要减去重叠部分的人数。

二、经典例题及解析1. 例题1题目：二（1）班同学参加课外活动，有20人参加英语班，25人参加电脑班，其中有10人两个班都参加了。

二（1）班一共有多少人参加课外活动？解析：我们可以画韦恩图来理解。

先画两个相交的圆，一个圆表示参加英语班的同学，另一个圆表示参加电脑班的同学，相交的部分就是两个班都参加的同学。

如果直接把参加英语班的20人和参加电脑班的25人相加：20 + 25=45（人），这里面把两个班都参加的10人重复计算了一次。

所以正确的计算方法是：20+25 10 = 35（人）。

2. 例题2题目：学校乐器队招收了42名新学员，其中会拉小提琴的有25名，会弹钢琴的有22名，两项都不会的有3名。

两项都会的有多少名？解析：我们知道总共有42名新学员，其中两项都不会的有3名，那么至少会一项乐器的学员有42 3 = 39（名）。

会拉小提琴的有25名，会弹钢琴的有22名，那么25+22 = 47（名），这个数字比至少会一项乐器的39名多。

多出来的部分就是两项都会的人数，即47 39 = 8（名）。

3. 例题3题目：把两块一样长的木板钉在一起，钉成一块长35厘米的木板，中间重叠部分长11厘米。

这两块木板各长多少厘米？解析：两块木板钉在一起后总长度是35厘米，但是中间重叠了11厘米。

三年级奥数4种重叠问题

三年级奥数4种重叠问题
以下是三年级奥数中的 4 种重叠问题:
1. 鸡兔同笼问题：假设有若干只鸡和若干只兔子，它们共有若干只脚。

如果假设其中的一些鸡变成了兔子，那么脚的总数会增加;如果假设其中的一些兔子变成了鸡，那么脚的总数会减少。

问有多少只鸡和兔子？
2. 重叠盒子问题：有若干个盒子，每个盒子都可以容纳若干只小动物。

现在要根据每个盒子的容量，将小动物平均分到每个盒子中。

问有多少个盒子和小动物？
3. 重叠蛋糕问题：有若干个蛋糕，每个蛋糕都可以切成若干份。

现在要根据每个蛋糕的切块数，将蛋糕平均分到每个小朋友手中。

问有多少个蛋糕和小朋友？
4. 重叠排队问题：有若干个小朋友，每个小朋友都可以排在若干种位置。

现在要根据每个小朋友的位置，将小朋友排队。

问有多少个小朋友和排队方式？。

小学数学重叠问题

小学数学重叠问题在小学数学的学习中，我们常常会遇到一种特殊的数学问题，那就是重叠问题。

这种问题通常涉及到两个或多个集合之间的重叠部分，以及这些部分与各个集合之间的关系。

解决重叠问题的关键是理解并应用集合论的基本概念和运算规则。

一、什么是重叠问题？重叠问题是指在一个集合中，另一个集合的元素与之有部分重合，或者两个集合的元素完全重合。

例如，在一群学生中，有的学生既参加数学小组也参加科学小组，这就是两个集合的重叠。

二、如何解决重叠问题？解决重叠问题的关键是正确理解和应用集合论的基本概念和运算规则。

以下是解决重叠问题的基本步骤：1、确定问题的集合：我们需要确定问题的集合，包括所有的元素和它们之间的关系。

例如，在一群学生中，我们需要确定哪些学生参加了数学小组，哪些学生参加了科学小组，以及哪些学生同时参加了两个小组。

2、识别重叠部分：接下来，我们需要识别出集合之间的重叠部分。

在上述例子中，我们需要找出哪些学生既参加了数学小组也参加了科学小组。

3、应用集合运算规则：我们需要应用集合运算规则来解决问题。

例如，如果我们想知道参加数学小组的学生总数，我们需要把只参加数学小组的学生和既参加数学小组又参加科学小组的学生都计算在内。

三、如何避免重叠问题的误解？解决重叠问题时，我们需要注意以下几点以避免误解：1、仔细阅读题目：理解题目中的每个集合和它们之间的关系是解决重叠问题的关键。

我们需要仔细阅读题目，理解每个集合的元素和它们之间的关系。

2、正确应用集合运算规则：在计算集合的元素个数时，我们需要正确应用集合运算规则，例如并集、交集等。

如果我们错误地应用了运算规则，可能会导致误解。

3、画出集合图：画出集合图可以帮助我们更好地理解集合之间的关系和重叠部分。

通过画出图形，我们可以更直观地看到哪些元素属于哪个集合，以及它们之间的重合部分。

四、例子：解决一个简单的重叠问题为了更好地理解重叠问题的解决方法，让我们看一个简单的例子。

假设在一个班级中，有30个学生，其中10个学生同时参加了数学小组和科学小组，5个学生只参加了数学小组，10个学生只参加了科学小组。

重叠问题

重叠问题像这样重叠问题是我们生活中经常遇到的问题，今天我们就来学习有关重叠问题中的“木头重叠”和“人员重叠”。

例1：请按照示例给每个木板标数。

示例：木板长80厘米。

（1）木板长70厘米。

（2）上面的木板长70厘米，下面的木板长60厘米。

练习1：请你按照示例给每块木板标数。

示例：木板重叠部分长30厘米，下面的木板长70厘米。

（1）木板重叠部分长40厘米。

（2）上面的木板长100厘米，下面的木板长100厘米，重叠部分长50厘米。

例2：如图，一块木板长70厘米，另一块木板长80厘米，把它们钉在一起变成一块大木板，中间钉在一起的木板长20厘米。

这块大木板长多少厘米？练习2：如图，两块都是5米长的木板，把它们钉在一起变成一块大木板，中间钉在一起的木板长1米.这块大木板长多少米？对这类题目，我们可以从已知条件入手，认真分析（有时还要作图分析，借助图来思考），找出解题方法。

例3.如图一根木棍长90厘米，另一个木棍长60厘米，两个木棍钉在一起，共长120厘米，那么中间钉在一起的木棍长度是多少厘米？练习3：如图，两块一样长的木板都是10米，:钉在一起时木板共长15米，中间钉在一起的木板长度是多少米？例4：把两根一样长的钢筋焊接成长为8米的钢筋，中间焊接处的重叠部分长2米（如下图），这两根钢筋原来分别长多少米？练习4：把两块一样长的木板:钉成长为120厘米的大木板，中间钉在一起的木板长度是40厘米（如下图），这两块木板原来分别长多少厘米？例5：下午张老师问他们班的学生：“语文作业作文请举手！”有47人举手。

又说：“数学作业做完了请举手！”有33人举手。

“两科作业都做完的请举手！”又有27人举手。

后来张老师发现，每位同学至少做完了一门功课的作业，你能知道张老师班有多少名学生吗？例6：张老师出了两道智力题，让63个学生来回答，其中答对第:一道题的有54个人，答对第二道题的有46个人。

请问：两道题都答对的有几个人？课堂内外：爱上数学主动思考1.请你按照示例给每块木板标数。

重叠问题

重叠问题
1、同学们排除做操，每行人数同样多。

小明的位置从左数是第4个，从右数是和经3个，从前数是第5个，从后数是第6个。

做操的同学一共有多少个？
2、同学们排除跳舞，每行、每列人数同样多。

小红的位置无论从前数、从后数、从左数还是从右数都是第3个。

共有多少个同学跳舞？
3、把两块一样长的木板如下图钉在一起，使其成了一块木板。

如果这块钉在一起的木板长120厘米，中间重叠部分的长度是16厘米。

这两块木板各
长多少厘米？
4、把两段一样长的纸条黏合在一起，使其成了一段更长的纸条。

这段更长的纸条长30厘米，中间重叠部分的长度是6厘米。

原来两段纸条各长多少厘米？
5、一次数学测试，全班36人中做对第一道题的有21人，做对第二道题有18人，每人至少做对一道题。

两道题都做对的有几人？
6、三（1）班有学生55人，每人至少参加赛跑和跳绳比赛中的一项比赛。

已知参加赛跑的学生有36人，参加跳绳的学生有38人。

两项比赛都参加的学生有多少人？
7、三（2）班订《数学报》的学生有32人，订《阅读报》的学生有30人，两种报纸都订的学生有10人，全班学生每人至少订一种报纸。

三（2）班有学生多少人？
8、三年级有107个小朋友去春游，带矿泉水的小朋友有78人，带水果的小朋友有77人，要求矿泉水和水果每人至少带一种。

既带矿泉水又带水果的小朋友有多少人？。

重叠问题练习题

重叠问题练习题重叠问题是数学中常见的问题类型之一，涉及到平面上两个或多个图形之间的重叠关系。

解决重叠问题需要运用一些几何概念和技巧。

本文将介绍几道常见的重叠问题练习题，并逐步解答这些问题。

练习题一：已知平面上有两个圆，圆A的半径为r，圆心为O1；圆B的半径为R，圆心为O2。

如果两个圆的圆心距离为d，求问这两个圆是否重叠？解答一：为了判断这两个圆是否重叠，我们可以分情况讨论。

首先，两个圆没有重叠的情况是，当两个圆心之间的距离大于两个圆的半径之和时，即d > r + R。

此时，两个圆之间没有交集，因此不重叠。

另一种情况是，两个圆完全包含在对方内部，即一个圆被另一个圆包围。

这种情况下，两个圆重叠。

具体来说，当两个圆心之间的距离小于两个圆的半径之差时，即d < |r - R|。

在这种情况下，大圆完全包围小圆，或者小圆完全包围大圆。

最后一种情况是，两个圆相互交叠但不能完全包含对方。

这种情况下，两个圆相交的部分形成一个圆环。

具体来说，当两个圆心之间的距离介于两个圆的半径之和和半径之差之间时，即|r - R| < d < r + R，两个圆形成一个圆环，重叠的部分就是这个圆环。

因此，通过对两个圆心距离和半径进行比较，我们可以判断出两个圆是否重叠。

练习题二：已知平面上有一个长方形ABCD，其中AB = a，BC = b。

另外，还有一个正方形EFGH，边长为s。

如果正方形完全位于长方形的内部，并且正方形的顶点之一恰好位于长方形的顶点A处，求问这两个图形的重叠面积是多少？解答二：首先，我们需要考虑正方形EFGH的位置。

根据题意，正方形的一个顶点位于长方形的顶点A处，那么我们可以确定正方形的位置。

由于正方形完全位于长方形的内部，那么正方形的另外三个顶点必然分别位于长方形的其他三个顶点，即B、C、D处。

接下来，我们需要求解两个图形的重叠面积。

重叠面积可以看作是正方形EFGH与长方形ABCD之间的交集部分。

重叠问题

重叠问题[ 例1 ] 洗好的8块手帕夹在绳子上晾干，同一个夹子夹住相邻的两块手帕的两边，这样一共要多少个夹子？分析：由图知道，两块手帕有一边重叠，用3个夹子。

三块手帕有两边重叠，用4个夹子，我们发现夹子数总比手帕数多1，因此8块手帕就要用9个夹子。

[ 例2 ] 把图画每两张重叠在一起钉在墙上，现在有5张画要多少个图钉呢？分析：每排两张画要6个图钉，每排三张画要8个图钉，每排四张画要10个图钉。

可以看出，图画每增加一张，图钉就要增加2颗，那么5张画要12个图钉。

[ 例3 ] 有两块一样长的木板，钉在一起，如果每块木板长25厘米，中间钉在一起的长5厘米，现在长木板有多长？分析：把两块木板钉起来，钉在一起的地方的长度就是重叠的部分。

现在的总长就是原来两个总长的和减去重叠的部分。

算式：25+25-5=45（厘米）所以现在木板长45厘米。

[ 例4 ] 张老师出了两道题，做对第一题的有13人，做对第二题的有22人，两道题都做对的有8人，这个班一共有多少人？22人8人13人分析：做对第一题的13个人里，有8个人也做对第二题，那么做对第二题的22个人里这8个人就又重复数了一次，因此把做对第一题的人数和做对第二题的人数和起来，再减去重复数的这8个人。

算式：13+22-8=27（人）所以这个班一共有27人。

[ 例5 ]四根长都是8厘米的绳子，把它们打结连在一起，成为一根长绳，打结处每根绳用去1厘米，绳结长度不计，现在这根长绳长多少厘米？分析：两根绳有一个结，三根绳有两个结，那么四根绳有三个结。

一个结用去1+1=2厘米，那么三个结用去2+2+2=6厘米，绳子总长8+8+8+8=32厘米，减去打结的6厘米，32-6=26，现在这根长绳是26厘米。

一年级重叠问题练习题及答案

一年级重叠问题练习题及答案一年级的同学们，今天我们来做一些有趣的重叠问题练习题。

这些问题会帮助你们更好地理解数学中的重叠概念。

让我们开始吧！问题1：小明有5个苹果和3个橙子，他想把它们放在一个篮子里。

如果篮子只能放6个水果，那么小明能把所有的水果都放进去吗？答案：小明有5个苹果和3个橙子，总共8个水果。

篮子只能放6个水果，所以他不能把所有的水果都放进去。

问题2：小华有3个红色气球和2个蓝色气球，她想把它们放在一个盒子里。

如果盒子只能放4个气球，那么小华能把所有气球都放进去吗？答案：小华有3个红色气球和2个蓝色气球，总共5个气球。

盒子只能放4个气球，所以她不能把所有的气球都放进去。

问题3：小刚有4本故事书和3本图画书，他想把它们放在书架上。

如果书架只能放5本书，那么小刚能把所有书都放进去吗？答案：小刚有4本故事书和3本图画书，总共7本书。

书架只能放5本书，所以他不能把所有的书都放进去。

问题4：小丽有6块巧克力和2块糖果，她想把它们放在一个盒子里。

如果盒子只能放7块零食，那么小丽能把所有零食都放进去吗？答案：小丽有6块巧克力和2块糖果，总共8块零食。

盒子只能放7块零食，所以她不能把所有的零食都放进去。

问题5：小强有5辆玩具车和3辆玩具飞机，他想把它们放在一个盒子里。

如果盒子只能放6个玩具，那么小强能把所有玩具都放进去吗？答案：小强有5辆玩具车和3辆玩具飞机，总共8个玩具。

盒子只能放6个玩具，所以他不能把所有的玩具都放进去。

问题6：小芳有4个篮球和3个足球，她想把它们放在一个篮子里。

如果篮子只能放6个球，那么小芳能把所有球都放进去吗？答案：小芳有4个篮球和3个足球，总共7个球。

篮子只能放6个球，所以她不能把所有的球都放进去。

结束语：同学们，你们做得很棒！通过这些练习题，你们应该对重叠问题有了更深的理解。

记得，数学不仅仅是数字，它也能帮助我们解决生活中的实际问题。

继续加油，你们会越来越棒的！。

重叠问题

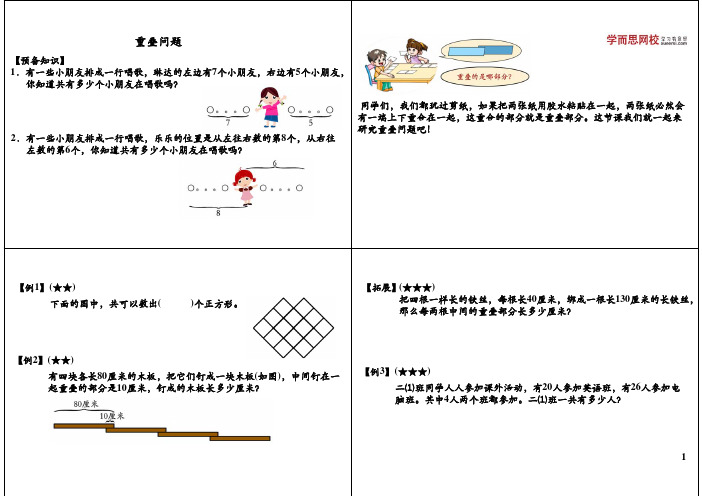
【例1】(★★) 下面的图中，共可以数出(
)个正方形。
【拓展】(★★★) 把四根一样长的铁丝，每根长40厘米，绑成一根长130厘米的长铁丝，那么每两根中间的重叠部分长多少厘米？
【例2】(★★) 有四块各长80厘米的木板，把它们钉成一块木板(如图)，中间钉在一起重叠的部分是10厘米，钉成的木板长多少厘米？
【例3】(★★★) 二⑴班同学人人参加课外活动，有20人参加英语班，有26人参加电脑班。其中4人两个班都参加。二⑴班一共有多少人？
பைடு நூலகம்
1
【拓展】(★★★) 史老师出了两道测试题，全班每个同学都至少答对了一道，答对第一道题的有30人，答对第二道题的有28人，两道都答对的有16人，那么全班同学总共有多少人？
重叠问题
【预备知识】 1．有一些小朋友排成一行唱歌，琳达的左边有7个小朋友，右边有5个小朋友，
你知道共有多少个小朋友在唱歌吗？
2．有一些小朋友排成一行唱歌，乐乐的位置是从左往右数的第8个，从右往左数的第6个，你知道共有多少个小朋友在唱歌吗？
同学们，我们都玩过剪纸，如果把两张纸用胶水粘贴在一起，两张纸必然会有一端上下重合在一起，这重合的部分就是重叠部分。这节课我们就一起来研究重叠问题吧！
【例5】(★★★★★) 学校开设了自然和趣味数学两门选修课，每个同学至少要选一门，二(3)班共有48人，有30人选了自然课，有13人两门都选了，那么选趣味数学课的同学有多少人？
【例4】(★★★) 20个同学报名参加美术组和舞蹈组，其中有16人参加了美术组，12 人参加了舞蹈组。问两个小组都参加的有多少个同学？
【例6】(★★★★★) 二年级二班有40名同学。其中有25人没参加数学小组，有18人参加航模小组，有10人两个小组都参加。那么只参加了这两个小组之一的学生共有多少人？

重叠问题

重叠问题

第20讲 重叠问题(含解题思路和参考答案)

重叠问题

重叠问题课件ppt

重叠问题

第20讲重叠问题含解题思路和参考答案

二年级数学重叠问题

三年级奥数4种重叠问题

小学数学重叠问题

重叠问题

重叠问题

重叠问题练习题

重叠问题

一年级重叠问题练习题及答案

重叠问题

第20讲重叠问题(含解题思路和参考答案)