周期信号功率式证明
通信原理 第四讲 功率信号的功率谱密度

试问它是功率信号还是能量信号,并求出其 功率谱密度或能量谱密度。 思路:由信号是能量有限还是功率有限来判断 解: 2 2t 2t
E x (t )dt 4e dt 2e
0
0
2
所以 x(t )为能量信号。 频谱密度为
s( f ) x(t )e
平均功率:
1 P lim T T
T /2
T / 2
s 2 (t )dt
傅立叶变换公式 F ( ) f (t )e jt dt
j 2 ft F ( f ) f ( t ) e dt 或 1 jt j 2 ft f (t ) F ( ) e d f ( t ) F ( f ) e df 2
jt0
Kf (t t0 ) KF ()e
j (t0 )
当这两条传输路径的信号合成后得
R(t ) Kf (t t0 ) Kf (t t0 )
对应于它的傅氏变换为 R(t ) KF ()e jt0 [1 e-j ] 信道的传递函数为 R( ) H ( ) Ke-jt [1 e-j ] F ( )
随机 包络
a(t ) a I (t ) a (t )
2 2 Q
相位
aQ (t ) (t ) arctan a ( t ) I
结论: (1)多径传播使单一频带信号变成窄带信号 (2)多径传播引起了频谱弥散 (3)多径传播引起选择性衰落
慢衰落:由于电离层浓度变化等因素所引起的信 号衰落。(季节、日夜、天气) 快衰落:由于多径效应引起的信号衰落。 为分析简单,下面假定只有两条传输路径, 且认为接收端的幅度与发端一样,只是在到达 f (t ) 时间上差一个时延 ,若发送信号为 ,它的 F ( ) 频谱为 ,记为
信号与系统第4章 周期信号的频域分析(3学时)

T0 /2
0
x(t )sin(n 0t )dt
四、信号对称性与傅里叶系数的关系
3、半波重迭信号
~ x (t ) ~ x (t T0 / 2)
~ x (t )
A t
T0
T0 / 2 0
T0 / 2
T0
特点: 只含有正弦与余弦的偶次谐波分量,而无奇次谐波分量。
四、信号对称性与傅里叶系数的关系
~ x (t )
2 1 -4 -3 -2 -1 1 2 3 4
~ x (t ) ~ x1 (t ) ~ x2 (t )
nπ nπt t~ x (t ) 1.5 Sa ( ) cos( ) 2 2 n 1
~ x1 (t )
2
x 1(t ) 2
1 2 3 4
-4 -3 -2 -1
三、周期信号的功率谱
一、周期信号频谱的概念
连续时间周期信号可以表示为虚指数信号之和,其 中Cn 为傅里叶系数 。
~ x (t )
n =
Cn e
jn0t
1 Cn T0
T0 t 0
t0
~ x (t )e jn 0t dt
问题1:不同信号的傅里叶级数形式是否相同? 相同 问题2:不同信号的傅里叶级数不同表现在哪里? 系数
例3 课本P129
例4 已知连续周期信号的频谱如图,试写出信号的 Fourier级数表示式。 Cn
3 2 1 1 3 4 3 2
9
6
0
3
6
9
n
解: 由图可知 C0 4
C 1 3
C2 1
C 3 2
~ x (t )
3.2 周期信号的傅里叶级数分析

f (t )
n
F e
n
jn1t
E T1
n1 jn1t Sa( 2 )e n
20
E f (t ) T1
n1 jn1t Sa( 2 )e n
E n1 Fn Sa( ) T1 2
2 E n1 cn Sa( ) T1 2 E c0 T1 n0
E cos(n t )dt
2 1 2
2E 2E n1 2 sin(n1t ) sin( ) T1n1 n 2 2
E1
n1 2 E n1 Sa( ) Sa( ) 2 T1 2
E 2 E f (t ) T1 T1
n1 Sa( 2 ) cos(n1t ) n 1
f1 t
f1 (t ) 1 f (t )
1
f (t)
练习P 3 7 171
2
-T
T T 0
2
T 2
T
2T
t
T 2
0 -1
T 2
T
2T
t
注意:不可左右移动,否则改变了 原信号的对称性。
11
四、傅里叶有限级数与最小方均误差
f (t ) a0 (an cos n1t bn sin n1t )
32
1 1 2 2 2 2 2 P a0 (an bn ) c0 cn 2 n 1 2 n 1 1 2 2 2 c0 (2 Fn 2 F n ) 2 n 1 c0 Fn F n
2 2 2 n 1 n 1 n
2 b2 T1
T1 2 T 1 2
第3章__周期信号的FS

N1 1 2 N k N
图:N1=2, N=10,20,40
3.5 连续时间傅立叶级数性质
x(t ) ak
FS
3.5.1 线性 FS FS ak y(t ) bk 若x(t),y(t)周期均为T, x(t ) FS Aak Bbk Ck 则:Z (t ) Ax(t ) By(t )
物理意义: 总平均功率=所有谐波的平均功率之和
3.6 离散时间福立叶级数性质 3.6.1 相乘
FS x[n] ak FS x [ n ] y [ n ] d k al bk l FS y[n] bk l N
周期卷积 • 计算
3.6.2 一次差分 x[n]-x[n-1]
k
结论:若连续(离散)时间LTI系统的输入 x(t)= ak es t x[n]= ak zk n k k 则 s t n a H ( z ) z a H ( s ) e k k k y(t)= k y[n]= k k k s,z可以是任意复数 j j s= ,z= e 时,即分别以 j n j t e 为基函数 e ——傅立叶分析
3.2 LTI系统对复指数信号的响应
复指数信号 e z 的重要性质 : LTI系统对其的响应是同样的复指数信号 ,增 加幅度因子:即 e st →H(s) e st n z →H(z) z n n e st z ——LTI系统的特征函数 复振幅因子H(s),H(z) ——系统的特征值
st
n
2
三角形式的傅立叶级数(实周期信号)
x(t ) c0 (an cos(n0t ) bn sin(n0t ))
n 1
1 c0 T0 2 an T0 2 bn T0
连续周期信号的频域分析

三、周期信号的频谱及其特点
3. 频谱的特性
(3) 信号的有效带宽
0~2 / 这段频率范围称为周期矩形脉冲信号的 有效频带宽度,即 2π B
信号的有效带宽与信号时域的持续时间成反比。 即 越大,其B越小;反之, 越小,其B 越大。
三、周期信号的频谱及其特点
3. 频谱的特性
(3) 信号的有效带宽 物理意义:在信号的有效带宽内,集中了信 号绝大部分谐波分量。若信号丢失有效带宽以 外的谐波成分,不会对信号产生明显影响。
n=—4 4
1 T /2 2 P T / 2 f (t )dt 0.2 T 包含在有效带宽(0 ~ 2 / )内的各谐波平均功率为
2 2 C0
2 | Cn | 2 0.1806
n=1
4
P 0.1806 1 90% P 0.200
例3 试求周期矩形脉冲信号在其有效带宽(0~2 /t)内
频谱的特性频谱的特性信号的有效带宽信号的有效带宽这段频率范围称为周期矩形脉冲信号的有效频带宽度有效频带宽度即信号的有效带宽与信号时域的持续时间信号的有效带宽与信号时域的持续时间成反比
连续周期信号的频域分析
周期信号的傅里叶级数展开 傅里叶级数的基本性质 周期信号的频谱及其特点 周期信号的功率谱
三、周期信号的频谱及其特点
三、周期信号的频谱及其特点
4. 相位谱的作用
幅频不变,零相位
幅频为常数,相位不变
四、周期信号的功率谱
帕什瓦尔(Parseval)功率守恒定理
2 1 T P 2T f (t ) dt Cn T 2 n 2
物理意义:任意周期信号的平均功率等于信号所 包含的直流、基波以及各次谐波的平均功率之和。
樊昌信《通信原理》(第6版)(课后习题 确知信号)【圣才出品】

其自相关函数为
2-7 已知一信号 s(t)的自相关函数为
(1)试求其功率谱密度 Ps(f)和功率 P; (2)试画出 RS(τ)和 Pn(f)的曲线。 解:(1)功率谱密度与自相关函数互为傅里叶变换,故
功率
。
(2)自相关函数和功率谱密度随频率的变化曲线如图 2-2 所示:
4/6
圣才电子书
又因
PБайду номын сангаас
1 T
T /
T
2 /2
s
2
(
t
)dt
1 ,故
s(t)是功率信号。
该信号周期为 T0 1,基波频率为 f0 1,则其傅里叶级数
即
Cn 1 , n 1
Cn 0 , others
故信号的功率谱密度为
P( f )
Cn 2 ( f nf
) ( f f0 )( f f0 ) 。
n
十万种考研考证电子书、题库视频学习平 台
图 2-2
2-8 已知一信号 s(t)的自相关函数是以 2 为周期的周期性函数:
试求 s(t)的功率谱密度 Pn(f)并画出其曲线。 解:周期性功率信号的功率谱密度是自相关函数的傅里叶变换,则
功率谱密度曲线如图 2-3 所示:
图 2-3
5/6
圣才电子书
十万种考研考证电子书、题库视频学习平
2-5 试求出 s(t)=Acoswt 的自相关函数,并从其自相关函数求出其功率。 解:(1)根据题意可知,s(t)为周期性功率信号,其自相关函数定义为
其中T0 2 / w 。
(2)由自相关函数的性质可知,平均功率为
。
功率谱密度为
P( f ) R( )e j2 f d A2 cos( 2 )e j2 f d
第四章(2)周期信号的频谱

周期性矩形脉冲信号的频谱还有自己的特点 周期性矩形脉冲信号的频谱还有自己的特点 : 1、各谱线的幅度按包络线 T 、
ωτ
= m π ( m = ±1, ± 2,...)
τ
Sa (
ωτ
2
) 的规律变化。 的规律变化。
各处, 的各处, 在 2 各处,即 的各处, τ 包络为零,其相应的谱线, 包络为零,其相应的谱线,亦即相应的频谱分量也等 于零。 于零。 2、周期矩形脉冲信号包含无限多条谱线,也就是说, 、周期矩形脉冲信号包含无限多条谱线,也就是说, 它可分解为无限多个频率分量。 它可分解为无限多个频率分量。 通常把频率范围 0 ≤ f ≤ τ (0 ≤ ω ≤ τ ) 称为周期矩形脉冲 带宽, 表示, 信号的带宽 信号的带宽,用符号 ∆F 表示,即周期矩形脉冲信 1 号的频带宽度为 ∆F = 。 τ
Fn F ( jω ) = lim = lim FnT T →∞ 1 / T T →∞
为频谱密度函数。 称 F ( jω )为频谱密度函数。
Fn lim = lim FnT 如何求频谱密度函数? 如何求频谱密度函数? F ( jω ) = T →∞ 1 / T T →∞
由式 f ( t ) =
n = −∞
T 2T f (t) T=8τ
0
3T
4T t
0 1/ 8
T f (t) T=16τ
0
2T
t
0 1/16
0
T
t
0
f (t) T→∞ τ/T
0 t 0
图4.3-5 周期与频谱的关系
思考: 思考:
1 1 1 f (t ) = [sin(Ωt ) + sin(3Ωt ) + sin(5Ωt ) + .... + sin(nΩt ) + ...] 3 5 n π 4
周期信号的频谱
当 n1 0
2
即 n1 0
基波分量的幅度:A Sa1
T 2
Fn
A
T
San1
2
Fn
为最大值 :A T
二次谐波分量的幅度:
A Sa 21
T 2
编辑版
15
3.3.2 双边频谱与信号的带宽
3.相位的确定
Fn
A
T
San1
2
是 n1 的实函数
Fn Fnejn Fn(consjsinn) Fn cosn
• 周期信号频谱的特点:
❖离散性:
由不连续的谱线组成,每一条谱线代表一个正弦分量,所以
此频谱称为不连续谱或离散谱;每条谱线间的距离为 ❖谐波性:
1
2
T
每一条谱线只能出现在基波频率 1 的整数倍频率上,即含 有 1 的各次谐波分量,而决不含有非 1 的谐波分量。
❖收敛性:
各次谐波分量的振幅虽然随 n1 的变化有起伏变化,但总的 趋势是随着 n1的增大而逐渐减小。
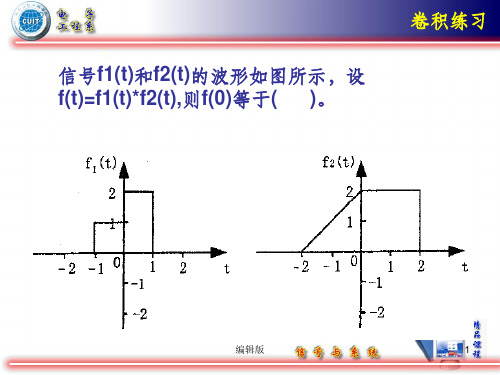
信号f1(t)和f2(t)的波形如图所示,设 f(t)=f1(t)*f2(t),则f(0)等于( )。
卷积练习
编辑版
1
3.3 周期信号的频谱
编辑版
2
3.3 周期信号的频谱
• 3.3.1 周期信号频谱的特点 • 3.3.2 双边频谱与信号的带宽 • 3.3.3 周期信号的功率
编辑版
3
3.3.1 周期信号频谱的特点
1
e jn1t
T n
1
2 T
编辑版
33
此课件下载可自行编辑修改,此课件供参考! 部分内容来源于网络,如有侵权请与我联系删除!感谢你的观看!
以相位为纵坐标所得到的谱线图
§3.2 周期信号的频谱和功率谱

不变,T增大,谱线间隔
1
2 T
减小,谱线逐渐密集,幅度
A T
பைடு நூலகம்
减
小
当 T
1 0
A 0 T
非周期信号连续频谱
非周期信号 n1 连续频率
2.当T不变, 减小时
T不变
1
2 间隔不变
T
A 振幅为0的谐波频率
T
2
,
4
,......
信号与系统
练习:周期信号的频谱描绘
不改变 不改变 不改变
Fn
2 T
2
f (t)dt
T
2 A
2
Adt
2
T
信号与系统
练习:周期信号的频谱描绘
a 2 nT
T
2 T
2
f (t) cos n1tdt
2A sin n n T
2 A
T
sin n
T
n
2A Sa(n )
T
T
T
f (t)
A
T
2 A
T
n 1
Sa( n
T
)
cos(n1t )
A 2A
TT
S a(
立叶展开式并画出其频谱图。
1
解: f(t) 在一个周期内可写为如下形式
Tt
f (t) 2 t T t T
T
22
f(t) 是奇函数,故 an 0
信号与系统
4
bn T
T 2 0
f (t) sin n1tdt
4 T
T 2 0
2t T
sin
n1tdt
(1
2
T
)
An &n 2
信号与系统知识要点

《信号与系统》知识要点第一章 信号与系统1、周期信号的判断 (1)连续信号思路:两个周期信号()x t 和()y t 的周期分别为1T 和2T ,如果1122T N T N =为有理数(不可约),则所其和信号()()x t y t +为周期信号,且周期为1T 和2T 的最小公倍数,即2112T N T N T ==。
(2)离散信号思路:离散余弦信号0cos n ω(或0sin n ω)不一定是周期的,当 ①2πω为整数时,周期02N πω=;②122N N πω=为有理数(不可约)时,周期1N N =; ③2πω为无理数时,为非周期序列注意:和信号周期的判断同连续信号的情况。
2、能量信号与功率信号的判断 (1)定义连续信号 离散信号信号能量: 2|()|k E f k ∞=-∞=∑信号功率: def2221lim ()d T T T P f t t T →∞-=⎰ /22/21lim|()|N N k N P f k N →∞=-=∑(2)判断方法能量信号: P=0E <∞, 功率信号: P E=<∞∞, (3)一般规律①一般周期信号为功率信号;②时限信号(仅在有限时间区间不为零的非周期信号)为能量信号;③还有一些非周期信号,也是非能量信号。
⎰∞∞-=t t f E d )(2def3 ① ②4、信号的基本运算1) 两信号的相加和相乘 2) 信号的时间变化a) 反转: ()()f t f t →- b) 平移: 0()()f t f t t →± c) 尺度变换: ()()f t f at →3) 信号的微分和积分注意:带跳变点的分段信号的导数,必含有冲激函数,其跳变幅度就是冲激函数的强度.正跳变对应着正冲激;负跳变对应着负冲激。
5、阶跃函数和冲激函数 (1)单位阶跃信号00()10t u t t <⎧=⎨>⎩0t =是()u t 的跳变点。
(2)单位冲激信号定义:性质:()1()00t dt t t δδ∞-∞⎧=⎪⎨⎪=≠⎩⎰ t1)取样性 11()()(0)()()()f t t dt f t t f t dt f t δδ∞-∞∞-∞=-=⎰⎰()()(0)()f t t f t δδ=000()()()()f t t t f t t t δδ-=-2)偶函数 ()()t t δδ=-3)尺度变换 ()1()at t aδδ=4)微积分性质 d ()()d u t t tδ= ()d ()t u t δττ-∞=⎰(3)冲激偶 ()t δ'性质: ()()(0)()(0)()f t t f t f t δδδ'''=-()()d (0)f t t t f δ∞-∞''=-⎰()d ()tt t t δδ-∞'=⎰()()t t δδ''-=- ()d 0t t δ∞-∞'=⎰(4)斜升函数 ()()()d tr t t t εεττ-∞==⎰(5)门函数 ()()()22G t t t τττεε=+--6、系统的特性 (重点:线性和时不变性的判断) (1)线性1)定义:若同时满足叠加性与均匀性,则称满足线性性质。
信号与系统复习资料第六章

信号与系统第五章(5.1~5.3)一、知识储备正交分解矢量正交信号正交正交定义31==∑=i yi xi Ty x v v V V 两矢量内积为0⎰=21d )()(*21t t t t t ϕϕ两函数内积为0正交集正交矢量集两两正交的矢量组成的矢量集合。
正交函数集⎰⎩⎨⎧=≠≠=21,0,0d )()(*t t i j i ji K j i t t t ϕϕ构成空间矢量空间例如矢量A 可表示为A =a Vx +b Vy +c Vz信号空间1122n ()...nf t C C C φφφ=+++二、傅里叶级数三角形式∑∑∞=∞=Ω+Ω+=110)sin()cos(2)(n nn nt n bt n aat f或∑∞=+Ω+=10)cos(2)(n n n t n A At f ϕ式中,A0=a0,22nn nba A +=,nnn a b arctan-=ϕ. 指数形式e )(j t n n n F tf Ω∞-∞=∑=以上为复傅里叶级数展开式,可以将f (t )理解成由一系列旋转向量合成的信号,各旋转向量的初始位置(严格来讲是t=0时刻所在的位置)就是复傅里叶系数Fn 。
画出三维频谱图如下图所示:三角形式和指数形式傅里叶系数之间的关系)j (21e 21e j n n n n n b a A F F n n -===ϕϕnnnnA b a F 212122=+=⎪⎪⎭⎫ ⎝⎛-=n nnab arctan ϕnn n A a ϕcos =nn n A b ϕsin -=n 的偶函数:an ,An ,|Fn |n 的奇函数:bn ,n波形对称性和谐波特性(四点)f(t)为偶函数——对称纵坐标)()(t f t f -=bn =0,展开为余弦级数f(t)为奇函数——对称于原点)()(t f t f --=an =0,展开为正弦级数此时其傅里叶级数中只含偶次谐波分量,而不含奇次谐波分量,即a1=a3=…=b1=b3=…=0周期信号的功率∑∑⎰∞-∞=∞==+=n nn n T FA A dt t f T2122002||212()(1周期信号一般是功率信号,上式为其平均功率,直流和n 次谐波分量在1Ω电阻上消耗的平均功率之和。
第2章 信号与系统分析基础2

[f2(t)] = F2(ω) • 时域卷积定理
[f1(t)﹡f2(t)]=F1(ω)F2(ω) • 频域卷积定理
[f1(t) ·f2(t)]=1/(2π) F1(ω)﹡F2(ω)
例2.5.13利用卷积定理求三角脉冲的频谱
f(t)=g(t)g(t)
F(ω)=G(ω)·G(ω)
g(t)
例2.5.14利用卷积定理求有限长余弦信号的 频谱
dt
= ∫∞-∞f(t)e-jωt dt
f(t)=
F(nω1)
e-jnω1t
n-
=
F(nω1)
/
ω1•
e-jnω1t
Δ(nω1)
nω1-
在极限情况下, nω1ω, Δ(nω1) dω1, nωF1(-nω1)∫∞/-∞ω1F(ω) / 2π
f(t)=1/(2π) ∫∞-∞F(ω)ejωt dω
结论:
(4)频带宽度(带宽)
频谱图上第一个零点以内的范围,记作B。 例:对周期矩形脉冲信号,
Bω=2 π /τ
或
Bf=1/τ
2.5.2傅里叶变换
• 傅里叶正变换
F(ω)= [f(t)]= ∫∞-∞f(t)e-jωt dt
F(ω)=|F(ω)|e jφ(ω)
• 傅里叶逆变换
f(t)= -1 [F(ω)]= 1/(2π)∫∞-∞F(ω)ejωt dω
f(t)
E
0
-T1
-τ/2 τ/2
T1
t
f(t)=a0+∑ [ancos(nω1t)+ bnsin(nω1t)] n=0
其中:
a0=1/T1∫T1/2-T1/2f(t)dt=1/T1∫τ/2τ/2Edt=Eτ/T1 an=2/T1 ∫T1/2-T1/2f(t)cos(nω1t)dt
周期信号的频谱

例题:O tf (t )T /31-TT如右图所示的周期性矩形脉冲信号(周期为T )经过一个低通滤波器,求其响应及响应的平均功率。
已知该滤波器的传递函数为()()⎪⎪⎩⎪⎪⎨⎧<≤<-≤=--时时时T T e T T e j H j j ωππωππωπωωωτωτ6,063,3/23,分析:周期信号可以分解成直流、基波、高次谐波等分量每个分量经过滤波器 复数解法解:求傅立叶系数:⎰-=3/001T tjn n dt eTC ωO tf (t )T /31-TT令ω0=2π/T3/0001T t jn eTjn ωω--=3/3sin 31ππjn e n c -⎪⎭⎫ ⎝⎛=3100==C A 2nj n n A eC ϕ=~基波和n 次谐波的复数表示低通滤波器只通过低于3ω0的信号,因此信号中只有直流、基波和二次谐波分量通过。
输出信号中的直流分量为:()3100==ωωj H A解:输出信号中的基波分量的复数表示为:()()τωπωωφπω0013/13sin 32+-=⎪⎭⎫ ⎝⎛=j j e c j H eA 输出信号中的二次谐波分量的复数表示为:()()τωπωωφπω00223/22232sin 94+-=⎪⎭⎫⎝⎛=j j e c j H e A 输出信号的时域表达式为:⎪⎭⎫ ⎝⎛--⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛--⎪⎭⎫ ⎝⎛+τωπωπτωπωπ00002322cos 32sin 943cos 3sin 3231t c t c 输出信号的平均功率为:280.02sin 41sin 211222≈⎥⎤⎢⎡⎪⎫⎛+⎥⎤⎢⎡⎪⎫ ⎛+⎪⎫ ⎛=ππc c P out第三章:信号的频谱§3-1 周期信号的频谱§3-2 非周期信号的频谱密度 傅立叶变换与频谱密度信号的频谱分布与带宽基本信号的频谱密度§3-3 频谱分析的基本定理§3-4 采样定理傅立叶变换的引出如何从频域描述一个非周期信号?tf (t )傅立叶级数?——显然不行怎么办?退而求其次,先考虑描述函数在有限区间[a,b)上的一段吧tf a,b (t )a btf T (t )a b考虑有限区间周期扩展再扩展成周期T =b -a 的函数f T (t )f T (t ):周期函数~可以用傅立叶级数表示在区间[a,b)上与f (t ) 相同傅立叶变换的引出tf T (t )a b()(),1100dt et f Tdte tf T C tjn bat jn ba T n ωω--⎰⎰==()()()⎪⎪⎩⎪⎪⎨⎧=-++∈-++=∑∞-∞=b a t b f a f b a t t f t f eC n tjn n或,2)0(0,,2)0(00ω傅立叶级数只在区间(a,b ) 上收敛于f (t ),因此C n 并不是f (t ) 的复频谱如果f T (t ) 满足狄利克雷条件,则可以展开成傅立叶级数:定义:则:ω0=2π/T傅立叶变换的引出进一步,选取对称区间[-T /2,T /2)。
通信原理教程第二章 信号

P(X xn) = 1
∵P(X xi) = P(X = x1) + P(X = x2) + … + P(X = xi),
∴
0
FX
(x)
i
pk
k1
1
x x1 x1 x xi1
x xn
性质:
FX(- ) = 0
FX(+) = 1
若x1 < x2,则有: FX(x1) FX(x2) ,
随机变量的概念:若某种试验A的随机结果用X表示,则称此
X为一呼叫次数是一个
随机变量。 随机变量的分布函数:
定义:FX(x) = P(X x) 性质: ∵ P(a < X b) + P(X a) = P(X b),
f(t)sin t)( 0t1
f(t)f(t1)
求频谱:
t
C ( jn 0 ) T 1 0 T T 0 0 // 2 2 s ( t ) e j n 0 td 0 1 t si t ) e n j2 n d ( t t ( 4 n 2 2 1 )
解:单位冲激函数常简称为函数,其定义是:
(t)dt 1 (t) 0
t 0
(t)的频谱密度: (f)(t)e j td 1 t(t)d 1 t
7
Sa(t)及其频谱密度的曲线:
(f)
(t)
1
0
t
0
f
函数的物理意义: 高度为无穷大,宽度为无穷小,面积为1的脉冲。
将上式两端求导,得到其概率密度:
性质:
n
pX(x) pi(xxi) i1
3.8帕塞瓦尔定理与能量频谱

功率信号与功率谱: 功率信号与功率谱: 功率信号:信号在时间区间( 功率信号:信号在时间区间(-∞,+ ∞)内的能量为∞, 内的能量为∞ 但在一个周期( T/2, 但在一个周期(-T/2,+T/2) 内的平均功率为有限值, 这样的信号称为功率信号。周期信号即为功率信号。 功率信号的平均功率为: 信号为一电流 i, i = I0 + ∑I nm cos(nΩt −ϕn ) 时域求得的信号功率 n=1 频域求得的信号功率 ∞ 1 ∞ 2 2 2 2 2 2 i 的有效值 I 为: I = i = I0 + ∑I nm = I0 +∑I n
1 ∞ 1 ∞ 2 2 W = ∫ [ f (t)] dt = ∫−∞ F( jω) dω =π ∫0 F( jω) dω −∞ 2π ∞ 即: W = ∫ G(ω)dω, ∴ G(ω) = 1 F( jω) 2 简称能量谱 0
2 ∞
π
能量谱为连续谱 它描述了单位频带内信号的能量随ω 它描述了单位频带内信号的能量随ω分布的规律。可见 能量谱为连续谱
Q f (t) = 10
ωτ
ห้องสมุดไป่ตู้
)
π
cos 997t ⋅
sin 5t 1 = cos 997t ⋅10Sa(5 t) 5t π
根据频域卷积定理: ( jω) = F 信号的能量为:
1 ⋅ 2π G (ω) ∗[δ (ω − 997) +δ (ω + 997)] 10 2π = G (ω −997) + G (ω + 997) 10 10
第三章第1讲 5
例
1
Gτ (t) ⇔τ Sa(
sin 5t 求信号 f (t) = 2cos 997t ⋅ 的能量。 πt 解:已知: 1 cos 997t ⇔[δ (ω − 997) + δ (ω + 997)]
周期信号的频谱分析——傅里叶级数

可画出频谱图 周期信号频谱具有离散性,谐波性,收敛性
X
二.指数函数形式的傅里叶级数
j nt 1.复指数正交函数集 e 0 ,1 , 2 n
1
第 14 页
2.级数形式 3.系数
j n t 1 f() t F ( n ) e 1 n
4
利用复变函数的正交特性
0 . 15 2 1 0 . 25
1
0 . 25
2 1 1
0
1
1
0
0 . 15
2 1
X
四.总结
(1)周期信号f(t)的傅里叶级数有两种形式
(2)两种频谱图的关系 (3)周期信号的频谱是离散谱,三个性质 (4)引入负频率
第 23 页
X
(1)周期信号f(t)的傅里叶级数有 两种形式
1 j 4 F2 1 e 2 1 j4 F 2 1 e 2
X
谱线
F (0) 1 0F
第 21 页
0 0
F ( ) 1 . 1 2 1 F 1
F F ( ) 1 . 1 2 1 1
0 .1 5 1
1 0.15
2 0.25
1
1
2
1
0
1
2 1
0 . 15
X
化为指数形式
1 j j t 1 f( t) 1 e 1t e 2 j
第 20 页
j t jn t 2 2 1 1 2 j 1 j t 4 4 1 e 1t e e e 2 整理 2 1 j j j t 1 j t 1 j 2 t 1 j 2 t 1 1 4 1 4 1 f ( t ) 1 1 e 1 e e e ee j j 2 2 2 2
信号与系统知识要点

《信号与系统》知识要点第一章 信号与系统1、周期信号的判断 (1)连续信号思路:两个周期信号()x t 和()y t 的周期分别为1T 和2T ,如果1122T N T N =为有理数(不可约),则所其和信号()()x t y t +为周期信号,且周期为1T 和2T 的最小公倍数,即2112T N T N T ==。
(2)离散信号思路:离散余弦信号0cos n ω(或0sin n ω)不一定是周期的,当 ①2πω为整数时,周期02N πω=;②122N N πω=为有理数(不可约)时,周期1N N =; ③2πω为无理数时,为非周期序列注意:和信号周期的判断同连续信号的情况。
2、能量信号与功率信号的判断 (1)定义连续信号 离散信号信号能量: 2|()|k E f k ∞=-∞=∑信号功率: def2221lim ()d T T T P f t t T →∞-=⎰ /22/21lim|()|N N k N P f k N →∞=-=∑(2)判断方法能量信号: P=0E <∞, 功率信号: P E=<∞∞, (3)一般规律①一般周期信号为功率信号;②时限信号(仅在有限时间区间不为零的非周期信号)为能量信号;③还有一些非周期信号,也是非能量信号。
⎰∞∞-=t t f E d )(2def3 ① ②4、信号的基本运算1) 两信号的相加和相乘 2) 信号的时间变化a) 反转: ()()f t f t →- b) 平移: 0()()f t f t t →± c) 尺度变换: ()()f t f at →3) 信号的微分和积分注意:带跳变点的分段信号的导数,必含有冲激函数,其跳变幅度就是冲激函数的强度。
正跳变对应着正冲激;负跳变对应着负冲激。
5、阶跃函数和冲激函数 (1)单位阶跃信号00()10t u t t <⎧=⎨>⎩0t =是()u t 的跳变点。
(2)单位冲激信号定义:性质:()1()00t dt t t δδ∞-∞⎧=⎪⎨⎪=≠⎩⎰ t1)取样性 11()()(0)()()()f t t dt f t t f t dt f t δδ∞-∞∞-∞=-=⎰⎰()()(0)()f t t f t δδ=000()()()()f t t t f t t t δδ-=-2)偶函数 ()()t t δδ=-3)尺度变换 ()1()at t aδδ=4)微积分性质 d ()()d u t t tδ= ()d ()t u t δττ-∞=⎰(3)冲激偶 ()t δ'性质: ()()(0)()(0)()f t t f t f t δδδ'''=-()()d (0)f t t t f δ∞-∞''=-⎰()d ()tt t t δδ-∞'=⎰()()t t δδ''-=- ()d 0t t δ∞-∞'=⎰(4)斜升函数 ()()()d tr t t t εεττ-∞==⎰(5)门函数 ()()()22G t t t τττεε=+--6、系统的特性 (重点:线性和时不变性的判断) (1)线性1)定义:若同时满足叠加性与均匀性,则称满足线性性质。
1.2.2 周期-非周期,能量-功率

例4:
P2
1 2
112 dt 0.5
0
0 P2
E2
f2 t 为功率信号。
12
3.小结
• 信号的表示方法 • 信号按时间特性分类
(1) 确定信号,随机信号 (2) 连续信号,离散信号 (3) 周期信号,非周期信号 (4) 能量信号,功率信号
13
学好信号与系统 低通高通路路通
北京邮电大学信号与系统 智慧教学研究组
9
(4)能量信号,功率信号
归一化瞬时功率
pt f t 2
信号f t 的归一化能量(或简称信号的能量):
为信号电压(或电流)加到1电阻上所消耗的能量
E f t 2 d t
信号的平均功率:
信号电压(或电流)在1电阻上所消耗的功率,
在整个时间轴上的平均功率为
P lim 1 f t 2 d t T T T
2
(3)周期信号,非周期信号
例2:信号f t cos10t cos 30t是否为周期信号?
若是周期信号请求出其周期T和基波角频率。 解
:
cos10t的周期:T1
2π 10
设f t 的周期为T,则
cos
30t的周期:T2
2π 30
T k1T1 k2T2, k1和k2均为正整数
T1 T2
k2 k1
10
(4)能量信号,功率信号
能量信号: 信号在时间区间,的能量为有限值,
但平均功率为0的信号。
大多数时限信号是能量信号。
例3:
E1
212 dt 2
0
0 E1
P1 0
f1 t 为能量信号。
11
(4)能量信号,功率信号
