北师大版数学选修1-2质量检测(四)

合集下载

高二数学北师大版选修1-2模块综合测评 Word版含答案

模块综合测评(时间分钟，满分分)一、选择题(本大题共小题，每小题分，共分．在每小题给出的四个选项中，只有一项是符合题目要求的)．为虚数单位，的共轭复数．．．．为( )．－．．．－【解析】因为＝×＋＝＝－，所以其共轭复数为，故选.【答案】．根据二分法求方程－＝的根得到的程序框图可称为( )．程序流程图．工序流程图．组织结构图．知识结构图【解析】由于该框图是动态的且可以通过计算机来完成，故该程序框图称为程序流程图．【答案】．下列框图中，可作为流程图的是( )→→→→→→→→→【解析】流程图具有动态特征，只有答案符合．【答案】.用反证法证明命题“，∈，如果可被整除”，那么，至少有一个能被整除．则假设的内容是( )．，都能被整除．，都不能被整除．不能被整除．，有一个不能被整除【解析】“至少有一个”的否定为“一个也没有”，故应假设“，都不能被整除”．【答案】．有一段演绎推理是这样的“有些有理数是真分数，整数是有理数，则整数是真分数”结论显然是错误的，是因为( )．小前提错误．大前提错误．非以上错误．推理形式错误【解析】一般的演绎推理是三段论推理：大前提——已知的一般原理；小前提——所研究的特殊情况；结论——根据一般原理对特殊情况作出的判断．此题的推理不符合上述特征，故选.【答案】．设是虚数单位，则复数在复平面内所对应的点位于( )．第二象限．第一象限．第四象限．第三象限【解析】＝＝＝－＋，由复数的几何意义知－＋在复平面内的对应点为(－)，该点位于第二象限，故选.【答案】．考察棉花种子是否经过处理跟生病之间的关系得到如表数据：( )．种子经过处理跟是否生病有关．种子经过处理跟是否生病无关．种子是否经过处理决定是否生病．以上都是错误的【解析】计算与可知相差很小，故选.【答案】．给出下面类比推理：①“若<，则<”类比推出“若<，则<”；②“(＋)＝＋(≠)”类比推出“＝＋(≠)”；。

精选高中数学章末质量评估4北师大版选修1_2

第四章数系的扩充与复数的引入(本栏目内容，在学生用书中以独立形式分册装订)一、选择题(本大题共10小题，每小题5分，共50分．在每小题给出的四个选项中，只有一项是符合题目要求的)1．已知i 2＝－1，则i(1－3i)＝( ) A.3－i B ．3＋i C ．－3－iD ．－3＋i解析： i(1－3i)＝i －3i 2＝3＋i. 答案： B2．z 1＝(m 2＋m ＋1)＋(m 2＋m －4)i ，m ∈R ，z 2＝3－2i ，则m ＝1是z 1＝z 2的( ) A ．充分不必要条件 B ．必要不充分条件 C ．充要条件D ．既不充分也不必要条件解析：因为z 1＝z 2，所以⎩⎪⎨⎪⎧m 2＋m ＋1＝3m 2＋m －4＝－2，解得m ＝1或m ＝－2，所以m ＝1是z 1＝z 2的充分不必要条件．答案： A3．已知复数z 满足|z |2＝z 2，则z 是( ) A ．0 B ．任意实数 C ．任意复数D ．实数和纯虚数解析：设z ＝a ＋b i(a ，b 为实数)，则 |z |2＝a 2＋b 2，z 2＝a 2－b 2＋2ab i.∵|z |2＝z 2，∴⎩⎪⎨⎪⎧a 2＋b 2＝a 2－b 2，2ab ＝0，即a ∈R 且b ＝0，故z ＝a 是任意实数．答案： B4．i 是虚数单位，复数－1＋3i1＋2i ＝( )A ．1＋iB ．5＋5iC ．－5－5iD ．－1－i 解析：－1＋3i1＋2i＝－1＋－5＝5＋5i5＝1＋i 答案： A 5．复数⎝⎛⎭⎪⎫3－i 1＋i 2＝( )A ．－3－4iB ．－3＋4iC ．3－4iD ．3＋4i解析： 3－i1＋i＝－－2＝2－4i 2＝1－2i ∴⎝⎛⎭⎪⎫3－i 1＋i 2＝(1－2i)2＝－3－4i答案： A6．(1＋i)20－(1－i)20的值是( ) A ．－1 024 B ．1 024 C ．0D ．1 024i解析： (1＋i)20－(1－i)20＝[(1＋i)2]10－[(1－i)2]10＝(2i)10－(－2i)10＝(2i)10－(2i)10＝0.答案： C7．若z 1＝(x －2)＋y i 与z 2＝3x ＋i(x ，y ∈R )互为共轭复数，则z 1对应的点在( ) A ．第一象限 B ．第二象限 C ．第三象限D ．第四象限解析：由z 1，z 2互为共轭复数，得⎩⎪⎨⎪⎧x －2＝3xy ＝－1，解得⎩⎪⎨⎪⎧x ＝－1y ＝－1，所以z 1＝(x －2)＋y i ＝－3－i.由复数的几何意义知z 1对应的点在第三象限．答案： C8．若复数z 满足1－z1＋z ＝i ，则|1＋z |等于( )A. 2 B ．1 C ．0D ．2解析：由1－z1＋z ＝i ，得1－z ＝i ＋i z ，∴(1＋i)z ＝1－i ，∴z ＝1－i1＋i ＝－i ，∴|1＋z |＝|1－i|＝ 2.答案： A9．设z 1＝i 4＋i 5＋i 6＋…＋i 12，z 2＝i 4·i 5·i 6·…·i 12，则z 1，z 2的关系是( ) A ．z 1＝－z 2 B ．z 1＝z 2 C ．z 1＝1＋z 2 D ．无法确定解析： z 1＝i41－i 91－i＝i41－i 1－i＝i 4＝1，z 2＝i 4＋5＋6＋7＋…＋12＝i 72＝1.答案： B10．定义运算⎪⎪⎪⎪a c b d ＝ad －bc ，则符合条件⎪⎪⎪⎪1z －1z i ＝4＋2i 的复数z 为( )A ．3－iB ．1＋3iC ．3＋iD ．1－3i解析： ⎪⎪⎪⎪1z－1z i ＝z i ＋z ＝z (1＋i)＝4＋2i ， ∴z ＝4＋2i 1＋i ＝4＋2i 1－i2＝4＋2－2i2＝3－i. 答案： A二、填空题(本大题共4小题，每小题5分，共20分．请把正确答案填在题中横线上) 11．若复数z 1＝4＋29i ，z 2＝6＋9i ，其中i 是虚数单位，则复数(z 1－z 2)i 的实部为________．解析：∵(z 1－z 2)i ＝[(4＋29i)－(6＋9i)]i ＝(－2＋20i)i ＝－20－2i ， ∴(z 1－z 2)i 的实部为－20. 答案：－2012．若复数z 满足z (1＋i)＝1－i(i 是虚数单位)，则其共轭复数z ＝________. 解析：设z ＝a ＋b i ，则(a ＋b i)(1＋i)＝1－i ，即a －b ＋(a ＋b )i ＝1－i.由⎩⎪⎨⎪⎧a －b ＝1，a ＋b ＝－1，解得⎩⎪⎨⎪⎧a ＝0，b ＝－1.所以z ＝－i ，z ＝i. 答案： i13．若复数2－b i31＋i (b ∈R )在复平面上对应的点在直线y ＝－x 上，则b 的值为________．解析： 2－b i31＋i＝＋b－2＝2－2i ＋b i ＋b 2＝2＋b ＋b －2，由题意得－(2＋b )＝b －2，∴b ＝0. 答案： 014．设z ∈C ，z ＋|z |＝2＋i ，则z ＝________. 解析：设z ＝a ＋b i(a ，b ∈R )，则|z |＝a 2＋b 2， ∴a ＋b i ＋a 2＋b 2＝2＋i ，∴⎩⎨⎧a ＋a 2＋b 2＝2，b ＝1∴⎩⎪⎨⎪⎧a ＝34b ＝1，∴z ＝34＋i.答案： 34＋i三、解答题(本大题共4小题，满分50分．解答时应写出必要的文字说明、证明过程或演算步骤)15．(本小题满分12分)已知z 1＝(x ＋y )＋(x 2－xy －2y )i ，z 2＝(2x －y )－(y －xy )i ，问x ，y 取什么实数值时，(1)z 1，z 2都是实数； (2)z 1，z 2互为共轭复数．解析： (1)由⎩⎪⎨⎪⎧x 2－xy －2y ＝0y －xy ＝0解得⎩⎪⎨⎪⎧x ＝0y ＝0或⎩⎪⎨⎪⎧x ＝1y ＝13，所以当⎩⎪⎨⎪⎧x ＝0y ＝0或⎩⎪⎨⎪⎧x ＝1y ＝13时，z 1，z 2都是实数．(2)由⎩⎪⎨⎪⎧x ＋y ＝2x －yx 2－xy －2y ＝y －xy解得⎩⎪⎨⎪⎧x ＝0y ＝0或⎩⎪⎨⎪⎧x ＝32y ＝34，所以当⎩⎪⎨⎪⎧x ＝0y ＝0或⎩⎪⎨⎪⎧x ＝32y ＝34时，z 1，z 2互为共轭复数．16．(本小题满分12分)计算：i －231＋23i＋(5＋i 19)－⎝ ⎛⎭⎪⎫1＋i 222.解析：原式＝＋231＋23i＋(5＋i 3)－11211＝i ＋(5－i)＋i ＝5＋i.17．(本小题满分12分)已知复数z ＝－2＋＋2－i.(1)求复数z ；(2)若z 2＋az ＋b ＝1－i ，求实数a ，b 的值．解析： (1)z ＝－2i ＋3＋3i 2－i ＝3＋i2－i＝＋＋5＝1＋i ；(2)把z ＝1＋i 代入得(1＋i)2＋a (1＋i)＋b ＝1－i ，即a ＋b ＋(2＋a )i ＝1－i ，所以⎩⎪⎨⎪⎧a ＋b ＝12＋a ＝－1，解得⎩⎪⎨⎪⎧a ＝－3b ＝4.18．(本小题满分14分)已知|z 1|＝1，|z 2|＝1，|z 1＋z 2|＝ 3.求|z 1－z 2|. 解析：方法一：设z 1＝a ＋b i ，z 2＝c ＋d i(a ，b ，c ，d ∈R )．由已知得a 2＋b 2＝1，c 2＋d 2＝1. (a ＋c )2＋(b ＋d )2＝3，又∵(a ＋c )2＋(b ＋d )2＝a 2＋b 2＋c 2＋d 2＋2ac ＋2bd ＝2＋2ac ＋2bd ＝3. ∴2ac ＋2bd ＝1.又|z 1－z 2|2＝(a －c )2＋(b －d )2＝a 2＋b 2＋c 2＋d 2－2ac －2bd ＝2－1＝1， ∴|z 1－z 2|＝1.方法二：在复平面内设z 1，z 2分别对应向量OZ 1→、OZ 2→，则对角线OZ →对应z 1＋z 2，Z 2Z 1→对应z 1－z 2，由已知|OZ 1→|＝1，|OZ 2→|＝1，|OZ |＝ 3. ∴∠OZ 1Z ＝120°.∴∠Z 2OZ 1＝60°. ∴在OZ 1Z 2中|Z 2Z 1→|＝1，即|z 1－z 2|＝1.方法三：由教材中的习题得结论|z 1＋z 2|2＋|z 1－z 2|2＝2(|z 1|2＋|z 2|2)，得|z 1－z 2|2＝1.∴|z 1－z 2|＝1.。

北师大版高中数学选修1-2课时跟踪检测(10套,附解析)

北师大版高中数学选修1-2课时跟踪检测（10套，附解析）一、回归分析1．已知两个有线性相关关系的变量的相关系数为r，则r取下列何值时，两个变量的线性相关关系最强( )A．－0.91 B．0.25C．0.6 D．0.86解析：选A 在四个r值中，|－0.91|最接近1，故此时，两个变量的线性相关关系最强．2．根据如下样本数据A．a>0，b>0 B．a>0，b<0C．a<0，b>0 D．a<0，b<0解析：选B 由表中数据画出散点图，如图．由散点图可知b<0，a>0，选B.3.设某大学的女生体重y(单位：kg)与身高x(单位：cm)具有线性相关关系，根据一组样本数据(x i，y i)(i＝1,2，…，n)，用最小二乘法建立的回归方程为y＝0.85x－85.71，则下列结论中不正确的是( )A．y与x具有正的线性相关关系B．回归直线过样本点的中心(x，y)C．若该大学某女生身高增加1 cm，则其体重约增加0.85 kgD．若该大学某女生身高为170 cm，则可断定其体重必为58.79 kg解析：选D 由于回归直线的斜率为正值，故y与x具有正的线性相关关系，选项A中的结论正确；回归直线过样本点的中心，选项B中的结论正确；根据回归直线斜率的意义易知选项C中的结论正确；由于回归分析得出的是估计值，故选项D中的结论不正确．4．为了解某社区居民的家庭年收入与年支出的关系，随机调查了该社区5户家庭，得到如下统计数据表：根据上表可得回归直线方程y ＝bx ＋a ，其中b ＝0.76，a ＝y －b x .据此估计，该社区一户年收入为15万元家庭的年支出为( )A ．11.4万元B ．11.8万元C ．12.0万元D ．12.2万元解析：选B 由题意知，x ＝8.2＋8.6＋10.0＋11.3＋11.95＝10，y ＝6.2＋7.5＋8.0＋8.5＋9.85＝8，∴a ＝8－0.76×10＝0.4，∴当x ＝15时，y ＝0.76×15＋0.4＝11.8(万元)．5．在一组样本数据(x 1，y 1)，(x 2，y 2)，…，(x n ，y n )(n ≥2，x 1，x 2，…，x n 不全相等)的散点图中，若所有样本点(x i ，y i )(i ＝1,2，…，n )都在直线y ＝12x ＋1上，则这组样本数据的样本相关系数为________．解析：根据样本相关系数的定义可知，当所有样本点都在直线上时，相关系数为1. 答案：16．某咖啡厅为了了解热饮的销售量y (个)与气温x (℃)之间的关系，随机统计了某4天的销售量与气温，并制作了对照表：________．解析：∵x ＝14(18＋13＋10－1)＝10，y ＝14(24＋34＋38＋64)＝40，∴40＝－2×10＋a ，∴a ＝60，当x ＝－4时，y ＝－2×(－4)＋60＝68.答案：687．某种产品的广告费用支出x 与销售额y 之间有如下的对应数据(单位：万元).(1)(2)求回归方程；(3)据此估计广告费用支出为10万元时，销售额y 的值．解：(1)作出散点图如下图．(2)由散点图可知，样本点近似地分布在一条直线附近，因此，x ，y 之间具有线性相关关系．由表中的数据可知，x －＝15×(2＋4＋5＋6＋8)＝5，y －＝15×(30＋40＋60＋50＋70)＝50.所以b ＝∑i ＝15x i －x－y i －y－∑i ＝15x i －x－2＝6.5，a ＝y －－b x －＝50－6.5×5＝17.5，因此线性回归方程为y ＝17.5＋6.5x .(3)x ＝10时，y ＝17.5＋10×6.5＝82.5(万元)．即当支出广告费用10万元时，销售额为82.5万元．8．某工厂为了对新研发的一种产品进行合理定价，将该产品按事先拟定的价格进行试销，得到如下数据：(1)求回归直线方程y ＝bx ＋a ，其中b ＝－20，a ＝y －b x ；(2)预计在今后的销售中，销量与单价仍然服从(1)中的关系，且该产品的成本是4元/件，为使工厂获得最大利润，该产品的单价应定为多少元？(利润＝销售收入－成本)解：(1)x ＝16(8＋8.2＋8.4＋8.6＋8.8＋9)＝8.5，y ＝16(90＋84＋83＋80＋75＋68)＝80，从而a ＝y ＋20x ＝80＋20×8.5＝250, 故y ＝－20x ＋250.(2)由题意知，工厂获得利润z ＝(x －4)y ＝－20x 2＋330x －1 000＝－20⎝⎛⎭⎪⎫x －3342＋361.25，所以当x ＝334＝8.25时，z max ＝361.25(元)．即当该产品的单价定为8.25元时，工厂获得最大利润．9．在钢铁碳含量对于电阻的效应研究中，得到如下数据表：解：由已知数据得x －＝17×∑i ＝17x i ≈0.543，y －＝17×145.2≈20.74，∑i ＝17x 2i ＝2.595，∑i ＝17y 2i ＝3 094.72，∑i ＝17x i y i ＝85.45.∴b ≈85.45－7×0.543×20.742.595－7×0.5432≈12.46， a ＝20.74－12.46×0.543≈13.97.线性回归方程为y ＝13.97＋12.46x . 下面利用相关系数检验是否显著．∑i ＝17x i y i －7x － y －＝85.45－7×0.543×20.74≈6.62，∑i ＝17x 2i －7x －2＝2.595－7×(0.543)2≈0.531， ∑i ＝17y 2i －7y －2＝3 094.72－7×(20.74)2＝83.687. ∴r ＝6.620.531×83.687≈0.993.由于r 接近于1，故钢铁碳含量对电阻的效应线性相关关系显著．二、条件概率与独立事件1．抛掷一颗骰子一次，A 表示事件：“出现偶数点”，B 表示事件：“出现3点或6点”，则事件A 与B 的关系是( )A ．相互互斥事件B ．相互独立事件C ．既相互互斥又相互独立事件D ．既不互斥又不独立事件解析：选B A ＝{2,4,6}，B ＝{3,6}，A ∩B ＝{6}，所以P (A )＝12，P (B )＝13，P (AB )＝16＝12×13，所以A 与B 是相互独立事件． 2．把一枚硬币抛掷两次，事件A ＝“第一次出现正面”，事件B ＝“第二次出现反面”，则P (B |A )的值为( )A.12 B ．14 C.13D ．1解析：选A P (B )＝P (A )＝12，P (AB )＝14，P (B |A )＝P ABP A ＝1412＝12.3．某农业科技站对一批新水稻种子进行试验，已知这批水稻种子的发芽率为0.8，出芽后的幼苗成活率为0.9，在这批水稻种子中，随机地取出一粒，则这粒水稻种子发芽能成长为幼苗的概率为( )A ．0.02B ．0.08C ．0.18D ．0.72解析：选D 设“这粒水稻种子发芽”为事件A ，“这粒水稻种子发芽又成长为幼苗”为事件AB ，“这粒种子能成长为幼苗”为事件B |A ，则P (A )＝0.8，P (B |A )＝0.9，由条件概率公式，得P (AB )＝P (B |A )·P (A )＝0.9×0.8＝0.72.4．甲射手击中靶心的概率为13，乙射手击中靶心的概率为12，甲、乙两人各射击一次，那么56等于( )A ．甲、乙都击中靶心的概率B ．甲、乙恰好有一人击中靶心的概率C ．甲、乙至少有一人击中靶心的概率D ．甲、乙不全击中靶心的概率解析：选D 设“甲、乙都击中靶心”为事件A ，则P (A )＝13×12＝16，甲、乙不全击中靶心的概率为P (A )＝1－P (A )＝1－16＝56.5．有一个数学难题，在半小时内，甲能解决的概率是12，乙能解决的概率是13，两人试图独立地在半小时内解决它，则两人都未解决的概率为________，问题得到解决的概率为________．解析：甲、乙两人都未能解决为⎝ ⎛⎭⎪⎫1－12⎝ ⎛⎭⎪⎫1－13＝12×23＝13，问题得到解决就是至少有1 人能解决问题． ∴P ＝1－13＝23.答案：13 236．盒中装有10只乒乓球，其中6只新球，4只旧球，不放回地依次取出2个球使用，在第一次摸出新球的条件下，第二次也取到新球的概率为________．解析：法一：设A ＝{第一次取到新球}，B ＝{第二次取到新球}，则n (A )＝6×9＝54，n (AB )＝6×5＝30，∴P (B |A )＝n AB n A ＝3054＝59.法二：在第一次取到新球的条件下，盒中装有9只乒乓球，其中5只新球，则第二次也取到新球的概率为P ＝59.答案：597．红队队员甲、乙、丙与蓝队队员A ，B ，C 进行围棋比赛，甲对A 、乙对B 、丙对C 各一盘．已知甲胜A 、乙胜B 、丙胜C 的概率分别为0.6，0.5，0.5.假设各盘比赛结果相互独立．求红队至少两名队员获胜的概率．解：设甲胜A 的事件为D ，乙胜B 的事件为E ，丙胜C 的事件为F ，则D ，E ，F 分别表示甲不胜A 、乙不胜B 、丙不胜C 的事件．因为P (D )＝0.6，P (E )＝0.5，P (F )＝0.5，由对立事件的概率公式知，P (D )＝0.4，P (E )＝0.5，P (F )＝0.5.红队至少两人获胜的事件有DE F ，D E F ，D EF ，DEF .由于以上四个事件两两互斥且各盘比赛的结果相互独立，因此红队至少两人获胜的概率为P ＝P (DE F )＋P (D E F )＋P (D EF )＋P (DEF )＝0.6×0.5×0.5＋0.6×0.5×0.5＋0.4×0.5×0.5＋0.6×0.5×0.5＝0.55.8．设进入某商场的每一位顾客购买甲种商品的概率为0.5，购买乙种商品的概率为0.6，且购买甲种商品与购买乙种商品相互独立，各顾客之间购买商品也是相互独立的．(1)求进入商场的1位顾客购买甲、乙两种商品中的一种的概率； (2)求进入商场的1位顾客至少购买甲、乙两种商品中的一种的概率．解：设“只购买甲种商品”为事件A ，“只购买乙种商品”为事件B ，“购买甲、乙两种商品中的一种”为事件C ，“至少购买甲、乙两种商品中的一种”为事件D .(1)因为C ＝(A B )＋(A B )，所以P (C )＝P (A B )＋P (A B )＝P (A )P (B )＋P (A )P (B ) ＝0.5×(1－0.6)＋(1－0.5)×0.6＝0.5. (2)因为D ＝A B ，所以P (D )＝P (A B )＝P (A )P (B )＝0.5×0.4＝0.2. 所以P (D )＝1－P (D )＝1－0.2＝0.8.9．2018年某中学对参加“社会实践活动”的全体志愿者进行学分考核，因该批志愿者表现良好，学校决定考核只有合格和优秀两个等次．若某志愿者考核为合格，授予1个学分；考核为优秀，授予2个学分，假设该校志愿者甲、乙、丙考核为优秀的概率分别为45，23，23，他们考核所得的等次相互独立．(1)求在这次考核中，志愿者甲、乙、丙三人中至少有一名考核为优秀的概率； (2)求在这次考核中甲、乙、丙三名志愿者所得学分之和至多为4分的概率．解：(1)记“甲考核为优秀”为事件A ，“乙考核为优秀”为事件B ，“丙考核为优秀”为事件C ，“甲、乙、丙至少有一名考核为优秀”为事件D .则P (D )＝1－P (A B C )＝1－P (A )P (B )P (C )＝1－⎝ ⎛⎭⎪⎫1－45×⎝ ⎛⎭⎪⎫1－23×⎝ ⎛⎭⎪⎫1－23＝4445.(2)由题意，得在这次考核中甲、乙、丙三名志愿者所得学分之和为3分的概率为P (AB C )＝P (A )P (B )P (C )＝⎝⎛⎭⎪⎫1－45×⎝⎛⎭⎪⎫1－23×⎝⎛⎭⎪⎫1－23＝145，在这次考核中甲、乙、丙三名志愿者所得学分之和为4分的概率为P (A B C )＋P (AB C )＋P (A B C )＝45×⎝⎛⎭⎪⎫1－23×⎝⎛⎭⎪⎫1－23＋⎝⎛⎭⎪⎫1－45×23×⎝⎛⎭⎪⎫1－23＋⎝⎛⎭⎪⎫1－45×⎝⎛⎭⎪⎫1－23×23＝845.所以在这次考核中甲、乙、丙三名志愿者所得学分之和至多为4分的概率为145＋845＝15.三、独立性检验独立性检验的基本思想及应用1．通过随机询问110名性别不同的大学生是否爱好某项运动，得到下表：由χ2＝n a ＋bc ＋d a ＋cb ＋d算得，χ2＝30－260×50×60×50≈7.8.附表：A ．有99.9%以上的把握认为“爱好该项运动与性别有关”B ．有99.9%以上的把握认为“爱好该项运动与性别无关”C ．有99%以上的把握认为“爱好该项运动和性别有关”D ．有99%以上的把握认为“爱好该项运动和性别无关”解析：选C 因为χ2≈7.8>6.635，所以有99%以上的把握认为有关．2．两个分类变量X 和Y, 值域分别为{x 1，x 2}和{y 1，y 2}, 其样本频数分别是a ＝10, b ＝21, c ＋d ＝35. 若X 与Y 有关系的可信程度不小于95%, 则c 等于( )A ．3B ．7C ．5D ．6解析：选A 列表如下：故χ2＝≥3.841. 把选项A、B、C、D代入验证可知选A.＋c－c3．某人研究中学生的性别与成绩、视力、智商、阅读量这4个变量的关系，随机抽查52名中学生，得到统计数据如表1至表4，则与性别有关联的可能性最大的变量是( )表1表3表4A．成绩C．智商D．阅读量解析：选D 因为χ21＝－216×36×32×20＝52×8216×36×32×20，χ22＝－216×36×32×20＝52×112216×36×32×20，χ23＝－216×36×32×20＝52×96216×36×32×20，χ24＝－216×36×32×20＝52×408216×36×32×20，则有χ24>χ22>χ23>χ21，所以阅读量与性别关联的可能性最大．4．在研究性别与吃零食这两个分类变量是否有关系时，下列说法中正确的序号是________．①若χ2>6.635，则我们有99%的把握认为吃零食与性别有关系，那么在100个吃零食的人中必有99人是女性；②由独立性检验可知，在有99%的把握认为吃零食与性别有关系时，如果某人吃零食，那么此人是女性的可能性为99%；③由独立性检验可知，在有99%的把握认为吃零食与性别有关系时，是指每进行100次这样的推断，平均有1次推断错误．解析：χ2是指确定有多大的把握认为“两个分类变量吃零食与性别有关系”的随机变量值，所以由独立性检验可知，当有99%的把握认为吃零食与性别有关系时，是指每进行100次这样的推断，平均有1次推断错误，故填③.答案：③5．下列是关于出生男婴与女婴调查的列联表：那么A＝________，BD＝________，E＝________.解析：由45＋E＝98得E＝53，由98＋D＝180可知D＝82.由A＋35＝D知A＝47.所以B＝45＋47＝92.C＝E＋35＝88.答案：47 92 88 82 536．为探究电离辐射的剂量与人体的受损程度是否有关，用两种不同剂量的电离辐射照射小白鼠，在照射后14天内的结果如下表所示.2≈________.解析：χ2＝－220×30×25×25≈5.333.答案：5.3337．在对人们的休闲方式的一次调查中，共调查了124人，其中女性70人，男性54人．女性中有43人主要的休闲方式是看电视，另外的27人主要的休闲方式是运动；男性中有21人主要的休闲方式是看电视，另外的33人主要的休闲方式是运动．(1)根据以上数据建立一个2×2列联表；(2)能否有95%的把握认为性别与休闲方式有关系．解：(1)2×2列联表为：(2)计算χ2＝－270×54×64×60≈6.201.因为6.201>3.841，所以有95%的把握认为“性别与休闲方式有关”．8．某地区甲校高二年级有1 100人，乙校高二年级有900人，为了统计两个学校高二年级在学业水平考试中的数学学科成绩，采用分层抽样的方法在两校共抽取了200名学生的数学成绩，如表．(已知本次测试合格线是50分，两校合格率均为100%)甲校高二年级数学成绩：(2)若数学成绩不低于80分为优秀，低于80分为非优秀，根据以上统计数据填写下面2×2列联表，并回答能否有95%的把握认为“两个学校的数学成绩有差异”？解：(1)所以x＝10，y＝15.甲校的平均分为1110×(55×10＋65×25＋75×35＋85×30＋95×10)≈75.乙校的平均分为190×(55×15＋65×30＋75×25＋85×15＋95×5)≈71.(2)数学成绩不低于80分为优秀，低于80分为非优秀，得到列联表如下：所以χ2＝110×90×60×140≈4.714，又因为4.714>3.841，故有95%的把握认为“两个学校的数学成绩有差异”．9．某学生对其30位亲属的饮食习惯进行了一次调查，并用如图所示的茎叶图表示他们的饮食指数(说明：图中饮食指数低于70的人，饮食以蔬菜为主；饮食指数高于70的人，饮食以肉类为主)．(1)根据茎叶图，帮助这位同学说明其30位亲属的饮食习惯；(2)根据以上数据完成如下2×2列联表；(3)解：(1)由茎叶图，可知30位亲属中50岁以上的人饮食多以蔬菜为主，50岁以下的人饮食多以肉类为主．(2)2×2列联表如下所示：(3)由题意，知χ2＝12×18×20×10＝10>6.635，故有99%以上的把握认为其亲属的饮食习惯与年龄有关系．四、流程图1．下列关于流程图的说法中不正确的是( )A．流程图用来描述一个动态过程B．算法框图是一种特殊的流程图C．流程图只能用带箭头的流程线表示各单元的先后关系D．解决某一问题的流程图的画法是唯一的解析：选D A，C均符合流程图的特征，算法框图是一种特殊的流程图，故B正确．2．某人带着包裹进入超市购物的流程图如图所示，则在空白处应填( )进入超市―→存放包裹―→在货架上选择物品―→付款―→―→离开超市A．退换物品B．归还货车C．取回包裹D．参加抽奖答案：C3.如图所示，已知集合A＝{x|框图中输出的x的值}，集合B＝{y|框图中输出的y的值}．全集U＝Z，Z为整数集．当x＝－1时，(∁U A)∩B＝( )A．{－3，－1,5}B．{－3，－1,5,7}C．{－3，－1,7}D．{－3，－1,7,9}解析：选D 根据程序框图功能知：y＝－3，x＝0；y＝－1，x＝1；y＝1，x＝2；…；y＝9，x＝6.所以A＝{0,1,2,3,4,5,6}．B＝{－3，－1,1,3,5,7,9}．则(∁U A)∩B＝{－3，－1,7,9}．4.执行如图所示的程序框图，如果输入的a＝－1，则输出的S等于( )A．2 B．3C．4 D．5解析：选B 运行程序框图，a＝－1，S＝0，K＝1，K≤6成立；S＝0＋(－1)×1＝－1，a＝1，K＝2，K≤6成立；S＝－1＋1×2＝1，a＝－1，K＝3，K≤6成立；S＝1＋(－1)×3＝－2，a＝1，K＝4，K≤6成立；S＝－2＋1×4＝2，a＝－1，K＝5，K≤6成立；S＝2＋(－1)×5＝－3，a＝1，K＝6，K≤6成立；S＝－3＋1×6＝3，a＝－1，K＝7，K≤6不成立，输出S＝3.5．某工程的工序流程图如图，则该工程的总工时最多为________天．解析：因为各个不同工序中用时最多的是①→②→④→⑥→⑦，即9天．答案：96．执行如图所示的程序框图，若输入n＝3，则输出T＝________.解析：输入n＝3，则i＝0，S＝0，T＝0，i≤n成立，故i＝1，S＝0＋1＝1，T＝0＋1＝1，此时i＝1≤n成立，故i＝2，S＝1＋2＝3，T＝1＋3＝4，此时i＝2≤n成立，故i＝3，S＝3＋3＝6，T＝4＋6＝10，此时i＝3≤n成立，故i＝4，S＝6＋4＝10，T＝10＋10＝20，此时i＝4≤n不成立，故输出T＝20.答案：207．如图是某工厂加工某种零件的一个工序操作流程图．按照这个工序流程图，回答下列问题： (1)一件成品最多经过几道加工和检验程序； (2)导致废品的产生有几种不同的情形．解：由流程图可得：(1)最多经过“粗加工”“检验”“返修加工”“返修检验”“精加工”“最后检验”六道加工和检验程序．(2)三种不同情形：①返修加工―→返修检验不合格． ②检验――→合格精加工―→最后检验不合格． ③返修检验――→合格精加工―→最后检验不合格．8．求两底面半径分别为1和4，高为4的圆台的表面积及体积，写出解决该问题的一个算法，并画出程序框图．解：算法步骤如下：第一步 r 1＝1，r 2＝4，h ＝4. 第二步计算l ＝r 2－r 12＋h 2.第三步计算S 1＝πr 21，S 2＝πr 22，S 3＝π(r 1＋r 2)l . 第四步计算S ＝S 1＋S 2＋S 3，V ＝13(S 1＋S 1S 2＋S 2)h .第五步输出S 和V . 该算法的程序框图如下：9．高考成绩公布后，考生如果认为公布的高考成绩与本人估算的成绩不符，可以在规定的时间内申请查分，其步骤如下：①本人填写《查分登记表》，交县(区)招生办申请查分，县(区)招生办呈交市招生办，再报省招生办．②省招生办复查，若无误，则查分工作结束后通知市招生办；若有误，则再具体认定并改正，也在查分工作结束后通知市招生办．③市招生办接通知后通知县(区)招生办，再由县(区)招生办通知考生．试画出该事件的流程图．解：流程图如图所示．五、结构图1．下列关于流程图和结构图的说法中不正确的是( )A．流程图用来描述一个动态过程B．结构图是用来刻画系统结构的C．流程图只能用带箭头的流程线表示各单元的先后关系D．结构图只能用带箭头的连线表示各要素之间的从属关系或逻辑上的先后关系解析：选D 结构图一般由构成系统的若干要素和表达各要素之间关系的连线(或方向箭头)构成，故D不正确．2．把平面内两条直线的位置关系填入结构图中的M，N，E，F中，顺序较为恰当的是( )①平行②垂直③相交④斜交A．①②③④B．①④②③C．①③②④D．②①④③解析：选C 平行无交点，而垂直、相交、斜交都有交点，垂直与斜交是并列的，都隶属于相交．3．下图是“集合”的知识结构图，如果要加入“子集”，则应该放在( )A．“集合的概念”的下位B．“集合的表示”的下位C．“基本关系”的下位D．“基本运算”的下位解析：选C 子集是集合与集合之间的关系，故应为“基本关系”的下位．4．下图是一商场某一个时间制订销售计划时的局部结构图，则“计划”受影响的主要要素有( )A．1个B．2个C．3个D．4个解析：选C 共有“策划部”“政府行为”“社会需求”，三个要素影响计划的执行．5．我国是华南虎的故乡，且华南虎是所有老虎的祖先，现在我国野生华南虎的数量已不足20只，弥足珍贵，老虎属于猫科动物，猫科动物的分类(如图所示)．据图回答：华南虎属于________科，________属．解析：该结构图是按从左到右的顺序画出的，从左到右第二层是科类，第三层是属类，分类由大到小，逐层细化，单线观察：猫科动物-豹亚科-豹属-虎种-华南虎，和华南虎相连的第二层是豹亚科，第三层是豹属．答案：豹亚豹6．下列关于结构图的说法中，正确的是________．①结构图只能是从左向右分解；②结构图只能是从上向下分解；③结构图只能是从下向上分解；④结构图一般呈“树”形结构；⑤结构图有时呈“环”形结构．解析：结构图分解方向一般依据具体情况选择从上向下或从左向右．答案：④⑤7．一家新技术公司计划研制一个名片管理系统，希望系统能够具备以下功能：(1)用户管理：能修改密码，显示用户信息，修改用户信息．(2)用户登录．(3)名片管理：能够对名片进行删除、添加、修改、查询．(4)出错信息处理．请根据这些要求画出该系统的结构图．解：由题意可得：8．如图所示是某大学的学校组织结构图，由图回答下列问题：(1)学生工作处的下位要素是什么？(2)学生工作处与其下位要素是什么关系？解：(1)由题图可知学生工作处的下位要素包括工业工程系、城建环保工程系、电气工程系、计算机工程系、机械工程系、汉教部．(2)学生工作处与其下位要素的关系是从属关系．9．画出三角函数的知识结构图．解：三角函数的知识结构图如下：六、归纳推理1．观察下列数列的特点：1,2,2,3,3,3,4,4,4,4，…，则第100项是( )A．10 B．13C．14 D．100解析：选C ∵＋2＝91，∴从第92项到第105项都是14，故选C.2.如图所示的三角形数组是我国古代数学家杨辉发现的，称为杨辉三角形，根据图中的数构成的规律，a所表示的数是( )11 11 2 11 3 3 11 4 a 4 11 5 10 10 5 1A．2 B．4C ．6D ．8解析：选C 由杨辉三角形可以发现：每一行除1外，每个数都是它肩膀上的两数之和．故a ＝3＋3＝6.3．观察下图中图形的规律，在其右下角的空格内适合的图形为( )A ．■ C ．□D ．○解析：选A 图形涉及三种符号□、○、△，其中符号○与△各有3个，且各自有二黑一白，所以□缺一个黑色符号，即应画上■才合适．4．设凸k 边形的内角和为f (k )，则凸k ＋1边形的内角和f (k ＋1)＝f (k )＋( ) A.π2B ．π C.32π D ．2π解析：选B 三角形内角和为π，四边形为2π，五边形为3π，…，故f (k ＋1)＝f (k )＋π.5．已知x ∈(0，＋∞)，有下列各式：x ＋1x ≥2，x ＋4x 2＝x 2＋x 2＋4x 2≥3，x ＋27x 3＝x 3＋x 3＋x3＋27x 3≥4成立，观察上面各式，按此规律若x ＋ax4≥5，则正数a ＝________.解析：观察给出的各个不等式，不难得到x ＋11x ≥2，x ＋22x 2≥3，x ＋33x3≥4，从而第4个不等式为x ＋44x 4≥5，所以当x ＋a x4≥5时，正数a ＝44.答案：446．如图①是第七届国际数学教育大会(简称ICME －7)的会徽图案，会徽的主体图案是由如图②的一连串直角三角形演化而成的，其中OA 1＝A 1A 2＝A 2A 3＝…＝A 7A 8＝1，如果把图②中的直角三角形依此规律继续作下去，记OA 1，OA 2，…，OA n ，…的长度构成数列{a n }，则此数列{a n }的通项公式为a n ＝__________.解析：根据OA 1＝A 1A 2＝A 2A 3＝…＝A 7A 8＝1和题图②中的各直角三角形，由勾股定理，可得a 1＝OA 1＝1，a 2＝OA 2＝OA 21＋A 1A 22＝12＋12＝2，a 3＝OA 3＝OA 22＋A 2A 23＝22＋12＝3，…，故可归纳推测出a n ＝n . 答案：n7．观察等式：1＋3＝4＝22,1＋3＋5＝9＝32,1＋3＋5＋7＝16＝42，你能得出怎样的结论？解：通过观察发现：等式的左边为正奇数的和，而右边是整数(实际上就是左边奇数的个数)的完全平方．因此可推测得出：1＋3＋5＋7＋9＋…＋(2n －1)＝n 2(n ≥2，n ∈N ＋)．8．已知a ，b 为正整数，设两直线l 1：y ＝b －ba x 与l 2：y ＝b ax 的交点为P 1(x 1，y 1)，且对于n ≥2的自然数，两点(0，b )，(x n －1,0)的连线与直线y ＝b ax 交于点P n (x n ，y n )．(1)求P 1，P 2的坐标； (2)猜想P n 的坐标(n ∈N ＋)．解：(1)解方程组⎩⎪⎨⎪⎧y ＝b －b ax ，y ＝ba x ，得P 1⎝ ⎛⎭⎪⎫a 2，b2.过(0，b )，⎝ ⎛⎭⎪⎫a 2，0两点的直线方程为2x a ＋y b ＝1，与y ＝b a x 联立解得P 2⎝ ⎛⎭⎪⎫a 3，b 3. (2)由(1)可猜想P n ⎝⎛⎭⎪⎫a n ＋1，b n ＋1.9．一种十字绣作品由相同的小正方形构成，图①②③④分别是制作该作品前四步所对应的图案，按照如此规律，第n 步完成时对应图案中所包含小正方形的个数记为f (n )．(1)求出f (2)，f (3)，f (4)，f (5)的值；(2)利用归纳推理，归纳出f (n ＋1)与f (n )的关系式； (3)猜想f (n )的表达式，并写出推导过程．解：(1)图①中只有一个小正方形，得f (1)＝1；图②中有3层，以第2层为对称轴，有1＋3＋1＝5(个)小正方形，得f (2)＝5；图③中有5层，以第3层为对称轴，有1＋3＋5＋3＋1＝13(个)小正方形，得f (3)＝13；图④中有7层，以第4层为对称轴，有1＋3＋5＋7＋5＋3＋1＝25(个)小正方形，得f (4)＝25；第五步所对应的图形中有9层，以第5层为对称轴，有1＋3＋5＋7＋9＋7＋5＋3＋1＝41(个)小正方形，得f(5)＝41.(2)∵f(1)＝1，f(2)＝5，f(3)＝13，f(4)＝25，f(5)＝41，∴f(2)－f(1)＝4＝4×1，f(3)－f(2)＝8＝4×2，f(4)－f(3)＝12＝4×3，f(5)－f(4)＝16＝4×4，…，∴f(n)－f(n－1)＝4×(n－1)＝4n－4.∴f(n＋1)与f(n)的关系式为f(n＋1)－f(n)＝4n.(3)猜想f(n)的表达式为f(n)＝2n2－2n＋1.由(2)可知f(2)－f(1)＝4＝4×1，f(3)－f(2)＝8＝4×2，f(4)－f(3)＝12＝4×3，f(5)－f(4)＝16＝4×4，……f(n)－f(n－1)＝4×(n－1)＝4n－4，将上述n－1个式子相加，得f(n)－f(1)＝4[1＋2＋3＋4＋…＋(n－1)]，则f(n)＝2n2－2n＋1.七、类比推理1．下列哪个平面图形与空间图形中的平行六面体作为类比对象较合适( )A．三角形B．梯形C．平行四边形D．矩形解析：选C 从构成几何图形的几何元素的数目、位置关系、度量等方面考虑，用平行四边形作为平行六面体的类比对象较为合适．2．设△ABC的三边长分别为a，b，c，△ABC的面积为S，内切圆半径为r，则r＝2Sa＋b＋c；类比这个结论可知：四面体PABC的四个面的面积分别为S1，S2，S3，S4，内切球的半径为r，四面体PABC的体积为V，则r＝( )A.VS1＋S2＋S3＋S4B.2VS1＋S2＋S3＋S4C.3VS1＋S2＋S3＋S4D.4VS1＋S2＋S3＋S4解析：选C 设内切球的球心为O，所以可将四面体PABC分为四个小的三棱锥，即OABC，OPAB，OPAC，OPBC，而四个小三棱锥的底面积分别是四面体PABC的四个面的面积，高是内切球的半径，所以V ＝13S 1r ＋13S 2r ＋13S 3r ＋13S 4r ＝13(S 1＋S 2＋S 3＋S 4)r ，∴r ＝3VS 1＋S 2＋S 3＋S 4.3．已知{b n }为等比数列，b 5＝2，则b 1b 2b 3…b 9＝29.若{a n }为等差数列，a 5＝2，则{a n }的类似结论为( )A ．a 1a 2a 3…a 9＝29B ．a 1＋a 2＋…＋a 9＝29C ．a 1a 2…a 9＝2×9D ．a 1＋a 2＋…＋a 9＝2×9解析：选D 类比等比数列{b n }中b 1b 2b 3…b 9＝b 95，可得在等差数列{a n }中a 1＋a 2＋…＋a 9＝9a 5＝9×2.4．类比三角形中的性质： ①两边之和大于第三边； ②中位线长等于底边长的一半； ③三内角平分线交于一点．可得四面体的对应性质：①任意三个面的面积之和大于第四个面的面积；②过四面体的交于同一顶点的三条棱的中点的平面面积等于该顶点所对的面面积的14；③四面体的六个二面角的平分面交于一点．其中类比推理方法正确的有( ) A ．① B ．①② C ．①②③D ．都不对解析：选C 以上类比推理方法都正确，需注意的是类比推理得到的结论是否正确与类比推理方法是否正确并不等价，方法正确结论也不一定正确．5．在△ABC 中，D 为BC 的中点，则AD ―→＝12()AB ―→＋AC ―→ ，将命题类比到四面体中去，得到一个命题为：______________________________________.．解析：平面中线段的中点类比到空间为四面体中面的重心，顶点与中点的连线类比顶点和重心的连线．答案：在四面体A BCD 中，G 是△BCD 的重心，则AG ―→＝13()AB ―→＋AC ―→＋AD ―→ 6．运用下面的原理解决一些相关图形的面积问题：如果与一条固定直线平行的直线被甲、乙两个封闭的图形所截得的线段的比都为k ，那么甲的面积是乙的面积的k 倍．你可以从给出的简单图形①②中体会这个原理．现在图③中的两个曲线方程分别是x 2a 2＋y 2b2＝1(a ＞b＞0)与x 2＋y 2＝a 2，运用上面的原理，图③中椭圆的面积为__________．解析：由于椭圆与圆截y 轴所得线段之比为b a，即k ＝b a，所以椭圆面积S ＝πa 2·b a＝πab . 答案：πab7．在Rt △ABC 中，若∠C ＝90°，则cos 2A ＋cos 2B ＝1，在空间中，给出四面体性质的猜想．解：如图，在Rt △ABC 中，cos 2A ＋cos 2B ＝⎝ ⎛⎭⎪⎫b c 2＋⎝ ⎛⎭⎪⎫a c 2＝a 2＋b2c 2＝1.于是把结论类比到四面体P A ′B ′C ′中，我们猜想，三棱锥P A ′B ′C ′中，若三个侧面PA ′B ′，PB ′C ′，PC ′A ′两两互相垂直，且分别与底面所成的角为α，β，γ，则cos 2α＋cos 2β＋cos 2γ＝1.8．在公比为4的等比数列{b n }中，若T n 是数列{b n }的前n 项积，则T 20T 10，T 30T 20，T 40T 30也成等比数列，且公比为4100；类比上述结论，相应地在公差为3的等差数列{a n }中，若S n 是{a n }的前n 项和．(1)写出相应的结论，判断该结论是否正确，并加以证明； (2)写出该结论一个更为一般的情形(不必证明)．解：(1)在公差为3的等差数列{a n }中，若S n 是{a n }的前n 项和，则数列S 20－S 10，S 30－S 20，S 40－S 30也是等差数列，且公差为300.该结论是正确的．证明如下：∵等差数列{a n }的公差d ＝3， ∴(S 30－S 20)－(S 20－S 10)＝(a 21＋a 22＋…＋a 30)－(a 11＋a 12＋…＋a 20)＝10d ＋10d ＋…＋10d ＝100d ＝300，10个同理可得：(S 40－S 30)－(S 30－S 20)＝300，所以数列S 20－S 10，S 30－S 20，S 40－S 30是等差数列，且公差为300. (2)在公差为d 的等差数列{a n }中，若S n 是{a n }的前n 项和，则对于任意k ∈N ＋，数列S 2k －S k ，S 3k －S 2k ，S 4k －S 3k 也成等差数列，且公差为k 2d .9．先阅读下列不等式的证法，再解决后面的问题：已知a 1，a 2∈R ，a 1＋a 2＝1，求证a 21＋a 22≥12.证明：构造函数f (x )＝(x －a 1)2＋(x －a 2)2，则f (x )＝2x 2－2(a 1＋a 2)x ＋a 21＋a 22＝2x 2－2x ＋a 21＋a 22. 因为对一切x ∈R ，恒有f (x )≥0，所以Δ＝4－8(a 21＋a 22)≤0，所以a 21＋a 22≥12.(1)若a 1，a 2，…，a n ∈R ，a 1＋a 2＋…＋a n ＝1，请写出上述结论的推广式； (2)类比上述证法，对你推广的结论加以证明．解：(1)若a 1，a 2，…，a n ∈R ，a 1＋a 2＋…＋a n ＝1，求证：a 21＋a 22＋…＋a 2n ≥1n.(2)证明：构造函数f (x )＝(x －a 1)2＋(x －a 2)2＋…＋(x －a n )2，则f (x )＝nx 2－2(a 1＋a 2＋…＋a n )x ＋a 21＋a 22＋…＋a 2n ＝nx 2－2x ＋a 21＋a 22＋…＋a 2n . 因为对一切x ∈R ，恒有f (x )≥0，所以Δ＝4－4n (a 21＋a 22＋…＋a 2n )≤0. 所以a 21＋a 22＋…＋a 2n ≥1n.八、数学证明1．下列四个推导过程符合演绎推理三段论形式且推理正确的是( )A ．大前提：无限不循环小数是无理数；小前提：π是无理数；结论：π是无限不循环小数B ．大前提：无限不循环小数是无理数；小前提：π是无限不循环小数；结论：π是无理数C ．大前提：π是无限不循环小数；小前提：无限不循环小数是无理数；结论：π是无理数D ．大前提：π是无限不循环小数；小前提：π是无理数；结论：无限不循环小数是无理数解析：选B 对于A ，小前提与结论互换，错误；对于B ，符合演绎推理过程且结论正确；对于C 和D ，均为大小前提及结论颠倒，不符合演绎推理三段论形式．故选B.2．“9的倍数都是3的倍数，某奇数是9的倍数，故此奇数是3的倍数”，上述推理是( )A ．小前提错B ．结论错C ．正确的D ．大前提错解析：选C ∵大前提，小前提，推理形式都正确， ∴结论正确．3．在不等边三角形中，a 为最大边，要想得到∠A 为钝角的结论，三边a ，b ，c 应满足的条件是( )A ．a 2＜b 2＋c 2B ．a 2＝b 2＋c 2C ．a 2＞b 2＋c 2D ．a 2≤b 2＋c 2解析：选C 由cos A ＝b 2＋c 2－a 22bc＜0，∴b 2＋c 2－a 2＜0，∴a 2＞b 2＋c 2.4．在证明f (x )＝2x ＋1为增函数的过程中，有下列四个命题：①增函数的定义是大前提；②增函数的定义是小前提；③函数f (x )＝2x ＋1满足增函数的定义是大前提；④函数f (x )＝2x ＋1满足增函数的定义是小前提．其中正确的命题是( )A ．①④B ．②④C ．①③D ．②③解析：选A 根据三段论特点，过程应为：大前提是增函数的定义；小前提是f (x )＝2x ＋1满足增函数的定义；结论是f (x )＝2x ＋1为增函数，故①④正确．5.如图，α⊥β，α∩β＝l ，P ∈α，PO ⊥l 交l 于O ，则可以得到的结论是________．。

【创新设计】-高中数学章末质量评估4 北师大版选修1-2

章末质量评估(四)(时间：100分钟满分：120分)一、选择题(每小题5分，共50分) 1．复数21－i 等于( )．A ．1＋iB ．1－iC ．－1＋iD ．－1－i 解析21－i＝＋－＋＝＋2＝1＋i.答案 A2．i 是虚数单位，i 3＋3i等于( )．A.14－312i B.14＋312i C.12＋36i D.12－36i 解析i3＋3i＝i 3－3i 3＋9＝3i －3i 212＝3＋3i 12＝14＋312i.答案 B3．复数z ＝1＋cos α＋isin α(π<α<2π)的模为 ( )．A ．2cos α2B ．－2cos α2C ．2sin α2D ．－2sin α2解析 |z |＝1＋cos α2＋sin 2α＝2＋2cos α＝4cos2α2＝2⎪⎪⎪⎪⎪⎪cos α2.∵π<α<2π，∴π2<α2<π，∴cos α2<0，∴2⎪⎪⎪⎪⎪⎪cos α2＝－2cos α2.答案 B4．已知复数z 满足|z |2－2|z |－3＝0，则复数z 对应点的轨迹为 ( )．A ．一个圆B ．线段C ．两点D ．两个圆解析 ∵|z |2－2|z |－3＝0，∴(|z |－3)(|z |＋1)＝0，∴|z |＝3表示一个圆．答案 A5．定义运算⎪⎪⎪⎪⎪⎪ab cd ＝ad －bc ，则符合条件⎪⎪⎪⎪⎪⎪1 －1z z i ＝4＋2i 的复数z 为( )．A ．3－iB ．1＋3iC ．3＋iD ．1－3i解析 ⎪⎪⎪⎪⎪⎪1 －1z z i ＝z i ＋z ＝z (1＋i)＝4＋2i ，∴z ＝4＋2i 1＋i ＝＋－2＝4＋2－2i2＝3－i.答案 A6．已知z ＝1＋i 2，则1＋z 50＋z 100的值是 ( )．A ．3B ．1C ．2＋iD ．i解析 z 50＝⎝ ⎛⎭⎪⎫1＋i 250＝⎣⎢⎡⎦⎥⎤⎝ ⎛⎭⎪⎫1＋i 2225＝i 25＝i.∴1＋z 50＋z 100＝i.答案 D7．复数z ＝m －2i1＋2i在复平面上对应的点不可能位于( )．A ．第一象限B ．第二象限C ．第三象限D ．第四象限解析 z ＝m －2i 1＋2i ＝15[(m －2i)(1－2i)]＝15[(m －4)－2(m ＋1)i]．若在第一象限，则⎩⎪⎨⎪⎧m －4>0，－m ＋，∴无解．答案 A8．若复数z 满足|z |－z ＝101－2i，则z 等于 ( )．A ．－3＋4iB ．－3－4iC ．3－4iD ．3＋4i答案 D9．满足条件|z |＝|3＋4i|的复数z 在复平面上对应点的轨迹是 ( )．A ．一条直线B ．两条直线C ．圆D ．椭圆解析 ∵|z |＝5，由模的几何意义知：复数z 对应点Z 到原点的距离为5，选C.答案 C10．若sin 2θ－1＋i(2cos θ＋1)是纯虚数，则θ的值为 ( )．A ．2k π－π4(k ∈Z )B ．2k π＋π4(k ∈Z )C ．2k π±π3(k ∈Z )D ．k π＋π4(k ∈Z )解析 ∵⎩⎨⎧sin 2θ－1＝0，2cos θ＋1≠0，∴⎩⎪⎨⎪⎧sin 2θ＝1，cos θ≠－22，∴⎩⎪⎨⎪⎧ 2θ＝2k π＋π2k ∈Z ，θ≠2k π±3π4k ∈Z ，∴⎩⎪⎨⎪⎧θ＝k π＋π4k ∈Z ，θ≠2k π±3π4k ∈Z ，∴θ＝2k π＋π4(k ∈Z )．答案 B二、填空题(每小题5分，共30分) 11．复数i 2(1＋i)的实部是________．解析 i 2(1＋i)＝－1－i ，所以实部是－1.答案－112．已知复数z 1＝3＋4i ，z 2＝t ＋i(t ∈R )，且z 1·z 2是实数，则实数t 等于 __________．解析 z 1·z 2＝(3＋4i)·(t －i)＝(3t ＋4)＋(4t －3)i 是实数，故4t －3＝0，t＝34.答案 3413．设a 是实数，且a1＋i ＋1＋i 2是实数，则a 等于__________．解析 ∵a 1＋i ＋1＋i 2＝a －a i 2＋1＋i 2＝a ＋12＋1－a 2i 为实数，∴1－a2＝0，∴a ＝1.答案 114. 已知复数z 1＝a 2＋2a －3＋(a －3)i ，z 2＝a －1＋(a 2＋2a －1)i(a ∈R )分别对应向量OZ 1→、OZ 2→(O 为原点)，若Z 1，Z 2两点关于x 轴对称，则a 的值为 ________．解析 ∵Z 1，Z 2关于x 轴对称，∴Z 1，Z 2实部相等，虚部互为相反数，∴⎩⎪⎨⎪⎧a 2＋2a －3＝a －1，a －3＝－a 2＋2a －，解得a ＝1.答案 115．若复数z 满足关系式z (1＋i)＝2，则z 的共轭复数为________．解析由题意得z ＝21＋i＝－＋－＝1－i ，因此复数z 的共轭复数等于1＋i.答案 1＋i16．已知关于x 的方程x 2＋(1＋2i)x －(3m －1)i ＝0有实根，则纯虚数m 的值是__________．解析方程有实根，不妨设其一个根为x 0，设m ＝a i(a ∈R )，代入，得x 20＋(1＋2i)x 0－(3a i －1)i ＝0，化简，得(2x 0＋1)i ＋x 20＋x 0＋3a ＝0.由性质可得⎩⎪⎨⎪⎧2x 0＋1＝0，x 20＋x 0＋3a ＝0，解得a ＝112，∴m ＝112i.答案112i 三、解答题(共40分)17．(10分)复数z 1＝a ＋b i(a ，b ∈R )，且a 2＋b 2＝25，z 2＝3＋4i ，z 1·z 2是纯虚数，求z 1.解 z 1·z 2＝(a ＋b i)(3＋4i)＝(3a －4b )＋(4a ＋3b )i. ∵z 1·z 2是纯虚数，∴3a －4b ＝0且4a ＋3b ≠0.①又a 2＋b 2＝25，②由①②解得⎩⎪⎨⎪⎧a ＝4，b ＝3或⎩⎪⎨⎪⎧a ＝－4，b ＝－3，∴z 1＝4＋3i 或z 1＝－4－3i.18．(10分)已知z 0＝2＋2i ，|z －z 0|＝ 2. (1)求复数z 在复平面内的对应点的轨迹；(2)求z 为何值时|z |有最小值，并求出|z |的最小值．解 (1)设z ＝x ＋y i(x ，y ∈R )，由|z －z 0|＝2，得：|x ＋y i －(2＋2i)|＝|(x －2)＋(y －2)i|＝2，解得：(x －2)2＋(y －2)2＝2.∴复数z 点的轨迹为以z 0(2,2)为圆心，2为半径的圆． (2)当z 点在Oz 0的连线上时，|z |有最大值或最小值， ∵|Oz 0|＝22，半径为 2.∴当z ＝1＋i 时，|z |min ＝ 2.19．(10分)已知复数z ＝1＋i ，求实数a 、b 使az ＋2b z ＝(a ＋2z )2. 解 ∵z ＝1＋i ，∴az ＋2b z ＝(a ＋2b )＋(a －2b )i ， (a ＋2z )2＝(a ＋2)2－4＋4(a ＋2)i ＝(a 2＋4a )＋4(a ＋2)i.∵a 、b 都是实数，∴由az ＋2b z ＝(a ＋2z )2，得⎩⎪⎨⎪⎧a ＋2b ＝a 2＋4a ，a －2b ＝4a ＋2.解得a 1＝－2，a 2＝－4，对应得b 1＝－1，b 2＝2.∴所求实数为a ＝－2，b ＝－1或a ＝－4，b ＝2.20．(10分)设存在复数z 同时满足下列条件： (1)复数z 在复平面内对应的点位于第二象限；(2)z z ＋2i z ＝8＋a i(a ∈R )．试求a 的取值范围．解设复数z ＝x ＋y i(x ，y ∈R )，则z ＝x －y i. 由(1)知x <0，y >0.又由(2)z z ＋2i z ＝8＋a i(a ∈R )，得(x ＋y i)(x －y i)＋2i(x ＋y i)＝8＋a i(a ∈R )，即(x 2＋y 2－2y )＋2x i ＝8＋a i(a ∈R )，所以⎩⎪⎨⎪⎧x 2＋y 2－2y ＝8，2x ＝a ，所以4(y －1)2＝36－a 2.因为4(y －1)2≥0，所以36－a 2≥0，即a 2≤36，所以－6≤a ≤6.又因为a ＝2x ，而x <0，所以a <0，所以－6≤a <0.故所求a的取值范围是[－6,0)．。

2020-2021学年北师大版数学选修1-2习题：第1-4章单元质量评估+综合测试(付,70)

选修1－2第一章单元质量评估本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分．满分150分，考试时间120分钟．第Ⅰ卷(选择题共60分)答题表题号123456789101112答案题给出的四个选项中，只有一项是符合要求的)1．散点图在回归分析过程中的作用是()A．查找个体个数B．比较个体数据大小关系C．探究个体分类D．粗略判断变量是否线性相关2．变量x，y的5组数据的散点图如图所示，去掉哪个点对应的数据后，剩下的4组数据的线性相关性最强()A．E B．CC．D D．A3．对有线性相关关系的两个变量建立的回归直线方程y＝a＋bx中，回归系数b()A．可以小于0 B．只能大于0C．能等于0 D．只能小于04．对两个变量y与x进行回归分析，分别选择不同的模型，它们的相关系数r如下，其中拟合效果最好的模型是() A．模型Ⅰ：相关系数r为0.96B．模型Ⅱ：相关系数r为－0.81C．模型Ⅲ：相关系数r为－0.53D．模型Ⅳ：相关系数r为0.355．在一次试验中，测得(x，y)的四组值对应的点分别是A(1,2)，B(2,3)，C(3,4)，D(4,5)，则y对x的线性回归方程为() A．y＝x＋1 B．y＝x＋2C．y＝2x＋1 D．y＝x－16．考察四个班的学生数学、物理成绩，得到列联表如下：A．34 B．20C．37 D．247．已知回归直线的斜率的估计值是1.23，样本点的中心为(4,5)，则线性回归方程是()A．y＝1.23x＋4 B．y＝1.23x＋5C．y＝1.23x＋0.08 D．y＝0.08x＋1.238．工人月工资y(元)与每小时的产值x(千元)的线性回归方程为y＝50＋80x，下列判断正确的是()A．每小时的产值为1千元时，月工资一定为130元B．每小时的产值每提高1千元，月工资平均提高80元C．每小时的产值每提高1千元，月工资平均提高130元D．当月工资为250元时，每小时的产值一定为2千元9．对两个变量y和x进行线性相关检验，n是观察值组数，r是相关系数，且已知：①n＝7，r＝0.953 3；②n＝15，r＝0.301 2；③n ＝17，r＝0.999 1；④n＝3，r＝0.995 0.则变量y和x具有相关关系的是()A．①和②B．①和③C．②和④D．③和④10．在一次对人体脂肪含量和年龄关系的研究中，研究人员获得了一组样本数据，并制作成如图所示的人体脂肪含量与年龄关系的散点图．根据该图，下列结论中正确的是()A．人体脂肪含量与年龄正相关，且脂肪含量的中位数等于20% B．人体脂肪含量与年龄正相关，且脂肪含量的中位数小于20% C．人体脂肪含量与年龄负相关，且脂肪含量的中位数等于20% D．人体脂肪含量与年龄负相关，且脂肪含量的中位数小于20% 11．下表是某厂1～4月份用水量(单位：百吨)的一组数据：其线性回归直线方程是y＝－0.7x＋a，则a等于()A．5 B．5.05C．5.25 D．6答案1．D由于散点图是由解释变量和预报变量绘制的图形，所以它可以粗略判断变量间是否具有线性相关关系，故选D.2．A E偏离得最多，故选A.3．A若b＝0，则相关系数r＝0，此时不具有线性相关关系，但b可以大于0也可以小于0.4．A|r|越大，拟合效果越好，故选A.5．A由四点A，B，C，D都在直线y＝x＋1上知选A.6．D7．C由题知b＝1.23，直线经过中心(4,5)，则a＝0.08，所以线性回归方程为y＝1.23x＋0.088．B回归直线的斜率为80，故每小时的产值每提高1千元，月工资平均提高80元．9．B②中r太小，④中观察值组数太少．10．B观察图形，可知人体脂肪含量与年龄正相关，且脂肪含量的中位数小于20%，故选B.11．C x＝2.5，y＝3.5，∵回归直线方程过定点(x，y)，∴3.5＝－0.7×2.5＋a.∴a＝5.25.————————————————————————————12．在一次男女生是否说谎的调查中，得到如下数据，根据表中数据可知下列结论中正确的是()说谎不说谎合计男6713女8917合计141630A.B．在此次调查中有99%的把握认为说谎与性别有关C．在此次调查中有90%的把握认为说谎与性别有关D．在此次调查中没有充分证据显示说谎与性别有关第Ⅱ卷(非选择题共90分)二、填空题(本大题共4小题，每小题5分，共20分，请把答案填写在题中横线上)13．如图，给出三个相关性判断：①正相关；②负相关；③不相关．与它们对应的散点图的顺序是________．14．若施化肥量x kg与水稻产量y kg之间的线性回归方程为y ＝5x＋250，则当施化肥量为80 kg时，预计水稻产量为________kg.15．为了判断选修文科是否与性别有关，现随机抽取50名同学，得到2×2列联表如下：已知P (χ2到χ2＝50×(13×20－10×7)230×27×20×23≈4.844，则认为选修文科与性别有关系出错的可能性为________．16．某化工厂为预测某产品的回收率y ，需要研究它和原料有效成分含量之间的相关关系．现取了8对观测值，计算得∑i ＝18x i ＝52，∑i ＝18yi ＝228，∑i ＝18x 2i ＝478，∑i ＝18x i y i ＝1 849，则y 对x 的线性回归方程是________．三、解答题(本大题共6小题，共70分．解答应写出文字说明、证明过程或演算步骤)17．(10分)调查在2～3级风时的海上航行中男女乘客的晕船情况，共调查了71人，其中女性34人，男性37人．女性中有10人晕船，另外24人不晕船；男性中有12人晕船，另外25人不晕船．(1)根据以上数据建立有关的2×2列联表； (2)判断晕船是否与性别有关系．18．(12分)某车间为了规定工时定额，需要确定加工零件所花费的时间，为此作了四次试验如下：(1)在给定坐标系(如图)中画出表中数据的散点图；(2)求y 关于x 的回归直线方程y ＝bx ＋a ； (3)试预测加工10个零件需要的时间．答案12．D 根据表中数据可求得2＝30×(6×9－7×8)213×17×14×16≈0.002 4，因为0.002 4<2.706，所以在此次调查中没有充分证据显示说谎与性别有关，故选D.13．a ，c ，b解析：a 正相关，c 负相关，b 不相关． 14．650解析：将x ＝80代入线性回归方程，得y ＝650(kg)． 15．5%解析：由题目条件，4.844>3.841，P (χ2>3.841)≈0.05. 16．y ＝11.47＋2.62x解析：∵b ＝∑i ＝1nx i y i －n x y∑i ＝1nx 2i －n x 2≈2.62，a ＝y －b x ＝11.47，∴线性回归方程为y ＝11.47＋2.62x .17．解：(1)2×2列联表如下：晕船情况性别晕船不晕船总计女102434男122537总计224971(2)计算χ2＝22×49×37×34≈0.08.因为χ2<2.706，所以我们没有充分证据说“晕船与性别有关”．18．解：(1)散点图如图．(2)由题中数据可得x＝2＋3＋4＋54＝3.5，y＝2.5＋3＋4＋4.54＝3.5，∑i＝14x i y i＝52.5，∑i＝14x2i＝54，进而可求得b＝52.5－4×3.5×3.554－4×3.52＝0.7，a＝3.5－0.7×3.5＝1.05，故回归直线方程为y＝0.7x＋1.05.(3)当x＝10时，y＝0.7×10＋1.05＝8.05，故预测加工10个零件需要8.05小时．————————————————————————————19.(12分)两所学校的计算机算法语言学习小组统一测验成绩如下：甲校：16,12,20,15,23,8,16,19.乙校：22,17,26,24,8,7,25,28.(1)求这16个数据的中位数；(2)统计中位数上下的频数；校别中位数以上中位数以下合计甲乙合计(3)20．(12分)(2016·新课标全国卷Ⅲ)下图是我国2008年至2014年生活垃圾无害化处理量(单位：亿吨)的折线图．(1)由折线图看出，可用线性回归模型拟合y与t的关系，请用相关系数加以说明；(2)建立y 关于t 的回归方程(系数精确到0.01)，预测2016年我国生活垃圾无害化处理量．参考数据：∑i ＝17y i ＝9.32，∑i ＝17t i y i ＝40.17，∑i ＝17(y i －y )2＝0.55，7≈2.646.附注：参考公式：相关系数r ＝∑i ＝1n(t i －t )(y i －y )∑i ＝1n(t i －t )2∑i ＝1n(y i －y )2.回归方程y ^＝a ^＋b ^t 中斜率和截距的最小二乘估计公式分别为：b^＝∑i ＝1n(t i －t )(y i －y )∑i ＝1n(t i －t )2，a ^＝y ^－b ^t .答案19．解：(1)将两组数据合在一起，从小到大的排列，寻找共同的中位数，由于n 1＋n 2＝8＋8＝16，则第8个与第9个位置上的数据之平均数即为共同的中位数，共同中位数为18.(2)(3)∵χ2＝8×8×8×8＝1≤2.706，∴两所学校的计算机算法语言学习小组的成绩无显著差异． 20．解：(1)由折线图中数据和附注中参考数据得 t ＝4，∑i ＝17(t i －t )2＝28,∑i ＝17(y i －y )2＝0.55，∑i ＝17(t i －t )(y i －y )＝∑i ＝17t i y i －t ∑i ＝17y i ＝40.17－4×9.32＝2.89，r ≈ 2.890.55×2×2.646≈0.99. 因为y 与t 的相关系数近似为0.99，说明y 与t 的线性相关程度相当高，从而可以用线性回归模型拟合y 与t 的关系．(2)由y ＝9.327≈1.331及(1)得b^＝∑i＝17(t i－t)(y i－y)∑i＝17(t i－t)2＝2.8928≈0.103，a^＝y－b^t≈1.331－0.103×4≈0.92.所以，y关于t的回归方程为y^＝0.92＋0.10t.将2016年对应的t＝9代入回归方程得y^＝0.92＋0.10×9＝1.82.所以预测2016年我国生活垃圾无害化处理量约为1.82亿吨．————————————————————————————21.(12分)某高校共有学生15 000人，其中男生10 500人，女生4 500人．为调查该校学生每周平均体育运动时间的情况，采用分层抽样的方法，收集300位学生每周平均体育运动时间的样本数据(单位：小时)．(1)应收集多少位女生的样本数据？(2)根据这300个样本数据，得到学生每周平均体育运动时间的频率分布直方图(如图所示)，其中样本数据的分组区间为：[0,2]，(2,4]，(4,6]，(6,8]，(8,10]，(10,12]．估计该校学生每周平均体育运动时间超过4小时的概率；(3)在样本数据中，有60位女生的每周平均体育运动时间超过4小时，请完成每周平均体育运动时间与性别列联表，并判断是否有95%的把握认为“该校学生的每周平均体育运动时间与性别有关”．附：K2＝n(ad－bc)2(a＋b)(c＋d)(a＋c)(b＋d)P(K2≥k0)0.100.050.0100.005 k0 2.706 3.841 6.6357.87922．(12分)某公司为确定下一年度投入某种产品的宣传费，需了解年宣传费x(单位：千元)对年销售量y(单位：t)和年利润z(单位：千元)的影响．对近8年的年宣传费x i和年销售量y i(i＝1,2，…，8)数据作了初步处理，得到下面的散点图及一些统计量的值．x46.6y563w 6.8∑i＝18(x i－x)2289.8∑i＝18(w i－w)2 1.6∑i＝18(x i－x)(y i－y) 1 469∑i＝18(w i－w)(y i－y)108.8表中w i＝x i，w＝18∑i＝18w i.(1)根据散点图判断，y＝a＋bx与y＝c＋d x哪一个适宜作为年销售量y关于年宣传费x的回归方程类型？(给出判断即可，不必说明理由)(2)根据(1)的判断结果及表中数据，建立y关于x的回归方程；(3)已知这种产品的年利润z与x，y的关系为z＝0.2y－x.根据(2)的结果回答下列问题：(ⅰ)年宣传费x＝49时，年销售量及年利润的预报值是多少？(ⅱ)年宣传费x为何值时，年利润的预报值最大？附：对于一组数据(u1，v1)，(u2，v2)，…，(u n，v n)，其回归直线v＝α＋βu的斜率和截距的最小二乘估计分别为β^＝∑i＝1n(u i－u)(v i－v)∑i＝1n(u i－u)2，α^＝v－β^u.答案21.解：(1)300×4 50015 000＝90，所以应收集90位女生的样本数据． (2)由频率分布直方图得1－2×(0.100＋0.025)＝0.75，所以该校学生每周平均体育运动时间超过4小时的概率的估计值为0.75.(3)由(2)知，300位学生中有300×0.75＝225人的每周平均体育运动时间超过4小时，75人的每周平均体育运动时间不超过4小时．又因为样本数据中有210份是关于男生的，90份是关于女生的，所以每周平均体育运动时间与性别列联表如下：每周平均体育运动时间与性别列联表K 2＝300×(45×60－165×30)275×225×210×90＝10021≈4.762>3.841.所以，有95%的把握认为“该校学生的每周平均体育运动时间与性别有关”．22．解：(1)由散点图可以判断，y ＝c ＋d x 适宜作为年销售量y 关于年宣传费x 的回归方程类型．(2)令w ＝x ，先建立y 关于w 的线性回归方程．由于d ^＝∑i ＝18(w i －w )(y i －y )∑i ＝18(w i －w )2＝108.81.6＝68，c ^＝y －d ^w ＝563－68×6.8＝100.6，所以y 关于w 的线性回归方程为y ^＝100.6＋68w ，因此y 关于x 的回归方程为y ^＝100.6＋68x .(3)(ⅰ)由(2)知，当x ＝49时，年销售量y 的预报值y ^＝100.6＋6849＝576.6，年利润z 的预报值z ^＝576.6×0.2－49＝66.32.(ⅱ)根据(2)的结果知，年利润z 的预报值 z ^＝0.2(100.6＋68x )－x ＝－x ＋13.6x ＋20.12.所以当x ＝13.62＝6.8，即x ＝46.24时，z ^ 取得最大值．故年宣传费为46.24千元时，年利润的预报值最大．第二章单元质量评估本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分．满分150分，考试时间120分钟．第Ⅰ卷(选择题共60分)答题表题给出的四个选项中，只有一项是符合要求的)1．下列关于流程图和结构图的说法中不正确的是( ) A ．流程图用来描述一个动态过程 B ．结构图用来刻画系统结构C ．流程图只能用带箭头的流程线表示各单元的先后关系D ．结构图只能用带箭头的连线表示各要素之间的从属关系或逻辑上的先后关系2．根据二分法求方程x 2－3＝0得到的框图可称为( ) A ．工艺流程图 B ．程序流程图 C ．知识结构图 D ．组织结构图 3．在下面的图示中，属于结构图的是( )A.B.C.D.4．要解决下面的四个问题，只用顺序结构画不出其流程图的是( )A ．利用公式1＋2＋…＋n ＝n (n ＋1)2计算1＋2＋…＋10的值 B ．当圆的面积已知时，求圆的周长C．给定一个数x，求其绝对值D．求函数f(x)＝x3＋4x－5的函数值5．计算机系统、硬件系统、软件系统、CPU、存储器的知识结构图为()6．进入互联网时代，发电子邮件是不可少的，一般而言，发电子邮件要分成以下几个步骤：a.打开电子信箱；b.输入发送地址；c.输入主题；d.输入信件内容；e.点击“写邮件”；f.点击“发送邮件”．则正确的流程是()A．a→b→c→d→e→fB．a→c→d→f→e→bC．a→e→b→c→d→fD．b→a→c→d→f→e7．如图是某创意大赛分类图，由图可知，影视动画属于()A．广告项B．设计项C．营销项D．平面图形8．在工商管理学中，MRP指的是物资需求计划，基本MRP的体系结构如图所示．从图中你能看出影响基本MRP的主要因素有()A．3个B．5个C．7个D．9个答案1．D各要素间的从属关系在结构图中可以用不带箭头的连线表示．2．B3．B A项为分析法证明问题的简易流程；C是频率分布直方图；D是集合的韦恩图．4．C求|x|，必须对x是否大于等于0进行判断，要用条件结构，不能只用顺序结构画流程图，故选C.5．D计算机系统包括“硬件”与“软件”两大系统，其中“存储器”与“CPU”为硬件系统．6．C进入电子邮箱后，必须先点击“写邮件”才可进行以后的操作．7．A由图知，影视动画属于广告项．8．A影响MRP的主要因素为产品结构、库存状态和主生产计划．————————————————————————————9.按照下面的流程图，则可得到()A．2,3,4,5,6 B．2,4,6,8,10C．1,2,4,8,16 D．2,4,8,16,3210．如下图，某人拨通了电话，准备手机充值需进行如下操作()A．1—5—1—1 B．1—5—1—5C．1—5—2—1 D．1—5—2—311．已知算法框图如图所示，则该算法框图的功能是()A ．求数列⎩⎨⎧⎭⎬⎫1n 的前10项和(n ∈N ＋)B ．求数列⎩⎨⎧⎭⎬⎫12n 的前10项和(n ∈N ＋) C ．求数列⎩⎨⎧⎭⎬⎫1n 的前11项和(n ∈N ＋) D ．求数列⎩⎨⎧⎭⎬⎫12n 的前11项和(n ∈N ＋) 12．设十人各拿水桶一只，同到水龙头前打水，设水龙头注满第i (i ＝1,2，…，10)个人的水桶需时T i 分钟，假设这些T i 各不相同，当水龙头只有一个可用时，应如何安排他(她)们的接水次序，使他(她)们的总的花费时间(包括等待时间和自己接水所花的时间)为最少( )A ．从T i 中最大的开始，按由大到小的顺序排队B ．从T i 中最小的开始，按由小到大的顺序排队C ．从靠近诸T i 平均数的一个开始，按依次小取一个大取一个的摆动顺序排队D ．任意顺序排队接水的总时间都不变第Ⅱ卷(非选择题共90分)二、填空题(本大题共4小题，每小题5分，共20分，请把答案填写在题中横线上)13．景泰蓝是深受人民喜爱的手工艺品．现在我们把它的制作流程叙述一下：第一步制胎，第二步掐丝，第三步点蓝，第四步烧蓝，第五步打磨，第六步镀金．请你用工序流程图画出以上工序．→→→→→14．如下图所示：则“函数的应用”包括的主要内容有________．15．下面结构图是________结构图，根据结构图可知，集合的基本运算是________，________，________.答案9．D 按照流程图顺序依次得到2,4,8,16,32.10．C 由操作图知：手机充值应按照“注册客户服务请按1”“代缴费请按5”“手机充值缴费按2”“手机充值按1”的先后顺序进行操作．故选C.11．B 由所给的算法框图可知其反映的算法为求S ＝12＋14＋16＋18＋110＋…＋12×10的和，故选B. 12．B 从T i 中最小的开始，由小到大的顺序排队接水可使总时间最少．如只有T 1，T 2两人接水，T 1需10分钟，T 2需5分钟，若T 1先接则需要10＋(10＋5)＝25(分钟)，若T 2先接则只需要5＋5＋10＝20(分钟)．13．制胎掐丝点蓝烧蓝打磨镀金14．函数与方程、函数模型及其应用15．知识并集交集补集解析：该结构图为知识结构图，集合的基本运算有：并集、交集和补集．————————————————————————————16.在下面的流程图中，令a ＝sin2θ，b ＝cos θ，c ＝sin θ，若在集合⎩⎨⎧⎭⎬⎫θ⎪⎪⎪－π2<θ<π4中，给θ取一个值，输出的结果是b ，则θ值所在范围是________．三、解答题(本大题共6小题，共70分．解答应写出文字说明、证明过程或演算步骤)17．(10分)中央电视台少儿频道主持人鞠萍，堪称一名节水高手．在一期节目中她谈到自己生活中的节水小窍门——做饭、淘米、洗菜的水留下来擦地或者浇花，洗衣服剩下的水留下冲卫生间．这样全家一个月节省消费10元多，一年下来就节省120多元．试用所学的框图知识表示她的节水过程．18．(12分)下图为某集团组织结构图，请据图分析财务部及人力资源部的隶属关系．19．(12分)如图所示知识结构图，说一下各知识之间的关系．答案 16.⎝ ⎛⎦⎥⎤－π2，π6 解析：由流程图知，输出的是a 、b 、c 中的最大值，则b ＝cos θ为最大值，－π2<θ<π4，－π<2θ<π2，∴θ∈⎝ ⎛⎦⎥⎤－π2，π6. 17．解：如下图所示：18．解：由组织结构图分析得：财务部直属总裁管理；而总裁又由董事长管理，董事长服从于董事会管理．人力资源部由董事长助理直接管理，董事长助理由董事长直接管理，董事长又服从于董事会管理，董事会是最高管理部门．19．解：此结构图主要说明坐标法在各知识中的应用，从图中可以看出，坐标法是研究问题的基本思想方法，可以类比平面几何和立体几何中的向量法来认识坐标法的应用；也可以类比平面几何和立体几何中的综合法来体会坐标法的优越性；也可以通过特殊化，得到点、直线、圆及圆锥曲线的坐标表示；还可以把平面直角坐标系推广到空间直角坐标系中，认识坐标法的更广阔的应用空间等．答案不唯一，合理即可．————————————————————————————20.(12分)某人在2016年买了一辆价值15万元的汽车，汽车将以每年20%的速度折旧．请用算法流程图描述汽车的价值变化，并输出4年后汽车的价值．21．(12分)阅读流程图如图所示．解答下列问题：(1)变量y在这个算法中的作用是什么？(2)这个算法的循环体是哪一部分，功能是什么？(3)这个算法的处理功能是什么？22．(12分)某“儿童之家”开展亲子活动，计划活动按以下步骤进行：首先，儿童与家长按事先约定的时间来到“儿童之家”，然后，一部分工作人员接待儿童，做活动前的准备；同时另一部分工作人员接待家长，交流儿童本周的表现；第三步，按照亲子活动方案进行活动；第四步，启导员填写亲子活动总结记录；同时家长填写反馈卡，最后启导员填写服务跟踪表．你能为“儿童之家”的这项活动设计一个活动流程图吗？答案20.解：流程图如图所示：21.解：(1)变量y是循环变量，控制着循环的开始和结束．(2)流程图的第②部分是循环体，是判断年份y是否是闰年，并输出结果．(3)由前面的分析可知道，这个算法的处理功能是：判断2000年至2005年中，哪些年份是闰年，哪些年份不是闰年，并输出结果．22．解：流程图如下：第三章单元质量评估本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分．满分150分，考试时间120分钟．第Ⅰ卷(选择题共60分)答题表题号123456789101112答案题给出的四个选项中，只有一项是符合要求的)1．归纳推理与类比推理的相似之处是()A．都是从一般到一般B．都是从一般到特殊函数C．都是从特殊到特殊D ．都不一定正确2．用数学归纳法证明1＋12＋13＋…＋12n －1<n (n ∈N ＋，n >1)时，第一步应验证不等式( )A ．1＋12<2B ．1＋12＋13<2 C ．1＋12＋13<3D ．1＋12＋13＋14<33．用反证法证明命题“设a ，b 为实数，则方程x 2＋ax ＋b ＝0至少有一个实根”时，要做的假设是( )A ．方程x 2＋ax ＋b ＝0至多有一个实根B ．方程x 2＋ax ＋b ＝0没有实根C ．方程x 2＋ax ＋b ＝0至多有两个实根D ．方程x 2＋ax ＋b ＝0恰好有两个实根4．观察按下列顺序排列的等式：9×0＋1＝1,9×1＋2＝11,9×2＋3＝21,9×3＋4＝31，…，猜想第n (n ∈N ＋)个等式应为( )A ．9(n ＋1)＋n ＝10n ＋9B ．9(n －1)＋n ＝10n －9C ．9n ＋(n －1)＝10n －10D ．9(n －1)＋(n －1)＝10n －105．类比平面内“垂直于同一条直线的两条直线互相平行”的性质，可得出空间内的下列结论( )①垂直于同一个平面的两条直线互相平行；②垂直于同一条直线的两条直线互相平行；③垂直于同一个平面的两个平面互相平行；④垂直于同一条直线的两个平面互相平行．A ．①②B ．②③C ．③④D ．①④6．观察下图的规律，在其下面一行的空格内画上合适的图形，应是()A．△★○◆ B．○◆△★C．○★△◆ D．◇●☆▲7．如图是今年元宵花灯展中一款五角星灯连续旋转闪烁所成的三个图形，照此规律闪烁，下一个呈现出来的图形是()8.如图，圆周上按顺时针方向标有1,2,3,4,5五个点．一只青蛙从1点开始按顺时针方向绕圆从一个点跳到另一点．若它停在奇数点上，则下一次只能跳一个点；若停在偶数点上，则下一次跳两个点．该青蛙从5这点跳起，经2 015次跳后它将停在的点是()A ．1B ．2C ．3D ．4答案1．D 归纳推理和类比推理都是合情推理，但是不一定正确． 2．B 由n ∈N ＋，n >1知n 的第一个值为2，此时不等式为1＋12＋122－1<2，故选B. 3．B “方程x 2＋ax ＋b ＝0至少有一个实根”的反面是“方程x 2＋ax ＋b ＝0没有实根”，故选B.4．B 由所给的等式可以根据规律猜想得9(n －1)＋n ＝10(n －1)＋1＝10n －9.5．D 显然①④正确．②中空间内垂直于同一条直线的两直线可能平行，可能相交，也可能异面；③垂直于同一个平面的两个平面可能平行，也可能相交，故D 正确．6．B 每行每列元素不同，且白黑相间．7．A 该五角星对角上的两盏花灯依次按逆时针方向亮一盏，故下一个呈现出来的图形是A.8．B 记a n 表示青蛙第n 次跳后所在的点数，则a 1＝1，a 2＝2，a 3＝4，a 4＝1，a 5＝2，a 6＝4，…，显然{a n }是一个周期为3的数列，故a 2 015＝a 2＝2.————————————————————————————9.设f(x)是定义在正整数集上的函数，且f(x)满足：“当f(k)≥k2成立时，总可推出f(k＋1)≥(k＋1)2成立”．那么，下列命题总成立的是()A．若f(1)<1成立，则f(10)<100成立B．若f(2)<4成立，则f(1)≥1成立C．若f(3)≥9成立，则当k≥1时，均有f(k)≥k2成立D．若f(4)≥25成立，则当k≥4时，均有f(k)≥k2成立10．将正偶数按下表排成5列：则A．第251行，第2列B．第251行，第3列C．第252行，第2列D．第252行，第3列11．如图甲，在平行四边形ABCD中，有AC2＋BD2＝2(AB2＋AD2)，那么在图乙所示的平行六面体ABCD－A1B1C1D1中，AC21＋BD21＋CA21＋DB21＝()A．4(AB2＋AD2＋AA21)B．3(AB2＋AD2＋AA21)C．2(AB2＋AD2＋AA21)D．4(AB2＋AD2)12．(2016·北京卷)某学校运动会的立定跳远和30秒跳绳两个单项比赛分成预赛和决赛两个阶段．下表为10名学生的预赛成绩，其中有三个数据模糊.学生序号12345678910立定跳远1.96 1.92 1.82 1.80 1.78 1.76 1.74 1.72 1.68 1.60 (单位：米)30秒跳绳63 a 7560637270a－1 b 65 (单位：次)跳远决赛和30秒跳绳决赛的有6人，则()A．2号学生进入30秒跳绳决赛B．5号学生进入30秒跳绳决赛C．8号学生进入30秒跳绳决赛D．9号学生进入30秒跳绳决赛第Ⅱ卷(非选择题共90分)二、填空题(本大题共4小题，每小题5分，共20分，请把答案填写在题中横线上)13．在平面上，若两个正三角形的边长的比为1∶2，则它们的面积比为1∶4，类似地，在空间中，若两个正四面体的棱长的比为1∶2，则它们的体积比为________．14．(2016·新课标全国卷Ⅱ)有三张卡片，分别写有1和2,1和3,2和3.甲，乙，丙三人各取走一张卡片，甲看了乙的卡片后说：“我与乙的卡片上相同的数字不是2”，乙看了丙的卡片后说：“我与丙的卡片上相同的数字不是1”，丙说：“我的卡片上的数字之和不是5”，则甲的卡片上的数字是________．15．观察以下不等式：1>12；1＋12＋13>1；1＋12＋13＋…＋17>32；1＋12＋13＋…＋115>2；1＋12＋13＋…＋131>52；…由此猜测第n 个不等式为________．16．一个二元码是由0和1组成的数字串x 1x 2…x n (n ∈N ＋)，其中x k (k ＝1,2，…，n )称为第k 位码元．二元码是通信中常用的码，但在通信过程中有时会发生码元错误(即码元由0变为1，或者由1变为0)．已知某种二元码x 1x 2…x 7的码元满足如下校验方程组：⎩⎪⎨⎪⎧x 4⊕x 5⊕x 6⊕x 7＝0，x 2⊕x 3⊕x 6⊕x 7＝0，x 1⊕x 3⊕x 5⊕x 7＝0，其中运算⊕定义为：0⊕0＝0,0⊕1＝1,1⊕0＝1,1⊕1＝0.现已知一个这种二元码在通信过程中仅在第k 位发生码元错误后变成了 1 101 101，那么利用上述校验方程组可判定k 等于________．答案9．D题设中“当f(k)≥k2成立时，总可推出f(k＋1)≥(k＋1)2成立”．实际上是给出了一个递推关系，从数学归纳法来考虑，因为f(4)≥25成立，所以f(4)≥16成立，即k的基础值为4，所以选项A、B、C都错误，故选D.10．D由2 014为偶数中从2数第1 007个数，又数表中每行4个，4×251＝1 004，则2 014为第252行第3个数．故选D.11．A已知平面上平行四边形的对角线的平方和等于从同一顶点出发的两条边的平方和的2倍，利用类比推理可知，空间中，平行六面体的体对角线的平方和等于从同一顶点出发的三条棱的平方和的4倍．12．B由数据可知，进入立定跳远决赛的8人为1～8号，所以进入30秒跳绳决赛的6人从1～8号里产生．数据排序后可知3号，6号，7号必定进入30秒跳绳决赛，则得分为63，a,60,63，a－1的5人中有3人进入30秒跳绳决赛．若1号，5号学生未进入30秒跳绳决赛，则4号学生就会进入决赛，与事实矛盾，所以1号，5号学生必进入30秒跳绳决赛．故选B.13．1∶8解析：由类比思想，面积比是边长比的平方，体积比是棱长比的立方．14．1和3解析：为方便说明，不妨将分别写有1和2,1和3,2和3的卡片记为A，B，C.从丙出发，由于丙的卡片上的数字之和不是5，则丙只可能是卡片A或B，无论是哪一张，均含有数字1，再由乙与丙的卡片上相同的数字不是1可知，乙所拿的卡片必然是C，最后由甲与乙的卡片上相同的数字不是2，知甲所拿的卡片为B ，此时丙所拿的卡片为A .15．1＋12＋13＋…＋12n －1>n2解析：由所给的不等式可以归纳得到1＋12＋13＋…＋12n －1>n2.16．5解析：若1≤k ≤3，则x 4＝1，x 5＝1，x 6＝0，x 7＝1，不满足x 4⊕x 5⊕x 6⊕x 7＝0；若k ＝4，则二元码为1 100 101，不满足x 1⊕x 3⊕x 5⊕x 7＝0；若k ＝5，则二元码为1 101 001，满足方程组，故k ＝5. ————————————————————————————三、解答题(本大题共6小题，共70分．解答应写出文字说明、证明过程或演算步骤)17．(10分)证明：1log 519＋1log 319＋1log 219<2.18．(12分)已知a ≠0，证明：关于x 的方程ax ＝b 有且只有一个根．19．(12分)如图，已知平面α∩β＝a ，b β，a ∩b ＝A ，且cα，c ∥a ，求证：b ，c 为异面直线．20．(12分)(2016·浙江卷)设函数f (x )＝x 3＋11＋x，x ∈[0,1]．证明：(1)f (x )≥1－x ＋x 2； (2)34<f (x )≤32.答案17．证明：方法1：(分析法)要证1log 519＋1log 319＋1log 219<2，只需证log 1930<log 19192，即证30<192，又30<192恒成立，∴原不等式成立．方法2：(综合法)1log 519＋1log 319＋1log 219＝log 195＋log 193＋log 192＝log 1930<log 19192＝2.18．证明：由于a ≠0，因此方程至少有一个根x ＝ba .如果方程不是只有一个根，不妨设x 1，x 2是它的两个不同根，即ax 1＝b ，ax 2＝b ，∴a (x 1－x 2)＝0.∵x 1≠x 2，∴x 1－x 2≠0，∴应有a ＝0，这与已知相矛盾，故假设不成立． ∴当a ≠0时，方程ax ＝b 有且只有一个根．19．证明：假设b 、c 不是异面直线，即b 、c 为共面直线，则b 、c 为相交直线或平行直线．(1)若b ∩c ＝P ，已知b β，cα，又α∩β＝a ，则P ∈b (bβ)，且P ∈c (cα)，从而，交点P 一定在平面α、β的交线上，即P ∈a ，于是a ∩c ＝P ，这与已知条件a ∥c 矛盾．因此b 、c 相交不成立．(2)若b ∥c ，已知a ∥c ，则a ∥b ，这与已知条件a ∩b ＝A 矛盾，因此b 、c 平行也不能成立．综合(1)(2)可知b 、c 为异面直线．20．证明：(1)因为1－x ＋x 2－x 3＝1－(－x )41－(－x )＝1－x41＋x，由于x ∈[0,1]，有1－x 41＋x ≤1x ＋1，即1－x ＋x 2－x 3≤1x ＋1，所以f (x )≥1－x ＋x 2.(2)由0≤x ≤1得x 3≤x ，故f (x )＝x 3＋1x ＋1≤x ＋1x ＋1＝x ＋1x ＋1－32＋32＝(x －1)(2x ＋1)2(x ＋1)＋32≤32，所以f (x )≤32.由(1)得f (x )≥1－x ＋x 2＝(x －12)2＋34≥34，又因为f (12)＝1924>34，所以f (x )>34. 综上，34<f (x )≤32.————————————————————————————21.(12分)阅读下列材料：根据两角和与差的正弦公式，有 sin(α＋β)＝sin αcos β＋cos αsin β， ① sin(α－β)＝sin αcos β－cos αsin β， ②由①＋②，得sin(α＋β)＋sin(α－β)＝2sin αcos β， ③ 令α＋β＝A ，α－β＝B ，有α＝A ＋B 2，β＝A －B2，代入③，得sin A ＋sin B ＝2sin A ＋B 2cos A －B2.(1)类比上述推证方法，根据两角和与差的余弦公式，证明：cos A －cos B ＝－2sin A ＋B 2sin A －B2；(2)若△ABC 的三个内角A ，B ，C 满足cos2A －cos2B ＝2sin 2C ，试判断△ABC 的形状．22．(12分)(2016·新课标全国卷Ⅲ)设函数f (x )＝ln x －x ＋1. (1)讨论f (x )的单调性；(2)证明当x ∈(1，＋∞)时，1<x －1ln x <x ； (3)设c >1，证明当x ∈(0,1)时，1＋(c －1)x >c x .。

2020-2021学年北师大版数学选修1-2习题：第四章数系的扩充与复数的引入单元质量评估

第四章单元质量评估本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分．满分150分，考试时间120分钟．第Ⅰ卷(选择题共60分)答题表题给出的四个选项中，只有一项是符合要求的)1．复数i(2－i)＝( ) A ．1＋2i B ．1－2i C ．－1＋2iD ．－1－2i2．若复数z ＝i(3－2i)(i 是虚数单位)，则z ＝( ) A ．2－3i B ．2＋3i C ．3＋2iD ．3－2i3．设i 是虚数单位，则复数2i1－i在复平面内所对应的点位于( ) A ．第一象限 B ．第二象限 C ．第三象限D ．第四象限4．已知(1－i )2z ＝1＋i(i 为虚数单位)，则复数z ＝( ) A ．1＋i B ．1－i C ．－1＋iD ．－1－i5．若a 为实数，且(2＋a i)·(a －2i)＝－4i ，则a ＝( ) A ．－1B ．0C ．1D ．26．原命题为“若z 1，z 2互为共轭复数，则|z 1|＝|z 2|”，关于其逆命题、否命题、逆否命题真假性的判断依次如下，正确的是( )A ．真，假，真B ．假，假，真C ．真，真，假D ．假，假，假7．设复数z 满足1＋2iz ＝i ，则z ＝( ) A ．－2＋i B ．－2－i C ．2＋iD ．2－i8．如果一个复数和它的模的和为5＋3i ，那么这个复数是( ) A.115 B.3i C.115＋3iD.115＋23i9．i 是虚数单位，若1＋7i2－i ＝a ＋b i(a ，b ∈R )，则乘积ab 的值是( )A ．－15B ．－3C ．3D ．1510．在复平面内ω＝－12＋32i 对应的向量为OA →，复数ω2对应的向量为OB→.那么向量AB →对应的复数是( ) A ．1 B ．－1 C.3iD ．－3i11．若x ∈C ，则方程|x |＝1＋3i －x 的解是( ) A.12＋32iB ．x 1＝4，x 2＝－1C ．－4＋3iD.12＋32i12．复数z 满足条件|2z ＋1|＝|z －i|，那么z 对应的点的轨迹是( )A ．圆B ．椭圆C ．双曲线D ．抛物线第Ⅱ卷(非选择题共90分)二、填空题(本大题共4小题，每小题5分，共20分，请把答案填写在题中横线上)13．i 是虚数单位，若复数(1－2i)·(a ＋i)是纯虚数，则实数a 的值为________．14．设复数z 满足z 2＝3＋4i(i 是虚数单位)，则z 的模为________． 15．关于实数x 的不等式mx 2－nx ＋p >0(m ，n ，p ∈R )的解集为(－1,2)，则复数n ＋p i 对应的点位于复平面内的第________象限．16．定义复数的一种运算z 1]|z 1|＋|z 2|,2)(等式右边为普通运算)，若复数z ＝a ＋b i ，且实数a ，b 满足a ＋b ＝3，则z *z 的最小值为________．答案1．A i(2－i)＝2i －i 2＝2i －(－1)＝1＋2i.2．A 因为z ＝i(3－2i)＝3i －2i 2＝2＋3i ，所以z ＝2－3i. 3．B 由复数除法的运算法则可得，2i 1－i ＝2i (1＋i )(1－i )(1＋i )＝2i －22＝－1＋i ，对应点为(－1,1)在第二象限．故选B.4．D 由已知得z ＝(1－i )21＋i ＝－2i 1＋i ＝－2i (1－i )(1＋i )(1－i )＝－2－2i2＝－1－i.5．B ∵(2＋a i)(a －2i)＝4a ＋(a 2－4)i ＝－4i ，∴⎩⎪⎨⎪⎧4a ＝0，a 2－4＝－4，解之得a ＝0. 6．B 易知原命题为真命题，所以逆否命题也为真，设z 1＝3＋4i ，z 2＝4＋3i ，则有|z 1|＝|z 2|，但是z 1与z 2不是共轭复数，所以逆命题为假，同时否命题也为假．7．C z ＝1＋2ii ＝2－i ，∴z ＝2＋i. 8．C 设这个复数为a ＋b i(a ，b ∈R )．由题意得a ＋b i ＋a 2＋b 2＝5＋3i ，即a ＋a 2＋b 2＋b i ＝5＋3i ，∴⎩⎪⎨⎪⎧a ＋a 2＋b 2＝5，b ＝3，解得⎩⎨⎧a ＝115，b ＝3，∴所求复数为115＋3i.9．B 1＋7i 2－i ＝(1＋7i )(2＋i )(2－i )(2＋i )＝－5＋15i5＝－1＋3i ＝a ＋b i ，∴a ＝－1，b ＝3，∴ab ＝－3.10．D ω2＝－12－32i ，对应向量OB →＝⎝ ⎛⎭⎪⎫－12，－32，OA →＝⎝ ⎛⎭⎪⎫－12，32，AB →＝OB →－OA →＝(0，－3)，对应复数为－3i.11．C 令x ＝a ＋b i(a ，b ∈R )，则a 2＋b 2＝1＋3i －a －b i ，∴⎩⎪⎨⎪⎧ a 2＋b 2＝1－a ，0＝3－b ，解得⎩⎪⎨⎪⎧a ＝－4，b ＝3，故原方程的解为－4＋3i.12．A 设z ＝x ＋y i ，|2z ＋1|＝|z －i|，则(2x ＋1)2＋4y 2＝x 2＋(y －1)2，即⎝ ⎛⎭⎪⎫x ＋232＋⎝ ⎛⎭⎪⎫y ＋132＝59表示以⎝ ⎛⎭⎪⎫－23，－13为圆心，半径为53的圆． 13．－2解析：(1－2i)(a ＋i)＝a ＋2＋(1－2a )i. ∵(1－2i)(a ＋i)是纯虚数，∴a ＋2＝0，且1－2a ≠0，∴a ＝－2. 14. 5解析：因为z 2＝3＋4i ，所以|z 2|＝32＋42＝5，所以|z |＝ 5. 15．二解析：∵mx 2－nx ＋p >0(m ，n ，p ∈R )的解集为(－1,2)，∴⎩⎪⎨⎪⎧m <0，(－1)＋2＝n m ，(－1)×2＝p m ，即n <0，p >0，∴复数n ＋p i 所对应的点位于复平面内的第二象限．16.322解析：根据题意，z *z ＝|z |＋|z |2＝|z |＝a 2＋b 2＝a 2＋(3－a )2＝2a 2－6a ＋9＝2⎝ ⎛⎭⎪⎫a －322＋92，因此，当a ＝32时，z *z 有最小值且最小值为322.———————————————————————————— 三、解答题(本大题共6小题，共70分．解答应写出文字说明、证明过程或演算步骤)17．(10分)计算⎣⎢⎡⎦⎥⎤(1＋2i )·i 100＋⎝⎛⎭⎪⎫1－i 1＋i 52－⎝ ⎛⎭⎪⎫1＋i 220.18．(12分)已知1＋i 是方程x 2＋bx ＋c ＝0的一个根(b ，c ∈R )． (1)求b ，c 的值；(2)试证明：1－i 也是方程的根．答案17．解：⎣⎢⎡⎦⎥⎤(1＋2i )·i 100＋⎝⎛⎭⎪⎫1－i 1＋i 52－⎝ ⎛⎭⎪⎫1＋i 220 ＝[(1＋2i)·1＋(－i)5]2－i 10 ＝(1＋i)2－i 10＝1＋2i.18．解：(1)∵1＋i 是方程x 2＋bx ＋c ＝0的根， ∴(1＋i)2＋b (1＋i)＋c ＝0，即b ＋c ＋(2＋b )i ＝0，∴⎩⎪⎨⎪⎧ b ＋c ＝0，2＋b ＝0，∴⎩⎪⎨⎪⎧b ＝－2，c ＝2.(2)由(1)知方程为x 2－2x ＋2＝0，把1－i 代入方程的左边得，左边＝(1－i)2－2(1－i)＋2＝0＝右边，∴1－i 也是方程的根．———————————————————————————— 19.(12分)已知复数z ＝1＋i. (1)设ω＝z 2＋3z －4，求ω；(2)如果z 2＋az ＋b z 2－z ＋1＝1－i ，求实数a ，b 的值．20．(12分)已知|z ＋2－2i|＝1，求|z |的最值．答案19．解：(1)∵z ＝1＋i ，∴ω＝z 2＋3z －4＝(1＋i)2＋3(1－i)－4＝－1－i. (2)由z 2＋az ＋b z 2－z ＋1＝1－i ，把z ＝1＋i 代入得(1＋i )2＋a (1＋i )＋b(1＋i )2－(1＋i )＋1＝1－i ，∴(a ＋b )＋(a ＋2)i i ＝1－i ， ∴(a ＋b )＋(a ＋2)i ＝(1－i)i ＝1＋i.∴⎩⎪⎨⎪⎧ a ＋b ＝1，a ＋2＝1.解得⎩⎪⎨⎪⎧a ＝－1，b ＝2.20．解：|z －(－2＋2i)|＝1，几何意义：z 在复平面上对应的点集是O ′(－2,2)为圆心，r ＝1的圆．|z |的几何意义是⊙O ′上的点与原点的距离： |OO ′|＝22＋22＝22， ∴|z |max ＝22＋1，|z |min ＝22－1.———————————————————————————— 21.(12分)已知复平面内▱ABCD ，点A 对应的复数为2＋i ，BA →对应的复数为1＋2i ，BC→对应的复数为3－i. (1)求点C ，D 对应的复数； (2)求▱ABCD 的面积．22．(12分)设P ，Q 是复平面上的点集，P ＝{z |z ·z ＋3i(z －z )＋5＝0}，Q ＝{ω|ω＝2i z ，z ∈P }．(1)P ，Q 分别表示什么曲线？(2)设z 1∈P ，z 2∈Q ，求|z 1－z 2|的最大值与最小值．答案21.解：(1)∵BA→对应的复数为1＋2i ，BC →对应的复数为3－i ，∴AC→对应的复数为(3－i)－(1＋2i)＝2－3i ，又OC→＝OA →＋AC →， ∴点C 对应的复数为(2＋i)＋(2－3i)＝4－2i.又BD →＝BA →＋BC →＝(1＋2i)＋(3－i)＝4＋i ，OB →＝OA →－BA →＝2＋i －(1＋2i)＝1－i ，∴OD→＝OB →＋BD →＝1－i ＋(4＋i)＝5， ∴点D 对应的复数为5. (2)∵BA →·BC→＝|BA →||BC →|cos B ，∴cos B ＝BA →·BC →|BA →||BC →|＝3－25×10＝152，∴sin B ＝752， ∴S ＝|BA →||BC →|sin B ＝5×10×752＝7. ∴▱ABCD 的面积为7.22．解：(1)设z ＝x ＋y i(x ，y ∈R )，代入P 中得x 2＋(y －3)2＝4，所以集合P 表示以(0,3)为圆心、2为半径的圆．设ω＝x ＋y i(x ，y ∈R )，由ω＝2i z 得 z ＝12y －12x i.因为z ∈P ，所以x 2＋y 2＋12x ＋20＝0，即(x ＋6)2＋y 2＝16.所以Q 表示以(－6,0)为圆心、4为半径的圆． (2)设A (0,3)，B (－6,0)，圆心距|AB |＝35>2＋4，即两圆外离，所以|z 1－z 2|max ＝6＋35，|z 1－z 2|min ＝35－6.。

北师大版高中数学选修1-2测试题及答案

2011年4月北师大版高中数学选修1-2 段考试题及答案一、选择题：本大题共14小题，每小题4分，共56分.在每小题给出的四个选项中，只有一项是符合要求的.1．若复数3i z =-，则z 在复平面内对应的点位于 A ．第一象限 B ．第二象限 C ．第三象限D ．第四象限2．按流程图的程序计算，若开始输入的值为3x =，则输出的x 的值是A ．6B ．21C ．156D ．2313．用演绎法证明函数3y x =是增函数时的小前提是 A ．增函数的定义B ．函数3y x =满足增函数的定义C ．若12x x <，则12()()f x f x <D ．若12x x >，则12()()f x f x >4．用火柴棒摆“金鱼”，如图所示：按照上面的规律，第n 个“金鱼”图需要火柴棒的根数为 A ．62n - B ．82n - C ．62n + D ．82n +5．（A 版）计算1i1i -+的结果是 A ．iB ．i -C ．2D ．2-（B 版）关于复数z 的方程31z -=在复平面上表示的图形是 A ．椭圆B ．圆C ．抛物线D ．双曲线6．有下列关系：①人的年龄与他（她）拥有的财富之间的关系；②曲线上的点与该点的坐标之间的关系；③苹果的产量与气候之间的关系；④森林中的同一种树木，其横断面直径与高度之间的关系，其中有相关关系的是 A ．①②③B ．①②C ．②③D ．①③④…① ② ③7．求135101S =++++的流程图程序如右图所示，其中①应为 A ．101?A = B ．101?A ≤ C ．101?A > D ．101?A ≥8．在线性回归模型y bx a e =++中，下列说法正确的是A ．y bx a e =++是一次函数B ．因变量y 是由自变量x 唯一确定的C ．因变量y 除了受自变量x 的影响外，可能还受到其它因素的影响，这些因素会导致随机误差e 的产生D ．随机误差e 是由于计算不准确造成的，可以通过精确计算避免随机误差e 的产生 9．对相关系数r ，下列说法正确的是A ．||r 越大，线性相关程度越大B ．||r 越小，线性相关程度越大C ．||r 越大，线性相关程度越小，||r 越接近0，线性相关程度越大D ．||1r ≤且||r 越接近1，线性相关程度越大，||r 越接近0，线性相关程度越小 10．用反证法证明命题：“一个三角形中不能有两个直角”的过程归纳为以下三个步骤：①9090180A B C C ++=︒+︒+>︒，这与三角形内角和为180︒相矛盾，90A B ==︒不成立；②所以一个三角形中不能有两个直角；③假设三角形的三个内角A 、B 、C 中有两个直角，不妨设90A B ==︒，正确顺序的序号为 A ．①②③B ．③①②C ．①③②D ．②③①11．（A 版）在独立性检验中，统计量2K 有两个临界值：3.841和6.635；当2K ＞3.841时，有95%的把握说明两个事件有关，当2K ＞6.635时，有99%的把握说明两个事件有关，当2K ≤3.841时，认为两个事件无关.在一项打鼾与患心脏病的调查中，共调查了2000人，经计算的2K =20.87，根据这一数据分析，认为打鼾与患心脏病之间 A ．有95%的把握认为两者有关B ．约有95%的打鼾者患心脏病C ．有99%的把握认为两者有关D ．约有99%的打鼾者患心脏病（B 版）在独立性检验中，统计量2χ有两个临界值：3.841和6.635；当2χ＞3.841时，有95%的把握说明两个事件有关，当2χ＞6.635时，有99%的把握说明两个事件有关，当2χ≤3.841时，认为两个事件无关.在一项打鼾与患心脏病的调查中，共调查了2000人，经计算的2χ=20.87，根据这一数据分析，认为打鼾与患心脏病之间 A ．有95%的把握认为两者有关B ．约有95%的打鼾者患心脏病C ．有99%的把握认为两者有关D ．约有99%的打鼾者患心脏病12．类比平面内 “垂直于同一条直线的两条直线互相平行”的性质，可推出空间下列结论：①垂直于同一条直线的两条直线互相平行 ②垂直于同一个平面的两条直线互相平行 ③垂直于同一条直线的两个平面互相平行 ④垂直于同一个平面的两个平面互相平行则正确的结论是 A ．①②B ．②③C ．③④D ．①④13．若定义运算：()()a a b a b b a b ≥⎧⊗=⎨<⎩，例如233⊗=，则下列等式不能成立．．．．的是 A ．a b b a ⊗=⊗B ．()()a b c a b c ⊗⊗=⊗⊗C ．222()a b a b ⊗=⊗D ．()()()c a b c a c b ⋅⊗=⋅⊗⋅（0c >）14．已知数列{}n a 的前n 项和为n S ，且11a =，2n n S n a =*()n ∈N ，可归纳猜想出n S 的表达式为 A ．21nn + B ．311n n -+ C ．212n n ++ D ．22nn + 二、填空题：本大题共4小题，每小题4分，共16分.把答案填在题中横线上.15．现有爬行、哺乳、飞行三类动物，其中蛇、地龟属于爬行动物；河狸、狗属于哺乳动物；鹰、长尾雀属于飞行动物，请你把下列结构图补充完整．16．已知,x y ∈R ，若i 2i x y +=-，则x y -= ． 17．（A 版）在等比数列{}n a 中，若91a =，则有121217(17n n a a a a a a n -⋅⋅⋅=⋅⋅⋅<，且)n *∈N 成立，类比上述性质，在等差数列{}n b 中，若70b =，则有．（B 版）在平面直角坐标系中，以点00(,)x y 为圆心，r 为半径的圆的方程为22200()()x x y y r -+-=，类比圆的方程，请写出在空间直角坐标系中以点000(,,)P x y z 为球心，半径为r 的球的方程为．18．观察下列式子：212311+=，313422+=，414533+=，515644+=，，归纳得出一般规律为．三、解答题：本大题共3小题，共28分.解答应写出文字说明，证明过程或演算步骤. 19．（本小题满分8分）某市居民1999～2003年货币收入x 与购买商品支出Y 的统计资料如下表所示：单位：亿元（Ⅰ）画出散点图，判断x 与Y 是否具有相关关系；（Ⅱ）（A 版）已知0.842,0.943b a ==-，请写出Y 对x 的回归直线方程，并计算出1999 年和2003的随机误差效应.（B 版）已知0.842,0.943b a ==-，请写出Y 对x 的回归直线方程，并估计货币收入为52（亿元）时，购买商品支出大致为多少亿元？20．（本小题满分10分）设数列{}n a 的前n 项和为n S ，且满足2n n a S =-()n *∈N ．（Ⅰ）求1a ，2a ，3a ，4a 的值并写出其通项公式；（Ⅱ）用三段论证明数列{}n a 是等比数列．21．（本小题满分10分）用反证法证明：如果12x >，那么2210x x +-≠.数学选修模块测试样题参考答案数学1-2 （人教A 版、B 版）一、选择题（每小题4分，共56分）1．D 2．D 3． B 4． D 5． B 6． D 7． B 8．C 9．D10．B11．C12．B13．C14．A二、填空题（每小题4分，共16分） 15. 如图所示.16. 3-17. （A 版）12b b ++…12n b b b +=++…13(13n b n -+<，且)n *∈N（B 版）2222000()()()x x y y z z r -+-+-= 18.11(1)(2)n n n n n+++=++ 三、解答题（解答题共28分） 19．（本小题满分8分）解：（Ⅰ）由某市居民货币收入预报支出，因此选取收入为自变量x ，支出为因变量Y ．作散点图，从图中可看出x 与Y 具有相关关系． ……………………………4分（Ⅱ）（A 版）Y 对x 的回归直线方程为 0.8420.943y x =- ……………………6分1999年和2003年的随机误差效应分别为0.263和-0.157.……………………8分（Ⅱ）（B 版）Y 对x 的回归直线方程为0.8420.943y x =- ……………………………6分货币收入为52（亿元）时，即x ＝52时，42.841y =，所以购买商品支出大致为43亿元……………………………8分20．（本小题满分10分）解：（Ⅰ）由2n n a S =-，得11a =；212a =；314a =；418a =，猜想11()2n n a -=()n *∈N ． ……………………………5分（Ⅱ）因为通项公式为n a 的数列{}n a ，若1n na p a +=，p 是非零常数，则{}n a 是等比数列；因为通项公式11()2n n a -=，又112n n a a +=；所以通项公式11()2n n a -=的数列{}n a 是等比数列．……………………………10分21．（本小题满分10分）证明：假设2210x x +-=，则1x =-容易看出112-<，下面证明112-<.要证明：112-成立，32<成立，只需证：924<成立，上式显然成立，故有112-<成立. ……………………………8分综上，112x =-<，与已知条件12x >矛盾.因此，2210x x +-≠. ……………………………10分。

2018年数学同步优化指导北师大版选修1-2练习：阶段质

阶段质量评估(四) 数系的扩充与复数的引入(时间：60分钟满分：80分)一、选择题(本大题共6小题，每小题5分，共30分．在每小题给出的四个选项中，只有一项是符合题目要求的)1．复数z 1，z 2满足z 1＝m ＋(4－m 2)i ，z 2＝2cos θ＋(λ＋3sin θ)i(m ，λ，θ∈R )，并且z 1＝z 2，则λ的取值范围是( )A ．[－1,1]B ．⎣⎡⎦⎤－916，1 C ．⎣⎡⎦⎤－916，7 D ．⎣⎡⎦⎤916，7 解析：由复数相等的充要条件可得⎩⎪⎨⎪⎧m ＝2cos θ，4－m 2＝λ＋3sin θ，化简得4－4cos 2θ＝λ＋3sin θ，由此可得λ＝－4cos 2θ－3sin θ＋4＝－4(1－sin 2θ)－3sin θ＋4＝4sin 2θ－3sin θ＝4⎝⎛⎭⎫sin θ－382－916.因为sin θ∈[－1,1]，所以λ∈⎣⎡⎦⎤－916，7. 答案：C2．设i 是虚数单位，则复数i 3－2i ＝( )A ．－iB ．－3iC ．iD ．3i解析：可通过分母实数化计算求解． i 3－2i ＝－i －2i ＝－i －2ii 2＝－i ＋2i ＝i.答案：C3．复数z ＝(2－i)×i(i 为虚数单位)在复平面内对应的点位于( ) A ．第一象限 B ．第二象限 C ．第三象限D ．第四象限解析：z ＝(2－i)×i ＝2i －i 2＝1＋2i ，则复数z 在复平面内对应的点的坐标为(1,2)，该点位于第一象限．答案：A4．设i 是虚数单位，若复数a ＋5i 1－2i (a ∈R )是纯虚数，则a ＝( )A ．－1B ．1C ．－2D ．2解析：∵a ＋5i1－2i ＝a ＋5i (1＋2i )(1－2i )(1＋2i )＝a ＋－10＋5i 5＝a －2＋i 是纯虚数，∴a ＝2.故选D ．答案：D5．定义运算⎪⎪⎪⎪⎪⎪a ，b c ，d ＝ad －bc ，则符合条件⎪⎪⎪⎪⎪⎪z ，1＋i 2，1 ＝0的复数z 对应的点在 ( )A ．第一象限B ．第二象限C ．第三象限D ．第四象限解析：由题意得z －2(1＋i)＝0，即z ＝2＋2i ，所以复数z 对应的点在第一象限．故选A ．答案：A6．(2015·山东卷)若复数z 满足z－1－i ＝i ，其中i 为虚数单位，则z ＝( )A ．1－iB ．1＋iC ．－1－iD ．－1＋i解析：由已知得z －＝i(1－i)＝1＋i ，则z ＝1－i ，故选A ．答案：A二、填空题(本大题共3小题，每小题5分，共15分．把正确答案填在题中的横线上) 7．(2017·江苏卷)已知复数z ＝(1＋i)(1＋2i)，其中i 是虚数单位，则z 的模是________. 解析：方法一 ∵z ＝(1＋i)(1＋2i)＝1＋2i ＋i －2＝－1＋3i ，∴|z |＝(－1)2＋32＝10. 方法二 |z |＝|1＋i||1＋2i|＝2×5＝10. 答案：108．若i 为虚数单位，图中网格纸的小正方形的边长是1，复平面内点Z 表示复数z ，则复数z 1＋2i＝________.解析：由图可知z ＝－1＋2i.则复数z1＋2i ＝－1＋2i 1＋2i ＝(－1＋2i )(1－2i )(1＋2i )(1－2i )＝3＋4i 5＝35＋45i.答案：35＋45i9．已知z ∈C ，且|z －2－2i|＝1，i 为虚数单位，则|z ＋2－2i|的最小值是________. 解析：设z ＝a ＋b i(a ，b ∈R )，满足|z －2－2i|＝1的点均在以C 1(2,2)为圆心，以1为半径的圆上，复数－2＋2i 的对应点为C 2(－2,2)，如图所示．所以|z ＋2－2i|的最小值是C 1，C 2连线的长为4与1的差，即为3. 答案：3三、解答题(本大题共3小题，共35分．解答时应写出文字说明、证明过程或演算步骤) 10．(本小题满分10分)已知i 是虚数单位，且复数z 1＝3－b i ，z 2＝1－2i ，若z 1z 2是实数，求实数b 的值．解：∵z 1＝3－b i ，z 2＝1－2i ，∴z 1z 2＝3－b i 1－2i ＝(3－b i )(1＋2i )(1－2i )(1＋2i )＝3＋2b 5＋6－b 5i. ∵z 1z 2是实数，∴6－b 5＝0，解得b ＝6. 11．(本小题满分12分)已知复数z ＝(m ＋2)＋(3－2m )i.实数m 分别取什么数值时， (1)复数z 与复数12＋17i 互为共轭复数？ (2)复数z 的模取得最小值？求出此时的最小值．解：(1)根据共轭复数的定义得⎩⎪⎨⎪⎧m ＋2＝12，3－2m ＝－17.解得m ＝10.(2)|z |＝(m ＋2)2＋(3－2m )2＝5⎝⎛⎭⎫m －452＋495， ∴当m ＝45时，复数的模取得最小值755.12．(本小题满分13分)已知m ∈R ，i 为虚数单位，且(m ＋2i)2＝－3＋4i. (1)求实数m 的值；(2)若|z －1|＝|m ＋2i|，求复数z 在复平面上所对应的点P 的轨迹方程．解：(1)∵(m ＋2i)2＝－3＋4i ， ∴m 2＋4m i －4＝－3＋4i.∴m ＝1. (2)若|z －1|＝|m ＋2i|，由(1)得|z－1|＝|1＋2i|，设z＝x＋y i，则|x－1＋y i|＝|1＋2i|，∴(x－1)2＋y2＝5.故复数z在复平面上所对应的点P的轨迹方程是以(1,0)为圆心，以5为半径的圆．。

2019—2020年北师大版高中数学选修1-2全册学业分层测评4及解析.docx

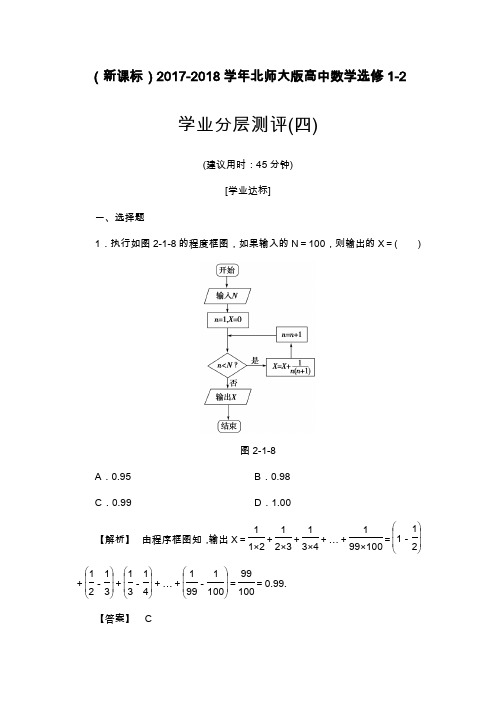
（新课标）2017-2018学年北师大版高中数学选修1-2学业分层测评(四)(建议用时：45分钟)[学业达标]一、选择题1．执行如图218的程度框图，如果输入的N ＝100，则输出的X ＝( )图218A ．0.95B ．0.98C ．0.99D ．1.00 【解析】由程序框图知，输出X ＝11×2＋12×3＋13×4＋…＋199×100＝⎝ ⎛⎭⎪⎪⎫1－12＋⎝ ⎛⎭⎪⎪⎫12－13＋⎝ ⎛⎭⎪⎪⎫13－14＋…＋⎝ ⎛⎭⎪⎪⎫199－1100＝99100＝0.99. 【答案】 C2．进入互联网时代，发电子邮件是不可少的，一般而言，发电子邮件要分成以下几个步骤：a.打开电子信箱；b.输入发送地址；c.输入主题；d.输入信件内容；e.点击“写邮件”；f.点击“发送邮件”．则正确的是( )A．a→b→c→d→e→f B．a→c→d→f→e→bC．a→e→b→c→d→f D．b→a→c→d→f→e【解析】依题意知发送电子邮件的步骤应是：a→e→b→c→d→f.【答案】 C3．如图219，小黑点表示网络的结点，结点之间的连线表示它们有网线相连，连线标注的数字表示该段网线单位时间内可以通过的最大信息量．现从结点A向结点B传递信息，信息可分开沿不同的路线同时传递，则单位时间内传递的最大信息量是( )图219A．26 B．24C．20 D．19【解析】由A→B有4条路线，4条路线单位时间内传递的最大信息量为6＋8＋12＝26.【答案】 A4．小明每天早晨起床后要做如下事情：洗漱用5分钟，收拾床褥用4分钟，听广播用15分钟，吃早饭用8分钟，要完成这些事情，小明要花费的最少时间为( )A ．17分钟B ．19分钟C ．23分钟D ．27分钟【解析】把过程简化，把能放在同一个时间内完成的并列，如听广播的同时可以洗涮、收拾被褥、吃早饭，共用5＋4＋8＝17(分钟)．【答案】 A5．执行下面的程序框图2110，若输入的a ，b ，k 分别为1,2,3，则输出的M ＝( )图2110A ．203B ．165C ．72D ．158【解析】当n ＝1时，M ＝1＋12＝32，a ＝2，b ＝32；当n ＝2时，M ＝2＋23＝83，a ＝32，b ＝83；当n＝3时，M＝32＋38＝158，a＝83，b＝158；n＝4时，终止循环．输出M＝15 8.【答案】 D 二、填空题6．椭圆x2a2＋y2b2＝1(a>b>0)的面积为S＝πab，当a＝4，b＝2时，计算椭圆面积的流程图如图2111所示，则空白处应为________.图2111【解析】由S＝πab知，需要输入a，b的值，由已知a＝4，b＝2，而且用的是框，故为赋值．【答案】a＝4，b＝27．如图2112是计算1＋13＋15＋…＋199的程序框图，判断框中应填的内容是________，处理框中应填的内容是________.图2112【解析】用i来表示计数变量，故判断框内为“i>99？”，处理框内为“i＝i ＋2”．【答案】i>99？i＝i＋28．执行如图2113所示的程序框图，若输入n＝3，则输出T＝________.图2113【解析】初始值：i＝0，S＝0，T＝0，n＝3，①i＝1，S＝1，T＝1；②i＝2，S＝3；T＝4；③i＝3，S＝6，T＝10；④i＝4，S＝10，T＝20，由于此时4≤3不成立，停止循环，输出T＝20.【答案】20三、解答题9．设计一个计算1＋2＋…＋100的值的程序框图．【解】程序框图设计如下：10．数学建模过程的流程图如图2114.图2114根据这个流程图，说明数学建模的过程．【解】数学建模的过程：根据实际情境提出问题，从而建立数学模型得出数学结果，然后检验是否合乎实际，如果不合乎实际，进行修改后重新提出问题．如果合乎实际，则成为可用的结果．[能力提升]1．某工厂加工某种零件的工序流程图如图2115：图2115按照这个工序流程图，一件成品至少经过几道加工和检验程序( )A．3 B．4C．5 D．6【解析】由流程图可知加工零件有三道工序：粗加工、返修加工和精加工，每道工序完成都要对产品进行检验，粗加工的合格品进入精加工，不合格品进入返修加工；返修加工的合格品进入精加工，不合格品作为废品处理；精加工的合格品为成品，不合格品为废品．由上可知一件成品至少要经过粗加工、检验、精加工、最后检验四道程序．【答案】 B2．执行两次如图2116所示的程序框图，若第一次输入的a的值为－1.2，第二次输入的a的值为1.2，则第一次、第二次输出的a的值分别为( )图2116A．0.2,0.2 B．0.2,0.8C．0.8,0.2 D．0.8,0.8【解析】第一次：a＝－1.2<0，a＝－1.2＋1＝－0.2，－0.2<0，a＝－0.2＋1＝0.8>0，a＝0.8≥1不成立，输出0.8.第二次：a＝1.2<0不成立，a＝1.2≥1成立，a＝1.2－1＝0.2≥1不成立，输出0.2.【答案】 C3．如图2117所示算法程序框图中，令a＝tan 315°，b＝sin 315°，c＝cos 315°，则输出结果为________.图2117【解析】程序框图的算法是求出a，b，c三个数中的最大值．对于tan 315°＝－1，sin 315°＝－22，cos 315°＝22，故输出的结果为22.【答案】2 24．栽种一棵梧桐树，其种树过程是：(1)取树苗；(2)挖直径1米，深1.5米的树坑；(3)将树苗放至树坑中央；(4)向树坑中培土到树坑边，离边缘0.2米；(5)向树坑中浇水；(6)判断水是否浇透，若水未浇透，则转(5)；否则转(7)；(7)栽种完毕．试画出该过程的流程图．【解】流程图如图所示．。

2016-2017学年北师大版高中数学选修1-2 章末质量评估4

第四章数系的扩充与复数的引入(本栏目内容，在学生用书中以独立形式分册装订)一、选择题(本大题共10小题，每小题5分，共50分．在每小题给出的四个选项中，只有一项是符合题目要求的)1．已知i 2＝－1，则i(1－3i)＝( ) A.3－i B ．3＋i C ．－3－iD ．－3＋i解析： i(1－3i)＝i －3i 2＝3＋i. 答案： B2．z 1＝(m 2＋m ＋1)＋(m 2＋m －4)i ，m ∈R ，z 2＝3－2i ，则m ＝1是z 1＝z 2的( ) A ．充分不必要条件 B ．必要不充分条件 C ．充要条件D ．既不充分也不必要条件解析：因为z 1＝z 2，所以⎩⎪⎨⎪⎧m 2＋m ＋1＝3m 2＋m －4＝－2，解得m ＝1或m ＝－2，所以m ＝1是z 1＝z 2的充分不必要条件．答案： A3．已知复数z 满足|z |2＝z 2，则z 是( ) A ．0 B ．任意实数 C ．任意复数D ．实数和纯虚数解析：设z ＝a ＋b i(a ，b 为实数)，则 |z |2＝a 2＋b 2，z 2＝a 2－b 2＋2ab i.∵|z |2＝z 2，∴⎩⎪⎨⎪⎧a 2＋b 2＝a 2－b 2，2ab ＝0，即a ∈R 且b ＝0，故z ＝a 是任意实数．答案： B4．i 是虚数单位，复数－1＋3i1＋2i ＝( )A ．1＋iB ．5＋5iC ．－5－5iD ．－1－i解析：－1＋3i 1＋2i＝(－1＋3i )(1－2i )5＝5＋5i5＝1＋i 答案： A5．复数⎝ ⎛⎭⎪⎫3－i 1＋i 2＝( )A ．－3－4iB ．－3＋4iC ．3－4iD ．3＋4i解析： 3－i 1＋i＝(3－i )(1－i )2＝2－4i2＝1－2i ∴⎝⎛⎭⎪⎫3－i 1＋i 2＝(1－2i)2＝－3－4i答案： A6．(1＋i)20－(1－i)20的值是( ) A ．－1 024 B ．1 024 C ．0D ．1 024i解析： (1＋i)20－(1－i)20＝[(1＋i)2]10－[(1－i)2]10＝(2i)10－(－2i)10＝(2i)10－(2i)10＝0. 答案： C7．若z 1＝(x －2)＋y i 与z 2＝3x ＋i(x ，y ∈R )互为共轭复数，则z 1对应的点在( ) A ．第一象限 B ．第二象限 C ．第三象限D ．第四象限解析：由z 1，z 2互为共轭复数，得⎩⎪⎨⎪⎧ x －2＝3x y ＝－1，解得⎩⎪⎨⎪⎧x ＝－1y ＝－1，所以z 1＝(x －2)＋y i ＝－3－i.由复数的几何意义知z 1对应的点在第三象限．答案： C8．若复数z 满足1－z1＋z ＝i ，则|1＋z |等于( )A. 2 B ．1 C ．0D ．2解析：由1－z1＋z ＝i ，得1－z ＝i ＋i z ，∴(1＋i)z ＝1－i ，∴z ＝1－i1＋i ＝－i ，∴|1＋z |＝|1－i|＝ 2. 答案： A9．设z 1＝i 4＋i 5＋i 6＋…＋i 12，z 2＝i 4·i 5·i 6·…·i 12，则z 1，z 2的关系是( ) A ．z 1＝－z 2 B ．z 1＝z 2 C ．z 1＝1＋z 2D ．无法确定解析： z 1＝i 4(1－i 9)1－i ＝i 4(1－i )1－i ＝i 4＝1，z 2＝i 4＋5＋6＋7＋…＋12＝i 72＝1.答案： B10．定义运算⎪⎪⎪⎪a c b d ＝ad －bc ，则符合条件⎪⎪⎪⎪1z －1z i ＝4＋2i 的复数z 为( ) A ．3－i B ．1＋3i C ．3＋iD ．1－3i解析： ⎪⎪⎪⎪1z －1z i ＝z i ＋z ＝z (1＋i)＝4＋2i ， ∴z ＝4＋2i 1＋i ＝(4＋2i )(1－i )2＝4＋2－2i 2＝3－i.答案： A二、填空题(本大题共4小题，每小题5分，共20分．请把正确答案填在题中横线上) 11．若复数z 1＝4＋29i ，z 2＝6＋9i ，其中i 是虚数单位，则复数(z 1－z 2)i 的实部为________．解析： ∵(z 1－z 2)i ＝[(4＋29i)－(6＋9i)]i ＝(－2＋20i)i ＝－20－2i ， ∴(z 1－z 2)i 的实部为－20. 答案：－2012．若复数z 满足z (1＋i)＝1－i(i 是虚数单位)，则其共轭复数z ＝________. 解析：设z ＝a ＋b i ，则(a ＋b i)(1＋i)＝1－i ，即a －b ＋(a ＋b )i ＝1－i.由⎩⎪⎨⎪⎧ a －b ＝1，a ＋b ＝－1，解得⎩⎪⎨⎪⎧a ＝0，b ＝－1. 所以z ＝－i ，z ＝i. 答案： i13．若复数2－b i 31＋i (b ∈R )在复平面上对应的点在直线y ＝－x 上，则b 的值为________．解析： 2－b i 31＋i ＝(2＋b i )(1－i )2＝2－2i ＋b i ＋b 2＝2＋b ＋(b －2)i2，由题意得－(2＋b )＝b －2，∴b ＝0.答案： 014．设z ∈C ，z ＋|z |＝2＋i ，则z ＝________. 解析：设z ＝a ＋b i(a ，b ∈R )，则|z |＝a 2＋b 2， ∴a ＋b i ＋a 2＋b 2＝2＋i ，∴⎩⎨⎧a ＋a 2＋b 2＝2，b ＝1∴⎩⎪⎨⎪⎧a ＝34b ＝1，∴z ＝34＋i.答案： 34＋i三、解答题(本大题共4小题，满分50分．解答时应写出必要的文字说明、证明过程或演算步骤)15．(本小题满分12分)已知z 1＝(x ＋y )＋(x 2－xy －2y )i ，z 2＝(2x －y )－(y －xy )i ，问x ，y 取什么实数值时，(1)z 1，z 2都是实数； (2)z 1，z 2互为共轭复数．解析： (1)由⎩⎪⎨⎪⎧ x 2－xy －2y ＝0y －xy ＝0解得⎩⎪⎨⎪⎧x ＝0y ＝0或⎩⎪⎨⎪⎧x ＝1y ＝13，所以当⎩⎪⎨⎪⎧x ＝0y ＝0或⎩⎪⎨⎪⎧x ＝1y ＝13时，z 1，z 2都是实数．(2)由⎩⎪⎨⎪⎧ x ＋y ＝2x －y x 2－xy －2y ＝y －xy 解得⎩⎪⎨⎪⎧x ＝0y ＝0或⎩⎨⎧x ＝32y ＝34，所以当⎩⎪⎨⎪⎧x ＝0y ＝0或⎩⎨⎧x ＝32y ＝34时，z 1，z 2互为共轭复数．16．(本小题满分12分)计算：i －231＋23i ＋(5＋i 19)－⎝ ⎛⎭⎪⎫1＋i 222.解析：原式＝i (1＋23i )1＋23i ＋(5＋i 3)－(2i )11211＝i ＋(5－i)＋i ＝5＋i.17．(本小题满分12分)已知复数z ＝(1－i )2＋3(1＋i )2－i .(1)求复数z ；(2)若z 2＋az ＋b ＝1－i ，求实数a ，b 的值．解析： (1)z ＝－2i ＋3＋3i 2－i ＝3＋i 2－i ＝(3＋i )(2＋i )5＝1＋i ；(2)把z ＝1＋i 代入得(1＋i)2＋a (1＋i)＋b ＝1－i ，即a ＋b ＋(2＋a )i ＝1－i ，所以⎩⎪⎨⎪⎧ a ＋b ＝12＋a ＝－1，解得⎩⎪⎨⎪⎧a ＝－3b ＝4. 18．(本小题满分14分)已知|z 1|＝1，|z 2|＝1，|z 1＋z 2|＝ 3.求|z 1－z 2|. 解析：方法一：设z 1＝a ＋b i ，z 2＝c ＋d i(a ，b ，c ，d ∈R )．由已知得a 2＋b 2＝1，c 2＋d 2＝1. (a ＋c )2＋(b ＋d )2＝3，又∵(a ＋c )2＋(b ＋d )2＝a 2＋b 2＋c 2＋d 2＋2ac ＋2bd ＝2＋2ac ＋2bd ＝3. ∴2ac ＋2bd ＝1.又|z 1－z 2|2＝(a －c )2＋(b －d )2＝a 2＋b 2＋c 2＋d 2－2ac －2bd ＝2－1＝1， ∴|z 1－z 2|＝1.方法二：在复平面内设z 1，z 2分别对应向量OZ 1→、OZ 2→，则对角线OZ →对应z 1＋z 2，Z 2Z 1→对应z 1－z 2，由已知|OZ 1→|＝1，|OZ 2→|＝1，|OZ |＝ 3. ∴∠OZ 1Z ＝120°.∴∠Z 2OZ 1＝60°. ∴在OZ 1Z 2中|Z 2Z 1→|＝1，即|z 1－z 2|＝1.方法三：由教材中的习题得结论|z 1＋z 2|2＋|z 1－z 2|2＝2(|z 1|2＋|z 2|2)，得|z 1－z 2|2＝1.∴|z 1－z 2|＝1.。

北师大版高中数学选修1-2同步练习第四章数系的扩充与复数的引入学业质量标准检测

第四章学业质量标准检测时间120分钟，满分150分。

一、选择题(本大题共12个小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的)1．复数1＋2i2－i ＝( A )A ．iB ．1＋iC ．－iD ．1－i[解析]1＋2i 2－i ＝(1＋2i )(2＋i )(2－i )(2＋i )＝5i5＝i. 2．(2018·北京卷，2)在复平面内，复数11－i 的共轭复数对应的点位于( D )A ．第一象限B ．第二象限C ．第三象限D ．第四象限[解析]11－i ＝12＋i 2，其共轭复数为12－i2，对应点位于第四象限．故选D ．3．已知i 为虚数单位，则i1＋3i ＝( B )A ．34－14iB ．34＋14iC ．32＋12i D ．32－12i [解析]i 1＋3i ＝i (1－3i )(1＋3i )(1－3i )＝i ＋34＝34＋14i.4．复数z 1＝3＋i ，z 2＝1－i ，则z ＝z 1·z 2在复平面内对应的点位于( D ) A ．第一象限 B ．第二象限 C ．第三象限D ．第四象限[解析] z ＝(3＋i)(1－i)＝4－2i ，所以复数z 对应的点Z (4，－2)在第四象限． 5．设z ＝1＋i(i 是虚数单位)，则2z ＋z 2等于( C )A ．－1＋iB ．－1－iC ．1＋iD ．1－i[解析] 2z ＋z 2＝21＋i＋(1＋i)2＝1－i ＋2i ＝1＋i.6．(2019·山师大附中高二期末测试)设复数z 满足(1＋i)z ＝i 2019，则复数z 的虚部为( B )A ．－12B ．12C ．12iD ．－12i[解析] ∵z 4＝1，∴i 2019＝(i 4)504·i 3＝－i ， ∴z ＝－i 1＋i＝－i (1－i )2＝－12－12i ，∴z ＝－12＋12i ，∴z 的虚部为12，故选B ．7．设x ∈R ，则“x ＝1”是“复数z ＝(x 2－1)＋(x ＋1)i 为纯虚数”的( A ) A ．充分必要条件 B ．必要不充分条件 C ．充分不必要条件D ．既不充分也不必要条件[解析] z 是纯虚数⇔⎩⎪⎨⎪⎧x 2－1＝0x ＋1≠0⇔x ＝1，故选A ．8．已知a ∈R ，复数z ＝(a －i )(1＋i )i ，若z ＝z ，则a ＝( B )A ．1B ．－1C ．2D ．－2[解析] 复数z ＝(a －i )(1＋i )i ＝(a －1)－(a ＋1)i ，由z ＝z ，可知a ＋1＝0，即a ＝－1.9．若z ＝cos θ－isin θ，则使z 2＝－1的θ值可能是( B ) A ．0 B ．π2C ．πD ．2π[解析] z 2＝cos 2θ－2isin θcos θ－sin 2θ＝cos2θ－i sin 2θ＝－1，∴⎩⎪⎨⎪⎧cos2θ＝－1－sin2θ＝0，∴θ＝π2.10．若θ∈⎝⎛⎭⎫3π4，5π4，则复数(cos θ＋sin θ)＋(sin θ－cos θ)i 在复平面内所对应的点在( B ) A ．第一象限 B ．第二象限 C ．第三象限D ．第四象限[解析] θ∈⎝⎛⎭⎫3π4，5π4时， sin θ＋cos θ<0，sin θ－cos θ>0，故对应点(cos θ＋sin θ，sin θ－cos θ)在第二象限．11．若A ，B 为锐角三角形的两个内角，则复数z ＝(cos B －sin A )＋i(sin B －cos A )对应的点位于复平面内的( B )A ．第一象限B ．第二象限C ．第三象限D ．第四象限[解析] ∵A 、B 为锐角三角形的内角， ∴π2<A ＋B <π， ∴A >π2－B ，B >π2－A ，∴sin A >sin(π2－B )＝cos B ，sin B >sin(π2－A )＝cos A ，∴⎩⎪⎨⎪⎧cos B －sin A <0sin B －cos A >0， ∴对应点在第二象限，故选B ．12．对任意复数ω1、ω2，定义ω1]2，其中ω－2是ω2的共轭复数，对任意复数z 1、z 2、z 3，有如下四个命题：①(z 1＋z 2)*z 3＝(z 1]( B ) A ．1 B ．2 C ．3D ．4[解析] ∵ω1]．∴①左边＝(z 1＋z 2)z 3，右边＝z 1z 3＋z 2z 3＝(z 1＋z 2)z 3，左边＝右边，正确． ②左边＝z 1(z 2＋z 3)＝z 1(z 2＋z 3)，右边＝z 1z 2＋z 1z 3＝z 1(z 2＋z 3)，左边＝右边，正确．③左边＝(z 1z 2)z 3，右边＝z 1(z 2z 3)＝z 1(z 2z 3)，左边≠右边，不正确． ④左边＝z 1z 2，右边＝z 2z 1，左边≠右边，不正确，选B ．二、填空题(本大题共4个小题，每小题5分，共20分，将正确答案填在题中横线上) 13．(2018·江苏，2)若复数z 满足i·z ＝1＋2i ，其中i 是虚数单位，则z 的实部为__2__. [解析] 由i·z ＝1＋2i ，得z ＝1＋2ii＝2－i ，∴z 的实部为2.14．(2019·宁夏罗平中学高二月考)若复数z ＝(3＋4i)(1－i)(i 为虚数单位)，则|z |＝[解析] 解法一：z ＝(3＋4i)(1－i)＝3－3i ＋4i ＋4＝7＋i ，∴|z |＝49＋1＝5 2. 解法二：∵z ＝(3＋4i)(1－i)，∴|z |＝|(3＋4i)(1－i)|＝|3＋4i|·|1－i|＝5 2.15．若复数z 满足z ＝|z |－3－4i ，则z ＝__76－4i .[解析] 设复数z ＝a ＋b i(a 、b ∈R )，则⎩⎨⎧a ＝a 2＋b 2－3b ＝－4，∴⎩⎪⎨⎪⎧a ＝76b ＝－4.∴z ＝76－4i.16．已知复数z ＝a ＋b i(a 、b ∈R )且a 1－i ＋b 1－2i ＝53＋i ，则复数z 在复平面对应的点位于第__四__象限．[解析] ∵a 、b ∈R 且a 1－i ＋b 1－2i ＝53＋i ，即a (1＋i )2＋b (1＋2i )5＝3－i2， ∴5a ＋5a i ＋2b ＋4b i ＝15－5i ，∴⎩⎪⎨⎪⎧ 5a ＋2b ＝155a ＋4b ＝－5，解得⎩⎪⎨⎪⎧a ＝7b ＝－10. ∴复数z ＝a ＋b i ＝7－10i 在复平面内对应的点位于第四象限．三、解答题(本大题共6个小题，共70分，解答应写出文字说明、证明过程或演算步骤) 17．(本题满分10分)m 为何实数时，复数z ＝(2＋i)m 2－3(i ＋1)m －2(1－i)是： (1)实数；(2)虚数；(3)纯虚数？ [解析] z ＝(2＋i)m 2－3(i ＋1)m －2(1－i) ＝2m 2＋m 2i －3m i －3m －2＋2i ＝(2m 2－3m －2)＋(m 2－3m ＋2)i. (1)由m 2－3m ＋2＝0得m ＝1或m ＝2，即m ＝1或2时，z 为实数．(2)由m 2－3m ＋2≠0得m ≠1且m ≠2，即m ≠1且m ≠2时，z 为虚数．(3)由⎩⎪⎨⎪⎧2m 2－3m －2＝0m 2－3m ＋2≠0，得m ＝－12，即m ＝－12时，z 为纯虚数．18．(本题满分12分)已知z ＝1＋i ，a 、b ∈R .若z 2＋az ＋bz 2－z ＋1＝1－i ，求a 、b 的值．[解析] ∵z ＝1＋i ，∴z 2＝2i ，所以 z 2＋az ＋b z 2－z ＋1＝2i ＋a ＋a i ＋b2i －1－i ＋1＝(a ＋2)i ＋(a ＋b )i＝a ＋2－(a ＋b )i ＝1－i.所以⎩⎪⎨⎪⎧ a ＋2＝1a ＋b ＝1，所以⎩⎪⎨⎪⎧a ＝－1b ＝2. 19．(本题满分12分)(2019·山东昌乐一中高二月考)已知z 1＝m 2＋1m ＋1i ，z 2＝(2m －3)＋12i ，m ∈R ，i 为虚数单位，且z 1＋z 2是纯虚数．(1)求实数m 的值； (2)求z 1·z 2的值．[解析] (1)z 1＋z 2＝(m 2＋2m －3)＋(1m ＋1＋12)i ，∵z 1＋z 2是纯虚数，∴⎩⎪⎨⎪⎧m 2＋2m －3＝01m ＋1＋12≠0，解得m ＝1. (2)由(1)知z 1＝1＋12i ，z 2＝－1＋12i ，∴z 2＝－1－12i ，∴z 1z 2＝(1＋12i)·(－1－12i)＝－1－12i －12i ＋14＝－34－i. 20．(本题满分12分)已知复数z 满足|z |＝2，z 2的虚部是2. (1)求复数z ；(2)设z ，z 2，z －z 2在复平面上的对应点分别为A 、B 、C ，求△ABC 的面积．[解析] (1)设z ＝a ＋b i(a 、b ∈R )，则z 2＝a 2－b 2＋2ab i ，由题意得a 2＋b 2＝2且2ab ＝2，解得a ＝b ＝1或a ＝b ＝－1，所以z ＝1＋i 或z ＝－1－i.(2)当z ＝1＋i 时，z 2＝2i ，z －z 2＝1－i ，所以A (1,1)、B (0,2)、C (1，－1)，所以S △ABC ＝1. 当z ＝－1－i 时，z 2＝2i ，z －z 2＝－1－3i ，所以A (－1，－1)，B (0,2)，C (－1，－3)，所以S △ABC ＝12×2×1＝1.21．(本题满分12分)已知复数z 1＝cos θ＋i ，z 2＝sin θ＋i.求： (1)z 1＋z 2；(2)|z 1＋z 2|的最大值．[解析] (1)z 1＋z 2＝(cos θ＋i)＋(sin θ＋i)＝sin θ＋cos θ＋2i ＝2sin(θ＋π4)＋2i.(2)|z 1＋z 2|2＝22＋[2sin(θ＋π4)]2＝4＋2sin 2(θ＋π4)，∵sin 2(θ＋π4)的最大值为1，∴|z 1＋z 2|2有最大值6.故θ＝π4＋k π，k ∈Z 时，|z 1＋z 2|max ＝ 6.22．(本题满分12分)已知复数z 1＝i(1－i)3， (1)求|z 1|；(2)若|z |＝1，求|z －z 1|的最大值． [分析] (1)利用模的定义求解；(2)可以利用三角代换，也可利用几何法数形结合． [解析] (1)z 1＝i(1－i)3＝i(－2i)(1－i)＝2(1－i)， ∴|z 1|＝22＋(－2)2＝2 2.(2)解法一：|z |＝1，∴设z ＝cos θ＋isin θ， |z －z 1|＝|cos θ＋isin θ－2＋2i| ＝(cos θ－2)2＋(sin θ＋2)2 ＝9＋42sin (θ－π4).当sin(θ－π4)＝1时，|z －z 1|取得最大值9＋42，从而得到|z －z 1|的最大值22＋1.解法二：|z |＝1可看成半径为1，圆心为(0,0)的圆，而z 1对应坐标系中的点(2，－2)． ∴|z －z 1|的最大值可以看成点(2，－2)到圆上的点距离最大，则|z －z 1|max ＝22＋1.。

(常考题)北师大版高中数学选修1-2第四章《数系的扩充与复数的引入》测试题(含答案解析)(4)

一、选择题1．1z 2z 是复数，则下列结论中正确的是（）A ．若22120z z +>，则2212z z >- B ．12||z z -=C ．22121200z z z z +=⇔==D ．2211||||z z =2．复数(),z a bi a b R =+∈，()m z z b =+，n z z =⋅，2p z =，则（）A ．m 、n 、p 三数都不能比较大小B ．m 、n 、p 三数的大小关系不能确定C ．m n p ≤=D ．m n p ≥=3．定义运算,,a b ad bc c d=-，则符合条件,10 ,?2z i i i+=-的复数 z 对应的点在（）A ．第一象限B ．第二象限C ．第三象限D ．第四象限4．若复数1z ，2z 满足1134z z i +=-，212z i ++=，则12z z -的最小值为（）．A ．110B ．1110C ．2110D ．2110-5．若复数2320211z i i i i =++++⋯+，则复数z 对应的点在第（）象限 A ．一B ．二C ．三D ．四6．下列关于复数z 的四个命题中，正确的个数是（）（1）若|1||1|2z z -++=，则复数z 对应的动点的轨迹是椭圆；（2）若|2||2|2z z --+=，则复数z 对应的动点的轨迹是双曲线；（3）若|1||Re 1|z z -=+，则复数z 对应的动点的轨迹是抛物线；（4）若|2|3z -≤，则||z 的取值范围是[1,5] A ．4 B ．1C ．2D ．37．若复数1a iz i+=-，且3·0z i >，则实数a 的值等于（） A ．1B ．-1C ．12 D ．12- 8．已知i 为虚数单位，a 为实数，复数(2)(1)z a i i =-+在复平面内对应的点为M ，则“1a =”是“点M 在第四象限”的（） A ．充分而不必要条件 B ．必要而不充分条件 C ．充要条件 D ．既不充分也不必要条件9．已知复数21iz i=+，则共轭复数z =( ) A ．1i -+B ．1i -C ．1i +D ．1i --10．若复数()()12i 2i z =-+(其中i 为虚数单位)在复平面中对应的点位于( ) A ．第一象限B ．第二象限C ．第三象限D ．第四象限11．已知实数[1,1]a ∈-，实数[1,2]b ∈-，则复数2a biz i+=-在复平面内对应的点位于第一象限的概率为（） A ．524B ．14C ．724D ．1312．设1z ，2z 为复数，则下列命题中一定成立的是（）A ．如果22120z z +=，那么120z z == B ．如果12=z z ，那么12=±z zC ．如果1z a ≤（a 为正实数），那么1a z a -≤≤D ．如果1z a =（a 为正实数），那么211z z a ⋅=二、填空题13．已知复数()(()()3422312i iz i i +-=++，那么复数z 的模为______.14．若复数z 满足24z z i +=-（i 为虚数单位），则z 的最小值为__________． 15．若复数z 满足i 12i01z+=，其中i 是虚数单位，则z 的虚部为________16．已知i 是虚数单位，则复数11ii+-的实部为______. 17．已知()21,1xyi x y R i+=∈-，则x y +=__________． 18．若复数是纯虚数(是虚数单位)，为实数，则复数的模为__________．19．设复数()21z i =-（i 是虚数单位），则z 的模为__________． 20．复数z 满足()12i z -=，则z 的虚部是__________．三、解答题21．已知复数z 满足|z |2=z 的实部大于0，z 2的虚部为2.（1）求复数z ；（2）设复数z ，z 2，z ﹣z 2之在复平面上对应的点分别为A ，B ，C ，求（OA OB +）⋅OC 的值.22．设z 为关于x 的方程20x mx n ++=（,m n ∈R ）的虚根，i 为虚数单位. （1）当1i z =-+时，求m 、n 的值；（2）若1n =，在复平面上，设复数z 所对应的点为P ，复数24i +所对应的点为Q ，试求||PQ 的取值范围.23．设复数n n n z x i y =+⋅，其中n x n y ∈R ，*n ∈N ，i 为虚数单位，1(1)n n z i z +=+⋅，134z i =+，复数n z 在复平面上对应的点为n Z .（1）求复数2z ，3z ，4z 的值；（2）是否存在正整数n 使得n OZ ∥1OZ ？若存在，求出所有满足条件的n ；若不存在，请说明理由；（3）求数列{}n n x y ⋅的前102项之和.24．已知复数()0,z a i a a R =+>∈，i 为虚数单位，且复数2z z+为实数．（1）求复数z ；（2）在复平面内，若复数()2m z +对应的点在第一象限，求实数m 的取值范围．25．已知复数Z 满足23z i z i -=++（其中i 为虚数单位）（1）求z ；（2）若2a iz+为纯虚数，求实数a 的值． 26．已知复数1z 满足()11i 13i z -=+，()2i z a a R =-∈（其中i 是虚数单位），若121z z ->，求a 的取值范围．【参考答案】***试卷处理标记，请不要删除一、选择题 1．D 解析：D 【分析】举反例12z i =+，22z i =-可判断选项A 、B ，举反例11z =，2z i =可判断选项C ，设1z a bi =+，(),a b R ∈，分别计算21||z 、21||z 即可判断选项D ，进而可得正确选项.【详解】对于选项A ：取12z i =+，22z i =-，()221232z i i =+=+，()222232z i i =-=-，满足221260z z +=>，但21z 与22z 是两个复数，不能比较大小，故选项A 不正确；对于选项B ：取12z i =+，22z i =-，12||22z z i -==，==B 不正确；对于选项C ：取11z =，2z i =，则22120z z +=，但是10z ≠，20z ≠，故选项C 不正确；对于选项D ：设1z a bi =+，(),a b R ∈，则()222212z a bi a b abi =+=-+2221z a b ===+，1z a bi =-，1z =，所以2221z a b =+，所以2211||||z z =，故选项D 正确.故选：D.2．C解析：C 【分析】根据复数的四则运算，结合基本不等式，即可得出结论. 【详解】z a bi =-，()2m a bi a bi b ab =++-=，22()()n a bi a bi a b =+-=+，22p a b =+222a b ab +，当且仅当a b =时，取等号m n p ∴≤=故选：C 【点睛】本题主要考查了复数的四则运算，涉及了基本不等式的应用，属于中档题.3．B解析：B 【解析】由题意可得：()()(),1210,2z i z i i i i i+=--+=-，即()()()121221222422i i i i i z i i i -----====---，∴1 22iz =-+，则复数z 对应的点的坐标为11,22⎛⎫-⎪⎝⎭在第二象限，故选B. 4．A解析：A 【分析】由复数模的定义求出1z 对应的点在一条直线上，2z 对应的点在圆上，利用圆的性质可求得直线上的点到圆上点的距离的最小值．【详解】复数1z 对应的点为1(,)Z x y ，因为1134z z i +=-，所以=6870x y +-=，所以点1Z 的轨迹是一条直线．复数2z 对应的点为2(,)Z x y ，因为212z i ++=表示点(),x y 到定点()1,1--的距离为2，所以点2Z 的轨迹表示以()1,1--为圆心、半径为2的圆，12z z -211221010-=-=．故选：A ．本题考查复数的模的运算，考查模的几何意义，利用几何意义把复数问题转化为直线上的点到圆上点的距离的最小值这个几何问题，利用几何性质得出求解方法．5．A解析：A 【分析】根据周期性得到1z i =+,得到答案. 【详解】2320211(11)(11)11z i i i i i i i i i i =++++⋯+=+--+⋯++--++=+，故复数z 对应的点在第一象限. 故选：A. 【点睛】本题考查了复数对应象限，意在考查学生的计算能力和转化能力.6．B解析：B 【分析】（1）根据椭圆的定义来判断；（2）根据双曲线的定义来判断；（3）根据抛物线的定义来判断；（4）利用圆的有关知识点判断. 【详解】（1）|1||1|2z z -++=，表示复平面内到点()()1,0,1,0-距离之和为2的点的轨迹，是由点()()1,0,1,0-构成的线段，故错误；（2）|2||2|2z z --+=，表示复平面内到点()2,0的距离比到点()2,0-的距离大2的点的轨迹，是双曲线的左支，故错误；（3）|1||Re 1|z z -=+，表示复平面内到点()1,0的距离等于到直线1x =-的距离的点的轨迹（点()1,0不在直线1x =-上），所以轨迹是抛物线，故正确；（4）|2|3z -≤，表示点的轨迹是圆心为()2,0，半径为3的圆及其内部（坐标原点在圆内），且z 表示轨迹上的点到原点的距离，所以min 0=，此时z 对应的点为原点，max 325r d =+=+=（d 表示原点到圆心的距离），所以 ||z 的取值范围是[0,5]，故错误. 故选B. 【点睛】复数对应的轨迹方程：（1）122z z z z a -+-=，当122a z z >-时，此时z 对应的点的轨迹是椭圆；（2）()1220z z z z a a ---=>，当122a z z <-时，此时z 对应的点的轨迹是双曲线.7．A【分析】由3·0z i >可判定3·z i 为实数，利用复数代数形式的乘除运算化简复数z ，再由实部为0，且虚部不为0列式求解即可. 【详解】()()()()()i 1i 11ii 1i 1i 1i 2a a a a z ++-+++===--+，所以3·z i =()()()()341i 1i 1i 122a a a a -++--++=，因为3·0z i >，所以3·z i 为实数，102a --= 可得1a =，1a =时3,?10z i =>,符合题意，故选A. 【点睛】复数是高考中的必考知识，主要考查复数的概念及复数的运算．要注意对实部、虚部的理解，掌握纯虚数、共轭复数、复数的模这些重要概念，复数的运算主要考查除法运算，通过分母实数化转化为复数的乘法，运算时特别要注意多项式相乘后的化简，防止简单问题出错，造成不必要的失分.8．A解析：A 【解析】因为(2i)(1+i)=a+2+(a-2)i z a =-，则点M 在第四象限时，满足2>a>-2,因此可知“1a =”是“点M 在第四象限”的充分而不必要条件，选A9．B解析：B 【解析】分析：首先求得复数z ，然后求解其共轭复数即可. 详解：由题意可得：()()()()2121211112i i i iz i i i i -+====+++-，则其共轭复数1z i =-. 本题选择B 选项.点睛：本题主要考查复数的运算法则，共轭复数的概念等知识，意在考查学生的转化能力和计算求解能力.10．D解析：D 【解析】分析：利用复数的出发计算得到z ，即可得到结论. 详解：()()12i 2i 24243,z i i i =-+=+-+=-故z 在复平面中对应的点位于第四象限. 故选D.点睛：本题考查复数乘法运算及复数的几何意义，是基础题.11．A解析：A 【解析】分析：化简复数z ，得()()225a b a b i z -++=，复数z 在复平面内对应的点位于第一象限，则2020a b a b ->+>，结合[]1,1a ∈-，[]1,2b ∈-，画出可行域，利用几何概型即可求出答案.详解：化简复数z ，得()()225a b a b i z -++=，复数z 在复平面内对应的点位于第一象限，则2020a b a b ->+>，又[] 1,1a ∈-，[]1,2b ∈-，故在平面直角坐标系上画出可行域，如图所示：∴复数z 在复平面内对应的点位于第一象限的概率1515222324P ⨯⨯==⨯. 故选：A.点睛：应用几何概型求概率的方法建立相应的几何概型，将试验构成的总区域和所求事件构成的区域转化为几何图形，并加以度量．(1)一般地，一个连续变量可建立与长度有关的几何概型，只需把这个变量放在数轴上即可；(2)若一个随机事件需要用两个变量来描述，则可用这两个变量的有序实数对来表示它的基本事件，然后利用平面直角坐标系就能顺利地建立与面积有关的几何概型；(3)若一个随机事件需要用三个连续变量来描述，则可用这三个变量组成的有序数组来表示基本事件，利用空间直角坐标系即可建立与体积有关的几何概型．12．D解析：D 【分析】对A,举出反例判断正误；对B,举出反例判断正误；对C,利用复数的几何意义判断正误；对D,设出复数即可化简结果,再判断正误即可．【详解】对于A,如果11z i =-,21z i =+,22120z z +=,所以120z z ==不正确。

北师大版数学高二-数学北师大版选修1-2练习章末检测卷(四)

章末检测卷(四)(时间：120分钟满分：150分)一、选择题(本大题共10小题，每小题5分，共50分)1．i 是虚数单位，若集合S ＝{－1,0,1}，则( )A ．i ∈SB ．i 2∈SC ．i 3∈S D.2i ∈S答案 B2．z 1＝(m 2＋m ＋1)＋(m 2＋m －4)i ，m ∈R ，z 2＝3－2i ，则“m ＝1”是“z 1＝z 2”的() A ．充分不必要条件 B ．必要不充分条件C ．充要条件D ．既不充分又不必要条件答案 A解析因为z 1＝z 2，所以⎩⎪⎨⎪⎧ m 2＋m ＋1＝3m 2＋m －4＝－2，解得m ＝1或m ＝－2，所以m ＝1是z 1＝z 2的充分不必要条件．3．i 是虚数单位，复数3＋i1－i 等于( )A ．1＋2iB ．2＋4iC ．－1－2iD ．2－i答案 A解析 3＋i1－i ＝(3＋i )(1＋i )(1－i )(1＋i )＝2＋4i 2＝1＋2i.故选A.4．已知a 是实数，a －i1＋i 是纯虚数，则a 等于( )A ．1B ．－1 C. 2 D ．－2答案 A解析 a －i 1＋i ＝(a －i )(1－i )(1＋i )(1－i )＝(a －1)－(a ＋1)i 2是纯虚数，则a －1＝0，a ＋1≠0，解得a ＝1.5．若(x －i)i ＝y ＋2i ，x ，y ∈R ，则复数x ＋y i 等于( )A ．－2＋iB ．2＋iC ．1－2iD ．1＋2i答案 B解析 ∵(x －i)i ＝y ＋2i ，x i －i 2＝y ＋2i ，∴y ＝1，x ＝2，∴x ＋y i ＝2＋i.6．若复数z 满足(3－4i)z ＝|4＋3i|，则z 的虚部为( )A ．－4B ．－45C ．4 D.45答案 D解析设z ＝a ＋b i ，故(3－4i)(a ＋b i)＝3a ＋3b i －4a i ＋4b ＝|4＋3i|，所以⎩⎪⎨⎪⎧ 3b －4a ＝03a ＋4b ＝5，解得b ＝45.7.若z 1＝(x －2)＋y i 与z 2＝3x ＋i(x ，y ∈R )互为共轭复数，则z 1对应的点在()A ．第一象限B ．第二象限C ．第三象限D ．第四象限答案 C解析由z 1，z 2互为共轭复数，得⎩⎪⎨⎪⎧ x －2＝3xy ＝－1，解得⎩⎪⎨⎪⎧ x ＝－1y ＝－1，所以z 1＝(x －2)＋y i ＝－3－i.由复数的几何意义知z 1对应的点在第三象限．8.已知f (n )＝i n －i －n (n ∈N ＋)，则集合{f (n )}的元素个数是( )A ．2B ．3C ．4D ．无数个答案 B解析 f (n )有三个值0,2i ，－2i.9．已知复数z ＝3＋i(1－3i )2，z 是z 的共轭复数，则z ·z 等于( )A.14 B.12 C ．1 D ．2答案 A10．设f (z )＝z ，z 1＝3＋4i ，z 2＝－2－i ，则f (z 1－z 2)等于( )A ．1－3iB ．11i －2C ．i －2D ．5＋5i答案 D二、填空题(本大题共5小题，每小题5分，共25分)11．i 是虚数单位，若1＋7i 2－i＝a ＋b i(a ，b ∈R )，则ab 的值是________．答案－3解析 1＋7i 2－i＝(1＋7i )(2＋i )5＝－1＋3i ， ∴a ＝－1，b ＝3，ab ＝－3.12．复平面内，若z ＝m 2(1＋i)－m (4＋i)－6i 所对应的点在第二象限，则实数m 的取值范围是________．答案 (3,4)解析 ∵z ＝m 2－4m ＋(m 2－m －6)i 所对应的点在第二象限，∴⎩⎪⎨⎪⎧m 2－4m <0m 2－m －6>0，解得3<m <4. 13．给出下面四个命题：①0比－i 大；②两个复数互为共轭复数，当且仅当其和为实数；③x ＋y i ＝1＋i 的充要条件为x ＝y ＝1；④如果让实数a 与a i 对应，那么实数集与纯虚数集一一对应．其中真命题的个数是________．答案 014．已知0<a <2，复数z 的实部为a ，虚部为1，则|z |的取值范围是______．答案 (1，5)解析由题意得z ＝a ＋i ，根据复数模的定义可知|z |＝a 2＋1.因为0<a <2，所以1<a 2＋1<5，故1<a 2＋1< 5. 15.下列说法中正确的序号是________．①若(2x －1)＋i ＝y －(3－y )i ，其中x ∈R ，y ∈∁C R ，则必有⎩⎪⎨⎪⎧2x －1＝y 1＝－(3－y )； ②2＋i>1＋i ；③虚轴上的点表示的数都是纯虚数；④若一个数是实数，则其虚部不存在；⑤若z ＝1i，则z 3＋1对应的点在复平面内的第一象限．答案 ⑤解析由y ∈∁C R ，知y 是虚数，则⎩⎪⎨⎪⎧ 2x －1＝y1＝－(3－y )不成立，故①错误；两个不全为实数的复数不能比较大小，故②错误；原点也在虚轴上，表示实数0，故③错误；实数的虚部为0，故④错误；⑤中z 3＋1＝1i 3＋1＝i ＋1，对应点在第一象限，故⑤正确．三、解答题(本大题共6小题，共75分)16．设复数z ＝lg(m 2－2m －2)＋(m 2＋3m ＋2)i ，当m 为何值时，(1)z 是实数？(2)z 是纯虚数？解 (1)要使复数z 为实数，需满足⎩⎪⎨⎪⎧m 2－2m －2>0m 2＋3m ＋2＝0，解得m ＝－2或－1.即当m ＝－2或－1时，z 是实数．(2)要使复数z 为纯虚数，需满足⎩⎪⎨⎪⎧m 2－2m －2＝1m 2＋3m ＋2≠0，解得m ＝3.即当m ＝3时，z 是纯虚数．17．已知复数z 1＝1－i ，z 1·z 2＋z 1＝2＋2i ，求复数z 2.解因为z 1＝1－i ，所以z 1＝1＋i ，所以z 1·z 2＝2＋2i －z 1＝2＋2i －(1＋i)＝1＋i.设z 2＝a ＋b i(a ，b ∈R )，由z 1·z 2＝1＋i ，得(1－i)(a ＋b i)＝1＋i ，所以(a ＋b )＋(b －a )i ＝1＋i ，所以⎩⎪⎨⎪⎧ a ＋b ＝1b －a ＝1，解得a ＝0，b ＝1，所以z 2＝i. 18．计算：(1)(2＋2i )4(1－3i )5； (2)(2－i)(－1＋5i)(3－4i)＋2i.解 (1)原式＝16(1＋i )4(1－3i )4(1－3i )＝16(2i )2(－2－23i )2(1－3i )＝－644(1＋3i )2(1－3i )＝－16(1＋3i )×4 ＝－41＋3i ＝－1＋3i.(2)原式＝(3＋11i)(3－4i)＋2i＝53＋21i ＋2i ＝53＋23i.19.实数m 为何值时，复数z ＝(m 2＋5m ＋6)＋(m 2－2m －15)i 对应的点在：(1)x 轴上方；(2)直线x ＋y ＋5＝0上．解 (1)若z 对应的点在x 轴上方，则m 2－2m －15>0，解得m <－3或m >5.(2)复数z 对应的点为(m 2＋5m ＋6，m 2－2m －15)，∵z 对应的点在直线 x ＋y ＋5＝0上，∴(m 2＋5m ＋6)＋(m 2－2m －15)＋5＝0，整理得2m 2＋3m －4＝0，解得m ＝－3±414. 20.已知复数z 满足|z |＝2，z 2的虚部是2.(1)求复数z ；(2)设z ，z 2，z －z 2在复平面上的对应点分别为A ，B ，C ，求△ABC 的面积．解 (1)设z ＝a ＋b i(a ，b ∈R )，则z 2＝a 2－b 2＋2ab i ，由题意得a 2＋b 2＝2且2ab ＝2，解得a ＝b ＝1或a ＝b ＝－1，所以z ＝1＋i 或z ＝－1－i.(2)当z ＝1＋i 时，z 2＝2i ，z －z 2＝1－i ，所以A (1,1)，B (0,2)，C (1，－1)，所以S △ABC ＝1.当z ＝－1－i 时，z 2＝2i ，z －z 2＝－1－3i ，所以A (－1，－1)，B (0,2)，C (－1，－3)，所以S △ABC ＝1.21.设z 1是虚数，z 2＝z 1＋1z 1是实数，且－1≤z 2≤1. (1)求|z 1|的值以及z 1的实部的取值范围；(2)若ω＝1－z 11＋z 1，求证：ω为纯虚数． (1)解设z 1＝a ＋b i(a ，b ∈R 且b ≠0)，则z 2＝z 1＋1z 1＝a ＋b i ＋1a ＋b i ＝(a ＋a a 2＋b 2)＋(b －b a 2＋b2)i. 因为z 2是实数，b ≠0，于是有a 2＋b 2＝1，即|z 1|＝1，还可得z 2＝2a .由－1≤z 2≤1，得－1≤2a ≤1，解得－12≤a ≤12，即z 1的实部的取值范围是[－12，12]．(2)证明 ω＝1－z 11＋z 1＝1－a －b i 1＋a ＋b i＝1－a 2－b 2－2b i (1＋a )2＋b 2＝－b a ＋1i. 因为a ∈[－12，12]，b ≠0，所以ω为纯虚数．。

2021北师大版高三数学选修1-2综合学习与测试卷及答案(4)

北师大版高三数学选修1-2综合学习与测试卷及答案(四)综合学习与测试(四)可能用到的公式或数据：1122211()()ˆ()ˆˆnni i i ii i n ni i i i x x y y x y nx yb x x x nx ay bx ====⎧---⎪⎪==⎪⎨--⎪⎪=-⎪⎩∑∑∑∑第Ⅰ卷(选择题共50分)一、选择题(本大题共10小题，每小题5分，共50分) 1、一位母亲记录了儿子3—9岁的身高，数据（略），由此建立的身高与年龄的回归模型为yˆ=7.19x+73.93，用这个模型预测这个孩子10岁时的身高，则正确的叙述是（）A 、身高一定是145.83cmB 、身高在145.83cm 以上C 、身高在145.83cm 左右D 、身高在145.83cm 以下2、复数534+i的共轭复数是（）A 、34-iB 、3545+i C 、34+i D 、3545-i 3、若数列{}n a 的通项公式为：241n a n n =++，则下列关于数列的说法正确的是（）A 、数列中可以出现偶数B 、数列的各项都是奇数C 、数列的各项都是质数D 、数列中都是合数4、若z C ∈且221z i +-=，则12z i --的最小值是（） A 、2 B 、3 C 、4D 、55、散点图在回归分析过程中的作用是（）A 、查找个体个数B 、比较个体数据大小关系C 、探究个体分类D 、粗略判断变量是否线性相关6、若大前提是：任何实数的平方都大于0，小前提是：a R ∈，结论是：20a >，那么这个演绎推理出错在（）10.8287.8796.6355.0243.8412.7062.0721.3230.7080.455k0.0010.0050.0100.0250.050.100.150.250.400.50()2P K k ≥()()()()()d b c a d c b a bc ad n K ++++-=22A、大前提B、小前提C、推理过程D、没有出错7、a=0是复数(),a bi ab R+∈为纯虚数的（）A、充分不必要条件B、必要不充分条件C、充要条件D、既不充分也不必要条件8、当213m<<时，复数()()32m i i+-+在复平面内对应的点位于：（）A、第一象限B、第二象限C、第三象限D、第四象限9、在如右图的程序图中，输出结果是A、5B、10C、20D、1510、把正整数按下图所示的规律排序，则从2003到2005的箭头方向依次为第Ⅱ卷(非选择题共100分)二、填空题(本大题共6小题，每小题5分，共30分)11、221(1)(4),.z m m m m i m R=++++-∈232.z i=-则1m=是12z z=的_________条件12、已知函数221)(xxxf+=，那么)4()31()3()21()2()1(ffffff+++++)41(f+=______________13、平面内一条直线把平面分成2部分，2条相交直线把平面分成4部分，1个交点；3条相交直线最多把平面分成7部分，3个交点；试猜想：n条相交直线最多把平面分成______________部分，____________个交点14、试求12345678,,,,,,,i i i i i i i i的值，由此推测4n i=_____, 41n i+=______,输出s否是s s a=⨯a=5,s=14?a≥a=a -142n i +=______, 43n i +=______, 12342000......i i i i i =___________15、一同学在电脑中打出如下若干个圆（图中●表示实心圆，○表示空心圆）：○●○○●○○○●○○○○●○○○○○●若将此若干个圆依次复制得到一系列圆，那么在前2006个圆中有个实心圆。